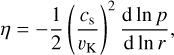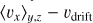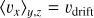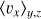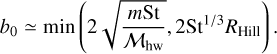| Issue |
A&A
Volume 665, September 2022
|
|
|---|---|---|
| Article Number | A122 | |
| Number of page(s) | 23 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202243849 | |
| Published online | 20 September 2022 | |
Dust ring and gap formation by gas flow induced by low-mass planets embedded in protoplanetary disks
I. Steady-state model
1
Department of Earth and Planetary Sciences, Tokyo Institute of Technology,
Ookayama, Meguro-ku, Tokyo
152-8551, Japan
e-mail: kuwahara.a.aa@m.titech.ac.jp
2
Earth-Life Science Institute, Tokyo Institute of Technology,
Ookayama, Meguro-ku, Tokyo
152-8550, Japan
3
National Institute of Technology, Ichinoseki College,
Takanashi, Hagisho, Ichinoseki-shi, Iwate
021-8511, Japan
Received:
22
April
2022
Accepted:
27
June
2022
Context. Recent high-spatial-resolution observations have revealed dust substructures in protoplanetary disks such as rings and gaps, which do not always correlate with gas. Because radial gas flow induced by low-mass, non-gas-gap-opening planets could affect the radial drift of dust, it potentially forms these dust substructures in disks.
Aims. We investigate the potential of gas flow induced by low-mass planets to sculpt the rings and gaps in the dust profiles.
Methods. We first perform three-dimensional hydrodynamical simulations, which resolve the local gas flow past a planet. We then calculate the trajectories of dust influenced by the planet-induced gas flow. Finally, we compute the steady-state dust surface density by incorporating the influences of the planet-induced gas flow into a one-dimensional dust advection-diffusion model.
Results. The outflow of the gas toward the outside of the planetary orbit inhibits the radial drift of dust, leading to dust accumulation (the dust ring). The outflow toward the inside of the planetary orbit enhances the inward drift of dust, causing dust depletion around the planetary orbit (the dust gap). Under weak turbulence (αdiff ≲ 10−4, where αdiff is the turbulence strength parameter), the gas flow induced by the planet with ≳1M⊕ (Earth mass) generates the dust ring and gap in the distribution of small dust grains (≲1 cm) with a radial extent of ~1–10 times the gas scale height around the planetary orbit without creating a gas gap and pressure bump.
Conclusions. The gas flow induced by low-mass, non-gas-gap-opening planets can be considered a possible origin of the observed dust substructures in disks. Our results may be helpful in explaining the disks whose dust substructures were found not to correlate with those of the gas.
Key words: protoplanetary disks / planets and satellites: formation / hydrodynamics
© A. Kuwahara et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
Recent high-spatial-resolution observations have revealed substructures in dust profiles (hereafter dust substructures), such as rings and gaps in both young and evolved protoplanetary disks (e.g., ALMA Partnership et al. 2015; Andrews et al. 2018; Long et al. 2018, 2020; van der Marel et al. 2019). Several mechanisms – planet-free and planet-dependent – have been proposed to explain the dust rings and gaps in disks.
The planet-free mechanisms are related to perturbations to the disk gas pressure and dust motion in the radial direction of the disk. Those include dust accumulation at the edge of the dead zone (Flock et al. 2015), dust growth at snow lines (Zhang et al. 2015), dust sintering (Okuzumi et al. 2016), self-induced dust pileup (Gonzalez et al. 2015, 2017), secular gravitational instability (SGI; Takahashi & Inutsuka 2014, 2016; Tominaga et al. 2018, 2019, 2020), magnetic disk winds (Suriano et al. 2017, 2018), a self-organization process due to nonideal magnetohydrodynamic effects (Béthune et al. 2017), a hypothetical axisymmetric radial pressure bump (Dullemond et al. 2018), and thermal wave instability (Watanabe & Lin 2008; Ueda et al. 2019, 2021; Wu & Lithwick 2021).
Disk–planet interaction is the other mechanism for interpreting the dust rings and gaps in disks. Paardekooper & Mellema (2004) were the first to discover that planets can open dust gaps in gas disks. A planet embedded in a disk perturbs the surrounding gas. The tidal torque by a giant planet can remove gas from the vicinity of the planetary orbit (Goldreich & Tremaine 1979, 1980; Lin & Papaloizou 1979), leading to the formation of a gas gap in a disk (e.g., Lin & Papaloizou 1986; Kley 1999; Nelson et al. 2000; Crida et al. 2006; Duffell & MacFadyen 2013; Fung et al. 2014; Kanagawa et al. 2015). The young protoplanetary disks contain abundant millimeter- to centimeter-sized dust particles (e.g., Testi et al. 2003). These particles drift from the outer to the inner region of the disk due to the global pressure gradient (the radial drift of dust; Whipple 1972; Weidenschilling 1977). Dust particles can be trapped at the edge of the gas gap, the so-called dust filtration mechanism, forming a dust ring and a gap (e.g., Rice et al. 2006; Paardekooper & Mellema 2006; Pinilla et al. 2012; Dong et al. 2015; Kanagawa et al. 2018). Thus, in the case of the dust substructure created by a gas gap, one would expect the spatial distribution of dust substructures to be correlated with that of gas.
However, this is not always the case (e.g., Zhang et al. 2021; Jiang et al. 2022), and it poses a challenge for the dust substructure formation model predictions by gas-gap-opening planets for several systems. Moreover, rings and gaps seem to be ubiquitous in the outer region of large, bright protoplanetary disks (≳10 au; e.g., Andrews et al. 2018), but the occurrence rate of giant planets per star is limited to ~10% (Johnson et al. 2010; Fernandes et al. 2019). The period-mass distribution of putative giant planets inferred from the observed dust gap widths is not reconciled with the current observed period-mass distribution of giant planets (Bae et al. 2018; Lodato et al. 2019; Disk Dynamics Collaboration 2020). Although this discrepancy might be solved by considering large-scale migration and planetary growth (Lodato et al. 2019), it is not conclusive that most dust substructures are derived from interactions between disks and gas-gap-opening planets.
The ambiguous relationship between the spatial distribution of gas and dust could be solved by considering low-mass planets that do not carve a deep gas gap in a disk. Here, we focus on the potential of gas flow induced by low-mass, non-gas-gap-opening planets to sculpt dust substructures in protoplanetary disks. Recent hydrodynamical simulations have revealed that a low-mass planet embedded in a disk induces gas flow with a complex three-dimensional (3D) structure (Ormel et al. 2015b; Fung et al. 2015, 2019; Lambrechts & Lega 2017; Cimerman et al. 2017; Kurokawa & Tanigawa 2018; Kuwahara et al. 2019; Béthune & Rafikov 2019; Moldenhauer et al. 2021). The key point is the outflow of the gas, which occurs in the radial direction to the disk. The outflow of the gas deflects the trajectories of dust particles significantly, even in the case of low-mass planets (~1 Mθ; Kuwahara & Kurokawa 2020a,b). Once the radial outward gas flow disrupts the motion of the particles, the inward drift of particles could be inhibited, leading to the formation of a dust substructure. This mechanism is studied in this paper.
Since planet-induced gas flow is a local phenomenon, a high-resolution simulation is required to capture the detailed 3D structure of the gas flow within the Bondi and Hill spheres. However, the influence of the 3D planet-induced gas flow is missing in previous studies on the effects of planets on the global dust distribution in disks. So far, the influence of planet-induced gas flow on dust particles has been investigated in terms of the accretion rate of particles onto the growing planet (Popovas et al. 2018, 2019; Kuwahara & Kurokawa 2020a,b; Okamura & Kobayashi 2021).
The structure of this paper is as follows. In Sect. 2 we describe our numerical methods. In Sect. 3, we show the results obtained from a series of numerical calculations. In Sect. 4, we discuss the implications for planet formation theory and observations of protoplanetary disks. We conclude in Sect. 5. Readers who are not interested in the details of modeling and the physical aspects of the results can skip Sects. 2.3–3.4 and proceed directly to Sect. 3.5.
2 Methods
2.1 Model overview
In this section, we provide an overview of our model. Our approach is summarized in Fig. 1. First, assuming a compressible, inviscid sub-Keplerian gas disk with the vertical stratification due to the vertical component of the stellar gravity, we performed 3D nonisothermal hydrodynamical simulations. Radiative cooling is implemented by using the β cooling model (Gammie 2001). The self-gravity of gas is neglected. Hydro-dynamical simulations were performed in the frame co-rotating with the planet (the black sphere in Fig. 1). These simulations resolve the region’s local gas flow, including the planet’s Hill and Bondi spheres (Sect. 2.3).
Second, we calculated the 3D trajectories of dust particles influenced by the planet-induced gas flow (Sect. 2.4.1). We numerically integrated the equation of motion of dust particles using the hydrodynamical simulation data. 3D orbital calculations were performed in the frame co-rotating with the planet (the local box in Fig. 1). Through each 3D orbital calculation, we sampled the positions and velocities of particles at specific time intervals. We then obtained the spatial distribution of dust influenced by the planet-induced gas flow in the local domain (Sect. 2.4.2).
Although our orbital calculations were performed in the local domain, in reality, the dust particles distribute outside the domain as well (i.e., in the full azimuthal direction of a disk). Thus, third, we assumed the uniform and Gaussian distributions of dust in the azimuthal and vertical directions outside the local domain of orbital calculations (Sect. 2.5.1), and then calculated the azimuthally and vertically averaged drift velocities of dust (Sect. 2.5.2) based on the obtained spatial distributions of dust both inside and outside the local domain of orbital calculations.
Finally, we computed the dust surface density by incorporating the obtained azimuthally and vertically averaged drift velocity into a one-dimensional (1D) advection-diffusion equation (Sect. 2.6).
2.2 Dimensionless unit system
Throughout all of our simulations, the length, times, velocities, and densities are normalized by the disk scale height, H, reciprocal of the orbital frequency, Ω−1, sound speed cs, and unperturbed gas density at the location of the planet, ρdisk, respectively. Section 2.9 describes the relation between dimensionless and dimensional quantities for the steady accretion disk model.
While the mass of the disk gas is normalized by ρdiskH3, our simulations that neglect the self-gravity of the gas allow us to introduce another normalization for the planetary mass (Ormel et al. 2015a) as given by:
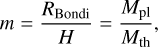 (1)
(1)
where 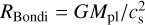 is the Bondi radius of the planet, Mpl is the mass of the planet, G is the gravitational constant, and Mth is the thermal mass of the planet (Goodman & Rafikov 2001):
is the Bondi radius of the planet, Mpl is the mass of the planet, G is the gravitational constant, and Mth is the thermal mass of the planet (Goodman & Rafikov 2001):
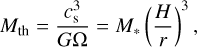 (2)
(2)
where M* is the mass of the central star and r is the orbital radius. The Hill radius is given by RHill = (m/3)1/3H in this unit. The relation between dimensionless planetary masses and dimensional ones for a steady viscous-accretion disk model is shown later in Sect. 2.9. We focus on low-mass planets (m ≤ 0.3) that do not shape the global pressure gradient and carve a gas gap in a disk1 The range of dimensionless planetary mass in this study is m = 0.03–0.3, which corresponds to a planet with ~0.1–10 M⊕ orbiting a solar-mass star at ~1–10 au.
 |
Fig. 1 Schematic illustration of our model. We performed 3D hydrodynamical simulations on the spherical polar grid (the black sphere), which hosts a planet located at its center (the brown-filled circle; Sect. 2.3). We consider the planet on a fixed circular orbit with the orbital radius, a. We adopt unperturbed sub-Keplerian shear flow at the outer boundary of the hydrodynamical simulations (the green arrows). We then calculated the trajectories of particles influenced by the planet-induced gas flow in the frame co-rotating with the planet (the local box; Sect. 2.4.1). We used the limited part of the computational domain of hydrodynamical simulation, Rhydro, in orbital calculations of dust particles (Sect. 2.4.1). The x and z coordinates of the starting point of particles, xs and zs, are the parameters. The starting point of orbital calculation is beyond Rhydro. The spatial interval of orbital calculation in the x direction is δx (Sect. 2.4.2). The x coordinate of the particle at the edge of the domain of orbital calculation is xe. The x coordinate of the particle after one synodical orbit, x′S, is given by Eq. (27) (Sect. 3.3). The schematic trajectories of particles are shown by the dashed blue lines (without the influence of planet-induced gas flow) and solid orange lines (perturbed by the planet-induced gas flow). The open circles on the trajectory correspond to the position of a particle at specific time intervals, ∆t(vy,0, zs) (Eq. (10)). The black arrows on the trajectories are the velocities in the x direction of a particle at each position, vx. It should be noted that we do not follow trajectories outside the calculation domain of orbital calculations. Instead, we assumed the uniform and Gaussian distributions of dust particles in the azimuthal and vertical directions outside the local domain of orbital calculation, respectively, where the particles have a fixed velocity in the x direction, vdrift. Based on the obtained spatial distribution of dust in the global domain, we calculated the azimuthally and vertically averaged drift velocity, 〈vx〉y,z (Eq. (17)). Finally, we calculated the dust surface density by incorporating 〈vx〉yz into the 1D advection-diffusion equation (Eq. (20)). |
2.3 Three-dimensional hydrodynamical simulations (the local domain)
We performed nonisothermal, inviscid 3D hydrodynamical simulations of the gas of the protoplanetary disk around an embedded planet. The inviscid assumption is justified in Sect. 2.4.2. The obtained gas flow data were used to simulate the orbits of dust particles influenced by the planet-induced gas flow (described later in Sect. 2.4).
Our methods of hydrodynamical simulations are the same as described by Kuwahara & Kurokawa (2020a,b). Our simulations were performed in a spherical polar coordinate co-rotating with a planet using the Athena++ code2 (Fig. 1; White et al. 2016; Stone et al. 2020). Hereafter we denote x, y, and z direction as radially outward (away from the star), azimuthal (the orbital direction of the planet), and vertical directions, respectively. We used varying sizes of the inner boundary, Rinn, as a function of the mass of the planet to follow a mass-radius relationship of the non-gaseous part of the planet:
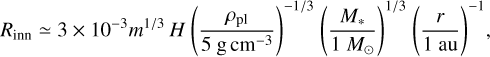 (3)
(3)
where ρpl is the density of the embedded planet and M⊙ is the solar mass3. A planet is embedded in an inviscid gas disk and is orbiting around a solar-mass star with a fixed orbital radius, a. The unperturbed gas velocity in the local frame is assumed to be the speed of the sub-Keplerian shear,
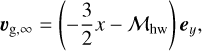 (4)
(4)
where Mhw is the Mach number of the headwind of the gas, vhw. The gas velocity has a constant value, υg,∞, at the outer edge of the computational domain of hydrodynamical simulations. The headwind of the gas is given by:
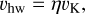 (5)
(5)
is a dimensionless quantity characterizing the global pressure gradient of the disk gas. In Eq. (6), p is the pressure of the gas and vK is the Keplerian velocity. The Mach number increases as the orbital distance increases for the steady viscous-accretion disk model (as shown later in Sect. 2.9). The range of the Mach number in this study is Mhw = 0.01–0.1, which covers a wide range of the disk (≲ 100 au). We list our parameter sets in Table 1.
List of hydrodynamical simulations.
2.4 Dust trajectory simulations (the local domain)
To clarify the influence of the planet-induced gas flow on the radial drift of dust particles in a disk, we calculated dust trajectories in gas flow obtained by hydrodynamical simulations (Sect. 2.4.1). We generated the spatial distribution of dust influenced by the planet-induced gas flow in the local domain (Sect. 2.4.2).
2.4.1 Three-dimensional orbital calculation of dust particles
We calculated the trajectories of dust particles influenced by the planet-induced gas flow in the frame co-rotating with the planet (Fig. 1). The x, y and z directions are similar to those used in the hydrodynamical simulations. A majority of our methods for orbital calculations are the same as described in detail by Kuwahara & Kurokawa (2020a,b), where we studied the accretion of dust particles onto a protoplanet embedded in a disk. We describe the differences in the numerical setting of orbital calculations with our previous works in Sect. 2.7.
In our co-rotating frame, the x- and y-components of the initial velocity of dust particles are given by the drift equations (Weidenschilling 1977; Nakagawa et al. 1986):
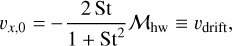 (7)
(7)
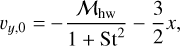 (8)
(8)
where St is the dimensionless stopping time of a dust particle, called the Stokes number,
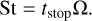 (9)
(9)
We assume St = 10−4–100. The relation between the Stokes numbers and dimensional particle sizes for a steady viscous-accretion disk model is shown later in Sect. 2.9. The parameter range in this study is St ~ 10−4–100, which corresponds to the dust particles of ~0.1 mm–1 m at ~1–10 au for the steady-state viscous-accretion disk (Sect. 2.9).
We numerically integrated the equation of motion of dust particles. We used the gas velocity obtained from the hydrody-namical simulation to calculate the gas drag force acting on the dust within the limited part of the computational domain, Rhydro (see Kuwahara & Kurokawa 2020a,b, for details). The sizes of the limited part of the computational domains, Rhydro, are listed in Table 1. We assumed the Stokes gas drag regime. The choice of the gas drag regime did not affect our results (discussed in Appendix A). The y coordinate of the starting point of particles is fixed at |ys| = 40 RHill (Ida & Nakazawa 1989). The x and z coordinates of the starting point of particles, xs and zs, are the parameters. The ranges of xs and zs are xs ∈ [−5 RHill, 5 RHill] and zs ∈ [0,1]. Owing to the symmetry of the system, we only consider z ≥ 0. We set the upper limit as z = 1. At high altitudes, z > 1, the dust density decreases significantly (described later in Eq. (11)). The ranges of xs and zs fully cover the size of the perturbed region, which can be scaled by the Bondi radius in our parameter sets (m ∈ [0.03,0.3]).
2.4.2 Spatial distribution of dust in the local domain
Through each orbital calculation, we sampled the positions and velocities of the particles at fixed small time intervals. We then obtained the spatial distribution of particles in the local calculation domain as schematically illustrated in the upper right corner of Fig. 1.
We first describe the spatial intervals of the starting points of the orbital calculations, which determine the radial and vertical distributions of the incoming dust (Fig. 1). We integrated the equation of motion for dust particles with their initial spatial intervals of δx = 0.01b in the x direction and of δz = 0.01 in the z direction. The maximum impact parameter of accreted particles in the unperturbed flow, b, is expressed by Eq. (B.1) in Appendix B. The spatial interval in the x direction, δx = 0.01b, has on the order of ~10−4–10−3 [H].
Next, we describe the time interval for sampling the position and velocity of a particle to generate the dust spatial distribution within a local domain of orbital calculations. The time interval is given by:
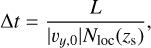 (10)
(10)
where L = 80 RHill (the size of the calculation domain) and Nloc(zs) is the number of dust particles on an unperturbed orbit (without the influences of gravity of the planet and the planet-induced gas flow) in the local calculation domain (described later in Eq. (11)). The dependence of ∆t on |vy,0| means that the dust mass flux is constant in the x direction of the local calculation domain. To take into account the vertical distribution of incoming dust, we assumed the Gaussian distribution:
![${N_{{\rm{loc}}}}\left( {{z_{\rm{s}}}} \right) = {N_0}\exp \left[ { - {1 \over 2}{{\left( {{{{z_{\rm{s}}}} \over {{H_{\rm{d}}}}}} \right)}^2}} \right],$](/articles/aa/full_html/2022/09/aa43849-22/aa43849-22-eq12.png) (11)
(11)
where N0 is the number of dust particles at the midplane. We adopt N0 = 500. In Eq. (11), the scale height of dust particles, Hd, is given by (Dubrulle et al. 1995; Cuzzi et al. 1993; Youdin & Lithwick 2007):
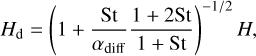 (12)
(12)
where αdiff is the dimensionless turbulent parameter, which describes turbulent diffusion in our model. We assume αdiff = 10−5, 10−4, and 10−3. We note that the obtained spatial distribution of dust in the local domain deviates from the Gaussian distribution in the vertical direction because of the gas flow in the vertical direction.
We assumed the inviscid fluid of an ideal gas and did not consider the effect of random motion of dust due to the turbulence in a series of hydrodynamical simulations and orbital calculations (Kuwahara & Kurokawa 2020a,b). The dimensionless turbulent parameter, αdiff, is used when we consider the vertical distribution of dust (Sects. 2.4.2 and 2.5) and the turbulent diffusion of dust in the radial direction (described later in Sect. 2.6). As long as we focus on the range of the turbulence strength considered in this study, the turbulence likely affects the dust only. The viscosity suppresses the 3D flow only when its α-viscous coefficient is large, αdiff ≳ 10−2 (Fung et al. 2015; Lambrechts & Lega 2017). We note that several previous studies reported another transition at even lower αdiff. Lambrechts & Lega (2017) found the oscillational flow pattern at αdiff ≲ 10−3. In our inviscid simulations, we also found the fluctuation after 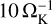 , but its amplitude is small: <10% in the x-component of the outflow velocity. McNally et al. (2019) considered the planets with m ≳ 0.3 and found the growth of a set of Rossby wave instability vortices outside the planetary orbits when αdiff ≲ 10−4 in their 2D global hydrodynamical simulations. Though these vortices do not appear in our local hydrodynamical simulations, their influences on dust drift may need to be investigated in a future study.
, but its amplitude is small: <10% in the x-component of the outflow velocity. McNally et al. (2019) considered the planets with m ≳ 0.3 and found the growth of a set of Rossby wave instability vortices outside the planetary orbits when αdiff ≲ 10−4 in their 2D global hydrodynamical simulations. Though these vortices do not appear in our local hydrodynamical simulations, their influences on dust drift may need to be investigated in a future study.
2.5 Model for global dust distribution
So far, we only considered the distribution of dust particles in the local domain of orbital calculation because we did not follow trajectories of dust outside the domain (Sect. 2.4.1). In reality, the dust particles distribute outside the domain as well (namely, in the full azimuthal direction of the disk). We then considered the spatial distribution of dust outside the local domain of orbital calculation (Sect. 2.5.1). Based on the obtained spatial distribution of dust both inside and outside the local domain of orbital calculation, we calculated the azimuthally and vertically averaged drift velocity of dust (Sect. 2.5.2).
2.5.1 Spatial distribution of dust in the global domain
We assumed the uniform distribution of dust particles in the azimuthal direction outside the local domain of orbital calculation, where the particles have the fixed velocity in the x direction, vdrift. We confirmed that the velocities of dust particles were almost identical to that of the initial values at the edge of the local domain of orbital calculation (Eqs. (7) and (8)). Thus, this assumption was justified.
To maintain consistency with orbital calculations, outside the domain, the number of dust particles on a hypothetical orbit (the orange solid line outside the local domain of orbital calculation, which is schematically illustrated in the upper left corner of Fig. 1) is given by:
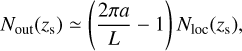 (13)
(13)
where we assume a ≫ x. As with the orbital calculations, we consider the ranges of x ∈ [−5 RHill, 5 RHill] and z ∈ [0,1]. The spatial intervals of hypothetical orbits are δx and δz in the x and z directions, respectively. Thus, the “global box” of size 10 RHill × (2πa − L) − 1 [H3] contains 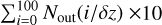 RHill/δx particles.
RHill/δx particles.
2.5.2 Azimuthally and vertically averaged drift velocity of dust
Based on the obtained spatial distribution of dust both inside and outside the local domain of orbital calculation (Sect. 2.5.1), we calculated the azimuthally and vertically averaged drift velocity of dust. We divided the obtained spatial distribution of dust in the global domain into grids in the x direction with equal spacing, ∆x = 10 × δx. The total number of sampling particles in each grid is given by:
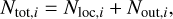 (14)
(14)
where Nloc,i is obtained from orbital calculations and Nout,i is given by Nout,i = Nout × (∆x/δx). The subscript i denotes the grid number. Each grid contains Ntot,i ~ 106 sampling particles. We confirmed that the sample number is large enough to achieve numerical convergence.
The azimuthally and vertically averaged x-component of the velocity on the ith grid is calculated by:
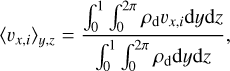 (15)
(15)
where ρd is the density distribution of dust
![${\rho _{\rm{d}}} = {\rho _{{\rm{d,0}}}}\exp \left[ { - {1 \over 2}{{\left( {{{{z_s}} \over {{H_{\rm{d}}}}}} \right)}^2}} \right],$](/articles/aa/full_html/2022/09/aa43849-22/aa43849-22-eq19.png) (16)
(16)
with the midplane density, ρd,0 = 1. We numerically calculated Eq. (15) as:
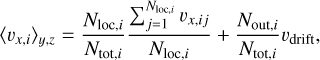 (17)
(17)
where the subscript j denotes the number of particles in the ith grid. The azimuthally and vertically averaged drift velocity of dust is schematically illustrated in the lower-right corner of Fig. 1.
2.6 Simulation of dust surface density
We computed the dust surface density by incorporating the azimuthally and vertically averaged drift velocity into the 1D advection-diffusion equation as schematically illustrated in the lower-left corner of Fig. 1. Instead of calculating the dust surface density directly from the obtained spatial distribution of dust, we solve the advection-diffusion equation for the following reason. The obtained spatial distribution of dust is a snapshot (Sect. 2.5.1). Though we considered the effect of turbulent diffusion in the vertical direction through Eq. (12), we did not consider it in the radial direction so far.
The dust surface density, Σd, can be obtained by solving the following 1D advection-diffusion equation:
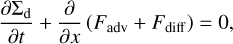 (18)
(18)
where Fadv = 〈vx〉y,z∑d and Fdiff = −D∂∑d/∂x. 〈vx〉y,z is given by Eq. (17), and D is the diffusion coefficient for the dust (Youdin & Lithwick 2007):
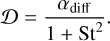 (19)
(19)
Because we focus on a radial range sufficiently narrow compared to the orbital radius of the planet, we assumed that the gas surface density is constant in these dust surface density simulations. Thus, the gas surface density can be omitted in Eq. (18). We assumed a steady state and integrated Eq. (18) once, and then obtained:
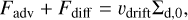 (20)
(20)
where ∑d,0 is the initial dust surface density.
The size of the calculation domain for solving Eq. (20) is x ∈ [−100 RHill, 100 RHill], which is much larger than that of the orbital calculations. Outside the domain of orbital calculations in the radial direction, |x| > 5 RHill, we set 〈vx〉y,z= vdrift (see also Sect. 2.8). As a boundary condition, we assumed ∑d = ∑d,0 = 1.
2.7 Numerical settings: Dust trajectory simulations
Most of our methods of orbital calculations are the same as described in detail by Kuwahara & Kurokawa (2020a,b), apart from the configuration of termination conditions. In Kuwahara & Kurokawa (2020a,b), where we studied the accretion of dust particles onto a protoplanet embedded in a disk, we terminated orbital calculation when either one of the following conditions was met: (1) the calculation time reached the sufficiently long time of computation, 104 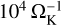 , (2) a dust particle reached the edge of the calculation domain, |y| ≥ 40 RHill (Fig. 1), or (3) accreted onto the planet, R ≤ 2 Rinn (see Kuwahara & Kurokawa (2020a,b, for details). However, we found that this treatment causes several problems when studying the influence of gas flow on dust drift (Sect. 2.6).
, (2) a dust particle reached the edge of the calculation domain, |y| ≥ 40 RHill (Fig. 1), or (3) accreted onto the planet, R ≤ 2 Rinn (see Kuwahara & Kurokawa (2020a,b, for details). However, we found that this treatment causes several problems when studying the influence of gas flow on dust drift (Sect. 2.6).
First, we found that the x-component of the gas velocity, vx,gas, is significant in the vicinity of the planet, R ≲ 0.3 RBondi (Figs. 2 and 3). The particles that enter the Bondi region circulate close to the planet and then accrete onto the planet (Figs. 2b and 3b). We found that the azimuthally and vertically averaged drift velocity of dust calculated by Eq. (17) fluctuated significantly in the vicinity of the planetary orbit, | x| ≲ 0.3 RBondi, due to the large vx,gas. To eliminate the fluctuation of the azimuthally and vertically averaged drift velocity, we assumed that the particles accreted onto the planet when R ≤ 0.3 RBondi in all cases.
Second, dust particles are trapped and circulate many times in the horseshoe region when the drift timescale of particles, tdrift ~ wHS /|vdrift|, where wHS ≃ 2 RBondi is the width of the horseshoe region4, is comparable to the horseshoe libration timescale, tlib ~ 8πa/(3ωwhs). We terminated orbital calculations to reduce the computational time when the horseshoe turn was detected twice.
 |
Fig. 2 Streamlines of gas (left) and trajectories of dust particles with St = 10−2 (right) at the midplane of the disk. The flow structure around a planet is obtained from m03-hw001. With this parameter set, the planet-induced gas flow is in the flow-shear regime (see Sect. 3.2). The color contour represents the flow speed in the x direction, vx,gas. We set zs = 0 for the orbital calculations. The dotted and dashed circles are the Bondi and Hill radii of the planet, respectively. The thick blue lines in the right panel correspond to the trajectories of the dust particles that satisfy x′s ≥ xs (see Fig. 1 and Sect. 3.3 for details). The 3D structure of the gas flow field is shown in Appendix E. |
 |
Fig. 3 Same as Fig. 2, but with the flow structure obtained from m003-hw01 and St = 10−4 set for the trajectories. In this figure, the planet-induced gas flow is in the flow-headwind regime (see Sect. 3.2). The 3D structure of the gas flow field is shown in Appendix E. |
2.8 Numerical settings: Azimuthally and vertically averaged drift velocity of dust
When we calculated the azimuthally and vertically averaged drift velocity of dust, 〈vx〉y,z, we found unexpected peaks in 〈vx〉y,z at the positions away from the planetary orbit (outside the region influenced by the planet-induced outward gas flow, |x| ≳ 1). These peaks are caused by the density waves excited by an embedded planet. While our hydrodynamical simulations can resolve the local gas flow pattern in detail, they do not handle the global structure in the azimuthal direction in a disk. Since the density waves extend in the azimuthal direction, they are interrupted at the edge of the computational domain of our hydrodynamical simulations. We found that the locations of the unexpected peaks coincide with those where the density waves are interrupted. Appendix C shows the locations of the outflows and the density waves.
Previous studies have reported that, in global disk simulations, the effects of density waves on dust drift were minor (Paardekooper & Mellema 2006; Muto & Inutsuka 2009; Rosotti et al. 2016; Dong et al. 2017a). Therefore, we assumed that the dust particles have a fixed velocity, vdrift, outside the region influenced by the planet-induced outward gas flow. In this region, the artificial effect of the interrupted density waves could be seen (schematically illustrated in the lower-right corner of Fig. 1).
2.9 Disk model
When we convert the dimensionless quantities into dimensional ones, we consider the steady accretion disks with a constant turbulence strength (Shakura & Sunyaev 1973), αacc, including viscous heating due to the accretion of the gas and irradiation heating from the central star (Fig. 4; Kusaka et al. 1970; Nakamoto & Nakagawa 1994; Oka et al. 2011; Ida et al. 2016). The dimensionless viscous alpha parameter, αacc, describes the global efficiency of angular momentum transport of the gas (Shakura & Sunyaev 1973). We assumed αacc = 10−3.
The disk midplane temperature and the aspect ratio of the disk are given by Eqs. (D.1)–(D.3) in Appendix D. In this disk model, the mass of the planet and the Mach number of the headwind can be described by (Figs. 4a and b):
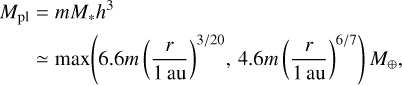 (21)
(21)
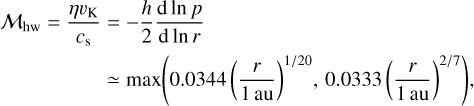 (22)
(22)
where we assume d ln p/d ln r ≃ −2.55 for the viscous region and d ln p/dln r ≃ −2.78 for the irradiation region (Ida et al. 2016).
In a steady accretion disk, the gas surface density is given by:
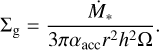 (23)
(23)
The stopping time of the dust particle depends on the thermal structure of the disk. Thus, the Stokes number is given by (Fig. 4c; Ida et al. 2016):
 (24/25)
(24/25)
where ρ• is the internal density of the particle, s is the radius of the particle, λ is the mean free path of the gas, λ = μmH/ρgσmol with μ, mH and σmol being the mean molecular weight, μ = 2.34, the mass of the proton, and the molecular collision cross section, σmol = 2 × 10−15 cm2 (Chapman & Cowling 1970; Weidenschilling 1977; Nakagawa et al. 1986).
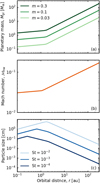 |
Fig. 4 Relation between the dimensionless quantities and dimensional ones. Each line represents the planetary mass (top; Eq. (21)), Mach number (middle; Eq. (22)), and particle size (bottom; Eqs. (24) and (25)) as a function of the orbital radius. In panel c, we only plotted St ≤ 10−2, which is the important parameter range in this study. |
 |
Fig. 5 Gas flow structure around a planet. The results were obtained from m01-hw001 (left), m01-hw003 (middle), and m01-hw01 (right). The color contour represents the flow speed in the x direction, vx,gas. The solid lines correspond to the specific streamlines. The vertical dashed blue line corresponds to the corotation radius for the gas. The dotted and dashed circles are the Bondi and Hill radii of the planet, respectively. |
3 Results
3.1 Results overview
The main subject of this study is to clarify the influence of the planet-induced gas flow on the radial distribution of dust particles in a disk. Section 3.2 summarizes the characteristic 3D structure of the planet-induced gas flow obtained by 3D hydrodynamical simulations. In Sects. 3.3 and 3.4, we show the results of our orbital calculations. Section 3.5 presents the results obtained by solving the 1D advection-diffusion equation for dust surface density.
3.2 Three-dimensional planet-induced gas flow
The planet-induced gas flow has a complex 3D structure. A substantial amount of gas from the disk enters the Bondi and Hill spheres at high latitudes (inflow), and exits through the midplane region of the disk (outflow). The 3D flow structure depends on Mhw (Ormel et al. 2015b; Kurokawa & Tanigawa 2018). In our previous work, we classified the planet-induced gas flow into the flow-shear and the flow-headwind regimes (Figs. 2 and 3; Kuwahara & Kurokawa 2020b). These flow regimes are important for understanding the tendency of simulation results of dust surface density (Sect. 3.5).
Qualitatively, the planet-induced gas flow has a vertically rotational symmetric structure in the flow-shear regime. The outflow occurs in the second and fourth quadrants of the x–y plane (Fig. 2a). The symmetry is broken in the flow-headwind regime, where the outflow occurs only in the fourth quadrant of the x–y plane (Fig. 3a). In both regimes the planet-induced gas flow affects the motion of dust particles (Kuwahara & Kurokawa (2020a,b, see also Figs. 2b and 3b). The 3D structure of the planet-induced gas flow is shown in Appendix E.
The transition from the flow-shear to the flow-headwind regime occurs when the dimensionless planetary mass drops below the flow transition mass (Kuwahara & Kurokawa 2020b):
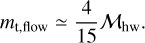 (26)
(26)
When m ≤ mt,flow, the planet-induced gas flow is in the flow-headwind regime. In our parameter set, only the case of m003-hw01 is classified as the flow-headwind regime, otherwise classified as the flow-shear regime based on the definition in Kuwahara & Kurokawa (2020b) (see also Table 1). The flow transition mass was originally derived to distinguish these hydrodynamical regimes.
The transition of the gas flow field from the flow-shear to the flow-headwind regime occurs smoothly. We found that the flow transition mass is not applicable for the classification of the effects on dust drift – which is the focus of this study – but it is still useful to understand the tendency of our results. In this study, the gas flow regime should be considered only as a qualitative guide to whether it is “shear-dominated” (two outflows occur both inside and outside the planetary orbit) or “headwind-dominated” (outflow occurs dominantly outside the planetary orbit).
Figure 5 shows the dependence of the gas flow structure around the planet with m = 0.1 on Mhw. In this figure, the planet-induced gas flow is in the flow-shear regime based on the definition in Kuwahara & Kurokawa (2020b). As shown in Fig. 5, the outflow speed toward the inside (outside) of the planetary orbit becomes weak (strong) as Mhw increases.
3.3 Existence of the forbidden region
We first show that the gas flow induced by low-mass planets affect the radial drift of the dust particles. Given a dust particle launched at (xs, ys), the x coordinate of a particle after one synodical orbit at y = ys can be described by:
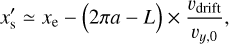 (27)
(27)
where xe is the x coordinate of a particle at the edge of the orbital calculation domain (upper right corner of Fig. 1). Equation (27) is valid because the velocity of dust is identical to that of the unperturbed value at the edge of the domain of orbital calculation (Sect. 2.4.2). We then set the following simple criteria: (1) when x′s < xs, the dust particles continue the radial drift. (2) When x′s ≥ xs, the planet-induced gas flow inhibits the radial drift. We only use the starting and ending points of an orbital calculation at this stage.
We found that a forbidden region exists outside the planetary orbit, where the radial drift of dust particles is inhibited (Fig. 6). Figure 6 shows the vector field of dust velocities influenced by the planet-induced gas flow in the x-z plane. The mass of the planet and Mach number of the headwind are m = 0.3 and Mhw = 0.01, respectively. We considered the Stokes numbers of St = 10−4, 10−2, and 3 × 10−2. In these cases, the planet-induced gas flow is in the flow-shear regime. A significant outward drift of dust particles can be seen near the midplane (dark green arrows in Fig. 6), because the outflow has the maximum speed near the midplane region of the disk. We discuss the motion of dust within the forbidden region in detail in Appendix F.
Similar to the flow-shear regime, we confirmed that a forbidden region exists outside the planetary orbit in the flow-headwind regime (see Sect. 3.4).
 |
Fig. 6 Vector field of dust velocities in the cases with St = 10−4 (left panel), 10−2 (middle panel), and 3 × 10−2 (right panel) under the common gas flow obtained from m03-hw001. The color contour from red to black represents the x component of the gas flow velocity averaged in the y direction within the calculation domain of hydrodynamical simulation around a planet, 〈vx,gas〉y. Arrows represent the direction of movement of dust particles. The color contour of the arrows from green to purple represents the distance of drift of a dust particle after one synodical orbit. The hatched region enclosed by black curves corresponds to the forbidden region. The two-headed blue arrow in panel b can be compared to the region shown by the thick blue lines in Fig. 2b. The dotted and dashed lines are the Bondi and Hill radii of the planet, respectively. Thanks to the symmetry of the system, we only focus on the region where z ≥ 0. We discuss the dust motion in the x-z plane in detail in Appendix F motion within the forbidden region. |
3.4 Width of the forbidden region
There is a clear dependence of the width of the forbidden region on the Stokes number. As shown in Fig. 6, the width of the forbidden region is wider for small Stokes number.
Figure 7 shows the changes of the vertically averaged width of the forbidden region weighted by the dust number density, 〈wf〉z, as a function of the Stokes number for different planetary masses and Mach numbers. The vertically averaged width of the forbidden region was calculated by:
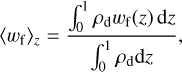 (28)
(28)
where wf (z) is the width of the forbidden region as a function of z. Same as Eq. (15), we only consider 0 ≤ z[H] ≤ 1. Overall trends indicate that 〈wf〉z is a decreasing function of the Stokes number, because the influences of gas flow are weaker for the large Stokes number. We note that the forbidden region does not exist in the limit of St → 0. The inflow to the Bondi sphere of the planet balances the outflow from it. This replenishment occurs through the meridional circulation of the gas (e.g., Fung et al. 2015). When St → 0, dust particles cycle along with the replenishment of the gas and, consequently with the outflow, meaning that the forbidden region does not exist in this limit. On the other hand, if the upper layer of the disk is dust-poor, we expect that the forbidden region does exist. This occurs when the dust scale height is smaller than the disk scale height, Hd < H. We discuss again the required conditions in our model later in Sect. 3.5.4 on turbulence strength.
For the larger Stokes numbers, St > 3 × 10−2, the forbidden region does not exist in our parameter spaces (m ∈ [0.03,0.3] and Mhw ∈ [0.01,0.1]). The following sections show only the results for St ≤ 3 × 10−2.
3.5 Influence of planet-induced gas flow on the dust surface density
The essential points of the previous sections are summarized in Fig. 1. So far, we have discussed the influence of the planet-induced gas flow on the radial drift of dust particles without the turbulent diffusion in the radial direction (Sects. 3.3 and 3.4, where we only used the starting and ending points of an orbital calculation). This section shows the steady-state dust surface density obtained by solving the 1D advection-diffusion equation (Eq. (20)). We found that the dust surface density profiles are different in the flow-shear (shear-dominated) and flow-headwind (headwind-dominated) regimes5. Hereafter, we refer to the regions where dust is depleted and accumulated as “dust gap” and “dust ring,” respectively.
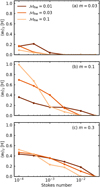 |
Fig. 7 Vertically averaged width of the forbidden region, 〈wf〉z. Different colors correspond to different Mhw. We adopt αdiff = 10−4. |
3.5.1 Dust ring and gap formation by planet-induced gas flow: Flow-shear regime
When the outflow occurs dominantly both outside and inside the planetary orbit, that is, when the planet-induced gas flow is in the flow-shear regime, the dust is accumulated outside the planetary orbit (dust ring) and depleted around the planetary orbit (dust gap; Fig. 8d). Panels a-d of Fig. 8 show the gas flow structure averaged in the y direction within the calculation domain of hydrodynamical simulation (m01-hw001; Fig. 8a), the difference of the azimuthally and vertically averaged drift velocity of dust particles from the unperturbed steady-state drift velocity (Eq. (17); Fig. 8b), advective and diffusive flux of dust (Fig. 8c), and the steady-state dust surface density (Fig. 8d), respectively. We set αdiff = 10−5 in Fig. 8b–d. We overplotted the forbidden regions for different Stokes numbers in Fig. 8a.
We found that the azimuthally and vertically averaged drift velocity of dust particles has positive and negative peaks outside and inside the planetary orbit (Fig. 8b). The positive peak is located at the position overlapping the forbidden region. The negative peak is caused by the outflow toward the inside of the planetary orbit, where the inward drift of dust particles is enhanced.
The advective flux dominates in the distant region far from the planet, |x| ≫ 1 (Fig. 8c). The dust particles drift inward to the central star with the steady-state velocity, vdrift, and thus the dust surface density has the fixed value, ∑d = ∑d,0.
The dust particles accumulate at the location where 〈vx〉y,z switches from negative to positive due to the outflow toward the outside of the planetary orbit, which is shown by the solid lines of St = 10−2 and 10−3 in Fig. 8d. The gradient of the dust surface density caused by dust accumulation results in an outward (inward) diffusive flux on the right (left) side across the peak of the dust surface density (Fig. 8c). The tail of the dust ring extends beyond the width of the forbidden region.
The dust particles pass through the forbidden region by turbulence diffusion and are transported inside the planetary orbit (Fig. 8c). Since the outflow occurs inside the planetary orbit in the flow-shear regime, the inward advective flux is enhanced by the outflow. As a result, the dust surface density decreases around the planetary orbit, followed by the formation of the dust gap.
We found that only the dust gap formation occurs in a few cases (e.g., St = 10−4 in Fig. 8d), such as when the amplitude of the positive peak in the azimuthally and vertically averaged drift velocity of dust is smaller than that of the negative peak.
The width and depth of the dust gap are larger for smaller Stokes numbers. The typical width of the dust gap is ~1 [H] in most cases, which corresponds to the width of the region influenced by the planet-induced outflow (e.g., Fig. 2). In Fig. 8, the width of the dust ring has on the order of ~0.1–1 [H], but it strongly depends on the Stokes number and the turbulence strength (shown later in Figs. 11 and 12, see Sect. 3.5.4 on turbulence strength).
 |
Fig. 8 Gas flow structure averaged in the y direction within the calculation domain of hydrodynamical simulation around a planet (panel a), the difference of the azimuthally and vertically averaged velocity of dust particles from the unperturbed steady-state drift velocity, |
3.5.2 Dust ring formation by planet-induced gas flow: Flow-headwind regime
When the outflow occurs dominantly outside the planetary orbit (flow-headwind regime), the dust is accumulated outside the planetary orbit without the depletion of dust around the planetary orbit, as shown in Fig. 9d. Similar to Fig. 8, panels a-d of Fig. 9 show the gas flow structure averaged in the y direction within the calculation domain of hydrodynamical simulation (m01-hw01; Fig. 9a), the difference between the azimuthally and vertically averaged drift velocity of dust particles and the unperturbed steady-state drift velocity (Fig. 9b), advective and diffusive flux of dust (Fig. 9c), and the dust surface density (Fig. 9d), respectively. We set αdiff = 10−4 in Figs. 9b–d.
In the flow-headwind regime, the azimuthally and vertically averaged drift velocity of dust particles has only a positive peak, which leads to dust accumulation outside the planetary orbit (Figs. 9b and d). We note that 〈vx〉y,z for St = 10-2 in Fig. 9 is always negative (see the small panel displayed in Fig. 9b). Even when the drift speed of dust is always negative, the dust particles accumulate slightly outside the planetary orbit (St = 10−2; Fig. 9d). This is caused by the traffic jam of dust that results from changes in 〈vx〉y,z. The width of the dust ring and the concentration of the dust into a ring are larger for the small Stokes number. The concentration strongly depends on the turbulence strength (shown later in Figs. 11 and 12, see also Sect. 3.5.3 on turbulence strength).
Similar to the flow-shear regime, the advective flux dominates in the distant region far from the planet, |x| ≫ 1, (Fig. 9c). The outward (inward) diffusive flux occurs on the right (left) side across the peak of the dust surface density (Fig. 9c). Inside the planetary orbit, the advective flux is not disturbed because the influence of the outflow toward the inside of the planetary orbit is weak. Thus, the dust gap does not form in a steady state.
 |
Fig. 9 Same as Fig. 8, but with the result obtained from m81-hw81 in panel a and αdiff = 10-4 adopted in panels b-d. Since we only plot the region where |x| ≤ 2, the outer part of the ring is interrupted. |
3.5.3 Dependence on planetary mass
Figures 10–12 (see also Figs. 13 and 14) show the dependence of dust surface density influenced by the planet-induced gas flow on the planetary mass. We found the following trends: (1) an apparent dust ring and (or) gap formation by the planet-induced gas flow occurs when:
 (29)
(29)
and (2) dust gap formation is susceptible to occur for a highermass planet.
Regarding the former trend, we recall that the width of the forbidden region increases with the planetary mass, except when the Stokes number is extremely small (St ≲ 10−3; Fig. 7). When m = 0.03, the smallest planetary mass considered in this study, the forbidden region does exist, but its width is small (〈wf〉z ≤ 0.2; Fig. 7a). The influence of the planet-induced gas flow on the radial drift of dust is weak. The turbulence diffusion can smooth the dust surface density, except when the turbulence strength is weak (αdiff ≤ 10−5; Figs. 10g–i).
The latter trend is related to the response of the topologies of the planet-induced gas flow to an increase in the Mach number. A larger Mhw is needed for a higher-mass planet to change the gas flow regime from the flow-shear to the flow-headwind regime (Eq. (26)). Within a range of the Mach numbers considered in this study, when m = 0.3, the influence of the outflow toward inside the planetary orbit remains and the dust gap forms. We found the following empirical relation between the planetary mass and the Mach number based on our results. The dust gap forms when (Fig. 13):
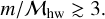 (30)
(30)
 |
Fig. 10 Dust surface density with m = 0.03 for the different Stokes numbers, the Mach numbers, and the turbulent parameters. Different colors correspond to different Stokes numbers. The minimum and the maximum values of the dust surface density are summarized in Figs. 13 and 14. |
 |
Fig. 11 Same as Fig. 10, but with m = 0.1. The gray-shaded region represents an excessive accumulation of dust particles, where the dust-to-gas ratio exceeds unity, assuming the initial value of ∑d,0/∑g = 0.01. Since we only plot the region where −1 ≤ x ≤ 4, the outer part of the ring is interrupted. The dashed black line corresponds to ∑d/∑d,0 = 1. |
 |
Fig. 12 Same as Fig. 10, but with m = 0.3. The gray-shaded region represents an excessive accumulation of dust particles, where the dust-to-gas ratio exceeds unity, assuming the initial value of ∑d,0/∑g = 0.01. Since we only plot the region where −1 ≤ x ≤ 4, the outer part of the ring is interrupted. The dashed black line corresponds to the initial value. |
3.5.4 Dependence on turbulence strength
Figures 13 and 14 show the dependence of dust surface density influenced by the planet-induced gas flow on the turbulence strength, αdiff. In common with Figs. 13 and 14, the influence of the planet-induced gas flow on the dust surface density is stronger for a small αdiff, in which case the dust settles in the midplane of the disk, and the velocity fluctuations caused by the planet-induced gas flow are large. This is because the outflow significantly influences the radial drift of dust near the midplane (Fig. 6). Then the large surface density gradient needs to achieve a steady state, which results in a significant accumulation or depletion of dust.
Within a range of the turbulence strengths considered in this study, the apparent dust ring and gap structures are found only when αdiff ≤ 10−4 (Figs. 13 and 14). When αdiff is very small, αdiff = 10−5, we found an excessive accumulation of dust outside the planetary orbit in some cases (Figs. 14g–i). We discuss an excessive dust concentration outside the planetary orbit in Sects. 4.4.3 and 4.6.
We assumed that a planet did not perturb the gas surface density (Sect. 2.6), and found that the influences of the planet-induced gas flow on the dust surface density were more pronounced for the small Stokes number (Figs. 13 and 14). However, one might expect that the spatial distribution of dust with the very small Stokes number (St ≪ 1) would match that of the gas.
We consider an endmember case where St = 10−4 and assume that the planet-induced gas flow is in the flow-shear regime. First, we only focus on the dust motion at the midplane region of the disk. Even when St = 10−4, the voids in the dust distribution are created by the outflow of the gas (e.g., Fig. 2b), because the outflow streamlines originated from the horseshoe streamlines at high altitudes (Fung et al. 2015). The 3D structure of the gas flow field is shown in Appendix E.
Next, we consider the vertical distribution of dust. The transient horseshoe gas flow transports the dust particles at high altitudes to the midplane region (orange arrows in Fig. 15)6. After transportation, the dust trajectories at the midplane region should match those shown in Fig. 2b. Thus, the voids remain in the dust distribution.
The downward motion of dust particles is identified even at z ~ H (Fig. 15). When the dust scale height is smaller than the disk scale height, Hd < H, dust-poor gas is supplied to the forbidden region. Then the surface density of dust deviates from thatof the gas even when St ≪ 1. Thus, from Eq. (12), our model for the dust substructure formation without the perturbation of the gas surface density would require the following condition: αdiff < St ≪ 1.
 |
Fig. 13 Minimum dust surface density, ∑d,min, as a function of the planetary mass and the Stokes number. Different rows correspond to different turbulent parameters, αdiff. Different columns correspond to different Mach numbers, Mhw. |
4 Discussion
4.1 Comparison to previous studies
Many authors have investigated the planet-driven dust ring and gap formation in a disk. One of the major differences between the conventional models and our model is that we focus on non-gas-gap-opening, low-mass planets. Consequently, the proposed mechanism works well for the particles with small Stokes numbers.
Gas-gap-opening planets have long been a plausible candidate to explain the dust rings and gaps in disks. A giant planet carves a density gap in a gas disk (e.g., Lin & Papaloizou 1986), and then the particles are trapped at the edge of the gas gap. The depth of the dust gap increases with the Stokes number (Zhu et al. 2012; Weber et al. 2018). When particles are tightly coupled with the gas, they can pass through the gas gap due to the turbulent diffusion or the viscous accretion flow (Rice et al. 2006; Zhu et al. 2012; Pinilla et al. 2016; Weber et al. 2018; Bitsch et al. 2018; Drazkowska et al. 2019).
Several studies have shown that a low-mass planet that does not carve a significant gas gap in a disk can form dust substructures. Paardekooper & Mellema (2006) found that ~15 M⊕ planet perturbs the dust surface density and then forms the dust gap in the distribution of the dust particles larger than 150 μm. From the analytical point of view, Muto & Inutsuka (2009) showed that ~2 M⊕ can open the dust gap when St ≳ 0.1 in the absence of the global pressure gradient. The axisymmetric dust depletion can be generated in an inviscid disk due to steepening of nonlinear density waves launched by ~8 M⊕ planet when St ≳ 2 × 10−3 (Zhu et al. 2014). The annular enhancements in the dust disk are caused by the pressure perturbation by a low-mass embedded planet (~15 M⊕) when St ≳ 2 × 10−2 (Rosotti et al. 2016). The depth of the dust gap or the concentration of the dust into a ring increases with the Stokes number (Zhu et al. 2014; Rosotti et al. 2016). Dust gap forms due to the tidal torque from a planet (~15 M⊕) when the Stokes number is large, St ≳ 1 (Dipierro et al. 2016; Dipierro & Laibe 2017). These previous studies did not consider the influences of the radial outward gas flow induced by an embedded planet, which is the mechanism we study in this paper.
Compared with the studies mentioned above, our study reveals the opposite trend: the dust ring and gap are likely to form when the Stokes number is small. The properties of the dust ring and gap, such as width, depth, and amplitude, are more pronounced for the small Stokes number (Figs. 10–12), because smaller dust particles are more sensitive to the gas flow. Our local approach cannot explicitly handle the global effects that investigated in the previous studies (e.g., shallow gas-gap opening by a low-mass planet), but a local model is needed to reveal the influence of the outflow of the gas.
Here we consider how our model can coexist with the other dust substructure formation mechanisms. In an inviscid disk, low-mass planets could open shallow gas gaps through nonlinear density wave steepening (Goodman & Rafikov 2001; Rafikov 2002; Zhu et al. 2014; Dong et al. 2017a, 2018). Linear waves excited by a low-mass planet steepen to shocks after they propagate a distance (Goodman & Rafikov 2001):
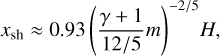 (31)
(31)
where γ = 1.4 is the adiabatic index. Equation (31) gives xsh ~ 1.5–3.8 [H] within a range of the planetary masses considered in this study, m = 0.03–0.3. These values are larger than the widths of the outflow of the gas, |x| ≲ 0.5 [H] (e.g., Fig. 5). We would expect that the large dust particles accumulate at |x| ≳ xsh due to the shallow gas-gap opening. Small particles that are tightly coupled with the gas, on the other hand, can diffuse or pass through the gas gap due to the turbulence, the viscous accretion flow, or both (e.g., Rice et al. 2006). These small dust are trapped by the outflow of the gas. Thus, when we consider the shallow gas-gap opening in an inviscid disk, we would expect that the locations of the dust rings and the widths of the dust gaps in the populations of the large and small dust grains do not match each other. The dust ring in the large dust population may appear ~1 [H] farther away than that in the small dust population. The width of the dust gap in the large dust population may be wider than that in the small dust.
 |
Fig. 14 Same as Fig. 13, but with panels showing the maximum dust surface density, ∑d,max, as a function of the planetary mass and the Stokes number. We note that the color contours are on a linear scale in panels a–f but on a log scale in panels g–i. |
 |
Fig. 15 Same as Fig. 6a, but the color contour from blue to red represents the z component of the gas flow velocity averaged in the y direction within the calculation domain of hydrodynamical simulation around a planet, 〈vz,gas〉y. The color contour of the arrows from purple to orange represents the difference in the z coordinates between the ending and starting points of orbital calculations. |
4.2 Turbulence in a protoplanetarydisk
Protoplanetary disks are thought to be turbulent, though the strength is highly uncertain. One of the possible origins of the disk turbulence is the magnetorotational instability (MRI), which produces strong turbulent intensities of αdiff ~ 103–10−2 (Balbus & Hawley 1991). However, Ohmic diffusion would suppress the MRI, which creates an MRI-inactive region (dead zone; Gammie 1996). The dead zone lies between a few times 0.1 au and about a few tens of au in a disk, in which the αdiff value should be smaller, αdiff ≲ 10−4 (Gammie 1996).
Even if the ionization degree is low, the turbulence can be generated through hydrodynamic instabilities, such as vertical shear instability (VSI; e.g., Urpin & Brandenburg 1998; Nelson et al. 2013). The strength is likely to be lower. The VSI can develop in the outer region of the disk, >10 au, and generate turbulence of αdiff ~ 10−4 (Malygin et al. 2017, and references therein). However, the VSI-driven turbulence may be suppressed by the toroidal magnetic fields in a disk (Cui & Bai 2020; Cui & Lin 2021), or dust evolution (Fukuhara et al. 2021). When the dust grows to ~0.1–1mm at > 10 au (corresponding to St ~ 10−4–10−3 in our disk model; Fig. 4c), the VSI may be stabilized completely (Fukuhara et al. 2021).
Recent observations suggest low levels of turbulence, αdiff ≲ 10−5–10−3, from dust settling (Pinte et al. 2015; Stephens et al. 2017; Dullemond et al. 2018; Villenave et al. 2022), or direct molecular emission line measurements (Flaherty et al. 2015, 2017, 2018). The above findings support the mechanism we proposed in this study as the origin of observed dust rings and gaps, where the weak turbulence condition is required (Figs. 13 and 14).
4.3 Size of dust in a protoplanetary disk
The planet-induced gas flow that is induced by a low-mass planet strongly influences on the distribution of aerodynamically small dust, St ~ 10−4–10−2. Such a small Stokes number corresponds to the dust particles of ~0.1–10 mm in the outer region of the disk, >10 au, for the steady viscous-accretion disk model assumed in this study (Fig. 4c).
The size of the dust particles in disks can be constrained observationally and theoretically. Recent observations constrain the maximum dust size in the HL Tau disk: ~0.1 mm (polarization observations at millimeter wavelengths; Kataoka et al. 2016) or ~1 mm (spectral energy distribution of the millimeter emission; Carrasco-Gonzâlez et al. 2019). Dust coagulation models can also constrain the size of the dust in a disk. Okuzumi & Tazaki (2019) has shown that the dust particles covered with the H2O-ice mantle can grow up to ~50 mm between the H2O and CO2 snow lines. Inside the H2O snow line, where the dust grains exist as nonsticky silicate grains, the maximum dust size in their model is ~1 mm. Outside the CO2 snow line, since the CO2 ice is as nonsticky as silicate grains (Musiolik et al. 2016a,b), the upper limit of the size of the dust in their model is ~0.1–1 mm. The above findings support the mechanism we propose in this study as the origin of observed dust rings and gaps, where small-sized particles are required.
4.4 Implications for planet formation
4.4.1 Pebble accretion
Dust particles with St ~ 10−3–100 can be referred to as pebbles. When the Stokes number is small (St ≲ 10−2), pebble accretion is suppressed significantly by the planet-induced gas flow (Popovas et al. 2018; Kuwahara & Kurokawa (2020a,b; Okamura & Kobayashi 2021). In our previous studies, assuming the uniform surface density of pebbles, we calculated the accretion probability of pebbles (Kuwahara & Kurokawa (2020a,b); however, the effect of the planet-induced gas flow on the dust surface density was not considered in these studies. In this section, assuming the typical disk model, where the Mhw increases with the orbital radius (Eq. (22)), we consider the accretion rate of pebbles onto a growing protoplanet. The planet-induced gas flow tends to be the flow-shear (flow-headwind) regime in the inner (outer) region of the disk for a fixed dimensionless planetary mass, m (Eq. (26)).
The dust gap forms around the planetary orbit when the planet-induced gas flow is in the flow-shear regime (Sect. 3.5.1). Under the influence of the planet-induced gas flow, the pebbles coming from a narrow window between the horseshoe and the shear regions can accrete onto the planet (Fig. 2b; Kuwahara & Kurokawa 2020a). The accretion cross section of pebbles lies within the dust gap formed by the planet-induced gas flow, because the outflow deflects the trajectories of pebbles outside the horseshoe region (Fig. 2b). Thus, the pebble accretion rate becomes lower than that estimated in Kuwahara & Kurokawa (2020a), where the uniform pebble surface density was assumed.
Here we consider the growth of the protoplanet with m = 0.3 at 1 au (Mpl ≃ 2 M⊕ and Mhw ≈ 0.03; Figs. 4a and b). Following Kuwahara & Kurokawa (2020a), we assume αdiff = 10−4 and St = 10−3 (see Sect. 4.4.3 of Kuwahara & Kurokawa (2020a) for a detailed description). Assuming uniform surface density of pebbles, the accretion rate of pebbles is Macc ~ 3 M⊕ Myr−1 (Kuwahara & Kurokawa 2020a; Okamura & Kobayashi 2021). When the effects of planet-induce gas flow on the dust distribution is considered, the pebble surface density would be reduced by a factor of ~2 due to the dust gap (Fig. 13e). Thus, the effective accretion rate could be reduced to ~1.5 M⊕ Myr−1. The growth timescale can be estimated as Mp/Macc ~ 1 Myr, which could be much longer when the turbulence strength or the Stokes number is smaller (αdiff < 10−4 or St < 10−3).
Only a dust ring is likely to be formed when the planet-induced gas flow is in the flow headwind regime (e.g., Figs. 11e and f). In this case, the accretion rate of pebbles could increase due to an increase in the pebble surface density near the planetary orbit.
We continue to consider the growth of the protoplanet, but we consider m = 0.1 (Mpl ≃ 3 M⊕ at 10 au). We assume Mhw = 0.1, which means that we focus on the outer region of the disk, ≳10 au, where the planet-induced gas flow tends to be the flow-headwind regime. Following Kuwahara & Kurokawa (2020a), we assume αdiff = 10−4 and St = 3 × 10−3. In the flow-headwind regime, the accretion probability of pebbles does not differ significantly from that obtained in the unperturbed flow except when the Stokes number is very small (St ≲ 10−3; Kuwahara & Kurokawa 2020b). The accretion rate of pebbles can be estimated as ~10 M⊕ Myr−1 for the uniform surface density of pebbles (Ormel 2017; Liu & Ormel 2018; Ormel & Liu 2018; Kuwahara & Kurokawa 2020a). The pebble surface density would be increased by a factor of ~2 due to the dust ring (Fig. 14f). Thus, the effective accretion rate could be increased to ~20 M⊕ Myr−1. In the outer region of the disk, the VSI-driven turbulence could be suppressed (Fukuhara et al. 2021, see also Sect. 4.2). This leads to a significant accumulation of pebbles (Fig. 14i) and could result in more efficient growth of the planet via pebble accretion.
4.4.2 Implications for the origins of the architectures of planetary systems
Based on the discussion in Sect. 4.4.1, we consider a formation scenario of planetary systems. In our previous studies, assuming uniform surface density of pebbles, we found that only the suppression of pebble accretion due to the planet-induced gas flow occurs in the late stage of planet formation (m ≳ 0.03–0.1), more specifically, in the inner region of the disk (≤1 au; Kuwahara & Kurokawa (2020a,b).
Our current results further supports the above discussions, which suggests that the growth of the protoplanets via pebble accretion is suppressed in the inner region of the disk (≲1 au). When the mass of the protoplanets reaches m ≳ 0.1 (≳ 0.7 M⊕ at 1 au), the subsequent growth of the protoplanets is highly suppressed by the reduction of the accretion probability of pebbles and pebble surface density due to the planet-induced gas flow. These protoplanets can avoid runaway gas accretion within the lifetime of the gas disk, which results in the formation of rocky terrestrial planets. The small rocky protoplanets may also experience giant impacts. These events lead to the formation of super-Earths.
In contrast, the efficient growth of the protoplanets via pebble accretion would be achieved in the outer region of the disk (≳ 10 au). Thus, we expect that the planets could exceed the critical core mass within the typical lifetime of the disk, leading to the formation of giant planets.
Our scenario may help explain the distribution of exoplanets (the dominance of super-Earths at <1 au; Fressin et al. 2013; Weiss & Marcy 2014 and a possible peak in the occurrence of gas giants at ~2–3 au Johnson et al. 2010; Fernandes et al. 2019), as well as the architecture of the Solar System: rocky planets in the inner regions, gas giants in the middle, and icy giants in the outer regions. The reduction of the pebble isolation mass in the inner region of the inviscid disk may cause the dichotomy that is apparent between the inner super-Earths and outer gas giants (Fung & Lee 2018). However, the small pebbles (St ≲ 10−3) may not be trapped at the local pressure maxima and thus, they continue to contribute to the growth of the planet (Bitsch et al. 2018). Since the smaller pebbles are more sensitive to the gas flow, the planet-induced gas flow has the potential to explain the dichotomy without the pressure maxima.
4.4.3 Dust growth and planetesimal formation
From Figs. 11 and 12, we found an excessive accumulation of small dust outside the planetary orbit in some cases. An increase in the dust-to-gas ratio may trigger planetesimal formation via direct growth and streaming instability (SI; Kretke & Lin 2007; Youdin & Goodman 2005; Youdin & Johansen 2007; Johansen & Youdin 2007). The growth rate of SI depends on the size of dust, which has the maximum value when St ~ 10−1–100 (Chen & Lin 2020; Umurhan et al. 2020). Thus, SI does not work for small dust grains.
In this study, we did not consider dust growth, but the accumulation of dust leads to subsequent dust growth due to an increase in the collision frequency of dust, and then the Stokes number increases. Assuming perfect sticking via collisions without collisional fragmentation and bouncing, the growth timescale can be described by 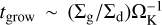 (Takeuchi & Lin 2005). Comparing the growth timescale to the drift timescale, when tgrow ≪ tdrift, the dust grains enter the “growth-dominated phase” (Taki et al. 2021). Taki et al. (2021) derived the Stokes number in the equilibrium state as follows:
(Takeuchi & Lin 2005). Comparing the growth timescale to the drift timescale, when tgrow ≪ tdrift, the dust grains enter the “growth-dominated phase” (Taki et al. 2021). Taki et al. (2021) derived the Stokes number in the equilibrium state as follows:
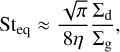 (32)
(32)
where η is given by (Ida et al. 2016)
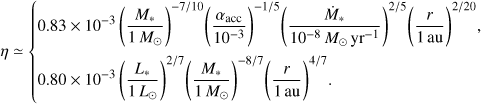 (33/34)
(33/34)
Equations (33) and (34) are valid in the region where viscous heating and stellar irradiation dominate, respectively. The dimensionless value of η has on the order of 10−3 and does not change significantly across the entire region of the disk (≲100 au). Thus, Steq strongly depends on the local dust-to-gas ratio. When Steq ≳ 1, the dust particles rapidly grow to planetesimal through the positive feedback between the reduced radial drift and the accelerated collisional growth (Taki et al. 2021).
From Figs. 11 and 12, the above condition is easily satisfied outside the planetary orbit under weak turbulence. As a result, the dust particles grow rapidly and begin to decouple from the gas. The planetesimals could form outside the planetary orbit, where dust accumulates due to the planet-induced gas flow.
4.5 Implications for protoplanetary disk observations
The gas flow induced by low-mass planets can be considered one of the possible origins of the observed dust substructures in disks. The characteristics of the dust ring and gap formed by the planet-induced gas flow are summarized as follows: (1) The planet-induced gas flow forms the ring and (or) gap in aerody-namically small dust grain distribution, St ≲ 10−2. (2) The gas flow induced by a low-mass embedded planet can generate the dust ring and (or) gap in a radial extent of ~ 1–10 [H] around the planetary orbit without creating a gas gap or pressure bump.
Our model for the dust ring and gap formation by low-mass planets can be tested when the following conditions are satisfied: (1) the dust substructures appear only for the distribution of small dust grains (≲ 1 cm) and (2) there is no correlation between the spatial distribution of gas and dust in a disk. This information can be obtained from observations of dust emission and scattering in different wavelengths to constrain the dust surface densities for different sizes and of spectral lines that trace the gas surface density.
In the following sections we discuss how our model can be distinguished from the other dust substructure formation mechanisms.
4.5.1 Correlation between the spatial distribution of gas and dust
Our model focuses on the low-mass planets that neither open gas gaps nor generate pressure bumps. Thus, correlations between the spatial distribution of gas and dust would not be observed.
When the dust substructures form due to the gas-gap-opening planet, however, there would be a correlation between the spatial distribution of gas and dust in disks, such as transition disks where the inner disks are depleted in dust relative to the outer disk (Francis & van der Marel 2020). In many transition disks, correlations between emission lines of gas and continuum rings are observed at the outer edge of the cavity, which suggests the existence of a massive planet within the cavity (van der Marel et al. 2016, 2018; Dong et al. 2017b; Boehler et al. 2017; Fedele et al. 2017).
4.5.2 Kinematic features in a protoplanetary disk
When a massive planet is embedded in a disk, kinematic features appear in the three velocity components of gas in the upper disk layers due to the large-scale meridional gas flow (Morbidelli et al. 2014; Szulágyi et al. 2014; Fung & Chiang 2016). The vertical flows toward the midplane with speeds of ~0.1cs at a region ~2–4 [H] above the midplane of the disk around HD 163296 have been detected by observations of 12CO emissions, which can be interpreted as a sign of the large-scale meridional gas flow that driven by Jupiter-mass planets (Teague et al. 2019).
Low-mass planets that do not carve a gap can induce the gas flow such as the small-scale meridional gas flow (Fung et al. 2015) or the subsonic polar inflow and radial outflow (e.g., Ormel et al. 2015b). These flows occur within the typical scale of the planetary atmosphere (≲ min(RBondi, RHill); Fung et al. 2015, 2019; Lambrechts & Lega 2017; Kuwahara et al. 2019; Béthune & Rafikov 2019; Krapp et al. 2022). Thus, as long as we focus on the low-mass planets, the kinematic features of gas that can be traceable in upper layers of disks by molecular emissions, for example 12CO (J = 2–1), would not be expected to be observable.
Meanwhile, the vertical location of the molecular emission surface depends on the molecular isotopologues and species. For instance, since the relative abundances of CO isotopologues are different, the emission surface approaches the midplane of the disk in the order of 12CO, 13CO, C18O, and C17O. Other molecules, such as HCN and C2H, can be used as tracers. The C2H lines come from a lower height than CO isotopologue (Law et al. 2021; Bosman et al. 2021). When observations with multiple chemical species constrain the velocity structure of the disk (Yu et al. 2021) and the kinematic features of the gas can only be seen in the region close to the midplane (z ≲ 1 [H]) at the orbital location of the dust substructure, such features of gas and dust support our model.
4.6 Caveats
4.6.1 Spatial distribution of dust in the global domain
The distribution of dust particles outside the local computational domain of orbital calculation is nontrivial. The planet-induced gas flow deflects the trajectories of particles and creates the voids in the x-y plane (Kuwahara & Kurokawa (2020a,b, see also Fig. 2b). Outside the local domain, however, these voids might be filled by the drift of particles in the x direction, and turbulent diffusion. Our local simulations could not handle the void closing. In estimating dust drift velocity, we assumed that the effects of the planet-induced gas flow are negligible outside the domain of the orbital calculations (namely, the void is closed outside the domain). This assumption is a conservative approach to give a minimum effect of the planet-induced gas flow on dust drift. In other words, if a planet can open a gap in our 1D model under this assumption, it means that gap could form even if we treat the global dust motion explicitly.
4.6.2 Steady-state solution
In this study, we only provide the steady-state solution of the 1D advection-diffusion equation (Eq. (20)). The timescale to reach the steady state depends on an inward advective flux of dust from the outer region of the disk. The drift speed of dust is low when the Stokes number is small. Thus, the advective flux of dust is small for a fixed initial dust surface density. It might take a long time to reach a steady state.
The timescale to reach the steady state can be estimated by the timescale for the dust concentration in a ring. The dust accumulates outside the planetary orbit with the timescale taccum:
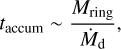 (35)
(35)
where Mring is the total mass of the mass of the ring and 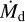 is the radial inward mass flux of dust. The ring mass can be described by:
is the radial inward mass flux of dust. The ring mass can be described by:
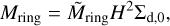 (36)
(36)
where 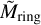 is the dimensionless mass of the ring that is obtained from our numerical results (Figs. 10–12). The initial dust surface density can be described by:
is the dimensionless mass of the ring that is obtained from our numerical results (Figs. 10–12). The initial dust surface density can be described by:
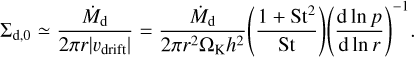 (37)
(37)
From Eq. (23), the gas surface density in a steady accretion disk can be rewritten as (Ida et al. 2016):
![${{\rm{\Sigma }}_{\rm{g}}} \simeq {{{{10}^{ - 5}}} \over {6{\pi ^2}}}\left( {{{{{\dot M}_{\rm{d}}}} \over {{{10}^{ - 8}}{M_ \odot }{\rm{y}}{{\rm{r}}^{ - 1}}}}} \right){\left( {{{{M_*}} \over {1\,\,{M_ \odot }}}} \right)^{ - 1/2}}{\left( {{r \over {{\rm{1}}\,\,\,{\rm{au}}}}} \right)^{1/2}}{\left( {{{{\alpha _{{\rm{acc}}}}} \over {{{10}^{ - 3}}}}} \right)^{ - 1}}{h^2}\left[ {{M_ \odot }{\rm{a}}{{\rm{u}}^{ - 2}}} \right].$](/articles/aa/full_html/2022/09/aa43849-22/aa43849-22-eq46.png) (38)
(38)
From Eqs. (37) and (38), ∑d,0 can be expressed as:
![${{\rm{\Sigma }}_{{\rm{d,0}}}} \simeq {{{{10}^{ - 5}}} \over {{\pi ^2}}}\left( {{{1 + {\rm{S}}{{\rm{t}}^2}} \over {{\rm{St}}}}} \right)\left( {{{{{\dot M}_{\rm{d}}}} \over {{{10}^2}{M_ \odot }{\rm{My}}{{\rm{r}}^{ - 1}}}}} \right){\left( {{{{M_*}} \over {1\,\,{M_ \odot }}}} \right)^{ - 1/2}}{\left( {{r \over {{\rm{1}}\,\,\,{\rm{au}}}}} \right)^{1/2}}{h^{ - 2}}\left[ {{M_ \oplus }{\rm{a}}{{\rm{u}}^{ - 2}}} \right].$](/articles/aa/full_html/2022/09/aa43849-22/aa43849-22-eq47.png) (39)
(39)
Thus, the timescale for the dust accumulation can be estimated by:
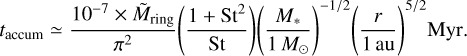 (40)
(40)
Here we consider the planet with m = 0.1, the Stokes number St = 10−4, and the turbulent parameter αdiff = 10−4. When Mhw = 0.03 (~1 au; Fig. 11e), Eq. (40) gives taccum ~ 6000 yr. When Mhw = 0.1 (~50 au; Fig. 11f), Eq. (40) gives taccum ~ 133 Myr.
From these estimations, in the inner region of the disk (≲ 1 au), the dust surface density can reach the steady state within the typical disk lifetime of a few megayears (Haisch et al. 2001), but it seems difficult to reach the steady state in the outer region (≳10 au). We plan to investigate the time evolution of the dust surface density influenced by the planet-induced gas flow in the second paper of this series. In reality, the time evolution of dust surface density is determined by complex processes such as dust growth and fragmentation. These additional processes should be included in further studies.
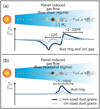 |
Fig. 16 Schematic illustrations of our model for the dust ring and gap formation. The planet-induced gas flow is in the flow-shear regime (panel a) and in the flow-headwind regime (panel b) to form dust substructures. |
5 Conclusions
We have investigated the influence of the gas flow induced by low-mass, non-gas-gap-opening planets on the spatial distribution of dust in protoplanetary disks. First, we performed 3D hydrodynamical simulations, which resolve the local gas flow in the region, including the Hill and Bondi spheres of the planet. We then calculated the trajectories of dust influenced by the planet-induced gas flow. We used the obtained hydrodynamical simulation data to calculate the gas drag force acting on the dust particle. Finally, we computed the steady-state dust surface density by incorporating the influences of the planet-induced gas flow into the 1D advection-diffusion equation. We summarize our main findings as follows (Fig. 16).
When St ≲ 3 × 10−2 (≲ 1 cm at ~1–10 au), a forbidden region exists outside the planetary orbit due to the outflow of the gas, where the planet-induced gas flow inhibits the radial drift of dust particles. The width of the forbidden region is wider for smaller Stokes numbers.
Under weak turbulence (αdiff ≲ 10−4), the gas flow induced by a non-gas-gap-opening planet with m ≳ 0.1 (≳ 0.7 M⊕ at 1 au, or ≳ 3.3 M⊕ at 10 au) generates dust accumulation (the dust ring) and depletion (the dust gap) with a radial extent of ~1–10 [H] around the planetary orbit in the distribution of small dust grains, St ≲ 10−2 (≲1 cm at ~1–10 au). When the outflow occurs dominantly both outside and inside the planetary orbit (m/Mhw ≳ 3), a dust ring and/or gap form(s). When the outflow occurs dominantly outside the planetary orbit (m/Mhw ≲ 3), only the dust ring forms outside the planetary orbit in the steady state.
The properties of the dust ring and gap, such as width, depth, and amplitude, are more pronounced for a small Stokes number, because smaller dust particles are more sensitive to the gas flow.
The dust ring and gap formation due to the planet-induced gas flow significantly impacts the processes of planet formation. The planetary growth via pebble accretion would be inefficient due to dust depletion around the planetary orbit. This is susceptible to occur in the inner region of the disk (≲1 au). In contrast, the dust accumulation could result in efficient growth of the planet via pebble accretion, and may trigger planetesimal formation via rapid growth of the dust particles. This is susceptible to occur in the outer region of the disk (≳ 1–10 au). Our result may be helpful in explaining the dichotomy between the inner super-Earths and outer gas giants.
The gas flow induced by low-mass, non-gas-gap-opening planets can be considered one of the possible origins of the observed dust substructures in disks. When (1) the dust ring and gap appear only for the distribution of small dust grains (≲1 cm), and (2) there is no correlation between the spatial distribution of gas and dust in a disk, such dust substructures may indicate the existence of a low-mass planet embedded in a protoplanetary disk (≳1 M⊕).
Acknowledgements
We would like to thank an anonymous referee for constructive comments. We thank Athena++ developers. This study has greatly benefited from fruitful discussions with Satoshi Okuzumi, Ayaka Okuya, and Yuya Fukuhara. Numerical computations were in part carried out on Cray XC50 at the Center for Computational Astrophysics at the National Astronomical Observatory of Japan. This work was supported by JSPS KAKENHI Grant number 20J20681, 20K04051, 9921K13976, and 21H04514.
Appendix A Gas drag regimes
The gas drag force is divided into two regimes, the Epstein and the Stokes regimes, depending on the relationship between the size of the particle and mean free path of the gas (Eqs. (24) and (25)), which differ in terms of the dependence on the gas density. In this study, we assumed that the gas drag force is independent of the gas density, which is strictly valid only in the Stokes regime but not in the Epstein regime. However, the region of particular interest in this study is typically beyond the Bondi region, where the gas density is almost constant and identical to the initial (unperturbed) value. We confirmed that the choice of the gas drag regime does not affect the results and thus, the results can be applicable for dust particles both in Epstein and Stokes regimes.
Appendix B Maximum impact parameter of accreted particles
The maximum impact parameter of accreted particles in the unperturbed flow, b, is expressed by (Ormel & Klahr 2010; Lambrechts & Johansen 2012; Guillot et al. 2014; Ida et al. 2016; Sato et al. 2016)
![$b = {b_0}\exp \left[ { - {{\left( {{{{\rm{St}}} \over 2}} \right)}^{0.65}}} \right],$](/articles/aa/full_html/2022/09/aa43849-22/aa43849-22-eq49.png) (B.1)
(B.1)
Appendix C Density waves excited by an embedded planet
An embedded planet excites the density waves as shown in Fig. C.1. Since the density waves extend in the azimuthal direction, they are interrupted at the edge of the computational domain of our hydrodynamical simulations, |x| ~ 3 [H]. Figure C.1 also shows that the outflow of the gas appears closer to the planetary orbit than the density waves.
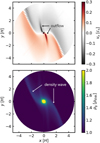 |
Fig. C.1 Flow structure at the midplane of the disk around a planet obtained from m03-hw001. The color contours represent the flow speed in the x direction (top) and the gas density (bottom) |
Appendix D Temperature and aspect ratio of the steady accretion disk
The disk midplane temperature is given by Tdisk = max(Tvis, Tirr), where Tvis and Tirr are temperatures determined by viscous heating and stellar irradiation (Garaud & Lin 2007; Oka et al. 2011; Ida et al. 2016),
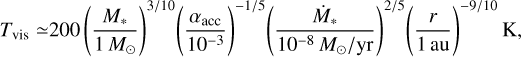 (D.1)
(D.1)
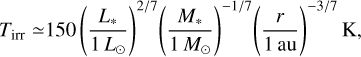 (D.2)
(D.2)
where  is the accretion rate of the disk and L* is the stellar luminosity. In this study, we assume a solar-mass host star, M* = 1 M⊙, the solar luminosity, L* = 1 L⊙, and the typical accretion rate of classical T Tauri stars,
is the accretion rate of the disk and L* is the stellar luminosity. In this study, we assume a solar-mass host star, M* = 1 M⊙, the solar luminosity, L* = 1 L⊙, and the typical accretion rate of classical T Tauri stars, 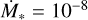 M⊙/yr.
M⊙/yr.
The aspect ratio of the disk is given by
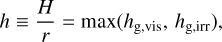 (D.3)
(D.3)
where hg,vis and hg,irr are aspect ratios given by (Ida et al. 2016)
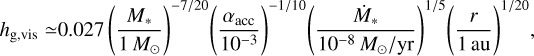 (D.4)
(D.4)
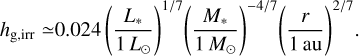 (D.5)
(D.5)
Appendix E Hydrodynamical regimes of the planet-induced gas flow
The gas flow around an embedded planet is perturbed by the planet, which forms the characteristic 3D structure of the flow field (Ormel et al. 2015b; Fung et al. 2015, 2019; Cimerman et al. 2017; Lambrechts & Lega 2017; Kurokawa & Tanigawa 2018; Kuwahara et al. 2019; Béthune & Rafikov 2019; Moldenhauer et al. 2021). The planet-induced gas flow is divided into two regimes, the flow-shear and flow-headwind regimes, depending on the relationship between the dimensionless planetary mass and the Mach number of the headwind of the gas (Eq. (26); Kuwahara & Kurokawa 2020b).
The fundamental features of the flow field are as follows: (1) gas from the disk enters the Bondi or Hill sphere (inflow) and exits through the midplane region of the disk (outflow; the red lines of Figs. E.1 and E.2). (2) The horseshoe flow exists in the anterior-posterior direction of the orbital path of the planet (the orange lines of Figs. E.1 and E.2). The horseshoe streamlines have a columnar structure in the vertical direction (Figs. E.1a and b). (3) The Keplerian shear flow extends inside and outside the orbit of the planet (the green lines of Figs. E.1 and E.2).
 |
Fig. E.1 Streamlines of 3D planet-induced gas flow around the planet with m = 0.3 and Mhw = 0. The planet-induced gas flow is in the flow-shear regime. The result is obtained from Kuwahara & Kurokawa (2020a). The solid green, orange, and red lines are the Keplerian shear, the horseshoe streamlines, and the recycling streamlines (Ormel et al. 2015b; Kuwahara et al. 2019) (or transient horseshoe streamlines (Fung et al. 2015)), respectively. The sphere is the Bondi sphere of the planet, whose size is 0.3 [H]. The arrows represent the direction of the gas flow. Panels a and b: Perspective views of the flow field. Panel c: x–y plane viewed from the +z direction. |
 |
Fig. E.2 Same as in Fig. E.1, but with m = 0.03 and Mhw = 0.1. The planet-induced gas flow is in the flow-headwind regime. The sphere is the Bondi sphere of the planet, whose size is 0.03 [H]. The vertical dashed line in panel c corresponds to the x coordinate of the position of the corotation radius for the gas, xg,cor = −2/3 Mhw. |
Appendix F Dust motion within the forbidden region
We first describe the motion of dust particles in the x direction. When the Stokes number is small (St = 10−4), the forbidden region lies in a wide range of Fig. 6a. Counterintuitively, we found that the forbidden region exists even above the outflow whose vertical scale is ~ 0.5 RBondi. To understand this phenomenon, we show the trajectories of dust particles with St = 10−4 at high altitudes in Fig. F.1. Figure F.1 compares the dust trajectories in the planet-induced gas flow (solid lines) with those in the unperturbed gas flow (dashed lines). In the distant region far from the planet, y > −4, the orbital radii of dust in the planet-induced gas flow are larger than those in the unperturbed gas flow (Fig. F.1a). Figure F.1b shows xe > xs in the planet-induced gas flow. This is caused by the gas flow structure at high altitudes. We note that the changes in the orbital radii of dust should be carefully considered. Since our hydrodynamical simulations were local, we did not trace the gas flow structure in the full azimuthal direction. Thus, our results may need to be compared with the results obtained by global hydrodynamical simulations in a future study.
 |
Fig. F.1 Trajectories of dust particles with St = 10−4 in the planet-induced gas flow (solid lines) and in the unperturbed sub-Keplerian shear flow (dashed lines). We used the result obtained from m03-hw001 to calculate dust trajectories. We set zs = 0.5 for the orbital calculations. Different colors correspond to different xs. The filled circles and cross symbols in panel b correspond to xs and xe, respectively. The dotted and dashed circles are the Bondi and Hill radii of the planet, respectively. Panel a: x–y plane viewed from the +z direction. Panel b: x–z plane viewed from the −y direction. Panel c: y–z plane viewed from the +x direction. This figure should be compared to Fig. 6a. |
When the Stokes number is large, the width of the forbidden region decreases significantly above the outflow (Fig. 6b). The width of the forbidden region for St = 10−2 (Fig. 6b) is narrower than that for St = 10−4 (Fig. 6a). When St = 3 × 10−2 (Fig. 6c), the width of the forbidden region is quite narrow (≲ 0.1 [H]). This is because, when the Stokes number is large, the dust particles are less affected by the gas flow.
Next, we describe the motion of dust particles in the z direction. The dust particles influenced by the planet-induced gas flow ascend when they pass through near the planet location (solid lines in Figs. F.1b and c). The upward motion of dust particles is caused by the meridional gas flow induced by the planet. In the case of low-mass planets, the meridional gas flow occurs as follows: the outflow streamlines connect to the horseshoe streamlines (called “transient horseshoe flow”; Fung et al. 2015). In the flow-shear regime, gas flows in at high latitudes of the gravitational sphere of the planet at its horseshoe turn. The transient flow is vertically compressed, then the upward gas flow occurs due to the decompression of the gas (see, e.g., Fig. 11 of Fung et al. 2015).
References
- ALMA Partnership (Brogan, C. L., et al.) 2015, ApJ, 808, L3 [Google Scholar]
- Andrews, S. M., Huang, J., Pérez, L. M., et al. 2018, ApJ, 869, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Ataiee, S., Baruteau, C., Alibert, Y., & Benz, W. 2018, A&A, 615, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bae, J., Pinilla, P., & Birnstiel, T. 2018, ApJ, 864, L26 [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214 [Google Scholar]
- Béthune, W., & Rafikov, R. R. 2019, MNRAS, 488, 2365 [Google Scholar]
- Béthune, W., Lesur, G., & Ferreira, J. 2017, A&A, 600, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Morbidelli, A., Johansen, A., et al. 2018, A&A, 612, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boehler, Y., Weaver, E., Isella, A., et al. 2017, ApJ, 840, 60 [Google Scholar]
- Bosman, A. D., Bergin, E. A., Loomis, R. A., et al. 2021, ApJS, 257, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Carrasco-González, C., Sierra, A., Flock, M., et al. 2019, ApJ, 883, 71 [Google Scholar]
- Chapman, S., & Cowling, T. G. 1970, The mathematical theory of non-uniform gases. An account of the kinetic theory of viscosity, thermal conduction and diffusion in gases (Cambridge: University Press) [Google Scholar]
- Chen, K., & Lin, M.-K. 2020, ApJ, 891, 132 [Google Scholar]
- Cimerman, N. P., Kuiper, R., & Ormel, C. W. 2017, MNRAS, 471, 4662 [Google Scholar]
- Crida, A., Morbidelli, A., & Masset, F. 2006, Icarus, 181, 587 [Google Scholar]
- Cui, C., & Bai, X.-N. 2020, ApJ, 891, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Cui, C., & Lin, M.-K. 2021, MNRAS, 505, 2983 [NASA ADS] [CrossRef] [Google Scholar]
- Cuzzi, J. N., Dobrovolskis, A. R., & Champney, J. M. 1993, Icarus, 106, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Dipierro, G., & Laibe, G. 2017, MNRAS, 469, 1932 [Google Scholar]
- Dipierro, G., Laibe, G., Price, D. J., & Lodato, G. 2016, MNRAS, 459, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Disk Dynamics Collaboration (Armitage, P. J., et al.) 2020, PASA, submitted [arXiv:2009.04345] [Google Scholar]
- Dong, R., Zhu, Z., & Whitney, B. 2015, ApJ, 809, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Dong, R., Li, S., Chiang, E., & Li, H. 2017a, ApJ, 843, 127 [Google Scholar]
- Dong, R., van der Marel, N., Hashimoto, J., et al. 2017b, ApJ, 836, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Dong, R., Li, S., Chiang, E., & Li, H. 2018, ApJ, 866, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Drazkowska, J., Li, S., Birnstiel, T., Stammler, S. M., & Li, H. 2019, ApJ, 885, 91 [CrossRef] [Google Scholar]
- Dubrulle, B., Morfill, G., & Sterzik, M. 1995, Icarus, 114, 237 [Google Scholar]
- Duffell, P. C., & MacFadyen, A. I. 2013, ApJ, 769, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C. P., Birnstiel, T., Huang, J., et al. 2018, ApJ, 869, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Fedele, D., Carney, M., Hogerheijde, M., et al. 2017, A&A, 600, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fernandes, R. B., Mulders, G. D., Pascucci, I., Mordasini, C., & Emsenhuber, A. 2019, ApJ, 874, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Flaherty, K. M., Hughes, A. M., Rosenfeld, K. A., et al. 2015, ApJ, 813, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Flaherty, K. M., Hughes, A. M., Rose, S. C., et al. 2017, ApJ, 843, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Flaherty, K. M., Hughes, A. M., Teague, R., et al. 2018, ApJ, 856, 117 [CrossRef] [Google Scholar]
- Flock, M., Ruge, J., Dzyurkevich, N., et al. 2015, A&A, 574, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Francis, L., & van der Marel, N. 2020, ApJ, 892, 111 [Google Scholar]
- Fressin, F., Torres, G., Charbonneau, D., et al. 2013, ApJ, 766, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Fukuhara, Y., Okuzumi, S., & Ono, T. 2021, ApJ, 914, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Fung, J., & Chiang, E. 2016, ApJ, 832, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Fung, J., & Lee, E. J. 2018, ApJ, 859, 126 [Google Scholar]
- Fung, J., Shi, J.-M., & Chiang, E. 2014, ApJ, 782, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Fung, J., Artymowicz, P., & Wu, Y. 2015, ApJ, 811, 101 [Google Scholar]
- Fung, J., Zhu, Z., & Chiang, E. 2019, ApJ, 887, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Gammie, C. F. 1996, ApJ, 457, 355 [Google Scholar]
- Gammie, C. F. 2001, ApJ, 553, 174 [Google Scholar]
- Garaud, P., & Lin, D. 2007, ApJ, 654, 606 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Tremaine, S. 1979, ApJ, 233, 857 [Google Scholar]
- Goldreich, P., & Tremaine, S. 1980, ApJ, 241, 425 [Google Scholar]
- Gonzalez, J.-F., Laibe, G., Maddison, S. T., Pinte, C., & Ménard, F. 2015, MNRAS, 454, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, J.-F., Laibe, G., & Maddison, S. T. 2017, MNRAS, 467, 1984 [NASA ADS] [Google Scholar]
- Goodman, J., & Rafikov, R. 2001, ApJ, 552, 793 [NASA ADS] [CrossRef] [Google Scholar]
- Guillot, T., Ida, S., & Ormel, C. W. 2014, A&A, 572, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haisch, Karl E. J., Lada, E. A., & Lada, C. J. 2001, ApJ, 553, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Ida, S., & Nakazawa, K. 1989, A&A, 224, 303 [NASA ADS] [Google Scholar]
- Ida, S., Guillot, T., & Morbidelli, A. 2016, A&A, 591, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jiang, H., Zhu, W., & Ormel, C. W. 2022, ApJ, 924, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., & Youdin, A. 2007, ApJ, 662, 627 [Google Scholar]
- Johnson, J. A., Aller, K. M., Howard, A. W., & Crepp, J. R. 2010, PASP, 122, 905 [Google Scholar]
- Kanagawa, K. D., Muto, T., Tanaka, H., et al. 2015, ApJ, 806, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Kanagawa, K. D., Muto, T., Okuzumi, S., et al. 2018, ApJ, 868, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Kataoka, A., Muto, T., Momose, M., Tsukagoshi, T., & Dullemond, C. P. 2016, ApJ, 820, 54 [Google Scholar]
- Kley, W. 1999, MNRAS, 303, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Krapp, L., Kratter, K. M., & Youdin, A. N. 2022, ApJ, 928, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Kretke, K. A., & Lin, D. 2007, ApJ, 664, L55 [CrossRef] [Google Scholar]
- Kurokawa, H., & Tanigawa, T. 2018, MNRAS, 479, 635 [Google Scholar]
- Kusaka, T., Nakano, T., & Hayashi, C. 1970, Progr. Theor. Phys., 44, 1580 [NASA ADS] [CrossRef] [Google Scholar]
- Kuwahara, A., & Kurokawa, H. 2020a, A&A, 633, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuwahara, A., & Kurokawa, H. 2020b, A&A, 643, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuwahara, A., Kurokawa, H., & Ida, S. 2019, A&A, 623, A179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambrechts, M., & Johansen, A. 2012, A&A, 544, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambrechts, M., & Lega, E. 2017, A&A, 606, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambrechts, M., Johansen, A., & Morbidelli, A. 2014, A&A, 572, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Law, C. J., Teague, R., Loomis, R. A., et al. 2021, ApJS, 257, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, D. N., & Papaloizou, J. 1979, MNRAS, 186, 799 [CrossRef] [Google Scholar]
- Lin, D. N., & Papaloizou, J. 1986, ApJ, 307, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, D. N. C., & Papaloizou, J. C. B. 1993, in Protostars and Planets III, eds. E. H. Levy, & J. I. Lunine, 749 [Google Scholar]
- Liu, B., & Ormel, C. W. 2018, A&A, 615, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lodato, G., Dipierro, G., Ragusa, E., et al. 2019, MNRAS, 486, 453 [Google Scholar]
- Long, F., Pinilla, P., Herczeg, G. J., et al. 2018, ApJ, 869, 17 [Google Scholar]
- Long, F., Pinilla, P., Herczeg, G. J., et al. 2020, ApJ, 898, 36 [CrossRef] [Google Scholar]
- Malygin, M. G., Klahr, H., Semenov, D., Henning, T., & Dullemond, C. P. 2017, A&A, 605, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masset, F. S., & Benítez-Llambay, P. 2016, ApJ, 817, 19 [NASA ADS] [CrossRef] [Google Scholar]
- McNally, C. P., Nelson, R. P., Paardekooper, S.-J., & Benítez-Llambay, P. 2019, MNRAS, 484, 728 [Google Scholar]
- Moldenhauer, T., Kuiper, R., Kley, W., & Ormel, C. 2021, A&A, 646, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morbidelli, A., Szulágyi, J., Crida, A., et al. 2014, Icarus, 232, 266 [Google Scholar]
- Musiolik, G., Teiser, J., Jankowski, T., & Wurm, G. 2016a, ApJ, 818, 16 [Google Scholar]
- Musiolik, G., Teiser, J., Jankowski, T., & Wurm, G. 2016b, ApJ, 827, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Muto, T., & Inutsuka, S.-I. 2009, ApJ, 695, 1132 [NASA ADS] [CrossRef] [Google Scholar]
- Nakagawa, Y., Sekiya, M., & Hayashi, C. 1986, Icarus, 67, 375 [Google Scholar]
- Nakamoto, T., & Nakagawa, Y. 1994, ApJ, 421, 640 [Google Scholar]
- Nelson, R. P., Papaloizou, J. C., Masset, F., & Kley, W. 2000, MNRAS, 318, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, R. P., Gressel, O., & Umurhan, O. M. 2013, MNRAS, 435, 2610 [Google Scholar]
- Oka, A., Nakamoto, T., & Ida, S. 2011, ApJ, 738, 141 [Google Scholar]
- Okamura, T., & Kobayashi, H. 2021, ApJ, 916, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Okuzumi, S., & Tazaki, R. 2019, ApJ, 878, 132 [Google Scholar]
- Okuzumi, S., Momose, M., Sirono, S.-I., Kobayashi, H., & Tanaka, H. 2016, ApJ, 821, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W. 2017, in Astrophysics and Space Science Library, 445, eds. M. Pessah, & O. Gressel, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W., & Klahr, H. H. 2010, A&A, 520, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ormel, C. W., & Liu, B. 2018, A&A, 615, A178 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ormel, C. W., Kuiper, R., & Shi, J.-M. 2015a, MNRAS, 446, 1026 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W., Shi, J.-M., & Kuiper, R. 2015b, MNRAS, 447, 3512 [Google Scholar]
- Paardekooper, S.-J., & Mellema, G. 2004, A&A, 425, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paardekooper, S.-J., & Mellema, G. 2006, A&A, 453, 1129 [CrossRef] [EDP Sciences] [Google Scholar]
- Pinilla, P., Benisty, M., & Birnstiel, T. 2012, A&A, 545, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinilla, P., Klarmann, L., Birnstiel, T., et al. 2016, A&A, 585, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinte, C., Dent, W. R., Ménard, F., et al. 2015, ApJ, 816, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Popovas, A., Nordlund, Å., Ramsey, J. P., & Ormel, C. W. 2018, MNRAS, 479, 5136 [Google Scholar]
- Popovas, A., Nordlund, Å., & Ramsey, J. P. 2019, MNRAS, 482, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Rafikov, R. R. 2002, ApJ, 572, 566 [NASA ADS] [CrossRef] [Google Scholar]
- Rice, W., Armitage, P. J., Wood, K., & Lodato, G. 2006, MNRAS, 373, 1619 [CrossRef] [Google Scholar]
- Rosotti, G. P., Juhasz, A., Booth, R. A., & Clarke, C. J. 2016, MNRAS, 459, 2790 [Google Scholar]
- Sato, T., Okuzumi, S., & Ida, S. 2016, A&A, 589, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Stephens, I. W., Yang, H., Li, Z.-Y., et al. 2017, ApJ, 851, 55 [Google Scholar]
- Stone, J. M., Tomida, K., White, C. J., & Felker, K. G. 2020, ApJS, 249, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Suriano, S. S., Li, Z.-Y., Krasnopolsky, R., & Shang, H. 2017, MNRAS, 468, 3850 [NASA ADS] [CrossRef] [Google Scholar]
- Suriano, S. S., Li, Z.-Y., Krasnopolsky, R., & Shang, H. 2018, MNRAS, 477, 1239 [NASA ADS] [CrossRef] [Google Scholar]
- Szulágyi, J., Morbidelli, A., Crida, A., & Masset, F. 2014, ApJ, 782, 65 [CrossRef] [Google Scholar]
- Takahashi, S. Z., & Inutsuka, S.-I. 2014, ApJ, 794, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Takahashi, S. Z., & Inutsuka, S.-I. 2016, AJ, 152, 184 [NASA ADS] [CrossRef] [Google Scholar]
- Takeuchi, T., & Lin, D. 2005, ApJ, 623, 482 [NASA ADS] [CrossRef] [Google Scholar]
- Taki, T., Kuwabara, K., Kobayashi, H., & Suzuki, T. K. 2021, ApJ, 909, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Teague, R., Bae, J., & Bergin, E. A. 2019, Nature, 574, 378 [NASA ADS] [CrossRef] [Google Scholar]
- Testi, L., Natta, A., Shepherd, D., & Wilner, D. 2003, A&A, 403, 323 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tominaga, R. T., Inutsuka, S.-I., & Takahashi, S. Z. 2018, PASJ, 70, 3 [NASA ADS] [Google Scholar]
- Tominaga, R. T., Takahashi, S. Z., & Inutsuka, S.-I. 2019, ApJ, 881, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Tominaga, R. T., Takahashi, S. Z., & Inutsuka, S.-I. 2020, ApJ, 900, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Ueda, T., Flock, M., & Okuzumi, S. 2019, ApJ, 871, 10 [Google Scholar]
- Ueda, T., Flock, M., & Birnstiel, T. 2021, ApJ, 914, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Umurhan, O. M., Estrada, P. R., & Cuzzi, J. N. 2020, ApJ, 895, 4 [Google Scholar]
- Urpin, V., & Brandenburg, A. 1998, MNRAS, 294, 399 [Google Scholar]
- van der Marel, N., van Dishoeck, E. F., Bruderer, S., et al. 2016, A&A, 585, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Marel, N., Williams, J. P., Ansdell, M., et al. 2018, ApJ, 854, 177 [Google Scholar]
- van der Marel, N., Dong, R., di Francesco, J., Williams, J. P., & Tobin, J. 2019, ApJ, 872, 112 [Google Scholar]
- Villenave, M., Stapelfeldt, K., Duchêne, G., et al. 2022, ApJ, 930, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Watanabe, S.-I., & Lin, D. 2008, ApJ, 672, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Weber, P., Benítez-Llambay, P., Gressel, O., Krapp, L., & Pessah, M. E. 2018, ApJ, 854, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Weidenschilling, S. J. 1977, MNRAS, 180, 57 [Google Scholar]
- Weiss, L. M., & Marcy, G. W. 2014, ApJ, 783, L6 [Google Scholar]
- Whipple, F. L. 1972, in From Plasma to Planet, ed. A. Elvius, 211 [Google Scholar]
- White, C. J., Stone, J. M., & Gammie, C. F. 2016, ApJS, 225, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y., & Lithwick, Y. 2021, ApJ, 923, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Youdin, A. N., & Goodman, J. 2005, ApJ, 620, 459 [Google Scholar]
- Youdin, A., & Johansen, A. 2007, ApJ, 662, 613 [Google Scholar]
- Youdin, A. N., & Lithwick, Y. 2007, Icarus, 192, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, H., Teague, R., Bae, J., & Öberg, K. 2021, ApJ, 920, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, K., Blake, G. A., & Bergin, E. A. 2015, ApJ, 806, L7 [Google Scholar]
- Zhang, K., Booth, A. S., Law, C. J., et al. 2021, ApJS, 257, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, Z., Nelson, R. P., Dong, R., Espaillat, C., & Hartmann, L. 2012, ApJ, 755, 6 [Google Scholar]
- Zhu, Z., Stone, J. M., Rafikov, R. R., & Bai, X.-N. 2014, ApJ, 785, 122 [NASA ADS] [CrossRef] [Google Scholar]
In our dimensionless unit, the pebble isolation mass is given by miso ≳ 0.6 (Lambrechts et al. 2014; Bitsch et al. 2018; Ataiee et al. 2018). When the Hill radius of the planet exceeds the disk scale height, a gas gap forms close to the planetary orbit. This happens when m > 3 (Lin & Papaloizou 1993).
We assumed r = 1 au in Eq. (3). The size of the inner boundary does not affect our results (Kuwahara & Kurokawa 2020a). Therefore, when we convert the dimensionless planetary mass into a dimensional one, we can use an arbitrary orbital radius regardless of a fixed Rinn (Sect. 2.9).
Our hydrodynamical simulations are performed in the local frame. The width of the horseshoe region obtained from our simulations differs from that obtained from global simulations (e.g., Masset & Benítez-Llambay 2016). See Kuwahara & Kurokawa (2020b) for the discussion.
Again, the following results cannot be directly classified based on the hydrodynamical regimes introduced by Kuwahara & Kurokawa (2020b) because the transition of the gas flow field from the flow-shear to the flow-headwind regime occurs smoothly. We use the gas flow regimes as a qualitative guide. The important point is whether the dominant outflow occurs inside or outside the planetary orbit.
The dust is stirred up by the meridional gas flow, but its magnitude is small (Fig. 15). Recent two-fluid (dust + gas) 3D global simulations also suggest that the meridional gas flow induced by a low-mass planet does not effectively stir dust particles (Krapp et al. 2022). We discuss the upward motion of dust in Appendix F.
All Tables
All Figures
 |
Fig. 1 Schematic illustration of our model. We performed 3D hydrodynamical simulations on the spherical polar grid (the black sphere), which hosts a planet located at its center (the brown-filled circle; Sect. 2.3). We consider the planet on a fixed circular orbit with the orbital radius, a. We adopt unperturbed sub-Keplerian shear flow at the outer boundary of the hydrodynamical simulations (the green arrows). We then calculated the trajectories of particles influenced by the planet-induced gas flow in the frame co-rotating with the planet (the local box; Sect. 2.4.1). We used the limited part of the computational domain of hydrodynamical simulation, Rhydro, in orbital calculations of dust particles (Sect. 2.4.1). The x and z coordinates of the starting point of particles, xs and zs, are the parameters. The starting point of orbital calculation is beyond Rhydro. The spatial interval of orbital calculation in the x direction is δx (Sect. 2.4.2). The x coordinate of the particle at the edge of the domain of orbital calculation is xe. The x coordinate of the particle after one synodical orbit, x′S, is given by Eq. (27) (Sect. 3.3). The schematic trajectories of particles are shown by the dashed blue lines (without the influence of planet-induced gas flow) and solid orange lines (perturbed by the planet-induced gas flow). The open circles on the trajectory correspond to the position of a particle at specific time intervals, ∆t(vy,0, zs) (Eq. (10)). The black arrows on the trajectories are the velocities in the x direction of a particle at each position, vx. It should be noted that we do not follow trajectories outside the calculation domain of orbital calculations. Instead, we assumed the uniform and Gaussian distributions of dust particles in the azimuthal and vertical directions outside the local domain of orbital calculation, respectively, where the particles have a fixed velocity in the x direction, vdrift. Based on the obtained spatial distribution of dust in the global domain, we calculated the azimuthally and vertically averaged drift velocity, 〈vx〉y,z (Eq. (17)). Finally, we calculated the dust surface density by incorporating 〈vx〉yz into the 1D advection-diffusion equation (Eq. (20)). |
| In the text | |
 |
Fig. 2 Streamlines of gas (left) and trajectories of dust particles with St = 10−2 (right) at the midplane of the disk. The flow structure around a planet is obtained from m03-hw001. With this parameter set, the planet-induced gas flow is in the flow-shear regime (see Sect. 3.2). The color contour represents the flow speed in the x direction, vx,gas. We set zs = 0 for the orbital calculations. The dotted and dashed circles are the Bondi and Hill radii of the planet, respectively. The thick blue lines in the right panel correspond to the trajectories of the dust particles that satisfy x′s ≥ xs (see Fig. 1 and Sect. 3.3 for details). The 3D structure of the gas flow field is shown in Appendix E. |
| In the text | |
 |
Fig. 3 Same as Fig. 2, but with the flow structure obtained from m003-hw01 and St = 10−4 set for the trajectories. In this figure, the planet-induced gas flow is in the flow-headwind regime (see Sect. 3.2). The 3D structure of the gas flow field is shown in Appendix E. |
| In the text | |
 |
Fig. 4 Relation between the dimensionless quantities and dimensional ones. Each line represents the planetary mass (top; Eq. (21)), Mach number (middle; Eq. (22)), and particle size (bottom; Eqs. (24) and (25)) as a function of the orbital radius. In panel c, we only plotted St ≤ 10−2, which is the important parameter range in this study. |
| In the text | |
 |
Fig. 5 Gas flow structure around a planet. The results were obtained from m01-hw001 (left), m01-hw003 (middle), and m01-hw01 (right). The color contour represents the flow speed in the x direction, vx,gas. The solid lines correspond to the specific streamlines. The vertical dashed blue line corresponds to the corotation radius for the gas. The dotted and dashed circles are the Bondi and Hill radii of the planet, respectively. |
| In the text | |
 |
Fig. 6 Vector field of dust velocities in the cases with St = 10−4 (left panel), 10−2 (middle panel), and 3 × 10−2 (right panel) under the common gas flow obtained from m03-hw001. The color contour from red to black represents the x component of the gas flow velocity averaged in the y direction within the calculation domain of hydrodynamical simulation around a planet, 〈vx,gas〉y. Arrows represent the direction of movement of dust particles. The color contour of the arrows from green to purple represents the distance of drift of a dust particle after one synodical orbit. The hatched region enclosed by black curves corresponds to the forbidden region. The two-headed blue arrow in panel b can be compared to the region shown by the thick blue lines in Fig. 2b. The dotted and dashed lines are the Bondi and Hill radii of the planet, respectively. Thanks to the symmetry of the system, we only focus on the region where z ≥ 0. We discuss the dust motion in the x-z plane in detail in Appendix F motion within the forbidden region. |
| In the text | |
 |
Fig. 7 Vertically averaged width of the forbidden region, 〈wf〉z. Different colors correspond to different Mhw. We adopt αdiff = 10−4. |
| In the text | |
 |
Fig. 8 Gas flow structure averaged in the y direction within the calculation domain of hydrodynamical simulation around a planet (panel a), the difference of the azimuthally and vertically averaged velocity of dust particles from the unperturbed steady-state drift velocity, |
| In the text | |
 |
Fig. 9 Same as Fig. 8, but with the result obtained from m81-hw81 in panel a and αdiff = 10-4 adopted in panels b-d. Since we only plot the region where |x| ≤ 2, the outer part of the ring is interrupted. |
| In the text | |
 |
Fig. 10 Dust surface density with m = 0.03 for the different Stokes numbers, the Mach numbers, and the turbulent parameters. Different colors correspond to different Stokes numbers. The minimum and the maximum values of the dust surface density are summarized in Figs. 13 and 14. |
| In the text | |
 |
Fig. 11 Same as Fig. 10, but with m = 0.1. The gray-shaded region represents an excessive accumulation of dust particles, where the dust-to-gas ratio exceeds unity, assuming the initial value of ∑d,0/∑g = 0.01. Since we only plot the region where −1 ≤ x ≤ 4, the outer part of the ring is interrupted. The dashed black line corresponds to ∑d/∑d,0 = 1. |
| In the text | |
 |
Fig. 12 Same as Fig. 10, but with m = 0.3. The gray-shaded region represents an excessive accumulation of dust particles, where the dust-to-gas ratio exceeds unity, assuming the initial value of ∑d,0/∑g = 0.01. Since we only plot the region where −1 ≤ x ≤ 4, the outer part of the ring is interrupted. The dashed black line corresponds to the initial value. |
| In the text | |
 |
Fig. 13 Minimum dust surface density, ∑d,min, as a function of the planetary mass and the Stokes number. Different rows correspond to different turbulent parameters, αdiff. Different columns correspond to different Mach numbers, Mhw. |
| In the text | |
 |
Fig. 14 Same as Fig. 13, but with panels showing the maximum dust surface density, ∑d,max, as a function of the planetary mass and the Stokes number. We note that the color contours are on a linear scale in panels a–f but on a log scale in panels g–i. |
| In the text | |
 |
Fig. 15 Same as Fig. 6a, but the color contour from blue to red represents the z component of the gas flow velocity averaged in the y direction within the calculation domain of hydrodynamical simulation around a planet, 〈vz,gas〉y. The color contour of the arrows from purple to orange represents the difference in the z coordinates between the ending and starting points of orbital calculations. |
| In the text | |
 |
Fig. 16 Schematic illustrations of our model for the dust ring and gap formation. The planet-induced gas flow is in the flow-shear regime (panel a) and in the flow-headwind regime (panel b) to form dust substructures. |
| In the text | |
 |
Fig. C.1 Flow structure at the midplane of the disk around a planet obtained from m03-hw001. The color contours represent the flow speed in the x direction (top) and the gas density (bottom) |
| In the text | |
 |
Fig. E.1 Streamlines of 3D planet-induced gas flow around the planet with m = 0.3 and Mhw = 0. The planet-induced gas flow is in the flow-shear regime. The result is obtained from Kuwahara & Kurokawa (2020a). The solid green, orange, and red lines are the Keplerian shear, the horseshoe streamlines, and the recycling streamlines (Ormel et al. 2015b; Kuwahara et al. 2019) (or transient horseshoe streamlines (Fung et al. 2015)), respectively. The sphere is the Bondi sphere of the planet, whose size is 0.3 [H]. The arrows represent the direction of the gas flow. Panels a and b: Perspective views of the flow field. Panel c: x–y plane viewed from the +z direction. |
| In the text | |
 |
Fig. E.2 Same as in Fig. E.1, but with m = 0.03 and Mhw = 0.1. The planet-induced gas flow is in the flow-headwind regime. The sphere is the Bondi sphere of the planet, whose size is 0.03 [H]. The vertical dashed line in panel c corresponds to the x coordinate of the position of the corotation radius for the gas, xg,cor = −2/3 Mhw. |
| In the text | |
 |
Fig. F.1 Trajectories of dust particles with St = 10−4 in the planet-induced gas flow (solid lines) and in the unperturbed sub-Keplerian shear flow (dashed lines). We used the result obtained from m03-hw001 to calculate dust trajectories. We set zs = 0.5 for the orbital calculations. Different colors correspond to different xs. The filled circles and cross symbols in panel b correspond to xs and xe, respectively. The dotted and dashed circles are the Bondi and Hill radii of the planet, respectively. Panel a: x–y plane viewed from the +z direction. Panel b: x–z plane viewed from the −y direction. Panel c: y–z plane viewed from the +x direction. This figure should be compared to Fig. 6a. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.