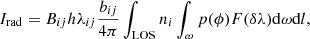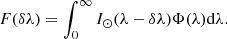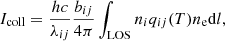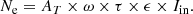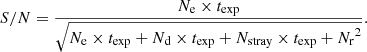EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 665 (September 2022) A&A, 665 (2022) A39 Full HTML
Open Access
Issue
A&A
Volume 665, September 2022
Article Number A39
Number of page(s) 14
Section The Sun and the Heliosphere
DOI https://doi.org/10.1051/0004-6361/202243029
Published online 06 September 2022

© J. Zhao et al. 2022

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.

1. Introduction

Coronal mass ejections (CME) are considered to be the main source of solar terrestrial space weather. Conventionally, they have three components, as observed by coronagraph images, namely: a bright core associated with the core of the flux rope, a large cavity associated with the envelope of the flux rope, and a bright front associated with the compression of the plasma (Illing & Hundhausen 1986). Evidence for erupting flux ropes was also demonstrated based on observations from the Solar Dynamics Observatory (SDO; Pesnell et al. 2012), as analyzed in Zhang et al. (2012), who discovered a hot channel in the extreme ultraviolet (EUV) high-temperature band before and during the eruption. Traced back to the sun, most CMEs are associated with the prominence (filament) eruptions, of which the quasi-static stage and onset process can be clearly observed at the solar limb.

Besides the three components mentioned above, soft X-ray observations (Hudson et al. 1999; Hudson & Schwenn 2000; Reeves et al. 2012) reveal a even higher temperature structure before the prominence eruption, known as “chewy nougats”, inside the cavity and above the prominence, which have a temperature of 1.6–2.0 MK. This central cavity can exist for a long time, and the lower boundary of the void will be visible in multi-EUV wavelengths before the eruption of the prominence (Gibson 2015).

The prominence-cavity system and its eruptive counterparts (the CME) have been observed in solar disk EUV images and in white light (WL) coronagraph for decades (see review in Gibson 2015), yet observations in UV wavelengths have been limited. UltraViolet Coronagraph Spectrometer (UVCS; Kohl et al. 1995) on board the Solar and Heliospheric Observatory (SOHO; Domingo et al. 1995) obtained UV observations of the corona and coronal mass ejections in UV H I Lyman-α and O VI (e.g., Susino & Bemporad 2016; Ying et al. 2020); in addition, the recently launched Metis on board Solar Orbiter also observes in both WL and Lyman-α. However, these instruments do not observe low enough in the corona to capture prominence cavities. The future Lyman-α Solar Telescope (LST; Li et al. 2019; Chen et al. 2019; Feng et al. 2019) on board the Advanced Space-based Observatory (ASO-S; Gan et al. 2019) will observe the sun in both WL and UV H I Lyman-α simultaneously and continuously from the low to high corona for the first time.

The WL coronal intensity is produced by Thomson scattering, which depends only on geometry and electron density and has been frequently observed in the past by the Large Angle Spectrometric Coronagraph (LASCO; Brueckner et al. 1995) on board SOHO as well as COR1 and COR2 on board the Solar TErrestrial RElations Observatory (STEREO) in space and K-cor at Mauna Loa Solar Observatory (MLSO) on the ground. The Lyman-α emission in the corona is more complex as it is produced by collisions and resonant scattering at the same time and depends both on density and temperature. It has only been observed by the UVCS in the inner corona with a slit spectrometer, while no full coronal image has been achieved in the past except the one obtained recently by Metis in the high corona (Romoli et al. 2021). To better understand future observations and further obtain physical parameters from observations of the inner corona, the emissions of the prominence-cavity system and an associated CME in WL and UV were synthesized and analyzed as a first step by Bemporad et al. (2018), who adopted MPI-AMRVAC software to simulate the prominence eruption. With the synthetic data from the MHD simulation, these authors verified the analysis of the data and presented a reliable method for obtaining the physical parameters of the CME, especially the electron temperature.

In this work, we synthesize the Lyman-α emission from the prominence-cavity system in the early phase of eruption by adopting an MHD simulation (Fan & Liu 2019) in which the structures of the prominence and cavity and the substructure of “chewy nougats” before the eruption are clearly identified. The Lyman-α emissions of the CME, its driven shock and the ambient solar wind based on the isotropic and anisotropic two-temperature MHD simulations of electrons and protons will be presented in our future papers. In Sect. 2, we show the details of the input MHD simulation. In Sect. 3, we describe the method used to do the synthesization. The results are shown in Sect. 4 and the instrumental response of future LST is present in Sect. 5. Our conclusions are discussed in Sect. 6.

2. MHD model

The input model is adopted from Fan & Liu (2019), who simulated the entire process of the emergence of magnetic flux rope, the consequent formation of prominence and cavity, and also the final eruption of the prominence-cavity system.

During the static stage, the prominence-cavity system with a horn-like central structure above the prominence is produced in synthetic multi-wavelength EUV images prior to eruption (see Fig. 7 in Fan & Liu 2019). In principle, the prominence is formed by condensation due to radiative cooling and the cavity that surrounds the prominence is formed as a result of density depletion. The horn-like structure is generated due to the evaporation of the prominence material to coronal temperatures. The above simulation is consistent with observations, such as Wang et al. (2016). There is also a “central cavity” enclosed by the horn that has higher temperature and density. The core of the central cavity appears as a dark structure in EUV wavelengths but has been observed as a bright structure in soft X-ray.

Fan & Liu (2019) examined the magnetic field structure associated with the various features of the prominence-cavity system. They find the prominence is formed at the dips of the twisted magnetic flux rope as well as the horn at even shallower dips, while the central cavity comprises the twisted field lines with no dips. The same MHD dataset has been studied in details in Liu & Su (2021) for the reconnection processes.

In this work, we study the plasma evolution and investigate the appearance of the UV emission for the entire process of the eruptive event. We selected four time steps of the simulation, which represent the static stage and eruptive phase, respectively. As the emission of line intensity only depends on the density, temperature, and the velocity, we show the distributions of the aforementioned input physical parameters in the middle cross-section of the flux rope in Fig. 1 from left to right. The different time steps are displayed from top to bottom. Although only the radial component of the velocity is shown in the right panels of the figure, the calculations in the following all consider the full vector velocity.

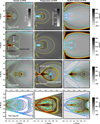thumbnail Fig. 1.

Physical parameters of the prominence-carrying flux rope system at different time steps, from the static stage (time steps 105 and 180) to the eruptive phase (time steps 189 and 192), shown from top to bottom. The electron density, temperature and radial velocity in the POS are displayed from left to right. The contours at different panels in this figure as well as in the following figures are displayed to better show the parameter distributions.

The pre-eruption phase is represented by time steps 105 and 180 (10.33 h and 17.83 h). In the quasi-static stage, physical structures such as the prominence and the cavity overarching the prominence are identified in the 2D electron density distribution. The prominence has a density on the order of 1010 cm−3, while the overarching cavity has a density on the order of 108 cm−3. The temperature of the simulated prominence is about 70 000 K, due to the artificial suppression of the radiative cooling below that temperature due to the limited numerical resolution (see Fan & Liu 2019). The temperature in the cavity is higher than its surroundings, reaching a peak value of about 3 MK, which is higher than the estimate (1.67–2.15 MK) based on the EUV observations from SDO/AIA (Bąk-Stęślicka et al. 2019). Substructure of the “central cavity” appears at time step 180 inside the overarching cavity, just above the prominence. Both the density and temperature of this central cavity lie in between those of the prominence and cavity.

The material in the overarching cavity is mainly downflow at the boundary, corresponding to converging flows towards the dips. Upflow (outflow) outside the flux rope system has been found, indicating that the streamer material is flowing away from the sun.

The prominence eruption is initiated at time step 189 (18.73 h). The reconnection current sheet, post-flare loops, boundary of the cavity, and prominence plasma are clearly seen in the electron density and the temperature distribution. Reconnection sites are identified at the high-temperature regions, with one site connecting the cusp structure (post-flare loops) near the solar surface and the other site at the boundary of the prominence-cavity system. Bidirectional outflow on the order of hundreds of km s−1 is found at the high temperature region, namely, the reconnection site. A high-speed outflow is also clearly shown at the front of the cavity. Although the plasma is heated during the reconnection process, some cool and dense plasma of the prominence still exists inside the cavity.

As the prominence eruption (or CME) propagates outwards, a large field of view (FOV) corresponding to 1 R⊙ ∼ 2.5 R⊙ along the solar equator is shown at time step 192 (19.03 h). Similar to time step 189, the high temperature appears at the same regions, but prominence plasma is nowhere at this time. The bidirectional flows look similar to the time step 189, but the high speed region at the cavity front bifurcates at the place where the plasma pressure of the ambient streamer is higher than its surroundings.

3. Methods

The physical properties of the prominence-cavity system and its eruptive counterpart – the CME – cover a wide range of density and temperature values. The prominence is cold and dense, while the structures surrounding it are hot and less dense. Hence, two methods are adopted in the present work for synthesizing the H I Lyman-α emission.

For the cold and dense plasma in the prominence, which is usually considered to be optically thick, non-local thermodynamic equilibrium (NLTE), radiative-transfer modeling has been extensively adopted for synthesizing the emission under various physical conditions. In relatively simple one-dimensional (1D) models, a plane-parallel slab standing vertically above the chromosphere is frequently used to represent the prominence plasma and radiative transfer processes are considered in the limited region (e.g., Heinzel & Rompolt 1987; Gontikakis et al. 1997, and the following works). On the basis of 1D NLTE modeling, detailed analyses of physical processes and parameter studies, such as those based on different temperatures and velocities, were achieved in the complete frequency redistribution (CRD) approximation and improved by using the partial frequency redistribution (PRD) approach. Such modeling procedures also provide line profiles, crucial for obtaining the plasma state when spectral observations are available. Two-dimensional (2D) models have been developed to take into account such effects as radiation escape at boundaries (Jones & Skumanich 1973, 1980, and subsequent works) and different illumination boundary conditions (Gouttebroze 2005). Complex 2D models have also been developed to study the physical properties of prominences with multi-thread structures in magnetohydrostatic equilibrium (such as Heinzel & Anzer 2001; Gunár et al. 2008). The results demonstrate the advantages of such approaches in explicitly interpreting the line profile (see review of Labrosse et al. 2010, and the references therein). However, 1D models have also been widely used in recent works (Heinzel et al. 2014, 2016; Ruan et al. 2019), since useful information on plasma parameters is obtained when comparing with observations of prominence fine structure. Considering the efficiency of computation and the applicability of the present calculation to future observations of Lyman-α intensity by LST, the 1D NLTE radiative-transfer code called PRODOP1 has been adopted in the present work for synthesizing the emission of the optically thick plasma in the prominence. PRODOP was written in the programming language FORTRAN and developed by Gouttebroze & Labrosse (2000) to solve the equations of 1D NLTE radiative transfer in solar prominences and filaments. It deals with both optically thick and optically thin plasma. It uses the angle-averaged partial redistribution approach (PRD) and solves a system of equations, for instance, the ionization equilibrium of hydrogen, the statistical equilibrium of the level populations for a twenty-level plus continuum hydrogen atom, NLTE radiative transfer, and other constraining equations to derive the electron densities at all depths and the emerging intensities for the hydrogen lines.

The prominence structure in this calculation consists of 1D isothermal and isobaric slabs standing vertically above the solar surface and illuminated by radiation from the surrounding atmosphere. Based on the input parameters including gas pressure, temperature, height above the solar surface, geometrical thickness of the 1D slab, microturbulent velocity, and radial velocity, this code computes the physical quantities and optical parameters such as electron density, total hydrogen density, ground state populations, total intensity, and optical thickness of H lines. Some relationships between the radiative and atmospheric quantities can thus be obtained in the hydrogen lines through the NLTE modeling of prominences. More details of this code are presented in Zhang et al. (2019). We need to mention that the emission from the 1D prominence model is still three-dimensional (3D). The direction of re-emission has a specific tendency and only the one along the LOS that points to the observer will be taken into consideration.

For the rest of the optically thin plasma, the emission is calculated through FORWARD analysis software2, which was introduced in Gibson et al. (2016) and adopted in Zhao et al. (2019, 2021).

4. Synthesization in the H I Lyman-α Line

The Lyman-α emission from the optically thin corona is contributed by two components: one is the collisional component that is produced by electron impact excitation of the residual neutral hydrogen atoms and the other one is the radiative component which is produced by resonant scattering of the incident radiation by neutral hydrogen. According to Noci et al. (1987), the radiative component is given by:

I rad = B ij h λ ij b ij 4 π ∫ LOS n i ∫ ω p ( ϕ ) F ( δ λ ) d ω d l , $$ \begin{aligned} I_{\rm rad} = B_{ij}h\lambda _{ij}\frac{b_{ij}}{4\pi }\int _{\rm LOS} n_{i}\int _{\omega } p(\phi )F(\delta \lambda ) \mathrm{d}\omega \mathrm{d}l ,\end{aligned} $$(1)

where Bij is the Einstein coefficient for photon absorption from the ground level i to the excited level j, h is the Plank constant, λij is the rest wavelength of the transition, bij is the branching fraction for de-excitation, ni is the number density of hydrogen atoms in the ground level, ω is the solid angle subtended by the incident radiation source, and p(ϕ) gives the angular dependence of the scattering process. In addition, F(δλ) is the so-called doppler dimming factor, expressed as follows:

F ( δ λ ) = ∫ 0 ∞ I ⊙ ( λ − δ λ ) Φ ( λ ) d λ . $$ \begin{aligned} F(\delta \lambda ) = \int _{0}^{\infty } I_{\odot }(\lambda - \delta \lambda )\Phi (\lambda )\mathrm{d}\lambda . \end{aligned} $$(2)

Here, I⊙ is the spectral profile of the incident radiation, δλ = λijν/c, where ν is the velocity of the moving scattering atom, and Φ(λ) is the normalized absorption profile. The collisional component can be expressed as:

I coll = hc λ ij b ij 4 π ∫ LOS n i q ij ( T ) n e d l , $$ \begin{aligned} I_{\rm coll} = \frac{hc}{\lambda _{ij}}\frac{b_{ij}}{4\pi }\int _{\rm LOS} n_{i}q_{ij}(T)n_{\rm e}\mathrm{d}l ,\end{aligned} $$(3)

where qij(T) is the collisional excitation rate.

The incident radiation in the calculation is assumed to have a Gaussian profile and line width of 0.4 Å, which is a first-order approximation. A reference profile recently provided by Gunár et al. (2020) will be considered in a future work. The incident radiation is cylindrical symmetric around the local vertical to the scatterer as discussed in Zhao et al. (2019, 2021), and is assumed to be unpolarized and independent of the heliocentric angle.

As the eruptive prominence-cavity system under study is assumed to correspond to a quiescent prominence not associated with active regions, the effect of anisotropic radiation from active regions is not included. Likewise, the contribution of the center-to-limb variation of H I Lyman-α radiation (a small limb brightening) to the anisotropy of the radiation field is not included, as this contribution can generally be ignored compared to the geometric effects due to the height of the scatterer in the corona (Casini & Judge 1999). Although UVCS results motivated our understanding of temperature anisotropy in Lyman-α (e.g., Zhao et al. 2021), the effect of temperature anisotropy is not considered in the present work for simplicity, namely, with the aim of interpreting the results with the more complex MHD model. As in Kohl et al. (1997), we excluded the contribution of turbulent velocity in this optically thin calculation for neutral hydrogen.

The calculation of the radiative component is carried out at each scattering point in the prominence-cavity system and the results of POS and LOS integration are described in the following. For each scattering point, the Doppler shift is considered between the incident radiation in the subtended solid angle and the absorption profile, with the latter being decided by the local temperature as well as the projected bulk velocity along the direction of the incident radiation. The direction of the re-emission after resonant scattering has a preference according to the scattering matrix: only the one along the LOS that points to the observer will be accounted for with regard to the integral intensity of the scattering point. The POS results are a collection of such integral intensity in the plane-of-sky while the LOS results are determined by summing up the re-emitted intensity at each scattering point along the same LOS.

For the collisional component, the collisional excitation rate is numerically computed by using a five-level hydrogen atom model with the continuum described in Gouttebroze et al. (1993) and adopted in Susino et al. (2018). The hydrogen ionization fraction is obtained from the CHIANTI atomic database (version 7) assuming ionization equilibrium, which has proved to be a reasonable approximation in general, although non-equilibrium ionization has been been found in eruptive hot prominence (Heinzel et al. 2016; Susino et al. 2018). Non-equilibrium ionization has also been found in the CME front (Pagano et al. 2020) and the associated shock (Pagano et al. 2008), which would affect the synthesized emission to a certain extent. As the MHD model adopted here has a similar temperature and velocity distribution at the CME front as the one in Pagano et al. (2020), non-equilibrium ionization is probably the case at time step 192. However, our synthesized results in the following show that the CME front in Lyman-α for the MHD simulation is relatively weak and will be hard to be observed (also see in Bemporad et al. 2018), which makes the assumption of ionization equilibrium an efficient approximation in the computational aspect.

In the following, we show the two components of the emission separately in different structures at different times under optically thin assumptions. For the optically thick calculations, only the total emission is calculated and the two components are not distinguished.

4.1. The cavity and substructures inside

The full line-of-sight (LOS) integration is shown later in this paper, but first we consider the synthesized Lyman-α emission for a slice at the plane of sky (POS), as shown in Fig. 2.

thumbnail Fig. 2.

Synthesized results of Lyman-α emission shown for a slice centered on the plane-of-sky at three different times of the static stage (time steps 105, 165, and 180) are displayed in the top, middle, and bottom rows, respectively. The radiative component, the collisional component, and ratio of the two components are shown in the left, middle, and right columns, respectively. In the first two columns, contours are overlaid on the intensity maps to emphasize the structures. The horizontal curve embedded in each of the right column panels shows the profile of the ratio along the Z = 0 line above the limb. The vertical solid lines in black and white indicate the bottom and top of the central cavity, while the dashed line passes through the cavity. The dashed-dotted line marks a location above the cavity and in the streamer. Profiles of the physical quantities and emissions along these vertical lines (except white solid line) are shown in Fig. 3.

The radiative component, the collisional component and their ratio are shown in the left, middle, and right columns. Results at different times before eruption are shown in different rows. Although the emission in the prominence is synthesized and displayed here, a more appropriate treatment is done with the PRODOP code when doing the LOS integration. We discuss this in greater detail in Sect. 4.2. Here, we discuss the optically thin structures in the FOV.

For all three time steps, the overall emission distribution of the radiative component is similar to the collisional one; for example, the cavity always has a weaker emission in both components. The ratio of the collisional component and radiative component in the FOV is less than 0.5, showing the resonant scattering is always dominant over the collisions in the pre-eruption phase. The ratio distribution in the prominence and ambient regions is zeroed out to better display the features in the rest part of FOV. The “central cavity,” which has been annotated in Fig. 1, is seen in the emission map and is clearly evident in the ratio map. The ratio of the two components is much higher in the central cavity, indicating a relatively strong effect of collisions which is primarily due to the higher density compared to the outer cavity.

thumbnail Fig. 3.

Comparison of physical parameters and synthesized emissions at different locations of the central cavity, cavity, and streamer background as described in the caption to Fig. 2. Results sampled at different locations as mentioned above are displayed from left to right. The distributions of density, temperature, radiative component, and collisional component emission are shown from top to bottom. Results at three different times are shown with different colors in each panels.

To diagnose the cavity and its substructures in detail, we examine the profiles of emission along a set of vertical lines marked in the right column panels of Fig. 2. These vertical line positions are selected based on the profile of emission ratio along the Z = 0 line, which is shown as a blue curve inset in each of the panels in the right column. By finding the first dip of the emission ratio profile after its peak, the top of the “central cavity” is identified and marked by the black vertical line. From this and the location of the “central cavity” bottom, the mid height of the central cavity is marked by the white dashed line. Hence, the black vertical line goes through the outer cavity, and the white dash-dotted line that goes through the streamer above cavity is selected for reference.

Once the bottom of the “central cavity” is defined, the above locations, represented by the vertical lines, are all obtained automatically, removing the artificial effect of selection.

The sampled profiles along the three vertical lines going through the “central cavity,” the outer cavity and the streamer are shown in the left, middle, and right columns of Fig. 3. In addition to the profiles of the two emission components (the two bottom rows), the profiles of density and temperature are also shown in the first and second rows of Fig. 3 for comparison. The time evolution is indicated with the different colors of the curves.

The first column shows the results passing through the “central cavity” as well as the ambient cavity (the dashed vertical line in Fig. 2). The symmetric cavity boundary and “central cavity” boundary (the horn) are annotated in the bottom panel. To align the emission and the physical parameters, the boundary of the cavity at the first time step is marked with black dotted lines for reference. The boundary of the “central cavity” at the last time step (red curves) is also marked with grey dotted lines. In principle, the evolution (blue – yellow – red) of the emission in the two components demonstrates that both the cavity and “central cavity” expand, with an accompanying decrease of emission intensity for the former but with an increase for the latter. The evolution of the physical parameters shows that both the density and temperature increase in the central cavity before the eruption, which is due to the prominence evaporation and heating in the core region of the flux rope. However, the density decreases while the temperature increases in the ambient cavity, which might be due to the flux-rope system reconnecting with the ambient field lines, causing the expansion and heating of the flux rope system. As the process of plasma condensation and evaporation continues, there will be sufficient evaporation of plasma above the prominence.

The strong emission of the “central cavity” is peaked at its boundary in both components and, hence, there is a well-pronounced “horn” above the prominence before the eruption. The main cause is the high temperature in the “central cavity,” which may bring a low collisional excitation rate for the collisional component and a low number density of neutral hydrogen for the radiative component.

The profiles passing through the cavity above the “central cavity” (the black vertical line in Fig. 2) are displayed in the middle column. Overall, the emission intensity and the physical conditions show a similar tendency as in the first column for the cavity, for instance, an expansion with decreasing emission and density. However, the intensity doesn’t change much inside the cavity, although mild increases can be found in the density and temperature above the “central cavity.” The reasoning behind this is the same as for the low emission in the “central cavity,” displayed in the first column. The results in the streamer are shown in the third column, with no apparent development of emission over time.

The LOS-integrated emission is calculated and shown in Fig. 4. It presents a similar structure as compared with the POS results. Total emission obtained by adding the two components is shown in the third column, and the structures that will be discussed are annotated, such as the prominence, cavity, “central cavity” and “horn.”

thumbnail Fig. 4.

LOS-integrated results of Fig. 2 are displayed from top to bottom: Irad, Icoll, Itotal and the ratio of Icoll and Irad are shown from left to right. The observable structures of prominence, cavity, central cavity and horn are marked in the panel of total emission at time step 165. The white dashed box gives the region where the PRODOP calculation is done for the static stage. The contours, the line curves and the vertical lines are indicated as in Fig. 2.

For a detailed study of the LOS integration results, a similar method has been adopted as that applied to the POS slices. The horizontal blue curve shows the profile of emission ratio along the Z = 0 line, the white and black solid lines sample the bottom and top of the “central cavity” and the dashed line samples the “central cavity.” The sampled profiles along the above lines are shown in Fig. 5. The column density appears to increase and then decrease before the eruption. The increase may be induced by the accumulation of evaporated plasma and the decrease might be due to the upward movement of the prominence which successively causes the leakage of the “central cavity” plasma along the core field lines of the flux rope. The tendency for a decrease in the density is also found in the POS results in Fig. 3. Emissions in both components show a tendency like the column density, that is, an increase followed by a decrease, confirming a strong dependency on the density parameter. Moreover, a dip appears in the place of the “central cavity” and then disappears before the eruption. The appearance of the dip has been explained in the previous part of this subsection and it survives the LOS integration at this early phase. The disappearance might be due to the highly non-homogeneous temperature along the LOS integration near pre-eruption. Therefore, the “horn” found in the POS at time step near eruption doesn’t survive the LOS integration.

thumbnail Fig. 5.

Profiles of the LOS integrated density (top); radiative and collisional components of the emission (middle); and the emission ratio (bottom), along the vertical line that goes through the central cavity (white dashed line in the right column of Fig. 4). The different colored curves correspond to the profiles at different times.

The ratio between the two components increases and then decreases before eruption, following a similar tendency as the column density and has no appearance of the “horn” structure. This may suggest that the ratio primarily relies on the density and that both components are influenced by the high temperature in a similar way.

Overall, from an observational aspect, all the profiles in the three panels show the expansion of the cavity and the “central cavity.” It is most pronounced in a finite region of the “central cavity” where the “horn” structure appears and then disappears just before the eruption.

4.2. The prominence

The prominence formation in the dips of the twisted field lines is produced by the runaway radiative cooling in the simulation. The prominence plasma remains briefly even after the flux rope starts to erupt. At the quasi-static stage, the simulated prominence plasma has a temperature around 7 × 104 K and the electron density is around 1010 cm−3. As the plasma is cool and dense, Lyman-α emission from the prominence is produced by absorbing the incident radiation and re-emitting. Therefore, NLTE radiative transfer code PRODOP is adopted here to obtain the re-emitted intensity.

Using the PRODOP code, we built a grid of 13 860 NLTE models, covering a temperature range of 7 × 104–1 × 105 K, a pressure range of 0.005–0.5 dyn cm−2, a height range of 5 × 104–2 × 105 km, and a radial velocity range of 0–250 km s−1. The turbulent velocity is set to be 10 km s−1 for all models and the thickness of the 1D slab is set to be 2000 km. For regions with thickness larger than 2000 km, several identical slabs are put together and the emergent synthetic spectrum is finally computed through all slabs along the LOS without radiative interaction. With the results of all models, we obtained a range of predicted line intensities that varied with the input parameters. PRODOP deals with the prominence as a 1D structure; hence, for each pixel in the POS, we limited the region of prominence plasma along the LOS by an upper threshold of density of 1 × 109 cm−3 and an upper threshold of temperature of 105 K. The required input parameters of the code such as the thickness of the slab, the mean density, and the mean radial velocity, as well as the density weighted temperature along the LOS are then determined from the MHD simulation, by which the integrated intensity is then calculated for each pixel. As the MHD simulation provides a prominence with minimum temperature around 70 000 K (see Fig. 1), our computations take into account the emission from the “warm” (10 000 ∼ 100 000 K) material of the PCTR by selecting a temperature range of 7 × 104 − 1 × 105 K for the prominence plasma.

The synthetic results, which are LOS-integrated, are shown in Fig. 6, with the top row panels showing the intensity of the re-emission and the middle row panels showing the optical depth. For time steps 105, 180, and 189 (10.33 h, 17.83 h, and 18.73 h) when the prominence is well identified, the optical depth is relatively high and the intensity of the prominence is one to two orders of magnitude lower compared with the optically thin assumption for most part of the prominence plasma, while emissions are comparable only at the prominence boundary under the two assumptions (optically thin and optically thick). This is primarily owing to the three-dimensional distribution of the prominence plasma which is shown for the POS cross-section in the first column of Fig. 1 and for the equatorial plane in the bottom panels of Fig. 6. For time step 192 (19.03 h), only a small amount of residual prominence plasma remains; hence, although the prominence plasma can still be recognized from the density criterion, the optical depth is relatively low and the intensity from the optically thick assumption is comparable to the FORWARD optically thin results. The above results obtained from optically thick calculations are then adopted to replace the prominence part in the LOS-integrated emission from the optically thin calculations. The combined results are displayed in Fig. 8.

thumbnail Fig. 6.

Radiative transfer calculation for the prominence plasma and corresponding optical depth. The synthesized intensity is shown in the top panels and the optical depth is shown in the middle. The contours are overlaid to emphasize the distribution. Density distributions at the equatorial plane at four time steps are shown in the bottom panels for reference here and for Fig. 7. The apex, leg, and foot of the prominence plasma are annotated in the right two panels.

The prominence as well as its eruptive counterparts have been observed in Lyman-α at lower altitudes with the Transition Region and Coronal Explorer (TRACE, Handy et al. 1999a) and Solar Ultraviolet Measurements of Emitted Radiation (SUMER, Raouafi 2002) on-board Solar and Heliospheric Observatory (SOHO). However, the former data is contaminated with longer wavelengths (Handy et al. 1999b; Kucera & Landi 2008) while the latter is affected by the instrumental effect of the attenuator (Heinzel et al. 2001). Without using the attenuator, an integral intensity of Lyman-α profile (7.36 × 104 erg cm−2 s−1 str−1) for the reference quiet sun has been obtained with observations from SOHO/SUMER Lyman-α raster scans (Gunár et al. 2020), which is comparable to the value of the incident radiation that has been adopted for the FORWARD and PRODOP calculations in the present work. The eruptive prominence embedded in the CME core is also observed in Lyman-α by the UVCS spectrometer on-board SOHO at higher altitudes. The emission intensity is acquired when the CME passes through the slit, and various intensity and optical depths have been obtained for different events and their different parts (Ciaravella et al. 1997, 2000; Heinzel et al. 2016), even at different bright knots inside the CME (Lee et al. 2009). Similar to Heinzel et al. (2016), where different optical depths have been obtained during the prominence eruption, the distribution of the optical depth in the present work at the same time (such as time step 189 in Fig. 6) also appears optically thick (τ >  1) at the inner part and optically thin (τ <  1) at the boundary of the prominence. Compared with the intensity of hot prominences obtained in Heinzel et al. (2016) with a maximum value around 102.5 erg cm−2 s−1 str−1, the synthesized results here at the eruptive phase seem to be well consistent (see Fig. 6 time step 189 and 192), which enables the quantitative comparison between the synthesized results in this work and future observations and also makes the signal-to-noise ratio (S/N) calculated in Sect. 5 dependable.

4.3. The CME

During the eruptive phase at time steps 189 and 192, the prominence-cavity system moves outward and is heated. The outer boundary of the cavity can still be identified, while the substructure inside cannot be fully distinguished; thus, the eruptive prominence-cavity system is treated as the whole CME.

As the CME ejects at hundreds of km/s, the Doppler dimming effect of the resonant scattering line becomes important. Such Doppler dimming effects are analyzed for Lyman-α emission at time steps 189 and 192. The results in the POS and that integrated along LOS are displayed in Fig. 7.

thumbnail Fig. 7.

Doppler dimming effect displayed at time steps 189 and 192 when the prominence erupts. The POS results are shown in the first and third rows while the LOS integrated results are shown in the second and fourth rows. The radiative component without and with Doppler dimming, as well as the extent of dimming are shown in the first three columns. The collisional component is present in the fourth column for comparison and the ratio of the two components is displayed in the last column. The black dashed boxes give the region where the PRODOP calculation is done for the eruptive phase.

In order to obtain the dimming extent, the radiative component of resonant scattering without Doppler dimming effect is calculated and displayed in the first column. The one with the Doppler dimming effect is shown in the second column and the dimming content is hence obtained as the emission in the first column minus the one in the second column and presented in third column. The collisional component is shown in the fourth column for comparison and the ratio is shown in the last column.

For the results in the POS, the dimming is most apparent at the locations outside the cavity at time step 189 and inside the cavity at time step 192, when comparing the results of Irad without and with Doppler dimming effect. At time step 189, the temperature is around 106 K both inside and outside the cavity, except the prominence plasma region and the reconnection regions at the cavity boundary and the bottom of the cavity. The corresponding velocity inside the cavity is even higher than the one outside the cavity. Therefore, the apparent dimmed Irad outside the cavity is mainly due to the low density there, although the locations with the highest radiative component experience more dimming. The dimming extent at the place with a high velocity, such as the CME front, is negligible as the electron temperature at these places is much higher. The above results are consistent with the theory that the dimming extent depends not only on the velocity, but also on the number density of hydrogen atoms and ion temperature. In our calculation, the ion temperature is assumed to be proportional to the electron temperature, so a higher electron temperature gives a much broader absorption profile during the resonant scattering, which gives a lower dimming extent. At time step 192, as the CME expands, the density decreases quickly and the emission is only apparent in limited regions inside the cavity even without the DD effect. The dimming extent is comparable with the emission extent without the DD effect, at the places where the temperature is around 106 K and the velocity is around 100 km s−1. The collisional component at both time steps have a similar distribution as the electron density and it progressively dominates over the radiative component after the DD effect at the high density region. The extremely large values (dark regions) in the 2D image of Icoll/Irad is mainly due to the tiny values of the Irad and Icoll there.

For the results integrated along the LOS, although the radiative component without and with the DD effect shows similar distributions with clear cavity boundaries at time step 189, the largest dimming extent happens at the bright core region. The ratio of Icoll and Irad is large at the front and the bottom of the bright core, with the former one primarily due to the contribution from the POS result (at the apex of the prominence as shown in Fig. 6) and the latter due to the contribution primarily from the result far away from the POS (at the foot of the prominence as shown in Fig. 6). At time step 192, the cavity boundary is faint but still can be recognized from the radiative component without the DD effect, and the dimming extent has a similar distribution like it. The synthesized Irad with DD effect shows a heavily dimmed bright core and the other places inside the cavity is fully dimmed. The Icoll/Irad is extremely large at the bright core region mainly due to the heavy dimming of the Irad.

And the other places with high ratio overlaid with colorful contours is due to the tiny values of Irad and Icoll there. We notice that there is a relatively low ratio region at the bottom of the bright core, where the radiative component is still comparable with the collisional component. This is primarily due to the high density at the foot of the flux rope, as the eruption continues and the mass falling down along the flux rope (as shown in the density distribution in the bottom right panel in Fig. 6).

Therefore, a completely different distribution can be found at the bright core during different stages of the eruption: that the collisional component is dominant at the front and bottom of the bright core at time step 189 and at almost everywhere except the bottom part of the bright core at time step 192.

As discussed above, CMEs often show a three-part structure in WL of bright core, dark cavity, and bright front. The prominence-cavity at the limb also shows a three-component structure, that is, the bright prominence, the dark cavity, and the relative bright front. These structures are obtained from the synthesized WL emission which is shown at the bottom of Fig. 8 for different time steps. The magnitude of the emission in WL from different structures does not vary a lot, for instance, emission from the CME core at time step 192 is only one to two orders of magnitude higher than the emission from the CME front. However, the emission in Lyman-α shows dramatic differences between the different structures, for instance, the emission from the prominence at time step 180 and 189 with PRODOP calculation can be three to four orders of magnitude higher than the background streamer. The core of the CME at time step 192 can be four to five orders of magnitudes higher than the CME front. For the detector of LST, a high gain and low gain mode is adopted simultaneously for observations, which will provide a high dynamic range for the future observations. The relevant instrumental performance of Solar Corona Imager (SCI, Li et al. 2019) of LST for eruptive prominence-cavity system is analyzed below.

thumbnail Fig. 8.

Total emission of Lyα at different time steps is shown on the top. The emission in the WL is shown at bottom for comparison.

5. Instrument response

The LST on board ASO-S is designed to observe the solar corona in Lyman-α 121.6 nm and WL 700 nm from 1.1 R⊙ to 2.5 R⊙ (Chen et al. 2019). As the emission decreases rapidly off the limb, the stray light is not negligible at the low corona. Hence, it is crucial to obtain sufficient S/N when observing different structures in the corona. The radiometric performance of LST/SCI is presented in the following for three different structures: the prominence-cavity system, eruptive prominence, and propagating coronal mass ejections (as discussed above). Such a range of different structures stands as a good example for planning future observational targets for the coronagraph.

The entrance pupil geometrical area AT of SCI is designed to be 28 cm2, corresponding to a diameter of 60 mm aperture. Considering the transmittance of the optical system, τ, the photoelectric conversion coefficient, ϵ, the pixel solid angle, ω, and the brightness of the structure, Iin, the electron counts per pixel Ne can be obtained by:

N e = A T × ω × τ × ϵ × I in . $$ \begin{aligned} N_{\rm e} = A_T\times \omega \times \tau \times \epsilon \times I_{\rm in} .\end{aligned} $$(4)

The detector pixel size of SCI is 11 μm, the pixel solid angle is calculated to be 1.29129 × 10−10 ster. According to laboratory tests, τ = 0.015, ϵ = 0.3. Then the S/N can be estimated according to the following equation:

S / N = N e × t exp N e × t exp + N d × t exp + N stray × t exp + N r 2 . $$ \begin{aligned} S/N = \frac{N_{\rm e}\times t_{\rm exp}}{\sqrt{N_{\rm e}\times t_{\rm exp} + N_{\rm d}\times t_{\rm exp} + N_{\rm stray}\times t_{\rm exp} + {N_{\rm r}}^2}} .\end{aligned} $$(5)

Here, Nd is the dark field noise, Nstray is the stray light noise, and Nr is the readout noise. As we use a complementary metal-oxide-semiconductor (CMOS) for the detector and adopt high gain and low gain for incident with low and high photons, two sets of Nr are considered in our evaluation of UV and WL as listed in Table 1. Parameters of low gain mode are adopted when the electron is greater than 2000, while high gain model parameters are adopted when the electron is less than 2000. The stray light noise that we used is from the simulation in Xue et al. (2020), with a designed roughness (0.1 nm) of the primary mirror.

Table 1.

Optical parameters adopted for estimating the SNR of UV and WL for LST/SCI.

The S/N for emissions of different structures in Lyα and WL 700 nm in the FOV of SCI with different exposure times (1 s, 3 s, and 5 s) are calculated and shown in Figs. 9 and 10, respectively. In UV Lyα wavelength, the S/N of the prominence is calculated from the optically thick synthetic results. Primarily, the cavity and “central cavity” before eruption, the erupting prominence, and the lower part of CME can all be observed with S/N greater than 3 in both wavelengths even with the shortest exposure time. Specifically, for the selected exposure times, the high value of the S/N is found in the erupting prominence and the central cavity in both wavelengths; this demonstrates that the S/N is higher in UV Lyα than in WL 700 nm in these places. Nevertheless, a larger region can be obtained in WL than in UV with SNR greater than 3. A discontinuity at R⊙ equals 1.2 is noticed in all S/N maps of WL, which is raised by the large stray light noise between 1.1 ∼ 1.2 R⊙.

thumbnail Fig. 9.

S/N at UV Lyα 121.6 nm for different structures, such as the prominence-cavity system at time step 180, the prominence eruption at time step 189 and the CME at time step 192, are displayed in the FOV of LST/SCI. Different exposure times are listed from left to right. A contour with S/N equal to 3 is also displayed.

thumbnail Fig. 10.

S/N at WL 700 nm for different structures, such as the prominence-cavity system at time step 180, the prominence eruption at time step 189 and the CME at time step 192, are displayed in the FOV of LST/SCI. Different exposure times are listed from left to right. A contour with S/N equal to 3 is also displayed.

6. Discussion and conclusions

The LST payload on board the ASO-S mission will observe the H I Lyα line and WL of the solar disk with LST/SDI and of solar corona from 1.1 R⊙ to 2.5 R⊙ with LST/SCI. It will provide Lyα images in the low corona and supply continuous and simultaneous observation in both wavelengths from the solar disk to the solar corona, for the first time ever. This observation will be complementary to the Solar Obiter observations, providing observations at lower latitudes for the purpose of diagnosing the initial physical properties of different features. The present work focuses on the transient event at the solar limb, which is one of the main scientific objectives of ASO-S. A consecutive evolution from the prominence-cavity system to the coronal mass elections has been studied, with a consideration of several crucial physical processes, such as the radiative transfer of prominence plasma and the Doppler dimming effect of resonant scattering for CME.

  1. The pre-eruptive prominence-cavity system has been synthesized in the Lyα line for the first time. Unlike the EUV lines, which are produced by collisional excitation, the Lyα line is produced by resonant scattering and its emission is dominated by the radiative component when the plasma has a low velocity. However, the synthetic emission in Lyα shows a similar pattern as has been found in EUV, namely, the horn enclosing the central cavity becomes well pronounced before the eruption, despite the fact that the strongest emission in Lyα comes from the prominence. Although the prominence and the cavity share the same flux rope system, their physical appearances shows dramatic differences. The process through which the plasma is transferred between the prominence and the cavity is still under debate. Schmit & Gibson (2013) investigated the connection between the prominence and the cavity with multi-EUV wavelengths, showing correlations between AIA/304, 171, and 193 Å of the horn structure. Wang et al. (2016) investigated the oscillation of the horn and showed the material flow from the prominence to the cavity. These authors concluded that the evaporation of the prominence generates the cavity, as opposed to the alternative that the cavity supplies mass to the prominence (e.g., Berger et al. 2012) and therefore becomes underdense. The MHD simulation of Fan & Liu (2019) shows shows both processes may occur, including the condensation of cavity plasma onto the prominence and prominence evaporation of mass into the central cavity. Since the Lyα line samples the material both in cool and hot temperatures, it is ideal for studying the plasma transfer between the prominence and the cavity, namely, for diagnosing the prominence-corona transition region (PCTR).

  2. The radiative transfer calculation is considered for the synthetic emission of the prominence plasma. During the process described in this paper, the optical depth varies from hundreds to a few, showing the transition of the prominence from optically thick to optically thin regimes, thus implying a heating of the prominence plasma during the eruption. The maximum difference of the synthetic emission between the optically thin and thick assumptions is obtained before the eruption, while the synthetic emission with an optically thin assumption would be overestimated by two orders of magnitude.

  3. The eruptive counterparts of the prominence-cavity system in the Lyα line show strong synthetic emission but are severely dimmed when they move out. The dimming happens everywhere but has a tendency toward a larger extent at regions of higher emission. The prominence plasma falls down along the flux rope during the eruption, and at the same time the apparent dimming (high ratio of Icoll/Irad) transfers from the front and bottom of the bright core to the whole bright core except the bottom part. Compared with the pre-eruptive phase when the radiative component dominates over the collisional component, the former one experiences dimming during the eruptive phase and the synthesized emission would be dominated by the collisional component, especially at the bright core inside the cavity when the velocity of CME front reaches around 600 km s−1 in the case shown here.

  4. The emissions in UV and WL are synthesized, and the three-component structure of the CME can be identified in both channels. However, the bright front of CME is about one to two orders of magnitude weaker than the bright core in WL, while the difference can be even greater, that is, around three or four orders of magnitude in UV.

  5. As is true for all telescopes, the S/N is a key index considering the rapid decrease of coronal emission off the solar limb. By analyzing the S/N, where the noise mainly comes from the straylight that is obtained with consideration of the instrument design of LST (Chen et al. 2019), we can see that the substructures inside the cavity before eruption and the bright core during the eruption can be clearly observed in both wavelengths for the reasonable exposure time in future observations.

Acknowledgments

We thank the referee for valuable suggestions. J.Z. was a visiting postdoc at HAO during 2017–2019, supported by the Chinese Scholarship Council (CSC NO. 201704910457). This work is supported by National Natural Science Foundation of China, Grant No. 11503089, 11921003, 11973012 and U1731241, and Chinese Academy of Science Strategic Pioneer Program on Space Science, Grant No. XDA15052200, XDA15320103, XDA15018300 and XDA15320301. This work is also supported by the mobility program (M-0068) of the Sino-German Science Center. This material is partly based upon work supported by the National Center for Atmospheric Research, which is a major facility sponsored by the National Science Foundation under Cooperative Agreement No. 1852977. We also benefit of discussion in ISSI team of “Solar eruptions: preparing for the next generation multi-waveband coronagraphs”.

References

  1. Bąk-Stęślicka, U., Gibson, S. E., & Stęślicki, M. 2019, Sol. Phys., 294, 164 [Google Scholar]
  2. Bemporad, A., Pagano, P., & Giordano, S. 2018, A&A, 619, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Berger, T. E., Liu, W., & Low, B. C. 2012, ApJ, 758, L37 [NASA ADS] [CrossRef] [Google Scholar]
  4. Brueckner, G. E., Howard, R. A., Koomen, M. J., et al. 1995, Sol. Phys., 162, 357 [NASA ADS] [CrossRef] [Google Scholar]
  5. Casini, R., & Judge, P. G. 1999, ApJ, 522, 524 [NASA ADS] [CrossRef] [Google Scholar]
  6. Chen, B., Li, H., Song, K.-F., et al. 2019, Res. Astron. Astrophys., 19, 159 [CrossRef] [Google Scholar]
  7. Ciaravella, A., Raymond, J. C., Fineschi, S., et al. 1997, ApJ, 491, L59 [NASA ADS] [CrossRef] [Google Scholar]
  8. Ciaravella, A., Raymond, J. C., Thompson, B. J., et al. 2000, ApJ, 529, 575 [NASA ADS] [CrossRef] [Google Scholar]
  9. Domingo, V., Fleck, B., & Poland, A. I. 1995, Sol. Phys., 162, 1 [Google Scholar]
  10. Fan, Y., & Liu, T. 2019, Front. Astron. Space Sci., 6, 27 [NASA ADS] [CrossRef] [Google Scholar]
  11. Feng, L., Li, H., Chen, B., et al. 2019, Res. Astron. Astrophys., 19, 162 [CrossRef] [Google Scholar]
  12. Gan, W.-Q., Zhu, C., Deng, Y.-Y., et al. 2019, Res. Astron. Astrophys., 19, 156 [Google Scholar]
  13. Gibson, S. 2015, in Coronal Cavities: Observations and Implications for the Magnetic Environment of Prominences, eds. J.-C. Vial, & O. Engvold, 415, 323 [NASA ADS] [Google Scholar]
  14. Gibson, S., Kucera, T., White, S., et al. 2016, Front. Astron. Space Sci., 3, 8 [NASA ADS] [CrossRef] [Google Scholar]
  15. Gontikakis, C., Vial, J. C., & Gouttebroze, P. 1997, A&A, 325, 803 [NASA ADS] [Google Scholar]
  16. Gouttebroze, P. 2005, A&A, 434, 1165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Gouttebroze, P., & Labrosse, N. 2000, Sol. Phys., 196, 349 [NASA ADS] [CrossRef] [Google Scholar]
  18. Gouttebroze, P., Heinzel, P., & Vial, J. C. 1993, A&AS, 99, 513 [NASA ADS] [Google Scholar]
  19. Gunár, S., Heinzel, P., Anzer, U., & Schmieder, B. 2008, A&A, 490, 307 [Google Scholar]
  20. Gunár, S., Schwartz, P., Koza, J., & Heinzel, P. 2020, A&A, 644, A109 [EDP Sciences] [Google Scholar]
  21. Handy, B. N., Acton, L. W., Kankelborg, C. C., et al. 1999a, Sol. Phys., 187, 229 [Google Scholar]
  22. Handy, B. N., Tarbell, T. D., Wolfson, C. J., Korendyke, C. M., & Vourlidas, A. 1999b, Sol. Phys., 190, 351 [NASA ADS] [CrossRef] [Google Scholar]
  23. Heinzel, P., & Anzer, U. 2001, A&A, 375, 1082 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Heinzel, P., & Rompolt, B. 1987, Sol. Phys., 110, 171 [NASA ADS] [CrossRef] [Google Scholar]
  25. Heinzel, P., Schmieder, B., Vial, J. C., & Kotrč, P. 2001, A&A, 370, 281 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Heinzel, P., Vial, J. C., & Anzer, U. 2014, A&A, 564, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Heinzel, P., Susino, R., Jejčič, S., Bemporad, A., & Anzer, U. 2016, A&A, 589, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Hudson, H., & Schwenn, R. 2000, AdSpR, 25, 1859 [NASA ADS] [Google Scholar]
  29. Hudson, H. S., Acton, L. W., Harvey, K. L., & McKenzie, D. E. 1999, ApJ, 513, L83 [Google Scholar]
  30. Illing, R. M. E., & Hundhausen, A. J. 1986, J. Geophys. Res., 91, 10951 [Google Scholar]
  31. Jones, H. P., & Skumanich, A. 1973, ApJ, 185, 167 [NASA ADS] [CrossRef] [Google Scholar]
  32. Jones, H. P., & Skumanich, A. 1980, ApJS, 42, 221 [NASA ADS] [CrossRef] [Google Scholar]
  33. Kohl, J. L., Esser, R., Gardner, L. D., et al. 1995, Sol. Phys., 162, 313 [Google Scholar]
  34. Kohl, J. L., Noci, G., Antonucci, E., et al. 1997, Sol. Phys., 175, 613 [Google Scholar]
  35. Kucera, T. A., & Landi, E. 2008, ApJ, 673, 611 [NASA ADS] [CrossRef] [Google Scholar]
  36. Labrosse, N., Heinzel, P., Vial, J. C., et al. 2010, Space Sci. Rev., 151, 243 [Google Scholar]
  37. Lee, J. Y., Raymond, J. C., Ko, Y. K., & Kim, K. S. 2009, ApJ, 692, 1271 [NASA ADS] [CrossRef] [Google Scholar]
  38. Li, H., Chen, B., Feng, L., et al. 2019, Res. Astron. Astrophys., 19, 158 [Google Scholar]
  39. Liu, T., & Su, Y. 2021, ApJ, 915, 55 [NASA ADS] [CrossRef] [Google Scholar]
  40. Noci, G., Kohl, J. L., & Withbroe, G. L. 1987, ApJ, 315, 706 [Google Scholar]
  41. Pagano, P., Raymond, J. C., Reale, F., & Orlando, S. 2008, A&A, 481, 835 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Pagano, P., Bemporad, A., & Mackay, D. H. 2020, A&A, 637, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Pesnell, W. D., Thompson, B. J., & Chamberlin, P. C. 2012, Sol. Phys., 275, 3 [Google Scholar]
  44. Raouafi, N. E. 2002, A&A, 386, 721 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Reeves, K. K., Gibson, S. E., Kucera, T. A., Hudson, H. S., & Kano, R. 2012, ApJ, 746, 146 [Google Scholar]
  46. Romoli, M., Antonucci, E., Andretta, V., et al. 2021, A&A, 656, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Ruan, G., Jejčič, S., Schmieder, B., et al. 2019, ApJ, 886, 134 [NASA ADS] [CrossRef] [Google Scholar]
  48. Schmit, D. J., & Gibson, S. 2013, ApJ, 770, 35 [NASA ADS] [CrossRef] [Google Scholar]
  49. Susino, R., & Bemporad, A. 2016, ApJ, 830, 58 [Google Scholar]
  50. Susino, R., Bemporad, A., Jejčič, S., & Heinzel, P. 2018, A&A, 617, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Wang, B., Chen, Y., Fu, J., et al. 2016, ApJ, 827, L33 [NASA ADS] [CrossRef] [Google Scholar]
  52. Xue, J., Romoli, M., Landini, F., et al. 2020, SPIE Conf. Ser., 11443, 114437E [NASA ADS] [Google Scholar]
  53. Ying, B., Bemporad, A., Feng, L., et al. 2020, ApJ, 899, 12 [NASA ADS] [CrossRef] [Google Scholar]
  54. Zhang, J., Cheng, X., & Ding, M.-D. 2012, Nat. Commun., 3, 747 [Google Scholar]
  55. Zhang, P., Buchlin, É., & Vial, J.-C. 2019, A&A, 624, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Zhao, J., Gibson, S. E., Fineschi, S., et al. 2019, ApJ, 883, 55 [NASA ADS] [CrossRef] [Google Scholar]
  57. Zhao, J., Gibson, S. E., Fineschi, S., et al. 2021, ApJ, 912, 141 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1.

Optical parameters adopted for estimating the SNR of UV and WL for LST/SCI.

In the text

All Figures

thumbnail Fig. 1.

Physical parameters of the prominence-carrying flux rope system at different time steps, from the static stage (time steps 105 and 180) to the eruptive phase (time steps 189 and 192), shown from top to bottom. The electron density, temperature and radial velocity in the POS are displayed from left to right. The contours at different panels in this figure as well as in the following figures are displayed to better show the parameter distributions.
In the text
thumbnail Fig. 2.

Synthesized results of Lyman-α emission shown for a slice centered on the plane-of-sky at three different times of the static stage (time steps 105, 165, and 180) are displayed in the top, middle, and bottom rows, respectively. The radiative component, the collisional component, and ratio of the two components are shown in the left, middle, and right columns, respectively. In the first two columns, contours are overlaid on the intensity maps to emphasize the structures. The horizontal curve embedded in each of the right column panels shows the profile of the ratio along the Z = 0 line above the limb. The vertical solid lines in black and white indicate the bottom and top of the central cavity, while the dashed line passes through the cavity. The dashed-dotted line marks a location above the cavity and in the streamer. Profiles of the physical quantities and emissions along these vertical lines (except white solid line) are shown in Fig. 3.
In the text
thumbnail Fig. 3.

Comparison of physical parameters and synthesized emissions at different locations of the central cavity, cavity, and streamer background as described in the caption to Fig. 2. Results sampled at different locations as mentioned above are displayed from left to right. The distributions of density, temperature, radiative component, and collisional component emission are shown from top to bottom. Results at three different times are shown with different colors in each panels.
In the text
thumbnail Fig. 4.

LOS-integrated results of Fig. 2 are displayed from top to bottom: Irad, Icoll, Itotal and the ratio of Icoll and Irad are shown from left to right. The observable structures of prominence, cavity, central cavity and horn are marked in the panel of total emission at time step 165. The white dashed box gives the region where the PRODOP calculation is done for the static stage. The contours, the line curves and the vertical lines are indicated as in Fig. 2.
In the text
thumbnail Fig. 5.

Profiles of the LOS integrated density (top); radiative and collisional components of the emission (middle); and the emission ratio (bottom), along the vertical line that goes through the central cavity (white dashed line in the right column of Fig. 4). The different colored curves correspond to the profiles at different times.
In the text
thumbnail Fig. 6.

Radiative transfer calculation for the prominence plasma and corresponding optical depth. The synthesized intensity is shown in the top panels and the optical depth is shown in the middle. The contours are overlaid to emphasize the distribution. Density distributions at the equatorial plane at four time steps are shown in the bottom panels for reference here and for Fig. 7. The apex, leg, and foot of the prominence plasma are annotated in the right two panels.
In the text
thumbnail Fig. 7.

Doppler dimming effect displayed at time steps 189 and 192 when the prominence erupts. The POS results are shown in the first and third rows while the LOS integrated results are shown in the second and fourth rows. The radiative component without and with Doppler dimming, as well as the extent of dimming are shown in the first three columns. The collisional component is present in the fourth column for comparison and the ratio of the two components is displayed in the last column. The black dashed boxes give the region where the PRODOP calculation is done for the eruptive phase.
In the text
thumbnail Fig. 8.

Total emission of Lyα at different time steps is shown on the top. The emission in the WL is shown at bottom for comparison.
In the text
thumbnail Fig. 9.

S/N at UV Lyα 121.6 nm for different structures, such as the prominence-cavity system at time step 180, the prominence eruption at time step 189 and the CME at time step 192, are displayed in the FOV of LST/SCI. Different exposure times are listed from left to right. A contour with S/N equal to 3 is also displayed.
In the text
thumbnail Fig. 10.

S/N at WL 700 nm for different structures, such as the prominence-cavity system at time step 180, the prominence eruption at time step 189 and the CME at time step 192, are displayed in the FOV of LST/SCI. Different exposure times are listed from left to right. A contour with S/N equal to 3 is also displayed.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.