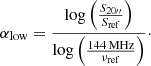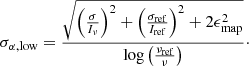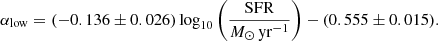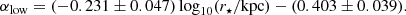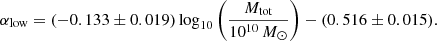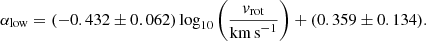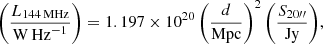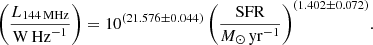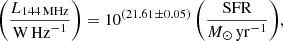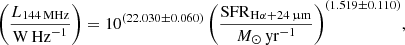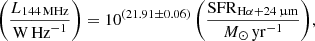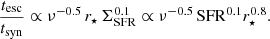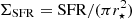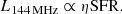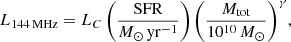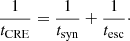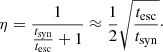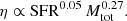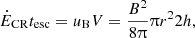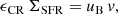EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 664 (August 2022) A&A, 664 (2022) A83 Full HTML
Free Access
Issue
A&A
Volume 664, August 2022
Article Number A83
Number of page(s) 64
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202142878
Published online 08 August 2022

© ESO 2022

1. Introduction

In the study of galaxy evolution, both cosmic rays and galactic magnetic fields are of special interest. Both comprise the non-thermal components of the interstellar medium (ISM) and have energy densities comparable to that of the gaseous parts of the ISM (Cox 2005). With their high energy density, they have a major influence on the dynamics of galaxy development and are a key factor in our understanding of galaxy evolution. Cosmic rays for example are believed to be a driving factor in the creation of galactic winds, transporting material from the galaxy outwards (e.g. Uhlig et al. 2012; Socrates et al. 2008; Everett et al. 2008; Salem & Bryan 2014; Girichidis et al. 2018). Cosmic rays are transported from the star-forming gaseous disc into the halo, where their pressure gradient slowly accelerates the gas. This process is particularly important for cool galactic winds that contain mostly warm and neutral gas (Veilleux et al. 2020). As galaxies require a steady influx of gas from the circumgalactic medium in order to compensate for gas depletion due to star formation and transport losses, the mechanisms of the entire disc–halo cycle, including the impact of these galaxy-wide winds, are an important factor in understanding the overall dynamics and evolution of galaxies (Tumlinson et al. 2017). Without magnetic fields, cosmic rays would quickly escape their host galaxy with relativistic velocities. Instead, they are spiralling along the magnetic field lines and are scattered in irregularities in the magnetic fields, making magnetic fields a key influence on the transport of cosmic rays (Zweibel 2013).

Over recent years, simulations of galaxies have advanced rapidly, and these include outflows and winds and take into account magnetic fields and cosmic rays (Vogelsberger et al. 2020). However, many fundamental questions remain open, such as those regarding the transport processes of cosmic rays. Much of our knowledge about cosmic-ray dynamics stems from observations of the Milky Way, but recently other galaxies have also come into focus as the view ‘from the outside’ now also includes the radio halo from these galaxies, which is harder to observe in the case of our Milky Way (e.g. Heesen et al. 2018a; Miskolczi et al. 2019; Schmidt et al. 2019; Mora-Partiarroyo et al. 2019; Stein et al. 2019a,b). This is one of the reasons why observations of cosmic-ray transport processes are of special interest. These relativistic cosmic rays also include cosmic-ray electrons (CREs), and radio frequencies are sensitive to the emission of CREs in the GeV energy range. This energy range also corresponds to the peak of the cosmic-ray spectrum in general. We can therefore probe the cosmic-ray transport parameters, where they are dynamically most important.

Radio continuum emission offers further advantages. Radio emission is not attenuated by dust, and as it originates from cosmic rays accelerated in supernova remnants of massive young stars, it can therefore be used as an extinction-free tracer of star formation (Condon 1992; Murphy et al. 2011). Current radio surveys can serve to calibrate the radio–star formation rate (SFR) relation in order to extrapolate it to more distant galaxies at higher redshifts. The radio–SFR relation has a spread of only ≈0.15 dex (Tabatabaei et al. 2017), which is comparable to uncertainty of the widely used hybrid star formation tracers such as the combination of Hα and 24-μm mid-infrared (MIR) emission (Calzetti et al. 2007). The synchrotron emission that we see as radio continuum depends both on the CRE and magnetic field content of galaxies. There is a degeneracy between having a high CRE energy density and weak magnetic fields, or vice versa, strong magnetic fields and a low CRE energy density. For reasons of dynamical stability, energy equipartition between the cosmic rays and the magnetic field is usually assumed, which is a good approximation for the Milky Way (Boulares & Cox 1990). Given the many dependencies of the synchrotron emission, it is astonishing that the radio–SFR relation is so tight. In particular, less-luminous galaxies should be deficient in radio luminosity as the CREs are expected to escape rapidly from their host. The fact that this does not appear to be the case when the SFR is measured by infrared (IR) star-formation tracers has been explained by authors invoking a ‘conspiracy’ between the escape of the CRE and dust-heating ultraviolet photons (Bell 2003; Lacki et al. 2010). While more sensitive, spatially resolved observations of dwarf galaxies have finally shown that the synchrotron emission is indeed suppressed (Hindson et al. 2018), the influence of cosmic-ray transport on the radio–SFR relation in L⋆ galaxies is still largely unknown (Lisenfeld et al. 1996; Li et al. 2016).

Low-frequency radio observations are particularly useful for studying synchrotron emission from galaxies because the fraction of thermal radiation (i.e. bremsstrahlung from non-relativistic electrons) is less than 10% (Tabatabaei et al. 2017). At 150 MHz, the radio–SFR relation shows a possible excess of radio emission in low-mass galaxies (Brown et al. 2017; Gürkan et al. 2018) which is not seen at higher frequencies (Schmitt et al. 2006; Li et al. 2016). Radio-continuum studies of dwarf galaxies are influenced by unrelated background sources (Hindson et al. 2018), and so spatially resolved studies are important. The most suitable telescope for these kinds of studies is the LOw Frequency ARray (LOFAR; van Haarlem et al. 2013), which is composed of 51 stations spread throughout Europe with two more stations under construction. The LOFAR Two-metre Sky Survey (LoTSS; see Shimwell et al. 2017) is currently exploring the northern sky and is more sensitive than any previous or ongoing radio survey at a similar angular resolution. The first data release (LoTSS-DR1; Shimwell et al. 2019) enabled successful work on cosmic-ray transport and the radio–SFR relation (e.g. Heesen et al. 2014) explored for four LOFAR galaxies (Heesen et al. 2019). Data release 2 (LoTSS-DR2; Shimwell et al. 2022) covers a larger sky area at 144 MHz with a bandwidth of 48 MHz at both 6 and 20 arcsec resolution with a sensitivity of 50−100 μJy beam−1.

This paper reports the first exploration of these data. We investigated a sample of nearby galaxies at distances of < 30 Mpc, which corresponds to a redshift of less than z ≈ 0.01. As our main aim is to study spatially resolved scaling relations, the sample selection was largely driven by the availability of ancillary data in the radio continuum and IR. We selected galaxies from the CHANG-ES radio continuum survey (Continuum HAlos in Nearby Galaxies: an EVLA Survey; Irwin et al. 2012), consisting of 35 edge-on galaxies, and from the KINGFISH far-infrared (FIR) survey (Key Insights on Nearby Galaxies: A Far-Infrared Survey with Herschel; Kennicutt & Evans 2012), which in turn is a descendent of the SINGS survey (The SIRTF Nearby Galaxies Survey; Kennicutt et al. 2003), the sample of the former consisting of 65 galaxies. From these samples, all galaxies also present in LoTSS-DR2 were included in our sample. The galaxy sample is very diverse in optical classification, ranging from elliptical and spiral galaxies to irregular galaxies. The sample has also a wide range of SFRs between 0.002 and 15 M⊙ yr−1. The galaxies also cover a wide range of nuclear types, ranging from the more quiescent H II and low-ionisation nuclear emission-line region (LINER) nuclei to the more active Seyfert nuclei. Similarly, the sample covers a wide range of total masses (within the optical radius) of between 108 and 1012 M⊙ and a large size range of between 1 and 70 kpc. The sample is not complete, but rather aims to capture a representative set of galaxies with a range of primary parameters such as SFR, morphology, mass, and size. Because of the limited sample size, secondary parameters such as nuclear type and environmental properties are not evenly sampled.

The structure of this paper is as follows: Sect. 2 presents the methodology, including a description of the sample, a summary of how the LoTSS-DR2 data were obtained and reduced, and how flux densities and radio spectral indices were measured. This is followed by Sect. 3, where we present the radio maps for one selected galaxy and also analyse integrated spectral indices (Sects. 3.1–3.3), spatially resolved spectral indices (Sect. 3.4), and the integrated radio–SFR relation (Sect. 3.5). We discuss our findings in more detail in Sect. 4, focusing on the non-linearity of the radio–SFR relation. Section 5 presents our conclusions and a brief outlook on possible follow-up work. Details about the complete sample are presented in Appendix A and our atlas of maps can be found in Appendix B.

2. Methodology

2.1. Galaxy sample

Appendix A presents the complete sample of galaxies in LoTSS that were considered as part of this study. We selected galaxies from samples that have either high-frequency radio continuum data, so that we can calculate radio spectral indices, or IR data so that we can calculate SFRs. For the edge-on sample, we chose from the CHANG-ES sample (Irwin et al. 2012), which contains 35 galaxies, 21 of which are located in the northern sky and are therefore accessible to LoTSS. For the IR data, we chose from the SINGS (Kennicutt et al. 2003) and KINGFISH (Kennicutt et al. 2011) samples. SINGS contains 75 representative star-forming galaxies within a distance of 30 Mpc, 48 of which are in the northern sky. Three galaxies were added, which are only in the KINGFISH survey (NGC 2146, IC 342, NGC 5457). Finally, we added another 4 galaxies, namely IC 10, NGC 598 (M 33), NGC 4214, and NGC 4449. Three of these are star-burst dwarf irregular galaxies and M 33 is the most nearby galaxy, which we can easily image as it is less than 1° in apparent size. This results in 76 galaxies, which will eventually be covered by LoTSS. The four subsamples are referred to as CHANG-ES, SINGS, KINGFISH+, and ‘Extra’.

In addition to the IR data, we also have rich ancillary data in the radio continuum. First, all CHANG-ES galaxies have 6-GHz data from Wiegert et al. (2015) at approximately 15 arcsec resolution, observed with the Karl G. Jansky Very Large Array (VLA) in D-configuration. There were also CHANG-ES data taken at 1.5 GHz in C-configuration with a similar resolution, which will be analysed in a forthcoming paper together with the LoTSS data (Stein et al., in prep.). The SINGS galaxies were observed at 1.4 GHz by the WSRT–SINGS survey (Braun et al. 2007), which includes 34 SINGS galaxies north of declination 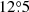with an optical diameter of > 5 arcmin. Approximately a third of the complete sample galaxies have active galactic nuclei (AGN) classified as either LINER, Seyfert or transition object (Ho et al. 1997), with more galaxies possibly containing hidden AGN that cannot be detected by optical spectroscopy (Satyapal et al. 2008). The AGN contribution to the radio flux was estimated from the work by Baldi et al. (2018) and Irwin et al. (2019), who present high-resolution maps for the Palomar (Ho et al. 1995) and CHANG-ES samples. We found that the galaxies with a radio-detected AGN in LoTSS-DR2 (10 galaxies in our sample of 45) have mostly AGN contributions of less than 1% at 1400 MHz. The exceptions are NGC 2683 (1.7%), NGC 3079 (19%), and NGC 5866 (35%). We therefore conclude that our galaxies are mostly not AGN contaminated, but the mentioned galaxies require special attention.

One of the important characteristics of galaxies is their star formation rate (SFR). We use two approaches for calculating this. Our main method is to use total infrared (TIR) fluxes in the wavelength range 3−1100 μm, which are more reliable for our edge-on sample, as the widely used MIR 24-μm emission becomes partially optically thick (Li et al. 2016; Vargas et al. 2018). Hence, in order to have consistent SFRs in our sample, this is the preferred method. Nevertheless, we also used SFRs from Hα and MIR tracers, which should be particularly reliable for spatially resolved SFRs in moderately inclined galaxies (Murphy et al. 2011; Leroy et al. 2012). As this paper is also a preparatory study of the spatially resolved radio–SFR relation, we compare the two methods. The TIR luminosities were calculated using the prescription of Dale & Helou (2002) using the flux densities from Dale et al. (2012), when available. For those galaxies that are not included in either SINGS or KINGFISH such as most of the CHANG-ES galaxies, we calculated their TIR luminosities from IRAS data using the formulae by Dale & Helou (2002). The TIR luminosities were converted into SFRs using the calibration presented in Kennicutt & Evans (2012), which is based on work by Hao et al. (2011) and Murphy et al. (2011). For SINGS and KINGFISH+, Kennicutt et al. (2011) provide SFRs from a combination of Hα and 24-μm emission based on measurements by Calzetti et al. (2010). The CHANG-ES galaxies have SFRs from 24-μm emission (Wiegert et al. 2015) using the calibration of Rieke et al. (2009).

Our galaxy sample covers a wide range of galaxy parameters (see Fig. 1). Nearly all types of optical galaxy classifications are included, and there is a range of almost 105 in total TIR luminosity as well as a range of 103 in physical size. SINGS was chosen specifically to have a fairly even distribution of optical galaxy types for the late-type spiral galaxies (Sa–Sd, and magellanic-type galaxies Sdm and Sm as well as irregular galaxies Ir). In addition, there are a few elliptical galaxies (E), lenticular galaxies (S0), and peculiar galaxies (P). This was not the case with CHANG-ES, where a radio flux density cut was used and so only galaxies with higher SFRs were included. This means that the CHANG-ES galaxies tend to be heavier and larger, and therefore our sample is biased towards massive galaxies with total masses of ≳1010 M⊙ and correspondingly larger SFRs. The four galaxies from the Extra sample add a few galaxies with lower masses to balance the distribution slightly (compare with Fig. 1). We note that the total mass is calculated as Mtot = 0.234(vrot/100 km s−1)2(r⋆/kpc) × 1010 M⊙, where we have estimated r⋆, the size of the star-forming disc, using the 3σ extent of the radio continuum emission at 144 MHz. Specifically, we projected the major axis of the a20″ integration region (Sect. 2.3) to obtain the physical size.

thumbnail Fig. 1.

Properties of the complete galaxy sample as presented in Appendix A. (a) Distribution of galaxy type; (b) SFR as a function of total mass enclosed within the radius of the star-forming disc; and (c) specific SFR (sSFR; per total mass) as a function of the optical galaxy diameter (projected apparent diameter D25). The galaxies are grouped according to the respective subsample to which they belong (Sect. 2.1).

2.2. LoTSS-DR2 data

The LoTSS-DR2 data were obtained and reduced as described in Shimwell et al. (2017, 2019). Here, we briefly summarise the procedure. The LoTSS data were obtained with the High Band Antenna (HBA) system of LOFAR. The data are taken with the HBA_DUAL_INNER configuration with 8 h dwell time and 120−168 MHz frequency coverage. The entire northern sky is covered with 3168 pointings. The publicly available LOFAR direction-independent calibration procedure was described in detail by van Weeren et al. (2016) and Williams et al. (2016) and makes use of the LOFAR Default Preprocessing Pipeline (DPPP; van Diepen et al. 2018) for averaging and calibration and BlackBoard Selfcal (BBS; Pandey et al. 2009). Because for LOFAR the direction-dependent effects (DDEs) are important, a lot of work has gone into improving their treatment during calibration. LoTSS uses the pipeline KILLMS Smirnov & Tasse (2015) to calculate DDE corrections and apply them to the data during imaging using DDFACET (Tasse et al. 2018). Compared with LoTSS-DR1 (Shimwell et al. 2019), LoTSS-DR2 (Shimwell et al. 2022) now provides a much improved imaging capability for diffuse extended emission (Tasse et al. 2021).

The LoTSS-DR2 data are provided in two ways: either as mosaics created from neighbouring pointings to improve sensitivity, or as re-calibrated (u, v) data sets, where the calibration is specially tailored to the target of interest (van Weeren et al. 2021). For most galaxies, we used the re-calibrated (u, v) data and re-imaged and deconvolved the data with WSCLEAN V2.9 (Offringa et al. 2014; Offringa & Smirnov 2017). For the imaging, we produced maps at 6 and 20 arcsec resolution, hereafter referred to as high- and low-resolution maps, respectively. For the high-resolution maps, we used Brigg’s robust weighting parameter of −0.5, whereas for the low-resolution maps we used a robust parameter of −0.25 together with a Gaussian taper of 10 arcsec. The maps were deconvolved with the multi-scale and auto masking options to remove any residuals comparable to the size of the galaxies. The maps were then restored with a Gaussian beam with a FWHM of 6 and 20 arcsec, respectively. We checked that the integrated flux densities of the 6- and 20-arcsec maps are identical for the same integration area (see Sect. 2.3) and found an average ratio of 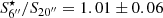, where 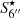is the integrated flux density in the 20-arcsec integration area of the 6-arcsec map and S20″ is the integrated 20-arcsec flux density. Hence, we are confident that we have sufficiently deconvolved both the high- and the low-resolution maps. In order to match the flux densities with the LoTSS-DR2 scale, we compared flux densities of point-like sources with the LoTSS-DR2 point-source catalogue and applied a scaling factor to our maps1. For a few galaxies (NGC 5055, NGC 5194/5, and NGC 5474), we found the mosaics to be superior to the re-calibrated data sets, and so we used them instead.

Galaxies included in this paper were detected and contained within usable LoTSS-DR2 mosaics. There were a few objects for which a mosaic was available but then no object was detected (M81DwA, IC 2574, DDO 154, and DDO 165). We did not attempt to improve detection rates by masking star-forming regions, reducing the area, and thus increasing the signal-to-noise ratio (S/N; Hindson et al. 2018). The analysis of dwarf irregular galaxies with low star-formation rates, which are particularly affected, is deferred to future work. For the 45 remaining galaxies, we made cutouts from the maps using the Common Astronomy Software Applications (CASA; McMullin et al. 2007). These cutouts were square regions centred on the galaxy with an edge length equal to the optical diameter of the galaxy (D25) plus 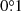rounded up to the nearest tenth of a degree. A minimum edge length of 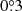was chosen to ensure that the background can be measured reliably. The size of the cutouts was sufficient to even include the faint diffuse emission in the outer discs.

2.3. Flux density estimation

For all galaxies in the sample, we estimated the total radio flux density for both the high and low resolutions within 3σ-contours. Around these contours, an elliptical region was created such that it encloses the 3σ-line surrounding the entire galaxy. This approach is a compromise between choosing a sufficiently large integration area so as not to underestimate the emission of the galaxy and minimising the contamination by background sources, which is ≈20 μJy beam−1 at 20 arcsec resolution (Williams et al. 2016). Another issue linked to extending the integration area below 3σ is that the flux is not properly deconvolved and the contribution from residual flux becomes a problem (Walter et al. 2008). Galaxies have fairly well-defined edges; the scale length of 2 kpc (Mulcahy et al. 2014) is equivalent to 44 arcsec at the median distance of our sample. We estimate that the flux between the 1σ and the 3σ contour lines is about 5% of the integrated flux density. Our integration areas enclose the 3σ contours, and so in many cases also include emission at the 2σ level, excluding some local radial extensions only. Hence, the 5% estimate is an upper limit.

The position angle of the region was chosen to be the position angle of the galaxy as listed in Table 1. Wherever other sources outside of the disc of the galaxy were apparent or where contours of the galaxy blended with those of other nearby sources, we excluded them from the region. In a few cases, this was not possible as the S/N was not sufficient to discern the galaxy from the surroundings with only the 3σ-lines. In these cases, the region was drawn by eye and we attempted to enclose the visibly discernible features of the galaxy as well as possible.

Table 1.

Integrated 144-MHz flux densities, map properties and star formation rates of the 45 galaxies in LoTSS-DR2.

The flux density Sν was then measured by integrating the intensity Iν in the integration regions. The error on the flux density was estimated by assuming a statistical error on the flux density caused by the background noise as well as a relative calibration error of ϵ = 0.1 (Shimwell et al. 2017), resulting in an error of the form

(1)

where Nbeams is the number of beams in the integration region. For most galaxies, except the faintest, the 10% relative error is the dominating contribution. Table 1 shows the resulting flux densities, S6″ and S20″, for the galaxy sample for both high (6 arcsec) and low (20 arcsec) resolutions, respectively. The table also shows the rms intensities for the background noise for the respective cutout.

2.4. Radio spectral indices

2.4.1. Integrated spectral indices

For further investigation, we calculated integrated radio continuum spectral indices. For those galaxies where L-band maps are available, we integrated the flux densities within the same ellipses as for the 20-arcsec LoTSS maps. These data were taken mostly from WSRT–SINGS (Braun et al. 2007) at 1365 MHz and CHANG-ES (Wiegert et al. 2015) at 1575 MHz. The CHANG-ES data are at a lower angular resolution of FWHM ≳ 30 arcsec; while we did not use them for the resolved spectral index maps, they are sufficient to provide us with integrated spectral indices. For the remaining maps, we used NVSS data at 1400 MHz, either from Yun et al. (2001) or integrating the NVSS map (Condon et al. 1998). We computed integrated spectral indices using the low-resolution flux densities and the flux density Sref from the reference data at νref ≈ 1400 MHz as

(2)

The low-resolution data were chosen as they have a higher surface brightness sensitivity and so have more reliable integrated flux densities. Table 2 contains the resulting integrated radio spectral indices. These values are presented in Table 2. We note that LOFAR data, and LoTSS data in particular, have been extensively compared with random field sources in order to gain confidence in the overall reliability of the spectral indices between LoTSS and higher frequency surveys (de Gasperin et al. 2018; Shimwell et al. 2019).

Table 2.

Radio spectral indices αlow between 144 MHz and the reference frequency and αhigh between the two reference frequencies.

We also calculated high-frequency radio spectral indices using our L band flux densities and C band flux densities from the literature. These high-frequency spectral indices, which are calculated between ≈1400 and ≈5000 MHz, are referred to as αhigh (Table 2). These data are taken either from the 6000-MHz flux densities presented in Wiegert et al. (2015), which are sensitive enough for the fairly small galaxies so that missing spacings play no role for the interferometric data. The remaining flux densities were mostly single-dish data obtained at 4850 MHz with either the 100-m Effelsberg telescope (Tabatabaei et al. 2017) or with the 110-m Green Bank Telescope (Gregory & Condon 1991).

2.4.2. Spatially resolved spectral index maps

We also determined radio spectral index maps for a subset of galaxies. We used both C-band data from CHANG-ES survey (Wiegert et al. 2015) at 6000 MHz and maps from the WSRT–SINGS survey (Braun et al. 2007) at 1365 MHz. For two galaxies, instead of the 6000-MHz data from Wiegert et al. (2015), we used the NGC 891 map from Schmidt et al. (2019) and the NGC 4631 map from Mora-Partiarroyo et al. (2019). The reason is that these maps are merged with single-dish data and so have reliable flux densities. In total, we were able to compute spectral index maps for 30 galaxies.

Prior to combination, at both frequencies, maps were masked below 3σ. The error map of the spectral index was calculated assuming a systematic map error of ϵmap = 0.05 for both LoTSS and the reference data:

(3)

This error underestimates the absolute error, but this smaller error, dominated by the uncertainties in the deconvolution, is a good estimate, because in spectral index maps we are most interested in the spatial variation. Table 2 presents the mean radio spectral index in these maps within the flux-integration areas and the corresponding standard deviation.

2.5. Image atlas

Figure 2 shows the maps of NGC 5194 (M 51). We present the LoTSS-DR2 intensity maps as contour and grey-scale maps at both resolutions, and include the spectral index maps as well. The maps are also shown overlaid on the rgb SDSS image. The full image atlas can be found in Appendix B.

thumbnail Fig. 2.

NGC 5194 (M 51). The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6 and 20 arcsec images without contours and the radio spectral index error. The third row shows the 6 and 20 arcsec contours overlaid on an rgb SDSS image as well as contours of the radio spectral index. Contours are at −1.0 (blue), −0.8 (green), −0.6 (yellow), and −0.4 (red). The filled circle shows the synthesised beam. The scale bar shows the projected size at the distance of the galaxy.

3. Results

At the low frequencies of LoTSS, we expect the radio continuum emission to be dominated by non-thermal (synchrotron) emission. For synchrotron emission from CREs with a distribution N ∝ E−p, the observed radio spectral index is α = (1 − p)/2. When spectral ageing is important, the CRE spectrum steepens to N ∝ E−p − 1 resulting in a spectral index of α = p/2 (Longair 2011). Therefore, for CRE with an injection spectrum, we expect α ≈ −0.5, which is corroborated by both observations and theory. For example, the average injection spectral index of cosmic-ray energy spectra is measured from γ-ray emission of young supernova remnants to be p = −2.3 ± 0.3 (see Fig. 4 in Mandelartz & Becker Tjus 2015), resulting in a non-thermal radio spectral index of αinj ≈ −0.65, consistent with models of diffusive shock acceleration (Bell 1978). The CRE spectrum is also constrained by radio spectral index measurements of supernova remnants, which provide a value of αinj = −0.5 ± 0.2 (Reynolds et al. 2012). Some remnants show low-frequency (< 100 MHz) spectral turnovers, but some do not. This is usually explained with an inhomogeneous, ionised medium in the Galactic foreground (Kassim 1989).

The non-thermal radio spectral index is altered by several processes which broadly fall into two categories. First, the observed radio continuum emission of a galaxy is affected by radiation transfer. At low frequencies, both free–free absorption (e.g. Carilli 1996; Adebahr et al. 2013) and synchrotron self-absorption (e.g. Carilli et al. 1991; Irwin et al. 2015; Callingham et al. 2015; Kapińska et al. 2017) can lower the radio continuum emission, and thus flatten the radio spectrum. The latter is in particular associated with AGN, although the spectrum may be better explained by a low-energy CRE cut-off (Lazio et al. 2006; McKean et al. 2016). Second, loss processes of the CRE, which have various dependencies on energy, will change the radio spectrum. Both ionisation losses and bremsstrahlung flatten the radio continuum spectrum to α ≈ −0.2 in dense star-formation regions (e.g. Basu et al. 2015). In contrast, both inverse Compton (IC) and synchrotron radiation depend on the energy of CREs, meaning that the radio spectrum is steepened to α ≈ −0.7 if the synchrotron loss time-scale of ≈100 Myr is similar to the CRE escape timescale. For the case where a galaxy is an electron calorimeter with no CRE escape, α = αinj − 0.50 ≈ −1.1 (e.g. Lisenfeld et al. 1996). Finally, adiabatic losses and escape of the CRE will result in an unchanged injection spectrum (e.g. Krause et al. 2018). We have to disentangle these various processes in order to understand the low-frequency radio continuum spectrum (Sects. 3.1–3.4) before we turn to the radio–SFR relation (Sect. 3.5).

3.1. Low-frequency radio spectral index

The mean integrated radio spectral index and standard deviation in our sample are ⟨αlow⟩= − 0.55 ± 0.14. Several galaxies in our sample have spectral indices that are lower than the injection spectral index. Most noticeable among them are NGC 855 and 5474, which have almost flat spectra with spectral indices of −0.22 ± 0.09 and −0.25 ± 0.06, respectively. Both are elliptical galaxies and so have low star formation rates and may host AGN, which are likely affected by absorption, which could explain their flat spectra. Late-type spiral and irregular galaxies also have spectral indices αlow > −0.5, which are NGC 598, NGC 2798, NGC 3077, NGC 3265, NGC 4214, and NGC 4625. Only a very large fraction of thermal radiation could, in theory at least, flatten the spectrum. While the thermal contribution is hard to estimate for our galaxies without radio data beyond 10 GHz, the thermal fraction is expected to be at only a few percent level at the LoTSS frequencies (e.g. Basu et al. 2012a; Tabatabaei et al. 2017; Klein et al. 2018). Thermal emission is therefore an insufficient explanation for the galaxies with significant deviations from the injection spectrum, which leaves absorption effects and CRE energy losses as the most likely cause.

Basu et al. (2015) modelled the relative importance of the various CRE energy loss mechanisms in galaxy discs and showed that, at 100 MHz, bremsstrahlung and ionisation losses are of similar importance and dominate over synchrotron losses. An integrated radio spectral index in agreement with the injection spectral index may be the result of a superposition of both spectral flattening and steepening, such as by a flat radio spectrum in the gaseous disc and a steep radio spectrum in the halo (Adebahr et al. 2013). The spectrum could also be explained by a fast escape of the CREs, where energy losses due to escape and adiabatic expansion dominate over synchrotron and IC radiation losses (Krause et al. 2018). However, this would mean small radiation losses due to synchrotron emission and so the galaxies would be underluminous in the radio continuum, as is the case in dwarf irregular galaxies (Hindson et al. 2018). However, this is not observed: the galaxies are in good agreement with the radio–SFR relation even at the low frequencies of LoTSS (Gürkan et al. 2018; Smith et al. 2021). We conclude that synchrotron losses of the CRE are still important. We return to this point in more detail in Sect. 4.

3.2. Spectral curvature

If both spectral flattening at low frequencies and spectral steepening at high frequencies occurs (Sect. 3.1), the resulting spectrum is convex and has spectral curvature. Figure 3 shows the high-frequency spectral indices as a function of our previously calculated low-frequency spectral indices between 144 and 1400 MHz. It can be seen that the αlow values are mostly smaller than the αhigh values. If we define the spectral curvature as Δα = αlow − αhigh, we find a mean value of ⟨Δα⟩ = 0.20 ± 0.18. This indicates a convex spectral curvature, in agreement with previous studies (Marvil et al. 2015; Chyży et al. 2018).

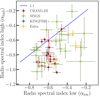thumbnail Fig. 3.

Radio colour–colour diagram with a comparison of the high-frequency radio spectral index αhigh (1400–5000 MHz) with the low-frequency radio spectral index αlow (144–1400 MHz) taken from Table 2. The blue solid line indicates points of equal spectral index, indicating a power-law radio continuum spectrum. Most of the data points lie below the blue line indicating spectra with a convex curvature. Data points above the blue line indicate concave spectra, as may be explained by a higher thermal fraction at high frequencies.

In order to distinguish free–free absorption from CRE bremsstrahlung and ionisation losses, we now investigate the effect of the inclination angle and thus the length of the line of sight on the spectral index (Israel & Mahoney 1990). We show in Fig. 4a the radio spectral index as a function of cos(i), where i is the inclination angle. If free–free absorption were important, we would expect to see a flattening of the spectrum for high inclination angles (see also Chyży et al. 2018). Clearly, the expected increase in α at low values of cos(i) is not observed; at best, a weak trend is visible (Spearman’s rank correlation coefficient of ρs = 0.29), where the spectral index seems to be increasing with cos(i), opposite to the expected trend. However, there is a bias in the CHANG-ES sample for massive galaxies to have high inclination angles, and these have intrinsically steeper spectra because they are more massive (we return to this in Sect. 4.3).

thumbnail Fig. 4.

Radio spectral index as a function of inclination angle. Panel a: integrated radio spectral index between 144 and 1400 MHz as a function of cos(i). Panel b: spectral curvature Δα = αlow − αhigh as a function of cos(i). The high-frequency radio spectral index αhigh is defined between 1400 and 5000 MHz. Both spectral index measurements show at most only a weak correlation with the inclination angle.

Hence, in order to take out this possible dependence of the spectral index, we also study the dependence of spectral curvature on the inclination angle. As free–free absorption depends strongly on frequency, the low-frequency radio spectral index should be affected, whereas the high-frequency one should be unchanged. As Fig. 4b shows, the spectral curvature has no correlation with cos(i) either (ρs = 0.08). Chyży et al. (2018) modelled the low-frequency radio continuum emission of galaxies and showed that spectral flattening towards lower frequencies cannot be solely due to free–free absorption. We note that inclination dependence alone is not a sufficient argument to rule out free–free absorption because in highly inclined galaxies, a mix of absorption in the inner disc and steep spectrum in the outer disc and halo (due to older CRE) could compensate. Further, more rigourous investigation is needed to support this claim, for instance by observing at 57 MHz (de Gasperin et al. 2021).

3.3. Radio spectral index and galaxy properties

In this section, we compare the radio spectral index with several fundamental galaxy parameters. Our galaxies span a wide range in mass, size, and star-formation activity, the influence of which we now explore. In Fig. 5a, we show the radio spectral index as a function of SFR. A clear trend is visible (ρs = −0.61), with the best-fitting relation

(4)

thumbnail Fig. 5.

Radio spectral index as a function of several fundamental galaxy parameters. Panel a: dependence on SFR as calculated from the TIR luminosity; (b): dependence of the star formation radius, which is derived from the extent of the 3σ contours in the 20 arcsec LoTSS images; (c): dependence on the total mass calculated; (d): dependence on the rotation speed. In all panels, the blue line is the best-fitting relation and the shaded areas show 1σ confidence intervals. The colours of the data points in panel b indicate the rotation velocity, in the other panels the colours indicate the different subsamples.

For higher SFRs, the radio continuum spectra become steeper. Similar results were obtained by Marvil et al. (2015), who studied 250 bright galaxies and measured mean spectral indices of −0.45 between 74 MHz and 325 MHz, −0.55 between 325 MHz and 1.4 GHz, and −0.69 between 1.4 GHz and 4.85 GHz. The spectra between 325 MHz and 1.4 GHz were found to become steeper with increasing radio luminosity and hence with increasing SFR.

Naively, one may expect galaxies with lower SFRs to exhibit steeper spectra due to the ceased acceleration and subsequent ageing of CRE. However, Fig. 5a shows the opposite trend where steeper spectra are found for galaxies with higher SFRs. Explanations for this effect could be the combination of CRE escape, free–free absorption, the fraction of thermal emission, and CRE energy losses. While the escaping CREs leave mostly the flat injection spectrum visible, absorption would further flatten this spectrum which may explain the observed spectral indices α > −0.5. A high fraction of thermal emission could have a similar effect, which is especially likely in dwarf galaxies (e.g. Basu et al. 2017), but also in other galaxies with very low surface SFR (below about 10−4 M⊙ kpc−2 yr−1), as these are deficient in injecting CREs to produce synchrotron radiation, leaving thermal radiation as a noticeable contribution to the spectrum (Schleicher & Beck 2016). However, all galaxies of our sample have larger values of surface SFR, and so dominant thermal emission cannot explain the trend seen in Fig. 5a. This leaves the competition between escape and synchrotron energy loss of CREs as the probable reason for the dependence of spectral index on SFR.

Figure 5b shows the radio spectral index as a function of the size of the star-forming disc. This correlation is significant (ρs = −0.62)

(5)

The radio spectral index also clearly depends on total mass enclosed within the star-forming disc (Fig. 5c) with (ρs = −0.70)

(6)

Similarly, we find a strong dependence on rotation speed (ρs = −0.70) as shown in Fig. 5d

(7)

It is unclear whether there is a primary relation that drives the remaining correlations. For instance, larger galaxies with large values of r⋆ tend to also be more massive, have larger values of SFR, and rotate faster. The correlation between mass and SFR is well known, and is usually referred to as the main sequence of galaxies (Brinchmann et al. 2004, compare with Fig. 1b). Similarly, there is a mass–size relation for star-forming galaxies (van der Wel et al. 2014), where larger galaxies have greater stellar mass. Also, there is a size–velocity relation, where larger galaxies have increased rotation speeds (Meurer et al. 2018). Thus if size were the primary driver of the spectral index variation, the other relations would follow.

Ordered magnetic fields could be an additional driver of the dependence of the radio spectral index on rotation speed. As shown by Tabatabaei et al. (2016), the strength of the ordered magnetic field in galaxy discs correlates with rotation speed. Diffusion and streaming of cosmic rays is enhanced along the field lines, meaning that CREs may be stored for longer in fast-rotating galaxies.

3.4. Spatially resolved radio spectral index and galaxy morphology

In the radio spectral index maps, we find regions with αlow ≳ −0.4 – which are clearly flatter than the injection spectrum – in many late-type spiral galaxies. Such regions are nearly always compact and cover only a small fraction of the galaxies, with the exception of NGC 2976 and 4559 where they are more widely distributed. In the moderately inclined galaxies, these areas appear to be mostly co-spatial with star-formation regions, whereas for most of the edge-on galaxies, these regions are co-spatial with the nucleus. Also, in the edge-on galaxies, the spectral index is relatively flat in the galactic midplane with αlow ≳ −0.7, but then decreases at larger distances from the midplane, reaching values of −0.9 ≲ αlow ≲ −0.7, with even steeper spectra (αlow ≈ −1.1) found far away from the disc.

The galaxies that are not classified as late-type spirals, with classifications such as Sa, S0, E, P, or Ir, have visibly different radio continuum emission, and have integrated spectral indices of α ≈ −0.3. As their radio continuum emission is compact, they may be more affected by free–free absorption, CRE bremsstrahlung, ionisation losses, and CRE escape. The only notable exception is NGC 4125, which has the steepest spectrum in our sample (αlow = −0.84). There appears to be little or no star formation, corroborated by the relatively red appearance of the optical image. It is possible that star formation has ceased and with it the injection of young CREs, causing strong spectral ageing. However, it is most likely that the emission is caused by the weak AGN, which is classified as a transition object between a H II and LINER object (Ho et al. 1997).

3.5. Radio–SFR relation

In this section, we study the integrated radio–SFR relation at 144 MHz. We use the low-resolution flux densities (S20″) measured from the 20-arcsec maps to calculate the spectral radio luminosity (L144 MHz = 4πd2S20″) as

(8)

where we have neglected the K-correction because our redshifts are low with z ≲ 0.01. These spectral luminosities are to be compared to the SFR as listed in Appendix A, which were calculated from the TIR luminosities (Sect. 2.1). We also used the SFRs calculated from Hα and 24-μm emission (Sect. 2.1 and Table 1).

Figure 6 shows both resulting plots for the integrated radio–SFR relation. We expect a scatter of at least 0.18 dex because that is the accuracy of the integrated SFR value from either method (Leroy et al. 2012). The scatter of the data points is slightly larger than that, as expected, and a clear general non-linear trend is found. We applied a least-square bisector fit, where it is best practice to fit the relation log–log space, which is equivalent to fitting log(L144 MHz) = log a + blog(SFR). Below are the results of the bisector fit (Isobe et al. 1990) for radio–SFR, with SFR determined using TIR:

(9)

thumbnail Fig. 6.

Integrated radio–SFR relation at 144 MHz. Blue lines indicate the best-fitting relations using a bisector fitting method as fitted in the log–log space. The dashed green line shows the best-fitting linear relation as fitted in linear space. Shaded bands represent the 3σ confidence intervals from the 1000 Monte–Carlo realisations. Panel a: the SFR is calculated from the TIR luminosity; in the panel b: the SFR is calculated using either the hybrid Hα + 24 μm SFR calibration or a 24 μm only calibration. For both SFR calibrations, the radio–SFR relation is clearly non-linear.

For this best-fitting relation, we find 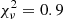and a rms scatter of σ = 0.27 dex. We assess the confidence intervals of the derived model parameters using the Markov chain Monte Carlo (MCMC) method. If we force a linear fit, we find the relation

(10)

this time with 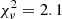. Similarly, below are the results of a bisector fit for radio–SFR, with SFR determined using Hα + 24 μm:

(11)

with 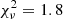and σ = 0.38 dex. If we force a linear fit, we find

(12)

with 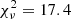. These best-fitting non-linear and linear relations are presented in Fig. 6 with their respective ±1σ confidence intervals. For the Hα + 24-μm derived SFRs, the scatter is slightly larger with 0.38 dex. As Fig. 6b shows, the CHANG-ES data points tend to mostly lie above the best-fitting non-linear relation. This means their radio luminosity is too large for a given SFR, or, as we would argue, their SFR measurement is too low. This was the case for the CHANG-ES galaxies investigated by Vargas et al. (2018) who conclude that the 24-μm MIR emission becomes partially optically thick in edge-on galaxies (see also Li et al. 2016). Hence, in what follows we only study the relation further using the TIR SFR measurements.

Now, we compare our results with previous studies of the low-frequency radio–SFR relation using LOFAR. Gürkan et al. (2018) studied approximately 1000 star-forming galaxies at 150 MHz using photometric SFRs in a redshift range of 0 ≲ z ≲ 0.3. These authors also found a super-linear relation with a L150/W Hz−1 = 1022.06±0.01(SFR/M⊙ yr−1)1.07±0.01. They also posited that the stellar mass is a second parameter in the relation, with higher masses having a higher radio luminosity. These results were largely confirmed by an even larger sample of galaxies at redshifts of z < 1 by Smith et al. (2021), with an intrinsic scatter around the relation of ≈0.3 dex, similar to our results.

The previous studies and our data show that it is possible to establish a robust radio–SFR relation for low radio frequencies. The scatter with 0.27 dex nevertheless exceeds the margin of error of the data which is the flux density uncertainty of 10% (0.041 dex). Hence, our scatter represents the intrinsic scatter of the radio–SFR relation. The scatter of 0.27 dex is almost equal to that of the most robust known star-formation tracers which have an uncertainty of 50%, equivalent to 0.18 dex (Leroy et al. 2012). What is clear now is that the slope of the integrated radio–SFR relation is significantly super-linear. This can also be seen in Fig. 6, where the linear fit is shown as a green dashed line. It is dominated by the data points at lower SFRs, with most points at higher SFRs lying above the curve, deviating from it much more than a few standard deviations. We do not expect this super-linear slope to be the result of contribution from AGN. The mean AGN luminosity for spiral galaxies is νLAGN = 1036 erg s−1, which is equivalent to a 144-MHz spectral luminosity of log10(LAGN/W Hz−1) = 20.5 (assuming α = −0.7; Baldi et al. 2021). The contribution from AGN to the radio continuum should therefore be subdominant except possibly at the lowest SFRs.

4. Discussion

4.1. The non-linear radio–SFR relation

The low-frequency radio–SFR relation is well represented by a slightly super-linear fit (Sect. 3.5), which is consistent with earlier studies of LOFAR data with significantly larger samples by both Gürkan et al. (2018) and Smith et al. (2021). This implies that the radio emission is enhanced in comparison to the injection of CREs linearly proportional to the star-formation rate, if the model of a CRE calorimeter applies (Völk 1989, see below). Based on the stellar mass dependence of the radio–SFR relation, Gürkan et al. (2018) suggested that the escape of the CREs from galaxies plays a role as well. Galaxies with higher stellar masses tend to be larger and so the CREs take longer to escape from the galaxy, boosting radio continuum luminosity.

The slope of the radio–SFR relation (in logarithmic scales) provides important information about the propagation of CREs and the relation between CRs and magnetic fields in galaxies. A linear slope indicates that CREs lose all their energy within the galaxy, which means that the radio luminosity depends only on the density of CREs, not on field strength (CRE calorimeter; Völk 1989). A super-linear relation can be interpreted as a signature of energy equipartition between CRs and magnetic fields (Niklas & Beck 1997), where the slope b depends on the synchrotron spectral index α and on the exponents of the relation between magnetic field and gas density (B ∝ ρκ) and of the global Kennicutt–Schmidt law (SFR ∝ ρn). Using α ≈ −0.7 (Sect. 3.1) and generic values of κ ≈ 0.5 and n = 1.4 ± 0.15 (Kennicutt 1998) yields b ≈ 1.3. A sublinear radio–SFR relation is expected under non-equipartition conditions; for example if the CRs diffuse rapidly away from their places of origin in star-forming regions (Berkhuijsen et al. 2013; Heesen et al. 2019). The slope of the radio–SFR correlation shown in Fig. 6 is in excellent agreement with the equipartition case.

The super-linear radio–SFR relation found here is consistent with the findings of Smith et al. (2021) for a large sample of galaxies at redshifts below 1. These latter authors also found a super-linear relation between SFR and radio luminosity, though with a slope closer to one, between the pure equipartition case (b ≈ 1.3) and the pure calorimeter case (b = 1.0). The actual conditions in the galaxies of the sample seem to be between these two cases. Galaxies with higher SFRs such as luminous infrared galaxies have stronger magnetic fields, which should bring them nearer to the calorimeter case, as argued by Li et al. (2016). Indeed, the mean synchrotron spectral index of a sample of 19 starburst galaxies is α ≈ −1.06 (Galvin et al. 2018).

From the mass dependence of the radio/SFR ratio as seen in their data, Smith et al. (2021) proposed that for lower mass galaxies, CREs escape the galaxy quickly, thus removing energy from the galaxy instead of radiating it as synchrotron radiation. This is in agreement with the findings of this work, as the previous results have also already advocated for the loss of cosmic rays by advection and winds (Gürkan et al. 2018). The mass dependence might also be an explanation for the high scatter in the data points: Smith et al. (2021) elaborate that higher mass galaxies have a higher luminosity at 150 MHz for a fixed SFR. It is possible that the scatter between our points in Sect. 3.5 is a result of large differences in mass at a given SFR.

Li et al. (2016) noted that the slope of the radio–SFR relation is frequency dependent. They find a slope of 1.13 ± 0.07 at 1.6 GHz, but a slope of only 1.06 ± 0.08 at 6 GHz. Similarly, Hindson et al. (2018) find a slope of only 0.93 ± 0.14 in their sample of dwarf irregular galaxies at 6 GHz. Hence, both relations are in agreement with linearity at 6 GHz. In contrast, Heesen et al. (2014) found a slope of 1.24 ± 0.04 at 1.4 GHz. In galaxies out to a redshift of 1.2, Basu et al. (2015) found a slope of 1.11 ± 0.04 at 1.4 GHz. However, Davies et al. (2017) find slopes of 1.3 and 1.5 at 1.4 GHz for TIR + ultraviolet and photometric SFRs, respectively. We can test this trend for our sample, exploiting the radio spectral index information. Using a standard least-square fit, we find slopes of 1.34 ± 0.06 at 144 MHz, 1.16 ± 0.06 at 1.4 GHz, and 1.08 ± 0.06 at 5 GHz. A flattening of the radio–SFR relation at 1.4 GHz in comparison to 144 MHz across one sample was also found by Gürkan et al. (2018). We propose that the flattening of the relation is caused by CRE propagation (Sect. 4.2).

4.2. The influence of energy losses and cosmic ray transport

The findings in Sect. 4.1 suggest that energy-dependent CRE escape may be behind the non-linearity of the radio–SFR relation. The best proxy for the importance of energy losses for the CREs is the radio spectral index.

We now review the conditions that regulate the radio spectral index. Krause et al. (2018) showed that the radio continuum scale height is related to the radius r⋆ of the radio disc, which is similar to the radius of the star-forming disc r⋆, as h = 0.05 r⋆. For advective transport, the escape time is therefore tesc ∝ h/v ∝ r⋆/v, with v being the outflow speed. The synchrotron lifetime scales as 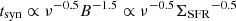. As the wind speed increases with SFR as 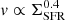(Heesen et al. 2018b; Heesen 2021), the ratio of escape timescale to synchrotron timescale is

(13)

For any galaxy that is a CRE calorimeter, tesc ≫ tsyn, all the CRE energy is radiated away via synchrotron emission and IC emission. On the contrary, for a highly non-calorimetric galaxy, tesc ≪ tsyn, meaning almost free CRE escape. The ratio tesc/tsyn can be related to the (non-thermal) radio spectral index α, because we expect α = αinj in the non-calorimetric case, meaning for a fast CRE escape the injection radio spectral index is observed. Conversely, in the calorimetric case when synchrotron radiation losses dominate, the radio spectral index is α = αinj − 0.5 (Lisenfeld & Völk 2000). Therefore, Eq. (13) predicts strong dependence of the radio spectral index on the radius with steeper spectra at larger radii as indeed found in Fig. 5b. On the other hand, there is no correlation between the radio spectral index and the SFR surface density (ρs = 0.16) as shown in Fig. 7. Again, this is in good agreement with the prediction by Eq. (13).

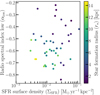thumbnail Fig. 7.

Radio spectral index as a function of the SFR surface density . Data points are coloured according to the radius of the star-forming disc r⋆. The radio spectral index depends only weakly on ΣSFR but significantly on r⋆ (compare with Fig. 5b). This is in agreement with the escape of CREs by advection in a wind (see Eq. (13)).

4.3. Semi-calorimetric radio–SFR relation

As shown in this paper, the radio–SFR relation has a slope (in logarithmic scales) of slightly above one, whereas results from previous works reveal some variation. The radio–SFR relation has a slope that is in agreement with unity in several cases, including spatially resolved observations (Dumas et al. 2011). While this could be explained with a calorimetric radio–SFR relation, our spectral indices in agreement with the injection spectrum argue against such a picture, although this might be accurate in starburst galaxies (Galvin et al. 2018). The radio spectral index variation suggests that more massive galaxies with steeper spectral indices are better electron calorimeters than less massive galaxies. Radio continuum luminosity is not only driven by SFR; the dependence on radio spectral index indicates that another physical parameter is required. One way to explain our data is to include the calorimetric synchrotron fraction η of the CRE, so that the semi-calorimetric radio–SFR relation, which takes CRE escape into account, becomes (e.g. Pfrommer et al. 2021)2

(14)

The calorimetric fraction is closely related to the radio spectral index, which itself is a function of star-forming radius, rotation speed, and total mass (Sect. 4.2).

We may therefore parametrise η with the total mass, as the second parameter of the ‘semi-calorimetric’ radio–SFR relation, as this is a quantity that is closely related to the stellar mass, which can be fairly easily measured from photometric measurements even for high-z galaxies. The parametrisation of Gürkan et al. (2018) is then used, where, assuming a linear dependence on the SFR,

(15)

results in γ = 0.25 ± 0.05 and a normalisation of LC = 1021.518 ± 0.044 W Hz−1. We also attempted to fit a non-linear SFR dependence, as Gürkan et al. (2018) have done, but this does not result in a significantly improved fit. The parametrisation of Eq. (15) therefore takes the CRE calorimetric fraction into account in a simple way. The CRE calorimetric fraction is the fraction of CRE energy that is radiated via synchrotron emission before the CREs are able to escape from the galaxy.

We now try a heuristic derivation of the relation found herein. For this we assume that the calorimetric fraction the CRE can be parametrised as η = tCRE/tsyn, where tCRE is the effective CRE lifetime considering both escape and synchrotron losses, and tsyn is the synchrotron lifetime. In our model, the effective CRE lifetime is then

(16)

It can be shown that for tesc ≈ tsyn, which is a reasonable assumption for galaxies as they fall in between the calorimetric and the non-calorimetric case (Lacki et al. 2010), we have

(17)

For η ≈ 0.5, the approximation in Eq. (17) is valid3. With 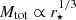(e.g. Mo et al. 1998), using Eq. (13) we obtain

(18)

This is in good agreement with the mass dependency that we find for the radio–SFR relation of Eq. (15). Obviously, such a derivation can only be approximate. Numerical models by Werhahn et al. (2021) support the semi-calorimetric model, although their calorimetric synchrotron fractions of the CRE may be as small as η ≈ 10−2 because of the low magnetic field strengths. We note that by combining Eqs. (14) and (16) we can also explain a small super-linearity of the radio–SFR relation. The mass dependence that we find is slightly smaller than that of Gürkan et al. (2018) and Smith et al. (2021), who find γ > 0.3.

Figure 8 shows the radio–SFR relation when using the parametrisation of Eq. (15). As can be seen, the super-linear relation is well described. The advantage of such a semi-calorimetric model is that it can explain both super-linear radio–SFR relations, particularly at low frequencies, and nearly linear relations at high frequencies (Sect. 4.1). In essence, at low frequencies the radiation efficiency has a larger relative variation compared to higher frequencies, resulting in a super-linear relation, whereas the radio–SFR relation at higher frequencies is closer to a linear relation. In contrast, at high frequencies the radiation efficiency is so high that only a small variation is expected. This means the radio–SFR relation is closer to linear. Similarly, if the samples are restricted to galaxies with a fairly uniform distribution of spectral indices, then the relation will be close to linear as well.

thumbnail Fig. 8.

Semi-calorimetric model fitted to the integrated radio–SFR relation at 144 MHz. The blue line shows the best-fitting semi-calorimetric relation as defined by Eq. (15). The shaded area indicates ±1σ. Data points are coloured according to the total mass of the galaxies.

4.4. Equipartition magnetic fields

Even though in our non-calorimetric model the magnetic field strength does not enter the formula for the radio continuum luminosity directly, the magnetic field still plays an important role by determining the CRE lifetime. Also, the magnetic field might regulate the escape of cosmic rays by diffusion, streaming, and advection in a wind. As there are good reasons to believe that galaxies are generally in energy equipartition, we now try to establish the conditions that must therefore generally hold. For energy equipartition to hold, the cosmic-ray energy has to be equivalent to the magnetic energy. In a stationary state, the cosmic-ray injection rate ĖCR and the escape timescale tesc determine the total cosmic-ray energy

(19)

where uB = B2/(8π) is the magnetic energy density, V = 2πr2h is the volume of the galaxy approximated by a cylinder, and h is the cosmic-ray scale height. The cosmic-ray lifetime is set by the escape time only because we neglect any cosmic ray losses other than escape. With tesc = h/v, we obtain

(20)

where we have used the assumption that the cosmic-ray injection rate is proportional to the SFR as ĖCR = ϵCRSFR with ϵCR = (1 − 3)×1040 erg s−1 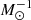yr (Socrates et al. 2008). If energy equipartition holds, then uB = uCR and this equation states that in a steady state the cosmic-ray injection is balanced by the escape of cosmic rays in a wind. We can now express the equipartition magnetic field strength as

(21)

Observations indicate that 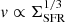, which is what is measured using galaxies viewed from an edge-on orientation with spectral ageing models in radio haloes (Heesen et al. 2018b). Consequently, we can derive 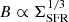, which is the equipartition scaling. However, we notice that in dwarf irregular galaxies the advection speed is generally smaller than what would be expected from the SFR surface density (Heesen et al. 2018c). This means these galaxies have higher magnetic field strengths than what would be estimated from energy equipartition. This has been shown by Hindson et al. (2018) for an entire sample of dwarf irregular galaxies.

This result is consistent with the findings of Tabatabaei et al. (2017), who obtain B ∝ SFR0.34 ± 0.04. It should be noted that we obtained the B − SFR relation indirectly from the radio continuum luminosity instead of directly using magnetic field strengths. It can be refined further by actually calculating magnetic field strengths and directly finding a B − SFR relationship and comparing it with this relation (see e.g., Chyży et al. 2011; Basu et al. 2017). However, an estimate of magnetic fields from the data at hand is beyond the scope of this work. The combination of 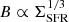with the global Schmidt–Kennicutt law yields B ∝ ρ0.5, which is consistent with Zeeman measurements of Galactic H I clouds (Crutcher et al. 2010) and with estimates in galaxies both for global averages (Niklas & Beck 1997) and spatially resolved measurements (Chyży et al. 2011; Basu et al. 2012b, 2017).

5. Conclusions

The LOFAR Two-metre Sky Survey (LoTSS) maps the entire northern hemisphere at 144 MHz with an unsurpassed combination of sensitivity and angular resolution (Shimwell et al. 2017, 2019, 2022). In this work, we define the LoTSS nearby galaxies sample, consisting of 76 nearby galaxies within 30 Mpc (z ≲ 0.01) distance. This sample is largely drawn from the CHANG-ES radio continuum survey of edge-on galaxies (Irwin et al. 2012) and the KINGFISH IR survey of moderately inclined galaxies (Kennicutt et al. 2011), providing us with rich ancillary data both in the radio continuum and IR. Here, we present our first look at the LoTSS data release 2 (LoTSS-DR2), in which 45 of these galaxies have maps that are suitable for further analysis. We measure integrated flux densities at 144 MHz, calculate integrated and spatially resolved spectral indices between 144 and 1400 MHz, and investigate the integrated radio–SFR relation.

We find that radio spectral indices are flat in general with a mean spectral index and standard deviation of ⟨αlow⟩= − 0.56 ± 0.14 (Sect. 3.1). Of the 43 galaxies with measured spectral indices, 6 galaxies have spectral indices >  − 0.5 even when considering the 1σ uncertainties. These flat spectral indices, which are not in agreement with the injection spectral index of αinj ≈ −0.6, cannot be explained by thermal free–free emission. Instead they require either a low-energy flattening of the CRE by ionisation losses or are caused by absorption of radio waves such as free–free or synchrotron self-absorption. We also find these flat spectral indices αlow ≳ −0.4 in the spatially resolved spectral index maps (Sect. 3.4). These are usually compact regions co-spatial with star formation regions (e.g. NGC 2976 and 4736), or they are located in the nucleus of galaxies (e.g. NGC 3556 and 4631). The nuclei of galaxies have plenty of ionised gas (Law et al. 2009) and AGN activity (Satyapal et al. 2008), both of which can affect the radio continuum spectra. The morphology of the spectral index maps suggests that the flat spectral index is confined to the star formation regions; in contrast, the full emitting volume of the galaxy, as measured by the global integrated radio spectral index, is instead dominated by steep spectrum regions, in particular in large galaxies. These areas of steep spectral indices (αlow ≲ −0.8) are best seen in the haloes of edge-on galaxies, but also show up in the outskirts of some spiral galaxies (e.g. NGC 5055 and 5194).

These findings are corroborated by the observed correlations of the radio spectral index with star formation rate, radius of the star-forming disc, rotation speed, and total mass. These relations are indeed closely connected because of the correlations between mass, SFR, radius, and rotation speed (Fig. 1 and Sect. 3.3). It is not clear which of these parameters is primarily responsible for determining the radio spectral index, if there is indeed one, or whether a combination of them is responsible. The competing factors are advection speed, which regulates the escape of the CRE, and magnetic fields, which regulate their synchrotron lifetime. In simple terms, more massive galaxies have stronger magnetic fields, which reduces the synchrotron lifetime of the CRE, but they also have higher winds speeds, reducing the escape timescale. The radio spectral index is determined by the ratio of the escape timescale to the synchrotron timescale, and so these effects do partially compensate each other. A wind velocity scaling with the SFR surface density of 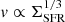would suggest that the radius of the star-forming disc is the main physical parameter, whereas the SFR surface density is of little importance (Eq. (13)). This is in good agreement with our observational data (Figs. 5b and 7). What makes such a velocity scaling so intriguing is also that it ensures energy equipartition between the cosmic rays and the magnetic field (Sect. 4.4), something that appears to be the natural outcome of stability considerations in galaxies (Crocker et al. 2021).

The variation of the radio spectral index as a function of galaxy mass means that more massive galaxies are closer to an electron calorimeter and so the CREs are losing a larger fraction of their energy due to synchrotron losses. This in turn means that galaxies are brighter with respect to the SFR, assuming that the CRE injection luminosity is proportional to the SFR. Such a dependence of the radio–SFR relation on mass was posited by Gürkan et al. (2018) and Smith et al. (2021) and we can now confirm their suggestion that this is indeed related to the escape of CREs. In our sample, this manifests itself as a super-linear radio–SFR relation (Sect. 3.5), with the more massive galaxies being those with a higher SFR (Fig. 1). In order to quantify the influence of CRE escape on the radio–SFR relation, we use the parametrisation of Gürkan et al. (2018), replacing the stellar mass with the closely related total mass within the star-forming radius (Sect. 4.3), which can account for the super-linearity of the radio–SFR relation (Fig. 8). In dwarf galaxies, we would expect the CRE escape to be fast and so they should be underluminous with respect to the SFR. Hindson et al. (2018) show this to be the case, where galaxies with SFR < 0.1 M⊙ yr−1 can be a factor of ten below the radio–SFR relation extrapolated from massive spiral galaxies. On the other hand, Gürkan et al. (2018) suggest just the opposite trend, where galaxies with SFR < 1 M⊙ yr−1 are radio bright. Part of this difference may be attributed to the fact that the stellar mass in these two studies is very different, with Gürkan et al. (2018) probing more massive galaxies (> 109 M⊙) and Hindson et al. (2018) dwarfs with stellar masses of ≈108 M⊙. This warrants some additional LOFAR observations of more dwarf irregular galaxies with LOFAR.

This study presents an analysis of integrated relations of the data from LoTSS-DR2 and should be seen as a preparatory work for exploiting the spatially resolved observations. For instance, the radio–SFR relation can be studied at kiloparsec resolution and the influence of the spectral index can be tested. As H I maps from the THINGS survey are available for many of our galaxies (Walter et al. 2008), we can compare equipartition magnetic fields with turbulent energy densities in the ISM and explore the B − ρ relation. Edge-on galaxies will provide us with an excellent view of the vertical transport of cosmic rays and so scaling laws such as that with SFR surface density can be explored, which is important for understanding whether or not energy equipartition might hold (Sect. 4.4).

1

We used the following script to perform the flux re-scaling: https://github.com/mhardcastle/ddf-pipeline/blob/master/scripts/align-extrationimage-fluxes.py

2

Where we have neglected the small super-linearity that Pfrommer et al. (2021) predicted because of the changing magnetic field strength of their model as a function of SFR.

3

Equation (17) can be expressed as η = x/(1 + x) with x = tesc/tsyn. The first Taylor expansion around x ≈ 1 leads to η ≈ 1/2(1 + x/2). The second Taylor expansions then gives .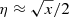

4

DSS images only used for NGC 891 and NGC 925 as these are outside of the SDSS footprint. In these cases, optical observations from DSS in the blue band were used in grey scale.

Acknowledgments

We thank the anonymous referee for a constructive report that helped to improve the paper. LOFAR is the Low Frequency Array designed and constructed by ASTRON. It has observing, data processing, and data storage facilities in several countries, which are owned by various parties (each with their own funding sources), and which are collectively operated by the ILT foundation under a joint scientific policy. The ILT resources have benefited from the following recent major funding sources: CNRS-INSU, Observatoire de Paris and Université d’Orléans, France; BMBF, MIWF-NRW, MPG, Germany; Science Foundation Ireland (SFI), Department of Business, Enterprise and Innovation (DBEI), Ireland; NWO, The Netherlands; The Science and Technology Facilities Council, UK; Ministry of Science and Higher Education, Poland; The Istituto Nazionale di Astrofisica (INAF), Italy. This research made use of the Dutch national e-infrastructure with support of the SURF Cooperative (e-infra 180169) and the LOFAR e-infra group. The Jülich LOFAR Long Term Archive and the German LOFAR network are both coordinated and operated by the Jülich Supercomputing Centre (JSC), and computing resources on the supercomputer JUWELS at JSC were provided by the Gauss Centre for Supercomputing e.V. (grant CHTB00) through the John von Neumann Institute for Computing (NIC). This research made use of the University of Hertfordshire high-performance computing facility and the LOFAR-UK computing facility located at the University of Hertfordshire and supported by STFC [ST/P000096/1], and of the Italian LOFAR IT computing infrastructure supported and operated by INAF, and by the Physics Department of Turin university (under an agreement with Consorzio Interuniversitario per la Fisica Spaziale) at the C3S Supercomputing Centre, Italy. The Jülich LOFAR Long Term Archive and the German LOFAR network are both coordinated and operated by the Jülich Supercomputing Centre (JSC), and computing resources on the supercomputer JUWELS at JSC were provided by the Gauss Centre for Supercomputing e.V. (grant CHTB00) through the John von Neumann Institute for Computing (NIC). MB acknowledges support from the Deutsche Forschungsgemeinschaft under Germany’s Excellence Strategy – EXC 2121 “Quantum Universe” – 390833306. AD acknowledges support by the BMBF Verbundforschung under the grant 05A20STA. MJH acknowledges support from the UK Science and Technology Facilities Council (ST/R000905/1). AB acknowledges support from the VIDI research programme with project number 639.042.729, which is financed by the Netherlands Organisation for Scientific Research (NWO). FdG acknowledges support from the Deutsche Forschungsgemeinschaft under Germany’s Excellence Strategy – EXC 2121 “Quantum Universe” – 390833306. B.A. acknowledges funding from the German Science Foundation DFG, within the Collaborative Research Center SFB1491 Cosmic Interacting Matters – From Source to Signal. We acknowledge the usage of the HyperLeda database (http://leda.univ-lyon1.fr). This research has made use of the NASA/IPAC Extragalactic Database (NED), which is funded by the National Aeronautics and Space Administration and operated by the California Institute of Technology.

References

  1. Adebahr, B., Krause, M., Klein, U., et al. 2013, A&A, 555, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Baldi, R. D., Williams, D. R. A., McHardy, I. M., et al. 2018, MNRAS, 476, 3478 [Google Scholar]
  3. Baldi, R. D., Williams, D. R. A., McHardy, I. M., et al. 2021, MNRAS, 500, 4749 [Google Scholar]
  4. Basu, A., Mitra, D., Wadadekar, Y., & Ishwara-Chandra, C. H. 2012a, MNRAS, 419, 1136 [NASA ADS] [CrossRef] [Google Scholar]
  5. Basu, A., Roy, S., & Mitra, D. 2012b, ApJ, 756, 141 [NASA ADS] [CrossRef] [Google Scholar]
  6. Basu, A., Beck, R., Schmidt, P., & Roy, S. 2015, MNRAS, 449, 3879 [NASA ADS] [CrossRef] [Google Scholar]
  7. Basu, A., Roychowdhury, S., Heesen, V., et al. 2017, MNRAS, 471, 337 [NASA ADS] [CrossRef] [Google Scholar]
  8. Beck, R., Klein, U., & Krause, M. 1985, A&A, 152, 237 [NASA ADS] [Google Scholar]
  9. Bell, A. R. 1978, MNRAS, 182, 147 [Google Scholar]
  10. Bell, E. F. 2003, ApJ, 586, 794 [Google Scholar]
  11. Berkhuijsen, E. M., Beck, R., & Tabatabaei, F. S. 2013, MNRAS, 435, 1598 [Google Scholar]
  12. Boulares, A., & Cox, D. P. 1990, ApJ, 365, 544 [NASA ADS] [CrossRef] [Google Scholar]
  13. Braun, R., Oosterloo, T. A., Morganti, R., Klein, U., & Beck, R. 2007, A&A, 461, 455 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [Google Scholar]
  15. Brown, M. J. I., Moustakas, J., Kennicutt, R. C., et al. 2017, ApJ, 847, 136 [Google Scholar]
  16. Callingham, J. R., Gaensler, B. M., Ekers, R. D., et al. 2015, ApJ, 809, 168 [Google Scholar]
  17. Calzetti, D., Kennicutt, R. C., Engelbracht, C. W., et al. 2007, ApJ, 666, 870 [Google Scholar]
  18. Calzetti, D., Wu, S. Y., Hong, S., et al. 2010, ApJ, 714, 1256 [NASA ADS] [CrossRef] [Google Scholar]
  19. Carilli, C. L. 1996, A&A, 305, 402 [NASA ADS] [Google Scholar]
  20. Carilli, C. L., Perley, R. A., Dreher, J. W., & Leahy, J. P. 1991, ApJ, 383, 554 [Google Scholar]
  21. Chyży, K. T., Beck, R., Kohle, S., Klein, U., & Urbanik, M. 2000, A&A, 355, 128 [NASA ADS] [Google Scholar]
  22. Chyży, K., Weżgowiec, M., Beck, R., & Bomans, D. 2011, A&A, 529, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Chyży, K. T., Jurusik, W., Piotrowska, J., et al. 2018, A&A, 619, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Condon, J. J. 1992, ARA&A, 30, 575 [Google Scholar]
  25. Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [Google Scholar]
  26. Cox, D. P. 2005, ARA&A, 43, 337 [Google Scholar]
  27. Crocker, R. M., Krumholz, M. R., & Thompson, T. A. 2021, MNRAS, 503, 2651 [CrossRef] [Google Scholar]
  28. Crutcher, R. M., Wandelt, B., Heiles, C., Falgarone, E., & Troland, T. H. 2010, ApJ, 725, 466 [NASA ADS] [CrossRef] [Google Scholar]
  29. Dale, D. A., & Helou, G. 2002, ApJ, 576, 159 [Google Scholar]
  30. Dale, D. A., Bendo, G. J., Engelbracht, C. W., et al. 2005, ApJ, 633, 857 [NASA ADS] [CrossRef] [Google Scholar]
  31. Dale, D. A., Aniano, G., Engelbracht, C. W., et al. 2012, ApJ, 745, 95 [NASA ADS] [CrossRef] [Google Scholar]
  32. Davies, L. J. M., Huynh, M. T., Hopkins, A. M., et al. 2017, MNRAS, 466, 2312 [Google Scholar]
  33. de Blok, W. J. G., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2648 [NASA ADS] [CrossRef] [Google Scholar]
  34. de Gasperin, F., Intema, H. T., & Frail, D. A. 2018, MNRAS, 474, 5008 [Google Scholar]
  35. de Gasperin, F., Williams, W. L., Best, P., et al. 2021, A&A, 648, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. de Vaucouleurs, G., de Vaucouleurs, A., Corwin, H. G., Jr., et al. 1991, Third Reference Catalogue of Bright Galaxies [Google Scholar]
  37. Dumas, G., Schinnerer, E., Tabatabaei, F. S., et al. 2011, AJ, 141, 41 [NASA ADS] [CrossRef] [Google Scholar]
  38. Everett, J. E., Zweibel, E. G., Benjamin, R. A., et al. 2008, ApJ, 674, 258 [CrossRef] [Google Scholar]
  39. Fletcher, A., Beck, R., Shukurov, A., Berkhuijsen, E. M., & Horellou, C. 2011, MNRAS, 412, 2396 [CrossRef] [Google Scholar]
  40. Galvin, T. J., Seymour, N., Marvil, J., et al. 2018, MNRAS, 474, 779 [Google Scholar]
  41. Girichidis, P., Naab, T., Hanasz, M., & Walch, S. 2018, MNRAS, 479, 3042 [NASA ADS] [CrossRef] [Google Scholar]
  42. Gregory, P. C., & Condon, J. J. 1991, ApJS, 75, 1011 [Google Scholar]
  43. Gregory, P. C., Scott, W. K., Douglas, K., & Condon, J. J. 1996, ApJS, 103, 427 [NASA ADS] [CrossRef] [Google Scholar]
  44. Gürkan, G., Hardcastle, M. J., Smith, D. J. B., et al. 2018, MNRAS, 475, 3010 [Google Scholar]
  45. Hao, C.-N., Kennicutt, R. C., Johnson, B. D., et al. 2011, ApJ, 741, 124 [Google Scholar]
  46. Heesen, V. 2021, Ap&SS, 366, 117 [NASA ADS] [CrossRef] [Google Scholar]
  47. Heesen, V., Brinks, E., Leroy, A. K., et al. 2014, AJ, 147, 103 [NASA ADS] [CrossRef] [Google Scholar]
  48. Heesen, V., Croston, J. H., Morganti, R., et al. 2018a, MNRAS, 474, 5049 [Google Scholar]
  49. Heesen, V., Krause, M., Beck, R., et al. 2018b, MNRAS, 476, 158 [CrossRef] [Google Scholar]
  50. Heesen, V., Rafferty, D. A., Horneffer, A., et al. 2018c, MNRAS, 476, 1756 [NASA ADS] [CrossRef] [Google Scholar]
  51. Heesen, V., Buie, E., II, Huff, C. J., et al. 2019, A&A, 622, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Hindson, L., Kitchener, G., Brinks, E., et al. 2018, ApJS, 234, 29 [NASA ADS] [CrossRef] [Google Scholar]
  53. Ho, L. C., Filippenko, A. V., & Sargent, W. L. 1995, ApJS, 98, 477 [NASA ADS] [CrossRef] [Google Scholar]
  54. Ho, L. C., Filippenko, A. V., & Sargent, W. L. W. 1997, ApJS, 112, 315 [NASA ADS] [CrossRef] [Google Scholar]
  55. Hunter, D. A., Ficut-Vicas, D., Ashley, T., et al. 2012, AJ, 144, 134 [CrossRef] [Google Scholar]
  56. Irwin, J., Beck, R., Benjamin, R. A., et al. 2012, AJ, 144, 43 [Google Scholar]
  57. Irwin, J. A., Henriksen, R. N., Krause, M., et al. 2015, ApJ, 809, 172 [NASA ADS] [CrossRef] [Google Scholar]
  58. Irwin, J., Wiegert, T., Merritt, A., et al. 2019, AJ, 158, 21 [NASA ADS] [CrossRef] [Google Scholar]
  59. Isobe, T., Feigelson, E., Akritas, M., & Babu, G. 1990, ApJ, 364, 104 [NASA ADS] [CrossRef] [Google Scholar]
  60. Israel, F. P., & Mahoney, M. J. 1990, ApJ, 352, 30 [Google Scholar]
  61. Jacobs, B. A., Rizzi, L., Tully, R. B., et al. 2009, AJ, 138, 332 [NASA ADS] [CrossRef] [Google Scholar]
  62. Kapińska, A. D., Staveley-Smith, L., Crocker, R., et al. 2017, ApJ, 838, 68 [CrossRef] [Google Scholar]
  63. Kassim, N. E. 1989, ApJ, 347, 915 [NASA ADS] [CrossRef] [Google Scholar]
  64. Kennicutt, R. C., Jr. 1998, ApJ, 498, 541 [Google Scholar]
  65. Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
  66. Kennicutt, R. C., Jr., Armus, L., Bendo, G., et al. 2003, PASP, 115, 928 [NASA ADS] [CrossRef] [Google Scholar]
  67. Kennicutt, R. C., Jr., Hao, C.-N., Calzetti, D., et al. 2009, ApJ, 703, 1672 [Google Scholar]
  68. Kennicutt, R. C., Calzetti, D., Aniano, G., et al. 2011, PASP, 123, 1347 [Google Scholar]
  69. Klein, U., Lisenfeld, U., & Verley, S. 2018, A&A, 611, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Krause, M., Irwin, J., Wiegert, T., et al. 2018, A&A, 611, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Lacki, B. C., Thompson, T. A., & Quataert, E. 2010, ApJ, 717, 1 [Google Scholar]
  72. Law, C. J., Backer, D., Yusef-Zadeh, F., & Maddalena, R. 2009, ApJ, 695, 1070 [NASA ADS] [CrossRef] [Google Scholar]
  73. Lazio, T. J. W., Cohen, A. S., Kassim, N. E., et al. 2006, ApJ, 642, L33 [NASA ADS] [CrossRef] [Google Scholar]
  74. Leroy, A. K., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2782 [Google Scholar]
  75. Leroy, A. K., Bigiel, F., de Blok, W. J. G., et al. 2012, AJ, 144, 3 [Google Scholar]
  76. Leroy, A. K., Walter, F., Martini, P., et al. 2015, ApJ, 814, 83 [Google Scholar]
  77. Li, J.-T., Beck, R., Dettmar, R.-J., et al. 2016, MNRAS, 456, 1723 [NASA ADS] [CrossRef] [Google Scholar]
  78. Lisenfeld, U., & Völk, H. J. 2000, A&A, 354, 423 [NASA ADS] [Google Scholar]
  79. Lisenfeld, U., Völk, H. J., & Xu, C. 1996, A&A, 306, 677 [NASA ADS] [Google Scholar]
  80. Longair, M. S. 2011, High Energy Astrophysics (Cambridge: Cambridge University Press) [Google Scholar]
  81. Makarov, D., Prugniel, P., Terekhova, N., Courtois, H., & Vauglin, I. 2014, A&A, 570, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  82. Mandelartz, M., & Becker Tjus, J. 2015, Astropart. Phys., 65, 80 [NASA ADS] [CrossRef] [Google Scholar]
  83. Marvil, J., Owen, F., & Eilek, J. 2015, AJ, 149, 32 [CrossRef] [Google Scholar]
  84. McKean, J. P., Godfrey, L. E. H., Vegetti, S., et al. 2016, MNRAS, 463, 3143 [Google Scholar]
  85. McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, in Astronomical Data Analysis Software and Systems XVI, eds. R. A. Shaw, F. Hill, & D. J. Bell (San Francisco: ASP), ASP Conf. Ser., 376, 127 [Google Scholar]
  86. Meurer, G. R., Obreschkow, D., Wong, O. I., et al. 2018, MNRAS, 476, 1624 [Google Scholar]
  87. Miskolczi, A., Heesen, V., Horellou, C., et al. 2019, A&A, 622, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  88. Mo, H. J., Mao, S., & White, S. D. M. 1998, MNRAS, 295, 319 [Google Scholar]
  89. Mora-Partiarroyo, S. C., Krause, M., Basu, A., et al. 2019, A&A, 632, A10 [NASA ADS] [EDP Sciences] [Google Scholar]
  90. Mulcahy, D. D., Horneffer, A., Beck, R., et al. 2014, A&A, 568, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  91. Murphy, E. J., Condon, J. J., Schinnerer, E., et al. 2011, ApJ, 737, 67 [Google Scholar]
  92. Neistein, E., Maoz, D., Rix, H.-W., & Tonry, J. L. 1999, AJ, 117, 2666 [NASA ADS] [CrossRef] [Google Scholar]
  93. Niklas, S., & Beck, R. 1997, A&A, 320, 54 [NASA ADS] [Google Scholar]
  94. Niklas, S., Klein, U., Braine, J., & Wielebinski, R. 1995, A&AS, 114, 21 [NASA ADS] [Google Scholar]
  95. Offringa, A. R., & Smirnov, O. 2017, MNRAS, 471, 301 [Google Scholar]
  96. Offringa, A. R., McKinley, B., Hurley-Walker, N., et al. 2014, MNRAS, 444, 606 [Google Scholar]
  97. Oh, S.-H., Hunter, D. A., Brinks, E., et al. 2015, AJ, 149, 180 [CrossRef] [Google Scholar]
  98. Pandey, V. N., van Zwieten, J. E., de Bruyn, A. G., & Nijboer, R. 2009, in The Low-Frequency Radio Universe, eds. D. J. Saikia, D. A. Green, Y. Gupta, & T. Venturi, ASP Conf. Ser., 407, 384 [NASA ADS] [Google Scholar]
  99. Pellerin, A., & Macri, L. M. 2011, ApJS, 193, 26 [NASA ADS] [CrossRef] [Google Scholar]
  100. Pfrommer, C., Werhahn, M., Pakmor, R., Girichidis, P., & Simpson, C. M. 2021, MNRAS, accepted [arXiv:2105.12132] [Google Scholar]
  101. Pu, S. B., Saglia, R. P., Fabricius, M. H., et al. 2010, A&A, 516, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  102. Reynolds, S. P., Gaensler, B. M., & Bocchino, F. 2012, Space Sci. Rev., 166, 231 [NASA ADS] [CrossRef] [Google Scholar]
  103. Rieke, G. H., Alonso-Herrero, A., Weiner, B. J., et al. 2009, ApJ, 692, 556 [NASA ADS] [CrossRef] [Google Scholar]
  104. Salem, M., & Bryan, G. L. 2014, MNRAS, 437, 3312 [CrossRef] [Google Scholar]
  105. Satyapal, S., Vega, D., Dudik, R. P., Abel, N. P., & Heckman, T. 2008, ApJ, 677, 926 [NASA ADS] [CrossRef] [Google Scholar]
  106. Schleicher, D. R. G., & Beck, R. 2016, A&A, 593, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  107. Schmidt, P., Krause, M., Heesen, V., et al. 2019, A&A, 632, A12 [NASA ADS] [EDP Sciences] [Google Scholar]
  108. Schmitt, H. R., Calzetti, D., Armus, L., et al. 2006, ApJ, 643, 173 [NASA ADS] [CrossRef] [Google Scholar]
  109. Shimwell, T. W., Röttgering, H. J. A., Best, P. N., et al. 2017, A&A, 598, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  110. Shimwell, T. W., Tasse, C., Hardcastle, M. J., et al. 2019, A&A, 622, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  111. Shimwell, T. W., Hardcastle, M. J., Tasse, C., et al. 2022, A&A, 659, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  112. Smirnov, O. M., & Tasse, C. 2015, MNRAS, 449, 2668 [Google Scholar]
  113. Smith, D. J. B., Haskell, P., Gürkan, G., et al. 2021, A&A, 648, A6 [EDP Sciences] [Google Scholar]
  114. Socrates, A., Davis, S. W., & Ramirez-Ruiz, E. 2008, ApJ, 687, 202 [NASA ADS] [CrossRef] [Google Scholar]
  115. Stein, Y., Dettmar, R. J., Irwin, J., et al. 2019a, A&A, 623, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  116. Stein, Y., Dettmar, R. J., Weżgowiec, M., et al. 2019b, A&A, 632, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  117. Tabatabaei, F. S., Krause, M., & Beck, R. 2007, A&A, 472, 785 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  118. Tabatabaei, F. S., Martinsson, T. P. K., Knapen, J. H., et al. 2016, ApJ, 818, L10 [NASA ADS] [CrossRef] [Google Scholar]
  119. Tabatabaei, F. S., Schinnerer, E., Krause, M., et al. 2017, ApJ, 836, 185 [Google Scholar]
  120. Tasse, C., Hugo, B., Mirmont, M., et al. 2018, A&A, 611, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  121. Tasse, C., Shimwell, T., Hardcastle, M. J., et al. 2021, A&A, 648, A1 [EDP Sciences] [Google Scholar]
  122. Tully, R. B., & Fisher, J. R. 1988, Catalog of Nearby Galaxies (Cambridge: Cambridge University Press) [Google Scholar]
  123. Tumlinson, J., Peeples, M. S., & Werk, J. K. 2017, ARA&A, 55, 389 [Google Scholar]
  124. Uhlig, M., Pfrommer, C., Sharma, M., et al. 2012, MNRAS, 423, 2374 [CrossRef] [Google Scholar]
  125. van der Wel, A., Franx, M., van Dokkum, P. G., et al. 2014, ApJ, 788, 28 [Google Scholar]
  126. van Diepen, G., Dijkema, T. J., & Offringa, A. 2018, Astrophysics Source Code Library [record ascl:1804.003] [Google Scholar]
  127. van Haarlem, M. P., Wise, M. W., Gunst, A. W., et al. 2013, A&A, 556, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  128. van Weeren, R. J., Williams, W. L., Hardcastle, M. J., et al. 2016, ApJS, 223, 2 [Google Scholar]
  129. van Weeren, R. J., Shimwell, T. W., Botteon, A., et al. 2021, A&A, 651, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  130. Vargas, C. J., Mora-Partiarroyo, S. C., Schmidt, P., et al. 2018, ApJ, 853, 128 [NASA ADS] [CrossRef] [Google Scholar]
  131. Veilleux, S., Maiolino, R., Bolatto, A. D., & Aalto, S. 2020, A&ARv, 28, 2 [NASA ADS] [CrossRef] [Google Scholar]
  132. Vogelsberger, M., Marinacci, F., Torrey, P., & Puchwein, E. 2020, Nat. Rev. Phys., 2, 42 [Google Scholar]
  133. Völk, H. J. 1989, A&A, 218, 67 [Google Scholar]
  134. Walter, F., Brinks, E., de Blok, W. J. G., et al. 2008, AJ, 136, 2563 [Google Scholar]
  135. Werhahn, M., Pfrommer, C., & Girichidis, P. 2021, MNRAS, 508, 4072 [NASA ADS] [CrossRef] [Google Scholar]
  136. White, R. L., & Becker, R. H. 1992, ApJS, 79, 331 [NASA ADS] [CrossRef] [Google Scholar]
  137. Wiegert, T., Irwin, J., Miskolczi, A., et al. 2015, AJ, 150, 81 [Google Scholar]
  138. Williams, W. L., van Weeren, R. J., Röttgering, H. J. A., et al. 2016, MNRAS, 460, 2385 [Google Scholar]
  139. Yun, M. S., Reddy, N. A., & Condon, J. J. 2001, ApJ, 554, 803 [Google Scholar]
  140. Zweibel, E. G. 2013, Phys. Plasmas, 20, 055501 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: The complete LoTSS galaxy sample

In this section, Table A.1 presents more information about the complete sample of galaxies contained in LoTSS. Of these 76 galaxies, a subset of 45 galaxies are in LoTSS-DR2 and presented in this paper.

Table A.1.

The complete LoTSS sample of 76 galaxies, a subset of 45 galaxies are included in LoTSS-DR2.

Appendix B: Atlas of galaxies

We present maps for 45 galaxies, which are included in LoTSS-DR2. There are two different sets of figures, with the first set containing six panels for galaxies where no spectral index maps were made (14 galaxies). The second set of figures includes three additional panels, showing the radio spectral index.

In the first row, we show the 144-MHz radio continuum intensity in units of Jy beam−1 as heat maps with contour lines, at 6 and 20 arcsec resolution, respectively. We also show intensity contour lines, beginning at 3σ and rising in increments of a power of two with each higher contour level. The same data are also presented as grey-scale images without contour lines in the second row. In the third row, we present overlays of these contours on optical colour images either from SDSS or DSS4. In all panels, flux regions are shown in blue, D25 optical diameters are shown as either black or white. Where available, we also present radio spectral maps in the third column. In the first row, we show the spectral index; in the second row the spectral index error map; the third row presents the radio spectral index as contours overlaid on the optical images from either SDSS or DSS. Contour lines are at values of α = −1 (blue), −0.8 (green), −0.6 (yellow) and −0.4 (red), respectively. We note that due to the 3σ-clipping prior to combination, the radio spectral index maps are blanked in parts of the maps, so that the contour lines may be interrupted in places.

All of these maps are presented in Figs B.1–B.45.

thumbnail Fig. B.1.

NGC 598 (M 33). The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively. Contours start at 3σ with with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6 and 20-arcsec images without contours. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image. The filled circle in the bottom-left corner shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.2.

NGC 855. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively. Contours start at 3σ with with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6 and 20-arcsec images without contours. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image. The filled circle in the bottom-left corner shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.3.

NGC 891. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb DSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.4.

NGC 925. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 23 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb DSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.5.

NGC 2683. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.6.

NGC 2798. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively. Contours start at 3σ with with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6 and 20-arcsec images without contours. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image. The filled circle in the bottom-left corner shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

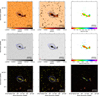thumbnail Fig. B.7.

NGC 2820. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.8.

NGC 2841. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.9.

NGC 2976. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.10.

NGC 3003. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.11.

NGC 3031 (M 81). The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively. Contours start at 3σ with with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6 and 20-arcsec images without contours. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image. The filled circle in the bottom-left corner shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.12.

NGC 3079. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.13.

NGC 3077. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively. Contours start at 3σ with with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6 and 20-arcsec images without contours. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image. The filled circle in the bottom-left corner shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.14.

NGC 3184. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.15.

NGC 3198. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.16.

NGC 3265. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively. Contours start at 3σ with with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6 and 20-arcsec images without contours. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image. The filled circle in the bottom-left corner shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.17.

Mrk 33. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively. Contours start at 3σ with with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6 and 20-arcsec images without contours. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image. The filled circle in the bottom-left corner shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

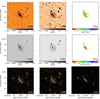thumbnail Fig. B.18.

NGC 3432. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.19.

NGC 3448. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.20.

NGC 3556. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.21.

NGC 3877. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.22.

NGC 3938. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.23.

NGC 4013. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

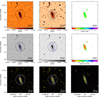thumbnail Fig. B.24.

NGC 4096. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.25.

NGC 4125. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.26.

NGC 4157. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.27.

NGC 4214. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively. Contours start at 3σ with with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6 and 20-arcsec images without contours. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image. The filled circle in the bottom-left corner shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.28.

NGC 4217. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.29.

NGC 4244. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.30.

NGC 4449. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively. Contours start at 3σ with with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6 and 20-arcsec images without contours. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image. The filled circle in the bottom-left corner shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.31.

NGC 4559. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 27 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.32.

NGC 4625. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively. Contours start at 3σ with with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6 and 20-arcsec images without contours. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image. The filled circle in the bottom-left corner shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.33.

NGC 4631. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.34.

NGC 4725. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 30 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.35.

NGC 4736. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.36.

NGC 5033. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 21 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.37.

NGC 5055. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.38.

NGC 5194. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.39.

NGC 5195. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

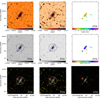thumbnail Fig. B.40.

NGC 5297. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.41.

NGC 5457. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively. Contours start at 3σ with with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6 and 20-arcsec images without contours. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image. The filled circle in the bottom-left corner shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.42.

NGC 5474. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively. Contours start at 3σ with with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6 and 20-arcsec images without contours. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image. The filled circle in the bottom-left corner shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.43.

NGC 5866. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively. Contours start at 3σ with with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6 and 20-arcsec images without contours. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image. The filled circle in the bottom-left corner shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.44.

NGC 5907. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

thumbnail Fig. B.45.

NGC 7331. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 23 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.

All Tables

Table 1.

Integrated 144-MHz flux densities, map properties and star formation rates of the 45 galaxies in LoTSS-DR2.

In the text
Table 2.

Radio spectral indices αlow between 144 MHz and the reference frequency and αhigh between the two reference frequencies.

In the text
Table A.1.

The complete LoTSS sample of 76 galaxies, a subset of 45 galaxies are included in LoTSS-DR2.

In the text

All Figures

thumbnail Fig. 1.

Properties of the complete galaxy sample as presented in Appendix A. (a) Distribution of galaxy type; (b) SFR as a function of total mass enclosed within the radius of the star-forming disc; and (c) specific SFR (sSFR; per total mass) as a function of the optical galaxy diameter (projected apparent diameter D25). The galaxies are grouped according to the respective subsample to which they belong (Sect. 2.1).
In the text
thumbnail Fig. 2.

NGC 5194 (M 51). The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6 and 20 arcsec images without contours and the radio spectral index error. The third row shows the 6 and 20 arcsec contours overlaid on an rgb SDSS image as well as contours of the radio spectral index. Contours are at −1.0 (blue), −0.8 (green), −0.6 (yellow), and −0.4 (red). The filled circle shows the synthesised beam. The scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. 3.

Radio colour–colour diagram with a comparison of the high-frequency radio spectral index αhigh (1400–5000 MHz) with the low-frequency radio spectral index αlow (144–1400 MHz) taken from Table 2. The blue solid line indicates points of equal spectral index, indicating a power-law radio continuum spectrum. Most of the data points lie below the blue line indicating spectra with a convex curvature. Data points above the blue line indicate concave spectra, as may be explained by a higher thermal fraction at high frequencies.
In the text
thumbnail Fig. 4.

Radio spectral index as a function of inclination angle. Panel a: integrated radio spectral index between 144 and 1400 MHz as a function of cos(i). Panel b: spectral curvature Δα = αlow − αhigh as a function of cos(i). The high-frequency radio spectral index αhigh is defined between 1400 and 5000 MHz. Both spectral index measurements show at most only a weak correlation with the inclination angle.
In the text
thumbnail Fig. 5.

Radio spectral index as a function of several fundamental galaxy parameters. Panel a: dependence on SFR as calculated from the TIR luminosity; (b): dependence of the star formation radius, which is derived from the extent of the 3σ contours in the 20 arcsec LoTSS images; (c): dependence on the total mass calculated; (d): dependence on the rotation speed. In all panels, the blue line is the best-fitting relation and the shaded areas show 1σ confidence intervals. The colours of the data points in panel b indicate the rotation velocity, in the other panels the colours indicate the different subsamples.
In the text
thumbnail Fig. 6.

Integrated radio–SFR relation at 144 MHz. Blue lines indicate the best-fitting relations using a bisector fitting method as fitted in the log–log space. The dashed green line shows the best-fitting linear relation as fitted in linear space. Shaded bands represent the 3σ confidence intervals from the 1000 Monte–Carlo realisations. Panel a: the SFR is calculated from the TIR luminosity; in the panel b: the SFR is calculated using either the hybrid Hα + 24 μm SFR calibration or a 24 μm only calibration. For both SFR calibrations, the radio–SFR relation is clearly non-linear.
In the text
thumbnail Fig. 7.

Radio spectral index as a function of the SFR surface density . Data points are coloured according to the radius of the star-forming disc r⋆. The radio spectral index depends only weakly on ΣSFR but significantly on r⋆ (compare with Fig. 5b). This is in agreement with the escape of CREs by advection in a wind (see Eq. (13)).
In the text
thumbnail Fig. 8.

Semi-calorimetric model fitted to the integrated radio–SFR relation at 144 MHz. The blue line shows the best-fitting semi-calorimetric relation as defined by Eq. (15). The shaded area indicates ±1σ. Data points are coloured according to the total mass of the galaxies.
In the text
thumbnail Fig. B.1.

NGC 598 (M 33). The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively. Contours start at 3σ with with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6 and 20-arcsec images without contours. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image. The filled circle in the bottom-left corner shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.2.

NGC 855. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively. Contours start at 3σ with with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6 and 20-arcsec images without contours. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image. The filled circle in the bottom-left corner shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.3.

NGC 891. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb DSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.4.

NGC 925. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 23 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb DSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.5.

NGC 2683. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.6.

NGC 2798. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively. Contours start at 3σ with with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6 and 20-arcsec images without contours. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image. The filled circle in the bottom-left corner shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.7.

NGC 2820. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.8.

NGC 2841. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.9.

NGC 2976. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.10.

NGC 3003. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.11.

NGC 3031 (M 81). The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively. Contours start at 3σ with with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6 and 20-arcsec images without contours. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image. The filled circle in the bottom-left corner shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.12.

NGC 3079. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.13.

NGC 3077. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively. Contours start at 3σ with with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6 and 20-arcsec images without contours. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image. The filled circle in the bottom-left corner shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.14.

NGC 3184. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.15.

NGC 3198. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.16.

NGC 3265. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively. Contours start at 3σ with with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6 and 20-arcsec images without contours. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image. The filled circle in the bottom-left corner shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.17.

Mrk 33. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively. Contours start at 3σ with with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6 and 20-arcsec images without contours. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image. The filled circle in the bottom-left corner shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.18.

NGC 3432. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.19.

NGC 3448. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.20.

NGC 3556. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.21.

NGC 3877. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.22.

NGC 3938. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.23.

NGC 4013. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.24.

NGC 4096. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.25.

NGC 4125. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.26.

NGC 4157. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.27.

NGC 4214. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively. Contours start at 3σ with with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6 and 20-arcsec images without contours. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image. The filled circle in the bottom-left corner shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.28.

NGC 4217. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.29.

NGC 4244. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.30.

NGC 4449. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively. Contours start at 3σ with with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6 and 20-arcsec images without contours. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image. The filled circle in the bottom-left corner shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.31.

NGC 4559. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 27 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.32.

NGC 4625. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively. Contours start at 3σ with with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6 and 20-arcsec images without contours. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image. The filled circle in the bottom-left corner shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.33.

NGC 4631. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.34.

NGC 4725. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 30 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.35.

NGC 4736. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.36.

NGC 5033. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 21 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.37.

NGC 5055. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.38.

NGC 5194. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.39.

NGC 5195. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.40.

NGC 5297. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 1365 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.41.

NGC 5457. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively. Contours start at 3σ with with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6 and 20-arcsec images without contours. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image. The filled circle in the bottom-left corner shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.42.

NGC 5474. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively. Contours start at 3σ with with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6 and 20-arcsec images without contours. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image. The filled circle in the bottom-left corner shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.43.

NGC 5866. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively. Contours start at 3σ with with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6 and 20-arcsec images without contours. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image. The filled circle in the bottom-left corner shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.44.

NGC 5907. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 20 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text
thumbnail Fig. B.45.

NGC 7331. The first row shows from left to right the 144-MHz maps at 6 and 20 arcsec resolution, respectively, and the radio spectral index map between 144 and 6000 MHz at 23 arcsec resolution. Contours start at 3σ with increments of a power of two. The black circle shows the optical D25 diameter and the blue ellipses show the 3σ contour extent used to integrate the flux density. The second row shows again the 6- and 20-arcsec images without contours and the radio spectral index error. The third row shows the 6- and 20-arcsec contours overlayed on an rgb SDSS image as well as contours of the radio spectral index. The filled circle shows the synthesised beam. A scale bar shows the projected size at the distance of the galaxy.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.