| Issue |
A&A
Volume 664, August 2022
|
|
|---|---|---|
| Article Number | A180 | |
| Number of page(s) | 17 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202142543 | |
| Published online | 30 August 2022 | |
RV-detected planets around M dwarfs: Challenges for core accretion models
1
Max-Planck-Institut für Astronomie,
Königstuhl 17,
69117
Heidelberg, Germany
e-mail: schlecker@arizona.edu
2
Department of Astronomy/Steward Observatory, The University of Arizona,
933 North Cherry Avenue,
Tucson,
AZ 85721
USA
3
Physikalisches Institut, University of Bern,
Gesellschaftsstrasse 6,
3012
Bern, Switzerland
4
Landessternwarte, Zentrum für Astronomie der Universität Heidelberg,
Königstuhl 12,
69117
Heidelberg, Germany
5
Lunar and Planetary Laboratory, University of Arizona,
1629 E. University Blvd.,
Tucson,
AZ 85721
USA
6
Universitäts-Sternwarte München, Ludwig-Maximilians-Universität München,
Scheinerstraße 1,
81679
München, Germany
7
Centre for Earth Evolution and Dynamics, Department of Geosciences, University of Oslo,
Sem Sælands vei 2b
0315
Oslo, Norway
8
Institut für Astrophysik, Georg-August-Universität,
Friedrich-Hund-Platz 1,
37077
Göttingen, Germany
Received:
28
October
2021
Accepted:
23
May
2022
Context. Planet formation is sensitive to the conditions in protoplanetary disks, for which scaling laws as a function of stellar mass are known.
Aims. We aim to test whether the observed population of planets around low-mass stars can be explained by these trends, or if separate formation channels are needed.
Methods. We address this question by confronting a state-of-the-art planet population synthesis model with a sample of planets around M dwarfs observed by the HARPS and CARMENES radial velocity (RV) surveys. To account for detection biases, we performed injection and retrieval experiments on the actual RV data to produce synthetic observations of planets that we simulated following the core accretion paradigm.
Results. These simulations robustly yield the previously reported high occurrence of rocky planets around M dwarfs and generally agree with their planetary mass function. In contrast, our simulations cannot reproduce a population of giant planets around stars less massive than 0.5 solar masses. This potentially indicates an alternative formation channel for giant planets around the least massive stars that cannot be explained with current core accretion theories. We further find a stellar mass dependency in the detection rate of short-period planets. A lack of close-in planets around the earlier-type stars (M* > 0.4 M⊙) in our sample remains unexplained by our model and indicates dissimilar planet migration barriers in disks of different spectral subtypes.
Conclusions. Both discrepancies can be attributed to gaps in our understanding of planet migration in nascent M dwarf systems. They underline the different conditions around young stars of different spectral subtypes, and the importance of taking these differences into account when studying planet formation.
Key words: stars: low-mass / techniques: radial velocities / planets and satellites: formation / methods: statistical / planets and satellites: gaseous planets / methods: numerical
© M. Schlecker et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model.
Open Access funding provided by Max Planck Society.
1 Introduction
M dwarf stars are not only the most abundant stars and planet hosts in the solar neighborhood (Reylé et al. 2021; Hsu et al. 2020), but also rewarding study objects regarding some of the most pressing questions on planet formation. They have been shown to host many small, potentially habitable planets (e.g., Ribas et al. 2018; Bluhm et al. 2020; Ment et al. 2020; Kemmer et al. 2020; Cloutier et al. 2021; Kossakowski et al. 2021), and much has been learned about their properties from recent demographic studies (e.g., Mulders et al. 2015a; Dressing & Charbonneau 2015; Gibbs et al. 2020; Hsu et al. 2020). In particular, the occurrence of small planets appears to increase with decreasing stellar mass (Mulders et al. 2015b; Hardegree-Ullman et al. 2019), and they might orbit closer to their hosts at very low stellar masses (Sabotta et al. 2021). On the other hand, the frequency of giant planets around M dwarfs seems to be low (Endl et al. 2006; Johnson et al. 2010; Bonfils et al. 2013; Obermeier et al. 2016; Ghezzi et al. 2018, but see Jordan et al. 2022). To understand how such trends come about, it is crucial to confront observational results with predictions made by planet formation theory. In this paper, we perform such a comparison using a well-defined observational sample and thorough characterization of its biases, as well as a planet population synthesis tailored to that sample.
On the observational side, the tightest constraints on exoplanet demographics have been based on data from the Kepler transit survey (Borucki et al. 2010), which detects planets down to very low masses and radii. However, Kepler has observed only a few thousand stars of spectral type M (e.g., Gaidos et al. 2016), and transit observations do not provide information about the mass of a planet. Instead of planetary radii, which are degenerate for giant planets (e.g., Hatzes & Rauer 2015), radial velocity (RV) surveys constrain projected planet masses. For comparisons to planet formation models, this is the more fundamental quantity due to its direct relationship to planetary accretion processes. RV surveys also require less restrictive geometrical configurations of detectable planetary systems, enabling more complete observations. They thus cover a unique parameter space and provide complementary input to exoplanet demographics. Spectroscopic surveys are able to identify active stars (e.g., Tal-Or et al. 2018; Jeffers et al. 2018) and binary stars (e.g., Baroch et al. 2018,2021), whose implicit or explicit exclusion from catalogs affect the planet statistics (Moe & Kratter 2021). This makes this detection technique ideal for the comparison with current population synthesis models, which currently do not include stellar multiplicity or activity.
One of the most comprehensive datasets currently available have been generated by the High Accuracy Radial velocity Planet Searcher (HARPS, Mayor et al. 2003) and the Calar Alto high-Resolution search for M dwarfs with Exoearths with Near-infrared and optical Echelle Spectrographs (CARMENES, Quirrenbach et al. 2010, 2013; Reiners et al. 2018b) surveys. Bonfils et al. (2013) reported planet occurrence rates for 102 low-mass stars and 14 planets, for which they took approximately 2000 spectra with the HARPS instrument. A more recent study by Sabotta et al. (2021) determined occurrence rates using ~6500 CARMENES spectra of 71 M dwarfs that host 27 planets. Combining these two surveys results in 9 confirmed planets around 147 target stars in the regime of 0.5–2.5 R⊕ and 0.5–10 d where Kepler found 13 confirmed planets around 561 target stars (Hardegree-Ullman et al. 2019), thus the overall detection rate is higher for the RV sample.
From the perspective of formation theory, the first fully operational planet population syntheses focused on isolated gas giant planets around solar-type stars (Ida & Lin 2005; Alibert et al. 2011). As theoretical understanding, computational resources, and algorithms improved, more and more physical mechanisms where added to the models, among them planet migration (Ida & Lin 2008; Dittkrist et al. 2014), long-term evolution of planet interiors (Mordasini et al. 2012), atmospheric escape (Jin et al. 2014), pebble accretion (Brügger et al. 2018; Bitsch et al. 2019), and disk chemistry (Cridland et al. 2016; Thiabaud et al. 2014). A major advancement was to simulate in the same disk multiple planets that gravitationally interact (Thommes et al. 2008; Ida & Lin 2010; Alibert et al. 2013), which is particularly important for realistic modeling of systems including small planets (Mordasini 2018). Models including such an N-body component are capable of computing systems that include the whole range of planetary masses. Most population synthesis efforts have limited themselves to planetary systems around stars with solar mass, but some studies took into account stellar mass dependencies (Ida & Lin 2005; Alibert et al. 2011; Liu et al. 2019; Miguel et al. 2020; Burn et al. 2021). The planetesimal accretion-based formation model of Emsenhuber et al. (2021a) used here includes all above mechanisms except for pebble accretion, and its extension to low-mass stars presented in Burn et al. (2021) allows to cover the full M dwarf mass range.
Direct comparison of its synthetic planets with observed samples is impeded by various selection effects and detection biases, some of which can be corrected. A common approach is to “de-bias” the observed sample, for example by weighting individual planet discoveries according to their detection probability (e.g., Cumming et al. 2008) or by injecting a test planet population to obtain the necessary correction factors (e.g., Bonfils et al. 2013). The drawback of such techniques is that slightly different assumptions can affect the calculated result, typically an occurrence rate in planetary parameter space (Hsu et al. 2020; Sabotta et al. 2021). A method that does not require extrapolations beyond the actually observed sample is to apply a detection bias to the synthetic planet population (e.g., Mulders et al. 2019), hence this is our method of choice.
In this paper, we compile a combined planet sample from the HARPS (Mayor et al. 2003) and CARMENES (Quirrenbach et al. 2010, 2013; Reiners et al. 2018b) M dwarf surveys. Instead of applying a simple RV amplitude cut, we use the actual RV measurements for each star to compute the detection bias and apply it to our synthetic population to simulate its observation. We further take into account the stellar mass distribution of the combined survey. Finally, we confront the observed and biased synthetic planet populations in minimum mass-period-stellar mass-space. The main purpose of our comparison of detection rates, planetary masses, and orbital period distributions is to show which of the CARMENES and HARPS planet detections our model can and cannot explain.
The paper is organized as follows: First, we introduce the observed samples in Sect. 2, followed by a brief description of the formation model and synthetic planet population in Sect. 3. We continue with presenting statistical comparisons of the observed and simulated samples in Sect. 4, and discuss the most relevant differences in Sect. 5. In Sect. 6, we provide conclusions to our findings.
2 Observed Sample
We compiled a sample of confirmed exoplanets orbiting M dwarf stars. By combining results from two of the largest RV surveys targeting low-mass stars, the HARPS survey (Bonfils et al. 2013) and the CARMENES search for exoplanets around M dwarfs (Quirrenbach et al. 2010), we obtained an observed sample of 35 planets around 147 stars. In the following, we describe how we compiled this sample.
2.1 The CARM70 Sample
One of the most comprehensive searches for exoplanets around M dwarfs is the CARMENES high-precision RV survey. The CARMENES instrument consists of two independent Echelle spectrographs, one for visual wavelengths 0.55–1.05 µm and one for near-Infrared wavelengths 0.95–1.7 µm (Quirrenbach et al. 2013). Both channels are fiber-fed from the Calar Alto 3.5 m telescope. In its Guaranteed Time Observations (GTO), CARMENES targets a sample of ~350 stars whose spectral type distribution peaks at M4V (Reiners et al. 2018b). This survey started beginning of 2016 and has since produced more than 18 000 spectra (Sabotta et al. 2021) and led to various exoplanet discoveries (e.g., Sarkis et al. 2018; Ribas et al. 2018; Luque et al. 2018; Morales et al. 2019; Zechmeister et al. 2019; Stock et al. 2020a; Nowak et al. 2020; Trifonov et al. 2021). The survey has already been defined with the goal to perform a population-level, statistical analysis on the datasets it produces. For a subset of the GTO stars, at least 50 RV measurements have been collected and observations are considered complete (Sabotta et al. 2021). In addition to the constraint on the RV measurements, all spectroscopic binaries (Baroch et al. 2018) were excluded as well as a set of very active stars with large RV scatter (Tal-Or et al. 2018). After accounting for duplicate stars in our combined stellar sample (see Sect. 2.3), a subset of 70 stars, here termed CARM70, remains. Several of the CARMENES discoveries were published in combination with other instruments. To ensure a homogeneous analysis, Sabotta et al. (2021) thus used only CARMENES data in their automated search for planetary signals with a false alarm probability (FAP) of less than 1% in the Generalized Lomb-Scargle periodograms (GLS; Zechmeister et al. 2009). There, we used a conservative period cutoff at half the time baseline to make sure that at least two orbits of the planet were observed. In this way, we identified 27 planets in 22 planetary systems.
2.2 The HARPS M Dwarf Sample
The High Accuracy Radial velocity Planet Searcher (HARPS) consists of an Echelle spectrograph fed from the ESO La Silla 3.6 m telescope with a second fiber for a reference spectrum (Mayor et al. 2003). It observes stars in different mass regimes, reaching from 0.1 M⊙ (Bonfils et al. 2013) up to intermediate masses (Leâo et al. 2018). The original M dwarf subsample of the HARPS search for exoplanets comprises a volume-limited (< 11 pc) target list, which was further cropped by declination (δ < +20 deg) and magnitude (V > 14mag). It contains 102 stars covering a mass range of mostly 0.1–0.6 M⊙ (Bonfils et al. 2013). Their stellar masses were calculated from empirical mass-luminosity relations (Delfosse et al. 2000). As in Bonfils et al. (2013), we excluded four stars with less than four RV measurements from the sample and additionally one target with five very low signal-to-noise observations (L 707-74). A scarcity of stars between ~0.35 M⊙ and 0.40 M⊙ in their sample has been shown to be a statistical fluctuation (Neves et al. 2013). Unlike CARM70, the HARPS M dwarf sample was not filtered to exclude very active stars. For this reason the stellar mass distribution of the HARPS sample has a lower median stellar mass of 0.29 M⊙. In the planet sample of Bonfils et al. (2013) there were 14 planets. Several of those planets were published as a result of analyzing a combination of time series with other instruments. Therefore, for our analysis, we retrieved again those signals that were present in HARPS data only. After this analysis, we excluded the two planets Gl 849b and Gl 832b from the sample, because the time baseline of the time series did not cover two whole orbits (they were published in combination with data from other instruments). GJ 876d was also excluded from our analysis as it is below the detection limit of HARPS data alone. Furthermore, we excluded GJ 58 Id as it is probably a false positive (Robertson et al. 2014; Hatzes 2016).
2.3 The Combined M Dwarf Sample
22 stars occur in both the HARPS and the CARMENES target list. To avoid duplicates while preserving sensitivity, we determined for each star the number of observations it received for each instrument and kept in the sample the dataset with the greater number of RV values. Some of these duplicate stars host planets, in which case we considered only the planets detectable with the retained dataset. No planets were lost from the sample due to this rule. In total, the combined HARPS&CARM70 sample consists of 147 target stars and 35 planets. All targets and duplicate stars in our sample are listed in Table A.1. Not only the mass distribution of the stellar sample is relevant for demographic assessments, but also how intensely each target was monitored. We show both the mass distributions of each stellar subsample and the number of observations for each mass bin in Fig. 11. Some of the planets have new parameter constraints from follow-up studies, in which case we used the updated values (see Table A.2).
 |
Fig. 1 Observed and simulated stellar sample. Top: combined observed stellar mass distribution is composed of different distributions for the HARPS (purple) and CARM70 samples (yellow), respectively. The host star masses in the synthetic NGM population are discrete. By weighted resampling of its systems according to the combined observed sample (red), we obtain a new distribution that approximates it (blue). Bottom: number of observations per stellar mass bin with the same color code as the top figure. Every target star is represented by a white box. |
3 Synthetic Planet Population
We computed a synthetic planet population using the Bern global model of planetary formation and evolution. Here, we briefly summarize the methodology, which has been described extensively in the previous works by Emsenhuber et al. (2021a,b), Schlecker et al. (2021a,b), Burn et al. (2021), and Mishra et al. (2021).
3.1 Formation and Evolution Model
The goal of a global model is to include all relevant physical processes that occur in the formation and evolution, albeit in a simplified fashion, so that their interactions can be studied. The current version of the model is based on several previous generations (Alibert et al. 2005,2013; Mordasini et al. 2009a). Its formation part computes concurrently the evolution of a protoplanetary disk consisting of gas and planetesimals, the accretion of solids and gas by the protoplanets, gas-driven migration, and the dynamical interactions between multiple protoplanets. The starting point of the simulations is an already-formed disk consisting of a gaseous part with mass Mdisk, a dust component (1%) used to calculate the opacity, and a disk of planetesimals with mass Mplts. The gas disk is modeled as an axissymmetric 1D radial profile following Lüst (1952) and Lynden-Bell & Pringle (1974), where the vertical structure is obtained following the procedure of Nakamoto & Nakagawa (1994) with direct irradiation from the star on the surface (Hueso & Guillot 2005). Turbulent viscosity is described by an a parametrization (Shakura & Sunyaev 1973). In addition, both internal (Clarke et al. 2001) and external (Matsuyama et al. 2003) photoevaporation are included. The combination of stellar accretion and photoevaporation leads to the dispersal of the gas disk after a few Myr, comparable to observed disk lifetimes (e.g., Haisch et al. 2001; Mamajek et al. 2009; Ribas et al. 2015).
Planets are assumed to form according to the core accretion paradigm (Perri & Cameron 1974; Mizuno 1980). At the start of each simulation, we inserted multiple planetary seeds with an initial mass of 0.01 M⊕. Their cores grow by accretion of planetesimals in the oligarchic regime (Ida & Makino 1993; Inaba et al. 2001; Fortier et al. 2013). Gas accretion rates are determined by the ability of the planet to cool by radiating away energy and, for planets exceeding a critical mass, by the gas supply from the disk. We computed nominal accretion rates by solving the internal structure equations of both the solid planetary core and the gaseous envelope Bodenheimer & Pollack (1986), where we assumed an onion-like structure, the deposition of accreted solids at the core-envelope boundary, and spherical symmetry. The maximum accretion rate that can be provided by the gas disk is given by the Bondi accretion in two or three dimensions, that is, the amount of gas that is intersected by the planet with a gas capture radius larger (two-dimensional problem) or smaller (three-dimensional problem) than the local disk scale height D’Angelo & Lubow (2008). Protoplanets embedded in a gas disk will undergo planetary migration. We account for type-I migration following Paardekooper et al. (2011) with a modulation due the planet’s orbital characteristics from Coleman & Nelson (2014). For very massive planets, we model type-II migration following Dittkrist et al. (2014). Planet eccentricities and inclinations are damped by the gas disk, following the prescription of Cresswell & Nelson (2008) in type-I migration and a fraction of the migration timescale in the type-II regime. Dynamical interactions between the protoplanets are tracked by means of the mercury N-body package (Chambers 1999), which includes a prescription of collisions described in Emsenhuber et al. (2021a). Beyond the gas disk phase, planetesimals accretion and orbital evolution are tracked until the end of the formation stage at 20 Myr. In the following evolution stage the thermodynamical evolution is tracked until 10Gyr (Mordasini et al. 2012) . This stage includes migration due to stellar tides for close-in planets (Benítez-Llambay et al. 2011) and photoevaporation to remove atmospheric material (Jin et al. 2014). While comprehensive, the Bern model currently lacks prescriptions for pebble accretion and the formation of planetesimals and planet seeds, both of which are currently in development (Brügger et al. 2020; Voelkel et al. 2021a,b).
3.2 The Synthetic M Dwarf Planet Population
The population synthesis approach randomizes initial conditions to sample the parameter space. In a Monte Carlo fashion, Mdisk and Mplts, as well as the external photoevaporation rate, the inner disk edge, and the starting location of each seed were varied between each run of the model. For the M dwarf planet population, termed NGM, we chose discrete stellar masses of 0.1, 0.3, 0.5, and 0.7 M⊙ (Burn et al. 2021). Some of the disk parameters have been shown to scale with stellar mass, and we aimed to scale our Monte Carlo parameter distributions accordingly. For the disk mass, we extrapolated the observed relation between disk mass and stellar mass found by Pascucci et al. (2016); Ansdell et al. (2017) to earlier times and adopted a linear relationship between star and disk masses. This choice of scaling is supported by observed stellar accretion rates (Alcalá et al. 2017), which compare reasonably well to the model output from Burn et al. (2021, see their Fig. 3). In order to account for the observed scatter in the measured disk masses of nearby star forming regions, we distributed our gas disk masses closely following the reported masses of Class-I objects in Tychoniec et al. (2018), resulting in a log-normal distribution N(µ = −1.49, σ2 = 0.123) (compare Emsenhuber et al. 2021b; Schlecker et al. 2021a). The total planetesimal mass Mplts directly relates the gas disk mass Mdisk with a dust-to-gas ratio, which in turn translates to a stellar metallicity under the assumption that stellar and disk metallicity are the same (Emsenhuber et al. 2021b). We distributed this parameter normally according to [Fe/H] measurements in the solar neighborhood (Santos et al. 2003). We assumed that inner disk edges are located at the co-rotation radius with the stellar spin (Günther 2013). In agreement with measured T Tauri rotation rates (Venuti et al. 2017), our inner edges are distributed log-normally (µ = 4.74 d, σ2 = 0.3 dex) in orbital period and do not scale with stellar mass. At each simulation run, we injected 50 planetary seeds into the disk at random radial positions between the inner edge and an orbital period of 253 yr. The external photoevaportion rate of the gas disk is chosen such that the resulting lifetimes of the disks are similar for all stellar masses with a median ~3.0Myr. More details on the distributions of the Monte Carlo parameters can be found in Burn et al. (2021).
Other parameters are fixed for each simulation run: the viscous a parameter was set to 2 × 10−3, and the initial slope of the planetesimal and gas disk are −1.5 and −0.9, respectively. This results in a high concentration of solid mass close to the star, where locally, planetesimals can make up to 10% of the total disk mass. Furthermore, we specified a planetesimal diameter of 600 m. This relatively low value leads to efficient damping by gas drag and therefore lower relative velocities between the growing planet and the planetesimals. A more detailed discussion on planetesimal sizes can be found in Emsenhuber et al. (2021b). In total, the NGM population consists of 4996 simulated systems.
Table 1 lists the simulation runs for each host star mass with the corresponding stellar effective temperature at a simulation time of 5 Gyr, Teff,5Gyr. The initial number of planetary seeds per system Nemb,ini was always 50.
3.3 Observing the Synthetic Population
In order to make a comparison to observed data meaningful, we had to take into account their selection effects and detection biases. We implemented this by weighted resampling of the simulated population and by performing injection-and-retrieval experiments with the observed data.
3.3.1 Stellar Mass Sampling
In contrast to the NGM population, the HARPS&CARM70 sample has a continuous distribution of stellar masses, as shown in Fig. 1. We approximated this distribution by weighted resampling of our synthetic population. For this purpose, we first computed a histogram of the observed stellar mass sample with the bin edges defined as the center between the discrete NGM stellar masses. The normalized histogram counts then served as sampling weights, which for HARPS&CARM70 amount to 0.204, 0.368, 0.388, 0.039, and 0 for NGM’s host star masses 0.1–1.0 M⊙ (see Table 1); that is, the 1.0 M⊙ population has no contribution. In total, we sampled 100 000 systems with replacement. As the synthetic planets will be compared to RV-detected exoplanets, for which only minimum masses M sin(i) are known, we assigned them random orbital inclination angles i. Here, we assumed an isotropic distribution of orbit orientations and, for each system, drew a sin(i) term from the distribution (Ho & Turner 2011)
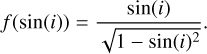 (1)
(1)
Hence, despite our oversampling of the NGM population, no planet occurs more than once with the exact same properties. The resulting M* distribution approximates the one of the HARPS&CARM70 sample (compare Fig. 1). While the over-sampled population contains 5 × 106 planets, in the following we consider only the 2433 170 planets that survived the formation and evolution phase until an assumed observation time tobs = 5 Gyr.
Synthetic planet population NGM.
3.3.2 Accounting for Detection Bias
Exoplanet surveys are affected by detection biases, distorting the distributions in planetary parameter space. Some of these biases can be characterized and corrected, which is commonly done for occurrence rate studies (e.g., Cumming et al. 2008; Zechmeister et al. 2009; Mayor et al. 2011; Bonfils et al. 2013; Sabotta et al. 2021; Fulton et al. 2021). To obtain a synthetic planet population that we can reasonably compare to our observed sample, we applied the same bias to the NGM planets. In this way, we obtain an observable NGM population that contains all the planets that a combined HARPS&CARM70 survey would have detected if it observed our synthetic systems.
In Sabotta et al. (2021), we conducted injection-and-retrieval experiments on the RV data for each of the stars in the CARM70 sample. The period and M sin(i) of the injected planets were taken from a grid of log-uniform distribution. For every grid point, we injected 50 test planets with random phase angles. If the test planet appeared in the GLS periodogram with a FAP of less than 1%, we counted it as a recovery. The detection probability for this grid point is then the number of recovered planets divided by the total number of injected planets. From the final survey sensitivity map, we excluded active periods that show up in the periodogram of the activity indicators. We further dismissed periods that are longer than half the time baseline by setting the detection probability to zero. At those periods we would not accept a real planetary signal (see Sect. 2), and therefore we do not accept corresponding test planets.
To make sure that the analysis is as self-consistent as possible, we computed survey sensitivities for the HARPS survey (Bonfils et al. 2013) in the same way using RV measurements and activity indicators produced with SERVAL (Zechmeister et al. 2018) by Trifonov et al. (2020b). To produce global sensitivity maps for a combined HARPS&CARM70 survey, we averaged the detection probability of each grid point for all targets of the combined sample. The resulting maps for the four stellar mass bins are shown in Fig. 2.
Each NGM planet received a detection probability depending on the period-minimum mass bin in which it falls on this map. We then assigned each synthetic planet a uniformly drawn random number from the interval [0.0,1.0) and considered the planet detected if this number is lower than the planet’s detection probability. Out of the 2433 170 synthetic planets, only 20021 are detectable according to this procedure.
4 Results
4.1 Observed and Theoretical Planet Detections
Occurrence rates are often computed from incomplete catalogs by characterizing a detection bias and correcting for it (e.g., Cumming et al. 2008; Bonfils et al. 2013; Burke et al. 2015; Obermeier et al. 2016; Lienhard et al. 2020; Wittenmyer et al. 2020; Gibbs et al. 2020). This has the disadvantage of having to extrapolate to domains of low sensitivity, leading to large uncertainties (Foreman-Mackey et al. 2014). Instead, here we apply the calculated bias of the combined HARPS&CARM70 survey to our synthetic population and directly compare the observed sample with detectable synthetic planets. We focus on comparing planetary detection rates n, which refer to the number of simulated or observed planet detections per finite interval in a parameter (e.g., the orbital period). Owing to the RV-detected exoplanet sample, our parameter space of choice is the one spanned by the minimum mass M sin(i) and the orbital period P. The corresponding detection rate density in this parameter space can be expressed as
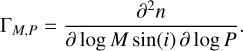 (2)
(2)
Across all masses and periods, we find a total number of observed planets per star of 0.24 ± 0.04 in the HARPS&CARM70 sample and a total number of observable synthetic planets per star of 0.201 ± 0.001, where the uncertainties are Poisson errors from the counting statistic. With 35 planets in 26 systems, the observed mean multiplicity of 1.35 is in agreement with the synthetic one of 1.38 (20021 synthetic planets in 14 513 systems). The total observed and theoretical detection rates thus appear consistent with each other. We note that the detection rate of giant planets in the CARMENES sample could be overestimated since the survey is not yet completed (see Sect. 5.5, Sabotta et al. 2021).
Figure 3 shows the distribution of biased simulated and observed planets in minimum mass-period space. The bulk of the unbiased theoretical occurrence density lies at roughly Earth-mass planets at orbital periods of a few hundred days (Burn et al. 2021). After applying the observational bias, the peak density is shifted to the super-Earth mass regime with periods of a few days. Super-Neptunes and giant planets (M sin(i) ≳ 20 M⊕) are expected to be much rarer. The model anticipates detections to be most likely at M sin(i) ≳ 200 M⊕ with orbits around ~100 d. It produces the fewest planets in the 20–200 M⊕ mass range, especially in orbits beyond ~20 d. However, such a dearth of Neptune to Saturn-mass planets at intermediate orbits is not obvious in the sample of detected CARM70 and HARPS planets. Although these are subject to selection effects (see Sect. 5.5), it is noticeable that the mass distribution here is rather continuous and does not reveal multiple modes. Concerning the agreement of simulated and observed planets, low-mass planets up to around 10 M⊕ are well reproduced by the model, whereas intermediate-mass planets occur in the observed sample but are hardly present in the synthetic population.
 |
Fig. 2 Combined detection probabilities for the HARPS&CARM70 survey binned to the stellar masses used in the simulations. The color code represents the detection probability of a planet with the corresponding period, minimum mass, and host star mass. The zero-detection threshold resides at slightly lower minimum masses for lower-mass stars, and the detection map for 0.7 M⊙ stars is patchy due to the small sample there. |
 |
Fig. 3 Observed and biased synthetic planets in minimum mass-period space. Markers show confirmed planets from the HARPS and CARM70 surveys, respectively. The color code shows the frequency of simulated planets in this parameter space after applying the detection bias of the combined HARPS &CARM70 survey. Low-mass planets are well reproduced by the model, but intermediate-mass planets appear more common than theoretically predicted. |
4.2 Planet Detections as a Function of Host Star Mass
To identify trends with planet host mass, we explore planet detections in the four stellar mass bins defined above (Fig. 4). The synthetic population shows a clear trend of increasing giant planet detection rate with host star mass. In general, giant planets are rare and occur only in the stellar mass bins 0.5 M⊙ and 0.7 M⊙. However, the giant planets in the HARPS&CARM70 sample are in stark contrast to this trend. The observed giant planet closest to a synthetic counterpart is GJ 876b, which orbits its host with a period of 61 d and has a projected mass of M sin(i) ≈ 761 M⊙ (Marcy et al. 2001; Rivera et al. 2005; Trifonov et al. 2018). With a stellar mass of 0.37 M⊙, the system just barely ended up in the stellar mass bin with zero detection rate density in the giant domain and is in fact relatively close to the few synthetic giant planets in the 0.5 M⊙ population.
There are four discovered planets on intermediate and large orbits (P = 10–1000 d) with projected masses M sin(i) = 20–200 M⊙, where NGM shows a deep valley in the detection rates: GJ 1148b,c (Haghighipour et al. 2010; Trifonov et al. 2018), HD 147379b (Reiners et al. 2018a), and GJ 3512b (Morales et al. 2019). While none of them would have been expected based on our simulations, the 147 M⊕ giant GJ 3512b is particularly difficult to reconcile with theoretical predictions: it orbits a late (M 5.5) M dwarf with a very low mass of (0.123 ± 0.009) M⊙ (Morales et al. 2019). Our theoretical model produces no giant planets in this stellar mass regime, and its existence remains a challenge for planet formation theories based on core accretion (Liu et al. 2020; Burn et al. 2021; Schib et al. 2021, but also see Kurtovic et al. 2021).
On the other hand, low-mass planets (M sin(i) ≲ 30 M⊕) are well represented by our synthetic systems. Populations from all stellar mass bins contribute to the synthetic planet detections in this domain, where in the unbiased population the maximum occurence rate density is invariably at orbits ~100–1000 d and terrestrial planet masses of a few M⊕. In the biased population presented here, this peak is shifted toward periods on the order of a few days. The observed low-mass planets in CARM70 and HARPS lie all in the domain where significant synthetic detection rate density exists.
If we normalize the planet detections by the number of stars of a given host star mass range (see Fig. 5), the simulated detections increase linearly with stellar mass. This can be directly attributed to the scaling of disk masses (see Sect. 3.2). In contrast, the observed detections vary across the considered range without a clear trend. While the total numbers of detections in both samples agree, significant deviations exist when they are partitioned by stellar mass. This is particularly true for giant planets.
 |
Fig. 4 As Fig. 3, but partitioned according to host star mass. In the biased synthetic population, the domination by low-mass planets on short to intermediate orbits is similar for all stellar masses, but giant planets occur only around stars with masses 0.5 M⊙ and higher. In contrast, the subgiant and giant planets in the observed sample occur most frequently around less massive stars. GJ 3512b, the giant planet in the 0.1 M⊙ panel, is particularly at odds with theoretical predictions. No simulated planets with M sin(i) > 10 M⊙ occur in this stellar mass bin. |
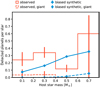 |
Fig. 5 Simulated and observed planet detections as a function of host star mass. In each stellar mass bin, vertical lines denote 68% confidence intervals based on the binomial distribution (not visible for the synthetic population), and the counts are normalized to the number of stars in that bin. The synthetic population features discrete M* values and shows a linear increase of detections with increasing stellar mass. The observed sample shows no clear trend. |
4.3 Planetary Mass Function
By marginalizing over the orbital period axis, a minimum mass distribution of the samples can be obtained. Figure 6 shows normalized histograms in M sin(i) for the observed and simulated planet samples. In the domain of terrestrial planets and super-Earths up to ~30 M⊙, the observed and theoretical distributions match well. Beyond that, the model predicts fewer planets than observed and shows a few very massive planets (>1000 M⊙) that are not observed. To quantify the difference between the observed and theoretical planetary mass functions, we performed a two-sample Anderson-Darling test (Anderson & Darling 1952), which is based on a nonparametric and distribution-free test statistic A2. Using the implementation in Scipy2 and critical values from Scholz & Stephens (2007), we find that the null hypothesis that the two samples stem from the same distribution can only be rejected at an estimated 25% significance level (A2 = 0.97). We cannot exclude an identical underlying base distribution. If we divide the samples into early (>0.4 M⊙) and late (<0.4 M⊙) host stars3, the agreement remains only for the early subsample. Due to the large difference in giant planet detection rates, the observed and simulated samples for later spectral subtypes are different at the 0.1% level.
Figure 6 further shows an apparent bimodality of the synthetic M sin(i) distribution for early host stars. We tested the significance of such a bimodality by applying Hartigan’s dip test (Hartigan & Hartigan 1985), which tests the null hypothesis of a unimodal distribution, on the different synthetic subsamples. For the overall synthetic sample, the resulting p-value of 7 × 10−3 suggests a multimodal distribution. Distinguishing between early and late stars, the dip test suggests a multimodal distribution for the early sample (pearly = 1 × 10−3) but not for the late sample (plate = 0.9). This is because at stellar masses below 0.4 M⊙ no giant planets occur and the distribution features a single slope. The minimum mass distribution of the observed sample is overall more flat and shows an almost continuous negative slope. Consequently, Hartigan’s dip test suggests a unimodal distribution (p0bs = 0.8).
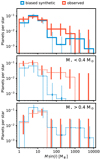 |
Fig. 6 Minimum mass distribution of synthetic and observed planets. Thick vertical lines show 68% confidence intervals based on the binomial distribution. Thin blue lines show standard deviations of 2000 bootstrapped synthetic samples, where each sample had the size of the observed sample. Top: total normalized counts. The distribution of the biased synthetic population appears bimodal in M sin(i). The observed sample shows a peak in the terrestrial planet regime of a few Earth masses and a continuous downward slope without a valley. At low masses, the theoretical and observed distributions agree. The formation model underproduces planets ≳30 M⊙ and features a “sub-Saturn valley.” Center and bottom: normalized counts for late (<0.4 M⊙) and early (>0.4 M⊙) M dwarfs separately. At minimum masses beyond ~30 M⊙, theory and observations disagree: while observed subgiant and giant planets occur mostly around stars with masses ~0.3 M⊙, the formation model produces such planets only around more massive stars. |
4.4 Orbital Period Distributions
One of the most directly accessible planetary properties is the orbital period. The period distributions of the synthetic and observed planets agree well, except for a peak at a few tens of days that occurs only in the observed sample (Fig. 7). Orbital periods of the biased synthetic population resemble a power law with a single slope, and a common origin of the distributions can be excluded on the 0.1% level (A2 = 7.85). The apparent log-linear slope is partly shaped by the period-sensitive completeness function, which masks a slight drop in occurrence for planets with periods shorter than ~10 d.
The observed sample shows a dearth of such short-period planets around stars of higher masses. This feature is not reproduced in our model with its current prescription for planet migration and the innermost parts of the protoplanetary disk (see discussion in Sect. 5.4).
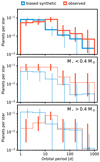 |
Fig. 7 Period distribution of observed and synthetic planets. As in Fig. 6, thick error bars denote 68% confidence intervals based on the binomial distribution, and thin lines show the standard deviations of bootstrapped simulated samples. Top: total normalized counts. The distributions are comparable over most of the range, except for a peak at ~10–30 d that only occurs in the observed sample. Center and bottom: nNormalized counts for early (>0.4 M⊙) and late (<0.4 M⊙) M dwarfs separately, both showing a high detection rate at a few tens of days in the observed sample. Significantly fewer short-period planets are found around higher-mass stars, which is in disagreement with our model. |
5 Discussion
The overall number of planet detections per star in the observed HARPS &CARM70 sample and in the biased synthetic NGM population are in good agreement. In M sin(i)-P-M* space, some discrepancies occur that we discuss here.
5.1 A missing Sub-Saturn Valley in the Planetary Mass Function
The simulated and observed minimum mass distributions agree for small planets up to ~30 M⊕. Beyond that, their shapes deviate: while the minimum mass distribution recovered from the discovered planets follows a smooth power law, the simulated planets show a significant bimodality. The valley between about 30 M⊕ and 200 M⊕ is also present in the unbiased synthetic population (Burn et al. 2021). Testing the existence or nonexistence of this demographic feature in M dwarf planetary systems may provide clues about the gas accretion process in the core accretion paradigm for different stellar types.
In the classical picture, the valley separates all planets that attained solid cores massive enough to enter runaway gas accretion and became giant planets from those that did not (Mizuno et al. 1978; Pollack et al. 1996). Due to the short duration of the runaway phase, only few planets retain intermediate masses (Mordasini et al. 2009b; Emsenhuber et al. 2021b, in prep.). Three-dimensional hydrodynamical simulations of planetary gas accretion have challenged this prediction by proposing significantly lower accretion rates (Szulágyi et al. 2014; Moldenhauer et al. 2021).
Preliminary observational evidence for the predicted valley has been provided by Mayor et al. (2011), who computed bias-corrected occurrence rates and the mass distribution for the HARPS RV survey, albeit for mostly solar-type stars. They reported a decrease of their bias-corrected mass distribution “between a few Earth masses and ~40 M⊕.” In contrast, the valley appears absent in the MOA-II microlensing survey (Suzuki et al. 2016,2018). Furthermore, the significance of the Mayor et al. (2011)-dip has recently been questioned (Bennett et al. 2021).
Future expansion of the observational sample will shed light on the existence, strength, and physical origin of a “sub-Saturn valley”. Planets on intermediate orbits of ~ 10–100 d period (e.g., Espinoza et al. 2016; Kipping et al. 2019; Brahm et al. 2020; Schlecker et al. 2020; Hobson et al. 2021) are suitable study objects, as they are less affected by direct interaction with the host star than their hotter siblings (Thorngren et al. 2016). The absence of a significant valley in our sample already indicates that it is not as pronounced as our canonical gas accretion formalism predicts.
5.2 Excess of Giant Planets Around Late M Dwarfs
The stellar mass dependence of giant planet detections with M sin(i) > 100 M⊕ in the synthetic NGM and observed samples are at odds with each other. While the formation model generally produces giant planets only around earlier stars, our RV-detected giant planets orbit only host stars with masses lower than 0.5 M⊙. This is despite a significantly higher survey sensitivity around earlier stars (Sabotta et al. 2021).
Further constraints on the occurrence of giant planets around stars over a wide range of masses are provided by the California Legacy Survey (CLS, Rosenthal et al. 2021; Fulton et al. 2021), which combined and extended previous surveys using Keck and HIRES data (Cumming et al. 2008; Howard et al. 2010; Hirsch et al. 2021). We plot its giant planet detections as a function of the stellar host mass in Fig. 8 together with the combined HARPS&CARM70 sample and our synthetic systems, where we included analogous populations for 1.0 M⊙ and 1.5 M⊙ stellar hosts (Emsenhuber et al. 2021b). We further add the linear giant planet occurrence trend found in Ghezzi et al. (2018). For the latter, we use the stellar mass-metallicity fit of their most recent planetary sample at [Fe/H] = −0.02, which is the mean metallicity in the synthetic sample of Burn et al. (2021). The fit deviates from the CLS sample for larger stellar masses due to enhanced metallicities in the latter. Thus, the derived, almost linear dependency (∝ 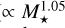 ) by Ghezzi et al. (2018) is better suited for comparison to the synthetic data than the full CLS sample. Similar to previous findings (Kennedy & Kenyon 2008), our synthetic giant planet occurrences show a trend in stellar mass that is significantly steeper than the observed one. This suggests that the gas accretion process needs to be revised in the model (Emsenhuber et al., in prep.).
) by Ghezzi et al. (2018) is better suited for comparison to the synthetic data than the full CLS sample. Similar to previous findings (Kennedy & Kenyon 2008), our synthetic giant planet occurrences show a trend in stellar mass that is significantly steeper than the observed one. This suggests that the gas accretion process needs to be revised in the model (Emsenhuber et al., in prep.).
Instead of changing the formation process itself, the proposed stellar mass scaling of the initial disk mass, which controls the number and masses of planetary cores (e.g., Kennedy & Kenyon 2008), may be questioned. It is based on millimeter dust continuum emission, which may be affected by unknown opacities, conversion of solid material into larger particles, or optical depth effects (e.g., Molyarova et al. 2017; Pascucci et al. 2016). A shallower stellar mass-scaling could resolve the discrepancy, however, realistic stellar accretion rates should be maintained. In our nominal scaling, these are consistent with observed data by Alcalá et al. (2017; see Burn et al. 2021), although slightly shallower. Indeed, other authors matched observed accretion rates with a steeper than linear slope: Alibert et al. (2011) found a good match to observational data (Muzerolle et al. 2003; Natta et al. 2004) for a slope of 1.2. Similarly, the scaling of Manara et al. (2012) used in Liu et al. (2020) results in a steeper relationship. Thus, a shallower than linear slope for the disk mass as a function of stellar mass is disfavored by accretion rate observations and not a viable option to enhance the giant planet formation rate around low-mass stars.
Giant planets occur more frequently around stars of higher metallicity (Gonzalez 1997; Santos et al. 2001, 2004; Fischer & Valenti 2005; Buchhave et al. 2018). Since for a fixed disk mass, metallicity controls the solid budget of the disk, larger metallicities promote the formation and growth of planetesimals and ultimately of planetary cores able to reach the runaway regime. It is thus reasonable to suspect that the giant planets in our sample have formed in particularly metal-rich environments that are not represented by the metallicity distribution of the synthetic systems. The reported values for the giant planet hosts mentioned above are 0.05 ± 0.2 dex or −0.11 ± 0.10 for Gl 876 b (Correia et al. 2010; Marfil et al. 2021), 0.36 ± 0.2 for Gl 317 (Anglada-Escudé et al. 2012), 0.13 ± 0.16 or −0.17 ± 0.10 for GJ 1148 (Passegger et al. 2018; Marfil et al. 2021) and −0.07 ± 0.16 or -0.12 ± 0.16 for GJ 3512 (Morales et al. 2019; Marfil et al. 2021), leaving only Gl 317 with an enhanced metallicity. Although the uncertainties are large, the other targets are consistent with solar metallicity. Recent discoveries in the literature like the sub-Neptune around TOI-2406 (M* = 0.16 M⊙, [Fe/H] = (−0.38 ± 0.07), Wells et al. 2021) and the giant planet around a late (M5.0 V) M dwarf with subsolar metallicity (Quirrenbach et al. 2022) complement the pattern. A high metal content alone thus cannot explain the existence of giant planets around very low-mass stars.
Already Johnson et al. (2010) reported an elevated giant planet occurrence at stellar masses below 0.5 M⊙, and both CARMENES and CLS find a slight excess of giant planets around stars with masses ~0.4 M⊙ compared to the linear trend in Ghezzi et al. (2018): Gl 876b and c (J22532-142, Marcy et al. 1998, 2001; Delfosse et al. 1998; Rivera et al. 2005; Millholland et al. 2018; Trifonov et al. 2018) are included in both the CLS and the CARMENES sample. Furthermore, Gl 317 (Johnson et al. 2007; Anglada-Escudé et al. 2012) and HIP 57050 (GJ 1148, Ross 1003, see also Trifonov et al. 2020a) both host a planet with mass >100 M⊕ and are included in CLS but not in the CARM70 sample (the latter is reported with a mass M sin(i)<100 M⊕ in CARMENES).
Stellar masses below ~0.3 M⊙ have not been thoroughly explored by RV surveys, and the currently small sample does not allow us to draw a definite conclusion about a deviation from the linear trend at very low stellar masses. However, Quirrenbach et al. (2022) recently reported the discovery of another giant planet around a late (M5.0 V) M dwarf. Although not part of our sample, the roughly Saturn-mass planet provides additional evidence for the existence of giant planets around stars of all masses.
It also allows a simple estimate: for 66 stars of spectral type M4.0 V or later, which roughly corresponds to our lowest-mass bin, CARMENES has already collected 30 or more RV measurements. This rather arbitrary threshold serves as a reasonable reference value above which CARMENES would detect gas giants in a wide range of periods. Two of these stars have been shown to host giant planets (Morales et al. 2019; Quirrenbach et al. 2022). We can thus estimate a lower limit on the giant planet occurrence rate of 2/66 ≈ 3% in this stellar mass bin. This assumes a generic completeness of 100% rate is likely higher when realistic detection sensitivities are taken into account. This crude estimate hints at a possible break of the linear occurrence rate trend reported before. However, no conclusions in this regard should be drawn ahead of a thorough sensitivity and occurrence rate assessment upon completion of the survey.
Discoveries of gas giants through gravitational microlensing support the existence of massive planets around low-mass stars (e.g., Udalski et al. 2005; Dong et al. 2009; Bennett et al. 2020; Bhattacharya et al. 2021; Han et al. 2021). These discoveries reinforce the puzzling disagreement of the new CARMENES results with theoretical predictions of giant planet occurrence as a function of stellar mass. This raises the question of whether planets with extreme planet-to-star mass ratios may form within the core accretion framework, or, as hypothesized in Morales et al. (2019), via a disk instability scenario (Cameron 1978).
 |
Fig. 8 Giant planet detections as a function of stellar mass. From the HARPS and CARMENES planets presented here (red), the California Legacy Survey (Rosenthal et al. 2021, gray), and our synthetic NGM planets (blue), we include detections with RV semi-amplitude K > 10 m s−1, M sin(i) > 100 M⊙, and P < 1000 d. We removed planets around close spectroscopic binaries (P < 20 yr) reported in Rosenthal et al. (2021). In addition, we show the fit of Ghezzi et al. (2018) for metallicities consistent with the assumptions made to draw the synthetic planets. Shaded areas and vertical lines denote 68% confidence intervals, respectively. We note that the HARPS &CARM70 sample is limited to M dwarfs ≲0.7 M⊙. The observed giant planets around very low-mass stars indicate a possible break of the monotonie stellar mass trend at around ~0.5 M⊙, which theoretical predictions fail to reproduce. If type-I migration is inhibited by a factor ×10 in the simulations (dashed blue line), giant planets occur also in systems with lower stellar masses. |
5.3 Potential of Core Accretion to Produce Giant Planets Around Low-mass Stars
There is a substantial body of literature that provides predictions about the existence of gas giant planets around low-mass stars. From the point of view of disk and exoplanet observations, Manara et al. (2018) found that the combined solid masses of planetary systems frequently exceed those of the most massive dust disks (30 M⊕ ≈ 10−4 M⊙ for M dwarfs), leading them to speculate about a dedicated formation pathway for massive giant planets around very low-mass stars. It should be noted that the total mass and distribution of planetesimals may strongly deviate from what is implied by the gas and dust distribution in disks (Lenz et al. 2019; Voelkel et al. 2020). At the times of observation, a large fraction of the dust might already be hidden in planetesimals (Gerbig et al. 2019).
Miguel et al. (2020) performed a population synthesis of planetary systems around (very) low-mass stars (M* = 0.05–0.25 M⊙) based on a semi-analytical model assuming classical planetesimal accretion. Their model was originally designed to study circumplanetary disks and features a low-viscosity gas disk model as well as type-I and type-II migration (Miguel & Ida 2016). They find efficient planet formation only in sufficiently massive disks (≳10−2 M⊙). Even under these conditions, their model fails to form any planets more massive than 5 M⊕.
Using a pebble accretion based model, Liu et al. (2019) model gas accretion onto planetary cores that have reached pebble isolation mass (Lambrechts et al. 2014). Their gas accretion method is optimistic (reduced opacity by a factor of ~20–100, no leftover thermal energy due to prior solid accretion) and therefore useful as an upper limit for giant planet formation in the pebble accretion scenario (see also Brügger et al. 2020). In this case and for varied disk properties, they found a minimum stellar mass for giant planet formation of ~0.3 M⊙.
In good agreement, Mulders et al. (2021) also use a pebble drift and accretion model to simulate planet growth around stars with different masses. They find that no giant planets form at stellar host masses ≲0.3 M⊙.
Adams et al. (2021) explore the planetary mass function of planets formed around host stars of different masses with a semi-empirical approach. They find a steeper planetary mass function for low-mass stars, suggesting a low probability of producing Jovian planets around stars with M* ≲ 0.5 M⊙.
Zawadzki et al. (2021) used N-body calculations to simulate the formation of planets around 0.2 M⊙ stars. Under the assumptions of early planetesimal formation (Lenz et al. 2019) and including type-I migration, they find efficient growth of planetary cores through early collisions of planetary seeds. Their setup assumes a rather high solid disk mass of ~2 × 10−2 M⊙ at the start of their simulations. While they do not model gas accretion onto planets, many of these cores grow to super-Earths, some of which in the mass range where runaway accretion could be triggered.
Finally, Burn et al. (2021) discuss modifications to the model used here that would enable the formation of giant planets around very low-mass stars. The dashed line in Fig. 8 shows the fraction of giant planets in simulations with type-I migration velocities inhibited by a factor ×10. For computational cost considerations, we initialized these otherwise identical simulations with only 20 planetary cores per disk, which is adequate for modeling gas giant systems (Emsenhuber et al. 2021b). Suppressing planet migration clearly has a strong effect on giant planet formation: In the modified simulations, planetary cores are able to reach masses beyond ~10 M⊕ even around late M stars without rapidly migrating into the star, enabling giant planet formation.
Even though there is no obvious evidence justifying such tuning of the migration scheme, it does mimic “planet traps” caused by inverted gas pressure gradients to some degree. Their existence is indicated by numerous observations of disk substructures (e.g., Andrews et al. 2018), which are suspected to be also common around very low-mass stars (Kurtovic et al. 2021; Pinilla et al. 2021). This way out of the giant planet conundrum still requires relatively high initial solid disk masses Msolid,0 > 66 M⊕ ≈ 2 × 10−4 M⊙. The efficiency of planet core formation could be further enhanced if large amounts of planetesimals are concentrated at intermediate orbital distances, possibly at the water iceline (Drazkowska & Alibert 2017).
Giant planet formation could be further facilitated if planet cores accrete not only planetesimals but also mm to cm-sized pebbles (Klahr & Bodenheimer 2006; Ormel & Klahr 2010; Lambrechts & Johansen 2012; Voelkel et al. 2020), but sufficiently high pebble fluxes are needed in order for growth to outweigh rapid inward migration (Bitsch et al. 2019).
We conclude that common theories of planet formation via core accretion do not predict planets like the gas giants around late M stars described here. Giant planet growth via direct collapse in a gravitationally instable disk remains an alternative scenario to form these planets, provided that the mass infall rate onto the disk at any one time exceeded its turbulence-driven accretion rate (Boss 1997). However, planets formed via disk instability are thought to form at large orbital radii and to be massive with M ~ 10 MJup (e.g., Adams & Benz 1992; Kratter et al. 2010). It is thus difficult to reconcile the planets considered here with this scenario.
A larger observational sample and systematic parameter studies of various formation models will be required to reveal the physical mechanisms responsible for this enigmatic subpopulation of planets. Stronger constraints can be expected from future microlensing surveys, which predominantly probe low-mass stars (Gould et al. 2010; Zang et al. 2021; Hwang et al. 2021). The high angular resolutions achieved by extremely large telescopes will allow one to resolve and measure masses of the hosts of essentially all microlensing planets discovered to date. Furthermore, astrometric data from Gaia Data Releases 3 and 4 will enable much better statistics on a sample of several thousand nearby M dwarfs (Sozzetti et al. 2014; Perryman et al. 2014). For these stars, giant planets on short and intermediate orbits can then be characterized, which will greatly enhance the sample size for precise occurrence rate studies of giant planets around low-mass stars.
5.4 A Stellar-mass Dependent Drop in the Period Distribution
The present-day picture of planet-disk interactions generally leads to migration of planets toward the star. Therefore, if and where they are stopped can in principle be constrained by the orbital period distribution of exoplanets. Our sample provides new constraints to this topic, which was previously predominantly explored with transit surveys. Mulders et al. (2015a) found a stellar mass dependent drop in occurrence rates of inner planets from the Kepler mission and determined a semi-major axis break point that scales as 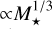 . The innermost planet of a given system appears to be located at a preferred orbital period ≃10 d (Mulders et al. 2018). As drivers of such a drop, migration traps (Plavchan & Bilinski 2013) or the removal of inner planets are being discussed.
. The innermost planet of a given system appears to be located at a preferred orbital period ≃10 d (Mulders et al. 2018). As drivers of such a drop, migration traps (Plavchan & Bilinski 2013) or the removal of inner planets are being discussed.
It seems possible to utilize trends with stellar host mass to pinpoint which process determines the location of the innermost planets. Mulders et al. (2015a) favored planetary tides or the stellar corotation radius to match their 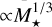 scaling. They further considered a removal of planets by stellar tides or dust sublimation in passive or viscously heated disks. Here, we briefly discuss new insights gained on the possible origins of this scaling in light of our sample.
scaling. They further considered a removal of planets by stellar tides or dust sublimation in passive or viscously heated disks. Here, we briefly discuss new insights gained on the possible origins of this scaling in light of our sample.
From Fig. 7 it becomes apparent that the Bern model fails to correctly predict the stopping mechanism: synthetic planets commonly migrate closer to the star than their observed counterparts. The model includes an inner edge set at corotation radii based on observed stellar rotation rates (Venuti et al. 2017, see the discussion in Burn et al. 2021). The drop of the gas surface density at this location causes a type-I outward migration zone (Masset et al. 2006), which should foster a local pile-up of planets (Mulders et al. 2019). However, we observe only little change of the innermost periods in simulations with increased inner disk edge position (see Appendix B). As indicated in Schlecker et al. (2021b), we find that the presence of planets within the corotation radius can be attributed to N-body interactions with planets further out: often, an inner planet gets locked in a mean-motion resonance with an outer migrating planet that pushes it further in. This model outcome is in agreement with the result of Ataiee & Kley (2021), who use 2D hydrodynamic models instead of migration rate prescriptions to address this issue. They found that commonly an inner edge is not able to stop migration of resonant chains of planets. This is in agreement with the resonant chain-shaped period distribution of planets around solar-mass stars in Carrera et al. (2019). Thus, the inner edge of the disk is only an efficient migration trap for solitary planets. With our multiseed setup, such a scenario is rare.
A more efficient migration trap could be the inner edge of a nonionized dead zone (Gammie 1996). Due to a change in ionization rate, the viscosity is expected to increase, which in turn leads to a lowered surface density and a pressure bump in a steady-state disk. The typical temperature at which this happens is ~ 1000 K (Flock et al. 2016, 2017). More detailed models were presented by Mohanty et al. (2018) and Jankovic et al. (2021): They find pressure bumps outside the dust sublimation front. Therefore, these pressure bumps can cause the first trap that resonant convoys of migrating planets would encounter. According to Ataiee & Kley (2021), the dead zone inner edge is efficient in halting migration of planets in resonant chains. The scaling of the orbital period of the pressure bump found by Mohanty et al. (2018) is 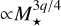 , where q is the exponent with which the stellar accretion rate depends on stellar mass q ~ 1.8 (Alcalá et al. 2017). Such a steep dependency of a trap mechanism on stellar mass is required to explain the tentative evidence from our sample shown in the right panel of Fig. 7. While the scaling found by Mohanty et al. (2018) looks promising to explain the trend, the absolute values of the found pressure bump locations are too large with orbital periods of ~60 d for solar-mass stars. However, the work of Mohanty et al. (2018) does not include dust evolution, which would change the outcome.
, where q is the exponent with which the stellar accretion rate depends on stellar mass q ~ 1.8 (Alcalá et al. 2017). Such a steep dependency of a trap mechanism on stellar mass is required to explain the tentative evidence from our sample shown in the right panel of Fig. 7. While the scaling found by Mohanty et al. (2018) looks promising to explain the trend, the absolute values of the found pressure bump locations are too large with orbital periods of ~60 d for solar-mass stars. However, the work of Mohanty et al. (2018) does not include dust evolution, which would change the outcome.
A related effect that is included in the Bern model is radial migration due to stellar tides (following e.g., Benítez-Llambay et al. 2011). Similar to the consideration of Mulders et al. (2015b), they lead to the removal of the planets closest to their host stars. In the simulations, tidal effects are at least partially responsible for shaping the period distribution at close orbits. Despite that, the observed distribution is not reproduced, which indicates that either tides are stronger in reality or that we are missing another important mechanism.
The modeled stellar tides in Burn et al. (2021) include the dependency on stellar mass and radius (determined using the stellar evolution tracks by Baraffe et al. 2015). Currently missing is the dependency on the ratio between the quadrupolar hydrostatic Love number and the tidal dissipation quality factor Q* (Gallet et al. 2017). These parameters depend on the interior structure and dynamics of the star, which vary with stellar mass. A detailed analysis taking this into account was done by Strugarek et al. (2017), who find that tides can become efficient for solar-mass stars and orbital periods below 20 d. However, the dynamical tide and therefore a large portion of the effect is suppressed for fully convective M dwarfs. Therefore, fewer planets would be removed at small orbital periods. This could explain the different distribution of planetary orbital periods for stars with M* < 0.4 M⊙.
Another effect leading to the same outcome as tides are magnetic planet-star interactions. Strugarek et al. (2017) find that they can dominate over tides in some regimes, but the order of magnitude is comparable to tides. For low stellar masses, magnetic effects are stronger than tides but are not efficient enough to lead to migration of planets on orbits with periods larger than a day.
Overall, our M dwarf sample provides tentative evidence for a steep scaling of a migration trap with stellar mass that could be caused by a magnetically induced pressure bump. Alternatively, efficient tidal migration could remove the innermost planets around larger stars but cease to be efficient for fully convective small stars. These findings should be seen as further motivation for a model revision of the planetary orbital migration and trapping mechanisms already mentioned in Emsenhuber et al. (2021a) and Schlecker et al. (2021a).
5.5 Caveats and Limitations
Radial velocity surveys are not free from biases, and the CARMENES and HARPS surveys are no exception. At the same time, no theoretical model can fully reflect all physical mechanisms relevant for planet formation, and simplifications have to be made. In the following, we list a number of limitations of our study that could affect our conclusions.
5.5.1 Selection Effects
Spectroscopic binaries have been removed from the HARPS and CARMENES samples, respectively. Moe & Kratter (2021) showed that this may lead to overestimated giant planet occurrence rates for G-type stars. Reported close binary fractions are relatively constant across the M dwarf mass range (Offner et al. 2022). Thus, the removal of binary stars from the samples can not lead to the apparent overabundance of giant planets around late M dwarfs. Since all our simulated planet hosts are single stars, this selection effect does not impair our comparison of observed and synthetic populations.
One potential bias is the intensified observation of targets that already show a tentative signal. Such a signal shows earlier for more massive planets, and these planets are thus more likely to be eventually detected. The CARM70 sample was selected out of a larger sample with about 340 targets based on the number of observations its stars received. Thus, “human intervention bias” may lead to an overprediction of more massive observed planets up to a factor of five, assuming there are no giant planets left in the rest of the sample (see also Sabotta et al. 2021). Since we have no indication of an enhancement of this effect for the least massive stars, it should not affect our conclusions. The analysis of the full CARMENES sample will result in more robust occurrence rates for giant planets.
5.5.2 Single-planet Approximation During Biasing
The NGM population consists of multiplanet systems where most systems maintain several planets each. In practice, their detectability not only depends on the individual planet properties but also on the combination of planets that occupy a system: The measured RV signal of a multiplanet system is a combination of contributions from the individual planets, and a successful disentanglement of these signals depends on their shape. Nevertheless, when applying the detection bias to synthetic systems, we treat each planet as isolated and assign its detectability based on the survey sensitivity at its orbital period and minimum mass. Injection-and-retrieval tests of each synthetic system might lead to a more realistic bias but would be computationally expensive and are not expected to have a significant impact on the statistical result.
5.5.3 Simplifications of the Formation Model
Due to computational limits, there remain relevant model parameters, such as the viscous a parameter or the planetesimal size, that are not included in our parameter search. While the chosen values result in a good fit for the solar mass case, there might be additional trends with stellar mass that need to be explored in the future. In addition, our model does not yet include the evolution of solids in the disk and the consistent formation of planetesimals and seeds (Burn et al. 2021). We note that the popular theoretical approximation of two grain sizes presented in Birnstiel et al. (2012) was derived for solar-type stars and its application to an order of magnitude lower stellar masses is not straightforward.
6 Conclusions
We have compared synthetic planet populations computed with a core accretion formation model with a sample of planets around low-mass stars discovered by the HARPS and CARMENES RV surveys. To correct for completeness, we performed injection tests on the actual RV time series of the surveys. Instead of extrapolating beyond the observed planet sample, we biased the population of simulated systems according to the detection limits of the observed sample. We then statistically compared the actual and synthetic surveys in M sin(i)-P-M* space. Our main findings are:
Theory and observations are in agreement for short-period rocky planets, which form the largest population. Their observed detection rates, planetary mass function, and orbital period distribution are consistent with our simulations.
Observed detections of giant planets around late (<0.5 M⊙) M dwarfs might be indicative of a break in the giant planet occurrence as a function of host star mass. The existence of these planets cannot be reconciled with our model, although the discrepancy is reduced when planet migration is suppressed.
The observed and synthetic planetary mass functions diverge for intermediate masses (30–200 M⊕). More sophisticated treatments of planetary gas accretion, in particular those that take into account 3D effects, are possibly needed for convergence.
The observed orbital period distribution depends on the stellar mass with a paucity of very short-period planets around stars ≳0.4 M⊙. While the model reproduces the distribution for less massive stars, it fails to remove planets or halt planetary migration efficiently enough for earlier M dwarfs. Candidate mechanisms to produce the observed trend are planet trapping due to a dead zone inner edge or stellar tides.
Both the inability to explain the existence of giant planets around very low-mass stars and the difference in the period distributions suggest that state-of-the-art planet formation models are still missing a complete picture of planet migration, or rather of the local disk conditions to which it is highly sensitive. Constraints on the abundance of substructures in disks around very low-mass stars through high angular resolution observations will be particularly insightful here.
With 147 stars and 35 planets, the statistical power of our sample is still limited. It will improve upon the completion of the CARMENES GTO survey, and beyond that by including the imminent results from astrometry and microlensing campaigns. On the theoretical side, future model improvements will allow one to study the physical mechanisms responsible for the discrepancies presented in this paper.
Our findings underscore the different conditions in protoplanetary disks around different stellar spectral types, which has a measurable impact on the outcome of planet formation. M dwarfs are not just small Suns.
Acknowledgements
We wish to thank Pedro Amado, Hans Baehr, Jose Caballero, Mario Flock, Andrew Gould, Diana Kossakowski, Nicolas Kurtovic, Kaitlin Kratter, Rafael Luque, Ilaria Pascucci, Ansgar Reiners, and Andreas Quirrenbach for stimulating discussions. We also thank the anonymous referee for their insightful comments that improved the manuscript. This work was supported by the Deutsche Forschungsgemeinschaft (DFG) via the DFG Research Unit FOR2544 “Blue Planets around Red Stars” (RE 2694/8-1), as well as through the DFG priority programs SPP 1992: “Exoplanet Diversity” (KL 1469/17-1) and SPP 1833 “Building a Habitable Earth” (KL 1469/13-(1-2)). This material is based upon work supported by the National Aeronautics and Space Administration under Agreement No. 80NSSC21K0593 for the program “Alien Earths.” The results reported herein benefitted from collaborations and/or information exchange within NASA’s Nexus for Exoplanet System Science (NExSS) research coordination network sponsored by NASA’s Science Mission Directorate. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. This research has made use of the VizieR catalogue access tool, CDS, Strasbourg, France (DOI:10.26093/cds/vizier). The original description of the VizieR service was published in 2000, A&AS 143, 23.
Appendix A Planet and Stellar Sample
Observed stars used in this study. Adapted from Sabotta et al. (2021) and Bonfils et al. (2013).
Observed planets used in this study. Adapted from Sabotta et al. (2021) and Bonfils et al. (2013).
Appendix B Influence of the Inner Disk Edge on Orbital Periods
In Sect. 4.4 we showed that our model produces synthetic detection rates that decrease approximately log-linearly with orbital period. This shape is caused by the combination of the underlying synthetic period distribution and applying the detection bias to the synthetic sample, which favors short-period planets over more distant ones. The relative occurrence rates differ from the Kepler sample, which peaks at ~10 d and declines for shorter orbital periods (Howard et al. 2012; Mulders et al. 2015a; Carrera et al. 2019). We observed a similar departure from a linear trend at the shortest orbital periods in the HARPS &CARM70 sample for the more massive stars.
This raises the question if the continuous decline in the model is merely defined by a numerical inner disk edge that is too close to the star. To explore this, we examine the period distribution of a comparison population with inner edges at periods >7.3 d instead of the nominal distribution with a median of 4.74d (Fig. B.l). Differences between the populations are visible, but no clear deviation from the original trend appears. In particular, the increased distance of the disk edge is not sufficient to overcome the effect of the detection bias and to cause a break in the distribution with a drop at small periods. An extended cavity hence fails to fully explain the observed lack of inner planets around the more massive stars in our sample.
 |
Fig. B.1 Dependence of the orbital period distribution on the position of the inner disk edge. For each stellar host mass bin, we show the nominal biased synthetic population and a comparison sample with inner disk edges greater than 7.3 d (dashed gray lines), which is the 68th percentile of the distribution. While differences occur, there is no clear deviation from the approximate linear trend. |
References
- Adams, F.C., & Benz, W. 1992, ASP Conf. Ser., 32, 170 [NASA ADS] [Google Scholar]
- Adams, F.C., Meyer, M.R., & Adams, A.D. 2021, ApJ, 909, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Alcalá, J.M., Manara, C.F., Natta, A., et al. 2017, A&A, 600, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alibert, Y., Mordasini, C., Benz, W., & Winisdoerffer, C. 2005, A&A, 434, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alibert, Y., Mordasini, C., & Benz, W. 2011, A&A, 526, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alibert, Y., Carron, F., Fortier, A., et al. 2013, A&A, 558, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Amado, P.J., Bauer, F.F., Rodriguez Lopez, C., et al. 2021, A&A, 650, A188 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anderson, T.W., & Darling, D.A. 1952, Ann. Math. Stat., 23, 193 [Google Scholar]
- Andrews, S.M., Huang, J., Pérez, L.M., et al. 2018, ApJ, 869, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Anglada-Escudé, G., Boss, A.P., Weinberger, A.J., et al. 2012, ApJ, 746, 37 [CrossRef] [Google Scholar]
- Anglada-Escudé, G., Tuomi, M., Gerlach, E., et al. 2013, A&A, 556, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ansdell, M., Williams, J.P., Manara, C.F., et al. 2017, AJ, 153, 240 [CrossRef] [Google Scholar]
- Astudillo-Defru, N., Forveille, T., Bonfils, X., et al. 2017, A&A, 602, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ataiee, S., & Kley, W. 2021, A&A, 648, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baraffe, I., Homeier, D., Allard, F., & Chabrier, G. 2015, A&A, 577, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baroch, D., Morales, J.C., Ribas, I., et al. 2018, A&A, 619, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baroch, D., Morales, J.C., Ribas, I., et al. 2021, A&A, 653, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bauer, F.F., Zechmeister, M., Kaminski, A., et al. 2020, A&A, 640, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benítez-Llambay, P., Masset, F., & Beaugé, C. 2011, A&A, 528, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bennett, D.P., Bhattacharya, A., Beaulieu, J.-P., et al. 2020, AJ, 159, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, D.P., Ranc, C., & Fernandes, R.B. 2021, AJ, 162, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Bhattacharya, A., Bennett, D.P., Beaulieu, J.P., et al. 2021, AJ, 162, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Birnstiel, T., Klahr, H., & Ercolano, B. 2012, A&A, 539, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Izidoro, A., Johansen, A., et al. 2019, A&A, 623, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bluhm, P., Luque, R., Espinoza, N., et al. 2020, A&A, 639, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bodenheimer, P., & Pollack, J.B. 1986, Icarus, 67, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Boisse, I., Bouchy, F., Hébrard, G., et al. 2011, A&A, 528, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfils, X., Forveille, T., Delfosse, X., et al. 2005, A&A, 443, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfils, X., Mayor, M., Delfosse, X., et al. 2007, A&A, 474, 293 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfils, X., Delfosse, X., Udry, S., et al. 2013, A&A, 549, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borucki, W.J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [Google Scholar]
- Boss, A.P. 1997, Science, 276, 1836 [NASA ADS] [CrossRef] [Google Scholar]
- Brahm, R., Nielsen, L.D., Wittenmyer, R.A., et al. 2020, AJ, 160, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Brügger, N., Alibert, Y., Ataiee, S., & Benz, W. 2018, A&A, 619, A174 [Google Scholar]
- Brügger, N., Burn, R., Coleman, G.A., Alibert, Y., & Benz, W. 2020, A&A, 640, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buchhave, L.A., Bitsch, B., Johansen, A., et al. 2018, ApJ, 856, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Burke, C.J., Christiansen, J.L., Mullally, F., et al. 2015, ApJ, 809, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Burn, R., Schlecker, M., Mordasini, C., et al. 2021, A&A, 656, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Butler, R.P., Vogt, S.S., Marcy, G.W., et al. 2004, ApJ, 617, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, A. 1978, Moon Planets, 18, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Carrera, D., Ford, E.B., & Izidoro, A. 2019, MNRAS, 486, 3874 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, J.E. 1999, MNRAS, 304, 793 [NASA ADS] [CrossRef] [Google Scholar]
- Cifuentes, C., Caballero, J.A., Cortés-Contreras, M., et al. 2020, A&A, 642, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clarke, C.J., Gendrin, A., Sotomayor, M., et al. 2001, MNRAS, 328, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Cloutier, R., Charbonneau, D., Stassun, K.G., et al. 2021, AJ, 162, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Coleman, G.A.L., & Nelson, R.P. 2014, MNRAS, 445, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Correia, A.C.M., Couetdic, J., Laskar, J., et al. 2010, A&A, 511, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cresswell, P., & Nelson, R.P. 2008, A&A, 482, 677 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cridland, A.J., Pudritz, R.E., & Alessi, M. 2016, MNRAS, 461, 3274 [CrossRef] [Google Scholar]
- Cumming, A., Butler, R.P., Marcy, G.W., et al. 2008, PASP, 120, 531 [NASA ADS] [CrossRef] [Google Scholar]
- D'Angelo, G., & Lubow, S.H. 2008, ApJ, 685, 560 [CrossRef] [Google Scholar]
- Delfosse, X., Forveille, T., Mayor, M., et al. 1998, A&A, 338, L67 [Google Scholar]
- Delfosse, X., Forveille, T., Ségransan, D., et al. 2000, A&A, 364, 217 [NASA ADS] [Google Scholar]
- Delfosse, X., Bonfils, X., Forveille, T., et al. 2013, A&A, 553, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dittkrist, K.M., Mordasini, C., Klahr, H., Alibert, Y., & Henning, T. 2014, A&A, 567, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dong, S., Gould, A., Udalski, A., et al. 2009, ApJ, 695, 970 [NASA ADS] [CrossRef] [Google Scholar]
- Drazkowska, J., & Alibert, Y. 2017, A&A, 608, A92 [CrossRef] [EDP Sciences] [Google Scholar]
- Dressing, C.D., & Charbonneau, D. 2015, ApJ, 807, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Díaz, R.F., Delfosse, X., Hobson, M.J., et al. 2019, A&A, 625, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Emsenhuber, A., Mordasini, C., Burn, R., et al. 2021a, A&A, 656, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Emsenhuber, A., Mordasini, C., Burn, R., et al. 2021b, A&A, 656, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Endl, M., Cochran, W.D., Kurster, M., et al. 2006, ApJ, 649, 436 [NASA ADS] [CrossRef] [Google Scholar]
- Espinoza, N., Brahm, R., Jordân, A., et al. 2016, ApJ, 830, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, D.A., & Valenti, J. 2005, ApJ, 622, 1102 [NASA ADS] [CrossRef] [Google Scholar]
- Flock, M., Fromang, S., Turner, N.J., & Benisty, M. 2016, ApJ, 827, 144 [CrossRef] [Google Scholar]
- Flock, M., Fromang, S., Turner, N.J., & Benisty, M. 2017, ApJ, 835, 230 [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D.W., & Morton, T.D. 2014, ApJ, 795, 64 [CrossRef] [Google Scholar]
- Fortier, A., Alibert, Y., Carron, F., Benz, W., & Dittkrist, K.M. 2013, A&A, 549, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Forveille, T., Bonfils, X., Delfosse, X., et al. 2009, A&A, 493, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fulton, B.J., Rosenthal, L.J., Hirsch, L.A., et al. 2021, ApJS, 255, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Gaidos, E., Mann, A.W., Kraus, A.L., & Ireland, M. 2016, MNRAS, 457, 2877 [NASA ADS] [CrossRef] [Google Scholar]
- Gallet, F., Bolmont, E., Mathis, S., Charbonnel, C., & Amard, L. 2017, A&A, 604, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gammie, C.F. 1996, ApJ, 457, 355 [Google Scholar]
- Gerbig, K., Lenz, C.T., & Klahr, H. 2019, A&A, 629, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghezzi, L., Montet, B.T., & Johnson, J.A. 2018, ApJ, 860, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Gibbs, A., Bixel, A., Rackham, B.V., et al. 2020, AJ, 159, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, G. 1997, MNRAS, 285, 403 [Google Scholar]
- González-Álvarez, E., Zapatero Osorio, M.R., Caballero, J.A., et al. 2020, A&A, 637, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gould, A., Dong, S., Gaudi, B.S., et al. 2010, ApJ, 720, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- Günther, H.M. 2013, Astron. Nachr., 334, 67 [CrossRef] [Google Scholar]
- Haghighipour, N., Vogt, S.S., Paul Butler, R., et al. 2010, ApJ, 715, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Haisch, K.E., Lada, E.A., & Lada, C.J. 2001, ApJ, 553, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Han, C., Udalski, A., Kim, D., et al. 2021, A&A, 655, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hardegree-Ullman, K.K., Cushing, M.C., Muirhead, P.S., & Christiansen, J.L. 2019, AJ, 158, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Hartigan, J.A., & Hartigan, P.M. 1985, Ann. Stat., 13, 70 [CrossRef] [Google Scholar]
- Hatzes, A.P. 2016, A&A, 585, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hatzes, A.P., & Rauer, H. 2015, ApJ, 810, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Hirsch, L.A., Rosenthal, L., Fulton, B.J., et al. 2021, AJ, 161, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, S., & Turner, E.L. 2011, ApJ, 739, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Hobson, M.J., Brahm, R., Jordán, A., et al. 2021, AJ, 161, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, A.W., Johnson, J.A., Marcy, G.W., et al. 2010, ApJ, 721, 1467 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, A.W., Marcy, G.W., Bryson, S.T., et al. 2012, ApJS, 201, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Hsu, D.C., Ford, E.B., & Terrien, R. 2020, MNRAS, 498, 2249 [CrossRef] [Google Scholar]
- Hueso, R., & Guillot, T. 2005, A&A, 442, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hwang, K.-H., Zang, W., Gould, A., et al. 2022, AJ, 163, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Ida, S., & Lin, D.N.C. 2005, ApJ, 626, 1045 [NASA ADS] [CrossRef] [Google Scholar]
- Ida, S., & Lin, D.N.C. 2008, ApJ, 673, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Ida, S., & Lin, D.N.C. 2010, ApJ, 719, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Ida, S., & Makino, J. 1993, Icarus, 106, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Inaba, S., Tanaka, H., Nakazawa, K., Wetherill, G.W., & Kokubo, E. 2001, Icarus, 149, 235 [CrossRef] [Google Scholar]
- Jankovic, M.R., Owen, J.E., Mohanty, S., & Tan, J.C. 2021, MNRAS, 504, 280 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffers, S.V., Schöfer, P., Lamert, A., et al. 2018, A&A, 614, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jin, S., Mordasini, C., Parmentier, V., et al. 2014, ApJ, 795, 65 [Google Scholar]
- Johnson, J.A., Butler, R.P., Marcy, G.W., et al. 2007, ApJ, 670, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J.A., Aller, K.M., Howard, A.W., & Crepp, J.R. 2010, PASP, 122, 905 [NASA ADS] [CrossRef] [Google Scholar]
- Jordan, A., Hartman, J.D., Bayliss, D., et al. 2022, AJ, 163, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Kaminski, A., Trifonov, T., Caballero, J.A., et al. 2018, A&A, 618, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kemmer, J., Stock, S., Kossakowski, D., et al. 2020, A&A, 642, A236 [EDP Sciences] [Google Scholar]
- Kennedy, G.M., & Kenyon, S.J. 2008, ApJ, 673, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D., Nesvorny, D., Hartman, J., et al. 2019, MNRAS, 486, 4980 [CrossRef] [Google Scholar]
- Klahr, H., & Bodenheimer, P. 2006, ApJ, 639, 432 [Google Scholar]
- Kossakowski, D., Kemmer, J., Bluhm, P., et al. 2021, A&A, 656, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kratter, K.M., Murray-Clay, R.A., & Youdin, A.N. 2010, ApJ, 710, 1375 [NASA ADS] [CrossRef] [Google Scholar]
- Kurtovic, N.T., Pinilla, P., Long, F., et al. 2021, A&A, 645, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lalitha, S., Baroch, D., Morales, J.C., et al. 2019, A&A, 627, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambrechts, M., & Johansen, A. 2012, A&A, 544, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambrechts, M., Johansen, A., & Morbidelli, A. 2014, A&A, 572, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leâo, I.C., Canto Martins, B.L., Alves, S., et al. 2018, A&A, 620, A139 [CrossRef] [EDP Sciences] [Google Scholar]
- Lenz, C.T., Klahr, H., & Birnstiel, T. 2019, ApJ, 874, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Lienhard, F., Queloz, D., Gillon, M., et al. 2020, MNRAS, 497, 3790 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, B., Lambrechts, M., Johansen, A., & Liu, F. 2019, A&A, 632, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, B., Lambrechts, M., Johansen, A., Pascucci, I., & Henning, T. 2020, A&A, 638, A88 [EDP Sciences] [Google Scholar]
- Luque, R., Nowak, G., Pallé, E., et al. 2018, A&A, 620, A171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lüst, R. 1952, Zeitschrift Naturforschung Teil A, 7, 87 [CrossRef] [Google Scholar]
- Lynden-Bell, D., & Pringle, J.E. 1974, MNRAS, 168, 603 [Google Scholar]
- Mamajek, E.E., Usuda, T., Tamura, M., & Ishii, M. 2009, AIP Conf. Proc., 1158, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Manara, C.F., Robberto, M., Da Rio, N., et al. 2012, ApJ, 755, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Manara, C.F., Morbidelli, A., & Guillot, T. 2018, A&A, 618, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marcy, G.W., Butler, R.P., Vogt, S.S., Fischer, D., & Lissauer, J.J. 1998, ApJ, 505, L147 [NASA ADS] [CrossRef] [Google Scholar]
- Marcy, G.W., Butler, R.P., Fischer, D., et al. 2001, ApJ, 556, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Marfil, E., Tabernero, H.M., Montes, D., et al. 2021, A&A, 656, A162 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masset, F.S., Morbidelli, A., Crida, A., & Ferreira, J. 2006, ApJ, 642, 478 [NASA ADS] [CrossRef] [Google Scholar]
- Matsuyama, I., Johnstone, D., & Hartmann, L. 2003, ApJ, 582, 893 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Mayor, M., Bonfils, X., Forveille, T., et al. 2009, A&A, 507, 487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mayor, M., Marmier, M., Lovis, C., et al. 2011, ArXiv e-prints [arXiv: 1189.2497] [Google Scholar]
- Ment, K., Irwin, J., Charbonneau, D., et al. 2020, AJ, 161, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Miguel, Y., & Ida, S. 2016, Icarus, 266, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Miguel, Y., Cridland, A., Ormel, C.W., Fortney, J.J., & Ida, S. 2020, MNRAS, 491, 1998 [NASA ADS] [Google Scholar]
- Millholland, S., Laughlin, G., Teske, J., et al. 2018, AJ, 155, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Mishra, L., Alibert, Y., Leleu, A., et al. 2021, A&A, 656, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mizuno, H. 1980, Prog. Theor. Phys., 64, 544 [Google Scholar]
- Mizuno, H., Nakazawa, K., & Hayashi, C. 1978, Prog. Theor. Phys., 60, 699 [Google Scholar]
- Moe, M., & Kratter, K.M. 2021, MNRAS, 507, 3593 [NASA ADS] [CrossRef] [Google Scholar]
- Mohanty, S., Jankovic, M.R., Tan, J.C., & Owen, J.E. 2018, ApJ, 861, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Moldenhauer, T.W., Kuiper, R., Kley, W., & Ormel, C.W. 2021, A&A, 646, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molyarova, T., Akimkin, V., Semenov, D., et al. 2017, ApJ, 849, 130 [Google Scholar]
- Morales, J.C., Mustill, A.J., Ribas, I., et al. 2019, Science, 365, 1441 [NASA ADS] [CrossRef] [Google Scholar]
- Mordasini, C. 2018, in Handbook of Exoplanets (Cham: Springer International Publishing), 2425 [CrossRef] [Google Scholar]
- Mordasini, C., Alibert, Y., & Benz, W. 2009a, A&A, 501, 1139 [CrossRef] [EDP Sciences] [Google Scholar]
- Mordasini, C., Alibert, Y., Benz, W., & Naef, D. 2009b, A&A, 501, 1161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mordasini, C.A., Alibert, Y., Klahr, H.H., & Henning, T. 2012, A&A, 547, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mulders, G.D., Pascucci, I., & Apai, D. 2015a, ApJ, 798, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Mulders, G.D., Pascucci, I., & Apai, D. 2015b, ApJ, 814, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Mulders, G.D., Pascucci, I., Apai, D., & Ciesla, F.J. 2018, AJ, 156, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Mulders, G.D., Mordasini, C., Pascucci, I., et al. 2019, The ApJ, 887, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Mulders, G.D., Drazkowska, J., van der Marel, N., Ciesla, F.J., & Pascucci, I. 2021, ApJ, 920, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Muzerolle, J., Hillenbrand, L., Calvet, N., Briceno, C., & Hartmann, L. 2003, ApJ, 592, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Nagel, E., Czesla, S., Schmitt, J.H., et al. 2019, A&A, 622, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakamoto, T., & Nakagawa, Y. 1994, ApJ, 421, 640 [Google Scholar]
- Natta, A., Testi, L., Muzerolle, J., et al. 2004, A&A, 424, 603 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neves, V., Bonfils, X., Santos, N.C., et al. 2013, A&A, 551, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nowak, G., Luque, R., Parviainen, H., et al. 2020, A&A, 642, A173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Obermeier, C., Koppenhoefer, J., Saglia, R.P., et al. 2016, A&A, 587, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Offner, S.S.R., Moe, M., Kratter, K.M., et al. 2022, ArXiv eprints [arXiv:2283.18866v1] [Google Scholar]
- Ormel, C.W., & Klahr, H.H. 2010, A&A, 520, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paardekooper, S.J., Baruteau, C., & Kley, W. 2011, MNRAS, 410, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Pascucci, I., Testi, L., Herczeg, G.J., et al. 2016, ApJ, 831, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Passegger, V.M., Reiners, A., Jeffers, S.V., et al. 2018, A&A, 615, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perri, F., & Cameron, A. 1974, Icarus, 22, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Perryman, M., Hartman, J., Bakos, G., & Lindegren, L. 2014, ApJ, 797, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Pinilla, P., Kurtovic, N.T., Benisty, M., et al. 2021, A&A, 649, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plavchan, P., & Bilinski, C. 2013, ApJ, 769, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Pollack, J.B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [Google Scholar]
- Quirrenbach, A., Amado, P.J., Mandel, H., et al. 2010, SPIE, 7735, 455 [Google Scholar]
- Quirrenbach, A., Amado, P.J., Caballero, J.A., et al. 2013, Proc. Int. Astron. Union, 8, 395 [CrossRef] [Google Scholar]
- Quirrenbach, A., Passegger, V.M., Trifonov, T., et al. 2022, A&A, 627, A49 [Google Scholar]
- Reiners, A., Ribas, I., Zechmeister, M., et al. 2018a, A&A, 609, L5 [EDP Sciences] [Google Scholar]
- Reiners, A., Zechmeister, M., Caballero, J.A., et al. 2018b, A&A, 612, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reylé, C., Jardine, K., Fouqué, P., et al. 2021, A&A, 650, A201 [Google Scholar]
- Ribas, Ä., Bouy, H., & Merin, B. 2015, A&A, 576, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ribas, I., Tuomi, M., Reiners, A., et al. 2018, Nature, 563, 365 [Google Scholar]
- Rivera, E.J., Lissauer, J.J., Butler, R.P., et al. 2005, ApJ, 634, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, P., Mahadevan, S., Endl, M., & Roy, A. 2014, Science, 345, 440 [Google Scholar]
- Rosenthal, L.J., Fulton, B.J., Hirsch, L.A., et al. 2021, ApJS, 255, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Sabotta, S., Schlecker, M., Chaturvedi, P., et al. 2021, A&A, 653, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N.C., Israelian, G., & Mayor, M. 2001, A&A, 373, 1019 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N.C., Israelian, G., Mayor, M., Rebolo, R., & Udry, S. 2003, A&A, 398, 363 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N.C., Israelian, G., & Mayor, M. 2004, A&A, 415, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sarkis, P., Henning, T., Kürster, M., et al. 2018, AJ, 155, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Schib, O., Mordasini, C., Wenger, N., Marleau, G.-D., & Helled, R. 2021, A&A, 645, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlecker, M., Kossakowski, D., Brahm, R., et al. 2020, AJ, 160, 275 [Google Scholar]
- Schlecker, M., Mordasini, C., Emsenhuber, A., et al. 2021a, A&A, 656, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlecker, M., Pham, D., Burn, R., et al. 2021b, A&A, 656, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scholz, F.W., & Stephens, M.A. 2007, J. Am. Stat. Assoc., 82, 918 [Google Scholar]
- Shakura, N.I., & Sunyaev, R. a. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Sozzetti, A., Giacobbe, P., Lattanzi, M.G., et al. 2014, MNRAS, 437, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Stock, S., Kemmer, J., Reffert, S., et al. 2020a, A&A, 636, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stock, S., Nagel, E., Kemmer, J., et al. 2020b, A&A, 643, A112 [EDP Sciences] [Google Scholar]
- Strugarek, A., Bolmont, E., Mathis, S., et al. 2017, ApJ, 847, L16 [Google Scholar]
- Suzuki, D., Bennett, D.P., Sumi, T., et al. 2016, ApJ, 833, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Suzuki, D., Bennett, D.P., Ida, S., et al. 2018, ApJ, 869, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Szulágyi, J., Morbidelli, A., Crida, A., & Masset, F. 2014, ApJ, 782, 65 [CrossRef] [Google Scholar]
- Tal-Or, L., Zechmeister, M., Reiners, A., et al. 2018, A&A, 614, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thiabaud, A., Marboeuf, U., Alibert, Y., et al. 2014, A&A, 562, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thommes, E.W., Matsumura, S., & Rasio, F.A. 2008, Science, 321, 814 [NASA ADS] [CrossRef] [Google Scholar]
- Thorngren, D.P., Fortney, J.J., Murrayclay, R.A., & Lopez, E.D. 2016, ApJ, 831, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Trifonov, T., Kürster, M., Zechmeister, M., et al. 2018, A&A, 609, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trifonov, T., Lee, M.H., Kürster, M., et al. 2020a, A&A, 638, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trifonov, T., Tal-Or, L., Zechmeister, M., et al. 2020b, A&A, 636, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trifonov, T., Caballero, J.A., Morales, J.C., et al. 2021, Science, 371, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Tychoniec, L., Tobin, J.J., Karska, A., et al. 2018, ApJS, 238, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Udalski, A., Jaroszynski, M., Paczynski, B., et al. 2005, ApJ, 628, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Udry, S., Bonfils, X., Delfosse, X., et al. 2007, A&A, 469, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venuti, L., Bouvier, J., Cody, A.M., et al. 2017, A&A, 599, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Voelkel, O., Klahr, H., Mordasini, C., Emsenhuber, A., & Lenz, C. 2020, A&A, 642, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Voelkel, O., Deienno, R., Kretke, K., & Klahr, H. 2021a, A&A, 645, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Voelkel, O., Deienno, R., Kretke, K., & Klahr, H. 2021b, A&A, 645, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wells, R.D., Rackham, B.V., Schanche, N., et al. 2021, A&A, 653, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wittenmyer, R.A., Butler, R.P., Horner, J., et al. 2020, MNRAS, 491, 5248 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, D.J., Wittenmyer, R.A., Tinney, C.G., Bentley, J.S., & Zhao, J. 2016, ApJ, 817, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Zang, W., Hwang, K.-H., Udalski, A., et al. 2021, AJ, 162, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Zawadzki, B., Carrera, D., & Ford, E.B. 2021, MNRAS, 503, 1390 [NASA ADS] [CrossRef] [Google Scholar]
- Zechmeister, M., Kürster, M., & Endl, M. 2009, A&A, 505, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zechmeister, M., Reiners, A., Amado, P.J., et al. 2018, A&A, 609, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zechmeister, M., Dreizler, S., Ribas, I., et al. 2019, A&A, 627, A49 [NASA ADS] [EDP Sciences] [Google Scholar]
For the distribution of the numbers of spectra in spectral subtype we refer to Fig. 10 in Sabotta et al. (2021).
0.4 M⊙ is centered between two of our simulated, discrete stellar masses and close to the threshold mass where stars become fully convective (Cifuentes et al. 2020).
All Tables
Observed stars used in this study. Adapted from Sabotta et al. (2021) and Bonfils et al. (2013).
Observed planets used in this study. Adapted from Sabotta et al. (2021) and Bonfils et al. (2013).
All Figures
 |
Fig. 1 Observed and simulated stellar sample. Top: combined observed stellar mass distribution is composed of different distributions for the HARPS (purple) and CARM70 samples (yellow), respectively. The host star masses in the synthetic NGM population are discrete. By weighted resampling of its systems according to the combined observed sample (red), we obtain a new distribution that approximates it (blue). Bottom: number of observations per stellar mass bin with the same color code as the top figure. Every target star is represented by a white box. |
| In the text | |
 |
Fig. 2 Combined detection probabilities for the HARPS&CARM70 survey binned to the stellar masses used in the simulations. The color code represents the detection probability of a planet with the corresponding period, minimum mass, and host star mass. The zero-detection threshold resides at slightly lower minimum masses for lower-mass stars, and the detection map for 0.7 M⊙ stars is patchy due to the small sample there. |
| In the text | |
 |
Fig. 3 Observed and biased synthetic planets in minimum mass-period space. Markers show confirmed planets from the HARPS and CARM70 surveys, respectively. The color code shows the frequency of simulated planets in this parameter space after applying the detection bias of the combined HARPS &CARM70 survey. Low-mass planets are well reproduced by the model, but intermediate-mass planets appear more common than theoretically predicted. |
| In the text | |
 |
Fig. 4 As Fig. 3, but partitioned according to host star mass. In the biased synthetic population, the domination by low-mass planets on short to intermediate orbits is similar for all stellar masses, but giant planets occur only around stars with masses 0.5 M⊙ and higher. In contrast, the subgiant and giant planets in the observed sample occur most frequently around less massive stars. GJ 3512b, the giant planet in the 0.1 M⊙ panel, is particularly at odds with theoretical predictions. No simulated planets with M sin(i) > 10 M⊙ occur in this stellar mass bin. |
| In the text | |
 |
Fig. 5 Simulated and observed planet detections as a function of host star mass. In each stellar mass bin, vertical lines denote 68% confidence intervals based on the binomial distribution (not visible for the synthetic population), and the counts are normalized to the number of stars in that bin. The synthetic population features discrete M* values and shows a linear increase of detections with increasing stellar mass. The observed sample shows no clear trend. |
| In the text | |
 |
Fig. 6 Minimum mass distribution of synthetic and observed planets. Thick vertical lines show 68% confidence intervals based on the binomial distribution. Thin blue lines show standard deviations of 2000 bootstrapped synthetic samples, where each sample had the size of the observed sample. Top: total normalized counts. The distribution of the biased synthetic population appears bimodal in M sin(i). The observed sample shows a peak in the terrestrial planet regime of a few Earth masses and a continuous downward slope without a valley. At low masses, the theoretical and observed distributions agree. The formation model underproduces planets ≳30 M⊙ and features a “sub-Saturn valley.” Center and bottom: normalized counts for late (<0.4 M⊙) and early (>0.4 M⊙) M dwarfs separately. At minimum masses beyond ~30 M⊙, theory and observations disagree: while observed subgiant and giant planets occur mostly around stars with masses ~0.3 M⊙, the formation model produces such planets only around more massive stars. |
| In the text | |
 |
Fig. 7 Period distribution of observed and synthetic planets. As in Fig. 6, thick error bars denote 68% confidence intervals based on the binomial distribution, and thin lines show the standard deviations of bootstrapped simulated samples. Top: total normalized counts. The distributions are comparable over most of the range, except for a peak at ~10–30 d that only occurs in the observed sample. Center and bottom: nNormalized counts for early (>0.4 M⊙) and late (<0.4 M⊙) M dwarfs separately, both showing a high detection rate at a few tens of days in the observed sample. Significantly fewer short-period planets are found around higher-mass stars, which is in disagreement with our model. |
| In the text | |
 |
Fig. 8 Giant planet detections as a function of stellar mass. From the HARPS and CARMENES planets presented here (red), the California Legacy Survey (Rosenthal et al. 2021, gray), and our synthetic NGM planets (blue), we include detections with RV semi-amplitude K > 10 m s−1, M sin(i) > 100 M⊙, and P < 1000 d. We removed planets around close spectroscopic binaries (P < 20 yr) reported in Rosenthal et al. (2021). In addition, we show the fit of Ghezzi et al. (2018) for metallicities consistent with the assumptions made to draw the synthetic planets. Shaded areas and vertical lines denote 68% confidence intervals, respectively. We note that the HARPS &CARM70 sample is limited to M dwarfs ≲0.7 M⊙. The observed giant planets around very low-mass stars indicate a possible break of the monotonie stellar mass trend at around ~0.5 M⊙, which theoretical predictions fail to reproduce. If type-I migration is inhibited by a factor ×10 in the simulations (dashed blue line), giant planets occur also in systems with lower stellar masses. |
| In the text | |
 |
Fig. B.1 Dependence of the orbital period distribution on the position of the inner disk edge. For each stellar host mass bin, we show the nominal biased synthetic population and a comparison sample with inner disk edges greater than 7.3 d (dashed gray lines), which is the 68th percentile of the distribution. While differences occur, there is no clear deviation from the approximate linear trend. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


