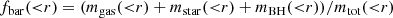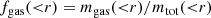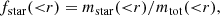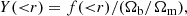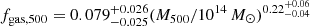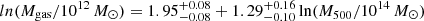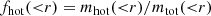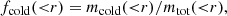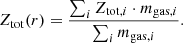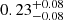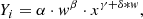| Issue |
A&A
Volume 663, July 2022
|
|
|---|---|---|
| Article Number | L6 | |
| Number of page(s) | 8 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202244068 | |
| Published online | 21 July 2022 | |
Letter to the Editor
Mapping ‘out-of-the-box’ the properties of the baryons in massive halos
1
Dipartimento di Fisica e Astronomia, Universitá di Bologna, Via Gobetti 92/3, 40121 Bologna, Italy
e-mail: matteo.angelinelli2@unibo.it
2
INAF, Osservatorio di Astrofisica e Scienza dello Spazio, Via Pietro Gobetti 93/3, 40121 Bologna, Italy
3
INFN, Sezione di Bologna, Viale Berti Pichat 6/2, 40127 Bologna, Italy
4
Universitäts-Sternwarte, Fakultät für Physik, Ludwig-Maximilians-Universität München, Scheinerstr.1, 81679 München, Germany
5
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Straße 1, 85741 Garching, Germany
6
Hamburger Sternwarte, University of Hamburg, Gojenbergsweg 112, 21029 Hamburg, Germany
7
Istituto di Radio Astronomia, INAF, Via Gobetti 101, 40121 Bologna, Italy
8
INAF, Osservatorio Astronomico di Trieste, Via G.B. Tiepolo 11, 34143 Trieste, Italy
9
IFPU, Institute for Fundamental Physics of the Universe, Via Beirut 2, 34014 Trieste, Italy
Received:
20
May
2022
Accepted:
23
June
2022
We study the distributions of the baryons in massive halos (Mvir > 1013 h−1 M⊙) in the Magneticum suite of smoothed particle hydrodynamical cosmological simulations, out to the unprecedented radial extent of 10R500, c. We confirm that, under the action of non-gravitational physical phenomena, the baryon mass fraction is lower in the inner regions (< R500, c) of increasingly less massive halos, and rises moving outwards, with values that span from 51% (87%) of the cosmological value in the regions around R500, c to 95% (100%) at 10R500, c in the systems with the lowest (highest; Mvir ∼ 5 × 1014 h−1 M⊙) masses. The galaxy groups almost match the gas (and baryon) fraction measured in the most massive halos only at very large radii (r > 6R500, c), where the baryon depletion factor Ybar = fbar/(Ωb/Ωm) approaches the value of unity, expected for ‘closed-box’ systems. We find that both the radial and mass dependence of the baryon, gas, and hot depletion factors are predictable and follow a simple functional form. The star mass fraction is higher in less massive systems, decreases systematically with increasing radii, and reaches a constant value of Ystar ≈ 0.09, where the gas metallicity is also constant, regardless of the host halo mass, as a result of the early (z > 2) enrichment process.
Key words: methods: numerical / large-scale structure of Universe / galaxies: clusters: intracluster medium / galaxies: groups: general / hydrodynamics / galaxies: clusters: general
© M. Angelinelli et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
Knowing the baryon content of groups and clusters of galaxies, the most massive gravitationally bound structures in the Universe, is key to connecting their evolution with cosmology. A general expectation is that the relative amount of baryons they contain, with respect to their total mass, must match the ratio between the cosmological baryon density, Ωb, and the total matter density, Ωm. However, for this to be true, sufficiently large volumes must be considered in order to treat such systems as ‘closed boxes’ (Gunn et al. 1972; Bertschinger 1985; Voit 2005) and allow the additional, time-integrated effect of feedback from galaxy formation to be neglected (e.g., Allen et al. 2011). Any departure from the ideal condition of a closed box should leave an imprint on the distribution of the different components of the baryon budget as a function of both radius and halo mass (Limber 1959). Galaxy groups with typical masses of 1013 − 14 M⊙, being characterised by a shallower gravitational potential than the one found in more massive systems, can hardly be considered as ‘closed’. They are thus unique laboratories for studying the interplay of the many different physical processes that affect the evolution of baryonic matter during the hierarchical structure formation (Springel 2005), as well as the energetic feedback from the many galaxies that co-evolve within them (or are continuously accreted over time). The fact that the galaxy groups are at the peak of the halo mass function makes their cosmological and astrophysical role particularly relevant.
Many observational studies (Sun et al. 2009; Ettori 2015; Lovisari et al. 2015; Eckert et al. 2016; Nugent et al. 2020) show how the baryon fraction in the central region of galaxy clusters and groups (< R500, c) increases with the mass of the system. In the external regions, the gas distribution is only slightly constrained by X-ray observations because of their low signal with respect to the local background, although they are physically more interesting because of the increased complexity of processes that regulate the status of the gas, including some expected residual amount of non-thermal pressure (e.g., Angelinelli et al. 2020). If the expectations for a self-similar formation scenario are met for the most massive systems, then, at the group scale, the baryon content is only half of that expected from the self-similar scenario (see e.g. the review by Eckert et al. 2021). While the low X-ray surface brightness hampers observational attempts to constrain the gas content of galaxy groups and clusters (though for the most massive systems, constraints around R200, c are available in e.g., Ghirardini et al. 2019), numerical simulations are overall able to correctly reproduce many different observed physical proprieties of the gas enclosed in galaxy groups, even if the proprieties of galaxies are not well constrained (see e.g., Oppenheimer et al. 2021; Gastaldello et al. 2021). Galaxy groups are the environment where the physical mechanisms that occur on galactic scales become less dominant, though are still important, with respect to the gravity that rules on cluster scales. Large-scale numerical cosmological simulations are then needed to recover the physical properties of these elusive and numerous systems (Ettori et al. 2006; Planelles et al. 2013; Haider et al. 2016; McCarthy et al. 2017; Pillepich et al. 2018; Biffi et al. 2018c; Vallés-Pérez et al. 2020; Galárraga-Espinosa et al. 2022, and references therein), as well as to facilitate realistic predictions for the next generation of X-ray observatories (Roncarelli et al. 2018).
In this work we perform a dedicated analysis of baryon and gas fractions in regions in the outskirts of galaxy clusters and beyond in a sample of halos simulated by the Magneticum1 suite. This work is structured as follows: in Sect. 2 we briefly describe the Magneticum simulations and our sample; in Sect. 3 we present the results of our analysis and a comparison with recent observational and numerical constraints. In Sect. 5 we discuss our main findings, the limitations of our analysis, and possible implications for future work.
2. Cosmological simulations: Magneticum
We selected a sub-sample of galaxy clusters and groups, part of the simulated Box2b/hr of Magneticum simulations at redshift z = 0.25, the last available snapshot for this simulated box. The high resolution run of Box2b includes a total of 2 ⋅ 28803 particles in a volume of (640 h−1 cMpc)3. The particle masses are 6.9 × 108 h−1 M⊙ and 1.4 × 108 h−1 M⊙, respectively, for dark matter and the gas component, and the stellar particles have a softening of ϵ = 2 h−1 ckpc. The cosmology adopted for these simulations is the WMAP7 from Komatsu et al. (2011), with a total matter density of Ωm = 0.272, of which 16.8% is baryons, the cosmological constant Λ0 = 0.728, the Hubble constant H0 = 70.4 km s−1 Mpc−1, the index of the primordial power spectrum n = 0.963, and the overall normalisation of the power spectrum σ8 = 0.809. The more relevant physical mechanisms included in Magneticum are: cooling, star formation, and winds with velocities of 350 km s−1 (Springel & Hernquist 2002); an explicit tracing of metal species (namely, C, Ca, O, N, Ne, Mg, S, Si, and Fe), a detailed tracking of the stellar population and chemical enrichment by Type Ia supernovae (SN-Ia), Type II supernovae (SN-II), and asymptotic giant branch (AGB) stars (Tornatore et al. 2003, 2007) and cooling tables from Wiersma et al. (2009); black holes and associated active galactic nucleus (AGN) feedback (Springel et al. 2005) with various improvements (Fabjan et al. 2010; Hirschmann et al. 2014) for the treatment of the black hole sink particles and the different feedback modes; isotropic thermal conduction of 1/20 of the standard Spitzer value (Dolag et al. 2004); a low viscosity scheme to track turbulence (Dolag et al. 2005b; Beck et al. 2016); higher-order smoothed particle hydrodynamic kernels (Dehnen & Aly 2012); and passive magnetic fields (Dolag & Stasyszyn 2009). Halos are identified using SUBFIND (Springel et al. 2001; Dolag et al. 2009), where the centre of a halo is defined as the position of the particle with the minimum of the gravitational potential. The virial mass, Mvir, is defined through the spherical overdensity as predicted by the generalised spherical top-hat collapse model (Eke et al. 1996). In particular, it is referred to Rvir, whose overdensity to the critical density follows Eq. (6) of Bryan & Norman (1998), which corresponds to ≈117 for the given redshift and cosmology. The radius R200, m (respectively R500, c) is defined as a spherical overdensity of 200 (respectively 500) to the mean (respectively critical) density in the chosen cosmology.
As shown in previous studies, the galaxy physics implemented in the Magneticum simulations leads to a successful reproduction of basic galaxy properties, such as the stellar mass function (Naab & Ostriker 2017; Lustig et al. 2022), the environmental impact of galaxy clusters on galaxy properties (Lotz et al. 2019), and the appearance of post-starburst galaxies (Lotz et al. 2021), as well as the associated AGN population at various redshifts (Hirschmann et al. 2014; Steinborn et al. 2016; Biffi et al. 2018a). At the cluster scale, Magneticum simulations have demonstrated its ability to reproduce the observable X-ray luminosity relation (Biffi et al. 2013), the pressure profile of the intracluster medium (ICM) (Gupta et al. 2017), the chemical composition of the ICM (Dolag et al. 2017; Biffi et al. 2018b), the high concentration observed in fossil groups (Ragagnin et al. 2019), and the gas properties in between galaxy clusters (Biffi et al. 2022). On larger scales, Magneticum simulations have been able to reproduce the observed Sunyaev–Zeldovich (SZ) power spectrum (Dolag et al. 2016) as well as the observed thermal history of the Universe (Young et al. 2021).
To build our sample, we divided the mass range between Mvir values of 1013 h−1 M⊙ and > 5 × 1014 h−1 M⊙ (corresponding to M500, c between 4.2 × 1012 h−1 M⊙ and 5.4 × 1014 h−1 M⊙ for the less massive and the most massive system, respectively) into 14 equal bins in logarithmic space. For each bin, we randomly selected ten objects from the simulated Box2b. The final sample is composed of a total of 140 galaxy groups and clusters, where the smallest halo is represented by 4.6 × 104 particles in the radial range shown in Fig. 1, which gives the density profiles for each object as well as the median values computed in the 14 mass bins.
 |
Fig. 1. Gas density profiles and maps. Top: radial profiles of gas density from 0.5R500, c up to 10R500, c. Grey lines indicate profiles of single objects, while coloured lines are the median values computed in different mass bins (see the colour legend). Bottom: median radial profiles of the gas density of different mass bins computed with respect to the median radial profile of the most massive bin (same colour legend as the upper plot). Insets: projected 2D electron gas density maps for the most massive (left; Mvir = 9.8 × 1014 h−1 M⊙, R500, c = 1120.4 h−1 ckpc) and the least massive (right; Mvir = 1013 h−1 M⊙, R500, c = 252.5 h−1 ckpc) objects in our sample. The blue circles represent 1, 3, 5, and 10R500, c. |
In addition, Fig. 1 also shows two gas density maps for the most massive and least massive objects in our sample, produced using the software SMAC (Dolag et al. 2005a). To also have an upper limit for the radial range of our analysis, we considered the position of the accretion shocks to be the boundary of our system. Different definitions of the position of accretion shocks can be found in the literature (Zhang et al. 2020; Aung et al. 2021). In our work, we assumed the position of the accretion shocks to be located at the same radius at which the gas entropy profile reaches its peak (Vazza et al. 2011). Expressing this distance as a function of R200, m, we find that the median distance of the accretion shock from the system centre is 3(±1)R200, m. Moreover, for our sample, we find also that R200, m is 2.3(±0.1)R500, c. As we wanted to characterise the baryon and gas fractions inside the entire volume of our galaxy groups and clusters, we combined these values and extended our analysis up to 10R500, c. A more detailed study of the position of accretion shocks in our sample will be part of a forthcoming paper.
3. The gas and baryon fractions out to 10R500, c
We defined the baryon, gas, and star fractions as
where r is the radial distance from the cluster or group centre. The different mi(< r) are referred to different particle types (gas, stars, or black holes), while mtot(< r) is the sum of the previous masses and the dark matter up to the radial shell, r. Regarding the black holes, which are no longer considered in our analysis, their median mass is 7 × 108 h−1 M⊙ and their contribution to the total baryon budget rapidly decreases at greater radial distances from the centre of the system, from 0.2% to 0.02%, without strong dependences on the halo mass. In the following we use the depletion parameter Y, defined as
where f(< r) could assume any definition given above and Ωb/Ωm = 0.168, the cosmological value of baryon over the total matter adopted for Magneticum simulations.
Firstly, we compared our results with the numerical and observational literature. In particular, in the left panel of Fig. 2, we compare our gas depletion with the values reported by Kravtsov et al. (2005) and Planelles et al. (2013). We can conclude from this comparison that the gas depletion factor we recover at R500, c for the most massive systems is in line with the numerical literature. However, on group mass scales, we expect the potential well to be less effective in bounding the accreting baryons and balancing the dispersive actions of feedback from AGN and winds from star-formation activity. Therefore, we expect a decrease in the gas depletion factor moving towards lower mass scales (see e.g., Eckert et al. 2021; Akino et al. 2022). In Fig. 2 we show how our simulated dataset is able to recover the expected and observed behaviour within R500, c.
 |
Fig. 2. Gas depletion in our sample compared with previous works. Left: radial profiles of gas depletion, from 0.5R500, c up to 1.4R500, c. Grey lines represent single objects in our sample, while the coloured ones are the median values computed in mass bins. Comparison numerical estimates from the literature are given by different symbols (black, Kravtsov et al. 2005; green, Planelles et al. 2013). From Kravtsov et al. (2005), we consider the mean value and its scatter for Ygas at R500, c in the simulations with gas dynamics and several physical processes (CSF). From Planelles et al. (2013), we plot the non-radiative run (NR), the run with star formation and feedback from a supernova explosion (CSF), and a run with the additional contribution from AGN (AGN). Right: gas depletion parameter at R500, c as a function of M500, c. Grey dots represent single objects in our sample, while the coloured ones are the median values computed in mass bins. The constraints from Kravtsov et al. (2005) (black points) are indicated in correspondence with the mass of single clusters in their analysis, whereas for Planelles et al. (2013) (green points) they are indicated in correspondence with our most massive bin. The lines and related shadow regions are the best fits proposed by Eckert et al. (2021) (purple; |
In Fig. 3 we show the distributions of the baryon (Ybar), gas (Ygas), and star (Ystar) depletion factors as functions of the radius (between 0.5R500, c and 10R500, c) and halo mass. We show that, although the baryon fraction is always ≥50% of the cosmological value Ωb/Ωm in each mass bin, it reaches the cosmological value only at radii larger than 5R500, c and only in the most massive systems. Indeed, Ybar is greater than 0.99 at r > 5R500, c in sub-sample D (comprising the most massive systems in our catalogue), whereas it has a value of about 0.83 at 5R500, c and 0.95 at 10R500, c (see Table A.1). Similar trends are observed for the gas depletion factor, Ygas. Also in this case, the larger the radii, the higher the depletion factor. Both for the baryonic matter and for the hot gas alone, less massive systems show a steeper increase in the depletion factor with increasing radius. On the contrary, the stellar depletion factor, Ystar, decreases with the radius and is higher in less massive systems. At larger radii, this behaviour is less prominent and both galaxy groups and clusters show constant and similar values of 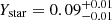 , confirming that the in situ enrichment does not play a significant role and that its uniform metal abundance is rather the consequence of the accretion of pre-enriched (at z > 2) gas (see Biffi et al. 2018c). On the other hand, a more efficient production of stars is required by the larger Ystar estimated in less massive halos within R500, c.
, confirming that the in situ enrichment does not play a significant role and that its uniform metal abundance is rather the consequence of the accretion of pre-enriched (at z > 2) gas (see Biffi et al. 2018c). On the other hand, a more efficient production of stars is required by the larger Ystar estimated in less massive halos within R500, c.
 |
Fig. 3. Depletion factors in our sample. Left: radial profiles of baryon, gas, and star depletion, from 0.5R500, c up to 10R500, c. The lines represent the median profiles in each mass bin, while the different line styles represent baryon (solid), gas (dashed), or star depletion (dash-dotted). Right: same as the plot on the left, but representing only three different gas particle selections: gas particles (dashed), hot gas with temperatures greater than 0.1 keV (dotted), and cold gas with temperatures below 0.1 keV (dash-dotted). |
Focusing on the gas component of our systems, we define fhot and fcold:
meaning a selection of gas particles based on the temperature, ‘hot’ for particles with temperatures greater than 0.1 keV and ‘cold’ for the others. In the right panel of Fig. 3, we show the radial behaviour of these quantities compared to Ygas. We note that the cold component of gas content became important at very large radii, over 6R500,c. Moreover, this cold component shows larger values for galaxy groups: it is larger than 0.2 at radii greater than 8R500, c. The hot phase presents a drop for all the mass bins at radii larger than 6R500, c, where we locate the accretion shocks in our systems on average (see Sect. 2). This means that, at the larger radii we investigate, there are also contributions from the environment in which galaxy groups and clusters reside, with a decreasing contribution to the expected gas emissivity in X-rays.
4. The radial trend of gas metallicity
The injection and evolution of metals by SN-Ia, SN-II, and AGB stars in Magneticum simulations are modelled following Tornatore et al. (2003, 2007). Although the simulation traces various elements individually, we consider here the total metallicity, that is to say, the sum of the elements heavier than helium relative to the hydrogen mass. Then, the total metallicity at each radial shell, r, Ztot(r), is the mass-weighted sum of the metallicity of the gas particles, i, with mass mgas, i that belong to the radial shell, r:
The radial shells are defined to include a fixed number of 250 particles to allow a significant statistical analysis of each of them. We normalised these values of metallicity to the solar values proposed by Asplund et al. (2009): Z⊙ = 0.0142.
In Fig. 4 we show the metallicity profiles recovered up to 10R500, c in all our halos. The profiles are remarkably similar, flattening to a constant value of about 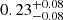 at r > 2R500, c and with a negligible dependence on the halo mass (see the median estimates in Table A.1). Some mass dependence would be expected as a consequence of any difference in star-formation activities from group to cluster scales, because groups are less effective in producing and releasing metals into their environment. The lack of evidence of such a dependence supports the expectations of the early enrichment scenario. Biffi et al. (2017; see also Biffi et al. 2018c) find that at r > 0.2R180 the metallicity is remarkably homogeneous, with almost flat profiles of the elements produced by either SN-Ia or SN-II, mostly as a consequence of the widespread displacement of metal-rich gas by early, powerful AGN bursts (z > 2 − 3) acting on small high-redshift halos, and with no significant evolution since redshift ∼2.
at r > 2R500, c and with a negligible dependence on the halo mass (see the median estimates in Table A.1). Some mass dependence would be expected as a consequence of any difference in star-formation activities from group to cluster scales, because groups are less effective in producing and releasing metals into their environment. The lack of evidence of such a dependence supports the expectations of the early enrichment scenario. Biffi et al. (2017; see also Biffi et al. 2018c) find that at r > 0.2R180 the metallicity is remarkably homogeneous, with almost flat profiles of the elements produced by either SN-Ia or SN-II, mostly as a consequence of the widespread displacement of metal-rich gas by early, powerful AGN bursts (z > 2 − 3) acting on small high-redshift halos, and with no significant evolution since redshift ∼2.
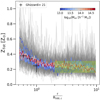 |
Fig. 4. Radial profiles of gas metallicity from 0.5R500, c up to 10R500, c. Grey lines represent single objects, while the coloured ones are the mean values computed in mass bins. The dashed green line and its related shadow region show the median and the 16th and 84th percentiles of the gas metallicity distribution over 2R500, c ( |
Given the large scatter observed in single radial profiles of metallicity in Fig. 4, we investigated the relations between the masses of the systems and metallicity. From the left panel of Fig. 5, where we show the metallicity as a function of gas mass, we note how the profiles are still highly scattered. However, looking at the values of metallicity computed at R500, c (the coloured dots in the plot), we also notice that galaxy groups (bluish dots) show a higher spread in metallicity than the galaxy clusters (reddish dots), with median values of 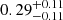 and
and 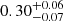 , respectively. This trend is similar to the findings discussed by Truong et al. (2019), who focused on the iron contribution in extremely central regions of simulated galaxy clusters and groups (r < 0.1R500). They also compared their results with observational work by Mernier et al. (2018). On the other hand, in the central and right panels of Fig. 5, we present the density-temperature phase diagram for the least (centre) and most (right) massive objects in our sample, colour-coding by the mass-weighted metallicity of each density-temperature bin. Here, we notice a high spread of metallicity values for both galaxy groups and clusters. Even when we consider the hot and cold gas phases separately, the scatter in metallicity is still present. From Fig. 5 as a whole, we conclude that the observed scatter in radial profiles of metallicity is due to an intrinsic scatter present in the gas particles. Moreover, the coexistence of different gas phases tends to enlarge the observed scatter.
, respectively. This trend is similar to the findings discussed by Truong et al. (2019), who focused on the iron contribution in extremely central regions of simulated galaxy clusters and groups (r < 0.1R500). They also compared their results with observational work by Mernier et al. (2018). On the other hand, in the central and right panels of Fig. 5, we present the density-temperature phase diagram for the least (centre) and most (right) massive objects in our sample, colour-coding by the mass-weighted metallicity of each density-temperature bin. Here, we notice a high spread of metallicity values for both galaxy groups and clusters. Even when we consider the hot and cold gas phases separately, the scatter in metallicity is still present. From Fig. 5 as a whole, we conclude that the observed scatter in radial profiles of metallicity is due to an intrinsic scatter present in the gas particles. Moreover, the coexistence of different gas phases tends to enlarge the observed scatter.
 |
Fig. 5. Metallicity as a function of mass and phase diagrams. Left: metallicity as a function of gas mass. The grey lines represent the profiles computed for single objects in our sample, whereas the coloured dots are the values computed at R500, c (again, for each group and cluster present in our sample). The colour-coding is given by the virial mass (Mvir) of the systems. Centre and right: density–temperature phase diagram for the less massive system (centre; Mvir = 1013 h−1 M⊙) and the most massive one in our sample (right; Mvir = 9.8 × 1014 h−1 M⊙). The colour-coding is given by the mass-weighted metallicity in each density–temperature bin. The dashed horizontal black lines represent the 0.1 keV (1.16 × 106 K) temperature cut, adopted to separate ‘hot’ and ‘cold’ gas phases. The dashed vertical line marks the gas density at R500, c. To the right of this line are the particles inside R500,c, and to the left the particles located at larger radii. |
5. Discussion and conclusions
While galaxy clusters, in particular the most massive and relaxed ones, are direct proxies of the cosmological baryon fraction (e.g., Allen et al. 2008; Ettori et al. 2009; Mantz et al. 2022), galaxy groups host an environment where the competing effects of gravity and the stellar and AGN feedbacks break the self-similar expectations regarding the gas distribution. Realistic numerical simulations are thus key to producing accurate 3D models of the likely distribution of gas in and around halos as a function of their mass.
We considered a large sample of 140 galaxy groups and clusters with Mvir > 1013 h−1 M⊙ at z = 0.25, simulated at high resolution with the Magneticum runs and analysed up to 10R500, c (i.e., roughly beyond the location of the accretion shock). We focused our analysis on the radial dependence of the depletion factors Ybar, Ygas, and Ystar (see the definitions in Sect. 3), well beyond the currently available constraints at ∼R200, c. We summarise here our main results:
-
We verified that the baryon fraction is always > 50% of the cosmological value adopted in our simulations at r > R500, c and at any mass bin. It reaches that value at ∼5R500, c, but only in the most massive systems. The Ybar in less massive systems, though it shows steeper radial profiles, remains 5% below Ωb/Ωm, even at 10R500, c (see Fig. 3 and Table A.1). Similar trends are observed for the gas component.
-
Once we divided the gas component into two different phases, hot when the temperature of the particle is greater than 0.1 keV and cold for the remaining gas, the contribution given by the cold phase is quite negligible inside 6R500, c, whereas beyond this limit, especially for less massive objects, it gradually becomes more important, reaching 45% of the entire gas contribution for galaxy groups and 25% for galaxy clusters at 10R500, c (see Fig. 3). The hot, X-ray-detectable phase is a good tracer of the total amount of gas at all the masses and always represents more than 90% (70%) of it in the most (least) massive objects within 5R500, c. At about 6R500, c, Yhot shows a drop for all mass bins. This drop is consistent with the position of the accretion shock.
-
We find that both the radial and mass dependences of Ybar, Ygas, and Yhot (see Fig. 3) are predictable and follow the following functional form:
where w = M500, c/5 × 1014 h−1 M⊙, x = r/R500, c, and α, β, γ, and δ are the free parameters quoted in Table A.2. The set of parameters (α, β, γ, δ) = (0.90, 0.12, 0.23, −0.22) provides a description within 2% of Ybar (see Fig. A.1).
-
The Ystar decreases systematically with increasing radii. While the contribution of the stellar mass fraction in the central region (< 2R500,c) is higher in less massive systems, this difference disappears at larger radii, and both galaxy groups and clusters reach a value of
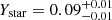 . In these regions, the metal distribution becomes constant, with a median value of
. In these regions, the metal distribution becomes constant, with a median value of 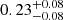 at r > 2R500, c, with no dependence on the halo mass (see Fig. 4 and Table A.1). These flat mass-independent metallicity profiles support a scenario in which the gas present in massive halos is enriched early, with a negligible contribution from recent star-formation processes (i.e., the gas is indeed expected to be mass-dependent). This result confirms, and extends to much larger radii, what has been obtained from recent work on numerical simulations (see e.g., Biffi et al. 2017, 2018c).
at r > 2R500, c, with no dependence on the halo mass (see Fig. 4 and Table A.1). These flat mass-independent metallicity profiles support a scenario in which the gas present in massive halos is enriched early, with a negligible contribution from recent star-formation processes (i.e., the gas is indeed expected to be mass-dependent). This result confirms, and extends to much larger radii, what has been obtained from recent work on numerical simulations (see e.g., Biffi et al. 2017, 2018c).
This study has explored the properties of the baryons in massive halos (Mvir > 1013 h−1 M⊙) well outside the virialised regions, where material from the cosmic field is still accreted. We have convincingly shown that these halos converge in a different way (depending on their mass) to common properties in terms of baryon, gas, stellar, and metal distribution as they approach the mean location of the accretion shock (∼6R500, c). This work allows us to make firm predictions on the average distribution of the baryons in their different phases in regions with both current (r < R500, c) and possible future observational constraints, indicating, for instance, where to look for gas that is not (X-ray) detected on the mass scales of the galaxy groups.
Acknowledgments
S.E. acknowledges financial contribution from the contracts ASI-INAF Athena 2019-27-HH.0, “Attività di Studio per la comunità scientifica di Astrofisica delle Alte Energie e Fisica Astroparticellare” (Accordo Attuativo ASI-INAF n. 2017-14-H.0), INAF mainstream project 1.05.01.86.10, and from the European Union’s Horizon 2020 Programme under the AHEAD2020 project (grant agreement n. 871158). M.A. and F.V. acknowledge the financial support by the H2020 initiative, through the ERC StG MAGCOW (n. 714196). A.R. acknowledges support from the grant PRIN-MIUR 2017 WSCC32. KD acknowledges supported by the Excellence Cluster ORIGINS which is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC-2094 – 390783311 and funding for the COMPLEX project from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program grant agreement ERC-2019-AdG 882679. The calculations for the hydro-dynamical simulations were carried out at the Leibniz Supercomputer Center (LRZ) under the project pr83li. We are especially grateful for the support by M. Petkova through the Computational Center for Particle and Astrophysics (C2PAP).
References
- Akino, D., Eckert, D., Okabe, N., et al. 2022, PASJ, 74, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Allen, S. W., Rapetti, D. A., Schmidt, R. W., et al. 2008, MNRAS, 383, 879 [Google Scholar]
- Allen, S. W., Evrard, A. E., & Mantz, A. B. 2011, ARA&A, 49, 409 [Google Scholar]
- Angelinelli, M., Vazza, F., Giocoli, C., et al. 2020, MNRAS, 495, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Aung, H., Nagai, D., & Lau, E. T. 2021, MNRAS, 508, 2071 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, A. M., Murante, G., Arth, A., et al. 2016, MNRAS, 455, 2110 [Google Scholar]
- Bertschinger, E. 1985, ApJS, 58, 39 [Google Scholar]
- Biffi, V., Dolag, K., & Böhringer, H. 2013, MNRAS, 428, 1395 [Google Scholar]
- Biffi, V., Planelles, S., Borgani, S., et al. 2017, MNRAS, 468, 531 [Google Scholar]
- Biffi, V., Dolag, K., & Merloni, A. 2018a, MNRAS, 481, 2213 [Google Scholar]
- Biffi, V., Mernier, F., & Medvedev, P. 2018b, Space Sci. Rev., 214, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Biffi, V., Planelles, S., Borgani, S., et al. 2018c, MNRAS, 476, 2689 [Google Scholar]
- Biffi, V., Dolag, K., Reiprich, T. H., et al. 2022, A&A, 661, A17 [Google Scholar]
- Bryan, G. L., & Norman, M. L. 1998, ApJ, 495, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Dehnen, W., & Aly, H. 2012, MNRAS, 425, 1068 [NASA ADS] [CrossRef] [Google Scholar]
- Dolag, K., & Stasyszyn, F. 2009, MNRAS, 398, 1678 [NASA ADS] [CrossRef] [Google Scholar]
- Dolag, K., Jubelgas, M., Springel, V., Borgani, S., & Rasia, E. 2004, ApJ, 606, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Dolag, K., Hansen, F. K., Roncarelli, M., & Moscardini, L. 2005a, MNRAS, 363, 29 [Google Scholar]
- Dolag, K., Vazza, F., Brunetti, G., & Tormen, G. 2005b, MNRAS, 364, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Dolag, K., Borgani, S., Murante, G., & Springel, V. 2009, MNRAS, 399, 497 [Google Scholar]
- Dolag, K., Komatsu, E., & Sunyaev, R. 2016, MNRAS, 463, 1797 [Google Scholar]
- Dolag, K., Mevius, E., & Remus, R.-S. 2017, Galaxies, 5, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Eckert, D., Ettori, S., Coupon, J., et al. 2016, A&A, 592, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eckert, D., Gaspari, M., Gastaldello, F., Le Brun, A. M. C., & O’Sullivan, E. 2021, Universe, 7, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Eke, V. R., Cole, S., & Frenk, C. S. 1996, MNRAS, 282, 263 [CrossRef] [Google Scholar]
- Ettori, S. 2015, MNRAS, 446, 2629 [NASA ADS] [CrossRef] [Google Scholar]
- Ettori, S., Dolag, K., Borgani, S., & Murante, G. 2006, MNRAS, 365, 1021 [NASA ADS] [CrossRef] [Google Scholar]
- Ettori, S., Morandi, A., Tozzi, P., et al. 2009, A&A, 501, 61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabjan, D., Borgani, S., Tornatore, L., et al. 2010, MNRAS, 401, 1670 [Google Scholar]
- Galárraga-Espinosa, D., Langer, M., & Aghanim, N. 2022, A&A, 661, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gastaldello, F., Simionescu, A., Mernier, F., et al. 2021, Universe, 7, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Ghirardini, V., Eckert, D., Ettori, S., et al. 2019, A&A, 621, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghizzardi, S., Molendi, S., van der Burg, R., et al. 2021, A&A, 646, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunn, J. E., Gott, J., & Richard, I. 1972, ApJ, 176, 1 [Google Scholar]
- Gupta, N., Saro, A., Mohr, J. J., Dolag, K., & Liu, J. 2017, MNRAS, 469, 3069 [Google Scholar]
- Haider, M., Steinhauser, D., Vogelsberger, M., et al. 2016, MNRAS, 457, 3024 [Google Scholar]
- Hirschmann, M., Dolag, K., Saro, A., et al. 2014, MNRAS, 442, 2304 [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [Google Scholar]
- Kravtsov, A. V., Nagai, D., & Vikhlinin, A. A. 2005, ApJ, 625, 588 [Google Scholar]
- Limber, D. N. 1959, ApJ, 130, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Lotz, M., Remus, R.-S., Dolag, K., Biviano, A., & Burkert, A. 2019, MNRAS, 488, 5370 [NASA ADS] [CrossRef] [Google Scholar]
- Lotz, M., Dolag, K., Remus, R.-S., & Burkert, A. 2021, MNRAS, 506, 4516 [NASA ADS] [CrossRef] [Google Scholar]
- Lovisari, L., Reiprich, T. H., & Schellenberger, G. 2015, A&A, 573, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lustig, P., Strazzullo, V., Remus, R. S., et al. 2022, MNRAS, submitted [arXiv:2201.09068] [Google Scholar]
- Mantz, A. B., Morris, R. G., Allen, S. W., et al. 2022, MNRAS, 510, 131 [Google Scholar]
- McCarthy, I. G., Schaye, J., Bird, S., & Le Brun, A. M. C. 2017, MNRAS, 465, 2936 [Google Scholar]
- Mernier, F., de Plaa, J., Werner, N., et al. 2018, MNRAS, 478, L116 [NASA ADS] [CrossRef] [Google Scholar]
- Naab, T., & Ostriker, J. P. 2017, ARA&A, 55, 59 [Google Scholar]
- Nugent, J. M., Dai, X., & Sun, M. 2020, ApJ, 899, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Oppenheimer, B. D., Babul, A., Bahé, Y., Butsky, I. S., & McCarthy, I. G. 2021, Universe, 7, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Pillepich, A., Nelson, D., Hernquist, L., et al. 2018, MNRAS, 475, 648 [Google Scholar]
- Planelles, S., Borgani, S., Dolag, K., et al. 2013, MNRAS, 431, 1487 [Google Scholar]
- Ragagnin, A., Dolag, K., Moscardini, L., Biviano, A., & D’Onofrio, M. 2019, MNRAS, 486, 4001 [Google Scholar]
- Roncarelli, M., Gaspari, M., Ettori, S., et al. 2018, A&A, 618, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [Google Scholar]
- Springel, V., & Hernquist, L. 2002, MNRAS, 333, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., White, S. D. M., Tormen, G., & Kauffmann, G. 2001, MNRAS, 328, 726 [Google Scholar]
- Springel, V., Di Matteo, T., & Hernquist, L. 2005, MNRAS, 361, 776 [Google Scholar]
- Steinborn, L. K., Dolag, K., Comerford, J. M., et al. 2016, MNRAS, 458, 1013 [Google Scholar]
- Sun, M., Voit, G. M., Donahue, M., et al. 2009, ApJ, 693, 1142 [NASA ADS] [CrossRef] [Google Scholar]
- Tornatore, L., Borgani, S., Springel, V., et al. 2003, MNRAS, 342, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Tornatore, L., Borgani, S., Dolag, K., & Matteucci, F. 2007, MNRAS, 382, 1050 [Google Scholar]
- Truong, N., Rasia, E., Biffi, V., et al. 2019, MNRAS, 484, 2896 [Google Scholar]
- Vallés-Pérez, D., Planelles, S., & Quilis, V. 2020, MNRAS, 499, 2303 [CrossRef] [Google Scholar]
- Vazza, F., Dolag, K., Ryu, D., et al. 2011, MNRAS, 418, 960 [NASA ADS] [CrossRef] [Google Scholar]
- Voit, G. M. 2005, Rev. Mod. Phys., 77, 207 [Google Scholar]
- Wiersma, R. P. C., Schaye, J., Theuns, T., Dalla Vecchia, C., & Tornatore, L. 2009, MNRAS, 399, 574 [NASA ADS] [CrossRef] [Google Scholar]
- Young, S., Komatsu, E., & Dolag, K. 2021, Phys. Rev. D, 104 [CrossRef] [Google Scholar]
- Zhang, C., Churazov, E., Dolag, K., Forman, W. R., & Zhuravleva, I. 2020, MNRAS, 494, 4539 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Estimates and fitting parameters of the depletion factors
Baryons (Ybar), gas (Ygas), hot gas phase (Yhot), cold gas phase (Ycold), stellar depletion factors (Ystar), and gas metallicity (Ztot) computed at four different radii (1, 3, 5, and 10 times R500,c) for four virial mass bins (A: 1013 < Mvir/h−1 M⊙ < 2·1013 (4.2·1012 < M500,c/h−1 M⊙ < 1.2·1013); B: 5·1013 < Mvir/h−1 M⊙ < 6·1013 (1.6·1013 < M500,c/h−1 M⊙ < 3.6·1013); C: 1014 < Mvir/h−1 M⊙ < 2·1014 (6.3·1013 < M500,c/h−1 < 1014); D: Mvir/h−1 M⊙ < 5·1014 (M500,c/h−1 M⊙ < 2.4·1014)). Errors are given as 16th and 84th distribution percentiles. Note that the depletion factors are computed within the given radii, unlike the metallicity values, which are given within a spherical shell (considering the same reference radii).
Best-fit parameters and related standard errors for the functional form of Eq. 8 fitted to Ybar, Ygas, and Yhot.
 |
Fig. A.1. Radial profiles of baryon depletion, from 0.5R500,c up to 2.5R500,c. The dashed lines represent the median profiles in each mass bin, according to the legend at the bottom-right corner. The solid lines are the fits performed according to the functional form of Eq. 8, with the same colour scale as the median profiles. |
We provide here details on the values of the depletion parameters under investigation in different mass bins and at various radii (see Table A.1).
We also provide the best-fit parameters obtained from the fitting function in Eq. 8 (see Table A.2). As our findings are potentially useful for making predictions and comparisons with observational work, we confined our fitting produce to a radial range similar to that available for present and near-future X-ray observations and limited to the central regions of our anazlysis, from 0.5R500,c to 2.5R500,c. The functional form is able to reproduce the behaviour of Ybar well at all considered masses, as also shown by the 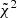 and the values of the median and maximum deviation of the model from the data (
and the values of the median and maximum deviation of the model from the data (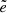 and emax, respectively) quoted in Table A.2. However, for the Ygas and Yhot, we note that our fitting procedure gives less strong results than for the Ybar case. We used the dispersion around the mean profile as weight to evaluate χ2.
and emax, respectively) quoted in Table A.2. However, for the Ygas and Yhot, we note that our fitting procedure gives less strong results than for the Ybar case. We used the dispersion around the mean profile as weight to evaluate χ2.
All Tables
Baryons (Ybar), gas (Ygas), hot gas phase (Yhot), cold gas phase (Ycold), stellar depletion factors (Ystar), and gas metallicity (Ztot) computed at four different radii (1, 3, 5, and 10 times R500,c) for four virial mass bins (A: 1013 < Mvir/h−1 M⊙ < 2·1013 (4.2·1012 < M500,c/h−1 M⊙ < 1.2·1013); B: 5·1013 < Mvir/h−1 M⊙ < 6·1013 (1.6·1013 < M500,c/h−1 M⊙ < 3.6·1013); C: 1014 < Mvir/h−1 M⊙ < 2·1014 (6.3·1013 < M500,c/h−1 < 1014); D: Mvir/h−1 M⊙ < 5·1014 (M500,c/h−1 M⊙ < 2.4·1014)). Errors are given as 16th and 84th distribution percentiles. Note that the depletion factors are computed within the given radii, unlike the metallicity values, which are given within a spherical shell (considering the same reference radii).
Best-fit parameters and related standard errors for the functional form of Eq. 8 fitted to Ybar, Ygas, and Yhot.
All Figures
 |
Fig. 1. Gas density profiles and maps. Top: radial profiles of gas density from 0.5R500, c up to 10R500, c. Grey lines indicate profiles of single objects, while coloured lines are the median values computed in different mass bins (see the colour legend). Bottom: median radial profiles of the gas density of different mass bins computed with respect to the median radial profile of the most massive bin (same colour legend as the upper plot). Insets: projected 2D electron gas density maps for the most massive (left; Mvir = 9.8 × 1014 h−1 M⊙, R500, c = 1120.4 h−1 ckpc) and the least massive (right; Mvir = 1013 h−1 M⊙, R500, c = 252.5 h−1 ckpc) objects in our sample. The blue circles represent 1, 3, 5, and 10R500, c. |
| In the text | |
 |
Fig. 2. Gas depletion in our sample compared with previous works. Left: radial profiles of gas depletion, from 0.5R500, c up to 1.4R500, c. Grey lines represent single objects in our sample, while the coloured ones are the median values computed in mass bins. Comparison numerical estimates from the literature are given by different symbols (black, Kravtsov et al. 2005; green, Planelles et al. 2013). From Kravtsov et al. (2005), we consider the mean value and its scatter for Ygas at R500, c in the simulations with gas dynamics and several physical processes (CSF). From Planelles et al. (2013), we plot the non-radiative run (NR), the run with star formation and feedback from a supernova explosion (CSF), and a run with the additional contribution from AGN (AGN). Right: gas depletion parameter at R500, c as a function of M500, c. Grey dots represent single objects in our sample, while the coloured ones are the median values computed in mass bins. The constraints from Kravtsov et al. (2005) (black points) are indicated in correspondence with the mass of single clusters in their analysis, whereas for Planelles et al. (2013) (green points) they are indicated in correspondence with our most massive bin. The lines and related shadow regions are the best fits proposed by Eckert et al. (2021) (purple; |
| In the text | |
 |
Fig. 3. Depletion factors in our sample. Left: radial profiles of baryon, gas, and star depletion, from 0.5R500, c up to 10R500, c. The lines represent the median profiles in each mass bin, while the different line styles represent baryon (solid), gas (dashed), or star depletion (dash-dotted). Right: same as the plot on the left, but representing only three different gas particle selections: gas particles (dashed), hot gas with temperatures greater than 0.1 keV (dotted), and cold gas with temperatures below 0.1 keV (dash-dotted). |
| In the text | |
 |
Fig. 4. Radial profiles of gas metallicity from 0.5R500, c up to 10R500, c. Grey lines represent single objects, while the coloured ones are the mean values computed in mass bins. The dashed green line and its related shadow region show the median and the 16th and 84th percentiles of the gas metallicity distribution over 2R500, c ( |
| In the text | |
 |
Fig. 5. Metallicity as a function of mass and phase diagrams. Left: metallicity as a function of gas mass. The grey lines represent the profiles computed for single objects in our sample, whereas the coloured dots are the values computed at R500, c (again, for each group and cluster present in our sample). The colour-coding is given by the virial mass (Mvir) of the systems. Centre and right: density–temperature phase diagram for the less massive system (centre; Mvir = 1013 h−1 M⊙) and the most massive one in our sample (right; Mvir = 9.8 × 1014 h−1 M⊙). The colour-coding is given by the mass-weighted metallicity in each density–temperature bin. The dashed horizontal black lines represent the 0.1 keV (1.16 × 106 K) temperature cut, adopted to separate ‘hot’ and ‘cold’ gas phases. The dashed vertical line marks the gas density at R500, c. To the right of this line are the particles inside R500,c, and to the left the particles located at larger radii. |
| In the text | |
 |
Fig. A.1. Radial profiles of baryon depletion, from 0.5R500,c up to 2.5R500,c. The dashed lines represent the median profiles in each mass bin, according to the legend at the bottom-right corner. The solid lines are the fits performed according to the functional form of Eq. 8, with the same colour scale as the median profiles. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.