| Issue |
A&A
Volume 663, July 2022
|
|
|---|---|---|
| Article Number | A177 | |
| Number of page(s) | 22 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202142450 | |
| Published online | 01 August 2022 | |
Cyanopolyyne line survey towards high-mass star-forming regions with TMRT
1
Centre For Astrophysics, Guangzhou University,
Guangzhou
510006, PR China
e-mail: jszhang@gzhu.edu.cn
2
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69,
53121
Bonn, Germany
3
School of Physics and Astronomy, Sun Yat-sen University,
Guangzhou
510275, PR China
Received:
15
October
2021
Accepted:
8
April
2022
Context. Cyanopolyynes (HC2n+1 N, n = 1,2,3), which are the linear carbon chain molecules, are precursors for the prebiotic synthesis of simple amino acids. They are important for understanding prebiotic chemistry and may be good tracers of the star formation sequence.
Aims. We aim to search for cyanopolyynes in high-mass star-forming regions (HMSFRs) at possibly different evolutionary stages, investigate the evolution of HC3N and its relation with shock tracers, and detect the existence of HC5N and HC7N in HMSFRs with a formed protostar.
Methods. We carried out a cyanopolyyne line survey towards a large sample of HMSFRs using the Shanghai Tian Ma 65 m Radio Telescope (TMRT). Our sample consisted of 123 targets taken from the TMRT C band line survey. It included three kinds of sources, namely those with detection of the 6.7 GHz CH3OH maser alone, with detection of the radio recombination line (RRL) alone, and with detection of both (hereafter referred to as Maser-only, RRL-only, and Maser-RRL sources, respectively). For our sample with detection of cyanopolyynes, their column densities were derived using the rotational temperature measured from the NH3 lines. We constructed and fitted the far-infrared (FIR) spectral energy distributions (SED; obtained from the Herschel FIR data and the Atacama Pathfinder Experiment data at 870 µm) of our HC3N sources. Moreover, by analysing the relation between HC3N and other shock tracers, we also investigate whether HC3N is a good tracer of shocks.
Results. We detected HC3N in 38 sources, HC5N in 11 sources, and HC7N in G24.790+0.084, with the highest detection rate being found for Maser-RRL sources and a very low detection rate found for RRL-only sources. The mean column density of HC3N was found to be (1.75 ± 0.42) × 1013, (2.84 ± 0.47) × 1013, and (0.82 ± 0.15) × 1013 cm−2 for Maser-only, Maser-RRL, and RRL-only sources, respectively. Based on a fit of the FIR SED, we derive their dust temperatures, H2 column densities, and abundances of cyanopolyynes relative to H2. The mean relative abundance of HC3N was found to be (1.22 ± 0.52) × 10−10 for Maser-only, (5.40 ± 1.45) × 10−10 for Maser-RRL, and (1.65 ± 1.50) × 10−10 for RRL-only sources, respectively.
Conclusions. The detection rate, the column density, and the relative abundance of HC3N increase from Maser-only to Maser-RRL sources and decrease from Maser-RRL to RRL-only sources. This trend is consistent with the proposed evolutionary trend of HC3N under the assumption that our Maser-only, Maser-RRL, and RRL-only sources correspond to massive young stellar objects, ultracompact H ii regions, and normal classical H ii regions, respectively. Our detections enlarge the sample of HC3N in HMSFRs and support the idea that unsaturated complex organic molecules can exist in HMSFRs with a formed protostar. Furthermore, a statistical analysis of the integrated line intensity and column density of HC3N and shock-tracing molecules (SiO, H2CO) enabled us to find positive correlations between them. This suggests that HC3N may be another tracer of shocks, and should therefore be the subject of further observations and corresponding chemical simulations. Our results indirectly support the idea that the neutral-neutral reaction between C2H2 and CN is the dominant formation pathway of HC3N.
Key words: astrochemistry / stars: formation / ISM: clouds / ISM: molecules
© Y. X. Wang et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
Molecules have been detected in space in various environments, including star-forming regions, the envelopes around evolved stars, well-developed protoplanetary discs around stars, and even distant galaxies. They serve as a useful probe of the physical conditions of their environments, and can be used to derive the ages of their natal molecular cloud (Herbst & van Dishoeck 2009; Jørgensen et al. 2020; Gerner et al. 2014; Sabatini et al. 2021; Gieser et al. 2021). So far, around 250 molecules have been detected in the interstellar medium and circumstellar shells1. Among them, carbon chain molecules contribute a very large portion of the known chemical complexity of the interstellar medium (Thaddeus & McCarthy 2001; Loomis et al. 2016; Law et al. 2018). As typical linear carbon chain molecules, cyanopolyynes (HC2n+1N, n = 1,2,3,…) have attracted great interest from astronomers in both observational studies and laboratory theoretical works (e.g. Travers et al. 1996; Bell et al. 1997; McCarthy et al. 1998; Loomis et al. 2016; Cernicharo et al. 2020). Due to their nitrile bond (-C=N), cyanopolyynes are considered to be precursors for the prebiotic synthesis of simple amino acids, which is thought to be important for understanding prebiotic chemistry (Calcutt et al. 2018).
Cyanoacetylene (HC3N), which is the shortest cyanopolyyne molecule, normally exists in warm and active star-forming regions (e.g. Yu et al. 2019; Feng et al. 2021). The University of Manchester Institute of Science and Technology (UMIST) database for astrochemistry2 suggests that HC3N has four main formation pathways, including the neutral–neutral reaction between C2H2 and CN, the neutral–neutral reaction between C2H and HNC, the ion–molecule reaction between 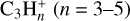 and nitrogen atoms, and the ion–molecule reaction between
and nitrogen atoms, and the ion–molecule reaction between 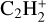 and HCN (McElroy et al. 2013). Up to now, it is not clear which formation pathway is the dominant one. Some theoretical models suggest that C2H2 is released from the grain mantle and produces HC3N by the neutral–neutral reaction between C2H2 and CN (Hassel et al. 2008; Chapman et al. 2009; Taniguchi et al. 2019a). Using the isotopic fractionation method (e.g. Takano et al. 1998; Sakai et al. 2007), the neutral–neutral reaction between C2H2 and CN was found to be the dominant formation pathway of HC3N (e.g. Takano et al. 1998; Araki et al. 2016; Taniguchi et al. 2016). A number of chemical models (Taniguchi et al. 2019a) suggested that there is enhancement of the key reactions of cyanopolyyne formation upon sublimation of CH4 and C2nH2 from dust grains. As shocks heat and compress the surrounding gas, thereby releasing molecules (such as CH4 and C2nH2) trapped in the dust mantles into the gas phase (e.g. Arce et al. 2008), the released CH4 and C2H2 would produce HC3N in the gas phase. Therefore, shocks may be associated with the formation process of HC3N. Investigation of the correlation between HC3N and shock tracers may therefore help us to constrain the formation pathway of HC3N.
and HCN (McElroy et al. 2013). Up to now, it is not clear which formation pathway is the dominant one. Some theoretical models suggest that C2H2 is released from the grain mantle and produces HC3N by the neutral–neutral reaction between C2H2 and CN (Hassel et al. 2008; Chapman et al. 2009; Taniguchi et al. 2019a). Using the isotopic fractionation method (e.g. Takano et al. 1998; Sakai et al. 2007), the neutral–neutral reaction between C2H2 and CN was found to be the dominant formation pathway of HC3N (e.g. Takano et al. 1998; Araki et al. 2016; Taniguchi et al. 2016). A number of chemical models (Taniguchi et al. 2019a) suggested that there is enhancement of the key reactions of cyanopolyyne formation upon sublimation of CH4 and C2nH2 from dust grains. As shocks heat and compress the surrounding gas, thereby releasing molecules (such as CH4 and C2nH2) trapped in the dust mantles into the gas phase (e.g. Arce et al. 2008), the released CH4 and C2H2 would produce HC3N in the gas phase. Therefore, shocks may be associated with the formation process of HC3N. Investigation of the correlation between HC3N and shock tracers may therefore help us to constrain the formation pathway of HC3N.
Unsaturated interstellar complex organic molecules (iCOMs, e.g. Herbst & van Dishoeck 2009; Ceccarelli et al. 2017)3, such as HC5N and HC7N, are generally abundant in quiescent infrared dark clouds (quiescent) (Suzuki et al. 1992; Hirota et al. 2009). During the earliest phases of the star formation process, unsaturated iCOMS become deficient and saturated iCOMs (such as CH3OH and CH3CN) become abundant instead in more evolved sources (e.g. Garrod & Herbst 2006; Herbst & van Dishoeck 2009). Such chemistry is known as ‘hot corino’ chemistry in low-mass star-forming regions (LMSFRs) and ‘hot core’ chemistry in high-mass star-forming regions (HMSFRs). However, various unsaturated iCOMs (e.g. C4H2 and HC5N) have been detected in many LMSFRs (Sakai et al. 2008, 2009; Graninger et al. 2016; Law et al. 2018; Zhang et al. 2021). The theory of warm carbon-chain chemistry (WCCC) has been proposed, which is based on the gas-grain model (Sakai et al. 2009), and can explain the formation of cyanopolyynes in LMSFRs with a formed protostar. As compared to the hot corino chemistry, in WCCC, unsaturated iCOMs can be formed in the gas phase when CH4 evaporates from grain mantle (Aikawa et al. 2008; Hassel et al. 2008) and are even more abundant in warm regions (20–30 K, Sakai et al. 2010).
The fact that unsaturated iCOMs can form in LMSFRs with a formed protostar naturally poses the question of whether unsaturated iCOMs can also form in HMSFRs in advanced evolutionary stages. There have been a few successful observations of unsaturated iCOMs towards HMSFRs with a formed protostar (Esplugues et al. 2013; Belloche et al. 2013; Green et al. 2014; Feng et al. 2015; Taniguchi et al. 2018c). However, the sample with detection of unsaturated iCOMs (especially HC7N) is still small. Several models involving chemical networks suggest that unsaturated iCOMs could be formed in HMSFRs with a formed protostar (e.g. Chapman et al. 2009; Taniguchi et al. 2019a). These theoretical results were obtained by simulating certain sources (e.g. G305.2+0.2 in Chapman et al. 2009 and G28.28-0.36 in Taniguchi et al. 2019a) characterised by their specific properties. Therefore, unlike LMSFRs, there is no sufficient understanding of the formation of unsaturated iCOMs in HMSFRs with a formed protostar. Hence, more studies of unsaturated iCOMs in HMSFRs are required in order to obtain more details of their primary formation path.
We performed a cyanopolyynes line survey in Ku band using the Shanghai Tian Ma 65 m Radio Telescope (TMRT) to investigate the evolution of HC3N in HMSFRs and the existence of HC5N and HC7N in HMSFRs with a formed protostar. In Sect. 2, we introduce our methods of sample selection and observations. We summarise our observational results and method of analysis in Sect. 3. We discuss the evolution of HC3N in HMSFRs in Sect. 4.1. In Sect. 4.2, the relation between HC3N and shocktracing molecules (H2CO and SiO) is studied. In Sect. 4.3, we discuss unsaturated iCOMs in HMSFRs with a formed protostar. A short summary is presented in Sect. 5.
2 Sample selection and observations
2.1 Sample selection and distance
Successful surveys of unsaturated iCOMs (HC5N, HC7N and HC9N etc., Li et al. 2016b; Zhang et al. 2017) in the C and Ku band were performed using TMRT. A systematic survey in C-band using TMRT was performed recently on a galactic radio recombination line (RRL) and a 6.7 GHz methanol maser towards a sample of 3348 sources obtained from the all-sky Wide-field Infrared Survey Explorer (WISE) point-source catalogue, applying colour criteria (Yang et al. 2017, 2019; Chen et al. 2020). The 6.7 GHz CH3OH maser and RRL were detected in 240 sources and 517 sources, respectively. A HMSFRs sample consisting of 654 sources was built by consolidating the 6.7 GHz CH3OH maser sample and the RRL sample (Chen et al. 2020). This incorporates three subsamples of sources, namely 137 sources with detection of the 6.7 GHz CH3OH maser alone (hereafter Maser-only), 414 sources with detection of the RRL alone (RRL-only), and 103 sources with detection of both (Maser-RRL). It was suggested that these three types of sources correspond to different star-forming stages, taking into consideration that the methanol maser should appear before the formation of the H ii region (Chen et al. 2020).
The sources with the strong 6.7 GHz CH3OH maser (flux density >0.4 Jy) or RRL emission (Tpeak > 0.02 K) that also have a galactocentric distance distribution (ranging from 3 to 12 kpc) similar to that of the original HMSFRs sample (3–13 kpc, Chen et al. 2020) were chosen as our targets in order to improve the detection rate of cyanopolyynes. We then chose 50 targets from each class.
The selected sources have accurate heliocentric distances, which were determined from trigonometric parallax measurements (Reid et al. 2014, 2019) or the latest parallax-based distance calculator V24. The galactocentric distances of our sources were then determined using the heliocentric distance according to the following formula (Roman-Duval et al. 2009):
![${D_{{\rm{GC}}}} = \sqrt {{{\left[ {{R_0}\cos \left( l \right) - D\cos \left( b \right)} \right]}^2} + R_0^2{{\sin }^2}\left( l \right)} ,$](/articles/aa/full_html/2022/07/aa42450-21/aa42450-21-eq3.png) (1)
(1)
where R0 is the galactocentric distance of the sun, which is equal to 8.122 ± 0.031 kpc (GRAVITY Collaboration 2018), l and b are the Galactic longitude and Galactic latitude, respectively, and D is the heliocentric distance (Table B.1).
Summary of target lines.
2.2 Observations
We carried out a cyanopolyyne line survey in August, September, and October 2018, April, May, November, and December 2019, and January 2020 using the 65 m TMRT located in Shanghai, China. Due to limited observation time, we observed 123 sources comprising 29 Maser-only, 50 Maser-RRL, and 44 RRL-only ones, while the remaining 27 sources, which are relatively weak, were not observed. In view of our detection rate, several detections among these 27 relatively weak sources could be missed. However, this should not introduce significant error in our results. Using a cryogenically cooled Ku band receiver with the frequency coverage of 12–18 GHz and the DIBAS (Digital Backend System) being a Field-Programmable Gate Array (FPGA)-based spectrometer (Bussa 2012), we were able to receive and record the signals. Mode 22, which has 16 spectral windows, was used in our observations. Each window has 16384 channels with bandwidths of 23.4375 MHz and a frequency resolution of 1.431 KHz. The centre frequency setups for our observations of cyanopolyynes are listed in Table 1. The half power beam widths (HPBWs) of TMRT at the transitions of HC3N (J = 2−1), HC5N (J = 6−5), and HC7N (J = 15−14) were about 52″ at 18195.31 MHz, 60″ at 15975.93 MHz, and 56″ at 16919.98 MHz, respectively. The typical root mean square (rms) was about 10 mK. The original velocity resolution was 0.02 km s−1 for HC3N (J = 2−1), and 0.03 km s−1 for HC5N (J = 6−5) and HC7N (J = 15−14). The system temperatures were about 30–80 K in the Ku band. A noise diode was used for calibration. The uncertainly on the antenna temperature 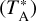 was about 20%. The main beam brightness temperature (Tmb) was obtained from the antenna temperature as
was about 20%. The main beam brightness temperature (Tmb) was obtained from the antenna temperature as 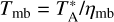 , where the main beam efficiency (ηmb) of the TMRT was about 0.6 in the Ku band (Wang et al. 2017). During our observations, we adopted a position-switching mode with the off-position at (−30′,0) or (30′,0) offset in azimuth and elevation from the source. Each cycle adopted 2 mins for both ON position and OFF position and each source was observed for 15 ON-OFF cycles. For a few weak objects, more scans were adopted to improve the signal-to-noise ratio (S/N) of the molecular lines.
, where the main beam efficiency (ηmb) of the TMRT was about 0.6 in the Ku band (Wang et al. 2017). During our observations, we adopted a position-switching mode with the off-position at (−30′,0) or (30′,0) offset in azimuth and elevation from the source. Each cycle adopted 2 mins for both ON position and OFF position and each source was observed for 15 ON-OFF cycles. For a few weak objects, more scans were adopted to improve the signal-to-noise ratio (S/N) of the molecular lines.
3 Results and analyses
The GILDAS/CLASS5 software was used for the data reduction. Poor scans (system temperature >80 K) were removed and the rest of the scans were averaged to improve the S/N. Linear or multi-order (<4) polynomial baselines were subtracted for the spectra. To further improve the S/N, the spectra were smoothed with a velocity resolution of ~0.4 km s−1. Among six hyperfine structure (HFS) lines of HC3N (J = 2−1) (e.g. Levshakov et al. 2010; Li et al. 2016b), only blended lines of the J = 2−1, F = 3−2 and J = 2−1, F = 2−1 transitions were detected towards our targets, except for G30.810-0.050. In this latter source, two extra groups of HFS components, that is, F = 1−1, and unresolved F = 2−2 and F = 1−0 were also detected. Due to the presence of the spectra with unresolved HFS components, the Gaussian method was used to fit the spectra instead of the HFS fitting method.
We successfully detected the HC3N (J = 2−1) emission line in 38 HMSFRs (S/N > 3) towards 123 sources, which results in a detection rate of 31 %. The sources with HC3N detection include 10 Maser-only, 22 Maser-RRL, and 6 RRL-only sources with detection rates of 34, 44 and 14%, respectively. As far as we know, among our 38 HC3N (J = 2−1) sources, 34 are newly detected (except G24.328+0.144, G24.790+0.084, G49.466−0.408 and G111.532+0.759, Widicus Weaver et al. 2017). Among the 38 sources with HC3N detection, the HC5N (J = 6−5) line was also detected in 11 sources with a detection rate of ~29%, including 2 Maser-only and 9 Maser-RRL sources with the detection rates of ~20 and ~41%, respectively. Apart from G24.790+0.084 (Green et al. 2014), another 10 sources were new HC5N detections. The HC7N (J = 15−14) transition was first detected in G24.790+0.084. All spectra for HC3N, HC5N, and HC7N are shown in Fig. 1, where solid and dashed lines show the local standard of rest (LSR) velocities of 6.7 GHz CH3OH maser (Yang et al. 2017, 2019) and RRL (Chen et al. 2020), respectively. The small differences in LSR velocity for these three molecules may be due to the fact that the molecules have different excitation mechanisms and exist in HMSFRs with different characteristics. The spectral line parameters of HC3N and unsaturated iCOMs (HC5N and HC7N) are listed in Tables B.1 and B.2, respectively.
 |
Fig. 1 Examples for HC3N, HC5N, and HC7N with TMRT telescope. Solid and dashed lines show the LSR velocity values of 6.7 GHz CH3OH maser (Yang et al. 2017, 2019), and of RRL (Chen et al. 2020), respectively. The full spectra are shown in Appendix Fig. A.1. |
 |
Fig. 2 HFS fitting of G30.810−0.050. |
3.1 Column density of cyanopolyynes
The HC3N (J = 2−1) line is generally considered to be optically thin (e.g. McGee et al. 1975; Gong et al. 2015; Li et al. 2016b). Among our detected sources, the strongest, G30.810−0.050, was found to have three groups of HFS structure components of HC3N (J = 2−1). We can determine the optical depth of its HC3N (J = 2−1) line using the HFS fitting method implemented in CLASS software (‘Method’ command) as shown in Fig. 2. A low optical depth value of <0.1 is obtained, which supports the idea that the optical depth effect is insignificant and cannot be used for further analysis.
The volume density of H2 can be estimated as 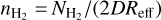 (Urquhart et al. 2014a; König et al. 2017), where
(Urquhart et al. 2014a; König et al. 2017), where 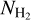 and Reff are the column density of H2 and the effective radius of the clump in rad (Table 2), respectively, and D is the heliocentric distance (Table B.1). The lowest value of the volume density for our sources is about 2.1 × 103 cm−3 (G24.328+0.144), which is larger than the critical density6 of HC3N (J = 2−1) (ncrit = 9.7 × 102 cm−3, with a kinetic temperature of 10 K, Shirley 2015). This suggests that the HC3N molecule is under local thermodynamic equilibrium (LTE). HC5N and HC7N are generally assumed to be in LTE as well (e.g. Li et al. 2016b; Taniguchi et al. 2018a; Wu et al. 2019; Zhang et al. 2021). Therefore, assuming LTE conditions and a negligible optical depth value, the column density can be estimated by the following equation (Cummins et al. 1986):
and Reff are the column density of H2 and the effective radius of the clump in rad (Table 2), respectively, and D is the heliocentric distance (Table B.1). The lowest value of the volume density for our sources is about 2.1 × 103 cm−3 (G24.328+0.144), which is larger than the critical density6 of HC3N (J = 2−1) (ncrit = 9.7 × 102 cm−3, with a kinetic temperature of 10 K, Shirley 2015). This suggests that the HC3N molecule is under local thermodynamic equilibrium (LTE). HC5N and HC7N are generally assumed to be in LTE as well (e.g. Li et al. 2016b; Taniguchi et al. 2018a; Wu et al. 2019; Zhang et al. 2021). Therefore, assuming LTE conditions and a negligible optical depth value, the column density can be estimated by the following equation (Cummins et al. 1986):
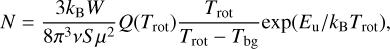 (2)
(2)
where kB is the Boltzmann constant, W is the integrated line intensity, ν is the rest frequency of the transition, and Trot and Tbg are the rotational temperature and the background temperature (2.73 K), respectively. Also, Eu/kB and Sµ2 (taken from Cologne Database for Molecular Spectroscopy, CDMS7) are the upper level energy in K and the product of the line strength and the square of the electric dipole moment, respectively (see Table 1). The partition functions, Q(Trot), of each molecule are taken from CDMS:
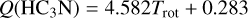 (3)
(3)
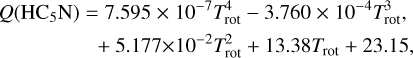 (4)
(4)
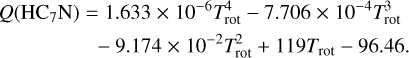 (5)
(5)
For molecular transitions under LTE conditions, the rotation temperature is usually determined by the rotation diagram method (e.g. Goldsmith & Langer 1999). Application of this method requires at least two transition lines of each molecule to be available. However, our observations provide only one transition line for each molecule.
Here, Trot was taken from the rotational temperature of NH3, which could be obtained from the NH3 inversion lines and was widely used as a good tracer of temperature in the molecular clouds (Tafalla et al. 2004; Mangum & Shirley 2015; Wang et al. 2020). Notably, NH3 and cyanopolyynes may come from different regions in the clumps and therefore lead to error in calculations of the column density of cyanopolyynes. However, HC3N and NH3 have similar critical densities, when the kinetic temperature is in the range of 10–50 K (Shirley 2015). Therefore, the use of Trot of NH3 should not cause any significant bias in our calculations of the column density of cyanopolyynes. The rotational temperature of NH3 was reported in 23 sources among the total of 38 sources with HC3N detection (Wienen et al. 2012; Urquhart et al. 2011; Li et al. 2016a; Chira et al. 2013). For another 6 sources (G20.234+0.085, G24.328+0.144, G24.528+0.337, G24.790+0.084, G28.287−0.348, and G192.600−0.048), only the optical depth (τ) and the main beam temperatures (Tmb) of NH3 lines were reported (Cyganowski et al. 2013; Svoboda et al. 2016; Yang et al. in prep.). For these sources, Trot of NH3 was derived as follows (e.g. Ragan et al. 2011):
![${T_{{\rm{rot}}}} = - 41.5{\left[ {\ln \left( {{{ - 0.283} \over {\tau \left( {1,1,m} \right)}}\ln \left[ {1 - {{{T_{mb}}\left( {2,2,m} \right)} \over {{T_{{\rm{mb}}}}\left( {1,1,m} \right)}}\left( {1 - {e^{ - \tau \left( {1,1,m} \right)}}} \right)} \right]} \right)} \right]^{ - 1}},$](/articles/aa/full_html/2022/07/aa42450-21/aa42450-21-eq13.png) (6)
(6)
where m represents the main hyperfine component. Therefore, we obtained the Trot values of NH3 for 29 sources from our sample with HC3N detection, including 9 Maser-only, 19 Maser-RRL, and 1 RRL-only sources. For 9 sources without Trot (1 Maser-only, 3 Maser-RRL, and 5 RRL-only), the average Trot value of each type was used as their Trot values (Table B.3). The column densities of cyanopolyynes molecules were obtained using the values of Trot of NH3 and Eq. (2) (Table B.3). We made a comparison with the published HC3N column densities towards our sample. These were found to be 2.00 × 1013 cm−2 for G28.287−0.348 (Taniguchi et al. 2018b) and 3.60 × 1013 cm−2 for G81.752−0.691 (DR21, Chung et al. 1991), which are comparable to our results (1.10 × 1013 cm−2 for G28.287−0.348 and 3.12 × 1013 cm−2 for G81.752−0.691, respectively). The mean column density of HC3N was found to be (1.75 ± 0.42) × 1013 cm−2 for Maser-only, (2.84 ± 0.47) × 1013 cm−2 for Maser-RRL, and (0.82 ± 0.15) × 1013 cm−2 for RRL-only sources. More details about the differences in the column density between these three types of sources is discussed in Sect. 4.1.
Far infrared properties of our HC3N sources.
3.2 Far-infrared spectral energy distributions
The Herschel infrared Galactic Plane Survey (Hi-GAL, Molinari et al. 2016) compact-source catalogue was obtained by performing photometry of Herschel images (70, 160, 250, 350 and 500 µm). Urquhart et al. (2014a) conducted a photometry of the Atacama Pathfinder Experiment (APEX, Güsten et al. 2006) images (870 µm) with the source-extraction routine SExtractor8 and obtained the APEX Telescope Large Area Survey of the Galaxy (ATLASGAL, Schuller et al. 2009; Contreras et al. 2013) compact-source catalogue. Using a search radius of 30″ (roughly half the HPBW of the HC3N), we cross-identified both catalogues with our HC3N sources. Twenty-one sources were found in both catalogues and their IR flux data are presented in Table 2. In a number of previous works (e.g. Wu et al. 2019; Elia et al. 2010), a single-temperature grey-body model was used to fit the spectral energy distributions (SEDs) of these sources. The Levenberg-Marquardt algorithm provided in the Python package lmfit was applied (Newville et al. 2016). The grey-body model can be expressed as follows:
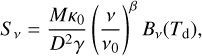 (7)
(7)
where M is the total (dust + gas) mass, κ0 = 1.85 cm2 g−1 is the dust opacity at 870 µm (Ossenkopf & Henning 1994), Bv(Td) is the Planck function at the dust temperature Td, β is the dust emissivity index (the mean value of 1.75 was used for all dust models, Ossenkopf & Henning 1994), and γ is the gas-to-dust ratio, which depends on the galactocentric distance of the source (Giannetti et al. 2017):
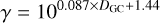 (8)
(8)
The derived values of γ are listed in Table 2. Figure 3 shows the fitting results of the far-infrared (FIR) SEDs of our sources. Similar to the previous works, the Herschel 70 µm data were excluded in our grey-body fitting because of their origin from a warm dust component and a large fraction of this emission coming from very small grains (e.g. Wu et al. 2019; Guzmán et al. 2015). The dust temperature Td and the total mass M were obtained from the SED fit, and are presented in Table 2. For comparison, we collected the results of Td and M of our 21 sources (listed in Table 2), which were derived in ATLASGAL (Urquhart et al. 2018). There are eight sources with M values consistent with those of Urquhart et al. (2018) within the error range, while all the others show a large difference in M values between ours and theirs. The values of Td for our sources are smaller than those of Urquhart et al. (2018). The difference should be mainly caused by the different fitting models used, that is, a two-component (grey-body and black-body) model was used by these latter authors, while we used a single component model.
3.3 Relative abundance of cyanopolyynes to H2
To obtain the relative abundance of cyanopolyynes with respect to H2 for our sources, we first estimated 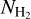 in these sources. Under the assumption of optically thin dust emission at 870 µm, the beam-averaged H2 column density can be calculated using the following expression Schuller et al. (2009):
in these sources. Under the assumption of optically thin dust emission at 870 µm, the beam-averaged H2 column density can be calculated using the following expression Schuller et al. (2009):
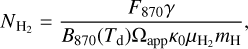 (9)
(9)
where F870 is the peak flux density (see Table 2) and Ωapp is the beam solid angle. For a source located at D, Ωapp = A/D2, where 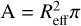 is the surface area of the source. The value of Reff is presented in Table 2. Here, mH is the mass of a hydrogen atom, and
is the surface area of the source. The value of Reff is presented in Table 2. Here, mH is the mass of a hydrogen atom, and 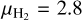 is the mean molecular weight per H2 molecule (Kauffmann et al. 2008). B870(Td) is the intensity of the black-body at 870 µm at the dust temperature Td, which was determined from the SED fit (Sect. 3.2). We obtained the column densities of H2 for 21 sources, including 6 Maser-only, 13 Maser-RRL, and 2 RRL-only sources (Table 2).
is the mean molecular weight per H2 molecule (Kauffmann et al. 2008). B870(Td) is the intensity of the black-body at 870 µm at the dust temperature Td, which was determined from the SED fit (Sect. 3.2). We obtained the column densities of H2 for 21 sources, including 6 Maser-only, 13 Maser-RRL, and 2 RRL-only sources (Table 2).
Using the results of the column density of cyanopolyynes (Table B.3) and H2 (Table 2), we derived the relative abundances of cyanopolyynes with respect to 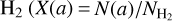 – where a refers to cyanopolyynes – for 21 sources (Table B.3). The mean relative abundance of HC3N was found to be (1.22 ± 0.52) × 10−10 for Maser-only sources, (5.40 ± 1.45) × 10−10 for Maser-RRL sources, and (1.65 ± 1.50) × 10−10 for RRL-only sources. In Sect. 4.1, we discuss the differences in relative abundance between our three types of sources.
– where a refers to cyanopolyynes – for 21 sources (Table B.3). The mean relative abundance of HC3N was found to be (1.22 ± 0.52) × 10−10 for Maser-only sources, (5.40 ± 1.45) × 10−10 for Maser-RRL sources, and (1.65 ± 1.50) × 10−10 for RRL-only sources. In Sect. 4.1, we discuss the differences in relative abundance between our three types of sources.
4 Discussion
4.1 Evolution of HC3N
The definitions of the evolutionary stages of HMSFRs, including physical and chemical classifications, are still not clear (Hoq et al. 2013; Miettinen 2014; Gerner et al. 2014; Urquhart et al. 2014b, 2019, 2022; Zhang et al. 2016; König et al. 2017). Based on the physical properties of the clumps, the sequence of a HMSFR is usually divided into four evolutionary stages: quiescent, high-mass protostellar object (protostellar), massive young stellar object (YSO), and H ii region (see Urquhart et al. 2019, 2022, and references therein).
Urquhart et al. (2019) carried out a 3 mm molecular-line survey towards a large sample consisting of 570 high-mass star-forming clumps and found a trend in the detection rate of HC3N (J = 10−9), namely an increase from quiescent, to protostellar, to YSO, and then a slight decrease in H ii region (including all H ii region stages). Yu et al. (2019) subdivided H ii regions into ultra-compact (UC) H ii regions and normal classical H ii regions. By analysing the archival available data from the Hi-GAL and the Millimetre Astronomy Legacy Team Survey at 90 GHz (MALT90)9, these latter authors found that the abundance of HC3N could increase in UC H ii regions, while it decreases or reaches a plateau in normal classical H ii regions.
The results of our analysis (Sect. 3) show that the detection rates of HC3N are 34, 44 and 14% for Maser-only, Maser-RRL, and RRL-only sources, respectively. The mean column density of HC3N is found to be (1.75 ± 0.42) × 1013 cm−2 for Maser-only sources, (2.84 ± 0.47) × 1013 cm−2 for Maser-RRL sources, and (0.82 ± 0.15) × 1013 cm−2 for RRL-only sources. The average values of the relative abundance of HC3N are (1.22 ± 0.52) × 10−10, (5.40 ± 1.45) × 10−10, and (1.65 ± 1.50) × 10−10 for Maser-only, Maser-RRL, and RRL-only sources, respectively. Those results are plotted as a function of source classification in Fig. 4. All the results show the same trend, namely an increase from Maser-only to Maser-RRL sources and a decease from Maser-RRL to RRL-only ones.
The 6.7 GHz CH3OH maser is excited according to the infrared radiative pumping mechanism in the disc when a formed protostar begins to warm its natal environment. This is normally considered to be related to the early stages of HMSFRs when there is significant mass accretion (e.g. Sobolev & Deguchi 1994; Minier et al. 2003; Ellingsen 2006; Xu et al. 2008). Based on the CH3OH maser line and radio continuum mapping observations towards a sample of HMSFRs, Walsh et al. (1998) found that the 6.7 GHz CH3OH maser is observable before the UC H ii regions (YSOs) and are probably destroyed as the UC H ii regions develop. Therefore, we assume our Maser-only sources in YSOs.
Based on the statistical investigations towards different types of masers, Ellingsen (2007) and Breen et al. (2010) proposed an evolutionary sequence for masers in HMSFRs and suggested that 6.7 GHz CH3OH maser can exist in UC H ii regions, although most of them are located at earlier YSO stages. Considering this, as well as the fact that RRL appears after the formation of the H ii region, we propose that our Maser-RRL sources are found in the more evolved UC H ii regions.
RRL are produced by scattering of free electrons off the ions, which come from the surrounding H i gas ionised by high-energy ultraviolet (UV) photons (>13.6 eV) from formed massive stars. RRL is a powerful tool to track H ii regions (Walsh et al. 1998; Bernasconi & Maeder 1996; Anderson et al. 2011, 2014, 2018; Condon & Ransom 2016; Luisi et al. 2018; Zhang et al. 2022). As RRLs are undetectable in young dense UC H ii regions and at their previous stages due to the effect of beam dilution and high optical depth (e.g. Churchwell 2002; Chen et al. 2020), our RRL-only sources should belong to more extended and evolved normal classical H ii regions.
Based on these assumptions, our results concerning Maser-only sources (YSO, 34%), which have a relatively high detection rate for HC3N compared to Maser-RRL and RRL-only sources (H ii region, ~30%), are identical to those of Urquhart et al. (2019). Our results concerning Maser-RRL, namely with the largest abundance of HC3N at this stage and a decrease from Maser-RRL (UC H ii region) to RRL-only (normal classical H ii region) sources, are consistent with those of Yu et al. (2019), that is a decrease from UC H ii to normal classical H ii regions. The UMIST database for astrochemistry suggested that HC3N molecules could be destroyed by a reaction with a UV photon, which produces CN and CCH or HC3N+ and an electron (McElroy et al. 2013). Therefore, the decrease in N(HC3N) between UC H ii regions and normal classical H ii regions may reflect the possibility of a destruction of HC3N by UV photons, which is consistent with the observations of Yu & Xu (2016). The increase in the column density of HC3N between YSOs and UC H ii regions is likely correlated with the increase in dust temperature, which results in a more desorbed progenitor (e.g. C2H2, CH4) of HC3N from the dust grain and a further increase in the amount of HC3N by gas phase reactions (Yu et al. 2019; Taniguchi et al. 2019b).
However, this evolutionary picture needs to be confirmed by comparing the physical parameters (such as luminosity, mass, and Tdust) of these three types of samples, as in Molinari et al. (2008). This issue will be discussed in a forthcoming paper (Chen et al., in prep.; and priv. comm.).
 |
Fig. 3 FIR SED and its fit curve (the solid curve, from one single temperature grey-body model) of sources with cyanopolyynes detection. The cross indicates 70 µm emission, which is not involved in the SED fit. |
 |
Fig. 4 The detection rates, column densities, and relative abundances of HC3N for different types of sources. |
4.2 HC3N: another tracer of shock?
Based on its spectra with large line-width and wing emissions (Beltrán et al. 2004; Yu & Wang 2015; Taniguchi et al. 2018c; Yu et al. 2019; Feng et al. 2021), and some theoretical modelling works on L1157-B1 (Viti et al. 2011; Benedettini et al. 2013; Mendoza et al. 2018), HC3N was proposed to be a species originating from outflow shock within active star-forming regions. Here, by analysing the relation between HC3N and other shock tracers, we study whether or not HC3N is a good tracer of shock.
Towards our HC3N sample, we collected the H2CO line intensity data from the TMRT C band survey (Dr. X. Chen priv. comm.). Using these data, we further calculated the column density of H2CO of our sample, as for cyanopolyynes in sample Sect. 3.1. Our column density results for H2CO are presented in Table B.4. The derived column densities range from 0.45 to 61.49 × 1013 cm−2, the mean value being equal to (7.78 ± 3.25) × 1013 cm−2. Our results are consistent with values calculated from previous observations towards one ATLASGAL HMSFR sample, which range from 0.48 to 61 × 1013 cm−2, the mean value being (7.8 ± 1.3) × 1013 cm−2, and the predictions of the RADEX non-LTE model (Tang et al. 2018).
Figure 5 (upper left panel) presents the column density of H2CO versus that of HC3N for our sample. A correlation between these characteristics can be seen, albeit with large scatter; that is, 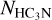 tends to be stronger in the sources with larger
tends to be stronger in the sources with larger 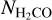 . A weighted least-squared linear fit gives
. A weighted least-squared linear fit gives 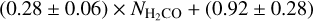 , with a correlation coefficient of 0.77, and the errors representing 1σ standard deviations. A similar correlation can also be found between the line intensities (with a Pearson correlation of 0.57, upper right panel), which reflects non-significant Malmquist bias on the correlation of their column densities.
, with a correlation coefficient of 0.77, and the errors representing 1σ standard deviations. A similar correlation can also be found between the line intensities (with a Pearson correlation of 0.57, upper right panel), which reflects non-significant Malmquist bias on the correlation of their column densities.
For another shock tracer, SiO, we collected the data for our sample, including the integrated line intensity and the corresponding column density (Csengeri et al. 2016). In Fig. 5, we plotted the column density (bottom left panel) and the integrated line intensity (bottom right panel) of HC3N versus those for SiO for our sample. Both panels show a significant correlation between SiO and HC3N, which reflects no significant selection bias. For the column density, a weighted least-squares linear fit (solid line) gives 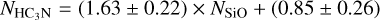 , with a larger correlation coefficient of 0.94 than that found for H2CO and HC3N.
, with a larger correlation coefficient of 0.94 than that found for H2CO and HC3N.
Similar strong correlations between the parameters for HC3N and SiO were also found before based on the results for a sample of 43 southern HMSFRs. These parameters included the line width, the integrated line intensity, the column density, and the relative abundance (He et al. 2021). For comparison, the column density results (empty circles) with the weighted least-squares linear fitting line (the dashed line) are also shown in Fig. 5 (bottom left panel). The strong correlation between HC3N and SiO is consistent, although their column densities cover larger ranges and their fit line has a larger slope. Both results in the literature and ours suggest a strong correlation between HC3N and SiO in terms of integrated line intensity and column density.
Taking H2CO and SiO molecules as good tracers of shock, positive correlations between them and HC3N support the idea of a shock origin of HC3N. Under the impact of shocks, C2H2, being the precursor molecule of HC3N, is released from dust grains to the gas phase and reacts with CN to form HC3N. This is in agreement with the findings of Taniguchi et al. (2019a) from chemical models that the sublimation of CH4 and C2H2 from dust grains enhances key reactions of the formation of cyanopolyynes. Therefore, our results indirectly suggest that the neutral-neutral reaction between C2H2 and CN is the dominant formation pathway of HC3N. In addition, shock models indicate that HC3N abundance would be strongly enhanced as a consequence of the passage of the shock (Mendoza et al. 2018). The presence of a C-type shock with a pre-shock density >104 cm−3 and a velocity of ~40 km s−1 (to reach the maximum shock temperature of 4000 K) can produce the observed high abundance of HC3N (Benedettini et al. 2013). Meanwhile, silicon monoxide (SiO) mainly originates from jets probing accretion processes (e.g. Codella et al. 1999; Duarte-Cabral et al. 2014; Cosentino et al. 2018). Under the action of high-velocity (20– 50 km s−1) shocks, Si atoms and Si-bearing molecules from the dust grains are evaporated to the gas phase and are subsequently oxidised to SiO (Martin-Pintado et al. 1992; Gusdorf et al. 2008; López-Sepulcre et al. 2016). However, H2CO is formed on the surface of dust grains by consecutive hydrogenation of CO, which can be released to the gas phase by shocks with relatively low velocity (~15 km s−1) (Mitchell 1984; Codella et al. 2010; Tafalla et al. 2010). Therefore, SiO and HC3N may trace similar high-velocity shock regions, while H2CO traces relatively low-velocity shock ones. This is in agreement with our results, which show a stronger correlation between SiO and HC3N than that seen between H2CO and HC3N.
To further confirm the dominant formation pathway of HC3N, we can investigate the correlation between C2H2 and HC3N towards sources with shocks and carry out observations of HC3N and its three isotopologues towards a large sample. Moreover, observations of the spatial distribution of different shock tracers are needed to find the similarities and differences in terms of their physical and chemical properties.
 |
Fig. 5 Column density (left panels) and the integrated line intensity (right panels) of HC3N are plotted against those of shock-tracing molecules (H2CO and SiO). The circles and empty circles indicate our sources and sources reported in He et al. (2021), respectively. The solid lines and the dashed line show the weighted linear fitting line for our data and theirs. |
4.3 Unsaturated iCOMs in HMSFRs with a formed protostar
As mentioned in Sect. 1, unsaturated iCOMs were previously thought to be destroyed in ‘hot core’ chemistry. However, some observational and theoretical studies seem to indicate that HC5N and even HC7N can be present in the protostellar or hot molecule cores (HMCs, which are the sources around YSOs with a rich molecular line spectrum; Kurtz et al. 2000; Cesaroni 2005; Hosokawa & Omukai 2009; Rathborne et al. 2011; Liu et al. 2021). Unlike LMSFRs, the formation pathway of unsaturated iCOMs in HMSFRs with a formed protostar is not yet clear.
Our survey successfully detected HC5N J = 6−5 transition (Eu/kB ~ 2.68 K) in 11 sources (10 of them are new) among 123 targeted HMSFRs (Sect. 3). Combined with previous observations (Green et al. 2014; Taniguchi et al. 2018c), HC5N was detected in 60 HMSFRs with a formed protostar. Furthermore, our first detection of the HC7N J = 15−14 transition (Eu/kB ~ 5.68 K) in G24.790+0.084 leads to three HC7N sources in three HMSFRs with a formed protostar (Orion KL in Feng et al. 2015 and G28.28−0.36 in Taniguchi et al. 2018a). Our detections enlarge the HC5N and HC7N samples and confirm that unsaturated iCOMs can exist in YSOs and UC H ii regions, which is consistent with the predictions of the chemical model of Chapman et al. (2009). However, our observations may be contaminated by the low-temperature gas without star-forming activity because of the large beam size (~53″) and low J transition with low level energy of molecular transitions (<10 K). Therefore, follow-up observations of high J molecular transitions with high spatial resolution would help to confirm the origin of HC5N and HC7N. More modelling works on iCOM chemistry are also needed to improve our understanding of unsaturated iCOMs.
It is also interesting that we find a significant difference in the column density ratio HC3N/HC5N between our subsamples (Table B.3). The mean value of the ratio of 10.45 ± 2.89 for Maser-RRL sources exceeds that of Maser-only sources of 4.11 ± 0.46 by a factor of about three. However, the ratio of N(HC3N)/N(HC5N) seems to decrease with time as obtained from the simulation result (Taniguchi et al. 2019a). Further investigations on large samples and more targeted chemical simulations are required to check whether the N(HC3N)/N(HC5N) ratio can be used as a chemical clock, given that the relative abundances of different molecules changes with time (Wakelam et al. 2004).
5 Summary
We present a cyanopolyyne (HC2n+1N) line survey in the Ku band (12–18 GHz) towards a large sample of 123 HMSFRs using the TMRT. The sample was divided into 29 sources with detection of the 6.7 GHz CH3OH maser alone (Maser-only), 44 sources with detection of RRL alone (RRL-only), and 50 sources with both maser and RRL (Maser-RRL). Our main results can be summarised as follows:
Among 123 targets, HC3N is detected in 38 sources (including 34 new ones), which include 10 Maser-only, 22 Maser-RRL, and 6 RRL-only sources. The detection rates are 34, 44, and 14% for Maser-only, Maser-RRL, and RRL-only sources, respectively.
The mean column densities of HC3N are (1.75 ± 0.42) × 1013 cm−2, (2.84 ± 0.47) × 1013 cm−2, and (0.82 ± 0.15) × 1013 cm−2 for Maser-only, Maser-RRL, and RRL-only sources, respectively. Based on the FIR data obtained from Hi-GAL and ATLASGAL, we constructed the FIR SED for our sample and obtained a number of physical parameters by fitting the SED, including the dust temperature, the H2 column density, and the relative abundance of cyanopolyynes. The mean relative abundances of HC3N are (1.22 ± 0.52) × 10−10, (5.40 ± 1.45) × 10−10, and (1.65 ± 1.50) × 10−10 for Maser-only, Maser-RRL, and RRL-only sources, respectively.
The detection rate, the mean column density, and the mean relative abundance of HC3N for three types of our sources show the same trend, that is, an increase from Maser-only to Maser-RRL sources and a decrease from Maser-RRL to RRL-only ones. This trend is consistent with the proposed evolutionary trend of HC3N (e.g. Urquhart et al. 2019; Yu et al. 2019) under the assumption that our Maser-only, Maser-RRL, and RRL-only sources correspond to YSOs, UC H ii regions, and normal classical H ii regions, respectively.
Our statistical analysis of the integrated line intensity and the column density of HC3N and shock-tracing molecules (SiO, H2CO) enabled us to find positive correlations between them. Such findings suggest that HC3N may be another tracer of shock. This supports the results of chemical models put forward by Taniguchi et al. (2019a), which suggest that the sublimation of CH4 and C2H2 from dust grains enhances key reactions of the formation of cyanopolyynes. We indirectly show that the neutral–neutral reaction between C2H2 and CN is the dominant formation pathway of HC3N.
We detect HC5N in 11 HMSFRs with a formed protostar, including 2 Maser-only and 9 Maser-RRL sources. Among these 11 sources, 10 sources are new detections (except G24.790+0.084). We detect HC7N in G24.790+0.084, which results in three HC7N sources in HMSFRs with a formed protostar. Our detections enlarge the samples of HC5N and HC7N and support the idea that unsaturated iCOMs can exist in YSOs and UC H ii regions.
Acknowledgements
This work is supported by the Natural Science Foundation of China (No. 12041302, 11590782). We thank the operators and staff at the TMRT stations for their assistance during our observations. We also thank Dr. J.Z. Wang, Dr. X.D. Tang and Dr. X. Chen for their nice comments and suggestions. Y.T.Y. is a member of the International Max Planck Research School (IMPRS) for Astronomy and Astrophysics at the Universities of Bonn and Cologne. Y.T.Y. would like to thank the China Scholarship Council (CSC) for support. J.J.Q. thanks for support from the NSFC (No. 12003080), the China Postdoctoral Science Foundation funded project (No. 2019M653144), the Guangdong Basic and Applied Basic Research Foundation (No. 2019A1515110588), and the Fundamental Research Funds for the Central Universities, Sun Yat-sen University (No. 2021qntd28). The authors would like to express their gratitude to EditSprings (https://www.editsprings.cn) for the expert linguistic services provided.
Appendix A Spectra of HC3N, HC5N, and HC7N
 |
Fig. A.1 All spectra for HC3N, HC5N, and HC7N with TMRT telescope. Solid and dashed lines show the LSR velocity values of the 6.7 GHz CH3OH maser (Yang et al. 2017, 2019), and of RRL (Chen et al. 2020), respectively. Blank panels represent non-detections. |
Appendix B The observed properties of detected lines in the survey
The HC3N (J = 2−1) transitions detected with the TMRT.
The HC5N (J = 3−2) and HC7N(J = 15−14) transitions detected with TMRT.
The column density and the relative abundance for HC3N, HC5N, and HC7N.
The integrated line intensities of other molecules.
Appendix C Source catalogue without cyanopolyyne detection
Sources without HC3N (J = 2−1) detection.
References
- Aikawa, Y., Wakelam, V., Garrod, R.T., & Herbst, E. 2008, ApJ, 674, 984 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, L.D., Bania, T.M., Balser, D.S., & Rood, R.T. 2011, ApJS, 194, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, L.D., Bania, T.M., Balser, D.S., et al. 2014, ApJS, 212, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, L.D., Armentrout, W.P., Luisi, M., et al. 2018, ApJS, 234, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Araki, M., Takano, S., Sakai, N., et al. 2016, ApJ, 833, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Arce, H.G., Santiago-Garcia, J., Jørgensen, J.K., Tafalla, M., & Bachiller, R. 2008, ApJ, 681, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, M.B., Feldman, P.A., Travers, M.J., et al. 1997, ApJ, 483, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Belloche, A., Müller, H.S.P., Menten, K.M., Schilke, P., & Comito, C. 2013, A&A, 559, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beltrân, M.T., Gueth, F., Guilloteau, S., & Dutrey, A. 2004, A&A, 416, 631 [CrossRef] [EDP Sciences] [Google Scholar]
- Benedettini, M., Viti, S., Codella, C., et al. 2013, MNRAS, 436, 179 [Google Scholar]
- Bernasconi, P.A., & Maeder, A. 1996, A&A, 307, 829 [Google Scholar]
- Breen, S.L., Ellingsen, S.P., Caswell, J.L., & Lewis, B.E. 2010, MNRAS, 401, 2219 [NASA ADS] [CrossRef] [Google Scholar]
- Bussa, S. 2012, AAS Meeting, 219, 446.10 [NASA ADS] [Google Scholar]
- Calcutt, H., Fiechter, M.R., Willis, E.R., et al. 2018, A&A, 617, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ceccarelli, C., Caselli, P., Fontani, F., et al. 2017, ApJ, 850, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J., Marcelino, N., Agündez, M., et al. 2020, A&A, 642, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cesaroni, R. 2005, in Massive Star Birth: A Crossroads of Astrophysics (Cambridge: Cambridge University Press), 227, 59 [NASA ADS] [Google Scholar]
- Chapman, J.F., Millar, T.J., Wardle, M., Burton, M.G., & Walsh, A.J. 2009, MNRAS, 394, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, H.-Y., Chen, X., Wang, J.-Z., Shen, Z.-Q., & Yang, K. 2020, ApJS, 248, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Chira, R.A., Beuther, H., Linz, H., et al. 2013, A&A, 552, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chung, H.S., Osamu, K., & Masaki, M. 1991, JKAS, 24, 217 [NASA ADS] [Google Scholar]
- Churchwell, E. 2002, ARA&A, 40, 27 [Google Scholar]
- Codella, C., Bachiller, R., & Reipurth, B. 1999, A&A, 343, 585 [NASA ADS] [Google Scholar]
- Codella, C., Lefloch, B., Ceccarelli, C., et al. 2010, A&A, 518, L112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Condon, J.J., & Ransom, S.M. 2016, Essential Rad. Astron., 4.3, 6 [Google Scholar]
- Contreras, Y., Schuller, F., Urquhart, J.S., et al. 2013, A&A, 549, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cosentino, G., Jiménez-Serra, I., Henshaw, J.D., et al. 2018, MNRAS, 474, 3760 [NASA ADS] [Google Scholar]
- Csengeri, T., Leurini, S., Wyrowski, F., et al. 2016, A&A, 586, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cummins, S.E., Linke, R.A., & Thaddeus, P. 1986, ApJS, 60, 819 [NASA ADS] [CrossRef] [Google Scholar]
- Cyganowski, C.J., Koda, J., Rosolowsky, E., et al. 2013, ApJ, 764, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Duarte-Cabral, A., Bontemps, S., Motte, F., et al. 2014, A&A, 570, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elia, D., Schisano, E., Molinari, S., et al. 2010, A&A, 518, L97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ellingsen, S.P. 2006, ApJ, 638, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Ellingsen, S.P. 2007, MNRAS, 377, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Esplugues, G.B., Cernicharo, J., Viti, S., et al. 2013, A&A, 559, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feng, S., Beuther, H., Henning, T., et al. 2015, A&A, 581, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feng, H., Wang, J., Li, S., et al. 2021, PASJ, 73, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Garrod, R.T., & Herbst, E. 2006, A&A, 457, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gerner, T., Beuther, H., Semenov, D., et al. 2014, A&A, 563, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giannetti, A., Leurini, S., König, C., et al. 2017, A&A, 606, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gieser, C., Beuther, H., Semenov, D., et al. 2021, A&A, 648, A66 [EDP Sciences] [Google Scholar]
- Goldsmith, P.F., & Langer, W.D. 1999, ApJ, 517, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Gong, Y., Henkel, C., Thorwirth, S., et al. 2015, A&A, 581, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Graninger, D.M., Wilkins, O.H., & Öberg, K.I. 2016, ApJ, 819, 140 [NASA ADS] [CrossRef] [Google Scholar]
- GRAVITY Collaboration (Abuter, R., et al.) 2018, A&A, 615, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Green, C.E., Green, J.A., Burton, M.G., et al. 2014, MNRAS, 443, 2252 [NASA ADS] [CrossRef] [Google Scholar]
- Gusdorf, A., Cabrit, S., Flower, D.R., & Pineau Des Forêts, G. 2008, A&A, 482, 809 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Güsten, R., Nyman, L.Â., Schilke, P., et al. 2006, A&A, 454, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guzmân, A.E., Sanhueza, P., Contreras, Y., et al. 2015, ApJ, 815, 130 [CrossRef] [Google Scholar]
- Hassel, G.E., Herbst, E., & Garrod, R.T. 2008, ApJ, 681, 1385 [NASA ADS] [CrossRef] [Google Scholar]
- He, Y.-X., Henkel, C., Zhou, J.-J., et al. 2021, ApJS, 253, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Herbst, E., & van Dishoeck, E.F. 2009, ARA&A, 47, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Hirota, T., Ohishi, M., & Yamamoto, S. 2009, ApJ, 699, 585 [Google Scholar]
- Hoq, S., Jackson, J.M., Foster, J.B., et al. 2013, ApJ, 777, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Hosokawa, T., & Omukai, K. 2009, ApJ, 691, 823 [Google Scholar]
- Jørgensen, J.K., Belloche, A., & Garrod, R.T. 2020, ARA&A, 58, 727 [CrossRef] [Google Scholar]
- Kauffmann, J., Bertoldi, F., Bourke, T.L., Evans, N.J.I., & Lee, C.W. 2008, A&A, 487, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- König, C., Urquhart, J.S., Csengeri, T., et al. 2017, A&A, 599, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kurtz, S., Cesaroni, R., Churchwell, E., Hofner, P., & Walmsley, C.M. 2000, in Protostars and Planets IV (Tucson: University of Arizona Press), 299 [Google Scholar]
- Law, C.J., Oberg, K.I., Bergner, J.B., & Graninger, D. 2018, ApJ, 863, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Levshakov, S.A., Lapinov, A.V., Henkel, C., et al. 2010, A&A, 524, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, F.C., Xu, Y., Wu, Y.W., et al. 2016a, AJ, 152, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Li, J., Shen, Z.-Q., Wang, J., et al. 2016b, ApJ, 824, 136 [Google Scholar]
- Liu, H.-L., Liu, T., Evans, Neal J., I., et al. 2021, MNRAS, 505, 2801 [NASA ADS] [CrossRef] [Google Scholar]
- Loomis, R.A., Shingledecker, C.N., Langston, G., et al. 2016, MNRAS, 463, 4175 [NASA ADS] [CrossRef] [Google Scholar]
- Löpez-Sepulcre, A., Watanabe, Y., Sakai, N., et al. 2016, ApJ, 822, 85 [CrossRef] [Google Scholar]
- Luisi, M., Anderson, L.D., Bania, T.M., et al. 2018, PASP, 130, 084101 [NASA ADS] [CrossRef] [Google Scholar]
- Mangum, J.G., & Shirley, Y.L. 2015, PASP, 127, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Martin-Pintado, J., Bachiller, R., & Fuente, A. 1992, A&A, 254, 315 [NASA ADS] [Google Scholar]
- McCarthy, M.C., Grabow, J.U., Travers, M.J., et al. 1998, ApJ, 494, L231 [NASA ADS] [CrossRef] [Google Scholar]
- McElroy, D., Walsh, C., Markwick, A.J., et al. 2013, A&A, 550, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McGee, R.X., Newton, L.M., & Butler, P.W. 1975, ApJ, 202, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Mendoza, E., Lefloch, B., Ceccarelli, C., et al. 2018, MNRAS, 475, 5501 [NASA ADS] [CrossRef] [Google Scholar]
- Miettinen, O. 2014, A&A, 562, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minier, V., Ellingsen, S.P., Norris, R.P., & Booth, R.S. 2003, A&A, 403, 1095 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mitchell, G.F. 1984, ApJS, 54, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Molinari, S., Pezzuto, S., Cesaroni, R., et al. 2008, A&A, 481, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molinari, S., Schisano, E., Elia, D., et al. 2016, A&A, 591, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Newville, M., Stensitzki, T., Allen, D.B., et al. 2016, Astrophysics Source Code Library [record ascl:1606.014] [Google Scholar]
- Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
- Ragan, S.E., Bergin, E.A., & Wilner, D. 2011, ApJ, 736, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Rathborne, J.M., Garay, G., Jackson, J.M., et al. 2011, ApJ, 741, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, M.J., Menten, K.M., Brunthaler, A., et al. 2014, ApJ, 783, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, M.J., Menten, K.M., Brunthaler, A., et al. 2019, ApJ, 885, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Rolffs, R., Schilke, P., Zhang, Q., & Zapata, L. 2011, A&A, 536, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roman-Duval, J., Jackson, J.M., Heyer, M., et al. 2009, ApJ, 699, 1153 [CrossRef] [Google Scholar]
- Sabatini, G., Bovino, S., Giannetti, A., et al. 2021, A&A, 652, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sakai, N., Ikeda, M., Morita, M., et al. 2007, ApJ, 663, 1174 [Google Scholar]
- Sakai, T., Sakai, N., Kamegai, K., et al. 2008, ApJ, 678, 1049 [Google Scholar]
- Sakai, N., Sakai, T., Hirota, T., & Yamamoto, S. 2009, ApJ, 702, 1025 [Google Scholar]
- Sakai, N., Sakai, T., Hirota, T., & Yamamoto, S. 2010, ApJ, 722, 1633 [Google Scholar]
- Schuller, F., Menten, K.M., Contreras, Y., et al. 2009, A&A, 504, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shirley, Y.L. 2015, PASP, 127, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Sobolev, A.M., & Deguchi, S. 1994, A&A, 291, 569 [NASA ADS] [Google Scholar]
- Suzuki, H., Yamamoto, S., Ohishi, M., et al. 1992, ApJ, 392, 551 [Google Scholar]
- Svoboda, B.E., Shirley, Y.L., Battersby, C., et al. 2016, ApJ, 822, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Tafalla, M., Myers, P.C., Caselli, P., & Walmsley, C.M. 2004, A&A, 416, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tafalla, M., Santiago-Garcia, J., Hacar, A., & Bachiller, R. 2010, A&A, 522, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takano, S., Masuda, A., Hirahara, Y., et al. 1998, A&A, 329, 1156 [NASA ADS] [Google Scholar]
- Tang, X.D., Henkel, C., Wyrowski, F., et al. 2018, A&A, 611, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taniguchi, K., Saito, M., & Ozeki, H. 2016, ApJ, 830, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Taniguchi, K., Miyamoto, Y., Saito, M., et al. 2018a, ApJ, 866, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Taniguchi, K., Saito, M., Majumdar, L., et al. 2018b, ApJ, 866, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Taniguchi, K., Saito, M., Sridharan, T.K., & Minamidani, T. 2018c, ApJ, 854, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Taniguchi, K., Herbst, E., Caselli, P., et al. 2019a, ApJ, 881, 57 [Google Scholar]
- Taniguchi, K., Saito, M., Sridharan, T.K., & Minamidani, T. 2019b, ApJ, 872, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Thaddeus, P., & McCarthy, M.C. 2001, SAA, 57, 757 [Google Scholar]
- Travers, M.J., McCarthy, M.C., Kalmus, P., Gottlieb, C.A., & Thaddeus, P. 1996, ApJ, 469, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Urquhart, J.S., Morgan, L.K., Figura, C.C., et al. 2011, MNRAS, 418, 1689 [NASA ADS] [CrossRef] [Google Scholar]
- Urquhart, J.S., Csengeri, T., Wyrowski, F., et al. 2014a, A&A, 568, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Urquhart, J.S., Moore, T.J.T., Csengeri, T., et al. 2014b, MNRAS, 443, 1555 [NASA ADS] [CrossRef] [Google Scholar]
- Urquhart, J.S., König, C., Giannetti, A., et al. 2018, MNRAS, 473, 1059 [NASA ADS] [CrossRef] [Google Scholar]
- Urquhart, J.S., Figura, C., Wyrowski, F., et al. 2019, MNRAS, 484, 4444 [NASA ADS] [CrossRef] [Google Scholar]
- Urquhart, J.S., Wells, M.R.A., Pillai, T., et al. 2022, MNRAS, 510, 3389 [NASA ADS] [CrossRef] [Google Scholar]
- Viti, S., Jimenez-Serra, I., Yates, J.A., et al. 2011, ApJ, 740, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Wakelam, V., Caselli, P., Ceccarelli, C., Herbst, E., & Castets, A. 2004, A&A, 422, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walsh, A.J., Burton, M.G., Hyland, A.R., & Robinson, G. 1998, MNRAS, 301, 640 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J.Q., Yu, L.F., Jiang, Y.B., et al. 2017, AcASn, 58, 37 [NASA ADS] [Google Scholar]
- Wang, S., Ren, Z., Li, D., et al. 2020, MNRAS, 499, 4432 [NASA ADS] [CrossRef] [Google Scholar]
- Widicus Weaver, S.L., Laas, J.C., Zou, L., et al. 2017, ApJS, 232, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Wienen, M., Wyrowski, F., Schuller, F., et al. 2012, A&A, 544, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wu, Y., Liu, X., Chen, X., et al. 2019, MNRAS, 488, 495 [Google Scholar]
- Xu, Y., Li, J.J., Hachisuka, K., et al. 2008, A&A, 485, 729 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yang, K., Chen, X., Shen, Z.-Q., et al. 2017, ApJ, 846, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, K., Chen, X., Shen, Z.-Q., et al. 2019, ApJS, 241, 18 [Google Scholar]
- Yu, N., & Wang, J.-J. 2015, MNRAS, 451, 2507 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, N., & Xu, J. 2016, ApJ, 833, 248 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, N., Wang, J.-J., & Xu, J.-L. 2019, MNRAS, 489, 4497 [CrossRef] [Google Scholar]
- Zhang, Y.-J., Zhou, J.-J., Esimbek, J., et al. 2016, Ap&SS, 361, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, X.-Y., Zhu, Q.-F., Li, J., et al. 2017, A&A, 606, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, C., Wu, Y., Liu, X.C., et al. 2021, A&A, 648, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, C., Evans, N.J., Liu, T., et al. 2022, MNRAS, 510, 4998 [NASA ADS] [CrossRef] [Google Scholar]
Unsaturated iCOMs are carbon-bearing molecules that have at least six atoms and are hydrogen poor (e.g. Rolffs et al. 2011; Rathborne et al. 2011).
The critical density is estimated from ncrit = Aij/Cij for optically thin emission, where Aij and Cij is the Einstein coefficient for spontaneous emission and the collision rate, respectively (Shirley 2015).
All Tables
All Figures
 |
Fig. 1 Examples for HC3N, HC5N, and HC7N with TMRT telescope. Solid and dashed lines show the LSR velocity values of 6.7 GHz CH3OH maser (Yang et al. 2017, 2019), and of RRL (Chen et al. 2020), respectively. The full spectra are shown in Appendix Fig. A.1. |
| In the text | |
 |
Fig. 2 HFS fitting of G30.810−0.050. |
| In the text | |
 |
Fig. 3 FIR SED and its fit curve (the solid curve, from one single temperature grey-body model) of sources with cyanopolyynes detection. The cross indicates 70 µm emission, which is not involved in the SED fit. |
| In the text | |
 |
Fig. 4 The detection rates, column densities, and relative abundances of HC3N for different types of sources. |
| In the text | |
 |
Fig. 5 Column density (left panels) and the integrated line intensity (right panels) of HC3N are plotted against those of shock-tracing molecules (H2CO and SiO). The circles and empty circles indicate our sources and sources reported in He et al. (2021), respectively. The solid lines and the dashed line show the weighted linear fitting line for our data and theirs. |
| In the text | |
 |
Fig. A.1 All spectra for HC3N, HC5N, and HC7N with TMRT telescope. Solid and dashed lines show the LSR velocity values of the 6.7 GHz CH3OH maser (Yang et al. 2017, 2019), and of RRL (Chen et al. 2020), respectively. Blank panels represent non-detections. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


