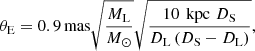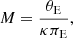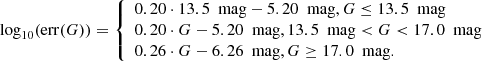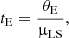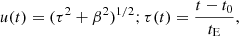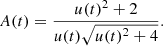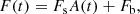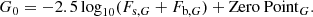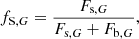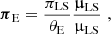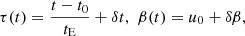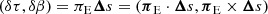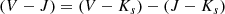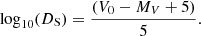| Issue |
A&A
Volume 662, June 2022
|
|
|---|---|---|
| Article Number | A59 | |
| Number of page(s) | 12 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202142602 | |
| Published online | 14 June 2022 | |
Lens parameters for Gaia18cbf – a long gravitational microlensing event in the Galactic plane⋆
1
Astronomical Observatory, University of Warsaw, Al. Ujazdowskie 4, 00-478 Warszawa, Poland
e-mail: kkruszynska@astrouw.edu.pl
2
Institute of Theoretical Physics and Astronomy, Vilnius University, Saulėtekio al. 3, Vilnius 10257, Lithuania
3
Las Cumbres Observatory, 6740 Cortona Drive, Suite 102, Goleta, CA 93117, USA
4
Department of Physics, University of Auckland, Private Bag 92019, Auckland, New Zealand
5
Institute of Astronomy, Faculty of Physics, Astronomy and Informatics, Nicolaus Copernicus University in Toruń, ul. Grudziądzka 5, 87-100 Toruń, Poland
6
Institute of Astronomy, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
7
Instytut Astronomiczny, Uniwersytet Wrocławski, Kopernika 11, Wrocław, Poland
8
Dipartimento di Fisica “E.R. Caianiello”, Università di Salerno, Via Giovanni Paolo II, 84084 Fisciano, Italy
9
Istituto Nazionale di Fisica Nucleare, Sezione di Napoli, Via Cintia, 80126 Napoli, Italy
10
University of St Andrews, Centre for Exoplanet Science, SUPA School of Physics & Astronomy, North Haugh, St Andrews KY16 9SS, UK
11
Facultad de Ingeniería y Tecnología, Universidad San Sebastian, General Lagos 1163, Valdivia 5110693, Chile
12
Komaba Institute for Science, The University of Tokyo, 3-8-1 Komaba, Meguro, Tokyo 153-8902, Japan
13
Instituto de Astrofísica de Canarias, Vía Láctea s/n, 38205 La Laguna, Tenerife, Spain
14
Zentrum für Astronomie der Universität Heidelberg, Astronomisches Rechen-Institut, Mönchhofstr. 12-14, 69120 Heidelberg, Germany
15
Astrobiology Center, 2-21-1 Osawa, Mitaka, Tokyo 181-8588, Japan
16
Nicolaus Copernicus Astronomical Center, Polish Academy of Sciences, Bartycka 18, 00-716 Warsaw, Poland
17
Center for Astrophysics and Cosmology, University of Nova Gorica, Vipavska 11c, 5270 Ajdovščina, Slovenia
Received:
7
November
2021
Accepted:
11
March
2022
Context. The timescale of a microlensing event scales as a square root of a lens mass. Therefore, long-lasting events are important candidates for massive lenses, including black holes.
Aims. Here, we present the analysis of the Gaia18cbf microlensing event reported by the Gaia Science Alerts system. It exhibited a long timescale and features that are common for the annual microlensing parallax effect. We deduce the parameters of the lens based on the derived best fitting model.
Methods. We used photometric data collected by the Gaia satellite as well as the follow-up data gathered by the ground-based observatories. We investigated the range of microlensing models and used them to derive the most probable mass and distance to the lens using a Galactic model as a prior. Using a known mass-brightness relation, we determined how likely it is that the lens is a main-sequence (MS) star.
Results. This event is one of the longest ever detected, with the Einstein timescale of tE = 491.41−84.94+128.31 days for the best solution and tE = 453.74−105.74+178.69 days for the second best. Assuming Galaxy priors, this translates to the most probable lens masses of ML = 2.65−1.48+5.09 M⊙ and ML = 1.71−1.06+3.78 M⊙, respectively. The limits on the blended light suggest that this event was most likely not caused by a MS star, but rather by a dark remnant of stellar evolution.
Key words: gravitational lensing: micro / Galaxy: stellar content / stars: black holes / stars: neutron
Full Table A.1 is only and Table A.2 is also available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/662/A59
© ESO 2022
1. Introduction
The first person to realise the possibility of gravitational microlensing was R. W. Mandl, who then inspired Einstein to make calculations that proved a technical possibility of such effect. Einstein himself, however, dismissed it as impossible to observe due to the rareness of such events and the limitations of the instruments present at that time (Einstein 1936). During the 1960s, much of theoretical groundwork was done (Liebes 1964; Refsdal 1964), but this phenomenon was not pursued as it is today until the idea was re-introduced towards the end of 1980 by Bohdan Paczyński as a way to reveal the nature of dark matter (Paczynski 1986). This has launched many successful surveys including MACHO (Alcock et al. 1992; Bennett et al. 1993), OGLE (Udalski et al. 1992), EROS (Aubourg et al. 1993), and MOA (Abe et al. 1997) and led to a detection of many microlensing events. Some of the events revealed planets around microlensing stars, which was predicted by Mao & Paczynski (1991). In order to obtain better light curves for observed events, follow-up with other telescopes was frequently used, including telescope networks such as μFUN (Gould et al. 2010) or Las Cumbres Observatory network of robotic telescopes (Tsapras et al. 2009). Recently, a new era of microlensing surveys started with the launch of KMTNet, which provides near 24 h monitoring of selected fields towards the Galactic bulge with cadences from 15 minutes up to 5 h (Kim et al. 2016).
Despite astonishing improvements in the way data are acquired, it is often hard to measure physical parameters of microlensing system, because it is difficult to uniquely determine the mass and distance to the lens based only on the event timescale. Information about the mass of the lens is encoded in a parameter called the Einstein radius, which is defined as
where ML is the mass of the lens, DS is the distance to the source, and DL is the distance to the lens (Paczynski 1996).
Deriving the absolute mass of the lens is, however, almost impossible without second-order effects or additional data. One such effect is the finite-source effect, which has to be included when the source is crossing over the lens or caustic or in other cases, when the gradient of lensing magnification over the source surface plays a significant role. One example where this occurs is well-sampled high magnification events or caustic-crossing events (Witt & Mao 1994).
Another method that can be used to obtain additional information about the lens system is parallax, which can be broken into three sub-groups: annual, terrestrial, and space. Annual parallax occurs when the event is long enough for Earth’s movement around the Sun to change the position of the observer and produces a distinct asymmetry in the observed light curve (Gould 1992; Alcock et al. 1995). Such an effect, combined with a large timescale tE can be used to constrain the mass of the lens and to find microlensing dark remnant candidates (Bennett et al. 2002; Poindexter et al. 2005; Wyrzykowski et al. 2016; Wyrzykowski & Mandel 2020; Lam et al. 2020; Karolinski & Zhu 2020; Abrams & Takada 2020; Mróz & Wyrzykowski 2021). The longest ever detected microlensing event had a timescale of 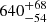 days (Mao et al. 2002), and only a few known events have timescales around 400 days (Wyrzykowski et al. 2015; Mróz et al. 2020). A terrestrial parallax occurs when a microlensing event is observed from two separate observatories on Earth. If the separation between the sites is large enough and the event is observed at high cadence, it is possible to see that the time of the peak and impact parameter differs between sites (Hardy & Walker 1995; Holz & Wald 1996; Gould et al. 2009). The space parallax is similar to the terrestrial one, but one of the observatories is located in space (Refsdal 1966). If the separation is as large as 1 au, it is possible to observe significant differences in the impact parameter u0 and the time of peak t0 even for standard events. Such observations have been provided for many events observed simultaneously by OGLE and Spitzer Space Telescope, most notably Dong et al. (2007). If the event is binary and both observatories manage to catch a caustic crossing, the separation may be smaller: as low as 0.01 au (Wyrzykowski et al. 2020). If it is possible to measure θE and πE, for example through finite-source effect and a parallax effect, one can directly measure the mass of the lens using the following relation (An et al. 2002; Gould 2004; Rybicki et al. 2022):
days (Mao et al. 2002), and only a few known events have timescales around 400 days (Wyrzykowski et al. 2015; Mróz et al. 2020). A terrestrial parallax occurs when a microlensing event is observed from two separate observatories on Earth. If the separation between the sites is large enough and the event is observed at high cadence, it is possible to see that the time of the peak and impact parameter differs between sites (Hardy & Walker 1995; Holz & Wald 1996; Gould et al. 2009). The space parallax is similar to the terrestrial one, but one of the observatories is located in space (Refsdal 1966). If the separation is as large as 1 au, it is possible to observe significant differences in the impact parameter u0 and the time of peak t0 even for standard events. Such observations have been provided for many events observed simultaneously by OGLE and Spitzer Space Telescope, most notably Dong et al. (2007). If the event is binary and both observatories manage to catch a caustic crossing, the separation may be smaller: as low as 0.01 au (Wyrzykowski et al. 2020). If it is possible to measure θE and πE, for example through finite-source effect and a parallax effect, one can directly measure the mass of the lens using the following relation (An et al. 2002; Gould 2004; Rybicki et al. 2022):
where 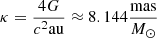 (Gould 2000).
(Gould 2000).
A different approach to obtaining the mass of the lens is to measure the flux of the lens FL (Koshimoto et al. 2017, 2020). This can be done with high angular resolution imaging using adaptive optics or the Hubble Space Telescope and requires knowledge of the mass-luminosity relation for the pass-band in which the event is observed. Such relations are known for the stars in the Galactic bulge, but not necessarily for the Galactic disc.
Yet another way of obtaining additional data needed to break degeneracies of the microlensing model is to observe how the event affects the astrometric position of the source. When the source is approaching the Einstein radius, its image gets deformed and splits into two separate images. Because the separation between two images is too small for events occurring in the Milky Way to be observable by the majority of modern telescopes, we observe a shift of the centroid of light instead. With enough precision, such effects can be measured, and it provides data for the direct measurement of the Einstein radius. So far, only one team has been successful in measuring an astrometric microlensing effect using the Hubble Space Telescope, and they revealed a microlensing event caused by a white dwarf (Sahu et al. 2017). In recent years, using the Very Large Telescope’s GRAVITY or PIONIER has helped to resolve two deformed images of the microlensed source, which provided an addidional way to measure θE (Dong et al. 2019; Cassan et al. 2021).
Gaia is a space satellite that was launched on 19 December 2019 from French Guiana by the European Space Agency. As a successor of the HIPPARCOS mission, its main purpose is to measure positions and parallaxes of 1 billion stars residing in the Milky Way with sub-milliarcsecond precision. It is also going to measure space velocities of observed stars and create a 3D structural map of the Milky Way (Gaia Collaboration 2016). It is equipped with two telescopes sharing a common focal plane. These telescopes have curved (1.45 × 0.5) m mirrors and their fields of view are separated by an angle of approximately 106.5°. The focal plane consists of 104 CCD matrices, which include two rows of Sky Mapper CCDs responsible for detecting observable objects, nine rows of astro-photometric fields (AF) measuring the brightness of a source in a wide G-band, two rows of low-resolution spectro-photometers (BP and RP), and three rows of high-precision radial velocity spectrograph used for sources brighter than V = 16 mag (RVS). The spacecraft is currently residing on a Lissajous orbit around the Lagrangian L2 point of the Earth-Sun system. It is rotating along its axis with a period of six hours, while the rotational axis is precessing with a period of 63 days. This allows Gaia to make full scans of the Milky Way repeatedly during the five years of its nominal mission (Gaia Collaboration 2016). Such a design yields the following consequences for the observations of a single source. First of all, each time Gaia passes a field, where an interesting object resides, we obtain two scans separated by a few hours. Secondly, instead of taking an image of the field, a source passing through a single row of CCDs is detected by the Sky Mappers, and then nine measurements of brightness are taken by AFs with a 3 s cadence – this means that the blend flux observed by Gaia may be smaller than in the case of a ground-based telescope. Lastly, on average, each source is observed once per 30 days – this means that ground-based follow-up is necessary for an evenly covered light curve suitable for modelling.
Since Gaia is observing the whole sky, the idea of an alerting system, called Gaia Science Alerts (GSA)1, was conceived (Wyrzykowski & Hodgkin 2012; Hodgkin et al. 2013, 2021). Gaia was expected to deliver not only astrometry with precision down to 24 microarcseconds, but also to provide a vast sample of interesting transients (Blagorodnova et al. 2016). Gaia Science Alerts has been operating since 2014 and has revealed around 18 000 transients, of which the majority are supernovae, active galactic nuclei, cataclysmic variables, and flaring young stellar objects. Microlensing events are also detected, and to date more than 300 candidates have been identified, with the vast majority located in the Galactic plane. Because of sparse Gaia sampling, global follow-up campaigns have been organised and provide supplementary photometric data, which then help one to study the events in detail (for example Wyrzykowski et al. 2020; Rybicki et al. 2022). The astrometric capabilities of the Gaia mission are going to be particularly useful for hundreds of events observed by Gaia, as the sub-milliarcsecond precision for the measurement of the position of observed source will lead to the measurement of the Einstein radius, which helps to determine the lens mass with improved precision (Belokurov & Evans 2002; Rybicki et al. 2018).
Here, we present a study of the photometric data of one of the longest microlensing events detected by the Gaia Science Alerts system, Gaia18cbf. We present a detailed analysis of this event and derive a probable range of parameters of the object that caused it. This paper is organised as follows. In Sect. 2, we present when and how the event was discovered and how photometric data were gathered. Next, we describe microlensing model we used and how we found best fitting models in Sect. 3. Section 4 is devoted to discussing the possible location and nature of the source star, while in Sect. 5 we discuss the nature of the lens. We discuss the results of the entire analysis in Sect. 6, and we provide closing arguments and conclusions in Sect. 7.
2. Discovery and follow-up
Gaia18cbf (AT2018etg according to the IAU transient name server was detected by the Gaia Science Alerts pipeline using the data collected on August 6 2018 (HJD′ = HJD – 2450000.0 = 8336.62). The event was located at equatorial coordinates RA = 16:04:38.86, δ = −41:06:17.39 and Galactic coordinates 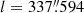 ,
, 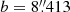 . We present a finding chart with the location of this event in Fig. 1. Two days later, on August 8, it was posted on GSA the website2.
. We present a finding chart with the location of this event in Fig. 1. Two days later, on August 8, it was posted on GSA the website2.
 |
Fig. 1. Location of Gaia18cbf and its neighbourhood during the event. Chart is a stack of two images obtained with 2 m LCO telescope located in Siding Springs Observatory in October 2019 and July 2020. White circle marks the target. |
Gaia Data Release 2 (GDR2) (Gaia Collaboration 2018) and Gaia Early Data Release 3 (GEDR3) (Gaia Collaboration 2021; Lindegren et al. 2021) contain an entry for this source under Gaia Source ID = 5995134605563805056. We present values of full five-parameter astrometric solutions along with estimated distances from Bailer-Jones et al. (2018, 2021) for this object in Table 1.
Gaia astrometric parameters for the source star in Gaia18cbf.
It is important to note that in GDR2 the parallax is negative, while the proper motions were measured with significant uncertainties. The precision of proper motions has improved in GEDR3; however, the parallax value is still negative. Estimated distances are not reliable for negative parallaxes and very faint sources. In case of microlensing, if the lens is luminous enough, the parallax measurement may be affected (Jeong et al. 1999). The lens can dominate over the source’s light, and the observed parallax and proper motion can be measured for the mean source and lens motion. This means that parameters presented in GDR2 and GEDR3 should be taken into account only after we have found a best fitting model for this event and after we have ruled out the case of a luminous lens.
2.1. Gaia photometry
Gaia’s photometric measurement is based on the mean of brightness from nine AFs and it is gathered in a wide G-band (Jordi et al. 2010). On average, Gaia observes a source once every 30 days. This event was discovered before the time of peak brightness. However, due to its unusual shape and low luminosity, it was first dismissed as a non-microlensing event. Only after the new Gaia data points collected in February 2019, from around the peak in brightness, did the event become a candidate microlensing event. As of October 15 2021, Gaia has collected 76 measurements for Gaia18cbf and the event has almost returned to its baseline. Gaia Science Alerts do not provide errors for published events, but the nominal error should vary from 0.02 mag for G = 17.7 mag at peak to 0.1 mag for G = 20.3 mag at baseline (Gaia Collaboration 2018).
We applied the following formula to provide estimates of error bars for Gaia measurements, since the light curve published by GSA provides none:
We present the Gaia data used for modelling in Table A.1.
2.2. Photometric follow-up
We require consistent follow-up in order to obtain proper values for a best fitting microlensing model, especially blending parameters. This means that the event should be observed not only at the time of peak brightness, but also during the baseline by the same telescope. Due to the target faintness and location, we chose to use the Las Cumbres Observatory Global Network (LCO) of robotic telescopes (Brown et al. 2013).
The follow-up observation started after the peak using the 2-m LCO telescope located at Siding Spring Observatory, Australia (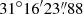 S,
S, 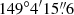 E, LCO SSO). The number of data points is presented in Table 2. Follow-up data were uploaded and calibrated using the Black Hole Target Observation Manager (BHTOM)3 tool for coordinated observations and processing of photometric time series. BHTOM uses Cambridge Photometric Calibration Server (Zieliński et al. 2019, 2020) and CCDPhot (Mikołajczyk et al., in prep.) as its main processing pipelines. In order to model this event, we chose to use the observations made in the i-band only. This is because there are significantly more points in the i-band compared to the V and G bands. The i-band data are presented in Table A.2.
E, LCO SSO). The number of data points is presented in Table 2. Follow-up data were uploaded and calibrated using the Black Hole Target Observation Manager (BHTOM)3 tool for coordinated observations and processing of photometric time series. BHTOM uses Cambridge Photometric Calibration Server (Zieliński et al. 2019, 2020) and CCDPhot (Mikołajczyk et al., in prep.) as its main processing pipelines. In order to model this event, we chose to use the observations made in the i-band only. This is because there are significantly more points in the i-band compared to the V and G bands. The i-band data are presented in Table A.2.
Summary of photometric data gathered for Gaia18cbf.
3. Microlensing model
The standard Paczyński light curve model (Paczynski 1986), which assumes a point source and a point lens, requires three parameters: the time of the peak of brightness t0, impact parameter β, which is the lens-source separation (scaled to θE) at t0, and the timescale of an event, called Einstein time tE, defined as:
where μLS is the relative proper motion of source and lens, which is typically unknown. Then, the time-varying projected lens-source separation, scaled to θE is expressed as:
which leads to the expression for the magnification of the source star as follows:
Finally, the relation for observed flux as a function of time is:
where Fs is the unmagnified flux of the source and Fb is the blend flux. The blend flux could be the light coming from the lensing star or, in dense fields, from nearby stars blended in the source image. If we consider binary lens or binary source models, the blend can also come from the lens’ or the source’s companion. Blending can also be a combination of the aforementioned factors.
In this paper, we use different flux parameters: G0, i0, fS, G and fS, i. The G0 is the brightness in baseline in G filter, which is derived from Fs and Fb from Eq. (6) using following relation:
Similarly, i0 is the brightness in the baseline in the i filter, calculated as G0. The fS, G is the blending parameter in G filter, which is related to Fs and Fb by the following relation:
and fS, i is the blending parameter in the i filter.
3.1. Annual parallax
The light curve presented in Fig. 2 reveals that the event lasted for over four years. This means that in modelling this event we have to include the annual parallax effect to take into account Earth’s movement around the Sun.
 |
Fig. 2. Light curve and best fitting models for Gaia18cbf with follow-up. Maroon dots represent data gathered by Gaia, while yellow dots mark data observed by Las Cumbres Observatory in Siding Spring Observatory (LCO SSO) in the i-band. Continuous lines represent different solutions for a point source-point lens model with parallax effect. Best fitting models for GF+, GF− and GL solutions are shown in red, blue, and green, respectively. In lighter colours, we show other solutions that we obtained through a Markov chain Monte Carlo method. The dashed line represents the point source–point lens model without including a parallax effect, called ‘GF0’. Bottom panel: we show the difference between the GF0 model and other models. The data shown in maroon and yellow dots represent the result of subtraction of the magnitude predicted by the GF0 model and the observed magnitude. We use the same colour representation for the GF+, GF−, and GL solutions, as in the top panel. |
First we have to introduce the parallax vector πE (Gould 2000), which has the same direction as the relative proper motion of the lens and source μLS and its magnitude is the relative parallax of the lens and source scaled by the Einstein radius:
where 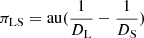 (Gould 2004). We adopt a geocentric coordinate system and follow equations introduced in Gould (2004). We have to add new terms to the microlensing model to take into account that during the year the observer located on Earth changes their position. These terms will correspond to changes of the source–lens projected separation and magnification. Relation (4) will then change to
(Gould 2004). We adopt a geocentric coordinate system and follow equations introduced in Gould (2004). We have to add new terms to the microlensing model to take into account that during the year the observer located on Earth changes their position. These terms will correspond to changes of the source–lens projected separation and magnification. Relation (4) will then change to
where
is the displacement vector due to parallax and Δs is the positional offset of the Sun in the geocentric frame (Gould 2004).
3.2. Modelling and results
We used a Markov chain Monte Carlo (MCMC) method to explore the parameter space of the model described above. We used the emcee package (Foreman-Mackey et al. 2013) for the MCMC method and the MulensModel package (Poleski & Yee 2019) to generate microlensing models including an annual parallax effect. We note that MulensModel returns flux parameters in form of Fs and Fb, as in Eq. (6). We then calculated fS, G and fS, i using Eqs. (7) and (8). We assumed Zero PointG and Zero Pointi as 22 mag following the MulensModel package parametrisation.
We modelled the event using two sets of photometric data: Gaia data only and Gaia and i-band follow-up data from LCO SSO. We first performed a preliminary exploration of the parameter space to discover possible solutions. After visually inspecting the resulting solutions, we found three classes of solutions for Gaia-only data: one with an unusually long Einstein timescale tE (dubbed GL), and two with shorter tE but symmetrical in relation to the impact parameter u0, (dubbed GS+ and GS−). For comparison, we also computed a model without including a parallax effect, called ‘G0’. We present parameters of best fitting models in Table 3.
Parameter values of best fitting solutions for Gaia18cbf using only Gaia photometric data.
When we added the follow-up data to the Gaia data, we noticed that the GL solution disappeared, but two symmetrical, with the regard to impact parameter, u0 solutions remained, called GF+ and GF−. We also added a model without including the parallax effect for comparison, called GF0. We present parameters of the best fitting models for this case in Table 4. The chi-squared contour plots in function of fitted parameters of the best solution, GF+, are presented in Fig. 3.
 |
Fig. 3. Chi-squared contours plotted as a function of the parameters fitted in the MCMC fit for the best model, GF+. Black, dark grey, and light grey solid colours represent 1σ, 2σ, and 3σ confidence regions, respectively. Black dots represent solutions outside of the 3/sigma confidence level. Blue lines and squares mark the median solution reported in Table 4. Plot was created using corner python package by Foreman-Mackey (2016). |
Parameter values of best fitting solutions for Gaia18cbf using Gaia and i-band follow-up photometric data.
The GL solution also has the highest χ2 value. The lowest χ2 value is found for a solution with u0 > 0 for both datasets used. When we use both Gaia and i-band follow-up data, the solution with u0 > 0 (GF+) also has the highest value of blending parameter fs = Fs/(Fs + Fb), implying that the observed flux is dominated by the flux from the source and the blended flux is negligible. This strongly supports the hypothesis that a dark object caused the Gaia18cbf microlensing event. Other solutions, however, have blending parameter values varying between 0.6 and 0.8, which would suggest that the lens is a dim star rather than a dark remnant of stellar evolution. We present the Gaia and follow-up data along with the best fitting light curves in Fig. 2.
4. Source star
To determine the physical properties of the lensing event, a distance estimation for the source star is essential. The most obvious place to find the distance of a star, in particular in case of an event discovered by Gaia, are the Gaia data releases. In this case we could not, however, use distances from GDR2 or GEDR3, because the parallax ϖ is negative and thus unreliable. Instead, we used archival photometric data and applied a spectro-photometric method to obtain the distance of the source star. This method assumes that the star is single and non-variable. We also assumed that the extinction is proportional to the colour excess. Additionally, we assumed that the light observed at all stages of the microlensing event is emitted by a single object, the background (source) star. The microlensing model can provide information on the amount of blended light (from lens or unrelated stars within the seeing disc), and, as shown in Sect. 3, different models indicate different values of blending. However, only in extreme cases can the blend dominate over the source; hence, in this study of the source we assumed the light at the baseline is dominated by the source star. In our case, the blending parameter fs does not fall below 0.6, so we can assume that the majority of the light during the event comes from the source.
In this work, we used the VISTA Hemisphere Survey (VHS) catalogue DR4.1 (McMahon et al. 2013) and the TESS Input Catalog–v8.0 (TIC-8; Stassun et al. 2019). The VISTA catalogue provides J and Ks magnitude values, as well as extinction, which allowed us to determine that the intrinsic colour of the source is star equal to (J − K)0 = 0.131 mag. According to (Pecaut & Mamajek 2013; hereafter PM), this colour most closely corresponds to a F0V-type star with an effective temperature of Teff = 7220 K and MV = 2.51 mag. For comparison, we empirically determined the intrinsic colours (J − H)0 and (H − Ks)0 using the 2MASS system (Straižys & Lazauskaité 2009), which provided us a F0V star value equal to (J − K)0 = 0.135 mag. Using the V magnitude from the TESS catalogue, we computed V0 taking into account the reddening E(B − V) = 0.482 mag. We adopted the coefficient RV = 3.15, which corresponds to the normal extinction law equal to AV = 1.534 mag. This gave us V0 = 18.955 mag and (V − Ks)0 = 0.785 mag. These values are colour indices in the middle of F0V and F1V spectral class. In our case, the uncertainties on magnitudes are eV = 0.062 mag, eJ = 0.081 mag and eKs = 0.279 mag. However, because the error for Ks is larger than the other two, we decided to use the (V − J)0 colour for comparison. We calculated it using following relation:
and PM data. Our obtained colour value of (V − J)0 = 0.654 mag again corresponds to a mean value between F0V (0.589 mag) and F1V (0.662 mag) stars. According to the three obtained colour index parameters, we assume that our source star spectral type is either F0V or F1V, which gives us absolute magnitudes of MV = 2.51 mag or MV = 2.79 mag, respectively. For further distance determination, we used an average value of MV = 2.65 ± 0.50 mag, including a conservative error due to unknown metallicity of the star. We determined the distance DS for the source star using the following relation:
We deduced thereby that the distance to the source star is 18.2 kpc.
The errors of the observed magnitudes, colour excesses, and extinction usually follow a Gaussian distribution, but taking into account non-linearity of the transformation and asymmetry of the distance (log10(DS)), we conclude the distance to the star is between 14.5 kpc and 23 kpc, which is in contrast with Bailer-Jones et al. (2018, 2021) (1 kpc < DS < 7.6) kpc and 6.4 kpc < DS < 9.8 kpc, respectively). We note that the exact value of the distance has, in practice, a small effect on the final models because πs ≪ θEπE. However, it is important to differentiate between nearby and faraway sources.
The uncertainties in distance estimation using this method are large. However, due to the dimness of the sources, we could not obtain a spectrum that would result in a more precise distance estimation.
We also derived the value of the interstellar extinction in the G-band, AG, towards this source. Since GDR2 does not provide any measurement of AG for Gaia18cbf, we instead calculated the average AG of all sources within 1 arcsecond of the source (8 stars in total), finding AG = 1.06 mag. We compared this value with extinction provided by Schlafly & Finkbeiner (2011) for SDSS bands: ASDSS, g = 1.810 mag, ASDSS, r = 1.252 mag, and ASDSS, i = 0.931 mag. Since the Gaia G-filter bandpass is wide (Jordi et al. 2010; Evans et al. 2018; Riello et al. 2021), spanning from 300 nm to 1000 nm, we conclude that the calculated value of extinction is correct.
5. Lens light analysis
In order to determine the nature of the lens in this event, we followed the procedure used in Wyrzykowski et al. (2016) and (Mróz & Wyrzykowski 2021; hereafter MW). In short, the microlensing parameters in the MCMC samples from the light-curve modelling were combined with the priors on missing parameters: namely, source distance, source proper motion, and lens proper motion. Since the blending parameter found in our main parallax solutions (GF+ and GF−) was above 0.7 in both cases, we adopted the source proper motions measured by Gaia EDR3. For the source distance, we did not use the distance provided in Bailer-Jones et al. (2021) as it was derived based on strongly negative geometric parallax and biased towards closer distances. Instead, for each iteration of the algorithm, we drew the source distance from the flat distribution covering the interval obtained through the analysis of archival photometric data in Sect. 4 as well as the extinction value in the G-band derived there.
Then we drew a random value of lens-source relative proper motion μLS from a flat distribution of values between 0 and 30 mas year−1 (MW). The combination of πE, tE, and μLS allowed us, for each MCMC sample, to compute the mass of the lens and, in combination with the source distance, its distance. This was in turn used to calculate the lens brightness if the lens was a main-sequence (MS) star. For our mass-luminosity relation, we used empirical data from PM provided on Eric Mamajek’s webpage4. We then compared the luminosity of the lens for a given mass with the blended light derived for a given MCMC sample. We assumed an extinction value for the source as calculated in Sect. 4. For the lens, we adopted a more sophisticated approach. We extracted reddening E(B − V) values in the direction of the event using online 3D maps of interstellar medium provided by Capitanio et al. (2017), and Lallement et al. (2014, 2018)5. Using this information, we assume that up to 300 pc the reddening E(B − V) = 0 mag and than it changes according with a fitted linear function. Based on that, we calculated AG using relation presented in Wang & Chen (2019); however, we did not allow the extinction to be larger than AG = 1.06 mag. For all the pairs ML–DL and corresponding lens light – blend light, we also computed a weight using set of priors from Skowron et al. (2011) and MW. These priors require tE and πE calculated in the heliocentric frame. We used formulas from Appendix A of Skowron et al. (2011) to find the correct values of these parameters. For the mass function slope, we assumed a power index of −1.75, as suggested in MW.
The results of the lens-light analysis for GF+ and GF− models are shown in Figs. 4 and 5, respectively, with the top panels showing the probability density for mass and distance of the lens. Table 5 gathers the most likely values for mass and distance of the lens in both solutions, as well as the value of the blend magnitude. For GF+ the most likely mass is 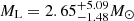 with the distance of
with the distance of 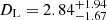 kpc. For GF−, the most likely mass is
kpc. For GF−, the most likely mass is 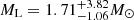 with the distance of
with the distance of 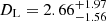 kpc. The more massive GF+ solution also has a larger value of the blending parameter fs (hence less light remains for the blend/lens), when compared to the GF− solution. The median distance, however, is similar for both solutions and depends mostly on the distance to the source.
kpc. The more massive GF+ solution also has a larger value of the blending parameter fs (hence less light remains for the blend/lens), when compared to the GF− solution. The median distance, however, is similar for both solutions and depends mostly on the distance to the source.
 |
Fig. 4. Posterior distribution of the lens mass, distance, lens light if it was a MS star and allowed blend light obtained using method outlined in Sect. 5. Top: Lens mass versus lens distance estimated from MCMC samples for Gaia18cbf for the best fitting model using the Gaia and follow-up data with u0 > 0 and including a microlensing parallax effect, called GF+. Bottom: blended light magnitude from the microlensing model GF+ versus the light of the lens expected if the lens was a MS star. The dashed line separates dark lens or remnant solutions from MS star solutions. The colours are the probability density shown on a logarithmic scale. |
 |
Fig. 5. Posterior distribution of the lens mass, distance, lens light if it was a MS star and allowed blend light obtained using method outlined in Sect. 5. Top: lens mass versus lens distance estimated from MCMC samples for Gaia18cbf for the best fitting model using the Gaia and follow-up data with u0 < 0 and including a microlensing parallax effect, called GF−. Bottom: blended light magnitude from the microlensing model versus the light of the lens expected if the lens was a MS star. The dashed line separates dark lens or remnant solutions from MS star solutions. The colours are the probability density shown on a logarithmic scale. |
Lens masses ML and distances DL for best fitting models for Gaia18cbf.
The bottom panels of Figs. 4 and 5 display the comparison between the blend light (as measured in the microlensing model) with the light expected for a MS star if the lens was fully responsible for the observed blending light. The dashed line divides the parameter space for a case where the MS scenario is justified given the blending, and where the MS scenario does not explain the mass for the given blending, and hence the remnant scenario is preferred. Given the faint baseline magnitude and relatively high value of the blending parameter, there is not much light in the light curve that could be attributed to the possible lens.
6. Discussion
The event Gaia18cbf clearly exhibited a very long-lasting increase in brightness, which went on for almost 2000 days. The most plausible explanation for the shape of the light curve is microlensing by a single lens, affected by the microlensing parallax effect due to the Earth’s orbital motion. The standard microlensing model (shown with a dashed line in Fig. 2) is not capable of reproducing the data, however, and the follow-up data filling the data gap at around JD = 2458750 help to better constrain the parallax model. Nevertheless, the discrepancy between GF+ and GF− models would probably have been resolved if the event had been followed-up nearer to the time of maximum brightness. Unfortunately, the part of the sky in which this event occurred is about 8 degrees away from the Galactic plane and was not observed by OGLE or any other surveys at that time.
As already mentioned in Sect. 3, the best results in terms of χ2 were given by the GF+ model. Both solutions have, however, large tE, making this event second longest known microlensing event, with Mao et al. (2002) being the first.
In our model, we did not include the effect of space parallax due to the difference in Gaia’s location at L2 and ground-based observatories. In order to see the shift between light curves observed with Earth-based and space-based observatories, we would have to have a high-amplification event sampled densely at the peak or a caustic crossing. Moreover, the parallax signal measured is small, and hence the impact of 1% of observer position difference would not be detectable.
The probability density depends on the assumed mass function slope, and in our mass-light analysis we assumed that the mass function for the lens follows the slope of ∝M−1.75, as suggested in MW. However, the actual value of this slope is poorly known (e.g. Bastian et al. 2010), and if we assume no prior on the mass (i.e. power of −1), the lens mass moves to higher values of 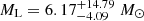 and
and 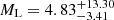 for GF+ and GF−, respectively. The lens distance changes to smaller values of
for GF+ and GF−, respectively. The lens distance changes to smaller values of 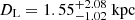 and
and 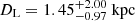 . Conversely, an extreme slope of −3 discourages larger masses and for the Gaia18cbf solutions GF+ and GF− yields
. Conversely, an extreme slope of −3 discourages larger masses and for the Gaia18cbf solutions GF+ and GF− yields 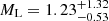 and
and 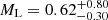 . For the GF− model, the lens distance increases to
. For the GF− model, the lens distance increases to 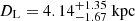 , which further discourages a massive remnant possibility, as a M2.5V-type MS star at that distance would have 26.6 mag and could hide within the allowed blending of
, which further discourages a massive remnant possibility, as a M2.5V-type MS star at that distance would have 26.6 mag and could hide within the allowed blending of 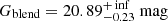 . However, for the GF+ solution, which we find more favourable, the MS scenario with
. However, for the GF+ solution, which we find more favourable, the MS scenario with 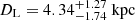 still cannot explain the observed blended light of
still cannot explain the observed blended light of 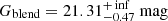 . High-resolution imaging with sensitivity to stars down to 26 mag would allow us to resolve this issue.
. High-resolution imaging with sensitivity to stars down to 26 mag would allow us to resolve this issue.
As we mentioned in Sect. 4, Gaia parallax ϖ cannot be used for distance estimation in microlensing events. However, if we wanted to use the values from Bailer-Jones et al. (2021), the lens would become more massive and slightly further away than in our initial assumptions. We present obtained values of lens mass ML and lens distance DL in Table 6.
Lens masses ML and distances DL for best fitting solutions assuming different distances to the source or lens mass distribution.
Figures 4 and 5 suggest that the lens is a dark remnant. Cases where the lens is a MS star have lower probability compared to the remnant solutions to cause the Gaia18cbf event. However, we can still test the assumption that the event was caused by a low-mass MS star located further away. If we assume that the extinction is AG = 1.06 mag and the lens is an M5V MS star with an absolute magnitude of MG = 12.04 mag (PM), then the minimal values of observable brightness of the lens, Gblend, presented in Sect. 5, would translate to distances of DL ≈ 440 pc for GF+ and DL ≈ 360 pc for GF−. However, such a lens would produce a larger microlensing parallax of πE = 1.33 for GF+ and πE = 1.46 for GF− if we assume that the source is 18.2 kpc away. From the analysis of the light curve, we obtained 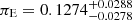 and
and 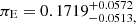 respectively. We can move the lens away; however, πE will never be smaller than 0.4. To reach the required parallax value, the lens has to weigh more than 2 M⊙. If we wanted to explain our event with an A- or B-type MS star as the lens, it would have to be at least 30 kpc away to reach maximal brightness allowed by Gblend of this event. This means that this event was most likely not caused by a MS star.
respectively. We can move the lens away; however, πE will never be smaller than 0.4. To reach the required parallax value, the lens has to weigh more than 2 M⊙. If we wanted to explain our event with an A- or B-type MS star as the lens, it would have to be at least 30 kpc away to reach maximal brightness allowed by Gblend of this event. This means that this event was most likely not caused by a MS star.
This leads us to a conclusion that we have detected a dark remnant candidate. Based on the masses we obtained, the lens could be a candidate white dwarf, neutron star, or a black hole. If the hypothesis of the dark remnant is correct, the mass of the object suggests a massive neutron star or a mass-gap object (Özel et al. 2010; Farr et al. 2011). This could be another case that supports the hypothesis that there is in fact no mass gap (Kreidberg et al. 2012) along with recently observed mass-gap objects (Thompson et al. 2019; Abbott et al. 2020; Jayasinghe et al. 2021).
We assumed that the relative proper motion of lens and source can reach up to 30 mas yr−1. The maximum value can be reached if source and lens are moving in exactly opposite directions and we are dealing with a fast moving lens. Natal kicks of neutron stars can typically reach up to 420 km s−1 (Hobbs et al. 2005), which translates to proper motion of μ = (40 − 80) mas yr−1 for an object located at 1–2 kpc. If the relative proper motion between the lens and source was this large, the Einstein radius would have to be enormous (θE > 40 mas) in order to reach an Einstein timescale of over 400 days. This would result in a more massive lens, however. In our case, the Einstein radius for the GF+ solution is 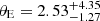 mas and for the GF− is
mas and for the GF− is 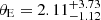 mas. This corresponds to relative proper motions of
mas. This corresponds to relative proper motions of 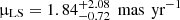 and
and 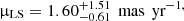 respectively.
respectively.
We cannot exclude the possibility that this event was caused by a binary lens; however, the data are too infrequent to obtain a good model. If the lens is a binary system, the caustic crossing could happen during the large gap in data before the peak, which lasts 139.31 days. Assuming that the distance to the source is DS = 18.2 kpc and using the lens and microlensing event parameters that we obtained, the separation of the binary system would have to be aGF+ ≤ 2.72 au for a GF+ solution and aGF− ≤ 1.33 au for a GF− solution. If the source is closer, the maximum separation would get smaller. This means that instead of a single lens, we could be dealing with a binary system consisting of two objects; for example, two neutron stars or two white dwarfs.
If we would like to confirm that the event was in fact caused by a dark remnant, we would have to wait ten years and use the Extremely Large Telescope to take high angular-resolution follow-up observations of this field to try and identify the source and lens as separate objects. If the lens is a neutron star, it may be emitting radio signals that are too weak to be detected by modern-day telescopes. We could try observing this area with more sensitive radio telescopes in the future. However, it is worth noting that only a small fraction of neutron stars can be observed as pulsars due to the fact that one of the magnetic poles has be aligned with our line of sight. If the lens consists of two neutron stars, the system might emit gravitational waves that could be detectable by the upcoming ESA mission, Laser Interferometer Space Antenna (Amaro-Seoane et al. 2017). Another option would be to wait for the final Gaia data release. Based on Rybicki et al. (2018), we expect that accuracy in the along scan direction (AL) should be between 0.3 mas for the brightest points and 3 mas for baseline magnitude. The largest astrometric displacement of the centroid of light due to microlensing occurs for 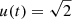 and is equal to δmax ≈ 0.354θE. This gives us maximal astrometric shift spanning between 0.45 mas and 2.44 mas for the GF+ and 0.35 mas and 2.07 mas for the GF−. This means that astrometric microlensing might be marginally measurable by Gaia.
and is equal to δmax ≈ 0.354θE. This gives us maximal astrometric shift spanning between 0.45 mas and 2.44 mas for the GF+ and 0.35 mas and 2.07 mas for the GF−. This means that astrometric microlensing might be marginally measurable by Gaia.
7. Conclusion
We presented an analysis of the Gaia18cbf microlensing event, discovered by the Gaia Science Alerts programme, operating within the Gaia space mission. The event exhibited one of the longest microlensing timescales ever seen as well as a significant annual microlensing parallax effect. The event has two best fitting solutions with a negative and positive impact parameter, u0, which we were not able to resolve due to insufficient follow-up data. The parameters of these solutions are presented in Table 4.
Using a Galactic-density and kinematics model, we estimated the probability density of the lens mass and distance. We present these densities in Figs. 4 and 5. The distance to the source was assessed using archival photometric data, because the parallax ϖ in the published Gaia catalogues for this source is negative. The estimated distance to the source varies between 14.5 kpc and 23 kpc, with a median value of 18.2 kpc. The estimated mass of the lens is 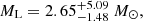 and the distance is
and the distance is 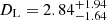 kpc for the solution with u0 > 0 (GF+). For the solution with u0 < 0 (GF−), the lens weighs
kpc for the solution with u0 > 0 (GF+). For the solution with u0 < 0 (GF−), the lens weighs 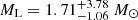 , while the distance to the lens is
, while the distance to the lens is 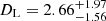 kpc. Because the event is dim and the blending parameter suggests that the majority of the light comes from the source, we propose that the lens is a dark remnant candidate, possibly a massive neutron star, or a mass-gap black hole. We conclude that it is impossible to confirm the hypothesis of the lens being a dark remnant right now, but follow-up observations in the future could resolve this issue. If the event was caused by a massive lens, we will be able see the signature of microlensing in the astrometric time series published with the final Gaia Data Release (2024).
kpc. Because the event is dim and the blending parameter suggests that the majority of the light comes from the source, we propose that the lens is a dark remnant candidate, possibly a massive neutron star, or a mass-gap black hole. We conclude that it is impossible to confirm the hypothesis of the lens being a dark remnant right now, but follow-up observations in the future could resolve this issue. If the event was caused by a massive lens, we will be able see the signature of microlensing in the astrometric time series published with the final Gaia Data Release (2024).
Acknowledgments
The authors would like to thank Dr Radek Poleski for discussion and his comments during the creation of this work. We would like to thank the referee for their comments, which helped to improve this paper. We acknowledge ESA Gaia, DPAC and the Photometric Science Alerts Team (http://gsaweb.ast.cam.ac.uk/alerts). This work was supported from the Polish NCN grants: Harmonia No. 2018/30/M/ST9/00311, Daina No. 2017/27/L/ST9/03221, MNiSW grant DIR/WK/2018/12 and NCBiR grant within POWER program nr POWR.03.02.00-00-l001/16-00. We acknowledge Research Council of Lithuania grant No S-LL-19-2 and European Commission’s H2020 OPTICON grant No. 730890 as well as OPTICON RadioNet Pilot grant No. 101004719. YT acknowledges the support of DFG priority program SPP 1992 “Exploring the Diversity of Extrasolar Planets” (TS 356/3-1). This work is partly supported by JSPS KAKENHI Grant No. JP18H05439, and the Astrobiology Center of National Institutes of Natural Sciences (NINS) (Grant No. AB031010).
References
- Abbott, R., Abbott, T. D., Abraham, S., et al. 2020, ApJ, 896, L44 [Google Scholar]
- Abe, F., Allen, W., Banks, T., et al. 1997, in Variables Stars and the Astrophysical Returns of the Microlensing Surveys, eds. R. Ferlet, J.-P. Maillard, & B. Raban, 75 [Google Scholar]
- Abrams, N. S., & Takada, M. 2020, ApJ, 905, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Alcock, C., Axelrod, T. S., Bennett, D. P., et al. 1992, in Robotic Telescopes in the 1990s, ed. A. V. Filippenko, ASP Conf. Ser., 103, 193 [NASA ADS] [Google Scholar]
- Alcock, C., Allsman, R. A., Alves, D., et al. 1995, ApJ, 454, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Amaro-Seoane, P., Audley, H., Babak, S., et al. 2017, ESA, submitted [arXiv:1702.00786] [Google Scholar]
- An, J. H., Albrow, M. D., Beaulieu, J. P., et al. 2002, ApJ, 572, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Aubourg, E., Bareyre, P., Brehin, S., et al. 1993, The Messenger, 72, 20 [NASA ADS] [Google Scholar]
- Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Mantelet, G., & Andrae, R. 2018, AJ, 156, 58 [Google Scholar]
- Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Demleitner, M., & Andrae, R. 2021, AJ, 161, 147 [Google Scholar]
- Bastian, N., Covey, K. R., & Meyer, M. R. 2010, ARA&A, 48, 339 [Google Scholar]
- Belokurov, V. A., & Evans, N. W. 2002, MNRAS, 331, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, D. P., Akerlof, C., Alcock, C., et al. 1993, in Texas/PASCOS ’92: Relativistic Astrophysics and Particle Cosmology, eds. C. W. Akerlof, & M. A. Srednicki, 688, 612 [Google Scholar]
- Bennett, D. P., Becker, A. C., Quinn, J. L., et al. 2002, ApJ, 579, 639 [NASA ADS] [CrossRef] [Google Scholar]
- Blagorodnova, N., Van Velzen, S., Harrison, D. L., et al. 2016, MNRAS, 455, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, T. M., Baliber, N., Bianco, F. B., et al. 2013, PASP, 125, 1031 [Google Scholar]
- Capitanio, L., Lallement, R., Vergely, J. L., Elyajouri, M., & Monreal-Ibero, A. 2017, A&A, 606, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cassan, A., Ranc, C., Absil, O., et al. 2021, Nat. Astron., 6, 121 [Google Scholar]
- Dong, S., Udalski, A., Gould, A., et al. 2007, ApJ, 664, 862 [NASA ADS] [CrossRef] [Google Scholar]
- Dong, S., Mérand, A., Delplancke-Ströbele, F., et al. 2019, ApJ, 871, 70 [CrossRef] [Google Scholar]
- Einstein, A. 1936, Science, 84, 506 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, D. W., Riello, M., De Angeli, F., et al. 2018, A&A, 616, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Farr, W. M., Sravan, N., Cantrell, A., et al. 2011, ApJ, 741, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D. 2016, J. Open Source Softw., 1, 24 [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 650, C3 [EDP Sciences] [Google Scholar]
- Gould, A. 1992, ApJ, 392, 442 [Google Scholar]
- Gould, A. 2000, ApJ, 542, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Gould, A. 2004, ApJ, 606, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Gould, A., Udalski, A., Monard, B., et al. 2009, ApJ, 698, L147 [Google Scholar]
- Gould, A., Dong, S., Gaudi, B. S., et al. 2010, ApJ, 720, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- Hardy, S. J., & Walker, M. A. 1995, MNRAS, 276, L79 [NASA ADS] [Google Scholar]
- Hobbs, G., Lorimer, D. R., Lyne, A. G., & Kramer, M. 2005, MNRAS, 360, 974 [Google Scholar]
- Hodgkin, S. T., Wyrzykowski, L., Blagorodnova, N., & Koposov, S. 2013, Phil. Trans. R. Soc. London Ser. A, 371, 20120239 [Google Scholar]
- Hodgkin, S. T., Harrison, D. L., Breedt, E., et al. 2021, A&A, 652, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holz, D. E., & Wald, R. M. 1996, ApJ, 471, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Jayasinghe, T., Stanek, K. Z., Thompson, T. A., et al. 2021, MNRAS, 504, 2577 [NASA ADS] [CrossRef] [Google Scholar]
- Jeong, Y., Han, C., & Park, S.-H. 1999, ApJ, 511, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Jordi, C., Gebran, M., Carrasco, J. M., et al. 2010, A&A, 523, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karolinski, N., & Zhu, W. 2020, MNRAS, 498, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, S.-L., Lee, C.-U., Park, B.-G., et al. 2016, J. Korean Astron. Soc., 49, 37 [Google Scholar]
- Koshimoto, N., Shvartzvald, Y., Bennett, D. P., et al. 2017, AJ, 154, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Koshimoto, N., Bennett, D. P., & Suzuki, D. 2020, AJ, 159, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Kreidberg, L., Bailyn, C. D., Farr, W. M., & Kalogera, V. 2012, ApJ, 757, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Lallement, R., Vergely, J. L., Valette, B., et al. 2014, A&A, 561, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lallement, R., Capitanio, L., Ruiz-Dern, L., et al. 2018, A&A, 616, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lam, C. Y., Lu, J. R., Hosek, Jr., M. W., Dawson, W. A., & Golovich, N. R. 2020, ApJ, 889, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Liebes, S. 1964, Phys. Rev., 133, 835 [Google Scholar]
- Lindegren, L., Klioner, S. A., Hernández, J., et al. 2021, A&A, 649, A2 [EDP Sciences] [Google Scholar]
- Mao, S., & Paczynski, B. 1991, ApJ, 374, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Mao, S., Smith, M. C., Woźniak, P., et al. 2002, MNRAS, 329, 349 [NASA ADS] [CrossRef] [Google Scholar]
- McMahon, R. G., Banerji, M., Gonzalez, E., et al. 2013, The Messenger, 154, 35 [NASA ADS] [Google Scholar]
- Mróz, P., & Wyrzykowski, Ł. 2021, Acta Astron., 71, 89 [Google Scholar]
- Mróz, P., Udalski, A., Szymański, M. K., et al. 2020, ApJS, 249, 16 [CrossRef] [Google Scholar]
- Özel, F., Psaltis, D., Narayan, R., & McClintock, J. E. 2010, ApJ, 725, 1918 [CrossRef] [Google Scholar]
- Paczynski, B. 1986, ApJ, 304, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Paczynski, B. 1996, ARA&A, 34, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Pecaut, M. J., & Mamajek, E. E. 2013, ApJS, 208, 9 [Google Scholar]
- Poindexter, S., Afonso, C., Bennett, D. P., et al. 2005, ApJ, 633, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Poleski, R., & Yee, J. C. 2019, Astron. Comput., 26, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Refsdal, S. 1964, MNRAS, 128, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Refsdal, S. 1966, MNRAS, 134, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Riello, M., De Angeli, F., Evans, D. W., et al. 2021, A&A, 649, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rybicki, K. A., Wyrzykowski, Ł., Klencki, J., et al. 2018, MNRAS, 476, 2013 [NASA ADS] [CrossRef] [Google Scholar]
- Rybicki, K. A., Wyrzykowski, Ł., Bachelet, E., et al. 2022, A&A, 657, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sahu, K. C., Anderson, J., Casertano, S., et al. 2017, Science, 356, 1046 [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [Google Scholar]
- Skowron, J., Udalski, A., Gould, A., et al. 2011, ApJ, 738, 87 [Google Scholar]
- Stassun, K. G., Oelkers, R. J., Paegert, M., et al. 2019, AJ, 158, 138 [Google Scholar]
- Straižys, V., & Lazauskaité, R. 2009, Baltic Astron., 18, 19 [Google Scholar]
- Thompson, T. A., Kochanek, C. S., Stanek, K. Z., et al. 2019, Science, 366, 637 [NASA ADS] [CrossRef] [Google Scholar]
- Tsapras, Y., Street, R., Horne, K., et al. 2009, Astron. Nachr., 330, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Udalski, A., Szymanski, M., Kaluzny, J., Kubiak, M., & Mateo, M. 1992, Acta Astron., 42, 253 [NASA ADS] [Google Scholar]
- Wang, S., & Chen, X. 2019, ApJ, 877, 116 [Google Scholar]
- Witt, H. J., & Mao, S. 1994, ApJ, 430, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Wyrzykowski, Ł., & Hodgkin, S. 2012, in New Horizons in Time Domain Astronomy, eds. E. Griffin, R. Hanisch, & R. Seaman, IAU Symp., 285, 425 [NASA ADS] [Google Scholar]
- Wyrzykowski, Ł., & Mandel, I. 2020, A&A, 636, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wyrzykowski, Ł., Rynkiewicz, A. E., Skowron, J., et al. 2015, ApJS, 216, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Wyrzykowski, Ł., Kostrzewa-Rutkowska, Z., Skowron, J., et al. 2016, MNRAS, 458, 3012 [NASA ADS] [CrossRef] [Google Scholar]
- Wyrzykowski, Ł., Mróz, P., Rybicki, K. A., et al. 2020, A&A, 633, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zieliński, P., Wyrzykowski, Ł., Rybicki, K., et al. 2019, Contrib. Astron. Obs. Skalnate Pleso, 49, 125 [NASA ADS] [Google Scholar]
- Zieliński, P., Wyrzykowski, Ł., Mikołajczyk, P., Rybicki, K., & Kołaczkowski, Z. 2020, in XXXIX Polish Astronomical Society Meeting, eds. K. Małek, M. Polińska, A. Majczyna, et al., 10, 190 [Google Scholar]
Appendix A: Photometry
Here, we present the photometric data used for modelling Gaia18cbf.
Gaia18cbf photometry from Gaia Science Alerts. The uncertainties (err[mag]) were estimated using Gaia DR2 (see Section 2.1). Full, machine-readable version of this table is available at the CDS.
Gaia18cbf photometry from LCO i-band. The machine-readable version of this table is available at the CDS.
All Tables
Parameter values of best fitting solutions for Gaia18cbf using only Gaia photometric data.
Parameter values of best fitting solutions for Gaia18cbf using Gaia and i-band follow-up photometric data.
Lens masses ML and distances DL for best fitting solutions assuming different distances to the source or lens mass distribution.
Gaia18cbf photometry from Gaia Science Alerts. The uncertainties (err[mag]) were estimated using Gaia DR2 (see Section 2.1). Full, machine-readable version of this table is available at the CDS.
Gaia18cbf photometry from LCO i-band. The machine-readable version of this table is available at the CDS.
All Figures
 |
Fig. 1. Location of Gaia18cbf and its neighbourhood during the event. Chart is a stack of two images obtained with 2 m LCO telescope located in Siding Springs Observatory in October 2019 and July 2020. White circle marks the target. |
| In the text | |
 |
Fig. 2. Light curve and best fitting models for Gaia18cbf with follow-up. Maroon dots represent data gathered by Gaia, while yellow dots mark data observed by Las Cumbres Observatory in Siding Spring Observatory (LCO SSO) in the i-band. Continuous lines represent different solutions for a point source-point lens model with parallax effect. Best fitting models for GF+, GF− and GL solutions are shown in red, blue, and green, respectively. In lighter colours, we show other solutions that we obtained through a Markov chain Monte Carlo method. The dashed line represents the point source–point lens model without including a parallax effect, called ‘GF0’. Bottom panel: we show the difference between the GF0 model and other models. The data shown in maroon and yellow dots represent the result of subtraction of the magnitude predicted by the GF0 model and the observed magnitude. We use the same colour representation for the GF+, GF−, and GL solutions, as in the top panel. |
| In the text | |
 |
Fig. 3. Chi-squared contours plotted as a function of the parameters fitted in the MCMC fit for the best model, GF+. Black, dark grey, and light grey solid colours represent 1σ, 2σ, and 3σ confidence regions, respectively. Black dots represent solutions outside of the 3/sigma confidence level. Blue lines and squares mark the median solution reported in Table 4. Plot was created using corner python package by Foreman-Mackey (2016). |
| In the text | |
 |
Fig. 4. Posterior distribution of the lens mass, distance, lens light if it was a MS star and allowed blend light obtained using method outlined in Sect. 5. Top: Lens mass versus lens distance estimated from MCMC samples for Gaia18cbf for the best fitting model using the Gaia and follow-up data with u0 > 0 and including a microlensing parallax effect, called GF+. Bottom: blended light magnitude from the microlensing model GF+ versus the light of the lens expected if the lens was a MS star. The dashed line separates dark lens or remnant solutions from MS star solutions. The colours are the probability density shown on a logarithmic scale. |
| In the text | |
 |
Fig. 5. Posterior distribution of the lens mass, distance, lens light if it was a MS star and allowed blend light obtained using method outlined in Sect. 5. Top: lens mass versus lens distance estimated from MCMC samples for Gaia18cbf for the best fitting model using the Gaia and follow-up data with u0 < 0 and including a microlensing parallax effect, called GF−. Bottom: blended light magnitude from the microlensing model versus the light of the lens expected if the lens was a MS star. The dashed line separates dark lens or remnant solutions from MS star solutions. The colours are the probability density shown on a logarithmic scale. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.