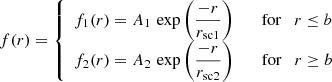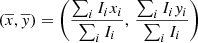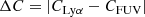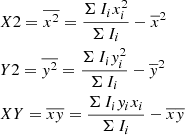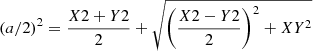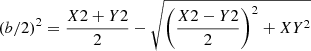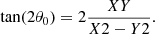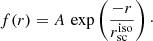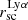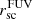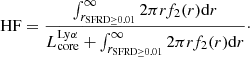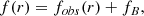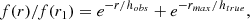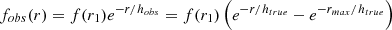| Issue |
A&A
Volume 662, June 2022
|
|
|---|---|---|
| Article Number | A64 | |
| Number of page(s) | 62 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202140734 | |
| Published online | 16 June 2022 | |
The Lyman Alpha Reference Sample
XII. Morphology of extended Lyman alpha emission in star-forming galaxies
1
Department of Astronomy, Oscar Klein Centre, Stockholm University, AlbaNova, 106 91 Stockholm, Sweden
e-mail: armin.rasekh@astro.su.se
2
European Southern Observatory, Av. Alonso de Córdova 3107, 763 0355 Vitacura, Santiago, Chile
3
Institut d’Astrophysique de Paris (IAP), 98bis Boulevard Arago, 75014 Paris, France
4
Centro de Astrobiología (CSIC–INTA), Departamento de Astrofísica, 28692 Villanueva de la Cañada, Spain
5
Observatoire de Genéve, Université de Genève, 51 Ch. des Maillettes, 1290 Versoix, Switzerland
6
Department of Physics & Astronomy, Macalester College, 1600 Grand Avenue, Saint Paul, MN 55105, USA
Received:
5
March
2021
Accepted:
10
September
2021
Aims. We use Hubble Space Telescope data of 45 nearby star-forming galaxies to investigate properties of Lyman-alpha (Lyα) halos, Lyα morphology, and the star-forming characteristics of galaxies. We study how the morphology of Lyα emission is related to other Lyα observables. Furthermore, we study the interdependencies of Lyα morphological quantities.
Methods. We studied the spatial extent of Lyα using surface brightness profiles in the following two ways (i) using circular apertures and (ii) within faint Lyα isophotes. We also measured the average intensity and the size of the regions with a high star formation rate density. The morphology of the galaxies was quantified by computing centroid position, axis ratio, and position angle in the Lyα, ultraviolet continuum, and I band maps.
Results. We found that galaxies with more extended star-forming regions possess larger Lyα halos. Furthermore, galaxies with more elongated Lyα morphology are also more extended in Lyα. Our data suggest that Lyα bright galaxies appear rounder in their Lyα morphology, and there is less of a contribution from their Lyα halo to their overall luminosity. We compared our results with studies at high redshift and found that whilst the Lyα extent in the inner regions of the galaxies in our sample are similar to the high-z Lyα emitters (LAEs), Lyα halos are more extended in high-z LAEs.
Conclusions. Our analysis suggests that the Lyα morphology affects the measurement of other observable quantities concerning Lyα emission, and some of the conclusions drawn from high redshift LAEs might be biased towards galaxies with specific Lyα shapes. In particular, faint Lyα emitters have larger Lyα scale lengths and halo fractions. This implies that faint Lyα emitters are harder to detect at high redshift than previously believed.
Key words: Galaxy: halo / Galaxy: evolution / Galaxy: structure
© ESO 2022
1. Introduction
The Lyman alpha (Lyα) recombination line in hydrogen (n = 2 → n = 1, with an energy difference of 10.2 eV, equivalent to the rest frame wavelength of λ0 = 121.567 nm) is the strongest recombination line in the intrinsic spectra of galaxies. Due to the potential strength of this line, Partridge & Peebles (1967) proposed to use this line for detecting and studying primaeval galaxies more than fifty years ago. Since the Lyα emission line from galaxies is only observable with ground-based telescopes at z > 2.5, the early searches for high-z galaxies showed little observational progress (Pritchet 1994). It was only in the mid-1990s that surveys started to deliver significant numbers of Lyα emitting star-forming galaxies (SFGs), while previously mainly quasi-stellar objects had been found (Hu & McMahon 1996; Djorgovski et al. 1996).
The Lyα emission line is a good tracer of ionising photons since there is a 68% chance that the ionised hydrogen atoms which capture an electron eventually emit Lyα photons (Dijkstra 2014). Indeed, studies show that Lyα photons are either emitted from the ionised gas around the star-forming region or active galactic nuclei (AGNs) (Miley & De Breuck 2008). In other words, Lyα is a valuable tool for studying the SFGs in general, and ionising photons and their origins in particular.
The Lyα emission line is a resonant line and is subject to scattering whenever it encounters neutral hydrogen (HI). Scattering either occurs within the host galaxy due to the presence of HI in the interstellar medium (ISM), or between the source and the observer due to the presence of HI in the circumgalactic medium (CGM) and intergalactic medium (IGM). Moreover, dust grains absorb Lyα photons and radiate in the far-infrared (FIR). Due to the scattering in the HI media and absorption by dust at the local scale, factors such as the geometry and the distribution of the ISM in the galaxy (Giavalisco et al. 1996; Hansen & Oh 2006; Hayes 2019; Marchi et al. 2019; Jaskot et al. 2019; Charlot & Fall 1993; Atek et al. 2008; Verhamme et al. 2008; Scarlata et al. 2009; Kornei et al. 2010; Hayes et al. 2011; Matthee et al. 2016; An et al. 2017), the HI kinematics (Kunth et al. 1998; Mas-Hesse et al. 2003; Wofford et al. 2013; Martin et al. 2015; Herenz et al. 2016), and the ISM kinematics (Wofford et al. 2013; Herenz et al. 2016) must be considered on how to interpret Lyα spectra and observations. Due to the complicated radiative transfer (RT), there is no clear one-to-one correlation between the Lyα escape fraction and other observed quantities such as Lyα luminosity or nebular extinction. Nevertheless, Sobral & Matthee (2019) found a clear correlation between the Lyα equivalent width and its escape fraction in Lyα emitters (LAEs) at redshifts z = [0.1−2.6], yielding an empirical relation. They find that for galaxies to follow the observed trend, high ionisation efficiencies and low dust extinction are required, consistent with very young galaxies and intense star formation episodes.
Due to the processes stated above, the Lyα emission is expected to be more extended than the star-forming regions where most of these photons are produced. Far-ultraviolet (FUV) instrumentations capable of spatially resolving galaxies are required to observationally confirm the existence of extended Lyα emission. In the nearby universe, it was only after the installation of the Advanced Camera for Surveys (ACS) and its Solar Blind Channel (SBC) on the Hubble Space Telescope (HST) that Lyα imaging of galaxies began to be carried out and Kunth et al. (2003) reported observations of ESO 350-IG038 (Haro 11) and SBS 0335–052. The analysis of ESO 338-IG04 and Haro11, presented in Hayes et al. (2005, 2007), clearly showed asymmetric Lyα halos around both galaxies. Östlin et al. (2009) summarised the findings for the first six galaxies observed (including the three above).
At high redshift, Møller & Warren (1998), and Fynbo et al. (1999) were the first to report more extended Lyα emission than ultraviolet (UV) emission for galaxies at z > 1.9. Later on, Steidel et al. (2011) reported that in a stack of 92 galaxies at z = 2.6 extracted from deep narrow band images, Lyα halos are also more extended than the UV continuum. Interestingly, extended Lyα emission was also seen from the stack of the subset of galaxies that showed Lyα central absorption in spectroscopic slits. The asymmetrical shape of the Lyα halos is not unexpected due to Lyα RT as well. Matthee et al. (2016) show extended and asymmetric Lyα emission in individual galaxies. In recent years, the Multi-Unit Spectroscopic Explorer (MUSE) instrument at the Very Large Telescope (VLT) with an increased sensitivity, resolution, and Field of View (FoV), transformed our understanding of the Lyα halos by enabling the extragalactic community to observe so many Lyα halos out to low surface brightnesses. It was shown that Lyα halos are ubiquitous at high redshift. It was also further demonstrated that in the high-z universe, Lyα halos are more extended than UV continuum, and the Lyα halos of individual galaxies are asymmetric (Wisotzki et al. 2016, 2018; Leclercq et al. 2017).
Studying the Lyα morphology and the geometry of the galaxies contributes to a better understanding of Lyα physics and the large scale distribution of the HI scattering media. To study the morphology of the galaxies at ⪅kpc scales, high spatial resolution data from nearby galaxies is required. Thus, to study the morphology of Lyα in the nearby galaxies, we used data from Lyman Alpha Reference Sample (LARS) (Östlin et al. 2014; Hayes et al. 2014), and its extension (Melinder et al., in prep.). In this paper, we make use of the high-resolution HST imaging data (FUV, UV, and optical) of this dataset. In general, LARS provides the opportunity to shed more light on the complex RT of Lyα. Indeed, a series of papers have been already published discussing many properties of these galaxies and how they relate to Lyα physics, such as studying the general properties of the sample and studying the correlation between these parameters (Hayes et al. 2014), studying the properties of the neutral ISM (Pardy et al. 2014), studying the impact of neutral ISM kinematics and geometry on Lyα (Rivera-Thorsen et al. 2015), studying the kinematic of the gas and its significance in the observed Lyα maps (Herenz et al. 2016), testing and modelling the dust content in the galaxies (Bridge et al. 2018) and predicting the Lyα properties of the SFGs (Runnholm et al. 2020).
An interesting question is how the morphology and orientation of galaxies affect the Lyα emission in star-forming galaxies. It has already been reported that in edge-on galaxies, such as M 82, Hα, IR and X-ray emission is seen to extend along the minor axis (Lehnert et al. 1999). In other words, there are geometrical effects that affect radiation at different wavelengths differently. In the context of Lyα, orientation effect has been also predicted in different studies (e.g. Laursen & Sommer-Larsen 2007; Verhamme et al. 2012; Behrens & Braun 2014).
This study is mainly motivated by the following questions: (i) how does the distribution of the star-forming regions and stellar populations impact the Lyα morphology and (ii) what is the impact of Lyα morphology on the global Lyα properties such as Lyα luminosity, equivalent width, escape fraction. To investigate these questions, we studied the Lyα and FUV morphology of galaxies in a large sample of nearby star-forming galaxies (SFGs) by looking at the light distribution of Lyα and how it compares to the FUV light distribution (tracing the star-forming regions). We perform measurements of the FUV and Lyα halos to characterise their spatial extent. We also investigate the FUV and Lyα morphology of these galaxies and how they relate to observables of Lyα radiative transfer (e.g. fesc). We devise methods to describe the surface brightness (SB) profiles and study the morphology of these galaxies in a non-parametric approach. We also check for correlations between different parameters devised and used in this study and measurements characterising the general properties of the galaxies.
In Sect. 2, we describe the observation and briefly touch upon the data reduction and photometry, in Sect. 3, methods used in this study are described, in Sect. 4, we discuss the outcomes of our analysis, in Sect. 5, we discuss our results and how they compare to the previous studies, and in Sect. 6, we summarise our findings and results. Finally, we assume a cosmology of (H0, ΩM, ΩΛ) = (70 km s−1 Mpc−1, 0.3, 0.7).
2. Data
Our sample consists of 45 galaxies, all in the nearby universe (z < 0.24). The data used to conduct this study are all obtained from the Hubble Space Telescope (HST). The first 14 galaxies- LARS01-14 -(initial LARS sample) were observed under the program GO-12310 (P.I.: G. Östlin), the next 28 galaxies (ELARS01-28) were observed under the programs GO-11110 (P.I.: S. McCandliss), and GO-13483 (P.I.: G. Östlin), Tol1214 (Tololo 1214−277) was observed under the program GO-14923 (P.I.: G. Östlin), Tol1247 (Tololo 1247−232) was observed under the program GO-13027 (P.I.: G. Östlin), and finally, J1156 was observed under the program GO-13656 (P.I.: M. Hayes) (Hayes et al. 2016).
All the galaxies in this sample are nearby SFGs that were selected based on their Hα equivalent width, and their FUV brightness (for more information see Östlin et al. 2014; Melinder et al., in prep.), Table 1 lists the redshift and Hα equivalent width based on SDSS (DR8) spectroscopic measurements, and the FUV luminosity determined from GALEX. The first 14 galaxies (LARS01-LARS14) were selected to have Hα equivalent width equal or higher than 100 Å and UV luminosity range between log (LFUV/L⊙) = 9.2 to (LFUV/L⊙) = 10.7, and redshift interval of z = [0.028−0.18]. ELARS01-28 galaxies were selected to have Hα equivalent width higher than 40 Å and the luminosity function was populated homogeneously below and above LFUV/L⊙ = 9.6, and redshift range z = [0.028−0.051]. In addition to these galaxies, the same type of HST observations also exist for the Tololo 1214−277, Tololo 1247−232, and J1156 (which has the highest redshift in the sample), and we added them to the sample as well.
Characteristics of the galaxies chosen for this sample.
In this study, we use the Lyα and FUV images of the galaxies to study the observed Lyα emission distribution and morphology of the galaxies (using Lyα images) compared to the sites where these photons were produced (star-forming regions) (using FUV maps). In addition, we use the I band images (using the reddest available HST filter for each galaxy) to study the morphology and distribution of the sum of both young and old stellar populations. Global measurements, such as stellar mass, Lyα escape fraction (fesc), nebular reddening, Lyα equivalent width (EWLyα), FUV and Lyα luminosities are taken from Melinder et al. (in prep.).
The method used to obtain Lyα maps of the first fourteen LARS galaxies (LARS01-14), which has been extended to the entire sample, was described in Östlin et al. (2014). The general idea behind this method is to use HST/SBC FUV long-pass filters, one containing Lyα emission and at least one without, to emulate a narrow band filter centred on the line. These filters also allow estimating the stellar continuum at Lyα. This continuum subtraction method builds on the experience from the first studies on six nearby SFGs (Hayes et al. 2005, 2007; Östlin et al. 2009) which led to the improved method developed and suggested by Hayes et al. (2009). This method became the strategy of LARS and is implemented in the Lyman alpha eXtraction software (LaXs) code. This software performs accurate and reliable pixel SED fitting in order to construct Lyα and FUV continuum maps (among other things) of the galaxies. In this study, all measurements on the FUV continuum are made in the LaXs-produced stellar continuum maps at Lyα wavelength.
This work is based on the latest recalibration of the HST/ACS/SBC data (Avila et al. 2019). The previously published Lyα maps of the LARS galaxies (LARS01-14) have been re-analysed by Melinder et al. (in prep.), taking advantage of the latest HST/ACS/SBC calibration.
As previously mentioned in Sect. 1, due to Lyα RT effects, Lyα emission from star-forming galaxies is usually more extended than the star-forming regions (where the majority of the Lyα photons are produced). In this study, we use the FUV maps of the galaxies to study the morphology of the star-forming regions. We note that as discussed in Otí-Floranes et al. (2012, 2014), the spatial distribution of the ionised gas (where the ionising photons are reprocessed into Lyα) is not necessarily similar to the distribution of the FUV continuum. This is only true if the star formation is still ongoing or relatively recent (< 4 Myr) since otherwise, the ionising photon output will have dropped significantly, and massive star winds and supernovae have had enough time to repel and push out the natal gas (Whitmore et al. 2011; Hollyhead et al. 2015). While the Hα data is available for the galaxies in our sample, there is almost no difference between the Hα and the FUV emission maps due to the scales we are probing in this study. However, since the FUV data are deeper, we use them to investigate the sites where Lyα photons originate.
3. Analysis and methods
The cornerstone of this study is the HST imaging data which has the advantage of a larger FoV compared to available spectroscopic observations at similar redshifts. The high-resolution HST imaging data of the 45 nearby SFGs galaxies enables us to study the Lyα light distribution and the morphology of the galaxies out to typical distances of ∼10 kpc (40 kpc for high redshift galaxies in the sample, e.g. LARS14, J1156).
We start by investigating the Lyα and FUV SB profiles (Sect. 3.1). In Sect. 3.2, we discuss the Lyα morphological parameters used in this study. In Sect. 3.3, we discuss the method used for studying the Lyα emission of the galaxies in the faint isophotes. Finally, in Sect. 3.4, we talk about the methods used to study the star-forming properties of the galaxies in our sample.
3.1. Fitting to the surface brightness profiles
In this section, we study the Lyα SB profiles of the galaxies and how they compare to their FUV SB profiles. In other words, we determine how the observed spatial distribution of Lyα emission differs from that of the FUV continuum, which traces the sites where most of the Lyα photons are produced. There are (at least) three common ways of forming and studying SB profiles, and each one has its own advantages and disadvantages. Below, we look into these options and highlight their pros and cons.
Circular annuli. The simplest approach is to integrate the light in circular annuli. The benefit is that it requires no assumption on the actual shape of a galaxy. The downside is that for galaxies that are not circular in shape, the light distribution will be artificially flattened, and the influence of background noise will be increased.
Elliptical annuli. A slightly more sophisticated method that overcomes the con above is to use elliptical annuli for integration. This works well for galaxies that are more elongated in shape. One may allow for a change in the position angle of the ellipses with radius to better capture certain features (e.g. bars and spiral arms), but for very irregular galaxies which are not well described by ellipses, it has the same con as the spherical model, without its pro.
Isophotal integration. A more general approach is isophotal integration. In this method, instead of stepping in radius, one steps in SB and calculates a characteristic radius as 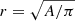 . It has the advantage of not relying on any assumption on the shape of the galaxy. Its cons, however, is that it does not go as deep and will not work at levels where the isophotal level is comparable to the background noise (then the isophotes will break up, and the area becomes ill-defined). It also requires extra care to compare results from different passbands as they generally do not probe the same area. For Lyα, there is an additional complication with isophotal integration: the Lyα absorption against the FUV continuum, which frequently occurs in the centre. In any case, isophotal integration is the best suited method to study the extended Lyα emission.
. It has the advantage of not relying on any assumption on the shape of the galaxy. Its cons, however, is that it does not go as deep and will not work at levels where the isophotal level is comparable to the background noise (then the isophotes will break up, and the area becomes ill-defined). It also requires extra care to compare results from different passbands as they generally do not probe the same area. For Lyα, there is an additional complication with isophotal integration: the Lyα absorption against the FUV continuum, which frequently occurs in the centre. In any case, isophotal integration is the best suited method to study the extended Lyα emission.
In this paper, we use the most straightforward (circular) (Sects. 3.1.1 and 3.1.2) and more general (isophotal) (Sect. 3.3) approach, while omitting the elliptical one, as our sample is in general quite irregular and the elliptical approach does not offer any significant advantage over the other two.
The steps taken to obtain the FUV and Lyα SB profiles using circular annuli are as follows: we masked the noisy edge of the images, started the SB profiles from the brightest point in the FUV maps, and determined the maximum radii from the largest circular aperture that could be fitted inside the masked region (usually set by the usable area in the SBC images), we define the radius of this aperture as rmax. Next, we performed photometry using 30 circular annulus bins (with 0.1 kpc as the smallest size) by using the python package photutils1 (Bradley et al. 2019). The number of bins was chosen to simultaneously provide a good signal-to-noise and radial resolution in the SB profiles. To estimate the error on the measured SB in each bin, we performed the same procedures on 100 Monte Carlo simulated science frames obtained from LaXs. It should be noted that all the aforementioned measurements were done using binned weighted Voronoi tessellated maps, utilising the Weighted Voronoi Tessellation (WVT) method developed by Diehl & Statler (2006) (for more information see Hayes et al. 2014).
3.1.1. Sérsic profile fitting
One of the most common models used to describe the SB profiles of the galaxies is Sérsic model (Sérsic 1963; Graham & Driver 2005):
where bn satisfies the relation 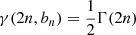 , where Γ, and γ are the Gamma function and the lower incomplete function.
, where Γ, and γ are the Gamma function and the lower incomplete function.
We fit the Sérsic function to FUV and Lyα SB profiles of the galaxies in our sample. We used the Sersic1D model in the python astropy package (Astropy Collaboration 2013, 2018). In Eq. (1), there are three free parameters: the amplitude or the luminosity at the effective radius (Ie), effective radius (reff), and Sérsic index (n). We limited some of these parameters to have a more physically meaningful interpretation of the results. For instance, the effective radii were limited to vary between 0.001 and 1000 kpc, or the Sérsic index to vary between 0.001 and 20. Moreover, since we clearly observe absorption in the Lyα maps of the galaxies, we set the criterion that out of 30 data points in the SB profiles, there must be at least six data points with positive net emission and signal-to-noise ratio higher than 2 (S/N > 2) for fitting the Sérsic profile to each FUV and Lyα profile in every galaxy.
Figure 1 shows examples of the fits for three galaxies. Our results clearly show that a single Sérsic profile does not describe the observed SB profiles very well. In addition, for a good fraction of the galaxies, the results indicated that the fitted parameters had reached the limits initially set as the requirements (e.g. 0.001 < n < 20).
 |
Fig. 1. Sérsic profile fitted to the Lyα and FUV SB profiles of three galaxies, LARS01, LARS09, and ELARS04. The resulted fits indicate Sérsic profile does not fully capture the behaviours of the SB profiles. Moreover, the limit set for the Sérsic index (e.g. 0.001 < n < 20) is reached in the fitted Sérsic profiles to the Lyα SB profile in LARS09, and FUV SB profile in both LARS09, and ELARS04. |
3.1.2. Double exponential fitting function
Around 60 years ago, de Vaucouleurs (1958) used an exponential function to describe the disk region of the profile in M 31. Since then, many studies have used an exponential function to successfully model the SB profiles of disk galaxies (Freeman 1970; Okamura 1988).
We found that a double exponential function describes the full SB profiles of both FUV and Lyα quite well in the majority of the galaxies. This double exponential function has the form described in Eq. (2), in this equation, b is a free parameter fitted to the profiles, f1(r), and f2(r) describe the innermost and outermost parts of the profiles. f1(r) might not be well-constrained for some of the Lyα profiles due to the absorption in the inner regions of the galaxies. However, f2(r) is the main term used in our analysis which describes the outermost part of the profiles. This term is used to extrapolate the SB profiles outside of the available instrument since the angular size of these galaxies could be quite large.
Similar to the Sérsic profile fitting (see Sect. 3.1.1), we took several measures to enhance the fits and characterise the SB profiles better. The weighted fitting method in the lmfit package was used, so the data with higher S/N contribute more to the overall fits. Moreover, the double exponential function was fitted only for those profiles where there were at least six data points with positive net emission in the full SB profiles, on top of requiring at least two data points in the halos (for the definition of the halo, see Sect. 4.1), these points are also required to have S/N higher than two. In Table A.1, we provide for each galaxy the Lyα SB of the faintest (furthest) annulus bin (or upper limit if S/N < 2) measured in the Voronoi tessellated maps.
We found that the fits fail to describe the outermost regions for several galaxies, especially in the FUV SB profiles. This is due to the relative low S/N in the outermost regions compared to the innermost and intermediate regions. In order to fit the outermost regions better, we manually down-weighted the data points in the intermediate regions, so the fits describe the outermost regions in these galaxies better. LARS01, 02, 05, 07, 12, 14, ELARS07, 09, 13 and J1156 are the galaxies with down-weighted intermediate data points in their FUV SB profiles. In LARS14 and J1156 cases, the intermediate regions were also downweighted in their Lyα SB profiles. Since for these two galaxies, the fit was not well-capturing the Lyα SB profile behaviour in the outermost regions, either.
To estimate the errors on the measured parameters, we ran 1000 Monte Carlo simulations. In these simulations, the measured SB were drawn randomly from a normal distribution based on the measured error in each bin. Figure 2 shows FUV and Lyα SB profiles with the fitted double exponential functions for the same galaxies shown in Fig. 1. Appendix C contains the same figures for the full sample. Table A.1 lists the measured Lyα core and halo scale lengths and their corresponding error bars.
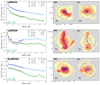 |
Fig. 2. Lyα, FUV SB profiles, and the fitted double exponential of different galaxies (same galaxies shown in Fig. 1) along with their FUV, and Lyα maps. Left panels: Lyα and FUV profiles and the fitted model to them. The dark and light colours distinguish the core from the halo, respectively. For bins with S/N < 1, the 2σ upper limit are displayed, and the bins with 1 ≤ S/N < 2 (data points not used in the fits) are displayed with the empty square symbol. Middle and right panels: FUV and Lyα maps of each galaxy, respectively. The blue rings represent the largest radii where a circle centred at the FUV brightest pixel fits within each map, used as the last bin where the photometry was performed on. The green ring shows the radius where the SFRD drops below 0.01 M⊙ yr−1 kpc−2. |
At faint Lyα SB levels, there is a systematic uncertainty resulting from background subtraction in the images during the data reduction. For the galaxies at z < 0.14 (all but LARS13, LARS14, and J1156), Lyα is in the F125LP filter. This filter also contains a relatively bright geocoronal background from OIλ1302 + 1306. The background is estimated from regions close to the edge of the chip in the images (Östlin et al. 2014). While the statistical error on the estimated background itself is negligible, it is possible that – if faint Lyα extends to the border of the chip – this practice could lead to subtraction of actual Lyα emission. The subtracted background is consistent with, or lower than, the target geocoronal background for the observational setup (HST SHADOW operations) for all galaxies but five (LARS04, ELARS04, ELARS08, ELARS12, and ELARS14). However, it is still possible that Lyα emission from the galaxy contributes to the subtracted background.
Given that the background cannot be independently estimated, we investigate the systematic effect of subtracting an unknown flat background on the exponential profile fit in the halo. For this analysis, we assume that the Lyα emission in the halo is bright enough that an exponential can be fit to the data, or equivalently that the subtracted background emission is low enough to not wash out the real Lyα emission. Furthermore, we assume that either 100% (the absolute worst case) or 10% of the subtracted emission is Lyα. In Appendix D, we calculate the effect of over-subtracting Lyα on the halo exponential that fits under these assumptions. The over-subtraction has a larger effect on the exponential fit if (a) the background level is estimated close to the fitting region and (b) the fitting region for the halo exponential spans a short radial range. We find that the systematic (positive) uncertainty from this effect is negligible (< 5%) for all of the galaxies for the 10% assumption. With the worst case assumption (which is very unlikely to be correct), four galaxies (ELARS05, ELARS08, ELARS09, and ELARS25) show uncertainties larger than 10%. We thus conclude that the background subtraction uncertainty does not affect the findings in this paper significantly.
3.2. Lyα morphology of the galaxies
In this work, we focus on Lyα and FUV (we have also investigated the I band) maps of the galaxies. This enables us to study and investigate the differences between the sites where the ionising photons were produced and how we observe them after the recombination and the ongoing Lyα RT. As discussed before, there is no one-to-one mapping of the FUV to Lyα morphologies. In some galaxies, the morphology of the galaxies are similar, and in some cases, we can clearly spot the differences between the morphology of the galaxies in these two maps. For example, there is one small knot to the south of LARS02, which is bright in both FUV and Lyα, while in other galaxies, FUV-bright regions tend to be associated with Lyα absorption, for example, ELARS08. Another example would be the spiral arms of the galaxy in ELARS05 that seem to be also evident in both FUV and Lyα, while in ELARS06 and other galaxies, for example, ELARS12, ELARS23, ELARS25, ELARS27, and ELARS28, the correlation is either not obvious or just non-existent.
Given the high-resolution HST data available for the LARS sample, one may ask whether it is possible to relate the Lyα properties of the galaxies to the ionised gas media. In general, connecting Lyα emission to the ionised gas properties is an important subject, especially since such comparisons are not generally available at high-z. We note that even though the physical resolution of many galaxies in our sample is sufficient for probing the ionised gas structures, as stated in Sect. 2 the Hα (and Hβ) observations of galaxies only covers star-forming regions and are not that sensitive to low surface brightness diffuse emission that tends to be present in the diffuse Lyα regions. A direct Lyα-Hα comparison could benefit from complementing the HST Hα imaging with that greater depth but of lower spatial resolution (e.g. using IFUs, see Bik et al. 2015) and will be the scope of a future paper.
As mentioned above, LARS provides an opportunity to study the Lyα morphology of the nearby star-forming galaxies in ⪅kpc scales. We investigate the asymmetry of the Lyα emission, and how it compares to the star-forming regions using three non-parametric approaches: (i) centroid shift between Lyα, and FUV, (ii) difference in the position angles of the major axis between FUV and Lyα, (iii) Lyα axis ratio (b/a)Lyα. In addition to these Lyα morphological parameters, we also measure the FUV and I band axis ratios.
We start by introducing the regions used for measuring the aforementioned morphological parameters and continue with how these parameters are assessed within these regions.
3.2.1. Regions used for assessing morphological parameters
Lyα. Regions where Lyα morphological parameters could be assessed were a significant challenge due to (i) intrinsically shallow Lyα halos and (ii) Lyα absorption in the centre of the galaxies. We note that regions with high continuum flux and high column density of neutral hydrogen tend to show up as Lyα absorbed regions unless a high spectroscopic resolution is used, even if there is intrinsic Lyα emission. The narrow-band technique used for making the Lyα emission images for our sample is thus highly susceptible to this issue, and many galaxies show Lyα absorption in the central parts.
To overcome these difficulties, we explored the Lyα maps of the galaxies to determine the faintest encompassing isophotes (FEI). To do so, unbinned Lyα images were smoothed with a kernel size defined in physical units (i.e. kpc) (the kernel sizes differ based on redshift of the galaxies) provided in Table 2 to address the low S/N, especially in the Lyα halos. The Lyα surface brightness limit for the FEI was then chosen by-eye as the faintest isophote, which contained as much diffuse emission as possible without breaking up into individual noise peaks. SBLyα = 1.5 × 1039 erg s−1 kpc−2 was found as a reasonable limit for Lyα FEI in our sample (except J1156, where SBLyα = 5.0 × 1039 was selected, see Table 2).
List of the galaxies, the kernel sizes used to smooth their maps, and the Lyα SB used for determining the faintest encompassing isophote in our morphological studies.
Another challenge was to find a way to include the regions affected by Lyα absorption so that they do not bias the morphological measurements. To do so, we first identify regions with relatively high FUV surface brightness, using a threshold corresponding to a star formation rate density (SFRD) of 0.1 M⊙ yr−1 kpc−2. We created a binary image for each galaxy, where the value is set to 1 if the Lyα brightness is higher than the FEI value, or if the SFRD is above 0.1; and 0 elsewhere. From now on, we refer to the region where the value is equal to one for measuring Lyα morphological parameters as Lyα Morphological Regions (LMR).
FUV and I band. Following the same strategy as for Lyα, unbinned FUV and I band images were smoothed with the same kernel size used for smoothing Lyα maps. Next, FUV and I band intensities in the FUV, and I band images were explored for finding the FUV and I band FEIs. SBFUV = 2.5 × 1037 erg s−1 kpc−2 Å−1, and SBI band = 1.5 × 1037 erg s−1 kpc−2 Å−1 were found as a good limit for all the galaxies in our sample.
Figure 3 shows examples of the regions used to determine the Lyα (LMR), FUV (FEIFUV), and I band (FEII band) morphological parameters displayed on the Lyα images.
 |
Fig. 3. Regions used to determine all the morphological parameters used in this study (ΔC, (b/a)Lyα, (b/a)FUV, (b/a)I, and ΔPA) displayed on the Lyα images for the three galaxies. The blue, green, and red contours are corresponding to the regions where the regions are brighter than SBLyα = 1.5 × 1039 erg s−1 kpc−2, SBFUV = 2.5 × 1037 erg s−1 kpc−2 Å−1, SBI band = 1.5 × 1037 erg s−1 kpc−2 Å−1 all displayed on the Lyα images (for more information on the limits, see Table 2). The blue, green, and red crosses represent the measured centroids (non-weighted first image moment) within LMR for Lyα, within FUV FEI for FUV, and within I band FEI for band, respectively. The determined PAs in the regions are also displayed with blue dashed, green dotted, and red dash-dotted lines for Lyα, FUV, and I band, respectively. Moreover, the axis ratio (b/a)Lyα for each region is printed in the lower left part of the panels with blue, green, and red for Lyα, FUV, and I band, respectively. Finally, the centroid shift (ΔC, in kpc) between Lyα and FUV, and the difference between the measured PA of Lyα, and FUV are printed on the lower right side of the panels. |
3.2.2. Centroid shift
The difference in the light distribution and morphology of Lyα and FUV emissions was initially approached by measuring the centroid in each map (within LMR for Lyα, and FUV FEI for FUV) and determining their difference. Determining the centroid position of a light distribution in an image is similar to determining the centre of mass of a distribution of mass of a system. Without any photon scattering or attenuation, the centroids of the Lyα (CLyα) and FUV (CFUV) emissions would coincide (assuming a symmetric distribution of ionised gas around the massive star clusters). But with the complex radiative transfer affecting Lyα morphology, the centroids do not necessarily coincide.
Due to the uncertainties on Lyα emission level in the central parts of the galaxies (where continuum absorption is significant (see Sect. 3.2.1)), we determined the Lyα centroid as the non-weighted first image moment (Stobie 1980) within the region described above. Moreover, to be consistent with the Lyα centroid measurement, we used the non-weighted first image moment within the FUV FEI region. The first image moment is generally defined as:
where xi, yi, 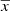 , and
, and 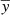 are the x, and y coordinates in the image coordinate system, and the weighted mean in the x and y axis, respectively. Finally, Ii is the flux measured in each pixel. As mentioned before, in our calculations, we used the non-weighted method where Ii = 1.
are the x, and y coordinates in the image coordinate system, and the weighted mean in the x and y axis, respectively. Finally, Ii is the flux measured in each pixel. As mentioned before, in our calculations, we used the non-weighted method where Ii = 1.
We determined the difference between the measured Lyα and FUV centroid as the centroid shift (ΔC):
This quantity indicates how the general distribution of Lyα photons has shifted from their main site of production. Table A.1 contains the measured centroid shift (ΔC) for each galaxy. Finally, to have a better understanding of the distribution of the sum of both young and old stellar populations, we determined the centroid for the whole stellar populations in the galaxies. To be consistent with our measurements in both Lyα and FUV, the centroid was computed as the non-weighted first image moment within the region selected by the I band FEI.
In Fig. 3, the measured centroid for each band is shown with a cross with the same colour used to display the contour for each band. Appendix E contains these results for the full sample.
3.2.3. Position angle and axis ratio
The first image moment collapses all the information on how the light is distributed in an image into a single value, the centroid position. However, by using the second image moment, the light distribution can be studied in greater detail (Stobie 1980). Hence, we expanded our non-parametric morphological studies utilising the second image moments and determined parameters that reveal more information on how the light distribution varies in different wavebands within the regions discussed in Sect. 3.2.1 in Lyα, FUV, and I band maps. The quantities studied through second image moments are axis ratio (b/a)Lyα, and the position angle (PA) (also used in other Lyα studies, e.g. Herenz et al. 2020) (difference of the measured position angle between FUV and Lyα), in addition to the FUV ((b/a)FUV) and I band ((b/a)I) axis ratios. Roughly, the axis ratio indicates the elongation, and the PA reveals the alignments of the light distribution in each bandpass. For instance, studying the difference in the measured PA between Lyα and FUV may reveal preferred directions of Lyα photon escape from the galaxies. The second-order image moments are defined as in Eq. (5):
As for the first moment, we use non-weighted image moments, hence Ii = 1. From the second image moments parameters in Eq. (5), parameters such as the minor and major axis, and the position angle of an ellipse can be analytically computed through Eq. (6), to Eq. (8).
In Eqs. (6) and (7), a, and b are the semi-major, and semi-minor axis, respectively. By measuring the semi-major (a) and semi-minor (b) axis, we assess the axis ratio. In general, axis ratios reveal different elongations or symmetricities of the light distribution in the regions of interest in the galaxies. The axis ratios and PAs in different wavebands are measured in the same regions described in Sect. 3.2.1 in each galaxy; the results are provided in Table A.1. From here on, we refer to the Lyα axis ratio ((b/a)Lyα) simply as the axis ratio unless we explicitly specify the axis ratios determined in other wavebands.
In Fig. 3, regions used for determining the axis ratios and PAs are shown with different contours, all displayed on the Lyα maps. The measured PAs within the region determined by Lyα, FUV, and I band FEIs are displayed with the blue dashed, green dotted, and dash-dotted lines, respectively. Appendix E contains these results for the full sample.
3.3. Isophotal analysis of the extent of the Lyα halos
As discussed in Sect. 1, it has already been established that Lyα halos are asymmetric in both local and high redshift universe. Furthermore, the stellar morphology in most of the galaxies in our sample is also quite irregular. Hence, circular apertures may not fully characterise the complicated Lyα distribution resulting from the radiative transfer. To avoid this issue, we also measure the extent of the Lyα halo, by studying the Lyα emission within the faint Lyα isophotes. This approach has the advantage that it explores the light distribution in the halo only. It also avoids the areas where the absorption becomes more prominent.
We used four isophotes, which provide us with an isophotal profile of the Lyα halo. The faintest encompassing Lyα isophote used in this analysis is SBLyα = 1.5 × 1039 erg s−1 kpc−2 for all galaxies but J1156, where Lyα SBLyα = 5.0 × 1039 erg s−1 kpc−2 Å−1 was selected (Sect. 3.2.1). The isophotes chosen for this analysis were selected as even multipliers (1, 2, 3, 4) of the faintest limit. Next, the areas covered within these isophotes were measured, and the equivalent radius (the radius of a circle with the same area encompassed by a given isophote) was determined.
Finally, we fit a simple exponential function to the Lyα isophotal SB profile of the halo to find the Lyα isophotal halo scale length (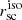 ) (Eq. (9)).
) (Eq. (9)).
Figure 4, shows the Lyα maps and the regions used for determining the extent of the halo and the exponential fit results. It is clear from this approach that more than one exponential function is needed to describe the full Lyα SB profiles. Appendix F contains these panels for the full sample.
 |
Fig. 4. Faint Lyα isophotes used to study the extent of the Lyα halo through the isophotal approach for each galaxy. In each figure, in the top panels, the region within the isophotal levels of even multipliers (1, 2, 3, 4) of the faintest limit (1.5 × 1039 erg s−1 kpc−2, except J1156 5.0 × 1039 erg s−1 kpc−2) denoted by red, orange, green and blue contours, all displayed on the Lyα maps of the galaxies. Bottom panels: data points corresponding to these isophotes displayed with the same colour, and a single exponential fit (Eq. (9)) to the points. The fitted scale lengths (and the measured error bar determined from the fit) are given in the lower left corner. The blue diamond represents the measured Lyα SB in the binned images at the innermost region (usually within r = 0.1 kpc from the brightest FUV point). |
3.4. Size and intensity of the star forming regions
So far, we have focused on measuring different quantities that quantify the Lyα morphology of the galaxies. With the high-resolution HST data available for our sample of galaxies, we also investigated how star-forming (SF) properties of the galaxies relate to the Lyα output.
We use two quantities for studying the SF properties, both based on the FUV, of the galaxies: (i) the size of the area with SFRD > 0.01 M⊙ yr−1 kpc−2 represented by the equivalent radius (the radius of a circle with the same area), and (ii) the average FUV SB (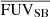 ) within these regions. The size of the area represents how large the SF regions are in each galaxy, while the (
) within these regions. The size of the area represents how large the SF regions are in each galaxy, while the (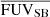 ) determines how intense the SF is in each galaxy.
) determines how intense the SF is in each galaxy.
For this analysis, we used the unbinned FUV images smoothed with the kernel sizes listed in Table 2. Figure 5 shows these regions, and the measured 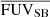 for three galaxies. Appendix G contains these results for the full sample.
for three galaxies. Appendix G contains these results for the full sample.
 |
Fig. 5. Regions used to determine the SF properties of the galaxies for the three galaxies. The green contours shows the regions with SFRD > 0.01 M⊙ yr−1 kpc−2 displayed on the unbinned FUV images. The measured average FUV SB ( |
4. Results
In this section, we discuss the outcomes of the analysis using the methods presented in Sect. 3.
4.1. Extent of the Lyα halos
To study the extended Lyα halos, we decomposed the profiles into core (inner) and halo (outer) regions. To do so, we studied the SFRD profiles of the galaxies obtained from the FUV SB profiles using the SFR calibration from Kennicutt & Evans (2012) and used a SFRD threshold of 0.01 M⊙ yr−1 kpc−2 to distinguish between core and halo. This threshold is roughly the SFRD in the Kennicutt–Schmidt relation where the slope changes from the efficient SFR to the inefficient SFR (Bigiel et al. 2008; Micheva et al. 2018). In Fig. 2, the radius in which the SFRD falls below the 0.01 M⊙ yr−1 kpc−2 is shown by a green circle on both FUV and Lyα images (middle, and right panels). This is also shown on the FUV and Lyα profiles (left panels), where the data points with the blue and sky blue in the Lyα profiles, and data points with the green and the light green represents core and halo, respectively.
As discussed in Sect. 3.1.2, we found that a double exponential function (Eq. (2)) describes both the Lyα and FUV SB profiles quite well. The second term (f2(r)) in this fitting function describes the behaviour of the halo. Based on the results from the profile fitting analysis, for the rest of the analysis, we exclude LARS04, LARS06, LARS13, ELARS01, ELARS03, ELARS07, ELARS12, ELARS14, ELARS15, ELARS16, ELARS18, ELARS20, ELARS21, ELARS23, ELARS28. These galaxies are faint Lyα emitters (the median of their Lyα luminosity is 2.30 × 1040 erg s−1 which is fainter by almost one order of magnitude compared to the median of the full sample 1.70 × 1040 erg s−1), and lack sufficient data points (less than 2) in their Lyα halo part of their Lyα SB profile with S/N > 2 for fitting the double exponential function (see Eq. (2)). This criterion makes us more confident that our extrapolation is based on the observed Lyα emission in the Lyα halos. We also exclude LARS10: this galaxy is also faint Lyα emitter (LLyα = 1.10 × 1040 erg s−1) and in spite of fulfilling the criterion of having more than two data points in its Lyα SB profiles, the measured fitted Lyα halo scale length has a large error bar where 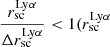 is the fitted scale length in the second term of the double exponential function defined in Eq. (2), to the Lyα SB profiles). Finally, LARS09 is excluded since its fitted
is the fitted scale length in the second term of the double exponential function defined in Eq. (2), to the Lyα SB profiles). Finally, LARS09 is excluded since its fitted 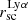 is huge (due to its Lyα morphology, with bright emission in the north and south of the centre and little sign of decreasing SB at large radii, see Figs. 2 and 3). The bin size of the circular annuli used for the SB profiles will certainly affect the S/N of individual data points, but using larger bins does not change this selection. Removing all these galaxies from the initial 45 galaxies in our sample, brings us to 28 galaxies that are explored in this study.
is huge (due to its Lyα morphology, with bright emission in the north and south of the centre and little sign of decreasing SB at large radii, see Figs. 2 and 3). The bin size of the circular annuli used for the SB profiles will certainly affect the S/N of individual data points, but using larger bins does not change this selection. Removing all these galaxies from the initial 45 galaxies in our sample, brings us to 28 galaxies that are explored in this study.
The range covered by Lyα halo scale length is between 1.03 to 9.05, with a median of 3.15 kpc. As previously stated, because of the physical processes involved in the Lyα RT, the Lyα SB profile usually drops more slowly than the FUV. Thus, we looked at the measured Lyα halo scale length 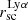 and how they compare to the FUV halo scale length
and how they compare to the FUV halo scale length 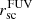 . Figure 6 shows
. Figure 6 shows 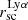 versus
versus 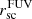 , and the distribution of these two quantities. We see that indeed, the distribution of Lyα emission is flatter than the FUV flux (
, and the distribution of these two quantities. We see that indeed, the distribution of Lyα emission is flatter than the FUV flux (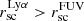 ). However, we note that when we compare the Lyα and FUV halo scale lengths, despite the difference in median value, the distributions are still consistent with each other (see the histograms). The KS test on two samples returns KS score of 0.21 corresponding to a p-value of 0.49, indicating that the distributions are similar, although this is driven by a few outliers. We also see that Lyα halo scale length correlates with the FUV halo scale length, indicating that more extended star-forming regions leads to more extended Lyα emission. Moreover, Bridge et al. (2018) finds that there is a correlation between the size of the Lyα halos and the scattering distance found in their analysis for the original LARS galaxies (LARS01-LARS14). We thus interpret the Lyα halo scale lengths to give a measure of the scattering distances of Lyα emission, and, consequently, that large Lyα halos (large
). However, we note that when we compare the Lyα and FUV halo scale lengths, despite the difference in median value, the distributions are still consistent with each other (see the histograms). The KS test on two samples returns KS score of 0.21 corresponding to a p-value of 0.49, indicating that the distributions are similar, although this is driven by a few outliers. We also see that Lyα halo scale length correlates with the FUV halo scale length, indicating that more extended star-forming regions leads to more extended Lyα emission. Moreover, Bridge et al. (2018) finds that there is a correlation between the size of the Lyα halos and the scattering distance found in their analysis for the original LARS galaxies (LARS01-LARS14). We thus interpret the Lyα halo scale lengths to give a measure of the scattering distances of Lyα emission, and, consequently, that large Lyα halos (large 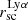 ) indicate large scattering distances.
) indicate large scattering distances.
 |
Fig. 6. Lyα halo scale length ( |
4.2. Lyα halo fraction
Studying Lyα halos is interesting on its own; however, perhaps the most important implication of the Lyα halo studies is to pin down the contribution of the halo to the total Lyα luminosity, that is the Lyα halo fraction. This quantity indicates what portion of the Lyα photons travels far away from where they were produced before escaping, and thus provide a clue on how far the ionising photons travel before ionising an H atom and how much radiative scattering goes on in each galaxy.
We define the Lyα halo fraction as the Lyα flux emitted in the halo divided by the total Lyα flux. The limited detector size of the SBC detector presents a problem for determining halo fractions. Many of our galaxies are close enough that their Lyα emission fills the detector chip. It is therefore likely that measurements in the images will miss part of the halo flux. Hence, we determine the halo fraction (HF) as: the measured Lyα luminosity through integrating the second term in our fitting function (which describes the halo, see Eq. (2)) from where we define halo (SFRD drops below 0.01 M⊙ yr−1 kpc−2) to infinity divided by the sum of this quantity and the observed Lyα luminosity in the core (Eq. (10)).
The left panel in Fig. 7 shows the distribution of HF for the galaxies in our sample. The measured HF ranges between 0.12 to 0.95 with a median size of 0.43. We looked at how HF compares with the observed halo fraction (HFobs). The observed halo fraction is determined by dividing the observed Lyα luminosity in the halo, to the observed Lyα luminosity out to the radius where (S/N)Lyα < 1. The right panel in Fig. 7 shows how the measured Lyα HF computed using the results from the fits compares with HFobs. Unsurprisingly, we see that the observed halo fractions are smaller than the profile fitted fractions. Assuming that the exponential nature of the halo holds out to at least a few scale radii, the fitted halo fractions provide a much more secure estimate of the actual fraction. Hence, in our study, we used HF determined from the fits and from here on, when we speak of HF, we refer to the Lyα HF determined from the fit.
 |
Fig. 7. Left panel: histogram showing the distribution of the measured HF for our sample of galaxies. Right panel: Lyα halo fraction HF computed from the fit (HF) vs. the observed halo fraction (HFobs). |
4.3. Lyα morphology of the galaxies
4.3.1. Centroid shift
The centroid shift (ΔC) is the offset between the measured centroid in Lyα, and FUV maps (see Sect. 3.2.2). The top panel in Fig. 8 shows the distribution of ΔC. Overall, we see that the Lyα emitting region is displaced from the FUV, and the measured ΔC ranges between 0.08, to 2.25, with the median size of 1.13 kpc. We discuss the relation between ΔC and the measured quantities in this study in addition to some Lyα observables in Sect. 5.
 |
Fig. 8. The difference in the position angles versus the centroid shift. The top and left histograms show the distributions and the measured median for ΔC, and ΔPA, respectively. |
4.3.2. Position angle difference
The difference between the measured Lyα and FUV position angle is another Lyα morphological parameter, assessed from the second image moment (see Sect. 3.2.3). From here on, we refer to the difference between the measured Lyα and FUV position angle as the absolute value of the difference in the position angles (ΔPA). This parameter indicates the difference between Lyα and FUV alignments. The right panel in Fig. 8 shows the distribution of ΔPA, ΔPA ranges between one, to 82 degrees, with the median size of 12°. Most of the galaxies have similar major axis in FUV and Lyα (small ΔPA), but we note that this parameter becomes very uncertain when the axis ratio is close to one. As an example, in the bottom left panel in Fig. 8 we show a scatter plot of ΔPA and ΔC. We discuss the relation between ΔC and the other quantities in Sect. 5.
4.3.3. Axis ratio
Another morphological parameter used in this study is the axis ratio. This parameter encapsulates more information about the light distribution than the centroid shift. Because, instead of collapsing all the information into a single value, it indicates how the spatial distribution (light distribution) differs in different directions. Axis ratio (b/a) is the ratio of the semi-minor axis to the semi-major axis; this parameter varies between zero and one.
The top left panel in Fig. 9 shows the distribution of Lyα axis ratio ((b/a)Lyα), the measured Lyα axis ratio ranges between 0.23, to 0.95, with the median size of 0.66. The top middle and top right panel show the measured ((b/a)Lyα) versus the FUV ((b/a)FUV), and I band ((b/a)I) axis ratios, respectively. The FUV axis ratio shows the spatial distribution of the young stellar population, while the I band axis ratio indicate the spatial distribution of both young and old stellar populations. The bottom panels show the histograms of FUV (bottom middle panel) and I band axis ratio (bottom right). We see that the distribution of the Lyα axis ratio is more similar to the FUV axis ratio distribution compared to the I band axis ratio distribution. The FUV axis ratio ranges from 0.19 to 0.90 with a median size of 0.64, while the I band axis ratio ranges between 0.24 to 0.89 with a median size of 0.54. The Lyα emission seems to follow the general FUV morphology of the galaxy (as measured by an axis ratio), despite radiative transfer effects.
 |
Fig. 9. Top left panel: histogram showing the distribution of Lyα axis ratio ((b/a)Lyα). Top middle panel: (b/a)Lyα versus the FUV axis ratio ((b/a)FUV). Top right panel: (b/a)Lyα versus the I band axis ratio ((b/a)I). Bottom middle panel: histogram showing (b/a)FUV distribution. Bottom right panel: histogram showing (b/a)I distribution. |
4.4. Isophotal analysis of the Lyα halo
Figure 10 shows the isophotal Lyα halo scale length (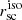 ) versus the extent derived from circular aperture analysis (
) versus the extent derived from circular aperture analysis (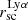 ). It should be noted that ELARS06, ELARS09, ELARS10, ELARS17, ELARS19, and ELARS26, are not included in this analysis (only this section and Sect. 5.3). These galaxies are among the faintest galaxies in our sample, and their Lyα emission level was not high enough to see them in all the four isophotes discussed in Sect. 3.3.
). It should be noted that ELARS06, ELARS09, ELARS10, ELARS17, ELARS19, and ELARS26, are not included in this analysis (only this section and Sect. 5.3). These galaxies are among the faintest galaxies in our sample, and their Lyα emission level was not high enough to see them in all the four isophotes discussed in Sect. 3.3.
 |
Fig. 10. Lyα halo scale lengths assessed through the isophotal approach versus the Lyα halo scale lengths derived from fitting the double exponential function to the Lyα SB profiles using the circular aperture. |
The majority of the galaxies appear more extended using circular apertures. This is expected because an isophotal profile is always narrower than a circular profile (the profiles are equal for a perfectly circular symmetric source). For example, in the extreme case of the edge-on galaxy LARS09, where the measured 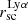 is too large (∼60 kpc, due to the morphology of the galaxy), it has a more reasonable measured
is too large (∼60 kpc, due to the morphology of the galaxy), it has a more reasonable measured 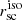 (2.8 kpc). The measured
(2.8 kpc). The measured 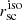 ranges between 0.62, to 4.25, with the median size of 1.4 kpc.
ranges between 0.62, to 4.25, with the median size of 1.4 kpc.
4.5. Characteristics of the star forming regions
4.5.1. Size and FUV intensity of the star forming regions
The majority of the Lyα photons are produced in the star-forming (SF) regions. Thus, we also study the star-forming regions and their properties. First, we investigate the size of the SF regions where most of the stars are formed, by measuring the size of the SF regions where the SFRD is higher than 0.01 M⊙ yr−1 kpc−2 (see Sect. 3.4). We represent this size by the equivalent radius (the radius of a circle with the same area, rSFRD > 0.01). Second, we study the FUV intensity within this region, by measuring the average FUV SB (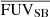 ) within the region where SFRD > 0.01 M⊙ yr−1 kpc−2. We use this average FUV surface brightness as a proxy for SFR density.
) within the region where SFRD > 0.01 M⊙ yr−1 kpc−2. We use this average FUV surface brightness as a proxy for SFR density.
Figure 11 shows how rSFRD > 0.01 varies with 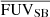 . The range covered by rSFRD > 0.01 is between 1.14 and 13.41, with a median of 3.73 kpc, the panel in histogram in right side shows the distribution of rSFRD > 0.01. The average FUV SB within the star forming region
. The range covered by rSFRD > 0.01 is between 1.14 and 13.41, with a median of 3.73 kpc, the panel in histogram in right side shows the distribution of rSFRD > 0.01. The average FUV SB within the star forming region 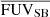 ranges between 7.98 × 1037 − 1.83 × 1039 with the median size of 3.02 × 1038 erg s−1 kpc−2 Å−1, the top panel in Fig. 11 shows the distribution of this quantity. We discuss the relation between rSFRD > 0.01,
ranges between 7.98 × 1037 − 1.83 × 1039 with the median size of 3.02 × 1038 erg s−1 kpc−2 Å−1, the top panel in Fig. 11 shows the distribution of this quantity. We discuss the relation between rSFRD > 0.01, 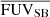 and the other quantities in Sect. 5.
and the other quantities in Sect. 5.
 |
Fig. 11. Size of the star forming region (rSFRD > 0.01), versus the average FUV SB ( |
5. Discussion
In this section, we explore the galaxies in our sample to find possible relation(s) between Lyα observables and the quantities used for studying the Lyα morphology. We also study the relation(s) between the Lyα morphological properties and host galaxy properties, such as stellar mass and I band axis ratio. In particular, we investigate how the Lyα morphology varies with the star-formation properties of the galaxies. Finally, we compare our results to similar measurements on the high redshift galaxies.
We use the following global observables (from Melinder et al., in prep.): stellar mass: estimated with the pixel SED fitting (LaXs), Lyα escape fraction (fesc): measured using the Lyα and Hα continuum maps, nebular reddening E(B − V)n: the average dust extinction in HII regions in the host galaxies (computed from the Balmer decrement), Lyα total luminosity (LLyα, using the Lyα emission map), Lyα equivalent width (EWLyα: measured using the Lyα and best-fit Lyα continuum maps), and FUV total luminosity (LFUV: using the best-fit Lyα continuum maps). The aperture used for the global observables is a circle centred on the brightest FUV pixel, and with a radius determined by growth curve analysis on the Lyα profiles (using the radius where the S/N of the Lyα SB drops below one).
In our investigation, we use the following quantities which carry information on the Lyα halo properties of the galaxies: Lyα halo scale length, Lyα halo fraction; and morphological parameters, such as: ΔC (see Sect. 3.2.2), axis ratio, ΔPA (see Sect. 3.2.3), and the isophotal Lyα halo scale length (see Sect. 3.3). Moreover, we use the following quantities that give insights on the star-forming properties of the galaxies: size of the SF regions, the average FUV SB within these regions, and the FUV axis ratio. We also look at the I band axis ratio as a quantity that characterises the stellar distribution of the host galaxies.
To quantify possible (anti-)correlations between each two parameters, we determine the Spearman’s rank correlation coefficient (ρs). This parameter varies between −1 to +1 (+1 showing correlation and −1 showing anti-correlation while zero indicates no correlation at all) and p-value (p0) indicating the probability of an uncorrelated system with the same measured Spearman’s correlation coefficient having arisen by chance (Ivezić et al. 2014). We use stats.Spearmanr task from the scipy package in python for assessing the Spearman’s correlation coefficients and p-values. We require a threshold of p0 below 0.05 (p0 < 0.05) for discussing the relation between any two given parameters (see Fig. 12).
 |
Fig. 12. Spearman p0 value for the Lyα observables and the quantities used for studying Lyα morphology. |
It should be noted that we investigate the relation between many quantities, and one might be concerned that looking for correlations between too many parameters would finally result in spurious correlations exceeding a given significance. We addressed this issue by (i) noting that some of the quantities investigated in our study are not independent of each other. For example, LLyα and LFUV, or fesc and EWLyα correlate (Sobral & Matthee 2019; Melinder et al., in prep.), and are not independent of each other. (ii) choosing a threshold for the assessed Spearman’s p-values (p0 < 0.05). We note that this threshold is only used as a tool to discuss the relation between different quantities. We are not claiming any physical relation between any given quantities based on the assessed p0. Furthermore, we would like to stress that our study is an exploratory one. We use the p0 criterion to select interesting findings in the data set, which we then discuss further.
It should be noted that the high spatial resolution data available for the LARS sample offers the opportunity to study the morphology of the galaxies at ⪅kpc scales. This is a piece of the puzzle that was missing in previous Lyα studies. Consequently, there is not much prior information, and, knowing the complexities of Lyα RT, it is hard to formulate strong hypotheses that can be tested.
5.1. Lyα observables and Lyα morphology
Here, we study the relations between global Lyα observables: Lyα total luminosity, Lyα equivalent width and Lyα escape fraction, and Lyα morphological properties: Lyα halo scale length, Lyα halo fraction, axis ratio, ΔC, and ΔPA. In other words, we investigate the relation between global Lyα observables and the quantities that are connected to how the Lyα photons redistribute within the host galaxies. Figure 12 shows the measured Spearman’s p-value between the Lyα observables and the quantities used for studying the Lyα morphology. As noted above, we only discuss cases with a p-value less than 0.05. For the interested readers, we also show how Lyα observables vary with all the morphological measurements in Appendix H.
5.1.1. Lyα luminosity
Our results show that Lyα luminosity (LLyα) anti-correlates with the HF (left panel in Fig. 13), meaning that Lyα halo contributes less to the overall luminosity in galaxies that are bright in Lyα while the majority of Lyα luminosity is coming from the Lyα halos in galaxies that are faint in Lyα. Thus, faint LAEs have more Lyα emission coming out from their halos, which causes them to exhibit overall low SB in Lyα. Consequently, detecting faint Lyα emitters at high redshift is even more challenging than what their global Lyα fluxes would indicate, and with limited spectroscopic apertures, this emission could even be missed completely. However, we note that the trend observed between HF and LLyα in our sample has not been observed in high-z surveys (Leclercq et al. 2017; Wisotzki et al. 2016), possibly due to the lack (or absence) of faint LAEs in these surveys. This result may also suggest that conclusions drawn from studying bright LAEs only, may be biased. Keep in mind that, unlike the MUSE sample that is selected on the Lyα emission of galaxies, our sample selection is agnostic to the Lyα properties.
 |
Fig. 13. How Lyα luminosity (LLyα) varies with the HF, and axis ratio (b/a)Lyα. The measured Spearman’s coefficient and p-value between LLyα and each quantity are displayed in the corresponding panels. |
We also observe a correlation between the Lyα luminosity and the axis ratio (right panel in Fig. 13), suggesting that bright galaxies appear rounder than the faint galaxies in Lyα.
5.1.2. Lyα escape fraction
We do not see any relation between any of the Lyα morphological quantities measured in this study and the Lyα escape fraction.
5.1.3. Lyα equivalent width
We see a weak anti-correlation between Lyα equivalent width (EWLyα) and the HF (see Fig. 14). In other words, EWLyα is lower in halo dominated galaxies (HF ∼ 1), indicating either lower escape fractions or an intrinsically older or higher metallicity stellar population (with a lower production efficiency of ionising photons, ξion, e.g. Matthee et al. 2017). This result is in line with the high-z findings reported by Steidel et al. (2011), where they find that galaxies with weak central Lyα or central absorption (e.g. LBGs) still have large halos (larger halo fractions).
 |
Fig. 14. How the measured Lyα equivalent width luminosity (EWLyα) varies with the HF. The measured Spearman’s coefficient and p-value between EWLyα and the HF are displayed in the top right. |
5.2. Lyα morphology and the stellar properties of the host galaxies
In this subsection, we study the interdependencies of the Lyα morphological quantities (Lyα halo scale length, Lyα halo fraction, axis ratio, ΔC, and ΔPA). Moreover, we also investigate how global parameters such as the stellar mass, the nebular reddening, and star-forming characteristics (size of the SF regions and the average intensity of the FUV SB) affect the Lyα morphology. Figure 15 shows the Spearman’s p values between these quantities. Once again, we only discuss cases with a p-value less than 0.05. For the interested reader, all cases are presented in Appendix I.
 |
Fig. 15. Spearman p0 value for the Lyα morphological quantities and the properties of the host galaxies. |
5.2.1. Extent of the Lyα halos
Our results show that Lyα halo extent (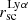 ) correlates with the stellar mass, size of the SF regions, and the HF, and anti-correlates with the average FUV SB within the SF regions, and the axis ratio (see Fig. 16). The correlation between
) correlates with the stellar mass, size of the SF regions, and the HF, and anti-correlates with the average FUV SB within the SF regions, and the axis ratio (see Fig. 16). The correlation between 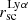 and the stellar mass suggests that massive galaxies possess more extended Lyα halos. Perhaps this also shows that the mass-size relation observed for normal galaxies at optical wavelengths (e.g. Fathi et al. 2010; Trujillo et al. 2020) also holds for Lyα emission.
and the stellar mass suggests that massive galaxies possess more extended Lyα halos. Perhaps this also shows that the mass-size relation observed for normal galaxies at optical wavelengths (e.g. Fathi et al. 2010; Trujillo et al. 2020) also holds for Lyα emission.
 |
Fig. 16. How the Lyα halo scale length ( |
One may expect that the Lyα halo extent should grow with the size of the SF regions. Since if the ionising photons cover a larger space in the galaxies, Lyα halos can get even more extended due to scattering. Indeed, we see a strong correlation between rSFRD > 0.01 and 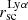 . In other words, we see that galaxies with more extended star-forming regions also have larger Lyα halos. We see an anti-correlation between the Lyα halo extent and
. In other words, we see that galaxies with more extended star-forming regions also have larger Lyα halos. We see an anti-correlation between the Lyα halo extent and 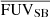 suggesting that galaxies with high SFR density do not have very extended Lyα emission. We see an anti-correlation between
suggesting that galaxies with high SFR density do not have very extended Lyα emission. We see an anti-correlation between 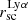 and the axis ratio suggesting that galaxies with more elongated Lyα morphology are also more extended in Lyα. This is likely driven by the use of circular annuli for the photometry (we do not see any relation between
and the axis ratio suggesting that galaxies with more elongated Lyα morphology are also more extended in Lyα. This is likely driven by the use of circular annuli for the photometry (we do not see any relation between 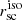 and (b/a)Lyα see Appendix J).
and (b/a)Lyα see Appendix J).
Finally, our data show a strong correlation between HF and 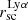 . In other words, we find galaxies that have more extended Lyα halos also have higher HF. This is in contrast with findings in previous studies where they see no trend between the measured Lyα halo scale length and the HF in their sample: Wisotzki et al. (2016), and Leclercq et al. (2017) (see Fig. 22). However, it is important to note that
. In other words, we find galaxies that have more extended Lyα halos also have higher HF. This is in contrast with findings in previous studies where they see no trend between the measured Lyα halo scale length and the HF in their sample: Wisotzki et al. (2016), and Leclercq et al. (2017) (see Fig. 22). However, it is important to note that 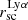 is used in the way we define HF (see Eq. (10)), and this correlation might reflect that these two quantities are implicitly related to each other.
is used in the way we define HF (see Eq. (10)), and this correlation might reflect that these two quantities are implicitly related to each other.
5.2.2. Lyα halo fraction
Our results indicate that the Lyα halo fraction (HF) anti-correlates with the total FUV luminosity, the average FUV SB within the SF regions (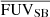 ) (see Fig. 17), and the axis ratio; and correlates with the Lyα halo scale length (see Sect. 5.2.1).
) (see Fig. 17), and the axis ratio; and correlates with the Lyα halo scale length (see Sect. 5.2.1).
 |
Fig. 17. How the Lyα halo fraction (HF) varies with the total FUV luminosity (LFUV), the average FUV SB within the SF regions ( |
The anti-correlation between the HF and LFUV implies that Lyα halos contribute more to the total Lyα luminosity in galaxies that have lower star formation rates (lower FUV luminosity) and therefore also lower intrinsic Lyα luminosity. Given the intrinsic relation between the Lyα and FUV luminosities, this relation re-portrays the anti-correlation between the LLyα and the HF (see Sect. 5.1.1). We also see an anti-correlation between HF and 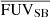 suggesting that the Lyα halos contribute more to the overall Lyα luminosity in SFGs galaxies that have lower SFR density. Finally, we find an anti-correlation between the HF and the axis ratio ((b/a)Lyα). This indicates that the halos in galaxies with high HF are on average, more elongated.
suggesting that the Lyα halos contribute more to the overall Lyα luminosity in SFGs galaxies that have lower SFR density. Finally, we find an anti-correlation between the HF and the axis ratio ((b/a)Lyα). This indicates that the halos in galaxies with high HF are on average, more elongated.
5.2.3. Centroid shift
We see that the centroid shift (ΔC see Eq. (3)) correlates with the stellar mass, and the size of the SF regions (see Fig. 18). As discussed in Sect. 5.2.1, both stellar mass and the size of the SF regions correlate with the Lyα halo scale length. In other words, we see that centroid shift correlates with the quantities that are connected to more extended Lyα halos. This suggests that the centroid shift grows in galaxies with larger 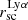 , since Lyα halos do not grow symmetrically, and a larger Lyα halo means a larger difference between the Lyα and FUV measured centroid. However, it should be noted that even though we see that some galaxies with large
, since Lyα halos do not grow symmetrically, and a larger Lyα halo means a larger difference between the Lyα and FUV measured centroid. However, it should be noted that even though we see that some galaxies with large 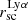 possess large centroid shifts (e.g. LARS11, ELARS25, and J1156), we do not see a direct correlation between ΔC and
possess large centroid shifts (e.g. LARS11, ELARS25, and J1156), we do not see a direct correlation between ΔC and 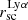 .
.
 |
Fig. 18. How the centroid shift (ΔC) varies with the stellar mass and the size of the SF regions. The measured Spearman’s coefficient and p-value between ΔC and each quantity are displayed in the corresponding panels. |
5.2.4. Position angle difference
We see that the difference in position angles (ΔPA) anti-correlates with stellar mass, nebular reddening (E(B − V)n), and size of the SF regions (see Fig. 19). The anti-correlation between ΔPA and the stellar mass suggests that Lyα and FUV misalignment is more significant in low-mass galaxies. We see an anti-correlation between ΔPA and the nebular reddening, mainly due to a lack of dusty galaxies with high ΔPA. Possibly, this is related to the paucity of dusty galaxies with high 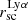 or HF, and that less Lyα scattering takes place in such galaxies. In galaxies that are dustier, the Lyα alignment is closer to the alignment of the star-forming regions; perhaps this is due to absorption of the Lyα photons by the dust particles, which results in less scattering of the Lyα photons, indicating that the Lyα photons follow the same path that the FUV photons take to escape the galaxies. Consequently, the Lyα and FUV alignments in these galaxies are more similar to each other.
or HF, and that less Lyα scattering takes place in such galaxies. In galaxies that are dustier, the Lyα alignment is closer to the alignment of the star-forming regions; perhaps this is due to absorption of the Lyα photons by the dust particles, which results in less scattering of the Lyα photons, indicating that the Lyα photons follow the same path that the FUV photons take to escape the galaxies. Consequently, the Lyα and FUV alignments in these galaxies are more similar to each other.
 |
Fig. 19. How the difference in the position angles (ΔPA) varies with the stellar mass, the nebular reddening E(B − V)n, and the size of the SF regions. The measured Spearman’s coefficient and p-value between ΔPA and each quantity are displayed in the corresponding panels. |
The anti-correlation between ΔPA and the size of the SF regions could be explained by there being more direct channels available for Lyα escape (and thus less scattering) in galaxies with larger SF regions. The Lyα photons are then escaping closer to where they were produced, and the overall emission is more similar to the FUV distribution. The anti-correlation between ΔPA and the size of the SF regions is augmented by a small number of galaxies with high ΔPA or high rSFRD > 0.01. A large ΔPA in a large SF region requires a more coherent change of preferred direction than in a small one, where the effect could more likely occur stochastically.
5.2.5. Lyα axis ratio
We see that axis ratio ((b/a)Lyα) correlates with the FUV axis ratio ((b/a)FUV), the average FUV SB within the SF regions (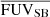 ), and the difference in the position angles (ΔPA) (see Fig. 20). The correlation between (b/a)Lyα and (b/a)FUV suggests that Lyα distribution in the galaxies depends on the FUV distribution. Given that the majority of the ionising photons are reprocessed into Lyα photons, it is hardly a surprise that the Lyα morphology depends on the distribution of the young stellar population (if there would have not been any scattering or dust absorption, this correlation would likely be even stronger). We see that galaxies with high SFR density (high
), and the difference in the position angles (ΔPA) (see Fig. 20). The correlation between (b/a)Lyα and (b/a)FUV suggests that Lyα distribution in the galaxies depends on the FUV distribution. Given that the majority of the ionising photons are reprocessed into Lyα photons, it is hardly a surprise that the Lyα morphology depends on the distribution of the young stellar population (if there would have not been any scattering or dust absorption, this correlation would likely be even stronger). We see that galaxies with high SFR density (high 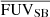 ) appear rounder in their Lyα morphology (high (b/a)Lyα). This could be the anti-correlation between the
) appear rounder in their Lyα morphology (high (b/a)Lyα). This could be the anti-correlation between the 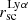 and
and 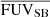 (see Sect. 5.2.1) from another perspective. Then, assuming that less scattering occurs in galaxies with high SFR density, these galaxies would also have less elongated Lyα morphology as well as less extended halos.
(see Sect. 5.2.1) from another perspective. Then, assuming that less scattering occurs in galaxies with high SFR density, these galaxies would also have less elongated Lyα morphology as well as less extended halos.
 |
Fig. 20. How the axis ratio ((b/a)Lyα) varies with the FUV axis ratio ((b/a)FUV), the average FUV SB within the SF regions ( |
Finally, the correlation between (b/a)Lyα and ΔPA seem to indicate that in galaxies where Lyα photons escape more in off-axis direction compared to the FUV morphology, the Lyα morphology is rounder and more symmetric. However, we note that ΔPA is unconstrained for high values of (b/a)Lyα.
5.3. Isophotal analysis of the Lyα halo
In this section, we look at the relation between the measured isophotal Lyα halo scale length (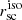 ) and Lyα observables, quantities used for studying the Lyα morphology, and also the some of the global observables (stellar mass, and nebular reddening). While we only discuss the cases with a p-value less than 0.05, we provide how
) and Lyα observables, quantities used for studying the Lyα morphology, and also the some of the global observables (stellar mass, and nebular reddening). While we only discuss the cases with a p-value less than 0.05, we provide how  varies which each quantity in Appendix J for the interested readers.
varies which each quantity in Appendix J for the interested readers.
Our analysis indicate that the isophotal Lyα scale lengths ( ) correlate with stellar mass, total Lyα luminosity (LLyα), total FUV luminosity (LFUV), the size of the star forming regions, and the centroid shift (ΔC) (see Fig. 21).
) correlate with stellar mass, total Lyα luminosity (LLyα), total FUV luminosity (LFUV), the size of the star forming regions, and the centroid shift (ΔC) (see Fig. 21).
 |
Fig. 21. How the measured isophotal Lyα halo scale length ( |
In other words, our data indicate that the size-mass relation in Lyα emission line holds using the isophotal Lyα scale lengths, too. We see that  strongly correlate with LLyα, and LFUV. We note that if a single exponential describes the isophotal Lyα halo SB profile well, the halo Lyα luminosity and the total Lyα luminosity will be directly proportional to the square of the scale length (
strongly correlate with LLyα, and LFUV. We note that if a single exponential describes the isophotal Lyα halo SB profile well, the halo Lyα luminosity and the total Lyα luminosity will be directly proportional to the square of the scale length (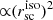 ). Hence, the strong correlation between
). Hence, the strong correlation between  and LLyα might simply reflect that a single exponential is a good choice for describing the isophotal Lyα halo SB profile. Due to the stellar morphology of the galaxies in our sample and the asymmetric Lyα halos, this was probably not captured in the circular aperture analysis. Moreover, given the intrinsic relation between the Lyα photons and FUV photons, and the strong correlation between the Lyα luminosity and FUV luminosity, the correlation between
and LLyα might simply reflect that a single exponential is a good choice for describing the isophotal Lyα halo SB profile. Due to the stellar morphology of the galaxies in our sample and the asymmetric Lyα halos, this was probably not captured in the circular aperture analysis. Moreover, given the intrinsic relation between the Lyα photons and FUV photons, and the strong correlation between the Lyα luminosity and FUV luminosity, the correlation between  and LFUV is not surprising, at all. It should be noted that we see the aperture size (where (S/N)Lyα drops below one) used for measuring the global properties of the galaxies (stellar mass, LLyα, LFUV, fesc, etc.) strongly depends on
and LFUV is not surprising, at all. It should be noted that we see the aperture size (where (S/N)Lyα drops below one) used for measuring the global properties of the galaxies (stellar mass, LLyα, LFUV, fesc, etc.) strongly depends on  . Consequently, at least part (or maybe all) of the observed correlation between
. Consequently, at least part (or maybe all) of the observed correlation between  , and the stellar mass, LLyα, and LFUV can be because of this aperture effect. Galaxies with more extended Lyα emission in the halo will have a larger area with significant (S/N > 1) emission and, therefore, a larger global aperture.
, and the stellar mass, LLyα, and LFUV can be because of this aperture effect. Galaxies with more extended Lyα emission in the halo will have a larger area with significant (S/N > 1) emission and, therefore, a larger global aperture.
Similar to  (see Sect. 5.2.1),
(see Sect. 5.2.1),  correlates with the size of the SF regions. Finally, we see that
correlates with the size of the SF regions. Finally, we see that  correlates with the centroid shift. This finding suggests Lyα morphology is more offset from the FUV morphology, and Lyα halos extend further away from the SF regions in galaxies with a more pronounced scattering of Lyα photons. The correlation with centroid shift is stronger for the isophotal scale length compared to
correlates with the centroid shift. This finding suggests Lyα morphology is more offset from the FUV morphology, and Lyα halos extend further away from the SF regions in galaxies with a more pronounced scattering of Lyα photons. The correlation with centroid shift is stronger for the isophotal scale length compared to  . The reason for this could be that (i) the difference between stellar and Lyα morphology is better captured in the isophotal analysis, and (ii) the isophotal analysis is done on a subset of the galaxies used for the circular analysis (see Sect. 4.4).
. The reason for this could be that (i) the difference between stellar and Lyα morphology is better captured in the isophotal analysis, and (ii) the isophotal analysis is done on a subset of the galaxies used for the circular analysis (see Sect. 4.4).
5.4. Comparison with high-z galaxies
By comparing observations of low redshift galaxies with similar systems at high redshift, it may be possible to constrain changes to Lyα physics due to galaxy evolution.
The selection criteria used for the galaxies included in our sample is very similar to a standard LBG selection criterion, targeting UV bright galaxies with ongoing star formation. The Lyα imaging of LBG selected galaxies have mainly been done with narrow-band observations or stacking (e.g. Steidel et al. 2011; Momose et al. 2014). In fact, Guaita et al. (2015) compared the Lyα images from the original LARS sample (first 14 galaxies in our sample) to these two studies. However, the data used in these studies are deeper than our study by almost two orders of magnitudes. In other words, these studies reach fainter SB levels further out and consequently, the physical scales probed in these studies are larger than those in our study. For example, Steidel et al. (2011) probed a physical scale in the range of ≥10 kpc. Their data indicate that Lyα scale lengths in the inner halos (< 20 kpc) are shorter (∼10 kpc) than those for the outer halos (⪆20 kpc, rather probing the CGM), but still much longer than for the continuum (∼3 kpc). Therefore, to compare galaxies on an individual level, we need to turn to Integral Field Spectroscopy (IFS) which can provide Lyα images of high-z galaxies, albeit at significantly worse spatial resolution than for the nearby galaxies in this study. In the IFS Lyα surveys performed by VLT/MUSE (e.g. Bacon et al. 2015), sources are detected based on their Lyα emission rather than UV brightness which means that the sample selection is somewhat different. Compared to a pure LBG selection, selection based on the Lyα emission will yield a sample with higher EWLyα galaxies. This also applies for comparing the MUSE Lyα results to LARS and should be kept in mind for the following section, where we discuss some of our results and how they compare to the z = 3−6 LAEs studied by Leclercq et al. (2017).
We begin by comparing the Lyα core and halo scale lengths (from fitting a double exponential function to the Lyα SB profiles, see Sect. 3.1.2) measured from our sample and the results obtained for LAEs in Leclercq et al. (2017). Figure 22 shows that similar to the MUSE findings, we see no relation between the measured Lyα halo scale lengths and the measured scale lengths in the core in our sample (top left panel). The parameter space covered by the LARS measurements is not similar to the MUSE findings (top right panel). We see that, unlike the core region where the fitted scale lengths coverage in MUSE and LARS are similar, and the measured medians are close, the galaxies in the MUSE study possess more extended Lyα halo, due to the larger FoV and possibly different selection criteria. The median of the Lyα core scale length in our sample is slightly higher than the MUSE sample, 0.47 kpc in our sample compared to the 0.43 kpc in the MUSE study. However, the median of the Lyα halo scale length in the MUSE sample is higher than our sample. The assessed median of the Lyα halo scale length in their sample is 4.37 kpc compared to 3.15 kpc in our sample.
 |
Fig. 22. Our results and how they compare to the MUSE study. Top left: how the Lyα halo scale length is compared to the Lyα core extent. Top right: the Lyα halo extent versus the Lyα core extent for both MUSE and our sample, the core extent is somewhat similar. However, Lyα is more extended in the MUSE sample compared to ours. Bottom left: the distribution of the HF in MUSE and our study, the bimodal distribution in HF in our study is not present in the LAEs observed in the MUSE study. Moreover, the median of the HF in the MUSE study (0.66) is larger than the measured median in our study (0.43). Bottom right: HF versus the Lyα halo extent measured in our sample and MUSE. The space covered in the HF- |
Furthermore, we see a difference both in the distribution and the median of the HF measured in our study compared to the MUSE study. The HF in our sample follows a bimodal distribution which is not observed in the LAEs observed in the MUSE studies (bottom left panel in Fig. 22), and the measured median of the HF in our sample is 0.43, which is lower than the median of the HF of the LAEs in the MUSE study (0.66). This could be due to a selection effect; the galaxies studied in the MUSE study are generally brighter in Lyα compared to the galaxies in our sample (the median of the Lyα luminosity in the MUSE sample is almost one order of magnitude higher than our sample).
Finally, the bottom right panel shows a comparison of HF versus  for our data to the same parameters for the MUSE survey. We find that the space coverage of our data in HF –
for our data to the same parameters for the MUSE survey. We find that the space coverage of our data in HF –  space is within the space coverage of the high-z LAEs studied in the MUSE study. The correlation between HF and
space is within the space coverage of the high-z LAEs studied in the MUSE study. The correlation between HF and  in our sample is not seen in the MUSE results. We note that the MUSE observations follow the Lyα much further out than we can in most LARS galaxies. This may introduce unknown implications for our measurements. HST imaging of z ∼ 0.3−0.5 galaxies could help bridge this gap and constrain this relation further.
in our sample is not seen in the MUSE results. We note that the MUSE observations follow the Lyα much further out than we can in most LARS galaxies. This may introduce unknown implications for our measurements. HST imaging of z ∼ 0.3−0.5 galaxies could help bridge this gap and constrain this relation further.
It should also be noted that there are several differences between how we measure the Lyα extent of the core and halo compared to the MUSE study. We fit a double exponential function (see Eq. (2)) where each component (core and halo) is described with a single exponential term. The MUSE study also uses a double exponential profile model. However, the core Lyα function is held constant and is set to an exponential fit derived from an HST FUV profile. The summed (core + halo) profile is also smoothed to match the ground-based spatial resolution.
Moreover, many of the galaxies in our sample shows Lyα absorption in the centre, which is not seen in the high-z LAEs. This could be because, in the MUSE study, regions were averaged over much larger distances (MUSE has a lower spatial resolution and the galaxies are further away), or a selection effect associated with their average higher Lyα equivalent widths, indicative of lower destruction of Lyα photons in the central regions.
In our analysis, we tried to limit the effect of absorption, but it does affect the core characteristics. Moreover, the MUSE sample is selected on Lyα emission, whereas our sample selection is agnostic to the Lyα properties, and this difference likely has an impact on the comparison.
The high-resolution HST data available for our sample also provides the opportunity to explore whether the assumption used in the high-z studies that Lyα and FUV continuum scale lengths in the core are similar is valid or not. In Fig. 23, the Lyα core scale length is plotted against the FUV core scale length. Our data suggest that even in the core regions of the galaxies, Lyα is more extended than FUV. The measured median of the Lyα core scale length exceeds the FUV core scale length by more than 70%. In other words, our data suggest that Lyα is more extended than the FUV not only in the halo, but also in the core regions. The MUSE study assumed them to be equal (since they cannot spatially resolve Lyα in the core) and have therefore likely underestimated the size of the Lyα core region.
 |
Fig. 23. Lyα core rsc vs. FUV core rsc. The data suggest that even in the core regions of the galaxies, Lyα is more extended than the FUV continuum. The measured median of the Lyα and FUV core scale lengths are displayed at the top left part of the figure with blue and green colours, respectively. |
Finally, to investigate how our galaxies would look like if they were at the same redshift as the MUSE sources (and observed with MUSE), we smoothed the Lyα maps of the LARS galaxies to match the MUSE seeing and physical scale at z = 3. In this step, the same method and the same fitting function used in the MUSE study was used for describing the convolved SB profiles. This comparison is not trivial because of the limited FoV of our HST observations. The spatial extent of the Lyα emission in the non-convolved maps is often so large that the smoothing moves most of the flux outside of the image, making it impossible to study the Lyα light distribution in the same way as in the MUSE analysis. The detailed information on Lyα in the core for the LARS galaxies is completely washed out by the smoothing. Also, smoothing galaxies with substantial absorption in the core result in profiles that are not comparable to the observed z ∼ 3 profiles. The failure of this test to give any useful information is due to the enormous disparity of spatial resolution and FoV size between LARS and the MUSE Lyα observations. At z ∼ 3 and with MUSE spatial resolution, most of the images of LARS galaxies only cover a few resolution elements. The situation is better for the galaxies at slightly higher redshift, and an intermediate redshift sample of HST observed Lyα emitters might be easier to use for comparison (Runnholm et al., in prep.).
6. Summary
In this article, we presented a study of how Lyα emission is spatially distributed in a sample of 45 nearby star-forming galaxies observed with the HST. We started by examining different ways to describe the Lyα and FUV SB profiles of the galaxies and concluded that a single Sérsic profile could not describe the Lyα and FUV SB profiles of the galaxies in our sample. However, a double exponential function (Eq. (2)) describes the majority of Lyα, and FUV SB profiles well, in particular, the outermost part of the Lyα SB profiles, which is the main focus of this study. Following Bigiel et al. (2008), Micheva et al. (2018) studies, FUV, and Lyα SB profiles were decomposed into core and halo parts by using a FUV-based SFRD threshold of 0.01 M⊙ yr−1 kpc−2, and the Lyα HF was defined based on the fitted results in the Lyα halo SB profile and the observed luminosity in the core (see Eq. (10)).
We studied the light distribution of the galaxies in different wavebands such as FUV, Lyα, and I band. The first and the second image moments were used to derive morphological parameters, such as the centroid shift between Lyα and FUV, and minor/major axis ratios (b/a) in Lyα, FUV and I band and the difference between the measured position angles in Lyα and FUV (ΔPAs) to study the Lyα morphology of the galaxies. Moreover, to characterise compactness and areal intensity of star formation, the size and average FUV SB of the regions with SFRD > 0.01 M⊙ yr−1 kpc−2 were also measured.
We also explored the galaxies in our sample to study the relations between the global Lyα observables: Lyα total luminosity, Lyα equivalent width and Lyα escape fraction; and the Lyα morphological properties: Lyα halo scale length, Lyα halo fraction, axis ratio, ΔC, and ΔPA. We observed a correlation between the Lyα luminosity and the axis ratio, suggesting that bright galaxies in Lyα appear rounder than the faint one. We also found that Lyα luminosity anti-correlates with the HF, meaning most Lyα luminosity is coming from the Lyα halos in galaxies that are faint in Lyα. Our findings also suggest that faint LAEs have more emission coming out from their halos, and potentially put these objects among the Lyα low SB galaxies. Therefore, detecting and observing faint LAEs at high redshift is more challenging than what their global LAE fluxes would indicate. Consequently, conclusions drawn from studying the bright LAEs only, might be biased. Our data suggest that there is no relation between the Lyα escape fraction and any of the Lyα morphological quantities. Finally, We saw a weak anti-correlation between EWLyα and the HF, indicating either lower escape fractions or an intrinsically older stellar population.
We also studied the interdependencies of the Lyα morphological quantities (Lyα halo scale length, Lyα halo fraction, axis ratio, ΔC, and ΔPA). Moreover, we investigated how the global parameters such as the stellar mass, the nebular reddening, and star-forming characteristics (size of the SF regions and the average intensity of the FUV SB) affect the Lyα morphology.
We saw that  correlates with the stellar mass, size of the SF regions, and the HF, and anti-correlates with the average FUV SB within the SF regions, and the axis ratio. These findings suggest that massive galaxies possess more extended Lyα halos, and the mass-size relation also holds for the Lyα emission. Moreover, galaxies with more extended star-forming regions also have larger Lyα halos, probably because the ionising photons cover larger space in the galaxies, and due to the scattering, Lyα halos get more extended. The anti-correlation between the
correlates with the stellar mass, size of the SF regions, and the HF, and anti-correlates with the average FUV SB within the SF regions, and the axis ratio. These findings suggest that massive galaxies possess more extended Lyα halos, and the mass-size relation also holds for the Lyα emission. Moreover, galaxies with more extended star-forming regions also have larger Lyα halos, probably because the ionising photons cover larger space in the galaxies, and due to the scattering, Lyα halos get more extended. The anti-correlation between the  and
and 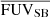 indicate that galaxies with high SFR density do not have very extended Lyα emission. Finally, the anti-correlation between
indicate that galaxies with high SFR density do not have very extended Lyα emission. Finally, the anti-correlation between  and the axis ratio suggests that galaxies with more elongated Lyα morphology are also more extended in Lyα. The strong correlation between
and the axis ratio suggests that galaxies with more elongated Lyα morphology are also more extended in Lyα. The strong correlation between  and HF suggest that galaxies that have more extended Lyα halos, have higher HF, too. However, this could simply be due to the way that we define HF (see Eq. (10)), and this correlation might reflect that these two quantities are implicitly related to each other.
and HF suggest that galaxies that have more extended Lyα halos, have higher HF, too. However, this could simply be due to the way that we define HF (see Eq. (10)), and this correlation might reflect that these two quantities are implicitly related to each other.
Our data show that HF anti-correlates with the total FUV luminosity, the average FUV SB within the SF regions, and the axis ratio; and correlates with  . These findings imply that Lyα halos contribute more to the total Lyα luminosity in galaxies with lower star formation rates (lower FUV luminosity) and therefore also lower intrinsic Lyα luminosity. Moreover, Lyα halos contribute more to the overall Lyα luminosity in SFGs galaxies with lower SFR density. Finally, we found that Lyα halos in galaxies with low HF are one average rounder.
. These findings imply that Lyα halos contribute more to the total Lyα luminosity in galaxies with lower star formation rates (lower FUV luminosity) and therefore also lower intrinsic Lyα luminosity. Moreover, Lyα halos contribute more to the overall Lyα luminosity in SFGs galaxies with lower SFR density. Finally, we found that Lyα halos in galaxies with low HF are one average rounder.
We found that the centroid shift correlates with the stellar mass and the size of the SF regions implying that the centroid shift correlates with two quantities which correlate with the  . This may suggest that the centroid shift grows in galaxies with larger
. This may suggest that the centroid shift grows in galaxies with larger  , since Lyα halo do not grow symmetrically, and larger Lyα halo means a larger difference between the Lyα and FUV measured centroid. However, we did not see a correlation between ΔC and
, since Lyα halo do not grow symmetrically, and larger Lyα halo means a larger difference between the Lyα and FUV measured centroid. However, we did not see a correlation between ΔC and  in our sample.
in our sample.
We saw that ΔPA anti-correlates with the stellar mass, E(B − V)n, and the size of the SF regions suggesting that Lyα and FUV misalignment is more significant in massive galaxies. The anti-correlation between ΔPA and the nebular reddening is mainly because of a lack of dusty galaxies with high ΔPA. Perhaps, this is because of the absorption of the Lyα photons by the dust particles resulting in less scattering of the Lyα photons. Consequently, Lyα photons follow the same path that the FUV photons take to escape the galaxies. The anti-correlation between ΔPA and the size of the SF regions could be illustrated by more direct channels available for Lyα to escape in galaxies with larger SF regions. The Lyα photons are then escaping closer to where they were produced, and the overall emission is more similar to the FUV distribution.
We saw that Lyα axis ratio correlates with (b/a)FUV,  , and ΔPA. The correlation between (b/a)Lyα and (b/a)FUV suggests that Lyα distribution in the galaxies depends on the FUV distribution. We see that galaxies with high SFR density (high
, and ΔPA. The correlation between (b/a)Lyα and (b/a)FUV suggests that Lyα distribution in the galaxies depends on the FUV distribution. We see that galaxies with high SFR density (high  ) appear rounder in their Lyα morphology (high (b/a)Lyα), assuming that less scattering occurs in galaxies with high SFR density, these galaxies would also have less elongated Lyα morphology as well as less extended halos. Finally, the correlation between (b/a)Lyα and ΔPA indicates that in galaxies where Lyα photons escape more in off-axis direction compared to the FUV morphology, the Lyα morphology is rounder and more symmetric.
) appear rounder in their Lyα morphology (high (b/a)Lyα), assuming that less scattering occurs in galaxies with high SFR density, these galaxies would also have less elongated Lyα morphology as well as less extended halos. Finally, the correlation between (b/a)Lyα and ΔPA indicates that in galaxies where Lyα photons escape more in off-axis direction compared to the FUV morphology, the Lyα morphology is rounder and more symmetric.
We also studied the extent of the Lyα halos through an isophotal approach. Since using circular apertures may give a skewed representation of the halos, because of the asymmetric nature of Lyα halos and the stellar morphology of the galaxies in our sample. We fit a simple exponential function to the Lyα isophotal SB profile of the halo to find the Lyα isophotal halo scale length ( ). Given that an isophotal profile is always narrower than a circular profile, the majority of the galaxies appear more extended using circular apertures. Furthermore, we also looked at the relation between the measured isophotal Lyα halo scale length (
). Given that an isophotal profile is always narrower than a circular profile, the majority of the galaxies appear more extended using circular apertures. Furthermore, we also looked at the relation between the measured isophotal Lyα halo scale length ( ) and Lyα observables, quantities used for studying the Lyα morphology, and also some of the global observables. We saw that
) and Lyα observables, quantities used for studying the Lyα morphology, and also some of the global observables. We saw that 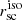 correlate with stellar mass, Lyα luminosity, FUV luminosity, the size of the star-forming regions, and the centroid shift. In other words, our data indicate that the size-mass relation in Lyα emission line holds using the isophotal Lyα scale lengths, too. Since we see the aperture size (where (S/N)Lyα drops below one) used for measuring the global properties of the galaxies strongly depends on
correlate with stellar mass, Lyα luminosity, FUV luminosity, the size of the star-forming regions, and the centroid shift. In other words, our data indicate that the size-mass relation in Lyα emission line holds using the isophotal Lyα scale lengths, too. Since we see the aperture size (where (S/N)Lyα drops below one) used for measuring the global properties of the galaxies strongly depends on 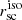 , at least part (or maybe all) of the observed correlation between
, at least part (or maybe all) of the observed correlation between 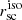 , and the stellar mass, LLyα, and LFUV can be because of this aperture effect.
, and the stellar mass, LLyα, and LFUV can be because of this aperture effect.
Finally, we compared our results with the high-z LAEs studied with MUSE (Leclercq et al. 2017). Whereas our sample selection is agnostic to the presence of Lyα emission, the MUSE sample is selected on Lyα emission, so some differences are to be expected. The parameter space covered by the core and halo Lyα scale lengths in our sample cover is similar to the LAEs in the MUSE study. Lyα core regions in our sample (median of the core scale length 0.47) extend similar to high-z LAEs (median of the core scale length 0.43). However, Lyα halos in the LAEs are more extended (median of the halo scale length 4.37) compared to our sample (median of the halo scale length 3.15). Furthermore, Lyα halos in the LAEs in the MUSE study contribute more to the total Lyα luminosity (median of HF = 0.66) compared to the nearby SFGs in our sample (median of HF = 0.43). Furthermore, the bimodal distribution observed in the HF in our sample is not observed in their sample. The comparison between the HF measured for the LAEs in our sample (median of 0.43) compared to the high-z LAEs in the MUSE study (median of 0.66) indicate the Lyα halos in the nearby SFGs contribute less to the total Lyα luminosity compared to high-z LAEs.
Utilising high-resolution data for the nearby galaxies in our sample, we tested whether the assumption that the FUV and Lyα scale length in cores are similar. Our results show that even in the core regions, Lyα is more extended, and the median of the measured core Lyα scale length is higher than 150% the median of the measured FUV scale length.
Acknowledgments
M.H. is a Fellow of the Knut and Alice Wallenberg Foundation. D.K. is supported by the Centre National d’Etudes Spatiales (CNES)/Centre National de la Recherche Scienti que (CNRS); convention no 131425. J.M.M.H. is funded by Spanish State Research Agency grants PID2019-107061GB-C61 and MDM-2017-0737 (Unidad de Excelencia Maria de Maeztu CAB). A.V. acknowledges support from the European Research Council under grant agreement ERC-stg-757258 (TRIPLE) and the Swiss National Foundation under grant PP00P2 176808.
References
- An, F. X., Zheng, X. Z., Hao, C.-N., Huang, J.-S., & Xia, X.-Y. 2017, ApJ, 835, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Atek, H., Kunth, D., Hayes, M., Östlin, G., & Mas-Hesse, J. M. 2008, A&A, 488, 491 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Avila, R. J., Bohlin, R., Hathi, N., et al. 2019, SBC Absolute Flux Calibration, Instrument Science Report ACS 2019-5, 13 [Google Scholar]
- Bacon, R., Brinchmann, J., Richard, J., et al. 2015, A&A, 575, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Behrens, C., & Braun, H. 2014, A&A, 572, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bigiel, F., Leroy, A., Walter, F., et al. 2008, AJ, 136, 2846 [NASA ADS] [CrossRef] [Google Scholar]
- Bik, A., Östlin, G., Hayes, M., et al. 2015, A&A, 576, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bradley, L., Sipocz, B., Robitaille, T., et al. 2019, https://doi.org/10.5281/zenodo.3368647 [Google Scholar]
- Bridge, J. S., Hayes, M., Melinder, J., et al. 2018, ApJ, 852, 9 [Google Scholar]
- Charlot, S., & Fall, S. M. 1993, ApJ, 415, 580 [Google Scholar]
- de Vaucouleurs, G. 1958, ApJ, 128, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Diehl, S., & Statler, T. S. 2006, MNRAS, 368, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Dijkstra, M. 2014, PASA, 31, e040 [Google Scholar]
- Djorgovski, S. G., Pahre, M. A., Bechtold, J., & Elston, R. 1996, Nature, 382, 234 [NASA ADS] [CrossRef] [Google Scholar]
- Fathi, K., Allen, M., Boch, T., Hatziminaoglou, E., & Peletier, R. F. 2010, MNRAS, 406, 1595 [NASA ADS] [Google Scholar]
- Freeman, K. C. 1970, ApJ, 160, 811 [Google Scholar]
- Fynbo, J. U., Møller, P., & Warren, S. J. 1999, MNRAS, 305, 849 [NASA ADS] [CrossRef] [Google Scholar]
- Giavalisco, M., Koratkar, A., & Calzetti, D. 1996, ApJ, 466, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, A. W., & Driver, S. P. 2005, PASA, 22, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Guaita, L., Melinder, J., Hayes, M., et al. 2015, A&A, 576, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hansen, M., & Oh, S. P. 2006, MNRAS, 367, 979 [NASA ADS] [CrossRef] [Google Scholar]
- Hayes, M. 2019, Saas-Fee Adv. Cour., 46, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Hayes, M., Östlin, G., Mas-Hesse, J. M., et al. 2005, A&A, 438, 71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hayes, M., Östlin, G., Atek, H., et al. 2007, MNRAS, 382, 1465 [NASA ADS] [Google Scholar]
- Hayes, M., Östlin, G., Mas-Hesse, J. M., & Kunth, D. 2009, AJ, 138, 911 [NASA ADS] [CrossRef] [Google Scholar]
- Hayes, M., Schaerer, D., Östlin, G., et al. 2011, ApJ, 730, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Hayes, M., Östlin, G., Duval, F., et al. 2014, ApJ, 782, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Hayes, M., Melinder, J., Östlin, G., et al. 2016, ApJ, 828, 49 [NASA ADS] [Google Scholar]
- Herenz, E. C., Gruyters, P., Orlitova, I., et al. 2016, A&A, 587, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herenz, E. C., Hayes, M., & Scarlata, C. 2020, A&A, 642, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hollyhead, K., Bastian, N., Adamo, A., et al. 2015, MNRAS, 449, 1106 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, E., & McMahon, R. G. 1996, Nature, 382, 281 [Google Scholar]
- Ivezić, Ž., Connelly, A. J., VanderPlas, J. T., & Gray, A. 2014, Statistics, Data Mining, and Machine Learning in Astronomy (Princeton: Princeton University Press) [Google Scholar]
- Jaskot, A. E., Dowd, T., Oey, M. S., Scarlata, C., & McKinney, J. 2019, ApJ, 885, 96 [Google Scholar]
- Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Kornei, K. A., Shapley, A. E., Erb, D. K., et al. 2010, ApJ, 711, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Kunth, D., Mas-Hesse, J. M., Terlevich, E., et al. 1998, A&A, 334, 11 [NASA ADS] [Google Scholar]
- Kunth, D., Leitherer, C., Mas-Hesse, J. M., Östlin, G., & Petrosian, A. 2003, ApJ, 597, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Laursen, P., & Sommer-Larsen, J. 2007, ApJ, 657, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Leclercq, F., Bacon, R., Wisotzki, L., et al. 2017, A&A, 608, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lehnert, M. D., Heckman, T. M., & Weaver, K. A. 1999, ApJ, 523, 575 [CrossRef] [Google Scholar]
- Marchi, F., Pentericci, L., Guaita, L., et al. 2019, A&A, 631, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martin, C. L., Dijkstra, M., Henry, A., et al. 2015, ApJ, 803, 6 [Google Scholar]
- Mas-Hesse, J. M., Kunth, D., Tenorio-Tagle, G., et al. 2003, ApJ, 598, 858 [NASA ADS] [CrossRef] [Google Scholar]
- Matthee, J., Sobral, D., Oteo, I., et al. 2016, MNRAS, 458, 449 [Google Scholar]
- Matthee, J., Sobral, D., Best, P., et al. 2017, MNRAS, 465, 3637 [NASA ADS] [CrossRef] [Google Scholar]
- Micheva, G., Östlin, G., Zackrisson, E., et al. 2018, A&A, 615, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miley, G., & De Breuck, C. 2008, A&ARv, 15, 67 [Google Scholar]
- Møller, P., & Warren, S. J. 1998, MNRAS, 299, 661 [CrossRef] [Google Scholar]
- Momose, R., Ouchi, M., Nakajima, K., et al. 2014, MNRAS, 442, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Okamura, S. 1988, PASP, 100, 524 [NASA ADS] [CrossRef] [Google Scholar]
- Östlin, G., Hayes, M., Kunth, D., et al. 2009, AJ, 138, 923 [NASA ADS] [CrossRef] [Google Scholar]
- Östlin, G., Hayes, M., Duval, F., et al. 2014, ApJ, 797, 11 [CrossRef] [Google Scholar]
- Otí-Floranes, H., Mas-Hesse, J. M., Jiménez-Bailón, E., et al. 2012, A&A, 546, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Otí-Floranes, H., Mas-Hesse, J. M., Jiménez-Bailón, E., et al. 2014, A&A, 566, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pardy, S. A., Cannon, J. M., Östlin, G., et al. 2014, ApJ, 794, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Partridge, R. B., & Peebles, P. J. E. 1967, ApJ, 147, 868 [Google Scholar]
- Pritchet, C. J. 1994, PASP, 106, 1052 [NASA ADS] [CrossRef] [Google Scholar]
- Rivera-Thorsen, T. E., Hayes, M., Östlin, G., et al. 2015, ApJ, 805, 14 [Google Scholar]
- Runnholm, A., Hayes, M., Melinder, J., et al. 2020, ApJ, 892, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Scarlata, C., Colbert, J., Teplitz, H. I., et al. 2009, ApJ, 704, L98 [NASA ADS] [CrossRef] [Google Scholar]
- Sérsic, J. L. 1963, Boletin de la Asociacion Argentina de Astronomia La Plata Argentina, 6, 41 [Google Scholar]
- Sobral, D., & Matthee, J. 2019, A&A, 623, A157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steidel, C. C., Bogosavljević, M., Shapley, A. E., et al. 2011, ApJ, 736, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Stobie, R. S. 1980, in Conference on Applications of Digital Image Processing to Astronomy, ed. D. A. Elliott, SPIE Conf. Ser., 264, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo, I., Chamba, N., & Knapen, J. H. 2020, MNRAS, 493, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Verhamme, A., Schaerer, D., Atek, H., & Tapken, C. 2008, A&A, 491, 89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verhamme, A., Dubois, Y., Blaizot, J., et al. 2012, A&A, 546, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Whitmore, B. C., Chandar, R., Kim, H., et al. 2011, ApJ, 729, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Wisotzki, L., Bacon, R., Blaizot, J., et al. 2016, A&A, 587, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wisotzki, L., Bacon, R., Brinchmann, J., et al. 2018, Nature, 562, 229 [Google Scholar]
- Wofford, A., Leitherer, C., & Salzer, J. 2013, ApJ, 765, 118 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Measured quantities in this study for each galaxy
All the quantities measured in this study.
Appendix B: Global quantities characterising the Lyα physics
Global quantities characterising the Lyα physics of each galaxy, used from Melinder et al. (in prep.).
Appendix C: Lyα and FUV profile and fits in the circular aperture
In this section, the Lyα and FUV profiles and the fitted double exponential, next to the FUV, and Lyα maps of all the galaxies in our sample are presented. In each figure, the left panels show the Lyα and FUV profiles and the fitted model to them. In these panels, blue and green represent Lyα, and FUV, respectively. The dark and light colours distinguish the core from the halo, respectively. For those bins with S/N < 1, the 1σ upper limit are displayed, and the bins with 1 ≤ S/N < 2 (data points not used in the fits) are displayed with the empty square symbol. In the bottom left of the left panels, the fitted Lyα and FUV halo scale lengths and their corresponding error bars are printed with sky blue and light green colours, respectively. The middle and right panels show the FUV and Lyα maps of each galaxy, respectively. The blue rings represent the largest radii where a circle centred at the FUV brightest pixel fits within each map, used as the last bin where the photometry was performed on, and the green ring shows the radius where the SFRD drops below 0.01 M⊙ yr−1 kpc−2.
 |
Fig. C.10. Same as Fig. 2, but for ELARS23 - ELARS26. |
 |
Fig. C.11. Same as Fig. 2, but for ELARS27, ELARS28, Tol1214, and Tol1247. |
 |
Fig. C.12. Same as Fig. 2, but for J1156. |
Appendix D: Systematic uncertainties on the halo exponential fits
In this section, we investigate the systematic uncertainties on the halo exponential fitting resulting from a possible over-subtraction of Lyα in the maps. Given the uncertainties in the core regions because of the Lyα continuum absorption, background over-subtraction is likely a negligible effect for the core profile fitting. As noted in the text, we make two assumptions to perform this estimate: (i) the halo profile can be fitted with an exponentially declining function, and (ii) the over-subtracted background is equal to the background flux subtracted during data reduction. In practice, the first assumption means that we cannot estimate this effect for the galaxies excluded from the sample in Sec. 4.1. As mentioned in the main text, the second assumption is the worst possible case and thus provides an upper bound on the uncertainty.
For the halo exponential profile, adding back in the over-subtracted flux can be written as:
where f(r) is the total surface brightness profile, fobs(r) is the exponential profile modelled on the subtracted data, and fB is the background level. Assumption (i) above means that fB cannot be much larger than fobs(r). Under assumption (ii) above fB is purely Lyα, and should also thus follow the exponential function, but evaluated at the radius r = rmax, which is always larger than the maximum radius used to obtain the fit. Hence,
where we have normalised the function by the surface brightness at the innermost point of the halo, f(r1). The scale length is denoted by htrue. With knowledge of the true scale length we can calculate the resulting scale length (hobs) for the profile with the background flux removed.
The scale lengths are found by fitting an exponential to the halo data points between the radii r1 and r2 (where the signal-to-noise of the Lyα surface brightness drops below 2). For this estimate we calculate the scale length from a simple line “fit” (in logarithmic space) to fobs between r1 and r2:
To get a first order estimate of the effect we use the best-fit halo scale length, rsc, Lyα in place of htrue and calculate the hobs/rsc, Lyα ratio. A ratio lower than one indicates that the fitted scale length has been underestimated due to over-subtraction of the background. The result for all of the galaxies is shown in Fig. D.1, where we show the ratios assuming that all of the background is Lyα (crosses), and with 10% of the background being Lyα (hexagons). We note that for all but 4 galaxies (ELARS05, ELARS08, ELARS09, and ELARS25), the systematic uncertainties on the scale lengths are less than 10%, even in the worst case. The worst case assumption puts an absolute upper bound on the uncertainty and likely over-estimates the systematic effects substantially. LARS09 is here marked as an excluded galaxy, even though it has a bright enough halo to get a profile fit (see Section 4.1). Because it has an extremely large fitted scale length, the over-subtraction uncertainty becomes very large (∼70%).
 |
Fig. D.1. The effect of over-subtracting Lyα on the fitted halo scale lengths. Galaxies marked with a vertical stripe are excluded from the sample due to low signal-to-noise in the halo (see Sec. 4.1). Crosses show the worst case assumption of all subtracted background flux being Lyα, and hexagons show the ratios when assuming 10% of the background being Lyα. |
In Table D.1 we show the subtracted background levels in luminosity units (also shown in Figures 2 and Appendix C) and the associated statistical uncertainty of this level. The third column lists the relative systematic (positive) error on the total Lyα luminosities (δLLyα, sys = [LLyα+BGLyα]/LLyα) assuming that 10/100 % of the background is intrinsic Lyα emission. The table also lists the scale length ratios (hobs/rsc, Lyα) calculated above.
Background fluxes and systematic uncertainty estimates on Lyα total luminosity and profile scale length.
Appendix E: Lyα morphology
In this section, for each galaxy we represent the regions used to determine the morphological parameters used in this study (ΔC, (b/a)Lyα, (b/a)FUV, (b/a)I, and ΔPA). These regions are determined on the non-binned images smoothed with the kernel size corresponding to a certain physical scale specified in Table 2. The blue contour represent the regions that are either brighter than SBLyα = 1.5 × 1039 erg/s/kpc2 (except J1156, SBLyα = 5.0 × 1039 erg/s/kpc2), or the SFRD is higher than 0.1 M⊙ yr−1 kpc−2. The green, and red contours represent the regions that are brighter than 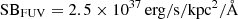 ,
, 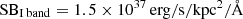 (The I band SB threshold used for ELARS01 is different and is equal to
(The I band SB threshold used for ELARS01 is different and is equal to 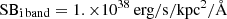 ) all displayed on the Lyα images. The blue, green, and red crosses represent the measured centroids (non-weighted first image moment) in the specified regions for Lyα, FUV, and I band, respectively. The PA determined in each region is also displayed with blue dashed, green dotted, and red dash-dotted lines for Lyα, FUV, and I band, respectively. The measured axis ratios determined in each region are given in the lower left part of the panels with blue, green, and red for Lyα, FUV, and I band, respectively. Finally, the centroid shift(ΔC) between Lyα and FUV, and difference between the measured PA of Lyα, and FUV (ΔPA) are given on the lower right side of the each panel.
) all displayed on the Lyα images. The blue, green, and red crosses represent the measured centroids (non-weighted first image moment) in the specified regions for Lyα, FUV, and I band, respectively. The PA determined in each region is also displayed with blue dashed, green dotted, and red dash-dotted lines for Lyα, FUV, and I band, respectively. The measured axis ratios determined in each region are given in the lower left part of the panels with blue, green, and red for Lyα, FUV, and I band, respectively. Finally, the centroid shift(ΔC) between Lyα and FUV, and difference between the measured PA of Lyα, and FUV (ΔPA) are given on the lower right side of the each panel.
 |
Fig. E.4. Same as Fig. 3, but for ELARS23 - ELARS28, Tol1214, Tol1247, and J1156. The Lyα SB limits used for J1156 is different from the rest of the sample and is equal to 5.0 × 1039 erg/s/kpc2. |
Appendix F: Extent of the halo through isophotal approach
In this section, we present the faint Lyα isophotes used to study the extent of the Lyα halo through the isophotal approach for each galaxy. In each figure, in the top panels the region within the isophotal levels of even multipliers (1, 2, 3, 4) of the faintest limit (1.5 × 1039 erg/s/kpc2, except J1156 5.0 × 1039 erg/s/kpc2). are denoted by red, orange, green and blue contours, all displayed on the Lyα maps of the galaxies. The bottom panels show the data points corresponding to these isophotes displayed with the same colour, and a single exponential fit (Eq. (9)) to the points. The fitted scale lengths (and the measured error bar determined from the fit) are given in the lower left corner. The blue diamond represents the measured Lyα SB in the binned images at the inner most region (usually within r = 0.1 kpc from the brightest FUV point).
 |
Fig. F.8. Same as Fig. 4, but for TOL1214, TOL1247, and J1156. The Lyα FEI used for J1156 is different from the rest of the sample and is equal to 5.0 × 1039 erg/s/kpc2). |
Appendix G: Star forming properties
In this section, we represent the regions where the SFRD > 0.01 M⊙ yr−1 kpc−2 used for studying the SF properties of the host galaxies in our sample. We used two parameters for studying the SF properties of the galaxies, the area where the SFRD > 0.01 M⊙ yr−1 kpc−2 presented by the equivalent radius rSFRD > 0.01 (the radius of a circle with the same area), and the average FUV SB ( ) by measuring the FUV SB within these regions and divided by the area. The measured
) by measuring the FUV SB within these regions and divided by the area. The measured  are given on the lower left side of each panel.
are given on the lower left side of each panel.
Appendix H: Lyα observables versus Lyα morphology
In this section, we present how the Lyα observables: Lyα luminosity (LLyα), Lyα escape fraction (fesc), and Lyα equivalent width (EWLyα), vary with the quantities used to study the Lyα halo properties or Lyα morphology of the galaxies: Lyα halo scale length 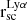 , Lyα halo fraction (HF), morphological parameters, such as: axis ratio ((b/a)Lyα), ΔC, ΔPA.
, Lyα halo fraction (HF), morphological parameters, such as: axis ratio ((b/a)Lyα), ΔC, ΔPA.
 |
Fig. H.1. How the total observed Lyα luminosity (LLyα) varies with the quantities used to study the Lyα morphology of the galaxies. |
 |
Fig. H.2. How Lyα escape fraction (fesc) varies with the quantities used to study the Lyα morphology of the galaxies. |
 |
Fig. H.3. How Lyα equivalent width (EWLyα) varies with the quantities used to study the Lyα morphology of the galaxies. |
Appendix I: Lyα morphology versus the stellar properties
In this section, we present how the quantities used to study the Lyα morphology and Lyα halo properties: Lyα halo scale length (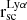 ), Lyα halo fraction (HF), axis ratio ((b/a)Lyα), the centroid shift (ΔC), and the difference in position angles of Lyα and FUV (ΔPA) vary with i) other Lyα morphology quantities, in addition to ii) some of the global quantities: stellar mass, and the nebular reddening, iii) star-forming characteristics: the size of the SF regions, and the average intensity of the FUV SB.
), Lyα halo fraction (HF), axis ratio ((b/a)Lyα), the centroid shift (ΔC), and the difference in position angles of Lyα and FUV (ΔPA) vary with i) other Lyα morphology quantities, in addition to ii) some of the global quantities: stellar mass, and the nebular reddening, iii) star-forming characteristics: the size of the SF regions, and the average intensity of the FUV SB.
 |
Fig. I.1. How Lyα halo scale length ( |
 |
Fig. I.2. How the Lyα halo fraction (HF) varies with other Lyα morphology quantities, and the stellar properties of the galaxies. |
 |
Fig. I.3. How Lyα axis ratio ((b/a)Lyα) varies with other Lyα morphology quantities, and the stellar properties of the galaxies. |
 |
Fig. I.4. How the centroid shift (ΔC) varies with other Lyα morphology quantities, and the stellar properties of the galaxies. |
 |
Fig. I.5. How the difference in position angles of Lyα and FUV (ΔPA) varies with other Lyα morphology quantities, and the stellar properties of the galaxies. |
Appendix J: Lyα isophotal halo scale length
In this section, we present how the Lyα halo scale length measured from the isophotal approach (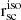 ) varies with i) the Lyα morphology and Lyα halo properties: Lyα halo fraction (HF), axis ratio ((b/a)Lyα), the centroid shift (ΔC), and the difference in position angles of Lyα and FUV (ΔPA) vary with ii) some of the global quantities: stellar mass, and the nebular reddening, iii) star-forming characteristics: the size of the SF regions, and the average intensity of the FUV SB.
) varies with i) the Lyα morphology and Lyα halo properties: Lyα halo fraction (HF), axis ratio ((b/a)Lyα), the centroid shift (ΔC), and the difference in position angles of Lyα and FUV (ΔPA) vary with ii) some of the global quantities: stellar mass, and the nebular reddening, iii) star-forming characteristics: the size of the SF regions, and the average intensity of the FUV SB.
 |
Fig. J.1. How the Lyα halo scale length measured from the isophotal approach ( |
All Tables
List of the galaxies, the kernel sizes used to smooth their maps, and the Lyα SB used for determining the faintest encompassing isophote in our morphological studies.
Global quantities characterising the Lyα physics of each galaxy, used from Melinder et al. (in prep.).
Background fluxes and systematic uncertainty estimates on Lyα total luminosity and profile scale length.
All Figures
 |
Fig. 1. Sérsic profile fitted to the Lyα and FUV SB profiles of three galaxies, LARS01, LARS09, and ELARS04. The resulted fits indicate Sérsic profile does not fully capture the behaviours of the SB profiles. Moreover, the limit set for the Sérsic index (e.g. 0.001 < n < 20) is reached in the fitted Sérsic profiles to the Lyα SB profile in LARS09, and FUV SB profile in both LARS09, and ELARS04. |
| In the text | |
 |
Fig. 2. Lyα, FUV SB profiles, and the fitted double exponential of different galaxies (same galaxies shown in Fig. 1) along with their FUV, and Lyα maps. Left panels: Lyα and FUV profiles and the fitted model to them. The dark and light colours distinguish the core from the halo, respectively. For bins with S/N < 1, the 2σ upper limit are displayed, and the bins with 1 ≤ S/N < 2 (data points not used in the fits) are displayed with the empty square symbol. Middle and right panels: FUV and Lyα maps of each galaxy, respectively. The blue rings represent the largest radii where a circle centred at the FUV brightest pixel fits within each map, used as the last bin where the photometry was performed on. The green ring shows the radius where the SFRD drops below 0.01 M⊙ yr−1 kpc−2. |
| In the text | |
 |
Fig. 3. Regions used to determine all the morphological parameters used in this study (ΔC, (b/a)Lyα, (b/a)FUV, (b/a)I, and ΔPA) displayed on the Lyα images for the three galaxies. The blue, green, and red contours are corresponding to the regions where the regions are brighter than SBLyα = 1.5 × 1039 erg s−1 kpc−2, SBFUV = 2.5 × 1037 erg s−1 kpc−2 Å−1, SBI band = 1.5 × 1037 erg s−1 kpc−2 Å−1 all displayed on the Lyα images (for more information on the limits, see Table 2). The blue, green, and red crosses represent the measured centroids (non-weighted first image moment) within LMR for Lyα, within FUV FEI for FUV, and within I band FEI for band, respectively. The determined PAs in the regions are also displayed with blue dashed, green dotted, and red dash-dotted lines for Lyα, FUV, and I band, respectively. Moreover, the axis ratio (b/a)Lyα for each region is printed in the lower left part of the panels with blue, green, and red for Lyα, FUV, and I band, respectively. Finally, the centroid shift (ΔC, in kpc) between Lyα and FUV, and the difference between the measured PA of Lyα, and FUV are printed on the lower right side of the panels. |
| In the text | |
 |
Fig. 4. Faint Lyα isophotes used to study the extent of the Lyα halo through the isophotal approach for each galaxy. In each figure, in the top panels, the region within the isophotal levels of even multipliers (1, 2, 3, 4) of the faintest limit (1.5 × 1039 erg s−1 kpc−2, except J1156 5.0 × 1039 erg s−1 kpc−2) denoted by red, orange, green and blue contours, all displayed on the Lyα maps of the galaxies. Bottom panels: data points corresponding to these isophotes displayed with the same colour, and a single exponential fit (Eq. (9)) to the points. The fitted scale lengths (and the measured error bar determined from the fit) are given in the lower left corner. The blue diamond represents the measured Lyα SB in the binned images at the innermost region (usually within r = 0.1 kpc from the brightest FUV point). |
| In the text | |
 |
Fig. 5. Regions used to determine the SF properties of the galaxies for the three galaxies. The green contours shows the regions with SFRD > 0.01 M⊙ yr−1 kpc−2 displayed on the unbinned FUV images. The measured average FUV SB ( |
| In the text | |
 |
Fig. 6. Lyα halo scale length ( |
| In the text | |
 |
Fig. 7. Left panel: histogram showing the distribution of the measured HF for our sample of galaxies. Right panel: Lyα halo fraction HF computed from the fit (HF) vs. the observed halo fraction (HFobs). |
| In the text | |
 |
Fig. 8. The difference in the position angles versus the centroid shift. The top and left histograms show the distributions and the measured median for ΔC, and ΔPA, respectively. |
| In the text | |
 |
Fig. 9. Top left panel: histogram showing the distribution of Lyα axis ratio ((b/a)Lyα). Top middle panel: (b/a)Lyα versus the FUV axis ratio ((b/a)FUV). Top right panel: (b/a)Lyα versus the I band axis ratio ((b/a)I). Bottom middle panel: histogram showing (b/a)FUV distribution. Bottom right panel: histogram showing (b/a)I distribution. |
| In the text | |
 |
Fig. 10. Lyα halo scale lengths assessed through the isophotal approach versus the Lyα halo scale lengths derived from fitting the double exponential function to the Lyα SB profiles using the circular aperture. |
| In the text | |
 |
Fig. 11. Size of the star forming region (rSFRD > 0.01), versus the average FUV SB ( |
| In the text | |
 |
Fig. 12. Spearman p0 value for the Lyα observables and the quantities used for studying Lyα morphology. |
| In the text | |
 |
Fig. 13. How Lyα luminosity (LLyα) varies with the HF, and axis ratio (b/a)Lyα. The measured Spearman’s coefficient and p-value between LLyα and each quantity are displayed in the corresponding panels. |
| In the text | |
 |
Fig. 14. How the measured Lyα equivalent width luminosity (EWLyα) varies with the HF. The measured Spearman’s coefficient and p-value between EWLyα and the HF are displayed in the top right. |
| In the text | |
 |
Fig. 15. Spearman p0 value for the Lyα morphological quantities and the properties of the host galaxies. |
| In the text | |
 |
Fig. 16. How the Lyα halo scale length ( |
| In the text | |
 |
Fig. 17. How the Lyα halo fraction (HF) varies with the total FUV luminosity (LFUV), the average FUV SB within the SF regions ( |
| In the text | |
 |
Fig. 18. How the centroid shift (ΔC) varies with the stellar mass and the size of the SF regions. The measured Spearman’s coefficient and p-value between ΔC and each quantity are displayed in the corresponding panels. |
| In the text | |
 |
Fig. 19. How the difference in the position angles (ΔPA) varies with the stellar mass, the nebular reddening E(B − V)n, and the size of the SF regions. The measured Spearman’s coefficient and p-value between ΔPA and each quantity are displayed in the corresponding panels. |
| In the text | |
 |
Fig. 20. How the axis ratio ((b/a)Lyα) varies with the FUV axis ratio ((b/a)FUV), the average FUV SB within the SF regions ( |
| In the text | |
 |
Fig. 21. How the measured isophotal Lyα halo scale length ( |
| In the text | |
 |
Fig. 22. Our results and how they compare to the MUSE study. Top left: how the Lyα halo scale length is compared to the Lyα core extent. Top right: the Lyα halo extent versus the Lyα core extent for both MUSE and our sample, the core extent is somewhat similar. However, Lyα is more extended in the MUSE sample compared to ours. Bottom left: the distribution of the HF in MUSE and our study, the bimodal distribution in HF in our study is not present in the LAEs observed in the MUSE study. Moreover, the median of the HF in the MUSE study (0.66) is larger than the measured median in our study (0.43). Bottom right: HF versus the Lyα halo extent measured in our sample and MUSE. The space covered in the HF- |
| In the text | |
 |
Fig. 23. Lyα core rsc vs. FUV core rsc. The data suggest that even in the core regions of the galaxies, Lyα is more extended than the FUV continuum. The measured median of the Lyα and FUV core scale lengths are displayed at the top left part of the figure with blue and green colours, respectively. |
| In the text | |
 |
Fig. C.1. Same as Fig. 2, but for LARS01 - LARS04. |
| In the text | |
 |
Fig. C.2. Same as Fig. 2, but for LARS05 - LARS08. |
| In the text | |
 |
Fig. C.3. Same as Fig. 2, but for LARS09 - LARS12. |
| In the text | |
 |
Fig. C.4. Same as Fig. 2, but for LARS13, LARS14, ELARS01, and ELARS02. |
| In the text | |
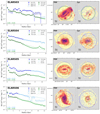 |
Fig. C.5. Same as Fig. 2, but for ELARS03 - LARS06. |
| In the text | |
 |
Fig. C.6. Same as Fig. 2, but for ELARS07 - ELARS10. |
| In the text | |
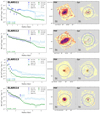 |
Fig. C.7. Same as Fig. 2, but for ELARS11 - ELARS14. |
| In the text | |
 |
Fig. C.8. Same as Fig. 2, but for ELARS15 - ELARS18. |
| In the text | |
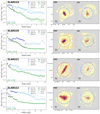 |
Fig. C.9. Same as Fig. 2, but for ELARS19 - ELARS22. |
| In the text | |
 |
Fig. C.10. Same as Fig. 2, but for ELARS23 - ELARS26. |
| In the text | |
 |
Fig. C.11. Same as Fig. 2, but for ELARS27, ELARS28, Tol1214, and Tol1247. |
| In the text | |
 |
Fig. C.12. Same as Fig. 2, but for J1156. |
| In the text | |
 |
Fig. D.1. The effect of over-subtracting Lyα on the fitted halo scale lengths. Galaxies marked with a vertical stripe are excluded from the sample due to low signal-to-noise in the halo (see Sec. 4.1). Crosses show the worst case assumption of all subtracted background flux being Lyα, and hexagons show the ratios when assuming 10% of the background being Lyα. |
| In the text | |
 |
Fig. E.1. Same as Fig. 3, but for LARS01 - LARS12. |
| In the text | |
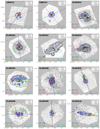 |
Fig. E.2. Same as Fig. 3, but for LARS13, LARS14, ELARS01 - ELARS10. |
| In the text | |
 |
Fig. E.3. Same as Fig. 3, but for ELARS11, ELARS22. |
| In the text | |
 |
Fig. E.4. Same as Fig. 3, but for ELARS23 - ELARS28, Tol1214, Tol1247, and J1156. The Lyα SB limits used for J1156 is different from the rest of the sample and is equal to 5.0 × 1039 erg/s/kpc2. |
| In the text | |
 |
Fig. F.1. Same as Fig. 4, but for LARS01 - LARS06. |
| In the text | |
 |
Fig. F.2. Same as Fig. 4, but for LARS07 - LARS12. |
| In the text | |
 |
Fig. F.3. Same as Fig. 4, but for LARS13, LARS14 and ELARS01- ELARS04. |
| In the text | |
 |
Fig. F.4. Same as Fig. 4, but for ELARS05 - ELARS10. |
| In the text | |
 |
Fig. F.5. Same as Fig. 4, but for ELARS11 - ELARS16. |
| In the text | |
 |
Fig. F.6. Same as Fig. 4, but for ELARS17 - ELARS22. |
| In the text | |
 |
Fig. F.7. Same as Fig. 4, but for ELARS23 - ELARS28. |
| In the text | |
 |
Fig. F.8. Same as Fig. 4, but for TOL1214, TOL1247, and J1156. The Lyα FEI used for J1156 is different from the rest of the sample and is equal to 5.0 × 1039 erg/s/kpc2). |
| In the text | |
 |
Fig. G.1. Same as Fig. 5, but for LARS01 - LARS12. |
| In the text | |
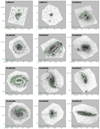 |
Fig. G.2. Same as Fig. 5, but for LARS13, LARS14, ELARS01 - ELARS10. |
| In the text | |
 |
Fig. G.3. Same as Fig. 5, but for ELARS11, ELARS22. |
| In the text | |
 |
Fig. G.4. Same as Fig. 5, but for ELARS23 - ELARS28, Tol1214, Tol1247, and J1156. |
| In the text | |
 |
Fig. H.1. How the total observed Lyα luminosity (LLyα) varies with the quantities used to study the Lyα morphology of the galaxies. |
| In the text | |
 |
Fig. H.2. How Lyα escape fraction (fesc) varies with the quantities used to study the Lyα morphology of the galaxies. |
| In the text | |
 |
Fig. H.3. How Lyα equivalent width (EWLyα) varies with the quantities used to study the Lyα morphology of the galaxies. |
| In the text | |
 |
Fig. I.1. How Lyα halo scale length ( |
| In the text | |
 |
Fig. I.2. How the Lyα halo fraction (HF) varies with other Lyα morphology quantities, and the stellar properties of the galaxies. |
| In the text | |
 |
Fig. I.3. How Lyα axis ratio ((b/a)Lyα) varies with other Lyα morphology quantities, and the stellar properties of the galaxies. |
| In the text | |
 |
Fig. I.4. How the centroid shift (ΔC) varies with other Lyα morphology quantities, and the stellar properties of the galaxies. |
| In the text | |
 |
Fig. I.5. How the difference in position angles of Lyα and FUV (ΔPA) varies with other Lyα morphology quantities, and the stellar properties of the galaxies. |
| In the text | |
 |
Fig. J.1. How the Lyα halo scale length measured from the isophotal approach ( |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} I(r) = I_{\rm e} \, . \, \exp \left(-b_n \, . \, \left[\left(\frac{r}{r_{\rm eff}}\right)^{(\frac{1}{n})}-1\right]\right) \end{aligned} $$](/articles/aa/full_html/2022/06/aa40734-21/aa40734-21-eq2.gif)