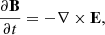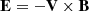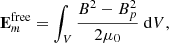| Issue |
A&A
Volume 658, February 2022
|
|
|---|---|---|
| Article Number | A200 | |
| Number of page(s) | 19 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202038744 | |
| Published online | 25 February 2022 | |
Data-driven, time-dependent modeling of pre-eruptive coronal magnetic field configuration at the periphery of NOAA AR 11726⋆
1
Department of Physics, University of Helsinki, PO Box 68 00014 Helsinki, Finland
e-mail: emilia.kilpua@helsinki.fi
2
Astrophysical and Planetary Sciences, University of Colorado, 2000 Colorado Avenue, Boulder, CO 80309, USA
3
Space Sciences Laboratory, University of California, 7 Gauss Way, Berkeley, CA 94720-7450, USA
4
Natural and Applied Sciences, University of Wisconsin, Green Bay, Green Bay, WI 54311, USA
Received:
25
June
2020
Accepted:
17
August
2021
Context. Data-driven, time-dependent magnetofrictional modeling has proved to be an efficient tool for studying the pre-eruptive build-up of energy for solar eruptions, and sometimes even the ejection of coronal flux ropes during eruptions. However, previous modeling works have illustrated the sensitivity of the results on the data-driven boundary condition, as well as the difficulty in modeling the ejections with proper time scales.
Aims. We aim to study the pre- and post-eruptive evolution of a weak coronal mass ejection producing eruption at the periphery of isolated NOAA active region (AR) 11726 using a data-driven, time-dependent magnetofrictional simulation, and aim to illustrate the strengths and weaknesses of our simulation approach.
Methods. We used state-of-the-art data processing and electric field inversion methods to provide the data-driven boundary condition for the simulation. We analyzed the field-line evolution, magnetic connectivity, twist, as well as the energy and helicity budgets in the simulation to study the pre- and post-eruptive magnetic field evolution of the observed eruption from AR11726.
Results. We find the simulation to produce a pre-eruptive flux rope system consistent with several features in the extreme ultraviolet and X-ray observations of the eruption, but the simulation largely fails to reproduce the ejection of the flux rope. We find the flux rope formation to be likely driven by the photospheric vorticity at one of the footpoints, although reconnection at a coronal null-point may also feed poloidal flux to the flux rope. The accurate determination of the non-inductive (curl-free) component of the photospheric electric field boundary condition is found to be essential for producing the flux rope in the simulation.
Conclusions. Our results illustrate the applicability of the data-driven, time-dependent magnetofrictional simulations in modeling the pre-eruptive evolution and formation process of a flux rope system, but they indicate that the modeling output becomes problematic for the post-eruptive times. For the studied event, the flux rope also constituted only a small part of the related active region.
Key words: Sun: coronal mass ejections (CMEs) / Sun: corona / magnetic fields / Sun: activity
Movies are available at https://www.aanda.org
© ESO 2022
1. Introduction
An accurate description of the magnetic field evolution in the corona is essential for studying solar eruptive activity and its space weather effects. Coronal mass ejections (CMEs), solar flares, and jets are all driven by the accumulation and abrupt release of magnetic energy in the corona (e.g., Chen 2011; Shibata & Magara 2011; Raouafi et al. 2016; Green et al. 2018), and the magnetic flux rope structures ejected in CMEs and eruptive flares largely determine the space weather effects of the eruptions in the heliosphere (e.g., Kilpua et al. 2017).
Direct remote-sensing estimates of the coronal magnetic field are sparsely available and offer only limited diagnostics for studying coronal eruption dynamics (Gibson et al. 2017; Wiegelmann et al. 2017). Consequently, any detailed quantitative study of eruption dynamics requires the modeling of the coronal magnetic field. In data-driven modeling, the routinely available observations of the photospheric magnetic field and plasma velocity are used as a lower radial boundary condition for coronal models (see Wiegelmann et al. 2017, for a review). Such modeling approaches vary in complexity ranging from static, data-constrained (nonlinear) force-free extrapolations of the magnetic field (see Wiegelmann & Sakurai 2012, for a review) to fully data-driven, time-dependent magnetohydrodynamic (MHD) simulations of the coronal plasma (e.g., Jiang et al. 2016; Sarp Yalim et al. 2017; Hayashi et al. 2018; Warnecke & Peter 2019).
A complete description of solar eruptions is needed to account for both the slow energy build-up process occurring over timescales of days, as well as the rapid release of energy in an eruption happening on much shorter timescales of minutes to hours. During the energy build-up phase, the coronal magnetic field accumulates current, free energy, and helicity, resulting in sheared magnetic field arcades or a flux rope (Green et al. 2018). The large-scale evolution in the low corona in this phase is largely quasi-static and governed by the dominant magnetic forces, and thus can be modeled using a zero-β and quasi-static approximations (see e.g., van Ballegooijen et al. 2000; Mackay & Yeates 2012; Wiegelmann et al. 2017, for discussion). The rapid eruption, however, is far from quasi-static, and it involves nonmagnetic forces, magnetic reconnection, as well as conversion of magnetic energy to kinetic and thermal energies, thus requiring time-dependent magnetohydrodynamic treatment (e.g., Pagano et al. 2013).
Due to the high computational cost of data-driven MHD modeling, the slow pre-eruptive energy build-up is rarely included in the simulation (see Jiang et al. 2016; Hayashi et al. 2018, for examples of such cases). Instead, MHD simulations often start from a state just before the eruption, where the simulation is initialized with an NLFFF or magnetohydrostatic extrapolation (e.g., Inoue et al. 2018; Jiang et al. 2018; Guo et al. 2019). However, due to the static nature of the NLFFF extrapolations, each extrapolated state depends only on the photospheric magnetic field vector data used as the lower boundary condition, and thus the extrapolations may miss some structures that formed in coronal processes (e.g., Yeates et al. 2018).
The pre-eruptive quasi-static energy build-up can be modeled in a time-dependent fashion also without the complexity and computational cost of the full MHD treatment using the time-dependent magnetofrictional (TMF) method. The TMF method approximates the coronal evolution via two competing processes: magnetofrictional relaxation of the magnetic field toward a minimum-energy force-free state (Yang et al. 1986), and a time-dependent photospheric boundary condition that injects energy and helicity to the system (van Ballegooijen et al. 2000). Together, these processes approximate the coronal magnetic field evolution in a truly time-dependent manner. The TMF method has been successfully used to model the formation of pre-eruptive coronal flux rope structures (Gibb et al. 2014; Cheung et al. 2015; Fisher et al. 2015; Yardley et al. 2018; Price et al. 2019; Kilpua et al. 2021), and in some studies the method has also been capable of modeling the ejection of the flux rope (Cheung & DeRosa 2012; Mackay & van Ballegooijen 2006; Weinzierl et al. 2016; Pomoell et al. 2019). However, since the method lacks a realistic momentum equation, it is unclear how reasonable its descriptions of flux rope ejections are, and several works report on failures to produce a flux rope ejection in the simulation, in contradiction with the observations (e.g., Kliem et al. 2013; Cheung et al. 2015; Price et al. 2019). These method-related issues are further amplified by the sensitivity of the simulation output to the photospheric data-driven boundary condition (discussed below), which can significantly affect eruptivity in the simulations. Despite the challenges and the open questions related to the TMF modeling, it still offers a very promising tool for studying the pre-eruptive behavior, and possibly also the eruption-time behavior of the coronal magnetic field.
The most important component of the TMF method is the data-driven time-dependent photospheric electric field boundary condition. It evolves the magnetic field at the lower photospheric boundary of the simulation according to the observations via Faraday’s law, and it also controls the injection of energy and helicity into the coronal simulation domain. Accurate estimation of the photospheric electric field from the available photospheric vector magnetic field and line-of-sight (LOS) plasma velocity is a challenging, under-constrained inversion problem, which is still under research (Schuck 2008; Kazachenko et al. 2014; Tremblay & Vincent 2015; Lumme et al. 2017, 2019; Fisher et al. 2020; Afanasyev et al. 2021). Consequently, previous TMF simulation studies have often employed nonoptimal and simplified photospheric electric field driving, in which the electric field has been inverted solely from LOS or vector magnetic field data (e.g., Yardley et al. 2018), or the harder-to-acquire electric field components related to the photosheric velocity have been substituted with ad hoc artificial methods (e.g., Cheung et al. 2015; Price et al. 2019). The limited accuracy of the photosheric electric field is a significant issue, as the electric field has been shown to be essential for producing realistic energization and twisting of the coronal magnetic field in the simulation (Cheung & DeRosa 2012; Pomoell et al. 2019).
Due to its fully time-dependent nature, the TMF method can effectively unravel the open questions related to the formation of erupting flux ropes, including the formation time (before or during the eruption; see e.g., Chen 2011 and Wang et al. 2017 for discussion), and the formation mechanism of the flux rope (flux cancellation, tether-cutting, bodily emergence, and others; see e.g., Green et al. 2007; Janvier et al. 2015, and references therein). Even though some of the previous works imply that it is questionable whether the TMF method can actually simulate the eruption process, modeling the pre-eruptive evolution alone can give valuable insights into the eruption dynamics. These include predicting flux rope rotation and deflection due to the magnetic forces in the domain (e.g., Liu et al. 2018), identifying possible triggering mechanisms for the eruption such as kink and torus instabilities (e.g., Jing et al. 2018), and studying the energy- and helicity-related thresholds for eruptivity (e.g., Moraitis et al. 2019; Price et al. 2019).
In this work, we employed the data-driven TMF method to study the formation and eruption of a flux rope as a weak CME (i.e., not associated with significant flares, C-class or larger) at the periphery of the NOAA active region 11726 on 22 April 2013, 08:40 UT. The active region emerges on the near side of the Sun, and it is well isolated, making it optimal for local data-driven modeling. The eruption of interest occurs at the periphery of the active region far from the strongest polarity inversion lines (PILs), which makes its formation mechanisms an interesting aspect to study. We conduct a fully data-driven TMF simulation for the active region employing high-quality photospheric electric field driving, which exploits the full potential of the available data input. Using the simulation output, we study the coronal energization process and the formation mechanism of the pre-eruptive flux rope and its eruption dynamics. We compare our simulation results to the remote sensing EUV and X-ray observations before, during, and after the eruption of interest, and we discuss the validity of the simulation results.
Section 2 details the basic properties and observations of NOAA AR 11726 and the eruption of interest. Section 3 presents the data processing, electric field inversion, and simulation methods, and Sect. 4 presents the results of the simulation. Section 5 discusses the results, and Sect. 6 lists the main conclusions of our study.
2. Observations
In this section, we describe the emergence and general magnetic properties of NOAA AR 11726 (Sect. 2.1) and present, in detail, the EUV and coronagraph observations of a CME-producing eruption at the periphery of the active region on 22 April 2013, 08:40 UT (Sect. 2.2). We also give a (non-exhaustive) summary of other eruptive activity of AR11726 relevant to our data-driven simulation in Table A.1, but these events receive no further analysis in this article.
2.1. Emergence and activity of NOAA AR 11726
NOAA AR 11726 emerged in the northeastern quadrant (∼N12E12) on 19 April 2013, 04:24 UT, and by 27 April 2013, ∼09:00 UT it had completely rotated behind the visible solar disk. We limit our analysis to the interval ranging from the pre-emergence state 18 April 2013, 03:00 UT until 24 April 2013 00:00 UT, which included the eruptive activity of interest (see below) and excluded the data gaps in the vector magnetogram data (below, and Sect. 3.2) occurring from 24 April 2013 03:00 UT onwards. During this time, AR11726 produced 31 C-class flares, one M1.0 flare (as reported by the Solar Monitor service1 based on the X-ray flux observations of the Geosynchronous Operational Environmental Satellite, GOES system), at least two clear CMEs, as well as several eruptions with signatures in the EUV and coronagraph data, from which we focus on a single eruption: a weak CME-producing eruption that was initiated at the periphery of the region on 22 April 2013, 08:40 UT (Sect. 2.2). Table A.1 gives a non-exhaustive list of other eruptive activity in NOAA AR 11726.
We analyzed the flux emergence in the AR11726 using vector magnetogram data of the Helioseismic and Magnetic Imager (HMI: Scherrer et al. 2012; Schou et al. 2012) instrument onboard the Solar Dynamics Observatory (SDO: Pesnell et al. 2012) processed and re-projected onto a local Cartesian frame tracking the active region (Fig. 1, see Sect. 3.2 for description of the data processing). The emergence was found to occur in several phases. First, two bipoles emerge sequentially on 19 April 2013, 04:24 UT and 12:00 UT (emergence times defined from the appearance of HMI SHARP strong-field patches; see Hoeksema et al. 2014; Bobra et al. 2014), and later merge to form the main AR complex of AR11726 (Fig. 1). Second, a small bipole emerges on 21 April 02:36 UT, west of the main AR complex constituting < 4% of the total unsigned flux of the entire region (Fig. 2, black and green curves).
 |
Fig. 1. Bz magnetogram of NOAA AR 11726 on 22 April, 2013 08:36 UT taken from the processed and re-projected SDO/HMI vector magnetogram series (Sect. 3.2) Please avoid the use of the slashes. For details, refer to Sect. 2.9 of the language guide. Please check for this throughout. The central structures related to the activity discussed in this paper have been pinpointed. The vertical white dashed line shows the photospheric cut of the x = 76 Mm plane used to find and track a pre-eruptive flux rope system in our data-driven simulation (Sect. 4). An animated version of the figure can be found online. |
 |
Fig. 2. Evolution of total unsigned magnetic flux and flux imbalance in NOAA AR 11726 derived from the processed and re-projected SDO/HMI Bz magnetogram series (Sect. 3.2), where the pixels |B|< 250 Mx cm−2 were masked to zero to avoid spurious effects arising from the noise-dominated weak-field pixels. The black curve shows the evolution of the unsigned flux over the entire active region patch, whereas the green curve shows the unsigned flux evolution of the small western bipole (see Fig. 1) multiplied by a factor of 30 to make its scale comparable to the unsigned flux of the entire active region. The red dashed curve shows the relative flux imbalance of the active region. The vertical dotted line shows the time of the weak CME eruption of 22 April 2013, 08:40 UT that we focus on in this study. |
2.2. Eruption in NOAA AR 11726 on 22 April 2013, 08:40 UT
In this work, we studied the CME-producing eruption that occurred between the western bipole and the western sunspot (Fig. 1) starting on 22 April 2013 at 08:40 UT. The eruption begins as expansion and disappearance of EUV loops at this position at 08:40 UT accompanied by clear coronal dimmings in the west-southwest (Fig. 3a). Shortly thereafter, at 09:07 UT, an expulsion of chromospheric or low-coronal material began at the same position, producing a strongly southward-moving structure in the EUV observations (Fig. 3b). Finally, we observe a likely unrelated M1.0 flare in a fan-spine configuration at the eastern end of the main AR complex (Fig. 3c). The low-coronal eruption features have a complex four-part response in the white-light coronagraph observations (Figs. 3g–i). Below, we present a detailed analysis of all eruption features listed above (grouped also in Table 1).
 |
Fig. 3. Remote sensing EUV and white-light observations of the eruption from NOAA AR 11726 from 22 April 2013, 08:40 UT onwards. Panels a–c show SDO/AIA observations with photospheric Bz plotted as ±100 Mx cm−2 contours (blue for negative) over the region included in the vector magnetogram series (Fig. 1). Panel a: pre-eruptive state at 08:36 UT, where the loop system erupting from 08:40 UT onwards is highlighted by the dashed white curve, the location of the solar limb in STEREO A/EUVI observations is shown by the lime dashed curve, and the main structures of the active region are pinpointed by arrows. Panel b: U-shaped location of the expulsion of the material from 09:07 UT onwards (the dashed U-shaped curve), and the likely correlated coronal structure at 09:30:32 UT to the southeast outlined by a red dashed curve. Panel c: post-eruption arcades as well as the site of the M1.0 flare on 10:22 UT. Panels d–f: STEREO A SECCHI/EUVI 195 Å observations at times consistent with panels a–c. Panel d: approximate position and shape of the Cartesian simulation box explained in Sect. 3. Panel e: approximate trajectory of the expelled plasma from panel b (white dashed lines). Panels g–i: composite images of STEREO A/EUVI 195 Å, COR 1, and COR2 white-light observations of the eruption (created using JHelioviewer software Müller et al. 2017). The main coronagraph structures and their visually traced trajectories are illustrated by the white dashed curves and the white dashed arrows, respectively. Movie versions of panels a–c, d–f, and g–h are available online. |
Eruption features observed in the EUV and white-light coronagraph data by SDO/AIA, STEREO A/SECCHI EUVI and COR2, and SOHO/LASCO instruments.
Figure 3, panels a–c, and their animated versions show the low-coronal signatures of the eruption as observed by the Atmospheric Imaging Assembly (AIA: Lemen et al. 2012) instrument onboard the SDO spacecraft in the 193 Å wavelength. The initiation of the eruption on 22 April 2013 at 08:40 UT is characterized by an expansion and disappearance of the AIA 193 Å coronal loops that originally connect the negative-polarity western sunspot and the southeastern positive part of the western bipole (Fig. 3a, white dashed curve). The subsequent loop expansion and coronal dimmings in the west-southwest imply that the eruption is directed west to southwest. Bright, post-eruption arcades (PEAs, often formed after the launch of a CME, e.g., Webb & Howard 2012) appear between the western sunspot and the western bipole 09:30 UT onwards, located at the position of the erupting loop system (Fig. 3c). The PEAs are also clearly visible in the 195 Å extreme ultraviolet imager (EUVI) observations of the Sun Earth Connection Coronal and Heliospheric Investigation (SECCHI: Howard et al. 2008) instrument onboard the Solar Terrestrial Relations Observatory Ahead (STEREO A: Kaiser et al. 2008) spacecraft (Fig. 3f). At the time, STEREO A was located at a Stonyhurst heliographic longitude of 134° (i.e., 134° west of the Sun-Earth line). Consequently, the spacecraft had a very good side view of the eruption, the eastern solar limb as seen by STEREO A located roughly at the western bipole (see Fig. 3, panels a–c, lime dashed curve).
An expulsion of chromospheric or low-coronal material occurs in a U-shaped region connecting the western sunspot and the western bipole from 09:07 UT onwards possibly in connection with the main eruption discussed above. The expulsion is visible in the AIA 304 Å, Hα, and also in the AIA 193 Å wavelengths (online movies 1 and 2 and Fig. 3b and its animated version), but no pre-existing filament is seen in this region in Hα observations from the Global Oscillation Network Group (GONG: Harvey et al. 1996) operated by the National Solar Observatory (NSO). After the initiation of this eruption, both the AIA 193 Å and 304 Å wavelengths show a southwest-propagating structure southwest of the eruption site at 09:30 UT (in the region X ∈ [0″,150″], Y ∈ [600″,700″], outlined by the red dashed curve in Fig. 3b). The eruption from the U-shaped region and the southwest-propagating plasma structure appear visually correlated, the plasma from the U-shaped region likely producing the structure to the southwest. There are no other clear sources visible to explain the southwestern structure, such as an eruption directly below the structure. This interpretation is further supported by STEREO A observations, which also show an apparent strongly southward motion of a narrow blob in the EUVI/195 Å observations (pinpointed by arrows in Fig. 3e; the trajectory is illustrated by the white dashed lines). STEREO A 195 Å data show the structure changing its direction of propagation rapidly at 09:30 UT, at a location co-spatial to the position where the southwest-propagating structure is detected. The structure is also visible in the low-cadence STEREO A EUVI 304 Å data at that position. We interpret these observations to correspond to strongly southward-erupting chromospheric or low-coronal material, which is then deflected near the equator, and expelled approximately radially outward, eventually appearing in the white-light coronagraph observations, as described below.
Finally, more than 100 min after the appearance of the first eruption signatures discussed above, the M1.0 flare occurs in the eastern end of the AR at 10:22 UT (Fig. 3c). The flare occurs in a compact region over a parasitic negative polarity patch (Fig. 1), where the EUV loops indicate a fan-spine topology (see e.g., Raouafi et al. 2016, and references therein), highlighted in supplementary Fig. A.1. However, since the flare eruption occurs far away from the source region of the 08:40 UT eruption, it is unlikely that these two are directly connected, although it is possible that the changes introduced by the 08:40 UT eruption act as a facilitator for the M1.0 flare. We leave further study of the flare for later studies.
The eruptive activity observed in the low corona from 08:40 UT onwards produces clear white-light coronagraph signatures illustrated in Fig. 3, panels g–i, and listed in Table 1. The main eruption starting at 08:40 UT appears to introduce two white-light blobs in the STEREO A SECCHI/COR2 coronagraph observations at 09:54 and 10:24 UT, which we label COR Blob 1 and 2, respectively (see Fig. 3h, and Table 1). Both structures can be traced back to weak expanding structures lower in the corona in SECCHI/COR1 and EUVI 195 Å observations (see the white dashed arrows in Fig. 3h). The locations of these expanding structures are roughly consistent with the initiation region of the 08:40 UT eruption between the western sunspot and bipole, but it is unclear whether only one of them or both correspond to the observed eruption of the AIA 193 Å loops. There is also a small chance that COR Blob 1 is related to another eruption and a flare occurring at the center of the STEREO A solar disk at 08:50 UT (see animated version of Fig. 3g), although this would require the eruption to have a high eastward inclination. The expulsion of plasma from a U-shaped region at 09:07 UT discussed above can be traced through the EUVI 195 Å and further COR1 observations to COR Blob 3 appearing in COR2 at 10:39 UT as a very narrow bright structure (Fig. 3i). Finally, a structure that we label COR Blob 4 appears at high latitudes in COR2 at 11:24 UT (Fig. 3i), and it can be traced back to very weak dimming above the AR11726 EUVI 195 Å observations from 10:30 UT onwards. The timing and position of the dimming imply that COR Blob 4 might be related to the M1.0 flare at 10:22 UT.
The coronagraph features above are recorded by the Computer Aided CME Tracking (CACTus: Robbrecht & Berghmans 2004) catalog as two events in STEREO A COR observations: at 10:24 UT with principal angle PA = 96° and at 11:24 UT with PA = 64°. The former corresponds well with the COR Blob 3 above, whereas the latter corresponds well with the later evolution of COR Blob 2. The C2 coronagraph of the Large Angle Spectrometric Coronagraph (LASCO: Brueckner et al. 1995) instrument onboard the Solar and Heliospheric Observatory (SOHO: Domingo et al. 1995) spacecraft also detects some of these ejections as viewed from the L1 position of SOHO. The SOHO/LASCO CME catalogue2 lists two events at 09:48 UT with PA = 261°, possibly corresponding to COR Blobs 1 and 2 (or the eruption at the center of the STEREO A disk at 08:50 UT), and another at 11:12 UT with PA = 328°, possibly corresponding COR Blobs 2 and/or 4, both labeled as “poor events”.
We also analyzed the EUV observations all the way from the emergence of the active region until the 22 April 2013, 08:40 UT eruption, as well as the coronal dimmings during the eruption (e.g., Dissauer et al. 2018). These results are presented along with the simulation output in Sect. 4.
3. Data-driven simulation of NOAA AR 11726
To study the coronal magnetic field evolution of the 22 April 2013, 08:40 UT eruption (Sect. 2.2), we conducted a data-driven, time-dependent magnetofrictional simulation for the entire AR11726 spanning from 18 April 2013, 03:00 UT to 24 April 2013, 00:00 UT, including the pre-emergence state, emergence, and the eruption of interest. In this section, we describe the setup of the coronal model used in the simulation (Sect. 3.1), as well as the data processing and electric field inversion methods used to acquire the photospheric, time-dependent, data-driven boundary condition of the simulation (Sect. 3.2).
3.1. Coronal model
We employed the time-dependent magnetofrictional (TMF) simulation code of Pomoell et al. (2019) based on the Cheung & DeRosa (2012) version of the TMF method. In the TMF method, the coronal magnetic field B is evolved in time according to Faraday’s law:
where the electric field is given by the resistive Ohm’s law:
In the TMF, method the V in Ohm’s law is not the true plasma velocity (evolved via MHD momentum equation), but it is substituted by an artificial velocity proportional to the Lorentz force (Yang et al. 1986):
where J = (∇×B)/μ0 is the current density and ν is the magnetofrictional coefficient (see Cheung & DeRosa 2012; Pomoell et al. 2019, for details). For static boundary conditions, this choice of V will monotonically decrease the total magnetic energy in the simulation domain forcing the system toward a minimum-energy force-free state. In the TMF, method the photospheric boundary condition of the simulation is time-dependent and fully constrained when the horizontal (i.e., tangential) components of the photospheric electric field Eh(t) are determined at the lower radial, photospheric boundary of the simulation box (van Ballegooijen et al. 2000; Cheung & DeRosa 2012). We point out that the magnetofrictional method used in this paper preserves the divergence of the magnetic field at zero throughout the computed evolution (see Pomoell et al. 2019, semi colon should be ‘and’; please remove comma for details details from). In addition, the driving electric field used as the boundary condition cannot introduce any divergence to the system, regardless of how it is defined or derived. The photospheric electric field is inverted from the photospheric remote-sensing observations of the magnetic field and plasma velocity (see Sect. 3.2), and it evolves the normal component of the photospheric magnetic field Bz according to the observations via Faraday’s law. This time-dependent boundary condition constantly injects new magnetic flux, energy, and helicity into the coronal simulation domain, which, combined with the continuous magnetofrictional relaxation, provides a truly time-dependent approximation for the coronal magnetic field evolution (e.g., van Ballegooijen et al. 2000; Mackay & van Ballegooijen 2006; Cheung et al. 2015; Fisher et al. 2015; Weinzierl et al. 2016; Yardley et al. 2018; Price et al. 2019). In this work, the simulation starts from a potential magnetic field. For further details regarding the model setup, we refer the reader to Pomoell et al. (2019).
3.2. Data-driven, time-dependent boundary condition
The data-driven, time-dependent boundary condition of the TMF simulation consists of the time-dependent horizontal components of the photospheric electric field Eh (for evolving the lower radial boundary according to observations), and the photospheric vertical Bz magnetic field component (for deriving the potential magnetic field used as initial condition, see Pomoell et al. 2019). We derived these boundary conditions from SDO/HMI photospheric vector magnetogram (=vector magnetic field, B) and Dopplergram (=LOS plasma velocity, VLOS) data (see Hoeksema et al. 2014, for an overview), using the ELECTRIC field Inversion Toolkit (ELECTRICIT) software (Lumme et al. 2017, 2019) and the PDFI (Poloidal-toroidal-decomposition-Doppler-Fourier-local-correlation-tracking-Ideal) electric field inversion method (Kazachenko et al. 2014; Fisher et al. 2020).
The PDFI electric field inversion is based on the use of Faraday’s law (Eq. (1)) and the assumption of an ideal Ohm’s law:
at the photosphere. The method uses these assumptions to solve two components of the PDFI electric field, the inductive component EI and the non-inductive component −∇ψ,
from the available input data. The inductive component is solved by uncurling Faraday’s law,
using poloidal-toroidal decomposition (PTD), for which ∂B/∂t is determined from the vector magnetogram observations. The non-inductive component is determined by the ideal Ohm’s law, essentially via the following Poisson equation for non-inductive potential ψ:
Although, in practice, the equation is first split into several components (see Kazachenko et al. 2014, for details). The input data for the solving the non-inductive potential consists of the vector magnetograms B, VLOS estimates from Dopplergrams, and the Vh optical flow estimates derived from the Bz magnetogram evolution using the FLCT method (Welsch et al. 2007; Fisher & Welsch 2008; Fisher et al. 2020), accompanied by the constraint of the ideal Ohm’s law, E ⋅ B = 0. The PDFI method employs all available input data (magnetograms and Dopplergrams) effectively, and the synthetic tests of various electric and velocity inversion methods indicate that it provides state-of-the-art accuracy in electric field inversion (see Welsch et al. 2007; Kazachenko et al. 2014; Lumme et al. 2019, for discussion).
To create a time series of processed vector magnetograms, Dopplergrams, and optical flow velocity estimates for the electric field inversion in AR11726, we used the data processing pipeline described by Lumme et al. (2017) and Lumme et al. (2019). The resulting time series consists of vector magnetogram and calibrated Dopplergram data Mercator re-projected onto a local Cartesian frame (Bx, By, Bz, VLOS) that tracks the disk transit of AR11726 (see Fig. 1 and its animated version). The 2D data maps had the shape of 872 × 481 pixels (pixel size ∼364 km on the Sun), and the series spanned the interval 18 April 2013, 00:00 UT – 24 April 2013, 03:00 UT with 12-minute cadence.
As indicated by the red dashed curve in Fig. 2, the re-projected Bz magnetograms show significant relative flux imbalance ∫Bz dA/∫|Bz| dA for the re-projected magnetogram patch (Fig. 1), ranging from ∼5–15% after the emergence of AR11726 from 19 April 2013, 04:24 UT onwards. This positive flux imbalance would produce a notable monopole term in the potential field initial condition of the simulation, which we deem problematic (similarly to Mackay et al. 2011; Gibb et al. 2014; Yardley et al. 2018; Pomoell et al. 2019; Price et al. 2019). We resolved the issue by artificially balancing the unmasked Bz magnetograms using the multiplicative method of Yeates (2017), which conserves the total unsigned flux ∫|Bz| dA and the positions of Bz PILs. This correction artificially removes all magnetic connections to regions outside our field of view, which may be an issue. However, since our active region is well isolated, we consider this a smaller issue than the constant upward monopole term produced by the imbalance. However, we note that the artificial balancing may affect the resulting energy and helicity content in the simulation.
We determined the optical flow horizontal velocity estimates Vh from the processed Bz magnetogram data using the FLCT method with σFLCT windowing parameter optimized to 5 pixels using the method of Lumme et al. (2019) and the noise-dominated weak-field pixels |Bz|< 250 Mx cm−2 masked to zero in the output. We inverted the photospheric electric field using the PDFI_SS software library (Fisher et al. 2020) as in Lumme et al. (2019), with the exception of using a lower masking threshold of |B|< 250 Mx cm−2 (Kazachenko et al. 2015) to remove the noise-dominated weak-field pixels from the input. In order to avoid undesired boundary effects in the electric field inversion and later in the simulation, we also padded the input magnetograms and velocity maps with a 100-pixel-wide region of zeroes before the inversion, and the padding region was then left in the output electric field maps and magnetograms.
Masking the weak-field pixels is essential to avoid spurious noise-related effects in the optical flow and electric field inversions (see Welsch et al. 2012; Kazachenko et al. 2015; Lumme et al. 2019; Fisher et al. 2020, for discussion). However, the electric field solved from masked input evolves the photospheric Bz of the simulation only in the unmasked pixels, and the weak-field regions are thus completely left out of the simulation. Our previous simulation works, Pomoell et al. (2019) and Price et al. (2019), showed that this masking also has undesirable effects: it leaves out several weak-field network pixels that sometimes have significant effects on the simulation output, and it also produces unrealistic, long low-lying loops over the masked regions. To avoid these effects, we decided to include the masked weak-field pixels (|B|< 250 Mx cm−2) in the simulation in a restrained fashion that avoids the issues they introduce in the optical flow and electric field inversions. Using the nomenclature of Fisher et al. (2020) and the TMF simulation work of the Coronal Global Evolutionary Model project (Fisher et al. 2015; Hoeksema et al. 2020; M.C.M. Cheung, priv. comm.), we include the weak-field pixels in the electric field boundary condition by adding an inductive “nudging” electric field component En to the PDFI estimate. The nudging electric field is solved from the unmasked ∂B/∂t input data so that the total electric field,
fulfills Faraday’s law for unmasked magnetograms, thus also evolving the simulation Bz in the weak-field regions. However, we note that the addition of the nudging electric field En after the EPDFI is inverted from masked B and ∂B/∂t input, makes the total electric field E partly inconsistent with the input constraints used to solve the non-inductive potential (see Eq. (7) and the related discussion above). However, the inconsistency is mostly minor, as En tends to be small relatively to EPDFI in regions where EPDFI has significant nonzero values.
Finally, in order to save computational resources in the simulation we re-binned the photospheric Bz magnetograms and Eh by a factor of 4, the final dimensions of the Bz magnetograms being 267 × 170 pixels with pixel size ∼1458 km on the Sun (which includes the full-resolution, 100-pixel zero padding added in the electric field inversion). The re-binning of the Bz magnetograms was done using a re-binning method that conserves the total unsigned flux. The electric field output of the PDFI inversion is specified at cell edges in a staggered grid (Yee 1966) with regard to the cell-centered Bz values. The re-binning was done by averaging the components along the 4 times re-binned cell edges so that the line integral around each re-binned pixel is equal to the full-resolution line integral at the original resolution (see Fisher et al. 2020, for details). This approach, combined with the re-binning method of Bz, conserves the perfect reproduction of  by the curl of
by the curl of  in Faraday’s law, and thus
in Faraday’s law, and thus  at lower photospheric plane of the simulation evolves exactly as in the re-binned magnetograms.
at lower photospheric plane of the simulation evolves exactly as in the re-binned magnetograms.
We also produced a low-resolution, 8 times re-binned series for performing quick diagnostic and parametric simulation test runs. These included a case where the non-inductive component was set to zero in the PDFI electric field (−∇ψ = 0 in Eq. (5), discussed further in Sect. 4.4).
3.3. Choice of simulation domain
We chose the shape of the final Cartesian simulation box according to the shape of the photospheric input data. For the default 4 times re-binned data input, the horizontal shape of the simulation box is 389 Mm × 248 Mm. We chose the height of the box to be 300 Mm, corresponding to 206 voxels for the 4 times re-binned input, larger than the dimension in the y-direction, but smaller than the x-dimension. This choice was found to be sufficient to avoid problematic boundary effects in the simulation. Fig. 1 shows the photospheric extent of the simulation domain excluding the padding region.
To summarize, we performed three runs that we discuss in the subsequent sections: the primary or default run using 4 times re-binned data (denoted ”rebin-4x”), otherwise the same run but instead employing a coarser resolution using 8 times re-binned data (denoted ”rebin-8x”), and a run using 8 times re-binned data but employing only the inductive electric field.
4. Simulation results
In this section, we study the results of the data-driven TMF simulation conducted for AR11726 (Sect. 3), with particular focus on the eruption occurring on 22 April 2013 at 08:40 UT (Sect. 2.2). In Sect. 4.1, we discuss the properties of a pre-eruptive flux rope (FR) system for the 22 April 2013, 08:40 UT eruption found in the simulation, and we compare its properties to the EUV and X-ray observations before and during the eruption. Section 4.2 discusses the evolution of the average quantitative properties (axial flux and twist) of the pre-eruptive FR system. In Sect. 4.3, we study the formation mechanism of the flux rope system. We find two plausible mechanisms for accumulating twist to the FR system: persistent positive vorticity (i.e., counter-clockwise twisting) at the negative-polarity footpoints of the FR field lines as well as reconnection at a coronal null above the flux rope. We find the former to be the more likely explanation. Finally, in Sect. 4.4 we present the overall energy and helicity budgets of the simulation and discuss how they relate to the evolution and properties of the FR system.
4.1. Coronal magnetic field evolution
4.1.1. Evolution of the flux rope
The remote sensing EUV observations discussed in Sect. 2.2 imply that the 22 April 2013, 08:40 UT eruption is initiated somewhere in the region between the western sunspot of the main AR complex and the western bipole (Fig. 1). The expansion of AIA 193 Å loops is observed from this position (Fig. 3a), the subsequent expulsion of chromospheric or low-coronal material observed in AIA 304 Å also arises from the U-shaped region in this location (Fig. 3b), and the PEAs also appear between the western sunspot and the bipole (Fig. 3c). Consequently, we computed several parameters on the x = 76 Mm yz-plane between the western sunspot and the western bipole, including log10(J/B), the logarithm of current density normalized to the magnetic field strength; the logarithm of the squashing factor Q of elemental magnetic flux tubes (Titov et al. 2002), which reaches high values Q ≫ 1 at quasi-separatrix layers (QSLs) that separate regions of different magnetic connectivity; and the twist (or winding) number Tw between two infinitesimally close field lines. The Q and Tw parameters were computed using the qfactor code of Liu et al. (2016) with slight modifications for better integration into our code framework.
On 22 April 2013 at 08:36 UT, i.e., just before the onset of the observed eruption, the simulation exhibits a clear isolated enhancement in log10(J/B) centered roughly at (x, y, z) = (76, 31, 25) Mm, accompanied by a clear rotation in the magnetic field direction from unit vectors Byz/|Byz|(x = 76 Mm) projected onto the x = 76 Mm plane (Fig. 4a). The log10Q squashing factor (Fig. 4b) shows that the log10(J/B) enhancement includes a region of low squashing factor log10Q ∼ 1 (outlined by the lime dashed curve in Fig. 4b) surrounded by a region of moderate- (log10Q ∼ 2) to-high (log10Q ∼ 6.5) squashing factor (the dashed magenta curve). This region also has large negative twist number Tw ≤ −1 (Fig. 4c). Consequently, this structure fulfills the Liu et al. (2016) definition of a flux rope, consisting of a bundle of field lines with similar connectivity and absolute twist number |Tw|≥1. Flux ropes are also often surrounded by a QSL separating the twisted field of the flux rope from the external less twisted field (e.g., Janvier et al. 2015, and references therein), which we also see as the moderate-to-high log10Q values surrounding the region. This interpretation is further supported by the Byz/|Byz| rotation and log10(J/B) enhancement. We label this structure the main flux rope, which is hereafter abbreviated as the main FR.
 |
Fig. 4. Simulation parameters at slice x = 76 Mm revealing the existence of a flux rope system on 22 April 2013 at 08:36 UT, just before the onset of the eruption discussed in Sect. 2.2. Panel a: logarithm of the current density scaled by the magnetic field magnitude log10(J/B) (white-purple color, saturated at −2.5 and −1) and the direction of the magnetic field projected to the plane Byz/Byz| as black arrows. The Bz component is plotted at the lower (z = 0) photospheric boundary of the simulation in black-white coloring saturated at ±0.01 T(=±100 Mx cm−2). Panel b: log-scaled magnetic squashing factor log10Q (black-white color, saturated at 1 and 5). Panel c: twist number of the magnetic field lines Tw (blue-red color, saturated at −1 and 1) and the direction of the Lorentz force projected to the plane (J × B)yz/|(J × B)yz| as black arrows. The lime and orange dashed curves in panels b and c enclose the regions over which the field lines of the observed flux rope system pass the x = 76 Mm plane. The lime curve encloses the main FR and the orange curve the intertwined FR (see text for exact definitions). Magenta dashed curves in these panels show the QSL boundary enclosing the FR system (also illustrated in Fig. 7b). Animated versions of each panel are available online. |
Figures 4b and c also reveal a second structure that fulfills the definition of a flux rope located next to the main FR (enclosed by the orange dashed curve). This second FR structure contains an internal QSL, thus it actually consists of two FR-like structures; however, for simplicity, we label them as a single FR structure, the intertwined FR, for the reasons explained below.
When tracing field lines from the main FR seed points at the x = 76 Mm plane (chosen with threshold [(log10Q ≤ 1.5)∧(Tw ≤ −1)]), we observe a clear flux rope structure illustrated in Fig. 5a. The main FR (rainbow-colored field lines) connects the negative-polarity western sunspot and the positive polarity at the eastern edge of the western bipole. The field lines traced from the smaller two-part FR structure weave with the main FR, i.e., the intertwined FR. Its negative-polarity footpoints are very close to those of the main FR, but the positive-polarity footpoints are spread over southwestern positive polarity network pixels.
 |
Fig. 5. Simulated field lines of flux rope system identified from the current density, squashing factor and twist maps at the x = 76 Mm plane on 22 April 2013 at 08:36 UT, just before the onset of the observed eruption at from 08:40 UT onwards (Sect. 2.2). Panel a: main FR field lines viewed from the southeast. The lines are rainbow-colored based on the seed point position of the lines at the x = 76 Mm plane. The Bz magnetic field component is plotted at the photospheric z = 0 lower boundary of the simulation domain in black-white coloring saturated at ±100 Mx cm−2 (=0.01 T). Panel b: intertwined FR with yellow-purple coloring. Panel c: both FRs viewed from the northwest. All plotted field lines are based on finding a coherent region on the x = 76 Mm plane where the condition [(log10Q ≤ 1.5)∧(Tw ≤ −1)] is fulfilled. Animated versions of each panel can be found online. For panels a and b, online movies 3 and 4 also offer the view from the northwest, as in panel c. |
In order to capture the formation process of the flux ropes (Tw ≤ −1) from initially weakly sheared arcades (|Tw|< 1), the animated version of the three panels of Fig. 5 were made by tracing the FR field lines from the x = 76 Mm plane using variable thresholds of twist and log10Q (see supplementary materials). For the main FR, they were selected as follows: [(log10Q ≤ 1.25)∧(Tw ≤ −0.25)] for 21 April 2013, 11:00–14:00 UT, [(log10Q ≤ 1.25)∧(Tw ≤ −0.5)] for 14:00–16:00 UT, and [(log10Q ≤ 1.25)∧(Tw ≤ −0.75)] for 16:00–21:00 UT, after which the default [(log10Q ≤ 1.5)∧(Tw ≤ −1)] was employed. The intertwined FR was tracked using [(log10Q ≤ 1.5)∧(Tw ≤ −0.25)] for 21 April 2013, 09:00–23:00 UT and [(log10Q ≤ 1.5)∧(Tw ≤ 1)] for 21 April 2013, 23:00–22 April 2013, 13:00 UT. These animations show how both the main and the intertwined FR structures are formed from initially weakly sheared arcades connecting the western sunspot and their respective positive footpoints in the west and southwest. The tracking of the field lines was not entirely successful for the intertwined FR, resulting in intermittent rogue field lines not really included in the FR structure, which are visible in the animated versions of panels b and c.
The twist numbers within both FRs reach values of Tw ≤ −1 around 21 April 2013, 18:00 UT. The cross-sectional width of the main FR increases over time, particularly at its western end, the western foot extending over a wide region just before the eruption (see the animated version of Fig. 5a). The main FR also develops a weak counter-clockwise writhe over time. Neither of these structures erupt in the simulation at the time of the observed eruption on 22 April 2013, 08:40–09:30 UT. We only observe a very slow rise of the western side of the main FR after the eruption time, which continues until 23 April 2013, 12:48 UT (at this time, the maximum twist of the FR field lines drops below one turn (|Tw|< 1), and we stop the tracking). Between 22 April 2013, 08:36 UT and 23 April, 12:48 UT, the average maximum height of the main FR field line rises 43 Mm, corresponding to the average upward rise velocity of 0.4 km s−1. The question of whether the TMF simulation is capable of reproducing the observed eruption is further discussed in Sect. 5, but henceforth we consider the simulation results predominantly as a representation of the pre-eruptive evolution.
4.1.2. Correspondence to EUV signatures
The pre-eruptive coronal configuration provided by the data-driven simulation appears consistent with several aspects of the observed eruption. First, we note that the simulated FR system has similar southward bending (see Fig. 5c) to the initial expansion of EUV loops from 22 April 2013 at 08:40 UT onwards (Sect. 2.2, Fig. 3a, white dashed line) as well as the U-shaped region that produces an expulsion of plasma from 22 April 2013, 09:07 UT onwards (Fig. 3b, red dashed line), possibly implying that these EUV eruption features correspond to or arise from the ejection of the simulated FR system. Another matching aspect is the strongly southward motion of certain eruption features, including the southward expulsion of the material erupted from the U-shaped region from 09:07 UT onwards (Figs. 3b and e), as well as the weak southward expansion of STEREO/EUVI 195 Å loops from 08:40 UT onwards. This forms a possible source of the COR Blob 1 coronagraph structure in Figs. 3h and i. As illustrated by Fig. 4c, the direction of the Lorentz force (J × B)yz/|(J × B)yz| projected onto the x = 76 Mm plane has a clear southward dominance around the FR system. This could explain the strongly southward eruption features. However, we note that we cannot conclusively connect the simulated flux rope to an individual observational structure: any of the COR Blob 1–3 coronagraph features and their back-traced low-coronal counterparts may correspond to the flux rope (Fig. 3i and Table 1).
Finally, we find some of the observed coronal dimmings to be partly consistent with the footpoint locations of the simulated FR system. Figure 6 illustrates the coronal dimmings in an AIA 193 Å base difference image constructed from pre- and post-eruptive observations on 22 April 2013 at 08:24 and 09:24 UT, respectively. Coronal dimmings are generally believed to correspond to the footpoints of the erupting FR system (Hudson & Webb 1997). We do not find any clear dimming close to the negative-polarity footpoints of the simulated FR system (enclosed by the lime curve in Fig. 6). On the other hand, we do see a clear dimming region in the western bipole, and the region extends more weakly over the positive polarity network patches south of the bipole (magenta dashed line in Fig. 6 encloses the entire dimming region). This region encloses the positive-polarity footpoints of both the main FR and the intertwined FR (outlined by the orange curve in Fig. 6). At 09:24 UT, the observed dimming region is significantly more extended than the FR footpoint region, but as illustrated by the animated version of Fig. 6, the dimming region is initially smaller, enclosing the FR footpoint region more tightly, after which point it is extended south and west. This could be a result of the footpoint drifting, where the footpoints of the erupting flux rope (and the resulting dimmings) drift away from the eruption site during the eruption (see e.g., Aulanier & Dudík 2019, and references therein). However, we do not detect such drifting in the simulation, most likely as the simulation is incapable of reproducing the eruption dynamics (as discussed in Sect. 5).
 |
Fig. 6. Base difference image between AIA 193 Å observations on 22 April at 08:24 UT and 09:24 UT. The AIA images are re-projected onto the local Cartesian coordinates of the re-projected magnetogram series forming the bottom of the simulation box (Sect. 3.2 and Fig. 1). The blue and red contours correspond to the −100 and 100 Mx cm−2 contours of the photospheric Bz magnetic field component, respectively. The lime and orange curves enclose the approximate position of the negative- and positive-polarity footpoints, respectively, of the pre-eruptive flux rope system (both main and intertwined FRs) at 08:36 UT, determined from the simulation. The magenta dashed curve encloses the dimming region that includes the negative-polarity footpoints of the FR system. An animated version of this figure can be found online. |
4.1.3. Null-points
At the x = 76 Mm slice both FR structures are embedded in a compact QSL (outlined by the dashed magenta curve in Fig. 4b), which carries a significant positive twist Tw ≲ 0.5 in its upper parts (Fig. 4c), indicating significant current density in the field lines. The field lines passing the x = 76 Mm slice at the QSL boundary above the FR system are illustrated in Fig. 7b (white box), and they share a visual consistency with the soft X-ray loops (Fig. 7a, white box) observed at this position by the X-Ray Telescope (XRT: Golub et al. 2007) onboard the Hinode spacecraft (Kosugi et al. 2007).
 |
Fig. 7. Panel a: Hinode/XRT soft X-ray observation of NOAA AR 11726 on 22 April 2013 at 05:52:15 UT. The white box encloses a collection of loops with enhanced emission emanating from the western bipole and connecting to the western sunspot. Panel b: snapshot of the simulation on 22 April 2013 at 06:00 UT, where the rainbow-colored field lines correspond to the upper section of the QSL boundary enclosing the FR system (magenta dashed curves in Figs. 4b and c). As indicated by the white box, the QSL field lines have a similar position and shape to the high-emission XRT loops in panel a. The gray scale background shows the photospheric Bz magnetic field component saturated at ±100 Mx cm−2 (black for negative), and the blue and red contours correspond similarly to ±100 Mx cm−2 limits (blue for negative). |
The enhanced X-ray emission at the QSL field lines might be a result of the enhanced current that causes dissipation, heating, and emission (e.g. Titov & Démoulin 1999; Green & Kliem 2014). However, there is also another possible source of heating of the overlying QSL field lines: magnetic null-points above the western bipole. At least two nulls arise at this position (shown in Figs. 8c,d and 14a) from the interaction between the south-north-pointing field within the western bipole and the oppositely oriented field of the main AR complex returning back to the negative-polarity western sunspot. These nulls form favorable conditions for magnetic reconnection. In particular, the one higher in the corona is directly connected to the overlying QSL loops, thus forming a possible source for nonthermal heating leading to enhanced emission. We note that the low-lying null-point appears to be a robust feature. It is found both in the high-resolution (rebin-4x) simulation and the low-resolution (rebin-8x) simulation without the non-inductive electric field, 2 Mm and 4 Mm above the lower boundary of the simulation box, respectively.
 |
Fig. 8. Structures near the two null-points over the western bipole in AIA 304 Å observations and in the simulation. Panel a: apparent J-shaped brightening in the AIA 304 Å observations on 21 April 2013 at 22:24 UT, east of the western bipole. The J-shape can be extrapolated to form a very weak S shape connecting to the western negative polarity sunspot (white dashed line). Panel b: clearer forward S at the same position 22:36 UT. Panel c: J-shaped structure in the simulation on 21 April at 22:00 UT (white-dashed curve) arising from the field lines connecting the western positive polarity to a low-lying null and the western sunspot (yellow-purple-colored field lines). Panel d: shows how the field lines in panel c are part of a larger positively twisted collection of arcades (yellow-purple-colored field lines). Rainbow-colored lines illustrate the positively-twisted QSL boundary field overlying the main FR (also shown in Fig. 7b at a later time), which connect to a null-point above the western bipole. |
One particularly interesting event is detected near the null points on 21 April 2013 at 22:24 UT, when an S-shaped structure of enhanced AIA 304 Å (and 131, 171, and 193 Å) emission appears, connecting the western bipole and western sunspot. This structure is brightest close to the western bipole (forming a clear J-shape), but overall quite weak (see the dashed white curve in Fig. 8a). Twelve minutes later, it developed into a clear forward-S-shape structure (white dashed curve in Fig. 8b), and it remained visible until ∼23:00 UT. However, we point out that the eastern end of the S-shape is unclear at both times, and it might be a visual coincidence related to pre-existing similarly curved AIA 304 Å structures near the western sunspot. As explained by, e.g., Green et al. (2007), a forward-S shape in EUV observations usually indicates positive twist, which is opposite to the negative twist of the simulated FR system (which also lies clearly more to the south -see Fig. 5- thus making it unlikely to be related to this structure). However, our simulation does also contain positively twisted structures at this position and at this time (see Fig. 4c, animated version). The field lines that pass a low-lying null close to the western bipole (Fig. 8c, yellow-purple field lines) resemble the initial S-shaped structure (Fig. 8a), including the sharp “hook” arising from the null-point close to the western bipole. At later times the hook close to the bipole evolves to be more curved (Fig. 8b) and cannot be reproduced by any single coherent field-line structure in the simulation. However, a large bundle of positively twisted field lines was present at this time (Fig. 8d yellow-purple field lines), which extend the field lines shown in Fig. 8c. This bundle does form a very weak forward-S shape, only much weaker and in a slightly different position than the observed one. We point out that the comparison between the EUV observations and the simulation field lines is challenging due to the projection effects of the EUV observations combined with the complexity of the configuration near the western bipole: The structure includes two null-points and positively twisted field lines in two vertical layers (the yellow-purple arcades and the rainbow-colored QSL field lines in Fig. 8d). We discuss the possible implications of the transient forward-S shape further in Sect. 5.
4.2. Properties of the flux rope system
Using the tracking of the flux rope field lines (described in Sect. 4.1 and Fig. 5), we are able to study how properties of the simulated flux ropes evolve in time. Figure 9 shows the time evolution of the mean  and minimum
and minimum  twist numbers of the field lines in the main FR, as well as its toroidal (i.e., axial) flux. We define the toroidal flux here as
twist numbers of the field lines in the main FR, as well as its toroidal (i.e., axial) flux. We define the toroidal flux here as
 |
Fig. 9. Time evolution of mean and minimum twist numbers |
where  is the average magnetic field direction over the FR field lines at the x = 76 Mm plane and dA is the differential area element. We point out that our estimate of the axial flux is rather crude. Better estimates could be retrieved by fitting and the a flux rope model to the field (e.g., the one by Gold & Hoyle 1960, although with issues of its own), or by using other means to find the axial flux (e.g., Liu et al. 2016). However, we consider our method sufficient for obtaining order-of-magnitude estimates and for studying temporal trends.
is the average magnetic field direction over the FR field lines at the x = 76 Mm plane and dA is the differential area element. We point out that our estimate of the axial flux is rather crude. Better estimates could be retrieved by fitting and the a flux rope model to the field (e.g., the one by Gold & Hoyle 1960, although with issues of its own), or by using other means to find the axial flux (e.g., Liu et al. 2016). However, we consider our method sufficient for obtaining order-of-magnitude estimates and for studying temporal trends.
Figure 9 shows that, consistently with the visual characteristics of the field-line evolution (Fig. 5b, animated version), both the absolute mean twist (purple curve) and the axial flux (black curve) of the main FR increase in time before the eruption, with the absolute value of the mean twist experiencing only a short period of slow decrease on 22 April 02:00–08:00 UT. On 22 April at 08:36 UT, i.e., four minutes before the eruption starts, the average twist reaches a value of −1.26 turns, which exceeds the 1.25-turn limit for kink instability in certain idealized configurations (e.g., Török et al. 2004; Török & Kliem 2005; Liu et al. 2016; Jing et al. 2018, and references therein), while the minimum twist in the FR is −1.76 turns. The axial flux is ∼1.3 × 1020 Mx at this time corresponding to 0.4% of the total unsigned flux of the entire AR 11726 and 33% of the total unsigned flux of the western bipole (Fig. 2). The axial flux in the FR is thus insignificant compared to the total flux in the larger AR, but it constitutes a significant portion of the western bipole. Assuming (crudely) that the FR has a cylindrical symmetry and that  represents the twist close to the axis of the cylinder, we can provide an order-of-magnitude estimate of the poloidal flux of
represents the twist close to the axis of the cylinder, we can provide an order-of-magnitude estimate of the poloidal flux of  (Liu et al. 2016), yielding 1.6 × 1020 Mx at the eruption time. After the observed eruption, the absolute twist number keeps increasing in the simulated FR, whereas the axial flux becomes roughly constant at 11:00 UT onwards. We stopped the analysis on 22 April 2013 at 13:00 UT due to the issues arising in the FR tracking and for estimating the axial flux after this time.
(Liu et al. 2016), yielding 1.6 × 1020 Mx at the eruption time. After the observed eruption, the absolute twist number keeps increasing in the simulated FR, whereas the axial flux becomes roughly constant at 11:00 UT onwards. We stopped the analysis on 22 April 2013 at 13:00 UT due to the issues arising in the FR tracking and for estimating the axial flux after this time.
Similar analysis of the intertwined FR gives  ,
,  , Φt = 2.9 × 1019 Mx cm−2, and
, Φt = 2.9 × 1019 Mx cm−2, and  Mx cm−2 on 22 April 2013, 08:36 UT, showing that the twists are comparable between the FRs, whereas the intertwined FR has clearly lower axial and poloidal fluxes (∼22–25% of the main FR values).
Mx cm−2 on 22 April 2013, 08:36 UT, showing that the twists are comparable between the FRs, whereas the intertwined FR has clearly lower axial and poloidal fluxes (∼22–25% of the main FR values).
4.3. Formation mechanism of the flux rope
Visual inspection of the formation of the main and intertwined FRs (Fig. 5, animated versions) implies that the twisting of the field lines originates from the negative-polarity footpoints, which are located close to each other at the western sunspot. More specifically, the animated version of Fig. 5a shows that the initially weakly sheared arcades (Tw ≤ −0.25) that later form the main FR accumulate twist at the negative-polarity footpoints while simultaneously piling up against the null-point topology at the western bipole (Fig. 8). This pile-up is, however, partly a projection effect, as illustrated by online movie 3, which shows this evolution viewed from the northwest. Nevertheless, we also investigated the possible injection of twist arising from the apparent interaction between the null-point and the FR field lines, summarized at the end of this section. However, the twist accumulation from the negative-polarity footpoints seems a more likely cause of the FR twisting. It would also explain why both FRs seem to form at approximately the same time (the twist numbers reaching Tw ≤ −1 around 21 April 2013, 18:00 UT for both) developing similar mean twist numbers, as well as why the twist is introduced similarly to both the arcades connecting the western sunspot and the western bipole (main FR), and the arcades connecting the western sunspot and southwestern positive polarity patches (intertwined FR).
In order to study the physical cause of the apparent twisting at the negative-polarity footpoints, we studied the photospheric velocity field. In our case, the relevant velocity estimate is the one implied by the driving electric field E = EPDFI + En (Eq. (8)) and ideal Ohm’s law:
where V⊥ ⊥ B contains only flows perpendicular to the magnetic field. Using this velocity estimate, we derived the vertical component of vorticity,
at the photosphere. As illustrated by Fig. 10 and its animated version, the negative-polarity footpoints of the both the main and intertwined FRs (pink and black points, respectively) lie in a region of persistent positive vertical vorticity (purple region, enclosed by a black dashed curve) throughout the formation of the FRs and well beyond the observed eruption on 22 April 2013 at 08:40 UT (we stopped the analysis on 22 April at 13:00 UT). The positive-polarity footpoints, in turn, do not exhibit any dominant sign of vorticity. Simple geometrical considerations, as well as modeling results of, e.g., Török & Kliem (2003) illustrate that positive vorticity, i.e., counter-clockwise twisting, at the photospheric footpoints of the magnetic arcades introduces negative twist to the field lines. Consequently, the observed persistent positive vorticity at the negative-polarity footpoints of the FR system is consistent with the apparent negative twisting observed to originate there in the visual inspection of field-line evolution (Fig. 5, animated version).
 |
Fig. 10. Map of vertical component of vorticity (∇×Vh, ⊥)⋅ez (orange-to-purple color scale, saturated at ±10−4 s−1) near the negative footpoints of the main FR (pink dots) and the intertwined FR (black dots) within the western sunspot (see Fig. 1) during the formation processes of the FRs on 21 April 2013 at 19:00 UT. The blue and red contours correspond to the photospheric Bz of ±100 Mx cm−2 (blue for negative). The black dashed curve encloses a persistent patch of positive vorticity that encloses the FR footpoints. An animated version of this figure is available online. |
In order to study the relationship between the observed photospheric vorticity at the negative-polarity footpoints and measured evolution of the mean twist number  in the main FR (Fig. 9), we developed a vorticity twisting proxy ω defined as follows:
in the main FR (Fig. 9), we developed a vorticity twisting proxy ω defined as follows:
where ⟨(∇ × V⊥, h)⋅ez⟩FP− is the average vorticity over the negative-polarity footpoints of the main FR. We multiplied the average vorticity by −1 to make its sign consistent with the twist it produces in the corona. We then approximated this quantity −⟨(∇×V⊥, h)⋅ez⟩FP− as the signed vorticity related to rigid rotation with constant angular velocity, in which case the angular velocity is defined as ω; i.e., half of the vorticity (see e.g., Spencer 2004). Deriving this proxy angular velocity ω from the average vorticity allows us to write ω in units of full rotations in unit time (2π rad h−1), directly comparable with the rate of change of the mean twist number  given in the same units. As illustrated by Fig. 11, the vorticity twisting proxy ω has similar magnitude to the twisting rate
given in the same units. As illustrated by Fig. 11, the vorticity twisting proxy ω has similar magnitude to the twisting rate  and they follow each other well in trends. The signs are also consistent (negative) for most of the time except for the 22 April 2013, 02:00–08:00 UT period, when
and they follow each other well in trends. The signs are also consistent (negative) for most of the time except for the 22 April 2013, 02:00–08:00 UT period, when  becomes momentarily weakly positive (see also Fig. 9). During this period, the vorticity twisting proxy ω is also at its weakest, suggesting that the momentary decrease in the absolute twist number could be a result of the coronal twist-lowering processes (such as magnetic diffusion: see e.g., Yardley et al. 2018) overcoming the photospheric twisting.
becomes momentarily weakly positive (see also Fig. 9). During this period, the vorticity twisting proxy ω is also at its weakest, suggesting that the momentary decrease in the absolute twist number could be a result of the coronal twist-lowering processes (such as magnetic diffusion: see e.g., Yardley et al. 2018) overcoming the photospheric twisting.
 |
Fig. 11. Twisting rate of mean twist |
We note that the uncertainties in this analysis are large; for example, we do not take into account the finite response time it takes for the photospheric twisting to affect the twist of the field lines (see Cheung & DeRosa 2012 for a discussion). Nevertheless, we conclude that the good correspondence between the photospheric vorticity (represented by the vorticity twisting proxy) and the mean twisting rate of main FR measured in the corona supports the hypothesis that the photospheric twisting at the negative-polarity footpoints causes the flux rope formation.
Finally, we note that we also studied the vorticity derived from the FLCT optical flow velocity estimate Vh, FLCT used as input to the electric field inversion (Sect. 3.2), and found no clear predominance of either sign in the vertical vorticity at the negative- or positive-polarity footpoints. This discrepancy is not a surprise considering the fact that Vh, FLCT is derived solely from the Bz magnetogram evolution, whereas the Vh, ⊥ estimate derived from the electric field includes also the contributions from the entire B evolution and Dopplergram VLOS.
4.4. Energy and helicity budgets
We studied the time evolution of magnetic energy Em and the free magnetic energy  (energy in excess to the minimum-energy potential field extrapolation; see e.g., Wiegelmann & Sakurai 2012), defined as
(energy in excess to the minimum-energy potential field extrapolation; see e.g., Wiegelmann & Sakurai 2012), defined as
where Bp = |Bp| is the magnitude of the potential magnetic field. We also studied the evolution of magnetic helicity HR, and its decomposition into helicity of the non-potential, current-carrying field Hj and the mutual helicity between the potential and non-potential fields 2Hpj (HR = Hj + 2Hpj, Pariat et al. 2015):
In the above, A is the magnetic vector potential B = ∇ × A, and the quantities with indices p refer to the potential part of the corresponding field (see e.g., Pariat et al. 2015; Valori et al. 2012). We also studied the relative magnitude of the non-potentiality using the following ratios  and Hj/HR (e.g., Pariat et al. 2017; Zuccarello et al. 2018; Price et al. 2019; Moraitis et al. 2019).
and Hj/HR (e.g., Pariat et al. 2017; Zuccarello et al. 2018; Price et al. 2019; Moraitis et al. 2019).
Figure 12 shows the time evolution of the parameters above for three of our simulations (Sect. 3): the default case (rebin-4x, presented in Sect. 4.1, black curves), the low-resolution version of the default (rebin-8x, red curves) and the low-resolution case driven using only the inductive electric field (−∇ψ = 0, green curves). We observe that the high- and low-resolution cases of the default run are very similar, the latter containing only slightly smaller energy and helicity budgets with otherwise identical trends. This is also reflected in the field-line evolution, the low-resolution run producing the same basic FR structure as the high-resolution run (Sect. 4.1). This justifies our use of the quicker low-resolution run to test the effect of the non-inductive component on the results. We ran the low-resolution simulation without the non-inductive component (−∇ψ = 0 in Eq. (5)), and the resulting energy and helicity budgets are represented by green curves in Fig. 12. Although the total energy evolution is only slightly smaller than in the default PDFI-driven case, the free energy and relative helicity budgets are only 42% and 7% of the PDFI-reference at the time of the eruption on 22 April 2013 at 08:40 UT (vertical dashed line). When considering the order-of-magnitude drop in the helicity budget, it was not a surprise that the simulation driven using the inductive electric field did not produce any of the flux ropes found in the PDFI-driven runs (e.g., Schuck & Antiochos 2019).
 |
Fig. 12. Coronal energy (upper panel) and helicity (lower panel) budgets and non-potentiality ratios (see text for details). Solid curves show the total budgets (Em and HR) for three of our simulations (see text for details). Dashed line shows the non-potential component of the total budget ( |
We also compared the coronal budgets to the estimates of photospheric energy and helicity injections (see Lumme et al. 2019), and we found these to be consistent subject to the discrepancies arising from the configuration of the photospheric boundary condition for the TMF method (discussed in detail by Pomoell et al. 2019).
As shown by Fig. 13, lower panel, AR 11726 exhibits predominantly positive helicity budget, thus opposing the hemispheric rule (e.g., Hoeksema et al. 2014), according to which the majority of the active regions in the northern hemisphere have negative helicity (e.g., Liu et al. 2014). This also means that the negatively twisted (negative-helicity) FR system between the western sunspot and the western bipole has helicity opposite to the predominant helicity of the active region. The difference in signs remains even when we limit the consideration of the simulation budgets only to the region containing the FR system, more specifically to region x > 3 Mm, enclosing the western sunspot and the bipole (Fig. 13, red curves). This result highlights the importance of the persistent positive vorticity patch at the western sunspot (Fig. 10), which likely causes the formation of the FR (see Sect. 4.3) and introduces helicity with sign opposite to the most of the corona embedding the flux rope system.
 |
Fig. 13. Coronal energy (upper panel) and helicity (lower panel) budgets and non-potentiality ratios (see the text for details) for the default simulation computed both in the entire domain (black curves), and in the western region x > 3 Mm enclosing the FR system of interest (red curves). Solid curves show the total budgets for three of our simulations (see text for details). Dashed line shows the non-potential component of the total budget (either |
Finally, when it comes to the energy and helicity budgets and the eruption dynamics, we observed few clear connections. The total and free energy budgets as well as the free-to-total energy ratios continue to increase even after the eruption on 22 April 2013 at 08:40 UT with no apparent effect introduced at the eruption time, both in the entire simulation box (Fig. 13, upper panel, black curves) and in the x > 3 Mm region focusing on the FR system (red curves). The total and non-potential helicity budgets follow similar, predominantly increasing trends. However, the total helicity budget limited to the western end of the domain (Fig. 13, lower panel, red solid curve) does experience a small momentary decrease at 08:40–12:00 UT, which in turn increases the non-potential-to-total-helicity ratio (red dotted curve). Since the flux rope does not exhibit clear eruption-like evolution in the simulation during this time, it is unclear what the significance of this is. The increase in the Hj/HR ratio after the eruption time is opposite to the hypothesis that certain types of FR eruptions occur when the ratio crosses a threshold value (Pariat et al. 2017; Zuccarello et al. 2018; Moraitis et al. 2019; Price et al. 2019). However, in the previous studies where the eruption was related to exceeding a certain Hj/HR threshold the erupting flux rope system had in most of the studied cases twist consistent with the dominant helicity sign in the coronal volume. In our case, a negatively twisted flux rope with negative helicity is embedded in a predominantly positive-helicity corona, which makes the interpretation more complicated. The pre-eruptive FR formation process, on the other hand, might be visible in the west-focused Hj/HR ratio (red dotted curve). It shows clear peaks on 21 April 2013 at 18:00 UT – 22 April 2013 at 03:00 UT, which arise from the momentary drops in the total helicity. This could arise from the FR system accumulating negative twist and helicity, which could then decrease the total signed helicity budget. We remind the reader that part of the differences between the computations done for the full domain and for only the western bipole arise from the previously discussed fact that the western bipole is dominated by the FR, but it constitutes only an insignificant part of the larger AR.
5. Discussion
Our data-driven, time-dependent magnetofrictional (TMF) simulation reproduced several observational features of the 22 April 2013, 08:40 UT eruption from NOAA AR 11726. These include the simulated pre-eruptive flux rope with footpoint locations consistent with the post-eruptive EUV arcades, one footpoint matching the observed coronal dimming, and the field lines passing the quasi-separatrix layer (QSL) above the flux rope that is visually consistent with the observed pre-eruption soft X-ray loops (Sect. 4.1). A particularly interesting feature was the weak transient (< 1 h visible) forward S-shape observed in the EUV data ten hours before the eruption. As discussed e.g. by Green et al. (2007), such forward S “sigmoid” shapes can be associated with the existence of positively twisted field lines (positive helicity), opposite to the negative twist of our pre-eruptive FR system. However, we did also discover positively twisted arcades in our simulation at this time, which, combined with the complex null-point configuration at the western end of the S shape, reproduced the observed S shape reasonably well. This result can be interpreted in two ways. Assuming that our simulation results are reliable, the result implies that such weak and transient EUV “sigmoids” can potentially form an unreliable proxy for the twist of pre-eruptive flux ropes. If they are used in predicting the twist sign (chirality) of the erupting flux rope and its interplanetary counterpart, additional proxies should be considered (similarly to, e.g., Palmerio et al. 2017, and references therein) and a careful analysis should be performed to ensure that the sigmoidal shape really corresponds to the erupting FR system. An opposite interpretation is that our simulation fails to reproduce a positively twisted structure that resulted in the EUV sigmoid, which, in the worst-case scenario, could even have been a coronal flux rope. Although we find this unlikely in light of other evidence, we still note that even the state-of-the-art electric field inversion schemes, such as our PDFI method, have such large uncertainties that they can produce helicity fluxes of inconsistent signs (Lumme et al. 2019): an issue that may well result in wrong twists in the simulated FR systems.
We found the quality of the photospheric electric field driving to be an integral part of the successful modeling results (Sect. 4.4). The proper estimation of the non-inductive (curl-free) electric field component was crucial for producing sufficient energy and helicity fluxes in the coronal simulation domain, and, consequently, in forming the pre-eruptive flux rope. The importance of the electric field inversion is further emphasized by the fact that the FR formation in the simulation was likely caused by a persistent patch of positive vorticity in the photospheric velocity field (derived from the electric field via Eq. (10)), which introduced a negative twist and helicity at the negative-polarity footpoints of the FR system. Our results are thus in agreement with previous studies implying the critical role of the non-inductive component in the photospheric energy and helicity fluxes (Fisher et al. 2010; Kazachenko et al. 2014; Lumme et al. 2017, 2019; Schuck & Antiochos 2019), as well as in reproducing the observed coronal activity in the simulations (Cheung & DeRosa 2012; Mackay et al. 2014; Cheung et al. 2015; Weinzierl et al. 2016; Pomoell et al. 2019). On the other hand, data-driven TMF simulations with only the inductive component by Gibb et al. (2014) and Yardley et al. (2018) resulted in the formation of pre-eruptive flux ropes. Yardley et al. (2018) even found that the amplification of helicity flux to the corona using a non-inductive component was relatively unimportant for the output. This discrepancy could be related to the difference in the FR formation mechanisms. The FRs of Gibb et al. (2014) and Yardley et al. (2018) formed via flux cancellation, whereas ours formed via photospheric twisting and/or coronal reconnection (Sect. 4.3 and discussion below).
The formation process and location of our pre-eruptive flux rope system (Sect. 4.3) does not appear to fall into some of the standard classes of FR formation processes in active regions. The FR system was formed over a relatively wide region of quiet Sun with no strong PIL, and starting from initially high-lying, weakly sheared arcades forming a non-stretched bundle with compactly located footpoints (see animated version of Figs. 5a,b and 10). This makes the formation via photospheric flux cancellation at the PIL an unlikely scenario, as it would require a clear flux-cancelling PIL, where sufficiently stretched sheared arcades reconnect to form long twisted FR field lines (see Fig. 1 of van Ballegooijen & Martens 1989 as well as Chintzoglou et al. 2019). We note that significant flux cancellation was observed at the western bipole (see the green curve in Fig. 2 and the animated version of Fig. 1); i.e. at the positive-polarity footpoints of the main part of the FR system (Fig. 5b). This may have affected the FR formation and evolution in some way, but we found no proof or plausible mechanism for it introducing significant twist to the FR system. The formation of twisted FR field lines from sheared arcades high in the corona, corresponding to a stable uneruptive tether-cutting (Moore et al. 2001), is similarly unlikely due to the lack of stretching in the arcades. Instead, we found the most likely cause of the FR formation to be the persistent positive vorticity in the photospheric velocity field at the negative-polarity footpoints of the FR system. The main part of the simulated FR system also developed counter-clockwise writhe, similarly to the idealized simulation of Török & Kliem (2003), where a negatively twisted flux rope was formed via positive photospheric vortical motions at the footpoints (see also Sect. 2.4 of Green et al. 2007, and references therein). These vortical motions were observed located within a sunspot (Figs. 10 and 1). Previous studies have shown the emergence of twisted flux to cause significant shearing and vortical motions as well as the rotation of sunspots (e.g., Fan 2009; Kumar et al. 2013; Leake et al. 2013), which suggests that the observed vortical motions and the resulting FR formation were likely a result of the emergence of twisted flux from the convection zone to the photosphere.
In addition to the vorticity-driven FR formation, there is another process potentially capable of transferring poloidal flux into the flux rope: the coronal reconnection at a null-point above the western bipole. The null-formed magnetic configuration above the western bipole is such that a reconnection at the null could introduce poloidal flux to the main FR, but not to the intertwined FR, which lies too far south for that. This is illustrated by the orange-to-green arrow in Fig. 14a and would correspond to passing the flux from Region 1 to Region 2 over the QSL boundary in 14b); i.e. the QSL would need to shift toward Region 1 in the FR formation phase. The clear signatures of such drifting of the QSL was however not found by visual inspection and quantitive tracking would be challenging due to the constant evolution of both the log10Q and the photospheric Bz distribution, thus preventing the estimation of the reconnection rate via tracking the QSL motion (as done e.g., by Lynch et al. 2016). Moreover, the location of the highest twist values and footpoints of the main FR do not match this scenario (i.e., they are close and along the QSL boundary between Region 2 and another Region 3 to the west, instead of the boundary between Regions 1 and 2, as would be expected in reconnection-driven twisting). Based on this semi-quantitative consideration of the magnetic connectivity and twist evolution above, we find it unlikely that the null-point reconnection would be the main driver of the twisting in the main FR field lines. However, we note that the reconnection may still introduce smaller amounts of poloidal flux to the FR system. The null-point reconnection may also be important for the eruption dynamics of the flux rope: the overlying QSL field lines surrounding the flux rope are directly connected to the null-point, and the reconnection-related weakening of the field may act as a trigger for the ejection of the FR system, similarly to the breakout eruption model of Antiochos et al. (1999). In our scenario, however, the null-point above the FR would add poloidal flux to the flux rope, whereas in the breakout model the null-point reconnection mainly serves to weaken the overlying strapping field, allowing the sheared field below it to expand and erupt (which is also possible in our case). Moreover, our flux rope forms prior to the observed eruption, and not during the eruption process.
 |
Fig. 14. Magnetic configuration of the higher coronal null-point (Fig. 8d) and its relationship with the main FR depicted on 21 April 2013 at 18:00 UT, when the main FR was just forming. Panel a: field-line configuration around the null-point (orange-white lines), the main FR (green-white lines), and field lines originating from Region 3 in panel b (black-white lines). The photospheric distribution of Bz is shown in gray scale (saturated at ±100 Mx cm−2, black for negative) and blue/red contours (±100 Mx cm−2, blue for negative). The purple-to-white color plot shows the magnetic squashing factor log10Q at horizontal plane z = 0.729 Mm ranging from 1 to 5, shown only in high-Q regions where log10Q ≥ 1.25. The blue-red color plot shows the twist number in the same horizontal plane including only the regions where [(log10Q ≤ 1.25)∧(Tw ≤ −0.25)]. Panel b: zooms into the positive-polarity photospheric footpoints of the field-line systems in panel a. The dashed lines outline regions of consistent magnetic connectivity for each field-line system, labeled Regions 1–3 with coloring consistent with that of panel a. The black patch in Region 2 shows the position where the footpoints of the main FR start to appear. An animated version of panel b is available online. |
As discussed in Sect. 4.1, our simulation approach was unable to reproduce the ejection of the flux rope from the simulation domain. The simulation only exhibited a very slow rise of the flux rope in the 28-hour period after the observed eruption time. Since the photosphere and corona continued to evolve during this time, thus re-organizing the coronal environment, it is uncertain whether this rise reflects the true eruption dynamics or the subsequent unrelated coronal evolution. A similar slow rise and ejection (or lift-off) of flux ropes has been observed in the TMF simulations by Mackay & van Ballegooijen (2006), Cheung & DeRosa (2012), and Pomoell et al. (2019), with timescales much shorter than the observed (ranging from several hours to days). The latter two also likely overestimated the true helicity content in the corona by several factors (see Lumme et al. 2017; Pomoell et al. 2019). Yardley et al. (2018), on the other hand, did not discover any flux rope ejections in their TMF simulations, but instead identified “eruption” as a slow rise and dissolution of the flux rope and the appearance of post-eruption loops (their result might be also related to the fact that their simulated eruptions were truly confined with no clear CMEs observed in the coronagraph data). These examples and our results suggest that it is challenging to realistically reproduce an ejection in the TMF simulation. This is not a surprise when considering the physical model against the full MHD picture. Setting the “velocity” proportional to the Lorentz force in the TMF method (Eq. (3)) means that even the strongest Lorentz forces expanding the flux rope (such as the hoop force that causes the ejection via torus instability, Kliem & Török 2006; Török & Kliem 2007) produce only convection of magnetic field lines to the direction of the force at velocity V ∝ J × B via the induction equation (Eqs. (1) and (2)):
whereas in the full MHD description, the Lorentz force would result in acceleration of the plasma (and the frozen-in magnetic field in case of ideal MHD) proportional to the Lorentz force, as defined by the momentum equation
where the pressure gradient term and gravity are approximated to be negligibly small using the force-free assumption (Sect. 1), applicable, for example, to the torus instability. This difference and the resulting increase of timescales in the TMF approach explains the challenge in modeling the ejections, and it emphasizes the suitability of the TMF method for modeling the pre-eruptive quasi-static energy build-up, but not the eruption (as discussed in Sect. 1). The simulation results of this particular case could be considerably affected by the fact that the eruption constituted only a small portion of the whole active region, in contrast to many previously studied events. However, even modeling the evolution just until the eruption time can give valuable information regarding the eruption dynamics. The large negative twist observed in our pre-eruptive flux rope system was found to exceed certain kink instability thresholds, thus suggesting that kink instability possibly had a role in the eruption dynamics. We also observed a clear southward dominance in the coronal Lorentz force around the pre-eruptive flux rope that may explain the strongly southward motions of certain eruption features in the EUV and coronagraph observations.
Having emphasized the importance of focusing the TMF simulation efforts on the pre-eruptive phase, we are led to another issue: the modeling of a sequence of eruptions from an active region. When the TMF-simulated corona cannot reproduce the ejection of flux and helicity (or at least does it with hugely overestimated timescales), the realism of the modeling output becomes uncertain for the post-eruptive times. In our case, we do not consider this issue important as the 22 April 2013, 08:40 UT eruption was the first major eruption from the western part of AR11726 (the region between the western sunspot and the western bipole), but the issue does become significant when considering the eruptions we associated with the central (“main AR complex”, Fig. 1) part of AR11726 (see supplementary Table A.1). We leave this issue and the studying of eruptions from the central part of AR11726 for further studies.
6. Conclusions
We conducted a data-driven, time-dependent magnetofrictional simulation for the emergence and subsequent eruptive behavior of NOAA active region 11726. When focusing on a single, weak, and CME-producing eruption occurring at the western periphery of the region on 22 April 2013 at 08:40 UT, our simulation was capable of capturing the pre-eruptive energy build-up for the eruption in the form of a coronal flux rope. The position and shape of the flux rope magnetic field configuration in the simulation was consistent with several observational EUV and X-ray features of the pre-eruptive and eruptive evolution, but the simulation was incapable of reproducing the eruption dynamics. We attribute this to the inherent properties of the magnetofrictional method, which inhibits the fast energy conversions required for simulating the ejection of a flux rope on realistic timescales. Consequently, our simulation results re-affirm the applicability of the magnetofrictional simulations to model the pre-eruptive evolution, but illustrates that the modeling output can become problematic for post-eruptive times.
When comparing the simulation results and the EUV observations for the pre-eruptive evolution, we noticed a weak and transient forward-S EUV sigmoid appearing ten hours before the eruption on 21 April 2013 at 22:24 UT. Due to the close proximity of the structure to the pre-eruptive flux rope system, using it alone could have yielded an incorrect positive twist for the flux rope. However, we found that, in the simulation, the sigmoid better corresponded to another structure besides the flux rope. This other structure consisted of positively twisted field lines and a related null-point configuration, and it had a reasonably consistent shape with the observed sigmoid. This illustrates that such weak transient sigmoids, observed long before the eruption, may give a misleading sign for the twist of the pre-eruptive flux rope system, and if they are used to deduce the sign, measures should be taken to ensure that the observed sigmoid does not correspond to some other structure besides the flux rope, as in our case. This issue is further amplified by the fact that our simulated flux rope had a negative twist and helicity, which is the opposite of the predominantly positive twist of the active region, and that our eruption of interest was relatively weak. We also note that the observed EUV sigmoid may, in the worst case scenario, imply that our simulation failed to produce a notable positively twisted structure (maybe even a flux rope), as a result of uncertainties in the electric field driving or the simulation method. However, we deem this unlikely in light of other supporting evidence, and we leave further considerations of such uncertainties for future works.
Our time-dependent simulation allowed a close inspection of the formation process of the pre-eruptive flux rope, and revealed it to arise from one or two processes: persistent positive vorticity in the photospheric velocity field at the negative-polarity footpoints of the flux rope system, and/or coronal reconnection at a null-point above the other end of the flux rope. Although we could not conclusively isolate the cause of the flux rope formation, we found the photospheric vorticity-driven twisting to be a more likely cause, and the possible coronal null-point reconnection acting more as an additional process. Since the observed vortical motions were observed within a sunspot, we conclude that the flux rope formation was likely driven by the emergence of twisted flux to the photosphere, which is known to be capable of creating shear and vortical motions in sunspots.
The fact that the flux rope formation was likely directly driven by photospheric vortical motions emphasizes the need for accurate photospheric boundary condition for the data-driven simulation. Our electric field boundary condition was derived from the remote sensing observations of the photospheric vector magnetic field and line-of-sight plasma velocity using the comprehensive PDFI inversion method. We found that the inclusion of a significant non-inductive (curl-free) component to the driving electric field was essential to producing the flux rope in the simulation. Employing the often-used approximation where the non-inductive component is neglected did not produce a flux rope and severely underestimated the coronal free energy and helicity budgets of the simulation, similarly to previous studies (Cheung & DeRosa 2012; Pomoell et al. 2019; Price et al. 2019).
Movies
Movie 1 associated with Fig. 1 (Figure_1_animated_version) Access here
Movie 2 associated with Fig. 3 (Figure_3_a_c_animated_version) Access here
Movie 3 associated with Fig. 3 (Figure_3_d_f_animated_version) Access here
Movie 4 associated with Fig. 3 (Figure_3_g_i_animated_version_close_view) Access here
Movie 5 associated with Fig. 3 (Figure_3_g_i_animated_version_wide_view) Access here
Movie 6 associated with Fig. 4 (Figure_4a_animated_version) Access here
Movie 7 associated with Fig. 4 (Figure_4b_animated_version) Access here
Movie 8 associated with Fig. 4 (Figure_4c_animated_version) Access here
Movie 9 associated with Fig. 5 (Figure_5a_animated_version) Access here
Movie 10 associated with Fig. 5 (Figure_5b_animated_version) Access here
Movie 11 associated with Fig. 5 (Figure_5c_animated_version) Access here
Movie 12 associated with Fig. 6 (Figure_6_animated_version) Access here
Movie 13 associated with Fig. 10 (Figure_10_animated_version) Access here
Movie 14 associated with Fig. 12 (Figure_12b_animated_version) Access here
Movie 15 (Supplementary_movie_1) Access here
Movie 16 (Supplementary_movie_2) Access here
Movie 17 (Supplementary_movie_3) Access here
Movie 18 (Supplementary_movie_4) Access here
Acknowledgments
All of the data download, magnetogram/Dopplergram processing steps, FLCT velocity inversion, and PDFI electric-field inversion are handled using the ELECTRIC field Inversion Toolkit, ELECTRICIT software (Lumme et al. 2017, 2019). When it comes to the Dopplergram calibration, FLCT velocity inversion and PDFI electric-field inversion, the toolkit acts as a wrapper for a Fortran Dopplergram calibration library by B. T. Welsch, the FLCT code v1.06 (http://solarmuri.ssl.berkeley.edu/~fisher/public/software/FLCT/) and the PDFI_SS software library (http://cgem.ssl.berkeley.edu/cgi-bin/cgem/PDFI_SS). The squashing factor and twist number maps were computed using the qfactor code by Liu et al. (2016) available at http://staff.ustc.edu.cn/~rliu/qfactor.html with modifications by D. J. Price. This research has made use of SunPy, an open-source and free community-developed solar data analysis package written in Python (Mumford et al. 2015). The vector magnetic-field, Dopplergram and EUV observations from the HMI and AIA instruments are courtesy of NASA/SDO and the HMI and AIA science teams. The STEREO SECCHI EUVI and COR data were accessed using UK Solar System Data Centre https://www.ukssdc.ac.uk/solar/stereo/data.html and ESA JHelioviewer (Müller et al. 2017) available at https://www.jhelioviewer.org/. E. Lumme acknowledges the doctoral program in particle physics and universe sciences (PAPU) of the University of Helsinki for financial support. B. T. Welsch acknowledges support from the NASA-LWS Targeted Research & Technology program under award 80NSSC19K0072. We acknowledge the ERC under the European Union’s Horizon 2020 Research and Innovation Programme Project 724391 (SolMAG), and Academy of Finland Project 310445 (SMASH). The results presented here have been achieved under the framework of the Finnish Centre of Excellence in Research of Sustainable Space (FORESAIL; Academy of Finland grant numbers 312390 and 336809), which we gratefully acknowledge.
References
- Afanasyev, A. N., Kazachenko, M. D., Fan, Y., Fisher, G. H., & Tremblay, B. 2021, ApJ, 919, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Antiochos, S. K., DeVore, C. R., & Klimchuk, J. A. 1999, ApJ, 510, 485 [Google Scholar]
- Aulanier, G., & Dudík, J. 2019, A&A, 621, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bobra, M. G., Sun, X., Hoeksema, J. T., et al. 2014, Sol. Phys., 289, 3549 [Google Scholar]
- Brueckner, G. E., Howard, R. A., Koomen, M. J., et al. 1995, Sol. Phys., 162, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, P. F. 2011, Liv. Rev. Sol. Phys., 8, 1 [Google Scholar]
- Cheung, M. C. M., & DeRosa, M. L. 2012, ApJ, 757, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Cheung, M. C. M., De Pontieu, B., Tarbell, T. D., et al. 2015, ApJ, 801, 83 [Google Scholar]
- Chintzoglou, G., Zhang, J., Cheung, M. C. M., & Kazachenko, M. 2019, ApJ, 871, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Dissauer, K., Veronig, A. M., Temmer, M., Podladchikova, T., & Vanninathan, K. 2018, ApJ, 855, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Domingo, V., Fleck, B., & Poland, A. I. 1995, Sol. Phys., 162, 1 [Google Scholar]
- Fan, Y. 2009, Liv. Rev. Sol. Phys., 6, 4 [Google Scholar]
- Fisher, G. H., & Welsch, B. T. 2008, in Subsurface and Atmospheric Influences on Solar Activity, eds. R. Howe, R. W. Komm, K. S. Balasubramaniam, & G. J. D. Petrie, ASP Conf. Ser., 383, 373, San Francisco [Google Scholar]
- Fisher, G. H., Welsch, B. T., Abbett, W. P., & Bercik, D. J. 2010, ApJ, 715, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, G. H., Abbett, W. P., Bercik, D. J., et al. 2015, Space Weather, 13, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, G. H., Kazachenko, M. D., Welsch, B. T., et al. 2020, ApJS, 248, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Gibb, G. P. S., Mackay, D. H., Green, L. M., & Meyer, K. A. 2014, ApJ, 782, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, S. E., Rachmeler, L. A., & White, S. M. 2017, Front. Astron. Space Sci., 4, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Gold, T., & Hoyle, F. 1960, MNRAS, 120, 89 [NASA ADS] [Google Scholar]
- Golub, L., Deluca, E., Austin, G., et al. 2007, Sol. Phys., 243, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Green, L. M., & Kliem, B. 2014, in Nature of Prominences and their Role in Space Weather, eds. B. Schmieder, J.-M. Malherbe, & S. T. Wu, IAU Symp., 300, 209 [Google Scholar]
- Green, L. M., Kliem, B., Török, T., van Driel-Gesztelyi, L., & Attrill, G. D. R. 2007, Sol. Phys., 246, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Green, L. M., Török, T., Vršnak, B., Manchester, W., & Veronig, A. 2018, Space Sci. Rev., 214, 46 [Google Scholar]
- Guo, Y., Xia, C., Keppens, R., Ding, M. D., & Chen, P. F. 2019, ApJ, 870, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, J. W., Hill, F., Hubbard, R. P., et al. 1996, Science, 272, 1284 [Google Scholar]
- Hayashi, K., Feng, X., Xiong, M., & Jiang, C. 2018, ApJ, 855, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Hoeksema, J. T., Liu, Y., Hayashi, K., et al. 2014, Sol. Phys., 289, 3483 [Google Scholar]
- Hoeksema, J. T., Abbett, W. P., Bercik, D. J., et al. 2020, ApJS, 250, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, R. A., Moses, J. D., Vourlidas, A., et al. 2008, Space Sci. Rev., 136, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Hudson, H. S., & Webb, D. F. 1997, Washington DC American Geophysical Union Geophysical Monograph Series, 99, 27 [NASA ADS] [Google Scholar]
- Inoue, S., Kusano, K., Büchner, J., & Skála, J. 2018, Nat. Commun., 9, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Janvier, M., Aulanier, G., & Démoulin, P. 2015, Sol. Phys., 290, 3425 [Google Scholar]
- Jiang, C., Wu, S. T., Feng, X., & Hu, Q. 2016, Nat. Commun., 7, 11522 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, C., Zou, P., Feng, X., et al. 2018, ApJ, 869, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Jing, J., Liu, C., Lee, J., et al. 2018, ApJ, 864, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, M. L., Kucera, T. A., Davila, J. M., et al. 2008, Space Sci. Rev., 136, 5 [Google Scholar]
- Kazachenko, M. D., Fisher, G. H., & Welsch, B. T. 2014, ApJ, 795, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Kazachenko, M. D., Fisher, G. H., Welsch, B. T., Liu, Y., & Sun, X. 2015, ApJ, 811, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Kilpua, E., Koskinen, H. E. J., & Pulkkinen, T. I. 2017, Liv. Rev. Sol. Phys., 14, 5 [Google Scholar]
- Kilpua, E. K. J., Pomoell, J., Price, D., Sarkar, R., & Asvestari, E. 2021, Front. Astron. Space Sci., 8, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Kliem, B., & Török, T. 2006, Phys. Rev. Lett., 96, 255002 [Google Scholar]
- Kliem, B., Su, Y. N., van Ballegooijen, A. A., & DeLuca, E. E. 2013, ApJ, 779, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Kosugi, T., Matsuzaki, K., Sakao, T., et al. 2007, Sol. Phys., 243, 3 [Google Scholar]
- Kumar, P., Park, S.-H., Cho, K.-S., & Bong, S.-C. 2013, Sol. Phys., 282, 503 [NASA ADS] [CrossRef] [Google Scholar]
- Leake, J. E., Linton, M. G., & Török, T. 2013, ApJ, 778, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [Google Scholar]
- Liu, Y., Hoeksema, J. T., Bobra, M., et al. 2014, ApJ, 785, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, R., Kliem, B., Titov, V. S., et al. 2016, ApJ, 818, 148 [Google Scholar]
- Liu, Y. A., Liu, Y. D., Hu, H., Wang, R., & Zhao, X. 2018, ApJ, 854, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Lumme, E., Pomoell, J., & Kilpua, E. K. J. 2017, Sol. Phys., 292, 191 [CrossRef] [Google Scholar]
- Lumme, E., Kazachenko, M., Fisher, G., et al. 2019, Sol. Phys., 294, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Lynch, B. J., Edmondson, J. K., Kazachenko, M. D., & Guidoni, S. E. 2016, ApJ, 826, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Mackay, D. H., & van Ballegooijen, A. A. 2006, ApJ, 641, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Mackay, D. H., & Yeates, A. R. 2012, Liv. Rev. Sol. Phys., 9, 6 [Google Scholar]
- Mackay, D. H., Green, L. M., & van Ballegooijen, A. 2011, ApJ, 729, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Mackay, D. H., DeVore, C. R., & Antiochos, S. K. 2014, ApJ, 784, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, R. L., Sterling, A. C., Hudson, H. S., & Lemen, J. R. 2001, ApJ, 552, 833 [Google Scholar]
- Moraitis, K., Sun, X., Pariat, É., & Linan, L. 2019, A&A, 628, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, D., Nicula, B., Felix, S., et al. 2017, A&A, 606, A10 [Google Scholar]
- Mumford, S. J., Christe, S., Pérez-Suárez, D., et al. 2015, Comput. Sci. Discovery, 8, 014009 [NASA ADS] [CrossRef] [Google Scholar]
- Pagano, P., Mackay, D. H., & Poedts, S. 2013, A&A, 554, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Palmerio, E., Kilpua, E. K. J., James, A. W., et al. 2017, Sol. Phys., 292, 39 [Google Scholar]
- Pariat, E., Valori, G., Démoulin, P., & Dalmasse, K. 2015, A&A, 580, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pariat, E., Leake, J. E., Valori, G., et al. 2017, A&A, 601, A125 [CrossRef] [EDP Sciences] [Google Scholar]
- Pesnell, W. D., Thompson, B. J., & Chamberlin, P. C. 2012, Sol. Phys., 275, 3 [Google Scholar]
- Pomoell, J., Lumme, E., & Kilpua, E. 2019, Sol. Phys., 294, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Price, D., Pomoell, J., Lumme, E., & Kilpua, E. 2019, A&A, 628, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raouafi, N. E., Patsourakos, S., Pariat, E., et al. 2016, Space Sci. Rev., 201, 1 [Google Scholar]
- Robbrecht, E., & Berghmans, D. 2004, A&A, 425, 1097 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sarp Yalim, M., Pogorelov, N., & Liu, Y. 2017, J. Phys. Conf. Ser., 837, 012015 [NASA ADS] [CrossRef] [Google Scholar]
- Scherrer, P. H., Schou, J., Bush, R. I., et al. 2012, Sol. Phys., 275, 207 [Google Scholar]
- Schou, J., Scherrer, P. H., Bush, R. I., et al. 2012, Sol. Phys., 275, 229 [Google Scholar]
- Schuck, P. W. 2008, ApJ, 683, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Schuck, P. W., & Antiochos, S. K. 2019, ApJ, 882, 151 [Google Scholar]
- Shibata, K., & Magara, T. 2011, Liv. Rev. Sol. Phys., 8, 6 [Google Scholar]
- Spencer, A. J. M. 2004, Continuum Mechanics (Courier Corporation) [Google Scholar]
- Titov, V. S., & Démoulin, P. 1999, A&A, 351, 707 [NASA ADS] [Google Scholar]
- Titov, V. S., Hornig, G., & Démoulin, P. 2002, J. Geophys. Res. (Space Phys.), 107, 1164 [Google Scholar]
- Török, T., & Kliem, B. 2003, A&A, 406, 1043 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Török, T., & Kliem, B. 2005, ApJ, 630, L97 [Google Scholar]
- Török, T., & Kliem, B. 2007, Astron. Nachr., 328, 743 [CrossRef] [Google Scholar]
- Török, T., Kliem, B., & Titov, V. S. 2004, A&A, 413, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tremblay, B., & Vincent, A. 2015, Sol. Phys., 290, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Valori, G., Démoulin, P., & Pariat, E. 2012, Sol. Phys., 278, 347 [Google Scholar]
- van Ballegooijen, A. A., & Martens, P. C. H. 1989, ApJ, 343, 971 [Google Scholar]
- van Ballegooijen, A. A., Priest, E. R., & Mackay, D. H. 2000, ApJ, 539, 983 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, W., Liu, R., Wang, Y., et al. 2017, Nat. Commun., 8, 1330 [Google Scholar]
- Warnecke, J., & Peter, H. 2019, A&A, 624, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Webb, D. F., & Howard, T. A. 2012, Liv. Rev. Sol. Phys., 9, 3 [Google Scholar]
- Weinzierl, M., Yeates, A. R., Mackay, D. H., Henney, C. J., & Arge, C. N. 2016, ApJ, 823, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Welsch, B. T., Abbett, W. P., De Rosa, M. L., et al. 2007, ApJ, 670, 1434 [NASA ADS] [CrossRef] [Google Scholar]
- Welsch, B. T., Kusano, K., Yamamoto, T. T., & Muglach, K. 2012, ApJ, 747, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Wiegelmann, T., & Sakurai, T. 2012, Liv. Rev. Sol. Phys., 9, 5 [Google Scholar]
- Wiegelmann, T., Petrie, G. J. D., & Riley, P. 2017, Space Sci. Rev., 210, 249 [CrossRef] [Google Scholar]
- Yang, W. H., Sturrock, P. A., & Antiochos, S. K. 1986, ApJ, 309, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Yardley, S. L., Green, L. M., van Driel-Gesztelyi, L., Williams, D. R., & Mackay, D. H. 2018, ApJ, 866, 8 [Google Scholar]
- Yeates, A. R. 2017, ApJ, 836, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Yeates, A. R., Amari, T., Contopoulos, I., et al. 2018, Space Sci. Rev., 214, 99 [CrossRef] [Google Scholar]
- Yee, K. 1966, IEEE Trans. Ant. and Prop., 14, 302 [Google Scholar]
- Zuccarello, F. P., Pariat, E., Valori, G., & Linan, L. 2018, ApJ, 863, 41 [Google Scholar]
Appendix A: Supplementary figures and tables
 |
Fig. A.1. SDO/AIA 211 Å EUV observation of the M1.0 flare at the eastern end of the AR11726 above a parasitic negative polarity on 22 April 2013, 10:30:01 UT. Lime dashed curves outline the associated fan-spine topology. |
Other major eruptive activity associated with NOAA AR 11726 omitted from this article. The table does not include all flares, for which a thorough listing of ≥C-class events can be found, e.g., from the Solar Monitor https://www.solarmonitor.org/. The classifications are based on our general study of the events as well as on the classifications of the low-coronal signatures defined by Yardley et al. (2018). Column entitled “simulation structures” contains information about the associated features in our data-driven simulation (Sect. 3).
All Tables
Eruption features observed in the EUV and white-light coronagraph data by SDO/AIA, STEREO A/SECCHI EUVI and COR2, and SOHO/LASCO instruments.
Other major eruptive activity associated with NOAA AR 11726 omitted from this article. The table does not include all flares, for which a thorough listing of ≥C-class events can be found, e.g., from the Solar Monitor https://www.solarmonitor.org/. The classifications are based on our general study of the events as well as on the classifications of the low-coronal signatures defined by Yardley et al. (2018). Column entitled “simulation structures” contains information about the associated features in our data-driven simulation (Sect. 3).
All Figures
 |
Fig. 1. Bz magnetogram of NOAA AR 11726 on 22 April, 2013 08:36 UT taken from the processed and re-projected SDO/HMI vector magnetogram series (Sect. 3.2) Please avoid the use of the slashes. For details, refer to Sect. 2.9 of the language guide. Please check for this throughout. The central structures related to the activity discussed in this paper have been pinpointed. The vertical white dashed line shows the photospheric cut of the x = 76 Mm plane used to find and track a pre-eruptive flux rope system in our data-driven simulation (Sect. 4). An animated version of the figure can be found online. |
| In the text | |
 |
Fig. 2. Evolution of total unsigned magnetic flux and flux imbalance in NOAA AR 11726 derived from the processed and re-projected SDO/HMI Bz magnetogram series (Sect. 3.2), where the pixels |B|< 250 Mx cm−2 were masked to zero to avoid spurious effects arising from the noise-dominated weak-field pixels. The black curve shows the evolution of the unsigned flux over the entire active region patch, whereas the green curve shows the unsigned flux evolution of the small western bipole (see Fig. 1) multiplied by a factor of 30 to make its scale comparable to the unsigned flux of the entire active region. The red dashed curve shows the relative flux imbalance of the active region. The vertical dotted line shows the time of the weak CME eruption of 22 April 2013, 08:40 UT that we focus on in this study. |
| In the text | |
 |
Fig. 3. Remote sensing EUV and white-light observations of the eruption from NOAA AR 11726 from 22 April 2013, 08:40 UT onwards. Panels a–c show SDO/AIA observations with photospheric Bz plotted as ±100 Mx cm−2 contours (blue for negative) over the region included in the vector magnetogram series (Fig. 1). Panel a: pre-eruptive state at 08:36 UT, where the loop system erupting from 08:40 UT onwards is highlighted by the dashed white curve, the location of the solar limb in STEREO A/EUVI observations is shown by the lime dashed curve, and the main structures of the active region are pinpointed by arrows. Panel b: U-shaped location of the expulsion of the material from 09:07 UT onwards (the dashed U-shaped curve), and the likely correlated coronal structure at 09:30:32 UT to the southeast outlined by a red dashed curve. Panel c: post-eruption arcades as well as the site of the M1.0 flare on 10:22 UT. Panels d–f: STEREO A SECCHI/EUVI 195 Å observations at times consistent with panels a–c. Panel d: approximate position and shape of the Cartesian simulation box explained in Sect. 3. Panel e: approximate trajectory of the expelled plasma from panel b (white dashed lines). Panels g–i: composite images of STEREO A/EUVI 195 Å, COR 1, and COR2 white-light observations of the eruption (created using JHelioviewer software Müller et al. 2017). The main coronagraph structures and their visually traced trajectories are illustrated by the white dashed curves and the white dashed arrows, respectively. Movie versions of panels a–c, d–f, and g–h are available online. |
| In the text | |
 |
Fig. 4. Simulation parameters at slice x = 76 Mm revealing the existence of a flux rope system on 22 April 2013 at 08:36 UT, just before the onset of the eruption discussed in Sect. 2.2. Panel a: logarithm of the current density scaled by the magnetic field magnitude log10(J/B) (white-purple color, saturated at −2.5 and −1) and the direction of the magnetic field projected to the plane Byz/Byz| as black arrows. The Bz component is plotted at the lower (z = 0) photospheric boundary of the simulation in black-white coloring saturated at ±0.01 T(=±100 Mx cm−2). Panel b: log-scaled magnetic squashing factor log10Q (black-white color, saturated at 1 and 5). Panel c: twist number of the magnetic field lines Tw (blue-red color, saturated at −1 and 1) and the direction of the Lorentz force projected to the plane (J × B)yz/|(J × B)yz| as black arrows. The lime and orange dashed curves in panels b and c enclose the regions over which the field lines of the observed flux rope system pass the x = 76 Mm plane. The lime curve encloses the main FR and the orange curve the intertwined FR (see text for exact definitions). Magenta dashed curves in these panels show the QSL boundary enclosing the FR system (also illustrated in Fig. 7b). Animated versions of each panel are available online. |
| In the text | |
 |
Fig. 5. Simulated field lines of flux rope system identified from the current density, squashing factor and twist maps at the x = 76 Mm plane on 22 April 2013 at 08:36 UT, just before the onset of the observed eruption at from 08:40 UT onwards (Sect. 2.2). Panel a: main FR field lines viewed from the southeast. The lines are rainbow-colored based on the seed point position of the lines at the x = 76 Mm plane. The Bz magnetic field component is plotted at the photospheric z = 0 lower boundary of the simulation domain in black-white coloring saturated at ±100 Mx cm−2 (=0.01 T). Panel b: intertwined FR with yellow-purple coloring. Panel c: both FRs viewed from the northwest. All plotted field lines are based on finding a coherent region on the x = 76 Mm plane where the condition [(log10Q ≤ 1.5)∧(Tw ≤ −1)] is fulfilled. Animated versions of each panel can be found online. For panels a and b, online movies 3 and 4 also offer the view from the northwest, as in panel c. |
| In the text | |
 |
Fig. 6. Base difference image between AIA 193 Å observations on 22 April at 08:24 UT and 09:24 UT. The AIA images are re-projected onto the local Cartesian coordinates of the re-projected magnetogram series forming the bottom of the simulation box (Sect. 3.2 and Fig. 1). The blue and red contours correspond to the −100 and 100 Mx cm−2 contours of the photospheric Bz magnetic field component, respectively. The lime and orange curves enclose the approximate position of the negative- and positive-polarity footpoints, respectively, of the pre-eruptive flux rope system (both main and intertwined FRs) at 08:36 UT, determined from the simulation. The magenta dashed curve encloses the dimming region that includes the negative-polarity footpoints of the FR system. An animated version of this figure can be found online. |
| In the text | |
 |
Fig. 7. Panel a: Hinode/XRT soft X-ray observation of NOAA AR 11726 on 22 April 2013 at 05:52:15 UT. The white box encloses a collection of loops with enhanced emission emanating from the western bipole and connecting to the western sunspot. Panel b: snapshot of the simulation on 22 April 2013 at 06:00 UT, where the rainbow-colored field lines correspond to the upper section of the QSL boundary enclosing the FR system (magenta dashed curves in Figs. 4b and c). As indicated by the white box, the QSL field lines have a similar position and shape to the high-emission XRT loops in panel a. The gray scale background shows the photospheric Bz magnetic field component saturated at ±100 Mx cm−2 (black for negative), and the blue and red contours correspond similarly to ±100 Mx cm−2 limits (blue for negative). |
| In the text | |
 |
Fig. 8. Structures near the two null-points over the western bipole in AIA 304 Å observations and in the simulation. Panel a: apparent J-shaped brightening in the AIA 304 Å observations on 21 April 2013 at 22:24 UT, east of the western bipole. The J-shape can be extrapolated to form a very weak S shape connecting to the western negative polarity sunspot (white dashed line). Panel b: clearer forward S at the same position 22:36 UT. Panel c: J-shaped structure in the simulation on 21 April at 22:00 UT (white-dashed curve) arising from the field lines connecting the western positive polarity to a low-lying null and the western sunspot (yellow-purple-colored field lines). Panel d: shows how the field lines in panel c are part of a larger positively twisted collection of arcades (yellow-purple-colored field lines). Rainbow-colored lines illustrate the positively-twisted QSL boundary field overlying the main FR (also shown in Fig. 7b at a later time), which connect to a null-point above the western bipole. |
| In the text | |
 |
Fig. 9. Time evolution of mean and minimum twist numbers |
| In the text | |
 |
Fig. 10. Map of vertical component of vorticity (∇×Vh, ⊥)⋅ez (orange-to-purple color scale, saturated at ±10−4 s−1) near the negative footpoints of the main FR (pink dots) and the intertwined FR (black dots) within the western sunspot (see Fig. 1) during the formation processes of the FRs on 21 April 2013 at 19:00 UT. The blue and red contours correspond to the photospheric Bz of ±100 Mx cm−2 (blue for negative). The black dashed curve encloses a persistent patch of positive vorticity that encloses the FR footpoints. An animated version of this figure is available online. |
| In the text | |
 |
Fig. 11. Twisting rate of mean twist |
| In the text | |
 |
Fig. 12. Coronal energy (upper panel) and helicity (lower panel) budgets and non-potentiality ratios (see text for details). Solid curves show the total budgets (Em and HR) for three of our simulations (see text for details). Dashed line shows the non-potential component of the total budget ( |
| In the text | |
 |
Fig. 13. Coronal energy (upper panel) and helicity (lower panel) budgets and non-potentiality ratios (see the text for details) for the default simulation computed both in the entire domain (black curves), and in the western region x > 3 Mm enclosing the FR system of interest (red curves). Solid curves show the total budgets for three of our simulations (see text for details). Dashed line shows the non-potential component of the total budget (either |
| In the text | |
 |
Fig. 14. Magnetic configuration of the higher coronal null-point (Fig. 8d) and its relationship with the main FR depicted on 21 April 2013 at 18:00 UT, when the main FR was just forming. Panel a: field-line configuration around the null-point (orange-white lines), the main FR (green-white lines), and field lines originating from Region 3 in panel b (black-white lines). The photospheric distribution of Bz is shown in gray scale (saturated at ±100 Mx cm−2, black for negative) and blue/red contours (±100 Mx cm−2, blue for negative). The purple-to-white color plot shows the magnetic squashing factor log10Q at horizontal plane z = 0.729 Mm ranging from 1 to 5, shown only in high-Q regions where log10Q ≥ 1.25. The blue-red color plot shows the twist number in the same horizontal plane including only the regions where [(log10Q ≤ 1.25)∧(Tw ≤ −0.25)]. Panel b: zooms into the positive-polarity photospheric footpoints of the field-line systems in panel a. The dashed lines outline regions of consistent magnetic connectivity for each field-line system, labeled Regions 1–3 with coloring consistent with that of panel a. The black patch in Region 2 shows the position where the footpoints of the main FR start to appear. An animated version of panel b is available online. |
| In the text | |
 |
Fig. A.1. SDO/AIA 211 Å EUV observation of the M1.0 flare at the eastern end of the AR11726 above a parasitic negative polarity on 22 April 2013, 10:30:01 UT. Lime dashed curves outline the associated fan-spine topology. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.