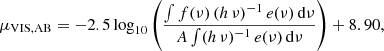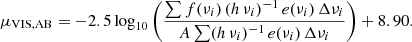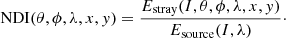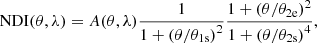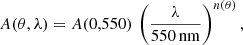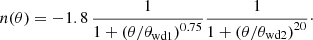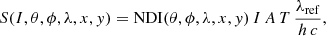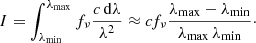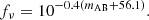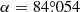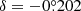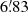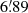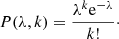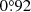| Issue |
A&A
Volume 657, January 2022
|
|
|---|---|---|
| Article Number | A92 | |
| Number of page(s) | 21 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/202141935 | |
| Published online | 18 January 2022 | |
Euclid preparation
XVI. Exploring the ultra-low surface brightness Universe with Euclid/VIS
1
NASA Ames Research Center, Moffett Field, CA 94035, USA
e-mail: a.s.borlaff@nasa.gov
2
ESAC/ESA, Camino Bajo del Castillo s/n., Urb. Villafranca del Castillo, 28692 Villanueva de la Cañada, Madrid, Spain
3
FRACTAL S.L.N.E., Calle Tulipán 2, Portal 13 1A, 28231 Las Rozas de Madrid, Spain
4
European Space Agency/ESTEC, Keplerlaan 1, 2201 AZ Noordwijk, The Netherlands
5
Departamento de Física Teórica, Atómica y Óptica, Universidad de Valladolid, 47011 Valladolid, Spain
6
Instituto de Astrofísica e Ciências do Espaço, Faculdade de Ciências, Universidade de Lisboa, Tapada da Ajuda, 1349-018 Lisboa, Portugal
7
AIM, CEA, CNRS, Université Paris-Saclay, Université de Paris, 91191 Gif-sur-Yvette, France
8
Observatoire de Paris, PSL Research University 61, Avenue de l’Observatoire, 75014 Paris, France
9
Observatoire Astronomique de Strasbourg (ObAS), Université de Strasbourg – CNRS, UMR 7550, Strasbourg, France
10
Institute of Cosmology and Gravitation, University of Portsmouth, Portsmouth PO1 3FX, UK
11
INAF-Osservatorio Astronomico di Brera, Via Brera 28, 20122 Milano, Italy
12
INAF-Osservatorio di Astrofisica e Scienza dello Spazio di Bologna, Via Piero Gobetti 93/3, 40129 Bologna, Italy
13
Mullard Space Science Laboratory, University College London, Holmbury St Mary, Dorking, Surrey RH5 6NT, UK
14
IFPU, Institute for Fundamental Physics of the Universe, Via Beirut 2, 34151 Trieste, Italy
15
SISSA, International School for Advanced Studies, Via Bonomea 265, 34136 Trieste, TS, Italy
16
INFN, Sezione di Trieste, Via Valerio 2, 34127 Trieste, TS, Italy
17
INAF-Osservatorio Astronomico di Trieste, Via G. B. Tiepolo 11, 34131 Trieste, Italy
18
Universidad de la Laguna, 38206 San Cristóbal de La Laguna, Tenerife, Spain
19
Instituto de Astrofísica de Canarias, Calle Vía Láctea s/n, 38204 San Cristóbal de la Laguna, Tenerife, Spain
20
Dipartimento di Fisica e Astronomia, Universitá di Bologna, Via Gobetti 93/2, 40129 Bologna, Italy
21
INFN-Sezione di Bologna, Viale Berti Pichat 6/2, 40127 Bologna, Italy
22
Universitäts-Sternwarte München, Fakultät für Physik, Ludwig-Maximilians-Universität München, Scheinerstrasse 1, 81679 München, Germany
23
Max Planck Institute for Extraterrestrial Physics, Giessenbachstr. 1, 85748 Garching, Germany
24
INAF-Osservatorio Astrofisico di Torino, Via Osservatorio 20, 10025 Pino Torinese, TO, Italy
25
Department of Astronomy, University of Geneva, Ch. d’Ecogia 16, 1290 Versoix, Switzerland
26
INFN-Sezione di Roma Tre, Via della Vasca Navale 84, 00146 Roma, Italy
27
Department of Mathematics and Physics, Roma Tre University, Via della Vasca Navale 84, 00146 Rome, Italy
28
INAF-Osservatorio Astronomico di Roma, Via Frascati 33, 00078 Monteporzio Catone, Italy
29
INAF-Osservatorio Astronomico di Capodimonte, Via Moiariello 16, 80131 Napoli, Italy
30
Centro de Astrofísica da Universidade do Porto, Rua das Estrelas, 4150-762 Porto, Portugal
31
Instituto de Astrofísica e Ciências do Espaço, Universidade do Porto, CAUP, Rua das Estrelas, 4150-762 Porto, Portugal
32
INFN-Bologna, Via Irnerio 46, 40126 Bologna, Italy
33
Dipartimento di Fisica e Scienze della Terra, Universitá degli Studi di Ferrara, Via Giuseppe Saragat 1, 44122 Ferrara, Italy
34
INAF, Istituto di Radioastronomia, Via Piero Gobetti 101, 40129 Bologna, Italy
35
Institut de Recherche en Astrophysique et Planétologie (IRAP), Université de Toulouse, CNRS, UPS, CNES, 14 Av. Edouard Belin, 31400 Toulouse, France
36
INFN-Sezione di Torino, Via P. Giuria 1, 10125 Torino, Italy
37
Dipartimento di Fisica, Universitá degli Studi di Torino, Via P. Giuria 1, 10125 Torino, Italy
38
Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS, Laboratoire Lagrange, Bd de l’Observatoire, CS 34229, 06304 Nice Cedex 4, France
39
INAF-IASF Milano, Via Alfonso Corti 12, 20133 Milano, Italy
40
Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Campus UAB, 08193 Bellaterra, Barcelona, Spain
41
Institute of Space Sciences (ICE, CSIC), Campus UAB, Carrer de Can Magrans, s/n, 08193 Barcelona, Spain
42
Institut d’Estudis Espacials de Catalunya (IEEC), Carrer Gran Capitá 2-4, 08034 Barcelona, Spain
43
Dipartimento di Fisica e Astronomia “Augusto Righi” – Alma Mater Studiorum Universitá di Bologna, Via Piero Gobetti 93/2, 40129 Bologna, Italy
44
Observatoire de Sauverny, Ecole Polytechnique Fédérale de Lausanne, 1290 Versoix, Switzerland
45
Department of Physics “E. Pancini”, University Federico II, Via Cinthia 6, 80126 Napoli, Italy
46
INFN Section of Naples, Via Cinthia 6, 80126 Napoli, Italy
47
INAF-Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
48
Institut National de Physique Nucléaire et de Physique des Particules, 3 Rue Michel-Ange, 75794 Paris Cédex 16, France
49
Centre National d’Etudes Spatiales, Toulouse, France
50
Institute for Astronomy, University of Edinburgh, Royal Observatory, Blackford Hill, Edinburgh EH9 3HJ, UK
51
Jodrell Bank Centre for Astrophysics, School of Physics and Astronomy, University of Manchester, Oxford Road, Manchester M13 9PL, UK
52
European Space Agency/ESRIN, Largo Galileo Galilei 1, 00044 Frascati, Roma, Italy
53
Univ. Lyon, Univ. Claude Bernard Lyon 1, CNRS/IN2P3, IP2I Lyon, UMR 5822, 69622 Villeurbanne, France
54
University of Lyon, UCB Lyon 1, CNRS/IN2P3, IUF, IP2I, Lyon, France
55
Departamento de Física, Faculdade de Ciências, Universidade de Lisboa, Edifício C8, Campo Grande, 1749-016 Lisboa, Portugal
56
Instituto de Astrofísica e Ciências do Espaço, Faculdade de Ciências, Universidade de Lisboa, Campo Grande, 1749-016 Lisboa, Portugal
57
Université Paris-Saclay, CNRS, Institut d’Astrophysique Spatiale, 91405 Orsay, France
58
Department of Physics, Oxford University, Keble Road, Oxford OX1 3RH, UK
59
INFN-Padova, Via Marzolo 8, 35131 Padova, Italy
60
INAF-Istituto di Astrofisica e Planetologia Spaziali, Via del Fosso del Cavaliere, 100, 00100 Roma, Italy
61
INAF-IASF Bologna, Via Piero Gobetti 101, 40129 Bologna, Italy
62
Institut d’Astrophysique de Paris, 98bis Boulevard Arago, 75014 Paris, France
63
Université de Paris, CNRS, Astroparticule et Cosmologie, 75013 Paris, France
64
Research Program in Systems Oncology, Faculty of Medicine, University of Helsinki, Helsinki, Finland
65
Department of Physics, University of Helsinki, PO Box 64, 00014 Helsinki, Finland
66
INAF-Osservatorio Astronomico di Padova, Via dell’Osservatorio 5, 35122 Padova, Italy
67
Institute of Theoretical Astrophysics, University of Oslo, PO Box 1029, Blindern, 0315 Oslo, Norway
68
Jet Propulsion Laboratory, California Institute of Technology, 4800 Oak Grove Drive, Pasadena, CA 91109, USA
69
von Hoerner & Sulger GmbH, SchloßPlatz 8, 68723 Schwetzingen, Germany
70
Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
71
Department of Physics and Helsinki Institute of Physics, University of Helsinki, Gustaf Hällströmin katu 2, 00014 Helsinki, Finland
72
Aix-Marseille Univ., CNRS/IN2P3, CPPM, Marseille, France
73
Université de Genève, Département de Physique Théorique and Centre for Astroparticle Physics, 24 Quai Ernest-Ansermet, 1211 Genève 4, Switzerland
74
Leiden Observatory, Leiden University, Niels Bohrweg 2, 2333 CA Leiden, The Netherlands
75
Helsinki Institute of Physics, University of Helsinki, Gustaf Hällströmin katu 2, Helsinki, Finland
76
NOVA Optical Infrared Instrumentation Group at ASTRON, Oude Hoogeveensedijk 4, 7991 PD Dwingeloo, The Netherlands
77
Centre de Calcul de l’IN2P3, 21 Avenue Pierre de Coubertin, 69627 Villeurbanne Cedex, France
78
Dipartimento di Fisica “Aldo Pontremoli”, Universitá degli Studi di Milano, Via Celoria 16, 20133 Milano, Italy
79
INFN-Sezione di Milano, Via Celoria 16, 20133 Milano, Italy
80
Argelander-Institut für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
81
Instituto de Física Teórica UAM-CSIC, Campus de Cantoblanco, 28049 Madrid, Spain
82
Aix-Marseille Univ., CNRS, CNES, LAM, Marseille, France
83
Instituto de Astrofísica de Andalucía, CSIC, Glorieta de la Astronomía, 18080 Granada, Spain
84
Centre for Extragalactic Astronomy, Department of Physics, Durham University, South Road, Durham DH1 3LE, UK
85
Institut für Theoretische Physik, University of Heidelberg, Philosophenweg 16, 69120 Heidelberg, Germany
86
Zentrum für Astronomie, Universität Heidelberg, Philosophenweg 12, 69120 Heidelberg, Germany
87
Istituto Nazionale di Astrofisica (INAF) – Osservatorio di Astrofisica e Scienza dello Spazio (OAS), Via Gobetti 93/3, 40127 Bologna, Italy
88
California Institute of Technology, 1200 E California Blvd, Pasadena, CA 91125, USA
89
ICC & CEA, Department of Physics, Durham University, South Road, DH1 3LE Durham, UK
90
INFN, Sezione di Lecce, Via per Arnesano, CP-193, 73100 Lecce, Italy
91
Department of Mathematics and Physics E. De Giorgi, University of Salento, Via per Arnesano, CP-I93, 73100 Lecce, Italy
92
Department of Physics and Astronomy, University of Aarhus, Ny Munkegade 120, 8000 Aarhus C, Denmark
93
Perimeter Institute for Theoretical Physics, Waterloo, Ontario N2L 2Y5, Canada
94
Department of Physics and Astronomy, University of Waterloo, Waterloo, Ontario N2L 3G1, Canada
95
Centre for Astrophysics, University of Waterloo, Waterloo, Ontario N2L 3G1, Canada
96
Institute of Space Science, Bucharest 077125, Romania
97
Institute for Computational Science, University of Zurich, Winterthurerstrasse 190, 8057 Zurich, Switzerland
98
Departamento de Astrofísica, Universidad de La Laguna, 38206 La Laguna, Tenerife, Spain
99
Dipartimento di Fisica e Astronomia “G. Galilei”, Universitá di Padova, Via Marzolo 8, 35131 Padova, Italy
100
Departamento de Física, FCFM, Universidad de Chile, Blanco Encalada, 2008 Santiago, Chile
101
Centre for Electronic Imaging, Open University, Walton Hall, Milton Keynes MK7 6AA, UK
102
Centro de Investigaciones Energéticas, Medioambientales y Tecnológicas (CIEMAT), Avenida Complutense 40, 28040 Madrid, Spain
103
Universidad Politécnica de Cartagena, Departamento de Electrónica y Tecnología de Computadoras, 30202 Cartagena, Spain
104
Kapteyn Astronomical Institute, University of Groningen, PO Box 800, 9700 AV Groningen, The Netherlands
105
Department of Physics, University of Jyväskylä, PO Box 35 (YFL), 40014 Jyväskylä, Finland
106
Infrared Processing and Analysis Center, California Institute of Technology, Pasadena, CA 91125, USA
107
Department of Physics and Astronomy, University College London, Gower Street, London WC1E 6BT, UK
Received:
2
August
2021
Accepted:
18
August
2021
Context. While Euclid is an ESA mission specifically designed to investigate the nature of dark energy and dark matter, the planned unprecedented combination of survey area (∼15 000 deg2), spatial resolution, low sky-background, and depth also make Euclid an excellent space observatory for the study of the low surface brightness Universe. Scientific exploitation of the extended low surface brightness structures requires dedicated calibration procedures that are yet to be tested.
Aims. We investigate the capabilities of Euclid to detect extended low surface brightness structure by identifying and quantifying sky-background sources and stray-light contamination. We test the feasibility of generating sky flat-fields to reduce large-scale residual gradients in order to reveal the extended emission of galaxies observed in the Euclid survey.
Methods. We simulated a realistic set of Euclid/VIS observations, taking into account both instrumental and astronomical sources of contamination, including cosmic rays, stray-light, zodiacal light, interstellar medium, and the cosmic infrared background, while simulating the effects of background sources in the field of view.
Results. We demonstrate that a combination of calibration lamps, sky flats, and self-calibration would enable recovery of emission at a limiting surface brightness magnitude of μlim = 29.5−0.27+0.08 mag arcsec−2 (3σ, 10 × 10 arcsec2) in the Wide Survey, and it would reach regions deeper by 2 mag in the Deep Surveys.
Conclusions.Euclid/VIS has the potential to be an excellent low surface brightness observatory. Covering the gap between pixel-to-pixel calibration lamp flats and self-calibration observations for large scales, the application of sky flat-fielding will enhance the sensitivity of the VIS detector at scales larger than 1″, up to the size of the field of view, enabling Euclid to detect extended surface brightness structures below μlim = 31 mag arcsec−2 and beyond.
Key words: instrumentation: detectors / techniques: image processing / space vehicles: instruments / techniques: photometric / methods: observational / galaxies: general
© ESO 2022
1. Introduction
Deep and wide imaging surveys are the next frontier for many studies in galaxy evolution and cosmology. The study of the structure of stellar halos (Arp & Bertola 1969; Ibata et al. 2007; Trujillo & Fliri 2016; Buitrago et al. 2017), the intracluster light (de Vaucouleurs & de Vaucouleurs 1970; Mihos 2004; Montes 2019; Montes et al. 2021), including the traces of their assembly such as tidal tails, shells, and faint satellites (Zwicky 1952; Arp 1966; Malin & Carter 1980; Schweizer & Seitzer 1988; Mihos et al. 2005; Martínez-Delgado et al. 2010, 2015; Bilek & Duc 2021), or the detection of the dim ultra-diffuse galaxies (Sandage & Binggeli 1984; van Dokkum et al. 2018; Trujillo et al. 2019) provide critical information about the past evolution of the Universe, and are strong tests for the cold dark matter standard cosmological model (ΛCDM, White & Rees 1978; Bullock & Johnston 2005; Cooper et al. 2010; Pillepich et al. 2014). With increasing astronomical image depth, these fields are less affected by the statistical uncertainties of the sky noise and more dominated by systematic biases, such as background gradients, flat-fielding residuals, or the loss of extended sources due to sky oversubtraction, which require special observing techniques and dedicated calibration procedures to recover the full low surface brightness potential of the observatory (Andreon 2002; Ferrarese et al. 2012; Duc et al. 2015; Trujillo & Fliri 2016). These effects severely harm the capability of space- and ground-based surveys to discover and study the structures that are hidden at the very low surface brightness (LSB) limits of the astronomical images.
Even in space-based observations, one of the most dominant systematic effects in deep cosmological surveys is light gradient contamination (we refer to Mihos 2019, for a review on the current challenges in deep imaging). The sky background is a combination of many natural and instrumental effects (i.e., zodiacal light, Earth atmosphere emission, infrared thermal emission, point-spread function contamination, and flat-fielding residuals). Space observations present a much lower sky background than ground-based observations, thus increasing the detection capabilities even with shorter exposure times. The most common method for background correction is the subtraction of a two-dimensional sky background model with a certain typical variation scale from the image itself (i.e., Source Extractor, Bertin & Arnouts 1996). While this approach is adequate for the compact source science, these methods are highly sensitive to the accuracy of the fit and the size of the mesh. They tend to oversubtract the outskirts of the extended objects and create regions with artificial negative fluxes around them (we refer to Aihara et al. 2018, for a discussion of this effect on the first versions of the Hyper Suprime-Cam Subaru Strategic Program Survey and possible solutions). This effect is particularly common in the mosaics of deep cosmological surveys (see Hubble Space Telescope ACS GOODS-North, GOODS-South, and WFC3/IR XDF mosaics, Giacconi et al. 2002; Giavalisco et al. 2004; Beckwith et al. 2006; Koekemoer et al. 2013; Illingworth et al. 2013) and can also severely affect the detection of faint compact sources. These artifacts result from the sky model inclusion of emission of extended sources such as galaxies or cirrus that are deeply buried in the background noise of the individual images at intensity levels significantly below the 1σ limit (Akhlaghi & Ichikawa 2015). If not appropriately masked, the extended source emission can be confused with the background and subtracted. Thus, careful masking of sources and robust statistics are required to avoid overestimating the sky background.
Euclid (Laureijs et al. 2011) is a space mission designed to investigate the nature of dark energy and dark matter through two specific cosmological probes, weak lensing and galaxy clustering, using the Euclid Visual instrument (VIS, Cropper et al. 2014) for optical imaging, and the Near-Infrared Spectrometer and Photometer instrument (NISP, Maciaszek et al. 2014). Euclid’s combination of large survey area (Wide Survey: 15 000 deg2, Deep Survey: 40 deg2, see Fig. 1), high spatial resolution (full width at half maximum, 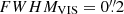 ,
, 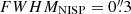 ), and depth of both VIS (optical, broad single bandpass 560 − 900 nm) and NISP (near-infrared – NIR – Y, J and H) is also ideal for the study of the low surface brightness limits of extended structures, such as Galactic dust cirri, extragalactic shells and tidal tails, ultra-diffuse galaxies, and even the cosmic infrared background (CIB). High spatial resolution reduces the effect of confusion by avoiding source blending, improving the sky background correction and allowing different tracers for low surface brightness structures, such as the identification of globular clusters (Montes et al. 2020). In the present article, we focus on the VIS detector, whose combination of high-resolution broadband sensitivity, wide field-of-view (FOV), purely reflective design, and exceptional point-spread function (PSF) stability is highly advantageous for the study of the structure of galaxies.
), and depth of both VIS (optical, broad single bandpass 560 − 900 nm) and NISP (near-infrared – NIR – Y, J and H) is also ideal for the study of the low surface brightness limits of extended structures, such as Galactic dust cirri, extragalactic shells and tidal tails, ultra-diffuse galaxies, and even the cosmic infrared background (CIB). High spatial resolution reduces the effect of confusion by avoiding source blending, improving the sky background correction and allowing different tracers for low surface brightness structures, such as the identification of globular clusters (Montes et al. 2020). In the present article, we focus on the VIS detector, whose combination of high-resolution broadband sensitivity, wide field-of-view (FOV), purely reflective design, and exceptional point-spread function (PSF) stability is highly advantageous for the study of the structure of galaxies.
 |
Fig. 1. Euclid/VIS stellar flux density map, based on Gaia (Gaia Collaboration 2016, 2018) and Sahlmann et al. (2016) catalogs: Black contours: footprint of a proxy of the Euclid/VIS Survey (Scaramella et al. 2021). The darkened regions, corresponding to the peak of the Milky Way emission, lie outside the footprint. The three regions marked with orange contours correspond to the Deep North, Deep South, and Deep Fornax fields. Color background: stellar flux density per HEALpix cell. The brightest region corresponds to the Galactic plane, a region avoided by the Euclid footprint. See the bottom color bar for the scaling. Red lines: projected trajectories of the main Solar System bodies (Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, and Neptune) as seen by Euclid during the mission, following the ecliptic plane (Giorgini et al. 2001). |
The VIS instrument uses calibration lamps to create flat fields with a high signal-to-noise ratio (S/N) for the correction of the pixel response non-uniformity (PRNU). The lamps directly illuminate the focal plane. The flats are acquired on sky as follows: the exposure starts with the shutter opening movement, which lasts three seconds, the lamp illuminates the focal plane (up to two seconds), the shutter closes, and the exposure stops. These flats therefore combine the sky background, astrophysical sources, shutter illumination nonuniformity, and the direct illumination by the flat lamp. By dithering the telescope, the astrophysical sources can be removed statistically, and the PRNU can be corrected for with high precision on spatial scales smaller than 100 pixels. On larger scales, the shutter illumination nonuniformity, the Lambertian cosine law for the calibration lamp, and any intrinsic illumination properties of the telescope optics will result in nonuniform illumination. Hence, the relative photometric zeropoint will vary across the FOV after application of the lamp flat field. These large-scale deviations will be calibrated to within 0.6% using widely dithered observations of a stellar field to measure how the fluxes of stable photometric sources change as a function of position in the focal plane after the lamp flats were applied (“self-calibration”).
While this approach meets the requirements for Euclid’s core science objectives, it can probably be improved upon for legacy science of the low surface brightness Universe, as we investigate in this paper. Sky flat-fields computed from hundreds of individual images (Pirzkal et al. 2011) are a challenging but very accurate technique for reducing artificial large-scale background structures following flat correction (Bouwens et al. 2011; Brooks & NIRCam Team 2016; Mack et al. 2018), also in ultra-deep ground-based observations (μlim = 31.5 mag arcsec−2 at 3σ in 10 × 10 arcsec2, Trujillo & Fliri 2016). For instance, the low surface brightness structures around the galaxies of the WFC3/IR Hubble Ultra Deep Field (HUDF, see XDF, Illingworth et al. 2013; HUDF12, Koekemoer et al. 2013) were considerably suppressed by the original reduction process. In Borlaff et al. (2019)1, the authors reduced the systematic biases associated with the reduction process using careful sky flat-fielding and optimized background correction techniques. These methods recovered a great number of new structures on the outskirts of the largest galaxies on the HUDF. As a result of the background improvements, some galaxies now present nearly twice the size than in the previous images, showing extended disks and stellar halos while increasing the depth of the images.
Although standard imaging pipelines are accurate enough to recover the properties of relatively compact sources, this is not the case for extended low surface brightness imaging. In absence of additional processing, the resulting data compromise the morphology and photometry of any structure with relatively extended spatial scales in the final mosaics. Euclid’s sky-mapping strategy is optimally suited for sky flat-fielding. Results can be compared with the internal calibration lamp flat fields and large-scale self-calibration measurements, and are readily applied to the data as an additional correction if necessary, monitoring possible contamination sources and other unwanted effects on the detectors in real time.
Based on the characteristics of the Euclid mission, it is the objective of this manuscript to propose specific reduction techniques to obtain high-quality mosaics that preserve the properties of extended low surface brightness sources. At the same time, we study which are the main contributors to the sky background that affect the low surface brightness performance, and how can we efficiently predict the presence and structure of unwanted stray-light contamination. Finally, we explore if in-flight sky flat-fielding using the Zodiacal light is a valid strategy to calibrate the variation in sensitivity across the FOV.
By analyzing these questions, we explore the efficacy of Euclid for low surface brightness science. In the present work, we generate 9916 VIS image simulations (enough to study the precision of sky flat-fields over an extended period of time; this approximately corresponds to the first four months into the mission) with the main objective of assessing the deep-imaging capabilities of the survey. The paper is organized as follows: We describe the process with which we generated the realistic VIS simulations in Sect. 2. Section 3 is dedicated to the description of the results. Sections 4 and 5 contain the discussion and conclusions, respectively. All magnitudes are in the AB system (Oke 1971) unless otherwise noted.
2. Methods
Euclid will be located in a Lissajous orbit in the Sun-Earth Lagrangian point L2. In this orbit, the optical/NIR background is mainly a combination of the zodiacal light, stray-light from stars and Solar System bodies, the CIB, and the interstellar medium (ISM) of the Milky Way. We must note that our objective is not to eliminate these components, but to be able to identify and separate them. If these components do not create a significant gradient (we test this in Sect. 3.2), we can assume that this sky background is a dim, but naturally flat illuminating source that theoretically should allow us to calibrate an imaging detector from variations in the pixel-to-pixel sensitivity across the field of view (Chromey & Hasselbacher 1996). This technique is called sky flat-fielding and provides the sensitivity correction of the detector using the science exposures themselves.
Our purpose is to evaluate whether the S/N of the sky background seen by VIS at L2 is sufficient to create a flat-field correction that does not increase the noise of the final mosaics, and how many coadded science exposures are needed to obtain a reasonable calibration. At the same time, we wish to test whether there will be systematic stray-light gradients and how they could affect this correction. In Sect. 2.1 we detail the results from our simulated observations of the zodiacal light, CIB, and ISM as seen by the VIS detectors. The stray-light component and the evaluation of its gradients are addressed in Sect. 2.2.
2.1. Sky background simulation
The fraction of the sky background dominated by the zodiacal light, stray-light, ISM, and the CIB in L2 is strongly dependent on the position on the sky and also on time, especially in the case of the zodiacal light. As a consequence of this, the Euclid survey avoids bright stars and regions of maximum zodiacal light (see Tereno et al. 2014; Scaramella et al. 2021). Zodiacal light and stray-light from stars are the dominant components of the sky background in the optical and NIR region of the spectrum. This background level increases the noise of the images, but also provides a useful reference uniform light component to create large-scale sky flats. Thus, creating realistic simulations of the sky background is the key point in this study.
In order to develop a realistic sky model, we took advantage of the background model calculator provided by the NASA/IPAC Infrared Science Archive (IRSA)2. The IRSA background model provides estimates based on observations for the different sky-background components considered in this study (zodiacal light, stray-light, CIB, and ISM) as a function of the observation time (day of the year), observation wavelength (from 0.5 to 1000 μm), and the sky coordinates. We refer to the project webpage for details of how the different components of the sky background are modeled. A table-based query system allows the user to calculate the spectral brightness (MJy sr−1) at the required pointing, wavelength, and time of the year3.
To estimate the flux that will be detected by the VIS detectors, we numerically integrated the sky-background intensity for all the pointings of the Euclid/VIS Survey footprint from 5640 Å to 9000 Å using seven sub-bands of 556 Å width each (see the left panel of Fig. 2). The intensity of each bandpass was multiplied with the expected value of the instrument response at the central wavelength to obtain the observed spectral energy distribution (SED) of each sky-background component. The instrument response (e) combines the effects of obstruction, mirrors absorption, dichroic reflectivity, and the quantum efficiency (QE) curve for the VIS CCD detectors, and it is defined as the flux ratio detected by the instrument (VIS) and that received at the entrance of the telescope as a function of wavelength.
 |
Fig. 2. Photometric characteristics of the Euclid/VIS detector. Left panel: Euclid/VIS transmission curve (solid red line). Gaia G-band transmission curve (Venancio et al. 2020, solid blue line). Euclid/VIS payload module (PLM) transmission curve (black dashed line). Quantum efficiency of the Euclid/VIS CCD detectors (including end-of-life contamination), derived from the initial engineering models (green dotted line). Wavelength ranges for the numerical integration of the transmission of VIS using the IRSA sky-background model (gray columns). SDSS g-band sensitivity for extended sources with zero airmass (light blue dotted line). Equivalent for SDSS r-band (orange dash-dotted line). Equivalent for SDSS i-band (magenta dash-dot-dotted line). Right panel: Euclid/VIS magnitude as a function of the Gaia G-band AB magnitudes for the synthetic stellar objects of the Euclid true universe simulation. See the legend for the fitted linear transformation model between both bands. |
We can calculate the sky-background surface brightness (μVIS, AB) in AB magnitudes per arcsec2 as it will be detected with the VIS instrument as
where f(ν) is the flux measured at a certain central frequency ν, e(ν) is the corresponding instrument response at the same frequency, and A is the angular area of the VIS pixels. Following a numerical integration over spectral bandpass bins (i) and taking the sky-background intensity at the center of the selected bandpass (νi) and the spectral widths (Δνi) into account, we can assume a discrete integration over the bins (i) defined on the VIS transmission curve,
The results from this analysis are detailed in Sect. 3.1.
2.2. Stray-light contamination
In this section we describe the process with which we simulated the stray-light from stars, including stars within and beyond the FOV. For Euclid/VIS, the stray-light is expected to be the second most important contributor to the sky background level after zodiacal light. The broad term of stray-light comprises any flux that does not belong to the on-axis source, which is usually the object of interest, either a point source or an extended source. If thermal isolation, baffles, and the remaining optical components of the telescope were ideal, creating no significant scattering or secondary optical paths, and if there were no diffraction effects, the photons collected at a single pixel would only originate at the source located in the on-axis line of sight from that point in the FOV.
To simulate real-world observations, we can divide stray-light sources into two different types (Bely 2003; Lemke et al. 2003; Spangelo et al. 2015). First, sources outside the line of sight, either astronomical or not, such as stars, planets, the Moon or the Earth, and second, thermal emission from the telescope components that surround the detectors. In the case of Euclid, the background generated by the thermal emission of the VIS equipment is estimated to be 1.52 × 10−28 e− px−1 s−1 (this estimate is based on an internal ESA study with the support of industry). This is deemed negligible for this study.
Specular and scattered light from off-axis light in the optical components contributes to the background level in the images and increases the noise. Stray-light contamination is one of the most important factors to take into account in the observation planning phase. This work presents a similar stray-light analysis as Klaas et al. (2014) for the PACS and SPIRE instruments of the Herschel telescope. The function that defines external stray-light transmission of a telescope is the normalized detector irradiance (NDI, Bely 2003). The NDI is defined as the ratio of the stray-light irradiance (power per unit area) at the detector to the irradiance of the source at the entrance of the telescope, allowing us to estimate the flux of photoelectrons that an off-axis source will generate in a certain region of the detector. This function is strongly dependent on the optical setup and wavelength. For a given telescope, the NDI depends on the angular distance between the optical axis and the source (θ), the position angle of the source in the focal plane reference frame (ϕ), the observation wavelength (λ), and the position on the FOV (x, y),
As a consequence of the complex dependence of the NDI on the specific characteristics of the detector, the optical system, and the sources, its solution is usually numerically estimated through ray-tracing simulations and realistic three-dimensional models of the system. In the case of the Euclid/VIS detector, two models are available for the NDI (Gaspar Venancio et al. 2016). First, an NDI model was created using the stray-light analysis software ASAP (Turner 2004). This model considers the variation of the NDI with the distance to the source and orientation of the detector (θ, ϕ), and its dependence on nine different positions across the focal plane of VIS (F1–F9, see Table 1). It is important to note that the current NDI models do not include diffraction peaks or ghosts created by the secondary reflections on the optical elements. Updated estimates of the NDI that include this component will be presented in a forthcoming publication. The nonaxisymmetric NDI model has been calculated for a finite number of θ and ϕ positions, thus numerical interpolation is required to estimate the NDI at each position and the stray-light contamination subsequently from the positions.
Parameters of the envelope NDI model defined in Eqs. (4)–(6) (Gaspar Venancio et al. 2016).
A second and simplified version of the VIS NDI model (worst-case scenario, or envelope NDI model) was created by choosing the higher NDI level of all the position angles (ϕ) at a certain angular distance from the optical axis to the source (θ). This model only depends on θ (hence one-dimensional), therefore it does not accurately represent the directional baffling effect of the telescope optics. This simplified model can be approximated using the following set of equations (we refer to Table 1 for the definition of the different parameters of this expression and their dependence throughout the FOV):
where
with λ being the stray-light source wavelength in nm and
When the NDI for a certain source is determined as a function of θ, ϕ, and its position on the FOV is known, we can simulate the stray-light contamination (S, e− px−1 s−1) created by a source of magnitude mAB that produces an irradiance (I, W m−2) at the entrance of the telescope as
where h is the Planck constant (kg m2 s−1), c is the speed of light (in m s−1), the reference bandpass wavelength is λref = 7.25 × 10−7 m, T is the average VIS transmission (which is approximately 76% at the peak of the curve), A is the physical pixel area expressed in m2 (1.44 × 10−10 m2 for Euclid/VIS), and
From the AB magnitude equation in units of W m−2 Hz−1, we can define the spectral flux density (fν) as
In order to simulate the stray-light produced by stars in the Euclid Survey, we used the Gaia catalog (Gaia Collaboration 2016, 2018). The Gaia catalog has 109 sources, including broadband photometry in the G band with a faint limit of G = 21 mag and a bright limit of G ∼ 6. We complemented the Gaia DR2 catalog with the additional catalog of 230 bright stars (G < 6 mag) from Sahlmann et al. (2016). To transform from Gaia G band to Euclid/VIS fluxes, we calibrated a transformation model using the synthetic catalogs from the Euclid true universe simulation4 (paper in prep., see the right panel of Fig. 2). The Euclid true universe simulation provides synthetic photometry for 4.1 × 107 stars in 1.8 × 104 deg2 by combining the stellar population models of Pickles & Depagne (2010) for the bright end and of the Besançon galaxy model5 (BGM web-service, OSU THETA 2019) for the faint end of the luminosity distribution. Finally, we included the stray-light emission from the major Solar System bodies, taking into account their predicted sky position as a function of time as seen from L2 by Euclid, based on the NASA/JPL HORIZONS ephemeris6 (Giorgini et al. 2001).
Integrating the stray-light created by ∼109 independent sources in several different positions of the FOV is a challenging computational task. In order to optimize the process, we adopted an approximation for the objects beyond a certain angular distance from the center of the FOV. We defined a certain high-resolution region surrounding the center of the Euclid/VIS FOV (R < 5) for which we calculated the stray-light from every star individually. Outside this region, the sky was divided into a grid of HEALPix7 cells (Górski et al. 2005) of approximately the same area. We adopted a characteristic parameter of Nside = 32, which is equivalent to dividing the sky sphere into 12 288 HEALpix cells and an approximate spatial resolution of 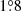 . We show the complete stellar flux map along with the Euclid/VIS footprint in Fig. 1. Every star that belongs to a cell located at R > 5 from the center of the FOV was grouped with the remaining stars inside the same cell, and their flux was estimated as a single source. The position of the group was calculated as the flux-weighted mean of the individual positions of the stars. In Appendix A we provide a quantitative test of the precision of this method, where we define the optimization of the high-resolution limit at Rmin = 5. We find that the stray-light estimate converges exponentially with Rmin, obtaining a variation at 5° of 0.1−0.01 e− per exposure per each degree that we increase Rmin. We can conclude that assuming Rmin = 5 provides a high confidence level to the stray-light estimate at an acceptable cost of computational effort.
. We show the complete stellar flux map along with the Euclid/VIS footprint in Fig. 1. Every star that belongs to a cell located at R > 5 from the center of the FOV was grouped with the remaining stars inside the same cell, and their flux was estimated as a single source. The position of the group was calculated as the flux-weighted mean of the individual positions of the stars. In Appendix A we provide a quantitative test of the precision of this method, where we define the optimization of the high-resolution limit at Rmin = 5. We find that the stray-light estimate converges exponentially with Rmin, obtaining a variation at 5° of 0.1−0.01 e− per exposure per each degree that we increase Rmin. We can conclude that assuming Rmin = 5 provides a high confidence level to the stray-light estimate at an acceptable cost of computational effort.
We provide an example of our simulations in Fig. 3. We simulated the first 9916 pointings of the mission plan, taking their sky position angle into account. For each simulation, we found all the HEALpix cells closer than Rmin = 5 to the center of the FOV. Then we generated a new catalog by combining the individual positions and fluxes of the closest stars (high-resolution map) with the positions and fluxes of the HEALpix cells for the sources at R > Rmin. Finally, based on the relative distance, position angle, and magnitude of each object in these new hybrid catalogs, we estimated the total stray-light that each star produces at the F1–F9 characteristic focal plane points (see Table 1), following Eqs. (4)–(7), and the numerical estimations from the nonaxisymmetric NDI model. The results of the stray-light analysis for the two NDI models are presented in Sect. 3.2.
 |
Fig. 3. Stray-light simulation of a Euclid/VIS observation in the environment of the Orion belt ( |
2.3. Extended source masking
In this section, we detail the methods we used to describe the masking of extended sources in our images. This is one of the most important points in order to accurately simulate the sky flat-fields. All science exposures that are used to create the sky flats will present astronomical sources. To avoid inhomogeneities in the final sky flats, all objects that are not part of the uniform sky background should be masked. This process decreases the number of valid pixels for the analysis, which systematically reduces the precision in detector sensitivity prediction.
To create a realistic distribution of sources that were obtained with a similar depth in a region of the spectrum, we used one of the most extended and deep surveys available for low surface brightness, the IAC SDSS Stripe 82 (S82) Legacy Survey (Fliri & Trujillo 2016; Román & Trujillo 2018). The S82 is a 275 deg2 region along the celestial equator (−50 < α < +60, 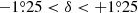 ) that has repeatedly been observed during the Sloan Digital Sky Survey (SDSS; York et al. 2000). Each region of the S82 was observed approximately 80 times, providing a limiting surface brightness 2.4 mag arcsec−2 fainter than that of standard SDSS data. The authors carefully corrected for residual sky-background substructures that might bias low surface brightness structures. The mosaics were generated using u, g, r, i, and z filters, plus an additional mosaic denominated rdeep, which combines the deepest frames of the g, r, and i bands into single mosaics. These frames are dedicated for the detection of extended low surface brightness structures, which are particularly suitable for our work because the maximum VIS sensitivity range overlaps the combined rdeep SDSS synthetic band well (see Fig. 2). In addition, the bands selected for the rdeep mosaics present the deepest limiting surface brightness magnitudes (μlim, S82 = 29.1, 28.6, 28.1 mag arcsec−2). As we detail in Sect. 3.4, the depth of these observations is compatible with the expected surface brightness limiting magnitude in the VIS exposures (μlim, S82 = 29.5 mag arcsec−2 per field in the Wide Survey, measured at a 3σ level, over 10 × 10 arcsec2).
) that has repeatedly been observed during the Sloan Digital Sky Survey (SDSS; York et al. 2000). Each region of the S82 was observed approximately 80 times, providing a limiting surface brightness 2.4 mag arcsec−2 fainter than that of standard SDSS data. The authors carefully corrected for residual sky-background substructures that might bias low surface brightness structures. The mosaics were generated using u, g, r, i, and z filters, plus an additional mosaic denominated rdeep, which combines the deepest frames of the g, r, and i bands into single mosaics. These frames are dedicated for the detection of extended low surface brightness structures, which are particularly suitable for our work because the maximum VIS sensitivity range overlaps the combined rdeep SDSS synthetic band well (see Fig. 2). In addition, the bands selected for the rdeep mosaics present the deepest limiting surface brightness magnitudes (μlim, S82 = 29.1, 28.6, 28.1 mag arcsec−2). As we detail in Sect. 3.4, the depth of these observations is compatible with the expected surface brightness limiting magnitude in the VIS exposures (μlim, S82 = 29.5 mag arcsec−2 per field in the Wide Survey, measured at a 3σ level, over 10 × 10 arcsec2).
Because some regions of the S82 Survey lie at a low Galactic latitude, the number of stars and Galactic cirrus is notably larger than in typical Euclid/VIS exposures. S82 is located at the edge of the footprint of the Euclid Wide Survey. The increased source count will systematically bias our results to a larger number of masked objects and consequently lower statistics for the sky flat fields. In addition, because the resolution of the S82 images is lower than that of Euclid, the size of the masked regions increases. For our purposes, we assumed that these conditions represent the worst-case scenario for this calibration, and we also assumed that we will obtain better statistics in the real Euclid sky flats. Despite these considerations, the wavelength coverage and depth of the IAC S82 Legacy Survey are optimal to simulate the number of pixels that will be covered by sources in average exposures.
In order to study the apparent size and basic morphology of the objects in the rdeep images, we used Gnuastro’s Noisechisel and Segment utilities (Akhlaghi & Ichikawa 2015; Akhlaghi 2019). To optimize the detection of the faintest wings of the extended sources, we set tilesize to 70 × 70 pixels2 and the minimum number of neighbors for interpolation to three in Noisechisel. For a more detailed description, we refer to the Gnuastro tutorial for detecting large extended targets8. Using the source-detection maps, we measured the fraction of pixels that belong to a detectable source in each image (the filling factor). Approximately 30−40% of the pixels were identified as part of a source (see Fig. 4). Using the source-detection maps, we generated a catalog by recording the area, major axis size, ellipticity, and position angle of all detected sources. We transformed the major axis sizes from the SDSS pixel scale to the Euclid/VIS pixel scale.
 |
Fig. 4. Fraction of identified pixels that are masked as part of a source per exposure in the IAC SDSS S82 mosaics (Fliri & Trujillo 2016; Román & Trujillo 2018). The dashed and dotted vertical lines represent the median value of the distribution and its ±1σ dispersion percentiles (see the legend). |
After we generated the source catalogs, the process of creating the masks for each simulated pointing can be summarized as follows. First, we selected a filling factor following the observational probability distribution (see Fig. 4). Second, we selected random sources until the sum of their equivalent areas on the CCD was equal to the required number of pixels to be masked. This number is set by the chosen filling factor. Because masks are placed randomly, a certain fraction of them will overlap. The overlapping areas systematically reduce the real number of pixels that are masked in each simulation. To partially compensate for the reduction of masked pixels, we generated a randomly placed single circular mask equal to the net area of mask-overlap. Finally, even after this correction, some of the objects overlapped the compensating circular mask. As a last step, we masked additional random pixels until we reached the required filling factor for the simulation.
As a last step, we simulated the effect of cosmic rays (CR) in the images by using the CR generation module of the VIS-PP9 Python package for Euclid/VIS simulations. CRs were added until they covered 2% of the FOV. This is a worst-case value considered in the technical requirements. We present an example of the resulting masks in the right panel of Fig. 5, with a completed sky background simulation (see Sect. 2.5).
 |
Fig. 5. Left panel: simulated flat-field structure using Perlin and pixel-to-pixel Gaussian noise. Right panel: example of one of the simulated precalibrated frames ( |
2.4. Flat field
In order to estimate our precision in recovering the structure of the VIS detector sensitivity using the sky background, we need to include the effects of a realistic photo-response nonuniformity (PRNU) in our simulations. Furthermore, the effective system transmission can be modified by molecular contamination, mostly in the form of water ice on optical surfaces due to molecular outgassing. This is a common problem encountered by spacecraft and can easily change photometry by up to a 10% (i.e., Gaia, Gilmore 2018). Most contamination can be cleared by heating of the optical surfaces when necessary. Unlike the Euclid lamp flats, sky flat fields take the full optical path into account, which can produce a significantly different calibration in the case of surface contamination. Therefore we must take a certain time variation of this sensitivity into account.
According to the Euclid payload element requirements, the VIS instrument pixel-to-pixel relative response is predicted to be stable to better than 10−4 on a 24-h timescale and better than 2.5 × 10−3 on a monthly timescale when averaged over 100 × 100 pixels2. Assuming the worst-case scenario based on these requirements, we can generate a function that simulates a realistic sensitivity for the VIS CCD, including their expected variation with time.
In order to do develop this sensitivity function, first we generated an initial flat field that will be the sensitivity at the start of the mission. To generate a realistic complex pattern with variations at different spatial scales, we used the self-similar (fractal) noise function of the Perlin-numpy package10. Perlin-numpy is an implementation of the simplex Perlin noise algorithm presented in Perlin (1985) and later improved in Perlin (2002). Using a combination of several layers of noise, this algorithm simulates the effect of fractal noise. We normalized the resulting structure to have an average value equal to one, with a minimum-to-maximum amplitude in the entire FOV of 0.2 (20%). This amplitude is arbitrary and does not affect our final results.
Secondly, to ensure pixel-to-pixel complexity, we added a pattern of random Gaussian noise with σ = 10−2 (the expected pixel-to-pixel variation). The result is the simulated PRNU at the initial mission time (the “base flat”, see the left panel of Fig. 5). To simulate the time variation of the flat field without increasing the pixel-to-pixel standard variation, we multiplied the base flat with two frames to take the small- and large-scale time variation into account. The first is a random Gaussian noise field on a per-pixel basis, with a standard deviation σ = 10−4 t, with t being the mission time in days. Second, we included the large-scale variation with a different Perlin noise pattern, spatially smoothed with a Gaussian kernel of 100 pixels in size, and an amplitude equal to σ = 8.2 × 10−5 t. We refer to these components as delta PRNUs.
Based on the Euclid/VIS payload requirements, very small variations are expected in periods of several days; they are almost negligible from exposure to exposure. To account for variations over these timescales and avoid to artificially increasing the noise linearly with time, we generated five delta PRNUs, simulating changes in flat expected in periods of 30 days. We independently multiplied each one of these delta PRNUs to the base flat, obtaining five different flats (one every 30 days for a period of four months). Finally, to estimate the flat field at a certain mission time, we performed a linear interpolation between the two closest estimations in time. By doing so, the PRNUs will present compatible noise levels, but they will have a difference in structure.
2.5. VIS-exposure simulation process
Based on the methods discussed in the previous sections, we simulated the exposures as follows: First, we selected the pointings (α, δ, PA) in sequential order, starting from the first exposure for the four months to simulate (9916 exposures). Then, we estimated the expected intensity level for the zodiacal light, ISM, and CIB, following the methods described in Sects. 2.1 and 2.2. We linearly interpolated the stray-light level at the different F1–F9 focal plane points in the simulated pointings (see Sect. 2.2) to obtain the predicted stray-light level and gradient for every independent pixel, including the components from the Solar System bodies, infield, and outfield stars (see Fig. 6 in Sect. 3.2). By combining this with the previous step, we estimated the total sky-background level (e−) and its structure.
 |
Fig. 6. Stray-light contamination levels in the Euclid/VIS Survey, taking sources inside (infield) or outside (outfield) the FOV into account, and the sum of all the objects (total). Left panel: average stray-light contamination level expected in the VIS exposures per pixel assuming the nominal 565 s exposure time (e− px−1). Right panel: average stray-light gradient level (e− px−1 deg−1) per exposure. Red bars: estimates based on the numerical nonaxisymmetric NDI model. Blue bars: estimates based on the worst-case scenario envelope NDI model. See the legend in the figures. |
After we combined the sky-background components, we simulated the effects of photon shot noise. We transformed the sky-background array from electrons to photons through dividing by the average QE. Then we generated an array of random Poisson values using the photon sky-background as the λ parameter as
Then we multiplied the photon sky-background image by the expected sensitivity nonuniformity of the camera (flat field) at the simulation time (see Sect. 2.4). After this, we transformed the units of the array from photon to electrons, and simulated contamination by CRs (see Sect. 2.3). We added dark current (1.38 × 10−6 e− s−1) and bias level (9.6 × 103 e−) according to the technical requirements. Once this is completed, we simulated the effects of readout noise by adding Gaussian white noise with a standard deviation of 4.5 e−.
At this point, the simulated image closely resembles the properties of the expected raw images from VIS, with the notable exception that they lack any kind of astronomical source except for CRs. We started the precalibration procedure by correcting the bias and dark current for the array. We transformed the units of the array from electrons to ADU (3.5 ADU per e−). Finally, we added the random pixel masks up to the filling factor described in Sect. 2.3 and Fig. 4.
We show a completed exposure example in the right panel of Fig. 5. The process described below was performed until we generated 9916 simulations, which correspond to approximately 120 days of mission time (approximately four VIS exposures every 4252 s), taking readout, dither, slew, and NISP observation time into account. When the simulated observations were generated, we normalized all the frames to their median value and carefully combined them using a bootstrapping median algorithm.
3. Results
In this section, we summarize the results from this work. In Sect. 3.1 we study the surface brightness magnitude of the sky background for the different zodiacal light, ISM, and CIB components. Section 3.2 details the analysis for the stray-light component. In Sect. 3.3 we study the viability of the sky flat-field calibration strategy for the VIS detector in terms of the field-sensitivity correction precision and time resolution. Finally, in Sect. 3.4 we provide an estimate of the expected limiting surface brightness magnitude for extended components that will be achievable for the survey.
3.1. Sky-background level
Figure 7 represents the predicted map of surface brightness sky background for the Euclid/VIS Survey, taking the zodiacal light, Milky Way ISM, and CIB into account. For pure representation purposes, we do not include the scattered light introduced by stars in this figure because its spatial variation is high. The average surface brightness of compact objects is not well defined for extended scales around 1 or larger, and their effect on the detectors depends on the position angle (see Sect. 2.2). We found that the average surface brightness of the sky background ranges from 21.5 mag arcsec−2 at low latitudes to about 22.5 mag arcsec−2 at higher latitude regions. The regions associated with brighter sky-background levels are dominated by the zodiacal light (Scaramella et al. 2014, 2021). These parts of the survey are closer to the edges of Euclid footprint toward the ecliptic plane, which is not only affected by the zodiacal light, but also by the stray-light of the Solar System bodies (see Fig. 6).
 |
Fig. 7. Predicted sky-background level map in equatorial coordinates for the Euclid/VIS Survey (Scaramella et al. 2021) as a combination of zodiacal light, Milky Way ISM, and CIB using the NASA/IPAC sky-background model. The resolution of the map is approximately |
The distribution of the surface brightness magnitude of the various background components is represented in the vertical histogram of Fig. 8. The dominant component to the total sky background is the zodiacal light (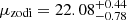 mag arcsec−2). Based on the NDI model that takes the variation with the position angle into account, the second most important component is the stray-light from stars (we detail this result in Sect. 3.2). The remaining components are much dimmer, with an average of
mag arcsec−2). Based on the NDI model that takes the variation with the position angle into account, the second most important component is the stray-light from stars (we detail this result in Sect. 3.2). The remaining components are much dimmer, with an average of 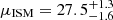 mag arcsec−2 for the ISM. Nevertheless, dust cirrus can be much brighter, up to μISM ∼ 24 mag arcsec−2, as observed in Mihos et al. (2017) and Román et al. (2020). The CIB appears as a constant background component of μCIB = 27.17 mag arcsec−2. Therefore the ISM background (i.e., Galactic cirri) is about 5 mag arcsec−2 fainter than the zodiacal light background. Taking into account that the ISM structures are also different from exposure to exposure, they average out and are negligible in the computed sky flats.
mag arcsec−2 for the ISM. Nevertheless, dust cirrus can be much brighter, up to μISM ∼ 24 mag arcsec−2, as observed in Mihos et al. (2017) and Román et al. (2020). The CIB appears as a constant background component of μCIB = 27.17 mag arcsec−2. Therefore the ISM background (i.e., Galactic cirri) is about 5 mag arcsec−2 fainter than the zodiacal light background. Taking into account that the ISM structures are also different from exposure to exposure, they average out and are negligible in the computed sky flats.
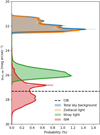 |
Fig. 8. Distribution of sky-background surface brightness in the Euclid/VIS exposures as predicted by the IRSA model for the zodiacal light (orange), ISM (red), and CIB (dashed black line), the simulations for the average stray-light contamination (green), and the combination of all components (blue histogram). |
3.2. Stray-light contamination
Our results show that stray-light will generate an average surface brightness magnitude of 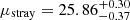 mag arcsec−2 in the VIS exposures, assuming the numerical NDI model (dependent on the position angle and the position in the FOV). Interestingly, if we assume the axisymmetric envelope model for the NDI (described in Eqs. (4)–(6)), the stray-light brightness estimate increases about 1.7 mag arcsec−2, to
mag arcsec−2 in the VIS exposures, assuming the numerical NDI model (dependent on the position angle and the position in the FOV). Interestingly, if we assume the axisymmetric envelope model for the NDI (described in Eqs. (4)–(6)), the stray-light brightness estimate increases about 1.7 mag arcsec−2, to 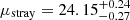 mag arcsec−2. This discrepancy is anticipated: The axisymmetric NDI is a worst-case scenario that does not take the full baffling effects of the telescope optics into account. This artificially increases the contamination by nearby stars in the FOV if we compare it with the more realistic nonaxisymmetric model.
mag arcsec−2. This discrepancy is anticipated: The axisymmetric NDI is a worst-case scenario that does not take the full baffling effects of the telescope optics into account. This artificially increases the contamination by nearby stars in the FOV if we compare it with the more realistic nonaxisymmetric model.
In Fig. 6 we present a summary of the results of the stray-light analysis, depending on the assumed model. In the left panel, we present the absolute stray-light flux as a function of the NDI model and the source. The estimatie of the stray-light gradients is presented in the right panel. We differentiate between the infield and outfield stray-light components. The results show three additional important results:
-
Out-of-field sources cause approximately 80% of the total amount of stray-light (76.1% according to the nonaxisymmetric NDI model and 88.9% according to the envelope NDI model).
-
The total intensity of the stray-light gradients produced by the infield and outfield sources is similar, but their value differs significantly depending on the NDI model. The symmetric NDI model predicts gradients twice as large (
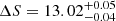 e− px−1 deg−1) as those estimated using the nonaxisymmetric NDI model (
e− px−1 deg−1) as those estimated using the nonaxisymmetric NDI model (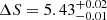 e− px−1 deg−1).
e− px−1 deg−1). -
Interestingly, we found that the sum of the stray-light gradients from infield and outfield sources differ from the stray-light gradients that we measured when all sources were taken into account. An explanation for this effect is that outfield sources create gradients with higher intensity toward the edges of the FOV, while infield sources are expected to create the opposite effect. Infield and outfield gradients neutralize partially on average when they are summed.
From the zodiacal model, we estimate that the average zodiacal induced gradient in the Euclid/VIS exposures is 0.598 ± 0.001 e− deg−1. This is approximately ten times less intense than the expected stray-light gradients per exposure. As a reference, for a surface brightness level of 22.5 mag arcsec−2 (corresponding to the darkest regions of the Euclid/VIS footprint), we would expect to a corner-to-corner change in FOV of Δμ = 0.005 mag arcsec−2 (or 0.073% of the total light per CCD). We therefore consider that compared to the stray-light gradients, the zodiacal light gradients are negligible for our estimates.
However, if the directions of the gradients are approximately random in the sky flats, then they will be partially suppressed when multiple exposures are coadded. Nevertheless, there are two different facts that may affect this hypothesis: first, the nonaxisymmetric design of the spacecraft sunshield of the Euclid spacecraft, and second, the preferential directions of the position angle of the exposures of the survey. Our simulations take all these effects into account by using the different NDI models and the real parameters of the survey plan (α, δ, position angle, epoch of each exposure start, and relative positions of the Solar System bodies).
We find that the median stray-light background varies within 2 e− throughout the focal plane (the largest difference between two focal plane points is 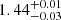 e− in the case of the nonaxisymmetric NDI model and
e− in the case of the nonaxisymmetric NDI model and 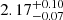 e− in the envelope NDI model). The spatial distribution of the median stray-light strongly depends on the NDI model (see Fig. A.2). The focal plane point F8 shows a significantly higher stray-light contamination than the remaining focal plane when the NDI envelope model is considered. In contrast, the nonaxisymmetric envelope NDI model shows a more uniform distribution. As discussed previously, the most reasonable cause for the model dependence of stray-light uniformity is that the azimuthal variation of the NDI takes the baffling effect of the telescope more accurately into account. In the case of the NDI envelope, which is a worst-case axisymmetric function, the stray-light blocking effect is removed from the simulation. In this case, the stray-light level is higher, with an extreme increase in contamination from out-of-field sources compared to the more complex nonaxisymmetric model, and the stray-light gradients are higher (as observed in Fig. 6). Based on these results and for the sake of completeness, the adoption of the more complete nonaxisymmetric NDI model for our models is justified.
e− in the envelope NDI model). The spatial distribution of the median stray-light strongly depends on the NDI model (see Fig. A.2). The focal plane point F8 shows a significantly higher stray-light contamination than the remaining focal plane when the NDI envelope model is considered. In contrast, the nonaxisymmetric envelope NDI model shows a more uniform distribution. As discussed previously, the most reasonable cause for the model dependence of stray-light uniformity is that the azimuthal variation of the NDI takes the baffling effect of the telescope more accurately into account. In the case of the NDI envelope, which is a worst-case axisymmetric function, the stray-light blocking effect is removed from the simulation. In this case, the stray-light level is higher, with an extreme increase in contamination from out-of-field sources compared to the more complex nonaxisymmetric model, and the stray-light gradients are higher (as observed in Fig. 6). Based on these results and for the sake of completeness, the adoption of the more complete nonaxisymmetric NDI model for our models is justified.
3.3. Sky flat-fielding
In this section we summarize the results of the sky flat-fielding simulations described in Sect. 2.5. In Fig. 9 we show the efficiency of the sky flat-field correction as a function of the number of combined exposures. The precision of the sky flat-fields is measured as the 1σ width (defined as the 84.1 − 15.9 percentile) of the probability distribution of the residuals between the sky flat-field estimate and the simulated PRNU of the detector (i.e., the “true” flat field), interpolated at the average epoch of the all exposures combined during that period.
 |
Fig. 9. Precision (in percent) of the VIS sky flat-field as a function of the number of combined exposures (as scaled by time) and the applied binning. The dotted horizontal magenta line represents the maximum measured variation of the LED flat-fields within the λ range of VIS (Szafraniec et al. 2016). The dashed black horizontal line represents the precision requirement for the calibration lamp flat-fielding correction. See the legend for details. |
The results shown in Fig. 9 reveal a complex calibration scenario. In theory, coadding more images provides a better approximation of the flat field, but in practice, degradation and stability effects over long periods of time actually increase the background residuals. The residuals of the sky flat fields decrease rapidly following a near square-root power law as a function of the number of images combined during the first ten days. Interestingly, our simulations show a strong deviation from the power law beyond that time (> 500 − 1000 images), where coadding more images to the sky flats does not help to reduce the background residuals in our images. This effect can be explained as a consequence of slight changes in the CCD detector sensitivity with time, which limits the integration time-span that we can use to generate the sky flats. Beyond a certain time period, changes in sensitivity are too high to be averaged in the independent images. Therefore the adopted timescale for observing a set of images to generate sky flat fields must be optimized in a trade-off between obtaining a higher S/N and avoiding the effect of the degradation of the effective throughput. As a consequence of this trade-off, the S/N of the sky flats cannot be improved beyond ∼0.2% on a pixel-to-pixel scale without applying some form of smoothing or spatial binning.
Nevertheless, recovering the pixel-scale structure in the sky flats is not a requirement for our purposes. The main objective of the sky flat fields is to use them to correct the sensitivity at large spatial scales (using the CU lamp flats for the small scales), resulting in a high-S/N flat field at considerably smaller spatial scales. Different types of sensitivity corrections can be used to obtain a valid calibration at all spatial scales (from pixel-to-pixel scales to the complete FOV). For this purpose, a viable strategy would be to first correct the exposures with the calibration lamp flat-fields and then coadd the resulting precalibrated images, obtaining a delta sky flat. This technique has proven to be a valid method for correcting large-scale gradient residuals in the flat fields of the WFC3/IR and the ACS instruments of the Hubble Space Telescope (Pirzkal et al. 2011; Mack et al. 2018). The flat-field calibration can thus be split into different components for large (r > x) and small (r < x) spatial scales,
where R is the raw image, F is the flat field, S is the calibrated science image, D is the dark current per exposure time t, and B is the bias. A large-scale delta sky flat field (Fr > x) can be generated after correcting the images with a first-order flat field (Fr < x) with spatial frequencies lower than a certain scale x. The precision of the first-order flat field (calibration lamp) allows us to increase the S/N of the delta sky flats by smoothing or binning up to a certain scale.
In Fig. 9 we simulate the precision that would be obtained by using the delta sky flat correction at different binning scales (from 0.2 to 2 arcsec). The high spatial resolution of Euclid/VIS, with a minimal binning (10 × 10 pixels2, 1 × 1 arcsec2) we enable us to meet the flat-field precision requirement every 5−10 days of the mission (in 3 days if the binning is made in 2 × 2 arcsec2 scales). We must note that the calibration lamps will provide high-precision flat fields for scales up to 60 × 60 pixels2 (6 × 6 arcsec2), allowing a continuous correction of spatial sensitivity variations.
In conclusion, our simulations show that sky flat fields can be periodically generated for scales larger than > 1 − 2 arcsec by combining the VIS science images obtained in periods of 3−10 days, complementing the calibration obtained using the on-board lamps. This result takes the technical specifications of the Euclid spacecraft, the VIS instrument and its survey (i.e., sensitivity, exposure time, attitude, and instrumental noise), as well as the observational strategy and the characteristics of the regions of the sky to be observed into account (zodiacal light, stray-light contamination, background source masking, cosmic-rays, ISM, and CIB). Delta sky flat fields generated using this method will be able to successfully complement the standard calibration procedure, providing a high-quality correction for large-scale sensitivity residuals. This will enable the Euclid/VIS Survey to detect large-scale low surface brightness structures. These sky flats will be combined with self-calibration methods (Manfroid 1995) to correct for the largest spatial scales. We propose that a calibration ladder (lamp flats for the small scales, self-calibration, and finally, sky flat fields) will enhance the precision of Euclid to explore the low surface brightness Universe.
3.4. Euclid/VIS Survey surface limiting magnitude for extended sources
One of the most important objectives of the present work is to provide a realistic prospect of the limiting surface brightness for extended sources in the Euclid/VIS Survey. Taking advantage of our simulated frames, we can estimate the effect of a large variety of systematic errors in the actual limiting surface brightness. We define this limit as the corresponding surface brightness of a 3σ (percentile interval 0.13−99.86%) intensity fluctuation measured over an area of 10 × 10 arcsec2, following the metric used in previous studies (Trujillo & Fliri 2016; Fliri & Trujillo 2016; Laine et al. 2018; Borlaff et al. 2019). This definition is arbitrary, and it is typically set to match the spatial scales of the low surface brightness features of nearby galaxies that extend over larger sizes than one single pixel (Mihos et al. 2017; Mihos 2019).
In Fig. 10 we show the results of the surface brightness limit analysis as functions of the different sky background components. We estimated the limit surface brightness of 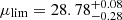 mag arcsec−2 per exposure, with a standard exposure time of 565 s. This limit was measured based on the results from the simulated images, after including the effects of the background light (see Sects. 2.1 and 2.2), Poisson noise, count discretization, and readout noise (see Sect. 2.5). We found that there is a clear strong dependence of the surface brightness limit with the intensity of the zodiacal light, which clearly dominates the remaining components (Laureijs et al. 2011; Scaramella et al. 2014). This effect is especially notable in the case of some of the calibration fields, which present much higher zodiacal light levels and thus lower surface brightness limits (Scaramella et al. 2021). Secondary effects such as stray-light and the intensity of the ISM (i.e., cirrus) do not present any correlation with the limiting magnitude, showing that they are not dominant factors for the surface brightness limit. This result confirms the hypothesis that the zodiacal light is the main limitation of the mission in terms of depth over the respective contributions on the stray-light, ISM, or the CIB.
mag arcsec−2 per exposure, with a standard exposure time of 565 s. This limit was measured based on the results from the simulated images, after including the effects of the background light (see Sects. 2.1 and 2.2), Poisson noise, count discretization, and readout noise (see Sect. 2.5). We found that there is a clear strong dependence of the surface brightness limit with the intensity of the zodiacal light, which clearly dominates the remaining components (Laureijs et al. 2011; Scaramella et al. 2014). This effect is especially notable in the case of some of the calibration fields, which present much higher zodiacal light levels and thus lower surface brightness limits (Scaramella et al. 2021). Secondary effects such as stray-light and the intensity of the ISM (i.e., cirrus) do not present any correlation with the limiting magnitude, showing that they are not dominant factors for the surface brightness limit. This result confirms the hypothesis that the zodiacal light is the main limitation of the mission in terms of depth over the respective contributions on the stray-light, ISM, or the CIB.
 |
Fig. 10. Surface brightness limit of the individual simulated VIS exposures as a function of the different components of the sky background. Top left panel: histogram of the surface brightness limit per exposure (9916 simulations). The solid and dashed vertical lines represent the median value of the distribution and its ±1σ dispersion percentiles. Top right panel: zodiacal light surface brightness vs. limiting surface brightness. Bottom left panel: average stray-light light level (from Solar System bodies and stars) surface brightness vs. limiting surface brightness. Bottom right panel: interstellar medium surface brightness vs. limiting surface brightness. Contours represent nine equidistant levels of probability density between 10% and 90%. |
The dithering pattern of the Wide Survey will ensure that almost every single position will be observed in three or four consecutive exposures of 565 s, dithered using an S-pattern (Δx, Δy = 0″, 0″; +50″, +100″; 0″, +100″; +50″, +100″, Markovič et al. 2017). This observing strategy ensures that about 40% of a survey field will be imaged three times, and 40% four times (Scaramella et al. 2021). When the results for the independent exposures are taken into account (see Fig. 10), the limit surface brightness for the Wide Survey will be nearly 0.74 mag arcsec−2 deeper than the individual frames, reaching 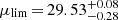 mag arcsec−2 (3σ, 10 × 10 arcsec2). For the regions in which the exposures overlap three times, the surface brightness magnitude limit will be
mag arcsec−2 (3σ, 10 × 10 arcsec2). For the regions in which the exposures overlap three times, the surface brightness magnitude limit will be 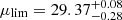 mag arcsec−2. The depth achieved in the Wide Survey will be then comparable to that of the observations made by the CFHT Megacam on NGC 7331 (Duc et al. 2018) or the S82 observations (275 deg2, Fliri & Trujillo 2016), but for 15 000 deg2 of the sky, with a better PSF, lower sky background, and a much higher spatial resolution (see Fig. 11). In addition to the Wide Field, three additional fields are especially interesting for the LSB science case, the North, South, and Fornax Euclid Deep Fields11, which will combine a higher density of exposures, reaching surface brightness levels up to 2 mag deeper than the Wide Survey.
mag arcsec−2. The depth achieved in the Wide Survey will be then comparable to that of the observations made by the CFHT Megacam on NGC 7331 (Duc et al. 2018) or the S82 observations (275 deg2, Fliri & Trujillo 2016), but for 15 000 deg2 of the sky, with a better PSF, lower sky background, and a much higher spatial resolution (see Fig. 11). In addition to the Wide Field, three additional fields are especially interesting for the LSB science case, the North, South, and Fornax Euclid Deep Fields11, which will combine a higher density of exposures, reaching surface brightness levels up to 2 mag deeper than the Wide Survey.
 |
Fig. 11. Comparison of the surface brightness limit (3σ, 10 × 10 arcsec2) for the Euclid/VIS Wide Survey (and two magnitudes deeper for the Deep Fields), compared with a selection of deep optical and near-infrared surveys including SDSS (York et al. 2000), IAC Stripe 82 (S82 Fliri & Trujillo 2016), the MATLAS deep-imaging Survey (Duc et al. 2015), DECaLS (Dey et al. 2019), Stellar Tidal Stream Survey (Martínez-Delgado 2019, STSS), Hyper Suprime-Cam DR2 (Aihara et al. 2018), Coma Cluster Dragonfly observations (van Dokkum et al. 2020), HST WFC3 ABYSS HUDF (Borlaff et al. 2019), XDF (Illingworth et al. 2013), UGC00180 10.4 m GTC exploration (Trujillo & Fliri 2016), the Burrell Schmidt Deep Virgo Survey (Mihos et al. 2017), the VEGAS-VST (Iodice et al. 2020; Ragusa et al. 2021), and LSST (10-year full survey integration, Ivezić et al. 2019). |
As a comparison, we show in Fig. 11 the expected depth for the Euclid Survey with some of the most notable results from the literature. The Deep Field mosaics have the potential of tracing extended structures deeper than the expected surface brightness limit of the Vera C. Rubin (LSST) final mosaics, complementing a lower covered area (65 deg2 between the three Euclid Deep Fields and 15 000 deg2 vs. 18 000 deg2 for Rubin) with a higher resolution and deeper limit in surface brightness in a similar wavelength range (although with notably lower spectral resolution), being comparable to the depths in the ACS HUDF (0.003 deg2, Illingworth et al. 2013). Future missions such as MESSIER (Valls-Gabaud & MESSIER Collaboration 2017) expect to reach much lower surface brightness magnitude levels closer to μlim = 34 mag arcsec−2 in optical bands and μlim = 37 mag arcsec−2 in UV. Nevertheless, we must stress that these results are only an approximation of reality. Real detection limits are subject to many factors not covered in our simulations, including additional sources of stray-light contamination, sensitivity degradation, sky background oversubtraction during image processing, or changes in the observing plan. The results in this section should be interpreted as the optimal result to be obtained with a pipeline optimized for low surface brightness detections (see Sect. 4).
4. Discussion
We confirm that the Euclid/VIS Survey enables unprecedented discovery space in addition to the core science. The combination of a Deep and Wide Survey offers a unique opportunity of studying the low surface brightness Universe with the benefits of space-based resolution. The Euclid Legacy Archive will provide high-quality imaging data up to depths and extensions that have not been observed before.
In general, the limiting surface brightness magnitude depends on the size of the objects to be detected. Integrating over larger areas allows increasing the precision for the detection of diffuse objects. This also applies to surface brightness profiles. As an example (assuming no cosmological dimming), for local galaxies with an angular size of D ∼ 1 arcmin, an image depth of μVIS, AB = 29.5 mag arcsec−2 (3σ detection, measured over an area of 10 × 10 arcsec2) in the VIS Wide Survey, and an outermost radial bin spatial resolution of 5 arcsec, the area to be integrated would be between 450 and 850 arcsec2, depending on the inclination (45° to face-on) of the galaxy. As a consequence, the limit for the surface brightness profiles of these nearby galaxies would range from 30.2 to 30.5 mag arcsec−2 (2−3 mag deeper than current SDSS r data, with a ten times higher spatial resolution). Based on SDSS observations, we estimate that there are approximately 24 000 galaxies outside the Local Group with diameters larger than 1 arcmin (measured as the Petrosian diameter in the SDSS r band) that will be observed in the Euclid Wide Survey. This means that we will find one of these extended objects in every pointing on average. This fact alone has the potential of moving the extragalactic structural analysis at ultra-low surface brightness (μ ≳ 30 mag arcsec−2) from individual explorations to the statistics domain. Simulation-based studies predict that a hypothetical survey with a limiting magnitude fainter than 29 mag arcsec−2 would detect up to ten accretion features around Milky Way-type galaxies at distances greater than 30 kpc from the host (Johnston et al. 2008). Volume-limited samples of nearby galaxies currently detect that almost 14% of the galaxies present diffuse features compatible with minor merger events at a limiting magnitude of 28 mag arcsec−2 (Morales et al. 2018). These results are compatible with those from Bilek & Duc (2021) and might suggest a conflict between the fractions predicted by cosmological models and observations.
The Euclid/VIS mosaics will provide unbiased photometry of the structure of objects with smaller sizes (we can expect 3 × 106 objects with DPetro, r > 1 arcsec in the Wide Survey), paying special attention to avoid sky background oversubtraction and/or residual gradients in the North, South, and Fornax Deep Surveys. Their potential depth and area will enable comprehensive investigations of the extended structure of vast numbers of galaxies at moderate redshift (z ∼ 1 − 2) reaching depths similar to the current observations available on the local Universe, overcoming the effect of cosmological dimming (Tolman 1930, 1934). As an example, two magnitudes deeper than the predictions for the Euclid/VIS Wide Field for objects at z = 1.5 is equivalent to a rest-frame observation at μlim = 27.8 mag arcsec−2, comparable to the S82 observations in the Local Universe. This combination of depth, area, and high spatial resolution will support studies of the evolution of the outskirts of galaxies in the most recent history of the Universe (z = 0 − 1.5). Star count methods are very efficient in exploring diffuse, local Universe structures, reaching far beyond integrated photometry where their stellar populations can be resolved (Butler et al. 2004; McConnachie et al. 2009; Ibata et al. 2009). The combination of deep, wide, and space-based observations is ideal for these explorations because the maximum distance where they are applicable is highly limited by the spatial resolution of the images (e.g., 16 Mpc using the Hubble Space Telescope; Zackrisson et al. 2012). In addition, the study of the tip of the red giant branch (Mouhcine et al. 2005) and globular cluster population (Rejkuba 2012) provides a precise independent distance estimation. These explorations require high-resolution observations, where space-telescopes have an advantageous position. These techniques are crucial for the study of the ultra-diffuse galaxies in the Local Universe, where Euclid could provide a statistical sample that could facilitate the debates about the presence of dark matter in these objects (see van Dokkum et al. 2018; Trujillo et al. 2019; Montes et al. 2020, and references therein). Moreover, higher-resolution and wider-area deep observations will reveal a great number of dwarf low surface brightness galaxies, which remain undetected beyond the local Universe.
Nevertheless, a significant number of challenges remains to be solved to ensure the quality of these mosaics. Addressing these challenges is beyond the scope of this paper. Even though our results show that Euclid is particularly well shielded against stray-light, gradients will still be observed in individual observations, necessitating their fitting and removal. Careful masking of the sources, including the extended wings buried in the background noise (Akhlaghi & Ichikawa 2015; Teeninga et al. 2015; Dey et al. 2019), is one of the greatest challenges of low surface brightness imaging. Because this “buried” emission is absorbed into the sky background model, sky background oversubtraction is a common issue in many surveys. The consequential negative effects on scientific results extend far beyond the outer structure of extragalactic sources. Coaddition of images with different background gradients increases the noise level of the final mosaics. Blind source-detection maps are more likely to lose small objects if they are in a highly oversubtracted region. Moreover, a certain fraction of the light in the sky background is caused by PSF effects (Slater et al. 2009; Sandin 2014, 2015), which smear the signal from the brightest pixels to the surrounding regions of the detector. While PSF deconvolution methods yield a reconstruction of the original distribution of light (Trujillo & Fliri 2016; Borlaff et al. 2017), or even stellar source removal (Román et al. 2020), this processing can only be successfully achieved if the sky background subtraction is not too aggressive in removing the spread light.
Ghosts created by secondary reflections add another layer of complexity to the PSF correction problem. Novel modeling and subtraction methods such as the one described in Karabal et al. (2017) for the CFHT MegaCam might be particularly useful to correct the individual frames of VIS before coadding. Nevertheless, all the techniques described require the precise determination of the PSF at scale lengths of approximately twice the size of the structure that is to be studied (see Janowiecki et al. 2010; Infante-Sainz et al. 2020). Their effect was beyond the scope of the current paper, but we will study the effect of the PSF and ghosts for low surface brightness science with Euclid images in a forthcoming publication.
Galactic cirri are one of the many extended low surface brightness structures that we expect to find in the Euclid Survey. Their complex filamentary structure (Miville-Deschênes et al. 2016) mimics that of the extragalactic tidal structures (Cortese et al. 2010), making them extremely hard to fit and separate, even counting with high-resolution far-infrared data (Mihos et al. 2017). Unfortunately, no such maps are available for most all-sky surveys, and because of its almost fractal-like structure, lower-resolution (4−5 arcmin) alternatives such as IRAS (Miville-Deschênes & Lagache 2005), Planck (Planck Collaboration I 2016), or WISE (Miville-Deschênes et al. 2016) might not be enough to correct the high-resolution images of Euclid/VIS. Multiwavelength methods based on deep, high-resolution optical photometry (Román et al. 2020) may be the key to isolate the optical diffuse emission by the cirri, enabling the study of the Galactic and extragalactic low surface structures by separation. Identification of low surface brightness large-scale cirri using multiwavelength data in VIS is a possibility that is yet to be explored.
An interesting problem that is yet to be studied is the effect of charge transfer inefficiency (Israel et al. 2015, CTI) in the extended, low surface brightness structures. CTI contamination causes spurious image trailing that increases over time due to radiation damage. In HST/ACS, CTI became a notable problem due to the trailing effect of warm pixels in the dark frames. We will explore self-correction methods such as those presented in Mack et al. (2018) in a future publication. While systematic effects such as hot, bad, saturated pixels, diffraction spikes, persistence effects, satellite trails, and residual fringe patterns can be automatically detected and masked using convolutional neural networks (CNNs) on the individual exposures (Paillassa et al. 2019), these methods can also be applied to detect merger signatures (Ackermann et al. 2018) and other tidal features (Walmsley et al. 2019; Martinez-Delgado et al., in prep.). However, mitigation of potential biases due to the lack of large training samples and contamination by foreground and background sources requires further refinement of these techniques.
Finally, there is the problem of wavelength variation of the flat field (Stubbs & Tonry 2006). On-ground characterization studies using calibration lamps on the CCD273 VIS detectors have shown a small but significant variation of the flat field with wavelength (Szafraniec et al. 2016). The amplitude of this wavelength variation ranges from 0.9% at 5500 Å to 0.6% at 8500 Å. At longer wavelengths, a pattern of concentric rings starts to be visible. The origin of this pattern is suspected to be silicon resistivity variations during the manufacturing process of the crystal. Interestingly, this wavelength-dependence is another aspect for which methods such as sky flat-fielding might be superior to the calibration lamps, at least for extended sources. In order to correct a wavelength dependence of the flat field, the SED of each pixel covering the sky would ideally be known before. As shown in Sect. 3.1, most of the detector area will be dominated by the zodiacal light whose SED may be matched using some combination flat field generated with the on-board set of calibration lamps. Sky flat fields perform this SED-dependent sky flat naturally by providing an estimate of the sensitivity independently of the calibration lamps, when constructed using the zodiacal light itself (the equivalent of a calibration lamp with the same SED as that of the observations). A combination of calibration lamp flat fields for bright sources and sky flats for the dim regions may be the best solution for a successful calibration for all spatial and intensity ranges.
5. Conclusions
We have studied the capabilities of the Euclid space telescope as a low surface brightness observatory. Although the detection of dim extended sources is beyond the original nominal mission design, the characteristics of the telescope in terms of FOV, survey footprint, exposure time, sensitivity, and wavelength coverage are ideal for this purpose. Nevertheless, systematic errors are often a major limitation for the study of the extended structure of dim objects and caused first by flat-field inaccuracy and second by stray-light residuals, which are extremely hard to predict and quantify.
Although sky flat-fielding techniques have been proven to be successful in calibrating large-scale residual variations of the sensitivity, most of their application extends to ground-based observations or NIR space observatories, where the sky background contribution is sufficiently bright for these calibrations (with a few exceptions, see Mack et al. 2018). In addition, the asymmetric design of the Euclid spacecraft external baffle could bias the sky flats. If this were the case, the position angles of the survey fields would need to be constrained for Euclid legacy science. In this paper, we showed that these effects are negligible.
We have studied the possibility of a low surface brightness reduction for Euclid/VIS, taking advantage of the imaging data of the mission as an additional legacy science product. A key product of this investigation includes the development of a set of simulated background observations that takes the effects of all-sky stray-light contamination, zodiacal light, ISM, CIB, QE, and payload transmission, instrumental and photon noise, cosmic-rays, flat-fielding, and detector degradation into account. The results show the following.
-
The Wide Survey VIS mosaics have the potential of achieving a limiting surface brightness magnitude of 29.5 mag arcsec−2 in an area of 15 000 deg2.
-
Sky flat-fielding is a valid strategy for the calibration of the Euclid/VIS Survey. The science exposures will allow us to independently generate a high-quality delta sky flat correction every 3−10 days (with a minimum spatial rebinning of 1 × 1 arcsec2), complying with the calibration quality requirements of the mission.
-
Stray-light will be efficiently shielded at ≤26 mag arcsec−2 in most frames. Gradients due to stray-light will be extremely low, and their average contribution to the sky flats is negligible. We confirm that the zodiacal light will be the main contributor to the sky background (Laureijs et al. 2011), with a magnitude of
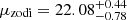 mag arcsec−2.
mag arcsec−2.
In addition to these results, the methods described in Sect. 2.2 provide a prediction of the shape of the stray-light background in the individual frames on a pixel-by-pixel basis. The methods presented in this work allow for individual corrections of the stray-light in the Euclid images, resulting in a more precise determination of the sky background over the standard Euclid processing pipeline.
The limiting surface brightness magnitude of the final Euclid mosaics will depend on how all the instrumental systematic effects are corrected. Considering the properties of the mission, we estimate that Euclid/VIS will provide high-resolution imaging with a limiting surface brightness close to μlim = 29.5 mag arcsec−2 in the Wide Survey and two magnitudes deeper in the Deep Surveys. The extraordinary combination of sensitivity, angular resolution and sky coverage of Euclid will support multiple transformative scientific investigations, including the study of extended disks, satellites, and stellar halos as tracers of the dark matter distribution in galaxies; unprecedented mapping of the zodiacal light and Galactic dust cirri; and a precise measurement of the anisotropies of the CIB.
Euclid has the potential to be the next breakthrough in the understanding of the formation and evolution of galaxies, providing high-resolution, deep, and extremely wide imaging of the low surface brightness Universe to the scientific community. It will become a cornerstone of low surface brightness astronomy for the next decades.
The ABYSS HST Ultra Deep Imaging Project: http://www.iac.es/proyecto/abyss/
NASA/IPAC Infrared Science Archive Background Model: https://irsa.ipac.caltech.edu/applications/BackgroundModel/
Euclid Flagship simulation: https://www.euclid-ec.org/?page_id=4133
Besançon Model of the Galaxy website: https://model.obs-besancon.fr/
NASA/JPL HORIZONS Online Ephemeris System: https://ssd.jpl.nasa.gov/?horizons
HEALPix is a project of NASA Jet Propulsion Laboratory available at: https://healpix.jpl.nasa.gov/
Gnuastro Tutorial – Detecting large extended targets: https://www.gnu.org/software/gnuastro/manual/html_node/Detecting-large-extended-targets.html
The Euclid Visible InStrument Python Package (VIS-PP) was created by Sami-Matias Niemi and it is available through GitHub: https://github.com/sniemi/EuclidVisibleInstrument
Euclid Deep fields: https://www.cosmos.esa.int/web/euclid/euclid-survey
Acknowledgments
The authors thank Françoise Combes, Emmanuel Bertin, and Mischa Schirmer for the provided input that helped to improve this publication significantly. We thank Koryo Okumura for his help with the stray-light modeling and prediction methods. We also thank Matthieu Marseille, Ruyman Azzollini, Stefano Andreon, Henry Joy McCracken and Kenneth Ganga for their contributions and comments to this manuscript. We give special thanks to Jason Rhodes and Jean-Gabriel Cuby for their support. Without your insight and feedback this project would have never been possible to finish. A. B. also thanks Michael Fanelli for his support and interesting comments on the project. A. B. was supported by an appointment to the NASA Postdoctoral Program at the NASA Ames Research Center, administered by Universities Space Research Association under contract with NASA, and the European Space Agency (ESA), through the European Space Astronomy Center Faculty. We acknowledge a number of agencies and institutes that have supported the development of Euclid, in particular the Academy of Finland, the Agenzia Spaziale Italiana, the Belgian Science Policy, the Canadian Euclid Consortium, the Centre National d’Etudes Spatiales, the Deutsches Zentrum für Luft- und Raumfahrt, the Danish Space Research Institute, the Fundação para a Ciência e a Tecnologia, the Ministerio de Economia y Competitividad, the National Aeronautics and Space Administration, the National Astronomical Observatory of Japan, the Netherlandse Onderzoekschool Voor Astronomie, the Norwegian Space Agency, the Romanian Space Agency, the State Secretariat for Education, Research and Innovation (SERI) at the Swiss Space Office (SSO), and the United Kingdom Space Agency. A complete and detailed list is available on the Euclid website (http://www.euclid-ec.org). This work has made use of data from the ESA mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This research made use of NumPy (Van Der Walt et al. 2011), Astropy, a community-developed core Python package for Astronomy (Astropy Collaboration 2013). All of the figures on this publication were generated using Matplotlib (Hunter 2007). This work was partly done using GNU Astronomy Utilities (Gnuastro, ascl.net/1801.009) version 0.11.22-dc86.
References
- Ackermann, S., Schawinski, K., Zhang, C., Weigel, A. K., & Turp, M. D. 2018, MNRAS, 479, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Aihara, H., Armstrong, R., Bickerton, S., et al. 2018, PASJ, 70, S8 [NASA ADS] [Google Scholar]
- Akhlaghi, M. 2019, ArXiv e-prints [arXiv:1909.11230] [Google Scholar]
- Akhlaghi, M., & Ichikawa, T. 2015, ApJS, 220, 1 [Google Scholar]
- Andreon, S. 2002, A&A, 382, 495 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arp, H. 1966, ApJS, 14, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Arp, H., & Bertola, F. 1969, Astrophys. Lett., 4, 23 [NASA ADS] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beckwith, S. V. W., Stiavelli, M., Koekemoer, A. M., et al. 2006, AJ, 132, 1729 [Google Scholar]
- Bely, P. Y. 2003, The Design and Construction of Large Optical Telescopes (New York: Springer-Verlag) [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- BGM web-service, OSU THETA 2019, Besançon Model of Stellar Population Synthesis of the Galaxy, https://model.obs-besancon.fr [Google Scholar]
- Bilek, M., & Duc, P. A. 2021, Publications de l’Observatoire Astronomique de Beograd, 100, 211 [Google Scholar]
- Borlaff, A., Eliche-Moral, M. C., Beckman, J. E., et al. 2017, A&A, 604, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borlaff, A., Trujillo, I., Román, J., et al. 2019, A&A, 621, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2011, ApJ, 737, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Brooks, B. H., & NIRCam Team 2016, Am. Astron. Soc. Meet. Abstr., 227, 147.13 [NASA ADS] [Google Scholar]
- Buitrago, F., Trujillo, I., Curtis-Lake, E., et al. 2017, MNRAS, 466, 4888 [NASA ADS] [Google Scholar]
- Bullock, J. S., & Johnston, K. V. 2005, ApJ, 635, 931 [Google Scholar]
- Butler, D. J., Martínez-Delgado, D., & Brandner, W. 2004, AJ, 127, 1472 [NASA ADS] [CrossRef] [Google Scholar]
- Chromey, F. R., & Hasselbacher, D. A. 1996, PASP, 108, 944 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, A. P., Cole, S., Frenk, C. S., et al. 2010, MNRAS, 406, 744 [Google Scholar]
- Cortese, L., Bendo, G. J., Isaak, K. G., Davies, J. I., & Kent, B. R. 2010, MNRAS, 403, L26 [Google Scholar]
- Cropper, M., Pottinger, S., Niemi, S. M., et al. 2014, Proc. SPIE, 9143, 91430J [NASA ADS] [CrossRef] [Google Scholar]
- de Vaucouleurs, G., & de Vaucouleurs, A. 1970, Astrophys. Lett., 5, 219 [NASA ADS] [Google Scholar]
- Dey, A., Schlegel, D. J., Lang, D., et al. 2019, AJ, 157, 168 [Google Scholar]
- Duc, P.-A., Cuillandre, J.-C., Karabal, E., et al. 2015, MNRAS, 446, 120 [Google Scholar]
- Duc, P.-A., Cuillandre, J.-C., & Renaud, F. 2018, MNRAS, 475, L40 [Google Scholar]
- Ferrarese, L., Côté, P., Cuillandre, J.-C., et al. 2012, ApJS, 200, 4 [Google Scholar]
- Fliri, J., & Trujillo, I. 2016, MNRAS, 456, 1359 [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaspar Venancio, L. M., Pachot, C., Carminati, L., et al. 2016, Proc. SPIE, 9904, 99040P [NASA ADS] [Google Scholar]
- Giacconi, R., Zirm, A., Wang, J., et al. 2002, ApJS, 139, 369 [Google Scholar]
- Giavalisco, M., Ferguson, H. C., Koekemoer, A. M., et al. 2004, ApJ, 600, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Gilmore, G. 2018, Contemp. Phys., 59, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Giorgini, J. D., Chodas, P. W., & Yeomans, D. K. 2001, AAS/Division for Planetary Sciences Meeting Abstracts, 33, 58.13 [NASA ADS] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R., Martin, N. F., Irwin, M., et al. 2007, ApJ, 671, 1591 [CrossRef] [Google Scholar]
- Ibata, R., Mouhcine, M., & Rejkuba, M. 2009, MNRAS, 395, 126 [Google Scholar]
- Illingworth, G. D., Magee, D., Oesch, P. A., et al. 2013, ApJS, 209, 6 [Google Scholar]
- Infante-Sainz, R., Trujillo, I., & Román, J. 2020, MNRAS, 491, 5317 [Google Scholar]
- Iodice, E., Spavone, M., Cattapan, A., et al. 2020, A&A, 635, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Israel, H., Massey, R., Prod’homme, T., et al. 2015, MNRAS, 453, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezić, Ž., Kahn, S. M., Tyson, J. A., et al. 2019, ApJ, 873, 111 [Google Scholar]
- Janowiecki, S., Mihos, J. C., Harding, P., et al. 2010, ApJ, 715, 972 [Google Scholar]
- Johnston, K. V., Bullock, J. S., Sharma, S., et al. 2008, ApJ, 689, 936 [Google Scholar]
- Karabal, E., Duc, P. A., Kuntschner, H., et al. 2017, A&A, 601, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klaas, U., Okumura, K., Ferlet, M., et al. 2014, Exp. Astron., 37, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Koekemoer, A. M., Ellis, R. S., McLure, R. J., et al. 2013, ApJS, 209, 3 [Google Scholar]
- Laine, S., Martinez-Delgado, D., Trujillo, I., et al. 2018, ArXiv e-prints [arXiv:1812.04897] [Google Scholar]
- Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, ArXiv e-prints [arXiv:1110.3193] [Google Scholar]
- Lemke, D., Kranz, T., Klaas, U., et al. 2003, in The Calibration Legacy of the ISO Mission, eds. L. Metcalfe, A. Salama, S. B. Peschke, & M. F. Kessler, ESA Spec. Publ., 481, 219 [NASA ADS] [Google Scholar]
- Maciaszek, T., Ealet, A., Jahnke, K., et al. 2014, Proc. SPIE, 9143, 91430K [NASA ADS] [CrossRef] [Google Scholar]
- Mack, J., Lucas, R. A., Grogin, N. A., Bohlin, R. C., & Koekemoer, A. M. 2018, ACS/WFC Sky Flats from Frontier Fields Imaging, Instrument Science Report ACS 2017-09 [Google Scholar]
- Malin, D. F., & Carter, D. 1980, Nature, 285, 643 [CrossRef] [Google Scholar]
- Manfroid, J. 1995, A&AS, 113, 587 [NASA ADS] [Google Scholar]
- Markovič, K., Percival, W. J., Scodeggio, M., et al. 2017, MNRAS, 467, 3677 [Google Scholar]
- Martínez-Delgado, D. 2019, in Highlights on Spanish Astrophysics X, eds. B. Montesinos, A. Asensio Ramos, F. Buitrago, et al., 146 [Google Scholar]
- Martínez-Delgado, D., Gabany, R. J., Crawford, K., et al. 2010, AJ, 140, 962 [Google Scholar]
- Martínez-Delgado, D., D’Onghia, E., Chonis, T. S., et al. 2015, AJ, 150, 116 [CrossRef] [Google Scholar]
- McConnachie, A. W., Irwin, M. J., Ibata, R. A., et al. 2009, Nature, 461, 66 [Google Scholar]
- Mihos, J. C. 2004, in Recycling Intergalactic and Interstellar Matter, eds. P. A. Duc, J. Braine, & E. Brinks, IAU Symp., 217, 390 [NASA ADS] [Google Scholar]
- Mihos, J. C. 2019, ArXiv e-prints [arXiv:1909.09456] [Google Scholar]
- Mihos, J. C., Harding, P., Feldmeier, J., & Morrison, H. 2005, ApJ, 631, L41 [Google Scholar]
- Mihos, J. C., Harding, P., Feldmeier, J. J., et al. 2017, ApJ, 834, 16 [Google Scholar]
- Miville-Deschênes, M.-A., & Lagache, G. 2005, ApJS, 157, 302 [Google Scholar]
- Miville-Deschênes, M. A., Duc, P. A., Marleau, F., et al. 2016, A&A, 593, A4 [Google Scholar]
- Montes, M. 2019, ArXiv e-prints [arXiv:1912.01616] [Google Scholar]
- Montes, M., Infante-Sainz, R., Madrigal-Aguado, A., et al. 2020, ApJ, 904, 114 [Google Scholar]
- Montes, M., Brough, S., Owers, M. S., & Santucci, G. 2021, ApJ, 910, 45 [Google Scholar]
- Morales, G., Martínez-Delgado, D., Grebel, E. K., et al. 2018, A&A, 614, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mouhcine, M., Ferguson, H. C., Rich, R. M., Brown, T. M., & Smith, T. E. 2005, ApJ, 633, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Oke, J. B. 1971, ApJ, 170, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Paillassa, M., Bertin, E., & Bouy, H. 2019, in Astronomical Data Analysis Software and Systems XXVII, eds. P. J. Teuben, M. W. Pound, B. A. Thomas, & E. M. Warner, ASP Conf. Ser., 523, 99 [NASA ADS] [Google Scholar]
- Perlin, K. 1985, ACM Siggraph Computer Graphics, 19, 287 [CrossRef] [Google Scholar]
- Perlin, K. 2002, Association for Computing Machinery, SIGGRAPH ’02, 681 [Google Scholar]
- Pickles, A., & Depagne, É. 2010, PASP, 122, 1437 [NASA ADS] [CrossRef] [Google Scholar]
- Pillepich, A., Vogelsberger, M., Deason, A., et al. 2014, MNRAS, 444, 237 [Google Scholar]
- Pirzkal, N., Mack, J., Dahlen, T., & Sabbi, E. 2011, Sky Flats: Generating Improved WFC3 IR Flat-fields, Space Telescope WFC Instrument Science Report [Google Scholar]
- Planck Collaboration I. 2016, A&A, 594, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ragusa, R., Spavone, M., Iodice, E., et al. 2021, A&A, 651, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rejkuba, M. 2012, Ap&SS, 341, 195 [Google Scholar]
- Román, J., & Trujillo, I. 2018, Res. Notes Am. Astron. Soc., 2, 144 [Google Scholar]
- Román, J., Trujillo, I., & Montes, M. 2020, A&A, 644, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sahlmann, J., Martín-Fleitas, J., Mora, A., et al. 2016, Proc. SPIE, 9904, 99042E [Google Scholar]
- Sandage, A., & Binggeli, B. 1984, AJ, 89, 919 [Google Scholar]
- Sandin, C. 2014, A&A, 567, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sandin, C. 2015, A&A, 577, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scaramella, R., Mellier, Y., Amiaux, J., et al. 2014, in Statistical Challenges in 21st Century Cosmology, eds. A. Heavens, J. L. Starck, & A. Krone-Martins, 306, 375 [NASA ADS] [Google Scholar]
- Scaramella, R., Amiaux, J., Mellier, Y., et al. 2021, A&A, submitted [arXiv:2108.01201] [Google Scholar]
- Schweizer, F., & Seitzer, P. 1988, ApJ, 328, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Slater, C. T., Harding, P., & Mihos, J. C. 2009, PASP, 121, 1267 [Google Scholar]
- Spangelo, S. C., Katti, R. M., Unwin, S. C., & Bock, J. J. 2015, J. Astron. Telesc. Instrum. Syst., 1, 037001 [NASA ADS] [CrossRef] [Google Scholar]
- Stubbs, C. W., & Tonry, J. L. 2006, ApJ, 646, 1436 [NASA ADS] [CrossRef] [Google Scholar]
- Szafraniec, M., Azzollini, R., Cropper, M., et al. 2016, Proc. SPIE, 9915, 991510 [NASA ADS] [CrossRef] [Google Scholar]
- Teeninga, P., Moschini, U., Trager, S., & Wilkinson, M. 2015, in Mathematical Morphology and its Applications to Signal and Image Processing, eds. J. Benediktsson, J. Chanussot, L. Najman, & H. Talbot (Cham: Springer), 9082, 157 [Google Scholar]
- Tereno, I., Carvalho, C. S., Dinis, J., et al. 2014, in Statistical Challenges in 21st Century Cosmology, eds. A. Heavens, J. L. Starck, & A. Krone-Martins, 306, 379 [NASA ADS] [Google Scholar]
- Tolman, R. C. 1930, Proc. Natl. Acad. Sci., 16, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Tolman, R. C. 1934, Relativity, Thermodynamics, and Cosmology (Oxford: Oxford Clarendon Press) [Google Scholar]
- Trujillo, I., & Fliri, J. 2016, ApJ, 823, 123 [Google Scholar]
- Trujillo, I., Beasley, M. A., Borlaff, A., et al. 2019, MNRAS, 486, 1192 [Google Scholar]
- Turner, M. G. 2004, Int. Soc. Opt. Photon., 5579, 333 [NASA ADS] [Google Scholar]
- Valls-Gabaud, D., & MESSIER Collaboration 2017, in Formation and Evolution of Galaxy Outskirts, eds. A. Gil de Paz, J. H. Knapen, & J. C. Lee, 321, 199 [Google Scholar]
- Van Der Walt, S., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [Google Scholar]
- van Dokkum, P., Danieli, S., Cohen, Y., et al. 2018, Nature, 555, 629 [Google Scholar]
- van Dokkum, P., Lokhorst, D., Danieli, S., et al. 2020, PASP, 132, 074503 [NASA ADS] [CrossRef] [Google Scholar]
- Venancio, L. M. G., Carminati, L., Amiaux, J., et al. 2020, in Space Telescopes and Instrumentation 2020: Optical, Infrared, and Millimeter Wave, eds. M. Lystrup, M. D. Perrin, N. Batalha, N. Siegler, & E. C. Tong (SPIE), Int. Soc. Opt. Photon., 45, 11443 [Google Scholar]
- Walmsley, M., Ferguson, A. M. N., Mann, R. G., & Lintott, C. J. 2019, MNRAS, 483, 2968 [NASA ADS] [CrossRef] [Google Scholar]
- White, S. D. M., & Rees, M. J. 1978, MNRAS, 183, 341 [Google Scholar]
- York, D. G., Adelman, J., Anderson, J. E., Jr., et al. 2000, AJ, 120, 1579 [NASA ADS] [CrossRef] [Google Scholar]
- Zackrisson, E., de Jong, R. S., & Micheva, G. 2012, MNRAS, 421, 190 [NASA ADS] [Google Scholar]
- Zwicky, F. 1952, PASP, 64, 242 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Limitations of stray-light approximation
In Sect. 2.2 we describe the method with which the stray-light that the VIS focal plane receives from the all-sky distribution of stars can be accurately estimated. We based our analysis on the Gaia DR2 catalog, with the addition of 260 objects from the bright end (G < 3 mag) detected by Sahlmann et al. (2016). To be able to simulate the stray-light from every single object in the sky in a reasonable computational time, we used a combination of full-resolution Gaia catalogs for the closest objects to the FOV and HEALpix binning for the stars beyond a certain critical radius (Rmin). In this appendix we test the uncertainties and limitations associated with this approximation, estimating them as a function of the relative size of the low- and high-resolution catalogs.
In Fig. A.1 we show the dependence of the stray-light results on the variation of the maximum radius where we estimate the stray-light from each independent star from the catalog. When we consider a very small minimum radius, clustering all the objects in their HEALpix cells beyond R > 1, we obtain less stray-light than when we consider a larger radius for the high-resolution map. Nevertheless, when higher values for Rmin are considered (simulating a larger region of the sky at full resolution), we find that the total stray-light level has a large increase for R < 2 but stays relatively constant beyond that limit. Moreover, analyzing the relative variation in total stray-light with Rmin (photons per pixel per degree increased in the high-resolution radius, see the lower panel of Fig. A.1), we find that the stray-light variation quickly converges to a constant value, finding differences smaller than 0.1 e− px−1 deg−1 beyond R > 5. The reason for this behavior is that the NDI decreases very rapidly with radius, so that slight changes in the position of the close stars make noticeable differences, but the effect of similar positional changes is negligible for stars at larger radii. We conclude that Rmin = 5 is a safe limit to generate our simulations, as a compromise between computational effort and the precision of our simulations.
 |
Fig. A.1. Variation in total stray-light estimated for a test sky pointing ( |
 |
Fig. A.2. Comparison of the median stray-light levels in the F1–F9 characteristic focal plane points of the Euclid/VIS survey, taking sources inside (infield) and outside (outfield) the FOV for the non-axisymmetric NDI model (left panel) and the envelope worst-case NDI model into account (right panel). See the color bar in the figures. |
All Tables
Parameters of the envelope NDI model defined in Eqs. (4)–(6) (Gaspar Venancio et al. 2016).
All Figures
 |
Fig. 1. Euclid/VIS stellar flux density map, based on Gaia (Gaia Collaboration 2016, 2018) and Sahlmann et al. (2016) catalogs: Black contours: footprint of a proxy of the Euclid/VIS Survey (Scaramella et al. 2021). The darkened regions, corresponding to the peak of the Milky Way emission, lie outside the footprint. The three regions marked with orange contours correspond to the Deep North, Deep South, and Deep Fornax fields. Color background: stellar flux density per HEALpix cell. The brightest region corresponds to the Galactic plane, a region avoided by the Euclid footprint. See the bottom color bar for the scaling. Red lines: projected trajectories of the main Solar System bodies (Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, and Neptune) as seen by Euclid during the mission, following the ecliptic plane (Giorgini et al. 2001). |
| In the text | |
 |
Fig. 2. Photometric characteristics of the Euclid/VIS detector. Left panel: Euclid/VIS transmission curve (solid red line). Gaia G-band transmission curve (Venancio et al. 2020, solid blue line). Euclid/VIS payload module (PLM) transmission curve (black dashed line). Quantum efficiency of the Euclid/VIS CCD detectors (including end-of-life contamination), derived from the initial engineering models (green dotted line). Wavelength ranges for the numerical integration of the transmission of VIS using the IRSA sky-background model (gray columns). SDSS g-band sensitivity for extended sources with zero airmass (light blue dotted line). Equivalent for SDSS r-band (orange dash-dotted line). Equivalent for SDSS i-band (magenta dash-dot-dotted line). Right panel: Euclid/VIS magnitude as a function of the Gaia G-band AB magnitudes for the synthetic stellar objects of the Euclid true universe simulation. See the legend for the fitted linear transformation model between both bands. |
| In the text | |
 |
Fig. 3. Stray-light simulation of a Euclid/VIS observation in the environment of the Orion belt ( |
| In the text | |
 |
Fig. 4. Fraction of identified pixels that are masked as part of a source per exposure in the IAC SDSS S82 mosaics (Fliri & Trujillo 2016; Román & Trujillo 2018). The dashed and dotted vertical lines represent the median value of the distribution and its ±1σ dispersion percentiles (see the legend). |
| In the text | |
 |
Fig. 5. Left panel: simulated flat-field structure using Perlin and pixel-to-pixel Gaussian noise. Right panel: example of one of the simulated precalibrated frames ( |
| In the text | |
 |
Fig. 6. Stray-light contamination levels in the Euclid/VIS Survey, taking sources inside (infield) or outside (outfield) the FOV into account, and the sum of all the objects (total). Left panel: average stray-light contamination level expected in the VIS exposures per pixel assuming the nominal 565 s exposure time (e− px−1). Right panel: average stray-light gradient level (e− px−1 deg−1) per exposure. Red bars: estimates based on the numerical nonaxisymmetric NDI model. Blue bars: estimates based on the worst-case scenario envelope NDI model. See the legend in the figures. |
| In the text | |
 |
Fig. 7. Predicted sky-background level map in equatorial coordinates for the Euclid/VIS Survey (Scaramella et al. 2021) as a combination of zodiacal light, Milky Way ISM, and CIB using the NASA/IPAC sky-background model. The resolution of the map is approximately |
| In the text | |
 |
Fig. 8. Distribution of sky-background surface brightness in the Euclid/VIS exposures as predicted by the IRSA model for the zodiacal light (orange), ISM (red), and CIB (dashed black line), the simulations for the average stray-light contamination (green), and the combination of all components (blue histogram). |
| In the text | |
 |
Fig. 9. Precision (in percent) of the VIS sky flat-field as a function of the number of combined exposures (as scaled by time) and the applied binning. The dotted horizontal magenta line represents the maximum measured variation of the LED flat-fields within the λ range of VIS (Szafraniec et al. 2016). The dashed black horizontal line represents the precision requirement for the calibration lamp flat-fielding correction. See the legend for details. |
| In the text | |
 |
Fig. 10. Surface brightness limit of the individual simulated VIS exposures as a function of the different components of the sky background. Top left panel: histogram of the surface brightness limit per exposure (9916 simulations). The solid and dashed vertical lines represent the median value of the distribution and its ±1σ dispersion percentiles. Top right panel: zodiacal light surface brightness vs. limiting surface brightness. Bottom left panel: average stray-light light level (from Solar System bodies and stars) surface brightness vs. limiting surface brightness. Bottom right panel: interstellar medium surface brightness vs. limiting surface brightness. Contours represent nine equidistant levels of probability density between 10% and 90%. |
| In the text | |
 |
Fig. 11. Comparison of the surface brightness limit (3σ, 10 × 10 arcsec2) for the Euclid/VIS Wide Survey (and two magnitudes deeper for the Deep Fields), compared with a selection of deep optical and near-infrared surveys including SDSS (York et al. 2000), IAC Stripe 82 (S82 Fliri & Trujillo 2016), the MATLAS deep-imaging Survey (Duc et al. 2015), DECaLS (Dey et al. 2019), Stellar Tidal Stream Survey (Martínez-Delgado 2019, STSS), Hyper Suprime-Cam DR2 (Aihara et al. 2018), Coma Cluster Dragonfly observations (van Dokkum et al. 2020), HST WFC3 ABYSS HUDF (Borlaff et al. 2019), XDF (Illingworth et al. 2013), UGC00180 10.4 m GTC exploration (Trujillo & Fliri 2016), the Burrell Schmidt Deep Virgo Survey (Mihos et al. 2017), the VEGAS-VST (Iodice et al. 2020; Ragusa et al. 2021), and LSST (10-year full survey integration, Ivezić et al. 2019). |
| In the text | |
 |
Fig. A.1. Variation in total stray-light estimated for a test sky pointing ( |
| In the text | |
 |
Fig. A.2. Comparison of the median stray-light levels in the F1–F9 characteristic focal plane points of the Euclid/VIS survey, taking sources inside (infield) and outside (outfield) the FOV for the non-axisymmetric NDI model (left panel) and the envelope worst-case NDI model into account (right panel). See the color bar in the figures. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.