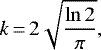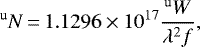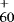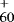| Issue |
A&A
Volume 656, December 2021
|
|
|---|---|---|
| Article Number | A100 | |
| Number of page(s) | 13 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202142078 | |
| Published online | 08 December 2021 | |
The C60:C60+ ratio in diffuse and translucent interstellar clouds
1
Laboratory Astrophysics Group of the Max Planck Institute for Astronomy at the Friedrich Schiller University Jena, Institute of Solid State Physics,
Helmholtzweg 3,
07743
Jena,
Germany
e-mail: gael.rouille@uni-jena.de
2
University of Lille, CNRS, UMR 8523 - PhLAM - Laboratoire de Physique des Lasers Atomes et Molécules,
59000
Lille,
France
Received:
24
August
2021
Accepted:
12
September
2021
Context. Insight into the conditions that drive the physics and chemistry in interstellar clouds is gained from determining the abundance and charge state of their components.
Aims. We propose an evaluation of the C60:C60+ ratio in diffuse and translucent interstellar clouds that exploits electronic absorption bands so as not to rely on ambiguous IR emission measurements.
Methods. The ratio is determined by analyzing archival spectra and literature data. Information on the cation population is obtained from published characteristics of the main diffuse interstellar bands attributed to C60+ and absorption cross sections already reported for the vibronic bands of the cation. The population of neutral molecules is described in terms of upper limits because the relevant vibronic bands of C60 are not brought out by observations. We revise the oscillator strengths reported for C60 and measure the spectrum of the molecule isolated in Ne ice to complete them.
Results. We scale down the oscillator strengths for absorption bands of C60 and find an upper limit of approximately 1.3 for the C60:C60+ ratio.
Conclusions. We conclude that the fraction of neutral molecules in the buckminsterfullerene population of diffuse and translucent interstellar clouds may be notable despite the non-detection of the expected vibronic bands. More certainty will require improved laboratory data and observations.
Key words: astrochemistry / ISM: abundances / ISM: lines and bands / ISM: molecules
© G. Rouillé et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1 Introduction
Mid-IR emission observations revealed the presence of fullerene C60 first in planetary and reflection nebulae (Cami et al. 2010; Sellgren et al. 2010) and then in various astrophysical objects (Cami 2014, and references therein). More recently, also exploiting mid-IR emission observations, Berné et al. (2017) found that C60 is present in the diffuse interstellar medium (ISM) as well. As to the fullerene cation C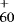 , after two decades of anticipation (Foing & Ehrenfreund 1994, 1997), it was identified recently as the carrier of diffuse interstellar bands (DIBs) observed at near-IR wavelengths (Campbell et al. 2015, 2016a,b; Walker et al. 2015, 2016, 2017). After several tests, the identification of C
, after two decades of anticipation (Foing & Ehrenfreund 1994, 1997), it was identified recently as the carrier of diffuse interstellar bands (DIBs) observed at near-IR wavelengths (Campbell et al. 2015, 2016a,b; Walker et al. 2015, 2016, 2017). After several tests, the identification of C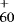 as the carrier is considered to be firm (Cordiner et al. 2019, and references therein), demonstrating the presence of C
as the carrier is considered to be firm (Cordiner et al. 2019, and references therein), demonstrating the presence of C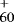 in the diffuse ISM. Lastly, Iglesias-Groth (2019) observed interstellar fullerenes C60 and C70, and the ions C
in the diffuse ISM. Lastly, Iglesias-Groth (2019) observed interstellar fullerenes C60 and C70, and the ions C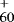 and C
and C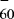 , in IR emission spectra of the star-forming region IC 348.
, in IR emission spectra of the star-forming region IC 348.
The ubiquity of C60 fullerene makes it an attractive species for probing various astrophysical environments (Brieva et al. 2016, and references therein). As an example of application, the C60:C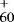 ratio in the ISM gives information on the local interstellar radiation field (ISRF) and electron density since it relates to photoionization and electron recombination (Bakes & Tielens 1995). Berné et al. (2017) evaluated the C60:C
ratio in the ISM gives information on the local interstellar radiation field (ISRF) and electron density since it relates to photoionization and electron recombination (Bakes & Tielens 1995). Berné et al. (2017) evaluated the C60:C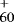 ratio for the diffuse ISM and, from the observed mid-IR emission bands of C60 and the measurement of DIBs attributed to C
ratio for the diffuse ISM and, from the observed mid-IR emission bands of C60 and the measurement of DIBs attributed to C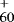 , they obtained absolute abundances that point to a C60:C
, they obtained absolute abundances that point to a C60:C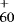 ratio between 0.3 and 6. Thus, the neutral species is possibly more abundant than the cation in the diffuse ISM, in agreement with a model predicting C60:C
ratio between 0.3 and 6. Thus, the neutral species is possibly more abundant than the cation in the diffuse ISM, in agreement with a model predicting C60:C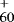 :C
:C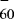 relative abundances of 0.62:0.11:0.27 (estimated from Fig. 5 in Bakes & Tielens 1995), that is, a C60:C
relative abundances of 0.62:0.11:0.27 (estimated from Fig. 5 in Bakes & Tielens 1995), that is, a C60:C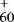 ratio of 5.6. The large uncertainty that affects the ratio given by Berné et al. (2017) originates chiefly in the evaluation of the column density of the neutral molecule from measurements of its IR emission spectrum. Even though improved emission observations may be a remedy, another issue arises. Indeed, the IR emission bands attributed to C60 may actually comprise contributions by analogous species (García-Hernández et al. 2013; Krasnokutski et al. 2019).
ratio of 5.6. The large uncertainty that affects the ratio given by Berné et al. (2017) originates chiefly in the evaluation of the column density of the neutral molecule from measurements of its IR emission spectrum. Even though improved emission observations may be a remedy, another issue arises. Indeed, the IR emission bands attributed to C60 may actually comprise contributions by analogous species (García-Hernández et al. 2013; Krasnokutski et al. 2019).
Electronic absorption bands are, by contrast, specific and better suited for probing the diffuse ISM, hence attempts to exploit those of C60 to evaluate the C60:C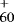 ratio. Resulting ratio values range from 1 (Léger et al. 1988) down to upper limits of 0.1 (Maier & Campbell 2017) and 0.0075 (Herbig 2000), the last two indicating strongly ionized populations, in contradiction with the prediction by Bakes & Tielens (1995) and the range of values proposed by Berné et al. (2017).
ratio. Resulting ratio values range from 1 (Léger et al. 1988) down to upper limits of 0.1 (Maier & Campbell 2017) and 0.0075 (Herbig 2000), the last two indicating strongly ionized populations, in contradiction with the prediction by Bakes & Tielens (1995) and the range of values proposed by Berné et al. (2017).
Facing this discrepancy, we propose another determination of the C60:C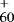 ratio in the diffuse ISM. Information on the cation population is provided to us by published detailed measurements of DIBs that C
ratio in the diffuse ISM. Information on the cation population is provided to us by published detailed measurements of DIBs that C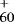 carries. As to the population of neutral buckminsterfullerene, it is characterized by an upper limit because the absorption bands of C60 that are most promising as gauges, expected at wavelengths near 4000 and 6000 Å, do not appear in the astronomical spectra at hand. Thus, we calculate an upper limit for C60:C
carries. As to the population of neutral buckminsterfullerene, it is characterized by an upper limit because the absorption bands of C60 that are most promising as gauges, expected at wavelengths near 4000 and 6000 Å, do not appear in the astronomical spectra at hand. Thus, we calculate an upper limit for C60:C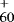 along lines of sight (LOSs) for which spectra of the 4000 and 6000 Å regions are available and for which the DIBs carried by C
along lines of sight (LOSs) for which spectra of the 4000 and 6000 Å regions are available and for which the DIBs carried by C are documentedin detail. For this purpose, we evaluate anew the oscillator strength of the relevant bands in the electronic spectrum of C60.
are documentedin detail. For this purpose, we evaluate anew the oscillator strength of the relevant bands in the electronic spectrum of C60.
Column densities of C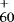 .
.
2 Lines of sight
We examined seven LOSs chosen for the availability of detailed measurements of the two strongest DIBs attributed to C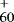 (Galazutdinov et al. 2017) and that of spectra that cover the 4000 and 6000 Å wavelength regions, where absorption bands of C60 are expected. These LOSs exhibit a color excess E(B−V) in the range 0.2–1.48, which translates approximately into total extinction AV values in the range 0.6–4.6 if we adopt the total-to-selective extinction ratio of the Milky Way (RV = 3.1, Cardelli et al. 1989). Although these values suggest the LOSs cross diffuse (AV ≲ 1) to translucent (1 ≲ AV ≲ 5) clouds, one must not presume the distribution of matter along them. Indeed, an alignment of diffuse clouds may not differ from a translucent cloud in terms of extinction. In any case, the spectra of all the corresponding target stars feature lines of the CH radical, indicating regions with diffuse molecular cloud conditions (Snow & McCall 2006). Furthermore, all except one include lines of the CN radical. As to translucent cloud conditions, they are actually met in at least one case, toward HD 169454 (Jannuzi et al. 1988).
(Galazutdinov et al. 2017) and that of spectra that cover the 4000 and 6000 Å wavelength regions, where absorption bands of C60 are expected. These LOSs exhibit a color excess E(B−V) in the range 0.2–1.48, which translates approximately into total extinction AV values in the range 0.6–4.6 if we adopt the total-to-selective extinction ratio of the Milky Way (RV = 3.1, Cardelli et al. 1989). Although these values suggest the LOSs cross diffuse (AV ≲ 1) to translucent (1 ≲ AV ≲ 5) clouds, one must not presume the distribution of matter along them. Indeed, an alignment of diffuse clouds may not differ from a translucent cloud in terms of extinction. In any case, the spectra of all the corresponding target stars feature lines of the CH radical, indicating regions with diffuse molecular cloud conditions (Snow & McCall 2006). Furthermore, all except one include lines of the CN radical. As to translucent cloud conditions, they are actually met in at least one case, toward HD 169454 (Jannuzi et al. 1988).
The measurements of the 9577 and 9632 Å DIBs by Galazutdinov et al. (2017) along the seven LOSs we have chosen are given in Table 1. They comprise the observed rest wavelengths, λ, full widths at half maximum (FWHMs), w, and equivalent widths, W.
Spectra of the LOS target stars measured in the 4000 and 6000 Å wavelength regions with a high signal-to-noise ratio (S/N) were found in the archives of the European Southern Observatory (ESO). For each LOS, spectra measured in series in the same observational session were summed to further increase the S/N. The errors on the flux values were then considered to be standard errors and were combined accordingly. The data sets are given in Appendix A.
The wavelength scales of the archival spectra are defined in the observer rest frame. For practical purposes, the standard of rest has been changed to an interstellar reference, a substance plausibly located in the same regions as interstellar fullerenes, so as to obtain scales that show the rest wavelengths of these species (Appendix B).
3 Laboratory spectra of C60 and C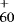
3.1 Positions and widths of the near-IR bands of C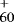
Campbell et al. (2016b) measured the near-IR spectrum of the C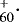 He complex in the gas phase below 10 K. They found that absorption bands of free C
He complex in the gas phase below 10 K. They found that absorption bands of free C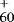 were similar in terms of wavelengths and relative intensities to those obtained for the complex, and that they matched DIBs as a consequence, leading to the first identification of one of their carriers (Cordiner et al. 2019, and references therein). We are presently interested in the two strongest bands of C
were similar in terms of wavelengths and relative intensities to those obtained for the complex, and that they matched DIBs as a consequence, leading to the first identification of one of their carriers (Cordiner et al. 2019, and references therein). We are presently interested in the two strongest bands of C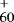 , which absorb at 9577.5 ± 0.1 Å and 9632.7 ± 0.1 Å according to Campbell et al. (2016b).
, which absorb at 9577.5 ± 0.1 Å and 9632.7 ± 0.1 Å according to Campbell et al. (2016b).
Exploiting the spectrum of C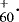 He further, Campbell et al. (2016b) determined the FWHMs of these two bands of C
He further, Campbell et al. (2016b) determined the FWHMs of these two bands of C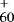 for a temperature of 10 K. Denoted w(C
for a temperature of 10 K. Denoted w(C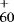 , 9577.5 Å) and w(C
, 9577.5 Å) and w(C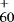 , 9632.7 Å), they are 2.5 ± 0.2 Å and 2.2 ± 0.2 Å, respectively.
, 9632.7 Å), they are 2.5 ± 0.2 Å and 2.2 ± 0.2 Å, respectively.
3.2 Positions and widths of the near-UV and orange bands of C60
Measurements in a molecular beam with resonant two-photon ionization spectroscopy showed that the 11 T1u ←1Ag transition of C60 gives narrow absorption bands near 4000 Å (Haufler et al. 1991). The two strongest bands, labeled A0 and A1 to follow Leach et al. (1992), were thoroughly examined by Sassara et al. (2001) to assist in searches for interstellar C60. They arise respectively at 4024 ± 0.5 Å and 3980 ± 0.5 Å, and, in interstellar conditions, the FWHMs w(C60, A0) and w(C60, A1) would be 4.05 ± 0.81 and 5.54 ± 0.80 Å, respectively (or 25 ± 5 and 35 ± 5 cm−1 in terms of wavenumbers in Sassara et al. 2001).
The absorption bands of C60 near 6000 Å have not been examined with the attention given those near 4000 Å, possibly because they originate in electric dipole-forbidden electronic transitions (Gasyna et al. 1991; Leach et al. 1992; Negri et al. 1992; Hansen et al. 1997; Orlandi & Negri 2002) and, hence, are expected to be weaker than the near-UV bands. Ground-based astronomical measurements, however, when atmospheric absorptions are avoided, are more effective in terms of sensitivity and resolution in the 6000 Å wavelength region than near 4000 Å. It is thus worthwhile to examine and characterize the orange bands of C60.
The assignment of the bands observed near 6000 Å is complex because three electronic transitions are involved (Orlandi & Negri 2002, and references therein). The bands were measured over a broad wavelength domain with C60 isolated in Ar ice at ~5 K (Gasyna et al. 1991)and, with greater detail, in Ne ice at 4 K (Sassara et al. 1997) and in He droplets at 0.37 K (Close et al. 1997). Measurements were also performed with C60 in hydrocarbon solvents at room temperature and at 77 K (Leach et al. 1992; Hora et al. 1996; Catálan & Pérez 2002). Prominent bands appeared to form a series, and the member at longest wavelength was labeled γ0 by Leach et al. (1992).
In a solvatochromism study, the γ0 band was predicted to arise at 607.3 ± 0.2 nm in the gas phase. In another such study, Renge (1995) observed the influence of temperature on the extrapolated gas-phase wavelength and proposed a transition energy of 16 482 ± 24 cm−1 for the γ0 band of cold C60 in the gas phase, which translates into a wavelength of 606.7 ± 0.9 nm. Finally, the spectrum of C60 isolated in He droplets, least affected by environment-induced shifts, yielded a wavelength of 607.17 nm (Close et al. 1997).
Haufler et al. (1991) had already observed narrow bands near 6000 Å in their study of C60 in a molecular beam, the strongest one rising near 6070 Å. Catálan (1994) identified this band with γ0, the assignment of which is still uncertain (Orlandi & Negri 2002, and references therein).
We presently determine a wavelength of 6070 ± 1.0 Å for the γ0 band from the examination of the photoionization spectrum (Fig. 2 in Haufler et al. 1991). It is consistent with the values extrapolated using solvatochromism, the value reported for C60 in He droplets, and particularly a later molecular-beam measurement (Hansen et al. 1997). The uncertainty does not include that of the spectrometer calibration, which was not indicated.
Haufler et al. (1991) remarked that the FWHM of some bands was less than 5 cm−1, which we find correct in the case of the band at 6070 Å. Consequently, assuming the FWHM of the absorption band is identical to that of the measured photoionization feature, we set w(C60, γ0) to 1.5 ± 0.5 Å in the cold gas phase. The temperature of the molecules in the molecular beam is uncertain, yet it is likely closer to 100 than 10 K because the vaporization process provides the molecules with much internal energy and cooling them in a carrier gas expansion becomes less effective as their mass increases. Nevertheless, the temperature may not be higher than 100 K in the case of C60 in a beam as estimated by Hansen et al. (1997). This is also suggested by the comparison of the FWHM presently adopted with that of simulated rotational contours (Edwards & Leach 1993). At 1.5 ± 0.5 Å, equivalent to 4.1 ± 1.4 cm−1, the FWHM and its uncertainty indicate temperatures between 50 and 100 K, such as those encountered in the less dense regions of diffuse molecular clouds. At the lower temperatures found in the denser regions of diffuse clouds and in translucent clouds, the FWHM would be smaller according to the simulations.
3.3 Oscillator strengths of the near-IR bands of C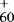
Campbell et al. (2016b) derived the absorption cross sections of the bands that arise at 9577.5 and 9632.7 Å in the spectrum of C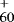 . They are denoted σ(C
. They are denoted σ(C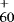 , 9577.5 Å) and σ(C
, 9577.5 Å) and σ(C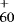 , 9632.7 Å) and their respective values are (5 ± 2) × 10−15cm2 and (4 ± 1.6) × 10−15cm2.
, 9632.7 Å) and their respective values are (5 ± 2) × 10−15cm2 and (4 ± 1.6) × 10−15cm2.
From their observational spectra, Galazutdinov et al. (2017) derived FWHMs for the two strongest DIBs attributed to C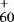 , w(DIB, 9577 Å) ranging from 2.3 ± 0.2 to 3.3 ± 0.2 Å, and w(DIB, 9632 Å) ranging from 1.8 ± 0.1 to 2.7 ± 0.2 Å. The deviation toward values larger than the laboratory measurements can be attributed to a higher temperature of the interstellar ions compared with the C
, w(DIB, 9577 Å) ranging from 2.3 ± 0.2 to 3.3 ± 0.2 Å, and w(DIB, 9632 Å) ranging from 1.8 ± 0.1 to 2.7 ± 0.2 Å. The deviation toward values larger than the laboratory measurements can be attributed to a higher temperature of the interstellar ions compared with the C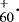 He complexes. It can also be attributed, at least partially, to the quality of the observational spectra. Indeed, assuming the two DIBs are caused by the same carrier, their widths should vary consistently from an LOS to another, when they do not. Moreover, deviations toward smaller values are not expected. Consequently, we assign the experimental absorption cross sections to the DIBs without considering any correction derived from their widths.
He complexes. It can also be attributed, at least partially, to the quality of the observational spectra. Indeed, assuming the two DIBs are caused by the same carrier, their widths should vary consistently from an LOS to another, when they do not. Moreover, deviations toward smaller values are not expected. Consequently, we assign the experimental absorption cross sections to the DIBs without considering any correction derived from their widths.
Spectra of C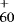 isolated in Ne ice were also reported and, as expected, the bands arising at 9577.5 and 9632.7 Å for the free cation are then slightly redshifted (Fulara et al. 1993; Strelnikov et al. 2015). Strelnikov et al. (2015) attributed oscillator strengths of 0.01 ± 0.003 and 0.015 ± 0.005 to the bluer and redder bands, respectively. Thus, the relative intensities are reversed compared to gas-phase measurements, an effect one may attribute to the interaction between the cations and the Ne matrix, unless the order of the bands itself is reversed, which would be unexpected.
isolated in Ne ice were also reported and, as expected, the bands arising at 9577.5 and 9632.7 Å for the free cation are then slightly redshifted (Fulara et al. 1993; Strelnikov et al. 2015). Strelnikov et al. (2015) attributed oscillator strengths of 0.01 ± 0.003 and 0.015 ± 0.005 to the bluer and redder bands, respectively. Thus, the relative intensities are reversed compared to gas-phase measurements, an effect one may attribute to the interaction between the cations and the Ne matrix, unless the order of the bands itself is reversed, which would be unexpected.
We can also compute effective oscillator strengths in a straightforward manner from the absorption cross sections and widths determined by Campbell et al. (2016b) through
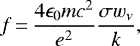 (1)
(1)
where m and e are the mass and charge of an electron, and c is the speedof light in vacuum. Equation (1) is obtained by making the approximation that band profiles are Gaussian in the wavenumber domain, and by using such a profile with FWHM wν when formulating the oscillator strength (Mulliken 1939, and references therein). In order to use w from the wavelength domain as given in Sect. 3.1, Eq. (1) can be approximated with
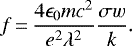 (3)
(3)
Values of 0.0164 ± 0.008 and 0.0114 ± 0.006 are obtained for f(C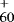 , 9577.5 Å) and f(C
, 9577.5 Å) and f(C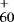 , 9632.7 Å), respectively. The reversal aside, they are consistent with those derived by Strelnikov et al. (2015). We retain the strengths derived from the absorption cross sections measured by Campbell et al. (2016b) on the C
, 9632.7 Å), respectively. The reversal aside, they are consistent with those derived by Strelnikov et al. (2015). We retain the strengths derived from the absorption cross sections measured by Campbell et al. (2016b) on the C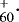 He complex because the spectrum of C
He complex because the spectrum of C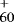 is less affected by the interaction with a single He atom than by the interaction with several Ne atoms, and because the gas-phase spectrum of the C
is less affected by the interaction with a single He atom than by the interaction with several Ne atoms, and because the gas-phase spectrum of the C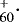 He complex is in better agreement with the DIB spectrum in terms of relative strengths compared to the matrix-isolation measurements.
He complex is in better agreement with the DIB spectrum in terms of relative strengths compared to the matrix-isolation measurements.
3.4 Oscillator strengths of the near-UV and orange bands of C60
Haufler et al. (1991) determined an oscillator strength of 0.006 ± 0.002 for the peaks of the 11 T1u ←1Ag transition, namely, the system of An bands of Leach et al. (1992). They did so by comparing their spectrum of C60 in a molecular beam with a spectrum obtained from a solution. Yet, from the spectrum of C60 in hexane at room temperature, Leach et al. (1992) obtained a value of 0.015 ± 0.005 for the same transition. The discrepancy between the two values possibly originates in the fact that Leach et al. (1992) did not correct the oscillator strength for the effect of the solvent (Chupka & Klots 1997). Considering a refractive index of 1.39 ± 0.01 for hexane at room temperature at 400 nm (estimated from Fig. 3 in Sowers et al. 1972), a correction factor of 0.582 ± 0.008 is obtained, which leads to an oscillator strength of 0.0087 ± 0.0031 for the 11 T1u ←1Ag transition of free C60. This value is in good agreement with that reported by Haufler et al. (1991), which is consequently chosen for our study.
We determined the oscillator strengths of the A0 and A1 bands by distributing the value given by Haufler et al. (1991) among the narrow peaks measured in a spectrum of C60 isolated in Ne ice, in proportion to their areas, which we assume to be similarly affected by the matrix environment. The spectroscopy is briefly described in Appendix C. Figure 1 shows the matrix-isolation spectrum and Gaussian profiles fitted onto seven peaks of the 11 T1u ←1Ag transition, that is, the system of An bands. The fitting procedure gave for the seven peaks together an area of 6.64 ± 0.21 cm−1, with individual peak areas of 1.386 ± 0.064 cm−1 for A0 and 2.938 ± 0.073 cm−1 for A1. Thus, values of 0.00131 ± 0.00056 and 0.0027 ± 0.0011 were derived for f(C60, A0) and f(C60, A1), respectively.They are visibly lower than those used by Berné et al. (2017), 0.005 and 0.007, yet on the same order.
Similarly, the oscillator strength of the orange band γ0 was obtained by comparing its area of 0.435 ± 0.022 cm−1 with that of the A1 band (Fig. 1). Consequently, f(C60, γ0) equals 0.00040 ± 0.00016.
4 Astronomical spectra
4.1 Observational data near 4000 Å
Several atomic lines arise in stellar spectra around 4000 Å. The strongest lines are the H I (Hϵ) and He I lines at 3970.075 and 4026.1914 Å rest wavelengths, respectively. While the H I and He I lines are observed in all spectra, the others appear with relative strengths that vary widely depending on the target star.
In each observational spectrum taken into account, the A0 band of C60 expected at 4024 Å would overlap the strong He I line mentioned above. Figure 2 illustrates the phenomenon in the spectrum of HD 169454; it also shows that the A0 band and a minor He I line (4023.973 Å rest wavelength) are superimposed, not to mention the overlap by an Fe III line (4022.35 Å rest wavelength, Thompson et al. 2008, and references therein).
In comparison, the A1 band of C60 at 3980 Å is better separated from the nearby O II line found at 3982.7140 Å rest wavelength, and from S III lines that rise at longer wavelengths. It is superimposed with a line of S II (3979.829 Å rest wavelength), which is apparent toward HD 183143 as observed in Fig. 3. Figure 3 also shows that the strength of the O II, S II, and S III lines depends on the spectral type of the target star and can be extremely weak.
Overlap with stellar lines is critical when the interstellar band is comparatively much weaker or, a fortiori, not observed because it lowers the S/N that is taken into account to determine the column density of the interstellar species or its upper limit. In such an instance, concerning the 4000 Å region, the A1 band of C60 at 3980 Å is preferred to A0, although broadening of the Hϵ line such as toward O9Ib-type HD 76341 may constitute a cause for concern.
 |
Fig. 1 (a) Absorption spectrum of C60 isolated in a Ne matrix, not corrected for scattering. Band labels according to Leach et al. (1992). (b) Gaussian profiles (thick gray solid curve) fitted to bands of the 11 T1u ←1Ag transition, including A0 and A1, and to the baseline. (c) Gaussian profiles (thick gray solid curve) fitted, with a common FWHM, to absorptions near the γ0 band. Fittedband positions are 16 431.1 ± 1.2 cm−1, 24 829.04 ± 0.98 cm−1, and 25 087.73 ± 0.65 cm−1 for γ0, A0, and A1, respectively.The wavelength scale of the spectrometer was calibrated with an accuracy of 0.3 nm. |
 |
Fig. 2 Spectrum toward HD 169454 (black solid curve) and synthetic absorption spectrum of C60 with the expected band positions, widths, and relative areas (thick gray solid curve). Narrow absorption lines in the 3967–3971 Å interval correspond to velocity components of the Ca II H line. |
4.2 Observational data near 6000 Å
Figure 4 shows the spectral region where the γ0 band of C60 is expected. A straight line continuum was defined over the 6058–6087 Å range of each original spectrum, still in the observer rest frame, and used to normalize the corresponding spectrum. The straight continuum was extrapolated to 6092 Å so as to be applied to the 6090 Ånarrow DIB, the position of which was to serve as reference for evaluating those of other DIBs (Sect. 6). Next the wavelength scale was changed from observer rest frame to interstellar (Appendix B).
While the 4000 Å spectral region is rich in stellar lines, the 6000 Å region comprises several DIBs and, in most cases, a line of stellar Ne I measured at 6074.338 Å in the laboratory (see Hobbs et al. 2009, for HD 183143). For all LOSs but HD 169454, the position of this line was predicted from the position of the He I line measured at 5875.62 Å in the laboratory. As to the spectrum toward HD 169454, we used lines of N II, Al III, and Si III that are observed clearly between 5665 and 5740 Å, for the He I line does not have a peak profile that would yield an accurate position.
A shift is apparent between the DIBs in the spectrum toward HD 183143 and the positions reported by Hobbs et al. (2009) for this veryLOS (Fig. 4). It is caused by a difference in the choice of reference for rest, the strongest velocity component of diatomic lines versus the strongest component of the 7698 Å K I line. The velocity difference is ~15 km s−1 (Hobbs et al. 2009), representing 0.3 Å at 6000 Å as observed in Fig. 4.
Finally, although H2O vapor gives numerous absorption lines near 6070 Å (Carleer et al. 1999), they are very weak and generally not detected. Thus telluric features are not seen.
Two DIBs are found at 6068.4 and 6071.1 Å (Galazutdinov et al. 2000; Tuairisg et al. 2000; Weselak et al. 2000; Hobbs et al. 2009), close to the position of the γ0 band, that is, 6070 ± 1 Å. Their FWHMs are on the order of 1–2 Å, as expected for the γ0 band. There is, however, no further indication at this stage that either of these DIBs could be identified with γ0. Although they represent rather weak absorptions, their presence influences the search for the C60 feature.
 |
Fig. 3 Normalized observational spectra (black solid curves). A straight line continuum was defined over the 3960–4000 Å range of each spectrum still in the observer rest frame. The top panel includes a synthetic A1 band of C60 with expected position and width, and arbitrary equivalent width (thick gray solid curve). Its position is indicated through all panels (vertical dotted line). The light gray area indicates the wavelength interval of two FWHMs taken into account to evaluate uW(C60, A1) at 3980 Å for each LOS. The spectral type of each target star is indicated. |
5 Column density of C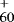
The column density of C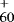 can be determined by comparing the equivalent widths of the relevant DIBs with Gaussian profiles defined using the absorption cross sections and associated widths derived by Campbell et al. (2016b) for a temperature of 10 K. We assume here that, for a given column density, W is conserved over a broad range of conditions. Considering an absorption feature with a Gaussian profile in the wavelength domain, where W is defined, the column density N of the absorbing species derived from the Lambert-Beer law is such that
can be determined by comparing the equivalent widths of the relevant DIBs with Gaussian profiles defined using the absorption cross sections and associated widths derived by Campbell et al. (2016b) for a temperature of 10 K. We assume here that, for a given column density, W is conserved over a broad range of conditions. Considering an absorption feature with a Gaussian profile in the wavelength domain, where W is defined, the column density N of the absorbing species derived from the Lambert-Beer law is such that
![\begin{equation*}N\,{=}\,-\frac{1}{\sigma}\ln\left[1-k\frac{W}{w}\right]. \end{equation*}](/articles/aa/full_html/2021/12/aa42078-21/aa42078-21-eq49.png) (4)
(4)
Given the large uncertainties on σ(C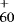 , 9577.5 Å) and σ(C
, 9577.5 Å) and σ(C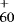 , 9632.7 Å), both 40%, on w(C
, 9632.7 Å), both 40%, on w(C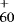 , 9577.5 Å) and w(C
, 9577.5 Å) and w(C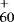 , 9632.7 Å), respectively 8 and 9%, and on W, 6–16%, ΔN is computedby using the propagation formula for large errors proposed by Seiler (1987). We assume here that the errors are independent and correspond to normal distributions. A correction is applied accordingly to N as calculated with Eq. (4) because the right hand term is a function that does not conserve the symmetry of normal distributions (Seiler 1987). The equivalent widths W of the DIBs observed at ~9577 and ~9632 Å, the column densities N(C
, 9632.7 Å), respectively 8 and 9%, and on W, 6–16%, ΔN is computedby using the propagation formula for large errors proposed by Seiler (1987). We assume here that the errors are independent and correspond to normal distributions. A correction is applied accordingly to N as calculated with Eq. (4) because the right hand term is a function that does not conserve the symmetry of normal distributions (Seiler 1987). The equivalent widths W of the DIBs observed at ~9577 and ~9632 Å, the column densities N(C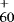 ) derived from them, and the corresponding errors, are given in Table 1.
) derived from them, and the corresponding errors, are given in Table 1.
In several cases, N(C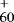 , 9577.5 Å) and N(C
, 9577.5 Å) and N(C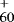 , 9632.7 Å) differ by a factor of ~2 although they are derived for the same LOS. Taking the uncertainties into account, the two values in each pair are nonetheless consistent. We note that the values presently obtained for N(C
, 9632.7 Å) differ by a factor of ~2 although they are derived for the same LOS. Taking the uncertainties into account, the two values in each pair are nonetheless consistent. We note that the values presently obtained for N(C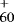 , 9577.5 Å) toward HD 169454 and HD 183143, respectively (7.8 ± 4.7) × 1012 and (30 ± 18) × 1012 cm−2, are in agreement with those derived by Berné et al. (2017), respectively 9 × 1012 and 20 × 1012 cm−2 (Table C.1 in Berné et al. 2017).
, 9577.5 Å) toward HD 169454 and HD 183143, respectively (7.8 ± 4.7) × 1012 and (30 ± 18) × 1012 cm−2, are in agreement with those derived by Berné et al. (2017), respectively 9 × 1012 and 20 × 1012 cm−2 (Table C.1 in Berné et al. 2017).
6 Column density of C60
Bands of interstellar C60 have been looked for near 4000 Å without success (e.g., Herbig 2000; Sassara et al. 2001; García-Hernández et al. 2012; García-Hernández & Díaz-Luis 2013; Díaz-Luis et al. 2015). Similarly, the seven spectra in Fig. 3 do not show any clear indication of an absorption band around 3980.0 Å that could be attributed to C60, and Fig. 4 does not reveal any new feature close to 6070.0 Å either. As a consequence, column densities N cannot be obtained for neutral buckminsterfullerene. Nevertheless, upper limits denoted uN can be estimated.
Values of uN can be evaluated by combining Eqs. (3) and (4). Observing that kW is small compared to w, and replacing N and W by the corresponding upper limits uN and uW, we obtain
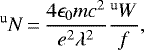 (5)
(5)
with uN, uW, and λ expressed in cm−2, mÅ, and Å, respectively. One recognizes the formula used by Herbig (2000), Díaz-Luis et al. (2015), or Berné et al. (2017). We calculate ΔuN and rectify uN following Seiler (1987) to take the large error on f into account.
Values of uW, the upper limit for the equivalent width of the band expected at wavelength λ, are taken equal to three equivalent-width detection thresholds, that is, 3σW, where σW is computed according to Lawton et al. (2008). Figure 5 presents σW curves for the 6000 Å region. Because σW depends on the difference between the observed spectrum and the chosen continuum, σW peaks at the position of any band or line that is not included in the continuum, as confirmed by a comparison with Fig. 4. Interestingly, the σW curves reveal a possible absorption feature at a position varying from 6078 to 6079 Å, which we have not identified. The varying wavelength suggests it is not a DIB, though, unless it is the effect of a poorly defined shape.
Moreover, the value of σW at a given wavelength considers the difference between the observed spectrum and the chosen continuum for all wavelengths in a surrounding interval spanning two FWHMs of the band to be detected. The value of σW at this wavelength can then be lowered by including in the continuum any nearby band with a profile that extends into the interval. Figure 5 includes cases in which fitted profiles of the DIBs nearest 6070 Å were included in the continuum. In the fitting procedure, each DIB was given a Gaussian profile with a position fixed to literaturevalue (Hobbs et al. 2009) – corrected using the shift observed for the 6090 Å DIB – while its FWHM andarea were free. A poor fit results in an incomplete elimination of the feature contribution to the σW curve.
Figure 6 shows σW curves for the 4000 Å region. They are given both with the stellar and interstellar atomic lines kept in the spectra and also with fitted profiles of the lines included in the continua. Large residuals from fitting the overlapping multiple components of the Ca II line cause the broad peak at 3968.5 Å that appears after the procedure.
Table 2 presents values for uW(C60) and uN(C60) obtained from the normalized observational spectra shown in Figs. 3 and 4. They were derived by giving f(C60, A1), w(C60, A1), f(C60, γ0), w(C60, γ0), and their uncertainties the values introduced and adopted in Sects. 3.2 and 3.4. The equivalent-width detection thresholds σW yielding the uW values were computed by using the data comprised within an interval centered at the rest wavelength of the relevant band and spanning two FWHMs.
According to the contents of Table 2, incorporation of specific spectral features into the continuum has the potential to lower substantially the upper limit for equivalent width. The most spectacular improvement is seen with HD 148379 where the uW and uN values derived from the UV spectrum are divided by a factor of close to four. The limits uN(C60, A1) and uN(C60, γ0) presented in Table 2 are in the ranges 14–81 × 1012 cm−2 and 9–26 × 1012 cm−2, respectively, when only the values obtained by including spectral features in the continuum, whenever available, are considered. The corresponding averages are 39 × 1012 cm−2 and 18 × 1012 cm−2. Thus uN(C60, A1) is approximately twice as large as uN(C60, γ0). The uncertainties are very large, with 63–65% for uN(C60, A1) and 70–74% for uN(C60, γ0).
 |
Fig. 4 Continuum-normalized spectra with interstellar wavelength scale for seven LOSs in the 6000 Å region. Each gray portion was obtained by extrapolating the straight continuum defined over the 6058–6087 Å interval (observer rest frame). The top panel includes a synthetic γ0 band of C60 of arbitrary equivalent width (thick gray solid curve, offset for clarity). Its position is indicated through all panels (vertical dotted line). Positions of DIBs according to Hobbs et al. (2009) are indicated in the bottom panel (short vertical lines). The predicted position of a line of stellar Ne I is marked in each panel (arrow). Synthetic spectra of DIBs and the Ne I line are represented in four panels (short-dashed curve). The light gray area indicates the wavelength interval of two FWHMs taken into account to evaluate uW(C60, γ0) at 6070 Å for each LOS. |
 |
Fig. 5 Equivalent-width detection threshold in the 6000 Å region for seven LOSs (solid curves). The vertical dotted line shows the expected position of the γ0 band of C60 in all spectra. Positions of DIBs according to Hobbs et al. (2009) are indicated in the bottom panel (short vertical lines). The predicted position of a line of stellar Ne I is marked in each panel (arrow). In four cases detection limits were computed as fitted profiles of the DIBs nearest 6070 Å were included in the continuum (short-dashed curves). An unidentified absorption would cause the rise near 6078 Å (asterisk). |
 |
Fig. 6 Equivalent-width detection threshold in the 4000 Å region scale for seven LOSs (solid curves). The vertical dotted line shows the expected position of the near-UV band of C60 in all spectra. The detection limits were also computed as fitted profiles of stellar lines were included in the continuum (short-dashed curves). |
Upper limits for column densities of interstellar C60 considering the A1 and γ0 bands.
7 Upper limits for the C60:C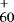 ratio
ratio
In order to compare populations of C60 and C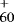 in interstellar clouds, we assume that the angular size of the clouds before a target star is large in comparison with the difference in LOS coordinates during the observations at UV and visible wavelengths, which remains smaller than 5″ (Table A.1). We also assume that the properties of the clouds do not vary significantly between the two sets of coordinates.
in interstellar clouds, we assume that the angular size of the clouds before a target star is large in comparison with the difference in LOS coordinates during the observations at UV and visible wavelengths, which remains smaller than 5″ (Table A.1). We also assume that the properties of the clouds do not vary significantly between the two sets of coordinates.
Our comparison is relevant to entire clouds and not to specific layers because the wavelengths of the DIBs attributed to C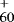 were determined by calibrating astronomical spectra with both atomic and molecular lines (Galazutdinov et al. 2017). The DIB wavelengths are given with an error in the range 0.1–0.3 Å, that is, on the order of the equivalent velocity difference between the diffuse atomic outer layer and the denser diatomic layer observed for HD 183143 (see Sect. 4.2). Moreover, the bands of C60 are currently not characterized with sufficient precision to allow us to search for them in a given layer.
were determined by calibrating astronomical spectra with both atomic and molecular lines (Galazutdinov et al. 2017). The DIB wavelengths are given with an error in the range 0.1–0.3 Å, that is, on the order of the equivalent velocity difference between the diffuse atomic outer layer and the denser diatomic layer observed for HD 183143 (see Sect. 4.2). Moreover, the bands of C60 are currently not characterized with sufficient precision to allow us to search for them in a given layer.
The upper limit of the C60:C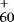 ratio then equals uN(C60)/N(C
ratio then equals uN(C60)/N(C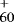 ). It is calculated by combining Eqs. (4) and (6) into which the values given in Tables 1 and 2 are entered, and by adding a correction that large errors make necessary (Seiler 1987). The errors that affect the ratios are then obtained by taking into account those attached to the band descriptors rather than ΔuN and ΔN. The results are given in Table 3, showing that the upper limit of the C60:C
). It is calculated by combining Eqs. (4) and (6) into which the values given in Tables 1 and 2 are entered, and by adding a correction that large errors make necessary (Seiler 1987). The errors that affect the ratios are then obtained by taking into account those attached to the band descriptors rather than ΔuN and ΔN. The results are given in Table 3, showing that the upper limit of the C60:C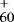 ratio noticeably depends on the band used to evaluate uN(C60). It ranges from 1.6 to 6.9 with an unweighted average value of 3.5 when using A1, and from 0.90 to 5.2 averaging 1.8 when using γ0. While the values in the latter case are lower and less spread than in the former when the extreme value of 5.2 is excluded, their relative uncertainties are greater. In either case the uncertainties are very large, respectively 76–81 and 83–90%, owing essentially to poorly determined oscillator strengths and absorption cross sections. The average ratio of 1.8 obtained by using γ0 is lowered to 1.3 when applying the inverted, squared errors as weights.
ratio noticeably depends on the band used to evaluate uN(C60). It ranges from 1.6 to 6.9 with an unweighted average value of 3.5 when using A1, and from 0.90 to 5.2 averaging 1.8 when using γ0. While the values in the latter case are lower and less spread than in the former when the extreme value of 5.2 is excluded, their relative uncertainties are greater. In either case the uncertainties are very large, respectively 76–81 and 83–90%, owing essentially to poorly determined oscillator strengths and absorption cross sections. The average ratio of 1.8 obtained by using γ0 is lowered to 1.3 when applying the inverted, squared errors as weights.
8 Discussion
8.1 The C60:C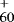 ratio in the diffuse ISM
ratio in the diffuse ISM
The detection of buckminsterfullerene and its cation in the ISM has extended the network of physical and chemical mechanisms at work in that environment. The relative populations of gas-phase C60, C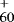 , and C
, and C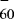 would be primarily governed by the ISRF strength and the electron density, which are directly related to mechanisms such as photoionization of C60 and electron detachment from C
would be primarily governed by the ISRF strength and the electron density, which are directly related to mechanisms such as photoionization of C60 and electron detachment from C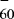 , electron attachment to C60 and electron recombination with C
, electron attachment to C60 and electron recombination with C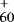 .
.
Figure 7 illustrates uN(C60, γ0)/N(C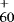 ) as a function of LOS and includes literature values of C60:C
) as a function of LOS and includes literature values of C60:C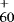 for comparison. The upper limits presently derived have an average value of 1.8, lowered to 1.3 when applying the inverted, squared errors as weights. Both averages are compatible with the interval of ratio values 0.3–6 presented by Berné et al. (2017), in particular its lower half. They suggest, however, that the ratio of 5.6 proposed by Bakes & Tielens (1995) in their theoretical study is somewhat large.
for comparison. The upper limits presently derived have an average value of 1.8, lowered to 1.3 when applying the inverted, squared errors as weights. Both averages are compatible with the interval of ratio values 0.3–6 presented by Berné et al. (2017), in particular its lower half. They suggest, however, that the ratio of 5.6 proposed by Bakes & Tielens (1995) in their theoretical study is somewhat large.
The value proposed by Bakes & Tielens (1995) was determined for a typical diffuse cloud with 100 K gas temperature, 7.5 × 10−3 cm−3 electron density, and 1 G0 ISRF, conditions that may not be observed along the real LOSs presently studied. For instance, Gredel & Münch (1986) determined a gas temperature of 15 K, thus well below 100 K, from the observation of C2 toward HD 169454. Additionally, in a study of C3 observed toward the same star, Schmidt et al. (2014) brought out two populations with excitation temperatures of 22.4 ± 1 K and 187 ± 25 K. Their analysis of the colder or less excited population led to an ISRF with a strength of 2 to 6 G0, greater than the 1 G0 ISRF used by Bakes & Tielens (1995). As to electron density, Harrison et al. (2013) proposed typical values in the range 0.01–0.06 cm−3, up to eight times that adopted by Bakes & Tielens (1995). Thus the conditions assumed by Bakes & Tielens (1995) may not be adequate to describe our LOSs, resulting through their interplay in a C60:C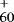 value greater than the weighted average upper limit derived in this study.
value greater than the weighted average upper limit derived in this study.
Moreover, properties of C60 and its ions relevant to the determination of their relative populations are not accurately known. The C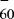 :C60 and C60:C
:C60 and C60:C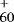 ratios are proportional, respectively, to the electron attachment rate of C60 and the electron recombination rate of C
ratios are proportional, respectively, to the electron attachment rate of C60 and the electron recombination rate of C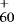 . To date, both values are uncertain. Bakes & Tielens (1995) attributed to neutral C60 an electron attachment cross sectionof 10−12 cm2 in their typical diffuse medium, a value proposed by Lezius et al. (1993). Because the analysis of measurements for electrons with low energy is complex (Kasperovich et al. 2001; Lezius 2003), the actual attachment cross section for an electron with an energy of ~0.013 eV (corresponding to 100 K) may be different, and, consequently, C
. To date, both values are uncertain. Bakes & Tielens (1995) attributed to neutral C60 an electron attachment cross sectionof 10−12 cm2 in their typical diffuse medium, a value proposed by Lezius et al. (1993). Because the analysis of measurements for electrons with low energy is complex (Kasperovich et al. 2001; Lezius 2003), the actual attachment cross section for an electron with an energy of ~0.013 eV (corresponding to 100 K) may be different, and, consequently, C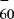 :C60 too. As to the electron recombination rate of C
:C60 too. As to the electron recombination rate of C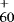 , which has yet to be measured, Bakes & Tielens (1995) used a theoretical value extrapolated from a model for grains (Draine & Sutin 1987). Yet they noted that this model gave rates an order of magnitude larger than measured ones when it was applied to the benzene (C6 H6) and naphthalene (C10H8) cations. Thus, the value they obtained for C60:C
, which has yet to be measured, Bakes & Tielens (1995) used a theoretical value extrapolated from a model for grains (Draine & Sutin 1987). Yet they noted that this model gave rates an order of magnitude larger than measured ones when it was applied to the benzene (C6 H6) and naphthalene (C10H8) cations. Thus, the value they obtained for C60:C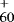 is possibly overestimated.
is possibly overestimated.
As to our result, one must be aware of the large uncertainties affecting the absorption cross sections and oscillator strengths we employed to evaluate C60:C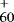 . Any correction applied to one of them changes uN(C60)/N(C
. Any correction applied to one of them changes uN(C60)/N(C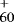 ), and therefore C60:C
), and therefore C60:C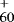 , in proportion.
, in proportion.
The influence of the chosen oscillator strengths on the C60:C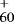 ratio is illustrated by the following evaluations, which differ from ours. Fulara et al. (1993) had estimated for the two bands of C
ratio is illustrated by the following evaluations, which differ from ours. Fulara et al. (1993) had estimated for the two bands of C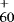 a total oscillator strength in the range 0.003–0.006, that is, five to nine times smaller than the value of 0.0278 we adopted (from adding 0.0164 to 0.0114, see Sect. 3.3). The former value was used by Herbig (2000) to estimate N(C
a total oscillator strength in the range 0.003–0.006, that is, five to nine times smaller than the value of 0.0278 we adopted (from adding 0.0164 to 0.0114, see Sect. 3.3). The former value was used by Herbig (2000) to estimate N(C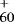 ) toward Cyg OB2/8A, which, combined with an evaluation of uN(C60) lower than ours by an order of magnitude, led to C60:C
) toward Cyg OB2/8A, which, combined with an evaluation of uN(C60) lower than ours by an order of magnitude, led to C60:C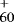 being 0.0075 at most. In that study, the author mentioned his doubts concerning the result and explained how the value for uN(C60) might be incorrect owing to a possibly much underestimated FWHM (see Sect. 8.2). In a second case, Maier & Campbell (Maier & Campbell 2017; Campbell & Maier 2017) inevitably derived a high degree of ionization, 98%, because they borrowed uN(C60) from Herbig (2000). They also stated that the degree of ionization should be at least 90% even if one of the DIBs observed near 6000 Å was absorption by C60 (Maier & Campbell 2017). The value was derived from elements in a discussion by Omont (2016), among which a theoretical oscillator strength of 0.01 attributed to the potential C60 DIB, which is 25 times greater than the strength presently determined for the γ0 band. We remark that abundances of neutral molecules and cations as evaluated by Omont (2016) would give 80% as the degree of ionization.
being 0.0075 at most. In that study, the author mentioned his doubts concerning the result and explained how the value for uN(C60) might be incorrect owing to a possibly much underestimated FWHM (see Sect. 8.2). In a second case, Maier & Campbell (Maier & Campbell 2017; Campbell & Maier 2017) inevitably derived a high degree of ionization, 98%, because they borrowed uN(C60) from Herbig (2000). They also stated that the degree of ionization should be at least 90% even if one of the DIBs observed near 6000 Å was absorption by C60 (Maier & Campbell 2017). The value was derived from elements in a discussion by Omont (2016), among which a theoretical oscillator strength of 0.01 attributed to the potential C60 DIB, which is 25 times greater than the strength presently determined for the γ0 band. We remark that abundances of neutral molecules and cations as evaluated by Omont (2016) would give 80% as the degree of ionization.
Finally, when using Eqs. (4) and (5), we assume that the area of the band is a valid measurement of the population of the absorbing species in absence of vibrational excitation, and that it is conserved over the range of temperature observed in diffuse and translucent clouds. Taking into account the conditions of the laboratory measurements on C60 and C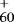 , the bands that interest us represent transitions from the electronic ground state with zero quantum of vibrational excitation. As a transfer of population to excited vibrational levels occurs when the temperature increases, the validity of the computed column densities may be affected when looking at the warmer regions of diffuse clouds. Nevertheless, provided the vibrational modes of the initial and final states of a transition are similar, the loss of area caused by an increase in the temperature may be compensated by the rise of overlapping bands that correspond to transitions from the thermally populated vibrational levels with conservation of the vibrational state. In this case, the C60:C
, the bands that interest us represent transitions from the electronic ground state with zero quantum of vibrational excitation. As a transfer of population to excited vibrational levels occurs when the temperature increases, the validity of the computed column densities may be affected when looking at the warmer regions of diffuse clouds. Nevertheless, provided the vibrational modes of the initial and final states of a transition are similar, the loss of area caused by an increase in the temperature may be compensated by the rise of overlapping bands that correspond to transitions from the thermally populated vibrational levels with conservation of the vibrational state. In this case, the C60:C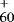 ratio may be valid for the range of temperatures encountered throughout molecular clouds. Verification is needed.
ratio may be valid for the range of temperatures encountered throughout molecular clouds. Verification is needed.
As mentioned in the introduction, Iglesias-Groth (2019) observed interstellar fullerenes C60 and C70, and the ions C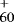 and C
and C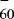 , in IR emission spectra of the star-forming region IC 348. Ion fractions of 20 and 10% were determined for C
, in IR emission spectra of the star-forming region IC 348. Ion fractions of 20 and 10% were determined for C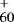 and C
and C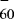 , respectively, giving a C60:C
, respectively, giving a C60:C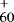 ratio of 3.5. We do not attempt a comparison with our results because the ISRF in the targeted regions is probably much stronger than in the typical diffuse or translucent interstellar clouds we are interested in. Actually Iglesias-Groth (2019) adopted ISRF strengths of 20 and 45 G0 in their analysis. Moreover, we are not aware of an evaluation of the electron density in the relevant regions. This value would have to be taken into account (Bakes & Tielens 1994, 1995).
ratio of 3.5. We do not attempt a comparison with our results because the ISRF in the targeted regions is probably much stronger than in the typical diffuse or translucent interstellar clouds we are interested in. Actually Iglesias-Groth (2019) adopted ISRF strengths of 20 and 45 G0 in their analysis. Moreover, we are not aware of an evaluation of the electron density in the relevant regions. This value would have to be taken into account (Bakes & Tielens 1994, 1995).
Upper limits for C60:C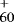 as uN(C60)/N(C
as uN(C60)/N(C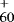 ) from the comparison of the A1 and γ0 bands of C60 with the 9577.5 and 9632.7 Å bands of C
) from the comparison of the A1 and γ0 bands of C60 with the 9577.5 and 9632.7 Å bands of C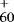 .
.
 |
Fig. 7 Values of C60:C |
8.2 Searches for vibronic bands of C60 in the diffuse ISM
Searches for interstellar C60 were attempted following the report of a narrow absorption by C60 at 3860 Å (Snow & Seab 1989; Somerville & Bellis 1989; Somerville & Crawford 1993). The measurements concerned van der Waals complexes of C60 with benzene and dichloromethane, from which the band of free C60 was predicted and attributed to the origin of the 11 T1u ←1Ag transition (Heath et al. 1987). Because it is firmly established that this transition is found at 4024 Å as the A0 band, the upper limit, on the order of 1014 cm−2, derived by Snow & Seab (1989) for N(C60) required a revision that Herbig (2000) attempted, though without obtaining a satisfying result.
Ehrenfreund & Foing (1997) searched for absorption by C60 near 3980 and near 6070 Å in a spectrum measured toward BD+63°1964. They found a weak band with 20 mÅ equivalent width close to 3980 Å. At 6070 Å, with a detection limit of 3 mÅ equivalent width, the spectrum did not show any absorption band. A possible DIB observed at 6220 Å appeared to coincide with a band seen beside the γ0 band in the spectrum of C60 (Haufler et al. 1991). Because laboratory spectra indicate that the γ0 band is the strongest component in the pair, the DIB at 6220 Å is likely caused by an interstellar substance that is not C60. Additionally, the wavelengths of the bands observed by Ehrenfreund & Foing (1997) do not coincide exactly with those derived from laboratory spectra of C60 (Herbig 2000).
Herbig (2000) looked for various bands of C60 toward several objects. Using band C reported by Leach et al. (1992) at 3284 Å in hexane at 300 K, an upper limit of 4.5 × 1011 cm−2 was found for N(C60) toward Cyb OB2/8A. The value is invalid, as actually suspected by the author, because it was derived by hypothesizing an FWHM of 1 Å for band C in the gas phase, which is too low a value considering that the band has a width of 1660 cm−1 in the spectrum of C60 in Ne ice (Sassara et al. 2001), that is, 173 Å (see also Fig. 1). Using this underestimated FWHM to evaluate uN(C60, C), Herbig (2000) obtained a C60:C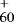 ratio on the order of 0.01 at maximum (see Sect. 8.1).
ratio on the order of 0.01 at maximum (see Sect. 8.1).
García-Hernández et al. (2012), García-Hernández & Díaz-Luis (2013), and Díaz-Luis et al. (2015) sought C60 toward the hot star DY Cen and the planetary nebulae Tc 1 and IC 418. From 1σ equivalent-width detection limits at 3980 Å, the authors derived upper limits of 1.5 × 1013, 1 × 1013, and 4 × 1013 cm−2 for the column densities of C60 toward DY Cen, Tc 1, and IC 418, respectively. The uN(C60, A1) values we obtained are on the same order (Table 2), though we took into account three equivalent-width detection thresholds in the form of uW. Analysis using the γ0 band gave lower values, albeit on the same order, despite again taking three equivalent-width detection thresholds into account.
Past searches for interstellar C60 focused on the detection of its UV and near-UV bands. To our knowledge, only Ehrenfreund & Foing (1997) and Herbig (2000) examined the possibility that DIBs near 6070 Å could be related to C60. Because it is narrow and lies at a visible wavelength, the γ0 band is a more convenient target than, for instance, A1, as demonstrated by the uW values in Table 2, despite the larger uncertainties that affect the description of this absorption. Furthermore, spectra in rare-gas matrices showed that the γ2 band is similar both in strength and width to γ0 (Gasyna et al. 1991; Sassara et al. 1997, and this work). Solvatochromism measurements (Catálan 1994; Renge 1995) and low-temperature gas-phase spectroscopy (Hansen et al. 1997) placed γ2 at ~584 nm. It is desirable that a future search for C60 targets both bands. Already surveys list DIBs at positions close to those of the γ0 and γ2 bands. A comparison is not straightforward, however, because of the uncertainties that affect the laboratory data (see also Herbig 2000). Our simple analysis of DIB measurements toward three targets (Tuairisg et al. 2000) indicates that the most strongly correlated DIBs near the positions of γ0 and γ2 are the bands at 5828.56 and 6068.45 Å. Not taking uncertainties into account, the separation is 10 Å too large for assigning the pair to the γ0 and γ2 bands.
9 Conclusions
After reevaluating the oscillator strengths of bands in the absorption spectrum of C60, we exploited spectra of background stars and available DIB measurements to estimate the C60:C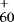 ratio in diffuse and translucent clouds. We obtained an average upper limit of ~1.3, corresponding to a minimum degree of ionization of ~40%. Combining observed emission and absorption bands of fullerene C60 and its cation, respectively, Berné et al. (2017) determined a C60:C
ratio in diffuse and translucent clouds. We obtained an average upper limit of ~1.3, corresponding to a minimum degree of ionization of ~40%. Combining observed emission and absorption bands of fullerene C60 and its cation, respectively, Berné et al. (2017) determined a C60:C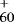 ratio equal to 0.3–6 in the diffuse ISM. The two results present common values, and they suggest that the fraction of neutral molecules in the fullerene population of the diffuse ISM may be notable even though its electronic transitions have not been detected. Our approach allows us, however, to not rely on IR emission spectra, which present a degree of ambiguity as to the species that cause them. As to the difference between our result and the theoretical prediction by Bakes & Tielens (1995), it can simply be the consequence of inadequate values given to parameters of the model. In that respect, more accurate measurements of interstellar absorption at near-UV and visible wavelengths would be useful to constrain the local ISRF strength and electron density. Furthermore, the comparison of these measurements with those of mid-IR emission bands would allow us to distinguish the part of emission in diffuse and translucent clouds that is actually caused by gas-phase C60 molecules.
ratio equal to 0.3–6 in the diffuse ISM. The two results present common values, and they suggest that the fraction of neutral molecules in the fullerene population of the diffuse ISM may be notable even though its electronic transitions have not been detected. Our approach allows us, however, to not rely on IR emission spectra, which present a degree of ambiguity as to the species that cause them. As to the difference between our result and the theoretical prediction by Bakes & Tielens (1995), it can simply be the consequence of inadequate values given to parameters of the model. In that respect, more accurate measurements of interstellar absorption at near-UV and visible wavelengths would be useful to constrain the local ISRF strength and electron density. Furthermore, the comparison of these measurements with those of mid-IR emission bands would allow us to distinguish the part of emission in diffuse and translucent clouds that is actually caused by gas-phase C60 molecules.
The very large uncertainties of the upper limits we derived are caused by the lack of accurate experimental data. New experiments are needed in order to better determine the absorption cross sections, oscillator strengths, and FWHMs of the various bands involved in this study, in particular that of the γ0 band of C60 at 6070 Å. Because it is narrow and arises in a wavelength domain favorable to observations, the γ0 band may be used to obtain the lowest equivalent-width detection threshold values. A better characterization of the γ2 band is also desirable. Since matrix-isolation measurements showed its strength and width are similar to those of γ0, a search for interstellar C60 at visible wavelengths would be considered successful if it revealed both bands. Another way to confirm the detection of γ0 would be to observe the near-UV A1 band too, which is especially worth attempting when the spectral type of the target star is favorable.
Finally, we need electronic spectra of C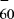 at low temperature in the gas phase in order to progress. To date, measurements of vibronic bands of the anion are scarce and their resolution modest (Tomita et al. 2005; Støchkel & Andersen 2013).
at low temperature in the gas phase in order to progress. To date, measurements of vibronic bands of the anion are scarce and their resolution modest (Tomita et al. 2005; Støchkel & Andersen 2013).
Acknowledgements
The authors gratefully acknowledge the use of observations collected at the European Southern Observatory under ESO programs 079.C-0597 (R. Gredel, for HD 169454 and HD 183143), 081.C-0475 (J. Smoker, for HD 76341, HD 136239, and HD 167264), 082.C-0566 (Y. Beletsky, for HD 136239 and HD 148379), 194.C-0833 (N. Cox, for HD 167264, HD 169454, and HD 183143), and 266.D-5655 (Paranal Observatory, ESO, for HD 168625). S.K. is thankful to the Deutsche Forschungsgemeinschaft (DFG) for its support through project No. 413610339. Special thanks are owed to R. Gredel for discussions on the wavelength calibration of astronomical spectra and for suggesting analysis methods, and to D. Strelnikov for exchanges on the determination of oscillator strengths.
Appendix A Observational data
For each LOS and wavelength domain examined in the present study, Table A.1 gives the resolution of the observational spectra, the angular distance to the target star, and the data sets. Information on the LOSs such as the spectral type of the target star and theobserved color excess can be found for instance in Hunter et al. (2006) for HD 76341, HD 136239, HD 148379, HD 167264,and HD 169454, and in Fan et al. (2019) for HD 168625 and HD 183143. Selected information on each target star is also found in Galazutdinov et al. (2017).
Observational data sets.
Appendix B Wavelengths and standards of rest
In this work, wavelengths are expressed in units of angstrom (Å) when explicit information shows that they were measured in air. Wavelengths are given in units of nanometer (nm) whenever the calibration conditions are not indicated in the source material. Wavenumbers in reciprocal centimeter (cm−1) may be for air or vacuum.
For each LOS we examined lines of identified interstellar species to evaluate their radial velocity relative to the observer, that is, the wavelength standard of rest in the archival spectra. This information was used to change this standard foran interstellar absorber plausibly coexisting with fullerenes, allowing us to locate bands of interstellar C60 in a straightforward manner by using the laboratory rest wavelengths.
We are looking for interstellar C60 in diffuse and translucent molecular clouds, for which K I, CH, and CH+ are the preferred tracers of the less dense regions, and CN of the denser ones (Pan et al. 2005; Rice et al. 2018). In some cases, DIBs exhibit a shift relative to the lines of these tracers, indicating that cloud structures may be complex (Galazutdinov et al. 2015). Red and blue shifts as great as ~10 km s−1 in terms of radial velocity have been observed. Because bands of interstellar C60 may be affected similarly, the γ0 and A1 bands may be shifted respectively up to 0.2 Å and 0.13 Å toward shorter or longer wavelengths. This is not a major issue considering the respective FWHMs of 1.5 ± 0.5 Å and 5.54 ± 0.80 Å that the two bands may show (Sect. 3.2).
The near-UV and violet regions show several lines of interstellar atoms and molecules that can serve as references, among which K I, CN, CH, and CH+ are found (see, e.g., Hobbs et al. 2009; Galazutdinov et al. 2015). The K I lines, at 4044.136 and 4047.208 Å rest wavelengths, are too weak to be seen in most of the present spectra though. In several cases, the CN, CH, and CH+ lines show velocity components, which can be distinguished by fitting peak profiles onto them when they are not well separated. As interstellar wavelength references, we chose the lines indicating the same velocity as the strongest CH and CN components, that is, we assume C60 is most likely to be found in the denser regions of diffuse clouds and in translucent clouds. Table B.1 presents the wavelengths of the interstellar diatomic lines seen by the observer and the associated average radial velocities 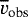 . They were determined by fitting Gaussian profiles to the diatomic lines as well as to the background stellar absorptions whenever it was necessary and possible.
. They were determined by fitting Gaussian profiles to the diatomic lines as well as to the background stellar absorptions whenever it was necessary and possible.
Wavelengths and average radial velocities in the observer rest frame for interstellar molecules.
Appendix C Matrix-isolation spectroscopy of C60 in solid Ne
The equipment used for measuring the spectrum of C60 isolated in Ne ice was described in previous studies (e.g., Rouillé et al. 2009). Conditions and parameters specific to the present case are as follows. Fullerene C60 powder (SES Research, Inc., purity 99.5%) was heated to 400 °C and the molecules thus released through an opening in the oven were deposited together with an excess of Ne atoms (Air Liquide, purity 99.999%) onto a 2 mm-thick CaF2 substrate (Korth Kristalle GmbH) cooled to 7.5 K. The Ne gas was fed into the vacuum chamber at the mass rate of 5 sccm (standard cubic centimeter per minute) and the matrix deposition process lasted 50 min. Absorption spectra were derived from transmission measurements with a spectrophotometer that scanned wavelengths with a step of 0.2 nm, a resolution of 0.2 nm, and a rate of 11 nm min−1. Factory calibration of the wavelength scale was given as accurate to 0.3 nm.
References
- Bakes, E. L. O., & Tielens, A. G. G. M. 1994, ApJ, 427, 822 [NASA ADS] [CrossRef] [Google Scholar]
- Bakes, E. L. O., & Tielens, A. G. G. M. 1995, Astrophys. Space Sci. Lib., 202, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Berné, O., Cox, N. L. J., Mulas, G., & Joblin, C. 2017, A&A, 605, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brieva, A. C., Gredel, R., Jäger, C., Huisken, F., & Henning, T. 2016, ApJ, 826, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Cami, J. 2014, in Proceedings of the International Astronomical Union, The Diffuse Interstellar Bands, eds. J. Cami, & N. Cox (Cambridge: Cambridge University Press), 9, 370 [Google Scholar]
- Cami, J., Bernard-Salas, J., Peeters, E., & Malek, S. E. 2010, Science, 329, 1180 [NASA ADS] [CrossRef] [Google Scholar]
- Campbell, E. K., & Maier, J. P. 2017, J. Chem. Phys., 146, 160901 [CrossRef] [Google Scholar]
- Campbell, E. K., Holz, M., Gerlich, D., & Maier, J. P. 2015, Nature, 523, 322 [NASA ADS] [CrossRef] [Google Scholar]
- Campbell, E. K., Holz, M., & Maier, J. P. 2016a, ApJ, 826, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Campbell, E. K., Holz, M., Maier, J. P., et al. 2016b, ApJ, 822, 17 [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [Google Scholar]
- Carleer, M., Jenouvrier, A., Vandaele, A.-C., et al. 1999, J. Chem. Phys., 111, 2444 [NASA ADS] [CrossRef] [Google Scholar]
- Catálan, J. 1994, Chem. Phys. Lett., 223, 159 [CrossRef] [Google Scholar]
- Catálan, J., & Pérez, P. 2002, FNCN, 10, 171 [Google Scholar]
- Chupka, W. A., & Klots, C. E. 1997, IJMSI, 167/168, 595 [Google Scholar]
- Close, J. D., Federmann, F., Hoffmann, K., & Quaas, N. 1997, Chem. Phys. Lett., 276, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Cordiner, M. A., Linnartz, H., Cox, N. L. J., et al. 2019, ApJ, 875, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Díaz-Luis, J. J., García-Hernández, D. A., Rao, N. K., Manchado, A., & Cataldo, F. 2015, A&A, 573, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. T.,& Sutin, B. 1987, ApJ, 320, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Edwards, S. A., & Leach, S. 1993, A&A, 272, 533 [NASA ADS] [Google Scholar]
- Ehrenfreund, P., & Foing, B. H. 1997, AdSpR, 19, 1033 [NASA ADS] [Google Scholar]
- Fan, H., Hobbs, L. M., Dahlstrom, J. A., et al. 2019, ApJ, 878, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Foing, B. H., & Ehrenfreund, P. 1994, Nature, 369, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Foing, B. H., & Ehrenfreund, P. 1997, A&A, 319, L59 [Google Scholar]
- Fulara, J., Jakobi, M., & Maier, J. P. 1993, Chem. Phys. Lett., 211, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Galazutdinov, G. A., Musaev, F. A., Krełowski, J., & Walker, G. A. H. 2000, PASP, 112, 648 [NASA ADS] [CrossRef] [Google Scholar]
- Galazutdinov, G., Krełowski, J., Beletsky, Y., & Valyavin, G. 2015, PASP, 127, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Galazutdinov, G. A., Shimansky, V. V., Bondar, A., Valyavin, G., & Krełowski, J. 2017, MNRAS, 465, 3956 [NASA ADS] [CrossRef] [Google Scholar]
- García-Hernández, D. A., & Díaz-Luis, J. J. 2013, A&A, 550, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Hernández, D. A., Rao, N. K., & Lambert, D. L. 2012, ApJ, 759, L21 [CrossRef] [Google Scholar]
- García-Hernández, D. A., Cataldo, F., & Manchado, A. 2013, MNRAS, 434, 415 [CrossRef] [Google Scholar]
- Gasyna, Z., Schatz, P. N., Hare, J. P., et al. 1991, Chem. Phys. Lett., 183, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Gredel, R., & Münch, G. 1986, A&A, 154, 336 [Google Scholar]
- Hansen, K., Müller, R., Brockhaus, P., Campbell, E. E. B., & Hertel, I. V. 1997, Z. Phys. D, 42, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, S., Faure, A., & Tennyson, J. 2013, MNRAS, 435, 3541 [NASA ADS] [CrossRef] [Google Scholar]
- Haufler, R. E., Chai, Y., Chibante, L. P. F., et al. 1991, J. Chem. Phys., 95, 2197 [NASA ADS] [CrossRef] [Google Scholar]
- Heath, J. R., Curl, R. F., & Smalley, R. E. 1987, J. Chem. Phys., 87, 4236 [NASA ADS] [CrossRef] [Google Scholar]
- Herbig, G. H. 2000, ApJ, 542, 334 [NASA ADS] [CrossRef] [Google Scholar]
- Hobbs, L. M., York, D. G., Thorburn, J. A., et al. 2009, ApJ, 705, 32 [Google Scholar]
- Hora, J., Pánek, P., Navrátil, K., et al. 1996, Phys. Rev. B, 54, 5106 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, I., Smoker, J. V., Keenan, F. P., et al. 2006, MNRAS, 367, 1478 [CrossRef] [Google Scholar]
- Iglesias-Groth, S. 2019, MNRAS, 489, 1509 [NASA ADS] [Google Scholar]
- Jannuzi, B. T., Black, J. H., Lada, C. J., & van Dishoeck, E. F. 1988, ApJ, 332, 995 [NASA ADS] [CrossRef] [Google Scholar]
- Kasperovich, V., Tikhonov, G., & Kresin, V. V. 2001, Chem. Phys. Lett., 337, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Krasnokutski, S. A., Gruenewald, M., Jäger, C., et al. 2019, ApJ, 874, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Lawton, B., Churchill, C. W., York, B. A., et al. 2008, AJ, 136, 994 [NASA ADS] [CrossRef] [Google Scholar]
- Leach, S., Vervloet, M., Desprès, A., et al. 1992, Chem. Phys., 160, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Léger, A., d’Hendecourt, L., Verstraete, L., & Schmidt, W. 1988, A&A, 203, 145 [Google Scholar]
- Lezius, M. 2003, IJMSp, 223–224, 447 [Google Scholar]
- Lezius, M., Scheier, P., & Märk, T. D. 1993, Chem. Phys. Lett., 203, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Maier, J. P., & Campbell, E. K. 2017, Angew. Chem. Int. Ed., 56, 4920 [CrossRef] [Google Scholar]
- Mulliken, R. S. 1939, J. Chem. Phys., 7, 14 [CrossRef] [Google Scholar]
- Negri, F., Orlandi, G., & Zerbetto, F. 1992, J. Chem. Phys., 97, 6496 [NASA ADS] [CrossRef] [Google Scholar]
- Omont, A. 2016, A&A, 590, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Orlandi, G., & Negri, F. 2002, Photochem. Photobiol. Sci., 1, 289 [CrossRef] [Google Scholar]
- Pan, K., Federman, S. R., Sheffer, Y., & Andersson, B.-G. 2005, ApJ, 633, 986 [NASA ADS] [CrossRef] [Google Scholar]
- Renge, I. 1995, J. Phys. Chem., 99, 15955 [CrossRef] [Google Scholar]
- Rice, J. S., Federman, S. R., Flagey, N., et al. 2018, ApJ, 858, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Rouillé, G., Steglich, M., Huisken, F., Henning, T., & Müllen, K. 2009, J. Chem. Phys., 131, 204311 [CrossRef] [Google Scholar]
- Sassara, A., Zerza, G., Chergui, M., Negri, F., & Orlandi, G. 1997, J. Chem. Phys., 107, 8731 [CrossRef] [Google Scholar]
- Sassara, A., Zerza, G., Chergui, M., & Leach, S. 2001, ApJS, 135, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, M. R., Krełowski, J., Galazutdinov, G. A., et al. 2014, MNRAS, 441, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Seiler, F. A. 1987, Risk Anal., 7, 509 [CrossRef] [Google Scholar]
- Sellgren, K., Werner, M. W., Ingalls, J. G., et al. 2010, ApJ, 722, L54 [NASA ADS] [CrossRef] [Google Scholar]
- Snow, T. P., & McCall, B. J. 2006, ARA&A, 44, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Snow, T. P., & Seab, C. G. 1989, A&A, 213, 291 [Google Scholar]
- Somerville, W. B., & Bellis, J. G. 1989, MNRAS, 240, 41 [Google Scholar]
- Somerville, W. B., & Crawford, I. A. 1993, Faraday Trans., 89, 2261 [CrossRef] [Google Scholar]
- Sowers, B. L., Williams, M. W., Hamm, R. N., & Arakawa, E. T. 1972, J. Chem. Phys., 57, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Støchkel, K., & Andersen, J. U. 2013, J. Chem. Phys., 139, 164304 [CrossRef] [Google Scholar]
- Strelnikov, D., Kern, B., & Kappes, M. M. 2015, A&A, 584, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thompson, H.M. A., Keenan, F. P., Dufton, P. L., et al. 2008, MNRAS, 383, 729 [Google Scholar]
- Tomita, S., Andersen, J. U., Bonderup, E., et al. 2005, Phys. Rev. Lett., 94, 053002 [NASA ADS] [CrossRef] [Google Scholar]
- Tuairisg, S. Ó., Cami, J., Foing, B. H., Sonnentrucker, P., & Ehrenfreund, P. 2000, A&AS, 142, 225 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walker, G. A. H., Bohlender, D. A., Maier, J. P., & Campbell, E. K. 2015, ApJ, 812, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, G. A. H., Campbell, E. K., Maier, J. P., Bohlender, D., & Malo, L. 2016, ApJ, 831, 130 [CrossRef] [Google Scholar]
- Walker, G. A. H., Campbell, E. K., Maier, J. P., & Bohlender, D. 2017, ApJ, 843, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Weselak, T., Schmidt, M., & Krełowski, J. 2000, A&AS, 142, 239 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Upper limits for column densities of interstellar C60 considering the A1 and γ0 bands.
Upper limits for C60:C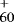 as uN(C60)/N(C
as uN(C60)/N(C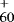 ) from the comparison of the A1 and γ0 bands of C60 with the 9577.5 and 9632.7 Å bands of C
) from the comparison of the A1 and γ0 bands of C60 with the 9577.5 and 9632.7 Å bands of C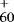 .
.
Wavelengths and average radial velocities in the observer rest frame for interstellar molecules.
All Figures
 |
Fig. 1 (a) Absorption spectrum of C60 isolated in a Ne matrix, not corrected for scattering. Band labels according to Leach et al. (1992). (b) Gaussian profiles (thick gray solid curve) fitted to bands of the 11 T1u ←1Ag transition, including A0 and A1, and to the baseline. (c) Gaussian profiles (thick gray solid curve) fitted, with a common FWHM, to absorptions near the γ0 band. Fittedband positions are 16 431.1 ± 1.2 cm−1, 24 829.04 ± 0.98 cm−1, and 25 087.73 ± 0.65 cm−1 for γ0, A0, and A1, respectively.The wavelength scale of the spectrometer was calibrated with an accuracy of 0.3 nm. |
| In the text | |
 |
Fig. 2 Spectrum toward HD 169454 (black solid curve) and synthetic absorption spectrum of C60 with the expected band positions, widths, and relative areas (thick gray solid curve). Narrow absorption lines in the 3967–3971 Å interval correspond to velocity components of the Ca II H line. |
| In the text | |
 |
Fig. 3 Normalized observational spectra (black solid curves). A straight line continuum was defined over the 3960–4000 Å range of each spectrum still in the observer rest frame. The top panel includes a synthetic A1 band of C60 with expected position and width, and arbitrary equivalent width (thick gray solid curve). Its position is indicated through all panels (vertical dotted line). The light gray area indicates the wavelength interval of two FWHMs taken into account to evaluate uW(C60, A1) at 3980 Å for each LOS. The spectral type of each target star is indicated. |
| In the text | |
 |
Fig. 4 Continuum-normalized spectra with interstellar wavelength scale for seven LOSs in the 6000 Å region. Each gray portion was obtained by extrapolating the straight continuum defined over the 6058–6087 Å interval (observer rest frame). The top panel includes a synthetic γ0 band of C60 of arbitrary equivalent width (thick gray solid curve, offset for clarity). Its position is indicated through all panels (vertical dotted line). Positions of DIBs according to Hobbs et al. (2009) are indicated in the bottom panel (short vertical lines). The predicted position of a line of stellar Ne I is marked in each panel (arrow). Synthetic spectra of DIBs and the Ne I line are represented in four panels (short-dashed curve). The light gray area indicates the wavelength interval of two FWHMs taken into account to evaluate uW(C60, γ0) at 6070 Å for each LOS. |
| In the text | |
 |
Fig. 5 Equivalent-width detection threshold in the 6000 Å region for seven LOSs (solid curves). The vertical dotted line shows the expected position of the γ0 band of C60 in all spectra. Positions of DIBs according to Hobbs et al. (2009) are indicated in the bottom panel (short vertical lines). The predicted position of a line of stellar Ne I is marked in each panel (arrow). In four cases detection limits were computed as fitted profiles of the DIBs nearest 6070 Å were included in the continuum (short-dashed curves). An unidentified absorption would cause the rise near 6078 Å (asterisk). |
| In the text | |
 |
Fig. 6 Equivalent-width detection threshold in the 4000 Å region scale for seven LOSs (solid curves). The vertical dotted line shows the expected position of the near-UV band of C60 in all spectra. The detection limits were also computed as fitted profiles of stellar lines were included in the continuum (short-dashed curves). |
| In the text | |
 |
Fig. 7 Values of C60:C |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.