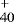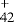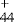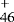| Issue |
A&A
Volume 650, June 2021
|
|
|---|---|---|
| Article Number | A193 | |
| Number of page(s) | 13 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202140675 | |
| Published online | 29 June 2021 | |
Intermediate-size fullerenes as degradation products of interstellar polycyclic aromatic hydrocarbons
1
Sorbonne Université, UPMC Université Paris 6 and CNRS, UMR 7095, Institut d’Astrophysique de Paris,
France
e-mail: omont@iap.fr
2
Institut für Organische Chemie, Universität Tübingen,
Auf der Morgenstelle 18,
72076
Tübingen,
Germany
e-mail: holger.bettinger@uni-tuebingen.de
Received:
26
February
2021
Accepted:
19
April
2021
The high interstellar abundances of polycyclic aromatic hydrocarbons (PAHs) and their size distribution are the result of complex chemical processes implying dust, UV radiation, and the main gaseous components (H, C+, and O). These processes must explain the high abundance of relatively small PAHs in the diffuse interstellar medium (ISM) and imply the continuous formation of some PAHs that are small enough (number of carbon atoms NC < ~35–50) to be completely dehydrogenated by interstellar UV radiation. The carbon clusters Cn thus formed are constantly exposed to the absorption of ~10–13.6 eV UV photons, allowing isomerization and favoring the formation of the most stable isomers. They might tend to form irregular carbon cages. The frequent accretion of interstellar C+ ions could favor further cage isomerization, as is known in the laboratory for C60, possibly yielding most stable fullerenes, such as C40, C44, and C50. These fullerenes are expected to be very stable in the diffuse ISM because C2 ejection is not possible by single UV photon absorption, but could need rare two-photon absorption. It is possible that at least one of these fullerenes or its cation is as abundant as C60 or C60+ in the diffuse ISM, although this abundance is limited by the lack of observed matching features in observed mid-infrared spectra. B3LYP calculations of the visible spectrum for a number of fullerene isomers with 40 ≤NC ≤ 50 show that they generally have a few spectral bands in the visible range, with f-values in the range of a few 10−2. This could make such fullerenes interesting candidates for the carriers of some diffuse interstellar bands.
Key words: astrochemistry / molecular processes / ISM: molecules / ISM: lines and bands / dust, extinction / line: identification
© A. Omont and H. F. Bettinger 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Interstellar carbonaceous macromolecules with a number of carbon atoms, NC ~ 30–150, which are intermediate between dust particles and the ~200 small molecules (NC ≲ 11) detected to date, mostly by radio astronomy, are an important component of the interstellar medium (ISM; e.g., Candian et al. 2018; Tielens 2013). They are mostly detected through their infrared (IR) vibrational emission from 3 to 20 μm that results from sporadic IR fluorescence following the absorption of a UV photon. They are found in various components of the ISM that are illuminated by UV radiation: in the general ISM of galaxies that is permeated by the UV radiation of massive stars, that is, mostly diffuse interstellar gas and photodissociation regions; and in the more specific environment of young stars and circumstellar matter of evolved stars in the post-asymptotic-giant-branch (post-AGB) and planetary nebula stages.
The carbon skeleton of these macromolecules is mostly composed of sp2 aromatic carbon, either plane polycyclic aromatic hydrocarbons (PAHs) or cage fullerenes (with a more marginal presence of sp3 micro-diamonds). Interstellar PAHs (Leger & Puget 1984; Allamandola et al. 1985; Tielens 2008) are thought to be mostly made of plane fused benzene rings with H-decorated edges, each typically with about 40 to 150 C atoms. Their presence in the ISM is inferred from the strong IR emission in the aromatic bands corresponding to the various CH or C-C vibration modes. However, no individual interstellar PAH is identified yet except for CN-naphthalene, which was detected very recently in a dense cloud well shielded from UV radiation (McGuire et al. (2021)). Altogether, PAHs typically contain ~10% of all interstellar carbon, which makes them one of the main reservoirs of interstellar carbon together with C+, CO, and carbon dust.
Interstellar fullerenes are much less conspicuous than PAHs. Their typical abundance is a few 10−4 of interstellar carbon in various environments (but up to 1% in special cases of planetary nebulae, where C60 was first identified by Cami et al. 2010). C60 is the only fullerene that is widely detected from its weak mid-IR features (see, e.g., the introduction of Cami et al. 2018; Berné et al. 2015b). Weaker mid-IR features of C are also detected in a few objects (and C70 in one object). C
are also detected in a few objects (and C70 in one object). C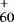 has been widely found in the diffuse ISM through its strong diffuse interstellar bands (DIBs) at 9577 and 9632 Å (Foing & Ehrenfreund 1994; Campbell et al. 2015).
has been widely found in the diffuse ISM through its strong diffuse interstellar bands (DIBs) at 9577 and 9632 Å (Foing & Ehrenfreund 1994; Campbell et al. 2015).
The formation of interstellar C60 is still debated (e.g., Candian et al. 2018). The most convincing scenarios imply the curvature and closure of sheets of graphene, in which NC is slightly larger than 60 heated by UV photons (see Sect. 3.1), or energetic processing of carbon or SiC dust in planetary nebulae (Cami et al. 2018; Bernal et al. 2019). Fullerenes are known to be very stable, especially C60. An energetic process is needed to destroy them, similar to PAHs (see below). However, the lack of CH bonds makes small fullerenes less sensitive to UV photodissociation than PAHs with a similar number of C atoms.
The identification of DIB carriers remains an outstanding problem in astrophysics (see Cox 2011; Cami & Cox 2014 and, e.g., Introduction of Omont et al. 2019). It is generally agreed that DIB carriers are probably large carbon-based molecules (with ~10–100 atoms) in the gas phase, such as PAHs, fullerenes, or carbon chains. The most stringent constraint on DIB carriers comes from the strength (equivalent width) of the bands, which can be expressed as the product of the carrier abundance by the band oscillator strength f (e.g., Cami 2014; Omont 2016). The equivalent width per unit reddening may be approximately written as (for NC ~ 60)
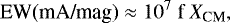 (1)
(1)
where XCM denotes the fraction of total interstellar carbon locked up in the M molecule.
The aim of this paper is to extend our previous review of the properties of interstellar fullerene compounds (Omont 2016) by pointing out that in addition to C60, other smaller fullerenes with NC between about 40 and 50 could be abundant in the diffuse ISM, resulting from the downsizing, dehydrogenation, and photoprocessing of the smallest interstellar PAHs. They could also be interesting candidates for the carriers of DIBs.
This paper is organized as follows. Section 2 and Appendix A summarize a few properties of the smallest interstellar PAHs in the diffuse ISM that are relevant for their eventual degradation into fullerenes. We focus on their size distribution, chemistry, and evolution. Section 3 argues that in the diffuse ISM, we may expect an efficient formation of carbon cages from the smallest PAHs with NC ~ 40–50 when they are fully dehydrogenated by photodissociation. Section 4 addresses the likely evolution of these cages into the most stable fullerenes, such as C50 or C44, through isomerization, which could be favored by C+ accretion. Sputtering of these fullerenes and the possible resulting abundances are then discussed. In Sect. 5 we finally consider the possible identification of these interstellar neutral or cation fullerenes through either their mid-IR spectrum or their optical spectrum (for which we performed B3LYP calculations), which could make them interesting carriers of DIBs. General conclusions and future prospects are outlined in Sect. 6.
 |
Fig. 1 Estimated orders of magnitude of reaction rates for a typical PAH/PAH+ of 50 C atoms in a diffuse interstellar cloud with NH = 50 cm−3, T = 50–100 K, and a UV intensity G0 = 3 Habing (Table A.1). |
2 Size distribution and evolution of the smallest PAHs in the diffuse ISM
The aim of this section is to recall how we understand the abundance and the size distribution of the smallest PAHs in the diffuse ISM, before they can eventually transform into fullerenes through downsizing and dehydrogenation. The details of what follows are outlined in Appendix A, which summarizes the properties of PAHs in the diffuse ISM and their chemical processes and recalls the conclusions of the models of their size distribution.
While the discussions of interstellar PAHs generally refer to regions with strong UV radiation, we here focus on typical interstellar diffuse clouds in which the interstellar absorption leading to DIBs mostly takes place, with a density nH = 30–100 cm−3, temperature T = 50–100 K, and UV intensity G0 = 1–10 Habing (Table A.1).
The key features of interstellar PAHs have been recognized since their discovery: They are part of a continuous distribution of aromatic carbonaceous particles that extends to the largest dust grains. Small PAHs with NC ≲ 30–40 are absent, however, because their CH bonds are photodissociated. Various chemical processes, including reactions with H, C+ and O, should explain their size evolution, but are not fully understood. The number NC of carbon atoms is strongly constrained by the ratios of the observed aromatic IR bands. The determination of the size distribution is made difficult by the complexity of the unknown PAH-emitting mixture (Appendix A.4), however.
The lower limit of the PAH size distribution is determined by UV photodissociation of the smallest PAHs. Photodissociation of interstellar PAHs has been modeled in many works since their discovery (Appendix A). It is agreed that carbon loss is much slower than aromatic hydrogen loss. However, the estimate of the critical number of carbon atoms below which total dehydrogenation occurs, NCcr, remains uncertain. We estimate in Appendix A.2 that a wide range must be considered for the value of NCcr, from ~35 to ~50.
The uncertain modeling of the PAH size distribution (Appendix A.4) agrees that the smallest PAHs, with NC close to NCcr, represent a significant fraction of all PAHs (see Sect. 3). More precisely, if we define the total abundance of all PAHs with a given value of NC, χ(NC) = n(NC)/nH, the order of magnitude of χ(NC) should be ~10−8 for values of NC close to NCcr, that is, XC(NC) is about 1.5 × 10−3 of the totalinterstellar carbon. In addition, the distribution of XC (NC) should mildly decrease with NC.
This size distribution is the result of a rich photochemistry whose main processes are detailed in Appendices A.2 and A.3 and which are summarized in Fig. 1 and Table A.1. PAH processing is dominated by frequent transient heating through UV photon absorption and by ionic accretion reactions, mainly H and O onto PAH cations and C+ onto neutral PAHs. They may increase the value of NC or decrease it by ejection of small hydrocarbon molecules Cx Hy or CO. Sporadic UV heating favors the most stable isomers. The complexity of these macromolecules and of their chemical processes makes a precise modeling very difficult if not impossible. Nevertheless, the relatively high abundances of PAHs with NC close to NCcr, which cannot be fed from lower NC values because growth of possible interstellar carbonaceous molecules with NC <NCcr seems to be ineffective (Appendix A.4), show the existence of a net downsizing rate from higher NC values. This effective downsizing processing, which most likely results from sputtering from reactions with O and C+, is needed to compensate for the eventual dehydrogenation of the smallest PAHs. Its analysis (Appendix A.4) allowsus to derive a rough estimate of the rate of formation of graphenic carbon clusters Cn, which mightsubsequently efficiently transform into fullerenes, as we argue in the next sections.
3 Formation of cages with NC < 60 from dehydrogenated PAHs in the diffuse ISM
This section describes the likely evolution of interstellar fully dehydrogenated graphene nanoflakes, Cn with n ~ 35–50, sporadically heated by UV-photon absorptions, into carbon cages, that is, close structures made of 2D carbon sheets, similar to fullerenes, but more irregular. We begin by first recalling the similar modeling of formation of interstellar C60 from graphene sheets Cn with n slightly greater than 60, and second, the complex models of PAH H-photolysis and isomerization. We then argue that C40−50 nanoflakes heated at a temperature close to 1000 K may spontaneously form irregular carbon cages through the same succession of steps as are well documented for C60, and eventually more stable fullerene isomers with the catalytic help of C+ temporary accretion.
3.1 Top-down formation of interstellar C60
As we recalled, the formation of interstellar C60 is still debated (e.g., Candian et al. 2018). The most convincing propositions imply curling and closure of sheets of graphene that might be formed from dehydrogenated interstellar PAHs in the ISM in the presence of strong UV radiation (Berné et al. 2012, 2015a; Zhen 2014). These models are based on laboratory data and molecular dynamics simulations. The following two works are especially illuminating about key features of the possible formation of C60 in the ISM: (i) in situ high-resolution transmission electron microscopy performed by Chuvilin et al. (2010) revealed the formation of spheroidal carbon cages directly from graphene nanoflakes. (ii) An accelerated molecular dynamics simulations in the range 300–3000 K allowed Pietrucci & Andreoni (2014) to perform a detailed investigation of the different steps of this process.
These processes are inefficient in forming C60 in the diffuse ISM because the dehydrogenation of PAHs with NC > 60 is impossible by single photon absorption. However, it is natural to wonder whether the same scheme might be applied to the formation ofsmaller fullerenes from fully dehydrogenated smaller PAHs, which are expected to be naturally produced in the diffuse ISM. This is the aim of this section.
3.2 Cage formation from carbon nanoflakes
Because of the striking success of the observation of the formation of C60 from a graphene sheet in the laboratory by Chuvilin et al. (2010) and the detailed understanding of its various steps by the simulations of Pietrucci & Andreoni (2014, hereafter PA14), it is worthwhile to analyze the possibility that the same processes may similarly proceed for forming smaller fullerenes with NC ~ 40–50. We do this below for each of the steps from the detailed results of Pietrucci & Andreoni and focus on their simulation at 1000 K because this temperature is relevant for PAHs with NC ~NCcr in the diffuse ISM (Appendix A).
Initial graphene nanoflake. As stated by PA14, representing the initial state of a fully dehydrogenated PAH by a pure plane graphene flake reproducing the PAH skeleton is certainly oversimplified. When heated to about 1000 K by the absorption of a ~10 eV photon, it immediately reorganizes into a more stable form with some general salient features, such as edge reorganization into a (5,7) rather than a (6,6) carbon pattern, or presence of at least one inner pentagon inducing a curved structure, such as corannulene. Although it is probable that such structures do appear before the end of the total dehydrogenation (Parneix et al. 2017), this should not change the subsequent evolution of the flake much if it eventually becomes completely dehydrogenated. Nothing in these features should significantly change from NC = 60 to NC = 40.
Formation of a convex or conical structure. The next step evolving toward a more complex structure to decrease the energy should also be general and little depend on whether there are 60 or 40 C. Its evolution into a conical structure with the formation of a 4C ring is quite general for NC = 60 and the flake shape chosen by PA14. We note, however, that the initial flake structure, with a bay, that was chosen by PA14 (their Fig. 1a), should favor the formation into a conical structure. A similar evolution also appears likely for NC ~ 50, although this is less certain when NC decreases strongly. In particular, the formation of a convex conical structure due to the presence of a four-membered ring can be hampered in smaller cages. The strain induced by the curvature might be too much there.
Formation and fate of short carbon chains. Similarly, the formation of various short chains, starting with C2, appears quite general and independent of NC. However, a key question is their fate and the probability that they might detach, which is zero for NC ~60 in the PA14 simulations. It is striking in these simulations that every time a C2 molecule detaches, it is reattached. The likelihood of reattachments for lower values of NC is difficult to evaluate because their probability depends on activation barriers and the efficiency of internal energy redistribution. This might prevent the overall cage formation or at least shrink the size of fullerenes that are eventually formed. This point would need to be determined by systematical simulations similar to those of PA14. They would imply a considerable amount of computer time, however.
Cage closure. This final state transforms chain networks into regular cages, as observed by PA14 for C60 simulations. It is expected to depend little on NC. Once formed, the cage is expected to resist subsequent transient heatings by photon absorption well. It is expected to frequently exchange ionization states through the equilibrium between photoionization and electron recombination. Accretion of H, H+, and e− is thought to be inefficient in the diffuse ISM because these particles should be immediately released by subsequent UV-photon absorptions.
Overall, the formation of cages from carbon nanoflakes with NC ~ 40–50 appears to be possible, especially for the highest values of NC, but it is not guaranteed, even in a small proportion, because C2 release might be dominant. In addition, it is not certain that the dehydrogenation of interstellar PAHs proceeds all the way to remove all H atoms. The possibility that the resulting carbon cage remains open and partially hydrogenated, eventually leading to tubular structures, might therefore deserve consideration.
4 Cage evolution into fullerene
4.1 Fullerene cage evolution
In their simulations of the evolution of a carbon nanoflake with 60 atoms at 1000 K, PA14 found that the final state is always a cage with 60 carbon atoms. However, it is never the well-known most stable Ih C60 isomer (buckminsterfullerene). Reaching the Ih shape implies difficult cage rearrangements with high activation barriers, such as in classical Stone-Wales transformations of pentagon-heptagon structures into two hexagons (EA > 6 eV, see, e.g., Bettinger et al. 2003). Such isomerizations can be achieved at higher temperature, as observed at 3000 K by PA14 (see also Berné et al. 2015a). These temperatures are much higher than can be achieved by single-photon absorption in the diffuse ISM (Appendix A).
However, it is known that a high temperature may be avoided through bond-rearrangement catalysis produced by the adsorption of a carbon atom (Eggen et al. 1996; Ewels et al. 2002; Dunk et al. 2012). As shown by 13C studies (Christian 1992; Dunk et al. 2012), the carbon adatom is scrambled with the C atoms of the cage through its incorporation into the C network, probably mostly by initial creation of a 7C ring. This lowers the activation energy for bond rearrangements by a large factor, ~3–4, so that rearrangements favoring the most stable isomers can be achieved at T ≲ 1000 K. This appears to be a key explanation for the high efficiency of the formation of fullerenes, especially Ih -C60 and D5h-C70, as stressed, for example, by Dunk et al. (2012). It is clear that this catalysis could operate for any fullerene and even for any sp2 system, including PAHs.
We suggest that similar processes might favor the formation of the most stable fullerene isomers from the cages formed from dehydrogenated PAHs (Sect. 3.2). Rather than atomic C, the dominant process should be the accretion of C+ on neutral cages. It should allow efficient bond rearrangement favoring the most stable cage isomers during subsequent transient heating by UV photon absorption.
The question is whether C+ accretion might not favor cage growth. The accretion of C+ on neutral even-numbered cage might eventually lead to the formation of relatively stable close-shell odd-numbered cationic carbon cages. However, odd-numbered cages must be much more unstable than even-numbered ones in the periods they become neutral through e-recombination. Therefore it is likely but not certain that the additional carbon is ejected following a subsequent UV-photon absorption before the next C+ accretion. We also note that the large predominance of even-numbered cages over odd-numbered ones is a constant feature of all fullerene formation experiments.
In the diffuse ISM, C+ accretion onto any neutral cage should proceed at a rate similar to PAHs of the same size, that is, ~10−4 yr−1 (Fig. 1 and Table A.1). As discussed in the following section, this is probably significantly faster than any cage-sputtering process. We may therefore conclude that C+ accretion might allow efficient bond rearrangement during subsequent transient heating by UV photon absorption. This could ensure that most cages formed with NC atoms eventually terminate into the most stable fullerene isomer with the same NC.
4.2 Fullerene sputtering and possible abundances
Fullerenes are known to be very stable structures. This may be quantified by the enthalpy change for the elimination of a C2 molecule (the dominant fragmentation channel of Cn cages). For instance, Candian et al. (2019) give the values 8.51, 9.57, 11.18, and 10.24 eV for the reaction Cn ⇒ Cn −2 + C2 with the most stable isomer of C44, C50, C60, and C70, respectively (see Díaz-Tendero et al. 2006 for a complete list). This is comparable to PAHs for C44, but significantly higher for the heavier fullerenes, even C50.
For these values of the dissociation energy, ≳8 eV, it is clear from the discussion of PAH dissociation of Appendix A that the ejection of a C2 molecule from a molecule with 40 to 50 C cannot be achieved by the absorption of a single UV photon with E < 13.6 eV. It requires the simultaneous absorption of two photons, which occurs only about every 107 yr or more in the diffuse ISM (Fig. 1 and Table A.1). Other well-established processes for PAH sputtering by energetic He+ or e− are slightly slower (Micelotta et al. 2010a,b and Fig. 1). It is possible that the most efficient decay process for interstellar fullerenes in the diffuse ISM is the combined result of O and C+ accretion, similarly to PAHs, but with important differences. The reaction of atomic oxygen with fullerene cations could similarly yield the loss of one C atom through CO release, but this could depend on the fullerene stability because the result of this reaction is questionable even for C60 (see references in Omont 2016). The result of C+ accretion byneutral fullerenes could be more entangled: the integration of an additional carbon in the network can favor isomerization, as quoted, and also compensate for carbon loss resulting from CO photolysis, but it could also favor C2 photo-ejection.
A rough estimate of the eventual abundance of each fullerene Fi from the balance between its formation and destruction can be formally derived. When we assume that fullerene Fi forms from dehydrogenation of PAHs with about NCcr carbon atoms with a total probability ηi, the number density of Fi, n(Fi), is derived from the equation
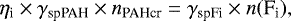 (2)
(2)
where nPAHcr is the number density of PAHs just above NCcr, γspPAH is their downsizing rate, which brings them below NCcr (Appendix A.4) and γspFi is the decay rate of n(Fi) (Appendix B.3). Therefore, we may write
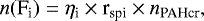 (3)
(3)
where rspi = γspPAH∕γspFi is the ratio of the decay rates. In Appendix A.4 we estimate the value of the fraction of interstellar carbon in PAHs for each value of NC above and close to NCcr, XC ~ 1.5 × 10−3 (i.e., about 1% of the total carbon in all PAHs). This yields for the carbon fraction in fullerene i
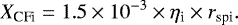 (4)
(4)
In the case of the most stable fullerenes, we may expect rspi ≥ 1 because their stability is greater than that of PAHs, while rspi might be closer to 1 for unstable fullerene isomers (see, e.g., Candian et al. 2019; Sun et al. 2005 and Table B.2 for an estimate of the formation energy of various fullerene isomers). If η is the total probability that PAH dehydrogenation ends in fullerenes, they should contain at least a total fraction XCF ~η × 1.5 × 10−3 of interstellar carbon. The value of η remains very uncertain. It might be very small if dehydrogenated PAHs were mainly photodissociated through successive C2 ejections (or formed nanotubes). Nevertheless, if they form efficiently from dehydrogenated PAHs, some of these fullerenes might have an abundance comparable to or greater than C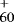 , whose abundance in the diffuse ISM may be roughly estimated as ~2 × 10−4 from its DIB strength (Walker et al. 2015; Campbell & Maier 2017; Omont 2016). Large abundances like this, if confirmed, should make some fullerenes smaller than C60 detectable through their IR emission bands or their visible absorption bands (DIBs), as we discuss in the next section.
, whose abundance in the diffuse ISM may be roughly estimated as ~2 × 10−4 from its DIB strength (Walker et al. 2015; Campbell & Maier 2017; Omont 2016). Large abundances like this, if confirmed, should make some fullerenes smaller than C60 detectable through their IR emission bands or their visible absorption bands (DIBs), as we discuss in the next section.
5 Optical and infrared spectra
5.1 Mid-infrared spectrum and abundance limit
In addition to the identification of C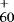 DIBs, all detections of C60 as well as C
DIBs, all detections of C60 as well as C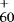 and C70 in the ISM have been achieved through their mid-IR emission bands in Spitzer 6–20 μm spectra (Cami et al. 2010; Sellgren et al. 2010; Berné et al. 2015a,b, 2017; and, e.g., references in Cami 2014; Candian et al. 2018). The possible presence of smaller (44-, 50-, and 56-atom) fullerenes was recently addressed by Candian et al. (2019). Their conclusion is that the spectra of most cages that are smaller than C60 show features in the 13–15 μm range, where the astronomical spectra of fullerene-rich planetary nebulae also contain characteristic signals. They were unable to conclusively identify any of them in Spitzer spectra, however, even the most symmetrical C5h C50, because the IR spectra of their various isomers are similar and the strength of their IR features is weaker than C60.
and C70 in the ISM have been achieved through their mid-IR emission bands in Spitzer 6–20 μm spectra (Cami et al. 2010; Sellgren et al. 2010; Berné et al. 2015a,b, 2017; and, e.g., references in Cami 2014; Candian et al. 2018). The possible presence of smaller (44-, 50-, and 56-atom) fullerenes was recently addressed by Candian et al. (2019). Their conclusion is that the spectra of most cages that are smaller than C60 show features in the 13–15 μm range, where the astronomical spectra of fullerene-rich planetary nebulae also contain characteristic signals. They were unable to conclusively identify any of them in Spitzer spectra, however, even the most symmetrical C5h C50, because the IR spectra of their various isomers are similar and the strength of their IR features is weaker than C60.
The same conclusions apply for the Spitzer IR spectra of diffuse regions of the ISM displayed by Berné et al. (2017). Comparing these spectra with those computed for the different isomers of C50 and C44 shown by Candian et al. (2019), we may conclude that none of them and their cations may have an abundance significantly greater than that of C60, which is estimated as2 × 10−4 at most of the total interstellar carbon by Berné et al. (2017). However, abundances close to this limit are not completely excluded. They should be more easily detectable by the James Webb Space Telescope (JWST).
5.2 Fullerene optical spectra
The visible range provides an incomparable sensitivity to detect absorption lines on the sightline of bright stars. About 600 such DIBs are known, whose mostly unknown carriers are believed to be carbonaceous macromolecules, such as the four confirmed C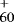 DIBs. However, even the identification of the carriers of the strongest DIBs needs high-accuracy laboratory spectral data, as is shown by the history of the confirmation of the identification of the C
DIBs. However, even the identification of the carriers of the strongest DIBs needs high-accuracy laboratory spectral data, as is shown by the history of the confirmation of the identification of the C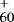 DIBs (Foing & Ehrenfreund 1994; Campbell et al. 2015).
DIBs (Foing & Ehrenfreund 1994; Campbell et al. 2015).
Fullerenes and their cations are known to have only relatively weak bands in the visible range (Koponen et al. 2008; Lan et al. 2015). However, no detailed laboratory or theoretical data about the optical spectrum of fullerenes except for C60 and C70 are available, including those with NC in the range40–50, which we propose are the most likely possible products of PAH dehydrogenation. Therefore we performed density functional theory (DFT) B3LYP/6-31G* calculations of the visible spectrum for 19 neutral fullerene isomers (and their cations, except for one), with even values of NC between 40 and 50 (Table B.2). The computation methods are described and analyzed in detail in Appendix B.1.
The results are presented in Figs. 2 and B.1–B.4. All cases display at least one and generally several significant bands between 400 and 800 nm, with f-values higher than 10−2. There is a trend for finding stronger bands for the most stable fullerenes, C50 and C44, and increasing values of NC. C50 isomers have several visible bands with f ~ (5–8)×10−2. Most of these relatively strong bands are concentrated at λ ≲ 550 nm, but a few are found at ~550–600 nm (Fig. 2). The visible bands of the isomers of the other fullerenes display a similar wavelength distribution, but with significantly lower f-values, by a factor ~2 for C44 and C48, ~3 for C46, and ~6 for C40 and C42 (see Figs. B.1–B.4). Our calculations generally confirm some similarity of the spectra of cation and neutral forms of the same molecule, as is known for PAHs (e.g., Malloci et al. 2004).
The extension of the calculations to C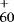 with the same methods has produced a strong double band at 893/892 nm with both f-values of 0.032, to be compared with the actual values of 963.2 and 957.7 nm with f ~ 0.03–0.02 (Walker et al. 2015; Campbell & Maier 2017). We may therefore conclude that i) the order of magnitude of the calculated f-values appears to be good, and ii) the most stable fullerene isomers with NC ~ 40–50 generally display one strong band at least in the visible-near-IR range comparable to C
with the same methods has produced a strong double band at 893/892 nm with both f-values of 0.032, to be compared with the actual values of 963.2 and 957.7 nm with f ~ 0.03–0.02 (Walker et al. 2015; Campbell & Maier 2017). We may therefore conclude that i) the order of magnitude of the calculated f-values appears to be good, and ii) the most stable fullerene isomers with NC ~ 40–50 generally display one strong band at least in the visible-near-IR range comparable to C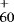 .
.
 |
Fig. 2 Computed absorption spectra (f-values) of three isomers of fullerene C50 (Table B.2). The results of complete calculations from ~350 to 2000 nm for the isomers of neutral C50 (D5h, 271; D3, 270; and Cs, 266) are displayed by open symbols, together with the cation spectra (C5h, 271; C2, 270; and Cs, 266) from ~500 to 2000 nm (full symbols). See similar Figs. B.1–B.4 for isomers of C40, C42, C44, C46, and C48 listed in Table B.2. |
5.3 Fullerenes as possible DIB carriers
Equation (1) shows that fullerenes with an f-value of a few 10−2 and an abundance, XCi, up to a few 10−4, may carry medium-strength DIBs with an equivalent width EWi in the range 10–100 mÅ/mag. This could make fullerenes with NC ~ 40–50 significant DIB carriers if they were able to form from dehydrogenated PAHs, with individual abundances reaching XCi ~ (1–2) × 10−4. We note, however, that the mid-IR spectrum of diffuse interstellar clouds appears to preclude larger fullerene abundances (Sect. 5.1) and that the number of species with XCi ~ 10−4 is probably limited in any case.
Figures 2 and B.1–B.4 show that the DIBs carried by such neutral and cation fullerenes might be distributed across the whole DIB wavelength range from 400 to 900 nm, with a significant number of cation bands at λ > 600 nm. As quoted, such abundances of 10−4 or slightly higher are comparable to those estimated in diffuse clouds for C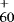 and C60 from near-IR DIBs and mid-IR emission bands, and larger than that of C
and C60 from near-IR DIBs and mid-IR emission bands, and larger than that of C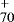 . Despite the poorer stability of the fullerenes with NC ~ 40–50, it is not impossible that their abundance is comparable to C60 because C60 cannot be directly formed from photodissociated PAHs in diffuse clouds. Therefore it is possible that these fullerenes carry some DIBs, especially cations such as C
. Despite the poorer stability of the fullerenes with NC ~ 40–50, it is not impossible that their abundance is comparable to C60 because C60 cannot be directly formed from photodissociated PAHs in diffuse clouds. Therefore it is possible that these fullerenes carry some DIBs, especially cations such as C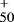 and C
and C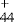 at longer wavelength. Their intensity could be somewhat similar to the weakest C
at longer wavelength. Their intensity could be somewhat similar to the weakest C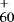 DIBs (Walker et al. 2016). Nothing is known about the width of their visible bands, but it might be comparable with the narrow width (a few cm−1) measured in the gas-phase for C
DIBs (Walker et al. 2016). Nothing is known about the width of their visible bands, but it might be comparable with the narrow width (a few cm−1) measured in the gas-phase for C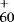 (Campbell et al. 2015) and C60 (Close et al. 1997) and in the ISM for C
(Campbell et al. 2015) and C60 (Close et al. 1997) and in the ISM for C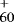 DIBs (Cox 2014), which could make them relatively easy to detect as DIBs.
DIBs (Cox 2014), which could make them relatively easy to detect as DIBs.
The mid-IR Spitzer data available on the diffuse ISM (Berné et al. 2017) place a limit on the total abundance of such fullerenes with NC ~ 40–50, which we estimate to be on the order of XCtot ≲ 10−3 (Sect. 5.1). When we assume an average oscillator strength 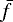 ~ 0.03, we obtain a total equivalent width EWful ≲ 300 mÅ mag−1 from Eq. (1) for all these fullerenes. This is only about 3% of the total equivalent width of the sum of all known DIBs (but λ4429 and λ7700 Å1) in the diffuseISM, which is estimated to be ~11 000 mÅ mag−1 in a typical sightline (Hobbs et al. 2009; Omont & Bettinger 2020). This confirms the conclusion of Omont (2016) that fullerenes can be only a minor component of the DIB carriers.
~ 0.03, we obtain a total equivalent width EWful ≲ 300 mÅ mag−1 from Eq. (1) for all these fullerenes. This is only about 3% of the total equivalent width of the sum of all known DIBs (but λ4429 and λ7700 Å1) in the diffuseISM, which is estimated to be ~11 000 mÅ mag−1 in a typical sightline (Hobbs et al. 2009; Omont & Bettinger 2020). This confirms the conclusion of Omont (2016) that fullerenes can be only a minor component of the DIB carriers.
These conclusions again show that the condition derived from Eq. (1) for the total abundance of all DIB carriers is extremely constraining. Assuming 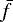 ~ 0.1, as proposedby Salama et al. (1996) for PAH-cation DIB carriers, yields XCtot ~ 10−2 for the carriers of all DIBs (but λ4429 Å and λ7700 Å). This is a significant fraction, ~10%, of the total carbon included in PAHs (but less than that if f > 0.1). It is very difficult indeed to escape the conclusion that the bulk of the DIB carriers must be related to the PAHs. Except for fullerenes, the only contenders, carbon chains (or rings), have never been identified through their mid-IR emission, which makes this high abundance unlikely. In addition to their overwhelming abundance, PAHs have many advantages as DIB carriers, including relatively strong bands at short wavelength (e.g., Malloci et al. 2007) and even at long λ for cations; a possible enhanced abundance for symmetric pericondensed PAHs (Andrews et al. 2015); families with very strong bands (f ≳ 1), such as polyacenes and rylenes (Omont et al. 2019; Ruiterkamp et al. 2002), which are favorable for carrying C2 DIBs and other narrow DIBs (Omont & Bettinger 2020). Their extreme isomer variety and possible large band width can prevent their individual detection, however, especially at short λ, which might explain the low DIB density at λ < 5500 Å.
~ 0.1, as proposedby Salama et al. (1996) for PAH-cation DIB carriers, yields XCtot ~ 10−2 for the carriers of all DIBs (but λ4429 Å and λ7700 Å). This is a significant fraction, ~10%, of the total carbon included in PAHs (but less than that if f > 0.1). It is very difficult indeed to escape the conclusion that the bulk of the DIB carriers must be related to the PAHs. Except for fullerenes, the only contenders, carbon chains (or rings), have never been identified through their mid-IR emission, which makes this high abundance unlikely. In addition to their overwhelming abundance, PAHs have many advantages as DIB carriers, including relatively strong bands at short wavelength (e.g., Malloci et al. 2007) and even at long λ for cations; a possible enhanced abundance for symmetric pericondensed PAHs (Andrews et al. 2015); families with very strong bands (f ≳ 1), such as polyacenes and rylenes (Omont et al. 2019; Ruiterkamp et al. 2002), which are favorable for carrying C2 DIBs and other narrow DIBs (Omont & Bettinger 2020). Their extreme isomer variety and possible large band width can prevent their individual detection, however, especially at short λ, which might explain the low DIB density at λ < 5500 Å.
Other DIB carriers remain possible, including nanotube segments and hetero atoms inserted in these various carbonaceous macromolecules. Nanotube segments present similarities with symmetrical PAHs and fullerenes. Their strong visible bands justify their consideration as DIB carriers (Zhou et al. 2006). As their formation appears to be possible from partially dehydrogenated PAHs (Sect. 3.2; Chen et al. 2020), we calculated the optical absorption spectra of a few of the shortest neutral and cation (4,4) and (5,5) hydrogenated armchair tube-segments with the same method as for fullerenes (Appendix B.2). Figures B.6 and B.7 show that all such neutral and cation tube-segments with NC > 40 have a strong band in the range ~400–800 nm with f ~ 0.5. There are many additional weaker bands, including cation bands at λ≳ 550 nm with f ≳ 0.02. As discussed in Appendix B.2, the size distribution of such nanotube-segments and the resulting interstellar absorption spectrum might depend not only on their formation, but also on their possible subsequent growth by C+ accretion. As it is expected that their band width is similar to that of PAHs or fullerenes, it is confirmed that they should also be considered as DIB carriers, as suggested by Zhou et al. (2006), if they actually formed in the diffuse ISM.
As the formation of semicapped nanotube segments from partially dehydrogenated PAHs is not excluded, we extended the calculations to a few semicapped armchair (5,5) nanotube segments, Cn H10, with n = 50 to 100, including C50H10, which was synthesized by Scott et al. (2011). Their visible absorption spectra (Fig. B.8) have similar general characteristics to open nanotube segments, with a trend to slightly weaker features.
6 Conclusion
The high interstellar abundance of PAHs and their size distribution are the result of complex chemical processes implying dust, UV radiation, and the main gaseous components (H, C+, O, etc.). A downsizing process, possibly dominated by sputtering following atomic oxygen accretion onto PAH cations, is required to compensate for efficient C+ accretion and to maintain a high C+ gaseous abundance. These processes must explain the high abundance of relatively small PAHs in the diffuse interstellar medium. They imply the continuous formation of some PAHs that are small enough (number of carbon atoms NC ≲ 35–50) to be completely dehydrogenated by interstellar UV radiation.
The carbon clusters CNC thus formed are constantly exposed to the absorption of ~10–13.6 eV UV photons, heating them to a temperature close to 1000 K, which allows isomerization and favors the formation of the most stable isomers with curved shapes. They might tend to form irregular carbon cages. The frequent accretion of interstellar C+ ions followed by UV photon absorption might favor further cage isomerization as known in the laboratory for C60, possibly yielding the formation of the most stable fullerenes, such as C40, C44, and C50.
These fullerenes are expected to be very stable in the diffuse ISM because C2 ejection is not possible by single UV photon absorption but might need rare two-photon absorption, while the increase in the size of the fullerene cages is impeded by the rarity of small carbonaceous molecules Cx Hy with x ≥ 2. It is therefore possible that at least one of these fullerenes or its cation is as abundant as C60 or C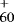 in the diffuse ISM, although higher abundances are precluded by the lack of observed matching mid-IR features. Our B3LYP calculations of the visible spectrum for a score of fullerene isomers with NC between 40 and 50 confirmed that they generally have a few spectral bands in the visible range with f-values in the range of a few 10−2. This could make some of them interesting candidates for the carriers of diffuse interstellar bands.
in the diffuse ISM, although higher abundances are precluded by the lack of observed matching mid-IR features. Our B3LYP calculations of the visible spectrum for a score of fullerene isomers with NC between 40 and 50 confirmed that they generally have a few spectral bands in the visible range with f-values in the range of a few 10−2. This could make some of them interesting candidates for the carriers of diffuse interstellar bands.
As is well known, the eventual identification of additional fullerenes as carriers of relatively weak DIBs cannot be achieved without laboratory measurement of the gas-phase wavelengths of their visible spectral bands. Even with the progress of methods such as He-tagging for cations, these measurements imply a considerable experimental effort, including the synthesis of such fullerenes. Nevertheless, this effort may be justified because it is important to understand the unique chemical properties of interstellar carbonaceous nanoparticles and macromolecules. Dehydrogenated PAHs are certainly the main source of interstellar carbon clusters with a few dozen carbon atoms. The evolution of these clusters is a key question in interstellar chemistry. Fullerenes appear to be a possible logical step in this evolution. If confirmed, their possible identification as DIB carriers would provide a powerful and specific tool to further reveal their detailed interstellar abundances and the astrochemical processes that determine them.
Finally, if the dehydrogenation of the smallest interstellar PAHs is not complete, it might lead to the formation of hydrogenated nanotube segments that are either open at both ends or are semicapped. If this formation appears to be more difficult than that of fullerenes, this possibility should also be explored. As most of these tubular PAHs with a few dozen carbon atoms have at least a strong visible band, with an expected width similar to PAHs or fullerenes, they should also be considered as DIB carriers.
Acknowledgements
We thank the referee for his/her very helpful comments and suggestions. We are indebted to Pierre Cox for his careful reading of the manuscript and his suggestions for improving it. We made a high use of “TOPCAT & STIL: Starlink Table/VOTable Processing Software” (Taylor 2005) and thank its developers. The authors acknowledge support by the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant no INST 40/575-1 FUGG (JUSTUS 2 cluster).
Appendix A Summary of the properties and chemistry of the smallest interstellar PAHs in the diffuse ISM
A.1 A main component of the ISM
The PAHs are a key component of the ISM because they are the main reservoir of carbonaceous macromolecules and typically contain ~10% of carbon inthe diffuse ISM. Since their identification (Leger & Puget 1984; Allamandola et al. 1985), they have been the object of many studies that interpreted their IR emission and discussed their physical and chemical properties (see, e.g., reviews by Omont 1986; Puget & Leger 1989; Allamandola et al. 1989; Salama et al. 1996; Li & Draine 2001; Tielens 2008, 2013; Joblin & Tielens 2011; Candian et al. 2018).
Practically our entire knowledge about astrophysical PAHs is based on their series of emission features in between 3.3 and 20 μm, which may be modeled as complex fluorescence following the absorption of a UV photon. The observed spectrum always results from a complex mixture of many PAHs with NC ~ 50–150 and provides key information about their size distribution (Sect. 2), their charge state, and also, with more difficulty, about their possible dehydrogenation and superhydrogenation.
Because of their large photoionization cross-section, interstellar PAHs always contain a substantial fraction of cations. This fraction depends both on the UV intensity and the gas density. In typical conditions of the diffuse ISM, PAHs undergo very frequent changes between neutral and cation charge states at a rate close to 1 yr−1 (see Fig. 1 and Table A.1). Any discussion of PAH chemistry must therefore jointly address neutrals and cations.
The overall formation or destruction processes of interstellar PAHs are complex. Their initial formation takes place mainly in circumstellar shells of AGB carbon stars, which eject a large amount of carbon dust into the ISM. Part of this dust may be converted into PAHs in shocks in the post-AGB or planetary nebula stages. A similar formation of PAHs may take place in supernova remnants. However, most of the observed PAHs are thought to result from the complex processing of dust grains and PAHs in the ISM through C+ /C accretion, various sputtering processes, accretion onto dust, and shock processing. PAH destruction ultimately occurs through energetic processes including mostly He+ and e− (Micelotta et al. 2010a,b), and possibly through O sputtering (see below). In the next section, we review the properties and chemistry of the smallest interstellar PAHs in the diffuse ISM. This is relevant for their eventual degradation into fullerenes.
A.2 Photo-processes
The chemistry of interstellar PAHs has been discussed by many authors (e.g., Omont 1986; Lepp & Dalgarno 1988; Le Page et al. 2001, 2003; Tielens 2008, 2013). It is dominated by photochemistry, as we discuss now, and ionic accretion processes (Appendix A.3), with rates whose orders of magnitude are recalled in Table A.1.
UV absorption. This is the most frequent and the key process for the chemical evolution of interstellar PAHs, even in the mild conditions of the diffuse ISM. At a frequency of about one month, at a rate that is practically proportional to NC and independent of the charge and hetero atoms, it injects an energy of ~6–13.6 eV, which may produce photoionization, photodissociation, or structure reorganization. As most of the photon energy is radiated in less than 1 s, the rate of simultaneous absorption of two UV photons, which may degrade the PAH carbon skeleton, is typically ≲10−7 yr−1.
Photoionization or electron recombination. If the energy of the photon is significantly greater than the PAH first-ionization potential, IP ~ 6.5 eV, the probability of photoionization before internal thermalization is significant. As electronic recombination occurs at a similar but uncertain rate ~1 yr−1, the fractions of neutrals and cations are both significant.
Photodissociation. H photolysis is the main reaction outcome from UV absorption. The photon energy EUV is mostly rapidly thermalized, yielding a vibrational temperature, TV (K) ~ 2000 × (EUV(eV)/NC)0.4 (Tielens 2005), close to 1000 K for EUV ~ 10 eV and NC ~ 50. Before this energy is progressively reemitted in the infrared within less than a fraction of a second, every possible reorganization can take place, either isomerization with an activation energy EA lower than a few eV, or photolysis with EA ≲ 5 eV. Both processes critically depend on TV and therefore on NC.
Because of the exponential dependence on TV, the dehydrogenation of PAHs is expected to vary extremely sharply around a critical value of NC, NCcr, so that the degree of hydrogenation is expected to abruptly vary from complete to zero around NCcr. We note, however, that these PAHs may retain their last few hydrogens, as quoted by Castellanos et al. (2018a). With the typical UV spectrum of the diffuse ISM, the value of NCcr probably depends little on the values assumed in Table A.1 for nH, T, and G0. Its value remains uncertain, however, because of the variety of PAH isomers and the numerous possible intermediate steps of their photodissociation. When only direct atomic H photolysis by breaking aromatic C-H bonds is considered, the value of NCcr could be as low as ~32 (e.g., Table 4 of Castellanos et al. 2018a). It has been proven, however, that various processes implying H migration and/or H2 formation may dominate for large PAHs (Castellanos et al. 2018a,b). In addition, it is predicted that the formation of pentagonal rings is competitive with the loss of a hydrogen atom (Parneix et al. 2017). Other possible isomer structure changes in the carbon skeleton, such as ring opening or Stone-Wales defects, may also be considered. Although these effects are probably extremely difficult to model, it is possible that the actual photodissociation activation energy is lowered in this H or C structure reorganization, implying higher values for NCcr. One argument supporting a high value of NCcr is the absence of any DIB compatible with the visible bands of C42H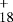 (HBC+) measured by Steglich et al. (2011; see also Gredel et al. 2011), which might be explained by photodissociation. On the other hand, it appears to be unlikely that a PAH such as circumcoronene (C54H18) is dissociated in the diffuse ISM because its direct H photodissociation rate is orders of magnitude lower than the IR emission (Castellanos et al. 2018a; Andrews et al. 2016). Therefore we consider a wide range of possible values of NCcr, from ~35 to ~50.
(HBC+) measured by Steglich et al. (2011; see also Gredel et al. 2011), which might be explained by photodissociation. On the other hand, it appears to be unlikely that a PAH such as circumcoronene (C54H18) is dissociated in the diffuse ISM because its direct H photodissociation rate is orders of magnitude lower than the IR emission (Castellanos et al. 2018a; Andrews et al. 2016). Therefore we consider a wide range of possible values of NCcr, from ~35 to ~50.
A.3 Overall chemistry: hierarchy of reaction rates
Figure 1 and Table A.1 display typical orders of magnitude for the main processes that the smallestPAHs, with about 50 C atoms, undergo in the diffuse ISM for averaged conditions: density nH = 50 cm−3, temperature T = 50–100 K, and UV intensity G0 = 3 Habing =1.6 × 1014 erg cm−3. The reaction rates of the relevant processes range over nine orders of magnitude so that there is a well-defined hierarchy. Together with photo-processes, the main processes are listed below (we do not discuss electron attachment and double ionization that are not very important in the diffuse ISM).
-
H accretion. Because of the overwhelming abundance of atomic hydrogen in the diffuse ISM, reactions between H and PAH+ are by far the most frequent pure chemical reactions undergone by PAHs. As expected, they occur at a significant fraction of the Langevin rate,
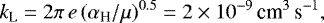 (A.1)
(A.1)where αH = 0.67 × 10−24 cm3 is the H polarizability and μ = 1 is the reduced atomic mass. However, we did not consider the processes that form loosely bound overhydrogenated states or immediately eject an H2 molecule (e.g., Castellanos et al. 2018b) because they are irrelevant for fullerene formation. We address only the rehydrogenation of partially dehydrogenated PAHs.
The actual rate of H association with large PAH cations is only about 7% of this value, as measured in the laboratory by Demarais (2014). We use this value, 1.4 × 10−10 cm3 s−1, in Table A.1 and Fig. 1 for the most important H process, rehydrogenation of PAHs through association of H with dehydrogenated PAH+, as adopted, for instance, by Montillaud et al. (2013) and Andrews et al. (2016). This process is implied in the discussion of PAH dehydrogenation of Appendix A.2.
-
C+ accretion. The Langevin rate for the reaction C+ + PAH is about 6 × 10−9 cm3 s−1 with α ~ 1.5 × 10−24 NC cm3 (e.g., Allamandola et al. 1989) and NC = 50. For anthracene (C14H10), Canosa et al. (1995) measured that the total reaction rate (charge exchange plus C+ accretion) is 3 × 10−9 cm3 s−1, which is close to the Langevin rate, while the branching ratio for C+ accretion is 40%. This ratio is expected to increase with the mass of the PAH. We may thus estimate that the rate of accretion of C+ onto neutral PAHs in the diffuse ISM remains close to 2 × 10−9 cm3 s−1. This yields about 2 × 10−4 yr−1 for the global rate of carbon accretion onto PAHs in the standard diffuse ISM (Table A.1 and Fig. 1).
Many structures are possible for the addition of the carbon atom to the carbon network. The reaction of C with naphtalene studied by Krasnokutski et al. (2017) shows that the formation of a seven-membered ring by insertion into a peripherical hexagon should be energetically favored with a total energy about −4 eV for naphtalene. Such a structure with NC ~ 40–50 should be unstable by interstellar photodissociation, but it could be stabilized by H addition. However, as discussed below (Appendix A.4), the overall net C+ growth rate,if any, cannot be higher than the O sputtering rate in order to sustain the PAH size distribution. Because the C+ accretion rate is significantly higher than the O rate (Table A.1 and Fig. 1), most C+ accretions therefore must eventually lead to the ejection of at least one carbon atom. Overall, it is difficult to predict whether the net result of C+ accretions leads to growth or sputtering of the carbon skeleton, and this result could depend on the PAH structure and size.
-
O sputtering. Atomic oxygen easily reacts with PAH cations. The results for a number of measured reactions O + PAH+ are summarized in Snow & Bierbaum (2008). Although CO is substantially produced in reactions with benzene and naphtalene cations, the direct result is only O accretion for coronene, with a rate 1.3 × 10−10 cm3 s−1. We may conservatively assume that the rate is at least comparable for heavier PAHs. This yields about 3 × 10−5 yr−1 for the global rate of oxygen accretion onto PAHs in the standard diffuse ISM (Table A.1 and Fig. 1).
Although there is no information on the initial product of this reaction, it is generally assumed that an epoxy binding on two adjacent C-C carbons is most probable. However, the epoxy binding energy is only ~2.4 eV (e.g., Li et al. 2006), so that the O-PAH association cannot survive the next UV photon absorption, unless the O atom forms a more stable binding. This is favored by its high mobility on the PAH surface, for which the hopping barrier is lower than about 1 eV (Li et al. 2006). A ketone therefore appears as a possible outcome, especially for heavy PAHs. For low values of NC, however, the ketone may be easily photodissociated with loss of CO, whose dissociation energy and barrier may be lower than 1.5 eV and 4 eV, respectively, as found by Chen et al. (2018) for bisanthenquinone. The net effect of reactions with O for the smallest stable PAHs with NC ≲ 50–60 should therefore be carbon sputtering. We may assume that its rate is practically equal to the rate of O accretion, γO ~ 0.7 × 10−4 yr−1, for relatively small PAHs with NC close to NCcr.
Typical orders of magnitude for rates of PAH chemical processes in the diffuse ISM(a).
A.4 Size distribution and dehydrogenation rate
-
Size distribution. The information about the size distribution of interstellar PAHs mainly comes from the observed IR spectrum and the ratios of its main features, especially implying the 3.3 μm band. However, despite the enormous amount of data accumulated on PAH IR spectra by successive space observatories, our understanding of the origin of this size distribution is still limited. As quoted by Draine et al. (2020), for example, the size distribution of interstellar PAHs results from various processes: fragmentation of dust grains, chemisputtering, He+ and e− sputtering in hot gas, growth by C+ accretion, agglomeration with other PAHs, and accretion onto dust grains... It is therefore impossible to derive a precise shape of the PAH size distribution because of our limited understanding of these processes. We therefore have to refer to empirical size distributions proposed on the basis of the IR feature ratios (e.g., Desert et al. 1990; Draine & Li 2007; Maragkoudakis et al. 2020).
These distributions and the corresponding PAH abundances as a function of NC, nPAH(NC)/nH, are well visualized in Fig. 5 of Pilleri et al. (2009), for example. We therefore approximate the PAH abundance as nPAH(NC)/nH = 10−8 for NC ≤ 50 and 10−8 × (NC/50)−1.67 for NC > 50. The difference with more elaborate models is not significant compared to their uncertainty. This corresponds to XC ~ 1.5 × 10−3 of total interstellar carbon for each value of NC ~ 50, that is, close to the dehydrogenation limit. For higher values of NC, the distribution of XC(NC) is expected to decrease mildly with NC, as (NC/50)−0.67 for the size distribution we assumed above.
Overall PAH dehydrogenation rate. Maintaining such a high abundance of PAHs close to the photodissociation limit needs to compensate for the dehydrogenation sink by an overall net downsizing of PAHs because there is no down-top feeding from smaller fullerenes or other carbonaceous carbon clusters. When we assume that carbon loss cannot result from the only effect of single-photon photodissociation and H reactions, this net downsizing should be dominated by C+ and O reactions because their rates are much faster than those of any others (Fig. 1). Atomic oxygen sputtering is an obvious contribution to the net PAH downsizing. The overall effect of C+ accretion is more uncertain because its net effect on the carbon skeleton may be either growth or sputtering. C+ growth, if any, must be slower than O sputtering to preserve a net downsizing, however. We note that this condition should also avoid the catastrophic depletion of gas carbon considered by Thaddeus (1995), for example. It is unlikely that C+ growth accidently almost compensates for O sputtering. We may therefore consider that it is likely that some fraction of the O sputtering rate, for instance, 0.3, provides a conservative lower limit for the actual sputtering rate, that is, γspPAH ≳ 0.3 γO = 0.2 × 10−4 yr−1. Because the sputtering rate, γspPAH, is also obviously the overall rate of PAH dehydrogenation, this is also a lower limit for the dehydrogenation rate.
Appendix B Computation of absorption spectra of fullerenes and nanotube segments
B.1 Fullerenes
As quoted in Sect. 5.2, in order to estimate the possibility of measuring the abundances of interstellar fullerenes through their optical absorption, we performed B3LYP/6-31G* calculations of the visible spectrum for 19 neutral fullerene isomers (and their cations except for one), with even values of NC between 40 and 50 (Table B.2).
 |
Fig. B.1 Computed absorption spectra (f-values) of neutral fullerenes C40 D2 38 and C42 D3h 45 and cations C |
 |
Fig. B.2 Computed absorption spectra (f-values) of three isomers of fullerene C44 (D2 75, D2 89, and D3h 72) and C |
Energies (in eV) of first 1T1u states of C60 buckminsterfullerene computed at various levels of theory.
For each of the fullerenes C40 to C50, the structures of those isomers that are within 10 kcal mol−1 in energy with respect to the most stable isomer as determined previously by Sun et al. (2005, see Table B.2) were optimized using the hybrid-density functional B3LYP (Becke 1993; Lee et al. 1988) in conjunction with the 6-31G* basis set implemented in Gaussian 16 (Frisch et al. 2016). For comparison, the structure of the Ih isomer of C60, buckminsterfullerene was also optimized at this level of theory.
The energy of excited states and oscillator strengths were computed using the optimized structures and time-dependent density functional theory (TD-DFT). We employed various functionals [B3LYP, CAM-B3LYP (Yanai et al. 2004), ωB97X (Chai & Head-Gordon 2008a), ωB97XD (Chai & Head-Gordon 2008b), PBE0 (Adamo & Barone 1999; Ernzerhof & Scuseria 1999), and M062X (Zhao & Truhlar 2008)] in conjunction with the 6-311+G** basis set forcomputing the electric dipole allowed transitions from the ground state to the two lowest lying 1T1u states of buckminsterfullerene to compare with experimental and sophisticated CASPT2 (Andersson 2020) data (Table B.1).
 |
Fig. B.3 Computed absorption spectra (f-values) of neutral fullerenes from 350 to 1200 nm, C46: Cs 99, C1 103, Cs 107, Cs 108, C2 109, C1 114, and C2 116 (left), and cations from ~480 to 1200 nm, C |
 |
Fig. B.4 Computed absorption spectra (f-values) of neutral fullerenes C48: C2 171, C1 196, Cs 197, and C2 199, from 350 to 1200 nm (left), and cations C |
We find that the deviation of the B3LYP values from experiment is the lowest of the functionals we investigated (0.4 eV and 0.6 eV for 11 T1u and 21 T1u, respectively). We also note that the energies hardly change when the much more economical 6-31G* basis set is employed. We thus chose the B3LYP/6-31G* level of theory to compute the excited state energies of the fullerenes for the semiquantitative purpose of this study.
The structures of the fullerene radical cations were optimized at the B3LYP/6-31G* level of theory starting from the structure of the neutrals without symmetry constraint. Vibrational analysis confirmed that they represent local minima of the potential energy surface. The point groups of the derived structures were directly identified, and they are reported in Table B.2. For C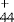 and C
and C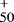 , these point groups agree with those given by Candian et al. (2019). Subsequently, the excited state energies were computed with the TD-DFT approach employing the B3LYP functional and the 6-31G* basis set.
, these point groups agree with those given by Candian et al. (2019). Subsequently, the excited state energies were computed with the TD-DFT approach employing the B3LYP functional and the 6-31G* basis set.
The structures of a few single-wall carbon nanotube segments were similarly optimized at the B3LYP/6-31G* level of theory for the neutrals and cations, and the excited state energies were subsequently computed at the B3LYP/6-31G* level of theory. The results are presented in Appendix B.2.
Fullerene isomers included in the calculations.
All calculated spectra of C40 to C50 fullerenes display at least one and generally several significant bands between 400 and 800 nm, with f-values higher than 10−2 (Figs. 2 and B.1–B.4). There is a trend for finding stronger bands for the most stable fullerenes, C50 and C44, and with increasing values of NC. C50 isomers have several visible bands with f ~ (5–8) × 10−2. Most of these relatively strong bands are concentrated at λ ≲ 550 nm, but a few are found at ~550–600 nm (Fig. 2). The visible bands of the isomers of the other fullerenes display a similar wavelength distribution, but with significantly lower f-values, by a factor ~2 for C44 and C48, ~3 for C46, and ~6 for C40 and C42 (see Figs. B.1–B.4).
Our calculations generally confirm some similarity of the spectra of cation and neutral forms of the same molecule, as is known for PAHs (e.g., Malloci et al. 2004). While the f-value of each the C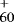 bands at 9577/9632 Å is ~3–2 × 10−2 (Campbell & Maier 2017), similar f-values are found for two bands of C
bands at 9577/9632 Å is ~3–2 × 10−2 (Campbell & Maier 2017), similar f-values are found for two bands of C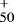 D5h at λ > 600 nm, and about half the computed cation spectra include a band at λ > 600 nm with f ≳ 10−2.
D5h at λ > 600 nm, and about half the computed cation spectra include a band at λ > 600 nm with f ≳ 10−2.
B.2 Nanotube segments
Nanotube segments (e.g., Fig. B.5) present similarities with symmetrical PAHs and fullerenes. Their strong visible bands justify their consideration as DIB carriers (Zhou et al. 2006). As their formation appears to be possible from partially dehydrogenated PAHs (Sect. 3.2; Chen et al. 2020), we calculated the optical absorption spectra of a few of the shortest neutral and cation (4,4) and (5,5) armchair tube-segments with the same method as fullerenes (Appendix B.1). Figures B.6 and B.7 display the spectra of (4,4) Cn H16, with n = 40, 48, and 56 and (5,5) Cn H20, with n = 30, 40, 50, 60, and 90. All these neutral and cation tube-segments with NC > 40 have a strong band in the range ~400–800 nm with f ~ 0.5. This confirms the results of Zhou et al. (2004, 2006) for (5,5) armchair tube-segments, but with significantlylower f-values. There are many additional weaker bands, including cation bands at λ≳ 550 nm with f ≳ 0.02. The size distribution of these nanotube-segments and the resulting interstellar absorption spectrum is expected to depend not only on their formation, but also on their subsequent chemistry and possible growth by C+ accretion. It is not excluded that they might carry some DIBs if they formed in the diffuse ISM.
 |
Fig. B.5 Example of nanotube segment: armchair (5,5) C50H20. |
 |
Fig. B.6 Computed absorption spectra (f-values) of some (5,5) armchair nanotube segments, Cn H20, with n = 30,40, 50, 60, and 90. Full symbols show cations, and open symbols show neutrals. |
We extended the calculations to a few neutral and cation semicapped armchair (5,5) nanotube segments, Cn H10, with n = 50, 60, 70, 80, 90, and 100, including C50H10, which was synthesized by Scott et al. (2011). Their visible absorption spectra (Fig. B.8) have similar general characteristics to open nanotube segments (Figs. B.6 and B.7), with a trend to slightly weaker features. The computed spectrum of neutral C50H10 appears to be compatible with that measured by Scott et al. (2011) in CH2Cl2.
 |
Fig. B.7 Computed absorption spectra (f-values) of some (4,4) armchair nanotube segments, Cn H16, with n = 40,48, and 56. Full symbols show cations, and open symbols show neutrals. |
 |
Fig. B.8 Computed absorption spectra (f-values) of some semicapped (5,5) armchair nanotube segments, Cn H10, with n = 50, 60, 70, 80, 90, and 100. Full symbols show cations, and open symbols show neutrals. The lower
λ limit of the computations is 400 nm for all neutrals. For cations, it varies from
~400 nm for C50H |
B.3 Summary of fullerene chemistry
The chemistry of interstellar fullerenes was addressed in Omont (2016), but mostly in view of C60. The main conclusions are that many atoms or ions, including H, C+, and O, probably accrete onto the cage, either ionized or neutral, with a rate comparable to the Langevin rate, similarly to PAHs (Appendix A.3). Low binding energies and the high C60 stability prevent the formation of stable compounds, however. Most accreted species are just quickly lost through photodissociation. The only exception might be Fe+, while it is not completely excluded that atomic oxygen might lead to sputtering through CO ejection.
Smaller fullerenes should have a similar uncertain chemistry, but their lower stability might increase the possibility of sputtering, especially following reactions with atomic oxygen. The case of C+ was quoted in Sect. 4.1. Its accretion rate could be similar to PAHs and might play an important role in cage evolution. However, its accretion is thought to remain transitory, before its ejection by the next UV photon with E ≳ 10 eV. Cage sputtering through loss of C3 is even possible for low values of NC, but this is uncertain. Cage growth by incorporation of a C2 unit after the accretion of a second C+ therefore appears to be inefficient. Replenishment in small PAHs from other types of Cn clusters with n <NCcr also appears to be unlikely because graphene flakes are probably unstable and tubular structures cannot easily return to the planar carbon skeleton of PAHs. Hydrogenated fullerenes (fulleranes) are probably more unstable than with C60, and the formation of interstellar endohedral compounds appears to be at least as difficult as for C60.
In conclusion, cage decay of these fullerenes could be as rapid as for PAHs for NC ~ 50, but probably not faster. Direct photodissociation decay through C2 loss might be considered for NC < 40.
References
- Adamo, C., & Barone, V. J. 1999, Chem. Phys., 110, 6158 [Google Scholar]
- Allamandola, L. J., Tielens, A. G. G. M., & Barker, J. R. 1985, ApJ, 290, L25 [Google Scholar]
- Allamandola, L. J., Tielens, A. G. G. M., & Barker, J. R. 1989, ApJS, 71, 733 [Google Scholar]
- Andersson, K. 2020, Chem. Phys. Lett., 739, 136976 [CrossRef] [Google Scholar]
- Andrews, H., Boersma, C., Werner, M. W., et al. 2015, ApJ, 807, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, H., Candian, A., & Tielens, A. G. G. M. 2016, A&A, 595, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Becke, A. D. J. 1993, Chem. Phys., 98, 5648 [Google Scholar]
- Bernal, J. J., Haenecour, P., Howe, J., et al. 2019, ApJ, 883, L43 [CrossRef] [Google Scholar]
- Berné, O., & Tielens, A. G. G. M. 2012, Proc. Natl. Acad. Sci., 109, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Berné, O., Montillaud, J., & Joblin, C. 2015a, A&A, 577, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berné, O., Montillaud, J., Mulas, G., et al. 2015b, SF2A-2015: Proceedings of the Annual meeting of the French Society of Astronomy and Astrophysics, 65 [Google Scholar]
- Berné, O., Cox, N. L. J., Mulas, G., et al. 2017, A&A, 605, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bettinger, H. F., Yakobson, B. I., & Scuseria, G. E. 2003, J. Am. Chem. Soc., 125, 5572 [CrossRef] [Google Scholar]
- Cami, J. 2014, IAU Symp., 297, 370 [Google Scholar]
- Cami, J., & Cox, N. L. J. 2014, IAU Symp., 297, 20 [Google Scholar]
- Cami, J., Bernard-Salas, J., Peeters, E., & Malek, S. E. 2010, Science, 329, 1180 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cami, J., Peeters, E., Bernard-Salas, J., et al. 2018, Galaxies, 6, 101 [CrossRef] [Google Scholar]
- Campbell, E. K., & Maier, J. P., 2017, J. Chem. Phys., 146, 160901 [NASA ADS] [CrossRef] [Google Scholar]
- Campbell, E. K., Holz, M., Gerlich, D., & Maier, J. P. 2015, Nature, 523, 322 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Candian, A., Zhen, J., & Tielens, A. G. G. M. 2018, Phys. Today, 71, 38 [CrossRef] [Google Scholar]
- Candian, A., Gomes Rachid, M., MacIsaac, H., et al. 2019, MNRAS, 485, 1137 [NASA ADS] [CrossRef] [Google Scholar]
- Canosa, A., Laubé, S., Rebrion, C., et al. 1995, Chem. Phys. Lett., 245, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Castellanos, P., Candian, A., Andrews, H., & Tielens, A. G. G. M. 2018a, A&A, 616, A166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castellanos, P., Candian, A., Zhen, J., Linnartz, H., & Tielens, A. G. G. M. 2018b, A&A, 616, A167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chai, J.-D., & Head-Gordon, M. J. 2008a, Chem. Phys., 128, 084106 [Google Scholar]
- Chai, J.-D., & Head-Gordon, M. J. 2008b, Phys. Chem. Chem. Phys., 10, 6615 [CrossRef] [Google Scholar]
- Chen, T., Zhen, J., Wang, Y., Linnartz, H., & Tielens, A. G. G. M. 2018, Chem. Phys. Lett., 692, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, T., Luo, Y., & Li, A. 2020, A&A, 633, A103 [CrossRef] [EDP Sciences] [Google Scholar]
- Christian, J. F., Wan, Z., & Anderson, S. L. 1992, J. Phys. Chem., 96, 3574 [CrossRef] [Google Scholar]
- Chuvilin, A., Kaiser, U., Bichoutskaia, E., et al. 2010, Nat. Chem., 2, 450 [NASA ADS] [CrossRef] [Google Scholar]
- Close, J. D., Federmann, F., Hoffmann, K., & Quaas, N. 1997, Chem. Phys. Lett., 276, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, N. L. J. 2011, The Molecular Universe, 280, 162 [Google Scholar]
- Cox, N. L. J., Cami, J., Kaper, L., et al. 2014, A&A, 569, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Demarais, N. J., Yang, Z., Snow, T. P., et al. 2014, ApJ, 784, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Desert, F.-X., Boulanger, F., & Puget, J. L. 1990, A&A, 500, 313 [Google Scholar]
- Díaz-Tendero, S., Sánchez, G., Alcamí, M., et al. 2006, Int. J. Mass Spectr., 252, 133 [CrossRef] [Google Scholar]
- Draine, B. T.,& Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., Li, A., Hensley, B. S., et al. 2020, ApJ, submitted [arXiv:2011.07046] [Google Scholar]
- Dunk, P. W., Kaiser, N. K., Hendrickson, C. L., et al. 2012, Nat. Commun., 3, 855 [NASA ADS] [CrossRef] [Google Scholar]
- Eggen, B. R., Heggie, M. I., Jungnickel, G., et al. 1996, Science, 272, 87 [CrossRef] [Google Scholar]
- Ernzerhof, M.,& Scuseria, G. E. J. 1999, Chem. Phys., 110, 5029 [Google Scholar]
- Ewels, C. P., Heggie, M. I., & Briddon, P. R. 2002, Chem. Phys. Lett., 351, 178 [CrossRef] [Google Scholar]
- Foing, B. H., & Ehrenfreund, P. 1994, Nature, 369, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Fowler, P. W., & Manolopoulos, D. E. 1995, An Atlas of Fullerenes (Oxford: Oxford University Press) [Google Scholar]
- Frisch, M. J., Trucks, G. W., Schlegel, H. B., et al. 2016, Gaussian 16 Rev. C.01, Wallingford, CT [Google Scholar]
- Fulara, J., Lessen, D., Freivogel, P., & Maier, J. P. 1993a, Nature, 366, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Gredel, R., Carpentier, Y., Rouillé, G., et al. 2011, A&A, 530, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hobbs, L. M., York, D. G., Thorburn, J. A., et al. 2009, ApJ, 705, 3 [Google Scholar]
- Joblin, C., & Tielens, A. G. G. M. 2011, EAS Pub. Ser., 46, 355 [CrossRef] [Google Scholar]
- Koponen, L., Puska, M. J., & Nieminen, R.M̃. 2008, J. Chem. Phys., 128, 154307 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Krasnokutski, S. A., Huisken, F., Jäger, C., et al. 2017, ApJ, 836, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Lan, Y., Kang, H., & Niu, T. 2015, Eur. Phys. J. D, 69, 69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leach, S. 1996, Z. Physikalische Chemie, 195, 15 [CrossRef] [Google Scholar]
- Lee, C., Yang, W., & Parr, R. G. 1988, Phys. Rev., B, 37, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Leger, A., & Puget, J. L. 1984, A&A, 500, 279 [NASA ADS] [Google Scholar]
- Le Page, V., Snow, T. P., & Bierbaum, V. M. 2001, ApJS, 132, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Le Page, V., Snow, T. P., & Bierbaum, V. M. 2003, ApJ, 584, 316 [NASA ADS] [CrossRef] [Google Scholar]
- Lepp, S., & Dalgarno, A. 1988, ApJ, 324, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Li, A., & Draine, B. T. 2001, ApJ, 554, 778 [Google Scholar]
- Li, J., Kudin, K. N., McAllister, M. J., et al. 2006, Phys. Rev. Lett., 96, 176101 [NASA ADS] [CrossRef] [Google Scholar]
- Maíz Apellániz, J., Barbá, R. H., Caballero, J. A., et al. 2021, MNRAS, 501, 2487 [CrossRef] [Google Scholar]
- Malloci, G., Mulas, G., & Joblin, C. 2004, A&A, 426, 105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malloci, G., Joblin, C., & Mulas, G. 2007, Chem. Phys., 332, 353 [Google Scholar]
- Maragkoudakis, A., Peeters, E., & Ricca, A. 2020, MNRAS, 494, 642 [CrossRef] [Google Scholar]
- McGuire, B. A., Loomis, R. A., Burkhardt, A. M., et al. 2021, Science, 371, 1265 [Google Scholar]
- Micelotta, E. R., Jones, A. P., & Tielens, A. G. G. M. 2010a, A&A, 510, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Micelotta, E. R., Jones, A. P., & Tielens, A. G. G. M. 2010b, A&A, 510, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Montillaud, J., Joblin, C., & Toublanc, D. 2013, A&A, 552, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Omont, A. 1986, A&A, 164, 159 [NASA ADS] [Google Scholar]
- Omont, A. 2016, A&A, 590, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Omont, A., & Bettinger, H. F. 2020, A&A, 637, A74 [CrossRef] [EDP Sciences] [Google Scholar]
- Omont, A., Bettinger, H. F., & Tönshoff, C. 2019, A&A, 625, A441 [Google Scholar]
- Parneix, P., Gamboa, A., Falvo, C., et al. 2017, Mol. Astrophys., 7, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Pietrucci, F., & Andreoni, W. 2014, J. Chem. Theory Comput., 10, 913 [CrossRef] [Google Scholar]
- Pilleri, P., Herberth, D., Giesen, T. F., et al. 2009, MNRAS, 397, 1053 [NASA ADS] [CrossRef] [Google Scholar]
- Pino, T., Carpentier, Y., Féraud, G., et al. 2011, EAS Pub. Ser., 46, 355 [CrossRef] [Google Scholar]
- Puget, J. L., & Leger, A. 1989, ARA&A, 27, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiterkamp, R., Halasinski, T., Salama, F., et al. 2002, A&A, 390, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salama, F., Bakes, E. L. O., Allamandola, L. J., & Tielens, A. G. G. M. 1996, ApJ, 458, 621 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Scott, L. T., Jackson, E. A., Zhang, Q., J. Am. Chem. Soc., 134, 107 [Google Scholar]
- Sellgren, K., Werner, M. W., Ingalls, J. G., et al. 2010, ApJ, 722, L54 [NASA ADS] [CrossRef] [Google Scholar]
- Snow, T. P., & Bierbaum, V. M. 2008, Ann. Rev. Anal. Chem., 229 [CrossRef] [Google Scholar]
- Steglich, M., Bouwman, J., Huisken, F., & Henning, T. 2011, ApJ, 742, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, G., Nicklaus, M. C., & Xie, R. 2005, J. Phys. Chem. A, 109, 4617 [CrossRef] [PubMed] [Google Scholar]
- Taylor, M. B., 2005, ASP Conf. Ser., 347, 29 [Google Scholar]
- Thaddeus, P. 1995, Astrophys. Space Sci. Libr., 202, 415 [Google Scholar]
- Tielens, A. G. G. M. 2005, The Physics and Chemistry of the Interstellar Medium (Cambridge, UK: Cambridge University Press) [CrossRef] [Google Scholar]
- Tielens, A. G. G. M. 2008, ARA&A, 46, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tielens, A. G. G. M. 2013, Rev. Mod. Phys., 85, 1021 [Google Scholar]
- Walker, G., Bohlender, D., Maier, J., & Campbell, E. 2015, ApJ, 812, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, G. A. H., Campbell, E. K., Maier, J. P., Bohlender, D., & Malo, L. 2016, ApJ, 831, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Yanai, T., Tew, D. P., & Handy, N. C. 2004, Chem. Phys. Lett., 393, 51 [CrossRef] [Google Scholar]
- Zhao, Y., & Truhlar, D. 2008, Theor. Chem. Acc., 120, 215 [CrossRef] [Google Scholar]
- Zhen, J., Castellanos, P., Paardekooper, D. M., et al. 2014, ApJ, 797, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Zhen, J., Rodriguez Castillo, S., Joblin, C., et al. 2016, ApJ, 822, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, Z., Steigerwald, M., Hybertsen, M., Brus, L. & Friesner, R. A. 2004, J. Am. Chem. Soc. 126, 3597 [CrossRef] [PubMed] [Google Scholar]
- Zhou, Z., Sfeir, M. Y., Zhang, L., et al. 2006, ApJ, 638, L105 [NASA ADS] [CrossRef] [Google Scholar]
Extremely strong and broad DIB recently discovered by Maíz Apellániz et al. (2021).
All Tables
Typical orders of magnitude for rates of PAH chemical processes in the diffuse ISM(a).
Energies (in eV) of first 1T1u states of C60 buckminsterfullerene computed at various levels of theory.
All Figures
 |
Fig. 1 Estimated orders of magnitude of reaction rates for a typical PAH/PAH+ of 50 C atoms in a diffuse interstellar cloud with NH = 50 cm−3, T = 50–100 K, and a UV intensity G0 = 3 Habing (Table A.1). |
| In the text | |
 |
Fig. 2 Computed absorption spectra (f-values) of three isomers of fullerene C50 (Table B.2). The results of complete calculations from ~350 to 2000 nm for the isomers of neutral C50 (D5h, 271; D3, 270; and Cs, 266) are displayed by open symbols, together with the cation spectra (C5h, 271; C2, 270; and Cs, 266) from ~500 to 2000 nm (full symbols). See similar Figs. B.1–B.4 for isomers of C40, C42, C44, C46, and C48 listed in Table B.2. |
| In the text | |
 |
Fig. B.1 Computed absorption spectra (f-values) of neutral fullerenes C40 D2 38 and C42 D3h 45 and cations C |
| In the text | |
 |
Fig. B.2 Computed absorption spectra (f-values) of three isomers of fullerene C44 (D2 75, D2 89, and D3h 72) and C |
| In the text | |
 |
Fig. B.3 Computed absorption spectra (f-values) of neutral fullerenes from 350 to 1200 nm, C46: Cs 99, C1 103, Cs 107, Cs 108, C2 109, C1 114, and C2 116 (left), and cations from ~480 to 1200 nm, C |
| In the text | |
 |
Fig. B.4 Computed absorption spectra (f-values) of neutral fullerenes C48: C2 171, C1 196, Cs 197, and C2 199, from 350 to 1200 nm (left), and cations C |
| In the text | |
 |
Fig. B.5 Example of nanotube segment: armchair (5,5) C50H20. |
| In the text | |
 |
Fig. B.6 Computed absorption spectra (f-values) of some (5,5) armchair nanotube segments, Cn H20, with n = 30,40, 50, 60, and 90. Full symbols show cations, and open symbols show neutrals. |
| In the text | |
 |
Fig. B.7 Computed absorption spectra (f-values) of some (4,4) armchair nanotube segments, Cn H16, with n = 40,48, and 56. Full symbols show cations, and open symbols show neutrals. |
| In the text | |
 |
Fig. B.8 Computed absorption spectra (f-values) of some semicapped (5,5) armchair nanotube segments, Cn H10, with n = 50, 60, 70, 80, 90, and 100. Full symbols show cations, and open symbols show neutrals. The lower
λ limit of the computations is 400 nm for all neutrals. For cations, it varies from
~400 nm for C50H |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.