| Issue |
A&A
Volume 656, December 2021
Solar Orbiter First Results (Cruise Phase)
|
|
|---|---|---|
| Article Number | A3 | |
| Number of page(s) | 11 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202140450 | |
| Published online | 14 December 2021 | |
Turbulence and wave transmission at an ICME-driven shock observed by the Solar Orbiter and Wind
1
Department of Space Science, The University of Alabama in Huntsville, Huntsville, AL 35899, USA
e-mail: lz0009@uah.edu
2
Center for Space Plasma and Aeronomic Research (CSPAR), The University of Alabama in Huntsville, Huntsville, AL 35805, USA
3
School of Earth and Space Sciences, Peking University Beijing, 100871 Beijing, PR China
4
National Institute for Astrophysics Astrophysical Observatory of Torino, Via Osservatorio 20, 10025 Pino Torinese, Italy
5
Department of Physics, University of Helsinki, Helsinki, Finland
6
Imperial College London, South Kensington Campus, London SW7 2AZ, UK
Received:
29
January
2021
Accepted:
30
April
2021
Aims. An interplanetary coronal mass ejection (ICME) event was observed by the Solar Orbiter at 0.8 AU on 2020 April 19 and by Wind at 1 AU on 2020 April 20. Futhermore, an interplanetary shock wave was driven in front of the ICME. Here, we focus on the transmission of the magnetic fluctuations across the shock and we analyze the characteristic wave modes of solar wind turbulence in the vicinity of the shock observed by both spacecraft.
Methods. The observed ICME event is characterized by a magnetic helicity-based technique. The ICME-driven shock normal was determined by magnetic coplanarity method for the Solar Orbiter and using a mixed plasma and field approach for Wind. The power spectra of magnetic field fluctuations were generated by applying both a fast Fourier transform and Morlet wavelet analysis. To understand the nature of waves observed near the shock, we used the normalized magnetic helicity as a diagnostic parameter. The wavelet-reconstructed magnetic field fluctuation hodograms were used to further study the polarization properties of waves.
Results. We find that the ICME-driven shock observed by Solar Orbiter and Wind is a fast, forward oblique shock with a more perpendicular shock angle at the Wind position. After the shock crossing, the magnetic field fluctuation power increases. Most of the magnetic field fluctuation power resides in the transverse fluctuations. In the vicinity of the shock, both spacecraft observe right-hand polarized waves in the spacecraft frame. The upstream wave signatures fall within a relatively broad and low frequency band, which might be attributed to low frequency MHD waves excited by the streaming particles. For the downstream magnetic wave activity, we find oblique kinetic Alfvén waves with frequencies near the proton cyclotron frequency in the spacecraft frame. The frequency of the downstream waves increases by a factor of ∼7–10 due to the shock compression and the Doppler effect.
Key words: shock waves / turbulence / waves / Sun: coronal mass ejections (CMEs)
© L.-L. Zhao et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Interplanetary shocks in the heliosphere have important consequences for the generation and evolution of solar wind turbulence. The direct effects of shock waves on nearby turbulence remains a controversial issue since the turbulence could be either self-generated at the shock due to particle streaming or preexisting in the solar wind and possibly amplified as it interacts with the shock. Exploring interaction of a shock with turbulence is interesting from a range of perspectives. First, large-scale magnetohydrodynamic (MHD) waves interacting with shocks can be modeled as the transmission and reflection of waves at an ideal discontinuity. In this regard, the shock is treated as an ideal discontinuity because large-scale MHD waves have wavelengths that are much longer than the shock transition region. The waves do not play a role in the dissipation of the shock. This problem has been investigated by several authors, such as McKenzie & Westphal (1968, 1969), who considered large-scale linear MHD waves associated with dispersion relations. A recent work from Zank et al. (2021) considers both linear propagating MHD modes and zero frequency or non-propagating modes (i.e., vortical and entropy modes, and in the appropriate geometry-magnetic island modes). The waves constitute a complete set for the linearized fluid equations. Since the large-scale MHD waves are assumed as small amplitude waves in their work, classical discontinuities, i.e., nonlinear structures (such as contact or tangential discontinuities), are not included. The authors discuss the transmission of linear MHD waves in cases involving a small background magnetic field, vortices, and magnetic island modes from upstream to downstream. The nonlinear cascade is neglected in these studies because the interaction time between waves (propagating or non-propagating) and the shock is much shorter than the nonlinear cascade time, provided the region just upstream and downstream of the shock is considered when dealing with the shock-turbulence transmission problem. In this case, there is no time for the nonlinear coupling between different wave modes to occur, so there is no need to assume weak nonlinearity. In fact, the observations presented by Pitňa et al. (2017) do show nonlinearity but only as the transmitted or self-generated turbulence is advected away from the shock.
In general, the wavelength of the transmitted waves tends to be smaller than the upstream waves. The fluctuation power downstream is typically larger than that upstream, which has been verified by satellite observations (e.g., Zank et al. 2006; Hu et al. 2013; Adhikari et al. 2016; Zhao et al. 2019a; Borovsky & Burkholder 2020; Borovsky 2020). However, this approach may not be applicable when the turbulent nonlinearity is not negligible, especially if the turbulence is strong. In this case, the back reaction of turbulence on shocks needs to be considered, which results in the Rankine-Hugniot jump conditions being modified by turbulence (e.g., Zank et al. 2002), and the amplitude of waves or fluctuations being greatly enhanced as it transmits to the downstream (e.g., Lu et al. 2009).
One important consequence of the turbulence-shock interaction is its effect on particle transport and acceleration. Self-generated fluctuations upstream of the shock can be amplified upon crossing the shock and these upstream and downstream waves may effectively scatter particles leading to efficient diffusive acceleration (e.g., McKenzie & Völk 1982; Li et al. 2003, 2005; Rice et al. 2003; Vainio & Laitinen 2007). Besides the increase of fluctuation power with the shock crossing, the change in the turbulence properties, such as the compressibility and anisotropy, will also affect the transport of particles. For example, the generation of magnetic islands may result in additional particle acceleration due to magnetic reconnection (Zank et al. 2014, 2015; Le Roux et al. 2015, 2016; Zhao et al. 2018, 2019a,b; Adhikari et al. 2019). Here, the magnetic islands represent convected magnetic field fluctuations with perpendicular wave vectors and may stand as a reasonable simplification of quasi-2D flux ropes (Zank et al. 2017, 2021).
Another aspect of the turbulence-shock interaction is related to kinetic-scale fluctuations. Kinetic-scale fluctuations are commonly observed in the solar wind and are thought to play an important role in dissipation processes through wave-particle interactions, which leads to the observed steepening of the magnetic fluctuation spectrum in the dissipation range. Previous observational analyses have identified different types of kinetic waves in the solar wind. Different wave modes can be identified based on their polarization properties. For example, ion cyclotron waves (ICWs) propagate nearly parallel to the magnetic field and possess a left-handed polarization in the solar wind frame (Jian et al. 2009, 2010; He et al. 2011a, 2019a; Bruno & Telloni 2015; Telloni et al. 2019), kinetic Alfvén waves (KAWs) propagate in a direction quasi-perpendicular to the magnetic field and are right-handed polarized (Bale et al. 2005; He et al. 2011b; Podesta 2013; Woodham et al. 2018; Telloni et al. 2020a), and whistler waves are circularly right-handed polarized and propagate quasi-parallel to the magnetic field (Gary & Smith 2009; Podesta & Gary 2011a,b; Salem et al. 2012; TenBarge et al. 2012; Zhu et al. 2019). Whistler waves can propagate obliquely or very perpendicularly and they may coexist with KAWs. However, according to linear kinetic theory, oblique whistler waves tend to have large magnetic compressibility with strong parallel fluctuations dB∥. In contrast, KAWs are mostly dominated by perpendicular fluctuations dB⊥ > dB∥ (Gary & Smith 2009; He et al. 2011b; Salem et al. 2012).
Although the interaction of kinetic waves and shocks has not been studied extensively, it is widely accepted that wave-particle interactions provide the primary dissipation mechanism for collisionless shocks. Observations of kinetic waves near interplanetary shocks have been reported by Wilson III et al. (2009) and Wilson (2016). In this paper, we study the details of waves and turbulence in the vicinity of an interplanetary shock observed by the Solar Orbiter and Wind between 2020 April 19–20. The shock is driven by an interplanetary coronal mass ejection (ICME), which was also observed by both spacecraft. Due to the fact that the Solar Orbiter was not taking plasma measurements during this period, we focus mainly on the transmission of magnetic fluctuation properties, such as the magnetic fluctuation power and compressibility. We also look into possible kinetic-scale wave activity both upstream and downstream of the shock based on the θB0lR distribution of the normalized magnetic helicity σm spectra, with θB0lR being the angle between the local mean magnetic field B0l (Horbury et al. 2008) and the radial direction.
The outline of this paper is as follows. Section 2 presents an overview of the large-scale ICME structure and its driven shock observed both by the Solar Orbiter and Wind. Section 3 provides the preliminary shock parameters and the magnetic field fluctuation spectra upstream and downstream of the shock observed by both spacecraft. The spectra of the normalized magnetic helicity σm are also shown as a diagnostic parameter of wave polarization characteristics. Section 4 shows the distribution of θB0lR in σm spectra and the wavelet-reconstructed magnetic field fluctuation hodograms in the T–N plane for the purpose of determining the wave modes. Section 5 provides a summary and discussion.
2. Observation of the ICME and its driven shock
Figure 1 illustrates the ICME and its driven shock in the X–Y plane of the Heliocentric Inertial (HCI) coordinate system at the time when they were observed. The locations of the Solar Orbiter and Wind are identified by the blue and red dots. The orange-colored region represents the ICME flux rope and the dashed lines represent the shock as it approaches the spacecraft. The Parker spiral magnetic field lines are also shown for reference. The shock reached Solar Orbiter on 2020 April 19, 05:06:18 UT. The Solar Orbiter was located then 0.80 AU from the Sun and had an HCI longitude of 130° and latitude of −3.94°. Then, Wind observed the shock on 2020 April 20, 01:33:04 UT from its location at ∼1.0 AU from the Sun and had an HCI longitude of 134.63° and latitude of −5.17°. The longitudinal separation between the Solar Orbiter and Wind is around 4.63° and the latitude separation is around 1.23°. Therefore, Wind and the Solar Orbiter are approximately radially aligned during this ICME event and the radial separation is 0.2 AU.
 |
Fig. 1. Solar Orbiter (blue dot) and Wind (red dot) positions in the X–Y plane of the Heliocentric Inertial (HCI) coordinate system at the time when the ICME event of 2020 April was observed by both. The schematic is plotted looking down on the ecliptic plane. The Parker magnetic field lines are also shown. The ICME-driven shock (dashed lines) was observed by both spacecraft. |
Figure 2 is an overview of the ICME event and its driven shock observed by the Solar Orbiter (SolO) during the period between 2020 April 18 and 2020 April 21. The ICME has been studied in detail in Davies et al. (2021) using multi-spacecraft measurements. Plasma measurements were not available for this period, so we show only the magnetic field data measured by the SolO/MAG instrument (Horbury et al. 2020). The top panel shows the magnetic field strength |B| and its three components BR, BT, and BN. The solid vertical line marks an abrupt increase in |B| that is identified as a forward interplanetary shock crossing. An ICME is first seen at ∼ April 19, 09:00 UT, and lasts about 24 hours. The vertical dashed lines in each panel enclose the observed ICME structure, which is characterized by a smooth magnetic field rotation through a large angle and the enhanced magnetic field strength compared to the surrounding solar wind (e.g., Burlaga et al. 1981; Kilpua et al. 2017). The averaged magnetic field magnitude within the ICME interval is about 18.4 nT. The second and third panels show the elevation (θ) and azimuthal (ϕ) angles of the magnetic field. The smooth rotation of the magnetic field within the ICME interval can be clearly seen from the elevation angle.
 |
Fig. 2. Solar Orbiter observation of the ICME (bounded by the dashed vertical lines) and its driven shock event (solid vertical line) during the period from 2020 April 18 to 2020 April 21. Top panel: time profiles of the magnetic field vector measured by the Solar Orbiter/MAG instrument. Second and third panels: elevation (θ) and azimuthal (ϕ) angles of the magnetic field direction in the RTN coordinate system. Bottom panel: spectrogram of the normalized magnetic helicity σm using the Morlet wavelet method. Contour lines are drawn at levels of |σm| = 0.8. |
In the bottom panel, we plot the normalized reduced magnetic helicity σm (Matthaeus et al. 1982) calculated by the wavelet method. We note that the strict definition of magnetic helicity is the volume integral of the scalar product between the magnetic vector potential and the magnetic field vector. It is an invariant of the ideal MHD equations and characterizes the degree of topological linkage of magnetic flux tubes (Moffatt 1978). It depends on the spatial properties of the magnetic field topology and thus cannot be estimated by single spacecraft observations only. However, using the Taylor hypothesis, Matthaeus et al. (1982) proposed a reduced form of magnetic helicity (being only along the direction of the plasma flow), which is defined in Fourier space and depends on the Fourier transform of the magnetic field transverse (with respect to the sampling direction) components. With the spectra of the reduced magnetic helicity, the handedness (chirality) of helical rotations in the magnetic field at a given scale can be specified. The reduced magnetic helicity can also be calculated in the time domain by means of wavelet transforms (e.g., He et al. 2011a; Telloni et al. 2012). In this figure and subsequent analysis, we use the complex Morlet wavelet function:
with the bandwidth A = 2.0 and center frequency C = 1.0 Hz; here, t′ is the time normalized by the wavelet scales (Torrence & Compo 1998).
The scale- and time-dependent normalized reduced magnetic helicity σm can be estimated by:
where the tilde represents wavelet transformed quantities, as does the tilde below; Im denotes the imaginary part of a complex number, s is the wavelet scale and is chosen to be between 1 hour and 64 hours in Figs. 2 and 3, and the asterisk represents the complex conjugate. The normalized reduced magnetic helicity σm ranges from −1 to 1. In describing the magnetic flux rope structure, the sign of magnetic helicity (or σm) can directly determine its handedness (chirality), that is, a positive value of σm corresponds to right-handed chirality and a negative value to left-handed chirality (e.g., Dasso et al. 2005; Hu et al. 2020). As shown in our previous studies (Telloni et al. 2020b; Zhao et al. 2020, 2021), the ICME, as a large-scale magnetic flux rope, usually possesses a high value of magnetic helicity due to the rotation of the magnetic field over a large angle. The black contour lines in the panel of σm enclose the high magnetic-helicity regions with |σm|≥0.8. The ICME observed by Solar Orbiter has a negative magnetic helicity (σm < 0) and is identified as a left-handed magnetic helical structure, which was also confirmed by Davies et al. (2021). The averaged σm in the region bounded by the black contour line is around −0.89.
 |
Fig. 3. Wind observation of the ICME and its driven shock during the period from 2020 April 19 to 2020 April 23. The panels from top to bottom show the magnetic field vector and magnitude, the flow speed, the proton number density and temperature, the proton plasma beta, and spectrograms of the normalized magnetic helicity σm, the normalized cross helicity σc, and the normalized residual energy σr. |
Figure 3 shows the Wind magnetic field and plasma measurements during the ICME passage. The top four panels show the magnetic field magnitude and the three components; the solar wind speed (Vsw); the proton number density (np) and temperature (Tp); and the proton plasma beta (βp). The forward shock is again indicated by a solid vertical line and is characterized by abrupt increases in the magnetic field strength, solar wind speed, proton density, and temperature. The ICME event starts at Wind at ∼07:45 UT and lasts around 28 hours. It shows the typical magnetic cloud signatures, that is, the abnormally low proton plasma beta attributed to the enhanced magnetic field strength and smoothly rotating field direction over an interval of a day (e.g., Burlaga et al. 1981), along with the low proton temperature. During the ICME interval, the averaged magnetic field magnitude ⟨|B|⟩ ≃ 13.5 nT, solar wind speed ⟨Vsw⟩≃345 km s−1, proton density ⟨np⟩≃12.4 cm−3, proton temperature ⟨Tp⟩≃54 434 K, and the proton plasma beta ⟨βp⟩≃0.24. The ICME is preceded by a slow solar wind (∼330 km s−1). The trailing wind is not particularly fast (peak speed ∼500 km s−1), but there is a clear positive speed gradient between the ICME and the solar wind behind. The ICME sheath, which is the region between the shock and the ICME ejecta, shows multiple plasma beta jumps that can be related to current sheet crossings (e.g., Li 2007; Liu et al. 2014; Huang et al. 2016). In the bottom three panels, we plot the wavelet spectrograms of the normalized magnetic helicity σm, the normalized cross helicity σc, and the normalized residual energy σr. The latter two quantities can be calculated from the Elsässer variables, 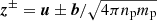 , with u and b as the fluctuating velocity and magnetic field vectors, np the proton number density, and mp the proton mass (Zank et al. 2012):
, with u and b as the fluctuating velocity and magnetic field vectors, np the proton number density, and mp the proton mass (Zank et al. 2012):
and
The normalized cross-helicity, σc, is a ratio of ideal invariants (cross-helicity and total fluctuating energy), whereas the normalized residual energy, σr, is not. After the shock passage, the cross helicity σc is almost zero, and the residual energy σr becomes more negative. Within the ICME interval: the averaged ⟨σm⟩≃ − 0.9 (left-handed helical structure), ⟨σc⟩≃0.07, ⟨σr⟩≃ − 0.73. The close-to-zero σc indicates that there is an almost equal amount of energy propagating parallel and anti-parallel to the magnetic field, that is, the turbulence is balanced. The highly negative σr indicates that the energy of the fluctuating magnetic field ⟨b2⟩ dominates compared to the kinetic fluctuation energy ⟨u2⟩. These two turbulent properties of the ICME flux rope structures have been widely studied (Telloni et al. 2020b; Zhao et al. 2020, 2021; Good et al. 2020). After the passage of the ICME, Wind tends to measure slightly faster solar wind with an increased σc.
Compared to the Solar Orbiter observation at 0.8 AU, theWind observations at 1 AU suggest that the ICME has expanded slightly as its duration increases from ∼24 hours to ∼28 hours. The magnetic helicity in the ICME interval is almost unchanged. Due to the lack of plasma data from Solar Orbiter in this period, we cannot compare the changes in the cross helicity and residual energy during the evolution of the ICME. The ICME-driven shock observed by both Solar Orbiter and Wind shows a small jump in the magnetic field magnitude, with the downstream increase being a factor of ∼2. However, the ICME sheath observed by both spacecraft shows obvious differences. The sheath observed by Wind is more dynamic and has multiple phases where it is increasing in plasma beta.
3. SolO and Wind observation near the shock
In the following analysis, we focus on the region in the vicinity of the ICME-driven shock observed by the Solar Orbiter and Wind. The shock parameters calculated at the two locations are summarized in Table 1. The shock normal at the Solar Orbiter position is obtained by the magnetic coplanarity method (Burlaga 1995):
Shock parameters at Wind and Solar Orbiter positions.
where Bd denotes the downstream mean magnetic field, Bu the upstream mean magnetic field, and ΔB = Bd − Bu.
The shock normal at the Wind position is calculated by a mixed coplanarity method:
where ΔV = Vd − Vu. The speed of the shock observed by Wind is estimated by means of the mass flux algorithm using plasma measurements:
where ρ = npmp is the proton mass density, 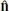 is the shock normal, and Δρ = ρd − ρu. Here, quantities with subscripts u and d correspond to their upstream and downstream mean values. The Solar Orbiter’s upstream interval for calculating the mean value is from 05:00 to 05:05 UT on April 19, and the downstream interval is between 05:07 and 05:12 UT. The Wind’s upstream interval for taking a mean is from 01:15 to 01:30 UT on April 20, and the downstream interval starts from 01:35 to 01:50 UT. These intervals are chosen on the basis that they exclude shock layers and do not include non-shock related disturbances, but are long enough to average out the turbulence and wave activities. In Table 1, the rows from top to bottom list the shock normal direction
is the shock normal, and Δρ = ρd − ρu. Here, quantities with subscripts u and d correspond to their upstream and downstream mean values. The Solar Orbiter’s upstream interval for calculating the mean value is from 05:00 to 05:05 UT on April 19, and the downstream interval is between 05:07 and 05:12 UT. The Wind’s upstream interval for taking a mean is from 01:15 to 01:30 UT on April 20, and the downstream interval starts from 01:35 to 01:50 UT. These intervals are chosen on the basis that they exclude shock layers and do not include non-shock related disturbances, but are long enough to average out the turbulence and wave activities. In Table 1, the rows from top to bottom list the shock normal direction 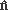 , shock obliquity ΘBn (the angle between upstream mean magnetic field and the shock normal), shock speed Vsh, upstream solar wind speed Vu, upstream magnetic field Bu, velocity jump Vd/Vu, magnetic jump Bd/Bu, flow speed changes along the shock normal
, shock obliquity ΘBn (the angle between upstream mean magnetic field and the shock normal), shock speed Vsh, upstream solar wind speed Vu, upstream magnetic field Bu, velocity jump Vd/Vu, magnetic jump Bd/Bu, flow speed changes along the shock normal 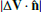 , proton density jump npd/npu, temperature jump Tpd/Tpu, upstream Alfvén speed VAu, upstream fast magnetosonic speed Vfu, upstream proton plasma beta βpu, and upstream fast mode mach number Mfu. As shown in the table, the normals for both shock indicate that the shock front is (at least locally), almost perpendicular to the Sun-Earth line. The shock is quasi-perpendicular at Wind’s position with ΘBn = 72° form (5) and 71° from (4), while at Solar Orbiter the shock is considerably more oblique (ΘBn = 44°). The magnetic field jump ratio is very similar at both locations. TheWind analysis further shows that shock is slow (speed 356 km s−1) and relatively weak (Mach number 2.0).
, proton density jump npd/npu, temperature jump Tpd/Tpu, upstream Alfvén speed VAu, upstream fast magnetosonic speed Vfu, upstream proton plasma beta βpu, and upstream fast mode mach number Mfu. As shown in the table, the normals for both shock indicate that the shock front is (at least locally), almost perpendicular to the Sun-Earth line. The shock is quasi-perpendicular at Wind’s position with ΘBn = 72° form (5) and 71° from (4), while at Solar Orbiter the shock is considerably more oblique (ΘBn = 44°). The magnetic field jump ratio is very similar at both locations. TheWind analysis further shows that shock is slow (speed 356 km s−1) and relatively weak (Mach number 2.0).
To study the wave activity upstream and downstream of the shock, we now consider an interval starting 2 hours prior to the shock and ending 2 hours after the shock passage. For both Wind and Solar Orbiter, the two-hour downstream interval is within the ICME sheath. Figure 4 shows Solar Orbiter’s observation of the magnetic field in this 4-hour interval. The ICME sheath includes a small magnetic flux rope just after 07:03 UT ahead of the ICME ejecta, which is not the focus in this study. The magnetic field data used here have a resolution of ∼0.125 s. The Solar Orbiter is mostly in the outward magnetic sector (BR > 0) during this period. The shock jump in the magnetic field magnitude is clearly seen in the top panel. There is a current sheet crossing around 06:23:54 UT, where the magnetic field BN and BR components change direction and the magnetic field magnitude |B| has a slight drop from ∼7 nT to 5.5 nT. A visual inspection of the magnetic field time-series shows that the downstream magnetic field exhibits a higher level of fluctuations compared with the upstream. The upstream magnetic field near the shock is more radially aligned compared to the downstream magnetic field, as indicated by the angle θBR. In the bottom two panels, we show the total magnetic field fluctuation power spectral density (PSD) and the normalized magnetic helicity σm from the wavelet analysis. The PSD shows that the downstream fluctuating power is higher compared to that upstream at a fixed frequency. As a reference, the proton cyclotron frequencies in the plasma frame are plotted in the third panel both upstream (fc, u) and downstream (fc, d), and the equivalent frequency in the spacecraft frame 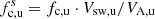 and
and 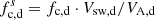 are shown in the bottom panel. Here, Vsw and VA are the solar wind speed and Alfvén speed estimated by Wind’s plasma measurements. The spectrogram of the normalized magnetic helicity shows a dominance of positive and relatively large σm around 0.1 Hz within an hour prior to the shock crossing (∼04:00–05:00). This indicates the existence of right-hand polarized waves in the outward magnetic sector. After crossing the shock, these positive and large σm values are observed and are prevalent at a frequency slightly higher than
are shown in the bottom panel. Here, Vsw and VA are the solar wind speed and Alfvén speed estimated by Wind’s plasma measurements. The spectrogram of the normalized magnetic helicity shows a dominance of positive and relatively large σm around 0.1 Hz within an hour prior to the shock crossing (∼04:00–05:00). This indicates the existence of right-hand polarized waves in the outward magnetic sector. After crossing the shock, these positive and large σm values are observed and are prevalent at a frequency slightly higher than 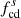 . The wave frequency increases by a factor of ∼10 with the shock crossing. This can be understood from the flow velocity Vsw increases in the downstream, causing the frequency fsc increase due to the Doppler effect. In addition, compression causes the wave number k to increase (or wavelength λ to decrease) across the shock (Zank et al. 2021), which also increases the observed frequency, according to Taylor’s hypothesis (fSC = Vsw/λ, λ = 2π/k).
. The wave frequency increases by a factor of ∼10 with the shock crossing. This can be understood from the flow velocity Vsw increases in the downstream, causing the frequency fsc increase due to the Doppler effect. In addition, compression causes the wave number k to increase (or wavelength λ to decrease) across the shock (Zank et al. 2021), which also increases the observed frequency, according to Taylor’s hypothesis (fSC = Vsw/λ, λ = 2π/k).
 |
Fig. 4. Solar Orbiter observation near the shock. Panels from top to bottom show the magnetic field components and magnitude, the angle θBR between the magnetic field and radial direction, the total magnetic field power spectral density (PSD), and the normalized magnetic helicity σm from the Morlet wavelet analysis. The cyan vertical line in each panel represents the current sheet crossing. The horizontal dashed lines in the third panel identify the proton cyclotron frequency in the plasma frame upstream fcu and downstream fcd. The dashed dotted lines in the fourth panel shows the equivalent frequency in the spacecraft frame |
The same analysis is done for the Wind data, as shown in Fig. 5. Here, magnetic field data with a resolution of 0.092 s are used. We also show the pitch angle distribution (PAD) of 97.37 eV electrons and the proton plasma beta βp to characterize a strong current sheet (SCS) crossing during this period. The SCS is identified by the directional change of the magnetic field, the decrease of the magnetic field magnitude |B|, and a sharp increase in the proton plasma beta βp. In the electron PAD panel, the unidirectional electron beam is initially aligned with 0° pitch angle and then switches to 180°. Based on the multiple proton plasma beta jumps in the ICME-sheath observed by Wind, it can be related to the heliospheric current sheet (HCS) since the flow is slow and may originate from the streamer belt, in which the HCS is often embedded. Unlike the Solar Orbiter, the Wind magnetic field appears to be quasi-perpendicular to the radial direction both upstream and downstream of the shock as shown in the θBR panel. The PSD panel shows that similar to Solar Orbiter, the magnetic fluctuation power increased in the downstream region. Compared to the PSD measured by Solar Orbiter, the magnetic fluctuation power observed by Wind is smaller, illustrating that the magnetic fluctuation power decreases as distance increases (e.g., Telloni et al. 2015). The characteristics of magnetic helicity are similar to those in Fig. 4. In the upstream region, an enhanced magnetic helicity (> 0) is also observed near 0.1 Hz. However, this phenomenon seems to be prevalent throughout the upstream 2-hour interval, which is different from that observed by the Solar Orbiter (within one hour). After crossing the shock, a large and positive magnetic helicity is observed near the downstream proton cyclotron frequency 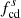 but lasts only about 40 minutes. The magnitude of σm is slightly smaller than upstream. After the SCS crossing, no significant positive enhancement is shown in the spectrogram of σm.
but lasts only about 40 minutes. The magnitude of σm is slightly smaller than upstream. After the SCS crossing, no significant positive enhancement is shown in the spectrogram of σm.
 |
Fig. 5. Wind observation near the shock. In the same format as Fig. 4. Third panel shows the pitch angle distribution of 97.37 eV electrons, and the fourth panel shows the proton plasma beta during this period. The cyan vertical lines represent the current sheet crossing. |
In Fig. 6, we show the frequency dependent magnetic fluctuation trace PSD and magnetic compressibility CB upstream and downstream of the shock observed by Solar Orbiter. We use both the standard Fourier method and the wavelet technique. To avoid the possible effects of the current sheet, the downstream spectrum is calculated within a 77-min interval (05:06:18–06:23:18 UT), corresponding to the region between the “shock” and “CS” shown in Fig. 4. The upstream spectrum is computed at the same interval length, i.e., 03:49:18–05:06:18 UT. The Fourier spectrum is calculated using the Blackman-Tukey method, namely, the Fourier transform of the correlation function PSD = ℱ[R(τ)]. The upstream spectrum is plotted in red and downstream in turquoise. The solid lines are the Fourier spectra and the dots are the wavelet spectra, which are consistent with one another. Clearly, the trace power of the magnetic field fluctuations is enhanced downstream. The amplitude of the magnetic fluctuations |δB|, i.e., the integral of the Fourier PSD, is ∼0.6 nT upstream and ∼1.68 nT downstream. The upstream spectrum shows a bump in the frequency range between fcu and 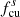 . The averaged θBR during the upstream interval is around 30° as shown in Fig. 4. The significant enhancement of the upstream magnetic fluctuation power at around 0.1 Hz indicates the presence of quasi-parallel propagating waves. The downstream inertial-range spectrum follows a power-law shape and is close to the Kolmogorov −5/3 spectrum. At higher frequencies, both upstream and downstream spectra steepen. In the frequency range of 0.3–4 Hz, the upstream spectrum has a slope of f−2.17. The downstream break frequency is around 0.5 Hz. The spectral break frequency can be estimated by fb = Vsw/2π/(di + ρi) with di the proton inertial length and ρi thermal proton gyroradius (Duan et al. 2018). The proton speed, density and temperature needed here are obtained from Wind measurements. After the break frequency, the downstream spectrum behaves like f−3.3. The magnetic compressibility CB is defined as the ratio between the power in the magnetic field magnitude fluctuations and the power in total fluctuation (P|B|/PTr) (Bavassano et al. 1982). As the solar wind turbulence is typically incompressible, CB is usually smaller than 0.1 in the inertial range. As it approaches the kinetic range with high frequencies, the compressibility increases obviously as shown in the figure. The upstream compressibility near 0.1 Hz is slightly smaller than downstream CB. In the frequency range 0.02–0.2 Hz, the upstream CB is around 0.04 and downstream CB is around 0.06. The downstream compressibility shows a significant increase after its spectral break frequency and exceeds the upstream CB at frequencies above 1 Hz.
. The averaged θBR during the upstream interval is around 30° as shown in Fig. 4. The significant enhancement of the upstream magnetic fluctuation power at around 0.1 Hz indicates the presence of quasi-parallel propagating waves. The downstream inertial-range spectrum follows a power-law shape and is close to the Kolmogorov −5/3 spectrum. At higher frequencies, both upstream and downstream spectra steepen. In the frequency range of 0.3–4 Hz, the upstream spectrum has a slope of f−2.17. The downstream break frequency is around 0.5 Hz. The spectral break frequency can be estimated by fb = Vsw/2π/(di + ρi) with di the proton inertial length and ρi thermal proton gyroradius (Duan et al. 2018). The proton speed, density and temperature needed here are obtained from Wind measurements. After the break frequency, the downstream spectrum behaves like f−3.3. The magnetic compressibility CB is defined as the ratio between the power in the magnetic field magnitude fluctuations and the power in total fluctuation (P|B|/PTr) (Bavassano et al. 1982). As the solar wind turbulence is typically incompressible, CB is usually smaller than 0.1 in the inertial range. As it approaches the kinetic range with high frequencies, the compressibility increases obviously as shown in the figure. The upstream compressibility near 0.1 Hz is slightly smaller than downstream CB. In the frequency range 0.02–0.2 Hz, the upstream CB is around 0.04 and downstream CB is around 0.06. The downstream compressibility shows a significant increase after its spectral break frequency and exceeds the upstream CB at frequencies above 1 Hz.
 |
Fig. 6. Solar Orbiter’s total magnetic field power spectra density (top panel) and magnetic comressibility CB (bottom panel) as a function of frequency upstream and downstream of the shock. The red and turquoise lines represent the upstream and downstream Fourier spectra using the Blackman-Tukey method. The red and green dots represent the corresponding Morlet wavelet results. Each spectrum is calculated in a 77-min interval upstream and downstream, respectively. Black straight lines in the top panel show power-law fits, and vertical dashed lines indicate the upstream and downstream proton cyclotron frequency in the plasma frame fcu, fcd and in the spacecraft frame |
The magnetic compressibility can also be represented by the ratio between fluctuations parallel and perpendicular to the mean magnetic field P∥/P⊥, as shown in Fig. 7. In the top panels, the parallel and transverse spectra are plotted in pink and green, respectively, and the sum of the two (trace spectra) in lime-green. The trace spectra are the same as in Fig. 6. Spectral power in fluctuations that are polarized transverse to the mean magnetic field dominates both upstream and downstream, indicating the dominance of nearly incompressible fluctuations. Another notable feature is that both the bump near 0.1 Hz in the upstream PSD and the spectral break of the downstream PSD at around 0.5 Hz are caused by the transverse fluctuations. The ratio of parallel fluctuation power to the perpendicular fluctuation power P∥/P⊥ (not shown here) upstream and downstream is consistent with their respective magnetic compressibility, CB = P|B|/PTr, as shown in Fig. 6. The bottom panels of Fig. 7 show the spectra of σm calculated with the Fourier (black line) and wavelet (red line) methods, respectively. Enhanced magnetic helicity is another signature of wave activities as the solar wind is usually in a state with σm ≃ 0 (e.g., Vasquez et al. 2018). Both upstream and downstream σm spectra exhibit a positive bump, suggesting the existence of right-hand polarized wave modes in the spacecraft frame. The upstream spectral bump and the enhancement of σm appear in a wide and low frequency range, that is, 0.01–0.4 Hz, while the downstream σm increases at relatively high frequencies near 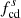 and peaks at around 1 Hz.
and peaks at around 1 Hz.
 |
Fig. 7. Decomposition of the magnetic field fluctuations into parallel and transverse fluctuations. Top panels: Solar Orbiter’s spectra for total magnetic field fluctuations (limegreen dashed lines) separated into compressible parallel (pink solid lines) and incompressible transverse fluctuations (green solid lines) in the upstream (left panels) and downstream (right panels) regions, respectively. The upstream and downstream proton cyclotron frequency in plasma frame fcu and fcd and the equivalent frequency in the spacecraft frame |
The same spectral analysis for Wind data near the shock is presented in Figs. 8 and 9. To avoid the effects of the strong current sheet observed by Wind shown in Fig. 5, each power spectrum here is calculated within a 40-min interval prior to the shock front (upstream) and after the shock passage (downstream). Table 2 lists the Wind measurements of the magnetic field and flow plasma parameters during this period. All the parameters are the mean of the 40-min interval. The magnetic fluctuation amplitude |δB| increases about 4 times downstream, while it increases about three times at the downstream observed by the Solar Orbiter.
 |
Fig. 8. Trace spectra of magnetic field fluctuations and magnetic compressibility. In the same format as Fig. 6, but for Wind observations upstream and downstream of the shock. Vertical dashed lines in the top panel indicate the proton cyclotron frequency in the plasma frame upstream fcu and downstream fcd and in the spacecraft frame upstream |
 |
Fig. 9. Decomposition of the total magnetic field fluctuations into parallel and transverse fluctuations. In the same format as Fig. 7, but for Wind observations. Top panels: upstream (left) and downstream (right) power spectra of the total magnetic fluctuations (limegreen dashed lines), compressible fluctuations (pink solid lines), and incompressible traverse fluctuations (green lines). Bottom panels: spectra of normalized magnetic helicity σm obtained from both Fourier and Wavelet methods. |
Magnetic field and solar wind parameters upstream and downstream of the shock observed by Wind.
Similarly to the Solar Orbiter results, we find an amplification in the magnetic field PSD downstream of the shock. However, due to the wave activity both upstream and downstream, the amplification is not a constant shift. We performed a power-law fitting on the upstream spectrum in the frequency range [0.005, 0.1] Hz and a flatter spectrum with f−1.0 was obtained. After about 0.1 Hz, the upstream spectrum starts to steepen. There are two other enhancements present at high frequencies in the upstream spectrum, but may be related to instrument noise. The downstream power spectrum also deviates from a single power-law spectrum. The spectrum starts to steepen after about 0.2 Hz. The magnetic compressibility CB at high frequencies (> 0.1 Hz) is larger in the upstream region compared to the downstream, but little difference is present at low frequencies.
Figure 9 displays the same format as Fig. 7. The top panels show the power spectra of the total magnetic fluctuations, PTr, compressible fluctuations, P∥, and transverse fluctuations, P⊥. Again, the magnetic field fluctuation power is dominated by the incompressible traverse fluctuations. The ratios P∥/P⊥ upstream and downstream are consistent with the magnetic compressibility obtained by CB = P|B|/PTr shown in Fig. 8, which is also found in the Solar Orbiter’s results. The upstream wave activity near 0.1 Hz is mostly in the traverse fluctuations. The downstream transverse spectrum shows a bump in the frequency range around 0.2 Hz. The wave activity is also reflected in the spectrum of the normalized magnetic helicity σm, shown in the bottom panel. We note that the quantity, σm, can be used to indicate both the handedness of magnetic helical structures (e.g., flux ropes) and the polarization of plasma waves. However, the association between the sign of σm and the plasma wave polarization is distinct from its association with the flux rope spatial handedness. As shown in previous studies (e.g., He et al. 2011a; Podesta & Gary 2011a; Woodham et al. 2019), plasma wave polarization depends not only on the sign taken by σm, but also on the direction of wave propagation with respect to the background magnetic field B0. For the outward propagating fluctuations (mostly observed in the solar wind), (i) if B0 is directed away from the Sun, the left-handed polarization corresponds to a negative σm and right-handed polarization to a positive σm; (ii) if B0 is directed towards the Sun, the left-handed polarization corresponds to a positive σm and right-handed polarization to a negative σm. In Figs. 7 and 9, all the identified waves show a positive enhancement of σm and also reside in the interval where the magnetic field is directed anti-sunward (see Figs. 4 and 5), thus indicating the right-handed polarization. The upstream σm wavelet spectrum peaks around 0.1 Hz and the downstream σm peaks around 0.7 Hz (close to 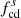 ). The downstream wave frequency is clearly larger than that upstream. The upstream wave signature falls over a relatively wide and low frequency range, resulting in a flat f−1 spectrum at frequencies less than 0.1 Hz. This indicates the low-frequency (0.01–0.1 Hz) right-hand polarized waves (He et al. 2019b), which are often observed in planetary foreshocks as ultra-low-frequency (ULF) waves (e.g., Greenstadt et al. 1995; Narita et al. 2003). In contrast, the downstream wave activity appears near
). The downstream wave frequency is clearly larger than that upstream. The upstream wave signature falls over a relatively wide and low frequency range, resulting in a flat f−1 spectrum at frequencies less than 0.1 Hz. This indicates the low-frequency (0.01–0.1 Hz) right-hand polarized waves (He et al. 2019b), which are often observed in planetary foreshocks as ultra-low-frequency (ULF) waves (e.g., Greenstadt et al. 1995; Narita et al. 2003). In contrast, the downstream wave activity appears near 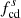 and is right-hand polarized, which might be kinetic Alfvén waves observed in the solar wind (e.g., He et al. 2011b; Podesta 2013; Telloni et al. 2020a).
and is right-hand polarized, which might be kinetic Alfvén waves observed in the solar wind (e.g., He et al. 2011b; Podesta 2013; Telloni et al. 2020a).
4. Upstream and downstream waves
In this section, we further analyze the nature of the waves observed in this shock event. The wave propagation angle relative to the mean magnetic field is crucial to the analysis. To find the angle, we calculate the local mean magnetic field based on the envelope of the wavelet function (1),
which depends on both the scale s and time t. We can then calculate the angle between the local mean magnetic field B0l and the radial direction θB0lR(s, t), which also depends on scale and time. The scale s is related to the time period p through s ∼ p/1.03 for the Morlet wavelet transform. By Taylor’s hypothesis, the observed wavevector is in the direction of the solar wind speed. For the sake of simplicity, we assume that the solar wind velocity is approximately radial. Therefore, the angle θB0lR(s, t) represents the wave propagation angle relative to the local mean magnetic field.
A histogram of the propagation angle θB0lR can be constructed as shown in Fig. 10, which illustrates the likelihood of different wave propagation direction at each scale. Here, waves in solar wind turbulence are identified by the enhanced magnetic helicity σm (e.g., He et al. 2011a,b; Vasquez et al. 2018; Telloni et al. 2019). The left and right panels show the σm spectra as a function of the propagation angle θB0lR for upstream and downstream of the shock, respectively. The time interval for calculating θB0lR in each region is the same as in Fig. 6. During this period, the solar wind is in the outward magnetic sector with BR > 0. The results show that the positive enhancement of the upstream σm in the period range [3, 26] s or frequency range [0.04, 0.3] Hz, which corresponds to the bump shown in the bottom left panel of Fig. 7, is mainly in the quasi-parallel direction, that is, θB0lR < 45°. On the other hand, the downstream enhanced σm has a more perpendicular θB0lR (∼60°), indicating that the waves downstream are more oblique. The downstream wave frequency is about ten times larger than the upstream wave frequency. Due to the quasi-parallel propagating angle upstream, the positively enhanced σm suggests the presence of right-hand polarized quasi-parallel propagating waves in the spacecraft frame. The frequency range of upstream waves is between fcu and 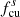 and the downstream right-hand polarized waves are mainly in the period less than 2 s or frequency larger than 0.5 Hz. The downstream waves can be transmitted from upstream with a higher frequency due to the shock compression and Doppler shift, but can also be locally generated downstream.
and the downstream right-hand polarized waves are mainly in the period less than 2 s or frequency larger than 0.5 Hz. The downstream waves can be transmitted from upstream with a higher frequency due to the shock compression and Doppler shift, but can also be locally generated downstream.
 |
Fig. 10. θB0lR distributions of σm spectra upstream (left) and downstream (right) of the shock observed by Solar Orbiter. θB0lR is the angle between the scale-dependent local mean magnetic field B0l and the radial direction. The inverse of the period gives the corresponding frequency. The horizontal dashed lines and dashed dotted lines show the periods corresponding to the proton cyclotron frequency in the plasma frame and in the spacecraft frame, respectively. |
Figure 11 shows the same analysis but for Wind observations upstream (left) and downstream (right) of the shock. The positively enhanced σm in the upstream region is observed in a wide period range between 2–100 s. The angle θB0lR is between 50° and 80°. The wave propagation angle is more oblique to the background magnetic field compared to the Solar Orbiter observations at 0.8 AU. The downstream wave activity mainly occurs in the periods of 0.8–4 s, and the propagation angle θB0lR is concentrated in the range 60°–80°. As discussed above, the downstream wave frequency increases about tenfold, but the downstream solar wind speed is only 1.15 times larger than that upstream, indicating a shorter wavelength downstream of the shock due to the compression (Zank et al. 2021). The positively enhanced σm observed by Wind also suggests the existence of right-hand polarized waves both upstream and downstream.
 |
Fig. 11. θB0lR distributions of σm spectra upstream (left) and downstream (right) of the shock. In the same format as Fig. 10, but for Wind observation. |
To further identify the wave modes, we analyze the hodograms of the BT and BN fluctuations obtained from wavelet decomposition. The method has been successfully applied to diagnose the kinetic waves in the solar wind (He et al. 2011b). Figure 12 shows two examples of the hodograph of the magnetic field fluctuations dBT–dBN in the Solar Orbiter’s upstream region. The first interval extends from 04:14:06 UT to 04:14:44 UT on 2020 April 19. The second interval extends from 05:03:35 UT to 05:03:59 UT. Both intervals are chosen by the enhanced magnetic helicity shown in Fig. 4. The magnetic fluctuations dBT and dBN are reconstructed from the wavelet transform by averaging in the period range between 3 s and 8 s. Both intervals show clearly right-handed polarization ellipses in the T–N plane (BR > 0). The local mean magnetic field B0l for each interval is listed in the figure, which has a small tilt angle to the R direction (assumed wavevector k direction), that is, the angle between B0l and R direction is around 20° for the first interval, and about 29° for the second interval. B0l is almost perpendicular to the T–N plane, indicating the dominance of perpendicular fluctuations dB⊥. Due to the relatively low frequency (0.125–0.3 Hz) and relatively small magnetic compressibility (CB ≃ 0.04), these signatures may indicate quasi-parallel Alfvén waves. However, we do not rule out the possibility of quasi-parallel fast-mode or whistler waves (He et al. 2015), which also possess the above properties. The exact wave mode identification needs further investigation.
 |
Fig. 12. Two cases of the dBT–dBN hodograms observed by the Solar Orbiter upstream of the shock. The magnetic field fluctuations dBT and dBN are reconstructed from the wavelet transform by averaging in the period range [3, 8] s. The first case is selected in the time interval between 04:14:06 UT and 04:14:44 UT on 2020 April 19 when 14° < θkB < 28°. The second case is selected in the time interval between 05:03:35 UT and 05:03:59 UT on 2020 April 19 when 22° < θkB < 34°. B0l is the local mean magnetic field averaged in the selected period range and time interval. |
Similarly, the magnetic hodograms of the Solar Orbiter downstream waves are presented in Fig. 13. The magnetic field fluctuations dBT and dBN are obtained by averaging the wavelet decomposition in the period range [0.5, 2] s. Because of the increased wave frequency downstream, the averaging period is smaller than that used upstream. This is also reflected in the lower number of data points on the ellipses compared to the upstream. The local downstream mean magnetic field B0l is quasi-perpendicular to the R direction, being 63.5° in the first interval and 70° in the second interval. Their directions in the T–N plane are shown as the black arrow in each panel. The two intervals show reasonably well defined polarization ellipses with the major axis perpendicular to the local mean magnetic field, indicating dB∥ < dB⊥. The wave frequency is in the range of 0.5–2 Hz and the compressibility is about 0.24. These features are consistent with oblique KAWs since oblique whistler waves usually have dB∥ > dB⊥ with the major axis of the polarization ellipse parallel to B0l (He et al. 2011b).
 |
Fig. 13. Magnetic hodograms in the same format as Fig. 12, but for Solar Orbiter observations downstream of the shock. The wavelet reconstructed magnetic field fluctuations dBT and dBN are averaged over the period range [0.5, 2] s. The black arrow indicates the direction of the local mean magnetic field B0l. |
The same analysis is also performed for Wind observations upstream and downstream of the shock. The results are shown in Figs. 14 and 15, respectively. The four intervals are again selected by the enhanced magnetic helicity σm(s, t) shown in Fig. 5. All of these intervals show right-hand polarized ellipses in the T–N plane (BR > 0) with the major axis perpendicular to the local mean magnetic field B0l. The upstream and downstream θkB observed by Wind is comparably larger than that observed by the Solar Orbiter, indicating that the wave modes here are more perpendicular with 50° < 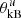 < 75° upstream and 65° <
< 75° upstream and 65° < 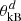 < 90° downstream. Similar to the Solar Orbiter, the upstream waves observed by Wind also fall in a low frequency band (0.01–0.14 Hz) within the MHD inertial scale, a relatively small magnetic compressibility (CB ≃ 0.05) and a dominant perpendicular fluctuation dB⊥, which can be oblique right-hand polarized Alfvén waves. Again, we do not exclude the possible existence of other MHD waves. The downstream wave frequency (0.5–1.4 Hz) is near the proton cyclotron frequency in the spacecraft frame and within the kinetic scale. The right-handed polarization with dB⊥ > dB∥ suggests the oblique KAWs downstream, as also observed by the Solar Orbiter.
< 90° downstream. Similar to the Solar Orbiter, the upstream waves observed by Wind also fall in a low frequency band (0.01–0.14 Hz) within the MHD inertial scale, a relatively small magnetic compressibility (CB ≃ 0.05) and a dominant perpendicular fluctuation dB⊥, which can be oblique right-hand polarized Alfvén waves. Again, we do not exclude the possible existence of other MHD waves. The downstream wave frequency (0.5–1.4 Hz) is near the proton cyclotron frequency in the spacecraft frame and within the kinetic scale. The right-handed polarization with dB⊥ > dB∥ suggests the oblique KAWs downstream, as also observed by the Solar Orbiter.
 |
Fig. 14. Magnetic hodograms in the same format as Fig. 12, but for Wind observations upstream of the shock. The wavelet reconstructed dBT and dBN are averaged over the period range of [7, 10] s. Black arrow lines indicate the local mean magnetic field B0l in the T–N plane. |
 |
Fig. 15. Magnetic hodograms in the same format as Fig. 12, but for Wind observations downstream of the shock. The reconstructed magnetic field fluctuations are averaged in the period range of [0.7, 2] s. |
5. Summary and discussion
In conclusion, here, we analyze the properties of waves and turbulence near an ICME-driven shock observed by Solar Orbiter at 0.8 AU and Wind at 1 AU on 2020 April 19–20. The ICME is identified as a left-handed magnetic helical structure. The ICME-driven shock is a fast forward oblique shock with estimated speed ∼356 km s−1 at 1 AU. The shock obliquity at Wind’s position is more perpendicular than that observed by the Solar Orbiter. The difference in the shock obliquity between the Solar Orbiter and Wind may be due to the slight differences in their latitude and longitude and also to propagation effects. The main results are summarized as follows:
-
Spectral analysis of the magnetic field fluctuations show an enhanced fluctuating power in the shock downstream, suggesting that the shock can amplify the upstream turbulence as it is transmitted through the shock. This is consistent with theoretical expectations (Zank et al. 2021) and previous observations (Hu et al. 2013; Zhao et al. 2019a; Borovsky 2020).
-
The total magnetic fluctuation power is dominated by the transverse fluctuations, which is consistent with nearly incompressible MHD turbulence models (Zank & Matthaeus 1992, 1993; Zank et al. 2017; Adhikari et al. 2017) and reported also in previous studies of downstream regions of interplanetary shocks (e.g., Moissard et al. 2019; Good et al. 2020).
-
The magnetic compressibility CB is usually less than 0.1 in the inertial range but increases significantly as it approaches the kinetic range. The difference in upstream and downstream magnetic compressibility depends on the specific frequency range and the wave activity. For Wind observations in the vicinity of the shock, the upstream CB is slightly larger than that downstream when the frequency exceeds 0.1 Hz. This also applies to Solar Orbiter, but not for frequencies greater than 1 Hz.
-
Both spacecraft have observed upstream wave activity near the shock, which produced a clear bump in the magnetic field trace spectra and also the spectra of the normalized magnetic helicity σm. The bump is located near 0.1 Hz and is mostly due to the transverse fluctuations. Wave activity is also found in the downstream region, which can be transmitted from the upstream region and also can be locally generated. The frequency of the downstream wave increases by a factor of 7–10 due to the shock compression and Doppler effect.
-
The waves identified in this study are all right-hand polarized with positively enhanced σm. The hodograms of the magnetic fluctuations and σm spectra indicate the existence of oblique kinetic Alfvén waves in the downstream region. The upstream waves observed by both spacecraft occur in a wide and low frequency range corresponding to ULF wave band, which can be low frequency Alfvén waves because of the small magnetic compressibility. However, we do not exclude the possibility of other low-frequency MHD waves being excited by ions and propagating upstream in the solar wind, such as the right-hand polarized fast mode wave, which requires further investigation.
Although we do present evidence of wave activity using both spectral analysis and magnetic hodograms, the nature of the waves observed here is not conclusive. The relatively low frequency of the upstream waves suggests that they may not be associated directly with shock dissipation. Instead, they may be generated by the streaming of particles and contribute to the scattering and acceleration of energetic particles. The connection between these waves and particle acceleration remains to be understood and ought to be the subject of additional investigations in the future.
Acknowledgments
We acknowledge the partial support of the NSF EPSCoR RII-Track-1 Cooperative Agreement OIA-1655280 and a NASA award 80NSSC20K1783. D.T. is partially supported by the Italian Space Agency (ASI) under contract I/013/12/0. The Solar Orbiter magnetometer was funded by the UK Space Agency (grant ST/T001062/1).
References
- Adhikari, L., Zank, G., Hunana, P., & Hu, Q. 2016, ApJ, 833, 218 [CrossRef] [Google Scholar]
- Adhikari, L., Zank, G., Hunana, P., et al. 2017, ApJ, 841, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Adhikari, L., Khabarova, O., Zank, G., & Zhao, L.-L. 2019, ApJ, 873, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Bale, S., Kellogg, P. J., Mozer, F., Horbury, T., & Reme, H. 2005, Phys. Rev. Lett., 94, 215002 [NASA ADS] [CrossRef] [Google Scholar]
- Bavassano, B., Dobrowolny, M., Fanfoni, G., Mariani, F., & Ness, N. 1982, Sol. Phys., 78, 373 [CrossRef] [Google Scholar]
- Borovsky, J. E. 2020, J. Geophys. Res. (Space Phys.), 125 [Google Scholar]
- Borovsky, J. E., & Burkholder, B. L. 2020, J. Geophys. Res.: Space Phys., 125, e2019JA027307 [Google Scholar]
- Bruno, R., & Telloni, D. 2015, ApJ, 811, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Burlaga, L. F. 1995, Interplanet. Magnetohydrodyn., 3 [Google Scholar]
- Burlaga, L., Sittler, E., Mariani, F., & Schwenn, a. R., 1981, J. Geophys. Res.: Space Phys., 86, 6673 [NASA ADS] [CrossRef] [Google Scholar]
- Dasso, S., Mandrini, C. H., Démoulin, P., Luoni, M. L., & Gulisano, A. M. 2005, Adv. Space Res., 35, 711 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, E., Möstl, C., Owens, M. J., et al. 2021, A&A, 656, A2 (SO Cruise Phase SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duan, D., He, J., Pei, Z., et al. 2018, ApJ, 865, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Gary, S. P., & Smith, C. W. 2009, J. Geophys. Res.: Space Phys., 114 [Google Scholar]
- Good, S., Kilpua, E., Ala-Lahti, M., et al. 2020, ApJ, 900, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Greenstadt, E., Le, G., & Strangeway, R. 1995, Adv. Space Res., 15, 71 [NASA ADS] [CrossRef] [Google Scholar]
- He, J., Marsch, E., Tu, C., Yao, S., & Tian, H. 2011a, ApJ, 731, 85 [NASA ADS] [CrossRef] [Google Scholar]
- He, J., Tu, C., Marsch, E., & Yao, S. 2011b, ApJ, 745, L8 [Google Scholar]
- He, J., Pei, Z., Wang, L., et al. 2015, ApJ, 805, 176 [NASA ADS] [CrossRef] [Google Scholar]
- He, J., Duan, D., Wang, T., et al. 2019a, ApJ, 880, 121 [NASA ADS] [CrossRef] [Google Scholar]
- He, J., Duan, D., Zhu, X., Yan, L., & Wang, L. 2019b, Sci. China Earth Sci., 62, 619 [NASA ADS] [CrossRef] [Google Scholar]
- Horbury, T. S., Forman, M., & Oughton, S. 2008, Phys. Rev. Lett., 101, 175005 [Google Scholar]
- Horbury, T., O’Brien, H., Blazquez, I. C., et al. 2020, A&A, 642, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hu, Q., Zank, G. P., Li, G., & Ao, X. 2013, in American Institute of Physics, 175 [Google Scholar]
- Hu, Q., He, W., Qiu, J., Vourlidas, A., & Zhu, C. 2020, Geophys. Res. Lett., e2020GL090630 [Google Scholar]
- Huang, J., Liu, Y. C.-M., Klecker, B., & Chen, Y. 2016, J. Geophys. Res.: Space Phys., 121, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Jian, L. K., Russell, C. T., Luhmann, J. G., et al. 2009, ApJ, 701, L105 [CrossRef] [Google Scholar]
- Jian, L., Russell, C., Luhmann, J., et al. 2010, J. Geophys. Res.: Space Phys., 115 [Google Scholar]
- Kilpua, E., Koskinen, H. E., & Pulkkinen, T. I. 2017, Liv. Rev. Sol. Phys., 14, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Le Roux, J., Zank, G., Webb, G., & Khabarova, O. 2015, ApJ, 801, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Le Roux, J., Zank, G., Webb, G., & Khabarova, O. 2016, ApJ, 827, 47 [CrossRef] [Google Scholar]
- Li, G. 2007, ApJ, 672, L65 [Google Scholar]
- Li, G., Zank, G., & Rice, W. 2003, J. Geophys. Res.: Space Phys., 108 [Google Scholar]
- Li, G., Hu, Q., & Zank, G. P. 2005, in The Physics of Collisionless Shocks: 4th Annual IGPP International Astrophysics Conference, eds. G. Li, G. P. Zank, & C. T. Russell, Am. Inst. Phys. Conf. Ser., 781, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Y.-M., Huang, J., Wang, C., et al. 2014, J. Geophys. Res.: Space Phys., 119, 8721 [NASA ADS] [CrossRef] [Google Scholar]
- Lu, Q., Hu, Q., & Zank, G. 2009, ApJ, 706, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Matthaeus, W. H., Goldstein, M. L., & Smith, C. 1982, Phys. Rev. Lett., 48, 1256 [Google Scholar]
- McKenzie, J., & Westphal, K. 1968, Phys. Fluids, 11, 2350 [NASA ADS] [CrossRef] [Google Scholar]
- McKenzie, J. F., & Westphal, K. O. 1969, Planet. Space Sci., 17, 1029 [CrossRef] [Google Scholar]
- McKenzie, J., & Völk, H. 1982, A&A, 116, 191 [NASA ADS] [Google Scholar]
- Moffatt, H. K. 1978, Field Generation in Electrically Conducting Fluids, 2 (Cambridge, London, New York, Melbourne: Cambridge University Press), 5 [Google Scholar]
- Moissard, C., Fontaine, D., & Savoini, P. 2019, J. Geophys. Res. (Space Phys.), 124, 8208 [NASA ADS] [CrossRef] [Google Scholar]
- Narita, Y., Glassmeier, K.-H., Schäfer, S., et al. 2003, Geophys. res. Lett., 30 [Google Scholar]
- Pitňa, A., Šafránková, J., Němeček, Z., & Franci, L. 2017, ApJ, 844, 51 [CrossRef] [Google Scholar]
- Podesta, J. J. 2013, Sol. Phys., 286, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Podesta, J. J., & Gary, S. P. 2011a, ApJ, 742, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Podesta, J. J., & Gary, S. P. 2011b, ApJ, 734, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Rice, W., Zank, G., & Li, G. 2003, J. Geophys. Res.: Space Phys., 108 [Google Scholar]
- Salem, C. S., Howes, G., Sundkvist, D., et al. 2012, ApJ, 745, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Telloni, D., Bruno, R., D’Amicis, R., Pietropaolo, E., & Carbone, V. 2012, ApJ, 751, 19 [Google Scholar]
- Telloni, D., Bruno, R., & Trenchi, L. 2015, ApJ, 805, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Telloni, D., Carbone, F., Bruno, R., et al. 2019, ApJ, 885, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Telloni, D., Bruno, R., D’Amicis, R., et al. 2020a, ApJ, 897, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Telloni, D., Zhao, L., Zank, G. P., et al. 2020b, ApJ, 905, L12 [NASA ADS] [CrossRef] [Google Scholar]
- TenBarge, J., Podesta, J., Klein, K., & Howes, G. 2012, ApJ, 753, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Torrence, C., & Compo, G. P. 1998, Bull. Am. Meteorol. Soc., 79, 61 [Google Scholar]
- Vainio, R., & Laitinen, T. 2007, ApJ, 658, 622 [NASA ADS] [CrossRef] [Google Scholar]
- Vasquez, B. J., Markovskii, S., & Smith, C. W. 2018, ApJ, 855, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, L. 2016, Washington DC American Geophysical Union Geophysical Monograph Series, 216, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson III, L., Cattell, C., Kellogg, P., et al. 2009, J. Geophys. Res.: Space Phy., 114, [Google Scholar]
- Woodham, L. D., Wicks, R. T., Verscharen, D., & Owen, C. J. 2018, ApJ, 856, 49 [CrossRef] [Google Scholar]
- Woodham, L. D., Wicks, R. T., Verscharen, D., et al. 2019, ApJ, 884, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Zank, G., & Matthaeus, W. 1992, J. Geophys. Res., 97, 17 [NASA ADS] [Google Scholar]
- Zank, G. P., & Matthaeus, W. 1993, Phys. Fluids A: Fluid Dyn., 5, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Zank, G., Zhou, Y., Matthaeus, W., & Rice, W. 2002, Phys. Fluids, 14, 3766 [NASA ADS] [CrossRef] [Google Scholar]
- Zank, G., Li, G., Florinski, V., et al. 2006, J. Geophys. Res.: Space Phys., 111 [CrossRef] [Google Scholar]
- Zank, G. P., Dosch, A., Hunana, P., et al. 2012, ApJ, 745, 35 [Google Scholar]
- Zank, G. l., Le Roux, J., Webb, G., Dosch, A., & Khabarova, O. 2014, ApJ, 797, 28 [CrossRef] [Google Scholar]
- Zank, G., Hunana, P., Mostafavi, P., et al. 2015, ApJ, 814, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Zank, G., Adhikari, L., Hunana, P., et al. 2017, ApJ, 835, 147 [Google Scholar]
- Zank, G., Nakanotani, M., Zhao, L. L., et al. 2021, ApJ, 913, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, L.-L., Zank, G. P., Khabarova, O., et al. 2018, ApJ, 864, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, L.-L., Zank, G., Chen, Y., et al. 2019a, ApJ, 872, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, L.-L., Zank, G., Hu, Q., et al. 2019b, ApJ, 886, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, L.-L., Zank, G., Adhikari, L., et al. 2020, ApJS, 246, 26 [Google Scholar]
- Zhao, L. L., Zank, G. P., Hu, Q., et al. 2021, A&A, 650, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhu, X., He, J., Verscharen, D., & Zhao, J. 2019, ApJ, 878, 48 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Magnetic field and solar wind parameters upstream and downstream of the shock observed by Wind.
All Figures
 |
Fig. 1. Solar Orbiter (blue dot) and Wind (red dot) positions in the X–Y plane of the Heliocentric Inertial (HCI) coordinate system at the time when the ICME event of 2020 April was observed by both. The schematic is plotted looking down on the ecliptic plane. The Parker magnetic field lines are also shown. The ICME-driven shock (dashed lines) was observed by both spacecraft. |
| In the text | |
 |
Fig. 2. Solar Orbiter observation of the ICME (bounded by the dashed vertical lines) and its driven shock event (solid vertical line) during the period from 2020 April 18 to 2020 April 21. Top panel: time profiles of the magnetic field vector measured by the Solar Orbiter/MAG instrument. Second and third panels: elevation (θ) and azimuthal (ϕ) angles of the magnetic field direction in the RTN coordinate system. Bottom panel: spectrogram of the normalized magnetic helicity σm using the Morlet wavelet method. Contour lines are drawn at levels of |σm| = 0.8. |
| In the text | |
 |
Fig. 3. Wind observation of the ICME and its driven shock during the period from 2020 April 19 to 2020 April 23. The panels from top to bottom show the magnetic field vector and magnitude, the flow speed, the proton number density and temperature, the proton plasma beta, and spectrograms of the normalized magnetic helicity σm, the normalized cross helicity σc, and the normalized residual energy σr. |
| In the text | |
 |
Fig. 4. Solar Orbiter observation near the shock. Panels from top to bottom show the magnetic field components and magnitude, the angle θBR between the magnetic field and radial direction, the total magnetic field power spectral density (PSD), and the normalized magnetic helicity σm from the Morlet wavelet analysis. The cyan vertical line in each panel represents the current sheet crossing. The horizontal dashed lines in the third panel identify the proton cyclotron frequency in the plasma frame upstream fcu and downstream fcd. The dashed dotted lines in the fourth panel shows the equivalent frequency in the spacecraft frame |
| In the text | |
 |
Fig. 5. Wind observation near the shock. In the same format as Fig. 4. Third panel shows the pitch angle distribution of 97.37 eV electrons, and the fourth panel shows the proton plasma beta during this period. The cyan vertical lines represent the current sheet crossing. |
| In the text | |
 |
Fig. 6. Solar Orbiter’s total magnetic field power spectra density (top panel) and magnetic comressibility CB (bottom panel) as a function of frequency upstream and downstream of the shock. The red and turquoise lines represent the upstream and downstream Fourier spectra using the Blackman-Tukey method. The red and green dots represent the corresponding Morlet wavelet results. Each spectrum is calculated in a 77-min interval upstream and downstream, respectively. Black straight lines in the top panel show power-law fits, and vertical dashed lines indicate the upstream and downstream proton cyclotron frequency in the plasma frame fcu, fcd and in the spacecraft frame |
| In the text | |
 |
Fig. 7. Decomposition of the magnetic field fluctuations into parallel and transverse fluctuations. Top panels: Solar Orbiter’s spectra for total magnetic field fluctuations (limegreen dashed lines) separated into compressible parallel (pink solid lines) and incompressible transverse fluctuations (green solid lines) in the upstream (left panels) and downstream (right panels) regions, respectively. The upstream and downstream proton cyclotron frequency in plasma frame fcu and fcd and the equivalent frequency in the spacecraft frame |
| In the text | |
 |
Fig. 8. Trace spectra of magnetic field fluctuations and magnetic compressibility. In the same format as Fig. 6, but for Wind observations upstream and downstream of the shock. Vertical dashed lines in the top panel indicate the proton cyclotron frequency in the plasma frame upstream fcu and downstream fcd and in the spacecraft frame upstream |
| In the text | |
 |
Fig. 9. Decomposition of the total magnetic field fluctuations into parallel and transverse fluctuations. In the same format as Fig. 7, but for Wind observations. Top panels: upstream (left) and downstream (right) power spectra of the total magnetic fluctuations (limegreen dashed lines), compressible fluctuations (pink solid lines), and incompressible traverse fluctuations (green lines). Bottom panels: spectra of normalized magnetic helicity σm obtained from both Fourier and Wavelet methods. |
| In the text | |
 |
Fig. 10. θB0lR distributions of σm spectra upstream (left) and downstream (right) of the shock observed by Solar Orbiter. θB0lR is the angle between the scale-dependent local mean magnetic field B0l and the radial direction. The inverse of the period gives the corresponding frequency. The horizontal dashed lines and dashed dotted lines show the periods corresponding to the proton cyclotron frequency in the plasma frame and in the spacecraft frame, respectively. |
| In the text | |
 |
Fig. 11. θB0lR distributions of σm spectra upstream (left) and downstream (right) of the shock. In the same format as Fig. 10, but for Wind observation. |
| In the text | |
 |
Fig. 12. Two cases of the dBT–dBN hodograms observed by the Solar Orbiter upstream of the shock. The magnetic field fluctuations dBT and dBN are reconstructed from the wavelet transform by averaging in the period range [3, 8] s. The first case is selected in the time interval between 04:14:06 UT and 04:14:44 UT on 2020 April 19 when 14° < θkB < 28°. The second case is selected in the time interval between 05:03:35 UT and 05:03:59 UT on 2020 April 19 when 22° < θkB < 34°. B0l is the local mean magnetic field averaged in the selected period range and time interval. |
| In the text | |
 |
Fig. 13. Magnetic hodograms in the same format as Fig. 12, but for Solar Orbiter observations downstream of the shock. The wavelet reconstructed magnetic field fluctuations dBT and dBN are averaged over the period range [0.5, 2] s. The black arrow indicates the direction of the local mean magnetic field B0l. |
| In the text | |
 |
Fig. 14. Magnetic hodograms in the same format as Fig. 12, but for Wind observations upstream of the shock. The wavelet reconstructed dBT and dBN are averaged over the period range of [7, 10] s. Black arrow lines indicate the local mean magnetic field B0l in the T–N plane. |
| In the text | |
 |
Fig. 15. Magnetic hodograms in the same format as Fig. 12, but for Wind observations downstream of the shock. The reconstructed magnetic field fluctuations are averaged in the period range of [0.7, 2] s. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



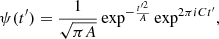
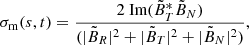
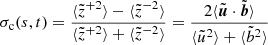
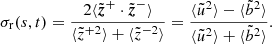
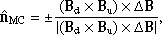
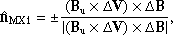
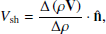
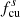
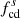
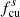
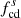
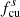
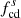
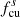
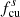
![$$ \begin{aligned} \bar{B}(s, t_{\rm n}) = \sum _{\rm m} B(t_{\rm m}) \exp \left[-\frac{(t_{\rm n} - t_{\rm m})^2}{2 s^2}\right], \end{aligned} $$](/articles/aa/full_html/2021/12/aa40450-21/aa40450-21-eq31.gif)