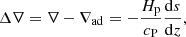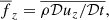| Issue |
A&A
Volume 655, November 2021
|
|
|---|---|---|
| Article Number | A78 | |
| Number of page(s) | 15 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202141337 | |
| Published online | 23 November 2021 | |
Prandtl number dependence of stellar convection: Flow statistics and convective energy transport
1
Georg-August-Universität Göttingen, Institut für Astrophysik, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
e-mail: pkaepyl@uni-goettingen.de
2
Nordita, KTH Royal Institute of Technology and Stockholm University, Stockholm, Sweden
Received:
18
May
2021
Accepted:
25
August
2021
Context. The ratio of kinematic viscosity to thermal diffusivity, the Prandtl number, is much smaller than unity in stellar convection zones.
Aims. The main goal of this work is to study the statistics of convective flows and energy transport as functions of the Prandtl number.
Methods. Three-dimensional numerical simulations of compressible non-rotating hydrodynamic convection in Cartesian geometry are used. The convection zone (CZ) is embedded between two stably stratified layers. The dominant contribution to the diffusion of entropy fluctuations comes in most cases from a subgrid-scale diffusivity whereas the mean radiative energy flux is mediated by a diffusive flux employing Kramers opacity law. Here, we study the statistics and transport properties of up- and downflows separately.
Results. The volume-averaged rms velocity increases with decreasing Prandtl number. At the same time, the filling factor of downflows decreases and leads to, on average, stronger downflows at lower Prandtl numbers. This results in a strong dependence of convective overshooting on the Prandtl number. Velocity power spectra do not show marked changes as a function of Prandtl number except near the base of the convective layer where the dominance of vertical flows is more pronounced. At the highest Reynolds numbers, the velocity power spectra are more compatible with the Bolgiano-Obukhov k−11/5 than the Kolmogorov-Obukhov k−5/3 scaling. The horizontally averaged convected energy flux (F̅conv), which is the sum of the enthalpy (F̅enth) and kinetic energy fluxes (F̅kin), is independent of the Prandtl number within the CZ. However, the absolute values of F̅enth and F̅kin increase monotonically with decreasing Prandtl number. Furthermore, F̅enth and F̅kin have opposite signs for downflows and their sum F̅↓conv diminishes with Prandtl number. Thus, the upflows (downflows) are the dominant contribution to the convected flux at low (high) Prandtl numbers. These results are similar to those from Rayleigh-Benárd convection in the low Prandtl number regime where convection is vigorously turbulent but inefficient at transporting energy.
Conclusions. The current results indicate a strong dependence of convective overshooting and energy flux on the Prandtl number. Numerical simulations of astrophysical convection often use a Prandtl number of unity because it is numerically convenient. The current results suggest that this can lead to misleading results and that the astrophysically relevant low Prandtl number regime is qualitatively different from the parameter regimes explored in typical contemporary simulations.
Key words: turbulence / convection
© ESO 2021
1. Introduction
The flows in solar and stellar convection zones (CZs) are characterised by very high Reynolds and Péclet numbers Re = uℓ/ν and Pe = uℓ/χ, respectively, where u and ℓ are typical velocity and length scales, and ν and χ are the kinematic viscosity and thermal diffusivity (e.g., Ossendrijver 2003; Käpylä 2011; Schumacher & Sreenivasan 2020). This implies very vigorous turbulence which means that resolving all scales down to the Kolmogorov scale is infeasible (e.g., Chan & Sofia 1986). Moreover, the ratio Pe/Re, which is the Prandtl number Pr = ν/χ, is typically much smaller than unity in stellar CZs (e.g., Augustson et al. 2019). For example, values of the order of Pr ≲ 10−6 are typical in the solar CZ. Most numerical simulations, however, are made with a Prandtl number of the order of unity because greatly differing viscosity and thermal diffusivity would lead to a wide gap in the smallest physically relevant scales of velocity and temperature. Therefore, reaching high Re and Pe simultaneously in simulations with low Pr is prohibitively expensive (e.g., Kupka & Muthsam 2017).
Recently, it has become clear that current simulations do not capture some basic features of solar convection with sufficient accuracy. Comparisons of helioseismic and numerical studies suggest that the simulations produce significantly higher velocity amplitudes at large horizontal scales (e.g., Hanasoge et al. 2012, 2016). While discrepancies also exist between helioseismic methods (see, e.g., Greer et al. 2015), there is another, more direct piece of evidence from simulations: global and semi-global simulations with solar luminosity and rotation rate preferentially lead to anti-solar differential rotation with a slower equator and faster poles (e.g., Fan & Fang 2014; Käpylä et al. 2014; Karak et al. 2018). This is indicative of an overly weak rotational influence on the flow leading to an excessive Rossby number. Simulations also suggest that inaccuracies in convective velocities of as little as 20–30% are sufficient for the rotation profile to flip (Käpylä et al. 2014). The discrepancy between simulations and observations has been dubbed the convective conundrum (O’Mara et al. 2016).
There are several possible causes of the overestimation of convective velocity amplitudes in current simulations. For example, the Rayleigh numbers in the simulations could be too low (e.g., Featherstone & Hindman 2016) or it could be that convection in the Sun is driven only in the thin near-surface layer, whilst the rest of the CZ is mixed by cool entropy rain emanating from the near-surface regions (Spruit 1997; Brandenburg 2016). In such scenarios, the bulk of the CZ would be weakly subadiabatic while the convective flux would still be directed outward because of a non-local non-gradient contribution to the convective energy flux (Deardorff 1961, 1966). Such layers have been named Deardorff zones (Brandenburg 2016), and have been detected in many simulations (e.g., Chan & Gigas 1992; Roxburgh & Simmons 1993; Tremblay et al. 2015; Hotta 2017; Käpylä et al. 2017). However, the effect of Deardorff layers on velocity amplitudes in rotating convection in spherical coordinates appears to be weak (Käpylä et al. 2019). Furthermore, while there is evidence of the importance of surface driving (e.g., Cossette & Rast 2016), it appears that this effect is also rather weak (Hotta et al. 2019).
Another possible cause of the discrepancy is unrealistic Prandtl numbers typically used in simulations. It is numerically convenient to use Pr = 1, although several recent studies have explored the possibility that stellar convection might operate in a high effective (turbulent) Prandtl number regime with Pr ≳ 1 (e.g., O’Mara et al. 2016; Bekki et al. 2017; Karak et al. 2018). One conclusion from these studies is that while the average velocity amplitude decreases as the Prandtl number increases, turbulent angular momentum transport is predominantly downward and leads to exacerbation of the anti-solar differential rotation issue at solar rotation rate and luminosity (Karak et al. 2018). Apart from the theoretical problem of explaining how the Sun switches from Pr ≪ 1 –suggested by microphysics– to Pr ≳ 1, the numerical studies appear to disfavour the possibility of an effective Prandtl number of greater than unity in the Sun.
The small Prandtl number limit, which is indicated by estimates of molecular diffusivities in stellar CZs (e.g., Augustson et al. 2019; Schumacher & Sreenivasan 2020), has also been considered in various studies. An early work by Spiegel (1962) explored the limit of zero Prandtl number in Boussinesq convection. This latter author showed that the temperature fluctuations are enslaved to vertical motions which leads to highly non-linear driving of convection. Subsequent numerical studies in the low-Pr regime showed that convection becomes highly inertial with a tendency for coherent large-scale flow structures to intensify (e.g., Breuer et al. 2004) along with vigorous turbulence. Studies of compressible convection have also explored the Prandtl number dependence, although its signifigance has gone largely unrecognised. For example, the results of Cattaneo et al. (1991) showed that the net energy flux due to downflows is reduced as a function of Pr, whereas the downward kinetic energy flux and upward enthalpy flux both increase as Pr decreases. These authors, however, did not connect this to the changing Prandtl number but rather concluded that these effects are a consequence of an increase in the Reynolds number or the degree of turbulence. Results similar to those of Cattaneo et al. (1991) were also reported by Singh & Chan (1993). On the other hand, Brandenburg et al. (2005) found that the correlation coefficients of velocity and temperature fluctuations with the enthalpy flux remained Pr-dependent at least to Reynolds numbers of the order of 103. Finally, Orvedahl et al. (2018) studied non-rotating anelastic convection in spherical coordinates and found that the overall velocity amplitude increases as the Prandtl number decreases while the spectral distribution of velocity is insensitive to Pr.
Here, the Prandtl number dependence of convective flow statistics, overshooting, and energy fluxes are studied systematically with a hydrodynamic convection setup in Cartesian geometry. A motivation of the current study is a prior work (Käpylä 2019a) where it was found that convective overshooting is sensitive to the Prandtl number and that earlier numerical results predicting weak overshooting for solar parameters were obtained from simulations where Pr ≳ 1 or Pr ≫ 1. This implies a change in the magnitudes, dominant scales, or other transport properties, such as correlations with thermodynamic quantities of convective flows, all of which are investigated in the present study. Overshooting is also closely related to the convective energy transport which is another focus of the current study. In particular, we study the overall transport properties as a function of Pr and the respective roles of up- and downflows.
2. The model
The setup used in the current study is the same as that in Käpylä (2019a). We solve the equations for compressible hydrodynamics
where D/Dt = ∂/∂t + u ⋅ ∇ is the advective derivative, ρ is the density, u is the velocity, 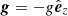 where g > 0 is the acceleration due to gravity, p is the pressure, T is the temperature, s is the specific entropy, and ν is the kinematic viscosity. Furthermore, Frad and FSGS are the radiative and turbulent sub-grid scale (SGS) fluxes, respectively, and Γcool describes cooling near the surface. [BOLD]S is the traceless rate-of-strain tensor with
where g > 0 is the acceleration due to gravity, p is the pressure, T is the temperature, s is the specific entropy, and ν is the kinematic viscosity. Furthermore, Frad and FSGS are the radiative and turbulent sub-grid scale (SGS) fluxes, respectively, and Γcool describes cooling near the surface. [BOLD]S is the traceless rate-of-strain tensor with
Radiation is modelled via the diffusion approximation, corresponding to an optically thick, fully ionised gas. The ideal gas equation of state p = (cP − cV)ρT = ℛρT is assumed, where ℛ is the gas constant, and cP and cV are the specific heat capacities at constant pressure and volume, respectively. The radiative flux is given by
where K(ρ, T) is the radiative heat conductivity,
with σSB being the Stefan-Boltzmann constant where κ is the opacity. The latter is assumed to obey the power law
where ρ0 and T0 are reference values of density and temperature. In combination, Eqs. (6) and (7) give
With the choices a = 1 and b = −7/2, this corresponds to the Kramers opacity law (Weiss et al. 2004), which was first used in convection simulations by Brandenburg et al. (2000).
The fixed flux at the bottom of the domain (Fbot) fixes the initial profile of radiative diffusivity, χ = K/(cPρ), which varies strongly as a function of height. Thus, additional SGS diffusivity is added in the entropy equation to maintain the numerical feasibility of the simulations. Here the SGS flux is formulated as
where 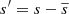 is the fluctuation of the specific entropy from the horizontally averaged mean which is denoted by an overbar. The mean
is the fluctuation of the specific entropy from the horizontally averaged mean which is denoted by an overbar. The mean 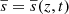 is computed at each time-step. The coefficient χSGS is constant throughout the simulation domain1. The net horizontally averaged SGS flux is negligibly small, such that
is computed at each time-step. The coefficient χSGS is constant throughout the simulation domain1. The net horizontally averaged SGS flux is negligibly small, such that 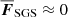 . This formulation differs from those used by Featherstone & Hindman (2016) and Karak et al. (2018), for example, where the SGS diffusion is applied to the total entropy. Physically, the current SGS diffusion can be envisaged to be operating on sufficiently small scales such that the gradients of the fluctuating entropy dominate over those of the mean. This is most likely fully justified only at very high Péclet numbers. While the Péclet numbers in the current simulations are at best modest, the current formulation minimises the effects of the SGS diffusion on the mean energy flux, which would also be reflected by the resolved convective flux. On the other hand, this formulation captures the effects of the SGS Prandtl number in the velocity and entropy fluctuations and therefore in the corresponding turbulent fluxes.
. This formulation differs from those used by Featherstone & Hindman (2016) and Karak et al. (2018), for example, where the SGS diffusion is applied to the total entropy. Physically, the current SGS diffusion can be envisaged to be operating on sufficiently small scales such that the gradients of the fluctuating entropy dominate over those of the mean. This is most likely fully justified only at very high Péclet numbers. While the Péclet numbers in the current simulations are at best modest, the current formulation minimises the effects of the SGS diffusion on the mean energy flux, which would also be reflected by the resolved convective flux. On the other hand, this formulation captures the effects of the SGS Prandtl number in the velocity and entropy fluctuations and therefore in the corresponding turbulent fluxes.
The cooling near the surface is given by
where Γ0 is a cooling luminosity, h(z) is a profile function, T = e/cV is the temperature, e is the internal energy, and Tcool = Ttop is the fixed reference temperature at the top boundary.
2.1. Geometry, initial, and boundary conditions
The computational domain is a rectangular box where zbot ≤ z ≤ ztop is the vertical coordinate. With zbot/d = −0.45 and ztop/d = 1.05, where d is the depth of the initially isentropic layer (see below), the vertical extent is Lz = ztop − zbot = 1.5d. The horizontal size of the domain is LH/d = 4 and the horizontal coordinates x and y run from −2d to 2d.
The initial stratification consists of three layers such that the two lower layers are polytropic with polytropic indices n1 = 3.25 (zbot/d ≤ z/d ≤ 0) and n2 = 1.5 (0 ≤ z/d ≤ 1). The uppermost layer above z/d = 1 is initially isothermal with T = Ttop. The latter mimics a photosphere where radiative cooling is efficient. The initial stratification is set by the normalised pressure scale height at the top boundary
All of the current runs have ξ0 = 0.054. The choices of n1 and n2 are close to those expected for the thermal stratifications in the radiative (see Barekat & Brandenburg 2014 and Appendix A of Brandenburg 2016) and convective layers, respectively. Prior experience confirms the validity of these choices (see, e.g., Käpylä et al. 2019), although the extent of the CZ is an outcome of the simulation rather than being fixed by the input parameters (Käpylä et al. 2017; Käpylä 2019a). Convection ensues because the system is initially in thermal inequilibrium.
The horizontal boundaries are periodic, and impenetrable and stress-free boundary conditions according to
are imposed on the vertical boundaries. The temperature gradient at the bottom boundary is set according to
where Fbot is the fixed input flux and Kbot(x, y, zbot, t) is the value of the heat conductivity at the bottom of the domain. On the upper boundary, constant temperature T = Ttop coinciding with the initial value is assumed.
2.2. Units, control parameters, and simulation strategy
The units of length, time, density, and entropy are given by
where ρ0 is the initial value of density at z = ztop. The models are fully defined by choosing the values of the kinematic viscosity ν, gravitational acceleration g, the values of a, b, K0, ρ0, T0, Γ0 and the SGS and effective Prandtl numbers
along with the cooling profile h(z). The values of K0, ρ0, T0 are subsumed into a new variable 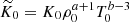 which is fixed by assuming Frad(zbot) = Fbot in the initial state. The profile h(z) = 1 for z/d ≥ 1 and h(z) = 0 for z/d < 1, connecting smoothly over a layer of width 0.025d. The normalised flux is given by
which is fixed by assuming Frad(zbot) = Fbot in the initial state. The profile h(z) = 1 for z/d ≥ 1 and h(z) = 0 for z/d < 1, connecting smoothly over a layer of width 0.025d. The normalised flux is given by
where ρbot and cs, bot are the density and the sound speed, respectively, at zbot in the initial non-convecting state. The current runs have ℱn ≈ 4.6 × 10−6 corresponding to runs K3 and K3h in Käpylä (2019a).
The advective terms in Eqs. (1)–(3) are formulated in terms of a fifth-order upwinding derivative with a hyperdiffusive sixth-order correction with a flow-dependent diffusion coefficient; see Appendix B of Dobler et al. (2006).
2.3. Diagnostics quantities
The following quantities are outcomes of the simulations that can only be determined a posteriori. These include the global Reynolds number and the SGS and effective Péclet numbers
where urms is the volume-averaged rms-velocity and k1 = 2π/d is an estimate of the wavenumber corresponding to the largest eddies in the system.
To assess the level of supercriticality of convection, the Rayleigh number is defined as:
The Rayleigh number varies as a function of height and is quoted near the surface at z/d = 0.85 for all models. Conventionally, the Rayleigh number in the hydrostatic, non-convecting state is one of the control parameters. In the current models with Kramers conductivity, the convectively unstable layer in the hydrostatic case is very thin and confined to the near-surface layers (Brandenburg 2016). Thus, the Rayleigh numbers are quoted from the thermally saturated statistically stationary states.
Contributions to the horizontally averaged vertical energy flux are:
Here the primes denote fluctuations and overbars horizontal averages. The total convected flux (Cattaneo et al. 1991) is the sum of the enthalpy and kinetic energy fluxes:
The CZ is defined as the region where 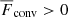 . The vertical position of the bottom of the CZ is given by zCZ. Error estimates for diagnostics are obtained by dividing the time-series into three parts of equal length and computing averages over each of them. The largest deviation of these averages from the time average over the whole time-series is taken to represent the error.
. The vertical position of the bottom of the CZ is given by zCZ. Error estimates for diagnostics are obtained by dividing the time-series into three parts of equal length and computing averages over each of them. The largest deviation of these averages from the time average over the whole time-series is taken to represent the error.
The PENCIL CODE (Pencil Code Collaboration 2021)2 was used to produce the simulations. At the core of the code is a switchable finite difference solver for partial differential equations that can be used to study a wide selection of physical problems. In the current study, a third-order Runge-Kutta time stepping method and centred sixth-order finite differences for spatial derivatives were used (cf. Brandenburg 2003).
3. Results
All of the runs discussed in the present study were branched off from run K3h of Käpylä (2019a); see Table 1 for a summary of the simulations. A thermally saturated snapshot of this run was used to produce new low-resolution models labeled the A set with SGS Prandtl numbers ranging between 0.1 and 10. The runs in the intermediate(high)-resolution set B(C) were remeshed from saturated snapshots of the corresponding runs in set A(B). Only a subset of PrSGS values were done at the highest grid resolution in set C.
Summary of the runs.
3.1. Flow characteristics
Figure 1 shows visualisations of the flows and entropy fluctuations in cases with PrSGS = 0.1, 1, and 10 (Re = 190, 175, and 167) corresponding to runs C01, C1, and C10. Visual inspection of the velocity patterns does not reveal notable differences at large scales such that the dominant granule sizes in the three cases are similar. Smaller scale structures in the velocity appear especially near the surface as the SGS Prandtl number increases; see the middle and bottom panels of Fig. 1. Nevertheless, the velocity patterns are remarkably similar in comparison to the entropy fluctuations which change dramatically as PrSGS increases from 0.1 to 10. In the PrSGS = 0.1 case the strong downflows coincide with smooth regions of negative (cool) entropy fluctuations, whereas the surrounding areas are almost featureless. In contrast, in the PrSGS = 10 case the smooth negative entropy regions have disintegrated into numerous smaller structures that are often detached from each other. The entropy fluctuations in the PrSGS = 1 run show an intermediate behaviour with traces of both large- and small-scale structures.
 |
Fig. 1. Left panels: normalised vertical velocity |
The averaged rms velocity as a function Preff from all runs is shown in Fig. 2. There is a tendency for urms to increase with decreasing PrSGS which was first reported by Singh & Chan (1993) in compressible convection. Data for approximately constant Pe is suggestive of a power law with exponent around −0.13; see the dotted lines in Fig. 2. A similar dependence can be seen in the suitably scaled data of non-rotating spherical shell simulations R0P[1,2,6] of Karak et al. (2018); see the crosses in Fig. 2. However, their run with the highest Pr (R0P20) appears to be an outlier. The results of Orvedahl et al. (2018) also indicate an increase in kinetic energy as the Prandtl number decreases. Furthermore, qualitatively similar results have been reported from Boussinesq convection (e.g., Breuer et al. 2004; Scheel & Schumacher 2016), although in the work of these latter authors the dependence of urms on Pr is much steeper. This is because, in Rayleigh-Bénard convection, the total flux transported by convection depends strongly on the Prandtl number.
 |
Fig. 2. Volume- and time-averaged rms velocity as a function Preff(zCZ) for all of the current runs (circles). The colours (sizes) of the symbols indicate the Péclet number (relative error) as indicated in the colour bar (legend). The dotted lines show power laws proportional to |
A distinct characteristic of convection is that the vertical flows are the main transporter of the energy flux. A diagnostic of the structure of vertical flows is the filling factor f of up- or downflows. Here the filling factor is defined as the area the downflows occupy at each depth such that the horizontally averaged vertical velocity is given by
where 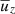 is the mean vertical velocity whereas
is the mean vertical velocity whereas 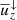 and
and 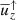 are the mean velocities in the down- and upflows, respectively. Figure 3a shows f for runs B01, B1, and B10 with PrSGS = 0.1, 1, and 10. These results indicate that the filling factor decreases with decreasing SGS Prandtl number. However, the change is relatively minor such that f differs by roughly 20% in the bulk of the CZ between the extreme cases with PrSGS = 0.1 and 10. The filling factor plays an important role in analytic and semi-analytic two-stream models of convection (e.g., Rempel 2004; Brandenburg 2016). For example, in the updated mixing length model of Brandenburg (2016), a very small filling factor is needed in cases where the Schwarzschild unstable part of the CZ is particularly shallow. The current simulations suggest that the filling factor goes in that direction when PrSGS decreases, but it appears that the smallest values of the order of 10−4 in some of the models of Rempel (2004) and Brandenburg (2016) are ruled out.
are the mean velocities in the down- and upflows, respectively. Figure 3a shows f for runs B01, B1, and B10 with PrSGS = 0.1, 1, and 10. These results indicate that the filling factor decreases with decreasing SGS Prandtl number. However, the change is relatively minor such that f differs by roughly 20% in the bulk of the CZ between the extreme cases with PrSGS = 0.1 and 10. The filling factor plays an important role in analytic and semi-analytic two-stream models of convection (e.g., Rempel 2004; Brandenburg 2016). For example, in the updated mixing length model of Brandenburg (2016), a very small filling factor is needed in cases where the Schwarzschild unstable part of the CZ is particularly shallow. The current simulations suggest that the filling factor goes in that direction when PrSGS decreases, but it appears that the smallest values of the order of 10−4 in some of the models of Rempel (2004) and Brandenburg (2016) are ruled out.
 |
Fig. 3. Filling factor of downflows for SGS Prandtl numbers 0.1 (solid line), 1 (dashed), and 10 (dash-dotted) as indicated by the legend from runs B01, B1, and B10 (a). Filling factor in runs with PrSGS = 0.1 with different PeSGS(b). The vertical dotted lines indicate the depths from which representative data for the top, middle, and bottom of the CZ are considered. |
The filling factor increases as a function of Re and PeSGS for a given PrSGS; see Fig. 3b for representative results for PrSGS = 0.1 where χSGS ≫ χ. It is plausible that a growing contribution from nearly isotropic small-scale eddies that become more prominent with increasing Re is partly responsible for the increasing trend of f as a function of the Reynolds number. However, preliminary studies using low-pass filtered data suggest that this effect is very subtle. Irrespective of the Re dependence of f, the energetics of the underlying larger scale granulation appear to be almost unaffected by Re; see Sect. 3.3.
3.2. Overshooting below the convection zone
It is of interest to study the extent of convective overshooting below the CZ given the systematic dependence of the overall convective velocities on PrSGS. The same definition of overshooting as in Käpylä (2019a) is used. This is outlined by defining the bottom of the CZ (zCZ) to be the depth where F̅conv changes from positive to negative. This depth is used to obtain a reference value of the horizontally averaged kinetic energy flux 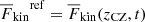 . The instantaneous overshooting depth zOS is then taken to be the depth where
. The instantaneous overshooting depth zOS is then taken to be the depth where 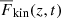 drops below
drops below 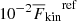 . The mean thickness of the overshoot layer is defined as
. The mean thickness of the overshoot layer is defined as
where Δt = t1 − t0, and t0 and t1 denote the beginning and end of the time-averaging period.
Figure 4 shows dos from all runs as a function of PrSGS. The current results confirm the conjecture of Käpylä (2019a) that dos is sensitive to the Prandtl number. However, the results still depend of the Péclet number especially for low PrSGS where it is challenging to reach high values of Pe. Nevertheless, comparing dos for approximately the same Pe, for example Pe ≈ 40 (light blue symbols in Fig. 4), shows that the overshooting is increasing monotonically as PrSGS decreases. The difference in dos between the cases PrSGS = 1 and PrSGS = 0.1 is about 30%. However, the difference decreases as the Péclet number increases; nevertheless it does not appear likely that the Pr dependence would disappear at even higher Péclet numbers.
 |
Fig. 4. Thickness of the overshoot layer dos normalised by the pressure scale height Hp(zCZ) for all runs as a function of Preff(zCZ). The colours (sizes) of the symbols indicate the Péclet number (relative error) as indicated in the colour bar (legend). |
Several numerical studies have shown that the deep parts of density-stratified CZs are often weakly stably stratified (e.g., Chan & Gigas 1992; Tremblay et al. 2015; Bekki et al. 2017; Hotta 2017; Käpylä et al. 2017). Such layers have also been found from semi-global and global simulations of rotating solar-like CZs (e.g., Karak et al. 2018; Käpylä et al. 2019; Viviani & Käpylä 2021) as well as from fully convective spheres (Käpylä 2021). We call this layer the Deardorff zone after Brandenburg (2016). This layer is characterised by a positive vertical gradient of entropy, ds/dz > 0, along with a positive convective energy flux, 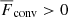 . The mean thickness of the Deardorff zone is defined in a similar way to dos via
. The mean thickness of the Deardorff zone is defined in a similar way to dos via
where zBZ is the depth where the entropy gradient changes sign. The results for dDZ are shown in Fig. 5. At first glance, dDZ shows an opposite trend in comparison to dos such that it decreases with the Prandtl number but the dependence on Péclet and Reynolds numbers is again strong, particularly for low PrSGS. However, considering only the largest Pe for each Preff, dDZ is roughly constant around 0.45Hp for Preff ≲ 3.
 |
Fig. 5. Thickness of the Deardorff layer dDZ normalised by the pressure scale height Hp(zCZ) for all runs as a function of Preff(zCZ). The colours (sizes) of the symbols indicate the Péclet number (relative error) as indicated in the colour bar (legend). |
3.3. Flow statistics and spectral distribution
A standard diagnostics in flow statistics is the probability density function (PDF) which is defined by:
The moments of the PDF carry information about the statistical properties of the flow. The instantaneous z-dependent moments are given by:
Here we study the skewness 𝒮 and the kurtosis 𝒦 of the velocity field:
Representative PDFs of the velocity components near the surface, at the middle, and near the base of the CZ from run C01 are shown in Fig. 6. The data are obtained by time-averaging over several snapshots. The horizontal flows have zero means and they have symmetric distributions around the mean. The vertical flows on the other hand show a bimodal distribution corresponding to the characteristic up- and downflow structure of convective granulation which is particularly clear near the surface. Similar results have been reported from a number of earlier numerical studies in different contexts and setups (e.g., Brandenburg et al. 1996; Miesch et al. 2008; Hotta et al. 2015).
 |
Fig. 6. Normalised PDFs of ux (left panel), uy (middle), and uz (right) from near the surface (black lines), middle (blue), and bottom (red) of the CZ as indicated by the key for run C01 with Re = 190 and PrSGS = 0.1. |
Figure 7 shows 𝒮 and 𝒦 as functions of depth from runs C01, C1, and C10. The skewness of the horizontal flows is essentially zero in all of the cases which is expected because no systematic horizontal anisotropy is present. 𝒮 is consistently negative and decreasing with depth for vertical flows within the CZ. This is indicative of a growing difference between the statistics of up- and downflows in the deeper parts. The kurtosis indicates a nearly Gaussian distribution with 𝒦 ≈ 3 for both vertical and horizontal flows near the surface (z/d ≈ 0.9). However, 𝒦 increases as a function of depth such that 𝒦 ≈ 5 for ux and uy, and has a value of greater than 10 for uz at the base of the CZ, indicating strong non-Gaussianity. The skewness and kurtosis do not change significantly in the CZ as a function of PrSGS. The results for 𝒮 and 𝒦 are in agreement with those of Hotta et al. (2015) and similar to the rotating spherical shell simulations of Miesch et al. (2008) notwithstanding the horizontal anisotropy in the latter. Finally, 𝒦 reaches very high values in the overshoot regions especially for low PrSGS; see left panel of Fig. 7. This is most likely due to the highly intermittent turbulence which in turn is due to the limited number of deeply penetrating plumes in these regions.
 |
Fig. 7. Kurtosis 𝒦 (solid lines) and skewness 𝒮 (dashed) of the velocity components from runs C01 (PrSGS = 0.1, left panel), C1 (PrSGS = 1, middle), and C10 (PrSGS = 10, right). |
Next we study the velocity amplitudes as functions of spatial scale from power spectra of the velocity field,
where 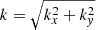 is the horizontal wavenumber and the hat denotes a two-dimensional Fourier transform. The power spectra are computed from between 10 and 40 snapshots –depending on the run– which are then time-averaged. Furthermore, normalisation is applied such that
is the horizontal wavenumber and the hat denotes a two-dimensional Fourier transform. The power spectra are computed from between 10 and 40 snapshots –depending on the run– which are then time-averaged. Furthermore, normalisation is applied such that
where kgrid = nxh/2 is the Nyquist scale of the horizontal grid with nxh grid points. With this normalisation the differences in the shape of the spectra are highlighted whereas the differences in the absolute magnitude are hidden. This is justified here because we are currently interested in the effects of the Prandtl number on the distribution of power as a function of spatial scale.
Representative results for PrSGS = 0.1, 1, and 10 are shown in Fig. 8 from runs C01, C1, and C10. The differences in EK are small and most clearly visible at high wavenumbers near the surface and near the base of the CZ. The power at the largest scales (k/kH < 3) is similar in all cases and the clearest differences are seen at the base of the CZ although even these features are not particularly pronounced. It is possible that the horizontal extent of the domain is too small to capture the largest naturally excited scales because the peak of the power spectrum is always near the box scale. The spectra show a scaling that is consistently steeper than the Kolmogorov-Obukhov k−5/3 spectrum. The Bolgiano-Obukhov scaling (Bolgiano 1959; Obukhov 1959) with k−11/5 is more compatible with the data especially at large Re. However, the inertial range even in the current highest resolution simulations is very limited and the conclusions regarding scaling properties are quite uncertain. Furthermore, there is a puzzling spread of scaling exponents from convection simulations: early studies with modest inertial ranges suggested a k−5/3 scaling (e.g., Cattaneo et al. 1991; Brandenburg et al. 1996; Porter & Woodward 2000) whereas more recent studies (e.g., Hotta et al. 2015; Featherstone & Hindman 2016) suggest clearly shallower scalings. On the other hand, power spectra of solar surface convection suggest significantly steeper (Yelles Chaouche et al. 2020, and references therein) scaling.
 |
Fig. 8. Normalised power spectra of velocity from depths z = 0.85d (left panel), z = 0.49d (middle), and z = 0.13d (right) for PrSGS = 0.1 (black lines), 1 (blue), and 10 (red) and Re = 167…190 corresponding to runs C01, C1, and C10, respectively. The insets show the low-wavenumber part of the spectra. The dashed and dotted lines respectively indicate the Bolgiano-Obukhov k−11/5 and Kolmogorov-Obukhov k−5/3 scalings for reference. |
To study the anisotropy of the flow, the power spectra of vertical and horizontal velocities are defined as
The same averaging and normalisation as above are applied here. Representative results from the same runs as in Fig. 8 are shown in Fig. 9. The horizontal and vertical velocity power spectra at all depths indicate a dominance of horizontal flows at large scales (k ≲ 3) whereas vertical flows are dominant for larger k. The scaling of EH is consistently steeper than the Kolmogorov-Obukhov k−5/3 dependence.
 |
Fig. 9. Normalised power spectra of vertical (EV, solid lines) and horizontal velocities (EH, dashed) from the same depths and runs as in Fig. 8. The inset shows low-wavenumber contributions. |
However, the differences between runs are again small with the exception of the bottom of the CZ (z = 0.13d) where a reduction of EH at large scales k/kH ≤ 4 for PrSGS = 0.1 is seen. The changes in the spectra are relatively subtle and an alternative way to study the spectral distribution of velocity is to consider the spectral anisotropy parameter AV which is defined as (Käpylä 2019b):
Results for AV for the same runs as in Figs. 8 and 9 are shown in Fig. 10. Near the surface the large scales are dominated by horizontal flows such that AV(k) > 0 for k < 4. The large-scale anisotropy for k/kH < 10 is almost identical for the three simulations shown in Fig. 10. The run with the highest PrSGS starts to deviate from the other two for k/kH > 10, and the two remaining runs deviate for k/kH ≳ 150. Given that the energy transport is dominated by scales for which k/kH ≲ 30 (see below), it is likely that the differences of AV at large k/kH are not of great importance. The anisotropy at the middle of the CZ is remarkably similar for all three cases such that significant deviations occur only for k/kH ≳ 100; see the middle panel of Fig. 10. The situation changes dramatically at the base of the CZ: while AV is essentially the same for all Prandtl numbers for k/kH > 8, the results systematically deviate at larger scales. That is, the flow at largest scales (k/kH = 1) continues to be horizontally dominated for all Prandtl numbers but AV is decreasing monotonically with PrSGS such the for PrSGS = 0.1, AV change of sign from positive to negative already for k/kH > 1. This is reflecting the stronger downflows and deeper overshooting in the low-PrSGS regime.
 |
Fig. 10. Spectral vertical anisotropy parameter AV(k) according to Eq. (35) from near the surface (z = 0.85d, left panel), middle (z = 0.49d, middle), and near the bottom of the CZ (z = 0.13d, right) for the same runs as in Fig. 8. |
Figure 11 shows normalised velocity power spectra compensated by k11/5 from five runs with PrSGS = 0.1 where the Reynolds number varies between 48 and 473. This figure shows that the scaling of the velocity spectra for the highest Reynolds numbers at low PrSGS is close to or even steeper than the Bolgiano-Obukhov k−11/5 scaling. This is particularly clear at the middle and at the base of the CZ while no clear scaling can be discerned near the surface. Evidence for the Bolgiano-Obukhov scaling for the kinetic energy spectrum has previously been reported from simulations Rayleigh-Bénard convection (e.g., Calzavarini et al. 2002) as well as from corresponding shell models (Brandenburg 1992). However, the generality of the results for the spectra remain in question as stated earlier.
 |
Fig. 11. Power spectra of the velocity compensated by k11/5 from near the surface (z = 0.85d, left panel), middle (z = 0.49d, middle), and near the bottom of the CZ (z = 0.13d, right) for PrSGS = 0.1 as a function of the SGS Péclet number as indicated by the legend. The spectra are normalised such that the contributions from k/kH = 1 coincide. |
The Bolgiano-Obukhov scaling is expected if the Bolgiano length is smaller than the typical turbulent length scale. In analogy with Rayleigh-Bénard convection (e.g., Calzavarini et al. 2002; Ching 2014), we define the Bolgiano length by
where 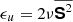 ,
, 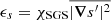 , and
, and 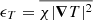 are the horizontally averaged dissipation rates of kinetic energy and entropy fluctuations due to SGS and radiative diffusion, respectively. The factors as = (cP/g2)3/4 and aT = (cP/d)3/2 enter due to dimensional arguments. The contribution from radiative diffusion ϵT is dominant in the denominator everywhere except near the surface where χ is very small. Representative results of ℓB are shown in Fig. 12 for runs C01, C1, and C10. We find that ℓB is of the order of 10−3…10−2d in the deep parts of the CZ and reaches maximum values of around 0.1d in the upper part of the CZ. Near the surface, lB increases with PrSGS. The integral scale of turbulence is given by
are the horizontally averaged dissipation rates of kinetic energy and entropy fluctuations due to SGS and radiative diffusion, respectively. The factors as = (cP/g2)3/4 and aT = (cP/d)3/2 enter due to dimensional arguments. The contribution from radiative diffusion ϵT is dominant in the denominator everywhere except near the surface where χ is very small. Representative results of ℓB are shown in Fig. 12 for runs C01, C1, and C10. We find that ℓB is of the order of 10−3…10−2d in the deep parts of the CZ and reaches maximum values of around 0.1d in the upper part of the CZ. Near the surface, lB increases with PrSGS. The integral scale of turbulence is given by
 |
Fig. 12. Normalised Bolgiano length ℓB/d according to Eq. (36) from runs C01 (black line), C1 (blue), and C10 (red). |
We find that ℓ is generally in the range 0.35…0.45d irrespective of depth. This suggests that the Bolgiano-Obukhov scaling is indeed expected in the deep parts of the CZ. However, near the surface ℓ/ℓB ≈ 4 such that it is not obvious that the Bolgiano-Obukhov scaling should appear there. This is to some degree reflected by the simulation results where no clear power-law scaling can be seen near the surface (cf. left panel of Fig. 11).
The current results indicate that increasing Re, and therefore increasing Ra, does not significantly change the distribution of velocity power in wavenumber space. This is in apparent contradiction with the results of Featherstone & Hindman (2016) who reported an increase of small-scale flow amplitudes at the expense of large-scale power as the Rayleigh number was increased. However, in their study the increase of the Rayleigh number was associated with a significant change in the fraction of the energy flux that is carried by convection because their SGS entropy diffusion contributes to the mean energy flux; see their Fig. 6. It also appears that when the Rayleigh number is sufficiently large, the decrease in the large-scale power ceases also for Featherstone & Hindman (2016); see their Fig. 3. In the present study the convective flux is not directly influenced by the SGS entropy diffusion and thus the current results differ qualitatively from those of Featherstone & Hindman (2016).
Figure 13 shows compensated power spectra of specific entropy fluctuations from runs C01, C1, and C10. The spectra are compensated by k11/6 which appears to be compatible with the highest Pe cases. For PrSGS = 0.1, there is no clear inertial range due to the low Péclet number in run C01. Runs C1 and C10, where the Péclet number is larger the entropy fluctuations, show roughly a k−11/6 scaling at intermediate scales near the surface and at the middle of the CZ (top and middle panels of Fig. 13). Near the base of the CZ, only run C10 with the highest Pe shows signs of k−11/6 spectra. The observed scaling is steeper than those from the Kolmogorov-Obukhov and Bolgiano-Obukhov models that predict k−5/3 and k−7/5, respectively. Based on the current results, it appears that the scaling of 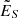 becomes progressively shallower as Pe increases such that neither of the theoretical predictions can be ruled out at the moment. However, simulations at even higher resolutions are needed to confirm this.
becomes progressively shallower as Pe increases such that neither of the theoretical predictions can be ruled out at the moment. However, simulations at even higher resolutions are needed to confirm this.
 |
Fig. 13. Power spectra of entropy fluctuations |
3.4. Convective energy transport
Figure 14 shows the enthalpy, kinetic energy, and total convected fluxes –from Eqs. (20), (21), and (24), respectively– for the runs in set B with Re = 79…93 and 5763 grid. Remarkably, F̅conv is almost identical within the CZ in all of the runs irrespective of the SGS Prandtl number. This indicates that the radiative flux and hence the thermal stratification and radiative conductivity are very similar in all of the runs. The constituents of the convective flux, however, show a very different behavior: the absolute values of the enthalpy and the kinetic energy fluxes increase monotonically with decreasing PrSGS. In particular, the kinetic energy flux more than doubles as PrSGS decreases from 10 to 0.1. For the lowest PrSGS, the downward kinetic energy flux exceeds Fbot near the middle of the CZ while F̅enth is almost twice Fbot. In contrast to the CZ, the convected flux in the overshoot layer shows much larger differences between different Prandtl numbers.
 |
Fig. 14. Normalised enthalpy (red), kinetic energy (blue), and convected (black) fluxes for the SGS Prandtl numbers ranging from 0.1 to 10 as indicated by the legend from the B set of runs with Re = 79…93. |
The contributions of up- and downflows to the enthalpy, kinetic energy, and total convected flux F̅conv are shown in Fig. 15. The contributions of the upflows to F̅enth and 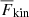 increase monotonically as PrSGS decreases, leading to a net increase in the convected flux
increase monotonically as PrSGS decreases, leading to a net increase in the convected flux 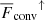 . The magnitudes of
. The magnitudes of 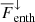 and
and 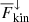 also increase as the SGS Prandtl number decreases but the net
also increase as the SGS Prandtl number decreases but the net 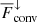 decreases because
decreases because 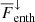 and
and 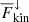 have opposite signs. Remarkably, F̅enth and
have opposite signs. Remarkably, F̅enth and 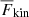 are almost identical above z/d ≈ 0.9 irrespective of PrSGS, suggesting that near-surface physics are not the cause of the differences discussed here. In total, the up- and downflows transport on average an equal fraction of F̅conv for SGS Prandtl number unity. The upflows are clearly dominant for the lowest SGS Prandtl numbers, such that for PrSGS = 0.1 the upflows transport roughly two-thirds of the convected flux within the CZ. An opposite, albeit weaker trend is seen for PrSGS > 1. The results for PrSGS ≠ 1 are thus qualitatively different from the case PrSGS = 1, and the difference increases towards larger and smaller Prandtl numbers. The current results are also in accordance with those of Cattaneo et al. (1991) who found that, in their more turbulent cases, the contribution of the downflows to Fconv diminishes. The increase in the level of turbulence in their cases was associated with a decreasing Prandtl number σ. In their simulations, the contribution of the downflows to the convected flux is practically negligible at σ = 0.1; see their Fig. 14d.
are almost identical above z/d ≈ 0.9 irrespective of PrSGS, suggesting that near-surface physics are not the cause of the differences discussed here. In total, the up- and downflows transport on average an equal fraction of F̅conv for SGS Prandtl number unity. The upflows are clearly dominant for the lowest SGS Prandtl numbers, such that for PrSGS = 0.1 the upflows transport roughly two-thirds of the convected flux within the CZ. An opposite, albeit weaker trend is seen for PrSGS > 1. The results for PrSGS ≠ 1 are thus qualitatively different from the case PrSGS = 1, and the difference increases towards larger and smaller Prandtl numbers. The current results are also in accordance with those of Cattaneo et al. (1991) who found that, in their more turbulent cases, the contribution of the downflows to Fconv diminishes. The increase in the level of turbulence in their cases was associated with a decreasing Prandtl number σ. In their simulations, the contribution of the downflows to the convected flux is practically negligible at σ = 0.1; see their Fig. 14d.
 |
Fig. 15. Contributions from upflows (a) and downflows (b) on the horizontally averaged convected (black lines), enthalpy (red), and kinetic energy (blue) fluxes for the same runs as in Fig. 14. |
An important caveat of the current results is that changing PrSGS implies also that the Péclet number is changing. Therefore, it is necessary to test whether the observed differences are really due to the Prandtl number and not because of a Péclet number dependence. Such a check is shown in Fig. 16 where the convected flux from the five simulations with PrSGS = 0.1 (A01, B01, C01, C01b, and C01c) is compared. The Reynolds and Péclet numbers differ by an order of magnitude in this set of runs. The differences are minor within the CZ, whereas somewhat larger deviations are seen in the depth of the overshoot region. Nevertheless, the results are robust enough within the parameter range explored here such that the conclusions drawn regarding the energy fluxes remain valid. However, the current results should still be considered with some caution as the Péclet numbers studied thus far are still modest compared to realistic stellar conditions.
 |
Fig. 16. Comparison of total convected flux (black) and the contributions of the upflows (red) and downflows (blue) between runs A01, B01, C01, C01b, and C01c with PrSGS = 0.1. |
Although the statistics of velocity and entropy fluctuations do not show drastic changes as a function of PrSGS, the convective energy transport is indeed strongly affected. In the following, the same procedure as in Nelson et al. (2018) is used to study the dominant scales in the different contributions to the convective flux. First, a low-pass filter is applied to the quantities that enter the expressions of the fluxes such that wavenumbers k < kmax are retained. For the enthalpy (kinetic energy) flux, this applies to the fluctuating vertical momentum flux (ρuz)′ and temperature fluctuation T′ (kinetic energy 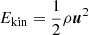 and vertical velocity uz). The normalised, horizontally averaged enthalpy and kinetic energy fluxes up to kmax are then computed according to
and vertical velocity uz). The normalised, horizontally averaged enthalpy and kinetic energy fluxes up to kmax are then computed according to
Representative results for PrSGS = 0.1, 1, and 10 are shown in Fig. 17 near the surface of the CZ. The current results indicate that for PrSGS = 0.1 the dominant contribution of the enthalpy flux comes from larger scales than for the kinetic energy flux. For PrSGS = 1 the situation is qualitatively unchanged but the difference in the dominant scales is much smaller. On the other hand, for PrSGS = 10 the behaviour is reversed although only at relatively large wavenumbers (k/kH ≳ 20). These results suggest that while the dominant velocity scale is quite insensitive to changes of the Prandtl number, a stronger dependence exists in the convective energy transport.
 |
Fig. 17. Spectrally decomposed, normalised enthalpy ( |
The current results thus suggest that convection becomes less efficient when the Prandtl number is decreased such that larger vertical velocities are required to carry the same flux. There are parallels between this and the Rayleigh-Bénard convection, where the Nusselt number decreases strongly for a given Rayleigh number when Pr is decreased (Schumacher & Sreenivasan 2020, and references therein). This means that low Prandtl number convection is very turbulent but at the same time inefficient in transporting heat. The analogy to the Reyleigh-Bénard case is, however, not complete as in the current simulations the ratio of convective to radiative flux is almost unchanged when the SGS Prandtl number changes. Therefore, the effects of the Prandtl number are necessarily much more subtle in the present cases and there is no straightforward way to connect, for example, the average rms-velocity and the Rayleigh number.
3.5. Velocity, temperature, and density fluctuations
The fact that the magnitudes of enthalpy and kinetic energy fluxes both increase as the SGS Prandtl number decreases while the total convected energy flux remains constant suggests a systematic change in the velocity and temperature fluctuations or their correlation as a function of PrSGS (for the latter, see Brandenburg et al. 2005). The rms-fluctuations of uz for the total velocity, upflows, and downflows are shown in Fig. 18a for runs C01, C1, and C10. The rms vertical velocity in the bulk of the CZ increases monotonically for both up- and downflows as PrSGS decreases. The increase is particularly pronounced for the downflows, 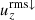 , which is also the main contributor to the increase in
, which is also the main contributor to the increase in 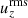 . This reflects the decreasing filling factor of downflows with PrSGS (see Fig. 3a) such that the downflows need to be faster due to mass conservation.
. This reflects the decreasing filling factor of downflows with PrSGS (see Fig. 3a) such that the downflows need to be faster due to mass conservation.
 |
Fig. 18. Horizontally averaged total rms vertical velocity (black lines) and the contributions from upflows (red) and downflows (blue) (a). Corresponding rms temperature (b) and density (c) fluctuations normalised by Ttop and ρtop = ρ0, respectively. Data for runs C01, C1, and C10 with PrSGS = 0.1, 1, and 10 are shown as indicated by the legend. |
The temperature fluctuations shown in Fig. 18b show a somewhat more complex behaviour: near the surface 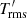 increases with PrSGS whereas in deeper parts the trend is reversed. This can be understood such that near the surface the temperature fluctuations are mostly in small-scale structures such as granules and intergranular lanes which are subject to stronger diffusion for smaller PrSGS, resulting in smaller
increases with PrSGS whereas in deeper parts the trend is reversed. This can be understood such that near the surface the temperature fluctuations are mostly in small-scale structures such as granules and intergranular lanes which are subject to stronger diffusion for smaller PrSGS, resulting in smaller 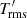 on average there. In the bulk of the CZ,
on average there. In the bulk of the CZ, 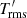 is the largest for the smallest PrSGS for both up- and downflows. This can partly explain the dominance of upflows in the energy transport for PrSGS = 0.1. For PrSGS = 1 and 10,
is the largest for the smallest PrSGS for both up- and downflows. This can partly explain the dominance of upflows in the energy transport for PrSGS = 0.1. For PrSGS = 1 and 10, 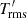 is always larger in the latter, which is due to the lower thermal diffusivity. Finally, Fig. 18c shows the depth dependence of the rms density fluctuations. Here a monotonic trend is seen such that
is always larger in the latter, which is due to the lower thermal diffusivity. Finally, Fig. 18c shows the depth dependence of the rms density fluctuations. Here a monotonic trend is seen such that 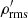 decreases with PrSGS.
decreases with PrSGS.
The correlation coefficient of vertical velocity and temperature fluctuations is given by
where 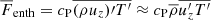 . The correlation coefficients C[uz, T′] for the total flow, and up- and dowflows for the same runs as in Fig. 18 are shown in Fig. 19. The overall correlation coefficient C[uz, T′] decreases monotonically as PrSGS increases, in agreement with Singh & Chan (1993). This trend is dominated by the downflows where
. The correlation coefficients C[uz, T′] for the total flow, and up- and dowflows for the same runs as in Fig. 18 are shown in Fig. 19. The overall correlation coefficient C[uz, T′] decreases monotonically as PrSGS increases, in agreement with Singh & Chan (1993). This trend is dominated by the downflows where ![$ C[u_z^\downarrow,T^{\prime\downarrow}] $](/articles/aa/full_html/2021/11/aa41337-21/aa41337-21-eq85.gif) increases with decreasing PrSGS while a much weaker and opposite trend is observed for the upflows. The increasing correlation
increases with decreasing PrSGS while a much weaker and opposite trend is observed for the upflows. The increasing correlation ![$ C[u_z^\downarrow,T^{\prime\downarrow}] $](/articles/aa/full_html/2021/11/aa41337-21/aa41337-21-eq86.gif) with decreasing PrSGS explains the simultaneous strong increase in the magnitude of
with decreasing PrSGS explains the simultaneous strong increase in the magnitude of 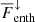 . At the same time, the correlation in the upflows is much less affected by the SGS Prandtl number and the overall increase in vertical velocity and temperature fluctuations for low PrSGS (see, Fig. 18) explains the increased
. At the same time, the correlation in the upflows is much less affected by the SGS Prandtl number and the overall increase in vertical velocity and temperature fluctuations for low PrSGS (see, Fig. 18) explains the increased 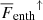 in that regime.
in that regime.
 |
Fig. 19. Correlation coefficient C[uz, T′] as a function of depth from run C01 (PrSGS = 0.1, solid lines), C1 (PrSGS = 1, dashed) and C10 (PrSGS = 10, dash-dotted) for the downflows (blue), upflows (red), and totals (black). |
3.6. Driving of convection
The dependence of the convective flows on the Prandtl number raises the question of what is driving them. A primary candidate is the entropy gradient at the surface which has indeed reported to be Prandtl number dependent (e.g. Brandenburg et al. 2005). A diagnostic of this is the maximum value of the superadiabatic temperature gradient
where ∇ = ∂lnT/∂lnp and ∇ad = 1 − 1/γ are the logarithmic and adiabatic temperature gradients, respectively. Figure 20 shows the maximum value of Δ∇ near the surface for the total entropy as well as for the upflow and downflow regions separately for all of the current runs. The results for max(Δ∇) show a decreasing trend as a function of Peeff and only a much weaker dependence on Preff. The data perhaps suggest a (lnPeeff)−1 dependence. A similar decreasing trend is seen in the upflow regions although the scatter in the data is stronger especially in the intermediate range of Peeff. On the other hand, the data for the downflows perhaps suggest a plateau for Peeff ≳ 30. However, these tentative dependences are rather uncertain due to the limited data available. Nevertheless, it appears that for approximately the same Péclet number, the entropy gradient increases with Prandtl number. This is opposite to the trend in the strength of downflows and thus the surface entropy gradient cannot be the dominant contribution in driving the downflows.
 |
Fig. 20. Maximum of the superadiabatic temperature gradient Δ∇=∇−∇ad as a function of the effective Péclet number at zsurf = 0.85d for the total (a), in upflows (b), and in downflows (c). The colour coding indicates Preff(zsurf). |
Next we turn to the force balance for vertical flows. The horizontally averaged force density is given by
where 𝒟/𝒟t = ∂/∂t − uz ∂z is the vertical advective time derivative. Representative results for the total force are shown in Fig. 21a for runs C01, C1, and C10. The runs with SGS Prandtl numbers 1 and 10 show a small difference near the surface in that the maximum total force is slightly larger for the lower Prandtl number. On the other hand, 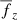 for PrSGS = 0.1 shows a markedly wider negative region in the upper part of the CZ between 0.65 ≲ z/d ≲ 0.9. The force on the upflows is shown in Fig. 21b. The differences between the two higher SGS Prandtl numbers are very small whereas the PrSGS = 0.1 case again shows a clear difference in the near-surface layers such that the region where upflows are decelerated is significantly wider. Remarkably,
for PrSGS = 0.1 shows a markedly wider negative region in the upper part of the CZ between 0.65 ≲ z/d ≲ 0.9. The force on the upflows is shown in Fig. 21b. The differences between the two higher SGS Prandtl numbers are very small whereas the PrSGS = 0.1 case again shows a clear difference in the near-surface layers such that the region where upflows are decelerated is significantly wider. Remarkably, 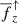 is in almost perfect anticorrelation with the superadiabatic temperature gradient in the upflows (Δ∇↑) such that upflows are decelerated (accelerated) in unstably (stably) stratified regions. This suggests that the upflows are not directly driven by the convective instability itself but rather by pressure forces induced by the deeply penetrating downflows (see also Korre et al. 2017; Käpylä et al. 2017). Finally, Fig. 21c shows the forces for the downflows. The downward force on the downflows is larger near the surface for PrSGS = 0.1 than in the cases with PrSGS = 1 and 10, which explains the stronger vertical velocities for low SGS Prandtl numbers. The force on the downflows is almost in anticorrelation with the overall superadiabatic temperature gradient; compare the grey and black lines in Fig. 21c3. The correlation with Δ∇↓ is clearly poorer.
is in almost perfect anticorrelation with the superadiabatic temperature gradient in the upflows (Δ∇↑) such that upflows are decelerated (accelerated) in unstably (stably) stratified regions. This suggests that the upflows are not directly driven by the convective instability itself but rather by pressure forces induced by the deeply penetrating downflows (see also Korre et al. 2017; Käpylä et al. 2017). Finally, Fig. 21c shows the forces for the downflows. The downward force on the downflows is larger near the surface for PrSGS = 0.1 than in the cases with PrSGS = 1 and 10, which explains the stronger vertical velocities for low SGS Prandtl numbers. The force on the downflows is almost in anticorrelation with the overall superadiabatic temperature gradient; compare the grey and black lines in Fig. 21c3. The correlation with Δ∇↓ is clearly poorer.
 |
Fig. 21. Horizontally averaged forces for the total flow (a), upflows (b) and downflows (c) for runs C01 (PrSGS = 0.1, solid lines), C1 (PrSGS = 1, dashed), and C10 (PrSGS = 10 dash-dotted). The blue and red lines show the corresponding superadiabatic temperature gradients with blue denoting negative and red positive values. The grey lines in panels b and c indicate Δ∇ for reference. |
Figure 18c showed that the density fluctuations are weakly decreasing with PrSGS such that the increased acceleration on the downflows cannot be explained by arguing that the matter in the downflows is cooler and heavier in the low-PrSGS cases in comparison to the higher PrSGS cases. On the other hand, Fig. 19 shows that the correlation between vertical velocity and temperature fluctuations increases with decreasing PrSGS which is the decisive factor in the enhanced acceleration of downflows. A similar enhancement of correlation is likely to carry over to other thermodynamic quantities as well. The exact mechanism is unclear, but it seems plausible to assume that a process similar to the positive feedback loop between vertical flows and the buoyancy force in the zero Prandtl number limit in Rayleigh-Bénard convection (Spiegel 1962) is also present in the compressible case.
4. Conclusions
Convective energy transport and flow statistics are sensitive to the SGS Prandtl number in the parameter range currently accessible to numerical simulations. The most striking effect is the decrease in net energy transport due to downflows with decreasing Prandtl number. This happens because the oppositely signed enthalpy and kinetic energy fluxes both increase in the downflows, leading to increased cancellation (Cattaneo et al. 1991). Another effect of a decreasing Prandtl number is the increase in the overall velocity which is mostly due to the increase in the downflow strength. The stronger downflows also lead to much stronger overshooting at the base of the CZ for lower Prandtl numbers.
On the other hand, the effects of the Prandtl number are very subtle in the statistics of the velocity field. The clearest systematic effect is that the filling factor of downflows decreases monotonically with decreasing SGS Prandtl number. However, the power spectra of velocity show very small differences, apart from the deep layers where the downflow dominance in the low-Prandtl number regime becomes more prominent. The current results do not indicate a decrease in the large-scale velocity power either with decreasing Prandtl or with increasing Rayleigh numbers. Such a decrease has been suggested to be at least a partial solution to the convective conundrum, or the overly high large-scale power in simulated flows (Featherstone & Hindman 2016). In the current simulations, the large-scale power is almost unaffected, most likely because the SGS entropy diffusion does not contribute to the mean energy flux unlike in the simulations of Featherstone & Hindman (2016). Notably, however, the dominant spatial scales of enthalpy and kinetic energy fluxes vary systematically with PrSGS which is likely to hold the key to understanding the changing convective dynamics.
The implications of the current results of solar and stellar convection are difficult to assess because of the greatly differing parameter regimes of the simulations compared to stellar CZs. Another aspect is that the current simulations are very likely not in an asymptotic regime such that the results show a dependence on the Reynolds and Péclet numbers. Nevertheless, even with these reservations, it appears likely that convection in the Sun is quite different from that obtained from simulations in which Pr ≈ 1. In particular, the overshooting depth can be substantially underestimated by the current simulations. It is also unclear as to how the Prandtl number effects manifest themselves in angular momentum transport which has thus far only been discussed in the Pr ≳ 1 regime (Karak et al. 2018).
The current simulations use SGS diffusion for the entropy fluctuations which is solely because of numerical convenience. The use of SGS diffusion has been criticised because it is typically not rigorously formulated and because it is possibly affecting the resolved convective energy flux indirectly. We will address these questions in a separate paper with simulations where the SGS diffusion is absent.
χSGS corresponds to 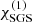 in Käpylä (2019a).
in Käpylä (2019a).
In earlier studies of non-rotating hydrodynamic convection (Käpylä et al. 2017; Käpylä 2019a) the total force on the downflows was found to adhere closely to Δ∇. These analyses, however, contain an error due to which the contribution from the viscous force is underestimated by a factor of between roughly 2 and 30 depending on the depth in the CZ. Thus the agreement between Δ∇ and 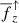 in these earlier studies is poorer than reported elsewhere and is comparable to that presented in the current study.
in these earlier studies is poorer than reported elsewhere and is comparable to that presented in the current study.
Acknowledgments
I thank the anonymous referee, Axel Brandenburg, and Nishant Singh for their comments on the manuscript. I acknowledge the hospitality of Nordita during the program “The Shifting Paradigm of Stellar Convection: From Mixing Length Concepts to Realistic Turbulence Modelling.” The simulations were made within the Gauss Centre for Supercomputing project “Cracking the Convective Conundrum” in the Leibniz Supercomputing Centre’s SuperMUC–NG supercomputer in Garching, Germany. This work was supported by the Deutsche Forschungsgemeinschaft Heisenberg programme (grant No. KA 4825/2-1).
References
- Augustson, K. C., Brun, A. S., & Toomre, J. 2019, ApJ, 876, 83 [Google Scholar]
- Barekat, A., & Brandenburg, A. 2014, A&A, 571, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bekki, Y., Hotta, H., & Yokoyama, T. 2017, ApJ, 851, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Bolgiano, R. 1959, J. Geophys. Res., 64, 2226 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A. 1992, Phys. Rev. Lett., 69, 605 [CrossRef] [Google Scholar]
- Brandenburg, A. 2003, Computational Aspects of Astrophysical MHD and Turbulence, eds. A. Ferriz-Mas, & M. Núñez (London: Taylor and Francis), 269 [Google Scholar]
- Brandenburg, A. 2016, ApJ, 832, 6 [Google Scholar]
- Brandenburg, A., Jennings, R. L., Nordlund, Å., et al. 1996, J. Fluid Mech., 306, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., Nordlund, A., & Stein, R. F. 2000, in Geophysical and Astrophysical Convection, Contributions from a workshop sponsored by the Geophysical Turbulence Program at the National Center for Atmospheric Research, October 1995, eds. P. A. Fox, & R. M. Kerr (The Netherlands: Gordon and Breach Science Publishers), 85 [Google Scholar]
- Brandenburg, A., Chan, K. L., Nordlund, Å., & Stein, R. F. 2005, Astron. Nachr., 326, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Breuer, M., Wessling, S., Schmalzl, J., & Hansen, U. 2004, Phys. Rev. E, 69, 026302 [NASA ADS] [CrossRef] [Google Scholar]
- Calzavarini, E., Toschi, F., & Tripiccione, R. 2002, Phys. Rev. E, 66, 016304 [NASA ADS] [CrossRef] [Google Scholar]
- Cattaneo, F., Brummell, N. H., Toomre, J., Malagoli, A., & Hurlburt, N. E. 1991, ApJ, 370, 282 [CrossRef] [Google Scholar]
- Chan, K. L., & Gigas, D. 1992, ApJ, 389, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Chan, K. L., & Sofia, S. 1986, ApJ, 307, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Ching, E. S. C. 2014, Statistics and Scaling in Turbulent Rayleigh-Bénard Convection (Singapore: Springer Singapore) [CrossRef] [Google Scholar]
- Cossette, J.-F., & Rast, M. P. 2016, ApJ, 829, L17 [Google Scholar]
- Deardorff, J. W. 1961, J. Atmos. Sci., 18, 540 [NASA ADS] [Google Scholar]
- Deardorff, J. W. 1966, J. Atmos. Sci., 23, 503 [NASA ADS] [CrossRef] [Google Scholar]
- Dobler, W., Stix, M., & Brandenburg, A. 2006, ApJ, 638, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, Y., & Fang, F. 2014, ApJ, 789, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Featherstone, N. A., & Hindman, B. W. 2016, ApJ, 818, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Greer, B. J., Hindman, B. W., Featherstone, N. A., & Toomre, J. 2015, ApJ, 803, L17 [Google Scholar]
- Hanasoge, S. M., Duvall, T. L., & Sreenivasan, K. R. 2012, Proc. Natl. Acad. Sci., 109, 11928 [Google Scholar]
- Hanasoge, S., Gizon, L., & Sreenivasan, K. R. 2016, Ann. Rev. Fluid Mech., 48, 191 [Google Scholar]
- Hotta, H. 2017, ApJ, 843, 52 [Google Scholar]
- Hotta, H., Rempel, M., & Yokoyama, T. 2015, ApJ, 803, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Hotta, H., Iijima, H., & Kusano, K. 2019, Sci. Adv., 5, 2307 [Google Scholar]
- Käpylä, P. J. 2011, Astron. Nachr., 332, 43 [CrossRef] [Google Scholar]
- Käpylä, P. J. 2019a, A&A, 631, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Käpylä, P. J. 2019b, Astron. Nachr., 340, 744 [CrossRef] [Google Scholar]
- Käpylä, P. J. 2021, A&A, 655, A66 [CrossRef] [Google Scholar]
- Käpylä, P. J., Käpylä, M. J., & Brandenburg, A. 2014, A&A, 570, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Käpylä, P. J., Rheinhardt, M., Brandenburg, A., et al. 2017, ApJ, 845, L23 [CrossRef] [Google Scholar]
- Käpylä, P. J., Viviani, M., Käpylä, M. J., Brandenburg, A., & Spada, F. 2019, Geophys. Astrophys. Fluid Dyn., 113, 149 [CrossRef] [Google Scholar]
- Karak, B. B., Miesch, M., & Bekki, Y. 2018, Phys. Fluids, 30, 046602 [NASA ADS] [CrossRef] [Google Scholar]
- Korre, L., Brummell, N., & Garaud, P. 2017, Phys. Rev. E, 96, 033104 [NASA ADS] [CrossRef] [Google Scholar]
- Kupka, F., & Muthsam, H. J. 2017, Liv. Rev. Comp. Astrophys., 3, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Miesch, M. S., Brun, A. S., DeRosa, M. L., & Toomre, J. 2008, ApJ, 673, 557 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, N. J., Featherstone, N. A., Miesch, M. S., & Toomre, J. 2018, ApJ, 859, 117 [Google Scholar]
- Obukhov, A. M. 1959, Akademiia Nauk SSSR Doklady, 125, 1246 [Google Scholar]
- O’Mara, B., Miesch, M. S., Featherstone, N. A., & Augustson, K. C. 2016, Adv. Space Res., 58, 1475 [CrossRef] [Google Scholar]
- Orvedahl, R. J., Calkins, M. A., Featherstone, N. A., & Hindman, B. W. 2018, ApJ, 856, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Ossendrijver, M. 2003, A&ARv., 11, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Pencil Code Collaboration (Brandenburg, A., et al.) 2021, J. Open Source Softw., 6, 2807 [Google Scholar]
- Porter, D. H., & Woodward, P. R. 2000, ApJS, 127, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Rempel, M. 2004, ApJ, 607, 1046 [Google Scholar]
- Roxburgh, L. W., & Simmons, J. 1993, A&A, 277, 93 [NASA ADS] [Google Scholar]
- Scheel, J. D., & Schumacher, J. 2016, J. Fluid Mech., 802, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Schumacher, J., & Sreenivasan, K. R. 2020, Rev. Mod. Phys., 92, 041001 [NASA ADS] [CrossRef] [Google Scholar]
- Singh, H. P., & Chan, K. L. 1993, A&A, 279, 107 [Google Scholar]
- Spiegel, E. A. 1962, J. Geophys. Res., 67, 3063 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. 1997, Mem. Soc. Astron. It., 68, 397 [Google Scholar]
- Tremblay, P.-E., Ludwig, H.-G., Freytag, B., et al. 2015, ApJ, 799, 142 [Google Scholar]
- Viviani, M., & Käpylä, M. J. 2021, A&A, 645, A141 [EDP Sciences] [Google Scholar]
- Weiss, A., Hillebrandt, W., Thomas, H.-C., & Ritter, H. 2004, Cox and Giuli’s Principles of Stellar Structure (Cambridge, UK: Cambridge Scientific Publishers Ltd) [Google Scholar]
- Yelles Chaouche, L., Cameron, R. H., Solanki, S. K., et al. 2020, A&A, 644, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Left panels: normalised vertical velocity |
| In the text | |
 |
Fig. 2. Volume- and time-averaged rms velocity as a function Preff(zCZ) for all of the current runs (circles). The colours (sizes) of the symbols indicate the Péclet number (relative error) as indicated in the colour bar (legend). The dotted lines show power laws proportional to |
| In the text | |
 |
Fig. 3. Filling factor of downflows for SGS Prandtl numbers 0.1 (solid line), 1 (dashed), and 10 (dash-dotted) as indicated by the legend from runs B01, B1, and B10 (a). Filling factor in runs with PrSGS = 0.1 with different PeSGS(b). The vertical dotted lines indicate the depths from which representative data for the top, middle, and bottom of the CZ are considered. |
| In the text | |
 |
Fig. 4. Thickness of the overshoot layer dos normalised by the pressure scale height Hp(zCZ) for all runs as a function of Preff(zCZ). The colours (sizes) of the symbols indicate the Péclet number (relative error) as indicated in the colour bar (legend). |
| In the text | |
 |
Fig. 5. Thickness of the Deardorff layer dDZ normalised by the pressure scale height Hp(zCZ) for all runs as a function of Preff(zCZ). The colours (sizes) of the symbols indicate the Péclet number (relative error) as indicated in the colour bar (legend). |
| In the text | |
 |
Fig. 6. Normalised PDFs of ux (left panel), uy (middle), and uz (right) from near the surface (black lines), middle (blue), and bottom (red) of the CZ as indicated by the key for run C01 with Re = 190 and PrSGS = 0.1. |
| In the text | |
 |
Fig. 7. Kurtosis 𝒦 (solid lines) and skewness 𝒮 (dashed) of the velocity components from runs C01 (PrSGS = 0.1, left panel), C1 (PrSGS = 1, middle), and C10 (PrSGS = 10, right). |
| In the text | |
 |
Fig. 8. Normalised power spectra of velocity from depths z = 0.85d (left panel), z = 0.49d (middle), and z = 0.13d (right) for PrSGS = 0.1 (black lines), 1 (blue), and 10 (red) and Re = 167…190 corresponding to runs C01, C1, and C10, respectively. The insets show the low-wavenumber part of the spectra. The dashed and dotted lines respectively indicate the Bolgiano-Obukhov k−11/5 and Kolmogorov-Obukhov k−5/3 scalings for reference. |
| In the text | |
 |
Fig. 9. Normalised power spectra of vertical (EV, solid lines) and horizontal velocities (EH, dashed) from the same depths and runs as in Fig. 8. The inset shows low-wavenumber contributions. |
| In the text | |
 |
Fig. 10. Spectral vertical anisotropy parameter AV(k) according to Eq. (35) from near the surface (z = 0.85d, left panel), middle (z = 0.49d, middle), and near the bottom of the CZ (z = 0.13d, right) for the same runs as in Fig. 8. |
| In the text | |
 |
Fig. 11. Power spectra of the velocity compensated by k11/5 from near the surface (z = 0.85d, left panel), middle (z = 0.49d, middle), and near the bottom of the CZ (z = 0.13d, right) for PrSGS = 0.1 as a function of the SGS Péclet number as indicated by the legend. The spectra are normalised such that the contributions from k/kH = 1 coincide. |
| In the text | |
 |
Fig. 12. Normalised Bolgiano length ℓB/d according to Eq. (36) from runs C01 (black line), C1 (blue), and C10 (red). |
| In the text | |
 |
Fig. 13. Power spectra of entropy fluctuations |
| In the text | |
 |
Fig. 14. Normalised enthalpy (red), kinetic energy (blue), and convected (black) fluxes for the SGS Prandtl numbers ranging from 0.1 to 10 as indicated by the legend from the B set of runs with Re = 79…93. |
| In the text | |
 |
Fig. 15. Contributions from upflows (a) and downflows (b) on the horizontally averaged convected (black lines), enthalpy (red), and kinetic energy (blue) fluxes for the same runs as in Fig. 14. |
| In the text | |
 |
Fig. 16. Comparison of total convected flux (black) and the contributions of the upflows (red) and downflows (blue) between runs A01, B01, C01, C01b, and C01c with PrSGS = 0.1. |
| In the text | |
 |
Fig. 17. Spectrally decomposed, normalised enthalpy ( |
| In the text | |
 |
Fig. 18. Horizontally averaged total rms vertical velocity (black lines) and the contributions from upflows (red) and downflows (blue) (a). Corresponding rms temperature (b) and density (c) fluctuations normalised by Ttop and ρtop = ρ0, respectively. Data for runs C01, C1, and C10 with PrSGS = 0.1, 1, and 10 are shown as indicated by the legend. |
| In the text | |
 |
Fig. 19. Correlation coefficient C[uz, T′] as a function of depth from run C01 (PrSGS = 0.1, solid lines), C1 (PrSGS = 1, dashed) and C10 (PrSGS = 10, dash-dotted) for the downflows (blue), upflows (red), and totals (black). |
| In the text | |
 |
Fig. 20. Maximum of the superadiabatic temperature gradient Δ∇=∇−∇ad as a function of the effective Péclet number at zsurf = 0.85d for the total (a), in upflows (b), and in downflows (c). The colour coding indicates Preff(zsurf). |
| In the text | |
 |
Fig. 21. Horizontally averaged forces for the total flow (a), upflows (b) and downflows (c) for runs C01 (PrSGS = 0.1, solid lines), C1 (PrSGS = 1, dashed), and C10 (PrSGS = 10 dash-dotted). The blue and red lines show the corresponding superadiabatic temperature gradients with blue denoting negative and red positive values. The grey lines in panels b and c indicate Δ∇ for reference. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



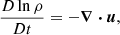
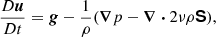
![$$ \begin{aligned} T \frac{D s}{D t}&= -\frac{1}{\rho } \left[\boldsymbol{\nabla } \boldsymbol{\cdot } \left({\boldsymbol{F}}_{\rm rad} + {\boldsymbol{F}}_{\rm SGS}\right) + \Gamma _{\rm cool} \right] + 2 \nu {\boldsymbol{\mathsf{S}}}^2, \end{aligned} $$](/articles/aa/full_html/2021/11/aa41337-21/aa41337-21-eq4.gif)
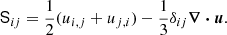
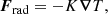
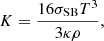
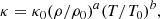
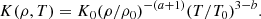
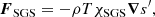
![$$ \begin{aligned} \Gamma _{\rm cool} = - \Gamma _0 h(z) [T_{\rm cool} - T(\boldsymbol{x},t)], \end{aligned} $$](/articles/aa/full_html/2021/11/aa41337-21/aa41337-21-eq15.gif)
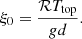
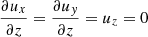
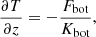
![$$ \begin{aligned}[x] = d,\ \ \ [t] = \sqrt{d/g},\ \ \ [\rho ] = \rho _0,\ \ \ [s] = c_{\rm P}, \end{aligned} $$](/articles/aa/full_html/2021/11/aa41337-21/aa41337-21-eq19.gif)
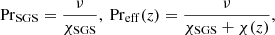
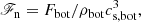
![$$ \begin{aligned} \mathrm{Re}\!=\!\frac{u_{\rm rms}}{\nu k_1},\ \mathrm{Pe}_{\rm SGS}\!=\!\frac{u_{\rm rms}}{\chi _{\rm SGS} k_1},\ \mathrm{Pe}(z)\!=\!\frac{u_{\rm rms}}{[\chi _{\rm SGS}+\chi (z)] k_1}, \end{aligned} $$](/articles/aa/full_html/2021/11/aa41337-21/aa41337-21-eq23.gif)
![$$ \begin{aligned} \mathrm{Ra}(z)&= \frac{gd^4}{\nu [\chi _{\rm SGS}+\chi (z)]}\left( - \frac{1}{c_{\rm P}}\frac{\mathrm{d}\overline{s}}{\mathrm{d}z} \right). \end{aligned} $$](/articles/aa/full_html/2021/11/aa41337-21/aa41337-21-eq24.gif)
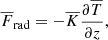
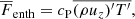
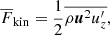
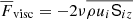
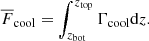
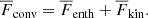
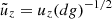
![$ \tilde{s}{\prime}({\boldsymbol{x}}) = [s({\boldsymbol{x}}) - \overline{s}(z)]/s^{\prime}_{\mathrm{rms}}(z) $](/articles/aa/full_html/2021/11/aa41337-21/aa41337-21-eq35.gif)
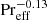
![$$ \begin{aligned} \overline{u}_z(z) = f(z) \overline{u}_z^\downarrow (z) + [1 - f(z)] \overline{u}_z^\uparrow (z), \end{aligned} $$](/articles/aa/full_html/2021/11/aa41337-21/aa41337-21-eq37.gif)
![$$ \begin{aligned} d_{\rm os} = \frac{1}{\Delta t}\int _{t_0}^{t_1} [z_{\rm CZ}(t) - z_{\rm OS}(t)] \mathrm{d}t, \end{aligned} $$](/articles/aa/full_html/2021/11/aa41337-21/aa41337-21-eq44.gif)
![$$ \begin{aligned} d_{\rm DZ} = \frac{1}{\Delta t}\int _{t_0}^{t_1} [z_{\rm BZ}(t) - z_{\rm CZ}(t)] \mathrm{d}t, \end{aligned} $$](/articles/aa/full_html/2021/11/aa41337-21/aa41337-21-eq46.gif)
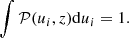
![$$ \begin{aligned} \mathcal{M}^n(u_i,z) = \int [u_i(\boldsymbol{x}) - \overline{u}_i(z)]^n \mathcal{P}(u_i,z) \mathrm{d}u_i. \end{aligned} $$](/articles/aa/full_html/2021/11/aa41337-21/aa41337-21-eq48.gif)
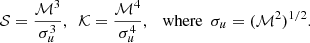
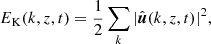
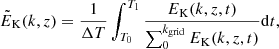
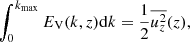
![$$ \begin{aligned} \int _0^{k_{\rm max}} E_{\rm H}(k,z) \mathrm{d}k&= {\frac{1}{2}}\left[\overline{u_x^2}(z) + \overline{u_{ y}^2}(z) \right]. \end{aligned} $$](/articles/aa/full_html/2021/11/aa41337-21/aa41337-21-eq54.gif)
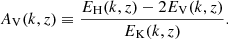
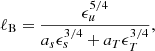
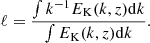
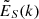
![$$ \begin{aligned} \tilde{\overline{F}}_{\rm enth}(k_{\rm max},z)&=\frac{1}{\Delta t} \int _{t_0}^{t_1} \left[ \frac{\overline{(\rho u_z)^\prime (z,k_{\rm max},t) T^\prime (z,k_{\rm max},t)}}{\overline{F}_{\rm enth}(z,t)} \right] \mathrm{d}t, \end{aligned} $$](/articles/aa/full_html/2021/11/aa41337-21/aa41337-21-eq72.gif)
![$$ \begin{aligned} \tilde{\overline{F}}_{\rm kin}(k_{\rm max},z)&=\frac{1}{\Delta t} \int _{t_0}^{t_1} \left[ \frac{\overline{E_{\rm kin}(z,k_{\rm max},t) u_z(z,k_{\rm max},t)}}{\overline{F}_{\rm kin}(z,t)} \right] \mathrm{d}t. \end{aligned} $$](/articles/aa/full_html/2021/11/aa41337-21/aa41337-21-eq73.gif)
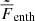
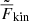
![$$ \begin{aligned} C[u_z,T^\prime ] = \frac{\overline{u_z T^\prime }}{u_z^\mathrm{rms}T^\prime _{\rm rms}} \approx \frac{\overline{F}_{\rm enth}}{c_{\rm P}\overline{\rho } u_z^\mathrm{rms}T^\prime _{\rm rms}}, \end{aligned} $$](/articles/aa/full_html/2021/11/aa41337-21/aa41337-21-eq83.gif)