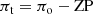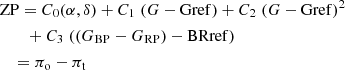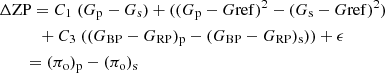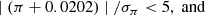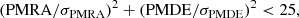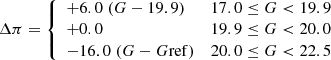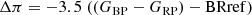| Issue |
A&A
Volume 654, October 2021
|
|
|---|---|---|
| Article Number | A20 | |
| Number of page(s) | 14 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202140862 | |
| Published online | 01 October 2021 | |
The parallax zero-point offset from Gaia EDR3 data⋆
Koninklijke Sterrenwacht van België, Ringlaan 3, 1180 Brussels, Belgium
e-mail: martin.groenewegen@oma.be
Received:
23
March
2021
Accepted:
14
June
2021
The second data release of Gaia revealed a parallax zero-point offset of −0.029 mas based on quasars. The value depended on the position on the sky, and also likely on magnitude and colour. The offset and its dependence on other parameters inhibited improvement in the local distance scale using for example the Cepheid and RR Lyrae period–luminosity relations. Analysis of the recent Gaia Early Data Release 3 (EDR3) reveals a mean parallax zero-point offset of −0.021 mas based on quasars. The Gaia team addresses the parallax zero-point offset in detail and proposes a recipe to correct for it based on ecliptic latitude, G-band magnitude, and colour information. This paper presents a completely independent investigation into this issue focusing on the spatial dependence of the correction based on quasars and the magnitude dependence based on wide binaries. The spatial and magnitude corrections are connected to each other in the overlap region in the range 17 < G < 19. The spatial correction is presented at several spatial resolutions based on the HEALPix formalism. The colour dependence of the parallax offset is unclear and in any case secondary to the spatial and magnitude dependence. The spatial and magnitude corrections are applied to two samples of brighter sources, namely a sample of approximately 100 stars with independent trigonometric parallax measurements from Hubble Space Telescope data, and a sample of 75 classical cepheids using photometric parallaxes. The mean offset between the observed GEDR3 parallax and the independent trigonometric parallax (excluding outliers) is about −39 μas, and after applying the correction it is consistent with being zero. For the classical cepheid sample the analysis presented here suggests that the photometric parallaxes may be underestimated by about 5%.
Key words: stars: distances / parallaxes
Table 1 and full Table 3 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/654/A20
© ESO 2021
1. Introduction
Data from the Gaia mission (Gaia Collaboration 2016) have impacted most areas in astronomy. One of the fields where the Gaia second data release (GDR2, Gaia Collaboration 2018) was eagerly awaited was in reliably establishing the local distance scale through calibration of the period–luminosity (PL) relation of classical cepheids (CCs) and RR Lyrae (RRL) variables.
Riess et al. (2018b) analysed a sample of 50 CCs and derived a parallax zero-point offset (hereafter PZPO) of −0.046 ± 0.013 mas, compared to the −0.029 mas derived for quasars by Lindegren et al. (2018). Riess et al. (2018b) concluded that the need to independently determine the PZPO largely countered the higher accuracy of the parallaxes when determining an improved zero-point of the PL relation. Independently, Groenewegen (2018) (hereafter G18) derived a PZPO of −0.049 ± 0.018 mas based on a comparison of nine CCs with the best non- parallaxes (mostly from Hubble Space Telescope (HST) data). Ripepi et al. (2019) re-classified all 2116 stars reported by Clementini et al. (2019) as Cepheids in the Milky Way (MW) and presented period–Wesenheit relations in the Gaia bands. Assuming a canonical distance modulus to the LMC of 18.50, they found a Gaia PZPO of ∼ − 0.07 to −0.1 mas. PZPOs based on GDR2 data were also reported for RRL stars (∼ − 0.056 mas, Muraveva et al. 2018; −0.042 ± 0.013 mas, Layden et al. 2019) and many other classes of objects (Stassun & Torres 2018, Graczyk et al. 2019, Xu et al. 2019, Schönrich et al. 2019). These values were mostly all-sky averages, but when sufficient data were available it was clear that the PZPO depended on position in the sky, magnitude, and colour (Zinn et al. 2019; Khan et al. 2019; Leung & Bovy 2019; Chan & Bovy 2020).
The Gaia Early Data Release 3 (GEDR3) presents the most recent information on parallax, proper motions (PMs), position and colour information for about 1.8 billion objects (Gaia Collaboration 2021a). Lindegren et al. (2021b) presents the general properties of the astrometric solution, while Lindegren et al. (2021a) (hereafter L20) specifically addresses the PZPO and present a Python script that is available to the community that calculates the PZPO. This module gives PZPO (without an error bar) as a function of input parameters, namely ecliptic latitude (β), G-band magnitude, the astrometric_params_solved parameter (Lindegren et al. 2021b), and either the effective wavenumber of the source used in the astrometric solution (νeff, nu_eff_used_in_astrometry for the five-parameter solution astrometric_params_solved = 31) or the astrometrically estimated pseudo colour of the source (pseudocolour) for the six-parameter solution (astrometric_params_solved = 95). The module is defined in the range 6 < G < 21 mag, 1.72 > νeff > 1.24 μm−1, corresponding to about 0.15 < (GBP − GRP) < 3.0 mag where G, GBP, and GRP are the magnitudes in the Gaia G-, Bp-, and Rp-band, respectively.
Several papers have already applied the L20 correction to the raw GEDR3 parallaxes. Riess et al. (2021) applied it to a sample of 75 CCs in the Milky Way (6.1 ≲ G ≲ 11.2 mag, 0.9 ≲ (GBP − GRP) ≲ 2.5 mag). For this sample, there is a strong dependence of the correction on β (ranging from −4 to −38 μas) with only a small dependence (of order 1.8 μas) on magnitude and colour, with a median correction of −24 μas. Allowing a remaining PZPO after application of the L20 correction and fitting the data to the independently calibrated PL relation of CCs in the Large Magellanic Cloud (LMC) reveals an offset of 14 ± 6 μas, in the sense that the L20 corrections are too negative, that is the values are over-corrected.
A similar conclusion is reached by Zinn (2021) who analysed a sample of 2000 first-ascent red giant branch stars with asteroseismic parallaxes in the Kepler field (9.0 ≲ G ≲ 13.0 mag, 1.0 ≲ (GBP − GRP) ≲ 2.3 mag), concluding that the L20 corrections are too negative by 15 ± 3 μas for G ≲ 10.8 mag.
Bhardwaj et al. (2021) apply a theoretical period–luminosity–metallicity relation in the K−band to a sample of about 350 Milky Way RR Lyrae stars (8.9 ≲ G ≲ 17.8 mag, 0.4 ≲ (GBP − GRP) ≲ 1.3 mag) to find a ZP of (−7 ± 3) μas when compared to the raw GEDR3 parallaxes. The mode of the L20 correction for this sample is −32 ± 4 μas, and so, again, the L20 formula over-corrects the parallaxes, in this case by 25 ± 5 μas.
Stassun & Torres (2021) continue their previous analysis using eclipsing binaries as reference objects. Stassun & Torres (2018) found an offset of (−82 ± 33) μas based on 89 stars from GDR2, while their latest analysis using GEDR3 indicates an offset of (−37 ± 20) μas based on 76 objects (5 ≲ G ≲ 12 mag, −0.1 ≲ (GBP − GRP) ≲ 2.2 mag). After applying the L20 correction, the PZPO becomes (−15 ± 18) μas, indicating no over- or under-correction.
Huang et al. (2021) use a sample of over 69 000 primary red clump (PRC; 9.5 ≲ G ≲ 15 mag, 1.32 ≲ νeff ≲ 1.5, or about 1.0 ≲ (GBP − GRP) ≲ 2.2 mag) stars based on LAMOST data from Huang et al. (2020). The distances come from Schönrich et al. (2019) and are based on a Bayesian analysis of DR2 data and include an PZPO of −0.054 mas. The reference distance is compared to the raw GEDR3 parallax, and the GEDR3 parallax after applying the L20 correction. The difference (Gaia – PRC) is −26 in the former and +3.7 μas in the latter case (no errors are reported). Huang et al. (2021) also show the trends of the parallax difference against G, νeff, and ecliptic latitude; they show that applying the L20 correction removes some of these trends (in particular against G magnitude), but not all, and show that there is a trend with ecliptic longitude, especially for ecliptic latitudes < 30°.
The aim of the present paper is to present an independent (and alternative) investigation into the PZPO, and in particular into the spatial dependence. This is achieved by using a large sample of reliable quasi-stellar objects (QSOs; selected differently from the sample used in various GEDR3 papers). In addition, physical binaries are considered to derive the dependence of the PZPO on G magnitude. At the bright end, the PZPO derived in the present paper is applied to a sample of stars that has not been systematically considered in previous works, namely stars that have an independent parallax measurement from the HST. In addition, the PZPO is applied to the sample of CCs by Riess et al. (2021), and results are compared to using the correction in L20.
The paper is structured as follows. In Sect. 2 the main methodology is introduced. In Sect. 3 the sample of stars is described. Section 4 presents the results of the calculations and the derivation of the PZPO, while Sect. 5 applies the PZPO to the QSO sample itself and the two samples of stars. A brief discussion and summary conclude the paper.
2. Methodology
The parallax zero-point offset is defined through
where πt is the true parallax and πo the observed parallax (as listed in the GEDR3 catalogue). The PZPO is parameterised in the present paper as a sum of linear functions that are assumed to hold over a range of magnitudes:
where Gref = 20.0 mag and BRref = 0.8 mag are reference values that are chosen to represent the typical colours of QSOs.
In the present analysis, binaries are also considered. In these cases, the true parallaxes for the two components are essentially the same and as they are essentially at the same position on the sky the C0 term may be assumed to cancel out. The difference in Eq. (2) for the two components (labelled as subscripts as primary, p, and secondary, s) becomes:
where ϵ is a term that can be thought of as the spatial correlation on the extent of the binary separation.
The difference between the formalism outlined in Appendix A in L20 and that is used here is two-fold. The main difference is that the spatial dependence is made explicit here rather than using a second-order polynomial in sin β. The other difference is that the spatial, magnitude and colour dependence are assumed to be separable while the L20 correction allows for cross-terms.
The term C0 is allowed to vary over the sky and the HEALPix formalism (Górski et al. 2005, the NESTED variant) is used to transform (α, δ) to a sky pixel. This is done using an implementation in Python, HEALPy (Zonca et al. 2019). The number of sky pixels depends on the chosen resolution; resolution levels 0, 1, 2, 3, and 4 are considered in the present paper and correspond to 12, 48, 192, 768 and 3072 pixels, respectively. The highest resolution corresponds to a mean spacing of 3.7 degrees between sky pixels.
The fitting of Eqs. (2) or (3) to the data is done with the singular value decomposition algorithm (routine svdfit) as implemented in Fortran77 in Press et al. (1992). This algorithm minimises the χ2 taking into account the errors in the ordinate (the parallax (difference)) and gives the best-fit parameter values with error bars. In order to also consider the errors in magnitudes and colours Monte Carlo simulations are performed where new datasets are generated taking into account Gaussian errors in the parallaxes, magnitudes, and colours. The parameter values quoted below (in Table 2) are the median values for the parameters among these simulations with the dispersion among the parameter values taken as error, calculated as 1.4826 times the median absolute deviation (MAD), equivalent to 1σ in a Gaussian distribution.
Result of the fitting to the QSO sample.
3. The sample
In order to apply Eqs. (2) or (3) and determine ZP as a function of sky position, magnitude, and colour, a large sample of sources with known true distances is required. In this paper, QSOs, physical binaries, and stars with an independent trigonometric parallax determination are considered.
For the samples discussed below the following parameters were retrieved from the GEDR3 main catalogue1: parallax and parallax error (parallax, parallax_error), PMs in Ra and Dec with errors (pmra, pmra_error, pmdec, pmdec_error), the source identifier (source_id)2, which parameters have been solved for (astrometric_params_solved; five- and six-parameter solutions are relevant for the present paper, see Lindegren et al. 2021b), the renormalised unit weight error (RUWE), the goodness of fit (GOF, astrometric_gof_al), the effective wavenumber of the source used in the astrometric solution (νeff, nu_eff_used_in_astrometry), the astrometrically estimated pseudocolour of the source (pseudocolour), and the G, GBP, and GRP magnitudes with errors (phot_g_mean_mag, phot_g_mean_mag_error, phot_bp_mean_mag, phot_bp_mean_mag_error, phot_rp_mean_mag, phot_rp_mean_mag_error).
3.1. Quasars
Several of the GEDR3-team papers use a QSO sample (Gaia Collaboration 2021b; Lindegren et al. 2021a,b) but the paper describing the selection of this sample has not been published at the time of submission. What is available is the list of 1.61 million source_ids which contains a reference to a catalogue but without any quality flag. For this reason, and because this project started before the release of GEDR3, a different QSO sample was created.
The Million Quasars (Milliquas) catalogue (version 7.0b, Flesch 2019) is used which contains of order 830 000 type-I QSOs and AGNs plus about 500 000 quasar candidates. From the full catalogue, the 1.37 million objects with a confirmed redshift > 0.1 or a probability of being a quasar of > 98% are selected. The cross-match facility (xMatch) at the Centre des Données (CDS) in Strasbourg was used to match this list with GEDR3 using a search radius of 0.15″, and this returned 998 220 matches, of which 855 518 QSOs have a parallax, and G, GBP, and GRP magnitudes available. The true parallax for these sources is assumed to be zero.
First the general properties of the QSO sample are discussed, and in particular the distribution of the GOF and the RUWE. The GOF parameter should follow a Gaussian distribution with zero mean and unit dispersion (Wilson & Hilferty 1931). In GDR2 this was not the case due to the “degree-of-freedom” bug (see Appendix A in Lindegren et al. 2018 and the discussion in Groenewegen 2018). The RUWE was introduced after GDR2 (Lindegren 2018) as another quality indicator of the astrometric solution. It compared the unit-weight-error (UWE, the square-root of the reduced χ2) to that of a sample of unproblematic stars as a function of magnitude and colour. Although the χ2 values were, in reality, numerically incorrect, the ratio of the UWEs was probably deemed representative of the relative quality of the astrometric solution. In Gaia EDR3, the “degree-of-freedom” bug has been corrected and the GOF is the main parameter describing the quality of the astrometric solution.
Although the QSO sample was selected to be pure, it still contains non-QSOs. As QSOs should have zero parallax and PMs (within the error bars) the following conditions are applied:
where −0.0202 mas is the average offset of QSOs (see below). Similar cuts were applied to the QSO sample in Lindegren et al. (2021a), but no selection on astrometric_params_solved or νeff is applied. The 5σ limit on the parallax and PMs in Ra and Dec corresponds to the expected level of outliers following Chauvenet’s criterion with ∼800 000 objects.
The upper panel in Fig. 1 shows the distribution of the GOF for the 841 000 QSOs that remain after applying the selection on parallax and PM, together with a Gaussian fit. The mean and dispersion are 0.483 and 1.187 with negligible formal errors. The mean is slightly larger than expected but the tail to negative GOF (the extreme value is −5.4) is not inconsistent with the distribution. On the other hand the tail to larger GOF (the extreme value is +200) is obvious. To obtain a better estimate of the mean and width of the distribution undisturbed by outliers, the lower panel shows the distribution when the GOF and the Gaussian fit to the distribution is restricted to < + 2.0. The mean is 0.388 with σ = 1.109. Based on this analysis a condition −4< GOF < 5 is imposed on all selections described in this paper, allowing for a small excess of sources towards larger GOF. Figure 2 shows the distribution in G, (GBP − GRP) colour, and RUWE after imposing these conditions, as well as RUWE < 1.4 to eliminate a few extreme outliers in that parameter. The distribution in RUWE has a peak slightly above one, consistent with the fact that the distribution in GOF peaks slightly above zero. This indicates that the error bars in the parallax are likely underestimated by a few percent (at least in this range of magnitude and colour), consistent with the findings in Fabricius et al. (2021) and El-Badry et al. (2021). A final sample of 824 819 QSOs is retained. The median parallax in that sample is −0.0202 mas with a dispersion (calculated as 1.4826 times the MAD) of 0.393 mas.
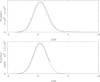 |
Fig. 1. Distribution of the GOF with a Gaussian fit. Top panel: approximately 841 000 QSOs with parallaxes and PMs consistent with zero. A significant tail toward large GOF is visible. Lower panel: fit with GOF restricted to < + 2.0. |
 |
Fig. 2. Distribution of G, (GBP − GRP) colour and RUWE for the QSO sample after applying selections on parallax, PM, GOF, and RUWE. |
3.2. Wide binaries
In this paper, the catalogue of wide binaries (WBs) of El-Badry et al. (2021) is used which is based on GEDR3 data. In its raw form, it contains 1.8 million candidate physical binaries. For wide and close-by binaries, the hypothesis that both components are at approximately the same physical distance may no longer be correct. The procedure outlined in Sect. 5 of El-Badry et al. (2021) is used to eliminate objects where the true parallax difference between the two stars (Eq. (13) of that paper) is estimated to contribute more than 5% to the error in the observed parallax differences (eliminating about 14 000 of the 1.8 million pairs). The sample is also restricted to the subset of about 784 000 pairs with a < 1% probability of chance alignment, which is stricter than the high-confidence sample (chance alignment < 10%) of 1.2 million objects considered in El-Badry et al. (2021).
Fabricius et al. (2021) and Lindegren et al. (2021a) also consider samples of binaries to validate the GEDR3 results and analyse the PZPO, respectively. Both samples are directly constructed from GEDR3 data (but they are not identical) and careful selection is needed to reach a pure sample.
3.3. Sources with trigonometric parallax determinations
The Fine Guidance Sensor (FGS) and the Wide Field Camera 3 (WFC3) onboard the HST have been used to determine parallaxes and PMs. The review of Benedict et al. (2017) describes the methodology and provides a list of 105 targets for which the parallax has been determined by using the FGS. Some close binaries are included in the list with both components. One component was removed from the list as the binary cannot be resolved by Gaia. Some recent works by van Belle et al. (2020) and Bond et al. (2018) (on Polaris B) are added to give a list of 102 targets. The methodology to use the WFC3 to obtain parallaxes was described in Riess et al. (2014) and Casertano et al. (2016) and has been used to obtain distances to eight CCs (Riess et al. 2014, 2018a). Although parallaxes from HIPPARCOS are in general no longer competitive when compared to Gaia, Table 1 includes one exception, Polaris A, the most nearby CC, which had no parallax listed in GDR1 or GDR2.
The independent trigonometric parallax data and basic GEDR3 data on the 111 objects are listed in Table 1. Only one object is not listed in GEDR3 (Polaris A), and eight objects have no parallax listed (all these have exceptionally large GOF values). Applying the selection on GOF and RUWE further eliminates 37 objects for a useful sample of 57 objects.
4. Results
This section presents a discussion of the results related to the derivation of the PZPO correction.
4.1. QSOs
Figure 3 provides another representation of the QSO sample, similar to Fig. 5 in L20. It shows a binned version of the PZPO (weighted mean and error) as a function of G magnitude, (GBP − GRP) colour (L20 shows it as a function of νeff), and β. The lines in the top and middle panels are not fits to the data but represent the finally applied corrections based on a full analysis (see later in this section, Eqs. (5) and (6)). In the middle panel, the line does not seem to fit the points very well. This is related to the fact that in the QSO sample the brighter QSOs are bluer than fainter ones. In addition, the error bar on this slope is quite large.
 |
Fig. 3. PZPO for the QSO sample as a function of G, (GBP − GRP) colour and ecliptic latitude (open circles). Only bins with ≥5 objects are plotted. Bins with 100 objects or less are plotted in blue, with 30 objects or less in red. The lines in the top panel and the lines in the middle panel are not a fit to the data, but are based on Eq. (5). The blue points in the lower panel indicate the PZPO for the 48 HEALPix level 1 pixels. The horizontal bar gives the range in sin β for each HEALPix pixel. |
Although the QSO sample is different from that used in GEDR3-team papers the behaviour is very similar to that shown in L20, as expected. There is a quite noticeable correlation with G for G ≳ 17 mag, a small (if any) correlation with colour (or νeff), and a relatively modest correlation with β. In particular, the latter correlation is interesting. An identical binning is used as in L20 (40 bins) and the distribution of the black open squares is almost identical to that shown in L20. The blue points show another representation, and highlight the main reason why a different spatial dependence of the PZPO is proposed here. The binning is now done based on HEALPix level 1, which has 48 pixels, very similar to the binning in L20. The point and the vertical error bar have the same meaning, while the horizontal line represents the range in β for that HEALPix pixel. One can clearly observe a significantly larger spread even for pixels with very similar ecliptic latitudes. This indicates that the PZPO is a more complicated function than of β alone. The result is qualitatively similar to Huang et al. (2021) who demonstrate that there is a trend of the PZPO with ecliptic longitude, especially for β < 30°.
To investigate this further Eq. (2) is fit to this sample, solving for C0 (only a spatial component), C0+C1+C2, and all parameters. This is done for several HEALPix levels, and the results are summarised in Table 2. As the fitting routine is based on minimising the χ2 one expects the value for C0 to be equal to the weighted mean of the parallaxes of all QSOs in that pixel when only the spatial component is solved for. As a sanity check for the implementation of the numerical code it was verified that this is indeed the case.
As the distribution of known quasars is not uniform over the sky (typically under-represented in the Galactic plane) the number of objects per sky pixel varies strongly. At HEALPix level 3 there are 10 pixels with no QSOs, and 63 with 40 objects or less. On the other hand 50% of pixels have 810 objects or more, with a maximum of 3762. Inspecting the error in the parallax offset and the signal-to-noise ratio suggests that 40 objects or more are required for the results to be robust. The median offset over these 706 pixels is −21.0 μas with a dispersion over the pixels (calculated via the MAD) of 12.4 μas when fitting only the spatial component. Averaging only over the pixels with 100 objects or more changes the parameter and the error by ∼0.3 μas.
The first entries in Table 2 (models 1–9) include all QSOs but based on the trends seen in Fig. 3 models restricted in G magnitude are more realistic, and several ranges have been explored. Models 10–28 show the main results, and based on these the following linear correction of the parallax is proposed (in μas mag−1) to be in the range G > 17 mag (Δπ to be subtracted from the catalogued GEDR3 parallax):
The presence of a colour dependence is less clear. As can be seen from the results in Table 2 the term is not very significant (at the 2σ level at best). Nevertheless, the colour correction (in μas mag−1) that is tested is:
Figure 3 shows no real trend with magnitude for brighter magnitudes. Fitting a constant at HEALPix level 0, as there are only about 3300 QSOs brighter than 17 mag, gives a value of about −31 μas (model 29).
Models 30–34 and 35–39 give the results when the parallaxes are corrected according to Eq. (5), and Eqs. (5) and (6), respectively. The results are listed for several HEALPix levels. The average spatial correction of the PZPO (at G = 20) is essentially independent of the chosen HEALPix level and suggests systematic errors of ≲0.5 μas. Tests using slopes of −6.1 and 17.0 at the bright and faint magnitude ends, respectively, and shifting the nodes by 0.1 mag indicate global differences of ≲0.2 μas and changes in the spatial PZPO in individual pixels of ≲ 0.2σ. Adding the colour correction increases the dispersion over the pixels, suggesting again that the colour term is not a significant factor.
The detailed results of models 30–39 are available through the CDS, and an example of the content is given in Table 3. These files list the PZPO and error for each individual HEALPix pixel for levels 0, 1, 2, 3, and 4, and the number of QSOs in each pixel.
Example of PZPO and error over the HEALPix pixels.
Table 4 lists the HEALPix level, the number of pixels, the number of pixels with only 0 or 1 object, and the range in the PZPO errors for the pixels with 40 or more objects, which typically increases with increasing spatial resolution.
Properties of the solutions.
Figure 4 illustrates how this spatial and magnitude correction works for the QSO sample with G > 17 mag. The black open circles give the observed parallaxes of the 821 000 QSOs averaged and binned over sin β. The blue open circles give the L20 correction for the individual QSOs again averaged and binned over sin β, while the black filled circles give the corrected parallaxes according to Eq. (5) and the red filled circles the spatial correction at HEALPix level 2. Weighted averages are used except for the blue circles of the L20 correction. The unweighted mean is shown as the L20 correction carries no error. The shape of the L20 correction is due to the fact that L20 uses a second-order polynominal in sin β (Eq. (A4) in L20 and the discussion in their Sect. 4.1). The spatial correction at HEALPix level 2 gives a good description of the parallaxes corrected according to Eq. (5) even though the fitting was done according to the HEALPix level and not specifically to ecliptic latitude. Section 5.1 discusses the results when the correction in L20 and the current one are applied to the QSO sample.
 |
Fig. 4. PZPO for the QSO sample with G > 17 mag as a function of sin β. Black open circles represent the observed data (the weighted mean) to be compared to the blue open circles that represent the L20 correction (the unweighted mean as the L20 correction carries no error). The black filled circles represent the corrected parallax data (according to Eq. (5)) to be compared to the red filled circles that represent the spatial correction at G = 20 mag at HEALPix level 2 (both are weighted means, but the error in the red filled circles is too small to be visible). |
4.2. Wide binaries
The top panel in Fig. 5 shows a binned version of the parallax difference between the primary and secondary component as a function of primary G in the top panel. A similar diagram was shown in Fabricius et al. (2021) (their Fig. 22) Most striking is the sharp decrease in the parallax difference for faint magnitudes. This is due to selection effects in the El-Badry et al. (2021) sample. Readily visible in the bottom panel are the conditions πp > 1 and πs > 1 mas that were imposed (but there are others on the (relative) parallax accuracy; see their Sect. 2), and also very clear is the fact that for a given πp there are many more objects with πs < πp than the inverse. Restricting the magnitudes to less than 19 mag seems to largely remove this asymmetric behaviour (top panel Fig. 6) and also removes the unexpected tendency of the parallax difference as a function of magnitude (bottom panel).
 |
Fig. 5. Top panel: parallax difference between the primary and secondary components in wide binaries as a function of primary G magnitude. Bins with more than 1000 objects are plotted in blue. Bottom panel: parallax of the secondary binary component plotted against that of the primary. Objects with primary G magnitude larger than 5, 15, 17, 19, and 20 mag are plotted as black, red, green, dark blue, and light blue dots, respectively. About 590 000 binaries are plotted where both components pass the criteria on GOF and RUWE. |
 |
Fig. 6. As in Fig. 5 but for Gs restricted to < 19.0 mag. After eliminating about 700 extreme outliers (those outside the two plotted lines in the top panel), a sample of about 480 000 objects remain. The bottom panel shows the parallax difference between primary and secondary component for that sample as a function of Gp. We note the different range in the ordinate compared to Fig. 5. |
It is now possible to iteratively study the PZPO based on WBs as a function of G magnitude. The first step is to correct the parallaxes according to Eq. (5). As the G magnitude of the binary sample is limited to G = 19 mag, this implies correcting the parallaxes of all objects with G > 17 by +6.0 μas mag−1. One can then plot the parallax difference against magnitude, only considering secondaries fainter than 17 mag. The top panel of Fig. 7 shows the result. The PZPO is essentially independent of G at the faint end, and the weighted mean of the 11 bins fainter than 17.1 mag is 1.6 ± 0.6 μas. In the range between ∼13.3 and ∼17 mag, the PZPO can be well approximated by a linear behaviour as indicated by the black line. In a second step this offset can be applied as well in this magnitude range, and the PZPO can be determined using secondaries fainter than 13.3 mag. The consecutive panels in Fig. 7 show how this procedure can be applied to brighter and brighter magnitudes. The bottom panel shows the final result. The weighted mean of the residuals is 0.05 μas with an rms of 2.7 μas (for G > 6), 4.3 μas (for G > 5), and 13 μas (for 5 < G < 6 mag). The correction that was applied with the range of G magnitudes determined so that the correction is continuous in G is given by Eq. (7) and is shown as the black line in the bottom panel.
 |
Fig. 7. As in Fig. 5 but with parallaxes corrected according to Eq. (7) in consecutive steps (see main text). The bottom panel shows the applied correction (Eq. (7)) as the black line. The small black, red, and green circles represent the L20 correction for β = 0, −60, and +60°. There is an offset as the L20 corrections are absolute, while the corrections applied to the WB sample are relative to the correction at G = 20 mag. |
The bottom panel of Fig. 7 also shows for comparison the correction by L20 for νeff = 1.55 (corresponding to (GBP − GRP) = 0.8 mag) and β = 0° (small black circles), +60° (green), and −60° (red circles). The behaviour for β = 0° of the L20 correction is very similar in shape and amplitude to the correction derived here. There is an offset due to the fact that the L20 corrections are absolute while the corrections in Eq. (7) are relative to the correction at G = 20 of ≈ − 12.6 μas (see Table 2) which is indeed approximately the difference at the faint end. What is remarkable is that the L20 correction also depends in a particular way on ecliptic latitude. For bright magnitudes the L20 correction for −60° lies above that for +60°, while for G ≳ 13 mag the inverse is true. In addition, the dependence on β increases with brighter magnitudes.
In this parallax correction, a 1 μas systematic error is added in quadrature to a random error of 2.7 μas for G > 6 and 13 μas for G ≤ 6.
5. Application of the PZPO correction
This section present a discussion of the results related to the application of the PZPO correction.
5.1. QSOs
The first application of the PZPO correction is to the QSO sample itself. We then compared the result to the effect of using the L20 correction. Table 5 provides the L20 correction, and the spatial, magnitude, and total correction in the present work, as well as the offset after applying the L20 correction and the correction in the present work for the different HEALPix levels. The weighted mean and the error therein are quoted in all cases. As the L20 correction comes without an error, one has been assigned. This was chosen to be a constant such that the error in the weighted mean of the L20 and the correction in the present work (Cols. 2 and 5) are the same for HEALPix level 0 and is equal to 3.0 μas. This choice has no practical impact. The error in the weighted mean after applying the corrections (Cols. 6 and 7) is independent of this choice, and is almost the same for both types of corrections (∼0.3 μas), as this error is dominated by the error in the observed parallaxes.
Parallax corrections for the QSO sample.
The results in Table 5 give the overall comparison for ∼821 000 QSOs in the sample, but as the main difference between the approach in L20 and in the present work is in the dependence of the correction on sky position this dependence is of interest. Figure 8 shows the corrected parallax after applying the correction in the present work (in black) and the correction provided in L20 (in blue) using 60 bins in sin β. The black points tend to be closer to the line of zero offset and Table 6 contains the details for the different HEALPix levels. The table lists the median over the bins and the scatter around the median (calculated as 1.4826⋅MAD), and shows that the scatter decreases with increasing spatial resolution when using the present correction. However, as shown in the following two sections, this is not the case in general. As the sample used to define the spatial correction is the same as the one to which it is applied there are no undefined spatial pixels being used. In general, increasing the spatial resolution (increasing the HEALPix level) will lead to an increasing number of stars being in spatial pixels that are undefined (insufficient number of QSOs), meaning that there is an optimal HEALPix level to be used.
 |
Fig. 8. Residual in the observed parallax after applying the correction in the present work (in black open circles, offset by −0.004 units horizontally) and the correction used in L20 (in blue filled circles, offset by +0.004 units) versus sin β for the QSO sample. Sixty bins have been used, and HEALPix level 2 has been used in the calculations. |
Parallax corrections for the QSO sample when binned against ecliptic latitude.
5.2. Independent trigonometric parallaxes
In Sect. 3.3, a sample of 111 stars with independent trigonometric paralax data is introduced (Table 1) of which 57 pass the selection on GOF and RUWE. Figure 9 compares these parallaxes to the GEDR3 ones in the top panel, while the residuals are shown in the bottom panel.
 |
Fig. 9. Independent trigonometric parallax plotted against GEDR3 parallax. The bottom panel displays the residual, where the error bar in the ordinate combines the error in the Gaia and the independent parallax in quadrature. Two stars where the residual is more than ten times the combined error bar are plotted as open triangles. |
Two stars are excluded from further analysis, VY Pyx and HD 285876. Benedict et al. (2017) mention that VY Pyx is an outlier, lying 1.19 mag away from the PL relation they derived. Adopting the parallax would shift this object 1.06 mag closer to the PL relation, thereby improving the agreement between them. Although Benedict et al. (2017) carefully analysed all steps in their procedure, it is likely that the FGS parallax is in error. For vA 645 (HD 285876) the difference between and FGS parallax is 20σ, much larger than one can reasonably attribute to a statistical outlier.
Figure 10 plots the residuals against G magnitude, (GBP − GRP) colour and sin β. Although these are the objects with the best independent trigonometric parallaxes the error bars on the differential parallax are dominated by the error in the external parallax and the range in the ordinate (∼4 mas) is much larger than when comparing GEDR3 parallaxes among themselves, where differences in parallax due to sky position, magnitude, and colour are of the order of 100 times smaller (∼0.04 mas, e.g., Figs. 3 or 7). This is probably the reason that no trends are obvious.
 |
Fig. 10. Difference between the independent trigonometric parallax and the GEDR3 parallax plotted against G, (GBP − GRP) colour, and sin β. The two outliers mentioned in Fig. 9 have been removed. |
Table 7 gives the median and weighted mean (with error bar) of the difference between the observed and the independent trigonometric parallax. The first five entries are for the entire sample, applying increasingly stricter selection criteria. The last two entries are specifically for the CCs, Type-II cepheids (T2Cs) and RRL stars in the sample. These objects are of special interest to the distance scale, and they are all radially pulsating stars of similar magnitude (7 ≲ G ≲ 10) and colour (0.5 ≲ (GBP − GRP) ≲ 2.3 mag). Appendix A gives some more details on this subsample.
PZPOs for the sample with independent trigonometric parallaxes.
Table 8 provides the spatial, magnitude, and total correction, as well as the offset between the corrected GEDR3 and independent trigonometric parallaxes. This is done for three representative samples, and for the different HEALPix levels. Ideally, the weighted mean of the difference between the corrected GEDR3 parallax and the independent trigonometric parallax (Col. 5) should be zero within the error bars, and this is indeed the case. However, some trends are observed. For the larger HEALPix levels, an increasing number of stars are missing and this results in a marked increase in the scatter. On the other hand, the best mapping of the spatial variations should be favoured. For the samples discussed here, this would imply using the results for HEALPix level 2. However, this choice will depend on the properties of the external sample (number of stars, distribution on the sky, accuracy of the external parallaxes).
Parallax corrections for the sample with independent trigonometric parallaxes.
5.3. Classical cepheids
The sample of Galactic CCs of Riess et al. (2021) was studied in a second application of the spatial and magnitude corrections derived in the present paper. These authors discuss a sample of 75 CCs with HST photometry which is used to calibrate the extragalactic distance scale along the lines outlined in earlier works (Riess et al. 2016, 2018b, 2019). They correct the GEDR3 parallaxes using the L20 formalism and fit the slope, zero point, and metallicity dependence of the PL relation as well as a constant offset between the photometric parallaxes and the corrected GEDR3 values. Fits where some of these parameters are fixed are also presented. In their analysis they increased the GEDR3 parallax uncertainties by 10%, which is not done here. One important conclusion in the present context is that Riess et al. (2021) find that the L20 procedure over-corrects the PZPO by 14 ± 6 μas.
Table 9 contains the result of the calculations for two samples. The first is the sample of 66 stars retained by Riess et al. (2021). This is the full sample of 75 stars minus 9 stars excluded in their best-fit analysis. Six were excluded because their GOF > 12.5 (SV Per, RW Cam, U Aql, DL Cas, SY Nor, RX Cam), one, CY Aur, because it is an outlier in the L20 correction, and S Vul and SV Vul which are marginal outliers of the PL relation3. The second sample is the 54 stars that remain after applying the criteria on GOF and RUWE used in this paper.
Parallax corrections for samples of Galactic CCs.
The reference parallax is the photometric parallax (with error) from Table 1 in Riess et al. (2021) which was derived from the HST photometry, the pulsation period, and the PL relation from Riess et al. (2016, 2019).
Column 2 of Table 9 gives the weighted mean offset between the observed GEDR3 parallax and the photometric parallax. It is unusually large (−6.4 to −7.7 μas, see below). Column 3 lists the weighted mean of the L20 correction, and the upper panel of Fig. 11 shows the dependence on β. A similar diagram was shown for the 75 CCs in Riess et al. (2021). What is striking is the close to parabolic shape of the correction which is built into in the L20 approach. The other columns show the weighted mean of the spatial, magnitude, and total correction, the offset between the corrected GEDR3 parallax and the photometric parallax, and the number of objects. If the GEDR3 parallaxes are corrected by the L20 formalism (on a star-by-star basis) the weighted mean offset with the photometric parallax becomes +14.3 ± 2.9 μas, consistent with Riess et al. (2021), and indicates an overcorrection by the L20 formalism. By increasing the photometric parallaxes by ∼3.3% one can obtain a weighted mean offset between the L20 corrected and photometric parallax consistent with zero (0.00 ± 2.93 μas). Such an increase is consistent with the result reported in the last entry of Table 2 in Riess et al. (2021) where the authors forced a fit without additional PZPO to determine the zero point of the PL relation. The value reported there (−5.865 ± 0.013) is consistent with the finding here that implies a zero point of −5.93 + 5log1.0325 = −5.861.
 |
Fig. 11. Top panel: PZPO correction by L20 for the sample of 66 CCs analysed by Riess et al. (2021) (cf. their Fig. 2). The colours represent different ranges in G: black (G ≤ 7), red (7 < G ≤ 8.5), green (8.5 < G ≤ 9.0), and blue (9 < G ≤ 11.5). Bottom panel: correction proposed here for the stricter selected sample of 54 stars at HEALPix level 2. |
The second block in Table 9 shows similar results for the smaller sample that fulfils the criteria on GOF and RUWE imposed here. The bottom panel of Fig. 11 shows that there is no dependence of the total correction (with error bar) proposed in the present paper on β. It is remarked that the error in the average total correction (Col. 6) is similar to or smaller than the average L20 correction (Col. 3) for HEALPix levels 0, 1, and 2.
Adopting the standard photometric parallax leads to overcorrection of ∼20 μas. Increasing the photometric parallax by a factor 1.0505 ± 0.0080 (implying a PL zero point of −5.823 ± 0.016, and H0 = 76.2 ± 1.3 km s−1 Mpc−1) will lead to a weighted mean offset between the corrected GEDR3 and the photometric parallax consistent with zero. It also implies a weighted mean offset of the observed GEDR3 and the photometric parallax of −29 ± 3 μas, which is very similar to other bright (G ≲ 10–11 mag) samples: for example, the stars with external trigonometric parallaxes and the subsample of pulsating stars (−39 ± 14, respectively, −29 ± 16 μas from Table 7) or the sample of EBs (−37 ± 20 μas, Stassun & Torres 2021) or WUMa-type EBs (−28.6 ± 0.6 μas for the 5-parameter solution, Ren et al. 2021).
6. Discussion and summary
The presence of a parallax zero-point offset that was identified in GDR2 received a lot of attention. The L20 paper analysing the new GEDR3 data offers a lot of insight into the issue and they present a Python script to calculate the correction based on G, β, and the pseudocolour or νeff (depending on the astrometric_params_solved parameter).
On the other hand, L20 note that ‘the results should … in no way be regarded as definitive’, and that ‘alternative routes [should be] explored towards getting a better handle on the systematics in Gaia data’. The present paper should be viewed in this light. An alternative procedure to the one in L20 is proposed which is offered to the community for further scrutiny.
The two approaches are similar in that both use samples of QSOs and wide binaries (albeit selected in different ways). The main differences of the approch outlined here to that used in L20 are that here, (1) there is no separation between five- and six-parameter solutions, (2) the colour dependence uses the (GBP − GRP) colour rather than pseudocolour or νeff, (3) the dependence on sky position and magnitude are separated, and are treated as additive terms, and that (4) the present approach gives a correction including an error estimate.
It is shown that the PZPO shows a more complicated behaviour than only on the ecliptic latitude (Fig. 3, also see Huang et al. 2021). L20 argue that such a dependence is theoretically expected and related to the scanning law but this would not explain the different behaviour at bright (Fig. 11; a range of ∼35 μas with the largest correction around β ∼ 5°) and faint magnitudes (Fig. 4; a range of ∼20 μas with a slow increase with β) in the L20 recipe.
Here, a practical approach is taken to calculate the PZPO over the sky using the HEALPix formalism. Using the dependence of the PZPO on G, a spatial PZPO at G = 20 mag is determined for several HEALPix levels based on the QSO sample for G > 17 mag. A large sample of WBs with very low chance alignments is used to derive the magnitude dependence of the PZPO for magnitudes < 19 mag. The range of 17 − 19 mag is used to connect the QSO to the WB sample.
The L20 recipe does not provide an error on the correction. It is shown here that error on the PZPO is dominated by the error on the spatial correction, and that it can be substantial (up to several tens of μas depending on sky position). Increasing the sample of QSOs, especially in the direction of the Galactic plane, will help in reducing the statistical error but only as 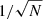 .
.
The recipes provided here cannot be easily transformed into a simple script. This may be seen as a disadvantage, but on the other hand, it requires the user to make informed choices. The procedure to be followed is outlined below:
-
Obtain the source_id, G magnitude, parallax and error, and (GBP − GRP) colour from GEDR3 for your source(s).
-
Get the pixel number in the HEALPix scheme from the source_id following footnote 2 for levels 0, 1, 2, 3, and 4.
-
Use the results from models 30–34 available from the CDS to obtain the spatial correction and error at G = 20 for the various HEALPix levels.
-
For G > 19.9 mag apply Eq. (5), otherwise apply Eq. (7). The error in this correction is a 1 μas systematic error to be added in quadrature to a random error of 2.7 μas for G > 6 and 13 μas for G ≤ 6.
-
If a colour term is to be included use the results from models 35–39, and additionally apply Eq. (6). This colour term is derived for the QSOs sample (G ≳ 17 mag, 0.2 ≲ (GBP − GRP) ≲ 1.6 mag) and is untested outside this range.
-
Add the spatial and magnitude (+colour) correction, and add the errors in quadrature. Subtract the total from the observed parallax to obtain the corrected parallax, that is, an estimate of the true parallax (Eq. (1)). Also in this last step the errors should be added in quadrature.
Following the examples described in Sect. 5, it is recommended to follow this procedure for all available HEALPix levels and then choose the highest level that does not compromise the S/N.
It was confirmed (Riess 2021, priv. comm.) that two corrections are necessary in Table 1 of Riess et al. (2021) to match their analysis; Z Sct is missing there but is available in Table 1 of Riess et al. 2018b, and the high GOF flag on AD Pup (GOF = 12.48) should instead appear on RX Cam (GOF = 28.7).
Acknowledgments
This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This research has made use of the SIMBAD database, the VizieR catalogue access tool and the cross-match service provided by CDS, Strasbourg. Thanks to Francois-Xavier Pineau for explaining the best use of the cross-match service. Some of the results in this paper have been derived using the healpy and HEALPix package. I would like to thank Drs. Kareen El-Badry and Valentin Ivanov for discussions on wide binaries and quasar catalogues, respectively, and the referee for a careful reading of the manuscript and helpful suggestions.
References
- Anderson, R. I. 2018, A&A, 611, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benedict, G. F., McArthur, B. E., Nelan, E. P., & Harrison, T. E. 2017, PASP, 129, 012001 [NASA ADS] [CrossRef] [Google Scholar]
- Bhardwaj, A., Rejkuba, M., de Grijs, R., et al. 2021, ApJ, 909, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Bond, H. E., Nelan, E. P., Remage Evans, N., Schaefer, G. H., & Harmer, D. 2018, ApJ, 853, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Casertano, S., Riess, A. G., Anderson, J., et al. 2016, ApJ, 825, 11 [Google Scholar]
- Chan, V. C., & Bovy, J. 2020, MNRAS, 493, 4367 [CrossRef] [Google Scholar]
- Clementini, G., Ripepi, V., Molinaro, R., et al. 2019, A&A, 622, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- El-Badry, K., Rix, H. W., & Heintz, T. M. 2021, MNRAS, 506, 2269 [NASA ADS] [CrossRef] [Google Scholar]
- Fabricius, C., Luri, X., Arenou, F., et al. 2021, A&A, 649, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flesch, E. W. 2019, ArXiv e-prints [arXiv:1912.05614] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021a, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Klioner, S. A., et al.) 2021b, A&A, 649, A9 [EDP Sciences] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Graczyk, D., Pietrzyński, G., Gieren, W., et al. 2019, ApJ, 872, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Groenewegen, M. A. T. 2018, A&A, 619, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huang, Y., Schönrich, R., Zhang, H., et al. 2020, ApJS, 249, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, Y., Yuan, H., Beers, T. C., & Zhang, H. 2021, ApJ, 910, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Khan, S., Miglio, A., Mosser, B., et al. 2019, The Gaia Universe, 13 [Google Scholar]
- Layden, A. C., Tiede, G. P., Chaboyer, B., Bunner, C., & Smitka, M. T. 2019, AJ, 158, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Leung, H. W., & Bovy, J. 2019, MNRAS, 489, 2079 [NASA ADS] [CrossRef] [Google Scholar]
- Lindegren, L. 2018, GAIA-C3-TN-LU-LL-124 [Google Scholar]
- Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Klioner, S. A., Hernández, J., et al. 2021a, A&A, 649, A2 [EDP Sciences] [Google Scholar]
- Lindegren, L., Bastian, U., Biermann, M., et al. 2021b, A&A, 649, A4 [EDP Sciences] [Google Scholar]
- Muraveva, T., Delgado, H. E., Clementini, G., Sarro, L. M., & Garofalo, A. 2018, MNRAS, 481, 1195 [Google Scholar]
- Press, W., Teukolsky, S., Vetterling, W., & Flannery, B. 1992, Numerical Recipes in C (Cambridge: Cambridge University Press) [Google Scholar]
- Ren, F., Chen, X., Zhang, H., et al. 2021, ApJ, 911, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Casertano, S., Anderson, J., MacKenty, J., & Filippenko, A. V. 2014, ApJ, 785, 161 [Google Scholar]
- Riess, A. G., Macri, L. M., Hoffmann, S. L., et al. 2016, ApJ, 826, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Casertano, S., Yuan, W., et al. 2018a, ApJ, 861, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Casertano, S., Yuan, W., et al. 2018b, ApJ, 855, 136 [Google Scholar]
- Riess, A. G., Casertano, S., Yuan, W., Macri, L. M., & Scolnic, D. 2019, ApJ, 876, 85 [Google Scholar]
- Riess, A. G., Casertano, S., Yuan, W., et al. 2021, ApJ, 908, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Ripepi, V., Molinaro, R., Musella, I., et al. 2019, A&A, 625, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schönrich, R., McMillan, P., & Eyer, L. 2019, MNRAS, 487, 3568 [Google Scholar]
- Stassun, K. G., & Torres, G. 2018, ApJ, 862, 61 [Google Scholar]
- Stassun, K. G., & Torres, G. 2021, ApJ, 907, L33 [NASA ADS] [CrossRef] [Google Scholar]
- van Belle, G. T., Schaefer, G. H., von Braun, K., et al. 2020, PASP, 132, 054201 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, E. B., & Hilferty, M. M. 1931, Proc. Natl. Acad. Sci., 17, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, S., Zhang, B., Reid, M. J., Zheng, X., & Wang, G. 2019, ApJ, 875, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Zinn, J. C. 2021, AJ, 161, 214 [Google Scholar]
- Zinn, J. C., Pinsonneault, M. H., Huber, D., & Stello, D. 2019, ApJ, 878, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Zonca, A., Singer, L., Lenz, D., et al. 2019, J. Open Source Software, 4, 1298 [Google Scholar]
Appendix A: Parallax difference for classical pulsators
Figure A.1 is similar to Figs. 9 and 10 but for the sample of 15 CCs, T2Cs, and RRL stars. Two outliers are plotted as open triangles. They are FF Aql and Polaris B. FF Aql is very bright (G = 5.1 mag) and this may be the reason for the offset. For Polaris B the reason is less clear. The GOF (3.55) and RUWE (1.15) easily fall within the applied selection criteria. The difference between the FGS parallax for Polaris B and the Hipparcos parallax for Polaris A has been discussed in the literature without reaching a conclusion on its implications (Bond et al. 2018; Anderson 2018; Appendix B in Groenewegen 2018).
 |
Fig. A.1. Difference between the independent trigonometric parallax and the GEDR3 parallax plotted against G, (GBP − GRP) colour, and sin β for the 15 CCs, T2Cs, and RRL stars. Two outliers are plotted as open triangles. |
All Tables
All Figures
 |
Fig. 1. Distribution of the GOF with a Gaussian fit. Top panel: approximately 841 000 QSOs with parallaxes and PMs consistent with zero. A significant tail toward large GOF is visible. Lower panel: fit with GOF restricted to < + 2.0. |
| In the text | |
 |
Fig. 2. Distribution of G, (GBP − GRP) colour and RUWE for the QSO sample after applying selections on parallax, PM, GOF, and RUWE. |
| In the text | |
 |
Fig. 3. PZPO for the QSO sample as a function of G, (GBP − GRP) colour and ecliptic latitude (open circles). Only bins with ≥5 objects are plotted. Bins with 100 objects or less are plotted in blue, with 30 objects or less in red. The lines in the top panel and the lines in the middle panel are not a fit to the data, but are based on Eq. (5). The blue points in the lower panel indicate the PZPO for the 48 HEALPix level 1 pixels. The horizontal bar gives the range in sin β for each HEALPix pixel. |
| In the text | |
 |
Fig. 4. PZPO for the QSO sample with G > 17 mag as a function of sin β. Black open circles represent the observed data (the weighted mean) to be compared to the blue open circles that represent the L20 correction (the unweighted mean as the L20 correction carries no error). The black filled circles represent the corrected parallax data (according to Eq. (5)) to be compared to the red filled circles that represent the spatial correction at G = 20 mag at HEALPix level 2 (both are weighted means, but the error in the red filled circles is too small to be visible). |
| In the text | |
 |
Fig. 5. Top panel: parallax difference between the primary and secondary components in wide binaries as a function of primary G magnitude. Bins with more than 1000 objects are plotted in blue. Bottom panel: parallax of the secondary binary component plotted against that of the primary. Objects with primary G magnitude larger than 5, 15, 17, 19, and 20 mag are plotted as black, red, green, dark blue, and light blue dots, respectively. About 590 000 binaries are plotted where both components pass the criteria on GOF and RUWE. |
| In the text | |
 |
Fig. 6. As in Fig. 5 but for Gs restricted to < 19.0 mag. After eliminating about 700 extreme outliers (those outside the two plotted lines in the top panel), a sample of about 480 000 objects remain. The bottom panel shows the parallax difference between primary and secondary component for that sample as a function of Gp. We note the different range in the ordinate compared to Fig. 5. |
| In the text | |
 |
Fig. 7. As in Fig. 5 but with parallaxes corrected according to Eq. (7) in consecutive steps (see main text). The bottom panel shows the applied correction (Eq. (7)) as the black line. The small black, red, and green circles represent the L20 correction for β = 0, −60, and +60°. There is an offset as the L20 corrections are absolute, while the corrections applied to the WB sample are relative to the correction at G = 20 mag. |
| In the text | |
 |
Fig. 8. Residual in the observed parallax after applying the correction in the present work (in black open circles, offset by −0.004 units horizontally) and the correction used in L20 (in blue filled circles, offset by +0.004 units) versus sin β for the QSO sample. Sixty bins have been used, and HEALPix level 2 has been used in the calculations. |
| In the text | |
 |
Fig. 9. Independent trigonometric parallax plotted against GEDR3 parallax. The bottom panel displays the residual, where the error bar in the ordinate combines the error in the Gaia and the independent parallax in quadrature. Two stars where the residual is more than ten times the combined error bar are plotted as open triangles. |
| In the text | |
 |
Fig. 10. Difference between the independent trigonometric parallax and the GEDR3 parallax plotted against G, (GBP − GRP) colour, and sin β. The two outliers mentioned in Fig. 9 have been removed. |
| In the text | |
 |
Fig. 11. Top panel: PZPO correction by L20 for the sample of 66 CCs analysed by Riess et al. (2021) (cf. their Fig. 2). The colours represent different ranges in G: black (G ≤ 7), red (7 < G ≤ 8.5), green (8.5 < G ≤ 9.0), and blue (9 < G ≤ 11.5). Bottom panel: correction proposed here for the stricter selected sample of 54 stars at HEALPix level 2. |
| In the text | |
 |
Fig. A.1. Difference between the independent trigonometric parallax and the GEDR3 parallax plotted against G, (GBP − GRP) colour, and sin β for the 15 CCs, T2Cs, and RRL stars. Two outliers are plotted as open triangles. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.