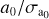EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 669 (January 2023) A&A, 669 (2023) A4 Full HTML
Open Access
Issue
A&A
Volume 669, January 2023
Article Number A4
Number of page(s) 10
Section Catalogs and data
DOI https://doi.org/10.1051/0004-6361/202244479
Published online 23 December 2022

© The Authors 2022

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.

1 Introduction

With the second data release (DR; Gaia Collaboration 2018) of the Gaia mission (Gaia Collaboration 2016), it was demonstrated that the mean parallax of quasi-stellar objects (QSOs) was not zero, but is slightly negative, −0.029 mas (Lindegren et al. 2018). This was confirmed in the third early DR (GEDR3; Gaia Collaboration 2021), where the average and median parallax zero-point offset (PZPO) of QSOs are −21 and −17 µas, respectively (Lindegren et al. 2021; hereafter L21). L21 presented a Python script to the community that returned the PZPO (without an error bar) as a function of input parameters, namely ecliptic latitude (β), G-band magnitude, the astrometric_params_solved parameter, and either the effective wavenumber of the source used in the astrometric solution (veff, nu_eff_used_in_astrometry for the five-parameter solution astrometric_params_solved = 31) or the astrometrically estimated pseudo-colour of the source (pseudocolour) for the six-parameter solution (astrometric_params_solved = 95). The module is defined in the range 6 < G < 21 mag, 1.72 > veff > 1.24 µm−1, corresponding to about 0.15 < (GBP – GRP) < 3.0 mag where G, GBP, and GRP are the magnitudes in the Gaia G, Bp, and Rp band, respectively. The script is based on the parallax values of QSOs and wide-binary systems (WBS; see L21 for all details).

In parallel, after the publication of GDR2 numerous studies appeared that studied the PZPO offset using other classes of stars, typically at brighter magnitudes than the QSOs. Examples using GDR2 data are studies of classical cepheids (CCs; Riess et al. 2018; Groenewegen 2018) that found a more negative value (−0.046 ± 0.013 and -0.049 ± 0.018 mas, respectively), RR Lyrae (~−0.056 mas, Muraveva et al. 2018, −0.042 ± 0.013 mas, Layden et al. 2019), red clump stars (Chan & Bovy 2020), (detached) eclipsing binaries (Stassun & Torres 2018; Graczyk et al. 2019), red giant asteroseismic parallaxes (Zinn et al. 2019; Khan et al. 2019), and stars with parallaxes from very long baseline interferometry (Xu et al. 2019), amongst others. With the advent of GEDR3 this line of research has continued (Huang et al. 2021; Stassun & Torres 2021; Ren et al. 2021; Zinn 2021; Riess et al. 2021; Maíz Apellániz 2022, hereafter MA22), including claims that the L21 procedure overcorrects the PZPO (Riess et al. 2021; Zinn 2021), at least for brighter objects. Alternative procedures for the L21 correction have been proposed by Groenewegen (2021, hereafter G21) and MA22. Clearly, the spatial, magnitude, and colour dependence of the PZPO remains of great interest.

One disadvantage of using alternative classes of objects is the intrinsic assumption is that the distances to those objects are known exactly, and with an accuracy comparable to that of Gaia. However, with the exception of the QSOs that truly have a parallax of zero for all practical purposes, this is based on direct or indirect assumptions or model dependences, such as reddening, a (linear) period-luminosity relation, an absolute magnitude, or a surface-brightness colour relation.

Binaries for which the astrometric and spectroscopic orbits are known offer the possibility of deriving the orbital parallax free from any assumption, based on Kepler laws. The only limitation in the accuracy of the distance is ultimately the quality of the data. GDR3 (Gaia Collaboration 2023b) offers the possibility of comparing Gaia trigonometric parallaxes to orbital parallaxes. In previous releases, the Gaia astrometric solution assumed single stars. Therefore, the quality parameters of the astrometric solution, such as the goodness of fit (GOF, astrometric_gof_al) or the renormalised unit weight error (RUWE), were (very) poor for (close) binary systems. In GDR3, non-single star (NSS) solutions are considered (Halbwachs et al. 2023; Gaia Collaboration 2023a), which means that for a subset of stars, (improved) parallaxes are determined that binary motion into account. Individual studies of astrometric and spectroscopic binary orbits also often derived the orbital parallax and compared it to HIPPARCOS or Gaia data, but no real systematic differences can be identified as the PZPO is a small quantity using mostly single objects (Gallenne et al. 2019 used four objects in the comparison of the orbital parallax and GDR2 data).

The paper is structured as follows. In Sect. 2, the sample of binaries is introduced and confronted with G(E)DR3 data. The impact and limitations of the DR3 NSS analysis are discussed in Sects. 3.1 and 3.2, and the PZPO is discussed in Sect. 3.3. A brief discussion and summary conclude the paper.

2 Sample

Recently, Piccotti et al. (2020) compiled a list of 69 SB2s with both visual and spectroscopic orbits, but the emphasis of that paper was on the masses and ages of the systems. The sample selection followed that of Piccotti et al. (2020) and was based on an extensive literature search using the Sixth Catalogue of Orbits of Visual Binary Stars (ORB6; Hartkopf et al. 2001, starting from orbits with grades 1, 2, and 3)1 and the Ninth Catalogue of Spectroscopic Binary orbits (SB9; Pourbaix et al. 2004)2. This initial correlation pointed to other literature that was then searched. Articles by specific authors were searched through the ADS, and the arXiv was monitored for relevant papers. The literature search ended May 10, 2022. Table 1 lists the adopted orbital elements and velocity amplitudes with references for a total of 186 systems. For six binaries, several components have been resolved (WDS 03272+0944, 06024+0939, 06290+2013, 17247+3802, 20396+0458, and 22388+4419), and therefore the table has 192 entries. This almost triples the number of systems compared to Piccotti et al. (2020). Although it was attempted to make this list complete, this cannot be guaranteed. Obviously, GDR3 provides orbital elements and velocity amplitudes for selected systems, and the impact of this is discussed in Sect. 3.2.

The orbital parallax follows from the orbital elements as 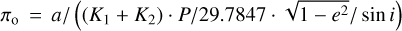πo=a/((K1+K2).P/29.7847.1−e2/sini)${\pi _{\rm{o}}} = {a \mathord{\left/{\vphantom {a {\left( {({K_1} + {K_2}).{P \mathord{\left/{\vphantom {P {29.7847.{{\sqrt {1 - {e^2}} } \mathord{\left/{\vphantom {{\sqrt {1 - {e^2}} } {\sin i}}} \right.\kern-\nulldelimiterspace} {\sin i}}}}} \right.\kern-\nulldelimiterspace} {29.7847.{{\sqrt {1 - {e^2}} } \mathord{\left/{\vphantom {{\sqrt {1 - {e^2}} } {\sin i}}} \right.\kern-\nulldelimiterspace} {\sin i}}}}} \right)}}} \right.\kern-\nulldelimiterspace} {\left( {({K_1} + {K_2}).{P \mathord{\left/{\vphantom {P {29.7847.{{\sqrt {1 - {e^2}} } \mathord{\left/{\vphantom {{\sqrt {1 - {e^2}} } {\sin i}}} \right.\kern-\nulldelimiterspace} {\sin i}}}}} \right.\kern-\nulldelimiterspace} {29.7847.{{\sqrt {1 - {e^2}} } \mathord{\left/{\vphantom {{\sqrt {1 - {e^2}} } {\sin i}}} \right.\kern-\nulldelimiterspace} {\sin i}}}}} \right)}}$(1)

where a is the semi-major axis in mas, K1 and K2 are the velocity semi-amplitudes of the two components (in km s−1), P is the orbital period in years, e is the eccentricity of the orbit, i is the inclination in degrees, and πo is the orbital parallax in mas. The error in πo is calculated through standard error propagation assuming all errors are independent. The orbital parallaxes and errors are listed in Table 2.

No selection on the accuracy of period, major axis, inclination, or velocity amplitude is made to be included in the sample, even if a large error implies a large error on the orbital parallax and likely a value that is not competitive in accuracy with the Gaia value. For objects for which no error bars on the orbital elements was published, an error of 1.3, 6, and 40% on period, 2.5, 15, and 40% on a, 5, 12, and 27° on i, and 0.01, 0.02, and 0.10 on e was adopted for orbits of grade 1, 2, and 3 in ORB6, respectively. If no error on the velocity amplitude was reported, an error of 5% was adopted. These cases are marked in Table 1 and are good targets for further observations to improve on the orbital parameters.

As a first step and as preparation for the DR3 release, the objects were identified in GEDR3 and also in the HIPPARCOS catalogue (the new reduction version by van Leeuwen 2008). The later proved essential in many cases as the epoch 1991.25 HIPPARCOS coordinates could be transformed to the epoch 2016.0 of GEDR3/GDR3 to properly identify the correct object that was achieved by comparing coordinates, parallax, and magnitude. It was then trivial to identify the correct object with the release of DR3, and Table 2 gives the orbital parallax (based on the data in Table 1 and Eq. (1)), and some information from HIPPARCOS and DR3 for the 192 objects. DR3 includes some parameters that were used in the pre-filtering stage of the astrometric binary pipeline (Halbwachs et al. 2023); they are discussed in detail below.

Inspection of Table 1 reveals that quite a number of objects (59, or about 30%) are not listed in GDR3, or are listed without parallax. The former are six of the very brightest objects (all have V ≲ 2.7 mag). The others only have two-parameter solutions (astrometric_params_solved = 3). However, these objects may potentially be in WBS. To investigate this further, the objects were correlated with the catalogue of El-Badry et al. (2021, based on GEDR3 data). Fourteen matches were found at distances up to 57″. However, objects without a parallax or proper motion in GEDR3 are obviously missing from El-Badry et al. (2021). In a second step, all sources within 1′ were retrieved from GDR3 and a potential list of WBS was compiled based on the orbital parallax and criteria on the parallax difference so that the search would retrieve all 14 matches in El-Badry et al. (2021). In a final step, the GDR3 and HIPPARCOS parallaxes and proper motions were inspected to make a final list of likely WBS, keeping only stars with Bp and Rp photometry. The information of these 37 sources is listed in Table A.1.

3 Results

3.1 Effects of pre-filtering in the NSS processing

Table A.2 shows that only 21 of the 180 (186 unique objects minus 6 stars not in DR3) known binaries have a non-zero NSS flag. In other words, 90% of the known binaries have not been flagged as such by the NSS pipeline(s). Although this is the reality of the current release, it might be instructive to investigate how these binaries were overlooked. Halbwachs et al. (2023) described the processing of astrometric binary stars. Stars were selected to be brighter than G = 19 mag and have 12 or more visibility periods. The first criteria has no impact, and the second removes 23 objects. There is a selection on keeping sources with RUWE < 1.4, removing 93 objects (of the 130 that have a RUWE listed), on ipd_frac_multi_peak ≤ 2, removing 64 objects, on ipd_gof_harmonic_amplitude <0.1, removing 57 objects, and on the significance of the modified Bp-Rp excess, ∣C*∣/σC* < 1.645, removing 113 objects.

Only 30 objects meet all pre-selection criteria. Additional objects are likely to have been removed in the processing and the post-processing steps (see details in Halbwachs et al. 2023). Similar criteria must have been adopted in the processing of spectroscopic binaries, but the paper describing this has not been published at the time of submission. As the aim of the paper is to use improved parallaxes from the astrometric binary pipeline, the details of the processing in the spectroscopic binary pipeline are less relevant here.

Table 1

Sample of stars (selected entries).

Table 2

Parallax data (selected entries).

3.2 Comparing the orbital elements of the NSS processing with the literature

Comparison of the orbital elements in Table A.2 with those in the literature reveals that a number of them (03396+1823, 04179−3348, 12313+5507, 17038−3809, 17422+3804, 18339+5144, 23456+1309, 23485+2539, and 18339+5144) refer to a different component than listed in Table 1, because period, eccentricity or velocity amplitude do not match. In all cases except one, the period in Table A.2 is the shorter one, suggesting that the elements refer to some inner orbit of the multiple system. Consultation of the ORB6 suggests that none of these orbits was known.

In the other cases, the elements found by the NSS analysis are not more precise than known in the literature, which were therefore kept. The median and 1.4826x median absolute deviation (MAD; equivalent to 1σ in a Gaussian distribution) were calculated of 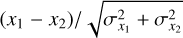(x2−x2)/σx12+σx22${{\left( {{x_2} - {x_2}} \right)} \mathord{\left/{\vphantom {{\left( {{x_2} - {x_2}} \right)} {\sqrt {\sigma _{{x_1}}^2 + \sigma _{{x_2}}^2} }}} \right.\kern-\nulldelimiterspace} {\sqrt {\sigma _{{x_1}}^2 + \sigma _{{x_2}}^2} }}$, where x represents period, eccentricity, or the velocity amplitudes, from the literature and the NSS analysis, and which are expected to be zero and unity, respectively.

Although the sample is small the errors on the parameters in the SB2 solution appear to be underestimated, as is indeed suggested at the end of Sect. 6 in Babusiaux et al. (2023). When we take the formal errors, the width of the distribution is about 4–9σ. When the errors are Scaled with 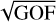GOF$\sqrt {{\rm{GOF}}}$, this is reduced to 0.8−1.5σ. For the non-SB2 solutions, the width is 0.6−1.6σ, suggesting that the error estimates are realistic.

3.3 PZPO

The main aim of the paper is to the investigate the PZPO. Figure 1 shows the difference of DR3 parallax minus orbital parallax for the objects plotted against G magnitude. The range in ordinate is ±12 mas to display all points. The Gaia parallax is the improved parallax from the NSS analysis (with its associated GOF parameter) for the eight stars in Table A.2 and from Table 1 otherwise. Added are the 37 WBS from Table A.1 for a total of 170 determinations plotted. When two Gaia parallaxes were available (from the counterpart of the orbital parallax source and from a WBS), they were not averaged as the PZPO depends on magnitude and possibly on colour. The figure shows that some of the parallax errors (dominated by the error in orbital parallax) are large and do not constrain any difference with the DR3 parallaxes. Unless specified otherwise, a standard selection (SS) is applied from now on choosing objects where the error in the orbital parallax should be smaller than five times the error in the DR3 parallax, the error in the orbital and DR3 parallaxes should be smaller than 2 mas, the ratio of the absolute difference between orbital and DR3 parallax to the combined error bar should be lower than five, and the GOF (either from the astrometric solution or the NSS solution) should be lower than 100, reducing the number of points to 68. In Fig. 1, these points are plotted in blue, and Fig. 2 shows a zoom with ordinates of ±0.15 mas using this selection. The data were also binned in G mag, using five bins that started at G = 0, 5.0, 6.0, 7.4, and 9.2 mag (this last bin includes all fainter objects), where the weighted mean (and error on the mean) was calculated, and plotted at the mean G magnitude of the objects in that bin. The first bin collects all of the brightest objects. Bright limits of 5.0 and 6.0 mag were used in G21 and L21/MA22, respectively, while 7.4 and 9.2 mag are cardinal magnitudes used in MA22. The weighted average over all objects results in an offset of −41.7 ± 10.7 µas (model 1 in Table 3, which also includes the values per magnitude bin).

Several corrections to the G(E)DR3 parallaxes have been proposed, and it is interesting to compare the corrected parallaxes to the orbital ones. To guide the eye, the solid line in Fig. 2 shows the magnitude correction from G21 with a constant spatial offset of −0.013 mas added (the average spatial correction of the sample following G21 at HEALPix level 0). We recall that the HEALPix formalism (Górski et al. 2005) is a convenient way to divide the sky into equal-area pixels. At HEALPix level 0, there are 12 pixels, and this increases by a factor of four for every next higher level. The HEALPix formalism is used by the Gaia team and is encoded in the source_id3.

Below, we apply different corrections on a star-by-star basis to the GDR3 parallaxes. If the corrections work the weighted mean difference should be consistent with zero. The first correction is the one by L21 (model 2). The number of sources is reduced to 30 as the correction is only defined for stars fainter than magnitude 6. After correction, the difference with the orbital parallax is −8.7 ± 11.5 µas. Model 3 shows the results for the MA22 correction, which is an extension of L21. The resulting difference is marginally closer to zero. We note that the errors on the correction are identical to applying no correction. This is related to the fact that the L21 and MA22 provided the offset without error bars. Finally, the G21 formalism was tested. The correction depends on the chosen HEALPix level and consists of a spatial correction defined at G = 20 mag (depending on the source coordinates (i.e. a certain pixel) at a chosen HEALPix level) and an additive magnitude correction. Following G21, only pixels with more than 40 QSOs have been considered. Models 4-8 show the results for HEALPix levels 0−4, respectively. As the G21 correction is defined for G > 5, there are more objects at the lower HEALPix levels, but then the number decreases with increasing HEALPix level as the number of objects in pixels with insufficient QSOs increases. HEALPix level 2 seems a good compromise between the sampling of the spatial correction and the loss of objects, and the result is comparable to the results for the other correction methods. If the G21 correction is limited to G > 6 mag, as it is for the other two methods, the resulting difference is very close to zero (model 6a).

The SS is useful to obtain insight into the overall behaviour of the PZPO but now a stricter final selection (FS) is introduced. As there are few objects fainter than tenth magnitude that nevertheless cover a wide range, and because there are very few extremely bright objects, the sample was restricted in magnitude and two bins from 4−6.162 and 6.162−10.591 mag (two breakpoints in Eq. (7) in G21) were considered. As there is a general offset between orbital and Gaia parallaxes, the condition on the difference of the two was modified to |(πGaia − (−0.04 mas)) − πorb|/σc < 5.0, where σc is the combined error of the Gaia and the orbital parallax 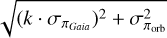(k⋅σπGaia)2+σπorb2$\sqrt {{{\left( {k \cdot {\sigma _{{\pi _{Gaia}}}}} \right)}^2} + \sigma _{\pi {\rm{orb}}}^2}$. The factor k is the error inflation factor, which was set to unity in the SS. Several papers have found that the error bars in the astrometric solution are underestimated (Fabricius et al. 2021; Maíz Apellániz et al. 2021; MA22). Here the formalism by El-Badry et al. (2021) was used. There correction was derived for G < 7 mag, but it will be used for brighter magnitudes as well. The effect is small in any case, k = 1.10−1.15 for G < 10 mag. Finally, a more stringent cut on the GOF was imposed. The distribution of the GOF of QSOs was discussed in G21, and in that paper an interval from −4 to +5 was chosen for acceptable solutions. Here the upper limit is slightly relaxed to +8, resulting in a sample of 20 objects. This is consistent with the other often-used selection criterion of RUWE <1.4, which would result in 23 objects.

Model 9 in Table 3 gives the results, and they are displayed in Fig. 3. This figure also shows the offset as a function of Bp-Rp colour with the range in ordinate chosen to show all objects, indicating that there is no evident dependence on colour. Models 10−16 show the results after applying the various correction methods. The results are very similar as before. All three proposed models bring the differences closer to zero, and consistent with zero within the error bars. When restricted to G magnitudes fainter than 6, G21 again provides the correction closest to zero for HEALPix level 2. Nevertheless, most of the results suggest that the corrections may be slightly underestimated (i.e. should be more negative), at least on average over the 6−10 magnitude range.

thumbnail Fig. 1

Parallax difference in the sense DR3 minus orbital parallax for the entire sample. The range in ordinate is ±12 mas. The stars from the SS are plotted in blue (see text).
thumbnail Fig. 2

Zoom of Fig. 1, with the SS applied as described in the text. There are points outside the plot range. The blue points are the weighted averages plotted at the mean magnitude of the objects in the magnitude bins. The solid lines represent the magnitude dependence of the PZPO from G21 with an average spatial correction of −0.013 mas added.
thumbnail Fig. 3

Parallax difference. Top panel: as Fig. 2 for the final selection as described in the text. There are points outside the plot range. Middle panel: offset plotted against Bp-Rp colour. The ordinate is chosen to be ±1 mas to show all data points in the sample, and the bottom panel has the same range in ordinate as in the top panel.
Table 3

Parallax differences for different assumptions.

4 Conclusions

The results from the NSS analysis specific to GDR3 show the potential but also the limitations of the current release. Of the sample of 186 known binaries compiled from the literature to have an orbital parallax, only 8 have an astrometric and 13 have an spectroscopic orbit determined from the NSS analysis. Most objects are eliminated at the pre-filtering stage of the NSS analysis. The analysis of the parallax difference between Gaia and orbital parallax is therefore strongly influenced by the large GOF parameter in the main astrometric catalogue, limiting the number of useful objects. The PZPO corrections proposed by L21, G21, and M22 give similar residuals. After these corrections were applied the remaining parallax differences were formally consistent with zero within the error bar for all three recipes. The current data and analysis therefore do not prefer a particular PZPO correction scheme over the other two.

Several improvements may be anticipated in the near future. The number of systems for which an orbital parallax will become available will likely grow, or orbital elements of existing systems will improve. For about one-third of the systems, separate astro-metric and spectroscopic orbits exist that were used to obtain the orbital parallax. For consistency, the existing data could be combined to obtain a single solution.

The situation might improve by DR4. The orbital parallax for 18 out of 20 stars in the final selection sample is accurate to better then 5%, and is even better than the Gaia value for 6 stars. In the full sample, 148 stars have an orbital parallax determination better than 5%. Having NSS solutions available for a eight times larger sample would lead to a significantly more precise determination of the PZPO at bright magnitudes. Whether this is realistic would depend on how much the criteria in the pre-filtering and post-processing stages could be relaxed. The impact of the former has been discussed, but some of the stars in the sample may also have been eliminated at the latter stage. Halbwachs et al. (2023) mentioned three criteria that have been applied as well. The one on parallax accuracy4 would eliminate about 45% of the sample. The selection on eccentricity accuracy5 would eliminate 1% of the sample, and the one on the significance of the photocenter major axis6 about 4%. Alternatively, with the planned release of the complete astrometric and spectroscopic time-series data with DR4, the community could combine Gaia data with literature data in order to obtain the best-determined orbit.

Acknowledgements

MG is grateful to the International Space Science Institute (ISSI) for support provided to the SH0T ISSI International Team (https://www.issibern.ch/teams/shot/). This work has made use of data from the European Space Agency (ESA) mission Gaia (http://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, http://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This research has made use of the SIMBAD database and the VizieR catalogue access tool operated at CDS, Strasbourg, France.

Appendix A Additional tables

Table A.1

Parameters for the WBS sample

Table A.2

Parameters from the NSS analysis

References

  1. Agati, J. L., Bonneau, D., Jorissen, A., et al. 2015, A&A, 574, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Anguita-Aguero, J., Mendez, R. A., Clavería, R. M., & Costa, E. 2022, AJ, 163, 118 [NASA ADS] [CrossRef] [Google Scholar]
  3. Babusiaux, C., Fabricius, C., Khanna, S., et al. 2023, A&A, in press, 10.1051/0004-6361/202243790 [Google Scholar]
  4. Bagnuolo, W. G. Jr., Taylor, S. F., McAlister, H. A., et al. 2006, AJ, 131, 2695 [NASA ADS] [CrossRef] [Google Scholar]
  5. Baron, F., Monnier, J. D., Pedretti, E., et al. 2012, ApJ, 752, 20 [CrossRef] [Google Scholar]
  6. Boden, A. F., Lane, B. F., Creech-Eakman, M. J., et al. 1999, ApJ, 527, 360 [NASA ADS] [CrossRef] [Google Scholar]
  7. Boden, A. F., Torres, G., & Latham, D. W. 2006, ApJ, 644, 1193 [NASA ADS] [CrossRef] [Google Scholar]
  8. Chan, V. C., & Bovy, J. 2020, MNRAS, 493, 4367 [Google Scholar]
  9. Docobo, J. A., Belega, Y., & Campo, P. P. 2018a, IAUDS Inf. Circ., 196, 1 [Google Scholar]
  10. Docobo, J. A., Campo, P. P., & Abushattal, A. A. 2018b, IAUDS Inf. Circ., 169, 1 [Google Scholar]
  11. El-Badry, K., Rix, H.-W., & Heintz, T. M. 2021, MNRAS, 506, 2269 [NASA ADS] [CrossRef] [Google Scholar]
  12. Fabricius, C., Luri, X., Arenou, F., et al. 2021, A&A, 649, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Farrington, C. D., ten Brummelaar, T. A., Mason, B. D., et al. 2014, AJ, 148, 48 [NASA ADS] [CrossRef] [Google Scholar]
  14. Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Gaia Collaboration (Arenou, F., et al.) 2023a, A&A, in press, 10.1051/0004-6361/202243782 [Google Scholar]
  18. Gaia Collaboration (Vallenari, A., et al.) 2023b, A&A, in press, 10.1051/0004-6361/202243940 [Google Scholar]
  19. Gallenne, A., Pietrzynski, G., Graczyk, D., et al. 2018, A&A, 616, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Gallenne, A., Pietrzynski, G., Graczyk, D., et al. 2019, A&A, 632, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [Google Scholar]
  22. Graczyk, D., Pietrzynski, G., Gieren, W., et al. 2019, ApJ, 872, 85 [NASA ADS] [CrossRef] [Google Scholar]
  23. Griffin, R. F. 2012a, J. Astrophys. Astron., 33, 29 [NASA ADS] [CrossRef] [Google Scholar]
  24. Griffin, R. F. 2012b, The Observatory, 132, 309 [NASA ADS] [Google Scholar]
  25. Griffin, R. F. 2018, The Observatory, 138, 192 [NASA ADS] [Google Scholar]
  26. Groenewegen, M. A. T. 2018, A&A, 619, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Groenewegen, M. A. T. 2021, A&A, 654, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Halbwachs, J. L., Boffin, H. M. J., Le Bouquin, J. B., et al. 2016, MNRAS, 455, 3303 [NASA ADS] [CrossRef] [Google Scholar]
  29. Halbwachs, J.-L., Kiefer, F., Lebreton, Y., et al. 2020, MNRAS, 496, 1355 [NASA ADS] [CrossRef] [Google Scholar]
  30. Halbwachs, J.-L., Pourbaix, D., Arenou, F., et al. 2023, A&A, in press, 10.1051/0004-6361/202243969 [Google Scholar]
  31. Hartkopf, W. I., Mason, B. D., & Worley, C. E. 2001, AJ, 122, 3472 [NASA ADS] [CrossRef] [Google Scholar]
  32. Hill, G., Barnes, J. V., Hutchings, J. B., & Pearce, J. A. 1971, ApJ, 168, 443 [NASA ADS] [CrossRef] [Google Scholar]
  33. Huang, Y., Yuan, H., Beers, T. C., & Zhang, H. 2021, ApJ, 910, L5 [NASA ADS] [CrossRef] [Google Scholar]
  34. Hummel, C. A., Armstrong, J. T., Buscher, D. F., et al. 1995, AJ, 110, 376 [Google Scholar]
  35. Jao, W.-C., Nelan, E. P., Henry, T. J., Franz, O. G., & Wasserman, L. H. 2016, AJ, 152, 153 [NASA ADS] [CrossRef] [Google Scholar]
  36. Khan, S., Miglio, A., Mosser, B., et al. 2019, in The Gaia Universe, 13 [Google Scholar]
  37. Kiefer, F., Halbwachs, J. L., Lebreton, Y., et al. 2018, MNRAS, 474, 731 [NASA ADS] [CrossRef] [Google Scholar]
  38. Konacki, M., & Lane, B. F. 2004, ApJ, 610, 443 [NASA ADS] [CrossRef] [Google Scholar]
  39. Layden, A. C., Tiede, G. P., Chaboyer, B., Bunner, C., & Smitka, M. T. 2019, AJ, 158, 105 [NASA ADS] [CrossRef] [Google Scholar]
  40. Lester, K. V., Fekel, F. C., Muterspaugh, M., et al. 2020, AJ, 160, 58 [NASA ADS] [CrossRef] [Google Scholar]
  41. Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Lindegren, L., Bastian, U., Biermann, M., et al. 2021, A&A, 649, A4 [EDP Sciences] [Google Scholar]
  43. Maíz Apellániz, J. 2022, A&A, 657, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Maíz Apellániz, J., Pantaleoni González, M., & Barbá, R. H. 2021, A&A, 649, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Mourard, D., Monnier, J. D., Meilland, A., et al. 2015, A&A, 577, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Muraveva, T., Delgado, H. E., Clementini, G., Sarro, L. M., & Garofalo, A. 2018, MNRAS, 481, 1195 [Google Scholar]
  47. Nemravová, J. A., Harmanec, P., Brož, M., et al. 2016, A&A, 594, A55 [Google Scholar]
  48. Pearce, J. A. 1936, PASP, 48, 214 [NASA ADS] [CrossRef] [Google Scholar]
  49. Piccotti, L., Docobo, J. Á., Carini, R., et al. 2020, MNRAS, 492, 2709 [NASA ADS] [CrossRef] [Google Scholar]
  50. Pourbaix, D. 1999, A&A, 348, 127 [NASA ADS] [Google Scholar]
  51. Pourbaix, D. 2000, A&AS, 145, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Pourbaix, D., Tokovinin, A. A., Batten, A. H., et al. 2004, A&A, 424, 727 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Ren, F., Chen, X., Zhang, H., et al. 2021, ApJ, 911, L20 [NASA ADS] [CrossRef] [Google Scholar]
  54. Riello, M., De Angeli, F., Evans, D. W., et al. 2021, A&A, 649, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Riess, A. G., Casertano, S., Yuan, W., et al. 2018, ApJ, 861, 126 [NASA ADS] [CrossRef] [Google Scholar]
  56. Riess, A. G., Casertano, S., Yuan, W., et al. 2021, ApJ, 908, L6 [NASA ADS] [CrossRef] [Google Scholar]
  57. Stassun, K. G., & Torres, G. 2018, ApJ, 862, 61 [Google Scholar]
  58. Stassun, K. G., & Torres, G. 2021, ApJ, 907, L33 [NASA ADS] [CrossRef] [Google Scholar]
  59. Tokovinin, A. A. 1993, Astron. Lett., 19, 73 [NASA ADS] [Google Scholar]
  60. Tokovinin, A. A. 2016a, AJ, 152, 10 [NASA ADS] [CrossRef] [Google Scholar]
  61. Tokovinin, A. A. 2016b, AJ, 152, 11 [NASA ADS] [CrossRef] [Google Scholar]
  62. Tokovinin, A. A. 2021, IAUDS Inf. Circ., 203, 1 [Google Scholar]
  63. Tokovinin, A. A. 2022, AJ, 163, 161 [NASA ADS] [CrossRef] [Google Scholar]
  64. Tokovinin, A. A., Gorynya, N. A., & Morrell, N. I. 2014, MNRAS, 443, 3082 [NASA ADS] [CrossRef] [Google Scholar]
  65. Tokovinin, A. A., Everett, M. E., Horch, E. P., Torres, G., & Latham, D. W. 2019, AJ, 158, 167 [NASA ADS] [CrossRef] [Google Scholar]
  66. Torres, R. M., Loinard, L., Mioduszewski, A. J., et al. 2012, ApJ, 747, 18 [NASA ADS] [CrossRef] [Google Scholar]
  67. van Leeuwen, F. 2008, VizieR Online Data Catalog: I/311 [Google Scholar]
  68. Wang, X., Ren, S., & Fu, Y. 2015, AJ, 150, 110 [NASA ADS] [CrossRef] [Google Scholar]
  69. Xu, S., Zhang, B., Reid, M. J., Zheng, X., & Wang, G. 2019, ApJ, 875, 114 [NASA ADS] [CrossRef] [Google Scholar]
  70. Zinn, J. C. 2021, AJ, 161, 214 [Google Scholar]
  71. Zinn, J. C., Pinsonneault, M. H., Huber, D., & Stello, D. 2019, ApJ, 878, 136 [Google Scholar]
3

Pixel number = source_id/(235 · 4(12-level)) for a given HEALPix level.

4

π/σπ > 20 000/P (days), using the orbital parallax to evaluate the inequality.

5

σe < 0.182 log P − 0.244.

6

a0/σa0${{{a_0}} \mathord{\left/{\vphantom {{{a_0}} {{\sigma _{{{\rm{a}}_0}}}}}} \right.\kern-\nulldelimiterspace} {{\sigma _{{{\rm{a}}_0}}}}}$ > 158/P (days), but using the major axis of the true orbit instead to evaluate the inequality.

All Tables

Table 1

Sample of stars (selected entries).

In the text
Table 2

Parallax data (selected entries).

In the text
Table 3

Parallax differences for different assumptions.

In the text
Table A.1

Parameters for the WBS sample

In the text
Table A.2

Parameters from the NSS analysis

In the text

All Figures

thumbnail Fig. 1

Parallax difference in the sense DR3 minus orbital parallax for the entire sample. The range in ordinate is ±12 mas. The stars from the SS are plotted in blue (see text).
In the text
thumbnail Fig. 2

Zoom of Fig. 1, with the SS applied as described in the text. There are points outside the plot range. The blue points are the weighted averages plotted at the mean magnitude of the objects in the magnitude bins. The solid lines represent the magnitude dependence of the PZPO from G21 with an average spatial correction of −0.013 mas added.
In the text
thumbnail Fig. 3

Parallax difference. Top panel: as Fig. 2 for the final selection as described in the text. There are points outside the plot range. Middle panel: offset plotted against Bp-Rp colour. The ordinate is chosen to be ±1 mas to show all data points in the sample, and the bottom panel has the same range in ordinate as in the top panel.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.