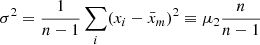| Issue |
A&A
Volume 653, September 2021
|
|
|---|---|---|
| Article Number | A68 | |
| Number of page(s) | 27 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/202141326 | |
| Published online | 23 September 2021 | |
SSTRED: Data- and metadata-processing pipeline for CHROMIS and CRISP
1
Institute for Solar Physics, Dept. of Astronomy, Stockholm University, Albanova University Center, 106 91 Stockholm, Sweden
e-mail: mats@astro.su.se
2
Institute of Theoretical Astrophysics, University of Oslo, Postboks 1029, Blindern, 0315 Oslo, Norway
Received:
17
May
2021
Accepted:
10
July
2021
Context. Data from ground-based, high-resolution solar telescopes can only be used for science with calibrations and processing, which requires detailed knowledge about the instrumentation. Space-based solar telescopes provide science-ready data, which are easier to work with for researchers whose expertise is in the interpretation of data. Recently, data-processing pipelines for ground-based instruments have been constructed.
Aims. We aim to provide observers with a user-friendly data pipeline for data from the Swedish 1-meter Solar Telescope (SST) that delivers science-ready data together with the metadata needed for proper interpretation and archiving.
Methods. We briefly describe the CHROMospheric Imaging Spectrometer (CHROMIS) instrument, including its (pre)filters, as well as recent upgrades to the CRisp Imaging SpectroPolarimeter (CRISP) prefilters and polarization optics. We summarize the processing steps from raw data to science-ready data cubes in FITS files. We report calibrations and compensations for data imperfections in detail. Misalignment of Ca II data due to wavelength-dependent dispersion is identified, characterized, and compensated for. We describe intensity calibrations that remove or reduce the effects of filter transmission profiles as well as solar elevation changes. We present REDUX, a new version of the MOMFBD image restoration code, with multiple enhancements and new features. It uses projective transforms for the registration of multiple detectors. We describe how image restoration is used with CRISP and CHROMIS data. The science-ready output is delivered in FITS files, with metadata compliant with the SOLARNET recommendations. Data cube coordinates are specified within the World Coordinate System (WCS). Cavity errors are specified as distortions of the WCS wavelength coordinate with an extension of existing WCS notation. We establish notation for specifying the reference system for Stokes vectors with reference to WCS coordinate directions. The CRIsp SPectral EXplorer (CRISPEX) data-cube browser has been extended to accept SSTRED output and to take advantage of the SOLARNET metadata.
Results. SSTRED is a mature data-processing pipeline for imaging instruments, developed and used for the SST/CHROMIS imaging spectrometer and the SST/CRISP spectropolarimeter. SSTRED delivers well-characterized, science-ready, archival-quality FITS files with well-defined metadata. The SSTRED code, as well as REDUX and CRISPEX, is freely available through git repositories.
Key words: instrumentation: high angular resolution / instrumentation: polarimeters / methods: observational / techniques: imaging spectroscopy / techniques: image processing
© ESO 2021
1. Introduction
Scientists working with data from ground-based high-resolution solar telescopes were for many years required to have detailed knowledge about the telescopes and instruments with which their data were collected. With the complexity of instruments and observing sequences developed during the past decades, this has become increasingly difficult. Only the home institutes of the instruments and a few other, strong groups were able to maintain the necessary knowledge.
Meanwhile, space-based solar telescopes have come with data pipelines that deliver well-characterized data, along with metadata that facilitate their interpretation. Such data have then been made available to researchers around the world through web-based virtual observatories with searchable databases, for instance, Hinode (Kosugi et al. 2007), the Interface Region Imaging Spectrograph (IRIS; De Pontieu et al. 2014), and the Solar Dynamics Observatory (SDO; Couvidat et al. 2016). This has significantly increased the scientific use of these data.
In recent years, data pipelines for the main ground-based telescopes have also been made available to observers, making the production of science-ready data a matter of some training and adequate computer resources. This is a crucial development to realize the scientific potential for solar data from ground-based telescopes. Some of these pipelines are the IBIS Software Package (Criscuoli & Tritschler 2014) for the Interferometric BIdimensional Spectropolarimeter (IBIS); CRISPRED (de la Cruz Rodríguez et al. 2015, hereinafter referred to as the CRISPRED paper) for the CRisp Imaging SPectropolarimeter (CRISP); the ROSA data reduction pipeline (Jess & Keys 2017) for the Rapid Oscillations in the Solar Atmosphere instrument (ROSA); and sTools (Kuckein et al. 2017) for the GREGOR Fabry-Pérot Interferometer (GFPI) and High-resolution Fast Imager (HiFI).
Working within the 2013–2017 EU FP7 SOLARNET project (Collados 2017), Haugan & Fredvik (2015) set out to define the metadata needed for the inclusion of ground-based solar data in future Solar Virtual Observatories (SVOs). This adds another set of requirements for the documentation, based on the expectation that data will be used without the observers being involved. Within the second SOLARNET project (2019–2022, EU Horizon 2020), Haugan & Fredvik (2020) further developed these recommendations as they were confronted with implementations in pipelines, primarily SSTRED and the pipeline for the Spectral Imaging of the Coronal Environment instrument (SPICE; SPICE Consortium et al. 2020).
With the August 2016 commissioning of the CHROMospheric Imaging Spectrometer (CHROMIS; Scharmer 2017) at the Swedish 1-m Solar Telescope (SST), a data-processing pipeline was needed. Like CRISP, CHROMIS is based on dual Fabry–Pérot interferometers (FPIs) in a telecentric mount and is also similar in the design in other aspects. It was evident that the CRISPRED code would be an excellent starting point, but much of the code had to be generalized to remove CRISP-specific assumptions about cameras, filters, data file formats, etc.
Inclusion of metadata according to the then recently formulated SOLARNET recommendations in CRISPRED required a more thorough rewrite. We decided to work in a new fork, dubbed CHROMISRED, so that observers reducing CRISP data would not be disturbed by the ongoing developments. When the new code base was fully operational for CHROMIS, we re-implemented full support for CRISP data in it.
This paper describes SSTRED: the new, combined pipeline for the two imaging spectro(polari)meters CRISP and CHROMIS. With it, we aim to provide the complex “machinery” needed to process multi-instrument, multi-wavelength data from a ground-based solar telescope, as well as compensate for the known imperfections in these data and prepare for their use together with space-based data.
SSTRED is being developed in parallel to the development of SOLARNET recommendations for metadata, and includes multiple calibration and correction steps beyond the standard pixel bias and gain, alignment and destretching, and image restoration. SSTRED is therefore well placed to serve as a model for pipelines of future instruments.
SSTRED was under development 2016–2021, and features were added as late as in March 2021. A draft version of this paper has been available since April 2018 (Löfdahl et al. 2018), with a second version uploaded in July 2019. We describe the state of SSTRED in June 20211.
Combining data from multiple instruments with access to different wavelength bands greatly enhances the scientific analysis. Examples of this science are published by Leenaarts et al. (2018), Esteban Pozuelo et al. (2019), Buehler et al. (2019), Kuridze et al. (2019), Kianfar et al. (2020), Pietrow et al. (2020), Joshi et al. (2020), Rouppe van der Voort et al. (2021), and Bose et al. (2021). This is evidence of the utility of SSTRED-processed data. Rouppe van der Voort et al. (2017) and Vissers et al. (2019) presented data that tapped into an even more complex but also more powerful application of SSTRED-processed data, which includes the analysis of CRISP and CHROMIS data together with space-based data from IRIS. More of the latter can be expected as Rouppe van der Voort et al. (2020) have released an archive of CRISP and CHROMIS data that are registered with IRIS data.
The organization of this paper is as follows. We first describe the instrumentation with relevant details of the CHROMIS and CRISP instruments (Sect. 2) and give an overview of the data-processing steps performed by SSTRED (Sect. 3) with references to the literature (in particular the CRISPRED paper, which is recommended reading for the interested reader) when possible. We then describe in detail aspects of the processing that are novel to SSTRED (calibration steps in Sect. 4 and image restoration in Sect. 5). The SSTRED output is rich in metadata that are stored in accordance with the SOLARNET recommendations, as described in Sect. 6. We present updates to the auxiliary CRIsp SPectral EXplorer (CRISPEX) data browser, relevant to exploring and analyzing the SSTRED science-ready output, in Sect. 7. We conclude with a discussion in Sect. 8. Some details about the implementation are found in the appendices.
2. Instrumentation
The optics of the SST (Scharmer et al. 2003) and its imaging setup are illustrated in Figs. 1 and 2, respectively. In the caption of Fig. 2, acronyms are defined for many optical elements that are discussed in the following two subsections, with details about the CRISP and CHROMIS instruments.
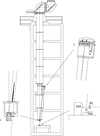 |
Fig. 1. Sketch of the SST (from Scharmer et al. 2003), from the 1 m lens, via the two alt-az mirrors, the field mirror on the bottom plate (inset A), the Schupmann corrector (B), the field lens and exit window (A), to the tip-tilt mirror (TM), deformable mirror (DM), and re-imaging lens (RL) on the optical table (C). The optical path continues in Fig. 2. |
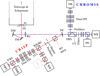 |
Fig. 2. Schematics of the setup used from the CHROMIS installation in August 2016 through the 2020 season. Acronyms: FL = field lens, FS = field stop, TM = tip-tilt mirror; DM = deformable mirror; RL = reimaging lens; DC = 500 nm dichroic beamsplitter; DBS = double beamsplitter, CT = correlation tracker; AO WFS = adaptive optics wavefront sensor; WB BS = wide-band beam splitter; FPI = Fabry–Pérot interferometer, LCs = liquid crystal modulators; P BS = polarizing beamsplitter, NB = narrowband, WB = wideband, NBT = NB transmitted, NBR = NB reflected, PD = phase diversity. White light enters the telescope from the top. It is split into a red and a blue beam at ∼500 nm by the DC. Distances and angles do not correspond to the physical setup. |
2.1. CRISP
CRISP operates in light with λ > 500 nm, reflected by the DC into a red beam. Details about CRISP are given by Scharmer et al. (2008) and (with an emphasis on data processing) in the CRISPRED paper. Here follows a brief update.
Before the 2015 season, new ferroelectric LCs were installed as a polarimetric modulator, replacing the old nematic LCs (de Wijn et al. 2021). Because they occupy more space on the optical table, they were installed directly after the WB BS rather than in the old position before the PBS.
We knew since 2013 that the original CRISP prefilters manufactured by Barr have significant optical power, which causes the focus to vary between the filters. This was compensated for by use of a variable focus on the DM, with the unfortunate consequence of leading to focus errors in the blue beam instead. In practice, this limited most CRISP observations to using prefilters that happened to have similar optical power or to not allow simultaneous blue data in all CRISP observations. New CRISP prefilters without optical power, made by Alluxa, were installed before the 2018 season. (The 587.66 nm He D3 filter was installed already in 2016, but it belongs to the new batch of Alluxa filters with no optical power.) Transmission profiles are shown in Fig. 3. See also Table 1, where additional information is given. Note that there have been problems with fitting the telescope model to calibration data for the 517 nm filter. Until proper calibrations can be made, we are using the model for the old 525 nm filter (see the CRISPRED paper).
 |
Fig. 3. CRISP prefilter transmission profiles as measured by the manufacturer for the filters installed before the 2018 season. The blue curves correspond to the smaller part number and (for the wavelength bands where we have spares) red curves the larger. The gray lines represent the average disk center atlas spectrum, normalized to the continuum. See also Table 1. (a) 517.2 nm filter profiles. (b) 587.6 nm filter profile. (c) 617.4 nm filter profiles. (d) 630.2 nm filter profiles. (e) 656.3 nm filter profiles. (f) 854.3 nm filter profiles. |
CRISP prefilters installed 2018.
The varying optical power caused a variation in image scale of up to several percent between some of the old CRISP prefilters. The image scale with the new filters agrees to within ∼0.1%.
There are four Sarnoff CAM1M100 cameras for CRISP, but only three at a time have been used regularly. The fourth has been used as a spare, but is no longer operational.
2.2. CHROMIS
CHROMIS (Scharmer et al. in prep.; Scharmer 2006) is based on a dual FPI mounted in a telecentric setup, similar to CRISP, but designed for use at wavelengths in the range 380–500 nm and currently without polarimetry. In particular, CHROMIS is optimized for use in the Ca II H and K lines, which are formed in the upper chromosphere, and for the H-β line.
The blue light with λ ≲ 500 nm is transmitted through the DC toward the DBS, which reflects most of the light to the narrow-band (NB) beam and transmits the remainder to the wide-band (WB) beam (where it is again split between the CT and the two WB cameras). The DBS was designed to reflect 90% to the NB path, but the current DBS does not reflect more than ∼60%. A new DBS with the proper splitting would improve the signal-to-noise ratio (S/N) in the NB and should be installed before a future polarimetry upgrade of the instrument.
The NB path goes through one of a set of filters mounted in a filter wheel. The filter characteristics are summarized in Table 2 and Fig. 4. These filters are all manufactured by Alluxa.
 |
Fig. 4. CHROMIS filter transmission profiles (normal incidence). Red lines: NB prefilters. Blue lines: WB filters. The filter profiles shown are measured in the center of the filter by the manufacturer. The FPI profiles are not wide enough to plot them here. The gray lines represent the average disk center atlas spectrum, normalized to the continuum. See also Table 2. (a) Ca II filter profiles. (b) H-β filter profiles. |
CHROMIS filters.
With the present set of prefilters, CHROMIS can be used in two wavelength regions. One region covers the Ca II H and K lines. Scanning through the wide Ca II lines and nearby continuum at 399 nm is done through five separate three-cavity NB prefilters, while simultaneous WB data, used for context and supporting image restoration, are collected through a single WB filter with a wavelength between the H & K lines. The other region covers the H-β line, with WB data collected in the continuum to the blue of the line.
The design FWHM of the FPI NB transmission profile is 8 pm at the Ca II H and K lines and 10 pm at H-β. However, the measured profile width in Ca II is estimated to be ∼13 pm (Rouppe van der Voort et al. 2017), which has been traced to a mismatch in the etalon reflectivities. (The profile width depends on the reflectivities in the high-resolution etalon, see Sect. 2.1 and Fig. A.1 in the CRISPRED paper.)
The WB re-imaging system provides a telecentric beam with the same focal ratio as the one of the CHROMIS FPIs. It provides an anchor object for image restoration, see Sect. 5. The PD camera collects WB data approximately one wave out of focus to further facilitate image restoration with phase diversity.
The Ca II H&K WB filter has been in use from the start, providing a photospheric image that works very well for on-disk image restoration. However, it gives very little signal outside the limb without saturation on the disk. Kuridze et al. (2019) managed to restore coronal loops, but it has been clear that a WB filter with better visibility of the fine structure outside the limb would be an advantage. The Ca II H core WB filters were installed in August 2020. Details about their use will be provided in the forthcoming CHROMIS paper.
All three cameras are Grasshopper3 2.3 MP Mono USB3 Vision (GS3-U3-23S6M-C) cameras, manufactured by PointGrey. They are equipped with Sony Pregius IMX174 globally shuttered 1920 × 1200-pixel CMOS detectors with 5.86 μm pitch. These cameras are synchronized electronically so that there is no need for an external shutter as in CRISP. The plate scale was ∼0 038/pixel during the 2016–2020 seasons, measured in pinhole array images using a pinhole spacing of 5
038/pixel during the 2016–2020 seasons, measured in pinhole array images using a pinhole spacing of 5 116 (see the CRISPRED paper, Sect. 3.3).
116 (see the CRISPRED paper, Sect. 3.3).
3. Overview of SSTRED processing
This section gives an overview of the processing steps for reducing CRISP and CHROMIS data with SSTRED. The processing divides naturally into steps performed before image restoration (with multi-object multi-frame blind deconvolution, MOMFBD), the MOMFBD processing itself, and post-MOMFBD steps. See Appendix A for notes on the pipeline code.
3.1. Pre-MOMFBD
The first step in processing CRISP and CHROMIS data for a particular observing day is running a setup script that locates and analyzes the directory tree with the day’s observed data, identifying science data as well as the various kinds of calibration data. A work directory (one per instrument) is created, where a configuration file and an IDL2 script with the recommended processing steps are written.
Most calibration data are collected as bursts of images with the same settings and exposure times as the science data. These bursts are then summed, resulting in calibration data where noise and (when relevant) imprints from granulation are reduced. This summing is performed for dark frames, flat fields, pinhole array images, and polarimetric calibrations. While summing, statistics are calculated. This allows checking for outliers and removal of suspicious frames. Flats and pinholes for the near-IR wavelength bands 7772 and 8542 Å recorded with CRISP are corrected for back-scatter. See Sect. 4.2 of the CRISPRED paper for details.
Based on the summed polarimetric calibration data, modulation matrices are then calculated for each CRISP pixel. See Sect. 4.1 of the CRISPRED paper.
The geometrical transform needed to align images from different cameras is estimated by a calibration step involving pinhole array images. We describe a procedure for this in Sect. 4.1, which is improved with respect to the procedure described in Sect. 3.2 of the CRISPRED paper.
The FPI cavity errors are measured from the summed flat fields. See Sect. 4.2 below.
The intensities registered by the detectors are affected by the transmission through the atmosphere, the telescope, other optics including in particular the prefilters, as well as the quantum efficiency (QE) of the detectors. These effects depend on both time and wavelength. We measure the effects from calibration data as described in Sects. 4.4.1 and 4.4.2 below.
3.2. MOMFBD
The MOMFBD image restoration is made outside of IDL, see details in Sect. 5. SSTRED uses a recent fork of the MOMFBD code written by van Noort et al. (2005), with several essential new features. The new code, REDUX, is described in Appendix A.3.
The MOMFBD processing includes image remapping based on pinhole calibration. This step aligns images from different cameras, see Sect. 4.1. Back-scatter correction for CRISP Sarnoff cameras in near IR wavelengths is performed as described in Sect. 4.2 of the CRISPRED paper.
3.3. Post-MOMFBD
The post-MOMFBD steps assemble the MOMFBD-restored images into science-ready data cubes with metadata. The cubes have dimensions [Nx, Ny, Ntun, Npol, Nscan], where Nx and Ny are the spatial dimensions, Ntun is the number of wavelength-tuning positions, Npol is the number of polarization states (four for Stokes data, one otherwise), and Nscan is the number of scans through the line. The physical coordinates are two spatial coordinates, the wavelengths, the polarization states, and the temporal coordinates. They are not strictly equivalent to the pixel coordinates. The spatial coordinates, solar longitude and latitude, vary with time (due to the solar rotation), and the time coordinate is advanced both while tuning and from scan to scan. This is specified in the metadata using the World Coordinate System (WCS), see Sect. 6.3.
The following steps are performed on the restored NB images to produce a science-ready data cube:
-
For polarimetric CRISP data: demodulation of four LC state images into Stokes component images. See Sect. 4.1 in the CRISPRED paper as well as Selbing (2005) and van Noort & Rouppe van der Voort (2008).
-
Removal of periodic image artifacts in polarimetric data. See Sect. 4.3
-
For CHROMIS Ca II data: Correction for time-variable misalignment due to chromatic dispersion in the atmosphere and in the telescope. See Sect. 4.5.
-
Correction for residual warping from anisoplanatic effects between NB images with different tuning and/or polarimetric states. See Sect. 5.4.
-
Compensation for field rotation caused by the alt-az mount of the telescope. See Sect. 4.7.
-
For cubes with multiple scans, geometrical alignment and destretching needed to make the transition from scan to scan smooth. See Sect. 4.6 in the CRISPRED paper.
-
For polarimetric CRISP data: removal of polarimetric cross-talk. See Sect. 4.6.
-
Spectral intensity scaling to compensate for prefilter transmission profiles and to obtain correct units by use of the prefilter calibration described in Sect. 4.4.1.
-
Temporal intensity scaling to compensate for changes in solar elevation. See Sect. 4.4.2
-
Finalize. A final adjustment of metadata to bring cubes made with earlier versions of SSTRED up to SOLARNET compliance. Statistics (see Sect. 6.4) and checksum calculations.
-
Archiving and export. Make thumbnail images and context videos. Upload science data cubes to local disks accessible from the internet. Upload metadata to databases (local and SVO).
3.4. SVO
As the last (optional) steps in the post-MOMFBD processing, we upload the science-ready data cubes to a web-accessible disk area at Stockholm University and their metadata to an SVO. At this point, we specify the SOLARNET keywords RELEASE (a date after which the data are released to the community) and RELEASEC (a comment describing the data policy and/or a link to more information about this policy).
We currently use the prototype SVO, hosted by the Royal Observatory of Belgium, developed by Mampaey et al. (2017) in the first SOLARNET project. We expect to move to the production SVO, developed by the same group (Mampaey et al., in prep.) in the second SOLARNET project when it is operational. The SVO facilitates searches in the metadata and can serve URLs for data downloads from the Stockholm servers. These search-and-download operations can also be performed by use of IDL scripts. The server is aware of the RELEASE keyword and knows to issue a password challenge if the release date is in the future.
4. Calibrations
Here we describe calibrations that were not mentioned in the CRISPRED paper or are performed differently in SSTRED. See Sect. 3 for how they fit within the pipeline processing as a whole.
4.1. Camera alignment
Optical setups that use beamsplitters, filters, and lenses are never perfectly stable in terms of alignment. We therefore need to routinely calibrate the alignment of the cameras separately for each prefilter. The tuning of the FPIs and the changes in the polarization states of the LCs in practice do not have a significant effect, therefore we average the measurements over those.
The coalignment of the cameras is measured by use of images of an alignment target mounted in the Schupmann focus, directly after the FS. This process is described by van Noort et al. (2005) and in Sect. 3.2 of the CRISPRED paper, although we have changed some aspects of this calibration. The alignment target, referred to as the pinhole array, is a rectangular grid of pinholes with a 5 12 spacing, completely filling the detector area. Three pinholes in an L configuration are intentionally slightly larger and therefore brighter. There is also some intensity variation from manufacturing and dirt. This variation is used to identify the correct orientation and alignment.
12 spacing, completely filling the detector area. Three pinholes in an L configuration are intentionally slightly larger and therefore brighter. There is also some intensity variation from manufacturing and dirt. This variation is used to identify the correct orientation and alignment.
The new method fits a generic transformation matrix to the relative pinhole positions as measured first by locating the peaks and then by maximizing the cross-correlation between subimages with the individual pinhole images. Previously, relative positions were measured as wavefront tilt components with the MOMFBD program, one hole at a time.
Another change is in how the results of the calibration are represented. Before, field-dependent shifts in the two axis directions were stored as detector-pixel maps of offsets in X and Y. This format can represent very general geometric deformations, but was in practice only used for global shifts (small ones, large ones represented by ALIGN_CLIPS), image-scale differences, skew, and field rotation. When the MOMFBD program had read a subfield in the anchor WB image, it would obtain the matching subfield in another camera or channel by looking up the X and Y shifts for the center position of the anchor camera and (1) applying the rounded offsets to the pixels coordinates to read out and (2) adding the sub-pixels remainders of the offsets to the wavefront tilt terms of the channel.
This scheme has problems near the edges of the field of view (FOV). This is mostly due to the fact that the images are first cropped to the greatest common FOV before applying the alignment offsets. If there is even a slight difference in rotation or scale between the cameras, the subfields near the corners can be shifted outside of the cropped image. The data that are missed through this operation, if only in a few pixels, will compromise the restoration. In addition, the shifts are not accurately described by a quadratic surface near the edges (which the old calibration assumes). The calibration itself was also not very robust with respect to a larger rotation misalignment between cameras. The new method, on the other hand, can handle arbitrary rotations and scale differences, and it can also be used to align CRISP and CHROMIS images.
The new method consists of determining the projective transforms (see, e.g., Hartley & Zisserman 2000) relating each channel to the reference channel in the form of a 3 × 3 matrix,
acting on the projective coordinate vector, [x, y, 1]T, followed by a normalization to maintain unity in the third element. The top left 2 × 2 block of H encodes rotation, magnification, and mirroring, h02 and h12 are translations into x and y (i.e., the top two rows of the matrix make up an affine transform), and the elements h20 and h21 are responsible for perspective skew and keystone effects. A simple sanity-check for the SST setup is that h00 and h11 should be close to +1 or −1, h02 and h12 should be within a few tens of pixels from 0 (or from the detector size, in case of mirroring), and that h20 and h21 should be tiny (∼10−5).
In addition to the advantages in accuracy and efficiency of the calibrations and the alignment during MOMFBD, there are some additional bonuses such as inverse or composed mappings, which are trivial matrix operations. Many software libraries (such as OpenCV) can be used to manipulate images based on these transformation matrices.
4.2. Cavity errors
CRISP and CHROMIS are based on dual FPIs, mounted in a telecentric configuration. The central wavelength of the FPI transmission profile can be tuned to different wavelengths by changes in the separation of the etalon cavities. Deviations from the nominal tuning wavelengths are caused by very fine spatial variations, δD, in the cavity, D, between the two plates of an etalon. Because the etalons are located near the focal plane, the variation over the etalon surfaces translates into variations over the FOV: the passband is not centered at exactly the same wavelength over the entire FOV.
These cavity errors, interpreted as distortions in the wavelength coordinate, λ, through δλ = δD ⋅ λ/D, have to be taken into account when the data are interpreted, in particular when CRISP and/or CHROMIS data are fit to models of the solar atmosphere.
4.2.1. Measurement
The method for measuring the cavity errors in CRISP from flat field data was developed by Schnerr et al. (2011) and is also described in Sect. 4.3 of the CRISPRED paper. It fits a pixel map of wavelength shifts, based on the assumption that the pixels in a scan all show the same spectrum. For this a sufficiently well sampled line, including slopes in both directions, is needed. We use the same method for CHROMIS; see Fig. 5 for cavity errors measured for CHROMIS. See Appendix B for how the cavity errors are stored as distortions to the WCS wavelength coordinate.
 |
Fig. 5. Cavity error of the high-resolution CHROMIS etalon through the Ca II H and K core prefilters as measured with data from 2016 June 19. Mapping the associated wavelength shift over the 1920 × 1200-pixel NB detector. |
The tuning of the CRISP and CHROMIS etalons is controlled digitally, with step sizes that were calibrated when the instruments were installed. The etalon separation might be thought to change with tuning, as was recently measured by Greco et al. (2019) in a laboratory setup. If the three piezo stacks that control the cavity width do not move by the same amount, we would obtain a time-variable linear component (tilt) in the cavity separation. However, the accuracy of the tuning control is estimated to ±0.0005 mÅ/du for CRISP and ±0.01 mÅ/du for CHROMIS (P. Sütterlin 2020, priv. comm.).
While the calibration is good enough that tilt variations with tuning are negligible within the tuning range of a prefilter, the cavity errors still do have a tilt component. The tilt component depends on the settings of parameters related to the piezos that control the gap when tuning, and these parameters are set by daily calibrations that are independent for each prefilter. For CHROMIS Ca II, where multiple prefilters are used in a single scan, the tilt (and possibly other low-order components) of the gap therefore varies from one prefilter to another. Compare the cavity maps for the two Ca II core filters in Fig. 5. This effect could have been reduced by sending control signals to each piezo stack individually. Sending a single control signal to all three is needed for fast scans.
The Ca II H and K wing filters have so far hardly been used, but it should be possible to calibrate them using some of the blends in the wing filter passbands. It should be possible also for the Ca II continuum filter, although it is not needed as long as it is not used to scan through any of the lines within its passband.
4.2.2. Flat fielding
When observations are made in the parts of spectral lines in which the intensity changes rapidly, the shifts in cavity error wavelength cause a spatial imprint on the intensities of both data and flats. The wavelength shifts cause intensity changes that are not accounted for in the monochromatic image-formation model assumed by MOMFBD. This can cause suboptimal solutions for the wavefronts (i.e., the PSFs) in the image restoration step because of mismatches with the image formation model, which assumes quasi-monochromatic data. For polarimetric observations, the time-dependent telescope polarization also has an effect on the flat fields. Moreover, deconvolving large discontinuities in the cavity errors can cause artifacts in the MOMFBD output. For these reasons, Schnerr et al. (2011) developed a method for taking all this into account.
Science data are often collected in areas in which the spectrum varies with both time and position in the FOV and is quite different from that of the quiet Sun, where flat-field data are collected. The CRISPRED paper (see their Sect. 3.1) improved upon the procedure by Schnerr et al. (2011) to take this into account as well. This is what is used for CRISP data in SSTRED.
The cavity errors of CHROMIS are both smoother and smaller than those of CRISP. CHROMIS cavity errors are ∼0.1 mÅ (see Fig. 5), while CRISP cavity errors are ∼10 mÅ (see Fig. 4 of the CRISPRED paper). For CHROMIS, we have therefore found that the faster method by Schnerr et al. (2011) is sufficient.
4.3. Periodic artifacts
Polarimetric CRISP datasets often show periodic artifacts in the Stokes Q, U, and V components, in particular U and V. A sample U image with such artifacts is shown in Fig. 6a. With dominating high-contrast features such as sunspots in the FOV, it is difficult to separate the signal from the artifact. However, the same artifact is visible in the polarization calibration (polcal) image data. As polcal data are always collected in regions with quiet Sun, the offending spatial frequency can quite easily be found manually in the 2D power spectrum of sums of polcal images. A sample image is shown in Fig. 6b. This spatial frequency is then removed from the Stokes images by use of a 2D notch filter, the result of which is shown in Fig. 6c.
 |
Fig. 6. Removal of periodic artifacts in polarimetric data. The sample CRISP Fe I 6302 Å, −210 mÅ from line core. Data were collected on 2019 May 10 at 09:07 UT with AR 2741 in the FOV. The image shown is 53″ squared. (a) Stokes U component, sunspot saturated to emphasize artifacts in the lower left corner. (b) The polarization calibration image on which the Fourier filter is based. (c) Fourier filtered U component without the artifacts. |
Similar Fourier filtering was implemented in CRISPRED, but it was left to the user to actually construct the filter. Díaz Baso (2018, his Fig. 2.19) and Pietrow et al. (2020, their Fig. 2) implemented their own similar corrections before the filter described here was included in SSTRED.
The artifact pattern seems stable over years of observations, but is measured independently for each new day of observations. A pattern with the same period and direction is visible also in the modulation matrix components. Our first thought was to apply the notch filter to this matrix before demodulating the data. However, this exacerbated the artifacts.
A close inspection of Fig. 6 shows cross-talk from Stokes I as a weak granulation pattern imprint outside the spot (in particular in the top part). See Sect. 4.6 for how this is removed.
4.4. Intensity calibration
4.4.1. Spectral intensity calibration
In order to characterize the wavelength-dependent instrument response in our observations, we use the Hamburg disk center atlas spectrum (Neckel 1999; Brault & Neckel 1987) as a reference. We degrade the atlas spectrum by convolution with a theoretical FPI transmission profile. We then estimate the parameters in a model prefilter profile by fitting the degraded atlas spectrum to quiet-Sun data collected at disk center. The prefilter model is a Lorentzian multiplied with an antisymmetric polynomial,
where
The parameters have the following effects on the fit: p0 is a scale factor from counts to the units of the atlas; p1 shifts the wavelength scale to align the spectral lines in the data with those in the atlas spectrum; p2 is a shift of the CWL of the prefilter; p3 is the FWHM of its transmission profile; p4 is the number of cavities in the filter; the polynomial with parameters p5 and p6 represent asymmetries in the profile as well as in other wavelength-dependent effects (such as the QE of the detector as well as the transmission of other optics and the atmosphere) on the number of collected photons; and the seldom used p7 stretches the wavelength grid. The Lorentzian represents the prefilter transmission profile, where not constraining the number of cavities to be an integer accounts for some deviations from an idealized filter.
Figure 7 shows examples of these fits for Ca II K and H-β. The derived prefilter curves are also plotted along with the fits in this figure.
 |
Fig. 7. Sample diagnostic plots from the spectral intensity calibration. The scan intensities are plotted in counts, while the fitted prefilter transmission is plotted in arbitrary units. (a) Ca II K core. (b) H-β. |
As described in Sect. 4.5 of the CRISPRED paper, the fitted profile (defined by parameters p0 and p2–p6) is used to compensate science data for the wavelength-dependent response of the instrument and to convert the camera counts into intensity in SI units (W m−2 Hz−1 sr−1). In addition, p1 is used to adjust the wavelength coordinate from the one set by the instrument calibration made each morning at the telescope.
4.4.2. Temporal intensity calibration
The spectral intensity calibration in the previous subsection is used to remove the effect of the prefilter transmission profiles and scale intensity counts to SI units. However, because of variations in solar elevation and the amount of dust in the line of sight, this conversion is really only valid for the time the calibration data were collected.
Our previous approach to correcting for this was to apply a correction factor that is the ratio of median WB intensities of the individual scan and that of the calibration data. This compensates for changes in elevation and dust, but has the drawback that it also removes the inherent intensity variations from solar disk center to limb. A better intensity calibration would need a similarly measured intensity ratio, but with both WB intensities obtained at disk center.
The present default calibration procedure is based on a polynomial fit to WB intensity data collected throughout the observing day. It does not matter if the data are science data or flats, as long as they are collected near disk center and temporally span the entire period of observations. We use the median intensity so that the procedure can tolerate science data obtained from active regions, as long as the FOV is not dominated by large sunspots or faculae. Sample data for both CRISP and CHROMIS are shown in Fig. 8. The data illustrate the decrease in extinction toward the red wavelengths, to essentially no effect in the IR. By default, second-order polynomials are used for the fit (first order if there are only two data points). Other fit functions can be specified if needed.
 |
Fig. 8. Disk center median WB calibration intensities from 2016 September 19. Prefilter wavelength bands in as indicated in the legends. The solid lines are fits to second-order polynomials as shown in the legends. (a) CHROMIS. (b) CRISP. |
It might be possible to relax the requirement that the calibration data are collected near disk center by correcting the intensities for limb darkening using measurements by, e.g., Neckel & Labs (1994) or Neckel (2005). However, this is not implemented at this point.
Figure 9 shows the effect of the corrections over two morning periods of observations. For the disk center data in Fig. 9a, the uncorrected intensities show the variation with solar elevation, similar to the WB calibration curve. The corrected intensities show much smaller temporal variation, crossing the uncorrected curve at the time the spectral intensity calibration data were collected. This holds for both the old and the new correction. In Fig. 9b we show a similar plot where data were collected during two center-to-limb scans. The disk center intensities are like those in Fig. 9a: following the increase with elevation for the uncorrected data, and are essentially identical for the two correction methods. The variations with μ are removed from the old method data (except very near the limb, an effect of the FOV including a gradient toward the limb as well as off-limb darkness), but preserved with the fit method.
 |
Fig. 9. CHROMIS Ca II NB continuum (median) intensities of restored data (individual scans), with and without temporal correction as indicated in the legends. The WB calibration curves are the fit functions (shown in Fig. 8a for the 2016 September 19 data), scaled to approximately match the disk center continuum intensities. The dot colors refer to data with no correction (green), the old correction based on the WB intensity in the data set itself, and the correction based on a fit to disk center data (red). (a) Data from 2016-09-19, μ ≈ 1 (near disk center). (b) Data from 2019-06-21, varying μ. |
In the new procedure, we also implemented a correction for varying exposure time. This was not necessary in CRISPRED as CRISP is operated with a constant rotating-shutter speed. The exposure time of CHROMIS can easily be changed, for instance, when the target is moved from disk center to limb.
For datasets consisting of multiple scans, the old method also corrects for rapid variations in intensity that would be unaccounted for if the ratio of fitted WB intensities alone were applied as for the individual scans. Therefore the fit correction takes the scan-to-scan variations in WB mean values into account. This results in corrections that remove the rapid variations; see the sample results in Fig. 10.
 |
Fig. 10. CHROMIS Ca II NB continuum (median) intensities of restored data (multiple scans), with and without temporal correction, as indicated in the legends. See also Fig. 9. |
We have implemented this step so that the new procedure is used by default, but for data not temporally spanned by WB disk center data, it will fall back to the old method. See Sect. 4.4.2 for a description that the metadata of the cube include information about which version of this step was actually performed.
4.4.3. Residual intensity variation
After the two intensity calibrations described in Sects. 4.4.1 and 4.4.2, Ca II continuum data still show systematic residual intensity variations. The 1% drop in intensity over the 30 min data collection interval in Fig. 10 (common to both methods) is consistent with the ∼5% intensity drop over 2.5 h shown in Fig. 9.
The WB and NB continuum passbands are separated by ∼5 nm and the gradient in the extinction wavelength-dependence is large around 400 nm. The effect can be replicated qualitatively with Rayleigh scattering and the semi-empirical expression for relative air mass as a function of zenith angle by Kasten & Young (1989), although not quantitatively well enough for an accurate correction.
We also found a systematic residual time-dependent variation in the ratio of intensities in the K line core and the continuum (separated even more in wavelength) in the same datasets (not shown).
4.5. Time-variable alignment
MOMFBD restoration, together with the pinhole calibration described in Sect. 4.1, usually delivers images recorded at different wavelengths that are very well aligned. However, the wavelength range of scans involving multiple Ca II prefilters can extend over more than 7 nm (see Fig. 4), which makes misalignment caused by wavelength-dependent dispersion significant. As a comparison, the wavelength ranges of scans through H-β and any of the CRISP lines are typically less than 1 nm.
The misalignment can be measured by use of cross-correlation of H&K WB and continuum data, which are both formed mostly in the photosphere. Figure 11 shows such measurements made with raw data collected during two morning hours. The misalignment is time-dependent, and there are two components, one of which varies with telescope elevation in a way that suggests atmospheric dispersion. The other component is periodic, and we found that the period matches that of the temperature of the telescope bottom plate, also shown in Fig. 11. The periodic variation was traced to an air-conditioning unit that switched on and off at regular time intervals. Our working hypothesis for the periodic component is that the temperature variations have a minute effect on the alignment of the field mirror that reflects the SST beam to the Schupmann corrector (see Fig. 1, inset A) or within the corrector itself. The alignment of the Schupmann corrector has a wavelength-dependent dispersion effect (Scharmer et al. 2003).
 |
Fig. 11. Covariation of the misalignment in continuum and WB measured with raw data and telescope bottom plate temperature. These data were collected during the morning hours of 2016 June 19. In bad seeing, measurements most often tend toward zero. The blue boxes correspond approximately to the plot ranges of Figs. 12b and c. (a) X misalignment. (b) Y misalignment. |
Regardless of the source of the dispersion, we measured the misalignment not only with WB and continuum, but also with images in the Ca II K blue wing and Ca II H red wing (formed at a similar height in the solar atmosphere) and found that it varies linearly with wavelength over the relevant range.
SSTRED includes a procedure for measuring and correcting the misalignment of the MOMFBD-restored Ca II scans. The process needs to be repeated for each scan because of the temporal variations. The misalignment between the WB and NB continuum images is measured by cross-correlation in the MOMFBD-restored data. The misalignments at the Ca II H wavelengths are then calculated by linear interpolation between the WB 395 nm and the NB continuum 399 nm. Similarly, linear extrapolation gives the misalignment at the Ca II K wavelengths.
Because the cross-correlation measurements depend on the data quality, they are smoothed with a method that ignores outliers and weights data points with respect to image RMS contrast. The variations around the smoothed line (disregarding the low-contrast outliers) suggest that the precision is a few tenths of a pixel, see Fig. 12.
 |
Fig. 12. Continuum alignment diagnostic plots for 121 Ca II scans collected from 09:28:36 on 2016 June 19, covering approximately one period of the undulations shown in Fig. 11. (a) WB RMS contrast. (b) Continuum/WB X misalignment. (c) Continuum/WB Y misalignment. Filled circles in (b) and (c): Misalignment measured by use of cross-correlation with MOMFBD restored data, colors represent RMS contrast as shown in (a). Lines in (b) and (c): Shifts in X and Y used for alignment, misalignment smoothed with a heuristic algorithm that gives more weight to the high-contrast data points. Diagnostic plots like these are automatically produced by SSTRED to allow the user to verify how well the contrast-aware smoothing worked. |
Correcting this misalignment after MOMFBD restoration is much easier and less time consuming than doing it in the raw data. The misalignment is only a few pixels, which is small in comparison to the MOMFBD subfield size. The MOMFBD assumption of a common wavefront in WB and NB is therefore not significantly violated.
4.6. Polarimetric cross-talk
The telescope polarization model limits the accuracy of the demodulation. In the resulting Stokes cubes, there is cross-talk between the components. Due to the larger numbers in the I component compared to the differential Q, U, and V components, the most significant cross-talk is from I to the other components. This is corrected for similarly to the procedure used by Sanchez Almeida & Lites (1992).
If the FOV is free from polarization signal, any structures that match I in the differential components are cross-talk and the rest is noise. With this assumption and X ∈ {Q, U, V}, the correction for the X component can be written as
where the weight wX can be estimated with a least-squares fit to the data in one or a few tuning states in (or as close as possible to) the continuum. We calculate
However, in our implementation, this is not exactly a least-squares fit. In the usual ℓ2 inner product definition, ⟨A, B⟩∝mean(A ⋅ B), we replaced the mean value with the histogram peak position, estimated with a Gaussian fit. This made the procedure more robust with respect to magnetic signal not completely removed by the masking, as well as artifacts that often occur near the edges of the FOV.
In addition, when evaluating Eq. (5), any spots, pores, or other areas where a significant magnetic field can be expected are masked from the FOV. A mask is automatically constructed based on the bisquare weights (see the biweight_mean function in the IDLAstro library) of the pixels in a time-averaged Stokes I image. The user can then adjust this mask or construct one from scratch by deselecting regions in a GUI.
The corrections in Eq. (4) are then applied to all tuning states. The weights are usually on the order ±10−3.
4.7. Orientation and pointing
The final science data cubes are by default oriented so that the pixel axis directions are along the HPLN and HPLT (solar longitude and latitude) coordinate axes. The second axis points toward solar North. The spatial coordinates can be calibrated with SDO/HMI continuum images as reference.
To calibrate the field rotation, we use datasets with some pores or spots in the FOV, features for which the orientation can be recognized in the lower resolution of HMI. See Fig. 8 in the CRISPRED paper for a comparison of CRISP and HMI images of the same FOV.
The pointing information logged by the primary image guider (PIG; Sliepen & Sütterlin 2013) is estimated to be correct to within 5″ if a four-limb calibration of the PIG/turret system was performed close in time before the data were collected but could otherwise be off by on the order of an arcminute. HMI continuum images with spots and pores can also be used to refine the pointing metadata in the spatial WCS information.
5. Image restoration
5.1. MFBD and MOMFBD
Isoplanatic image formation with optical aberrations can be modeled as a convolution of an object with a PSF, where the PSF is determined by the variation of the wavefront phase over the pupil. The wavefront can be expanded into linear combinations of a finite set of modes that span a subspace of all possible aberrations. Multi-frame blind deconvolution (MFBD) methods, including phase diversity (PD, see Sect. 5.2), are based on estimating the wavefront parameters by fitting the model to a data set, where the assumption that multiple images depict the same object is a powerful constraint (see, e.g., Löfdahl 2002, and references therein). With the assumption of additive white noise, the intensity of the unknown object can be calculated by deconvolution of the data so that the pixel values do not have to be estimated as independent model parameters.
The wavefront aberrations are caused by turbulence in the Earth’s atmosphere, randomly mixing air with different temperature and therefore different refractive index. We therefore have to make the assumption that the exposures are short enough that the PSF does not have time to change significantly. Due to turbulence at high altitudes, the line of sight from the telescope to different parts of the FOV passes through different turbulent structures, which means that the image formation is not really isoplanatic. However, within sufficiently small subfields, the assumption of isoplanatic image formation is a good approximation. We solve the model fitting and deconvolution problem independently within multiple subfields and form restored versions of the full FOV by mosaicking the results from the individual subfields.
For imaging spectro(polari)meters, each NB wavelength tuning and polarization state produces its own cospatial “object”. The number of collected frames in each state is then determined by a trade-off: we need many frames to boost the S/N, particularly in the core of deep lines, but we wish to complete a full scan before the solar scene evolves too much. Usually, only a few frames per state are collected, too few for MFBD to effectively restore the images independently for the individual NB states. In addition to the NB images, we also collect WB images in synchronization with the NB images, with the result that an NB line scan is always accompanied by a simultaneous WB data set that spans the entire scan. The MOMFBD algorithm uses the WB and NB data together to make a joint restoration (Löfdahl 2002; van Noort et al. 2005). A CHROMIS MOMFBD dataset is illustrated in Fig. 13, CRISP is similar but without a PD channel (see Sect. 5.2). The WB anchor images aid the image restoration in two ways: (1) the large number of images of the same object and many realizations of the random wavefronts constrain the solution, and (2) the estimated wavefront tilt components align all the WB images and therefore also the NB images to the WB. The result is that the different NB images are also aligned to each other.
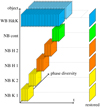 |
Fig. 13. Schematic representation of CHROMIS datasets for MOMFBD processing. The depicted mock dataset has an NB continuum tuning point (green), two tuning points each in an NB K filter (yellow) and an NB H filter (orange). The H&K WB filter (blue) anchors the entire scan. This meas that it forces MOMFBD to align the restored images of the scan. |
Some particular challenges related to MOMFBD image restoration with spectropolarimetric data are described by van Noort & Rouppe van der Voort (2008), Schnerr et al. (2011), and in Sect. 4.4 of the CRISPRED paper. We use a MOMFBD code not published before (see Appendix A.3) and a few developments in how the MOMFBD processing is set up and run. The latter are described in the following subsections.
5.2. Phase diversity
The PD wavefront-sensing and image-restoration technique is a form of MFBD that is constrained by the intentional defocusing of one or more images, corresponding to a known parabolic difference in phase over the pupil. The technique was invented by Gonsalves (1982) and the theory was clarified and extended to multiple diversities and multiple exposures by Paxman et al. (1992a) and (1992b). It was independently developed for high-resolution solar data by Löfdahl & Scharmer (1994) and Seldin & Paxman (1994). Both implementations were verified versus each other and versus speckle interferometry by Paxman et al. (1996). Löfdahl (2002) formulated it in terms of linear equality constraints (LECs), thereby incorporating it into what later became the MOMFBD method.
The diversity in phase does not have to be focus. However, this is easily implemented and by far the most commonly used. The magnitude of the phase difference also does not have to be known, although it does constrain the solution much better if it is.
CHROMIS includes a WB PD camera. See Fig. 14 for a demonstration of the image quality obtained with three different MOMFBD restorations of CHROMIS Ca H+K WB data: 60-mode MOMFBD with and without PD, and MOMFBD without PD and only the two tip and tilt modes corrected, corresponding to shift-and-add together with correction for the theoretical, aberration-free modulation transfer function (MTF) of the telescope. Both 60-mode restorations bring out fine structure that is not visible in the MTF-corrected image, but PD improves the contrast further, although it is still far from the expected Ca II continuum granulation RMS contrast in excess of 27% (Scharmer et al. 2019).
 |
Fig. 14. Contrast and image quality after different levels of MOMFBD restoration of CHROMIS Ca II continuum images from 110 scans collected on 2016 September 19. The FOV is 700 × 700 pixels (26 |
5.3. Modes
By default, we use Karhunen–Loève (KL) modes to parameterize the unknown wavefronts to be estimated by the MOMFBD processing. Like Zernike polynomials, they are orthogonal on a circular pupil. In addition, they are statistically independent with respect to wavefronts from atmospheric turbulence. As the SST adaptive optics (AO) monomorph deformable mirror is designed to correct such atmospheric wavefronts, the KL modes are also well suited to correcting residual wavefronts from the AO.
The KL modes implemented are based on expansion in Zernike polynomials (Roddier 1990) and are therefore indexed as the dominating Zernike polynomial as ordered by Noll (1976). In this order, the expected variance from turbulent seeing does not decrease monotonically. To make the best subset selection, we therefore have to order them first. Then we select the most significant subset by truncating the list to the desired length.
We used to sort the selected subset of KL-modes back in index order, for no better reason than to make the list look cleaner. We have since realized that this is not optimal with respect to an important aspect of the inner workings of the MOMFBD (and REDUX) program: In order to stabilize the solution, a few iterations are run with first 5, then 10, then 15, etc., modes until all the specified modes are included. The purpose is to allow the most significant modes to determine the coarse shape of the wavefront before the finer features are fit. This internal increase in the number of modes should therefore also be performed in variance order, which means the selected set should be specified in variance order.
5.4. Residual alignment and destretching
With perfectly estimated wavefronts, the anchor WB images should force the restored images of all objects to be perfectly aligned. However, model fitting with real data is rarely perfect, so that there are small but noticeable residual misalignments between the NB images. There is also residual stretching (from anisoplanatic wavefront aberrations) on scales smaller than the subfields that MOMFBD cannot compensate for.
Henriques (2012) included a technique for a post-MOMFBD dewarping step that compensates for the residual geometrical differences between the NB images in a scan. This has since been used routinely in the CRISPRED pipeline, see Sect. 4.4.2 of the CRISPRED paper. The method is based on the MOMFBD program outputting additional deconvolved WB images, in addition to the restored anchor WB image based on all exposures in the scan. The additional WB images, one per NB state, are generated by deconvolving only the subset of the raw WB images that are simultaneous to the raw NB images of that state. The additional deconvolved WB images are locally distorted in exactly the same way as the deconvolved NB images and have the same residual misalignment. Unlike NB images from different states, however, these WB images can be successfully destretched against the anchor WB image to measure the local warping, which is then applied to the NB images to obtain a significantly better aligned data cube.
We modified the way to make the MOMFBD program generate these additional WB images. We used to specify them as part of the MOMFBD data set, using LECs to make their estimated wavefronts identical to those of the simultaneous NB images. With zero weight in the error metric, mathematically, they should not affect the solution. However, numerically, it turns out that adding these additional objects, even with zero weights, does have a small but measurable effect on the converged solution. We attribute this to the changed LECs and to the null spaces they generate.
The solution is modified slightly when zero-weight objects are added to the LECs, but there is another downside to the previous approach. The MOMFBD code treats the additional objects just as any other, that is, it will load and process the WB data twice (once for the anchor object and once for the additional WB objects), which leads to a significant increase in both RAM usage and CPU load. For both CRISP and CHROMIS, the number of data increases by 33% by this method (three cotemporal exposures are basically turned into four).
To overcome these issues, REDUX has a new mechanism in which the additional WB objects are not specified with LECs. Instead, REDUX can be configured to generate the desired images as a final step after the wavefronts have been estimated. At this point, it deconvolves subsets of the WB images that match the frame numbers of the NB images. As no modifications are made to the problem itself, this will not interfere with the solution at all.
In practice, although the converged solutions differ, the quality of the restored data is similar. The real advantage of not including the additional WB objects in the problem with LECs is that fewer gradients of the error metric need to be calculated. For a typical CRISP or CHROMIS data set with three cameras, this means a ∼25% reduction in the processing time.
6. Metadata
For metadata, we follow the SOLARNET recommendations of Haugan & Fredvik (2020). The idea is that data should have enough metadata for “a Solar Virtual Observatory (SVO) [to] be able to [...] find sets of successful observations matching a hypothetical ideal observation proposal (if such observations exist).” The SOLARNET recommendations are an attempt to standardize metadata for multiple telescopes and instruments so that searches can be “instrument agnostic”. The metadata should also facilitate correct interpretation of data by a researcher who was not involved in the observations or the pipeline processing. That is, they should be complete enough that all important circumstances of the observations are included. Moreover, the processing done by the pipeline should be documented in the metadata, in particular when a processing step might be run with different parameter settings.
We store science-ready data in FITS format (Pence et al. 2010) with metadata information in the form of FITS header keywords and extensions. Some information is difficult to fit in standard FITS header keywords. A number of conventions have therefore been developed to facilitate storing particular types of information in FITS files. We use the record-valued keywords of Calabretta et al. (2004) to represent coordinate distortions. We also use the JavaScript Object Notation (JSON; Bray 2014) to encode FITS keywords with structured contents as strings, such as the SOLARNET PRPARAn keywords. JSON was developed for JavaScript, but is now implemented in all major programming languages. Finally, we use the SOLARNET variable keywords (Haugan & Fredvik 2015; 2020), a mechanism for associating auxiliary data with the main data in a FITS file for intensity statistics and some metadata from the log files of auxiliary instruments. The SOLARNET variable keywords are stored in FITS binary-table extensions and are associated with single-value regular header keywords. The regular header keyword value is not defined, but it is supposed to represent the whole cube in a way that makes sense for the particular quantity.
6.1. SOLARNET compliance and support
A FITS file can be partially or fully SOLARNET compliant. For partial compliance, it is enough to include four mandatory header keywords, and if one of the keywords is different from the definitions in the SOLARNET recommendations, a fifth keyword with a list of these different keywords. For full compliance, a larger set of mandatory keywords must be used depending on the nature of the observation. The level of SOLARNET compliance itself is indicated with the mandatory header keyword SOLARNET and values of 0.5 for partial compliance and 1 for full compliance.
The SSTRED SOLARNET-compliant science data cubes are supported by CRISPEX (Vissers & Rouppe van der Voort 2012) version 1.7.4 (released in January 2018) or later, see also Sect. 7. SOLARNET compliance should make it easier for future data viewing and analysis programs to support data from multiple sources.
In addition to SSTRED, several data pipelines are or will be preparing their metadata in compliance with the SOLARNET recommendations. The sTools pipeline is partially SOLARNET-compliant (Denker et al. 2018). The pipeline of SPICE produces SOLARNET-compliant output. The Astronomical Institute of the Slovak Academy of Sciences (AISAS) is updating their data pipelines, developed for the Coronal Multi-channel Polarimeter for Slovakia (CoMP-S; Kučera et al. 2010) and the Solar Chromospheric Detector (SCD; Kučera et al. 2015) instruments of the Lomnický Štít Observatory, according to the SOLARNET Metadata Recommendations (Rybák & Gömöry, priv. comm.). The recently funded Solar Activity Monitor NETwork (SAMNET) project are planning to follow the SOLARNET recommendations for their data structure (Erdélyi, priv. comm.). The Royal Observatory of Belgium (ROB) are aiming at producing, from early 2021, image datasets from the Uccle Solar Equatorial Table (USET; Berghmans et al. 2005) in white light, Hα, and Ca II K with SOLARNET-compliant headers (Vansintjan, priv. comm.). The Solar ALMA Pipeline (SoAP; Szydlarski 2019) will follow the SOLARNET recommendations (Haugan & Fredvik 2020).
This is evidence that the SOLARNET metadata recommendations have gained momentum and do provide a means of metadata standardization. This should significantly aid the analysis of data, in particular the co-analysis of data from multiple instruments and telescopes.
6.2. Observations
Passing metadata from the observations through the SSTRED processing, including the many calibration steps, requires access to metadata pertaining to the details of the observations. These metadata have to be collected from multiple sources, such as log files from auxiliary instruments as well as the raw image data files themselves.
6.2.1. Image data
The metadata collected from the raw data files include prefilter, tuning, and polarimetry states, the detector that was used, time stamps, and exposure times. CHROMIS raw data are stored in multi-frame FITS files with metadata in the headers, and CRISP raw data are stored one frame per file in an ANA fz format. The latter format has less strictly structured headers and many metadata are therefore encoded in the file names.
The reading of metadata from the raw files in a structured way is a major bottleneck in SSTRED processing, in particular for CRISP, where each frame has a file header to be read and a file name to be parsed. We therefore started experimenting with ways of speeding this up.
A first attempt was to implement a dynamically loadable module (DLM) that could be used to cache this information, so that SSTRED at least did not have to read the same information more than once in the same IDL session. This was mainly useful for development and testing, but did not really help regular users, who generally only process the same data once.
Recently, we implemented code that reads all the raw-file metadata already at the time of the observations, and writes it in a database. For users with access to the database, this is a very significant speed-up in SSTRED processing that depends on the file system and the current load. A few tests with reading metadata for 50 000 CRISP frames (corresponding to 7.5 min of observations) took 20–45 min from the files and 25–40 s from the database. For large datasets, we therefore have a reduction from hours to minutes by reading metadata from the database.
When during normal operations, metadata for older data are accessed that are not already in the database, SSTRED automatically falls back to reading the metadata from the data files and then adds them to the database (effectively serving as a cache that is persistent between IDL sessions).
The database runs on a MariaDB server. To avoid redundancy, it is organized in hierarchical, linked tables with columns of metadata appropriate for each level, see Table 3. In addition, there are auxiliary tables with information about image detectors and prefilters.
Metadata database tables.
The tables have unique constraints to prevent writing the same information in multiple rows. They also have foreign key constraints that prevent deletion of information from connected rows in different tables.
As of this writing, the database is only available for users at the Institute for Solar Physics in Stockholm. We plan to make it more widely available after a testing period.
6.2.2. Auxiliary instruments
We extract some metadata from auxiliary instruments for the available points in time within the span of the science data in a data cube. These metadata are stored as SOLARNET variable keywords.
From the turret system log file, we read the elevation angle. The AO log file provides the AO lock rate as well as two estimates of the Fried parameter r0. One of the r0 values measures mostly ground layer seeing, while the other also includes high-altitude seeing (Scharmer et al. 2019).
6.3. World Coordinate System
Following the SOLARNET recommendations, we use the World Coordinate System (WCS) to describe the observations. The WCS is part of the FITS standard 3.0 (Pence et al. 2010, their Sect. 8), and it allows the specification of coordinates for all (multi-dimensional) pixels of a data cube. More details can be found in a series of papers started by Greisen & Calabretta (2002) and continued by authors cited in the subsections below.
For our five-dimensional science-ready data cubes, the relevant coordinates are spatial, temporal, spectral, and polarimetric. The WCS part of a sample FITS header produced by SSTRED is shown in Fig. 15. As specified with the PSi_0 keywords, all our coordinates (except Stokes) are tabulated in a FITS extension named WCS-TAB, in columns numbered as given by the PVi_3 keywords.
 |
Fig. 15. WCS part of sample FITS header without polarimetry. |
6.3.1. Spatial coordinates
The WCS for spatial coordinates was defined by Calabretta & Greisen (2002). Thompson (2006, 2010b) extended the notation with coordinates relevant to solar observations.
Our spatial coordinates are obtained from PIG. PIG fits a circle to the circumference of the primary image of the solar disk, as projected on the bottom plate of the telescope vacuum tube. Knowing the location of the exit window, it infers the pointing with ∼10″ accuracy and ∼1″ precision and logs it every second. However, the accuracy depends on a recent calibration, with several positions on the limb as reference. Failing that, the pointing can be 1–2′ off.
It is rare, but PIG sometimes loses track of the solar disk for extended periods of time. When it does, SSTRED falls back to the less accurate spatial coordinates from the turret system, logged every 30 s.
The SSTRED interpolates the logged coordinates to obtain the pointing for any point in time.
All frames that belong to the same scan are aligned by the MOMFBD processing so that they all have a common FOV. The temporal alignment procedure follows the features in the photospheric WB images, trying to keep them stationary in the FOV. This means that the spatial coordinates are constant during a scan but can change with scan number due to the solar rotation and possibly the motion of the tracked feature over the solar surface. However, with the expected limited accuracy of the pointing information, we initially set the spatial coordinates to the median of the logged pointing coordinates. Varying coordinates can be introduced later with calibrations to other instruments.
We specify the spatial coordinates by tabulating them for the array corner pixels for each scan. A capable WCS reader can then interpolate to obtain the coordinates for any pixel.
Before May 2020, SSTRED did not have an absolute calibration of the orientation of the cameras with respect to the solar coordinate system. It can now do this (also for older data) by fitting SST images of a suitable target to simultaneous SDO/HMI continuum images. Before, only the average of the four corner coordinates could be trusted as the coordinates of the center of the FOV. The lack of orientation information is signaled by setting the systematic accuracy (keyword CSYERn) for the spatial coordinates to 60″ or worse (comparable to the entire FOV). When the calibration is complete, CSYERn is set to 5″ or less.
6.3.2. Spectral coordinates
The spectral coordinates (Greisen et al. 2006) are initially set by the tuning sequence decided by the observer. Because they are in general not equidistant, they have to be tabulated.
Small adjustments of the wavelength scale are made based on a calibration of disk center data versus an atlas spectrum (see Sect. 4.4.1). The cavity errors (see Sect. 4.2) are stored as distortions to the wavelength coordinate by use of notation that extends the WCS formalism, see Appendix B.
Before we implemented a correction of the wavelengths based on the spectral calibration (Sect. 4.4.1), the wavelength of the line core had to be calibrated for each target individually, and it depends on the position of the observed target on the solar disk. For example, de la Cruz Rodríguez et al. (2011) provided a calibration method based on synthetic spectra derived from 3D MHD simulations of the solar photosphere, and later studies by Löhner-Böttcher et al. (2017, 2018) proposed to calibrate observations using laser-based measurements.
Recent atmospheric model inversion codes such as NICOLE (Socas-Navarro et al. 2015) and the STockholm Inversion Code (STiC; de la Cruz Rodríguez et al. 2016) need information about pixel- and line-dependent wavelength shifts originating from cavity errors, for instance. When the observations all have the same cavity errors, a correction can be applied afterward to the estimated velocities. For multi-line and multi-instrument data, however, the inversions need instrumental profiles customized for each spectral region and pixel.
6.3.3. Polarimetric coordinates
In the WCS, the polarimetric coordinates for Stokes vectors are defined as indices [1,2,3,4] for the [I, Q, U, V] components (Greisen & Calabretta 2002). The Stokes Q, U, and V components are defined with respect to a frame of reference, such as a Cartesian coordinate system with axes (x, y, z), where Q > 0 (Q < 0) denotes linear polarization along the x-axis (y-axis), U > 0 (U < 0) denotes linear polarization along the line y = x (y = −x), and V > 0 (V < 0) denotes right-handed (left-handed) circular polarization around the z-axis.
Our reference system is oriented so that x is parallel to the HPLT axis (solar north) and y is antiparallel to the HPLN axis, which forms a right-handed system together with a z-axis pointing along the propagation axis. However, the WCS surprisingly does not seem to have a general notation to describe the orientation of the Stokes reference system.
Two Stokes reference system conventions are in use in the night-time community, both based on the equatorial coordinate system (Right Ascension and Declination), but with the third axis pointing in different directions (toward or away from the observer, respectively). To break the ambiguity, Górski et al. (2010) defined the FITS header keyword POLCCONV for the Hierarchical Equal Area iso-Latitude Pixelization (HEALPix) data structure that is used for sky maps from various sources. Their POLCCONV has two possible string values, ‘IAU’ and ‘COSMO’, for these two conventions.
Equatorial coordinates are not practical for high-resolution solar observations, where we are more interested in coordinates on the solar disk than in the Sun’s position on the sky. The latest version of the SOLARNET recommendations (Haugan & Fredvik 2020) recommends a right-handed coordinate system with the z-axis oriented toward the observer, as for the IAU convention (Heeschen et al. 1973). The axes are specified with an extended use of POLCCONV in the form ‘(±XXXX,±YYYY,±ZZZZ)’, where XXXX, YYYY, and ZZZZ are names of WCS coordinates, and a plus (minus) means that the axis is parallel (antiparallel) to the named coordinate.
Thus, we specify our reference system with POLCCONV = ‘(+HPLT,-HPLN,+HPRZ)’, where HPRZ is defined as the axis pointing toward the observer (Thompson 2006).
This use of POLCCONV could serve as a general notation. For example, the right-handed equatorial IAU system mentioned above can be specified as POLCCONV = ‘(+RA--,+Dec-,-DIST)’, where DIST, defined as the “radial distance from the observer”, points away from the observer. The left-handed COSMO system is then POLCCONV = ‘(+RA--,+Dec-,+DIST)’.
When developing notation for the POLCCONV keyword, we initially specified only the first two axes. For SST data, this means that when the third axis is omitted, +HPRZ is implied.
6.3.4. Temporal coordinates
Temporal WCS coordinates are described by Rots et al. (2015).
Due to varying delays from FPI tuning and prefilter changes during spectral scans, the temporal coordinates in our data cubes are not equidistant and therefore have to be tabulated. Time is read from the metadata of each raw-data frame and averaged for the frames that were combined (by MOMFBD restoration) to make a frame in the data cube.
Time is advanced not only from one scan to the next, but also from one tuning position to the next. Polarimetric states are varied several times per tuning state, so that the restored images are made from data with overlapping time. These images are then mixed in approximately equal proportions by demodulation into Stokes components. Because of this, we assign the same time coordinate to all Stokes components of the same tuning state.
6.3.5. Telescope location
The telescope location is specified in three dimensions with the keywords OBSGEO-X, OBSGEO-Y, OBSGEO-Z (Rots et al. 2015, their Sect. 4.1.3). We calculated the values of these keywords (as shown in Fig. 15) following their recipe. As input we used the geodetic location of the SST (latitude, longitude, altitude) = (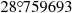 ,
, 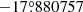 , 2380 m).
, 2380 m).
These numbers come from two services provided by Google. The latitude and longitude is available with high precision by selection of a location in Google Maps3. They also run a separate elevation service4, by use of which the altitude of the SST location was determined to a few meters above 2360 m. Allowing for the SST tower, the adopted altitude value is 2380 m. The accuracy is estimated to ∼10 m, which should be sufficient for calculations of relative speeds versus the Sun.
6.4. Statistics
The SOLARNET recommendations include the statistics metadata keywords in Table 4. One purpose of this is to enable including intensity statistics in data archive search criteria.
Statistics metadata keywords.
In addition to the keywords in Table 4, there is a DATARMS keyword in the SOLARNET recommendations. However, because DATANRMS is just DATARMS normalized with DATAMEAN, it would be redundant to include all three quantities. In our opinion, DATANRMS, corresponding to what is commonly known as the RMS contrast, is the more useful quantity. Potential uses are searches in an SVO, for data quality in quiet-Sun data, and perhaps in active regions to detect transient features such as flares.
These statistical keywords are stored as SOLARNET variable keywords, one value per frame in science data cubes. These values are easy to calculate as the cube is written to file, frame by frame.
We also need regular header keyword values that accompany these variable keywords and represent statistics for the whole cube. The minimum and maximum values for the whole cube are easy to calculate, they are just the minimum and maximum of the per-frame minimum and maximum values. Moments and percentiles require special attention because their calculation with built-in IDL commands requires that the whole cubes are in memory. The NB cubes are potentially too large for this (this is the reason CRISPEX needs the two differently ordered versions of the cubes for fast access, see Appendix C.2). We therefore need alternative ways to compute them.
Pébay et al. (2016) reported numerically stable one-pass expressions for the mean, 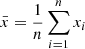 , as well as the central moments,
, as well as the central moments, 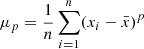 for any p ≥ 2, from which RMS, skewness, and kurtosis can be calculated. However, we wish to calculate the quantities for the whole cube from those of the individual frames, therefore we instead use their “pairwise” formulas to combine the per-frame quantities as described in Appendix D.
for any p ≥ 2, from which RMS, skewness, and kurtosis can be calculated. However, we wish to calculate the quantities for the whole cube from those of the individual frames, therefore we instead use their “pairwise” formulas to combine the per-frame quantities as described in Appendix D.
The cube percentiles cannot be calculated from the per-frame percentiles. Instead, we calculate (approximate) percentile values (including the median) from a cumulative histogram for the entire cube, accumulated frame by frame, using a large number of bins (now 216 = 65536 bins). The percentile values can then be found as the data values corresponding to the first bins that exceed the percentiles. The accuracy of percentiles calculated in this way should be on the order of the bin size (i.e., the range of values in the cube divided by the number of bins). Assuming the data values are evenly distributed within the bins, we further improve the accuracy by at least an order of magnitude by use of interpolation.
The mean absolute deviation from the mean (MAD) was a late addition to the included statistics. Like the percentiles, it cannot be calculated for the whole cube from the per-frame values. This value is instead built up during the histogram accumulation pass through the cube, the mean being known from the first pass. The fact that we make two passes removes one advantage with the pair-wise expressions in Appendix D, as we could then also use the two passes for the moments. If computing time is of the essence, a simple mean of the per-frame values for the regular header keyword might be considered.
7. CRISPEX
An important part of the workflow with complex data products like the science-ready data cubes produced by SSTRED is being able to view and analyze them. Not a part of SSTRED per se, CRISPEX (Vissers & Rouppe van der Voort 2012) is an IDL tool that offers such data cube browsing and analysis functionality. Details such as the changelog, how to keep an up-to-date distribution of CRISPEX, and a short usage tutorial can be found on the CRISPEX github page5.
From version 1.7.4, released in January 2018, CRISPEX supports the SOLARNET-compliant science data cubes output by SSTRED. CRISPEX was originally developed for CRISP science data cubes stored in LP format files. Along with the fz format, the LP (for “La Palma”) format has been used for SST/SVST data since at least the early 1990s. CRISPEX was earlier extended to support data from IRIS (De Pontieu et al. 2014), reading both its Level 3 spectrograph (SG) FITS cube files and the Level 2 slit-jaw image (SJI) files6. In fact, CRISPEX can handle any synthetic or observational data cube, provided it has been formatted according to either the legacy LP format, the SOLARNET-compliant FITS format, or the IRIS FITS format (e.g., IRIS SJI-formatted SDO and Hinode data, or IRIS SG-formatted Bifrost cubes).
The richer metadata in the SOLARNET cubes should result in an improved user experience compared to the LP format cubes (and to some extent, also compared to the IRIS format), both when calling the program and during run-time. During run-time, the changes are visible mostly when dealing with the WCS information, see Sect. 6.3. For instance, while the LP and IRIS formats provide only scan-averaged time, the SOLARNET format’s WCS information contains image timing information as function of wavelength tuning and modulation state (for tuning instruments) or of spatial position and modulation state (for (scanning) slit spectrographs). The time-dependent spatial position is also available, which allows accounting for solar rotation during the observations when returning the solar spatial coordinates. This is particularly beneficial for browsing multi-instrument datasets (e.g., CRISP plus CHROMIS or CRISP/CHROMIS plus IRIS). First, because the image to be displayed (determined through nearest-neighbor interpolation in time) can be selected more closely in time when considering tuning filter instruments or (rastering) spectrographs. Second, because creating co-aligned cubes might in principle be skipped, assuming the (time-dependent) spatial coordinates are well defined: the pixel size difference, xy-translation, FOV rotation with respect to solar north and solar rotation would automatically be taken into account during run-time through the WCS information of the respective files.
Moreover, to accommodate the larger CHROMIS images (larger than CRISP and IRIS), the zooming functionality has been extended to allow zoom true to size (i.e., 1:1 data-vs-monitor pixel scale) also on screens that would normally not fit the image. This could in the future also be useful for visualizing data from the Daniel K. Inouye Solar Telescope (DKIST; Rimmele et al. 2020) or the European Solar Telescope (EST; Matthews et al. 2016), which are set to deliver 4k × 4k images or larger.
The metadata needed, particularly the coordinate system of the data, is provided in different ways for the different file formats. For smooth display and for plotting of large data cubes, the data themselves need to be ordered optimally for fast access. Details are given in Appendix C.
8. Discussion
8.1. Processing
The SSTRED is a data processing pipeline that processes raw data from CRISP and CHROMIS and outputs science data cubes in FITS files.
We identified two deficiencies with CHROMIS data that we had not encountered in CRISP data. Wavelength- and time-dependent dispersion in both atmosphere and optics caused misalignment within Ca II scans. An alignment procedure was implemented as part of SSTRED. Wavelength-dependent dispersion also appears to limit the accuracy of the intensity calibration, which is measured in the WB but is applied to all wavelengths. The cause for these two issues is the wide wavelength range in Ca II scans compared to other line scans collected with CRISP and CHROMIS, together with the large wavelength gradient of the dispersion in the 400 nm region.
Creating science cubes from MOMFBD-restored images involves multiple spatial corrections, such as alignment, rotation, temporal destretching to remove anisoplanatic distortions, and inter-tuning destretching to remove MOMFBD-residual geometrical distortions. Some of these operations require one correction to be applied before another is measured, causing multiple consecutive interpolation operations. As each interpolation is a blurring operation, we wish to minimize the number of such operations. Instead of performing these resampling operations consecutively, SSTRED can combine measured image shifts, rotations, and spatial distortions into a single interpolation operation, resulting in less blurring and fewer artifacts. Future pipeline developers, designing code from scratch, should build in these capabilities at a low level, perhaps by making images class objects. The objects could include both original image data, a version with operations so far performed on them, as well as a record of these operations. When further operations are added, a new version can be calculated in this way, using the original data and the combined operations.
Limb data are not as well supported as on-disk data. This has to do with difficulties with alignment. The alignment between WB and NB outside the limb is hampered by weak signals in the WB and continuum. On disk, there can be problems with low contrast of features on the disk and also with finding a rectangular subfield on the disk on which to perform the cross correlation.
8.2. Metadata
The SSTRED processes metadata, and the output science data cubes are compliant with the SOLARNET metadata recommendations as formulated by Haugan & Fredvik (2020). This is meant to facilitate interpretations as well as the search for science data in future Solar Virtual Observatories (SVOs). As part of SOLARNET compliance, we specify the coordinates of the output data cubes within the WCS system.
The number of pipelines that produce SOLARNET-compliant output is growing. Any new instrument and pipeline should implement this from the start. The metadata and SVO upload will facilitate the findability, accessibility, interoperability, and reusability (FAIR; Wilkinson et al. 2016) of the data.
Metadata processing posed a few new challenges to the pipeline development, leading to new developments. The time-consuming reading of header data led to the implementation of a database for raw-data metadata. Cavity errors, pixel-dependent deviations from the nominal wavelength coordinate, required an extension of an already proposed notation for WCS coordinate distortions. While not (yet) part of WCS proper, adoption of this notation by other pipelines would simplify the task of writing software for the analysis of data from multiple instruments. By storing intensity statistics in the metadata, frame by frame as variable keywords, we can calculate some of the statistics (the moments) of data cubes from the statistics of the individual frames. An SVO that implements this capability can facilitate searches by quickly calculating statistics of subsets of data cubes from those of the individual frames.
8.3. Development
The SSTRED was first developed for CHROMIS data, generalizing the old CRISPRED pipeline and adding metadata support. It should be fairly easy to extend it to process data from other, similar instruments.
The development was made by a very small team after CHROMIS was installed. The development of the IDL parts of SSTRED has occupied one of us (MGL) for a large fraction of his time since the installation of CHROMIS. Another (TH) spent considerable time on REDUX. Together with the time spent by the remaining authors, and counting also the development of CRISPRED prior to the CHROMIS installation, this represents an effort of several person-years. This is costly, but an effort that is clearly needed to maximize the scientific output of modern ground-based solar instrumentation.
Development of new calibrations has lead to new recommendations for SST observations, such as collecting small datasets of disk-center, quiet-Sun data every now and then throughout the observing period to facilitate the intensity calibration. Artifacts are to be expected, and it is important to identify and characterize them as soon as possible and if possible, develop procedures for compensating for them.
The SOLARNET recommendations include versioning of data files. We take this to also include intermediate data files, such as calibration data that can perhaps be fitted in various ways or are based on parameters that depend on the specific use case of the data. To make the final data completely specified, versions of these data files need to be specified in the metadata. This is rather complicated and probably needs to be implemented at the core level of the pipeline. We have chosen not to do this, but next-generation pipelines should be designed with this in mind.
We rely on a few external IDL libraries that are self-contained and available through git version control (IDLAstro and Coyote) or direct download from a web site (mpfit). We made an early decision not to require users to install SolarSoft (Freeland & Handy 1998) to run SSTRED. While this prevented us from using the WCS routines of Thompson (2010a) within the pipeline, we still wished SolarSoft users to be able to use its WCS support when reading SSTRED output. Testing showed that while our five-dimensional data cubes complied with the WCS definitions, SolarSoft could not perform the required interpolation in more than three coordinate dimensions with routines included in IDL. We found the multi-dimensional interpolation implementation of Smith (2003), which is now included in SolarSoft.
The SST granulation images can be aligned to HMI images with very god precision, as demonstrated by Rutten (priv. comm.), but this requires HMI data with high enough cadence so that a frame can be found that is close enough in time for the granulation pattern not to have changed too much. Not using SolarSoft within SSTRED also limited our use of HMI data to 15-min cadence publicity jpeg images available through predictable URLs. We did not find a way to programmatically download HMI 45-s cadence science data without SolarSoft. This is the reason that our pointing calibration versus HMI data so far only works for data with spots or pores in the FOV.
8.4. Data access
Access to science-ready CRISP and CHROMIS data depends on the data policies of the owners of the data. Data that belong to the Institute for Solar Physics are currently proprietary, but are shared with researchers based in Sweden. Data collected within the SOLARNET access program are proprietary for one year after successful pipeline processing and are then released to the solar community. Access to data collected by other research groups depends on their data policies.
The SVO (see Sect. 3.4) database has access information and can serve download URLs. Our own data, as well as data collected under the second SOLARNET project access program are hosted by Stockholm University, from where they can be downloaded, depending on the release status. The data download is straightforward for data that are released to the solar community, but download of proprietary data is password-protected.
The Institute of Theoretical Astrophysics in Oslo and the Lockheed Martin Solar and Astrophysics Laboratory have released co-aligned SST/IRIS datasets elsewhere (Rouppe van der Voort et al. 2020).
8.5. Concluding remarks
We have described the SSTRED data-processing pipeline. We also demonstrated what needs to go into the pipelines of a major ground-based solar telescope and its instruments.
A pipeline that encodes optimized processing of data and calibrations is absolutely necessary for a nontrivial instrument to reach its full scientific potential. Known sources of error need to be at least characterized and when possible compensated for.
Well-defined metadata are crucial for data to be usable for scientists with little knowledge about the instruments and the circumstances of the observations. We aim to follow and establish mechanisms and notation to fully characterize the output from the pipeline.
The SSTRED was developed while the instruments and the pipeline were used, which means that early versions of the pipeline were less capable than the current version. For future telescopes, we must improve on this by having full support very soon after commissioning and also very well controlled data-collection procedures. A pipeline can only work with the data that were collected, and the quality of the processed data strongly depends on the calibration data that are collected. We cannot and should not stop development of better processing procedures, therefore we should collect more calibration and environment data than we know we need. As an example, having a log of the temperature sensor data from the telescope bottom plate made it much easier to understand the wavelength- and time-dependent misalignment of Ca II CHROMIS data.
All software must be expected to have bugs. Therefore it is extremely important to archive not only reduced data, but also raw data, including calibration data, at least for observations that are of lasting value and/or are difficult to repeat (unusual events, part of long time-sequences, etc.). While developing SSTRED, we have often found reasons to reprocess data, sometimes multiple times, because of corrected bugs or the addition of improved procedures. Retaining this possibility is one way of ensuring the best-quality data for scientific interpretation.
In our opinion, SSTRED represents the most ambitious data-processing pipeline for solar imaging instruments. It can thus serve as a reference for future similar developments.
See Appendix A for information about access and versions of the pipeline code.
See also the IRIS Technical Notes (ITN) 11 and 12 – concerning data levels and header keywords, respectively – on the IRIS website: https://iris.lmsal.com/documents.html.
Acknowledgments
Guus Sliepen implemented the new data acquisition system used for CHROMIS. We have had valuable discussions about metadata and FITS headers with Mats Carlsson and Bill Thompson. We are grateful to several users – in particular Vasco Henriques and Pradeep Chitta – for patiently testing SSTRED and reporting bugs. Lewis Fox helped with the coding in the early stages of development. This work was carried out as a part of the SOLARNET project supported by the European Commission’s 7th Framework Programme under grant agreement No. 312495. This research has received financial support from the European Union’s Horizon 2020 research and innovation program under grant agreement No. 824135 (SOLARNET). The Swedish 1-m Solar Telescope is operated on the island of La Palma by the Institute for Solar Physics in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias. The Institute for Solar Physics is supported by a grant for research infrastructures of national importance from the Swedish Research Council (registration number 2017-00625). JdlCR is supported by grants from the Swedish Research Council (2015-03994), the Swedish National Space Board (128/15) and the Swedish Civil Contingencies Agency (MSB). This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (SUNMAG, grant agreement 759548).
References
- Berghmans, D., van der Linden, R. A. M., Vanlommel, P., et al. 2005, Ann. Geophys., 23, 3115 [CrossRef] [Google Scholar]
- Bose, S., Joshi, J., Henriques, V. M. J., & Rouppe van der Voort, L. 2021, A&A, 647, A147 [EDP Sciences] [Google Scholar]
- Brault, J. W., & Neckel, H. 1987, Spectral Atlas of Solar Absolute Disk averaged and Disk-Center Intensity from 3290 to 12510 Å [Google Scholar]
- Bray, T. 2014, The JavaScript Object Notation (JSON) Data Interchange Format, RFC 7159, RFC Editor [Google Scholar]
- Buehler, D., Esteban Pozuelo, S., de la Cruz Rodriguez, J., & Scharmer, G. B. 2019, ApJ, 876, 47 [Google Scholar]
- Calabretta, M. 2021, WCSLIB 7.6, Australia Telescope National Facility, CSIRO [Google Scholar]
- Calabretta, M. R., & Greisen, E. W. 2002, A&A, 395, 1077 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calabretta, M. R., Valdes, F. G., Greisen, E. W., & Allen, S. L. 2004, Representations of Distortions in FITS World Coordinate Systems, https://fits.gsfc.nasa.gov/wcs/dcs_20040422.pdf (draft dated 2004-04-22) [Google Scholar]
- Collados, M. 2017, SOLARNET IV: The Physics of the Sun from the Interior to the Outer Atmosphere, 1 [Google Scholar]
- Couvidat, S., Schou, J., Hoeksema, J. T., et al. 2016, Sol. Phys., 291, 1887 [Google Scholar]
- Criscuoli, S., & Tritschler, A. 2014, IBIS Data Reduction Notes, NSO5 [Google Scholar]
- de la Cruz Rodríguez, J., Kiselman, D., & Carlsson, M. 2011, A&A, 528, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de la Cruz Rodríguez, J., Löfdahl, M., Sütterlin, P., Hillberg, T., & Rouppe van der Voort, L. H. M. 2015, A&A, 573, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de la Cruz Rodríguez, J., Leenaarts, J., & Asensio Ramos, A. 2016, ApJ, 830, L30 [NASA ADS] [CrossRef] [Google Scholar]
- De Pontieu, B., Title, A. M., Lemen, J. R., et al. 2014, Sol. Phys., 289, 2733 [NASA ADS] [CrossRef] [Google Scholar]
- de Wijn, A. G., de la Cruz Rodríguez, J., Scharmer, G. B., Sliepen, G., & Sütterlin, P. 2021, AJ, 161, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Denker, C., Kuckein, C., Verma, M., et al. 2018, ApJS, 236, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Díaz Baso, C. J. 2018, Ph.D. Thesis, Universidad de La Laguna [Google Scholar]
- Esteban Pozuelo, S., de la Cruz Rodriguez, J., Drews, A., et al. 2019, ApJ, 870, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Fanning, D. W. 2011, Coyote’s Guide to Traditional IDL Graphics (Coyote Book Publishing) [Google Scholar]
- Freeland, S. L., & Handy, B. N. 1998, Sol. Phys., 182, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Gonsalves, R. A. 1982, Opt. Eng., 21, 829 [NASA ADS] [CrossRef] [Google Scholar]
- Górski, K. M., Wandelt, B. D., Hivon, E., Hansen, F. K., & Banday, A. J. 2010, The HEALPix Primer, Jet Propulsion Laboratory, v. 2.15a [Google Scholar]
- Greco, V., Sordini, A., Cauzzi, G., Reardon, K., & Cavallini, F. 2019, A&A, 626, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Greisen, E. W., & Calabretta, M. R. 2002, A&A, 395, 1061 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Greisen, E. W., Calabretta, M. R., Valdes, F. G., & Allen, S. L. 2006, A&A, 446, 747 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hack, W., Dencheva, N., Fruchter, A., & Greenfield, P. 2012, Distortion Correction in HST FITS Files, Tech. Rep. TSR 2012–01 (Space Telescope Science Institute) [Google Scholar]
- Hartley, R., & Zisserman, A. 2000, Multiple View Geometry in Computer Vision, 2nd edn. (Cambridge University Press) [Google Scholar]
- Haugan, S. V. H., & Fredvik, T. 2015, Document on Standards for Data Archiving and VO, Deliverable D20.4, SOLARNET (EC 7th FP grant 312495). [Google Scholar]
- Haugan, S. V. H., & Fredvik, T. 2020, ArXiv e-prints [arXiv:2011.12139v1] [Google Scholar]
- Heeschen, D. S., Howard, W. E., Smith, F. G., et al. 1973, Trans. IAU, 15A, 165 [Google Scholar]
- Henriques, V. M. J. 2012, A&A, 548, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jess, D., & Keys, P. 2017, ROSA data reduction pipeline (Queen’s University Belfast Astrophysics Research Centre) [Google Scholar]
- Joshi, J., Rouppe van der Voort, L. H., & de la Cruz Rodríguez, J. 2020, A&A, 641, L5 [EDP Sciences] [Google Scholar]
- Kasten, F., & Young, A. T. 1989, Appl. Opt., 28, 4735 [CrossRef] [Google Scholar]
- Kianfar, S., Leenaarts, J., Danilovic, S., de la Cruz Rodríguez, J., & José Díaz Baso, C. 2020, A&A, 637, A1 [CrossRef] [EDP Sciences] [Google Scholar]
- Kosugi, T., Matsuzaki, K., Sakao, T., et al. 2007, Sol. Phys., 243, 3 [Google Scholar]
- Kučera, A., Ambróz, J., Gömöry, P., Kozák, M., & Rybák, J. 2010, Contrib. Astron. Obs. Skalnaté Pleso, 40, 135 [Google Scholar]
- Kučera, A., Tomczyk, S., Rybák, J., et al. 2015, IAU Gen. Assembly, 29, 2246687 [Google Scholar]
- Kuckein, C., Denker, C., Verma, M., et al. 2017, Fine Structure and Dynamics of the Solar Atmosphere, eds. S. Vargas Domínguez, A. G. Kosovichev, L. Harra, P. Antolin, Proc. IAUS, 327 [Google Scholar]
- Kuridze, D., Mathioudakis, M., Morgan, H., et al. 2019, ApJ, 874, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Landsman, W. B. 1993, in Astronomical Data Analysis Software and Systems II, eds. R. J. Hanisch, R. J. V. Brissenden, & J. Barnes, ASP Conf. Ser., 52, 246 [Google Scholar]
- Leenaarts, J., de la Cruz Rodríguez, J., Danilovic, S., Scharmer, G., & Carlsson, M. 2018, A&A, 612, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Löfdahl, M. G. 2002, in Image Reconstruction from Incomplete Data II, eds. P. J. Bones, M. A. Fiddy, & R. P. Millane, Proc. SPIE, 4792, 146 [Google Scholar]
- Löfdahl, M. G., & Scharmer, G. B. 1994, A&AS, 107, 243 [NASA ADS] [Google Scholar]
- Löfdahl, M. G., Hillberg, T., de la Cruz Rodríguez, M. G., et al. 2018, ArXiv e-prints [arXiv:1804.03030v1] [Google Scholar]
- Löhner-Böttcher, J., Schmidt, W., Doerr, H.-P., et al. 2017, A&A, 607, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Löhner-Böttcher, J., Schmidt, W., Stief, F., Steinmetz, T., & Holzwarth, R. 2018, A&A, 611, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mampaey, B., Vansintjan, R., & Delouille, V. 2017, in SOLARNET IV: The Physics of the Sun from the Interior to the Outer Atmosphere, 91 [Google Scholar]
- Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [Google Scholar]
- Matthews, S. A., Collados, M., Mathioudakis, M., & Erdelyi, R. the EST Team 2016, in Ground-based and Airborne Instrumentation for Astronomy VI, eds. C. J. Evans, L. Simard, & H. Takami, Proc. SPIE, 9908, 990809 [Google Scholar]
- Neckel, H. 1999, Sol. Phys., 184, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Neckel, H. 2005, Sol. Phys., 229, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Neckel, H., & Labs, D. 1994, Sol. Phys., 153, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Noll, R. J. 1976, J. Opt. Soc. Am., 66, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Paxman, R. G., Schulz, T. J., & Fienup, J. R. 1992a, J. Opt. Soc. Am. A, 9, 1072 [NASA ADS] [CrossRef] [Google Scholar]
- Paxman, R. G., Schulz, T. J., & Fienup, J. R. 1992b, in Signal Recovery and Synthesis IV, Optical Society of America, Tech. Digest Ser., 11, 5 [Google Scholar]
- Paxman, R. G., Seldin, J. H., Löfdahl, M. G., Scharmer, G. B., & Keller, C. U. 1996, ApJ, 466, 1087 [NASA ADS] [CrossRef] [Google Scholar]
- Pébay, P., Terriberry, T. B., Kolla, H., & Bennett, J. 2016, Comput. Stat., 31, 1305 [Google Scholar]
- Pence, W. D., Chiappetti, L., Page, C. G., Shaw, R. A., & Stobie, E. 2010, A&A, 524, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pietrow, A. G. M., Kiselman, D., de la Cruz Rodríguez, J., et al. 2020, A&A, 644, A43 [CrossRef] [EDP Sciences] [Google Scholar]
- Rimmele, T. R., Warner, M., Keil, S. L., et al. 2020, Sol. Phys., 295, 172 [Google Scholar]
- Roddier, N. 1990, Opt. Eng., 29, 1174 [NASA ADS] [CrossRef] [Google Scholar]
- Rots, A. H., Bunclark, P. S., Calabretta, M. R., et al. 2015, A&A, 574, A36 [CrossRef] [EDP Sciences] [Google Scholar]
- Rouppe van der Voort, L., De Pontieu, B., Scharmer, G. B., et al. 2017, ApJ, 851, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Rouppe van der Voort, L. H. M., De Pontieu, B., Carlsson, M., et al. 2020, A&A, 641, A146 [EDP Sciences] [Google Scholar]
- Rouppe van der Voort, L. H. M., Joshi, J., Henriques, V. M. J., & Bose, S. 2021, A&A, 648, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanchez Almeida, J., & Lites, B. W. 1992, ApJ, 398, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Scharmer, G. 2017, in SOLARNET IV: The Physics of the Sun from the Interior to the Outer Atmosphere, 85 [Google Scholar]
- Scharmer, G. B. 2006, A&A, 447, 1111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scharmer, G. B., Bjelksjö, K., Korhonen, T. K., Lindberg, B., & Pettersson, B. 2003, in Innovative Telescopes and Instrumentation for Solar Astrophysics, eds. S. Keil, & S. Avakyan, Proc. SPIE, 4853, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Scharmer, G. B., Narayan, G., Hillberg, T., et al. 2008, ApJ, 689, L69 [Google Scholar]
- Scharmer, G. B., Löfdahl, M. G., Sliepen, G., & de la Cruz Rodríguez, J. 2019, A&A, 626, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schnerr, R., de la Cruz Rodríguez, J., & van Noort, M. 2011, A&A, 534, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Selbing, J. 2005, Master’s Thesis, Stockholm University [arXiv:1010.4142] [Google Scholar]
- Seldin, J. H., & Paxman, R. G. 1994, in Image Reconstruction and Restoration, eds. T. J. Schultz, & D. L. Snyder, Proc. SPIE, 2302, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Sliepen, G., & Sütterlin, P. 2013, Synergies Between Ground and Space BasedSolar Research, 1st SOLARNET – 3rd EAST/ATST meeting [Google Scholar]
- Smith, J. D. 2003, Ninterpolate Function https://tir.astro.utoledo.edu/idl/ninterpolate.pro, See also “Multidimensional Interpolation” thread from 2003 in news:comp.lang.idl-pvwave [Google Scholar]
- Socas-Navarro, H., de la Cruz Rodríguez, J., Asensio Ramos, A., Trujillo Bueno, J., & Ruiz Cobo, B. 2015, A&A, 577, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- SPICE Consortium (Anderson, M., et al.) 2020, A&A, 642, A14 [CrossRef] [EDP Sciences] [Google Scholar]
- Szydlarski, M. 2019, in ALMA2019: Science Results and Cross-Facility Synergies, 126 [Google Scholar]
- Thompson, W. T. 2006, A&A, 449, 791 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thompson, W. 2010a, The SolarSoft WCS Routines: A Tutorial, Adnet Systems Inc. (NASA Goddard Space Flight Center) [Google Scholar]
- Thompson, W. T. 2010b, A&A, 515, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Noort, M. J., & Rouppe van der Voort, L. H. M. 2008, A&A, 489, 429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Noort, M., Rouppe van der Voort, L., & Löfdahl, M. G. 2005, Sol. Phys., 228, 191 [Google Scholar]
- Vissers, G., & Rouppe van der Voort, L. H. M. 2012, ApJ, 750, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Vissers, G. J. M., de la Cruz Rodriguez, J., Libbrecht, T., et al. 2019, A&A, 627, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilkinson, M. D., Dumontier, M., Aalbersberg, I. J., et al. 2016, Sci. Data, 3, 160018 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Pipeline code
The non-MOMFBD parts of SSTRED are coded in IDL, with some parts implemented as DLMs coded in C/C++ for speed and/or to use existing code. SSTRED works with IDL version 8.3 or later.
The SSTRED IDL code is available from github7. The hash of the latest commit, tagged 1.1.0-634, is g3a676b9f2e5e.
The SSTRED uses IDL objects, with the major steps in the processing implemented as class methods. There are separate classes for CRISP and CHROMIS, inheriting common code from a top class whenever possible and practical.
Adding support for another, similar instrument should not be very hard. It is a matter of entering information about detectors, file formats, and filters, identifying common processing steps, and writing a few new class methods that cover the differences. Identifying any particular data imperfections for the new instrument and developing calibrations and corrections for them could be time-consuming.
A.1. Required IDL libraries
The following IDL code/libraries are required:
A.2. DLMs
Some parts of the pipeline are implemented as DLMs coded in C/C++. There are several reasons for this, primarily because it gives access to lower-level C++ functionality, which allows for optimization. There is also the benefit of obtaining access to high-level C++ libraries, such as boost and OpenCV. In particular, the pinhole calibration mentioned in Sect. 4.1 utilizes camera calibration tools that are readily available in OpenCV.
The DLM also allows direct access to code intrinsic to the REDUX/MOMFBD software (see the Appendix A.3 for access and version information). This means that we can be certain that function calls within IDL are doing the exact same thing as the REDUX code does.
Sample tasks implemented as DLMs:
-
Sum images.
-
Read and mosaic MOMFBD output.
-
Read and write fz format files.
-
Do pinhole alignment.
-
Geometric transform of images.
-
Measurements and application of stretch vectors.
-
Log file conversion.
-
Some metadata handling.
-
Access to some internal REDUX MOMFBD code.
A.3. REDUX code
CHROMIS and CRISP data are restored from optical aberrations caused by turbulence in the atmopshere and partially corrected for by the SST AO. We used the MOMFBD code of van Noort et al. (2005) as the workhorse for SST image data for several years. One of us (TH) now maintains a fork of that project (called REDUX), where parts of the original code are replaced with open-source libraries.
REDUX implements several improvements and new features compared to MOMFBD. This includes a method for making sparser null-space matrices from the LECs, leading to a speed-up of ∼33%. Another is the re-implementation of the additional WB objects used for dewarping (see Sect. 5.4) with an additional ∼25% speed-up.
As with the old MOMFBD code, pinhole calibration is used to specify the relative geometry between the cameras involved in a data set to be restored. The REDUX code can read the new projective transforms described in Sect. 4.1. (It still supports the xoffs/yoffs files of the old MOMFBD program.)
The REDUX code, including the DLMs, is available from github8. The hash of the latest commit, tagged 1.0.18-13, is g27ba623e9b22. See the Redux wiki page9 for installation and usage instructions.
Appendix B: Wavelength distortions
This appendix describes how SSTRED stores cavity errors (see Sect. 4.2) as distortions in the wavelength coordinate.
The etalons are fixed with respect to the detectors, so that the cavity errors can be described as distortions that are a function of the spatial pixel coordinates. The distorted coordinate is not a pixel coordinate, however, it is the wavelength in physical units, that is, the wavelength world coordinate.
Calabretta et al. (2004) defined a notation for describing coordinate distortions as part of the WCS. (Unlike the other WCS papers we refer to, this is published only in draft form. However, the notation is in fact used for data from the Hubble Space Telescope (Hack et al. 2012) and will be used for SPICE. It is also implemented in the WCSLIB C library (Calabretta 2021)10.) However, while this notation can specify distortions that are a function of pixel coordinates, the coordinate being distorted also has to be a pixel coordinate.
This would not be a problem if the wavelength pixel-coordinate grid were equidistant in wavelength. Then a distortion in the tuning pixel coordinate would be equivalent to a distortion in the wavelength world coordinate. In our case, however, the wavelength is tabulated without restriction on the spacing between tuning points. This would lead to a table look-up that has a discontinuous derivative, defined by the spacing in wavelength between the two nearest tuning points. Alternatively, if the distortion were defined in the tuning pixel coordinate, it would have to be specified for each tuning, resulting in an additional dimension in the distortion table, and this would still cause problems at tuning points surrounded by different-length wavelength intervals.
 |
Fig. B.1. WCS distortions part of a sample FITS header with cavity maps for two Ca II prefilters, 3934 and 3969. These lines come after the CDELT3 line in Fig. 15. |
We use an extended notation, described by Haugan & Fredvik (2020, version 1.5, in prep.). This notation allows distortions to be associated with and applied to any of a set of numbered stages in the conversion of pixel coordinates to world coordinates in the WCS. In contrast to the cases considered by Calabretta et al. (2004), the associate and apply stages are specified individually. Below we give a brief description focused on the parts used for the cavity errors.
The new notation generalizes the record-valued DPj/DQi keywords and the associated CPDISj/CQDISi keywords of Calabretta et al. (2004) and defines keywords with similar meaning, but with W substituted for P and Q. The DWj (and i) keywords have a few additional records compared to DQi and DPj, namely DWj⋅ASSOCIATE and DWj⋅APPLY, the values of which are the relevant stage numbers. See Fig. B.1 for the corresponding part of a FITS header.
The cavity maps are a function of the spatial pixel coordinates at stage 1 (the associate stage), but they are a distortion of the spectral world coordinate at stage 6 (the applied stage). Consequently, we set DW3⋅ASSOCIATE to 1 and DW3⋅APPLY to 6.
Following Calabretta et al. (2004), we store the distortion array in a FITS image extension called WCSDVARR. Multiple distortions, to be applied in sequence, can be stored in multiple WCSDVARR extensions with different version numbers (EXTVER keyword). Each distortion array can be defined to apply to only a partial range of the apply coordinates. For this, the DWj⋅SCALEi and DWj⋅OFFSETi keywords are used (see Calabretta et al. 2004; Haugan & Fredvik 2020 for details). We use this mechanism for the multiple cavity maps resulting from CHROMIS line scans using multiple prefilters (Sect. 4.2.1).
The SSTRED has code for reading at least the distortions written by SSTRED itself. It should not be hard to port this to any language in which the SSTRED output is to be read. Documentation can be found in the SST wiki11. The corrected wavelength coordinate for a data pixel, λcorr(ix, iy, itun, ipol, iscan) = λ(itun)+δλ(ix, iy, itun), where λ(itun) is the nominal tuning wavelength, and δλ is the contents of the image extension WCSDVARR.
Appendix C: CRISPEX-supported file formats
C.1. Metadata
The CRISPEX program needs metadata to correctly handle and display the data. In particular, it needs coordinates: spatial, temporal, spectral, and polarimetric.
As the legacy LP format cubes come with a minimalistic header (describing only the cube dimensions and the data type), the CRISPEX IDL command takes a number of keywords, some are Boolean flags (to obtain a particular behavior), and some are used to supply auxiliary data files with additional information (e.g., time in seconds and wavelength values).
For FITS cubes – both of the IRIS and the SOLARNET compliant varieties – CRISPEX (un)sets these switches and populates auxiliary information variables automatically from the file metadata, thereby simplifying the call sequence. Table C.1 lists which header keywords are used (and how) by CRISPEX. Details are given in Sects. C.1.1 and C.1.2 below.
C.1.1. IRIS FITS files
Most header keywords are used to determine or read the spatial WCS information that can then be processed by the SolarSoft IDL functions wcs_get_coord() and wcs_get_pixel() to go back and forth between cube pixel and data value, especially for the coordinate transform between files of differently sized FOVs. Most other header keywords are used to obtain correct labeling in plot windows and control panel selection options, or as switches to enable/disable certain behavior. The remainder are to deal with multiple spectral windows for the particular case of IRIS Level 3 data, where the wavelength axis is usually a concatenation of noncontiguous spectral diagnostic windows corresponding to the various observed lines.
IRIS Level 3 files contain four extensions, the first three of which are used by CRISPEX: (0) the main data (in BUNIT), (1) the wavelength array (in CUNIT3), and (2) the timing array (in CUNIT4 since STARTOBS). IRIS Level 2 SJI files contain three extensions, of which CRISPEX only uses the first two. The main extension again contains the main data. The first auxiliary extension holds the time- and raster step-dependent information on the slit.
FITS header keywords required by CRISPEX
 |
Fig. C.1. Schematic representation of the CRISPEX data ordering of a spectrotemporal Stokes cube with three tuning positions. The third dimension has been “unfolded” into a tuning/polarimetry axis and a scan axis, showing that the data are ordered sequentially as wavelength scans for each Stokes parameter separately before proceeding to the next scan. On the polarimetry axis, ipol = [1, 2, 3, 4]⇔Stokes [I, Q, U, V] (Q and U not shown in the figure). |
C.1.2. SOLARNET-compliant FITS files
The SOLARNET-compliant FITS cubes use WCS for all coordinates, see Sect. 6.3. The WCS information is in main header keywords and/or binary extensions, depending on whether it is on regular grids or has to be tabulated.
CRISPEX does not access the WCS headers and extensions directly, but rather retrieves the coordinate information through the SolarSoft functions fitshead2wcs() and wcs_get_coord(). CRISPEX ensures loading a modified version of wcs_proj_tab as well as auxiliary routines (all provided with the CRISPEX distribution) that allow interpolation in the five-dimensional coordinate look-up table when accessed through wcs_get_coord().
C.2. Data cube ordering
Regardless of the file format (LP, IRIS-style FITS, or SOLARNET FITS), CRISPEX expects a certain data-cube ordering for it to correctly access the data when the cursor is moved or changed, for example, the frame number or wavelength tuning position. CRISPEX cubes can be written as three-, four- or five-dimensional cubes, but are upon access considered to be three-dimensional, a sequence of two-dimensional frames with any higher dimension combined, or “folded” into a third dimension.
At this time, the ordering in the image cubes and spectral cubes is hard-coded. Should the need arise, CRISPEX could be updated to obtain the ordering information from WCS CTYPEn header keywords.
C.2.1. Image cubes
From the point of view of CRISPEX, the basic data cube is a sequence of two-dimensional images. With notation from Sect. 6.3, its dimensions are [Nx, Ny, N3], where N3 = Ntun ⋅ Npol ⋅ Nscan. CRISPEX will then subscript the third dimension with index i3 = iscan ⋅ Ntun ⋅ Npol + ipol ⋅ Ntun + itun to obtain the xy-image at spectrotemporal position (itun, ipol, iscan).
In words, intensity images are stacked according to wavelength tuning first, Stokes parameter second, and scan number (i.e., repetition) third. See Fig. C.1 for an illustration involving polarimetric data.
C.2.2. Spectral cubes
For single-wavelength time-series or single-wavelength scans, all dimensions present can be accessed quickly enough so that an image cube on its own suffices. However, for multi-dimensional cubes (e.g., time series of wavelength scans, or time series of imaging spectropolarimetry), traversing the image cube to extract the local spectrum or construct the spectrum as function of time for any pixel during run-time would take a considerable amount of time, and the recommended procedure therefore is to create a reordered, so-called “spectral”, data-cube file for swifter access to the time-dependent spectra.
A CRISPEX spectral cube has dimensions [Ntun, Nscan, N3], where N3 = Nx ⋅ Ny ⋅ Npol. The spectrum-time data frame at position (ix, iy, ipol) is obtained by indexing the third dimension with i3 = iy ⋅ Nx ⋅ Npol + ix ⋅ Npol + ipol, that is, spectrum-time diagrams are stacked according to Stokes parameter first, followed by the two spatial dimensions, x-coordinate second, and y-coordinate third.
Appendix D: Calculation of mean and moments
In this appendix we detail how we calculate the mean, variance (and its positive square root, the standard deviation from the mean), skewness, and excess kurtosis for the SOLARNET statistical keywords. We wish to do this for a data cube or a subset thereof, without having the entire cube in memory at the same time, by combining the same statistics calculated for the individual frames. This would potentially also be useful for an SVO that supports serving subsets of data defined on the fly.
Following Pébay et al. (2016) we write the mean of a set of n data points as
and define the central moments for any p ≥ 2 as
where
We partition the n data points into two subsets 𝒜 and ℬ with n𝒜 and nℬ data points, respectively, and define 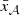 (
(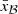 ) and
) and 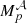 (
(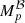 ) as
) as  and Mp, but for the subset 𝒜 (ℬ). We also define
and Mp, but for the subset 𝒜 (ℬ). We also define
With these definitions, Pébay et al. (2016) write “pairwise and update formulas” for the mean value of the n data points as the following combination of the means for the two subsets,
and n times the central moments as
We use equations (D.5) and (D.6) repeatedly to incrementally calculate the statistics for the whole cube one frame at a time. The mean,  , as defined above for a data cube with n pixels, is what we need. The variance, skewness, and excess kurtosis are not the same as the central moments, μp, however, although the conversions are easy enough. By definition, the unbiased estimate of the variance can be written as
, as defined above for a data cube with n pixels, is what we need. The variance, skewness, and excess kurtosis are not the same as the central moments, μp, however, although the conversions are easy enough. By definition, the unbiased estimate of the variance can be written as
and the standard deviation is its positive square root, σ. The Fisher–Pearson coefficient of skewness is defined as
The kurtosis for a normal distribution is 3. It is common to subtract 3 to obtain 0 for the normal distribution. The result is referred to as the excess kurtosis,
This is the quantity returned by the IDL kurtosis() and moment() functions, as well as by default by the python scipy.stats.kurtosis() function12.
All Tables
All Figures
 |
Fig. 1. Sketch of the SST (from Scharmer et al. 2003), from the 1 m lens, via the two alt-az mirrors, the field mirror on the bottom plate (inset A), the Schupmann corrector (B), the field lens and exit window (A), to the tip-tilt mirror (TM), deformable mirror (DM), and re-imaging lens (RL) on the optical table (C). The optical path continues in Fig. 2. |
| In the text | |
 |
Fig. 2. Schematics of the setup used from the CHROMIS installation in August 2016 through the 2020 season. Acronyms: FL = field lens, FS = field stop, TM = tip-tilt mirror; DM = deformable mirror; RL = reimaging lens; DC = 500 nm dichroic beamsplitter; DBS = double beamsplitter, CT = correlation tracker; AO WFS = adaptive optics wavefront sensor; WB BS = wide-band beam splitter; FPI = Fabry–Pérot interferometer, LCs = liquid crystal modulators; P BS = polarizing beamsplitter, NB = narrowband, WB = wideband, NBT = NB transmitted, NBR = NB reflected, PD = phase diversity. White light enters the telescope from the top. It is split into a red and a blue beam at ∼500 nm by the DC. Distances and angles do not correspond to the physical setup. |
| In the text | |
 |
Fig. 3. CRISP prefilter transmission profiles as measured by the manufacturer for the filters installed before the 2018 season. The blue curves correspond to the smaller part number and (for the wavelength bands where we have spares) red curves the larger. The gray lines represent the average disk center atlas spectrum, normalized to the continuum. See also Table 1. (a) 517.2 nm filter profiles. (b) 587.6 nm filter profile. (c) 617.4 nm filter profiles. (d) 630.2 nm filter profiles. (e) 656.3 nm filter profiles. (f) 854.3 nm filter profiles. |
| In the text | |
 |
Fig. 4. CHROMIS filter transmission profiles (normal incidence). Red lines: NB prefilters. Blue lines: WB filters. The filter profiles shown are measured in the center of the filter by the manufacturer. The FPI profiles are not wide enough to plot them here. The gray lines represent the average disk center atlas spectrum, normalized to the continuum. See also Table 2. (a) Ca II filter profiles. (b) H-β filter profiles. |
| In the text | |
 |
Fig. 5. Cavity error of the high-resolution CHROMIS etalon through the Ca II H and K core prefilters as measured with data from 2016 June 19. Mapping the associated wavelength shift over the 1920 × 1200-pixel NB detector. |
| In the text | |
 |
Fig. 6. Removal of periodic artifacts in polarimetric data. The sample CRISP Fe I 6302 Å, −210 mÅ from line core. Data were collected on 2019 May 10 at 09:07 UT with AR 2741 in the FOV. The image shown is 53″ squared. (a) Stokes U component, sunspot saturated to emphasize artifacts in the lower left corner. (b) The polarization calibration image on which the Fourier filter is based. (c) Fourier filtered U component without the artifacts. |
| In the text | |
 |
Fig. 7. Sample diagnostic plots from the spectral intensity calibration. The scan intensities are plotted in counts, while the fitted prefilter transmission is plotted in arbitrary units. (a) Ca II K core. (b) H-β. |
| In the text | |
 |
Fig. 8. Disk center median WB calibration intensities from 2016 September 19. Prefilter wavelength bands in as indicated in the legends. The solid lines are fits to second-order polynomials as shown in the legends. (a) CHROMIS. (b) CRISP. |
| In the text | |
 |
Fig. 9. CHROMIS Ca II NB continuum (median) intensities of restored data (individual scans), with and without temporal correction as indicated in the legends. The WB calibration curves are the fit functions (shown in Fig. 8a for the 2016 September 19 data), scaled to approximately match the disk center continuum intensities. The dot colors refer to data with no correction (green), the old correction based on the WB intensity in the data set itself, and the correction based on a fit to disk center data (red). (a) Data from 2016-09-19, μ ≈ 1 (near disk center). (b) Data from 2019-06-21, varying μ. |
| In the text | |
 |
Fig. 10. CHROMIS Ca II NB continuum (median) intensities of restored data (multiple scans), with and without temporal correction, as indicated in the legends. See also Fig. 9. |
| In the text | |
 |
Fig. 11. Covariation of the misalignment in continuum and WB measured with raw data and telescope bottom plate temperature. These data were collected during the morning hours of 2016 June 19. In bad seeing, measurements most often tend toward zero. The blue boxes correspond approximately to the plot ranges of Figs. 12b and c. (a) X misalignment. (b) Y misalignment. |
| In the text | |
 |
Fig. 12. Continuum alignment diagnostic plots for 121 Ca II scans collected from 09:28:36 on 2016 June 19, covering approximately one period of the undulations shown in Fig. 11. (a) WB RMS contrast. (b) Continuum/WB X misalignment. (c) Continuum/WB Y misalignment. Filled circles in (b) and (c): Misalignment measured by use of cross-correlation with MOMFBD restored data, colors represent RMS contrast as shown in (a). Lines in (b) and (c): Shifts in X and Y used for alignment, misalignment smoothed with a heuristic algorithm that gives more weight to the high-contrast data points. Diagnostic plots like these are automatically produced by SSTRED to allow the user to verify how well the contrast-aware smoothing worked. |
| In the text | |
 |
Fig. 13. Schematic representation of CHROMIS datasets for MOMFBD processing. The depicted mock dataset has an NB continuum tuning point (green), two tuning points each in an NB K filter (yellow) and an NB H filter (orange). The H&K WB filter (blue) anchors the entire scan. This meas that it forces MOMFBD to align the restored images of the scan. |
| In the text | |
 |
Fig. 14. Contrast and image quality after different levels of MOMFBD restoration of CHROMIS Ca II continuum images from 110 scans collected on 2016 September 19. The FOV is 700 × 700 pixels (26 |
| In the text | |
 |
Fig. 15. WCS part of sample FITS header without polarimetry. |
| In the text | |
 |
Fig. B.1. WCS distortions part of a sample FITS header with cavity maps for two Ca II prefilters, 3934 and 3969. These lines come after the CDELT3 line in Fig. 15. |
| In the text | |
 |
Fig. C.1. Schematic representation of the CRISPEX data ordering of a spectrotemporal Stokes cube with three tuning positions. The third dimension has been “unfolded” into a tuning/polarimetry axis and a scan axis, showing that the data are ordered sequentially as wavelength scans for each Stokes parameter separately before proceeding to the next scan. On the polarimetry axis, ipol = [1, 2, 3, 4]⇔Stokes [I, Q, U, V] (Q and U not shown in the figure). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} H = \left[ \begin{array}{cc|c} h_{00}&h_{01}&h_{02} \\ h_{10}&h_{11}&h_{12} \\ \hline h_{20}&h_{21}&1 \end{array}\right], \end{aligned} $$](/articles/aa/full_html/2021/09/aa41326-21/aa41326-21-eq4.gif)
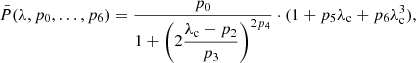
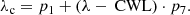
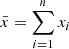
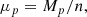
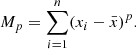
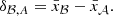
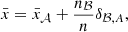
![$$ \begin{aligned} M_p&= M_p^{\mathcal{A} } + M_p^{\mathcal{B} } + n_{\mathcal{A} }\left( \frac{-n_{\mathcal{B} }}{n} \delta _{\mathcal{B} ,A} \right)^p + n_{\mathcal{B} }\left( \frac{ n_{\mathcal{A} }}{n} \delta _{\mathcal{B} ,A} \right)^p \nonumber \\&\quad + \sum _{k=1}^{p-2} \left({\begin{array}{c}p\\ k\end{array}}\right) \; \delta _{\mathcal{B} ,A}^k \left[ M_{p-k}^{\mathcal{A} }\left(\frac{-n_{\mathcal{B} }}{n}\right)^k + M_{p-k}^{\mathcal{B} }\left(\frac{n_{\mathcal{A} }}{n}\right)^k\right]. \end{aligned} $$](/articles/aa/full_html/2021/09/aa41326-21/aa41326-21-eq25.gif)