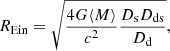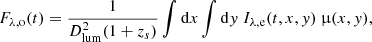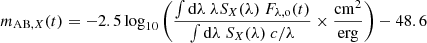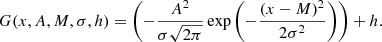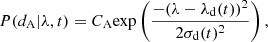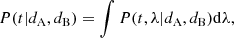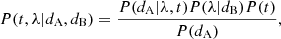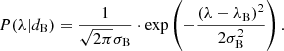| Issue |
A&A
Volume 653, September 2021
|
|
|---|---|---|
| Article Number | A29 | |
| Number of page(s) | 19 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202040169 | |
| Published online | 03 September 2021 | |
HOLISMOKES
V. Microlensing of type II supernovae and time-delay inference through spectroscopic phase retrieval
1
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild Str. 1, 85748 Garching, Germany
e-mail: jana@mpa-garching.mpg.de
2
Physik-Department, Technische Universität München, James-Franck-Straße 1, 85748 Garching, Germany
3
Exzellenzcluster ORIGINS, Boltzmannstr. 2, 85748 Garching, Germany
4
Institute of Astronomy and Astrophysics, Academia Sinica, 11F of ASMAB, No.1, Section 4, Roosevelt Road, Taipei 10617, Taiwan
5
STAR Institute, Quartier Agora – Allée du six Août, 19c, 4000 Liège, Belgium
6
Institute of Physics, Laboratory of Astrophysics, Ecole Polytechnique Fédérale de Lausanne(EPFL), Observatoire de Sauverny, 1290 Versoix, Switzerland
7
Department of Physics and Astronomy, Michigan State University, East Lansing, MI 48824, USA
8
Department of Computational Mathematics, Science, and Engineering, Michigan State University, East Lansing, MI 48824, USA
Received:
18
December
2020
Accepted:
8
May
2021
We investigate strongly gravitationally lensed type II supernovae (LSNe II) for time-delay cosmography, incorporating microlensing effects; this expands on previous microlensing studies of type Ia supernovae (SNe Ia). We use the radiative-transfer code TARDIS to recreate five spectra of the prototypical SN 1999em at different times within the plateau phase of the light curve. The microlensing-induced deformations of the spectra and light curves are calculated by placing the SN into magnification maps generated with the code GERLUMPH. We study the impact of microlensing on the color curves and find that there is no strong influence on them during the investigated time interval of the plateau phase. The color curves are only weakly affected by microlensing due to the almost achromatic behavior of the intensity profiles. However, the lack of nonlinear structure in the color curves during the plateau phase of type II-plateau supernovae makes time-delay measurements more challenging compared to SN Ia color curves, given the possible presence of differential dust extinction. Therefore, we further investigate SN phase inference through spectral absorption lines under the influence of microlensing and Gaussian noise. As the spectral features shift to longer wavelengths with progressing time after explosion, the measured wavelength of a specific absorption line provides information on the epoch of the SN. The comparison between retrieved epochs of two observed lensing images then gives the time delay of the images. We find that the phase retrieval method that uses spectral features yields accurate delays with uncertainties of ≲2 days, making it a promising approach.
Key words: gravitational lensing: strong / gravitational lensing: micro / distance scale / supernovae: individual: type II
© J. Bayer et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1. Introduction
Over the last few years, several new and independent techniques for measuring the Hubble constant, H0, have been presented to address the problem of the > 4σ discrepancy (Verde et al. 2019) between the value measured from observations of the cosmic microwave background (Planck Collaboration VI 2020) and distance ladder measurements from the supernova H0 for the equation of state (SH0ES) program (Riess et al. 2016, 2018, 2019; see also Freedman et al. 2019, 2020). One of these techniques is to conduct time-delay cosmography on strongly lensed variable objects (Refsdal 1964) to infer H0 through time-delay measurements, lens mass modeling, and reconstructing the line-of-sight mass distributions. The calculated time-delay distance is inversely proportional to H0.
The method can be applied to different variable sources. One possibility is to use quasars, which has already been done in the H0LiCOW program (Suyu et al. 2017; Birrer et al. 2019; Sluse et al. 2019; Chen et al. 2019; Wong et al. 2020; Rusu et al. 2020) in cooperation with the COSmological MOnitoring of GRAvItational Lenses (COSMOGRAIL; Eigenbrod et al. 2005; Courbin et al. 2018; Bonvin et al. 2018), the Strong lensing at High Angular Resolution Program (SHARP; Chen et al. 2019), and the STRong-lensing Insights into the Dark Energy Survey (STRIDES) collaboration (Shajib et al. 2020). The newly established Time-Delay COSMOgraphy (TDCOSMO) organization is further testing systematic effects and expanding the lensed quasar sample for future studies (Millon et al. 2020b,a; Gilman et al. 2020; Birrer et al. 2020). A second way to conduct time-delay measurements is through strongly lensed supernovae (LSNe), which was first envisioned by Refsdal (1964) when he introduced the concept of time-delay cosmography.
Until today, only two LSNe with multiple resolved images have been observed. The first, called “SN Refsdal”, is a type II supernova (SN II), discovered by Kelly et al. (2016a,b), which was lensed by the galaxy cluster MACS J1149.5+222.3. The second LSN, iPTF16geu, was discovered by Goobar et al. (2017) and is a type Ia supernova (SN Ia) at redshift 0.409 lensed by a galaxy at a redshift of 0.216. Several lensing studies on SN Refsdal have been performed (e.g., Rodney et al. 2016; Kelly et al. 2016b; Treu et al. 2016; Pierel & Rodney 2019; Grillo et al. 2016, 2020; Baklanov et al. 2021); iPTF16geu has been studied extensively (Goobar et al. 2017; More et al. 2017; Yahalomi et al. 2017; Dhawan et al. 2018; Johansson et al. 2021) and shows strong signs of microlensing. Further studies on SNe Ia and their usability to measure time delays have been conducted by Goldstein et al. (2018), Foxley-Marrable et al. (2018), Huber et al. (2019, 2021). The main focus of those papers has been the characterization of the perturbations introduced by microlensing.
Microlensing of SNe results from the additional lensing of strongly lensed SNe induced by the compact masses that the lens galaxy is composed of (e.g., stars). The influence of microlensing is independent for each observed image of the SN. This causes the spectrum to be magnified to an unknown amount and makes time-delay measurements difficult. Goldstein et al. (2018), Huber et al. (2021) show that microlensing of LSNe Ia is mostly achromatic. In three of five color curves, Huber et al. (2021) find characteristic minima or maxima within the achromatic phase of SNe Ia, making time-delay measurements with LSNe Ia feasible.
With this work, which is part of Highly Optimised Lensing Investigations of Supernovae, Microlensing Objects, and Kinematics of Ellipticals and Spirals (HOLISMOKES; Suyu et al. 2020), we take a closer look at SNe II for time-delay measurements that incorporate microlensing effects. Characteristic features in the light curves and spectra of SNe II could be used to conduct time-delay measurements. With the upcoming Rubin Observatory Legacy Survey of Space and Time (LSST; LSST Science Collaboration 2009) we expect to detect over 1000 LSNe II (Wojtak et al. 2019; Goldstein et al. 2018; Goldstein & Nugent 2017). This number is larger than the number of LSNe Ia expected to be observed, which is estimated to be around 500 to 900 (Oguri & Marshall 2010; Wojtak et al. 2019). Therefore, it would be a missed opportunity to not include SNe II for time-delay cosmography.
We use radiative-transfer models to investigate the potential of LSNe II for cosmographic measurements. In recent years computational capabilities have grown, allowing us to conduct more and more complex calculations for modeling SNe of different types. The study of LSNe Ia by Huber et al. (2019) used the Applied Radiative Transfer In Supernovae (ARTIS) code, which was developed by Kromer & Sim (2009).
For this study of LSNe II, we use the Monte Carlo radiative transfer code TARDIS (Kerzendorf & Sim 2014), as modified by Vogl et al. (2019). The spatial specific-intensity profiles for each wavelength are microlensed by magnification maps generated with the inverse ray-tracing code GERLUMPH (Vernardos et al. 2015), and deformed spectra are constructed. We then evaluate the microlensed spectra, light curves, and color curves on their usability for time-delay measurements. In doing so, we investigate a new approach to inferring phases on the basis of the spectral evolution of the SN. Throughout the paper, we assume a radiation-free flat Lambda cold dark matter (ΛCDM) cosmology with H0 = 72 km s−1 Mpc−1 (Bonvin et al. 2017), Ωm = 0.26, and ΩΛ = 0.74, as assumed by Oguri & Marshall (2010).
The structure of the paper is as follows. First, we discuss the TARDIS simulations and present the synthetic SN II spectra in Sect. 2. In Sect. 3 we explain our application of microlensing to those spectra and show the resulting light curves and color curves. Further, we show the impact of microlensing on the absorption features. In Sect. 4 we investigate the phase inference of SNe from the absorption wavelengths. Finally, we discuss our results in Sect. 5 and conclude in Sect. 6.
2. Type II supernova models
In this section we describe the creation of the SN II models we use for the microlensing investigation in Sect. 3. We performed the calculations with the extended version of the radiative-transfer code TARDIS from Vogl et al. (2019) and applied it to the prototypical type II-plateau supernova (SN II-P) 1999em. The reconstructed spectra are part of the plateau phase. The characteristic temporal evolution of the light curve of a SN II-P is shown in Fig. 1 with the region of interest marked with a red crisscross pattern (Barbon et al. 1979; Anderson et al. 2014; Valenti et al. 2015; Gall et al. 2015; Utrobin et al. 2017; Hicken et al. 2017).
 |
Fig. 1. Schematic light curve of a typical SN II-P. The red hatched area is the region of interest for the models in this paper and is part of the plateau phase marked by the gray area. |
2.1. TARDIS simulations
TARDIS is a Monte Carlo based radiative transfer code based on the indivisible energy packet scheme of Lucy (1999, 2002, 2003), originally written for spectral modeling of SNe Ia (Kerzendorf & Sim 2014). Vogl et al. (2019) modified the code to perform spectral synthesis for SNe II and specifically applied it to spectra of SN 1999em (Vogl et al. 2020).
The original TARDIS code considers Thomson scattering and bound-bound line interactions as an approximation for SNe Ia (Barna et al. 2017; Boyle et al. 2017; Magee et al. 2016, 2017). To account for the hydrogen-rich composition of SNe II, the modified code additionally accounts for bound-free, free-free, and collisional processes (Lucy 2002, 2003). The modified TARDIS code accounts for nonlocal thermodynamic equilibrium (NLTE) effects in the ionization and excitation balance of hydrogen and, in selected cases, helium. Additionally, the thermal structure is calculated from the equilibrium of the heating and cooling of the shells.
To synthesize the spectra, the properties of the propagating energy packets are tracked and finally binned. The resulting spectra are affected by Monte Carlo noise. To improve the signal-to-noise ratio (S/N), multiple virtual Monte Carlo packets (v-packets) are emitted for each emitted or interacting packet. These additional packets propagate along randomly selected rays and get attenuated by the integrated optical depth. When the v-packet exits the computational region through the outer boundary, the emission radius r, the propagation direction cos(θ), the frequency ν, and the energy ϵ are saved. These are used to calculate the specific intensity and the impact parameter p to construct the specific intensity profiles in Sect. 2.3.
We assumed power-law density profiles and a homogeneous composition to calculate the TARDIS models for this study. The abundances of H, He, C, N, and O were set to their CNO cycle equilibrium values (taken from Prantzos et al. 1986). All other elements follow the solar chemical composition (Asplund et al. 2009). Due to computational expense, the code produces only parameters at a specific epoch and no temporal development. In order to provide a time-dependent evolution of spectra for the analysis of microlensing effects, we computed several spectra at different epochs and used these snapshots as the temporal evolution.
2.2. Observed and model spectra of SN 1999em
For the analysis of the effect of microlensing, we used the TARDIS models for SN 1999em. We selected SN 1999em as it is a prototypical SN II-P (e.g., Dessart & Hillier 2006). Additionally, it is one of the most well-observed and well-studied SNe II. Its distance has been determined several times, and it has been observed over a long period of time, resulting in many spectra (Leonard et al. 2002; Baron et al. 2004; Hamuy et al. 2001). Given the availability of a huge amount of data, it is a good candidate for SN II modeling (e.g., Utrobin 2007).
The observed spectra of SN 1999em (Leonard et al. 2002; Hamuy et al. 2001) were used as a reference for the simulated spectra as TARDIS only creates snapshots at specific epochs and does not perform fully time-dependent radiative transfer computations. To achieve a sensible temporal evolution of the snapshots, they were fit to the observed spectra of a specific SN.
The observed spectra are shown in Fig. 2 in comparison to the model spectra selected from extensive model grids, including the one from Vogl et al. (2020). The observed spectra have been de-reddened under the assumption of the Cardelli et al. (1989) extinction law. The color excess is set to E(B − V) = 0.08 and the total-to-selective extinction ratio to RV = 3.1, as in Vogl et al. (2019). The flux of the model spectra was calculated for the SN at a distance of 10 pc and shifted by eye to match the observed spectra. The wavelength resolution of the spectra was chosen to be about 3 Å per bin.
 |
Fig. 2. Model (blue) and observed (orange) spectra of SN 1999em at various epochs. The model spectra are obtained from TARDIS. (a) Spectrum at day 11 after the explosion. (b) Spectrum at day 13 after the explosion. (c) Spectrum at day 17 after the explosion. (d) Spectrum at day 22 after the explosion. (e) Spectrum at day 27 after the explosion. |
At early times, around day 11 after the explosion, the spectrum is characterized by a broad hydrogen Balmer series and a He I line at 5876 Å. Roughly two weeks after the explosion, Fe II absorption lines become visible and stronger with time. All five spectra were taken during the plateau phase of SN 1999em (Leonard et al. 2002; Hamuy et al. 2001).
2.3. Specific intensity profiles
We calculated the specific intensity profiles from the TARDIS simulations using a similar approach as Huber et al. (2019). In contrast to these authors, we used v-packets instead of regular Monte Carlo packets. We further neglected flight-time differences between packets that are emitted at different distances to the observer. The parameters of the v-packets used for the calculation are the emission radius r, the energy ϵ, the frequency ν, the time elapsed since explosion t, and cos(θ), where θ is the angle between the position vector of the observer and the position vector of the v-packet leaving the computational domain.
In Fig. 3 the spatial distributions of the normalized intensity profiles for the six LSST filters, u, g, r, i, z, and y (LSST Science Collaboration 2009), are shown. The profiles for the different filters are calculated by convolving the transmission profile of each filter with the specific intensity. Based on the plot, we chose 25 bins of the impact parameter p as an appropriate binning resolution for each epoch. The resulting intensity was normalized by the maximum of the specific intensity for each filter. The normalized specific intensity profiles are very achromatic, especially at the first three investigated epochs, which show barely any difference between the profiles for the different filters.
 |
Fig. 3. Normalized specific intensity profiles as a function of the impact parameter, p, in units of REin (with REin = 2.9 × 1016 cm defined in Eq. (1), setting the SN to a redshift of zs = 0.77 and the lens to a redshift of zl = 0.32). (a) Day 11 after explosion. (b) Day 13 after explosion. (c) Day 17 after explosion. (d) Day 22 after explosion.(e) Day 27 after explosion. |
3. Microlensing of type II supernovae
With the upcoming LSST, thousands of LSNe will be detected, including SNe Ia and SNe II. The possible use of SNe Ia for time-delay measurements, and the influence of microlensing on it, has already been investigated by Huber et al. (2019), Goldstein et al. (2018) using characteristic structures within color curves to infer a time delay between two lensing images. However, microlensing on SNe II is still an open question from a theoretical viewpoint and is the motivation for this work.
The microlensed flux was calculated according to Huber et al. (2019) using specific intensities, retrieved with the TARDIS simulation at the source plane, which were microlensed using magnification maps. To investigate the effect of microlensing on time-delay measurements of LSNe II, we inserted 10 000 random SN positions into a microlensing map.
3.1. Microlensing magnification maps
We used the magnification maps from GERLUMPH (Vernardos et al. 2015) to calculate the microlensed SN spectra. These maps, which were calculated using the inverse ray-shooting technique (Kayser et al. 1986; Wambsganss et al. 1992; Vernardos & Fluke 2013), contain the magnification μ(x, y) in the source plane as a function of the Cartesian coordinates x and y in units of the Einstein radius REin. The characteristic scale of the map, REin, is defined as:
where Ds is the angular-diameter distance from the observer to the source, Dds the angular-diameter distance from the lens to the source, Dd the angular-diameter distance from the observer to the lens, and c the speed of light. We further assumed a Salpeter initial mass function with a mean mass of the point mass microlenses of ⟨M⟩ = 0.35 M⊙ as described by Huber et al. (2021).
The magnification maps are primarily defined by three parameters: the convergence κ, the shear γ, and the smooth matter fraction 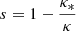 , where κ* is the convergence of the stellar component. The maps used in this work have a resolution of 20 000 × 20 000 pixels, corresponding to a size of 10REin × 10REin.
, where κ* is the convergence of the stellar component. The maps used in this work have a resolution of 20 000 × 20 000 pixels, corresponding to a size of 10REin × 10REin.
In this work we consider two SN images of a lens system with different microlensing maps. Galaxy-scale strong lens systems typically have two or four images of the background source. For a two-image lensed system, the first and second images that appear are time-delay minimum (type I) and saddle (type II) images1, respectively. For a four-image lensed system, the first two images are of type I and the next two images are of type II. For our current study, we consider two SN images from either a double or a quad system, with the first SN image as type I and the second one as type II. Therefore, we simulated microlensing for these two SN images using two different microlensing magnification maps, which are shown in Fig. 4.
 |
Fig. 4. Magnification maps for two different κ and γ values with smooth matter fraction s = 0.50. The magnification μ(x, y) is indicated by the color scale on the right-hand side. (a) Type I microlensing map. (b) Type II microlensing map. |
For the first image, we chose κ = 0.36 and γ = 0.35, which are the median values of type I lensing images of the OM10 catalog (Oguri & Marshall 2010). For the second image, we chose κ = 0.7 and γ = 0.7, which are the median values of type II lensing images of the OM10 catalog (Huber et al. 2021; Suyu et al. 2020). We adopted s = 0.5 for both cases.
The observed microlensed flux Fλ, o(t) was computed by placing the SN into the magnification map and solving:
where Dlum is the luminosity distance to the source and Iλ, e(t, x, y) is the specific intensity in the source plane. For the calculation we interpolated the specific intensity onto a 2D Cartesian grid of the same spatial resolution as the magnification map and integrated over the SN (Huber et al. 2019).
The AB magnitudes were then calculated by:
(Bessell & Murphy 2012), where SX(λ) is the transmission function of the LSST filter X (LSST Science Collaboration 2009).
3.2. Type II supernova light curves and color curves
In this subsection we study the effect of microlensing on the light curves and color curves retrieved from the TARDIS simulations and investigate if they can be used for time-delay measurements. The impact on the color curves is of particular interest as the achromatic behavior of the specific intensity profiles suggests that microlensing has little influence on the color curves.
The curves were created using the filters u, g, r, i, z, and y of LSST (LSST Science Collaboration 2009). The transmission of each filter was convolved with the supernova flux to obtain the light curve for that filter. The microlensed flux was calculated according to Eq. (2) with Dlum = 10 pc to get the absolute magnitudes when calculating the light curves. For the non-microlensed flux, the magnification was set to μ(x, y) = 1. The luminosity distance was chosen such that further computations could be made with the flux instead of the luminosity density. The microlensed and non-microlensed AB magnitudes for the light curves were then calculated via Eq. (3). As an example for the microlensed light curve, we chose a position in the magnification map of type I lensing where the expanding layers cross a caustic with time. The position is shown in Fig. 5, with the circles representing the radius of the SN containing 99.9 % of the luminosity for the five different epochs. We see that the caustic is crossed from day 13 onward.
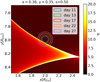 |
Fig. 5. Magnification map for type I lensing with the position of the SN for the microlensed light curve. The different circles represent the sizes of the SN at the five different epochs we investigate. |
The caustic crossing can also be seen within the light curves shown in Fig. 6 for the non-microlensed and microlensed case. We normalized the light curves by shifting the magnitude of the first epoch to zero. The light curves show that after day 11 the difference in the absolute magnitude between the non-microlensed and microlensed case is increased. This means that the SN is magnified by the caustic crossing after day 11. The intrinsic light curves do not have characteristic structures, such as peaks, as they include only epochs of the plateau phase of SN 1999em. The plateau phase is the part in the light curve of a SN II-P where the magnitude barely changes over a certain period of time. The light curves within the plateau phase of our investigation can be strongly affected by microlensing, which adds large uncertainties to time-delay measurements.
 |
Fig. 6. Microlensed and non-microlensed normalized light curves in the LSST filters u, g, r, i, z, and y for SN 1999em at the position marked in the microlensing map in Fig. 5. |
Even though the non-microlensed light curves are almost linear, which leads to nearly linear color curves, we wanted to show the influence of microlensing on these color curves, following Goldstein et al. (2018), Huber et al. (2019, 2021). Due to the achromatic specific intensity profiles, the influence is expected to be low. We calculated the LSN signal at 10 000 different random positions in the microlensing map. For each position, we calculated the magnitude difference, mAB, X(ti)−mAB, Y(ti), for two filters, X and Y. For each filter combination, we plot the median and the 1σ and 2σ deviations retrieved from the 10 000 individual color curves. Four comparisons of the microlensed color curves to the non-microlensed color curves are shown in Fig. 7. Additional color curves are shown in Appendix A. It can been seen that the influence of microlensing on the color curves is small overall. Yet, these color curves cannot be used in time-delay measurements in a straightforward way because they do not show large characteristic structures that would simplify the time-delay measurements, given the possibility of differential dust extinction between the multiple SN images (Elíasdóttir et al. 2006). Therefore, to use color curves, a longer time span, covering more than the first part of the plateau phase that we consider in this work, would be helpful for inferring the time delays. We defer this to future studies.
 |
Fig. 7. Color curves of the non-microlensed and microlensed spectra with median, 1σ, and 2σ ranges obtained from 10 000 random positions in the type I lensing magnification map. In addition, the bottom part of each panel (Figs. 7a–d) shows the deviation of the microlensed color from the non-microlensed color with 1σ uncertainties. |
3.3. Type II supernova spectra and absorption features
As the light curves and color curves lack significant features within the plateau phase, we investigate another approach to perform time-delay measurements on SNe II. We used the temporal evolution of the minima of the absorption lines of Hα, Hβ, and Fe II as they are common features used for velocity measurements that can be detected in at least three epochs. The hydrogen lines can even be detected in all five of the epochs (see Fig. 8).
 |
Fig. 8. Model spectra for the five epochs with the three absorption lines of interest, labeled Hα, Hβ, and Fe II. |
We applied a two-step procedure to determine the wavelength of an absorption line from noisy spectra. In the first step, we visually estimated the absorption minimum and selected a range of wavelength bins around that minimum to refine the estimate through the function signal.find_peaks of the python module scipy (Virtanen et al. 2020). We adopted the output of signal.find_peaks as λinit, the initial wavelength of the absorption minimum. In the second step, we fit a Gaussian to the absorption line profile to further refine the wavelength measurement, especially in the presence of noise. As the lines have individual asymmetrical P-Cygni profiles, different fitting ranges were selected for each feature. For Hα we chose 15 bins toward smaller wavelengths and 25 bins toward longer wavelengths, for Hβ 8 bins toward smaller and 18 bins toward longer wavelengths, and for Fe II 20 bins toward smaller and 15 toward longer wavelengths. The bins are counted from λinit, and each bin has a width of 3Å. The success of the fitting is dependent on the fitting range. If the range is too small, then the fit might fail. Noisy spectra in particularly can sometimes have two small minima within the absorption feature. If the range is too large, then the fit might shift to longer wavelengths as a result of the asymmetric P-Cygni line shape. The optimal wavelength range to use for the Gaussian fit was determined through simulations of noisy spectra. We applied different fit windows onto the noisy spectra and chose the window that best reproduced the known absorption minimum of the model spectrum2. The result of the Gaussian fit yields the wavelength of the absorption line, as detailed below.
The Gaussian fit was performed using the optimize.curve_fit function of the python module scipy, a least-squares minimization using a Levenberg-Marquardt optimizer with a fitting function:
The input x is the wavelength range over which the fit is computed. The parameter A is the square root of the amplitude, M the mean of the Gaussian, σ the standard deviation, and h the offset. If the fitting failed, which is indicated by a determined minimum that is larger than λinit + 60 Å (outside the fitting range) or smaller than λinit − 60 Å, the fitting was repeated with a fit range shifted by five bins, which equals 15 Å, to longer wavelengths. In these few cases, it is the effect of microlensing that deforms the spectral feature and shifts it to the red or blue once the SN crosses a caustic. The shift to redder wavelengths cannot be compensated for by the fitting method itself, making this additional calculation necessary. In Fig. 9 examples of fits to the non-microlensed absorption lines are shown. We see in these plots that some fits, especially for later times, tend to the bluer or redder part of the absorption line due to the asymmetrical line profile and fitting range. As this shift is always in the same direction, this does not affect the following phase retrieval method.
 |
Fig. 9. Noiseless absorption lines without microlensing in blue for Hα, Hβ, and Fe II including the Gaussian fits in orange used to measure the minima of the absorption lines, marked by the vertical red line. The vertical dashed lines in gray mark the borders of the fitting range. |
The fitting was performed for every position in the microlensing map, for each of the five epochs and for each absorption line in the microlensed spectra without noise. The temporal evolution of the absorption minima of Hα, Hβ, and Fe II is shown in Fig. 10 for the two magnification maps of Fig. 4. The plots include the median of all determined minima of the positions in the microlensing map and the 1σ and 2σ uncertainties. The temporal evolution of the wavelengths of the absorption minima of the spectra without microlensing is shown in yellow for reference. The evolution is similar for the two images, but microlensing tends to introduce larger uncertainties for the second lensing image.
 |
Fig. 10. Temporal evolution of the absorption minima of the Hα, Hβ, and Fe II lines for non-microlensed and microlensed spectra using the two different magnification maps of Fig. 4 (left: Fig. 4a; right: Fig. 4b). For the microlensed spectra without noise (labeled S/N = ∞), the median of the 10 000 positions and the 1σ and 2σ ranges are shown in black and gray, respectively. The temporal evolution of the absorption lines with added noise of S/N = 10 is shown in orange and red. |
In addition to the noise-free case, we repeated the calculations assuming an S/N per pixel of 10 for the spectra. To simulate a noisy spectrum, we added Gaussian noise to the flux of each wavelength bin of the microlensed spectrum; in other words, we drew a random Gaussian number with standard deviation given by σG = flux/(S/N) and added it to the flux. We simulated a noisy microlensed spectrum for each position in the microlensing map and applied a Savitzky-Golay filter to make the fitting procedure easier. We obtained the distribution of the absorption minima shown in red in Fig. 10. In all panels of Fig. 10 (particularly the top panels for Hα images), the uncertainties due to microlensing (gray bands) are smaller than the uncertainties due to noise in the spectra (red bands) when S/N = 10.
Furthermore, we investigated the correlation between the absorption minima of the three lines for different S/N in Fig. 11. We show the plots for S/N = 10, 20, 30, and ∞ at day 22. We consider these three additional S/N values besides the noiseless case as feasible for future observations. We also use these S/N and day 22 for the phase retrieval in the following section. In contrast to the noisy cases, the noiseless case has a very tight data distribution, and therefore we only show the 2σ contour. For S/N = ∞, the absorption minima of Hα, Hβ, and Fe II are strongly correlated within the 1σ and 2σ contours. For S/N = 30, the 1σ contour already shows no correlation, whereas in the 2σ contour slight correlations are still present. As the S/N gets smaller, the 1σ stays uncorrelated and the 2σ contour become increasingly more uncorrelated.
 |
Fig. 11. Correlations between the absorption minima of Fe II, Hα, and Hβ at day 22 for the four investigated S/N: 10, 20, 30, and ∞. The solid 1σ contours in the 2D histograms contain 68% of the data and the dashed 2σ contours 95%. The 1D histograms contain the 1σ (vertical solid lines) and the 2σ (vertical dashed lines) ranges. For S/N = ∞ we only show the contour containing 95% of the data and the 2σ range. Above the 1D histograms the mean wavelength of the absorption minimum with 1σ uncertainties is indicated. While there are significant correlations in the absorption minima of the different lines in the case of noiseless spectra, the correlations become weak or negligible with noisy spectra. (a) S/N = 10. (b) S/N = 20. (c) S/N = 30. (d) S/N = ∞. |
4. Supernova phase inference from spectra and time-delay measurement
In this section we investigate the possibility of inferring phases from the wavelengths of the absorption minima of the spectral lines. The basic idea is based on Fig. 10, which shows that the wavelengths of the absorption minima evolve over time. When we detect a LSN system based on its first appearing image, which we denote as SN-A, we can obtain spectra of this SN-A image at different epochs to determine the evolution of the absorption features (as shown in Fig. 10). A subsequent spectrum taken at time tB of the next appearing SN image, which we denote as SN-B, can then be used to infer the phase of SN-B based on the measured wavelength (i.e., the time tA at which image SN-A had the same absorption wavelength value as that measured in the SN-B spectrum). The difference between these two times, tB − tA, then gives the time delay between the SN-B and SN-A images. Below, we describe in more detail how we quantitatively inferred the phase and time delays, taking microlensing and noise in the spectrum into account.
Here we consider the scenario where we have obtained spectra of SN-A at five epochs (as in the previous sections), denoted by ti, where i = 1, 2, …, Nepoch and Nepoch = 5. The spectra have the same S/N. Through the microlensing simulations described in the last two sections, we obtained the distribution of absorption line wavelengths, accounting for microlensing and noise as shown in the left panels of Fig. 10. In particular, for the microlensing of the SN-A image, we adopted the magnification map with κ = 0.36 and γ = 0.35 since the first appearing SN-A image must be a time-delay minimum image. By sampling 10 000 positions on the microlensing map and thus simulating 10 000 noisy microlensed spectra for the given S/N at each ti, we obtained the distribution of absorption line wavelengths λ(ti) following the absorption line fitting method described in Sect. 3.3.
We approximated the distribution of λ(ti) at each epoch as a Gaussian with mean λd, i and standard deviation σd, i. To obtain a continuous distribution of λd(t) and σd(t) for any time t, we linearly interpolated between the discrete λd, i and σd, i values. This allows us to describe the likelihood of the data dA (i.e., the spectra and microlensing maps of SN-A) for a given time t and absorption wavelength λ as
where CA is the normalization constant.
Next we consider a spectrum taken of the SN-B image at tB. Similar to the procedure described above for the SN-A image, we repeated the microlensing simulations to produce 10 000 microlensed spectra of SN-B for a given S/N to account for uncertainties associated with microlensing and noise in the spectrum. The main difference from the procedure of SN-A is that the microlensing map for SN-B is for the time-delay saddle image with κ = 0.70, γ = 0.70. This is appropriate since at least one of the next appearing SN images is a time-delay saddle. Furthermore, considering the saddle image allows us to probe uncertainties due to both types of lensing images (time-delay minimum and time-delay saddle images) given that the microlensing maps are sensitive to the image types. From the distribution of 10 000 microlensed noisy realizations of the SN-B single epoch spectrum, we can measure the mean wavelength λB and standard deviation σB. We used the wavelength measurement λB ± σB to infer the times in SN-A that are consistent with these values.
Quantitatively, we are interested in obtaining the probability distribution of time t of SN-A given the data dA and measurement dB (of λB ± σB) – that is, P(t|dA, dB) – which can be expressed by
where λ are the absorption line wavelengths associated with SN-A.
Using Bayes’ rule, we can rewrite the integrand as:
where we have separated dependences (dA and t do not depend on dB). The expression for P(dA|λ, t) is given by Eq. (5). Through our Gaussian approximation of the measurement dB, we can write
Given that our data dA is fixed, P(dA) is a constant. Assuming a uniform prior on t (i.e., P(t) is constant), we can simplify Eq. (6) to
where CAB is a constant.
We can compute P(t|dA, dB) through importance sampling (e.g., Lewis & Bridle 2002). We first generated samples of P(dA|λ, t) by (1) randomly drawing a value of t, assuming they follow a Gaussian distribution, which we denote as tsamp, (2) computing λd(tsamp) and σd(tsamp), and (3) using these sampled values to draw a random Gaussian deviate, λsamp. We repeated steps (1)–(3) to obtain 31 981 samples of (tsamp, λsamp) (or 19 980 samples for the specific case of the Fe II absorption line). The number of samples was the result of setting the amount between the third and fourth epoch to 10 000 samples. The number of samples within the other epochs resulted from choosing the same density of samples along the wavelength axis. Each of these samples was then weighted by P(λsamp|dB) as given by Eq. (8). The weighted distribution of t finally yields P(t|dA, dB).
As an example, we applied this procedure with tB set equal to the fourth epoch at day 22.0 of the SN-A image modeled with TARDIS. We chose this epoch as it is the central epoch of the temporal evolution of the Fe II absorption line and enabled us to evaluate all three absorption lines of interest, Hα, Hβ, and Fe II. For the noise addition, we again selected the three different S/N values of 10, 20, and 30.
The retrieved phases of all three absorption lines are shown in Fig. 12 as histograms indicating the distribution of the weighted samples. The input epoch (thick vertical red line) is recovered very well by our phase retrieval method. In particular, assuming a S/N = 20 or higher, the histogram shows a sharp peak centered around the input phase value. We additionally combined the three separate phase retrievals in Fig. 12d. This assumes the best case scenario with negligible correlation in the noise and microlensing, which means that we can simply multiply the three distributions with one another. The assumption of uncorrelated data is justified based on the correlation plots in Fig. 11, which show that in the case of noisy spectra the absorption minima are only very weakly correlated. Only the noiseless spectra show correlations, which we can safely disregard since S/N = ∞ is a limiting case, only included in this study to give an upper limit for the accuracy. Additionally, its median and width are very similar to the case of S/N = 30, suggesting that the correlation does not matter much for the present work. The peak around the epoch that should be retrieved is sharper than for the single line retrievals. Another possibility for reducing the uncertainties would be to combine several spectra of the SN-B image, if they are available, but taking possible correlations introduced by microlensing into account.
 |
Fig. 12. Histograms of the retrieved phases of the second SN image using the absorption lines Fe II, Hα, and Hβ. The phase inference is done for S/N = 10, 20, and 30 and for noiseless spectra. The red vertical lines in the histograms indicate the epochs of the five available spectra of the first SN image. The thick vertical line marks the input value. By using the wavelengths of absorption features, the phase of the second SN image is correctly recovered. (a) Retrieved phase using the absorption line of Fe II. (b) Retrieved phase using the absorption line of Hα. (c) Retrieved phase using the absorption line of Hβ. (d) Retrieved phase combining all three absorption lines. |
In Table 1 we list the weighted average and the corresponding 1σ deviations of the phases retrieved for the different absorption lines and their combination. For Fe II and Hβ the averages deviate more than the average of Hα from the input value of 22.0 days. For Hα the input value is recovered within its 1σ uncertainties. For all considered S/N, we recover the input value when combining the phase retrieval results of the three absorption lines.
Weighted average and the 1σ uncertainties of the phase retrievals considering all five epochs of the first image.
Even though a S/N of 10 already yields a good result for the phase retrieval with uncertainties smaller than 2.5 days, the uncertainties of S/N = 20 and 30 are both smaller than 2 days. The difference in 1σ of S/N = 20 and 30 is marginal or even negligible, with S/N = 20 also being very close (within 0.2 days in uncertainty) to the noiseless 1σ deviation, suggesting that a S/N of 20 would be sufficient to apply our phase retrieval method.
Our method also does not require very high resolution spectra. Well-calibrated spectra with resolution R ≳ 500 are sufficient for determining the relative phase of SN images to fractions of a day since the line profiles of SNe are broad.
To further explore the effect of microlensing on the phase retrieval, we investigate a scenario with extremely high micro-magnification using two additional magnification maps in Appendix B. We find the phase retrieval to be only negligibly affected by microlensing even in this high microlensing scenario since we obtain the same retrieved phases within 0.2 days for the original and the high-magnification microlensing scenarios.
Furthermore, we consider a case where the fourth epoch that we want to retrieve with the second image is not measured within the first image to check how well the method works if the available data are limited. Another reason for this scenario is that with real measurements we might not have data of the second image covering the same epochs as for the first image. For this case we only used the third and fifth epoch and interpolated linearly between them to create samples as explained previously in this section. We justify the linear interpolation by the linear behavior of the absorption minima of the last three epochs as shown in Fig. 10. In particular, Hα follows a linear trend to a high degree of precision. We thus expect Hα to give the best results in this case. The resulting phase retrieval histograms are shown in Fig. 13 with the weighted average and the 1σ uncertainties for the different absorption lines, their combination, and for the different S/N realizations shown in Table 2. As expected, the recovered weighted average of the phase using the Hα absorption line agrees well with the exact value of 22.0 days. Even though the precision is almost unchanged, the accuracy is strongly biased in the case of Fe II and Hβ. This most likely results from the nonlinear evolution of the last three bins, which is not as linear as for Hα.
 |
Fig. 13. Histograms of the retrieved phases of the second SN image using the absorption lines Fe II, Hα, and Hβ and using only the third and fifth epoch of the first image. The phase inference is done for S/N = 10, 20, and 30 and for noiseless spectra. The thin red vertical lines in the histograms indicate the epochs of the two used spectra of the first image. The thick vertical line marks the input value of the second image. (a) Retrieved phase using the absorption line of Fe II. (b) Retrieved phase using the absorption line of Hα. (c) Retrieved phase using the absorption line of Hβ. (d) Retrieved phase combining all three absorption lines. |
Weighted average and the 1σ uncertainties of the phase retrievals considering the third and the fifth epoch of the first image.
In general we detect three sources for bias: microlensing, fitting ranges, and the cadence of the observations. The cadence is an especially important factor for the first image. At the moment we can only estimate the strength of each of these bias contributions from our results. How much each bias affects the measurements will depend on the details of actual data once they are available. Combining the phase inference from multiple spectral features can potentially reduce the bias compared to the measurements for a single line. As illustrated in Fig. 13 and Table 2, when we multiply the phase-retrieval histograms together, the bias cancels out since the underprediction of the phase from the Hβ absorption line counterbalances the overprediction of the phase from Fe II. Depending on the spectral features used, such a perfect cancelation of the biases might not occur. Therefore, when applying our method to real data, we recommend investigating individual spectral features through simulations to quantify potential biases, as we have done here.
For accurate phase retrievals, we ideally need as many measured epochs of the first image as possible to ensure that we cover the range of phases where we might be able to measure the second image and use it in the phase retrieval. This further ensures that linear interpolations only cover short periods, which minimizes the bias induced by a long gap between epochs. From the example in Fig. 12 we can see that a cadence of around five days for the first image already reduces the bias significantly compared to a cadence of approximately ten days as used in Fig. 13. Having as many epochs as possible for the first image also ensures that we do not need to extrapolate (which would lead to another source of bias) to cover an epoch of the second image that could be missing in the measurements of the first image. As the combination of the phase retrieval of several different absorption lines can lead to the canceling of the bias, we recommend using at least three different absorption lines and also considering them individually, which gives a general hint of the amount of bias to expect.
5. Discussion
As of today, only one strongly lensed SN II has been observed, namely SN Refsdal, which was first detected by Kelly et al. (2016a,b). With its five detected and resolved images, time-delay cosmography with a SN II is being conducted for the first time. The system has so far primarily been used to crash test and validate lens modeling codes’ predictions of the place and time of the reappearance of the last trailing SN image. The short time delays between the first four appearing images have been measured by Rodney et al. (2016) based on their light curves and by Baklanov et al. (2021) using model light curves, and there are ongoing efforts to measure the time delay of the last trailing SN image using light curves (P. Kelly, priv. comm.).
Type Ia supernova iPTF16geu, discovered by Goobar et al. (2017), has four spatially resolved images from which time-delay measurements have been conducted. The delays have been calculated through two independent channels: from photometry of consecutive image appearances by Dhawan et al. (2020) and from spectral features by Johansson et al. (2021). The authors mention that microlensing effects (More et al. 2017; Mörtsell et al. 2020) on the light curves cause inaccuracies in the time-delay measurements. Therefore, they used the spectra for the first time to retrieve time delays. They fit the blended spectra of three of the four SN images and, separate from that group, the spectrum of the remaining SN image with two different sets of templates: the template spectra of Hsiao et al. (2007) and the spectral energy distribution template of SN 2011fe (Amanullah et al. 2015). Significant features of the fits were then used to measure the time delay between the image groups. In the case of iPTF16geu, the spectroscopic time delay is not as precise as the photometric time delay, but the spectra seem to be less sensitive to microlensing than the color curves (Johansson et al. 2021). In contrast to our new method, which takes advantage of the temporal evolution of the blue shift of absorption lines, the method by Johansson et al. (2021) needs very good sets of spectral templates. These only exist for SNe Ia.
In the context of our new method of retrieving time delays from absorption lines of SNe II, the studies of iPTF16geu indicate that light curves and color curves with strong features are in general more promising than spectral lines for the calculation of time delays. Microlensing has a minor impact on the color curves, especially if the intensity profiles appear to be mostly achromatic. The spectral approach is also highly dependent on the observational data quality. If the measurements are dominated by noise, features and absorption lines may become undetectable, making spectra unusable for time-delay measurements. Nevertheless, in cases where the color curves do not show useful nonlinear structures for delay measurement, which is the case in the early plateau phase of SNe II-P, we demonstrate that the phase of a spectrum can be accurately inferred. The uncertainties of the retrieved phase using a single absorption line lie within ±2 days (provided several spectra of one of the other LSN images in the system have been obtained to determine the evolution of the absorption line). Considering that delays of galaxy-scale LSNe typically range from days to weeks, our new method is very promising for obtaining delays with < 10 % uncertainty for systems with delays longer than 20 days.
By comparing our LSNe II-P work to previous LSNe studies (e.g., Goldstein et al. 2018; Foxley-Marrable et al. 2018; Huber et al. 2019, 2021), we find that LSNe Ia and II-P have separate advantages for measuring time delays. The homogeneity of SNe Ia facilitates the comparison with templates, making it easier to retrieve time delays with them. In contrast to SNe Ia, the plateau phase of SNe II-P lacks characteristic maxima or minima within the light and color curves, which makes this phase not ideal for time-delay measurements using color curves. However, this phase showed less “chromatic” evolution within the intensity profiles than SNe Ia (Huber et al. 2019, 2021), making LSNe II-P less susceptible to microlensing effects within the early plateau phase. Therefore, our newly developed time-delay measurement method using the absorption lines of the spectra of LSNe II-P is a promising way of conducting cosmography in the LSST era (LSST Science Collaboration 2009) as more LSNe II than LSNe Ia are expected to be detected (Oguri & Marshall 2010; Wojtak et al. 2019; Goldstein et al. 2018; Goldstein & Nugent 2017). Methods of conducting time-delay measurements during the plateau phase of SNe II-P will be most useful as this is the time range where observations will be easiest to perform due to the brightness and duration of that phase.
6. Conclusion
In this work we investigated strongly lensed SNe II and the possible impact of microlensing on time-delay measurements. We used model spectra of SN 1999em from the TARDIS code modified by Vogl et al. (2019). These were microlensed using magnification maps generated with the code GERLUMPH (Vernardos et al. 2015). We then investigated the effect of microlensing on light and color curves. We find that the color curves are mostly unaffected by microlensing since the specific intensity profiles in different bands are very similar during the plateau phase. During the investigated time span, the light curves, and therefore also the color curves, are almost linear, with no strong characteristic features that could be used as easily as for SNe Ia around the same epochs for time delay retrieval. Further investigation of time-delay measurements using SNe II-P color curves is deferred to future studies. We thus developed a new method for calculating the time delay of two SN images from the absorption lines in their spectra. For both images, we simulated spectra that were distorted by microlensing and had noise with different S/N values. We discovered that the phase can be determined from a single spectral feature with a 1σ uncertainty of < 2 days and the weighted average reproducing the input phase value within the 1σ uncertainty, assuming a realistic S/N of 20. If several measurements of different absorption lines are combined, the uncertainty can be further minimized and the accuracy improved as possible biases can cancel one another out. By neglecting any correlations between the errors of the different absorption lines, the 1σ uncertainty can be minimized to ±1.0 days for S/N = 20. Given the complementarity between the spectral and photometric delay inference, we advocate for the combination of both approaches in future measurements of LSNe.
Acknowledgments
We thank A. Kozyreva, C. McCully, and S. Sim for discussions. We also thank the anonymous referee for helpful and detailed comments. We thank the Max Planck Society for support through the Max Planck Research Group for SHS. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (LENSNOVA: grant agreement No. 771776; COSMICLENS: grant agreement No. 787886). This research is supported in part by the Excellence Cluster ORIGINS which is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC-2094 – 390783311. J. H. H. Chan acknowledges support from the Swiss National Science Foundation (SNSF). This research made use of TARDIS, a community-developed software package for spectral synthesis in supernovae (Kerzendorf & Sim 2014; Kerzendorf et al. 2020). TARDIS is fiscally sponsored by NumFOCUS, a nonprofit that promotes open practices in research, data, and scientific computing. The development of TARDIS received support from the Google Summer of Code initiative and from ESA’s Summer of Code in Space program. TARDIS makes extensive use of Astropy and PyNE.
References
- Amanullah, R., Johansson, J., Goobar, A., et al. 2015, MNRAS, 453, 3300 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, J. P., González-Gaitán, S., Hamuy, M., et al. 2014, ApJ, 786, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Baklanov, P., Lyskova, N., Blinnikov, S., & Nomoto, K. 2021, ApJ, 907, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Barbon, R., Ciatti, F., & Rosino, L. 1979, A&A, 72, 287 [Google Scholar]
- Barna, B., Szalai, T., Kromer, M., et al. 2017, MNRAS, 471, 4865 [NASA ADS] [CrossRef] [Google Scholar]
- Baron, E., Nugent, P. E., Branch, D., & Hauschildt, P. H. 2004, ApJ, 616, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Bessell, M., & Murphy, S. 2012, PASP, 124, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Birrer, S., Treu, T., Rusu, C. E., et al. 2019, MNRAS, 484, 4726 [NASA ADS] [CrossRef] [Google Scholar]
- Birrer, S., Shajib, A. J., Galan, A., et al. 2020, A&A, 643, A165 [CrossRef] [EDP Sciences] [Google Scholar]
- Bonvin, V., Courbin, F., Suyu, S. H., et al. 2017, MNRAS, 465, 4914 [NASA ADS] [CrossRef] [Google Scholar]
- Bonvin, V., Chan, J. H. H., Millon, M., et al. 2018, A&A, 616, A183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boyle, A., Sim, S. A., Hachinger, S., & Kerzendorf, W. 2017, A&A, 599, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, G. C. F., Fassnacht, C. D., Suyu, S. H., et al. 2019, MNRAS, 490, 1743 [NASA ADS] [CrossRef] [Google Scholar]
- Courbin, F., Bonvin, V., Buckley-Geer, E., et al. 2018, A&A, 609, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dessart, L., & Hillier, D. J. 2006, A&A, 447, 691 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dhawan, S., Bulla, M., Goobar, A., et al. 2018, MNRAS, 480, 1445 [NASA ADS] [CrossRef] [Google Scholar]
- Dhawan, S., Johansson, J., Goobar, A., et al. 2020, MNRAS, 491, 2639 [Google Scholar]
- Eigenbrod, A., Courbin, F., Vuissoz, C., et al. 2005, A&A, 436, 25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elíasdóttir, Á., Hjorth, J., Toft, S., Burud, I., & Paraficz, D. 2006, ApJS, 166, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Foxley-Marrable, M., Collett, T. E., Vernardos, G., Goldstein, D. A., & Bacon, D. 2018, MNRAS, 478, 5081 [NASA ADS] [CrossRef] [Google Scholar]
- Freedman, W. L., Madore, B. F., Hatt, D., et al. 2019, ApJ, 882, 34 [Google Scholar]
- Freedman, W. L., Madore, B. F., Hoyt, T., et al. 2020, ApJ, 891, 57 [Google Scholar]
- Gall, E. E. E., Polshaw, J., Kotak, R., et al. 2015, A&A, 582, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilman, D., Birrer, S., & Treu, T. 2020, A&A, 642, A194 [CrossRef] [EDP Sciences] [Google Scholar]
- Goldstein, D. A., & Nugent, P. E. 2017, ApJ, 834, L5 [Google Scholar]
- Goldstein, D. A., Nugent, P. E., Kasen, D. N., & Collett, T. E. 2018, ApJ, 855, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Goobar, A., Amanullah, R., Kulkarni, S. R., et al. 2017, Science, 356, 291 [Google Scholar]
- Grillo, C., Karman, W., Suyu, S. H., et al. 2016, ApJ, 822, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Grillo, C., Rosati, P., Suyu, S. H., et al. 2020, ApJ, 898, 87 [Google Scholar]
- Hamuy, M., Pinto, P. A., Maza, J., et al. 2001, ApJ, 558, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Hicken, M., Friedman, A. S., Blondin, S., et al. 2017, ApJS, 233, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Hsiao, E. Y., Conley, A., Howell, D. A., et al. 2007, ApJ, 663, 1187 [NASA ADS] [CrossRef] [Google Scholar]
- Huber, S., Suyu, S. H., Noebauer, U. M., et al. 2019, A&A, 631, A161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huber, S., Suyu, S. H., Noebauer, U. M., et al. 2021, A&A, 646, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johansson, J., Goobar, A., Price, S. H., et al. 2021, MNRAS, 502, 510 [CrossRef] [Google Scholar]
- Kayser, R., Refsdal, S., & Stabell, R. 1986, A&A, 166, 36 [NASA ADS] [Google Scholar]
- Kelly, P. L., Brammer, G., Selsing, J., et al. 2016a, ApJ, 831, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Kelly, P. L., Rodney, S. A., Treu, T., et al. 2016b, ApJ, 819, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Kerzendorf, W. E., & Sim, S. A. 2014, MNRAS, 440, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Kerzendorf, W., Sim, S., Vogl, C., et al. 2020, https://zenodo.org/record/3902923 [Google Scholar]
- Kromer, M., & Sim, S. A. 2009, MNRAS, 398, 1809 [Google Scholar]
- Leonard, D. C., Filippenko, A. V., Gates, E. L., et al. 2002, PASP, 114, 35 [Google Scholar]
- Lewis, A., & Bridle, S. 2002, Phys. Rev. D, 66, 103511 [Google Scholar]
- LSST Science Collaboration (Abell, P. A., et al.) 2009, ArXiv e-prints [arXiv:0912.0201] [Google Scholar]
- Lucy, L. B. 1999, A&A, 345, 211 [NASA ADS] [Google Scholar]
- Lucy, L. B. 2002, A&A, 384, 725 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lucy, L. B. 2003, A&A, 403, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magee, M. R., Kotak, R., Sim, S. A., et al. 2016, A&A, 589, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magee, M. R., Kotak, R., Sim, S. A., et al. 2017, A&A, 601, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Millon, M., Courbin, F., Bonvin, V., et al. 2020a, A&A, 642, A193 [CrossRef] [EDP Sciences] [Google Scholar]
- Millon, M., Galan, A., Courbin, F., et al. 2020b, A&A, 639, A101 [CrossRef] [EDP Sciences] [Google Scholar]
- More, A., Suyu, S. H., Oguri, M., More, S., & Lee, C.-H. 2017, ApJ, 835, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Mörtsell, E., Johansson, J., Dhawan, S., et al. 2020, MNRAS, 496, 3270 [Google Scholar]
- Oguri, M., & Marshall, P. J. 2010, MNRAS, 405, 2579 [NASA ADS] [Google Scholar]
- Pierel, J. D. R., & Rodney, S. 2019, ApJ, 876, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prantzos, N., Doom, C., Arnould, M., & de Loore, C. 1986, ApJ, 304, 695 [NASA ADS] [CrossRef] [Google Scholar]
- Refsdal, S. 1964, MNRAS, 128, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Macri, L. M., Hoffmann, S. L., et al. 2016, ApJ, 826, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Casertano, S., Yuan, W., et al. 2018, ApJ, 861, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Casertano, S., Yuan, W., Macri, L. M., & Scolnic, D. 2019, ApJ, 876, 85 [Google Scholar]
- Rodney, S. A., Strolger, L. G., Kelly, P. L., et al. 2016, ApJ, 820, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Rusu, C. E., Wong, K. C., Bonvin, V., et al. 2020, MNRAS, 498, 1440 [Google Scholar]
- Shajib, A. J., Birrer, S., Treu, T., et al. 2020, MNRAS, 494, 6072 [Google Scholar]
- Sluse, D., Rusu, C. E., Fassnacht, C. D., et al. 2019, MNRAS, 490, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Suyu, S. H., Bonvin, V., Courbin, F., et al. 2017, MNRAS, 468, 2590 [Google Scholar]
- Suyu, S. H., Huber, S., Cañameras, R., et al. 2020, A&A, 644, A162 [CrossRef] [EDP Sciences] [Google Scholar]
- Treu, T., Brammer, G., Diego, J. M., et al. 2016, ApJ, 817, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Utrobin, V. P. 2007, A&A, 461, 233 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Utrobin, V. P., Wongwathanarat, A., Janka, H. T., & Müller, E. 2017, ApJ, 846, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, S., Sand, D., Stritzinger, M., et al. 2015, MNRAS, 448, 2608 [NASA ADS] [CrossRef] [Google Scholar]
- Verde, L., Treu, T., & Riess, A. G. 2019, Nat. Astron., 3, 891 [Google Scholar]
- Vernardos, G., & Fluke, C. J. 2013, MNRAS, 434, 832 [NASA ADS] [CrossRef] [Google Scholar]
- Vernardos, G., Fluke, C. J., Bate, N. F., Croton, D., & Vohl, D. 2015, ApJS, 217, 23 [CrossRef] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- Vogl, C., Sim, S. A., Noebauer, U. M., Kerzendorf, W. E., & Hillebrandt, W. 2019, A&A, 621, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vogl, C., Kerzendorf, W. E., Sim, S. A., et al. 2020, A&A, 633, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wambsganss, J., Witt, H. J., & Schneider, P. 1992, A&A, 258, 591 [NASA ADS] [Google Scholar]
- Wojtak, R., Hjorth, J., & Gall, C. 2019, MNRAS, 487, 3342 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wong, K. C., Suyu, S. H., Chen, G. C. F., et al. 2020, MNRAS, 498, 1420 [Google Scholar]
- Yahalomi, D. A., Schechter, P. L., & Wambsganss, J. 2017, ArXiv e-prints [arXiv:1711.07919] [Google Scholar]
Appendix A: Color curves
 |
Fig. A.1. Color curves of the non-microlensed and microlensed spectra with median, 1σ, and 2σ ranges obtained from 10 000 random positions in the type I lensing magnification map with κ = 0.36 and γ = 0.35. In addition, the bottom part of each panel (Figs. A.1a–k) shows the deviation of the microlensed color from the non-microlensed color with 1σ uncertainties. |
Appendix B: Microlensing maps with high magnification
In addition to the already investigated microlensing case using the magnification maps with κ = 0.36 and γ = 0.35 (image I) and κ = γ = 0.70 (image II) from Fig. 4, in this section we investigate a high magnification scenario. Therefore, we applied our method following the steps explained in Sects. 3.3 and 4 to GERLUMPH magnification maps with κ = γ = 0.43 (image I) and κ = 0.57 and γ = 0.58 (image II) as shown in Fig. B.1. These two microlensing maps correspond to the high magnification case of the 1σ contours of LSNe in the OM10 catalog for images I and II, respectively (Huber et al. 2021).
 |
Fig. B.1. Magnification maps for two different κ and γ values with smooth matter fraction s = 0.50. The magnification μ(x, y) is indicated by the color scale on the right-hand side. (a) Type I microlensing map. (b) Type II microlensing map. |
We show the temporal evolution of the absorption minima of Hα, Hβ, and Fe II of the high magnification case in Fig. B.2. Compared to the case discussed in Sect. 3.3, there is barely any visible difference.
 |
Fig. B.2. Temporal evolution of the absorption minima of the Hα, Hβ, and Fe II lines for non-microlensed and microlensed spectra using the two different magnification maps of Fig. B.1 (left: Fig. B.1a; right: Fig. B.1b). |
The histograms of the phase retrieval using this second microlensing scenario are shown in Fig. B.3. In this scenario the input epoch is also recovered very well, especially for S/N = 20 and higher S/N cases.
 |
Fig. B.3. Histograms of the retrieved phases under high microlensing magnifications of the second SN image and second microlensing scenario using the absorption lines Fe II, Hα, and Hβ. By using the wavelengths of the absorption features, the phase of the second SN image of the second microlensing scenario is correctly recovered. (a) Retrieved phase using the absorption line of Fe II. (b) Retrieved phase using the absorption line of Hα. (c) Retrieved phase using the absorption line of Hβ. (d) Retrieved phase combining all three absorption lines. |
In Table B.1 we list the weighted average and the 1σ deviations of the retrieved phases. Compared to the averages and uncertainties of the originally investigated microlensed spectra in Table 1, we see that this second case has the same or smaller uncertainties and retrieves the phase with the same accuracy. As the second scenario microlensing maps correspond to a high magnification case, we expected higher or at least equal uncertainties. The smaller uncertainties can be explained by fluctuations caused by the spectral fitting procedures. As the absorption lines have the asymmetric P-Cygni profile, the fitting ranges influence the phase retrieval uncertainties by ≲0.2 days. The chosen fitting ranges discussed in Sect. 3.3 appear to work better for the second scenario than for the first scenario, especially for Hβ, resulting in smaller phase retrieval uncertainties in some cases. In general, both investigated microlensing cases have comparable phase retrieval results.
Phase retrieval under high microlensing magnifications.
All Tables
Weighted average and the 1σ uncertainties of the phase retrievals considering all five epochs of the first image.
Weighted average and the 1σ uncertainties of the phase retrievals considering the third and the fifth epoch of the first image.
All Figures
 |
Fig. 1. Schematic light curve of a typical SN II-P. The red hatched area is the region of interest for the models in this paper and is part of the plateau phase marked by the gray area. |
| In the text | |
 |
Fig. 2. Model (blue) and observed (orange) spectra of SN 1999em at various epochs. The model spectra are obtained from TARDIS. (a) Spectrum at day 11 after the explosion. (b) Spectrum at day 13 after the explosion. (c) Spectrum at day 17 after the explosion. (d) Spectrum at day 22 after the explosion. (e) Spectrum at day 27 after the explosion. |
| In the text | |
 |
Fig. 3. Normalized specific intensity profiles as a function of the impact parameter, p, in units of REin (with REin = 2.9 × 1016 cm defined in Eq. (1), setting the SN to a redshift of zs = 0.77 and the lens to a redshift of zl = 0.32). (a) Day 11 after explosion. (b) Day 13 after explosion. (c) Day 17 after explosion. (d) Day 22 after explosion.(e) Day 27 after explosion. |
| In the text | |
 |
Fig. 4. Magnification maps for two different κ and γ values with smooth matter fraction s = 0.50. The magnification μ(x, y) is indicated by the color scale on the right-hand side. (a) Type I microlensing map. (b) Type II microlensing map. |
| In the text | |
 |
Fig. 5. Magnification map for type I lensing with the position of the SN for the microlensed light curve. The different circles represent the sizes of the SN at the five different epochs we investigate. |
| In the text | |
 |
Fig. 6. Microlensed and non-microlensed normalized light curves in the LSST filters u, g, r, i, z, and y for SN 1999em at the position marked in the microlensing map in Fig. 5. |
| In the text | |
 |
Fig. 7. Color curves of the non-microlensed and microlensed spectra with median, 1σ, and 2σ ranges obtained from 10 000 random positions in the type I lensing magnification map. In addition, the bottom part of each panel (Figs. 7a–d) shows the deviation of the microlensed color from the non-microlensed color with 1σ uncertainties. |
| In the text | |
 |
Fig. 8. Model spectra for the five epochs with the three absorption lines of interest, labeled Hα, Hβ, and Fe II. |
| In the text | |
 |
Fig. 9. Noiseless absorption lines without microlensing in blue for Hα, Hβ, and Fe II including the Gaussian fits in orange used to measure the minima of the absorption lines, marked by the vertical red line. The vertical dashed lines in gray mark the borders of the fitting range. |
| In the text | |
 |
Fig. 10. Temporal evolution of the absorption minima of the Hα, Hβ, and Fe II lines for non-microlensed and microlensed spectra using the two different magnification maps of Fig. 4 (left: Fig. 4a; right: Fig. 4b). For the microlensed spectra without noise (labeled S/N = ∞), the median of the 10 000 positions and the 1σ and 2σ ranges are shown in black and gray, respectively. The temporal evolution of the absorption lines with added noise of S/N = 10 is shown in orange and red. |
| In the text | |
 |
Fig. 11. Correlations between the absorption minima of Fe II, Hα, and Hβ at day 22 for the four investigated S/N: 10, 20, 30, and ∞. The solid 1σ contours in the 2D histograms contain 68% of the data and the dashed 2σ contours 95%. The 1D histograms contain the 1σ (vertical solid lines) and the 2σ (vertical dashed lines) ranges. For S/N = ∞ we only show the contour containing 95% of the data and the 2σ range. Above the 1D histograms the mean wavelength of the absorption minimum with 1σ uncertainties is indicated. While there are significant correlations in the absorption minima of the different lines in the case of noiseless spectra, the correlations become weak or negligible with noisy spectra. (a) S/N = 10. (b) S/N = 20. (c) S/N = 30. (d) S/N = ∞. |
| In the text | |
 |
Fig. 12. Histograms of the retrieved phases of the second SN image using the absorption lines Fe II, Hα, and Hβ. The phase inference is done for S/N = 10, 20, and 30 and for noiseless spectra. The red vertical lines in the histograms indicate the epochs of the five available spectra of the first SN image. The thick vertical line marks the input value. By using the wavelengths of absorption features, the phase of the second SN image is correctly recovered. (a) Retrieved phase using the absorption line of Fe II. (b) Retrieved phase using the absorption line of Hα. (c) Retrieved phase using the absorption line of Hβ. (d) Retrieved phase combining all three absorption lines. |
| In the text | |
 |
Fig. 13. Histograms of the retrieved phases of the second SN image using the absorption lines Fe II, Hα, and Hβ and using only the third and fifth epoch of the first image. The phase inference is done for S/N = 10, 20, and 30 and for noiseless spectra. The thin red vertical lines in the histograms indicate the epochs of the two used spectra of the first image. The thick vertical line marks the input value of the second image. (a) Retrieved phase using the absorption line of Fe II. (b) Retrieved phase using the absorption line of Hα. (c) Retrieved phase using the absorption line of Hβ. (d) Retrieved phase combining all three absorption lines. |
| In the text | |
 |
Fig. A.1. Color curves of the non-microlensed and microlensed spectra with median, 1σ, and 2σ ranges obtained from 10 000 random positions in the type I lensing magnification map with κ = 0.36 and γ = 0.35. In addition, the bottom part of each panel (Figs. A.1a–k) shows the deviation of the microlensed color from the non-microlensed color with 1σ uncertainties. |
| In the text | |
 |
Fig. B.1. Magnification maps for two different κ and γ values with smooth matter fraction s = 0.50. The magnification μ(x, y) is indicated by the color scale on the right-hand side. (a) Type I microlensing map. (b) Type II microlensing map. |
| In the text | |
 |
Fig. B.2. Temporal evolution of the absorption minima of the Hα, Hβ, and Fe II lines for non-microlensed and microlensed spectra using the two different magnification maps of Fig. B.1 (left: Fig. B.1a; right: Fig. B.1b). |
| In the text | |
 |
Fig. B.3. Histograms of the retrieved phases under high microlensing magnifications of the second SN image and second microlensing scenario using the absorption lines Fe II, Hα, and Hβ. By using the wavelengths of the absorption features, the phase of the second SN image of the second microlensing scenario is correctly recovered. (a) Retrieved phase using the absorption line of Fe II. (b) Retrieved phase using the absorption line of Hα. (c) Retrieved phase using the absorption line of Hβ. (d) Retrieved phase combining all three absorption lines. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.