EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 652 (August 2021) A&A, 652 (2021) A132 Full HTML
Free Access
Issue
A&A
Volume 652, August 2021
Article Number A132
Number of page(s) 9
Section The Sun and the Heliosphere
DOI https://doi.org/10.1051/0004-6361/202141006
Published online 24 August 2021

© ESO 2021

1. Introduction

Helioseismology is one of the few available techniques that can be used to infer the properties of the solar interior. It is based on the analysis of the oscillations on the surface. The first studies in this field were focused on the interpretation of the eigenfrequencies of the resonant modes. They led to remarkable results, such as insight into the interior solar rotation (Christensen-Dalsgaard 2002). Despite its successes, the study of the eigenfrequencies only allows the inference of the global properties of the Sun. To bypass this limitation, the new field of ‘local helioseismology’ has been developed over the last three decades (Braun et al. 1987, 1992; Hill 1988; Duvall et al. 1993). Local helioseismology focuses on the interpretation of not only eigenfrequencies, but the whole wave field, with the aim of exploring localized structures below the surface.

The interest in local helioseismology led to the development of a number of techniques and applications (see Gizon & Birch 2005, for a review). One of those is helioseismic holography (Lindsey & Braun 1990), a technique based on the fundamental idea that the wave field at the solar surface has the signature of the wave field of any region in the solar interior at any given time. Phase-sensitivity holography is a particular case of local helioseismology used to infer time-travel perturbations. A detailed description of helioseismic holography, and of phase-sensitivity holography in particular, can be found in Lindsey & Braun (2000a).

Far-side imaging is an application of phase-sensitivity holography with the purpose of detecting active regions in the non-visible hemisphere of the Sun (Lindsey & Braun 2000b; Braun & Lindsey 2001). To this end, it uses data from a ‘pupil’ (a region of the solar surface where the wave field is observed) on the near side of the Sun to infer the properties of a ‘focus point’ on the far side. Similar studies of far-side active regions have been performed using time-distance helioseismology instead of helioseismic holography (Duvall & Kosovichev 2001; Zhao 2007; Ilonidis et al. 2009). The success of these methods relies on the transparency of the solar interior to seismic waves from a range of frequencies. These waves are reflected off the top layers of the solar interior and are refracted back to the surface, far from the original source, leading to a ‘bounce-like’ propagation. In regions with strong magnetic field concentrations, such as sunspots, the solar surface is depressed (an effect known as Wilson depression) and waves are reflected at a deeper layer (Lindsey et al. 2010; Schunker et al. 2013; Felipe et al. 2017). This shortening of the wave path can be detected in far-side seismic maps as a reduction in the travel time. Far-side imaging relies on multi-skip waves, using waves that are reflected off the surface at least once on their propagation from the focus point to the pupil or vice versa. Zhao et al. (2019) have recently developed new schemes to perform time-distance far-side analyses that include waves whose paths follow a higher number of skips.

The space weather in the Solar System, and its influence on the biological and technological systems on Earth, is a direct consequence of the activity on the solar surface. Learning about and preventing these effects is the main goal of space weather forecasting. Far-side helioseismology is a key ingredient in the forecasting because it allows the detection of active regions that could represent a potential risk before they rotate into the visible solar hemisphere. Moreover, the inclusion of far-side active regions has been proven to greatly improve the performance of space weather forecasting (Fontenla et al. 2009; Arge et al. 2013). A discussion of the space weather applications of far-side seismic imaging is available in Lindsey & Braun (2017).

Although promising and successful, all seismic techniques for the detection of far-side active regions are only able to detect the strongest active regions, leaving fainter far-side activity un-probed (González Hernández et al. 2007; Liewer et al. 2014, 2017). In an effort to improve detection capabilities, Felipe & Asensio Ramos (2019) leveraged deep learning to develop a convolutional neural network (CNN) that improves the sensitivity of the method. We refer to this neural network hereafter as ‘FarNet’.

The main goal of this paper is to analyse FarNet in depth, comparing its performance on the detection of active regions with standard far-side helioseismic techniques. We have employed direct Solar Terrestrial Relations Observatory (STEREO; Kaiser 2004) far-side extreme ultraviolet (EUV) images to test the reliability of the network predictions. The paper is organized as follows: Sect. 2 explains the data used to obtain the predictions of far-side active regions and gives insight about FarNet and the standard seismic method, Sect. 3 shows the data that we used as proxies for active regions for the comparison, Sect. 4 describes the comparison between both methods, and the results are discussed in Sect. 5.

2. Detection of far-side active regions

2.1. Far-side seismic maps

The fundamental data for the seismological identification of far-side active regions are phase-shift maps of the non-visible solar hemisphere measured through a helioseismic technique. Regions with a negative phase shift (a reduction in the travel time of the waves) are potentially associated with the presence of an active region. We used maps obtained from the Joint Science Operation Center (JSOC) repository1, computed using helioseismic holography from Doppler data obtained by the Helioseismic and Magnetic Imager (HMI; Schou et al. 2012). These seismic maps are published in Carrington coordinates with a periodicity of 12 h. Two kinds of phase-shift maps are made public in the JSOC repository, one computed using a temporal window of 24 h of Doppler data and another computed using 5 days of the same data.

2.2. Standard seismic method

The presence of strong far-side active regions is routinely detected using Stanford’s Strong-Active-Region Discriminator (SARD)2 on seismic maps processed with five days of HMI Doppler data.

The method searches for regions where the negative phase-shift is greater than 0.085 rad and calculates their corresponding seismic strength (S), which is given by the integrated negative phase shift over the area of the region. The area unit used in this calculation is the millionth of a hemisphere (μHem), so the seismic strength is given in μHem rad. A signal is classified as a far-side seismic region if the seismic strength, S, exceeds a threshold of 400 (Liewer et al. 2017). One of the goals of our study is the evaluation of the performance of the standard seismic method as the selection of the S threshold varies. We applied the SARD routine to five-day phase-shift maps of the analysed range of dates. The routine returns output maps with the same size (in longitude and latitude) as the input seismic map, where each region with S stronger than a user-specified threshold is labelled with an integer number. We extracted far-side active region maps as a function of the threshold, with S thresholds increasing from 0 to 1275 (including the standard value of 400).

2.3. FarNet network

FarNet3 is a fully convolutional neural network that follows the standard encoder-decoder U-net architecture (Ronneberger et al. 2015). Both the encoder and the decoder are built by the successive applications of convolutional layers, batch normalization (BN; Ioffe & Szegedy 2015), and rectified linear unit (ReLU) activation functions (Nair & Hinton 2010). The encoder decreases the size of the input images in several steps (while increasing the number of channels of the tensors) by using max-pooling (Goodfellow et al. 2016). The decoder recovers the original size via transpose convolutions (Zeiler et al. 2010). As standard in the U-net architecture, skip connections are used to accelerate training by avoiding vanishing gradients.

FarNet takes as input 11 consecutive phase-shift maps computed from HMI Doppler data using helioseismic holography. Each map is obtained from observations acquired over 24 h, and the temporal cadence between consecutive maps is 12 h. Only a region of the seismic maps, centred on the central meridian of the far side and spanning 120° in longitude and 144° in latitude, is given to the network as input. The output of the neural network consists of a probability map of the same size as the input maps. To produce such probability maps, the output of the network is equipped with a sigmoid activation function. The network was developed and trained using PyTorch (Paszke et al. 2019).

As explained in Felipe & Asensio Ramos (2019), FarNet was trained using, as expected values on the training set, binary segmented near-side HMI magnetograms, on which activity is indicated with ones and no activity with zeros. The magnetograms were obtained 13.5 days after the central date of the inputs to allow for a half rotation of the solar surface. Active regions that emerged on the near side were carefully removed to keep only those that emerged on the far side before rotating into the visible hemisphere.

Detections in the network output were evaluated by computing the ensuing integrated probability (Pi). To do so, we searched for regions of contiguous pixels with a probability larger than 0.2 and integrated over the area obtained after applying a Gaussian smoothing of a full width at half maximum of 1.5 pixels to the probability map. Given that the output map has pixels with an area of 1 deg2, and is probability dimensionless, the integrated probability has units of deg2. To discriminate true active regions from potential artefacts, Felipe & Asensio Ramos (2019) selected regions with an integrated probability above Pi = 100. Figure 1 shows an example of seismic maps used as input for the network and the resulting output, as well as the corresponding region of the five-day cumulative phase-shift map that would be used to compute the standard method prediction for the same date.

thumbnail Fig. 1.

Comparison between the inputs of both methods of detecting far-side activity and Farnet’s output. Top: eleven phase-shift maps used as input to FarNet. Each map is computed with 24 h of Doppler observations. The time cadence of the seismic maps is 12 h. The colour scale indicates the phase shift, ranging from −0.28 rad (dark blue) to 0.17 rad (yellow). Bottom: five-day cumulative phase-shift map (a) computed for the central time of the series (input time 0 h, December 25, 2013) and (b) the prediction of FarNet for the same time using the 11 phase-shift maps.

3. EUV data for far-side activity calibration

As a proxy for the location of active regions, we used 304 Å Carrington maps from the Solar Museum Server of NASA (Liewer et al. 2017), composed of observations from the Extreme Ultraviolet Imager (EUVI; Wuelser et al. 2004) on board STEREO and the instrument Atmospheric Imaging Assembly (AIA; Lemen et al. 2012) on board Solar Dynamics Observatory (SDO; Pesnell et al. 2012). STEREO 304 Å data have been used as an indication of far-side magnetic activity by several works that analysed seismic detections of far-side active regions (Liewer et al. 2012, 2014; Zhao et al. 2019). Magnetized regions exhibit an increased brightness in the EUV, and images in the 304 Å band show a good correlation with magnetic flux maps (Ugarte-Urra et al. 2015). Liewer et al. (2012) used visual comparison between helioseismic predictions of far-side active regions and STEREO data from February to July 2011, and Liewer et al. (2014) extended the range of study by adding the period from January to April 2012. Later, Zhao et al. (2019) compared three months of far-side helioseismic images with STEREO data. Here, we have performed a more statistically significant study by extending the analysis to a larger amount of cases. We use data from the whole temporal period when there was good STEREO far-side coverage, spanning from April 2011 to May 2016. The far-side coverage by STEREO spacecraft after late 2014 is not complete, but it is sufficient for our goals since our analysis is focused on the central region of the far hemisphere.

3.1. Identification of far-side active regions in EUV data

The comparison of the large set of outputs from the two far-side methods considered in this work and the STEREO 304 Å images was automatized. To this end, we transformed the STEREO/SDO data on activity masks (hereafter ‘EUV masks’). The images were segmented by considering an intensity threshold such that every pixel above this threshold is considered to be part of an active region. The ideal EUV thresholds were determined from the comparison of EUV masks with different thresholds (restricted to the near side of the composite Carrington maps) with HMI magnetograms acquired simultaneously. The whole procedure is illustrated for one representative case in Fig. 2. For the HMI magnetograms, we employed the JSOC series hmi.Mldailysynframe_720s. The synoptic magnetograms from this series are presented in longitude and the sine of the latitude, and the first 120° in longitude are substituted by a nearly instantaneous magnetogram centred on the central meridian of the visible hemisphere. A total of 1600 STEREO/SDO images and HMI magnetograms were used for the threshold calibration (only the region acquired with SDO/AIA from the STEREO/SDO Carrington maps was actually employed), using one image per day from June 1, 2010, to May 15, 2016. There is a gap of missing STEREO/SDO composite maps from August 2014 to November 2015.

thumbnail Fig. 2.

Processing steps performed to calculate the best threshold to compute EUV activity masks. Data are from September 22, 2013. (a): HMI magnetogram. (b): magnetogram after resizing and applying Gaussian smoothing over the absolute values. (c): final magnetogram mask, using 25 G as the threshold for feature determinations. (d): square root of the STEREO/SDO composite image from the same solar region. (e): region of the STEREO/SDO image after applying the square-root transformation, resizing, and applying Gaussian smoothing. (f): section of the final EUV mask, using the best threshold determined by the date-threshold fit.

In order to properly calibrate the EUV threshold, we first defined activity masks from the magnetograms. For reproducibility purposes, we explain how we did so in the following. Magnetograms were re-sized to a resolution of 1 deg on both the latitude and longitude axis. A Gaussian filter with a standard deviation of three degrees was applied to the absolute value of the magnetogram signal to remove small-scale magnetic field variations that could complicate the image segmentation (middle panel in the top row of Fig. 2). From the results of the Gaussian smoothing, activity masks were computed with the IDL (Interactive Data Language) routine rankdown.pro, part of the feature tracking software YAFTA4. A threshold of 25 G was selected to compute these masks. This value was based on a visual inspection of continuum images of multiple magnetic features, such as sunspots and pores, with the support of the JHelioviewer software (Müller et al. 2017). An example of the resulting magnetogram activity masks is shown in the top-right panel of Fig. 2.

The EUV data were also processed for the inter-comparison, with the consecutive application of: i) a square-root non-linear transformation, ii) a downsizing to a resolution of 1 deg in latitude and longitude, and iii) a Gaussian filter with a standard deviation of three degrees. We then generated 21 EUV masks with the YAFTA routine, with thresholds ranging from 20 to 40 in units of square root of EUVI digital numbers per second (DN/s).

Various EUV masks were computed using different thresholds for a sample of dates covering the temporal span between June 2010 and May 2016. The best threshold for each image of the selected EUV sample was chosen such that the ensuing mask was as close as possible to that from the associated magnetogram. This similarity was automatically determined by comparing the features in both mask maps. We found that the ideal EUV threshold depends on the date of the observations (Fig. 3). The threshold shows a clear trend with the date, with a negative slope. No clear trend, though, is found with proxies of activity, such as the number of sunspots. This trend could be due to the degradation of the STEREO detectors over time. Another reason could be that although photospheric active regions have a huge effect on the EUV irradiance, they do not explain the whole emission. Approximately 80% of the total solar irradiance is due to photospheric magnetic activity, but chromospheric and coronal processes need to be taken into account, these processes being especially relevant on the EUV part of the spectrum (Domingo et al. 2009). Finally, we computed the EUV masks for the STEREO dataset employed for the evaluation of the seismic detections of far-side active regions (April 2011 to May 2016, with a gap in between) using the threshold given by the linear fit shown as an orange line in Fig. 3.

thumbnail Fig. 3.

Ideal threshold of the EUV images derived from the comparison of near-side EUV and activity masks as a function of time. Blue dots represent the ideal threshold determined for individual cases. Darker blue regions illustrate a higher concentration of cases. The orange line shows the linear fit of the thresholds, which gives the actual threshold applied to far-side EUV data to compute the EUV masks. Fit coefficients can be found at the top of the figure. Dates range from June 2010 to May 2016, with a gap in STEREO/SDO composite images from August 2014 to November 2015.

4. Comparison of methods

Figure 4 illustrates the predictions of far-side active regions given by FarNet (last column) and the standard method (second-to-last column) for three independent cases. They are compared with simultaneous direct observations of the far side as observed in EUV with STEREO (first column) and the EUV masks constructed for the evaluation of the results (second column).

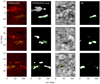thumbnail Fig. 4.

Visual comparison between methods applied on data from April 13, 2011 (top), June 8, 2013 (middle), and April 1, 2014 (bottom). From left to right: square root of the re-sized STEREO/SDO image, the EUV mask, the seismic map computed with 5 days of Doppler data, and the FarNet output. Yellow and green lines show the standard seismic method detections with S > 400 and FarNet detections with Pi > 100, respectively.

A visual inspection of Fig. 4 confirms the well-known fact that the seismic signature of far-side active regions in the visible hemisphere can be employed to detect them. The output from both methods reveals locations where far-side active regions are expected since a reduced travel time is found. Those far-side active regions are confirmed by the enhanced EUV emission measured with STEREO. Interestingly, the outputs from FarNet show a better resemblance with EUV data, including the detection of small regions that are missed by the standard seismic approach.

We evaluated the performances of both methods as a function of the threshold Pi and S, using true detections and false positives as performance indicators. As explained above, the standard helioseismic method uses data computed from five days of observations (a single seismic map is computed from five days of Doppler data) and the neural network approach uses data from six days (11 seismic maps computed with observations of 24 h with a time cadence of 12 h). In both methods, the use of a longer temporal span improves the signal-to-noise ratio. However, this leads to uncertainties in the determination of the dates when the seismically detected far-side active regions are present. For completeness, we evaluated the reliability of the methods by comparing their prediction with a set of EUV masks. We considered the time of the prediction to be the central date and time of the data employed for the computation (in the case of FarNet, for example, it is the time corresponding to 0 h in Fig. 1). This prediction was compared with several EUV masks centered on that date. Three studies were made, comparing the outputs with 24, 72, and 120 h of EUV data (3, 7, and 11 images, respectively, since the cadence of the employed EUV data is 12 h). A total of 2342 far-side predictions were used in the comparisons. Each of them was considered as an independent case, meaning that they were compared individually with the corresponding EUV masks and that a single active region can be counted several times. In this sense, our statistical approach is similar to that from Zhao et al. (2019) but differs from Liewer et al. (2017) since we are not tracking active regions.

4.1. Definitions of true detections and false positives

A true detection is reported for the output if one of these two conditions is satisfied: i) the presence of a feature in the EUV masks with a centroid within ±15° in longitude and ±5° in latitude of the centroid of any blob on the output (criteron based on the previous work of Liewer et al. 2017), or ii) if a source on the output of any of the methods has an area larger than 127 deg2, a superposition between part of the area of the detected regions and the features on the EUV mask will be taken as a true detection. The area selected to take superposition into account is the typical area of a Pi = 100 region on the network outputs. This Pi is the threshold chosen for seismic detections in Felipe & Asensio Ramos (2019). If any of the segmented regions of the output satisfies either of the two criteria, it is considered to be a true detection. If none of the criteria are fulfilled, it is considered a false positive.

4.2. Results

Figure 4 shows the results of applying the standard method and the network to seismic data of three independent dates. For those three days, the network shows a greater sensitivity, and all strong active regions detected by the network (Pi > 100) are associated with EUV emission signatures. Of the three cases illustrated in Fig. 4, only one strong active region (S>400) is detected by the standard method.

Figure 5 shows the number of true detections and false positives for each method. The upper panels show the results for FarNet, and the lower panels show those for the standard seismic method. All plots indicate the number of regions above a certain threshold in Pi or S, depending on the method. Results are shown for the comparison with windows of 24, 72, and 120 h of EUV data. These figures clearly show that once a sufficiently small false detection rate is reached, the number of true detection for FarNet greatly exceeds those of the standard seismic method. For instance, we find that Pi = 120 produces a negligible amount of false positives for FarNet, giving near to 2000 true detections in the 24 h window. In the same conditions, a negligible false positive rate is reached for S = 400 for the standard seismic method, which then produces fewer than 1500 true detections.

thumbnail Fig. 5.

True detections (blue dots) and false positives (orange dots) from FarNet (first row) and from the standard seismic method (second row) over the whole range of dates of the study. Each dot corresponds to the detections with Pi or S over the X axis value. Each column represents the results of the comparison with 24 h (first column), 72 h (second column), and 120 h (third column) of STEREO data.

Figure 7 shows a different view of the results for a better inter-comparison of the two methods. We display the number of true detections for each method as a function of the ratio of false positives to total positives (true detections plus false positives). Each point on the figure is associated with a particular Pi or S threshold. The lower panels are close-ups for the cases with Pi > 100 and S > 400, which are the thresholds previously suggested for each method (Liewer et al. 2017; Felipe & Asensio Ramos 2019). The lower-left panel of Fig. 7 shows that for larger values of Pi and S both methods return similarly good results. In the rest of the range of false positive ratios (and in the whole range, in the case of windows of 72 and 120 h of EUV data; middle and right panels), it is clear that the FarNet performance is superior to that of the standard seismic method. This proves that FarNet is able to reliably detect smaller activity signatures than the standard method.

Table 1 shows a comparison of both methods, employing the threshold defined in previous studies for the standard method (S = 400) and that which leads to the closer percentage of false positives for the network results (Pi = 113) for the 24-h study. For those thresholds, FarNet achieved an improvement of ∼47% in the number of true detections.

Table 1.

Amount of detections and false positives for the 24-h-range study, with S > 400 for the seismic method (SS) and Pi > 113 for the neural network (NN) approach.

Figure 8 illustrates the rate of false positives as a function of the signature (Pi or S) of the detected active regions. In this figure, the horizontal axis represents the centre of the range employed for each individual measurement. In the case of FarNet (top row), each dot indicates the ratio of false positives for the set of detections with Pi in the range [Pi − 10, Pi + 10], and the bottom panels illustrate the same quantity but for seismically detected active regions in the range [S − 25, S + 25]. This representation differs from previous analyses (Figs. 5 and 7) since the considered detections for each data point are restricted to those inside the defined bin, instead of including all the active regions with Pi or S above the corresponding threshold. The results from Fig. 8 provide an indication of the reliability of an independent far-side seismic detection (characterized by its Pi and/or S), supported by the statistical analysis of similar detections over approximately four years of data.

Figure 6 shows the false negatives of both methods as a function of the area of the features on the EUV masks for a comparison of each EUV mask with the output related to the same date. False negatives are defined as regions where EUV emission is found, but with no association with a seismically detected active region. Detections were claimed for regions on the outputs with Pi > 113 or S > 400. These false negatives were studied for intervals of 100 deg2 of area, from 0 to 1100. We found that for regions on the EUV masks with an area over 600 deg2, both the network and the standard method can detect virtually all the sources. This is in agreement with Zhao et al. (2019), who found a similar area threshold for the complete detection of EUV active regions. For smaller regions, the network leaves fewer regions without detection, as expected from previous results.

thumbnail Fig. 6.

False negatives from the network (blue line) and from the standard method (orange line) as a function of the area of the regions on the activity masks, for the whole range of dates of the study. Only the output from the same date as the EUV mask was used for this result, for each method and each EUV mask.

5. Discussion and conclusions

Since the pioneering works of Lindsey & Braun (2000b) and Braun & Lindsey (2001), the detection of far-side active regions based on the analysis of the oscillations in the visible hemisphere has become a common approach. These predictions are regularly published as one of the data products from SDO and the Global Oscillation Network Group (GONG; Harvey et al. 1996). Later works have subsequently validated the method and evaluated its performance. Due to the absence of direct far-side observations during the first years of this century, those first analyses compared the seismic predictions with observations taken after the probed solar regions had rotated into the visible solar hemisphere. Those studies revealed the relation between the seismic signature and the magnetic field strength (González Hernández et al. 2007) and found that 40% of the total active regions appearing at the east limb of the Sun can be detected with a confidence level higher than 60% (González Hernández et al. 2010). With the advent of the STEREO spacecraft, direct observations of the far side have been available, allowing a better evaluation of the reliability of the seismic predictions. These methods have shown a remarkable performance in detecting strong far-side active regions (Liewer et al. 2014, 2017; Zhao et al. 2019).

In this study we have evaluated two different approaches for identifying active regions in holography far-side seismic maps: the standard method of computing the seismic strength of the regions and the recently developed neural network FarNet. The predictions from those two approaches have been compared with direct EUV far-side observations acquired with STEREO. In both cases, we have quantified the results as a function of the threshold selected for the identification of active regions. Our study benefits from the analysis of a larger sample than those of previous works. The evaluation of the standard method confirms the reliability of this approach for detecting strong active regions. Our results support the selection of S = 400 as the threshold for the identification of far-side active regions since it provides a high number of detections with a low risk of false positives (around 4%; see Table 1).

Felipe & Asensio Ramos (2019) validated the neural network FarNet using a limited sample of STEREO data. That sample covered a time period during the solar minimum (and, thus, with a low availability of active regions) and without full STEREO coverage of the far side. Felipe & Asensio Ramos (2019) showed the promising results provided by FarNet, and here we have confirmed the potential of the method using a greatly improved statistical sample. A comparison of FarNet results with the standard approach shows that both methods are similarly good for strong active regions (S ≳ 500). In the case of weaker active regions, FarNet exhibits a significantly better performance than the standard method. For thresholds (in S and Pi) that give a similar success rate, FarNet manages to identify a much higher number of active regions (Fig. 7).

thumbnail Fig. 7.

Number of true detections from both methods as a function of the ratio of false positives (FP) to total positives (TP). The second row shows a close-up look at the results from thresholds higher than S = 400 (standard seismic method) and Pi = 100 (FarNet). Each column represents the results of the comparison with 24 h (first column), 72 h (second column), and 120 h (third column) of STEREO data.

thumbnail Fig. 8.

Rate of false positives over all positives as a function of their seismic signature. Each data point represents the ratio of false positives in the ranges [Pi − 10, Pi + 10] (FarNet, top row) and [S − 25, S + 25] (standard seismic method, bottom row), with Pi and S given by the value in the horizontal axis. Each column represents the comparison results for the studies done with 24 h (first column), 72 h (second column), and 120 h (third column) of STEREO data.

These results show FarNet’s potential for a great number of applications. The detection of far-side active regions is fundamental for space weather studies, including the forecast of the spectral irradiance (Fontenla et al. 2009) and the solar wind (Arge et al. 2013). One way to probe far-side active regions is through EUV far-side imaging. STEREO spacecraft have produced massive amounts of EUV data from the far-side hemisphere since their launch in 2006. Using this data, Kim et al. (2019) were able to infer far-side magnetograms with fair success with a machine learning tool. This technique can be very helpful for when EUV far-side data are available, but unfortunately far-side observations are a limited resource. STEREO spacecraft are currently returning to the Earth side, and STEREO-B has stopped transmitting. The ESA (European Space Agency) mission Solar Orbiter (launched in February 2020; Müller et al. 2013) will provide far-side magnetograms, but only during some periods of its orbit. Seismic inference will remain a key tool over the coming decades since it will be the only approach for obtaining a constant monitoring of the solar far-side hemisphere.

In this context, there is a growing interest in improving the methods for the seismic detection of far-side active regions. Recent developments have taken steps in this direction by exploring various time-distance measurement schemes with more multi-skip waves (Zhao et al. 2019) and by employing machine learning tools (Felipe & Asensio Ramos 2019). Here, we have further analysed the network presented in Felipe & Asensio Ramos (2019), confirming its promising results. Our study is restricted to active regions around the centre of the far side (up to 60° from the far-side centre in longitude), and our statistics do not discern the locations of the regions. However, one would expect a better performance near the centre of the far side than near the limbs. Future efforts will be devoted to evaluating the sensitivity of both methods with the closeness of the active regions to the limb. Additionally, FarNet still has room for improvement. The training of the network was made using, as outputs, binary magnetograms of the near side taken 13.5 days after the prediction date. That is, they are not co-temporal to the seismic images. This limitation can potentially be bypassed by employing the STEREO EUV masks defined in this work and/or future far-side magnetograms acquired with Solar Orbiter for the training. We are actively working along this line, and the preliminary results look promising. Other possible developments include the direct use of Doppler maps as inputs, instead of phase-shift seismic maps, and the design of neural networks capable of returning an estimation of far-side magnetic flux and/or magnetograms.

2

Further insight on the system can be found at http://jsoc.stanford.edu/data/farside/explanation.pdf

Acknowledgments

We thank P.C. Liewer and collaborators for making publicly available the composite STEREO/EUVI and SDO/AIA maps necessary to carry out this research. We thank C. Lindsey and D.C. Braun for providing the Stanford’s Strong-Active-Region Discriminator routine to compute predictions of active regions on the far side. This work was supported by the State Research Agency (AEI) of the Spanish Ministry of Science, Innovation and Universities (MCIU) and the European Regional Development Fund (FEDER) under grant with reference PGC2018-097611-A-I00 and by Consejería de Economía, Conocimiento y Empleo del Gobierno de Canarias and the European Regional Development Fund (ERDF) under grant with reference PROID2020010059. We acknowledge the community effort devoted to the development of the following open-source packages that were used in this work: numpy (numpy.org, Harris et al. 2020), matplotlib (matplotlib.org, Hunter 2007), PyTorch (pytorch.org, Paszke et al. 2019), and SunPy (sunpy.org, The SunPy Community 2020).

References

  1. Arge, C. N., Henney, C. J., Hernandez, I. G., et al. 2013, Sol. Wind, 13, 11 [Google Scholar]
  2. Braun, D. C., & Lindsey, C. 2001, ApJ, 560, L189 [NASA ADS] [CrossRef] [Google Scholar]
  3. Braun, D. C., Duvall, T. L., Jr., & Labonte, B. J. 1987, ApJ, 319, L27 [NASA ADS] [CrossRef] [Google Scholar]
  4. Braun, D., Lindsey, C., Fan, Y., & Jefferies, S. 1992, ApJ, 392, 739 [NASA ADS] [CrossRef] [Google Scholar]
  5. Christensen-Dalsgaard, J. 2002, Rev. Mod. Phys., 74, 1073 [NASA ADS] [CrossRef] [Google Scholar]
  6. Domingo, V., Ermolli, I., Fox, P., et al. 2009, Space Sci. Rev., 145, 337 [CrossRef] [Google Scholar]
  7. Duvall, T. L., & Kosovichev, A. G. 2001, in Recent Insights into the Physics of the Sun and Heliosphere: Highlights from SOHO and Other Space Missions, eds. P. Brekke, B. Fleck, & J. B. Gurman, IAU Symp., 203, 159 [NASA ADS] [Google Scholar]
  8. Duvall, T. L., Jr., Jefferies, S. M., Harvey, J. W., & Pomerantz, M. A. 1993, Nature, 362, 430 [NASA ADS] [CrossRef] [Google Scholar]
  9. Felipe, T., & Asensio Ramos, A. 2019, A&A, 632, A82 [CrossRef] [EDP Sciences] [Google Scholar]
  10. Felipe, T., Braun, D. C., & Birch, A. C. 2017, A&A, 604, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Fontenla, J. M., Quémerais, E., González Hernández, I., Lindsey, C., & Haberreiter, M. 2009, Adv. Space Res., 44, 457 [NASA ADS] [CrossRef] [Google Scholar]
  12. Gizon, L., & Birch, A. C. 2005, Liv. Rev. Sol. Phys., 2, 6 [Google Scholar]
  13. González Hernández, I., Hill, F., & Lindsey, C. 2007, ApJ, 669, 1382 [NASA ADS] [CrossRef] [Google Scholar]
  14. González Hernández, I., Hill, F., Scherrer, P. H., Lindsey, C., & Braun, D. C. 2010, Space Weather, 8, 06002 [CrossRef] [Google Scholar]
  15. Goodfellow, I., Bengio, Y., & Courville, A. 2016, Deep Learning (MIT Press) http://www.deeplearningbook.org [Google Scholar]
  16. Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [CrossRef] [PubMed] [Google Scholar]
  17. Harvey, J. W., Hill, F., Hubbard, R. P., et al. 1996, Science, 272, 1284 [Google Scholar]
  18. Hill, F. 1988, ApJ, 333, 996 [NASA ADS] [CrossRef] [Google Scholar]
  19. Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
  20. Ilonidis, S., Zhao, J., & Hartlep, T. 2009, Sol. Phys., 258, 181 [NASA ADS] [CrossRef] [Google Scholar]
  21. Ioffe, S., & Szegedy, C. 2015, in Proceedings of the 32nd International Conference on Machine Learning (ICML-15), eds. D. Blei, & F. Bach, JMLR Workshop Conf. Proc., 448 [Google Scholar]
  22. Kaiser, M. 2004, Adv. Space Res., 36, 1483 [Google Scholar]
  23. Kim, T., Park, E., Lee, H., et al. 2019, Nat. Astron., 3, 397 [NASA ADS] [CrossRef] [Google Scholar]
  24. Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [Google Scholar]
  25. Liewer, P., Hernandez, I., Hall, J., & Thompson, W. 2012, Sol. Phys., 281, 3 [NASA ADS] [Google Scholar]
  26. Liewer, P. C., González Hernández, I., Hall, J. R., Lindsey, C., & Lin, X. 2014, Sol. Phys., 289, 3617 [NASA ADS] [CrossRef] [Google Scholar]
  27. Liewer, P. C., Qiu, J., & Lindsey, C. 2017, Sol. Phys., 292, 146 [NASA ADS] [CrossRef] [Google Scholar]
  28. Lindsey, C., & Braun, D. C. 1990, Sol. Phys., 126, 101 [NASA ADS] [CrossRef] [Google Scholar]
  29. Lindsey, C., & Braun, D. C. 2000a, Sol. Phys., 192, 261 [NASA ADS] [CrossRef] [Google Scholar]
  30. Lindsey, C., & Braun, D. C. 2000b, Science, 287, 1799 [Google Scholar]
  31. Lindsey, C., & Braun, D. 2017, Space Weather, 15, 761 [NASA ADS] [CrossRef] [Google Scholar]
  32. Lindsey, C., Cally, P. S., & Rempel, M. 2010, ApJ, 719, 1144 [NASA ADS] [CrossRef] [Google Scholar]
  33. Müller, D., Marsden, R. G., St Cyr, O. C., & Gilbert, H. R. 2013, Sol. Phys., 285, 25 [NASA ADS] [CrossRef] [Google Scholar]
  34. Müller, D., Nicula, B., Felix, S., et al. 2017, A&A, 606, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Nair, V., & Hinton, G. E. 2010, in Proceedings of the 27th International Conference on Machine Learning (ICML-10), June 21–24 (Haifa, Israel), 807 [Google Scholar]
  36. Paszke, A., Gross, S., Massa, F., et al. 2019, in Advances in Neural Information Processing Systems 32, eds. H. Wallach, H. Larochelle, A. Beygelzimer, et al. (Curran Associates, Inc.), 8024 [Google Scholar]
  37. Pesnell, W. D., Thompson, B. J., & Chamberlin, P. C. 2012, Sol. Phys., 275, 3 [Google Scholar]
  38. Ronneberger, O., Fischer, P., & Brox, T. 2015, ArXiv e-prints [arXiv:1505.04597] [Google Scholar]
  39. Schou, J., Scherrer, P. H., Bush, R. I., et al. 2012, Sol. Phys., 275, 229 [Google Scholar]
  40. Schunker, H., Gizon, L., Cameron, R. H., & Birch, A. C. 2013, A&A, 558, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. The SunPy Community (Barnes, W. T., et al.) 2020, ApJ, 890, 68 [Google Scholar]
  42. Ugarte-Urra, I., Upton, L., Warren, H. P., & Hathaway, D. H. 2015, ApJ, 815, 90 [NASA ADS] [CrossRef] [Google Scholar]
  43. Wuelser, J. P., Lemen, J. R., Tarbell, T. D., et al. 2004, in Telescopes and Instrumentation for Solar Astrophysics, eds. S. Fineschi, & M. A. Gummin, International Society for Optics and Photonics (SPIE), 5171, 111 [NASA ADS] [CrossRef] [Google Scholar]
  44. Zeiler, M., Krishnan, D., Taylor, G., & Fergus, R. 2010, Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2528–2535, Conference date: 13–06-2010 Through 18–06-2010 [Google Scholar]
  45. Zhao, J. 2007, ApJ, 664, L139 [NASA ADS] [CrossRef] [Google Scholar]
  46. Zhao, J., Hing, D., Chen, R., & Hess Webber, S. 2019, ApJ, 887, 216 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1.

Amount of detections and false positives for the 24-h-range study, with S > 400 for the seismic method (SS) and Pi > 113 for the neural network (NN) approach.

In the text

All Figures

thumbnail Fig. 1.

Comparison between the inputs of both methods of detecting far-side activity and Farnet’s output. Top: eleven phase-shift maps used as input to FarNet. Each map is computed with 24 h of Doppler observations. The time cadence of the seismic maps is 12 h. The colour scale indicates the phase shift, ranging from −0.28 rad (dark blue) to 0.17 rad (yellow). Bottom: five-day cumulative phase-shift map (a) computed for the central time of the series (input time 0 h, December 25, 2013) and (b) the prediction of FarNet for the same time using the 11 phase-shift maps.
In the text
thumbnail Fig. 2.

Processing steps performed to calculate the best threshold to compute EUV activity masks. Data are from September 22, 2013. (a): HMI magnetogram. (b): magnetogram after resizing and applying Gaussian smoothing over the absolute values. (c): final magnetogram mask, using 25 G as the threshold for feature determinations. (d): square root of the STEREO/SDO composite image from the same solar region. (e): region of the STEREO/SDO image after applying the square-root transformation, resizing, and applying Gaussian smoothing. (f): section of the final EUV mask, using the best threshold determined by the date-threshold fit.
In the text
thumbnail Fig. 3.

Ideal threshold of the EUV images derived from the comparison of near-side EUV and activity masks as a function of time. Blue dots represent the ideal threshold determined for individual cases. Darker blue regions illustrate a higher concentration of cases. The orange line shows the linear fit of the thresholds, which gives the actual threshold applied to far-side EUV data to compute the EUV masks. Fit coefficients can be found at the top of the figure. Dates range from June 2010 to May 2016, with a gap in STEREO/SDO composite images from August 2014 to November 2015.
In the text
thumbnail Fig. 4.

Visual comparison between methods applied on data from April 13, 2011 (top), June 8, 2013 (middle), and April 1, 2014 (bottom). From left to right: square root of the re-sized STEREO/SDO image, the EUV mask, the seismic map computed with 5 days of Doppler data, and the FarNet output. Yellow and green lines show the standard seismic method detections with S > 400 and FarNet detections with Pi > 100, respectively.
In the text
thumbnail Fig. 5.

True detections (blue dots) and false positives (orange dots) from FarNet (first row) and from the standard seismic method (second row) over the whole range of dates of the study. Each dot corresponds to the detections with Pi or S over the X axis value. Each column represents the results of the comparison with 24 h (first column), 72 h (second column), and 120 h (third column) of STEREO data.
In the text
thumbnail Fig. 6.

False negatives from the network (blue line) and from the standard method (orange line) as a function of the area of the regions on the activity masks, for the whole range of dates of the study. Only the output from the same date as the EUV mask was used for this result, for each method and each EUV mask.
In the text
thumbnail Fig. 7.

Number of true detections from both methods as a function of the ratio of false positives (FP) to total positives (TP). The second row shows a close-up look at the results from thresholds higher than S = 400 (standard seismic method) and Pi = 100 (FarNet). Each column represents the results of the comparison with 24 h (first column), 72 h (second column), and 120 h (third column) of STEREO data.
In the text
thumbnail Fig. 8.

Rate of false positives over all positives as a function of their seismic signature. Each data point represents the ratio of false positives in the ranges [Pi − 10, Pi + 10] (FarNet, top row) and [S − 25, S + 25] (standard seismic method, bottom row), with Pi and S given by the value in the horizontal axis. Each column represents the comparison results for the studies done with 24 h (first column), 72 h (second column), and 120 h (third column) of STEREO data.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.