| Issue |
A&A
Volume 651, July 2021
|
|
|---|---|---|
| Article Number | A121 | |
| Number of page(s) | 19 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202140961 | |
| Published online | 29 July 2021 | |
Asteroseismic analysis of variable hot subdwarf stars observed with TESS
I. The mean g-mode period spacings in hot subdwarf B stars⋆
1
Instituto de Física y Astronomía, Universidad de Valparaíso, Gran Bretaña 1111, 2360102 Playa Ancha, Valparaíso, Chile
e-mail: murat.uzundag@postgrado.uv.cl
2
European Southern Observatory, Alonso de Cordova 3107, Santiago, Chile
3
Astronomical Institute of the Czech Academy of Sciences, CZ-251 Ondřejov, Czech Republic
4
Astroserver.org, Fő tér 1, 8533 Malomsok, Hungary
5
Instituto de Astrofísica de La Plata, UNLP-CONICET, La Plata, Paseo del Bosque s/n B1900FWA, Argentina
6
INAF-Osservatorio Astrofisico di Torino, strada dell’Osservatorio 20, 10025 Pino Torinese, Italy
7
ARDASTELLA Research Group, Institute of Physics, Pedagogical University of Cracow, ul. Podchorżych 2, 084 Kraków, Poland
8
Embry-Riddle Aeronautical University, Department of Physical Science, 32114 Daytona Beach, FL, USA
9
Nordic Optical Telescope, Rambla José Ana Fernández Pérez 7, 38711 Breña Baja, Spain
10
Department of Physics and Astronomy, Aarhus University, Ny Munkegade 120, 8000 Aarhus C, Denmark
11
Department of Physics, Astronomy and Materials Science, Missouri State University, 901 S. National, 65897 Springfield, MO, USA
12
Nicolaus Copernicus Astronomical Centre of the Polish Academy of Sciences, ul. Bartycka 18, 716 Warsaw, Poland
Received:
31
March
2021
Accepted:
25
May
2021
Context. We present photometric and spectroscopic analyses of gravity (g-mode) long-period pulsating hot subdwarf B (sdB) stars, also called V1093 Her stars, observed by the TESS space telescope in both 120 s short-cadence and 20 s ultra-short-cadence mode during the survey observation and the extended mission of the southern ecliptic hemisphere.
Aims. We performed a detailed asteroseismic and spectroscopic analysis of five pulsating sdB stars observed with TESS in order to compare the observations with model predictions based on our stellar evolution computations coupled with adiabatic pulsation computations.
Methods. We processed and analyzed TESS observations of long-period pulsating hot subdwarf B stars. We used standard pre-whitening techniques on the datasets to extract the pulsation periods from the TESS light curves. We applied standard seismic tools for mode identification, including asymptotic period spacings and rotational frequency multiplets. Based on the values obtained from Kolmogorov-Smirnov and Inverse Variance tests, we searched for a constant period spacing for dipole (l = 1) and quadrupole (l = 2) modes. We calculated the mean period spacing for l = 1 and l = 2 modes and estimated the errors by means of a statistical resampling analysis. For all stars, atmospheric parameters were derived by fitting synthetic spectra to the newly obtained low-resolution spectra. We computed stellar evolution models using the LPCODE stellar evolution code, and computed l = 1 g-mode frequencies with the adiabatic nonradial pulsation code LP-PUL. Derived observational mean period spacings were then compared to the mean period spacings from detailed stellar evolution computations coupled with the adiabatic pulsation computations of g-modes.
Results. We detect 73 frequencies, most of which are identified as dipole and quadrupole g-modes with periods spanning from ∼3000 s to ∼14 500 s. The derived mean period spacing of dipole modes is concentrated in a narrow region ranging from 251 s to 256 s, while the mean period spacing for quadrupole modes spans from 145 s to 154 s. The atmospheric parameters derived from spectroscopic data are typical of long-period pulsating sdB stars with an effective temperature ranging from 23 700 K to 27 600 K and surface gravity spanning from 5.3 dex to 5.5 dex. In agreement with the expectations from theoretical arguments and previous asteroseismological works, we find that the mean period spacings obtained for models with small convective cores, as predicted by a pure Schwarzschild criterion, are incompatible with the observations. We find that models with a standard, modest convective boundary mixing at the boundary of the convective core are in better agreement with the observed mean period spacings and are therefore more realistic.
Conclusions. Using high-quality space-based photometry collected by the TESS mission coupled with low-resolution spectroscopy from the ground, we provide a global comparison of the observations with model predictions by means of a robust indicator such as the mean period spacing. All five objects that we analyze in this work show remarkable homogeneity in both seismic and spectroscopic properties.
Key words: asteroseismology / stars: oscillations / stars: interiors / stars: evolution / stars: horizontal-branch / subdwarfs
© ESO 2021
1. Introduction
Hot subdwarf stars (sdB) are core-helium burning stars with a very thin hydrogen (H) envelope (Menv < 0.01 M⊙), and a mass close to the core-helium (He)-flash mass ∼0.47 M⊙. The sdB stars are evolved, compact (log g = 5.0−6.2 dex), and hot (Teff = 20 000 – 40 000 K) objects with radii between 0.15 R⊙ and 0.35 R⊙, and are located on the so-called extreme horizontal branch (EHB; see Heber 2016, for a review). They have experienced extreme mass-loss mostly due to binary interactions at the end of the red giant phase, where they lost almost the entire H-rich envelope, leaving a He burning core with an envelope too thin to sustain H-shell burning. Hot subdwarf B stars will spend about 108 yr burning He in their cores. Once the He has been exhausted in their core, they will start burning He in a shell surrounding a carbon and oxygen (C/O) core as subdwarf O (sdO) stars, and will eventually end their lives as white dwarfs (Heber 2016).
One of the major advances in our understanding of sdB stars was initiated by Kilkenny et al. (1997), who discovered rapid pulsations in hot sdBs known as V361 Hya stars (often referred to as short-period sdBV stars). The V361 Hya stars show multiperiodic pulsations with periods spanning from 60 s to 800 s. In this region, the pulsational modes correspond to low-degree, low-order pressure p-modes with photometric amplitudes up to a few per cent of their mean brightness (Reed et al. 2007; Østensen et al. 2010; Green et al. 2011). These modes are excited by a classical κ-mechanism due to the accumulation of the iron group elements (mostly iron itself), in the Z-bump region (Charpinet et al. 1996, 1997). These latter authors also showed that radiative levitation is a key physical process in enhancing the abundances of iron group elements, which is needed to be able to excite the pulsational modes. The p-mode sdB pulsators are found in a temperature range between 28 000 K and 35 000 K and with the surface gravity log g in the interval 5–6 dex. Subsequently, the long-period sdB pulsators known as V1093 Her stars were discovered by Green et al. (2003). These show brightness variations with periods of up to a few hours and have amplitudes smaller than 0.1% of their mean brightness (Reed et al. 2011). The oscillation frequencies are associated with low-degree (l < 3) medium- to high-order (10 < n < 60) g-modes, which are driven by the same mechanism (Fontaine et al. 2003; Charpinet et al. 2011). The g-mode sdB pulsators are somewhat cooler, with temperatures ranging from 22 000 K to 30 000 K and log g from 5 dex to 5.5 dex. Between the two described families of pulsating sdB stars, some “hybrid” sdB pulsators have been found that simultaneously show g- and p-modes. These hybrid sdB pulsators are located in the middle of the region of the HR diagram between p- and g-mode sdB pulsators (Green et al. 2011, Fig. 5). These objects are of particular importance as they enable us to study both the core structure and the outer layers of the sdBVs via asteroseismology. A few examples have been found from the ground (Oreiro et al. 2005; Baran et al. 2005; Schuh et al. 2006; Lutz et al. 2008).
During the nominal Kepler mission (Borucki et al. 2010), 18 pulsating subdwarf B stars were monitored in one-minute short-cadence mode. The majority of the stars (16) were found to be long-period g-mode pulsators, while just two of them were short-period p-mode pulsators (Østensen et al. 2010, 2011; Baran et al. 2011; Reed et al. 2011; Kawaler et al. 2010). Additionally, 3 known sdBs stars in the old open cluster NGC 6791 were found to pulsate (Pablo et al. 2011; Reed et al. 2012). The temperature of these sdBs ranges from 21 500 K to 37 000 K with a median of 27 400 K and surface gravities between log g of 4.67 dex and 5.82 dex, with a median of 5.42 dex. In 2013, the Kepler mission was reinitiated after the second reaction-wheel failure and it continued as the K2 mission observing along the ecliptic (Haas et al. 2014). During the K2 mission, more than 25 sdBs were found to pulsate and analyses are still ongoing. To date, 18 of these sdBVs have been published together with their atmospheric parameters (Reed et al. 2016, 2019, 2020b; Ketzer et al. 2017; Bachulski et al. 2016; Baran et al. 2019; Silvotti et al. 2019; Østensen et al. 2020). These stars have Teff in between 22 300 K and 37 000 K and log g from 5.2 dex to 5.7 dex (Reed et al. 2018, for a review).
For many sdBVs observed with Kepler, the asymptotic period sequences for g-mode pulsations have been successfully applied, especially for dipole (l = 1) and quadrupole (l = 2) modes, as more than 60% of the periodicities are associated with these modes (Reed et al. 2018). The asymptotic approximation can be perfectly applied for homogeneous stars. The period separation of g-modes becomes approximately constant for high radial orders. This is called the asymptotic regime of pulsations, and is masterfully documented in Tassoul (1980). It is important to note that the asymptotic g-mode theory is strictly valid for completely radiative and chemically homogeneous stars. However, sdB stars are stratified, and diffusion processes (gravitational settling and radiative levitation) contribute significantly to compositional discontinuities, which disturb the pulsational modes and could break the sequences of periods with constant spacing. This effect has been found in several g-mode-dominated sdBV stars. Furthermore, when the compositional discontinuities become stronger in transition zones, some modes are trapped; this was also detected for a few sdBV stars observed with Kepler (Østensen et al. 2014; Uzundag et al. 2017; Baran et al. 2017; Kern et al. 2018). Mode trapping is characterized by strong departures from a constant period spacing. Trapped modes can be useful, in that they provide a test for stellar evolution models, and offer a unique opportunity to determine mixing processes due to convective overshooting beyond the boundary of the helium-burning core (Ghasemi et al. 2017).
Another important asteroseismic tool, rotational multiplets, became available for sdB stars thanks to the long baseline of Kepler data (Baran 2012). During the nominal mission of Kepler, the rotation periods of sdBs were found to range from 10 d to 100 d (Reed et al. 2014). For the short-period sdB systems with WD companions (Porb < 15 d), the rotational periods of the sdBs were found to be in the range from 28 d to 50 d (2019, references therein). For the short-period sdB binary systems with M-dwarf companions (Porb < 0.8 d), rotational periods in the range between 7 and 40 d have been identified (Baran et al. 2019). Moreover, detecting rotational multiplets in both g- and p-modes in hybrid sdB pulsators is of special importance as these provide a way to determine the rotation of both the core and the envelope of these stars. Also, rotational splittings allow us to assign a harmonic degree to a pulsation mode. These remarkable stars have been found to be either solid-body rotators (Baran 2012; Ketzer et al. 2017) or radially differential rotators (Foster et al. 2015; Baran et al. 2017). The rotation properties of evolved stars are further discussed in a recent review of Charpinet et al. (2018).
The Transiting Exoplanet Survey Satellite (TESS) was launched successfully on 18 April 2018. The primary goal of this mission is to discover exoplanets around nearby and bright stars by means of the transit method (Ricker et al. 2014). The spacecraft has four identical 100 mm aperture cameras and is in a highly eccentric lunar-resonance Earth orbit. The orbit allows the telescope to observe the targets over ∼27 d continuously, covering a huge area in the sky (24° × 96°). During the first year, TESS surveyed 13 sectors in the southern hemisphere at both a short cadence (SC) of 2 min and a long cadence (LC) of 30 min. Results from LC observations of the first year were reported by Sahoo et al. (2020b).
During the first year, TESS observed 1702 compact objects including hot subdwarfs, prewhite dwarfs, and white dwarfs at two-minute cadence. The first results of asteroseismic analysis of hot sdB pulsating stars observed by TESS were reported in three papers (Charpinet et al. 2019; Reed et al. 2020a; Sahoo et al. 2020a). In the present paper, we analyze five pulsating sdB stars, which were observed in a single sector in SC mode by TESS during the survey phase of the southern ecliptic hemisphere. For each of these TESS targets, we obtained low-resolution spectra and fitted model atmospheres in order to derive their fundamental atmospheric parameters. We present the details of spectroscopic and photometric observations as well as the main characteristics of the studied sdBVs in Sect. 2. We discuss the analysis of the TESS data in Sect. 3 and give details on the frequency analysis along with detailed seismic mode identification. In Sects. 4 and 5, we present our analysis of the spectroscopic data and atmospheric parameters for each star, derived by fitting synthetic spectra to the newly obtained low-resolution spectra. We calculate asteroseismic models in Sect. 6 and compare them with the observations. Finally, we summarize our findings in Sect. 7.
2. Observations
2.1. Photometric observations – TESS
The TESS mission Cycle 1, covering most of the southern hemisphere, started on 25 July 2018 and ended on 18 July 2019. During this time, a total of 13 sectors were observed, where each sector covered ∼27 d of continuous observations in SC mode. During Cycle 1, TESS observed 806 subdwarf (sd) candidates including sdB stars, sdO stars, and their He-rich counterparts. Among them, we have found several rich oscillators including short- and long-period sdB pulsators. By “rich”, we mean that there are sufficient pulsation frequencies present for asteroseismic methods (e.g., rotational multiplets and/or asymptotic period spacing) to be applicable. To date, five rich, long-period sdB pulsators have been reported. Four of these stars have been analyzed by Sahoo et al. (2020a) and Reed et al. (2020a), who applied the asymptotic period spacing. For one target, Charpinet et al. (2019) produced a detailed model by best-matching all the observed frequencies with those computed from models. In the present paper, we concentrate on five other long-period pulsating sdB stars, TIC 260795163, TIC 080290366, TIC 020448010, TIC 138707823, and TIC 415339307, that were observed by TESS. During Cycle 2, the second year of the primary mission, TESS observed the northern hemisphere, sectors 14–26, after which it re-observed the southern hemisphere in what is referred to as the extended mission. During the extended TESS mission, three of the selected stars (TIC 260795163, TIC 080290366 and TIC 138707823) were observed with 20s ultra-short-cadence (USC) mode. While TIC 080290366 and TIC 138707823 were observed in USC mode over only one sector (29), TIC 260795163 was observed in USC mode over two consecutive sectors (27 and 28).
Among the stars analyzed in this paper, the only star for which photometric variability was discovered before TESS is TIC 080290366 (Koen & Green 2010). The remaining four V1093 Her stars are new discoveries. The details of the photometric TESS observations are summarized in Table 1, where we also give the literature name of the targets, which are taken from SIMBAD1, the TESS Input Catalog (TIC) number, right ascension, declination, and T-magnitude along with their corresponding observed sectors. Using available magnitude values from the literature, we calculated TESS magnitude of all targets as described by Stassun et al. (2018) using the tool of ticgen2.
Five sdB stars studied in this work.
2.2. Spectroscopic observations
The spectroscopic follow-up observations of the sdB pulsators analyzed in this paper were obtained with two instruments, the Boller and Chivens (B&C) spectrograph mounted at the 2.5 m (100 inch) Iréne du Pont telescope at Las Campanas Observatory in Chile3, and the European Southern Observatory (ESO) Faint Object Spectrograph and Camera (v.2) (EFOSC2; Buzzoni et al. 1984) mounted at the Nasmyth B focus of the New Technology Telescope (NTT) at La Silla Observatory in Chile.
We obtained low-resolution spectra in order to calculate the atmospheric parameters, such as effective temperature Teff, surface gravity log g, and He abundance. Although the atmospheric parameters for TIC 260795163, TIC 080290366, TIC 020448010, TIC 138707823 and TIC 415339307 are available in the literature (Heber et al. 1984; Heber 1986; Kilkenny et al. 1995, 1988; Németh et al. 2012; Lei et al. 2018), we reobserved them in order to ensure homogeneity in our analysis. The B&C spectra were obtained using the 600 lines mm−1 grating corresponding to the central wavelength of 5000 Å, covering a wavelength range from 3427 to 6573 Å. We used ax 1 arcsec slit, which provided a resolution of 3.1 Å. Depending on the brightness of the targets, the exposure times were between 300 s and 480 s, which was enough to obtain an optimal signal-to-noise ratio (S/N) to measure Teff and log g with 5% precision. For the EFOSC2 setup, we used grism #7 and a 1 arcsec slit and the exposure times were between 200 s and 300 s. This setup provided a wavelength coverage from 3270 to 5240 Åwith a S/N of about 150. TIC 260795163, TIC 080290366, and TIC 138707823 were observed with 2 × 2 binning mode at a resolution of 5.4 Å, while TIC 020448010 was observed using 1 × 2 binning, such that the spectral resolution slightly improved to 5.2 Å. The details of the spectroscopic observations are given in Table 2 including, instrument, date, exposure time, resolution, and S/N at 4200 Å.
Observing log of the spectroscopic data obtained for the five sdB stars studied in this work.
2.3. The targets
– TIC 260795163 (EC 23073-6905) was discovered during the Edinburgh-Cape survey-II (Kilkenny et al. 1995) and was classified as an sdB star with low-dispersion spectrograms and UBV photometry. Kilkenny et al. (1995) derived Teff ∼ 27 000 K and log g ∼ 5 dex, respectively. These latter authors reported a radial velocity variation of about ± 26 km s−1. Subsequently, Magee et al. (1998) and Copperwheat et al. (2011) measured the radial velocity of the star and did not find significant variation. The Gaia DR2 parallax and corresponding distance for this object are π = 2.002 ± 0.058 mas and d = 499.6 ± 14.4 pc.
– TIC 080290366 (alias JL 194, EC 00292-4741, CD-48 106) is a well-known relatively bright hot subdwarf star with a T-band magnitude of 11.85. The star was observed several times and can be found in many surveys, including Hill & Hill (1966), Jaidee & Lyngå (1969), Kilkenny & Hill (1975), Wegner (1980), Kilkenny et al. (1988, 2016). The atmospheric parameters of TIC 080290366 were derived by Heber et al. (1984) and also given by Kilkenny et al. (1988). The authors showed that the effective temperature and surface gravity of TIC 080290366 are Teff = 25 200 K and log g = 5.20 dex. The evolutionary status of TIC 080290366 was discussed by (Newell 1973). The presence of a potential weak magnetic field was investigated by Mathys et al. (2012); however, the detection limit was not enough to be conclusive. The parallax and corresponding distance for this star extracted from Gaia DR2 are π = 1.992 ± 0.05 mas and d = 502.1 ± 12.6 pc.
– TIC 020448010 (EC 11119-2405) was discovered during the Edinburgh-Cape Blue Object Survey as a hot sdB star with V-band magnitude of 12.72 (Kilkenny et al. 1997). The atmospheric parameters were obtained by Németh et al. (2012). The authors found Teff = 23 430 ± 900 K, log g = 5.29 ± 0.15 dex and a low surface He abundance of log(He/H) = − 2.52 ± 0.25. Kawka et al. (2015) included the target in their survey for hot subdwarf binaries, but did not detect significant velocity variations. From Gaia DR2, the parallax and distance of this object are π = 1.964 ± 0.055 mas and d = 509.1 ± 14.2 pc, respectively.
– The discovery of TIC 138707823 (alias EC 00008-2355, FB 1, Ton S 135, PHL 2580, MCT 0000-2355) was led by Haro & Luyten (1962) who searched for faint blue stars in the region near the south galactic pole. TIC 138707823 was confirmed by Lamontagne et al. (2000) as an sdB star. Estimations of the atmospheric parameters of TIC 138707823 have been provided in several papers (Greenstein & Sargent 1974; Kilkenny et al. 1977, 1988): effective temperature of 23 000 to 27 000 K and surface gravity of 5.4 to 5.6 dex. Heber (1986) measured Teff and log g as 25 600 ± 1250 K and 5.60 ± 0.20 dex, respectively. Edelmann et al. (2005) found that TIC 138707823 is a binary system comprised of an sdB and a main sequence (MS) or a white dwarf (WD) companion with an orbital period of Porb = 4.122 ± 0.008 d. Geier & Heber (2012) calculated the atmospheric parameters of TIC 138707823 from UVES spectroscopy and found Teff = 27 600 ± 500 K and log g = 5.43 ± 0.05 dex. From Gaia DR2, the parallax and distance of TIC 138707823 are π = 1.437 ± 0.057 mas and d = 695.9 ± 27.7 pc, respectively.
– TIC 415339307 (HS 0352 + 1019) was included in the KISO Survey and Hamburg Quasar Survey (Wegner & Boley 1993; Edelmann et al. 2003). The atmospheric parameters were determined by Edelmann et al. (2003), who found Teff = 24 900 ± 600 K, log g = 5.34 ± 0.1 dex, and log(nHe/nH) = −2.7± 0.2. Recently, Lei et al. (2018) derived 26 340 ± 150 K, 5.33 ± 0.01 dex and log(nHe/nH) = −2.68 ± 0.06. From Gaia DR2, the parallax and distance of TIC 415339307 are π = 1.296 ± 0.056 mas and d = 771.36 ± 33.04 pc, respectively.
3. Analysis of TESS data
We analyzed TESS observations using the SC mode, which samples every 2 mins, allowing us to analyze the frequency range up to the Nyquist frequency at about 4167 μHz. Given that the TESS USC data, with 20 s sampling time, recently became available for three of the stars analyzed here, we include the analysis of the USC data when available. The Nyquist frequency of the USC data is at about 25 000 μHz which allows us to analyze the short period range of the pulsation spectra. The light curves were processed using the Science Processing Operations Center (SPOC) pipeline (Jenkins et al. 2016), which is based on the Kepler Mission science pipeline and made available by the NASA Ames SPOC center and at the MAST archive4.
We first downloaded the target pixel file (TPF) of interest from the MAST archive, which is maintained by the Lightkurve Collaboration Lightkurve Collaboration 2018). The TPFs include an 11 × 11 postage stamp of pixels from one of the four CCDs per camera that the target is located on. The TPFs are examined to determine the amount of crowding and other potential bright sources near the target. We used TPFs to optimize the aperture if needed. In most cases, we used the pipeline aperture as it gave the most optimal result with respect to S/N. Given that the pixel size of TESS is very large (21 arcsec) we need to pay special attention to possible contamination. The contamination factor is indicated with the keyword CROWDSAP, which gives the ratio of the target flux to the total flux in the TESS aperture. For the each target, we checked the contamination by looking at the CROWDSAP parameter which is listed in Table 3. For the three stars (TIC 260795163, TIC 080290366 and TIC 138707823) that were also observed during the extended mission, we give the relevant parameters in parentheses in Table 3. For four targets, TIC 080290366, TIC 020448010, TIC 138707823 and TIC 415339307, the CROWDSAP value is higher than 0.9, which implies that less than 10% of the total flux originally measured in the TESS aperture comes from other unresolved sources. For TIC 260795163, the CROWDSAP is smaller than 0.7 (for SC mode observations) and almost 40% of the flux comes from the other background sources. As the difference in magnitude between the target and nearby object is more than four, we can safely conclude that the flux variations indeed come from the sdB star. For the extended mission, the CROWDSAP is much better for TIC 260795163, with 0.81, and for TIC 080290366 and TIC 138707823 it is the same as for the SC data, i.e., greater than 0.9.
Parameters of Fourier Transforms of g-mode sdB pulsators studied in this work.
We generated the light curves by integrating the fluxes (‘PDCSAP FLUX’5) within the aperture mask as a function of time in barycentric corrected Julian days (‘BJD – 2457000’). After that, we removed the outliers that vary significantly from the local standard deviation (σ) by applying a running 5σ clipping mask. We then detrended the light curves to remove any additional low-frequency systematic error that may be present in the data. To do this, we applied a Savitzky-Golay filter with a three-day window length computed with the Python package LIGHTKURVE. Detrending with this method suppressed any spurious frequencies below 1 μHz, which is the typical region where spurious frequencies are seen in TESS data. We also examined the light curves before applying the low-frequency fitting in order to search for any potential binary signals that might be affected by detrending. However, we did not find binary signatures in the FT of any of the five stars. The fluxes were then normalized and transformed to amplitudes in parts-per-thousand (ppt) unit ((ΔI/I − 1) × 1000). For TIC 260795163, which was observed during two consecutive sectors in USC mode, we combined the light curves.
3.1. Frequency analysis
The Fourier transforms (FT) of the light curves were computed to examine the periodicities present in the data, aiming at identifying the frequency of all pulsation modes, along with their amplitude and phase.
We adopt a relatively conservative detection threshold of 0.1% false alarm probability (FAP), which means that if the amplitude reaches this limit, there is a 0.1% chance that it is simply the result of noise fluctuations. We calculated the 0.1% FAP threshold following the method described in Kepler (1993).
The temporal resolution of the data is around 0.6 μHz (1.5/T, where T is the data length, which is between 24 and 27 d). In Table 3, we list all relevant information regarding the Fourier transform, including the number of data points and the 0.1% FAP level of each dataset.
For all the peaks that are above the accepted threshold and up to the frequency resolution of the particular dataset, we performed a nonlinear least square (NLLS) fit in the form of Aisin(ωit + ϕi), with ω = 2π/P, where P is the period. In this way, we determined the values of frequency (period), phase, and amplitude corresponding to each periodicity. Using the parameters of NLLS fit, we prewhitened the light curves until no signal above the 0.1% FAP level was left in the FT of each star unless there were unresolved peaks. For all frequencies that still had some signal left above the threshold after prewhitening we carefully checked if there was a close-by frequency within the frequency resolution and in such cases only the highest amplitude frequency was fitted and prewhitened, as shown in Figs. 3 and 5. All prewhitened frequencies for each of the five stars are given in Tables 4–8, showing frequencies (periods) and amplitudes with their corresponding errors and the S/N. The Fourier transforms of the prewhitened light curves of all five analyzed stars are shown in Figs. 13–17.
Frequency solution from the TESS light curve of TIC 260795163 including frequencies, periods, amplitudes (and their uncertainties), and S/N.
Frequency solution from the TESS light curve of TIC 080290366 including frequencies, periods, and amplitudes (and their uncertainties) and the signal-to-noise ratio.
Frequency solution from the TESS light curve of TIC 020448010 including frequencies, periods, amplitudes (and their uncertainties), and S/N.
Frequency solution from the TESS light curve of TIC 138707823 including frequencies, periods, amplitudes (and their uncertainties), and S/N.
Frequency solution from the TESS light curve of TIC 415339307 including frequencies, periods, amplitudes (and their uncertainties), and S/N.
For all five stars analyzed in this paper, a total of 73 frequencies were extracted from their light curves. The detected frequencies are distributed in a narrow region between 68 μHz and 315 μHz. This corresponds to the g-mode region seen in V1093 Her-type sdB pulsators (e.g., Reed et al. 2018). The amplitude spectra of all five stars are shown in Fig. 1, where we also give atmospheric parameters derived in Sect. 4 for each star. Reed et al. (2020a) recently reported a correlation between effective temperature and the frequency of the highest amplitude of g-modes detected in V1093 Her-type sdB pulsators observed by Kepler and K2. As can be seen in Fig. 1, the five g-mode sdB pulsators analyzed in this paper do not deviate from this finding.
 |
Fig. 1. Fourier transform of all five sdB stars observed in single SC sectors, concentrating on the g-mode region of the frequency spectrum. The panels are sorted with decreasing effective temperature from top to bottom. In each panel, we give the TESS input catalog number, effective temperature (in kelvin), and surface gravity (in dex), respectively. The horizontal red lines correspond to 0.1% FAP confidence level. |
TIC 260795163 (Tmag = 11.73) was observed in SC during sector 1 between July 25 and August 22 2018. The observations yielded 18 099 data points with the temporal resolution of 0.62 μHz (1.5/T, where T is 27.87 d). From sector 1 data, we detected 12 frequencies above 0.1% FAP confidence level, which corresponds to 0.467 ppt. The median noise level including the entire FT is equal to 0.09 ppt. The S/N of detected frequencies ranges from 4.75 to 30.87.
TIC 260795163 was also observed during two consecutive sectors of the extended mission. These observations started on 4 July 2020 and ended on 26 August 2020. From this 49 d dataset, we calculate the FT of the USC data up to Nyquist frequency of 25 000 μHz. The frequency resolution of USC data is 0.35 μHz. The average noise level of the entire FT of the USC dataset is 0.055 ppt and the 0.1% FAP threshold level is 0.26 ppt. All frequencies with amplitudes above this threshold are concentrated in a narrow region between 100 and 320 μHz, which is almost identical to what we detected from the SC observations. Beyond 320 μHz, there is no peak detected above the 0.1% FAP threshold up to the Nyquist frequency. We find only one peak reaching the 4.5 σ level at 23 975.8 μHz. However, this frequency seems too high to be excited in an sdB pulsator.
Concerning the g-mode region, we extracted 23 significant frequencies from both sector 1 and the extended mission (sector 27 and 28) dataset. The 13 frequencies that are found in both sectors (sector 1 and sector 27 + 28) are provided in Table 4. We found seven frequencies in the extended mission dataset that were not detected in sector 1. These frequencies are also provided in Table 4. As can be seen in the Fig. 2, there are several frequencies above the threshold level in the extended mission (sector 27 and 28) that are not detected in sector 1 (see Table 4 frequencies tagged with †).
 |
Fig. 2. Top: Fourier transform of sector 1 of TIC 260795163. The horizontal red line indicates the 0.1% FAP level. The orange line is the residual after extraction of the signals. Bottom: Fourier transform of sectors 27 and 28 of TIC 260795163. The horizontal red line indicates the 0.1% FAP level. The orange line is the FT of the prewhitened light curve. |
The amplitude spectrum of this object is dominated by a number of frequencies between 100 and 315 μHz, as shown in Fig. 2. The top panel presents the amplitude spectrum from sector 1, while the bottom panel shows the amplitude spectrum from sectors 27 and 28. In the lower frequency region, the four peaks (f1, f2, f3 and f8) were detected in sectors 27 and 28. The frequency f5 is within 4.5 σ level in 120 s cadence data and in the USC data it is becoming a significant peak above 0.1% FAP level. However, there is a frequency, f4, that is detected only in sector 1, with a S/N of 4.75, while it is not detected in sectors 27 and 28. Also, there are residuals in the FT of the USC data after prewhitening. These residuals are shown in Fig. 3. The strong residuals at f13 and f23 could either be due to unresolved close-by frequencies or to amplitude, frequency, or phase variations over the length of the data. For these residuals, we did not prewhiten further. Overall, combining the nominal and extended mission dataset, we detect 23 g-modes spanning from 127 to 315 μHz.
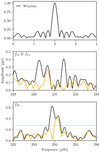 |
Fig. 3. Fourier transform of USC data of TIC 260795163. The top panel: window function calculated from USC data. The second and third panels from the top display two different frequency regions in which the signals show strong residuals after the extraction. These frequencies are given in Table 4. The horizontal red line indicates the 0.1% FAP level. The orange line is the FT of the prewhitened light curve. |
TIC 080290366 was found to be a pulsating star by Koen & Green (2010), who detected five oscillation frequencies ranging from 127 μHz to 233 μHz. TIC 080290366 (Tmag = 11.85) was observed in SC mode during sector 2 (2018-Aug-22 to 2018-Sep-20) for 27.4 d, with a frequency resolution of 0.63 μHz. Other parameters such as the length of the observations, contamination, number of data points, and 0.1% FAP confidence level are given in Table 3. From sector 2, we detected 16 frequencies between 81 and 257 μHz.
TIC 080290366 was also observed during the extended mission in sector 29 (2020-Aug-26 to 2020-Sep-22). The data length of sector 29 is 24.3 d, implying a lower frequency resolution of 0.72 μHz. The FT average noise level is 0.067 ppt. The 0.1% FAP confidence level is 0.316 ppt. We did not detect any high-frequency p-mode from the USC observations, while we detected 17 g-mode frequencies, most of them being present already in sector 2. All the frequencies that were detected in both the nominal and extended mission are listed in Table 5. In total, we detected 18 frequencies spanning from 81.6 μHz (∼12 200 s) to 257.4 μHz (∼3900 s) with amplitudes between 0.3 and 2.5 ppt. Fifteen frequencies are detected in both datasets, the frequency near 141.7 μHz was detected only in sector 2, while the three frequencies near 90.9, 114.7, and 168.0 μHz were found only in sector 29.
The FTs of sector 2 (upper panel) and sector 29 (lower panel) are shown in Fig. 4, where several frequencies clearly show differences. In Fig. 5, we show the amplitude spectrum of sector 29 in more detail around the regions in which a power excess is left after prewhitening compared with the window function.
 |
Fig. 4. Top: Fourier transform of data taken in sector 2 of TIC 080290366. The horizontal red line indicates the 0.1% FAP level. The orange line is the residual after extraction of the signals. Bottom: Fourier transform of data taken in sector 29 of TIC 080290366. The horizontal red line indicates the 0.1% FAP level. The orange line is the FT of the prewhitened light curve. |
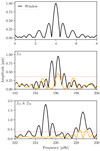 |
Fig. 5. Fourier Transform of sector 29 of TIC 080290366, compared with the window function (top panel). The lower panels show an excess of power after prewhitening (orange line), see Sect. 3.3 for more details. The horizontal red line indicates the 0.1% FAP level. |
 |
Fig. 6. Top: Fourier transform of sector 2 data of TIC 138707823. The horizontal red line indicates the 0.1% FAP level. The orange line is the residual after extraction of the signals. Bottom: Fourier transform of sector 29 data of TIC 138707823. The horizontal red line indicates the 0.1% FAP level. The orange line is the FT of the prewhitened light curve. |
TIC 020448010 (Tmag = 12.18) was observed in SC mode during sector 9 for a period of 24.2 d, which provides a frequency resolution of 0.717 μHz. The FT average noise level is 0.088 ppt. The rest of the parameters, including length of the observations, contamination, number of data points, and 0.1% FAP confidence level, are given in Table 3. The star was discovered by TESS as a g-mode sdB pulsator with 15 frequencies concentrated in a narrow region ranging from 68 μHz to 187 μHz and with amplitudes of between 0.36 ppt and 1.26 ppt. The extracted frequencies are listed in Table 6 with their associated errors and S/N. In Fig. 15, we show all detected frequencies (light gray) and residuals (orange) after prewhitening.
TIC 138707823 (Tmag = 12.7) was observed in SC mode during sector 2 between August 22 and September 20, 2018, for 27.4 days. From these SC observations of TIC 138707823, we extracted seven periodicities from the light curve. All frequencies above 0.1% FAP significance level of 0.563 ppt are listed in Table 7. The frequencies are located in a narrow range from 87 to 237 μHz.
TIC 138707823 was also observed during Sector 29 (2020-Aug-26 to 2020-Sep-22) with USC mode. The length of these observations (23.85 d) is almost 4 d shorter than the sector 2 dataset, resulting in somewhat poorer frequency resolution (0.728 μHz) than that obtained for the SC dataset (0.634 μHz). The average noise level of the FT is 0.13 ppt. We extracted three significant frequencies above the threshold of 0.62 ppt. These three frequencies, which were also detected in sector 2, are marked with †† in Table 7. The four frequencies at 87, 132, 181, and 191 μHz, which were not detected during the extended mission, are given without symbols in Table 7.
The amplitude spectrum of the sector 2 data for TIC 138707823 is relatively poor in comparison with that of the four stars presented in this work, displaying only seven frequencies above the threshold level. These seven frequencies can be seen in the upper panel of Fig. 16. The bottom panel of the same figure shows only three significant frequencies from sector 29. Combining the results from sector 2 and 29, we detect seven frequencies which are concentrated between 87 μHz and 237 μHz.
TIC 415339307 (Tmag = 14.2) was observed by TESS in SC mode during sector 5 between 15 November 2018 and 11 December 2018, covering about 26 days. The amplitude spectrum of this object, shown in Fig. 17, contains nine frequencies above the 0.1% FAP significance level of 1.27 ppt. The average noise level of the FT is 0.26 ppt. We note that there is a frequency at 184.122 μHz (f3) just below the 0.1% FAP confidence level, albeit at 4.5 σ, which we keep as a candidate frequency and discuss its nature in Sect. 3.3.
The photometric and FT parameters, including average noise level, contamination factor, number of data points, and 0.1% FAP confidence level, are given in Table 3. In Table 8, we list all (10) frequencies (periods) and their amplitudes with corresponding errors and we show all detected frequencies in Fig. 17.
3.2. Rotational multiplets
Our main goal is to identify modes of detected pulsations in order to constrain theoretical models of pulsating sdB stars. For rotating stars, the existence of nonradial oscillations allows identification of the pulsation modes via rotational multiplets (Aerts et al. 2010). The nonradial pulsations are described by three quantized numbers, n, l, and m, where n is the number of radial nodes between center and surface, l is the number of nodal lines on the surface, and m is the azimuthal order, which denotes the number of nodal great circles that connect the pulsation poles of the star.
In rotating stars, the pulsation frequencies are split into 2l + 1 azimuthal components due to rotation, revealing an equally spaced cluster of 2l + 1 components. This 2l + 1 configuration can be resolved with high-precision photometry if the star has no strong magnetic field and the rotational period is not longer than the duration of the observation.
The detection of rotational splitting is important as it is one of the two methods used to identify the pulsational modes of a star and at the same time provides information about the rotation period of the star. In particular for the g-mode pulsators, such a detection unveils the rotation of the deep part of the radiative envelope close to the convective core.
Rotational multiplets have been detected in several sdBVs (Charpinet et al. 2018, references therein). Typical rotation periods detected in sdB stars are of the order of 40 d (Baran et al. 2019), unless the stars are in close binary systems. Even though TESS allows us to obtain uninterrupted time-series, especially for stars observed in multiple sectors, it is not ideally suited for the detection of rotationally split multiplets in sdBVs. For the stars that have been observed in just 1 sector (∼27 d), which translates to a frequency resolution of ∼0.6 μHz, we are limited to the detection of rotational periods shorter than about 13 d. For each star, we searched for a coherent frequency splitting, Δν, in the g-mode region but did not find any consistent solution. Therefore, we conclude that it is not possible to perform mode identification for either of the sdBV stars analyzed in this paper, or to determine the rotational period based on rotational splitting. Given that four of the analyzed stars are not members of close binaries, we do not expect them to have short rotation periods such that they could be detected in a single sector TESS data. However, for TIC 138707823, which is a short-period binary system with an orbital period of about 4 d (Edelmann et al. 2005), we do not detect any significant signal that might be attributed to this orbital period.
3.3. Frequency and amplitude variations
From the continuous light curves produced by the space missions such as Kepler and K2, and now TESS, it has been observed that oscillation frequencies in compact stars, including pulsating sdB stars, and DBV and DOV pulsating white dwarfs, may not be stable (Silvotti et al. 2019; Zong et al. 2016b; Córsico et al. 2021). It is known that the frequency and amplitude variations mostly occur because of beatings of unresolved peaks or unresolved multiplets. Recently, the complex patterns that have been observed were interpreted as evidence of frequency, amplitude, or phase modulations due to weak nonlinear mode interactions, as discussed in Zong et al. (2016a). Furthermore, the variability may be due to the photon-count noise caused by contamination of the background light in the aperture.
The continuous photometric measurements of five stars allow us to construct sliding FTs (sFTs) to examine the temporal evolution of the detected frequencies over the course of the TESS observations. Therefore, we computed and examined the sFT of each target. As three targets were observed in more than one sector, for these stars we selected the sectors in which we see the largest number of pulsation modes, i.e., sectors 27 and 28 for TIC 260795163, sector 29 for TIC 080290366, and sector 2 for TIC 138707823.
The sFTs are computed in a similar way as described in Silvotti et al. (2019): we run a five-day sliding window with a step size of 0.2 d. The amplitudes are illustrated by a color-scale in ppt units. We set a lower limit on the amplitudes by running the three-times-average noise level of the five-day window. Afterwards, we calculate the Fourier transform of each subset and trail them in time.
Figures 7–11 show the sFTs for the g-mode region of each star. In most of the cases, the high-amplitude frequencies (S/N ≥ 10) are stable in both frequency and amplitude over the length of the data for all stars. However, some pulsational frequencies are not stable throughout the TESS run and here we discuss each case.
 |
Fig. 7. Sliding Fourier transform of TIC 260795163 from USC data. The color-scale illustrates amplitude in ppt units. See text for more details on sFT computations. |
 |
Fig. 8. Sliding Fourier transform of TIC 080290366. The sFT is calculated from USC data. |
In the case of TIC 260795163, the highest amplitude frequencies (at 250.447, 268.360, 288.186 and 315.537 μHz) are stable in frequency, although the one at 250 μHz shows a small wobble. A few frequencies, mostly lower than 250 μHz, are not stable, at least in amplitude. However, they have a low S/N and therefore are below the detection threshold throughout part of the run. In the case of the frequency at 293.996 μHz (f22), it is quite stable up to day ∼2050 and then becomes weaker in amplitude. Indeed, we can see this effect in the bottom panel of Fig. 3, in which we show the strong residual after prewhitening, implying that either the amplitude, phase, or frequency could be variable over the length of the data. In the case of TIC 080290366 (see Fig. 8), the amplitudes of the frequencies at 196.144 (f14) and 228.658 μHz (f17) are variable and it is exactly these two frequencies that show residuals after prewhitening in Fig. 5. The highest amplitude frequency at 105.313 μHz (f5) of TIC 020448010 is relatively stable over the run, along with the frequency at 133.516 μHz (f10) (Fig. 9). The low-amplitude frequencies are mostly unstable in amplitude; for example the frequency at 83.096 μHz is absent between days 1551 and 1555.
In the case of TIC 138707823 (Fig. 10), we safely extracted seven peaks from the SC observations and all the frequencies are visible in the sFT except for the frequency at 237.895 μHz, whose S/N is low. The highest amplitude frequency at 151.497 μHz is stable over the length of the data, while the rest of the frequencies (87.82, 132.67, 173.09, 181.38 and 191.02 μHz) are not stable in amplitude, while they seem to be stable in frequency.
In the case of TIC 415339307 (Fig. 11), the frequency at 175.929 μHz shows strong variability in amplitude, being at very low S/N in the first half of the run while in the second half it has the highest amplitude of about 4 ppt. In Fig. 17, this effect is seen as a significant residual at 5684 s. Frequencies at 203.126 and 214.359 μHz are not stable in either frequency or amplitude. The frequency at 184.122 μHz (f3) (S/N = 4.45 in the entire FT) is definitely present in the sFT, however it is not stable in either frequency or amplitude during the first half of the run, while it appears more stable in frequency during the second half of the run. The frequency at 255.863 μHz is stable up to almost 1448 d, while it is absent beyond 1448 d. As this frequency is above the 0.1% FAP level in the FT, we include it in our analysis as well.
We do not find strong evidence of rotational splitting in any of the targets analyzed in this paper, and hence all of them must have considerably longer rotation periods than the length of their TESS dataset. Consequently, any peak we have observed must be considered an unresolved multiplet consisting of a summation of three, for l = 1, or more sinusoids with independent phase and amplitude, and with each sinusoid having slightly different unresolved frequency. This produces a beating effect on timescales longer than the analyzed TESS dataset, which then may appear as any form of frequency and/or amplitude variation. Beating of unresolved multiplets is therefore the default cause of any such variations observed in datasets that are too short to reveal rotational splitting.
3.4. Asymptotic g-mode period spacing
Fontaine et al. (2003) showed that the oscillation modes detected in long-period pulsating subdwarf B stars are associated with high-order g-modes. In the asymptotic limit, when n > > l the consecutive radial overtones of high-order g-modes are evenly spaced in period such that the consecutive g-modes follow the equation:
where ΔP0 is just the asymptotic period spacing for g-modes, which is defined as ![$ \Delta P_{0} \propto [\smallint_{r_1}^{r_2} \frac{|N|}{r} dr]^{-1} $](/articles/aa/full_html/2021/07/aa40961-21/aa40961-21-eq2.gif) , N being the Brunt-Väisälä frequency, the critical frequency of nonradial g-modes (Tassoul 1980), and ϵl is a constant (Unno et al. 1979).
, N being the Brunt-Väisälä frequency, the critical frequency of nonradial g-modes (Tassoul 1980), and ϵl is a constant (Unno et al. 1979).
The existence of a nearly constant period spacing of g-modes in the asymptotic regime means that we can search for the patterns of modes with a given harmonic degree in the observed period spectra of pulsating stars. This method, referred to as the asymptotic period spacing method, has been used to identify the degree of pulsational modes in many g-mode pulsators such as γ-Dor stars, slowly pulsating B stars (SPBs), and white dwarfs (Aerts 2021, and references therein).
However, only with the onset of space-based light curves such as those obtained by Kepler did it become possible to use this method to identify the degrees of the pulsational modes in sdB stars (e.g., Reed et al. 2011). However, this method cannot be used to determine the absolute radial order n of a given mode from the Eq. (1) without detailed modeling. What we can do is choose a relative number for a radial order (nl) corresponding to a modal degree l such that all other consecutive radial orders for this modal degree have an offset with respect to nl. The ratio between consecutive overtones is then derived from equation (1), such that the ratio for dipole (l = 1) and quadrupole (l = 2) modes is 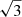 . Based on the theoretical models by Charpinet et al. (2000), the period spacing of l = 1 modes is around 250 s for sdB pulsators. The Kepler and K2 observations of g-mode pulsating sdB stars find that the average period spacing for l = 1 modes ranges from 227 s to 276 s (Reed et al. 2018). Recent results from the TESS mission on five g-mode sdB pulsators find similar results, with the average period spacing ranging from 232 s to 268 s (Charpinet et al. 2019; Sahoo et al. 2020a; Reed et al. 2020a). Here, we search for constant period spacing in our five target stars observed by TESS using the Kolmogorov-Smirnov (K-S; Kawaler et al. 1988) and the inverse variance (I-V; O’Donoghue 1994) significance tests.
. Based on the theoretical models by Charpinet et al. (2000), the period spacing of l = 1 modes is around 250 s for sdB pulsators. The Kepler and K2 observations of g-mode pulsating sdB stars find that the average period spacing for l = 1 modes ranges from 227 s to 276 s (Reed et al. 2018). Recent results from the TESS mission on five g-mode sdB pulsators find similar results, with the average period spacing ranging from 232 s to 268 s (Charpinet et al. 2019; Sahoo et al. 2020a; Reed et al. 2020a). Here, we search for constant period spacing in our five target stars observed by TESS using the Kolmogorov-Smirnov (K-S; Kawaler et al. 1988) and the inverse variance (I-V; O’Donoghue 1994) significance tests.
In the K-S test, Q is the quantity that defines the probability distribution of observed modes. If the data have a nonrandom distribution in the period spectrum, then the distribution will have a peak at the minimum value of Q. In the I-V test, on the other hand, a maximum of the inverse variance will indicate a consistent period spacing.
In Fig. 12, we show the K-S (top panel) and I-V (bottom panel) results obtained for the five stars in our sample. For both panels, we applied a vertical, arbitrary offset for visualization purposes. The same color coding is applied for both panels. For all targets, the statistical tests display a clear indication of the mean period spacing at around 250 s. For the case of TIC 260795163 and TIC 080290366, the I-V test is not as conclusive as for the other three stars. However, the K-S test does show an indication of a possible mean period spacing of l = 1 at 250 s. Moreover, TIC 260795163 and TIC 080290366 show peaks at around 150 s referring to the possible period spacing of quadrupole modes.
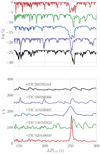 |
Fig. 12. Kolmogorov-Smirnov (top panel) and inverse variance (lower panel) tests to search for a constant period spacing in the five stars of our sample. The offset on log Q for the Kolmogorov-Smirnov is 6 and the offset on y-axis for the inverse variance test is 80. All stars present a significant probability of having a constant period spacing. |
Based on the potential period spacings obtained from the K-S and I-V tests, we search for the sequences of dipole and quadrupole modes in the entire FT of each star. First, we search for the l = 1 and l = 2 sequences examining consecutive modes in the period domain of the FT of each star. Given that the higher degree modes are more sensitive to geometrical suppression due to the mode cancelation effect (Aerts et al. 2010), we assume that the highest amplitude frequencies are corresponding to low-degree modes (l = 1 and l = 2). This assumption is only valid if all the modes have the same intrinsic amplitude. For sdB pulsators, the majority of the detected frequencies have been identified with low-degree modes (l≤ 2). However, a few exceptional examples have been reported. For instance, in two sdB pulsators observed during the nominal mission of Kepler, the high-degree g-modes were assigned up to l = 6 (Kern et al. 2018) or l = 8 (Telting et al. 2014) using the method of rotational multiplets. Silvotti et al. (2019) also reported several high-degree modes up to l = 12 using solely asymptotic period spacing in the brightest (V = 10.2) sdB pulsator HD 4539 (EPIC 220641886) observed during the K2 mission. We proceed in the following way: we assign arbitrary radial orders (n) for each identified l degree and calculate the mean period spacing using a linear regression fit. In this way, we calculated the mean period spacing (ΔP) for all stars and find that the mean period spacing for the l = 1 mode ranges from 251 s to 255 s. In order to assess the errors of the mean period spacing obtained in our analysis, we performed a bootstrap resampling analysis as described by Efron (1979), Simpson & Mayer-Hasselwander (1986). We used this method because many possible modes are not detected in the amplitude spectra. Furthermore, in some cases, the individual pulsational period has no unique modal degree solution, and in some specific cases the modes could be altered due to mode trapping.
In order to make a realistic error assignment, we simulated 104 datasets from the determined l modes. For each target, we created sets of randomly chosen observed periods that are already identified as l = 1 or l = 2 modes in order to obtain the mean period spacing from each different subsequence. The same data point can occur multiple times and ordering is not important, such that for N data points the total number of possible different bootstrap samples is 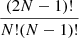 (Andrae 2010). For instance, for a given dipole sequence consisting of ten modes, the highest possible number of different bootstrapping subsets is about 105. For the five stars analyzed in this paper, we detected dipole sequences that range from 7 to 13 modes depending on the star. Therefore, we restricted ourselves to 104 subsets. For each of the subsets that include a series of dipole or quadrupole modes, we derive the mean period spacing with the linear regression fit. The most probable solution is obtained as a mean period spacing (which corresponds to the 50th percentile of the ΔPl = 1 distribution). The errors are then estimated as 1 σ and given in Table 9.
(Andrae 2010). For instance, for a given dipole sequence consisting of ten modes, the highest possible number of different bootstrapping subsets is about 105. For the five stars analyzed in this paper, we detected dipole sequences that range from 7 to 13 modes depending on the star. Therefore, we restricted ourselves to 104 subsets. For each of the subsets that include a series of dipole or quadrupole modes, we derive the mean period spacing with the linear regression fit. The most probable solution is obtained as a mean period spacing (which corresponds to the 50th percentile of the ΔPl = 1 distribution). The errors are then estimated as 1 σ and given in Table 9.
Seismic properties of five pulsating sdB stars studied in this work.
The right panels of Figs. 13–17 show the residuals between the observed periods and the periods derived from the mean period spacing for the ΔPl = 1 where we can see the deviation of the modes. The scatter of the residuals for all stars is up to 50 s and for the stars for which more l = 1 modes are detected, we notice the oscillatory pattern, which is a characteristic feature that was found in several V1093 Hya-type sdB pulsators (e.g., Telting et al. 2012; Baran 2012). Detecting all modes of the l = 1 sequence with an expected period spacing of 250 s (Charpinet et al. 2002) is unlikely as the sdB stars are chemically stratified, which causes the observed modes to be scattered around this value. Such small deviations from the mean period spacing are to be expected in those stars where diffusion processes have had enough time to smooth out the H–He transition zone (Miller Bertolami et al. 2012). On the other hand, the efficiency of trapping diminishes with increasing radial order, as discussed in Charpinet et al. (2014). This is because the local wavelength of the modes decreases with increasing radial order, and therefore the higher order g-modes become less affected by the H–He transition zone. In this way, the higher order g-modes may present an almost constant period spacing even without smoothing the H-He transition zone.
 |
Fig. 13. Fourier transform of TIC 260795163 (presented here are the sectors 1, 28 and 29 together). The residuals after prewhitening are shown in orange. The red and blue dots show the dipole and quadrupole modes respectively. If there is no unique identification, the period is shown in both colors. The horizontal red line correspond to 0.1% FAP confidence level. The right panel shows the residuals between the observed and the fitted periods. See text for more details on mode identification and the mean period spacing computations. |
3.4.1. TIC 260795163
The K-S test for TIC 260795163 shows an indication of both dipole and quadrupole modes; see the upper panel of Fig. 12. Assuming that the highest amplitude frequency at 288.186 μHz (f21 in Table 4) is an l = 1 mode, then the sequence of l = 1 mode is fulfilled with the following frequencies: f10, f14, f17 and f19. Beyond 6000 s, six additional frequencies (f1 to f6) were found to fit the dipole sequence. The six frequencies f8, f9, f11, f15, f16, and f20 showed consistent period spacing for quadrupole modes with a unique solution. For four frequencies, we cannot find a unique solution, namely f4, f6, f10, and f21, and they could be interpreted as either l = 1 or l = 2 modes.
Of the total of 23 periodicities detected in TESS data for TIC 260795163, there were five frequencies that did not fit either l = 1 or l = 2 sequences. These periodicities could be either higher-degree modes or l = 1 and/or l = 2 modes which are severely affected by mode trapping and do not fit the l = 1 or l = 2 patterns. However, without detecting rotational multiplets, it is impossible to test either of the two possibilities. The amplitude spectra of TIC 260795163 with our mode identification are presented in Fig. 13. Based on this mode identification, we calculate the mean period spacing of dipole modes, ΔPl = 1 = 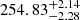 s and quadrupole modes, ΔPl = 2 =
s and quadrupole modes, ΔPl = 2 = 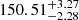 s.
s.
3.4.2. TIC 080290366
Based on the results from the K-S and I-V tests in which there is a peak at around 255 s indicating a possible ΔPl = 1, and also a peak at 155 s indicating a possible ΔPl = 2 (see upper and lower panel of Fig. 12), we searched for dipole and quadrupole sequences in the FT of TIC 080290366. Starting from the highest amplitude frequency at 149.133 μHz (f7 in Table 5) as an l = 1 mode, we find two frequencies that fit the dipole mode sequence, f8 and f9. Beyond 7 500 s, there are five frequencies that are also following dipole mode sequences: f1, f2, f3, f4, and f5. We found only three frequencies that uniquely fit the l = 2 sequence. For five frequencies (f5, f8, f9, f14 and f17) the solution is degenerate as the frequencies fit both dipole and quadrupole mode sequences. Of the 18 detected frequencies, there are 4 that did not fit dipole or quadrupole mode sequences. These frequencies could be high-order degree modes or trapped modes. The amplitude spectra of TIC 080290366 with our mode identification are presented in Fig. 14. Based on the mode identification explained above, we calculated both 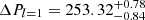 s and
s and 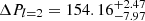 s. The final seismic result for TIC 080290366 and the other stars analyzed in this paper is given in Table 9.
s. The final seismic result for TIC 080290366 and the other stars analyzed in this paper is given in Table 9.
3.4.3. TIC 020448010
The K-S and IV tests display a clear indication of a period spacing at 253 s as shown in Fig. 12. Starting with the highest amplitude peak at 9495.5 s (f5 in Table 6), we search for a dipole sequence in the FT. Out of 15 detected frequencies, 12 frequencies uniquely fit the l = 1 sequence, while only 2 frequencies can be evaluated as l = 2 mode as the difference corresponds to 2 × ΔPl = 2. However, one periodicity (at 8778.2 s) does not have a unique solution: it could be either l = 1 or l = 2 mode.
The amplitude spectra of TIC 020448010 together with the mode identification are presented in Fig. 15. Based on our mode identification we calculate the average period spacing for dipole modes, 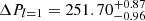 s. In Table 9, we also give ΔPl = 2 using the ratio between consecutive overtones derived from equation (1).
s. In Table 9, we also give ΔPl = 2 using the ratio between consecutive overtones derived from equation (1).
3.4.4. TIC 138707823
The K-S and IV tests show a clear indication of a possible ΔPl = 1 at 255 s as can be seen in Fig. 12. Assuming the highest peak at 6600.78 s (f3) to be an l = 1 mode, we find that the dipole sequence can be completed with f4, f5, and f6. In the longer period region beyond 6600 s, there are two more frequencies with the large gap in between that fit the l = 1 sequence. We interpreted these two frequencies as l = 1 modes and added them to the fitting procedure in order to find the mean period spacing of ΔPl = 1. The same case is valid for the shorter period region and between f6 and f7 there is a large gap of about 1000 s (which is four times ΔPl = 1). We note that the periodicity (at 6600.78 s) deviates from the mean period spacing significantly. This mode can be interpreted as a candidate trapped mode, but knowledge of where the quadrupole modes are is required in order for us to come to any firm conclusions. The two frequencies f2 and f4 could be also interpreted as l = 2 modes because three times ΔPl = 1 is equal to five times ΔPl = 2. If we exclude these two degenerate modes and calculate the average period spacing of l = 1, we find ΔPl = 1 = 256.38 ± 1.43 s. If we include these two modes and calculate the average period spacing, we find 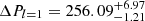 s. We list all modes identified in Table 7 and show them in Fig. 16.
s. We list all modes identified in Table 7 and show them in Fig. 16.
3.4.5. TIC 415339307
The FT of TIC 415339307 shows that all the frequencies are concentrated in a narrow region between 156 μHz (3371 s) and 296 μHz (6399 s) as can be seen in Fig. 17. In Fig. 12, K-S and I-V tests show signs of a potential average period spacing at 250 s. We identified five dipole modes and two quadrupole modes, while three modes were able to fit both solutions. Between 4500 s and 6000 s, there are four frequencies that can only be fitted by a dipole mode sequence. We find that the frequencies f1, f6, f8, and f10 also fit the dipole sequence. The frequencies f7 and f9 can only be quadrupole modes as the difference between the modes is around 300 s. The frequencies f1, f6, and f10 can be identified as l = 2 modes.
Including all these identified modes, we calculated ΔPl = 1 = 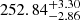 s and
s and 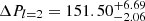 s. We list all identified modes in Table 8 and show them in Fig. 17.
s. We list all identified modes in Table 8 and show them in Fig. 17.
4. Analysis of spectroscopic data
We reduced and analyzed the data from the EFOSC2 spectrograph using standard PyRAF6 (Science Software Branch at STScI 2012) procedures. First, we applied bias correction and flat-field correction, and then we removed the pixel-to-pixel sensitivity variations by dividing each pixel with the response function. Subsequently, we applied wavelength calibrations using the spectra obtained with the internal He-Ar comparison lamp. In a last step, we performed a flux calibration using the standard stars EG 21 and EG 274. The S/N of the final spectra is between 80 and 150 (see Table 2).
The data obtained with the B&C spectrograph were reduced in a similar way using PyRAF. WE bias subtracted and flat-field corrected all frames, and removed cosmic ray events. Afterwards, we performed a wavelength calibration with calibration spectra taken immediately after target observations. We then corrected all wavelength-calibrated spectra for atmospheric extinction using coefficients provided by PyRAF. Finally, we flux calibrated all spectra using the spectrophotometric standard star EG 21. The final spectra have S/N ranging from 70 to 120.
5. Spectral analysis with XTGRID
We analyzed all the stars of our sample and derived atmospheric parameters by fitting synthetic spectra to the newly obtained low-resolution spectra. Synthetic spectra were calculated from TLUSTY nonlocal thermodynamic equilibrium stellar atmosphere models (Hubeny & Lanz 2017) using H and He composition. These models were used in the steepest-descent χ2-minimizing fitting procedure XTGRID (Németh et al. 2012) using the web service provided by Astroserver7. The iterative procedure starts out from a starting model and by successive corrections converges on the best fit. We applied a convergence limit of 0.5% relative change of all model parameters over three successive iterations. Error bars were calculated by mapping the χ2 landscape around the best fit until the 3σ confidence limit for the given degree of freedom was reached. The error calculations are performed in one dimension for the He abundance, but include the correlations between surface temperature and gravity.
Figure 18 shows the new observations together with their best-fit TLUSTY/XTGRID models and Table 10 lists the atmospheric parameters. The sample is very homogeneous, all spectra in Fig. 18 are dominated by Balmer-lines and only weak He I lines are seen. This together with the Balmer-decrement suggest that the stars must have very similar atmospheric parameters, which is in agreement with earlier observations suggesting that sdBVs stars (g-mode pulsators) form a compact group on the EHB. However, the spectral analysis reveals a systematic difference between the parameters derived from EFOSC2 and B&C data. The poor blue coverage of the NTT/EFOSC2 wavelength calibration lamp results in serious flexure along the dispersion axis and causes discrepancies in fitting. For completeness, we include all results in Table 10. Where B&C spectra are available, we consider them superior in quality and the results from B&C data as final.
 |
Fig. 18. Best-fit TLUSTY/XTGRID models for the five hot subdwarf stars analyzed in this paper. The spectra are dominated by the H Balmer-series marked at the bottom and a few weak He I lines marked at the top of the figure. The observed continua adjusted to the theoretical models. |
Spectroscopic results of five sdBV stars analyzed in this paper.
Among the stars analyzed in this paper, there is a confirmed binary system TIC 138707823. Figure 18 shows that TIC 138707823 has a clean sdB spectrum without any significant optical contribution from a companion. This confirms earlier results (Edelmann et al. 2005; Geier & Heber 2012) that the companion is a compact object, most likely a WD.
6. Asteroseismic models
A proper asteroseismic interpretation of the observed frequencies found in g-mode sdB pulsators requires the computation of oscillations in stellar models (Charpinet et al. 2000, 2002). To this end, we computed stellar evolution models with the LPCODE stellar evolution code (Althaus et al. 2005), and computed l = 1 g-mode frequencies with the adiabatic nonradial pulsation code LP-PUL (Córsico & Althaus 2006). Opacities, nuclear reaction rates, thermal neutrino emission, and equation of state are adopted as in Miller Bertolami (2016) and Moehler et al. (2019). In particular, it is worth noting that atomic diffusion was not included in the present computations. Diffusion is expected to reduce mode-trapping features in the latter stages of the He-core burning phase (Miller Bertolami et al. 2012). In the present work we aim to compare the model predictions with observations on a global level by means of a robust indicator such as the mean period spacing (ΔP), leaving detailed period-to-period comparisons of individual stars for future work. As such, we expect trapping features to play no important role in the comparisons. SdB models were constructed from an initially Mi = 1 M⊙ ZAMS model with ZZAMS = 0.02, and Y = 0.245 + 2 × Z, as in Miller Bertolami (2016). Mass loss was artificially enhanced prior to the He-core flash in order to produce sdB models during the core-He-burning stage in the Teff range of g-mode sdB pulsators. The resulting models at the beginning of the He-core-burning stage have masses of MZAHB = 0.46738, 0.4675, 0.468, 0.469, 0.47, and 0.473 M⊙. For the sake of comparison, models during the He-core-burning stage were computed under two different assumptions regarding convective boundary mixing (CBM): one is the extreme assumption of a strict Schwarzschild criterion (Schwarzschild 1906) at the convective core, and the other corresponds to the inclusion of CBM at the boundary of the convective core. In the latter case, CBM is adopted as an exponentially decaying velocity field following Freytag et al. (1996) and Herwig et al. (1997), with free parameters taken as in Miller Bertolami (2016). This corresponds to the assumption of a moderate CBM (see Sect. 3.1 in De Gerónimo et al. 2019). It is worth noting that although strong theoretical arguments indicate that the strict Schwarzschild criterion is not physically sound, it serves as a useful estimation of the smallest possible convective core size (Castellani et al. 1971, 1985; Gabriel et al. 2014). The value of ΔP was computed from the periods of individual l = 1 g-modes in the range 2000 s–10 000 s, which is a typical range for the periods observed in V1093 Her stars. The computed value of ΔP shows oscillations due to two completely separate factors. On one hand, as the models evolve, structural changes push different periods inside or outside the range in which we computed ΔP, leading to small fluctuations in the value of ΔP. For the sake of clarity, in Fig. 19 we show its time-averaged value in a moving window of 3 Myr. The variance around the mean value is shown by the confidence bands in the bottom right panel of Fig. 19. On the other hand, larger fluctuations occurring on longer timescales also appear in the sequences that include moderate CBM due to the oscillating behavior of the boundary of the convective core.
 |
Fig. 19. Properties of the two sets of stellar evolution models discussed in the text as compared with those observed in pulsating sdB stars. Blue circles indicate the stars studied in this work while green circles indicate those from previous studies (Reed et al. 2018; Charpinet et al. 2019; Reed et al. 2020a; Sahoo et al. 2020a). Red tracks correspond to models computed with a moderate CBM prescription while cyan tracks correspond to those computed under the extreme assumption of a strict Schwarzschild criterion. Masses of the models are MZAHB = 0.467, 0.4675, 0.468, and 0.47 M⊙, and darker colors correspond to more massive models. Thick magenta lines show the locus of the model at the zero-age extreme horizontal branch (ZAEHB). Light-colored bands around the curves in the bottom right panel indicate the typical variance of ΔP around the mean value. |
The two sets of sdB models are shown in Fig. 19 together with the properties observed in the V1093 Her stars studied in the present and previous works. From Fig. 19, it becomes apparent that models with a small convective core close to those predicted by a strict Schwarzschild criterion, are too compact (and consequently too dim) to fit the surface gravities observed in known pulsators. This is reinforced by the comparison between the evolution of the mean period spacing (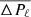 ) against log g and log Teff in Fig. 19. Models with small convective cores give mean period spacings that are too small to account for the observations. On the contrary, models with a moderate CMB prescription are able to reach the range of mean period spacings observed in V1093 Her stars (Fig. 19). The reason for this is two fold, and can be understood by looking at the expression of the asymptotic mean period spacing
) against log g and log Teff in Fig. 19. Models with small convective cores give mean period spacings that are too small to account for the observations. On the contrary, models with a moderate CMB prescription are able to reach the range of mean period spacings observed in V1093 Her stars (Fig. 19). The reason for this is two fold, and can be understood by looking at the expression of the asymptotic mean period spacing 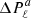 ,
,
The buoyancy (Brunt-Väisälä) frequency for an ideal monoatomic gas with radiation can be written as
where, in the case of sdB stars, radiation pressure is almost negligible and β ∼ 1. We see that period spacing, in general, scales as 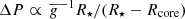 . As models that include CBM have cores that grow larger than those using a strict Schwarzschild criterion, the g-mode propagation cavity (of size ∼R⋆ − Rcore) is reduced and leads to larger values of the period spacings. This is why models that include CBM show oscillations in the value of ΔP, as those models show oscillations in the size of the convective core (see Fig. 19). In addition, models with larger convective cores are able to increase the mean molecular weight of the star to larger values than their small convective core counterparts. This leads to greater luminosities in the sdB models that include CBM, and consequently to smaller surface gravities for the same effective temperature. The decrease in the mean value of the local surface gravity then also leads to an increase in the period spacing of the models. Finally, close to the end of the He-core burning stage, sdB models with CBM develop one of more breathing pulse instabilities (Castellani et al. 1985). This creates the loops in the log g − log Teff diagram at relatively low gravities and leads to an extension of the He-core-burning lifetime.
. As models that include CBM have cores that grow larger than those using a strict Schwarzschild criterion, the g-mode propagation cavity (of size ∼R⋆ − Rcore) is reduced and leads to larger values of the period spacings. This is why models that include CBM show oscillations in the value of ΔP, as those models show oscillations in the size of the convective core (see Fig. 19). In addition, models with larger convective cores are able to increase the mean molecular weight of the star to larger values than their small convective core counterparts. This leads to greater luminosities in the sdB models that include CBM, and consequently to smaller surface gravities for the same effective temperature. The decrease in the mean value of the local surface gravity then also leads to an increase in the period spacing of the models. Finally, close to the end of the He-core burning stage, sdB models with CBM develop one of more breathing pulse instabilities (Castellani et al. 1985). This creates the loops in the log g − log Teff diagram at relatively low gravities and leads to an extension of the He-core-burning lifetime.
From the previous discussion it is apparent that small convective cores close to those predicted by a bare Schwarzschild criterion can be discarded on the basis of the observations. This is in agreement with theoretical arguments (Castellani et al. 1985; Gabriel et al. 2014) as well as with independent observational constraints (Charpinet et al. 2011; Bossini et al. 2015; Constantino et al. 2015, 2016). Although models with a moderate CBM prescription at the burning core cover the range of observed period spacings, closer inspection shows that observed mean period spacings are about 10 to 20 s larger (∼5 to 10%) than those predicted by the models. Such a shift could be attained by a small increase in the size of the convective core. The consequent small decrease in the surface gravity of the models would still be in agreement with observations.
7. Summary and conclusions
Here, we present the analysis of data collected for five pulsating hot subdwarf B stars, TIC 260795163, TIC 080290366, TIC 020448010, TIC 138707823, and TIC 415339307, observed with the TESS mission. Of the five analyzed stars, four are new detections of long-period pulsating sdB (V1093 Her) stars, namely TIC 260795163, TIC 020448010, TIC 138707823, and TIC 415339307. This high-duty cycle space photometry delivered by the TESS mission provides data of excellent quality with which to detect and identify the modes in long-period sdBV stars.
The pulsations detected in these five stars are concentrated in the short frequency region from ∼70 to ∼300 μHz, which is in line with what was discovered during the second half of the survey phase of Kepler (Baran et al. 2011). We detected 73 oscillation frequencies which we associate with g-modes in sdBVs. We did not find any p-modes for any of the targets. With the 120-second observations, it is difficult to find p-modes because we are limited to a Nyquist frequency of about 4200 μHz. However, we did not find any p-modes either in the 20-second data for TIC 260795163, TIC 080290366, and TIC 138707823, even though the Nyquist frequency for that data set is about 25 000 μHz. This might imply that the analyzed stars are most likely pure g-mode sdB pulsators.
We analyzed the data using the asteroseismic methods of rotational multiplets and asymptotic period spacing in order to identify pulsational modes. Although we detect many pulsation frequencies, we do not find evidence for complete rotational multiplets in any of the analyzed stars. Relying solely on asymptotic period spacing relationships, we identify the observed periods as mainly dipole and quadrupole g-modes.
We constructed sFTs to examine the temporal evolution of the pulsation modes. None of the pulsation spectra or sFTs for any of the analyzed stars show a clear pattern indicating rotational multiplets. Moreover, the highest S/N frequencies seem to be stable over the course of these TESS observations (from 25 to 49 d). However, the low-amplitude frequencies do show complex patterns in their sFTs. With a higher number of data points and with a longer baseline such as for stars that have been observed in multiple sectors with TESS, a better frequency resolution will be achieved and also noise levels will be lower, which will make detection of possible rotational multiples viable. In particular, we believe that for the stars that lie in the continuing viewing zone of TESS it will be possible to detect rotational multiplets and make the mode identification more secure. In forthcoming papers, we will concentrate on the stars that have been observed in more than a single sector, and on a star which is in the southern continuous viewing zone of TESS.
For the 5 V1093 Her stars analyzed in this paper, namely TIC 260795163, TIC 080290366, TIC,020448010 TIC 138707823, and TIC 415339307, we identified 49 frequencies out of the 73 detected ones as l = 1 modes using solely asymptotic period spacing. In some cases, we were not able to identify the modes with a unique modal degree. We mention that for 15 periodicities, we do not find a unique identification, and therefore these can be interpreted as either l = 1 or l = 2 modes.
We apply the method of bootstrapping with 104 times randomization in order to calculate the mean period spacing obtained in our analysis and also to assess the errors. The mean period spacing for l = 1 modes obtained in this way for the five analyzed stars ranges from 251 s to 255 s, while the average period spacing for l = 2 modes spans from 145 s to 155 s.
We derived atmospheric parameters for all five stars by fitting synthetic spectra to the newly obtained low-resolution Dupont/B&C and NTT/EFOSC2 spectra. The effective temperatures of the observed sdB stars span from 23 700 K to 27 600 K and their surface gravity (log g) is in the range from 5.3 to 5.5 dex, confirming that they are indeed occupying the g-mode sdBV parameter space.
We computed stellar evolution models with LPCODE stellar evolution code (Althaus et al. 2005), and computed l = 1 g-mode frequencies with the adiabatic nonradial pulsation code LP-PUL (Córsico & Althaus 2006). We compared the derived mean period spacings (ΔP) of dipole g-modes derived from TESS observations for the five sdBV stars of our sample and 33 found in the literature with the predictions of the adiabatic pulsation computations performed on stellar evolutionary models. In agreement with expectations from theoretical arguments and previous asteroseismological works (Castellani et al. 1985; Gabriel et al. 2014; Charpinet et al. 2011; Bossini et al. 2015; Constantino et al. 2015; Schindler et al. 2015), and recently (Ostrowski et al. 2021), we find that models relying on a simplistic implementation of the Schwazschild criterion lead to small convective cores and values of ΔP which are too low to match the observations. On the contrary, models with a standard treatment of convective boundary mixing at the convective core are able to match the observed values of ΔP, although more intense convective boundary mixing cannot be discarded.
We did not attempt to constrain envelope properties for any of the targets analyzed in this work for the following reasons. First, we did not detect any p-modes. Although lower order g-modes are sensitive to envelope properties, a model fit of the observed periods is required, as was done by Charpinet et al. (2019), which is beyond the scope of this paper. Second, we did not detect any trapped modes either, which can be used to investigate the envelope by identifying the period spacing between the trapped modes.
For a description of instrumentation, see: http://www.lco.cl/?epkb_post_type_1=boller-and-chivens-specs
Acknowledgments
We wish to acknowledge the suggestions and comments of an anonymous referee that improved the original version of this work. We thank Alejandro H. Córsico for kindly providing us with the codes for the K-S and I-V tests and for his valuable comments on the earlier version of this manuscript. M.U. thanks Özgür Bastürk and M.Ekrem Esmer for valuable discussions. M.U. acknowledges financial support from CONICYT Doctorado Nacional in the form of grant number No: 21190886 and ESO studentship program. P.N. acknowledges support from the Grant Agency of the Czech Republic (GAČR 18-20083S). This research has used the Sandbox services of www.Astroserver.org. Financial support from the Polish National Science Centre under projects No. UMO-2017/26/E/ST9/00703 and UMO-2017/25/B ST9/02218 is acknowledged. This paper includes data collected by the TESS mission. Funding for the TESS mission is provided by the NASA Explorer Program. Funding for the TESS Asteroseismic Science Operations Centre is provided by the Danish National Research Foundation (Grant agreement no.: DNRF106), ESA PRODEX (PEA 4000119301) and Stellar Astrophysics Centre (SAC) at Aarhus University. We thank the TESS team and staff and TASC/TASOC for their support of the present work. We thank Brad Barlow, who made possible TESS Cycle 3 observations of variable hot subdwarf stars observations with the proposal number G03221. And finally we thank the TASC WG8 team for supporting this project and providing valuable feedback.
References
- Aerts, C. 2021, Rev. Mod. Phys. 93. 15001 [CrossRef] [Google Scholar]
- Aerts, C., Christensen-Dalsgaard, J., & Kurtz, D. W. 2010, Asteroseismology (Springer) [Google Scholar]
- Althaus, L. G., Serenelli, A. M., Panei, J. A., et al. 2005, A&A, 435, 631 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrae, R. 2010, ArXiv e-prints [arXiv:1009.2755] [Google Scholar]
- Bachulski, S., Baran, A. S., Jeffery, C. S., et al. 2016, Acta Astron., 66, 455 [Google Scholar]
- Baran, A., Pigulski, A., Kozieł, D., et al. 2005, MNRAS, 360, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Baran, A. S. 2012, Acta Astron., 62, 179 [Google Scholar]
- Baran, A. S., Kawaler, S. D., Reed, M. D., et al. 2011, MNRAS, 414, 2871 [NASA ADS] [CrossRef] [Google Scholar]
- Baran, A. S., Reed, M. D., Østensen, R. H., Telting, J. H., & Jeffery, C. S. 2017, A&A, 597, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baran, A. S., Telting, J. H., Jeffery, C. S., et al. 2019, MNRAS, 489, 1556 [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bossini, D., Miglio, A., Salaris, M., et al. 2015, MNRAS, 453, 2290 [NASA ADS] [CrossRef] [Google Scholar]
- Buzzoni, B., Delabre, B., Dekker, H., et al. 1984, The Messenger, 38, 9 [NASA ADS] [Google Scholar]
- Castellani, V., Giannone, P., & Renzini, A. 1971, Ap&SS, 10, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Castellani, V., Chieffi, A., Tornambe, A., & Pulone, L. 1985, ApJ, 296, 204 [Google Scholar]
- Charpinet, S., Fontaine, G., Brassard, P., & Dorman, B. 1996, ApJ, 471, L103 [Google Scholar]
- Charpinet, S., Fontaine, G., Brassard, P., et al. 1997, ApJ, 483, L123 [Google Scholar]
- Charpinet, S., Fontaine, G., Brassard, P., & Dorman, B. 2000, ApJS, 131, 223 [Google Scholar]
- Charpinet, S., Fontaine, G., Brassard, P., & Dorman, B. 2002, ApJS, 139, 487 [Google Scholar]
- Charpinet, S., Van Grootel, V., Fontaine, G., et al. 2011, A&A, 530, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charpinet, S., Brassard, P., Van Grootel, V., & Fontaine, G. 2014, in 6th Meeting on Hot Subdwarf Stars and Related Objects, eds. V. van Grootel, E. Green, G. Fontaine, & S. Charpinet, Astron. Soc. Pac. Conf. Ser., 481, 179 [Google Scholar]
- Charpinet, S., Giammichele, N., Zong, W., et al. 2018, Open Astron., 27, 112 [CrossRef] [Google Scholar]
- Charpinet, S., Brassard, P., Fontaine, G., et al. 2019, A&A, 632, A90 [CrossRef] [EDP Sciences] [Google Scholar]
- Constantino, T., Campbell, S. W., Christensen-Dalsgaard, J., Lattanzio, J. C., & Stello, D. 2015, MNRAS, 452, 123 [Google Scholar]
- Constantino, T., Campbell, S. W., Lattanzio, J. C., & van Duijneveldt, A. 2016, MNRAS, 456, 3866 [Google Scholar]
- Copperwheat, C. M., Morales-Rueda, L., Marsh, T. R., Maxted, P. F. L., & Heber, U. 2011, MNRAS, 415, 1381 [Google Scholar]
- Córsico, A. H., & Althaus, L. G. 2006, A&A, 454, 863 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Córsico, A. H., Uzundag, M., Kepler, S. O., et al. 2021, A&A, 645, A117 [EDP Sciences] [Google Scholar]
- De Gerónimo, F. C., Battich, T., Miller Bertolami, M. M., Althaus, L. G., & Córsico, A. H. 2019, A&A, 630, A100 [EDP Sciences] [Google Scholar]
- Edelmann, H., Heber, U., Hagen, H. J., et al. 2003, A&A, 400, 939 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Edelmann, H., Heber, U., Altmann, M., Karl, C., & Lisker, T. 2005, A&A, 442, 1023 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Efron, B. 1979, Ann. Statist., 7, 1 [Google Scholar]
- Fontaine, G., Brassard, P., Charpinet, S., et al. 2003, ApJ, 597, 518 [Google Scholar]
- Foster, H. M., Reed, M. D., Telting, J. H., Østensen, R. H., & Baran, A. S. 2015, ApJ, 805, 94 [Google Scholar]
- Freytag, B., Ludwig, H. G., & Steffen, M. 1996, A&A, 313, 497 [NASA ADS] [Google Scholar]
- Gabriel, M., Noels, A., Montalbán, J., & Miglio, A. 2014, A&A, 569, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Geier, S., & Heber, U. 2012, A&A, 543, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghasemi, H., Moravveji, E., Aerts, C., Safari, H., & Vučković, M. 2017, MNRAS, 465, 1518 [Google Scholar]
- Green, E. M., Fontaine, G., Reed, M. D., et al. 2003, ApJ, 583, L31 [Google Scholar]
- Green, E. M., Guvenen, B., O’Malley, C. J., et al. 2011, ApJ, 734, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Greenstein, J. L., & Sargent, A. I. 1974, ApJS, 28, 157 [Google Scholar]
- Haas, M. R., Barclay, T., Batalha, N. M., et al. 2014, in American Astronomical Society Meeting Abstracts #223, 228.01, Am. Astron. Soc. Meet. Abs., 223 [Google Scholar]
- Haro, G., & Luyten, W. J. 1962, Boletin de los Observatorios Tonantzintla y Tacubaya, 3, 37 [Google Scholar]
- Heber, U. 1986, A&A, 155, 33 [NASA ADS] [Google Scholar]
- Heber, U. 2016, PASP, 128 [Google Scholar]
- Heber, U., Hunger, K., Jonas, G., & Kudritzki, R. P. 1984, A&A, 130, 119 [NASA ADS] [Google Scholar]
- Herwig, F., Bloecker, T., Schoenberner, D., & El Eid, M. 1997, A&A, 324, L81 [NASA ADS] [Google Scholar]
- Hill, P. W., & Hill, S. R. 1966, MNRAS, 133, 205 [Google Scholar]
- Hubeny, I., & Lanz, T. 2017, ArXiv e-prints [arXiv: 1706.01859] [Google Scholar]
- Jaidee, S., & Lyngå, G. 1969, Arkiv for Astron., 5, 345 [Google Scholar]
- Jenkins, J. M., Twicken, J. D., McCauliff, S., et al. 2016, Proc. SPIE, 9913, 99133E [Google Scholar]
- Kawaler, S. D. 1988, IAU Symp., 123, 329 [Google Scholar]
- Kawaler, S. D., Reed, M. D., Quint, A. C., et al. 2010, MNRAS, 409, 1487 [Google Scholar]
- Kawka, A., Vennes, S., O’Toole, S., et al. 2015, MNRAS, 450, 3514 [NASA ADS] [CrossRef] [Google Scholar]
- Kepler, S. O. 1993, Baltic Astron., 2, 515 [Google Scholar]
- Kern, J. W., Reed, M. D., Baran, A. S., Telting, J. H., & Østensen, R. H. 2018, MNRAS, 474, 4709 [Google Scholar]
- Ketzer, L., Reed, M. D., Baran, A. S., et al. 2017, MNRAS, 467, 461 [NASA ADS] [Google Scholar]
- Kilkenny, D., & Hill, P. W. 1975, MNRAS, 173, 625 [Google Scholar]
- Kilkenny, D., Hill, P. W., & Brown, A. 1977, MNRAS, 178, 123 [Google Scholar]
- Kilkenny, D., Heber, U., & Drilling, J. S. 1988, S. Afr. Astron. Observat. Circular, 12, 1 [Google Scholar]
- Kilkenny, D., Luvhimbi, E., O’Donoghue, D., et al. 1995, MNRAS, 276, 906 [Google Scholar]
- Kilkenny, D., Koen, C., O’Donoghue, D., & Stobie, R. S. 1997, MNRAS, 285, 640 [Google Scholar]
- Kilkenny, D., Worters, H. L., O’Donoghue, D., et al. 2016, MNRAS, 459, 4343 [Google Scholar]
- Koen, C., & Green, E. M. 2010, MNRAS, 406, 2701 [Google Scholar]
- Lamontagne, R., Demers, S., Wesemael, F., Fontaine, G., & Irwin, M. J. 2000, AJ, 119, 241 [Google Scholar]
- Lei, Z., Zhao, J., Németh, P., & Zhao, G. 2018, ApJ, 868, 70 [Google Scholar]
- Lightkurve Collaboration (Cardoso, J. V. d. M., et al.) 2018, Astrophysics Source Code Library [record ascl:1812.013] [Google Scholar]
- Lutz, R., Schuh, S., Silvotti, R., Kruspe, R., & Dreizler, S. 2008, Commun. Asteroseismol., 157, 185 [NASA ADS] [Google Scholar]
- Magee, H. R. M., Dufton, P. L., Keenan, F. P., et al. 1998, A&A, 338, 85 [NASA ADS] [Google Scholar]
- Mathys, G., Hubrig, S., Mason, E., et al. 2012, Astron. Nachr., 333, 30 [Google Scholar]
- Miller Bertolami, M. M. 2016, A&A, 588, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller Bertolami, M. M., Córsico, A. H., & Althaus, L. G. 2012, in Fifth Meeting on Hot Subdwarf Stars and Related Objects, eds. D. Kilkenny, C. S. Jeffery, & C. Koen, Astron. Soc. Pac. Confer. Ser., 452, 175 [Google Scholar]
- Moehler, S., Landsman, W. B., Lanz, T., & Miller Bertolami, M. M. 2019, A&A, 627, A34 [CrossRef] [EDP Sciences] [Google Scholar]
- Németh, P., Kawka, A., & Vennes, S. 2012, MNRAS, 427, 2180 [Google Scholar]
- Newell, E. B. 1973, ApJS, 26, 37 [Google Scholar]
- O’Donoghue, D. 1994, MNRAS, 270, 222 [Google Scholar]
- Oreiro, R., Pérez Hernández, F., Ulla, A., et al. 2005, A&A, 438, 257 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Østensen, R. H., Silvotti, R., Charpinet, S., et al. 2010, MNRAS, 409, 1470 [NASA ADS] [CrossRef] [Google Scholar]
- Østensen, R. H., Silvotti, R., Charpinet, S., et al. 2011, MNRAS, 414, 2860 [NASA ADS] [CrossRef] [Google Scholar]
- Østensen, R. H., Telting, J. H., Reed, M. D., et al. 2014, A&A, 569, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Østensen, R. H., Jeffery, C. S., Saio, H., et al. 2020, MNRAS, 499, 3738 [Google Scholar]
- Ostrowski, J., Baran, A. S., Sanjayan, S., & Sahoo, S. K. 2021, MNRAS, 503, 4646 [Google Scholar]
- Pablo, H., Kawaler, S. D., & Green, E. M. 2011, ApJ, 740, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Reed, M. D., Terndrup, D. M., Eggen, J. R., & Unterborn, C. T. 2007, Commun. Asteroseismol., 150, 269 [Google Scholar]
- Reed, M. D., Baran, A., Quint, A. C., et al. 2011, MNRAS, 414, 2885 [Google Scholar]
- Reed, M. D., Baran, A., Østensen, R. H., Telting, J., & O’Toole, S. J. 2012, MNRAS, 427, 1245 [Google Scholar]
- Reed, M. D., Foster, H., Telting, J. H., et al. 2014, MNRAS, 440, 3809 [Google Scholar]
- Reed, M. D., Baran, A. S., Østensen, R. H., et al. 2016, MNRAS, 458, 1417 [Google Scholar]
- Reed, M. D., Baran, A. S., Telting, J. H., et al. 2018, Open Astron., 27, 157 [Google Scholar]
- Reed, M. D., Telting, J. H., Ketzer, L., et al. 2019, MNRAS, 483, 2282 [NASA ADS] [Google Scholar]
- Reed, M. D., Shoaf, K. A., Németh, P., et al. 2020a, MNRAS, 493, 5162 [Google Scholar]
- Reed, M. D., Yeager, M., Vos, J., et al. 2020b, MNRAS, 492, 5202 [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2014, SPIE Conf. Ser., 9143, 914320 [Google Scholar]
- Sahoo, S. K., Baran, A. S., Heber, U., et al. 2020a, MNRAS, 495, 2844 [Google Scholar]
- Sahoo, S. K., Baran, A. S., Sanjayan, S., & Ostrowski, J. 2020b, MNRAS, 499, 5508 [Google Scholar]
- Schindler, J.-T., Green, E. M., & Arnett, W. D. 2015, ApJ, 806, 178 [Google Scholar]
- Schuh, S., Huber, J., Dreizler, S., et al. 2006, A&A, 445, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schwarzschild, K. 1906, Astronomische Mitteilungen der Universitaets-Sternwarte zu Goettingen, 13, 1 [NASA ADS] [Google Scholar]
- Science Software Branch at STScI 2012, Astrophysics Source Code Library [record ascl:1207.011] [Google Scholar]
- Silvotti, R., Uzundag, M., Baran, A. S., et al. 2019, MNRAS, 489, 4791 [Google Scholar]
- Simpson, G., & Mayer-Hasselwander, H. 1986, A&A, 162, 340 [NASA ADS] [Google Scholar]
- Stassun, K. G., Oelkers, R. J., Pepper, J., et al. 2018, AJ, 156, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Tassoul, M. 1980, ApJS, 43, 469 [Google Scholar]
- Telting, J. H., Østensen, R. H., Baran, A. S., et al. 2012, A&A, 544, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Telting, J. H., Baran, A. S., Nemeth, P., et al. 2014, A&A, 570, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Unno, W., Osaki, Y., Ando, H., & Shibahashi, H. 1979, Nonradial oscillations of stars (University of Tokyo Press) [Google Scholar]
- Uzundag, M., Baran, A. S., Østensen, R. H., et al. 2017, MNRAS, 472, 700 [NASA ADS] [CrossRef] [Google Scholar]
- Wegner, G. 1980, AJ, 85, 538 [CrossRef] [Google Scholar]
- Wegner, G., & Boley, F. I. 1993, AJ, 105, 660 [CrossRef] [Google Scholar]
- Zong, W., Charpinet, S., & Vauclair, G. 2016a, A&A, 594, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zong, W., Charpinet, S., Vauclair, G., Giammichele, N., & Van Grootel, V. 2016b, A&A, 585, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Observing log of the spectroscopic data obtained for the five sdB stars studied in this work.
Frequency solution from the TESS light curve of TIC 260795163 including frequencies, periods, amplitudes (and their uncertainties), and S/N.
Frequency solution from the TESS light curve of TIC 080290366 including frequencies, periods, and amplitudes (and their uncertainties) and the signal-to-noise ratio.
Frequency solution from the TESS light curve of TIC 020448010 including frequencies, periods, amplitudes (and their uncertainties), and S/N.
Frequency solution from the TESS light curve of TIC 138707823 including frequencies, periods, amplitudes (and their uncertainties), and S/N.
Frequency solution from the TESS light curve of TIC 415339307 including frequencies, periods, amplitudes (and their uncertainties), and S/N.
All Figures
 |
Fig. 1. Fourier transform of all five sdB stars observed in single SC sectors, concentrating on the g-mode region of the frequency spectrum. The panels are sorted with decreasing effective temperature from top to bottom. In each panel, we give the TESS input catalog number, effective temperature (in kelvin), and surface gravity (in dex), respectively. The horizontal red lines correspond to 0.1% FAP confidence level. |
| In the text | |
 |
Fig. 2. Top: Fourier transform of sector 1 of TIC 260795163. The horizontal red line indicates the 0.1% FAP level. The orange line is the residual after extraction of the signals. Bottom: Fourier transform of sectors 27 and 28 of TIC 260795163. The horizontal red line indicates the 0.1% FAP level. The orange line is the FT of the prewhitened light curve. |
| In the text | |
 |
Fig. 3. Fourier transform of USC data of TIC 260795163. The top panel: window function calculated from USC data. The second and third panels from the top display two different frequency regions in which the signals show strong residuals after the extraction. These frequencies are given in Table 4. The horizontal red line indicates the 0.1% FAP level. The orange line is the FT of the prewhitened light curve. |
| In the text | |
 |
Fig. 4. Top: Fourier transform of data taken in sector 2 of TIC 080290366. The horizontal red line indicates the 0.1% FAP level. The orange line is the residual after extraction of the signals. Bottom: Fourier transform of data taken in sector 29 of TIC 080290366. The horizontal red line indicates the 0.1% FAP level. The orange line is the FT of the prewhitened light curve. |
| In the text | |
 |
Fig. 5. Fourier Transform of sector 29 of TIC 080290366, compared with the window function (top panel). The lower panels show an excess of power after prewhitening (orange line), see Sect. 3.3 for more details. The horizontal red line indicates the 0.1% FAP level. |
| In the text | |
 |
Fig. 6. Top: Fourier transform of sector 2 data of TIC 138707823. The horizontal red line indicates the 0.1% FAP level. The orange line is the residual after extraction of the signals. Bottom: Fourier transform of sector 29 data of TIC 138707823. The horizontal red line indicates the 0.1% FAP level. The orange line is the FT of the prewhitened light curve. |
| In the text | |
 |
Fig. 7. Sliding Fourier transform of TIC 260795163 from USC data. The color-scale illustrates amplitude in ppt units. See text for more details on sFT computations. |
| In the text | |
 |
Fig. 8. Sliding Fourier transform of TIC 080290366. The sFT is calculated from USC data. |
| In the text | |
 |
Fig. 9. As in Fig. 8 but for TIC020448010. The sFT is calculated from SC data. |
| In the text | |
 |
Fig. 10. The same figure as 8 but for TIC 138707823. The sFT is calculated from SC data. |
| In the text | |
 |
Fig. 11. As in Fig. 8 but for TIC 415339307. The sFT is calculated from SC data. |
| In the text | |
 |
Fig. 12. Kolmogorov-Smirnov (top panel) and inverse variance (lower panel) tests to search for a constant period spacing in the five stars of our sample. The offset on log Q for the Kolmogorov-Smirnov is 6 and the offset on y-axis for the inverse variance test is 80. All stars present a significant probability of having a constant period spacing. |
| In the text | |
 |
Fig. 13. Fourier transform of TIC 260795163 (presented here are the sectors 1, 28 and 29 together). The residuals after prewhitening are shown in orange. The red and blue dots show the dipole and quadrupole modes respectively. If there is no unique identification, the period is shown in both colors. The horizontal red line correspond to 0.1% FAP confidence level. The right panel shows the residuals between the observed and the fitted periods. See text for more details on mode identification and the mean period spacing computations. |
| In the text | |
 |
Fig. 14. Same as Fig. 13 but for TIC 080290366 (presented here is sector 29). |
| In the text | |
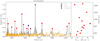 |
Fig. 15. Same as Fig. 13 but for TIC 020448010 (presented here is sector 9). |
| In the text | |
 |
Fig. 16. Same as Fig. 13 but for TIC 138707823 (presented here is sector 2). |
| In the text | |
 |
Fig. 17. Same as Fig. 13 but for TIC 415339307 (presented here is sector 5). |
| In the text | |
 |
Fig. 18. Best-fit TLUSTY/XTGRID models for the five hot subdwarf stars analyzed in this paper. The spectra are dominated by the H Balmer-series marked at the bottom and a few weak He I lines marked at the top of the figure. The observed continua adjusted to the theoretical models. |
| In the text | |
 |
Fig. 19. Properties of the two sets of stellar evolution models discussed in the text as compared with those observed in pulsating sdB stars. Blue circles indicate the stars studied in this work while green circles indicate those from previous studies (Reed et al. 2018; Charpinet et al. 2019; Reed et al. 2020a; Sahoo et al. 2020a). Red tracks correspond to models computed with a moderate CBM prescription while cyan tracks correspond to those computed under the extreme assumption of a strict Schwarzschild criterion. Masses of the models are MZAHB = 0.467, 0.4675, 0.468, and 0.47 M⊙, and darker colors correspond to more massive models. Thick magenta lines show the locus of the model at the zero-age extreme horizontal branch (ZAEHB). Light-colored bands around the curves in the bottom right panel indicate the typical variance of ΔP around the mean value. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



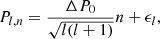
![$$ \begin{aligned} \Delta P_\ell ^a = \frac{P_o}{\sqrt{\ell (\ell +1)}}= \frac{2\pi ^2}{\sqrt{\ell (\ell +1)}}\left[\int _{r_1}^{r_2} \frac{N}{r} dr\right]^{-1}. \end{aligned} $$](/articles/aa/full_html/2021/07/aa40961-21/aa40961-21-eq23.gif)
![$$ \begin{aligned} N^2={ g}^2\frac{\upmu (4-3\beta )}{\mathfrak{R} \, T} \left[\nabla _{\rm ad}-\nabla +\frac{\beta \,\nabla _\upmu }{4-3\beta }\right], \end{aligned} $$](/articles/aa/full_html/2021/07/aa40961-21/aa40961-21-eq24.gif)