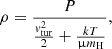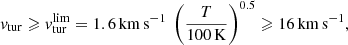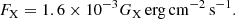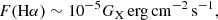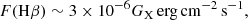| Issue |
A&A
Volume 651, July 2021
|
|
|---|---|---|
| Article Number | A13 | |
| Number of page(s) | 25 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202039730 | |
| Published online | 01 July 2021 | |
Excitation mechanisms in the intracluster filaments surrounding brightest cluster galaxies
1
LERMA, Observatoire de Paris, PSL research Université, CNRS, Sorbonne Université, 75104 Paris, France
2
SOFIA Science Center, USRA, NASA Ames Research Center, M.S. N232-12, Moffett Field, CA 94035, USA
e-mail: fpolles@usra.edu
3
Sorbonne Université, CNRS, UMR 7095, Institut d’Astrophysique de Paris, 98bis bd Arago, 75014 Paris, France
4
Institut Universitaire de France, Ministère de l’Education Nationale, de l’Enseignement Supérieur et de la Recherche, 1 rue Descartes, 75231 Paris Cedex 05, France
5
École normale supérieure, Université PSL, Sorbonne Université, CNRS, LERMA, 75005 Paris, France
6
Université Paris-Saclay, CNRS, Institut d’Astrophysique Spatiale, 91405 Orsay, France
7
Kavli Institute for Particle Astrophysics and Cosmology, Stanford University, 452 Lomita Mall, Stanford, CA 94305-4085, USA
8
Collège de France, 11 Place Marcelin Berthelot, 75005 Paris, France
9
Institute for Computational Cosmology, Department of Physics, Durham University, South Road, Durham DH1 3LE, UK
10
Institute of Astronomy, University of Cambridge, Madingley Road, Cambridge CB1 0HA, UK
11
Department of Physics and Astronomy, University of Kentucky, Lexington, KY 40506, USA
Received:
20
October
2020
Accepted:
27
February
2021
Context. The excitation of the filamentary gas structures surrounding giant elliptical galaxies at the center of cool-core clusters, also known as brightest cluster galaxies (BCGs), is key to our understanding of active galactic nucleus (AGN) feedback, and of the impact of environmental and local effects on star formation.
Aims. We investigate the contribution of thermal radiation from the cooling flow surrounding BCGs to the excitation of the filaments. We explore the effects of small levels of extra heating (turbulence), and of metallicity, on the optical and infrared lines.
Methods. Using the CLOUDY code, we modeled the photoionization and photodissociation of a slab of gas of optical depth AV ≤ 30 mag at constant pressure in order to calculate self-consistently all of the gas phases, from ionized gas to molecular gas. The ionizing source is the extreme ultraviolet (EUV) and soft X-ray radiation emitted by the cooling gas. We tested these models comparing their predictions to the rich multi-wavelength observations from optical to submillimeter, now achieved in cool core clusters.
Results. Such models of self-irradiated clouds, when reaching sufficiently large AV, lead to a cloud structure with ionized, atomic, and molecular gas phases. These models reproduce most of the multi-wavelength spectra observed in the nebulae surrounding the BCGs, not only the low-ionization nuclear emission region like optical diagnostics, [O III]λ 5007 Å/Hβ, [N II]λ 6583 Å/Hα, and ([S II]λ 6716 Å+[S II]λ 6731 Å)/Hα, but also the infrared emission lines from the atomic gas. [O I]λ 6300 Å/Hα, instead, is overestimated across the full parameter space, except for very low AV. The modeled ro-vibrational H2 lines also match observations, which indicates that near- and mid-infrared H2 lines are mostly excited by collisions between H2 molecules and secondary electrons produced naturally inside the cloud by the interaction between the X-rays and the cold gas in the filament. However, there is still some tension between ionized and molecular line tracers (i.e., CO), which requires optimization of the cloud structure and the density of the molecular zone. The limited range of parameters over which predictions match observations allows us to constrain, in spite of degeneracies in the parameter space, the intensity of X-ray radiation bathing filaments, as well as some of their physical properties like AV or the level of turbulent heating rate.
Conclusions. The reprocessing of the EUV and X-ray radiation from the plasma cooling is an important powering source of line emission from filaments surrounding BCGs. CLOUDY self-irradiated X-ray excitation models coupled with a small level of turbulent heating manage to simultaneously reproduce a large number of optical-to-infrared line ratios when all the gas phases (from ionized to molecular) are modeled self-consistently. Releasing some of the simplifications of our model, like the constant pressure, or adding the radiation fields from the AGN and stars, as well as a combination of matter- and radiation-bounded cloud distribution, should improve the predictions of line emission from the different gas phases.
Key words: galaxies: clusters: intracluster medium / intergalactic medium / ISM: structure / ISM: lines and bands / techniques: spectroscopic
© F. L. Polles et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
X-ray observations of galaxy clusters show that for more than one-third of the clusters, the X-ray surface brightness peaks in the center. This emission is due to the cooling of the hot intracluster medium (ICM) with a short radiative cooling time. At the center of these “cool-core” clusters lies a giant elliptical galaxy, the brightest cluster galaxy (BCG). Chandra and XMM-Newton X-ray observations of BCGs revealed huge ICM cavities produced by the jet of the central black hole (e.g., McNamara & Nulsen 2007; Fabian et al. 2015). These cavities highlight the impact of active galactic nuclei (AGNs) on large-scale environments and suggest that the necessary heating source to prevent the overcooling in the cool-core cluster could be provided by the AGN. Observations at different wavelengths of these regions show that the cavities are often surrounded by multi-wavelength line-emitting filamentary structures (e.g., Heckman et al. 1989; Conselice et al. 2001; Lim et al. 2012; Mittal et al. 2012; Rose et al. 2020), illustrating the multi-phase nature of these streams. Studies of the correlation between Hα and CO(1–0) line emission (e.g., Salomé et al. 2011; Tremblay et al. 2018; Olivares et al. 2019; Russell et al. 2019) showed that these two tracers are co-spatial and co-moving with most of the mass of the filaments lying in the molecular phase. These filaments may have formed from the cooling of the hot gas in very local regions around the AGN cavities, when the gas is locally thermally unstable (e.g., Gaspari et al. 2012; Beckmann et al. 2019; Qiu et al. 2020).
In recent decades several studies have investigated the powering source of the multi-wavelength spectrum of these filamentary nebulae (e.g., Heckman et al. 1989; Voit et al. 1994; Ferland et al. 1994, 2002, 2008; Bayet et al. 2011; Canning et al. 2016), proposing and exploring different sources of photoionization and heating: (1) the central AGN, (2) X-rays from the ICM, (3) heat conduction from the ICM to the cold filament, (4) shocks and turbulent mixing layers, (5) collisional heating by cosmic rays, and (6) hybrid models (several energy sources). Some of these sources have already been excluded: photoionization from the AGN is not powerful enough to produce the observed Hα+[N II] line emission (e.g., Heckman et al. 1989; Conselice et al. 2001) and is in disagreement with the lack of a strong radial gradient profile in the optical emission line ratios (e.g., Heckman et al. 1989). The relatively constant Hα/H2 (Lim et al. 2012) and Hα/CO (e.g., Olivares et al. 2019) over the entire nebula also suggests that the excitation process is local. A local ionization mechanism could be the photoionization by young massive stars, but this scenario is not favored either, because the observations show a strong [N II]λ 6583 Å/Hα and weak [O III]λ 5007 Å/Hβ, indicating that the optical spectra of these nebulae are more similar to low-ionization nuclear emission region (LINER) spectra than HII spectra (e.g., Heckman et al. 1987; Crawford & Fabian 1992). Mcdonald et al. (2012) claimed that a model with a mix of heating by shocks (100–400 km s−1; Allen et al. 2008) and photoionization by stars (Kewley et al. 2001) can reproduce the optical line ratios [N II]λ 6583 Å/Hα, [O I]λ 6300 Å/Hα, ([S II]λ 6716 Å+[S II]λ 6731 Å)/Hα, and [O III]λ 5007 Å/Hβ of a sample of nine BCGs. However, this study was limited to optical lines. In the near-infrared (NIR), Jaffe & Bremer (1997) investigated the line ratio H2 1–0 S(1)/Hα, measuring a ratio of ∼0.1, which is larger than that observed in Galactic HII regions (∼0.01) and excludes fast shocks (> 50 km s−1) as the possible excitation mechanism. The possible sources of excitation of the ro-vibrationally excited H2 lines in the filaments have also been discussed by Wilman et al. (2002) and Lim et al. (2012).
Focusing on one filament around NGC 1275, the so-called Horseshoe-region, Ferland et al. (2008, 2009) extended the observational constraints from optical to infrared, and proposed the collisions of the cold gas in the filaments with ionizing particles as the main heating mechanism. These latter authors showed that this model is consistent with the filaments being made of cloudlets of varying densities and excited by cosmic rays. One strong motivation and success of this model was to reproduce the surprisingly strong molecular hydrogen lines detected by Spitzer in Perseus and Centaurus filaments (Johnstone et al. 2007), together with the ratios of the NIR H2 line emission, as well as the lack of [O III]λ 5007 Å emission line noticed in most of the filaments of Perseus by Hatch et al. (2006). Fabian et al. (2011) showed that the surrounding hot ICM is a possible source of these energetic particles. Bayet et al. (2011) used the same kind of model (energetic particles with/without extra-heating) to predict molecular emission lines like CN (2–1), HCO+ (3–2), and C2H (3–2). With the advent of the Herschel Space Observatory, the detection of the far-infrared (FIR) [C II]λ 157.7 μm and [O I]λ 63.2 μm line emission was made possible in BCGs and was even mapped in the filaments of the Perseus and Centaurus clusters. Mittal et al. (2012) showed that the observed ratio [O I]λ 63.2 μm/[C II]λ 157.7 μm was barely reproduced by the energetic particles model only. In order to reproduce this ratio with such a model, it is necessary to add an extra heating source such as turbulent heating, with typical velocity dispersion of 2–10 km s−1 as shown in Canning et al. (2016). This model succeeds in reproducing the observations, albeit a result of a weighted sum of a power-law distribution of cloud densities for which the CLOUDY computation was stopped at the illuminated face of the cloud (first zone), that is, only emission from the skin of the clouds was combined. In Canning et al. (2016), the authors investigated the behavior of the predicted line emissivity throughout a cloud at fixed density, but not for an integral of clouds of many densities.
In this paper we re-investigate the effect of the excitation due to thermal radiation as expected from the cooling of the hot plasma and we explore the outcomes of photoionization at different depths of the cloud in terms of visual extinction (AV). The photoionization by the X-ray photons emitted by the condensing and cooling gas, the so-called cooling flow, has already been considered (i.e., Voit & Donahue 1990; Ferland et al. 1994; Donahue & Voit 1991 and references therein). The cool-core clusters have measured mass deposition rates of 10–100 M⊙ yr−1, or smaller when considering regions inside the filaments. Even if large amounts of energy are expected via this cooling gas, Crawford & Fabian (1992) argued against the capacity of this process to power the nebula. From unresolved X-ray data, these latter authors showed that the photoionization by the surrounding X-ray gas was not powerful enough to excite the nebula of the core of the Perseus cluster. Recent deep and high-resolution observations of X-ray filaments by the satellite Chandra (Walker et al. 2015), showing an average intensity of 12 filaments in Perseus of 4 × 10−16 erg cm−2 s−1 arcsec−2, reignited interest in the exploration of this mechanism. In the present study, we do not add any further source of excitation so that we may measure and discuss the effects of reprocessing the X-ray cooling energy from the ionized to the molecular phase. We are aware that this model is too simple to be able to reproduce all of the gas phases simultaneously. We emphasize that we explore the physical properties of the cloud and the predicted line emission at different AV. We also discuss the impact of adding some turbulent heating and of varying the metallicity (Z) on the physical and chemical properties of the cloud. We compare model predictions with observations of line emission from the filaments, combining the state-of-the-art models with recent observations at different wavelengths, from the optical to the infrared, extending the range of constraints and predictions for a single model.
The model setup is described in Sect. 2.1. The effects of varying the different free parameters are analyzed in Sects. 2.2 and 2.3. The predicted optical-to-submillimeter line emission from our grid of models is compared with the observations provided by the literature in Sect. 3. Our results are discussed in Sect. 4 and the conclusions are summarized in Sect. 5.
2. Modeling
In this section, we present the setup of the CLOUDY models as well as the evolution of the chemical and physical structure of the cloud with the free parameters of the models.
2.1. Setup of the models
We use the photoionization and photodissociation code CLOUDY v17.01 (Ferland et al. 2017), which allows self-consistent calculation of the thermal and chemical structure of a plane-parallel layer of a gas and dust. Previous studies focused analyses on the neutral and molecular phases; however, the initial conditions of each phase are a consequence of the processes that take place on the previous phase. Moreover, some line emission, such as [C II]λ 157.7 μm, can arise from both ionized and neutral phases. Therefore, computations that do not take into account multiple gas phases could lead to incorrect interpretation of the phase properties. In our analysis, each model is performed at a constant total pressure1 of 106.5 K cm−3, which is the average pressure of the hot gas surrounding the filaments of NGC 1275, as deduced from X-ray observations (Sanders & Fabian 2007). Similar pressure values have been estimated from the electron density calculated with the line ratio [S II]λλ 6716,6731 Å (e.g., Heckman et al. 1989). All models are stopped at the visual extinction of AV = 30 mag. Other input parameters for the models are: the shape and intensity of the incident radiation field, the chemical composition of dust and gas, the metallicity (Z), and the turbulent velocity dispersion (vtur). AV = 30 mag corresponds to slightly different physical size based on the initial conditions of the model. To give an order of magnitude, for a model of GX = 10, vtur = 10 km s−1, and Z = Z⊙, the size of the full cloud is ∼48 pc. The model parameters are described in detail below and a summary is provided in Table 1.
Model summary.
2.1.1. Input radiation field: shape
One of the key parameters of the present modeling is the shape of the input radiation field. Energetic particles or hard X-ray fail to reproduce the observed [O III]λ 5007 Å/Hβ ratio because they produce overly low amounts of highly ionized oxygen [O III]λ 5007 Å with respect to the other ionized species. To solve this problem, extreme ultraviolet (EUV) as well as soft X-ray photons are necessary because they manage to create and excite the different ions. The slope of the input field has thus a direct impact on the ionized line ratios. Such photons can be emitted by the gas in cooling flows (self-irradiation). This model is described in Johnstone et al. (1992). The total emission due to the gas that cools constantly from the temperature of the hot surrounding medium is the result of the sum of the gas emission at each temperature normalized by the mass deposition rate. In our models, the soft X-ray/EUV band of the input radiation field is thus a power law resulting from the co-added series of Raymond-Smith collisional-equilibrium continua (Raymond & Smith 1977). This continuum shape is available in CLOUDY2 as an input spectral energy distribution (SED) shape and has already been used in Ferland et al. (1994, 2002) to model cooling flow environments. Figure 1 shows that almost all of this soft X-ray and EUV radiation is self-absorbed and reprocessed at larger wavelengths when it encounters a cloud of sufficient depth. As explained in Sect. 2.1.2, we fine-tune the input radiation intensity and the AV to reproduce the X-ray surface brightness observed in the filaments of Perseus. Our simplified model does not explore the spatial distribution or the size distribution of the clouds. We note that one strong hypothesis of this model is that a large fraction of the hot cooling gas radiation is absorbed and reprocessed by the slab of atomic and molecular gas. Our models explore a range of cloud optical depths, which allows us to match both the observed X-ray fluxes and multi-wavelength line emission. We defer a more complex model of a fog of atomic and molecular clouds spread in a bath of hot cooling gas to future work.
 |
Fig. 1. Spectral energy distribution of the input radiation field for GX = 10 (black line) and the total outward radiation field (continuum and line emission) stopping the model at different AV (blue line): 0.1, 5, and 30 mag. The two vertical green lines show the energy necessary to create O++ and N+, two of the ions whose emission is used to constrain the modeling. The dots represent the average observed integrated flux for the filaments surrounding NGC 1275 of 4.0 × 10−16 erg cm−2 s−1 arcsec−2 in the 0.6–2.0 keV band (red dot; Walker et al. 2015) and of 5 × 10−15 erg cm−2 s−1 arcsec−2 in the 2–10 keV band (magenta dot; Sanders et al. 2005). The orange background highlights the range over which the integrated intensity is calculated to scale GX. |
We also added an intergalactic background continuum, taken to be the 2005 version of the Haardt & Madau (1996) background at zero redshift, with both starburst and quasar continua. The input SED also includes the cosmic microwave background (CMB) and the infrared dust emission of the standard interstellar radiation field.
2.1.2. Input radiation field: Intensity
The intensity of the X-ray/EUV emission is varied with the parameter GX. By definition, GX = 1 corresponds to an integrated intensity of between 0.2 and 2 keV of 4πνFν = 1.6 × 10−3 erg cm−2 s−1. To compare the input and output values of the radiation field in CLOUDY with the observed surface brightness, one has to divide this value by 4π in order to get a value in erg cm−2 s−1 sr−1. For instance GX = 1 corresponds to an input field of 1.3 × 10−4 erg cm−2 s−1 sr−1, that is 3 × 10−15 erg cm−2 s−1 arcsec−2.
We compared the CLOUDY outward radiation field in the range 0.6–2.0 keV with the X-ray surface brightness observed in the same band by Walker et al. (2015) in the filaments of the Perseus cluster. The authors estimated that the average surface brightness in this band of the filaments is 4.0 × 10−16 ergs cm−2 s−1 arcsec−2; this is the red dot at 2.1 × 10−4 erg cm−2 s−1 in Fig. 1. To give an order of magnitude, Sanders et al. (2005) estimated the surface brightness of the hard X-ray emission in the band 2–10 keV and found that it decreases with radius, from ∼5 × 10−15 ergs cm−2 s−1 arcsec−2 at a radius of 20 arcsec (magenta dot on Fig. 1) to 10−16 ergs cm−2 s−1 arcsec−2 at 200 arcsec.
In our grid of models, GX varies between 10−2 and 103, in steps of 0.2 dex. We note that the range of GX that is explored here is higher than in Ferland et al. (1994, 2002) where self-irradiated clouds have also been modeled. The values used by these latter authors at that time were scaled on unresolved X-ray observations. The more recent X-ray observations in Perseus are by Sanders & Fabian (2007). Also, Walker et al. (2015) showed that the X-ray radiation is not homogeneously spread over the entire 100 kpc region and soft X-ray emission arising from the filaments surrounding NGC 1275 has surface brightness values reaching up to a few 10−16 ergs cm−2 s−1 arcsec−2 as mentioned above. The comparison between the input SED used by Ferland et al. (1994) and the input SED of one of our models is shown in Fig. C.1. Figure 1 shows that low GX are too small compared to the X-ray observations in Perseus. We nevertheless include grids of models with such low GX in order to show the effect of turning on GX radiation.
2.1.3. Outward radiation field: cloud optical depth effects
The novel aspect of our modeling is that we self-consistently compute the chemical and thermodynamical structure and the emissivity of the entire cloud as a function of AV ≤ 30 mag. Figure 1 shows how the outward transmitted spectrum changes with the total3AV of the cloud. With increasing AV, that is of the hydrogen column density, the cloud absorbs more continuum in the energy range between X-ray and NIR, all of the hydrogen-ionizing radiation is absorbed, and the dust emission in FIR increases. Stopping the calculation at AV = 30 mag implies going through different gas phases.
2.1.4. Elemental abundances
Our chemical setup is based on the previous studies of Ferland et al. (2009) and Canning et al. (2016). The gas elemental abundances and the chemical composition of dust are set to those derived in the Orion Nebula by Baldwin et al. (1991), Rubin et al. (1991), Osterbrock et al. (1992), and Rubin et al. (1993; see Tables A.1 and A.2). The grain size distribution is set to the standard distribution in the Milky Way presented in Weingartner & Draine (2001), which consists of a mixture of graphites and silicates and is known to reproduce the standard Galactic extinction curve with RV = 3.1. The polycyclic aromatic hydrocarbon (PAH) size distribution is given by a power law described in Abel et al. (2008).
While most parameters are calibrated with Galactic values, it is important to note that the elemental composition and dust properties in the filaments could be different. Indeed, the average metallicity of the ICM is ∼0.3 Z⊙. However, and as shown in Fig. 10 of Sanders & Fabian (2007), the metallicity of the filaments varies with radius, reaching a maximum at a distance of 40 kpc. In their study the metallicity covers a range between 0.3 and 0.7 Z⊙. To investigate the effect of metallicity on the predicted line emission in our models, which is compared with the line emission arising from the filaments, we explore values between 0.3 and 1 Z⊙ in steps of 0.05.
2.1.5. Turbulence
The input of mechanical energy in filaments surrounding BCGs originates from various processes such as the cascade of kinetic energy injected at large scales by AGN jets and inflated bubbles (e.g., Revaz et al. 2008; Beckmann et al. 2019), the turbulent mixing between the hot and cold phases (Begelman & Fabian 1990; Banerjee & Sharma 2014; Hillel & Soker 2020), and the collisions between intertwined filaments. All these processes generate small-scale turbulence which not only induces pressure fluctuations but may also leads to the propagation of low-velocity molecular shocks that could be responsible for bright H2 emission of filaments (Johnstone et al. 2007; Guillard et al. 2012). In CLOUDY, turbulence is modeled through a velocity dispersion parameter vtur which acts as a pressure support, a homogeneous heating rate, and a contribution to the line broadening for the radiative transfer. In the collisional ionization models presented in Canning et al. (2016), the authors considered turbulent velocity dispersion of 2−10 km s−1, which is enough to decrease the optical depth of the lines and improve the cooling efficiency.
The lines originating from the warm gaseous nebula surrounding NGC 1275 have typical full width at half-maximum (FWHM) ranging between 50 and 200 km s−1 (Lim et al. 2012). In comparison, a FWHM of ∼30 km s−1 was measured from CO(1–0) in the same region (Salomé et al. 2008). More recently, FWHMs of 100–140 km s−1 were obtained from several emission lines of CO for a sample of various BCGs (Olivares et al. 2019) and FWHMs of 3–150 km s−1 from several molecular absorption lines seen against the bright radio core of Hydra-A (Rose et al. 2019, 2020). Whether these line widths originate from the internal velocity dispersion of cold filaments or result from relative motions between filaments is an unsolved issue. In the latter case, the velocity dispersion of the cold components would be intrinsically smaller. To explore all possible scenarios, we extend the range of turbulent velocity dispersion studied by Canning et al. (2016) and adopt values of vtur between 0 and 100 km s−1.
2.2. Thermal and ionization profiles
The main parameters of the models are the intensity of the input X-ray radiation field, the turbulence strength, and the metallicity. Figure 2 summarizes how these parameters influence the thermal and ionization structures of a cloud of constant total pressure P = 106.5 K cm−3. To facilitate the interpretation, in Figs. 3, D.1, and D.3 we also display the main heating and cooling processes, and the chemical profiles associated with seven models representative of the entire parameter domain.
 |
Fig. 2. Temperature (left column), hydrogen density (middle column), and ionization fraction ne−/nH (right column) of the gas predicted by CLOUDY as functions of the visual extinction AV and the X-ray radiation field scaling factor GX (top row), the turbulent velocity dispersion vtur (middle row), and the metallicity Z (bottom row). Nonvarying parameters are set to their standard values. In particular, the total pressure of the gas is set to 106.5 K cm−3, GX = 10 (for middle and bottom rows), vtur = 10 km s−1 (for top and bottom rows), and Z = Z⊙ (for top and middle rows). The black curves correspond to isocontours. The transition from ionized to atomic phase and that from atomic to molecular are defined by ne−/nH0 = 1 and nH0/nH2 = 1, respectively, indicated with a blue curve. The blue I, A, and M identify the different gas phases: ionized, atomic, and molecular, respectively. |
 |
Fig. 3. Effects of the radiation field intensity. Physical properties as a function of AV for models in thermal equilibrium and constant pressure fixed at 106.5 K cm−3, with solar metallicity, turbulent velocity 10 km s−1, and different values of X-ray radiation field intensity: GX = 10−1 (left column), GX = 101 (central column) and GX = 102 (right column). Top row: gas temperatures. Second row: total hydrogen density in black and ionization fraction (ne/nH) in blue. Third row: relative abundances of hydrogen. Bottom row: relative abundances of carbon (yellow), oxygen (blue), sulfur (green), and CO (black). The white background indicates the ionized phase, the gray background the atomic phase, and the dark gray the molecular phase. The transition from ionized to atomic phases and that from atomic to molecular correspond to density ratios of e−/H0 = 1 and H0/H2 = 1, respectively. |
Because X-ray photons dominate both the heating and the ionization rates of the gas, the structures shown in Fig. 2 are similar to the standard profiles predicted in photo-dominated regions (PDRs). As a function of the visual extinction AV, the cloud undergoes a transition from a hot (T ∼ 104 K), diffuse, and partially or fully ionized phase to a cold (T ∼ 10−100 K), dense, and partially or fully molecular medium. High temperatures at the border of the cloud result from an equilibrium between the heating induced by the photoelectric effect on gas particles and the cooling induced by electronic transitions. In contrast, low temperatures inside the cloud result from a balance between the heating due to photoelectric effect on grains and the cooling induced by fine structure lines and molecular lines. The fact that the photoelectric effect is still efficient at large AV is a known property of X-ray-dominated regions (XDRs): because hard X-rays have small interaction cross-sections, they penetrate deep into the cloud where they locally induce the production of UV photons that participate in the ionization of dust and gas, and photodissociation.
The transition between the two thermochemical states is driven by the absorption of the X-ray radiation field. Again, because of the low interaction cross-sections of high-energy photons, this transition requires a larger total column density than that required in clouds illuminated only by UV radiation field (Meijerink et al. 2006, 2007). Moreover, because X-rays are mostly absorbed by atoms, self-shielding effects are important. It follows that the cloud structure not only depends on AV but also on the density profile from the border of the cloud: the smaller the density, the wider the transition. If GX increases, both the ionization and molecular fronts necessarily occur at larger extinction. This is due to the increase in the input X-ray flux at high energy, the decrease in density at the border to ensure a constant total pressure, and the local production of UV photons induced by the thermalization of photoelectrons.
In this framework, the impact of the turbulent velocity dispersion is straightforward. Because the total pressure is assumed to be constant, the mass density is
where P is the total pressure, μ is the mean molecular mass of the gas, and mH the mass of hydrogen atoms. Therefore, the primary effect of the velocity dispersion in CLOUDY is to globally reduce the density of the gas over the entire cloud. Equation (1) also reveals a threshold effect: as vtur increases, the turbulence pressure (Ptur) increases and the thermal gas pressure (Pth) decreases. When the Ptur becomes higher than the Pth, the cloud switches from a medium at constant thermal pressure with sharp profiles to a medium at constant density with smoother profiles. Such a transition occurs for Ptur > Pth, thus
in agreement with the middle panel of Fig. 2. Finally, as ρ decreases when vtur increases, both the ionization and molecular fronts necessarily shift towards larger AV.
As shown in Figs. 2 and D.3, the metallicity appears to have a very limited impact on the thermochemical properties of the cloud. This result is slightly misleading because the metallicity is explored over a narrow range of values. When the metallicity decreases, the abundances of dust and heavy elements decrease by the same factor. A given AV therefore corresponds to higher hydrogen column density, which means the ionization front occurs correspondingly sooner.
2.3. Cumulative emission
The physics of a cloud illuminated by high-energy photons is driven by the reprocessing of the input radiation field into continuum and line emission. A PDR (illuminated by UV photons) and an XDR (illuminated X-ray photons) differ by the nature of this reprocessing and the amount of matter required. In classical PDRs, the input energy flux is reprocessed over typical visual extinction AV ∼ 1 mag, mostly through continuum dust emission; only a few percent is converted into atomic and molecular lines. In contrast, and because the impinging radiation field consists of photons of higher energies (X-ray; see Fig. 1), the reprocessing of the input radiative flux in XDRs not only requires large total column densities (AV typically larger than 30 mag), but also occurs through efficient atomic and molecular line emissions.
Following the definitions of Meijerink & Spaans (2005), the X-ray energy flux impinging the cloud is
The resulting absorption and emission processes are shown in Figs. 4, D.2, and D.4 where we display the local cooling and the cumulative emissions of fine-structure, metastable, and electronic lines of several atoms and ions for different values of GX, vtur, and Z.
 |
Fig. 4. Effects of the radiation field intensity on heating mechanisms and line emission. Heating and cooling mechanisms as a function of AV for the same models as those in Fig. 3. Top row: heating mechanisms. CLOUDY provides the first five main heating mechanisms as output. If one of the heating mechanisms is not one of these five for some values of AV, the mechanism is not shown in the figure. This is the reason for some vertical straight lines in the panels. Second row: emissivity of carbon, oxygen, and sulphur lines, Hα and Hβ. Bottom row: cumulative emission of carbon, oxygen, and sulphur lines, Hα and Hβ. The cumulative emission values are theoretical, and some of these values are too low to be detected by the instruments. The instrumental limitations mean that access is only given to the brightest values, thus to the emission arising from the denser parts of the cloud. It is important to remember that by comparing the observations with this predicted line emission we only constrain the properties of the denser phase of the cloud. |
The excitation of Hα and Hβ occurs through collisions with high-energy secondary electrons and through recombination of H+. As a result, the integrated fluxes of these lines are simply proportional to the input radiation field,
and
regardless of the metallicity or the density profile set by vtur (Figs. D.2 and D.4). Because of these simple relations, Hα and Hβ are valuable proxies for the input radiation field and can thus be used as normalization factors for other atomic and ionized lines. The results of CLOUDY on the optical line ratios are presented in Sect. 3.1 where we introduce and discuss the predicted Baldwin-Phillips-Terlevich (BPT) diagrams (Baldwin et al. 1981).
Unlike Hα and Hβ, the metastable and electronic lines of [S II], [N II], and [O III] are primarily excited by collisions of S+, N+, and O++ with thermalized electrons. Because the excited levels lie at ∼2.5 × 104 K above the ground state, the corresponding emissivity not only depends on the ionization profiles of the cloud but also on its temperature, and, in particular, on the amount of gas above ∼5000 K. The integrated intensities of all these lines are therefore built up at the border of the cloud where the gas is both ionized and warm. As the ionization potential of O+ is considerably larger than that of O, N, or S, [O III] lines necessarily trace the outskirts of the [O II]-, [N II]-, and [S II]-emitting regions. In this framework, the dependencies on the input parameters are straightforward and simply follow the results presented in the previous section. Low-density or strong X-ray radiation fields naturally favor large abundances of ionized species at the border of the cloud and the depth over which the gas resides at high temperature. The integrated intensities of [O II], [N II], [S II], and [O III] lines therefore increase with GX but also with vtur if 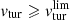 (Figs. 4 and D.2).
(Figs. 4 and D.2).
All the lines described above are tracers that carry only a small fraction ∼10−2 of the input X-ray energy flux. Indeed, because of the assumed initial SED, the impinging X-ray radiation field is preferentially reprocessed into the fine structure lines of [O I] and [C II], providing that AV is sufficiently large. As a result, for most of the models considered here, these lines not only carry a substantial amount of the input radiative flux, but also strongly depend on the size of the cloud. Evidently, the integrated intensities of both [O I] and [C II] increase with GX. The increase of vtur, instead, has a different effect on the two cooling lines. When vtur increases, the density decreases while the temperature increases. For large densities, C+ is converted into C very early in the cloud (see Fig. D.1, left), while the transition happens later in a low-density medium (see Fig. D.1, right). Thus, the integrated intensities of [C II] increase with vtur. The integrated intensities of [O I], instead, slightly decrease because of the increasing temperature.
3. Comparison with the observables
In this section, we compare the predicted line emission from our grid of models with the observations of several BCGs at optical to submillimeter wavelengths.
3.1. Optical tracers
The combination of the line ratios [O III]λ 5007 Å/Hβ, [N II]λ 6583 Å/Hα ([S II]λ 6716 Å+[S II]λ 6731 Å)/Hα, and [O I]λ 6300 Å/Hα is commonly used in the so-called BPT diagrams to identify the excitation mechanism of the optical line-emitting gas. Mcdonald et al. (2012) used this technique to investigate the sources of ionization contributions in the filaments of nine cool-core galaxy clusters. Overlapping on the BPT diagram grid of models of previous studies and the observed values, the authors eliminated most of the heating mechanisms suggested. In Fig. 5, we compare our grid of models with the observed values of the BCG sample provided by these latter authors. To make the reading of these plots easier, we show BPT diagrams as examples in Appendix E, varying Z and GX for a fixed turbulence of 10 km s−1 (Fig. E.1), and those varying only the turbulence and the metallicity for single values of GX = 100 (Fig. E.2). These figures show the line ratios predicted at different AV: 0.001 mag (top row), 0.1 mag (second row), 1 mag (third row), and 5 mag (bottom row).
 |
Fig. 5. BPT diagrams. The gray dots (filament values) and the stars (nucleus values) represent the data from Mcdonald et al. (2012). The size of the dots decreases with increasing distance of the corresponding object from the nuclei. The solid black line is the upper limit for HII regions by Kewley et al. (2001) and the dashed black line is the lower limit for AGNs by Kauffmann et al. (2003). The predicted cumulative line ratios from the models are overlapped. The color bar corresponds to the different values of GX (the logarithm of the value is written on the bar); each symbol corresponds to one turbulence value and the size of the symbols increases with the metallicity (from 0.3 to 1 Z⊙). Top row: cumulative emission at AV = 0.001 mag; second row: cumulative emission at AV = 0.1 mag; third row: cumulative emission at AV = 1 mag; bottom row: cumulative emission at AV = 5 mag. Left column: [O III]λ 5007 Å/Hβ vs. [N II]λ 6583 Å/Hα; central column: [O III]λ 5007 Å/Hβ vs. [S II]/Hα; right column: [O III]λ 5007 Å/Hβ vs. [O I]/Hα. |
In Fig. 5 we can immediately see that, in general, our grid of models can reproduce the observables, with the exception of the [O I]λ 6300 Å/Hα ratio. The observed values in the [N II] diagram are well reproduced at all of the explored AV. We note that varying AV changes the best model that reproduces the specific observed ratio. Also, the predicted ([S II]λ 6716 Å+[S II]λ 6731 Å)/Hα are in agreement with the data, even if increasing AV increases the predicted ([S II]λ 6716 Å+[S II]λ 6731 Å)/Hα ratio. The predicted [O I]λ 6300 Å/Hα, instead, are only in agreement with the observables for very low AV (AV = 10−3 mag). Table 2 summarizes, among all of the models, the restricted parameter space that can reproduce the optical observations. The range of GX values that can reproduce most of the observables, for any metallicity, moves to lower values with increasing turbulence and to higher values with increasing AV. The different position of the models on the BPT diagrams highlights the impact of GX, turbulence, and AV on the physical properties of the cloud (i.e., temperature, electron fraction, and density). Indeed, the different combination of the free parameters affects the physical properties of the cloud, and therefore the predicted optical line ratios.
Restricted ranges of free parameters are given for four values of AV = 0.001, 0.1, 1, and 5 mag.
The optical line ratios of the BPT diagrams trace different sections of the cloud. As described in the previous section, [O III]λ 5007 Å arises from the outskirts of the environment compared to [N II]λ 6583 Å and [S II] lines, while [O I]λ 6300 Å, which traces warm dense gas, comes from the ionized front. Thus, varying AV affects the line ratios for a given combination of GX and turbulence. For those models with low-excitation sources (low GX and turbulence), the cloud does not have an ionized phase, and therefore there is no impact of the variation of AV on the line ratios. The increase of GX and/or the turbulence moves the ionized front deeper into the cloud. Thus, for those models with excitation sources strong enough to ionize the gas, varying AV changes the relative phase distribution of the clouds, and consequently the predicted optical line ratios vary. In particular, the increasing overestimation of [O I]λ 6300 Å/Hα with AV suggests that the observed optical emission arises from a cloud with low AV. In other words, a large fraction of the gas in the filaments can be reproduce by a matter-bounded cloud.
We note that the observed [O III]λ 5007 Å/Hβ ratio given by Mcdonald et al. (2012) can be very small (0.1–0.03). This was already discussed by Hatch et al. (2006) who noticed the unexpected complete lack of [O III]λ 5007 Å in most of the regions inside the filaments around NGC 1275. The observed optical line ratios may have several excitation mechanisms, such as star formation and particle excitation, which may be varying the [O III]λ 5007 Å/Hβ line ratio. The small values in Mcdonald et al. (2012) correspond to regions where there is no evidence of star formation. Powering the optical nebula without a strong [O III]λ 5007 Å line can be explained if cosmic ray ionization is invoked as described by Ferland et al. (2009). Another solution is the strategy adopted in this work, that is, to use an EUV continuum that can reproduce the observed optical line ratios (see Sect. 2.1.1). We leave a detailed comparison of the current model predictions with the observed emission lines in the filaments of NGC 1275 to a future study.
3.2. Infrared tracers
Unlike the optical lines, infrared observations are not significantly affected by extinction and they cover a wide range of ionization potentials and critical densities. Moreover, line ratios of infrared lines are almost independent of temperature.
3.2.1. [Ne II]λ 12.8 μm/[Ne III]λ 15.5 μm
The line ratio [Ne II]λ 12.8 μm/[Ne III]λ 15.5 μm is a perfect tracer of the intensity of the radiation source because the two lines are emitted by the same element but with different ionization stages. The [Ne III]λ 15.5 μm has higher ionization potential than [Ne II]λ 12.8 μm, 41 eV and 21.6 eV, respectively, and they have similar critical density: 3 × 105 cm−3 for [Ne III]λ 15.5 μm and 7 × 105 cm−3 for [Ne II]λ 12.8 μm. Both lines are found exclusively in HII regions, with [Ne III]λ 15.5 μm arising from the layer closer to the radiative source compared to [Ne II]λ 12.8 μm. These two lines have been detected for several BCGs with the IRS instrument onboard Spitzer. We collected the observed ratio [Ne II]/[Ne III] for a total of ten BCGs (values from Donahue et al. 2011, Egami et al. 2006, and Johnstone et al. 2007) and compare them with the predicted line ratio from our grid of models. The comparison is shown in the top row of Fig. 6. The observed ratio of the full sample covers the range between 1.10 and 5.25, and is represented by the blue background. We do not present the theoretical line ratio for all of the models, but only for a few representative cases, and simply aim to understand how the ratio changes as a function of the free parameters, namely GX, turbulence, metallicity, and AV. On the left panel we fix vtur and Z, and we vary only GX. For low GX, the model cannot reproduce the observables. Increasing the intensity of the radiation field, the model produces more energetic photons, boosts [Ne III]λ 15.5 μm, and the ratio decreases, with lower values at low AV. After the ionization front, the ratio becomes constant. Similar behavior is shown varying only the turbulence (central panel). We see that the combination of GX = 10 and vtur = 0−2 km s−1 can reproduce the observed range at every AV. Increasing vtur boosts [Ne III]λ 15.5 μm and moves the predicted values that can reproduce the observations inside the cloud. The effect of varying the metallicity on the [Ne II]/[Ne III] ratio is almost negligible and all of the model with vtur = 10 km s−1 and GX = 10 can reproduce the observed ratio (right panel). The restricted range of the parameter space that can reproduce the observations, taking into account all of the models, is presented in Table 3. The models with GX between 1 and 103 can reproduce the line ratio for an extended range of AV. The smallest value of AV that matches the observed [Ne II]/[Ne III] ratio varies with the combination of GX and vtur. Variation of the metallicity affects the behavior of the predicted line ratio only slightly. The impact of the metallicity on the range of AV is indicated in Table 3 with different letters.
 |
Fig. 6. Comparison of observed and predicted cumulative line ratios: [NeII]/[NeIII] (top), [O I]λ 63.2 μm/[C II]λ 157.7 μm (middle), and H2 S(1) 17.0 μm/H2 S(2) 12.3 μm (bottom), as a function of AV. The blue background highlights the observed line ratio of [NeII]/[NeIII], with values between 1.10 and 5.25 (data from Donahue et al. 2011, Egami et al. 2006, and Johnstone et al. 2007). The observed line ratio [O I]λ 63.2 μm/[C II]λ 157.7 μm ranges between 0.22 and 1.64 (values from Edge et al. 2010, Mittal et al. 2011, 2012, and Werner et al. 2014), and is shown in green, and the yellow background highlights the observed ratio of the two pure rotational H2 lines, between 0.2 and 0.9 (values from Donahue et al. 2011, Egami et al. 2006, and Johnstone et al. 2007). Column on the left: predicted ratios for models with vtur = 10 km s−1 and solar metallicity, central column: predicted ratios for models with GX = 10 and solar metallicity, and column on the right: predicted ratios for models with vtur = 10 km s−1 and GX = 10. |
Restricted parameter space of the free parameters that reproduce the infrared observations.
3.2.2. [O I]λ 63.2 μm/[C II]λ 157.7 μm
The FIR line ratio [O I]λ 63.2 μm/[C II]λ 157.7 μm observed by Herschel is a good tracer of the electron density if the lines are optically thin because the critical densities of these two lines are different. The critical density for [O I]λ 63.2 μm is ∼5 × 105 cm−3, and that for [C II]λ 157.7 μm is ∼3 × 103 cm−3, much lower. The range of observed [O I]λ 63.2 μm/[C II]λ 157.7 μm line ratios (0.22–1.64) is shown in the central row of Fig. 6 as the green background (values from Edge et al. 2010, Mittal et al. 2011, 2012, and Werner et al. 2014). Our models match those observations for a large range of free parameters, as summarized in Table 3. As carbon and oxygen abundances are scaled by the same factor, the metallicity has very little impact on this line ratio, while the variation of GX and turbulence has a clear effect on the profile of the [O I]λ 63.2 μm/[C II]λ 157.7 μm line ratios. For a fixed value of GX, the range of AV values that fit the data increases with increasing turbulence. The same behavior can be observed for models with a fixed value of vtur and different GX, that is, increasing GX moves the minimum value of the range of AV values that fit the data to higher AV.
3.2.3. Pure rotational H2 lines
In the infrared we can also detect the line emission of the warm molecular gas (≥100 K) emitted by the rotational and vibrational H2 transitions. In the bottom row of Fig. 6, we compare the observed H2 pure rotational line ratio S(1)17 μm/S(2)12 μm (values from Donahue et al. 2011, Egami et al. 2006, and Johnstone et al. 2007) with our model predictions. The observed line ratio is between 0.2 and 0.9, and is represented by the orange background, and the predicted line ratios from representative models are shown as a function of AV. At a constant moderate turbulent heating rate (vtur = 10 km, left panel), because the S(1) line has a lower excitation temperature than the S(2) line, all models show an increase in the H2 S(1)/S(2) line ratio with AV, except for very low GX where it is roughly constant (in that case the cloud temperature is almost constant at AV > 0.01). We note that the models match the observed range of ratios where the medium is mostly atomic. For a fixed GX = 10 and solar metallicity (middle panel), the observed ratio can be reproduced by all of the turbulence values, but for a different range of AV. Finally, the metallicity affects the behavior of the predicted line ratio only slightly (right panel). A summary of the combination of free parameter values that can reproduce the observed ratio H2 S(1) 17.0 μm/S(2) 12.3 μm is provided in Table 3.
3.2.4. Ro-vibrational H2 lines
The ro-vibrational H2 lines that emit ∼2 μm have also been observed in several BCGs, and presented by Edge et al. (2002). In Fig. 7, we compare the observed values of H2 1–0 S(3), H2 1–0 S(2), H2 1–0 S(1), and H2 1–0 S(0) normalized by Paα to our predicted H2/Paα, ratios. In our models, these line emissions are excited by the collision with the secondary electrons produced by the interaction of the X-ray radiation field with the medium. For most of our models, this excitation mechanism is enough to produce the H2 emission inside the cloud and we do not need to add cosmic rays. Increasing the X-ray radiation field intensity (left column), the peak of the emission moves to higher AV. Consequently, the cumulative intensity of the H2 lines reaches higher values deeper into the cloud. However, increasing GX decreases the density of the cloud at low AV, and therefore the cumulative emission profiles of these lines become steeper. Variation of the turbulence, instead, does not change the values of the secondary electron rate (central column), but affects the structure of the cloud (see Sect. 2.2). The combination of these two factors pushes the intensity of the ro-vibrational lines down for higher turbulence. Finally, with increasing metallicity (right column) the line emission decreases. All of the models that we show in Fig. 7 can reproduce the normalized ro-vibrational line emission, even if at different AV.
 |
Fig. 7. Comparison of observed and predicted ro-vibrational H2 lines, normalized by Paα, as a function of AV for the models described in Sect. 2.2. The different background highlights the observed ratios, between 0.1 and 2.3 (values from Edge et al. 2002). For each ratio, the color of the background and that of the corresponding theoretical cumulative ratio are the same. Column on the left: predicted cumulative emission for models with turbulence of 10 km s−1, solar metallicity, and various values of GX: 0.1 (top), 10 (middle), and 100 (bottom); central column: predicted cumulative emission for models with GX = 10, solar metallicity, and various values of turbulence: 0 (top), 10 (medium), and 50 (bottom) km s−1; column on the right: predicted cumulative emission for models with turbulence 10 km s−1, GX = 10, and various values of metallicity: 0.3 (top), 0.65 (middle), and 1 (bottom) Z⊙. |
3.3. Submillimeter lines
Finally, we compare the predicted CO(1–0), (2–1), and (3–2) transitions, which trace the cold (∼10 K) molecular gas, to the observations presented in Salomé et al. (2008). Figure 8 shows the observed range of CO (1–0) and CO (2–1) with a green and a blue background, respectively, and the predicted values of the three transitions for models with fixed turbulence and metallicity but different values of GX (left panel), and for models with fixed GX and metallicity but varying the turbulence (right panel). As the cold molecular gas traced by the CO transitions is expected to arise from the deepest region of the cloud, we compared the observations with the predicted cumulative emission at AV = 30 mag. For a fixed vtur = 10 km s−1 and Z = Z⊙, all the models with GX ≥ 10 can reproduce the observed CO(1–0) and all the models with GX ≥ 1.6 can reproduce the observed emission CO(2–1). On the other hand, fixing Z = Z⊙ and GX = 10, only the model with vtur = 10 and 30 km s−1 can reproduce both transitions. These comparisons restrict the “good” parameter space drastically, in particular the turbulence. We would like to reiterate that these results are based on a single model component, and a more complex multi-component model could lead to different results. An additional limitation in these models is that the turbulence is treated as a constant heating rate everywhere in the cloud, which is unrealistic.
 |
Fig. 8. Comparison of observed (green and blue background) and predicted cumulative CO emission: 1–0, 2–1, and 3–2. The predicted values are for AV = 30 mag (end of the cloud). Panel on the left: predicted values as a function of GX for models with turbulence of 10 km s−1 and solar metallicity. Panel on the right: predicted values as a function of turbulence for models with GX = 10 and solar metallicity. |
4. Origin of the soft X-ray/EUV emission
The actual model assumes that the soft X-ray and the EUV photons that power the nebula are produced by the cooling of the hot ICM in the filaments. In this section, we investigate whether the input X-ray intensity of our models can power the total line intensities, and we compare with observational estimates from the Perseus cluster.
To give orders of magnitude, a GX = 10 corresponds to an input X-ray surface brightness in the range 0.6–3.4 keV of ∼4 × 10−14 erg cm−2 s−1 arcsec−2. For a typical filament in Perseus of 27″ × 1″ at the distance of 80 Mpc, this means a luminosity of ∼1×1042 erg s−1. Sanders & Fabian (2007) analyzed the X-ray emission in a region of 27.3 × 1 arcsec2. They computed that the difference in temperature between the cooling X-ray-emitting gas and the surrounding gas was ∼2.7 keV. This implies a released energy of ∼2.5 × 1054 erg by the X-ray-emitting gas of the filament as it cools down from the temperature of the surrounding hot gas. Assuming a timescale for this process of ∼105 yr, these latter authors conclude that the gas cooling provides enough energy to power about 1042 erg s−1.
The authors also discuss the fact that the X-ray surface brightness in 0.5–2 keV is almost similar to the Hα+[N II]λ 6583 Å surface brightness given by Conselice et al. (2001) (Fig. 18 of Sanders & Fabian 2007). In order to account for the total reprocessed emission in all the different lines, Sanders & Fabian (2007) estimate that the input power must be a factor of 20 larger than that required for the Hα only. This leads to a required input power of ∼1042 erg s−1 for a typical filament in the Perseus cluster. The present models show that the predicted surface brightness in the range 0.6–2 keV is similar to the predicted Hα+[N II]λ 6548, 6583 Å surface brightness for AV > 20, which corresponds to hydrogen column density of ∼1022 cm−2. A cloud with large optical depth is needed to reprocess the X-rays and excite the infrared H2 lines (Fig. 7). As an example, Fig. 9 shows the behavior of the two emissions for the model with GX = 10, vtur = 10 km s−1, and Z = Z⊙. The predicted surface brightness of the reprocessed soft X-ray from the model is comparable to the observed value, 4.3 × 10−16 erg cm−2 s−1 arcsec−2, within a factor of three for AV ≥ 18 mag. The Hα+[N II]λ 6548, 6583 Å surface brightness, instead, is underpredicted by a factor of about four. It is important to remember that large uncertainties are related to the observations, such as the extinction correction for both Galactic and internal reddening (e.g., Johnstone et al. 2007). Nevertheless, this discrepancy between the observed and the predicted Hα+[N II]λ 6548, 6583 Å points out a weakness in our models, which could be related to the a priori assumptions.
 |
Fig. 9. Predicted cumulative surface brightness of Hα+[N II]λ 6548, 6583 Å (dashed line) and predicted ionizing continuum 0.6–2 keV X-ray band (solid line) as a function of AV for a model with GX = 10, vtur = 10 km s−1, and Z = Z⊙. The dark gray and soft gray background show the range of predicted ionizing continuum 0.6–2 keV X-ray and cumulative surface brightness of Hα+[N II]λ 6583 Å, respectively, for models with GX in the range 1–100. The red dots show the predicted transmitted continuum 0.6–2 keV X-ray band estimated at AV = 1, 5, 10, and 30 mag. The area covered by red (blue) diagonal lines represents a factor of three of the observed surface brightness of Hα+[N II]λ 6548, 6583 Å from Conselice et al. (2001) for region 15 of that paper, 1.3 × 10−15 erg cm−2 s−1 arcsec−2 (of 0.6–2 keV X-ray band from Walker et al. 2015, 4.3 × 10−16 erg cm−2 s−1 arcsec−2). |
Table F.1 presents the list of the 20 brightest predicted lines at different AV for the seven models described in this paper, ordered from the brightest to the faintest. The total energy released clearly depends on the parameters of a given model but is enough to power all the different lines.
There is a range of specific models for which (i) the input X-ray energy is similar to the value estimated in Sanders & Fabian (2007) if coming from self-irradiation by the cooling gas, and for which (ii) this energy is enough to power the total line emission, and produce outwards X-ray surface brightness comparable to the observed value for AV ≥ 5 mag.
Finally, the actual models produce very faint or even no O VIλ1032,1038 Å doublet. For example, for GX = 100 the surface brightness of these lines is of the order of 10−24 erg cm−2 s−1 arcsec−2, while that of Hα is ∼10−15 erg cm−2 s−1 arcsec−2. This is in agreement with the nondetection of these lines shown by Lecavelier des Etangs et al. (2004). However, observations reveal a tension in this regard, because other works have detected the O VI doublet at the center of some cool-core clusters (e.g., Bregman et al. 2006). The O VI line emission can be enhanced in radiative shocks and mixing layers (e.g., McQuinn & Werk 2018; Ji et al. 2019), which are not considered in our models.
5. Conclusions
This article presents the modeling of the physical and chemical structure and line emission of filaments surrounding BCGs. We use the CLOUDY code to revisit a self-irradiated model where the source of photoionization and heating of the filaments is the cooling radiation from the hot ICM plasma (the so-called cooling flow). We explore the effect of the penetration of the photons into the clouds by varying AV. As a result, the grid of models predicts the emission lines arising from the ionized, neutral, and molecular regions. We also explore turning on additional (turbulent) heating and we discuss the impact of this additional source of heating that acts as an extra pressure.
The structure of the clouds changes as the free parameters change. Increasing the intensity of the radiation field, the temperature and the ionization fraction of the gas also increase, while the density decreases (the models are isobaric). For low X-ray intensity the edge of the cloud is atomic and becomes molecular inside. Increasing the intensity, the ionization and molecular fronts move to higher AV. Increasing the turbulence has similar effects. Changing the metallicity has less dramatic consequences on the model predictions.
We note that the important parameters are (i) the slope of the input radiation field, that is, the power law used in CLOUDY to model X-ray cooling flows, which produce the soft X-ray and EUV photons that play a major role in the gas ionization; (ii) the strength of the input X-ray radiation field; (iii) the Av; and (iv) the level of turbulence, which provides extra-heating through dissipation of energy. There is an unavoidable degeneracy in the impact of these parameters, but it is clear that without any X-ray source it is not possible to reproduce the observations.
We compared our grid of models to the varied range of observations now achieved in cool-core clusters. Filaments in BCGs have been mapped from the soft X-ray to the millimeter and many lines in the optical and the infrared have been detected. We used such data to restrict the plausible range of parameters. The different combinations of the free parameters presented in this paper can reproduce the multi-wavelength observables without requiring an excess in X-ray luminosity. The emitted intensity in the X-ray from Sanders et al. (2005) and Walker et al. (2015) is in agreement with the estimated reprocessed emitted intensity in the 2–10 keV band as well as the 0.6–2 keV band of the models with GX ∼ 10 and the X-ray input energy is enough to power the line emission.
Within a reduced range of parameters, some models can simultaneously reproduce most of the ionized and molecular lines. The combination of GX between 1 and 103, any metallicity, and turbulence that varies according to the selected GX, for Av between 0.1 and 10 mag reproduces the typical BCG LINER-like low-ionization line ratio observed in BPT diagrams, including [O III], with [O I] being more difficult to reproduce if not at very low Av (less then 0.1 mag). This restricted range of parameter space reproduces the infrared ratios as well. We note that the MIR and FIR lines arising from the atomic and molecular gas phases are highly dependent on the AV. Finally, only the models with vtur = 10 or 30 km s−1 and GX ≥ 10 can reproduce the observed CO transitions.
It is clear that the mechanisms powering the nebula are more complex than these simple single-component plane-parallel models of constant-pressure self-irradiated clouds. A better representation of the filaments may come from a combination of such models as expected for a population of clouds with a range of AV illuminated by different GX and extra heating. We are aware that a constant pressure model is a simplification and we also expect a contribution of energetic particles and of star formation in some regions, but this was out of the scope of the present study. In future, new constraints from high-resolution multi-wavelength line emission as well as molecular absorption lines from Multi Unit Spectroscopic Explorer (MUSE) and Atacama Large Millimeter/submillimeter Array (ALMA) for several BCGs will help in the development of a more complex modeling.
In a future paper we will use the restricted grid of models identified in this study to model the multi-wavelength observations of the filamentary regions surrounding NGC 1275.
In CLOUDY, the total pressure includes ram, magnetic, turbulent, particle, and radiation pressure. More information can be found in the CLOUDY manual ( www.nublado.org ).
Acknowledgments
The authors thank the anonymous referee for providing helpful comments that contribute to improving the paper. This work was supported by the ANR grant LYRICS (ANR-16-CE31-0011). The grids of models have been run on the computing cluster Totoro funded by the European Research Council, under the European Community’s Seventh framework Programme, through the Advanced Grant MIST (FP7/2017-2022, No 742719)
References
- Abel, N. P., van Hoof, P. A. M., Shaw, G., Ferland, G. J., & Elwert, T. 2008, ApJ, 686, 1125 [Google Scholar]
- Allen, M. G., Groves, B. A., Dopita, M. A., Sutherland, R. S., & Kewley, L. J. 2008, ApJS, 178, 20 [Google Scholar]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baldwin, J. A., Ferland, G. J., Martin, P. G., et al. 1991, ApJ, 374, 580 [Google Scholar]
- Banerjee, N., & Sharma, P. 2014, MNRAS, 443, 687 [Google Scholar]
- Bayet, E., Viti, S., Hartquist, T. W., & Williams, D. A. 2011, MNRAS, 417, 627 [Google Scholar]
- Beckmann, R. S., Dubois, Y., Guillard, P., et al. 2019, A&A, 631, A60 [EDP Sciences] [Google Scholar]
- Begelman, M. C., & Fabian, A. C. 1990, MNRAS, 244, 26P [NASA ADS] [Google Scholar]
- Bregman, J. N., Fabian, A. C., Miller, E. D., & Irwin, J. A. 2006, ApJ, 642, 746 [Google Scholar]
- Canning, R. E. A., Ferland, G. J., Fabian, A. C., et al. 2016, MNRAS, 455, 3042 [Google Scholar]
- Conselice, C. J., Gallagher, J. S., & Wyse, R. F. G. 2001, ApJ, 122, 2281 [Google Scholar]
- Crawford, C. S., & Fabian, A. C. 1992, MNRAS, 259, 265 [NASA ADS] [Google Scholar]
- Donahue, M., & Voit, G. M. 1991, ApJ, 381, 361 [Google Scholar]
- Donahue, M., de Messières, G. E., O’Connell, R. W., et al. 2011, ApJ, 732, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Edge, A. C., Wilman, R. J., Johnstone, R. M., et al. 2002, MNRAS, 337, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Edge, A. C., Oonk, J. B. R., Mittal, R., et al. 2010, A&A, 518, L46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Egami, E., Rieke, G. H., Fadda, D., & Hines, D. C. 2006, ApJ, 652, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., Sanders, J. S., Williams, R. J. R., et al. 2011, MNRAS, 417, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., Walker, S. A., Pinto, C., Russell, H. R., & Edge, A. C. 2015, MNRAS, 451, 3061 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J., Fabian, A. C., & Johnstone, R. M. 1994, MNRAS, 266, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J., Fabian, A. C., & Johnstone, R. M. 2002, MNRAS, 333, 876 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J., Fabian, A. C., Hatch, N. A., et al. 2008, MNRAS, 386, 72 [CrossRef] [Google Scholar]
- Ferland, G. J., Fabian, A. C., Hatch, N. A., et al. 2009, MNRAS, 392, 1475 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J., Chatzikos, M., Guzmán, F., et al. 2017, Rev. Mex. Astron. Astrofis, 53, 385 [Google Scholar]
- Gaspari, M., Ruszkowski, M., & Sharma, P. 2012, ApJ, 746, 94 [Google Scholar]
- Guillard, P., Ogle, P. M., Emonts, B. H. C., et al. 2012, ApJ, 747, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Haardt, F., & Madau, P. 1996, ApJ, 461, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Hatch, N. A., Crawford, C. S., Johnstone, R. M., & Fabian, A. C. 2006, MNRAS, 367, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Heckman, T. M. 1987, in Observational Evidence of Activity in Galaxies, eds. E. E. Khachikian, K. J. Fricke, & J. Melnick, IAU Symp., 121, 421 [Google Scholar]
- Heckman, T. M., Baum, S. A., van Breugel, W. J. M., & McCarthy, P. 1989, ApJ, 338, 48 [Google Scholar]
- Hillel, S., & Soker, N. 2020, ApJ, 896, 104 [Google Scholar]
- Jaffe, W., & Bremer, M. N. 1997, MNRAS, 284, L1 [Google Scholar]
- Ji, S., Oh, S. P., & Masterson, P. 2019, MNRAS, 487, 737 [Google Scholar]
- Johnstone, R. M., Fabian, A. C., Edge, A. C., & Thomas, R. A. 1992, The spectral Signature of the Cooling Flow in Abell 478, Tech. Rep. [Google Scholar]
- Johnstone, R. M., Hatch, N. A., Ferland, G. J., et al. 2007, MNRAS, 382, 1246 [Google Scholar]
- Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003, MNRAS, 346, 1055 [Google Scholar]
- Kewley, L. J., Dopita, M. A., Sutherland, R. S., Heisler, C. A., & Trevena, J. 2001, ApJ, 556, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Lecavelier des Etangs, A., Gopal-Krishna, & Durret, F. 2004, A&A, 421, 503 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Petit, F., Nehmé, C., Le Bourlot, J., & Roueff, E. 2006, ApJS, 164, 506 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lim, J., Ohyama, Y., Chi-Hung, Y., Dinh-V-Trung, T., & Shiang-Yu, W. 2012, ApJ, 744, 112 [Google Scholar]
- Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 500, 259 [NASA ADS] [Google Scholar]
- Mcdonald, M., Veilleux, S., & Rupke, D. S. N. 2012, ApJ, 746 [Google Scholar]
- McNamara, B. R., & Nulsen, P. E. J. 2007, ARA&A, 45, 117 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- McQuinn, M., & Werk, J. K. 2018, ApJ, 852, 33 [Google Scholar]
- Meijerink, R., & Spaans, M. 2005, A&A, 436, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meijerink, R., Spaans, M., & Israel, F. P. 2006, ApJ, 650, L103 [Google Scholar]
- Meijerink, R., Spaans, M., & Israel, F. P. 2007, A&A, 461, 793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mittal, R., O ’dea, C. P., Ferland, G., et al. 2011, MNRAS, 418, 2386 [Google Scholar]
- Mittal, R., Oonk, J. B. R., Ferland, G. J., et al. 2012, MNRAS, 426, 2957 [Google Scholar]
- Olivares, V., Salome, P., Combes, F., et al. 2019, A&A, 631, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Osterbrock, D. E., Tran, H. D., & Veilleux, S. 1992, ApJ, 389, 305 [Google Scholar]
- Qiu, Y., Bogdanović, T., Li, Y., McDonald, M., & McNamara, B. R. 2020, Nat. Astron., 4, 900 [CrossRef] [Google Scholar]
- Raymond, J. C., & Smith, B. W. 1977, Soft X-ray Spectrum of a Hot Plasma, Tech. Rep. [Google Scholar]
- Revaz, Y., Combes, F., & Salomé, P. 2008, A&A, 477, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rose, T., Edge, A. C., Combes, F., et al. 2019, MNRAS, 485, 229 [Google Scholar]
- Rose, T., Edge, A. C., Combes, F., et al. 2020, MNRAS, 496, 364 [Google Scholar]
- Rubin, R. H., Simpson, J. P., Haas, M. R., & Erickson, E. F. 1991, ApJ, 374, 564 [Google Scholar]
- Rubin, R. H., Dufour, R. J., & Walter, D. K. 1993, ApJ, 413, 242 [Google Scholar]
- Russell, H. R., McNamara, B. R., Fabian, A. C., et al. 2019, MNRAS, 490, 3025 [Google Scholar]
- Salomé, P., Combes, F., Revaz, Y., et al. 2008, A&A, 484, 317 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salomé, P., Combes, F., Revaz, Y., et al. 2011, A&A, 531 [Google Scholar]
- Sanders, J. S., & Fabian, A. C. 2007, MNRAS, 381, 1381 [Google Scholar]
- Sanders, J. S., Fabian, A. C., & Dunn, R. J. H. 2005, MNRAS, 360, 133 [Google Scholar]
- Tremblay, G. R., Combes, F., Oonk, J. B. R., et al. 2018, ApJ, 865, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Voit, G. M., & Donahue, M. 1990, ApJ, 360, L15 [Google Scholar]
- Voit, G. M., Donahue, M., & Slavin, J. D. 1994, ApJS, 95, 87 [Google Scholar]
- Walker, S. A., Kosec, P., Fabian, A. C., & Sanders, J. S. 2015, MNRAS, 453, 2481 [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [Google Scholar]
- Werner, N., Oonk, J. B. R., Sun, M., et al. 2014, MNRAS, 439, 2291 [Google Scholar]
- Wilman, R. J., Edge, A. C., Johnstone, R. M., et al. 2002, MNRAS, 337, 63 [Google Scholar]
Appendix A: Chemical ISM composition
The gas and dust elemental abundances used in our models are those given by CLOUDY for the ISM case. We report in Table A.1 the values for the gas phase and in Table A.2 the values for the dust composition.
Gas-phase abundances used in our models.
Grain abundances used in our models.
Appendix B: Input parameters for the model with GX = 10, vtur = 10 km s−1 and Z = 1 Z⊙
table HM05 z = 0
table SED “cool.sed”
intensity −1.8, range 14.71 to 147.06 Ryd
table sed “test_modif.sed”
f(nu) −16.8611 0.1755
cosmic ray background 0
turbulence 10 km s−1
hden 2
constant pressure no continuum set 6.5
no grain molecules
database H2
abundances he = −1.022 li = −10.268 be = −20.000 b = −10.051 c = −3.523 n = −4.155
continue o = −3.398 f = −20.000 ne = −4.222 na = −6.523 mg = −5.523 al = −6.699
continue si = −5.398 p=−6.796 s=−5.000 cl=−7.000 ar=−5.523 k = −7.959
continue ca = −7.699 sc = −20.000 ti = −9.237 v = −10.000 cr = −8.000 mn = −7.638
continue fe = −5.523 co = −20.000 ni = −7.000 cu = −8.824 zn = −7.6990 no grains
grains ism
grains pah
metals and grains 1
set pah constant −4.6
set H2 Jura rate
Appendix C: Comparison between our initial radiation field and the SED used by Ferland et al. (1994)
Figure C.1 shows the input SED used in Ferland et al. (1994) in green, and the input SED of one of our models, i.e., GX = 10, as an example, in black. The input SED used by Ferland et al. (1994) is extremely faint compared to the more recent surface brightness measurements by Walker et al. (2015) represented by the red star.
 |
Fig. C.1. Comparison of the X-ray component of one of the input SEDs used in this study, i.e., GX = 10 (black curve), with that of the input SED used in Ferland et al. (1994; green dashed curve). The red star represents the observed surface brightness measurements by Walker et al. (2015). |
Appendix D: Metallicity and turbulence effects in the structure of the cloud
Figures D.1 and D.2 show the consequences of different turbulent velocities on the structure of the cloud and Figs. D.3 and D.4 show the effects of varying the metallicity. The figures are described in Sect. 2.2.
 |
Fig. D.1. Same as Fig. 3, but this time GX is fixed at 10 and the turbulence varies: 0 km s−1 (left column), 10 km s−1 (central column), and 50 km s−1 (right column). |
 |
Fig. D.2. Same as Fig. 4, but this time GX is fixed at 10 and the turbulence varies: 0 km s−1 (left column), 10 km s−1 (central column), and 50 km s−1 (right column). |
 |
Fig. D.3. Same as Fig. 3, but this time GX is fixed at 10 and the metallicity varies: Z = 0.3 Z⊙ (left column), Z = 0.65 Z⊙ (central column), and Z = Z⊙ (right column). |
 |
Fig. D.4. Same as Fig. 4, but this time GX is fixed at 10 and the metallicity varies: Z = 0.3 Z⊙ (left column), Z = 0.65 Z⊙ (central column), and Z = Z⊙ (right column). |
Appendix E: Behavior of [O III]λ 5007 Å/Hβ, [N II]λ 6583 Å/Hα, [S II]/Hα and [O I]λ 6300 Å/Hα in the parameter space
 |
Fig. E.1. BPT diagrams. Comparison of the observed line ratios with the model predictions. The gray dots (filament values) and the stars (nucleus values) represent the data from Mcdonald et al. (2012). The size of the dots decreases with increasing distance of the corresponding object from the nuclei. The solid black line is the upper limit for HII regions by Kewley et al. (2001) and the dashed black line is the lower limit for AGNs by Kauffmann et al. (2003). The predicted cumulative line ratios from the models are overlaid. The gray lines correspond to a single value of metallicity and different values of X-ray emission (the logarithm of the value is written on the left and reproduced with different colors); from left to right the X-ray emission is constant and the metallicity increases (from 0.3 to 1 Z⊙). The turbulent velocity is fixed to 10 km s−1. Left column: cumulative emission of [O III]λ 5007 Å/Hβ vs. [N II]λ 6583 Å/Hα; central column: [O III]λ 5007 Å/Hβ vs. [S II]/Hα; right column: [O III]λ 5007 Å/Hβ vs. [O I]/Hα. Top row: cumulative emission at AV = 0.001 mag; second row: cumulative emission at AV = 0.1 mag; third row: cumulative emission at AV = 1 mag; bottom row: cumulative emission at AV = 5 mag. |
 |
Fig. E.2. BPT diagrams. Comparison of the observed line ratios with the model predictions. The gray dots (filament values) and the stars (nucleus values) represent the data from Mcdonald et al. (2012). The size of the dots decreases with increasing distance of the corresponding object from the nuclei. The solid black line is the upper limit for HII regions by Kewley et al. (2001) and the dashed black line is the lower limit for AGNs by Kauffmann et al. (2003). The predicted cumulative line ratios from the models are overlaid. The gray lines correspond to a single value of metallicity and different values of turbulence (the velocity value is written on the left and reproduced with different colours); from left to right the velocity is constant and the metallicity increases (from 0.3 to 1 Z⊙). The GX is fixed to 100. Left column: cumulative emission of [O III]λ 5007 Å/Hβ vs. [N II]λ 6583 Å/Hα; central column: [O III]λ 5007 Å/Hβ vs. [S II]/Hα; right column: [O III]λ 5007 Å/Hβ vs. [O I]/Hα. Top row: cumulative emission at AV = 0.001 mag; second row: cumulative emission at AV = 0.1 mag; third row: cumulative emission at AV = 1 mag; bottom row: cumulative emission at AV = 5 mag. |
Appendix F: Predicted cumulative line emission
Table F.1 presents the 30 brightest predicted lines, from brightest to faintest, for the seven models described in the paper. The predicted lines are for AV = 0.1, 1, 5, and 30 mag.
Brightest predicted cumulative line emission.
All Tables
Restricted ranges of free parameters are given for four values of AV = 0.001, 0.1, 1, and 5 mag.
Restricted parameter space of the free parameters that reproduce the infrared observations.
All Figures
 |
Fig. 1. Spectral energy distribution of the input radiation field for GX = 10 (black line) and the total outward radiation field (continuum and line emission) stopping the model at different AV (blue line): 0.1, 5, and 30 mag. The two vertical green lines show the energy necessary to create O++ and N+, two of the ions whose emission is used to constrain the modeling. The dots represent the average observed integrated flux for the filaments surrounding NGC 1275 of 4.0 × 10−16 erg cm−2 s−1 arcsec−2 in the 0.6–2.0 keV band (red dot; Walker et al. 2015) and of 5 × 10−15 erg cm−2 s−1 arcsec−2 in the 2–10 keV band (magenta dot; Sanders et al. 2005). The orange background highlights the range over which the integrated intensity is calculated to scale GX. |
| In the text | |
 |
Fig. 2. Temperature (left column), hydrogen density (middle column), and ionization fraction ne−/nH (right column) of the gas predicted by CLOUDY as functions of the visual extinction AV and the X-ray radiation field scaling factor GX (top row), the turbulent velocity dispersion vtur (middle row), and the metallicity Z (bottom row). Nonvarying parameters are set to their standard values. In particular, the total pressure of the gas is set to 106.5 K cm−3, GX = 10 (for middle and bottom rows), vtur = 10 km s−1 (for top and bottom rows), and Z = Z⊙ (for top and middle rows). The black curves correspond to isocontours. The transition from ionized to atomic phase and that from atomic to molecular are defined by ne−/nH0 = 1 and nH0/nH2 = 1, respectively, indicated with a blue curve. The blue I, A, and M identify the different gas phases: ionized, atomic, and molecular, respectively. |
| In the text | |
 |
Fig. 3. Effects of the radiation field intensity. Physical properties as a function of AV for models in thermal equilibrium and constant pressure fixed at 106.5 K cm−3, with solar metallicity, turbulent velocity 10 km s−1, and different values of X-ray radiation field intensity: GX = 10−1 (left column), GX = 101 (central column) and GX = 102 (right column). Top row: gas temperatures. Second row: total hydrogen density in black and ionization fraction (ne/nH) in blue. Third row: relative abundances of hydrogen. Bottom row: relative abundances of carbon (yellow), oxygen (blue), sulfur (green), and CO (black). The white background indicates the ionized phase, the gray background the atomic phase, and the dark gray the molecular phase. The transition from ionized to atomic phases and that from atomic to molecular correspond to density ratios of e−/H0 = 1 and H0/H2 = 1, respectively. |
| In the text | |
 |
Fig. 4. Effects of the radiation field intensity on heating mechanisms and line emission. Heating and cooling mechanisms as a function of AV for the same models as those in Fig. 3. Top row: heating mechanisms. CLOUDY provides the first five main heating mechanisms as output. If one of the heating mechanisms is not one of these five for some values of AV, the mechanism is not shown in the figure. This is the reason for some vertical straight lines in the panels. Second row: emissivity of carbon, oxygen, and sulphur lines, Hα and Hβ. Bottom row: cumulative emission of carbon, oxygen, and sulphur lines, Hα and Hβ. The cumulative emission values are theoretical, and some of these values are too low to be detected by the instruments. The instrumental limitations mean that access is only given to the brightest values, thus to the emission arising from the denser parts of the cloud. It is important to remember that by comparing the observations with this predicted line emission we only constrain the properties of the denser phase of the cloud. |
| In the text | |
 |
Fig. 5. BPT diagrams. The gray dots (filament values) and the stars (nucleus values) represent the data from Mcdonald et al. (2012). The size of the dots decreases with increasing distance of the corresponding object from the nuclei. The solid black line is the upper limit for HII regions by Kewley et al. (2001) and the dashed black line is the lower limit for AGNs by Kauffmann et al. (2003). The predicted cumulative line ratios from the models are overlapped. The color bar corresponds to the different values of GX (the logarithm of the value is written on the bar); each symbol corresponds to one turbulence value and the size of the symbols increases with the metallicity (from 0.3 to 1 Z⊙). Top row: cumulative emission at AV = 0.001 mag; second row: cumulative emission at AV = 0.1 mag; third row: cumulative emission at AV = 1 mag; bottom row: cumulative emission at AV = 5 mag. Left column: [O III]λ 5007 Å/Hβ vs. [N II]λ 6583 Å/Hα; central column: [O III]λ 5007 Å/Hβ vs. [S II]/Hα; right column: [O III]λ 5007 Å/Hβ vs. [O I]/Hα. |
| In the text | |
 |
Fig. 6. Comparison of observed and predicted cumulative line ratios: [NeII]/[NeIII] (top), [O I]λ 63.2 μm/[C II]λ 157.7 μm (middle), and H2 S(1) 17.0 μm/H2 S(2) 12.3 μm (bottom), as a function of AV. The blue background highlights the observed line ratio of [NeII]/[NeIII], with values between 1.10 and 5.25 (data from Donahue et al. 2011, Egami et al. 2006, and Johnstone et al. 2007). The observed line ratio [O I]λ 63.2 μm/[C II]λ 157.7 μm ranges between 0.22 and 1.64 (values from Edge et al. 2010, Mittal et al. 2011, 2012, and Werner et al. 2014), and is shown in green, and the yellow background highlights the observed ratio of the two pure rotational H2 lines, between 0.2 and 0.9 (values from Donahue et al. 2011, Egami et al. 2006, and Johnstone et al. 2007). Column on the left: predicted ratios for models with vtur = 10 km s−1 and solar metallicity, central column: predicted ratios for models with GX = 10 and solar metallicity, and column on the right: predicted ratios for models with vtur = 10 km s−1 and GX = 10. |
| In the text | |
 |
Fig. 7. Comparison of observed and predicted ro-vibrational H2 lines, normalized by Paα, as a function of AV for the models described in Sect. 2.2. The different background highlights the observed ratios, between 0.1 and 2.3 (values from Edge et al. 2002). For each ratio, the color of the background and that of the corresponding theoretical cumulative ratio are the same. Column on the left: predicted cumulative emission for models with turbulence of 10 km s−1, solar metallicity, and various values of GX: 0.1 (top), 10 (middle), and 100 (bottom); central column: predicted cumulative emission for models with GX = 10, solar metallicity, and various values of turbulence: 0 (top), 10 (medium), and 50 (bottom) km s−1; column on the right: predicted cumulative emission for models with turbulence 10 km s−1, GX = 10, and various values of metallicity: 0.3 (top), 0.65 (middle), and 1 (bottom) Z⊙. |
| In the text | |
 |
Fig. 8. Comparison of observed (green and blue background) and predicted cumulative CO emission: 1–0, 2–1, and 3–2. The predicted values are for AV = 30 mag (end of the cloud). Panel on the left: predicted values as a function of GX for models with turbulence of 10 km s−1 and solar metallicity. Panel on the right: predicted values as a function of turbulence for models with GX = 10 and solar metallicity. |
| In the text | |
 |
Fig. 9. Predicted cumulative surface brightness of Hα+[N II]λ 6548, 6583 Å (dashed line) and predicted ionizing continuum 0.6–2 keV X-ray band (solid line) as a function of AV for a model with GX = 10, vtur = 10 km s−1, and Z = Z⊙. The dark gray and soft gray background show the range of predicted ionizing continuum 0.6–2 keV X-ray and cumulative surface brightness of Hα+[N II]λ 6583 Å, respectively, for models with GX in the range 1–100. The red dots show the predicted transmitted continuum 0.6–2 keV X-ray band estimated at AV = 1, 5, 10, and 30 mag. The area covered by red (blue) diagonal lines represents a factor of three of the observed surface brightness of Hα+[N II]λ 6548, 6583 Å from Conselice et al. (2001) for region 15 of that paper, 1.3 × 10−15 erg cm−2 s−1 arcsec−2 (of 0.6–2 keV X-ray band from Walker et al. 2015, 4.3 × 10−16 erg cm−2 s−1 arcsec−2). |
| In the text | |
 |
Fig. C.1. Comparison of the X-ray component of one of the input SEDs used in this study, i.e., GX = 10 (black curve), with that of the input SED used in Ferland et al. (1994; green dashed curve). The red star represents the observed surface brightness measurements by Walker et al. (2015). |
| In the text | |
 |
Fig. D.1. Same as Fig. 3, but this time GX is fixed at 10 and the turbulence varies: 0 km s−1 (left column), 10 km s−1 (central column), and 50 km s−1 (right column). |
| In the text | |
 |
Fig. D.2. Same as Fig. 4, but this time GX is fixed at 10 and the turbulence varies: 0 km s−1 (left column), 10 km s−1 (central column), and 50 km s−1 (right column). |
| In the text | |
 |
Fig. D.3. Same as Fig. 3, but this time GX is fixed at 10 and the metallicity varies: Z = 0.3 Z⊙ (left column), Z = 0.65 Z⊙ (central column), and Z = Z⊙ (right column). |
| In the text | |
 |
Fig. D.4. Same as Fig. 4, but this time GX is fixed at 10 and the metallicity varies: Z = 0.3 Z⊙ (left column), Z = 0.65 Z⊙ (central column), and Z = Z⊙ (right column). |
| In the text | |
 |
Fig. E.1. BPT diagrams. Comparison of the observed line ratios with the model predictions. The gray dots (filament values) and the stars (nucleus values) represent the data from Mcdonald et al. (2012). The size of the dots decreases with increasing distance of the corresponding object from the nuclei. The solid black line is the upper limit for HII regions by Kewley et al. (2001) and the dashed black line is the lower limit for AGNs by Kauffmann et al. (2003). The predicted cumulative line ratios from the models are overlaid. The gray lines correspond to a single value of metallicity and different values of X-ray emission (the logarithm of the value is written on the left and reproduced with different colors); from left to right the X-ray emission is constant and the metallicity increases (from 0.3 to 1 Z⊙). The turbulent velocity is fixed to 10 km s−1. Left column: cumulative emission of [O III]λ 5007 Å/Hβ vs. [N II]λ 6583 Å/Hα; central column: [O III]λ 5007 Å/Hβ vs. [S II]/Hα; right column: [O III]λ 5007 Å/Hβ vs. [O I]/Hα. Top row: cumulative emission at AV = 0.001 mag; second row: cumulative emission at AV = 0.1 mag; third row: cumulative emission at AV = 1 mag; bottom row: cumulative emission at AV = 5 mag. |
| In the text | |
 |
Fig. E.2. BPT diagrams. Comparison of the observed line ratios with the model predictions. The gray dots (filament values) and the stars (nucleus values) represent the data from Mcdonald et al. (2012). The size of the dots decreases with increasing distance of the corresponding object from the nuclei. The solid black line is the upper limit for HII regions by Kewley et al. (2001) and the dashed black line is the lower limit for AGNs by Kauffmann et al. (2003). The predicted cumulative line ratios from the models are overlaid. The gray lines correspond to a single value of metallicity and different values of turbulence (the velocity value is written on the left and reproduced with different colours); from left to right the velocity is constant and the metallicity increases (from 0.3 to 1 Z⊙). The GX is fixed to 100. Left column: cumulative emission of [O III]λ 5007 Å/Hβ vs. [N II]λ 6583 Å/Hα; central column: [O III]λ 5007 Å/Hβ vs. [S II]/Hα; right column: [O III]λ 5007 Å/Hβ vs. [O I]/Hα. Top row: cumulative emission at AV = 0.001 mag; second row: cumulative emission at AV = 0.1 mag; third row: cumulative emission at AV = 1 mag; bottom row: cumulative emission at AV = 5 mag. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.