EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 648 (April 2021) A&A, 648 (2021) A20 Full HTML
Free Access
Issue
A&A
Volume 648, April 2021
Article Number A20
Number of page(s) 15
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/202040099
Published online 07 April 2021

© ESO 2021

1 Introduction

The development of second and third-generation echelle spectrographs has produced a significant boost in the radial velocity (RV) searches for Earth-like planets around M-dwarfs. Since the first discovery of an exoplanet orbiting an M-type star using the RV method (Delfosse et al. 1998; Marcy et al. 1998), a total of 116 planets have been discovered around M-dwarfs using this technique1. The vast majority of them (75%) have been detected in the last decade via such instruments as HARPS-N (e.g., Affer et al. 2019; Pinamonti et al. 2019), HARPS (e.g., Dreizler et al. 2020; Grandjean et al. 2020), CARMENES (e.g., Lalitha et al. 2019; Zechmeister et al. 2019), SOPHIE (e.g., Hobson et al. 2019), and PFS (e.g., Feng et al. 2019).

Despite the fact that M-dwarfs are the most common stars in the Milky Way (Chabrier & Baraffe 2000; Winters et al. 2015), only 10% of all known planetary companions have been detected around this type of star. From the complete four-year Kepler dataset, Dressing & Charbonneau (2015) found 156 planet candidates orbiting M-type stars, estimating an average of ~2.5 planets per star in the Porb < 200 d and R = 1–4 R⊕ regime. This occurrence rate, combined with their closer habitable zones due to their lower luminosities, makes such low-mass stars ideal targets for the search of temperate Earth-like planets. However, the complexity of the characteristic stellar activity pattern of these stars requires a careful analysis of the chromospheric activity indicators to identify false planetary signals induced by the rotation of the star (Bonfils et al. 2007; Robertson et al. 2014; Suárez Mascareño et al. 2018; Toledo-Padrón et al. 2019).

The planetary formation scenario provided by the core accretion theory (Pollack et al. 1996) indicates that the most common planets around M-dwarfs are super-Earth and Neptune-mass planets (Reiners et al. 2018; Luque et al. 2018; Perger et al. 2019; González-Álvarez et al. 2020), most of them located in the Porb< 100 d region. Nonetheless, there have also been some detections of gas giants orbiting late-type stars (Butler et al. 2006; Gaudi et al. 2008; Howard et al. 2010; Morales et al. 2019), although their location tends to be beyond the snow line of the system (where volatile compounds such as water or carbon dioxide could condense into solid ice grains). Endl et al. (2006) estimated a frequency <1.27% of Jovian planets around M-dwarfs, which is lower than that of FKG-type stars. The elusiveness of giant planets orbiting M-type stars is contrasted by the higher occurrence rate of super-Earth planets (Tuomi et al. 2014), with some Earth-like planets also being reported (Anglada-Escudé et al. 2016; Astudillo-Defru et al. 2017a; Bonfils et al. 2018; Zechmeister et al. 2019; Dreizler et al. 2020), but still lacking in tems of proper statistics of their population and occurrence rate at present.

We report the discovery of a short-period super-Earth orbiting the nearby M-type star GJ 740, as part of the HADES (HArps-n red Dwarf Exoplanet Survey) program, complemented by data from HARPS and the CARMENES survey. HADES is a collaboration between the Instituto de Astrofísica de Canarias (IAC), the Institut de Ciències de l’Espai (IEEC-CSIC), and the Italian GAPS (Global Architecture of Planetary Systems) program (Covino et al. 2013) and it is aimed at detecting and characterizing exoplanets around M-dwarfs, as well as improving the available statistical information on the properties of these objects. The reported detection contributes to the planetary discoveries made by the collaboration (Affer et al. 2016, 2019; Perger et al. 2017a, 2019; Suárez Mascareño et al. 2017; Pinamonti et al. 2018, 2019). In this work, we also explore the possibility of an outer high-mass planetary companion characterized by a long orbital period and its impact on the planetary configuration.

The paper is structured as follows. Section 2 presents the dataset used in this work, including both spectroscopy and photometry. Section 3 details the stellar properties of GJ 740. Section 4 demonstrates the techniques used for the RV and stellar activity indicator measurements. Section 5 describes the analysis of these and the photometric measurements. Section 6 features a discussion of these results and Sect. 7 provides our conclusions.

2 Data

2.1 Spectroscopic dataset

The HADES RV program monitored GJ 740 from 26 May 2013 (BJD = 2 456 438.7) to 16 June 2019 (BJD = 2 458 650.7) using the HARPS-N spectrograph (Cosentino et al. 2012) installed at the 3.6 m Telescopio Nazionale Galileo (TNG) in the Roque de los Muchachos Observatory, Spain. The high resolution of R ~ 115 000 provided by this fiber-fed echelle spectrograph, along with its spectral range from 3830 to 6900 Å are ideal for high-precision RV searches. We obtained a total of 129 HARPS-N spectra over a time span of 6 yr. Every spectrum was taken using an exposure time of 900 s to average out the short-time periodic oscillations of the star (Dumusque et al. 2011), although this phenomenon has not yet been detected in M-dwarfs (Berdiñas et al. 2017). The average signal-to-noise ratio (S/N) achieved at 5500 Å per pixel was 110, enough to ensure a good exposure level of the blue part of the spectra, which contains the Ca II H&K lines that are especially weak for M-type stars (Giampapa et al. 1989; Lovis et al. 2011). Some of the spectra were obtained using a Fabry-Pérot (FP) interferometer (Wildi et al. 2010) for the wavelength calibration due to the lack of availability of the Th-Ar lamp for the simultaneous calibration. In those cases, the Th-Ar lamp was used to obtain the absolute calibration prior to the observations, and then all the FP spectra were referred to the Th-Ar calibration spectrum with a drift value. The interferometer provides a high level of short-term RV precision and has the advantage of avoiding possible contamination of the Ca II H&K lines, but lacks the precise drift correction provided by the Th-Ar lamp. However, the mean inter-night instrumental drift calculated by Perger et al. (2017b) for the whole HADES sample was about 1 m s−1.

We also acquired 32 spectra with the CARMENES spectrograph at the Calar Alto Observatory (Quirrenbach et al. 2018) overlapping at the epoch during which the HARPS-N observations were carried out. CARMENES allows for the simultaneous observation in two different channels that cover the visible (between 5200 and 9600 Å) and near-infrared (between 9600 and 17 100 Å) regions of the spectra, with resolutions of R ~ 94 600 and R ~ 80 400, respectively. The RV precision provided by both channels is ~1 m s−1, similar to the one obtained in HARPS-N. The CARMENES spectra were acquired from 11th April 2016 (BJD = 2 457 489.7) to 27th July 2017 (BJD = 2 457 962.5). This dataset is characterized by an average S/N per pixel of 122. Hollow cathode lamps combined with an FP etalon were used to obtain the wavelength calibration of these spectra (Bauer et al. 2015).

Additionally, this star has been monitored from the southern hemisphere using the HARPS spectrograph (Mayor et al. 2003) installed at the 3.6 m telescope of La Silla Observatory, Chile. This fiber-fed echelle spectrograph has similar characteristics to its northern counterpart. It is contained in a vacuum vessel to minimize the RV drifts produced by temperature and pressure variations. We used 57 HARPS spectra from the ESO public database taken over a time span of more than 4 yr: from 30 June 2008 (BJD = 2 454 647.7) to 10 August 2012 (BJD = 2 456 149.7). The exposure time used was the same as for the HARPS-N spectra, achieving an average S/N per pixel at 5500 Å of 81.5. In this case, the majority of the spectra were calibrated with an FP interferometer.

2.2 Photometric dataset

To complement the spectroscopic analysis, we used 474 photometric measurements from All Sky Automated Survey (ASAS; Pojmanski 1997). The measurements come from one of the three observing stations of the project (ASAS-S/ASAS-3), located at the Las Campanas Observatory, Chile. This survey carries out observations in V and I bands simultaneously, with a plate scale of 14”/pixel and an average accuracy of ~0.05 mag per exposure, achieving the best results in the range of V ~ 8–12 mag (which includes GJ 740). The light curve provided by ASAS includes a quality flag associated with every measurement. Using these flags, we are able to discard the worst-quality data (labeled as grade ‘C’ and ‘D’). This leaves us with 459 measurements covering a time span of eight years: from 26 September 2001 (BJD = 2 452 178.6) to 2 November 2009 (BJD = 2 455 137.5). Since the original data were given in the heliocentric Julian date (HJD), we performed a conversion to the barycentric Julian date (BJD) considering the difference between the two systems of up to 8 s due to the motion of the Sun (the reference frame in this case), caused mainly by Jupiter and Saturn (Eastman et al. 2010).

We also relied on the publicly available light curve from the SuperWASP database (Pollacco et al. 2006). The data were taken with the survey facilities located at the South African Astronomical Observatory and the Roque de los Muchachos Observatory. The cameras used feature a plate scale of 13.7”/pixel and an average accuracy better than 1% for objects with V ~ 7.0–11.5. We analyzed 2350 photometric data points taken between 18 June 2006 (BJD = 2 453 904.7) and 23 July 2008 (BJD = 2 454 670.7). A time conversion from HJD to BJD was performed based on the procedure used for the ASAS dataset.

Within the framework of the EXORAP project, we collected ~5 yr of B, V, R, and I-band photometry at the INAF-Catania Astrophysical Observatory with an 80 cm f/8 Ritchey-Chretien robotic telescope (APT2) located at Serra la Nave on Mt. Etna. We performed data reduction by overscan, bias, dark subtraction, and flat fielding with IRAF2 procedures and we visually inspected the data to check the quality (see Affer et al. 2016 for details). Errors in the individual photometric points include the intrinsic noise (photon noise and sky noise) and the root-mean-square (RMS) of the ensemble stars used for computing the differential photometry. The final dataset contains ~200 photometric points for each of the B, V, and R bands distributed over five consecutive seasons, between BJD = 2 456 480.5 and BJD = 2 458 003.5. Due to technical reasons, the I-band photometry contains only 100 points covering the first four seasons.

3 GJ 740

GJ 740 (HD 176029, BD+05 3993) is a bright (mV = 9.2) M1V-type high-proper motion star, located at 11.1 pc from the Sun (Gaia Collaboration 2018). The search for companions of this star has produced null detections (Carson et al. 2005; Lamman et al. 2020), reporting only some faint field background objects (Carson et al. 2005). Stellar parameters from the literature are shown in Table 1 along with new values established in this work.

This star has been studied by Astudillo-Defru et al. (2017b), who obtained a rotation period of 24 d using 55 HARPS spectra. GJ 740 was included within a sample of 107 M dwarfs studied by Giacobbe et al. (2020) as part of the APACHE photometric transit search project (Sozzetti et al. 2013), recovering a period of 35.6422 ± 0.0063 d from a 765 dtime span dataset. Through another photometric study based on the ASAS survey, Díez Alonso et al. (2019) obtained a rotation period of 35.20 ± 0.30 d. Suárez Mascareño et al. (2018) carried out a stellar activity analysis on the whole HADES sample, deriving an expected rotational period of Prot = 36.3 ± 1.7 d for this staradding 93 HARPS-N to the existing HARPS spectra, along with 458 ASAS photometricmeasurements. This study provided also a mean level of chromospheric activity of 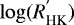log(R^{'}_HK)$\log(R^{&#x0027;}_{\textrm{HK}})$ = −4.88 ± 0.04 computed through the Ca II H&K lines, along with a magnetic cycle of 2044 d detected in several stellar activity indicators. We extend this stellar activity study with new HARPS-N and CARMENES spectra in order to model the chromospheric effects on the RV measurements.

Table 1

Stellar properties of GJ 740.

4 Determination of RVs and stellar activity indicators

For the RV calculation in the HARPS-N and HARPS datasets, we followed two different approaches. The first one is based on the HARPS-N DRS (Data Reduction Software) pipeline (Lovis & Pepe 2007), which builds a cross-correlation function (CCF) for a certain template mask driven by the spectral type. For GJ 740, we used the M2 mask, which contains 9196 wavelength intervals of 0.02 Å width with different depths located at the positions of isolated stellar lines. This mask is shifted 161 times in an RV range of ~40 km s−1, providing a CCF for each echelle order. The resulting CCFs are fitted by a Gaussian along with an offset constant to obtain an RV measurement per echelle order. These measurements are weighted in terms of the flux of each order to obtain the final RV value. We modify this last step of the process by weighting each CCF order according to its mean flux, performing a secular acceleration correction based on the proper motion of the star, and fitting the combined CCF with a Gaussian along with a second-order polynomial, which provides slightly better results. The RVs computed through this methodology exhibit an RMS = 4.3 m s−1 with a mean RV uncertainty of 1.4 m s−1 in the case of HARPS and an RMS = 6.3 m s−1 with a mean RV uncertainty error of 1.2 m s−1 in the case of HARPS-N. The difference between both datasets is caused by the RV trend present in the HARPS-N measurements.

The second approach that we implemented for computing the RVs of the HARPS-N and HARPS spectra is based on the TERRA reduction software (Anglada-Escudé & Butler 2012), which corrects the spectra for the blaze function, secular acceleration (Kürster et al. 2003), and then puts the spectra in the solar system barycentric frame by correcting for the barycentric and stellar RV. Then it performs a template matching with the highest S/N spectra, carrying out a least-squares fit on the residuals for every shift and providing an RV value from the minimum χ2 value. The RVs computed by TERRA yield an RMS = 4.3 m s−1 and a mean uncertainty error of 0.9 m s−1 in the case of HARPS and RMS = 5.8 m s−1 and mean uncertainty error of 0.8 m s−1 in the case of HARPS-N. These results support the superiority of performance on the part of the TERRA pipeline for M-dwarfs (Perger et al. 2017b) and for this reason, we opted for this reduction procedure in our analysis.

In the case of the CARMENES dataset, the spectra were reduced using the CARACAL pipeline (Caballero et al. 2016) and the RVs were computed using the SERVAL tool (Zechmeister et al. 2018), which is a public code3 similar to TERRA. This tool performs a template-matching using a high S/N template built from the available spectra of the star as a reference. The CARMENES RV time series computed by SERVAL presents an RMS = 4.3 m s−1, with a mean uncertainty of 1.8 m s−1.

In order to model the stellar activity effects on the RV measurements, we studied the flux variations of certain spectral lines connected with several chromospheric activity indicators. The measurements were made on the spectra corrected from the blaze function (using a blaze spectrum given by the DRS pipeline), the barycentric velocity of the Earth, and the radial velocity of the star. We also carried out a re-binning of the spectra in order to obtain the same wavelength width per pixel (0.01 Å). To avoid any wavelength shifts that can affect the flux measurements, we correlated the spectra using the first spectrum taken by each spectrograph as a reference. All these spectra were co-added into an average spectrum that was normalized and used for calculating the weight of each echelle order for the individual spectra. Once all these corrections had been applied to the individual spectra, we derived three activity indicators: Hα (Kürster et al. 2003; Gomes da Silva et al. 2011), the Smw index associated with the Ca II H&K lines (Noyes et al. 1984; Lovis et al. 2011), and the NaD index associated with the doublet of NaI D1 and D2 lines (Díaz et al. 2007; Houdebine et al. 2009). The continuum passbands of this last index were modified following Toledo-Padrón et al. (2019) in order to have them in the same echelle order of the core lines, avoiding the overlap zones between spectral orders. Moreover, we calibrated the Mount-Wilson S-index following Lovis et al. (2011) and Suárez Mascareño et al. (2015). The CARMENES spectra do not cover this index in their wavelength range. The error on all the measurements was calculated using the RMS on the spectral bands related to each index (core lines and continuum passbands), along with error propagation.

The stellar activity can also be tracked using properties related to the CCF such as the full width at half maximum (FWHM) or the bisector span (BIS). We measured the FWHM using the CCFs from the DRS pipeline weighted, corrected for secular acceleration, and fitted by a Gaussian with a second-order polynomial. For the BIS measurements, we used the bisector fits provided by the same pipeline, although this time series did not provide any relevant information for the stellar activity study since the BIS is not well defined for M-dwarfs due to the bumps present on the wings of the CCF (Rainer et al. 2020).

To remove outliers in all time series, we applied a 3σ-clipping in values and another 3σ-clipping in errors to each one of them, using the median value and error as a reference. This serves to discard points that can be related to stellar flares, a phenomenon that is especially important in the case of active M-type stars (Reiners 2009; Hawley et al. 2014). For consistency, a measurement cataloged as an outlier in one of the time series was discarded in the rest of the time series. The final measurements resulting from this process are shown in Fig. 1, along with the photometric time series, and the properties of each dataset are listed in Table 2.

Table 2

Properties of all the datasets used in this work.

5 Time-series analysis

We analyzed the periodic signals present in the time series of RVs, photometric observations, and chromospheric activity indicators related to stellar rotation and magnetic activity. First, we built the generalized Lomb Scargle (GLS) periodograms (Lomb 1976; Zechmeister & Kürster 2009) and established three threshold levels related to the false alarm probability (FAP) of these signals (Horne & Baliunas 1986). The threshold levels were obtained by randomizing each time series separately in a bootstrapping process of 10 000 iterations (Endl et al. 2001). We then studied the most significant peaks in the periodograms based on these threshold levels. For this study, we adopted the significance standards established in Toledo-Padrón et al. (2019), with the 0.1 and 10% levels FAP separating the statistically significant signals, those whose significance is unclear, and the non-significant ones. The first periodograms from the stellar activity indicators, along with the photometric data and the RVs are shown in Fig. 2.

Using the S-index values, we computed a mean chromospheric activity level of 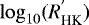log10(R_HK^{'})$\log_{10} (R_{\textrm{HK}}^{&#x0027;})$ = −4.88 ± 0.05, which matches the one published in Suárez Mascareño et al. (2018). That publication presents an analysis of the whole HADES sample to establish a relation between the activity level and the rotation period of the stars of the sample, including GJ 740, which we found to have a Prot = 36.3 ± 1.7 d. Figure 2 clearly shows that all the periodograms present significant peaks near to this value (yellow line), along with two bumps at 330 d and 440 d. In all the spectroscopic periodograms, the statistical significance of the rotationsignal is exceeded by a long-period signal that could be associated with the magnetic cycle of the star.

thumbnail Fig. 1

Top: time series of the RV and the chromospheric activity indicators with combined measurements from HARPS (representedin violet), HARPS-N (represented in cyan), and CARMENES (represented in yellow). Bottom: time series of the photometric magnitudes taken with ASAS (represented in dark red) and EXORAP (represented in orange) in the B, V, R, and I filters.
thumbnail Fig. 2

Periodograms of the RV, FWHM, Hα, Smw, NaD, ASAS V, EXORAP B, EXORAP V, and EXORAP R-band magnitude time series. The periods related to stellar rotation, planetary companion, and possible magnetic cycle have been represented as yellow, cyan, and brown vertical lines, respectively. The green, brown, and red horizontal lines indicate the 0.1, 1, and 10% FAP levels, respectively.

5.1 Long-term variation

The most significant peak in all the spectroscopic GLS periodograms of Fig. 2 is related to a long-term signal whose periodicity around 8 yr makes it compatible with a magnetic cycle similar to the one observed in the Sun. The length of the photometriccampaigns is not enough to detect a signal with this periodicity. This signal has a significance much greater than the 0.1% FAP level in all cases. We fitted this signal with a sinusoidal model that includes offset and jitter terms for each spectrograph. We first used an implementation of the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm (Schraudolph et al. 2007)available in the minimize package from the scipy library to optimize the parameters of the model. Then we carried out an Markov chain Monte Carlo (MCMC) analysis based on the results of the BFGS algorithm using the emcee package (Foreman-Mackey et al. 2013), performing simulations within a Bayesian framework to infer the probability distribution over all the parameters considered. We used 10 000 steps for the burn-in stage, 50 000 steps for the constructionstage, and 512 walkers to sample the parameter space. We established a convergence criterion based on the auto-correlation function to ensure that the previous setup produces a correct parameter distribution. This analysis provided the results shown in Fig. 3 when the long-term component is modeled along with the rotation component.

In the middle panels of Fig. 3, we show how the long-term signal in the RV time series presents a shift in periodicity with respect to the signals detected in the activity indicators, displaying a compatibility with them at 2σ. The periodicity of the signal in the activity indices is around 2820 d (2701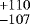−107+110$^{&#x002B;110}_{-107}$ in FWHM, 2832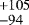−94+105$^{&#x002B;105}_{-94}$ in Hα, 2848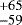−59+65$^{&#x002B;65}_{-59}$ in Smw, and 2913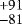−81+91$^{&#x002B;91}_{-81}$ in NaD), while in the RV time-series is located at 3363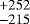−215+252$^{&#x002B;252}_{-215}$ d. Our time span of ~4000 d did not allow us to detect a second cycle to ensure the periodicity of the signal.

The right panels of Fig. 3 show the periodograms related to the residuals obtained after subtracting the models represented in the left panels from each time series. The jitter terms provided by the MCMC were added quadratically to the errors ofeach dataset and the offset applied to all the measurements. In these plots, the bumps at 330 d and 440 d from Fig. 2 have completely disappeared from the periodograms, which indicates that these signals were aliases of the long-term signal. We found signals related to the rotation of the star around 40 d in the RV, Hα, Smw, and NaD time series as the main peaks. In the FWHM case, the signal related to the first harmonic of the stellar rotation shows a greater amplitude than the forest of peaks around 40 d.

thumbnail Fig. 3

Analysis of the long-term signal. Left: RV, FWHM, Hα, Smw, and NaD time series with their respective model of the long-term signal. Center: posterior distribution for the periodicity of the long-term signal. Right: periodograms of the residuals after subtracting the model. The blue, green, and red horizontal lines indicate the 0.1, 1, and 10% FAP levels, respectively. The highest peak of the periodogram is marked with a blue shaded area.
thumbnail Fig. 4

Analysis of the rotation signal. Left: RV, FWHM, Hα, Smw, and NaD time series with their respective model of the long-term signal and the rotation signal. The shaded regions indicate the 1σ confidence band of the GP model. Center: posterior distribution for the periodicity of the rotation signal. Right: periodograms of the residuals after subtracting the model. The blue, green, and red horizontal lines indicate the 0.1, 1, and 10% FAP levels, respectively. The highest peak of the periodogram is marked with a blue shaded area.

5.2 Rotation period

For the nextstep of the analysis, we used the original time series to characterize the rotation through a Gaussian process (GP) regression (Haywood et al. 2014; Rajpaul et al. 2015; Ambikasaran et al. 2015) and to simultaneously recompute the activity cycle model that was used previously. To model the stellar rotation, we used the following quasi-periodic kernel: κ(τ)=Krot22+Ce−τ/ts[cos(2πτProt)+(1+C)]+(σRV2(t)+σj2)δτ,\begin{equation*} \kappa(\tau)=\frac{K_{\textrm{rot}}^{2}}{2&#x002B;C}e^{-\tau/t_{s}}\left[\cos\left(\frac{2 \pi \tau}{P_{\textrm{rot}}}\right)&#x002B;(1&#x002B;C)\right]&#x002B;\left(\sigma_{\textrm{RV}}^{2}(t)&#x002B;\sigma_{\textrm{j}}^{2}\right)\delta_{\tau},\end{equation*}(1)

which contains the squared amplitude of the signal 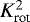Krot2$K_{\textrm{rot}}^{2}$, the periodicity of the signal Prot, and the timescale of the surface phenomena in the star ts. The kernel also contains a term named C whose role is to measure the relative importance between the two components of the kernel: the periodic (i.e., the cosine) and non-periodic (i.e., the exponential). This kernel has been proven to provide good results in the activity analysis of Proxima Centauri performed by Suárez Mascareño et al. (2020). We fitted the parameters of the kernel using the celerite code (Foreman-Mackey et al. 2017) with the same setup of steps, walkers, and convergence criterion as the one described in the previous subsection. The parameters obtained for all of the time series (including the new values of the parameters related to the long-term signal) are listed in Table 3 and the results are shown in Fig. 4.

The middle panels of Fig. 4 show that the rotation period in the RV time series is not well-constrained, with a wide distribution reaching its maximum peak close to the first harmonic of the rotation period. The coherence time recovered from the RV kernel is much shorter than the one obtained in the rest of the time series. In the chromospheric activity-indicator time series, we detected the rotation signal with a periodicity of ~37 d (36.9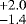−1.4+2.0$^{&#x002B;2.0}_{-1.4}$ in FWHM, 36.1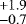−0.7+1.9$^{&#x002B;1.9}_{-0.7}$ in Hα, 37.1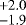−1.9+2.0$^{&#x002B;2.0}_{-1.9}$ in Smw, and 36.5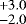−2.0+3.0$^{&#x002B;3.0}_{-2.0}$ in NaD). The fact that the parameter ts is a few stellar rotations in the activity indices is consistent with the evolutionary timescale of the active regions (Scandariato et al. 2017). Of these activity indicators, the Hα index exhibits the most significant stellar rotation signal (see Fig. 3) and provides the most stable stellar activity characterization, with lower relatives errors in the rotation parameters fitted (see Table 3). A zoom-in of the Hα model is shown in Fig. 5.

We then computed the Bayesian evidence logZ (Perrakis et al. 2014) for all the time series. When comparing the log Z values of two different models, a difference between their logZ values greater than 10 indicates a significant preference for the model with the higher log Z. The results indicate that the rotation+long-term signal model is preferred over the long-term signal model. The first model is characterized by greater logZ values in allthe time series, presenting a difference greater than 30 with respect to the values computed for the second model. This Bayesian parameter is shown in Table 4 for all the models considered in this work.

In Fig. 2 we previously observed how the ASAS photometric dataset exhibit the same rotation signal as the one found in the chromospheric time series. The GP regression with the rotation kernel reveals a periodicity of Prot = 35.60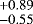−0.55+0.89$^{&#x002B;0.89}_{-0.55}$ d for this signal. No additional significant signals were detected after this model was subtracted.

The analysis of the SuperWASP photometric time series did not reveal any clear information about the rotation of GJ 740 since all the short-term signals have low significance. This time series presents the problem that results from the majority of its photometricmagnitudes having been measured in a time span of 130 d, with only 9 d of observations outside this range. The time span of the dataset and the density of points is not enough to have a good characterization of the long-term behavior of the star, a fact that is reflected in the lack of long-term significant peaks after the trend correction. We found a similar time span problem in the APACHE dataset analyzed in Giacobbe et al. (2020) with regard to the long-term signal.

We also carried out a pre-whitening analysis of the four EXORAP light curves. The main feature of the periodograms of the pre-whitened B and V light curves is a forest of strong peaks between 20 and 60 days, which are aliases of the strongest peak at ~36 days with FAP < 0.1%. The same applies to the R-band light curve, where the 36 d period has a slightly higher FAP ~ 1%. In the I-band all the signals are non-statistical significant (i.e., FAP > 10%) due to the short time span of the light curve.

We then performed a more sophisticated analysis by fitting the light curves with a cubic polynomial function in a Monte Carlo framework, using the emcee package (Foreman-Mackey et al. 2013). We included a GP to characterize the red noise in the data introduced by stellar activity, allowing independent offsets for the two different instrumental setups used during the survey. The posterior distribution of the B, V, and R light curves shows that the correlated noise is consistent with the periodicity of 36 days returned by the periodograms. The combination of these distributions provides an orbital period of 35.563 ± 0.071 d. The fit of the I-band light curve does not lead to any conclusive result. This is due to the fact that this light curve is shorter in time coverage, contains fewer data, and the activity signal in this red band is expected to be lower than in the previous cases.

The periodograms of the stellar indices residuals in the right panels of Fig. 4 show that following the rotation subtraction, no more signals were detected with a statistical significance higher than the 10% FAP level (except in the RV case). This indicates that the signals previously detected at ~19 d were related to the first harmonic of the rotation period. In the case of the RV time series, we found a short-period signal of 2.4 d with a significance greater than the 0.1% level of FAP, which could have a planetary origin since it is not present in the activity proxy time series.

Table 3

Priors and parameters related to the long-term and rotation signals obtained from the final stellar activity MCMC analysis of all the time series.

Table 4

log Z values computed for the different models implemented in this paper within their corresponding time series.

thumbnail Fig. 5

Top: model obtained for the Hα time series using Gaussian Processes to treat the rotation signal and a sinusoidal function to treat the long-term signal. The shaded regions indicate the 1σ confidence band of the GP model. Bottom: zoom on different time windows.

5.3 Planetary signal

We explored the possible presence of a planetary signal at 2.38 d in the RV time series by adding a Keplerian component to our previous MCMC model that included the stellar rotation and long-term signal terms. We performed an MCMC analysis using the Hα model shown in Fig. 5 to establish the boundaries for the RV rotation parameters. The Keplerian parameters of the candidate planet converged to the distributions shown in Fig. 6. The rest of the parameters are displayed in Table A.1 and Fig. A.1.

The posterior distributions from this MCMC analysis exhibit a good convergence based on the auto-correlation of the chains to an orbital period of 2.37756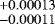−0.00011+0.00013$^{&#x002B;0.00013}_{-0.00011}$ d for GJ 740 b. The signal is characterized by an amplitude of 2.13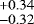−0.32+0.34$^{&#x002B;0.34}_{-0.32}$ m s−1 and an eccentricity of 0.24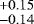−0.14+0.15$^{&#x002B;0.15}_{-0.14}$. The logZ value computed for this model indicates a significantly better Bayesian result than the one obtained for the previous models implemented for the RV time series, with a ΔlogZ greater than 20 in favor of the planetary model. The planetary nature of this signal is further supported by the steady increase of its statistical significance and the consistency of the RV semi-amplitude with the number of measurements shown in Fig. A.2. Figure 7 depicts the RV time series phased to the period of this planetary signal.

The nominal eccentricity obtained is larger than the one expected for a short orbital period planet such as GJ 740 b, but it is consistent with zero at the 2σ level. For this reason, we tried an additional model using a sinusoidal function to represent the planetary signal. This model is characterized by a Bayesian evidence of log Z = −535, which is slightly worse than the value obtained for the Keplerian model. The difference between the two models is below the limit to consider one of them more significant than the other.

Using the orbital period obtained we computed the semi-axis of the planet using the mass of the host star from Table 1. This parameter allowed us to calculate the flux received by the planet, its equilibrium temperature, and the probability that the planet could transit its host star. We listed in Table 5 all the MCMC parameters, along with these derived properties.

Figure 7 shows how the RV values are fitted nicely by the planetary model, leaving minor residuals. As shown in the bottom panel of Fig. 7, the RMS of the residuals after subtracting the final model is only 1 m s−1. The periodogram of these residuals produces only non-significant signals (i.e., lower than the PSD value related to the 10% level of FAP), which is similar to the distribution found in the other activity indices after subtracting the rotationand the long-term signal. We added both a Keplerian and a sinusoidal model to try to track the presence of an additional planetary signal in the RV residuals, but the simulations did not match the convergence criteria.

thumbnail Fig. 6

Posterior distributions of the GJ 740 b fitted parameters. The 16th–84th percentiles are represented through vertical dashed lines.
thumbnail Fig. 7

Top: phase-folded curve of the RV time series using the GJ 740 b orbital period after subtracting the long-term signal and the rotation period. The jitter terms of each spectrograph have been added to the original RV errors. The red solid line represents the planetary model. Bottom: residuals after subtracting the model.
Table 5

MCMC and derived planetary parameters of GJ 740 b obtained from the final RV time-series analysis.

5.4 Photometric transits

Taking into account the high transit probability shown in Table 5, we computed the BoxLeastSquares (BLS) periodogram (Kovács et al. 2002) for the ASAS time series and carried out an MCMC analysis similar to the one performed in the RV timeseries (without modeling any long-term signal since it was not detected in photometry) to search for the planetary signal. The posterior distribution of the planetary parameters did not meet the convergence criteria and therefore there is no evidence of detection. The SuperWASP and EXORAP datasets do not show any hint of a short-period signal in the P < 10 d region with enough statistical significance to be reliable.

5.5 Exploring additional signals

To ensure that the GP regression is not overfitting and absorbing signals that are not related to stellar activity, we replaced the GP rotation model with a simpler one based on a double sinusoidal function. The periodogram of the RV residuals after subtracting this new model reveals the presence of a previously non-detected 15 d signal. The inclusion of an additional sinusoidal function in our MCMC model to fit this signal (along with the long-term sinusoidal, the GP rotation term, and the GJ 740 b Keplerian) provides a greater logZ value than the one related to the previous model (without the short-term sinusoidal). However, the amplitude of this signal is below the 3σ significance level and its periodicity requires a narrow prior to be constrained. Additionally, this 15 d signal is also present in the Hα and Smw indicators. We performed the same MCMC analysis on these time series, and we obtained a good convergence based on the auto-correlation of the chains, which indicates that this signal is most likely caused by stellar activity.

6 Discussion

6.1 Stellar activity

We compared our results with those reported in Suárez Mascareño et al. (2018), where the long-term signal of GJ 740 was detected with a periodicity of 2040 d in the FWHM, Hα, and Smw time series with lower semi-amplitudes (2.58 m s−1, 0.165, and 0.00658, respectively). The differences with the results presented in this paper could be explained by the larger dataset used in our analysis. Although the baseline of our data is sufficient to have a good estimation of the period of the presumed magnetic cycle, the most significant long-term peak differs between the different time series. Merging the probability distribution of the FWHM, Hα, Smw, and NaD datasets, we obtain a mean value of 2800 ± 150 d.

In the analysis presented in Suárez Mascareño et al. (2018), we also detected the rotation period at 38 d in the Hα and Smw time series, with an additional peak in the first harmonic at ~19 d. In the case of the FWHM time series, the peaks were shifted to 35 and 18 d, respectively. The presence of the first harmonic of rotation in these time series could be caused by the geometric distribution of active regions. The photometry analysis carried out in the article supported the detection of the rotation signal at 35 d. The average results from our analysis including the NaD time series characterized the rotation of the star with a periodicity of 36.5 ± 1.0 d.

Regarding the photometric variability, the EXORAP results suggest a scenario where this variability is affected by the effects of an irregularly spotted stellar surface coupled with stellar rotation. This scenario is consistent with the fact that the activity signal is stronger at bluer wavelengths, where the contrast between the photosphere and cool spots is larger. Furthermore, we notice that B and V photometry get dimmer with time, suggesting that the spot coverage increases during the observation campaign. This is consistent with an increasing level of stellar activity as also suggested by the chromospheric indices shown in Fig. 1.

The coherence time obtained in the posterior distribution of the rotation parameters in the EXORAP analysis is comparable with the stellar rotation, which contrasts with the results obtained in Scandariato et al. (2017), where the evolutionary timescale of active regions found shows typically longer values, on the order of a few stellar rotations. This indicates that the photosphereof GJ 740 is more dynamic than what is typically found for field M-dwarfs. The amplitude of the correlated noise decreases with increasing wavelength. Consistently with the periodogram analysis, this suggests that the correlated signal is due to the presence of cool spots corotating with the stellar surface. The stellar dimming during the survey is confirmed, supporting the scenario where the spot coverage (and the activity level) increases with time.

6.2 GJ 740 b

With regardto the planetary signal, the semi-major axis value shown in Table 5 positions GJ 740 b in a close-in orbit to its parent star. We computed the habitable zone of GJ 740 based on the methodologies published by Selsis et al. (2007) and Kopparapu (2013). The first one provides a range between 0.14 and 0.66 AU, while the second one results in a conservative range between 0.25 and 0.48 AU, and an optimistic range between 0.20 and 0.51 AU. Therefore, we found that GJ 740 b is located out of the habitable zone of its parent star. The lack of a radius measurement does not allow for a precise description of the composition of GJ 740 b with theoretical models, but its mass and short orbital period suggest a rocky composition (Weiss & Marcy 2014). The posterior distribution of the eccentricity of the planet presented in Fig. 6 shows compatibility with a null value at 2σ. This has been proven to be usual for short-period Keplerian orbits (Kipping 2013) and cases similar to the one of GJ 740 b can be found in the literature (Astudillo-Defru et al. 2017c; Meléndez et al. 2017; Feng et al. 2019). To compare GJ 740 b with other detected planets around M-dwarfs with measured masses we created the mass-period diagram represented in Fig. 8.

Figure 8 shows that GJ 740 b falls within the peak of the orbital period distribution and is very closeto the mass peak. It is positioned as the planet with the second shortest orbital period around an M1 star after L 168-9 b (Astudillo-Defru et al. 2020). The super-Earth region of the diagram (between 2 and 10 M⊕) is the most crowded zone, lacking any detected sub-Neptunes, Neptune-like, and Jovian planets at short periods. The diagram also shows agap of low-mass planets with long periods due to instrument limitations.

The search for a photometric counterpart of the planetary signal caused by the transits of the planet did not reveal any match within our photometric datasets. Using the mass-radius relation for exoplanets found by Otegi et al. (2020), we estimate a radius of 1.43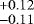−0.11+0.12$^{&#x002B;0.12}_{-0.11}$ R⊕ for GJ 740 b, assuming a density of ρP > 3.3 g cm−3. Such a radius value leads to a transit depth of 0.5 mmag, which is out of the precision range provided by the photometric instruments used in this work. The lack of a TESS light curve for this target precludes a deeper analysis of this possible photometric signal. Future TESS observations on this target are planned between 9 July and 5 August of 2022 within Sector 54. The CHEOPS telescope would be an ideal instrument to check for the occurrence of transits.

thumbnail Fig. 8

Mass-period diagram including the detected exoplanets from NASA exoplanets archive with published masses and orbital periods orbiting around M-type stars. The sub-spectral type of the parent star is indicated with a unique symbol and color. GJ 740 b has been represented with an unfilled black square, and the HADES detections (GJ 3998 b and GJ 3998 c, Affer et al. 2016; GJ 625 b, Suárez Mascareño et al. 2017: GJ 3942 b, Perger et al. 2017a; Gl 15 A b and Gl 15 A c, Pinamonti et al. 2018; Gl 686 b, Affer et al. 2019; Gl 49 b, Perger et al. 2019; and GJ 685 b, Pinamonti et al. 2019) have been marked with pink unfilled dots. The four horizontal dashed lines indicate the mass of Jupiter, Saturn, Neptune, and the Earth as a reference. The top and right panels contain the mass and orbital period distribution of the sample.

6.3 Possible second planetary companion

We studied the possibility of having a second planet causing the ~3400 d signal in theRV time series since it is not clear that the origin of the signal is related to the presumed activity cycle of the star due to the differences with respect to the results obtained from the activity indicators. We calculated the range of masses associated with the plausible orbital period of this planet in Fig. 9 using a sinusoidal model.

Figure 9 indicates that this second planet would be characterized by a mass of ~100 M⊕. The existence of this high-mass companion is favored by the greater statistical possibility of finding super-Earths like GJ 740 b in multi-planetary systems (Batalha et al. 2013; Ribas et al. 2018). Nevertheless, super-Earths with short orbital periods have been proven to be more likely to be on single-planetary systems than their analogs with longer orbital periods (Weiss et al. 2018); although only a few giant planets have been detected around M-dwarfs (Correia et al. 2010; Forveille et al. 2011; Anglada-Escudé et al. 2012; Lee et al. 2013; Morales et al. 2019). In Fig. 8, only two planets with a period greater than 1000 d orbiting a M1 star are shown: GJ 328 b (Robertson et al. 2013a) and GJ 832 b (Bailey et al. 2009). Both of them are Jupiter like planets with a mass of 2.30 ± 0.13 MJup and 0.64 ± 0.06 MJup, and orbital separation of 4.5 ± 0.2 AU and 3.4 ± 0.4 AU, respectively.Implementing a Keplerian model to trace the signal results in a not well-defined eccentricity for the model due to the long period of the signal in comparison with the time span of the observations.

To explore the possible origins of this signal, we performed a correlation study between the RV and the stellar activity indicators based on the Pearson coefficient (Pearson 1895). We calculated this coefficient along with the p-value crossing all the time series for each individual spectrograph first, obtaining a low non-significant correlation in HARPS and an intermediate significant correlation in HARPS-N. This indicates a different behavior in the stellar activity in the epoch when the HARPS-N measurements were taken. We then subtract the Smw contributionto the RV time series, which causes a decrease in the PSD associated with the long-term signal in the periodogram but keeping a FAP below the 0.1% level. Thus, we cannot conclude that this signal is entirely related to the stellar activity of GJ 740.

Considering that GJ 740 is sufficiently bright to be observed by both Gaia and HIPPARCOS, we quantified the detection limits in the mass-separation diagram based on the proper motion difference technique. Using the formalism presented inKervella et al. (2019) (Eqs. (13)–(15)) we produced the diagram shown in Fig. 10.

Although there is no evidence for a statistically significant proper motion anomaly in GJ 740, Fig. 10 indicates that an object at 3–4 AU (encompassing the orbital period of 9.3 yr of the candidate planet) with a mass of around 0.6 MJup can be ruledout at the 1-sigma level. This means that we can place an approximate limit on the inclination of the possible companion around 30 deg. To acquire sensitivity to a Saturn-mass object, such as the one we might be seeing in the RV time series, we will have to wait for future Gaia data release, starting with DR3 (in less than two years’ time). An improvement in mass sensitivity of a factor of 2 at that period is likely to be achieved by combining improved calibration schemes for bright stars such as GJ 740 and more data undergoing processing.

The possibility that the signal is related to the magnetic cycle of the star is not clear due to the uncertainties in the periodicity of the signal from all the time series and the time coverage of our dataset, which is not enough to trace two periods of the cycle. This explanation for the signal is difficult to prove if we look at the low number of M-dwarfs with published and well-measured long-period cycles in the literature (Gomes da Silva et al. 2012; Savanov 2012; Robertson et al. 2013b; Toledo-Padrón et al. 2019), along with the probability that an M-dwarf that presents long-term activity variability may not present RV changes related to the magnetic cycle (Gomes da Silva et al. 2012). The peak of the cycle length for early M-type stars has been located around 6 yr (Gomes da Silva et al. 2012; Suárez Mascareño et al. 2016). The case of BD-114672, studied by Barbato et al. (2020), is a similar case to GJ 740, showing how a late K-type star with a mass similar to GJ 740 can exhibit both a long-period planet and cycle. Consequently, we concludethat the origin of the long-term RV signal is unclear until further observations are carried out on GJ 740.

Considering the mass of the candidate, the moderately old age of the system, and a favorable projected separation of ~0.3", this target is still out of reach for current instrumentation such as SPHERE or GPI – unless the planet is much brighter than expected (e.g., the possible detection of Proxima Centauri c with SPHERE presented in Gratton et al. 2020). The new generation instruments at 30–40 m class telescopes presents much better perspectives for this kind of detection.

thumbnail Fig. 9

Distribution of the RMS of the residuals in the RV time series after subtracting the long-term signal with a sinusoidal function whose amplitude is calculated from the considered values of mass and period.
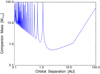thumbnail Fig. 10

Diagram of the minimum mass of a planetary companion for GJ 740 at different orbital radius based on the proper motion difference method.

7 Conclusions

Our analysis of the 129 HARPS-N, 57 HARPS, and 32 CARMENES spectra of GJ 740 taken over 11 yr shows the presence of a super-Earth orbiting the star with an orbital period of 2.37756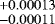−0.00011+0.00013$^{&#x002B;0.00013}_{-0.00011}$ d and an RV semi-amplitude of 2.13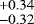−0.32+0.34$^{&#x002B;0.34}_{-0.32}$ m s−1. This planet presents a minimum mass of Mp sini = 2.96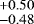−0.48+0.50$^{&#x002B;0.50}_{-0.48}$ M⊕ and a transit probability of 9%. We analyzed 474 photometric measurements from ASAS, 2350 SuperWASP measurements, and 5 yr’ worth of EXORAP measurements to search for a possible periodic signal caused by the transit of the planet in these time series, however, none of the peaks in the periodogram around the orbital period of the planet present enough statistical significance.

Our study of five different spectroscopic time series reveals that GJ 740 presents variations consistent with a long-term cycle of 7.67 ± 0.41 yr and a rotation period of 36.5 ± 1.0 d. The photometric dataset of ASAS and EXORAP confirms the rotation of the star at 35.60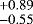−0.55+0.89$^{&#x002B;0.89}_{-0.55}$ d and 35.563 ± 0.071 d, respectively. The RV time-series presents hints of a possible second planetary signal at 9.3 yr that is also compatible with the presumed cycle signal detected in the stellar indices at 2σ. The MCMC analysis carried out on this signal did not converge to a clear eccentricity value and its origin cannot be determined given the time span of our current dataset.

Acknowledgements

B.T.P. acknowledges Fundación La Caixa for the financial support received in the form of a Ph.D. contract. A.S.M. acknowledges financial support from the Spanish Ministry of Science and Innovation (MICINN) under the 2019 Juan de la Cierva Programme. J.I.G.H. acknowledges financial support from Spanish MICINN under the 2013 Ramón y Cajal program RYC-2013-14875. B.T.P., A.S.M., J.I.G.H. and R.R. acknowledge financial support from the Spanish MICINN AYA2017-86389-P. I.R. and M.Pe. acknowledge support from the Spanish MICINN and the Fondo Europeo de Desarrollo Regional (FEDER) through grant PGC2018-098153-B-C33, as well as the support of the Generalitat de Catalunya/CERCA program. G.A.P.S. acknowledges support from INAF through the Progetti Premiali funding scheme of the Italian Ministry of Education, University, and Research. G.A.P.S. acknowledges financial support from Progetto Premiale 2015 FRONTIERA (OB.FU. 1.05.06.11) funding scheme of the Italian Ministry of Education, University, and Research. G.S. acknowledges the funding support from Italian Space Agency (ASI) regulated by “Accordo ASI-INAF n. 2013-016-R.0 del 9 luglio 2013 e integrazione del 9 luglio 2015”. This research has received financial support from the agreement ASI-INAF n.2018-16-HH.0. The results of this paper were based on observations made with the Italian Telescopio Nazionale Galileo (TNG), operated on the island of La Palma by the INAF-Fundación Galileo Galilei at the Roque de Los Muchachos Observatory of the Instituto de Astrofísica de Canarias (IAC); observations made with the HARPS instrument on the ESO 3.6-m telescope at La Silla Observatory (Chile); and observations made with the CARMENES instrument. CARMENES is an instrument for the Centro Astronómico Hispano-Alemán de Calar Alto (CAHA, Almería, Spain). CARMENES is funded by the German Max-Planck-Gesellschaft (MPG), the Spanish Consejo Superior de Investigaciones Científicas (CSIC), the European Union through FEDER/ERF FICTS-2011-02 funds, and the members of the CARMENES Consortium (Max-Planck-Institut für Astronomie, Instituto de Astrofísica de Andalucía, Landessternwarte Königstuhl, Institut de Ciències de l’Espai, Insitut für Astrophysik Göttingen, Universidad Complutense de Madrid, Thüringer Landessternwarte Tautenburg, Instituto de Astrofísica de Canarias, Hamburger Sternwarte, Centro de Astrobiología and Centro Astronómico Hispano-Alemán), with additional contributions by the Spanish MICINN through projects RYC2013-14875, AYA2015-69350-C3-2-P, AYA2016-79425-C3-1/2/3-P, ESP2016-80435-C2-1-R, ESP2017-87143-R, ESP2017-87676-C05-1/2/5-R, and AYA2017-86389-P, the German Science Foundation through the Major Research Instrumentation Program and DFG Research Unit FOR2544 “Blue Planets around Red Stars”, the Klaus Tschira Stiftung, the states of Baden-Württemberg and Niedersachsen, and by the Junta de Andalucía. This paper made use of the IAC Supercomputing facility HTCondor (http://research.cs.wisc.edu/htcondor/), partly financed by the MICINN with FEDER funds, code IACA13-3E-2493. This research has made use of the NASA Exoplanet Archive, which is operated by the California Institute of Technology, under contract with the National Aeronautics and Space Administration under the Exoplanet Exploration Program. This paper makes use of data from the first public release of the WASP data (Butters et al. 2010)as provided by the WASP consortium and services at the NASA Exoplanet Archive, which is operated by the California Institute of Technology, under contract with the National Aeronautics and Space Administration under the Exoplanet Exploration Program. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular, the institutions participating in the Gaia Multilateral Agreement.

Appendix A Additional material

thumbnail Fig. A.1

Posterior distributions of the cycle and rotation fitted parameters from the cycle+rotation+Keplerian model applied to the RV time series. The 16th–84th percentiles are represented through vertical dashed lines.
thumbnail Fig. A.2

Evolution of the PSD associated with the planetary signal along the number of RV measurements considered. The blue, green, and red horizontal lines indicate the 0.1, 1, and 10% FAP levels, respectively.
Table A.1

Priors and parameters related to the long-term and rotation signals obtained from the final RV MCMC analysis.

References

  1. Affer, L., Micela, G., Damasso, M., et al. 2016, A&A, 593, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Affer, L., Damasso, M., Micela, G., et al. 2019, A&A, 622, A193 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Ambikasaran, S., Foreman-Mackey, D., Greengard, L., Hogg, D. W., & O’Neil, M. 2015, IEEE Trans. Pattern Anal. Mach. Intell., 38, 252 [NASA ADS] [CrossRef] [Google Scholar]
  4. Anglada-Escudé, G., & Butler, R. P. 2012, ApJS, 200, 15 [NASA ADS] [CrossRef] [Google Scholar]
  5. Anglada-Escudé, G., Boss, A. P., Weinberger, A. J., et al. 2012, ApJ, 746, 37 [NASA ADS] [CrossRef] [Google Scholar]
  6. Anglada-Escudé, G., Amado, P. J., Barnes, J., et al. 2016, Nature, 536, 437 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  7. Astudillo-Defru, N., Díaz, R. F., Bonfils, X., et al. 2017a, A&A, 605, L11 [EDP Sciences] [Google Scholar]
  8. Astudillo-Defru, N., Delfosse, X., Bonfils, X., et al. 2017b, A&A, 600, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Astudillo-Defru, N., Forveille, T., Bonfils, X., et al. 2017c, A&A, 602, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Astudillo-Defru, N., Cloutier, R., Wang, S. X., et al. 2020, A&A, 636, A58 [CrossRef] [EDP Sciences] [Google Scholar]
  11. Bailey, J., Butler, R. P., Tinney, C. G., et al. 2009, ApJ, 690, 743 [Google Scholar]
  12. Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Mantelet, G., & Andrae, R. 2018, AJ, 156, 58 [NASA ADS] [CrossRef] [Google Scholar]
  13. Barbato, D., Pinamonti, M., Sozzetti, A., et al. 2020, A&A, 641, A68 [EDP Sciences] [Google Scholar]
  14. Batalha, N. M., Rowe, J. F., Bryson, S. T., et al. 2013, ApJS, 204, 24 [NASA ADS] [CrossRef] [Google Scholar]
  15. Bauer, F. F., Zechmeister, M., & Reiners, A. 2015, A&A, 581, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Berdiñas, Z. M., Rodríguez-López, C., Amado, P. J., et al. 2017, MNRAS, 469, 4268 [NASA ADS] [CrossRef] [Google Scholar]
  17. Bonfils, X., Mayor, M., Delfosse, X., et al. 2007, A&A, 474, 293 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Bonfils, X., Astudillo-Defru, N., Díaz, R., et al. 2018, A&A, 613, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Butler, R. P., Johnson, J. A., Marcy, G. W., et al. 2006, PASP, 118, 1685 [NASA ADS] [CrossRef] [Google Scholar]
  20. Butters, O. W., West, R. G., Anderson, D. R., et al. 2010, A&A, 520, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Caballero, J. A., Guàrdia, J., López del Fresno, M., et al. 2016, SPIE Conf. Ser., 9910, 99100E [Google Scholar]
  22. Carson, J. C., Eikenberry, S. S., Brandl, B. R., Wilson, J. C., & Hayward, T. L. 2005, AJ, 130, 1212 [NASA ADS] [CrossRef] [Google Scholar]
  23. Chabrier, G., & Baraffe, I. 2000, ARA&A, 38, 337 [NASA ADS] [CrossRef] [Google Scholar]
  24. Cifuentes, C., Caballero, J. A., Cortés-Contreras, M., et al. 2020, A&A, 642, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Correia, A. C. M., Couetdic, J., Laskar, J., et al. 2010, A&A, 511, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Cosentino, R., Lovis, C., Pepe, F., et al. 2012, Proc. SPIE, 8446, 84461V [Google Scholar]
  27. Covino, E., Esposito, M., Barbieri, M., et al. 2013, A&A, 554, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Delfosse, X., Forveille, T., Mayor, M., et al. 1998, A&A, 338, L67 [Google Scholar]
  29. Díaz, R. F., Cincunegui, C., & Mauas, P. J. D. 2007, MNRAS, 378, 1007 [Google Scholar]
  30. Díez Alonso, E., Caballero, J. A., Montes, D., et al. 2019, A&A, 621, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Dreizler, S., Jeffers, S. V., Rodríguez, E., et al. 2020, MNRAS, 493, 536 [NASA ADS] [CrossRef] [Google Scholar]
  32. Dressing, C. D., & Charbonneau, D. 2015, ApJ, 807, 45 [NASA ADS] [CrossRef] [Google Scholar]
  33. Dumusque, X., Santos, N. C., Udry, S., Lovis, C., & Bonfils, X. 2011, in The Astrophysics of Planetary Systems: Formation, Structure, and Dynamical Evolution, eds. A. Sozzetti, M. G. Lattanzi, & A. P. Boss (Cambridge: Cambridge University Press), 276, 527 [Google Scholar]
  34. Eastman, J., Siverd, R., & Gaudi, B. S. 2010, PASP, 122, 935 [NASA ADS] [CrossRef] [Google Scholar]
  35. Endl, M., Kürster, M., Els, S., Hatzes, A. P., & Cochran, W. D. 2001, A&A, 374, 675 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Endl, M., Cochran, W. D., Kürster, M., et al. 2006, ApJ, 649, 436 [Google Scholar]
  37. Feng, F., Crane, J. D., Xuesong Wang, S., et al. 2019, ApJS, 242, 25 [Google Scholar]
  38. Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
  39. Foreman-Mackey, D., Agol, E., Ambikasaran, S., & Angus, R. 2017, AJ, 154, 220 [Google Scholar]
  40. Forveille, T., Bonfils, X., Lo Curto, G., et al. 2011, A&A, 526, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Gaudi, B. S., Bennett, D. P., Udalski, A., et al. 2008, Science, 319, 927 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  43. Giacobbe, P., Benedetto, M., Damasso, M., et al. 2020, MNRAS, 491, 5216 [Google Scholar]
  44. Giampapa, M. S., Cram, L. E., & Wild, W. J. 1989, ApJ, 345, 536 [NASA ADS] [CrossRef] [Google Scholar]
  45. Gomes da Silva, J., Santos, N. C., Bonfils, X., et al. 2011, A&A, 534, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Gomes da Silva, J., Santos, N. C., Bonfils, X., et al. 2012, A&A, 541, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. González-Álvarez, E., Micela, G., Maldonado, J., et al. 2019, A&A, 624, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. González-Álvarez, E., Zapatero Osorio, M. R., Caballero, J. A., et al. 2020, A&A, 637, A93 [EDP Sciences] [Google Scholar]
  49. Grandjean, A., Lagrange, A. M., Keppler, M., et al. 2020, A&A, 633, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Gratton, R., Zurlo, A., Le Coroller, H., et al. 2020, A&A, 638, A120 [EDP Sciences] [Google Scholar]
  51. Hawley, S. L., Davenport, J. R. A., Kowalski, A. F., et al. 2014, ApJ, 797, 121 [NASA ADS] [CrossRef] [Google Scholar]
  52. Haywood, R. D., Collier Cameron, A., Queloz, D., et al. 2014, MNRAS, 443, 2517 [NASA ADS] [CrossRef] [Google Scholar]
  53. Hobson, M. J., Delfosse, X., Astudillo-Defru, N., et al. 2019, A&A, 625, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Horne, J. H., & Baliunas, S. L. 1986, ApJ, 302, 757 [Google Scholar]
  55. Houdebine, E. R., Stempels, H. C., & Oliveira, J. H. 2009, MNRAS, 400, 238 [Google Scholar]
  56. Howard, A. W., Johnson, J. A., Marcy, G. W., et al. 2010, ApJ, 721, 1467 [NASA ADS] [CrossRef] [Google Scholar]
  57. Kervella, P., Arenou, F., Mignard, F., & Thévenin, F. 2019, A&A, 623, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Kipping, D. M. 2013, MNRAS, 434, L51 [NASA ADS] [CrossRef] [Google Scholar]
  59. Kopparapu, R. K. 2013, ApJ, 767, L8 [NASA ADS] [CrossRef] [Google Scholar]
  60. Kovács, G., Zucker, S., & Mazeh, T. 2002, A&A, 391, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Kürster, M., Endl, M., Rouesnel, F., et al. 2003, A&A, 403, 1077 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Lalitha, S., Baroch, D., Morales, J. C., et al. 2019, A&A, 627, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Lamman, C., Baranec, C., Berta-Thompson, Z. K., et al. 2020, AJ, 159, 139 [CrossRef] [Google Scholar]
  64. Lee, B. C., Han, I., & Park, M. G. 2013, A&A, 549, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Lomb, N. R. 1976, Ap&SS, 39, 447 [Google Scholar]
  66. Lovis, C., & Pepe, F. 2007, A&A, 468, 1115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Lovis, C., Dumusque, X., Santos, N. C., et al. 2011, ArXiv e-prints [arXiv:1107.5325] [Google Scholar]
  68. Luque, R., Nowak, G., Pallé, E., et al. 2018, A&A, 620, A171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Maldonado, J., Scandariato, G., Stelzer, B., et al. 2017, A&A, 598, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Marcy, G. W., Butler, R. P., Vogt, S. S., Fischer, D., & Lissauer, J. J. 1998, ApJ, 505, L147 [NASA ADS] [CrossRef] [Google Scholar]
  71. Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
  72. Meléndez, J., Bedell, M., Bean, J. L., et al. 2017, A&A, 597, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Morales, J. C., Mustill, A. J., Ribas, I., et al. 2019, Science, 365, 1441 [NASA ADS] [CrossRef] [Google Scholar]
  74. Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984, ApJ, 279, 763 [NASA ADS] [CrossRef] [Google Scholar]
  75. Otegi, J. F., Bouchy, F., & Helled, R. 2020, A&A, 634, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Passegger, V. M., Reiners, A., Jeffers, S. V., et al. 2018, A&A, 615, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Pearson, K. 1895, Proc. R. Soc. London Ser. I, 58, 240 [Google Scholar]
  78. Perger, M., Ribas, I., Damasso, M., et al. 2017a, A&A, 608, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Perger, M., García-Piquer, A., Ribas, I., et al. 2017b, A&A, 598, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Perger, M., Scandariato, G., Ribas, I., et al. 2019, A&A, 624, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  81. Perrakis, K., Ntzoufras, I., & Tsionas, E. G. 2014, Comput. Stat. Data Analy., 77, 54 [Google Scholar]
  82. Pinamonti, M., Damasso, M., Marzari, F., et al. 2018, A&A, 617, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  83. Pinamonti, M., Sozzetti, A., Giacobbe, P., et al. 2019, A&A, 625, A126 [CrossRef] [EDP Sciences] [Google Scholar]
  84. Pojmanski, G. 1997, Acta Astron., 47, 467 [Google Scholar]
  85. Pollacco, D. L., Skillen, I., Collier Cameron, A., et al. 2006, PASP, 118, 1407 [NASA ADS] [CrossRef] [Google Scholar]
  86. Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
  87. Quirrenbach, A., Amado, P. J., Ribas, I., et al. 2018, SPIE Conf. Ser., 10702, 107020W [Google Scholar]
  88. Rainer, M., Borsa, F., & Affer, L. 2020, Exp. Astron., 49, 73 [Google Scholar]
  89. Rajpaul, V., Aigrain, S., Osborne, M. A., Reece, S., & Roberts, S. 2015, MNRAS, 452, 2269 [NASA ADS] [CrossRef] [Google Scholar]
  90. Reiners, A. 2009, A&A, 498, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  91. Reiners, A., Ribas, I., Zechmeister, M., et al. 2018, A&A, 609, L5 [EDP Sciences] [Google Scholar]
  92. Ribas, I., Tuomi, M., Reiners, A., et al. 2018, Nature, 563, 365 [NASA ADS] [CrossRef] [Google Scholar]
  93. Robertson, P., Endl, M., Cochran, W. D., MacQueen, P. J., & Boss, A. P. 2013a, ApJ, 774, 147 [NASA ADS] [CrossRef] [Google Scholar]
  94. Robertson, P., Endl, M., Cochran, W. D., & Dodson-Robinson, S. E. 2013b, ApJ, 764, 3 [NASA ADS] [CrossRef] [Google Scholar]
  95. Robertson, P., Mahadevan, S., Endl, M., & Roy, A. 2014, Science, 345, 440 [NASA ADS] [CrossRef] [Google Scholar]
  96. Savanov, I. S. 2012, Astron. Rep., 56, 716 [NASA ADS] [CrossRef] [Google Scholar]
  97. Scandariato, G., Maldonado, J., Affer, L., et al. 2017, A&A, 598, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  98. Schraudolph, N. N., Yu, J., & Günter, S. 2007, in Artificial intelligence and statistics (Berlin: Springer), 436 [Google Scholar]
  99. Selsis, F., Kasting, J. F., Levrard, B., et al. 2007, A&A, 476, 1373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  100. Sozzetti, A., Bernagozzi, A., Bertolini, E., et al. 2013, Euro. Phys. J. Web Conf., 47, 03006 [Google Scholar]
  101. Suárez Mascareño, A., Rebolo, R., González Hernández, J. I., & Esposito, M. 2015, MNRAS, 452, 2745 [NASA ADS] [CrossRef] [Google Scholar]
  102. Suárez Mascareño, A., Rebolo, R., & González Hernández, J. I. 2016, A&A, 595, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  103. Suárez Mascareño, A., González Hernández, J. I., Rebolo, R., et al. 2017, A&A, 605, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  104. Suárez Mascareño, A., Rebolo, R., González Hernández, J. I., et al. 2018, A&A, 612, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  105. Suárez Mascareño, A., Faria, J. P., Figueira, P., et al. 2020, A&A, 639, A77 [CrossRef] [EDP Sciences] [Google Scholar]
  106. Toledo-Padrón, B., González Hernández, J. I., Rodríguez-López, C., et al. 2019, MNRAS, 488, 5145 [Google Scholar]
  107. Tuomi, M., Jones, H. R. A., Barnes, J. R., Anglada-Escudé, G., & Jenkins, J. S. 2014, MNRAS, 441, 1545 [NASA ADS] [CrossRef] [Google Scholar]
  108. Weiss, L. M., & Marcy, G. W. 2014, ApJ, 783, L6 [NASA ADS] [CrossRef] [Google Scholar]
  109. Weiss, L. M., Isaacson, H. T., Marcy, G. W., et al. 2018, AJ, 156, 254 [Google Scholar]
  110. Wildi, F., Pepe, F., Chazelas, B., Lo Curto, G., & Lovis, C. 2010, Proc. SPIE, 7735, 77354X [Google Scholar]
  111. Winters, J. G., Henry, T. J., Lurie, J. C., et al. 2015, AJ, 149, 5 [NASA ADS] [CrossRef] [Google Scholar]
  112. Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  113. Zechmeister, M., Kürster, M., & Endl, M. 2009, A&A, 505, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  114. Zechmeister, M., Reiners, A., Amado, P. J., et al. 2018, A&A, 609, A12 [CrossRef] [Google Scholar]
  115. Zechmeister, M., Dreizler, S., Ribas, I., et al. 2019, A&A, 627, A49 [NASA ADS] [EDP Sciences] [Google Scholar]
2

IRAF is distributed by the National Optical Astronomy Observatories, which are operated by the Association of Universities for Research in Astronomy, Inc., under a cooperative agreement with the National Science Foundation.

All Tables

Table 1

Stellar properties of GJ 740.

In the text
Table 2

Properties of all the datasets used in this work.

In the text
Table 3

Priors and parameters related to the long-term and rotation signals obtained from the final stellar activity MCMC analysis of all the time series.

In the text
Table 4

log Z values computed for the different models implemented in this paper within their corresponding time series.

In the text
Table 5

MCMC and derived planetary parameters of GJ 740 b obtained from the final RV time-series analysis.

In the text
Table A.1

Priors and parameters related to the long-term and rotation signals obtained from the final RV MCMC analysis.

In the text

All Figures

thumbnail Fig. 1

Top: time series of the RV and the chromospheric activity indicators with combined measurements from HARPS (representedin violet), HARPS-N (represented in cyan), and CARMENES (represented in yellow). Bottom: time series of the photometric magnitudes taken with ASAS (represented in dark red) and EXORAP (represented in orange) in the B, V, R, and I filters.
In the text
thumbnail Fig. 2

Periodograms of the RV, FWHM, Hα, Smw, NaD, ASAS V, EXORAP B, EXORAP V, and EXORAP R-band magnitude time series. The periods related to stellar rotation, planetary companion, and possible magnetic cycle have been represented as yellow, cyan, and brown vertical lines, respectively. The green, brown, and red horizontal lines indicate the 0.1, 1, and 10% FAP levels, respectively.
In the text
thumbnail Fig. 3

Analysis of the long-term signal. Left: RV, FWHM, Hα, Smw, and NaD time series with their respective model of the long-term signal. Center: posterior distribution for the periodicity of the long-term signal. Right: periodograms of the residuals after subtracting the model. The blue, green, and red horizontal lines indicate the 0.1, 1, and 10% FAP levels, respectively. The highest peak of the periodogram is marked with a blue shaded area.
In the text
thumbnail Fig. 4

Analysis of the rotation signal. Left: RV, FWHM, Hα, Smw, and NaD time series with their respective model of the long-term signal and the rotation signal. The shaded regions indicate the 1σ confidence band of the GP model. Center: posterior distribution for the periodicity of the rotation signal. Right: periodograms of the residuals after subtracting the model. The blue, green, and red horizontal lines indicate the 0.1, 1, and 10% FAP levels, respectively. The highest peak of the periodogram is marked with a blue shaded area.
In the text
thumbnail Fig. 5

Top: model obtained for the Hα time series using Gaussian Processes to treat the rotation signal and a sinusoidal function to treat the long-term signal. The shaded regions indicate the 1σ confidence band of the GP model. Bottom: zoom on different time windows.
In the text
thumbnail Fig. 6

Posterior distributions of the GJ 740 b fitted parameters. The 16th–84th percentiles are represented through vertical dashed lines.
In the text
thumbnail Fig. 7

Top: phase-folded curve of the RV time series using the GJ 740 b orbital period after subtracting the long-term signal and the rotation period. The jitter terms of each spectrograph have been added to the original RV errors. The red solid line represents the planetary model. Bottom: residuals after subtracting the model.
In the text
thumbnail Fig. 8

Mass-period diagram including the detected exoplanets from NASA exoplanets archive with published masses and orbital periods orbiting around M-type stars. The sub-spectral type of the parent star is indicated with a unique symbol and color. GJ 740 b has been represented with an unfilled black square, and the HADES detections (GJ 3998 b and GJ 3998 c, Affer et al. 2016; GJ 625 b, Suárez Mascareño et al. 2017: GJ 3942 b, Perger et al. 2017a; Gl 15 A b and Gl 15 A c, Pinamonti et al. 2018; Gl 686 b, Affer et al. 2019; Gl 49 b, Perger et al. 2019; and GJ 685 b, Pinamonti et al. 2019) have been marked with pink unfilled dots. The four horizontal dashed lines indicate the mass of Jupiter, Saturn, Neptune, and the Earth as a reference. The top and right panels contain the mass and orbital period distribution of the sample.
In the text
thumbnail Fig. 9

Distribution of the RMS of the residuals in the RV time series after subtracting the long-term signal with a sinusoidal function whose amplitude is calculated from the considered values of mass and period.
In the text
thumbnail Fig. 10

Diagram of the minimum mass of a planetary companion for GJ 740 at different orbital radius based on the proper motion difference method.
In the text
thumbnail Fig. A.1

Posterior distributions of the cycle and rotation fitted parameters from the cycle+rotation+Keplerian model applied to the RV time series. The 16th–84th percentiles are represented through vertical dashed lines.
In the text
thumbnail Fig. A.2

Evolution of the PSD associated with the planetary signal along the number of RV measurements considered. The blue, green, and red horizontal lines indicate the 0.1, 1, and 10% FAP levels, respectively.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.