EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 646 (February 2021) A&A, 646 (2021) A9 Full HTML
Free Access
Issue
A&A
Volume 646, February 2021
Article Number A9
Number of page(s) 35
Section Galactic structure, stellar clusters and populations
DOI https://doi.org/10.1051/0004-6361/202039392
Published online 29 January 2021

© ESO 2021

1. Introduction

The signature of multiple stellar populations in globular clusters (GCs) is the star-to-star difference in the abundances of light elements (from C to Si, and in a few cases, up to K, Ca, and Sc) in them and with respect to the field stars of similar metallicity. The observational evidence accumulated in the past half a century is reviewed in Gratton et al. (2004, 2012, 2019) and in Bastian & Lardo (2018). The whole chemical pattern of multiple populations and its reflection in the photometric sequences of the colour-magnitude diagrams (CMD) can be explained as caused by the nucleosynthesis through proton-capture reactions in H-burning at high temperature (Denisenkov & Denisenkova 1989; Langer et al. 1993).

This origin is strongly favoured because the alterations are not randomly distributed in chemical space. The depletion in elements that are consumed in proton-capture reactions (C, O, and Mg) is always accompanied by enhancement in the abundance of species that are produced by these same reactions (N, Na, Al, and Si). This is obviously the reason why the main observed signature is represented by the well-known anti-correlations C-N, O-Na, Mg-Al, etc., as well as correlations between Na-Al, Al-Si, and so on. Some doubts about the nucleosynthetic origin of these patterns have been cast by discrepancies with the output of theoretical models that tried to explain them. However, the extreme regularity with which we observe O and Mg abundances that are only depleted, never enhanced, or viceversa, Na and Al only enhanced, never depleted with respect to field halo stars, leaves us with no doubt that the mechanism must reside in nucleosynthesis operating through proton-capture reactions. The simple truth is that models still cannot faithfully reproduce the whole complexity of GCs (e.g. Bastian et al. 2015).

A direct inference is that multiple stellar populations in GCs must also differ in age, the amount of the difference depending on the proposed candidate polluter for nuclearly processed matter. This stems from the inability of currently evolving low-mass stars to achieve the high temperatures for H-burning in their interior that are required to operate the proton-capture reactions, in particular for the most energetic cycles, such as Mg-Al or the leakage from this on 28Si (Karakas & Lattanzio 2003). This in turn implies that the nucleosynthesis in question must have occurred in stars more massive than the currently observed stars, which were born, evolved, and ended their life in previous stellar generations (e.g. Gratton et al. 2001).

While the constraint on the temperature for nuclear burning is physically robust, the imperfect match between observations and models still precludes a clear identification of the stellar sites at which this burning occurred. Proposed candidate polluters cover a wide range in mass, ranging from asymptotic giant branch (AGB) stars (e.g. Cottrell & Da Costa 1981; Ventura et al. 2001) to massive fast-rotating stars (Decressin et al. 2007) or in binary interaction (de Mink et al. 2009), and more exotic candidates such as very massive stars (Denissenkov & Hartwick 2014; Gieles et al. 2018) and supergiants (Szécsi & Wünsch 2019).

Producing elements higher in mass than Si from proton-captures would require very high temperatures in order to overcome the Coulomb barrier. The interest in the group K-Ca-Sc has constantly grown since the triggering discovery of large variations in K abundances in NGC 2419. From high-resolution spectra, Cohen & Kirby (2012) found K, Ca, and Sc enhanced in Mg-poor stars of this cluster, while the medium-resolution spectroscopic survey by Mucciarelli et al. (2012) detected a wide spread in Mg and K abundances, anti-correlated with each other, in giants of NGC 2419 sharing the same Fe and Ca abundances. Their analysis revealed that the star with huge [K/Fe] and high Mg depletion found in Cohen et al. (2011) is not the only notable exception in this GC.

Initially, the impact of K production in the context of multiple populations was disregarded because it was thought to require temperatures too high outside supernovae. However, Ventura et al. (2012) advocated that the observed K-Mg anti-correlation might be explained by the simultaneous activation of the Mg-Al-Si and Ar-K cycles in particular conditions, for example low metallicity and enhanced efficiency of the hot bottom-burning in the AGB phase. A first scrutiny (Carretta et al. 2013a) of K abundances in a few other GCs, based on a limited number of stars in each GC, appeared to confirm the uniqueness of the pattern in NGC 2419, as well as the anti-correlation of Ca and Sc with Mg abundances in this GC (see also Cohen & Kirby 2012).

Mucciarelli et al. (2015) targeted NGC 2808, which is one of the GCs with the most extended Na-O anti-correlation (Carretta et al. 2006), and found that K is not only anti-correlated with Mg, but is also correlated with Al and Na abundances. Together with the correlation Ca-Sc and the Sc-Mg anti-correlation discovered by Carretta (2015) in NGC 2808, these observations left no doubt that K, Ca, and Sc are affected by real variations linked to the proton-capture processes in multiple population in GCs, even if their mass is lower than that of NGC 2419.

However, to fully explore this high-temperature regime at which the first-generation (FG) polluters operated in the early protoclusters, it is highly desirable to gain more statistics. Carretta et al. (2013a) have pointed out that the paucity of K abundances available in GCs can be bypassed by exploiting the Ca and Mg abundance determinations, which are available for many more stars and are usually based on several atomic transitions. A first attempt was successfully made in Carretta et al. (2014a), who plotted in their Fig. 10 the [Ca/Mg] ratio as a function of [Ca/H] for more than 200 red giants in about 20 GCs. In addition to NGC 2419, five GCs stand out in this plane, with stars showing an excess of Ca with respect to Mg: NGC 4833, NGC 7078 (M 15), NGC 2808, NGC 6715 (M 54), and NGC 5139 (ω Centauri).

With the same purpose, Carretta & Bragaglia (2019) defined a similar diagnostic plot, this time based not on a comparison with GC stars, but using field stars. The idea was to obtain more efficient detection plots because field halo stars are an almost pure FG population. Many recent studies (e.g. Martell et al. 2011; Koch et al. 2019a) estimated the contribution of GC stars with a second-generation (SG) composition only at the 2–2.5% level in the halo. The rarity of these stars makes it improbable that the control sample is much affected by SG interlopers and thus can be safely used as a baseline to probe the possible outcome of the multiple-population phenomenon of the Ca and Sc anti-correlations with Mg. We tested the efficiency of these diagnostics by showing that a Ca excess is easily detected in the SG stars of NGC 2808, as expected, but not in those of the massive bulge cluster NGC 6388. In addition, we highlighted that this approach also provides an accurate enough estimate of the temperature range achievable by the FG polluters. When Al-Mg-Si variations are detected but no variations in Ca and Sc are observed, the inferred temperatures must be high enough to activate the Mg-Al cycle, possibly leaking on Si (T >  100 − 110 MK), but not high enough to trigger the K production from Ar (T = 120 − 150 MK; Ventura et al. 2012; D’Antona et al. 2016; Prantzos et al. 2017). In this way, we can hope to supply useful additional constraints to theoretical models to devise more appropriate scenarios for the origin of multiple populations in GCs.

Encouraged by this first attempt, here we extend this approach with a systematic search based on existing abundances of Mg, Ca, and Sc from published analyses of high-resolution spectra of GC stars, to be compared with a control sample of field stars. In addition to the two notable cases already known (NGC 2419 and NGC 2808), we retrieve all the GCs reported in Carretta et al. (2014a). We also find a few other GCs for which statistically robust evidence of the operation of proton-capture reactions at very high temperature has been clearly assessed. A first scrutiny of their properties in general suggests that these particular classes of polluters were preferentially at work in massive and/or metal-poor GCs.

The paper is organised as follows: Sect. 2 presents the detection procedure of excesses in Ca and Sc against a control sample of field stars. Section 3 presents the results of our census for GCs analysed by our group and for the optical sample from the literature; the new detections are discussed and additional plots are presented in the appendices. Section 4 extends the analysis to the IR, using APOGEE results, and potassium is added. Section 5 discusses a few cases of borderline detections, and Sect. 6 discusses and summarises our findings.

2. Setting the stage

In this section we introduce our procedure to demonstrate possible excesses of light elements resulting from proton-capture reactions occurring under extreme conditions in early phases of GC lifetimes. Our approach follows and expands on the approach used in Carretta & Bragaglia (2019), where we defined diagnostic plots named detectors of high-temperature H-burning (DOHT). In the following, we describe our improved procedure in detail, that is, the adopted reference sample, the different samples of scrutinised GCs, and the statistical tests we used in the analysis.

2.1. Reference sample of field stars

As in Carretta & Bragaglia (2019), we tested the presence of signatures of high temperature burning products in GC multiple populations by comparing their abundance ratio patterns for [Ca/H], [Sc/H], and [Mg/H] with that of field stars because the latter are expected to incorporate only the yields from supernova (SN) nucleosynthesis (e.g. Gratton et al. 2000; Smith & Martell 2003). Our preferred reference sample is the one by Gratton et al. (2003). These stars cover a range in metallicity from [Fe/H] = − 2.6 up to [Fe/H]∼0.0 dex, encompassing the whole interval of metal abundances spanned by GCs in the Milky Way (see e.g. Harris 1996, online 2010 edition). Abundances of Mg, Ca, and Sc were derived for many stars of this sample. The abundance analysis is as homogeneous as possible with the one for GCs in our golden and silver samples (from our FLAMES survey, see below) because the adopted line list, reference solar abundances, and correction for hyperfine structure (HFS) for Sc are exactly the same. In Fig. 1 (upper panel) we show the relation between [Ca/H] and [Mg/H] for stars in Gratton et al. (2003), together with the linear regression line that we used to subtract the fit from the observed [Ca/H] values and linearize them for an easier measurement of the Ca excesses.

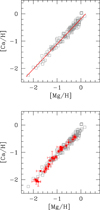thumbnail Fig. 1.

Upper panel: [Ca/H] ratios as a function of [Mg/H] for the field stars in the sample of Gratton et al. (2003). The linear fit to the data we used to rectify the [Ca/H] values is superimposed. Lower panel: same as in the upper panel. The mean values and rms scatter of GCs in our golden and silver samples are superimposed (see text).

2.2. Detection procedure

In our procedure for detecting excesses of elements produced by H-burning at very high temperature in GCs, we focused in particular on Ca because this is a widely studied species, analysed in all the scrutinised GCs. Its abundances are often based on several transitions. A possible concern is that the [Ca/Fe] ratio is overabundant in metal-poor halo stars, either in clusters or in the halo field (e.g. Gratton et al. 2004), because the contribution of Fe from type Ia SNe at these low metallicities is reduced, whereas the expected variations in Ca are likely small. Changes of comparable amounts would be easier to detect if the involved elements had intrinsically lower abundance, as in the case of K or Sc. However, this concern is entirely overcome by our differential procedure, which is tailored to compare field and cluster stars, where the primordial level of Ca is established by explosive nucleosynthesis in the core-collapse SN phase of massive stars (e.g. Woosley & Weaver 1995), regardless of the diverse environment. The initial abundance ratios of α-elements to iron is determined by the massive star initial mass function (IMF), which is largely invariant (see e.g. Kordopatis et al. 2015), so that the abundance-scaling relations remain constant for metal-poor stars in the Galaxy. This evidence is confirmed by the lower panel in Fig. 1, where we superimpose the average values from GCs in our so-called golden and silver samples on the field star distribution (see Sects. 3.1 and 3.3 below).

On the other hand, Sc is not analysed in all the samples we have access to, and its derived abundance is affected by additional differences due to the treatment of corrections for HFS and even of the iron abundance used as reference in the [Sc/Fe] ratio. It is often unclear whether neutral or singly ionised Fe is used, and sometimes only the average from both is published, which makes the use of [Sc/H] ratio more uncertain. However, results based on Sc may be used in support of the conclusions based on Ca abundances; they are presented in the appendix.

To illustrate our procedure, we use NGC 4833. This GC shows the effects we are looking for more clearly. In Fig. 2 the main steps of the procedure are shown. In the upper left panel the observed distribution of stars in NGC 4833 from Carretta et al. (2014a) is superimposed on the distribution from Gratton et al. (2003) in the [Ca/H] vs [Mg/H] plane. In this case, the solar reference abundances are the same for the two samples. In the upper right panel we apply the linear fit in Fig. 1 to both samples. In the lower left panel, these “corrected” [Ca/H]corr values are plotted as generalised histograms for field and cluster stars, assuming a typical error of 0.08 dex. We used the complete set of field stars after verifying that the ratio [Ca/H]corr runs flat, without modification of average and dispersion. In this step, the two samples were aligned using the mode of the distributions; in practice, the GC peak was shifted to correspond to the maximum of the field star distribution. This also accounts for residual small differences that are due to the adoption of a different temperature scale in the analyses, for instance.

thumbnail Fig. 2.

Steps of our procedure applied to NGC 4833. Upper left panel: stars in NGC 4833 (Carretta et al. 2014a: filled blue squares) superimposed to field stars (Gratton et al. 2003: empty grey squares) in the [Ca/H]–[Mg/H] plane. Upper right panel: same stars (and symbols) after subtracting the linear fit in Fig. 1 from [Ca/H] to obtain linearised values [Ca/H]corr. Lower left panel: generalised histograms of the [Ca/H]corr values for field (filled grey area) and GC stars (empty blue area). Lower right panel: cumulative distribution of corrected Ca abundances for field and GC stars. The probability for the two-tail Kolmogorov-Smirnov test is also listed.

Simple visual inspection is clearly enough in this example (as well as in most of the cases we analysed) to detect an evident excess of Ca in a fraction of GC stars, excess that is absent in the field stars. To better quantify these effects, we applied a two-sample Kolmogorov–Smirnov (K–S) test to each GC under the null hypothesis that the two sample populations (GC and field stars) are drawn from the same parent distribution. In the case of NGC 4833, the cumulative distributions of the corrected [Ca/H] values are compared in the lower right panel of Fig. 2, where the probability for the two-tail K–S test is also indicated. For NGC 4833, the result of the test unambiguously shows that the two distributions are not extracted from the same parent population. A fraction of stars of this cluster shows an excess of Ca above the level established by SNe in field halo stars with similar metallicity. The same procedure can also be used also with Sc, if available; for NGC 4833 the Sc distribution confirms the results obtained with Ca (the K–S test indicates a high significance, with P(K − S) = 4.3 × 10−5.

We also computed the number of outliers in the GC linearised distributions, defined as those GC stars whose corrected [Ca/H]corr ratios exceed the 3σ range with respect to the average for field stars (where the last value is zero by definition in our procedure). We adopted rms = 0.084 dex for [Ca/H] from Gratton et al. (2003). This value is only slightly above the error in Ca because of the uncertainties in the analysis. We verified that this is also a typical and reasonable value to be used for most of the literature Ca abundances. In the example above, NGC 4833 has 8 stars (of the 52 in our sample, i.e. 15%) that exceed the 3σ limit.

The same steps can be applied to all other GCs (see next section). Whenever possible (and explicitly published), we used the solar reference abundances from the original studies to remove a source of offset by shifting the abundances on the solar reference scale used by Gratton et al. (2003) and in our FLAMES survey of GCs (i.e. log ϵ(Fe) = 7.54, log ϵ(Mg) = 7.43, log ϵ(Ca) = 6.27, and log ϵ(Sc) = 3.13). The distribution peak alignment (Fig. 2) takes care of residual small offsets caused by differences in the adopted solar abundances.

3. Analysis and results

The procedure described in the previous section for NGC 4833 was applied to all GCs for which we found published abundances of Fe, Mg, and Ca (and Sc whenever possible: see Appendix B) based on high-resolution spectra. The GCs and the (sometimes multiple) abundance analyses used in the present study are listed in Table 1. For each GC we list the NGC number or name, a unique alphanumeric code identifying each individual study in each different GC in the plots shown both in the main paper body and in the appendices, the number of stars analysed in each GC, and the reference of the paper.

Table 1.

Adopted abundance analyses.

The GCs in Table 1 are grouped into three separated sub-samples. Our FLAMES survey conducted to study the O-Na anti-correlation in GCs, described in Carretta et al. (2006); Carretta et al. (2010a), allowed us to analyse an unprecedented sample of more than 2800 giants in 27 GCs in an extremely homogeneous way, with high-resolution FLAMES spectra. Not all stars have the full set of abundances derived for all elements, but in our so-called golden sample, we collected 9 GCs with published abundances of Fe, Mg, Ca, and Sc that have been derived from either UVES or GIRAFFE spectra. To these we also added NGC 6388, whose data are still unpublished (paper in preparation). A total of 817 stars with homogeneously derived abundances in 10 GCs constitutes our prime sample.

Second, our silver sample consists of 16 GCs in which Fe, Mg, and Ca abundances were derived from UVES spectra in Carretta et al. (2009a) and Carretta et al. (2010b) for a total of 190 giants. In this case, while the high degree of homogeneity is preserved, the sample is limited to a maximum of 14 stars in each GC because only few UVES fibres are available. This subset represents our second-best sample for its homogeneity, although the rather small samples are not ideal.

Finally, in the third group we include all the samples retrieved in the literature with abundances of Fe, Mg, and Ca based on high-resolution optical spectroscopy (plus one near-IR for NGC 6553). The number of stars in each study varies strongly, from 2 (Arp 2 and E3) to more than 100 (NGC 6121). The near-IR results in the latest APOGEE data release are presented and discussed in Sect. 4.

The results of the K–S test on Ca abundance distribution for all studies (labelled by their code) of all GCs (indicated by NGC number or name) are listed in Table 2, together with the number of outliers in the GC [Ca/H]corr ratios. The literature sample in Table 2 is split into two subsets, according to the number of stars examined in each GC (more and fewer than 5). In Appendix A we show the observed [Ca/H] ratios as a function of [Mg/H] for all literature samples.

Table 2.

Results for [Ca/H]–[Mg/H].

3.1. Golden sample

The observed distribution of stars in GCs of our golden sample is shown in the plane [Ca/H]–[Mg/H] in Fig. 3. Visual inspection shows that the cluster stars are clearly superimposed on the locus populated by field stars in most cases, with three exceptions: NGC 2808, NGC 4833, and NGC 6715 (M 54).

thumbnail Fig. 3.

Observed [Ca/H] ratios as a function of [Mg/H] ratios for the GCs in our golden sample (filled blue squares) compared to the field stars in Gratton et al. (2003: empty grey squares).

NGC 2808 is a case study for correlations and anti-correlations involving products forged in H-burning in conditions of very high temperature. Carretta (2015) showed that among the multiple populations in this GC, the Sc abundances are anti-correlated with those of Mg and are well correlated with Si and Ca abundances. At high statistic significance, all these relations indicate that a fraction of stars in NGC 2808 is contaminated by nuclear matter processed at very high temperature in proton-capture reactions. Figure 3 is another way to present these observations. It also immediately shows the excess of this production with respect to field stars where Si and Ca originated only in SN nucleosynthesis.

To this template case we now add NGC 4833, which seems to be an analogy on a smaller scale. This is expected because the original analysis by Carretta et al. (2014a) has clearly shown that this GC stands out in the [Ca/Mg] versus [Ca/H] plane, another diagnostic plot introduced in Carretta et al. (2013a) to single out GCs with an excess of Ca and/or a high Mg depletion. A group of Mg-poor stars was also found in a more limited sample by Roederer & Thompson (2015).

The third detection is represented by NGC 6715 (M 54). Some giants clearly show excesses of Ca with respect to field stars over the range in metallicity covered by this former nuclear cluster of the dwarf galaxy Sagittarius.

The probability (p-value) associated with the two-tail K–S test is listed in the first part of Table 2 for the GCs of the golden sample. We adopted the usual convention that a p-value < 0.05 means that there is sufficient evidence to reject the null hypothesis that the GC and field star samples are extracted from the same parent population. The low values we found for NGC 2808, NGC 4833, and NGC 6715 confirm the detected difference between field and cluster stars on statistically robust grounds. In all these three samples, a fraction of 15–16% of the stars is classified as outliers, following the criteria described above. The case for NGC 1851, with a p-value below 0.05 and no outlier above the 3σ threshold (as is immediately clear from the visual inspection) is discussed in the next subsection.

These three detections are also mirrored, albeit not so clearly, in the [Sc/H] versus [Mg/H] plane (see Fig. B.1). The K–S test and the numerous outliers in the Sc distribution also strengthen our findings based on Ca.

3.2. Proof-of-concept case: NGC 1851

The particular case of NGC 1851 appears to show a discrepancy: while in Fig. 3 the cluster stars are well superimposed on the field stars of similar metallicity, the K–S test in Table 2 formally indicates that the probability that we can reject the null hypothesis is low (i.e. that the samples are extracted from the same parent population).

The explanation is that two different sub-populations coexist in this GC. Carretta et al. (2011) showed that the difference in Fe alone is too small for a clear distinction of these two populations; however, the separation is evident in a classification scheme with a combination of Fe and Ba, where the latter is much more abundant in the more metal-rich component. In other words, NGC 1851 appears to be a smaller-scale example of the so-called iron complex GCs, such as NGC 6656 (M 22: e.g. Marino et al. 2011), NGC 6273 (M 19: Johnson et al. 2015, 2017c), and NGC 5824 (Roederer et al. 2016). In these GCs, a spread in Fe is accompanied by a dispersion in s-process elements, whose content is higher in the most metal-rich fraction. Carretta et al. (2011) found that each component in NGC 1851 hosts a fully developed O-Na anti-correlation by its own, but the two populations also have different levels of [Ca/H], [Mg/H], [Si/H] with a statistically high level of confidence.

Because we used both Ca and Mg in our tests, we repeated our procedure for NGC 1851 and separated the two components as found and defined in Carretta et al. (2011). The results are shown in Fig. 4. Each individual component does not seem to be significantly different from the field stars, as established by the probabilities of the K–S test. On the other hand, the two components are clearly segregated and clustered around two slightly different values in the entire sample. This in turn results in a less than perfect match with the underlying field stars, and this spurious signal is most probably what is intercepted by the K–S test based on the total sample of NGC 1851. The discussion in this section can be also used as a sanity check of our procedure and as a proof of concept that it efficiently works in detecting the excesses we are interested in.

thumbnail Fig. 4.

Analysis for the detection and test of the Ca excess in NGC 1851: the whole procedure is now applied separately to the two stellar components (red and blue symbols and lines) found by Carretta et al. (2011) in this cluster.

3.3. Silver sample

In terms of homogeneity, our silver sample GCs are next because their stars were analysed with the same tools (line lists, solar reference abundances, HFS corrections, and abundance analysis code) as the stars in the golden sample and in the field. The only relevant difference is that these stars were observed with the dedicated UVES-FLAMES fibres, hence the number of stars in each cluster is smaller1. As a compensation, the number of transitions for Fe, Ca, and Sc is higher because the spectral coverage of UVES spectra is larger, providing more robust estimates of the abundances.

The diagnostic plots showing the observed distributions of GC stars and field stars in the [Mg/H], [Ca/H] plane are presented in Fig. 5. The p-values for the K–S test are listed in the second part of Table 2: no GC in this sample shows evidence of excess of Ca with respect to field stars.

thumbnail Fig. 5.

Observed [Ca/H] ratios as a function of [Mg/H] ratios for the GCs in our silver sample (filled blue squares) compared to the field stars in Gratton et al. (2003), shown in grey.

Interestingly, the GCs in this set are the same as were used in Carretta et al. (2009a) to explore the various relations among the light elements O, Na, Mg, Al, and Si whose abundances are potentially changed in proton-capture reactions involving a large temperature interval for nuclear burning. The only significant slopes in the Si-Al correlation were found for NGC 2808, NGC 6388, NGC 6752, and NGC 7078 (Carretta et al. 2009a, Fig. 10). Translated into temperature, this finding means that FG polluters were only in these GCs able to reach the 65 MK threshold (Arnould et al. 1999), providing the right environment for leakage on 28Si in the Mg-Al cycle (see Karakas & Lattanzio 2003).

Carretta & Bragaglia (2019) have examined the cases of NGC 2808 and NGC 6388, which stimulated the census of the present work. By applying the same line of reasoning, we may conclude that in NGC 6752 we can also pinpoint a rather narrow range for the operating temperatures of the polluters, as we did in NGC 6388: high enough to modify Si, but not high enough to touch on heavier elements. Mucciarelli et al. (2017) offered a nice support to this conclusion because they found that in NGC 6752 the results are formally compatible with a null spread in K abundance.

The verdict on NGC 7078 (M 15) is more uncertain. Two outliers, at slightly more than 3σ in [Ca/H]corr, might indicate a low excess in Ca, in agreement also with the diagnostic plot [Ca/Mg] versus [Ca/H] shown in Carretta et al. (2014a). However, the K–S test does not formally support this conclusion, and we cannot currently strongly state that stars in NGC 7078 are genuinely different from the distribution of field stars. Unfortunately, the various literature studies do not help solve this issue either (see below). It would be interesting to make a survey of K abundances in this GC: the K I resonance line at 7698.98 Å should be still strong enough to be reliably measured in giant stars of such a low-metallicity cluster as well.

3.4. Literature sample

To enlarge the set of GCs, we collected literature samples in which Mg, Ca, and possibly Sc were derived from high-resolution spectra (in this section we consider optical spectra, APOGEE is discussed in Sect. 4). Multiple studies of the same cluster were considered to improve our chance of detecting stars with a clear excess in Ca and/or Sc. Only in two cases did we try to combine different analyses for the same cluster to reach a more statistically meaningful number of stars. However, for NGC 5466 the optical sample by L15 and the near-IR from APOGEE (Mészáros et al. 2020, see next section) display an offset, therefore we did not combine them. Conversely, for NGC 6558, we summed the samples B07 and B18 because they are from the same group; we only took unique stars.

Whenever possible, abundances were corrected for offsets due to solar reference abundances with respect to those in Gratton et al. (2003). However, the procedure that normalises the GC stars to the bulk of field star in [Ca/H]corr helps to smooth out residual small differences due to the analysis.

In Appendix A (Figs. A.1–A.10) we show the observed distributions of [Ca/H] and [Mg/H] superimposed on the field stars by Gratton et al. (2003). In the panels, each GC study is identified with the alphanumeric code in Tables 1 and 2. NGC 2419 is plotted with a different scale that is required to show the full extent of its huge spreads in Ca and Mg (and Sc, see Appendix B). This cluster clearly stands out with its large alterations in these elements, as was discovered in Cohen & Kirby (2012) and Mucciarelli et al. (2012).

The results of the two-tail K–S test are listed in Table 2. From these tests, a (moderate) number of GCs show a clear signature of the operation of proton-capture reactions at very high temperature, meaning that the low p-values allow us to safely state that the difference between the two distributions (field versus GC stars) is real. In addition, if different studies exist for the same GC, all the corresponding statistical tests give results that agree with each other.

In addition to NGC 2419, we detected such a clear signal in NGC 4833, NGC 5139 (ω Cen), NGC 5824, NGC 5986, and NGC 6402, all GCs with a large number of stars analysed. The analysis of NGC 4833 by Roederer & Thompson (2015) independently confirms the result we obtained for this GC in our golden sample. The excess in ω Centauri, the most massive GC in the Milky Way, is detected by two independent studies (which become three when the APOGEE contribution is included, see next section). In its case, the large variations are clearly evident from the Mg and Ca distribution (see Fig. A.2).

Moreover, we found a few GCs where the conclusion is unclear: either because different analyses for the same cluster provide different answers, or because the sample in the GC shows a large dispersion that is not skewed only towards excess values. In the latter case, we cannot be sure that the effect is astrophysical and not simply due to large errors associated with the abundance analysis.

The list of these GCs includes NGC 4590 (M 68), NGC 6205 (M 13), NGC 6218 (M 12), NGC 6440, NGC 6441, NGC 6553, and Pal 14. We discuss these objects below, but in the following we do not consider the presence of matter produced at very high temperature H-burning in these GCs conclusive. Two of them are also in our silver sample (NGC 6218 and NGC 6838), where they do not show any Ca excess.

Globular clusters for which only a limited number of stars (< 5) is available are plotted in different colours in the figures in Appendices A and B and are listed in the last lines of Table 2. The K–S test shows that the cluster and field star distributions do not differ for any of these GCs. The soundness of this conclusion is limited by the small available samples. However, for Ter 8 the result is rather well assessed on the basis of the larger sample analysed by Carretta et al. (2014b). Because of the small numbers involved, the lack of evidence for the remaining GCs must be considered only as an indication, to be confirmed when (if) larger size samples become available.

4. View from the IR: Mg, Ca, and K from APOGEE

While we were completing the collection of the high-resolution optical dataset, Mészáros et al. (2020) published the abundance analysis of 44 GCs from high-resolution IR spectra acquired in the SDSS-IV APOGEE-2 survey. The studied elements include Ca and Mg. Scandium is not present, but they derived abundances of K, which initially was the only indicator in the literature for the possible presence of alterations produced in very high temperature H-burning. Given the dimension of the dataset and the homogeneous analysis, we decided to explore their sample to complement the optical observations and support our previous finding.

Following Mészáros et al. (2020), we restricted the APOGEE-2 sample to 26 clusters according to the same selection criteria as they used, excluding GCs with a higher reddening value (E(B − V) > 0.4) as well as those with fewer than five member stars whose spectra have a signal-to-noise ratio S/N >  70 (see Table 3 for the survived clusters). Almost all of the remaining GCs are already in the optical sample, so that they can be used as a further check, especially when a larger number of stars is present, which is often the case. Two GCs are new entries with respect to the optical samples: NGC 5024 and Pal 5.

Table 3.

Results for the APOGEE-2 sample (Mészáros et al. 2020).

In Appendix C we plot the observed distribution of GC stars from the APOGEE-2 sample in the [Ca/H] versus [Mg/H] plane (Figs. C.1 and C.2). We only plot and use in the following stars in the range suggested by Mészáros et al. (2020), that is, S/N >  70, Teff <  5500 K, and actual measurements for Ca and Mg, excluding stars flagged as limits. No correction for the solar abundances is applied (the solar reference values are not explicitly provided in Mészáros et al.). However, when these selection criteria are applied to the APOGEE sample, the differences are small enough that the abundances from IR spectra nicely fall on the field star distribution. Residual offsets in Ca due to the different methods of analysis are taken care of by aligning the mode of the distributions.

We then repeated all the steps and statistical tests we performed for the optical samples. The results are listed in Table 3 and generally confirm and strengthen our previous findings.

4.1. Differences between optical and IR

Three cases need further discussion, however. NGC 2808 and NGC 6715 (M 54) show no statistically significant Ca excess, in contrast with the optical datasets and the direct visual comparison in Figs. C.1 and C.2. On the other hand, the distribution in NGC 6752 appears to differ from that of field stars according to the K–S statistical test, at variance with the results from optical samples.

The case for NGC 6715 can be easily understood. Only one star out of six surviving the selection criteria in the APOGEE sample falls outside the distribution defined by field stars. Neither oxygen nor sodium abundances were derived for these stars in Mészáros et al. (2020). However, four stars are in common in APOGEE and Carretta et al. (2010c), and the outlier star fortunately is one of these. The abundances [O/Fe] = –0.748 dex and [Na/Fe] = +0.774 dex explain the classification of this star as an SG star with extreme alterations in light elements (E component), according to the definitions given in Carretta et al. (2009b)2. This status is also confirmed by the high ratio [Al/Fe] found for this star both in Mészáros et al. (2020) and Carretta et al. (2010c). It is then not surprising that its [Ca/H]corr ratio exceeds 3σ (see Sect. 3), suggesting that the extreme abundances of O, Na, and Al are likely also accompanied by excess of Ca. On the other hand, all the remaining stars display an abundance pattern that is perfectly consistent with that of the field stars, and because they represent ∼80% of this limited sample, the statistical test indicates a similarity with the distribution of field stars, despite the contrasting evidence from the optical data and the simple visual inspection of the APOGEE data themselves.

NGC 6752 shows a small skewness in the Ca distribution and the K–S test indicates a (quite marginal) difference with the field star distribution. Furthermore, a few outliers are present, as also immediately evident from the visual inspection, and this is not found in the optical samples. We cross-matched the APOGEE data with ours from the O-Na anti-correlation study by Carretta et al. (2007), finding 60 stars in common within the range in S/N and temperature acceptable for accurate IR data. All outliers with high values of Ca are SG stars (as is also the outlier star located below the field star distribution) according to our classification in P, I, and E components (Carretta et al. 2009b). For the remaining stars, the distribution of population is as expected: the vast majority of higher-Ca belongs to SG, while SG and FG stars are about two-thirds to one-third for the lower-Ca. Finally, we note that none of the analyses based on optical spectra presented evidence of an excess of Ca in the sample (Table 2). This result is also confirmed by data for Sc, available for the two optical samples in the literature: the K–S test excludes a statistically significant excess of Sc in stars of NGC 6752. In conclusion, because NGC 6752 shows an Si-Al correlation (Carretta et al. 2009a), but apparently K is not touched (Mucciarelli et al. 2017) and Ca and Sc are compatible with the level found in field stars of similar metallicity in all the available analyses but the one from APOGEE, the IR data deserve further studies.

Finally, the case for NGC 2808 is more complicated; the cluster is a prime example for extended anti-correlations and the data in our golden set also show excess in Ca (and Sc, in addition to K, see Mucciarelli et al. 2015 for the last). The APOGEE data are compatible with the field star distribution, at least according to the K–S test (see Table 3). However, the excess of Ca is clearly evident from Fig. C.1, with 5 stars in the sample found at more than 3σ above the field star distribution. To better understand this, we cross-matched the two samples, finding 51 stars in common. By assigning the common APOGEE stars to the population groups defined in Carretta (2015): P1, P2, I1, I2, and E, indicating the unpolluted and increasingly polluted stars), we found that the analysis by Mészáros et al. (2020) contains an overabundance of stars belonging to the FG component (groups P1 and P2), while in Carretta (2015) these object are shifted in the SG component. More than to selection effects, this difference is likely to be due to uncertainties in the abundance analysis. On average, we found that the scatter for the Mg abundances in APOGEE (0.111 dex, 66 stars) is about twice the scatter in the optical analysis (0.056 dex, 83 stars). Larger uncertainties mean that the Ca abundance excess is probably not perfectly correlated with the population groups, generating the confusion signalled in the statistical tests. The presence of matter processed at high temperature is well assessed also in the APOGEE sample. In addition to the K-Mg anti-correlation in NGC 2808 claimed by Mészáros et al. (2020), confirming previous results of Mucciarelli et al. (2015), using their APOGEE data we found a correlation between K and Ca abundances that is significant to a high level of confidence (p-value = 4.4 × 10−3), much more than the weak anti-correlation between K and Mg (p-value = 0.122).

4.2. NGC 4833: another GC with K-Mg anti-correlation

The APOGEE data have the additional advantage of providing the K abundance derived for many stars in several GCs; this is not routinely done. Mucciarelli et al. (2012, 2015) found a Mg-K anti-correlation in NGC 2419 and NGC 2808, respectively, with strongly depleted Mg abundances. Mészáros et al. (2020) added ω Cen to the small list of clusters showing this feature. They applied very restrictive quality cuts because the two K lines in the H band are fairly weak, especially at low metallicity, so that confirmation from optical spectroscopy is required before the extent of the Mg-K anti-correlation in this third GC can be discussed. Interestingly, Mészáros et al. (2020) also found a weak anti-correlation in NGC 1904, but they attributed this more probably to correlated errors in the measurements.

Unfortunately, the GCs analyzed by Mészáros et al. (2020) do not include NGC 4833. The results we obtained here indicate that this cluster as a good candidate to host a well-defined K-Mg anti-correlation, although it is probably less extended than those found in NGC 2808 and NGC 2419 (and possibly ω Cen). However, we found GIRAFFE spectra with the HR18 setup in the ESO archive (programme 095.D-0539(A), PI Mucciarelli) that were taken to study the K abundance and its relation to other light elements. In the same observational programme, spectra in the K I line region were also acquired for stars in NGC 7078 (M 15), NGC 6715 (M 54), and NGC 5139 (ω Cen); these are the only GCs that differ in the diagnostic plot presented in Carretta et al. (2014a, Fig. 10) in addition to NGC 4833, NGC 2808, and NGC 2419. Results from that programme are not yet published, therefore we downloaded spectra of NGC 4833 from the ESO archive to make a simple test. In Fig. 6 we compare the GIRAFFE spectra in the region around the K I 7698.98 Å line for two pairs of stars selected from Carretta et al. (2014a) to have similar atmospheric parameters but differences in their Mg content as large as possible.

thumbnail Fig. 6.

Lower panels: comparison of ESO archive GIRAFFE HR18 spectra in the potassium resonance K I 7698.98 Å line region for two pairs of stars in NGC 4833 analysed in Carretta et al. (2014a). Each pair contains two stars selected to have similar atmospheric parameters (listed in each panel) and to span a range as wide as possible in [Mg/H] (also listed). The position of each pair of stars in the [Ca/H] vs [Mg/H] plane is shown in the upper panels.

In both cases the outcome of this comparison is as expected if a K-Mg anti-correlation does exist in the stars of NGC 4833: the stars with lower Mg abundances are also those whose K content is higher (and vice versa), judging from the line depth. The difference does not seem very large, but in one case the chosen stars are not even at the extreme of the Mg range in NGC 4833 (upper left panel in Fig. 6).

Here we limit ourselves to conclude for the first time that NGC 4833 is another GC likely to host a fully developed K-Mg anti-correlation, joining the set of GC with this signature of extreme nuclear processing in multiple stellar populations. The K-Mg relation should be explored for the full sample in NGC 4833, but this is beyond the immediate aim of the present work. Similarly, the analysis of the extant data for NGC 7078 (M 15) would also be important to ascertain the existence (and extent) of a K-Mg anti-correlation.

5. GCs with uncertain or borderline results

As already stated in Sect. 3.4, some GCs in the optical literature sample show uncertain results and need further discussion. In some cases, the uncertainty derives from contradictory indications from different studies of apparently similar quality and merit. It is not always possible to solve the discrepancies. The solution will probably only be achieve when larger samples are studied in a homogeneous way. This will be possible with high-resolution spectroscopic surveys, such as WEAVE (Dalton et al. 2012) and 4MOST (de Jong 2011), which are soon to start in the Northern and Southern hemisphere, respectively.

NGC 4590. The cluster has three datasets, only one of which (Schaeuble et al. 2015) shows GC stars that are statistically different from the field, according to the K–S test. In this sample, only one star lies more than 3σ above the field star distribution, which might be an indication of processing at high temperatures. Furthermore, we note that Mg seems to present a wider range of values (see Fig. A.2) than the other studies. A possibility is the inclusion in the sample by S15 of blue HB stars, whose scatter in both Mg and Ca is noticeably higher than RGB and red HB stars. However, the K–S test applied to the [Sc/H] distribution also appears to exclude that cluster and field stars are extracted from the same parent distribution.

NGC 6205. The three datasets (two optical, one IR) have similar size, but only the stars in Cohen & Melendez (2005a,b) show a possible indication of high-temperature H-burning from the K–S test and four outliers in Ca. According to the Sc values, however, there is no significant difference between field and cluster stars. This GC surely merits further study because it shows very extended anti-correlations, with an extreme depletion in oxygen.

NGC 6218. For this cluster the two available optical samples contain 11 stars each, but while nothing is seen in the silver sample dataset, in good agreement with the results from APOGEE, the K–S test gives contradictory results for the Johnson & Pilachowski (2006) case. However, no star is found to exceed the 3σ threshold. Furthermore, no significant variations in Sc are evident from the comparison with field stars (Fig. B.5). We have no explanation for this, and while the GC probably does not show Ca enhancement, larger samples are required to firmly settle the issue.

NGC 6440. Only seven stars are present in Muñoz et al. (2018) for this GC, for which the statistical test indicates a difference with the field star distribution. NGC 6440 is metal rich, at the limit of the Gratton et al. (2003) sample. However, the situation remains the same when we compare it to more extended samples of field stars (e.g. Bensby et al. 2014). When we instead consider Sc, the cluster distribution does not statistically differ from the field stars. We also note that the outlier farther away from the field distribution has a ratio [Na/Fe] = +0.15 dex that identifies it as an FG star, unlikely to have severe alterations in any of the proton-capture elements. Given the contradictory results of Ca and Sc and the small sample, further tests are required.

NGC 6441. Abundances for this cluster come from Gratton et al. (2006, 2007). At variance with NGC 6388, which is often considered a sibling, it apparently shows indications of hot-H cycling, with a statistically significant excess in Ca according to the K–S test, and with many outliers, while Sc seems to be the same as in the field star distribution. The comparison with the analysis of NGC 6388, an almost twin cluster in metallicity, age, and location in the Galactic bulge, may be of some help. The observed spreads in [Mg/H], [Ca/H], and [Sc/H] are 0.06, 0.06, and 0.08 dex, respectively, for NGC 6388 (Carretta & Bragaglia, in prep.). These values increase to 0.18, 0.24, and 0.21 dex for NGC 6441 in Gratton et al. (2006, 2007). However, we remark that only 34% of the requested observations were obtained for NGC 6441, while observations were completed for NGC 6388 (and are further complemented by many archival datasets in the forthcoming analysis we used here, Carretta & Bragaglia, in prep.). As a consequence, the median S/N for HR13 spectra in NGC 6441 is 55, compared to 76 for NGC 6388. We therefore conclude that the larger dispersions observed in NGC 6441 are probably not intrinsic, but are mostly due to the lower quality of the spectra. A definitive answer must unfortunately await until better quality data are available also for NGC 6441.

NGC 6553. For this metal-rich GC, the dataset by Tang et al. (2017) shows no difference from the field stars, while the dataset by Johnson et al. (2014), similar in size, does (even if the K–S test is only marginally conclusive). However, when we consider the enhanced set of metal-rich field stars (Bensby et al. 2014), the evidence weakens as the K–S test is passed. Therefore NGC 6553 is probably not a strong enough case for Ca enhancement.

Pal 14. For this very distant GC, the Ca and Sc distributions give contradictory answers. Given the rather large spread in Mg and because the outliers are below the field star distribution and not above, we tend to attribute the result to a combination of small sample and large errors.

6. Discussion and summary

Star-to-star variations in the light proton-capture elements C, N, O, and Na are so ubiquitous in Milky Way GCs that the presence of the O-Na anti-correlation has been proposed to be the distinctive definition of a genuine GC (Carretta et al. 2010a) because the overwhelming majority of GCs show this feature (see the reviews by Bastian & Lardo 2018; Gratton et al. 2019). Only a subset of GCs, the most massive and/or metal-poor, are known to host anti-correlated variations in the abundances of the higher mass Mg and Al (Carretta et al. 2009a; Pancino et al. 2017; Nataf et al. 2019; Mészáros et al. 2020). The present census searched for indications of much higher temperatures reached in the FG polluters of multiple population in GCs, in a regime where the production of Al was disfavoured and an excess of K, Ca, and Sc were instead likely produced. Recalling that some GCs had controversial results according to the test we adopted, we focus in the following on the eight GCs with robust detections, those where the statistical criteria all converged at a high level of confidence.

6.1. Excesses and multiple populations

In Table 4 we summarise the GCs and studies in which variations in K, Ca, and Sc abundances, related to alterations in the Mg amount, were detected, confirmed, or simply noted. Significant variations in Ca with respect to the level of field stars are found in all these GCs, whereas K and Sc abundance variations are uncovered only in about half of the sample.

Table 4.

Globular clusters with detected excesses in K, Ca, and Sc.

Indications for such variations have been reported in a few of the original papers. In NGC 4833, evidence of a Sc-Ca correlation was detected by Carretta et al. (2014a), but it was deemed to be scarcely significant given the large internal errors involved. This was consistent with burning of Mg under conditions advocated by Ventura et al. (2012) to explain the K-Mg anti-correlation in NGC 2419, however. Again for NGC 4833, Roederer & Thompson (2015) noted that [K/Fe] appeared to be anti-correlated with [Mg/Fe], but they found the difference in K abundances in the Mg-rich and Mg-poor groups significant only at about 1.5σ. However, when we perform a linear regression on their limited sample (excluding star 4-224 with [K/Fe] = +1.39, as they did), we find a p-value = 0.018, which is statistically significant. A large spread in [Mg/Fe] was detected in NGC 5824 by Mucciarelli et al. (2018) and Roederer et al. (2016). The latter study did not detect evidence of internal spread for other α-element ratios. Johnson et al. (2017a) did not measure K and Sc abundances in NGC 5986, but they clearly stated that a wide range in [Ca/Mg] was found in this cluster. Although weaker than the spreads in NGC 2808 or NGC 2419, they concluded that significant processing at high temperature was probably at work in this cluster as well, as implied by the diagnostic plot [Ca/Mg] versus [Ca/H] shown in Carretta et al. (2014a). Finally, in their analysis of NGC 6402, Johnson et al. (2019) detected a correlation between [Al/Fe] and [Ca/Fe], which may indicate possible Ca variations. However, they also noted the need for similar correlations involving K and/or Sc to confirm the high-temperature nuclear processing.

The novelty and effectiveness of the approach adopted in the present work also rests on the unambiguous confirmation of all the previous indications of suggested detections. To verify that the variations in Ca (as well as in Sc, whenever possible) are produced by the multiple-population phenomenon, we also mapped in every GC the stars with Ca and Mg abundances onto the O-Na anti-correlation, the main signature of multiple populations in GCs. We used the P, I, and E classification defined in Carretta et al. (2009a); see also Section 4, this work), except for NGC 2808 (Carretta 2015), NGC 5986 (Johnson et al. 2017a) and NGC 6404 (Johnson et al. 2019), for which we followed the subdivision into components given in the original studies.

The association between Ca excesses (as detected by the linearised [Ca/H]corr and the P, I, or E classification is summarised in Fig. 7 for seven GCs. In this plot, only stars with derived abundances of light elements (O and Na) required for P,I, and E classification are shown. For NGC 5824, O and Na abundances are available only for two stars with MIKE spectra, so that it is not possible to separate the sample into P, I, and E groups in this cluster. For NGC 2419 (CK12) only three stars have O abundances; for this GC we can only distinguish between first- (i.e. P) and second-generation (i.e. I) stars. In the majority of cases, the stars showing the highest Ca excess fall in the E component or among the most polluted I stars, where the composition changes due to a previous stellar generation were driven towards more extreme Na enhancements and O depletions. This figure is proof that in these GCs the changes in light proton-capture elements such as O and Na, as well as the alterations in Ca (and by extension, in K and Sc, as in NGC 2808), are linked by the same mechanisms.

thumbnail Fig. 7.

Linearised ratios [Ca/H]corr as a function of [Mg/H] ratios for GCs with robust excess detections (this work). Cluster stars are coloured according to whether they belong to the P, I, or E components defined by the O and Na abundances. For NGC 2808 (Carretta 2015), NGC 5986 (Johnson et al. 2017a) and NGC 6404 (Johnson et al. 2019), we followed the original division into components.

To better quantify this association, we made linear fits to the observed data, using the [Ca/H] ratio as independent variable. We found statistically significant correlations and/or anti-correlations with [Mg/H] in NGC 2419 (p = 0.003); with [O/H] (p = 0.040), [Na/H] (p = 4 × 10−4), and [Al/H] (p = 0.017) in NGC 2808; with [Na/H] (p = 0.033), [Si/H] (p = 0.004), and [K/H] (p = 0.009) in NGC 4833 (ROE15); with [Na/H] and [Al/H] (p <  1 × 10−6) in NGC 5139 (Ndc95); with [Na/H] (p = 0.011) and [Al/H] (p = 3 × 10−4 in NGC 5986 (J17A); with [Na/H] (p = 0.001) and [Al/H] (p = 0.008) in NGC 6402 (J19); and with [Na/H] (p <  1 × 10−6) in NGC 6715 (Carretta et al. 2010c). The tight association between light and higher mass proton-capture elements then indicates that this phenomenon is seen in GCs where the production of nuclearly processed matter in the polluters, regardless of they were, did proceed more than in other clusters, resulting in extreme modifications in stellar composition.

Carretta (2006) introduced a parameter that is well suited to quantify the range of abundance ratios reached in GC multiple population: the interquartile range of the [O/Na] ratio. The higher IQR[O/Na], the lower the O and the higher the Na levels observed in a GC. The extent of the O-Na anti-correlation is found to be primarily driven by the total GC mass, as indicated by the tight correlation between IQR[O/Na] and the total absolute cluster magnitude MV (Carretta et al. 2010a). Because we have a truly homogeneous analysis only for GCs in our golden and silver samples, we adopted the IQR[O/Na] values (IQR2) from the recent empirical calibration by Carretta (2019). Using homogeneous O and Na values for 22 GCs, an empirical calibration as a function of MV, cluster concentration, and HB index was given for non-post-core-collapse GCs, providing empirical IQR2s on the same scale for 95 GCs in the Milky Way. These homogeneous IQR2s are available for most GCs in the present census3, and they are plotted in Fig. 8 as a function of the cluster masses, using the total absolute magnitude MV (as a proxy for total mass) and both the present-day and the initial mass from Baumgardt et al. (2018).

thumbnail Fig. 8.

Extension of the Na-O anti-correlation as given by the empirically calibrated IQR2[O/Na] values from Carretta (2019) as a function of total absolute magnitude MV from Harris (1996, 2010 online edition; left panel) and of the present-day and original total GC masses (middle and right panels, respectively) from Baumgardt et al. (2018). GCs with robust detection of changes in Ca (K and Sc) in the present census are indicated with filled red circles.

The eight GCs with robust detection of variations in Ca have the highest extent of the O-Na anti-correlation in the Galaxy, with the exception of NGC 5824, and are among the most massive GCs in the Milky Way. The processes of mass loss do not seem to have affected the location of these GCs in the plane IQR2-mass strongly, except for a small increase in the present-day mass spread. All the GCs with a high probability of hosting internal abundance variations in Ca (K, Sc) are then at the high-mass end of the Galactic distribution. However, some other factor(s) must be involved, probably related to the cluster metallicity. Although NGC 6388 is one of the most massive GCs in the Milky Way, it does not show any significant change in the content of these higher mass proton-capture elements, and we note that its metallicity is about 0.6 dex higher than that of NGC 2808, the cluster with the highest [Fe/H] values of the GCs highlighted in Fig. 8.

The metallicity effect is also evident from the fact that all these eight GCs belong to the OoII groups, according to the mean period of their RR Lyrae stars, with the exception of the two most metal-rich clusters, NGC 2808 and NGC 6402 (e.g. Catelan 2009). All of them are classified as old halo GCs and are associated with present-day disrupting dwarf galaxies or with inferred past accretion events (see Massari et al. 2019; Forbes 2020; Kruijssen et al. 2020). This origin does not appear to be a strong constraint because orbital properties and age-metallicity relations appear to indicate that most GCs entered the main Galaxy following the accretion of their once parent smaller galaxies. The nomenclature of the ancestral systems almost alone varies in different studies.

To better explore the problem, we computed the fraction of outliers (i.e. GC stars with high and very high values of Ca with respect to the distribution of field stars) in the eight GCs. For NGC 2419 and NGC 5139, where the different analyses provide similar fractions that agree excellently, we averaged them; for NGC 4833, where differences are large, we opted for our analysis from the golden sample, based on a sample three times larger than in ROE15. We checked whether these fractions correlate with many global cluster parameters. We found that good correlations exist with mass and metallicity (from Baumgardt et al. 2018, and the Harris 1996, 2010 online edition, respectively). The best correlation is a multivariate relation where the fraction of stars with more altered Ca excesses is a function of both parameters, shown in Fig. 9. The Pearson correlation coefficient is rP = 0.95, which for eight objects implies a very high statistical confidence level for the derived relation (p = 3 × 10−4), corroborating the reality of this new observable we introduced in the context of multiple populations in GCs. This type of dependence on mass and [Fe/H] has been found previously for other manifestations of the multiple population phenomenon in GCs, for example for the minimum level of O reached in GCs (Carretta et al. 2009b) and the maximum value of Al production (Carretta et al. 2009a). Altogether, these observations reinforce the findings of Carretta et al. (2010a), who showed that the multiple population signatures are driven by a few cluster parameters and that mass and metallicity are among the most important ones.

thumbnail Fig. 9.

Relation between mass and metallicity and the fraction of outliers in [Ca/H]corr in the eight clusters with robust detection. The multivariate relation is indicated in the figure x-axis; the Pearson r coefficient is shown.

Eight out of a sample of 77 GCs is a 10% fraction of clusters showing significant variations in high-mass proton-capture elements. In the same subset, a rough estimate is that the Mg-Al anti-correlation is observed in 30 GCs, that is, 39% of the sample. The source of the variations surveyed in the present work seems to be rare (and dependent on mass and metallicity), and some sort of on-off mechanism is apparently required.

Two modalities are possible: either the polluters are normal stars sampled from the normal IMF of GCs and this particular processing occurred only under particular conditions, or some type of polluter only appeared in a few GCs for some reasons. The best candidates for the first hypothesis could be massive AGB and super-AGB stars because at very low metallicities their hot-bottom burning may reach temperatures so high that nucleosynthesis may advance up to high-mass species such as K (Ventura et al. 2012). A problem might then arise for the higher metallicity GCs such as NGC 2808 and NGC 6402 because the mechanism was used to explain the chemical pattern in NGC 2419, with [Fe/H] ∼ –2 dex.

In the second case, a plausible on-off mechanism might be represented by the supermassive stars born at the centre of some GCs. Gieles et al. (2018) showed that the required conditions for these objects to form may be limited to the most massive clusters (≳106 stars) with high accretion rates (≳105 M⊙ Myr−1). The first condition is clearly satisfied by the above eight GCs, which are among the most massive in the Galaxy, and with scarce evidence for a significant mass loss. Denissenkov & Hartwick (2014) showed that such stars might produce gas whose content matches the composition of E stars. However, the synthesis was followed only up to Mg and Al abundances, nothing was said about higher mass elements.

On the theoretical side, it would be interesting to have a self-consistent and detailed pattern of nucleosynthesis including all species involved in the phenomenon of multiple population for the whole metallicity range spanned by GCs. Now we know that changes in the chemical content of SG stars may concern a range of species that is wider than previously thought, at least in some GCs.

For the observers, we need to ascertain the existence of these excesses also in GCs with uncertain evidence, and we need to gather better statistics for each GC in general. An effort to analyse all the GIRAFFE spectra for GCs in our silver sample is already in progress with the aim to move them to the golden sample. This would increase the number of stars with homogeneous abundances of Mg, Ca, and Sc derived in each cluster by about one order of magnitude.

6.2. Summary

We have extended the analysis presented in Carretta & Bragaglia (2019) of the two GCs NGC 2808 and NGC 6388 to all available data of GCs where information on Ca (an possibly Sc) is available. We collected useful data for 77 individual clusters, which is a significant fraction of the MW globulars. Our prime sample contains 10 GCs that were homogeneously analysed by our group and with large number of stars observed with GIRAFFE and UVES, followed by 16 GCs where only UVES spectra are available. To this we added literature samples, both from optical and IR spectra (the latter from the homogeneous APOGEE survey). For many clusters, more than one source is available.

We verified whether overabundances of Ca (and Sc) over the normal field stars level are present in these GCs, using the diagnostic plot [Ca/H] versus [Mg/H]. We then quantified the enhancement using a K–S test and computing the fraction of the outliers (at 3σ level) in each GCs with respect to the field star distribution. We found a clear indication of Ca enhancement (i.e. of very high temperature H-burning) in NGC 4833, NGC 6715, NGC 6402, NGC 5296, NGC 5824, and ω Cen, which join the previously studied NGC 2419 and NGC 2808 (Cohen & Kirby 2012; Mucciarelli et al. 2012; Carretta 2015, 2019, respectively). For these clusters we connected the Ca enhancement with the normal variations in light elements (O, Na), which are ubiquitous in GCs. We found that the higher levels of Ca are associated with the more polluted SG stars that belong to the E and more extreme I populations.

A few more clusters are uncertain cases either because too few stars for robust statistical analysis are available, or because different datasets give contradictory results (or both). We expect that the situation becomes clearer and a better census is possible when (a) the full analysis of the GIRAFFE spectra of the 16 GCs in our silver sample is completed, which will increase the number of stars tenfold, and (b) in the longer run, when data from large spectroscopic surveys such as WEAVE and 4MOST become available.

The eight GCs with a robust detection of Ca (and possibly Sc) enhancement are among the most massive in the MW, as measured both from present-day and initial mass. They also have very extended O-Na anti-correlations, as measured by IQR[O/Na], strengthening the relation between Ca excess and multiple populations in GCs. The fraction of outliers in Ca abundance also correlates well with cluster mass and metallicity. It would be very useful if models for polluters could systematically explore the yields up to at least Ca over different masses and metallicities.

Finally, we suggest for the first time that an anti-correlation between Mg and K also exists in NGC 4833 (in addition to the three known cases of NGC 2419, NGC 2808, and ω Cen; Cohen & Kirby 2012; Mucciarelli et al. 2012; Mészáros et al. 2020). We hope that the case will be studied in detail, together with other good candidates such as NGC 7078, NGC 6715 (see Carretta et al. 2014a), NGC 1904 (Mészáros et al. 2020), and all other GCs for which we found Ca enhancements in the present work.

1

We recall that for each FLAMES plate, there are about 130 fibres for the GIRAFFE and only 8 for the UVES spectrographs.

2

Primordial P stars are those with [O/Fe] and [Na/Fe] ratios as in normal halo field stars, the intermediate I component has depleted [O/Fe] and enhanced [Na/Fe] ratios, and stars with [O/Na] < –0.9 dex represent the extreme E component.

3

NGC 5139 does not have an HB index, therefore we simply adopted the observed IQR[O/Na] value from data by Johnson & Pilachowski (2010) for this cluster.

Acknowledgments

We thank D. Romano, L. Moscardini, P. Montegriffo, M. Bellazzini, and R. Schiavon for useful comments. We thank the referee for their careful reading and useful discussion of the manuscript. This research has made use of the SIMBAD database (Wenger et al. 2000), operated at CDS, Strasbourg, France and of the VizieR catalogue access tool, CDS, Strasbourg, France (DOI: 10.26093/cds/vizier). The original description of the VizieR service was published in Ochsenbein et al. 2000). This research has made use of NASA’s Astrophysics Data System. We made extensive use of TOPCAT (http://www.starlink.ac.uk/topcat/, Taylor 2005).

References

  1. Arnould, M., Goriely, S., & Jorissen, A. 1999, A&A, 347, 572 [NASA ADS] [Google Scholar]
  2. Barbuy, B., Zoccali, M., Ortolani, S., et al. 2007, AJ, 134, 1613 [NASA ADS] [CrossRef] [Google Scholar]
  3. Barbuy, B., Zoccali, M., Ortolani, S., et al. 2009, A&A, 507, 405 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Barbuy, B., Cantelli, E., Vemado, A., et al. 2016, A&A, 591, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Barbuy, B., Muniz, L., Ortolani, S., et al. 2018, A&A, 619, A178 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Bastian, N., & Lardo, C. 2018, ARA&A, 56, 83 [Google Scholar]
  7. Bastian, N., Cabrera-Ziri, I., & Salaris, M. 2015, MNRAS, 449, 3333 [NASA ADS] [CrossRef] [Google Scholar]
  8. Baumgardt, H., Hilker, M., Sollima, A., & Bellini, A. 2018, MNRAS, 482, 5138 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bensby, T., Feltzing, S., & Oey, M. S. 2014, A&A, 562, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Bragaglia, A., Carretta, E., D’Orazi, V., et al. 2017, A&A, 607, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Çalişkan, Ş., Christlieb, N., & Grebel, E. K. 2012, A&A, 537, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Carretta, E. 2006, AJ, 131, 1766 [NASA ADS] [CrossRef] [Google Scholar]
  13. Carretta, E. 2015, ApJ, 810, 148 [NASA ADS] [CrossRef] [Google Scholar]
  14. Carretta, E. 2019, A&A, 624, A24 [CrossRef] [EDP Sciences] [Google Scholar]
  15. Carretta, E., & Bragaglia, A. 2019, A&A, 627, L7 [CrossRef] [EDP Sciences] [Google Scholar]
  16. Carretta, E., Gratton, R. G., Bragaglia, A., Bonifacio, P., & Pasquini, L. 2004, A&A, 416, 925 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2006, A&A, 450, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Carretta, E., Bragaglia, A., Gratton, R. G., Lucatello, S., & Momany, Y. 2007, A&A, 464, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Carretta, E., Bragaglia, A., Gratton, R. G., & Lucatello, S. 2009a, A&A, 505, 139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2009b, A&A, 505, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Carretta, E., Lucatello, S., Gratton, R. G., Bragaglia, A., & D’Orazi, V. 2011, A&A, 533, 69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2010a, A&A, 516, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2010b, ApJ, 712, L21 [NASA ADS] [CrossRef] [Google Scholar]
  24. Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2010c, A&A, 520, 95 [Google Scholar]
  25. Carretta, E., Gratton, R. G., Bragaglia, A., et al. 2013a, ApJ, 769, 40 [NASA ADS] [CrossRef] [Google Scholar]
  26. Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2013b, A&A, 557, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2014a, A&A, 564, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2014b, A&A, 561, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2015, A&A, 578, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Carretta, E., Bragaglia, A., Lucatello, S., et al. 2017, A&A, 600, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Catelan, M. 2009, Ap&SS, 320, 261 [NASA ADS] [CrossRef] [Google Scholar]
  32. Cohen, J. G. 2004, AJ, 127, 1545 [NASA ADS] [CrossRef] [Google Scholar]
  33. Cohen, J. G., & Kirby, E. N. 2012, ApJ, 760, 86 [NASA ADS] [CrossRef] [Google Scholar]
  34. Cohen, J. G., & Melendez, J. 2005a, AJ, 129, 303 [NASA ADS] [CrossRef] [Google Scholar]
  35. Cohen, J. G., & Melendez, J. 2005b, AJ, 129, 1607 [NASA ADS] [CrossRef] [Google Scholar]
  36. Cohen, J. G., Huang, W., & Kirby, E. N. 2011, ApJ, 740, 60 [NASA ADS] [CrossRef] [Google Scholar]
  37. Cottrell, P. L., & Da Costa, G. S. 1981, ApJL, 245, L79 [NASA ADS] [CrossRef] [Google Scholar]
  38. Crestani, J., Alves-Brito, A., Bono, G., Puls, A. A., & Alonso-García, J. 2019, MNRAS, 487, 5463 [Google Scholar]
  39. Dalton, G., Trager, S. C., Abrams, D. C., et al. 2012, in WEAVE:the next generation wide-field spectroscopy facility for the William Herschel Telescope, SPIE Conf. Ser., 8446, 84460P [Google Scholar]
  40. D’Antona, F., Vesperini, E., & D’Ercole, A. 2016, MNRAS, 458, 2122 [NASA ADS] [CrossRef] [Google Scholar]
  41. Decressin, T., Meynet, G., Charbonnel, C., Prantzos, N., & Ekstrom, S. 2007, A&A, 464, 1029 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. de Jong, R. 2011, The Messenger, 145, 14 [NASA ADS] [Google Scholar]
  43. de Mink, S. E., Pols, O. R., Langer, N., & Izzard, R. G. 2009, A&A, 507, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Denisenkov, P. A., & Denisenkova, S. N. 1989, A.Tsir., 1538, 11 [Google Scholar]
  45. Denissenkov, P. A., & Hartwick, F. D. A. 2014, MNRAS, 437, L21 [NASA ADS] [CrossRef] [Google Scholar]
  46. Feltzing, S., Primas, F., & Johnson, R. A. 2009, A&A, 493, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Forbes, D. A. 2020, MNRAS, 493, 847 [NASA ADS] [CrossRef] [Google Scholar]
  48. Gieles, M., Charbonnel, C., Krause, M. G. H., et al. 2018, MNRAS, 478, 2461 [NASA ADS] [CrossRef] [Google Scholar]
  49. Gonzalez, G., & Wallerstein, G. 1998, AJ, 116, 765 [NASA ADS] [CrossRef] [Google Scholar]
  50. Gratton, R. G., Sneden, C., Carretta, E., & Bragaglia, A. 2000, A&A, 354, 169 [NASA ADS] [Google Scholar]
  51. Gratton, R. G., Bonifacio, P., Bragaglia, A., et al. 2001, A&A, 369, 87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Gratton, R. G., Carretta, E., Claudi, R., Lucatello, S., & Barbieri, M. 2003, A&A, 404, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Gratton, R. G., Sneden, C., & Carretta, E. 2004, ARA&A, 42, 385 [NASA ADS] [CrossRef] [Google Scholar]
  54. Gratton, R. G., Bragaglia, A., Carretta, E., et al. 2005, A&A, 440, 901 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Gratton, R. G., Lucatello, S., Bragaglia, A., et al. 2006, A&A, 455, 271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Gratton, R. G., Lucatello, S., Bragaglia, A., et al. 2007, A&A, 464, 953 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Gratton, R. G., Carretta, E., & Bragaglia, A. 2012, A&ARv., 20, 50 [NASA ADS] [CrossRef] [Google Scholar]
  58. Gratton, R. G., Bragaglia, A., Carretta, E., et al. 2019, A&ARv., 27, 8 [NASA ADS] [CrossRef] [Google Scholar]
  59. Hanke, M., Koch, A., Hansen, C. J., & McWilliam, A. 2017, A&A, 599, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
  61. Ivans, I. I., Sneden, C., Kraft, R. P., et al. 1999, AJ, 118, 1273 [NASA ADS] [CrossRef] [Google Scholar]
  62. Johnson, C. I., & Pilachowski, C. A. 2006, AJ, 132, 2346 [NASA ADS] [CrossRef] [Google Scholar]
  63. Johnson, C. I., & Pilachowski, C. A. 2010, ApJ, 722, 1373 [NASA ADS] [CrossRef] [Google Scholar]
  64. Johnson, C. I., Rich, M. R., Kobayashi, C., Kunder, A., & Koch, A. 2014, AJ, 148, 67 [NASA ADS] [CrossRef] [Google Scholar]
  65. Johnson, C. I., Rich, M. R., Pilachowski, C. A., et al. 2015, AJ, 150, 63 [NASA ADS] [CrossRef] [Google Scholar]
  66. Johnson, C. I., Caldwell, N., Rich, R. M., Pilachowski, C. A., & Hsyu, T. 2016, AJ, 152, 21 [NASA ADS] [CrossRef] [Google Scholar]
  67. Johnson, C. I., Caldwell, N., Rich, M. R., et al. 2017a, ApJ, 842, 24 [NASA ADS] [CrossRef] [Google Scholar]
  68. Johnson, C. I., Caldwell, N., Rich, M. R., & Walker, M. G. 2017b, AJ, 154, 155 [NASA ADS] [CrossRef] [Google Scholar]
  69. Johnson, C. I., Caldwell, N., Rich, M. R., et al. 2017c, ApJ, 836, 168 [CrossRef] [Google Scholar]
  70. Johnson, C. I., Rich, R. M., Caldwell, N., et al. 2018, AJ, 155, 71 [CrossRef] [Google Scholar]
  71. Johnson, C. I., Caldwell, N., Rich, R. M., Mateo, M., & Bailey, J. I. 2019, MNRAS, 485, 4311 [CrossRef] [Google Scholar]
  72. Kacharov, N., Koch, A., & McWilliam, A. 2013, A&A, 554, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Karakas, A. I., & Lattanzio, J. C. 2003, PASA, 20, 279 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  74. Koch, A., & McWilliam, A. 2014, A&A, 565, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  75. Koch, A., Côtè, P., & McWilliam, A. 2009, A&A, 506, 729 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Koch, A., Hansen, T. T., & Kunder, A. 2018, A&A, 609, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Koch, A., Grebel, E. K., & Martell, S. L. 2019a, A&A, 625, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  78. Koch, A., Xu, S., & Rich, R. M. 2019b, A&A, 627, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Kordopatis, G., Wyse, R. F. G., Gilmore, G., et al. 2015, A&A, 582, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Kraft, R. P., Sneden, C., Smith, G. H., et al. 1997, AJ, 113, 279 [NASA ADS] [CrossRef] [Google Scholar]
  81. Kraft, R. P., Sneden, C., Smith, G. H., Shetrone, M. D., & Fulbright, J. 1998, AJ, 115, 1500 [NASA ADS] [CrossRef] [Google Scholar]
  82. Kruijssen, J. M. D., Pfeffer, J. L., Chevance, M., et al. 2020, MNRAS, 498, 2472 [CrossRef] [Google Scholar]
  83. Lai, D. K., Smith, G. H., Bolte, M., et al. 2011, AJ, 141, 62 [NASA ADS] [CrossRef] [Google Scholar]
  84. Lamb, M. P., Venn, K. A., Shetrone, M. D., Sakari, C. M., & Pritzl, B. J. 2015, MNRAS, 448, 42 [NASA ADS] [CrossRef] [Google Scholar]
  85. Langer, G. E., Hoffman, R., & Sneden, C. 1993, PASP, 105, 301 [NASA ADS] [CrossRef] [Google Scholar]
  86. Lee, J.-W., Carney, B. W., & Habgood, M. J. 2005, AJ, 129, 251 [NASA ADS] [CrossRef] [Google Scholar]
  87. Lind, K., Charbonnel, C., Decressin, T., et al. 2011, A&A, 527, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  88. Magurno, D., Sneden, C., Braga, V. F., et al. 2018, ApJ, 864, 57 [CrossRef] [Google Scholar]
  89. Marino, A. F., Villanova, S., Piotto, G., et al. 2008, A&A, 490, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  90. Marino, A. F., Sneden, C., Kraft, R. P., et al. 2011, A&A, 532, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  91. Marino, A. F., Milone, A. P., Karakas, A. I., et al. 2015, MNRAS, 450, 815 [NASA ADS] [CrossRef] [Google Scholar]
  92. Marino, A. F., Milone, A. P., Yong, D., et al. 2017, ApJ, 843, 66 [NASA ADS] [CrossRef] [Google Scholar]
  93. Marino, A. F., Yong, D., Milone, A. P., et al. 2018, ApJ, 859, 81 [NASA ADS] [CrossRef] [Google Scholar]
  94. Marino, A. F., Milone, A. P., Sills, A., et al. 2019, ApJ, 887, 91 [NASA ADS] [CrossRef] [Google Scholar]
  95. Martell, S. L., Smolinski, J. P., Beers, T. C., & Grebel, E. K. 2011, A&A, 534, 136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  96. Massari, D., Mucciarelli, A., Dalessandro, E., et al. 2017, MNRAS, 468, 1249 [NASA ADS] [CrossRef] [Google Scholar]
  97. Massari, D., Koppelman, H. H., & Helmi, A. 2019, A&A, 630, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  98. Mészáros, S., Masseron, T., García-Hernández, D. A., et al. 2020, MNRAS, 492, 1641 [CrossRef] [Google Scholar]
  99. Monaco, L., Saviane, I., Correnti, M., Bonifacio, P., & Geisler, D. 2011, A&A, 525, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  100. Monaco, L., Villanova, S., Carraro, G., Mucciarelli, A., & Moni Bidin, C. 2018, A&A, 616, A181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  101. Mottini, M., Wallerstein, G., & McWilliam, A. 2008, AJ, 136, 614 [NASA ADS] [CrossRef] [Google Scholar]
  102. Mucciarelli, A., Bellazzini, M., Ibata, R., et al. 2012, MNRAS, 426, 2889 [NASA ADS] [CrossRef] [Google Scholar]
  103. Mucciarelli, A., Bellazzini, M., Catelan, M., et al. 2013, MNRAS, 435, 3667 [NASA ADS] [CrossRef] [Google Scholar]
  104. Mucciarelli, A., Bellazzini, M., Merle, T., et al. 2015, ApJ, 801, 68 [NASA ADS] [CrossRef] [Google Scholar]
  105. Mucciarelli, A., Merle, T., & Bellazzini, M. 2017, A&A, 600, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  106. Mucciarelli, A., Lapenna, E., Ferraro, F. R., et al. 2018, ApJ, 859, 75 [NASA ADS] [CrossRef] [Google Scholar]
  107. Muñoz, C., Geisler, D., & Villanova, S. 2013, MNRAS, 433, 2006 [NASA ADS] [CrossRef] [Google Scholar]
  108. Muñoz, C., Villanova, S., Geisler, D., et al. 2017, A&A, 605, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  109. Muñoz, C., Geisler, D., Villanova, S., et al. 2018, A&A, 620, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  110. Mura-Guzmán, A., Villanova, S., & Muñoz, C. 2018, MNRAS, 474, 4541 [NASA ADS] [CrossRef] [Google Scholar]
  111. Nataf, D. M., Wyse, R. F. G., Schiavon, R. P., et al. 2019, AJ, 158, 14 [NASA ADS] [CrossRef] [Google Scholar]
  112. Ness, M., Asplund, M., & Casey, A. R. 2014, MNRAS, 445, 2994 [NASA ADS] [CrossRef] [Google Scholar]
  113. Norris, J. E., & Da Costa, G. S. 1995, ApJ, 441, L81 [Google Scholar]
  114. Ochsenbein, F., Bauer, P., & Marcout, J. 2000, A&AS, 143, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  115. O’Malley, E. M., Knaizev, A., McWilliam, A., & Chaboyer, B. 2017, ApJ, 846, 23 [NASA ADS] [CrossRef] [Google Scholar]
  116. Pancino, E., Romano, D., Tang, B., et al. 2017, A&A, 601, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  117. Prantzos, N., Charbonnel, C., & Iliadis, C. 2017, A&A, 608, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  118. Puls, A. A., Alves-Brito, A., Campos, F., Dias, B., & Barbuy, B. 2018, MNRAS, 476, 690 [NASA ADS] [CrossRef] [Google Scholar]
  119. Rain, M. J., Villanova, S., Muñoz, C., & Valenzuela-Calderon, C. 2019, MNRAS, 483, 1674 [CrossRef] [Google Scholar]
  120. Ramírez, S., & Cohen, J. G. 2002, AJ, 123, 3277 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  121. Ramírez, S., & Cohen, J. G. 2003, AJ, 125, 224 [NASA ADS] [CrossRef] [Google Scholar]
  122. Roederer, I. U., & Thompson, I. B. 2015, MNRAS, 449, 3889 [NASA ADS] [CrossRef] [Google Scholar]
  123. Roederer, I. U., Mateo, M., Bailey, J. I., et al. 2016, MNRAS, 455, 2417 [NASA ADS] [CrossRef] [Google Scholar]
  124. Sakari, C. M., Venn, K. A., Irwin, M., et al. 2011, ApJ, 740, 106 [NASA ADS] [CrossRef] [Google Scholar]
  125. San Roman, I., Muñoz, C., Geisler, D., et al. 2015, A&A, 579, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  126. Sbordone, L., Bonifacio, P., Buonanno, R., et al. 2007, A&A, 465, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  127. Schaeuble, M., Preston, G., Sneden, C., et al. 2015, AJ, 149, 204 [CrossRef] [Google Scholar]
  128. Shetrone, M. D., & Keane, M. J. 2000, AJ, 119, 840 [NASA ADS] [CrossRef] [Google Scholar]
  129. Smith, G. H., & Martell, S. L. 2003, PASP, 115, 1211 [NASA ADS] [CrossRef] [Google Scholar]
  130. Sneden, C., Kraft, R. P., Shetrone, M. D., et al. 1997, AJ, 114, 1964 [NASA ADS] [CrossRef] [Google Scholar]
  131. Sneden, C., Kraft, R. P., Guhathakurta, P., Peterson, R. C., & Fulbright, J. P. 2004, AJ, 127, 2162 [NASA ADS] [CrossRef] [Google Scholar]
  132. Szécsi, D., & Wünsch, R. 2019, ApJ, 871, 20 [NASA ADS] [CrossRef] [Google Scholar]
  133. Tang, B., Cohen, R. E., Geisler, D., et al. 2017, MNRAS, 465, 19 [NASA ADS] [CrossRef] [Google Scholar]
  134. Taylor, M. B. 2005, ASPC, 347, 29 [Google Scholar]
  135. Thygesen, A. O., Sbordone, L., Andrievsky, S., et al. 2014, A&A, 572, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  136. Valenti, E., Origlia, L., & Rich, R. M. 2011, MNRAS, 414, 2690 [NASA ADS] [CrossRef] [Google Scholar]
  137. Ventura, P., D’Antona, F., Mazzitelli, I., & Gratton, R. 2001, ApJ, 550, L65 [NASA ADS] [CrossRef] [Google Scholar]
  138. Ventura, P., D’Antona, F., Di Criscienzo, M., et al. 2012, ApJ, 761, L30 [NASA ADS] [CrossRef] [Google Scholar]
  139. Villanova, S., & Geisler, D. 2011, A&A, 535, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  140. Villanova, S., Carraro, G., Scarpa, R., & Marconi, G. 2010, NewA, 15, 520 [NASA ADS] [CrossRef] [Google Scholar]
  141. Villanova, S., Geisler, D., Carraro, G., Moni Bidin, C., & Munoz, C. 2013, ApJ, 778, 186 [NASA ADS] [CrossRef] [Google Scholar]
  142. Villanova, S., Monaco, L., Moni Bidin, C., & Assmann, P. 2016, MNRAS, 460, 2351 [NASA ADS] [CrossRef] [Google Scholar]
  143. Villanova, S., Moni Bidin, C., Mauro, F., Muñoz, C., & Monaco, L. 2017, MNRAS, 464, 2730 [NASA ADS] [CrossRef] [Google Scholar]
  144. Villanova, S., Monaco, L., Geisler, D., et al. 2019, ApJ, 882, 174 [NASA ADS] [CrossRef] [Google Scholar]
  145. Wenger, M., Ochsenbein, F., Egret, D., et al. 2000, A&AS, 143, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  146. Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] [Google Scholar]
  147. Yong, D., Grundahl, F., Nissen, P. E., Jensen, H. R., & Lambert, D. L. 2005, A&A, 438, 875 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  148. Yong, D., Roederer, I. U., Grundahl, F., et al. 2014a, MNRAS, 441, 3396 [NASA ADS] [CrossRef] [Google Scholar]
  149. Yong, D., Alves-Brito, A., Da Costa, G. S., et al. 2014b, MNRAS, 439, 2638 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Observed distributions for the literature samples

In this appendix we show a visual catalogue of the literature samples examined in the present work that are based on optical high-resolution spectroscopy (Figs. A.1–A.10).

thumbnail Fig. A.1.

Observed [Ca/H] ratios as a function of [Mg/H] ratios for nine GCs in the literature sample, ordered by NGC name. In each panel we list the alphanumeric code of Table 1 to identify the corresponding study. The [Mg/H] scale for NGC 2419 is different, to encompass the whole range of variation in this cluster. The GC stars are plotted in blue whenever the sample includes fewer than five objects.

thumbnail Fig. A.2.

As in Fig. A.1 for the other GCs in the literature sample.

thumbnail Fig. A.3.

As in Fig. A.1 for the other GCs in the literature sample. For NGC 5466 we also show the small APOGEE sample by Mészáros et al. (2020), in magenta.

thumbnail Fig. A.4.

As in Fig. A.1 for the other GCs in the literature sample.

thumbnail Fig. A.5.

As in Fig. A.1 for the other GCs in the literature sample.

thumbnail Fig. A.6.

As in Fig. A.1 for the other GCs in the literature sample.

thumbnail Fig. A.7.

As in Fig. A.1 for the other GCs in the literature sample.

thumbnail Fig. A.8.

As in Fig. A.1 for the other GCs in the literature sample.

thumbnail Fig. A.9.

As in Fig. A.1 for the other GCs in the literature sample.

thumbnail Fig. A.10.

As in Fig. A.1 for the other GCs in the literature sample.

Appendix B: View from Sc

In this appendix we show the visual catalogue of the data for the Sc-Mg distribution observed in all GCs examined in the present work. In Fig. B.1 we show the clusters in the golden sample, and in Figs. B.2–B.8 the same for the literature sample.

thumbnail Fig. B.1.

Observed distributions [Sc/H] as a function of [Mg/H] ratios for the ten GCs in our golden sample, superimposed on field stars in Gratton et al. (2003).

thumbnail Fig. B.2.

Observed distributions [Sc/H] as a function of [Mg/H] ratios for the first nine GCs in the literature sample, superimposed on field stars in Gratton et al. (2003). In each panel we list the alphanumeric code of Table 1 to identify the corresponding study. GC stars are shown in blue whenever the sample includes fewer than five objects.

thumbnail Fig. B.3.

As in Fig. B.2 for the other nine GCs.

thumbnail Fig. B.4.

As in Fig. B.2 for the other nine GCs.

thumbnail Fig. B.5.

As in Fig. B.2 for the other nine GCs.

thumbnail Fig. B.6.

As in Fig. B.2 for the other nine GCs.

thumbnail Fig. B.7.

As in Fig. B.2 for the other nine GCs.

thumbnail Fig. B.8.

As in Fig. B.2 for the last three GCs in the literature sample.

Appendix C: Observed distributions from APOGEE

In this appendix we show the catalogue of the observed Ca-Mg distribution for the GCs in the APOGEE sample (Figs. C.1 and C.2).

thumbnail Fig. C.1.

Observed [Ca/H] ratios as a function of [Mg/H] ratios for the GCs in the APOGEE-2 sample (Mészáros et al. 2020) compared to the field stars in Gratton et al. (2003).

thumbnail Fig. C.2.

As in Fig. C.1 for the other ten GCs in Mészáros et al. (2020).

All Tables

Table 1.

Adopted abundance analyses.

In the text
Table 2.

Results for [Ca/H]–[Mg/H].

In the text
Table 3.

Results for the APOGEE-2 sample (Mészáros et al. 2020).

In the text
Table 4.

Globular clusters with detected excesses in K, Ca, and Sc.

In the text

All Figures

thumbnail Fig. 1.

Upper panel: [Ca/H] ratios as a function of [Mg/H] for the field stars in the sample of Gratton et al. (2003). The linear fit to the data we used to rectify the [Ca/H] values is superimposed. Lower panel: same as in the upper panel. The mean values and rms scatter of GCs in our golden and silver samples are superimposed (see text).
In the text
thumbnail Fig. 2.

Steps of our procedure applied to NGC 4833. Upper left panel: stars in NGC 4833 (Carretta et al. 2014a: filled blue squares) superimposed to field stars (Gratton et al. 2003: empty grey squares) in the [Ca/H]–[Mg/H] plane. Upper right panel: same stars (and symbols) after subtracting the linear fit in Fig. 1 from [Ca/H] to obtain linearised values [Ca/H]corr. Lower left panel: generalised histograms of the [Ca/H]corr values for field (filled grey area) and GC stars (empty blue area). Lower right panel: cumulative distribution of corrected Ca abundances for field and GC stars. The probability for the two-tail Kolmogorov-Smirnov test is also listed.
In the text
thumbnail Fig. 3.

Observed [Ca/H] ratios as a function of [Mg/H] ratios for the GCs in our golden sample (filled blue squares) compared to the field stars in Gratton et al. (2003: empty grey squares).
In the text
thumbnail Fig. 4.

Analysis for the detection and test of the Ca excess in NGC 1851: the whole procedure is now applied separately to the two stellar components (red and blue symbols and lines) found by Carretta et al. (2011) in this cluster.
In the text
thumbnail Fig. 5.

Observed [Ca/H] ratios as a function of [Mg/H] ratios for the GCs in our silver sample (filled blue squares) compared to the field stars in Gratton et al. (2003), shown in grey.
In the text
thumbnail Fig. 6.

Lower panels: comparison of ESO archive GIRAFFE HR18 spectra in the potassium resonance K I 7698.98 Å line region for two pairs of stars in NGC 4833 analysed in Carretta et al. (2014a). Each pair contains two stars selected to have similar atmospheric parameters (listed in each panel) and to span a range as wide as possible in [Mg/H] (also listed). The position of each pair of stars in the [Ca/H] vs [Mg/H] plane is shown in the upper panels.
In the text
thumbnail Fig. 7.

Linearised ratios [Ca/H]corr as a function of [Mg/H] ratios for GCs with robust excess detections (this work). Cluster stars are coloured according to whether they belong to the P, I, or E components defined by the O and Na abundances. For NGC 2808 (Carretta 2015), NGC 5986 (Johnson et al. 2017a) and NGC 6404 (Johnson et al. 2019), we followed the original division into components.
In the text
thumbnail Fig. 8.

Extension of the Na-O anti-correlation as given by the empirically calibrated IQR2[O/Na] values from Carretta (2019) as a function of total absolute magnitude MV from Harris (1996, 2010 online edition; left panel) and of the present-day and original total GC masses (middle and right panels, respectively) from Baumgardt et al. (2018). GCs with robust detection of changes in Ca (K and Sc) in the present census are indicated with filled red circles.
In the text
thumbnail Fig. 9.

Relation between mass and metallicity and the fraction of outliers in [Ca/H]corr in the eight clusters with robust detection. The multivariate relation is indicated in the figure x-axis; the Pearson r coefficient is shown.
In the text
thumbnail Fig. A.1.

Observed [Ca/H] ratios as a function of [Mg/H] ratios for nine GCs in the literature sample, ordered by NGC name. In each panel we list the alphanumeric code of Table 1 to identify the corresponding study. The [Mg/H] scale for NGC 2419 is different, to encompass the whole range of variation in this cluster. The GC stars are plotted in blue whenever the sample includes fewer than five objects.
In the text
thumbnail Fig. A.2.

As in Fig. A.1 for the other GCs in the literature sample.
In the text
thumbnail Fig. A.3.

As in Fig. A.1 for the other GCs in the literature sample. For NGC 5466 we also show the small APOGEE sample by Mészáros et al. (2020), in magenta.
In the text
thumbnail Fig. A.4.

As in Fig. A.1 for the other GCs in the literature sample.
In the text
thumbnail Fig. A.5.

As in Fig. A.1 for the other GCs in the literature sample.
In the text
thumbnail Fig. A.6.

As in Fig. A.1 for the other GCs in the literature sample.
In the text
thumbnail Fig. A.7.

As in Fig. A.1 for the other GCs in the literature sample.
In the text
thumbnail Fig. A.8.

As in Fig. A.1 for the other GCs in the literature sample.
In the text
thumbnail Fig. A.9.

As in Fig. A.1 for the other GCs in the literature sample.
In the text
thumbnail Fig. A.10.

As in Fig. A.1 for the other GCs in the literature sample.
In the text
thumbnail Fig. B.1.

Observed distributions [Sc/H] as a function of [Mg/H] ratios for the ten GCs in our golden sample, superimposed on field stars in Gratton et al. (2003).
In the text
thumbnail Fig. B.2.

Observed distributions [Sc/H] as a function of [Mg/H] ratios for the first nine GCs in the literature sample, superimposed on field stars in Gratton et al. (2003). In each panel we list the alphanumeric code of Table 1 to identify the corresponding study. GC stars are shown in blue whenever the sample includes fewer than five objects.
In the text
thumbnail Fig. B.3.

As in Fig. B.2 for the other nine GCs.
In the text
thumbnail Fig. B.4.

As in Fig. B.2 for the other nine GCs.
In the text
thumbnail Fig. B.5.

As in Fig. B.2 for the other nine GCs.
In the text
thumbnail Fig. B.6.

As in Fig. B.2 for the other nine GCs.
In the text
thumbnail Fig. B.7.

As in Fig. B.2 for the other nine GCs.
In the text
thumbnail Fig. B.8.

As in Fig. B.2 for the last three GCs in the literature sample.
In the text
thumbnail Fig. C.1.

Observed [Ca/H] ratios as a function of [Mg/H] ratios for the GCs in the APOGEE-2 sample (Mészáros et al. 2020) compared to the field stars in Gratton et al. (2003).
In the text
thumbnail Fig. C.2.

As in Fig. C.1 for the other ten GCs in Mészáros et al. (2020).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.