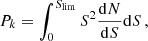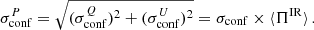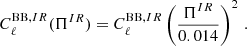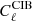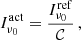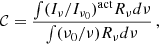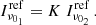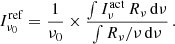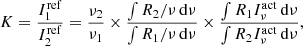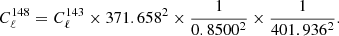| Issue |
A&A
Volume 642, October 2020
|
|
|---|---|---|
| Article Number | A232 | |
| Number of page(s) | 25 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201937147 | |
| Published online | 23 October 2020 | |
Impact of polarised extragalactic sources on the measurement of CMB B-mode anisotropies
1
Aix Marseille Univ, CNRS, CNES, LAM, Marseille, France
e-mail: guilaine.lagache@lam.fr
2
CNRS, IRAP, 9 Av. colonel Roche, BP 44346, 31028 Toulouse cedex 4, France
3
Jet Propulsion Laboratory, California Institute of Technology, Pasadena, CA 91109, USA
4
Département de Physique Théorique and Center for Astroparticle Physics, Université de Genève, 24 quai Ansermet, 1211 Genève 4, Switzerland
Received:
19
November
2019
Accepted:
12
August
2020
One of the main goals of cosmology is to search for the imprint of primordial gravitational waves in the polarisation filed of the cosmic microwave background to probe inflation theories. One of the obstacles in detecting the primordial signal is that the cosmic microwave background B-mode polarisation must be extracted from among astrophysical contaminations. Most efforts have focus on limiting Galactic foreground residuals, but extragalactic foregrounds cannot be ignored at the large scale (ℓ ≲ 150), where the primordial B-modes are the brightest. We present a complete analysis of extragalactic foreground contamination that is due to polarised emission of radio and dusty star-forming galaxies. We update or use current models that are validated using the most recent measurements of source number counts, shot noise, and cosmic infrared background power spectra. We predict the flux limit (confusion noise) for future cosmic microwave background (CMB) space-based or balloon-borne experiments (IDS, PIPER, SPIDER, LiteBIRD, and PICO), as well as ground-based experiments (C-BASS, NEXT-BASS, QUIJOTE, AdvACTPOL, BICEP3+Keck, BICEPArray, CLASS, Simons Observatory, SPT3G, and S4). The telescope aperture size (and frequency) is the main characteristic that affects the level of confusion noise. Using the flux limits and assuming mean polarisation fractions independent of flux and frequency for radio and dusty galaxies, we computed the B-mode power spectra of the three extragalactic foregrounds (radio source shot noise, dusty galaxy shot noise, and clustering). We discuss their relative levels and compare their amplitudes to that of the primordial tensor modes parametrised by the tensor-to-scalar ratio r. At the reionisation bump (ℓ = 5), contamination by extragalactic foregrounds is negligible. While the contamination is much lower than the targeted sensitivity on r for large-aperture telescopes at the recombination peak (ℓ = 80), it is at a comparable level for some of the medium- (∼1.5 m) and small-aperture telescope (≤0.6 m) experiments. For example, the contamination is at the level of the 68% confidence level uncertainty on the primordial r for the LiteBIRD and PICO space-based experiments. These results were obtained in the absence of multi-frequency component separation (i.e. considering each frequency independently). We stress that extragalactic foreground contaminations have to be included in the input sky models of component separation methods dedicated to the recovery of the CMB primordial B-mode power spectrum. Finally, we also provide some useful unit conversion factors and give some predictions for the SPICA B-BOP experiment, which is dedicated to Galactic and extragalactic polarisation studies. We show that SPICA B-BOP will be limited at 200 and 350 μm by confusion from extragalactic sources for long integrations in polarisation, but very short integrations in intensity.
Key words: cosmic background radiation / submillimeter: galaxies / radio continuum: galaxies
© G. Lagache et al. 2020
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
The ΛCDM model is the standard model of cosmology. It is the simplest parametrisation of the Hot Big Bang model, with two principal ingredients: Λ refers to a cosmological constant (i.e. the energy density of the vacuum), and CDM stands for cold dark matter, that is, dark matter particles that move slowly. Because it is very successful in predicting a wide variety of observations related to the cosmic microwave background (CMB), the large-scale structure, and gravitational lensing, the ΛCDM model has reached the status of a paradigm. In this paradigm, an era of early exponential expansion of the Universe, dubbed cosmic inflation, has been proposed to explain why the Universe as revealed by the CMB radiation is almost exactly Euclidean and so nearly uniform in all directions. While the basic ΛCDM model fits all the data (with parameters known at the percent level), the physics of inflation is still unknown. Thus, one of the central goals of modern cosmology is to determine the nature of inflation. One generic prediction is the existence of a background of gravitational waves, which produces a distinct, curl-like signature in the polarisation of the CMB. This is referred to as primordial B-mode polarisation (which is due to tensor perturbations). The detection of this primordial B-mode polarisation would provide clear proof that inflation did occur in the early Universe. Unfortunately, cosmic inflation does not provide a unique prediction for the amplitude of the primordial tensor modes parametrised by the tensor-to-scalar ratio r. We are in a situation where there is no natural range for r, in particular, there is no relevant lower bound. The natural goal is to be able to measure r beyond doubt for the Higgs inflation (which is an inflation scenario where the inflaton field is the Higgs boson), that is, r ≥ ∼ 2 × 10−3 at 5σ. If this does not lead to a detection, it will discard the whole class of large-field models. If the inflaton field was nothing but the Higgs field, this would have tremendous consequences for physics. Thus a precise measurement of (or upper bound on) r is essential to constrain inflation physics. The current 95% CL upper limit on r as measured by Planck1 combined with ground-based CMB experiments is r < 0.056 (Planck Collaboration X 2020) at a pivot scale of k = 0.002 Mpc−1. The search for the primordial B-mode is an outstanding challenge that has motivated a number of experiments designed to measure the anisotropies of the CMB in polarisation with an ever-increasing precision.
B-modes are also generated by gravitational lensing of E-mode polarisation, providing a unique window into the physics of the evolved Universe and invaluable insights into late-time physics, such as the effect of dark energy and the damping of structure formation by massive neutrinos. These lensing B-modes are a nuisance for the primordial B-modes. Several approaches have been studied for the CMB B-mode delensing using large-scale structure surveys (galaxies or the cosmic infrared background (CIB), e.g. Smith et al. 2012; Sherwin & Schmittfull 2015; Manzotti et al. 2017), or assuming that the lensing potential can be estimated internally from CMB data (e.g. Carron et al. 2017; Sehgal et al. 2017).
In addition to instrumental challenges, future experiments targeting r ∼ 10−3 will have to solve the critical problem of component separation. In addition to lensing, polarised Galactic foreground contamination dominates the amplitude of the large-scale CMB B-modes by several orders of magnitude. The capabilities of future experiments to remove the contamination due to polarised Galactic emissions have been investigated for example by Errard et al. (2016), Remazeilles et al. (2016) and Philcox et al. (2018). We investigate the polarisation fluctuations caused by extragalactic contaminants: radio galaxies and dusty star-forming galaxies (DSFG). While polarised compact extragalactic sources are expected to be a negligible foreground for CMB B-modes near the reionisation peak (ℓ < 10), they are expected to be the dominant foreground for r = 10−3 when delensing has been applied to the data, from the recombination peak to higher multipoles, ℓ > 50 (Curto et al. 2013).
Extragalactic radio sources are typically assumed to be Poisson distributed in the sky. The clustering of radio sources is strongly diluted by the broad distribution in redshifts of objects that contribute at any flux density. The contribution of clustering to the angular power spectrum is therefore small and can be neglected if sources are not subtracted down to very faint flux limits, S ≪ 10 mJy (González-Nuevo et al. 2005).
For DSFG, we have to consider polarisation fluctuations not only for the Poisson distribution of point sources, but also for the clustering, that is, the CIB anisotropies (e.g. Knox et al. 2001; Negrello et al. 2004; Viero et al. 2013; Planck Collaboration XXX 2014). The CIB power spectrum can be represented as the sum of two contributions that are usually called the one-halo and two-halo terms. The one-halo represents the correlation of galaxies in the same dark matter halo (pairs of galaxies inside the same halo); the two-halo, capturing the galaxy correlations in different dark-matter haloes, describes the large-scale clustering. While we expect some polarisation fluctuations from the one-halo (which is close to Poisson fluctuations), polarised two-halo fluctuations are expected to be null, provided there is no correlation of the polarisation of galaxies within distinct halos. We could have a contribution from the large-scale clustering because of galaxy spin alignments in the filamentary dark-matter structure (e.g. Codis et al. 2018; Piras et al. 2018, and references therein). However, as recently shown by Feng & Holder (2020), this contribution is >100 and ≳1000 times lower than the shot noise of DSFG at ℓ = 100 and ℓ = 1000, respectively. Thus we consider that it has a negligible effect because it is extremely weak.
We compute the expected level of polarised fluctuations from the shot noise of radio galaxies and DSFG and from the CIB one-halo using current or updated models for a large set of future CMB space-based or balloon-borne experiments (IDS, PIPER, SPIDER, LiteBIRD, and PICO)2, as well as ground-based experiments (C-BASS, NEXT-BASS, QUIJOTE, AdvACTPOL, BICEP3+Keck, BICEPArray, CLASS, SO, SPT3G, and S4)3. Our predictions use a point-source detection limit that is self-consistently computed for each experiment (taking the sensitivities into account and determining confusion noises using our number count models). We also include some predictions for SPICA B-POP. An accurate computation of the flux detection limit is mandatory to predict the shot noise of radio sources because changing the flux cut by 30% affects the shot noise by 30%, while it is less important for DSFG: a small variation in the flux cut leads to only a small variation in shot-noise power (Planck Collaboration XVIII 2011).
Our work extends previous studies that concentrated either on a single experiment (e.g. De Zotti et al. 2015), a restricted frequency area (e.g. Bonavera et al. 2017a; Curto et al. 2013), a given galaxy population (e.g. radio galaxies; Puglisi et al. 2018), or on high multipoles (e.g. Gupta et al. 2019 for ℓ ≳ 2000; e.g. Datta et al. 2019 for CMB EE). We are the first to use our radio and DSFG models in combination with the CIB and CMB contamination and instrument noise to iteratively predict the confusion noise that is due to extragalactic sources for all experiments and then derive the level of polarised fluctuations.
The paper is organised as follows. We present the evolutionary models for radio sources and DSFG and discuss their polarised emission in Sects. 2 and 3. In Sect. 4 we give the formalism for computing polarised shot noise from galaxy number counts in intensity. We then describe our halo model of CIB anisotropies that is used to compute the polarisation power spectra that arise from the clustering of DSFG (Sect. 5). We use these models to compute the flux limit (caused by the fluctuations of the background sky brightness below which sources cannot be detected individually, i.e. the confusion noise) for a large number of future CMB experiments and for SPICA B-POP (Sect. 6). The flux limits allow us to compute the expected level of radio and dusty galaxy polarised shot noises, which we discuss (together with the polarised one-halo) in Sect. 7.1, and which we compare to the CMB primordial B-mode power spectrum in Sect. 7.2 for all experiments. We conclude in Sect. 8.
2. Radio sources
In this section, we present the evolutionary model we are choosing to describe the number counts of radio galaxies (Sect. 2.1), and its update (Sect. 2.2). We then discuss the polarised emission of radio galaxies (Sect. 2.3). Finally, we compute the shot noise using our model and compare it with observations from CMB experiments (Sect. 2.4).
2.1. Number counts at cm to mm wavelengths
Number counts of extragalactic radio sources are well determined at radio frequencies ν ≲ 10 GHz down to flux densities of S ≲ 1 mJy (and even S ≲ 0.03 mJy at 1.4 GHz) based on data from deep and large area surveys (e.g. Bondi et al. 2008; De Zotti et al. 2010; Bonavera et al. 2011; Massardi et al. 2011; Miller et al. 2013; Smolčić et al. 2017; Puglisi et al. 2018; Huynh et al. 2020). At higher frequencies, that is, from tens of GHz to millimetre (mm) wavelengths, observational data on radio sources are mainly provided by CMB experiments (e.g. Planck Collaboration XXVI 2016; Datta et al. 2019; Gralla et al. 2020; Everett et al. 2020). Space missions such as WMAP and Planck, which cover the full sky, were able to detect only bright sources, with flux densities higher than a few hundred mJy at best. On the other hand, the better angular resolution of ground-based experiments allows them to reach deeper in flux density, but on smaller areas of the sky. The uncertainties on number counts are therefore still large, especially in the frequency range where the CMB dominates, that is, between 70 and 300 GHz.
Evolutionary models for extragalactic radio sources (e.g. Toffolatti et al. 1998; De Zotti et al. 2005; Massardi et al. 2010) are able to provide a good fit to data on luminosity functions and multi-frequency source counts from ∼100 MHz to ≳5 GHz. They adopt a schematic description of radio source populations, divided into steep- and flat-spectrum (or blazars) sources, according to the spectral index of the power-law spectrum, S(ν) ∝ να, at GHz frequencies that is lower or higher than −0.5. A simple power law is also used to extrapolate spectra to high frequencies, ν ≫ 5 GHz. However, especially for blazars, real source spectra are generally more complex than a power law, which can hold only for limited frequency ranges. As a consequence, these models tend to over-predict the number counts of radio sources at ν ≳ 100 GHz, as measured by the Atacama Cosmology Telescope (ACT) at 148 GHz (Marriage et al. 2011), for instance, or by Planck in all the High Frequency Instrument (HFI) channels (Planck Collaboration XIII 2011; Planck Collaboration Int. VII 2013). The main reason for this disagreement is the spectral steepening observed in Planck radio source catalogues above ∼70 GHz (Planck Collaboration XIII 2011; Planck Collaboration XV 2011; Planck Collaboration Int. XLV 2016) that was previously suggested by other data sets (González-Nuevo et al. 2008; Sadler et al. 2008).
A first attempt of taking this steepening in blazar spectra into account was made by Tucci et al. (2011). They described the spectral behaviour of blazars at cm–mm wavelengths statistically by considering the main physical mechanisms responsible for the emission. In agreement with classical models of the synchrotron emission in the inner jets of blazars (Blandford & Königl 1979; Konigl 1981; Marscher & Gear 1985), the spectral high-frequency steepening was interpreted as caused, at least partially, by the transition from the optically thick to the optically thin regime. The frequency νM at which the spectral break occurs depends on the relevant physical parameters of AGNs: the redshift, the Doppler factor (δ), and the linear dimension of the region (approximated as homogeneous and spherical) that is mainly responsible for the emission at the break frequency. In particular, Tucci et al. (2011) showed that the break frequency can be written in an approximated form as
where DL is the luminosity distance of the sources, and C is a function of the spectral indices before and after the break frequency (αfl and αst respectively) and of the flux density Sν0 at a reference frequency (typically 5 GHz; see their Appendix B). Finally, the parameter rM is the distance from the AGN core of the jet region that dominates the emission at the frequency νM (for a conical jet model, this parameter can be easily related to the dimension of the emitting jet region). It defines the dimension and thus the compactness of the emitting region at that frequency. This is the most critical parameter for determining νM because the uncertainty on its actual value is large.
Based on 5 GHz number counts and on information of spectral properties of radio sources at GHz frequencies, the Tucci et al. (2011) model provided predictions of number counts at cm/mm wavelengths by extrapolating flux densities of radio sources from low (1–5 GHz) to high frequencies. The model considered three populations of radio sources (steep-, inverted-, and flat-spectrum sources), and a different high-frequency spectral behaviour for each of them. Here we focus on blazars, which are the dominant class at ν ≳ 70 GHz. The most successful model studied in the paper (referred to as “C2Ex”) assumes different distributions of the break frequency for BL Lac objects and flat-spectrum radio quasars (FSRQs). According to this, most FSRQs should bend their otherwise flat spectra between 10 and 100 GHz, whereas in BL Lac, spectral breaks are expected typically at ν ≳ 100 GHz (implying that the observed synchrotron radiation comes from more compact emitting regions than FSRQs). This dichotomy has indeed been found in the Planck radio catalogues (Planck Collaboration XIII 2011; Planck Collaboration Int. XLV 2016). This model provides a very good fit to all the data of bright (S ≳ 100 mJy) radio sources for number counts and spectral index distributions up to ∼500– 600 GHz (Planck Collaboration XIII 2011; Planck Collaboration Int. VII 2013).
A partial agreement is also found when other surveys, deeper in flux than Planck, are considered. In Fig. 1 we compare the number counts from the model with observational data at frequencies between 70 and 220 GHz. Beyond Planck, data are from ACT (150, 218 GHz; Marsden et al. 2014; Datta et al. 2019) and SPT and SPT (95, 150, 220 GHz; Mocanu et al. 2013a). The model tends to underestimate SPT/ACT counts in the flux density range Bonavera et al. (2017a), Gupta et al. (2019) mJy. Very recently, however, Everett et al. (2020) presented the number counts from the full 2500 square degrees of the SPT-SZ survey; they extended previous SPT results (see the green points in Fig. 1). These new data agree better with the C2Ex model estimates at 220 GHz.
 |
Fig. 1. Normalized differential number counts (S5/2n(S)) from the Tucci et al. (2011) model (black lines) and observations (Planck, black points; ACT, cyan points; SPT, blue and green points) between 70 and 220 GHz. Red lines represent the model, but with the updated parameter values as described in the text. The very recent measurements from ACT at 148 GHz (cyan dots from Datta et al. 2019) and from SPT-SZ (green dots from Everett et al. 2020) are not used in the fit, but are shown for comparison. |
2.2. Updated model for number counts
The recent data from ACT and SPT experiments give us the opportunity to better constrain the model parameters for blazars. We described above that the break frequency depends on a set of physical parameters related to AGNs. Tucci et al. (2011) imposed most of them on the basis of observational constraints (as the redshift distribution of the different radio source populations; the Doppler factor; spectral indices) and on the basis of typical assumptions for AGN model (equipartition condition, narrow conical jets, etc.). The only free parameter used in the model is the distance rM to the AGN core of the emitting jet region at the break frequency. In the best model of Tucci et al. (2011), rM is taken to be log-uniformly distributed in the range of [0.3, 10] pc for FSRQs and in the range of [0.01, 0.3] pc for BL Lacs.
We now determine the best estimate of the rM range by fitting number counts from Planck, ACT (Marsden et al. 2014) and SPT (Mocanu et al. 2013a) between 70 and 220 GHz. This is done only for BL Lacs, while for FSRQs we maintain the same range of rM values as before. We verified that a change in the rM interval for this class of objects does not improve the fit of the number counts at sub-Jy level significantly (i.e. for ACT/SPT data). This is not surprising because FSRQs provide the dominant contribution to number counts of bright sources, with S ≫ 100 mJy (see Fig. 1). At these flux levels, the strong constraints come from Planck measurements, which are already well described by the model. On the other hand, at fainter fluxes, the relevance of BL Lacs increases, and we expect them to become the dominant population at a few dozen mJy. This is exactly the range of fluxes in which the model slightly underestimates the observed number counts. By increasing the contribution of BL Lacs, we should remove or reduce the discrepancy between model and SPT/ACT data without affecting the predictions for the very bright sources.
Jointly with rM, we considered the spectral index αst of blazars after the break frequency (i.e. in the optically thin regime) as an additional free parameter in the fit. Tucci et al. (2011) assumed this to be distributed as a Gaussian around ⟨αst⟩ = − 0.8 with a dispersion of 0.2, in agreement with the canonical values for the optically thin synchrotron spectral index. No differences between the two classes of blazars were considered. However, Planck Collaboration XIII (2011), Planck Collaboration Int. XLV (2016) found that the average spectral index of blazars after the spectral break is somewhat flatter than −0.8.
The results of the fit give more compact radio-emission regions in BL Lacs than previous values, with 0.0025 ≤ rM ≤ 0.05 pc, that is, about a factor 5 smaller than before. In addition, the average high-frequency spectral index is flatter, ⟨αst⟩ = − 0.7, consistent with the trend observed in Planck data.
Number counts predicted by the updated model differ mainly at low- to intermediate-flux densities, S < 0.1 mJy, and provide an improved fit to observational data at 95 and 150 GHz (see Fig. 1). The reduced χ2 is now very close to 1. SPT data at 95 GHz are still slightly higher, between 20 and 60 mJy, but the discrepancy is reduced and is not significant. The change in the average value of ⟨αst⟩ also produces a small increase in the number counts of FSRQs at ν > 100 GHz. Number counts from the updated model are provided online4.
2.3. Statistical properties of polarised emission
Polarisation in radio sources is typically observed to be a few percent of the total intensity at cm or mm wavelengths (e.g. Murphy et al. 2010; Battye et al. 2011; Sajina et al. 2011; Massardi et al. 2013; Galluzzi et al. 2019), and only very few objects show a fractional polarisation, Π = P/S, as high as ∼10%. Steep-spectrum radio sources are on average more polarised than flat-spectrum sources at ν ≲ 20 GHz (Tucci et al. 2004; Klein et al. 2003). Their fractional polarisation strongly depends on the frequency, from ∼2.5% at 1.4 GHz to ∼5.5% at 10.5 GHz (Klein et al. 2003). At low frequencies, flat-spectrum sources are instead characterised by an almost constant and low degree of polarisation (∼2.5%).
Extensive studies of high-frequency polarisation properties have been conducted by Tucci & Toffolatti (2012) and Massardi et al. (2013) using the Australia Telescope 20 GHz (AT20G) survey (Murphy et al. 2010). This is a quite deep survey in intensity (with a completeness level of 91% at S ≥ 100 mJy and 79% at S ≥ 50 mJy in regions south of declination −15°) with a high detection rate in polarisation. Moreover, simultaneous measurements at 5 and 8 GHz are also available for a consistent fraction of objects. These analyses found that the distribution of the polarisation degree (in blazars) is well described by a log–normal function (see also Battye et al. 2011) with an average fractional polarisation of ∼3%. No clear correlation between the fractional polarisation and the flux density was observed, with a slight dependence on the frequency of the polarisation degree.
At frequencies ν > 20 GHz, polarisation measurements of very bright sources (S ≳ 1 Jy) seem to indicate an increase in fractional polarisation with frequency. Using the VLA for polarisation measurements of a complete sample of the WMAP catalogue, Battye et al. (2011) found that ⟨Πrad⟩ = 2.9, 3.0, and 3.5% at 8.4, 22, and 43 GHz, respectively, and a fractional polarisation that is typically higher at 86 GHz than at 43 GHz. This was confirmed by measurements at 86 GHz from Agudo et al. (2010), obtained with the IRAM 30 m Telescope. They found that for sources with detected polarisation at 15 GHz, the fractional polarisation at 86 GHz is higher than at 15 GHz by a mean factor of ∼2. However, these results were not confirmed using new data and/or improved data analysis procedures (Hales et al. 2014; Bonavera et al. 2017b; Galluzzi et al. 2017; Puglisi et al. 2018; Trombetti et al. 2018; Datta et al. 2019; Gupta et al. 2019). No significant trends of the polarisation degree with flux density or with frequency are found at the frequencies of interest for CMB B-mode search. Latest measurements of fractional polarisation at ν > 50 GHz vary from ∼1.5 to 3.5% and are obtained either using log-normal fits to the distribution of observed polarisation fractions, or using stacking or statistical approaches. To compute the radio source contamination in polarisation to the CMB B-mode (Sect. 7), we assumed a constant ⟨Πrad⟩ = 2.8%, in agreement with the recent Planck (e.g. Puglisi et al. 2018), SPT (Gupta et al. 2019) and ACT (Datta et al. 2019) measurements, and radio source follow-ups from 90 to 220 GHz.
2.4. Shot-noise predictions
In this section, we compare the shot-noise level from residual radio sources found in observational data with values expected from our reference model, to confirm the validity of the model. As the radio shot noise level is highly sensitive to the flux limit, we also provide some useful empirical relations that allow us to compute the shot-noise level as a function of the flux limit.
2.4.1. Shot-noise levels in current CMB experiments
We report the residual shot-noise level in ACT and SPT data estimated by Dunkley et al. (2013) and George et al. (2015), and compare them with predictions from the Tucci et al. (2011) model before and after our update in Table 1. The agreement is quite good for both cases, although the shot-noise level of the updated model is closer to the observational estimates.
Shot-noise power of residual radio sources, Dℓ = ℓ(ℓ + 1)Cℓ/2π [μ ], at ℓ = 3000, estimated in ACT and SPT data, and predicted by models.
], at ℓ = 3000, estimated in ACT and SPT data, and predicted by models.
In Table 2 we report auto- and cross-power spectra (shot noise only) due to residual radio sources in Planck data according to the updated model. We also compute the error of these predictions due to an uncertainty in the flux cut of 20 and 30%. Moreover, we give a tentative estimate of the error associated with the uncertainty on the model that is computed as the difference between results from the old and the updated model. The uncertainties we find are probably quite conservative, but they are nevertheless smaller than the errors due to a 20% uncertainty in Scut at frequencies where radio sources are dominant (i.e. ν ≤ 217 GHz).
Auto- and cross-power spectra due to residual radio sources for Planck according to the updated model for the flux cuts reported in the Table.
The consistency between the measured Poisson amplitude in the Planck auto- and cross-power spectra at 100, 143, and 217 GHz with the updated model discussed here has previously been investigated in Planck Collaboration XI (2016, see their Table 20). The agreement is good, except at 100 GHz, where the predicted amplitude is significantly lower than the observed value. However, this discrepancy was attributed by the authors to a residual unmodelled systematic effect in the data rather than to a foreground modelling error. Moreover, the Poisson power at 100 GHz is found to be smaller in Planck Collaboration V (2020), which agrees better with the model prediction (7.8 Jy2 sr−1 for our model with a flux cut of 340 mJy compared to 10.5 Jy2 sr−1 for Planck, but with an unknown flux cut).
2.4.2. Shot-noise level as a function of flux limits
It can be useful to know the dependence of the shot-noise level from residual radio sources on the flux cut Slim. We considered the Planck frequencies, and a range of flux limits between 1 mJy and 1 Jy, that is, more or less the range covered by CMB experiments.
We start with auto-power spectra. We know that differential number counts for radio sources scale approximately as n(S) ∝ S−2, and power spectra as Cℓ ∝ Slim. Therefore it is convenient to consider the quantity 𝒟SN = Cℓ/Slim. At a given frequency, we fit 𝒟SN ≡ 𝒟SN(Slim) as a double power law:
𝒟SN(Slim) from the updated model and the best fits given by Eq. (2) are shown in Fig. 2. The parameters of the fits are provided in Table 3.
 |
Fig. 2. Left panel: power spectra (divided by the flux limit) of residual radio sources as a function of the flux limit from 30 to 857 GHz (from top to bottom). Points are from the updated T11 model; solid lines are fits using Eq. (2) with parameters given in Table 3. Right panel: cross-power spectra at the frequencies indicated in the figure as a function of the flux limit |
Cross-power spectra depend on the flux cuts at the two considered frequencies. In order to describe  , we chose to use a sixth-degree polynomial function. After computing cross-power spectra in an uniform grid of log(Slim/Jy) between −3 and 0, we determined the polynomial fit using the IDL routine SFIT. For arbitrary flux limits (but always between 1 mJy and 1 Jy) at frequencies ν1 and ν2, cross-power spectra can be estimated by means of
, we chose to use a sixth-degree polynomial function. After computing cross-power spectra in an uniform grid of log(Slim/Jy) between −3 and 0, we determined the polynomial fit using the IDL routine SFIT. For arbitrary flux limits (but always between 1 mJy and 1 Jy) at frequencies ν1 and ν2, cross-power spectra can be estimated by means of
where Ki, j are the coefficients of the fit5. We verified that the fit has a typical error of 2–3%, with maximum errors of about 10–15% (usually at the borders of the grid). Figure 2 also shows examples of cross-power spectra and the corresponding fits when 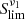 is fixed.
is fixed.
3. Dusty star-forming galaxies
Similarly to the previous section, we present here the evolutionary model we chose to describe the number counts of DSFGs (Sect. 3.1). We then discuss their polarised emission (Sect. 3.2). Finally, we compute the shot noise using our model and compare it with recent observations (Sect. 3.3).
3.1. Model for the number counts
Since their discoveries in the 1990s, DSFGs have revolutionized the field of galaxy formation and evolution (e.g. Casey et al. 2014). The continuous advent of new experiments (either space-based – ISO, Spitzer, Herschel, Planck – or ground-based, e.g. SCUBA/JCMT, Laboca/APEX, IRAM, and ALMA) makes the study of high-z dusty galaxies one of the most important areas of extragalactic astronomy. Accompanying the new measurements, many empirical or semi-analytical models have been developed in the past 20 years (e.g. Lagache et al. 2003; Béthermin et al. 2011; Gruppioni et al. 2011; Lapi et al. 2011; Cai et al. 2013; Casey et al. 2018; Popping et al. 2020). We chose to use the model of Béthermin et al. (2012a) here because it provides one of the best fits to the number counts from the mid-IR to radio wavelengths, including counts per redshift slice in the SPIRE bands. Moreover, it gives a reasonable CIB redshift-distribution, which is important for computing cross-power spectra (Béthermin et al. 2013). Finally, as it has been developed in-house, it can be run for numerous wavelengths and different bandpasses, which is mandatory for our analysis.
The model is based on the main assumption that star-forming galaxies have two modes of star formation: main sequence (MS) and starburst (SB). Main-sequence galaxies are secularly evolving galaxies with a tight correlation between stellar mass (M⋆) and star formation rate (SFR) at a given redshift. The evolution of MS and SB galaxies is based on the Sargent et al. (2012) formalism, which jointly used the mass function of star-forming galaxies, the redshift evolution of the sSFR (specific star formation rate, sSFR = SFR/M⋆), and its distribution at fixed M⋆, with a separate contribution from MS and SB galaxies to reproduce IR luminosity functions. The model uses redshift-dependent templates for the spectral energy distributions (SED) of MS and SB, based on fits of Draine & Li (2007) models to Herschel observations of distant galaxies as presented in Magdis et al. (2012). Finally, as strongly lensed sources contribute ∼20% to (sub-)mm counts around 100 mJy, magnification caused by strong lensing (μ > 2) is also included in the model (see Béthermin et al. 2012a for more details).
We show in Fig. 3 the comparison of the model with some measured far-IR/sub-millimetre counts. We also show the counts from Béthermin et al. (2017), obtained using an updated version of the two star-formation mode galaxy evolution model of Béthermin et al. (2012a), combined with abundance matching to populate a dark matter light cone and thus simulate the clustering. Béthermin et al. (2017) produced 2 deg2 simulated maps (called SIDES) and extracted the sources as done in the observations. They convincingly showed that the limited angular resolution of single-dish instruments has a strong effect on far IR and sub-millimetre continuum observations. In particular, at 350 and 500 μm, they reported that the number counts measured by Herschel between 5 and 50 mJy are biased towards high values by a factor ∼2. When these resolution effects are taken into account, they reproduce a large set of observables very well, such as number counts and their evolution with redshift and CIB power spectra. This demonstrates that any model should thus underestimate the measured single-dish number counts from ∼100 to 1000 μm in a given range of fluxes (see Figs. 4 and 5 in Béthermin et al. 2017). This is indeed the case for Béthermin et al. 2012a (Fig. 3), which agrees very well with the intrinsic SIDES model (and not with the observed SIDES counts). We also show in Fig. 3 the recent counts obtained from the ALMA ALPINE program (Béthermin et al. 2020) at 850 μm, which are not affected by blending due to limited angular resolution, and agree well with the model. For bright fluxes (≳1 Jy), the redshift grid of the model is too coarse to estimate the Euclidian plateau properly. We therefore directly computed the value of the plateau using Eq. (6) of Planck Collaboration Int. VII (2013). Although it is mostly systematically ∼1σ lower, the model agrees to first order with the Euclidian plateau measured by Planck (Planck Collaboration Int. VII 2013). For the purpose of this paper, number counts at such bright fluxes are not relevant, as their contribution to shot noise and confusion noise is negligible. For example, at 272 GHz (1.1 mm), the confusion noise has converged for a flux cut of ∼10 mJy (i.e. the confusion noise for sources with flux < 10 mJy is nearly equal to that of sources with flux < 10 Jy). Therefore we are very confident in our use of the Béthermin et al. (2012a) model to compute the shot-noise levels from DSFG. We clearly validate the use of our model to compute the confusion noises in Sect. 6.3.1. The Béthermin et al. (2017) model could not be used for this purpose as it does not give any analytical predictions and the volume of the dark-matter simulation is too small to derive accurate predictions for the large-volume surveys discussed here.
 |
Fig. 3. Galaxy number counts at 350, 500, and 850 μm. The model we used (Béthermin et al. 2012a) is shown with the continuous line. It agrees very well with the most recent Béthermin et al. (2017) model (SIDES, long-dashed line). Measurements are from Herschel at 350 and 500 μm (Oliver et al. 2010; Clements et al. 2010; Glenn et al. 2010; Béthermin et al. 2012c), SCUBA2, and ALMA at 850 μm (Geach et al. 2017; Béthermin et al. 2020), and Planck at very bright fluxes (Planck Collaboration Int. VII 2013). The models are below the Herschel measurements at intermediate fluxes because these measurements are biased high due to the relatively low angular resolution combined with galaxy clustering (as demonstrated in Béthermin et al. 2017). |
3.2. Polarised emission
Little is known about the polarisation emission of dusty galaxies. Dust enshrouding star-forming galaxies absorbs UV radiation from stars, and re-emits light at longer wavelengths, which is responsible for the far-IR SED of CIB galaxies. Thermal emission from interstellar dust in CIB galaxies, as in our Galaxy, is polarised because the dust grains are aligned with interstellar magnetic fields. The degree of polarisation is not very well known; it is likely to be low because the complex structure of galactic magnetic fields with reversals along the line of sight and the disordered alignment of dust grains reduce the global polarised flux when it is integrated over the whole galaxy.
Very few measurements exist for individual galaxies. Measurements at 850 μm of M82 by Greaves et al. (2002) gave a global net polarisation degree of only 0.4%, while Arp 220 measurements at 850 μm by Seiffert et al. (2007) gave a 99% confidence upper limit of 1.54%. Using the stacking technique with Planck data on a sample of ∼4700 DSFG, Bonavera et al. (2017a) estimated the average fractional polarisation at 143, 217, and 353 GHz. They obtained a mean fractional polarisation ⟨Π⟩ of 3.10 ± 0.75 and 3.65 ± 0.66% at 217 and 353 GHz, respectively, after correcting for noise bias. The uncorrected value of ⟨Π⟩ at 217 GHz is 1.15±0.74%, implying that the detection is significant at the 1.55σ level. At 353 GHz, the detection significance increases from 2.8σ to 5.5σ before and after the correction. Trombetti et al. (2018) revisited these estimates, exploiting the intensity distribution analysis of the Planck polarisation maps. They did not detect any polarisation signal from DSFG at a similarly high significance as Bonavera et al. (2017a). They derived a 90% confidence upper limit on the median fractional polarisation at 353 GHz of ⟨Π⟩≲2.2%. The upper limit at the same confidence level is looser at 217 GHz, ⟨Π⟩≲3.9%, where dusty galaxies are substantially fainter. These upper limits are consistent with the median values reported in Bonavera et al. (2017a), which are 1.3 ± 0.7 and 2.0 ± 0.8% at 217 and 353 GHz, respectively. Recently, Gupta et al. (2019) identified 55 sources as DSFG in their SPT sample, and no polarisation signal was detected for these sources. Their 95% confidence level upper limits are quite high and consistent with earlier results. Finally, De Zotti et al. (2018) made an estimate for spiral galaxies seen edge-on based on the average value of the Stokes Q parameter measured using the Planck dust polarisation maps of the Milky Way. They estimated a mean polarisation degree averaged over all possible inclination angles of 1.4%. These low values of fractional polarisation are understood as due to the complex structure of galactic magnetic fields and to the disordered alignment of dust grains. To study the contamination from polarised emission of DSFG to the CMB B-modes (Sect. 7), we accordingly adopted ⟨ΠIR⟩ = 1.4%.
3.3. Shot-noise predictions
Béthermin et al. 2017 (see also Negrello et al. 2005; Valiante et al. 2016) showed that counts obtained from single-dish antenna observations in the far-IR to mm are biased high because of source multiplicity and clustering in the large beams (10–30 arcsec). This may cause strong discrepancies between shot noises measured from the integral of the observed number counts and shot noises measured from CIB power spectra. For Herschel/SPIRE, another complexity is introduced into the comparison: the beam profile and aperture efficiency vary across the passband and return a relative spectral response function (RSRF) that is different for point sources and extended emission. To compare model predictions to shot-noise measurements from CIB power spectra, we therefore also ran the model with the RSRF for extended source. Comparisons between model and observations are given in Tables 4 and 5 for Herschel/SPIRE and Planck/HFI, respectively. The shot-noise levels from observations are obtained either by fitting the CIB power spectra using the halo model (Viero et al. 2013; Planck Collaboration XXX 2014) or by fitting the total power spectra using a parametric model and assuming a power law for the CIB (Mak et al. 2017). In the first case, there is a strong degeneracy between the one-halo term and the shot noise, especially at the Planck angular resolution.
Herschel/SPIRE shot-noise levels as measured from CIB anisotropies and predicted using the integral of the number counts as modelled by Béthermin et al. (2012a).
Observed and predicted Planck/HFI shot-noise levels.
It is very difficult to derive any conclusion from Tables 4 and 5 because (i) some measured values are incompatible (i.e. when the shot noise derived with a higher flux limit is lower than that derived with a lower flux limit). This is the case for Planck at 545 and 353 GHz and for Herschel at the three wavelengths. ii) the model is not systematically higher or lower than the measurements. In the frequencies of interest (ν≲500 GHz), observations and model predictions agree by 20%, which we assume to be the uncertainty in our prediction. We stress that in contrast to the radio, a small variation in the flux limit Slim leads to only a small variation in shot-noise power. For example, changing Slim by 30% leads to a variation of the shot-noise level seen by Planck by less than 1% at 217 GHz (Planck Collaboration XVIII 2011).
4. Polarised shot noise from point sources: formalism
We explain below why we expect a polarisation term if galaxies have random orientations. We define the complex linear polarisation of a source with flux S,
where Π is the fractional polarisation, and ψ is the polarisation angle.
If the polarisation angles of different sources are uncorrelated, then
but the variance is non-zero (de Zotti et al. 1999),
We derive the shot-noise fluctuations of polarised point sources following Tucci et al. (2004). For Poisson-distributed sources, the temperature power spectrum follows
We can consider a similar expression for the polarisation power spectrum,
where 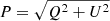 and
and 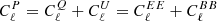 .
.
Because the emission will contribute equally to EE and BB on average, we can consider
The power spectrum due to sources with a given fractional polarisation is
assuming that Π does not vary with S. When the distribution of fractional polarisation for all sources is considered, the power spectrum becomes
where is 𝒫(Π) is the probability density function of fractional polarisation.
This formulation is very convenient, as 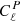 is defined as a function of a flux cut derived in total intensity. Thus it assumes that sources are masked from polarisation maps using total intensity data. This is the case with current CMB experiments and will probably also be most likely the case with future CMB data with the use of higher angular resolution and sensitivity surveys to remove the source contamination. With this formulation, we can also consider different source populations with different fractional polarisations.
is defined as a function of a flux cut derived in total intensity. Thus it assumes that sources are masked from polarisation maps using total intensity data. This is the case with current CMB experiments and will probably also be most likely the case with future CMB data with the use of higher angular resolution and sensitivity surveys to remove the source contamination. With this formulation, we can also consider different source populations with different fractional polarisations.
The probability density function can be constrained from the observed distributions of fractional polarisations. However, because of the lack of constraints at CMB frequencies (∼90–200 GHz) for radio and dusty galaxies, we considered a fix polarisation fraction for each population (see Sect. 7).
5. Clustering of dusty star-forming galaxies
To compute polarisation power spectra due to the clustering of CIB galaxies, we used the halo model, which provides a phenomenological description of the galaxy clustering at all relevant angular scales (Cooray & Sheth 2002). Assuming that all galaxies are located in virialised dark matter halos, the CIB clustering power spectrum is expressed as the sum of two components: a one-halo term, accounting for correlations between galaxies in the same halo, and a two-halo term, due to correlations between galaxies belonging to separated dark matter halos. The first term, together with the shot-noise power spectrum, dominates the small-scale clustering, and the second is prominent at large angular scales. Thus, the total CIB angular power spectrum at frequencies ν and ν′ can be written as
In the following section, after briefly introducing the model and its main parameters (we refer to Shang et al. 2012; Viero et al. 2013; Planck Collaboration XXX 2014 for a detailed discussion), we show that the amplitudes of CIB polarisation power spectra are a small fraction of the one-halo term of the clustering spectra at most, and we derive upper limits on these amplitudes by fitting the model to current measurements of CIB angular power spectra from Herschel/SPIRE (Viero et al. 2013).
5.1. Halo model with luminosity dependence
In the Limber approximation (Limber 1954), the CIB clustering power spectrum at frequencies ν and ν′ is
where the term χ(z) denotes the comoving distance at redshift z, and a(z) is the scale factor. The total emissivity from all CIB galaxies 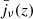 is computed from the luminosity function dn/dL as
is computed from the luminosity function dn/dL as
where the galaxy luminosity Lν(1 + z) is linked to the observed flux Sν as
Finally, the term 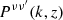 is the 3D power spectrum of the emission coefficient, expressed as
is the 3D power spectrum of the emission coefficient, expressed as
This term includes the two-halo and one-halo term. Expressing the luminosity of central and satellite galaxies as Lcen, ν(1 + z)(MH, z) and Lsat, ν(1 + z)(mSH, z) (where MH and mSH denote the halo and sub-halo masses, respectively), Eq. (14) can be written as the sum of the contributions from central and satellite galaxies as
Here dN/dm and dn/dm denote the halo and sub-halo mass function from Tinker et al. (2008) and Tinker et al. (2010), respectively, and Ncen is the number of central galaxies inside a halo, which was assumed to be equal to zero if the mass of the host halo is lower than Mmin = 1011 M⊙ (Shang et al. 2012) and one otherwise.
Introducing 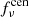 and
and 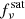 as the number of central and satellite galaxies weighted by their luminosity as
as the number of central and satellite galaxies weighted by their luminosity as
the 3D CIB power spectrum at the observed frequencies ν, ν′ in Eq. (16) can be expressed as the sum of one-halo term and two-halo term as
where
The term u(k, M, z) is the Fourier transform of the halo density profile (Navarro et al. 1997) with a concentration parameter from Duffy et al. (2010), and b(M, z) denotes the halo bias (Tinker et al. 2010). The linear dark matter power spectrum Plin(k) in Eq. (21) is computed using CAMB6.
The parametrisation of the term L(1 + z)ν(M, z) is the key ingredient of the model. Following Shang et al. (2012), we assumed a simple parametric function to describe the link between galaxy luminosity and its host dark matter halo, where the dependence of the galaxy luminosity on frequency, redshift, and halo mass is factorised in three terms as
The free normalisation parameter L0 is constrained by the data and has no physical meaning. The galaxy SED is modelled as (see Blain et al. 2003, and reference therein)
where the Planck function Bν has an emissivity index β = 1.5, (Planck Collaboration Int. XVII 2014; Serra et al. 2016). The power-law functional form at frequencies ν ≥ ν0 has previously been used in a number of similar analyses (Hall et al. 2010; Viero et al. 2013; Shang et al. 2012; Planck Collaboration XXX 2014), and it agrees better with observations than the exponential Wien tail. The free parameter Td is the mean temperature of the dust in CIB galaxies, averaged over the considered redshift range. We assumed a redshift-dependent, global normalisation of the L–M relation of the form
and we considered a log-normal function to describe the luminosity-mass relation as
The term σL/M (fixed to σL/M = 0.5, as in Shang et al. 2012; Viero et al. 2013; Planck Collaboration XXX 2014; Serra et al. 2016) accounts for the range of halo masses that contribute most to the IR luminosity. The parameter Meff describes a narrow range of halo masses around Meff ∼ 1012 M⊙ associated with a peak in the star-formation efficiency that is caused by various mechanisms that suppress star formation in high and low halo masses (Benson et al. 2003; Silk 2003; Bertone et al. 2005; Croton et al. 2006; Dekel & Birnboim 2006; Béthermin et al. 2012b; Behroozi et al. 2013).
5.2. Results
We constrained the main parameters of our halo model using six measurements of CIB angular auto- and cross-power spectra at 250, 350, and 500 μm from Herschel/SPIRE (Viero et al. 2013) in the multipole range 200 < l < 23 000, and assumed the extended flux limit case. To further constrain the model, we also computed the star formation rate density in the range 0 < z < 6, and we fit to the compilation of star formation rate density measurements from Madau & Dickinson (2014).
We performed a Monte Carlo Markov chain (MCMC) analysis of the parameter space using a modification of the publicly available code CosmoMC (Lewis & Bridle 2002), and varied the following set of four halo model parameters:
together with six free parameters Ai = 1, …6 for the amplitudes of the shot-noise power spectra. We obtained a good fit to the data, with a total χ2 of 104.9 for 97 degrees of freedom. Mean values and marginalised limits for all free parameters used in the fit and comparison between Herschel/SPIRE measurements of the CIB power spectra with our best estimates of the one-halo, two-halo, and shot-noise, are shown in Serra et al. (2016). Shot noises derived from this model are very close to those found for the Béthermin et al. (2017) simulations. This gives us confidence about the level of the one-halo term.
5.3. CIB power spectrum in polarisation
The polarisation fraction Π for a given intensity of dust emission I can be expressed in terms of the Stokes parameters Q and U as
where Q and U are related to the polarisation angle ψ, through
Polarisation power spectra can be computed with the same formalism as we used to compute the CIB intensity power spectrum by substituting the galaxy luminosity L(1 + z)ν(M, z) for Q and U as
It is easy to see that if the polarisation among different sources is uncorrelated (as discussed in Sect. 1), the two-halo term cannot produce any polarisation power spectrum because computing it involves an average over the polarisation angle of all sources, which is zero.
The contribution from the one-halo term is slightly more complicated. The dark matter halos that contribute most to the CIB power spectra have a mass in the range 12.5 < Log(MH) < 13.5, and the typical number of satellite galaxies in this range is too small (typically fewer than 5) to average the quantities 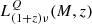 and
and 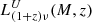 to zero. As a result, when the one-halo contribution is computed, it is possible that terms proportional to
to zero. As a result, when the one-halo contribution is computed, it is possible that terms proportional to
give a positive contribution to the polarisation power spectra. We did not consider here the terms proportional to fsatfcen because it has been shown in simulations and observationally that the tidal field of a large central galaxy can torque its satellites such that the major axis of satellite galaxies points towards their hosts (see e.g. Fig. 8 in Pereira et al. 2008 or Fig. 6 in Joachimi et al. 2015) and we therefore do not expect any polarised signal. While accurate estimates of the amplitude of the polarisation power spectrum would require numerical simulations, we here estimate the maximum contribution from the one-halo term, and we show that it is almost negligible with respect to the contribution from the shot noise (see Sect. 7.1). The maximum amplitude of polarisation can be obtained assuming the (unphysical) case where the polarisation angle ψ of all sources is perfectly correlated and equal to zero (for Q) or π/2 (for U). Assuming ⟨ΠIR⟩ the mean fractional polarisation of all DSFG, it is easy to see that the maximum amplitude of the polarisation power spectra is simply ⟨ΠIR⟩2 times the amplitude of the one-halo contribution to the CIB intensity power spectrum, keeping only the term proportional to 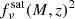 . Thus, the EE of BB CIB power spectra are computed following:
. Thus, the EE of BB CIB power spectra are computed following:
Maximising the contribution of the one-halo term is supported by the evidence of strong clustering of dusty star-forming galaxy on sub-arcmin scales (Chen et al. 2016) as well as the observed abundance of proto-cluster cores on such scales (Negrello et al. 2017). Deriving the polarised CIB power spectrum by simply scaling the total (two- and one-halo) CIB power spectrum in temperature using a fractional polarisation (as done in Curto et al. 2013 or Trombetti et al. 2018) obviously overestimates its contribution.
6. Confusion noise for future polarised experiments
Using our models for radio and DSFG number counts and for the CIB anisotropies, we can now compute the confusion noise and the point-source flux limit (Sect. 6.3) for any CMB experiments, given their characteristics (Sects. 6.1 and 6.2). We describe our method and its validation in Sect. 6.3.1, and we discuss the contributions of the different components (instrument noise, radio, DSFG, CMB) to the point-source sensitivity limit in Sect. 6.3.2. Section 6.3.3 is dedicated to our predictions of confusion noise (in intensity and polarisation) for SPICA B-BOP.
6.1. Future CMB experiments
We considered all future CMB experiments, either already selected, funded, or in advanced discussion. Their name, frequency, angular resolution, sky coverage, and instrument noise (in intensity) are given in Table 6 for balloon-borne and space-based experiments and in Table 7 for ground-based experiments. We also considered Planck for reference and for cross-checks of our computations. The characteristics of each experiment were extracted from: Planck Collaboration I (2020) for Planck; Taylor (2018) for C-BASS; López-Caniego et al. (2014) for QUIJOTE; Calabrese et al. (2014) for AdvACTPOL; Hui et al. (2018) for BICEP+keck and BICEPArray; Essinger-Hileman et al. (2014) for CLASS; Errard et al. (2016) for PIPER; Ade et al. (2019) for Simons Observatory; Rahlin et al. (2014) for SPIDER; Young et al. (2018) for PICO; Abazajian et al. (2019) for CMB-S4; Hill-Valler (2019) for NEXT-BASS; the online presentation for SPT-3G7; the online presentation for LiteBIRD8; the online presentation for IDS9.
CMB space-based and balloon-borne experiments.
6.2. Unit conversions and bandpass corrections
In the mm wavelength domain, two different units are often used. While for studies of Galactic emission or extragalactic sources, the unit is Jansky (Jy), KCMB is the natural unit for CMB. Transforming Jy into KCMB is not only a unit conversion, but also requires a colour correction (to account for the different spectral energy distribution that is implicitly assumed in the two units). This transformation is detailed in Appendix A. The conversion factors that are given in Tables 10 and 11 assume a square bandpass, with a δν and a central frequency ν given in the tables. Colour corrections are not computed for each experiment as it requires precisely knowing the bandpasses (e.g. for Planck, assuming a square bandpass rather than the true bandpass leads to error in the colour corrections that are of the same order as the correction). Consequently, all the numbers given in the tables in Jy are given for the true spectra (but σinst and σCMB, which are given for the convention νIν= constant, use the square bandpasses).
For current experiments with known bandpass, accurate unit conversions are given in Appendix A. For current experiments, a comparison of foreground levels (CIB and SZ especially) also necessitates their extrapolation between nearby frequencies of different experiments. To this end, useful conversion factors are given in Appendix A.
6.3. Confusion noise and flux limit
As we showed in Eq. (11), we chose to use a flux cut in total intensity rather than in polarised intensity mainly for two reasons: (i) we assumed that sources are removed or masked from polarisation maps using total intensity data, for which we could have a high-resolution survey complete to some level in total intensity, as opposed to the equivalent in polarised intensity (e.g. Battye et al. 2011; Datta et al. 2019), and (ii) source number counts in polarisation are very scarce, and more polarisation data are required to constrain dN/dP. By contrast, thanks to the numerous data in intensity obtained in the past decade, accurate modelling is available for number counts in intensity. Consequently, we computed the confusion noise and flux limit in intensity for each CMB experiment listed in Sect. 6.1.
6.3.1. Method and validation
The confusion noise10 is usually defined as fluctuations of the background sky brightness below which sources cannot be detected individually. These fluctuations are caused by intrinsically discrete extragalactic sources. In the far-IR, sub-mm, and mm, the confusion noise is an important part of the total noise budget because of the limited size of the telescopes compared to the wavelength. The confusion noise is even often greater than the instrument noise and therefore severely limits the survey depth (e.g. Lagache et al. 2003; Dole et al. 2003; Negrello et al. 2004; Nguyen et al. 2010).
When the flux of a point source is measured, the root mean square (rms) fluctuations due to extragalactic point sources are the sum of three components:
where σSNrad, σSNir, and σClus are the rms fluctuations associated with the radio shot noise, dusty galaxy shot noise, and dusty galaxy clustering, respectively (we recall that clustering from radio sources is neglected, see Sect. 1). They are related to the power spectrum Pk following
where Wk is the power spectrum of the beam (we assume Gaussian beams), and i stands for SNrad, SNir, and Clus, respectively. Tk is the transfer function linked to the flux measurement of the sources. We assumed that fluxes are measured using aperture photometry,
where ∏ is the rectangular function, and R1 and R2 are the radii of the two circular apertures (with R2 > R1) and
The Fourier transform of f(r) is
which gives the following power spectrum for our aperture photometry filter:
The confusion noise can be determined using two criteria, the so-called photometric and source density criteria (Dole et al. 2003; Lagache et al. 2003). The photometric case is derived from the fluctuations of the signal due to the sources below the detection threshold Slim in the beam. The source density case is derived from a completeness limit and evaluates the density of the sources detected above the detection threshold Slim, such that only a small fraction of sources is missed because they cannot be separated from their nearest neighbour. The choice of the criterion depends on the shape of the source counts and the solid angle of the beam (Dole et al. 2003). The transition between the two is at about 200 μm, depending on telescope diameters (Lagache et al. 2003). In this paper, we therefore use the photometric criterion.
The photometric criterion is related to the quality of the photometry of detected sources, the flux measured near Slim being severely affected by fainter sources in the beam. It is defined by the implicit equation,
where qphot measures the photometric accuracy (we assume qphot = 511), and Slim is the confusion limit. σtot is defined as
where 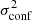 is given in Eq. (36) and σinst is the instrument noise per beam (given in Tables 6 and 7). We also added the noise introduced by CMB fluctuations, σCMB, which is given by Eq. (37), where we replaced Pk by the power spectrum of the CMB. F is a correction factor that accounts for the flux lost by the aperture photometry procedure (which does not cover the entire beam size). With our choice of R1 and R2 (see below), and assuming Gaussian beams, F ≃ 3 for all experiments considered here.
is given in Eq. (36) and σinst is the instrument noise per beam (given in Tables 6 and 7). We also added the noise introduced by CMB fluctuations, σCMB, which is given by Eq. (37), where we replaced Pk by the power spectrum of the CMB. F is a correction factor that accounts for the flux lost by the aperture photometry procedure (which does not cover the entire beam size). With our choice of R1 and R2 (see below), and assuming Gaussian beams, F ≃ 3 for all experiments considered here.
In the range of confusion limits of CMB experiments, only 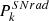 and
and 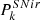 depend on Slim. They are derived following
depend on Slim. They are derived following
where dN/dS are the number counts given by the models described in Sect. 2.2 and Sect. 3.1 for radio and dusty galaxies, respectively.
Confusion noises and flux limits are given in Tables 6 and 7. They were obtained using R1 = FWHM/2 and R2 = 2 × R1.
We confirmed that our confusion noises agree very well with those measured by ISO/ISOPHOT, Herschel/SPIRE, and Planck. For SPIRE, we obtain σconf = 6.4, 6.6, and 5.3 mJy beam−1, while Nguyen et al. (2010) measured 5.8 ± 0.3, 6.3 ± 0.4, and 6.8 ± 0.4 mJy beam−1 at 250, 350 and 500 μm, respectively. For Planck, we compared our flux limit to the flux cuts given in the PCCS2 source catalogue for 90% completeness (in the extragalactic zone) in Table 8. This comparison is indicative as the 90% completeness flux limit is not strictly equivalent to the confusion noise[]. The overall agreement is better than ∼2σ. However, our flux cut is systematically below the PCCS2 flux limit for the highest frequencies (217, 353, 545, and 857 GHz). We verified that this underestimate can be easily explained by the cirrus contamination, which may be quite high in the extragalactic zone (covering |b|> 30°) and which is ignored in the present paper. Finally, we also verified our results for SPT by substituting σinst from SPT-3G in the SPT-SZ survey. Considering 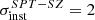 , 1.2, and 4 mJy, we obtain Slim = 11, 7.1 and 20.5 mJy, at 95, 150, and 220 GHz, respectively, which agrees very well with Mocanu et al. (2013b, see their Table 3, for 95% completeness limit). The very good agreement with previous far-IR, sub-mm, and mm experiments gives us confidence in our computations.
, 1.2, and 4 mJy, we obtain Slim = 11, 7.1 and 20.5 mJy, at 95, 150, and 220 GHz, respectively, which agrees very well with Mocanu et al. (2013b, see their Table 3, for 95% completeness limit). The very good agreement with previous far-IR, sub-mm, and mm experiments gives us confidence in our computations.
Flux limits for Planck frequencies from the PCCS2 source catalogue (Planck Collaboration XXVI 2016) for 90% completeness in the extragalactic zone and using our model.
6.3.2. Contributions to the point-source sensitivity
Ground-based experiments have a maximum frequency of 280 GHz. The contribution of the different components to the point-source sensitivity mostly depends on the frequency and size of the telescope apertures.
The smallest telescopes, with sizes < 1 m (BICEP, CLASS, SO-SAT, and CMB-S4-SAT) or the low-frequency telescopes (C-BASS, NEXT-BASS, and QUIJOTE, with ν < 40 GHz) have quite poor angular resolutions. The contribution of radio sources dominates up to ∼10–15 GHz, then the confusion noise from the CMB becomes dominant. If we can remove the CMB, the CIB clustering dominates the noise budget at the higher frequencies (ν > 200 GHz). Instrument noise is always much lower than the astrophysical components.
As expected, a telescope with a larger aperture returns lower flux limits because the confusion noise is much lower (and the instrument noise is generally lower as well). For larger aperture telescopes (AdvACTPOL, SO-LAT, SPT-3G, and CMB-S4-LAT), the instrument noise is at the same order of magnitude as confusion noises. For ν > 145 GHz, the dominant contribution to the σtot comes from the shot noise of DSFG.
In space, telescopes have smaller apertures in general and instrument noise is always negligible compared to confusion noise. Confusion from the CMB always dominates, except at the highest frequencies (ν ≳ 300 GHz). Except for the CMB, galaxy clustering above ∼150–200 GHz contributes much. PIPER, SPIDER, and LiteBIRD have large Slim (> 1 Jy) that will consequently lead to a large contamination to the CMB-B mode measurements.
6.3.3. The case of B-POP
We also considered the SPICA B-POP polarised experiment, which is at shorter wavelength. B-POP will provide 100–350 μm images of linearly polarised dust emission with an angular resolution, signal-to-noise ratio, and dynamic ranges comparable to those achieved by Herschel images of the cold ISM in total intensity. The angular resolution of B-BOP at 200 μm will also be a factor ∼30 better than Planck polarisation data.
At these wavelengths and with this high angular resolution, only the shot noise of DSFG contributes to the confusion noise (σconf). Flux limits are about 0.4, 19.6, and 35.3 mJy at 100, 200, and 350 μm, respectively (see Table 9). This is sightly above the SPIRE/Herschel 350 μm flux limit due to the smaller telescope aperture. For one pointing (2.5′ × 2.5′), confusion noise levels are reached in 9.9, 0.02, and 0.02 seconds at 100, 200, and 350 μm, respectively12. For a 1 Sq. Deg. survey, they are reached in 1.6 hours, 9.7 seconds, and 12.1 seconds. This shows that the 200 and 350 μm maps, even on large areas, will be severely limited in depth by extragalactic confusion.
Confusion noise, flux limit, and DSFG shot noise level for the SPICA B-POP experiment.
In polarisation, after masking all the sources detected in intensity, up to Slim, the r.m.s of polarised intensity due to confusion is
Assuming a fractional polarisation for DSFG ⟨ΠIR⟩ = 1.4% (see Sect. 3.2) and 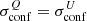 , we obtain a confusion noise in polarisation
, we obtain a confusion noise in polarisation 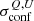 = 0.79, 38.6, 70.3 μJy after masking all the sources detected in intensity at 100, 200, and 350 μm, respectively. These
= 0.79, 38.6, 70.3 μJy after masking all the sources detected in intensity at 100, 200, and 350 μm, respectively. These 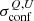 levels are reached in 57 h, 5.8 min, and 7.0 min for a single pointing, and 33 737, 57, and 69 hours for a 1 Sq. Deg. survey, at 100, 200, and 350 μm, respectively. In polarisation, confusion is therefore not expected to be reached at 100 μm, but could be reached for the deepest integrations at longer wavelengths. Confusion from galaxies could ultimately limit the sensitivity of the high-latitude polarimetric deep surveys of the interstellar medium of our Galaxy at 200 and 350 μm.
levels are reached in 57 h, 5.8 min, and 7.0 min for a single pointing, and 33 737, 57, and 69 hours for a 1 Sq. Deg. survey, at 100, 200, and 350 μm, respectively. In polarisation, confusion is therefore not expected to be reached at 100 μm, but could be reached for the deepest integrations at longer wavelengths. Confusion from galaxies could ultimately limit the sensitivity of the high-latitude polarimetric deep surveys of the interstellar medium of our Galaxy at 200 and 350 μm.
7. Contamination of the CMB B-modes
In order to provide reliable predictions of the radio source and DSFG contamination to CMB anisotropy polarisation measurements, we have to assume a fractional polarisation for each population of galaxies. For radio sources, at the frequencies where the contamination of the B-modes is minimum (i.e. ∼90–300 GHz), there are still few polarisation measurements and very scarce polarisation fraction measurements for the different types of radio sources (see Sect. 2.3). Thus, we used a constant ⟨Πrad⟩ = 2.8%, in agreement with the recent Planck, SPT, and ACT measurements and radio source follow-ups from 90 to 220 GHz. For DSFG, the situation is even worse and polarisation properties are almost completely unexplored. As discussed in Sect. 3.2, we adopted ⟨ΠIR⟩ = 1.4%. As all our BB power spectra are proportional to the square of the fractional polarisation, it is very easy to obtain polarised power spectra for other choices of fractional polarisation:
7.1. Polarised power spectra of the extragalactic components
We list in Tables 10 and 11 the level of BB power spectra for radio (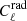 ) and DSFG (
) and DSFG (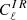 ) shot noise, and the clustering (
) shot noise, and the clustering (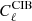 ) for three multipoles (ℓ = 80, 1000, and 4000).
) for three multipoles (ℓ = 80, 1000, and 4000).
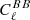 of the extragalactic foreground components for space-based and balloon-borne experiments: radio galaxies, dusty galaxies (IR), and CIB one-halo (completely negligible for ν ≤ 90 GHz and thus not computed).
of the extragalactic foreground components for space-based and balloon-borne experiments: radio galaxies, dusty galaxies (IR), and CIB one-halo (completely negligible for ν ≤ 90 GHz and thus not computed).
We first compare in Fig. 4 the relative level of DSFG shot noise and clustering power spectra at ℓ = 80. We recall that the clustering power spectra are an upper limit as we estimated the maximum contribution of the one-halo term (see Sect.5.3). The ratio 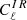 /
/ 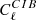 is mostly constant, and between 2 and 3 for 120 < ν < 700 GHz. At lower frequencies, it is much higher (from 4 to 30) and thus
is mostly constant, and between 2 and 3 for 120 < ν < 700 GHz. At lower frequencies, it is much higher (from 4 to 30) and thus 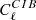 can be neglected. Consequently, we did not compute the clustering power spectra for frequencies ν ≤ 90 GHz. The ratio increases very slowly with ℓ, by up to ∼30% at ℓ = 4000 and ν < 400 GHz.
can be neglected. Consequently, we did not compute the clustering power spectra for frequencies ν ≤ 90 GHz. The ratio increases very slowly with ℓ, by up to ∼30% at ℓ = 4000 and ν < 400 GHz.
 |
Fig. 4. Ratio of shot noise and clustering (one-halo CIB anisotropies) for dusty galaxies at ℓ = 80 for all CMB experiments (ℓ = 80 corresponds to the recombination B-peak). |
We then compare in Fig. 5 the level of the radio power spectra and DSFG+clustering power spectra as a function of frequency. As expected, the general trend is an increase in 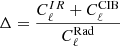 with frequency, roughly proportional to ν7 for 80 < ν< 400 GHz. We can distinguish three families of points, depending on the telescope size, with Δ varying by a factor ∼250:
with frequency, roughly proportional to ν7 for 80 < ν< 400 GHz. We can distinguish three families of points, depending on the telescope size, with Δ varying by a factor ∼250:
 |
Fig. 5. Ratio between the BB power spectra of [IR shot noise + clustering] and radio shot noise, at ℓ = 80 for all CMB experiments. |
-
For the large-aperture telescopes (≥6 m, i.e. SPT-3G, S4-LAT, SO-LAT, AdvActPol),
![$ \Delta \simeq 100 \times \left ( \frac{\nu}{220\,\mathrm{[GHz]}} \right)^7 $](/articles/aa/full_html/2020/10/aa37147-19/aa37147-19-eq95.gif) .
. -
For the medium-aperture telescopes (∼1.5 m, i.e. Planck, IDS, PICO),
![$ \Delta \simeq 4 \left ( \frac{\nu}{220\,\mathrm{[GHz]}} \right)^7 $](/articles/aa/full_html/2020/10/aa37147-19/aa37147-19-eq96.gif) .
. -
For the small-aperture telescopes (≤0.6 m, i.e. LiteBIRD, SPIDER, CLASS, SO-SAT, S4-SAT, BICEP),
![$ \Delta \simeq 0.4 \times \left ( \frac{\nu}{220\,\mathrm{[GHz]}} \right)^7 $](/articles/aa/full_html/2020/10/aa37147-19/aa37147-19-eq97.gif) .
.
Thus, the DSFG power spectra level is higher than that of radio galaxies at a frequency that decreases with telescope size: ∼247, 180, and 114 GHz, from small to large apertures. These results do not depend on the multipole (as 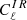 /
/ 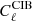 varies weakly with ℓ).
varies weakly with ℓ).
7.2. Comparison with the CMB B-modes
We first illustrate the contaminations of extragalactic components to the CMB B-mode power spectrum at two frequencies, ∼220 GHz (Fig. 6) and 145 GHz (Fig. 7). At each frequency, we plot the power spectra for two different aperture telescopes to illustrate the turnover between radio/DSFG dominant contaminations. The CMB B-mode power spectrum was calculated for the Planck 2018 cosmology (using TT, TE, EE+lowE+lensing+BAO and a pivot scale for r of 0.002 Mpc−1, Planck Collaboration VI 2020).
 |
Fig. 6. Extragalactic foreground power spectra for Planck (coloured dashed lines) and LiteBIRD (coloured continuous lines) at 217 and 235 GHz, respectively. The three continuous black lines are the primordial CMB B-mode power spectrum for r = 0.1, 0.01, and 0.001 from top to bottom. The dash-three-dots line is the lensing B-mode. |
 |
Fig. 7. Extragalactic foreground power spectra for S4-SAT (coloured dashed lines) and S4-LAT (coloured continuous lines) at 145 GHz. The three continuous black lines are the primordial CMB B-mode power spectrum for r = 0.1, 0.01, and 0.001 from top to bottom. The dash-three-dots line is the lensing B-mode. As the two experiments are at the same frequency, the two |
We compare in Fig. 6Planck at 217 GHz with LiteBIRD at 235 GHz. While the contamination by radio galaxies is twice lower than by DSFG for Planck, the power spectrum of radio galaxies is five times larger than that of DSFG for LiteBIRD (even if the frequency of 235 GHz is higher). It is at the same level of the r = 0.01 (r = 0.001) B-mode power spectrum for ℓ = 160 (ℓ = 83). For Planck, the total contamination is negligible compared to the last 95% CL upper limit r0.002 < 0.056 (Planck Collaboration X 2020). In Fig. 7 we show the level of the extragalactic components for the ground-based S4-SAT and S4-LAT experiments. Contamination by radio sources dominates for S4-SAT at a level of r = 1.7 × 10−3 at ℓ = 80. For S4-LAT, the dominant contamination comes from DSFG shot noise, at a level of r = 1.2 × 10−5 at ℓ = 80.
We finally compute the equivalent tensor-to-scalar ratio (req) of the total extragalactic contamination (radio galaxy shot noise, DSFG shot noise, and clustering) for each individual frequency at given multipoles. We show in Fig. 8 the variation in req as a function of frequencies at the recombination B-peak, ℓ = 80. Minimum req is reached for 90 ≲ ν≲300 GHz depending on the experiment. Similarly to Fig. 5 (and see Sect 7.1), we can distinguish three cases according to the telescope aperture size:
 |
Fig. 8. Equivalent tensor-to-scalar ratio (req) of the sum of the extragalactic foregrounds at the recombination B-peak, ℓ = 80, for the different CMB experiments (req is computed for each individual frequency). |
– Large-aperture telescopes. The minimum contamination is at the level of req = 7.4 × 10−6 for SPT-3G at 95 GHz. For SO-LAT, AdvACT, and S4-LAT, req is about 1.5 and 2 × 10−5 at 90–93 and 145–150 GHz, respectively. These levels are well below the targeted σr of these experiments (by a factor of ≳20–400).
– Medium-aperture telescopes. The minimum contamination is at the level of req ≃ 10−4 and is reached at ν≃200 GHz. While this is ∼40 times higher than σr for IDS alone, it is at the same level as σr for PICO (Hanany et al. 2019).
– Small-aperture telescopes. The contamination reaches a level of 4.3−5.4 × 10−4 for S4-SAT, SO-SAT, and BICEPArray at ∼220 GHz. It increases to 8.5 × 10−4 for CLASS at 217 GHz, and 1.1 × 10−3 for LiteBIRD at 235 and 280 GHz and PIPER at 200 and 270 GHz. Finally, it is about 2.5 × 10−3 for SPIDER at 150 GHz. The level of contamination (of 4 to 8 × 10−4 from 150 to 270 GHz) is below the targeted σr for the Bicep/Keck experiment, for which they project 0.002 < σr < 0.006 by the end of the planned BICEP Array program, assuming current modelling of polarised Galactic foregrounds and depending on the level of delensing that can be achieved with higher angular resolution maps from the South Pole Telescope (Hui et al. 2018). For LiteBIRD, the contamination reaches the 68% confidence level uncertainty, that is σr < 10−3 (this σr includes statistical, instrumental systematic, and Galactic foreground uncertainties, Matsumura et al. 2016).
This comparison between req and σr was made considering each frequency for req independently, while σr is usually estimated for each experiment by combining the whole set of available bands and under specific assumptions (e.g. taking systematic effects or foregrounds residual impacts into account). Multi-frequency component separations should be able to decrease the level of extragalactic foreground contamination.
To offer a complementary view, rather than comparing req with σr, we could compare req with the equivalent instrument noise 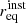 computed independently at each frequency. We calculate
computed independently at each frequency. We calculate 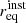 following
following
where 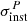 is the instrument noise in polarisation (given in Tables 6 and 7). We show in Fig. 9 the ratio of req and
is the instrument noise in polarisation (given in Tables 6 and 7). We show in Fig. 9 the ratio of req and 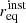 for all frequencies and experiments. A contamination of at least 10% (req/
for all frequencies and experiments. A contamination of at least 10% (req/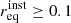 ) for 70 ≤ ν ≤ 250 GHz is reached for BICEP at 95 and 150 GHz, CLASS, SO-SAT, and SPIDER at 93 GHz, LiteBIRD from 78 to 140 GHz, S4-SAT from 85 to 155 GHz, and PICO from 75 to 129 GHz. Combining higher and lower frequencies to decrease the Galactic foreground residuals may also add more contamination from extragalactic sources (because of their different mean polarised SEDs and because they are not correlated from high to low frequencies). For example, for PICO,
) for 70 ≤ ν ≤ 250 GHz is reached for BICEP at 95 and 150 GHz, CLASS, SO-SAT, and SPIDER at 93 GHz, LiteBIRD from 78 to 140 GHz, S4-SAT from 85 to 155 GHz, and PICO from 75 to 129 GHz. Combining higher and lower frequencies to decrease the Galactic foreground residuals may also add more contamination from extragalactic sources (because of their different mean polarised SEDs and because they are not correlated from high to low frequencies). For example, for PICO, 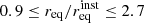 for 21 ≤ ν ≤ 52 GHz and for S4-SAT, it is > 10 for ν = 30–95 GHz.
for 21 ≤ ν ≤ 52 GHz and for S4-SAT, it is > 10 for ν = 30–95 GHz.
 |
Fig. 9. Ratio of equivalent r of the extragalactic foregrounds (req) and instrument noise ( |
The scale dependency of extragalactic foregrounds compared to the CMB makes the ratio of the primordial CMB signal over foregrounds more favourable at larger scale, in particular at the reionisation B-bump (ℓ = 5). Only nearly full-sky (fsky≥70%) experiments can provide some measurements at such low multipoles. The r equivalent in this case is very small (2.7 × 10−6 for PICO at 186 GHz, 3.7–3.4 ×10−5 for LiteBIRD at 195-235 GHz, and 2.5 ×10−5 for CLASS at 217 GHz; see Fig. 10). They are much smaller than the targeted limits on the primordial r for PICO and LiteBIRD, and σr = 8.5 × 10−3 for CLASS (including diffuse Galactic thermal dust and synchrotron foregrounds, Watts et al. 2015). For Planck, the level of contamination by polarised extragalactic sources is much lower than the current B-mode upper limit (Planck Collaboration VI 2020).
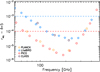 |
Fig. 10. Equivalent tensor-to-scalar ratio (req) of the sum of the extragalactic foregrounds at ℓ = 5, corresponding to the reionisation B-bump. We also show the σr for LiteBIRD, PICO, and CLASS (dashed lines). For Planck, the current 1σ upper limit is r < 0.028 and is thus not visible in the figure. |
Finally, we consider the ratio of the extragalactic foreground and CMB lensing BB power spectra (at ℓ = 1000). This ratio is ∼120 times higher than the equivalent tensor-to-sclar ratio req at ℓ = 80. It extends from ∼10−3 for large-aperture experiments to ∼10−1 for small-aperture experiments. As is already known, ground-based large-aperture telescopes will provide the ability to delens the maps from future satellite CMB missions, such as LiteBIRD (e.g. Namikawa & Nagata 2014).
8. Conclusion
We have computed the expected level of polarised fluctuations from the shot noise of radio galaxies and DSFG and from the CIB clustering using current or updated models. Using these models, we predicted the point-source detection limits (confusion noises, in intensity) for future CMB space-based or balloon-borne experiments (IDS, PIPER, SPIDER, LiteBIRD, and PICO) and ground-based experiments (C-BASS, NEXT-BASS, QUIJOTE, AdvACTPOL, BICEP3+Keck, BICEPArray, CLASS, SO, SPT3G, and S4). These limits were computed by taking the instrument noise, the three extragalactic foregrounds, and the CMB into account. The models, as well as the point-source detection flux limits, were validated using most recent measurements on number counts, CIB power spectra, confusion noises, and shot noise levels. As expected, we found that the confusion noise levels are mostly driven by the telescope-aperture sizes and frequency.
Assuming a constant polarisation fraction consistent with current observational results for the radio sources of ⟨Πrad⟩ = 2.8%, and assuming for the dusty source ⟨ΠIR⟩ = 1.4%, we then predicted the shot noises and CIB one-halo clustering B-mode power spectra. We compared the amplitude of the different extragalactic foregrounds as a function of frequency and telescope-aperture size. We found that CIB clustering is almost negligible. The relative levels of radio and DSFG shot noises are mainly driven by the telescope sizes, which can be classified into three categories: large-aperture (≥6 m, i.e. SPT-3G, S4-LAT, SO-LAT, AdvActPol), medium-aperture (∼1.5 m, i.e. Planck, IDS, PICO), and small-aperture (≤0.6 m, i.e. LiteBIRD, SPIDER, CLASS, SO-SAT, S4-SAT, BICEP-Keck) telescopes. While we have an equal contribution between radio shot noise and DSFG shot noises (+ clustering) at ν ≃ 120 GHz for large-aperture telescopes, it reaches ν ≃ 280 GHz for small-aperture telescopes, which are thus dominated by the radio shot noise at the frequencies dedicated to the CMB measurement. González-Nuevo et al. (2005) showed that the contribution of radio source clustering to the temperature angular power spectrum is small and can be neglected if sources are not subtracted down to very faint flux limits, S ≪ 10 mJy. However, future ground-based experiments such as S4-LAT will be able to reach flux limits of the order of 2-3 mJy. At these levels, the clustering of radio sources might not be negligible for ℓ < 30 compared to the shot-noise level (González-Nuevo et al. 2005).
We also predict the confusion noise for SPICA B-BOP and showed that confusion could ultimately limit the sensitivity of deep polarised surveys at 200 and 350 μm (with the confusion noise in polarisation reached in 57 and 69 h for a 1 square degree field at 200 and 350 μm, respectively).
Finally, we computed the equivalent tensor-to-scalar ratio (req) of the total extragalactic contamination (radio galaxy shot noise, DSFG shot noise, and clustering) for given multipoles. At the reionisation B-bump (ℓ = 5), the extragalactic contamination will not limit the measurements. At the recombination B-peak (ℓ = 80), the contamination for large-aperture telescope experiments is much below the targeted primordial r, but this is not the case for some of the small- and medium- aperture telescopes. For example for the LiteBIRD and PICO space experiments, the contamination is at the level of the 68% confidence level uncertainty on the primordial r (not considering a multi-frequency component separation that should globally decrease req). On the other side of the multipole range, extragalactic components represent 10–20% of the CMB lensing BB power spectrum at ℓ = 1000 for LiteBIRD. Moreover, a similar slope is observed between the extragalactic components and the CMB lensing BB power spectrum up to ℓ = 200 and between the extragalactic components and the primordial B-mode power spectrum for 15 ≲ℓ≲ 50, leading to degeneracies in any model fitting. Removing this extragalactic contamination from the data is thus mandatory for some of the small- and medium-aperture telescope experiments.
Foreground mitigation was studied for the Galactic components. We showed that it requires a multi-frequency coverage (but see Philcox et al. 2018 for a method based on anisotropy statistics, or Aylor et al. 2019 for the use of neural network). It will be difficult to apply this multi-frequency approach to extragalactic foregrounds, as the three extragalactic components are degenerated (i.e. same power spectra at the multipole of interest) and the sum of the three does not have a well-defined frequency dependency. Moreover, even if more precise polarised source counts for radio galaxies will be obtained in the near future, the variation in radio shot noise with flux limit (changing the flux cut by 30% affects the shot noise by 30%, see Table 2), together with the variability of radio sources, may prevent us from using more accurate modelling to precisely predict the shot-noise level.
Polarised Galactic foregrounds are dominated by dust and synchrotron emissions with spatial variation of their SEDs. Using a parametric maximum-likelihood approach, Errard et al. (2016) found that combinations from ground- and space-based and balloon-borne experiments can significantly improve component separation performance, delensing, and cosmological constraints over individual datasets. In particular, they reported that a combination of post-2020 ground- and space-based experiments could achieve constraints such as σr ∼ 1.3 × 10−4 after component separation and iterative delensing. However, such results (see also e.g. Stompor et al. 2016) are often derived ignoring complexities in the Galactic foreground emission due to synchrotron and dust, and neglecting potential other contaminants such as anomalous microwave emission and extragalactic foregrounds. Moreover, they adopted component separation methods that essentially assume a model that matches the simulated foregrounds under study well. Remazeilles et al. (2016) tested some of these assumptions explicitly and reported biases in the derived value of r of more than 1σ by neglecting the curvature of the synchrotron emission law, for instance. Given their levels for some of mid- and small-aperture telescopes, extragalactic foregrounds have clearly to be considered in the component separation methods dedicated to the extraction of the CMB B-modes. For this purpose, our detailed computation of flux limits and shot-noise levels will allow including these foregrounds precisely into the input sky models.
Planck (http://www.esa.int/Planck) is a project of the European Space Agency (ESA) with instruments provided by two scientific consortia funded by ESA member states and led by Principal Investigators from France and Italy, telescope reflectors provided through a collaboration between ESA and a scientific consortium led and funded by Denmark, and additional contributions from NASA (USA).
The meaning of all abbreviations is: inflation and dust surveyor, primordial inflation polarisation explorer, lite (light) satellite for the studies of B-mode polarisation and inflation from cosmic background radiation detection, and probe of inflation and cosmic origins for IDS, PIPER, LiteBIRD and PICO, respectively.
The meaning of all abbreviations is: C-band all-sky survey, next band all-sky-survey, Q-U-I joint Tenerife, advanced Atacama cosmology telescope polarimeter, background imaging of cosmic extragalactic polarisation, cosmology large angular scale surveyor, Simons observatory, south pole telescope and stage-4 for C-BASS, NEXT-BASS, QUIJOTE, AdvACTPOL, BICEP, CLASS, SO, SPT, and S4, respectively.
Ki, j are provided at https://people.lam.fr/lagache.guilaine/Products.
We only considered the confusion noise due to extragalactic sources because in the high Galactic latitude cosmological fields, the cirrus confusion noise is negligible, contributes very little to the total noise (Dole et al. 2003), or can be mitigated using component separation methods.
We chose a standard signal-to-noise ratio S/N = 5σ, which is usually sufficient to obtain a reliability close from 100% (e.g. > 95% at S/N = 5 in Planck Collaboration XXVI 2016). It is extremely difficult to assess the reliability of a survey as a function of S/N before actual data are available because it is sensitive to many unknown parameters (non-Gaussian noise and systematics, non-Gaussian foregrounds, exact statistics of the sources, and choice of source extraction method). In addition, the exact threshold associated with a given reliability can also vary with regions in case of heterogeneous depth and/or foreground contamination, as for Planck.
These values were computed using the André et al. (2019) sensitivity forecasts (see their Table 1). They correspond to the time needed to reach σinst = σconf.
Acknowledgments
GL warmly thank F. Boulanger for insightful discussions on the CIB polarisation, J. Delabrouille and J. Gonzales-Nuevo for discussions on the transfer function linked to the source flux measurements, G. De Zotti for discussions around the results presented in this paper, and N. Ponthieu and M. Tristram for their help in manipulating polarised quantities. PS acknowledges hospitality from LAM, where part of this work was completed. GL, MB and LM acknowledge support from the OCEVU Labex (ANR-11-LABX-0060) and the A*MIDEX project (ANR-11-IDEX-0001-02) funded by the “Investissements d’Avenir” French government program managed by the ANR. GL has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 788212). We acknowledge financial support from the "Programme National de Cosmologie and Galaxies" (PNCG) funded by CNRS/INSU-IN2P3-INP, CEA and CNES, France.
References
- Abazajian, K., Addison, G., Adshead, P., et al. 2019, ArXiv e-prints [arXiv:1907.04473] [Google Scholar]
- Ade, P., Aguirre, J., Ahmed, Z., et al. 2019, J. Cosmol. Astropart. Phys., 2019, 056 [Google Scholar]
- Agudo, I., Thum, C., Wiesemeyer, H., & Krichbaum, T. P. 2010, ApJS, 189, 1 [NASA ADS] [CrossRef] [Google Scholar]
- André, P., Hughes, A., Guillet, V., et al. 2019, PASA, 36, e029 [CrossRef] [Google Scholar]
- Aylor, K., Haq, M., Knox, L., Hezaveh, Y., & Perreault-Levasseur, L. 2019, ArXiv e-prints [arXiv:1909.06467] [Google Scholar]
- Battye, R. A., Browne, I. W. A., Peel, M. W., Jackson, N. J., & Dickinson, C. 2011, MNRAS, 413, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Behroozi, P. S., Wechsler, R. H., & Conroy, C. 2013, ApJ, 770, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Benson, A. J., Bower, R. G., Frenk, C. S., et al. 2003, ApJ, 599, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Bertone, S., Stoehr, F., & White, S. D. M. 2005, MNRAS, 359, 1201 [NASA ADS] [CrossRef] [Google Scholar]
- Béthermin, M., Dole, H., Lagache, G., Le Borgne, D., & Penin, A. 2011, A&A, 529, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Daddi, E., Magdis, G., et al. 2012a, ApJ, 757, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Béthermin, M., Doré, O., & Lagache, G. 2012b, A&A, 537, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Le Floc’h, E., Ilbert, O., et al. 2012c, A&A, 542, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Wang, L., Doré, O., et al. 2013, A&A, 557, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Wu, H.-Y., Lagache, G., et al. 2017, A&A, 607, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Fudamoto, Y., Ginolfi, M., et al. 2020, A&A, 643, A2 [CrossRef] [EDP Sciences] [Google Scholar]
- Blain, A. W., Barnard, V. E., & Chapman, S. C. 2003, MNRAS, 338, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Königl, A. 1979, ApJ, 232, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Bonavera, L., Massardi, M., Bonaldi, A., et al. 2011, MNRAS, 416, 559 [NASA ADS] [Google Scholar]
- Bonavera, L., González-Nuevo, J., De Marco, B., Argüeso, F., & Toffolatti, L. 2017a, MNRAS, 472, 628 [NASA ADS] [CrossRef] [Google Scholar]
- Bonavera, L., González-Nuevo, J., Argüeso, F., & Toffolatti, L. 2017b, MNRAS, 469, 2401 [NASA ADS] [CrossRef] [Google Scholar]
- Bondi, M., Ciliegi, P., Schinnerer, E., et al. 2008, ApJ, 681, 1129 [NASA ADS] [CrossRef] [Google Scholar]
- Cai, Z.-Y., Lapi, A., Xia, J.-Q., et al. 2013, ApJ, 768, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Calabrese, E., Hložek, R., Battaglia, N., et al. 2014, J. Cosmol. Astropart. Phys., 2014, 010 [Google Scholar]
- Carron, J., Lewis, A., & Challinor, A. 2017, J. Cosmol. Astropart. Phys., 2017, 035 [NASA ADS] [CrossRef] [Google Scholar]
- Casey, C. M., Narayanan, D., & Cooray, A. 2014, Phys. Rep., 541, 45 [Google Scholar]
- Casey, C. M., Zavala, J. A., Spilker, J., et al. 2018, ApJ, 862, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, C.-C., Smail, I., Swinbank, A. M., et al. 2016, ApJ, 831, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Clements, D. L., Rigby, E., Maddox, S., et al. 2010, A&A, 518, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Codis, S., Jindal, A., Chisari, N. E., et al. 2018, MNRAS, 481, 4753 [CrossRef] [Google Scholar]
- Cooray, A., & Sheth, R. 2002, Phys. Rep., 372, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Croton, D. J., Springel, V., White, S. D. M., et al. 2006, MNRAS, 365, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Curto, A., Tucci, M., González-Nuevo, J., et al. 2013, MNRAS, 432, 728 [NASA ADS] [CrossRef] [Google Scholar]
- Datta, R., Aiola, S., Choi, S. K., et al. 2019, MNRAS, 486, 5239 [CrossRef] [Google Scholar]
- de Zotti, G., Gruppioni, C., Ciliegi, P., Burigana, C., & Danese, L. 1999, New A, 4, 481 [NASA ADS] [CrossRef] [Google Scholar]
- De Zotti, G., Ricci, R., Mesa, D., et al. 2005, A&A, 431, 893 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Zotti, G., Massardi, M., Negrello, M., & Wall, J. 2010, A&ARv, 18, 1 [NASA ADS] [CrossRef] [Google Scholar]
- De Zotti, G., Castex, G., González-Nuevo, J., et al. 2015, J. Cosmol. Astropart. Phys., 2015, 018 [NASA ADS] [CrossRef] [Google Scholar]
- De Zotti, G., González-Nuevo, J., Lopez-Caniego, M., et al. 2018, J. Cosmol. Astropart. Phys., 2018, 020 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., & Birnboim, Y. 2006, MNRAS, 368, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Dole, H., Lagache, G., & Puget, J.-L. 2003, ApJ, 585, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Duffy, A. R., Schaye, J., Kay, S. T., et al. 2010, MNRAS, 405, 2161 [NASA ADS] [Google Scholar]
- Dunkley, J., Calabrese, E., Sievers, J., et al. 2013, J. Cosmol. Astropart. Phys., 7, 025 [Google Scholar]
- Errard, J., Feeney, S. M., Peiris, H. V., & Jaffe, A. H. 2016, J. Cosmol. Astropart. Phys., 2016, 052 [NASA ADS] [CrossRef] [Google Scholar]
- Essinger-Hileman, T., Ali, A., Amiri, M., et al. 2014, Proc. SPIE, 9153, 91531I [CrossRef] [Google Scholar]
- Everett, W. B., Zhang, L., Crawford, T. M., et al. 2020, ApJ, 900, 55 [CrossRef] [Google Scholar]
- Feng, C., & Holder, G. 2020, ApJ, 897, 140 [CrossRef] [Google Scholar]
- Galluzzi, V., Massardi, M., Bonaldi, A., et al. 2017, MNRAS, 465, 4085 [NASA ADS] [CrossRef] [Google Scholar]
- Galluzzi, V., Puglisi, G., Burkutean, S., et al. 2019, MNRAS, 489, 470 [CrossRef] [Google Scholar]
- Geach, J. E., Dunlop, J. S., Halpern, M., et al. 2017, MNRAS, 465, 1789 [Google Scholar]
- George, E. M., Reichardt, C. L., Aird, K. A., et al. 2015, ApJ, 799, 177 [Google Scholar]
- Gispert, R., Lagache, G., & Puget, J. L. 2000, A&A, 360, 1 [NASA ADS] [Google Scholar]
- Glenn, J., Conley, A., Béthermin, M., et al. 2010, MNRAS, 409, 109 [NASA ADS] [CrossRef] [Google Scholar]
- González-Nuevo, J., Toffolatti, L., & Argüeso, F. 2005, ApJ, 621, 1 [NASA ADS] [CrossRef] [Google Scholar]
- González-Nuevo, J., Massardi, M., Argüeso, F., et al. 2008, MNRAS, 384, 711 [NASA ADS] [CrossRef] [Google Scholar]
- Gralla, M. B., Marriage, T. A., Addison, G., et al. 2020, ApJ, 893, 104 [CrossRef] [Google Scholar]
- Greaves, J. S., & Holland, W. S. 2002, in Astrophysical Polarized Backgrounds, eds. S. Cecchini, S. Cortiglioni, R. Sault, & C. Sbarra, Am. Inst. Phys. Conf. Ser., 609 [Google Scholar]
- Gruppioni, C., Pozzi, F., Zamorani, G., & Vignali, C. 2011, MNRAS, 416, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, N., Reichardt, C. L., Ade, P. A. R., et al. 2019, MNRAS, 490, 5712 [CrossRef] [Google Scholar]
- Hales, C. A., Norris, R. P., Gaensler, B. M., & Middelberg, E. 2014, MNRAS, 440, 3113 [NASA ADS] [CrossRef] [Google Scholar]
- Hall, N. R., Keisler, R., Knox, L., et al. 2010, ApJ, 718, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Hanany, S., Alvarez, M., Artis, E., et al. 2019, ArXiv e-prints [arXiv:1902.10541] [Google Scholar]
- Hill-Valler, J. R. 2019, Ph.D. Thesis, University of Oxford [Google Scholar]
- Hui, H., Ade, P. A. R., Ahmed, Z., et al. 2018, Proc. SPIE, 10708, 1070807 [Google Scholar]
- Huynh, M. T., Seymour, N., Norris, R. P., & Galvin, T. 2020, MNRAS, 491, 3395 [CrossRef] [Google Scholar]
- Joachimi, B., Cacciato, M., Kitching, T. D., et al. 2015, Space Sci. Rev., 193, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Klein, U., Mack, K.-H., Gregorini, L., & Vigotti, M. 2003, A&A, 406, 579 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Knox, L., Cooray, A., Eisenstein, D., & Haiman, Z. 2001, ApJ, 550, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Konigl, A. 1981, ApJ, 243, 700 [NASA ADS] [CrossRef] [Google Scholar]
- Lagache, G., Dole, H., & Puget, J.-L. 2003, MNRAS, 338, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Lapi, A., González-Nuevo, J., Fan, L., et al. 2011, ApJ, 742, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, A., & Bridle, S. 2002, Phys. Rev. D, 66, 103511 [NASA ADS] [CrossRef] [Google Scholar]
- Limber, D. N. 1954, ApJ, 119, 655 [NASA ADS] [CrossRef] [Google Scholar]
- López-Caniego, M., Rebolo, R., Aguiar, M., et al. 2014, ArXiv e-prints [arXiv:1401.4690] [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Magdis, G. E., Daddi, E., Béthermin, M., et al. 2012, ApJ, 760, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Mak, D. S. Y., Challinor, A., Efstathiou, G., & Lagache, G. 2017, MNRAS, 466, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Manzotti, A., Story, K. T., Wu, W. L. K., et al. 2017, ApJ, 846, 45 [CrossRef] [Google Scholar]
- Marriage, T. A., Baptiste Juin, J., Lin, Y.-T., et al. 2011, APJ, 731, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P., & Gear, W. K. 1985, ApJ, 298, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Marsden, D., Gralla, M., Marriage, T. A., et al. 2014, MNRAS, 439, 1556 [NASA ADS] [CrossRef] [Google Scholar]
- Massardi, M., Bonaldi, A., Negrello, M., et al. 2010, MNRAS, 404, 532 [NASA ADS] [Google Scholar]
- Massardi, M., Ekers, R. D., Murphy, T., et al. 2011, MNRAS, 412, 318 [NASA ADS] [CrossRef] [Google Scholar]
- Massardi, M., Burke-Spolaor, S. G., Murphy, T., et al. 2013, MNRAS, 436, 2915 [NASA ADS] [CrossRef] [Google Scholar]
- Matsumura, T., Akiba, Y., Arnold, K., et al. 2016, J. Low Temp. Phys., 184 [Google Scholar]
- Miller, N. A., Bonzini, M., Fomalont, E. B., et al. 2013, ApJS, 205, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Mocanu, L. M., Crawford, T. M., Vieira, J. D., et al. 2013a, ApJ, 779, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Mocanu, L. M., Crawford, T. M., Vieira, J. D., et al. 2013b, ApJ, 779, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, T., Sadler, E. M., Ekers, R. D., et al. 2010, MNRAS, 402, 2403 [NASA ADS] [CrossRef] [Google Scholar]
- Namikawa, T., & Nagata, R. 2014, J. Cosmol. Astropart. Phys., 2014, 009 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Negrello, M., Magliocchetti, M., Moscardini, L., et al. 2004, MNRAS, 352, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Negrello, M., González-Nuevo, J., Magliocchetti, M., et al. 2005, MNRAS, 358, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Negrello, M., Gonzalez-Nuevo, J., De Zotti, G., et al. 2017, MNRAS, 470, 2253 [NASA ADS] [CrossRef] [Google Scholar]
- Neugebauer, G., Habing, H. J., van Duinen, R., et al. 1984, ApJ, 278, L1 [Google Scholar]
- Nguyen, H. T., Schulz, B., Levenson, L., et al. 2010, A&A, 518, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oliver, S. J., Wang, L., Smith, A. J., et al. 2010, A&A, 518, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pereira, M. J., Bryan, G. L., & Gill, S. P. D. 2008, ApJ, 672, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Philcox, O. H. E., Sherwin, B. D., van Engelen, A., et al. 2018, MNRAS, 479, 5577 [CrossRef] [Google Scholar]
- Piras, D., Joachimi, B., Schäfer, B. M., et al. 2018, MNRAS, 474, 1165 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XIII. 2011, A&A, 536, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XV. 2011, A&A, 536, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XVIII. 2011, A&A, 536, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXX. 2014, A&A, 571, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XI. 2016, A&A, 594, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXVI. 2016, A&A, 594, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration I. 2020, A&A, 641, A1 [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration V. 2020, A&A, 641, A5 [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration X. 2020, A&A, 641, A10 [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. VII. 2013, A&A, 550, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XVII. 2014, A&A, 566, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XLV. 2016, A&A, 596, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popping, G., Walter, F., Behroozi, P., et al. 2020, ApJ, 891, 135 [CrossRef] [Google Scholar]
- Puglisi, G., Galluzzi, V., Bonavera, L., et al. 2018, ApJ, 858, 85 [CrossRef] [Google Scholar]
- Rahlin, A. S., Ade, P. A. R., Amiri, M., et al. 2014, Proc. SPIE, 9153, 915313 [CrossRef] [Google Scholar]
- Remazeilles, M., Dickinson, C., Eriksen, H. K. K., & Wehus, I. K. 2016, MNRAS, 458, 2032 [NASA ADS] [CrossRef] [Google Scholar]
- Sadler, E. M., Ricci, R., Ekers, R. D., et al. 2008, MNRAS, 385, 1656 [NASA ADS] [CrossRef] [Google Scholar]
- Sajina, A., Partridge, B., Evans, T., et al. 2011, ApJ, 732, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Sargent, M. T., Béthermin, M., Daddi, E., & Elbaz, D. 2012, ApJ, 747, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Sehgal, N., Madhavacheril, M. S., Sherwin, B., & van Engelen, A. 2017, Phys. Rev. D, 95, 103512 [CrossRef] [Google Scholar]
- Seiffert, M., Borys, C., Scott, D., & Halpern, M. 2007, MNRAS, 374, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Serra, P., Doré, O., & Lagache, G. 2016, ApJ, 833, 153 [CrossRef] [Google Scholar]
- Shang, C., Haiman, Z., Knox, L., & Oh, S. P. 2012, MNRAS, 421, 2832 [NASA ADS] [CrossRef] [Google Scholar]
- Sherwin, B. D., & Schmittfull, M. 2015, Phys. Rev. D, 92, 043005 [NASA ADS] [CrossRef] [Google Scholar]
- Silk, J. 2003, MNRAS, 343, 249 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Silverberg, R. F., Hauser, M. G., Boggess, N. W., et al. 1993, in Infrared Spaceborne Remote Sensing, ed. M. S. Scholl, Proc. SPIE, 2019, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, K. M., Hanson, D., LoVerde, M., Hirata, C. M., & Zahn, O. 2012, J. Cosmol. Astropart. Phys., 2012, 014 [NASA ADS] [CrossRef] [Google Scholar]
- Smolčić, V., Novak, M., Bondi, M., et al. 2017, A&A, 602, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stompor, R., Errard, J., & Poletti, D. 2016, Phys. Rev. D, 94, 083526 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, A. C. 2018, ArXiv e-prints [arXiv:1805.05484] [Google Scholar]
- Tinker, J., Kravtsov, A. V., Klypin, A., et al. 2008, ApJ, 688, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Tinker, J. L., Robertson, B. E., Kravtsov, A. V., et al. 2010, ApJ, 724, 878 [NASA ADS] [CrossRef] [Google Scholar]
- Toffolatti, L., Argueso Gomez, F., de Zotti, G., et al. 1998, MNRAS, 297, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Trombetti, T., Burigana, C., De Zotti, G., Galluzzi, V., & Massardi, M. 2018, A&A, 618, A29 [CrossRef] [EDP Sciences] [Google Scholar]
- Tucci, M., & Toffolatti, L. 2012, Adv. Astron., 2012, 624987 [Google Scholar]
- Tucci, M., Martínez-González, E., Toffolatti, L., González-Nuevo, J., & De Zotti, G. 2004, MNRAS, 349, 1267 [NASA ADS] [CrossRef] [Google Scholar]
- Tucci, M., Toffolatti, L., de Zotti, G., & Martínez-González, E. 2011, A&A, 533, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valiante, E., Smith, M. W. L., Eales, S., et al. 2016, MNRAS, 462, 3146 [NASA ADS] [CrossRef] [Google Scholar]
- Viero, M. P., Wang, L., Zemcov, M., et al. 2013, ApJ, 772, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Watts, D. J., Larson, D., Marriage, T. A., et al. 2015, ApJ, 814, 103 [CrossRef] [Google Scholar]
- Young, K., Alvarez, M., Battaglia, N., et al. 2018, Proc. SPIE, 10698, 1069846 [Google Scholar]
Appendix A: Colour corrections and unit conversions for Planck/HFI, ACT, SPT, and Herschel/SPIRE
A.1. Colour corrections
Following the IRAS convention, the spectral intensity data Iν are often expressed at fixed nominal frequencies, assuming the source spectrum is νIν= constant (i.e. constant intensity per logarithmic frequency interval, labelled “ref” hereafter). The colour-correction factor 𝒞 is defined such that
where 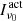 is the actual specific intensity of the sky at frequency ν0,
is the actual specific intensity of the sky at frequency ν0, 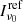 is the corresponding value given with the IRAS (Neugebauer et al. 1984) or DIRBE (Silverberg et al. 1993) convention13, and ν0 is the frequency corresponding to the nominal wavelength of the band. With these definitions,
is the corresponding value given with the IRAS (Neugebauer et al. 1984) or DIRBE (Silverberg et al. 1993) convention13, and ν0 is the frequency corresponding to the nominal wavelength of the band. With these definitions,
where (Iν/Iν0)act is the actual specific intensity of the sky (SED) normalised to the intensity at frequency ν0, and Rν is the spectral response.
A.2. Colour corrections for CIB and IR shot-noise
We give here colour corrections that are useful for joined CIB analyses in HFI, ACT, SPT, and Herschel/SPIRE. To have an idea of the errors linked to the SED used to compute 𝒞, we used two different CIB SEDs,
-
from Gispert et al. (2000) fit of FIRAS measurements
-
from Béthermin et al. (2012a) empirical model of galaxy evolution.
We recommend using the CIB from Béthermin et al. (2012a) as it comes from a unified model based on our current understanding of the evolution of main-sequence and starburst galaxies. It reproduces all recent measurements of galaxy counts from the mid-IR to the radio, including counts per redshift slice. It is probably more accurate than the FIRAS measurements. Colour corrections 𝒞 are given in Table A.1. We can use the same colour corrections for the star-forming galaxy shot noise and the clustered power spectrum (as the SEDs are very similar).
Colour corrections 𝒞 (Eq. (A.2)) for dusty star-forming galaxies are given for two different CIB spectral energy distributions (“model” refers to the model of Béthermin et al. (2012a), while “measure” refers to the Gispert et al. (2000) fit of FIRAS measurements).
A.3. Colour corrections for radio shot noise
For the radio galaxy shot noise SED we can use a power law Sν ∝ να, with α = −0.5/−0.6. This is the average spectral index for radio sources that mainly contribute to the shot-noise power spectrum. With this SED, we find that the colour corrections are all lower than 0.7% for 20 ≤ ν ≤ 857 GHz. We can thus neglect them.
A.4. Unit conversions (tSZ, KCMB, MJy sr−1)
In unit conversion, data are presented in a different unit, but remain consistent with a given SED (e.g. MJy sr−1 can be expressed as an equivalent brightness in K). With colour correction, data are expressed with respect to a different assumed SED at the same reference frequency. Changing from KCMB to MJy sr−1 with a different spectral index involves both a unit conversion and a colour correction. We give some unit conversions for SPT, ACT, and HFI in Tables A.2 and A.3. Spectral responses are the official 2013 released ones for Planck/HFI. For ACT and SPT, they have been provided by the teams. For SPT, we use the SPT-SZ bandpasses.
MJy sr−1[νIν= constant] to KCMB unit conversion.
ySZ to KCMB unit conversion.
A.5. Converting CIB power spectra between HFI, ACT, SPT, and SPIRE
The purpose here is to convert the measurement through one bandpass into a measurement as it would be obtained through another bandpass (often close in frequency, e.g. HFI at 143 GHz versus SPT at 150 GHz). This means that we wish to find K such that
For clarity, we write I1 and I2 the fiducial monochromatic flux densities from spectral response 1 and 2 (with the convention νIν = constant) at their respective reference frequencies ν1 and ν2. Combining Eq. (A.1) and A.2 gives
It then follows
where R1 and R2 are the normalised spectral responses 1 and 2, respectively. Values for K for HFI, ACT, and SPT are given in Table A.4. For HFI 545 and 857 GHz and Herschel/SPIRE 500 and 350 μm channels, K(545 GHz, 500 μm) = 0.899808 and K(857 GHz, 350 μm) = 1.00685.
Factors to convert the CIB intensity (in Jy/sr with the convention νIν = constant) into the HFI, ACT, and SPT bandpasses (see Eqs. (A.3) and (A.5)). ν1 and ν2 are given in the first column and first line, respectively (e.g. K(ν1, ν2) = K(857, 545) = 1.989.
We can note that K(143, 148) and K(143, 150) are < 1 because the HFI 143 GHz bandpass is sensitive to lower frequencies than ACT 148 GHz and SPT 150 GHz.
Example of the use of K factors. the HFI-alone likelihood gives the best Cℓ CIB amplitude at 143 GHz in μKCMB. To convert it for ACT at 148 GHz into μKCMB follows
All Tables
Shot-noise power of residual radio sources, Dℓ = ℓ(ℓ + 1)Cℓ/2π [μ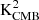 ], at ℓ = 3000, estimated in ACT and SPT data, and predicted by models.
], at ℓ = 3000, estimated in ACT and SPT data, and predicted by models.
Auto- and cross-power spectra due to residual radio sources for Planck according to the updated model for the flux cuts reported in the Table.
Herschel/SPIRE shot-noise levels as measured from CIB anisotropies and predicted using the integral of the number counts as modelled by Béthermin et al. (2012a).
Flux limits for Planck frequencies from the PCCS2 source catalogue (Planck Collaboration XXVI 2016) for 90% completeness in the extragalactic zone and using our model.
Confusion noise, flux limit, and DSFG shot noise level for the SPICA B-POP experiment.
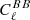 of the extragalactic foreground components for space-based and balloon-borne experiments: radio galaxies, dusty galaxies (IR), and CIB one-halo (completely negligible for ν ≤ 90 GHz and thus not computed).
of the extragalactic foreground components for space-based and balloon-borne experiments: radio galaxies, dusty galaxies (IR), and CIB one-halo (completely negligible for ν ≤ 90 GHz and thus not computed).
Colour corrections 𝒞 (Eq. (A.2)) for dusty star-forming galaxies are given for two different CIB spectral energy distributions (“model” refers to the model of Béthermin et al. (2012a), while “measure” refers to the Gispert et al. (2000) fit of FIRAS measurements).
Factors to convert the CIB intensity (in Jy/sr with the convention νIν = constant) into the HFI, ACT, and SPT bandpasses (see Eqs. (A.3) and (A.5)). ν1 and ν2 are given in the first column and first line, respectively (e.g. K(ν1, ν2) = K(857, 545) = 1.989.
All Figures
 |
Fig. 1. Normalized differential number counts (S5/2n(S)) from the Tucci et al. (2011) model (black lines) and observations (Planck, black points; ACT, cyan points; SPT, blue and green points) between 70 and 220 GHz. Red lines represent the model, but with the updated parameter values as described in the text. The very recent measurements from ACT at 148 GHz (cyan dots from Datta et al. 2019) and from SPT-SZ (green dots from Everett et al. 2020) are not used in the fit, but are shown for comparison. |
| In the text | |
 |
Fig. 2. Left panel: power spectra (divided by the flux limit) of residual radio sources as a function of the flux limit from 30 to 857 GHz (from top to bottom). Points are from the updated T11 model; solid lines are fits using Eq. (2) with parameters given in Table 3. Right panel: cross-power spectra at the frequencies indicated in the figure as a function of the flux limit |
| In the text | |
 |
Fig. 3. Galaxy number counts at 350, 500, and 850 μm. The model we used (Béthermin et al. 2012a) is shown with the continuous line. It agrees very well with the most recent Béthermin et al. (2017) model (SIDES, long-dashed line). Measurements are from Herschel at 350 and 500 μm (Oliver et al. 2010; Clements et al. 2010; Glenn et al. 2010; Béthermin et al. 2012c), SCUBA2, and ALMA at 850 μm (Geach et al. 2017; Béthermin et al. 2020), and Planck at very bright fluxes (Planck Collaboration Int. VII 2013). The models are below the Herschel measurements at intermediate fluxes because these measurements are biased high due to the relatively low angular resolution combined with galaxy clustering (as demonstrated in Béthermin et al. 2017). |
| In the text | |
 |
Fig. 4. Ratio of shot noise and clustering (one-halo CIB anisotropies) for dusty galaxies at ℓ = 80 for all CMB experiments (ℓ = 80 corresponds to the recombination B-peak). |
| In the text | |
 |
Fig. 5. Ratio between the BB power spectra of [IR shot noise + clustering] and radio shot noise, at ℓ = 80 for all CMB experiments. |
| In the text | |
 |
Fig. 6. Extragalactic foreground power spectra for Planck (coloured dashed lines) and LiteBIRD (coloured continuous lines) at 217 and 235 GHz, respectively. The three continuous black lines are the primordial CMB B-mode power spectrum for r = 0.1, 0.01, and 0.001 from top to bottom. The dash-three-dots line is the lensing B-mode. |
| In the text | |
 |
Fig. 7. Extragalactic foreground power spectra for S4-SAT (coloured dashed lines) and S4-LAT (coloured continuous lines) at 145 GHz. The three continuous black lines are the primordial CMB B-mode power spectrum for r = 0.1, 0.01, and 0.001 from top to bottom. The dash-three-dots line is the lensing B-mode. As the two experiments are at the same frequency, the two |
| In the text | |
 |
Fig. 8. Equivalent tensor-to-scalar ratio (req) of the sum of the extragalactic foregrounds at the recombination B-peak, ℓ = 80, for the different CMB experiments (req is computed for each individual frequency). |
| In the text | |
 |
Fig. 9. Ratio of equivalent r of the extragalactic foregrounds (req) and instrument noise ( |
| In the text | |
 |
Fig. 10. Equivalent tensor-to-scalar ratio (req) of the sum of the extragalactic foregrounds at ℓ = 5, corresponding to the reionisation B-bump. We also show the σr for LiteBIRD, PICO, and CLASS (dashed lines). For Planck, the current 1σ upper limit is r < 0.028 and is thus not visible in the figure. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



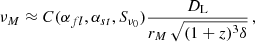
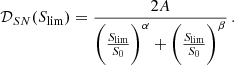
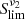
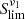
![$$ \begin{aligned} \log \left[C^{\nu _1,\,\nu _2}_{\ell }(S_{\rm lim}^{\nu _1},\,S_{\rm lim}^{\nu _2})\right]= \sum _{i,j=0}^6\,K_{i,\,j}\,\left[{\log (S^{\nu _1}_{\rm lim})+3 \over 0.2}\right]^j \,\left[{\log (S^{\nu _2}_{\rm lim})+3 \over 0.2}\right]^i\,, \end{aligned} $$](/articles/aa/full_html/2020/10/aa37147-19/aa37147-19-eq7.gif)
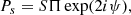
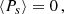
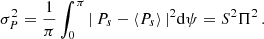
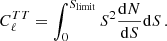
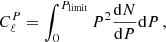
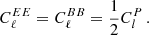
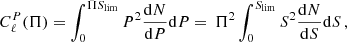
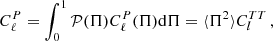
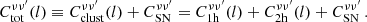
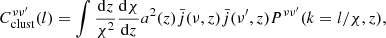
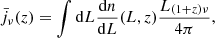
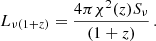
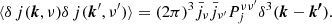
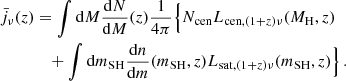
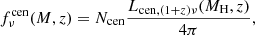
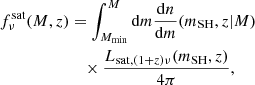
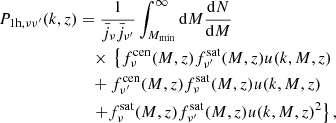
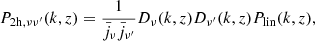
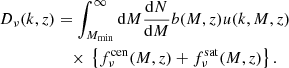
![$$ \begin{aligned} L_{(1+z)\nu }(M,z)= L_0 \Phi (z) \Sigma (M) \Theta [(1+z)\nu ]. \end{aligned} $$](/articles/aa/full_html/2020/10/aa37147-19/aa37147-19-eq35.gif)
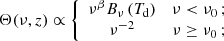
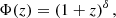
![$$ \begin{aligned} \Sigma (M) = M \frac{1}{(2\pi \sigma ^2_{L/M})^{0.5}}\mathrm{exp} \left[-\frac{({\mathrm{log} }_{10}M - \mathrm{log} _{10}M_{\mathrm{eff} })^2}{2\sigma _{L/M}^2}\right]. \end{aligned} $$](/articles/aa/full_html/2020/10/aa37147-19/aa37147-19-eq38.gif)
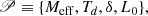
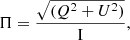
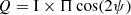
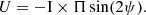
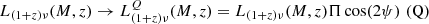
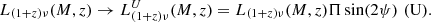
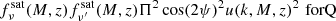
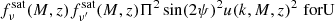
![$$ \begin{aligned} C_\ell ^{EE} = C_\ell ^{BB} = \frac{1}{2} \times P_{\rm 1h}[\propto f^{\mathrm{sat} }(M,z)^2] \times \langle \Pi ^{\mathrm{IR} } \rangle ^2 \,. \end{aligned} $$](/articles/aa/full_html/2020/10/aa37147-19/aa37147-19-eq50.gif)
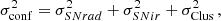
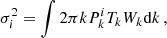
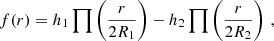
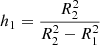
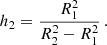
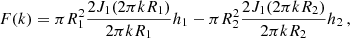
![$$ \begin{aligned} T_k=\left( \frac{\pi R_{1}^2 R_{2}^2}{R_{2}^2-R_{1}^2} \right)^2 \left[\frac{2J_{1}(2 \pi kR_{1})}{2 \pi kR_{1}}- \frac{2J_{1}(2 \pi kR_{2})}{2 \pi kR_{2}} \right]^2 . \end{aligned} $$](/articles/aa/full_html/2020/10/aa37147-19/aa37147-19-eq60.gif)
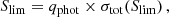
![$$ \begin{aligned} \sigma _{\rm tot} = \sqrt{F^2 \times [\sigma _{\rm conf}^2 + \sigma ^2_{\rm CMB}] + \sigma ^2_{\rm inst} } \,, \end{aligned} $$](/articles/aa/full_html/2020/10/aa37147-19/aa37147-19-eq62.gif)