| Issue |
A&A
Volume 641, September 2020
|
|
|---|---|---|
| Article Number | A89 | |
| Number of page(s) | 11 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202038303 | |
| Published online | 11 September 2020 | |
Geometry of the X-ray source 1H 0707–495
1
Nicolaus Copernicus Astronomical Center, Polish Academy of Sciences, Bartycka 18, 00-716 Warszawa, Poland
e-mail: mitsza@camk.edu.pl
2
Faculty of Physics and Applied Informatics, Łódź University, Pomorska 149/153, 90-236 Łódź, Poland
3
Centre for Extragalactic Astronomy, Department of Physics, University of Durham, South Road, Durham, DH1 3LE, UK
4
Institute of Physics, University of Zielona Góra, Licealna 9, 65-417 Zielona Góra, Poland
5
Hakubi Center, Kyoto University, Yoshida-honmachi, Sakyo-ku, Kyoto 606-8501, Japan
6
Department of Astronomy, Kyoto University, Kitashirakawa-oiwakecho, Sakyo-ku, Kyoto 606-8502, Japan
Received:
30
April
2020
Accepted:
29
June
2020
Aims. We investigate the constraints on the size and location of the X-ray source in 1H 0707–495 determined from the shape of the relativistically smeared reflection from the accretion disc.
Methods. We developed a new code to model an extended X-ray source and we applied this code to all archival XMM observations of 1H 0707–495.
Results. In contrast to earlier works we find that the relativistic reflection in this source is not consistent with an extended uniform corona. Instead, we find that the X-ray source must be very compact, at most a gravitational radius in size, and located at most a few gravitational radii from the black-hole horizon. A uniform extended corona produces an emissivity that is similar to a twice-broken power-law, but the inner emissivity is fixed by the source geometry rather than being a free parameter. In 1H0707–495, the reflection from the inner disc is much stronger than expected for a uniformly extended source. Including the effect of ionised absorption from the wind does not change this conclusion, but including scattered emission (and more complex absorption) from the wind can dramatically change the reflection parameters.
Key words: accretion, accretion disks / black hole physics / galaxies: Seyfert / X-rays: individuals: 1H 0707–495
© ESO 2020
1. Introduction
1H 0707–495 is a narrow-line Seyfert 1 galaxy well known for a sharp drop in its spectrum around 7 keV (Boller et al. 2002). This spectral feature can be imprinted either by an absorbing material on our line of sight (e.g. Tanaka et al. 2004; Done et al. 2007; Hagino et al. 2016; Mizumoto et al. 2019) or by irradiation of an accretion disc (e.g. Fabian et al. 2009; Zoghbi et al. 2010; Dauser et al. 2012). We consider the latter and we study constraints on the size and location of the X-ray source, which can be derived under this spectral interpretation.
Relativistic reflection spectroscopy is an important tool to constrain the geometry of accretion flows in their inner parts (e.g. Tanaka et al. 1995; Fabian & Ross 2010; Brenneman 2013). Two approximations are commonly used for such studies to simplify the model parametrisation and computations. First, in so-called lamppost geometry, irradiation of the disc surface by a point-like source is assumed (Martocchia & Matt 1996, and many later works). This allows us to estimate the distance of the X-ray source, but not its size. Secondly, even more often a phenomenological radial emissivity, typically a power law, is assumed, without any explicit assumption about the X-ray source. In this case, departures of the estimated emissivity from the dissipation profile of a Keplerian disc indicate that effects of the source-to-disc radiation transfer may be involved in shaping a reflection spectrum. Then, fitted emissivity can be used to infer the source geometry.
Such an approach was proposed by Wilkins & Fabian (2012, hereafter WF12). These authors showed the apparent similarity between an empirical, double-broken, power-law radial emissivity and the actual emissivity of the disc irradiated by an extended source, and used this to find the time averaged size of the X-ray source in 1H 0707–495 of about 30 gravitational radii. Then, Wilkins et al. (2014, hereafter W14) used spectra binned by the flux to show that the inferred outer break radius of the emissivity decreases with flux, and again compared these emissivities with their extended source illumination to claim that the size of the extended X-ray source decreases with decreasing source luminosity.
To gauge the accuracy of their approach, we develop in this work a similar relativistic reflection model with an extended X-ray source. However, rather than limiting our study to the qualitative comparison of this model with empirical emissivities (as WF12 and W14 did), we use this model directly to carry out a spectral description of 1H 0707–495. A part of this work addresses WF12 and W14, therefore, we adopt their data reduction method and assumptions about the X-ray source, and we use the same rest-frame reflection model rather than the newer models now available.
We also discuss in detail the reflection strength, which is the normalisation of the observed reflection with respect to the direct spectral component from the X-ray source. This quantity is strictly determined for a given geometry (see e.g. Dauser et al. 2014) and then gives a crucial test of the self-consistency of a model. However, this important constraint is often neglected in the X-ray data analysis. This concerns, in particular, all relativistic reflection models of 1H 0707–495 noted above.
Finally, evidence for a blue-shifted, photo-ionised outflow in 1H 0707–495 was reported by Dauser et al. (2012), Hagino et al. (2016), and Kosec et al. (2018). We take these results into account and investigate how the presence of such a blue-shifted absorber affects the fitted parameters of our reflection model.
2. Data reduction
We considered 15 XMM-Newton (Jansen et al. 2001) observations of 1H 0707–495 between 2000 and 2011 with an exposure time longer than 10 ks, (see e.g. Table 1 in Hagino et al. 2016). The 15 spectra from the EPIC pn detector (Strüder et al. 2001) were extracted using the XMM-Newton Science Analysis Software (SAS) version 17.0.0, and the current calibration file released on 29 March 2019. The data were reduced separately for each observation. We applied the standard selection criteria with the PATTERN ≤4 condition and excluding periods with the 10–12 keV background rate above 0.4 counts per second. The source spectra were extracted for a circular region that is 60 arcsec in diameter. For the background spectra, we found the optimal circular region via the ebkgreg tool, which was typically chosen to be a region of about 120 arcsec in diameter. The response files for each spectrum were generated with the rmfgen1 and arfgen2 tools.
The observation performed in January 2011 (Obs. ID 0554710801) caught the source in an extremely low state (Fabian et al. 2012) and is treated separately in this work; we refer to this as a very low (VL) state. The remaining 14 observations were combined to build the spectra of three non-overlapping count rate intervals that have <4, 4–6, and 6–10 counts s−1 (in the 0.2–10 keV energy range), which we refer to as the low (L), medium (M), and high (H) state, respectively. This selection of flux-resolved spectra is similar to that used in W14 and it is based on the assumption that the state of the X-ray source is determined by the X-ray flux. Spectral differences between these spectra could be then used to verify whether systematic changes of the source geometry correspond to the change of the observed flux.
Light curves of 1H 0707–495 with the time bin equal to 100 s were extracted with the same size of the source and background regions as the spectra and corrected with the epiclccorr tool. Using the light curves we created good time intervals (GTI) files for each of the 14 observations, applying the above count rate criteria. The spectra selected by count rate were extracted using these GTI files, with appropriate response files. Finally, the spectra for each count rate range were summed with the epicspeccombine tool. The resulting spectra have total exposure times of 64.5 (VL), 313.5 (L), 318 (M), and 237.8 (H) ks.
Our selection criteria for flux-resolved spectra are almost the same as those applied in W14, except for the energy range used for spectral selection, which in our case is slightly larger than the 0.3–10 keV range used in that work. Our extracted light curves are then essentially the same as those shown in Fig. 1 of W14, except for a slightly larger (by about 0.5 counts s−1) amplitude of our light curves.
Following W14, we considered the 1.1–10 keV range. For spectral binning we adopted two approaches. For our basic version of the binning, referred to as binning (1), we used the specgroup tool of SAS with the minimal signal-to-noise ratio for each channel set to 5 and the oversample parameter set to 3. To address the results of W14, we used also binning (2) following their procedure, that is via the grppha tool of the HEASOFT package, with the condition of having at least 25 counts in each spectral bin. We note large differences regarding assessments of the agreement of the considered spectral model with the spectra binned using procedures (1) and (2).
3. Model
The model developed in this work, referred to as reflkerr_elp (for extended lamppost), closely follows the lamppost model reflkerr_lp of Niedźwiecki et al. (2019), except for taking into account the spatial extent and rotation of an X-ray source, instead of treating it as point-like and static (lamppost). We consider a Keplerian disc in the Kerr metric, irradiated by a cylindrical corona with radius rc, located symmetrically around the black-hole rotation axis between a lower height hmin and upper height hmax. The inclination angle of a distant observer is denoted by i. All length scales r, h are in units of the gravitational radius, Rg = GM/c2. All the results presented below are for a = 0.998. We assume that the corona is uniform, that is its rest-frame emissivity is constant in Boyer-Lindquist coordinates.
The finite size of the corona means that we should also include its dynamics. We assume that the corona co-rotates with the disc, that is the angular velocity of the corona at (r, θ) equals the Keplerian velocity, ΩK(ρ), where ρ = rsinθ. For ρ < rISCO we assume rigid rotation with ΩK(rISCO), where rISCO is the radius of the innermost stable circular orbit.
The inner radius of the disc is denoted by rin and we assume that rin ≥ rISCO. 1H 0707–495 may be accreting at a rate close to the Eddington limit (see e.g. Done & Jin 2016), which may mean that the region of the flow at r < rISCO is optically thick so it can contribute to the observed reflection (Reynolds & Begelman 1997). This effect is not included in all previous studies of this object. We check that this is negligible in our models, all of which have extreme a, and inclination angles i ≃ (40−50)°.
Our computation of the fluxes of the X-ray radiation, either reaching the distant observer directly or illuminating the disc surface, strictly follows the model of Niedźwiecki & Życki (2008, hereafter NZ08); see Appendix A for technical details of our xspec implementation and comparison with similar computations.
To compute the observed reflected component, we apply the procedure used in the reflkerr_lp model, with reflionx (Ross & Fabian 2005) used for the rest-frame reflection. In Sects. 5.1 and 5.4 we apply the reflkerr model (Niedźwiecki et al. 2019), in which we also use reflionx for the rest-frame reflection (instead of hreflect originally used in reflkerr). In our fitting procedure, we use a free normalisation of the reflection component, which allows us to compare our results with previous works. We scale the reflection normalisation by ℛ, where ℛ = 1 corresponds to the actual normalisation for a given geometry. For the discussion below we also define the reflection strength, ℛobs, defined here as the ratio of the observed reflected and direct fluxes in the 20–30 keV range.
Figure 1 illustrates changes of the reflection spectra corresponding to the contraction of the X-ray source in the vicinity of the black-hole horizon. We start with the magenta line showing a fairly large and thick corona, where hmax = rc = 30 and hmin = 0. We successively shrink hmax = rc to 8 (blue) 3 (green) 2 (red), and 1.3 (black). The increase in relativistic broadening for smaller sizes is clear, as is the increasing ℛobs. The latter results from the combination of Doppler beaming and light bending. The latter effect is well known to increase the fraction of photons hitting the disc (Martocchia & Matt 1996), however, for a static source, the related enhancement of the observed reflection is rather weak (except for large i, see below). If the X-ray source rotates, its radiation is Doppler beamed to outer parts of the disc. Then, the observed reflection is not so strongly dependent on i. At the same time, the change of the irradiation profile resulting from the source rotation leads to a considerable change of the observed spectral shape of reflection.
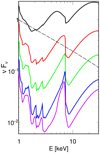 |
Fig. 1. Illustration of changes of the reflection spectrum resulting from the contraction of the X-ray source, described by the decrease of both hmax and rc, for Γ = 2.6, ξ = 50, ZFe = 9, i = 50°, ℛ = 1, a = 0.998, hmin = 0, and rin = rISCO. The reflection spectra, shown by solid curves, correspond to hmax = rc = 1.3 (black), 2 (red), 3 (green), 8 (blue), and 30 (magenta) from top to bottom. The primary spectrum is the same in all cases and is shown by the dashed line. |
Figure 2 illustrates the effect of azimuthal motion of the X-ray source; see also NZ08, who extensively studied the effects of the off-axis location of the X-ray source and its orbital motion. Our assumptions about co-rotation with the disc at ρ ≥ rISCO and rigid rotation at ρ < rISCO appear to be natural and are the only choices that can be justified ab initio, unlike the unknown dynamics associated with magnetic flares. The angular velocity within rISCO in this model is equal to ΩK(rISCO), giving V ≃ 0.1c at ρ = 0.2, where V is the velocity measured in the locally non-rotating frame (Bardeen et al. 1972). At h = 1.5 and ρ = 1.5, V ≃ 0.8c is much larger than the Keplerian V in the equatorial plane. This is because V of a co-rotating source for a Kerr black hole increases with h at h ≲ ρ (see Sect. 2.2.3 in NZ08).
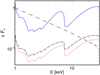 |
Fig. 2. Example illustration of the effect of the rotation of the X-ray source. The dotted red curve shows the reflection spectrum computed with reflkerr_lp (i.e. for a static point-like source, at h = 2.) The dashed black and solid blue curves show the reflection spectra computed with reflkerr_elp with rc = 0.2 and 1.5, respectively, in both hmin = hhor and hmax = 2. In all three cases Γ = 2.6, ξ = 50, AFe = 9, i = 50°, a = 0.998, rin = rISCO and ℛ = 1. The observed primary spectrum is the same in all three models and is shown by the dot-dashed black curve. The difference between the reflkerr_lp and the reflkerr_elp spectra is primarily due to the azimuthal motion of the emitting plasma in the latter, where V ≃ 0.1c for rc = 0.2 and ≃0.8c for rc = 1.5. |
Figure 2 shows the results at i = 50°, relevant for 1H0707–495. For a static point-like source at h = 2, ℛobs/ℛobs, nr ≃ 2, although in this case Nirr/Nobs ≃ 5, where ℛobs, nr is the reflection strength for an isotropic source above a semi-infinite slab in flat space-time, and Nirr and Nobs are, respectively, the number of photons hitting the disc and observed directly from the source. This factor of 2 enhancement of the reflection strength is lower than the factor of 5 enhancement of the irradiating photon number compared to those observed as for a static lamppost; the enhanced irradiation occurs mostly at r ≲ h and the reflected radiation is directed mostly to large i (see e.g. Niedźwiecki & Zdziarski 2018), therefore, the related increase of ℛobs is rather modest for i ≲ 70°.
The black dashed curve in Fig. 2 shows a mostly vertical extended source from the horizon that is hmin = hhor up to hmax = 2, with very small radial extent rc = 0.2. This geometry is very similar to the lamppost for light bending but the rotation velocity of V ≃ 0.1c Doppler beams the radiation more towards the outer parts of the disc, where reflection gives a stronger contribution for small i and, hence, ℛobs is larger.
This effect is even more marked when the radial extent of the source is increased to rc = 1.5 because this has V ≃ 0.8c and ℛobs/ℛobs, nr ≃ 15. The increasing distortion of the reflection spectrum, as compared to the static source, is clearly seen.
Concluding the above discussion we note that significant changes of the angular distribution of radiation at the X-ray source (in particular, those related to the motion of the emitting plasma) may significantly change ℛobs. However, they also lead to significant changes of the observed shape of the reflected spectrum owing to the change of the radial irradiation profile. Then, treating the reflection strength as a free parameter is unphysical and we again note that we scale it by ℛ only to compare our results with earlier works. Models with ℛ ≫ 1, such as found in Sects. 5.1 and 5.2, are clearly unphysical.
4. Comparison with empirical radial emissivity
The red curve in Fig. 3a shows the twice-broken power-law emissivity fitted to average spectra of 1H0707–495 by Wilkins & Fabian (2011), with the inner, middle, and outer indices of q1 = 7.8, q2 = 0, and q3 = 3.3, respectively and the breaking radii of rbr, 1 = 5.6 and rbr, 2 = 35. In WF12, the authors argued that this inferred emissivity profile is consistent with that produced by an X-ray source with rc ≃ rbr, 2 (specifically, with hmin = 2, hmax = 10, and rc = 30). We use our code to explicitly calculate the emissivity of such an extended corona, shown by the blue curve in Fig. 3a. Our assumptions concerning the X-ray source are exactly the same as those of WF12 and our radial profile agrees with theirs (Fig. 15(b) in WF12). However, it differs substantially from the empirical profile of Wilkins & Fabian (2011). The empirical profile fitted to 1H0707–495 indicates a major contribution of radiation reflected from r < 5, which suffers strong redshift. However, while the irradiation profile produced by an extended source steepens at r ≲ 5 (because of the blueshift of photons arriving at this region from X-rays produced in the corona at larger distances), this effect is too weak to reproduce the extremely steep (with q ≃ 8) inner part of the empirical profile. The contribution of reflection arising from r < 5 is only 15 per cent for the actual profile of an extended corona irradiating the disc, whereas it equals 97 per cent for the empirical profile.
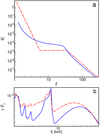 |
Fig. 3. Panel a: red line shows the twice-broken power-law, radial emissivity profile fitted to 1H0707–495 by Wilkins & Fabian (2011), see text. The blue line shows the emissivity profile produced by the X-ray source with hmin = 2, hmax = 10, rc = 30, and Γ = 3.1. Panel b: reflection spectra for the emissivity profiles shown in panel a, and for Γ = 3.1, ξ = 53, AFe = 9, i = 54° and rin = rISCO; the difference of spectral shapes is only due to different amounts of relativistic distortion corresponding to the difference of the radial profiles. |
The model matches well to the change in q seen a larger radii, from q ≃ 0 at r ≲ rc to q ≃ 3 at r ≳ rc. This is a simple geometrical effect that is also reproduced in flat space-time, however, it is of minor importance for the total reflection spectrum because so little of the total reflection signal is produced at these radii.
The large difference in emissivity from the central regions translates into a clear difference in predicted spectra, as shown in Fig. 3b. The extended corona of WF12 does not give the same reflected spectrum as derived from the empirical emissivity profile fit to the data from 1H0707–495.
5. Spectral analysis
In Sects. 5.1 and 5.2 we address W14, therefore, we follow their assumption that reflection is produced by weakly ionised disc and (still following W14) we adopt the Zoghbi et al. (2010) parameters of the reflection model as follows: ionisation parameter, ξ, iron abundance, ZFe, and i. In Sect. 5.3 we relax these assumptions and allow a free fit of our extended corona model to the data.
5.1. Phenomenological radial emissivity
Following W14 we fitted the L, M, and H spectra assuming a twice-broken power-law, radial emissivity, for which we also adopted their constraints on the emissivity parameters (see the footnote of Table 1), and we fixed ξ = 53.4, i = 53.96°, ZFe = 8.88, and rin = rISCO. We applied model reflkerr (Niedźwiecki et al. 2019), which computes the reflection spectrum for an arbitrary twice-broken power-law, radial emissivity. Our results, see Table 1, are consistent with those of W14. In particular, we find rbr, 2 between ≃20 and ≃30, increasing with the observed flux. The fit quality with spectral binning (2) is also consistent with W14 and seemingly excellent. For binning (1) we found only insignificant differences in the values of the fitted parameters, however, in this case they give a much worse χ2/DoF > 2.
Results of spectral fitting of the coronal model reflkerr using empirical radial emissivities.
We now fit our extended disc corona reflection model directly to the data to explicitly test if this geometry can indeed produce the observed emissivity. The reflkerr model computes the transfer of both the reflected and direct radiation from the corona, therefore, properly calculates the reflection strength for this geometry. We find that the data can only be fit with an unphysically strong reflection component, namely ℛ > 10. This rules out the parameters of W14 for the disc-corona model in 1H0707–495. The empirical twice-broken power-law emissivity is only an approximation of models with a radially extended X-ray corona over the disc, and is a poor approximation for models with very steep inner emissivity as these produce much more inner disc reflection than is expected from an isotropic (in its rest frame), radially extended source.
For the VL spectrum, the twice-broken radial profile, with constraints on (q1, q2, q3) of W14, does not give a good fit. We therefore fitted a single-broken profile (see Table 1). The fitted profile is very steep, having q2 > 7 at r > 2.3. However, the inner q1 = −0.8 indicates a strongly reduced contribution from r ≲ 2. This break in the emissivity is highly significant. Using a single power law and setting rin = rISCO we get a much worse fit with Δχ2 ≃ +50 for binning (1). The fit also significantly improves after allowing ξ to vary; it then decreases to the minimum value allowed in reflionx, that is ξ = 10. The spectral feature observed in VL between ∼2 keV and ∼7 keV (see Fig. 4) can be reproduced by a relativistic line from a weakly ionised disc. However, in the disc-corona model such a spectral description requires an unrealistic reduction of the primary continuum, namely ℛ > 750 (see Fig. 5a), which again rules out this geometry.
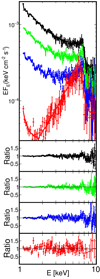 |
Fig. 4. Top panel: unfolded data and model spectra for our best-fitted models for VL (red), L (blue), M (green), and H (black) using zxipcf*reflkerr_elp. Spectral binning (1) was used. The model parameters are given in Table 4. The model is shown by the solid curve. Bottom panel: fit residuals given as the data-to-model ratio for VL, L, M, and H from bottom to top. |
 |
Fig. 5. Primary (dashed) and reflected (solid) spectra in our best models for VL with panel a: reflkerr (Sect. 5.1), panel b: reflkerr_elp with a weakly ionised disc (Sect. 5.2), and panel c: reflkerr_elp with a strongly ionised disc and an ionised absorber (Sect. 5.3). The spectra correspond to the fitted parameters for VL given in Tables 1, 3, and 4, respectively, except for ℛ, which was set to the physical value, i.e. ℛ = 1. As can be seen in Fig. 4, the observed VL spectrum has a strong depression at ∼2 keV. For the models shown in panels a and b, the contribution of the primary component must be artificially reduced by a factor >750 and >25, respectively, to obtain a similar spectral depression in the total spectra. In panel c the black curves show the unabsorbed and the red curves show the absorbed spectra. In this case, the relativistic effects combined with absorption allow us to reproduce the observed shape with ℛ = 1. |
5.2. Extended lamppost: plain reflection
We now use our model reflkerr_elp. We first aim to quantitatively test whether irradiation by an extended disc corona out to rc can give a broken power-law emissivity with rc ≃ rbr, 2 as proposed by WF12 and W14. Therefore, (1) we keep the same assumptions about the rest-frame reflection as in the previous section, and (2) we set rc equal to rbr, 2 of the reflkerr model fitted to a given state (Table 1). This gives much larger values of χ2 than obtained with reflkerr in Sect. 5.1, specifically Δχ2 ≃ (150−200) for spectra L, M, and H with binning (1) as shown in Table 2. There is no good fit for VL as discussed above, so we do not tabulate results for this spectrum.
The worsening of the fit shows that the disagreement between the empirical and physical emissivity profiles discussed in Sect. 4 is important even for the analysis limited to the 1–10 keV range. Using rbr, 2 to estimate rc (as proposed by WF12 and W14) does not work for an extended corona geometry. The very large inner emissivities inferred from the twice-broken power law require a more radially concentrated X-ray illumination pattern than produced from a uniform corona, even in full general relativity.
This is the case even when we allow rc to vary, rather than fixing it to rbr, 2. The inferred reflection in the data is dominated by the inner, extremely steep emissivity so the fitted rc as well as hmax are very small for all spectra, as detailed in Table 3. This means that the source geometry is now close to that of the standard lamppost, except that it is rotating.
Results of spectral fitting of our model reflkerr_elp.
For such small rc and hmax, any value of hmin between rhor and hmax gives identical results because radiation from h close to hmax dominates both the observed and irradiating flux. For simplicity, for all results presented in this section, we assumed hmin = rhor for L, M, and H. For VL, where the fitted rc is slightly larger, we assumed hmin = 0; allowing hmin to vary does not change the results.
Figure 6 shows the probability distributions and correlations between rc, hmax and ℛ, obtained using the Markov chain Monte Carlo (MCMC) method. The major degeneracy concerns the anti-correlation between rc and ℛ in L, M, and H, which is related to the increase of V with rc (for the assumed velocity field close to the symmetry axis, see Sect. 3). This is due to the increase of reflection strength with V (see Fig. 2). The VL spectrum requires a negligible contribution of the primary component, namely ℛ ≳ 25, see Fig. 5b, so for this state we do not get the ℛ − rc anti-correlation.
 |
Fig. 6. Probability distributions showing correlations between the rc, hmax, and ℛ parameters of the reflkerr_elp model with a weakly ionised disc (see Table 3) fitted in the 1.1–10 keV range to the VL (top left), L (top right), M (bottom left), and H (bottom right) spectrum, obtained in the MCMC analysis using xspec_emcee implemented by Jeremy Sanders. The results of this analysis are presented using package corner (Foreman-Mackey 2016). The contours in the 2D plots correspond to the significance of σ = 1, 2, 3. The histograms show the probability distributions for the individual parameters. |
For VL we also allowed rin to vary and we find that rin > rISCO is formally significant; setting rin = rISCO gives, for binning (1), Δχ2 = 17.
All these fits are somewhat worse than those of the phenomenological broken power-law emissivity reflection fits, typically by Δχ2 ∼ 10−20 for binning (1). This is because the model geometry is now reproducing the inner, very steep emissivity, where most of the reflection signal is produced, at the expense of the weak outer reflection component. More concerning is that they all require ℛ > 1 so are physically unrealistic except for the brightest state (H).
The pure reflection models clearly show that the best-fit, extended source geometry is not very extended for all the spectra of 1H0707–495. The illumination pattern derived from these fits requires a very centrally concentrated X-ray corona, close to the lamppost geometry except for its rotation kinematics modifying the illumination pattern. Hence there is also no evidence that the size of the corona is correlated with the luminosity, as claimed in W14.
5.3. Extended lamppost: reflection and ionised absorption
We now include photo-ionised absorption in addition to our model for reflection from the extended disc-corona, reflkerr_elp, as multiple studies have shown that this is significantly present (Dauser et al. 2012; Hagino et al. 2016; Kosec et al. 2018). We first model this absorption using the zxipcf model implemented in xspec, although we note that this assumes only a rather small turbulent velocity broadening of 200 km s−1, that is much smaller than those inferred from the data (around 10 0000 km s−1 in Kosec et al. 2018). This model also assumes solar abundances for all elements, whereas the reflection fits typically require large overabundance of iron and uses an ion population calculated assuming Γ = 2.2, which is rather harder than that inferred for 1H0707–495. Nonetheless, it gives a simple model to approximately characterize some of the spectral complexity associated with partially ionised absorption.
We do not impose any constraints on the model parameters except for linking the reflection i and ZFe across all four states, and fixing a = 0.998. The spectral fitting results are given in Table 4, Fig. 4 shows the spectra and best-fit models to all states.
Results of spectral fitting of the model reflkerr_elp, with a partially covering ionised absorption computed with zxipcf.
Adding the photo-ionised absorber significantly improves the spectral description in all four states, both compared to the extended disc-corona fits with free corona size shown above, and even compared to the phenomenological twice-broken power-law emissivity fits. We allow here the scaling parameter of reflection, ℛ, to vary but all fits correspond to a physically self-consistent ℛ ≃ 1. This is even the case for the VL spectrum, which always previously required ℛ ≫ 1.
Figure 5 shows the sequence of model fits to the VL spectrum, with the direct power law (dashed) and reflection component (solid) shown separately. Panel a shows the low-ionisation reflkerr fit with reflection calculated from the phenomenological emissivity as in Sect. 5.1, but for a reflection normalisation set to the physical ℛ = 1 rather than the extreme values required from the fits. Even though the emissivity best fit is a single, very centrally concentrated power law, gravitational effects alone are not sufficient to enhance the reflection to the extent required by the data. Panel b shows the fit with reflection calculated from the self-consistent illumination pattern of an extended, rotating corona. The disc ionisation parameter is similarly low to that derived from the phenomenological emissivity fits. Thus the reflected component shape is much the same, but its amplitude is now dramatically enhanced by the source kinematics, with the intrinsic rotation changing the illumination pattern on the disc. However, this is still insufficient to explain the inflection in the VL data at 2 keV. Instead, panel c shows the fit including ionised absorption. Unlike the L, M, and H fits, the ionised absorber in VL is only moderately rather than highly ionised (ξ ∼ 40 rather than 104). Its effect on the spectrum is to produce strong continuum curvature rather than distinct ionised absorption line features, with a strong low-energy cut-off below 4 keV from bound-free transitions in metals such as Si, S, and Fe L. This continuum curvature gives a much better fit to the data and changes the shape of the best-fit reflection spectrum so that it now is better described by a highly ionised disc. This increases the amount of reflection at low energies compared to the Compton hump and shifts the line thereby shifting the line and edge energies. The total continuum spectrum then has a strong dip at 2 keV as well as at 9 keV, as observed in the data (see also Fig. 4).
Figure 4 also shows the other datasets fit with this model including ionised absorption. The change in behaviour of the continuum at low energies between VL and L, M, and H is obvious; L, M and H instead give the best-fit ionised absorption, which is highly ionised ξ ∼ 104.
For all the datasets, the geometry of the extended source is changed very little from that derived in the previous section. Both rc and hmax are small, making the model much more like a lamppost (but with rotation) than a corona with a large-scale extent over the disc. Similar to Sect. 5.2, we assume hmin = rhor for L, M, and H and hmin = 0 for VL; allowing hmin to vary does not change our results.
However, despite the lack of change in source geometry, all the spectral fits are now consistent with ℛ ≃ 1. This is because of the much larger inferred ionisation state of the reflector, with ξ > 1000, in all four states instead of ξ = 10−60 in fits without the additional ionised absorption. The disc albedo is strongly enhanced by ionisation, which enhances the reflection spectrum in soft X-rays for the same radial and vertical extent of the X-ray source.
The ionised absorber in L, M, and H is highly ionised; therefore this absorber has little continuum absorption and is instead dominated by ionised line features. The inferred columns are extremely high, with Nh ∼ 1.1 × 1024 cm−2 for L, which is optically thick to electron scattering. The inferred columns for M and H are lower, but only by a factor 2-5. Scattering of the continuum from the ionised absorbing material must be important at these columns, so the model is not self-consistent. These derived columns could be overestimated as they depend strongly on the velocity structure of the absorbing material. Absorption lines saturate when the core of the line becomes optically thick, that is when photons at the line centre cannot escape at the rest energy of the transition. Increasing the column beyond this cannot lead to much more absorption as there are no more photons at the line centre to remove. Absorption increases in the wings of the line, but Doppler wings are very steep so the line equivalent width does not increase much as the column increases. A larger spread of velocity in the absorbing material gives a wider but shallower line for the same column, so it remains optically thin at higher columns. Fits to 1H0707–495 by Kosec et al. (2018) indicate that the velocity width of the line is around 13 000 km s−1 as opposed to the 200 km s−1 used in zxipcf, which reduces the columns to around 2−4 × 1023 cm−2. However, this still has an optical depth to electron scattering of ∼0.2. The geometry of the material then determines how much the scattered emission contributes to the spectrum, and it is not just scattered continuum but also resonance line scattering. Calculating the contribution of these cannot be done analytically for non-spherical geometries, rather this requires a Monte Carlo radiation transfer code.
5.4. Disc reflection and wind absorption and scattering
We apply the Monte Carlo radiation transport code monaco (Odaka et al. 2011) to model the absorption and scattering self-consistently from a bipolar wind geometry (Hagino et al. 2015, 2016, 2017; Tomaru et al. 2018). We use the specific bipolar wind simulation of Mizumoto et al. (2019), which is tailored to fit to the time average spectrum of 1H0707–495 (similar to the M and H spectra used here). The model assumes a black-hole mass of 2 × 106 M⊙, with a wind filling an axi-symmetric bicone between 45−56.3° (so that the solid angle from the focal point d below the black hole is Ω/2π = 0.15), launched at d = rmin = 50, corresponding to an escape velocity of 0.2c. The mass-loss rate in the wind is set to Ṁwind/ṀEdd = 0.2 and this, combined with the velocity law, gives the density structure along the wind streamlines. This is illuminated by a power law with Γ = 2.6 and LX = 0.003LEdd to get the self-consistent ionisation structure. Mizumoto et al. (2019) show that the scattered spectrum in this simulation can also account for the time lags seen in this source around the iron line energy.
We now use this combined absorption and scattering wind model to modify the intrinsic emission and its reflection from the disc. We model the latter via reflkerr with a phenomenological emissivity fixed to a single power law with q = 3. This is justified because after adding the wind component we find that the inner radius of the reflecting material increases to a very large value, implying only a very mild relativistic distortion of the reflected spectrum. The fits now have to be restricted to energies above 2 keV due to the energy band limitations of the tabulated model.
We could not get a good fit for the VL spectrum, as we no longer include the less ionised material (probably clumps within the wind), which produces the very marked spectral curvature in these data. These less ionised clumps are probably still present in L, M, and H, but at a lower level (smaller covering fraction, see Hagino et al. 2016) so the spectrum can be fit without including this material. Hagino et al. (2016) show that the brightest, steepest spectra are least affected by these clumps, so we plot the best fit for H in Fig. 7. All parameters are given in Table 5, but the reduced energy range means that the goodness of fit cannot be directly compared with previous models. Hence we also refit the zxipcf*reflkerr_elp model to the same energy range; the χ2/DoF for the joint fit to L, M, and H (with linked i and ZFe) is 369/326 for binning (1). Hence the fit with the wind model is somewhat worse in terms of Δχ2, but the number of degrees of freedom in the model are also lower because it is computed only for a single fixed wind geometry.
 |
Fig. 7. Unfolded data and model spectrum for our best-fitted model for H using monaco*reflkerr. The red curve shows the total (i.e. primary power law + reflection) transmitted component attenuated by absorption. The blue curve shows the total scattered component. |
Results of spectral fitting in the 2–10 keV range of the model reflkerr, with wind absorption and scattering computed with monaco.
Including the scattered emission from the wind dramatically changes the requirement for reflection from the disc to be distorted by extreme relativistic effects. However, the model is still not self-consistent as the inferred amount of reflection from the disc is strongly enhanced over that expected, with ℛ ∼ 6 rather than ≃1. Imposing the constraint of ℛ = 1, we find that small values of both the inner radius of the disc and the source size are again required. The model also has very different assumptions about metallicity, namely ZFe = 5 is fitted for the reflector, compared to solar in the wind.
6. Summary
This paper shows the model of reflection from an extended corona geometry, which can be directly fit to X-ray spectral data. All previous models assumed either a point-like source (lamppost) or some phenomenological radial emissivity. The authors of WF12 associated a twice-broken power-law emissivity with the illumination pattern expected from a uniform extended corona, with the outer break indicating the radial extent of the corona, a uniform illumination interior to this, and then a marked enhancement at small radii due to light bending and other GR effects. However, we show that this qualitative match to extended corona models is not a good quantitative fit to real data. We use 1H0707–495 as apparently the most extreme relativistic reflection source, and directly fit it with both a twice-broken power-law phenomenological emissivity and the full illumination pattern produced by an extended disc corona. The outer break radius of the emissivity, rbr, 2 ∼ 30, so according to WF12 indicates a corona of size rc = 30. Explicitly fitting a uniform extended corona with rc = 30 to the data produces a reflection spectrum that strongly deviates from that observed for any scale height because the self-consistent, centrally peaked illumination pattern is not as steep as required by the phenomenological fits.
Instead, allowing the size (as well as the height) of the corona to be a free parameter makes the corona collapse in size. The best-fit corona geometry derived from these fits to the data is a very compact source of ≲1Rg in size, and is located at most ∼2Rg from the black-hole horizon in all flux states. These fits show a corona that is highly centrally peaked, rather than uniformly extended. This is close to the original lamppost model used initially for computational convenience, although we also point out the importance of the source rotation in our model, which makes a large increase in the amount of relativistic reflection that escapes to infinity.
The fitted location of the X-ray source is interestingly consistent with that estimated previously by fitting the lamppost model to the time-averaged (Dauser et al. 2012) and time-dependent (Caballero-García et al. 2018) spectra in 1H0707–495, which in both cases gives h ≃ 3. The latter, however, depends on the black-hole mass, and the lamppost model of Caballero-García et al. (2018) cannot explain the measured delay spectra if it is 5.3 × 106 M⊙ (Pan et al. 2016) rather than 2 × 106 M⊙ estimated in earlier works.
In our analysis we considered only a fixed, maximum value of black-hole spin, a = 0.998. Such a high value was estimated in the lamppost model by Dauser et al. (2012) and the fitted values of the inner radius of the disc, (1.3−1.4)Rg (Sect. 5.3) indicate that a > 0.99 is required in this version of the model.
We do not find any sizable changes of the corona geometry between different X-ray flux levels, which would lead to varying distortion of the reflection component, such as shown in Fig. 1. The spectral variations appear to be mostly from the change of both the amplitude and slope of the primary emission spectrum and the change of the disc ionisation state. We note some hints of geometrical changes only for a VL state, with a weak truncation of the disc at about 2Rg (which is ruled out at higher states) and a weak decrease of the height and increase of the radius. However, the large difference between this VL and higher flux spectra is primarily due to the difference of the ionisation state of the absorber.
Our fits then strongly favour a compact source on the spin axis of the black hole. Yet it is difficult to produce a physical model of such a source. There are strong limits on the amount of X-rays that could be produced by Comptonisation of disc photons (Dovčiak & Done 2016), and the radiative efficiency is strongly reduced owing to photon trapping by the black hole (Niedźwiecki et al. 2016).
Including the effect of simple models of ionised absorption from the wind (see also Dauser et al. 2012; Kosec et al. 2018) does not change the conclusions about the source size fit to the data, but does indicate that these models are not self-consistent because the large columns of ionised material inferred contribute substantially to the spectrum via electron scattering and line emission and resonance line scattering. We use the specific bipolar wind Monte Carlo calculation of Mizumoto et al. (2019) and find that the inclusion of the scattered flux from the wind can dramatically change the parameters. With this model, the reflection spectrum from the disc is only mildly distorted by relativistic effects, and indicates the disc extending down to 700Rg only, rather than requiring most of the reflection to come from within 5Rg; the fit however is somewhat worse than for the phenomenological absorption only models.
Nonetheless, even this model is incomplete as the inferred amount of reflection from the disc is much larger than expected in this geometry, and the metallicities of the reflector and wind are different, and most importantly, we neglect any additional absorption from clumps of less ionised material entrained in the hot wind. While such winds cannot be easily modelled ab initio, they may hold the key to the dramatic spectral features seen in the most extreme active galactic nuclei.
The model can be downloaded at https://users.camk.edu.pl/mitsza/reflkerr_elp
Acknowledgments
We thank Andrzej Zdziarski and the referee, Thomas Dauser, for valuable comments. This research has been supported in part by the Polish National Science Centre grants 2014/13/B/ST9/00570, 2015/18/A/ST9/00746 and 2016/21/B/ST9/02388. A. N. is a member of the International Team 458 at the International Space Science Institute (ISSI), Bern, Switzerland, and thanks ISSI for the support during the meeting in Bern. M. M. acknowledges support from Japan Society for the Promotion of Science (JSPS) overseas research fellowship and Hakubi project at Kyoto University.
References
- Bardeen, J. M., Press, W. H., & Teukolsky, S. A. 1972, ApJ, 178, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Boller, T., Fabian, A. C., Sunyaev, R., et al. 2002, MNRAS, 329, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Brenneman, L. 2013, Measuring the Angular Momentum of Supermassive Black Holes (Springer) [CrossRef] [Google Scholar]
- Caballero-García, M. D., Papadakis, I. E., Dovčiak, M., et al. 2018, MNRAS, 480, 2650 [Google Scholar]
- Dauser, T., Svoboda, J., Schartel, N., et al. 2012, MNRAS, 422, 1914 [NASA ADS] [CrossRef] [Google Scholar]
- Dauser, T., Garcia, J., Parker, M. L., Fabian, A. C., & Wilms, J. 2014, MNRAS, 444, L100 [NASA ADS] [CrossRef] [Google Scholar]
- Done, C., & Jin, C. 2016, MNRAS, 460, 1716 [NASA ADS] [CrossRef] [Google Scholar]
- Done, C., Sobolewska, M. A., Gierliński, M., & Schurch, N. J. 2007, MNRAS, 374, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Dovčiak, M., & Done, C. 2016, Astron. Nachr., 337, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., & Ross, R. R. 2010, Space Sci. Rev., 157, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., Zoghbi, A., Ross, R. R., et al. 2009, Nature, 459, 540 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fabian, A. C., Zoghbi, A., Wilkins, D., et al. 2012, MNRAS, 419, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D. 2016, J. Open Source Softw., 24 [Google Scholar]
- Hagino, K., Odaka, H., Done, C., et al. 2015, MNRAS, 446, 663 [Google Scholar]
- Hagino, K., Odaka, H., Done, C., et al. 2016, MNRAS, 461, 3954 [NASA ADS] [CrossRef] [Google Scholar]
- Hagino, K., Done, C., Odaka, H., Watanabe, S., & Takahashi, T. 2017, MNRAS, 468, 1442 [NASA ADS] [CrossRef] [Google Scholar]
- Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kosec, P., Buisson, D. J. K., Parker, M. L., et al. 2018, MNRAS, 481, 947 [NASA ADS] [CrossRef] [Google Scholar]
- Laor, A. 1991, ApJ, 376, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Laor, A., Netzer, H., & Piran, T. 1990, MNRAS, 242, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Martocchia, A., & Matt, G. 1996, MNRAS, 282, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Miniutti, G., & Fabian, A. C. 2004, MNRAS, 349, 1435 [NASA ADS] [CrossRef] [Google Scholar]
- Mizumoto, M., Ebisawa, K., Tsujimoto, M., et al. 2019, MNRAS, 482, 5316 [CrossRef] [Google Scholar]
- Niedźwiecki, A., & Życki, P. T. 2008, MNRAS, 386, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Niedźwiecki, A., & Miyakawa, T. 2010, A&A, 509, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Niedźwiecki, A., & Zdziarski, A. A. 2018, MNRAS, 477, 4269 [CrossRef] [Google Scholar]
- Niedźwiecki, A., Zdziarski, A. A., & Szanecki, M. 2016, ApJ, 821, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Niedźwiecki, A., Szanecki, M., & Zdziarski, A. A. 2019, MNRAS, 485, 2942 [NASA ADS] [CrossRef] [Google Scholar]
- Odaka, H., Aharonian, F., Watanabe, S., et al. 2011, ApJ, 740, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Pan, H.-W., Yuan, W., Yao, S., et al. 2016, ApJ, 819, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, C. S., & Begelman, M. C. 1997, ApJ, 488, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, C. S., Young, A. J., Begelman, M. C., & Fabian, A. C. 1999, ApJ, 514, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Ross, R. R., & Fabian, A. C. 2005, MNRAS, 358, 211 [Google Scholar]
- Ruszkowski, M. 2000, MNRAS, 315, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suebsuwong, T., Malzac, J., Jourdain, E., & Marcowith, A. 2006, A&A, 453, 773 [CrossRef] [EDP Sciences] [Google Scholar]
- Tanaka, Y., Nandra, K., Fabian, A. C., et al. 1995, Nature, 375, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, Y., Boller, T., Gallo, L., Keil, R., & Ueda, Y. 2004, PASJ, 56, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Tomaru, R., Done, C., Odaka, H., Watanabe, S., & Takahashi, T. 2018, MNRAS, 476, 1776 [CrossRef] [Google Scholar]
- Wilkins, D. R., & Fabian, A. C. 2011, MNRAS, 414, 1269 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkins, D. R., & Fabian, A. C. 2012, MNRAS, 424, 1284 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkins, D. R., Kara, E., Fabian, A. C., & Gallo, L. C. 2014, MNRAS, 443, 2746 [NASA ADS] [CrossRef] [Google Scholar]
- Zoghbi, A., Fabian, A. C., Uttley, P., et al. 2010, MNRAS, 401, 2419 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: reflkerr_elp
The construction of the reflkerr_elp model3 closely follows that of reflkerr_lp. In particular, the convolution of the general-relativistic effects with the rest-frame radiation spectra makes use of the transfer functions; these transfer functions, following Laor et al. (1990) and Laor (1991), are constructed by tabulating a large number of photon trajectories. The transfer functions are computed only for a single value of the spin parameter, a = 0.998. The source-to-disc and source-to-observer transfer functions are tabulated in a grid including 51 bins in both ρ and h. We use 50 bins logarithmically spaced between ρ = 0.1 and 50, and the additional bin for ρ = [0, 0.1], and similarly 50 bins logarithmically spaced between h = 0.1 and 50, and the additional bin for h = [0, 0.1]. Then, in our parametrisation of the model, both the rc and hmax parameters can be fitted in the range of [0.1, 50]. To compute these transfer functions, we generated photon trajectories sampling the region at 0 ≤ h ≤ 50 and 0 ≤ ρ ≤ 50 with uniform probability density; at each point the initial direction in the source rest frame was generated with an isotropic probability distribution. The photon trajectories were computed via the code developed by NZ08. For the disc-to-observer transfer we use the same transfer functions as in reflkerr and reflkerr_lp.
Our model relies on the numerical accuracy of the code of NZ08, therefore, we now briefly compare this code with other similar computations. Irradiation of an accretion disc by a single point-like source, located off the symmetry axis of the Kerr metric, has been considered in a number of works, many of which are aimed at explaining some observed variability effects by the change of the location of the source (e.g. Reynolds et al. 1999; Ruszkowski 2000; Miniutti & Fabian 2004; Niedźwiecki & Miyakawa 2010; NZ08). There were some differences in the interpretation of the reduced variations of the reflected component in the model with a co-rotating source, which effect was attributed to light bending by Miniutti & Fabian (2004), whereas NZ08 clarified that it is mostly due to the assumed dependence of the source rotation velocity on its height. However, the quantitative results of these studies, for example the dependence of the reflection strength (typically represented by the Fe line flux in these works) on the source location, were in fairly good agreement.
Suebsuwong et al. (2006) and NZ08 show radial profiles for disc irradiation, which can be compared to those presented by WF12, and again there seems to be a good agreement between these three works. In Fig. A.1 we show the emissivity profiles, computed with the code of NZ08, in the form suitable for the comparison with Fig. 10 in WF12. We see that the profiles computed with these two codes match very well. The same was found for the case of the extended corona (Fig. 3a) and we note again that the difference between the conclusions of our work and that of Wilkins et al. do not result from any differences between the computational models, but from the different methods of their application to data interpretation.
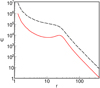 |
Fig. A.1. Radial emissivity profiles for a point-like and an extended source, to be compared with Fig. 10 in WF12. The dashed black curve is for a disc-like source with h = 10 and ρ ≤ 25. The red solid curve is for a point-like source at h = 10 and ρ = 25. |
All Tables
Results of spectral fitting of the coronal model reflkerr using empirical radial emissivities.
Results of spectral fitting of the model reflkerr_elp, with a partially covering ionised absorption computed with zxipcf.
Results of spectral fitting in the 2–10 keV range of the model reflkerr, with wind absorption and scattering computed with monaco.
All Figures
 |
Fig. 1. Illustration of changes of the reflection spectrum resulting from the contraction of the X-ray source, described by the decrease of both hmax and rc, for Γ = 2.6, ξ = 50, ZFe = 9, i = 50°, ℛ = 1, a = 0.998, hmin = 0, and rin = rISCO. The reflection spectra, shown by solid curves, correspond to hmax = rc = 1.3 (black), 2 (red), 3 (green), 8 (blue), and 30 (magenta) from top to bottom. The primary spectrum is the same in all cases and is shown by the dashed line. |
| In the text | |
 |
Fig. 2. Example illustration of the effect of the rotation of the X-ray source. The dotted red curve shows the reflection spectrum computed with reflkerr_lp (i.e. for a static point-like source, at h = 2.) The dashed black and solid blue curves show the reflection spectra computed with reflkerr_elp with rc = 0.2 and 1.5, respectively, in both hmin = hhor and hmax = 2. In all three cases Γ = 2.6, ξ = 50, AFe = 9, i = 50°, a = 0.998, rin = rISCO and ℛ = 1. The observed primary spectrum is the same in all three models and is shown by the dot-dashed black curve. The difference between the reflkerr_lp and the reflkerr_elp spectra is primarily due to the azimuthal motion of the emitting plasma in the latter, where V ≃ 0.1c for rc = 0.2 and ≃0.8c for rc = 1.5. |
| In the text | |
 |
Fig. 3. Panel a: red line shows the twice-broken power-law, radial emissivity profile fitted to 1H0707–495 by Wilkins & Fabian (2011), see text. The blue line shows the emissivity profile produced by the X-ray source with hmin = 2, hmax = 10, rc = 30, and Γ = 3.1. Panel b: reflection spectra for the emissivity profiles shown in panel a, and for Γ = 3.1, ξ = 53, AFe = 9, i = 54° and rin = rISCO; the difference of spectral shapes is only due to different amounts of relativistic distortion corresponding to the difference of the radial profiles. |
| In the text | |
 |
Fig. 4. Top panel: unfolded data and model spectra for our best-fitted models for VL (red), L (blue), M (green), and H (black) using zxipcf*reflkerr_elp. Spectral binning (1) was used. The model parameters are given in Table 4. The model is shown by the solid curve. Bottom panel: fit residuals given as the data-to-model ratio for VL, L, M, and H from bottom to top. |
| In the text | |
 |
Fig. 5. Primary (dashed) and reflected (solid) spectra in our best models for VL with panel a: reflkerr (Sect. 5.1), panel b: reflkerr_elp with a weakly ionised disc (Sect. 5.2), and panel c: reflkerr_elp with a strongly ionised disc and an ionised absorber (Sect. 5.3). The spectra correspond to the fitted parameters for VL given in Tables 1, 3, and 4, respectively, except for ℛ, which was set to the physical value, i.e. ℛ = 1. As can be seen in Fig. 4, the observed VL spectrum has a strong depression at ∼2 keV. For the models shown in panels a and b, the contribution of the primary component must be artificially reduced by a factor >750 and >25, respectively, to obtain a similar spectral depression in the total spectra. In panel c the black curves show the unabsorbed and the red curves show the absorbed spectra. In this case, the relativistic effects combined with absorption allow us to reproduce the observed shape with ℛ = 1. |
| In the text | |
 |
Fig. 6. Probability distributions showing correlations between the rc, hmax, and ℛ parameters of the reflkerr_elp model with a weakly ionised disc (see Table 3) fitted in the 1.1–10 keV range to the VL (top left), L (top right), M (bottom left), and H (bottom right) spectrum, obtained in the MCMC analysis using xspec_emcee implemented by Jeremy Sanders. The results of this analysis are presented using package corner (Foreman-Mackey 2016). The contours in the 2D plots correspond to the significance of σ = 1, 2, 3. The histograms show the probability distributions for the individual parameters. |
| In the text | |
 |
Fig. 7. Unfolded data and model spectrum for our best-fitted model for H using monaco*reflkerr. The red curve shows the total (i.e. primary power law + reflection) transmitted component attenuated by absorption. The blue curve shows the total scattered component. |
| In the text | |
 |
Fig. A.1. Radial emissivity profiles for a point-like and an extended source, to be compared with Fig. 10 in WF12. The dashed black curve is for a disc-like source with h = 10 and ρ ≤ 25. The red solid curve is for a point-like source at h = 10 and ρ = 25. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


