| Issue |
A&A
Volume 638, June 2020
|
|
|---|---|---|
| Article Number | A26 | |
| Number of page(s) | 9 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202037541 | |
| Published online | 04 June 2020 | |
Detection of Fe I and Fe II in the atmosphere of MASCARA-2b using a cross-correlation method
1
Instituto de Astrofísica de Canarias,
Vía Láctea s/n,
38205
La Laguna,
Tenerife,
Spain
e-mail: mstangret@iac.es
2
Departamento de Astrofísica, Universidad de La Laguna,
38200
San Cristobal de La Laguna,
Spain
3
Institut für Astrophysik, Georg-August-Universität,
Friedrich-Hund-Platz 1,
37077
Göttingen, Germany
4
Instituto de Astrofísica de Andalucía (IAA-CSIC),
Glorieta de la Astronomía s/n,
18008
Granada,
Spain
Received:
21
January
2020
Accepted:
27
February
2020
Ultra-hot Jupiters are gas giants planets whose dayside temperature is greater than 2200 K as a consequence of the strong irradiation received from the host star. These kinds of objects are perfect laboratories to study the chemistry of exoplanetary upper atmospheres via transmission spectroscopy. Exo-atmospheric absorption features are buried in the noise of the in-transit residual spectra. However we can retrieve information of hundreds of atmospheric absorption lines by performing a cross-correlation with an atmospheric transmission model, which allows us to greatly increase the exo-atmospheric signal. The Rossiter–McLaughlin effect and centre-to-limb variation contribute strongly at the high spectral resolution of our data. We present the first detection of Fe I and confirmation of absorption features of Fe II in the atmosphere of the ultra-hot Jupiter MASCARA-2b/KELT-20b, by using three transit observations with HARPS-N. After combining all transit observations we find a high cross-correlation signal of Fe I and Fe II with signal-to-noise ratios of 10.5 ± 0.4 and 8.6 ± 0.5, respectively. The peak absorption for both species appear to be blue-shifted with velocities of − 6.3 ± 0.8 km s−1 for Fe I and − 2.8 ± 0.8 km s−1 for Fe II, suggesting the presence of winds from the day- to night-side of the atmosphere of the planet. These results confirm previous studies of this planet and add a new atomic species (Fe I) to the long list of detected species in the atmosphere of MASCARA-2b, making it, together with KELT-9b, the most feature-rich ultra-hot Jupiter to date.
Key words: planetary systems / planets and satellites: individual: MASCARA2-b / planets and satellites: atmospheres / techniques: spectroscopic
© ESO 2020
1 Introduction
High-resolution spectroscopy facilitates the detection and characterisation of planetary atmospheres owing to to the different Doppler velocities of the Earth, the host star, and the planet. In particular, because of their extended atmospheres, high temperatures, and short orbital periods, hot Jupiters are perfect laboratories to study the nature, structure, and composition of the gas giants using these techniques (Birkby 2018; Snellen et al. 2010).
More recently, a new subclass of objects, so-called ultra-hot Jupiters (UHJ), emerged from the hot Jupiters population. Located close to their parent star, UHJs are continually exposed to intense irradiation. This increases their temperatures to extreme values causing significant differences in chemical composition between the day- and night-side of the atmosphere (Arcangeli et al. 2018; Bell & Cowan 2018; Helling et al. 2019b). The established criteria to distinguish between HJ and UHJ is that the temperature on the day-side of the planet is higher than 2200 K (Parmentier et al. 2018) for UHJ. Many studies also point out that H2O is not expected to exist on the day-side of UHJ, contrary to the case of hot Jupiters, because of the thermal dissociation of molecules as predicted by Parmentier et al. (2018).
Studies of UHJs atmospheres have been carried out for several planets: HAT-P-7b (Armstrong et al. 2016; Helling et al. 2019b), WASP-18b (Sheppard et al. 2017; Arcangeli et al. 2018; Helling et al. 2019a), WASP-33b (Haynes et al. 2015; Nugroho et al. 2017), and WASP-103b (Kreidberg et al. 2018); a variety of atomic and molecular species have been detected in the atmospheres of these planets.
Chemical composition studies of the hottest planet known to date, KELT-9b (Gaudi et al. 2017), reveal an extended hydrogen atmosphere (Balmer Hα line; Yan & Henning 2018). Moreover, Hoeijmakers et al. (2018, 2019) report the detection of Cr II, Fe I, Fe II, Mg II, Na I, Sc II, Ti II, and Y II, as well as evidence of Ca I, Cr I, Co I, and Sr II in its atmosphere. Additionally, Cauley et al. (2019) detect in H β and Mg I triplet in this planet. These atmospheric species have also been detected in the cooler UHJs WASP-18b (Arcangeli et al. 2018), WASP-33b (von Essen et al. 2019), WASP-12b (Jensen et al. 2012), WASP-76b (Seidel et al. 2019), and MASCARA-2b (Casasayas-Barris et al. 2018, 2019).
In this paper, we present the study of MASCARA-2b (Talens et al. 2018) also known as KELT-20b (Lund et al. 2017). The planet orbits a fast-rotating A-type star (v sin i = 116 km s−1) in 3.47 days at a distance of 0.0542 AU. Because of the strong stellar irradiation, the equilibrium temperature of the planet is 2260 K. All stellar and planetary parameters are provided in Table 1. The atmosphere of this planet has recently been studied using high-dispersion transit spectroscopy by Casasayas-Barris et al. (2018, 2019), who detected Ca II, Fe II, Na I, H α, H β, and indications of H γ and Mg I. We analyse the same three transit observations of HARPS-N used in Casasayas-Barris et al. (2019), using the cross-correlation method. The detection of the same species via a different technique gives confidence in previous results, but also allows us to probe for other atomic/ionic species that might not have strong enough signals in individual lines to be detected in transmission. We are focussing on Fe I and Fe II to study the differences between the neutral and ionised species of the same atom. Fe I and Fe II both consist of long list of absorption lines, which make them perfect species to study using cross-correlation.
Physical and orbital parameters of MASCARA-2.
2 Observations
We observed three full transits of MASCARA-2b during the nights of 16 August 2017, 12 June 2018, and 19 June 2018 (nights 1, 2, and 3, from here after), using the HARPS-North spectrograph (Cosentino et al. 2012) mounted at the 3.58 m Telescopio Nazionale Galileo (TNG) at Observatorio del Roque de los Muchachos (ORM) in La Palma, Spain. During nights 2 and 3, we used the GIARPS mode, which allowed us to make simultaneous observations at optical (HARPS-N) and near-infrared (GIANO-B) wavelengths.
The observation set-up was as follows: for night 1 we took 90 exposures of 200 s, resulting in 32 out-of-transit and 58 in transit spectra (ϕ = −0.0318 to + 0.0350, where ϕ is the planet orbital phase), with an average signal-to-noise ratio (S/N) of 51.0; for night 2 we took 116 exposures of 200 s with 61 out of transit and 55 in transit spectra (ϕ = −0.0541 to + 0.0393) with an averageS∕N = 78.6, and for night 3 we took 78 exposures of 300 s with 37 out of transit and 41 in transit spectra (ϕ = −0.0394 to + 0.0441) with an averageS∕N = 80.5. During night 2, possibly because of passing clouds, the S/N for eight spectra drastically dropped. We decided to discard these spectra (22:58 UT - 23:24 UT), as well as one spectra with a S/N lower than 35 taken at 01:28 UT, from the analysis. Thus, for night 2 we discarded nine spectra, while for nights 1 and 3 we used all available spectra. A log of the observations is presented in Table 2.
The observations were reduced using the HARPS-North Data Reduction Software (DRS; Cosentino et al. 2014; Smareglia et al. 2014), version 3.7, which order-by-order extracts the spectra and performs operations such as flat-fielded using the daily calibrationset. In the end, all the orders for each spectrum were combined into a one-dimensional spectrum. As a result we obtained one-dimensional spectra in optical wavelength given in air (380–690 nm in a step of 0.01 nm) and referred to the Barycentric rest frame.
3 Methods
3.1 Model spectra
Transmission spectra models of Fe I and Fe II used in our analysis were calculated using petitRADTRANS (Mollière et al. 2019), which allows us to create high-resolution models of atoms and molecules at the typical temperatures of exoplanet atmospheres. To calculate the model for MASCARA-2b, we assumed a surface gravity (log g) of 3.0 (corresponding to a mass of about 1.2 MJ), considering that the actual mass of the planet is unknown. According to theoretical calculations in Lothringer & Barman (2019), the upper atmospheres of UHJs orbiting A-type stars are significant hotter than the equilibrium temperatures. Therefore, we used an isothermal temperature of 4000 K, which is higher than the planetary equilibrium temperature (2260 K) but close to the simulations in Lothringer & Barman (2019). The continuum level was set to 1 mbar, following Yan et al. (2019) and Hoeijmakers et al. (2019), which state that for UHJ the continuum level is typically between 1 mbar and 10 mbar owing to H absorption. We assumed a solar abundance and calculated the spectra of Fe I and Fe II separately by setting the mixing ratios of Fe I and Fe II to the solar Fe abundance. Finally, the spectra were convolved with the HARPS-N instrumental profile. In the case of Fe II we assumed a complete ionisation of Fe. The synthetic model spectra of Fe I, Fe II are presented in Fig. 1.
3.2 Outlier rejection and normalisation
As a first step of our analysis, owing to computing limitations we divided the spectrum and models into 37 chunks of 8160 pixels each. From now on, we refer to these spectral chunks in our analysis as “orders”, not to be confused with the original echelle orders in the charge-coupled device (CCD). By analysing the time evolution of each pixel we removed outliers, which we define as values deviating by more than 5σ from a fitted quadratic polynomial in time, and which are mostly related to cosmic rays. We normalised the spectrum fitting a quadratic polynomial for each order independently. Once we normalised the spectrum, following Alonso-Floriano et al. (2019) and Sánchez-López et al. (2019) we masked all the lines in which the absorption was larger that 80% of the flux, which are related only to the telluric absorption; the lines of studied species are not masked. We also masked the sky emission lines in which the flux was larger than 5% of the flux continuum.
To correct telluric contamination we used Molecfit (Smette et al. 2015; Kausch et al. 2015), ESO tool, which fits syntetic transmission spectra to data. Following the same method as described in Casasayas-Barris et al. (2019). In the next step to remove the stellar signals from our data, we used SYSREM (Tamuz et al. 2005; Mazeh et al. 2007). This algorithm removes linear trends affecting the spectral matrix in time and wavelength. Each of the spectral point is weighted by its error. By iterating SYSREM we can remove most of the stellar signal and any residual telluric signals that could remain after the Molecfit corrections. As pointed in Birkby et al. (2017) even though the signal from the planet is Doppler-shifted and much smaller in amplitude than the telluric and stellar signals, it can be also removed after a numbers of iterations. Therefore it is necessary to find the optimal number of SYSREM iterations.
In our analysis we ran SYSREM for each order independently for 15 iterations. We then tested two ways of choosing the best SYSREM iteration: using the same iteration number for both species or using a different iteration number choosing that for which the S/N of the signal is the strongest. The final results are the same within error bars, so we chose to use the optimal iteration number for each species. We found that the optimal SYSREM iterations for each night and each species are slightly different, respectively, for Fe I and Fe II we used iteration 4 and 5 for night 1, 4, and 2 for night 2, 7, and 6 for night 3. We used the same number of iterations for all orders. The S/N for each SYSREM iteration for all nights and both species after summing all good orders are presented in Fig. 2.
Summary of the transit observations of MASCARA-2b.
 |
Fig. 1 Synthetic models of Fe I (top panel) and Fe II (bottom panel). The black regions show the orders used in the analysis and the light grey regions show the discarded orders. |
3.3 Cross-correlation
For each order and each SYSREM iteration separately we cross-correlate the residuals with the models of Fe I and Fe II. The cross-correlation is performed in the Earth’s rest frame, using a radial velocity range of ± 200 km s−1 in steps of 0.8 km s−1, which correspond to the velocity step-size of the pixels for HARPS-N. Once we retrieved the cross-correlation map, we shifted it to planet rest frame using the planet radial velocities vp,
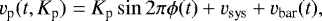 (1)
(1)
where Kp is the semi-amplitude of the exoplanet radial velocity, ϕ(t) is the orbitalphase of a planet, vsys is the systemic velocity, and vbar(t) is the barycentric velocity. To be sure that we retrieved the signal from the planet, we assumed that the Kp value is unknown. We then shifted the cross-correlation map to the planet rest frame for a range of Kp values, from 0 to 300 km s−1, in steps of 1 km s−1. We expect the maximum signal from the planetary atmosphere at the predicted values of Kp = 170 km s−1 and radial velocity 0 km s−1.
In the next step, by visual inspection, we discard the orders where the telluric and stellar signals were not totally removed after applying 15 SYSREM iterations. For all of the species and nights we discarded 9 orders out of 37. The discarded orders are presented in Fig. 1. For each Kp value we co-addedthe in-transit cross-correlation values, excluding the ingress and egress data, where the spectrum could present different geometries as pointed in Yan & Henning (2018) and Salz et al. (2018).
As described in Birkby et al. (2017), Brogi et al. (2018), Alonso-Floriano et al. (2019), and Sánchez-López et al. (2019) we checked the significance of detected signals by calculating its S/N. To do this, we divided the co-added cross-correlation values by the standard deviation away from the expected signal (0 km s−1) in the region from −50 km s−1 to −150 km s−1 and from 50 km s−1 to 150 km s−1. The results are shown in the top panel of Figs. A.1 and A.2 for individual nights and for the combinationof the three nights in Fig. 5.
 |
Fig. 2 Maximum value of the S/N, after summing all good orders, for each SYSREM iteration and for each night; Fe I (left) and Fe II (right). The SYSREM iteration number chosen is denoted with a diamond point. |
 |
Fig. 3 Cross-correlation residuals map of Fe I for each night. Top three panels: cross-correlation residuals for each night. Middle three panels: models of RME + CLV. Three bottom panels: cross-correlation residuals after removing the effects. The horizontal red dashed line shows first and last contacts of the transit; the tilted red dashed lines show the expected planet velocities. |
3.4 Rossiter-McLaughlin effect and centre-to-limb variation
MASCARA-2 is a fast-rotating star. Consequently, we detected a strong Rossiter–McLaughlin (RM) effect, which affects our cross-correlation results (see Fig. 3). In addition to the RM effect, the centre-to-limb variation (CLV) also changes the stellar line profile during transit (Czesla et al. 2015; Yan et al. 2017). Both effects depend on the region of the stellar disc blocked by the planet.
To retrieve the signal from the planet with high precision it is necessary to remove both of these effects from our data. For this correction, we modelled the stellar spectra over the full HARPS-N wavelength coverage, containing both CLV and RM effects on the stellar lines profiles for different planet orbital phases. To compute these stellar models we applied the methodology described in Casasayas-Barris et al. (2019). In brief, we modelled stellar spectra for different limb-darkening angles using the line list from VALD3 (Ryabchikova et al. 2015) and models of Kurucz ATLAS9 computed with the Spectroscopy Made Easy tool (SME; Valenti & Piskunov 1996), as presented in Yan et al. (2017), and assuming local thermodynamical equilibrium (LTE) and solar abundance. Then, the stellar models containing the CLV and RM deformations on the stellar line profiles are calculated considering the regions of the stellar disc blocked by the planet at various orbital phases, due to the geometry of the system. For this calculation we assume 1 Rp = 1.83 RJ (Talens et al. 2018). For the remaining system parameters, such as the spin-orbit angle (λ), P, R⋆, i, a, e and v sin i, we assume the values presented in Table 1. The residuals of these models (after dividing all modelled stellar spectra by one out-of-transit stellar spectrum) are then cross-correlated with the planetary atmospheric model following the same method applied to the observed data.
We observe that owing to different assumptions in the models calculation, such as the LTE condition, the solar abundance, and the 1 Rp value (which could change because of the opacity of the atmosphere at different wavelengths, as presented in Snellen 2004 and Di Gloria et al. 2015), the cross-correlated model residual maps show smaller intensity amplitudes than the cross-correlated data. To account for this more muted amplitude, we fitted the cross-correlated models to the data using Markov chain Monte Carlo (MCMC; Foreman-Mackey et al. 2013).
Finally, because of the large uncertainties on the geometry of the system, especially in the λ value, we shifted the RM + CLV models to the same velocity slope observed in the data, after applying the cross-correlation, within the uncertainties of λ.
4 Results
Casasayas-Barris et al. (2019) report the detection of Fe II absorption features in the transmission spectrum of MASCARA-2b. We use a cross-correlation technique to confirm that detection and extend it to Fe I. We analyse each night individually, as well as the three nights combined, in a search for these signatures.
The cross-correlation residual maps of Fe I and Fe II are presented in Figs. 3 and 4, respectively.In all figures, the three top panels show the residuals of the observations after cross-correlation. A strong signature, induced by the RM effect (bright tilted signal) is visible in all nights. At lower contrast, the absorption signal from the planet (dark tilted signal) is also present and has a different velocity. The three middle panels show the computed model residuals of RM + CLV, as described in Sect. 3.4. The bottom panels show the cross-correlation residual map after removing the RM + CLV model signals. The absorption features of Fe I and Fe II are strong enough to be detected, before and after correcting for the RM + CLV effects, for all individual nights.
As mentioned in Sect. 3.4, the cross-correlation maps (after RM + CLV correction) are shifted to the planet rest frame for different Kp values in the range 0–300 km s−1. In Figs. A.1and A.2, we present Kp maps (top panels) and S/N plot for a broad range around the expected Kp value for each night and each atomic transition independently. We detected the signal consistent with the exoplanet radial velocity change for each night separately at 5.1, 6.2 and 5.6 σ for Fe I and 4.2, 6.2 and 4.3 σ for Fe II.
To obtain smaller uncertainties in the Kp determination, and higher S/N, we co-add the in-transit data for each Kp value from the three nights. In Fig. 5 we present the Kp maps and S/N plots for expected Kp value separately for Fe I and Fe II. In the panels, where we present the Kp maps, the yellow cross is located at the expected Kp value and 0 km s−1. The grey contour represents the area with 1σ error bars from maximum value of S/N. We can clearly see that the signal with the highest S/N is located near the expected Kp value indicating the presenceof Fe I and Fe II in the atmosphere of MASCARA-2b. The right panels present the S/N plots for a broad range around the expected Kp value. For Fe I we detect a signal at 10.5σ and for Fe II at 8.6 σ. In the S/N plot of Fe II, we can see a slope along the negative values of radial velocities, which is related to a non-perfect removal of the RME model in this region; however this does not affect the final results. All the values of S/N, Kp and vwind for each night and species, as well as for the combination of the three nights, are presented in Table 3.
For all two models, the cross-correlation peaks appear to be blue-shifted: − 6.3 ± 0.8 km s−1 for Fe I and − 2.8 ± 0.8 km s−1 for Fe II, which suggests the presence of strong winds in the atmosphere of MASCARA-2b. This is consistent with the previous detection and the corresponding wind velocity derived by Casasayas-Barris et al. (2019), who detected Fe II with vwind = −2.8 ± 0.8 km s−1 and blue-shifted adsorptions of H α, H β, H γ, Ca II and Na I.
It must be noted that in both works, the value for the systemic velocity of MASCARA-2 was taken from Talens et al. (2018), who report values of − 21.07 ± 0.03 km s−1 (obtained by fitting RM effect) and − 21.3 ± 0.4 km s−1 (obtained by fitting radial velocities). However, Lund et al. (2017) report a systemic velocity for MASCARA-2b of − 23.3 ± 0.3 km s−1 (obtained by fitting radial velocities). After considering those differences and their uncertainties, the cross-correlation peaks can be detected ranging from −7.13 km s−1 to −2.87 km s−1 for Fe I and −4.63 km s−1 to −0.37 km s−1 for Fe II. All these results are consistent with the previous statement of blue-shifted absorption and the presence of winds in the atmosphere of the planet.
There is a significant difference between the wind velocities obtained for Fe I and Fe II, and at the same time, the widths of the fitted Gaussians to the CCF values are significantly different (FWHM = 15.1± 0.6 km s−1 for Fe I and FWHM = 8.5 ± 0.6 km s−1 for Fe II). These two facts suggest that the signals come from different altitudes in the planetary atmosphere, where Fe II would be located in the upper part of the atmosphere and Fe I would be located deeper in the atmosphere, where pressure is larger causing spectral broadening of its lines. This would be in line with Gibson et al. (2020) and Sing et al. (2019) studies of the atmosphere of the UHJ WASP-121 b, in which they discuss how Fe I and Fe II signals are formed at physically different regions, where Fe I becomes strongly ionised into Fe II in the upper atmosphere.
In our case the wind velocity of neutral Fe is higher than the velocity of ionised Fe. This result contradicts predictions from the physical models of the winds in the atmosphere of giant planets (Showman et al. 2019), where we expect that in the higher part of the atmosphere, where the atoms are strongly irradiated and ionised, the wind velocities would be larger. At present we do not have a physical explanation for this observation.
Casasayas-Barris et al. (2019) report detections of Fe II using transmission spectroscopy method. The detected three lines of Fe II (λ = 501.8 nm, λ = 516.9 nm and λ = 531.6 nm) are three of the strongest lines and are well separated from the other lines in the absorption spectrum of Fe II. However there was no detection on individual Fe I. This was probably because of a combination of the location of strong Fe I lines, combined with the S/N of the orders where these lines lie and the location of telluric atmospheric lines. It is surprising that some lines of Fe II were detected alone in transmission. This gives the cross-correlation method a big advantage over transmission because all lines have an additive contribution to the final result. In contrast, the results obtained using the cross-correlation method with atoms or molecules which have few spectral lines is challenging.
While our results show that the cross-correlation signal for Fe I is stronger than for Fe II, we cannot determine which species is more abundant because the detected signal depends on the number and strength of the spectral lines for each species (see Fig. 1). Further, the correlation signal is also affected by various telluric residuals and other astrophysical/instrumental noises, making the comparison of abundances challenging. As pointed out by Alonso-Floriano et al. (2019) and Birkby (2018) the CCF is practically insensitive to changes of p-T profile at present S/N levels, meaning we cannot determine the temperatures where the lines are formed either.
 |
Fig. 5 Cross-correlation residuals, Kp maps, and S/N plots after combining the three nights for each species. Left column: cross-correlation residual maps for Fe I and Fe II. Middle column: Kp map after cross-correlating residuals with the model of Fe I and Fe II. The yellow x is located at the predicted Kp value and 0 km s−1. The grey contour represents the area with 1σ from maximum signal. Right column: CCF values (black) for the predicted Kp value with the fitted Gaussian profile (red). |
Results obtained in the analysis for different nights and species with 1σ uncertainties.
5 Conclusions
According to Helling et al. (2019a) on the day-side of the atmospheres of UHJs, owing to thermal dissociation we expect the presence of both Fe I and Fe II. We present the detection of both species in the atmosphere of the UHJ MASCARA-2b using the cross-correlation method. The absorption features for both species are found to be blue-shifted. This suggests that we are observing strong day-to-night winds at the planet terminator with values that agree with previous studies of the atmosphere of this planet (Casasayas-Barris et al. 2018, 2019). The strong signal from Fe II in the planet terminator, where temperature is significantly lower than on the day-side, also suggests the existence of winds in the atmosphere of MASCARA-2b, which would transport ionised Fe from the day-side to the night-side of the planet.
Fe I and Fe II have been previously detected in the atmosphere of KELT-9b by Hoeijmakers et al. (2018, 2019) using the cross-correlation method and by Cauley et al. (2019) using transmission spectroscopy. KELT-9b, however, has an extremely high day-side equilibrium temperature (Teq = 3920 K), while that of MASCARA-2b is much lower (Teq = 2260 K). At these cooler temperatures, Fe II has only been detected in WASP-121b (Sing et al. (2019); Teq = 2700 K) using near-ultraviolet transmission spectrum from Hubble Space Telescope. This makes MASCARA-2b one of the most interesting exoplanets known for detailed further studies of hot Jupiter atmospheres.
Acknowledgements
Based on observations made with the Italian Telescopio Nazionale Galileo (TNG) operated on the island of La Palma by the Fundación Galileo Galilei of the INAF (Istituto Nazionale di Astrofisica) at the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofisica de Canarias. This work is partly financed by the Spanish Ministry of Economics and Competitiveness through projects ESP2014-57495-C2-1-R, ESP2016-80435-C2-2-R and ESP2017-87143. R. M.S. and N.C.B. acknowledge the support of the Instituto de Astrofísica de Canarias via an Astrophysicist Resident fellowship. F.Y. acknowledges the support of the DFG priority program SPP 1992 “Exploring the Diversity of Extrasolar Planets (RE 1664/16-1)”. This work made use of PyAstronomy and of the VALD database, operated at Uppsala University, the Institute of Astronomy RAS in Moscow, and the University of Vienna.
Appendix A Individual transmission spectra
Following the same format as Fig. 5, we show the Kp versus radial velocity maps for each individual night, together with the S/N versus radial velocity plots.
 |
Fig. A.1 For Fe I, Kp maps and S/N plots for each of the nights separately. |
 |
Fig. A.2 For Fe II, Kp maps and S/N plots for each of the nights separately. |
References
- Alonso-Floriano, F. J., Sánchez-López, A., Snellen, I. A. G., et al. 2019, A&A, 621, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arcangeli, J., Désert, J.-M., Line, M. R., et al. 2018, ApJ, 855, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Armstrong, D. J., de Mooij, E., Barstow, J., et al. 2016, Nat. Astron., 1, 0004 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, T. J., & Cowan, N. B. 2018, ApJ, 857, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Birkby, J. L. 2018, ArXiv e-prints [arXiv:1806.04617] [Google Scholar]
- Birkby, J. L., de Kok, R. J., Brogi, M., Schwarz, H., & Snellen, I. A. G. 2017, AJ, 153, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Brogi, M., Giacobbe, P., Guilluy, G., et al. 2018, A&A, 615, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casasayas-Barris, N., Pallé, E., Yan, F., et al. 2018, A&A, 616, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casasayas-Barris, N., Pallé, E., Yan, F., et al. 2019, A&A, 628, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cauley, P. W., Shkolnik, E. L., Ilyin, I., et al. 2019, AJ, 157, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Cosentino, R., Lovis, C., Pepe, F., et al. 2014, Proc. SPIE, 9147, 91478C [Google Scholar]
- Cosentino, R., Lovis, C., Pepe, F., et al. 2012, SPIE Conf. Ser., 8446, 84461V [Google Scholar]
- Czesla, S., Klocová, T., Khalafinejad, S., Wolter, U., & Schmitt, J. H. M. M. 2015, A&A, 582, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Gloria, E., Snellen, I. A. G., & Albrecht, S. 2015, A&A, 580, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Gaudi, B. S., Stassun, K. G., Collins, K. A., et al. 2017, Nature, 546, 514 [NASA ADS] [Google Scholar]
- Gibson, N. P., Merritt, S., Nugroho, S. K., et al. 2020, MNRAS, 493, 2215 [NASA ADS] [CrossRef] [Google Scholar]
- Haynes, K., Mandell, A. M., Madhusudhan, N., Deming, D., & Knutson, H. 2015, ApJ, 806, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Helling, C., Gourbin, P., Woitke, P., & Parmentier, V. 2019a, A&A, 626, A133 [CrossRef] [Google Scholar]
- Helling, C., Iro, N., Corrales, L., et al. 2019b, A&A, 631, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hoeijmakers, H. J., Ehrenreich, D., Heng, K., et al. 2018, Nature, 560, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Hoeijmakers, H. J., Ehrenreich, D., Kitzmann, D., et al. 2019, A&A, 627, A165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jensen, A. G., Redfield, S., Endl, M., et al. 2012, ApJ, 751, 86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kausch, W., Noll, S., Smette, A., et al. 2015, A&A, 576, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kreidberg, L., Line, M. R., Parmentier, V., et al. 2018, AJ, 156, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Lothringer, J. D., & Barman, T. 2019, ApJ, 876, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Lund, M. B., Rodriguez, J. E., Zhou, G., et al. 2017, AJ, 154, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Mazeh, T., Tamuz, O., & Zucker, S. 2007, ASP Conf. Ser., 366, 119 [NASA ADS] [Google Scholar]
- Mollière, P., Wardenier, J. P., van Boekel, R., et al. 2019, A&A, 627, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nugroho, S. K., Kawahara, H., Masuda, K., et al. 2017, AJ, 154, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Parmentier, V., Line, M. R., Bean, J. L., et al. 2018, A&A, 617, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ryabchikova, T., Piskunov, N., Kurucz, R. L., et al. 2015, Phys Scr., 90, 054005 [Google Scholar]
- Salz, M., Czesla, S., Schneider, P. C., et al. 2018, A&A, 620, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez-López, A., Alonso-Floriano, F. J., López-Puertas, M., et al. 2019, A&A, 630, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seidel, J. V., Ehrenreich, D., Wyttenbach, A., et al. 2019, A&A, 623, A166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sheppard, K. B., Mandell, A. M., Tamburo, P., et al. 2017, ApJ, 850, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Showman, A. P., Tan, X., & Zhang, X. 2019, ApJ, 883, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Sing, D. K., Lavvas, P., Ballester, G. E., et al. 2019, AJ, 158, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Smareglia, R., Bignamini, A., Knapic, C., Molinaro, M., & GAPS Collaboration 2014, ASP Conf. Ser., 485, 435 [NASA ADS] [Google Scholar]
- Smette, A., Sana, H., Noll, S., et al. 2015, A&A, 576, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Snellen, I. A. G. 2004, MNRAS, 353, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Snellen, I. A. G., de Kok, R. J., de Mooij, E. J. W., & Albrecht, S. 2010, Nature, 465, 1049 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Talens, G. J. J., Justesen, A. B., Albrecht, S., et al. 2018, A&A, 612, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tamuz, O., Mazeh, T., & Zucker, S. 2005, MNRAS, 356, 1466 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, J. A., & Piskunov, N. 1996, A&AS, 118, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von Essen, C., Mallonn, M., Welbanks, L., et al. 2019, A&A, 622, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yan, F., & Henning, T. 2018, Nat. Astron., 2, 714 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, F., Pallé, E., Fosbury, R. A. E., Petr-Gotzens, M. G., & Henning, T. 2017, A&A, 603, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yan, F., Casasayas-Barris, N., Molaverdikhani, K., et al. 2019, A&A, 632, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Results obtained in the analysis for different nights and species with 1σ uncertainties.
All Figures
 |
Fig. 1 Synthetic models of Fe I (top panel) and Fe II (bottom panel). The black regions show the orders used in the analysis and the light grey regions show the discarded orders. |
| In the text | |
 |
Fig. 2 Maximum value of the S/N, after summing all good orders, for each SYSREM iteration and for each night; Fe I (left) and Fe II (right). The SYSREM iteration number chosen is denoted with a diamond point. |
| In the text | |
 |
Fig. 3 Cross-correlation residuals map of Fe I for each night. Top three panels: cross-correlation residuals for each night. Middle three panels: models of RME + CLV. Three bottom panels: cross-correlation residuals after removing the effects. The horizontal red dashed line shows first and last contacts of the transit; the tilted red dashed lines show the expected planet velocities. |
| In the text | |
 |
Fig. 4 Same as Fig. 3, but for Fe II. |
| In the text | |
 |
Fig. 5 Cross-correlation residuals, Kp maps, and S/N plots after combining the three nights for each species. Left column: cross-correlation residual maps for Fe I and Fe II. Middle column: Kp map after cross-correlating residuals with the model of Fe I and Fe II. The yellow x is located at the predicted Kp value and 0 km s−1. The grey contour represents the area with 1σ from maximum signal. Right column: CCF values (black) for the predicted Kp value with the fitted Gaussian profile (red). |
| In the text | |
 |
Fig. A.1 For Fe I, Kp maps and S/N plots for each of the nights separately. |
| In the text | |
 |
Fig. A.2 For Fe II, Kp maps and S/N plots for each of the nights separately. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


