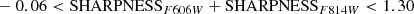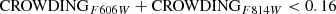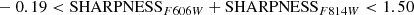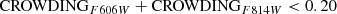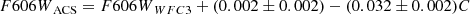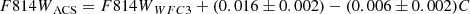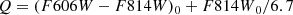| Issue |
A&A
Volume 637, May 2020
|
|
|---|---|---|
| Article Number | A8 | |
| Number of page(s) | 20 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201936994 | |
| Published online | 01 May 2020 | |
Tracing the anemic stellar halo of M 101
1
Leibniz-Institut für Astrophysik Potsdam (AIP), An der Sternwarte 16, 14482 Potsdam, Germany
e-mail: hanlbomi@gmail.com
2
Department of Physics and Astronomy, University of Louisville, 102 Natural Science Building, Louisville, KY 40292, USA
3
Instituto de Investigación Multidisciplinar en Ciencia y Tecnología, Universidad de La Serena, Raúl Bitrán 1305, La Serena, Chile
4
Departamento de Física y Astronomía, Universidad de La Serena, Av. Juan Cisternas 1200 Norte, La Serena, Chile
5
Department of Astronomy, University of Michigan, 311 West Hall, 1085 South University Ave., Ann Arbor, MI 48109-1107, USA
6
Department of Physics and Astronomy, University of Alabama, Box 870324, Tuscaloosa, AL 35487-0324, USA
Received:
25
October
2019
Accepted:
18
January
2020
Models of galaxy formation in a cosmological context predict that massive disk galaxies should have structured extended stellar halos. Recent studies in integrated light, however, report that a few galaxies, including the nearby disk galaxy M 101, have no measurable stellar halos to the detection limit. We aim to quantify the stellar content and structure of M 101’s outskirts by resolving its stars. We present the photometry of its stars based on deep F606W and F814W images taken with Hubble Space Telescope (HST) as part of the GHOSTS survey. The HST fields are placed along the east and west sides of M 101 out to galactocentric distance (R) of ∼70 kpc. The constructed color-magnitude diagrams of stars reach down to two magnitudes below the tip of the red giant branch. We derived radial number density profiles of the bright red giant branch (RGB) stars. The mean color of the RGB stars at R ∼ 40−60 kpc is similar to those of metal-poor globular clusters in the Milky Way. We also derived radial surface brightness profiles using the public image data provided by the Dragonfly team. Both the radial number density and surface brightness profiles were converted to radial mass density profiles and combined. We find that the mass density profiles show a weak upturn at the very outer region, where surface brightness is as faint as μg ≈ 33 mag arcsec−2. An exponential disk + power-law halo model on the mass density profiles finds the total stellar halo mass of Mhalo = 8.2−2.2+3.5 × 107 M⊙. The total stellar halo mass does not exceed Mhalo = 3.2 × 108 M⊙ when strongly truncated disk models are considered. In combining the halo mass with the total stellar mass of M 101, we obtain the stellar halo mass fraction of Mhalo/Mgal = 0.20−0.08+0.10% with an upper limit of 0.78%. We compare the halo properties of M 101 with those of six GHOSTS survey galaxies as well as the Milky Way and M 31 and find that M 101 has an anemic stellar halo similar to the Milky Way.
Key words: stars: Population II / Galaxy: halo / galaxies: spiral / galaxies: structure / galaxies: individual: M 101
© ESO 2020
1. Introduction
The standard paradigm of the Λ-cold dark matter (ΛCDM) cosmology predicts the hierarchical assembly of stellar and dark matter halos during structure formation (White & Rees 1978; Blumenthal et al. 1984). Massive galaxies, either elliptical or disk galaxies, have grown through the accretion of gas and the merger of preexisting less massive galaxies. The latter process leads to the formation of extended stellar envelopes around massive galaxies, called stellar halos. Because the dynamical and star formation time-scales at galaxy outskirts are considered to be long, stellar halos are ideal systems in which to study the growth and assembly history of galaxies (Bullock et al. 2001; Freeman & Bland-Hawthorn 2002; Bullock & Johnston 2005).
The Galaxy Halos, Outer disks, Substructure, Thick disks, and Star clusters (GHOSTS) survey is an ongoing Hubble Space Telescope (HST) survey program, which images the outskirts of nearby galaxies to provide a better understanding of the disk growth and the halo assembly histories through resolved stars (de Jong et al. 2007; Radburn-Smith et al. 2011). Our recent studies based on six Milky Way (MW)-mass disk galaxies have shown that these six galaxies as well as the two massive galaxies in the Local Group (the MW and M 31) have stellar halos dominated by old and metal-poor red giant branch (RGB) stars and they show large variations in mass, mass fraction, median color (metallicity), color gradient, and power-law surface brightness profile slope (Monachesi et al. 2016; Harmsen et al. 2017). All these properties agree well with the predictions of cosmological simulations that firstly, massive galaxies should have stellar halos, and secondly, their properties should vary considerably from galaxy to galaxy (Bullock et al. 2001; Bullock & Johnston 2005; Purcell et al. 2007; Cooper et al. 2010; Monachesi et al. 2019).
It is therefore puzzling that recent studies in integrated light with a novel array of telephoto lenses (the Dragonfly array Abraham & van Dokkum 2014) report a few galaxies that have no measurable stellar halos to faint limits (μg ∼ 32 mag arcsec−2). van Dokkum et al. (2014) investigated the outskirts of the massive spiral galaxy M 101 with the Dragonfly array. By fitting the mass density profile with a multicomponent model, they find the stellar halo mass fraction, 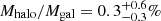 , to be significantly lower than those of other massive disk galaxies (Mhalo/Mgal ≃ 1 to a few %). The stellar halo of M 101 was revisited by the Dragonfly team in Merritt et al. (2016). From the same integrated light image data, they measured the stellar halo mass outside of five half-mass radius (Rh) and derived a value of the halo mass fraction, Mhalo, > 5Rh/Mgal = 0.04 ± 0.08%. Although they did not explicitly derive the total stellar halo mass fraction, it is expected to be several times larger than the >5Rh value (Harmsen et al. 2017), which would agree with van Dokkum et al. (2014). Considering the low halo mass fractions and large uncertainties, the very presence of an M 101 stellar halo is controversial. Merritt et al. (2016) also report two more galaxies that have no detectable stellar halos: NGC 1042 (Mhalo, >5Rh/Mgal = 0.01 ± 0.01%) and NGC 3351 (Mhalo, >5Rh/Mgal = 0.02 ± 2.25%). The low inclinations (close to face-on) of these three galaxies make detecting a stellar halo very challenging, but taken at face value, such a population of galaxies without stellar halos would present a critical challenge to the picture of ubiquitous stellar halos formed from the debris of disrupting dwarf galaxies.
, to be significantly lower than those of other massive disk galaxies (Mhalo/Mgal ≃ 1 to a few %). The stellar halo of M 101 was revisited by the Dragonfly team in Merritt et al. (2016). From the same integrated light image data, they measured the stellar halo mass outside of five half-mass radius (Rh) and derived a value of the halo mass fraction, Mhalo, > 5Rh/Mgal = 0.04 ± 0.08%. Although they did not explicitly derive the total stellar halo mass fraction, it is expected to be several times larger than the >5Rh value (Harmsen et al. 2017), which would agree with van Dokkum et al. (2014). Considering the low halo mass fractions and large uncertainties, the very presence of an M 101 stellar halo is controversial. Merritt et al. (2016) also report two more galaxies that have no detectable stellar halos: NGC 1042 (Mhalo, >5Rh/Mgal = 0.01 ± 0.01%) and NGC 3351 (Mhalo, >5Rh/Mgal = 0.02 ± 2.25%). The low inclinations (close to face-on) of these three galaxies make detecting a stellar halo very challenging, but taken at face value, such a population of galaxies without stellar halos would present a critical challenge to the picture of ubiquitous stellar halos formed from the debris of disrupting dwarf galaxies.
Stellar halos are in general very faint so a quantitative measurement of the halo component in a galaxy requires intensive efforts. Models predict that most of the stars in a stellar halo are at small galactocentric radii, where they are very difficult to disentangle from the much brighter bulge and disk components. Stellar halos are dominant only at larger radii, where the surface brightnesses can reach well below μ ∼ 30 mag arcsec−2. Integrated light photometry is a useful approach for detecting stellar halos owing to surface brightness being distance independent and the relatively modest observational cost for covering large areas of sky. Yet, detecting and quantifying halo light up to 10 000× fainter than the sky requires stringent control of systematic error. A small change in the background modeling, foreground star or background galaxy subtraction can lead to a large difference in the derived halo profile. The scattered light from the optics (de Jong 2008; Slater et al. 2009; Abraham & van Dokkum 2014; Sandin 2014) or the atmospheric conditions (DeVore et al. 2013; Zhang et al. 2018) and low surface brightness galactic cirrus (Trujillo & Fliri 2016) are other possible contaminants, which make the measurement of the low surface brightness stellar structures using integrated light more difficult and much more uncertain.
A complementary and more reliable approach is to count and characterize resolved stars in order to quantify the halo structure. It enables to obtain information of age- and metallicity-resolved stellar populations, which allows clearer separation between the stellar disk and halo, and exploration of variations in stellar population from halo to halo (Monachesi et al. 2016; Harmsen et al. 2017). While resolved stars from wide-field ground-based imaging is possible for the nearest galaxies (e.g., M 31 – Ibata et al. 2014, M 81 – Okamoto et al. 2015, NGC 55 – Tanaka et al. 2011, NGC 253 – Greggio et al. 2014, NGC 891 – Mouhcine et al. 2010, NGC 2403 – Barker et al. 2012, NGC 4631 – Tanaka et al. 2017, and Cen A – Crnojević et al. 2016), star counting with HST is able to detect a faint stellar structure that has surface brightness levels down to μV ≈ 32−34 mag arcsec−2 (Streich et al. 2016; Harmsen et al. 2017), a factor of roughly ten deeper than limits achieved with integrated light, μV ≈ 30−32 mag arcsec−2 (Mihos et al. 2013, 2017; Merritt et al. 2016). These limits can even be achieved on relatively small patches on the sky, without having to average over very large annuli to obtain enough signal to noise, and is mainly limited by the Poisson noise in the number of detected objects and the statistical removal of contaminating sources. The primary disadvantages of resolved star studies are that they are strongly limited in distance to galaxies within 10−15 Mpc (Dalcanton et al. 2009; Radburn-Smith et al. 2011) and that coverage with HST or many other facilities is limited to small fields of view, making it difficult to survey large areas. These two independent approaches each have their own pros and cons in detecting faint stellar substructures, and it would be ideal to combine both techniques whenever practical.
In this study, we select M 101, a face-on massive disk galaxy, to study its faint outskirts based on both star count and integrated light photometry. M 101 has similar properties to the MW in terms of absolute magnitude (MV ∼ −21.0 mag Makarov et al. 2014), maximum rotation velocity (Vmax ∼ 235 km s−1 Bosma et al. 1981; Zaritsky et al. 1990), and morphological type (SABcd de Vaucouleurs et al. 1991). There are ∼10 known dwarf galaxies within 100 kpc projected distance from M 101 (Karachentsev et al. 2015; Danieli et al. 2017; Bennet et al. 2019), possibly associated with the formation of the M 101 outskirts. M 101 has globular clusters, which show the global spatial distribution similar to the MW globular clusters (Simanton et al. 2015). The line-of-sight velocities of the M 101 globular clusters do not follow the HI disk kinematics, so some of them could be located well above the disk plane, being counterparts of the halo globular clusters in the MW (Simanton-Coogan et al. 2017).
The lack of a detectable stellar halo in M 101 is hard to understand given satellite and globular cluster populations. While numerical simulations predict that halos of MW mass galaxies can have a wide range of masses, halos are inevitable when galaxies are formed through mergers of smaller systems (Purcell et al. 2007, 2008; Deason et al. 2016; D’Souza & Bell 2018). If the lack of stellar halo in M 101 is taken at face value it would be impossible to interpret, and would indicate an important flaw in hierarchical models. Consequently, we study M 101’s distant outskirts using resolved stars in concert with public integrated light image data, to provide a much more robust measurement of its outskirts properties.
The distance modulus to M 101 is estimated to be (m − M)0 = 29.11 ± 0.04 (d = 6.64 ± 0.12 Mpc) from recent studies based on near-infrared Cepheids (Riess et al. 2016) and optical Tip of the Red Giant Branch (TRGB) measurements (Beaton et al. 2019; Freedman et al. 2019). At this distance, its disk and halo can readily be resolved into individual stars through HST imaging with reasonable exposure times.
The stellar halo of M 101 is, however, far more difficult to be detected compared to other massive galaxies because of its face-on nature (incl. ≈ 17°, i.e., Zaritsky et al. 1990). The stellar disk of M 101 extends in radius well beyond 15′ (29 kpc, see Fig. 1) with a mean disk scale length of 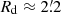 (4.2 kpc) (Mihos et al. 2013; Laine et al. 2016), which is almost a factor of two larger than that of the MW, Rd ≈ 2.2 kpc (Bovy & Rix 2013). M 101 is a textbook example of a lopsided galaxy (Jog & Combes 2009), presenting a strong asymmetry of the outer disk structure. Its disk scale length varies significantly with azimuthal angles from
(4.2 kpc) (Mihos et al. 2013; Laine et al. 2016), which is almost a factor of two larger than that of the MW, Rd ≈ 2.2 kpc (Bovy & Rix 2013). M 101 is a textbook example of a lopsided galaxy (Jog & Combes 2009), presenting a strong asymmetry of the outer disk structure. Its disk scale length varies significantly with azimuthal angles from 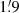 (3.7 kpc) to
(3.7 kpc) to 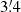 (6.6 kpc) (Mihos et al. 2013). The stellar halo of M 101, if any, is expected to be embedded in the extended, asymmetric, and face-on stellar disk and to dominate the luminosity only at the very outer regions. The resolved stellar populations can help to detect stellar halo in this galaxy, providing a much more robust measurement of its stellar halo properties.
(6.6 kpc) (Mihos et al. 2013). The stellar halo of M 101, if any, is expected to be embedded in the extended, asymmetric, and face-on stellar disk and to dominate the luminosity only at the very outer regions. The resolved stellar populations can help to detect stellar halo in this galaxy, providing a much more robust measurement of its stellar halo properties.
 |
Fig. 1. Location of HST ACS (red squares) and WFC3 (purple squares) fields overlaid on a deep 75′ × 75′ g-band image provided by the DNGS (Abraham & van Dokkum 2014). North is up and east is to the left. High surface brightness regions of the g-band image are replaced by the color image from the SDSS. The white and black dashed lines represent circles with |
This paper is organized as follows. In Sect. 2 we describe the data we used and how we derive the stellar photometry. Section 3 presents color-magnitude diagrams of target fields. We show radial star count profiles for young, intermediate, and old stellar populations in M 101. We also present integrated light photometry based on the public images provided by the Dragonfly Nearby Galaxy Survey (DNGS). Then we combine both the star count and integrated light profiles and derive the mass contribution of the stellar halo. Section 4 discusses the halo properties of M 101 in comparison with those in previous studies, the other observed halos, and model predictions. Primary results are summarized in the last section.
2. Observations and data reduction
2.1. Observations
The observations were taken between 14 February and 9 September 2015 with HST under the program ID 13696 (PI: B. Holwerda) as part of the GHOSTS survey (PI: R. de Jong). Six target fields were chosen to sample resolved stellar populations at the outskirts of M 101 along the east and west sides from the center, as shown in Fig. 1 (F1–F7 except for F5). The six fields cover 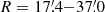 , corresponding to galactocentric distances R = 34−71 kpc from the M 101 center. Two broadband filters, F606W and F814W in the Advanced Camera for Surveys (ACS) and the Wide Field Camera 3 (WFC3), have been used for simultaneously measuring the density via star count and metallicity via color of the RGB following Monachesi et al. (2013, 2016) and Harmsen et al. (2017). Exposure times are ∼2700 s for each filter, long enough to detect resolved RGB stars with a signal to noise ratio of 10 at ∼2 mag below the TRGB. We also used three HST fields in the archive: one shallow ACS field (F5) located at R =
, corresponding to galactocentric distances R = 34−71 kpc from the M 101 center. Two broadband filters, F606W and F814W in the Advanced Camera for Surveys (ACS) and the Wide Field Camera 3 (WFC3), have been used for simultaneously measuring the density via star count and metallicity via color of the RGB following Monachesi et al. (2013, 2016) and Harmsen et al. (2017). Exposure times are ∼2700 s for each filter, long enough to detect resolved RGB stars with a signal to noise ratio of 10 at ∼2 mag below the TRGB. We also used three HST fields in the archive: one shallow ACS field (F5) located at R = 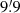 from the galaxy center (ID = 13364, PI: D. Calzetti) and two very deep fields (F8 and F9) taken with ACS and WFC3 located at the northeast side of M 101 (ID = 13701, PI: C. Mihos). A summary of the HST data used in this work for M 101 is listed in Table 1.
from the galaxy center (ID = 13364, PI: D. Calzetti) and two very deep fields (F8 and F9) taken with ACS and WFC3 located at the northeast side of M 101 (ID = 13701, PI: C. Mihos). A summary of the HST data used in this work for M 101 is listed in Table 1.
Summary of HST data for M 101 (NGC 5457).
2.2. Data reduction and photometry
The data reduction and the photometry were performed using the GHOSTS pipeline. The pipelines for the ACS/WFC and WFC3/UVIS data are described in detail in Radburn-Smith et al. (2011) and Monachesi et al. (2016), respectively. We briefly summarize the general procedure and minor changes we applied to the pipeline in this study.
The pipeline is composed of three main steps: source detection, stellar photometry, and point source selection. The first and second steps are based on DOLPHOT (Dolphin 2000), and the last step utilizes SExtractor (Bertin & Arnouts 1996), as well as photometric culls. All these steps are executed automatically by Python-based routines.
The source detection was carried out on the combined, drizzled images. We downloaded the charge transfer efficiency-corrected individual frame images (FLC images) of ACS/WFC and WFC3/UVIS observations from MAST1. We noted that some of the FLC images are not properly aligned, showing small offsets of ∼0.5 pixel, so that the drizzled images have slightly broader PSFs. We made a bright source list for each FLC image and updated the WCS in the image header with Tweakreg. The resulting astrometry was good to 0.1 pixel. We then ran astrodrizzle to make drizzled images. In this process, data quality (DQ) extension images were also updated.
The stellar photometry was carried out using the ACS and WFC3 modules of DOLPHOT on the WCS-corrected FLC images. Cosmic rays and hot pixels in the science extension of the FLC images were masked using the DQ extension. We used TinyTim PSFs (Krist et al. 2011) implemented in DOLPHOT for the ACS reduction. In the case of the WFC3 reduction, we used Jay Anderson’s PSFs (Anderson & King 2006), because we found that they provide better photometric measurements showing smaller systematic offsets in overlapping regions of WFC3 images (Monachesi et al. 2016). The DOLPHOT parameters used for the ACS/WFC and WFC/UVIS reductions in this study are the same as those given in Table A.2 of Monachesi et al. (2016).
The raw DOLPHOT output catalogs contain various types of sources, such as background galaxies, saturated stars, artifacts, as well as point sources. We selected the clean point sources by applying several selection criteria. We first applied photometric culls as follows:
for the ACS/WFC reduction, and
for the WFC3/UVIS reduction. Additionally, we selected sources with type = 1 (good star). These culls were determined from the analysis of empty archival fields, which are dominated by background galaxies. Our previous studies found that these culls are very efficient in the point source selection, eliminating 90%−95% of the background galaxies (Radburn-Smith et al. 2011; Monachesi et al. 2016). Even after the culls, there are some remaining background galaxies (5%−10%). Characterizing their contribution to the point source photometry is also important to derive the true radial number density profile of the M 101 stars. We used extra empty fields to determine the likely background of the M 101 data more accurately. Details of the selected fields and the basic procedure of the background estimation are presented in Appendix A.
Second, we made a mask file of extended sources using SExtractor and rejected sources lying in the pixel position of the masked sources in the final catalog. Finally, we visually inspected all the remaining sources brighter than F814W = 26.5 mag in five fields, F2, F3, F4, F6, and F7, which are expected to show very low stellar density, and confirmed that all the detected sources are genuine point-like sources. In the case of F7, however, we discovered a clustering of point sources centered at α = 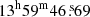 and δ =
and δ = 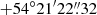 , possibly a dwarf galaxy associated with M 101 or a background galaxy (Jang et al., in prep.). We discarded point sources in R = 3″ region around the galaxy candidate in the following analysis.
, possibly a dwarf galaxy associated with M 101 or a background galaxy (Jang et al., in prep.). We discarded point sources in R = 3″ region around the galaxy candidate in the following analysis.
The HST data used in this study were taken with two instruments, ACS/WFC and WFC3/UVIS. We converted the WFC3/UVIS magnitudes to the ACS/WFC magnitude system using the photometric transformation in Jang & Lee (2015):
and
where C ≡ F606WACS − F814WACS. This empirical transformation is based on stars in two Milky Way globular clusters (NGC 2419 and 47 Tuc), which were observed with both ACS/WFC and WFC3/UVIS. The photometry of resolved stars in this paper is given in the Vega magnitude system.
2.3. Artificial star tests (ASTs)
We carried out extensive ASTs to estimate the level of photometric completeness and uncertainties. The procedure of the tests is described in detail in Radburn-Smith et al. (2011). In short, we placed a number of artificial stars in each frame and passed them through DOLPHOT. This process was repeated until we obtained in total ∼1 000 000 artificial stars per field. We set the spatial distribution of the input artificial stars based on surface brightness, placing more stars in the higher surface brightness regions. The distribution of color and magnitude of the artificial stars were similar to those of the real stars.
We found that the 50% completeness levels for the RGB candidates in fields F1 to F7 except for F5 are approximately at F814W = 27 mag, two magnitudes below the TRGB. The same completeness level for Field 5 was reached at F814W ≃ 26.4 mag, slightly brighter than those of the other fields, but still deep enough to investigate the RGB population. The low completeness of Field 5 is due to its high stellar density and shorter exposure time. Fields F8 and F9 were taken with much longer exposure times than the other fields. We obtained the deepest stellar photometry from these two fields such that the 50% completeness levels reach down to F814W = 28.3 mag, more than three magnitudes below the TRGB.
We also confirmed that our photometry is precise and accurate. The 1σ dispersion in magnitude is as small as 0.05 mag at F814W = 25 mag in fields F1–F7. The dispersion becomes slightly larger at F814W = 26 mag, but still an order of 0.1 mag: 0.08 ∼ 0.1 mag for F1–F7 except for F5, and 0.13 mag for F5. The two deep fields, F8 and F9, are much more precise than the other fields, showing the dispersion smaller than 0.05 mag for all magnitude bins brighter than F814W = 26.5 mag. Systematic offsets in photometry, which are the mean magnitude differences between the input sources and the recovered sources, are also measured to be small. The offsets are smaller than 0.03 mag for stars brighter than F814W = 25 mag in all the fields. The offsets do not exceed 0.07 mag at F814W = 26.5, well within the typical errors at the same magnitude level.
3. Results
3.1. Color magnitude diagrams of the M 101 fields
In Fig. 2 we display color magnitude diagrams (CMDs) for the selected point sources in the nine fields of M 101. The mean Galactocentric distances, assuming a face-on symmetric geometry, are marked in each panel. The galactic foreground extinction toward M 101 is known to be very low, AF606W = 0.021 mag and AF814W = 0.013 (Schlafly & Finkbeiner 2011, NED), and the extinction of the nine fields are nearly the same. The host galaxy extinction is expected to be very low, because most of the target fields cover the outermost regions of the galaxy. We corrected the magnitudes for the foreground extinction only.
 |
Fig. 2. CMDs for the selected point sources corrected for Galactic extinction and reddening in the nine HST fields around M 101. Blue, orange, and pink shaded regions indicate selection bins for the young (main sequence and helium burning stars), intermediate (asymptotic giant branch stars), and old (RGB stars) stellar populations, respectively. The region enclosed by red lines represent the selection bin we used for the color measurement only. Dashed lines represent the 50% completeness limits. Photometric errors as derived from ASTs at (F606W − F814W)0 = 1.0 are marked at (F606W − F814W)0 = 2.0. We overlaid a 10 Gyr stellar isochrone with [Fe/H] = −1.6 dex in the Padova models (Bressan et al. 2012), to give an indication of the RGB domain in the CMD. |
CMDs allow us to investigate the age-resolved stellar population. We defined three CMD bins as indicated by shaded regions in each panel to preferentially sample young, intermediate, and old stellar populations. The bluest CMD bin samples bright main-sequence and helium-burning stars, typically younger than 300 Myr (blue region). The two CMD bins in the red color range are designed for asymptotic giant branch (AGB) stars with ages of between ∼1 and ∼3 Gyr (orange region), and old RGB stars, mostly older than 3 Gyr (pink region). We set a narrow color range for the RGB bin, as fields F2 and F9 show already very narrow, blue (metal-poor) RGB distributions and fields at larger radii can be expected similarly metal-poor. All the CMD bins, except for the bin sampling RGB stars in F5, are well above the 50% completeness level (orange dashed line). The CMD of F5 is somewhat shallower than the other fields due to the short exposure time and high stellar density in the inner region of M 101. Nevertheless, the CMD is deep enough to detect stars down to ∼1.5 mag below the TRGB and the applied incompleteness corrections are small.
The CMDs show a few notable features. First, the CMDs for the inner region of M 101 show signs of younger stellar populations, as well as old RGB stars. This is evident in F5, covering the innermost region at R ∼ 19 kpc. There is a plume of blue MS stars, and red helium burning (RHeB) stars, so F5 is estimated to be dominated by or significantly contaminated by disk stars. The CMD of F8 at R ∼ 34 kpc shows similar features, but the mean RGB color is much bluer and the MS and RHeB stars in F8 do not reach as bright magnitude as in F5, thus indicating that F8 lacks the youngest populations seen in F5. The CMD of F1 shows an evident population of AGB stars. We noted that two fields, F1 and F8 cover extended faint structures of M 101, called “E-spur” and “NE plume” in Mihos et al. (2013), which show bluer B − V color with a stronger far-ultraviolet emission than other regions at the same galactocentric distance. Thus, the sign of younger stellar populations in the two fields is consistent with the result of the integrated light study.
Second, CMDs for F2 and F9 show a well-defined narrow and blue RGB stellar population. We find that the RGB sequence of these fields is well matched to the 10 Gyr isochrone with a metallicity of [Fe/H] ≈ −1.6 dex in the Padova models (Bressan et al. 2012). F5 and F1 in the inner region at R = 19 kpc and 34 kpc, respectively, show mostly redder and broader RGB stars compared to the other fields. In this sense, RGB stars appear to become bluer from inner to outer region (F5–F1–F8–F2–F9) as can be seen from their location relative to the isochrone shown in Fig. 2. Fields beyond 50 kpc (F3, F4, and F7) are expected to be dominated by metal-poor RGB stars, but it is not obvious in the CMDs due to their low stellar densities with underlying contaminants, mostly either foreground stars in the Milky Way or unresolved background galaxies.
Third, fields F2, F6, and F9 cover nearly the same projected distances along the east, west, and northeast sides of M 101, respectively, but their RGB sequences in CMDs are distinctly different. The CMDs of F2 and F9 have a well-populated RGB, but F6’s RGB is more sparely populated. Moreover, the mean color of bright RGB stars in F2 and F9 appear slightly bluer than that of F6. This means that in its faint outskirts M 101 is still asymmetric, at least at R = 45 ∼ 50 kpc.
3.2. Radial number density profiles of resolved stars
Figure 3 shows radial number density profiles of detected point sources in the three CMD bins with distinct ages. We corrected profiles using the photometric completeness data for each star we derived in Sect. 2.2. We divided the profiles into three groups according to azimuthal angles: one on the east side (circles), another one on the west side (squares), and the third on the northeast side (triangles) of M 101.
 |
Fig. 3. Top panels: radial projected stellar density profiles for the MS/HeB (left), AGB (middle), and RGB (right) populations before background subtraction. Circles, squares, and triangles with field IDs in each panel indicate the profiles along the east, west, and northeast sides from the center of M 101, respectively. Error bars indicate 1σ Poisson uncertainties. The approximate background levels measured from the control fields are marked by shaded regions. Bottom panels: same as the top panels, except after background subtraction. In the last panel, we indicate the radial coverage of each field by a small horizontal line. |
The upper panels of Fig. 3 show the number density profiles for the young (MS/HeB), intermediate-aged (AGB), and old (RGB) populations, as selected from the boxes shown in Fig. 2, without the additional background subtraction. Approximate background levels measured from the control fields (see Appendix A for details) are indicated by a shaded region in each panel. The profile for the young stellar populations (top left) shows no measurable excess on the top of the background beyond R ≈ 40 kpc, while that of the AGB population (top middle) shows a marginal excess at R ≈ 45 kpc (F2 and F9). The excess is clear in the RGB profile where all four data points between R = 40 kpc and 55 kpc are above the background level (top right).
In the lower panels of Fig. 3, we display the number density profile for each population after background subtraction. We subtracted the background levels for the ACS and WFC fields separately to get more accurate measurements of the M 101 stellar densities. The effective number projected densities range from ρ ≈ 103N arcmin−2 to below zero. These negative values occur due to low number statistics (a few stars per field) giving rise to large uncertainties and are shown as 1σ upper limits only. The extended RGB profile gives a significant detection above ρ = 1 arcmin−2 out to R ≈ 55 kpc and a marginal detection thereafter. We used the RGB profile as an indicator of surface mass profiles at the outskirts of M 101 in the following analysis.
3.3. Radial color profiles of resolved stars
The colors of the bright old RGB stars are known to have relatively little dependence on age compared to metallicity (Hoyle & Schwarzschild 1955; Sandage & Smith 1966), so they are often used as a metallicity indicator (Harris et al. 1999; Monachesi et al. 2013; Gilbert et al. 2014; Lee & Jang 2016). We investigate the radial color distribution of the RGB stars to get an insight into the metallicity profile of the outer parts of M 101.
We selected stars brighter than F814W0 = 26.1 mag, corresponding to ∼1 mag below the TRGB. The boundary of the selection box is shown by red lines in Fig. 2. We used both blue and red RGB stars to minimize the selection bias in the color measurements. The faint stars with F814W0 ≥ 26.1 mag were not used in the analysis due to their relatively low completeness with large color uncertainties. We transformed the (F606W − F814W)0 color of each selected star to the Q-index, a modified color for the RGB stars that is relatively insensitive to the F814W band magnitude (Monachesi et al. 2013). The Q-index is defined by rotating CMDs an angle of 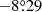 , so that a sequence of metal-poor RGB stars becomes vertical. The Q-index can be expressed by a numerical form,
, so that a sequence of metal-poor RGB stars becomes vertical. The Q-index can be expressed by a numerical form,
where a value of 6.7 is a correction factor determined from a stellar model for old (10 Gyr) and metal poor ([Fe/H] = −1.2 dex) RGB stars. A detailed description of the Q-index can be found in Monachesi et al. (2013, 2016).
We determined the median Q-index color and corresponding uncertainty using the bootstrap resampling method. We constructed CMDs of M 101 fields subtracted for the contribution of foreground stars and unresolved background galaxies statistically using CMDs of the empty fields displayed in Appendix A. The remaining stars were used for an initial guess of the median Q-index color. We iterated this procedure one thousand times to get a distribution of the measured Q-index colors. Fitting the Gaussian model to the distribution of the colors, we obtained the median color (the Gaussian mean) and corresponding 1σ uncertainty (the Gaussian width). We also included a systematic uncertainty due to the photometric calibration of 0.04 mag in color (Radburn-Smith et al. 2011; Monachesi et al. 2016). Once we measured the median Q-index color, we rotated back to the original coordinate and derived a median (F606W − F814W)0 color at 0.5 mag below the TRGB (F814W0, −3.5 = 25.6 mag). By the definition of the Q-index, the median (F606W − F814W)0 color of M 101 is 3.82 mag (25.6/6.7) smaller than the median Q-index color. Figure 4 shows a distribution of the measured (F606W − F814W)0 colors as a function of galactocentric distance. We converted the median (F606W − F814W)0 color to metallicity using the empirical relation in Streich et al. (2014) assuming [α/Fe] = 0.3 and marked the values in the right side of the figure.
 |
Fig. 4. Median (F606W − F814W)0 color profiles of RGB stars along the east (circles), west (squares), and northeast (triangles) sides of M 101. The mean RGB color of the fields beyond 40 kpc is indicated by a dashed line. |
The measured median colors have a narrow range from (F606W − F814W)0 ≈ 0.95 (F2 and F9) to 1.15 (F5 and F3). The uncertainty becomes larger due to low stellar densities toward the outskirts. As expected from the CMDs seen in Fig. 2, the color of F5 in the innermost region is clearly redder than most of the other fields. We noted, however, that the CMD of F5, as well as F8, shows highly populated upper helium-burning stars and some of them are placed in the blue-side of the RGB selection bin in CMDs. Thus, we argue that the true median colors of RGB stars in F5 and F8 would be slightly redder than the measured colors. We determined the median color of M 101 outskirts using six fields beyond 40 kpc (F2, F3, F4, F6, F7, and F9), where the contribution of the young stellar population is not significant. The weighted mean of the median color of the six fields gives (F606W − F814W)0 = 0.98 ± 0.03 with a standard deviation of 0.09 mag. Here the color measurement is not based on some fields that have only a small number of stars, but on a combination of both sparse and well populated fields taking the weighted mean. We adopted a conservative color, (F606W − F814W)0 = 1.00 ± 0.05. At this color, the mean metallicity is estimated to be [Fe/H] = 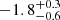 dex.
dex.
3.4. Radial surface brightness profiles from integrated light studies
The radial density profiles of the resolved stars can be combined with those of the integrated light, so we can investigate more detailed structural properties of M 101. There are two independent studies of M 101 based on the integrated light photometry by Mihos et al. (2013) and Merritt et al. (2016). Mihos et al. (2013) presented a comprehensive analysis of the extended disk using deep B and M (≈V) images taken with the Burrell Schmidt telescope. The 1σ limiting surface brightness of the B-band data was μB = 29.5 mag arcsec−2, where a 9 × 9 binned image was used (resulting in a pixel scale of 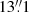 ). Merritt et al. (2016) carried out a similar study using g and r-band data taken with the Dragonfly array. They also measured the 1σ limiting surface brightness in 12″ × 12″ boxes and obtained μg = 28.6−29.2 mag arcsec−2, similar to that of Mihos et al. (2013).
). Merritt et al. (2016) carried out a similar study using g and r-band data taken with the Dragonfly array. They also measured the 1σ limiting surface brightness in 12″ × 12″ boxes and obtained μg = 28.6−29.2 mag arcsec−2, similar to that of Mihos et al. (2013).
Both studies mentioned above presented radial surface brightness profiles of M 101 out to ∼50 kpc. Merritt et al. (2016) presented the azimuthally averaged profile only, whereas Mihos et al. (2013) provided profiles along several azimuthal bins showing a variation of surface brightness at a given radius. Mihos et al. (2013) pointed out that the M 101 disk is strongly asymmetric, showing a variation in surface brightness of ∼2 mag arcsec−2 outside R = 5′ (9.7 kpc). Because our HST data cover only a small fraction of the M 101 outskirts, the azimuthally decomposed profiles shown in Mihos et al. (2013) would be more suitable for a comparison.
It is also noted, however, that the Dragonfly array is specifically designed to have less scattered light at large radii, typically by a factor of 5−10, than most other telescopes can achieve (Abraham & van Dokkum 2014; Sandin 2014). This is especially important at the outskirts of M 101, where the surface brightness is as low as μ ∼ 30 mag arcsec−2. We, therefore, take a hybrid approach, which utilizes the image data provided by the Dragonfly survey and follows the method of Mihos et al. (2013).
We obtained public g and r-band images of M 101 from the DNGS webpage2. The images are coadded and resampled to have a pixel scale of 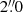 . We performed surface photometry on star-subtracted images with circular apertures. We first tried to reproduce the profile shown in Merritt et al. (2016) to make sure that our independent analysis reproduces statistically consistent result of the original author. We found that the star-subtracted images still contain compact sources around M 101, which are mostly background galaxies or known satellite galaxies of M 101. We masked these sources to sample faint stellar emission at the outskirts of M 101 as much as possible. The sky background was determined from the outer area with galactocentric distances between 25′ (48 kpc) and 35′ (68 kpc). We divided this area into 20 subregions as a function of distance and derived the mean sky value of each region. The mean and standard deviation of the 20 sky values were used as the mean and uncertainty of the sky background. We also carried out point spread function (PSF) fitting photometry using DAOPHOT (Stetson 1987) on star un-subtracted images and derived instrumental magnitudes, which we used in turn to obtain photometric zero-points by comparing to the PSF photometry provided by the Sloan Digital Sky Survey (York et al. 2000).
. We performed surface photometry on star-subtracted images with circular apertures. We first tried to reproduce the profile shown in Merritt et al. (2016) to make sure that our independent analysis reproduces statistically consistent result of the original author. We found that the star-subtracted images still contain compact sources around M 101, which are mostly background galaxies or known satellite galaxies of M 101. We masked these sources to sample faint stellar emission at the outskirts of M 101 as much as possible. The sky background was determined from the outer area with galactocentric distances between 25′ (48 kpc) and 35′ (68 kpc). We divided this area into 20 subregions as a function of distance and derived the mean sky value of each region. The mean and standard deviation of the 20 sky values were used as the mean and uncertainty of the sky background. We also carried out point spread function (PSF) fitting photometry using DAOPHOT (Stetson 1987) on star un-subtracted images and derived instrumental magnitudes, which we used in turn to obtain photometric zero-points by comparing to the PSF photometry provided by the Sloan Digital Sky Survey (York et al. 2000).
The top panel of Fig. 5 shows an azimuthally averaged g-band surface brightness profile of M 101 from our analysis (red dots with error bars) and in Merritt et al. (2016; solid line with a shaded region). It is clear that the two profiles are in good agreement within uncertainties. We display the difference between the two profiles in the bottom panel of Fig. 5, subtracting the profile in Merritt et al. (2016) from ours. Two points are noted. First, there is Δμg = 0.08 mag arcsec−2 systematic offset in the inner region (R ≲ 30 kpc), where the signal to noise ratio of the residual profile is high. The origin of this offset is unclear but may be related to the photometric zero-point adopted in each study.
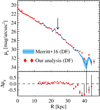 |
Fig. 5. Top: azimuthally averaged g-band radial surface brightness profiles of M 101 in Merritt et al. (2016; solid line with a shaded region) and in this study (red dots with error bars), reproduced from the image data provided by the DNGS. Two profiles agree well. A weak break in the brightness profile is detected at R ∼ 24 kpc (arrow). Bottom: difference between the two profiles, in the sense that our profile is ∼0.08 mag fainter than that of Merritt et al. (2016). |
Second, there is a large offset between the two profiles in the outer region (R ≳ 35 kpc), where the surface brightness is fainter than μg ∼ 30 mag arcsec−2. The profile in this region is very sensitive to the adopted sky background level, and an unambiguous determination of sky level and its uncertainty are challenging. We therefore emphasize that the uncertainty we derived from the image and shown in Fig. 5 by error bars should be considered as a lower limit.
The azimuthally averaged profile of M 101 in Fig. 5, as well as that in Fig. 3 of Merritt et al. (2016), shows a weak break at R ∼ 24 kpc (12′, ∼5Rd). Beyond this region, the profile becomes steeper, similar to those of the Type II disks (Freeman 1970; van der Kruit 1979; Pohlen & Trujillo 2006). Our finding is in contrast to that of Mihos et al. (2013). They pointed out that there is no obvious break in the azimuthally averaged disk profiles, though there is a very slight down-bending at R = 7′−9′ (14−17 kpc). This is due to a difference in methodology: Mihos et al. (2013) derived the averaged profile by taking the median of profiles along several azimuthal bins, while we take the profile of the azimuthally-averaged surface brightness.
We next consider the surface brightness profiles along the northeast, east, and west sides from the center of M 101. We selected, from the Dragonfly data, wedge-shaped regions with position angles of ϕ = 45° ± 22.5° (northeast side, counterclockwise from the north), ϕ = 90° ± 22.5° (east side) and ϕ = 270° ± 22.5° (west side), and derived surface brightness profiles in a similar way as we did for the azimuthally averaged profile. The background levels were determined locally from the outer area with 25′ ≲ R ≲ 35′ associated with the target direction. In Fig. 6 we display g-band surface brightness and g − r color profiles of M 101 taken along the northeast (green dotted line), east (orange dashed line), west (blue dot-dashed line) sides. We also display the profile averaged over all azimuths by a gray solid line.
 |
Fig. 6. Top: radial g-band surface brightness profiles of M 101 taken along different azimuthal selections: azimuthally averaged (solid gray line), along the northeast side (green dotted line), along the east side (orange dashed line), and along the west side (blue dot-dashed line). Shaded regions represent uncertainties. A schematic picture of M 101 has the same color coding as the profiles. Three profiles along the northeast, east, and west sides show large differences at the outskirts. Bottom: radial color profiles. The black solid line is an approximation of g − r color from the Eq. (10) of the text. |
A few distinguishable features are noted. First, the surface brightness profiles for the northeast, east and west sides are 1.5 ∼ 2 mag shallower compared to the azimuthally averaged one. The brighter limiting magnitudes of the azimuthally decomposed profiles are mainly due to the limited photon flux associated with the small area used for the photometry and for the sky estimation. Second, there is a large difference between the three azimuthally decomposed profiles, as already mentioned in Mihos et al. (2013). The northeast and east sides show radially more extended and brighter profiles outside 18 kpc compared to that of the west side. The azimuthally-averaged profile is similar to that of the east side. Third, the decomposed profiles show larger fluctuations in both surface brightness and color than the averaged profile. This is also related to the aperture size used for the averaged photometry. The decomposed profiles are more affected by structure (spiral arms, etc.) in the galaxy than the averaged profile. Indeed, we confirmed that the sharp blueward dips at R ∼ 7 kpc and 22 kpc in the color profile on the east side are due to star forming knots in the spiral arms. The fluctuation is more evident in color, so we approximate the color profiles using a form below:
The approximation is shown in the bottom panel of Fig. 6 by a black line and was used to derive stellar mass density profiles in the next section.
3.5. Radial mass density profiles
We converted the stellar number density (star count) and the surface brightness (integrated light) profiles to stellar mass density profiles. We then combined them to see the mass distribution of M 101 from inner to outer regions. The conversion from stellar number density to mass density was derived using the Padova stellar models (Bressan et al. 2012), similar to the method described in Harmsen et al. (2017). Briefly, we constructed a well-populated CMD for old (10 Gyr) and metal-poor ([Fe/H] = −1.8) stars, assuming a Chabrier initial mass function (Chabrier 2003). We then derived a relation between the number of RGB stars in the RGB bins of the CMDs (see Fig. 3) and the present-day stellar mass of the entire number of generated stars. Here we considered the RGB population only, excluding younger stellar populations, because CMDs of the observed stars showed that the outer region of M 101 is dominated by metal-poor RGB stars. We assign a systematic uncertainty of 0.3 dex to these density estimates, accounting for a reasonable range of age (5 Gyr−12 Gyr) and metallicity ([Fe/H] = −2.0 to −1.5) variations in stellar populations.
The conversion between the g-band surface brightness and the mass density is made using Eq. (1) in van Dokkum et al. (2014):
where Σ is stellar mass surface density in M⊙ kpc−2, and μg, (m − M)0, and g − r are measured surface brightness, distance modulus, and color, respectively. This relation is based on observed galaxies at low redshift (0.045 < z < 0.055) with similar stellar masses (10 < log(M/M⊙) < 10.7) and colors (0.2 < (g − r) < 1.2) in the SDSS DR7, assuming a Chabrier initial mass function (Chabrier 2003).
Figure 7 displays the mass density profiles of M 101 taken over the entire azimuthal range (a), the northeast side (b), the east side (c), and the west side (d). Circles and squares indicate the profiles from the integrated light and the resolved RGB stars, respectively. The density profiles extend out to R ∼ 70 kpc, where the mass densities are as low as 103 M⊙ kpc−2. The profiles from the two independent approaches overlap in the region between R ≈ 25 kpc to 45 kpc and they are in good agreement with each other, especially considering the decomposed profiles only. This agreement between the results for integrated light and star counts is not by design as two completely separate calibrations are used; a color-stellar M/L conversion for the integrated stellar light, and scaling of the RGB star counts to total stellar mass using isochrones.
 |
Fig. 7. Radial mass surface density profiles taken from the entire region (a), the northeast side (b), the east side (c), and the west side (d) of M 101. Circles and squares represent the profiles from the integrated light and the resolved blue RGB stars, respectively. Error bars are smaller than the symbol sizes in most cases so they are not readily seen. |
There are non-negligible offsets in panel a such that the mass densities of F5 and F6 are slightly lower and F8, F9, and F2 are slightly higher than those of the integrated light. These offsets are much smaller in the azimuthally decomposed cases in panels b, c, and d, indicating that the offsets are mainly due to local variations. The remaining offset between F5 and the integrated light in panel d can be explained by the sampling issue, as the star count profile samples the blue RGB stars only, while F5 RGBs have a broad range of color, and also the young stars present at this radius contribute to the integrated light.
The outskirts of the profiles are largely determined by scaling resolved RGB star counts. The profile for the M 101 west side (d) is almost flat in the outskirts, clearly not continuing the exponential disk profile from the inner regions. This extended stellar structure has a surface brightness of μg ≈ 33 mag arcsec−2 and is similar to stellar halos as seen often in nearby disk galaxies (McConnachie et al. 2009; Barker et al. 2012; Monachesi et al. 2013, 2016; Okamoto et al. 2015; Harmsen et al. 2017). A similar flattening in mass density is seen in the outskirts of the M 101 east side (c) but the signal is weaker and the uncertainty is larger than on the west side. The profile for the northeast side (b) does not extend far enough in radius to tell whether or not it flattens.
3.6. Modeling the M 101 halo
The detection of stellar halos in face-on galaxies is very difficult because the distinguishing feature of the accreted populations – higher velocity dispersion and scale height – is observationally inaccessible if we only have photometric information. We are forced into much less certain inferences based on either mass density profiles or stellar populations. The case of M 101 is even worse because of its extended and asymmetric stellar disk. Nevertheless, our analysis implies that M 101 has a stellar halo such that the radial mass density profiles become flatter at the outer regions (R ≳ 50 kpc), deviating from the exponential distribution and the stellar populations at the outskirts (R ≳ 40 kpc) are dominated by metal-poor RGB stars. From these observational measures, we model the halo structure of M 101. We considered two possible approaches: one using the radial mass density profiles under the assumption that stellar halos have radially more extended profiles than stellar disks, and another from the stellar population perspective assuming that stellar halos of the MW mass galaxies are dominated by metal-poor RGB stars. In this case, we introduced truncated disk models to explain metal-poor stellar populations of M 101 beyond R = 40 kpc. The halo geometry of M 101 is not known and it is very hard to constrain from the current data so we assumed a spherical geometry in the following analysis.
3.6.1. Modeling the stellar halo based on the mass density profiles
We consider a two component model, with an exponential disk and a power-law halo, to express the density profiles of M 101:
where Rd is the disk scale length, αh is the projected power-law index for the halo, and Σ0, d and Σ0, h are surface density scale factors for the disk and halo, respectively. M 101 is widely considered to be a bulgeless pure disk galaxy (Kormendy et al. 2010); consequently, we do not include a bulge component in our model. We model the outer region of the profile with R ≥ 25 kpc, where the disk is reasonably well described by a single exponential law and less affected by local variations in the light profile.
We first set all four parameters (Rd, αh, Σ0, d, and Σ0, h) to be free, and fit the outer region of density profiles (R ≥ 25 kpc) using the IDL based routine mpfitexpr (Markwardt 2009). The routine yielded the best fit values of the four parameters, but the values were sensitive to initial conditions and errors were very large. We noted that there are only a few data points beyond R = 40 kpc of the density profiles, so that the parameters for the halo component (αh and Σ0, h) are difficult to constrain. We therefore constrain the power-law index for the halo to a fixed value. While later for error analyses we choose a range of αh = −2 to −4 following the range of αh values shown by other GHOSTS galaxies (Harmsen et al. 2017), we for now fix αh = −3 at the mid-point of that range and fit the profiles again.
The best fit results are shown by dashed lines in Fig. 8. The halo component was detected in the profiles for the entire region (a), the east side (c) and the west side (d) of M 101. In the case of the northeast side (b), however, we do not detect the halo component quantitatively. This shows that our HST data sampling the outer regions beyond R ≳ 50 kpc is critical in detecting the M 101 halo.
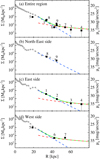 |
Fig. 8. Same as Fig. 7, but with two component fits to the density profiles: outer disk (blue dashed lines, exponential law), halo (red dashed lines, power law). The sum of the two component fits beyond 25 kpc are indicated by green lines. The halo component is not detected in the northeast side (b) so we plotted a fit for the outer disk only. |
We numerically integrated the halo profile from 40 kpc to 70 kpc, where the contribution of the stellar halo is estimated to be dominant, and derived the stellar halo mass, Mhalo, 40−70. The profile for the entire region yields a halo mass of 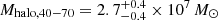 . Here the upper and the lower boundaries are purely 1σ fitting errors. When we assume that the halo profiles of the east and west sides are good measurements of a spherically symmetric halo, we obtained halo masses of
. Here the upper and the lower boundaries are purely 1σ fitting errors. When we assume that the halo profiles of the east and west sides are good measurements of a spherically symmetric halo, we obtained halo masses of 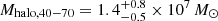 and
and 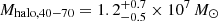 , respectively. We also confirmed that the measured halo mass on the east side does not change much, when we exclude F4 in the outermost region from the fit (
, respectively. We also confirmed that the measured halo mass on the east side does not change much, when we exclude F4 in the outermost region from the fit (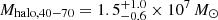 ).
).
We next consider halo profiles with different power-law slopes. Harmsen et al. (2017) showed that the MW sized disk galaxies have a range of halo power-law slopes from αh = −2.0 to −3.7. We set the halo power-law slope αh = −2.0 to −4.0 in steps of 0.5 and estimated the stellar halo mass, Mhalo, 40−70, as shown in Fig. 9. The estimated halo masses show only a weak dependence on the power-law slopes assumed. The mass variations are approximately ±15% in a given slope range and are smaller than 1σ measurement errors.
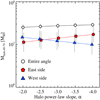 |
Fig. 9. Estimated stellar halo mass between 40 kpc and 70 kpc as a function of the halo power-law slope (αh) assumed in each fit. Circles, pentagons and triangles represent the halo mass from the analysis of the entire region, the east and west sides of M 101, respectively. |
The estimated halo masses from the entire region of M 101 are systematically higher than the values from the east and west sides. This systematic difference is likely due to the asymmetric disk geometry of M 101 combined with the sparse sampling of the galaxy outskirts. The integrated light profile can be averaged over the entire azimuthal range of the galaxy, while the star count profile is not. Modeling the halo using profiles from different spatial sampling could lead to a bias. This possible bias can be minimized when we use profiles taken along specific directions, where the HST fields are located. Indeed, the stellar halo masses measured from the east and west sides show a good agreement in a given slope range. We determine the halo mass of M 101 by taking the weighted mean of the two estimations from the east and west sides with αh = −3.0: 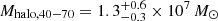 . This value is approximately the same in the given range of power-law slopes. The higher halo mass measured from the entire region (Mhalo, 40−70 ∼ 3 × 107 M⊙) can be seen as an upper limit, and we consider this in detail in the next section.
. This value is approximately the same in the given range of power-law slopes. The higher halo mass measured from the entire region (Mhalo, 40−70 ∼ 3 × 107 M⊙) can be seen as an upper limit, and we consider this in detail in the next section.
The weak mass dependence on the halo profile is encouraging. The large range in aperture radii used for the mass estimation (R = 40 kpc and 70 kpc) strongly contributes to this relatively small halo mass uncertainty. The power-law profiles are not very steep in this outer region so that the shape dependent variations in mass can be minimized. In the following analysis, we used a fixed value of the halo power-law slope, αh = −3.0.
3.6.2. Modeling the stellar halo from the population perspective
One of the major advantages of the resolved stellar populations over the integrated light is allowing us to separate the stars into different ages. CMDs of HST fields in Fig. 2 show that there is a transition of stellar populations from inner to outer regions such that inner fields at R ≲ 40 kpc (F1, F5, and F8) show multiple stellar populations, whereas outer fields at 40 kpc ≲ R ≲ 60 kpc (F2, F6, and F7) have no sign of young stars and they are old and metal-poor. The disk-halo decomposition presented in the previous section suggests that five fields (F1, F2, F5, F8 and F9) are dominated by disk stars, and three fields beyond R = 50 kpc (F3, F4, and F7), together with a half of F6, belong to the halo component.
Two fields, F2 and F9, are notable. They are located at large distances of R = 46 kpc, corresponding to ∼10 disk scale lengths, and their CMDs show in general old and metal-poor characteristics (although F9 exhibits a slight excess of AGB stars). In a stellar population perspective, they could be a stellar halo. However, they do follow an exponential trend from inner brightness profiles. The disk-halo decomposition based on the two simple profiles – a single exponential disk and a power-law halo – suggests that the two fields are solely dominated by disk stars and it would lead to an underestimation of the halo mass. We modeled the halo structure of M 101 with truncated disk models so outer fields (R ≳ 40 kpc) have more weight in the stellar halo.
We considered model disks that have an exponential form with a truncation at R = 40 kpc as illustrated in Fig. 10. Here, the disk truncation we considered is hypothetical. There is no observational evidence of a disk truncation at this radius of M 101, and it is very difficult to detect, even though it really exists, due to the halo component. Nevertheless, we explored the possible impact of the disk truncation to estimate an upper limit of the stellar halo mass. The disk scale lengths before and after the truncation are defined by Rd, in and Rd, out, respectively. Model disks have different truncation strengths from ΔRd = Rd, in − Rd, out = 0.0 kpc to 2.5 kpc, in steps of 0.5 kpc. The halo component is assumed to have a power-law slope of αh = −3. We then fit the mass density profiles to find the disk scale lengths before and after the truncation (Rd, in and Rd, out), and the scale factors for the disk (Σ0, d ) and halo (Σ0, h). Because the two disk scale lengths (Rd, in and Rd, out) are correlated, there are three unknown parameters to find (Rd, in, Σ0, d and Σ0, h). The stellar halo mass between 40 kpc and 70 kpc was also calculated by integrating the halo profile numerically as was done for the previous section. We repeated this calculation for stellar disks with truncations at Rtr = 35 kpc and 45 kpc as well. Stellar disks with truncations at inner regions with R < 35 kpc were not considered because CMDs of the inner regions show younger stellar populations.
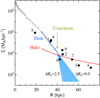 |
Fig. 10. Illustration of truncated disk models. The observed mass density profile for the entire region of M 101 is indicated by open circles (integrated light) and filled squares (star counts). Blue and red lines are models for the disk and halo. The disk model has a truncation starting at R ∼ 40 kpc with a range of strengths from ΔRd = Rd, in − Rd, out = 0.0 kpc (no truncation) to ΔRd = 2.5 kpc (strong truncation). |
Figure 11 shows the estimated stellar halo masses from the truncated disk models as a function of the truncation strength. We detected the halo component in the profiles for the entire region (a), the east side (b), and the west side (c) of M 101. The halo component was not quantitatively detected in the northeast side even with strongly truncated disk models. This is most likely due to the lack of data points at a large radial distance (R ≳ 50 kpc). It is naturally expected that the inferred halo mass increases when the truncation is stronger and the truncation starts earlier. A similar trend is seen in the figure. Disks with strong and earlier truncations yield in general higher halo masses. We, however, noted that the estimated halo masses are saturated at strongly truncated cases so that they do not exceed the mass of Mhalo, 40−70 = 5 × 107 M⊙ (dashed lines). From this result, we consider a mass of Mhalo, 40−70 = 5 × 107 M⊙ as the upper limit of the M 101 halo mass.
 |
Fig. 11. Estimated stellar halo mass between 40 kpc and 70 kpc as a function of the truncation strengths. Three panels represent results from the analysis of the entire region (a), the east (b) and the west (c) sides of M 101. Disk models with a truncation starting at 35 kpc, 40 kpc, and 45 kpc are also considered as marked by pentagons, squared, and triangles, respectively. The upper limit of the estimated halo masses, Mhalo, 40−70 = 5 × 107 M⊙, is indicated by a dashed line in each panel. |
3.6.3. Estimating the total stellar halo mass and the halo mass fraction
Now we have two mass estimates of the M 101 stellar halo. The inference based on the mass density profiles gave the mean stellar halo mass of 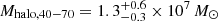 . From the stellar population perspective, we examined truncated disk models and obtained an upper limit of the halo mass, Mhalo, 40−70 = 5 × 107 M⊙. These halo mass estimates are based on a limited radial range (40 kpc ≤ R ≤ 70 kpc) with a face-on and circular geometry assumed. Next we convert the halo masses measured in a limited radial range to total halo masses, which we do by using stellar halo models in a similar way as in our previous studies (Monachesi et al. 2013; Harmsen et al. 2017).
. From the stellar population perspective, we examined truncated disk models and obtained an upper limit of the halo mass, Mhalo, 40−70 = 5 × 107 M⊙. These halo mass estimates are based on a limited radial range (40 kpc ≤ R ≤ 70 kpc) with a face-on and circular geometry assumed. Next we convert the halo masses measured in a limited radial range to total halo masses, which we do by using stellar halo models in a similar way as in our previous studies (Monachesi et al. 2013; Harmsen et al. 2017).
Bullock & Johnston (2005) provide 11 halo realizations from their numerical simulations3. They used a hybrid semianalytic plus N-body approach to reproduce stellar halos for MW-type galaxies from a series of accretion and disruption events of satellite galaxies in the context of ΛCDM. The halo models have a fixed dark matter mass, Mvir = 1.4 × 1012 M⊙ at z = 0 with a range of stellar halo luminosities from L = 0.6 × 109 to 1.2 × 109 L⊙. Each halo model has 1.8 ∼ 4.6 million stellar particles that carry basic information, such as positions (X, Y and Z), velocities (VX, VY and VZ), age, metallicity, and stellar mass. We generated a sample of stars having the same age, metallicity, and mass as each stellar particle using the Padova stellar models (Bressan et al. 2012). We assumed a Chabrier initial mass function (Chabrier 2003) for the stars in stellar particles.
Figure 12 (left) shows an example of one halo realization, Halo02 in Bullock & Johnston (2005). A two-dimensional mass density map is plotted in the XY plane so the halo appears face-on, similar to the case of M 101. We considered only the diffuse component of the halo models by selecting the stellar particles that are unbounded from the satellite galaxies (tub < 0). The mass density map implies that a significant fraction of the mass of accreted stellar halos is located near the center of the host galaxy.
 |
Fig. 12. Left: face-on view of the Halo02 model in Bullock & Johnston (2005). A dashed line represents R = 40 kpc radius centered on the halo model. Three ACS-like fields at R = 45, 55, and 65 kpc are marked by white squares. Top right: CMDs of inferred stars from the three ACS-like fields in the halo model. Stars are shifted to the M 101 distance. Shaded regions are the RGB selection bins used in this study. Bottom right: radial mass density profiles measured from the bright RGB stars in the selected fields. A solid line indicates the power-law fit with a slope of αh = −3.0. |
We examined the bias and uncertainty in the derived total stellar halo mass estimates when they are inferred only from the sparse sampling of the outer global structure. We placed three emulated HST observations at R = 45 kpc, 55 kpc, and 65 kpc on the model halos as marked by white squares in Fig. 12 (left). Each observation has 6 kpc × 6 kpc size, similar to the mean physical size of the ACS and WFC3 fields at the distance of M 101. We generated a sample of stars that satisfies age, metallicity, and stellar mass of individual stellar particles in the halo realizations using the Padova stellar models. CMDs of the generated stars in the three HST observations are presented in the top-right panels of Fig. 12. We shifted stars to the M 101 distance and considered observational effects including photometric uncertainties and incompleteness measured from the ASTs, so that the output mock-CMDs appear similar to those from real HST observations. Stars in the mock-CMDs were treated identically to the real M 101 stars. We selected stars in the RGB bins of the CMDs and derived mass density profiles as shown in the bottom-right panels of the figure. The best fit result of a power-law with a slope of αh = −3.0 is plotted by a solid line. The stellar halo mass, Mhalo, 40−70, was derived from the numerical integration of the power-law fit. We repeated this mass estimate for different halo orientation angles relative to the X-axis from 10° to 360° in steps of 10° and for different halo models. Since we have 11 stellar halo models, we obtained 396 (=36 × 11) estimates of Mhalo, 40−70.
We found that our analysis technique, employing the two measurements along the opposite sides of the galaxy, induces little bias in mass estimates. The mean stellar halo mass Mhalo, 40−70 inferred from the simulated sparse HST observations is only 2% lower than the true Mhalo, 40−70 in the model. Hence, the expected bias is estimated to be at the level of ∼2% of Mhalo, 40−70, which we ignored in the following analysis. Our estimates of Mhalo, 40−70 are on average 15.6% of the total stellar mass of the model halos with a standard deviation of 4.7%. The estimated total stellar halo mass of M 101, Mhalo, derived from Mhalo, 40−70 and the mean halo mass fraction in simulations (15.6%) is then: 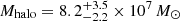 . We adopted 42% of Mhalo as a systematic uncertainty considering uncertainties associated with the uncertain stellar populations (30%, see Sect. 3.5) and the total halo mass estimation when using sparse HST observations (30%). The upper limit of the total halo mass is measured to be Mhalo = 3.2 × 108 M⊙.
. We adopted 42% of Mhalo as a systematic uncertainty considering uncertainties associated with the uncertain stellar populations (30%, see Sect. 3.5) and the total halo mass estimation when using sparse HST observations (30%). The upper limit of the total halo mass is measured to be Mhalo = 3.2 × 108 M⊙.
The total stellar mass of M 101 was derived from its K-band luminosity. The apparent K-band magnitude of M 101 is 5.51 mag (Jarrett et al. 2003), corresponding to an absolute magnitude of MK = −23.6 mag. Assuming a K-band mass to light ratio of M/L = 0.7 (Bell & de Jong 2001), we obtained the total stellar mass of M 101, Mgal = 4.1 ± 1.2 × 1010 M⊙, where the error is dominated by the uncertain stellar populations. This mass is in agreement with van Dokkum et al. (2014; 5.3 ± 1.5 × 1010 M⊙) and Merritt et al. (2016; 5.89 ± 1.87 × 1010 M⊙). The stellar halo mass fraction is estimated to be 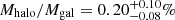 with an upper limit of 0.78%. The measured halo mass fraction is very low but meaningfully higher than zero.
with an upper limit of 0.78%. The measured halo mass fraction is very low but meaningfully higher than zero.
4. Discussion
Through the analysis of both integrated light and resolved stars, we found a significant evidence for an extended stellar component at the outskirts of M 101. This extended component also shows a clear population-II, old and low-metallicity characteristics indicating that M 101 has a stellar halo. We measured the stellar halo mass at the outskirts of M 101 and derived the total stellar halo mass by comparing with the accreted stellar halo models in Bullock & Johnston (2005). In this section, we compare the measured halo properties of M 101 with those of previous studies (Sect. 4.1), those of other MW mass disk galaxies (Sect. 4.2), and model predictions (Sect. 4.3).
4.1. Comparison with previous studies of the M 101 halo
There have been several studies investigating the faint outskirts of M 101. The claim that M 101 might lack a stellar halo was first made by van Dokkum et al. (2014). They used deep g and i-band images taken from the Dragonfly array and derived a radial mass density profile reaching out to R ∼ 70 kpc (see Figs. 2 and 3 of their paper). The profile appears very steep in the inner 5 kpc region and to follow an exponential profile out to R ≃ 45 kpc. Beyond this radius, the profile becomes flatter, deviating from the exponential trend. This extended structure could be the stellar halo, but its low surface brightness (μg ≳ 32 mag arcsec−2) and corresponding large uncertainties (σμg ≳ 1 mag arcsec−2) makes it difficult to quantify the halo structure. They fit the mass density profile with a two-component model consisting of a Sersic (1968) bulge and an exponential disk. The residuals from the fit were considered to be a halo component. They fit the residuals again with a model “U” in Courteau et al. (2011), which has a power-law shape. The total stellar halo mass and the stellar halo mass fraction they derived were  and
and 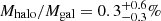 , respectively.
, respectively.
The stellar halo of M 101 was revisited by the Dragonfly team in Merritt et al. (2016). They reanalyzed the M 101 data with a revised method to be consistent with seven other galaxies studied in the paper. The radial surface brightness and mass density profiles of M 101 appear to follow an exponential trend out to the end of the profile (R ∼ 50 kpc). They carried out the bulge, disk, and halo decomposition in a similar way as in van Dokkum et al. (2014). The stellar halo mass was computed by integrating the halo profile outside 5 half-light radii (32.7 kpc), yielding a halo mass fraction of Mhalo, > 5Rh/Mgal = 0.04 ± 0.08%. We corrected this value to the total halo mass fraction using the halo models in Bullock & Johnston (2005). We confirmed that the 11 halo models in Bullock & Johnston (2005) have 39 ± 11% of the total stellar halo mass outside R = 32.7 kpc. This mass fraction leads to the total stellar halo mass fraction of M 101 of Mhalo/Mgal = 0.1 ± 0.2%.
The total stellar halo mass fractions in the two previous studies are very low and not much different from zero within uncertainties. In this study, we used additional resolved star data as well as the integrated light images to get a better estimate of the halo properties and obtained the stellar halo mass fraction, 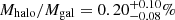 . This value is similar to the values in the two previous studies based on the integrated light only. However, its uncertainty is smaller so that the halo mass fraction is more significant. We also provide an upper limit of the halo mass fraction, 0.78%, from the stellar population perspective. If this value is taken, the halo mass fraction of M 101 is not much different from that of the Milky Way (∼1%, Harmsen et al. 2017).
. This value is similar to the values in the two previous studies based on the integrated light only. However, its uncertainty is smaller so that the halo mass fraction is more significant. We also provide an upper limit of the halo mass fraction, 0.78%, from the stellar population perspective. If this value is taken, the halo mass fraction of M 101 is not much different from that of the Milky Way (∼1%, Harmsen et al. 2017).
Mihos et al. (2018) used two very deep HST fields at R = 35 kpc and 46 kpc from the M 101 center to study the stellar populations of M 101’s outer disk. These two fields are the same as Fields F8 and F9 used in this study. They noted that the stellar contents in the two fields, which are only ∼10 kpc away from each other along the radial direction, are remarkably different. The inner field exhibits multiple stellar populations, while the outer field shows no sign of a young stellar population. The mean metallicity of the RGB stars in the inner and outer fields they measured are [M/H] = −1.3 ± 0.2 and −1.7 ± 0.2, respectively. The apparent metallicity difference between the two fields may imply that the stars in the fields have different origin. Based on the old and low-metallicity characteristics of the outer field, they inferred that the outer field samples the halo stars. However, they also pointed out that the disk-halo discrimination based on the stellar populations alone is not easy, so they claimed that it was still unclear whether M 101 has a stellar halo or not.
The outer field in Mihos et al. (2018; F9 in this study) lies close to the extended stellar disk of M 101 (NE plume). It makes it difficult to rule out the possibility that F9 is contaminated by disk stars, especially due to the presence of bright AGB stars. The mass density of F9 shown in Fig. 8 in this study is not much different from the exponential fit, supporting the disk origin. It is worth comparing it to fields F2 and F6, which also lie at approximately the same galactocentric distance (R ∼ 43−46 kpc), but sample different azimuthal directions from the M 101 center. The CMDs of these fields are dominated by old and metal poor RGB stars with a weaker sign of the bright AGB stars.
The origin of stars in F9 is still unclear because of its compatible properties such that its stellar population is close to the stellar halos, but its stellar density is more similar to the stellar disks. Given the dominant population of old and metal-poor RGB stars and the presence of very bright AGB stars in F9, it is likely that F9 is mostly halo, but that there might be some low-level star formation that happened in the last Gyr, or some small contribution from disk stars. If we assume that F9 is dominated by the disk stars, based on its stellar density only, then the outer disk stellar populations become very similar to the halo. If instead we consider the stellar populations as a better probe so that F9 becomes the halo, then M 101’s stellar disk is truncated somewhere between F8 (35 kpc) and F9 (46 kpc). Further observations beyond F9 would be useful to decompose the stellar disk and halo components in the density profile and to investigate the asymmetry in the disk and halo structures of M 101.
4.2. Comparison of the M 101 stellar halo with other observed stellar halos
Detailed halo properties of six MW mass disk galaxies have been studied through the GHOSTS survey (de Jong et al. 2007). Now we have one more sample galaxy, M 101, which has a stellar halo with a very low mass fraction and low metallicity, making the stellar halo properties of the MW mass galaxies even more diverse. In this section, we compare the stellar halo properties of M 101 to those of the six other GHOSTS disk galaxies, as well as the MW and M 31.
We obtained the stellar halo properties of the six GHOSTS galaxies from Harmsen et al. (2017). The properties of the MW and M 31 are available in the literature, and well summarized in Harmsen et al. (2017). Briefly, we adopted the total stellar mass of the MW and M 31 of MMW = 6.1 ± 1.1 × 1010 M⊙ (Licquia & Newman 2015) and MM 31 = 10.3 ± 2.3 × 1010 M⊙ (Sick et al. 2015), respectively. Rotation velocities are estimated to be VC = 218 ± 6 km s−1 for the Milky Way (Bovy et al. 2012) and VC = 257 ± 6 km s−1 for M 31 (HyperLeda, Makarov et al. 2014). The halo metallicity at 30 kpc for the MW is [Fe/H] = −1.7 dex (Sesar et al. 2011; Xue et al. 2015). This value is much lower than that of M 31, [Fe/H] = −0.5 dex (D’Souza & Bell 2018). The stellar halo mass for the MW and M 31 are estimated to be Mhalo, MW = 4−7 × 108 M⊙ (Bland-Hawthorn & Gerhard 2016) and Mhalo, M 31 = 1.5 × 1010 M⊙ (Ibata et al. 2014), respectively.
In panel a of Fig. 13, we compare the ratio of stellar halo mass to the total galaxy stellar mass as a function of the total galaxy stellar mass. The total galaxy stellar masses range from log10(Mgal/M⊙) = 10.6 to 11.0, varying by a factor of ∼2.5. The stellar halos show much larger variations in mass fractions by a factor of ∼7 for the previous six GHOSTS galaxies alone, ∼16 for the six GHOSTS galaxies and two galaxies in the Local group (the MW and M 31), and more than 50 for all nine galaxies including M 101. M 101 shows extreme properties in the total galaxy mass and the stellar halo mass fractions among the sample galaxies.
 |
Fig. 13. Comparison of observed stellar halo properties in nearby galaxies. (a) ratio of stellar halo mass and total galaxy stellar mass vs. total galaxy stellar mass. (b) mean stellar halo metallicity at 30 kpc vs. maximum rotation velocity. (c) mean stellar halo metallicity at 30 kpc vs. stellar halo mass. |
In panel b of Fig. 13, we plot the stellar halo metallicity at 30 kpc as a function of maximum rotation velocity, which is a proxy of the total galaxy mass. The halo metallicity of M 101 is measured at R ∼ 50 kpc, because inner R = 30 kpc regions are not accessible due to the disk stars. The radial color profile of RGB stars in Fig. 4 does not show a clear gradient beyond R = 40 kpc. We estimated the halo metallicty at 30 kpc of M 101 from the metallicity at 50 kpc ([Fe/H] = 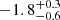 dex) assuming that there is no metallicity gradient between 30 kpc and 50 kpc. Instead, we assigned an additional metallicity uncertainty of 0.2 dex for M 101 considering the mean color gradient of the GHOSTS stellar halos, ΔQ = −0.002 mag kpc−1 (Monachesi et al. 2016). It is worth mentioning that the halo metallicities for the six GHOSTS galaxies were measured along the minor axis, the vertical axis away from the disk, while the value for M 101 is from the major axis, which is only accessible. In the figure, we see that there is no measurable trend. The stellar halo of M 101 is similar to the MW in rotation velocity and metallicity.
dex) assuming that there is no metallicity gradient between 30 kpc and 50 kpc. Instead, we assigned an additional metallicity uncertainty of 0.2 dex for M 101 considering the mean color gradient of the GHOSTS stellar halos, ΔQ = −0.002 mag kpc−1 (Monachesi et al. 2016). It is worth mentioning that the halo metallicities for the six GHOSTS galaxies were measured along the minor axis, the vertical axis away from the disk, while the value for M 101 is from the major axis, which is only accessible. In the figure, we see that there is no measurable trend. The stellar halo of M 101 is similar to the MW in rotation velocity and metallicity.
Panel c of Fig. 13 displays the stellar halo metallicity at 30 kpc as a function of inferred stellar halo mass. The two halo properties show a strong correlation as reported and also discussed in detail in Harmsen et al. (2017). The stellar halo of M 101 follows this correlation, extending the low mass end. This correlation is broadly consistent with expectations in cosmological simulations that most of the halo mass is accreted from the few most-massive progenitors (Vogelsberger et al. 2014; Deason et al. 2016; Bell et al. 2017; D’Souza & Bell 2018). The low stellar halo mass and halo metallicity of M 101 together with the MW indicate that these two galaxies had amongst the quietest accretion histories in the Local Universe.
4.3. Comparison of the M 101 stellar halo with models
In Fig. 14, we explore the stellar halo properties of observed galaxies in the context of model predictions accounting for the accretion of low-mass dwarf galaxies during halo formation. We derived model predictions of stellar halos compiled in Harmsen et al. (2017) and plotted their approximated boundaries in the figure by shaded regions: Bullock & Johnston (2005, red area), Purcell et al. (2007, 2008, light green area), Cooper et al. (2010, blue small circles), Cooper et al. (2013, pink area), Deason et al. (2016, light yellow area). Observed galaxies are also marked by filled symbols with error bars.
 |
Fig. 14. a: total stellar halo mass fraction as a function of total galaxy stellar mass. b: stellar halo metallicity as a function of the total stellar mass of the galaxy. Observed galaxies are marked by symbols with error bars: six GHOSTS galaxies (red circles), the MW and M 31 (yellow circles), and M 101 in this study (starlet symbol). Shaded regions indicate model predictions in the literature: Bullock & Johnston (2005, red area), Purcell et al. (2007, 2008, light green area with a green line), Cooper et al. (2010, blue circles), Cooper et al. (2013, pink area), Deason et al. (2016, light yellow area). |
As already mentioned in Sect. 4.2, the observed stellar halos have a broad range of the total stellar halo mass fractions (Mhalo/Mgal). This diversity is also found in the model predictions in panel a, as well as in Monachesi et al. (2019), where this is also found with the Auriga hydrodynamical simulations. M 101 has the lowest stellar halo mass fraction among the observed galaxies. The measured halo mass fraction of M 101, together with its upper limit, marks the low-mass end of the Purcell et al. (2007, 2008) models (within 95% boundary) and also agrees with the general trend of the Cooper et al. (2010) models. A strong correlation between the stellar halo mass (Mhalo) and metallicity ([Fe/H]) is well reproduced by models, as shown in panel b. The M 101 stellar halo marks the low mass and the low metallicity end of the observed halos, but nicely agrees with the model predictions.
The overall agreement of the M 101 halo with models is quite encouraging. Clearly M 101 has a low mass and low metallicity stellar halo compared with those of other disk galaxies; such a halo occurs naturally in current halo formation models as the outcome of a relatively quiet accretion history dominated by the accretion of few to several low-mass, low-metallicity satellite galaxies (Deason et al. 2016; D’Souza & Bell 2018; Monachesi et al. 2019).
5. Summary
Using deep image data taken with HST/ACS and HST/WFC3, we examine the photometric and structural properties of M 101 outskirts. We obtain resolved star photometry from these high-resolution images and confirm that the outskirts of M 101 are dominated by old and metal-poor RGB stars. The radial mass density profiles of M 101 show evidence for an extended structural component in M 101’s outskirts, a strong candidate for being the stellar halo. We compared the basic properties of this extended structural component with those of other disk galaxies. Our primary results are summarized as follows.
-
We derived deep CMDs of resolved stars, reaching down to ∼2 magnitude below the TRGB. The CMDs beyond 40 kpc show clear Population II, old and low metallicity characteristics.
-
The radial star count profile of the Population II RGB stars reaches out to ∼60 kpc. The mean metallicity of the RGB stars at R ∼ 50 kpc is estimated to be [Fe/H] =
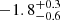 dex.
dex. -
We independently derived radial surface brightness profiles of M 101 using public image data provided by the DNGS and combined them with our resolved stellar photometry to derive radial mass density profiles.
-
The radial mass density profiles of the M 101 east and west sides show an extended stellar component, which we interpret as being the stellar halo. In the case of the northeast side, however, we do not detect the halo component quantitatively.
-
We derived the halo mass of M 101 from the exponential disk + power-law halo model fits and obtained a halo mass of
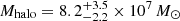 , and a halo mass fraction of
, and a halo mass fraction of 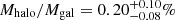 . In this case, the outer disk of M 101 is assumed to have very old and metal-poor stellar populations, similar to halo populations.
. In this case, the outer disk of M 101 is assumed to have very old and metal-poor stellar populations, similar to halo populations. -
We also estimated an upper limit of the halo mass fraction, Mhalo/Mgal = 0.78%, from the assumption that stellar halos can be traced better by the old and metal-poor populations. This modeling favors a truncated disk at R ∼ 40 kpc to explain the population change.
-
We compared the halo properties of M 101 with those of other disk galaxies. From the mass, mass fraction, and mean metallicity of the M 101 halo, we conclude that M 101 has a low-mass, low-metallicity stellar halo with properties similar to that of the Milky Way.
-
M 101’s low-mass and low-metallicity stellar halo is in agreement with the range of halos expected for Milky Way mass galaxies, where M 101 would have had a rather quiet accretion history dominated by the accretion of a few (but more than two) low-mass, low-metallicity satellite galaxies.
The halo models are available at http://user.astro.columbia.edu/~kvj/halos/ (see also Robertson et al. 2005; Font et al. 2006).
Acknowledgments
We acknowledge discussions with Richard D’Souza. This work was supported by HST grant GO-13696 provided by NASA through a grant from the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26555. Additionally, some of the data presented in this paper were obtained from the Mikulski Archive for Space Telescopes (MAST). We are grateful to the Dragonfly team for obtaining and releasing the excellent quality deep images of M 101 that we used in this study. We are also thankful to the anonymous referee for his/her useful comments. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. This work was supported by NSF grant AST 1008342 and HST Grants GO-11613 and GO-12213 provided by NASA through a Grant from the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26555. AM acknowledges financial support from FONDECYT Regular 1181797 and funding from the Max Planck Society through a Partner Group grant.
References
- Abraham, R. G., & van Dokkum, P. G. 2014, PASP, 126, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, J., & King, I. R. 2006, Instrument Science Report ACS 2006-01, 34 [Google Scholar]
- Barker, M. K., Ferguson, A. M. N., Irwin, M. J., Arimoto, N., & Jablonka, P. 2012, MNRAS, 419, 1489 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., & de Jong, R. S. 2001, ApJ, 550, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E., Monachesi, A., D’Souza, R., et al. 2017, Galaxies, 5, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Beaton, R. L., Seibert, M., Hatt, D., et al. 2019, ApJ, 885, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Bennet, P., Sand, D. J., Crnojević, D., et al. 2019, ApJ, 885, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bland-Hawthorn, J., & Gerhard, O. 2016, ARA&A, 54, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blumenthal, G. R., Faber, S. M., Primack, J. R., & Rees, M. J. 1984, Nature, 311, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Bosma, A., Goss, W. M., & Allen, R. J. 1981, A&A, 93, 106 [NASA ADS] [Google Scholar]
- Bovy, J., & Rix, H.-W. 2013, ApJ, 779, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Bovy, J., Allende Prieto, C., Beers, T. C., et al. 2012, ApJ, 759, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Bullock, J. S., & Johnston, K. V. 2005, ApJ, 635, 931 [NASA ADS] [CrossRef] [Google Scholar]
- Bullock, J. S., Kolatt, T. S., Sigad, Y., et al. 2001, MNRAS, 321, 559 [Google Scholar]
- Calzetti, D. 2013, HST Proposal [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, A. P., Cole, S., Frenk, C. S., et al. 2010, MNRAS, 406, 744 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, A. P., D’Souza, R., Kauffmann, G., et al. 2013, MNRAS, 434, 3348 [NASA ADS] [CrossRef] [Google Scholar]
- Courteau, S., Widrow, L. M., McDonald, M., et al. 2011, ApJ, 739, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Crnojević, D., Sand, D. J., Spekkens, K., et al. 2016, ApJ, 823, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Dalcanton, J. J., Williams, B. F., Seth, A. C., et al. 2009, ApJS, 183, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Danieli, S., van Dokkum, P., Merritt, A., et al. 2017, ApJ, 837, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Deason, A. J., Mao, Y.-Y., & Wechsler, R. H. 2016, ApJ, 821, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Jong, R. S., Seth, A. C., Bell, E. F., et al. 2007, Stellar Populations as Building Blocks of Galaxies, 241, 503 [NASA ADS] [Google Scholar]
- de Jong, R. S. 2008, MNRAS, 388, 1521 [NASA ADS] [Google Scholar]
- de Vaucouleurs, G., de Vaucouleurs, A., Corwin, Jr., H. G., et al. 1991, Third Reference Catalogue of Bright Galaxies (RC3) (New York: Springer) [Google Scholar]
- DeVore, J. G., Kristl, J. A., & Rappaport, S. A. 2013, J. Geophys. Res. (Atm.), 118, 5679 [NASA ADS] [CrossRef] [Google Scholar]
- Dolphin, A. E. 2000, PASP, 112, 1383 [NASA ADS] [CrossRef] [Google Scholar]
- D’Souza, R., & Bell, E. F. 2018, MNRAS, 474, 5300 [NASA ADS] [CrossRef] [Google Scholar]
- Font, A. S., Johnston, K. V., Bullock, J. S., & Robertson, B. E. 2006, ApJ, 638, 585 [Google Scholar]
- Freeman, K. C. 1970, ApJ, 160, 811 [NASA ADS] [CrossRef] [Google Scholar]
- Freeman, K., & Bland-Hawthorn, J. 2002, ARA&A, 40, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Freedman, W. L., Madore, B. F., Hatt, D., et al. 2019, ApJ, 882, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Gilbert, K. M., Kalirai, J. S., Guhathakurta, P., et al. 2014, ApJ, 796, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Greggio, L., Rejkuba, M., Gonzalez, O. A., et al. 2014, A&A, 562, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, G. L. H., Harris, W. E., & Poole, G. B. 1999, AJ, 117, 855 [NASA ADS] [CrossRef] [Google Scholar]
- Harmsen, B., Monachesi, A., Bell, E. F., et al. 2017, MNRAS, 466, 1491 [NASA ADS] [CrossRef] [Google Scholar]
- Holwerda, B. 2014, HST Proposal [Google Scholar]
- Hoyle, F., & Schwarzschild, M. 1955, ApJS, 2, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R. A., Lewis, G. F., McConnachie, A. W., et al. 2014, ApJ, 780, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Jang, I. S., & Lee, M. G. 2015, ApJ, 807, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Jarrett, T. H., Chester, T., Cutri, R., Schneider, S. E., & Huchra, J. P. 2003, AJ, 125, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Jog, C. J., & Combes, F. 2009, Phys. Rep., 471, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Karachentsev, I. D., Riepe, P., Zilch, T., et al. 2015, Astrophys. Bull., 70, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., Drory, N., Bender, R., & Cornell, M. E. 2010, ApJ, 723, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Krist, J. E., Hook, R. N., & Stoehr, F. 2011, Proc. SPIE, 8127, 81270J [CrossRef] [Google Scholar]
- Laine, J., Laurikainen, E., & Salo, H. 2016, A&A, 596, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, M. G., & Jang, I. S. 2016, ApJ, 822, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Licquia, T. C., & Newman, J. A. 2015, ApJ, 806, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Makarov, D., Prugniel, P., Terekhova, N., Courtois, H., & Vauglin, I. 2014, A&A, 570, A13 [CrossRef] [EDP Sciences] [Google Scholar]
- Markwardt, C. B. 2009, Astronomical Data Analysis Software and Systems XVIII, 411, 251 [NASA ADS] [Google Scholar]
- McConnachie, A. W., Irwin, M. J., Ibata, R. A., et al. 2009, Nature, 461, 66 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Merritt, A., van Dokkum, P., Abraham, R., & Zhang, J. 2016, ApJ, 830, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Mihos, J. C., Harding, P., Spengler, C. E., Rudick, C. S., & Feldmeier, J. J. 2013, ApJ, 762, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Mihos, C. 2014, HST Proposal [Google Scholar]
- Mihos, J. C., Harding, P., Feldmeier, J. J., et al. 2017, ApJ, 834, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Mihos, J. C., Durrell, P. R., Feldmeier, J. J., Harding, P., & Watkins, A. E. 2018, ApJ, 862, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Monachesi, A., Bell, E. F., Radburn-Smith, D. J., et al. 2013, ApJ, 766, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Monachesi, A., Bell, E. F., Radburn-Smith, D. J., et al. 2016, MNRAS, 457, 1419 [NASA ADS] [CrossRef] [Google Scholar]
- Monachesi, A., Gómez, F. A., Grand, R. J. J., et al. 2019, MNRAS, 485, 2589 [NASA ADS] [CrossRef] [Google Scholar]
- Mouhcine, M., Ibata, R., & Rejkuba, M. 2010, ApJ, 714, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Okamoto, S., Arimoto, N., Ferguson, A. M. N., et al. 2015, ApJ, 809, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Pohlen, M., & Trujillo, I. 2006, A&A, 454, 759 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Purcell, C. W., Bullock, J. S., & Zentner, A. R. 2007, ApJ, 666, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Purcell, C. W., Bullock, J. S., & Zentner, A. R. 2008, MNRAS, 391, 550 [NASA ADS] [CrossRef] [Google Scholar]
- Radburn-Smith, D. J., de Jong, R. S., Seth, A. C., et al. 2011, ApJS, 195, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Macri, L. M., Hoffmann, S. L., et al. 2016, ApJ, 826, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, B., Bullock, J. S., Font, A. S., Johnston, K. V., & Hernquist, L. 2005, ApJ, 632, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Sandage, A., & Smith, L. L. 1966, ApJ, 144, 886 [NASA ADS] [CrossRef] [Google Scholar]
- Sandin, C. 2014, A&A, 567, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Sesar, B., Jurić, M., & Ivezić, Ž. 2011, ApJ, 731, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Sersic, J. L. 1968, Atlas de Galaxias Australes (Cordoba, Argentina: Observatorio Astronomico) [Google Scholar]
- Sick, J., Courteau, S., Cuillandre, J. C., et al. 2015, Galaxy Masses as Constraints of Formation Models, 311, 82 [NASA ADS] [Google Scholar]
- Simanton, L. A., Chandar, R., & Whitmore, B. C. 2015, ApJ, 805, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Simanton-Coogan, L. A., Chandar, R., Miller, B., & Whitmore, B. C. 2017, ApJ, 851, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Slater, C. T., Harding, P., & Mihos, J. C. 2009, PASP, 121, 1267 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B. 1987, PASP, 99, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Streich, D., de Jong, R. S., Bailin, J., et al. 2014, A&A, 563, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Streich, D., de Jong, R. S., Bailin, J., et al. 2016, A&A, 585, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tanaka, M., Chiba, M., Komiyama, Y., et al. 2011, ApJ, 738, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, M., Chiba, M., & Komiyama, Y. 2017, ApJ, 842, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo, I., & Fliri, J. 2016, ApJ, 823, 123 [NASA ADS] [CrossRef] [Google Scholar]
- van der Kruit, P. C. 1979, A&AS, 38, 15 [NASA ADS] [Google Scholar]
- van Dokkum, P. G., Abraham, R., & Merritt, A. 2014, ApJ, 782, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Vogelsberger, M., Genel, S., Springel, V., et al. 2014, MNRAS, 444, 1518 [NASA ADS] [CrossRef] [Google Scholar]
- White, S. D. M., & Rees, M. J. 1978, MNRAS, 183, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Xue, X.-X., Rix, H.-W., Ma, Z., et al. 2015, ApJ, 809, 144 [NASA ADS] [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., Anderson, Jr., J. E., et al. 2000, AJ, 120, 1579 [CrossRef] [Google Scholar]
- Zaritsky, D., Elston, R., & Hill, J. M. 1990, AJ, 99, 1108 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, J., Abraham, R., van Dokkum, P., et al. 2018, ApJ, 855, 78 [Google Scholar]
Appendix A: CMDs of the control fields and background estimation
We describe here the method used to estimate the background levels of the radial number density profiles in the main text. We first selected HST fields in the archive satisfying the following criteria: (1) located at high galactic latitude with |b|≳40°, similar to M 101’s b ∼ 59.8°, (2) located at large distance from bright stars or galaxies in the sky, (3) located at large distance from known tidal streams or star clusters in the galactic halo, (4) located at large distance from known galaxy clusters, and (5) observed with similar exposure times as the M 101 data (∼2500 s). Table A.1 summarizes the selected HST fields taken with ACS (8 fields) and WFC3 (8 fields) from the selection criteria above. Some of the fields have been used in Radburn-Smith et al. (2011) and Monachesi et al. (2016) to determine the best selection criteria (photometry culls).
We calibrated and extracted point source photometry of the HST data for the 16 “empty” fields in the same way as the M 101 fields, and plotted their CMDs in Figs. A.1 (for ACS fields) and A.2 (for WFC3 fields). Most of the sources in the CMDs must be either foreground stars or unresolved background galaxies that have passed the culls. Shaded regions in each figure denote the population bins used for the M 101 fields. Sources are sparsely distributed in the CMDs without showing remarkable structures. We counted the number of sources in the population bins of each CMD and calculated the spatial number densities considering the photometric incompleteness and the effective field area. Derived results are summarized in Fig. A.3. We confirmed that all populations show field to field variations in spatial number densities. We estimate the mean number density of sources in the ACS fields, ρ = 0.95 ± 0.31 N arcmin−2 in the MS + HeB bin, 0.44 ± 0.31 N arcmin−2 in the AGB bin, and 0.73 ± 0.26 N arcmin−2 in the RGB bin of the ACS fields, where the uncertainties are taken to be the standard deviation of the individual densities. We obtained the similar values from the WFC3 fields, ρ = 1.08 ± 0.40 N arcmin−2 in the MS + HeB bin, 0.20 ± 0.14 N arcmin−2 in the AGB bin, and 0.60 ± 0.26 N arcmin−2 in the RGB bin. The measured source densities from the ACS and WFC3 fields agree well within uncertainties. We used these values for the background estimation.
Summary of HST data for the control fields.
 |
Fig. A.1. CMDs for the selected point sources corrected for the extinction and reddening and after the culls have been applied in the eight empty fields taken with ACS/WFC. Shaded regions are the same as those in Fig. 2: Blue for young stellar population including main sequence and helium burning stars, orange for intermediate aged AGB stars and red for old RGB stars. Dashed lines represent the 50% completeness limits. Photometric errors as derived from ASTs at (F606W − F814W)0 = 1.0 are marked at (F606W − F814W)0 = 2.0. |
 |
Fig. A.3. a: distributions of the unresolved object densities in the MS + HeB (circles), AGB (triangles), RGB (squares) bins in the eight empty fields taken with ACS. Error bars denote 1σ Poisson uncertainties of the object count. The mean level of each object population is indicated by a shaded region. Right: same as (a) but for WFC3 fields. |
All Tables
All Figures
 |
Fig. 1. Location of HST ACS (red squares) and WFC3 (purple squares) fields overlaid on a deep 75′ × 75′ g-band image provided by the DNGS (Abraham & van Dokkum 2014). North is up and east is to the left. High surface brightness regions of the g-band image are replaced by the color image from the SDSS. The white and black dashed lines represent circles with |
| In the text | |
 |
Fig. 2. CMDs for the selected point sources corrected for Galactic extinction and reddening in the nine HST fields around M 101. Blue, orange, and pink shaded regions indicate selection bins for the young (main sequence and helium burning stars), intermediate (asymptotic giant branch stars), and old (RGB stars) stellar populations, respectively. The region enclosed by red lines represent the selection bin we used for the color measurement only. Dashed lines represent the 50% completeness limits. Photometric errors as derived from ASTs at (F606W − F814W)0 = 1.0 are marked at (F606W − F814W)0 = 2.0. We overlaid a 10 Gyr stellar isochrone with [Fe/H] = −1.6 dex in the Padova models (Bressan et al. 2012), to give an indication of the RGB domain in the CMD. |
| In the text | |
 |
Fig. 3. Top panels: radial projected stellar density profiles for the MS/HeB (left), AGB (middle), and RGB (right) populations before background subtraction. Circles, squares, and triangles with field IDs in each panel indicate the profiles along the east, west, and northeast sides from the center of M 101, respectively. Error bars indicate 1σ Poisson uncertainties. The approximate background levels measured from the control fields are marked by shaded regions. Bottom panels: same as the top panels, except after background subtraction. In the last panel, we indicate the radial coverage of each field by a small horizontal line. |
| In the text | |
 |
Fig. 4. Median (F606W − F814W)0 color profiles of RGB stars along the east (circles), west (squares), and northeast (triangles) sides of M 101. The mean RGB color of the fields beyond 40 kpc is indicated by a dashed line. |
| In the text | |
 |
Fig. 5. Top: azimuthally averaged g-band radial surface brightness profiles of M 101 in Merritt et al. (2016; solid line with a shaded region) and in this study (red dots with error bars), reproduced from the image data provided by the DNGS. Two profiles agree well. A weak break in the brightness profile is detected at R ∼ 24 kpc (arrow). Bottom: difference between the two profiles, in the sense that our profile is ∼0.08 mag fainter than that of Merritt et al. (2016). |
| In the text | |
 |
Fig. 6. Top: radial g-band surface brightness profiles of M 101 taken along different azimuthal selections: azimuthally averaged (solid gray line), along the northeast side (green dotted line), along the east side (orange dashed line), and along the west side (blue dot-dashed line). Shaded regions represent uncertainties. A schematic picture of M 101 has the same color coding as the profiles. Three profiles along the northeast, east, and west sides show large differences at the outskirts. Bottom: radial color profiles. The black solid line is an approximation of g − r color from the Eq. (10) of the text. |
| In the text | |
 |
Fig. 7. Radial mass surface density profiles taken from the entire region (a), the northeast side (b), the east side (c), and the west side (d) of M 101. Circles and squares represent the profiles from the integrated light and the resolved blue RGB stars, respectively. Error bars are smaller than the symbol sizes in most cases so they are not readily seen. |
| In the text | |
 |
Fig. 8. Same as Fig. 7, but with two component fits to the density profiles: outer disk (blue dashed lines, exponential law), halo (red dashed lines, power law). The sum of the two component fits beyond 25 kpc are indicated by green lines. The halo component is not detected in the northeast side (b) so we plotted a fit for the outer disk only. |
| In the text | |
 |
Fig. 9. Estimated stellar halo mass between 40 kpc and 70 kpc as a function of the halo power-law slope (αh) assumed in each fit. Circles, pentagons and triangles represent the halo mass from the analysis of the entire region, the east and west sides of M 101, respectively. |
| In the text | |
 |
Fig. 10. Illustration of truncated disk models. The observed mass density profile for the entire region of M 101 is indicated by open circles (integrated light) and filled squares (star counts). Blue and red lines are models for the disk and halo. The disk model has a truncation starting at R ∼ 40 kpc with a range of strengths from ΔRd = Rd, in − Rd, out = 0.0 kpc (no truncation) to ΔRd = 2.5 kpc (strong truncation). |
| In the text | |
 |
Fig. 11. Estimated stellar halo mass between 40 kpc and 70 kpc as a function of the truncation strengths. Three panels represent results from the analysis of the entire region (a), the east (b) and the west (c) sides of M 101. Disk models with a truncation starting at 35 kpc, 40 kpc, and 45 kpc are also considered as marked by pentagons, squared, and triangles, respectively. The upper limit of the estimated halo masses, Mhalo, 40−70 = 5 × 107 M⊙, is indicated by a dashed line in each panel. |
| In the text | |
 |
Fig. 12. Left: face-on view of the Halo02 model in Bullock & Johnston (2005). A dashed line represents R = 40 kpc radius centered on the halo model. Three ACS-like fields at R = 45, 55, and 65 kpc are marked by white squares. Top right: CMDs of inferred stars from the three ACS-like fields in the halo model. Stars are shifted to the M 101 distance. Shaded regions are the RGB selection bins used in this study. Bottom right: radial mass density profiles measured from the bright RGB stars in the selected fields. A solid line indicates the power-law fit with a slope of αh = −3.0. |
| In the text | |
 |
Fig. 13. Comparison of observed stellar halo properties in nearby galaxies. (a) ratio of stellar halo mass and total galaxy stellar mass vs. total galaxy stellar mass. (b) mean stellar halo metallicity at 30 kpc vs. maximum rotation velocity. (c) mean stellar halo metallicity at 30 kpc vs. stellar halo mass. |
| In the text | |
 |
Fig. 14. a: total stellar halo mass fraction as a function of total galaxy stellar mass. b: stellar halo metallicity as a function of the total stellar mass of the galaxy. Observed galaxies are marked by symbols with error bars: six GHOSTS galaxies (red circles), the MW and M 31 (yellow circles), and M 101 in this study (starlet symbol). Shaded regions indicate model predictions in the literature: Bullock & Johnston (2005, red area), Purcell et al. (2007, 2008, light green area with a green line), Cooper et al. (2010, blue circles), Cooper et al. (2013, pink area), Deason et al. (2016, light yellow area). |
| In the text | |
 |
Fig. A.1. CMDs for the selected point sources corrected for the extinction and reddening and after the culls have been applied in the eight empty fields taken with ACS/WFC. Shaded regions are the same as those in Fig. 2: Blue for young stellar population including main sequence and helium burning stars, orange for intermediate aged AGB stars and red for old RGB stars. Dashed lines represent the 50% completeness limits. Photometric errors as derived from ASTs at (F606W − F814W)0 = 1.0 are marked at (F606W − F814W)0 = 2.0. |
| In the text | |
 |
Fig. A.2. Same as Fig. A.1, but for WFC3 fields. |
| In the text | |
 |
Fig. A.3. a: distributions of the unresolved object densities in the MS + HeB (circles), AGB (triangles), RGB (squares) bins in the eight empty fields taken with ACS. Error bars denote 1σ Poisson uncertainties of the object count. The mean level of each object population is indicated by a shaded region. Right: same as (a) but for WFC3 fields. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.