| Issue |
A&A
Volume 636, April 2020
|
|
|---|---|---|
| Article Number | A62 | |
| Number of page(s) | 13 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202037474 | |
| Published online | 17 April 2020 | |
Investigating the connection between γ-ray activity and the relativistic jet in 3C 273 during 2015−2019⋆
1
Department of Physics and Astronomy, Seoul National University, Gwanak-gu, Seoul 08826, Korea
e-mail: dwkim@astro.snu.ac.kr
2
INAF Istituto di Radioastronomia, Via P. Gobetti, 101, Bologna 40129, Italy
3
Astro Space Center, Lebedev Physical Institute, Russian Academy of Sciences, Profsouznaya st., 84/32, Moscow 117997, Russia
Received:
10
January
2020
Accepted:
5
March
2020
Context. The powerful radiation over the entire electromagnetic spectrum and its radio jet activity of the blazar 3C 273 offer the opportunity of studying the physics of γ-ray emission from active galactic nuclei. Since the historically strong outburst in 2009, 3C 273 showed relatively weak emission in the γ-ray band over several years. However, recent Fermi-Large Area Telescope observations indicate higher activity during 2015−2019.
Aims. We constrain the origin of the γ-ray outbursts toward 3C 273 and investigate their connection to the parsec-scale jet.
Methods. We generated Fermi-LAT γ-ray light curves with multiple binning intervals and studied the spectral properties of the γ-ray emission. Using a 3 mm ALMA light curve, we studied the correlation between radio and γ-ray emission. The relevant activity in the parsec-scale jet of 3C 273 was investigated with 7 mm VLBA observations that were obtained close in time to notable γ-ray outbursts.
Results. We find two prominent γ-ray outbursts in 2016 (MJD 57382) and 2017 (MJD 57883) accompanied by millimeter-wavelength flaring activity. The γ-ray photon index time series show a weak hump-like feature around the γ-ray outbursts. The monthly γ-ray flux–index plot indicates a transition from softer-when-brighter to harder-when-brighter states at 1.03 × 10−7 ph cm−2 s−1. A significant correlation between the γ-ray and millimeter-wavelength emission is found, and the radio lags the γ-rays by about 105−112 days. The 43 GHz jet images reveal the known stationary features (i.e., the core, S1, and S2) in a region upstream of the jet. We find an indication for a propagating disturbance and a polarized knot between the stationary components at about the times of the two γ-ray outbursts.
Conclusions. Our results support a parsec-scale origin for the observed higher γ-ray activity, which suggests that this is associated with standing shocks in the jet.
Key words: techniques: interferometric / galaxies: jets / quasars: individual: 3C 273 / γ-rays: galaxies / radio continuum: galaxies
Data for Figs. 1 and 2 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/636/A62
© ESO 2020
1. Introduction
Blazars are a subclass of active galactic nuclei (AGN) and arguably the most energetic persistent objects in the Universe. They are characterized by powerful nonthermal emission through the entire electromagnetic spectrum, rapid variability, and strong polarization (Trippe et al. 2012). This phenomenology can be explained by the presence of a relativistic jet whose emission is subject to Doppler boosting that is the result of a small viewing angle between the jet axis and the line of sight (e.g., Blandford et al. 2019). The relativistic jets are responsible for the formation of the observed spectral energy distributions (SEDs) of blazars (Chen 2018; Lewis et al. 2018; Meyer et al. 2019). The standard model of blazar SEDs (i.e., leptonic scenarios) predicts that the jets radiate through two main processes: synchrotron radiation at radio to UV/X-ray and inverse Compton scattering (IC) at X-rays to γ-rays (e.g., Potter & Cotter 2013; Piano et al. 2018; Liodakis et al. 2019; but see also H.E.S.S. Collaboration 2019, for discussion of its limitations and alternative models). Because the spatial resolution of high energy telescopes is inadequate, however, our understanding of the high-energy emission is limited, and the site of its production is a matter of active debate.
γ-ray emission from blazars is known to vary on short timescales ranging from minutes to days (e.g., Nalewajko 2013; Petropoulou & Dimitrakoudis 2015; Meyer et al. 2019), and it occasionally shows distinct spectral variations such as hardening or softening (e.g., Rani et al. 2013a; Kim et al. 2018a; Shah et al. 2019; but see also Nalewajko 2013; Paliya 2015, for limitations in the spectral analysis). Furthermore, multiwaveband studies have reported strong positive correlations between γ-ray emission and emission at lower frequencies (e.g., Algaba et al. 2018; Prince 2019). The observations provide indications for the emission physics: a small or narrow emission region, variations in acceleration or cooling processes, and spatial separation between emitting regions at different observing frequencies. The γ-ray-to-radio correlations (e.g., Pushkarev et al. 2010; León-Tavares et al. 2012; Ramakrishnan et al. 2015; Lico et al. 2017) in particular played an important role in linking the γ-ray production site to the Very Large Baseline Interferometry (VLBI) radio core. This core is generally identified as the brightest compact synchrotron self-absorbed feature in the VLBI images of blazar jets (Kovalev et al. 2009; Kim et al. 2018b; but see also Lee et al. 2016a, for optically thin spectra of blazars at millimeter-wavelengths that dominate the core). In addition, the absence of γ-ray absorption by broad-line region (BLR) photons further supports a location of the γ-ray dissipation zone downstream of the relativistic jet (i.e., > 104 Rs, with Rs being the Schwarzschild radius), where the parsec-scale radio core appears (e.g., Harris et al. 2012; Costamante et al. 2018; Meyer et al. 2019; see also Jorstad et al. 2013; Kravchenko et al. 2016; Kim et al. 2018a, for VLBI studies consistent with the idea). However, the BLR region, which is closer to the central black hole, is also a well-known γ-ray production site, as revealed by observations of several objects (e.g., Rani et al. 2013a; Berton et al. 2018; but see also Hodgson et al. 2018; Rani et al. 2018, for discussion of multiple γ-ray sites).
The flat-spectrum radio quasar 3C 273 is one of the most extreme blazars, showing strong and flaring radiation throughout the electromagnetic spectrum. 3C 273 displays a bright extended relativistic jet in centimeter to millimeter VLBI images and is known to be a powerful high-energy emitter (Bruni et al. 2017), making it one of the best sources for studying the nature of the γ-ray emission from blazars. Several recent studies (Rani et al. 2013a; Chidiac et al. 2016; Lisakov et al. 2017) have indicated that a region close to the jet apex and not the 7 mm core is the place of origin of bright γ-ray outbursts. Using the energy dependence of electron cooling times, we can determine the site of the inverse Compton (IC) scattering that generates the γ-ray emission (Dotson et al. 2012). This provides information on the place of origin of the IC seed photons (the BLR or a dusty torus) and thus provides a distance scale (subparsec or parsec) for the γ-ray production in the jet (Dotson et al. 2015; Coogan et al. 2016). A common assumption in many scenarios that were envoked to explain the blazar γ-ray flaring activity is that a plasma blob moves downstream from the jet; these structures that travel along the jet are frequently observed. As it propagates along the jet, the blob can pass and interact with standing shocks (e.g., Wehrle et al. 2016; Hodgson et al. 2017; see also Böttcher 2019, for a discussion of γ-ray flares with different origins). The latter may appear as stationary features (e.g., Gómez et al. 1997; Hervet et al. 2016) in the VLBI jets.
In this study, we investigate the 2015−2019 γ-ray emission of 3C 273 that is associated with its relativistic jet to explore the origin of γ-ray outbursts. The observations and data are described in Sect. 2. In Sect. 3 we present our results and analysis. Finally, we discuss and conclude on the observed phenomena in Sects. 4 and 5, respectively. We use the following cosmological parameters: H0 = 71 km Mpc s−1, ΩΛ = 0.73, and Ωm = 0.27, corresponding to an angular scale of 2.71 pc mas−1 at the redshift of 3C 273, z = 0.158 (Strauss et al. 1992).
2. Observations
2.1. Fermi-LAT
We analyzed Pass 8 γ-ray data obtained by the Fermi-LAT (Atwood et al. 2009). The data were calibrated following the standard unbinned likelihood procedure1. We selected SOURCE class events at 0.1−300 GeV measured between 2015 January 1 and 2018 December 10 (MJD: 57023−58462). Filter parameters DATA_QUAL> 0 && LAT_CONFIG==1 and zmax=90° were selected for the good-time intervals and to minimize the Earth limb γ-ray contamination. We defined a region of interest (ROI) of 15° ×15° centered at 3C 273, and included all sources in the 4FGL catalog (i.e., The Fermi-LAT Collaboration 2020) within the ROI. To take diffuse background sources into account, Galactic diffuse emission gll_iem_v07 and isotropic background emission iso_P8R3_SOURCE_V2_v1 templates were applied. The significance of γ-ray signals was evaluated with the maximum likelihood test statistic (TS). First, we optimized the background model using the ScienceTools (v11r5p3). We performed a maximum likelihood fit to the data covering half of the whole period and left the spectral parameters of all sources free. For the two diffuse backgrounds, the normalizations, including the index of the Galactic diffuse emission, were left free. The sources with TS < 10 in the background model obtained from the first optimization were removed, then a second optimization was performd with the updated model. To produce the final γ-ray light curves, we left the spectral parameters free for sources within 3° from the ROI center, plus the normalizations for the diffuse backgrounds. All the other parameters were fixed to the results of the second optimization. The spectral model of 3C 273 was assumed to be a power-law model2 defined as dN/dE ∝ E+Γ, with N being the number of photons, E the photon energy, and Γ the photon index. We computed 2σ upper limits for γ-ray signals detected with TS < 9 or ΔFγ/Fγ > 0.5, where Fγ and ΔFγ indicate the flux and its error, respectively. As binning intervals for the γ-ray light curves, we selected 30 and 7 days for the full time range (i.e., 2015−2019), and one day for flaring periods to provide a zoom-in view. Based on the average flare duration of 12 days reported in Abdo et al. (2010a), weekly and monthly time bins are appropriate to describe the global γ-ray activity of blazars, as also noted in previous studies (Rani et al. 2013a; Chidiac et al. 2016; Meyer et al. 2019). 3C 273 was not very bright during 2015−2019. Thus, we preferred an interval of at least 7 days to achieve a high signal-to-noise ratio. Weekly binning also coincides with the average sampling interval of the ALMA data used in this study (see Sect. 3.3).
2.2. ALMA band 3
We make use of a radio light curve of 3C 273 provided by the Atacama Large Millimeter/submillimeter Array (ALMA)3 spanning from 2015 January to 2018 December. The flux data were obtained at ALMA band 3 (84−116 GHz), and most them have been taken at 91 and 103 GHz. When several flux measurements were made on a single day, the data point with the smallest error was considered here. Further details of the observations can be found in Bonato et al. (2018).
2.3. VLBA 43 GHz
The VLBA-BU-BLAZAR program (i.e., Jorstad & Marscher 2016) monitors bright γ-ray blazars (34 blazars and 3 radio galaxies) every month with the Very Long Baseline Array (VLBA) at 43 GHz. We used fully calibrated data for 3C 273, which are publicly available4. The data were imaged with the software package Difmap (Shepherd 1997). The image analysis was performed with several datasets observed close to the time of two γ-ray outbursts: 2015 December to 2016 April and 2017 April to 2017 August (ten epochs in total). We considered a conservative flux density accuracy of 10%. For the positions of the brightest and compact knots, about one in ten of the synthesized beam dimensions were used (e.g., Lister et al. 2009). A full description of the VLBA-BU-BLAZAR data can be found in Jorstad et al. (2017). We further produced linear polarization maps similar to those of Kim et al. (2018a) for all epochs. We also used the CLEANed model components provided by the BU group on their website5 to investigate the 43 GHz fluxes during 2015−2019. We followed Lee et al. (2016b) in our calculations of brightness temperatures and resolution limits for observed jet components. The rms noise of a jet component was estimated from an area spanning 3 × 3 beam sizes centered at the position of the component.
3. Results
3.1. Light curves
Figure 1 shows the γ-ray and radio light curves of 3C 273 from 2015 January 11 to 2018 December 24 (MJD: 57033−58476). The 3 mm ALMA light curve comprises one major flare and three minor flares during this time, with an average radio flux of 11 ± 3 Jy and a minimum of about 7 Jy. The major flare spans from mid-2015 to late-2016, and the peak reaches ∼20 Jy on 2016 March 27 (MJD 57474). This implies an increase in the flux density by a factor of about 2.5. We also note the presence of a substructure in this flare: an additional peak of ∼18 Jy on 2016 January 21 (MJD 57408). Interestingly, it seems that each ALMA flare has some substructure (“subflares”). The other minor flares lasted for less than a year, with relatively weak peaks below 13 Jy. The 43 GHz VLBA fluxes essentially follow the ALMA light curve, but the relatively long cadence (∼30 days) prevents a more exact comparison. We note that the 43 GHz fluxes are both higher and lower than the ALMA fluxes at different times. This implies a variable radio spectrum at millimeter-wavelengths. It is worth noting that a significant fraction of the total VLBI flux, about 1−6 Jy depending on the time, is contributed by the extended jet structure beyond 0.3−0.4 mas from the core (see Fig. 7).
 |
Fig. 1. γ-ray and radio light curves of 3C 273 in 2015−2019. From top to bottom: ALMA band 3 (∼100 GHz) overlaid on the VLBA 43 GHz total flux, Fermi-LAT fluxes using monthly binning, and Fermi-LAT fluxes using weekly binning. For the γ-ray light curves, the 2 σ upper limits are indicated by red downward arrows. The vertical dashed lines show three γ-ray outbursts that are identified in the weekly light curve. Each of the shaded areas spans 100 days centered at the peak of a γ-ray outburst. |
The monthly and weekly binned γ-ray light curves yield average fluxes of (2.0 ± 1.2)×10−7 ph cm−2 s−1 and (2.6 ± 1.4)×10−7 ph cm−2 s−1, respectively. It is worth noting that 3C 273 has been in a relatively low-γ-ray flux state since the historical powerful outburst around 2009 September (see Lisakov et al. 2017; Meyer et al. 2019). However, we find three notable and distinguishable γ-ray events in our light curves. The first event (2016A) can be found in the monthly light curve, and the peak reaches 5.6 × 10−7 ph cm−2 s−1 on 2016 January 11 (MJD 57398). This γ-ray outburst overlaps in time with the major ALMA flare. The other events can be identified more clearly in the weekly light curve. We find the second event (2016B) on 2016 October 9 (MJD 57670) with a peak of 5.3 × 10−7 ph cm−2 s−1. The third event (2017A) appeared on 2017 May 7 (MJD 57880) with a peak of 7.0 × 10−7 ph cm−2 s−1. These outbursts seems to have 3 mm radio counterparts that are weaker than the counterpart to the first γ-ray event. In particular, the third event is evident only in the light curve with weekly binning. Similarly, the peak of the first γ-ray outburst can be localized more precisely in the weekly light curve, with a flux of 8.7 × 10−7 ph cm−2 s−1 on 2015 December 27 (MJD 57383).
To analyze the γ-ray flares in more detail and to minimize the binning effect, we produced γ-ray light curves with one-day time binning for each outburst (e.g., Marscher et al. 2010; Wehrle et al. 2016). Figure 2 shows the daily γ-ray light curves, which cover the time ranges indicated by the shaded areas in Fig. 1. The first outburst peaks on 2015 December 26 (MJD 57382) with a flux of 1.4 × 10−6 ph cm−2 s−1. For the second and third outbursts, the peaks occur on 2016 October 8 (MJD 57669) with a flux of 9.4 × 10−7 ph cm−2 s−1 and on 2017 May 10 (MJD 57883) with a flux of 2.5 × 10−6 ph cm−2 s−1, respectively. The 2016A event is by far the most prominent, showing variable enhanced activity around its peak, whereas the γ-ray activity around the peaks of the 2016B and 2017A events appears to be substantially weaker. We do not see any notable temporal variation in the photon indices derived from the three daily light curves; the average photon index values are −2.80, −3.58, and −2.85. The first and third outbursts are easily identified in their daily light curves because of their brightness and high statistical significance, whereas the 2016B outburst is weak and shows relatively low TS. Furthermore, the quality of the BU data obtained on 2016 October 6 is rather poor because two VLBA antennas were not available. We therefore focus on the 2016A and 2017A γ-ray outbursts in our further analysis.
 |
Fig. 2. Zoomed-in γ-ray light curves of 3C 273, binned into one-day time bins, for the three γ-ray flaring periods indicated by the shaded areas in Fig. 1. Upper panels, in each diagram: photon indices at the same time resolution. Average photon index values are marked by horizontal solid lines. The vertical dashed lines mark the peak times of the γ-ray outbursts in the daily light curves. |
3.2. Photon indices from weekly and monthly γ-ray light curves
In Fig. 3 we present the photon indices derived from the LAT light curves (see Sect. 2.1 for details) as a function of γ-ray flux. The indices range from −4.5 to −2.0 for weekly binning, and from −3.5 to −2.0 for monthly binning. Their averages are −2.85 and −2.78, respectively. We do not see any correlations (i.e., softer-when-brighter or harder-when-brighter trends) for the weekly γ-ray fluxes. However, simple visual inspection of the monthly data suggests different trends above and below a flux of about 1.03 × 10−7 ph cm−2 s−1. For fluxes below the threshold, flux and photon index show a negative correlation with a Pearson coefficient of −0.49 at a confidence level of 87%; above the threshold, the correlation is positive, with a Pearson coefficient of 0.48 at a confidence level of 99%. Accordingly, the source appears to have been in a harder-when-brighter spectral state at γ-ray fluxes above 1.03 × 10−7 ph cm−2 s−1. There is also an indication of a softer-when-brighter trend at lower fluxes, but the confidence level is too low for us to conclude about this.
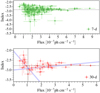 |
Fig. 3. Photon index vs. flux for the weekly binned (top) and monthly binned (bottom) γ-ray light curves. The dashed lines indicate the average photon index values. The vertical solid line in the bottom panel marks a break flux value of 1.03 × 10−7 ph cm−2 s−1. The light blue lines show the linear regression lines for photon indices above and below the break flux. |
The evolution of the photon index with time during 2015−2019 is shown in Fig. 4 using weekly and monthly binning. Overall, the uncertainties of the photon indices are too large for a meaningful quantitative analysis. We therefore limit ourselves to a qualitative discussion of potential patterns or trends in the data. There is an indication for gradual temporary increases of the monthly photon indices during the two γ-ray outbursts. The first hump spans ∼180 days (MJD: 57278−57458) with a peak value of −2.74 on MJD 57338, while the second hump spans ∼120 days (MJD: 57818−57938) with a peak value of −2.73 on MJD 57878. Interestingly, the 2016 γ-ray outburst lags the local peak of the first bump by about 44 days, whereas the 2017 outburst coincides with the local peak of the second hump. This might indicate that many regions emit in γ-rays in the jet, which would suggest that a first dissipation zone is responsible for these local peaks.
 |
Fig. 4. Photon index vs. time of the weekly and monthly γ-rays. Top panel: entire time range of our observations. Bottom panels: zoomed-in views on the data around the times of the 2016A and 2017A γ-ray outbursts defined in Fig. 2 (marked by vertical dashed lines). Error bars correspond to 1σ uncertainties. |
The weekly indices seem to be fluctuating randomly without showing any noteworthy trends throughout our observations. We attribute this to the combination of typically modest variations in the spectral index (e.g., Abdo et al. 2010b; Lisakov et al. 2017) and low-photon-number statistics, which causes a substantial scattering of the photon index values (Nandikotkur et al. 2007; Rani et al. 2013a). The photon statistics improves with stronger source activity (e.g., Paliya 2015). However, 3C 273 was relatively weak during 2015−2019 (cf. Sect. 3.1). Nandikotkur et al. (2007) found that binning data into longer time intervals can reduce the large error bars of the spectral index values. Thus, the monthly indices arguably describes the γ-ray spectral variations in our data better than the weekly indices.
3.3. Correlation between the radio and γ-ray light curves
We employed the discrete correlation function (DCF; Edelson & Krolik 1988) to investigate the relationship between γ-ray and radio emission. The average sampling interval for the ALMA light curve is ∼9.8 days. When we disregard the upper limits, the average sampling intervals of the weekly and monthly γ-ray light curves are ∼11.7 and ∼32.3 days, respectively. We therefore used time steps of 12 and 33 days for the DCF analysis for the weekly and monthly binned γ-ray fluxes, respectively. To determine the height and location of a DCF peak, we fit a Gaussian function defined as DCF(t) = a × exp[ − (t − c)2/2w2] to the DCF durve, with a being the amplitude, c the time lag, and w the width of the Gaussian profile. The statistical significance of the correlation was calculated following Rani et al. (2013b) by calculating the Pearson correlation coefficient for the ALMA data and LAT data and its uncertainty after applying the time shift derived from the Gaussian fit to the DCF curve.
The results of the correlation analysis are shown in Fig. 5 and summarized in Table 1. The Gaussian fits to the DCF curves find time delays of −105 ± 4 and −112 ± 6 days (γ-ray leading) for the weekly and monthly binned γ-ray light curves, respectively. These estimates are consistent with each other within the errors. We note that the location of the DCF peak varies considerably (with a standard deviation of ∼12.5 days) when different time-delay bins are used to calculate the DCF for the weekly and monthly γ-ray fluxes. However, the time delays found from the Gaussian fits are only weakly affected by the binning of the DCF (with a standard deviation of ∼0.9 days). When we apply the best-fit delays, the Pearson correlation analysis resulted in coefficient values of 0.67 for the pair with the monthly γ-ray fluxes and 0.48 for the pair with the weekly γ-ray fluxes at significance levels of > 99% for both (see Fig. 5).
 |
Fig. 5. DCF curves and flux–flux plots comparing the 3 mm radio and γ-ray light curves in 2015−2019 for the monthly γ-ray fluxes (top panels) and the weekly γ-ray fluxes (bottom panels). Orange curves in the left panels indicate the best Gaussian fits to the DCF curves. For the flux-flux plots (right panels), the ALMA light curve has been shifted in time by the delays found from the Gaussian fits. The Pearson correlation coefficients (rp) and corresponding p-values (pp) are shown in the flux-flux plots. |
Results of our correlation analysis for 2015−2019 data.
Simple visual inspection of Fig. 1 caused us to suspect that the DCF is dominated by data from the time range 2015−2017. We therefore repeated our correlation analysis using the parts of the light curves in that time range (see Fig. 6). We used the weekly γ-ray light curve, which includes the fine structure of the flares and is sampled about as densely as the ALMA fluxes. We find a clear correlation comparable to the results in Table 1, which confirms the initial impression that the major γ-ray and radio flares in 2015−2017 dominate the correlation between the full (2015−2019) light curves. The results of the analysis are summarized in Table 2. We also checked the 2017−2019 data, but found the DCF to be consistent with random fluctuations.
Results of our correlation analysis for the 2015−2017 data.
3.4. Parsec-scale jet near the 43 GHz core
We investigated the parsec-scale jet of 3C 273 during times of elevated γ-ray and radio band activity using VLBA maps. Considering the time-lags between γ-ray and radio fluxes, we chose two sets of VLBA-BU-BLAZAR observations that span about four months after each γ-ray outburst, shown in Figs. 7 and 8. All maps are aligned at the position of the core, which is taken to be the upstream end of the jet. In each data set, the structure of the jet was represented by a number of two-dimensional circular Gaussians fitted to the visibility domain. The resultant models consist of 7−10 components whose parameters are summarized in Table A.1. We found three stationary features: the core, and two additional components labeled S1 and S2, which have been identified in a previous study (i.e., Lisakov et al. 2017), with S1 and S2 located at about 0.16 and 0.33 mas from the core, respectively.
 |
Fig. 7. 7 mm VLBA images of 3C 273 during the 2016 γ-ray outburst. The contours and color scale represent the total intensity and linearly polarized intensity, respectively. Contour levels are 1%, 2%, 4%, 8%, etc., 64%, 80% of the peak intensity. A zoomed-in view on the core region is provided in the subplots. White line segments indicate the EVPA directions uncorrected for Faraday rotation. Circular Gaussian jet components are indicated by green (for the three stationary components) and yellow (for the others) cirles with a cross. The vertical dot-dashed lines show the average positions of the S1 (=0.1 mas) and S2 (=0.21 mas) components projected onto the x-axis. The vertical solid line indicates the core position. All maps are restored with a 0.2 × 0.2 mas beam (indicated at the bottom left). |
 |
Fig. 8. Same as in Fig. 7, but for the 2017 γ-ray outburst. Contour levels are 2.5%, 5%, 10%, etc., 40%, 80% of the peak intensity. |
Figures 7 and 8 shows a spatial displacement of the 7 mm emission during the two γ-ray outbursts. The sequence of maps in Fig. 7 begins on MJD 57361. The second epoch is just 6 days after the 2016 γ-ray outburst. In this epoch, the total intensity peak is located at the S1 position. Then, the peak moves down to the S2 position on MJD 57501 and increases its intensity to ∼9 Jy beam−1. The proper motion of this displacement is about 0.59 mas yr−1, which corresponds to an apparent speed of ∼6.0c (with c being the speed of light). Interestingly, a displacement of the emission peak like this is also observed for the 2017 γ-ray outburst, but it is weaker. In Fig. 8, the initial position on MJD 57859 of the peak intensity coincides with the core. Then, until MJD 57886, which is 3 days after the 2017 γ-ray outburst, it moves downstream to a location between the core and S1. The further motion of the emission peak cannot be clearly recognized until MJD 57937, when the flux increases to ∼4.8 Jy beam−1. At this time, both the core and S1 have became simultaneously brighter. On MJD 57971, the flux peak is localized at the position of S1 and shows a decrease in total intensity. This corresponds to a proper motion of about 0.37 mas yr−1, translating into an apparent speed of ∼3.8c. The proper motions are consistent with the radial speeds of the newborn components reported in Lisakov et al. (2017).
Figure 9 shows the fluxes and distances from the core as function of time for the core, S1, and S2 as determined from the VLBA data. The S1 flux peaks almost simultaneously with the 2016 γ-ray outburst. The flux of S2 increases rapidly, by a factor of 10, just after the 2016 γ-ray outburst. The core remains quiescent. The 2017 γ-ray outburst coincides with the rise of a flare of S1. In addition, the core fluxes during the first two epochs (i.e., MJD 57859 and 57886) are consistent with each other within the errors, but increase rapidly thereafter. This suggests that the 2017 γ-ray outburst also coincides with the onset of the core flare. This connection can also be made for γ-ray outburst and the S2 flare in 2016. Notably, S2 doubles its flux in a month until MJD 57971. As evident in Figs. 7 and 8, the positions of the presumably stationary components show some variation in both epochs we studied. S2 moved toward the core from MJD 57388 to 57419 by about ∼0.1 mas, accompanied by a rapid increase in its flux. S2 then slowly returned to its initial core distance. In the 2017 observations, we note a tendency for both S1 and S2 to move toward the core. In general, S1 moves less than S2.
 |
Fig. 9. Left: flux density (top) and distance from the core (bottom) of the core, S1, and S2 derived from Gaussian modeling of the jet components as shown in Fig. 7. Right: same as the left panels, but for the observations in Fig. 8. The vertical dashed lines correspond to the times of the 2016 and 2017 γ-ray outbursts. The average distances of S1 and S2 (i.e., 0.16 and 0.33 mas from the core) are indicated by the horizontal solid lines. |
Because the combined total flux density of the core, S1, and S2 components dominate the millimeter-wavelength emission of 3C 273, we can conclude that the two radio flares and the γ-ray production occur in this region of the jet. We note that S2 is responsible for the major ALMA flare (peaking on MJD 57474). We suggest that the subflare (peaking on MJD 57408) within the major ALMA flare might be associated with the activity in S1. For the second ALMA flare (around MJD 57888), associated with the 2017 γ-ray outburst, both the core and S1 contribute equally.
3.5. Polarization
Figures 7 and 8 present distributions of the linearly polarized intensity overlaid on the total intensity contours. We only mapped out polarized emission that exceeded a conservative significance threshold of 9σ. In the core region, the polarized emission is weak and only observed in a single epoch (MJD 57886), which is consistent with other studies (i.e., Attridge et al. 2005; Jorstad et al. 2005). In the 2016 observations, we find a polarized knot that is spatially connected to S1 and S2 and shows systematic variations in position and intensity. Just after the 2016 γ-ray outburst (MJD 57388), the polarized knot appears to encounter S2 while still covering the S1 region. It then appears to pass through the S2 region (MJD 57419) while showing an increase in polarized intensity. This suggests that the emergence of the polarized knot precedes the total intensity peak, which leads us to the conclusion that we observe the downstream propagation of a disturbance in both total and polarized intensity. The polarized intensity peaks in the time from MJD 57466 to 57501 at ∼300 mJy in the S2 region.
In 2017, the polarized emission is weaker and shows a more complicated structure. We detect a polarized knot upstream of the core on MJD 57886, immediately after the 2017 γ-ray outburst. It disappears before the following observations. This behavior might indicate an energetic physical process (e.g., acceleration) that occurs upstream of the core, thus suggesting an association between the millimeter-wavelength core and the high-energy emission. Weak polarization is detected around S2 at two epochs (MJD 57886 and 57937), probably implying physical or geometrical changes in that region.
4. Discussion
4.1. Positional variations of the stationary components
The 7 mm VLBA observations reveal two stationary components in the jet of 3C 273, S1 and S2, which have been reported before by Lisakov et al. (2017). These features are thought to be multiple recollimation shocks (RCS) that have been predicted by relativistic magnetohydrodynamics (MHD) simulations (e.g., Gómez et al. 1995; Mizuno et al. 2015). We found a wiggling (up- and downstream) motion of S2 (see also Fig. 2 of Lisakov et al. 2017, for a similar pattern). S2 moved toward the core (inward motion) by about ∼0.1 mas from MJD 57388 to 57419 while increasing its flux. It then shifted downstream back to its original position (see Fig. 9). Because a new moving knot (J1, which appeared on MJD 57419) was passing through the S2 region in MJD 57388, both components can appear blended into a single feature, leading to a shift of the centroid downstream of the initial position of S2. After the passage, the two components appear to split, resulting in an apparent inward motion of S2. The apparent displacement of a stationary jet component matches the signature expected for an RCS zone breakout (e.g., Abeysekara et al. 2018). When a moving blob with high kinetic energy starts interacting with the standing RCS localized in the region where the magnetic field becomes unstable, there could be (1) an enhancement of nonthermal emission, (2) a strong instability of the magnetic field configuration (e.g., tearing instability; Del Zanna et al. 2016), and (3) a positional displacement by the underlying flow with increasing kinetic power of the jet (Hervet et al. 2016). This scenario also predicts some fast γ-ray emission induced by magnetic reconnection, but the observed photon indices around MJD 57405 in Fig. 2 appear too soft (Ding et al. 2019). A more conventional interpretation for the S2 motions would be an opacity effect (e.g., Lobanov 1998). Variations in opacity can occur when flaring components pass through these regions (e.g., Plavin et al. 2019), resulting in an apparent spatial drift.
Yet another possible explanation for the apparent motion of S2 in 2016 is the so-called core shuttle effect. Changes in the physical state, and thus in the opacity of the core, that are due to a propagating disturbance may cause a wiggling of the core position. However, the core was in a quiescent state during the time of the S2 motion, implying the absence of newly formed jet components. Moreover, a core shuttle should also affect the separation of S1 from the core, which is not observed. In 2017, however, a core shuttle might have affected the separations of both S1 and S2 from the core, which changed simultaneously (see Fig. 9) and coincided with an increase in the flux density of the core.
4.2. 2016 γ-ray outburst
Our VLBA analysis in Sects. 3.4 and 3.5 found that the millimeter-wavelength activity in 3C 273 is confined to the most upstream few parsecs of the jet. For the 2016 γ-ray outburst, the flaring of the stationary components S1 and S2 strongly suggests that the γ-ray outburst has a physical connection with these regions. This is further supported by the clear γ-ray and radio correlation, which can be attributed to the major ALMA flare close to the 2016 γ-ray outburst (see also Meyer et al. 2019, for their LCCF result on 3C 273). Moreover, the contemporaneous displacements of the total intensity peak and the polarized knot indicate that a moving disturbance played an important role in producing the high-energy emission.
Many studies have reported the connection between parsec-scale radio jets and γ-ray outbursts: γ-ray outbursts tend to be accompanied by radio flares and strongly polarized jet features (Agudo et al. 2011a; Jorstad et al. 2013; Wehrle et al. 2016; Kim et al. 2018a; Park et al. 2019). In our case, an obvious connection is provided by the contemporaneous flares in γ-ray and radio bands. Based on the timing of its radio variability, we can regard S1 as the place of origin of the 2016 γ-ray outburst. When we consider the sampling interval of the VLBA observations (i.e., ∼30 days), the S1 flare clearly coincides with the γ-ray outburst, implying a cospatial emission region. Such an event can be caused by the passage of a powerful disturbance through a standing feature, which is visually confirmed in Fig. 7. We provide the source-frame brightness temperatures for each stationary component in Fig. 10. Clearly, S1 reaches 2.3 × 1012 K, which implies that particle energy dominated during the γ-ray outburst. This strengthens the argument that S1 is responsible for the γ-ray outburst. The plasma in the region of the standing shock is likely to be turbulent (Marscher 2016). In this case, particles in S1 can be accelerated by second-order Fermi acceleration (e.g., Asano et al. 2014) and/or magnetic reconnections (e.g., Sironi & Spitkovsky 2014) in disordered magnetic fields. A moving shock is able to further compress and energize the already excited particles, thus producing strong γ-ray emission.
 |
Fig. 10. Source-frame brightness temperatures (Tb) of the core, S1, and S2. Vertical dashed lines indicate the times of the γ-ray outbursts. Upward arrows mark limits on Tb, calculated using the spatial resolution limit for each component whenever the observed size is smaller than this limit. |
However, we cannot rule out the possibility that S2 is responsible for the 2016 γ-ray outburst. A polarized knot that enters the S2 region is detected just after the γ-ray outburst. This might be attributed to a shock interaction between S2 and a disturbance, which would cause a γ-ray flare in S2 (e.g., Agudo et al. 2011a; see also Hughes 2005, for a discussion of plasma compression resulting in magnetic field enhancement). Such a scenario is natural as the disturbance continues to travel along the jet. However, we noted several interesting phenomena accompanying this particular disturbance. From MJD 57388 to 57419, the total intensity peak and the polarized knot propagated downstream simultaneously but were located at different positions. Subsequently, the strong radio flare occurred in S2, which dominates the estimate for the γ-ray to radio time delay of ∼100 days. Taken together, the observations suggest a large size of the emitting blob (e.g., Lisakov et al. 2017). It has been suggested that the high-energy electrons can be confined to a narrow and thin region of a shock front (Wehrle et al. 2012; Marscher 2014). As the moving blob begins to interact with S2, a strong γ-ray emission could have occurred in the shock front, which is the injection site (e.g., Agudo et al. 2011b). The strong S2 flare reaching up to ≈10.5 Jy is remarkable. During the passage of a disturbance in the S2 region, the increase in particle density and/or magnetic field strength appears to be huge and might have caused a temporary change of the opacity in the shocked region (e.g., Kravchenko et al. 2016). Lisakov et al. (2017) found that one of the flares in the 43 GHz core (event B7 in their nomenclature) peaked when it reached its most downstream position. We find such a pattern for S2 in Fig. 7 (i.e., from MJD 57419 to 57501). This is indicates that S2, like the core, is indeed a recollimation shock.
The association of the γ-ray emission with the S1 or S2 regions in the jet (≥104Rs) disfavors the BLR as the source of seed photons. At the distances of S1 and S2, the BLR is not thought to be an effective source of seed photons for IC scattering unless the BLR is more extended than expected (León-Tavares et al. 2013). Recent studies found indications that the majority of γ-ray bright Flat-Spectrum Radio Quasars (FSRQs) radiate γ-rays beyond the BLR region. This supports the parsec-scale scenario (Costamante et al. 2018; Meyer et al. 2019). Dotson et al. (2012) suggested energy-dependent cooling times for γ-ray emission produced through infrared (IR) seed photons from the dusty torus. Inverse Compton scattering of IR seed photons occurs in the Thomson regime, whereas the Klein−Nishina regime is relevant for higher-energy seed photons (e.g., UV photons from the BLR region), resulting in energy-independent cooling times (see Blumenthal & Gould 1970). We tried to test this theory by using γ-ray data binned into very short intervals (e.g., 3 h). However, insufficient photon statistics prevented the creation of meaningful γ-ray light curves. More powerful flares or brighter blazars might be suitable for such an analysis. Lower-energy seed photons could originate from the dusty torus or the jet itself (e.g., Marscher et al. 2010; Wehrle et al. 2016; see also Banasiński & Bednarek 2018, for discussion of another emitting blob in the jet that provides seed photons).
4.3. 2017 γ-ray outburst
We found a fast and short γ-ray outburst on MJD 57883 (see Fig. 2). The contemporaneous radio flaring activity in both the core and S1 makes it difficult to interpret the γ-ray outburst, however. The total intensity radio maps obtained just after the γ-ray outburst suggest a strong disturbance that is localized between the core and S1. As discussed before, we assumed that the core was in the onset of its flare while S1 was already in the middle of its flare at the time of the γ-ray outburst. This can be explained by several moving disturbances. The polarization image of the jet observed in MJD 57886 shows a weak polarized knot near the core, which indicates the emergence of a new disturbance. We therefore considered two propagating disturbances around the time of the γ-ray outburst: one interacting with the core (K1), and one interacting with S1 (K2). This picture is consistent with the jet features observed on MJD 57971: (1) for K1, the total intensity peak located at S1, and (2) for K2, the enhanced flux of S2. An increasing trend in the core size from MJD 57886 to 57937 might further support the presence of K1.
Figure 2 shows that the 2017 γ-ray outburst lasted for a short time (probably less than a day), very different from the 2016 outburst. The short timescale suggests a small emitting region (e.g., Petropoulou & Dimitrakoudis 2015), implying a region in the jet located closer to the central engine (Tavecchio et al. 2010). The relatively low apparent component speeds around the γ-ray outburst further support this idea (Rani et al. 2018). We also note that the γ-ray outburst triggered a millimeter-wavelength flare in the core that might have been accompanied by the emergence of a polarized knot nearby. The core is therefore likely to be responsible for the γ-ray outburst. A timing of events like this (γ-ray outbursts occurring at the very beginning of a radio flare) is common in blazars (e.g., Marscher 2016; Lisakov et al. 2017). The γ-ray outburst could have been caused by the interaction of the standing shock and a strong disturbance (i.e., K1) propagating down the jet, in the same manner as explained in Sect. 4.2. In addition, the brightness temperature of the core peaks at the time of the γ-ray outburst, which further supports this scenario.
It is worth noting that there seems to be a discrepancy in position between the polarized knot and the core component. This might be due to variable opacity in the core region (e.g., Lisakov et al. 2017), when the core region temporarily becomes partially optically thin. The 3 mm to 7 mm spectral index indeed varied rapidly around the time of the γ-ray outburst (see Fig. 1). When we modeled the minor ALMA flare that is associated with the γ-ray outburst as a combination of an exponentially rising and an exponentially declining part, we found a 3 mm peak at MJD 57897±7 (see Fig. 11). This corresponds to a time delay of about 40 days relative to the 7 mm core flare observed on MJD 57937. The nonzero time lag implies optically thick emission, but the source of the ALMA flare is unknown (i.e., between the core, S1, and S2). Nevertheless, this is relevant with respect to the result of Chidiac et al. (2016), who found a time delay of ∼50 days between the 43 and 230 GHz light curves of 3C 273. In short, we are not able to determine the opacity condition in the core during the γ-ray outburst.
 |
Fig. 11. 3 mm ALMA light curve around the time of the 2017 γ-ray outburst (vertical dashed line). The model that combines an exponential rise with a subsequent exponential decay (as introduced by Valtaoja et al. 1999, but without fixing the decay timescale) is indicated by the red curve. |
In the conventional view, the core shift might play a role, although it is expected to occur at very small submilliarcsec scales at wavelengths below 7 mm (Vol’vach et al. 2013; Lisakov et al. 2017). Interestingly, the 2017 γ-ray outburst coincides with not only the onset of the 7 mm flare in the core, but also with the peak of the 3 mm flare at the same time. Thus, we suggest that a moving blob (i.e., K1) started to interact with the 7 mm core, while the blob (probably its tail part) still passed through the 3 mm core. This scenario could explain the polarized feature that appeared on MJD 57886 upstream from the 7 mm core. Furthermore, a passage of K1 through the 3 mm core can explain the contemporaneous γ-ray and 3 mm flares (e.g., Jorstad et al. 2013; Wehrle et al. 2016). Based on our observations of the γ-ray outburst, however, we cannot definitively locate the origin of the γ-ray outburst between the 3 and 7 mm core. When the millimeter-wavelength core is considered the γ-ray production site, IR emission from the dusty torus (e.g., Marscher 2014), stationary knots (e.g., Wehrle et al. 2016), or from the jet sheath are candidate sources of seed photons, as discussed in the previous section.
4.4. γ-ray spectra
Overall, spectral index values around −2.8 (Fig. 3) are close to the value reported in Harris et al. (2012). The typical photon indices of γ-ray bright FSRQs, which are around −2.4, mean that 3C 273 shows a softer photon index, however (see Harris et al. 2012; Linford et al. 2012). Although 3C 273 was less γ-ray bright than these extreme FSRQs (e.g., 3C 279 and 3C 454.3), it seems that the difference in photon index values is a sign of different source physics, like a spectral break or additional emitting components (Harris et al. 2012; H.E.S.S. Collaboration 2018; see also Costamante et al. 2018, for the exception of 3C 273 at constraining high/low states). We also note that our parsec-scale scenario supports what Harris et al. (2012) reported: γ-ray absorption by BLR photons is disfavored in γ-ray bright FSRQs.
γ-ray outbursts, accompanied by variability of the γ-ray spectral index, have been reported in many previous studies (Rani et al. 2013a, 2018; Kim et al. 2018a; Ding et al. 2019). The usual combination is an increase in γ-ray flux density and hardening of photon indices. Unfortunately, we are not able to draw a clear quantitative conclusion from our data becuase the photon statistics are insufficient. However, a simple visual inspection of the monthly binned photon indices in Fig. 4 suggests such an evolution for both the 2016 and 2017 γ-ray outbursts. The peak of the 2016 γ-ray outburst lags a local maximum in the spectral index time series on MJD 57338 by about 40 days, whereas the γ-ray peak of the 2017 outburst coincides with a local photon index peak on MJD 57878. If we identify each of the local photon index peaks with the first shock interaction between a strong disturbance propagating down the jet and the millimeter-wave core, we can make a smooth connection to our parsec-scale scenario for both γ-ray outbursts.
The overall spectral behavior of the monthly binned γ-rays shown in Fig. 3 indicates a transition from a softer-when-brighter state to a harder-when-brighter state at a critical γ-ray flux of around 1.03 × 10−7 ph cm−2 s−1, but the softer-when-brighter trend is only marginally significant (see also Abdo et al. 2010c; Paliya 2015; Kim et al. 2018a, for similar trends in other sources). This transition can be explained by a balance between acceleration and cooling of relativistic particles, which in turn implies that cooling is dominant for the softer-when-brighter trend. This transition might also be related to a shift of the IC peak in the SED (Shah et al. 2019). As the source power increases during strong flares, the IC peak can be shifted to higher energies, which results in a harder-when-brighter trend.
5. Conclusions
The detailed analysis of the γ-ray and radio activity of the blazar 3C 273 during 2015−2019 enables us to address the nature of flaring activity and its connection to the parsec-scale jet. During our observations, 3C 273 experienced two significant γ-ray outbursts, accompanied by strong flaring activity at millimeter-wavelengths. We identified three quasi-stationary components in the compact inner region of the jet: the core, S1, and S2. These features are confirmed to be the main sources of the observed millimeter-wavelength emission, exhibiting powerful flaring variability. The joint analysis of the γ-ray and radio data revealed a strong correlation between the two energy regimes and provided strong evidence that the inner jet region is the production site of γ-ray emission. Overall, the observed behavior can be explained by a scenario in which the radio and γ-ray flares are produced in the core–S1–S2 region by moving disturbances and their interaction with the standing shocks. The emergence of notable polarized knots and high brightness temperatures (up to ∼1012 K) around the times of the γ-ray outbursts further support this scenario. As the blob propagates down the jet, it causes changes in the physical conditions in the ambient flow, resulting in the observed spatial displacements of stationary components (the core and S2) and variations in spectral properties.
Acknowledgments
We would like to thank the anonymous referee for providing fruitful comments on the manuscript. This work makes use of public Fermi data obtained from Fermi Science Support Center (FSSC). This paper makes use of the following ALMA data: ADS/JAO.ALMA#2011.0.00001.CAL. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), MOST and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. This study makes use of 43 GHz VLBA data from the VLBA-BU Blazar Monitoring Program (VLBA-BU-BLAZAR; http://www.bu.edu/blazars/VLBAproject.html), funded by NASA through the Fermi Guest Investigator Program. The VLBA is an instrument of the National Radio Astronomy Observatory. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated by Associated Universities, Inc. Dae-Won Kim acknowledges support from the National Research Foundation of Korea (NRF) through fellowship 2019R1A6A3A13095962. Sascha Trippe and Dae-Won Kim acknowledges support from the NRF grant 2019R1F1A1059721. EVK acknowledges support through the contract ASI-INAF 2015-023-R.1-2019.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010a, ApJ, 722, 520 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010b, ApJ, 710, 1271 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Agudo, I., et al. 2010c, ApJ, 721, 1425 [NASA ADS] [CrossRef] [Google Scholar]
- Abeysekara, A. U., Benbow, W., Bird, R., et al. 2018, ApJ, 856, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Agudo, I., Jorstad, S. G., Marscher, A. P., et al. 2011a, ApJ, 726, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Agudo, I., Marscher, A. P., Jorstad, S. G., et al. 2011b, ApJ, 735, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Algaba, J.-C., Lee, S.-S., Kim, D.-W., et al. 2018, ApJ, 852, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Asano, K., Takahara, F., Kusunose, M., Toma, K., & Kakuwa, J. 2014, ApJ, 780, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Attridge, J. M., Wardle, J. F. C., & Homan, D. C. 2005, ApJ, 633, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Banasiński, P., & Bednarek, W. 2018, ApJ, 864, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Berton, M., Liao, N. H., La Mura, G., et al. 2018, A&A, 614, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blandford, R., Meier, D., & Readhead, A. 2019, ARA&A, 57, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Blumenthal, G. R., & Gould, R. J. 1970, Rev. Mod. Phys., 42, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Bonato, M., Liuzzo, E., Giannetti, A., et al. 2018, MNRAS, 478, 1512 [NASA ADS] [CrossRef] [Google Scholar]
- Böttcher, M. 2019, Galaxies, 7, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Bruni, G., Gómez, J. L., Casadio, C., et al. 2017, A&A, 604, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, L. 2018, ApJS, 235, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Chidiac, C., Rani, B., Krichbaum, T. P., et al. 2016, A&A, 590, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coogan, R. T., Brown, A. M., & Chadwick, P. M. 2016, MNRAS, 458, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Costamante, L., Cutini, S., Tosti, G., Antolini, E., & Tramacere, A. 2018, MNRAS, 477, 4749 [NASA ADS] [CrossRef] [Google Scholar]
- Del Zanna, L., Papini, E., Landi, S., Bugli, M., & Bucciantini, N. 2016, MNRAS, 460, 3753 [NASA ADS] [CrossRef] [Google Scholar]
- Ding, N., Gu, Q. S., Geng, X. F., et al. 2019, ApJ, 881, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Dotson, A., Georganopoulos, M., Kazanas, D., & Perlman, E. S. 2012, ApJ, 758, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Dotson, A., Georganopoulos, M., Meyer, E. T., & McCann, K. 2015, ApJ, 809, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Edelson, R. A., & Krolik, J. H. 1988, ApJ, 333, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Gómez, J. L., Martí, J. M., Marscher, A. P., Ibáñez, J. M., & Marcaide, J. M. 1995, ApJ, 449, L19 [Google Scholar]
- Gómez, J. L., Martí, J. M., Marscher, A. P., Ibáñez, J. M., & Alberdi, A. 1997, ApJ, 482, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, J., Daniel, M. K., & Chadwick, P. M. 2012, ApJ, 761, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Hervet, O., Boisson, C., & Sol, H. 2016, A&A, 592, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- H.E.S.S. Collaboration (Abdalla, H., et al.) 2018, A&A, 619, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- H.E.S.S. Collaboration (Abdalla, H., et al.) 2019, A&A, 627, A159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hodgson, J. A., Krichbaum, T. P., Marscher, A. P., et al. 2017, A&A, 597, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hodgson, J. A., Rani, B., Lee, S.-S., et al. 2018, MNRAS, 475, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Hughes, P. A. 2005, ApJ, 621, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Jorstad, S., & Marscher, A. 2016, Galaxies, 4, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Jorstad, S. G., Marscher, A. P., Lister, M. L., et al. 2005, AJ, 130, 1418 [NASA ADS] [CrossRef] [Google Scholar]
- Jorstad, S. G., Marscher, A. P., Smith, P. S., et al. 2013, ApJ, 773, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Jorstad, S. G., Marscher, A. P., Morozova, D. A., et al. 2017, ApJ, 846, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, D.-W., Trippe, S., Lee, S.-S., et al. 2018a, MNRAS, 480, 2324 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, J.-Y., Lee, S.-S., Hodgson, J. A., et al. 2018b, A&A, 610, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kovalev, Y. Y., Aller, H. D., Aller, M. F., et al. 2009, ApJ, 696, 17 [Google Scholar]
- Kravchenko, E. V., Kovalev, Y. Y., Hovatta, T., & Ramakrishnan, V. 2016, MNRAS, 462, 2747 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, S.-S., Wajima, K., Algaba, J.-C., et al. 2016a, ApJS, 227, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, S.-S., Lobanov, A. P., Krichbaum, T. P., & Zensus, J. A. 2016b, ApJ, 826, 135 [Google Scholar]
- León-Tavares, J., Valtaoja, E., Giommi, P., et al. 2012, ApJ, 754, 23 [NASA ADS] [CrossRef] [Google Scholar]
- León-Tavares, J., Chavushyan, V., Patiño-Álvarez, V., et al. 2013, ApJ, 763, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, T. R., Finke, J. D., & Becker, P. A. 2018, ApJ, 853, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Lico, R., Giroletti, M., Orienti, M., et al. 2017, A&A, 606, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Linford, J. D., Taylor, G. B., & Schinzel, F. K. 2012, ApJ, 757, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Liodakis, I., Romani, R. W., Filippenko, A. V., Kocevski, D., & Zheng, W. 2019, ApJ, 880, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Lisakov, M. M., Kovalev, Y. Y., Savolainen, T., Hovatta, T., & Kutkin, A. M. 2017, MNRAS, 468, 4478 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lister, M. L., Cohen, M. H., Homan, D. C., et al. 2009, AJ, 138, 1874 [NASA ADS] [CrossRef] [Google Scholar]
- Lobanov, A. P. 1998, A&AS, 132, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marscher, A. P. 2014, ApJ, 780, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P. 2016, Galaxies, 4, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P., Jorstad, S. G., Larionov, V. M., et al. 2010, ApJ, 710, L126 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, M., Scargle, J. D., & Blandford, R. D. 2019, ApJ, 877, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Mizuno, Y., Gómez, J. L., Nishikawa, K.-I., et al. 2015, ApJ, 809, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Nalewajko, K. 2013, MNRAS, 430, 1324 [NASA ADS] [CrossRef] [Google Scholar]
- Nandikotkur, G., Jahoda, K. M., Hartman, R. C., et al. 2007, ApJ, 657, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Paliya, V. S. 2015, ApJ, 808, L48 [NASA ADS] [CrossRef] [Google Scholar]
- Park, J., Lee, S.-S., Kim, J.-Y., et al. 2019, ApJ, 877, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Petropoulou, M., & Dimitrakoudis, S. 2015, MNRAS, 452, 1303 [NASA ADS] [CrossRef] [Google Scholar]
- Piano, G., Munar-Adrover, P., Pacciani, L., et al. 2018, A&A, 616, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plavin, A. V., Kovalev, Y. Y., Pushkarev, A. B., & Lobanov, A. P. 2019, MNRAS, 485, 1822 [NASA ADS] [CrossRef] [Google Scholar]
- Potter, W. J., & Cotter, G. 2013, MNRAS, 431, 1840 [NASA ADS] [CrossRef] [Google Scholar]
- Prince, R. 2019, ApJ, 871, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Pushkarev, A. B., Kovalev, Y. Y., & Lister, M. L. 2010, ApJ, 722, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Ramakrishnan, V., Hovatta, T., Nieppola, E., et al. 2015, MNRAS, 452, 1280 [CrossRef] [Google Scholar]
- Rani, B., Lott, B., Krichbaum, T. P., Fuhrmann, L., & Zensus, J. A. 2013a, A&A, 557, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rani, B., Krichbaum, T. P., Fuhrmann, L., et al. 2013b, A&A, 552, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rani, B., Jorstad, S. G., Marscher, A. P., et al. 2018, ApJ, 858, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Shah, Z., Jithesh, V., Sahayanathan, S., Misra, R., & Iqbal, N. 2019, MNRAS, 484, 3168 [NASA ADS] [CrossRef] [Google Scholar]
- Shepherd, M. C. 1997, ASP Conf. Ser., 125, 77 [Google Scholar]
- Sironi, L., & Spitkovsky, A. 2014, ApJ, 783, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Strauss, M. A., Huchra, J. P., Davis, M., et al. 1992, ApJS, 83, 29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tavecchio, F., Ghisellini, G., Bonnoli, G., & Ghirlanda, G. 2010, MNRAS, 405, L94 [NASA ADS] [CrossRef] [Google Scholar]
- The Fermi-LAT Collaboration (Abdollahi, S., et al.) 2020, ApJS, 247, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Trippe, S., Neri, R., Krips, M., et al. 2012, A&A, 540, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valtaoja, E., Lähteenmäki, A., Teräsranta, H., & Lainela, M. 1999, ApJS, 120, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Vol’vach, A. E., Kutkin, A. M., Vol’vach, L. N., et al. 2013, Astron. Rep., 57, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Wehrle, A. E., Marscher, A. P., Jorstad, S. G., et al. 2012, ApJ, 758, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Wehrle, A. E., Grupe, D., Jorstad, S. G., et al. 2016, ApJ, 816, 53 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Additional table
Parameters of the 43 GHz components obtained from Gaussian model fits.
All Tables
All Figures
 |
Fig. 1. γ-ray and radio light curves of 3C 273 in 2015−2019. From top to bottom: ALMA band 3 (∼100 GHz) overlaid on the VLBA 43 GHz total flux, Fermi-LAT fluxes using monthly binning, and Fermi-LAT fluxes using weekly binning. For the γ-ray light curves, the 2 σ upper limits are indicated by red downward arrows. The vertical dashed lines show three γ-ray outbursts that are identified in the weekly light curve. Each of the shaded areas spans 100 days centered at the peak of a γ-ray outburst. |
| In the text | |
 |
Fig. 2. Zoomed-in γ-ray light curves of 3C 273, binned into one-day time bins, for the three γ-ray flaring periods indicated by the shaded areas in Fig. 1. Upper panels, in each diagram: photon indices at the same time resolution. Average photon index values are marked by horizontal solid lines. The vertical dashed lines mark the peak times of the γ-ray outbursts in the daily light curves. |
| In the text | |
 |
Fig. 3. Photon index vs. flux for the weekly binned (top) and monthly binned (bottom) γ-ray light curves. The dashed lines indicate the average photon index values. The vertical solid line in the bottom panel marks a break flux value of 1.03 × 10−7 ph cm−2 s−1. The light blue lines show the linear regression lines for photon indices above and below the break flux. |
| In the text | |
 |
Fig. 4. Photon index vs. time of the weekly and monthly γ-rays. Top panel: entire time range of our observations. Bottom panels: zoomed-in views on the data around the times of the 2016A and 2017A γ-ray outbursts defined in Fig. 2 (marked by vertical dashed lines). Error bars correspond to 1σ uncertainties. |
| In the text | |
 |
Fig. 5. DCF curves and flux–flux plots comparing the 3 mm radio and γ-ray light curves in 2015−2019 for the monthly γ-ray fluxes (top panels) and the weekly γ-ray fluxes (bottom panels). Orange curves in the left panels indicate the best Gaussian fits to the DCF curves. For the flux-flux plots (right panels), the ALMA light curve has been shifted in time by the delays found from the Gaussian fits. The Pearson correlation coefficients (rp) and corresponding p-values (pp) are shown in the flux-flux plots. |
| In the text | |
 |
Fig. 6. Same as Fig. 5, but using only the weekly γ-ray fluxes in the time range 2015−2017. |
| In the text | |
 |
Fig. 7. 7 mm VLBA images of 3C 273 during the 2016 γ-ray outburst. The contours and color scale represent the total intensity and linearly polarized intensity, respectively. Contour levels are 1%, 2%, 4%, 8%, etc., 64%, 80% of the peak intensity. A zoomed-in view on the core region is provided in the subplots. White line segments indicate the EVPA directions uncorrected for Faraday rotation. Circular Gaussian jet components are indicated by green (for the three stationary components) and yellow (for the others) cirles with a cross. The vertical dot-dashed lines show the average positions of the S1 (=0.1 mas) and S2 (=0.21 mas) components projected onto the x-axis. The vertical solid line indicates the core position. All maps are restored with a 0.2 × 0.2 mas beam (indicated at the bottom left). |
| In the text | |
 |
Fig. 8. Same as in Fig. 7, but for the 2017 γ-ray outburst. Contour levels are 2.5%, 5%, 10%, etc., 40%, 80% of the peak intensity. |
| In the text | |
 |
Fig. 9. Left: flux density (top) and distance from the core (bottom) of the core, S1, and S2 derived from Gaussian modeling of the jet components as shown in Fig. 7. Right: same as the left panels, but for the observations in Fig. 8. The vertical dashed lines correspond to the times of the 2016 and 2017 γ-ray outbursts. The average distances of S1 and S2 (i.e., 0.16 and 0.33 mas from the core) are indicated by the horizontal solid lines. |
| In the text | |
 |
Fig. 10. Source-frame brightness temperatures (Tb) of the core, S1, and S2. Vertical dashed lines indicate the times of the γ-ray outbursts. Upward arrows mark limits on Tb, calculated using the spatial resolution limit for each component whenever the observed size is smaller than this limit. |
| In the text | |
 |
Fig. 11. 3 mm ALMA light curve around the time of the 2017 γ-ray outburst (vertical dashed line). The model that combines an exponential rise with a subsequent exponential decay (as introduced by Valtaoja et al. 1999, but without fixing the decay timescale) is indicated by the red curve. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


