| Issue |
A&A
Volume 634, February 2020
|
|
|---|---|---|
| Article Number | A134 | |
| Number of page(s) | 16 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201936669 | |
| Published online | 25 February 2020 | |
Contribution from stars stripped in binaries to cosmic reionization of hydrogen and helium
1
The Observatories of the Carnegie Institution for Science, 813 Santa Barbara St., Pasadena, CA 91101, USA
e-mail: ygoetberg@carnegiescience.edu
2
Center for Astrophysics, Harvard & Smithsonian, 60 Garden Street, Cambridge, MA 02138, USA
3
Anton Pannekoek Institute for Astronomy, University of Amsterdam, 1090 GE Amsterdam, The Netherlands
4
GRAPPA, GRavitation and AstroParticle Physics Amsterdam, University of Amsterdam, 1090 GE Amsterdam, The Netherlands
5
Department of Astronomy, University of Washington, Seattle, WA 98195, USA
6
Geneva Observatory, University of Geneva, 1290 Sauverny, Switzerland
7
School of Physics, Trinity College Dublin, The University of Dublin, Dublin 2, Ireland
8
Department of Physics & Astronomy, Johns Hopkins University, Baltimore, MD 21218, USA
9
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
Received:
10
September
2019
Accepted:
14
November
2019
Massive stars are often found in binary systems, and it has been argued that binary products boost the ionizing radiation of stellar populations. Accurate predictions for binary products are needed to understand and quantify their contribution to cosmic reionization. We investigate the contribution of stars stripped in binaries because (1) they are, arguably, the best-understood products of binary evolution, (2) we recently produced the first radiative transfer calculations for the atmospheres of these stripped stars that predict their ionizing spectra, and (3) they are very promising sources because they boost the ionizing emission of stellar populations at late times. This allows stellar feedback to clear the surroundings such that a higher fraction of their photons can escape and ionize the intergalactic medium. Combining our detailed predictions for the ionizing spectra with a simple cosmic reionization model, we estimate that stripped stars contributed tens of percent of the photons that caused cosmic reionization of hydrogen, depending on the assumed escape fractions. More importantly, stripped stars harden the ionizing emission. We estimate that the spectral index for the ionizing part of the spectrum can increase to −1 compared to ≲ − 2 for single stars. At high redshift, stripped stars and massive single stars combined dominate the He II-ionizing emission, but we expect that active galactic nuclei drive cosmic helium reionization. Further observational consequences we expect are (1) high ionization states for the intergalactic gas surrounding stellar systems, such as C IV and Si IV, and (2) additional heating of the intergalactic medium of up to a few thousand Kelvin. Quantifying these warrants the inclusion of accurate models for stripped stars and other binary products in full cosmological simulations.
Key words: binaries : close / dark ages / reionization / first stars / galaxies: stellar content / ultraviolet: stars
© ESO 2020
1. Introduction
Cosmic reionization refers to the process in the history of our Universe when the intergalactic medium (IGM) became ionized. How this process occurred is still uncertain and depends on two main questions: which were the sources of ionizing photons, and what fraction of these photons escaped to become available for the ionization of the IGM. For the sources that emitted the ionizing radiation, which are the focus of this paper, the current consensus is that stellar populations produced most of the photons that ionized intergalactic hydrogen and neutral helium, while active galactic nuclei (AGN) produced the majority of the photons that fully ionized helium (Barkana & Loeb 2001; Faucher-Giguère et al. 2009; Worseck et al. 2016; McQuinn 2016; Dayal & Ferrara 2018). However, the relative contributions from AGN and stellar populations are not fully constrained so far.
Numerical and analytical models of the early Universe (e.g., Gnedin & Ostriker 1997; McQuinn et al. 2007; Robertson et al. 2010; Haardt & Madau 2012; Finlator et al. 2018; Katz et al. 2019) reproduce the observed completion of hydrogen reionization around a redshift, z, of ∼ 6 (Fan et al. 2006a). However, to achieve this, the models require that a large portion of the produced ionizing photons escape the host galaxies and reach the IGM. Only when a high escape fraction (fesc) of 20% or higher at high redshifts is assumed do the simulations reach complete reionization by z ∼ 6, as observations indicate (Bolton & Haehnelt 2007a; Ouchi et al. 2009; Haardt & Madau 2012; Robertson et al. 2013). With a low escape fraction of a few percent, similar to what is observed locally and at intermediate redshifts (e.g., Izotov et al. 2016a; Steidel et al. 2018), reionization is significantly delayed, which does not match several observational constraints (Fan et al. 2006b). While it is possible that the escape fraction was indeed higher in the early Universe (Inoue et al. 2006), other effects could impact the amount of ionizing photons that reach the IGM at high redshifts. Examples are a higher cosmic star formation rate than is usually assumed because of faint and therefore undetected galaxies in the distant Universe (see Atek et al. 2015; Livermore et al. 2017; Dayal & Ferrara 2018) and higher ionizing emission from quasars at high redshift than is usually considered (Madau & Haardt 2015). Here we explore additional contribution from stellar sources that have not been investigated in detail: stars stripped of their hydrogen-rich envelopes in binary interaction with a close companion.
Recent advances in stellar astrophysics indicate that several types of stars that emit ionizing radiation are still often neglected in models of the ionizing output from galaxies. Efforts have been made to include stellar rotation (Meynet & Maeder 2005; Levesque et al. 2012; Georgy et al. 2013; Leitherer et al. 2014) and very massive stars with masses above 100 M⊙ (Crowther et al. 2016, see also Vanzella et al. 2019a for a possible high-redshift super-starcluster) in models for the spectra of stellar populations. Observational surveys show evidence that massive and intermediate stars have binary companions that are located so closely that interaction between the two stars is inevitable as the stars swell during their evolution (e.g., Sana et al. 2012; Moe & Di Stefano 2017). Such binary interaction can lead to severe exchange or loss of stellar material and possibly even to coalescence of the stars.
Pioneering work has been done by the team that developed the binary population and spectral synthesis (BPASS) code (Eldridge & Stanway 2009, 2012; Eldridge et al. 2017), who provided observationally testable predictions for stellar populations that account for binary interaction. These include emission rates of ionizing photons (Stanway et al. 2016, see also Van Bever et al. 1999), the production efficiency of H-ionizing photons (ξion, Wilkins et al. 2016), and nebular emission line ratios for nearby and distant stellar populations (Stanway et al. 2014; Xiao et al. 2018). Using these results, sophisticated models including the effect of interacting binaries have been created for cosmic reionization and the evolution of galaxies (Ma et al. 2016; Rosdahl et al. 2018). The main result is that when interacting binaries are included, the reionization occurs earlier compared to when only single stars are considered. Another result is that interacting binaries may cause additional heating of the IGM, and that the delay in the production of ionizing photons from interacting binaries relative to isolated massive stars may allow for higher escape fractions.
However, the different contributions from individual sources need to be carefully analyzed separately to understand which stars are responsible for the ionizing emission, and maybe more importantly, how uncertain the predicted emission rates of ionizing photons are. Here, we therefore chose to focus on modeling the contribution from one type of binary products: stars that are stripped of their hydrogen-rich envelopes. Envelope-stripping is predicted to be the most common type of interaction in binaries, as the fate of one-third of all massive stars (Sana et al. 2012). During either stable or unstable mass-transfer, the hydrogen-rich envelope of one star is lost or partially transferred to the second star, leaving the hot, helium-rich core exposed (Kippenhahn & Weigert 1967; Paczyński 1967; Podsiadlowski et al. 1992; Ivanova et al. 2013). These stripped stars are so hot (∼50 − 100 kK) that the majority of their emitted photons are able to ionize hydrogen (Götberg et al. 2017, hereafter Paper I). The envelope-stripping is usually completed after or when the donor star reaches central hydrogen exhaustion, meaning that stripped stars are formed with a time delay that roughly corresponds to the main-sequence duration of the donor star. Because stars over a wide range of masses can become stripped, this means that the ionizing radiation from stripped stars is emitted over an extended period of time after a starburst (several 100 Myr, Götberg et al. 2019). It is likely that the ionizing radiation from stripped stars therefore escapes the birth environment and reaches the IGM, as strong stellar winds and the first supernovae are expected to remove most of the surrounding gas within several megayears (Myr) after star formation started (e.g., Krumholz et al. 2019). If some gas is still present when stripped stars are created, it is likely that their hard ionizing emission produces a characteristic nebular emission line morphology (Xiao et al. 2018, see also Stanway et al. 2014).
Envelope-stripping is probably also the type of binary interaction that is most well understood because models suggest that it is a common and often inevitable evolutionary phase and also because several stripped stars have been observed (Gies et al. 1998; Groh et al. 2008; Peters et al. 2008, 2013; Wang et al. 2017, 2018; Chojnowski et al. 2018). The number of observed stripped stars is small, but the reason is likely that most stripped stars are hidden by their bright companion stars in optical wavelengths and are therefore difficult to discover (Paper I, see also Wang et al. 2018). The frequently observed hydrogen-poor supernovae are also evidence for the existence of a large population of stripped stars (Smith et al. 2011; Lyman et al. 2016; Liu et al. 2016; Shivvers et al. 2017; Graur et al. 2017). Their low ejecta masses (e.g., Drout et al. 2011; Modjaz et al. 2016) and the apparent difficulty of directly observing their progenitors (e.g., Eldridge et al. 2013) suggest that most of these explosions are not the deaths of massive Wolf-Rayet (WR) stars, but that they originate from lower mass stars that are hydrogen poor, which is also in agreement with the old ages inferred for hydrogen-poor supernova sites using nebular emission features (Xiao et al. 2019). In the classical framework of isolated binary evolution, stripped stars are additionally thought to play important roles as the progenitors of gravitational wave events (Dewi & Pols 2003; Belczynski et al. 2016; Tauris et al. 2017; Kruckow et al. 2018). With the rapidly increasing number of detected gravitational wave events, understanding the impact of stripped stars both nearby and over cosmic time is becoming urgent.
In addition to stripped stars, several other binary products likely contributed to the photon budget during the reionization, but they are not the topic of this work. An example is stars that gain mass through mass transfer with a companion star and binary stars that merge. These stars are thought to appear as massive blue stragglers, that is, more massive main-sequence stars than their progenitors, leading to an increase in ionizing emission from massive OB-type main-sequence stars (Braun & Langer 1995; Van Bever et al. 1999; Belkus et al. 2003; Chen & Han 2009; Schneider et al. 2014; de Mink et al. 2014). Another effect of binary interaction is rapid rotation induced by mass accretion, coalescence, or tidal forces, which can cause the interior of the rotating stars to mix. This in turn provides the burning regions with fresh fuel (Packet 1981; de Mink et al. 2009, 2013). If wind mass-loss and the associated loss of angular momentum is low, as is the case at low metallicity, and depending on the properties of internal magnetic fields and the efficiency of rotational mixing, the star continues to rotate rapidly and may evolve chemically homogeneously (Yoon & Langer 2005; Cantiello et al. 2007; Eldridge et al. 2008; de Mink et al. 2009; Groh et al. 2019). The result is that the stars remain small and hot throughout their lives, which maintains their high ionizing emission rates (Szécsi et al. 2015; Kubátová et al. 2019). Last, accreting white dwarfs, neutron stars, or black holes are expected to radiate X-rays and dominate the output of 1 keV photons from stellar populations. They are likely an unimportant source of the extreme ultraviolet photons that are responsible for the reionization of hydrogen, but might be interesting for helium reionization (e.g., Fragos et al. 2013; Chen et al. 2015; Madau & Fragos 2017; Schaerer et al. 2019, see also Woods & Gilfanov 2013, 2014; Senchyna et al. 2019). However, calculations suggest that accreting compact objects are likely subdominant to quasars (Upton Sanderbeck et al. 2018).
Well-established spectral synthesis codes that are commonly used to represent the radiative emission from stars during reionization are, for example, STARBURST99 (Leitherer et al. 1999, 2014) and GALAXEV (Bruzual & Charlot 2003). Efforts have been made to account for the effect of interacting binaries (van Bever & Vanbeveren 1998; Zhang et al. 2004; Vanbeveren et al. 2007; Chen & Han 2009), with particular progress in the field of the distant Universe made by BPASS, as previously mentioned.
Modeling the radiative contribution from stripped stars has been a challenge because no spectral models created for stripped stars have been available, and their spectra have been represented with spectral models made for other types of stars (e.g., Eldridge et al. 2017). However, Götberg et al. (2018, hereafter Paper II) presented grids of evolutionary and spectral models created for stars that are stripped in binaries, which we synthesized to estimate the contribution from stripped stars to stellar populations in Götberg et al. (2019, hereafter Paper III). These models are publicly available on CDS1 and via the STARBURST99 online interface2.
In this paper, we estimate the importance of stars that are stripped in binaries over cosmic history and discuss their roles during the reionization of hydrogen and helium. This is the fourth paper in a series in which we describe and discuss the effect of the ionizing radiation that is emitted by stripped stars, but it can be read independently. We use our evolutionary and spectral models made with the stellar evolution code MESA (Paxton et al. 2011, 2013, 2015, 2018, 2019) and the radiative transfer code CMFGEN (Hillier 1990; Hillier & Miller 1998), presented in Paper II, and our population synthesis presented in Paper III, together with a simple model for cosmic reionization to understand the relative contributions from stripped stars during the evolution of the Universe. We emphasize that our novel approach of developing customized atmosphere models for stripped stars using CMFGEN allows us to study them in more depth and thus to understand their role in stellar populations over cosmic time better than previous studies.
We structure the article as follows. In Sect. 2 we describe how we model the ionizing radiation from stellar populations, from AGN, and over cosmic time. In Sect. 3 we present the ionizing emission and the influence of stripped stars on the hardness of the ionizing radiation that emerges into the IGM. In Sect. 4 we describe the role of stripped stars during reionization by quantifying the fraction of ionizing photons that they contribute and their effect on the time at which reionization is completed. Our models suggest that stripped stars affect the conditions in the IGM, which in some cases may influence observable quantities. In Sect. 5 we therefore discuss the possible effect of stripped stars on intergalactic absorption features from metals and heating of the IGM. In Sect. 6 we summarize our findings and conclusions.
2. Modeling cosmic reionization
In this section, we first describe the models that we adopted for the sources of ionizing radiation in Sect. 2.1. Then, we describe the semi-analytical approach we chose to simulate the reionization of hydrogen and helium in Sect. 2.2. We visualize the method in Fig. 1.
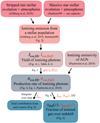 |
Fig. 1. Flowchart visualizing the method we use to model the reionization of hydrogen and helium accounting for ionizing radiation from stellar populations and AGN. The quantities that we consider uncertain are written in red. See Sect. 2 for details and also, e.g., Madau et al. (1999) and Haardt & Madau (2012) where similar methods have been employed. (The massive stars in STARBURST99 are represented by evolutionary models from the Geneva grids (Ekström et al. 2012; Levesque et al. 2012; Georgy et al. 2013), atmosphere models from CMFGEN for Wolf-Rayet stars (Hillier & Miller 1998; Smith et al. 2002), and atmosphere models from WM-BASIC for OB-stars (Pauldrach et al. 2001; Leitherer et al. 2010).) |
2.1. Sources of ionizing radiation
We considered stars that are stripped in binaries, massive main-sequence stars, WR stars, and AGN as sources of ionizing radiation during the reionization of hydrogen and helium. Below, we describe how we model the ionizing emissivity over cosmic time for each of these sources.
2.1.1. Stellar populations including stars that are stripped in binaries
We considered stripped stars that are created through stable mass-transfer and common-envelope evolution. In these formation channels, the compact helium core of the donor star is exposed. This stripped star is hot (≳30 000 K) and long lived if interaction occurred prior to the completion of central helium burning, which is an evolutionary phase that constitutes about 10% of the total stellar lifetime (see Paper I and Paper II). Stripped stars are formed over an extended time period after a burst of star formation, mainly because they originate from lower mass stars than massive WR and O-type stars. This allows the ionizing radiation to be emitted up to several hundred Myr after a starburst (Paper III). This is shown in Fig. 2, which shows the emission rates of H I- and He II-ionizing photons from a starburst. The massive stars modeled by STARBURST99 are predicted to emit ionizing photons early, primarily within the first ∼10 Myr. Stripped stars are formed after ∼10 Myr and emit ionizing photons for several hundred Myr. This is consistent with some of the predictions from the binary population synthesis code BPASS. For more details, see Paper III, from which Fig. 2 is adapted.
 |
Fig. 2. Emission rates of ionizing photons from a starburst of 106 M⊙ as a function of time. We show the emission rates from stripped stars in dark blue, from massive stars in light blue (using STARBURST99), and we also show the predicted emission rates from the code BPASS in gray. The shaded regions span the emission rates for metallicities between Z = 0.0002 and Z = 0.014, and the solid lines show the emission rates for solar metallicity (Z = 0.014). Top panel: emission rate of H I-ionizing photons, and bottom panel: emission rate of He II-ionizing photons. Stripped stars are clearly responsible for late emission of ionizing photons in a starburst. This figure is adapted from Paper III. |
We modeled the ionizing output from stripped stars using the detailed evolutionary and spectral models presented in Paper II. These models are customized for stars that are stripped in binaries. They were computed for initial donor star masses between 2 and 18 M⊙ using the binary stellar evolutionary code MESA (Paxton et al. 2011, 2013, 2015, 2018, 2019) and the non-LTE radiative transfer code CMFGEN (Hillier 1990; Hillier & Miller 1998). We consider four metallicities Z = 0.014, 0.006, 0.002, and 0.0002, which approximately correspond to the metallicity of the Sun, the Large and Small Magellanic Clouds, and a very low metallicity environment that likely existed at high redshifts.
We computed the total radiative output from stripped stars by simulating a stellar population based on our detailed models. Details can be found in Paper III, but we summarize the main assumptions here. We drew initial stellar masses, Minit, assuming a Kroupa (2001) initial mass function (IMF) with lower and upper mass limits at 0.1 and 100 M⊙. We determined which stars are the most massive stars in binary systems by assuming the mass-dependent binary fraction of Moe & Di Stefano (2017). We drew companion stars to these primaries by assuming a flat mass ratio (q ≡ Minit, 2/Minit, 1) distribution between 0.1 and 1, in agreement with observations from Kiminki & Kobulnicky (2012), Sana et al. (2012), and as summarized in Moe & Di Stefano (2017). We assumed that the initial orbital period for the binary systems follows the distribution of Sana et al. (2012) for binaries, in which the most massive star in the system is more massive than 15 M⊙, and the distribution of Öpik (1924) when its mass is lower than 15 M⊙. We assumed the initial period range to span from binaries that touch at birth up to 103.7 days (Moe & Di Stefano 2017). We determined when interaction is initiated by comparing the sizes of the Roche lobes of the stars (Eggleton 1983) with the sizes of the stars, which we measured from evolutionary models of single stars that have the same assumptions for the interior as our binary models (Paper II). Whether the system initiates stable mass-transfer or common-envelope evolution was determined by comparing the mass ratio to a critical value, qcrit, above which stable mass-transfer follows and below which a common envelope develops (qcrit = 0.65 and 0.4 for main-sequence and Hertzsprung gap donors, following de Mink et al. 2007 and de Mink et al. 2013, respectively). In case of stable mass-transfer, the result is a binary system containing a stripped star. For the systems that initiated a common envelope, we determined whether the envelope is successfully ejected by taking the classical α-prescription (Webbink 1984) and setting the efficiency parameter, αCE, and the structure parameter, λCE, to be αCEλCE = 0.5, which is comparable with the current literature (e.g., Dewi & Tauris 2000; Hurley et al. 2002; Izzard 2004; Fragos et al. 2019). This choice results in low numbers of stripped stars that are created through common envelope ejections in our models (Paper III), but we note that the common-envelope parameters are poorly constrained, which could affect the predictions for the number of stripped stars in stellar populations. We assumed that all stripped stars with progenitor stars of the same mass have the same properties, independent of the formation channel.
We consider our predicted emission rates of H I- and He I-ionizing photons from stripped stars to be relatively robust because the properties of stripped stars are predicted to be insensitive to the orbital period or the assumed mass ratio in most cases (but see Yoon et al. 2017; Sravan et al. 2019, who showed that the properties of stripped stars are affected at very low metallicities or at very long initial periods). The number of stripped stars in stellar populations also affects the emission rates of ionizing photons. We consider the predicted number of stripped stars to be relatively robust because initial conditions for massive binaries, such as the binary fraction, orbital period distribution, and mass ratio distribution, have been constrained observationally (Sana et al. 2012, see also Moe & Di Stefano 2017). Using binary population synthesis models together with observed data, Sana et al. (2012) found that one-third of the massive stars become stripped. Stellar wind mass-loss from stripped stars is not well known, which is important to take into account because dense stellar winds can block ionizing emission. In Paper I, we found that H I- and He I-ionizing emission from stripped stars only varies by a factor of two for a range of wind mass-loss rates, however. In contrast, the He II-ionizing emission is sensitive to variations in the wind mass-loss rate, and we therefore consider our predicted emission rates of He II-ionizing photons to be less certain (see Paper I, for a discussion). However, as we show in this study, the contribution from stripped stars to the ionization of He II is far smaller than that from quasars in any case.
Our models concern only stripped stars with progenitors of initial masses ≤20 M⊙, which excludes the contribution from higher mass stripped stars that could provide an additional boost of ionizing emission. Because it is uncertain how common and how hot such massive stripped stars are, predictions for their contribution are also uncertain. In addition, our models for stripped stars are made for stable mass-transfer, which likely means that a small amount of the hydrogen-envelope remains, in contrast to what is expected from the violent common-envelope evolution (cf. Ivanova 2011; Yoon et al. 2017; Paper I). Because the stripped stars created through common-envelope evolution most likely have less of their hydrogen envelope left after interaction, they are expected to be hotter, which also causes them to emit harder ionizing radiation. The difference in ionizing emission rates between the stripped stars that are created through the two evolutionary channels is small at high metallicity, but it might be significant for low-metallicity environments (cf. Paper III). We expect that including more accurate models for stripped stars that are created through common-envelope evolution would affect the emission rate of H I-ionizing photons only weakly, but the emission rate of He II-ionizing photons would be affected more significantly. The reason is that the bulk of the emission from our stripped star models is already H I-ionizing, but the He II-ionizing emission is sensitive to temperature variations. To accurately account for the ionizing emission from high-mass stripped stars and the higher temperatures of stripped stars that are created through common-envelope evolution, more detailed evolutionary models are required. Studies like these are important, but they are beyond the scope of this paper.
To represent the ionizing output from a full stellar population including massive main-sequence stars and WR stars, we combined our predictions for stripped stars with estimates for single stars using the spectral synthesis code STARBURST99 (Leitherer et al. 1999, 2010, 2014), as detailed in Paper III. Binaries that have not yet interacted are mostly main-sequence stars and can therefore also be considered to be well modeled by STARBURST99. Our approach does not account for the emission from other binary products, such as merger stars or stars that gained mass through accretion.
Yields of ionizing photons, Iion. A simple way to compare the ionizing radiation from different types of stars is to integrate their emission rates of ionizing photons (shown in Fig. 2) over time and normalize by the total mass of formed stars. This quantity is referred to as the yield of ionizing photons, Iion, and describes the number of produced ionizing photons per solar mass of formed stars, or equivalently, the emission rate of ionizing photons per star formation rate (see Madau & Dickinson 2014).
For the yields of H I-ionizing photons, we find that stripped stars produce Iion,H I ≈ 1051.9 s−1 (M⊙ year−1)−1, while massive stars produce Iion,H I ≈ 1053 s−1 (M⊙ year−1)−1 in the case of solar metallicity. This means that stripped stars are responsible for about 5% of the total production of H I-ionizing radiation from stellar populations. Despite providing a small fraction of the total budget, we argue that the delay in the photon production from stripped stars likely enhances their importance for reionization (see Sect. 4). For the yield of He II-ionizing photons at solar metallicity, our models predict that Iion,He I ≈ 1049.1 s−1 ( M⊙ year−1)−1 for stripped stars, which is about an order of magnitude higher than what massive stars produce. The yields of ionizing photons are affected by metallicity (for details, see Appendix A).
Relation between redshift and metallicity. The emission rate of H I-ionizing photons from massive main-sequence stars is known to increase with decreasing metallicity (e.g., Topping & Shull 2015). The emission from stripped stars is only mildly affected by metallicity, leading to emission rates of H I-ionizing photons at Z = 0.002 that are about a factor of two higher than at solar metallicity (Paper I; Paper II). The yields of He II-ionizing photons show large fluctuations with metallicity for single-star populations and large variations between different spectral synthesis models, but remain relatively constant for stripped stars with Z ≥ 0.002 (see Appendix A).
The early stellar populations that reionized the Universe were likely metal poor (e.g., Balestra et al. 2007; Gallazzi et al. 2008). We account for the change in metallicity over redshift by assuming that all stellar populations have an average metallicity that evolves with redshift following the relation log10⟨Z/Z⊙⟩ = 0.153 − 0.074z1.34 of Madau & Fragos (2017, see also Kewley & Kobulnicky 2007), where we assumed solar metallicity to be Z⊙ ≡ 0.014 (Asplund et al. 2009). We then interpolated the yields of ionizing photons over metallicity using log-scales for the metallicity and the yields to reach a trend as smooth as possible. Next, we used the scaling between metallicity and redshift to obtain the appropriate yields of ionizing photons for each redshift. Our method is approximate because a spread of metallicity has been observed at each redshift (see Madau & Dickinson 2014, and references therein). However, the weak sensitivity of the H I-ionizing radiation to metallicity described above allows us to consider only a mean metallicity per redshift. The already uncertain predictions for the He II-ionizing emission are significantly affected by metallicity variations.
Production rates of ionizing photons, ṅion. We describe the rate with which stellar populations produce ionizing photons over cosmic time, ṅion, by multiplying the yields of ionizing photons, Iion, with the cosmic star formation rate density, ψ(z),
We employed the cosmic star-formation history of Madau & Dickinson (2014, their Eq. (15)) together with the yields of ionizing photons that we presented previously. The star formation rate density of Madau & Dickinson (2014) reaches a peak at about z ∼ 2−3 and decreases for both higher and lower redshifts. Star formation in galaxies at high redshift that are too faint to be observed has been suggested to provide a large portion of the ionizing emission and to affect the reionization (e.g., Bouwens et al. 2012; Wise et al. 2014). However, the relative importance of stripped stars to massive stars remains the same independent of the star-formation history. Therefore we do not expect significant changes in the relative contribution from stripped stars when a different star-formation history is considered, although the estimated time of reionization may change.
Equation (1) assumes that all ionizing photons that stellar populations produce are emitted in the instant the stars are formed. In reality, stars emit ionizing photons during the entirety or parts of their lifetimes, as shown in Fig. 2. However, approximating the ionizing emission to be instantaneous is justified when a time interval is considered that is much longer than the stellar lifetimes. This is the case for cosmic reionization, which lasts for several hundred Myr, and most of the emission of ionizing photons from stellar populations extends over about 50 Myr (Paper III and Fig. 2).
Escape fraction, fesc. We followed the approach of Haardt & Madau (2012) when we simulated the escape fraction of ionizing photons over cosmic time. Their function for the escape fraction increases from 0% in the local Universe to 20% at z ∼ 7 and stalls at 100% at z ∼ 11. We modified the function slightly to match what we consider realistic for massive stars and for stripped stars separately. We shifted the escape fraction up to 2% for massive stars and 50% for stripped stars in the local Universe. We chose the lower limit for massive stars because star-forming regions in the nearby Universe have been observed to have an escape fraction of a few percent (e.g., Mostardi et al. 2013; Doran et al. 2013; Leitherer et al. 2016; Izotov et al. 2016a,b; Steidel et al. 2018; Tanvir et al. 2019), which simulations agree well with (Paardekooper et al. 2011, 2015; Shull et al. 2012; Roy et al. 2015; Ma et al. 2015; Rutkowski et al. 2016). However, simulations also show that the escape fraction increases with time after star formation has stopped, and it is likely to reach ∼50% after a few tens of Myr because of the strong stellar winds and supernovae from massive stars (Kimm & Cen 2014; Trebitsch et al. 2017; Kimm et al. 2019; Kim et al. 2019). At this time, stripped stars are present in the stellar populations, and many are yet to be created (see Paper III). Studies presenting compilations over a range of redshifts indicate that the escape fraction was higher at early times (Inoue et al. 2006; Faisst 2016; Fletcher et al. 2019, see however Gnedin et al. 2008). Because galaxies were small in the early Universe (Bouwens et al. 2017), they had a larger relative surface area, which leads to a higher leakage of ionizing photons (Wise & Cen 2009; Wise et al. 2014). This motivates the increase in the function for the escape fraction with higher redshift. To avoid completely transparent galaxies, we also truncated the functions for the escape fractions so that they did not exceed 80%. The function of Haardt & Madau (2012) is relatively steep, and we therefore also multiplied the function with a factor of 0.5 to allow for lower escape fractions at higher redshifts. The results are the following functions:
Haardt & Madau (2012) did not allow He II-ionizing photons produced in galaxies to emerge into the IGM. We allowed the emission of He II-ionizing photons, using the same escape fractions, with the motivation that photons may be able to escape through open holes in the interstellar medium, which means that no material can prevent the radiation from reaching the IGM. Recent observational studies of high-redshift galaxies support this idea (see Vanzella et al. 2019b; Ji et al. 2020; Rivera-Thorsen et al. 2019). We show our assumed escape fractions as a function of redshift in Fig. 3.
 |
Fig. 3. Redshift-dependent escape fractions that we assume in our standard model for stripped stars (dark blue), massive stars (light blue), and AGN (beige). The functions for the escape fraction for stripped stars and massive stars are given in Eqs. (2) and (3), respectively. We also show the escape fraction of Haardt & Madau (2012) for stellar populations as a gray dotted line; it is marked HM12. |
The escape fraction is an uncertain parameter that affects the resulting time of reionization and the contribution from the different sources of ionizing radiation. To explore the dependence on the escape fraction, we also considered three models with constant escape fractions, one with high escape fractions, one with low escape fractions, and one in which stripped stars have a high escape fraction and massive stars have a low escape fraction (see Tables 1 and 2).
Four models for our calculation of cosmic reionization.
2.1.2. Active galactic nuclei
The accretion disks around supermassive black holes in the center of galaxies are so hot that they radiate both hydrogen- and helium-ionizing photons. Their emission is likely harder than that from stellar populations because parts of the accretion disks can reach higher temperatures than stars. The ionizing spectra of AGN are usually approximated by a power law, Lν ∝ να, for which the slope varies for individual objects (−3 ≲ α ≲ −1) but can be averaged to α = −1.7 (Lusso et al. 2015, see also Telfer et al. 2002). We note that the spectra of AGN are unexplored observationally for the wavelength range shortward of ∼350 Å and for photon energies lower than ∼0.1 keV (e.g., Upton Sanderbeck et al. 2018). In this regime, the spectral slope is typically extrapolated from longer wavelengths (e.g., Haardt & Madau 2012). The number density of AGN has been observed to peak at z ∼ 2 − 3 and steeply declines for both higher and lower redshifts (e.g., Hopkins et al. 2007).
Calculating the ionizing emissivity of AGN, ṅion and ṅion,He II, requires combining the number density of AGN and their spectra. We employed the ionizing emissivity of Puchwein et al. (2019, see their Eq. (25)) to represent the production rate of H I-ionizing photons from AGN over cosmic time. For the production rate of He II-ionizing photons from AGN, we used the H I-ionizing emissivity and extrapolated to higher frequencies using the average spectral shape of AGN from Lusso et al. (2015).
The escape fraction from AGN is commonly assumed to be unity because of their violent outflows and strong ionizing emission. However, recent studies suggest that the escape fraction might be somewhat smaller (Cristiani et al. 2016; Micheva et al. 2017). We followed the findings of Cristiani et al. (2016) and adopted an escape fraction of 80% for AGN (which is also the upper limit for our stellar populations), assuming that it is constant over cosmic time.
2.2. Cosmic reionization: a simple semi-analytic model
We estimated the contribution from stripped stars to the reionization of hydrogen and helium by calculating their impact on the volume filling factor of ionized gas, x, over cosmic time. The volume filling factor is a dimensionless parameter that describes the fraction of gas in the IGM that is ionized in terms of volume. We followed a simple approach, described for example in Madau et al. (1999) and Haardt & Madau (2012), where the rate of change of the volume filling factor of ionized gas is described as the balance between the rate with which ionizing photons reach the atoms or ions in the IGM and the rate with which the ions recombine. The rate of change of the volume filling factors of ionized hydrogen and helium can be written in the form of the following differential equations:
where ⟨n⟩ is the mean number density of a considered element in the IGM, and ⟨trec⟩ is the mean recombination timescale for a given ion. The combination of the escape fraction and the production rate of ionizing photons, fesc ṅion, describes the rate at which ionizing photons reach the IGM. We use the subscripts H and He to denote the quantities for hydrogen and helium, respectively. The escape fraction is assumed to be the same for both hydrogen and helium because we assume that it primarily is an effect of geometry within the host galaxy (cf. Vanzella et al. 2019b; Ji et al. 2020; Rivera-Thorsen et al. 2019). However, we discuss the possibility and impact of wavelength-dependent escape fractions in Sect. 3. We use quantities for a comoving cosmological volume throughout this paper, unless otherwise stated.
We calculated the mean recombination time of ionized hydrogen and helium following Haardt & Madau (2012):
In Eq. (5), the clumpy structure of the hydrogen and helium in the IGM is approximated by a redshift dependent clumping factor, CIGM = 1 + 43z−1.71 (Haardt & Madau 2012). It is likely that the hydrogen and singly-ionized helium gas are somewhat differently distributed during their respective reionizations, but for simplicity, we use the same clumping factor. However, the choice of clumping factor does not significantly affect our results. We assumed that the IGM has a temperature of ∼20 000 K during reionization (see, e.g., Miralda-Escudé & Rees 1994; D’Aloisio et al. 2019), meaning that the recombination coefficients were set to αB,H II = 1.43 × 10−13 cm3 s−1 and αB,He III = 9.08 × 10−13 cm3 s−1 (for Case B-type recombination, following Osterbrock & Ferland 2006). The electron density, ne, accounts for the free electrons from ionization of both hydrogen and helium. We assumed that the reionizations of H I and He I were coupled because the number of He I-ionizing photons were sufficient for He I reionization to occur prior to H I reionization, but the mean-free paths of the photons were limited by the more abundant hydrogen (Miralda-Escudé & Rees 1994). We then assumed that reionization of He II occurred after that of H I and He I. Furthermore, we assumed that the ionization fronts were thin compared to the size of the ionized bubbles they enclosed, which is a good approximation for all but the very first stages of reionization (for a discussion, see Madau et al. 1999). This means that there were free electrons from ionized hydrogen and singly-ionized helium in the ionized bubbles during H I reionization, which results in an electron density of ne = 1.08 ⟨nH⟩, where the mean number density of hydrogen is ⟨nH⟩ = 1.9 × 10−7 (1 + z)3 cm−3 (Haardt & Madau 2012). We assumed that the composition in the IGM is primordial (e.g., Wagoner et al. 1967), meaning that there are approximately 12 hydrogen atoms for every helium atom. During He II reionization, the electron density was higher inside the ionized bubbles because helium was fully ionized, and therefore ne = 1.17 ⟨nH⟩. The resulting recombination timescale is about 500 Myr at z ∼ 6 for recombination of hydrogen and about seven times shorter for recombination of He III to He II at the same time.
To solve Eq. (4), we integrated over time assuming a flat cosmology in the standard ΛCDM theory and applied H(z) = H0(ΩM(1 + z)3 + ΩΛ)1/2. For the cosmological parameters, we used the latest results from the Planck satellite (ΩM = 0.31, ΩΛ = 0.69, and H0 = 68 km s−1 Mpc−1, Planck Collaboration XIII 2016).
In Sect. 2.1 we described how we estimated the production rates of ionizing photons and the escape fraction of ionizing photons for the various ionizing sources that we considered. We used these together with the calculated recombination times to numerically solve Eq. (4) and present the solutions in Sect. 4. We created four models for the cosmic emissivity of ionizing photons that are distinguished by different assumptions for the escape fraction of ionizing photons, as summarized in Table 1. The standard model uses the functions for the escape fraction as described by Eqs. (2) and (3). Because the escape fraction is uncertain, we also considered a high-fesc and a low-fesc model, which both assume constant escape fractions such that the reality likely resides somewhere between the two models. For the high-fesc model, we assumed an escape fraction of 20% for massive stars and 80% for stripped stars, while for the low-fesc model, we instead assumed an escape fraction of 5% for massive stars and 30% for stripped stars. We also created a combination model in which we assumed that the escape fraction is 5% for massive stars and 80% for stripped stars. For all models we assumed a constant escape fraction of 80% for AGN.
3. Ionizing emissivity over cosmic time
3.1. Cosmic emission rates of H I- and He II-ionizing photons
In Fig. 4 we show the rates at which ionizing photons reach the IGM for the different models described in Table 1 and as a function of redshift. These rates were calculated by multiplying the escape fraction with the production rates of ionizing photons (Eq. (1) and Eq. (25) from Puchwein et al. 2019 for stars and AGN, respectively).
 |
Fig. 4. Rate with which ionizing photons reach the intergalactic medium. Panels a, b, and c: rate for H I-ionizing photons and panels d, e, and f: for He II-ionizing photons. Left column: results for our standard model, middle column: for our high-fesc model, and right column: for our low-fesc model (see Table 1). We show the contribution from stripped stars in dark blue, from massive stars in light blue, and from AGN in brown. The extent of the colored regions represents the spread caused by metallicity variations. The results for the combination model (see Table 1) are the same as in the high-fesc model for the stripped stars and the same as in the low-fesc model for the massive stars. |
The figure shows that stripped stars potentially played important roles as sources of both H I- and He II-ionizing photons, but during different epochs in cosmic time. Figure 4a shows the emission rate of H I-ionizing photons from stars and AGN as a function of redshift for our standard model. The model predicts that stripped stars were responsible for a few up to about 25% of the total emission rate of H I-ionizing photons prior to z = 6. Massive stars are predicted to have been the main provider of H I-ionizing photons at early times, and AGN became important for z < 6. Around z = 2 − 3, AGN provided the majority of the H I-ionizing photons, and therefore likely played a major role in keeping the intergalactic hydrogen ionized. Panels b and c of Fig. 4 show the cosmic emission rates of H I-ionizing photons in our high-fesc and low-fesc models. Panels a–c show that the contribution from stripped stars to the cosmic emission rate of H I-ionizing photons is relatively high in all our models. We show the range of emission rates caused by metallicity as colored bands for the massive stars and stripped stars in Fig. 4, although in our models we employ a mean metallicity at each redshift. The figure shows that the emission rate of H I-ionizing photons is only weakly affected by the choice of metallicity, suggesting that accounting for a spread of metallicities at each redshift might have little effect on the result. However, we note that a difference of a factor of two in the emission rate of ionizing photons can have important consequences for the predictions for the time at which reionization occurred and which sources provided the ionizing photons. Our models predict that stripped stars produce H I-ionizing photons at the highest rate when the metallicity is Z = 0.002, when their emission rate of H I-ionzing photons is about 35% higher than at solar metallicity (see Table A.1).
The photoionization rate of the IGM has been observed to be remarkably constant over cosmic time (e.g., Becker & Bolton 2013, see also Mason et al. 2019). Because the photoionization rate of the IGM is proportional to the cosmic emission rate of ionizing photons (times the mean free path of ionizing photons, which also increases with decreasing redshift at z ∼ 5), it appears that the flatter emission rates presented in our standard model are favored (Fig. 4a), which could suggest that the escape fraction indeed increases with redshift.
Figures 4d–f show the emission rate of He II-ionizing photons from the individual ionizing sources over cosmic time and for our three models. For stars, the He II-ionizing photons are produced in the steep Wien part of the spectra, and the emission rate of He II-ionizing photons is therefore very sensitive to temperature variations. At lower metallicity, massive stars are hotter and therefore are predicted to emit He II-ionizing photons at higher rates. However, recombination of helium in the stellar atmospheres, which is dependent on the wind mass-loss rates, can easily block large portions of the emitted He II-ionizing flux. Because wind mass-loss rates are uncertain for many types of stars, the emission rate of He II-ionizing photons from stellar populations is subject to uncertainties. The large spread of emission rates of He II-ionizing photons from massive stars and stripped stars seen in Figs. 4d–f is therefore due to both the effect of metallicity and uncertainties in stellar atmosphere models (cf. Paper I). We followed the average metallicity-redshift relation of Madau & Fragos (2017), but note that in reality, the importance of stripped stars and massive stars may vary significantly at a given redshift, depending on the metallicity of the individual stellar populations. Figures 4d–f show that in all cases, AGN are responsible for most of the emitted He II-ionizing photons because they dominate the emission for a long time. However, at very high redshifts, z ≳ 10, stripped stars and/or massive stars could have dominated the output of He II-ionizing photons.
3.2. Spectral energy distribution of the cosmic emissivity
The integrated spectrum of the radiation that emerges into the IGM contains is imprinted by the sources that produced the ionizing radiation. The hardness of the ionizing radiation can, for example, be used to infer what type of source emitted the radiation because the different sources are characterized by different spectral shapes.
We show the integrated spectrum of the ionizing emissivity for four snapshots in the cosmic history in Fig. 5, using our standard model. The figure displays the emerging emissivities of stripped stars, massive stars, and AGN at redshifts z = 1.7, 4.3, 7, and 11.7 and in units of erg s−1 Hz−1 per comoving Mpc3. The emissivity, ε, is here defined as the ionizing spectrum integrated over all sources within a comoving Mpc3. We calculated the emissivity in a similar fashion as the production rate of ionizing photons (see Eq. (1)) by multiplying the average wavelength-dependent luminosity of stellar populations, Lν, with the cosmic star formation rate density. In Fig. 5 we highlight the additional radiation that stripped stars contribute in dark green. To create the figure, we used spectra for continuous star formation during 1 Gyr. After this long time, the spectrum has long reached equilibrium in the ionizing wavelengths.
 |
Fig. 5. Spectral energy distribution of the ionizing radiation that emerges into the IGM during cosmic evolution. We show the contribution from stellar populations in green shades and from AGN in gray. The contribution from stripped stars is highlighted in dark green. They cause the spectra to harden. The dashed lines show spectral slopes of α = −3, −2, and −1, assuming Lν ∝ να. The panels represent four snapshots during cosmic evolution, taken at z = 1.7, 4.3, 7.0, and 11.7. Following the relation between average metallicity and redshift of Madau & Fragos (2017, see also Sect. 2.1.1), the average metallicity at these times is Z = 0.014, 0.006, 0.002, and 0.0002 (Z⊙ ≡ 0.014, Asplund et al. 2009). This figure adopts our standard model for the escape fractions, see Table 1. |
With their hard ionizing spectra, stripped stars cause the total emerging emissivity from stellar populations to harden. The effect is primarily important for z ≲ 7 and becomes stronger with decreasing redshift, as shown in Fig. 5. We assumed that the emerging emissivity roughly follows ∝Eα, where E is the photon energy and α is the spectral index. Then, at z ∼ 2, stripped stars cause the emission to harden from α ∼ −3 to α ∼ −1 for photon energies lower than about 50 eV. The effect is similar up to z ∼ 4, and at z = 7, stripped stars cause the spectral index to increase by about 0.5.
The panels of Fig. 5 show the evolution of the ionizing emission as the Universe grew older. With lower redshift, the average metallicity increased, causing the emission from massive stars to soften from spectral indices of α = −2 (panel d) to α = −3 (panel a). However, when stripped stars are accounted for, this effect is washed out and the spectral index from stellar populations remains at α ≥ −2. The results for our high-fesc and low-fesc models are less pronounced but similar to those of the standard model. In the high-fesc and low-fesc models, the stripped stars cause the spectral index to remain at α ∼ −2 over cosmic time.
The influence of AGN is small for the hardness of the H I- and He I-ionizing spectrum. At these wavelengths, stellar populations dominate at all times in our models. However, the He II-ionizing emission is dominated by AGN for most of the cosmic evolution. Only at very high redshifts, z ≳ 10, do stellar populations dominate the emission of He II-ionizing photons. It is likely that the contribution from stellar populations was larger than predicted by our models at these high redshifts. The reason is that a spread of metallicities exist at each point in time, which allows for a larger contribution from stripped stars, while our models assume an average metallicity for each point in time. We also note that other sources of ionizing radiation may affect the hardness of the ionizing spectrum. Rotating massive stars could cause the H I- and He I-ionizing emission to be slightly harder (see e.g., D’Aloisio et al. 2019), while accreting white dwarfs and X-ray binaries could affect the hardness of the He II-ionizing emission (Chen et al. 2015; Madau & Fragos 2017; Schaerer et al. 2019).
The emitted light is also expected to harden when the escape fraction is strongly dependent on the photon energy. The escape fraction is expected to be dependent on the photon energy because higher energy photons have longer mean-free paths (Osterbrock & Ferland 2006; McCandliss & O’Meara 2017), but it is not yet clear how strong the effect is. When photons escape through large holes in the galactic gas, the emerging radiation is not hardened because no gas prevents them from propagating.
4. Reionization including stripped stars
Here, we describe the results of our models for the cosmic evolution of the fraction of ionized hydrogen and helium. We focus in particular on the results from our standard model, but also compare the results from the high-fesc and low-fesc models. First, we describe the effect of stripped stars on hydrogen reionization. Then, we discuss their impact on helium reionization.
4.1. Hydrogen reionization
We show the increase in volume filling factor of ionized hydrogen, xH II, with decreasing redshift in Fig. 6. We find that hydrogen reionization occurs about 100 Myr earlier when stripped stars are included, which corresponds to about 10% of the total age of the Universe at the time. In our standard model, H I-reionization occurs at z ∼ 5.8 when stripped stars are not included, but at z ∼ 6.5 when they are. The impact of stripped stars is small at early times, but they become important as hydrogen reionization progresses. At redshift z = 12, about 25% of the Universe is reionized independent of whether stripped stars are included, but when hydrogen is completely reionized in the model including stripped stars, only 85% of the IGM is reionized when stripped stars are not included. In Table 2 we display the redshifts at which hydrogen reionization is completed for our four models and for when stripped stars are accounted for and when they are not. The table shows that the effect of the escape fraction is large for the time of reionization. However, in all models, stripped stars give rise to earlier reionization than when they are not included.
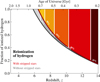 |
Fig. 6. Reionization of hydrogen shown as the cosmic evolution of the volume filling factor of ionized hydrogen in the IGM, xH II. We show the evolution of xH II in our standard model (see Table 1). We use red shades for the version that includes stripped stars and gray shades for the version without them. We mark the times when 20%, 40%, 60%, and 80% of the hydrogen in the IGM is ionized using white lines and labels. Stripped stars cause reionization to occur about 100 Myr earlier than when only single stars and AGN are considered. |
To evaluate the total relative importance of the different ionizing sources to the reionization of hydrogen, we integrated the individual contributions to the cosmic emission rate of H I-ionizing photons from the early Universe until the end of reionization. The resulting contribution from stripped stars to the budget of H I-ionizing photons prior and up to reionization is about 20% in our standard model. The effect of the choice of the escape fraction is visible when the relative contribution from stripped stars in our models is compared. In the combination model, the stripped stars have a much larger escape fraction than massive stars, which means that their contribution is as high as about 40%. On the other hand, in our high-fesc model, the escape fraction for stripped stars is the same as in our combination model, but the escape fraction for massive stars is lower. The result is that the reionization occurs earlier and the contribution from stripped stars is lower (∼15%, see Table 2).
Figure 7 shows the relative contribution from the different ionizing sources to the budget of H I-ionizing photons, measured from the early Universe until reionization is completed at z = 6.5 for our standard model. The figure shows that stripped stars played an important role as contributors with ionizing photons during the reionization of hydrogen, providing about 20% of the ionizing photons. Massive stars were the most important, producing about 75% of the ionizing photons. In our models, AGN are less important as sources of H I-ionizing photons and produce only a few percent of the photons that reionized the Universe. We also show the evolution of the relative contributions from the different ionizing sources to the total number of produced H I-ionizing photons in Fig. 8a. This figure shows that the importance of stripped stars increased with the age of the Universe.
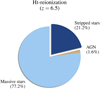 |
Fig. 7. Relative contribution of ionizing photons from stripped stars (dark blue), massive stars (light blue), and AGN (beige) to the photon budget that caused hydrogen reionization. Stripped stars contributed about 20% of the H I-ionizing photons, see Sect. 4. This figure shows the results from our standard model, for which reionization is complete at z = 6.5 when stripped stars are included (see Tables 1 and 2). |
 |
Fig. 8. Cosmic evolution of the relative contribution from stripped stars (dark blue), massive stars (light blue), and AGN (beige) to the budget of H I-ionizing photons (panel a) and He II-ionizing photons (panel b). We label the time of hydrogen and helium reionization and shade the times predicted by our model for the reionization of the Universe. This figure shows the results from our standard model; the trend in massive stars is in part due to the strongly redshift-dependent fesc (see Table 1). |
The contribution from AGN has been debated, and several models consider a higher number density of AGN at earlier times, which leads to a higher contribution to the hydrogen reionization (e.g., Giallongo et al. 2015; Madau & Haardt 2015). However, higher emission from AGN at early times leads to earlier reionization of helium than what has been observed because of the hard spectra of AGN. We therefore did not consider any model with a higher AGN contribution.
In the code BPASS (Eldridge et al. 2017; Stanway & Eldridge 2018, version 2.2.1, Tuatara), the inclusion of binary products results in emission rates of hydrogen-ionizing photons that are higher by a few percent to 30%, depending on the considered metallicity (see the yields of ionizing photons presented in Fig. A.1). This is consistent with what we predict for stripped stars at solar metallicity, which produce about 5% of the total number of emitted ionizing photons from stellar populations (see also Stanway et al. 2016). At lower metallicity, BPASS predicts higher yields of H I-ionizing photons than what we predict that stripped stars can be responsible for. The individual yields of ionizing photons for different types of stars are not available in the BPASS models. However, the most likely reason for their higher yields is that for Z ≤ 0.004, BPASS accounts for other binary products than stripped stars, and especially for efficient rotational mixing and subsequent chemically homogeneous evolution of low-metallicity stars that accreted material or merged with its companion star (Eldridge et al. 2017, see also Cantiello et al. 2007). In consequence, BPASS predicts complete reionization for low escape fractions within the observed timescale or even gives rise to early reionization (fesc ∼ 5 − 10%, Rosdahl et al. 2018, see also Ma et al. 2016 and Wilkins et al. 2016, but we note that these authors all used an earlier version of BPASS, which had a higher binary fraction than in the version Tuatara). This shows that the effect of chemically homogeneous stars is significant, with important implications for cosmic reionization and the spectra of stellar populations, if rotational mixing is indeed as efficient as these models predict. Although several studies have claimed circumstantial evidence (e.g., Martins et al. 2009; Hainich et al. 2015, see, however, also Schootemeijer & Langer 2018; Shenar et al. 2019, and Abdul-Masih et al. 2019), direct solid proof for chemically homogeneous evolution is still lacking.
4.2. Helium reionization
All our models indicate that stripped stars contributed ≲3% in total of the photons that fully reionized helium. This means that the time of helium reionization is not affected by stripped stars. Our models reach complete helium reionization at z ∼ 3, and the main producer of the He II-ionizing photons that caused helium reionization in our models is AGN.
We show the relative contributions to the budget of He II-ionizing photons from the different ionizing sources that we consider in Fig. 8b. The figure shows that the contribution from stellar populations dominated before z ∼ 10, and between z ∼ 6 − 8, stripped stars were responsible for about 10% of the He II-ionizing photons that reached the IGM. This means that the early emission of He II-ionizing photons could have resulted in heating the IGM before the reionization of helium was complete. In our standard model, the reionization of helium starts around z = 5, when slightly more than 10% of the intergalactic helium has been fully ionized.
5. Observable consequences
5.1. Highly ionized absorbers in the IGM
In Sect. 3 we showed that stripped stars harden the ionizing radiation that emerges from galaxies (Fig. 5), which could produce significant effects on the observable ionization structure of the IGM. This is particularly interesting because high-ionization species such as C IV and Si IV have been observed in the IGM at high redshift (e.g., Ryan-Weber et al. 2006, 2009; D’Odorico et al. 2013; Doughty et al. 2018). The metals in the IGM are likely expelled from galaxies through large-scale outflows, which explains why they are detected in small and dense clumps that could indicate the locations of galaxies. The intergalactic metals are then ionized by radiation emitted by the galaxies, reaching various levels of ionization depending on the hardness and intensity of the emerging ionizing radiation.
The observed abundance of C IV at high redshifts is in some cases unexpectedly high compared to what cosmological simulations predict (e.g., Finlator et al. 2016; Doughty et al. 2018). A reason might be that the emission from galaxies is harder than what is assumed for the galaxy spectra for the H I- and He I-ionizing emission at energies between 1 − 4 Rydberg (D’Odorico et al. 2013).
Stripped stars emit sufficiently hard ionizing radiation to ionize both Si III to Si IV and C III to C IV (see Fig. 7 of Paper III). Figure 5 shows that our models predict that stripped stars boost the flux at these photon energies by a factor of a few up to ten, depending on the metallicity of the stellar population. However, detailed radiative transfer modeling is needed to accurately determine the influence from stripped stars on the ionization state of the IGM. We also note that other sources of hard ionizing radiation, such as accreting compact objects (e.g., Di Stefano & Kong 2003; Fragos et al. 2013; Chen et al. 2015) or post-AGB stars (e.g., Byler et al. 2019), may play a role in the creation of highly ionized elements in the IGM.
We note that the absorption lines discussed here are different from the strong emission lines observed in some star-forming galaxies, for example, O III and He II (Stark et al. 2015; Senchyna et al. 2017; Vanzella et al. 2017; Berg et al. 2019; Saxena et al. 2019). To make predictions for these requires modeling the nebular spectrum, which is beyond our current scope.
5.2. Temperature of the intergalactic medium
During reionization, the IGM was heated by excess photon energy after each ionization of individual atoms. The gas simultaneously cooled through line excitations and collisional ionization from photoelectrons (Miralda-Escudé & Rees 1994). Harder spectra of the ionizing sources therefore leave imprints on the IGM in terms of higher temperatures. After reionization was complete, the IGM cooled again, reaching temperatures of about 7000 − 10 000 K at z ∼ 5 (Becker et al. 2011; Boera et al. 2014; Iršič et al. 2017).
With the hardening of the ionizing spectrum when stripped stars are considered, the IGM may reach higher temperatures depending on the speed with which the ionization fronts move (faster fronts lead to larger temperature increases, D’Aloisio et al. 2019). Following Fig. 2 of D’Aloisio et al. (2019) and assuming that the ionization fronts move with speeds between 103 and 104 km s−1, we estimate that stripped stars could cause an increase of the IGM temperature of ∼1000 up to ∼5000 K because they harden the ionizing emission and cause significant changes to the spectral index (see Fig. 5).
Stripped stars may therefore affect observables for the temperature of the IGM. The additional heating from the hard spectra of stripped stars would cause lines in the Lyα forest to be more thermally broadened. Temperature measurements from the forest have been performed to redshifts as high as z ≈ 6 (Bolton & Haehnelt 2007b; Bolton et al. 2012; Viel et al. 2013; Boera et al. 2019). A precise understanding of the timing of reionization is likely required to be able to use a temperature measurement to probe the hardness of the source spectra because the post-reionization temperature that is measured in the forest also depends on when gas was ionized (affecting how much it is able to cool; Upton Sanderbeck et al. 2016). Such an understanding may be possible in combination with future cosmic microwave background and redshifted 21 cm observations (McQuinn 2016).
The ionization fronts during reionization cool through collisionally excited Lyα emission. With a higher IGM-temperature, the line emissivity of Lyα is therefore expected to increase (Cantalupo et al. 2008; Visbal & McQuinn 2018). We estimate that the increased IGM temperature that stripped stars are responsible for gives rise to an increased Lyα emissivity of about a factor of a few up to ten (cf. Fig. 1 of Cantalupo et al. 2008, see also Davies et al. 2016). However, the Lyα emission from cooling ionization fronts during the reionization is hard to detect (Silva et al. 2013; Pullen et al. 2014; Davies et al. 2016). This signal then needs to be distinguished from galactic Lyα emission (however, see Comaschi & Ferrara 2016), but there may be unique signatures that allow it to be extracted (Visbal & McQuinn 2018). The weak signal from the reionizing IGM is predicted to be detectable with instruments that reach higher sensitivity than currently available, such as the future space mission SPHEREx (Kovetz et al. 2017, launch expected in 2023).
6. Summary and conclusions
With their high temperatures and late formation times, stars that are stripped of their hydrogen-rich envelopes during interaction in binaries have been predicted to play an important role during reionization. We have estimated their contribution to the budget of photons that caused cosmic reionization of hydrogen and helium. We used detailed spectral models that we customized for these stripped stars (Paper II). We combined the radiative contribution from stripped stars to realistic stellar and AGN populations (Paper III) with a commonly used simple method to calculate the cosmic evolution of the volume filling factors of ionized hydrogen and helium. We accounted for the cosmic star formation history, the recombination timescales, the intergalactic density of hydrogen and helium, and assumed clumping of the IGM. We considered four models that differ from each other by the different assumptions of the escape fraction. With these various approaches for the uncertain escape fraction, we hope to have bracketed the actual conditions between stellar populations and intergalactic space.
In agreement with previous studies, we have found that stars that are stripped in binaries likely had important effects on cosmic reionization. However, we took a different approach than earlier work on the effect of interacting binaries on cosmic history (cf. Ma et al. 2016; Rosdahl et al. 2018). By carefully implementing detailed stellar evolutionary and atmosphere models especially made for stripped stars in a model for reionization, we were able to (1) follow a single type of binary product and understand their impact on the evolving Universe, and (2) better understand which predictions for them are robust and which are uncertain. Our reionization model is simple. More sophisticated cosmological simulations would aid in understanding details about the role of stripped stars during reionization. In particular, such simulations could self-consistently model the escape of ionizing photons, which is a critical uncertainty in our analysis. However, with the simple model we employ, the effect originating from individual ionizing sources is easy to distinguish. This has allowed us to identify possibly observable traces that stripped stars left in cosmic history. Below, we summarize our conclusions.
-
Stripped stars cause the emerging spectra from galaxies to harden. At solar metallicity, the slope of the ionizing part of the spectrum can harden from a spectral index of −3 to −1 when stripped stars are included. The effect decreases with lower metallicity.
-
Our standard model suggests that stripped stars provided ∼20% of the photons that reionized hydrogen in the Universe. This estimate is sensitive to our assumptions about the escape fraction, but the uncertainties in binary interaction and in the emission rates of H I-ionizing photons from stripped stars are expected to be small.
-
The He II-ionizing emission from stripped stars is not sufficient to compete with AGN and significantly impact the complete reionization of helium, even given the large uncertainties in our models about the absorption of He II-ionizing photons in a wind. However, if most of these photons are not absorbed, the stripped stars could have contributed significantly to the initial part of He II reionization at z ∼ 6 − 8.
-
The harder ionizing radiation that stripped stars introduce in the spectra of galaxies could give rise to high ionization levels of high-redshift circumgalactic gas. This might help explain the unexpectedly high abundance of C IV that has been detected in dense regions at z ∼ 6 (see, e.g., D’Odorico et al. 2013).
-
The harder spectra that we expect from stellar populations because of the presence of stripped stars likely lead to an increased temperature of the intergalactic medium during the reionization of hydrogen. We estimate that accounting for stripped stars leads to an increase of 1000 to 5000 K in the temperature of the IGM at the time of ionization. Current high-redshift temperature measurements using the Lyα forest are likely unable to detect these differences. The increased temperature could also lead to an increased emissivity of Lyα from cooling ionization fronts, which may be detectable with future intensity mapping surveys.
We have focused on the ionizing contribution from stripped stars during the reionization of hydrogen and helium. A detailed analysis of other products of binary interaction is important to improve our understanding further. However, the models we presented for stripped stars already provide new clues on the nature of ionizing photons on cosmological scales. In combination with careful modeling of the nebula, our predictions may provide observable signatures in the large numbers of spectra anticipated from the James Webb Space Telescope (JWST, Gardner et al. 2006), which would allow probing the role of interacting binaries throughout cosmic time.
Acknowledgments
The authors thank the anonymous referee for useful comments that helped improve the manuscript. We also acknowledge various people for inspiring and helpful discussion during the preparation of this manuscript, including Danielle Berg, Renyue Cen, John Chisholm, Pratika Dayal, J. J. Eldridge, Jim Fuller, Anne Hutter, Alicia Lanz, Claus Leitherer, Tony Piro, Mathieu Renzo, Gwen Rudie, Abel Schootemeijer, Amy Secunda, Peter Senchyna, Elizabeth Stanway, Dan Stark, Allison Strom, Santiago Torres, Eros Vanzella, and Manos Zapartas. YG acknowledges the funding from the Alvin E. Nashman fellowship for Theoretical Astrophysics. SdM acknowledges funding by the European Union’s Horizon 2020 research and innovation programme from the European Research Council (ERC), Grant agreement No. 715063), and by the Netherlands Organisation for Scientific Research (NWO) as part of the Vidi research program BinWaves with project number 639.042.728. EZ acknowledges support from the Federal Commission for Scholarships for Foreign Students for the Swiss Government Excellence Scholarship (ESKAS No. 2019.0091) for the academic year 2019–2020. This work made use of v2.2.1 of the Binary Population and Spectral Synthesis (BPASS) models for comparison purposes as last described in Eldridge et al. (2017) and Stanway & Eldridge (2018).
References
- Abdul-Masih, M., Sana, H., Sundqvist, J., et al. 2019, ApJ, 880, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Atek, H., Richard, J., Jauzac, M., et al. 2015, ApJ, 814, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Balestra, I., Tozzi, P., Ettori, S., et al. 2007, A&A, 462, 429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barkana, R., & Loeb, A. 2001, Phys. Rep., 349, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, G. D., & Bolton, J. S. 2013, MNRAS, 436, 1023 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, G. D., Bolton, J. S., Haehnelt, M. G., & Sargent, W. L. W. 2011, MNRAS, 410, 1096 [NASA ADS] [CrossRef] [Google Scholar]
- Belczynski, K., Holz, D. E., Bulik, T., & O’Shaughnessy, R. 2016, Nature, 534, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Belkus, H., Van Bever, J., Vanbeveren, D., & van Rensbergen, W. 2003, A&A, 400, 429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berg, D. A., Chisholm, J., Erb, D. K., et al. 2019, ApJ, 878, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Boera, E., Murphy, M. T., Becker, G. D., & Bolton, J. S. 2014, MNRAS, 441, 1916 [NASA ADS] [CrossRef] [Google Scholar]
- Boera, E., Becker, G. D., Bolton, J. S., & Nasir, F. 2019, ApJ, 872, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Bolton, J. S., & Haehnelt, M. G. 2007a, MNRAS, 382, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Bolton, J. S., & Haehnelt, M. G. 2007b, MNRAS, 374, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Bolton, J. S., Becker, G. D., Raskutti, S., et al. 2012, MNRAS, 419, 2880 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2012, ApJ, 752, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2017, ArXiv e-prints, unpublished [arXiv:1711.02090] [Google Scholar]
- Braun, H., & Langer, N. 1995, A&A, 297, 483 [NASA ADS] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Byler, N., Dalcanton, J. J., Conroy, C., et al. 2019, AJ, 158, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Cantalupo, S., Porciani, C., & Lilly, S. J. 2008, ApJ, 672, 48 [Google Scholar]
- Cantiello, M., Yoon, S.-C., Langer, N., & Livio, M. 2007, A&A, 465, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, H.-L., Woods, T. E., Yungelson, L. R., Gilfanov, M., & Han, Z. 2015, MNRAS, 453, 3024 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, X., & Han, Z. 2009, MNRAS, 395, 1822 [NASA ADS] [CrossRef] [Google Scholar]
- Chojnowski, S. D., Labadie-Bartz, J., Rivinius, T., et al. 2018, ApJ, 865, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Comaschi, P., & Ferrara, A. 2016, MNRAS, 463, 3078 [NASA ADS] [CrossRef] [Google Scholar]
- Cristiani, S., Serrano, L. M., Fontanot, F., Vanzella, E., & Monaco, P. 2016, MNRAS, 462, 2478 [NASA ADS] [CrossRef] [Google Scholar]
- Crowther, P. A., Caballero-Nieves, S. M., Bostroem, K. A., et al. 2016, MNRAS, 458, 624 [NASA ADS] [CrossRef] [Google Scholar]
- D’Aloisio, A., McQuinn, M., Maupin, O., et al. 2019, ApJ, 874, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, F. B., Furlanetto, S. R., & McQuinn, M. 2016, MNRAS, 457, 3006 [NASA ADS] [CrossRef] [Google Scholar]
- Dayal, P., & Ferrara, A. 2018, Phys. Rep., 780, 1 [NASA ADS] [CrossRef] [Google Scholar]
- de Mink, S. E., Pols, O. R., & Hilditch, R. W. 2007, A&A, 467, 1181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Mink, S. E., Cantiello, M., Langer, N., et al. 2009, A&A, 497, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Mink, S. E., Langer, N., Izzard, R. G., Sana, H., & de Koter, A. 2013, ApJ, 764, 166 [NASA ADS] [CrossRef] [Google Scholar]
- de Mink, S. E., Sana, H., Langer, N., Izzard, R. G., & Schneider, F. R. N. 2014, ApJ, 782, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Dewi, J. D. M., & Tauris, T. M. 2000, A&A, 360, 1043 [NASA ADS] [Google Scholar]
- Dewi, J. D. M., & Pols, O. R. 2003, MNRAS, 344, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Di Stefano, R., & Kong, A. K. H. 2003, ApJ, 592, 884 [NASA ADS] [CrossRef] [Google Scholar]
- D’Odorico, V., Cupani, G., Cristiani, S., et al. 2013, MNRAS, 435, 1198 [NASA ADS] [CrossRef] [Google Scholar]
- Doran, E. I., Crowther, P. A., de Koter, A., et al. 2013, A&A, 558, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Doughty, C., Finlator, K., Oppenheimer, B. D., Davé, R., & Zackrisson, E. 2018, MNRAS, 475, 4717 [NASA ADS] [CrossRef] [Google Scholar]
- Drout, M. R., Soderberg, A. M., Gal-Yam, A., et al. 2011, ApJ, 741, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P. 1983, ApJ, 268, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eldridge, J. J., & Stanway, E. R. 2009, MNRAS, 400, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Eldridge, J. J., & Stanway, E. R. 2012, MNRAS, 419, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Eldridge, J. J., Izzard, R. G., & Tout, C. A. 2008, MNRAS, 384, 1109 [NASA ADS] [CrossRef] [Google Scholar]
- Eldridge, J. J., Fraser, M., Smartt, S. J., Maund, J. R., & Crockett, R. M. 2013, MNRAS, 436, 774 [NASA ADS] [CrossRef] [Google Scholar]
- Eldridge, J. J., Stanway, E. R., Xiao, L., et al. 2017, PASA, 34, e058 [NASA ADS] [CrossRef] [Google Scholar]
- Faisst, A. L. 2016, ApJ, 829, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, X., Strauss, M. A., Becker, R. H., et al. 2006a, AJ, 132, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fan, X., Carilli, C. L., & Keating, B. 2006b, ARA&A, 44, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Faucher-Giguère, C.-A., Lidz, A., Zaldarriaga, M., & Hernquist, L. 2009, ApJ, 703, 1416 [NASA ADS] [CrossRef] [Google Scholar]
- Finlator, K., Oppenheimer, B. D., Davé, R., et al. 2016, MNRAS, 459, 2299 [NASA ADS] [Google Scholar]
- Finlator, K., Keating, L., Oppenheimer, B. D., Davé, R., & Zackrisson, E. 2018, MNRAS, 480, 2628 [NASA ADS] [CrossRef] [Google Scholar]
- Fletcher, T. J., Tang, M., Robertson, B. E., et al. 2019, ApJ, 878, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Fragos, T., Lehmer, B., Tremmel, M., et al. 2013, ApJ, 764, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Fragos, T., Andrews, J. J., Ramirez-Ruiz, E., et al. 2019, ApJ, 883, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Gallazzi, A., Brinchmann, J., Charlot, S., & White, S. D. M. 2008, MNRAS, 383, 1439 [NASA ADS] [CrossRef] [Google Scholar]
- Gardner, J. P., Mather, J. C., Clampin, M., et al. 2006, Space Sci. Rev., 123, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Georgy, C., Ekström, S., Eggenberger, P., et al. 2013, A&A, 558, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giallongo, E., Grazian, A., Fiore, F., et al. 2015, A&A, 578, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gies, D. R., Bagnuolo, Jr., W. G., Ferrara, E. C., et al. 1998, ApJ, 493, 440 [NASA ADS] [CrossRef] [Google Scholar]
- Gnedin, N. Y., & Ostriker, J. P. 1997, ApJ, 486, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Gnedin, N. Y., Kravtsov, A. V., & Chen, H.-W. 2008, ApJ, 672, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Götberg, Y., de Mink, S. E., & Groh, J. H. 2017, A&A, 608, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Götberg, Y., de Mink, S. E., Groh, J. H., et al. 2018, A&A, 615, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Götberg, Y., de Mink, S. E., Groh, J. H., Leitherer, C., & Norman, C. 2019, A&A, 629, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Graur, O., Bianco, F. B., Modjaz, M., et al. 2017, ApJ, 837, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Groh, J. H., Oliveira, A. S., & Steiner, J. E. 2008, A&A, 485, 245 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Groh, J. H., Ekström, S., Georgy, C., et al. 2019, A&A, 627, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haardt, F., & Madau, P. 2012, ApJ, 746, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Hainich, R., Pasemann, D., Todt, H., et al. 2015, A&A, 581, A21 [Google Scholar]
- Hillier, D. J. 1990, A&A, 231, 116 [NASA ADS] [Google Scholar]
- Hillier, D. J., & Miller, D. L. 1998, ApJ, 496, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Richards, G. T., & Hernquist, L. 2007, ApJ, 654, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, J. R., Tout, C. A., & Pols, O. R. 2002, MNRAS, 329, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Inoue, A. K., Iwata, I., & Deharveng, J.-M. 2006, MNRAS, 371, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Iršič, V., Viel, M., Haehnelt, M. G., et al. 2017, Phys. Rev. D, 96, 023522 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ivanova, N. 2011, ApJ, 730, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanova, N., Justham, S., Chen, X., et al. 2013, A&ARv, 21, 59 [Google Scholar]
- Izotov, Y. I., Orlitová, I., Schaerer, D., et al. 2016a, Nature, 529, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Schaerer, D., Thuan, T. X., et al. 2016b, MNRAS, 461, 3683 [NASA ADS] [CrossRef] [Google Scholar]
- Izzard, R. G. 2004, PhD Thesis, University of Cambridge. [Google Scholar]
- Ji, Z., Giavalisco, M., Vanzella, E., et al. 2020, ApJ, 888, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Katz, H., Kimm, T., Haehnelt, M. G., et al. 2019, MNRAS, 483, 1029 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L., & Kobulnicky, H. A. 2007, in The Metallicity History of Disk Galaxies, ed. R. S. de Jong, 435 [Google Scholar]
- Kim, J.-G., Kim, W.-T., & Ostriker, E. C. 2019, ApJ, 883, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Kiminki, D. C., & Kobulnicky, H. A. 2012, ApJ, 751, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Kimm, T., Blaizot, J., Garel, T., et al. 2019, MNRAS, 486, 2215 [NASA ADS] [CrossRef] [Google Scholar]
- Kimm, T., & Cen, R. 2014, ApJ, 788, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., & Weigert, A. 1967, ZAp, 65, 251 [Google Scholar]
- Kovetz, E. D., Viero, M. P., Lidz, A., et al. 2017, ArXiv e-prints [arXiv:1709.09066] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kruckow, M. U., Tauris, T. M., Langer, N., Kramer, M., & Izzard, R. G. 2018, MNRAS, 481, 1908 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., McKee, C. F., & Bland-Hawthorn, J. 2019, ARA&A, 57, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Kubátová, B., Szécsi, D., Sander, A. A. C., et al. 2019, A&A, 623, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Leitherer, C., Ortiz Otálvaro, P. A., Bresolin, F., et al. 2010, ApJS, 189, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Leitherer, C., Ekström, S., Meynet, G., et al. 2014, ApJS, 212, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Leitherer, C., Hernandez, S., Lee, J. C., & Oey, M. S. 2016, ApJ, 823, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Levesque, E. M., Leitherer, C., Ekstrom, S., Meynet, G., & Schaerer, D. 2012, ApJ, 751, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Y.-Q., Modjaz, M., Bianco, F. B., & Graur, O. 2016, ApJ, 827, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Livermore, R. C., Finkelstein, S. L., & Lotz, J. M. 2017, ApJ, 835, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Lusso, E., Worseck, G., Hennawi, J. F., et al. 2015, MNRAS, 449, 4204 [NASA ADS] [CrossRef] [Google Scholar]
- Lyman, J. D., Bersier, D., James, P. A., et al. 2016, MNRAS, 457, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, X., Kasen, D., Hopkins, P. F., et al. 2015, MNRAS, 453, 960 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, X., Hopkins, P. F., Kasen, D., et al. 2016, MNRAS, 459, 3614 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Fragos, T. 2017, ApJ, 840, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Haardt, F. 2015, ApJ, 813, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., Haardt, F., & Rees, M. J. 1999, ApJ, 514, 648 [NASA ADS] [CrossRef] [Google Scholar]
- Martins, F., Hillier, D. J., Bouret, J. C., et al. 2009, A&A, 495, 257 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mason, C. A., Naidu, R. P., Tacchella, S., & Leja, J. 2019, MNRAS, 489, 2669 [NASA ADS] [CrossRef] [Google Scholar]
- McCandliss, S. R., & O’Meara, J. M. 2017, ApJ, 845, 111 [NASA ADS] [CrossRef] [Google Scholar]
- McQuinn, M. 2016, ARA&A, 54, 313 [NASA ADS] [CrossRef] [Google Scholar]
- McQuinn, M., Lidz, A., Zahn, O., et al. 2007, MNRAS, 377, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Meynet, G., & Maeder, A. 2005, A&A, 429, 581 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Micheva, G., Iwata, I., & Inoue, A. K. 2017, MNRAS, 465, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Miralda-Escudé, J., & Rees, M. J. 1994, MNRAS, 266, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Modjaz, M., Liu, Y. Q., Bianco, F. B., & Graur, O. 2016, ApJ, 832, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Moe, M., & Di Stefano, R. 2017, ApJS, 230, 15 [Google Scholar]
- Mostardi, R. E., Shapley, A. E., Nestor, D. B., et al. 2013, ApJ, 779, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Öpik, E. 1924, Publications of the Tartu Astrofizica Observatory, 25 [Google Scholar]
- Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics of gaseous nebulae and active galactic nuclei (Sausalito, CA: University Science Books) [Google Scholar]
- Ouchi, M., Mobasher, B., Shimasaku, K., et al. 2009, ApJ, 706, 1136 [NASA ADS] [CrossRef] [Google Scholar]
- Paardekooper, J.-P., Pelupessy, F. I., Altay, G., & Kruip, C. J. H. 2011, A&A, 530, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paardekooper, J.-P., Khochfar, S., & Dalla Vecchia, C. 2015, MNRAS, 451, 2544 [NASA ADS] [CrossRef] [Google Scholar]
- Packet, W. 1981, A&A, 102, 17 [NASA ADS] [Google Scholar]
- Paczyński, B. 1967, Acta Astron., 17, 355 [NASA ADS] [Google Scholar]
- Pauldrach, A. W. A., Hoffmann, T. L., & Lennon, M. 2001, A&A, 375, 161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
- Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Peters, G. J., Gies, D. R., Grundstrom, E. D., & McSwain, M. V. 2008, ApJ, 686, 1280 [Google Scholar]
- Peters, G. J., Pewett, T. D., Gies, D. R., Touhami, Y. N., & Grundstrom, E. D. 2013, ApJ, 765, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Podsiadlowski, P., Joss, P. C., & Hsu, J. J. L. 1992, ApJ, 391, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Puchwein, E., Haardt, F., Haehnelt, M. G., & Madau, P. 2019, MNRAS, 485, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Pullen, A. R., Doré, O., & Bock, J. 2014, ApJ, 786, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Rivera-Thorsen, T. E., Dahle, H., Chisholm, J., et al. 2019, Science, 366, 738 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, B. E., Ellis, R. S., Dunlop, J. S., McLure, R. J., & Stark, D. P. 2010, Nature, 468, 49 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Robertson, B. E., Furlanetto, S. R., Schneider, E., et al. 2013, ApJ, 768, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Rosdahl, J., Katz, H., Blaizot, J., et al. 2018, MNRAS, 479, 994 [NASA ADS] [Google Scholar]
- Roy, A., Nath, B. B., & Sharma, P. 2015, MNRAS, 451, 1939 [NASA ADS] [CrossRef] [Google Scholar]
- Rutkowski, M. J., Scarlata, C., Haardt, F., et al. 2016, ApJ, 819, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Ryan-Weber, E. V., Pettini, M., & Madau, P. 2006, MNRAS, 371, L78 [NASA ADS] [CrossRef] [Google Scholar]
- Ryan-Weber, E. V., Pettini, M., Madau, P., & Zych, B. J. 2009, MNRAS, 395, 1476 [NASA ADS] [CrossRef] [Google Scholar]
- Sana, H., de Mink, S. E., de Koter, A., et al. 2012, Science, 337, 444 [Google Scholar]
- Saxena, A., Pentericci, L., Mirabelli, M., et al. 2019, A&A, submitted [arXiv:1911.09999] [Google Scholar]
- Schaerer, D. 2003, A&A, 397, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaerer, D., Fragos, T., & Izotov, Y. I. 2019, A&A, 622, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, F. R. N., Izzard, R. G., de Mink, S. E., et al. 2014, ApJ, 780, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Schootemeijer, A., & Langer, N. 2018, A&A, 611, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Senchyna, P., Stark, D. P., Vidal-García, A., et al. 2017, MNRAS, 472, 2608 [NASA ADS] [CrossRef] [Google Scholar]
- Senchyna, P., Stark, D. P., Mirocha, J., et al. 2019, MNRAS, submitted [arXiv:1909.10574] [Google Scholar]
- Shenar, T., Sablowski, D. P., Hainich, R., et al. 2019, A&A, 627, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shivvers, I., Modjaz, M., Zheng, W., et al. 2017, PASP, 129, 054201 [NASA ADS] [CrossRef] [Google Scholar]
- Shull, J. M., Harness, A., Trenti, M., & Smith, B. D. 2012, ApJ, 747, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Silva, M. B., Santos, M. G., Gong, Y., Cooray, A., & Bock, J. 2013, ApJ, 763, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, L. J., Norris, R. P. F., & Crowther, P. A. 2002, MNRAS, 337, 1309 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, N., Li, W., Filippenko, A. V., & Chornock, R. 2011, MNRAS, 412, 1522 [NASA ADS] [CrossRef] [Google Scholar]
- Sravan, N., Marchant, P., & Kalogera, V. 2019, ApJ, 885, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Stanway, E. R., & Eldridge, J. J. 2018, MNRAS, 479, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Stanway, E. R., Eldridge, J. J., Greis, S. M. L., et al. 2014, MNRAS, 444, 3466 [NASA ADS] [CrossRef] [Google Scholar]
- Stanway, E. R., Eldridge, J. J., & Becker, G. D. 2016, MNRAS, 456, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, D. P., Walth, G., Charlot, S., et al. 2015, MNRAS, 454, 1393 [Google Scholar]
- Steidel, C. C., Bogosavljević, M., Shapley, A. E., et al. 2018, ApJ, 869, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Szécsi, D., Langer, N., Yoon, S.-C., et al. 2015, A&A, 581, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tanvir, N. R., Fynbo, J. P. U., de Ugarte Postigo, A., et al. 2019, MNRAS, 483, 5380 [NASA ADS] [CrossRef] [Google Scholar]
- Tauris, T. M., Kramer, M., Freire, P. C. C., et al. 2017, ApJ, 846, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Telfer, R. C., Zheng, W., Kriss, G. A., & Davidsen, A. F. 2002, ApJ, 565, 773 [NASA ADS] [CrossRef] [Google Scholar]
- Topping, M. W., & Shull, J. M. 2015, ApJ, 800, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Trebitsch, M., Blaizot, J., Rosdahl, J., Devriendt, J., & Slyz, A. 2017, MNRAS, 470, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Upton Sanderbeck, P. R., D’Aloisio, A., & McQuinn, M. J. 2016, MNRAS, 460, 1885 [NASA ADS] [CrossRef] [Google Scholar]
- Upton Sanderbeck, P. R., McQuinn, M., D’Aloisio, A., & Werk, J. K. 2018, ApJ, 869, 159 [NASA ADS] [CrossRef] [Google Scholar]
- van Bever, J., & Vanbeveren, D. 1998, A&A, 334, 21 [NASA ADS] [Google Scholar]
- Van Bever, J., Belkus, H., Vanbeveren, D., & Van Rensbergen, W. 1999, New Astron., 4, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Vanbeveren, D., Van Bever, J., & Belkus, H. 2007, ApJ, 662, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Vanzella, E., Castellano, M., Meneghetti, M., et al. 2017, ApJ, 842, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Vanzella, E., Calura, F., Meneghetti, M., et al. 2019a, MNRAS, 483, 3618 [NASA ADS] [CrossRef] [Google Scholar]
- Vanzella, E., Caminha, G. B., Calura, F., et al. 2019b, MNRAS, 491, 1093 [Google Scholar]
- Viel, M., Becker, G. D., Bolton, J. S., & Haehnelt, M. G. 2013, Phys. Rev. D, 88, 043502 [NASA ADS] [CrossRef] [Google Scholar]
- Visbal, E., & McQuinn, M. 2018, ApJ, 863, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Wagoner, R. V., Fowler, W. A., & Hoyle, F. 1967, ApJ, 148, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, L., Gies, D. R., & Peters, G. J. 2017, ApJ, 843, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, L., Gies, D. R., & Peters, G. J. 2018, ApJ, 853, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Webbink, R. F. 1984, ApJ, 277, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkins, S. M., Feng, Y., Di-Matteo, T., et al. 2016, MNRAS, 458, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Wise, J. H., & Cen, R. 2009, ApJ, 693, 984 [NASA ADS] [CrossRef] [Google Scholar]
- Wise, J. H., Demchenko, V. G., Halicek, M. T., et al. 2014, MNRAS, 442, 2560 [NASA ADS] [CrossRef] [Google Scholar]
- Woods, T. E., & Gilfanov, M. 2013, MNRAS, 432, 1640 [NASA ADS] [CrossRef] [Google Scholar]
- Woods, T. E., & Gilfanov, M. 2014, MNRAS, 439, 2351 [NASA ADS] [CrossRef] [Google Scholar]
- Worseck, G., Prochaska, J. X., Hennawi, J. F., & McQuinn, M. 2016, ApJ, 825, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Xiao, L., Stanway, E. R., & Eldridge, J. J. 2018, MNRAS, 477, 904 [NASA ADS] [CrossRef] [Google Scholar]
- Xiao, L., Galbany, L., Eldridge, J. J., & Stanway, E. R. 2019, MNRAS, 482, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, S.-C., & Langer, N. 2005, A&A, 443, 643 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoon, S.-C., Dessart, L., & Clocchiatti, A. 2017, ApJ, 840, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, F., Han, Z., Li, L., & Hurley, J. R. 2004, A&A, 415, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Yields of ionizing photons for a range of metallicities
The yields of ionizing photons for stellar populations are dependent on metallicity. There are many reasons for this dependence. The emission rate of ionizing photons increases with hotter and more luminous stars, and the stellar temperature and luminosity both depend on metallicity. The stellar lifetime increases with increasing metallicity because the core masses are smaller at higher metallicity, causing the stars to burn slower. The longer lifetime allows the star to radiate ionizing emission for a longer time.
In the case of stripped stars, the yields of ionizing photons are mostly determined by the emission rate of ionizing photons from the stars. The emission rate of H I-ionizing photons from stripped stars increases with decreasing metallicity; it peaks at Z ∼ 0.002. At an even lower metallicity, our models predict that stripped stars are sufficiently cool for the emission rate of ionizing photons to be affected and to decrease again. This effect is subtle for H I-ionizing emission. Stripped stars are the least efficient in producing H I-ionizing photons at solar metallicity, with a yield of ionizing photons of Iion,H I ∼ 7.8 × 1051 s−1 (M⊙ yr−1)−1. They are most efficient in producing H I-ionizing photons at Z = 0.002, reaching a 30% higher value for the yield of H I-ionizing photons.
This metallicity dependence on the yields of ionizing photons is presented in Table A.1 and Fig. A.1, where we display the yields of H I-, He I-, and He II-ionizing photons at different metallicities. We show the yields for stripped stars using our models. For massive main-sequence and WR stars, we show the predictions from the code STARBURST99 (Leitherer et al. 1999, 2010) and the single-star version of the code BPASS (version 2.2.1, Tuatara, Eldridge et al. 2017; Stanway & Eldridge 2018). In Fig. A.1a we also show the predictions from the models from Schaerer (2003) because these are used for a similar calculation as ours. The calculation was presented in Madau & Dickinson (2014). We also display the predictions from the version of BPASS that account for interacting binaries. For all populations, we assumed the initial mass function from Kroupa (2001) with lower and upper mass limits of 0.1 and 100 M⊙, respectively.
 |
Fig. A.1. Yields of H I-, He I-, and He II-ionizing photons (Iion,H I, Iion,He I, and Iion,He II respectively). We show these yields as functions of metallicity. The photon yields from stripped stars are shown in green and those from massive stars in pink (using models from Starburst99). Panels a, b and c: yield of H I-, He I-, and He II-ionizing photons, respectively. The values are presented in Table A.1. (Z⊙ ≡ 0.014, Asplund et al. 2009.) |
Yields of H I-, He I-, and He II-ionizing photons (Iion,H I, Iion,He I, and Iion,He II respectively).
Figure A.1a shows that the yield of H I-ionizing photons increases with decreasing metallicity for massive stars. This can be understood from the fact that stars are hotter and more luminous at lower metallicity, causing their emission rate of ionizing photons to increase. Table A.1 also shows that the predictions for Iion,H I from the various codes agree relatively well.
In the considered range of metallicities, the yields of H I-ionizing photons from stripped stars is roughly 5% of that from massive main-sequence and WR stars. Our models predict that their contribution is slightly higher at Z = 0.002. The models from BPASS predict that interacting binaries increase the yield of H I-ionizing photons by about 5% at solar metallicity. This is in agreement with the contribution we predict for stripped stars. At Z = 0.006, BPASS predicts a larger difference of about 15%, which disagrees with our models. The reason for this could be that BPASS includes stripped stars of higher masses than we do. At Z = 0.002, BPASS predicts that binaries increase the yield of H I-ionizing photons by ∼20%. At these low metallicities, BPASS assumes that rapidly rotating stars evolve chemically homogeneously, which causes an increase in Iion,H I.
The yield of He I-ionizing photons, Iion,He I, follows a similar trend with metallicity as the yield of H I-ionizing photons, as seen in Fig. A.1b. Down to Z = 0.002, the contribution from stripped stars to Iion,He I is about 20% compared to that from massive main-sequence and WR stars. The reason why their contribution to Iion,He I is relatively higher than that to Iion,H I is that stripped stars are hotter than main-sequence stars. With the high temperatures of stripped stars, a larger portion of their emitted H I-ionizing photons are also He I-ionizing photons than in massive main-sequence and WR stars.
Figure A.1c shows that the yields of He II-ionizing photons, Iion,He II, are probably uncertain for most stars. The predictions for massive main-sequence and WR stars from STARBURST99 and BPASS are different by up to an order of magnitude. The He II-ionizing emission is produced in the steep Wien part of the stellar spectra, which is sensitive to temperature variations and the assumptions for wind mass-loss. This can easily lead to large uncertainties in Iion,He II. Taking the large uncertainties into account, we consider that stripped stars emit He II-ionizing photons at roughly the same or a somewhat higher rate than massive main-sequence and WR stars.
All Tables
Yields of H I-, He I-, and He II-ionizing photons (Iion,H I, Iion,He I, and Iion,He II respectively).
All Figures
 |
Fig. 1. Flowchart visualizing the method we use to model the reionization of hydrogen and helium accounting for ionizing radiation from stellar populations and AGN. The quantities that we consider uncertain are written in red. See Sect. 2 for details and also, e.g., Madau et al. (1999) and Haardt & Madau (2012) where similar methods have been employed. (The massive stars in STARBURST99 are represented by evolutionary models from the Geneva grids (Ekström et al. 2012; Levesque et al. 2012; Georgy et al. 2013), atmosphere models from CMFGEN for Wolf-Rayet stars (Hillier & Miller 1998; Smith et al. 2002), and atmosphere models from WM-BASIC for OB-stars (Pauldrach et al. 2001; Leitherer et al. 2010).) |
| In the text | |
 |
Fig. 2. Emission rates of ionizing photons from a starburst of 106 M⊙ as a function of time. We show the emission rates from stripped stars in dark blue, from massive stars in light blue (using STARBURST99), and we also show the predicted emission rates from the code BPASS in gray. The shaded regions span the emission rates for metallicities between Z = 0.0002 and Z = 0.014, and the solid lines show the emission rates for solar metallicity (Z = 0.014). Top panel: emission rate of H I-ionizing photons, and bottom panel: emission rate of He II-ionizing photons. Stripped stars are clearly responsible for late emission of ionizing photons in a starburst. This figure is adapted from Paper III. |
| In the text | |
 |
Fig. 3. Redshift-dependent escape fractions that we assume in our standard model for stripped stars (dark blue), massive stars (light blue), and AGN (beige). The functions for the escape fraction for stripped stars and massive stars are given in Eqs. (2) and (3), respectively. We also show the escape fraction of Haardt & Madau (2012) for stellar populations as a gray dotted line; it is marked HM12. |
| In the text | |
 |
Fig. 4. Rate with which ionizing photons reach the intergalactic medium. Panels a, b, and c: rate for H I-ionizing photons and panels d, e, and f: for He II-ionizing photons. Left column: results for our standard model, middle column: for our high-fesc model, and right column: for our low-fesc model (see Table 1). We show the contribution from stripped stars in dark blue, from massive stars in light blue, and from AGN in brown. The extent of the colored regions represents the spread caused by metallicity variations. The results for the combination model (see Table 1) are the same as in the high-fesc model for the stripped stars and the same as in the low-fesc model for the massive stars. |
| In the text | |
 |
Fig. 5. Spectral energy distribution of the ionizing radiation that emerges into the IGM during cosmic evolution. We show the contribution from stellar populations in green shades and from AGN in gray. The contribution from stripped stars is highlighted in dark green. They cause the spectra to harden. The dashed lines show spectral slopes of α = −3, −2, and −1, assuming Lν ∝ να. The panels represent four snapshots during cosmic evolution, taken at z = 1.7, 4.3, 7.0, and 11.7. Following the relation between average metallicity and redshift of Madau & Fragos (2017, see also Sect. 2.1.1), the average metallicity at these times is Z = 0.014, 0.006, 0.002, and 0.0002 (Z⊙ ≡ 0.014, Asplund et al. 2009). This figure adopts our standard model for the escape fractions, see Table 1. |
| In the text | |
 |
Fig. 6. Reionization of hydrogen shown as the cosmic evolution of the volume filling factor of ionized hydrogen in the IGM, xH II. We show the evolution of xH II in our standard model (see Table 1). We use red shades for the version that includes stripped stars and gray shades for the version without them. We mark the times when 20%, 40%, 60%, and 80% of the hydrogen in the IGM is ionized using white lines and labels. Stripped stars cause reionization to occur about 100 Myr earlier than when only single stars and AGN are considered. |
| In the text | |
 |
Fig. 7. Relative contribution of ionizing photons from stripped stars (dark blue), massive stars (light blue), and AGN (beige) to the photon budget that caused hydrogen reionization. Stripped stars contributed about 20% of the H I-ionizing photons, see Sect. 4. This figure shows the results from our standard model, for which reionization is complete at z = 6.5 when stripped stars are included (see Tables 1 and 2). |
| In the text | |
 |
Fig. 8. Cosmic evolution of the relative contribution from stripped stars (dark blue), massive stars (light blue), and AGN (beige) to the budget of H I-ionizing photons (panel a) and He II-ionizing photons (panel b). We label the time of hydrogen and helium reionization and shade the times predicted by our model for the reionization of the Universe. This figure shows the results from our standard model; the trend in massive stars is in part due to the strongly redshift-dependent fesc (see Table 1). |
| In the text | |
 |
Fig. A.1. Yields of H I-, He I-, and He II-ionizing photons (Iion,H I, Iion,He I, and Iion,He II respectively). We show these yields as functions of metallicity. The photon yields from stripped stars are shown in green and those from massive stars in pink (using models from Starburst99). Panels a, b and c: yield of H I-, He I-, and He II-ionizing photons, respectively. The values are presented in Table A.1. (Z⊙ ≡ 0.014, Asplund et al. 2009.) |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



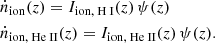
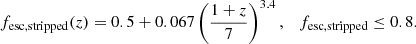
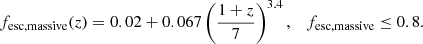
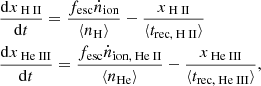
![$$ \begin{aligned} \begin{aligned}&\langle t_{\mathrm{rec, }{\text{ H}}\,{{{\textsc{II}}}}} \rangle = [n_{\rm e}\; \alpha _{B, {\text{ H}}\,{{{\textsc{II}}}}} \; C_{\mathrm{IGM}}]^{-1} \\&\langle t_{\mathrm{rec, }{\text{ He}}\,{{{\textsc{III}}}}} \rangle = [n_{\rm e} \; \alpha _{B, {\text{ He}}\,{{{\textsc{III}}}}} \; C_{\mathrm{IGM}}]^{-1}, \end{aligned} \end{aligned} $$](/articles/aa/full_html/2020/02/aa36669-19/aa36669-19-eq5.gif)