| Issue |
A&A
Volume 633, January 2020
|
|
|---|---|---|
| Article Number | A118 | |
| Number of page(s) | 17 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201936884 | |
| Published online | 22 January 2020 | |
Molecular complexity in pre-stellar cores: a 3 mm-band study of L183 and L1544★,★★
1
Center for Astrochemical Studies, Max-Planck-Institut für Extraterrestrische Physik,
Gießenbachstraße 1,
85748 Garching, Germany
e-mail: lattanzi@mpe.mpg.de
2
Ural Federal University, Ekaterinburg,
Russia
3
Department of Physics, PO Box 64, University of Helsinki, Helsinki, Finland
4
IRAP, Université de Toulouse, CNRS, UPS, CNES,
Toulouse, France
Received:
8
October
2019
Accepted:
9
December
2019
Context. Pre-stellar cores (PSCs) are units of star formation. Besides representing early stages of the dynamical evolution leading to the formation of stars and planets, PSCs also provide a substrate for incipient chemical complexity in the interstellar space.
Aims. Our aim is to understand the influence of external conditions on the chemical composition of PSCs. For this purpose, we compared molecular column densities in two typical PSCs, L183 and L1544, which are embedded in different environments.
Methods. A single-pointing survey of L183 at λ = 3 mm was conducted using the IRAM 30-m single-dish antenna. This led to the detection of more than 100 emission lines from 46 molecular species. The molecular column densities and excitation temperatures derived from these lines were compared to the corresponding parameters in L1544. The data for L1544 were obtained from literature or publicly available surveys, and they were analysed using the same procedure as adopted for L183. An astrochemical model, previously developed for the interpretation of organic molecule emissions towards the methanol peak of L1544, was used to interpret the combined data.
Results. Our analysis reveals clear chemical differences between the two PSCs. While L1544 is richer in carbon-bearing species, in particular carbon chains, oxygen-containing species are generally more abundant in L183. The results are well-reproduced by our chemical model.
Conclusions. The observed chemical differentiation between the two PSCs is caused by the different environmental conditions: the core of L183 is deeply buried in the surrounding cloud, whereas L1544 lies close to the edge of the Taurus Molecular Cloud. The obscuration of L183 from the interstellar radiation field (ISRF) allows the carbon atoms to be locked in carbon monoxide, which ultimately leads to a large abundance of O-bearing species. In contrast, L1544, being more affected by the ISRF, can keep a fraction of carbon in atomic form, which is needed for the production of carbon chains.
Key words: ISM: molecules / line: identification / molecular data / molecular processes / radio lines: ISM
The reduced spectrum is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/633/A118
© V. Lattanzi et al. 2020
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1 Introduction
Cold dark clouds represent a very unique environment to test our knowledge of the chemical and physical evolution of the structures that ultimately led to life. In particular, pre-stellar cores (PSCs), which are dynamically evolved starless cores (such as L183; also known as L134N), represent the first phases of the star-formation process and breeding grounds of chemical complexity. Despite their apparent simplicity and the lack of internal energy sources, PSCs exhibit a surprisingly complex molecular inventory and large variations in the abundances. Chemical differentiations are observed within (e.g. Spezzano et al. 2016a), as well as among, different starless and pre-stellar cores (e.g. Tafalla et al. 2006, and references therein). Here, we focus on the pre-stellar core L183, well known to be rich in S-bearing as well as O-bearing molecules (e.g. Swade 1989), and with a physical structure similar to that of L1544 (Crapsi et al. 2005, 2007; Pagani et al. 2007).
The physical and chemical conditions of PSCs have been probed over the past years by many molecular features, spanning from simple diatomic species to ions, and, more recently, to larger organic molecules. In the following, we refer to C-bearing species with at least six atoms as interstellar complex organic molecules (iCOMs), in accordance with the definition stated in Ceccarelli et al. (2017). This class of molecules was first detected in the warm and dense (≳100 K and ≳106 cm−3) hot cores (Blake et al. 1987); more recently a good fraction of these relatively complex species have been also detected in cooler (~10 K) environments (Öberg et al. 2010; Bacmann et al. 2012; Vastel et al. 2014; Jiménez-Serra et al. 2016). These new detections posed a serious challenge for the existing astrochemical models. In the more recent of them, simple radicals, formed during the cold pre-collapse phase on the cold (≲20 K) grain surface, are thought to acquire mobility and react, forming iCOMs when the dust temperature reaches ~30 K (e.g. Garrod et al. 2007). But the detection of iCOMs such as methanol (CH3OH), methyl formate (CH3 OCHO), and dimethyl ether (CH3 OCH3) in regions where the dust temperature is below 30 K cannot be described by such a theory. Recently, Balucani et al. (2015), building up on the model from Vasyunin & Herbst (2013), developed a new model where gas-phase reactions, triggered bynon-thermal desorption of methanol from the ices, play a major role in the formation of methoxy, methyl formate, and dimethyl ether in cold regions. The authors then showed how grain-surface chemistry contributes to the formation of hydrogenated species during the pre-stellar phase, but is not necessarily important for all iCOMs.
Nevertheless, the first step to molecular complexity remained unsolved. Methanol (CH3 OH) is believed to form on the grain surfaces via subsequent additions of hydrogen to iced CO (Watanabe & Kouchi 2002) or, alternatively, in the bulk of water-rich ices (Watanabe et al. 2003). However, Hiraoka et al. (2002, 2005) have claimed that the formation pathway through CO hydrogenation cannot be the major source of methanol in the ISM, since the reaction rates are too slow. Among the other possible routes proposed in the past years, very recent experiments show that CH3 OH can also be formed with the irradiation of methane (CH4) and water ices (Martín-Doménech et al. 2016). On the other hand, other experiments have also revealed that thermal desorption at 10 K is negligible for species more massive than molecular hydrogen, and that irradiation of methanol (pure or mixed) ices produces mainly photofragments of the species (Bertin et al. 2016). Refined astrochemical models have then been used to investigate other non-thermal desorption mechanisms. Garrod et al. (2006) and Garrod & Herbst (2006) considered that the energy of formation released by the association reaction of grain-surface radicals is sufficient for breaking the surface-molecule bond of the product. Following the same idea, Dulieu et al. (2013) used experiments, and Minissale et al. (2016) used an analytic model to come to the conclusion that chemical desorption processes allow a significant fraction of surface species, methanol included, to be ejected into the gas phase. More recently, Dartois et al. (2019) showed experimental evidence that cosmic rays penetrating deep into dense clouds can also provide an efficient mechanism to desorb complex organic molecules, such as methanol and methyl acetate.
The challenge of reproducing the observed abundances of iCOMs in cold molecular clouds has also been addressed recently by Vasyunin et al. (2017), making use of an advanced gas-grain astrochemical model with an updated gas-phase chemistry. The model uses a multi-layer approach to the ice-surface chemistry, and assumes, based on the results of Minissale et al. (2016), that the efficiency of reactive desorption depends on the composition of the ice. In this work, Vasyunin et al. (2017) applied the chemical model to the L1544 PSC, finding a good agreement between theoretical and observational data. According to this work, saturated organic molecules can build up fractional abundances of (3–4) × 10−10 through the reactive desorption process of CH3OH and gas-phase chemistry, about 5000 au away from the core centre, defined by the position of the millimetre dust continuum emission peak.
L183 is a low-mass, centrally condensed starless core with a high central-column density. It belongs to a loose group of high-latitude (b ~ 37°) dense clouds with a total mass of ~80 M⊙ (Pagani et al. 2004), associated with the surface of the local bubble at a distance of 110 pc (Franco 1989). This object has been the target of several studies in molecular lines (Swade 1989; Dickens et al. 2000; Lee et al. 2001; Pagani et al. 2005, 2007; Requena-Torres et al. 2007), and in the far-infrared and sub-millimetre continuum (Juvela et al. 2002; Ward-Thompson et al. 2002; Lehtinen et al. 2003; Pagani et al. 2003a; Kirk et al. 2005; Kauffmann et al. 2008). Dickens et al. (2000) mapped the core in 13 molecular species. Comparing the abundances derived from these observations with those obtained for the quiescent core TMC–1, the authors found that the latter core is more carbon-rich, and thus less chemically evolved than L183. A similar analysis, and full comparison with Dickens et al. (2000), is to be presented in a coming paper (in preparation) where the emission maps of several chemical compounds observed in L183 will be presented. Also, Crapsi et al. (2005) found large molecular D/H ratio (20%) and high central densities (1 × 106 cm−3) toward L183, characteristics of PSCs. Kirk et al. (2009), in their N2 H+(1–0) mapping with the Berkeley-Illinois-Maryland Array (BIMA), detected three spatially and kinematically distinct clumps, one of them at the systemic velocity of L183 (vlsr ≃ 2.4 km s−1), and coincident with the dust emission peak.
Here, we present single-pointing observations towards L183 performed with the IRAM 30 m telescope at the wavelength λ = 3 mm. We compare the chemical abundances derived for L183 with those found previously in L1544, in order to study similarities and differences between these two PSCs. We also compare our results with the predictions of the astrochemical model developed by Vasyunin et al. (2017). This would test how applicable the model is to PSCs other than L1544.
In the next section of this paper, we briefly summarise the observations. This is followed by a detailed description of the data analysis (Sect. 3) and the construction of the physical model for the core (Sect. 4). In Sect. 5, we present the observational results and compare these with predictions from our astrochemical model (Sect. 6) and with corresponding data from L1544. Finally, in Sect. 7, we present the main conclusions from this work.
2 Observations
Single-pointing observations towards the quiescent core L183 (α2000 = 15h54m08s.6, δ2000 = −02°52′10′′.0) were carriedout with the IRAM 30 m antenna, at Pico Veleta (Spain), in May 2015. We used the EMIR receiver at 3 mm (E090) and three different tuning configurations (with some overlap) to cover a total of ~ 19 GHz (83.8–86.6, 87.0–89.9, 92.6–94.4, 95.9–97.7, 99.4–102.3, 102.7–105.6, 108.3–110.1, 111.6–113.4 GHz). The FTS spectrometer in its high-resolution configuration was used as backend, allowing an instantaneous bandwidth of 7.2 GHz distributed in four sub-bands, with a final unsmoothed resolution of 49 kHz. We observed L183 in frequency switching mode, since the lines are sufficiently narrow, using frequency throws of 3.9 MHz. Also thanks to good weather conditions, system temperatures were typically around 80–120 K. Pointing and focus were checked regularly every ~ 1.5 and 4 h, respectively, on strong and nearby quasars: in the observed frequency range, the half power width of the main beam can be approximated to a good accuracy to 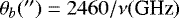 . The acquired spectra were then converted from the antenna temperature
. The acquired spectra were then converted from the antenna temperature 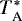 to the main beam temperature Tmb adopting the inverse of the main beam efficiency (Beff) as derived in Velilla Prieto et al. (2017):
to the main beam temperature Tmb adopting the inverse of the main beam efficiency (Beff) as derived in Velilla Prieto et al. (2017):
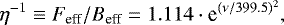 (1)
(1)
where ν is the frequency in GHz, and Feff is the forward efficiency of the antenna. We spent an uneven amount of time on each of the three tunings (0.5, 2.7 and 8.1 h), and the final sensitivity of the whole survey is in the 1.7–11 mK range.
3 Analysis
3.1 L183 data
The single pointing observations of L183 allowed the detection (above 3.5σ) of more than 100 lines from 46 different molecular species, including iCOMs, carbon chains, molecular ions, and deuterium substituted species (see Table 1). The data processing, analysis, and line identification through the CDMS (Müller et al. 2005) and JPL (Pickett et al. 1998) molecular spectral line databases, were performed using the GILDAS1 and the CASSIS2 software.
For the species where more than two transitions have been observed (see Table B.1), the analysis was carried out through a Markov chain Monte Carlo (MCMC) method implemented within CASSIS (Vastel et al. 2018b). The MCMC method consists of an iterative process that goes through all the parameter space (column density, excitation temperature, source size, linewidth, and vlsr) with a random walk and heads into the solutions, by a χ2 minimisation. All the parameters can be varied as boundary conditions to the model: for all the species analysed, the emission is compatible with a source size, obtained directly from the output of the MCMC fitting routine, much larger than the IRAM beam (~ 30′′). In the cases where the molecular species were detected only through one or two rotational transitions, the analysis was carried out assuming two excitation temperatures: 5 and 10 K. These values were chosen in accordance with those derived previously in the same source (e.g. Swade 1989; Crapsi et al. 2005, for N2 H+ and N2 D+) and those derived through our hyperfine fitting analysis (see later in this section). The column density was determined under the assumption, unless stated otherwise, that the lines are optically thin, using, as in Caselli et al. (2002b):
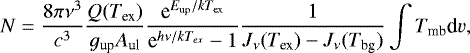 (2)
(2)
where ν is the frequency of the transition, c the speed of light, h and k the Planck and Boltzmann constants, respectively, gup the upper level degeneracy, Aul the spontaneous emission Einstein coefficient, Tex the excitation temperature, Q(Tex) the partition function at Tex, and Eup the energy of the upper level. Jν(T) is the equivalent Rayleigh-Jeans temperature defined as:
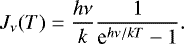 (3)
(3)
For every transition analysed here, the assumption of optically thin lines was checked deriving the optical depth from
![\begin{equation*} \tau=-{\textrm{ln}}\left[1-\frac{T_{\textrm{mb}}}{f[J_{\nu}(T_{\textrm{ex}})-J_{\nu}(T_{\textrm{bg}})]}\right]\!,\end{equation*}](/articles/aa/full_html/2020/01/aa36884-19/aa36884-19-eq7.png) (4)
(4)
where f is the source filling factor, being the source size obtained from the MCMC fits considerably larger than the telescope beam (typically by two orders of magnitude; see discussion above), f was fixed to unity for all the species analysed here. For H13CN, N2 H+, and NH2D, the opacity was obtained directly using the hyperfine splitting routine (HFS) implemented in the GILDAS/CLASS software. Under the assumption that all the hyperfine components have the same excitation temperature, the same width, and do not overlap, the HFS fitting routine provides the linewidth and the opacity, from which the Tex can be directly derived (see Eq. (6), below). When two lines were detected for the same molecular species, the column density derived for the transition involving the lower Eup was chosen as representative, and, in case of similar Eup, the one with the lowest opacity. The error on the column density was obtained from 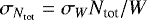 , where W is the integrated intensity and its associated error,
, where W is the integrated intensity and its associated error,
Molecules detected towards L183.
![\begin{equation*} \sigma_W = \sqrt{(\textrm{cal}\times W)^2+[\textrm{rms}\times\sqrt{2\times FWHM\times \Delta \rm{v}}]^2,}\end{equation*}](/articles/aa/full_html/2020/01/aa36884-19/aa36884-19-eq9.png) (5)
(5)
is provided directly from the analysis with CASSIS. Here, cal = 15% includes the calibration and pointing uncertainties, and Δv is the velocity resolution in km s−1. All the molecular species have at least a transition that is optically thin (τ ≲ 0.1), with the exception of SO and HNCO, where both the detected lines were optically thick. For SO, the abundances were derived by means of its rarer isotopologues S18 O, and assuming a 16 O/18O ≃ 500, as in Dickens et al. (2000) for the same source. For HNCO, the final column density was obtained correcting the one derived in the optically thin approximation by the optical depth correction factor τ∕(1 −e−τ) (Mangum & Shirley 2015), obtaining τ from the line main beam temperature, as described above (see Eq. (4)).
The separate hyperfine analysis for H13CN, N2 H+, and NH2D was carried out as in Caselli et al. (2002b): the excitation temperature was obtained from hyperfine fitting of the spectra with well-constrained opacities (τ∕στ > 3), under the assumption of a unique excitation temperature for all the hyperfine components. H13 CN was detected through its fundamentalrotational transition (J = 1–0) with a well resolved hyperfine structure, due to the coupling of the nitrogen nuclear spin (I = 1) with the overall rotation of the molecule. To obtain the column density of the species, the HFS routine of the CLASS software was used to derive the opacity of the main component (τ = 1.95 ± 0.10, relative intensity Ri = 1). This value leads to opacities of 1.17 ± 0.06 and 0.39 ± 0.02 for the middle (Ri = 0.6) and weakest (Ri = 0.2) component of the hyperfine structure, respectively. The main beam temperature of the principal component, the output of the same fitting routine, was then used to derive, under the assumption that the emitting region of the source fills the antenna beam, the excitation temperature, through
,\end{equation*}](/articles/aa/full_html/2020/01/aa36884-19/aa36884-19-eq10.png) (6)
(6)
giving a Tex = (3.03 ± 0.45) K, including calibration and pointing uncertainty. This value matches the one obtained in the same source by Swade (1989) exactly. Now, from this Tex and from Caselli et al. (2002b, Eq. (A1)), we derive a total column density of N = (9.4 ± 0.5) × 1011cm−2. Swade (1989) obtained N ≳ 7.7 × 1011cm−2 but, with the lines being optically thick, the value is an underestimation of the real column density.
Seven hyperfine components of the fundamental rotational transition of N2 H+ were detected with our observations of L183. Following the same approach as described above, a total opacity of τ = 16.20 ± 0.30 (4.19 ± 0.07 for the main hyperfine component) and an excitation temperature of Tex = (4.57 ± 0.69) K was obtained. From the opacity of the weakest component (τ = 0.60 ± 0.01), we obtained a total column density of N = (1.2 ± 0.2) × 1013cm−2. These values are in very good agreement with those derived for the same species in L183 by Crapsi et al. (2005), although the pointing of these observations was slightly different from ours (~20′′): in this previous study, a total opacity of 20.3 ± 0.2 was derived, with an excitation temperature of 4.8 ±0.1 K, and a total column density of N = (2.0 ± 0.6) × 1013cm−2.
The 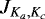 = 11,1–10,1 rotational transition, in five hyperfine components, of ortho-NH2D was detected in L183, with a total opacity of τ = 3.30 ± 0.02 (1.49 ± 0.01 for the main hyperfine component). The excitation temperature derived is Tex = (5.61 ± 0.84) K for a total column density of N = (2.3 ± 0.1) × 1014 cm−2; these values are in perfect accordance with those reported previously by Gerin et al. (2009) for the same source (Tex = (5.5 ± 0.5) K and N = (2.4 ± 0.4) × 1014cm−2).
= 11,1–10,1 rotational transition, in five hyperfine components, of ortho-NH2D was detected in L183, with a total opacity of τ = 3.30 ± 0.02 (1.49 ± 0.01 for the main hyperfine component). The excitation temperature derived is Tex = (5.61 ± 0.84) K for a total column density of N = (2.3 ± 0.1) × 1014 cm−2; these values are in perfect accordance with those reported previously by Gerin et al. (2009) for the same source (Tex = (5.5 ± 0.5) K and N = (2.4 ± 0.4) × 1014cm−2).
3.2 L1544 data
The molecular abundances of the different species detected in L183 were then compared to those found towards the dust peak of L1544. This source is a pre-stellar core in Taurus, extensively studied with several single pointing (e.g. Crapsi et al. 2005; Keto & Caselli 2010; Vastel et al. 2014, 2015, 2016, 2018a,b, 2019; Jiménez-Serra et al. 2016; Quénard et al. 2017) and mapping observations (e.g. Caselli et al. 1999, 2002a; Vastel et al. 2006; Spezzano et al. 2017; Chacón-Tanarro et al. 2019), which also showed the chemical richness and complexity of this source. Mapping CO and CS isotopologues, NH3 and N2 H+ around the dust core of L1544, Tafalla et al. (2002) revealed an active molecular differentiation, confirmed and extended recently by Spezzano et al. (2017) with the mapping of the central 6.25 arcmin2, with 39 emission features of 22 molecular species, and the identification of five distinct emitting “peaks”. Thanks to the number of studies performed in the past years towards the prototypical pre-stellar core L1544, the majority of the species detected in L183 were available in the literature, and have been used in Table B.2 for comparing the two sources. For the molecular species for which no data were available in previous works, the column densities for L1544 were obtained from the publicly available data of the IRAM Large Program ASAI (Astrochemical Surveys At IRAM; Lefloch et al. 2018). This Large Program performed single pointing observations towards the dust peak of L1544 (α2000 = 05h04m17s.2, δ2000 = 25°10′42′′.8) using the 3 mm-band EMIR receiver, and covering (rms = 2.1–7.0 mK) the 80.0–106.0 GHz frequency range with high sensitivity. The analysis of these observations was carried out following the same method described above for L183.
In Table B.1, the full list of the molecular transitions observed toward L183, and analysed for the abundance comparisonwith L1544, is presented along with the result from the line Gaussian fit. In this inventory, all the molecular species detected in L183 that have also been observed in L1544 are shown, either in literature studies or in the ASAI survey. The observed column densities for both sources are presented in Table B.2. The diatomic system, CN and 13 CN, was excluded from our study, since a full detailed work has been published by Hily-Blant et al. (2008), analysing the N = 1 → 0 rotational transition of both isotopologues in L1544 and L183. Same considerations apply for the case of HC15N: a full analysis on the comparison of its abundance in L183 and L1544 was reported by Hily-Blant et al. (2013), focusing on the J = 1 → 0 emission line in the 3 mm band.
The observed chemical abundances were finally compared to an advanced gas-grain astrochemical model, successfully applied to L1544, a full description of which can be found in Vasyunin et al. (2017). This model benefits from an updated gas-phase chemistry, with a multilayer approach to ice-surface chemistry and an up-to-date treatment of reactive desorption, based on recent experiments. In the following section, we provide the input of the chemical code, namely the physical structure of L183.
4 Physical model of the L183 core
The aforementioned astrochemical model is based on a spherically symmetric representation of the density and temperaturedistributions in the central part of L183 based on Herschel/SPIRE maps of the cloud at 250, 350, and 500 μm (Griffin et al. 2010). The cloud has been mapped as part of the Herschel photometric survey of planck-detected Galactic cold clouds (Juvela et al. 2010). We used level 2 pipeline-reduced data, downloaded from the Herschel Science Archive (HSA), created using the Standard Product Generation (SPG) software version 14.1.0. The SPIRE maps were used to calculate the dust colour temperature, TC, and the H2 column density, N(H2), distributions. A modified blackbody function with the dust emissivity spectra index β =1.5, as used previously for L1544, was fitted to each pixel after smoothing the 250 and 350 μm images to the resolution of the 500 μm image (~ 40′′), and resampling all images to the same grid. For the dust emissivity coefficient per unit mass of gas at λ = 250 μm, we adopted the value from Hildebrand (1983), κ250μm = 0.1 cm2 g−1.
The N(H2) map (Fig. 1) reveals a filamentary structure extending in a north-south direction. The dense core investigated here is part of this structure. We first defined the backbone of the filament by spline interpolation through manually selected positions. The structure was analysed assuming a cylindrically symmetric density distribution around this backbone. A full description of the methodology adopted here can be found in Redaelli et al. (2018). Column density profiles along cuts perpendicular to the backbone were fitted by Plummer profiles. These profiles were inverted to radial density profiles, 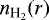 , using the formula presented in Arzoumanian et al. (2011, Eq. (1)). A three-dimensional model for the density structure was interpolatedusing the radial density profiles at different positions along the backbone.
, using the formula presented in Arzoumanian et al. (2011, Eq. (1)). A three-dimensional model for the density structure was interpolatedusing the radial density profiles at different positions along the backbone.
The dust temperature distribution in this model was calculated using a Monte Carlo programme for continuum radiative transfer developed by Juvela (2005). The spectrum of the unattenuated interstellar radiation field (ISRF) was taken from Black (1994). We used the dust opacity data from Ossenkopf & Henning (1994) for unprocessed dust grains with thin ice coatings3, which agree with the opacities at 250, 350 and 500 μm used in the derivation of the TC and N(H2) maps described above (Fig. 1). The intensity of the ISRF was adjusted until the surface brightnesses predicted from the model approximately agreed with the SPIRE maps at 250, 350, and 500 μm. The gas and dust temperatures are assumed to be equal throughout the cloud in the present model, although this assumption is likely to be valid at densities above ~105 cm−3 (the innermost ~5000 AU for L183, see Fig. 2) only (Goldsmith 2001). Finally, to facilitate the modelling of the single-pointing observations presented here and to provide the input to the chemical code described in Sect. 6, the three-dimensional models of the density and temperature distributions were averaged within spherical shells around the density maximum. The resulting one-dimensional density and temperature profiles are shown in Fig. 2.
The full structure of the physical model briefly described here is to be presented in a following work.
 |
Fig. 1 Herschel/SPIRE maps, at the same linear scale, of the H2 column density (top row) and dust temperature (bottom row) in L183 (left column) and L1544 (right column). The beam of SPIRE is shown as a white (top row) and black (bottom row) circle in the bottom-left corner. The white star in the middle of L183 figures represents our pointing, while the one in L1544 identifies the dust peak of the source. White contours are 0.5, 1.5, 2.5 × 1022 cm−2 for the H2 column density (top row) maps and 12, 14, 16, 18 K for the dust temperature (bottom row) maps, respectively. |
5 Results
The molecular column densities derived towards the dust peak of L183 with our observations were first compared with those obtained in L1544, and successively with those predicted by our astrochemical model.
 |
Fig. 2 Molecular hydrogen density and dust temperature radial profiles for L183 and L1544, derived from the Herschel/SPIRE maps in Fig. 1 as described in the text. For L1544, the radial profile from Keto & Caselli (2010) is also shown. |
5.1 L183 and L1544
The full list of chemical inventory for L183 and L1544 is shown side by side in Table B.2. A graphic representation of this table is provided in Fig. 3, where the ratios of molecular column densities in the two sources are shown. This plot was created following the structure of Table B.2; two different ratios were derived for molecules inthe upper block of the table, comparing the column densities for the two excitation temperatures, and both points are plotted in Fig. 3. For the middle block species, the two points in the plot represent the two column densities derived for L183 both compared to the single value found in L1544; finally for molecular species in the lower block of Table B.2, only one value per molecule is provided in Fig. 3. The figure is basically structured in four different blocks of molecular species families: from left to right, we find the group of iCOMs, followed by carbon-chain species. Next are nitrogen-bearing molecules, and finally, at the right end of the plot, the abundance ratios of the sulphur-bearing species are shown. Obviously, this schematic division is not fully strict, and there are overlaps in between the groups, but such a scheme might help to guide the analysis of the results.
As a general comment, the column densities of the detected species in the two sources do not differ by more than one order of magnitude. On the other hand, it is also noticeable that, except in a few cases (CH3CHO, t-HCOOH, CH3OH, C3 O, HNCO, HOCN, HOCO+, 13 C18O, SO, S18O, SO2, OCS), L1544 appears to have larger column densities than L183.
The ratio for the iCOMs is larger than unity for the oxygen-bearing species, such as CH3CHO, t-HCOOH, and CH3OCHO; however, from the plot, it is clear that when the iCOMs are richer in carbon than in oxygen, such as methyl acetylene (CH3CCH), the ratio becomes similar to the carbon chains, meaning that L1544 is richer than L183.
The quality of our observations allowed us also to detect, for the first time in L183, the methyl formate (CH3OCHO) and the single deuterated methanol (CH2DOH). The former species was also detected by Jiménez-Serra et al. (2016) in L1544, both in the dust and the methanol peak. The columndensity value that we derive for the methyl formate in L183 is about four times less than the one observed towards the dust peak of L1544 by Jiménez-Serra et al. (2016); nevertheless, considering the large uncertainty associated with the value for L1544, the L183 methyl formate column density is within 1σ of that derivedtowards L1544. Also, it can be noticed in Table B.2 that the excitation temperatures derived in the sources for this species are quite different, at 14 and 5 K in L183 and L1544, respectively. If the excitation temperature parameter space in the MCMC analysis for the L183 data, is limited to values closer to the one derived for L1544, we obtain the same column densities for the two sources, but with a consequent worsening of the line fitting. This difference is consistent with the iCOMs tracing the outer envelope of the cores, and L1544 being warmer than L183 for the most part outside the radius of 1000 au (see Fig. 1).
From our observations, we were able to detect four transitions of the e0 state of CH2DOH. All four lines of CH2DOH peak at lower velocity (~ 300 m s−1, more than 10 times larger than the frequency uncertainty) with respect to the main isotopologues, possibly indicating that the two species are actually tracing slightly different parts of the core. A similar behaviour was also reported in Bizzocchi et al. (2014) for L1544. For these reasons, we also performed detailed mapping observations of L183, which are to be compared with those of L1544 recently published by Chacón-Tanarro et al. (2019), and are the topic of a follow-up paper.
The column densities derived in L183 for carbon-chain molecules is, on average, ~ 10% of that obtained for L1544 towards the dust peak. This result is even more dramatic since the abundances in L1544 of some of the species in this family, for example, CCH and C4 H, might actually be underestimated. In fact, six fine components of the N = 1−0 transition of CCH were observed in L1544, the same is shown in Table B.1 for L183: all of them have an opacity higher than 0.5, so the final abundance should be augmented by about 30%. Twelve fine lines were detected for the longer carbon-chain radical C4 H in L1544, from the N = 9−8, N = 10−9, and N = 11−10 transitions, and also, for this species, the final column density should be corrected by a factor 1.3. The numbers for propadienylidene, the linear C3 H2, were obtained treating the ortho and para species separately, with different partition functions, and energy for the ortho states renormalised. The final column density is the sum of the two individual ones. From our analysis, we derived, for L183, an ortho-to-para c-C3H2 ratio of ≲ 7, consistent within the errors obtained by Turner et al. (2000) for L183 (4.3). The cyclic-to-linear C3 H2 ratio in L183 from our analysis is ~25 ± 6, similar (in two sigmas) to that derived by Spezzano et al. (2016b) in L1544 (~32±4), but lower than the one derived by Turner et al. (2000) (~50), probably reflecting our lower para l−C3H2 abundance.
The column density for the nitrogen-bearing molecular species derived in L183 is around 20% less than the one in L1544. This result is not surprising, since several studies have shown that the L1544 dust peak is rich in nitrogen-containing compounds (e.g. Spezzano et al. 2017; Vastel et al. 2019) and, as previously noted, appears overall to be more chemically rich than L183. Again, also for this class of molecular species, when oxygen is present, as is the case for the isocyanic and cyanic acid (HNCO and HOCN, respectively), L183 presents abundances larger than L1544. Deuterated ammonia, NH2D shows similar (in a factor 2) column density and excitation temperature in the two sources. As stated above, the column density derived through the HFS analysis of our observations is in perfect agreement with the values reported in Tiné et al. (2000), though observing a nearby position in L183 (α2000 = 15h54m08s.6, δ2000 = −02°52′01′′.1).
The last “family” of molecular species, which is represented in the plot, is composed of the sulphur-bearing molecules. In this case, there is a well-defined dichotomy carbon–oxygen, which somehow summarises what we discussed while analysing the previous cases. All the species containing oxygen, such as SO and SO2, are more abundant in L183, yet if carbon is present, L1544 has higher column densities than the previous source, as shown by HCS+, and the isotopologues of H2CS. In this framework, it is interesting how OCS has the same column density in the two sources, and it is also the only molecule observed containing the three elements. One exception to this scheme is the case of C34 S, whose column density ratio for the two sources is very close to unity.
Finally, we present a few considerations on the choice of the excitation temperature. From Fig. 3, it is clear that, in general, adopting 5 or 10 K as the excitation temperature does not significantly change the results of the above discussion regarding the column densities of the different species. Nevertheless, this is not true for only two molecular species, namely C3 O and HC3N. In the former case, the value obtained at 5 K for L183 is considerably larger than the one for L1544, which is actually found for the latter source, assuming an excitation temperature of 10 K (see Table B.2). The ratio at 5 K is even more suspicious, considering that C3O would be the only carbon chain for which L183 is richer than L1544. For HC3N, the column density derived for L183 at 10 K is more than two orders of magnitude lower than the one for L1544. From the considerations described above in this section, it is not a total surprise that a nitrogen-carbon-chain species is more abundant in L1544 than in L183. Assuming the same excitation temperature in L183 as the one found for L1544 (i.e. 7.2 K, see Table B.2), we obtain a column density in L183 ~ 50 times lower than in L1544.
 |
Fig. 3 Logarithmic column density ratios of L183 relative to L1544. Where no uncertainty was provided in the literature data (see Table B.2), an error of 25% of the reported column density was assigned for the error bars in the plot. In cases where the column density was derived for two temperatures, both ratios are shown for the same species. The red dashed line represents the ratio equal to unity. |
 |
Fig. 4 Rotational diagram with the five rotational transitions of methanol detected towards L183. The red dashed line corresponds to the best linear fit, which yields the excitation temperature and column density shown in the plot. |
5.2 Methanol analysis
To better understand the excitation processes involving methanol rotational levels, due to the key role of this species in the building up of the chemical complexity in interstellar environments, a more detailed analysis was carried out. Firstly, since the detected transitions span a large range of Eup energy (7–40K, see Table B.1), we constructed a population diagram. As shown in Fig. 4, the LTE model does not reproduce the excitation conditions of the species in L183 very well, exhibiting some scatter among the points of the plot representing the observed transitions. In these conditions, the rotational diagram analysis yields a rotational temperature of Trot = (7.3 ± 1.7) K, and a column density of N = (9.1 ± 6.0) × 1013cm−2. The rotational partition function is derived by summing up all (A + E) rotational levels (Xu & Lovas 1997), whose energies are available at the CDMS.
A second analysis using the radiative transfer code MOLLIE (Keto & Rybicki 2010) was hence performed to check the results obtained in the LTE approximation. De-excitation rates for the collisional systems para-H2/A-CH3OH and para-H2/E-CH3OH (Rabli & Flower 2010a), available in the LAMDA database (Schöier et al. 2005), were then used for the statistical equilibrium calculation: the lack of data for ortho-H2 does not hamper our modelling, because of the very low H2 ortho-to-para ratio (OPR) expected in PSCs (e.g. Sipilä et al. 2013). Also, it should be noted that the data in the LAMDA database are available for kinetic temperatures as low as 10 K. A and E symmetries of methanol were treatedseparately in the simulations, considering rotational levels below 38 and 45 K, respectively. As done previously (Bizzocchi et al. 2014), the initial CH3OH abundance, which is the input parameter to MOLLIE, is translated to a radial abundance profile: the A-CH3OH radial abundance corresponding to the best-fit input abundance is shown in Fig. 5 as an example. The resulting beam-averaged value of the CH3OH column density (including both A and E species) is (4.9 ± 0.7) × 1013 cm−2, assuming a 15% calibration error; despite the scatter of points in the rotational diagram described above, this value is in good agreement with the one found in the LTE approximation (roughly a factor 2) (see Fig. 4). From the spectral distribution of the emerging radiation field data cube, the modelled spectra were extracted from the central pixel, convolved with the 30m telescope main beam, and compared to the observations. Optimal χ2 -fit between observed and modelled spectral profiles were found for the 21,2 –11,1 (E2), 20,2 –10,1 (A+), and 20,2 –10,1 (E1) transitions using input abundances of 1.45 × 10−9 and 1.40 × 10−9, for A and E species, respectively (see Fig. 6). A deeper look at the modelled brightness of the observed methanol transitions shows, despite the aforementioned agreement, large discrepancies for the other two observed lines. In particular, the intensity of the 00,0 –11,1 (E1–E2) transition at 108.9 GHz, as noted previously in Bizzocchi et al. (2014), is largely underestimated, and, as shown in Fig. 7, this line is predicted to be considerably sub-thermally excited, even at the high gas density of the cloud centre. This is due to an artefact of the coupled state approximation used in the calculation of the collisional rates (Rabli & Flower 2010b); the rate coefficients for the collisional transition connecting the state 00,0 to the lower 11,1 are set to zero in the dataset used (Rabli & Flower 2010a), but it is very likely that this transition has a small, but non-zero, rate coefficient. Post-alteration of this collisional rate, even by a fraction of the 21,2 –11,1 upward rate (75%), makes it possible to better model the emission of the 00,0 –11,1 rotational transition, without altering the modelling of the other transitions considered above (see Figs. A.1 and A.2; see also an extended discussion in Bizzocchi et al. 2014 and Fig. 8 therein).
 |
Fig. 5 Modelled methanol radial abundance profile. |
 |
Fig. 6 Observed (in blue) and modelled spectrum with MOLLIE of CH3OH in L183. Thevelocity axis is centred on the 20,2–10,1 (A+) transition at 2.4 km s−1. |
6 The L183 chemical model
The chemical column densities derived through our L183 observations were also compared to those predicted by the chemical model recently developed by Vasyunin et al. (2017, see Table 2). In addition to iCOMs, which were the focus of Vasyunin et al. (2017) paper on L1544, the molecular set now also includes sulfur-bearing species as well some simpler molecules, routinely observed in cold clouds. To reproduce the observed column densities of species in L183, we used the radial distributions of density and temperature derived using Herschel/SPIRE data, as described previously. The beam size of the Herschel observatory does not resolve the densest central part of L183, seen with the IRAM 30 m telescope at millimetre wavelengths (e.g. Crapsi et al. 2005; Pagani et al. 2007). As found in previous work, the central density of L183 is close to that of L1544 (e.g. Table 9 in Crapsi et al. 2005). We therefore assume that the central 3000 au of L183 has a density profile similar to L1544 as deduced by Keto & Caselli (2010, see Fig. 8). The inner1000 AU of L1544 was recently targeted by Caselli et al. (2019) ALMA observations, revealing a larger flat radius than predicted by Keto & Caselli (2010), thus suggesting that it is at an earlier evolutionary phase, or maybe that the L1544 dynamical evolution differs from that of a contracting Bonnor-Ebert sphere.
While the chemical model was successful in explaining the observed column densities of iCOMs in L1544 (hereafter “Model 1”), the wider set of species that we are now trying to model provided a new challenge. In this work, we define the best-fit modelled column densities as obtained with the model at the time when two conditions are satisfied. Firstly, times are selected when the number of molecules with modelled column densities within one order of magnitude from the observed ones is the highest. Secondly, the selected time is the one at which the sum of squared differences between the modelled and observed column densities is minimal. For that best-fit time, the species that are hard to reproduce by our model are OCS, SO2, CH3OCHO, and H2CCO (see Table 3, in bold; a full description of “Model 1” can be found in Vasyunin et al. 2017). For all the molecules “indirectly” observed via their isotopic substituted species, since the chemical model does not include isotopic elements, ratios of 18 O/16O = 500, and 13 C/12C = 64 were assumed (Dickens et al. 2000).
To improve the agreement between the model and observations, we varied the initial conditions for the simulations (“Model 2”). While in the original model of Vasyunin et al. (2017), the initial chemical composition was calculated under the conditions of a diffuse cloud with Av = 2 mag and gas density 102 cm−3, here in Model 2, we adopted the initial chemical composition of a dark cloud model (Av = 10 mag, gas density 104 cm−3). This is based on the fact that L183 appears more embedded in the dense gas compared to L1544, based on the Herschel maps. However, this approach seems unable to improve the agreement (see Table 3): other species are in disagreement with the observed column densities, including CO, which appears highly depleted in the model, and, in addition, the agreement for the species that were not well described by the “Model 1” was not improved.
A closerlook at the output from our model revealed that it significantly overestimated the column densities of water (H2 O) and molecular oxygen (O2) in comparison to observational data reported in the literature. Interestingly, H2 O, SO2 and O2 are chemically related to each other via the OH radical, which is involved in the formation of all three species. Water column density was estimated by Snell et al. (2000) for different dark clouds, and found to be in the range 1 × 10−9–1 × 10−8 relative to atomic hydrogen. Also, Caselli et al. (2012), using Herschel observations of L1544, estimated water abundance to be ~ 3 × 10−10. For O2, upper limits obtained by Pagani et al. (2003b) were below 8.5 × 10−8 in L183. On the other hand, our models 1 and 2 predict fractional abundances of 3.0 × 10−7 and 1.6 × 10−7 for H2O, and 2.0 × 10−6, and 1.9 × 10−6 for O2, respectively. These predicted high abundances of O2 and H2O in the gas phase exist mainly at early evolutionary times, when icy mantles are not yet completely formed. The reason is a very high (> 50%) efficiency of reactive desorption for the surface reaction H + O → OH (Minissale et al. 2016). At later time, the surface is becoming covered with water, which reduces reactive desorption efficiency and, also, the gas-phase atomic oxygen is gradually depleted from the gas.
To solve these issues, we updated the original model (Vasyunin et al. 2017) as follows: the new reaction C + H2O → HCO + H, as proposed by Hickson et al. (2016), was added, and in the original model, the rate of the reaction CH + CH3OH → CH3CHO + H was overestimated for Tgas=10 K. Hence, the rate of this reaction was fixed at 2.5 × 10−10 cm3 s−1 at 10 K (E. Roueff, priv. comm.). The results of the simulations obtained with the updated model are shown in the last column (“Model 3”) of Table 3, and in Fig. 9, along with the abundances of H2 O and O2 for the old and new models (Fig. 10). The inclusion of the new reaction C + H2O → HCO + H helps to reduce the peak water abundance, which is reached at early times and likely overproduced by the original model by almost an order of magnitude. After 105 yr, for both models, the water abundance is about 10−7 relative to hydrogen nuclei, which is similar to the numbers showed in Bergin et al. (2000). Nevertheless, the column density of water in the model is about 8 × 1015 cm−2, which is over two orders of magnitude higher than the lower limit estimated for L1544 by Caselli et al. (2012). The radial profile of the H2 O abundance produced with our model is similar to the shape proposed in Caselli et al. (2012), with a low abundance in the centre of the cloud (~1 × 10−7) and a maximum at intermediate radii (see Fig. 9). Once the reaction rate of CH + CH3OH → CH3CHO + H was fixed as described above, the column densities of CH3CHO and chemically related H2CCO reasonably fitted the observational values, and still no improvement is observed for O2.
“Model 3”, which is the chemical model presented in Vasyunin et al. (2017) with the updated chemical network discussed above, was applied also to the L1544 data presented in Table B.2, with the proper physical parameters as input. This comparison, whose results are presented in Table 4, extends the work presented in Vasyunin et al. (2017), since now the molecular sample is larger. The overall agreement is a little worse now than for L183, with the observed column densities of HCS+, CH3OCHO, and HC3N, other than SO2, not being well-reproduced by the model.
 |
Fig. 7 Excitation temperature of four rotational transitions of methanol, as a function of the cloud radius, derived with our best-fit radiative transfer modelling; the purple dashed line corresponds to the cosmic microwave background temperature. |
 |
Fig. 8 Combined density profiles for L183: blue line corresponds to the density profile derived with Herschel/PACS maps; L1544 density profile (orange) from Keto & Caselli (2010). |
Description of the chemical models.
7 Discussion and conclusions
A sensitive, single-pointing survey of the pre-stellar core L183 was conducted in the 3 mm-wave region with the IRAM 30 m antenna. Several emission lines were assigned to different molecular species, roughly 30 of them arising from iCOMs. Methyl formate (CH3OCHO) and the singly deuterated methanol (CH2DOH) were detected for the first time in this source. The column densities of the species derived in L183 were compared to those found in the densepre-stellar core L1544.
In general, carbon-bearing molecules are more abundant in L1544, while oxygen-bearing species are more abundant in L183. This is especially true for the iCOMs and the sulphur-bearing molecules, which show a clear division, depending whether they are sulphur-oxygen (e.g. SO, SO2) or sulphur-carbon compounds (e.g. CS, HCS+, H2 CS). However, our chemical model gives, for both cores, a similar age of ~105 yr. A comparison of the H2 map of L183 (Fig. 1) to that of L1544 (Spezzano et al. 2016a, Fig. 1) helps to explain the chemical difference: the L183 dense core is well embedded within the molecular cloud, which screens the entire dense core from the interstellar radiation field. As a consequence, most of C is likely to be converted into CO, leaving few C atoms for building carbon chains. In contrast, the southern part of L1544 lies close to the sharp edge of the cloud, making it more freely exposed to the interstellar radiation field. Chemical differentiation in the two PSCs is therefore likely to be affected more by environmental conditions than by the time evolution.
Another important finding from this comparison is the similar behaviour of methanol and its single deuterated species in the two objects. Our analysis of L183 methanol emission features clearly confirms what the previous study carried out by Bizzocchi et al. (2014) and Vastel et al. (2014) found for L1544; that the excitation of methanol in cold dense molecular clouds can not be modelled in local thermodynamic equilibrium conditions. For this reason, a non-LTE analysis of the emission lines of CH3OH was carried out, in a similar manner to that adopted previously for L1544. Also, there is an evident shift (~ 300 m s−1) in radial velocity of the detected emission peaks of deuterated methanol, compared to those of the main isotopologue. This systemic velocity distinction might be, as already suggested for L1544 by Bizzocchi et al. (2014), and recently confirmed by Chacón-Tanarro et al. (2019), the result of different parts of the cloud traced by methanol and deuterated methanol. While CH3OH traces the outer shell of the dense core as explained by Vasyunin et al. (2017) and Vastel et al. (2014), CH2DOH becomes more abundant closer to the core centre, where larger amounts of CO freeze-out boost the deuterium fractionation (e.g. Roberts et al. 2003). From our observations of the methanol system, we find a deuteration towards the dust peak of L183 of [3.9 ± 0.7] × 10−2 (see Table B.2), which should be compared to the one reported in Bizzocchi et al. (2014) for L1544 of [10 ± 3] × 10−2.
The molecular line observations of L183 were also compared to the chemical model of Vasyunin et al. (2017), which was recently used to interpret molecular abundances in L1544. The chemical network of the model was modified by adjusting certain reaction rates and by adding some new reactions. The upgrade improved the agreement with the observations, and the current version is able to reproduce, within one order of magnitude, the column densities of 21 species out of the total 22 included in the analysis. This updated model, using appropriate physical parameters, was also applied to the L1544 data, and the model reproduced the column densities of 18 molecules observed towards this source. Remarkably, the best-fit time for L1544 from the model is ~ 8.5 × 104 yr, which is approximately half the age derived by Vasyunin et al. (2017). This age is, however, very close to the best-fit time for L183 (9.5 × 104 yr). This suggests that environmental conditions are more important for chemical differentiation than chemical evolutionary effects. The comparison between the observations and the chemical modelling shows a good agreement except for O2 and SO2. These species are overproduced by both the original and the updated model (see Fig. 10 and Table 2 for O2 and SO2, respectively). Both molecules are formed in the gas phase via the reactions with OH: O + OH → O2 + H, and SO + OH → SO2 + H. One may ask, therefore, if the problem arises from an overestimate of the OH abundance in the model. However, the peak abundance of OH is about 10−7 relative to atomic hydrogen, which is consistent with estimations by Crutcher (1999). Another possible reason for the reduction of the “extra” SO2 is that the model neglects some important destructive reactions of this molecule. We tested this hypothesis by adding some reactions of sulphur dioxide with molecular kations, such as HCO+ and H3 O+. However, this did not substantially modify the expected yield of SO2 in the model (Laas, priv. comm.). Another source of uncertainty is the little known rate coefficient for the reaction SO + OH → SO2 + H. We adopted the rate coefficient from the most recent study available in literature (Ballester & Varandas 2007, see Table 3), although this value was determined at room temperature. Very recent analyses indicate that the rate coefficient is four times higher at 10 K than at 300 K (Fuente, A. et al. 2019). Adopting this new coefficient would lead to an even higher yield of SO2 at low temperatures, and to a larger discrepancy with the observed values. What is said above clearly shows how poorly understood the chemistry of sulphur-bearing molecules is in cold, dense regions.
In order to have a broader picture of the chemical distribution in L183 and to confirm our hypotheses regarding the effect of the environmental conditions on the chemical evolution of the molecular cloud, follow-up observations have been carried out. The main focus of these observations, which are to be presented in a forthcoming paper, was to trace the methanol and its single deuterated species emission around the dust peak, in order to study the distribution of these two species. At the same time, thanks to the large frequency bandwidth of the IRAM 30 m receiver system, many other molecular species are detected and mapped in the same region. These observations should allow us to have a clearer idea of the chemical distribution around the L183 dust peak and correlate this with the environmental conditions: if our assumption is correct, we could expect a more uniform molecular distribution around the dust peak in L183 than toward L1544. The analysis of the observational data is currently underway and the results are to be presented in a forthcoming paper.
 |
Fig. 9 Radial profiles of abundances of species obtained with the updated model, in the text labelled as “Model 3” (solid), and with the original model (dashed) developed in Vasyunin et al. (2017). The profiles were obtained at the “best-fit ” time of 9.5 × 104 yr. For each radial point, the column densities of the species are divided by the corresponding column density of hydrogen (see Fig. 1). Then, convolution over 26′′ Gaussian beam is performed to mimic IRAM 30 m observations. |
 |
Fig. 10 Molecular oxygen (left column) and water (right column) abundances in the original model by Vasyunin et al. (2017) (blue) and its updated version (red). |
Observed and modelled column densities for L183.
Observed and modelled column densities for L1544.
Acknowledgements
The authors thank François Dulieu and Jacob C. Laas for fruitful comments on the SO2 chemistry. Evelyne Roueff is also gratefully acknowledged for discussions on reaction rates of some complex organic molecules in our model. We also thank Elena Redaelli for providing the L1544 SPIRE density profile. The work by A.I.V. is supported by Latvian Council of Science via the Project lzp-2018/1-0170.
Appendix A: Additional methanol transitions
 |
Fig. A.1 Observed (in blue) and modelled spectrum with MOLLIE of CH3OH in L183. |
 |
Fig. A.2 Observed (in blue) and modelled spectrum with MOLLIE of CH3OH in L183. In green the modified model with the altered sets of collisional data (see Sect. 5.2.) |
Appendix B: Additional tables
Spectroscopic parameters of the selected molecular species detected towards L183, along with the results of the line Gaussian fits from CASSIS.
Excitation temperatures and column densities of molecules detected toward L183 and L1544.
References
- Arzoumanian, D., André, P., Didelon, P., et al. 2011, A&A, 529, L6 [Google Scholar]
- Bacmann, A., Taquet, V., Faure, A., Kahane, C., & Ceccarelli, C. 2012, A&A, 541, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ballester, M., & Varandas, A. 2007, Chem. Phys. Lett., 433, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Balucani, N., Ceccarelli, C., & Taquet, V. 2015, MNRAS, 449, L16 [Google Scholar]
- Bergin, E. A., Melnick, G. J., Stauffer, J. R., et al. 2000, ApJ, 539, L129 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, M., Romanzin, C., Doronin, M., et al. 2016, ApJ, 817, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Bizzocchi, L., Caselli, P., Spezzano, S., & Leonardo, E. 2014, A&A, 569, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bizzocchi, L., Lattanzi, V., Laas, J., et al. 2017, A&A, 602, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Black, J. H. 1994, ASP Conf. Ser., 58, 355 [NASA ADS] [Google Scholar]
- Blake, G. A., Sutton, E. C., Masson, C. R., & Phillips, T. G. 1987, ApJ, 315, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Brünken, S., Gottlieb, C. A., McCarthy, M. C., & Thaddeus, P. 2009, ApJ, 697, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Walmsley, C. M., Tafalla, M., Dore, L., & Myers, P. C. 1999, ApJ, 523, L165 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Walmsley, C. M., Zucconi, A., et al. 2002a, ApJ, 565, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Walmsley, C. M., Zucconi, A., et al. 2002b, ApJ, 565, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Keto, E., Bergin, E. A., et al. 2012, ApJ, 759, L37 [Google Scholar]
- Caselli, P., Pineda, J. E., Zhao, B., et al. 2019, ApJ, 874, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Cazzoli, G., & Puzzarini, C. 2005, J. Mol. Spectr., 233, 280 [NASA ADS] [CrossRef] [Google Scholar]
- Cazzoli, G., & Puzzarini, C. 2008, A&A, 487, 1197 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cazzoli, G., Cludi, L., Cotti, G., Esposti, C. D., & Dore, L. 1994, J. Mol. Spectr., 167, 468 [NASA ADS] [CrossRef] [Google Scholar]
- Cazzoli, G., Dore, L., Puzzarini, C., & Beninati, S. 2002, Phys. Chem. Chem. Phys., 4, 3575 [CrossRef] [Google Scholar]
- Cazzoli, G., Cludi, L., Buffa, G., & Puzzarini, C. 2012, ApJS, 203, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Ceccarelli, C., Caselli, P., Fontani, F., et al. 2017, ApJ, 850, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J., Lefloch, B., Agúndez, M., et al. 2018, ApJ, 853, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Chacón-Tanarro, A., Caselli, P., Bizzocchi, L., et al. 2019, A&A, 622, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crapsi, A., Caselli, P., Walmsley, C. M., et al. 2005, ApJ, 619, 379 [Google Scholar]
- Crapsi, A., Caselli, P., Walmsley, M. C., & Tafalla, M. 2007, A&A, 470, 221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crutcher, R. M. 1999, ApJ, 520, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Dartois, E., Chabot, M., Id Barkach, T., et al. 2019, A&A, 627, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dickens, J. E., Irvine, W. M., Snell, R. L., et al. 2000, ApJ, 542, 870 [NASA ADS] [CrossRef] [Google Scholar]
- Dulieu, F., Congiu, E., Noble, J., et al. 2013, Sci. Rep., 3, 1338 [NASA ADS] [CrossRef] [Google Scholar]
- Franco, G. A. P. 1989, A&A, 223, 313 [NASA ADS] [Google Scholar]
- Fuente, A., Navarro, D. G., Caselli, P., et al. 2019, A&A, 624, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fusina, L., Di Lonardo, G., Johns, J. W. C., & Halonen, L. 1988, J. Mol. Spectr., 127, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Garrod, R. T., & Herbst, E. 2006, A&A, 457, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garrod, R., Park, I. H., Caselli, P., & Herbst, E. 2006, Faraday Discuss., 133, 51 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Garrod, R. T., Wakelam, V., & Herbst, E. 2007, A&A, 467, 1103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gerin, M., Marcelino, N., Biver, N., et al. 2009, A&A, 498, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldsmith, P. F. 2001, ApJ, 557, 736 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Golubiatnikov, G. Y., Lapinov, A. V., Guarnieri, A., & Knöchel, R. 2005, J. Mol. Spectr., 234, 190 [Google Scholar]
- Gottlieb, C. A., Gottlieb, E. W., Thaddeus, P., & Kawamura, H. 1983, ApJ, 275, 916 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Gupta, H., Gottlieb, C. A., McCarthy, M. C., & Thaddeus, P. 2009, ApJ, 691, 1494 [NASA ADS] [CrossRef] [Google Scholar]
- Hickson, K. M., Loison, J.-C., Nunez-Reyes, D., & Mereau, R. 2016, ArXiv e-prints [arXiv:1608.08877] [Google Scholar]
- Hildebrand, R. H. 1983, QJRAS, 24, 267 [NASA ADS] [Google Scholar]
- Hily-Blant, P., Walmsley, M., Pineau Des Forêts, G., & Flower, D. 2008, A&A, 480, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hily-Blant, P., Bonal, L., Faure, A., & Quirico, E. 2013, Icarus, 223, 582 [Google Scholar]
- Hily-Blant, P., Faure, A., Vastel, C., et al. 2018, MNRAS, 480, 1174 [NASA ADS] [CrossRef] [Google Scholar]
- Hiraoka, K., Sato, T., Sato, S., et al. 2002, ApJ, 577, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Hiraoka, K., Wada, A., Kitagawa, H., et al. 2005, ApJ, 620, 542 [NASA ADS] [CrossRef] [Google Scholar]
- Hocking, W. H., Gerry, M. C. L., & Winnewisser, G. 1975, Can. J. Phys., 53, 1869 [NASA ADS] [CrossRef] [Google Scholar]
- Ilyushin, V., Kryvda, A., & Alekseev, E. 2009, J. Mol. Spectr., 255, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Jiménez-Serra, I., Vasyunin, A. I., Caselli, P., et al. 2016, ApJ, 830, L6 [Google Scholar]
- Johns, J. W. C., Nemes, L., Yamada, K. M. T., et al. 1992, J. Mol. Spectr., 156, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Juvela, M. 2005, A&A, 440, 531 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Juvela, M., Mattila, K., Lehtinen, K., et al. 2002, A&A, 382, 583 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Juvela, M., Ristorcelli, I., Montier, L. A., et al. 2010, A&A, 518, L93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kauffmann, J., Bertoldi, F., Bourke, T. L., Evans, II, N. J., & Lee, C. W. 2008, A&A, 487, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Keto, E., & Caselli, P. 2010, MNRAS, 402, 1625 [NASA ADS] [CrossRef] [Google Scholar]
- Keto, E., & Rybicki, G. 2010, ApJ, 716, 1315 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, J. M., Ward-Thompson, D., & André, P. 2005, MNRAS, 360, 1506 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, J. M., Crutcher, R. M., & Ward-Thompson, D. 2009, ApJ, 701, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Klapper, G., Lewen, F., Belova, S. P., & Winnewisser, G. 2000, Zeitschrift Naturforschung Teil A, 55, 441 [NASA ADS] [Google Scholar]
- Kleiner, I., Lovas, F. J., & Godefroid, M. 1996, J. Phys. Chem. Ref. Data, 25, 1113 [CrossRef] [Google Scholar]
- Lapinov, A. V., Golubiatnikov, G. Y., Markov, V. N., & Guarnieri, A. 2007, Astron. Lett., 33, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, C. W., Myers, P. C., & Tafalla, M. 2001, ApJS, 136, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Lefloch, B., Bachiller, R., Ceccarelli, C., et al. 2018, MNRAS, 477, 4792 [NASA ADS] [CrossRef] [Google Scholar]
- Lehtinen, K., Mattila, K., Lemke, D., et al. 2003, A&A, 398, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maeda, A., Medvedev, I. R., Winnewisser, M., et al. 2008, ApJS, 176, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Mangum, J. G., & Shirley, Y. L. 2015, PASP, 127, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Marcelino, N., Cernicharo, J., Tercero, B., & Roueff, E. 2009, ApJ, 690, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Marcelino, N., Brünken, S., Cernicharo, J., et al. 2010, A&A, 516, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Margulès, L., Lewen, F., Winnewisser, G., Botschwina, P., & Müller, H. S. P. 2003, Phys. Chem. Chem. Phys., 5, 2770 [CrossRef] [Google Scholar]
- Martín-Doménech, R., Muñoz Caro, G. M., & Cruz-Díaz, G. A. 2016, A&A, 589, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minissale, M., Dulieu, F., Cazaux, S., & Hocuk, S. 2016, A&A, 585, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., & Brünken, S. 2005, J. Mol. Spectr., 232, 213 [CrossRef] [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. S. P., Maeda, A., Thorwirth, S., et al. 2019, A&A, 621, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Öberg, K. I., Bottinelli, S., Jørgensen, J. K., & van Dishoeck, E. F. 2010, ApJ, 716, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Ossenkopf, V.,& Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
- Padovani, M., Walmsley, C. M., Tafalla, M., Galli, D., & Müller, H. S. P. 2009, A&A, 505, 1199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pagani, L., Lagache, G., Bacmann, A., et al. 2003a, A&A, 406, L59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pagani, L., Olofsson, A. O. H., Bergman, P., et al. 2003b, A&A, 402, L77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pagani, L., Bacmann, A., Motte, F., et al. 2004, A&A, 417, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pagani, L., Pardo, J.-R., Apponi, A. J., Bacmann, A., & Cabrit, S. 2005, A&A, 429, 181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pagani, L., Bacmann, A., Cabrit, S., & Vastel, C. 2007, A&A, 467, 179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pearson, E. F., Creswell, R. A., Winnewisser, M., & Winnewisser, G. 1976, Zeitschrift Naturforschung Teil A, 31, 1394 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, J. C., Yu, S., & Drouin, B. J. 2012, J. Mol. Spectr., 280, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, J. Quant. Spec. Radiat. Transf., 60, 883 [Google Scholar]
- Quénard, D., Vastel, C., Ceccarelli, C., et al. 2017, MNRAS, 470, 3194 [NASA ADS] [CrossRef] [Google Scholar]
- Rabli, D., & Flower, D. R. 2010a, MNRAS, 406, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Rabli, D., & Flower, D. R. 2010b, MNRAS, 403, 2033 [NASA ADS] [CrossRef] [Google Scholar]
- Redaelli, E., Bizzocchi, L., Caselli, P., et al. 2018, A&A, 617, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Requena-Torres, M. A., Marcelino, N., Jiménez-Serra, I., et al. 2007, ApJ, 655, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, H., Herbst, E., & Millar, T. J. 2003, ApJ, 591, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Sakai, N., Sakai, T., Hirota, T., & Yamamoto, S. 2008, ApJ, 672, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Schmid-Burgk, J., Muders, D., Müller, H. S. P., & Brupbacher-Gatehouse, B. 2004, A&A, 419, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schöier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sipilä, O., Caselli, P., & Harju, J. 2013, A&A, 554, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Snell, R. L., Howe, J. E., Ashby, M. L. N., et al. 2000, ApJ, 539, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Spahn, H., Müller, H. S. P., Giesen, T. F., et al. 2008, Chem. Phys., 346, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Spezzano, S., Tamassia, F., Thorwirth, S., et al. 2012, ApJS, 200, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Spezzano, S., Brünken, S., Schilke, P., et al. 2013, ApJ, 769, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Spezzano, S., Bizzocchi, L., Caselli, P., Harju, J., & Brünken, S. 2016a, A&A, 592, L11 [CrossRef] [EDP Sciences] [Google Scholar]
- Spezzano, S., Gupta, H., Brünken, S., et al. 2016b, A&A, 586, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spezzano, S., Caselli, P., Bizzocchi, L., Giuliano, B. M., & Lattanzi, V. 2017, A&A, 606, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Swade, D. A. 1989, ApJ, 345, 828 [NASA ADS] [CrossRef] [Google Scholar]
- Tafalla, M., Myers, P. C., Caselli, P., Walmsley, C. M., & Comito, C. 2002, ApJ, 569, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Tafalla, M., Santiago-García, J., Myers, P. C., et al. 2006, A&A, 455, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tang, T. B., Inokuchi, H., Saito, S., Yamada, C., & Hirota, E. 1985, Chem. Phys. Lett., 116, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Thorwirth, S., Müller, H. S. P., & Winnewisser, G. 2000, J. Mol. Spectr., 204, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Tiemann, E. 1974, J. Mol. Spectr., 51, 316 [NASA ADS] [CrossRef] [Google Scholar]
- Tiné, S., Roueff, E., Falgarone, E., Gerin, M., & Pineau des Forêts, G. 2000, A&A, 356, 1039 [NASA ADS] [Google Scholar]
- Turner, B. E., Herbst, E., & Terzieva, R. 2000, ApJS, 126, 427 [NASA ADS] [CrossRef] [Google Scholar]
- van der Tak, F. F. S., Müller, H. S. P., Harding, M. E., & Gauss, J. 2009, A&A, 507, 347 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vastel, C., Caselli, P., Ceccarelli, C., et al. 2006, ApJ, 645, 1198 [NASA ADS] [CrossRef] [Google Scholar]
- Vastel, C., Ceccarelli, C., Lefloch, B., & Bachiller, R. 2014, ApJ, 795, L2 [Google Scholar]
- Vastel, C., Yamamoto, S., Lefloch, B., & Bachiller, R. 2015, A&A, 582, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vastel, C., Ceccarelli, C., Lefloch, B., & Bachiller, R. 2016, A&A, 591, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vastel, C., Kawaguchi, K., Quénard, D., et al. 2018a, MNRAS, 474, L76 [NASA ADS] [CrossRef] [Google Scholar]
- Vastel, C., Quénard, D., Le Gal, R., et al. 2018b, MNRAS, 478, 5514 [NASA ADS] [CrossRef] [Google Scholar]
- Vastel, C., Loison, J. C., Wakelam, V., & Lefloch, B. 2019, A&A, 625, A91 [Google Scholar]
- Vasyunin, A. I., & Herbst, E. 2013, ApJ, 769, 34 [Google Scholar]
- Vasyunin, A. I., Caselli, P., Dulieu, F., & Jiménez-Serra, I. 2017, ApJ, 842, 33 [Google Scholar]
- Velilla Prieto, L., Sánchez Contreras, C., Cernicharo, J., et al. 2017, A&A, 597, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vrtilek, J. M., Gottlieb, C. A., Gottlieb, E. W., Killian, T. C., & Thaddeus, P. 1990, ApJ, 364, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Ward-Thompson, D., André, P., & Kirk, J. M. 2002, MNRAS, 329, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Watanabe, N., & Kouchi, A. 2002, ApJ, 571, L173 [NASA ADS] [CrossRef] [Google Scholar]
- Watanabe, N., Shiraki, T., & Kouchi, A. 2003, ApJ, 588, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Winnewisser, M., Winnewisser, B. P., & Winnewisser, G. 1985, in NATO Advanced Science Institutes (ASI) Series C, eds. G. H. F. Diercksen, W. F. Huebner, & P. W. Langhoff (Berlin: Springer), 157, 375 [Google Scholar]
- Winnewisser, M., Winnewisser, B. P., Stein, M., et al. 2002, J. Mol. Spectr., 216, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, L.-H., & Lovas, F. J. 1997, J. Phys. Chem. Ref. Data, 26, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, L.-H., Fisher, J., Lees, R. M., et al. 2008, J. Mol. Spectr., 251, 305 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Spectroscopic parameters of the selected molecular species detected towards L183, along with the results of the line Gaussian fits from CASSIS.
Excitation temperatures and column densities of molecules detected toward L183 and L1544.
All Figures
 |
Fig. 1 Herschel/SPIRE maps, at the same linear scale, of the H2 column density (top row) and dust temperature (bottom row) in L183 (left column) and L1544 (right column). The beam of SPIRE is shown as a white (top row) and black (bottom row) circle in the bottom-left corner. The white star in the middle of L183 figures represents our pointing, while the one in L1544 identifies the dust peak of the source. White contours are 0.5, 1.5, 2.5 × 1022 cm−2 for the H2 column density (top row) maps and 12, 14, 16, 18 K for the dust temperature (bottom row) maps, respectively. |
| In the text | |
 |
Fig. 2 Molecular hydrogen density and dust temperature radial profiles for L183 and L1544, derived from the Herschel/SPIRE maps in Fig. 1 as described in the text. For L1544, the radial profile from Keto & Caselli (2010) is also shown. |
| In the text | |
 |
Fig. 3 Logarithmic column density ratios of L183 relative to L1544. Where no uncertainty was provided in the literature data (see Table B.2), an error of 25% of the reported column density was assigned for the error bars in the plot. In cases where the column density was derived for two temperatures, both ratios are shown for the same species. The red dashed line represents the ratio equal to unity. |
| In the text | |
 |
Fig. 4 Rotational diagram with the five rotational transitions of methanol detected towards L183. The red dashed line corresponds to the best linear fit, which yields the excitation temperature and column density shown in the plot. |
| In the text | |
 |
Fig. 5 Modelled methanol radial abundance profile. |
| In the text | |
 |
Fig. 6 Observed (in blue) and modelled spectrum with MOLLIE of CH3OH in L183. Thevelocity axis is centred on the 20,2–10,1 (A+) transition at 2.4 km s−1. |
| In the text | |
 |
Fig. 7 Excitation temperature of four rotational transitions of methanol, as a function of the cloud radius, derived with our best-fit radiative transfer modelling; the purple dashed line corresponds to the cosmic microwave background temperature. |
| In the text | |
 |
Fig. 8 Combined density profiles for L183: blue line corresponds to the density profile derived with Herschel/PACS maps; L1544 density profile (orange) from Keto & Caselli (2010). |
| In the text | |
 |
Fig. 9 Radial profiles of abundances of species obtained with the updated model, in the text labelled as “Model 3” (solid), and with the original model (dashed) developed in Vasyunin et al. (2017). The profiles were obtained at the “best-fit ” time of 9.5 × 104 yr. For each radial point, the column densities of the species are divided by the corresponding column density of hydrogen (see Fig. 1). Then, convolution over 26′′ Gaussian beam is performed to mimic IRAM 30 m observations. |
| In the text | |
 |
Fig. 10 Molecular oxygen (left column) and water (right column) abundances in the original model by Vasyunin et al. (2017) (blue) and its updated version (red). |
| In the text | |
 |
Fig. A.1 Observed (in blue) and modelled spectrum with MOLLIE of CH3OH in L183. |
| In the text | |
 |
Fig. A.2 Observed (in blue) and modelled spectrum with MOLLIE of CH3OH in L183. In green the modified model with the altered sets of collisional data (see Sect. 5.2.) |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


