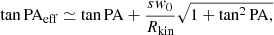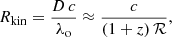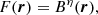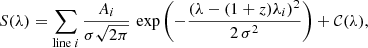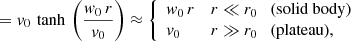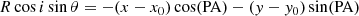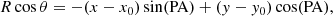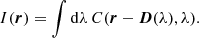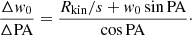| Issue |
A&A
Volume 633, January 2020
|
|
|---|---|---|
| Article Number | A43 | |
| Number of page(s) | 12 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201936318 | |
| Published online | 09 January 2020 | |
Forward modeling of galaxy kinematics in slitless spectroscopy
Univ Lyon, Université Claude Bernard Lyon 1, CNRS/IN2P3, IP2I Lyon, 69622 Villeurbanne, France
e-mail: m.outini@ipnl.in2p3.fr, y.copin@ipnl.in2p3.fr
Received:
15
July
2019
Accepted:
14
October
2019
Context. Slitless spectroscopy has long been considered a complicated and confused technique. Nonetheless, with the advent of Hubble Space Telescope (HST) instruments, characterized by a low sky background level and a high spatial resolution (most notably WFC3), slitless spectroscopy has become an adopted survey tool to study galaxy evolution from space.
Aims. We aim to investigate its application to single-object studies to measure not only redshift and integrated spectral features, but also spatially-resolved quantities such as galaxy kinematics.
Methods. We built a complete forward model to quantitatively compare actual slitless observations. This model depends on a simplified thin cold disk galaxy description – including flux-distribution, intrinsic-spectrum, and kinematic parameters – and on the instrumental signature. It is used to improve redshifts and constrain basic rotation curve parameters, meaning the plateau velocity v0 (in km s−1) and the central velocity gradient w0 (in km s−1 arcsec−1).
Results. The model is tested on selected observations from 3D-HST and GLASS surveys to estimate redshift and kinematic parameters on several galaxies measured with one or more roll angles.
Conclusions. Our forward approach makes it possible to mitigate the self-contamination effect, a primary drawback of slitless spectroscopy, and therefore has the potential to increase precision on redshifts. In a limited sample of well-resolved spiral galaxies from HST surveys, it is possible to significantly constrain galaxy rotation curve parameters. This proof-of-concept work is promising for future large slitless spectroscopic surveys, such as Euclid and WFIRST.
Key words: galaxies: high-redshift / galaxies: kinematics and dynamics / galaxies: evolution / instrumentation: spectrographs
© M. Outini and Y. Copin 2020
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Spectroscopy surveys play a fundamental role in the understanding of galaxy formation and evolution with cosmic time and in cosmology. These surveys have been achieved using different techniques. Fiber-fed multi-object spectrographs are commonly used to measure redshift and integrated properties on pre-selected targets. For instance, the Sloan Digital Sky Survey (SDSS) has measured more than a million local galaxy spectra (York et al. 2000; Strauss et al. 2002), and has revealed how the star formation rates, metallicities, and stellar populations vary with environment, mass, and redshift (Gómez et al. 2003; Brinchmann et al. 2004; Kauffmann et al. 2004). Similar surveys like the 2dF and 6dF Galaxy Redshift Surveys (Folkes et al. 1999; Jones et al. 2004) also made it possible to constrain cosmological parameters by mapping the distribution of galaxies along cosmic time (Cole et al. 2005). More recently, the VIPERS survey (de la Torre et al. 2013) made it possible to map, with unprecedented precision, the large-scale distribution of galaxies by measuring more than 100 000 redshifts at 0.5 < z < 1.2. Nevertheless, these fiber-based surveys suffer from drawbacks: galaxy central regions are integrated, so two-dimensional internal structure cannot be properly recovered, and objects need to be selected and targeted a priori.
Alternatively, integral-field spectrographs (IFS) are ideal for the study of resolved objects over their spatial extent, but still require explicit pointing of individual galaxies. In the last years, the development of highly successful IFS surveys (ℛ ≳ 1500) – such as SAURON (de Zeeuw et al. 2002), ATLAS3D (Cappellari et al. 2011), SAMI (Croom et al. 2012), CALIFA (Sánchez et al. 2012), and MaNGA (Bundy et al. 2015) – has pushed our understanding of galaxy properties further. Not limited to integrated measurements, these surveys in the nearby Universe (z ≲ 0.1) made it possible to accurately map the gas, stellar populations, and kinematics, and led to a new kinematical classification scheme of early-type galaxies (Emsellem et al. 2007, 2011).
Contrary to inherently-targeted multi-object spectrographs, “panoramic” IFS can be used to continue untargeted surveys, but only on very limited sky areas because of observation time/cost constraints. For example, MUSE (Bacon et al. 2010) has probed the evolution of gas kinematics of low-mass galaxies (M⋆ ≤ 1010 M⊙) up to z = 1.4 on the Hubble Deep Field South (Contini et al. 2016).
In contrast to graceful IFS, slitless spectroscopy has generally been seen as a clumsy technique with well-recognized drawbacks. As a matter of fact, the absence of an independent spatial sampling before spectral dispersion induces two major contamination issues: self-contamination – the effective spectral resolution is directly related to the size and shape of the spatially-resolved object in the dispersion direction – and cross-contamination – signal pollution from nearby objects; both effects make the data reduction difficult and the redshift measurement less accurate. In addition, slitless spectroscopy is affected by a comparatively high integrated background level (particularly from the ground), limiting the depth or signal-to-noise ratio of observations. However, this technique has some pros of its own: the ease of instrumental design and observational use, a large field of view, and a very high multiplexing capability: all leading to very large object catalogs (∼100 000 galaxies in recent surveys and ≳15 M in future surveys). Furthermore, it has the potential to provide flux-limited surveys with high spectro-photometric accuracy, insensitive to fiber or slit losses.
Thereby, since the advent of the Hubble Space Telescope (HST) grism instruments, slitless spectroscopy has de facto become a tool of choice to study galaxy evolution from space: a low background level and a fine spatial resolution both mitigate the aforementioned shortcomings (Freudling et al. 2008; Kümmel et al. 2011; Dressel 2012). Dedicated HST surveys such as WISP (Atek et al. 2010), 3D-HST (Brammer et al. 2012; Momcheva et al. 2016), GLASS (Schmidt et al. 2014; Treu et al. 2015), FIGS (Pirzkal et al. 2017) have led to this technique being considered as appropriate to derive redshift and integrated-galaxy properties over large samples, and it is ready to be used in future missions, such as Euclid (Grupp et al. 2012) and WFIRST (Spergel et al. 2015).
Traditional approaches in slitless spectroscopy (e.g. Kümmel et al. 2009) use standard “inverse” data-reduction and analysis methods, extracting parameters from observations using successive and dedicated data manipulation steps. Typically, it involves empirical modeling of the spectral trace, a cross-dispersion summation to estimate the 1D galaxy spectrum, the ad-hoc combination of spectra obtained at different position angles, and any subsequent spectral analyses performed on the averaged spectrum. Not only is the proper error propagation difficult between the different data-reduction steps, but such a reverse approach can hardly correct or quantify the impact of spatially-resolved galactic properties, such as internal dynamics or metallicity gradients.
Alternatively, a “forward” approach makes it possible to constrain physical or instrumental parameters directly in the observation space, properly accounting for degeneracy and covariances, and allowing for the inclusion of bayesian-like priors. By constructing a predictive model of the galaxy 2D dispersed image (hereafter coined, “spectrogram”) depending on a set of observationally or physically motivated parameters, we investigate the possibility of measuring not only intrinsic mean spectral quantities – for example, redshift, emission line intensities, and widths – independently of self-confusion, but also spatially-resolved quantities such as internal kinematics. Thus, by combining forward methods to derive resolved quantities on a single object and the large multiplexing power of multi-object spectrographs, slitless spectroscopy surveys offer a unique opportunity to study galaxy properties on an unprecedented scale.
In this paper, we detail how to forward-model slitless spectrograms from a galaxy model – including flux-distribution, intrinsic-spectrum, and kinematic parameters – and an instrumental signature. Considering our targets are mainly line-emitting disk galaxies, we will use two major assumptions: an axi-symmetric thin cold disk geometry for the galaxy, and a separability hypothesis under which the intrinsic galaxy spectrum is supposed uniform over its whole extent. Using this approach, we will investigate the application of slitless spectroscopy to single object studies to measure internal kinematic parameters, namely the plateau velocity v0 (Kalinova et al. 2017; Varidel et al. 2019) and the central velocity gradient (CVG) w0 (Lelli et al. 2013; Erroz-Ferrer et al. 2016).
The paper is organized as follows. In Sect. 2, we present galaxy kinematics in slitless spectroscopy and describe the model parametrization. We test our method on simulated spectrograms in Sect. 3, and apply it to selected galaxies from 3D-HST and GLASS survey in Sect. 4. We discuss the results in Sect. 5, and conclude and open some perspectives in Sect. 6.
2. Resolved kinematics in slitless spectroscopy
In this section, we investigate the kinematic signature in a slitless resolved galaxy spectrum. The internal velocity induces differential Doppler shifts (in addition to the systemic cosmological redshift), inducing small offsets of observed wavelengths as a function of position, and therefore distorting the overall spectral shape.
The slitless spectrogram I(x, y) can be derived from two key ingredients, first the spectro-spatial flux distribution cube of the galaxy C(r, λ), which contains all the observable information – spatial profile, intrinsic spectrum, velocity field, instrumental transmission and PSF, etc. – and second the 2D dispersion law D(λ) from the spectrograph, relating the wavelength to the (x, y)-offset on the detector. More details on how the spectrogram is computed are given in Sect. 2.3.
2.1. Pedagogic case
To illustrate the effect of resolved kinematics in slitless spectroscopy, we build a pedagogic simulation mimicking the observation of an Hα-emitting disk galaxy at z ∼ 0.9 with an exponential thin-disk density profile, with an inclination of 60° and a scale length of rd = 6 px, and a dispersion direction perpendicular to the major axis; a uniform intrinsic spectrum made of a constant continuum, and an Hα + [N II] emission line complex at z = 0.9; a typical plateau velocity curve with v→v0 = 300 km s−1 beyond transition radius r0 = 10 px (see Sect. 2.3.4). For illustration purposes, the simulated instrument is similar to an HST-like slitless spectrograph, but with an unrealistic spectral sampling of D = 2.5 Å px−1, ten times better than actual slitless instruments.
Simulated slitless spectrograms are shown in Fig. 1. In both cases, one can distinguish the Hα + [N II] emission line complex from the constant continuum that spreads out on each side. When the velocity field is ignored (upper panel), the emission lines have a shape similar to the flux distribution; on the opposite, when the kinematic effects are included (lower panel), the velocity-induced Doppler offset significantly distorts the emission line spectral shape. As can be seen, the kinematic signature on the slitless spectrogram is somewhat similar to the one traditionally observed in long slit spectroscopy.
 |
Fig. 1. Toy simulation of spectrogram of typical Hα-emitting disk galaxy at z ∼ 0.9 (intrinsic spectrum in uppermost panel, spatial profile on the leftmost panels) as observed with an HST-like slitless spectrograph, but with an improved spectral resolution of ℛ ∼ 2500 (see text). Top: without kinematic effects; bottom: signature of the intrinsic velocity field is clearly visible as a distortion of the spectrogram. The red dashed lines correspond to the galaxy rotation curves at each emission lines’ position, and are tracing the distortion in the spectrogram. |
Two important lessons can be learned from this simple simulation. In this particular model, the disk scale length rd was chosen two times smaller than the turnover radius of the velocity curve r0. As a consequence, only the inner solid body rotation part of the velocity field has a clear observational signature, the plateau region being too far out of the exponential disk extent to have any significant impact on spectrogram shape (see galaxy rotation curves plotted as red dashed lines in the lower panel of Fig. 1). This is discussed more in Sect. 3.
Secondly, it appears that the relative position angle (PA), defined as the angle between the (projected) galaxy’s major axis and the cross-dispersion direction, plays a critical role in the kinematic signature, PA = 0 (the major axis is perpendicular to the dispersion direction) being the most favorable case. In the central region of the galaxy, where the kinematics is dominated by the solid body rotation, we can approximate the effective PA observed in the spectrogram (PAeff) from the relative PA of the galaxy and the CVG w0 (see Fig. 2):
 |
Fig. 2. Sketch of broadband galaxy shape (open contours) and the spectrogram for an infinitely thin emission line (shaded contours) distorted by intrinsic velocity curve (red dashed line); x (resp. y) is direction of dispersion (resp. cross-dispersion), PA is the intrinsic relative position angle defined as the angle between the broadband galaxy major axis and the cross-dispersion direction, and PAeff the apparent position angle on the spectrogram. |
where s is the spatial sampling of the instrument (in arcsec px−1), w0 is expressed in km s−1 arcsec−1, and kinematic sampling Rkin is defined below in Eq. (2). Since relative PA and CVG w0 are so correlated, they cannot be constrained independently from the spectrogram alone: the kinematic major axis needs to be set a priori from external photometric observations (more discussions in Sect. 2.3.4).
Overall, due to self confusion effects inherent to slitless spectroscopy, the kinematic parameters are entangled with spectro-spatial flux distribution of the galaxy. This is the goal of our analysis to estimate them using an accurate modeling of the slitless spectrogram.
2.2. Kinematic sampling
The impact of resolved kinematics on slitless spectra can be roughly quantified using the kinematic sampling Rkin, defined as the line-of-sight velocity resolution in km s−1 px−1:
where D is the spectral sampling (in Å px−1), λo = (1 + z)λe is the cosmologically redshifted wavelength of a line at rest-frame wavelength λe, and ℛ ≡ λ/Δλ ≈ λo/D is the resolving power. As defined, a smaller Rkin corresponds to a higher sensitivity to internal kinematics.
The kinematic sampling estimated for various current and future slitless surveys is presented in Table 1. Unfortunately, current HST-based surveys only have a kinematic sampling ≳800 km s−1 px−1, which might prove barely sufficient to derive precise velocity parameters for a large fraction of the sample. Future surveys, however, will all reach Rkin ∼ 150–300 km s−1 px−1, which is more appropriate for detailed kinematic analyses.
Main instrumental properties of past, current, and future slitless surveys.
In order to properly constrain galaxy-internal kinematics from slitless spectroscopy, we now build a predictive model sufficiently realistic to be quantitatively compared to actual observations in a forward approach. As noticed earlier, this model only depends on a galaxy model (Sect. 2.3) – including flux distribution, intrinsic spectrum and kinematic parameters – and on an instrumental signature (Sect. 2.4) – allowing a complete simulation of the observed spectrogram.
2.3. Galaxy model
2.3.1. Core assumptions
By design, slitless observations essentially target Hα-emitting galaxies at high redshift (0.5 < z < 1.5, see Sect. 4). Additionally, given the limited spatial resolution and kinematic sampling (Table 1), the observations cannot yet constrain elaborate models. Therefore, we are making the physical assumption (reasonable for galaxies considered in this analysis) of an axisymmetric thin cold disk. As a consequence, the galaxy flux distribution, spectrum, and velocity field only depend on the internal radius R.
We further adopt the separability assumption: the rest-frame galaxy spectrum is supposed to be entirely uniform, and only modulated by Doppler shift from internal kinematics. As a result, the observer-frame galaxy datacube C(r, λ) – with two spatial dimensions and a spectral one – can easily be reconstructed from the normalized spatial flux distribution F(r), the cosmologically redshifted intrinsic spectrum S(λ), and the line-of-sight velocity field v(r) of the galaxy:
2.3.2. Spatial flux distribution
As mentioned earlier, slitless spectrography is plagued by self-confusion, mixing different spatial and spectral contributions from the target on the same part of the detector. A key component of our model is therefore a precise description of the internal flux distribution F(r) of the resolved galaxy at considered wavelengths.
Under the assumption of an axisymmetric thin cold disk, the galaxy morphology is characterized by its inclination, position angle and intrinsic radial flux profile. Such a model will be used to estimate F(r) in simulations (Sect. 3). For real observations (Sect. 4.3), however, given the morphological variety of galaxies – for example. spiral arms or disk warps – we choose to estimate the galaxy flux distribution directly from the thumbnail broadband images B(r) systematically acquired along slitless spectroscopic observations.
It should be noted that, even though our model will essentially be constrained by emission lines (see Sect. 2.3.3), the broadband image, acquired in a band covering the spectrograph band pass, is a direct observation of the integrated flux mostly originating from the continuum. For high-redshift galaxies (z ≳ 1), the spatial Hα emission line profile is shown to be similar to the continuum, but more extended on average (Nelson et al. 2012). To allow for this difference, we related the internal flux distribution of the galaxy F(r) to the peak-normalized broadband image B(r) through a simple power law:
where a flux distribution index η < 1 corresponds to a more diffuse distribution than broadband one’s. We further discuss the impact of our choices – in particular the fact that the flux distribution might not be the same in the continuum and in the emission line – in Sect. 5.
2.3.3. Intrinsic spectrum
The 3D-HST and GLASS surveys use grisms G141 and G102 in the infrared domain and cover the 7500 to 17 500 Å wavelength range (see Sect. 4.1). As shown in Sect. 2.2, the kinematic impact is expected to be at its most subtle in the slitless spectrograms, and only significant for strong emission lines, namely the complex Hαλ6563 + [N II]λλ6548, 6584 + [S II]λλ6718, 6732 (for a redshift 0.3 < z < 1.7), or the doublet [O III]λλ4959, 5007 (for 0.7 < z < 2.5). We do not consider fainter emission lines such as Hβ.
The intrinsic galaxy spectrum is modeled as a sum of individual Gaussian lines on top of a smooth continuum:
where Ai and λi are respectively the amplitude and the rest-frame wavelength for each line i, σ the supposedly constant line width, and 𝒞(λ) an ad hoc continuum. For the line doublets, we assume a constant amplitude ratio of A[N II]λ6584/A[N II]λ6548 = A[O III]λ5008/A[O III]λ4960 and A[S II]λ6718/A[S II]λ6732 = 1.
Since the spectrogram adjustment is performed on a very restricted range around the modeled emission lines, and the instrumental transmission is assumed to be known (see Sect. 2.4), the continuum 𝒞 is simply modeled by a constant 𝒞0, which is the same for all lines. Overall, only a handful of parameters are needed to describe the intrinsic spectrum, namely six for an Hα-emitting galaxy: effective redshift z, line amplitudes AHα, A[N II]λ6584, and A[S II]λ6718, effective dispersion σ, and continuum constant 𝒞0.
2.3.4. Velocity field
In this section, we present how we constructed a model for the galaxy velocity field v(r). Even under simplifying hypotheses, a physical modeling of galaxy rotation curves (hereafter, RC) requires a detailed description of the contributions from the disk, bulge, and halo components to the galaxy dynamics, to be constrained only with high-precision morphologic and spectroscopic observations (e.g. Courteau 1997), out of reach to low-dispersion slitless spectrography.
Under the assumption of an axisymmetric thin cold disk, one can revert to an analytic expansion to reproduce the overall shape of the intrinsic rotation velocity curve vrot(r) with a restricted number of empirical parameters. In our case, we used a simple hyperbolic tangent profile, very similar to the commonly used arc-tangent profile (Stott et al. 2016; Pelliccia et al. 2017):
where v0 is the plateau value of the RC, and r0 is the transition (or turnover) radius. In practice, we use expression (7), since the CVG w0 ≡ v0/r0 is the dominant term at small radius, leading to less degeneracy between the parameters.
We note that v0 can only be significantly constrained if the observations go beyond r ∼ r0. As briefly explained in Sect. 2, there is a competition between the RC turnover radius r0 and the galaxy disk scale length rd: if r0 ≲ rd, then both v0 and w0 can be reasonably constrained; alternatively, if r0 is significantly larger than rd, only the solid body rotation parameter w0 can be sensibly measured.
For a thin cold disk, the observed mean velocity field v(r) along the line of sight is straightforwardly given as:
where cz is the systemic velocity, vrot(R) is the rotation curve, i the galaxy inclination, and θ the azimuthal angle in the plane of the galaxy:
with PA the relative position angle, r = (x, y) the Cartesian coordinates in the sky, and (x0, y0) the galactic center coordinates. With the galaxy being modeled as a cold rotating thin disk, the kinematic and morphologic position angles are assumed to be the same.
Since PA is highly degenerate with w0 (see Fig. 1), it is crucial to constrain it independently from photometry. To do so, we estimated the projection angle i and relative position angle PA from a Sersic fit (Sersic 1968) to the broadband image used for the flux distribution. However, since only vrot(R) sin i is adjusted, we stress that the inclinaison i is not needed in the fit per se, but only for post-analysis velocity deprojection if needed.
2.4. Instrumental model
The second key ingredient needed to simulate the slitless spectrogram is the dispersion law D(λ) from the spectrograph. As well as its transmission curve 𝒯(λ).
Dispersion law. The dispersion law D(λ) gives the (x, y)-offset on the detector (with respect to a reference position) as a function of wavelength. This is mostly an instrumental quantity, derived from dedicated calibration procedures (e.g. Kuntschner et al. 2009a,b).
Even though the forward approach described in Copin (in prep.) would be an appropriate way to calibrate the dispersion law, we rely in this analysis on the WCS solution computed and delivered for each galaxy by standard data reduction. Given the required precision of our model, we observed minor inconsistencies for some spectrograms, in the form of a px-scale offset in the cross-dispersion direction, as a result of a small registration error between broadband and dispersed images. To account for this effect, we introduced a nuisance parameter Δy (in px). It should be noted that a similar mis-registration along the dispersion axis was corrected to first-order by the effective redshift z adjusted in the procedure.
Transmission. The transmission 𝒯(λ) conveys the chromatic evolution of the instrumental response, and is derived from specific flux calibration (Kuntschner et al. 2011). In our model, we simply included the provided transmission into the galaxy datacube C(r, λ) derived from Sect. 2.3.
2.5. Forward modeling
2.5.1. Spectrogram reconstruction
Once the galaxy datacube C(r, λ) and the dispersion law D(λ) were known, we computed the resulting spectrogram using (e.g. Freudling et al. 2008):
In practice, the spatial convolution and wavelength integration are performed in Fourier space (Copin, in prep.). Since both quantities C(r, λ) and D(λ) depend on various parameters p, we were able to simulate a spectrogram to be compared to the observations. This “forward” approach makes it possible to constrain physical or instrumental parameters directly in the observation space, in opposition to more traditional “inverse” methods extracting fully or partially free parameters from data using ad hoc procedures.
2.5.2. Maximum likelihood
For an observed spectrogram Dij with estimated variance 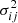 , we computed a spectrogram model Iij(p) and constrained the set of free parameters p by minimizing the following χ2:
, we computed a spectrogram model Iij(p) and constrained the set of free parameters p by minimizing the following χ2:
The maximum likelihood procedure further provides the full parameter covariance matrix, from which one can compute the 1σ uncertainties. Since only the emission lines are significantly distorted by resolved kinematics, the adjustment is performed on a restricted area about 40 × 60 px around emission lines of interest, equivalent to  (resp. 1400 Å) for galaxy respectively observed with grism G102 (resp. G141).
(resp. 1400 Å) for galaxy respectively observed with grism G102 (resp. G141).
3. Validation of simulations
3.1. Fiducial case
We present realistic simulations designed to mimic WFC3-GLASS observations with grism G102 (see Table 1) in a favorable case, where the disk scale length rd is similar to the RC turnover radius r0. We first simulate spectrograms with the following properties (see Fig. 3):
 |
Fig. 3. Galaxy model to construct fiducial test spectrogram. Left: spatial flux distribution F(x, y) and velocity field v(x, y) with v0 sin i = 250 km s−1 and w0 sin i = 420 km s−1 arcsec−1. Right: effective galaxy spectrum S(λ)×𝒯(λ), including instrumental transmission. |
– flux distribution: axisymetric exponential profile with a disk scale length 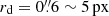 , an inclination i = 60°, and a relative position angle PA = 0°;
, an inclination i = 60°, and a relative position angle PA = 0°;
– intrinsic spectrum: from 7500 to 11 500 Å with 5 emission lines to simulate Hα+[N II]+[S II] complex at z = 0.6, with a constant line width σ = 5 Å, and a constant continuum;
– velocity field: v0 sin i = 250 km s−1 and w0 sin i = 420 km s−1 arcsec−1 corresponding to a turnover radius r0 = rd;
– instrumental model: linear dispersion law D(λ) aligned along the x-axis, and simplified apodized transmission.
A constant Gaussian noise component is finally added, so that the peak signal-to-noise ratio (PSNR) is around 40 (a typical value for high quality slitless HST spectra).
The fit residuals without (resp. with) kinematics are shown in the middle (resp. bottom) panel of Fig. 4. The minimal χ2 computed on a rectangular region of 40 × 60 px around the Hα and [S II] lines decreases from 2688 for 40 × 60 − 7 = 2392 degrees of freedom (DoF) to 2380 with only two additional kinematic parameters (w0, v0). This Δχ2 = −106 decrement for a model with only two extra parameters has a one-tailed p-value of ∼10−23, corresponding to a 10.0σ detection level. As expected, the residual map without kinematics displays a clear signature of the velocity field as a coherent quadrupolar structure around Hα line position; this structure disappears in the residual map with kinematics.
 |
Fig. 4. Top: input peak-normalized dispersed image data (gray) and model with kinematics (contours) adjusted on the fit region (rectangle). Bottom left: residual map for the model without kinematics, with a quadrupolar structure visible at Hα line location. Bottom right: residual map for model including kinematics. The cross represents the position and relative PA of the galaxy at Hα wavelength. The decrease in the χ2 with two additional kinematic parameters corresponds to a 10.0σ detection. |
The fiducial fit with kinematics gives v0 sin i = (243±39) km s−1, w0 sin i = (397±53) km s−1 arcsec−1 and z = 0.599 98 ± 0.000 04 (statistical error), all within 1σ of the input values.
The correlation matrices are presented in Fig. 5 for the fit without and with kinematics. It should be noted that the kinematics parameters v0 sin i and w0 sin i are slightly anti-correlated, but are almost uncorrelated to the other adjusted parameters: no other galactic or instrumental parameter can mimic a kinematic signature.
 |
Fig. 5. Correlation matrix for both fits without (left) and with (right) kinematics for fiducial simulation. |
 |
Fig. 6. Marginalized distributions of kinematic parameters v0 sin i, w0 sin i and redshift z for 500 realizations of a Gaussian noise with PSNR of 40. Blue lines show input values for the simulation, the dashed lines show the 16th, 50th and 84th percentiles of the posterior distribution. Red lines (resp. shadded region) indicate fit result (resp. ±1σ error band) derived from the fiducial noise realization. |
To test the parameter distribution, we performed the fit for 500 different realizations of the Gaussian noise with a PSNR of 40 in the same configuration, and we present the marginalized distributions of measured parameters v0 sin i, w0 sin i and redshift z in Fig. 4. All distributions are consistent with the input parameters in the simulation, and reasonably Gaussian. As expected from correlation matrix (Fig. 5), there is a slight anti-correlation between kinematic parameters.
3.2. Impact of simulation parameters
The following paragraphs are dedicated to different effects which can impact the measure of both the kinematic parameters and redshift. These effects are the signal-to-noise-ratio and the impact of rd/r0.
Impact of signal-to-noise ratio. We considered the same model as described previously, but performed the fit for 500 realizations of a Gaussian noise with a lower PSNR of 20. As expected, the kinematic parameter marginalized distributions are broader around the true values, but there is no hint of biases at lower signal-to-noise ratio.
Impact of rd/r0. We constructed simulations with the same attributes as the fiducial case but with rd/r0 = 1/2 or 2, with fixed 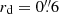 and v0 sin i = 250 km s−1. The marginalized distributions of v0 sin i, w0 sin i and redshift z are presented in Fig. 7. As previously illustrated in the pedagogic case (Sect. 2.1), the case r0/rd = 1/2 (left panels) is favorable: the plateau of the galaxy RC is reached within the photometric extent of the galaxy, and the maximum velocity v0 sin i is well measured. In the opposite case r0/rd = 2 (right panels), the velocity turn-over radius lies outside the extent of the galaxy disk, and velocity v0 sin i is only marginally constrained. However, since the inner solid body rotation part always lies within the disk extent, the CVG w0 sin i is always estimated with similar accuracy.
and v0 sin i = 250 km s−1. The marginalized distributions of v0 sin i, w0 sin i and redshift z are presented in Fig. 7. As previously illustrated in the pedagogic case (Sect. 2.1), the case r0/rd = 1/2 (left panels) is favorable: the plateau of the galaxy RC is reached within the photometric extent of the galaxy, and the maximum velocity v0 sin i is well measured. In the opposite case r0/rd = 2 (right panels), the velocity turn-over radius lies outside the extent of the galaxy disk, and velocity v0 sin i is only marginally constrained. However, since the inner solid body rotation part always lies within the disk extent, the CVG w0 sin i is always estimated with similar accuracy.
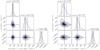 |
Fig. 7. Same as Fig. 6 with r0 = 1/2 rd (left, w0 sin i = 840 km s−1 arcsec−1) or r0 = 2 rd (right, w0 sin i = 210 km s−1 arcsec−1). As noticed earlier, the plateau velocity v0 is barely constrained when rd ≲ r0 (right), i.e., when the disk extent only covers the inner solid-rotation part of the velocity field. This has, however, only a small impact on the determination of redshift z and CVG w0. |
4. Application to HST-based observations
In this section, we present the results obtained by applying the forward model to real galaxy spectrograms from both 3D-HST and GLASS surveys.
4.1. 3D-HST and GLASS surveys
The 3D-HST survey is a 248-orbit HST treasury program used to measure Wide-Field-Camera3 (WFC3) G141 grism spectra in four of the five deep fields of the CANDELS Multi-Cycle Treasury project (AEGIS, COSMOS, GOODS-S and UDS, Grogin et al. 2011; Koekemoer et al. 2011) conducted between 2010 and 2012 (Brammer et al. 2012). The WFC3 G141 grism has a spectral coverage from 1.0 to 1.75 μm (corresponding to ground-based J and H bands) with a dispersion of about 46 Å px−1 (two times smaller in the actual spectrograms after resampling), corresponding to a spectral resolution of ∼130 in the primary spectral order. This survey also made observations in parallel mode with the instrument ACS using the grism G800L covering 0.5 to 1.0 μm wavelengths. More details on this survey, observation strategy, and data reduction are given in (van Dokkum et al. 2011; Skelton et al. 2014; Momcheva et al. 2016).
The GLASS survey is a HST large program (140 orbits) with the goal of measuring grism spectra over the field of ten massive galaxy clusters at redshift z = 0.31 − 0.69 (for Hα emitters) (Schmidt et al. 2014; Treu et al. 2015). The WFC3 is also used in this survey covering wavelength between 0.75 and 1.75 μm using both grism G102 and G141 to observe the cluster cores. The spectra are acquired at two almost orthogonal roll angles (90 ± 10)° to ease cross-decontamination. It results in a catalog of 1272 redshifts down to MAB ≤ 26 (1060 redshifts with MAB ≤ 24). The WFC3 G102 grism has a spectral coverage from 0.75 to 1.15 μm, a dispersion about 24.5 Å px−1 (two times smaller in resampled spectrograms) and a resolution of 210 in the primary spectral order. The analysis was performed using the 3D-HST reduction pipeline (Brammer et al. 2012).
We would have liked to test other HST-based surveys, such as FIGS (Pirzkal et al. 2017), but the reduced spectrograms are not yet publicly available. The ongoing FIGS survey is providing more than 10 000 spectrograms of 2000 different sources (each object is observed at five different roll angles). It has a huge potential for our analysis, since multi-roll joint adjustments (as presented in Sect. 4.3.2) would improve constraints on the redshift and kinematic parameters.
4.2. Kinematic sample preselection
Keeping in mind that the kinematic signature is expected to often be evasive on the HST spectrograms, we do not expect to detect it for all targets. We therefore applied some criteria to both 3D-HST1 and GLASS2 catalogs to select the most promising targets.
From the 33 559 initial Hα and [O III] emitters in the G102 and G141 wavelength domains, we first selected highly significant emission lines (Fline > 25 × 10−17 erg s−1 cm−2 and > 15σ detection level on flux for 3D-HST and quality factor Q ≥ 3 for GLASS). We further selected well-resolved and bright galaxies – allowing an accurate measurement of relative PA – by applying cuts on their effective radius (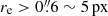 at WFC3 scale) and integrated magnitude (MF140W < 22), as well as moderately inclined galaxies (20 ° < i < 80°): face-on galaxies have a vanishing apparent velocity field, while edge-on galaxies are generally not well approximated by a thin cold disk.
at WFC3 scale) and integrated magnitude (MF140W < 22), as well as moderately inclined galaxies (20 ° < i < 80°): face-on galaxies have a vanishing apparent velocity field, while edge-on galaxies are generally not well approximated by a thin cold disk.
A final visual inspection of the spectrograms of the 386 pre-selected candidates was performed to discard severely contaminated spectra, and other data issues. Broadband images were also examined to remove galaxies with highly asymmetric flux distributions, ongoing mergers, or any other complex structures that could not be handled within our model assumptions.
This selection process picked out 87 galaxies (57 with Hα emission line only, 11 with [O III] only, and 19 with both Hα + [O III] lines) from 3D-HST survey, and 28 galaxies (24 Hα, 2 [O III] and 2 Hα + [O III]) from GLASS survey. This sub-sample is only a minimal pre-selection, from which we present the most promising cases in terms of kinematic signature. In this proof-of-concept analysis, we do not try to estimate the overall fraction of targets over which the kinematic analysis is prone to providing accurate measurements; this should be the subject of a forthcoming study once the methodology is applied systematically over large simulated and or observed samples.
4.3. Results
4.3.1. Fitting procedure
The adopted method to probe kinematics from the spectrograms as follows. Firstly, the position angle is estimated from a Sersic fit to the broadband image, and is kept fixed afterwards. This preliminary measurement was necessary since it is a critical parameter of the model. Then, a kinematic-less fit (v0 = w0 ≡ 0) is performed as a reference, providing an estimate of spectral and nuisance parameters. The final fit including kinematic parameters v0 and w0 is performed using previous estimates as initial guess. Finally, the one-tailed p-value is computed from the best-fit χ2 without and with kinematics to assess the significance of the fit improvement with the addition of two kinematic parameters. The p-value is converted into a kinematic detection z-score, expressed in σ.
In the following sections, we present some particular kinematic detections by computing the objective χ2 on a rectangular region of 40 × 60 px around the emission line of interest, Hα complex or [O III] doublet. Table 2 summarizes the main parameters values and uncertainties of the various fits detailed below.
Adjusted parameters for test galaxies from the GLASS and 3D-HST surveys.
4.3.2. GLASS results
Single line from single roll angle. We present the result of the fit performed on galaxy #1134 from the GLASS survey, illustrating a very significant kinematic detection. This galaxy has a strong emission complex Hα+[N II]+[S II] and a disk scale length 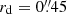 . The fit residuals without (resp. with) kinematics is shown in the bottom left (resp. right) panel of Fig. 8. It should be noted that the residual map without kinematics displays a coherent structure around Hα line position, which is significantly reduced in the residual map with kinematics: indicating that this structure was a signature of the velocity field. The fit gives the following results for the kinematic parameters: v0 sin i = (250±28) km s−1, w0 sin i = (242±28) km s−1 arcsec−1, which corresponds to an RC turnover radius of
. The fit residuals without (resp. with) kinematics is shown in the bottom left (resp. right) panel of Fig. 8. It should be noted that the residual map without kinematics displays a coherent structure around Hα line position, which is significantly reduced in the residual map with kinematics: indicating that this structure was a signature of the velocity field. The fit gives the following results for the kinematic parameters: v0 sin i = (250±28) km s−1, w0 sin i = (242±28) km s−1 arcsec−1, which corresponds to an RC turnover radius of 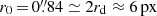 . The χ2 improvement between the two models (without and with kinematics) corresponds to a 12.7 σ detection (p ∼ 10−33) of the kinematic signature.
. The χ2 improvement between the two models (without and with kinematics) corresponds to a 12.7 σ detection (p ∼ 10−33) of the kinematic signature.
 |
Fig. 8. Top left: adjusted velocity field v(r) (contours) over-imposed on broadband image B(r) (gray) of galaxy #1134 from the GLASS survey. Top right: input observed (gray) and modeled (contours) peak-normalized spectrogram, centered on the Hα+[N II]+[S II] complex. Red dashed lines represent the adjusted rotation curve at the Hα position. Given the poor kinematic sampling, the offset induced by the kinematics is only ± ∼ 0.5 px. Bottom left: residual map for model without kinematics. Bottom right: residual map after adding kinematic parameters to the model. Black cross represents position angle of the galaxy at Hα emission line position and the dotted line the spectral trace. The decrease in the χ2 corresponds to a 12.7σ kinematic signature detection. |
Multiple lines from single roll angle. In the case where both Hα and [O III] lines are detected in the spectrogram, we can apply a joint fit on both emission line regions by minimizing the total χ2 = χ2(Hα) + χ2(O III), where each contribution is computed from its own region. Both components share the same intrinsic parameters (redshift, v0 sin i, etc.), with the exception of the continuum level 𝒞0, and cross-dispersion offset Δy, which can be different. We show an example of this approach on galaxy #451 from the GLASS survey. The fit residuals with kinematics on each emission line region is shown in Fig. 9.
 |
Fig. 9. Top: input observed (gray) and modeled (contours) peak-normalized spectrogram of galaxy #451 from the GLASS survey for which Hα complex (right frame) and [O III] doublet (left frame) are simultaneously adjusted. Bottom: residual map for model with kinematics centered on [O III] doublet (left) and on Hα+[N II]+[S II] complex (right). The black crosses represent PA of the galaxy at [O III] and Hα emission line positions. The decrease in the total χ2 corresponds to a joint detection at 13.2σ. |
Multiple roll angles. As noticed earlier, each galaxy in the GLASS survey was observed with two almost orthogonal satellite roll angles, corresponding to different dispersion directions and therefore relative PAs. Parameters describing its intrinsic spectrum, flux distribution, and velocity field are common to both spectrograms: only the transverse offsets Δy of the dispersion law may be different. As a matter of fact, we also observed inconsistencies between roll angles in the longitudinal component of the dispersion law (i.e. wavelength solution), leading to spuriously different redshifts when estimated from individual spectrograms. To account for this effect, we introduced another nuisance parameter, the wavelength solution offset Δx (in Å), such that the observed wavelength of an emission line may differ in both roll angles:
where z is the joint (effective) redshift, and λ0 is the restframe wavelength.
We are now able to construct a model describing both spectrograms and fit them simultaneously. This was done by minimizing the joint χ2 = χ2(PA1) + χ2(PA2), where each χ2(PAi) is the objective function defined in Sect. 2.5.2 for an individual spectrogram with given relative PAi.
We applied this simultaneous fit to the [O III] emission line of galaxy #399 from the cluster MACS0717 of the GLASS survey, measured with a disk scale length  . Each roll-angle spectrogram is first adjusted on its own, leading to a 14.7 σ and 21.6 σ internal kinematic detection respectively; the joint fit on the two spectrograms provides a kinematic z-score of 25.5 σ (see Fig. 10). The fit gives the following results for the common adjusted kinematic parameters: v0 sin i = (287±15) km s−1, w0 sin i = (605±32) km s−1 arcsec−1, which corresponds to an RC turnover radius of
. Each roll-angle spectrogram is first adjusted on its own, leading to a 14.7 σ and 21.6 σ internal kinematic detection respectively; the joint fit on the two spectrograms provides a kinematic z-score of 25.5 σ (see Fig. 10). The fit gives the following results for the common adjusted kinematic parameters: v0 sin i = (287±15) km s−1, w0 sin i = (605±32) km s−1 arcsec−1, which corresponds to an RC turnover radius of 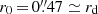 . We find a final redshift of z = 1.691 75 ± 0.000 06, accounting for the wavelength offset Δx = (−12.37±0.32) Å; this corresponds to a shift of about ± ∼ 0.5 px between the wavelength solutions. It is therefore crucial to include it in the model to constrain subtle sub-pixel effects such as kinematics from multi-roll angle spectrograms.
. We find a final redshift of z = 1.691 75 ± 0.000 06, accounting for the wavelength offset Δx = (−12.37±0.32) Å; this corresponds to a shift of about ± ∼ 0.5 px between the wavelength solutions. It is therefore crucial to include it in the model to constrain subtle sub-pixel effects such as kinematics from multi-roll angle spectrograms.
 |
Fig. 10. Same as Fig. 8 for joint fit on [O III] emission line of galaxy #399 from GLASS survey observed with a roll angle of 52° (left panels) and 152° (right panels). It should be noted that for the first spectrogram, the large residual structure, which is visible at the bottom of the results from an incomplete source decontamination does not significantly affect the model adjustment result, but only increases the final χ2 value. The decrease in the joint χ2 corresponds to a 25.5 σ-level detection. |
4.3.3. 3D-HST results
We present the result for galaxy #19843 from the 3D-HST survey, illustrating a weaker kinematic detection than previously shown. This galaxy has a strong Hα+[N II]+[S II] emission complex and a disk scale length of 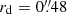 . As shown in Fig. 11, the kinematic detection is only at the 6.2σ level (p ∼ 2 × 10−10).
. As shown in Fig. 11, the kinematic detection is only at the 6.2σ level (p ∼ 2 × 10−10).
 |
Fig. 11. Same as Fig. 8 for galaxy #19843 from 3D-HST survey. The addition of kinematic parameters in the model decreases the objective χ2 at a limited 6.2σ level. |
5. Discussions
5.1. Core model assumptions
Axisymmetric thin cold disk. Under the cold rotating thin-disk hypothesis, morphological and kinematic position angles are assumed to be the same. However, the misalignment between these two position angles can be quite significant (> 30°). Contini et al. (2016) and Harrison et al. (2017) estimated that such misalignment can be attributed to either low/high inclinaison, dispersion dominated systems, or complex morphological substructures such as central bars, spiral arms, or clumps in a low-surface brightness disk.
As the CVG w0 is strongly correlated with the assumed kinematic axis (see Eq. (1)), our method is particularly sensitive to the presence of central asymmetric structures, such as bars, and other kinematically distinct components (KDC), which are incompatible with the cold thin-disk approximation. The method presented here therefore remains best-suited to rotation-dominated isolated late-type spiral galaxies.
Separability assumption. The second strong hypothesis of our model is more of a technical one, helping to construct the three-dimensional galaxy datacube; assuming the rest-frame galaxy spectrum is entirely uniform. This assumption is acceptable for homogeneous objects, but less valid for KDCs or star-forming galaxies. Nelson et al. (2012) studied a sample of 57 galaxies from the 3D-HST survey, and compared Hα and stellar continuum maps: for high-redshift galaxies (z ∼ 1), Hα emission globally follows the rest-frame R-band light but tends to be more extended and clumpier. Comparing Hα and continuum effective radii, they found that ⟨re(Hα)/re(R)⟩ = 1.3 ± 0.1. However, this difference has not been confirmed with IFU observations for galaxies at z ∼ 2 (Förster Schreiber et al. 2011).
For our study, we selected only reasonably compact objects, and systematically found η ∼ 1 ± 0.1, indicating that Hα and continuum flux distribution are reasonably similar.
Overall, the two core assumptions are well justified for large and bright isolated late-type galaxies. Furthermore, given the available instrumental setup, with limited spatial and kinematic samplings, slitless observations can only constrain simplified models (disk rotation curves, age or metallicity gradients, etc.).
5.2. Systematics from the position angle
As mentioned in Sect. 2, galaxy-relative PA and CVG w0 induce similar line shape distortions in the spectrogram, and are therefore strongly correlated. By differentiating Eq. (1) at constant effective PA, one can estimate the systematic error Δw0 associated to an error on the relative PA of the galaxy:
For the galaxy #1134 from the GLASS survey, we found a systematic error on the CVG Δw0 ≈ 38 km s−1 arcsec−1. For both the galaxies #451 and #399, Δw0 ≈ 123 km s−1 arcsec−1. Finally, for the galaxy #19843 of the 3D-HST survey, we computed Δw0 ≈ 108 km s−1 arcsec−1.
Overall, the systematic uncertainties on the CVG w0 are larger than the statistical ones (except for galaxy #19843) but remains in a similar range since the PA is very well constrained from the broadband images (see Table 2), and the kinematic sampling is the governing term in Eq. (14) where s = 0.13 arcsec px−1.
5.3. Implications on redshift precision
Self-confusion effect in slitless spectroscopy is generally assumed to induce redshift measurements that are less accurate than in more traditional spectroscopic observations. However, the forward model presented here significantly attenuate this effect, as the effective spectral resolution does not depend on the object extent anymore, even in the absence of kinematic parameters. In Table 2, we compare the redshift uncertainties from the forward model described in Sect. 4.3 to the total uncertainties (including systematics) estimated by 3D-HST and GLASS analysis. We emphasize that only the statistical error on the redshift measurement is quoted in our case, as we do not have access to the data reduction details for HST-based surveys. Nonetheless, it is important to note that the forward modeling delivers a redshift accuracy down to ∼10−4 or less. Using a similar forward approach for slitless spectroscopic reduction would probably provide an equivalent precision gain on instrumental calibrations (notably dispersion solution), which would in turn decrease the final systematic errors to a comparable level. Ultimately, our study suggests that a consistently forward analysis of slitless observations – including for data reduction procedures – could allow a significant gain in redshift precision.
5.4. Kinematic measurements
Notwithstanding its direct degeneracy with the assumed kinematic angle, the CVG w0 is reasonably constrained by the core 2D shape of the emission lines in the slitless spectrogram. On the other hand, the plateau velocity v0 remains difficult to measure, since spectroscopic observations are rarely deep enough in available redshift surveys to probe regions well beyond effective radius rd ≈ r0, where the velocity flattening would be manifest. Furthermore, current instrumental setups, with a limited kinematic sampling (Rkin > 650 km s−1 px−1), do not favor precise measurements of internal kinematic signatures, inducing sub-px spectral distortions.
We note that in this proof-of-concept analysis, we did not take into account the “beam smearing”, meaning, the degradation of kinematic resolution due to limited spatial resolution. Formally, one would need to construct an “infinitely” spatially-resolved model cube before applying the spatial PSF, while, in our case, we built the model cube from an already PSF-convolved flux model (Eq. (3)). This would mostly change the estimated value of w0 for very steep unresolved CVGs.
Lastly, the natural drawback of the forward approach is that the model is assumed to be a fair representation of the observed data. If this is not the case (specifically, non cold thin disk-like objects and/or non-radial structures), errors are dominated by systematics and the resulting kinematic parameters have no adequate physical interpretations.
6. Conclusions and perspectives
In this article, we explored the possibility of probing single objects with slitless spectroscopy, by measuring not only integrated spectral features, but also spatially-resolved quantities such as internal kinematics. To achieve that, we presented a forward-model of slitless spectrograms from a galaxy model – including flux-distribution, intrinsic-spectrum and kinematic parameters – and an instrumental signature. This method relies on two major assumptions: the axisymmetric thin cold-disk approximation, and the separability hypothesis. We applied this method to HST-surveys’ galaxies to measure internal kinematics parameters: the plateau velocity v0 and the central velocity gradient w0.
The kinematic signature on slitless spectrograms is very specific, as a quadrupole structure in the kinematic-less residuals around emission lines. It is therefore difficult to confuse with other effects such as line flux distribution or radial structures. Even if the kinematic signature is subtle, it extends over the full galaxy scale, which makes the statistical detection significant even with limited kinematic sampling.
The main results of our method can be summarized as follows.
We present the first detection of resolved internal kinematics in galaxies from slitless spectroscopic observations. Using a simple asymptotic velocity curve, we note that the CVG w0 is more precisely determined than the plateau velocity v0, but is directly sensitive to systematic errors on the assumed relative position angle of the galaxy, which must be estimated from external photometry.
The forward model naturally corrects for the self-confusion effect: the spectral resolution does not explicitly depend on the object shape/extent anymore. It implies a more precise redshift measurement (down to 10−4) with a simple model without kinematics, and even better one with a model including kinematics. Improved redshifts from slitless surveys will have a direct impact on cosmological probes, such as baryon acoustic oscillation and redshift space distortion measurements, where the expected precision is 10−3 to 10−4.
We observe sub-px inconsistencies in the dispersion law of the spectrograms from 3D-HST and GLASS surveys in the cross-dispersion direction, and use a nuisance parameter to account for it. However, calibration errors along the dispersion axis induce a systematic error in the effective redshift determination, but do not affect the kinematic parameters. It should be kept in mind that this analysis is a proof of concept applied at the data analysis level only: optimal results would be obtained with a full forward model of slitless spectrograms, including in data calibration stages.
We demonstrate the great flexibility of our forward model, where one can simultaneously fit different emission lines, spectrograms observed with different dispersion direction, and even spectrograms from different instruments, allowing improved constraints on redshift and kinematic parameters.
The spectroscopic resolving power ℛ is a key parameter determining the amplitude of the Doppler distortion in the spectrogram, and is therefore a deciding quantity to precisely constrain the CVG and the plateau velocity. Furthermore, the spectroscopic observations must be deep enough to probe the velocity curve well beyond the photometric disk radius and reach the asymptotic regime.
We stress that, building on a finer understanding of the spectrogram formation, this forward model of slitless spectra has the potential to obtain more precise redshift measurements than standard approaches. This is to be widely tested on future slitless surveys, such as Euclid, which is to acquire spectrograms for 30M galaxies in the Wide Field, and also produce deeper spectroscopic observations in the Deep Fields (Laureijs et al. 2011). Moreover, these surveys should be characterized by a finer kinematic sampling Rkin ∼ 200 km s−1 pxd−1, more suited to kinematic-measurement and galaxy-scaling relation studies such as the Tully-Fisher relation (e.g. Aquino-Ortíz et al. 2018; Lelli et al. 2019) or morpho-kinematic classification (e.g. Cortese et al. 2014; Kalinova et al. 2017; Schulze et al. 2018).
Acknowledgments
We thank the referee for the careful reading of the paper and useful suggestions. We also thank Orane Monteil for an early contribution to this work. This research made use of the MINUIT algorithm (James & Roos 1975) via the iminuit (https://github.com/iminuit/iminuit) Python interface. This work is based on observations taken by the 3D-HST Treasury Program (GO 12177 and 12328) with the NASA/ESA HST, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26555.
References
- Aquino-Ortíz, E., Valenzuela, O., Sánchez, S. F., et al. 2018, MNRAS, 479, 2133 [NASA ADS] [CrossRef] [Google Scholar]
- Atek, H., Malkan, M., McCarthy, P., et al. 2010, ApJ, 723, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Bacon, R., Accardo, M., Adjali, L., et al. 2010, Ground-based and Airborne Instrumentation for Astronomy, III, 773508 [NASA ADS] [CrossRef] [Google Scholar]
- Brammer, G. B., van Dokkum, P. G., Franx, M., et al. 2012, ApJS, 200, 13 [Google Scholar]
- Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Bundy, K., Bershady, M. A., Law, D. R., et al. 2015, ApJ, 798, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., Emsellem, E., Krajnović, D., et al. 2011, MNRAS, 413, 813 [NASA ADS] [CrossRef] [Google Scholar]
- Cole, S., Percival, W. J., Peacock, J. A., et al. 2005, MNRAS, 362, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Contini, T., Epinat, B., Bouché, N., et al. 2016, A&A, 591, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cortese, L., Fogarty, L. M. R., Ho, I.-T., et al. 2014, ApJ, 795, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Courteau, S. 1997, AJ, 114, 2402 [NASA ADS] [CrossRef] [Google Scholar]
- Croom, S. M., Lawrence, J. S., Bland-Hawthorn, J., et al. 2012, MNRAS, 421, 872 [NASA ADS] [Google Scholar]
- de la Torre, S., Guzzo, L., Peacock, J. A., et al. 2013, A&A, 557, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Zeeuw, P. T., Bureau, M., Emsellem, E., et al. 2002, MNRAS, 329, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Doyon, R., Hutchings, J. B., Beaulieu, M., et al. 2012, in Space Telescopes and Instrumentation 2012: Optical, Infrared, and Millimeter Wave, Proc. SPIE, 8442, 84422R [CrossRef] [Google Scholar]
- Dressel, L. 2012, Wide Field Camera 3 Instrument Handbook for Cycle 21 v. 5.0 (Baltimore: Space Telescope Science Institute) [Google Scholar]
- Emsellem, E., Cappellari, M., Krajnović, D., et al. 2007, MNRAS, 379, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Emsellem, E., Cappellari, M., Krajnović, D., et al. 2011, MNRAS, 414, 888 [Google Scholar]
- Erroz-Ferrer, S., Knapen, J. H., Leaman, R., et al. 2016, MNRAS, 458, 1199 [NASA ADS] [CrossRef] [Google Scholar]
- Folkes, S., Ronen, S., Price, I., et al. 1999, MNRAS, 308, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Freudling, W., Kümmel, M., Haase, J., et al. 2008, A&A, 490, 1165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Förster Schreiber, N. M., Shapley, A. E., Erb, D. K., et al. 2011, ApJ, 731, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Grogin, N. A., Kocevski, D. D., Faber, S. M., et al. 2011, ApJS, 197, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Grupp, F., Prieto, E., Geis, N., et al. 2012, Infrared, and Millimeter Wave, 8442, 84420X [Google Scholar]
- Gómez, P. L., Nichol, R. C., Miller, C. J., et al. 2003, ApJ, 584, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, C. M., Johnson, H. L., Swinbank, A. M., et al. 2017, MNRAS, 467, 1965 [NASA ADS] [CrossRef] [Google Scholar]
- James, F., & Roos, M. 1975, Comp. Phys. Commu., 10, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, D. H., Saunders, W., Colless, M., et al. 2004, MNRAS, 355, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Kalinova, V., Colombo, D., Rosolowsky, E., et al. 2017, MNRAS, 469, 2539 [Google Scholar]
- Kauffmann, G., White, S. D. M., Heckman, T. M., et al. 2004, MNRAS, 353, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Koekemoer, A. M., Faber, S. M., Ferguson, H. C., et al. 2011, ApJS, 197, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Kuntschner, H., Bushouse, H., Kümmel, M., & Walsh, J. R. 2009a, Space Telescope WFC Instrument Science Report, 18 [Google Scholar]
- Kuntschner, H., Bushouse, H., Kümmel, M., & Walsh, J. R. 2009b, Space Telescope WFC Instrument Science Report, 17 [Google Scholar]
- Kuntschner, H., Kümmel, M., Walsh, J. R., & Bushouse, H. 2011, Space Telescope WFC Instrument Science Report, 5 [Google Scholar]
- Kümmel, M., Walsh, J. R., Pirzkal, N., Kuntschner, H., & Pasquali, A. 2009, PASP, 121, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Kümmel, M., Rosati, P., Fosbury, R., et al. 2011, A&A, 530, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, ArXiv e-prints [arXiv:1110.3193] [Google Scholar]
- Lelli, F., Fraternali, F., & Verheijen, M. 2013, MNRAS, 433, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Lelli, F., McGaugh, S. S., Schombert, J. M., Desmond, H., & Katz, H. 2019, MNRAS, 484, 3267 [NASA ADS] [CrossRef] [Google Scholar]
- Momcheva, I. G., Brammer, G. B., van Dokkum, P. G., et al. 2016, ApJS, 225, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, E. J., van Dokkum, P. G., Brammer, G., et al. 2012, ApJ, 747, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Pelliccia, D., Tresse, L., Epinat, B., et al. 2017, A&A, 599, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pirzkal, N., Burgasser, A. J., Malhotra, S., et al. 2009, ApJ, 695, 1591 [NASA ADS] [CrossRef] [Google Scholar]
- Pirzkal, N., Malhotra, S., Ryan, R. E., et al. 2017, ApJ, 846, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, K. B., Treu, T., Brammer, G. B., et al. 2014, ApJ, 782, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Schulze, F., Remus, R.-S., Dolag, K., et al. 2018, MNRAS, 480, 4636 [NASA ADS] [CrossRef] [Google Scholar]
- Sersic, J. L. 1968, Atlas de Galaxias Australes (Cordoba, Argentina: Observatorio Astronomico) [Google Scholar]
- Skelton, R. E., Whitaker, K. E., Momcheva, I. G., et al. 2014, ApJS, 214, 24 [Google Scholar]
- Spergel, D., Gehrels, N., Baltay, C., et al 2015, ArXiv e-prints [arXiv:1503.03757] [Google Scholar]
- Stott, J. P., Swinbank, A. M., Johnson, H. L., et al. 2016, MNRAS, 457, 1888 [NASA ADS] [CrossRef] [Google Scholar]
- Straughn, A. N., Meurer, G. R., Pirzkal, N., et al. 2008, AJ, 135, 1624 [NASA ADS] [CrossRef] [Google Scholar]
- Strauss, M. A., Weinberg, D. H., Lupton, R. H., et al. 2002, AJ, 124, 1810 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez, S. F., Kennicutt, R. C., de Gil Paz, A., et al. 2012, A&A, 538, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thompson, R. I., Rieke, M., Schneider, G., Hines, D. C., & Corbin, M. R. 1998, ApJ, 492, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Treu, T., Schmidt, K. B., Brammer, G. B., et al. 2015, ApJ, 812, 114 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G., Brammer, G., Fumagalli, M., et al. 2011, ApJ, 743, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Varidel, M. R., Croom, S. M., Lewis, G. F., et al. 2019, MNRAS, 485, 4024 [NASA ADS] [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., Anderson, Jr., J. E., et al. 2000, AJ, 120, 1579 [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Toy simulation of spectrogram of typical Hα-emitting disk galaxy at z ∼ 0.9 (intrinsic spectrum in uppermost panel, spatial profile on the leftmost panels) as observed with an HST-like slitless spectrograph, but with an improved spectral resolution of ℛ ∼ 2500 (see text). Top: without kinematic effects; bottom: signature of the intrinsic velocity field is clearly visible as a distortion of the spectrogram. The red dashed lines correspond to the galaxy rotation curves at each emission lines’ position, and are tracing the distortion in the spectrogram. |
| In the text | |
 |
Fig. 2. Sketch of broadband galaxy shape (open contours) and the spectrogram for an infinitely thin emission line (shaded contours) distorted by intrinsic velocity curve (red dashed line); x (resp. y) is direction of dispersion (resp. cross-dispersion), PA is the intrinsic relative position angle defined as the angle between the broadband galaxy major axis and the cross-dispersion direction, and PAeff the apparent position angle on the spectrogram. |
| In the text | |
 |
Fig. 3. Galaxy model to construct fiducial test spectrogram. Left: spatial flux distribution F(x, y) and velocity field v(x, y) with v0 sin i = 250 km s−1 and w0 sin i = 420 km s−1 arcsec−1. Right: effective galaxy spectrum S(λ)×𝒯(λ), including instrumental transmission. |
| In the text | |
 |
Fig. 4. Top: input peak-normalized dispersed image data (gray) and model with kinematics (contours) adjusted on the fit region (rectangle). Bottom left: residual map for the model without kinematics, with a quadrupolar structure visible at Hα line location. Bottom right: residual map for model including kinematics. The cross represents the position and relative PA of the galaxy at Hα wavelength. The decrease in the χ2 with two additional kinematic parameters corresponds to a 10.0σ detection. |
| In the text | |
 |
Fig. 5. Correlation matrix for both fits without (left) and with (right) kinematics for fiducial simulation. |
| In the text | |
 |
Fig. 6. Marginalized distributions of kinematic parameters v0 sin i, w0 sin i and redshift z for 500 realizations of a Gaussian noise with PSNR of 40. Blue lines show input values for the simulation, the dashed lines show the 16th, 50th and 84th percentiles of the posterior distribution. Red lines (resp. shadded region) indicate fit result (resp. ±1σ error band) derived from the fiducial noise realization. |
| In the text | |
 |
Fig. 7. Same as Fig. 6 with r0 = 1/2 rd (left, w0 sin i = 840 km s−1 arcsec−1) or r0 = 2 rd (right, w0 sin i = 210 km s−1 arcsec−1). As noticed earlier, the plateau velocity v0 is barely constrained when rd ≲ r0 (right), i.e., when the disk extent only covers the inner solid-rotation part of the velocity field. This has, however, only a small impact on the determination of redshift z and CVG w0. |
| In the text | |
 |
Fig. 8. Top left: adjusted velocity field v(r) (contours) over-imposed on broadband image B(r) (gray) of galaxy #1134 from the GLASS survey. Top right: input observed (gray) and modeled (contours) peak-normalized spectrogram, centered on the Hα+[N II]+[S II] complex. Red dashed lines represent the adjusted rotation curve at the Hα position. Given the poor kinematic sampling, the offset induced by the kinematics is only ± ∼ 0.5 px. Bottom left: residual map for model without kinematics. Bottom right: residual map after adding kinematic parameters to the model. Black cross represents position angle of the galaxy at Hα emission line position and the dotted line the spectral trace. The decrease in the χ2 corresponds to a 12.7σ kinematic signature detection. |
| In the text | |
 |
Fig. 9. Top: input observed (gray) and modeled (contours) peak-normalized spectrogram of galaxy #451 from the GLASS survey for which Hα complex (right frame) and [O III] doublet (left frame) are simultaneously adjusted. Bottom: residual map for model with kinematics centered on [O III] doublet (left) and on Hα+[N II]+[S II] complex (right). The black crosses represent PA of the galaxy at [O III] and Hα emission line positions. The decrease in the total χ2 corresponds to a joint detection at 13.2σ. |
| In the text | |
 |
Fig. 10. Same as Fig. 8 for joint fit on [O III] emission line of galaxy #399 from GLASS survey observed with a roll angle of 52° (left panels) and 152° (right panels). It should be noted that for the first spectrogram, the large residual structure, which is visible at the bottom of the results from an incomplete source decontamination does not significantly affect the model adjustment result, but only increases the final χ2 value. The decrease in the joint χ2 corresponds to a 25.5 σ-level detection. |
| In the text | |
 |
Fig. 11. Same as Fig. 8 for galaxy #19843 from 3D-HST survey. The addition of kinematic parameters in the model decreases the objective χ2 at a limited 6.2σ level. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.