| Issue |
A&A
Volume 632, December 2019
|
|
|---|---|---|
| Article Number | A45 | |
| Number of page(s) | 17 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201935550 | |
| Published online | 26 November 2019 | |
Lyman continuum escape fraction and mean free path of hydrogen ionizing photons for bright z ∼ 4 QSOs from SDSS DR14
1
Dipartimento di Fisica e Astronomia, Università di Padova, Vicolo dell’Osservatorio 3, 35122 Padova, Italy
e-mail: michael.romano@studenti.unipd.it
2
INAF–Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
3
INAF–Osservatorio Astronomico di Roma, Via Frascati 33, 00078 Monte Porzio Catone, Italy
4
INAF–Osservatorio Astronomico di Trieste, Via G.B. Tiepolo 11, 34143 Trieste, Italy
5
Las Campanas Observatory, Carnegie Observatories, Colina El Pino Casilla 601, La Serena, Chile
Received:
26
March
2019
Accepted:
7
October
2019
Context. One of the main challenges in observational cosmology is related to the redshift evolution of the average hydrogen (HI) ionization in the Universe, as evidenced by the changing in ionization level of the intergalactic medium (IGM) through cosmic time. Starting from the first cosmic reionization, the rapid evolution of the IGM physical properties in particular poses severe constraints for the identification of the sources responsible for maintaining its high level of ionization up to lower redshifts.
Aims. In order to probe the ionization level of the IGM and the ionization capabilities of bright quasi-stellar objects (QSOs) at z = 4, we selected a sample of 2508 QSOs drawn from the Sloan Digital Sky Survey (SDSS, DR14) in the redshift interval 3.6 ≤ z ≤ 4.6 and absolute magnitude range −29.0 ≲ M1450 ≲ −26.0. Particularly, we focus on the estimate of the escape fraction of HI-ionizing photons and their mean free path (MFP), which are fundamental for characterizing the surrounding IGM.
Methods. Starting from UV/optical rest-frame spectra of the whole QSO sample from the SDSS survey, we estimated the escape fraction and free path individually for each of the QSOs. We calculated the Lyman continuum (LyC) escape fraction as the flux ratio blueward (∼900 Å rest frame) and redward (∼930 Å rest frame) of the Lyman limit. We then obtained the probability distribution function (PDF) of the individual free paths of the QSOs in the sample and studied its evolution in luminosity and redshift, comparing our results with those in literature.
Results. We find a lower limit to the mean LyC escape fraction of 0.49, in agreement with the values obtained for both brighter and fainter sources at the same redshift. We show that the free paths of ionizing photons are characterized by a skewed distribution function that peaks at low values, with an average of ∼49 − 59 proper Mpc at z ∼ 4, after possible associated absorbers (AAs) were excluded. This value is higher than the one obtained at the same redshift by many authors in the literature using different techniques. Moreover, the PDF of free path gives information that is complementary to the MFP derived through the stacking technique. Finally, we also find that the redshift evolution of this parameter might be milder than previously thought.
Conclusions. Our new determination of the MFP at z ∼ 4 implies that previous estimates of the HI photoionization rate ΓHI available in the literature should be corrected by a factor of 1.2−1.7. These results have important implications when they are extrapolated at the epoch of reionization.
Key words: quasars: general / dark ages / reionization / first stars
© ESO 2019
1. Introduction
The epoch of reionization (EoR) marks a fundamental event for the Universe that is characterized by a transition phase of the intergalactic medium (IGM) from cold and almost neutral to warm and fully ionized (Meiksin 2009; McQuinn 2016). During this dramatic event, which is approximately determined to have occurred at z ∼ 6 − 8, the first UV photon sources with energies higher than 13.6 eV were able to clear the fog of the widespread neutral hydrogen (HI) and end the so-called period of the Dark Ages (Dayal & Ferrara 2018). The analysis of the optical depth of the cosmic microwave background (CMB) by Planck (Planck Collaboration VI 2019) and the analysis of high-z quasi-stellar objects (QSOs; Fan et al. 2006; Becker et al. 2015) have recently clarified that the EoR was a very rapid event. This phase transition lasted for a short time Δz ≤ 2.8, and it was also a patchy process. This is consistent with the progressive decrease in photoionization rate ΓHI that is observed at z ≥ 5.5 (Calverley et al. 2011; Davies et al. 2018; D’Aloisio et al. 2018).
The debate of what caused the EoR is ongoing. While the majority of the astrophysical community favors star-forming galaxies as the main drivers of HI reionization (Dayal & Ferrara 2018), alternative explanations based on active galactic nuclei (AGNs) have been proposed (Giallongo et al. 2012, 2015; Madau & Haardt 2015; Grazian et al. 2018; Boutsia et al. 2018). It is widely accepted that QSOs and AGNs dominate the HI ionizing background at z < 3 (Haardt & Madau 2012; Fontanot et al. 2012; Cristiani et al. 2016; Faucher-Giguère 2019). It is still debated, however, whether the HI-ionizing background at higher redshift is mainly driven by rest-frame star-forming galaxies or by AGNs. One of the main arguments against HI reionization driven by accreting super-massive black holes (SMBHs) is the fast drop in the space density of bright QSOs (Fan et al. 2001; Cowie et al. 2009) at z ≥ 3 and the lack of numerous L ∼ L* AGNs at z ≥ 4 (Parsa et al. 2018; Akiyama et al. 2018; Kim et al. 2019; Matsuoka et al. 2018; Yang et al. 2019). Contrasting results have been obtained in literature so far, leading to significant uncertainties in the estimate of the HI photoionization rate, into which the luminosity function directly enters (Boutsia et al. 2018; Giallongo et al. 2019; Kulkarni et al. 2019).
In order to quantify the contribution of active SMBHs to the cosmological photoionizing background, two other physical parameters are required in addition to the QSO luminosity function: (1) the escape fraction of HI-ionizing photons, that is, at the Lyman continuum (LyC) λ ∼ 900 Å rest frame, fesc(LyC), and (2) the mean free path (MFP) of HI-ionizing photons. The latter is the average physical distance that HI-ionizing photons typically travel before they are absorbed by a factor 1/e, that is, by an optical depth of τHI = 1. This quantity directly enters into the calculation of the photoionization rate ΓHI, and it can thus change the amount of UV photons per unit time that is released by QSOs into the IGM in a significant way.
At z ∼ 1, Cowie et al. (2009) found fesc(LyC) ∼ 100% for bright QSOs, while Stevans et al. (2014) indicated similar results for a sample of fainter Seyfert 1 and Seyfert 2 galaxies. The LyC escape fraction of bright QSOs (M1450 ≲ −26) and faint AGNs (M1450 ∼ −24) at z ∼ 4 has been studied by Cristiani et al. (2016) and Grazian et al. (2018), respectively. They found that the LyC escape fraction of QSOs and AGNs is ∼75% or greater, and it does not show any dependence on the absolute luminosities of the objects, at least up to L ∼ L*. In particular, Cristiani et al. (2016) found that the distribution of the escape fraction of bright QSOs from the Sloan Digital Sky Survey (SDSS) is bimodal, with an 18−25% probability of a negligible escape fraction and the remaining 75−82% with fesc(LyC)∼100%. However, as discussed in Grazian et al. (2018), this bimodality might be due to the choice of the spectral window that they adopted to measure the ionizing photon leakage, that is, λrest = 865 − 885 Å. Sources with an high escape fraction and a proximate Lyman limit system (LLS) or a damped Lyman-α system, which is close to the emission redshift of a QSO, can spuriously mimic an fesc(LyC)∼0. It is thus important to study the relation between the LyC escape fraction and the presence of nearby absorbers in detail. An effective parameter that is useful to quantify the presence of LLSs surrounding QSOs could be the MFP.
The individual free path (IFP) of HI-ionizing photons can be obtained by deriving the optical depth along a line of sight by counting the individual intervening absorbers (Faucher-Giguère et al. 2008; Songaila & Cowie 2010; Rudie et al. 2013; O’Meara et al. 2013; Inoue et al. 2014; Prochaska et al. 2015; Crighton et al. 2019). This approach yielded different results depending on the input HI column density distribution used in the models. The robust detection of absorbers, and in particular (partial) LLSs, is a delicate problem, however, and it has been limited to the line of sight of very luminous QSOs. They can reside in very massive halos, thus biasing our view of the MFP with respect to the MFP in the other less strongly biased regions of the Universe. Alternatively, the MFP can be obtained by stacking a large number of high-z QSOs and measuring the decrement of a factor 1/e with respect to the mean flux level at λrest ∼ 912 Å, as carried out by Prochaska et al. (2009) and Worseck et al. (2014). They obtained a fast evolution of the MFP with cosmic epoch MFP(z) ∝ (1 + z)−5.4 over a wide redshift range 2.3 < z < 5.5. This rapid decrement according to Worseck et al. (2014) implies an evolution in number density or in the physical size of the absorbers.
These two methods (individual absorber distribution versus stacking) do not provide fully consistent results, however. The redshift evolution of the MFP derived by Worseck et al. (2014) is far more rapid than the evolution found by the statistics of the absorbers (e.g., Songaila & Cowie 2010). For example, Songaila & Cowie (2010) found a number density of LLSs per unit redshift n(z)∝(1 + z)−1.94, corresponding to a MFP evolution of MFP(z)∝(1 + z)−4.44. For comparison, Crighton et al. (2019) measured a redshift evolution for the incidence of LLSs of l(z)∝(1 + z)1.70. These differences are expected, however, because different absorber populations (e.g., partial LLSs, LLSs, and damped systems) might contribute in a different way to the MFP and scale differently with redshift (Prochaska et al. 2010; Inoue et al. 2014).
The MFP of HI-ionizing photons is a physical quantity averaged over a sample of QSOs at high z. It is a measure of the distribution of Lyman limit opacity and thus of the IGM ionization state in the LyC. More information is carried by the probability distribution function of the IFPs of the population, PDF(IFP). This latter depends on the distribution of neutral patches, which are sparse HI residuals that are surrounded by a widespread ionized gas. These patches consist of diffuse gas clouds in the IGM and/or denser large-scale structures, that is, the external regions of galaxies or regions around filaments, as proposed by Fumagalli et al. (2011) and Worseck et al. (2014).
The study of PDF(IFP) is important as a benchmark for numerical simulations of the IGM. Strong constraints on cosmological simulations can be provided by a detailed knowledge of the IFP distribution across a wide redshift range. For example, radiation-hydrodynamical simulations by Rahmati & Schaye (2018) indicated that close to the reionization epoch (at z = 6), the distribution of IFP peaks at ∼5 pMpc, with an extended tail toward lower values, if measured along a random line of sight. When the line of sight is instead centered on massive galaxies, the authors predict a bimodal distribution with a peak at a few kiloparsec and another less pronounced peak at ∼5 proper Mpc.
In this paper we study the distribution function of the HI-ionizing IFPs centered on relatively bright (M1450 ≲ −26) QSOs at 3.6 ≤ z ≤ 4.6, and we try to understand the connection between the IFP and the LyC escape fraction. This work can be useful to understand the physical conditions that allow HI-ionizing photons to escape from QSOs and to subsequently ionize the IGM.
The paper is organized as follows: in Sect. 2 we describe the SDSS data we used, in Sect. 3 we outline the method we adopted to measure the QSO physical properties (i.e., spectral slope, LyC escape fraction, and IFP of HI-ionizing photons). Section 4 describes the results, and Sect. 5 investigates the connection between fesc(LyC) and the free path. Discussions, summary, and conclusions are provided in Sects. 6 and 7. In Appendix A we provide an example of an SDSS QSO spectrum, while in Appendix B we discuss the difference between the MFP obtained from stacked spectra and an MFP obtained from the mean value of the IFP distribution.
Throughout the paper, we assume H0 = 70 km s−1 Mpc−1, Ωm = 0.3, and ΩΛ = 0.7. Physical distances are expressed in proper Mpc (pMpc).
2. Data
The 14th Data Release of the Sloan Digital Sky Survey (SDSS, DR14) contains observations of different sources until July 2016, including all the previous detections in the preceding phases for a total of 526.356 QSOs detected over 9376 deg2 (Paris et al. 2018). These sources have been selected by combining many color criteria at different redshifts from several surveys; in particular, the automated procedure of the SDSS compares the observed spectra and a set of synthetic spectra to determine the redshift and the type of a source. At each assumed redshift, a least-squares fit to each observed spectrum is made using a general set of models for galaxies, QSOs, and cataclysmic variables. For each extragalactic model, a range of redshifts is explored and a chi-squared analysis is computed; the five best templates of each category are then stored in order of increasing reduced chi-squared. Finally, these last models are refitted enhancing the resolution of the spectra (diminishing the initial velocity step). The overall best fit is obtained in this way, and the class and redshift of each source are specified (for a more accurate description of the spectral classification and redshift measurement made by SDSS, see Bolton et al. 2012). The spectroscopic data of the QSOs have been taken in the wavelength range 3600 ≲ λobs ≲ 10 000 Å, and the spectral resolution varies from ∼1300 at 3600 Å up to ∼2500 at 10 000 Å.
We selected a sample of bright QSOs with 17.0 ≤ I ≤ 20.0 (−29.0 ≲ M1450 ≲ −26.0) and 3.6 ≤ z ≤ 4.6 from DR14 for a total of 2840 objects and analyzed their UV/optical spectra in order to characterize their physical properties and the surrounding IGM. The relatively wide ranges in magnitude and redshift allowed us to investigate a possible luminosity and redshift evolution of our targets. The choice of this redshift coverage was mainly made for the following reasons: (1) QSOs at redshift 3.0 < z < 3.6 present a bias against having (u − g) < 1.5. Sources with strong Lyman limit absorptions are therefore mostly selected with respect to other sources, and this alters the estimate of their physical properties in this redshift range (Prochaska et al. 2009). (2) At this epoch of the Universe, the transmission of the IGM is still relatively high. This allows observing the characteristic features of QSOs.
3. Method
3.1. Cleaning of the sample
In order to proceed for a statistical analysis on the characterizing properties of our QSO sample, each spectrum was examined individually. We also extracted several fundamental pieces of information (i.e., the spectral slope, the free path of UV-ionizing photons, and the LyC escape fraction).
At first, we visually inspected all the 3.6 ≤ z ≤ 4.6 QSOs to obtain a sample with as little bias as possible. To do this, we checked for the source type and redshift, which are automatically assigned by the SDSS pipeline. Several targets have been incorrectly classified as QSOs by the SDSS procedure: they do not present any typical feature of a QSO UV/optical spectrum at these redshifts. We therefore discarded these spurious sources from the final sample. Furthermore, a precise determination of the systemic redshifts of the sources is of great importance in order to reduce the uncertainties on the estimate of the parameters describing the QSOs. We therefore checked each spectrum for an inaccurate position of the strongest lines in emission of the QSO. To finally refine the spectroscopic redshift of a source, we used the OI emission line (1305.5 Å rest frame). This line forms in the outermost portion of the broad line region and is thus less affected by changes in its spectral shape due to possible QSO outflows (Matsuoka et al. 2005). Taking the wavelength relative to the OI line centroid (λOI, in Angstrom), the new redshift was obtained as znew = λOI/1305.5 − 1. Moreover, the modified redshifts of a few objects fell outside of the redshift interval we used to select our QSOs. Without these latter sources and the spurious ones, the final sample consists of 2508 QSOs, each of which was analyzed in order to obtain information about their evolution and the environment in which they reside.
3.2. Estimating the spectral slope
The spectral slope of each QSO was obtained by fitting the region redward of the Lyα line (∼1216 Å rest frame) with the power law Fλ = F0λ−αλ, and then extrapolating it in the bluer side of the spectra by imposing a softening at shorter wavelengths with 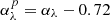 at λrest ≲ 1000 Å (Cristiani et al. 2016; Stevans et al. 2014; Shull et al. 2012; Telfer et al. 2002). We first corrected each spectrum for interstellar extinction using the Cardelli et al. (1989) extinction law and the absorptions available in the SDSS database. Following Cristiani et al. (2016), the five spectral windows that are free of emission lines were then used for the fit. The windows are reported in Table 1 of Cristiani et al. (2016). To estimate the intrinsic continuum, we used the average values (both in flux and wavelength) obtained in each window after an iterative 2σ clipping. We left the normalization constant F0 and the spectral slope αλ as free parameters and used a nonlinear least-squares minimization routine to obtain the best-fit parameters that described the local continuum of each QSO. By extrapolating the power law in the region blueward of the Lyα line, we also obtained the flux decrements DA and DB (Oke & Korycansky 1982) in the spectral windows between the Lyα and Lyβ lines (1170−1050 Å rest frame) and between the Lyβ line and the Lyman limit (1015−920 Å rest frame). We derived the flux decrements DA and DB in order to determine possible dependencies of the escape fraction and of the free ionizing path on these (and other) physical parameters. As an example, Fig. 1 shows the results of this procedure applied on the QSO SDSS J105340.8+010335.7 at zQSO = 3.66983. Here, the cyan regions are the five spectral windows used to fit the continuum, where the third window (1440−1465 Å rest frame) is zoomed to show the effect of the iterative 2σ clipping. Moreover, in several cases, the first window (1284−1291 Å rest frame) might be affected by the emission of the NV line, therefore we computed the fit with and without this region. The longest wavelength region might instead be affected by poor sky subtraction problems, especially at high z. However, by default, the spectral slope for each QSO was estimated considering the fit over all the spectral windows, in order to rely on all the exploitable data. The values obtained for the all windows (no first window) are shown in the upper left (right) panel of Fig. 1. Finally, the yellow portions of the spectrum represent the regions in which the flux decrements DA and DB were calculated.
at λrest ≲ 1000 Å (Cristiani et al. 2016; Stevans et al. 2014; Shull et al. 2012; Telfer et al. 2002). We first corrected each spectrum for interstellar extinction using the Cardelli et al. (1989) extinction law and the absorptions available in the SDSS database. Following Cristiani et al. (2016), the five spectral windows that are free of emission lines were then used for the fit. The windows are reported in Table 1 of Cristiani et al. (2016). To estimate the intrinsic continuum, we used the average values (both in flux and wavelength) obtained in each window after an iterative 2σ clipping. We left the normalization constant F0 and the spectral slope αλ as free parameters and used a nonlinear least-squares minimization routine to obtain the best-fit parameters that described the local continuum of each QSO. By extrapolating the power law in the region blueward of the Lyα line, we also obtained the flux decrements DA and DB (Oke & Korycansky 1982) in the spectral windows between the Lyα and Lyβ lines (1170−1050 Å rest frame) and between the Lyβ line and the Lyman limit (1015−920 Å rest frame). We derived the flux decrements DA and DB in order to determine possible dependencies of the escape fraction and of the free ionizing path on these (and other) physical parameters. As an example, Fig. 1 shows the results of this procedure applied on the QSO SDSS J105340.8+010335.7 at zQSO = 3.66983. Here, the cyan regions are the five spectral windows used to fit the continuum, where the third window (1440−1465 Å rest frame) is zoomed to show the effect of the iterative 2σ clipping. Moreover, in several cases, the first window (1284−1291 Å rest frame) might be affected by the emission of the NV line, therefore we computed the fit with and without this region. The longest wavelength region might instead be affected by poor sky subtraction problems, especially at high z. However, by default, the spectral slope for each QSO was estimated considering the fit over all the spectral windows, in order to rely on all the exploitable data. The values obtained for the all windows (no first window) are shown in the upper left (right) panel of Fig. 1. Finally, the yellow portions of the spectrum represent the regions in which the flux decrements DA and DB were calculated.
 |
Fig. 1. Spectral slope and flux decrements for the QSO SDSS J105340.8+010335.7 at zQSO = 3.66983. The cyan portions of the spectrum are the five windows that are free of emission lines. The yellow regions are the places of the spectrum in which the flux decrements DA and DB have been calculated. The solid orange and green lines represent the fit with and without the first window (1284−1291 Å rest frame), respectively. |
Absorption features and/or noise in the spectra might even alter the slope of several sources, leading to an incorrect estimate of the intrinsic continuum of many QSOs. To avoid this complication, the sources were inspected one by one, and the spectral windows that were affected by strong noise were removed. We then recomputed the fit to estimate the spectral slope.
3.3. Estimating the LyC escape fraction of SDSS QSOs at z ∼ 4
The LyC escape fraction for each QSO of our sample was derived following Grazian et al. (2018). In summary, we estimated the mean flux density shortward, Fν(900), and longward, Fν(930), of the Lyman limit (912 Å rest frame) and measured the escape fraction as fesc = Fν(900)/Fν(930).
More precisely, Fν(900) is the mean flux density of the QSO in the HI-ionizing continuum region, between 892 and 905 Å rest frame, while Fν(930) is the average flux density in the non-ionizing region redward of the Lyman limit, between 915 and 960 Å rest frame. It is worth noting that this latter spectral window was slightly enlarged with respect to the window used by Grazian et al. (2018), that is, 915−945 Å. After several tests, we verified that with this new choice, the measurement of the mean flux density Fν(930) for our sources became more stable than the previous because it was less strongly affected by possible absorption lines in the Lyman-α forest. However, on average, the old and new escape fractions are quite similar to each other. Finally, when we calculated Fν(930), we avoided the region between 935 and 940 Å because of the Lyϵ emission line of the QSO. At z ∼ 3.6 − 4.6, the adopted rest-frame wavelengths 892−960 Å correspond to observed wavelengths of λobs ∼ 4100 − 5400 Å, which are well sampled by the SDSS spectra we used here. In order to avoid intervening absorbers in these regions, both Fν(900) and Fν(930) were derived with an iterative 2σ clipping procedure.
It is worth noting here that we did not attempt to reconstruct the intrinsic QSO continuum, but measured the observed mean flux level in these two spectral windows, assuming an equal residual Lyman series absorption above and below the Lyman limit. The observed distribution of the escape fraction might be different from the intrinsic one due to the errors in the estimate of the local continua, both red- and blueward of the LyC. With this aim, we estimated the flux variation in the Lyman forest. For each QSO studied in this paper, we measured the mean flux (after the 2σ clipping procedure) in the rest-frame wavelength 915−960 Å and 960−1005 Å and computed their flux ratio. This flux ratio does not depend on the absolute magnitudes or spectroscopic redshifts, and its scatter is ∼0.15 dex. We assumed that the same error can be applied when we estimated the individual QSO continua (both red- and blueward of the LyC). For comparison, Prochaska et al. (2010) estimated a 10% uncertainty on the estimate of the SDSS QSO continuum in the Lyman forest. Adopting this ∼0.15 dex continuum uncertainty, we find that the typical scatter of the escape fraction is ∼15−17% for fesc > 75%, while it progressively decreases to 1−2% at fesc < 20%. Moreover, the output values of the escape fraction are fully consistent with the input values, without any systematics. We verified that the mean value of the escape fraction distribution was not significantly perturbed by the scatter due to flux ratio uncertainties. Interestingly, the intrinsic distribution (i.e., after deconvolution by the observed scatter) gives slightly higher mean values of fesc than the observed distribution. In the following, we prefer to plot only the observed distribution because the (reconstructed) intrinsic distribution is too noisy.
As discussed in Grazian et al. (2018), this technique is equivalent to measuring fesc = exp(−τLL), where τLL is the average opacity at the Lyman limit. It could include the cumulative effect of small absorbers (τLL < 2), which cannot be individually detected in the SDSS QSO spectra (Prochaska et al. 2010).
We avoided using the spectral window close to the 912 Å rest frame of the QSO (i.e., 905−912 Å rest frame) because this region can be affected by the QSO proximity effect. Moreover, the uncertainties in spectroscopic redshift determination of SDSS spectra, typically of σz ∼ 0.01, does not allow us to precisely locate the position of the Lyman limit, therefore we decided to place our spectral window far from this region.
It is worth noting here that our estimate of the LyC escape fraction fesc for the SDSS QSOs at z ∼ 4 can be considered a lower limit to the real value for several reasons: (1) we did not correct this value for the spectral slope of the QSOs. In the λrest ≤ 1200 Å region, a typical value for the spectral slope is αν ∼ −1.7 (Lusso et al. 2015). If we were to correct for this slope, the true values of fesc for our QSOs should be revised upward by ∼6%. (2) There are possible Lyman-α absorbers that serendipitously fall between the two spectral windows adopted to estimate fesc, that is, 905−915 Å in the QSO frame. Following Inoue et al. (2014), we computed a flux decrement of ∼0.6 between 930 and 900 Å rest frame, due to intervening IGM (see their Fig. 4 for zspec = 4.0). (3) We excluded the proximity region of the QSO from the escape fraction calculations, which is instead a clear signature of the ionization of the surrounding IGM. (4) As we discuss in Sect. 5.1, when we estimate the mean flux density Fν(900) in a shorter spectral window between 898 and 905 Å rest frame, the escape fraction is slightly larger than the fraction computed in the wider region between 892 and 905 Å rest frame.
3.4. Estimating the IFP of HI-ionizing photons
The free path of photons at 912 Å rest frame is a fundamental parameter for estimating the HI photoionization rate. The IFP is defined as the physical distance that a 912 Å rest-frame photon can travel before it is attenuated by a factor of e−1 in flux. This attenuation can be caused by encountering a LLS with optical depth τHI = 1, or alternatively, by the cumulative effect of a great number of more transparent absorbers, with τHI ≪ 1, even if it is not possible to detect them individually.
In order to carry out a statistical analysis, the free path was estimated individually for each spectrum. At first, the spectral energy distribution (SED) of each source was corrected for its intrinsic spectral slope, considering a break in the continuum at ∼1000 Å rest frame, as found by Stevans et al. (2014) and Shull et al. (2012). This was done by flattening the spectral slope of each QSO (obtained as described in Sect. 3.2) for the value Δαν = 0.72 (Cristiani et al. 2016) at λ ≤ 1000 Å rest frame. Starting from λin = 3600/(1 + z), the region blueward of the Lyman limit was divided into several spectral windows of width Δλ and upper limit λfin = λin + Δλ. By default, Δλ was chosen to be 10 Å because this value is a good compromise to follow the spectral features of the specific QSO without under- or overestimating the IFP. In this way, the spectral window was moved upward of 1 Å in every cycle until the Lyman limit, that is, λfin = 912 Å, was reached. In each window, the average fluxes and wavelengths were calculated through an iterative 2σ clipping on the respective data, and they were then interpolated with a spline. In this case, an asymmetric clipping was computed to avoid underestimating the continuum level of the spectrum: all the negative residuals were rejected. The average flux obtained in the upper window near the Lyman limit, f912, was used to compute the flux reduced by a factor e−1, as fred = f912/e. The intersection between the spline and fred defines the wavelength relative to the (Lyman limit) absorber along the line of sight, λLLS, whose redshift was obtained as zLLS = λLLS/912 − 1. Therefore, the comoving distances between the absorber and the source were computed as Dc = Dc(zQSO)−Dc(zLLS), where zQSO is the redshift of the QSO. Finally, the free path of ionizing photons is the proper distance between the QSO and the LLS, and it was derived as IFP = 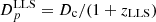 . We verified that the IFP value does not depend on the choice of Δαν = 0.72. We derived the individual IFPs for all the QSOs with Δαν = 0.5 and Δαν = 1.0, which are still allowed by the uncertainties provided by Stevans et al. (2014), Shull et al. (2012), and Telfer et al. (2002), for instance, and found that the effect is negligible, with a difference of ∼0.1 pMpc in the mean value of IFPs.
. We verified that the IFP value does not depend on the choice of Δαν = 0.72. We derived the individual IFPs for all the QSOs with Δαν = 0.5 and Δαν = 1.0, which are still allowed by the uncertainties provided by Stevans et al. (2014), Shull et al. (2012), and Telfer et al. (2002), for instance, and found that the effect is negligible, with a difference of ∼0.1 pMpc in the mean value of IFPs.
In several cases, absorption features blueward of the Lyman limit could drag the interpolated fluxes below fred, and then bring it above this threshold; this trend could create many intersections of the spline with fred, for each of which the IFP was computed. Both the minimum and maximum IFP values were derived, as we show in Fig. 2 for the QSO SDSS J114514.2+394715.9 at zQSO = 4.06557. For all our QSOs, the real IFP of ionizing photons is clearly associated with the maximum IFP value: the minimum value is the result of an absorption feature. For this reason, we set the maximum IFP as the definitive value for each QSO by default.
 |
Fig. 2. IFP estimate for the QSO SDSS J114514.2+394715.9 at zQSO = 4.06557. The green circles and solid line represent the average fluxes in the 10 Å windows and the spline, respectively. The red line marks the Lyman limit. The horizontal blue and cyan lines represent fred and its uncertainty, respectively. In this case, the choice of IFP corresponds to λrest ∼ 800 Å. The flux on the y-axis is in arbitrary units. |
4. Results
4.1. Spectral slope distribution
To study the ensemble properties of our QSO sample, we first obtained the spectral slope distribution in order to carry out a statistical analysis of this parameter and to explore a possible evolution in magnitude and/or redshift.
Figure 3 shows the distribution function. The red line marks the mean value of the spectral slope, αν = −0.69 ± 0.47 (i.e., αλ ≈ 1.31). The uncertainties were computed as half the difference between the 84th and 16th percentiles. This result is in agreement with previous estimates of Cristiani et al. (2016), who found αλ = 1.30 at 3.6 < z < 4.0, and with those of Telfer et al. (2002) and Stevans et al. (2014), who obtained αλ ≈ 1.31 and 1.17 at lower redshift, respectively.
 |
Fig. 3. Spectral slope distribution. The vertical red solid and dashed lines are the mean value and its uncertainties, respectively. |
To investigate the evolution of the spectral slope, the whole QSO sample was split into two halves including fainter and brighter sources with respect to different absolute magnitude thresholds M1450 (from ≈ − 29.0 up to ≈ − 26.0). The two distributions corresponding to each M1450 were compared using a two-sample Kolmogorov–Smirnov (KS) test, in which we chose to reject the null hypothesis (i.e., the hypothesis that two independent samples are drawn from the same parent distribution) for a pvalue below 1%. With this test, a luminosity evolution of the spectral slope was rejected.
The same procedure was used to study the evolution of αν with redshift. In this case, the QSO sample was split into five redshift bins with Δz = 0.2 in order to test possible differences among the various distribution functions, as shown in Fig. 4. The horizontal solid lines in the upper panel of the figure represent the average values of the spectral slope in each redshift bin, increasing from αν ≈ −0.74 in the first bin up to αν ≈ −0.57 in the last bin. The corresponding distributions are plotted in the lower panel, which also shows the KS tests between the first and the other redshift bins. It is interesting to note that the KS tests between the first and the last three distributions are significant, defining a possible redshift evolution of the analyzed parameter.
 |
Fig. 4. Upper panel: spectral slope as a function of redshift. The horizontal red, orange, green, cyan, and blue lines are the average values from the lowest to the highest redshift bins. Bottom panel: distribution of the spectral slope in each redshift bin (with the same color as in the upper panel). |
This is probably caused by the shorter range in wavelengths that was used to compute the power-law fit, which affects the QSO spectra at high redshift, that is, the fact that the reddest spectral window in the spectra might no longer be included in the wavelength coverage of the SDSS for these sources. In order to test this hypothesis, we recomputed the spectral slopes for our QSO sample and excluded the spectral window at the highest wavelengths when we fit the power law. In this case we obtain an increase of αν from ≈ − 0.65 at z ∼ 3.7 to ≈ − 0.57 at z ∼ 4.5. Thus, at low redshift (z ≲ 3.9), the average value of the slope is slightly higher than the value obtained with all the free emission windows, while it remains unchanged at high redshift. In this case, the KS test is no longer significant within the different bins in redshift. For these reasons, the above-mentioned redshift trend of the spectral slope seems to be mostly caused by a systematic effect that is due to the reduced spectral range and not by a physical evolution.
4.2. LyC escape fraction distribution
Depending on the intrinsic properties of each specific QSO and on its possible absorption features, the computed LyC escape fractions cover a broad range of values that extends from approximately zero to 100%. We found an average value fesc = 0.49 ± 0.36 in our sample, as reported in Fig. 5, which shows the escape fraction distribution function of all our sources (red histogram); this value results in a multi-modal distribution with a peak at low values (14.5% of the QSOs with fesc < 0.10), a minimum between 0.10 ≤ fesc ≤ 0.3, and a broad dispersion at higher values, as also found by Cristiani et al. (2016). This figure also shows the distribution from the subsample without sources with IFP < 10 pMpc, resulting in an average value of fesc = 0.58 ± 0.25 (in blue, see Sect. 5.1). By individually inspecting the sources within the first bin, we attributed the low fesc peak to the presence of several QSOs with LLSs that are intrinsic to the QSO itself or that intervene along the line of sight, which absorb almost all the UV radiation escaping from them. This causes a rapid decline of the emitted flux in the region blueward of the Lyman limit, which in turn produces a negligible escape fraction (see Sect. 5.2 for a discussion of the effect of these sources on the final statistical analysis of the physical parameters of the QSOs).
 |
Fig. 5. LyC escape fraction distribution for the whole sample (in red) and for sources with IFP ≥ 10 pMpc (in blue). The solid and dashed gray lines represent the mean values of the first and second distributions, respectively. |
As for the spectral slope, we also tested the dependence of the LyC escape fraction on both redshift and magnitude by splitting the whole sample into sources with lower and higher redshifts (z ≤ 4.1 and z > 4.1), and into QSOs that are brighter and fainter than a given absolute magnitude threshold, respectively. The different object populations were compared with a KS test whose results have allowed us to exclude a possible evolution of fesc with redshift. To determine the dependency of the escape fraction on the magnitude, we split the sample into different magnitude bins and obtained a pvalue = 0.007 in the brightest bin (M1450 < −27.4). This might be significant for a possible trend of the escape fraction with luminosity. However, at fainter magnitudes, the pvalue increases to values higher than 1%, which prevents us from confirming an evolution of fesc with luminosity.
4.3. IFP distribution
The analysis implemented in this paper allowed us to estimate for the first time the MFP of UV-ionizing photons of a QSO sample at redshift z ∼ 4 in a statistical way, that is, based on the distribution functions of IFPs. These functions are displayed in Fig. 6 for redshift bins of Δz = 0.2, where the dashed red lines mark the mean value in each bin; a peak in the distributions is present at low free paths, with a broad tail at higher values, and MFP ∼ 43 pMpc at z ∼ 4.
 |
Fig. 6. Free path distribution functions for the whole QSO sample at 3.6 ≤ z ≤ 4.6 in redshift bins of Δz = 0.2. The dashed red lines represent the mean value in each redshift bin. |
It is well known that this parameter evolves in redshift because the Universe is increasingly composed of more neutral hydrogen, which absorbs UV photons when the EoR is approached (see Sect. 5.2). At z < 5 the HI-ionizing background is quasi-uniform (e.g., Meiksin & White 2004; Becker et al. 2015), resulting in a skewed but unimodal distribution of free paths that reflects the Poisson variance in the incidence of (partial) LLSs along individual lines of sight. The dependency of the free paths on the luminosity of the QSOs is discussed in the next section.
5. Free path versus LyC escape fraction connection
5.1. Dependence of LyC escape fraction on IFPs of QSOs
The distribution of the LyC escape fraction of our QSOs is multi-modal, with a narrow peak at fesc ≲ 0.2 and a broad distribution from 0.3 to 1.0, as discussed in the previous section. In order to investigate the origin of this multi-modality, we checked for any dependencies of fesc on the other physical parameters. No dependence was found by comparing against spectral slope αν, redshift, absolute magnitude M1450, and Lyman decrements (DA and DB). The only exception is against the IFPs, as shown in Fig. 7. It is interesting to note the trend of the escape fraction with the IFP at ≤20 pMpc. In particular, a deficiency of high escape fractions at low IFP and a lack of low fesc at high free paths is evident. Moreover, an increase in escape fraction proportional to the IFP seems to be present up to IFP of ∼10 − 20 pMpc.
 |
Fig. 7. Escape fraction vs. IFP for QSOs at z > 3.80. The gray points show the escape fractions calculated with the ionizing window 892−905 Å rest frame, and the orange points represent the escape fractions with the reduced ionizing window 898−905 Å rest frame. The black filled square represents the mean fesc in IFP bins of 30 pMpc (the open square is the mean of fesc in IFP bins containing fewer than ten sources). The vertical bars are the error on the mean in each IFP bin. QSOs with z < 3.8 have been excluded here to avoid possible biases due to their underestimated IFP, as discussed in Sect. 6.1.1. |
The lack of sources at low free paths and high escape fractions might be interpreted as an effect caused by the choice of the spectral window in the ionizing region, between 892 and 905 Å rest frame, that we adopted to derive fesc. Figure 8 shows the IFP estimate for QSO SDSS J034402.9−065300.6 at zQSO = 3.92455. This source has IFP = 6.7 ± 0.3 pMpc and fesc = 0.0, thus consistent with the above consideration. In this case, the wavelength associated with the IFP is inside the ionizing window of the escape fraction (highlighted in orange in the figure), creating a correlation between the two parameters. At the same time, a reduced spectral window, closer to the Lyman limit at 912 Å, could increase the average flux in this region, leading to an enhanced escape fraction for the specific QSO. As an example, the rest-frame 892−905 Å window was reduced to 898−905 Å and the escape fractions were recomputed using this modified window for the whole sample. This is displayed in Fig. 7. Here, the escape fractions adopted in this paper (gray points, calculated as explained in Sect. 3.3) and the modified fractions (orange points) are plotted for each source at z > 3.80 (see Sect. 6.1.1) as a function of their free paths. The orange points tend to populate the low IFP region at high escape fractions, which reduces the previously discussed deficit of these sources. This confirms that the lack of these QSOs is mostly due to the spectral window (892−905 Å rest frame) that we adopted to calculate the escape fraction and not to a physical mechanism. In principle, adopting an even shorter window close to 912 Å rest frame for the fesc derivation would further reduce the number of sources with low IFP and low fesc, but at the same time, the scatter would increase significantly. For these reasons, we decided to fix the spectral windows for the escape fraction measurements to the rest-frame 892−905 Å wavelength range. Interestingly, Cristiani et al. (2016) adopted a wavelength interval much larger than we adopted here (850−880 Å rest frame), and their peak at low fesc is slightly higher than ours. At fesc ≥ 0.20, Cristiani et al. (2016) have a fraction of 69.5% of their sample, while we have 78.8% of the QSOs above this threshold.
 |
Fig. 8. Free path estimate for the QSO SDSS J034402.9−065300.6 at zQSO = 3.92455, a QSO with a short IFP and a low value of the escape fraction, thus representing an example of correlation between IFP and fesc. The orange spectral region marks the ionizing window we used to calculate the escape fraction (i.e., 892−905 Å rest frame). |
In Fig. 5 we also plot the escape fraction distribution without the sources with short IFP. When we limit the sample to IFP ≥ 10 pMpc, the peak at fesc ∼ 0 disappears, and a continuous trend is in place, indicating that the sources with a low escape fraction are probably due to absorbers that by chance lie at small distance from the QSO, or are associated with it. In the following sections we discuss the nature of these absorbers.
Another interesting feature emerges from Fig. 7: when the very few objects with fesc ∼ 20% and large IFP are excluded, a trend of a larger escape fraction appears for longer IFP, as highlighted by the mean of fesc in IFP bins of 30 pMpc (black filled and open square) and by the lower envelope of the individual QSOs (gray points). In particular, at very large IFP (> 170 pMpc), only a few QSOs have fesc ≤ 40%. We verified that this correlation does not depend on the choice of the parameter Δαν = 0.72 we adopted. The observed trend remains when we changed this parameter to 0.5 or 1.0. This correlation, however, might be limited to only the few QSOs with an IFP greater than 170 pMpc, while for the bulk of the QSOs with 30 < IFP < 150 pMpc, the escape fraction shows no strong dependency on the IFP; it remains almost constant at ∼60 − 70%. Finally, we also computed a KS test to determine whether the sample of QSOs with IFP > 150 pMpc and the sample with 30 < IFP < 150 pMpc were drawn by the same parent population. We find a pvalue of 0.064, thus we can conclude that the differences between the two samples are not significant. At present, however, we cannot exclude that this trend is due to some systematic effects of the data (e.g., due to the color selection of z ∼ 4 QSOs). More checks are needed in the future to substantiate this statement.
In the following sections, we consider two extreme options to interpret the nature of the QSOs with IFP ≤ 10 pMpc when we study the IGM properties: (1) all the sources with IFP ≤ 10 pMpc are affected by intervening absorbers (option 1). (2) All these QSOs are instead related to associated (intrinsic) absorption (option 2), which is due to the presence of dense neutral absorbers in their vicinity. In the first, the IFP is the physical distance between the emitter and the absorbing system, while in the second the IFP reflects the outflow velocity of material that sits close to the QSO. In option 1, the QSOs with IFP ≤ 10 pMpc were included in the statistical analysis of the PDF for the free paths. In option 2, they were instead excluded from representing the mean properties of the IGM because the central engines are affected by their surrounding circum galactic medium or host galaxy. Absorbers might also be associated with an optical depth τ ≤ 1, which would mildly suppress the flux blueward of the Lyman limit, thus mimicking intervening absorbers with IFP ≥ 10 pMpc. We assume here that all the systems with IFP ≥ 10 pMpc are intervening absorbers. This assumption reduces the observed IFP with respect to the intrinsic IFP. In Sect. 6.2 we discuss the nature of the close absorbers with IFP ≤ 10 pMpc in detail.
5.2. Redshift evolution of the MFP
Because our data cover a relatively wide redshift range, we investigate here the evolution of the MFP of ionizing photons with cosmic age. An evolution in redshift of the MFP is certainly expected because of the properties of the IGM and its evolution with cosmic expansion, and a precise estimate of it is fundamental because it is one of the primary sources of uncertainty in the calculation of the photoionization rate ΓHI, as we discuss in the next subsection.
In the past, the MFP of ionizing photons has mainly been estimated by the number statistics of LLSs with redshift (e.g., Songaila & Cowie 2010; Prochaska et al. 2013; Inoue & Iwata 2008; Inoue et al. 2014) or by stacking a large number of QSO spectra at the same redshifts (e.g., Prochaska et al. 2009; Worseck et al. 2014). Given the high quality of the SDSS spectra analyzed here to determine the escape fraction, we decided to measure the free path for each individual QSO at 3.6 ≤ z ≤ 4.6 in order to derive the mean value and scatter of this parameter, leading to a statistical analysis of the free path distribution. Moreover, the PDF of the IFP gives better complementary information than a single average value (MFP).
We first computed the IFPs for SDSS QSOs at 3.6 ≤ z ≤ 4.2 and I ≤ 19.5 and found that the mean values of the IFP distribution are higher than the MFP obtained by Prochaska et al. (2009) and Worseck et al. (2014) through the stacking technique. We then extended the magnitude limit of our QSO sample to I = 20.0 and derived mean values of the IFP that were consistent with the results of Prochaska et al. (2009) and Worseck et al. (2014). We then determined the dependence of the IFP on the absolute magnitude M1450 of the SDSS QSOs because we have indications of a possible trend of the IFP with QSO luminosity.
Figure 9 shows the dependence of the IFP on the absolute magnitude M1450 of SDSS QSOs at 3.8 < z < 4.0 and I ≤ 20.0. The small black dots represent the measurements for individual QSOs, while the big blue circles indicate the mean values of the free paths and absolute magnitudes when the sample is divided into bins of ∼1.0 in M1450. A trend of larger IFP for brighter sources is possibly suggested by this plot, with IFP ∼ 60 pMpc at M1450 ∼ −28 and IFP ∼ 45 pMpc at M1450 ∼ −26. This trend is probably due to sources with low IFP, which are more frequent at fainter magnitudes (in the lower right corner of Fig. 9), rather than the lack of faint QSOs with long free paths.
 |
Fig. 9. Free path vs. absolute magnitude M1450 for individual SDSS QSOs at 3.8 < z < 4.0 and I ≤ 20.0 (small black dots). The large blue points show the average value of the free paths in bins of ΔM1450 = 1.0. The error bars of the large blue points show the 84th and 16th percentiles of the IFP distributions for each bin of absolute magnitude. |
A similar trend was found at higher redshifts, at least up to z = 4.6, the maximum redshift for our sample. Figure 10 shows the mean values of the free paths for all the SDSS QSOs with 3.6 ≤ z ≤ 4.6 and I ≤ 20.0, divided into redshift and absolute magnitude M1450 bins. The continuous lines are the best fit with a linear relation to the mean values. The trend with luminosity becomes milder at higher redshifts, and at z ∼ 4.5, it is almost negligible.
 |
Fig. 10. Average values of the free paths for all SDSS QSOs at 3.6 ≤ z ≤ 4.6 and I ≤ 20.0, divided into redshift and absolute magnitude M1450 bins. The vertical bars are the standard error of the mean in each bin of absolute magnitude. The lines show the best linear fit to the observed mean points for each redshift bin. |
While a redshift evolution of the MFP is expected both by theoretical and observational arguments, as discussed above, however, an evolution in magnitude of the MFP is not so obvious. In principle, we should expect that the physical properties of the IGM (e.g., the MFP) are independent from the properties of the tools adopted to study it, that is, the high-z QSOs analyzed in this paper. We carried out a simple simulation in order to determine whether the dependence of the IFP on the QSO luminosity might instead be due to an instrumental effect, for example, to the decreasing signal-to-noise ratio (S/N) of the spectra. We started from the observed spectra of five SDSS QSOs at I ≤ 17.5, that is, with a high S/N. We selected them in order to span the observed range of IFPs from 20 to 200 pMpc as well as possible. These spectra have a relatively high S/N, and we can measure their IFP with very high accuracy. We used these spectra as input to our simulations: for each simulated I-band magnitude in the range I = 18 − 20, we rescaled the input spectra by the factor 100.4(Iobs − Isim), where Iobs and Isim are the observed and simulated I-band magnitudes, respectively. Then we added random noise considering the original (i.e., without any rescaling) rms of the observed spectra released by SDSS and derived the IFP of the simulated QSOs with the same tools as for our measurements, as described above. We repeated this operation for 100 times for each simulated magnitude. In Fig. 11 we plot the mean values of the output IFP for each of the five QSOs and for each simulated magnitude in the range Isim = 18 − 20, corresponding to the magnitude range of our sample. The error bars indicate the 16th and 84th percentiles of the IFP distribution. We find no dependence of the resulting IFP on the luminosity of the objects. This reassures us that the observed trend with luminosity shown in Fig. 9 is not spurious and cannot come from the low S/N of the data at M1450 ∼ −26. Only at very large IFP (∼200 pMpc) and at I ∼ 20 is the free path slightly underestimated, by ∼0.1 dex. This effect is too small to explain the strong trend found in Fig. 9, however. Moreover, it is not expected that the SDSS algorithms preferentially select sources with lower free paths with respect to bright QSOs at faint observed magnitudes. It is not so obvious to find a plausible explanation for the observed trend with luminosity.
 |
Fig. 11. Free path of simulated QSOs at different I-band magnitudes. Circles show the mean value of 100 simulations for each QSO and magnitude bin, and the error bars indicate the 16th and 84th percentiles of the resulting IFP distribution. No strong trend of the IFP with the observed I-band magnitude has been detected. |
Figure 12 summarizes the mean values of the IFP for three different absolute magnitude bins of SDSS QSOs from z = 3.6 to z = 4.6 and magnitude I ≤ 20.0. The mean IFP values were fit with a power-law relation MFP(z) = MFP(z = 4) × [(1 + z)/5]η, and the continuous lines show the best fit at different luminosities. The redshift evolution η we find is milder than that reported by Worseck et al. (2014). When we exclude the redshift interval between z = 3.6 and 3.8 (we show in the next sections that this bin might be prone to a systematic effect) from the plot, the resulting η is consistent with that reported by Worseck et al. (2014), as shown in the bottom part of Table 1. It should also be noted that the redshift range studied by Worseck et al. (2014) is 2.3 < z < 5.5, while our redshift interval is smaller (3.6 < z < 4.6) and thus might be more easily prone to uncertainties in the derivation of η.
 |
Fig. 12. Mean values of the IFP for SDSS QSOs at 3.6 ≤ z ≤ 4.6 and I ≤ 20.0 (option 1), divided into redshift for three bins of absolute magnitude M1450. The vertical bars are the standard error of the mean in each bin of absolute magnitude. The continuous lines show the best power-law fit to the observed mean points for each M1450 bin. |
Redshift evolution of the MFP for all QSOs at 3.6 ≤ z ≤ 4.6 and I ≤ 20.0 (option 1).
Interestingly, Table 1 shows that for our fainter absolute magnitude bin −26.5 ≤ M1450 ≤ −25.5, the best fit to our mean values has a normalization MFP(z = 4) = 39.4 pMpc, which is quite close to the best-fit value of 37 pMpc provided by Worseck et al. (2014). This is awaited because their results are expected to be dominated by faint QSOs with M1450 ∼ −26, which is close to the completeness limit of SDSS survey at z ∼ 4. The MFPs measured both by Prochaska et al. (2009) and Worseck et al. (2014) are based indeed on a stack of 150 QSOs for each adopted redshift bin, with a bootstrap on the whole SDSS sample. Because these 150 QSOs were chosen randomly from the whole SDSS QSO survey in the adopted redshift bin, the sample might be dominated by fainter QSOs, and thus by lower IFPs, if the observed IFP-luminosity relation is correct. In order to deepen the observed correlation between the IFP and luminosity, we cut our sample to IFP > 30 pMpc, finding that the luminosity dependency on the IFP disappears. This reassures us that this trend is due to QSOs with low values of the IFP, mainly at low luminosities, which might be affected by associated absorbers (AAs). However, we cannot exclude that this effect is due to some biases caused by color selection effects, which depend on the observed magnitudes. A further investigation is needed in the future to completely explain the observed correlation.
In order to ensure that the examined QSO sample did not present too many different features from the samples of Prochaska et al. (2009) or Worseck et al. (2014), the stacking technique was also implemented to infer the evolution of the MFP in redshift. The MFP was computed from the rest-frame stacked spectra in different redshift bins of Δz = 0.2 from z = 3.6 to z = 4.6, modeling the observed flux in the region blueward of the Lyman limit as f = f912 exp(−τeff, LL), taking into account the spectral slope αν and the softening of the QSO spectrum at λrest ≲ 1000 reported by Cristiani et al. (2016). In particular, the stacked spectra were averaged without weighting to avoid introducing biases caused by sources without strong LLS absorption, which have a higher S/N (Prochaska et al. 2009). The MFP from the stacked spectra were obtained by calculating the λLLS at which τeff, LL = 1, as described in Sect. 3.4, and converting this wavelength into a redshift zLLS by assuming a rest frame λrest = 912 Å.
As discussed in Sect. 3.4 (and in Sect. 6.1.1), the MFP estimate for QSOs at 3.6 < z < 3.8 might be biased low due to the limited coverage of the observed SDSS spectra (λobs ≥ 3560 Å). We therefore excluded the redshift bin 3.6 < z < 3.8 from the fit in Fig. 10 and obtained a steeper evolution of the MFP with redshift (Table 1, bottom part). As shown by our results, the redshift evolution is still milder than that reported by Worseck et al. (2014).
When we exclude all the QSOs with IFP ≤ 10 pMpc from our sample, assuming that they are affected by associated absorptions (option 2), the trends highlighted above further move toward a milder evolution of MFP with redshift. Figure 13 shows the updated mean values of IFP, divided into different bins of absolute magnitude, versus redshift. It is immediately evident that the mean values of the IFP are significantly higher than the best fit reported by Worseck et al. (2014) (MFP ∼ 50 pMpc at z = 4 vs. MFP = 37 ± 2 pMpc by Worseck et al. 2014) and the redshift evolution is far milder. Table 2 summarizes the best-fit values of our MFP with a power-law relation. At all luminosities the slope is η ∼ −2.6 ÷ −4.3, which is significantly milder than the slope described by Worseck et al. (2014) (η = −5.4 ± 0.4).
 |
Fig. 13. The mean values of the IFP for SDSS QSOs at 3.6 ≤ z ≤ 4.6, I ≤ 20.0, and IFP > 10 pMpc (“option 2”), divided in redshift for three bins of absolute magnitude M1450. The vertical bars are the standard error of the mean in each bin of absolute magnitude. The continuous lines show the best power-law fit to the observed mean points for each M1450 bin. |
Redshift evolution of the MFP for QSOs at 3.6 ≤ z ≤ 4.6 with IFP > 10 pMpc (option 2).
We also determined the effect of eliminating broad absorption line (BAL) QSOs from our sample. First of all, it is worth noting that the analysis carried out by Worseck et al. (2014) might include sources with possible AAs, but excludes all the BAL QSOs. We found that neither the normalization nor the slope of the MFP(z) relation are affected by BAL QSOs, and the best-fit values of the sample without BAL QSOs (and without AAs) are very similar to those in Table 2. This effect is expected because neither the LyC escape fraction nor the IFP distributions depend on the BAL QSOs fraction. This indicates implicitly that the BAL phenomenon and the AAs are not related.
Figure 14 summarizes the main results of this section. When we consider all the QSOs at 3.6 ≤ z ≤ 4.6 and I ≤ 20.0 (option 1), the mean value of the PDF(IFP) and the stack give similar results (as we discuss in Appendix B), while when we exclude QSOs with IFP ≤ 10 pMpc, assuming they are affected by AAs (option 2), we obtain a huge difference between mean and stack and a milder redshift evolution than Worseck et al. (2014). Table 3 summarizes the MFP obtained through stack and mean values of the PDF(IFP), compared with the results of Worseck et al. (2014).
 |
Fig. 14. Redshift dependence of the MFP for SDSS QSOs at 3.6 ≤ z ≤ 4.6 and I ≤ 20.0. The filled black points (connected by a continuous black line) summarize the mean value of the free paths excluding objects with IFP ≤ 10 pMpc, which might be affected by AAs (option 2). The open black circles (connected by a dashed black line) show the MFP for all the QSOs of our sample (option 1). The filled red points (connected by a continuous red line) are instead derived from the stack of QSOs with IFP > 10 pMpc, and the open red circles (connected by a dashed red line) show the MFP obtained by the stack of all the QSOs. The dotted blue curve is the evolution of the MFP with redshift found by Worseck et al. (2014), while the blue open triangles indicate their mean values in different redshift bins. |
Summary of the MFP vs. redshift.
The differences between our best fit and the results of Worseck et al. (2014) could be due to two main reasons: (1) we excluded from our sample the QSOs that are suspected to be affected by AAs, with IFP ≤ 10 pMpc (option 2). (2) We used the mean values of the PDF(IFP) instead of the stack, as done by Prochaska et al. (2009) and Worseck et al. (2014). As discussed in Appendix B, an underestimated MFP from stacking compared to the mean value of the PDF is expected, in particular for skewed distributions, as we find at z ≳ 4. Following these arguments, the PDF of the IFP of UV-ionizing photons can give more information on the IGM than the stacking technique. For this reason, we use the PDF(IFP) below in order to compute the contribution of QSOs/AGNs to the HI-ionizing background.
Figure 13 also shows that the difference between the bright and faint QSO samples is reduced at z > 4.2 and seems almost negligible at z ∼ 4.5. Moreover, the mean value of the IFP distributions progressively diverges from the estimates of Worseck et al. (2014) from z = 3.6 to z = 4.6 for option 2. This might have deep implications for the MFP estimate at the EoR. For example, following the relation between MFP and redshift found by Worseck et al. (2014), a MFP of ∼6 pMpc is expected at z = 6, while an MFP three times larger (MFP ∼ 18 pMpc) is expected from extrapolating our relation in Table 3 and Fig. 14. When the outlined trend shown in Fig. 13 for option 2 is also kept at higher redshifts, this might have important implications for the computation of the photoionization rate at the EoR, as we discuss in the next subsection.
5.3. Corrected ionizing background at z = 4 and implications on reionization
The contribution of bright QSOs, faint AGNs and/or star-forming galaxies to the HI-ionizing background can be quantified by computing the photoionization rate of neutral hydrogen atoms, ΓHI. This parameter primarily depends on the overall emissivity of the sources and on their MFP, that is, ΓHI ∝ MFP ⋅ fesc ⋅ ϵ912, where fesc is the escape fraction of LyC photons and ϵ912 is the overall intrinsic contribution of the ionizing sources emitted at 912 Å rest frame. The latter depends on the luminosity function of high-z AGNs or star-forming galaxies and on the spectral slope of the sources close to 912 Å rest frame. Because it is not the aim of this paper to revise the estimate of the emissivity of the different populations of galaxies and AGNs, we only compute here the scaling factor due to our revised estimates of the MFP and fesc at z ∼ 4, 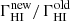 .
.
If the main sources of HI-ionizing photons are star-forming galaxies at high redshift, the scaling factor for ΓHI is simply the ratio MFPmean/MFPW14 from Table 4. It varies from 0.98 to 1.27 when all the QSOs are used for an estimate of the MFP (option 1). The correction is significantly higher when the MFP is derived only from QSOs with IFP > 10 pMpc (option 2). In the latter case, the ratio MFPmean/MFPW14 increases from ∼1.1 at z = 3.7 to 1.6 at z = 4.5.
Total corrections to the HI photoionizing background.
In the opposite case, when QSOs and AGNs are the main producers of the ionizing background at z ≳ 4, the ratio 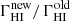 does not simply scale as MFPmean/MFPW14. We need to take two additional correction factors into account: (1) the possible correlation between IFP and escape fraction (see Fig. 7), and (2) the fraction of QSOs with IFP greater than 10 pMpc for option 2. The first factor (CORR1 in Table 4) was computed as ⟨IFP * fesc⟩/(⟨IFP⟩*⟨fesc⟩) and is always greater than 1, given the observed correlation between these two parameters. The fraction CORR2 of QSOs with IFP > 10 pMpc is instead about 0.7−0.8 for option 2, while CORR2 is always 1.0 for option 1, by definition.
does not simply scale as MFPmean/MFPW14. We need to take two additional correction factors into account: (1) the possible correlation between IFP and escape fraction (see Fig. 7), and (2) the fraction of QSOs with IFP greater than 10 pMpc for option 2. The first factor (CORR1 in Table 4) was computed as ⟨IFP * fesc⟩/(⟨IFP⟩*⟨fesc⟩) and is always greater than 1, given the observed correlation between these two parameters. The fraction CORR2 of QSOs with IFP > 10 pMpc is instead about 0.7−0.8 for option 2, while CORR2 is always 1.0 for option 1, by definition.
When we consider all the QSOs (option 1), then the new estimate of MFPmean is not significantly larger than previous estimates, but this is balanced by a strong correction for the correlation between IFP and escape fraction (CORR1 ∼ 1.2 − 1.3). In this case the global correction is ∼1.2 − 1.7 (upper part of Table 4). When we instead exclude QSOs with IFP ≤ 10 pMpc from our calculations (option 2), the higher value of MFP is compensated by the fact that only 70−80% of the lines of sight contribute to the photoionization rate. In this case (bottom part of Table 4), the total correction to ΓHI is 1.2 in the redshift interval z = 3.6 − 3.8, which increases to 1.4−1.7 at higher redshift. In addition, this ratio increases from z = 3.7 to z = 4.5. Interestingly, the global correction to the ionizing background 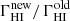 does not depend on whether QSOs with IFP ≤ 10 pMpc are included (option 1) or excluded (option 2) in our calculations, but it is practically consistent between the two cases.
does not depend on whether QSOs with IFP ≤ 10 pMpc are included (option 1) or excluded (option 2) in our calculations, but it is practically consistent between the two cases.
It is worth noting that the values of MFPmean/MFPW14 inferred in this work are only lower limits. The averaged values of the MFP computed from the IFP distribution functions may even be greater if all the possible caveats in the estimate of this parameter are taken into account (i.e., observational limitations and selection effects of some QSOs, see Sect. 6.1).
In summary, our results indicate a milder evolution of the MFP with redshift, giving a revised estimates of the photoionization rate by a factor of 1.4−1.7 upward at z ∼ 4.0 − 4.5. When the trend obtained with these QSOs is extrapolated at z ∼ 6, then the new estimates of the MFP, and consequently of the ionizing background, might be higher by 2−3 times than the recent estimates for star-forming galaxies and QSOs/AGNs (e.g., Finkelstein et al. 2019; Giallongo et al. 2019). In the future it will be important to check whether this trend is still present at z > 5.
6. Discussions
6.1. Possible systematic effects
This work is based on a sample of z ∼ 4 QSOs selected by the SDSS because of their optical photometry (Paris et al. 2018). The specific selection criteria adopted by the SDSS may affect our results, especially for the escape fraction and MFP estimates. We take the effect of the limited extension of SDSS spectra in the UV and the color selections of z ∼ 4 QSOs into account here. Both these issues could prevent a correct and robust estimate of the total contribution of AGNs to the HI-ionizing background at z ∼ 4. We do not attempt here to correct for these two effects, but it is easy to conclude from what we show in the following that the net effect of these two issues leads to an underestimated escape fraction and MFP. Dedicated observations and well-defined surveys are needed at the end to properly correct for these problems.
6.1.1. Limited coverage of SDSS spectra in the UV
The SDSS spectra released in the DR14 distribution are limited to the wavelength range 3600 ≲ λobs ≲ 10 000 Å. The cut at lower wavelengths in the UV can affect our estimate of the free path of QSOs at z ∼ 4, as shown in Fig. B.1. In this case, this QSO (SDSS J113654.6+485322.3 at zQSO = 3.61964) has a long path along the line of sight that is free from damped Lyman-α or LLSs. Its ionizing radiation is thus able to travel tens of proper megaparsec without being attenuated by a factor 1/e (defining the IFP) and can reach the observed lower limit of the SDSS spectrum at λobs ∼ 3550 Å. It is not known, with the present data, whether the ionizing radiation of this QSO is able to reach bluer wavelengths, and for this reason, an IFP of 145.94 pMpc is assigned. This is a lower limit, simply imposed by an instrumental limitation; the real value of the IFP for this object might be higher than the value assigned here. In our sample, the provided IFP is a lower limit due to this effect for 12.8% of the QSOs. In the redshift bin 3.6 < z < 3.8 this fraction is 15.4%, and it progressively decreases to 10% in the highest redshift bins we considered. In the future spectroscopic follow-up of these objects is required to definitively measure their IFP and to ensure that the SDSS spectra are not affected by any systematics.
This issue causes the artificial lack of QSOs with long IFP at lower redshifts, especially close to z ∼ 3.6, as shown in Fig. 15. Many sources with high free paths could present a spectrum that extends far beyond the lower instrumental limit of the observed wavelengths; this results in an altered estimate of the IFP distribution. Because we find at z ∼ 4 QSOs with IFP ∼ 200 pMpc or larger, we do expect that these sources are also present at lower redshifts. Their absence, however, is due only to instrumental limitation, as shown by Fig. 15. The blue line in this plot represents the maximum values of the IFP that can be obtained considering a minimum observable wavelength of about 3550 Å at different redshifts. These limits exactly follow the distributions of the sources with the highest IFP, confirming that this trend is not a physical effect, but an instrumental feature, as explained before. To correct for this systematic effect the sources close to the instrumental limit shown in Fig. 15, deep spectra with spectrographs sensitive to UV bluer wavelengths are required, that is, with the Multi-Object Double Spectrograph (MODS1) at the Large Binocular Telescope (LBT) or with the FOcal Reducer low dispersion Spectrograph (FORS1) at the Very Large Telescope (VLT), as shown by Grazian et al. (2018).
 |
Fig. 15. Individual free path (black points) vs. spectroscopic redshift for SDSS QSOs at 3.6 ≤ z ≤ 4.6. The blue line represents the maximum value of the IFP that can be obtained at each redshift because of the observational limits of the SDSS spectra, i.e., λobs ≳ 3550 Å. |
In conclusion, this particular problem can artificially reduce the average value and the scatter of the free path that is obtained through the PDF of the QSO sample, especially at z ≤ 3.9. This effect is particularly noticeable in Figs. 12 and 13. For example, when we compute the MFP in the redshift interval 4.0 ≤ z ≤ 4.1, we obtain MFP = 40.73 pMpc, while when we exclude sources with IFP ≥ 150 pMpc (thus simulating the bias observed at z ∼ 3.6), the average value is artificially lower, MFP = 34.61 pMpc. Thus, the MFP adopted in the present paper at z ≤ 3.9 could be higher, of ∼18%.
This underestimated MFP at z ≤ 3.7 can also artificially flatten the redshift evolution of this parameter shown in Fig. 14. We excluded the first redshift bin and computed the best fit for the sample of QSOs with IFP > 10 pMpc (option 2), and find η ∼ −4.3 ÷ −3.2, with slightly larger uncertainties (ση ∼ 0.8). In the future, deep spectra that extend into the UV at λobs ∼ 3300 Å for these QSOs would provide a more robust estimate of the redshift evolution of the MFP.
6.1.2. Color selection effects
The selection criteria adopted by the SDSS team to select the QSOs we analyzed in this paper are based on optical colors (Paris et al. 2018). In particular, the selection of QSOs at 3.6 ≤ z ≤ 4.2 is mainly based on the color criterion u − g > 1.5 (Richards et al. 2002), which is especially useful because it involves the Gunn filters u and g, which are centered at the average wavelengths 3551 and 4686 Å, respectively. The u − g color takes advantage of the expected flux decrement of the source in the region blueward of the Lyman limit. Problems arise when the observed QSO presents a large IFP. This effect causes a bluer u − g color, which might be lower than the SDSS threshold used to select QSOs at z > 3.6. Figure 16 shows the effect discussed here. In this plot, our QSO sample is split into two parts using a threshold in IFP of 150 pMpc for sources with higher and lower redshift than the median redshift of the sample (z ∼ 3.90). The u − g distribution with larger (smaller) free paths with respect to the threshold is represented by the green (orange hatched) histogram, and its mean value is marked by the dot-dashed (solid) black line. At higher values of the IFP, the mean value of the distribution moves to bluer u − g colors (green histograms), approaching the 1.5 threshold adopted by the SDSS to select the observed QSOs. In particular, this effect is more pronounced at lower redshift (bottom panel), where a possible lack of sources with high IFP would change the evolution of this parameter with redshift. For these reasons, QSOs with large IFP could be lost in the standard selection procedure adopted by the SDSS, which might artificially decrease the average value and scatter of the free path distribution and thus the overall contribution of these sources to the UV-ionizing photon production. This effect is particularly severe at z ≲ 3.5, as has been pointed out by Prochaska et al. (2009) and Cristiani et al. (2016).
 |
Fig. 16. Distribution functions of the u − g color for QSOs with high (green histogram, IFP ≥ 150 pMpc) and low (orange hatched histogram, IFP < 150 pMpc) IFPs. The solid and dot-dashed black lines refer to the average values of the orange and green distributions, respectively. Top (bottom) panel: u − g distributions for QSOs at higher (lower) redshift with respect to the median one at z ∼ 3.90. |
It is useful to note here that the few QSOs at 3.6 ≤ z ≤ 4.6, with u − g ≤ 1.5 shown in Fig. 16 (123 out of 2508 sources in the all redshift range) were observed by the SDSS with other selection criteria that are complementary to the optical color selection of the SDSS, as described by Dawson et al. (2013) and Paris et al. (2018). It is therefore not possible to estimate the systematic effects due to this color selection criterion with a simple analytic calculation. Just as an example, of the 16 faint AGNs found at 3.6 ≤ z ≤ 4.2 in the COSMOS field by Boutsia et al. (2018), only 5 (approximately 30%) would be selected when the color selection of the SDSS were adopted, with an incompleteness of ∼70%. Interestingly, the missed AGNs are selected mainly by X-ray emission (Civano et al. 2016; Marchesi et al. 2016) and show high values of LyC escape fraction (Grazian et al. 2018) and IFP. A dedicated survey, unbiased toward high IFP sources, is required in the future to resolve this shortcoming, which might be particularly severe for a proper estimate of the average value of the free path (and its scatter) and for a correct quantification of the number density of QSOs at high redshifts. This survey, however, will have the severe problem of strong contamination by nearby galaxies and stars, which affect the samples that are selected by adopting bluer u − g colors.
6.2. Population of z ∼ 4 QSOs with low escape fractions and short free paths
In the previous sections we chose a threshold above 10 pMpc for the IFP in order to study the properties of the IGM. We suspect indeed that the QSOs with a free path lower than this limit might be affected by associated (intrinsic) absorbers. In this context, it is worth noting here that we do not claim that the AAs act on scales of 10 pMpc. Our hypothesis is that AAs that reside a few kiloparsec away from the QSO can have high peculiar velocities (outflows up to ∼104 km s−1) and can therefore mimic a cosmological distance ≲10 pMpc from the QSO itself.
With the aim of verifying this guess, we cross-correlated our sample with the XQ-100 sample (Lopez et al. 2016), which is a legacy survey of 100 quasars at 3.5 < z < 4.5 observed with VLT/X-shooter for a deep exposure time. We find 44 objects in common, and we then refer to Perrotta et al. (2016) for the properties of their absorbers. The authors find a statistically significant (up to 8σ) excess of associated NV absorbers at a velocity of |v| ≤ 104 km s−1, corresponding to ∼20 pMpc. This is slightly different from our adopted threshold of 10 pMpc, but it can be comparable to it, considering the redshift uncertainties of ∼0.005 for the SDSS sample and the intrinsic uncertainties on the IFP determination of 2−3 pMpc that are due to our procedure.
Out of the 44 QSOs in common in our sample and the XQ-100 sample, we examined in detail the absorbers of the 6 QSOs with free path less than 10 pMpc. We find that for all six, the CIV absorbers studied by Perrotta et al. (2016) lie within 1−2 pMpc from our estimates, which indicates that these absorbers are the responsible for the short free path measured by our methods, and for the low value of the escape fraction, as we discussed above. More precisely, 2 out of 6 QSOs have an NV system, which according to Perrotta et al. (2016) is a robust signature of AAs. Our recovered NV fraction (33%) is similar to the fractions found by Perrotta et al. (2016, 2018), that is, 33% and 38%, respectively. The other four systems have no individual detection of NV in Perrotta et al. (2016); however, a more recent work by Perrotta et al. (2018) indicates that CIV absorptions with N(CIV) ≥ 1014 cm−2 within 5000 km s−1 of the emission redshift of the QSO (mimicking a distance of ∼10 pMpc) are detected in NV at 15σ through stacking, supporting our guess that all these systems are probably bona fide associated because of their high column densities and high excitations. High ionization absorption lines indeed require close proximity to the QSOs based on detailed photoionization constraints (Chen et al. 2018).
7. Summary and conclusions
The aim of this paper was to measure the LyC escape fraction and the free path of HI-ionizing photons for a complete sample of the z ∼ 4 QSO population, as a follow-up study of the work by Cristiani et al. (2016). The fesc and MFP are fundamental parameters involved in the characterization of the IGM and in particular, in the estimate of the HI photo-ionization rate ΓHI at high redshifts. With this aim, we selected 2508 QSOs at 3.6 ≤ z ≤ 4.6 and in the magnitude range 17.0 ≤ I ≤ 20.0 (−29.0 ≲ M1450 ≲ −26.0).
In order to quantify the number of UV photons able to ionize the surrounding IGM, the LyC escape fraction of each QSO was computed as the ratio between the average flux blueward (892 ≤ λrest ≤ 905 Å) and redward (915 ≤ λrest ≤ 960 Å) of the Lyman limit. The PDF(fesc) resulted in a multi-modal distribution with a mean value fesc = 0.49 ± 0.36. In particular, the narrow peak at fesc ≤ 0.2 could depend on the wavelength coverage used to compute the average flux in the ionizing region, blueward of the Lyman limit. A shorter spectral window, closer to the 912 Å rest frame, results in a larger number of sources with high escape fraction, reducing the height of the peak at low fesc (Fig. 6). This in turn increases the average value of the PDF(fesc), and makes the result obtained in this paper just a lower limit to the real value of the fesc. The mean fesc we find (∼0.5) is consistent with the average flux decrement between 930 and 900 Å rest frame due to intervening IGM absorption derived by Inoue et al. (2014) at z = 4 (∼0.6, see their Fig. 4), suggesting that the escape fraction might even reach 100% in bright QSOs when we correct for this effect. This last consideration is then strengthened by the connection between fesc and the IFP of HI-ionizing photons that we find in this paper. Sources with IFP ≤ 10 pMpc also show a low LyC escape fraction (Fig. 7). As reported in Sect. 5, this is again an effect of the spectral window chosen to compute fesc. Furthermore, QSOs with IFP ≤10 pMpc (possibly affected by AAs) are probably not ideal tracers of the properties of the IGM. Finally, a redshift and magnitude evolution of fesc was excluded. Therefore, the ionizing properties of faint AGNs and bright QSOs seem to be the same at z ∼ 4, in agreement with Grazian et al. (2018).
The estimate of the MFP of HI-ionizing photons from its distribution function is a method that might represent an improvement with respect to the analysis performed so far in the literature. The classical approach to calculating the MFP relies on assumptions on the frequency distribution of IGM absorbers or on the direct estimate of this parameter from the stacked spectra of QSOs in different redshift bins. On the one hand, the first approach is uncertain because of several problems in deriving the exact HI frequency distribution. On the other hand, the stacking technique seems to depend on the fraction of QSOs with low IFPs. For this reason, the statistical analysis of the IFP distribution has been considered a more informative method to study the ionization status of the IGM.
Summarizing, we have found that (1) the IFP distribution function carries more information than the MFP from stacking. (2) The MFPs at z ∼ 4 are larger than the MFP found by Worseck et al. (2014) by a factor of 1.1−1.7, probably because these authors sampled fainter luminosities at higher redshifts and did not clean their sample from possible associated (intrinsic) absorbers. (3) The redshift evolution of the MFP we derive is milder than the evolution obtained by Worseck et al. (2014). (4) If the trends found at z ∼ 4 and M1450 ∼ −27 are also confirmed at higher redshifts and at fainter luminosities, this could have strong implications for the role of bright QSOs and faint AGNs in the hydrogen reionization process.
As for the LyC escape fraction, we determined the dependence of the free path on luminosity and redshift. For the first case, we divided the sample into redshift bins of Δz = 0.2, each of which was in turn split into magnitude bins ΔM1450 = 1.0. The IFP of bright QSOs is found to be larger than the IFP of faint QSOs, at least up to z = 4. This trend becomes milder at higher redshifts and seems to be unaffected by systematic effects.
As previously said about the free path, we used the same redshift and absolute magnitude bins to test its redshift evolution by computing the MFPs from the PDF in each bin. We then compared our results with those of Worseck et al. (2014), with respect to which we found a milder trend of MFP versus redshift. This is mainly due to the technique involved to calculate the MFP by Worseck et al. (2014), that is, the stacking method, which might underestimate the real value of the MFP at different redshifts (see Appendix B). When we exlcude QSOs with IFP ≤ 10 pMpc, assuming that these sources are affected by AAs, the difference between the MFPs from the PDFs and those obtained by the stack even increases (MFP = 49−59 pMpc at z = 4, from our work, compared to MFP = 37 ± 2 pMpc by Worseck et al. 2014), with milder evolution with redshift (η ∼ −2.6 ÷ −4.3 versus the best fit of Worseck et al. 2014, i.e., η = −5.4). Extrapolating these results at higher redshifts could have important implications for the reionization process.
In this regard, we computed the scaling factor 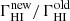 in order to correct previous estimates of the photoionization rate according to our new measurements of MFPs from the PDFs. To do this, we considered two extreme cases: (1) all the QSOs with IFP ≤ 10 pMpc were affected by intervening absorbers (option 1), and (2) that these latter sources were all associated (intrinsic) systems that should be rejected for correct estimates of the MFP (option 2). For an ionizing background mainly produced by QSOs and AGNs, the correction factor in both cases extends from 1.2 at z = 3.7 to 1.7 at z = 4.5, respectively, with a possible monotonic trend with redshift. It is worth noting that recent results of Perrotta et al. (2016, 2018) indicate that at least 30% of the CIV absorbers at |v| ≤ 104 km s−1 (i.e., at ≤ 10 − 20 pMpc when we translate the velocity offset into a cosmological distance) from the QSOs might be affected by associated (intrinsic) systems.
in order to correct previous estimates of the photoionization rate according to our new measurements of MFPs from the PDFs. To do this, we considered two extreme cases: (1) all the QSOs with IFP ≤ 10 pMpc were affected by intervening absorbers (option 1), and (2) that these latter sources were all associated (intrinsic) systems that should be rejected for correct estimates of the MFP (option 2). For an ionizing background mainly produced by QSOs and AGNs, the correction factor in both cases extends from 1.2 at z = 3.7 to 1.7 at z = 4.5, respectively, with a possible monotonic trend with redshift. It is worth noting that recent results of Perrotta et al. (2016, 2018) indicate that at least 30% of the CIV absorbers at |v| ≤ 104 km s−1 (i.e., at ≤ 10 − 20 pMpc when we translate the velocity offset into a cosmological distance) from the QSOs might be affected by associated (intrinsic) systems.
Finally, it is worth noting that our estimate of the PDF of the free path at z ≥ 3.5 is of paramount importance because it gives a reference benchmark for the theoretical models that investigate the reionization epoch with the most recent cosmological hydrodynamical simulations with complex radiative transfer calculations. It will be interesting to follow whether these models are able to reproduce the mean value, the scatter, and the redshift evolution of the IFP distribution functions outlined in this paper. Detailed comparison with modern simulations, such as are carried out by Inoue et al. (2014), will be the subject of a future paper.
Although these are important clues for studying the evolution of the MFP with redshift, it is necessary to go deeper in magnitude by observing fainter AGNs at z ≥ 4 in order to increase the statistics on these sources and thus to better investigate their possible luminosity evolution. This will be done by a follow-up survey that extends the seminal work done by Grazian et al. (2018). In addition, extending the analyzed sample of QSOs in redshift at z ∼ 5 − 6 is of paramount importance to confirm the trends we have found at z ≤ 4.6.
Acknowledgments
We warmly thank the referees for their deep insight into the paper, for the careful reading of our manuscript, for the constructive comments and useful suggestions that contribute to improve the quality of our paper. Funding for the Sloan Digital Sky Survey IV has been provided by the Alfred P. Sloan Foundation, the US Department of Energy Office of Science, and the Participating Institutions. SDSS-IV acknowledges support and resources from the Center for High-Performance Computing at the University of Utah. The SDSS web site is www.sdss.org. SDSS-IV is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS Collaboration including the Brazilian Participation Group, the Carnegie Institution for Science, Carnegie Mellon University, the Chilean Participation Group, the French Participation Group, Harvard-Smithsonian Center for Astrophysics, Instituto de Astrofísica de Canarias, The Johns Hopkins University, Kavli Institute for the Physics and Mathematics of the Universe (IPMU)/University of Tokyo, the Korean Participation Group, Lawrence Berkeley National Laboratory, Leibniz Institut für Astrophysik Potsdam (AIP), Max-Planck-Institut für Astronomie (MPIA Heidelberg), Max-Planck-Institut für Astrophysik (MPA Garching), Max-Planck-Institut für Extraterrestrische Physik (MPE), National Astronomical Observatories of China, New Mexico State University, New York University, University of Notre Dame, Observatário Nacional/MCTI, The Ohio State University, Pennsylvania State University, Shanghai Astronomical Observatory, United Kingdom Participation Group, Universidad Nacional Autónoma de México, University of Arizona, University of Colorado Boulder, University of Oxford, University of Portsmouth, University of Utah, University of Virginia, University of Washington, University of Wisconsin, Vanderbilt University, and Yale University.
References
- Akiyama, M., He, W., Ikeda, H., et al. 2018, PASJ, 70S, 34 [Google Scholar]
- Becker, G. D., Bolton, J. S., Madau, P., et al. 2015, MNRAS, 447, 3402 [NASA ADS] [CrossRef] [Google Scholar]
- Bolton, A. S., Schlegel, D. J., Aubourg, E., et al. 2012, AJ, 144, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Boutsia, K., Grazian, A., Giallongo, E., et al. 2018, ApJ, 869, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Calverley, A. P., Becker, G. D., Haehnelt, M. G., & Bolton, J. S. 2011, MNRAS, 412, 2543 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, C., Hamann, F., Simon, L., et al. 2018, MNRAS, 481, 3865 [NASA ADS] [CrossRef] [Google Scholar]
- Civano, F., Marchesi, S., Comastri, A., et al. 2016, ApJ, 819, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Cowie, L. L., Barger, A. J., & Trouille, L. 2009, ApJ, 692, 1476 [NASA ADS] [CrossRef] [Google Scholar]
- Crighton, N. H. M., Prochaska, J. X., Murphy, M. T., et al. 2019, MNRAS, 482, 1456 [NASA ADS] [CrossRef] [Google Scholar]
- Cristiani, S., Serrano, L. M., Fontanot, F., Vanzella, E., & Monaco, P. 2016, MNRAS, 462, 2478 [NASA ADS] [CrossRef] [Google Scholar]
- D’Aloisio, A., McQuinn, M., Davies, F. B., & Furlanetto, S. R. 2018, MNRAS, 473, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, F. B., Hennawi, J. F., Eilers, A.-C., & Lukić, Z. 2018, ApJ, 855, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Dawson, K. S., Schlegel, D. J., Ahn, C. P., et al. 2013, AJ, 145, 10 [Google Scholar]
- Dayal, P., & Ferrara, A. 2018, Phys. Rep., 780, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, X., Strauss, M. A., Schneider, D. P., et al. 2001, AJ, 121, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, X., Strauss, M. A., Becker, R. H., et al. 2006, AJ, 132, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Faucher-Giguère, C. A. 2019, Arxiv e-prints [arXiv:1903.08657] [Google Scholar]
- Faucher-Giguère, C.-A., Lidz, A., Hernquist, L., & Zaldarriaga, M. 2008, ApJ, 688, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Finkelstein, S. L., D’Aloisio, A., Paardekooper, J.-P., et al. 2019, ApJ, 879, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Fontanot, F., Cristiani, S., & Vanzella, E. 2012, MNRAS, 425, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Fumagalli, M., Prochaska, J. X., Kasen, D., et al. 2011, MNRAS, 418, 1796 [NASA ADS] [CrossRef] [Google Scholar]
- Giallongo, E., Menci, N., Fiore, F., et al. 2012, ApJ, 755, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Giallongo, E., Grazian, A., Fiore, F., et al. 2015, A&A, 578A, 83 [Google Scholar]
- Giallongo, E., Grazian, A., Fiore, F., et al. 2019, ApJ, 884, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Grazian, A., Boutsia, K., Giallongo, E., et al. 2018, A&A, 613A, 44 [Google Scholar]
- Haardt, F., & Madau, P. 2012, ApJ, 746, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Inoue, A. K., & Iwata, I. 2008, MNRAS, 387, 1681 [NASA ADS] [CrossRef] [Google Scholar]
- Inoue, A. K., Shimizu, I., Iwata, I., & Tanaka, M. 2014, MNRAS, 442, 1805 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, Y., Im, M., Jeon, Y., et al. 2019, ApJ, 870, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Kulkarni, G., Worseck, G., & Hennawi, J. F. 2019, MNRAS, 488, 1035 [NASA ADS] [CrossRef] [Google Scholar]
- Lopez, S., D’Odorico, V., Ellison, S. L., et al. 2016, A&A, 594, 91 [Google Scholar]
- Lusso, E., Worseck, G., Hennawi, J. F., et al. 2015, MNRAS, 449, 4204 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Haardt, F. 2015, ApJ, 813, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Matsuoka, Y., Oyabu, S., Tsuzuki, Y., et al. 2005, PASJ, 57, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Matsuoka, Y., Onoue, M., Kashikawa, N., et al. 2018, PASJ, 70S, 35 [NASA ADS] [Google Scholar]
- Marchesi, S., Civano, F., Elvis, M., et al. 2016, ApJ, 817, 34 [NASA ADS] [CrossRef] [Google Scholar]
- McQuinn, M. 2016, ARA& A, 54, 31 [Google Scholar]
- Meiksin, A. 2009, Rev. Mod. Phys., 81, 1405 [NASA ADS] [CrossRef] [Google Scholar]
- Meiksin, A., & White, M. 2004, MNRAS, 350, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- O’Meara, J. M., Prochaska, J. X., Worseck, G., et al. 2013, ApJ, 765, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Oke, J. B., & Korycansky, D. J. 1982, ApJ, 255, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Paris, I., Petitjean, P., Aubourg, E., et al. 2018, A&A, 613A, 51 [Google Scholar]
- Parsa, S., Dunlop, J. S., & McLure, R. J. 2018, MNRAS, 474, 2904 [NASA ADS] [CrossRef] [Google Scholar]
- Perrotta, S., D’Odorico, V., Prochaska, J. X., et al. 2016, MNRAS, 462, 3285 [NASA ADS] [CrossRef] [Google Scholar]
- Perrotta, S., D’Odorico, V., Hamman, F., et al. 2018, MNRAS, 481, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration VI. 2019, A&A, submitted [arXiv:1807.06209] [Google Scholar]
- Prochaska, J. X., Worseck, G., & O’Meara, J. M. 2009, ApJ, 705, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Prochaska, J. X., O’Meara, J. M., & Worseck, G. 2010, ApJ, 718, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Prochaska, J. X., Hennawi, J. F., Lee, K.-G., et al. 2013, ApJ, 776, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Prochaska, J. X., O’Meara, J. M., Fumagalli, M., et al. 2015, ApJS, 221, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Rahmati, A., & Schaye, J. 2018, MNRAS, 478, 5123 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, G. T., Fan, X., Newberg, H. J., et al. 2002, AJ, 123, 2945 [NASA ADS] [CrossRef] [Google Scholar]
- Rudie, G. C., Steidel, C. C., Shapley, A. E., et al. 2013, ApJ, 769, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Shull, J. M., Stevans, M. L., & Danforth, C. W. 2012, ApJ, 752, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Songaila, A., & Cowie, L. L. 2010, ApJ, 721, 1448 [NASA ADS] [CrossRef] [Google Scholar]
- Stevans, M. L., Shull, J. M., Danforth, C. W., & Tilton, E. M. 2014, ApJ, 794, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Telfer, R. C., Zheng, W., Kriss, G. A., et al. 2002, ApJ, 565, 773 [NASA ADS] [CrossRef] [Google Scholar]
- Worseck, G., Prochaska, J. X., O’Meara, J. M., Becker, G. D., et al. 2014, MNRAS, 445, 1745 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, J., Wang, F., Fan, X., et al. 2019, ApJ, 871, 199 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Example of SDSS QSO spectra
In this appendix, we report another example (beyond the example previously shown in Fig. 2) that explains the procedure we adopted to estimate the IFP for each SDSS QSO. In particular, Fig. B.1 is an example of the problem related to the estimate of the free path for several sources in our sample, that is, the limited wavelength coverage of some SDSS spectra. Here the LyC emission extends at wavelengths bluer than the lower limit of the SDSS spectrum, that is, λobs = 3560 Å, indicated by the dashed orange line, but does not intersect the blue line, which marks the 1/e level with respect to the flux at 912 Å rest frame. In this case the estimated IFP of 145.94 pMpc is only a lower limit because of instrumental limitations, and the true free path for this QSO might be even larger.
Appendix B: MFP from stacked spectra and from the mean value of the PDF
The results from the statistical analysis on the IFP distribution functions for the high-z QSOs highlight a possible disagreement between these latter values and those from the stacks. In principle, this might be caused by the shape of the IFP distributions, which are highly asymmetric or skewed and wide at z ≥ 3.6. To test this hypothesis, we compared the MFP from the stacked spectra and from the mean value of the distributions of subsamples selected in narrow intervals of IFP in the redshift range 3.60 ≤ z ≤ 3.80. Table B.1 summarizes the results. As reported in the first three rows of this table, bins of 10 pMpc in IFP were considered, that is, between 50−60, 90−100, and 140−150 pMpc (Col. 1); in each of these bins, a number Nobj of QSOs was found (Col. 2). When we compare the MFP from the stacks and distributions (Cols. 3 and 4, respectively), it can be seen that the discrepancies are clearly reduced.
Stack vs PDF from simulations.
Furthermore, two distant peaks were also analyzed in order to study the effect of the asymmetry or skewness of the distribution on the stacked spectrum. The obtained values are reported in the last row of Table B.1 for two peaks at 15 and 105 pMpc, with 36 and 8 QSOs in each bin, respectively. In this case, the results from the stack and the distribution are quite different from each other: the first value is significantly lower than the second. These observations seem to lead to the conclusion that in a wide and really asymmetric distribution, the stack is dominated by sources with small IFP, resulting in a lower value than is obtained with the distribution function. Moreover, the stacking technique seems to depend on the number of sources with a low free path with respect to those with higher values of this parameter. When the number of QSOs in the bin with low free paths is about the same or lower than twice of that in the highest bin, the stacked spectrum is dominated by these latter sources, resulting in the estimate of a large MFP. On the other hand, if the ratio between the two numbers is greater than three (which is the case discussed here), sources with low free paths dominate the stack, which provides a result lower than the one computed from the mean of the associated distribution. This is a simple consequence of the definition of IFP, which is the distance where the emitted flux is reduced by a factor of 1/e ∼ 1/3, that is, dominated by the bulk of the IFP distribution.
 |
Fig. B.1. Free path estimate of the QSO SDSS J113654.6+485322.3 at zQSO = 3.61964. Same color legend as in Fig. 2. |
Finally, it is reasonable to believe that the disagreement between the two methods discussed above might increase at higher redshift (i.e., z > 4) because the asymmetry of the IFP distribution functions is likely more pronounced. Certainly, approaching the end of the reionization at z ∼ 6 − 7, the discrepancy should be reduced because of the decrement of the free paths for all the sources, resulting in a PDF that is peaked at low values.
The simulations carried out here are quite simplistic, and it is possible that they are not able to fully reproduce the real IFP distributions. However, they are useful for understanding the behavior of the stacking procedure when it is applied to skewed distributions, as those that we show in Fig. 6.
All Tables
Redshift evolution of the MFP for all QSOs at 3.6 ≤ z ≤ 4.6 and I ≤ 20.0 (option 1).
Redshift evolution of the MFP for QSOs at 3.6 ≤ z ≤ 4.6 with IFP > 10 pMpc (option 2).
All Figures
 |
Fig. 1. Spectral slope and flux decrements for the QSO SDSS J105340.8+010335.7 at zQSO = 3.66983. The cyan portions of the spectrum are the five windows that are free of emission lines. The yellow regions are the places of the spectrum in which the flux decrements DA and DB have been calculated. The solid orange and green lines represent the fit with and without the first window (1284−1291 Å rest frame), respectively. |
| In the text | |
 |
Fig. 2. IFP estimate for the QSO SDSS J114514.2+394715.9 at zQSO = 4.06557. The green circles and solid line represent the average fluxes in the 10 Å windows and the spline, respectively. The red line marks the Lyman limit. The horizontal blue and cyan lines represent fred and its uncertainty, respectively. In this case, the choice of IFP corresponds to λrest ∼ 800 Å. The flux on the y-axis is in arbitrary units. |
| In the text | |
 |
Fig. 3. Spectral slope distribution. The vertical red solid and dashed lines are the mean value and its uncertainties, respectively. |
| In the text | |
 |
Fig. 4. Upper panel: spectral slope as a function of redshift. The horizontal red, orange, green, cyan, and blue lines are the average values from the lowest to the highest redshift bins. Bottom panel: distribution of the spectral slope in each redshift bin (with the same color as in the upper panel). |
| In the text | |
 |
Fig. 5. LyC escape fraction distribution for the whole sample (in red) and for sources with IFP ≥ 10 pMpc (in blue). The solid and dashed gray lines represent the mean values of the first and second distributions, respectively. |
| In the text | |
 |
Fig. 6. Free path distribution functions for the whole QSO sample at 3.6 ≤ z ≤ 4.6 in redshift bins of Δz = 0.2. The dashed red lines represent the mean value in each redshift bin. |
| In the text | |
 |
Fig. 7. Escape fraction vs. IFP for QSOs at z > 3.80. The gray points show the escape fractions calculated with the ionizing window 892−905 Å rest frame, and the orange points represent the escape fractions with the reduced ionizing window 898−905 Å rest frame. The black filled square represents the mean fesc in IFP bins of 30 pMpc (the open square is the mean of fesc in IFP bins containing fewer than ten sources). The vertical bars are the error on the mean in each IFP bin. QSOs with z < 3.8 have been excluded here to avoid possible biases due to their underestimated IFP, as discussed in Sect. 6.1.1. |
| In the text | |
 |
Fig. 8. Free path estimate for the QSO SDSS J034402.9−065300.6 at zQSO = 3.92455, a QSO with a short IFP and a low value of the escape fraction, thus representing an example of correlation between IFP and fesc. The orange spectral region marks the ionizing window we used to calculate the escape fraction (i.e., 892−905 Å rest frame). |
| In the text | |
 |
Fig. 9. Free path vs. absolute magnitude M1450 for individual SDSS QSOs at 3.8 < z < 4.0 and I ≤ 20.0 (small black dots). The large blue points show the average value of the free paths in bins of ΔM1450 = 1.0. The error bars of the large blue points show the 84th and 16th percentiles of the IFP distributions for each bin of absolute magnitude. |
| In the text | |
 |
Fig. 10. Average values of the free paths for all SDSS QSOs at 3.6 ≤ z ≤ 4.6 and I ≤ 20.0, divided into redshift and absolute magnitude M1450 bins. The vertical bars are the standard error of the mean in each bin of absolute magnitude. The lines show the best linear fit to the observed mean points for each redshift bin. |
| In the text | |
 |
Fig. 11. Free path of simulated QSOs at different I-band magnitudes. Circles show the mean value of 100 simulations for each QSO and magnitude bin, and the error bars indicate the 16th and 84th percentiles of the resulting IFP distribution. No strong trend of the IFP with the observed I-band magnitude has been detected. |
| In the text | |
 |
Fig. 12. Mean values of the IFP for SDSS QSOs at 3.6 ≤ z ≤ 4.6 and I ≤ 20.0 (option 1), divided into redshift for three bins of absolute magnitude M1450. The vertical bars are the standard error of the mean in each bin of absolute magnitude. The continuous lines show the best power-law fit to the observed mean points for each M1450 bin. |
| In the text | |
 |
Fig. 13. The mean values of the IFP for SDSS QSOs at 3.6 ≤ z ≤ 4.6, I ≤ 20.0, and IFP > 10 pMpc (“option 2”), divided in redshift for three bins of absolute magnitude M1450. The vertical bars are the standard error of the mean in each bin of absolute magnitude. The continuous lines show the best power-law fit to the observed mean points for each M1450 bin. |
| In the text | |
 |
Fig. 14. Redshift dependence of the MFP for SDSS QSOs at 3.6 ≤ z ≤ 4.6 and I ≤ 20.0. The filled black points (connected by a continuous black line) summarize the mean value of the free paths excluding objects with IFP ≤ 10 pMpc, which might be affected by AAs (option 2). The open black circles (connected by a dashed black line) show the MFP for all the QSOs of our sample (option 1). The filled red points (connected by a continuous red line) are instead derived from the stack of QSOs with IFP > 10 pMpc, and the open red circles (connected by a dashed red line) show the MFP obtained by the stack of all the QSOs. The dotted blue curve is the evolution of the MFP with redshift found by Worseck et al. (2014), while the blue open triangles indicate their mean values in different redshift bins. |
| In the text | |
 |
Fig. 15. Individual free path (black points) vs. spectroscopic redshift for SDSS QSOs at 3.6 ≤ z ≤ 4.6. The blue line represents the maximum value of the IFP that can be obtained at each redshift because of the observational limits of the SDSS spectra, i.e., λobs ≳ 3550 Å. |
| In the text | |
 |
Fig. 16. Distribution functions of the u − g color for QSOs with high (green histogram, IFP ≥ 150 pMpc) and low (orange hatched histogram, IFP < 150 pMpc) IFPs. The solid and dot-dashed black lines refer to the average values of the orange and green distributions, respectively. Top (bottom) panel: u − g distributions for QSOs at higher (lower) redshift with respect to the median one at z ∼ 3.90. |
| In the text | |
 |
Fig. B.1. Free path estimate of the QSO SDSS J113654.6+485322.3 at zQSO = 3.61964. Same color legend as in Fig. 2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


