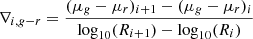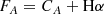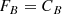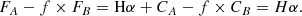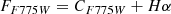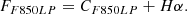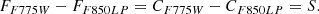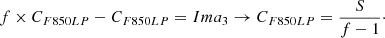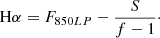| Issue |
A&A
Volume 632, December 2019
|
|
|---|---|---|
| Article Number | A15 | |
| Number of page(s) | 13 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201935288 | |
| Published online | 21 November 2019 | |
The stellar host in star-forming low-mass galaxies: Evidence for two classes⋆
1
Instituto de Astrofísica de Canarias, Calle Váa Láctea s/n, 38205 La Laguna, Tenerife, Spain
e-mail: alumbrerascalle@gmail.com
2
Universidad de La Laguna, Departamento de Astrofísica, Avenida Astrofísico Francisco Sánchez, s/n, 38206 La Laguna, Tenerife, Spain
Received:
15
February
2019
Accepted:
17
April
2019
Context. The morphological evolution of star-forming galaxies provides important clues to understand their physical properties, as well as the triggering and quenching mechanisms of star formation.
Aims. We analyze the morphology of galaxies hosting star-forming events at low redshift (z < 0.36). We aim at connecting morphology and star-formation properties of low-mass galaxies (median stellar mass ∼108.5 M⊙) beyond the local Universe.
Methods. We use a sample of mediumband selected star-forming galaxies from the GOODS-North field. Hα images for the sample are created combining both spectral energy distribution fits and HST data. Using them, we mask the star forming regions to obtain an unbiased two-dimensional model of the light distribution of the host galaxies. For this purpose we use PHI, a new Bayesian photometric decomposition code. We applied it independently to 7 HST bands, from the ultraviolet to the near-infrared, assuming a Sérsic surface brightness model.
Results. Star-forming galaxy hosts show low Sérsic index (with median n ∼ 0.9), as well as small sizes (median Re ∼ 1.6 kpc), and negligible change of the parameters with wavelength (except for the axis ratio, which grows with wavelength in 46% of the sample). Using a clustering algorithm, we find two different classes of star-forming galaxies: A more compact, redder, and high-n (class A) and a more extended, bluer and lower-n one (class B). This separation holds across all seven bands analyzed. In addition, we find evidence that the first class is more spheroidal-like (according to the distribution of observed axis ratios). We compute the color gradients of the host galaxies finding that 48% of the objects where the analysis could be performed show negative gradients, and only in 5% they are positive.
Conclusions. The host component of low-mass star-forming galaxies at z < 0.36 separates into two different classes, similar to what has been found for their higher mass counterparts. The results are consistent with an evolution from class B to class A. Several mechanisms from the literature, like minor and major mergers, and violent disk instability, can explain the physical process behind the likely transition between the classes.
Key words: galaxies: star formation / galaxies: photometry / galaxies: structure / galaxies: evolution / galaxies: starburst / galaxies: fundamental parameters
Full Tables 1 and 2 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/632/A15
© ESO 2019
1. Introduction
During the recent decades, numerous studies have explored the different morphological, structural, and color properties of star-forming galaxies (SFGs). The relation between star formation and the structural properties of galaxies, as well as the dependence on galaxy mass and cosmic time are key to understanding galaxy evolution. Large surveys show that the bulk of star formation happens in disk galaxies, as defined by their “near-exponential” surface brightness profiles (Brennan et al. 2017), with stellar masses below 1010.5 M⊙, and stellar mass surface densities lower than 108.8 M⊙ kpc−2 (Kauffmann et al. 2003; Ilbert et al. 2013).
In the nearby universe, HII galaxies, blue compact dwarfs, and dwarf irregular galaxies dominate the low-mass star-forming galaxy population. In order to understand the possible relation between structure and star formation processes, detailed photometric studies of SFGs have revealed the necessity of either masking the star-forming regions (Cairós et al. 2002, 2003; Caon et al. 2005; Amorín et al. 2009 or analyzing only the outermost parts of the galaxies (Janowiecki & Salzer 2014). These works revealed old, disk-like host galaxies underneath the starburst events that dominate the optical emission of these systems.
At higher redshifts (z > 0.5), the morphological analysis of SFGs faces problems such as Malmquist bias, cosmological dimming, and lack of the needed spatial resolution (Paulino-Afonso et al. 2017, and references therein). This implies that galaxies analyzed in these studies are typically more massive (M⋆ > 109.5 M⊙) than those at lower redshifts. Still, most of the previous works at these redshifts show that star formation tends to happen in disk galaxies with Sérsic index n ∼ 1 (e.g. Wuyts et al. 2011). Even compact, starbursting systems, such as green pea galaxies have been shown to host an underlying disk-like stellar structure, as do their local counterparts (Amorín et al. 2012). As redshift increases, the typical specific star formation rate (sSFR) increases as well because the SFR is higher for galaxies with the same stellar mass (Oliver et al. 2010; Whitaker et al. 2014; Tasca et al. 2015). Galaxy morphology also changes at higher redshift, with galaxies showing large and massive star-forming knots (Abraham et al. 1996; van den Bergh et al. 1996; Elmegreen et al. 2004a,b, 2007). As in low-redshift systems, an accurate description of the structural properties of the host galaxy can only be achieved once an analysis of the clumps (the current star formation) separate from that of the host galaxy (previously formed stars) is carried out. It has been also shown that star-forming clumps closer to the center of a galaxy are generally older, redder, denser (Guo et al. 2012), and more massive (Hinojosa-Goñi et al. 2016; Cava et al. 2018) than those at larger galactocentric distances. This supports the idea that these massive clumps are created through violent disk instabilities (Bournaud et al. 2007). Their coalescence and infall to the galaxy center eventually gives rise to central concentrations of stars thus reshaping the morphology of the galaxy (Ceverino et al. 2010).
The structural and morphological properties of galaxies are also linked to the triggering and quenching of star formation. Indeed, several observational works have pointed out the existence of a transitional population of galaxies (Dellenbusch et al. 2008; Meyer et al. 2014; Lian et al. 2015; Koleva et al. 2013; Pandya et al. 2017; Wang et al. 2017, 2018; Kelvin et al. 2014; Pawlik et al. 2018; Maltby et al. 2018). They show intermediate properties (in size, Sérsic index, star formation rate) between passive galaxies and normal SFGs, thus hinting to a possible evolutionary path where these properties are connected. In low-mass galaxies it has been extensively determined, both observationally and in simulations, that the star formation history of low-mass galaxies is more bursty than in higher mass galaxies (Di Matteo et al. 2008; Bauer et al. 2013; Sparre et al. 2017; Faucher-Giguère 2018). The triggering mechanisms can be due to the accretion of pristine gas (Sánchez Almeida et al. 2013, 2015), the compression of hot gas around the galaxies due to interactions with the intergalactic medium (Wright et al. 2019), or encounters with other galaxies (Stierwalt et al. 2015). The quenching processes at these masses is thought to be dominated by the environment where they reside (Fillingham et al. 2018). At high galaxy masses, more complex quenching mechanisms have been proposed, which may still play a role in the lower mass range. The compaction scenario suggests that galaxies grow their central stellar densities (through minor or major mergers, or violent disk instability) compacting the galaxy, and stopping star formation as a result (Dekel & Burkert 2014). Another possibility is the morphological quenching theory (Martig et al. 2009), where the growth of central stellar mass density inhibits further star formation by stabilizing the gas in the disk against gravitational collapse. The analysis of the structure of SFGs, and their diverse properties can help constrain the possible evolutionary pathways between them and the physical reasons driving these changes.
In this work, we present an accurate modeling of the surface brightness distribution and structural properties of the host component of low-mass emission line galaxies (ELGs) at low redshift (z < 0.36). Our aim is to fill the gap between large surveys (at masses higher than 109 M⊙) and local dwarf galaxies analysis, with particular emphasis on the presence of transitional types (i.e. galaxies transforming from star forming to passive) at these masses and redshifts. The sample, obtained in Lumbreras-Calle et al. (2019; hereafter Paper I) includes low-mass star-forming systems identified thanks to the data from the Survey for High-z Absorption Red and Dead Sources (SHARDS, Pérez-González et al. 2013), a deep, mediumband multiwavelenght survey. In order to robustly analyze the morphological properties of the galaxies, we use the high-resolution, deep HST images from the CANDELS (Grogin et al. 2011; Koekemoer et al. 2011) and 3D-HST (Skelton et al. 2014) surveys.
The paper is structured as follows. In Sect. 2 we describe the sample selection and the code used in the photometric decomposition. In Sect. 3, we describe the process of masking the star-forming regions and performing the actual photometric fits. In Sect. 4 we analyze the results of the photometric fits in the context of the galaxy properties. In Sect. 5 we discuss the results and in Sect. 6 we present our conclusions.
Throughout this paper we consider standard ΛCDM cosmology, with ΩΛ = 0.73, ΩM = 0.27 and H0 = 71 km s−1 Mpc−1. All uncertainties reported refer to the limits of the central 68% of the probability distribution.
2. Sample selection and photometric decomposition
2.1. Sample selection and databases
The initial sample of young SFGs analyzed in this paper is extracted from Paper I. They identified 160 ELGs at z < 0.36 within SHARDS (Pérez-González et al. 2013). The SHARDS survey consists of deep imaging of the GOODS-North field using 25 contiguous mediumband filters, and it was performed using the Optical System for Imaging and low-Intermediate-Resolution Integrated Spectroscopy (OSIRIS, Cepa et al. 2000) instrument, at the 10.4 m Gran Telescopio de Canarias (GTC) at the Observatorio del Roque de los Muchachos, in La Palma.
A full description of the sample selection and characterization can be found in Paper I. Briefly, the authors developed an algorithm to simultaneously detect the Hα and [OIII] emission lines, as star formation tracers, in the well-sampled (R ∼ 50) SED provided by SHARDS. They removed contamination by active galactic nucleii from the sample, ensuring that the emission lines come from star-forming events. In addition, models with two single stellar populations (SSPs), one young and one old, were used to fit the SED of the galaxies and to obtain their stellar population properties. Thanks to the depth and quasi-spectroscopic resolution of SHARDS they were able to detect SFGs with equivalent widths (EWs) as low as 12 Å (median values of ∼35 Å in [OIII] 5007 and ∼56 Å in Hα) and stellar masses as low as 107 M⊙ (with median value of 108.5 M⊙).
The SHARDS survey covers the Hubble Space Telescope (HST) legacy field GOODS-North. Thus, multiwavelength high spatial resolution imaging is available for all 160 ELGs in the sample. In particular, in this paper we use images in the F606W and F850LP filters from the Advanced Camera for Surveys (ACS) obtained from the CANDELS survey (Grogin et al. 2011; Koekemoer et al. 2011), the F435W and F775W filters from ACS, and the F125W, F140W, and F160W filters from the Wide Fide Camera 3 (WFC3) retrieved from the 3D-HST survey (Brammer et al. 2012; Skelton et al. 2014). This is the dataset we used to perform our photometric decomposition, described in the next subsection.
2.2. PHI photometric decomposition code
Since the development of two-dimensional (2D) photometric decomposition programs such as GALFIT (Peng et al.; 2002), BUDDA (de Souza et al. 2004), or GASP2D (Méndez-Abreu et al. 2008), a vast amount of work has been performed with them, and the limitations in their application to SFGs have been studied in detail (Paulino-Afonso et al. 2017; Amorín et al. 2009, among others). However, some problems related with the algorithms still exist, such as local minima trapping of the solution and inaccurate derivation of the final errors. Therefore, a new approach is needed to provide an accurate description of the stellar host in ELGs at intermediate redshift. In order to overcome some of these difficulties, we used the PHI code described in Argyle et al. (2018). PHI is based on an adaptive Markov chain Monte Carlo (MCMC) algorithm that efficiently explores the parameter space providing robust results and statistically meaningful errors.
A complete description of the code can be found in Argyle et al. (2018). Here we summarize its most important aspects. As most 2D fitting codes, PHI uses the flux and the error images of a galaxy, as well as the point spread function (PSF). The code starts exploring the parameter space and in each iteration it produces a model image for the galaxy. Then, this model is convolved with the PSF and (given its Bayesian framework) the likelihood and posterior probability are calculated for the model and the data. After that, the MCMC engine starts varying the parameters, repeating the model creation and likelihood and posterior probability computation until the code converges or a maximum number of iterations is reached.
The exploration of the parameter space is performed at three different levels:
-
(1)
Blocked Adaptive Metropolis. At this stage, PHI works by fixing all parameters but one, and only modifies this parameter in order to estimate its typical scale of variation. This makes the further exploration of the parameter space more efficient.
-
(2)
Adaptive Metropolis. The code varies all parameters in each iteration to obtain a good description of the covariance matrix.
-
(3)
Chain convergence. Three Markov chains are run simultaneously, using the last covariance matrix from level 2, in order to perform the exploration of the parameter space in the most efficient way. We only consider a fit to be successful when at least two of these chains converge and give compatible results.
In this paper we use a single Sérsic function (Sersic 1968) to describe the surface brightness distribution of the host galaxy:
where Ie is the intensity at the effective radius Re, enclosing half of the total light of the model; n is the Sérsic index, describing the concentration of the light profile; and bn is a parameter determined by n. This model is implemented in concentric elliptical isophotes with position angle θ and ellipticity ϵ = 1 − q, where q = b/a is the ratio of the semiminor to the semimajor axis of the ellipse. It is worth noting that we use uniform priors in all parameters involved in the fit. In the case of Ie and Re the fit is performed in logarithmic units. The Sérsic index n is allowed to vary between 0.4 and 8, and q between 0.2 and 1.
3. Masking and fitting process
To robustly describe the surface brightness distribution of the host galaxies in our sample of ELGs, we first masked out the star-forming regions in the HST images. Not masking them would add spurious flux, possibly biasing the result of the fit (see Amorín et al. 2009, and references therein). The full process of masking and fitting is summarized in Fig. 1 and described in this section. We created the masks running the SExtractor code (Bertin & Arnouts 1996) with different threshold levels on Hα images created using HST broadband data. For those galaxies where no clear Hα was detected, we created the masks based on the near-UV HST data (F435W filter). Then, we performed the photometric decompositions, removed the poor fits, and chose the appropriate masks (see Fig. 1).
 |
Fig. 1. Flowchart summarizing the process of choosing the appropriate fits and masks. The numbers in boxes (a) and (b) give the median number of galaxies in the sample, considering all masks, for each one of the four filters in ACS (from top to bottom, F435W, F606W, F775W, and F850LP) and the three in WFC3 (F125W, F140W, and F160W). The numbers in box (c) give the number of galaxies in each band fulfilling all criteria, after choosing the final mask. |
3.1. Creation of masks for the star-forming regions
Our first step was to create pure Hα images using the available broadband HST images. To this end, we used data from two HST filters, one including the Hα line emission and the other probing only the stellar continuum. The process started by aligning and PSF-matching the two images. Then we subtracted the continuum image from the emission line one. In particular, for galaxies at z < 0.266, the Hα line lies in the F775W filter and F850LP was used as continuum. For those with z > 0.298, Hα lies in F850LP and F775W contains the continuum. Between those redshifts, the process is more complex since Hα is covered with both filters (see Appendix A for more details).
As a simple subtraction of the two images (with and without Hα) is not accurate enough, we took into account the continuum variation between the two filters, using the best-fit models derived in Paper I. These were obtained by fitting stellar population models to SHARDS data, which provides higher spectral resolution than HST, thus making this process feasible. To include the uncertainties in the SED fitting, we perturbed the scaling factor (±10%) between filters choosing the value that produced less continuum oversubtraction when generating the Hα images.
Once the pure Hα images are built, the mask creation process consists in detecting sources over a given threshold. We ran SExtractor with different thresholds over the sky background (1.1σ, 1.5σ, and 2 σ). The output segmentation maps were directly used as star-forming region masks. Since our ELG detection process (described in Paper I) is based on the SHARDS survey, which detects emission lines very efficiently, some galaxies showed no measurable Hα in the HST images. In these cases we used the near-UV HST data (F435W filter) to select the most prominent UV emitting regions as masks.
3.2. Quality check and mask selection
All galaxies in our sample were photometrically analyzed using PHI in the seven HST filters (F435W, F606W, F775W, F850LP, F125W, F140W, F160W). We used four different masking modes (no mask, 1.1σ, 1.5σ, and 2σ over the threshold mask). An example of the different masking regions is shown in Fig. 2. In total, we carried out 4480 (160 galaxies × 7 bands × 4 masks) photometric decompositions using the PHI code. Most of these fits converged, but a few either failed or showed high χ2 values, and they were removed from the sample. In order to choose the most accurate one, we evaluated the results obtained for different masks. The whole process is summarized in Fig. 1, where we also show the number of galaxies retained in each step for each band, and the effect of the different mask modes in the fitted values of radius and Sérsic index.
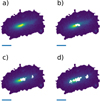 |
Fig. 2. Example of a galaxy from our sample without a mask (panel a) and with the three different Hα detection masks over it: 2σ (panel b), 1.5σ (panel c) and 1.1σ (panel d). The horizontal line represents a 1 kpc distance. |
3.2.1. Removing poor fits
We find that for some of the galaxies (15 in median, considering the different bands and masks) the code does not reach a solution. This is either due to galaxies being too small, faint, or due to errors in the photometry in certain bands. Among those runs where the code does provide a solution we find ∼29 (depending on the filter and mask) where either none or only one of the three chains converges successfully. We also removed those fits since we could not ensure they are reliable, and we were left with the number of galaxies listed in box (a) of Fig. 1 for each filter.
In addition, we evaluated the goodness of the model by analyzing its χ2. The offset between filters was accounted for by normalizing the values in order to apply the same criterion in all bands. We measured the distribution of χ2 in each band, defining σ* as the distance between the 16th and 50th percentiles. After visually inspecting the residual images, we placed the threshold at 2σ* over the median χ2. The fits presenting higher values were removed from the sample, and the number of galaxies left in the sample is presented in box (b) of Fig. 1.
3.2.2. Mask selection
We then analyzed the fitted parameters of the galaxies as a function of the mask used to cover the star-forming regions. We find a significant difference between the photometric parameters when the galaxies are fitted with or without mask (independently of which one is used). For instance, we find differences greater than 20% in 22.5% and 9.5% of the galaxies when considering the Sérsic index n and effective radius Re, respectively. However, these values drop to 5.1% and 2.4% when comparing the best-fitting values among different masks. This means that the presence or absence of a mask has a noticeable influence on the fit for some of the galaxies, and therefore it is necessary to use them to derive precise morphological properties of the host galaxy. The precise shape and size of the mask has, however, a small impact on the fitted parameters. Therefore, as a compromise, we chose to use our intermediate Hα mask (with detection threshold of 1.5σ over the sky noise). In this way we avoided both large masks that leave very few galaxy pixels to fit and small masks that leave many pixels contaminated by strong star-forming regions possibly biasing the fit.
Using the 1.5σ masks, we were left with the number of galaxies per filter shown in box (c) of Fig. 1. They fulfill the three criteria previously mentioned: PHI finds a solution, two or three chains converge, and the normalized χ2 of the model is smaller than the threshold. Considering this, 143 galaxies were successfully fitted in at least in one band. To select the final sample of galaxies over which we would perform the rest of the analysis, we only keep those that present good fits in at least three bands: two or more filters from ACS, and one or more from WFC3. This was done to ensure that an analysis of the galaxy colors is feasible without extrapolating values to distant wavelength ranges. Applying this criteria, 95 galaxies constitute the final sample studied in this paper.
4. Results
In this section we summarize the results of applying our photometric decomposition to the ELGs. In Table 1 we give the best-fitting values (with uncertainties) for all the parameters in all galaxies and bands, as well as the χ2 values. The uncertainties in the photometric parameters for each galaxy were derived using their marginalized posterior distributions. We find that more than 70% of galaxies present uncertainties lower than 25% on every parameter in all bands, except for the Sérsic index and Sérsic total intensity in the WFC3 filters. In fact, considering only ACS bands, more than 70% of galaxies present uncertainties lower than 10% in all parameters, but the Sérsic index and Sérsic effective intensity. The final sample fitted is composed of 95 galaxies out of the original 160 detected ELGs (60%).
Photometric parameters obtained from PHI fitting.
Physical properties, synthetic magnitudes, and class to which each galaxy belongs.
4.1. Photometric properties of the host galaxies
Figure 3 presents the distribution of the photometric parameters: effective radius Re, Sérsic index n, axis ratio q, and effective surface brightness μe for the 95 galaxies analyzed. Different colors represent the results in the different HST bands. Two examples of the photometric decomposition are shown in Fig. 4.
 |
Fig. 3. Distribution of the main photometric parameters derived for our ELG sample. Upper left panel: values of the effective radius of the best-fit Sérsic model for the galaxies in each filter, in kpc. Upper right panel: histogram of the Sérsic index, lower left panel: axis ratio q, and lower right panel: surface brightness at the effective radius (after applying the cosmological dimming and K corrections). |
 |
Fig. 4. Example of two galaxies from our sample, with the original image and the Hα detection mask overlaid on it (left column), the Sérsic model (central column) and the residuals from the fit (right column). All images are presented with the same color scale, shown in the central color bar (in counts). |
We find that the median effective radii of the host galaxies are smaller than 1.7 kpc in all bands. These values are low compared to those reported in previous studies (e.g. Wuyts et al. 2011), but in agreement with the expectations at the mass range where our sample resides (Lange et al. 2015; Shibuya et al. 2015). Closely inspecting the distribution, we detect a characteristic double-peaked distribution in all bands with maxima at ∼0.8 kpc and ∼1.9 kpc. We investigate this further in Sect. 5.1 (Fig. 4).
Regarding the Sérsic index, more than 75% of the galaxies present values lower than 2 in all bands (and more than 50% equal or lower than 1), with very few (∼4%) in the range 3 < n < 5. These Sérsic index values are consistent with the results of other emission-line-selected galaxy samples (e.g. Paulino-Afonso et al. 2017). Some specific bands present wider distributions (such as F606W and F850LP), but median values remain very similar, spanning from 0.83 to 1.01 except for the bluest filter (F435W), where the Sérsic index is lower than for the other bands (0.59).
The axis ratio q of the host galaxies shows a wide range of values in all bands (from 0.2 to 1, the minimum and maximum possible values) but with different characteristics in the different filters. The bluest filter (F435W) presents a lower median value (0.46) and flatter distribution than the rest of the bands.
The surface brightness at the effective radius μe presents a similar distribution in all bands, slightly skewed toward brighter values in the WFC3 values. It is important to note that the values in this histogram have been corrected by cosmological dimming and K-correction (following the procedure described in Sect. 4.2).
4.2. Integrated colors of the host galaxies
Our multiwavelength photometric decomposition yields results in seven non-rest-frame HST filters, which need to be transformed into standard rest-frame filters to perform color analysis. In order to obtain the U, V, and J rest-frame magnitudes for our models, we apply the K-correction (Hogg et al. 2002). To this end, we take advantage of the SED fits performed on each of the galaxies in Paper I, using the SHARDS data, with higher spectral resolution. We obtain the synthetic magnitudes of the whole galaxies in the U, V, and J rest-frame filters and the HST non-rest frame filters by convolving the population models with the filter transmissions. The difference between the U, V, and J magnitudes and the nearest HST band is the K-correction (see Fig. 5). We apply it to the integrated magnitude of the Sérsic model of the host galaxy in the appropriate HST bands. U, V, and J magnitudes for each host galaxy are presented in Table 2.
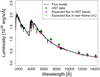 |
Fig. 5. Example of the K-correction process. The composite stellar population model (from Paper I) is shown as a black line. The green triangles represent the integrated flux of the galaxy in each HST band. The pink circles are the expected flux in each HST band, considering only the stellar population model. The gray dots are the expected U, V and J fluxes considering the model. The K-correction is the difference between these fluxes and the expected values in the nearest HST filters. |
Figure 6 shows the UVJ diagram for the host galaxies and the integrated flux of the whole galaxy, including star-forming regions (from Paper I). Even though our sample is exclusively composed of SFGs, we show how some of their hosts actually lie in the passive region of the diagram (top left) once they are free from the star-forming regions.
 |
Fig. 6. UVJ diagram for the Sérsic models of the host galaxies of the sample (gray triangles). The blue circles represent the integrated colors of the entire galaxies derived from the SED models obtain in Paper I. The black lines represent the separation between passive galaxies (top left) and SFGs taken from Whitaker et al. (2014). |
4.3. Wavelength dependence of the photometric parameters
We take advantage of the multiwavelength data to analyze the possible trends in the photometric parameters with wavelength. We computed whether the median values of each parameter for the sample correlate with the wavelength, and we computed as well the correlation between parameter value and wavelength for each individual galaxy. Throughout the paper, we calculate the correlation between variables by performing 1000 Monte Carlo and bootstrap simulations and deriving the Spearman rank coefficient in each one. If more than 95% of the simulations present a positive (negative) coefficient, we consider that a positive (negative) correlation is present.
The host galaxy axis ratio q is higher at longer wavelengths, meaning that the galaxies become rounder when seen in the infrared, compared to the UV-optical range. The median value of the sample grows from q = 0.47 at F435W to q = 0.67 at F140W. For individual galaxies, 46% of them present a statistically significant positive correlation (the longer the wavelength of the filter considered, the higher the q). Considering the Sérsic index, the median values of the sample oscillate between n = 1.0 and n = 0.8, with no dependence on wavelength. The only exception is the F435W band, with a lower median value of n = 0.6. The median values of the effective radius Re also do not show dependence on wavelength. We find the smallest value in F435W with Re = 1.34 kpc, but F160W shows the second smallest one, Re = 1.45 kpc. The same applies for individual galaxies.
Vulcani et al. (2014) find very clear trends with increasing wavelength: a ∼ 30% decrease in size and a ∼ 100% increase in Sérsic index in our wavelength range. Lange et al. (2015) find a less striking relation, with a 16% decrease in size from g to Ks band in late-type galaxies. van der Wel et al. (2014) find a similar variation with wavelength, but it fades at lower masses. We use their Eq. (1) to compute the expected change in effective radius with wavelength. Assuming the median values in both mass and redshift of our sample, and considering the F850LP and F125W filters, we find Δlog10(Reff [kpc]) = 0.0098. This is compatible with the measured values of the galaxies in our sample, ![$ \Delta\log_{10}(R_{\mathrm{eff}}\,[\mathrm{kpc}])= 0.000^{+0.072 }_{-0.046} $](/articles/aa/full_html/2019/12/aa35288-19/aa35288-19-eq52.gif) (Table 2).
(Table 2).
4.4. Color gradients of the host galaxies
Color gradients have been widely used to understand the structural properties and evolution of galaxies (Franx & Illingworth 1990; MacArthur et al. 2004; La Barbera et al. 2005; Tortora et al. 2010; Patel et al. 2013). These studies have found negative color gradients, and have been linked to age and metallicity gradients, supporting an inside-out mode of star formation.
We computed the g − r color gradients of the galaxies along the semimajor axis using the modeled surface brightness in each band. In this way, we considered only the structure of the host galaxy, without contamination due to the star-forming regions. We chose the g and r SDSS bands in order to compare our results with results from the literature. For the K-correction, we followed the same procedure described in Sect. 4.2. In addition, we excluded the F435W filter from this analysis since its lower signal-to-noise ratio in the outermost regions of the galaxies prevents us from using it to accurately compute colors. We derived color gradients only in the subsample of galaxies where the segmentation map radius obtained from 3D-HST (Skelton et al. 2014) is larger than 0.9 arcsecs. We also removed all galaxies where the basic morphological parameters (PA and position of the center) do not match between the two filters used to derive the color. This left us with a subsample of 58 galaxies for the study.
We computed the logarithmic slope in bins of 500 pc to derive partial color gradients:
where R is the radius in kpc, and μg and μr are respectively the surface brightness in g and r at that radius. We avoided both the innermost region of the galaxies (R < 500 pc) and regions where more than 30% of the pixels are covered by the star formation mask.
We present two examples of g − r color as a function of radius in Fig. 7; the first galaxy shows a clear negative gradient and the second shows a flat profile. We classified a galaxy with a global gradient when the median value of each partial gradient is higher (in absolute value) than the standard deviation of the whole set of partial gradients. Considering this, we find that only 31 out of the 58 galaxies show a color gradient, with a median value of ∇g − r = −0.48. Out of these 31 galaxies, 28 have a negative color gradient, i.e. the outskirts are bluer than the inner regions. Color gradients, as well as g and r magnitudes for each host galaxy are presented in Table 2.
 |
Fig. 7. Examples of g − r color profiles for two galaxies in the sample. Top: galaxy with a flat color profile. Bottom: galaxy with a negative color gradient. The vertical dashed (solid) line shows the effective radius in the g(r) band. The green line represents the percentage of the area of the galaxy masked as a function of radius. |
If we consider all 58 galaxies analyzed (assigning ∇g − r = 0 to those where there was no significant gradient) we get a mean value of −0.32. This is comparable to other studies such as Kennedy et al. (2015), who find ∇g − r between −0.22 and −0.29 for their sample of galaxies with n < 2.5 (as most of our sample is), or Tortora et al. (2010), who find ∇g − i ∼ −0.2 ± 0.15 for late-type galaxies with the same median effective radius as ours.
5. Discussion
In this section, we analyze the properties of the sample, discovering through clustering analysis the existence of two different classes, that are based radius, Sérsic index, and color. We discuss possible scenarios to explain these differences and possible evolutionary paths between the galaxies in our sample belonging to each class. We also analyze the evidence in favor and against each one of the possibilities.
5.1. Two classes of host galaxies
Exploring in detail the distribution of effective radius of our sample of galaxies (Fig. 3, panel a), we found a double peak, visible in all bands, at ∼0.8 kpc and ∼1.9 kpc. Selecting galaxies around the two peaks resulted in subsamples that present a suggestive difference in median values of Sérsic index and U − V color. In order to disentangle more precisely these two possible classes of galaxies, we used a clustering algorithm. We performed the computation using a Gaussian mixture model (Bouveyron et al. 2007), implemented using the sklearn package in Python (Pedregosa et al. 2011). This model assumes that the sample is generated from several Gaussian distributions, and the code estimates their parameters, determining also the cluster to which each galaxy belongs, with a certain confidence level. We assumed the sample can be separated into two different clusters (classes A and B) based on the effective radius, the Sérsic index, and the U − V color. For each galaxy, we used the median value across ACS filters for the effective radius and Sérsic index, and the result is presented in Fig. 8. We discovered the existence of the two classes. Class A corresponds to the subsample of galaxies with lower radius, higher n, and redder U − V color; instead, class B is made up of larger, bluer, and lower n galaxies. Class A consists of 23 galaxies and class B of 72.
 |
Fig. 8. Classification of galaxies based on effective radius, Sérsic index, and U − V color into classes A and B (see text). Red and blue dots are galaxies belonging to class A and B with probability p > 0.8, respectively. Pink and cyan dots are galaxies that belong to class A and B with 0.8 ≥ p > 0.5, respectively. The parameters used in this plot are the median values for each galaxy across all bands. |
We ran a series of tests to further confirm and strengthen this conclusion. First, we performed Kolmogorov–Smirnov (KS) tests, which show that classes A and B are statistically different in n, Re, and U − V (p-values < 10−4 in all cases). In contrast, separating the sample into either n, effective radii, or U − V colors does not result in statistically different samples in all three parameters simultaneously. The g − r color is also statistically different from one class to the other (redder in class A), giving consistency to our analysis in U − V and g − r. The two subsamples are also present if we run the clustering analysis in each band individually. The KS tests also show that the two subsamples are statistically different in the three parameters (Re, n, and U − V) in all filters. Although the subsamples are not identical in all bands, ∼80% of the galaxies in each class are present in the majority of filter-selected subsamples.
Having confirmed the significance of the two classes, we also analyzed some of the different parameters of each class. We first considered the apparent shape of the galaxies, focusing on the axis ratio q. The lowest q value in a sample can be used as a proxy for the intrinsic shape of the galaxies in it, regardless of orientation (Sánchez-Janssen et al. 2010). Separating into classes A and B, we find that the minimum q value, in all bands, is lower for class B than for class A, indicating that galaxies in class A are more spheroidal than those in class B. Furthermore, if we consider the q25% value (first quartile of the distribution) in each band, the percentage of galaxies in each class that are below that threshold indicates the relative amount of elongated galaxies in each subsample. We find that this percentage is higher in class B than in class A (∼ 31% versus ∼ 18% in median), strengthening the previous observation of the minimum q values. We also find that the median sSFR is lower in class A than in class B, with 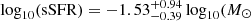 yr−1) and log
yr−1) and log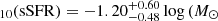 yr−1), respectively. Similarly, the median stellar mass of class A is lower than in class B, with
yr−1), respectively. Similarly, the median stellar mass of class A is lower than in class B, with 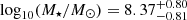 and
and 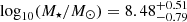 , respectively. It is worth noting that in both cases the distributions show significant overlap.
, respectively. It is worth noting that in both cases the distributions show significant overlap.
We compare our results with the work by Hinojosa-Goñi et al. (2016) on starburst galaxies within the COSMOS field. They built their sample using data from Subaru mediumband filters (Taniguchi et al. 2015) in a manner similar to our method in Paper I. Using the HST F814W images, they morphologically classified their sample in three categories: Sknot, when the galaxy consists of a single star-forming clump; Sknot+diffuse, when the single clump is surrounded by diffuse emission; and Mknot, when multiple clumps are identified in a single galaxy. Using their data, we find their Sknot and Sknot+diffuse galaxies to be redder than their Mknot subsample (Fig. 9). We applied the K − S test to confirm their distributions are statistically different. The effective radii of their subsamples also show a differentiated behavior: Mknot galaxies are larger than Sknot+diffuse, which in turn are larger than Sknot. The dispersion in values is, however, very high for the Mknot subsample (∼1.8 kpc). Both results indicate trends coherent with our findings. This will be explored further in Méndez Abreu et al. (in prep.).
 |
Fig. 9. Histogram of U − V color for the starburst galaxies in Hinojosa-Goñi et al. (2016). In red, Sknot galaxies, in green Sknot+diffuse, and in blue Mknot. The vertical lines represent the median values of each subsample, with the same color code. |
Considering the results presented in this section, we find convincing evidence for the existence of two different classes of galaxies hosting star-forming events in our sample: (i) larger, bluer, and disk-like host galaxies, and (ii) smaller, redder, and spheroid galaxies. The class to which each host galaxy belongs is shown in Table 2.
5.2. Mass-size relation
Figure 10 shows the mass-size relation for our sample, with class A galaxies in red and class B in blue. The two classes follow different mass-size relations, with similar slope but a clear offset. The linear fit to each class is shown in red and blue lines, with the 1σ errors of the fit computed using Monte Carlo and bootstrap simulations and shown as shaded areas.
 |
Fig. 10. Mass-size relation of our sample of galaxies: galaxies that belong to class B (blue dots), and class A (red dots). The shaded blue (red) area is the 1σ limit for a linear fit to the blue (red) dots, using bootstrap and Monte Carlo simulations. The lines represent mass-size relations found in the literature (see legend). Lines are continuous until they reach the mass limit for each sample, from where we point extrapolations to lower masses as dashed lines. |
The comparison with the literature is also shown in Fig. 10. We note that our mass range is one or two orders of magnitude lower than theirs. Class B galaxies follow a relation compatible with the extrapolation to low masses of the SFG sample in van der Wel et al. (2014), as well as the disk components of galaxies in the sample studied in Lange et al. (2016). The galaxies in class A, however, follow a relation more similar to the spheroidal and quiescent galaxies. In addition, there is an offset in the median values of the effective radius of the two classes, with class A and showing a median of 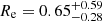 kpc and
kpc and 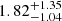 kpc, respectively.
kpc, respectively.
5.3. Comparison with previous studies on star-forming galaxy subsamples
In our work, class B galaxies show properties similar to typical SFGs in the literature, while class A present intermediate values between SFG and quiescent galaxies. There are a number of studies in the literature that find transition-type galaxies as well, that could be linked with our class A. The different ways of selecting these samples, and the physical characteristics of the transition-type galaxies can provide useful clues that place the results of the present paper in a broader context.
There are a variety of methods for selecting transition galaxies presented in the literature: Pandya et al. (2017) selected galaxies below the main sequence of star formation, Wang et al. (2017) identified SFGs in MaNGA with larger 4000 ß break at 1.5 Re than in the center, and Wang et al. (2018) selected compact SFGs. Regarding post-starburst galaxies (PSBs), Pawlik et al. (2018; their ePSB class) and Maltby et al. (2018; their low-mass, low-redshift PSB) defined transition samples according to principal component analysis of their spectra and SED, respectively.
In all the studies where the Sérsic index or the radius is measured, the transition samples present intermediate values between star-forming and quiescent galaxies in both parameters (in the Wang et al. (2018) case, the radius is smaller than in other SFGs by design). In some cases (Pandya et al. 2017; Pawlik et al. 2018; Maltby et al. 2018) the color of the galaxies is measured and presents intermediate values as well. The sSFR shows higher values than in normal SFGs in Wang et al. (2018) and Wang et al. (2017), while it is lower by design in Pandya et al. (2017). The metallicities are only measured in Wang et al. (2017), and they are higher than in normal SFGs. In terms of the relative abundance of these transition galaxies, we find 24% of the sample to be of the intermediate type. Some samples are similar to ours (20% of all the SFGs in Pandya et al. 2017, 14% in Wang et al. 2017) while others, specifically the post-starburst samples (Maltby et al. 2018; Pawlik et al. 2018) are less common, around 4%.
It should be noted that our analysis differs from those described before in the way the sub-samples are selected. We do not impose hard limits in some parameters a priori, but analyze the two populations that arise from clustering analysis when considering radius, Sérsic index, and color.
5.4. Physical explanation for the two-classes subdivision
In this subsection we review the possible scenarios capable of explaining the existence of two populations of SFGs like those presented in this paper. We discuss the processes that entail the evolution of galaxies from class B to class A, but also some models that explain the existence of galaxies that remain in class B without necessarily evolving from galaxies in class A.
5.4.1. Evolution from galaxies in one class to another
Major mergers. If two SFGs (like our class B population) of similar mass merge, the gas can fall to the center, triggering a fast central starburst. According to Hopkins et al. (2010), the resulting system can be dominated by a central, dense, quasi-spheroidal bulge. If the residual disk is faint, it can be undetectable in our images, and thus the galaxy may have smaller effective radius, while still presenting star formation, as our class A population (see also Pawlik et al. 2018). Dwarf–dwarf galaxy mergers have also been presented as a possible cause of transition-type galaxies, for example in Dellenbusch et al. (2008). However, our galaxies in class A are not systematically more massive than class B (if anything, the opposite is true; see Table 3), which would be expected if they were the result of a major merger.
Properties of the full sample of galaxies, and of the two separate classes.
Violent disk instability. Cold gas accretion onto a galaxy can produce violent disk instability (VDI), which in turn drives dissipative gas inflows into the disk center (partly as giant star-forming clumps coalesce to the center). This results in a compact star-forming system (“blue nugget”) that is later quenched, turning into a “red nugget” (Bournaud et al. 2007; Ceverino et al. 2010; Dekel & Burkert 2014, among others). This scenario implies an increase in central surface brightness in the galaxies undergoing this quenching process. We see in Fig. 11 that the galaxies in our class A subsample are in fact located in the quenched region of the surface mass density versus mass diagram, considering the relation derived by Fang et al. (2013).
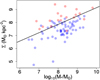 |
Fig. 11. Surface mass density of the galaxies in the sample as a function of galaxy mass. The line is an extrapolation of the relation presented in Fig. 4 of Fang et al. (2013) to fit galaxies in the red sequence and the green valley. Red and blue circles represent galaxies in class A and B, respectively. |
The main limitations to applying this model to our sample is the different mass and redshift range for which it was developed (M⋆ > 1010M⊙, z = 1−3) compared to our less massive, closer sample (107 < M⋆/M⊙ < 1010, z = 0.1−0.36). This affects the availability of cold gas in the intergalactic medium (which is higher at higher redshift) and the ability of our galaxies to accrete it. However, recent works (Sánchez Almeida et al. 2013, 2015) present strong evidence of cold flow accretion from the cosmic web into local dwarf galaxies which would make the scenario more plausible.
Minor mergers and gas accretion. Several authors have presented evidence supporting the importance of minor mergers in the star formation history and morphological evolution of galaxies, specifically in recent times (z < 1) (Bournaud et al. 2007; Kaviraj 2014; Smethurst et al. 2015). As Smethurst et al. (2015) point out, minor mergers could be responsible for the evolution across the green valley of galaxies in an intermediate speed quenching regime (∼1.5 Gyr). More specifically, minor mergers would trigger star formation, which would exhaust the remaining gas and contribute to the quenching of the galaxy (Smethurst et al. 2015).
Starkenburg et al. (2016) performed simulations of dwarf galaxies merging with dark satellites (galaxies consisting only of dark matter), and found that these interactions triggered starbursts and morphological changes, leaving a more spheroidal and compact system than the original dwarf galaxy. Although this is consistent with our data, it should be noted that dark satellites, even if predicted by cosmological simulations, have not yet been detected.
It is worth noting that other scenarios for this evolution (e.g. environment-related processes) cannot be applied to our sample, given the lack of high-density environments in the GOODS-N field.
5.4.2. No link between the two classes
Contrary to what has been previously discussed, it is possible that galaxies in different classes just represent different evolutionary paths.
The existence of a slightly red, small, compact population but with measurable star formation activity (class A) can be explained in several ways. For example, minor merger accretion of gas-rich dwarf galaxies could cause a low level of star formation in an otherwise red, quiescent galaxy. There is evidence of accreted, kinematically misaligned gas in early-type and green valley galaxies (Davis et al. 2011; Jin et al. 2016). This could be comparable to the ex-situ clumps of star formation described in Mandelker et al. (2014).
Other authors have recently presented numerical simulations (Wright et al. 2019; Ledinauskas & Zubovas 2018) that show reignition of star formation in quiescent, dwarf galaxies due to interactions with streams of gas in the intergalactic medium. This scenario is plausible, considering that the star formation history of local dwarf ellipticals (e.g. Tolstoy et al. 2009; Grebel 1998) presents, in some cases, small star-forming events at redshift similar to those of our galaxies (even isolated galaxies, as shown in Greco et al. 2018).
Reaching a conclusion on the precise evolution and nature of the two classes of galaxies cannot be obtained with the data in this paper. However, the similarity with several results in the literature at higher masses, makes us consider that the compaction and quenching scenario is the most likely cause of the two classes. The precise mechanisms that causes it (VDI, minor or major mergers) remain unclear, and all of them may be at play. The exact nature of the compaction, i.e. whether it is a physical contraction with radial migration of the stars or a relative accumulation of mass in the inner regions compared to the outskirts (Wang et al. 2018), is also a matter of debate.
6. Conclusions
In this paper our aim was to better constrain the relation between the morphology of galaxies and their star formation properties. We performed single Sérsic 2D fitting to the HST images of the ELG sample defined in Paper I using the software PHI (Argyle et al. 2018), a Bayesian 2D fitting code, that provides us with realistic uncertainties in the parameters of the fit.
To accurately measure the light distribution of the underlying host galaxy harboring star-forming events, we need to mask the clumps of star formation. To do so, we created Hα images of the galaxies, subtracting a continuum broadband filter from the filter contaminated by the line, taking into account the slope of the SED. For the galaxies where the Hα image did not present clumps, we used the brightest clumps in the F435W images (our bluest filter) as mask. We find that using larger or smaller masks does not change the results significantly, but not using any mask biases the Sérsic index values in many galaxies (22% of them would present discrepancies larger than 20%).
The sample shows low median Sérsic index (n ∼ 1), with 80% of the sample showing n < 2 in all bands, consistent with the literature for SFGs. In agreement with the low masses derived in Paper I, the measured radius are small, lower than 3 kpc in at least 80% of the galaxies. The axis ratio q shows an extended distribution, with growing values of q at longer wavelengths.
We also computed the color of the host component of the galaxies, as well as the color gradients for those galaxies where this analysis is feasible. Most host galaxies belong to the star-forming area of the UVJ diagram, although they are redder than the complete galaxy (considering star-forming clumps as well). Color gradients are clearly seen in only 31 of the 58 galaxies where we performed the analysis, and the vast majority of them (28) are negative: the outskirts are bluer than the inner regions.
We find, using a clustering algorithm, that the sample can be separated in two classes (A and B) according to their size, Sérsic index, and color. Class A shows lower radius, higher n and redder U − V color, while class B shows the opposite properties. This separation holds in all bands. In addition, the minimum value of the axis ratio q is higher in class A for all bands, indicating that they are more spheroidal. In the mass-size diagram, class A galaxies follow a relation similar to passive and spheroidal galaxies. We find several studies in the literature that also describe two different populations of SFGs that are similar to our two classes.
We reviewed the possible causes of this separation, and find our data coherent with the scenario known as compaction and quenching. If this were the case, extended SFGs would become more compact (through mergers or violent disk instability) and spheroidal, and they would later be quenched. This would mean that there is an evolutionary link between the galaxies in the two classes. In order to confirm this scenario, a larger sample is needed. In future work, we will extend this morphological analysis to a sample of higher redshift SFGs.
Acknowledgments
We thank the anonymous referee whose comments and suggestions helped improve this paper. This work was partly financed by the Spanish Ministerio de Economía y Competitividad (MINECO) within the ESTALLIDOS project (AYA2013-47742-C4-2P and AYA2016-79724-C4-2-P). AL-C acknowledges financial support from MINECO PhD contract BES-2014-071055 and from grant EEBB-I-16-10913 for a short stay at St. Andrews University. JMA acknowledges support from the Spanish Ministerio de Economia y Competitividad (MINECO) under the grant AYA2017-83204-P. We thank J. Argyle for the help running the code PHI. We also thank R. García-Dias for help with the clustering algorithm and A. Dorta for his work with the computing system CONDOR. AL-C thanks A. S. Borlaff, S. Roca-Fábrega, and C. Gómez-Guijarro for the helpful discussions. This work has made use of the programming software R (R Core Team 2015) and the Python package astropy (Astropy Collaboration 2013; Price-Whelan et al. 2018).
References
- Abraham, R. G., Tanvir, N. R., Santiago, B. X., et al. 1996, MNRAS, 279, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Amorín, R., Aguerri, J. A. L., Muñoz-Tuñón, C., & Cairós, L. M. 2009, A&A, 501, 75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Amorín, R., Pérez-Montero, E., Vílchez, J. M., & Papaderos, P. 2012, ApJ, 749, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Argyle, J. J., Méndez-Abreu, J., Wild, V., & Mortlock, D. J. 2018, MNRAS, 479, 3076 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bauer, A. E., Hopkins, A. M., Gunawardhana, M., et al. 2013, MNRAS, 434, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bournaud, F., Elmegreen, B. G., & Elmegreen, D. M. 2007, ApJ, 670, 237 [Google Scholar]
- Bouveyron, C., Girard, S., & Schmid, C. 2007, Comput. Stat. Data Anal., 52, 502 [CrossRef] [MathSciNet] [Google Scholar]
- Brammer, G. B., van Dokkum, P. G., Franx, M., et al. 2012, ApJS, 200, 13 [Google Scholar]
- Brennan, R., Pandya, V., Somerville, R. S., et al. 2017, MNRAS, 465, 619 [NASA ADS] [CrossRef] [Google Scholar]
- Cairós, L. M., Caon, N., García-Lorenzo, B., Vílchez, J. M., & Muñoz-Tuñón, C. 2002, ApJ, 577, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Cairós, L. M., Caon, N., Papaderos, P., et al. 2003, ApJ, 593, 312 [NASA ADS] [CrossRef] [Google Scholar]
- Caon, N., Cairós, L. M., Aguerri, J. A. L., & Muñoz-Tuñón, C. 2005, ApJS, 157, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Cava, A., Schaerer, D., Richard, J., et al. 2018, Nat. Astron., 2, 76 [Google Scholar]
- Cepa, J., Aguiar, M., Escalera, V. G., et al. 2000, in Optical and IR Telescope Instrumentation and Detectors, eds. M. Iye, & A. F. Moorwood, Proc. SPIE, 4008, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Ceverino, D., Dekel, A., & Bournaud, F. 2010, MNRAS, 404, 2151 [NASA ADS] [Google Scholar]
- Davis, T. A., Alatalo, K., Sarzi, M., et al. 2011, MNRAS, 417, 882 [NASA ADS] [CrossRef] [Google Scholar]
- de Souza, R. E., Gadotti, D. A., & dos Anjos, S. 2004, ApJS, 153, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., & Burkert, A. 2014, MNRAS, 438, 1870 [NASA ADS] [CrossRef] [Google Scholar]
- Dellenbusch, K. E., Gallagher, III, J. S., Knezek, P. M., & Noble, A. G. 2008, AJ, 135, 326 [NASA ADS] [CrossRef] [Google Scholar]
- Di Matteo, P., Bournaud, F., Martig, M., et al. 2008, A&A, 492, 31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elmegreen, D. M., Elmegreen, B. G., & Hirst, A. C. 2004a, ApJ, 604, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, D. M., Elmegreen, B. G., & Sheets, C. M. 2004b, ApJ, 603, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, D. M., Elmegreen, B. G., Ravindranath, S., & Coe, D. A. 2007, ApJ, 658, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Fang, J. J., Faber, S. M., Koo, D. C., & Dekel, A. 2013, ApJ, 776, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Faucher-Giguère, C.-A. 2018, MNRAS, 473, 3717 [NASA ADS] [CrossRef] [Google Scholar]
- Fillingham, S. P., Cooper, M. C., Boylan-Kolchin, M., et al. 2018, MNRAS, 477, 4491 [NASA ADS] [CrossRef] [Google Scholar]
- Franx, M., & Illingworth, G. 1990, ApJ, 359, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Grebel, E. K. 1998, Highlights Astron., 11, 125 [NASA ADS] [Google Scholar]
- Greco, J. P., Goulding, A. D., Greene, J. E., et al. 2018, ApJ, 866, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Grogin, N. A., Kocevski, D. D., Faber, S. M., et al. 2011, ApJS, 197, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Y., Giavalisco, M., Ferguson, H., et al. 2012, ApJ, 757, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Hinojosa-Goñi, R., Muñoz-Tuñón, C., & Méndez-Abreu, J. 2016, A&A, 592, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hogg, D. W., Baldry, I. K., Blanton, M. R., & Eisenstein, D. J. 2002, ArXiv e-prints [arXiv:astro-ph/0210394] [Google Scholar]
- Hopkins, P. F., Croton, D., Bundy, K., et al. 2010, ApJ, 724, 915 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., McCracken, H. J., Le Fèvre, O., et al. 2013, A&A, 556, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Janowiecki, S., & Salzer, J. J. 2014, ApJ, 793, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Jin, Y., Chen, Y., Shi, Y., et al. 2016, MNRAS, 463, 913 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., White, S. D. M., et al. 2003, MNRAS, 341, 54 [Google Scholar]
- Kaviraj, S. 2014, MNRAS, 440, 2944 [NASA ADS] [CrossRef] [Google Scholar]
- Kelvin, L. S., Driver, S. P., Robotham, A. S. G., et al. 2014, MNRAS, 439, 1245 [NASA ADS] [CrossRef] [Google Scholar]
- Kennedy, R., Bamford, S. P., Baldry, I., et al. 2015, MNRAS, 454, 806 [NASA ADS] [CrossRef] [Google Scholar]
- Koekemoer, A. M., Faber, S. M., Ferguson, H. C., et al. 2011, ApJS, 197, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Koleva, M., Bouchard, A., Prugniel, P., De Rijcke, S., & Vauglin, I. 2013, MNRAS, 428, 2949 [NASA ADS] [CrossRef] [Google Scholar]
- La Barbera, F., de Carvalho, R. R., Gal, R. R., et al. 2005, ApJ, 626, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Lange, R., Driver, S. P., Robotham, A. S. G., et al. 2015, MNRAS, 447, 2603 [NASA ADS] [CrossRef] [Google Scholar]
- Lange, R., Moffett, A. J., Driver, S. P., et al. 2016, MNRAS, 462, 1470 [NASA ADS] [CrossRef] [Google Scholar]
- Ledinauskas, E., & Zubovas, K. 2018, A&A, 615, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lian, J. H., Kong, X., Jiang, N., Yan, W., & Gao, Y. L. 2015, MNRAS, 451, 1130 [NASA ADS] [CrossRef] [Google Scholar]
- Lumbreras-Calle, A., Muñoz-Tuñón, C., Méndez-Abreu, J., et al. 2019, A&A, 621, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- MacArthur, L. A., Courteau, S., Bell, E., & Holtzman, J. A. 2004, ApJS, 152, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Maltby, D. T., Almaini, O., Wild, V., et al. 2018, MNRAS, 480, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Mandelker, N., Dekel, A., Ceverino, D., et al. 2014, MNRAS, 443, 3675 [NASA ADS] [CrossRef] [Google Scholar]
- Martig, M., Bournaud, F., Teyssier, R., & Dekel, A. 2009, ApJ, 707, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Méndez-Abreu, J., Aguerri, J. A. L., Corsini, E. M., & Simonneau, E. 2008, A&A, 478, 353 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meyer, H. T., Lisker, T., Janz, J., & Papaderos, P. 2014, A&A, 562, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oliver, S., Frost, M., Farrah, D., et al. 2010, MNRAS, 405, 2279 [NASA ADS] [Google Scholar]
- Pandya, V., Brennan, R., Somerville, R. S., et al. 2017, MNRAS, 472, 2054 [NASA ADS] [CrossRef] [Google Scholar]
- Patel, S. G., van Dokkum, P. G., Franx, M., et al. 2013, ApJ, 766, 15 [Google Scholar]
- Paulino-Afonso, A., Sobral, D., Buitrago, F., & Afonso, J. 2017, MNRAS, 465, 2717 [NASA ADS] [CrossRef] [Google Scholar]
- Pawlik, M. M., Taj Aldeen, L., Wild, V., et al. 2018, MNRAS, 477, 1708 [NASA ADS] [CrossRef] [Google Scholar]
- Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Mach. Learning Res., 12, 2825 [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2002, AJ, 124, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez-González, P. G., Cava, A., Barro, G., et al. 2013, ApJ, 762, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Price-Whelan, A. M., Sipőcz, B. M., Günther, H. M., et al. 2018, AJ, 156, 123 [Google Scholar]
- R Core Team. 2015, R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing (Vienna, Austria) [Google Scholar]
- Sánchez Almeida, J., Muñoz-Tuñón, C., Elmegreen, D. M., Elmegreen, B. G., & Méndez-Abreu, J. 2013, ApJ, 767, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez Almeida, J., Elmegreen, B. G., Muñoz-Tuñón, C., et al. 2015, ApJ, 810, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez-Janssen, R., Méndez-Abreu, J., & Aguerri, J. A. L. 2010, MNRAS, 406, L65 [NASA ADS] [Google Scholar]
- Sersic, J. L. 1968, Atlas de Galaxias Australes [Google Scholar]
- Shibuya, T., Ouchi, M., & Harikane, Y. 2015, ApJS, 219, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Skelton, R. E., Whitaker, K. E., Momcheva, I. G., et al. 2014, ApJS, 214, 24 [Google Scholar]
- Smethurst, R. J., Lintott, C. J., Simmons, B. D., et al. 2015, MNRAS, 450, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Sparre, M., Hayward, C. C., Feldmann, R., et al. 2017, MNRAS, 466, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Starkenburg, T. K., Helmi, A., & Sales, L. V. 2016, A&A, 595, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stierwalt, S., Besla, G., Patton, D., et al. 2015, ApJ, 805, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Taniguchi, Y., Kajisawa, M., Kobayashi, M. A. R., et al. 2015, PASJ, 67, 104 [NASA ADS] [Google Scholar]
- Tasca, L. A. M., Le Fèvre, O., Hathi, N. P., et al. 2015, A&A, 581, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tolstoy, E., Hill, V., & Tosi, M. 2009, ARA&A, 47, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Tortora, C., Napolitano, N. R., Cardone, V. F., et al. 2010, MNRAS, 407, 144 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bergh, S., Abraham, R. G., Ellis, R. S., et al. 1996, AJ, 112, 359 [NASA ADS] [CrossRef] [Google Scholar]
- van der Wel, A., Franx, M., van Dokkum, P. G., et al. 2014, ApJ, 788, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Vulcani, B., Bamford, S. P., Häußler, B., et al. 2014, MNRAS, 441, 1340 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, E., Kong, X., Wang, H., et al. 2017, ApJ, 844, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, E., Li, C., Xiao, T., et al. 2018, ApJ, 856, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Whitaker, K. E., Franx, M., Leja, J., et al. 2014, ApJ, 795, 104 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Wright, A. C., Brooks, A. M., Weisz, D. R., & Christensen, C. R. 2019, MNRAS, 482, 1176 [NASA ADS] [CrossRef] [Google Scholar]
- Wuyts, S., Förster Schreiber, N. M., van der Wel, A., et al. 2011, ApJ, 742, 96 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Creating the Hα images
In this appendix we explain in detail the process we followed to create the Hα images, depending on the redshift of the galaxy.
z < 0.266 and z > 0.298
For galaxies with z < 0.266 or z > 0.298, the process is quite straightforward. Band A (with Hα contamination) is F775W in the lower redshift case and F850LP in the higher redshift case. Band B (with only stellar continuum in its wavelength range) is F850LP in the lower redshift case and F775W in the higher redshift case. We then have
where FA and FB are the total fluxes in each band, CA and CB the continua, and Hα the line flux. Subtracting, and taking into account the scaling factor f = CA/CB between the continua computed from the SHARDS SED fits in Paper I we obtain:
0.266 < z < 0.298
For galaxies with 0.266 < z < 0.298, both F775W and F850LP are contaminated by Hα; therefore, the previous approach is unfeasible. The use of the F606W filter as continuum is impossible because it is affected by [OIII] and Hβ contamination (and other filters would be too distant in wavelength). We consider then:
We have then:
Computing the scaling factor f = CF775W/CF850LP between the continua:
Substituting in the second equation, we obtain:
All Tables
Physical properties, synthetic magnitudes, and class to which each galaxy belongs.
All Figures
 |
Fig. 1. Flowchart summarizing the process of choosing the appropriate fits and masks. The numbers in boxes (a) and (b) give the median number of galaxies in the sample, considering all masks, for each one of the four filters in ACS (from top to bottom, F435W, F606W, F775W, and F850LP) and the three in WFC3 (F125W, F140W, and F160W). The numbers in box (c) give the number of galaxies in each band fulfilling all criteria, after choosing the final mask. |
| In the text | |
 |
Fig. 2. Example of a galaxy from our sample without a mask (panel a) and with the three different Hα detection masks over it: 2σ (panel b), 1.5σ (panel c) and 1.1σ (panel d). The horizontal line represents a 1 kpc distance. |
| In the text | |
 |
Fig. 3. Distribution of the main photometric parameters derived for our ELG sample. Upper left panel: values of the effective radius of the best-fit Sérsic model for the galaxies in each filter, in kpc. Upper right panel: histogram of the Sérsic index, lower left panel: axis ratio q, and lower right panel: surface brightness at the effective radius (after applying the cosmological dimming and K corrections). |
| In the text | |
 |
Fig. 4. Example of two galaxies from our sample, with the original image and the Hα detection mask overlaid on it (left column), the Sérsic model (central column) and the residuals from the fit (right column). All images are presented with the same color scale, shown in the central color bar (in counts). |
| In the text | |
 |
Fig. 5. Example of the K-correction process. The composite stellar population model (from Paper I) is shown as a black line. The green triangles represent the integrated flux of the galaxy in each HST band. The pink circles are the expected flux in each HST band, considering only the stellar population model. The gray dots are the expected U, V and J fluxes considering the model. The K-correction is the difference between these fluxes and the expected values in the nearest HST filters. |
| In the text | |
 |
Fig. 6. UVJ diagram for the Sérsic models of the host galaxies of the sample (gray triangles). The blue circles represent the integrated colors of the entire galaxies derived from the SED models obtain in Paper I. The black lines represent the separation between passive galaxies (top left) and SFGs taken from Whitaker et al. (2014). |
| In the text | |
 |
Fig. 7. Examples of g − r color profiles for two galaxies in the sample. Top: galaxy with a flat color profile. Bottom: galaxy with a negative color gradient. The vertical dashed (solid) line shows the effective radius in the g(r) band. The green line represents the percentage of the area of the galaxy masked as a function of radius. |
| In the text | |
 |
Fig. 8. Classification of galaxies based on effective radius, Sérsic index, and U − V color into classes A and B (see text). Red and blue dots are galaxies belonging to class A and B with probability p > 0.8, respectively. Pink and cyan dots are galaxies that belong to class A and B with 0.8 ≥ p > 0.5, respectively. The parameters used in this plot are the median values for each galaxy across all bands. |
| In the text | |
 |
Fig. 9. Histogram of U − V color for the starburst galaxies in Hinojosa-Goñi et al. (2016). In red, Sknot galaxies, in green Sknot+diffuse, and in blue Mknot. The vertical lines represent the median values of each subsample, with the same color code. |
| In the text | |
 |
Fig. 10. Mass-size relation of our sample of galaxies: galaxies that belong to class B (blue dots), and class A (red dots). The shaded blue (red) area is the 1σ limit for a linear fit to the blue (red) dots, using bootstrap and Monte Carlo simulations. The lines represent mass-size relations found in the literature (see legend). Lines are continuous until they reach the mass limit for each sample, from where we point extrapolations to lower masses as dashed lines. |
| In the text | |
 |
Fig. 11. Surface mass density of the galaxies in the sample as a function of galaxy mass. The line is an extrapolation of the relation presented in Fig. 4 of Fang et al. (2013) to fit galaxies in the red sequence and the green valley. Red and blue circles represent galaxies in class A and B, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} I(R)=I_{\rm e} \exp \left\{ -b_n \left[ \left(\frac{R}{R_{\rm e}}\right)^{1/n}-1 \right] \right\} \end{aligned} $$](/articles/aa/full_html/2019/12/aa35288-19/aa35288-19-eq51.gif)