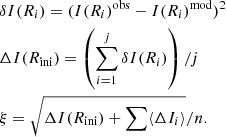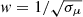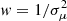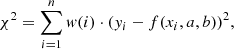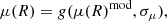| Issue |
A&A
Volume 632, December 2019
|
|
|---|---|---|
| Article Number | A128 | |
| Number of page(s) | 20 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201935144 | |
| Published online | 16 December 2019 | |
A new fitting concept for the robust determination of Sérsic model parameters⋆
1
Instituto de Astrofísica e Ciências do Espaço – Centro de Astrofísica da Universidade do Porto, Rua das Estrelas, 4150-762 Porto, Portugal
e-mail: Iris.Breda@astro.up.pt
2
Departamento de Física e Astronomia, Faculdade de Ciências, Universidade do Porto, Rua do Campo Alegre, 4169-007 Porto, Portugal
3
University of Vienna, Department of Astrophysics, Türkenschanzstr. 17, 1180 Vienna, Austria
4
Instituto de Astrofísica e Ciências do Espaço, Universidade de Lisboa, OAL, Tapada da Ajuda, PT1349-018 Lisboa, Portugal
5
Departamento de Física, Faculdade de Ciências da Universidade de Lisboa, Edifício C8, Campo Grande, PT1749-016 Lisboa, Portugal
Received:
28
January
2019
Accepted:
30
September
2019
Context. The Sérsic law (SL) offers a versatile, widely used functional form for the structural characterization of galaxies near and far. Whereas fitting this three-parameter function to galaxies with a genuine SL luminosity distribution (e.g., several local early-type galaxies–ETGs) yields a robust determination of the Sérsic exponent η and effective surface brightness μeff, this is not necessarily the case for galaxies whose surface brightness profiles (SBPs) appreciably deviate, either in their centers or over an extended radius interval, from the SL (e.g., ETGs with a “depleted” core and nucleated dwarf ellipticals, or most late-type galaxies-LTGs). In this general case of “imperfect” SL profiles, the best-fitting solution may significantly depend on the radius (or surface brightness) interval fit, the photometric passbands considered and the specifics of the fitting procedure (photometric uncertainties of SBP data points or image pixels, and corrections for point spread function (PSF) convolution effects). Such uncertainties may then affect, in a non-easily predictable manner, automated structural studies of large heterogeneous galaxy samples and introduce a scatter, if not a bias, in galaxy scaling relations and their evolution across redshift (z).
Aims. Our goal is to devise a fitting concept that permits a robust determination of the equivalent SL model for the general case of galaxies with imperfect SL profiles.
Methods. The distinctive feature of the concept proposed here (iFIT) is that the fit is not constrained through standard χ2 minimization between an observed SBP and the SL model of it, but instead through the search for the best match between the observationally determined and theoretically expected radial variation of the mean surface brightness and light growth curve. This approach ensures quick convergence to a unique solution for both perfect and imperfect Sérsic profiles, even shallow and resolution-degraded SBPs. iFIT allows for correction of PSF convolution effects, offering the user the option of choosing between a Moffat, Gaussian, or user-supplied PSF. iFIT, which is a standalone FORTRAN code, can be applied to any SBP that is provided in ASCII format and it has the capability of convenient graphical storage of its output. The iFIT distribution package is supplemented with an auxiliary SBP derivation tool in python.
Results. iFIT has been extensively tested on synthetic data with a Sérsic index 0.3 ≤ η ≤ 4.2 and an effective radius 1 ≤ Reff (″)≤20. Applied to non PSF-convolved data, iFIT can infer the Sérsic exponent η with an absolute error of ≤ 0.2 even for shallow SBPs. As for PSF-degraded data, iFIT can recover the input SL model parameters with a satisfactorily accuracy almost over the entire considered parameter space as long as FWHM(PSF) ≤ Reff. This study also includes examples of applications of iFIT to ETGs and local low-mass starburst galaxies. These tests confirm that iFIT shows little sensitivity on PSF corrections and SBP limiting surface brightness, and that subtraction of the best-fitting SL model in two different bands generally yields a good match to the observed radial color profile.
Conclusions. It is pointed out that the publicly available iFIT offers an efficient tool for the non-supervised structural characterization of large galaxy samples, as those expected to become available with Euclid and LSST.
Key words: galaxies: photometry / galaxies: structure / galaxies: fundamental parameters / techniques: photometric / galaxies: starburst / galaxies: elliptical and lenticular / cD
A copy of the code is available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/632/A128
© ESO 2019
1. Introduction
The Sérsic fitting law (SL; also referred to as generalized de Vaucouleurs law, Sérsic 1963, 1968) is a widely used functional form in structural studies of galaxies, and intimately linked to our understanding on several key astrophysical subjects, such as the nature of bulges (e.g., Davies et al. 1988, for a review) and the size growth of early-type galaxies (ETGs) since z ∼ 2 (e.g., Trujillo et al. 2006; Buitrago et al. 2017). Following initial applications of it to surface brightness profiles (SBPs) of ETGs (Caon et al. 1993), this functional form is now implemented in several state-of-the-art 1D and 2D surface photometry packages1 and routinely applied to galaxy images as a whole (e.g., Hoyos et al. 2011; van der Wel et al. 2012; Guo et al. 2013; Lange et al. 2015) or in bulge-disk decomposition studies (e.g., Andredakis et al. 1995; Courteau et al. 1996; Gadotti 2009).
Its simple, three-parameter functional form, that defines a SBP at the photometric radius R⋆ (″) as
with μ0 (mag/□″) and α (″) denoting the central surface brightness and an angular pseudo-scale length, and the shape parameter η regulating the profile curvature offers a versatile means for approximating a wide variety of galaxy profiles, from those of nearly exponential type I galactic disks (η ≈ 1) to the centrally steeply increasing SBPs of massive ETGs, with the specific case of η ≈ 4 corresponding to the de Vaucouleurs (1948) law. Another popular formulation of the SL involves the mean surface brightness μeff at the effective radius Reff therein (cf. Eq. (2)); η being coupled to these parameters through a normalization factor (Caon et al. 1993; Trujillo et al. 2001a, for details).
Since the 1990s, the SL has attracted a great deal of interest, with several studies exploring its mathematical formulation and the couplings between its free parameters (e.g., Graham & Colless 1997; Trujillo et al. 2001a; Graham & Driver 2005; Graham et al. 2005), stellar-dynamical origin (e.g., Márquez 2000; Cen 2014), intrinsic luminosity density distribution it corresponds to (e.g., Ciotti 1991; Papaderos 1993; Papaderos et al. 1996a; Chakrabarty & Jackson 2009; Baes & Gentile 2011; Baes & Van Hese 2011), and the connection between η and light concentration indices (Graham et al. 2001), and the Gini coefficient (Lotz et al. 2004; Cibinel et al. 2013).
Some examples echoing the importance placed on the SL include the broad usage of η as a discriminator between classical bulges and pseudo-bulges (e.g., Gadotti 2009; Fisher & Drory 2008, 2011; Neumann et al. 2017) and proxy to the bulge-to-total (B/T) ratio (Lang et al. 2014), bulge morphology (e.g., Fabricius et al. 2012; Lange et al. 2015), central velocity dispersion (Graham 2002) and super-massive black hole mass (SMBH; Graham et al. 2001; Savorgnan et al. 2016). The importance of the SL in our understanding on galaxy taxonomy and scaling relations is also reflected in the debate on the classical giant vs. dwarf galaxy dichotomy (established mainly from fitting King models to SBPs, cf. e.g., Binggeli & Cameron 1991, 1993) that vanishes on the μ0 vs. η plane, suggesting that dwarf ellipticals (dEs) are essentially the lower-luminosity extension of bright ETGs (Graham & Guzman 2003; Graham 2011). Likewise, the trend for increasing η with increasing optical ETG luminosity – already apparent from early photographic work by Binggeli & Cameron (1993) and the analysis by Caon et al. (1993) has prompted the proposal of it being a useful extragalactic distance indicator (Young & Currie 1994, see, however, Binggeli & Jerjen 1998). Moreover, the SL was found to yield a good approximation to the stellar mass surface density (Σ⋆, B) profiles of galaxy bulges since z ∼ 2 (Lang et al. 2014), which underscores its versatility as a tool for the systematization of galaxy physical properties.
Despite the indisputable virtues of the SL, some lines of evidence suggest caution in the way its shape parameter η is derived and interpreted in the evolutionary context of galaxies. One limitation stems both from its mathematical nature and the specifics of its fitting to galaxy SBP data points via standard χ2-minimization (e.g., through the Levenberg–Marquardt nonlinear fitting algorithm; Levenberg 1944; Marquardt 1963). For instance, Graham et al. (2001) demonstrate that inherent to the mathematical nature of the SL is a correlation between η and Reff (cf. Eq. (2)). This parameter coupling was also described from an empirical point of view in Noeske et al. (2003) as a degeneracy between η and the pseudo-scale length α in Eq. (1). As the latter authors and Cairós et al. (2003) remark, fitting Eq. (1) to a genuine (perfect) Sérsic profile robustly recovers its three parameters, almost regardless of the radius (or μ) interval considered. However, in the case of an imperfect Sérsic profile (iSP), that is a SBP that strictly follows the SL over only a limited interval in R⋆, the fit can substantially depend on the radius (or μ) interval considered. This rather obvious fact has actually non-trivial implications regarding the uniqueness of the best-fitting SL model and its applicability to the structural characterization of galaxies.
One may enumerate several examples of local galaxies with iSP light distributions – both mono-component systems with a nearly spatially uniform stellar mass-to-light ratio (ℳ/ℒ; e.g., ETGs), as well as composites of young and old stellar populations of differing spatial extent that mimic a high-η Sérsic profile. A third class of pseudo-SL profiles can result from the excitation of an extended nebular halo around a compact starburst or active galaxy (Papaderos & Östlin 2012). Whereas such extreme objects are scarce in the local universe, they are presumably ubiquitous at high redshift, that is, in the epoch when most galaxies have experienced the dominant phase of their build-up (e.g., Stark et al. 2009; Schaerer & de Barros 2010; Steidel et al. 2014).
An example for the first type of iSPs is given by massive luminous (MV ≲ −21.5) ETGs with a “depleted” core, prompting the need for a modified SL function (e.g., the 6-parameter core-SL function proposed in Graham et al. 2003, see also Trujillo et al. 2004). A precise quantification of these central deviations from the SL is of considerable interest in the light of their documented connection with the ETG radio and X-ray power (Bender et al. 1989) that could hold clues to the buildup history and nuclear energy sources of these systems. For instance, the “light deficit” relative to inward extrapolation of the SL model, if due to core evacuation by a binary SMBH (Begelman et al. 1980; Ebisuzaki et al. 1991; Merritt 2006), could be used to constrain the SMBH mass and yield insights into the growth of SMBHs and their interaction with the galaxy host, as well as on the role of mergers on the buildup of ETGs (e.g., Bonfini et al. 2018, and references therein).
A similar type of iSPs is presented by a subset of dEs with exponential profiles with a flat core (type V SBPs in the notation by Binggeli & Cameron 1993)2. While this kind of SBPs can, in first order, be approximated by a single SL with a η< 1, the best-fitting set of η and α (or Reff) depend on the μ interval considered: fits to shallow images being restricted to the core-dominated region typically yield a η≲ 0.5, whereas deeper images, capturing the outer exponential intensity fall-off yield a η ∼ 1 (e.g., Noeske et al. 2003).
A significant dependence of the fit on the μ range considered is also to be expected when a single SL model is applied to an iSP galaxy with an additional luminosity component, as for example a compact bulge or bar, circumnuclear star formation (SF) ring or the sharp central luminosity excess of nucleated dEs (Binggeli & Cameron 1991; De Propris et al. 2005) or Seyfert galaxies (e.g., Xanthopoulos 1996; Slavcheva-Mihova & Mihov 2010). For instance, Balcells et al. (2003), point out from a combined analysis of SBPs from ground based and Hubble Space Telescope (HST) data that smearing of a central point source with the adjacent emission in a bulge of η = 1.7 can lead to an artificial increase of η to ∼4, mimicking a de Vaucouleurs profile. Likewise, Méndez-Abreu et al. (2008) and Breda (2014) find that decomposition of a barred late-type galaxy (LTG) solely into a bulge and a disk (i.e., omitting the bar) can strongly bias the best-fitting SL model for the bulge. More generally, errors arising from an incomplete or inadequate 1D or 2D parametric decomposition scheme can be systematic, therefore potentially of greater concern than formal fitting uncertainties.
In all these cases of iSPs, prior knowledge of the photometric structure of a galaxy facilitates integration in an image decomposition scheme of the parametric ingredients needed for an exact modeling of a galaxy, including the luminosity fraction owing to a bona fide SL component (as an example, the parametrization of a nucleated type-V dE as due to the superposition of a core-SL model plus a central Gaussian). This is a rather theoretical option, however, at least in what concerns compact (or higher-z) galaxies: structural details in the centers of these systems are rarely visually accessible due to limited spatial resolution and smearing with the point spread function (PSF), and can only be obtained after a multi-stage photometric analysis (inspection of fitting residuals and color morphology, unsharp masking, wavelet decomposition or Lucy 1974 deconvolution). As a result, a suitable adaptation of SBP decomposition schemes is impractical in studies of individual galaxies and prohibitively complex in the case of automated structural studies of large galaxy samples, which by necessity mostly employ a single SL to model galaxy images (e.g., Simard 1998; Marleau & Simard 1998; Griffith et al. 2012; van der Wel et al. 2012).
Quite importantly, since possible deviations from the SL in central parts of galaxies involve precisely those pixels with the highest signal-to-noise ratio (S/N) and therefore smallest photometric uncertainties σμ, they could have a strong and non-easily predictable impact on any error-weighted image decomposition (for instance, bulge-disk decomposition into two SL components, one of them with a fixed η = 1 that accounts for the disk). This problem is further aggravated by the fact that the central low-σμ data points are most strongly affected by PSF convolution effects. As pointed out in Papaderos et al. (1996a, see also Ribeiro et al. 2016), the fact that in error-weighted profile decomposition the solution is driven by these innermost (lowest-σμ) data points may lead to a systematic failure of the model to describe the lower-surface brightness (LSB) periphery of galaxies: in bulge-disk decomposition studies, preference to the innermost points can lead to an artificial “compactification” of the disk (overestimation of its central surface brightness together with underestimation of its exponential scale length), which in turn results in the underestimation of the luminosity of the bulge.
The second category of iSPs is due to the superposition of evolutionary and spatially distinct stellar populations, and rather frequent among local star-forming galaxies, such as blue compact dwarfs (BCDs; Loose & Thuan 1986a; Papaderos et al. 1996a; Cairós et al. 2001; Gil de Paz et al. 2003). Except for very few cases (see below) starburst activity in these systems takes place in one or several knots embedded within a more extended old elliptical stellar host. BCDs showing a central confinement of SF (∼20% of the local BCD population, classified as nuclear-elliptical according to the scheme of Loose & Thuan 1986a) typically exhibit high-η (3–4) iSP SBPs (e.g., Haro 2 and Haro 3, Loose & Thuan 1986b; Papaderos et al. 1996a), reaching in some cases a η > 6 (Bergvall & Östlin 2002). Given the strong radial color gradients (up to ∼2 B − R mag kpc−1 out to 1–2 host galaxy exponential scale lengths α; cf. Papaderos et al. 1996b, 2002), the best-fitting η for these systems can substantially depend on the photometric passband and the radius interval considered in the fit. Without multi-band photometry or spectroscopic information, BCDs and their “cohorts” (e.g., compact narrow emission-line galaxies or green peas (GPs); cf. Koo et al. 1994; Cardamone et al. 2009; Izotov et al. 2011; Amorín et al. 2012), being omnipresent at higher-z’s, are therefore solely on the basis of their high η hardly distinguishable from compact passive ETGs.
Finally, an even more extreme class of iSPs – exceptionally rare in the nearby universe yet probably omnipresent at high z’s – are those presented by compact galaxies with a very high specific star formation rate (sSFR), such as the extremely metal-poor (12 + log(O/H) ≈ 7.2) BCDs I Zw 18 (Sargent & Searle 1970; Izotov et al. 2001) and SBS 0335-052 E (e.g., Izotov et al. 1990; Papaderos et al. 1998; Herenz et al. 2017). These systems experience a vigorous starburst episode that gives rise to a large ionized gas envelope reaching out to several kpc away from their stellar component. Since the nebular halo of starburst galaxies shows a nearly exponential Hα profile (Papaderos et al. 2002; Knollmann 2005), its superposition with the more compact stellar emission results in a two-slope exponential profile that is barely distinguishable from a high-η Sérsic profile, as discussed in Papaderos & Östlin (2012). As shown by these authors, fitting a SL to this kind of iSP profiles can lead to an increasing Sérsic exponent η with decreasing limiting surface brightness μlim, from η≃ 1 when shallow imaging allows only for detection of the inner (stellar emission dominated) exponential part of the SBP to 1 ≤ η ≤ 5 when deeper imaging data additionally enable detection of the surrounding shallower exponential nebular halo. Therefore, depending on the rest-frame μlim of the imaging data in hand, such extreme starburst galaxies at high-z could readily be misclassified as massive ETGs on the basis of their high-η pseudo-Sérsic profiles3. This obviously applies to any system hosting a powerful central source of energy and momentum that is capable of exciting an extended nebular envelope, such as quasars. Moreover, the fact that escaping and resonantly scattered Lyman-α radiation, both in quasars (Steidel et al. 2011; Borisova et al. 2016; Wisotzki et al. 2016; Villar-Martín et al. 2018; Arrigoni Battaia et al. 2018; Wisotzki et al. 2018; Cantalupo et al. 2019) and starburst galaxies (Hayes et al. 2007), leads to nearly exponential rest-frame UV halos suggests that iSPs similar to those of I Zw 18 could be ubiquitous among galaxies in the early universe.
Summarizing, whereas the Sérsic law arguably gives a good first-order match to a wide range of observed galaxy SBPs and offers a convenient means for their quantitative characterization, it is actually only a subset of local galaxies (e.g., a part of ETGs) that display genuine (perfect) SL profiles in all optical-NIR photometric bands and across their entire radial extent. In fact, a large number of galaxies in the local universe, and the more so at high z’s, shows appreciable-to-strong deviations from the SL. The modeling of such imperfect Sérsic-like SBPs can strongly depend on the specifics of fitting, correction for PSF convolution effects and depth (μlim) of the data in hand. These fitting uncertainties pose a significant obstacle to the automatized application of the SL to large galaxy samples and can propagate into significant scatter in fundamental galaxy relations.
In view of such considerations it appears worthwhile to explore a robust and computationally inexpensive SL fitting concept that can be applied in an unsupervised manner (e.g., without need for an initial guess to the SL model parameters, like in GALFIT, or a prior “training” on local galaxies, like in the case of convolutional neural networks, e.g., Huertas-Company et al. 2015, among others) and having little sensitivity to μlim and PSF convolution effects. Such a tool would be valuable to the automated structural characterization of the vast number of high-z irregular iSP galaxies expected to be detected with, for instance, the Euclid satellite and the Large Synoptic Survey Telescope (LSST).
The fact that the galaxy morphology drastically changes toward high-z’s, with an increasing fraction of, for example, clumpy disks (Elmegreen et al. 2009; Wisnioski et al. 2013; Shibuya et al. 2015; Guo et al. 2015) and cometary (also referred to as tadpole) and “chain” galaxies (Elmegreen et al. 2007; Straughn et al. 2006) underscores the need for fitting the SL without prior assumptions on morphology and structure (e.g., the B/T ratio or Gini coefficient) that are largely empirically established from analysis of lower-z galaxy samples.
In this article, we present such a concept, which is realized in the publicly available code iFIT4 and validated both on local Hubble-type galaxies (Breda & Papaderos 2018; Breda 2019, and this study) and irregular star-forming galaxies, such as BCDs. A distinctive feature of iFIT is that the fit to a galaxy is not determined through standard error-weighted χ2 minimization with respect to individual SBP data points, but instead through the search for the best-fitting equivalent SL model (hereafter eSP) that gives the best match both to the observed light growth curve and variation of the mean surface brightness ⟨Ii⟩ with R⋆. Basing the fitting procedure on the latter robust quantities facilitates quick convergence to a unique solution both for perfect and imperfect Sérsic profiles without the need for an initial guess to fitting parameters. Quite importantly, a key advantage of iFIT over standard SL fitting tools is that the solution is not driven by the innermost (R⋆ ≲ FWHM) data points that enclose a typically minor fraction (< 10%) of the total luminosity and can strongly suffer from PSF degradation. iFIT, supplemented with the capability of retrieving SL model parameters even from strongly PSF-degraded galaxy images offers a handy tool for the structural characterization of galaxies (or sub-components thereof, e.g., bulges) near and far.
In Sect. 2 we outline the concept of iFIT and in Sect. 3 we provide a brief description of its invocation and output. A quantitative assessment of the ability of iFIT to retrieve the Sérsic model parameters from synthetic SBPs (both unconvolved and convolved with a PSF model) spanning a relevant range in η and μlim is given in Sect. 4. This section also provides examples of the application of iFIT to irregular starburst galaxies, exemplified by the BCDs He 2–10 and I Zw 18. Finally, Sect. 5 summarizes the main conclusions from this study, Appendix A gives a description of results obtained with iFIT for a sample of local ETGs and two distant (z = 0.768 & 1.091) galaxies and Appendix B provides an empirical rationale for the advantage of adopting alternative weights when performing weighted least squares to retrieve the correct parameters in the case of iSP’s.
At this stage iFIT is merely a standalone code that can be applied to any SBP provided in ASCII format. It is intended as a module of a versatile galaxy decomposition package under development that will offer a suite of functional forms, including a core-SL function (Graham et al. 2003), a centrally flattening modified exponential function (Papaderos et al. 1996a), Ferrer profiles, the Nuker law (Lauer et al. 1995), and King profiles (Elson 1999), among others, for approximating galaxy SBPs and their structural components. For convenience, the iFIT distribution package is supplemented by a python tool that allows for the computation of SBPs with the algorithm by Bender & Möllenhoff (1987).
2. Methodology
A widely used alternative formulation of the SL is:
where, Reff is defined as the photometric radius that encloses 50% of the total luminosity of a SBP, μeff is the surface brightness at Reff and bη is given by Γ(2η) = 2γ(2η, bη), with Γ and γ standing for the incomplete and complete gamma functions, respectively (Ciotti 1991). The factor bη ensures that the radius Reff encloses 50% of the total (out to R⋆ = ∞) luminosity of the SBP. At variance to the approximation bη = 1.9992η − 0.3271 proposed by Graham et al. (2005) we adopted the asymptotic expansion given by Eq. (18) of Ciotti & Bertin (1999).
Below, we summarize the main features of the adopted methodology.
2.1. Preparatory steps & Integration
iFIT starts by converting the input surface brightness profile (μ, mag/□″) into a radial intensity distribution I(R) (counts/□″), which is subsequently integrated out to the maximum observed radius Rmax (Fig. 1):
 |
Fig. 1. Pseudo-code illustrating principal steps of the convergence procedure in iFIT. |
where I(R⋆) is 10(μ(R⋆)−C)/ − 2.5 and C denotes a calibration constant in mag. Before integration, spline interpolation is performed by means of TSPACK, a curve-fitting package based on exponential tension splines with automatic selection of tension factors (Renka 2009) that is publicly available for several programming languages. Due to the drastic steepening of high Sérsic η profiles at small R⋆, traditional cubic spline interpolation techniques fail to accurately reproduce the I(R⋆) curve, which results in major errors in 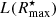 . Whenever errors (σμ) are provided along with an SBP, they are interpolated and taken into account in the fit.
. Whenever errors (σμ) are provided along with an SBP, they are interpolated and taken into account in the fit.
2.2. Estimation of flux-enclosing parameters
The latter permits estimation of a sequence of radii R40, R50, R60, R70, R80, R90 and R100 that enclose an increasing fraction of 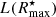 (40, 50, 60, 70, 80, 90% and 100%, respectively) along with the corresponding mean intensity levels (⟨I40⟩, ⟨I50⟩, ⟨I60⟩, ⟨I70⟩, ⟨I80⟩, ⟨I90⟩ and ⟨I100⟩) therein. The mean intensity ⟨Ii⟩ corresponding to each
(40, 50, 60, 70, 80, 90% and 100%, respectively) along with the corresponding mean intensity levels (⟨I40⟩, ⟨I50⟩, ⟨I60⟩, ⟨I70⟩, ⟨I80⟩, ⟨I90⟩ and ⟨I100⟩) therein. The mean intensity ⟨Ii⟩ corresponding to each 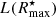 percentages (i) is computed as
percentages (i) is computed as
As we will detail next, at variance to traditional SL fitting techniques, iFIT determines the solution by evaluating the difference (model vs. observed SBP) for these ⟨Ii⟩, this way preventing the few innermost points to dictate the fit. As apparent from the middle panel of Fig. 2, these central points with the highest intensity, which are most affected by PSF convolution effects, actually encompass a rather small fraction of 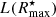 (≲10%, depending on η). Furthermore, the concept of iFIT secures a more robust solution against deviant SBP points due to, for instance, an incompletely removed overlapping Galactic star or a high-z background source that pops up only in red passbands, since the latter have generally a small effect on
(≲10%, depending on η). Furthermore, the concept of iFIT secures a more robust solution against deviant SBP points due to, for instance, an incompletely removed overlapping Galactic star or a high-z background source that pops up only in red passbands, since the latter have generally a small effect on 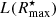 and the galaxy’s light growth curve.
and the galaxy’s light growth curve.
 |
Fig. 2. Example a Sérsic profile μ(R⋆) with a η = 3 and an effective radius Reff = 3″ (solid line). Top panel: vertical dashed lines correspond to the radii enclosing 40, 50, 60, 70, 80 and 90% of |
2.3. Determination of Reff & μeff
One of the advantages of the presented algorithm is that in early stages of the convergence procedure it fixes two (Reff & μeff) of the three free parameters of Eq. (2), which in turn alleviates the degeneracy between Reff and η. This is done through a preliminary linear regression in y = μ(R⋆) vs. x = R1/η, where η is allowed to vary from 0.3 to 8.0. By employing least squares method for the functional form μ(R⋆) = m ⋅ R1/η + b, one obtains for each adopted η the effective radius Reff and the corresponding μ from the slope m and the y-axis intercept b as:
If a σμ array is provided by the user, the previous step is repeated by performing weighted linear regression with the weight of each SBP point set to (a) 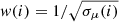 , (b) w(i) = 1/σμ(i) and (c) w(i) = 1/σμ(i)2. Repeating the convergence procedure three times (obtaining three solutions) allows iFIT to estimate errors for the parameters of the SL equation5. For this reason we advice the user to supply σμ values in the 3rd column of the ASCII file holding the SBP to be fit.
, (b) w(i) = 1/σμ(i) and (c) w(i) = 1/σμ(i)2. Repeating the convergence procedure three times (obtaining three solutions) allows iFIT to estimate errors for the parameters of the SL equation5. For this reason we advice the user to supply σμ values in the 3rd column of the ASCII file holding the SBP to be fit.
If the input SBP is convolved with a PSF, in order to ensure that the degraded resolution does not affect the determination of Reff and μeff, the linear regression is computed only for SBP data points within a radius R⋆ > 3 × FWHM of the PSF. We note that in cases of strong PSF degradation (when FWHM/Reff > 1 − 2) and a shallow input SBP that contains less than 90% of the total luminosity (that is, a SBP truncated at the radius R90 ≃ 4 × Reff in the case of the example in Fig. 2), iFIT might not be able to obtain a sensible solution (see Fig. 5 for acquaintance of iFIT limitations). This should not be perceived, however, as a limitation that is exclusive to iFIT, since any surface photometry code presumably fails under such conditions.
2.4. Estimating the Sérsic η for non-seeing convolved profiles
This module integrates a fundamental and novel aspect of the concept presented here: its goal is to estimate η through the search for the best match between the seven observationally determined ⟨Ii⟩’s (i = 40, 50, 60, 70, 80, 90 and 100) with the theoretically expected values. Basing the solution on the 7 aforementioned robust quantities is an important advantage as compared to standard χ2 minimization with respect to SBP data points, and results in a unique eSP to any SBP, namely, both to a perfect and imperfect SL profile. In the first case, the deviation between model and SBP data points is obviously zero. Specifically, convergence is achieved through comparison of the theoretical Ri and ⟨Ii⟩ for a grid of synthetic SL profiles in the range 0.3 ≤η≤ 8.0, adopting the respective Reff and μeff for each η obtained in the previous step.
where i stands for a percentage of 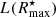 and n is the number of terms inside the square root. The η that yields the closest match between the theoretical and observed quantities (the absolute minimum in ξ) is selected as the best-fitting eSP to a SBP. This set of multiple constraints yields a robust and unique solution for η, eliminating the risk of being trapped in a local minimum, as may occur with standard nonlinear fitting algorithms whose best-fitting solution might depend on the initial guess and the selection (or σμ) of individual data points.
and n is the number of terms inside the square root. The η that yields the closest match between the theoretical and observed quantities (the absolute minimum in ξ) is selected as the best-fitting eSP to a SBP. This set of multiple constraints yields a robust and unique solution for η, eliminating the risk of being trapped in a local minimum, as may occur with standard nonlinear fitting algorithms whose best-fitting solution might depend on the initial guess and the selection (or σμ) of individual data points.
2.5. Estimating the Sérsic model parameters for seeing convolved profiles
iFIT allows to recover the SL parameters from a SBP that is convolved by a Gaussian or Moffat (Moffat 1969) PSF. The latter is given by
Additionally, iFIT allows for correction for a user-supplied PSF in ASCII format. In the latter case, a Moffat model is fit to that PSF and the parameters αM & βM are determined with MINPACK (Moré et al. 1984), a publicly available set of subroutines that solves nonlinear least-squares problems using a modified version of the Levenberg–Marquardt algorithm. If, on the other hand, the user does not have an observationally determined ASCII profile for the PSF, iFIT offers the alternative of rendering the FWHM (″) of the PSF for a Moffat or Gaussian function (in the first case βM is assumed to be 4.765, Trujillo et al. 2001b; and ∞ for a Gaussian).
Once an analytic model for the PSF has been defined, iFIT constructs, similar to the treatment of non-convolved profiles, a set of synthetic SBPs by varying η and subsequently convolving each one with the PSF. The procedure to find the correct η is the same as the one described under Sect. 2.4 with the only difference being that the quantities ⟨ΔIi⟩ now refer to PSF-convolved synthetic SBPs. Another difference lies in Eq. (6) which in this case includes an extra term that facilitates quick convergence: as shown in Fig. 2, although the innermost points account for a small fraction of the total luminosity, they dominate in terms of intensity. This implies that, especially for high-ηSL profiles, ⟨ΔI40⟩ and ⟨ΔI50⟩ are similar for different η’s. The introduction of an additional single term that compares the observed surface brightness at the innermost SBP points with those of the model at the same radius eases convergence to the correct solution (ΔI(Rini) is defined as the sum of the differences between observations (I(Ri)obs) and model (I(Ri)mod) for the set of points that lay within the first observed point (i = 1) and point i = j – the first observational point where the derivative increases, that is, f′(i)|i = j > f′(i)|i = j − 1).
Finally, after convergence to a solution, iFIT computes the difference between model and observation providing an estimate for the goodness of the fit.
3. Application of iFIT
iFIT requires as minimum input the SBP of the galaxy in a two-column ASCII file holding the photometric radius R⋆ (″) and corresponding surface brightness μ(R⋆) (mag/□″), with the option of including photometric uncertainties σμ(i) in a third column. If the SBP is to be modeled taking into account PSF convolution effects, the user needs to additionally provide the PSF in the same two-column format as the input SBP, or indicate the FWHM (″) of a Moffat or Gaussian approximation to the PSF. In its current public release, iFIT is provided along with an auxiliary routine that permits computation of SBPs through a python implementation of the 2D photometry code by Bender & Möllenhoff (1987).
iFIT exports the results from the fit into three files, one of those holding a graphical representation of the input SBP and the SL model of it in postscript (.ps) format (see Appendix A for a complete explanation). Of the two additional ASCII files, the first one (name_of_input_file.SProf.dat) stores the obtained SL model in a two-column format for non-PSF-convolved SBPs and with four columns in the case of PSF-convolved data where the last two columns list the convolved SL model. The second ASCII output file, name_of_input_file.Results.dat, contains the three parameters of the SL best-fitting model (η, Reff and μeff), apparent magnitude, absolute magnitude (whenever the distance to the galaxy is provided), central surface brightness μ(R⋆ = 0) of the model as well as an estimate on the quality of the fit (0, 1 and 2 for, respectively, a adequate, moderate and inadequate fit).
A cookbook provided along with the distribution of iFIT (v.1) contains examples of the invocation of the code for different choices on the PSF (cf. Fig. 3).
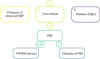 |
Fig. 3. Scheme of input and output quantities, and available provisions for the PSF model to be taken into account, where “y” stands for “yes”, “n” for “no”, “G/M” for a Gaussian or Moffat PSF model, and “U” for a non-PSF-convolved SBP. |
Some examples are:
-
fitting a SBP that is convolved with a Moffat PSF with a FWHM of 0.5 arcsec:
$ iFIT SBP_file.dat y M 0.5 0
-
fitting a SBP that is convolved with a PSF provided by the user in ASCII format:
$ iFIT SBP_file.dat y U PSF_file.dat 0
-
fitting the SBP of a galaxy at a distance of 10 Mpc without taking PSF convolution effects into account:
$ iFIT SBP_file.dat n 10
4. Assessment of the accuracy of iFIT
In order to assess the ability of iFIT to infer the Sérsic model parameters we created an extended grid of synthetic profiles covering the relevant parameter range 0.3 ≤ η ≤ 4.2 and 1 ≤ Reff ≤ 20 in steps of 0.1 and 1″, respectively. A second grid of synthetic profiles was created by convolving these SBPs with Moffat PSF models with a FWHM between 0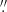 5 and 2″ in steps of 0
5 and 2″ in steps of 0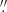 5. Furthermore, these mock SBPs were truncated at the radius enclosing 90, 95 and 99% of the total luminosity in order to simulate different limiting
5. Furthermore, these mock SBPs were truncated at the radius enclosing 90, 95 and 99% of the total luminosity in order to simulate different limiting 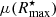 . The results are discussed in the following sections.
. The results are discussed in the following sections.
4.1. Testing iFIT on unconvolved synthetic profiles
Here we examine the absolute deviation Δη between input and output η for the studied range in η and Reff. We consider three cases of non-PSF-convolved Sérsic SBPs enclosing 90%, 95% and 99% of 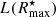 . It should be noted that for the case illustrated in Fig. 2 truncation of the profile at R90 implies a limiting surface brightness μlim ≲ 25 mag/□″ that corresponds to a rather shallow exposure. As apparent from Fig. 4, for perfect Sérsic profiles containing 99% of the total SBP luminosity, the code recovers η over the entire considered parameter range with no error, whereas fits to shallow (90% & 95% of
. It should be noted that for the case illustrated in Fig. 2 truncation of the profile at R90 implies a limiting surface brightness μlim ≲ 25 mag/□″ that corresponds to a rather shallow exposure. As apparent from Fig. 4, for perfect Sérsic profiles containing 99% of the total SBP luminosity, the code recovers η over the entire considered parameter range with no error, whereas fits to shallow (90% & 95% of 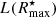 ) SBPs yield an error of typically less than 0.1 in η. Regarding the other two SL parameters, iFIT recovers Reff & μeff with a maximum absolute error of 0
) SBPs yield an error of typically less than 0.1 in η. Regarding the other two SL parameters, iFIT recovers Reff & μeff with a maximum absolute error of 0 4, 0
4, 0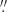 01 and ∼0″ & 0.06 mag, 0.01 mag and ∼0 mag for profiles enclosing 90%, 95% and 99% of
01 and ∼0″ & 0.06 mag, 0.01 mag and ∼0 mag for profiles enclosing 90%, 95% and 99% of 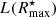 , respectively. Given that the correct recovery of η is tightly connected to that of the other parameters, with other words, failure to determine one of the three SL parameters normally implies global failure of the fit, the topology of ΔReff and Δμeff is similar to that of Δη.
, respectively. Given that the correct recovery of η is tightly connected to that of the other parameters, with other words, failure to determine one of the three SL parameters normally implies global failure of the fit, the topology of ΔReff and Δμeff is similar to that of Δη.
 |
Fig. 4. Absolute deviation Δη between estimated and input η as a function of η and the effective radius Reff (″) for the case of unconvolved Sérsic profiles encompassing 90, 95 and 99% of the total luminosity (upper, middle and lower panel, respectively). The vertical color bar corresponds to Δη = |ηin − ηout| between 0 and 1. |
4.2. Testing iFIT on PSF-convolved synthetic profiles
The situation is obviously more demanding in the case of seeing-degraded Sérsic SBPs, where the ability of any code to recover the input η depends on the degree of PSF smearing.
Figure 5 shows the results for synthetic SBPs covering the range 0.3 ≤ η ≤ 4.2, 1 ≤ Reff(″)≤20 and 0.025 ≤ FWHM/Reff ≤ 2.
 |
Fig. 5. Absolute deviation Δη between estimated and input η as a function of η and FWHM/Reff for the case of Sérsic SBPs enclosing 90% (left panel), 95% (middle panel) and 99% (right panel) of the total luminosity after convolution with a Moffat PSF with 0.5 ≤ FWHM/Reff ≤ 2, whereby 1 ≤ Reff (″)≤20. |
As apparent from Fig. 5, iFIT faithfully recovers η across the entire range of input values as long as the FWHM of the PSF does not appreciably exceed the profile effective radius. On the other hand, even for SBPs that contain 99% of the total luminosity (right panel) there is a region in the parameter space where iFIT fails to recover the correct η (and consequently also Reff and μeff), especially but not exclusively for very low-η profiles. This happens when FWHM/Reff> 1, suggesting that in order for iFIT to converge into an accurate η, the PSF must be lower than Reff. This is actually a generous limit given that, for a FWHM/Reff> 1, a structural analysis becomes increasingly problematic. For instance, in the case of a disk-dominated LTG this situation would imply that the FWHM of the PSF is equivalent to 1.7 exponential disk scale lengths. In the even more extreme case of both strongly PSF-degraded and shallow SBPs, specifically, when Rmax is on the order of 3 × FWHM, iFIT is unsurprisingly unable to correctly estimate Reff and μeff, therefore also η (see Sect. 2.3, item 3). Such a situation applies, however, to high-z compact galaxies observed under natural seeing (FWHM ∼ 1.3″ in the case of the Sloan Digital Sky Survey-SDSS) and for which the rest-frame 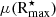 is probably restricted due to cosmological dimming. If, however, higher-angular resolution data with, for example, the HST (maximum
is probably restricted due to cosmological dimming. If, however, higher-angular resolution data with, for example, the HST (maximum 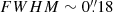 ) are available for such galaxies, iFIT permits an accurate (Δη ≤ 0.1) determination of η. As for |ΔReff|, in the range 0.025 < FWHM/Reff < 1 the maximal errors were found to be 0
) are available for such galaxies, iFIT permits an accurate (Δη ≤ 0.1) determination of η. As for |ΔReff|, in the range 0.025 < FWHM/Reff < 1 the maximal errors were found to be 0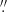 76, 0
76, 0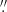 37 and 0
37 and 0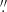 34 for profiles enclosing 90%, 95% and 99% of
34 for profiles enclosing 90%, 95% and 99% of 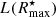 , respectively. Regarding |Δμeff|, in the same range of FWHM/Reff, maximal deviations between input and retrieved values are 0.78 mag, 0.43 mag and 0.22 mag. As in the previous situation, the variation of the quantities |ΔReff| and |Δμeff| across FWHM/Reff is similar to that of |Δη|. On the grounds of this error analysis, and from Fig. 5, it is advisable to not use iFIT when the PSF (FWHM) is larger than the Reff of the observed profile, specially when the imaging data are shallow.
, respectively. Regarding |Δμeff|, in the same range of FWHM/Reff, maximal deviations between input and retrieved values are 0.78 mag, 0.43 mag and 0.22 mag. As in the previous situation, the variation of the quantities |ΔReff| and |Δμeff| across FWHM/Reff is similar to that of |Δη|. On the grounds of this error analysis, and from Fig. 5, it is advisable to not use iFIT when the PSF (FWHM) is larger than the Reff of the observed profile, specially when the imaging data are shallow.
4.3. Testing iFIT on early-type galaxies
iFIT was tested on g and r band images for 121 local ETGs from the SDSS (see Appendix A for details). The images were sky-subtracted, rotated to the astronomical orientation, corrected for Galactic extinction following the prescriptions by Schlafly & Finkbeiner (2011) and, whenever necessary, corrected for foreground Galactic stars by substituting them by the mean intensity of the adjacent stellar continuum. Finally, the frames were trimmed and SBPs were computed from 2D models obtained with the function FIT/ELL3 (based on an algorithm by Bender & Möllenhoff 1987) within the package SURFPHOT of ESO-MIDAS6. Photometric uncertainties for SBP data points were computed following Papaderos et al. (1996a, hereafter P96a). Modeling with iFIT was performed by taking into account the PSF, as determined from typically three non-saturated Galactic stars in each frame.
It was found that, although some PSF models yield a visually better fit at small radii, they generally play a minor role on the determination of the SL parameters (see Fig. A.1). This demonstrates the robustness of the algorithm. As an additional check, fits were repeated for 24 randomly selected ETGs from SDSS in the r- and g-band that were intentionally inaccurately sky subtracted, such as to leave residuals at the level up to ∼3 times the sky noise. This test has shown that the result does not greatly depend on the quality of the background subtraction, given an average difference of 0.1 ± 0.11 in η and 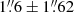 in Reff as compared to the previously determined values.
in Reff as compared to the previously determined values.
Another key test has addressed whether subtraction of the best-fitting SL model of SBPs in two different passbands yields a radial color profile that well matches the observed one. This was found to be indeed the case for the majority of the sample, as illustrated in Fig. 6 for three randomly selected ETGs. More specifically, a comparison of the derived η for the ETG sample in the two filters yields an average difference |ηr − ηg|/ηr of 0.08. This value, and its small dispersion (σ = 0.07) attests a smooth variation of η across wavelength and is consistent with the similarity of the SBPs of these systems in both bands, as apparent from the very weak g–r radial color gradients of the galaxies (Fig. 6) for R⋆ ≳ 3″. This is also due to the concept of iFIT, specifically, the fact that the SL solution is constrained on the basis of robust ⟨Ii⟩’s rather than by directly fitting the SBP data points. This an advantage over standard concepts: for instance, a study with GALFIT of 17 massive galaxies from dos Reis et al. (in prep.) yields an average difference |ηH − ηI|/ηH of ∼0.38 between solution in the I and H band, whereas for the same sample iFIT returns 0.22. The fact that standard fitting tools may give in some cases discordant η’s in different bands (which might be partly due to imperfections in the PSF models used) is a known issue that has been dealt with by different teams. For instance, the MegaMorph extension of GALFIT (Häußler et al. 2013) integrates a prescription that forces η to vary smoothly across wavelength within a narrow, empirically estimated interval. Such a mechanism is unnecessary in the case of iFIT, which in all studied cases yields a good match between predicted and observed radial color profiles.
 |
Fig. 6. Observed g-r radial color profile (filled circles) vs. difference between the best-fitting Sérsic model with iFIT for g- and r-band images (blue curve) for three randomly selected ETGs from SDSS. |
4.4. Application of iFIT to irregular starburst galaxies
iFIT may have a wide range of applications on irregular galaxies, such as local BCDs/GPs and the majority of unevolved galaxies in the early universe. The structural analysis of such systems with standard tools poses a significant challenge given their clumpiness and asymmetry, the absence of a clear geometrical center and an axis-symmetric morphological pattern that could be easily integrated in a parametric decomposition scheme. The fact that the intensity maximum (i.e., the usually visually chosen “galaxy center”) for such rapidly assembling systems may spatially differ across wavelength, due to SF propagation and strong detached nebular emission (cf. e.g., Papaderos et al. 1996a, 1998, 2002, for such cases among BCDs), as well as the redshift-dependent μlim, due to cosmological dimming, further complicate the situation. A robust determination of the best-fitting eSP model for such galaxies would be desirable in the context of an automated structural characterization of large galaxy samples with data from, for instance, Euclid and LSST. Since, from the morphological point of view, local BCDs can be considered the best local analogs of unevolved low-mass galaxies at high-z, it is worth testing applications of iFIT to such systems. As an illustrative example, we show in Fig. 7 the SL model obtained with iFIT for the BCD Henize 2–10 by fitting B and R images taken with the Danish 1.54 m telescope at La Silla (see Papaderos & Fricke 1998, for details). It can be seen that, iFIT yields for both filters similar Sérsic model parameters, despite a difference by 4 mag in the adopted μlim. The stability of the best-fitting SL solution with iFIT is to be contrasted with studies of BCDs with GALFIT, which, as pointed out by Amorín et al. (2007), show a strong dependence on the surface brightness interval considered.
 |
Fig. 7. Left panel: true-color image composite of archival broad- and narrow-band HST images for the central region of the BCD Henize 2–10, illustrating the morphological complexity of stellar emission (green and blue) within its starburst component, as well as the presence of strong Hα emission (red) excited by the chain of super-star clusters (zoom-in in the upper panel) discovered by Conti & Vacca (1994). Middle panel: contour map of He 2–10, computed from ground-based data. The morphology of the starburst component and of the underlying older host galaxy is delineated by contours in blue and red, respectively. The horizontal bar corresponds to 20″. Right panel: B- and R-band SBPs of He 2–10, computed with the 2D surface photometry code by Bender & Möllenhoff (1987). The overlaid curves show SL fits with iFIT down to a surface brightness μlim between 24 and 28 mag/□″. It can be seen that in all cases the Sérsic model parameters inferred for both bands are mutually consistent and show little dependence on μlim. |
Another case is represented by I Zw 18, an extremely metal-poor BCD that is immersed within an extended nebular halo contributing ≳1/3 of its total R-band luminosity (Papaderos et al. 2002). As shown in Papaderos & Östlin (2012), the R-band profile of this galaxy (SBP1) reflects the superposition of two nearly exponential luminosity components differing in their scale length α and central surface brightness μ0, namely the steep inner component that is primarily due to stellar emission and dominates down to ∼24.5 mag/□″, and the surrounding shallower nebular envelope. The best-fitting η for the combined SBP depends on the limiting surface brightness, being ∼1.2 for a μlim ≤ 24.5 mag/□″ and reaching an η ∼ 2 for a μlim ≃ 29 mag/□″ (dashed gray curve in Fig. 8). Would the nebular envelope present a shallower profile under preservation of its total luminosity (for instance, a by a factor 2 larger exponential scale length α and by 1.5 mag dimmer central surface brightness μ0), then the best-fitting η for the combined stellar+nebular profile (SBP2) would increase from 2.5 for μlim = 26 mag/□″ to up to ∼5 for μlim > 28 mag/□″ (dashed-dotted gray curve in Fig. 8). In the latter case, a marginally resolved distant morphological analog of I Zw 18 (e.g., a high-sSFR compact galaxy or quasar surrounded by an extended Lyα envelope) could, purely on the basis of its high η, be misclassified as an evolved ETG.
 |
Fig. 8. Left panel: true-color image composite of I Zw 18 produced from archival HST data, showing the extended nebular halo of the BCD (adapted from Papaderos & Östlin 2012). The horizontal bar corresponds to 5″. Upper-right panel: SL model with iFIT (blue) to the observed R-band SBP of I Zw 18 (SBP1; from Papaderos & Östlin 2012). The inset shows a Moffat model of the PSF (see appendix for further explanations) and the fit residuals are displayed in the lower diagram. Bottom panel: variation of the best-fitting Sérsic index η vs. limiting surface brightness μlim obtained by Papaderos & Östlin (2012) for SBP1 and SBP2 using standard χ2 minimization (gray dashed and dashed-dotted curve, respectively). Open and filled circles show the result obtained with iFIT by modeling both SBPs down to a μlim between 23.5 mag/□″ and 29 mag/□″. |
Repeated modeling of SBP1&2 with iFIT (Fig. 8) reveals a far weaker dependence of the SL solution on μlim: even for a μlim ≃ 29 mag/□″, the inferred η reaches maximal values of ∼1.7 and ∼2.5 for SBP1 and SBP2, respectively. These lower η’s better reflect the fact that ∼2/3 of the optical luminosity of I Zw 18 originates from the steeper stellar emission-dominated inner exponential component. Therefore, the concept of luminosity- and ⟨Ii⟩-weighted inference of Sérsic model parameters in iFIT gives credit to those parts of a SBP that contribute most to the total emission while at the same time providing a good match to a SBP as a whole. On the other hand, this fact alone does not mean that fitting an eSP to such composite stellar + nebular profiles offers a meaningful approach to the structural characterization of compact, high-sSFR galaxies like I Zw 18. Supplementary or alternative approaches might be worth considering, as for example an analysis of the variation of η as a function of μlim, as a possible diagnostic for an outer shallow exponential slope, in conjunction with the core-envelope color contrast technique by Papaderos & Östlin (2012, cf. their Fig. 15) that permits identification of systems surrounded by an extended nebular envelope. Indeed, the recent realization that such systems are virtually omnipresent at high z’s (e.g., Wisotzki et al. 2018), as conjectured by Papaderos & Östlin (2012), calls for an exploration of suitable approaches for their structural and morphological characterization.
This also applies to the morphologically diverse population of generally irregular galaxies at high z. For instance, a fraction of ∼10% of these systems show cometary morphology (also referred to as tadpoles; Elmegreen et al. 2007; Straughn et al. 2006, see also Förster-Schreiber et al. 2011 for further examples at z ∼ 2) that is due to the confinement of intense SF activity at the one tip of an elongated stellar host or clumpy proto-disk. Interestingly, cometary morphology is rather common among extremely metal-poor (12 + log(O/H) ≤ 7.6) young dwarf galaxy candidates in the local universe (Papaderos et al. 2008; Morales-Luis et al. 2011), which points to its association with early and intermediate stages of dwarf galaxy evolution.
1D surface photometry is obviously insufficient for a full characterization of such irregular elongated galaxies, since, following the standard definition, a SBP records the photometric radius R⋆ of the circle subtending the same area 𝒜 as the isophote of a galaxy at each surface brightness level μ. This sacrifices important morphological information (e.g., the variation of ellipticity ϵ, position angle PA and α4 across μ), unless the SBP determination is supplemented by a Fourier analysis of the best-fitting ellipses to galaxy isophotes (e.g., Carter 1978; Loose & Thuan 1986b; Bender et al. 1988; Caon et al. 1993). In the case of cometary/tadpole galaxies and other irregular systems that strongly depart from axis-symmetry, the determination of 𝒜 via fitting of ellipses to isophotes (or extraction of an SBP within concentric elliptical apertures with fixed center, PA and ϵ) is non-optimal. Preferable SBP extraction techniques in those cases involve the computation of 𝒜 through a line integral along isophotes or summation of pixels above an intensity threshold (cf. methods ii & iii in P96a, see also Loose & Thuan 1986b). A probably even better approach is to compute photon statistics within irregular isophotal annuli (isan) that closely trace the morphology of a galaxy at each μ-intervall (Papaderos et al. 2002, see also Noeske et al. 2003, 2005, 2006 for its application to local and higher-z star-forming galaxies). This technique, eventually supplemented by a Fourier analysis of isan jointly with quantitative morphology indicators (e.g., asymmetry index) might offer a promising avenue to the characterization cometary and irregular galaxies near and far. Such an approach, combined with iFIT, would probably be preferable to currently existing parametric 2D photometry tools since all latter are essentially tied to the simplifying assumption that galaxies can be approximated by a superposition of axis-symmetric components. It should also be noted that most structural quantities inferred from 2D photometry and considered in galaxy studies are actually converted into 1D quantities. For instance, one finally adopts one single value for the Sérsic index η instead of its best-fitting value along the major and minor axis light profile, although these two can substantially differ from one another (e.g., Ferrari et al. 2004). The same applies to the model-dependent Reff, which despite its intrinsic coupling with η is widely used as a measure of the “size” of a galaxy.
In the light of the above considerations it appears worthwhile to further explore quantitative morphological and structural indicators for irregular cometary/tadpole galaxies. Devising methods for the identification and characterization of such elongated systems near and far appears to be timely given that they may have an appreciable impact on the weak lensing signal (Pandya et al. 2019) with, for instance, Euclid.
5. Summary and conclusions
In this article, we present iFIT, a simple yet robust algorithm for fitting a Sérsic model of galaxy SBPs. At variance to standard SL fitting routines that employ direct χ2 minimization between fit and individual SBP data points (or image pixels), the distinctive characteristic of iFIT is that it identifies the best-fitting SL model of a SBP through the search for the best match between the observationally determined and theoretically expected light growth curve and radial variation of the mean surface brightness. This novel concept therefore effectively ties the fit solution to robust photometric quantities (instead of individual SBP data points that can be subject to large uncertainties) and warrants quick convergence to a unique solution, even for shallow and resolution-degraded SBPs of galaxies showing significant deviations from the SL. Indeed, a series of tests on synthetic and observed SBPs indicate that solutions with iFIT generally show little dependence both on limiting surface brightness, quality of sky subtraction and PSF convolution effects, as well as on the photometric band considered. The reliability of the code is further underscored by the fact that subtraction of the SL models independently obtained with iFIT for local early-type galaxies in two different filters closely reproduces the observed radial color profile. Furthermore, the capability of iFIT to robustly infer the best-fitting equivalent Sérsic model for irregular galaxies that strongly deviate from the SL (as most high-z galaxies) is demonstrated on the analysis of the local BCDs He 2–10 and I Zw 18. For these reasons, and given that iFIT does not require an initial guess to SL model parameters, it offers a robust and computationally inexpensive tool for the automated structural analysis of galaxies near and far.
Examples include GIM2D (Simard 1998; Simard et al. 2002), GALFIT (Peng et al. 2002, 2010, and extensions of it, e.g., GALAPAGOS, Barden et al. 2012, MegaMorph, Häußler et al. 2013, GALFIT-CORSAIR Bonfini 2014, and BUDDI, Johnston et al. 2017), BUDDA (de Souza et al. 2004), GASP2D (Méndez-Abreu et al. 2008), ARCHANGEL (Schombert & Smith 2012), IMFIT (Erwin 2015), PROFILER (Ciampur 2016) and PROFIT (Robotham et al. 2017).
Such centrally flattening exponential SBPs were also found in the underlying host of several BCDs (Papaderos et al. 1996a; Noeske et al. 2003) and hypothesized to arise from its adiabatic expansion in response to starburst-driven mass loss (Fukunaga-Nakamura & Tosa 1989; Papaderos et al. 1996b).
Due to severe ionized gas contamination of these sources, and depending on their redshift and available photometric passbands, their observed colors could superficially support this erroneous conclusion (cf. discussion and Fig. 15 in Papaderos & Östlin 2012).
Available at www.iastro.pt/research/tools.html, along with instructions for its usage, as well as observed and synthetic images for demonstration and test purposes.
Appendix B contains a detailed explanation supporting the use of the modified weights.
Acknowledgments
We would like to thank the anonymous referee for numerous valuable comments and suggestions. We thank the European taxpayer, who in the spirit of solidarity between EU countries has offered to Portugal a substantial fraction of the financial resources that allowed it to sustain a research infrastructure in astrophysics. Specifically, the major part of this work was carried out at an institute whose funding is provided to ∼85% by the EU via the FCT (Fundação para a Ciência e a Tecnologia) apparatus, through European and national funding via FEDER through COMPETE by the grants UID/FIS/04434/2013 & POCI-01-0145-FEDER-007672 and PTDC/FIS-AST/3214/2012 & FCOMP-01-0124-FEDER-029170. Additionally, this work was supported by FCT/MCTES through national funds (PIDDAC) by this grant UID/FIS/04434/2019. We acknowledge support by European Community Programme (FP7/2007-2013) under grant agreement No. PIRSES-GA-2013-612701 (SELGIFS). I.B. was supported by the FCT Ph.D.::SPACE Doctoral Network (PD/00040/2012) through the fellowship PD/BD/52707/2014 funded by FCT (Portugal) and POPH/FSE (EC) and by the fellowship CAUP-07/2014-BI in the context of the FCT project PTDC/FIS-AST/3214/2012 & FCOMP-01-0124-FEDER-029170, as well as by the fellowship CIAAUP-19/2019-BIM within the scope of the research unit Instituto de Astrofísica e Ciências do Espačo (IA). P.P. was supported through Investigador FCT contract IF/01220/2013/CP1191/CT0002 and by a contract that is supported by FCT/MCTES through national funds (PIDDAC) and by grant PTDC/FIS-AST/29245/2017. J.M.G. is supported by the fellowship CIAAUP-04/2016-BPD in the context of the FCT project UID/FIS/04434/2013 & POCI-01-0145-FEDER-007672 and acknowledges the previous support by the fellowships SFRH/BPD/66958/2009 funded by FCT and POPH/FSE (EC) and DL 57/2016/CP1364/CT0003. SA gratefully acknowledge support from the Science and Technology Foundation (FCT, Portugal) through the research grants PTDC/FIS-AST/29245/2017 and UID/FIS/04434/2019. We thank Sandra dos Reis for granting us access to her results with GALFIT prior to publication. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
References
- Amorín, R., Muñoz-Tuñón, C., Aguerri, J. A. L., Cairós, L. M., & Caon, N. 2007, A&A, 467, 541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Amorín, R., Pérez-Montero, E., Vílchez, J. M., Papaderos, P. 2012, ApJ, 749, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Andredakis, Y., Peletier, R., & Balcells, M. 1995, MNRAS, 275, 874 [NASA ADS] [CrossRef] [Google Scholar]
- Arrigoni Battaia, F., Hennawi, J. F., Prochaska, J. X., et al. 2018, MNRAS, 482, 3162 [Google Scholar]
- Aitken, A. 1936, Proc. R. Soc. Edinburgh, 55, 42 [Google Scholar]
- Baes, M., & Gentile, G. 2011, A&A, 525, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baes, M., & Van Hese, W. 2011, A&A, 534, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balcells, M.,Graham, A. W., Domínguez-Palmero, L., & Peletier, R. F. 2003, ApJ, 582, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Barden, M., Häußler, B., Peng, C. Y., et al. 2012, MNRAS, 422, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Begelman, M. C., Blandford, R. D., & Rees, M. J. 1980, Nature, 287, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Bender, R., & Möllenhoff, C. 1987, A&A, 177, 71 [NASA ADS] [Google Scholar]
- Bender, R., Döbereiner, S., & Möllenhof, C. 1988, A&AS, 74, 385 [NASA ADS] [Google Scholar]
- Bender, R., Surma, P., Doebereiner, S., et al. 1989, A&A, 217, 35 [NASA ADS] [Google Scholar]
- Bergvall, N., & Östlin, G. 2002, A&A, 390, 891 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Binggeli, B., & Cameron, L. M. 1991, A&A, 252, 27 [NASA ADS] [Google Scholar]
- Binggeli, B., & Cameron, L. M. 1993, A&AS, 98, 297 [NASA ADS] [Google Scholar]
- Binggeli, B., & Jerjen, H. 1998, A&A, 333, 17 [NASA ADS] [Google Scholar]
- Bond, N. A., Gardner, J. P., De Mello, D. F., et al. 2014, ApJ, 791, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Bonfini, P. 2014, PASP, 126, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Bonfini, P., Bitsakis, T., Zezas, A., et al. 2018, MNRAS, 473, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Borisova, E., Cantalupo, S., Lilly, S. J., et al. 2016, ApJ, 831, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Breda, I. 2014, MSc Thesis, University of Porto [Google Scholar]
- Breda, I. 2019, Ph.D. Thesis, University of Porto [Google Scholar]
- Breda, I., & Papaderos, P. 2018, A&A, 614, 48 [Google Scholar]
- Buitrago, F., Trujillo, I., Curtis-Lake, E., et al. 2017, MNRAS, 466, 4888 [NASA ADS] [Google Scholar]
- Cairós, L. M., Vílchez, J. M., & Gonzàlez Pérez, L. M., 2001, ApJS, 133, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Cairós, L. M., Caon, N., Papaderos, P., et al. 2003, ApJ, 593, 312 [NASA ADS] [CrossRef] [Google Scholar]
- Cantalupo, S., Pezzulli, G., Lilly, S. L., et al. 2019, MNRAS, 483, 5188 [NASA ADS] [CrossRef] [Google Scholar]
- Carter, D. 1978, MNRAS, 182, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Cardamone, C., Schawinski, K., & Sarzi, M. 2009, MNRAS, 399, 1191 [NASA ADS] [CrossRef] [Google Scholar]
- Caon, N., Capaccioli, M., & D’Onofrio, M. 1993, MNRAS, 265, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Cen, R. 2014, ApJ, 790, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Chakrabarty, D., & Jackson, B. 2009, A&A, 498, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ciampur, B. C. 2016, PASA, 33, e062 [NASA ADS] [CrossRef] [Google Scholar]
- Cibinel, A., Carollo, C. M., Lilly, S. J., et al. 2013, ApJ, 776, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Ciotti, L. 1991, A&A, 249, 99 [NASA ADS] [Google Scholar]
- Ciotti, L., & Bertin, G. 1999, A&A, 352, 447 [NASA ADS] [Google Scholar]
- Conti, P. S., & Vacca, W. D. 1994, ApJ, 423, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Courteau, S., de Jong, R. S., & Broeils, A. H. 1996, ApJ, 457, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, J. I., Phillipps, S., Cawson, M. G. M., et al. 1988, MNRAS, 232, 239 [NASA ADS] [CrossRef] [Google Scholar]
- De Propris, R., Phillipps, S., Drinkwater, M. J., et al. 2005, ApJ, 623, L105 [NASA ADS] [CrossRef] [Google Scholar]
- de Vaucouleurs, G. 1948, Ann. Astrophys., 11, 247 [Google Scholar]
- de Souza, R. E., Gadotti, D. A., & dos Anjos, S. 2004, ApJS, 153, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Ebisuzaki, T., Makino, J., & Okumura, S. K. 1991, Nature, 354, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, D. M., Elmegreen, B. G., Ravindranath, S., & Coe, D. A. 2007, ApJ, 658, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, D. M., Elmegreen, B. G., Marcus, M. T., et al. 2009, ApJ, 701, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Elson, R. A. 1999, in Stellar Dynamics in Globular Clusters, eds. C. Martinez Roger, P. Fournon, & F. Sanchez (Cambridge: Cambridge University Press), 10th Canary Islands Winter School of Astrophysics: Globular clusters, 209 [CrossRef] [Google Scholar]
- Erwin, D. 2015, ApJ, 799, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Fabricius, M. H., Saglia, R. P., Fisher, D. B., et al. 2012, ApJ, 754, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrari, F., Dottori, H., Caon, N., et al. 2004, MNRAS, 347, 824 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, D. B., & Drory, N. 2008, AJ, 136, 773 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, D. B., & Drory, N. 2011, ApJ, 716, 942 [Google Scholar]
- Förster-Schreiber, N., Shapley, A. E., Genzel, R., et al. 2011, ApJ, 739, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Fukunaga-Nakamura, A., & Tosa, M. 1989, PASJ, 41, 953 [NASA ADS] [Google Scholar]
- Gadotti, D. A. 2009, MNRAS, 393, 1531 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, A. W., Trujillo, I., & Caon, N. 2001, AJ, 122, 1707 [NASA ADS] [CrossRef] [Google Scholar]
- Gil de Paz, A., Madore, B. F., & Pevunova, O. 2003, ApJS, 147, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, A. W. 2002, MNRAS, 334, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, A. W. 2011, in A Universe of Dwarf Galaxies, Conf. Proc. (Lyon, June 14-18, 2010), EAS, 48, 231G [Google Scholar]
- Graham, A., & Colless, M. 1997, MNRAS, 287, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, A., & Driver, S. 2005, PASA, 22, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, A. W., & Guzman, R. 2003, AJ, 125, 2936 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, A. W., Erwin, P., Caon, N., & Trujillo, I. 2001, ApJ, 563, 11 [Google Scholar]
- Graham, A. W., Erwin, P., Trujillo, I., & Asensio, Ramos A. 2003, AJ, 125, 2951 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, A., Driver, S., Petrosian, V., et al. 2005, AJ, 130, 1535 [NASA ADS] [CrossRef] [Google Scholar]
- Griffith, R. L., Cooper, M. C., & Newman, J. A. 2012, VizieR Online Data Catalog, II/200 [Google Scholar]
- Guo, Y., Ferguson, H. C., Giavalisco, M., et al. 2013, ApJS, 207, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Y., Ferguson, H. C., Bell, E. F., et al. 2015, ApJ, 800, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Häuß ler, B., Bamford, S. P., Vika, M., et al. 2013, MNRAS, 430, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Hayes, M., Östlin, G., Atek, H., et al. 2007, MNRAS, 382, 1465 [NASA ADS] [Google Scholar]
- Herenz, E. C., Hayes, M., Papaderos, P., et al. 2017, A&A, 606, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hoyos, C., den Brok, M., Kleijn, G. V., et al. 2011, MNRAS, 411, 2439 [NASA ADS] [CrossRef] [Google Scholar]
- Huertas-Company, M., Gravet, R., Cabrera-Vives, G., et al. 2015, ApJS, 221, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Illingworth, G. D., Magee, D., Oesch, P. A., et al. 2013, ApJS, 209, 6 [Google Scholar]
- Izotov, Y. I., Lipovetsky, V. A., Guseva, N. G., et al. 1990, Nature, 343, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Chaffee, F. H., Foltz, C. B., et al. 2001, ApJ, 560, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Guseva, N. G., & Thuan, T. X. 2011, ApJ, 728, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Jiménez-Teja, Y., Benítez, N., Molino, A., & Fernandes, C. A. C. 2015, MNRAS, 453, 1136 [NASA ADS] [CrossRef] [Google Scholar]
- Johnston, E. J., Häußler, B., Aragón-Salamanga, A., et al. 2017, MNRAS, 465, 2317 [NASA ADS] [CrossRef] [Google Scholar]
- Knollmann, S. R. 2005, Diploma Thesis, University of Göttingen [Google Scholar]
- Koo, D. C., Bershady, M. A., Wirth, G. D., et al. 1994, ApJ, 427, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Lang, P., Wuyts, S., Somerville, R., et al. 2014, ApJ, 788, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Lange, R., Driver, S. P., Robotham, A. S. G., et al. 2015, MNRAS, 447, 2603 [NASA ADS] [CrossRef] [Google Scholar]
- Lauer, T. R., Ajhar, E. A., Byun, Y.-I., et al. 1995, AJ, 110, 2622 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levenberg, K. 1944, QApMa, 2, 164 [Google Scholar]
- Loose, H. H., & Thuan, T. X. 1986a, in Star Forming Dwarf Galaxies and Related Objects, eds. D. Kunth, T. X. Thuan, & J. T. T. Van (Editions Frontières), 73 [Google Scholar]
- Loose, H.-H., & Thuan, T. X. 1986b, ApJ, 309, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Lotz, J. M., Primack, J., & Madau, P. 2004, AJ, 128, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B. 1974, AJ, 79, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Marleau, F. R., & Simard, L. 1998, ApJ, 507, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Marquardt, D. 1963, J. SIAM, 11, 431 [Google Scholar]
- Márquez, I., et al. 2000, A&A, 353, 873 [NASA ADS] [Google Scholar]
- Méndez-Abreu, J., Aguerri, J. A. L., Corsini, E. M., & Simonneau, E. 2008, A&A, 478, 353 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Merritt, D. 2006, ApJ, 648, 976 [NASA ADS] [CrossRef] [Google Scholar]
- Moffat, A. F. J. 1969, A&A, 3, 455 [NASA ADS] [Google Scholar]
- Morales-Luis, A. B., Sánchez Almeida, J., Aguerri, J. A. L., & Muñoz-Tuñón, C. 2011, ApJ, 743, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Moré, J. J., Sorensen, D. C., Hillstrom, K. E., & Garbow, B. S. 1984, MINPACK Project Sour. Dev. Math. Softw., 25, 88 [Google Scholar]
- Neumann, J., Wisotzki, L., Choudhury, O. S., et al. 2017, A&A, 604, 30 [Google Scholar]
- Noeske, K. G., Papaderos, P., Cairós, L. M., & Fricke, K. J. 2003, A&A, 410, 481 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noeske, K. G., Papaderos, P., Cairós, L. M., & Fricke, K. J. 2005, A&A, 429, 115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noeske, K. G., Koo, D. C., Phillips, A. C., et al. 2006, ApJ, 640, L143 [NASA ADS] [CrossRef] [Google Scholar]
- Pandya, V., Primack, J., Behroozi, P., et al. 2019, MNRAS, 488, 5580 [NASA ADS] [CrossRef] [Google Scholar]
- Papaderos, P. 1993, Diploma Thesis, University of Göttingen [Google Scholar]
- Papaderos, P., & Fricke, K. J. 1998, in X-rays from Blue Compact Dwarf Galaxies, eds. B. Aschenbach, & M. J. Freyberg (Garching: Max-Planck-Institut für extraterrestrische Physik), Highlights in X-ray Astronomy: International Symposium in Honour of Joachim Trümper’s 65th Birthday, June 17–19, 1998, Garching, Germany, Symposium proceedings, 73 [Google Scholar]
- Papaderos, P., & Östlin, G. 2012, A&A, 537, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papaderos, P., Loose, H.-H., Thuan, T. X., & Fricke, K. J. 1996a, A&AS, 120, 207 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papaderos, P., Loose, H.-H., Fricke, K. J., & Thuan, T. X. 1996b, A&A, 314, 59 [NASA ADS] [Google Scholar]
- Papaderos, P., Izotov, Y. I., Fricke, K. J., Thuan, T. X., & Guseva, N. G. 1998, A&A, 338, 43 [NASA ADS] [Google Scholar]
- Papaderos, P., Izotov, Y. I., Thuan, T. X., et al. 2002, A&A, 393, 461 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papaderos, P., Guseva, N. G., Izotov, Y. I., & Fricke, K. J. 2008, A&A, 491, 113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peng, C. Y., Ho, L., Impey, C. D., & Rix, H. W. 2002, AJ, 124, 266 [Google Scholar]
- Peng, C. Y., Ho, L., Impey, C. D., & Rix, H. W. 2010, AJ, 139, 2097 [Google Scholar]
- Saglia, R. P., Bender, R., & Dressler, A. 1993, A&A, 279, 75 [NASA ADS] [Google Scholar]
- Straughn, A. N., Cohen, S. H., Ryan, R. E., et al. 2006, ApJ, 639, 724 [NASA ADS] [CrossRef] [Google Scholar]
- Renka, R. J. 2009, ACM Trans. Math. Softw., 36, 7 [CrossRef] [Google Scholar]
- Ribeiro, B., Lobo, C., Antón, S., et al. 2016, MNRAS, 456, 3899 [NASA ADS] [CrossRef] [Google Scholar]
- Robotham, A. S. G., Taranu, D. S., Tobar, R., et al. 2017, MNRAS, 466, 1513 [NASA ADS] [CrossRef] [Google Scholar]
- Savorgnan, G. A. D., Graham, A. W., Marconi, A., & Sani, E. 2016, ApJ, 817, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Sargent, W. L. W., & Searle, L. 1970, ApJ, 162, L155 [NASA ADS] [CrossRef] [Google Scholar]
- Schaerer, D., & de Barros, S. 2010, A&A, 515, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sérsic, J. L. 1963, Bol. Asoc. Argent. Astron., 6, 41 [Google Scholar]
- Sérsic, J.-L. 1968, Atlas de galaxias australes (Cordoba: Observatorio Astronomico) [Google Scholar]
- Schlafly, E., & Finkbeiner, D. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Schombert, J., & Smith, A. K. 2012, PASA, 29, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Shibuya, T., Ouchi, M., & Harikane, Y. 2015, ApJ Suppl., 219, 15 [Google Scholar]
- Simard, L. 1998, in Astronomical Data Analysis Software and Systems VII, eds. R. Albrecht, R. N. Hook, & H. A. Bushouse (San Francisco, CA: ASP), 145, 108 [NASA ADS] [Google Scholar]
- Simard, L., Willmer, C. N. A., Vogt, N. P., et al. 2002, ApJS, 142, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Slavcheva-Mihova, L., & Mihov, B. 2010, A&A, 526, A43 [Google Scholar]
- Stark, D. P., Ellis, R. S., Bunker, A., et al. 2009, ApJ, 697, 1493 [NASA ADS] [CrossRef] [Google Scholar]
- Steidel, C. C., Bogosavljevic, M., Shapley, A. E., et al. 2011, ApJ, 736, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Steidel, C. C., Rudies, G. C., Strom, A. L., et al. 2014, ApJ, 795, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo, I., Graham, A. W., & Caon, N. 2001a, MNRAS, 326, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo, I., Aguerri, J. A. L., Cepa, J., & Gutiérrez, C. M. 2001b, MNRAS, 328, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo, I., Erwin, P., Asensio, Ramos A., & Graham, A. W. 2004, AJ, 127, 1917 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo, I., Förster-Schreiber, N. M., & Rudnik, G. 2006, ApJ, 650, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Xanthopoulos, E. 1996, MNRAS, 280, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Wisnioski, E., Glazebrook, K., Blake, C., & Swinbank, A. M. 2013, MNRAS, 436, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Wisotzki, L., Bacon, R., Blaizot, J., et al. 2016, A&A, 587, 98 [Google Scholar]
- Wisotzki, L., Bacon, R., Brlinchmann, J., et al. 2018, Nature, in press [Google Scholar]
- van der Wel, A., Bell, E. F., Häussler, B., et al. 2012, ApJS, 203, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Villar-Martín, M., Cabrera-Lavers, A., Humphrey, A., et al. 2018, MNRAS, 474, 2302 [NASA ADS] [CrossRef] [Google Scholar]
- Young, C. K., & Currie, M. J. 1994, MNRAS, 268, L11 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Testing iFIT on real galaxies
iFIT was tested on SDSS g & r-band data for 121 local ETGs. The images were sky-subtracted, rotated in astronomical orientation and corrected for Galactic foreground extinction (adopting the values by Schlafly & Finkbeiner 2011, available at NASA Extragalactic Data Base–NED). Galactic foreground stars that overlap some ETGs were substituted by the mean intensity of the adjacent stellar continuum. Finally the frames were trimmed and the SBPs were extracted using the function FIT/ELL3 within the package SURFPHOT of ESO-MIDAS. Below we show only results from fitting in the g-band, whereby the effect of the adopted PSF was examined by running iFIT three times for each galaxy using a different non-saturated field star to approximate the PSF. Although some PSFs render better results than others at small radii, it can be seen from Fig. A.1 and Table A.1 that the result from iFIT does not appreciably depend on PSF corrections, except for the cases when MINPACK is unable to properly fit the PSF.
 |
Fig. A.1. Fitting of the SBP of NGC 4956 with iFIT using two different PSFs. The SBPs (both from the galaxy and individual stars used for the PSF determination) were obtained with the routine FIT/ELL3 in ESO-MIDAS for g-band frames from SDSS DR7. The graphical output from iFIT provides in the header the following information: name of the input file, name of the PSF file, and estimated characteristics for the input PSF (FWHM and βM). The color of the inner dot in the r.h.s. circle informs on the method used to estimate Reff and μeff: blue – non-weighted linear regression; purple – |
SL model parameters obtained with iFIT by fitting g-band SDSS images for three times each using different PSFs that were computed from nearby field stars.
Figure A.1 shows the output from iFIT for the ETG NGC 4956 for two PSF models:
Additionally iFIT was tested on F435W and F606W from ACS/WFC imaging data for higher-z galaxies extracted from the Hubble eXtreme Deep Field (XDF) Data release 1.0 (Illingworth et al. 2013). Figure A.2 shows two examples of such galaxies.
 |
Fig. A.2. Fits with iFIT of the SBP of two higher-z galaxies from XDF in the F606W filter after background subtraction. The upper and lower panel displays, respectively, the galaxy ACS-GC 90045619 (RA: 53.157796°, Dec: −27.797536°) at z = 0.768 (Bond et al. 2014) and UDF:[JBM2015] 18620 (RA: 53.167567°, Dec: −27.792520°) at z = 1.091 (Jiménez-Teja et al. 2015) (encircled). The horizontal bar corresponds to 1″. |
Appendix B: Empirical assessment of the alternative weights in the weighted linear regression
Weighted least squares (WLS) (a variation of the ordinary least squares, OLS) should be applied when the assumption of constant variance in the errors is violated (heteroscedasticity), the measurements come from a Gaussian distribution and the stochastic variation from point to point is independent.
Providing that there is a functional relation (f) between the observational points (y) such as y = f(x, a, b), being x and y the independent and dependent variables, respectively, and a and b the model parameters to be determined, WLS minimizes the χ2 statistics by varying the parameters a and b:
where the optimal weight to be adopted is the reciprocal of the variance of the measured errors – w(i) = 1/σμ(i)2 (Aitken 1936).
The aforementioned procedure is optimal in theory, that is, when the measured data points perfectly match the model to be fit. However, the essential message from this article is that galaxy SBPs do not necessarily obey the SL, but in many cases show substantial systematic deviations from it, especially but not exclusively in their brightest central part due to, for example, depleted cores in massive ETGs, central nuclei in dwarf ellipticals, circumnuclear star-forming rings in LTGs (cf. Introduction). Using standard χ2-minimization algorithms to fit the SL to such iSPs unavoidably leads to solutions being primarily dictated by the central, hence lowest-σμ(i), SBP data points which often fail to adequately describe the extended lower-surface brightness component of galaxies, being unable to properly model the underlying SL component. While such fits might be irreproachable in terms of their reduced χ2, they can result in substantial and possibly systematic errors in several widely used quantities for the structural characterization of galaxies (e.g., the model-dependent Reff as a measure of the size of a galaxy) and in the colors implied by SL models for their LSB periphery. The fact that these lowest-σμ(i) SBP data points (or image pixels) are precisely those mostly affected by PSF convolution effects further aggravates the problem. Although this drawback is rather obvious, it has actually not been addressed in any 1D/2D structural characterization of galaxies via the SL, and we are unaware of a quantitative assessment of the bias it could introduce in automated surface photometry studies of galaxies.
In the interest of overcoming this obstacle and developing a suitable approach for the determination of the best-fitting equivalent SL model of an iSP, we use here alternative weights, such as 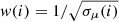 and w(i) = 1/σμ(i), in order to decrease the relative impact of the innermost low-σμ(i) data points on the fitting solution. Below we attempt to empirically demonstrate the superiority of these alternative weights for recovering the true SL parameters by fitting a few typical iSP’s. To avoid biases due to, for example, the lack of resolution or the shallowness of the input SBPs, we designed those such as to have a fine radius step (0
and w(i) = 1/σμ(i), in order to decrease the relative impact of the innermost low-σμ(i) data points on the fitting solution. Below we attempt to empirically demonstrate the superiority of these alternative weights for recovering the true SL parameters by fitting a few typical iSP’s. To avoid biases due to, for example, the lack of resolution or the shallowness of the input SBPs, we designed those such as to have a fine radius step (0 01) and to contain ∼95% of the total theoretical luminosity):
01) and to contain ∼95% of the total theoretical luminosity):
(1) The left panel of Fig. B.1 illustrates the case of a perfect SL profile (η = 3, Reff = 20″, μeff = 22.6 mag), denoted in the following as pA. In the following tables, the middle column (η3) lists the results obtained by performing linear regression via OLS/WLS where x = R1/η with a fixed η = 3 and y = μ(R⋆), and subsequently applying Eq. (5) (see Sect. 2.3, item 3), adopting the different weights as specified in the leftmost column. The right-hand column lists the final solutions obtained by iFIT (Table B.1).
 |
Fig. B.1. Left panel: theoretical SL profile with η = 3, Reff = 20″, μeff = 22.6 mag (hereafter pA), with σμ estimated following Papaderos et al. (1996a), and its fit (red curve) with iFIT. Right panel: profile pA after convolution with a Moffat PSF with FWHM of 1 |
Comparison of results for different error weights.
It is important to note that in the case of a perfect SL profile, performing WLS with alternative weights returns the same solution as the one obtained by adopting the statistically optimal (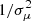 ) weights or OLS, confirming that the inclusion of the alternative weights wont introduce a bias.
) weights or OLS, confirming that the inclusion of the alternative weights wont introduce a bias.
(2) For the same SL profile but convolved with a Moffat PSF with a FWHM of 1.57″ (pB, right panel of Fig. B.1) the same exercise yields the results listed in Table. B.2.
Same configuration as Table B.1 displaying the results for pB.
These results show that even a slight alteration of the central low-σμ part of the profile (in this case, convolution with a Moffat function with FWHM/Reff≈ 0.08) results in appreciable deviations from the correct solution (Reff = 20 and μeff = 22.6) becoming larger when WLS fitting assumes 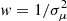 . Alternative weights have the advantage of decreasing the impact of the brightest, lowest-σμ points in the convergence procedure, resulting in a solution which is closer to the true value.
. Alternative weights have the advantage of decreasing the impact of the brightest, lowest-σμ points in the convergence procedure, resulting in a solution which is closer to the true value.
To assess whether the obtained results emerge simply as a consequence of testing purely theoretical models, the exercise was repeated by inducing perturbations to the SBPs (see Fig. B.2) so that:
 |
Fig. B.2. pA (left panel) and pB (right panel) after random perturbation out of a Gaussian distribution with mean μ(R) and standard deviation σμ. |
where g(μ(R)mod, σμ) is a random deviate from a Gaussian distribution with mean μ(R) and standard deviation σμ (Tables B.3 and B.4).
Same configuration as Table B.1 displaying the results for pA after adding a random perturbation out of a Gaussian distribution.
Same configuration as Table B.1 displaying the results for pB after adding a random perturbation out of a Gaussian distribution.
(3) Adding a subtle luminosity component modeled by Eq. (1) with η = 0.25, μ0 = 21.54, α = 5.79 to the previous convolved SL profile yields a luminosity increase by ∼4% (Fig. B.3) yields the solutions in Table B.5.
 |
Fig. B.3. Theoretical SL profile pB plus a subtle additional component overplotted in purple, modeled by Eq. (1) with η = 0.25, μ0 = 21.54, α = 5.79 (SL profile pC), with the iFIT solution overplotted. |
Same configuration as Table B.1 displaying the results for pC.
The results obtained by adopting standard weights are the ones that farthest depart from the correct solution. This occurs because, as previously mentioned, by using standard WLS to fit an iSP that deviates from the SL at low radii such as the iSP in Fig. B.3, low-σμ, bright SBP points which hold the imprints of the extra luminosity component and thus mostly deviate from the SL will dictate the fit. From the table above it is also apparent that alternative weights recover far better the characteristics of the photometrically dominant, underlying SL component (Table B.6).
Same configuration as Table B.1 displaying the results for pC after adding a random perturbation out of a Gaussian distribution.
The perturbed counterpart is displayed in Fig. B.4.
 |
Fig. B.4. pC after random Gaussian perturbation with mean μ(R) and standard deviation σμ. |
(4) Adding an additional component given by Eq. (1) with η = 0.25, μ0 = 21.04, α = 6.20 to pB, enhancing the total luminosity by ∼6%, (profile pD at the left-hand side of Fig. B.5) yields the fitting solutions in Table B.7, which documents a similar behavior as the one discussed for the iSP profile pC.
 |
Fig. B.5. Left panel: theoretical SL profile pB plus an additional component modeled by Eq. (1) with η = 0.25, μ0 = 21.04, α = 6.20 (SL profile pD) and respective iFIT fit. Right panel: pD plus an extra luminosity excess in the faint end of the SL modeled by the polynomial equation μ(R) = 0.148 ⋅ R2 − 5.960 ⋅ R + 84.180, (SL profile pE) with the iFIT solution overplotted. Overplotted dashed-dot purple lines display the additional components. |
Same configuration as Table B.1 displaying the results for pD.
(5) Likewise, profile pE (right-hand side of Fig. B.5) simulates a wiggle at intermediate radii of profile pC through addition of a component modeled by the polynomial equation μ(R) = 0.148 ⋅ R2 − 5.960 ⋅ R + 84.180, that enhances the total luminosity by ∼9% (Table B.8).
Same configuration as Table B.1 displaying the results for pE.
It can again be seen that an alternative weight recovers best the characteristics of the dominant SL component, whereas WLF with standard weights underestimates η and Reff by, respectively, 23% and 36%, while they overestimate μeff by one mag (Fig. B.6).
 |
Fig. B.6. pD (left panel) and pE (right panel) after random perturbation out of a Gaussian distribution with mean μ(R) and standard deviation σμ. |
The same result is observed for a set of diverse iSP’s with or without noise (cf. Tables B.9 and B.10): the standard WLS yields incorrect solutions, in the sense of the largest deviations from the characteristics of the photometrically dominant, underlying SL component. As discussed above, this occurs due to the nature of the χ2 minimization method, that largely bases the solution on the brightest, lowest-σμ points of a SBP (or galaxy image).
Same configuration as Table B.1 displaying the results for pD after adding a random perturbation out of a Gaussian distribution.
Same configuration as Table B.1 displaying the results for pE after adding a random perturbation out of a Gaussian distribution.
Although with these examples we tried to simulate some of the typically observed iSP’s, it is obviously impossible to illustrate and carry out a comparative SL modeling of all possible iSP’s. For this reason, and given that for some iSP’s the standard WLS or an intermediate weight is the one that better recovers the true SL parameters, iFIT is designed such as to employ the four weighting methods and subsequently converge to the solution which best matches the observed light growth curve.
All Tables
SL model parameters obtained with iFIT by fitting g-band SDSS images for three times each using different PSFs that were computed from nearby field stars.
Same configuration as Table B.1 displaying the results for pA after adding a random perturbation out of a Gaussian distribution.
Same configuration as Table B.1 displaying the results for pB after adding a random perturbation out of a Gaussian distribution.
Same configuration as Table B.1 displaying the results for pC after adding a random perturbation out of a Gaussian distribution.
Same configuration as Table B.1 displaying the results for pD after adding a random perturbation out of a Gaussian distribution.
Same configuration as Table B.1 displaying the results for pE after adding a random perturbation out of a Gaussian distribution.
All Figures
 |
Fig. 1. Pseudo-code illustrating principal steps of the convergence procedure in iFIT. |
| In the text | |
 |
Fig. 2. Example a Sérsic profile μ(R⋆) with a η = 3 and an effective radius Reff = 3″ (solid line). Top panel: vertical dashed lines correspond to the radii enclosing 40, 50, 60, 70, 80 and 90% of |
| In the text | |
 |
Fig. 3. Scheme of input and output quantities, and available provisions for the PSF model to be taken into account, where “y” stands for “yes”, “n” for “no”, “G/M” for a Gaussian or Moffat PSF model, and “U” for a non-PSF-convolved SBP. |
| In the text | |
 |
Fig. 4. Absolute deviation Δη between estimated and input η as a function of η and the effective radius Reff (″) for the case of unconvolved Sérsic profiles encompassing 90, 95 and 99% of the total luminosity (upper, middle and lower panel, respectively). The vertical color bar corresponds to Δη = |ηin − ηout| between 0 and 1. |
| In the text | |
 |
Fig. 5. Absolute deviation Δη between estimated and input η as a function of η and FWHM/Reff for the case of Sérsic SBPs enclosing 90% (left panel), 95% (middle panel) and 99% (right panel) of the total luminosity after convolution with a Moffat PSF with 0.5 ≤ FWHM/Reff ≤ 2, whereby 1 ≤ Reff (″)≤20. |
| In the text | |
 |
Fig. 6. Observed g-r radial color profile (filled circles) vs. difference between the best-fitting Sérsic model with iFIT for g- and r-band images (blue curve) for three randomly selected ETGs from SDSS. |
| In the text | |
 |
Fig. 7. Left panel: true-color image composite of archival broad- and narrow-band HST images for the central region of the BCD Henize 2–10, illustrating the morphological complexity of stellar emission (green and blue) within its starburst component, as well as the presence of strong Hα emission (red) excited by the chain of super-star clusters (zoom-in in the upper panel) discovered by Conti & Vacca (1994). Middle panel: contour map of He 2–10, computed from ground-based data. The morphology of the starburst component and of the underlying older host galaxy is delineated by contours in blue and red, respectively. The horizontal bar corresponds to 20″. Right panel: B- and R-band SBPs of He 2–10, computed with the 2D surface photometry code by Bender & Möllenhoff (1987). The overlaid curves show SL fits with iFIT down to a surface brightness μlim between 24 and 28 mag/□″. It can be seen that in all cases the Sérsic model parameters inferred for both bands are mutually consistent and show little dependence on μlim. |
| In the text | |
 |
Fig. 8. Left panel: true-color image composite of I Zw 18 produced from archival HST data, showing the extended nebular halo of the BCD (adapted from Papaderos & Östlin 2012). The horizontal bar corresponds to 5″. Upper-right panel: SL model with iFIT (blue) to the observed R-band SBP of I Zw 18 (SBP1; from Papaderos & Östlin 2012). The inset shows a Moffat model of the PSF (see appendix for further explanations) and the fit residuals are displayed in the lower diagram. Bottom panel: variation of the best-fitting Sérsic index η vs. limiting surface brightness μlim obtained by Papaderos & Östlin (2012) for SBP1 and SBP2 using standard χ2 minimization (gray dashed and dashed-dotted curve, respectively). Open and filled circles show the result obtained with iFIT by modeling both SBPs down to a μlim between 23.5 mag/□″ and 29 mag/□″. |
| In the text | |
 |
Fig. A.1. Fitting of the SBP of NGC 4956 with iFIT using two different PSFs. The SBPs (both from the galaxy and individual stars used for the PSF determination) were obtained with the routine FIT/ELL3 in ESO-MIDAS for g-band frames from SDSS DR7. The graphical output from iFIT provides in the header the following information: name of the input file, name of the PSF file, and estimated characteristics for the input PSF (FWHM and βM). The color of the inner dot in the r.h.s. circle informs on the method used to estimate Reff and μeff: blue – non-weighted linear regression; purple – |
| In the text | |
 |
Fig. A.2. Fits with iFIT of the SBP of two higher-z galaxies from XDF in the F606W filter after background subtraction. The upper and lower panel displays, respectively, the galaxy ACS-GC 90045619 (RA: 53.157796°, Dec: −27.797536°) at z = 0.768 (Bond et al. 2014) and UDF:[JBM2015] 18620 (RA: 53.167567°, Dec: −27.792520°) at z = 1.091 (Jiménez-Teja et al. 2015) (encircled). The horizontal bar corresponds to 1″. |
| In the text | |
 |
Fig. B.1. Left panel: theoretical SL profile with η = 3, Reff = 20″, μeff = 22.6 mag (hereafter pA), with σμ estimated following Papaderos et al. (1996a), and its fit (red curve) with iFIT. Right panel: profile pA after convolution with a Moffat PSF with FWHM of 1 |
| In the text | |
 |
Fig. B.2. pA (left panel) and pB (right panel) after random perturbation out of a Gaussian distribution with mean μ(R) and standard deviation σμ. |
| In the text | |
 |
Fig. B.3. Theoretical SL profile pB plus a subtle additional component overplotted in purple, modeled by Eq. (1) with η = 0.25, μ0 = 21.54, α = 5.79 (SL profile pC), with the iFIT solution overplotted. |
| In the text | |
 |
Fig. B.4. pC after random Gaussian perturbation with mean μ(R) and standard deviation σμ. |
| In the text | |
 |
Fig. B.5. Left panel: theoretical SL profile pB plus an additional component modeled by Eq. (1) with η = 0.25, μ0 = 21.04, α = 6.20 (SL profile pD) and respective iFIT fit. Right panel: pD plus an extra luminosity excess in the faint end of the SL modeled by the polynomial equation μ(R) = 0.148 ⋅ R2 − 5.960 ⋅ R + 84.180, (SL profile pE) with the iFIT solution overplotted. Overplotted dashed-dot purple lines display the additional components. |
| In the text | |
 |
Fig. B.6. pD (left panel) and pE (right panel) after random perturbation out of a Gaussian distribution with mean μ(R) and standard deviation σμ. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



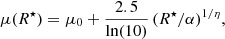
![$$ \begin{aligned} \mu (R^{\star }) = \mu _{\rm eff} + \frac{2.5 b_{\eta }}{ln(10)} \left[ \left( \frac{R^{\star }}{R_{\rm eff}}\right)^{1/ \eta } - 1 \right], \end{aligned} $$](/articles/aa/full_html/2019/12/aa35144-19/aa35144-19-eq2.gif)
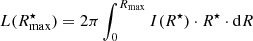
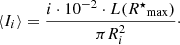
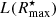
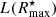
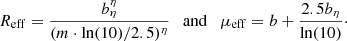
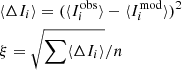
![$$ \begin{aligned}&{F}_{\mathrm{M}}({R}^{\star }) = \left[ 1 + \left( \frac{{R}^{\star }}{\alpha _{\mathrm{M}}}\right)^{2} \right]^{- \beta _{\mathrm{M}}}\nonumber \\&\alpha _{\mathrm{M}} = \frac{{FWHM}}{(2 \sqrt{2^{1/\beta _{\mathrm{M}}}-1})}\cdot \end{aligned} $$](/articles/aa/full_html/2019/12/aa35144-19/aa35144-19-eq16.gif)