| Issue |
A&A
Volume 631, November 2019
|
|
|---|---|---|
| Article Number | A50 | |
| Number of page(s) | 27 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201936338 | |
| Published online | 17 October 2019 | |
HALOGAS: the properties of extraplanar HI in disc galaxies
1
ASTRON, Netherlands Institute for Radio Astronomy, Oude Hoogeveensedijk 4, 7991 PD Dwingeloo, The Netherlands
2
Kapteyn Astronomical Institute, University of Groningen, Postbus 800, 9700 AV Groningen, The Netherlands
e-mail: marasco@astro.rug.nl
3
Department of Physics and Astronomy, University of Bologna, Via P. Gobetti 93/2, 40129 Bologna, Italy
4
CSIRO Astronomy and Space Science, PO Box 1130, Bentley, WA 6102, Australia
5
Dept. of Astronomy, Univ. of Cape Town, Private Bag X3, Rondebosch 7701, South Africa
6
Ruhr-University Bochum, Faculty of Physics and Astronomy, Astronomical Institute, 44780 Bochum, Germany
7
Department of Physics and Electronics, Rhodes University, PO Box 94, Makhanda 6140, South Africa
8
South African Radio Astronomy Observatory, 2 Fir Street, Black River, Park Observatory, Cape Town 7405, South Africa
9
Argelander-Institut für Astronomie, Auf dem Hügel 71, 53121 Bonn, Germany
10
Department of Astronomy and Steward Observatory, University of Arizona, Tucson, AZ, USA
11
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
12
Department of Astronomy, New Mexico State University, Las Cruces, NM 88001, USA
Received:
17
July
2019
Accepted:
6
September
2019
We present a systematic study of the extraplanar gas (EPG) in a sample of 15 nearby late-type galaxies at intermediate inclinations using publicly available, deep interferometric H I data from the Hydrogen Accretion in LOcal GAlaxieS (HALOGAS) survey. For each system we masked the H I emission coming from the regularly rotating disc and used synthetic datacubes to model the leftover “anomalous” H I flux. Our model consists of a smooth, axisymmetric thick component described by three structural and four kinematical parameters, which are fit to the data via a Markov chain Monte Carlo (MCMC) based Bayesian method. We find that extraplanar H I is nearly ubiquitous in disc galaxies as we fail to detect it in only two of the systems with the poorest spatial resolution. The EPG component encloses ∼5−25% of the total H I mass with a mean value of 14%, and has a typical thickness of a few kpc which is incompatible with expectations based on hydrostatic equilibrium models. The EPG kinematics is remarkably similar throughout the sample, and consists of a lagging rotation with typical vertical gradients of ∼ − 10 km s−1 kpc−1, a velocity dispersion of 15−30 km s−1, and, for most galaxies, a global inflow in both the vertical and radial directions with speeds of 20−30 km s−1. The EPG H I masses are in excellent agreement with predictions from simple models of the galactic fountain that are powered by stellar feedback. The combined effect of photo-ionisation and interaction of the fountain material with the circumgalactic medium can qualitatively explain the kinematics of the EPG, but dynamical models of the galactic fountain are required to fully test this framework.
Key words: galaxies: halos / galaxies: ISM / galaxies: evolution / ISM: structure / ISM: kinematics and dynamics
© ESO 2019
1. Introduction
Disc galaxies are characterised by the presence of a thin disc of neutral hydrogen (H I) that can extend in radius far beyond the classical optical radius. In the inner regions of discs, the H I layers have a typical scaleheight of 100−200 pc. This thickness is well explained by assuming that the gas is in vertical hydrostatic equilibrium within the galactic potential, that is, the gas turbulent motions balance the vertical gravitational pull by the stellar disc and dark matter halo (Olling 1995). In the outer regions of discs, the H I layer is expected to flare due to the decrease of the vertical force. However, within the optical radius, the scaleheight is unlikely to vary by more than a factor two (Bacchini et al. 2019). Thus, in the inner disc, where most of the star formation takes place, we should expect H I to be confined within a few hundred parsec from the midplane.
The above mentioned expectation is, in fact, not met by H I observations as it was found that a number of disc galaxies keep a fraction (typically 10% or more) of their H I in a rather thick layer reaching up a few kiloparsecs above the midplane (Swaters et al. 1997; Fraternali et al. 2001). In the few systems studied in detail, this layer of neutral gas turns out to show three key features: firstly, it has a scaleheight of typically 1−2 kpc, which is far beyond what one would expect from gas in hydrostatic equilibrium (e.g. Oosterloo et al. 2007); secondly, it rotates more slowly than the gas in the disc, showing a velocity gradient with height of order −(10−20) km s−1 kpc−1 (e.g. Schaap et al. 2000; Fraternali et al. 2005; Zschaechner et al. 2011); thirdly, it is located mostly in the inner regions of the disc, showing a clear correspondence with the star forming disc (e.g. Fraternali et al. 2002; Boomsma et al. 2008). In this paper we generically refer to this component as extraplanar gas (EPG), but in the literature one can also find reference to it as an H I halo, as a thick H I disc (Kamphuis et al. 2013), or as a “lagging” component (because of its peculiar rotation, Matthews & Wood 2003).
Other than the above mentioned properties, in some galaxies, non-circular motions have also been detected. The EPG of NGC 2403, UGCA 105, and NGC 4559 seems to have a coherent (radial) infall motion towards the centre of the galaxy (Fraternali et al. 2002; Barbieri et al. 2005; Schmidt et al. 2014; Vargas et al. 2017). In NGC 6946 (a galaxy seen close to face-on) vertical motions of H I are ubiquitously observed across the star forming disc and are in clear connection to the EPG component (Boomsma et al. 2008). The EPG of NGC 891 shows the presence of outflow and inflow motions with an increase in velocity dispersion with height (Oosterloo et al. 2007). On the whole, extraplanar H I appears to be a somewhat separate component (both spatially and kinematically) from the thin H I disc.
The presence of H I at large distances from the disc has also been known to occur in the Milky Way for decades. Lockman (1984, 2002) found H I clouds towards the inner galaxy reaching up to distances of a few hundred parsec from the midplane (see also Di Teodoro et al. 2018). Other clouds, known as high-velocity and intermediate-velocity clouds (HVCs and IVCs; Wakker & van Woerden 1997), are observed at anomalous velocities with respect to the normal rotation of the disc material. HVCs and IVCs have distinct properties: while the former are typically located at distances of several kpc from the midplane and have sub-Solar metallicity, the latter are confined within a few kpc from the Sun and their metallicity is close to Solar (Wakker 2001). This evidence, together with their different velocities, may indicate different origins. Marasco & Fraternali (2011, hereafter MF11) modelled the extraplanar layer of the Milky Way as seen in the all-sky LAB H I survey (Kalberla et al. 2005). Their model reveals that the Galactic EPG contains about 10% of the total H I, rotates with a gradient dvϕ/dz ≃ −15 km s−1 kpc−1, and has complex kinematics characterised by vertical and radial inflow towards the central regions of the disc. While IVCs clearly appear as “local” features of the Galactic EPG, which is mostly built by unresolved clouds at larger distances, the HVCs seem to be a more distinct component with an origin that is still debated (e.g. Putman et al. 2012; Fraternali et al. 2015).
Along with H I, emission in Hα and other optical lines is commonly observed around disc galaxies, probing the existence of extra-planar diffuse ionised gas (DIG) layers at temperatures of ∼104 K extending 1−2 kpc from the discs. There are several indications that these gas layers are the ionised counterpart of the H I EPG: galaxies with larger SFRs show a more prominent DIG component (Rossa & Dettmar 2003) and the kinematics of this ionised gas is consistent with that of EPG, featuring both a lagging rotation (Heald et al. 2006, 2007; Kamphuis et al. 2007) and non-circular motions (Fraternali et al. 2004). Thus, the photoionisation of H I EPG from bright stars in the disc is the most likely explanation for the DIG layers.
The formation of H I EPG in disc galaxies has been investigated by different authors. The mechanisms considered fall into three classes of models: equilibrium models, inflow models and galactic fountain. The possibility that the EPG layer could be in equilibrium has been first explored by Barnabè et al. (2006) who built models of non-barotropic (baroclinic) gas layers and applied them to the observations of NGC 891, finding that the gas temperature required to reproduce the data was ∼105 K, an order of magnitue above that of the warm H I medium. In a second step in this direction, Marinacci et al. (2010a) investigated the possibility of an equilibrium model where the random motions of the EPG are non-thermal and thus also suitable for a colder, “clumpy” component. Within this framework, one can derive prescriptions equivalent to the hydrostatic equilibrium using the Jeans equations, with the further possibility of introducing anisotropic velocity dispersion. The final result was that no model could fully reproduce the kinematics of NGC 891’s H I EPG, but the best result could be obtained by introducing a strong anisotropy in the vertical direction, which is akin to what one finds in galactic fountain models (see below).
The second type of model proposed that the EPG layer is produced by gas accretion onto the galaxy discs from the external environment. Galaxies are likely surrounded by large gas reservoirs as most baryons are found to be outside galaxies in the local Universe (e.g. Bregman 2007; Werk et al. 2013). For galaxies similar to the Milky Way, this reservoir is likely in the form of hot gas at nearly the virial temperature and contains a significant fraction of the missing baryons (e.g. Gatto et al. 2013; Miller & Bregman 2015). In this scenario, the extraplanar gas could be produced by the cooling of this so-called “corona” in a cooling flow model. Kaufmann et al. (2006) explored this possibility with SPH simulations and found that the kinematics of this accreting gas would in fact be similar to that observed for NGC 891, but this idea later incurred two drawbacks. First, it became clear that most of the cold gas in those simulations was caused by numerical effects (Agertz et al. 2007; Kaufmann et al. 2009) and, in fact, unphysical. Indeed, thermal instabilities are unlikely to develop in a corona akin to that surrounding the Milky Way (Binney et al. 2009; Joung et al. 2012, but see also Sormani et al. 2018 and references therein). Second, the large mass of the extraplanar gas combined with the short dynamical time for accretion onto the disc (essentially the free fall time) would lead to accretion rates exceeding the star formation rate (SFR) of these galaxies by orders of magnitude (Fraternali & Binney 2008). Thus, it appears very unlikely that all the extraplanar H I in local galaxies could be explained by gas accretion. However, a fraction of EPG may well have such an origin (e.g. Marasco et al. 2012). Galaxies of lower mass are not expected to host a massive hot corona, but rather a number of “cold” (∼105 K) gas filaments that connect the outer regions of their disc to the intergalactic space. These cold flows would constitute the main mode of gas accretion onto galaxies at high redshift, and should still be significant at low redshift in low mass systems. Again, it is unlikely that these flows, which are expected to merge with galaxy discs at large galactocentric radii, can be the origin of the extraplanar H I, which is seen preferentially in the inner regions.
The other explanation for the presence of the EPG layer is that of a galactic fountain powered by stellar feedback (e.g. Shapiro & Field 1976; Collins et al. 2002). In this picture, the EPG is pushed up from the thin disc of the galaxy by the expansion of superbubbles around stellar OB associations. Superbubbles are produced by the combined action of supernova explosions and stellar winds and can reach sizes much larger than a typical supernova bubble, thus exceeding the disc scaleheight (Mac Low & McCray 1988). When a superbubble reaches the blowout, the cold material gathered in its shell is ejected into the halo region and so is its interior, which consists of rarefied hot gas. In this scheme, the extraplanar H I is made up mostly of material from the supershells (Melioli et al. 2009) and partially of material from the hot bubble that is promptly cooling after the ejection (Houck & Bregman 1990). In a series of papers, the kinematics of the extraplanar gas has been contrasted with the prediction of galactic fountain models with and without interaction between the fountain flow and the surrounding galactic corona (Fraternali & Binney 2006, 2008; Marinacci et al. 2010b). Both in the Milky Way and NGC 891, the extent of the EPG layer can be well reproduced by these models, while its kinematics shows signs of interaction between the outflowing material and gas cooling from the corona. In this scenario, the EPG would be formed mostly by fountain material with a percentage of 10−20% of cooled coronal gas (Fraternali et al. 2013; Fraternali 2017). The outflow velocities required by these models to reproduce the data are ≲100 km s−1, compatible with those measured for the high-velocity H I component around the star forming regions of nearly face-on galaxies, like NGC 6946 (Boomsma et al. 2008). These relatively low speeds rule out the possibility of a powerful outflow into the circumgalactic medium (CGM), suggesting a more gentle disc-halo gas circulation for the origin of the EPG.
In this paper, we use data from the Hydrogen Accretion in LOcal GAlaxieS (HALOGAS) survey (Heald et al. 2011a, hereafter H11) to investigate the presence and the properties of the EPG in a sample of 15 nearby galaxies. This represents the first systematic investigation of the EPG properties in a sample of galaxies, and increases substantially the number of systems for which a detailed study of the EPG has been carried out. We hereby show that the vast majority of late-type galaxies present a thick layer of EPG characterised by a slow rotation and a coherent inflow motion towards the galaxy centre. We describe our sample and modelling methodology in Sect. 2, and apply our method to the HALOGAS systems in Sect. 3. The interpretation of our findings in the context of the galactic fountain framework, together with a discussion on the limitations of our method, are presented in Sect. 4. We summarise our results in Sect. 5.
2. Method
We infer the properties of the EPG by following a method analogous to that used by MF11 to study the extraplanar H I of the Milky Way. This method is based on two main steps. The first step consists of filtering out from the datacube the emission that comes from the regularly rotating thin H I disc. The second is to build simple parametric models of EPG, based on a limited number (7 in our case) of free parameters, that are fit to the data by producing synthetic H I cubes and comparing them directly to the observations. Our galaxy sample and the details of our method are described below. In Appendix B we test our method on mock data.
2.1. The sample
The HALOGAS sample of H11 comprises 24 late-type galaxies, partitioned into 9 nearly edge-on and 15 intermediate inclination systems. With the exception of NGC 2403 and NGC 891, for which pre-existing deep H I data were already available, all galaxies have been re-observed at the Westerbork Synthesis Radio Telescope (WSRT) for a total integration time per galaxy of 10 × 12 h in order reach H I column density sensitivities of a few ×1019 cm−2. These rank amongst the deepest interferometric H I observations of galaxies in the local Universe and constitute the best dataset to study the faint EPG emission in nearby galaxies1. Comparisons between the WSRT and GBT (single-dish) H I-fluxes indicate that not more than ∼2% of the H I masses in and around galaxies should be missed by the HALOGAS survey due to the lack of short baselines and/or sensitivity (Pingel et al. 2018).
In this work we focus on the subset of 15 galaxies seen at intermediate inclinations (50 ° < i < 72°), that allow the separation of extraplanar gas given its peculiar kinematics. The main physical properties of these galaxies are listed in Table 1 and column density maps are shown in Fig. C. While our modelling technique can also be applied to highly inclined systems, some of the steps in the method described below would require significant modifications. In fact, in edge-on galaxies, the EPG separation can not be done on the basis of kinematics alone (Sect. 2.2); rotation curves must be derived with a different fitting technique and information on the gas motion in the direction perpendicular to the disc is no longer accessible (Sect. 2.3). In order to provide a homogenous analysis throughout the entire sample, we limit our study to systems at intermediate inclination. Separate studies of the edge-on galaxies in HALOGAS have been undertaken (Zschaechner et al. 2011, 2012, 2015; Kamphuis et al. 2013).
Physical properties of galaxies in our sample, from H11 and Heald et al. (2012).
The HALOGAS survey provides H I datacubes at two different spatial resolutions, ∼15″ and ∼30″. In this work we use exclusively the cubes at ∼30″. This gives us two advantages: a higher column density sensitivity, mandatory to study the faint-level emission around galaxies, and fewer independent resolution elements to model, which alleviates the computational cost of our software. A lower spatial resolution also washes out the small-scale fluctuations in the gas density distribution that would never be represented by our smooth, axisymmetric models, while still providing enough information to trace the global EPG parameters that we try to derive. Dealing with fewer independent data points also implies a significant gain in computational speed.
Most original HALOGAS cubes are significantly oversampled, with about ∼9 spaxels2 per FWHM along the beam major axis. Also, the target galaxy often occupies only a small part of the total field of view. To increase the computational speed, we have trimmed the cubes in order to discard most of the empty background and maintain preferentially the central galaxies, and re-binned them to 3 spaxel per beam FWHM (mean on both axes), sufficient to represent the data without information loss.
2.2. Separation of extraplanar gas
The separation of the EPG emission from the disc emission is largely inspired by the technique firstly pioneered by Fraternali et al. (2002) and is based on the assumption that the kinematics of the EPG differs from that of the gas that regularly rotates within the disc. The collisional nature of gas implies that two components with distinct kinematics along the same line-of-sight are likely to occupy distinct locations within the galaxy.
To give an example, in Fig. 1 we sketch how line-profiles get modified by having a layer of slowly rotating gas superimposed on the normally rotating thin disc. If the disc is very thin, the resolution of the data is good and the inclination is not extreme (say i < 80°), then the profiles are broadened only by the gas turbulence and are reasonably well described by Gaussian distributions. The presence of a slowly rotating component shows up then as an asymmetric tail extending towards the systemic velocity (i.e. at lower rotational velocities). This tail is clearly visible along the kinematic major axis of the galaxy and it tends to fade around the minor axis (unless non-circular motions are also present, see Fraternali et al. 2001). The line profile (dots) in Fig. 1 is extracted from a location along the major axis in the HALOGAS datacube of NGC 3198 (Gentile et al. 2013, hereafter G13), normalised and shifted in velocity to a systemic velocity of vsys = 0 km s−1. The Gaussian fit (blue solid line) is obtained by excluding the prominent tail visible at velocities between ∼50 and 120 km s−1. The fit perfectly reproduces the high-velocity side of the profile. A separation of the EPG can be achieved either by subtracting this Gaussian fit from the whole profile, or by masking the emission at velocities where the Gaussian fit has a high signal-to-noise ratio (e.g. the region within the vertical dashed lines in Fig. 1). The latter approach is typically more conservative and is that adopted in this study.
 |
Fig. 1. Sketch of observation of extraplanar gas in galaxy seen at intermediate inclination. The typical line profile (along the kinematic major axis of the galaxy) will be composed by a nearly Gaussian part coming from the thin disc with overlaid a tail at low rotation velocity produced by the lagging EPG layer. The width of the disc emission is roughly symmetrical, produced by gas turbulence and well fitted by a Gaussian function (blue solid line). The EPG separation is achieved by masking a portion of the profile with substantial contribution from this Gaussian function (“internal mask” region). |
The above procedure represents the original disc/EPG separation strategy of Fraternali et al. (2002). It works well for moderately inclined galaxies seen at a high spatial resolution, so that beam-smearing effects do not influence the shape of the line profiles. Here, we have revisited their strategy and implemented some improvements, preferentially to deal with cases where the spatial resolution is not optimal. We firstly produce a 3D mask in order to filter out in each velocity channel the regions where H I emission is absent. To do so, we smooth spatially the datacube by a factor of 5 (using a 2D Gaussian kernel) and set to unity (zero) all voxels with intensity above (below) a 4σ threshold, with σ being the new rms-noise in the smoothed dataset. We have checked by eye that, in all galaxies, this procedure outputs a mask that is generous enough to account for the entire emission coming from the galaxy while simultaneously filtering out any noise spikes occurring in the outer regions. This “external” mask is immediately applied to the original data before any additional procedure.
The next step is modelling the Gaussian part of all the line profiles, in order to describe the main H I disc. We select all profiles in the (masked) data with peaks above 4 times the original rms-noise and fit a Gaussian function to their “upper” 40% portion, which means that we only consider flux densities above 40% of the line peak. Profiles with intensity peaks below the imposed 4σ threshold are excluded from the analysis and are effectively incorporated within the internal mask (see below). Extensive experiments with visualisation tools and with mock data allowed us to establish that these values assure a proper characterisation of the Gaussian and the most efficient separation of the EPG. We have also experimented with Gauss-Hermite polynomials and attempted to fit only the high-velocity narrower portion of the line profiles, finding the above procedure to give the best results.
We then build a cube made of all these Gaussian fits. This cube represents a non-parametric, approximated model for the H I disc, which we use to develop an “internal” mask to separate disc and EPG emission in the data. Unfortunately, our simplistic approach to the disc modelling does not account for beam-smearing effects, which may produce deviations from Gaussianity in the shape of the line profiles even in the absence of a genuine, kinematically anomalous component. If the spatial resolution is not optimal, these effects become a major concern especially in the inner regions of galaxies where the rotation curve has a steep gradient. In order to mitigate these issues we further convolve the Gaussian cube with the data beam. Tests done on synthetic data showed that this step helps in filtering out the disc emission in the innermost regions of poorly resolved systems and significantly improves the estimations of the EPG parameters (see Appendix B). Finally, we convert the Gaussian cube into a mask by setting to unity (blank) all voxels with intensity below (above) twice the data rms-noise. Applying this internal mask to the data means effectively blanking all regions dominated by H I emission coming from the regularly rotating disc: the remaining H I flux is dominated by the EPG. We illustrate this procedure on the H I data of NGC 3198 in Sect. 3.1.
It is important to stress that the procedure above highlights only a fraction of the emission coming from the EPG or, vice-versa, overestimates the contribution of the disc component to the total emission. This can be easily appreciated in Fig. 1, as the lagging EPG probably contributes to the total emission also at velocities larger than 120 km s−1, but it is subdominant with respect to the disc contribution and virtually inseparable from the latter. In fact, in the case of a purely lagging EPG the tail in the profiles would completely disappear along the galaxy minor axis, where no signature of rotation is visible, and one may naively conclude that EPG in galaxies is systematically more abundant along the major axis, which would certainly be a bizzarre result. These considerations highlight the difficulties of measuring directly the properties of the EPG, like its mass, on the basis of a pure kinematical decomposition. The approach adopted in this work attempts to bypass these limitations by building synthetic datacubes of EPG based on parametric models and fitting them to the data, having both the observed and the synthetic cubes filtered in the same manner.
2.3. The model of the EPG layer
We model the EPG layer as an axisymmetric, smooth distribution characterised by three geometrical and four kinematical parameters. The density distribution of the EPG follows the model developed by Oosterloo et al. (2007) and applied to the EPG of NGC 891, where the surface density profile Σ(R) is given by
where Σ0 is the central surface density, γ is an exponent regulating the density decline towards the centre and Rg is an exponential scale-length. For γ > 1, the surface density increases with radius peaking at R = Rg(γ − 1), and declines exponentially further out.
At a given R, the density distribution in the z direction is given by
where h is the EPG scale-height. This is an empirical formula that represents well the vertical EPG distribution in NGC 891, and gives a density that is zero in the galactic midplane, reaching a maximum at z = 0.88h and declining exponentially at larger distances. Equation (2) may seem to be an unusual parametrisation for a gas density distribution, but has two main advantages. The first is that it features a “hole” for z → 0, where the EPG would in fact vanish within the regularly rotating disc. We find this preferable with respect to an exponential or a Gaussian distribution, which would leave us with the additional issue of defining a (somewhat arbitrary) separation threshold between the disc and the EPG layer in the z direction. The second advantage is purely numerical, as the inverse of the cumulative distribution function has an analytical form, which dramatically speeds up the extraction of random numbers from this distribution. For simplicity, and to minimise the number of free parameters, we have decided not to consider a flare in the EPG distribution, but rather a radially constant scale-height h. We discuss the implications of this assumption in Sect. 4.1. As in MF11, the normalisation of the density distribution – which ultimately sets the mass of the EPG – is computed by re-scaling the flux of the synthetic cube to that of the data, and therefore is not a free parameter of the model.
The EPG kinematics is described by four parameters: the vertical gradient in the gas rotational speed (dvϕ/dz), the velocities in the radial and in the vertical directions (vR and vz), and gas velocity dispersion σ. Thus the EPG is allowed to rotate with a different speed with respect to the material within the disc (or to not rotate at all, for dvϕ/dz ≪ 0). It can globally accrete onto or escape from the galaxy, can move in or out, and have a different velocity dispersion. These simple kinematical parameters allow us to model different scenarios, from a nearly-spherical accretion with negligible angular momentum, to a galactic fountain cycle, to powerful nuclear galactic winds.
Along with the rotational lag, a further ingredient is required to model the rotation of the gas: the galaxy rotation curve. While HALOGAS galaxies are well studied nearby systems, studies of their rotation curves are rather scattered in the literature and feature different methods applied to a variety of datasets. In the philosophy of carrying out a homogeneous analysis of the HALOGAS dataset, we have re-derived the rotation curves of all galaxies in our sample using the 3D tilted ring modelling code 3DBAROLO (Di Teodoro & Fraternali 2015), adopting as a first estimate for their inclination the values from H11 reported in Table 1 and fixing the kinematical centre to their optical centre. In Table 1 we also list the median inclination (INC) and position angle (PA) found by 3DBAROLO for each galaxy, which will be adopted in the EPG modelling procedure (Sect. 2.4). The new inclinations are compatible with those of H11 within a few degrees, with the noticeable exception of NGC 5055 for which our estimate (65°, compared to 55° of H11) is representative only for the innermost 20 kpc (see Sect. 3.2 and Fig. 83 in de Blok et al. 2008). In Fig. 2 we show the rotation curves for the 12 systems for which we detect an EPG component: they are largely compatible with those available in the literature once re-scaled to the appropriate distance, as expected in well-resolved nearby disc galaxies.
 |
Fig. 2. Rotation curves for our sample of HALOGAS galaxies derived with 3DBAROLO and used in our EPG modelling. Each system is labelled with its NGC number. |
2.4. From the model to the synthetic cube
For a given choice of x = (Rg, γ, h, dvϕ/dz, vR, vz, σ) we build a stochastic realisation of our model in the full 6D phase-space. This is achieved by extracting random “particles” in a Cartesian space (x, y, z) – where x and y define the galaxy plane – following the density distribution defined by Eqs. (1) and (2). Each particle has an associated (vx, vy, vz) velocity vector that depends on the kinematical parameters adopted. We stress that the particles are by no means representative of single H I clouds, and are simply used as a convenient way to sample a continuous gas distribution. In Appendix A we discuss in detail how we determine the optimal number of particles associated to each model.
The next step is to apply a rotation matrix to the particle positions and velocities in such a way that the system, to an observer located along the z-axis, would appear at a given INC and PA. This is obtained by first rotating the particle set along the x axis by INC degrees, and then around the z axis by (PA+90) degrees3. The underlying assumption is that the EPG layer is not warped, thus its sky projection can be described by single values for INC and PA, which is justified by the fact that EPG is typically observed within the inner regions of galaxies where warps are negligible (see also Sect. 4.1). Clearly, such assumption simplifies significantly the computation of the projection effects. We account for the gas velocity dispersion by adding to the line-of-sight velocity of each particle a random (isotropic) velocity extracted from a Gaussian distribution with standard deviation given by σ. Here σ represent a total velocity dispersion along the line-of-sight, and incorporates all microscopic (e.g. temperature) and macroscopic (e.g. cloud-to-cloud random motions) effects that can affect the broadening of the H I profiles.
Using the galaxy distance D, this particle set is then transferred into a sky (RA, Dec, vhel) 3D grid with voxel size equal to that in the observed datacube. At this stage, the intensity in a given voxel of the synthetic cube has still no physical units, and simply represents the number of particles in that voxel. For a given H I mass MHI, we convert all intensities into Jy beam−1 units by multiplying them by 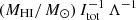 , where Itot is the sum of all intensities in the cube and Λ is a conversion factor given by
, where Itot is the sum of all intensities in the cube and Λ is a conversion factor given by
where ΔRA and ΔDec are the spaxel size, Δv is the channel separation, and Bmaj and Bmin are the FWHM along the beam major and minor axes (see Eqs. (3) and (5) in Iorio et al. 2017). The resulting cube is then spatially smoothed to the resolution of the observations, using a 2D Gaussian kernel with axis ratio and orientation given by the Bmaj, Bmin and Bpa keywords in the data header. To better match the velocity resolution of our syntehtic cube to that of the HALOGAS data we further perform Hanning smoothing, convolving consecutive velocity channels with a 0.25−0.50−0.25 triangular kernel. This has a negligible impact on our results, given the typical velocity dispersion of the EPG (15−30 km s−1) compared to the typical velocity resolution in HALOGAS (FWHM of ∼8 km s−1, corresponding to a standard deviation of 3.4 km s−1).
We now illustrate the effect of the various model parameters on the synthetic cubes. For this purpose we build a series of toy-models made of two components, a thin disc and a thick EPG layer, the latter enclosing 15% of the total H I mass which we take as 3 × 109 M⊙ using NGC 2403 as a reference. The disc is kept fixed in all models and follows the rotation curve of NGC 2403; the radial surface density and the vertical density profiles follow Gaussian distributions (e.g. Martinsson et al. 2013) centred at (R, z) = (0, 0) with standard deviations of 7.3 kpc and 0.1 kpc respectively, The properties of the EPG layer varies model by model and are listed in Table 2. All systems are seen at an inclination of 60°. We have adopted the same resolution and grid size of the VLA cube of NGC 2403 to build the synthetic data (30″ ≃ 0.5 kpc), in order to show the signatures of the various parameters in a well-resolved, clean case.
Figure 3 shows, for each model, a position-velocity (pv) diagram parallel to the major axis (on top) and another parallel to the minor axis (bottom), both with an axis-offset of +2′. The red contours highlight the H I emission from the disc alone, without the EPG contribution, and are the same in all panels. In all models the EPG emerges as a faint, kinematically distinct H I feature which is extended preferentially towards the systemic velocity, producing the so-called “beard” (Schaap et al. 2000) in the major axis pv slices. Clearly, different parameters leave different imprints on the synthetic cube. As expected, the effects of varying the EPG rotation can be better appreciated along the major axis (see models slowrot and fastrot), while radial motions are readily visible in slices parallel to the minor axis (models rad_in and rad_out). We note that in all pv-slices the approaching and the receding sides are perfectly symmetric by construction, except for the cases where radial or vertical motions are present. Position-velocity plots exactly along the major axis (i.e. no offset, not shown here) are symmetric in all cases.
 |
Fig. 3. Position-velocity (pv) slices for the disc+EPG toy models discussed in Sect. 2.4 and based on the parameters listed in Table 2. For each model we show a pv slice parallel to the major (on the top) and to the minor (on the bottom) axes. The insets in the top-left panels sketch the slice directions. Axis-offset is 2′ in both cases. The slice thickness is 3 spaxels, corresponding to a resolution element. Black contours are spaced by powers of 2, the outermost being at an intensity level of 0.4 mJy beam−1. Red contours show the emission from the disc alone, without the contribution of the EPG. |
Summary of the geometrical and kinematical parameters for our EPG model and of the priors adopted.
Other effects, like those produced by varying vz, are more subtle. Given the symmetry of our models, in an optically-thin regime one would expect that gas that moves perpendicularly to the midplane, either outflowing from it (vz > 0) or inflowing onto it (vz < 0), leaves the same signature on the cube. An intuitive example is that of a face-on galaxy: gas in the foreground moving towards the observer (i.e. moving away from the disc) would be indistinguishable from background gas accreting onto the galaxy. Quite remarkably, Fig. 3 demonstrates instead that even the sign of vertical motions can be distinguished, as one can appreciate by comparing models vert_in and vert_out. We show why this is possible in Fig. 4, where we sketch the case of a galaxy seen at an intermediate inclination where the EPG is inflowing vertically towards the disc and has a radially declining H I surface density. For a given inclination, thickness and – most noticeably – radial density profile of the EPG, a sight-line piercing through the system will encounter different densities above and below the midplane, which would cause a preferentially blue-shifted or red-shifted H I signal. Since the EPG kinematics, thickness and density profile are all fit to the data simultaneously, we are confident that our approach can exploit the subtle signatures in the data and correctly recover the gas vertical motions. The fact that we derive coherent kinematical properties in most HALOGAS galaxies (Sect. 3.2) indicates that this is the case (see also Appendix B).
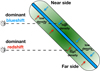 |
Fig. 4. Sketch showing how vertical motions produce a distinct signature on the inferred H I kinematics depending on the EPG thickness, inclination, orientation and surface density profile. In this case, the presence of a vertical inflow (red and blue arrows) and a radially declining surface density profile (shades of green) produce a redder or bluer-shifted signal depending on which galaxy side is considered. |
Figure 3 also highlights possible degeneracies in the parameter space. The effect of varying the vertical rotational gradient is somewhat degenerate with varying the halo thickness, meaning that thicker, rapidly rotating halos appear similar to thinner, slowly rotating ones (see also MF11). Another possible degeneracy is that between vertical and radial motions, as both produce similar asymmetries in the pv-slices. In general, the signature of these parameters on the data is not unique but depends on the surface density profile and on the thickness of the EPG, for reasons analogous to those discussed above for the vertical motions. Therefore, in order to infer their values from the data, it is of fundamental importance to fit both the EPG geometry and the EPG kinematics at the same time by employing a method that can automatically account for the degeneracy in the parameter space. We describe our fitting strategy in the section below.
Finally, we stress that the sign of both radial and vertical motions is ultimately determined from the knowledge of the near/far sides of the system. For instance, in the example sketched in Fig. 4, the signature of vertical motions would be the same if we considered vertical outflows rather than inflows and switched the two galaxy sides. In other words, if the “true” 3D orientation of the galaxy is unknown, the values of vR and vz can be determined up to a sign. We determine the near/far side of each HALOGAS galaxy using the commonly adopted assumption of trailing spiral arms, which are readily recognisable in all systems from optical/UV images. After fitting the model to the data as described in the section below, we change the sign of the inferred (vR, vz) couple, depending on whether the 3D orientation of our model matches that of the galaxy under consideration.
2.5. Fitting the model to the data
We use a Bayesian approach to determine the optimal parameters for the EPG of each galaxy in our sample. The probability 𝒫 of our parameters x given some data 𝒟 is given by
(Bayes’ theorem) where 𝒫(𝒟|x) is the likelihood function and 𝒫(x) is the prior.
As in Marasco et al. (2017), we write the likelihood as
where ℳ(x) indicates the model cube obtained with a given choice of parameters, ℛ(x) is the sum of the absolute residuals between the model and the data, ϵ is the uncertainty in the data (assumed to be constant over the whole dataset) and the sum is extended to all voxels outside the internal mask (see Sect. 2.2). The external mask, which sets to zero the intensities in the regions outside the galaxy, is not applied to the synthetic cubes in order to penalise models where the EPG emission extends too far out either in radius or in velocity.
Equation (5) does not represent a standard χ2 likelihood, which is instead based on the sum of the squared residuals. Our choice is driven by the necessity of giving a larger weight to the faint-level emission around galaxies, with respect to what a χ2 likelihood would provide. We have experimented with other residuals – (𝒟 − ℳ)2 or |𝒟 − ℳ|/max(𝒟, ℳ) – finding the absolute residuals to perform better on the basis of visual inspection of position-velocity diagrams. We note that the use of absolute residuals has featured in previous works (e.g. MF11, Marasco et al. 2012), and is the “default” fitting method in 3DBAROLO.
The value of ϵ in Eq. (5) is particularly relevant as it affects the width of the posterior distributions, which give the uncertainty on the fitted parameters (see also Sect. 4.2). In principle ϵ should be the rms-noise of the datacube, corrected for the fact that adjacent voxels are correlated. However, given that our model is a simple axisymmetric approximation of the EPG, the requirement that it fits the data to the noise level is not realistic and would lead to a severe underestimation of the uncertainty associated to our parameters. To account for this, we use instead an “effective” uncertainty that takes into account the deviation from axisymmetry in the EPG component, computed as follows. Consider I(i, j, k) to be the intensity in a given voxel with RA, Dec and velocity coordinates given by i, j and k, where I(0, 0, 0) is the intensity at the galaxy centre and at the systemic velocity. In a pure axisymmetric system we expect that δI ≡ I(i, j, k)−I(−i, −j, −k)≃0 or, more precisely, that the standard deviation of the distribution of δI, σδI, is equal to the rms-noise in the data. We can then use σδI as an estimator for the deviation from pure axisymmetry. While other methods to quantify H I asymmetries in galaxies have been proposed in the past (e.g. Holwerda et al. 2011; van Eymeren et al. 2011; Giese et al. 2016), our approach is better suited for the current study as it uses simultaneously the information on the spatial and kinematic distribution of the gas. Using the centre and systemic velocity of each galaxy, we compute σδI using all voxels that have not been filtered out by either the external or the internal masks, obtaining values ranging typically from 1 to 8 times the rms-noise in the data. We then set ϵ = σδI × nvpr, nvpr being the number of voxel per resolution element, approximated by
where the factor 2 at the beginning accounts for Hanning smoothing. As we have nvpr ∼ 20, the values of ϵ ranges from 20 to 160 times the data rms noise.
Table 3 summarises the model parameters and our choice of priors, all uniform within reasonable ranges. We sample the posteriors with an affine-invariant Markov chain Monte Carlo (MCMC) method, using the python implementation by Foreman-Mackey et al. (2013). We use 100 walkers and a number of chain steps varying from 1000 to 2000, depending on the galaxy in exam. The chains are initialised by distributing the walkers in a small region around a minimum in the parameter space, which is determined via a Downhill Simplex minimisation routine (Nelder & Mead 1965)4. As discussed in Sect. 2.3, the EPG mass of each model is set by normalising the flux in the synthetic cube to that of the data, and is stored at each step of the chains. At the end of the process, the chains are inspected by eye in order to determine the initial “burn-in” chunk that must be discarded5, while the remaining portion is used to sample the posterior probability.
In Appendix B we test our fitting strategy on artificial data and show that the various degeneracies discussed in Sect. 2.4 are not complete: our method can recover the various input parameters with (very) good accuracy, thanks to the simultaneous fit to the EPG morphology and kinematics.
3. Results
3.1. The EPG of NGC 3198
To illustrate our method, we first treat in detail a single, reference system: NGC 3198. This galaxy was already studied by G13 using the same HALOGAS data as in the current study. G13 experimented with different models and concluded that the H I emission from this galaxy could not be reproduced by a single disc component, but it required the contribution of a thick (3 kpc scale-height) layer of EPG featuring a vertical rotational lag of −15 km s−1 kpc−1 in the approaching side and −7 km s−1 kpc−1 in the receding side. The EPG, which was assumed to have the same surface density profile of the whole gas distribution, would account for ∼15% of the total H I content.
We follow the method described in Sect. 2.2 to filter out the emission from the thin disc and from regions not associated to the galaxy. To illustrate the effect of this procedure, in Fig. 5 we show a pv-slice along the major axis of the galaxy where we have highlighted the regions associated to the internal (white area) and to the external (green dashed contour) masks. Clearly, the masking of the disc leaves out a low-velocity tail of H I emission (the so-called “beard”) preferentially from within the inner regions of the galaxy. As discussed above, the internal mask is applied to both the data and the models, while the external mask is used to filter out from the data potential H I sources not associated to the galaxy but it is not applied to the models.
 |
Fig. 5. Position-velocity slice along the major axis of NGC 3198 (1′≃4.2 kpc at the distance adopted). The white area shows the emission from the thin H I disc (internal mask), derived as discussed in Sect. 2.2. The region outside the green dashed contour (external mask) is not associated to the galaxy and is set to zero in the data. The orange squares show the rotation curve derived with 3DBAROLO. Black contours are spaced by powers of 2, the outermost being at an intensity level of 0.28 mJy beam−1 (2σnoise). A negative contour (−2σnoise) is shown as a dashed grey contour. |
Figure 5 also shows the rotation curve derived with 3DBAROLO (orange squares). 3DBAROLO uses a tilted ring approach to model the whole H I emission in the 3D data. As the emission is vastly dominated by the thin disc component, we expect that the presence of the EPG has a negligible impact on the inferred rotation curve. Still, in order to give a higher weight to the bright emission from the disc, we have configured 3DBAROLO so that it uses χ2-like residuals to infer the quality of the fit. Since we use axisymmetric templates, unlike G13 we do not attempt to model the approaching and the receding sides of the galaxy separately but fit the whole system simultaneously. Aside from this, our rotation curve is perfectly compatible with that determined by previous studies (Begeman 1989; de Blok et al. 2008, G13).
Once the data have been masked and the rotation curve has been derived, we can proceed to model the leftover H I emission with our MCMC routine. As our EPG modelling technique requires a single estimate for the inclination and position angle of the entire galaxy, for consistency we adopt the median values determined by 3DBAROLO (INC = 70°, PA = 214°, see Table 1), which are compatible with those reported by de Blok et al. (2008). In the top panel of Fig. 6 we show the corner-plots for the EPG parameters of NGC 3198, along with their marginalised posterior distribution. All posteriors are unimodal, indicating that there is a well-defined choice of parameters that best reproduce the properties of the EPG in this galaxy. Hereafter we quote the median of the posterior distributions as best-fit values, and take the 16th and 84th percentiles as a nominal uncertainty. The corner-plots also show some partial degeneracy, especially between Rg and γ and between the rotational lag and the scale-height (which we have already anticipated with our toy models in Sect. 2.4), which increases the uncertainty associated to these parameters. We find a value of −9.2 ± 1.4 km s−1 kpc−1 for the rotational lag, a precise estimate that falls well within the range quoted by G13 for the two sides of the galaxy, while the magnitude of the vertical and radial velocities are compatible with zero within their uncertainty. As for the mass fraction of the EPG (fEPG), derived as the ratio between the H I flux in the unmasked EPG model and the total flux in the unmasked data cube, we find a value of 8.6%, in slight tension with respect to the 10−20% quoted in G13. Also, we infer a scale-height of ≃1.4 kpc that is about half their estimated value. Arguably, there are substantial differences between our model/method and those of G13. We discuss this further in Sect. 4.3.
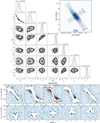 |
Fig. 6. Top: corner-plots showing the correlation between the various parameters (shaded regions, with contours at arbitrary iso-density levels) along with their marginalised probability distribution (histograms on top) for the EPG of NGC 3198. Top-right inset: total H I map of NGC 3198 showing the cuts parallel to the major and minor axes used in pv-slices below. Bottom: pv-slices for the data (black contours) and for our best-fit model (red contours). Slice off-sets are indicated on the top-left of each panel. The white area and the green dashed contour indicate the internal and external mask, respectively. Orange squares show the rotation velocities determined with 3DBAROLO. Contours are spaced by powers of 2, the outermost being at an intensity level of 0.28 mJy beam−1 (2σnoise). A negative contour (−2σnoise) is shown for the data as a dashed grey line. |
The bottom panel of Fig. 6 compares the data (black contours) and our best-fit model (red contours) via a series of pv-slices parallel to the major (top panels) and minor (bottom panels) axes. The orientations and separations of the various slices are shown in the top-right inset of Fig. 6, overlaid on top of the total H I map (see Appendix C). In the data, the EPG seems to be systematically more abundant in the approaching side of the galaxy (see major-axis slices at ±1′), a feature that our axisymmetric model clearly cannot reproduce. Apart from this difference, there is excellent agreement between the model and the data. The former reproduces very well the emission from the low-velocity gas, visible in the major-axis slices. The absence of prominent asymmetric features in the minor-axis slices, evident in both the data and the model, testify the lack of global inflow/outflow motions.
3.2. EPG properties across the HALOGAS sample
We now present the results for the rest of the HALOGAS sample. Unless specified differently, the procedure adopted is the same as that described for NGC 3198 in Sect. 3.1.
Three galaxies out of 15 were left out from the analysis: NGC 1003, NGC 4274 and NGC 4448. A visual inspection of the H I datacube of NGC 1003 revealed the presence of a strong line-of-sight warp in the eastern part of the galaxy, where the orientation becomes nearly edge-on. This effect seems to be less prominent on the western side. This line-of-sight warp, already noticed by Heald et al. (2011b), also explains the appearance of the total H I map (Fig. C.1), which suggests a much higher inclination than that inferred from the optical image (70 ° −75°). As our EPG separation method fails when consecutive rings overlap along the line of sight, we decided to discard this system from our study.
 |
Fig. 7. Position-velocity slices for the galaxies in our sample (see description for the bottom panel of Fig. 6). Individual cases are discussed in the text. |
 |
Fig. 7. continued. |
 |
Fig. 7. continued. |
 |
Fig. 7. continued. |
In NGC 4274 and NGC 4448, instead, the masking of the H I disc leaves virtually no EPG emission to work with. These are two of the systems with the fewest resolution elements; their datacubes show very asymmetric H I profiles which – according to our mask – are largely caused by beam-smearing rather than by the presence of kinematically anomalous gas. Our method relies on the modelling of a kinematically distinct component and can not be used here, but we can not exclude that some EPG may actually be present in these systems. More advanced modelling techniques, based on fitting simultaneously both the disc and the EPG component to the data, may be preferred in these cases, but are beyond the scope of this paper.
Figure 7 shows the pv slices for the remaining HALOGAS galaxies and for their best-fit model. Some individual cases require further discussion.
NGC 0672 is interacting with a companion, IC 1727, an irregular dwarf which strongly contaminates the H I flux at negative (approaching) velocities (see also maps in Appendix C). The rotation curve of NGC 0672 has been derived using only the receding side of the disc, and a significant portion of the approaching side has been blanked and added to the internal mask (as it appears from the white square regions in the slices along the major axis). An H I filament is visible in the major axis slices at −2′ and −1′ at about the systemic velocity, possibly caused by the interaction between the two galaxies. The filament is not reproduced by our model, as expected. Note that in this galaxy we have used γ > 0 as an additional prior. The best-fit model would naturally prefer a negative γ (i.e. a larger central concentration for the EPG), which slightly improves the pv-slice along the major axis but at the cost of producing no emission in the slices at ±2′ offsets, where anomalous H I is clearly visible.
NGC 0925 shows an extended H I tail towards the south, possibly caused by a recent interaction with a very faint system (Sancisi et al. 2008, H11). This tail seems to be efficiently masked by our procedure, as can be seen from the extent of the white regions in minor axis pv-slices, and the model appears to fit reasonably well the leftover anomalous emission.
In NGC 0949, the tilted ring fit with 3DBAROLO indicates clearly the presence of a warp (> 10°) in both inclination and position angle. Given the limited number of resolution elements (7 per side), we have decided to fix the INC and PA to median values for both the rotation curve and the EPG modelling. We have verified that the EPG mass and kinematics do not change significantly if we use a rotation curve that accounts for the warp.
The anomalous gas of NGC 2403 has been studied in detail first by Schaap et al. (2000) and then by Fraternali et al. (2002), and represents the prototypical case for a slow rotating and inflowing EPG. We compare our findings with those of Fraternali et al. (2002) in Sect. 4.3. The overall H I emission is contaminated by the Galactic H I foreground in a few channels at negative velocities, which we have blanked (white horizontal stripes). Also here a prominent filament is visible in minor axis pv-slices at offsets ≤0 and along the major axis (see also de Blok et al. 2014a). As expected, the filament is not reproduced by our model.
In NGC 2541, too, 3DBAROLO finds a warp in both INC and PA, with magnitudes of ∼5 ° −10°. Our model seems to reproduce well the emission from the anomalous component, which is fairly axisymmetric and smooth.
The anomalous gas in NGC 4062 is barely visible in pv slices parallel to the major axis, and is virtually absent along the minor axis. Given the limited resolution and number of voxels to fit, the application of our model to this system must be taken with some skepticism. However, tests on mock data have shown that even in this condition our model can recover the correct parameter within a 2σ uncertainty, as we discuss in Appendix B.
NGC 4258 features a complex kinematical pattern, with streaming motions in the innermost few kpc (as visible from the markedly asymmetric pv slice along the minor axis) and a ∼15° warp in both PA and INC distributed along its entire disc. It also contains an active nucleus and it is classified as a Seyfert 2 object. Despite this complexity, the properties of its EPG appear to be analogous to those of the rest of the sample.
As already noticed by de Blok et al. (2014b), NGC 4414 has substantial (∼10°) warp in position angle, and its rotation curve indicates the presence of a prominent stellar bulge. As for NGC 5055 (another warped galaxy, see below), modelling the whole system resulted in a very poor fit and we decided to focus on the innermost 20 kpc region, where variations in PA are less severe. Our model seems to miss a significant fraction of the anomalous H I flux, especially along the major axis (at about the systemic velocity) and in parallel slices at ±1′ offsets.
The EPG of NGC 4559 was already studied by Barbieri et al. (2005) and Vargas et al. (2017), with which we compare our findings in Sect. 4.3. The pv-slices parallel to the major axis show that the EPG is systematically more abundant on the approaching side, a feature that our axisymmetric model can not reproduce. As discussed, our model gives pv-slices along the major axis (offset of 0′) that are symmetric by construction.
NGC 5055 is well known to host a prominent warp in its outskirt (e.g. Battaglia et al. 2006), which can be traced accurately with 3DBAROLO (see Fig. 4 in Di Teodoro & Fraternali 2015). Modelling the EPG of the whole dataset resulted in a very poor fit, and we decided to focus on the innermost 20 kpc where the INC and PA are relatively stable. In fact, anomalous H I flux may spuriously arise at R > 20 kpc due to the overlap of consecutive annuli along the line of sight, given the rapid variation of the INC and PA in these regions. Despite this treatment, a significant fraction of the anomalous H I emission, including a filament visible along the major axis, does not seem to be reproduced by our model: it is likely that the EPG mass of this galaxy is underestimated. We also note that the background noise in the datacube is not constant and is difficult to treat properly. We discuss this “difficult” system in more detail in Sect. 4.1.
The best-fit parameters for the EPG of these 12 galaxies are listed in Table 4, along with their associated 1σ uncertainty, computed as half the difference between the 16th and 84th percentiles of their probability distribution. The nominal uncertainty on the EPG mass that we derive from the marginalised posterior is small, typically around 5%, and is not quoted in Table 4. More realistic errors come from the uncertainty on the distances, for which we assume a fiducial value of 10% (corresponding to a 20% error on the mass). The EPG fraction, fEPG, varies from 9% (NGC 3198) to 27% (NGC 0949) with a mean value of 14%, and is fairly consistent with the values typically quoted in the literature (e.g. Fraternali 2010). This confirms that the EPG is a common feature of late-type galaxies.
Best-fit parameters and associated uncertainty for the EPG of the galaxies studied in this work.
For three galaxies (NGC 2541, NGC 4062 and NGC 4414) we find a flat posterior in the Rg parameter, meaning that the EPG scale radius for these systems is unconstrained. Interestingly, this has little impact on the EPG mass, mostly because of the flux normalisation and because the model is always truncated at the outermost radius measured in the rotation curve (we do not extrapolate the EPG mass beyond that radius). With the exception of NGC 5055 and NGC 4414, which are both poorly fit by our model, the EPG scale-height is always confined within 1−3 kpc. The EPG is more turbulent than the gas in the disc, with velocity dispersions varying from 15 to 35 km s−1, a factor of 1.5−3 higher than the H I in the disc. Even accounting for this larger velocity dispersion, if the EPG were in hydrostatic equilibrium we would expect scale-heights of ≲1 kpc (e.g. Bacchini et al. 2019). Hence the EPG is not in hydrostatic equilibrium, and this has fundamental implications for its origin (see Sect. 4.4 for further discussions).
All galaxies show a negative gradient in rotational velocity, i.e. the EPG systematically rotates at a lower speed than the disc. The rotational lag varies from a few to ∼ − 20 km s−1 kpc−1, with a median value of −10 km s−1 kpc−1, meaning that rotation is still the main motion of this anomalous component. The only two outliers in this scheme are again NGC 5055 and NGC 4414, with a lag of ≈ − 50 km s−1 kpc−1 (but notice the large errors), which is compensated by the small scale-height given the (partial) degeneracy between these two parameters. Remarkably, once we have determined the near/far sides of these systems and subsequently adjusted the sign of vR and vz, we find that all galaxies are compatible with having vR ≤ 0 within the uncertainties, and that 11 galaxies out of 12 are compatible with having vz ≤ 0 within the uncertainties. That is, the EPG appears to be globally inflowing towards the galaxy centre with typical speeds of 20−30 km s−1.
Figure 8 summarises the kinematical properties of the systems analysed. Galaxies that cluster in the bottom-left region of the plot (vR < 0, vz < 0) have also more precise kinematical measurements, as it appears from the error-bars. The fact that several late-type galaxies show similar kinematical properties for their EPG strongly supports the idea of a common physical origin for this H I component. We discuss this further in Sect. 4.4.
 |
Fig. 8. Kinematics of the EPG in the HALOGAS galaxies as derived from our models. EPG tends to be globally inflowing with a speed of 20−30 km s−1. Interacting and poorly fitted galaxies are shown with separate symbols. Values for the Milky Way (MW) are from MF11. |
4. Discussion
4.1. Limitations of our method
Our method represents an important step forward in the analysis of kinematically anomalous gas in galaxies. While we tailored our procedure around systems at intermediate inclinations, it is in principle possible to extend our fitting strategy to edge-on galaxies once a method for filtering the emission from the disc is decided. However, our approach comes with a number of limitations that we discuss below.
Two key assumptions are that the EPG is smooth and axisymmetric. These are clearly not valid in the cases where the kinematically anomalous gas is built by a few, isolated H I complexes scattered around the disc. This does not seem to be a typical scenario, but there are cases where isolated H I complexes/filaments are visible and can have an impact on the fitting procedure. An example is NGC 2403, where an anomalous, bright H I filament is visible in most of the pv-slices parallel to the minor axis. This filament is kinematically detached from the rest of the smooth EPG component and is likely to have a separate origin (e.g. de Blok et al. 2014a). Even if it accounts only for a few per cent of the total EPG H I mass, Its presence may impact the modelling by artificially increasing the EPG thickness, rotational lag or velocity dispersion. We note in fact how, in the pv-slice along the major axis, the model appears to slightly “overshoot” the data.
Much more common are the cases where the EPG appears to be more abundant on one side of the galaxy. A striking example is that of NGC 4559, where most of the anomalous H I is located on the approaching side of the disc as it appears from the major axis pv-slice. As we discussed, in an axisymmetric model the pv along the major axis is always symmetric. In this particular case, our model attempts to find a compromise between the two galaxy sides, overestimating (underestimating) the emission from the receding (approaching) region.
In a scenario where the EPG is produced by a galactic fountain cycle, we may expect that the anomalous gas originates preferentially from the regions of intense star formation, like spiral arms. While this may introduce an additional asymmetry in the EPG distribution, in principle the relative speed between the disc material, the spiral arm pattern and the halo gas should wash out any imprint of the original ejection region. Total maps of the kinematically anomalous gas, in fact, do not show hints of a spiral structure (e.g. Fraternali et al. 2002; Boomsma et al. 2005), although asymmetries may be present (also in the ionised component, see Kamphuis et al. 2007). Another feature that a galactic fountain is expected to produce is a flare in the EPG distribution (e.g. Marasco et al. 2012, 2015). In order to model such feature we should include an additional free parameter to describe the radial dependency of h. In the philosophy of keeping the model as simple and generic as possible, in this work we have not explored the possibility of a flare, but it is a feature that we plan to introduce in future studies.
Another limitation of our model is the assumption of a single choice of INC and PA for the whole galaxy, i.e. we assume that the EPG component is not warped. In our sample, at least six galaxies show a substantial (∼10° or more) warp in their H I distributions: NGC 0949, NGC 1003, NGC 2541, NGC 4258, NGC 4414 and – the most extreme case – NGC 5055. In principle, a warped disc should not produce asymmetries in the line profiles unless consecutive rings overlap significantly along the line of sight, and it is expected to be automatically filtered out by our masking procedure. In addition, if the EPG component originates from a galactic fountain, we expect it to be confined within the inner (star forming) disc, where variations in INC and PA are weak. In practice, applying our procedure to the whole cubes of NGC 5055 and NGC 4414 resulted in very poor fits to the anomalous H I emission of these galaxies (while this does not seem to be the case for the other warped systems). The fit improves when we limit the model to the innermost ∼20 kpc, where the warp is less pronounced. However, even when we fit only the inner parts, we find that the model does not reproduce a significant fraction of the anomalous H I flux, and that the best-fit values for the rotational gradient and for the scale-height are distinct from those of the rest of the sample. It is possible that a fraction of the EPG in these two galaxies has a different origin with respect to the others, perhaps related to the same physical process that have built the warp. Our model may not be appropriate to describe all the anomalous H I in these systems. In general, uncertainties in the adopted value of inclination have little impact on our results and seem to affect exclusively the inferred rotational gradient. We have experimented by varying the fiducial INC of NGC 3198 and NGC 4062 by ±5°, adjusting their rotation curve accordingly, finding a variation of about ±1.5 km s−1 kpc−1 in the best-fit dvϕ/dz while all the other parameters (including the EPG masses) remained unaffected.
An important question is how robust – or model dependent – our results are, with particular focus on the EPG mass. We have already discussed how modelling the anomalous H I emission directly in the 3D data domain is fundamental to derive the EPG mass, given that the total H I flux measured after the disc subtraction largely depends on the kinematics of the EPG itself and on the galaxy inclination. That said, our model is parametric and it is clear that a different parametrisation can lead to different results. For instance, in our parametrisation of the vertical density distribution (Eq. (2)), ρ(z)∝exp(−|z|/h) for |z|≫h and the density profile deviates from an exponential law only close to the midplane, where a depression occurs to accomodate for the thin disc. As discussed, a pure exponential layer would make the boundaries between the disc and the EPG ambiguous and is not used in this work. At any rate, the surface density that one obtains by neglecting the inner depression, i.e. by assuming an exponential profile all the way down to the midplane, would be a factor of 2 larger than what we currently infer. As a test, we have tried to fit NGC 3198 using an EPG model with exponential surface and vertical density profiles, rather than the profiles described by Eqs. (1) and (2), finding a factor 2 difference in the EPG mass. The best-fit scale height and the kinematical parameters, though, were compatible with those derived in our original parametrisation within 2σ on both measures. Interestingly, in this new parametrisation we find a much stronger degeneracy between scale-height and rotational lag (already noticed by G13), and wider and more asymmetric posterior probability distributions. We have repeated this test on NGC 4062, for which our results are supposedly less robust given the limited resolution and extent of the EPG emission in this galaxy. The results show a 50% larger EPG mass but, quite remarkably, the same kinematical parameters of our previous determination. This strengthen our findings for this particular galaxy and indicates that, in general, the inferred EPG kinematics do not depend strongly on the model parametrisation.
Additional uncertainties come from the choice of the flux-density threshold at which we “clip” our disc model to produce the mask. We have tested whether our results for NGC 3198 vary if we change our fiducial threshold (2× the data rms-noise) to a smaller (1× the rms-noise) or to a larger (3× the rms-noise) value, finding that in all cases the kinematical parameters and the scale-height remain compatible within the error-bars. Rg and γ are instead less stable, leading to some fluctuations in fEPG (0.07, 0.09 and 0.10 for thresholds of 1×, 2× and 3× the rms-noise). Uncertainties on the distances lead to similar or larger error-bars on the H I masses. A more in-depth discussion on the error-bars associated to our measurements is presented in Sect. 4.2.
Finally, we would like to draw attention to our disc/EPG separation method, which is based on building a Gaussian model for the thin disc emission that is then used to filter out the disc contribution in the data. As for warps, we expect that our masking procedure is robust against large-scale non-circular motions (like a global radial flow) within the thin H I disc, given that their effect would be to shift the velocity centroids of the H I lines without affecting their shape. Local non-circular motions within the disc on scales comparable to or smaller than the beam size would instead affect the shape of the profiles and produce “anomalous H I” that would be incorporated in our EPG modelling. While it is difficult to quantify the incidence of these effects, we do not expect them to have a systematic impact on our results. Systematics are instead caused by beam-smearing: even in a razor-thin disc, line-profiles can deviate from a Gaussian if the spatial resolution is poor. Galaxies like NGC 4275 and NGC 4448 show remarkably asymmetric line profiles, but such asymmetries are consistent with being produced by beam-smearing rather than by a distinct, anomalous H I component. Experiments made with mock H I cubes indicate that even a small contamination from the disc emission can strongly affect the recovery of the EPG parameters, typically leading to lower values of dvϕ/dz, h and σ. This is why we have adopted a conservative mask, achieved by further smoothing the Gaussian model with the instrumental beam: in many cases this leaves little H I flux to work with (or no flux at all for NGC 4275 and NGC 4448) but it is indispensable. In general, a more complete modelling approach would consist of fitting simultaneously both the disc and the EPG components to the data. Such method may provide a better alternative to infer the EPG properties in poorly resolved galaxies, at the cost of a higher number of free parameters with respect to the current method. In the near future, MeerKAT will provide deep H I data at a higher angular resolution for several systems, significantly improving our understanding of the EPG properties in galaxies.
4.2. Reliability of the uncertainties in the EPG parameters
Our fitting approach is extremely sensitive to tiny differences between models and data. Despite our careful treatment of the likelihood (Sect. 2.5), the a-posteriori probability of our models drops very quickly as the parameters depart from their best-fit values. As a consequence, models that are labelled to differ by several σ from the best-fit one may still appear as “good” at a visual inspection. To illustrate this, in Fig. 9 we compare the best-fit model for the EPG of NGC 672, for which we have found a clear evidence of vertical and radial inflow with (vz, vR) = (−35, −25) km s−1 and error-bars of a few km s−1, with models that have the same best-fit parameters but where vz or vR are either zeroed or reverted. While the best-fit model (first column in Fig. 9) clearly outperforms those where the vR or vz have “wrong” sign (third and fifth column), it is only marginally better than those with no radial or vertical motions (second and fourth column). The latter in particular appears almost identical to the best-fit models, except for a few locations indicated by the arrows. The situation would not differ if we had chosen a different pv-slice. However, given the nominal error-bars associated to our measurements, a model with vz = 0 is at ∼15σ from the best-fit values!
 |
Fig. 9. Comparison between the best-fit model for the EPG of NGC 0672 (first column) and other models that use the same parameters but different values for vz and vR, as labelled on top of each panel. For simplicity we show only the pv-slices at 1′-offset. Contours are the same as in Fig. 6. Arrows show the locations where the various models are inferior to the best-fit one. |
The example discussed represents a somewhat extreme case, but similar considerations apply to other parameters as well. In Fig. 10 we compare the best-fit EPG for NGC 3198 (top panels) with a model featuring a thicker, more slowly rotating EPG (bottom-left panel) and with a model where the EPG is thinner and the lag is more pronounced (bottom-right panel). These models deviates by ∼4−5σ from the best-fit one and are selected in the direction of the thickness-lag degeneracy. Also in this case the differences with respect to the best-fit model are marginal.
 |
Fig. 10. Comparison between the best-fit model for the EPG of NGC 3198 (top panels) and two models that use the same parameters but different values for h and dvϕ/dz (bottom panels). Contours are the same as in Fig. 6. Arrows show the locations where the models are inferior to the best-fit one. We have focussed on pv-slices where the differences are more evident. |
In general, it is hard to distinguish by eye models that differ by less than ∼3σ from their quoted best-fit values. In this work we used a statistical approach to the modelling and preferred not to adopt any arbitrary by-eye criterion to define the uncertainty associated to the estimated parameters. The examples illustrated above may help the reader to have a better perspectives on the error-bars quoted in this study.
4.3. Comparison with previous work
The presence of anomalous H I features around the disc of late-type galaxies has been known for several decades, and we refer the reader to the review of Sancisi et al. (2008) for a more complete discussion on the topic. However, it was only in the last ∼20 years that more focussed studies on the anomalous H I component were carried out for a limited number of systems, where deep H I data were available.
NGC 891 is arguably the best-studied case of EPG in galaxies (Sancisi & Allen 1979; Swaters et al. 1997; Oosterloo et al. 2007). Edge-on systems like this have the considerable advantage that the disc/EPG separation can be done directly on the total H I map rather than resorting to anomalies in the gas kinematics. Consequently, once the boundaries between disc and EPG have been set, the EPG mass can be readily computed and does not suffer from sensitivity drops along the minor axis as in galaxies at intermediate inclinations. It has been suggested that the large EPG fraction of NGC 891 (28% of the total, Marinacci et al. 2010a) indicates that at least part of its anomalous gas may originate from an interaction with the companion UGC 1807. While the typical fEPG of our HALOGAS sample is ∼14%, for NGC 2403 and NGC 0949 we measure 22% and 27% respectively. This suggests that the case of NGC 891 is not unique.
Another relevant study was that of Fraternali et al. (2002), who studied the EPG of NGC 2403 using VLA H I observations. They used a kinematical disc/halo decomposition – on which the procedure adopted in this work is largely based – and inferred the presence of an EPG component with fEPG ∼ 10%, characterised by a lagging rotation and a radial inflow with speeds of 10−20 km s−1. These properties were determined by applying a tilted ring model to the velocity field of the anomalous H I emission. We used the same data as in Fraternali et al. (2002) and reached very similar conclusions. Our 3D modelling, though, allows us to determine the EPG kinematics with a greater accuracy: we find lagging rotation with dvϕ/dz of ∼ − 12 km s−1 kpc−1 and a global inflow in both the radial (−20 km s−1) and vertical (−10 km s−1) directions. We also predict an EPG fraction of 22%, ∼ twice the value inferred by Fraternali et al. We believe that this difference is fully due to our modelling scheme and that our results are more reliable.
Barbieri et al. (2005) used WSRT H I observations to study the anomalous gas in NGC 4559, finding evidence for a thick (2 < h < 3 kpc), slowly rotating component with fEPG of ∼10%, and with possible hints of a radial inflow at the level of ∼15 km s−1. Similar results were obtained by Vargas et al. (2017) who used the same HALOGAS data as in the current study and performed an analysis similar to that of G13 for NGC 3198 (see below). Our results are in agreement with these findings, and we can even confirm the presence of radial (and vertical) inflow motions. We stress, though, that this system is significantly lopsided in both its density distribution and kinematics, which makes it difficult to model it via axisymmetric templates. As shown by Vargas et al. (2017), most of the anomalous H I flux in this galaxy is spatially coincident with the regions of star formation as traced by Hα and UV images, suggesting a galactic fountain origin for the EPG.
As already discussed (Sect. 3.1), G13 determined an H I mass and a scale-height for the EPG of NGC 3198 that are about twice the values determined in this work. Since we used the same data of G13, the difference must be in the method. Firstly, G13 used a two-component model comprising a disc and an EPG layer to model the whole H I dataset. While in principle this approach is more powerful than that adopted here, in practice – given the large number of parameters involved – it relies on modifying by hand the model parameters one by one until a satisfactory reproduction of the data is achieved. This complicates the assessment of the uncertainty associated to the various parameters and, most importantly in this particular case, of their degeneracy. Secondly, G13 used an exponential vertical profile and a surface density that is a re-scaled version of that of the total H I component. As discussed in Sect. 4.1, fitting the EPG of NGC 3198 with a double-exponential layer results in twice the EPG mass and a strong correlation between dvϕ/dz and h: a model with dvϕ/dz = −10 km s−1 kpc−1 and h = 3 kpc (as in G13) is indistinguishable from one with dvϕ/dz = −60 km s−1 kpc−1 and h = 0.4 kpc, as we could verify directly in the pv slices. Interestingly, the best-fit velocity dispersion for the EPG in this parametrisation is σ ∼ 12 km s−1 (with a large error-bar), equal to the fiducial value adopted by G13 but half of our current estimate. These considerations highlight the importance of properly taking into account the correlations in the parameter space.
The HALOGAS H I data of NGC 4414 were already studied by de Blok et al. (2014b), who noticed the presence of a prominent U-shaped warp in the system’s outskirt. They used different techniques to estimate the fraction of EPG in the innermost ∼20 kpc, finding values ranging from 3% up to 12% depending on the method adopted. Our estimate (12%) agrees with their quoted upper limit, but we reiterate that the quality of our fit is poor and our model may be not optimal to describe the EPG in this galaxy.
MF11 have used 3D models to infer the global properties of the EPG of the Milky Way. They built a thin disc model to filter out the H I emission from the regularly rotating disc and fitted the leftover emission with the same model that we adopt here, although they had fixed Rg and γ to some fiducial values in order to minimise the number of free parameters. They were the first to highlight that the Galactic H I halo features a lagging rotation (−15 km s−1 kpc−1) and a global inflow towards the disc with speeds of 20−30 km s−1, properties that – according the our new results – are quite common in late-type galaxies.
It is interesting to compare our findings for systems at intermediate inclinations with those reported in the literature in edge-on galaxies. Edge-on systems constitute an ideal laboratory to study the vertical distribution and rotational lag of the EPG, provided that line-of-sight warps are properly taken into account (e.g. Kamphuis et al. 2013). A compilation of EPG studies in edge-on systems is offered in Zschaechner et al. (2015), who highlighted how the rotational lag is maximised close to the galaxy centre, reaching values up to −40 km s−1 kpc−1, and gradually weakens outwards, flattening beyond ∼R25 at values ≳ − 10 km s−1 kpc−1. As we do not model the radial variation of dvϕ/dz, the values that we infer are more sensitive to the outer parts of the EPG layer, where most of the H I flux is enclosed. In this respect, our measurements for the rotational lag are compatible with those of Zschaechner et al. (2015). Instead, the EPG scale-heights listed in Zschaechner et al. (2015) are smaller than those determined in this work by a factor ∼2−3. A possible explanation for this discrepancy is again the different vertical density profile adopted (exponential vs our Eq. (2)), as discussed in Sect. 4.1.
4.4. The origin of the EPG
The best-fit parameters found for the EPG give us fundamental clues on the origin of this component. Our analysis reveals that in all HALOGAS systems the EPG “knows” about the presence of the disc, as it rotates along with it at a (slighty) lower speed, with a dvϕ/dz that varies from system to system but has a typical value of −10 km s−1 kpc−1. In addition, in most galaxies the EPG appears to be globally inflowing in both the radial and vertical directions, with velocities around 20−30 km s−1. This peculiar kinematics, along with a significant thickness (1 < h < 3 kpc), imply that the EPG properties are not compatible with predictions based on hydrostatic equilibrium models (e.g. Barnabè et al. 2006; Marinacci et al. 2010a; Bacchini et al. 2019). Non-stationary models are therefore required to explain the properties of this component.
A possibility is that the whole EPG originates from the spontaneous condensation of the innermost layers of the CGM, leading to a continuous, smooth accretion of pristine gas onto the disc. In galaxies where we find vz < 0, we can compute the infall rate of the EPG, Ṁ, as 1.4 MHI, EPG vz ⟨z⟩−1, where the factor 1.4 accounts for the helium and ⟨z⟩≃1.32h is the median EPG displacement from the midplane. We find inflow rates ranging from 3 to about 50 times the SFR of each system, with a median Ṁ/SFR of 9. This implies that, if the EPG were produced solely by external gas accretion, galaxies would double their cold gas reservoir in a mere few hundred Myr, indefinitely growing in mass and size at a very fast pace. From the theoretical point of view, it is very unlikely that such a disparity between gas accretion and star formation rate can lead to a realistic galaxy population. These considerations, along with theoretical arguments against the spontaneous condensation of the CGM (e.g. Binney et al. 2009; Nipoti 2010), strongly disfavour this scenario. We do not exclude, though, that a small fraction of the EPG may come from external accretion (see below).
Following the work firstly pioneered by Fraternali & Binney (2006) and then followed up by Fraternali & Binney (2008) and Marasco et al. (2012), we can readily interpret all the discussed features in the framework of the galactic fountain cycle. In this context the EPG is built by material ejected from the disc by stellar feedback that travels through the halo region, eventually returning back to the disc on timescales of several tens of Myrs. The fountain material is ejected from regions of active star formation and thus, at the beginning of its journey through the halo, can be photo or shock-ionised and therefore invisible in the H I phase. This produces an observational bias in H I against the fountain material that leaves the disc (vz > 0) in favour of that returning back to it (vz < 0), which justifies the vertical velocities inferred for most galaxies. A higher velocity dispersion for the fountain material is expected due to fountain cloud-to-cloud relative motions and, for single clouds, to ram-pressure stripping from the hot CGM.
The fountain clouds inevitably develop some rotational lag as a consequence of the angular momentum conservation (for details see Fraternali 2017), but this is typically insufficient to explain the measured values of dvϕ/dz. In addition, simple ballistic orbits for clouds ejected perpendicularly to the disc show that the fountain material moves preferentially outwards (vR > 0), in disagreement with our measurements. Both these issues can be solved by assuming that the fountain clouds interact with a CGM having locally a lower specific angular momentum: as the clouds exchange momentum with the CGM, they lose rotational speed and flow backwards, acquiring a net vR < 0 in the latest part of their trajectory (see Fig. 6 in Fraternali & Binney 2008). In this more refined model, the fountain orbits are characterised by positive values of (vz, vR) in the ascending part and by negative (vz, vR) in the descending part, while mixed signs for the radial and vertical velocities are less common. This pattern is consistent with that shown in Fig. 8, where the top-left and bottom-right regions are practically empty (the exception being NGC 925, which is still compatible with vz ≃ 0 and is an interacting system). Photo-Ionisation in the early (ascending) phase can explain the bias towards the descending portion of the fountain, hence the position of most galaxies in Fig. 8, while systems like NGC 5585 and NGC 3198 may be characterised by a different distribution in their ionisation flux that drives them towards the opposite side of the plot. The effect of photo-ionisation could be investigated further in Hα spectroscopic cubes (e.g. from Fabry-Pérot observations, or with WEAVE, Dalton et al. 2012), using the same modelling approach adopted in this work, by looking at signatures of opposite (vz, vR) as compared to the HALOGAS results, although part of the outflowing gas can be very hot and thus not visible in Hα.
It is not straightforward to predict a priori a timescale for the recombination of the fountain gas, as this depends on the initial launching conditions and on the combined effect of different ionising mechanisms. A lower limit can be set by the typical recombination timescales for the warm interstellar medium in absence of any source of radiation, which range between 0.1 and 1 Myr depending on the electron density (Spitzer 1978). A rough upper limit can be set by the lifetime of OB associations (of the order of 10 Myr) under the assumption that the gas is fully photo-ionised, although extragalactic UV background may be important above the disc by somewhat increasing this value. Early hydrodynamical calculations for thermally-powered galactic fountains (Houck & Bregman 1990) have also suggested a few tens of Myr as the time required by the hot and rarefied material ejected into the halo to condense and form discrete dense clouds. Finally, 17 Myr is the best-fit recombination timescale in the fountain model of Marasco et al. (2012) required to reproduce the Galactic EPG H I data. All these timescales are typically smaller than the fountain orbital times (30−70 Myr, see Eq. (9) below).
Marasco et al. (2012) successfully modelled the EPG in the Milky Way using a dynamical model of the galactic fountain interacting with the CGM. As the kinematics of the Galactic EPG is similar to that of most HALOGAS systems (Fig. 8), we may expect that the same model can be applied to the galaxies studied in this work. This will be the subject of a future study.
To further test the galactic fountain framework, we compare the EPG masses reported in Table 4 to the mass expected to be produced by a galactic fountain cycle, which we write in a general form as
where Σfount is the gas surface density of the fountain component. Given that the fountain cycle is powered by stellar feedback, we expect that Σfount depends on both the star formation rate density ΣSFR and on the vertical orbital time torb:
where β is the mass-loading factor and represents the amount of gas that joins the fountain cycle per unit star formation rate.
For a flat rotation curve in an isothermal potential, the orbital time is nearly a linear function of radius and can be roughly approximated as
Equation (8) can be further simplified by assuming that ΣSFR is an exponential function of radius:
where the value of the total SFR for each galaxy is taken from Table 1. Combining Eqs. (7), (9) and (10) leads to a simple approximation for the fountain mass:
As for RSFR, we use the results of Leroy et al. (2008) who studied the FUV+NIR star formation density profiles for a sample of 23 nearby galaxies and found RSFR ≃ (0.22 ± 0.06)R25.
The left panel of Fig. 11 compares SFRs and EPG masses for our galaxy sample. While these two quantities are arguably related in a galactic fountain framework, only a mild correlation appears to be present (Pearson coefficient of 0.23, or 0.66 using only the “regular” systems). The correlation improves significantly (Pearson coefficient of 0.44, or 0.84 for the regular systems) when we compare the EPG masses with the theoretical prediction from Eq. (11), where we used a constant ad-hoc mass-loading factor β = 7 (right panel of Fig. 11) which we discuss below. Now most HALOGAS systems align well on the one-to-one line, notable exceptions being NGC 5055, NGC 4414 and NGC 672. As discussed already, the EPG masses of the first two systems are likely underestimated by our model, while that of NGC 672 may be augmented by the interaction or merging with its (massive) companion. The trend is remarkably tight if one focuses solely on the non-interacting, well-fitted HALOGAS galaxies, corroborating the validity of the galactic fountain framework. Interestingly, NGC 925 follows very well the trend of the non-interacting systems despite the presence of a low-mass nearby perturber. We have used distinct symbols in Fig. 11 to emphasise that the magnitude of perturbation expected for NGC 925 is small compared to that of NGC 672.
 |
Fig. 11. Left panel: SFR vs EPG mass for our HALOGAS sample. Right panel: theoretical EPG mass predicted by a galactic fountain model (Eq. (11) with β = 7) vs that inferred from the data. The two panels span the same range (∼1.5 dex) on both axes. Error-bars are determined by assuming a 10% uncertainty on the distances and a 20% uncertainty on the total SFR, in addition to the uncertainty on the RSFR discussed in the text. Interacting galaxies and systems with a poorly fit EPG are shown with separate symbols. We have also included NGC 891 (MEPG from Marinacci et al. 2010a) and the Milky Way, for which we used MEPG = 3.2 ± 1.0 × 108 M⊙ (MF11), and assumed fiducial values for SFR, RSFR and vflat of 2 ± 1 M⊙ yr−1, 2.5 ± 0.5 kpc and 240 ± 10 km s−1 respectively. |
The value of the mass loading factor adopted in Eq. (11) deserves further discussion. In general, β is very difficult to constrain observationally and we have fixed its value to 7 in order to maximise the agreement between the observed and the theoretical EPG masses. Remarkably, this empirically estimated value is perfectly compatible with those determined by Fraternali & Binney (2006) by applying their dynamical fountain models to NGC 891 and 2403: they found ratios between the fountain outflow rate and the star formation rate ranging from 4 to 9, depending on the details of the gravitational potential. It is interesting to combine our estimate for β with the typical EPG inflow rate determined at the beginning of this section. If stellar feedback ejects material at a typical rate of 7 times the SFR, and the inflow rate of the EPG is ∼9 times the SFR, there is a net gas accretion onto the disc at (approximately) the same rate as the star formation. While these numbers represent only a crude estimate for the actual outflow and inflow rates, the scenario described is compatible with expectations from a fountain-driven gas accretion framework (Fraternali & Binney 2008; Marasco et al. 2012; Fraternali 2017), where fountain clouds trigger the condensation and stimulate the subsequent accretion of a small fraction of the CGM. This accreting gas plays a key role in the galaxy evolution by replenishing the material used in the process of star formation (e.g. Sancisi et al. 2008).
As discussed, NGC 4274 and NGC 4448 have been excluded from our analysis as our masking procedure leaves little H I emission to work with. The theoretical EPG masses predicted by our fountain model for these two systems are log(MEPG/M⊙) = 8.85 and 7.02 respectively, with an uncertainty of 0.15 dex. The small mass predicted for NGC 4448 comes from its exceptionally small star formation rate (0.056 M⊙ yr−1) and scale length (1.2 kpc). One may ask whether EPG layers with such masses would be actually detectable in the data or, equivalently, what is the upper limit on the EPG mass for these two systems. Answering these questions is hard, given that the detectability of EPG at a given mass depends on its kinematics and density distribution, which are unknown. As a test, we have produced synthetic cubes for a series of EPG layers of different masses, using as representative scale-height and kinematical parameters the median values of the sample (h = 1.6 kpc, dvϕ/dz = −10 km s−1 kpc−1, vz = −18 km s−1, vR = −20 km s−1, σ = 25 km s−1) and experimenting with different values for Rg and γ. We verified visually the detectability of these models in the pv-slices of NGC 4274 and NGC 4448. The results of these experiments show that, for log(MEPG/M⊙)≳8.5 (7.4), anomalous H I always appears in the pv-slices of NGC 4274 (NGC 4448) regardless the details of the surface density distribution. The quoted detection limits correspond to about 40% and 60% of the total H I content of NGC 4274 and NGC 4448, well above the typical EPG fractions measured for the rest of the sample. With respect to our predictions, NGC 4274 is somehow poor of anomalous H I while NGC 4448 seems consistent with the fountain model, i.e. its fountain mass from Eq. (11) is below the detection limit.
5. Conclusions
In this work we have analysed a sample of 15 late-type galaxies at intermediate inclination using publicly available H I data from the HALOGAS survey (Heald et al. 2011a). The unprecedented depth of these data allowed us to study the properties of the extraplanar gas (EPG), the faint, kinematically anomalous H I component that lies at the interface between the disc and the large-scale circumgalactic medium (CGM). This is the first time that a systematic and homogeneous study of the EPG has been carried out on a sample of galaxies.
In order to separate the H I emission from the EPG, we have built Gaussian models for the H I line profiles and used them to filter out the disc contribution in the datacubes. The leftover, kinematically anomalous H I emission has been modelled by building synthetic H I cubes of idealised EPG and fitting them to the data via a Bayesian MCMC approach. Our models use 3 parameters to describe the EPG density distribution (Eqs. (1) and (2)) and 4 parameters for its global kinematics (vertical rotational lag dvϕ/dz, radial velocity vR, vertical velocity vz and velocity dispersion σ).
Our results can be summarised as follows:
-
1.
The EPG is ubiquitous in late-type galaxies. We have failed to detect it only in 2 galaxies (NGC 4274 and NGC 4448) out of 15, arguably because of the poor spatial resolution that complicates the disc-EPG separation. We have also excluded NGC 1003 from our analysis due to the nearly edge-on orientation of its outermost H I component.
-
2.
The EPG typically accounts for ∼10−15% of the total H I mass, reaching up to ∼25% in a small number of individual cases.
-
3.
The scale-height of the EPG is in the range 1−3 kpc. These values are not compatible with expectations based on hydrostatic equilibrium.
-
4.
The kinematics of the EPG is vastly dominated by rotation. All systems show a vertical lag in rotational speed, dvϕ/dz, with an average value of about −10 km s−1 kpc−1. There are no galaxies with dvϕ/dz ≥ 0.
-
5.
In most galaxies (9 out of 12) the EPG appears to be globally inflowing towards the centre, with typical speeds of ∼20−30 km s−1 in both the radial and vertical direction.
A galactic fountain appears to be the most probable origin for the EPG in late-type galaxies, although gas accretion is likely to contribute (Sancisi et al. 2008; Fraternali 2017). The EPG masses of the HALOGAS galaxies are in good agreement with theoretical expectations based on a simple galactic fountain model. The kinematics of the anomalous H I can be explained qualitatively by two processes: photo-ionisation of the gas outflowing from the disc, and interaction between the fountain material and a CGM with a lower specific angular momentum. Both these processes were key to the success of the dynamical models of Marasco et al. (2012) at reproducing the properties of the Galactic EPG. Our analysis shows that the EPG of most late-type galaxies has properties analogous to those of the Milky Way. The application of dynamical models of the galactic fountain to the HALOGAS data will allow us to understand better the physics of the interface between the disc and the CGM, and constitutes a natural follow-up to the current study.
All H I cubes and moment maps are publicly available as part of the HALOGAS Data Release 1 (Heald 2019) at https://zenodo.org/record/2552349#.XY3jnOczZ0s
Acknowledgments
The authors thank Renzo Sancisi, Richard Rand and Paolo Serra for providing constructing comments to the manuscript. FF and AM thank Martina Valleri who, in her Master’s thesis in 2013, had already found the presence of extraplanar gas in several nearby galaxies from the THINGS survey. The Westerbork Synthesis Radio Telescope is operated by the ASTRON (Netherlands Foundation for Research in Astronomy) with support from the Netherlands Foundation for Scientific Research NWO.
References
- Agertz, O., Moore, B., Stadel, J., et al. 2007, MNRAS, 380, 963 [NASA ADS] [CrossRef] [Google Scholar]
- Bacchini, C., Fraternali, F., Iorio, G., & Pezzulli, G. 2019, A&A, 622, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baillard, A., Bertin, E., de Lapparent, V., et al. 2011, A&A, 532, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barbieri, C. V., Fraternali, F., Oosterloo, T., et al. 2005, A&A, 439, 947 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barnabè, M., Ciotti, L., Fraternali, F., & Sancisi, R. 2006, A&A, 446, 61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Battaglia, G., Fraternali, F., Oosterloo, T., & Sancisi, R. 2006, A&A, 447, 49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Begeman, K. G. 1989, A&A, 223, 47 [NASA ADS] [Google Scholar]
- Binney, J., Nipoti, C., & Fraternali, F. 2009, MNRAS, 397, 1804 [NASA ADS] [CrossRef] [Google Scholar]
- Boomsma, R., Oosterloo, T. A., Fraternali, F., van der Hulst, J. M., & Sancisi, R. 2005, A&A, 431, 65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boomsma, R., Oosterloo, T. A., Fraternali, F., van der Hulst, J. M., & Sancisi, R. 2008, A&A, 490, 555 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bregman, J. N. 2007, ARA&A, 45, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, M. J. I., Moustakas, J., Smith, J.-D. T., et al. 2014, ApJS, 212, 18 [Google Scholar]
- Collins, J. A., Benjamin, R. A., & Rand, R. J. 2002, ApJ, 578, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Cook, D. O., Dale, D. A., Johnson, B. D., et al. 2014, MNRAS, 445, 881 [Google Scholar]
- Dalton, G., Trager, S. C., Abrams, D. C., et al. 2012, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Proc. SPIE, 8446, 84460P [Google Scholar]
- de Blok, W. J. G., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2648 [NASA ADS] [CrossRef] [Google Scholar]
- de Blok, W. J. G., Keating, K. M., Pisano, D. J., et al. 2014a, A&A, 569, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Blok, W. J. G., Józsa, G. I. G., Patterson, M., et al. 2014b, A&A, 566, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Teodoro, E. M., & Fraternali, F. 2015, MNRAS, 451, 3021 [NASA ADS] [CrossRef] [Google Scholar]
- Di Teodoro, E. M., McClure-Griffiths, N. M., Lockman, F. J., et al. 2018, ApJ, 855, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Fraternali, F. 2010, in American Institute of Physics Conference Series, eds. V. P. Debattista, & C. C. Popescu, 1240, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Fraternali, F. 2017, in Gas Accretion onto Galaxies, eds. A. Fox, & R. Davé, Astrophys. Space Sci. Lib., 430, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Fraternali, F., & Binney, J. J. 2006, MNRAS, 366, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Fraternali, F., & Binney, J. J. 2008, MNRAS, 386, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Fraternali, F., Oosterloo, T., Sancisi, R., & van Moorsel, G. 2001, ApJ, 562, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Fraternali, F., van Moorsel, G., Sancisi, R., & Oosterloo, T. 2002, AJ, 123, 3124 [NASA ADS] [CrossRef] [Google Scholar]
- Fraternali, F., Oosterloo, T., & Sancisi, R. 2004, A&A, 424, 485 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fraternali, F., Oosterloo, T. A., Sancisi, R., & Swaters, R. 2005, in Extra-Planar Gas, ed. R. Braun, ASP Conf. Ser., 331, 239 [NASA ADS] [Google Scholar]
- Fraternali, F., Marasco, A., Marinacci, F., & Binney, J. 2013, ApJ, 764, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Fraternali, F., Marasco, A., Armillotta, L., & Marinacci, F. 2015, MNRAS, 447, L70 [NASA ADS] [CrossRef] [Google Scholar]
- Gatto, A., Fraternali, F., Read, J. I., et al. 2013, MNRAS, 433, 2749 [NASA ADS] [CrossRef] [Google Scholar]
- Gentile, G., Józsa, G. I. G., Serra, P., et al. 2013, A&A, 554, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giese, N., van der Hulst, T., Serra, P., & Oosterloo, T. 2016, MNRAS, 461, 1656 [NASA ADS] [CrossRef] [Google Scholar]
- Heald, G. 2019, https://doi.org/10.5281/zenodo.2552349 [Google Scholar]
- Heald, G. H., Rand, R. J., Benjamin, R. A., & Bershady, M. A. 2006, ApJ, 647, 1018 [NASA ADS] [CrossRef] [Google Scholar]
- Heald, G. H., Rand, R. J., Benjamin, R. A., & Bershady, M. A. 2007, ApJ, 663, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Heald, G., Józsa, G., Serra, P., et al. 2011a, A&A, 526, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heald, G., Allan, J., Zschaechner, L., et al. 2011b, in Tracing the Ancestry of Galaxies, eds. C. Carignan, F. Combes, & K. C. Freeman, IAU Symp., 277, 59 [NASA ADS] [Google Scholar]
- Heald, G., Józsa, G., Serra, P., et al. 2012, A&A, 544, C1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holwerda, B. W., Pirzkal, N., de Blok, W. J. G., et al. 2011, MNRAS, 416, 2415 [NASA ADS] [CrossRef] [Google Scholar]
- Houck, J. C., & Bregman, J. N. 1990, ApJ, 352, 506 [NASA ADS] [CrossRef] [Google Scholar]
- Iorio, G., Fraternali, F., Nipoti, C., et al. 2017, MNRAS, 466, 4159 [NASA ADS] [Google Scholar]
- Joung, M. R., Bryan, G. L., & Putman, M. E. 2012, ApJ, 745, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kamphuis, P., Peletier, R. F., Dettmar, R. J., et al. 2007, A&A, 468, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kamphuis, P., Rand, R. J., Józsa, G. I. G., et al. 2013, MNRAS, 434, 2069 [NASA ADS] [CrossRef] [Google Scholar]
- Kaufmann, T., Mayer, L., Wadsley, J., Stadel, J., & Moore, B. 2006, MNRAS, 370, 1612 [NASA ADS] [CrossRef] [Google Scholar]
- Kaufmann, T., Bullock, J. S., Maller, A. H., Fang, T., & Wadsley, J. 2009, MNRAS, 396, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C., Armus, L., Bendo, G., et al. 2003, PASP, 115, 928 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2782 [NASA ADS] [CrossRef] [Google Scholar]
- Lockman, F. J. 1984, ApJ, 283, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Lockman, F. J. 2002, ApJ, 580, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Mac Low, M.-M., & McCray, R. 1988, ApJ, 324, 776 [NASA ADS] [CrossRef] [Google Scholar]
- Marasco, A., & Fraternali, F. 2011, A&A, 525, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marasco, A., Fraternali, F., & Binney, J. J. 2012, MNRAS, 419, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Marasco, A., Debattista, V. P., Fraternali, F., et al. 2015, MNRAS, 451, 4223 [NASA ADS] [CrossRef] [Google Scholar]
- Marasco, A., Fraternali, F., van der Hulst, J. M., & Oosterloo, T. 2017, A&A, 607, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marinacci, F., Fraternali, F., Ciotti, L., & Nipoti, C. 2010a, MNRAS, 401, 2451 [NASA ADS] [CrossRef] [Google Scholar]
- Marinacci, F., Binney, J., Fraternali, F., et al. 2010b, MNRAS, 404, 1464 [NASA ADS] [Google Scholar]
- Martinsson, T. P. K., Verheijen, M. A. W., Westfall, K. B., et al. 2013, A&A, 557, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matthews, L. D., & Wood, K. 2003, ApJ, 593, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Melioli, C., Brighenti, F., D’Ercole, A., & de Gouveia Dal Pino, E. M. 2009, MNRAS, 399, 1089 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, M. J., & Bregman, J. N. 2015, ApJ, 800, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Nelder, J. A., & Mead, R. 1965, Comput. J., 7, 308 [Google Scholar]
- Nipoti, C. 2010, MNRAS, 406, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Olling, R. P. 1995, AJ, 110, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Oosterloo, T., Fraternali, F., & Sancisi, R. 2007, AJ, 134, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Pingel, N. M., Pisano, D. J., Heald, G., et al. 2018, ApJ, 865, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Putman, M. E., Peek, J. E. G., & Joung, M. R. 2012, ARA&A, 50, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, M. S. 1975, in Radio Observations of Neutral Hydrogen in Galaxies, eds. A. Sandage, M. Sandage, & J. Kristian (The University of Chicago Press), 309 [Google Scholar]
- Rossa, J., & Dettmar, R.-J. 2003, A&A, 406, 493 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sancisi, R., & Allen, R. J. 1979, A&A, 74, 73 [NASA ADS] [Google Scholar]
- Sancisi, R., Fraternali, F., Oosterloo, T., & van der Hulst, T. 2008, A&ARv, 15, 189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaap, W. E., Sancisi, R., & Swaters, R. A. 2000, A&A, 356, L49 [NASA ADS] [Google Scholar]
- Schmidt, P., Józsa, G. I. G., Gentile, G., et al. 2014, A&A, 561, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shapiro, P. R., & Field, G. B. 1976, ApJ, 205, 762 [NASA ADS] [CrossRef] [Google Scholar]
- Sormani, M. C., Sobacchi, E., Pezzulli, G., Binney, J., & Klessen, R. S. 2018, MNRAS, 481, 3370 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, L. 1978, Physical Processes in the Interstellar Medium (New York: Wiley) [Google Scholar]
- Swaters, R. A., Sancisi, R., & van der Hulst, J. M. 1997, ApJ, 491, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Thilker, D. A., Bianchi, L., Meurer, G., et al. 2007, ApJS, 173, 538 [NASA ADS] [CrossRef] [Google Scholar]
- van Eymeren, J., Jütte, E., Jog, C. J., Stein, Y., & Dettmar, R. J. 2011, A&A, 530, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vargas, C. J., Heald, G., Walterbos, R. A. M., et al. 2017, ApJ, 839, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Wakker, B. P. 2001, ApJS, 136, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Wakker, B. P., & van Woerden, H. 1997, ARA&A, 35, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Werk, J. K., Prochaska, J. X., Thom, C., et al. 2013, ApJS, 204, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Zschaechner, L. K., Rand, R. J., Heald, G. H., Gentile, G., & Kamphuis, P. 2011, ApJ, 740, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Zschaechner, L. K., Rand, R. J., Heald, G. H., Gentile, G., & Józsa, G. 2012, ApJ, 760, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Zschaechner, L. K., Rand, R. J., & Walterbos, R. 2015, ApJ, 799, 61 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: The optimal sampling
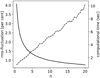 |
Fig. A.1. rms-fluctuation in the cubes (solid line, left-hand axis) and median computational time per model (dashed line, right-hand axis) as a function of η, the mean number of particle per resolution element used in the modelling. The improvements in the modelling accuracy are negligible for η ≳ 4. |
A quantity that is relevant in our modelling procedure is the number of particles N used in the stochastic realisation of the model. It is convenient to express N as η × nres, with η being the mean number of particles per resolution element and nres being the number of independent resolution elements in the cube. The latter depends on the angular and kinematical “size” of the system and on the resolution, and can be approximated as
where Rout is the outermost radius that we model (in our case the outermost point of the rotation curve), vmax is the maximum rotation velocity, i is the inclination, and the 50 km s−1 term represents a typical FWHM of the H I line broadening for the EPG component. Thus N can be readily computed for any choice of η via Eq. (A.1).
Clearly, the larger η is, the smaller the stochastic fluctuations between different realisations of the same model are, at the expenses of the computational time. In order to test how the magnitude of these fluctuations varies as a function of η we proceed as follows. As a fiducial case we consider the best-fit parameters found for the EPG of NGC 3198 and reported in Table 4. Using these parameters we first construct a very-high resolution cube using η = 50, which is used as a reference. Then we explore the range 0.5 < η < 20 and, for any given η, we build multiple realisations of the same model, for each storing the absolute residual between the current and the reference cube. Figure A.1 shows how the rms-fluctuation of these residuals decreases (solid line) and how the median computational time grows (dashed line) for increasing values of η. While the computational time increases linearly with η, the rms-fluctuations show an inflection point around η ∼ 4 above which the accuracy in the model improves very slowly with increasing the number of particles. For this reason we set η = 4 for all models used in this work.
Appendix B: Testing the method on mock data
We now test whether our method can recover the input parameters in mock H I observations. We first focus on a well resolved galaxy with a prominent EPG component, and then discuss a less resolved, more difficult system. For both cases we build models made of two H I components: a regularly rotating thin disc and a layer of EPG.
For the first case we take as a reference NGC 3198 and build our model using the same distance and rotation curve of this galaxy. The synthetic cube is also based on the same resolution and grid size of the HALOGAS data of NGC 3198. For the thin disc, we assume Gaussian distributions for the radial surface density and the vertical density profiles, with standard deviations of 15 kpc and 0.1 kpc respectively. For the EPG we adopt h = 2 kpc, dvϕ/dz = −15 km s−1 kpc−1, vR = vz = −20 km s−1, σ = 20 km s−1, and use the same best-fit values for Rg and γ found for NGC 3198. The H I mass of the system is 1010 M⊙ with the EPG accounting for 15% of the total, similar to the median fEPG in our sample (but a factor 1.7 larger than the fEPG found for NGC 3198). This choice for the parameters produces quite prominent “beards” in the pv slices, as shown by the bottom panel of Fig. B.1).
We further inject artificial noise in our synthetic cube with the following procedure. We first create a separate cube made of Gaussian noise, which we then convolve with the observation beam and perform Hanning smoothing. We then re-scale the intensities so that their standard deviation matches the rms-noise of the HALOGAS data, and finally sum it to our synthetic.
We analyse the mock data with the procedure described in Sect. 2. Figure B.1 shows the inferred posterior probability of the EPG parameters. The input parameters, marked with blue squares, always fall within the 16th and 84th percentiles (corresponding to a 1σ uncertainty) of the posterior distribution, indicating that our method can robustly mask the emission coming from the disc and efficiently recover the properties of the extra-planar gas.
How much can we degrade our resolution and signal-to-noise and still be able to recover the correct input parameters? To answer this question, we have repeated the exercise above but used as a reference galaxy NGC 4062, the most distant and less resolved galaxy in our sample for which we are still able to characterise the EPG component. We have used EPG parameters analogous to those inferred for this galaxy6, a total H I mass of 1.4 × 109 M⊙ with an fEPG of 15%, a thin disc scale length of 4.7 kpc, and the same resolution and grid size of the HALOGAS data for this system. In this case the input and output parameters were compatible with each other only within the 2σ uncertainty, indicating that our procedure is still quite reliable at this resolution and signal-to-noise but should not be applied to data of lower quality.
Appendix C: Column density maps
Figure C.1 shows the H I column density maps for the 15 HALOGAS systems studied here (black contours) overlaid on top of their optical images.
 |
Fig. C.1. H I column density maps for the 15 HALOGAS galaxies in our sample (black contours) overlaid on top of their optical images. The outermost contour is set to a signal-to-noise ratio (S/N) of 3, its value varies and is indicated on each panel in units of M⊙ pc−2. The remaining contours are spaced by powers of 2, the first (thicker line) being at a column density of 1 M⊙ pc−2. The beam size (FWHM) of the H I data is indicated in the bottom-left corner of each panel. |
The H I column density at a given sight-line (i, j), ΣHI(i, j), is derived by integrating the H I profile in velocity after the application of the external mask (see Sect. 2.2), and is converted to physical units following Roberts (1975) as
where I(i, j, k) is the voxel intensity, Δv is the channel separation and the sum is extended to all velocity channels.
The outermost column density contours in Fig. C.1 are determined under the assumption of Gaussian noise by substituting the sum that appears in Eq. (C.1) with the term 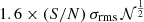 , where (S/N) is the desired signal-to-noise level (3 in our case), σrms is the rms-noise in the datacube, 𝒩 is the median number of channels used in the computation of the column density map (which we derive from the external mask) and the factor 1.6 accounts for Hanning smoothing. This gives column density sensitivities in the range 0.1−0.2 M⊙ pc−2, depending on the system.
, where (S/N) is the desired signal-to-noise level (3 in our case), σrms is the rms-noise in the datacube, 𝒩 is the median number of channels used in the computation of the column density map (which we derive from the external mask) and the factor 1.6 accounts for Hanning smoothing. This gives column density sensitivities in the range 0.1−0.2 M⊙ pc−2, depending on the system.
Optical images come from various ground-based telescopes and are taken from Cook et al. (2014, NGC 0672, NGC 4258, NGC 5055, NGC 5585), Kennicutt et al. (2003, NGC 0925, NGC 3198, NGC 4559), the DSS (NGC 0949, NGC 1003, NGC 4062, NGC 4274, NGC 4414, NGC 4448), Brown et al. (2014, NGC 2403) and Baillard et al. (2011, NGC 2541).
Additional visualisation of these and all other HALOGAS galaxies, including presentation of ancillary multiwavelength data products, will be provided in the HALOGAS Atlas paper (Heald et al., in prep.).
All Tables
Physical properties of galaxies in our sample, from H11 and Heald et al. (2012).
Summary of the geometrical and kinematical parameters for our EPG model and of the priors adopted.
Best-fit parameters and associated uncertainty for the EPG of the galaxies studied in this work.
All Figures
 |
Fig. 1. Sketch of observation of extraplanar gas in galaxy seen at intermediate inclination. The typical line profile (along the kinematic major axis of the galaxy) will be composed by a nearly Gaussian part coming from the thin disc with overlaid a tail at low rotation velocity produced by the lagging EPG layer. The width of the disc emission is roughly symmetrical, produced by gas turbulence and well fitted by a Gaussian function (blue solid line). The EPG separation is achieved by masking a portion of the profile with substantial contribution from this Gaussian function (“internal mask” region). |
| In the text | |
 |
Fig. 2. Rotation curves for our sample of HALOGAS galaxies derived with 3DBAROLO and used in our EPG modelling. Each system is labelled with its NGC number. |
| In the text | |
 |
Fig. 3. Position-velocity (pv) slices for the disc+EPG toy models discussed in Sect. 2.4 and based on the parameters listed in Table 2. For each model we show a pv slice parallel to the major (on the top) and to the minor (on the bottom) axes. The insets in the top-left panels sketch the slice directions. Axis-offset is 2′ in both cases. The slice thickness is 3 spaxels, corresponding to a resolution element. Black contours are spaced by powers of 2, the outermost being at an intensity level of 0.4 mJy beam−1. Red contours show the emission from the disc alone, without the contribution of the EPG. |
| In the text | |
 |
Fig. 4. Sketch showing how vertical motions produce a distinct signature on the inferred H I kinematics depending on the EPG thickness, inclination, orientation and surface density profile. In this case, the presence of a vertical inflow (red and blue arrows) and a radially declining surface density profile (shades of green) produce a redder or bluer-shifted signal depending on which galaxy side is considered. |
| In the text | |
 |
Fig. 5. Position-velocity slice along the major axis of NGC 3198 (1′≃4.2 kpc at the distance adopted). The white area shows the emission from the thin H I disc (internal mask), derived as discussed in Sect. 2.2. The region outside the green dashed contour (external mask) is not associated to the galaxy and is set to zero in the data. The orange squares show the rotation curve derived with 3DBAROLO. Black contours are spaced by powers of 2, the outermost being at an intensity level of 0.28 mJy beam−1 (2σnoise). A negative contour (−2σnoise) is shown as a dashed grey contour. |
| In the text | |
 |
Fig. 6. Top: corner-plots showing the correlation between the various parameters (shaded regions, with contours at arbitrary iso-density levels) along with their marginalised probability distribution (histograms on top) for the EPG of NGC 3198. Top-right inset: total H I map of NGC 3198 showing the cuts parallel to the major and minor axes used in pv-slices below. Bottom: pv-slices for the data (black contours) and for our best-fit model (red contours). Slice off-sets are indicated on the top-left of each panel. The white area and the green dashed contour indicate the internal and external mask, respectively. Orange squares show the rotation velocities determined with 3DBAROLO. Contours are spaced by powers of 2, the outermost being at an intensity level of 0.28 mJy beam−1 (2σnoise). A negative contour (−2σnoise) is shown for the data as a dashed grey line. |
| In the text | |
 |
Fig. 7. Position-velocity slices for the galaxies in our sample (see description for the bottom panel of Fig. 6). Individual cases are discussed in the text. |
| In the text | |
 |
Fig. 7. continued. |
| In the text | |
 |
Fig. 7. continued. |
| In the text | |
 |
Fig. 7. continued. |
| In the text | |
 |
Fig. 8. Kinematics of the EPG in the HALOGAS galaxies as derived from our models. EPG tends to be globally inflowing with a speed of 20−30 km s−1. Interacting and poorly fitted galaxies are shown with separate symbols. Values for the Milky Way (MW) are from MF11. |
| In the text | |
 |
Fig. 9. Comparison between the best-fit model for the EPG of NGC 0672 (first column) and other models that use the same parameters but different values for vz and vR, as labelled on top of each panel. For simplicity we show only the pv-slices at 1′-offset. Contours are the same as in Fig. 6. Arrows show the locations where the various models are inferior to the best-fit one. |
| In the text | |
 |
Fig. 10. Comparison between the best-fit model for the EPG of NGC 3198 (top panels) and two models that use the same parameters but different values for h and dvϕ/dz (bottom panels). Contours are the same as in Fig. 6. Arrows show the locations where the models are inferior to the best-fit one. We have focussed on pv-slices where the differences are more evident. |
| In the text | |
 |
Fig. 11. Left panel: SFR vs EPG mass for our HALOGAS sample. Right panel: theoretical EPG mass predicted by a galactic fountain model (Eq. (11) with β = 7) vs that inferred from the data. The two panels span the same range (∼1.5 dex) on both axes. Error-bars are determined by assuming a 10% uncertainty on the distances and a 20% uncertainty on the total SFR, in addition to the uncertainty on the RSFR discussed in the text. Interacting galaxies and systems with a poorly fit EPG are shown with separate symbols. We have also included NGC 891 (MEPG from Marinacci et al. 2010a) and the Milky Way, for which we used MEPG = 3.2 ± 1.0 × 108 M⊙ (MF11), and assumed fiducial values for SFR, RSFR and vflat of 2 ± 1 M⊙ yr−1, 2.5 ± 0.5 kpc and 240 ± 10 km s−1 respectively. |
| In the text | |
 |
Fig. A.1. rms-fluctuation in the cubes (solid line, left-hand axis) and median computational time per model (dashed line, right-hand axis) as a function of η, the mean number of particle per resolution element used in the modelling. The improvements in the modelling accuracy are negligible for η ≳ 4. |
| In the text | |
 |
Fig. B.1. As in Fig. 6, but using the mock data as described in Appendix B. |
| In the text | |
 |
Fig. C.1. H I column density maps for the 15 HALOGAS galaxies in our sample (black contours) overlaid on top of their optical images. The outermost contour is set to a signal-to-noise ratio (S/N) of 3, its value varies and is indicated on each panel in units of M⊙ pc−2. The remaining contours are spaced by powers of 2, the first (thicker line) being at a column density of 1 M⊙ pc−2. The beam size (FWHM) of the H I data is indicated in the bottom-left corner of each panel. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



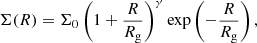
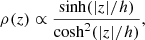
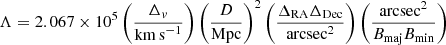
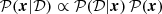
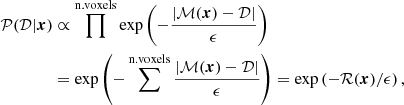
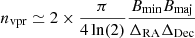
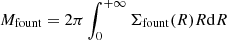
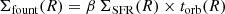
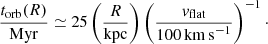
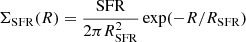
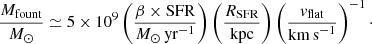
![$$ \begin{aligned} n_{\rm res} \simeq &1.18 \times 10^5 \left(\frac{R_{\rm out}}{\mathrm{kpc}}\right)^2 \left(\frac{{ v}_{\rm max}\sin (i)+50}{\mathrm{km\,s}^{-1}}\right)\nonumber \\&\times \left[\left(\frac{\Delta _{\mathrm{ v}}}{\mathrm{km\,s}^{-1}}\right) \left(\frac{D}{\,\mathrm{Mpc}}\right) \left(\frac{B_{\rm maj} B_{\rm min}}{\mathrm{arcsec}^2}\right)\right]^{-1} \end{aligned} $$](/articles/aa/full_html/2019/11/aa36338-19/aa36338-19-eq16.gif)