| Issue |
A&A
Volume 630, October 2019
|
|
|---|---|---|
| Article Number | A62 | |
| Number of page(s) | 21 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201936054 | |
| Published online | 24 September 2019 | |
The biasing phenomenon
1
Tartu Observatory, 61602 Tõravere, Estonia
e-mail: jaan.einasto@to.ee
2
ICRANet, Piazza della Repubblica 10, 65122 Pescara, Italy
3
Estonian Academy of Sciences, 10130 Tallinn, Estonia
Received:
9
June
2019
Accepted:
5
August
2019
Context. We study biasing as a physical phenomenon by analysing geometrical and clustering properties of density fields of matter and galaxies.
Aims. Our goal is to determine the bias function using a combination of geometrical and power spectrum analyses of simulated and real data.
Methods. We apply an algorithm based on the local densities of particles, δ, to form simulated, biased models using particles with δ ≥ δ0. We calculate the bias function of model samples as functions of the particle-density limit δ0. We compare the biased models with Sloan Digital Sky Survey (SDSS) luminosity-limited samples of galaxies using the extended percolation method. We find density limits δ0 of biased models that correspond to luminosity-limited SDSS samples.
Results. The power spectra of biased model samples allow estimation of the bias function b(> L) of galaxies of luminosity L. We find the estimated bias parameter of L* galaxies, b* = 1.85 ± 0.15.
Conclusions. The absence of galaxy formation in low-density regions of the Universe is the dominant factor of the biasing phenomenon. The second-largest effect is the dependence of the bias function on the luminosity of galaxies. Variations in gravitational and physical processes during the formation and evolution of galaxies have the smallest influence on the bias function.
Key words: large-scale structure of Universe / dark matter / cosmology: theory / galaxies: clusters: general / methods: numerical
© ESO 2019
1. Introduction
The formation of galaxies is very complex, including gravitational and hydrodynamical processes. Hydrodynamical processes dominate on small scales, while gravitational processes dominate on large scales. Thus, the biasing phenomenon can be divided into local bias and large-scale bias, as emphasised in the very detailed review by Desjacques et al. (2018). Most papers cited by Desjacques et al. (2018) were devoted to the study of local bias. In this paper, we are interested in the global bias phenomenon, where gravitational processes dominate.
Various statistical tools have been applied to quantify the large-scale galaxy bias, such as the galaxy autocorrelation function, starting from Kaiser (1984), Bardeen et al. (1986), and Szalay (1988). Another statistic used to study the relationship between matter and galaxies is the void probability function (VPF), as done by Gramann (1990) and Einasto et al. (1991), and more recently by Walsh & Tinker (2019). Here, we use the power spectrum analysis method. The power spectrum analysis confers several advantages over the correlation function analysis (Feldman et al. 1994). The power spectrum measures the fractional density contributions on different scales, and is a natural quantity to describe the density field, especially on large scales.
Different authors have used different data and different methods to estimate power spectra, which has led to various definitions of the bias parameter. The geometrical properties of the distribution of galaxies and matter have been discussed separately using a large variety of methods. This area of research is very rich, as seen from discussions at a recent symposium on the cosmic web (van de Weygaert et al. 2016). The connection between determinations of power spectra and geometrical properties of the cosmic web has rarely been discussed.
In the present paper we try to obtain a more general view of the biasing phenomenon in the context of the structure of the cosmic web. The biasing phenomenon is a physical problem concerning the relation between distributions of matter and galaxies on large scales. In discussing the global biasing phenomenon we assume that gravity is the dominating force determining the formation and evolution of the cosmic web on large scales. According to the presently accepted Λcold dark matter (ΛCDM) model, the primordial density field forms a statistically homogeneous, isotropic, and nearly random field. Density waves of different scales began with random and uncorrelated spatial phases. As density waves evolve, they interact with others in a non-linear way. This interaction leads to the generation of non-random and correlated phases which form the spatial pattern of the present cosmic web with clusters, filaments, sheets, and voids. Matter flows out from under-dense regions towards over-dense regions, which changes the pattern of the evolving cosmic web. In high-density regions there exists conditions favourable to the formation of galaxies.
We consider the bias function b as a fundamental cosmological function, which quantitatively relates differences between distributions of matter and galaxies. The numerical value of the bias function can be found by the power spectrum analysis, and the relation between galaxies and matter can be found using geometrical properties of the cosmic web. Firstly, we briefly discuss the formation of the biasing concept and the basic physical processes involved in the biasing phenomenon: the formation of galaxies in the cosmic web, the phase synchronisation of density perturbations, and the evolution of voids.
An important element of the classical version of the cosmology paradigm is the distribution of galaxies. Available data on the distribution of galaxies on the sky suggested that this distribution is essentially a random one (field galaxies) to which some clusters and perhaps even superclusters were added; see the angular distribution of the numbers of galaxies brighter than B ≈ 19 by Seldner et al. (1977). The angular distribution of galaxies can be considered as a random Gaussian process described by the angular correlation function of galaxies, as done by Peebles (1973), Peebles & Hauser (1974), Peebles & Groth (1975), and Davis & Peebles (1983).
In the 1970s the number of galaxies with measured redshifts was sufficiently large to study the distribution of galaxies in three dimensions. The topic was discussed in the IAU Symposium 79 “Large Scale Structure of the Universe” in Tallinn by Jõeveer & Einasto (1978), Tarenghi et al. (1978), Tifft & Gregory (1978), and Tully & Fisher (1978). Three-dimensional data demonstrated that the distribution of galaxies and clusters of galaxies is filamentary and that there are almost no galaxies outside filaments. A theory of the formation of galaxies due to gravitational instability was suggested by Zeldovich (1970). Numerical simulations in the framework of this model by Doroshkevich et al. (1980) demonstrated the formation of a cellular network of high- and low-density regions. Due to the similarity of the observed large-scale distribution of galaxies to the structure found in simulations, the structure was called “cellular” (Jõeveer et al. 1977, 1978). Subsequently, more general terms “supercluster-void network” (Einasto et al. 1980) and “cosmic web” (Bond et al. 1996) were used.
Jõeveer et al. (1977, 1978) estimated that knots, filaments, and sheets fill only about 1% of the total volume of the Universe; the rest forms voids. The authors noticed that gravity works very slowly and is very unlikely to completely evacuate such large volumes as in cell interiors; there must exist unclustered matter in voids. In this way, the difference between distributions of matter and galaxies was detected. The structure of superclusters and voids was investigated quantitatively by Zeldovich et al. (1982) by comparing distributions of simulated particles with real galaxies. The multiplicity test confirmed the existence of a smooth population of void particles in simulations. The multiplicity test also showed the absence of a large low-density population of void galaxies in the observed sample. To explain these differences Zeldovich et al. (1982) assumed that the matter density in voids and sheets is too small to start galaxy formation. The term “biasing” was suggested later by Kaiser (1984) to denote the difference between the correlation functions of clusters of galaxies and those of galaxies. Subsequently, this term was used in a more general sense to denote differences in the distribution of galaxies and matter (Davis et al. 1985).
Galaxy formation is a two-stage process – gravitating material in the Universe condenses first into dark matter (DM) halos (White & Rees 1978). To form a galaxy, the density of matter must exceed a critical value, the Press–Schechter limit (Press & Schechter 1974). This result is confirmed by hydrodynamical models of galaxy formation (for early model see Cen & Ostriker 1992). The arguments by White and Rees are supported by direct observational evidence – all galaxies are DM-dominated, especially dwarf galaxies (McConnachie 2012). The luminous content of galaxies results from the combined action of gravitational and hydrodynamical processes within potential wells provided by DM.
Arguments by Zeldovich, White, and Rees lead to a simple biasing model, where galaxies do not form in low-density regions at all, or are too faint to be included into flux-limited galaxy surveys.
The expansion of the Universe in its early phase is an adiabatic process (Zeldovich 1970; Peebles 1982a). The growth of adiabatic perturbations proceeds at a low temperature of the primordial “gas”, and the flow of particles is very smooth (Zeldovich 1970, 1978; Zeldovich et al. 1982). Small initial perturbations combined with the smooth flow of particles develop into the non-linear stage and dense regions will be built up by the concentration of matter into caustics by intersection of particle trajectories (Zeldovich 1978; Zeldovich et al. 1982; Arnold et al. 1982). In this way, the skeleton of the cellular cosmic web is formed. An early three-dimensional numerical simulation by Doroshkevich et al. (1982) showed only the formation of very large supercluster type systems with bulky connections without a web of fine filaments. This simulation was made under the assumption that DM is made of massive neutrinos, that is, the hot dark matter (HDM) model. Weakly interacting massive particles, referred to as CDM, were suggested by Peebles (1982b). Quantitative analysis of a CDM model by Melott et al. (1983) showed that the CDM model is in good agreement with observations. In particular, all quantitative tests applied to the HDM model by Zeldovich et al. (1982) showed that the CDM model is in good agreement with observed samples of galaxies. In the CDM model the intersection of particle trajectories leads directly to the early formation of thin filaments and knots, as shown by Melott et al. (1983), and subsequently studied in more detail by White et al. (1987), Kofman et al. (1990), and Bond et al. (1996).
When the presence of voids was discovered, Dekel & Silk (1986) assumed that voids can be populated with dwarf galaxies. However, observations suggested that voids are marked by the absence of both normal and dwarf galaxies (Einasto et al. 1989; Lindner et al. 1995, 1996; Peebles 2001; Tinker et al. 2006).
There is a simple explanation for the absence of dwarf galaxies in voids. The growth of density perturbations is an acoustic phenomenon and can be studied by the wavelet technique (Einasto et al. 2011a,b). Voids are regions in space where due to phase synchronisation, medium- and large-scale density waves combine in similar under-density phases. Here, the growth of all small-scale density perturbations responsible for the formation of galaxies is suppressed. Small-scale density perturbations form initially everywhere, but in regions of under-dense phases of large and medium perturbations the density contrast of small-scale perturbations decreases during evolution. Galaxies, clusters, and superclusters form in regions where medium- and large-scale density waves combine in similar over-density phases. Near maxima of large-scale density perturbations, medium and small-scale perturbations grow. This leads to the formation of numerous halos and subhalos around the high- and medium-density peaks. It is possible that the phase synchronisation is the basic process which leads to the formation of galaxy systems with centrally located giant galaxies surrounded by dwarf galaxies. The formation of satellite galaxies and relations between satellite and main galaxies are presently the subjects of intensive studies, both observational and theoretical; for a recent review see Wechsler & Tinker (2018).
Gravity works slowly and more-or-less smoothly distributed particles can always be found in low-density regions. Sheth & van de Weygaert (2004), Rieder et al. (2013), and Aragon-Calvo et al. (2016) among others investigated how galaxies form and evolve inside the cosmic web. Galaxies accrete star-forming gas at early times via the network of primordial filaments and the flow of gas along filaments is continuous. It is evident, that not all matter in filaments (and walls) is presently located in halos – the process is still ongoing. Density distributions of Sloan Digital Sky Survey (SDSS) samples can be compared with density-distribution models. Cautun et al. (2014), Falck & Neyrinck (2015), and Ganeshaiah Veena et al. (2019) highlighted regions belonging to simulated voids, walls, filaments, and halos. In all models there exist large under-dense regions, where halo (and thus galaxy) formation is not possible. These studies suggest that the fraction of particles in low-density regions not associated with halos is about 25–30% of all particles. This non-clustered matter forms a more-or-less uniformly distributed medium, part of it being located in weak filaments of dark and baryonic matter (Aragon-Calvo et al. 2010).
The goal of this paper is to study biasing as a physical phenomenon and to estimate the bias function using clustering and geometrical properties of the distribution of DM and galaxies. We divide this task into three subtasks: (i) the generation of biased model distributions of matter and the study of the geometrical properties of the distribution of DM, and of simulated and real galaxies; (ii) the calculation of power spectra of simulated biased models and the determination of the bias function using simulated biased models; and (iii) the comparison of the geometrical properties of simulated and real galaxy samples to find the simulated model which best represents the observed distribution.
In simulations we select particles from the same set for biased samples and for unbiased samples, and full data on the distribution of particles, selection, and boundary effects and so on are known. Thus, the comparison of biased and unbiased models is fully differential. As a result of the comparison we find the relation between the biased model selection parameter and the galaxy sample selection parameter. The bias function depends on the selection parameter used to define biased models to simulate galaxies. This method circumvents the main difficulty of the power spectrum analysis of the biasing phenomenon: from observations we can determine the power spectrum directly only for galaxies of varying luminosity, but not for matter. Following this idea, we have to decide: (i) how to construct biased model samples, and (ii) how to compare biased models with observations.
We use a simple biased DM simulation model and divide matter into a low-density population with no galaxy formation or a population of galaxies below a certain luminosity limit, and a high-density population with clustered matter, associated with galaxies above the luminosity limit. From observations we get information on the distribution of galaxies at the present epoch (the mean age of our observational SDSS sample corresponds to age at redshift z = 0.1). Following this consideration we use present-day (Eulerian) particle local densities, δ, and label each particle with this density value. Halos surrounding galaxies like our own Galaxy and M31 have an effective radius of the order of 1 h−1 Mpc (Einasto et al. 1974a; Karachentsev et al. 2002). Inside such halos hydrodynamical processes leading to the formation of visible galaxies are dominant. In our study we use density fields with the size of individual cells 1 h−1 Mpc, and therefore all the details of galaxy formation are hidden inside cells. Local density is expressed in units of the mean density of the whole unbiased model sample (or of the mean luminosity density of the whole SDSS sample); it is a dimensionless quantity and is independent of particle mass and galaxy luminosity.
We apply a sharp particle-density limit, δ0. Biased model samples include particles with density labels, δ ≥ δ0. These samples are found from the full DM sample by excluding particles of density labels less than the limit δ0. In this way biased model samples mimic observed samples of galaxies, where there are no galaxies fainter than a certain luminosity limit. We use a series of particle-density limits δ0 to find limits, which correspond in the best way to observational samples of galaxies. Galaxy formation is a complex phenomenon, which depends on the local and the global cosmic environment and on the history of the structure evolution. To estimate the possible influence of these factors, we also apply fuzzy particle-density limits to select particles for the high-density population.
To investigate geometrical properties of the cosmic web and to compare models with observations we apply the extended percolation analysis developed by Einasto et al. (1986a, 2018), and Einasto & Saar (1987). The extended percolation analysis aims to describe geometrical properties of the whole cosmic web and is complementary to methods whose aims are to describe the properties of elements of the cosmic web, such as knots, filaments, sheets, and voids. The extended percolation method allows the comparison of samples with very different border configurations, such as observational samples with conical shell borders and cubic model samples. The extended percolation analysis uses density fields of model and observational samples. Thus, all the difficulties in the comparison of models with observations reside in the methods used to calculate density fields. The extended percolation analysis uses completely different properties of the cosmic web to compare models with observations, and is suitable to find proper biased models representing observational data.
As a basic reference model sample we use a numerical simulations of the evolution of the web applying ΛCDM cosmology in a box of size 512 h−1 Mpc, almost equal in volume to the volume of the flux-limited SDSS main galaxy survey, (509 h−1 Mpc)3, used by Liivamägi et al. (2012) to find superclusters of galaxies. We use cosmological parameters: Hubble parameter H0 = 100 h km s−1 Mpc−1, matter density parameter Ωm = 0.28, and dark energy density parameter ΩΛ = 0.72. For comparison, we also use halo-mass-selected samples from the Horizon Run 4 (HR4) simulation by Kim et al. (2015) in a box of size 512 h−1 Mpc. As observational data we use absolute magnitude (volume)-limited SDSS samples with limits Mr − 5 log h = −18.0, − 19.0, − 20.0, − 21.0.
The paper is organised as follows. In the following section we describe the calculation of the density fields of observed and simulated samples, and the method to find clusters, voids, and their parameters. In Sect. 3, we investigate the geometrical properties of the cosmic web as delineated by matter and galaxies using the extended percolation method. In Sect. 4 we calculate power spectra and estimate the bias function of model samples. In Sect. 5 we compare parameters of observed and simulated clusters, and find biased models which correspond to luminosity-selected SDSS galaxies in the best way. In Sect. 6 we discuss our results. The final section presents our main conclusions.
2. Data and methods
2.1. Particle-density-selected model samples
Simulations of the evolution of the cosmic web were performed in a box of size L0 = 512 h−1 Mpc, with resolution Ngrid = 512 and with 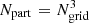 particles. The initial density fluctuation spectrum was generated using the COSMICS code by Bertschinger (1995), assuming cosmological parameters Ωm = 0.28, ΩΛ = 0.72, σ8 = 0.84, and the dimensionless Hubble constant h = 0.73. To generate initial data we used the baryonic matter density Ωb = 0.044 (Tegmark et al. 2004a). Calculations were performed with the GADGET-2 code by Springel (2005).
particles. The initial density fluctuation spectrum was generated using the COSMICS code by Bertschinger (1995), assuming cosmological parameters Ωm = 0.28, ΩΛ = 0.72, σ8 = 0.84, and the dimensionless Hubble constant h = 0.73. To generate initial data we used the baryonic matter density Ωb = 0.044 (Tegmark et al. 2004a). Calculations were performed with the GADGET-2 code by Springel (2005).
The accepted σ8 for the model is in good agreement with σ8 determinations for matter; see Planck Collaboration VI (2018) for Planck 2018 results. Spectra of cosmic microwave background (CMB) temperature and polarisation in combination with CMB gravitational lensing yield σ8 = 0.8111 ± 0.0060. If data on baryonic acoustic oscillations (BAOs) at lower redshifts is added, then the result is σ8 = 0.8102 ± 0.0060. Zubeldia & Challinor (2019) derived cosmological constraints using the Planck sample of clusters, detected via the Sunyaev–Zeldovich (SZ) effect. These latter authors find σ8 = 0.76 ± 0.04. The signal from CMB comes from redshift z = 1100, while SZ clusters have a characteristic redshift of z ≈ 0.2. Thus, data from different distances are in very good agreement.
For all simulation particles and all simulation epochs, we calculated local density values at particle locations, δ, using positions of 27 nearest particles, including the particle itself. Densities were expressed in units of the mean density of the whole simulation. In the study presented here we used particle-density-selected samples at the present epoch. Biased model samples contain particles above a certain limit, δ ≥ δ0, in units of the mean density of the simulation. For the analysis we used density limits δ0 = 0.5, 1.0, 2.0, 5.0, 7.5, 10.0, 15.0, 20.0, 50.0, 100.0. Particle-density-selected samples are referred to as biased model samples and are denoted as L512.i, where i denotes the particle-density limit δ0. The full DM model includes all particles and corresponds to the particle-density limit δ0 = 0, and therefore it is denoted as L512.00. The main data on biased model samples are given in Table 1, where we also provide the fraction of particles, FC = NC/Npart, where NC is the number of particles with density limit δ ≥ δ0, and Npart is the total number of particles in the simulation. FC is equal to the number density of selected particles, δ ≥ δ0, per cubic h−1 Mpc, Dens. We also provide the total filling factor of over-density regions at density threshold Dt = 0.1, FFC, and the bias parameters b(δ0), calculated using Eq. (3) below.
L512 particle-density-limited models.
The use of the local density as the only parameter to determine the fate of particles in the web is a simplification; see the distribution of particles in regions of different density by Cautun et al. (2014) and Ganeshaiah Veena et al. (2019). However, as shown among others by Tinker & Conroy (2009), just the local density, not the global one, is essential in the determination of the formation of galaxies inside DM haloes. In observational SDSS samples and comparison HR4 model samples we used sharp limits of absolute magnitudes and halo masses. The formation of galaxies inside DM halos is determined by a variety of processes. For this reason, particles of slightly varying densities can be located in halos of fixed lower mass limit and the actual particle-density limit is fuzzy. To take this effect into account we made additional calculations with L512 models with fuzzy particle-density limits; see below.
2.2. Luminosity-limited SDSS galaxy samples
We use luminosity limited (usually referred to as volume-limited) galaxy samples by Tempel et al. (2014), selected from data release 10 (DR10) of the SDSS galaxy redshift survey (Ahn et al. 2014). Data on four luminosity-limited SDSS samples are given in Table 2. Limiting absolute magnitudes in red r−band, Mr, maximum comoving distances, dlim, and numbers of galaxies in samples, Ngal, are taken from Tempel et al. (2014); volumes of samples, V0, and sample lengths, L0, are determined by counting cells inside the conical survey volume, and the maximum lengths of over-density regions (“clusters” in the terminology used here). The SDSS samples with Mr − 5logh luminosity limits −18.0, −19.0, −20.0, and −21.0 are referred to as SDSS.18, SDSS.19, SDSS.20 and SDSS.21. Respective luminosity limits in solar units were calculated using the absolute magnitude of the Sun in r-band, M⊙ = 4.64 (Blanton & Roweis 2007). Table 2 also provides the number density of sample galaxies per cubic h−1 Mpc, Dens. The SDSS galaxy samples are conical and have different sizes: for example the volume of the sample SDSS.21 is 52 times larger than the volume of the sample SDSS.18.
SDSS luminosity limited samples.
2.3. Halo mass limited model samples
To check the comparison of observed and biased model data we applied the extended percolation analysis also for a series of halo-mass-limited model samples, taken from the Horizon Run 4 simulation by Kim et al. (2015). This simulation was made in a cubic box of size 3150 h−1 Mpc, using 63003 particles in a ΛCDM cosmology with Ωm = 0.26, Ωb = 0.044, ΩΛ = 0.74, amplitude parameter σ8 = 0.794, and current Hubble expansion constant H0 = 100 h km s−1 Mpc−1, where h = 0.72. We selected halos from this simulation for the present epoch in a box of size L0 = 512 h−1 Mpc. Halos were found containing at least 30 particles, and the minimal mass of halos is Ms = 2.706 × 1011 h−1 M⊙. This simulation contains 8 particles per cell of length 1 h−1 Mpc, and the mean density of matter per cell is Mmean = 0.7216 × 1011 h−1 M⊙. We use four halo-mass-limited samples from the HR4 simulation. The main data on HR4 samples are given in Table 3, where we also give the fraction of mass in the clustered population, FC, and the number density of halos per cubic h−1 Mpc, Dens.
HR4 halo-mass-limited samples.
2.4. Calculation of percolation functions
The first step in the extended percolation analysis is the calculation of density fields. Here we applied the B3 spline (see Martínez & Saar 2002). This function is different from zero only in the interval x ∈ [ − 2, 2]. To calculate the high-resolution density field we use the kernel of the scale, equal to the cell size of the simulation, L0/Ngrid = 1 h−1 Mpc, where L0 is the size of the simulation box, and Ngrid is the number of grid elements in one coordinate. The smoothing with index i has a smoothing radius ri = L0/Ngrid × 2i. The effective scale of smoothing is equal to ri. We applied this smoothing up to index 6. For our L512 model, smoothing indexes i = 1, 2, and 3 correspond to B3 kernels of radii RB = 2, 4, and 8 h−1 Mpc, respectively. The B3 kernel of radius RB = 1 h−1 Mpc corresponds to a Gaussian kernel with dispersion RG = 0.6 h−1 Mpc (Tempel et al. 2014). The non-smoothed density field corresponds to kernel RB = 1 h−1 Mpc. Densities were expressed in mean density units.
The calculation of percolation functions consists of several steps. We scanned density fields in a range of threshold densities from Dt = 0.1 to Dt = 10 in mean density units to find over- and under-density systems, called clusters and voids, respectively. We used a logarithmic step of densities, ΔlogDt = 0.02. Two cells of the same type are considered as members of a system if they have a common sidewall. For each cluster and void we calculate the centre coordinates, xc, yc, zc (mean values of extreme x, y, z coordinates); sizes along coordinate axes, Δx, Δy, Δz (differences between extreme x, y, z coordinates); geometrical diameters, 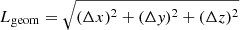 ; maximal sizes along coordinate axes, Lmax = max(Δx, Δy, Δz); volumes, VC, defined as the volume of space where the density is equal to or greater than the threshold density Dt; and total masses (or luminosities), Mt, that is, the masses (luminosities) inside the density contour Dt of the cluster, both in mean density units.
; maximal sizes along coordinate axes, Lmax = max(Δx, Δy, Δz); volumes, VC, defined as the volume of space where the density is equal to or greater than the threshold density Dt; and total masses (or luminosities), Mt, that is, the masses (luminosities) inside the density contour Dt of the cluster, both in mean density units.
During the cluster search we found the cluster with the largest volume for the given threshold density, and, for each threshold density, stored the number of clusters found, and data on the largest cluster: the geometrical diameter (the maximal size along coordinate axes), the volume, and the total mass (luminosity). The diameters (lengths) of the largest clusters, L(Dt) = Lmax, filling factors of the largest clusters, ℱ(Dt) = Vmax/V0, and the numbers of clusters at the threshold density, 𝒩(Dt), as a function of the threshold density, Dt, were used as percolation functions. Diameters are expressed in h−1 Mpc, and volumes (filling factors) are expressed in units of the volume of the whole sample, V0. During the search of high- and low-density systems, we excluded very small systems, using exclusion volume limit, Nlim = 50 or 500 computation cells (cubic h−1 Mpc). Samples calculated with a lower exclusion limit include small systems with volumes less than (8 h−1 Mpc)3, which increases the number of clusters approximately tenfold, but has little effect on the shapes of number functions, 𝒩(Dt). Length functions L(Dt) and filling factor functions ℱ(Dt) are not influenced by the choice of Nlim.
We use as a percolation function the volume of the largest cluster, Vmax, not its mass, Mmax. The mass function depends on the mass concentration inside halos. The volume is free from this dependence; here we consider the question of whether the cluster lies above or below the limit dividing particles or halos into over- and under-dense regions. This aspect is treated by the fuzziness of the particle selection limit.
A similar procedure was applied to find the largest low-density regions or voids in our terminology.
3. Geometrical properties of density fields of matter and galaxies
In this section we compare distributions of matter and galaxies using the extended percolation method. We pay special attention to similarities and differences between distributions of DM and galaxies, both simulated and real.
3.1. Percolation analysis of distributions of matter and galaxies
The original percolation analysis was designed to measure the connectivity of percolating clusters (Stauffer 1979), and was used by Zeldovich et al. (1982) and Melott et al. (1983) to investigate the connectivity of HDM and CDM models, respectively. The extended percolation method was designed by Einasto et al. (1986a, 2018), and Einasto & Saar (1987) to compare more general geometrical properties of models with observations. The density field is divided into high- and low-density regions using a variable density threshold. Each element of the cosmic web belongs to a high- and low-density region, depending on the threshold. In this way the extended percolation analysis is a method to study various geometrical properties of the whole cosmic web over a large range of densities, and to compare models with observations.
Percolation functions describe how geometrical properties, such as sizes and volumes of largest clusters and voids, depend on the threshold used to divide the density field into high- and low-density regions. At high threshold density only the highest peaks (central regions of the largest cluster) are considered as over-density regions, and sizes and filling factors of largest clusters are small. As the density threshold decreases, outer lower-density regions of the clusters are included as parts of clusters, and the lengths and filling factors of clusters increase. At a certain density threshold, the cluster merges with a neighbouring cluster, and the length and filling factor of the largest cluster abruptly increases. After several mergers, the largest cluster spans the whole sample, that is, it percolates (Liivamägi et al. 2012).
Figure 1 presents percolation functions: filling factors of the largest clusters and voids, ℱ(Dt), lengths of the largest clusters and voids, L(Dt), and the number of clusters and voids, 𝒩(Dt), as a function of the threshold density, Dt, to divide the density field into over- and under-density regions. Functions are given for the full unbiased model L512.00, and for simulated and real galaxy samples represented by the biased model L512.10, by the luminosity limited sample SDSS.21, and by the halo-mass-limited model HR4.12. These simulated and real galaxy samples correspond approximately to L⋆ galaxies; see below.
 |
Fig. 1. Percolation functions for unbiased L512.00 samples, biased L512.10 samples, and SDSS.21 and HR4.12 samples, from top to bottom panels, respectively. Left panels are for filling factor functions, middle panels for cluster length functions, right panels for number functions. Number functions are calculated with small system exclusion limit Nlim = 50 (L512.10 and SDSS.21 samples); and with Nlim = 500 (L512.00 and HR4.12 samples). Functions for clusters are plotted with solid lines, and for voids with dashed lines. |
The basic difference between the full model sample L512.00 and galaxy samples lies in the presence of the weak filamentary web in the L512.00 sample, which is absent in galaxy samples. Percolation functions describe this difference in various ways. In the full model L512.00, weak filaments and sheets fill the whole space, as seen in Fig. 14 below, which isolate small low-density regions (voids). This property of the web is characterised by the number function as follows: at small threshold densities, the number of voids of the model L512.00 is high; see the upper right panel of Fig. 1. In contrast, at small threshold density, high-density regions form one connected system, that is, a cluster, since low-density filaments join knots of the density field into one connected system, thus 𝒩 = 1. With increasing threshold density some filaments became fainter than the threshold density, and the connected cluster splits into smaller units. Simultaneously, tunnels appear between small voids and the voids merge. This leads to a rapid increase in the number of clusters, and a decrease in the number of voids with increasing Dt (for smoothing length 1).
The presence of weak filaments and sheets in the full DM model L512.00 is expressed also in the filling factor and length functions. At small threshold densities the single high-density region (cluster) fills almost the whole sample volume, and the volume of the largest void is very small. The largest clusters percolate at a threshold density of Dt = 2−5, while the largest voids percolate at Dt = 0.1−0.4, depending on the smoothing scale.
In simulated and real galaxy samples, low-density DM filaments and sheets are not present. This leads to important differences in percolation functions. First of all, voids are connected (percolated) at all threshold densities, and thus the length of the largest void is equal to the size of the sample, and the number of voids is 𝒩 = 1. Only at very large smoothing kernels do some additional voids appear at low Dt, created by excessively smoothed clusters. The filling factors of the largest clusters are much lower than for the full sample L512.00, and the filling factors of the largest voids are higher. The absence of connecting filaments between high-density knots of the web makes these knots isolated systems. For this reason the number of clusters at low threshold densities is rather large in all galaxy samples, in contrast to the sample L512.00. These small isolated clusters are seen in Fig. 14 in the model sample L512.10 and in the observed sample SDSS.21. The number of clusters, 𝒩(Dt), is almost constant at Dt ≤ 1 for all real and simulated galaxy samples SDSS.21, L512.10, and HR4.12 in high-resolution density fields. Larger smoothing restores some filamentary connections between knots, and therefore the number of clusters decreases with decreasing Dt ≤ 1.
We highlight the fact that all percolation functions of simulated and real galaxy samples L512.10, SDSS.21, and HR4.12 are qualitatively very similar. Some minor quantitative differences are mainly due to the fact that the biased model selection parameter (particle-density limit of the sample L512.10) is not exactly tuned for the best mutual agreement of percolation functions. This similarity is remarkable, since volumes and shapes of SDSS and L512 samples are very different, as mentioned above. The insensitivity of percolation functions to sample volumes, shapes, and selection methods is an important property of the percolation method. This robustness of percolation functions has a simple explanation: percolation functions measure the growth of clusters (and voids) with decreasing threshold limit of the density field, Dt. The size, shape, and volume of the largest over-density region (cluster) and of the largest under-density region (void) does not depend on the overall size (volume) and shape of the whole sample.
We conclude that the percolation analysis allows a reliable comparison of model and observed samples. The percolation analysis shows quantitatively the presence of large differences between the full DM-dominated model L512.00 on the one hand, and three versions of galaxy samples, L512.10, SDSS.21, and HR4.12, on the other.
3.2. Recipes to select galaxy samples
Samples of real and simulated galaxies were selected for the percolation and power spectrum analyses using three different sources and respective recipes: galaxy luminosity limits, halo mass limits, and particle local density limits. In principle we could use a simulated galaxy model, where halos are filled with galaxies using the halo occupation distribution (HOD), as done by Tinker & Conroy (2009) in the study of the void phenomenon. However, such synthetic galaxies are generated only inside DM halos, and thus this model is actually a variant of the halo based HR4 model. Comparison of galaxy and DM samples was made using respective density fields. The difference in the calculation of respective density fields lies in the use of spatial coordinates. In halo-mass-limited samples, only the positions of halo centres were used. Large halos host many galaxies and have dimensions exceeding the resolution scale of density fields, 1 h−1 Mpc. Thus, density fields calculated from halo data are more approximate, as seen in high-resolution density field maps. If data on locations of individual galaxies are used, as in the case of SDSS samples, we get a smoother density field. When positions of all individual particles are used, as in the case of the density fields based on the L512, we get an even smoother density field. However, differences in the density fields of LCDM and SDSS samples are small (see Fig. 14), and have little influence on percolation functions and the distribution of densities. Differences in the nature of the objects have a larger effect in the HR4 model. The HR4 sample is based on rather massive halos with at least 30 particles per halo; thus fine details of density fields are invisible. At high threshold densities, HR4 over-density regions (clusters) are shorter and their number is smaller for a given threshold density, as seen from the comparison of L512, SDSS, and HR4 samples in Figs. 6 and 7. The largest difference is in the number functions for small smoothing kernels, RB = 1, 2 h−1 Mpc.
4. Power spectra and bias parameters of models
In this section, we calculate power spectra of biased L512 model samples. We investigate the influence of the fuzzy particle-density limit. Our goal is to find the bias as a function of the particle-density limit δ0, used in the selection of biased model samples.
4.1. Power spectra of biased L512 models
We calculated power spectra of the full L512.00 model with all DM particles included, 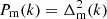 , and for biased model L512.i samples (clustered particle samples),
, and for biased model L512.i samples (clustered particle samples), 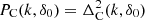 , using particle-density limits, δ0, according to Table 1. We applied standard procedures, used to calculate power spectra of numerical simulations (Eisenstein & Hu 1999). Power spectra for the full model L512.00 and for biased models L512.i, are shown in the left panel of Fig. 2.
, using particle-density limits, δ0, according to Table 1. We applied standard procedures, used to calculate power spectra of numerical simulations (Eisenstein & Hu 1999). Power spectra for the full model L512.00 and for biased models L512.i, are shown in the left panel of Fig. 2.
 |
Fig. 2. Left: power spectra of particle-density-limited L512 model spectra. The blue solid line with error ticks is for the spectrum of the model with all matter, L512.00 (particle-density limit δ0 = 0). For comparison, dashed black line shows the linear power spectrum. Thin coloured lines are for power spectra, calculated for biased L512.i models according to Table 1. Open and filled symbols with error bars are power spectra of flux-limited X-ray-selected clusters of galaxies, samples L050 and L120, according to Schuecker et al. (2001). Right: relative bias functions for power spectra of density-limited L512 models. |
The right panel of Fig. 2 shows relative bias functions 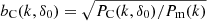 . Bias functions depend on the wavenumber k. They have a plateau around k ≈ 0.03 h Mpc−1, similar to the plateau found by Percival et al. (2001). We used the plateau at k ≈ 0.03 h Mpc−1 to find bias parameters for model samples as a function of particle-density limits,
. Bias functions depend on the wavenumber k. They have a plateau around k ≈ 0.03 h Mpc−1, similar to the plateau found by Percival et al. (2001). We used the plateau at k ≈ 0.03 h Mpc−1 to find bias parameters for model samples as a function of particle-density limits, 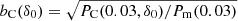 . Results are seen as dark circles in the upper curve on the right panel of Fig. 3.
. Results are seen as dark circles in the upper curve on the right panel of Fig. 3.
 |
Fig. 3. Left: probability function G(δ) for the L512.5 model with a particle-density limit δ0 = 5 and scatter of the particle-density limit σ = 0, 1, 2. Right: bias parameters b as functions of the particle-density limit, δ0, found from power spectra of biased models for particle-density limits, δ0. Coloured filled circles show calculated bias parameters from spectra for three values of the scatter of the particle-density limit, and coloured curves show bias functions according to Eq. (3). |
4.2. Influence of a fuzzy particle-density limit
The use of the local density δ0 as the only parameter to determine the fate of particles in the web is a simplification. Particles of slightly variable densities can indeed end up in halo-type density enhancements, which can be considered as model equivalents to real galaxies. For this reason the density limit to divide particles into high- and low-density populations is fuzzy.
To find the influence of a fuzzy particle-density limit we made the power spectrum and percolation function analyses for the L512 model, using a series of particle local density limits. We selected particles for this model as follows: particles with local densities x ≤ xmin are excluded, particles with densities x within limits xmin…xmax are included with a probability G(x), which depends on the location within the window, and particles with densities x > xmax are all included. Here we use the designation x = D(x)/Dm, where D(x) is the density at location x, and Dm is the mean density. Limits xmin and xmax are determined by the choice of the fuzziness distribution function p(x). The probability function G(x) to include particles in the clustered population was calculated applying the standard procedure:
For the fuzziness distribution function we used the normal distribution,
where x0 = δ0 is the location of the sharp limit, and the dispersion of the particle-density limit σ depends on the location of the limit, σ = f × δ0; f is the fuzziness parameter.
Power spectra were calculated for a series of particle-density limits, δ0, using fuzziness parameter values f = 0.1, 0.2, 04. The limit f = 0 corresponds to a sharp particle-density limit at δ0. Probability distributions G(δ) are shown in the left panel of Fig. 3 for the particle-density limit δ0 = 5. It should be noted that the form of the function G(δ) is the same for all particle-density limit values, since the dispersion σ is proportional to the density limit, δ0. Using power spectra we calculated the clustering bias parameter b, shown by coloured filled symbols in the right panel of Fig. 3.
The bias parameter as function of the particle-density limit can be approximated as follows:
This approximation gives a good fit of biased L512 models within particle-density limits 0.5 ≤ δ0 ≤ 100; see coloured lines in Fig. 3. Parameters [a, c, d, n] depend on the fuzziness parameter f, used in calculations of power spectra. For f = 0 and f = 0.1, parameters have values [a, c, d, n] = [3.89, 0.163, 4.18E−5, 1.74], for f = 0.2 we get [a, c, d, n] = [3.70, 0.163, 3.47E−5, 1.75], and for f = 0.4 we have [a, c, d, n] = [3.60, 0.157, 7.98E−6, 1.95].
We calculated density fields and performed the percolation analysis for the model L512.5 using the particle-density limit δ0 = 5, the scatter of particle-density limit σ = 1, 2, and applying smoothing kernels RB = 1, 2, 4, 8 h−1 Mpc. Percolation functions ℱ(Dt) and L(Dt) are shown in Fig. 4. Solid lines are for functions using sharp particle-density limits with σ = 0, dashed lines using particle-density limit scatter of σ = 1, and dotted lines with a scatter of σ = 2, which correspond to fuzziness parameter values of f = 0.0, 0.2, 0.4, respectively. Our results indicate that the scatter σ = 1 yields percolation functions that are almost identical to those with a sharp particle-density limit, σ = 0. Even a very large scatter of σ = 2 causes very small changes to percolation functions. These calculations show that power spectra and percolation functions for the fuzzy particle-density limit are close to results obtained with a sharp limit. At low particle-density limits δ0 ≤ 2 the fraction of matter in high-density regions determines the effective biasing factor, b ≈ 1/FC, as shown already by Einasto et al. (1999); see also Table 1. We consider the particle-density limit δ0 as an effective limit.
 |
Fig. 4. Percolation functions using fuzzy particle-density limits of the model L512.5 with δ0 = 5. Left: filling factor functions. Right: length functions of largest superclusters. Solid lines are for functions with fuzziness dispersion σ = 0, i.e. sharp particle-density limit, dashed lines are for dispersion σ = 1, and dotted lines for σ = 2. |
The bias function,
is given in Table 1 and in Fig. 3. It was calculated using the plateau at k = 0.03 Mpc−1 and applying a smoothed value according to Eq. (3). The bias function yields a one-to-one relationship between the bias parameter b and the particle-selection parameter δ0 of biased models. The bias function depends on the cosmological parameters of the model, but only weakly, since we use ratios of power spectra of the same model. It depends also on the particle-selection method. The fuzziness analysis shows that the selection method is rather robust.
5. Percolation analysis of simulated and real galaxy fields
In this section we continue the extended percolation analysis of observed and simulated clusters. We compare percolation functions for different limiting parameters (luminosities of galaxies, particle-density limits, masses of halos), and for different samples, that is, observed versus simulated samples. Our goal is to find density limits δ0 of biased models, which correspond to luminosity-limited SDSS samples, and mass-limited HR4 samples.
5.1. Percolation properties of observed and model samples
Percolation properties depend on the smoothing kernel size, since smoothing makes clusters and connecting filaments larger and helps clusters to percolate. We calculated density fields of observed and model samples, expressing densities in units of the mean density of particular samples. The L512 model sample includes all particles of the model, the HR4 model sample includes all halos, containing at least 30 particles, and the SDSS sample includes all galaxies within the apparent r magnitude interval 12.5 ≤ mr ≤ 17.77. Using density fields with these normalisations we calculated all percolation functions.
The comparison of percolation functions of observed SDSS samples and HR4 model samples with percolation functions of L512 model samples showed that percolation functions of SDSS and HR4 samples are shifted towards higher threshold densities relative to L512 model samples. This is a well-known effect. All densities are expressed in mean density units. In the L512 model samples, the mean density includes, in addition to clustered matter, DM in low-density regions, where there are no galaxies, or galaxies are fainter than the magnitude limit of the observational SDSS survey. In calculations of the mean density of observed SDSS samples and HR4 model samples, unclustered and low-density DM is not included. This means that in the calculation of densities in mean density units, densities are divided into smaller numbers, which increases the density values of SDSS and HR4 samples.
The total number and mass of the particles of the HR4 model samples is known, and therefore it is easy to calculate the density normalisation factor, which brings density fields to the level corresponding to all particles. We found that the fraction of particles in our HR4 samples is fc = 0.37156. To bring HR4 density fields to the same normalisation as L512 density fields, we multiplied all threshold densities by the factor fc. Corrected density thresholds can be used as arguments in percolation functions. Since we plot percolation functions using as argument log(Dt), the shape of functions does not depend on the normalisation factor, and we can use the same functions as in our preliminary analysis, only the argument is shifted.
The comparison of percolation functions of SDSS and HR4 samples shows that the SDSS sample contains galaxies that correspond to less massive halos than the HR4 sample. For this reason the correction factor fc for SDSS samples must be closer to unity. The exact value of this factor is difficult to calculate. Our analysis of percolation functions and respective parameters using various density normalisation factors shows that final results only rather modestly depend on the exact value of the factor fc. We accepted the factor fc = 0.45 for SDSS samples.
Using corrected density normalisations, Fig. 5 shows filling factor functions of the largest clusters and voids, ℱ(Dt) = Vmax/V0, while Fig. 6 shows length functions, that is, the lengths of the largest clusters, L(Dt) = Lmax in h−1 Mpc, and Fig. 7 shows number functions ℱ(Dt). Length functions of voids are not defined since voids percolate at all threshold densities. The left panels of these latter figures are for luminosity-limited SDSS samples, while the middle panels are for particle-density-limited L512 samples using particle-density limits of δ0 = 2, 5, 10, and 20, and the right panels are for halo-mass-limited HR4 model samples. In functions, we use the threshold density, Dt, as argument, corrected for sample mean density normalisation.
 |
Fig. 5. Filling-factor functions of largest clusters and voids, ℱ(Dt) = Vmax/V0, as functions of the threshold density, Dt. Left panels: luminosity-limited SDSS samples. Middle panels: particle-density limited (biased) L512 model samples. Right panels: HR4 model samples. Left panels from top to bottom are for luminosity limits of Mr − 5logh = −18.0, − 19.0, − 20, 0, − 21.0; middle panels from top to bottom are for samples with particle-density limits of δ0 = 2, 5, 10, 20; right panels from top to bottom are for halo- mass-limited samples HR4.11, HR4.12, HR4.123, and HR4.13. Functions for clusters are plotted with solid lines, and those for voids with dashed lines; colours mark different smoothing lengths. |
 |
Fig. 6. Length functions of largest clusters, L(Dt) = Lmax in h−1 Mpc. Panels and lines are as in Fig. 5. |
 |
Fig. 7. Number of clusters and voids, 𝒩(Dt). Number functions are calculated with small system exclusion limit Nlim = 50 (L512 and SDSS samples); and with Nlim = 500 (HR4 samples). Lines are as in Fig. 5. |
Figures 5–7 show that the percolation functions of the observed and model samples have surprisingly similar shapes, and depend in a simple and regular way on sample parameters. The difference between filling factor functions of observed and model samples is the largest at lowest threshold density, Dt = 0.1. Therefore, we use filling factor function values at threshold density, Dt = 0.1, as test parameters to compare samples in a quantitative manner. The behaviour of length functions is more complicated and is discussed further below.
5.2. Filling factor test of clusters and voids
The cluster filling factor test parameter is defined as FC = ℱC(0.1), and the void filling factor test parameter as FV = ℱV(0.1). Each sample with a different particle-density limit δ0 and smoothing kernel size RB yields a value for FC and FV. We calculated these parameters of the L512 model for a range of particle-density limits δ0, and define filling factor test functions as follows: FC(δ0) and FV(δ0). Our goal is to find particle-density limits δ0 of L512 models which correspond to galaxy luminosity limits of SDSS samples and halo mass limits of HR4 samples. We shall use the following strategy: we plot filling factor test functions FC(δ0) and FV(δ0) of biased models L512, separately for smoothing kernels RB = 1, 2, 4, 8 h−1 Mpc. Results are shown in Fig. 8. Solid lines are for biased L512 models, different colours mark functions calculated using smoothing scales RB = 1, 2, 4, 8 h−1 Mpc. Left panels are for cluster filling factors, and right panels for void filling factors. Filling factors of SDSS and HR4 samples of various luminosity limits are known, and it is straightforward to interpolate in order to find out at which particle-density limits δ0 filling factors of SDSS (HR4) samples are equal to filling factors of biased L512 samples. This comparison was made separately for each smoothing kernel value, RB, and for filling factors of clusters and voids. We tried several interpolation schemes, and found that good results are obtained by linear interpolation along the logδ0 axis.
Using this interpolation scheme we found for each SDSS luminosity limit (HR4 sample halo mass limit) particle-density limits δ0 of biased L512 samples, which correspond to these SDSS (HR4) samples, separately for clusters and voids, and for different smoothing kernel length, RB. Figure 8 shows that there is good agreement between values obtained using clusters and voids, and using various smoothing kernels. We consider density fields smoothed with RB = 1 and RB = 2 h−1 Mpc kernels as the best ones for comparison, and accept mean values of particle-density limits δ0, found on the basis of clusters and voids of L512 models for these smoothing kernels, as representative of observed SDSS (HR4) samples of various luminosity (mass) limits. We estimated the errors of obtained δ0 values from deviations of individual δ0 values for clusters and voids using smoothing kernels RB = 1 and RB = 2 h−1 Mpc. Results are given in Col. (2) of Table 4.
 |
Fig. 8. Filling factor test function of clusters FC(δ0) and voids FV(δ0). Solid lines show test functions of L512 models for four smoothing scales, RB = 1, 2, 4, 8 h−1 Mpc. Left panels are for cluster filling factors, right panels for void filling factors. Upper panels: filling factors of SDSS samples, while lower panels show filling factors of HR4 samples, both according to the symbols in the respective keys. |
Particle-density limit and bias parameters of SDSS and HR4 samples.
5.3. Length function test
We now compare SDSS and HR4 samples with reference samples of biased L512 models using the length function. For this purpose, only cluster length functions can be used, since voids percolate at all threshold levels, and void lengths are equal to sample effective lengths. Most valuable information comes from the location of length functions for smoothing kernels RB = 1 h−1 Mpc and RB = 2 h−1 Mpc, in relation to functions for larger smoothing scales. But the problem here is that clusters only percolate at low limiting luminosities (halo masses), and therefore the percolating density threshold Dt can only be found for these samples.
Positions of SDSS and HR4 samples relative to L512 samples can be found using percolation threshold densities. Percolation threshold densities of biased L512 samples as functions of the particle-density limit δ0 are shown separately for various smoothing kernel lengths in the left panels of Fig. 9. Percolation threshold densities of SDSS and HR4 samples were found using length functions for largest and second-largest clusters, following Klypin & Shandarin (1993). By interpolation along the δ0 coordinate we found particle-density limits of L512 samples, corresponding to SDSS and HR4 samples.
 |
Fig. 9. Left panels: cluster percolation threshold test, right panels: cluster length test for high-luminosity (mass) samples. Upper panels are for SDSS samples, lower panels for HR4 samples. Solid lines show cluster length test functions of L512 models for various smoothing scales. Coloured symbols show SDSS samples of various luminosity and HR4 samples of various halo mass limits. |
At high luminosities (halo masses), the largest clusters at small smoothing lengths are shorter than the total length of the sample, as seen in plots of density fields of samples L512.10 and SDSS.21 in Fig. 14. For SDSS and HR4 samples with no percolation, we applied cluster lengths at threshold density Dt = 0.1 using interpolation schemes similar to interpolation of filling factor functions. This procedure was applied for high-luminosity samples SDSS.20 and SDSS.21, and for high-mass samples HR4.12, HR4.123, and HR4.13. Results of this interpolation are shown in the right panels of Fig. 9. We used locations of length functions for smoothing kernels RB = 1 and RB = 2 h−1 Mpc. Errors were calculated from the scatter of individual values for different smoothing kernels. Results for particle-density limits are given in Col. 3, (δ0)L, of Table 4 for SDSS and HR4 samples.
One possibility to get simple estimates of positions of SDSS (and HR4) samples relative to L512 samples is to use the general shape of cluster length functions. Here we compare the shape and location of length functions for smoothing kernels RB = 1, 2 h−1 Mpc with the shape and location of length functions for larger smoothing kernels. For instance, let us compare the length function of the SDSS.18.1 (here the second index 1 shows the smoothing scale, RB = 1 h−1 Mpc) sample relative to SDSS.18 samples for larger smoothing kernels, SDSS.18.2, SDSS.18.4, and SDSS.18.8. Figure 6 shows that the length function of the sample SDSS.18.1 is located between the length functions of samples SDSS.18.4 and SDSS.18.8. Near the percolation level the length function of the model sample L512.2.1 lies to the right of the length functions of samples L512.2.2, L512.2.4, and L512.2.8. However, in the model sample with a higher particle-density limit L512.5.1 the length function is located at approximately the same location as that of the length function of the L512.5.2 sample.
Comparing locations of SDSS sample length functions at smoothing kernels RB = 1 h−1 Mpc and RB = 2 h−1 Mpc with locations of respective L512 samples, we find that the shape of the length function of the SDSS.18 sample corresponds best with the model sample of particle-density limit δ0 = 5. The length functions of the SDSS.18 samples correspond to those of the model sample L512 only within particle-density limits 3 < δ0 < 7. Therefore, our estimated corresponding model of the L512 series for the SDSS.18 sample is the model with δ0 = 5 ± 2. This simple length function shape comparison test uses the information for the whole length function, not only at percolation or Dt = 0.1 level; it was made for all SDSS and HR4 samples, and results are given in Col. 4, (δ0)Ls, of Table 4.
Length function tests confirm results obtained with the filling factor test. As we see from Table 4, cluster length tests yield slightly higher particle-density limits δ0 for SDSS samples than the filling factor test. Figure 10 shows the particle-density limit parameter δ0 and its error for all luminosity-limited SDSS samples, and for halo-mass-limited HR4 samples, applying filling function and length function tests. All tests show that the particle-density limit of biased model samples increases with the increase of the luminosity (halo mass) of the sample; the increase is regular and has a small scatter. Graphs for SDSS and HR4 samples can be brought to a single diagram if a mass-to-luminosity ratio of SDSS samples, M/Lr = 103 ± 10, is applied.
 |
Fig. 10. Particle-density limit parameter δ0 for SDSS-luminosity-limited samples (left panel), and for halo-mass-limited HR4 model samples (right panel). Absolute magnitude and halo mass limits are used as arguments. Red circles are based on filling factor test for clusters and voids, blue boxes on length function tests, and green diamonds on length function shape estimates, as given in Table 4. |
5.4. Redshift space distortions
Model samples yield true spatial coordinates, and observational SDSS samples are based on angular positions and redshifts. In using redshifts to calculate spatial coordinates, one must take into account two types of redshift space distortion: the fingers of God effect, caused by the random motion of galaxies in clusters, and redshift space distortions (RSD) or the Kaiser (1987) effect, caused by the coherent motion of galaxies towards clusters and superclusters.
The finger of God effect is taken into account in catalogues of groups and clusters, used in calculations of the SDSS density field (Tempel et al. 2014). The Kaiser effect leads to an apparent flattening of the structure, referred to as the pancakes of God. For this reason, the SDSS density field is distorted. Filamentary connections between over-dense regions are disturbed by the Kaiser effect. Filling factor test functions are shown in Fig. 8, cluster length test functions in Fig. 9. In these figures, filling factors and lengths of L512 model samples represent true model filling factors and lengths. To correct for this effect, points corresponding to SDSS samples must be shifted, which leads to changes of particle-density limits δ0. The questions remains as to by how much these points should be shifted?
In answering this question, the comparison of filling factor and length tests of HR4 model samples is of help. The analysis described above was based on true positions of halos in real space. We made a new analysis, using positions and velocities of halos of the HR4.11 sample to calculate a version of the sample in redshift space. Positions of all halos were shifted from real to redshift space for an observer, located outside of the box by 100 h−1 Mpc, at the centre below the x = y = 0 plane. We calculated percolation functions for both versions of the HR4.11 sample. Results are shown in Fig. 11.
 |
Fig. 11. Percolation function tests to check the influence of redshift space distortions. Left panel: filling factor functions and the right panel length functions of HR4.11 models. Solid lines are calculated for real space, dashed lines for redshift space. |
We used filling factors at threshold density level Dt = 0.1 to find particle-density limits of L512 samples, corresponding to HR4 models. This test shows that for smoothing lengths 1 and 2 h−1 Mpc, HR4.11 models in real and redshift space yield almost identical δ0 limits. In the cluster percolation threshold (length) test, HR4.11 samples in redshift space have lower threshold densities Dt, especially for samples with smoothing kernels 1 and 2 h−1 Mpc. This yields a mean value of δ0 = 9.6 ± 1.9, which is slightly larger than for real space, δ0 = 8.0 ± 1.5; see Table 4. If such relative corrections are applied to all observed samples then particle-density limits (δ0)L in real space would be 4.1, 4.9, 6.7, 14.1 for samples SDSS.18, SDSS.19, SDSS.20, and SDSS.21, respectively. Such corrections bring particle-density limits, (δ0)L, closer to limits found from the filling factor test, (δ0)F.
The length function test compares the percolation length of samples, while the filling factor test compares the volumes of clusters and voids at very low threshold density Dt = 0.1. Our check using HR4 samples shows that differences found from the comparison of results for real and redshift space are small. Filling factor and length tests represent very different properties of the cosmic web; it is surprising that both tests yield such close results. We can make a tentative conclusion that the redshift space distortion effect is small, and that differences in filling factor and length tests of SDSS samples are mainly due to random factors.
5.5. Luminosity dependence
We applied the function (3) with parameter set for f = 0 to find bias parameter values of biased L512 models, bF, bL and bLs, corresponding to SDSS and HR4 samples. Results are given in Table 4. Bias parameter values of SDSS samples are shown in the left panel of Fig. 12 as a function of the absolute magnitude limit Mr of samples. Red circles show bF calculated from L512 spectra for biased models using the filling factor test; blue and green symbols show bLand bLs found from spectra of biased L512 models using two length function tests. Errors were found from the mean scatter of bF, bL, and bLs values for luminosity-limited SDSS samples, as shown in Table 4. We accept an arithmetic mean of our three tests, bF, bL, BLs, shown by red circles in the right panel of Fig. 12. The accepted error corresponds to a characteristic error from one measurement; this is internal error – possible systematic errors due to the method must be discussed separately.
 |
Fig. 12. Left panel: bias parameter b values as a function of the absolute magnitude limit Mr − 5logh of the sample. Red circles show bias parameter values as found from biased L512 spectra using the filling factor test, bF, blue boxes indicate bias parameters as found from spectra using the length function test, bL, and green diamonds show bias parameters using the length function general shape test bLs. Right panel: bias function found in this paper compared with bias functions found in other studies. Bias parameter values for SDSS galaxies of various absolute magnitude limits found in this paper are marked by red circles with error bars. Bias parameter values of SDSS galaxies found by Shi et al. (2018) and applying normalising factor b° = 1.4 are marked by black squares with error bars; that for BOSS galaxies according to Gil-Marín et al. (2017) is shown by a blue diamond, and that for X-ray clusters of galaxies by Schuecker et al. (2001) by a green triangle. Dashed line shows the fit by Norberg et al. (2001), applying bias normalising factor b° = 1.85. Black, blue, and red lines show fits by Norberg et al. (2001), Tegmark et al. (2004b), and Zehavi et al. (2011), respectively. |
Available data indicate that the relative bias function f(> L) = b(L)/b° is approximately constant at low luminosities L < L* at level f(L < L*)) ≈ 0.9, which leads to b(L < L*) ≈ 0.9 × b°. Here b° is the bias normalising factor. The flattening of the b(L) relation at low luminosities L is probably due to the nature of the distribution of faint galaxies. As shown by Tempel et al. (2009), first ranked galaxies have a tendency to have a cutoff at magnitudes M − 5log10h ≈ −17 in the photometric system of the 2dF survey bJ. Satellite galaxies can have fainter luminosities, but satellites are located only around main galaxies (Einasto et al. 1974b). Thus, power spectra and percolation properties of very faint galaxies cannot be very different from properties of galaxies corresponding to the faint end of the luminosity function of central galaxies.
The luminosity dependence of our data is very well fitted by the bias function of Norberg et al. (2001):
where L is the luminosity limit of galaxies of the sample, L* is the characteristic luminosity of the sample (Schechter 1976). Fitting our bias parameters for SDSS samples to the Norberg et al. (2001) bias function yields a normalising factor b° = 1.85 ± 0.15, and we get for the luminosity dependence of SDSS galaxies:
The error was found from the scatter of tests for bF, bL, BLs. Norberg et al. (2001) defined the relative bias function so that f(L*) = 1. Thus, our analysis suggests that the bias parameter of L* galaxies is b* = 1.85 ± 0.15.
Our bias function is based on the comparison of power spectra of biased model samples L512.i and the full model sample L512.00. Since the comparison is differential, possible errors in cosmological parameters of the model are minimal. The critical element of the method is the sharp density limit δ0 used to select particles for biased samples. We checked the influence of the sharpness of the density limit using fuzzy limits. However, the question remains as to how well such biased model samples represent luminosity-limited SDSS galaxy samples. It is possible that a sharp particle-density limit and a sharp SDSS galaxy luminosity limit yield slightly different samples near the lower borders of limits.
We can check possible differences using number functions. Figure 7 shows that at low and medium threshold densities, 0.1 ≤ Dt ≤ 1, and small smoothing lengths, the number functions of all biased model samples and luminosity-limited SDSS samples are almost flat. In this threshold density interval, samples are dominated by small isolated clusters. Various threshold density levels select the same clusters, and therefore the number of clusters remains the same. In samples with larger smoothing length, the number of clusters at low Dt is smaller, because smoothing joins these previously isolated clusters at a low threshold limit to filaments, and isolated clusters almost disappear. At threshold density Dt = 0.1 and smoothing length RB = 8 h−1 Mpc, samples SDSS.18 and L512.2 contain only a few isolated clusters due to faint galaxy filaments connecting knots to single objects. In samples of higher limiting luminosity or particle-density limit, the number of clusters at Dt = 0.1 gets larger, since filaments connecting knots became invisible; see Fig. 7. In this respect, simulated and real galaxy samples yield qualitatively very similar results. We may conclude that our method to find biased model samples using sharp particle-density limits is a fair representative of SDSS luminosity-limited samples.
As discussed above, redshift space distortions can increase length function test parameters (δ0)L and corresponding bias parameters bL. Thus, if one prefers the filling factor test, one can use the value b* = 1.70 ± 0.15 for the bias parameter of L* galaxies. This does not influence our main conclusion that the bias parameter of L* galaxies is b* ≫ 1.0.
5.6. Comparison with other data
In the right panel of Fig. 12 we compare our results for the bias function b(L) with the results of other authors. The dashed line shows our bias function (6), whereas the black, blue, and red lines show fits by Norberg et al. (2001), Tegmark et al. (2004b), and Zehavi et al. (2011).
Tegmark et al. (2004b) calculated power spectra in six bins of absolute magnitude, and found that the relative bias function is better given by the expression: f(L) = b(L)/b° = 0.895 + 0.150(L/L*)−0.040(M − M*); see their Figs. 28 and 29. Here, Mr = M* − 2.5 × log10(L/L*) and M* are r-magnitudes of SDSS galaxies and respective Schechter magnitudes.
Zehavi et al. (2011) investigated the galaxy clustering of the completed SDSS survey, and found for the bias function the form bg(> L)×(σ8/0.8) = 1.06 + 0.21(L/L*)1.12, where L is the r-band luminosity corrected to z = 0.1, and L* corresponds to M* = −20.44 ± 0.01 (Blanton et al. 2003). Pollina et al. (2019) found relative linear bias factors between clusters and galaxies using the first years of observations of the Dark Energy Survey, bcl/bgal = 1.6 for L > 0.5L* galaxies.
Shi et al. (2016, 2018) developed a method to map real space distribution of galaxies. The method was applied to measure the clustering amplitude of matter and bias parameters of flux-limited sample of galaxies in SDSS DR7 in the redshift range 0.01 ≤ z ≤ 0.2. We show in Fig. 12 the bias parameter values found by Shi et al. (2018), applying a normalising factor of b° = 1.4.
Gil-Marín et al. (2015, 2017) investigated the clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic (BOSS) Survey. The BOSS survey selects luminous red giant (LRG) galaxies and consists of near and distant samples, the LOWZ sample of effective redshifts zLOWZ = 0.32, and the distant sample CMASS with zCMASS = 0.57. Gil-Marín et al. (2017) found the linear biasing parameter b1 = 2.08 for LOWZ survey, and b1 = 2.01 for CMASS survey. Gil-Marín et al. (2017) compared observed bias parameters with bias parameters for N-body halos of mock samples: the low-bias model with a halo mass limit of Mmin = 3.80 × 1012 M⊙ h−1 has b1 = 1.75, and the high-bias model with Mmin = 8.36 × 1012 M⊙ h−1 has b1 = 2.07; see Table 1 by Gil-Marín et al. (2017). These values are close to bias parameter values found for our HR4.123 and HR4.13 samples; see Table 4 and Fig. 3. We show in Fig. 12 the bias parameter for BOSS LOWZ galaxies according to Gil-Marín et al. (2017). BOSS galaxies were selected using LRG galaxies. We found for these galaxies the mean red magnitude Mr − 5logh = −21.0, with a spread of about one magnitude. Our SDSS galaxy samples contain galaxies with luminosities greater than or equal to absolute magnitude limits. Therefore, we can accept the magnitude lower limit Mr − 5logh = −20.5 for LRG galaxies, almost equal to the magnitude of L* galaxies.
Power spectra of X-ray detected clusters of galaxies were derived in the framework of the REFLEX survey by Schuecker et al. (2001). Power spectra have a maximum around k = 0.05 h Mpc−1, shown in Fig. 2 for two flux-limited cluster samples: L050 with X-ray luminosity limit, LX ≥ 0.5 × 1044 erg s−1, and L120 with limit LX ≥ 1.2 × 1044 erg s−1. The amplitude of the spectrum is higher for higher X-ray-limit clusters. Both spectra correspond to our model samples with very high particle-density limit δ0 ≈ 50; see Fig. 2. For X-ray clusters we estimated the mean magnitude Mr − 5logh = −21.5.
6. Discussion
We show in Fig. 13 power spectra of L512 models again; the spectrum for biased model L512.10 is highlighted in red. This biased model corresponds approximately to L* luminosity-limited galaxy samples. Figure 13 also shows the power spectrum obtained by Tegmark et al. (2004b) according to their Table 3, which corresponds to L* SDSS galaxies.
 |
Fig. 13. Power spectra of particle-density-limited L512 model spectra. The power spectrum of the sample L512.10 is shown by the bold red line. Filled symbols show the power spectrum of SDSS galaxies by Tegmark et al. (2004b). |
When the presence of the cosmic web was first discussed in the IAU Tallinn Symposium, Zeldovich in his talk emphasised the importance of developing statistical tools to quantitatively measure the new phenomena: the filamentary character of the galaxy distribution and the presence of voids. So far, the basic quantitative descriptor of the distribution of galaxies has been the two-point projected correlation function wp(rp). This function is adequate to describe 2D data, as presented by Seldner et al. (1977) and analysed by Soneira & Peebles (1978). Following this initiative, Zeldovich et al. (1982) applied the percolation analysis to test the filamentarity of the web, and the multiplicity analysis to test the clustering properties. The Soneira & Peebles (1978) model failed in both tests. The model of Zeldovich, based on a HDM simulation by Doroshkevich et al. (1982), failed in a multiplicity test. Both tests showed the agreement of the model with observations only when a CDM model was used (Melott et al. 1983).
The cosmic web is very rich in detail and has complex properties. For this reason there exist no statistical tools able to describe all the properties of the web. Each statistical tool is an instrument to test certain well-fixed properties of the web. To evaluate possible strengths and limits of power-spectrum determinations by various authors we have to understand what features of the web can be tested by particular tools. The general properties of the cosmic web as delineated by galaxies and DM were elucidated early on. As discussed above, the main difference between distributions of matter and galaxies is the presence of DM in low-density regions, with no corresponding population of galaxies.
Geometrical properties of density fields of matter, model galaxies, and SDSS galaxies are discussed in previous sections. Here we discuss some aspects of the distribution that are critical to power-spectrum analyses. In Fig. 14 we compare the high-resolution density fields of these samples, represented by the full model sample L512.00, the biased model sample L512.10, and the SDSS.21 sample. L⋆ galaxies have approximately the magnitude Mr − 5logh = − 20.5, and thus the luminosity density field of SDSS.21 contains slightly higher-luminosity galaxies than the L512.10 field. This figure shows that qualitatively the pattern of the distribution of simulated and real clusters is similar. The presence of large regions with zero spatial density is clearly seen in simulated and real galaxy density fields.
 |
Fig. 14. Upper panels: central sections of the high-resolution non-smoothed density fields of identical 256 × 256 × 1 h−1 Mpc slices of DM models L512.00 and L512.10, found for particle-density limits δ0 = 0, 10. Lower panel: slice through the zoomed density field of the SDSS.21 galaxy sample, smoothed with 1 h−1 Mpc kernel. The size of the sample in the vertical direction is about 240 h−1 Mpc. This figure illustrates the effect of zero-density regions in simulated and real density fields of galaxies. Densities are expressed in logarithmic scale in the interval 0.005–15 in mean density units. The colour code is identical in all panels. |
In Fig. 15 we compare cumulative distributions of densities in the density fields of model samples L512 with the respective distributions for observed SDSS samples and comparison HR4 samples. In the full sample there are particles with all density labels, thus the cumulative distribution smoothly approaches unity with decreasing particle density. In all biased samples, low-density particles are absent, thus a large fraction of cells of the density field have zero density. The cumulative distribution has a peak at the lowest density value, corresponding to pixels with zero density, and continues at a lower level. Density distributions of SDSS and HR4 samples are qualitatively similar to distributions of biased L512 samples.
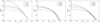 |
Fig. 15. Cumulative distributions of densities of high-resolution density fields of L512, SDSS, and HR4 samples (left, middle, and right panels, respectively). For the L512 model, dashed black line shows the distribution for the full sample with all particles, L512.00, and coloured solid lines for biased model samples L512.5, L512.10, L512.20, and L512.50. Similar coloured lines are used for SDSS, and HR4 samples of various magnitude (halo mass) limits. |
Figure 16 shows a cross section of the density field at spatial y, z-coordinates through the centre of the field presented in Fig. 14. We plot here the density contrast δ(x) = D(x) − 1. The blue line shows the density contrast at the early epoch, corresponding to a redshift of z = 30. At this early epoch, the amplitude of density fluctuations is small, and density fluctuations are approximately equal everywhere. The black line gives the density contrast for the same cross section at the present epoch for the sample with all particles, L512.00. The density field is dominated by fluctuations of the density contrasts in the range −1 < δ(x) < 2, with a mean around δ ≈ −0.5, superposed by isolated very high-density peaks. The red line shows the same cross section but for the biased sample L512.10. In the sample L512.10, high-density peaks of the density field of biased models are the same as in the full model. Weak DM knots of medium density, seen in the sample L512.00, are gone. In contrast to the L512.00 sample, over most of the density field the density of the sample L512.10 has zero density and density contrast δ = −1.
 |
Fig. 16. Cross sections of length 300 h−1 Mpc of the density contrast δ(x) = D(x)−1 of the model L512 along the x-spatial coordinate at the same z-coordinate as shown in Fig. 14. The blue line shows the density field of the model L512.00 at a redshift of z = 30. The black line shows the density field of the full model L512.00 at the present epoch, and the red line shows the same but for the biased model L512.10. |
Table 1 provides the fraction of particles in biased samples, FC, and filling factor FFC of all clusters (non-zero density cells) of the density field at threshold density Dt = 0.1. Both quantities are given as functions of the particle-density limit δ0 of biased model samples. The table shows that the filling factor of clusters decreases with increasing δ0 much faster than the fraction of particles. This is a well-known effect: the density of clusters increases towards their centres and the volume decreases more rapidly than the number of particles. For comparison we note that filling factors of all clusters at the threshold density level Dt = 0.1 of samples SDSS.18, SDSS.19, SDSS.20, and SDSS.21 are 0.1795, 0.1449, 0.0976, and 0.0399, respectively. The fraction of zero-density cells is increasingly closer to unity when we increase the sample particle-density limit δ0 or the luminosity limit L. In the sample L512.10, 95% of all cells of the density field have zero density, in the SDSS.21 field this value is even 96% of all cells.
In our method, power spectra are calculated using ΛCDM models. The power spectrum is a sum over all density contrasts. The greater the fraction of cells with zero density and density contrast δ = −1, the greater the sum. For this reason, the power spectrum of all biased model samples has a higher amplitude than the full DM model; the larger the fraction of zero-density regions, the higher the amplitude. Thus, the power spectrum is a measure of the fraction of zero-density cells in the sample. It is interesting to note that Einasto et al. (1986b) arrived at the same conclusion from the analysis of the three-dimensional correlation function.
A summary of measurements of power spectra is presented in Figs. 12 and 13. The power spectrum for our full DM model L512.00 is in very good agreement with the updated matter power spectrum at z = 0, as compiled by Chabanier et al. (2019). The comparison of various determinations shows that all methods permitted us to determine very accurately the luminosity dependence of galaxy power spectra, when appropriate bias normalising factors b° are applied. The amplitude of the spectrum can be characterised by the bias normalising factor. Figures show that normalising factors can be divided into two groups: around b° ≈ 1 – Norberg et al. (2001), Tegmark et al. (2004b), and Zehavi et al. (2011); and around b° ≈ 2 – Schuecker et al. (2001), Gil-Marín et al. (2015, 2017), and our work. This variety of bias normalising factors suggests that authors used different tools to handle zero density regions of the luminosity density field of galaxies.
The devil is in the details, and the methods to estimate power spectra of galaxies contain numerous technical details and assumptions. Each method has finite scope, and the results of each method are characteristic of the method used. In this respect, a combined method using different properties of the cosmic web carries the advantage of taking into account the bias phenomenon in a more comprehensive manner. It is clear that future development will add new details to the picture we have today.
7. Concluding remarks
The present study is based on the assumptions that the ΛCDM model is a good approximation of the real Universe on scales where gravitational forces are dominating and where the local density is the dominant factor in galaxy formation. Our study shows that the absence of galaxy formation in low-density regions of the cosmic web is an essential property of the ΛCDM universe. The combined action of several physical processes gives rise to (i) the smoothness of the flow of particles until the intersection of particle trajectories; (ii) the formation of halos along caustics of particle trajectories; (iii) the phase synchronisation of density perturbations on various scales; and (iv) the two-step nature of galaxy formation by condensation of baryonic matter within DM halos.
We studied the distribution of galaxies and matter using several density fields and applying percolation and power spectrum analyses. To calculate the density fields of simulated galaxies we used the particle local density δ as a dimensionless characteristic of particles of numerical simulations of the cosmic web. We applied a sharp particle-density limit, δ ≥ δ0, to select particles, which form biased model samples. We tested this selection algorithm using fuzzy particle-density limits and analysed the number functions of simulated and real galaxies. Our analysis shows that this sample-selection method yields biased model samples in a wide range of particle-density limits, and allows us to calculate the bias function of biased model samples as functions of the particle-density limit, b(> δ0). The bias function only weakly depends on cosmological parameters of the model, since we use ratios of power spectra of the same model.
We compared biased model samples with luminosity-selected SDSS galaxy samples using the extended percolation analysis, based on density fields of matter and galaxies. Density fields of ΛCDM models were calculated using local density values of each particle. Density fields of SDSS samples were calculated using positions and luminosities of galaxies. Density fields of HR4 models were calculated using positions of halo centres and their masses. In spite of these differences, fields found for various samples appear very similar and allow an easy quantitative comparison. We found that the extended percolation method allows comparison of observational and model samples with very different sample sizes and configurations. This method is almost unaffected by the redshift space distortions present in observational samples. The percolation method is very sensitive to geometrical properties of clusters and voids of observed and model samples, and allows density limits δ0 of biased models to be found which correspond to luminosity-limited SDSS samples.
As a result of the physical processes described above there exists at all cosmological epochs a low-density population, consisting of a mixture of dark and baryonic matter. Phase synchronisation, which leads to the formation of small, filamentary, high-density regions and large contiguous regions with very low spatial densities, plays a crucial role in the evolution of the Universe. Galaxy formation is possible only in the high-density medium. This is the main factor in the biasing phenomenon, leading to an increase in zero-density cells in density fields of simulated and real galaxies, and an increase in the amplitude of the power spectrum of galaxies with respect to the power spectrum of matter. The second-largest effect is the dependence of the bias function on the luminosity of galaxies. Variations in gravitational and physical processes during the formation and evolution of galaxies, represented in our biasing model by the fuzziness of the biasing threshold, have the smallest influence on the large-scale bias.
The combined geometrical and power spectrum analysis clearly demonstrates the presence of large differences between distributions of matter and galaxies, expressed quantitatively by percolation functions and power spectra. Power spectra of biased models representing SDSS samples of various luminosity limits allowed us to calculate the expected bias function, b(> L). The bias function is in very good agreement with earlier studies when appropriate bias normalising factors are applied. Our main conclusions can be summarised as follows.
-
1.
Non-clustered matter in low-density regions is smoothly distributed, which rises the amplitude of power spectra of the clustered matter in galaxies with respect to the amplitude of power spectra of all matter. This is the dominant factor influencing the biasing phenomenon, and can be used as a cosmological constraint.
-
2.
The dependence of the bias parameter on the luminosity of galaxies has the second-largest effect on the bias parameter. Variations in gravitational and physical processes during the formation and evolution of galaxies have the smallest influence on the bias parameter.
-
3.
The combined analysis of geometrical properties of the cosmic web and power spectra of biased model samples and SDSS samples of galaxies allowed us to estimate the bias parameter of L* galaxies to b* = 1.85 ± 0.15.
Acknowledgments
Our special thanks are to Gert Hütsi for calculations of power spectra and for many stimulating discussions. We thank Changbom Park for the permission to use Horizon 4 simulations for this study, Mirt Gramann, Enn Saar, Antti Tamm, Elmo Tempel and Rien van de Weygaert for discussion and the anonymous referee for useful suggestions (We report with sorrow that during final preparations of the paper our collaborator Ivan Suhhonenko (1974–2019) passed away.). This work was supported by institutional research funding IUT26-2 and IUT 40-2 of the Estonian Ministry of Education and Research. We acknowledge the support by the Centre of Excellence “Dark side of the Universe” (TK133) financed by the European Union through the European Regional Development Fund. The study has also been supported by ICRAnet through a professorship for Jaan Einasto. We thank the SDSS Team for the publicly available data releases. Funding for the SDSS and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the U.S. Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS Web Site is http://www.sdss.org/. The SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, University of Cambridge, Case Western Reserve University, University of Chicago, Drexel University, Fermilab, the Institute for Advanced Study, the Japan Participation Group, Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, Ohio State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington.
References
- Ahn, C. P., Alexandroff, R., Allende Prieto, C., et al. 2014, ApJS, 211, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Aragon-Calvo, M. A., van de Weygaert, R., Araya-Melo, P. A., Platen, E., & Szalay, A. S. 2010, MNRAS, 404, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Aragon-Calvo, M. A., Neyrinck, M. C., & Silk, J. 2016, OJA, submitted [arXiv:1607.07881] [Google Scholar]
- Arnold, V. I., Shandarin, S. F., & Zeldovich, I. B. 1982, Geophys. Astrophys. Fluid Dyn., 20, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Bardeen, J. M., Bond, J. R., Kaiser, N., & Szalay, A. S. 1986, ApJ, 304, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Bertschinger, E. 1995, ArXiv e-prints [arXiv:astro-ph/9506070] [Google Scholar]
- Blanton, M. R., & Roweis, S. 2007, AJ, 133, 734 [NASA ADS] [CrossRef] [Google Scholar]
- Blanton, M. R., Hogg, D. W., Bahcall, N. A., et al. 2003, ApJ, 592, 819 [NASA ADS] [CrossRef] [Google Scholar]
- Bond, J. R., Kofman, L., & Pogosyan, D. 1996, Nature, 380, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Cautun, M., van de Weygaert, R., Jones, B. J. T., & Frenk, C. S. 2014, MNRAS, 441, 2923 [NASA ADS] [CrossRef] [Google Scholar]
- Cen, R., & Ostriker, J. P. 1992, ApJ, 399, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Chabanier, S., Millea, M., & Palanque-Delabrouille, N. 2019, MNRAS, submitted [arXiv:1905.08103] [Google Scholar]
- Davis, M., & Peebles, P. J. E. 1983, ApJ, 267, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, M., Efstathiou, G., Frenk, C. S., & White, S. D. M. 1985, ApJ, 292, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., & Silk, J. 1986, ApJ, 303, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Desjacques, V., Jeong, D., & Schmidt, F. 2018, Phys. Rep., 733, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Doroshkevich, A. G., Kotok, E. V., Poliudov, A. N., et al. 1980, MNRAS, 192, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Doroshkevich, A. G., Shandarin, S. F., & Zeldovich, I. B. 1982, Comments Astrophys., 9, 265 [NASA ADS] [Google Scholar]
- Einasto, J., & Saar, E. 1987, in Observational Cosmology, eds. A. Hewitt, G. Burbidge, & L. Z. Fang, IAU Symp., 124, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Einasto, J., Kaasik, A., & Saar, E. 1974a, Nature, 250, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Einasto, J., Saar, E., Kaasik, A., & Chernin, A. D. 1974b, Nature, 252, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Einasto, J., Jõeveer, M., & Saar, E. 1980, MNRAS, 193, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Einasto, J., Gramann, M., Einasto, M., et al. 1986a, Estonian Acad. Sci.Preprint, A-9, 3 [Google Scholar]
- Einasto, J., Saar, E., & Klypin, A. A. 1986b, MNRAS, 219, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Einasto, J., Einasto, M., & Gramann, M. 1989, MNRAS, 238, 155 [NASA ADS] [Google Scholar]
- Einasto, J., Einasto, M., Gramann, M., & Saar, E. 1991, MNRAS, 248, 593 [NASA ADS] [Google Scholar]
- Einasto, J., Einasto, M., Tago, E., et al. 1999, ApJ, 519, 456 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Einasto, J., Hütsi, G., Saar, E., et al. 2011a, A&A, 531, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Einasto, J., Suhhonenko, I., Hütsi, G., et al. 2011b, A&A, 534, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Einasto, J., Suhhonenko, I., Liivamägi, L. J., & Einasto, M. 2018, A&A, 616, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eisenstein, D. J., & Hu, W. 1999, ApJ, 511, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Falck, B., & Neyrinck, M. C. 2015, MNRAS, 450, 3239 [NASA ADS] [CrossRef] [Google Scholar]
- Feldman, H. A., Kaiser, N., & Peacock, J. A. 1994, ApJ, 426, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Ganeshaiah Veena, P., Cautun, M., Tempel, E., van de Weygaert, R., & Frenk, C. S. 2019, MNRAS, 487, 1607 [NASA ADS] [CrossRef] [Google Scholar]
- Gil-Marín, H., Noreña, J., Verde, L., et al. 2015, MNRAS, 451, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Gil-Marín, H., Percival, W. J., Verde, L., et al. 2017, MNRAS, 465, 1757 [NASA ADS] [CrossRef] [Google Scholar]
- Gramann, M. 1990, MNRAS, 244, 214 [NASA ADS] [Google Scholar]
- Jõeveer, M., & Einasto, J. 1978, in Large Scale Structures in the Universe, eds. M. S. Longair, & J. Einasto, IAU Symp., 79, 241 [NASA ADS] [Google Scholar]
- Jõeveer, M., Einasto, J., & Tago, E. 1977, Estonian Acad. Sci. Preprint, 3 [Google Scholar]
- Jõeveer, M., Einasto, J., & Tago, E. 1978, MNRAS, 185, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, N. 1984, ApJ, 284, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, N. 1987, MNRAS, 227, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Karachentsev, I. D., Sharina, M. E., Makarov, D. I., et al. 2002, A&A, 389, 812 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kim, J., Park, C., L’Huillier, B., & Hong, S. E. 2015, J. Korean Astron. Soc., 48, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Klypin, A., & Shandarin, S. F. 1993, ApJ, 413, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Kofman, L., Pogosian, D., & Shandarin, S. 1990, MNRAS, 242, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Liivamägi, L. J., Tempel, E., & Saar, E. 2012, A&A, 539, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindner, U., Einasto, J., Einasto, M., et al. 1995, A&A, 301, 329 [NASA ADS] [Google Scholar]
- Lindner, U., Einasto, M., Einasto, J., et al. 1996, A&A, 314, 1 [NASA ADS] [Google Scholar]
- Martínez, V. J., & Saar, E. 2002, Statistics of the Galaxy Distribution (Boca Raton: Chapman & Hall/CRC) [Google Scholar]
- McConnachie, A. W. 2012, AJ, 144, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Melott, A. L., Einasto, J., Saar, E., et al. 1983, Phys. Rev. Lett., 51, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Norberg, P., Baugh, C. M., Hawkins, E., et al. 2001, MNRAS, 328, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E. 1973, ApJ, 185, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E. 1982a, ApJ, 258, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E. 1982b, ApJ, 263, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E. 2001, ApJ, 557, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E., & Hauser, M. G. 1974, ApJS, 28, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E., & Groth, E. J. 1975, ApJ, 196, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Percival, W. J., Baugh, C. M., Bland-Hawthorn, J., et al. 2001, MNRAS, 327, 1297 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration VI. 2018, A&A, submitted [arXiv:1807.06209] [Google Scholar]
- Pollina, G., Hamaus, N., Paech, K., et al. 2019, MNRAS, 487, 2836 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., & Schechter, P. 1974, ApJ, 187, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Rieder, S., van de Weygaert, R., Cautun, M., Beygu, B., & Portegies Zwart, S. 2013, MNRAS, 435, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Schechter, P. 1976, ApJ, 203, 297 [Google Scholar]
- Schuecker, P., Böhringer, H., Guzzo, L., et al. 2001, A&A, 368, 86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seldner, M., Siebers, B., Groth, E. J., & Peebles, P. J. E. 1977, AJ, 82, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Sheth, R. K., & van de Weygaert, R. 2004, MNRAS, 350, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Shi, F., Yang, X., Wang, H., et al. 2016, ApJ, 833, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Shi, F., Yang, X., Wang, H., et al. 2018, ApJ, 861, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Soneira, R. M., & Peebles, P. J. E. 1978, AJ, 83, 845 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Stauffer, D. 1979, Phys. Rep., 54, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Szalay, A. S. 1988, ApJ, 333, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Tarenghi, M., Tifft, W. G., Chincarini, G., Rood, H. J., & Thompson, L. A. 1978, in Large Scale Structures in the Universe, eds. M. S. Longair, & J. Einasto, IAU Symp., 79, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Tegmark, M., Strauss, M. A., Blanton, M. R., et al. 2004a, Phys. Rev. D, 69, 103501 [CrossRef] [Google Scholar]
- Tegmark, M., Blanton, M. R., Strauss, M. A., et al. 2004b, ApJ, 606, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Tempel, E., Einasto, J., Einasto, M., Saar, E., & Tago, E. 2009, A&A, 495, 37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tempel, E., Tamm, A., Gramann, M., et al. 2014, A&A, 566, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tifft, W. G., & Gregory, S. A. 1978, in Large Scale Structures in the Universe, eds. M. S. Longair, & J. Einasto, IAU Symp., 79, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Tinker, J. L., & Conroy, C. 2009, ApJ, 691, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Tinker, J. L., Weinberg, D. H., & Warren, M. S. 2006, ApJ, 647, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Tully, R. B., & Fisher, J. R. 1978, in Large Scale Structures in the Universe, eds. M. S. Longair, & J. Einasto, IAU Symp., 79, 214 [NASA ADS] [Google Scholar]
- van de Weygaert, R., Shandarin, S., Saar, E., & Einasto, J. 2016, in The Zeldovich Universe: Genesis and Growth of the CosmicWeb, IAU Symp., 308 [Google Scholar]
- Walsh, K., & Tinker, J. 2019, MNRAS, 488, 470 [NASA ADS] [CrossRef] [Google Scholar]
- Wechsler, R. H., & Tinker, J. L. 2018, ARA&A, 56, 435 [NASA ADS] [CrossRef] [Google Scholar]
- White, S. D. M., & Rees, M. J. 1978, MNRAS, 183, 341 [NASA ADS] [CrossRef] [Google Scholar]
- White, S. D. M., Frenk, C. S., Davis, M., & Efstathiou, G. 1987, ApJ, 313, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Zehavi, I., Zheng, Z., Weinberg, D. H., et al. 2011, ApJ, 736, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Zeldovich, Y. B. 1970, A&A, 5, 84 [NASA ADS] [Google Scholar]
- Zeldovich, Y. B. 1978, in Large Scale Structures in the Universe, eds. M. S. Longair, & J. Einasto, IAU Symp., 79, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Zeldovich, Y. B., Einasto, J., & Shandarin, S. F. 1982, Nature, 300, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Zubeldia, I., & Challinor, A. 2019, MNRAS, 489, 401 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Percolation functions for unbiased L512.00 samples, biased L512.10 samples, and SDSS.21 and HR4.12 samples, from top to bottom panels, respectively. Left panels are for filling factor functions, middle panels for cluster length functions, right panels for number functions. Number functions are calculated with small system exclusion limit Nlim = 50 (L512.10 and SDSS.21 samples); and with Nlim = 500 (L512.00 and HR4.12 samples). Functions for clusters are plotted with solid lines, and for voids with dashed lines. |
| In the text | |
 |
Fig. 2. Left: power spectra of particle-density-limited L512 model spectra. The blue solid line with error ticks is for the spectrum of the model with all matter, L512.00 (particle-density limit δ0 = 0). For comparison, dashed black line shows the linear power spectrum. Thin coloured lines are for power spectra, calculated for biased L512.i models according to Table 1. Open and filled symbols with error bars are power spectra of flux-limited X-ray-selected clusters of galaxies, samples L050 and L120, according to Schuecker et al. (2001). Right: relative bias functions for power spectra of density-limited L512 models. |
| In the text | |
 |
Fig. 3. Left: probability function G(δ) for the L512.5 model with a particle-density limit δ0 = 5 and scatter of the particle-density limit σ = 0, 1, 2. Right: bias parameters b as functions of the particle-density limit, δ0, found from power spectra of biased models for particle-density limits, δ0. Coloured filled circles show calculated bias parameters from spectra for three values of the scatter of the particle-density limit, and coloured curves show bias functions according to Eq. (3). |
| In the text | |
 |
Fig. 4. Percolation functions using fuzzy particle-density limits of the model L512.5 with δ0 = 5. Left: filling factor functions. Right: length functions of largest superclusters. Solid lines are for functions with fuzziness dispersion σ = 0, i.e. sharp particle-density limit, dashed lines are for dispersion σ = 1, and dotted lines for σ = 2. |
| In the text | |
 |
Fig. 5. Filling-factor functions of largest clusters and voids, ℱ(Dt) = Vmax/V0, as functions of the threshold density, Dt. Left panels: luminosity-limited SDSS samples. Middle panels: particle-density limited (biased) L512 model samples. Right panels: HR4 model samples. Left panels from top to bottom are for luminosity limits of Mr − 5logh = −18.0, − 19.0, − 20, 0, − 21.0; middle panels from top to bottom are for samples with particle-density limits of δ0 = 2, 5, 10, 20; right panels from top to bottom are for halo- mass-limited samples HR4.11, HR4.12, HR4.123, and HR4.13. Functions for clusters are plotted with solid lines, and those for voids with dashed lines; colours mark different smoothing lengths. |
| In the text | |
 |
Fig. 6. Length functions of largest clusters, L(Dt) = Lmax in h−1 Mpc. Panels and lines are as in Fig. 5. |
| In the text | |
 |
Fig. 7. Number of clusters and voids, 𝒩(Dt). Number functions are calculated with small system exclusion limit Nlim = 50 (L512 and SDSS samples); and with Nlim = 500 (HR4 samples). Lines are as in Fig. 5. |
| In the text | |
 |
Fig. 8. Filling factor test function of clusters FC(δ0) and voids FV(δ0). Solid lines show test functions of L512 models for four smoothing scales, RB = 1, 2, 4, 8 h−1 Mpc. Left panels are for cluster filling factors, right panels for void filling factors. Upper panels: filling factors of SDSS samples, while lower panels show filling factors of HR4 samples, both according to the symbols in the respective keys. |
| In the text | |
 |
Fig. 9. Left panels: cluster percolation threshold test, right panels: cluster length test for high-luminosity (mass) samples. Upper panels are for SDSS samples, lower panels for HR4 samples. Solid lines show cluster length test functions of L512 models for various smoothing scales. Coloured symbols show SDSS samples of various luminosity and HR4 samples of various halo mass limits. |
| In the text | |
 |
Fig. 10. Particle-density limit parameter δ0 for SDSS-luminosity-limited samples (left panel), and for halo-mass-limited HR4 model samples (right panel). Absolute magnitude and halo mass limits are used as arguments. Red circles are based on filling factor test for clusters and voids, blue boxes on length function tests, and green diamonds on length function shape estimates, as given in Table 4. |
| In the text | |
 |
Fig. 11. Percolation function tests to check the influence of redshift space distortions. Left panel: filling factor functions and the right panel length functions of HR4.11 models. Solid lines are calculated for real space, dashed lines for redshift space. |
| In the text | |
 |
Fig. 12. Left panel: bias parameter b values as a function of the absolute magnitude limit Mr − 5logh of the sample. Red circles show bias parameter values as found from biased L512 spectra using the filling factor test, bF, blue boxes indicate bias parameters as found from spectra using the length function test, bL, and green diamonds show bias parameters using the length function general shape test bLs. Right panel: bias function found in this paper compared with bias functions found in other studies. Bias parameter values for SDSS galaxies of various absolute magnitude limits found in this paper are marked by red circles with error bars. Bias parameter values of SDSS galaxies found by Shi et al. (2018) and applying normalising factor b° = 1.4 are marked by black squares with error bars; that for BOSS galaxies according to Gil-Marín et al. (2017) is shown by a blue diamond, and that for X-ray clusters of galaxies by Schuecker et al. (2001) by a green triangle. Dashed line shows the fit by Norberg et al. (2001), applying bias normalising factor b° = 1.85. Black, blue, and red lines show fits by Norberg et al. (2001), Tegmark et al. (2004b), and Zehavi et al. (2011), respectively. |
| In the text | |
 |
Fig. 13. Power spectra of particle-density-limited L512 model spectra. The power spectrum of the sample L512.10 is shown by the bold red line. Filled symbols show the power spectrum of SDSS galaxies by Tegmark et al. (2004b). |
| In the text | |
 |
Fig. 14. Upper panels: central sections of the high-resolution non-smoothed density fields of identical 256 × 256 × 1 h−1 Mpc slices of DM models L512.00 and L512.10, found for particle-density limits δ0 = 0, 10. Lower panel: slice through the zoomed density field of the SDSS.21 galaxy sample, smoothed with 1 h−1 Mpc kernel. The size of the sample in the vertical direction is about 240 h−1 Mpc. This figure illustrates the effect of zero-density regions in simulated and real density fields of galaxies. Densities are expressed in logarithmic scale in the interval 0.005–15 in mean density units. The colour code is identical in all panels. |
| In the text | |
 |
Fig. 15. Cumulative distributions of densities of high-resolution density fields of L512, SDSS, and HR4 samples (left, middle, and right panels, respectively). For the L512 model, dashed black line shows the distribution for the full sample with all particles, L512.00, and coloured solid lines for biased model samples L512.5, L512.10, L512.20, and L512.50. Similar coloured lines are used for SDSS, and HR4 samples of various magnitude (halo mass) limits. |
| In the text | |
 |
Fig. 16. Cross sections of length 300 h−1 Mpc of the density contrast δ(x) = D(x)−1 of the model L512 along the x-spatial coordinate at the same z-coordinate as shown in Fig. 14. The blue line shows the density field of the model L512.00 at a redshift of z = 30. The black line shows the density field of the full model L512.00 at the present epoch, and the red line shows the same but for the biased model L512.10. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} p(x)\mathrm{d}x = \frac{1}{\sigma \sqrt{2\pi }} \exp \left[-\frac{(x - x_0)^2}{2\sigma ^2}\right]\mathrm{d}x, \end{aligned} $$](/articles/aa/full_html/2019/10/aa36054-19/aa36054-19-eq8.gif)