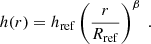| Issue |
A&A
Volume 627, July 2019
|
|
|---|---|---|
| Article Number | L10 | |
| Number of page(s) | 6 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/201935169 | |
| Published online | 16 July 2019 | |
Letter to the Editor
Polarization reversal of scattered thermal dust emission in protoplanetary disks at submillimetre wavelengths
Institut für Theoretische Physik und Astrophysik, Christian-Albrechts-Universität zu Kiel, Leibnizstr. 15, 24118 Kiel, Germany
e-mail: rbrunngraeber@astrophysik.uni-kiel.de
Received:
30
January
2019
Accepted:
5
July
2019
Investigation of the polarized light of protoplanetary disks is key for constraining dust properties, disk morphology, and embedded magnetic fields. However, different polarization mechanisms and the diversity of dust grain shapes and compositions lead to ambiguities in the polarization pattern. The so-called “self-scattering” of thermal, re-emitted radiation in the infrared and millimetre and submillimetre wavelengths is discussed as a major polarization mechanism. If the net flux of the radiation field is in the radial direction, it is commonly assumed that the polarization pattern produced by scattering in a protoplanetary disk shows concentric rings for disks seen in face-on orientation. We show that a change of 90° of the polarization vector orientation may occur and mimic the typical pattern of dichroic emission of dust grains aligned by a toroidal magnetic field in disks seen close to face-on. Furthermore, this effect of polarization reversal is a fast-changing function of wavelength and grain size, and is thus a powerful tool to constrain grain composition and size distribution present in protoplanetary disks. In addition, the effect may also provide unique constraints for the disk inclination, especially if the disk is seen close to face-on.
Key words: radiative transfer / protoplanetary disks / polarization / radiation mechanisms: thermal / scattering
© ESO 2019
1. Introduction
Polarized dust emission of protoplanetary disks and molecular clouds in the millimetre (mm) and submillimetre (submm) wavelength regime was long believed to originate exclusively from dichroic emission and absorption of non-spherical dust grains that are at least partially aligned by a magnetic field. However, dust growth in protoplanetary disks leads to particles of micrometre (μm) to mm size, and hence to optically thick disks at mm and submm wavelengths (e.g. Wolf et al. 2008). The re-emitted thermal radiation of the dust gets scattered by these large grains and therefore polarized, a process that is commonly referred to as self-scattering (Kataoka et al. 2015). This scattering is considered to give rise to the observed polarization of selected protoplanetary disks (e.g. HL Tau; Stephens et al. 2014; Yang et al. 2016a). The scattering of thermal radiation produces polarization vectors oriented perpendicular to the dominating direction of the anisotropic local radiation field, that is, it is expected to show concentric rings for face-on protoplanetary disks in the case of the Rayleigh limit (Yang et al. 2016a,b). Furthermore, Yang et al. (2016a, 2017) investigated several properties of polarized radiation resulting from scattering in the mm and submm wavelength range; for example, the near-far-side asymmetry for moderately inclined disks. These studies were performed considering mostly single grain sizes and analytical temperature distributions, and are limited to special cases concerning dust composition and disk geometry that might not reflect the true nature of protoplanetary disks. The consideration of self-consistently calculated temperatures, grain size distributions, multiple scattering, multi-wavelength effects, and the exploration of a broad disk and dust parameter space are only possible with the full extent of Monte Carlo radiative transfer simulations and have seldom been performed to date (e.g. Kataoka et al. 2016; Yang et al. 2017). However, a large number of recently published observations of polarized radiation rely on the results of these early, limited studies and try to explain the observed patterns with mm and submm scattering (Ohashi et al. 2018; Lee et al. 2018; Hull et al. 2018; Bacciotti et al. 2018).
In this Letter, we present the effect of a polarization reversal by 90° which is the natural outcome of the anisotropic behaviour of the scattering function in the case of Mie scattering (Daniel 1980; Fischer et al. 1994). This effect may mimic the polarization pattern of aligned dust grains in a toroidal magnetic field for disks seen close to face-on and may thus completely change the interpretation of the observations. Furthermore, considering the full scattering properties of the dust may provide a unique and powerful tool to constrain several important parameters for dust and disk evolution, such as the spatial distribution of grain size and composition.
In Sect. 2.1, the general effect of the polarization reversal is described. Subsequently, the influence of the observing wavelength and grain size (Sect. 2.2), grain size distribution (Sect. 2.3), grain composition and porosity (Sect. 2.4), and disk inclination (Sect. 2.5) are investigated. We conclude our findings in Sect. 3.
This study is performed with version 4.02.01 of the versatile, publicly available, Monte Carlo 3D radiative transfer code POLARIS 1 (Reissl et al. 2016).
2. Reversal of the polarization orientation due to anisotropic scattering
2.1. General description of the effect
The polarization state of light scattered by single dust grains depends on wavelength, grain size and shape, chemical composition, and geometrical substructure. In a smooth, undisturbed protoplanetary disk observed at submm to mm wavelengths the radiation field is dominated by the radial component, that is, the flux density of the thermal re-emission is decreasing monotonously from inside out. In the simplest case, a protoplanetary disk is seen face-on and the scattered intensity is dominated by single scattering. In this case, the typical disk flaring results in scattering angles close to 90° for a major fraction of the observed radiation. Under these assumptions it is possible to predict the polarization pattern of a protoplanetary disk directly by the analysis of the Müller matrix 𝒮 of the dust. In this case, the degree and orientation of linear polarization are defined by
The scattering plane is defined by the radiation source, the point of scattering, and the location of the observer. If p > 0, the polarization vector of the scattered light is perpendicular to the scattering plane while it is parallel for p < 0. Thus, a 90° flip of the polarization vector (so-called polarization reversal) is expected to occur once p changes sign.
The upper row of Fig. 1 shows the maximum degree of polarization p as a function of the scattering angle θ for astronomical silicate (refractive indices from Draine & Lee 1984; Laor & Draine 1993; Weingartner & Draine 2001) together with the resulting intensity map and superimposed polarization vectors of a typical density and temperature distribution of a protoplanetary disk (see Appendix A for details) in the case of Rayleigh scattering, that is, where the grain radius s is much smaller than the observing wavelength λ and thus the size parameter
 |
Fig. 1. Left: maximum degree of polarization p = −𝒮12/𝒮11 for single scattering as a function of the scattering angle θ for astronomical silicate (astrosil). The incident light is unpolarized. The dashed vertical and horizontal lines indicate θ = 90° and p = 0, respectively. The symbols on the left indicate the orientation of the polarization vector after scattering, that is, perpendicular (p > 0) and parallel (p < 0) to the scattering plane. Right: intensity map of a face-on protoplanetary disk model with superimposed polarization vectors, calculated with the radiative transfer code POLARIS for the case of Rayleigh scattering, that is, x = 0.3 (top) and for the case of x = 1.9 (bottom) where a 90° change of the polarization vector orientation occurs. These maps include direct re-emission and scattered light. The length of the polarization vectors are scaled to the maximum polarization degree present in each figure. |
As expected for Rayleigh scattering, the polarization vectors are aligned in concentric rings and are thus oriented perpendicular to the scattering plane. This is the standard case discussed in the literature. Kataoka et al. (2015) showed that polarization vectors may also have radially outward directed orientations for the Rayleigh regime if the local radiation field is dominated by its azimuthal component (see their Fig. 7). We find that this case does not occur with the density distribution used here as the resulting intensity distribution has no steep radial gradients except for the regions close the inner rim of the disk which is not spatially resolved in this study. This finding was also confirmed by Yang et al. (2016a, their Fig. 2) who found polarization vectors which are exclusively aligned in concentric rings for face-on disks.
However, for an increased size parameter, for example in the Mie regime, the scattering function is significantly more complex and the resulting polarization degree p is no longer symmetric with respect to forward versus backward scattering. For size parameters x ≳ 1, p shows a wavy pattern with multiple minima and maxima for different scattering angles. This results not only in different polarization degrees for the different viewing angles, but the quantity p may even become negative which results in a polarization reversal. This effect is illustrated in the lower row of Fig. 1 for x = 1.9. While the polarization reversal was found in previous studies (e.g. Daniel 1980; Fischer et al. 1994; Kirchschlager & Wolf 2014), it was not discussed in detail in terms of mm or submm scattering except for a short paragraph in Yang et al. (2016a).
As the Müller matrix elements depend on various quantities, such as grain size, wavelength, chemical composition, and grain shape, we emphasise that the effect of polarization reversal may be a common feature and may not be neglected during the analysis of polarization observations of protoplanetary disks. In the following sections, we briefly discuss the occurrence of polarization reversal as a function of selected parameters.
2.2. Grain size and observing wavelength
Due to the wavelength dependency of the optical properties, the polarization degree p is a function of grain size s and wavelength λ individually, and of the size parameter x. We present the polarization degree for selected grain sizes and wavelengths to emphasise the strong and fast variation of 𝒮12/𝒮11 with variation of these parameters. The polarization fraction for scattering angles of 80, 90 and 100° is shown for s = 50 and 100 μm as a function of wavelength in Fig. 2. In the wavelength range targeted by the far-infrared and mm/submm polarimeters SOFIA/HAWC+ and ALMA between 100 μm and 1 mm, the sign of 𝒮12/𝒮11 changes several times. Although SOFIA/HAWC+ operates at the necessary wavelength regime to trace the polarization reversal for 100 μm grains, it does not, unlike ALMA, spatially resolve protoplanetary disks.
 |
Fig. 2. Left: maximum degree of polarization p for silicate grains of size s = 50 μm as a function of wavelength for different scattering angles θ around 90°. The orange and green rectangles indicate the bands A, C, D, and E of SOFIA/HAWC+, and 10, 9, 8, and 7 of ALMA, respectively. Right: same as left but for grain size s = 100 μm. |
2.3. Grain size distribution
For a grain size distribution the resulting signed polarization degree for single scattering p can no longer be calculated by Eq. (1). If multiple grain sizes are present in the disk, the scattering properties must be averaged and weighted by the size distribution n(s) and the different scattering cross sections Csca(s) of the grains. The signed polarization degree p is thus given by
The averaging process over all grain sizes for a given function f(s) is defined as
Considering a grain size distribution rather than single grain sizes will reduce the previously discussed effect of the rapidly changing polarization degree p due to the averaging of the Müller matrix elements. The polarization reversal corresponds to a certain size parameter range, and therefore observations at different wavelengths must be performed for different grain sizes. Commonly used size distributions for the upper layers of protoplanetary disks span grain radii from nanometre (nm) scale to hundreds of nm or at most some μm (Mathis et al. 1977; Glauser et al. 2008; Brunngräber et al. 2016; Keppler et al. 2018; Casassus et al. 2018). For these grain size distributions, the scattering lies in the Rayleigh regime for wavelengths λ ⪆ 10 μm. However, with high-resolution polarimeters working in the visible and near-infrared wavelength region such as VLT/SPHERE, the polarization reversal might be detectable for scattered stellar light (see Fig. 6). Including even larger grains may still result in a polarization reversal for narrow wavelength ranges in the mm regime. In Fig. 3, the polarized fraction p and the intensity map of a face-on disk at λ = 1.6 mm is shown for grains ranging from 10 nm to 1 mm with a power law grain size distribution n(s) ∝ s−2.5ds.
 |
Fig. 3. Left: maximum degree of polarization p (cf. Eq. (3)) for silicate grains with sizes between 10 nm and 1 mm and a size distribution of n(s) ∝ s−2.5ds as a function of scattering angle θ at a wavelength of λ = 1.6 mm. Right: corresponding intensity map of a face-on disk with superimposed polarization vectors. The length of the polarization vectors are scaled to the maximum polarization degree present in the figure. |
2.4. Grain composition and porosity
The most abundant dust grain materials present in the ISM and in protoplanetary disks are silicates and graphite, possibly covered with icy mantles of H2O and other volatile species. Up to this point, all calculations were done assuming pure astronomical silicate. In this section, we additionally consider pure graphite (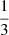 parallel and
parallel and  perpendicular, see Draine & Malhotra 1993; refractive indices from Draine & Lee 1984; Laor & Draine 1993), a mixture of silicates (62.5%) and graphite (37.5%) which is a very common assumption for the dust composition in protoplanetary disks (Draine & Lee 1984; Williams & Cieza 2011; Varga et al. 2018; Brunngräber & Wolf 2018), and pure water ice grains (refractive indices from Warren & Brandt 2008). For pure graphite grains we find that the polarization reversal stops at smaller wavelengths compared to silicates, that is, the Rayleigh regime extends to slightly larger size parameters x. For grain radii of 100 μm, the largest wavelengths where the polarization reversal can be observed is about 450 μm for graphite and 650 μm for silicates. Furthermore, the overall course of the polarization fraction p in the case of graphite is smoother, with shallower gradients. The polarization fraction of a mixture of silicates and graphites shows an intermediate behaviour and changes less rapidly with wavelength and scattering angle if compared to the case of pure silicate; see left panel of Fig. 4.
perpendicular, see Draine & Malhotra 1993; refractive indices from Draine & Lee 1984; Laor & Draine 1993), a mixture of silicates (62.5%) and graphite (37.5%) which is a very common assumption for the dust composition in protoplanetary disks (Draine & Lee 1984; Williams & Cieza 2011; Varga et al. 2018; Brunngräber & Wolf 2018), and pure water ice grains (refractive indices from Warren & Brandt 2008). For pure graphite grains we find that the polarization reversal stops at smaller wavelengths compared to silicates, that is, the Rayleigh regime extends to slightly larger size parameters x. For grain radii of 100 μm, the largest wavelengths where the polarization reversal can be observed is about 450 μm for graphite and 650 μm for silicates. Furthermore, the overall course of the polarization fraction p in the case of graphite is smoother, with shallower gradients. The polarization fraction of a mixture of silicates and graphites shows an intermediate behaviour and changes less rapidly with wavelength and scattering angle if compared to the case of pure silicate; see left panel of Fig. 4.
 |
Fig. 4. Maximum degree of polarization p of different grain compositions (left) and for silicate grains with different porosities (right). |
Another important parameter determining the optical properties of dust grains in protoplanetary disks is porosity, resulting from various grain growth mechanisms (e.g. Blum et al. 2000; Ormel et al. 2008). We consider spherical, porous silicate dust grains similar to those used by Kirchschlager & Wolf (2013, 2014). The optical properties were calculated with DDSCAT 2 (Draine & Flatau 1994). The polarization fraction p for grains with three different porosities can be seen in the right panel of Fig. 4. Although material and size remain unchanged, vacuum inclusions inside the grain result in a very different scattering behaviour for both different scattering angles and wavelengths.
2.5. Disk inclination
If the disk is slightly inclined, the dominating scattering angle will shift to a smaller (larger) value than 90° for the near-side (far-side) of the disk. Thus, asymmetric scattering will occur. This can be seen in Fig. 5 for the wavelengths λ = 154 μm (central wavelength of the SOFIA/HAWC+ D band), λ = 300 and 322 μm (ALMA band 10), and λ = 447 μm (ALMA band 9). All disks are inclined by i = 15° from face-on. In the SOFIA/HAWC+ D band image (middle left), the near-side of the disk (lower half of the intensity maps) displays a larger polarization degree (as indicated by the length of the polarization vectors) than the far-side (upper half). This is due to the fact that p = −𝒮12/𝒮11 is larger for scattering angles around θ = 90 ° −i = 75° than for scattering angles around θ = 90 ° +i = 105°. If the disk were seen face-on, the polarization vectors would point radially outwards as p is negative for θ = 90°.
 |
Fig. 5. Top: maximum degree of polarization p of different wavelengths corresponding to the SOFIA/HAWC+ band D (λ = 154 μm), and the ALMA bands 10 (λ = 300 μm and λ = 322 μm) and 9 (λ = 447 μm). Middle and bottom: corresponding intensity maps with superimposed polarization vectors. The inclination for all four sub-plots is i = 15°. The lengths of the polarization vectors are scaled to the maximum polarization degree present in each figure. We note that the resolution of SOFIA/HAWC+ is not sufficient to spatially resolve the polarization pattern of protoplanetary disks. |
The images for the wavelengths λ = 300 and 447 μm (ALMA bands 10 and 9, respectively) show the polarization reversal and an additional asymmetry in the polarization degree. For λ = 300 μm, the far-side shows a higher degree of polarization and for λ = 447 μm, the near-side is slightly more polarized.
A change of sign of the polarization fraction p close to θ = 90° will result in different polarization patterns for the far- and near-side. This is clearly visible for the second wavelength of the ALMA band 10 (λ = 322 μm; see lower left panel of Fig. 5). The polarization vectors at the far-side show the polarization reversal while the near-side shows a pattern of concentric rings because p becomes negative for scattering angles larger than ≈90°. The same effect but for a larger disk inclination of i = 50° is shown in Fig. 6. This disk is composed of astronomical silicate and graphite with grain sizes from 10 nm to 1 μm for an observing wavelength of λ = 1.25 μm (J band).
 |
Fig. 6. Polarization degree (left) and intensity map for an inclined disk with an inclination of i = 50° (right) composed of a mixture of astronomical silicate and graphite of sizes between 10 nm and 1 μm at a wavelength of λ = 1.25 μm (J band). The dotted, vertical lines in the left panel represent the predominant scattering angles at the near- and far-side of the disk, i.e. θ = 90 ° ±i. The length of the polarization vectors are scaled to the maximum polarization degree present in the figure. |
Thus, with precise measurements of the polarized light in the continuum, one is potentially able to stringently constrain the disk inclination even if it is as small as 15°.
3. Conclusion
We investigated the influence of the anisotropic scattering function due to Mie scattering on the observable polarization pattern of protoplanetary disks resulting from scattered thermal dust emission in the mm and submm wavelength regime. If the signed polarization degree p becomes negative, the resulting polarization pattern undergoes a change of 90° in orientation compared to the commonly assumed pattern due to scattering. This reversal is highly dependent on several parameters such as observing wavelength, grain size and composition, and disk inclination. Therefore, this effect and the anisotropic character of the scattering function in general may serve as a powerful tool to enable observers to set strict constraints on these parameters. This requires multi-wavelength polarization observations with high-enough spatial and spectral resolution between roughly 100 and 1000 μm. At the moment, only SOFIA is able to perform polarization measurements in the shorter wavelengths but with a restricted spatial resolution. For wavelengths larger than 350 μm, ALMA is the perfect instrument to trace this polarization reversal.
Acknowledgments
This research was funded through the DFG grant WO 857/18-1. RB thanks R. Brauer for providing general support in the application of POLARIS.
References
- Andrews, S. M., Wilner, D. J., Espaillat, C., et al. 2011, ApJ, 732, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Bacciotti, F., Girart, J. M., Padovani, M., et al. 2018, ApJ, 865, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Blum, J., Wurm, G., Kempf, S., et al. 2000, Phys. Rev. Lett., 85, 2426 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Brunngräber, R., & Wolf, S. 2018, A&A, 611, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brunngräber, R., Wolf, S., Ratzka, T., & Ober, F. 2016, A&A, 585, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casassus, S., Avenhaus, H., Pérez, S., et al. 2018, MNRAS, 477, 5104 [NASA ADS] [CrossRef] [Google Scholar]
- Daniel, J.-Y. 1980, A&A, 87, 204 [NASA ADS] [Google Scholar]
- Draine, B. T., & Flatau, P. J. 1994, J. Opt. Soc. Am. A, 11, 1491 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Lee, H. M. 1984, ApJ, 285, 89 [Google Scholar]
- Draine, B. T., & Malhotra, S. 1993, ApJ, 414, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, O., Henning, T., & Yorke, H. W. 1994, A&A, 284, 187 [NASA ADS] [Google Scholar]
- Glauser, A. M., Ménard, F., Pinte, C., et al. 2008, A&A, 485, 531 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartmann, L., Calvet, N., Gullbring, E., & D’Alessio, P. 1998, ApJ, 495, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Hull, C. L. H., Yang, H., Li, Z.-Y., et al. 2018, ApJ, 860, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Kataoka, A., Muto, T., Momose, M., et al. 2015, ApJ, 809, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Kataoka, A., Muto, T., Momose, M., Tsukagoshi, T., & Dullemond, C. P. 2016, ApJ, 820, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Keppler, M., Benisty, M., Müller, A., et al. 2018, A&A, 617, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kirchschlager, F., & Wolf, S. 2013, A&A, 552, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kirchschlager, F., & Wolf, S. 2014, A&A, 568, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laor, A., & Draine, B. T. 1993, ApJ, 402, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, C.-F., Li, Z.-Y., Ching, T.-C., Lai, S.-P., & Yang, H. 2018, ApJ, 854, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D., & Pringle, J. E. 1974, MNRAS, 168, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Ohashi, S., Kataoka, A., Nagai, H., et al. 2018, ApJ, 864, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W., Cuzzi, J. N., & Tielens, A. G. G. M. 2008, ApJ, 679, 1588 [NASA ADS] [CrossRef] [Google Scholar]
- Reissl, S., Wolf, S., & Brauer, R. 2016, A&A, 593, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stephens, I. W., Looney, L. W., Kwon, W., et al. 2014, Nature, 514, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Varga, J., Ábrahám, P., Chen, L., et al. 2018, A&A, 617, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Warren, S. G., & Brandt, R. E. 2008, J. Geophys. Res. Atmos., 113, D14220 [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, J. P., & Cieza, L. A. 2011, ARA&A, 49, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, S., Schegerer, A., Beuther, H., Padgett, D. L., & Stapelfeldt, K. R. 2008, ApJ, 674, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, H., Li, Z.-Y., Looney, L., & Stephens, I. 2016a, MNRAS, 456, 2794 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, H., Li, Z.-Y., Looney, L. W., et al. 2016b, MNRAS, 460, 4109 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, H., Li, Z.-Y., Looney, L. W., Girart, J. M., & Stephens, I. W. 2017, MNRAS, 472, 373 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Disk set-up
The density distribution of the dust is based on the studies by Lynden-Bell & Pringle (1974), Hartmann et al. (1998), and Andrews et al. (2011) and given by
with the vertical integrated surface density
and the scale height
In Eq. (A.1), r and z are the usual cylindrical coordinates, and ρ0 is the number density at r = Rref and z = 0 au and is scaled to the given total dust mass. The disk parameter values used in this study are compiled in Table A.1.
Disk parameter values.
All Tables
All Figures
 |
Fig. 1. Left: maximum degree of polarization p = −𝒮12/𝒮11 for single scattering as a function of the scattering angle θ for astronomical silicate (astrosil). The incident light is unpolarized. The dashed vertical and horizontal lines indicate θ = 90° and p = 0, respectively. The symbols on the left indicate the orientation of the polarization vector after scattering, that is, perpendicular (p > 0) and parallel (p < 0) to the scattering plane. Right: intensity map of a face-on protoplanetary disk model with superimposed polarization vectors, calculated with the radiative transfer code POLARIS for the case of Rayleigh scattering, that is, x = 0.3 (top) and for the case of x = 1.9 (bottom) where a 90° change of the polarization vector orientation occurs. These maps include direct re-emission and scattered light. The length of the polarization vectors are scaled to the maximum polarization degree present in each figure. |
| In the text | |
 |
Fig. 2. Left: maximum degree of polarization p for silicate grains of size s = 50 μm as a function of wavelength for different scattering angles θ around 90°. The orange and green rectangles indicate the bands A, C, D, and E of SOFIA/HAWC+, and 10, 9, 8, and 7 of ALMA, respectively. Right: same as left but for grain size s = 100 μm. |
| In the text | |
 |
Fig. 3. Left: maximum degree of polarization p (cf. Eq. (3)) for silicate grains with sizes between 10 nm and 1 mm and a size distribution of n(s) ∝ s−2.5ds as a function of scattering angle θ at a wavelength of λ = 1.6 mm. Right: corresponding intensity map of a face-on disk with superimposed polarization vectors. The length of the polarization vectors are scaled to the maximum polarization degree present in the figure. |
| In the text | |
 |
Fig. 4. Maximum degree of polarization p of different grain compositions (left) and for silicate grains with different porosities (right). |
| In the text | |
 |
Fig. 5. Top: maximum degree of polarization p of different wavelengths corresponding to the SOFIA/HAWC+ band D (λ = 154 μm), and the ALMA bands 10 (λ = 300 μm and λ = 322 μm) and 9 (λ = 447 μm). Middle and bottom: corresponding intensity maps with superimposed polarization vectors. The inclination for all four sub-plots is i = 15°. The lengths of the polarization vectors are scaled to the maximum polarization degree present in each figure. We note that the resolution of SOFIA/HAWC+ is not sufficient to spatially resolve the polarization pattern of protoplanetary disks. |
| In the text | |
 |
Fig. 6. Polarization degree (left) and intensity map for an inclined disk with an inclination of i = 50° (right) composed of a mixture of astronomical silicate and graphite of sizes between 10 nm and 1 μm at a wavelength of λ = 1.25 μm (J band). The dotted, vertical lines in the left panel represent the predominant scattering angles at the near- and far-side of the disk, i.e. θ = 90 ° ±i. The length of the polarization vectors are scaled to the maximum polarization degree present in the figure. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




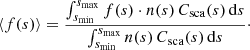
![$$ \begin{aligned} \varrho (r) =\frac{\Sigma (r)}{\sqrt{2\pi }\,h(r)}\!\cdot \exp {\left[-\frac{1}{2}\left(\frac{z}{h(r)}\right)^2\right]} , \end{aligned} $$](/articles/aa/full_html/2019/07/aa35169-19/aa35169-19-eq7.gif)
![$$ \begin{aligned} \Sigma (r) = \sqrt{2\pi }\,\rho _0h_{\mathrm{ref}}\cdot \left(\frac{r}{R_{\mathrm{ref}}}\right)^{-\gamma }\cdot \exp {\left[-\left(\frac{r}{R_{\mathrm{ref}}}\right)^{2-\gamma }\right]} \end{aligned} $$](/articles/aa/full_html/2019/07/aa35169-19/aa35169-19-eq8.gif)