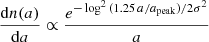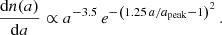| Issue |
A&A
Volume 634, February 2020
|
|
|---|---|---|
| Article Number | L15 | |
| Number of page(s) | 7 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/201937314 | |
| Published online | 21 February 2020 | |
Letter to the Editor
Polarized emission by aligned grains in the Mie regime: Application to protoplanetary disks observed by ALMA
1
Université Paris-Saclay, CNRS, Institut d’astrophysique spatiale, 91405 Orsay, France
e-mail: Vincent.Guillet@ias.u-psud.fr
2
Laboratoire Univers et Particules de Montpellier, Université de Montpellier, CNRS/IN2P3, CC 72, Place Eugène Bataillon, 34095 Montpellier Cedex 5, France
3
Institut de Ciències de l’Espai (ICE, CSIC), Can Magrans s/n, 08193 Cerdanyola del Vallès Catalonia, Spain
4
Institut d’Estudis Espacials de Catalunya (IEEC), 08034 Barcelona Catalonia, Spain
5
Laboratoire AIM, CEA/DSM-CNRS-Université Paris Diderot, IRFU, Astrophysics department, 91191 Gif-sur-Yvette, France
6
Harvard-Smithsonian Center for Astrophysics, Cambridge, MA 02138, USA
7
Max-Planck-Institut fuÌr extraterrestrische Physik, Giessenbachstr. 1, 85748 Garching, Germany
Received:
13
December
2019
Accepted:
22
January
2020
Context. The azimuthal polarization patterns observed in some protoplanetary disks by the Atacama Large Millimetre Array (ALMA) at millimeter wavelengths have raised doubts about whether they are truly produced by dust grains that are aligned with the magnetic field lines. These conclusions were based on the calculations of dust polarized emission in the Rayleigh regime, that is, for grain sizes that are much smaller than the wavelength. However, the grain size in such disks is typically estimated to be in the range of 0.1−1 mm from independent observations.
Aims. We study the dust polarization properties of aligned grains in emission in the Mie regime, that is, when the mean grain size approaches the wavelength.
Methods. By using the T-MATRIX and DustEM codes, we computed the spectral dependence of the polarization fraction in emission for grains in perfect spinning alignment for various grain size distributions. We restricted our study to weakly-elongated oblate and prolate grains of astrosilicate composition that have a mean size ranging from 10 μm to 1 mm.
Results. In the submillimeter and millimeter wavelength range, the polarization by B-field aligned grains becomes negative for grains larger than ∼250 μm, meaning that the polarization vector becomes parallel to the B-field. The transition from the positive to the negative polarization occurs at a wavelength of λ ∼ 1 mm. The regime of negative polarization does not exist for grains that are smaller than ∼100 μm.
Conclusions. When using realistic grain size distributions for disks with grains up to the submillimeter sizes, the polarization direction of thermal emission by aligned grains is shown to be parallel to the direction of the magnetic field over a significant fraction of the wavelengths typically used to observe young protoplanetary disks. This property may explain the peculiar azimuthal orientation of the polarization vectors in some of the disks observed with ALMA and attest to the conserved ability of dust polarized emission to trace the magnetic field in disks.
Key words: polarization / dust / extinction / ISM: magnetic fields / submillimeter: planetary systems
© V. Guillet et al. 2020
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Polarization observations by the Atacama Large Millimetre Array (ALMA) have allowed for the detection and resolution of linearly polarized dust emission at core scales of a few thousands of astronomical units and disk scales at a few tens of astronomical units. Thus, ALMA has revealed intriguing polarization features in the star forming cores, such as magnetized accretion filaments and significantly polarized outflow cavities (Maury et al. 2018; Le Gouellec et al. 2019; Hull et al. 2019). In the frame of the modern theory of grain alignment (Lazarian & Hoang 2007), these observations imply the presence of large grains, thus several tens of microns, that are located in protostellar cores (Valdivia et al. 2019; Galametz et al. 2019). At disks scales, the self-scattering of large grains, ∼100 μm, appears to be the dominant mechanism in a significant fractions of young stellar disks (Kataoka et al. 2015, 2016; Yang et al. 2016, 2017; Girart et al. 2018; Hull et al. 2018; Bacciotti et al. 2018; Dent et al. 2019; Harrison et al. 2019; Sadavoy et al. 2019). However, there are a number of sources in which self-scattering cannot explain the observed polarization properties. ALMA polarization observations of Class I objects, such as HH 111 VLA 1 and [BHB2007] 11, can be interpreted as a combination of poloidal magnetic field morphology, which was produced by infall gas motions, and a toroidal one, which was produced by disk rotation (Lee et al. 2018; Alves et al. 2018). The polarization levels observed for the latter is at least a factor of ∼2 larger than self-scattering predictions. Therefore, a significant effort should be made to revise models of disk polarization in an attempt to satisfactorily match observations of both the dust and magnetic field properties in disks.
Models of dust polarized emission that were designed for the interstellar medium (Draine & Fraisse 2009; Guillet et al. 2018) cannot be used to interpret observations of dust in protoplanetary disks where the grain size is a thousand times larger, typically on the order of a millimeter (Testi et al. 2014). In this article, we modeled the emission of polarized radiation by aligned grains in the Mie regime, that is, when the grain size is on the order of the wavelength, and we compare our predictions with polarization observations in protoplanetary disks.
This Letter is structured as follows: our dust model is presented in Sect. 2. Section 3 compares its predictions with polarization observations in disks. Finally, Sect. 4 provides a summary of our results.
2. Polarized emission by aligned grains in the Mie regime
In this section, we build on the study by Guillet et al. (2018) to present a simple dust model allowing for the calculation of the polarized emission by aligned grains up to 1 mm in size.
2.1. Dust model
We modeled dust grains by oblate (disk-like) and prolate (needle-like) spheroids, which spin around their small axis that is their axis of maximal inertia. For simplicity, we assume that the orientation of their spin axis remains fixed in space in perfect alignment. We note that a is the half-size of the symmetry axis and b is the half-size of the two other axes. The axis ratio b/a is larger than 1 for oblate grains and smaller than 1 for prolate grains.
The material composing the grain is another important ingredient in the calculation of dust emission. We used the so-called astronomical silicates (Draine & Lee 1984), which are characterized by a constant spectral index β = 2 from the far-infrared to the millimeter domain. We restricted our analysis to homogeneous and compact grains. While calculations for composite fluffy aggregates with carbon and ferromagnetic inclusions as well as ice coating are more relevant to disks, they are beyond the scope of this first analysis of Mie polarized emission.
We used the DustEM tool (Compiègne et al. 2011; Guillet et al. 2018) to predict the polarized emission of a size distribution of grains. DustEM consistently computes the equilibrium temperature of each grain size in any radiation field and the spectral dependence of both polarized and unpolarized dust extinction and emission. The grain absorption and scattering cross-sections were computed with the T-MATRIX code, a numerical adaptation of the extended boundary condition method (Waterman 1971) for nonspherical particles in a fixed orientation (Mishchenko 2000). When the grain approaches the Mie regime, the grain cross-sections vary both rapidly and strongly with the wavelength because of interferences between scattered waves (Kruegel 2003). To obtain a smooth spectral dependence of the grain optical polarization properties, calculations were performed for 400 grain sizes between 0.3 μm and 3 mm.
While the total intensity and polarized intensity strongly depend on the intensity of the radiation field heating the grains, its effect is much smaller on the polarization fraction in the submillimeter and millimeter wavelength range. Therefore, as a first step, we used the interstellar standard radiation field (ISRF) scaled with G0 = 100, for which the grain temperature that was computed by DustEM (∼30 K for a 10 μm grain and ∼10 K for a 1 mm grain) is within the range of current observational constraints (Testi et al. 2014).
2.2. Effect of the size distribution with a magnetic field in the plane of the sky
We present the spectral dependence of the polarization fraction for different size distributions. We first consider log-normal size distributions
with σ = 0.1, for different mean size apeak ranging from 10 μm to 1 mm. Such narrow log-normal distributions are well suited for the modeling of single size distributions and allow for the averaging of the physical oscillations of the grain cross-sections happening in the Mie regime (see Sect. 2.1 and Appendix A).
The spectral dependence of the polarization fraction P/I(λ) is presented in the top panel of Fig. 1 for weakly elongated oblate grains (b/a = 1.1). The polarization spectrum for prolate grains of comparable elongation (b/a = 0.9) is very similar and is, for the sake of brevity, hence not shown. For grains that are smaller than 10 μm, the polarization fraction P/I is constant in the submillimeter and millimeter range, which is as expected for the Rayleigh regime (2πa ≪ λ). As the grain size increases, this regime is shifted to longer and longer wavelengths. At shorter wavelengths, the polarization fraction is reduced and even negative for the larger grain sizes. A negative polarization fraction means that the direction of polarization of the thermal emission of the grain is parallel to the direction of alignment, and not perpendicular to it as in the Rayleigh regime. This means that weakly-elongated grains, rather counter-intuitively, emit on average preferentially with a polarization parallel to the minor axis than to the major axis. For apeak ≥ 100 μm, the polarization fraction is negative from the submillimeter up to λmax ≃ 2πapeak and peaks at a wavelength of λpeak ≃ 4apeak before becoming positive again and progressively increasing toward the value that is characteristic for the Rayleigh regime. The larger the grains, the wider and deeper the regime of negative polarization. In Appendix A, we show that this specific property is not actually related to the grain size, but to the lower values of the imaginary part of the dust refractive index, k(λ), in the submillimeter and millimeter wavelength range. The systematic decrease of k(λ) with increasing λ makes the transition from positive to negative polarization unavoidable. We note that this qualitative explanation is only valid for materials with a low value of the imaginary part k of the refractive index. It can therefore not apply to the carbonaceous grains that Yang & Li (2019) propose to alleviate the tension between the grain size inferred from polarization and unpolarized observations in protoplanetary disks. Numerical calculations are needed to attest to whether the Mie polarized emission of such highly-absorbing materials is negative or not. This is part of a more general question regarding the impact of the grain shape, structure, and composition on the Mie negative polarization regime, as we emphasize in Sect. 2.3.
 |
Fig. 1. Polarization fraction in emission for oblate grains (axis ratio b/a = 1.1) that are perfectly aligned in the plane of the sky. Results are presented for log-normal (top) and MRN-like (bottom) size distributions. The grain size corresponding to the peak of the mass distribution is indicated in μm. Negative polarization fractions correspond to a rotation of the polarization vector by 90°. The wavelength of ALMA bands 3, 6, and 7 are indicated with dashed vertical lines. Mean values of the polarization fraction observed for [BHB2007] 11 are overplotted in positive and negative for the log-normal size distributions. |
Power-law size distributions, which include the widely-used Mathis-Rumpl-Nordsieck (MRN) size distribution (Mathis et al. 1977), may be more relevant than log-normal or single-sized grain distributions to model what we can expect from a competition between coagulation and fragmentation (Ormel et al. 2009). We now present our results for MRN-like size distributions, which were completed by exponential decay to insure a smooth upper cut of the size distribution:
The bottom panel of Fig. 1 presents our results for apeak ranging from 10 μm to 1 mm, for weakly elongated oblate grains with b/a = 1.1. The polarization fraction in the submillimeter is now positive regardless of the size distribution. It is dominated by the contribution of small grains, which remain in the positive regime. The negative regime, which only appears for apeak larger than a few hundred of microns, starts at a wavelength that does not vary much with apeak, and it is close to 1 mm. Further calculations, which are not shown here, indicate that the position of this transition wavelength also depends on the index of the power-law and on the value of the radiation field intensity, but only slightly. The spectral dependence of the polarization fraction for prolate grains with b/a = 0.9 is very similar, and hence not shown.
2.3. Effect of grain shape when the magnetic field is inclined
The inclination of the magnetic field is a fundamental geometric ingredient in the modeling of polarized emission by aligned grains in the turbulent interstellar medium (Planck Collaboration XII 2020) and in protoplanetary disks (Yang et al. 2019). While the effect of the inclination of the magnetic field onto the polarization fraction is independent of the wavelength in the Rayleigh regime (Lee & Draine 1985), this is not the case in the Mie regime (Voshchinnikov 1989), which may have some important consequences for the interpretation of polarization observations in inclined disks.
Figure B.1 shows the spectral dependence of the polarization fraction for an inclination angle of 45° for weakly-elongated prolate (b/a = 0.9) and oblate (b/a = 1.1) grains with log-normal and MRN size distributions. For prolate grains with a log-normal size distribution, the γ = 45° case is similar to the γ = 0° case of Fig. 1, with a reduced amplitude. For oblate grains, the negative regime is more irregular and weaker. Due to the important weight of small particles in MRN size distributions, the negative polarization regime disappears in ALMA bands 7 and 6 in the prolate case. It does not exist at all in the oblate case. This distinct behavior of prolate and oblate grains, which does not appear when the magnetic field is in the plane of the sky (Sect. 2.2), is unusual in polarized emission. It points at the importance in the Mie regime of the grain shape and spinning, precessing and nutating dynamics around the alignment direction, and therefore deserves to be investigated further in the future.
3. Applications to ALMA polarization observations of protoplanetary disks
In this section, we compare our results to polarization observations of protoplanetary disks where the polarization patterns cannot be explained by the self-scattering of the dust continuum.
3.1. Azimuthal direction of polarization in protoplanetary disks
The azimuthal direction of the polarization vectors observed in HL tau with ALMA at 3 mm, if interpreted to be caused by aligned grains in the Rayleigh regime, leads to a configuration of the magnetic field that is almost radial, which would be difficult to interpret (Kataoka et al. 2017; Stephens et al. 2017). This anomalous polarization topology, which is not unique to HL Tau, raises doubts about the ability of dust polarization to trace the magnetic field in disks (Stephens et al. 2017; Cox et al. 2018; Sadavoy et al. 2019). Alignment by RATs along the radiation field anisotropy (Tazaki et al. 2017) or by the gas flow (Kataoka et al. 2019) have been invoked, although some of the detailed comparisons with observations remain elusive (Yang et al. 2019).
Negative polarization produced by ≳ 500 μm grains may be a solution to the observed azimuthal polarization topology if we assume an azimuthal magnetic field, which is not unrealistic. This specific property of Mie polarized emission has the advantage of being based on well-established optics and alignment physics with the magnetic field. Any departure from the expected azimuthal distribution would indicate a more complex magnetic field morphology. This is what may happen in the disk around the Class II AS 209 YSO (Mori et al. 2019), where the polarization distribution might not be related to the dust properties or alignment mechanism, but rather to the underlying structure of gas and dust rings to which the magnetic field is coupled. Our model also provides an explanation for the observed variations of the polarization fraction with the wavelength, for example in HL Tau between bands 3 and 7, while a pure Rayleigh polarization regime predicts a flat behavior that is inconsistent with observations (Yang et al. 2019). If this scenario is correct, we expect to observe a flip of the polarization vectors by 90° at longer wavelengths (for λ > 2πapeak) together with high polarization fractions (≳10%), which are characteristic for the polarized emission by aligned grains in the Rayleigh regime (Fig. 1). Still, the lack of azimuthal variation in the polarization fraction observed at λ = 3 mm that Yang et al. (2019) also pointed out has yet to be explained. Negative polarization predicts a severe drop of the polarization fraction with γ (see Sect. 2.3), which may not be compatible with ALMA observations. This needs to be investigated by a detailed model including the spectral dependence of polarization by self-scattering and polarized emission by aligned grains in the Mie regime.
Figure 2 schematically summarizes our results by showing the polarization vectors that, according to our model, should be observed in ALMA bands for grains of 50 μm, 250 μm, and 1 mm, in the case of a protoplanetary disk that is inclined by an angle of 45°. For simplicity and clarity, this figure is based on the case of prolate grains with log-normal size distributions, which appears to be more regular. An azimuthal distribution of the magnetic field in the disk is observed with an inclination angle ranging from γ = 0° along the minor axis to γ = 45° along the major axis of the disk. In the Rayleigh regime (a ≪ λ, top row), the direction of the polarization vector is perpendicular to the magnetic field, which is not exactly along the radial direction (see the discussion in Yang et al. 2019). The polarization fraction is high, independent of the wavelength, and scales as cos2 γ (Draine & Lee 1984). This is contrary to the Mie regime of negative polarization (bottom row) in which polarization vectors are parallel to the magnetic field. The polarization fraction is lower than in the Rayleigh regime; it decreases somewhat faster with γ (Fig. B.1) and increases with increasing wavelength until it peaks (Fig. 1).
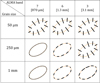 |
Fig. 2. Schematic representation of the polarization vectors from polarized emission by prolate (b/a = 0.9) aligned grains that would be observed in the three ALMA bands for a protoplanetary disk inclined by an angle of 45° with a perfectly azimuthal magnetic field (dashed orange ellipses), for three values of the grain size corresponding to the peak of log-normal size distribution. The length of the vectors scales with the polarization fraction, reproducing the trends predicted by our model. Dotted lines indicate a polarization fraction that is close to zero. The contribution of self-scattering to the observed polarization is ignored. |
Finally, we stress that the low levels of polarization from self-scattering of the dust grains (whose contribution is ignored in the schematic view of Fig. 2), which are widely-observed in protoplanetary disks around 1 mm, could be made possible because the otherwise much stronger polarization due to aligned grains cancels itself out in the Mie regime around this wavelength (see Fig. 1 bottom). The complication induced by the superposition of the polarization signal by aligned grains and by self-scattering is underlined by the studies of Kataoka et al. (2016) and Ohashi et al. (2018) who analyzed the polarization patterns observed by ALMA band 7 at 870 μm in the protoplanetary disk around HD142527. To explain the change from a radial to an azimuthal polarization pattern from the southern to the northern part of the disk, these authors invoke an azimuthal magnetic field that is modulated by the presence of two different size distributions. Small (≲100 μm) aligned grains in the Rayleigh regime would produce a high level (∼10%) of polarized emission in the south, while large (∼100 μm) grains in the north would generate a low level of polarization of a few percentage points by self-scattering. Similar to the contradiction raised by Yang et al. (2019) for HL Tau, this scenario cannot explain why the polarized emission by these large grains, which is much more intense than that produced by self-scattering, is not observed in the northern part. This would impose that such grains are not aligned, which is not compatible with the current view on grain alignment in disks (Hoang & Lazarian 2016). When the impact of the grain size on polarized emission is taken into account, as is the purpose of this Letter, the contradiction however disappears. The large grains responsible for self-scattering contribute very little to the polarization observed at 870 μm because it is around this wavelength that the transition from positive to negative polarization occurs (Fig. 1). Even if the polarized emission by aligned grains is not strictly negligible in that particular region, its direction whether parallel (negative polarization) or perpendicular (positive polarization) to the azimuthal direction generated by self-scattering would not change the observed polarization pattern (azimuthal or radial), but it would only result in a smaller or larger polarization fraction, respectively.
3.2. [BHB2007] 11
The [BHB2007] 11 is a protostellar binary system, which is classified as Class I (Brooke et al. 2007; Hara et al. 2013), with a relatively tenuous but elongated envelope surrounding a circumbinary disk, which is formed by a network of complex filaments (Alves et al. 2019). A molecular outflow appears to be launched at the centrifugal barrier that is just outside of the circumbinary disk (Alves et al. 2017). ALMA multiwavelength polarization observations show polarization within the circumbinary disk (Alves et al. 2018). Remarkably, the polarization directions are observed to be the same in bands 7, 6, and 3. The analysis of the polarization properties (polarization degree and pattern) indicates that this is produced by aligned grains with the magnetic fields instead of self-scattering and radiation fields.
We built beam-matching maps that were obtained in the three bands using the same visibility range as in Alves et al. (2018) but with a smaller robust weighting producing a common synthesized beam of 0.20″×0.15″ with a position angle of −80° for the three bands. We measured the polarization fraction in the three bands along the two main filaments detected by Alves et al. (2019), excluding the southern side, which is close to source B, with much larger values (but at the edge of the filament). The averaged polarization fraction is 7.5±1.3%, 5.7±1.1%, and 4.3±0.6% at 3.1, 1.3, and 0.87 mm, respectively. Figure 1 compares these observations with our model predictions. In the absence of any flip of the polarization vectors between bands, the frequency dependence is incompatible with the regime of positive polarization, but it is in rough agreement with the negative regime of large, almost single-sized, grains (≳500 μm). The presence of large grains in a Class I disk is not surprising since grains of several tens of microns seem to already be present in the youngest protostars (Valdivia et al. 2019). The large values of polarization at the three frequencies suggest that the grain distribution should be closer to the log-normal rather than a modified MRN, and that grains should have more efficient polarization properties than the ones used here. A more detailed modeling in combination with observations at other wavelengths is needed to confirm this scenario, which would challenge the current interpretation of the magnetic morphology in this region (Alves et al. 2018).
4. Summary
The direction of the magnetic field is routinely assumed to be perpendicular to the polarization vectors of dust thermal emission, as expected in the Rayleigh regime of dust emission (x = 2πa ≪ 1). Our work shows that this assumption may be incorrect when the size of the grain approaches the wavelength (Mie regime, x ∼ 1). In the Mie regime, the polarization vectors become parallel to the magnetic field for weakly elongated spheroidal grains of prolate and oblate shapes, with size distributions either peaked or that follow a power-law. This so-called negative polarized emission is present over a large range in wavelength that includes ALMA bands. Polarized emission by aligned grains is predicted to become positive as soon as λ > 2πa. This can be tested with millimeter observations using the Karl G. Jansky Very Large Array.
The polarization direction and wavelength dependence of the negative polarization in the Mie regime may reconcile some observations of protoplanetary disks, such as HL Tau and [BHB2007] 11, with standard dust physics: dust grains are aligned with the magnetic field and their polarized emission still traces the magnetic field, though in an unusual way. The transition from the positive to the negative polarization regime, which for our dust model happens to be around λ = 1 mm for submillimeter and millimeter grains, may also explain why dust polarized emission by aligned grains is often not detected in disks. Further studies are needed to assess how the detailed grain properties, such as the shape, composition, fractal dimension, and porosity, will affect the properties of the negative polarization Mie regime, in particular its amplitude and its dependence with the magnetic field inclination.
Acknowledgments
We thank the anonymous referee for her/his constructive comments, suggesting Fig. 2 and enriching the discussion section. V. Guillet thanks S. Cabrit, A. Kataoka, H. Yang, F. Ménard and G. Bertrang for stimulating discussions. J.M.G. is supported by the Spanish grant AYA2017-84390-C2-R (AEI/FEDER, UE). F.O.A. acknowledges financial support from the Max Planck Society. This work was funded by the European Research Council (ERC) under the European Union Horizon 2020 research and innovation programme (MagneticYSOs project grant agreement N.679937), and supported by the Programme National PCMI of CNRS/INSU. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2013.1.000291.S and #2016.1.01186.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada) and NSC and ASIAA (Taiwan) and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ.
References
- Alves, F. O., Girart, J. M., Caselli, P., et al. 2017, A&A, 603, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alves, F. O., Girart, J. M., Padovani, M., et al. 2018, A&A, 616, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alves, F. O., Caselli, P., Girart, J. M., et al. 2019, Science, 366, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Bacciotti, F., Girart, J. M., Padovani, M., et al. 2018, ApJ, 865, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Brooke, T. Y., Huard, T. L., Bourke, T. L., et al. 2007, ApJ, 655, 364 [NASA ADS] [CrossRef] [Google Scholar]
- Compiègne, M., Verstraete, L., Jones, A., et al. 2011, A&A, 525, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cox, E. G., Harris, R. J., Looney, L. W., et al. 2018, ApJ, 855, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Dent, W. R. F., Pinte, C., Cortes, P. C., et al. 2019, MNRAS, 482, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Fraisse, A. A. 2009, ApJ, 696, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Lee, H. M. 1984, ApJ, 285, 89 [Google Scholar]
- Galametz, M., Maury, A. J., Valdivia, V., et al. 2019, A&A, 632, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Girart, J. M., Fernández-López, M., Li, Z. Y., et al. 2018, ApJ, 856, L27 [CrossRef] [Google Scholar]
- Guillet, V., Fanciullo, L., Verstraete, L., et al. 2018, A&A, 610, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hara, C., Shimajiri, Y., Tsukagoshi, T., et al. 2013, ApJ, 771, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, R. E., Looney, L. W., Stephens, I. W., et al. 2019, ApJ, 877, L2 [CrossRef] [Google Scholar]
- Hoang, T., & Lazarian, A. 2016, ApJ, 831, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Hull, C. L. H., Yang, H., Li, Z.-Y., et al. 2018, ApJ, 860, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Hull, C. L. H., Le Gouellec, V. J. M., Girart, J. M., Tobin, J. J., & Bourke, T. L. 2019, ApJ, accepted [arXiv:1910.07290] [Google Scholar]
- Kataoka, A., Muto, T., Momose, M., et al. 2015, ApJ, 809, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Kataoka, A., Tsukagoshi, T., Momose, M., et al. 2016, ApJ, 831, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Kataoka, A., Tsukagoshi, T., Pohl, A., et al. 2017, ApJ, 844, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Kataoka, A., Okuzumi, S., & Tazaki, R. 2019, ApJ, 874, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Kirchschlager, F., Bertrang, G. H. M., & Flock, M. 2019, MNRAS, 488, 1211 [NASA ADS] [CrossRef] [Google Scholar]
- Kruegel, E. 2003, The Physics of Interstellar Dust, Series in Astronomy and Astrophysics (Bristol, UK: The Institute of Physics) [Google Scholar]
- Lazarian, A., & Hoang, T. 2007, MNRAS, 378, 910 [Google Scholar]
- Le Gouellec, V. J. M., Hull, C. L. H., Maury, A. J., et al. 2019, ApJ, 885, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, H. M., & Draine, B. T. 1985, ApJ, 290, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, C.-F., Li, Z.-Y., Ching, T.-C., Lai, S.-P., & Yang, H. 2018, ApJ, 854, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Maury, A. J., Girart, J. M., Zhang, Q., et al. 2018, MNRAS, 477, 2760 [Google Scholar]
- Mishchenko, M. I. 2000, Appl. Opt., 39, 1026 [NASA ADS] [CrossRef] [Google Scholar]
- Mori, T., Kataoka, A., Ohashi, S., et al. 2019, ApJ, 883, 16 [Google Scholar]
- Ohashi, S., Kataoka, A., Nagai, H., et al. 2018, ApJ, 864, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W., Paszun, D., Dominik, C., & Tielens, A. G. G. M. 2009, A&A, 502, 845 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XII. 2020, A&A, in press https://doi.org/10.1051/0004-6361/201833293 [Google Scholar]
- Sadavoy, S. I., Stephens, I. W., Myers, P. C., et al. 2019, ApJS, 245, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Stephens, I. W., Yang, H., Li, Z.-Y., et al. 2017, ApJ, 851, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Tazaki, R., Lazarian, A., & Nomura, H. 2017, ApJ, 839, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Testi, L., Birnstiel, T., & Ricci, L. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning, 339 [Google Scholar]
- Valdivia, V., Maury, A., Brauer, R., et al. 2019, MNRAS, 488, 4897 [NASA ADS] [CrossRef] [Google Scholar]
- Voshchinnikov, N. V. 1989, Astron. Nachr., 310, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Waterman, P. C. 1971, Phys. Rev. D, 3, 825 [Google Scholar]
- Yang, H., & Li, Z. Y. 2019, AAS J., submitted [arXiv:1909.08192] [Google Scholar]
- Yang, H., Li, Z.-Y., Looney, L., & Stephens, I. 2016, MNRAS, 456, 2794 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, H., Li, Z.-Y., Looney, L. W., Girart, J. M., & Stephens, I. W. 2017, MNRAS, 472, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, H., Li, Z.-Y., Stephens, I. W., Kataoka, A., & Looney, L. 2019, MNRAS, 483, 2371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: The reason behind negative polarization
We have demonstrated that the polarized emission by aligned weakly-elongated grains can present a regime of negative polarization when the grain size becomes on the order of the wavelength. In this regime, the direction of polarization is parallel to the alignment direction, that is to the magnetic field, and not perpendicular to it as is usually assumed.
Recently, Kirchschlager et al. (2019) independently found the signature of a negative polarization in the optical properties of 100 μm prolate and oblate porous grains, which are composed of silicate, carbon, or ice. These authors limited their calculations to grains smaller than 100 μm and did not include the calculation of the grain temperature. As a consequence, the negative polarization is absent from their prediction for the spectral dependence of the polarized fraction of an MRN-like size distribution, which, consistently with Fig. 1, remains positive at all wavelengths.
According to Fig. 1, negative polarization does not happen for all grains sizes. To understand the reason for this, Fig. A.1 presents how the grain polarization efficiency varies with the size parameter of x = 2πa/λ. The polarization efficiency of an individual, perfectly aligned, grain writes: p = (C2,abs − C1,abs)/(C2,abs + C1,abs), where C1,abs (resp. C2,abs) is the grain absorption and emission cross-section for an electromagnetic wave that is linearly polarized along (resp. perpendicular to) the direction of alignment projected onto the plane of the sky (for more details, see Guillet et al. 2018). We recall that for a given value of the complex refraction index m = n + ik, the dust optical cross-section only depends on the value of x, that is, on the ratio a/λ, and not on the value of a and λ. Interferences between the waves scattered by the grain in the Mie regime produce strong oscillations (Kruegel 2003). For x ≪ 1, the polarization efficiency is positive, which is as expected in the Rayleigh regime. For x ≥ 1, the polarization efficiency oscillates between positive and negative values, which converge toward zero at high x, as expected in the geometric optical regime where a ≫ λ. We can observe two things. First, the values of x for which the polarization fraction cancel out does not depend on the grain size. Second, the smaller the grain, the smaller the oscillations. As we comment below, this is explained by the variation of the complex refraction index with the wavelength.
 |
Fig. A.1. Top: dust polarization efficiency (C2,abs − C1,abs)/(C2,abs + C1,abs) as a function of the size parameter x = 2πa/λ for individual grains with a size comprised between 10 and 1000 μmm. We note that the x axis has been reverted for an easier comparison with the bottom panel. Bottom: same as a function of the wavelength λ, for 3 mean grain sizes apeak of 25, 100, and 500 μm. The grain of oblate shape has an axis ratio b/a = 1.1 and is perfectly aligned with its direction of alignment in the plane of the sky (γ = 0°). |
The bottom panel of Fig. A.1 shows how the polarization fraction varies as a function of the wavelength for different values of the width σ of the log-normal distribution and mean grain size apeak. The real part n and imaginary part k of the optical constant of so-called astronomical silicates (Draine & Lee 1984) are also plotted. The real part n, which controls the position of the zeros in the oscillations of the polarization efficiency (Kruegel 2003), is constant between 100 μm to 1 cm. The imaginary part, which controls the spectral dependence of the grain absorption cross-section and the amplitude of the oscillations in the Mie regime (Kruegel 2003), decreases as k(λ) ∝ λ1 − β ∝ 1/λ. Larger values of k tend to damp the oscillations (top panel of Fig. A.1). The smaller grains (25 μm here) are in the Mie regime in the far-infrared (λ ∼ 100 μm), where the absorption is still high (k ∼ 0.3). The larger grains (500 μm) fall in this regime in the millimeter, where k has dropped by a factor of 10, leaving stronger oscillations. These positive and negative oscillations average out when the size distribution gets wider (larger value of σ), with a positive mean value for smaller grains at small wavelength, and a negative mean value for larger grains at large wavelengths.
Our modeling was restricted to homogeneous, compact, weakly elongated grains. The detailed physical properties of dust aggregates, including the shape, composition, structure, and fluffiness, are known to affect the absorption and scattering properties of dust grains. Their impact on the regime of negative polarization deserves more investigation.
Appendix B: Additional figure
 |
Fig. B.1. Same as Fig. 1, but for a direction of alignment inclined by 45° with respect to the plane of the sky. Log-normal (top row) and MRN (bottom row) size distributions of prolate (left column) and oblate (right column) grains. |
All Figures
 |
Fig. 1. Polarization fraction in emission for oblate grains (axis ratio b/a = 1.1) that are perfectly aligned in the plane of the sky. Results are presented for log-normal (top) and MRN-like (bottom) size distributions. The grain size corresponding to the peak of the mass distribution is indicated in μm. Negative polarization fractions correspond to a rotation of the polarization vector by 90°. The wavelength of ALMA bands 3, 6, and 7 are indicated with dashed vertical lines. Mean values of the polarization fraction observed for [BHB2007] 11 are overplotted in positive and negative for the log-normal size distributions. |
| In the text | |
 |
Fig. 2. Schematic representation of the polarization vectors from polarized emission by prolate (b/a = 0.9) aligned grains that would be observed in the three ALMA bands for a protoplanetary disk inclined by an angle of 45° with a perfectly azimuthal magnetic field (dashed orange ellipses), for three values of the grain size corresponding to the peak of log-normal size distribution. The length of the vectors scales with the polarization fraction, reproducing the trends predicted by our model. Dotted lines indicate a polarization fraction that is close to zero. The contribution of self-scattering to the observed polarization is ignored. |
| In the text | |
 |
Fig. A.1. Top: dust polarization efficiency (C2,abs − C1,abs)/(C2,abs + C1,abs) as a function of the size parameter x = 2πa/λ for individual grains with a size comprised between 10 and 1000 μmm. We note that the x axis has been reverted for an easier comparison with the bottom panel. Bottom: same as a function of the wavelength λ, for 3 mean grain sizes apeak of 25, 100, and 500 μm. The grain of oblate shape has an axis ratio b/a = 1.1 and is perfectly aligned with its direction of alignment in the plane of the sky (γ = 0°). |
| In the text | |
 |
Fig. B.1. Same as Fig. 1, but for a direction of alignment inclined by 45° with respect to the plane of the sky. Log-normal (top row) and MRN (bottom row) size distributions of prolate (left column) and oblate (right column) grains. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.