| Issue |
A&A
Volume 626, June 2019
|
|
|---|---|---|
| Article Number | A6 | |
| Number of page(s) | 13 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201834365 | |
| Published online | 30 May 2019 | |
Effects of dust evolution on protoplanetary disks in the mid-infrared
1
Kapteyn Astronomical Institute, University of Groningen,
Postbus 800,
9700 AV
Groningen,
The Netherlands
e-mail: greenwood@astro.rug.nl
2
SRON Netherlands Institute for Space Research,
PO Box 800,
9700 AV
Groningen,
The Netherlands
3
Anton Pannekoek Institute for Astronomy, University of Amsterdam,
PO Box 94249,
1090 GE
Amsterdam,
The Netherlands
4
SUPA, School of Physics & Astronomy, University of St. Andrews,
North Haugh, St. Andrews
KY16 9SS,
UK
5
Max Planck Institute for Extraterrestrial Physics,
Gießenbachstraße 1,
85741
Garching,
Germany
Received:
3
October
2018
Accepted:
25
March
2019
In this paper, we couple the dust evolution code two-pop-py with the thermochemical disk modelling code ProDiMo. We create a series of thermochemical disk models that simulate the evolution of dust over time from 0.018 to 10 Myr, including the radial drift, growth, and settling of dust grains. We examine the effects of this dust evolution on mid-infrared gas emission, focusing on the mid-infrared spectral lines of C2H2, CO2, HCN, NH3, OH, and H2O, which are readily observable with Spitzer and the upcoming E-ELT and JWST. The addition of dust evolution acts to increase line fluxes by reducing the population of small dust grains. We find that the spectral lines of all species except C2H2 respond strongly to dust evolution; line fluxes increase by more than an order of magnitude across the model series as the density of small dust grains decreases over time. The C2H2 line fluxes are extremely low because of a low abundance in the infrared line-emitting regions, even though C2H2 is commonly detected with Spitzer, suggesting that warm chemistry in the inner disk may need further investigation. Finally, we find that the CO2 flux densities increase more rapidly than the other species as the dust disk evolves. This suggests that the flux ratios of CO2 to other species may be lower in disks with less-evolved dust populations.
Key words: astrochemistry / line: formation / molecular processes / astroparticle physics / protoplanetary disks
© ESO 2019
1 Introduction
Throughout the lifetime of a protoplanetary disk of a few million years, its evolution is dominated by the gas and dust that accrete onto the star, coalesce into larger bodies, or are dissipated by photoevaporation and stellar winds. The dust in these disks is a significant factor in their evolution. Although dust particles (assuming typical interstellar medium (ISM) abundances) make up only a small portion of the total disk mass, small grains composed of dust and ice dominate the radiative transfer of the disk and provide seeds for planets to form.
It is crucial that we can determine the distribution of this dust. In the eras of ALMA, JWST, and E-ELT we have both the sensitivity and angular resolution to spatially resolve nearby protoplanetary disks, to spectrally resolve the emission lines from molecules, and to detect the broad emission features from silicate grains. The distributions of gas and dust in the disk are not necessarily co-spatial and nor is the ratio constant with height, because dust grains are expected to grow and fall toward the midplane (Blum & Wurm 2008; Dominik & Dullemond 2008) and the scale heights of the dust and gas disks may differ (de Gregorio-Monsalvo et al. 2013; Avenhaus et al. 2018). T Tauri stars and brown dwarfs have flatter dust disks and relatively thicker gas disks than Herbig stars (Mulders & Dominik 2012). A crucial step that we must take is to understand the physics behind these effects and how we can incorporate them into a thermochemical disk model.
In the infrared, we can observe the spectral lines of many species that trace the warm upper layers of the inner disk. For example, typical mid-infrared water line fluxes in T Tauri disks have been observed to range between about 2 × 10−13 erg cm−2 s−1 and 2 × 10−15 erg cm−2 s−1 (Pontoppidan et al. 2010). The authors also note that there appears to be a subclass of disks that have strong 14.98 μm CO2 emission, but with no detectable contributions in the 14–16 μm range from water, HCN, and C2H2. Previous results by Meijerink et al. (2009) and Bosman et al. (2017) suggested that a high gas-to-dust ratio of 1000: 1 in the line-emitting regions might be necessary to reproduce the mid-infrared line fluxes observed with Spitzer. This ratio has often been adopted by the modelling community (Bruderer et al. 2015; Bosman et al. 2017).
To justify this ratio, we need to explain what has happened to the dust: if the disk formed from a molecular cloud with a gas-to-dust ratio of 100:1, this dust cannot disappear without reason. We know that dust settles in disks (Dubrulle et al. 1995), and that especially in older disks, the midplanes are typically more dust-rich than the upper layers (Dullemond & Dominik 2005). We need to account for this dust settling to quantify the gas-to-dust ratio of the line-emitting regions. In this paper, we couple a dust evolution code with a thermochemical modelling code and for the first time analyse the effects of dust evolution on the mid-infrared spectral lines.
Accurately determining the gas and dust masses of protoplanetary disks is difficult. Primarily, this is because much of the line and continuum emission is optically thick: there is no known way to derive gas and dust masses from line and continuum observationsthat is free of significant degeneracies. Although observing disks with gaps can help to measure scale heights and thus estimate midplane densities, there can be a lot of optically thick gas and dust in the midplane that cannot be observed directly – for example, Pinte et al. (2016) found that the dust density in the gaps of HL Tau is at least a factor of 10 lower than in the rings surrounding the gaps. However, it is difficult to place an upper limit on the dust density in the rings.
Likewise, it is difficult to observe accurately the dust grain size distribution as a function of radius and height. For example, although there has been progress in spatially resolving the dust surface density of disks (Pinilla et al. 2014), the measured spectral index is dependent upon assumptions about the dust temperature. Scattered light imaging using SPHERE has been used to observe the surface of dust disks (Ginski et al. 2016; Stolker et al. 2016; Avenhaus et al. 2018; Muro-Arena et al. 2018). Particularly, the survey of eight T Tauri disks introduced by Avenhaus et al. (2018) is a valuable set of observations. Although a detailed analysis of each source is left for forthcoming papers, Avenhaus et al. (2018) have provided insights such as showing that all of the observed T Tauri disks appear to have τ = 1 surface flaring indices between ~1.1 and ~1.6, and showingstriking geometric structures such as gaps, rings, and even the lower disk surface of three disks. If an inclined disk has rings or gaps in the dust structure, the height of the dust scattering surface can be estimated by geometrically fitting these structures (Ginski et al. 2016; Avenhaus et al. 2018).
In comparison to micron-sized dust grains, decimetre-sized bodies have very little effect on the radiative transfer of the disk in the mid-infrared regions. However, their effect on the evolution of the disk is much more significant. Because they are less affected by processes such as viscosity and turbulence, decimetre-sized bodies are more likely to be found close to the midplane of the disk and are a crucial step toward the eventual formation of planets.
To analyse the effect of dust evolution and migration on the mid-infrared spectral lines of a T Tauri protoplanetary disk, we model the evolution of dust over time, and create a thermochemical model of the disk at discrete time steps in the evolution. In this way, we incorporate a self-consistent description of dust evolution into our thermochemical disk models, where the gas-to-dust ratio and dust size distribution vary not only at each timestep, but also radially and vertically through the disk. By analyzing the mid-infrared spectral lines of each individual model, we can build an understanding of how dust evolution affects these lines.
2 Modelling strategy
A total of four separate codes were used in a set to produce the models in this paper. The underlying disk model is based upon the “DIANA standard” T Tauri disk described in Woitke et al. (2016). However, this DIANA standard disk model does not address the dust structure in detail. Table 1 describes the parameters of our T Tauri disk model. This section serves as a technical description of what each code does and how they are interfaced.
First, we used the two-population dust evolution code two-pop-py1 (Birnstiel et al. 2012, 2015, 2017). The two-pop-py code produces a one-dimensional description of the dust at each age increment. It is a simplified version of the dust evolution code described in Birnstiel et al. (2010), calibrated with the use of these more complex models and based upon the use of two dust grain populations: a small monomer population and a large grain population. The small grain population is coupled to the gas, not affected by drift velocities, and is constant in time and space. The population of large grains can grow in size, and is affected by the limiting mechanisms of radial drift and grain fragmentation. The reconstruction of the grain size distribution from the simple two-population model is described by Birnstiel et al. (2015).
From two-pop-py, we obtained the gas and dust surface densities as functions of radius, and the dust mass fraction as a function of both radius and grain size. The dust mass fraction records the fraction of the total mass that is accounted for by each grain size increment, as a function of radius. For each age increment, we calculated a separate disk model. For this, we used the code MCMax (Min et al. 2009) to create a two-dimensional model of the disk structure and calculate the dust continuum radiative transfer for the dust temperature. We ensured that the grain sizes are conserved between two-pop-py and MCMax.
There are two standard methods in MCMax to calculate the scale heights of the gas and dust: to have parameterized scale heights or to solve for hydrostatic equilibrium. We took a hybrid approach, first forcing the scale heights of the gas to remain parameterized, then solving the dust for hydrostatic equilibrium and allowing the dust to settle in a self-consistent manner (described by Mulders & Dominik 2012). We do not argue for the physical correctness of this procedure (which is unknown), rather for the simplicity it brings. The first argument is that we want to remain as close to the DIANA standard of models as possible, where only the dust distribution deviates from the standard. The second argument is that it simplifies the results and analysis. Although the total gas mass in the disk decreases with age, the gas scale heights remain constant. This allows us better to analyse the effects that different dust distributions have on the mid-infrared molecular lines, under the assumption that everything else is equal.
The third code in the pipeline is ProDiMo (Woitke et al. 2009; Kamp et al. 2010; Aresu et al. 2011), which takes the MCMax output and calculates a full thermochemical disk model. We took the disk structure directly from MCMax, then ran the disk chemistry, taking the reaction rates for 235 species from the UMIST2012 chemical network (McElroy et al. 2013) to calculate the thermal and chemical equilibrium state of the disk. Because theoverall opacity and density structure of the disk is fixed, there is no need for global disk structure iterations.
The final element is FLiTs, which calculates a high-resolution spectrum from a ProDiMo model (Woitke et al. 2018) across the infrared wavelength range. The ProDiMo model provides the gas and dust temperatures, stellar spectrum and local radiation field, opacities, molecular number densities, and level populations. The FLiTs program reads this file and calculates the spectrum of the disk for the desired molecules and wavelength range.
3 Dust migration and disk surface densities
The effects of dust migration over time are visible in both the surface densities and dust grain size distributions, as computed by two-pop-py. These are one-dimensional results, while we later used MCMax to compute the two-dimensional disk structure. The precise timescales are not strictly relevant for this discussion because the ages are very uncertain, both in the models and any observed disks. It is better to compare disks with different surface densities than to compare disks of different ages, because these parameters are more readily observable. For example, disks in Ophiuchus are thought to be less than 1 Myr old (Furlan et al. 2009), but basic properties such as the disk mass may vary by about two orders of magnitude (Testi et al. 2016). We need many different models in order to accurately represent such a diverse disk population. Nevertheless, for brevity we refer to each model by its two-pop-py age.
In each ProDiMo model we used steady-state chemistry: the ProDiMo chemistry may run for longer than the “age” of the two-pop-py model. However, the timescales for disk surface chemistry (on the order of years) are much shorter than the timescale of dust evolution (≳ 104 yr): it is only when considering longer wavelengths such as submillimetre that we might need to calculate time-dependent chemistry.
Figure 1 shows the gas and dust surface densities from t0 = 0.018 Myr to tmax = 10 Myr. Although the gas mass slowly decreases over time owing to viscous evolution, the loss of dust from radial drift is much greater2, and this causes the total gas-to-dust ratio of the disk to increase over time, from 100 at t = 0 to over 6000 at 10 Myr. For the column of gas at a radius of 1 AU, the youngest model has a gas-to-dust ratio of about 40, whereas the oldest model reaches about 4 × 104.
The youngest two-pop-py model is close to the initial state of the system, and the low gas-to-dust ratio in the initial state of the inner disk isthe result of a high level of inward dust mass flux. As the disk ages, radial drift continues to deplete the total dust mass in the disk. One other notable trend in Fig. 1 is the bump in gas-to-dust ratio, which becomes significant at 0.32 Myr and a radius of 40 AU, and moves inward with time. This bump is due to a localized depletion in the dust, reported by Birnstiel et al. (2012) as a pileup effect caused by increases in the disk temperature from viscous heating, similar to the grain pileup in Youdin & Chiang (2004).
Figure 2 describes how the gas mass, dust mass, and gas-to-dust ratio vary over time, integrated over the entire disk. Figure 3 shows vertical cuts of the grain size distribution at radii of 0.1, 1, 10, and 100 AU. At radii of 10 AU or less, the trends are similar: the grain size distribution shows both an overall decrease in surface densities and a disproportionate depletion of larger grains, which are transported inward owing to radial drift. As a consequence, in the inner disk at 0.1 AU there are many large grains up to 10 cm in size at an age of 10 Myr. However, at 1 AU this cutoff is at a grain size of 1 cm, and about 0.05 cm at 10 AU. This happens because a population of large grains can only be maintained so long as there is an inward flux of grains coming from larger radii. The situation is slightly different at 100 AU. Although there is no significant population of centimetre-sized, grains, the population of millimetre-sized grains grows until an age of 0.56 Myr.
Summary of important model parameters used in each step of the procedure.
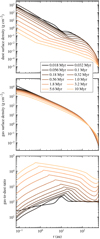 |
Fig. 1 Dust surface column density, gas surface column density, and gas-to-dust ratio as a function of radius for each age increment. |
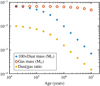 |
Fig. 2 Dust and gas masses and dust-to-gas ratio of the entire disk over time. |
4 Size of the dust disk
One consequence of our dust settling method is that the dust disk is less vertically extended than the gas disk. This is not an artefact of parameterizing the gas structure, but a result of the self-consistent description of dust settling. Disks with processed dust and dust disks that are thinner than the gas disk have been reported in previous literature (de Gregorio-Monsalvo et al. 2013; Ginski et al. 2016; Muro-Arena et al. 2018; Avenhaus et al. 2018), but the number of observations are still relatively few.
The dust disk calculated using our self-consistent settling is thinner than a disk model that uses Dubrulle settling (Dubrulle et al. 1995). The main differences between the self-consistent settling method (Mulders & Dominik 2012) and Dubrulle setting is that Dubrulle settling uses only the midplane density and temperature. Away from the midplane, the analytical solution for the midplane density and temperature becomes less accurate. Self-consistent settling agrees well with Dubrulle settling in the midplane, but submicron particles can also decouple from the gas in the upper disk (Mulders & Dominik 2012), contrary to Dubrulle settling. The distribution of < 0.1 μm particles is nearly uniform throughout a Dubrulle-settled disk, and larger grain sizes are affected less by settling than the self-consistent model (Mulders & Dominik 2012).
All of our models have a dust disk that is thinner than the gas disk. Figure 3 shows vertical cuts of the gas-to-dust ratio through the disks at each age. In every case, in the upper layers of the disk where some tenuous gas still exists, the gas-to-dust ratio can easily be 105 or more. In the midplane of the inner disk, particularly at 0.1 AU, the gas-to-dust ratio of models younger than 0.56 Myr can be less than 10. This is in contrast to at 100 AU, where most of the disk at 0.018 Myr has a gas-to-dust ratio of 100. At young ages, there are few large grains in the outer disk: the dust only decouples significantly from the gas in older models, once millimetre-sized dust grains have formed. However, at small radii, there is already a significant population of large grains at t = 0.18 Myr. This gives rise to the low gas-to-dust ratio in the midplane at small radii.
When comparing the gas and dust disk thickness with observations, our youngest models are comparable to disks such as IM Lup that appear to be less settled (Cleeves et al. 2016), while the older models are more comparable to disks such as HD 163296, where the dust disk may be significantly settled in comparison to the gas disk (de Gregorio-Monsalvo et al. 2013).
The settled dust structure causes every disk to have some regions where the gas-to-dust ratio is 1000 or more, whichas we find in Fig. 5 is the minimum gas-to-dust ratio from which all species except C2H2 tend to emit.
Both dust evolution and the new self-consistent method of settling contribute to changes in the mid-infrared line fluxes, because both of these processes affect small micron-sized dust grains. Dust evolution affects the surface density of these grains in the disk, while settling affects the vertical distribution of those grains. Figures 4 and 5 show the effects of dust evolution and the settling method on dust densities, absorption coefficient, and gas temperatures, while Fig. 6 shows those same effects on the mid-infrared line fluxes.
Counterintuitively, the mid-infrared line fluxes can in fact increase owing to Dubrulle settling. Even though Dubrulle settling leads to lower gas temperatures in the mid-infrared line-emitting region for each species, in Fig. 6 we see that models with Dubrulle settling tend to have somewhat stronger lines than those same models with self-consistent settling. Although the total vertical optical depth remains the same in models with both Dubrulle and self-consistent settling, the dust in the latter models is more concentrated toward the midplane. Thus, reduced optical depths in the upper layers of models with Dubrulle settling can allow the mid-infrared line-emitting regions to grow in size. However, it is important to note that although the method of settling can affect the line fluxes, the effects of dust evolution remain more significant.
 |
Fig. 3 Left: vertical cuts of the grain size distribution at r = 1 AU (top), r= 10 AU (middle), and r = 100 AU (bottom). Right: vertical cuts of the gas-to-dust ratio at r = 1 AU (top), r= 10 AU (middle), and r = 100 AU (bottom). |
5 Mid-infrared spectra
The migration and evolution of dust has a profound effect on the mid-infrared spectra and line-emitting regions of our disk model. To discuss the line-emitting regions of each species, it is necessary to define the exact molecular lines we are using, and how the line-emitting regions themselves are derived.
We define the line-emitting region as the area from which 70% of the flux originates in both the radial and vertical directions. The lower limit, x15, is defined so that 85% of the total line flux of that spectral line is emitted at radii greater than x15. The upper limit, x85, is the opposite – only 15% of the total line flux of that spectral line is emitted at a radius greater than x85. At each radius, z15 and z85 define the heights in the disk above which 15 and 85% of the flux is emitted, respectively. The properites of the line-emitting region for a given species (such as Tgas) are averaged and weighted with the volume density of that species across the line-emitting region.
Table 2 details the molecular lines chosen for analysis, one for each species. For consistency, where possible, we analyse spectroscopic lines that have previously been analysed in other literature (see references in Table 2). Whenever an individual molecular line is referenced in this paper, it refers to the line in this table.
The flux of a particular molecular line is driven primarily by three factors: the gas-to-dust ratio, gas temperature in the line-emitting region, and optical depth in the line-emitting region ⟨τ20 μm⟩. Figure 7 shows how the average gas-to-dust ratio ⟨g∕d⟩, average gas temperature ⟨Tgas⟩, and the linefluxes change with age in the disk. Although the gas-to-dust ratio of the entire disk begins at 100: 1, the self-consistent dust settling is not informed by the age of the model. It solves for the vertical dust structure without considering the settling timescales, which may be a few × 105 yr (Dullemond & Dominik 2004).
We measure fluxes in two different ways. Where we mention the flux of an individual spectral line, these fluxes are calculated using a vertical escape probability method (Woitke et al. 2009). These line fluxes are accurate only for a face-on disk, because no detailed radiative transfer is taken into account. In contrast, where we discuss FLiTs spectra, these have been calculated for an inclined disk and account for both the radial and vertical optical depth. These spectra are also convolved to an instrumental resolution, so that we measure the peak flux of a complex of lines and not the integrated flux of a single line. The purpose of the first method is to measure how line emission responds to changes in the dust distribution by picking these representative lines to measure the properties of the line-emitting region. The purpose of the second method is to put these measurements into an observational context. By accounting for the many spectral lines that are in the bandheads of some species and convolving the resulting spectrum, we can relate the peak fluxes of the spectra to observations and sensitivities of Spitzer or JWST.
In comparison to observed Spitzer spectra (e.g., Pontoppidan et al. 2010; Salyk et al. 2011; Pascucci et al. 2013), the FLiTs spectra of all of our species except C2H2 can producespectral lines that are at least as bright as we have observed. The spectra are highly responsive to changes in the dust distribution, where the loss of small dust particles over time acts to reduce the opacity of the disk and dramatically increases line fluxes. The only exception to this trend is C2H2, where our models do not produce lines that are as bright as Spitzer observations (despite C2H2 being readily detected), suggesting that the chemical networks of C2H2 may be inaccurate or incomplete.
 |
Fig. 4 From top to bottom: midplane dust density, gas temperature of a vertical column of gas at 1 AU, and a vertical cut of the dust density at 1 AU. For comparison with the standard 0.018 and 1 Myr models, the same models (but with Dubrulle settling instead) are plotted to illustrate the effects of both dust settling and evolution on the mid-infrared regions. |
 |
Fig. 5 Absorption opacity, plotted for the standard 0.018 and 1 Myr models, and the same models but with Dubrulle settling instead. |
 |
Fig. 6 Mid-infrared line fluxes for both the standard 0.018 and 1 Myr models, and the same models with Dubrulle settling. |
5.1 Line fluxes: C2H2 in comparison to other species
Throughout the dust evolution simulation, the line flux of each species except C2H2 increases by at least an order of magnitude, whereas C2H2 remains more or less constant in line flux. For all species except C2H2, the gas-to-dust ratio in the line-emitting region increases significantly as the dust evolves.
On the other hand C2H2 simply does not exist in these models in the upper layers of the disk. It is easily destroyed when the dust evolves and the disk becomes more optically thin. As the disk ages the remaining C2H2 is concentrated further toward the midplane, and the line-emitting region is pushed both toward the midplane and out to larger radii (up to ~0.6 AU). In these models, we see the same bifurcated structure of C2H2 discussed in Greenwood et al. (2018) and seen also in Walsh et al. (2015). A significant proportion of the line-emitting population of C2H2 is below the AV = 10 line, meaning that the dust continuum in this region is very optically thick in the mid-infrared. As the dust evolves and becomes more optically thin, the C2H2 responds and shifts closer toward the midplane. Hence, there is no chance for the line flux to increase. Greenwood et al. (2018) have shown that a more dust-rich disk model has stronger C2H2 lines, where for all other species, more dust-rich models have weaker lines. Our models from this work do not predict C2H2 line fluxes that are observable with any current spacecraft. However, there are clear Spitzer detections of C2H2 in T Tauri disks with similar detection rates to the other species (Pontoppidan et al. 2010). More work is needed to understand this particular species.
5.2 Properties of the line-emitting regions
Figure 7 shows changes in the gas-to-dust ratio, gas temperature, vertical dust optical depth, escape probability line flux, and line-emitting area of each line over time. Although for each species the gas-to-dust ratio in the line-emitting region increases steadily over time, C2H2 has a consistently lower ratio than the other species because its line-emitting area is closer toward the midplane.
The trends in gas temperature are more complex. For C2H2, at 1.8 Myr the gas temperature of the line-emitting region drops dramatically, from about 900 to 350 K. The temperature drops even more as the disk ages further. This trend is also reflected in the fact that C2H2 is in absorption for the oldest few disk models (see Fig. 9). The reason for this is changes in the line-emitting area: the C2H2 abundances in the oldest disk models drop significantly, and the line-emitting area moves outward and toward the midplane. The gas temperatures of the CO2 and NH3 line-emitting regions stay relatively stable over time. For HCN and H2O, we see an increase in gas temperature, particularly for the oldest models. This is because the line-emitting regions become larger and move toward slightly warmer, higher layers in the disk.
Figure 7 shows that where we compute the spectra of our models using FLiTs, we expect the fluxes of every species except C2H2 to increase significantly as the dust in the disk evolves. This is illustrated by Figs. 8 and 9, which show that between the youngest and oldest disks models, the peak flux densities for every species except C2H2 increase by factors ranging from 30 for H2O to 200 for OH. The escape probability line fluxes in Fig. 7 increase by similar amounts, showing that measuring the escape probability line flux of these single lines forms a reasonable proxy for measuring trends in the overall strength of the line-emitting region.
For comparison to infrared observatories, the median 1σ mid-infrared line sensitivity of Spitzer isabout 8.5 × 10−19 W m−2, thus many individual spectral lines are far too faint for Spitzer to detect3. However, the ro-vibrational bandheads of species such as CO2 contain many lines that at a low spectral resolution are blended together, which is why we can see these species with Spitzer. In some of the more evolved disks, even individual OH, o-H2O, NH3, and HCN lines are significantly above this sensitivity limit (see Fig. 7). Following the flux densities of the convolved spectra presented in Figs. 8 and 9, and assuming a 5σ Spitzer sensitivity of 5 mJy in 512 s, we expect that only C2H2 would be undetectable at every age. OH, H2O, and NH3 are only detectable in more evolved disks, while HCN and CO2 should be detectable in every model. At R = 600, the complexes of water lines can easily become blurred at Spitzer’s low spectral resolution, making it difficult to determine the continuum flux (in comparison to R = 2800 spectra). The 10σ continuum sensitivity of the Mid-Infrared Instrument (MIRI) on JWST is around 0.1 mJy at 15 μm, with an exposure time of 104 s (Glasse et al. 2015). Thus with JWST, we can expect that in every model, all species except C2H2 would be detectable with exposure times much less than 104 s.
C2H2 even goes into absorption at 5.6 and 10 Myr. The line emission features in disk models up to 1.8 Myr old appear to be dominated by emission from near the inner wall, while in the older disk models the line-emitting region extends out to 0.6 AU and is close to the midplane. The absorption lines in the 5.6 and 10 Myr old models are likely attributable to the fact that the C2H2 emission comes from close to the midplane. As described in Greenwood et al. (2018), there exists an inversion in the gas temperature around the AV = 1 line, such that there may exist clouds of colder gas above the warmer gas in the disk. Absorption lines may result if these clouds of colder gas exist between our line of sight and the line-emitting region of the species.
CO2 is the brightest species by a significant margin, suggesting that our younger models may be representative of the subclass discovered by Pontoppidan et al. (2010), where in six disks only CO2 was unambiguously detected. This subclass may consist of disks in which the dust is significantly settled in comparison to the gas, similar to the structure produced in our models by the self-similar dust settling. In this case, we would expect CO2 to be the brightest species in the mid-infrared, and thus other species may remain undetected. The reason that CO2 fluxes can be so high is that it is a robust species that is able to survive in relatively optically thin regions because it has a small cross section for photodissociation (van Dishoeck et al. 2006). As the dust structure evolves and becomes more optically thin, the line-emitting area of CO2 also grows; Fig. 7 shows that CO2 can have a line-emitting area close to 1000 AU2, and the CO2 emission extends to about 15 AU at 1 Myr.
Emission line of each species chosen for analysis, including upper level energies Eup and the Einstein A coefficient.
6 Discussion
As the dust evolves, grains are depleted from the disk and the mid-infrared molecular line emission grows substantially for every species except C2H2. This happens because dust particles (particularly small micron-sized grains) are the main carriers of opacity in the disk, so reduced continuum optical depths lead directly to a larger line-emitting area and increased molecular line fluxes.
The lack of C2H2 emission is because this species exists closer toward the midplane than the other molecules. Thus, it is more affected by both the optical depth of the dust in the disk and the gas temperature inversions around AV = 1. The T Tauri spectra observed by Carr & Najita (2011) have peak C2H2 flux densities of up to about 20 mJy, and C2H2/HCN line flux ratios between about 0.08 and 0.8. As Figs. 7–9 show, when we compare the peak flux densities of the FLiTs spectra of our strongly evolved models, we see much lower ratios: although the ratio of the spectral flux densities of C2H2–HCN is ~ 0.02 at 0.18 Myr, it decreases with age to as low as 5 × 10−5 at 10 Myr (with the caveat that for the oldest models, C2H2 is in weak absorption). The fact that C2H2 behaves so differently from other species suggests either that our chemical network misses some key C2H2 formation pathways, or that the dust structure of our models is not representative of disks with C2H2 detections. Although it is possible that uncertainties in the chemical network and reaction rates lead to significant inaccuracies in the distribution of C2H2 calculated by ProDiMo, our C2H2-deficient models mayalso be a natural result of the dust structure. Walsh et al. (2015) found that C2H2 is significantly less abundant in Herbig Ae disks because of increased levels of photodissociation, which also increases when the population of small dust grains is reduced. This suggests that the low C2H2 line fluxes are a result of an evolved dust structure, but it does not adequately explain the fact that C2H2 is all but absent in even our youngest 0.018 Myr model.
Another notable result is that CO2 is much brighter than all other species in our models, suggesting that our older models may be representative of the disks found by Pontoppidan et al. (2010) where only CO2 was detected. If these sources have an evolved and settled dust structure, our results show that we would expect CO2 to be much brighter than other species. The sources where CO2 was not the only detected species may have a less evolved and settled dust structure, giving lower CO2 line fluxes and more equal ratios between the line fluxes of different species. In all of our models, the CO2 spectrum has a brighter flux density than all other species by at least a factor of ten. The explanation for the relative brightness of CO2 likely lies in the dust and temperature structure of the models.
While Pontoppidan et al. (2010) noted a strong correlation between spectral type and line detections, there also appears to be a dichotomy in their results between B, A, and F type objects and G, K, and M spectral types. For spectral types earlier than G, there is a dramatic and as yet unexplained drop in the detection rates of all species except CO. This may appear to be in conflict with Mulders & Dominik (2012), who suggested that late-type (brown dwarf and T Tauri) disks have flatter dust disks and relatively thicker gas disks than earlier (Herbig) disks do4. In this paper we suggest that a highly evolved and strongly settled dust structure may lead to CO2 emission being much brighter than other species. However, if younger disks have less-evolved dust (thus more small dust grains) and a less-settled dust structure, and because our models show that CO2 line fluxes increase with age more than other species, we suggest that the flux ratios between CO2 and the other species that we have modeled are lower in early-type disks.
The work by Mulders & Dominik (2012) is based upon SEDs, and they state that “regions with the same temperature have a self-similar vertical structure independent of stellar mass”. It is difficult to distinguish changes in the SEDs of our dust evolution models at wavelengths below 30 μm; thus we are probing different parametre spaces. The lack of detections around early-type stars could be because the stronger UV radiation of early-type stars is enough to prevent species that are vulnerable to photodissociation from forming in sufficient quantities. Such species include C2H2, H2O, NH3, and HCN, which all have photodissociation cross sections >10−17 cm−2 (van Dishoeck et al. 2006). Walsh et al. (2015) found that weaker UV fields indeed allow for more molecule-rich disk atmospheres. Thermochemical models by Antonellini et al. (2015) found that strong UV radiation does not weaken water line fluxes and that a likely explanation for the lack of water detections around Herbig stars is noisy spectra combined with high continuum flux levels. Future modelling and observational work is required to thoroughly to understand the interplay between the disk dust structure, radiation field, and mid-infrared molecular lines. What appears most clear is that as the main opacity carrier in the disk, the evolution and settling of dust can have a substantial impact.
 |
Fig. 7 Left, top: gas-to-dust ratio in the line-emitting region of each species, over time. The significant bump seen in the gas-to-dust ratio of OH is misleading. Our measurement of the line-emitting area is biased by the fact that there is a small amount of OH emission coming from warm upper layers at relatively large radii. These upper layers have a disproportionately high gas-to-dust ratio. Left, middle: the line-emitting area, in square astronomical units, of each species overtime. This area is calculated from a face-on perspective, assuming that the line emission comes from an annulus encompassed by the inner and outer radii of the line emission (x15 and x85). Much like the gas-to-dust ratio for less-evolved models, the line-emitting area calculation of OH is biased by small amounts of emission at larger radii. Left, bottom: the escape probability line flux of each species over time. The dashed horizontal line indicates the nominal 1σ Spitzer sensitivity of 8.5 × 10−19 W m−2 achievable with a 512 second integration. Right, top: the density-averaged gas temperature in the line-emitting region of each species over time. Right, middle: the density-averaged vertical optical depth of the dust at 20 μm in the line-emitting region of each species over time. |
 |
Fig. 8 FLiTs spectra of the disk models up to 0.32 Myr old, convolved to a spectral resolution R = 2800 (black lines) and R = 600 (red lines). Where indicated, the spectra were multiplied by 5, 10, or 50 to improve visibility. This disk is at an inclination of 45°. The reason why the spectral lines become weaker at 0.032 Myr, only to become stronger again at 0.056 Myr, is likelydue to the dust evolution; Fig. 1 shows that radii smaller than 1 AU, the gas-to-dust ratio drops between the 0.018 and 0.032 Myr models, before increasing again at the 0.056 Myr mark. Because the onset of radial drift suddenly decreases the gas-to-dust ratio, we see a corresponding drop in line fluxes. |
 |
Fig. 9 FLiTs spectra of the disk models from 0.56 Myr old, convolved to a spectral resolution R = 2800 (black lines) and R = 600 (red lines). Where indicated, the spectra were multiplied by 5, 10, or 50 in order to improve visibility. This disk is at an inclination of 45°. The y-axis limits are different than those in Fig. 8. |
7 Conclusions
We have coupled the dust evolution code two-pop-py with the radiative transfer code MCMax, the thermochemical disk modelling code ProDiMo, and the line-tracing code FLiTs. We produced a series of models that simulate the evolution of dust over time in a two-dimensional thermochemical disk model, and have created infrared spectra of these models including C2H2, CO2, HCN, NH3, OH, and H2O mid-infraredline emission.
This paper shows that dust evolution has a very clear and straightforward effect on the mid-infrared line fluxes, where the evolving and diminishing dust population in the surface acts to decrease continuum optical depths and thus increase line fluxes by up to a factor of 100. Even in the least-evolved disk models, the mid-infrared lines prefer to emit from a gas-to-dust ratio of at least 1000:1. This provides a physical explanation for the need in previous literature to use such ratios to produce enough line flux to match models withobservations.
This is a double-edged sword: although the dust structure is a significant degeneracy when fitting models to observations, if we can observe the dust directly (for example, by observing the τ = 1 surface withscattered-light imaging), the dust structure also becomes a powerful diagnostic in understanding the mid-infrared emission of T Tauri disks. Upcoming observatories such as JWST and E-ELT will significantly improve our ability to observe these disks, and combined with more sophisticated models, we can build a two- or three-dimensional understanding of dust structure in the inner disk and the mid-infrared spectral lines.
Acknowledgements
We would like to thank Lucia Klarmann, Gabriela Muro Arena, Paola Pinilla, Til Birnstiel, and Michiel Min for their discussions and comments on the manuscript. We also thank the Center for Information Technology of the University of Groningen for their support and for providing access to the Peregrine high performance computing cluster.
References
- Antonellini, S., Kamp, I., Riviere-Marichalar, P., et al. 2015, A&A, 582, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aresu, G., Kamp, I., Meijerink, R., et al. 2011, A&A, 526, A163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Avenhaus, H., Quanz, S. P., Garufi, A., et al. 2018, ApJ, 863, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Bate, M. R., Bonnell, I. A., & Bromm, V. 2003, MNRAS, 339, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Birnstiel, T., Dullemond, C. P., & Brauer, F. 2010, A&A, 513, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birnstiel, T., Klahr, H., & Ercolano, B. 2012, A&A, 539, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birnstiel, T., Andrews, S. M., Pinilla, P., & Kama, M. 2015, ApJ, 813, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Birnstiel, T., Klahr, H., & Ercolano, B. 2017, Astrophysics Source Code Library [record ascl:1708.015] [Google Scholar]
- Blum, J., & Wurm, G. 2008, ARA&A, 46, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bosman, A. D., Bruderer, S., & van Dishoeck, E. F. 2017, A&A, 601, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruderer, S., Harsono, D., & van Dishoeck, E. F. 2015, A&A, 575, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carr, J. S., & Najita, J. R. 2011, ApJ, 733, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Cleeves, L. I., Öberg, K. I., Wilner, D. J., et al. 2016, ApJ, 832, 110 [NASA ADS] [CrossRef] [Google Scholar]
- de Gregorio-Monsalvo, I., Ménard, F., Dent, W., et al. 2013, A&A, 557, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dominik, C., & Dullemond, C. P. 2008, A&A, 491, 663 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dorschner, J., Begemann, B., Henning, T., Jaeger, C., & Mutschke, H. 1995, A&A, 300, 503 [Google Scholar]
- Draine, B. T. 1978, ApJS, 36, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Dubrulle, B., Morfill, G., & Sterzik, M. 1995, Icarus, 114, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C. P., & Dominik, C. 2004, A&A, 421, 1075 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dullemond, C. P., & Dominik, C. 2005, A&A, 434, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Furlan, E., Watson, D. M., McClure, M. K., et al. 2009, ApJ, 703, 1964 [NASA ADS] [CrossRef] [Google Scholar]
- Ginski, C., Stolker, T., Pinilla, P., et al. 2016, A&A, 595, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Glasse, A., Rieke, G. H., Bauwens, E., et al. 2015, PASP, 127, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Greenwood, A. J., Kamp, I., Waters, L. B. F. M., Woitke, P., & Thi, W.-F. 2018, A&A, submitted [Google Scholar]
- Jacquemart, D., Mandin, J. Y., Dana, V., et al. 2003, J. Quant. Spectr. Rad. Transf., 82, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Kamp, I., Tilling, I., Woitke, P., Thi, W. F., & Hogerheijde, M. 2010, A&A, 510, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McElroy, D., Walsh, C., Markwick, A. J., et al. 2013, A&A, 550, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meijerink, R., Pontoppidan, K. M., Blake, G. A., Poelman, D. R., & Dullemond, C. P. 2009, ApJ, 704, 1471 [NASA ADS] [CrossRef] [Google Scholar]
- Min, M., Hovenier, J. W., & de Koter, A. 2005, A&A, 432, 909 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Min, M., Dullemond, C. P., Dominik, C., de Koter, A., & Hovenier, J. W. 2009, A&A, 497, 155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Min, M., Rab, C., Woitke, P., Dominik, C., & Ménard, F. 2016, A&A, 585, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mulders, G. D., & Dominik, C. 2012, A&A, 539, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muro-Arena, G. A., Dominik, C., Waters, L. B. F. M., et al. 2018, A&A, 614, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Notsu, S., Nomura, H., Ishimoto, D., et al. 2017, ApJ, 836, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Pascucci, I., Herczeg, G., Carr, J. S., & Bruderer, S. 2013, ApJ, 779, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Pinilla, P., Benisty, M., Birnstiel, T., et al. 2014, A&A, 564, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinte, C., Dent, W. R. F., Ménard, F., et al. 2016, ApJ, 816, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Pontoppidan, K. M., Salyk, C., Blake, G. A., et al. 2010, ApJ, 720, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Rothman, L. S., Jacquemart, D., Barbe, A., et al. 2005, J. Quant. Spectr. Rad. Transf., 96, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Salyk, C., Pontoppidan, K. M., Blake, G. A., Najita, J. R., & Carr, J. S. 2011, ApJ, 731, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Stolker, T., Dominik, C., Min, M., et al. 2016, A&A, 596, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Testi, L., Natta, A., Scholz, A., et al. 2016, A&A, 593, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Dishoeck, E. F., Jonkheid, B., & van Hemert, M. C. 2006, Faraday Discuss., 133, 231 [Google Scholar]
- Walsh, C., Nomura, H., & van Dishoeck, E. 2015, A&A, 582, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woitke, P., Kamp, I., & Thi, W. F. 2009, A&A, 501, 383 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woitke, P., Min, M., Pinte, C., et al. 2016, A&A, 586, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woitke, P., Min, M., Thi, W. F., et al. 2018, A&A, 618, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Youdin, A. N., & Chiang, E. I. 2004, ApJ, 601, 1109 [NASA ADS] [CrossRef] [Google Scholar]
- Zubko, V. G., Mennella, V., Colangeli, L., & Bussoletti, E. 1996, MNRAS, 282, 1321 [NASA ADS] [CrossRef] [Google Scholar]
two-pop-py is available on Github at http://birnstiel.github.io/two-pop-py/
One caveat to their analysis is that the best-fit brown dwarf, T Tauri, and Herbig disk models have identical outer radii. Their brown dwarf model has a very low surface density and is strongly flared, while the outer radius of 400 AU is not representative of a typical brown dwarf disk (Bate et al. 2003).
All Tables
Emission line of each species chosen for analysis, including upper level energies Eup and the Einstein A coefficient.
All Figures
 |
Fig. 1 Dust surface column density, gas surface column density, and gas-to-dust ratio as a function of radius for each age increment. |
| In the text | |
 |
Fig. 2 Dust and gas masses and dust-to-gas ratio of the entire disk over time. |
| In the text | |
 |
Fig. 3 Left: vertical cuts of the grain size distribution at r = 1 AU (top), r= 10 AU (middle), and r = 100 AU (bottom). Right: vertical cuts of the gas-to-dust ratio at r = 1 AU (top), r= 10 AU (middle), and r = 100 AU (bottom). |
| In the text | |
 |
Fig. 4 From top to bottom: midplane dust density, gas temperature of a vertical column of gas at 1 AU, and a vertical cut of the dust density at 1 AU. For comparison with the standard 0.018 and 1 Myr models, the same models (but with Dubrulle settling instead) are plotted to illustrate the effects of both dust settling and evolution on the mid-infrared regions. |
| In the text | |
 |
Fig. 5 Absorption opacity, plotted for the standard 0.018 and 1 Myr models, and the same models but with Dubrulle settling instead. |
| In the text | |
 |
Fig. 6 Mid-infrared line fluxes for both the standard 0.018 and 1 Myr models, and the same models with Dubrulle settling. |
| In the text | |
 |
Fig. 7 Left, top: gas-to-dust ratio in the line-emitting region of each species, over time. The significant bump seen in the gas-to-dust ratio of OH is misleading. Our measurement of the line-emitting area is biased by the fact that there is a small amount of OH emission coming from warm upper layers at relatively large radii. These upper layers have a disproportionately high gas-to-dust ratio. Left, middle: the line-emitting area, in square astronomical units, of each species overtime. This area is calculated from a face-on perspective, assuming that the line emission comes from an annulus encompassed by the inner and outer radii of the line emission (x15 and x85). Much like the gas-to-dust ratio for less-evolved models, the line-emitting area calculation of OH is biased by small amounts of emission at larger radii. Left, bottom: the escape probability line flux of each species over time. The dashed horizontal line indicates the nominal 1σ Spitzer sensitivity of 8.5 × 10−19 W m−2 achievable with a 512 second integration. Right, top: the density-averaged gas temperature in the line-emitting region of each species over time. Right, middle: the density-averaged vertical optical depth of the dust at 20 μm in the line-emitting region of each species over time. |
| In the text | |
 |
Fig. 8 FLiTs spectra of the disk models up to 0.32 Myr old, convolved to a spectral resolution R = 2800 (black lines) and R = 600 (red lines). Where indicated, the spectra were multiplied by 5, 10, or 50 to improve visibility. This disk is at an inclination of 45°. The reason why the spectral lines become weaker at 0.032 Myr, only to become stronger again at 0.056 Myr, is likelydue to the dust evolution; Fig. 1 shows that radii smaller than 1 AU, the gas-to-dust ratio drops between the 0.018 and 0.032 Myr models, before increasing again at the 0.056 Myr mark. Because the onset of radial drift suddenly decreases the gas-to-dust ratio, we see a corresponding drop in line fluxes. |
| In the text | |
 |
Fig. 9 FLiTs spectra of the disk models from 0.56 Myr old, convolved to a spectral resolution R = 2800 (black lines) and R = 600 (red lines). Where indicated, the spectra were multiplied by 5, 10, or 50 in order to improve visibility. This disk is at an inclination of 45°. The y-axis limits are different than those in Fig. 8. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


