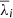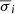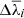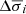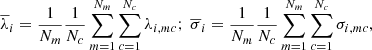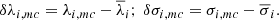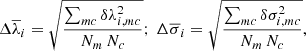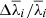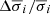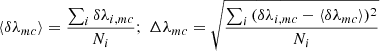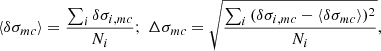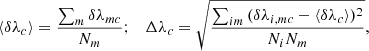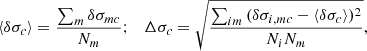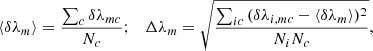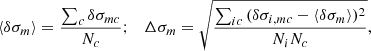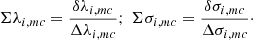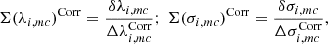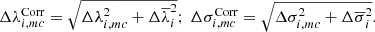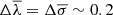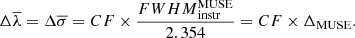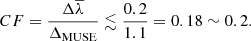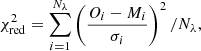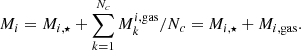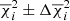EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 625 (May 2019) A&A, 625 (2019) A83 Full HTML
Free Access
Issue
A&A
Volume 625, May 2019
Article Number A83
Number of page(s) 20
Section Numerical methods and codes
DOI https://doi.org/10.1051/0004-6361/201834478
Published online 17 May 2019

© ESO 2019

1. Introduction

The kinematic characterization of different galaxy populations is a key observational input in distinguishing between different evolutionary paradigms, such as the “major merger” (Tacconi et al. 2006, 2008; Kartaltepe et al. 2012) and the “steady cold gas accretion” (Kereš et al. 2005; Ocvirk et al. 2008; Dekel et al. 2009a; Ceverino et al. 2010) scenarios, since it allows one to determine the fraction of rotating disks to mergers at different cosmic epochs (see e.g., Genzel et al. 2001; Tacconi et al. 2008; Dekel et al. 2009b; Förster Schreiber et al. 2009; Lemoine-Busserolle & Lamareille 2010; Lemoine-Busserolle et al. 2010; Bournaud et al. 2011; Epinat 2011; Glazebrook 2013; Bellocchi et al. 2016). Kinematics is also important in the study of physical processes that govern the formation and evolution of the galaxies, providing a powerful diagnostic to infer the main source of dynamic support (Puech et al. 2007; Epinat et al. 2009; Cappellari et al. 2013; Zhu et al. 2018), to distinguish between relaxed virialized systems and merger events (Flores et al. 2006; Shapiro et al. 2008; Bellocchi et al. 2012, 2016; Barrera-Ballesteros et al. 2015), to infer fundamental galaxy quantities like the dynamical mass (Colina et al. 2005; Bellocchi et al. 2013; Aquino-Ortíz et al. 2018), and also to detect and characterize radial motions associated with feedback mechanisms, like massive gas outflows (Shapiro et al. 2009; Rupke & Veilleux 2013; López-Cobá et al. 2017a,b; Maiolino et al. 2017).

With the aid of integral field spectroscopy (IFS), we can resolve the kinematical status and internal processes at work within galaxies and more clearly understand the role of the dominant mechanisms involved at early epochs of galaxy formation. This technique provides much more information on the observed galaxies than was previously available through classical long-slit spectroscopy: on the one hand, the full 2D spatial information (i.e., maps rather than radial profiles) can be reconstructed at high resolution in regions of bright emission; on the other hand, one of the advantages of IFS is that large areas may be combined in order to properly characterize weak signals, such as the galaxy outskirts. The observed spectrum at each spaxel (or area) includes gas in different phases, traced by distinctive features at different wavelengths (e.g., Hα emission allows one to study the warm ionized emission, NaD absorption traces the neutral gas, the CO emission helps to trace the cold molecular clouds, etc.; see Bekeraité et al. 2016; Leung et al. 2018; Levy et al. 2018) as well as the underlying stellar population (a smooth continuum with absorption features). To properly characterize their physical properties, we need to apply methods that are able to separate the contributions of gas and stars to the total emission. To this aim, in the last ten years many routines have been developed to subtract the stellar continuum. Some of them, like STARLIGHT (Cid Fernandes et al. 2005), FIT3D (Sánchez et al. 2016a), pPXF (Cappellari & Emsellem 2004), STECKMAP (Ocvirk et al. 2006), sedfit (Walcher et al. 2006), and PyPARADISE (Husemann et al. in prep.) are widely used nowadays. These routines allow for detailed studies of the underlying stellar population(s) of the source and for interesting parameters/properties to be derived such as the total stellar mass, the star formation rate (e.g., Pérez et al. 2013; González Delgado et al. 2017), the age and metallicities, and the kinematics of the stars.

In this paper we want to investigate how the choice of different stellar-subtraction methods affects the derivation of the gas kinematics traced by the ionized component through the Hα and [NII] lines. We also analyze how the choice of different line fitting approaches influences the derivation of the kinematic parameters (mean velocity and velocity dispersion). The target of this study is a nearby galaxy observed with VLT/MUSE, for which we obtain high-resolution spectra that are perfectly suited to our aims (a related discussion has recently been presented by Belfiore et al. 2019 in the context of the MaNGA Data Analysis Pipeline). We describe the observations in Sect. 2. In Sect. 3 we present the selection of the spectra, a brief description of the methods used for the stellar continuum subtraction, and the line-fitting approaches considered. Section 4 is devoted to the discussion of the results obtained using different methods, and our main conclusions are summarized in Sect. 5. Appendix A presents some details of the line-fitting analysis along with complementary kinematic results and the quality of the fits is discussed in Appendix B. Throughout the paper we consider H0 = 70 km s−1 Mpc−1, ΩM = 0.3, and ΩΛ = 0.7.

2. Observations

NGC 29061 is a nearby (z = 0.007138, d = 30 Mpc) “normal” star-forming galaxy which was observed during the science verification of the MUSE instrument (Bacon et al. 2004), and included in the pilot study of the All-weather MUse Supernova Integral-field of Nearby Galaxies (AMUSING; Galbany et al. 2016) given that it hosts the type-IIn supernova (SN) 2005ip (Boles et al. 2005; Modjaz et al. 2005). According to its morphology, this object is classified as a Scd galaxy. In Fig. 1 the continuum and the Hα2 emissions of this object are shown.

thumbnail Fig. 1.

Top panel: continuum MUSE image of NGC 2906. The continuum image was obtained as the mean of the median values in two wavelength ranges: 5620–5750 Å and 6890–7000 Å. Left panel: nuclear peak shown by a cross symbol and the position of the supernova SN2005ip represented by the star symbol. A zoom of the region selected by the white box is shown on the right. Right panel: region showing the distribution of the spectra (white dots) which have been chosen for the analysis. Each spectrum is identified by a letter (a, b, ..., k, l) in order to allow the reader to easily find its position. Bottom panel: Hα peak emission of the same regions as described in the top figure.

The MUSE instrument provides a field of view (FoV) of 1 arcmin2 with spaxels of 0.2″ × 0.2″ in wide-field mode (WFM). At this redshift, the arcsecond to kiloparsec conversion gives 0.147 kpc arcsec−1. In this configuration the data cube is composed by 320 × 322 spaxels with 3680 elements of spectral sampling. The wavelength coverage ranges between 4750 and 9350 Å with a mean resolution of R ∼ 30003 and sampling of 1.25 Å. The object was observed with a seeing (FWHM) of 0.88″ (∼0.13 kpc). With the MUSE instrument it is possible to combine good seeing conditions with a large FoV and a spatial sampling sufficient to properly sample the point spread function (PSF). Thus, it is a well-suited instrument to study the kinematics of our object in detail.

3. Analysis

In this section we first present the selection criteria for the spectra. We then describe the codes used to subtract the stellar continuum emission from the observed unsubtracted data, as well as the stellar libraries involved. Finally, we discuss the different approaches used to fit the Hα-[NII] line complex.

3.1. Selected spectra

This work focuses on the analysis of twelve spectra, half of which are located in the nuclear region, with the remaining half being located in different parts of the galaxy. For practical reasons, we refer to the different spaxels using letters (a, b, ..., k, l), as shown in Figs. 1, 2, and 4, ordered according to their (decreasing) log([NII]λ6583/Hα) flux ratios4.

thumbnail Fig. 2.

From left to right: Unsubtracted MUSE spectra at the different positions (identified by the letters; see Fig. 1) along with the pure gas spectra obtained from applying the three different stellar-subtraction methods, respectively: FIT3D, STARLIGHT (MILES and STELIB) and pPXF methods. The Hαλ6563 and the two forbidden [NII]λλ6548, 6583 lines are shown. The line-fitting results are shown using the colored solid line: the unsubtracted data are in orange, FIT3D data are in green, STARLIGHT (MILES) data are in dark blue, STARLIGHT (STELIB) data are in magenta, and pPXF data are in red. The line fitting case[1] (all parameters fixed) is considered. The flux is in units of 10−20 erg s−1 cm−2 Å−1 and the wavelength is in Å.

The spatial distribution of the selected spaxels is shown in Fig. 1. The intensity peak in the continuum image (spectrum d) has been considered as the origin of our system of reference, and the offsets of all spectra with respect to that origin are listed in Table 3. The minimum separation between the spectra is 0.6″, reached in the region close to the nucleus, up to a maximum separation of 11.8″ from the center.

We have tried to ensure that these spectra are representative of a wide range of physical conditions and signal–to–noise ratios (S/Ns). The original spectra, extracted from the MUSE datacube, are shown in the left column of Fig. 2, whereas the other columns display the results obtained after subtracting the stellar continuum with each of the four methods described below. Although the precise line fluxes and equivalent widths are relatively sensitive to the adopted method, it is evident from Fig. 2 that the values of the log([NII]λ6583/Hα) ratio illustrate the whole range of values typically found in a Baldwin et al. (1981) diagram (see also Table 3).

3.2. Stellar continuum subtraction methods

In order to characterize nebular emission, the stellar continuum emission needs to be subtracted. The Hα and Hβ emission line profiles may be significantly affected from Balmer absorption especially in evolved stellar populations (e.g., Sarzi et al. 2007; Cresci et al. 2015; Gomes et al. 2016).

This is clearly visible in NGC 2906, where the Hα emission in the central spectra is relatively highly absorbed (from a to d spectra in Fig. 2), while for the outer spectra this effect does not seem to be so relevant (from f to l spectra in Figs. 2 and 3).

thumbnail Fig. 3.

As in Fig. 2.

Here we remove the stellar contribution using three different software programs that are publicly available and have been widely used in the literature:

  1. FIT3D5 (Sánchez et al. 2016c,a).

  2. STARLIGHT6 (Cid Fernandes et al. 2004, 2005, 2013).

  3. Penalized Pixel–Fitting7 (pPXF; Cappellari & Emsellem 2004; Cappellari 2017).

These spectral-synthesis codes combine the spectra from a base of simple stellar populations of various ages and metallicities in order to match an observed spectrum. The search for an optimal model and the coefficients of the population vector associated with the base elements also allow for interesting outputs to be derived, such as the star-formation and chemical-enrichment histories of a galaxy or region, and allow us to recover non-linear parameters, such as the amount of dust extinction and the main kinematic parameters (velocity shift and dispersion) of both stars and gas. The reader is referred to the corresponding articles for an in-depth discussion of each method.

In any case, the characteristics of the stellar libraries adopted as a basis are as important as the fitting algorithm. The choice of the stellar library generally depends on the resolution of the data. In our case, MUSE has a nominal spectral resolution FWHM ∼ 2.68 Å, and we combined each code with one of the following stellar libraries in order to achieve a similar (or lower) resolution:

  1. STELIB: empirical library from Bruzual & Charlot (2003; hereafter BC03);

  2. MILES: “Medium-resolution Isaac Newton Telescope Library of Empirical Spectra” from Vazdekis et al. (2010);

  3. GRANADA & MILES: a combination of the theoretical stellar libraries from González Delgado et al. (2005) and González Delgado & Cid Fernandes (2010) with Vazdekis et al. (2010).

The STELIB9 library (Le Borgne et al. 2003) consists of a homogeneous library of 249 stellar spectra in the visible range (3200–9500 Å), with an intermediate spectral resolution (≤3 Å) and sampling (1 Å). A measured metalicity is available for only 187 of the 249 stars; this can be used to compute the predicted spectra. This library includes stars of various spectral types and luminosity classes, spanning a relatively wide range in metallicity (Z = 0.0001 − 0.05).

The MILES10 stellar library (Vazdekis et al. 2010) consists of stars spanning a large range in atmospheric parameters. The 985 spectra were obtained at the 2.5 m Isaac Newton Telescope (INT) and cover the range 3525–7500 Å (Sánchez-Blázquez et al. 2006) at 2.51 Å (FWHM) spectral resolution (Falcón-Barroso et al. 2011). These models cover ages between ∼0.1 and ∼18 Gyr and metallicities in the range 0.0004–0.03. Vazdekis/Miles models are based on the previous models from Vazdekis (1999) and Vazdekis et al. (2003) and they use Padova2000 isochrones. The Padova isochrones (1994 and 2000) are presented in Girardi et al. (2002)11.

GRANADA12 & MILES stellar library (gsd156) comprises 156 templates that cover 39 stellar ages (1 Myr–13 Gyr), and four metallicities (Z = 0.002, 0.008, 0.02 and 0.03). These templates have been extracted from a combination of the synthetic stellar spectra from the GRANADA (Martins et al. 2005) and the SSP libraries provided by the MILES project. This SSP library uses the Salpeter (1955) initial mass function (IMF) and Girardi et al. (2000) and Geneva13 tracks and is described in detail in Cid Fernandes et al. (2013).

The “code-stellar library” combinations we used are as follows.

  1. The FIT3D code with the GRANADA and MILES libraries;

  2. the STARLIGHT code with the MILES library (see Galbany et al. 2016 and references therein for more information14);

  3. the STARLIGHT code with the STELIB library;

  4. the pPXF code with the MILES library.

In Table 1 we summarize all combinations of the “code-stellar library” used in this analysis, including details on the isochrones and the age of the stellar populations considered.

Table 1.

Set of SSP models and stellar libraries used for the spectral fitting.

3.3. Line fitting cases

In this work we focus on the Hαλ6563Å and the forbidden [NII]λλ6548, 6583Å emission lines15. The routine MPFITEXPR (implemented in IDL code by Markwardt 2009) is commonly used to derive the kinematic parameters (e.g., Arribas et al. 2008; Bellocchi et al. 2012, 2013, 2016; Cazzoli et al. 2014; Cairós et al. 2015; Poggianti et al. 2017). This algorithm allows one to fit the observed lines of the individual spectra to Gaussian profiles and the continuum emission as a line with a certain slope. It derives the best set of lines that match the available data. In cases of adjusting multiple lines, the line flux ratios can be fixed according to the atomic physics (as in the case of the [NII] doublet). The outputs of this routine are the wavelength (i.e., centroid λ), the width (σ), and flux of the line. The routine also allows for the λ and σ parameters to be combined in different ways, keeping them fixed or leaving them free to vary. Therefore, when fitting the Hα-[NII] complex, there are four cases that can be taken into account:

  1. λ & σFIXED: he wavelengths of the different lines are fixed according to the atomic physics and their widths are constrained to be equal for all lines (e.g., Bellocchi et al. 2013, 2016);

  2. λFREE, σFIXED: the wavelengths of the different lines are free to vary but their widths are constrained to be equal for all lines;

  3. λFIXED, σFREE: the wavelengths of the different lines are fixed according to the atomic physics but their widths are left free to vary;

  4. λ & σFREE: both wavelengths and widths are free to vary for all lines.

All these cases are summarized in Table 2. In the following section the results of our analysis are shown and discussed. It is worth mentioning that in this work the MUSE instrumental profile (σINS) has not been subtracted. To obtain a rough estimate of the instrumental profile we apply the line fitting case 1 to the [OI]λ6300 sky line in a relatively large region of the galaxy, where the [OI] emission is present. We derive a typical (median) value for the wavelength of λINS  ∼  6299.99 Å and σINS  ∼  0.88 Å, with the respective mean values of 6299.99 (±0.91) Å and 0.96 (±0.48) Å.

Table 2.

Different cases considered for the line-fitting analysis for the wavelength and for the width.

4. Results

In this section we present and discuss the kinematic results obtained when different stellar-subtraction methods and line-fitting approaches are considered. The raw observed data (hereafter, unsubtracted) are also included in the analysis in order to study the case in which the stellar emission is not removed at all, and thus to understand the importance of removing (or not) the stellar component from the data for the derivation of the kinematics of the gas component.

In Sect. 4.1 we focus on the results derived for each individual spectrum to better study the dispersion related to the choice of a specific stellar-subtraction method and to study the effect of using a particular line-fitting approach. In Sect. 4.2 we then analyze the mean trends obtained when considering all spectra averaged according to the number of methods or the number of cases considered.

4.1. Mean and dispersion for individual spectra

In this section the derivation of the kinematic results of each individual spectrum (λi, mc, σi, mc) is presented, where the index i runs over our 12 individual spectra, and a combination of twenty values per spectrum is analyzed (i.e., 5 methods × 4 cases; Nmc = Nm Nc = 20). We reiterate the fact that according to our selection criterion the [NII] contribution is very significant in the first six spectra (from spectrum [a] to [f]), while the Hα flux emission dominates in the remaining six spectra (from spectrum [g] to [l]).

We first determined the wavelength λi, mc and the velocity dispersion σi, mc for both lines in each spectrum (Fig. 4) as derived when applying different line–fitting approaches (“cases”) and continuum–subtraction methods. The increasingly asymmetric shape of the Hα profile in the first spectra, characterized by lower S/N as a consequence of the Hα absorption, reflects the larger dispersions when deriving the kinematic values using different stellar subtraction methods and line fitting cases. Conversely, the quality of the fit of the [NII] line is also affected by the corresponding S/N, although the differences are not as marked as for the Balmer line.

thumbnail Fig. 4.

Kinematic results for the individual spectra when using different stellar-subtraction methods and line-fitting approaches for the Hα (top) and [NII] (bottom) emission lines. The four line-fitting cases and the five stellar-subtraction methods used are highlighted according to the different symbols and colors (as in Fig. 2), respectively (twenty values for each spectrum). The mean wavelength and dispersion ( λ ¯ i $ \overline\lambda_i $, σ ¯ i $ \overline\sigma_i $) as well as their standard deviation ( Δ λ ¯ i $ \Delta\overline\lambda_i $, Δ σ ¯ i $ \Delta\overline\sigma_i $) are represented using dashed light gray lines and the shaded area (light red and cyan), respectively.

Considering that each measurement provides a wavelength λi, mc and a velocity dispersion σi, mc, we defined the mean values for each spectrum among all twenty combinations as

λ ¯ i = 1 N m 1 N c ∑ m = 1 N m ∑ c = 1 N c λ i , m c ; σ ¯ i = 1 N m 1 N c ∑ m = 1 N m ∑ c = 1 N c σ i , m c , $$ \begin{aligned} \overline{\lambda }_i = \frac{1}{N_m} \frac{1}{N_c} \sum _{m=1}^{N_m} \sum _{c=1}^{N_c} \lambda _{i, mc};~\overline{\sigma }_i = \frac{1}{N_m} \frac{1}{N_c} \sum _{m=1}^{N_m} \sum _{c=1}^{N_c} \sigma _{i, mc}, \end{aligned} $$(1)

and we characterize the behavior of the different methods and cases in terms of the offset from the appropriate mean value:

δ λ i , m c = λ i , m c − λ ¯ i ; δ σ i , m c = σ i , m c − σ ¯ i . $$ \begin{aligned} \delta \lambda _{i, mc} = \lambda _{i, mc} - \overline{\lambda }_i ;~ \delta \sigma _{i, mc} = \sigma _{i, mc} - \overline{\sigma }_i. \end{aligned} $$(2)

As the true kinematic parameters of every individual spectrum are unknown, we cannot determine the optimal combination of subtraction method and fitting approach (in each particular case), but we may quantify the uncertainties associated to such a choice in a statistical sense, computing the standard deviations,

Δ λ ¯ i = ∑ mc δ λ i , m c 2 N m N c ; Δ σ ¯ i = ∑ mc δ σ i , m c 2 N m N c , $$ \begin{aligned} \Delta \overline{\lambda }_i = \sqrt{ \frac{\sum _{mc} \delta \lambda _{i, mc}^2}{N_m\,N_c} } ;~ \Delta \overline{\sigma }_i = \sqrt{ \frac{\sum _{mc} \delta \sigma _{i, mc}^2}{N_m\,N_c} } ,\end{aligned} $$(3)

arising from our Nmc = 20 combinations.

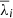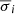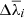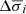The mean values of the wavelength λ ¯ i $ \overline{\lambda}_i $ and the velocity dispersion σ ¯ i $ \overline{\sigma}_i $ obtained for each spectrum, along with the measurement dispersions (uncertainty ranges) Δ λ ¯ i $ \Delta\overline\lambda_i $ and Δ σ ¯ i $ \Delta\overline\sigma_i $, are listed in Table 3 and shown in Fig. 4. 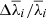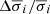The latter, as well as the fractional uncertainties ( Δ λ ¯ i / λ ¯ i $ \Delta\overline\lambda_i/\overline{\lambda}_i $ and Δ σ ¯ i / σ ¯ i $ \Delta\overline\sigma_i/\overline{\sigma}_i $) are plotted in Fig. 5. We find that, for Hα, 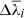Δ λ ¯ i $ \Delta\overline\lambda_i $ decreases from 0.3 Å down to 0.03 Å when moving from spectrum [a] to [l], and a (much milder) decreasing trend is also found for the velocity dispersion uncertainty 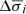Δ σ ¯ i $ \Delta\overline\sigma_i $, which varies from ∼0.4 down to ∼0.1. The respective fractional uncertainties for the wavelength parameter, 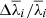Δ λ ¯ i / λ ¯ i $ \Delta\overline\lambda_i/\overline\lambda_i $, thus cover the range of values from 4.9 × 10−5 Å down to 3.9 × 10−6 Å from spectrum [a] to [l], while those obtained for the velocity dispersion, 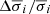Δ σ ¯ i / σ ¯ i $ \Delta\overline\sigma_i/\overline\sigma_i $, vary from ∼0.21 down to ∼0.08. The opposite trend is derived for the [NII] line, reflecting the line intensity ratios, although more stable and constant values are obtained for both line wavelength and width for different spaxels.

Table 3.

Mean values and standard deviations for the wavelength and line width of the Hα and [NII] emission lines obtained when combining all line-fitting cases and stellar-continuum subtraction methods for each individual spaxel.

thumbnail Fig. 5.

Trend of the linear (top) and fractional (bottom) dispersion values of the λ ( Δ λ ¯ i $ \Delta\overline\lambda_i $ and Δ λ ¯ i / λ ¯ i $ \Delta\overline\lambda_i/\overline\lambda_i $; left) and σ ( Δ σ ¯ i / σ ¯ i $ \Delta\overline\sigma_i/\overline\sigma_i $; right) parameters. For each spectrum the Hα values are in light red and the [NII] ones are in light blue.

It is important to bear in mind that on the one hand we are quantifying the dispersion of the measured parameters with respect to the average value, which may be different from the true solution. On the other hand, it is conservative to assume that the estimated central wavelengths and line widths inferred from the various codes and combinations of stellar population synthesis (SPS) models are statistically independent, in the sense that any off-diagonal terms in the covariance matrix would likely reduce the quoted systematic uncertainties. For these reasons, our estimate of the dispersion between codes may actually be regarded as an upper limit to the true systematic uncertainty associated to the choice of a specific method.

4.2. Trends for different methods and cases

Figure 6 shows the mean and standard deviation

〈δ λ mc 〉= ∑ i δ λ i,mc N i ; Δ λ mc = ∑ i (δ λ i,mc −〈 δ λ mc 〉 ) 2 N i $$ \begin{aligned} \langle \delta {\lambda _{mc}}\rangle = \frac{{\sum_i \delta {\lambda _{i,mc}}}}{{{N_i}}};\;\Delta {\lambda _{mc}} = \sqrt {\frac{{\sum_i {(\delta {\lambda _{i,mc}} - \langle } \delta {\lambda _{mc}}\rangle {)^2}}}{{{N_i}}}} \end{aligned} $$(4)

〈δ σ mc 〉= ∑ i δ σ i,mc N i ; Δ σ mc = ∑ i (δ σ i,mc −〈 δ σ mc 〉 ) 2 N i , $$ \begin{aligned} \langle \delta {\sigma _{mc}}\rangle = \frac{{\sum_i \delta {\sigma _{i,mc}}}}{{{N_i}}};\;\Delta {\sigma _{mc}} = \sqrt {\frac{{\sum_i {(\delta {\sigma _{i,mc}} - \langle } \delta {\sigma _{mc}}\rangle {)^2}}}{{{N_i}}}} , \end{aligned} $$(5)

thumbnail Fig. 6.

Left panels: mean kinematic results averaged over all individual spectra (see Table 4) for the Hα (top) and [NII] (bottom) emission lines. Right panels: results for different methods/cases separately, as indicated, for the Hα (top) and [NII] (bottom). Symbol shapes and colors denote case and method, respectively. Symbol types are as in Fig. 4.

averaged over the Ni = 12 spaxels, for each emission line, stellar continuum subtraction method, and line-fitting case. Numerical values are reported in Table 4.

Table 4.

Mean and standard deviation of the mean kinematic results averaged over all individual spectra.

Tables 5 and 6 show the results from further averaging over the Nm = 5 methods

〈δ λ c 〉= ∑ m δ λ mc N m ; Δ λ c = ∑ im (δ λ i,mc −〈 δ λ c 〉 ) 2 N i N m , $$ \begin{aligned} \langle \delta {\lambda _c}\rangle = \frac{{\sum_m \delta {\lambda _{mc}}}}{{{N_m}}};\quad \Delta {\lambda _c} = \sqrt {\frac{{\sum_{im} {(\delta {\lambda _{i,mc}} - \langle } \delta {\lambda _c}\rangle {)^2}}}{{{N_i} {N_m}}}} , \end{aligned} $$(6)

〈δ σ c 〉= ∑ m δ σ mc N m ; Δ σ c = ∑ im (δ σ i,mc −〈 δ σ c 〉 ) 2 N i N m , $$ \begin{aligned} \langle \delta {\sigma _c}\rangle = \frac{{\sum_m \delta {\sigma _{mc}}}}{{{N_m}}};\quad \Delta {\sigma _c} = \sqrt {\frac{{\sum_{im} {(\delta {\sigma _{i,mc}} - \langle } \delta {\sigma _c}\rangle {)^2}}}{{{N_i} {N_m}}}} , \end{aligned} $$(7)

Table 5.

Mean and root mean square values for each stellar-subtraction method.

Table 6.

Mean and root mean square values for each line-fitting case.

for each line fitting case, as well as over the Nc = 4 cases

〈δ λ m 〉= ∑ c δ λ mc N c ; Δ λ m = ∑ ic (δ λ i,mc −〈 δ λ m 〉 ) 2 N i N c , $$ \begin{aligned} \langle \delta {\lambda _m}\rangle = \frac{{\sum_c \delta {\lambda _{mc}}}}{{{N_c}}};\quad \Delta {\lambda _m} = \sqrt {\frac{{\sum_{ic} {(\delta {\lambda _{i,mc}} - \langle } \delta {\lambda _m}\rangle {)^2}}}{{{N_i} {N_c}}}} , \end{aligned} $$(8)

〈δ σ m 〉= ∑ c δ σ mc N c ; Δ σ m = ∑ ic (δ σ i,mc −〈 δ σ m 〉 ) 2 N i N c , $$ \begin{aligned} \langle \delta {\sigma _m}\rangle = \frac{{\sum_c \delta {\sigma _{mc}}}}{{{N_c}}};\quad \Delta {\sigma _m} = \sqrt {\frac{{\sum_{ic} {(\delta {\sigma _{i,mc}} - \langle } \delta {\sigma _m}\rangle {)^2}}}{{{N_i} {N_c}}}} , \end{aligned} $$(9)

with a fixed stellar-subtraction method, respectively. These results are also shown in Fig. 7.

thumbnail Fig. 7.

Top and middle panels: mean Hα and [NII] deviations obtained when averaging over all cases (left) and over all methods (right). Bottom panel: mean deviations of the Hα-[NII] complex for all cases (left) and all methods (right).

Our results show clear systematic trends depending on the stellar continuum subtraction algorithm. The measurements obtained from the FIT3d method and those derived after applying the STARLIGHT (MILES) method are relatively similar, and both prescriptions tend to yield slightly larger wavelengths and lower widths (with respect to the mean values) for either line, regardless of the line-fitting case. On the other hand, higher line widths are found when the STARLIGHT (STELIB) and pPXF algorithms are used, with a mild bias towards lower wavelengths.

In particular, for the Hα line the wavelength deviations follow a decreasing trend, from higher to lower wavelengths (from 0.06 Å to –0.083 Å) when moving from the Unsubtracted to the pPXF methods. On the other hand, the width deviations increase from a mean value of –0.19 Å for the Unsubtracted method up to ∼0.24 Å for the pPXF method. When taking into account the [NII] line, all but the pPXF method derived similar wavelength and width deviations with respect to the total mean values. However, they still follow a similar trend (i.e., decreasing or increasing if we consider the wavelength or width deviations, respectively) to that shown for the Hα line but covering a smaller range of values (see Table 5). It is important to note once again that this does not necessarily imply that these deviations are closer to the unknown true solution.

Focusing on the results derived from the STARLIGHT code with different stellar libraries (i.e., MILES, STELIB) and comparing with the measurements obtained with pPXF based on the MILES library, it is evident that the details of the minimization algorithm are at least as important as the choice of spectral basis. Starting from the same data, each program converges to a different solution. Subtle differences in the residual spectra are apparent in Fig. 2, and it is not surprising that these differences propagate into the final kinematic parameters. In our case, the difference when using the same method with different stellar libraries (STARLIGHT using MILES or STELIB) or the same stellar library with different stellar-subtraction methods (STARLIGHT and pPXF using MILES) is at least a factor of two, deriving a larger gap among the kinematic values (λ, σ) when different methods are considered.

Regarding the line-fitting approach, we found a certain similarity between the cases that share the same kinematics for the velocity dispersion parameter: that is, when σ is fixed (cases [1] and [2]) and when σ is free to vary (cases [3] and [4]). We derived the same trends for the wavelength and the velocity dispersion of both Hα and [NII] emission lines. The magnitude of the uncertainties is similar to those stemming from the stellar-subtraction method, but the effect is much more random than systematic.

In general, the two lines yield consistent measurements, although the differences in the recovered kinematics arising from using different methods are somewhat stronger for the Balmer line. For [NII], all methods result in fairly similar values, with the only possible exception being the velocity dispersion obtained when pPXF is used to subtract the stellar continuum. Velocity dispersion is actually more sensitive to the adopted prescription than the mean velocity derived from the line centroid, causing the larger spread already observed in Figs. 4 and 5.

The kinematic results obtained from fitting the Hα-[NII] complex (see Fig. 7, bottom) show a more robust determination of the global kinematic properties with respect to the adopted line-fitting approach (right panel), as the strongest (and thus more stable) line tends to dominate the result, and random deviations in each individual line tend to compensate each other on average (see also Belfiore et al. 2019). However, the systematic differences arising from the continuum-subtraction method (left panel) persist, as they are present in both emission lines.

5. Discussion

In order to gauge whether or not these uncertainties are statistically compatible with the errors returned by the MPFITEXPR routine, we normalized (i.e., standardized) the deviation of each individual measurement from the mean (δλi, mc, δσi, mc) using the line-fitting errors derived from the output covariance matrix (Δλi, mc, Δσi, mc):

Σ λ i , m c = δ λ i , m c Δ λ i , m c ; Σ σ i , m c = δ σ i , m c Δ σ i , m c · $$ \begin{aligned} \Sigma \lambda _{i, mc} = \frac{\delta \lambda _{i, mc}}{\Delta \lambda _{i, mc}};~ \Sigma \sigma _{i, mc} = \frac{\delta \sigma _{i, mc}}{\Delta \sigma _{i, mc}}\cdot \end{aligned} $$(10)

The normalized deviations give us an estimate of the “number of σ” by which each result departs from the mean value, assuming that the line-fitting errors are representative of the expected standard deviation. As can easily be seen in Fig. 8, the dispersion of these variables is often well above unity, as expected from Gaussian statistics, for both Hα and [NII] lines.

thumbnail Fig. 8.

Kinematic parameter deviations, Σ(λi, mc) and Σ(σi, mc) computed with respect to their mean values and normalized to the line-fitting errors derived using IDL for each individual spectrum. The mean deviations as well as their standard deviations are represented using dashed lines (light red for the Hα and cyan for the [NII] lines) and the shaded area in gray, respectively. Top panels: Hα results. Bottom panels: [NII] results.

In the next step we modified the Eq. (10) including, along with the line-fitting errors, an extra correction term accounting for the contribution coming from the choice of a specific stellar-subtraction method (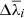 Δ λ ¯ i $ \Delta\overline\lambda_i $ and Δ σ ¯ i $ \Delta\overline\sigma_i $) in the computation of the standard deviation. The new (i.e., corrected) formulas are then modified:

Σ ( λ i , m c ) Corr = δ λ i , m c Δ λ i , m c Corr ; Σ ( σ i , m c ) Corr = δ σ i , m c Δ σ i , m c Corr , $$ \begin{aligned} \Sigma (\lambda _{i, mc})^\mathrm{Corr} = \frac{\delta \lambda _{i, mc}}{\Delta \lambda _{i, mc}^\mathrm{Corr}}; ~\Sigma (\sigma _{i, mc})^\mathrm{Corr} = \frac{\delta \sigma _{i, mc}}{\Delta \sigma _{i, mc}^\mathrm{Corr}}, \end{aligned} $$(11)

where

Δ λ i , m c Corr = Δ λ i , m c 2 + Δ λ ¯ i 2 ; Δ σ i , m c Corr = Δ σ i , m c 2 + Δ σ ¯ i 2 . $$ \begin{aligned} \Delta \lambda _{i, mc}^\mathrm{Corr} = \sqrt{\Delta \lambda _{i, mc}^2 + \Delta \overline{\lambda }_i^2}; ~\Delta \sigma _{i, mc}^\mathrm{Corr} = \sqrt{\Delta \sigma _{i, mc}^2 + \Delta \overline{\sigma }_i^2}. \end{aligned} $$(12)

For both lines we derive a mean dispersion of 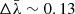Δ λ ¯ ∼ 0.13 $ \Delta\bar\lambda\sim0.13 $ Å for the wavelength while 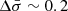Δ σ ¯ ∼ 0.2 $ \Delta\bar\sigma\sim0.2 $ Å for the velocity dispersion. In order to consider a general value for both parameters and for both lines we take into account the highest dispersion value derived for the wavelength and velocity dispersion parameters (∼0.2 Å), as derived for the velocity dispersion of the Hα line.

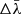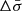As can be seen in in Fig. 9, applying the same mean value for Δ λ ¯ $ \Delta\bar\lambda $ and Δ σ ¯ $ \Delta\bar\sigma $ we finally derived smaller dispersions (of order unity) for both axes and for both lines. Within the (corrected) 1σ error bar, the results of all methods can be considered to be statistically consistent with each other.

thumbnail Fig. 9.

Corrected deviations Σ(λi, mc)i, mc and Σ(σi, mc)Corr for the Hα (top) and [NII] (bottom) lines derived by applying the same mean dispersion factor ( Δ λ ¯ = Δ σ ¯ ∼ 0.2 $ \Delta\overline\lambda=\Delta\overline\sigma\sim0.2 $ Å; see also Fig. 5) for the wavelength and the velocity dispersion. In this correction the dispersion generated from using different stellar-subtraction methods and line-fitting cases is included. The error bars are now ≲1 Å for all spectra and for both parameters (shaded light red and cyan areas for the Hα and [NII] lines, respectively). The mean corrected deviations are represented by dashed white lines for both lines.

We then propose the following prescription to compute the correction factor (CF) that needs to be considered to take into account the uncertainty associated with the choice of a specific stellar-subtraction method. The formula can be related to the instrumental profile of the instrument, ΔMUSE:

Δ λ ¯ = Δ σ ¯ = C F × FWHM instr MUSE 2.354 = C F × Δ MUSE . $$ \begin{aligned} \Delta \overline{\lambda }= \Delta \overline{\sigma }= CF \times \frac{{FWHM}_{\rm instr}^\mathrm{MUSE}}{2.354}= CF \times \Delta _{\rm MUSE}. \end{aligned} $$(13)

In the case of the MUSE data the (theoretical) instrumental resolution is of the order of 1.1 Å (FWHM = 2.6 Å). Considering the mean uncertainty value of 0.2 Å, the correction factor (CF) can be derived as:

C F = Δ λ ¯ Δ MUSE ≲ 0.2 1.1 = 0.18 ∼ 0.2 . $$ \begin{aligned} CF = \frac{\Delta \overline{\lambda }}{\Delta _{\rm MUSE}} \lesssim \frac{0.2}{1.1} = 0.18 \sim 0.2. \end{aligned} $$(14)

In this particular case, the (observed, computed) instrumental resolution ΔMUSE is of the order of 0.9 Å, deriving a CF of the order of ∼0.22. To check the validity of this equation, the same analysis should be applied to other local sources observed with MUSE and other instruments in order to test whether or not our simple prescription can be extended to other instrumental resolutions.

6. Summary and conclusions

We have compared the kinematic results obtained when applying three different stellar-subtraction methods to a sample of twelve spectra in the nearby, normal star-forming galaxy NGC 2906, observed with MUSE instrument on the VLT. The spectra were selected according to their different ionization phases, located in different parts of the galaxy, from the nuclear regions to the outer spiral arms.

In order to study and compare the kinematics of the gas component, such as that derived from applying the stellar-subtraction methods with that derived from the unsubtracted (gas and stars) one, we considered the following stellar-subtraction methods: FIT3D, STARLIGHT and pPXF. Each of them was combined with a specific stellar library: MILES for the STARLIGHT and pPXF methods, STELIB for the STARLIGHT method, and a combination of two stellar libraries, GRANADA & MILES for the FIT3D one. From their combination we obtained four different data sets of the gaseous ionized component. To better characterize the dispersion when deriving the kinematic parameters we also included different line-fitting approaches. In particular, we considered all possible ways to combine the wavelength and the velocity dispersion parameters allowing them to be free to vary or keeping them fixed according to the atomic physics.

The main results of the present study can be summarized as follows.

  • When comparing the kinematic deviations (for both Hα and [NII] lines) derived for the raw unsubtracted data (gas and star; no stellar subtraction is applied) with those derived when applying different stellar-subtraction methods for the whole sample of spectra we see that the kinematic results obtained with FIT3D are very similar to that derived in the STARLIGHT (MILES) case, whereas high kinematic deviations are found when using the STARLIGHT (STELIB) and pPXF.

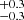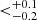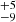  • When averaging over all cases, the velocity dispersion σ is the parameter most affected by the choice of the different combinations of method and line-fitting approach, whose deviations are found to be in the range − 0.3 + 0.3 $ ^{+0.3}_{-0.3} $ Å, while the wavelength λ parameter is less affected ( < − 0.2 + 0.1 $ { < }^{+0.1}_{-0.2} $ Å or − 9 + 5 $ ^{+5}_{-9} $ km s−1).

  • When averaging over all methods, the kinematic deviations obtained for the Hα and [NII] lines (⟨δλm⟩, ⟨δσm⟩) show point–symmetric distribution for the cases [1]–[4] and the cases [2]–[3].

  • When analyzing the kinematic results for each individual spectrum we derive a larger dispersion (error bars) in the kinematic parameters when the line taken into account shows a low S/N: this was the case for both Hα and [NII] lines, deriving a typical value of ≲0.2 Å. These uncertainties represent the systemic error associated to the choice of a specific stellar-subtraction method.

The implications of these results allow us to draw the following conclusions.

  1. Subtraction of the stellar continuum is not crucial when properly deriving the kinematics of the ionized gas component, although it is when the real flux of the line has to be recovered; however, determination of the Hα width is relatively severely affected by the choice of the stellar-subtraction method. This factor has to be considered in the presence of an outflow.

  2. Any method (including none) can be used to measure the gas kinematics as long as an additional term ( 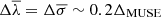Δ λ ¯ = Δ σ ¯ ∼ 0.2 Δ MUSE $ \Delta\overline\lambda=\Delta\overline\sigma\sim0.2\Delta_{\mathrm{MUSE}} $) is added to the error budget. Further analysis with other local sources observed with MUSE and other instruments should be considered to establish the validity of this equation.

  3. The kinematic results obtained from combining the line-fitting results of the Hα-[NII] complex show a robust determination of the global kinematic properties, as the strongest (and thus more stable) line tends to dominate the result and the most extreme deviations, which could be derived when individual lines are considered, are thus diluted. This is supported by the fact that the [NII] line is not affected by stellar absorption.

1

This galaxy was previously observed with the integral field spectrograph PMAS/PPak mounted on the 3.5 m telescope at the Calar Alto Observatory. It is part of the Third Public Data Release (DR3) of the Calar Alto Legacy Integral Field Area (CALIFA) survey (Sánchez et al. 2016b).

2

The Hα flux emission is actually the flux peak of the line having removed the continuum emission computed in a region close to the Hα-[NII] complex.

3

See the MUSE spectral resolution (R) as a function of the wavelength at: https://www.eso.org/sci/facilities/paranal/instruments/muse/inst.html. At the Hα wavelength, it corresponds to a spectral resolution R ∼ 2500, deriving a FWHM of 2.6 Å.

4

Flux ratios were computed applying the most general line-fitting approach (case [4]; see Sect. 3.3).

5

Specifically, the pipeline Pipe3D was used which is based on the FIT3D code. http://www.astroscu.unam.mx/~sfsanchez/FIT3D/

8

The intrinsic spectral resolution is slightly lower than the theoretical one (FWHM ∼ 2.2 Å).

9

The STELIB stellar library can be found at http://webast.ast.obs-mip.fr/stelib.

10

The MILES stellar library can be found at http://miles.iac.es/pages/webtools/tune-ssp-models.php.

11

Available at http://pleiadi.pd.astro.it/ based on the (solar scaled mixture) tracks from Bertelli et al. (1994) and Girardi et al. (2000), respectively.

12

The GRANADA library is a high-resolution library.

13

Geneva isochrones were computed with the isochrone program presented in Meynet (1995) and they follow the prescriptions quoted in Cerviño et al. (2001) from the evolutionary tracks from Schaller et al. (1992), Charbonnel et al. (1993), Schaerer et al. (1993a,b).

14

This model is considered a “modified” version of the BC03 models (i.e., CB07; see Bruzual 2007 for further details).

15

We do not discuss the results of [NII]λ6548Å since this line is three times fainter than [NII]λ6583Å (according to atomic physics) and is subjected to higher uncertainties in the fit. Furthermore, in most cases, it would share the same kinematics as the [NII]λ6583Å line.

Acknowledgments

We thank the anonymous referee for useful comments and suggestions which helped us to improve the quality and presentation of the manuscript. This paper is based on observations carried out at the European Southern Observatory, Paranal (Chile), Program 60.A-9100(B) with MUSE at Very Large Telescope (VLT). This research made use of the NASA/IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. EB acknowledges support from the Spanish Ministerio de Economía y Competitividad through the grant AYA2016-79724-C4-1-P as well as the exchange programme “Study of Emission–Line Galaxies with Integral–Field Spectroscopy” (SELGIFS, FP7–PEOPLE–2013–IRSES–612701), funded by the EU through the IRSES scheme. YA is also supported by the Ramón y Cajal programme (RyC–2011–09461; Mineco, Spain). HIM wants to acknowledge the Mexican CONACyT grant (Ciencia Básica) 285080 and PAPIIT–DGAPA–IA104118 (UNAM) project for funding the develop of the Pipe3D code. SFS thanks Conacyt CB–285080, FC–2016–01–1916 and PAPIIT–DGAPA–IN100519 projects.

References

  1. Aquino-Ortíz, E., Valenzuela, O., Sánchez, S. F., et al. 2018, MNRAS, 479, 2133 [NASA ADS] [CrossRef] [Google Scholar]
  2. Arribas, S., Colina, L., Monreal-Ibero, A., et al. 2008, A&A, 479, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Bacon, R., Bauer, S. M., Bower, R., et al. 2004, in Ground-based Instrumentation for Astronomy, eds. A. F. M. Moorwood, & M. Iye, Proc. SPIE, 5492, 1145 [NASA ADS] [CrossRef] [Google Scholar]
  4. Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Barrera-Ballesteros, J. K., García-Lorenzo, B., Falcón-Barroso, J., et al. 2015, A&A, 582, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Bekeraité, S., Walcher, C. J., Falcón-Barroso, J., et al. 2016, A&A, 593, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Belfiore, F., Westfall, K. B., Schaefer, A., et al. 2019, AJ, submitted [arXiv:1901.00866] [Google Scholar]
  8. Bellocchi, E., Arribas, S., & Colina, L. 2012, A&A, 542, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Bellocchi, E., Arribas, S., Colina, L., & Miralles-Caballero, D. 2013, A&A, 557, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Bellocchi, E., Arribas, S., & Colina, L. 2016, A&A, 591, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Bertelli, G., Bressan, A., Chiosi, C., Fagotto, F., & Nasi, E. 1994, A&AS, 106, 275 [NASA ADS] [Google Scholar]
  12. Boles, T., Nakano, S., & Itagaki, K. 2005, Cent. Bureau Electron. Telegrams, 275 [Google Scholar]
  13. Bournaud, F., Chapon, D., Teyssier, R., et al. 2011, ApJ, 730, 4 [NASA ADS] [CrossRef] [Google Scholar]
  14. Bruzual, G. 2007, in From Stars to Galaxies: Building the Pieces to Build Up the Universe, eds. A. Vallenari, R. Tantalo, L. Portinari, & A. Moretti, ASP Conf. Ser., 374, 303 [NASA ADS] [Google Scholar]
  15. Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
  16. Cairós, L. M., Caon, N., & Weilbacher, P. M. 2015, A&A, 577, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Cappellari, M. 2017, MNRAS, 466, 798 [NASA ADS] [CrossRef] [Google Scholar]
  18. Cappellari, M., & Emsellem, E. 2004, PASP, 116, 138 [NASA ADS] [CrossRef] [Google Scholar]
  19. Cappellari, M., McDermid, R. M., Alatalo, K., et al. 2013, MNRAS, 432, 1862 [NASA ADS] [CrossRef] [Google Scholar]
  20. Cazzoli, S., Arribas, S., Colina, L., et al. 2014, A&A, 569, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Cerviño, M., Gómez-Flechoso, M. A., Castander, F. J., et al. 2001, A&A, 376, 422 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Ceverino, D., Dekel, A., & Bournaud, F. 2010, MNRAS, 404, 2151 [NASA ADS] [Google Scholar]
  23. Charbonnel, C., Meynet, G., Maeder, A., Schaller, G., & Schaerer, D. 1993, A&AS, 101, 415 [NASA ADS] [Google Scholar]
  24. Cid Fernandes, R., Gu, Q., Melnick, J., et al. 2004, MNRAS, 355, 273 [NASA ADS] [CrossRef] [Google Scholar]
  25. Cid Fernandes, R., Mateus, A., Sodré, L., Stasińska, G., & Gomes, J. M. 2005, MNRAS, 358, 363 [NASA ADS] [CrossRef] [Google Scholar]
  26. Cid Fernandes, R., Pérez, E., García Benito, R., et al. 2013, A&A, 557, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Colina, L., Arribas, S., & Monreal-Ibero, A. 2005, ApJ, 621, 725 [NASA ADS] [CrossRef] [Google Scholar]
  28. Cresci, G., Marconi, A., Zibetti, S., et al. 2015, A&A, 582, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Dekel, A., Sari, R., & Ceverino, D. 2009a, ApJ, 703, 785 [Google Scholar]
  30. Dekel, A., Birnboim, Y., Engel, G., et al. 2009b, Nature, 457, 451 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  31. Epinat, B. 2011, IAU Symp., 277, 128 [NASA ADS] [Google Scholar]
  32. Epinat, B., Contini, T., Le Fèvre, O., et al. 2009, A&A, 504, 789 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Falcón-Barroso, J., Sánchez-Blázquez, P., Vazdekis, A., et al. 2011, A&A, 532, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Flores, H., Hammer, F., Puech, M., Amram, P., & Balkowski, C. 2006, A&A, 455, 107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Förster Schreiber, N. M., Genzel, R., Bouché, N., et al. 2009, ApJ, 706, 1364 [NASA ADS] [CrossRef] [Google Scholar]
  36. Galbany, L., Anderson, J. P., Rosales-Ortega, F. F., et al. 2016, MNRAS, 455, 4087 [NASA ADS] [CrossRef] [Google Scholar]
  37. Genzel, R., Tacconi, L. J., Rigopoulou, D., Lutz, D., & Tecza, M. 2001, ApJ, 563, 527 [NASA ADS] [CrossRef] [Google Scholar]
  38. Girardi, L., Bressan, A., Bertelli, G., & Chiosi, C. 2000, A&AS, 141, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Girardi, L., Bertelli, G., Bressan, A., et al. 2002, A&A, 391, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Glazebrook, K. 2013, PASA, 30, e056 [NASA ADS] [CrossRef] [Google Scholar]
  41. Gomes, J. M., Papaderos, P., Kehrig, C., et al. 2016, A&A, 588, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. González Delgado, R. M., & Cid Fernandes, R. 2010, MNRAS, 403, 797 [NASA ADS] [CrossRef] [Google Scholar]
  43. González Delgado, R. M., Cerviño, M., Martins, L. P., Leitherer, C., & Hauschildt, P. H. 2005, MNRAS, 357, 945 [NASA ADS] [CrossRef] [Google Scholar]
  44. González Delgado, R. M., Pérez, E., Cid Fernandes, R., et al. 2017, A&A, 607, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Kartaltepe, J. S., Dickinson, M., Alexander, D. M., et al. 2012, ApJ, 757, 23 [CrossRef] [Google Scholar]
  46. Kereš, D., Katz, N., Weinberg, D. H., & Davé, R. 2005, MNRAS, 363, 2 [NASA ADS] [CrossRef] [Google Scholar]
  47. Le Borgne, J.-F., Bruzual, G., Pelló, R., et al. 2003, A&A, 402, 433 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Lemoine-Busserolle, M., & Lamareille, F. 2010, MNRAS, 402, 2291 [NASA ADS] [CrossRef] [Google Scholar]
  49. Lemoine-Busserolle, M., Bunker, A., Lamareille, F., & Kissler-Patig, M. 2010, MNRAS, 401, 1657 [NASA ADS] [CrossRef] [Google Scholar]
  50. Leung, G. Y. C., Leaman, R., van de Ven, G., et al. 2018, MNRAS, 477, 254 [NASA ADS] [CrossRef] [Google Scholar]
  51. Levy, R. C., Bolatto, A. D., Teuben, P., et al. 2018, ApJ, 860, 92 [NASA ADS] [CrossRef] [Google Scholar]
  52. López-Cobá, C., Sánchez, S. F., Cruz-González, I., et al. 2017a, ApJ, 850, L17 [NASA ADS] [CrossRef] [Google Scholar]
  53. López-Cobá, C., Sánchez, S. F., Moiseev, A. V., et al. 2017b, MNRAS, 467, 4951 [NASA ADS] [Google Scholar]
  54. Maiolino, R., Russell, H. R., Fabian, A. C., et al. 2017, Nature, 544, 202 [NASA ADS] [CrossRef] [Google Scholar]
  55. Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [NASA ADS] [Google Scholar]
  56. Martins, L. P., González Delgado, R. M., Leitherer, C., Cerviño, M., & Hauschildt, P. 2005, MNRAS, 358, 49 [NASA ADS] [CrossRef] [Google Scholar]
  57. Meynet, G. 1995, A&A, 298, 767 [NASA ADS] [Google Scholar]
  58. Modjaz, M., Kirshner, R., Challis, P., & Calkins, M. 2005, Cent. Bureau Electron. Telegrams, 276 [Google Scholar]
  59. Ocvirk, P., Pichon, C., Lançon, A., & Thiébaut, E. 2006, MNRAS, 365, 46 [NASA ADS] [CrossRef] [Google Scholar]
  60. Ocvirk, P., Pichon, C., & Teyssier, R. 2008, MNRAS, 390, 1326 [NASA ADS] [Google Scholar]
  61. Pérez, E., Cid Fernandes, R., González Delgado, R. M., et al. 2013, ApJ, 764, L1 [NASA ADS] [CrossRef] [Google Scholar]
  62. Poggianti, B. M., Moretti, A., Gullieuszik, M., et al. 2017, ApJ, 844, 48 [NASA ADS] [CrossRef] [Google Scholar]
  63. Puech, M., Hammer, F., Lehnert, M. D., & Flores, H. 2007, A&A, 466, 83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Rupke, D. S. N., & Veilleux, S. 2013, ApJ, 768, 75 [NASA ADS] [CrossRef] [Google Scholar]
  65. Sánchez, S. F., Pérez, E., Sánchez-Blázquez, P., et al. 2016a, Rev. Mex. Astron. Astrofis., 52, 21 [NASA ADS] [Google Scholar]
  66. Sánchez, S. F., García-Benito, R., Zibetti, S., et al. 2016b, A&A, 594, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Sánchez, S. F., Pérez, E., Sánchez-Blázquez, P., et al. 2016c, Rev. Mex. Astron. Astrofis., 52, 171 [Google Scholar]
  68. Sánchez-Blázquez, P., Peletier, R. F., Jiménez-Vicente, J., et al. 2006, MNRAS, 371, 703 [NASA ADS] [CrossRef] [Google Scholar]
  69. Sarzi, M., Allard, E. L., Knapen, J. H., & Mazzuca, L. M. 2007, MNRAS, 380, 949 [NASA ADS] [CrossRef] [Google Scholar]
  70. Schaerer, D., Meynet, G., Maeder, A., & Schaller, G. 1993a, A&AS, 98, 523 [NASA ADS] [Google Scholar]
  71. Schaerer, D., Charbonnel, C., Meynet, G., Maeder, A., & Schaller, G. 1993b, A&AS, 102, 339 [NASA ADS] [Google Scholar]
  72. Schaller, G., Schaerer, D., Meynet, G., & Maeder, A. 1992, A&AS, 96, 269 [Google Scholar]
  73. Shapiro, K. L., Genzel, R., Förster Schreiber, N. M., et al. 2008, ApJ, 682, 231 [NASA ADS] [CrossRef] [Google Scholar]
  74. Shapiro, K. L., Genzel, R., Quataert, E., et al. 2009, ApJ, 701, 955 [NASA ADS] [CrossRef] [Google Scholar]
  75. Tacconi, L. J., Neri, R., Chapman, S. C., et al. 2006, ApJ, 640, 228 [NASA ADS] [CrossRef] [Google Scholar]
  76. Tacconi, L. J., Genzel, R., Smail, I., et al. 2008, ApJ, 680, 246 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  77. Vazdekis, A. 1999, ApJ, 513, 224 [NASA ADS] [CrossRef] [Google Scholar]
  78. Vazdekis, A., Cenarro, A. J., Gorgas, J., Cardiel, N., & Peletier, R. F. 2003, MNRAS, 340, 1317 [NASA ADS] [CrossRef] [Google Scholar]
  79. Vazdekis, A., Sánchez-Blázquez, P., Falcón-Barroso, J., et al. 2010, MNRAS, 404, 1639 [NASA ADS] [Google Scholar]
  80. Walcher, C. J., Böker, T., Charlot, S., et al. 2006, ApJ, 649, 692 [NASA ADS] [CrossRef] [Google Scholar]
  81. Zhu, L., Ven, G. V. D., Bosch, R. V. D., et al. 2018, Nat. Astron., 2, 233 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Complementary line-fitting results

Here we present complementary kinematic results which have not been shown in the main text. In Fig. A.1 we present the line-fitting results obtained for the spectrum “a” as an example when considering cases 2,3 and 4 applied to the Hα-[NII] complex. This kind of analysis has been applied to the whole sample of spectra to derive the kinematic results discussed in the text.

thumbnail Fig. A.1.

(General comments about the panels as in Fig. 2) Line-fitting results for the spectrum “a” obtained following the assumptions of case 2 [λ free, σ fixed] (top), case 3 [λ fixed, σ free] (middle), and case 4 [λ and σ free] (bottom). For each case and method the centroid of the Hα and [NII] lines is highlighted using the dashed lines. The line-fitting results are shown using the colored solid line: the “unsubtracted” data are in orange, FIT3D data in green, STARLIGHT (MILES) data in dark blue, STARLIGHT (STELIB) data in magenta and pPXF data in red.

In Fig. A.2 we show the kinematic results (λrest, σobs) obtained for all spectra when applying the four cases for the five methods. When no stellar-subtraction method (Unsubtracted) is applied to the Hα line, we derive the smallest value of the velocity dispersions (i.e., σ ∼ 1.3 Å) followed by that obtained when applying the STARLIGHT (MILES) method. When considering the pPXF routine we obtain the highest velocity dispersion (i.e., σ ∼ 1.7 Å). The [NII] velocity dispersion values cover a similar range (1.4–1.8 Å) and show an analogous trend to that derived for the Balmer line.

thumbnail Fig. A.2.

Individual kinematic values for the Hα (top) and [NII] (bottom) lines as derived from combining the four cases with the different methods. The error bar for each value is derived from the line-fitting method (see text for details). The symbol types are described in the text. The color code is as in previous figures: the “unsubtracted” data are in orange, FIT3D data in green, STARLIGHT (MILES) data in dark blue, STARLIGHT (STELIB) data in magenta and pPXF data in red.

We also present in Tables A.1–A.3 the main results obtained when combining different line-fitting approaches with different stellar-subtraction methods. In particular, in Table A.1 the respective mean values for the wavelength and width of the two emission lines are shown for all different cases and methods. In Tables A.2 and A.3 we complement the information given in the previous table considering the mean values of the four cases for each method and vice versa (i.e., mean values of the five methods for each case).

Table A.1.

Mean value (and standard deviations) for the Hα and [NII] lines among the different methods and different cases.

Table A.2.

Mean values (and standard deviations) for the Hα and [NII] lines when considering the four cases of line fitting for each method.

Table A.3.

Mean values (and standard deviations) for Hα and [NII] lines when considering the five methods for each line-fitting case.

Appendix B: Chi-square results

In this section we present the results obtained for each spaxel when computing the chi-square ( χ2) values in order to test which stellar continuum subtraction code most faithfully explains the raw observed data (within the errors).

The goodness of the fits has been evaluated by means of the reduced χ2 (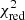 χ red 2 $ \chi^2_{\rm red} $), where the number of degrees of freedom are the number of data points used in the fit, following the equation:

χ red 2 = ∑ i = 1 N λ ( O i − M i σ i ) 2 / N λ , $$ \begin{aligned} \chi ^2_{\rm red} = \sum _{i=1}^{N_\lambda } \left( \frac{O_i - M_i}{\sigma _i}\right)^2{/}N_\lambda , \end{aligned} $$(B.1)

where Nλ is the number of observed data points, Oi and Mi are the raw observed flux data and the total flux model values for the ith point, and σi is the corresponding observed error.

We constrain the derivation of the 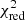χ red 2 $ \chi^2_{\rm red} $ values in the range defined by the lines of our interest, which involves the Hα-[NII] complex (rest frame wavelength range from 6540 Å to 6600 Å).

In particular, the total model emission in the wavelength range of our interest (Mi) is given by the combination of the stellar continuum model (Mi, ⋆) and the pure gas model (Mi, gas) emissions. The pure gas emission (Mi, gas) was derived as the average of the models obtained when applying the four line-fitting cases (Nc = 4, see text for details). Thus, each model can be described as follows:

M i = M i , ⋆ + ∑ k = 1 N c M k i , gas / N c = M i , ⋆ + M i , gas . $$ \begin{aligned} M_i = M_{i,\star } + \sum _{k=1}^{N_c} M_{k}^{i,\mathrm{gas}}/N_c = M_{i,\star } + M_{i,\mathrm{gas}}. \end{aligned} $$(B.2)

In Figs. B.1 and B.1 we compare the data Oi with the different models Mi, derived as described in Eq. (B.2), for each spaxel. The χ values as a function of the wavelength (λ) are also shown for each model.

thumbnail Fig. B.1.

Top panels: comparison between the raw observed data (within the errors; shaded gray area) and the results derived when using the five models. The color code is as in previous figures (Unsubtracted model is in orange, FIT3d is in green, STARLIGHT/MILES in dark blue, STARLIGHT/STELIB in magenta and pPXF is in red). The vertical dotted lines identify the rest–frame wavelength of the Hα-[NII] complex. Bottom panels: Chi ( χ) distribution obtained for each method in the rest frame wavelength range 6540–6600 Å (see text in Appendix B). The vertical dot lines identify the rest–frame wavelength of the Hα-[NII] complex. The horizontal area highlighted by the dashed gray lines represents the ±1 χ range values.

thumbnail Fig. B.1.

continued.

The reduced chi-square 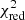χ red 2 $ \chi^2_{\rm red} $ values for all spaxels are reported in Table B.1 and they are also shown in Fig. B.2. The best solution (lowest 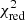χ red 2 $ \chi^2_{\rm red} $) as well as the second-best 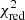χ red 2 $ \chi^2_{\rm red} $ results are highlighted in Table B.1.

thumbnail Fig. B.2.

Reduced chi-square distribution for each individual spaxel as derived when applying the five stellar-subtraction methods (color-coded as in Fig. B.1). The gray area represents the range of values covered by the mean chi-square within the respective standard deviation derived for each ith spaxel ( χ ¯ i 2 ± Δ χ ¯ i 2 $ \overline\chi^2_i \pm \Delta\overline\chi^2_i $).

Our results suggest that for the majority of the spectra, especially those characterized by a log([NII]/Hα) ratio in between –0.49 and ∼0.0 (low Hα/[NII] ratio; spectra from a to f), the best solution is achieved when using the FIT3d method. The pPXF method seems to give good fits only when spectra with higher Hα/[NII] ratios are considered (i.e., j, k, l). In between these two ranges (i.e., spectra g, h, i) FIT3d and STARLIGHT (MILES and STELIB) methods derive the best fits.

However, the Unsubtracted model does not give good solutions in any case, deriving for the innermost spectra (i.e., from [a] to [d] with low Hα/[NII] ratio) the most discrepant results (a factor of ×∼2) among all methods considered in this analysis. When considering spectra with higher Hα/[NII] ratios, the Unsubtracted model can also give reasonable secondary fits in a few cases, although for the majority of the spectra the best candidates for a secondary best 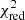χ red 2 $ \chi^2_{\rm red} $ are FIT3D and STARLIGHT (MILES and STELIB).

Table B.1.

Reduced chi-square 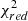χ red 2 $ \chi^2_{red} $ values for the different spaxels and models.

All Tables

Table 1.

Set of SSP models and stellar libraries used for the spectral fitting.

In the text
Table 2.

Different cases considered for the line-fitting analysis for the wavelength and for the width.

In the text
Table 3.

Mean values and standard deviations for the wavelength and line width of the Hα and [NII] emission lines obtained when combining all line-fitting cases and stellar-continuum subtraction methods for each individual spaxel.

In the text
Table 4.

Mean and standard deviation of the mean kinematic results averaged over all individual spectra.

In the text
Table 5.

Mean and root mean square values for each stellar-subtraction method.

In the text
Table 6.

Mean and root mean square values for each line-fitting case.

In the text
Table A.1.

Mean value (and standard deviations) for the Hα and [NII] lines among the different methods and different cases.

In the text
Table A.2.

Mean values (and standard deviations) for the Hα and [NII] lines when considering the four cases of line fitting for each method.

In the text
Table A.3.

Mean values (and standard deviations) for Hα and [NII] lines when considering the five methods for each line-fitting case.

In the text
Table B.1.

Reduced chi-square χ red 2 $ \chi^2_{red} $ values for the different spaxels and models.

In the text

All Figures

thumbnail Fig. 1.

Top panel: continuum MUSE image of NGC 2906. The continuum image was obtained as the mean of the median values in two wavelength ranges: 5620–5750 Å and 6890–7000 Å. Left panel: nuclear peak shown by a cross symbol and the position of the supernova SN2005ip represented by the star symbol. A zoom of the region selected by the white box is shown on the right. Right panel: region showing the distribution of the spectra (white dots) which have been chosen for the analysis. Each spectrum is identified by a letter (a, b, ..., k, l) in order to allow the reader to easily find its position. Bottom panel: Hα peak emission of the same regions as described in the top figure.
In the text
thumbnail Fig. 2.

From left to right: Unsubtracted MUSE spectra at the different positions (identified by the letters; see Fig. 1) along with the pure gas spectra obtained from applying the three different stellar-subtraction methods, respectively: FIT3D, STARLIGHT (MILES and STELIB) and pPXF methods. The Hαλ6563 and the two forbidden [NII]λλ6548, 6583 lines are shown. The line-fitting results are shown using the colored solid line: the unsubtracted data are in orange, FIT3D data are in green, STARLIGHT (MILES) data are in dark blue, STARLIGHT (STELIB) data are in magenta, and pPXF data are in red. The line fitting case[1] (all parameters fixed) is considered. The flux is in units of 10−20 erg s−1 cm−2 Å−1 and the wavelength is in Å.
In the text
thumbnail Fig. 3.

As in Fig. 2.
In the text
thumbnail Fig. 4.

Kinematic results for the individual spectra when using different stellar-subtraction methods and line-fitting approaches for the Hα (top) and [NII] (bottom) emission lines. The four line-fitting cases and the five stellar-subtraction methods used are highlighted according to the different symbols and colors (as in Fig. 2), respectively (twenty values for each spectrum). The mean wavelength and dispersion ( λ ¯ i $ \overline\lambda_i $, σ ¯ i $ \overline\sigma_i $) as well as their standard deviation ( Δ λ ¯ i $ \Delta\overline\lambda_i $, Δ σ ¯ i $ \Delta\overline\sigma_i $) are represented using dashed light gray lines and the shaded area (light red and cyan), respectively.
In the text
thumbnail Fig. 5.

Trend of the linear (top) and fractional (bottom) dispersion values of the λ ( Δ λ ¯ i $ \Delta\overline\lambda_i $ and Δ λ ¯ i / λ ¯ i $ \Delta\overline\lambda_i/\overline\lambda_i $; left) and σ ( Δ σ ¯ i / σ ¯ i $ \Delta\overline\sigma_i/\overline\sigma_i $; right) parameters. For each spectrum the Hα values are in light red and the [NII] ones are in light blue.
In the text
thumbnail Fig. 6.

Left panels: mean kinematic results averaged over all individual spectra (see Table 4) for the Hα (top) and [NII] (bottom) emission lines. Right panels: results for different methods/cases separately, as indicated, for the Hα (top) and [NII] (bottom). Symbol shapes and colors denote case and method, respectively. Symbol types are as in Fig. 4.
In the text
thumbnail Fig. 7.

Top and middle panels: mean Hα and [NII] deviations obtained when averaging over all cases (left) and over all methods (right). Bottom panel: mean deviations of the Hα-[NII] complex for all cases (left) and all methods (right).
In the text
thumbnail Fig. 8.

Kinematic parameter deviations, Σ(λi, mc) and Σ(σi, mc) computed with respect to their mean values and normalized to the line-fitting errors derived using IDL for each individual spectrum. The mean deviations as well as their standard deviations are represented using dashed lines (light red for the Hα and cyan for the [NII] lines) and the shaded area in gray, respectively. Top panels: Hα results. Bottom panels: [NII] results.
In the text
thumbnail Fig. 9.

Corrected deviations Σ(λi, mc)i, mc and Σ(σi, mc)Corr for the Hα (top) and [NII] (bottom) lines derived by applying the same mean dispersion factor ( Δ λ ¯ = Δ σ ¯ ∼ 0.2 $ \Delta\overline\lambda=\Delta\overline\sigma\sim0.2 $ Å; see also Fig. 5) for the wavelength and the velocity dispersion. In this correction the dispersion generated from using different stellar-subtraction methods and line-fitting cases is included. The error bars are now ≲1 Å for all spectra and for both parameters (shaded light red and cyan areas for the Hα and [NII] lines, respectively). The mean corrected deviations are represented by dashed white lines for both lines.
In the text
thumbnail Fig. A.1.

(General comments about the panels as in Fig. 2) Line-fitting results for the spectrum “a” obtained following the assumptions of case 2 [λ free, σ fixed] (top), case 3 [λ fixed, σ free] (middle), and case 4 [λ and σ free] (bottom). For each case and method the centroid of the Hα and [NII] lines is highlighted using the dashed lines. The line-fitting results are shown using the colored solid line: the “unsubtracted” data are in orange, FIT3D data in green, STARLIGHT (MILES) data in dark blue, STARLIGHT (STELIB) data in magenta and pPXF data in red.
In the text
thumbnail Fig. A.2.

Individual kinematic values for the Hα (top) and [NII] (bottom) lines as derived from combining the four cases with the different methods. The error bar for each value is derived from the line-fitting method (see text for details). The symbol types are described in the text. The color code is as in previous figures: the “unsubtracted” data are in orange, FIT3D data in green, STARLIGHT (MILES) data in dark blue, STARLIGHT (STELIB) data in magenta and pPXF data in red.
In the text
thumbnail Fig. B.1.

Top panels: comparison between the raw observed data (within the errors; shaded gray area) and the results derived when using the five models. The color code is as in previous figures (Unsubtracted model is in orange, FIT3d is in green, STARLIGHT/MILES in dark blue, STARLIGHT/STELIB in magenta and pPXF is in red). The vertical dotted lines identify the rest–frame wavelength of the Hα-[NII] complex. Bottom panels: Chi ( χ) distribution obtained for each method in the rest frame wavelength range 6540–6600 Å (see text in Appendix B). The vertical dot lines identify the rest–frame wavelength of the Hα-[NII] complex. The horizontal area highlighted by the dashed gray lines represents the ±1 χ range values.
In the text
thumbnail Fig. B.1.

continued.
In the text
thumbnail Fig. B.2.

Reduced chi-square distribution for each individual spaxel as derived when applying the five stellar-subtraction methods (color-coded as in Fig. B.1). The gray area represents the range of values covered by the mean chi-square within the respective standard deviation derived for each ith spaxel ( χ ¯ i 2 ± Δ χ ¯ i 2 $ \overline\chi^2_i \pm \Delta\overline\chi^2_i $).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.