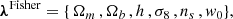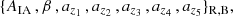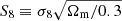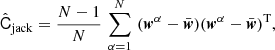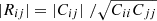| Issue |
A&A
Volume 624, April 2019
|
|
|---|---|---|
| Article Number | A30 | |
| Number of page(s) | 25 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201834714 | |
| Published online | 04 April 2019 | |
KiDS+GAMA: Intrinsic alignment model constraints for current and future weak lensing cosmology
1
Department of Physics and Astronomy, University College London, Gower Street, London WC1E 6BT, UK
e-mail: hj@star.ucl.ac.uk
2
Leiden Observatory, Leiden University, PO Box 9513, Leiden 2300 RA, The Netherlands
3
Department of Physics, University of Oxford, Keble Road, Oxford OX1 3RH, UK
4
Max-Planck-Institut für extraterrestrische Physik, Postfach 1312 Giessenbachstrasse, 85741 Garching, Germany
5
Scottish Universities Physics Alliance, Institute for Astronomy, University of Edinburgh, Blackford Hill, Edinburgh EH9 3HJ, UK
6
Argelander-Institut für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
Received:
23
November
2018
Accepted:
14
February
2019
We directly constrain the non-linear alignment (NLA) model of intrinsic galaxy alignments, analysing the most representative and complete flux-limited sample of spectroscopic galaxies available for cosmic shear surveys. We measure the projected galaxy position-intrinsic shear correlations and the projected galaxy clustering signal using high-resolution imaging from the Kilo Degree Survey (KiDS) overlapping with the GAMA spectroscopic survey, and data from the Sloan Digital Sky Survey. Separating samples by colour, we make no significant detection of blue galaxy alignments, constraining the blue galaxy NLA amplitude AIAB = 0.21−0.36+0.37 to be consistent with zero. We make robust detections (∼9σ) for red galaxies, with AIAR = 3.18−0.46+0.47, corresponding to a net radial alignment with the galaxy density field, and we find no evidence for any scaling of alignments with galaxy luminosity. We provide informative priors for current and future weak lensing surveys, an improvement over de facto wide priors that allow for unrealistic levels of intrinsic alignment contamination. For a colour-split cosmic shear analysis of the final KiDS survey area, we forecast that our priors will improve the constraining power on S8 and the dark energy equation of state w0, by up to 62% and 51%, respectively. Our results indicate, however, that the modelling of red/blue-split galaxy alignments may be insufficient to describe samples with variable central/satellite galaxy fractions.
Key words: gravitational lensing: weak / cosmology: observations / large-scale structure of Universe
© ESO 2019
1. Introduction
Light travelling towards Earth passes through the inhomogeneous universe, and consequent tidal gravitational field. In accordance with General Relativity, the light is differentially deflected, producing coherent distortions in the apparent shapes of source galaxies. This weak cosmological lensing – or cosmic shear – signal encodes information pertaining to the total matter distribution, universal geometry, and cosmic expansion and acceleration, as each evolves with redshift. Thus cosmic shear is one of the vital probes in the challenge to de-shroud the dark energy and dark matter species of the Λ cold dark matter (ΛCDM) cosmological model.
Since its first detections around the turn of the century (Bacon et al. 2000; Kaiser et al. 2000; Wittman et al. 2000; Van Waerbeke et al. 2000), cosmic shear has matured into a powerful tool for cosmology (Heymans et al. 2013; Jee et al. 2016; Hildebrandt et al. 2018; Köhlinger et al. 2017; Troxel et al. 2018; Hikage et al. 2019), been combined with complementary probes to great effect (Abbott et al. 2018; Joudaki et al. 2018; van Uitert et al. 2018) and formed the basis of design for many next-generation wide-field sky surveys (LSST; LSST Science Collaboration 2009, Euclid; Laureijs et al. 2011, WFIRST; Spergel et al. 2013).
The primary astrophysical systematic effect for cosmic shear is the intrinsic alignment of galaxies (Heavens et al. 2000; Croft & Metzler 2000; Catelan et al. 2001; Hirata & Seljak 2004). Cosmic shear relies upon picking up coherent, percent-level shape distortions (shears) over a statistical ensemble of galaxies. However, galaxies may interact with the gravitational field during formation, becoming aligned with their local environment. The same environment/structure also contributes to the lensing distortions observed in background galaxies. Both processes contaminate cosmic shear signals by sourcing non-random shear correlations in imaging data; between the intrinsic shapes of locally aligned galaxies (II), and between those intrinsic shapes and the gravitational shear field (GI). II correlations are restricted to physically close pairs, and are subdominant to the latter GI term, which can operate over wide separations in redshift, posing a greater threat of contamination for deep cosmic shear studies.
Tidal alignments, as they apply to galaxies, are thought to manifest through two principal mechanisms; galaxy halos are tidally (i) stretched (see Catelan et al. 2001), and (ii) torqued (see Schäfer 2009 for a review of the latter) by the interaction of the tidal shear quadrupole with the moment of inertia of the halo. Pressure-supported, red elliptical galaxies equilibrate their stellar distributions according to the ellipsoidal halo potential. Rotationally supported, blue spirals align their spin axes with the halo angular momentum (see Kiessling et al. 2015). Each type is thus imprinted with the alignments of the halo. The former effect is linear, and the latter quadratic in the matter density contrast, suggesting strong tidal alignment of blue galaxy spin axes at small scales, which quickly dissipate with increasing separation. These contrast with the further-reaching shape alignments of red galaxies. Both types of alignments should be stronger around more pronounced peaks of the matter distribution (Piras et al. 2018).
This picture is supported by observations; many studies show strong alignments out to 100 h−1 Mpc for SDSS galaxies, with luminous red galaxies (LRGs) and bright subsamples showing the largest alignment amplitudes (Mandelbaum et al. 2006; Hirata et al. 2007; Joachimi et al. 2011; Li et al. 2013; Singh et al. 2015). Significant (⩾3σ) alignments of nearby spiral galaxy spin axes, with reconstructed tidal fields, have been reported on scales ≲3 h−1 Mpc (Lee & Pen 2002; Lee & Erdogdu 2007; Lee 2011), but attempted measurements of large-scale intrinsic ellipticity correlations of spirals have thus far been consistent with zero (Hirata et al. 2007; Mandelbaum et al. 2011; Tonegawa et al. 2018). Hydrodynamical simulations corroborate these observational findings for red galaxies, but exhibit disagreements as to the form and amplitude of blue galaxy alignments (Chisari et al. 2015; Velliscig et al. 2015; Tenneti et al. 2016; Hilbert et al. 2017).
The risk of shear contamination by intrinsic alignment (IA) of galaxies, and the associated threat posed to cosmological parameter inference, has long been known (Heavens et al. 2000; Heymans et al. 2004; Hirata & Seljak 2004). Much work has been devoted to measuring the strength of IA and forecasting its impact under various scenarios of modelling or lack thereof (Joachimi & Bridle 2010; Joachimi et al. 2011; Kirk et al. 2012; Krause et al. 2016; Blazek et al. 2017). Broadly summarised, the findings suggest (i) significant biasing of cosmological parameters if IA are not accounted for; (ii) IA mitigation schemes, involving nuisance parameters for marginalisation, which will degrade cosmological constraints but can effectively mitigate biasing of parameter inference; (iii) joint analyses of shear probes with positional information and cross-correlations, to aid with degeneracy-breaking and self-calibration of IA models; (iv) the need for increasingly detailed modelling of IA – particularly with respect to non-linearities – accompanied by simulations (for model-testing and predictions) and observational constraints upon IA parameters over a long redshift baseline.
Recent, dedicated studies of cosmic shear have allowed for the effects of intrinsic alignments with nuisance parameterisations (Heymans et al. 2013; Jee et al. 2016; Joudaki et al. 2016; Hildebrandt et al. 2018; Troxel et al. 2018; Samuroff et al. 2018). The currently preferred models, with wide prior ranges, wield great power to modulate lensing observables – this has resulted in heavy degradation of cosmological constraining power. Moreover, we cannot be certain that other systematic effects, known (e.g. photo-z errors – see Efstathiou & Lemos 2018; van Uitert et al. 2018) or otherwise, are not leaking into the IA parameterisations. Informative priors for the models are the first step to assuaging these concerns, and they must be derived from galaxy samples representative of cosmic shear datasets.
This work aims to motivate such a prior for current and future studies by constraining the alignment amplitudes exhibited by the flux-limited GAMA spectroscopic sample (Driver et al. 2011), with high-resolution KiDS (de Jong et al. 2013) imaging and shapes. We supplement our GAMA data with galaxies from the SDSS Main sample (York et al. 2000; Strauss et al. 2002) – the only other readily available, wide-area, flux-limited, spectroscopic dataset. This study is made unique by the lack of selection a priori, high completeness (>98%) and spectroscopic redshifts of GAMA and SDSS Main, and so yields a set of constraints which are uniquely instructive for future shear studies. With the aforementioned dependencies of alignments in mind, we also split our samples by colour and redshift, and fit to them with colour-specific parameters, in an effort to more comprehensively describe the contributions of the two galaxy populations.
We measure galaxy position-intrinsic shear correlations in our samples, using galaxies as a proxy to the total matter density field and measuring their tendency to align with that field over a range of scales. We simultaneously fit to clustering measurements in the same samples for self-calibration of the galaxy bias, elsewise degenerate with the intrinsic alignment amplitude. We fit to our signals with the non-linear alignment (NLA) model (Hirata & Seljak 2004; Bridle & King 2007), with and without a luminosity power-law. We forecast, via Fisher matrix analysis, the improvement in cosmological parameter constraints for a finished KiDS survey, when adopting our derived IA constraints as informative priors.
The structure of this paper is as follows; we describe our galaxy survey data in Sect. 2, along with our measurement pipeline. Section 3 details our models and methods of fitting, and we summarise the results of fitting in Sect. 4. Section 5 outlines our forecasting for a future shear analysis, and our concluding remarks are presented in Sect.6.
Throughout our intrinsic alignment analysis, we work with rest-frame AB magnitudes, k-corrected to z = 0, and assume a flat ΛCDM cosmology with Ωm = 0.25, h = 0.7, Ωb = 0.044, ns = 0.95, σ8 = 0.8, w0 = −1 and wa = 0. This is the cosmology adopted by the MICE1 simulations, whose mocks we make use of in our analysis (see Appendix A.2). It is also similar to that assumed by Joachimi et al. (2011), allowing for direct comparison of intrinsic alignment constraints.
2. Data
2.1. KiDS +GAMA
The ongoing Kilo Degree Survey (KiDS; de Jong et al. 2017) is a wide-field optical imaging survey, taking data in four passbands (ugri) with the OmegaCAM camera at the VLT Survey Telescope (VST). The VST-OmegaCAM system is optimised for producing 1 deg2 images of exceptional quality, facilitating accurate galaxy shape measurements for the primary science driver of KiDS: weak lensing studies.
KiDS aims to image 1350 deg2 of sky in 2 rougly equal-sized strips. KiDS-North, centered on the celestial equator, shares complete overlap with the Galaxy and Mass Assembly (GAMA; Driver et al. 2011) equatorial fields – a total 180 deg2, split equally between G9, G12 and G15. GAMA is a now-complete spectroscopic survey which operated on the Anglo-Australian Telescope, with the AAOmega spectrograph. GAMA galaxies possess thoroughly tested spectroscopic redshifts and are highly complete (>98%) in the r-band limit r < 19.8.
Our KiDS+GAMA dataset consists of the final release (Liske et al. 2015), equatorial GAMA spectroscopic sample, with shapes measured from KiDS-4502 imaging. Galaxy shapes are measured from r-band images, for which the best dark-time seeing conditions are reserved in KiDS. Singh & Mandelbaum (2016) analysed the SDSS-III BOSS LOWZ luminous red galaxy (LRG) sample (Alam et al. 2015) with different shape measurement methods, finding variability in ellipticities, intrinsic alignment conclusions and the impacts of observational systematics. The connection between such variabilities and the radial weighting employed in shape estimation is explored in our companion paper: Georgiou et al. (2019).
We measure shapes using the moments-based DEIMOS (DEconvolution In MOments Space) method introduced by Melchior et al. (2011). We briefly describe the DEIMOS method here, as applied to KiDS+GAMA, and refer the reader to Georgiou et al. (2019) for details of the production of our ellipticity catalogue. The moments Q of the distribution of brightness (flux) G(x) across an image, where x = (x , y) is a coordinate vector, are expressed in Cartesian coordinates as
where n = i + j gives the order of the moment. One recovers the complex ellipticity of an object from 2nd-order brightness moments as
which relates to the semi-major a and semi-minor b axes as |ϵ| = (a − b)(a + b)−1.
Observed galaxy flux profiles G*(x) are distorted by convolution with the point spread function P(x) – determined by observing conditions, telescope optics and detector properties, the PSF describes the blurring of point-like sources in imaging. The PSF-convolved flux profile is
Melchior et al. (2011) transform the flux profile into Fourier space and show, with the convolution theorem, that the moments of the observed flux distribution 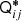 are
are
where {P}ij denotes the moments of the PSF. Thus the nth-order deconvolved moments Qij of the image can be recovered from the image- and PSF-moments up to the same order. In practice, one must also account for noise in the image, from sky background, pixel noise etc. The pixel signal-to-noise ratio (SNR) is lowest at large distances from the galaxy centroid, which would tend to dominate the measurement of 2nd-order brightness moments (Eq. (1)). We suppress pixel noise using Gaussian elliptical weight functions W(x), and recover an approximation to the unweighted brightness profile by computing a truncated Taylor expansion of W−1(x) (see Georgiou et al. 2019).
Galaxy shapes can be obscured by overlapping objects in images. These shapes can still be measured by applying masks to the nuisance objects, but the loss of information could have an impact upon the quality of the shape measurement. We verify that excluding blended galaxies – where isophotal radii overlap – does not significantly change our measurements of alignment correlation functions, and continue to include these galaxies in our analysis. We refer the reader to Georgiou et al. (2019) for further details on our use of weight functions and associated bias considerations, deblending, and any other details of the shape measurements.
We choose a rest-frame colour cut of g − r > 0.66 on inspection of the colour-r-band absolute magnitude diagram, in order to cleanly isolate the red sequence (Fig. 1), and we define 2 redshift bins with edges [ 0.02 , 0.26 , 0.5 ] (see Appendix A for more detail on this choice). These cuts yield colour/redshift samples (Z1B, Z1R, Z2B, Z2R) of roughly equal size, and we apply the same colour cut to SDSS galaxies. For measuring position-intrinsic shear correlations in each sample, we define a “shapes” subset of galaxies residing in unmasked3 pixels (for details of the masking procedure, see Kuijken et al. (2015) We further exclude any galaxies flagged as having a bad shape measurement (see Georgiou et al. 2019), and correlate the remaining (∼85−87%) shapes against the positions of all galaxies in the same colour/redshift bin – the “density” sample. We also measure correlations against randomly distributed points, using random catalogues specifically designed for GAMA (Farrow et al. 2015), and randomly downsampled to retain at least 10× the number of galaxies in a corresponding galaxy sample. Where used in additional, demonstrative sample selections, stellar-mass estimates for GAMA galaxies are taken from StellarMassesLambdarv20 (Wright et al. 2017).
 |
Fig. 1. Left panel: galaxy rest-frame colour–magnitude diagram, where we choose a cut in g − r to isolate the red sequence in GAMA and SDSS. Right panel: sample absolute r-band magnitude-redshift diagram. The total distribution of GAMA and SDSS galaxies is shown, binned in hexagonal cells with a colour scale corresponding to the counts in cells. Coloured contours indicate 75% and 95% of galaxies in a sample. Colour/redshift cuts are shown as dashed green lines, and the apparent leakage of contours is due to the grid-size used in kernel density estimation. |
2.2. SDSS Main
The Sloan Digital Sky Survey (SDSS; York et al. 2000) imaged about π steradians of the sky, drift-scanning in five bands (ugriz), with the purpose-built, wide-field SDSS photometric camera (Gunn et al. 1998). Of the ∼1 million objects followed up spectroscopically, the Main galaxy sample (Strauss et al. 2002) was designed to be flux-limited and highly complete (>99%) to r < 17.77, thus forming a complementary dataset to GAMA, shallower and over a wider area of ∼3340 deg2. These are the same SDSS Main samples measured for IA by Mandelbaum et al. (2006), Hirata et al. (2007) and Joachimi et al. (2011), where the latter two works also included LRG-selected samples in their analysis. We make no magnitude selections, and employ a different colour-cut in our analysis, hence we re-measure the alignment signals. We use PSF-corrected ellipticity measurements made by Mandelbaum et al. (2005) with the REGLENS pipeline – REGLENS measures galaxy shapes via “re-Gaussianisation” (Hirata & Seljak 2003). This is a moments-based method, which assumes Gaussianity in the PSF and galaxy profiles, treating non-Gaussianities with perturbative corrections. We refer the reader to Hirata & Seljak (2003), Mandelbaum et al. (2005) for further details.
We define red and blue SDSS samples (SR, SB) with the same rest-frame cut at g − r = 0.66. The SDSS density samples retain galaxies with bad shapes flags, which are excluded from the shapes samples. Figure 1 illustrates the colour-redshift-magnitude spaces of our selected samples, which are detailed in Table 1.
Details of our density (bracketed numbers) and intrinsic shape field tracer samples, composed of GAMA and SDSS galaxies split by redshift and/or colour.
2.3. Estimators
We adapt the notation of Schneider et al. (2002), defining a bin filter Δrp, Π(x) = 1 for a pair separation vector x = (x∥ , x⊥) where the (absolute) comoving radial component x∥ is less than the maximum under consideration Πmax, and the comoving transverse component x⊥ satisfies rp/10Δlog(rp)/2 < x⊥ ⩽ rp × 10Δlog(rp)/2 for a transverse bin centred on rp (log-space bin width Δlog(rp) is constant). For any other separation vector, Δrp, Π(x) = 0. We adopt the estimator defined by Mandelbaum et al. (2006) 4, and given as
where we use subscripts to denote and index shape (s), density (d) and density-/shapes-random (r , rs) galaxy samples, and
gives the paircount between samples i and j, which is then normalised according to the relative sample populations5. The tangential shear component6γ+, ij of a galaxy i relative to the vector connecting it to a galaxy j is given as
where, for galaxy i, the ellipticity ϵi = ϵi1 + iϵi2 (see Sect. 2.1) and φij is the polar angle of the pair separation vector. Note that the sign convention here is γ+ > 0 for radial alignments, in contrast with the standard for galaxy-galaxy lensing. The shear responsivity 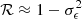 in Eq. (7) quantifies the response of galaxy ellipticities to gravitational shearing, for a given galaxy sample. The responsivity is doubled when ellipticities are measured via polarisation (see Mandelbaum et al. 2006), as is the case for our SDSS samples. The resulting shear corrections are then ≲8% for GAMA, and ≲35% for SDSS, respectively.
in Eq. (7) quantifies the response of galaxy ellipticities to gravitational shearing, for a given galaxy sample. The responsivity is doubled when ellipticities are measured via polarisation (see Mandelbaum et al. 2006), as is the case for our SDSS samples. The resulting shear corrections are then ≲8% for GAMA, and ≲35% for SDSS, respectively.
We consider our measurements in line-of-sight projection
thus compressing the measurement into fewer data points, with generally higher signal-to-noise ratios (S/N).
We test for alignment systematics by measuring (i) the position-intrinsic correlation cross-component wg× (replacing γ+ with γ× in Eq. (5), where γ× is the imaginary analogue to Eq. (7); equivalent to γ+ after a 45 degree rotation of the ellipticity), which must vanish on average since galaxy formation does not break parity. We also measure (ii) wg+ for galaxy pairs with large line-of-sight separations 60 ⩽ |Π| ⩽ 90 h−1 Mpc. Spectroscopic redshifts allow us to choose a narrower range for this test, relative to previous works (e.g. Joachimi et al. 2011), starting at 60 h−1 Mpc given recent detections of alignments on large transverse scales (Singh et al. 2015). One expects astrophysically induced alignment signals to be dominated by short-range correlations, and consistent with zero over much larger scales, providing the second, “large-Π” systematics test.
We measure galaxy clustering with the standard Landy & Szalay (1993) estimator
where the rp, Π binning of paircounts is implicit. Equation (9) is well known to improve the bias and covariance properties of the galaxy auto-correlation through subtraction of the random field from the density field, and this concept carries over to our alignment estimator (Eq. (5)).
Singh et al. (2017) demonstrated that the subtraction of the galaxy-galaxy lensing signal measured around random points (i.e. a randomly distributed lens sample) also holds advantages in reducing the impact of systematics and correlated shape noise, especially on large transverse scales. This is done in the context of galaxy-galaxy lensing; long-range lens clustering introduces noise through lensed, and therefore correlated, background shapes. The GI analogy would suppose that intrinsic shears of the shape sample are correlated over super-sample scales – e.g. galaxies aligning with filaments/knots etc. This correlated shape noise would show in the random-intrinsic correlation, and be subtracted by our estimator (Eq. (5)).
We compute the total projected correlation functions by summing over line-of-sight separations −60 ⩽ Π ⩽ +60 h−1 Mpc, in bins of ΔΠ = 4 h−1 Mpc (Eq. (8) and analogous for wgg) and consider the results in 11 log-spaced bins between 0.1 ⩽ rp ⩽ 60 h−1 Mpc.
We compute all intrinsic alignment correlations using our own code, and make use of the public SWOT7 (Coupon et al. 2012) kd-tree code for clustering correlations, which we verify against our own (brute-force) code and against external clustering measurements in GAMA (Farrow et al. 2015).
2.4. Covariances
We estimate signal covariances with delete-one jackknife methods, which we describe briefly here, referring the reader to Appendix A for more detail.
Jackknife samples are defined by the consecutive exclusions and replacements of many “patches” within the survey footprint, such that each sample constitutes most of the galaxy data. The covariance is thus estimated by considering the deviation from the mean signal upon removal of independent subsets of the data. Each subset must then correctly and independently sample the signal of interest; each patch must be larger than the largest scales under examination. Simultaneously, the number of patches must be much greater than the size of the data vector, or else estimates of the inverse covariance will suffer from excessive noise. Attempting to satisfy both requirements, we implement a 3D jackknife routine, slicing patches in redshift and multiplying the available number of independent subsets. We remain, however, unable to reliably sample large pair separations at low-redshift in GAMA (see Fig. A.1), thus we discard the largest scales (∼40−60 h−1 Mpc) for GAMA samples with a significant proportion of low-redshift galaxies – see Appendix A for more detail, and for assessments of the jackknife performance.
3. Modelling
We observe the weak lensing angular power spectrum as the sum of shear-shear (GG), intrinsic-intrinsic (II) and shear-intrinsic (GI) contributions, such that
for correlations between samples i and j. The cosmic shear GG term encodes the average coherent gravitational shearing of galaxies’ light by structure along the line-of-sight, and is the statistic of interest for cosmological analyses. Intrinsically correlated orientations of galaxies result in the extra intrinsic shear correlation II and interference GI terms. These angular power spectra are theoretically determined for a flat universe, by Limber projection of the matter Pδ, intrinsic PII and matter-intrinsic PδI power spectra, as
each weighted by an efficiency kernel describing the coincidence of sample redshift (comoving distance) distributions p(χ) and/or lensing efficiencies q(χ), where p(χ) dχ = p(z) dz and
for present-day Hubble parameter H0, matter energy-density fraction Ωm and comoving distances χ, with χh denoting the horizon distance. The redshift distributions of our galaxy samples are shown in Fig. A.1 as dashed red/blue histograms.
We constrain models for PδI by fitting to the real-space alignment and clustering correlation functions described in Sect. 2.3.
3.1. Tidal alignments
The linear alignment (LA) model assumes a linear relation between the tidal shearing of galaxies and the gravitational potential quadrupole at their epoch of formation. This form is motivated as follows: fluctuations in the large-scale potential govern the perturbation of halo ellipticites, within which galaxy ellipticities follow suit. With the large-scale fluctuations necessarily small, higher-order terms dwindle and the intrinsic shearing of galaxies by large-scale structure is thus assumed to be a localised, linear function of the potential. In the simplest case, this leads to intrinsic shear PII and cross matter-intrinsic shear PδI power spectra (Hirata & Seljak 2004)
and
respectively, where AIA is a free, dimensionless amplitude parameter, normalised to unity by the constant 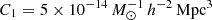 – this factor is derived by comparing to the work of Brown et al. (2002) who measured II correlations in the low-redshift (z ∼ 0.1) SuperCOSMOS survey (Hambly et al. 2001), where cosmic shear is negligible.
– this factor is derived by comparing to the work of Brown et al. (2002) who measured II correlations in the low-redshift (z ∼ 0.1) SuperCOSMOS survey (Hambly et al. 2001), where cosmic shear is negligible. 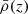 is the mean density of the universe and D(z) is the growth factor.
is the mean density of the universe and D(z) is the growth factor.
In the original LA model, Pδ(k, z) is the linear matter power spectrum. Hirata et al. (2007) and Bridle & King (2007) suggested and implemented a substitution of the non-linear corrected spectrum 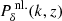 , birthing the non-linear alignment (NLA) model. Whilst without theoretical motivation, this model was seen to provide a better description of the alignments measured in LRG samples on scales approaching the non-linear. We conduct and present our analysis with both the LA and NLA models, choosing to focus on the NLA given its widespread use in the literature. Results between the N/LA models will differ only mildly for this work, since meaningful fits of these models must be restricted to quasi-linear scales – neither model provides a true consideration of non-linear evolution/dependence or of intra-halo baryonic physics (e.g. stellar/AGN feedback). However, the choice of model is expected to levy significant changes in cosmic shear analyses that extract a large fraction of their constraining power from highly non-linear scales. The development of appropriate models for IA remains an active topic of research.
, birthing the non-linear alignment (NLA) model. Whilst without theoretical motivation, this model was seen to provide a better description of the alignments measured in LRG samples on scales approaching the non-linear. We conduct and present our analysis with both the LA and NLA models, choosing to focus on the NLA given its widespread use in the literature. Results between the N/LA models will differ only mildly for this work, since meaningful fits of these models must be restricted to quasi-linear scales – neither model provides a true consideration of non-linear evolution/dependence or of intra-halo baryonic physics (e.g. stellar/AGN feedback). However, the choice of model is expected to levy significant changes in cosmic shear analyses that extract a large fraction of their constraining power from highly non-linear scales. The development of appropriate models for IA remains an active topic of research.
We make fits of the NLA and also a luminosity-dependent analogue, henceforth NLA-β, including a power-law scaling β on the average luminosity L of samples, such that
where Lpiv ∼ 4.6 × 1010 L⊙ is an arbitrary pivot luminosity, corresponding to an absolute r-band magnitude of −22 (see Table 1).
We note that fitting linear models to spiral galaxy alignments is at best an approximation to lowest order8, and that next-stage lensing studies should consider splitting the modelling of alignments to include a quadratic alignment prescription for blue galaxies – such an analysis was recently completed by Samuroff et al. (2018); applying the mixed alignment model of Blazek et al. (2017) to DESY1 data (Abbott et al. 2018), they find the first marginal evidence for quadratic alignments of both late- and early-type galaxies.
3.2. Line-of-sight projection
We project matter and matter-intrinsic power spectra along the line-of-sight using Hankel transformations
and jointly model position-intrinsic alignments and clustering, thereby self-calibrating for galaxy bias. Jn denotes an nth-order Bessel function of the first kind, and bg is the linear, assumed scale-independent galaxy bias. The weight function 𝒲(z), as derived by Mandelbaum et al. (2011), is given by
where p(z)’s are the normalised redshift probability distributions of the galaxy samples being correlated, i.e. a density and a shapes sample for alignments, or two density samples for clustering. The galaxy samples we analyse in this work are flux-limited, therefore p(z) does not increase as dVcom/dz – the gain in comoving volume with respect to redshift. χ(z) , χ′(z) are the comoving radial coordinate and its derivative with respect to z, such that χ2(z)χ′(z) is proportional to dVcom/dz. Thus, 𝒲(z) is inversely proportional to dVcom/dz and acts to down-weight higher redshifts, where flux-limited samples miss faint galaxies.
3.3. Likelihoods
We constrain the N/LA models, fitting to wg+ and wgg (see Sect. 2.3) by sampling multi-dimensional parameter posterior distributions, using the COSMOSIS9 (Zuntz et al. 2015) implementation of the affine-invariant EMCEE (Foreman-Mackey et al. 2013) Monte Carlo Markov chain sampler. The COSMOSIS framework supports the flexible construction of a pipeline to compute theoretical power spectra and other statistics, and to calculate likelihoods against a data vector whilst sampling over parameters. We exclude the first 30% of samples for a burn-in phase.
The non-linear processes unaccounted for by the N/LA models include non-linear density evolution and galaxy biasing, quadratic tidal torquing, and any other higher-order effects contributing to alignment signatures. The galaxy density-weighted sampling of the intrinsic alignment field is included at lowest order in the original derivation by Hirata & Seljak (2004), however Blazek et al. (2015) highlight additional, linear-scale, galaxy bias-dependent contributions in a perturbative expansion. In light of the models’ limitations, and inline with previous analyses, we limit our NLA (and LA) fits to transverse scales above 6 h−1 Mpc.
Our parameter vectors for the NLA/NLA-β (and LA/-β) models are then
where we fit a galaxy bias and “integral constraint” (IC) to the galaxy clustering measured in each sample i. The integral constraint is a free parameter, taking the form of a small additive scalar applied to the clustering correlation function, to correct for the effects of a partial-sky survey window (Roche & Eales 1999). Subscripts R, B denote a red and blue version of each parameter, which are fit to all relevant samples. This brings the total number of parameters to 14 (16) for the NLA (NLA-β)10. Previous dedicated IA studies have used galaxy clustering to fit and fix galaxy bias (e.g. Joachimi et al. 2011) – we instead opt to marginalise over galaxy biases and integral constraints, thereby propagating our uncertainty in these parameters into our IA model constraints. Since our samples form independent datasets, by virtue of colour separation and disjoint areas, we can reduce the dimensionality of the problem by fitting our models to red and blue samples separately.
We choose not to include a redshift power-law scaling ηother in our models, as has been done in previous works (Hirata et al. 2007; Joachimi et al. 2011; Mandelbaum et al. 2011), since the redshift baseline of our measurements is short – GAMA starts to become sparse after z ∼ 0.4. While the results of previous work do not preclude the possibility of a significant redshift evolution, we argue that there is good reason to expect it to be small. Tidal torque theories suggest angular momentum generation as the source of spiral galaxy alignments. Since the spinning-up of a proto-galaxy halo is a perturbative effect, these alignments exist in the initial conditions of the matter field. After collapse of the overdense region, the angular momentum of the galaxy dominates over tidal torquing effects, and the galaxy orientation should be “frozen-in”. Subsequently, only merger events should change the orientation of the galaxy.
Mergers would be expected to erase the memory of previous alignments, disrupt galaxy and halo angular momenta and prompt a relaxation phase. The system should relax into a configuration with a reduced spin magnitude, diluting the quadratic alignment signature (Cervantes-Sodi et al. 2010). However, with merger timescales much shorter than relaxation, the spiral quickly transitions to a pressure-supported elliptical. The stellar distribution will then gradually re-equilibrate according to the ellipsoidal halo potential, itself moulded by the tidal field.
Therefore we might expect to observe “fixed” blue galaxy alignments, opposite red galaxy alignments with their evolution tied to the tidal field (and divided out of our models by the growth factor), or some diluted middling alignment for transitioning galaxies, where the change of sign takes the amplitude close to zero. Joachimi et al. (2011) constrain ηother to be consistent with zero for early-type galaxies over a long redshift baseline. Mandelbaum et al. (2011) analysed late-type galaxy alignments in the WiggleZ survey (Drinkwater et al. 2010), with SDSS shapes, and also found ηother to be consistent with zero. Furthermore, their null detection at a mean redshift z̄ ∼ 0.6 was recently matched by a null detection from the FastSound galaxy redshift survey (Tonegawa et al. 2015) at z ∼ 1.4 (Tonegawa et al. 2018), suggesting no strong evolution of spiral galaxy alignments. Considering all of the above, we suggest that a physically motivated prior on ηother should be narrow and centred on zero.
4. IA constraints for flux-limited samples
With our aim to motivate tighter, more realistic priors for intrinsic alignment parameters, we fit the standard and the luminosity-dependent N/LA models to galaxy position-intrinsic shear and clustering correlations in KiDS+GAMA and SDSS Main. We compute signal detection significances across all scales, and restrict fits of the models to transverse scales > h−1 Mpc. Our various measurements are shown in Figs. 2–4. The results of fitting are shown in Figs. 5, 6 and Table 2.
 |
Fig. 2. Measured galaxy clustering for our blue (top panel) and red (bottom panel) galaxy samples. Solid curves illustrate the best-fit linear clustering per sample (Eq. (19)). The vertical dashed line indicates rp = 6 h−1 Mpc, below which scales are excluded from fitting (Sect. 3.3). |
 |
Fig. 3. Measured galaxy position-intrinsic shear correlations for our blue (top panel) and red (bottom panel) galaxy samples. Best-fit NLA models are shown as solid curves, and the vertical dashed line indicates rp = 6 h−1 Mpc, below which scales are excluded from fitting (Sect. 3.3). The best-fit LA model to SR is shown as a dot-dashed line. |
 |
Fig. 4. Galaxy clustering (top panel) and position-intrinsic shear correlations (bottom panel) measured in the full KiDS+GAMA and SDSS Main datasets. Solid lines illustrate the best-fit NLA model, and dot-dashed lines the LA. The vertical dashed line indicates rp = 6 h−1 Mpc, below which scales are excluded from fitting (Sect. 3.3). |
 |
Fig. 5. Posterior probability contours of our fitted galaxy bias bg, NLA amplitude A and luminosity power-law β parameters, for red (left panel) and blue (right panel) galaxies. The filled (unfilled) contours are for the NLA (NLA-β) models. Dashed grey lines mark values of zero for IA parameters. |
 |
Fig. 6. Constraints on the NLA model alignment amplitude AIA, from various subsamples of GAMA and SDSS (Table 1), plotted against sample properties. The constraints illustrated here are also given in Table B.1. Top left panel: AIA vs. shape sample red galaxy fraction. We interpolate (green line/shading) between our fits to blue (blue square) and red (red square) galaxy samples, according to |
NLA model parameter and galaxy bias 1D marginalised constraints for our samples, with 68% confidence intervals and the reduced χ2 (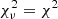 per degree of freedom) statistics for the global fit.
per degree of freedom) statistics for the global fit.
4.1. Clustering
Relating the matter-intrinsic power spectrum PδI to wg+ requires estimations of the galaxy bias bg of our density tracers. Hence we measure galaxy clustering in our density samples and perform fits of a linear, scale-independent bias with the full matter power spectrum (Eq. (19)). We verify that our clustering pipeline reproduces the GAMA measurements of Farrow et al. (2015) for their sample selection.
Figure 2 shows our measurements of wgg in GAMA and SDSS, with best-fit linear clustering overlaid. Our fits include the integral constraint correction (Sect. 3.3), which is small (|IC|≲3 h−1 Mpc) and therefore negligible on small scales. Fits of the linear clustering model are restricted to scales >6 h−1 Mpc, indicated by vertical dashed lines. Our sample galaxy bias fits are summarised in Table 2. The biases form a consistent and expected picture – more luminous samples are more biased at the same redshifts.
4.2. Alignments
Figure 3 shows our colour-split measurements of wg+, overlaid with the best-fitting NLA (solid lines). We also perform fits to our data with the LA model, shown as dot-dashed lines in Fig. 3 (to SR only) and Fig. 4. Table 3 lists signal detection significances for the alignment signals and systematics tests (described in Sect. 2.3).
Reduced χ2 statistics to assess the significance of signal detections against the null hypothesis (i.e. a zero-signal), for wg+ and for systematics tests; wg× and wg+ limited to large line-of-sight separations (60 ⩽ |Π| ⩽ 90 h−1 Mpc), denoted Π+.
4.2.1. Signals and NLA results
We find blue galaxy alignments to be consistent with zero, in agreement with previous studies of this population (Mandelbaum et al. 2011; Tonegawa et al. 2018). The NLA-β amplitude Aβ and power-law β are also consistent with zero, at 95% confidence. For blue galaxies on the whole, or for individual blue samples, we make no significant detections of wg+, whether restricting to linear scales, or considering the full range in rp (Table 3). Fits to GAMA-only: 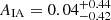 , and SDSS-only:
, and SDSS-only: 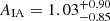 , are consistent with each other, and the total-fit, at 68% confidence.
, are consistent with each other, and the total-fit, at 68% confidence.
In agreement with previous work (Hirata et al. 2007; Joachimi et al. 2011), we measure a significantly positive amplitude of alignments for red galaxies, in both modes of fitting and at >95% confidence. The total significance of detection we find for red galaxy alignments is close to 9σ over the full range in rp, and 6.79σ when limited to linear scales (⩾6 h−1 Mpc). The β luminosity-scaling is found to be comfortably consistent with zero, and thus results in a poorer fit (owing to a lost degree of freedom) than for the 1-parameter NLA. This is in contrast with previous observations of near-linear scalings of red galaxy/LRG alignments with luminosity (e.g. Hirata et al. 2007; Joachimi et al. 2011; Singh et al. 2015). The perturbative IA model of Blazek et al. (2015) uncovered additional contributions to the observed large-scale intrinsic shape correlation, arising from source density weighting (Hirata & Seljak 2004) – as galaxies preferentially exist in overdense space, our sampling of the intrinsic ellipticity field is necessarily biased, as briefly discussed in Sect. 3.3. This contribution was found to be galaxy bias-dependent, and mooted as responsible for such observed luminosity-scalings – indeed we measure SDSS red to have the weakest alignment signature (see Sect. 4.2.2) of our red samples, although the significance of this is questionable. A GAMA-only fit results in a slightly higher red galaxy alignment amplitude of 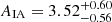 , whilst SDSS-only returns
, whilst SDSS-only returns 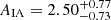 , again comfortably consistent with each other and the total fit.
, again comfortably consistent with each other and the total fit.
For the “full” (all-galaxy) samples, we measure a positive NLA amplitude at just over 95% confidence, whilst the NLA-β is poorly constrained, owing to a sparse luminosity baseline. A point of interest is the apparently larger amplitude of wg+ measured for SDSS, compared with GAMA, for which the N/LA models are unable to account – the green and purple curves in Fig. 4 differ only by their dependence on the (subdominant) weight function 𝒲(z) and the fitted galaxy bias per sample. Individual fits to these samples yield 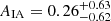 , and
, and 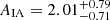 , for GAMA and SDSS, respectively – mildly discrepant at ∼1.8σ. GAMA is brighter, and constrained to be more biased, than SDSS, seemingly ruling-out luminosity/bias-dependences as explanations. It must, however, be noted that these all-galaxy signals constitute muddy combinations of clearly dichotomous alignment signatures, and that GAMA and SDSS sample different environments – something we explore in the next section.
, for GAMA and SDSS, respectively – mildly discrepant at ∼1.8σ. GAMA is brighter, and constrained to be more biased, than SDSS, seemingly ruling-out luminosity/bias-dependences as explanations. It must, however, be noted that these all-galaxy signals constitute muddy combinations of clearly dichotomous alignment signatures, and that GAMA and SDSS sample different environments – something we explore in the next section.
A primary motive for this work was to take advantage of highly complete, flux-limited data in order to constrain IA as it pertains to cosmic shear contamination. The only comparable analyses to date are the SDSS Main studies of Mandelbaum et al. (2006) – M06, and Hirata et al. (2007) 11 – H07, each of which was conducted slightly differently to this work. For example, neither study made use of the N/LA models as they are typically formulated today, allowing for no easy comparison of fitted alignment amplitudes AIA. In any case, our sample selections are also quite different – both M06 & H07 made use of the long luminosity baseline in SDSS to create subsamples, and whilst H07 also split their samples into red/blue galaxies, their cut was performed using observer-frame magnitudes. Nevertheless, we make some broadly similar findings; H07 made robust detections of IA in red galaxies, as did M06 for their brightest sample, itself dominated by red galaxies. Additionally, H07 also failed to make a significant detection for blue galaxies.
We do however seem to find some indirect disagreement in the alignment amplitude vs. sample luminosity trend inferred from the data. Each of M06 & H07 saw trends of increasing signal amplitudes with sample luminosity, whilst we find no evidence for luminosity evolution in our model fits. Furthermore, the far brighter Z2R sample exhibits an amplitude of alignment entirely consistent with the Z1R fit, and as mentioned above, we measure a larger amplitude of alignment for the fainter (uncut) SDSS sample than for GAMA. We explore these individual fits, and how they correlate with sample properties, in Sect. 4.2.2.
4.2.2. Individual sample fits
We make additional, individual fits of AIA to each of our galaxy samples, to gain further insight into trends with colour, luminosity and redshift. Fig. 6 illustrates the results of fitting individual amplitudes to (i, squares in top left panel) red and blue signals, (ii, filled points in right panels) signals from each of our colour/redshift-split samples in GAMA and SDSS, (iii, unfilled triangles/circles) individual signals from uncut GAMA and SDSS, (iv, pentagon in top left panel) all signals from the uncut samples, and (v, stars in right panels) signals from GAMA galaxies with stellar-mass M* ⩾ 1011 M⊙. Only the filled data points are independent of each other, as the unfilled points are each fitted to some collection/subset of the independent samples – Table B.1 details the constraints from each sample, with independent samples denoted by †.
In each panel of the figure, there is a clear dichotomy in the fitted amplitudes for red and blue galaxies, highlighted in the right-hand panels by dashed lines and shading. The top right panel shows AIA vs. sample luminosity, and reveals a vaguely positive correlation in the filled data points, but at very low significance, especially if one (i) considers blue and red separately, and (ii) notes that the Z1B fitted amplitude is anomalously low with respect to the other blue sample amplitudes12.
The bottom right panel shows AIA vs. sample mean-redshifts, with any correlation even less pronounced. To date, no direct IA analyses have found evidence for redshift evolution of intrinsic alignments (Joachimi et al. 2011; Mandelbaum et al. 2011; Tonegawa et al. 2018), and our results seem to agree – although it should be noted that our baseline is short, and limited to the relatively near universe. Some works have reported evidence for scaling of IA with sample luminosity (Hirata et al. 2007; Joachimi et al. 2011; Singh et al. 2015), findings unsupported by our measurements – we do make a clean detection for massive, red GAMA galaxies (red stars), at 9.1σ and with a large fitted amplitude of alignment, but these galaxies are effectively a subset of (primarily) the Z2R sample. Thus the large-M* points are highly correlated with their high-redshift counterparts; these points (upward triangles) disagree with the notion of luminosity dependence. As discussed above, it may be that such an observed dependence is due to environmental properties which correlate with luminosity. Our data points might weakly support this assertion for red galaxies, given that we constrain SDSS red to be less biased than the red GAMA samples (see Table 2), however the significance is extremely low; more work is needed for a concrete answer to this question.
In the top left panel, we interpolate between the fitted red and blue alignment amplitudes according to
where fred ∈ [ 0 , 1 ] is the sample red fraction, and we assume that the red and blue galaxy populations contribute linearly to the measurable alignment of the full sample. Thus we provide predictions13 for the AIA one might measure in a flux-limited sample of mixed galaxy-type, given the red galaxy fraction, and provided that the red/blue dichotomy is the dominant driver of the alignment profile.
Shown also in the top-left panel are the two AIA fitted to the total GAMA (green triangle) and total SDSS (pink circle) signals (shown in the bottom panel of Fig. 4), and the single amplitude fitted to both signals (gold pentagon). One clearly sees that GAMA galaxies are less radially aligned than is predicted by the interpolation. We find this discrepancy to be driven by a significant fraction of satellite galaxies in GAMA, with differing alignment behaviour – previous work has found satellite galaxy alignments to be weaker than those of central galaxies, or altogether non-existent (Sifón et al. 2015; Singh et al. 2015; Huang et al. 2018), in particular when considering larger pair-separations as we do when fitting our models.
Figure 7 breaks down the central14 and satellite, red and blue contributions to the total GAMA alignment signature. The low amplitude fitted to GAMA is simply understood in this context – the left-hand panels demonstrate linear-scale (≳ a few h−1 Mpc) alignments to be sourced entirely by red central galaxy shapes. All other galaxy shapes – red satellites, blue centrals and blue satellites – are unaligned on these scales (seen in all panels), and thus dampen the overall alignment signature with zero-mean white noise. Thus the linear-scale alignment correlation can be thought of as “set” by the red central galaxies, and then repeatedly damped upon the inclusion of other species; blue galaxies have zero-signal, and so force an effective rescaling of wg+ by a factor ∼fred; red satellites do source a strong signal (bottom-left panel) through the inclusion of their positions (which are highly correlated with centrals on these scales), but this is slashed by their own lack of alignment (right-panels), making the overall dampening a more complicated function of red central/satellite fractions.
 |
Fig. 7. Various position-intrinsic shear correlations measured between GAMA samples of exclusively central or satellite galaxies, with errors estimated via jackknife. The title of each panel indicates the central/satellite composition of the position-shear (i.e. density-shape) samples, and we measure correlations in the mixed samples, and for red- (red dashed) and blue-only (blue dashed) subsets. |
Being ∼2 magnitudes shallower than GAMA, and at less than a tenth of the on-sky density, SDSS is comparatively deficient in fainter satellite galaxies at low redshift (see right-panel of Fig. 1). Thus the linear-scale alignment dampening described above is more severe for GAMA than for SDSS, explaining the behaviour seen in Figs. 4 and 6. Indeed, we find an alignment amplitude fit to the mixed central galaxy signal in GAMA (Fig. 7, top-left panel, green curve) to sit comfortably atop the interpolation of Fig. 6, with an almost unchanged red fraction.
Inspecting the signals themselves, we note first that blue galaxies exhibit null signals under every division of the data. We also see that red central galaxies align radially with each other at large-rp (top-left), and with satellites at small-rp (bottom-left) – we re-measure this signal with |Πmax| = 12 h−1 Mpc to confirm that these centrals are aligning with their own satellite distribution. In comparison, red satellites align strongly, but more noisily, with each other on smaller scales (bottom-right), and are elsewise unaligned. With these measurements we can make the following statements about red galaxies: satellite galaxies exist preferentially along the semi-major axis direction of the central galaxy, and the satellite galaxies are, on average, aligned with this direction. These are interesting considerations for future work, given that the satellite distribution is thought to trace that of the underlying dark matter.
Satellite considerations thus explain the discordance between the blue-to-red amplitude interpolation in Fig. 6 and the amplitudes fitted to GAMA signals, and call for additional work; a motivated prior for the amplitude of intrinsic alignments in a cosmic shear study may need to consider not only the red fraction of the galaxy sample, but also the satellite fraction. Such population fractions will correlate with each other to an extent, with redshift as the universal galaxy population evolves, and with spatially variable limiting magnitudes for any given survey. To complicate matters further, Georgiou et al. (2019) find these influential red satellite galaxies to drive variation in measurable alignment signatures as a function of the passband of observation; cosmic shear studies in different bands can expect different contributions of alignments to shear signals. Thus predicting the IA contamination of shear in a galaxy survey is highly non-trivial.
4.2.3. LA results
Linear alignment model fits to the data (fully detailed in Table C.1) result in consistency with analogous parameters from the NLA/NLA-β at 68% in all cases. The slightly larger amplitudes seen for red galaxies reflect the smaller amplitude of fluctuations in the linear matter power spectrum (see Sect. 3.1). This can be seen most clearly in the bottom panel of Fig. 3, where the LA fit to SR (brown dot-dashed line) happens to closely match the NLA-Z1R fit (orange solid line) in amplitude. The linear model shows a clear deficit in power at scales ≲20 h−1 Mpc, relative to the NLA. Consistency between the blue LA and NLA models is even stronger, as expected for null-signals.
The χ2 statistics in Tables 2 and C.1 purport the LA model to describe these data almost as well as the NLA on scales ⩾6 h−1 Mpc, though it is clear from the N/LA illustrations in Figs. 3 and 4 that (i) neither model is sufficient to capture the complex variation of alignments as a function of galaxy sample properties and (ii) only the red GAMA signals would seem to explicitly prefer the enhancement offered by the NLA on scales of a few h−1 Mpc. The inclusion of blue galaxies efficiently washes out the wg+ signal on those scales (green points in Fig. 4), such that something in-between the N/LA models would appear closer to the truth. This result reaffirms the need for more complex modelling of IA in cosmic shear, highlighting the non-trivial contributions of various (i.e. colour, environment) sub-samples to overall alignment signatures.
4.3. Systematics tests
Table 3 lists the detection significances of our measured signals – wg+ , wg+{60 < |Π| < 90 h−1 Mpc} and wg× – across all rp-scales, and when limited to the scales of fitting (>6 h−1 Mpc; bracketed numbers). We make no significant (>2σ) detections of any systematic signals (see Sect. 2.3) in our samples.
5. Impact on cosmology
Here we forecast the impact of our informative IA priors upon a colour-split cosmic shear analysis over a completed KiDS survey. We assume that the alignments in the data are perfectly described by the N/LA models – something we will investigate in future work. This assumption is questionable for the NLA, but given its widespread use in current surveys, and since we are not concerned with biasing of parameters here, but rather the pure impact of priors, we continue as such. The model survey is described by an area of 1, 350 deg2 with a total galaxy number density of 9 arcmin−2 (Hildebrandt et al. 2017), and a total shape dispersion of 0.41. We model the n(z), over z ∈ [ 0.1 , 1.2 ] , according to (Smail et al. 1995)
where α = 2, γ = 1.5 and z0 = 0.375. We define 5 tomographic bins in redshift, with edges (KiDS+VIKING-450; Hildebrandt et al. 2018): [ 0.1 , 0.3 , 0.5 , 0.7 , 0.9 , 1.2 ], each scattered about the bin centre with σz = 0.05(1 + z) and with no catastrophic outliers. Using KV450 galaxies, we estimate ⟨L/Lpiv⟩ for each colour/redshift bin, with the unchanged pivot Lpiv ∼ 4.6 × 1010 L⊙. We also assume the KV450 red galaxy fraction per redshift bin for our toy survey; approx. [ 0.13 , 0.23 , 0.27 , 0.26 , 0.26 ] (Wright et al. 2018). Splitting the model survey by colour more than doubles the available information when computing auto- and cross-correlations – our data vector d consists of shear angular power spectra C(ℓ) with intrinsic contributions (Eqs. (10)–(13)), for all colour/redshift bin combinations, in 10 logarithmic bins ℓ ∈ [50, 2000]
for a total of 550 data points. We compute a full analytical covariance matrix (see Hildebrandt et al. 2017, Sect. 5), with non-Gaussian and super-sample contributions, for computation of the Fisher information (see Tegmark et al. 1997, and references therein). Our cosmological parameter vector is
and we fix Ωk = 0. We append the parameter vector with nuisance parameters for the NLA/NLA-β, and for characterising the impact of additive photometric redshift biases – modern shear surveys rely upon photo-z, and as such are prone to systematic bias in redshift distributions and resultant constraints. We parameterise the additive photo-z bias per colour/redshift bin, such that nx(z)→nx(z − azx), where nx(z) is the redshift distribution of bin x ∈ [ 1, 5 ]R, B. Our nuisance parameters are then
giving a total of 18 (20) parameters with NLA (NLA-β) alignments in the data. We take the MICE cosmology from our IA analysis as the fiducial cosmology about which Fisher derivatives are computed, and apply Gaussian priors as listed in Table 4. Adding a Gaussian prior to the Fisher information is necessary in the case of 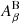 and βB, as small-amplitude signals result in a total degeneracy between these parameters. We limit their variability – in the NLA-β forecast, only – in order to demonstrate a meaningful application of our derived IA priors. The results of our forecasts are shown in Figs. 8 and 9, and condensed in Fig. 10 to show the IA prior impacts on the
and βB, as small-amplitude signals result in a total degeneracy between these parameters. We limit their variability – in the NLA-β forecast, only – in order to demonstrate a meaningful application of our derived IA priors. The results of our forecasts are shown in Figs. 8 and 9, and condensed in Fig. 10 to show the IA prior impacts on the 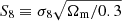 parameter, and dark energy equation of state w0. We note that the Fisher approximation – the mean curvature of the likelihood function about the fiducial cosmology – is inexact in the case of non-Gaussian posterior probability distributions, such that the banana-like Ωm − σ8 degeneracy observed in cosmic shear analyses (Hildebrandt et al. 2017; Abbott et al. 2018) is not exactly captured. Thus our forecasts are demonstrative in purpose, and may differ from analogous full, simulated likelihood forecasts (e.g. Krause et al. 2016).
parameter, and dark energy equation of state w0. We note that the Fisher approximation – the mean curvature of the likelihood function about the fiducial cosmology – is inexact in the case of non-Gaussian posterior probability distributions, such that the banana-like Ωm − σ8 degeneracy observed in cosmic shear analyses (Hildebrandt et al. 2017; Abbott et al. 2018) is not exactly captured. Thus our forecasts are demonstrative in purpose, and may differ from analogous full, simulated likelihood forecasts (e.g. Krause et al. 2016).
Gaussian priors on cosmological and IA/photo-z nuisance parameters adopted for our Fisher forecasts.
 |
Fig. 8. Fisher forecasted cosmological constraints for a KiDS-like survey, with (cyan) and without (grey) the application of our derived IA priors, assuming intrinsic alignments obey the non-linear alignment (NLA) model. Filled contours correspond to forecasts without any priors upon photo-z bias parameters (cf. the “Modest” and “Informative” prior cases in Table 4). Forecasts with photo-z bias fixed to zero are represented by navy and red unfilled contours, where navy also assumes perfect knowledge of IA model parameters. Dashed grey lines mark values of zero for nuisance parameters. |
 |
Fig. 9. The same as Fig. 8, but assuming luminosity-dependent non-linear alignments (NLA-β) in the data. |
 |
Fig. 10. Comparison of marginalised 68% confidence intervals on |
Figures 8 and 9 depict forecasted constraints for final KiDS-like colour-split cosmic shear, with NLA and NLA-β alignments in the modelled data, respectively. Clear improvements are seen in Ωm , σ8 , w0 constraining power when applying our 68% confidence intervals as informative priors on the IA parameters (grey vs. cyan contours). This demonstrates the degrading influence of free-to-roam IA nuisance parameters in cosmic shear analyses – the application of our priors results in up to ∼50% reductions in the size of errorbars on S8 and w0 for the NLA forecast, and 20% for the LA whose weaker contribution levies smaller gains when constrained. The gains in constraints upon crucial parameters are illustrated in Fig. 10 (circles vs. stars) and fully detailed in Table 5, for each of the photo-z bias prior setups detailed in Table 4. The “Modest” case features a rough estimate for a monotonically increasing uncertainty in the real positions of tomographic bin-centres, and serves as a yard-stick between the case without any priors and the “Informative” case, where we adapt the constraints of van Uitert et al. (2018) for use as priors.
Forecasted improvements in constraining power for key cosmological parameters when employing IA model constraints as informative prior ranges on IA nuisance parameters.
Figures 8–10 also plot some idealised cases – assuming perfect knowledge of both intrinsic alignments and photometric redshift distributions we plot navy, unfilled contours in Figs. 8,9, and cyan/grey diamonds in Fig. 10. For perfect photo-z alone, we include red, unfilled contours (Figs. 8 and 9) and mauve/red diamonds (Fig. 10). In the latter case, our analysis priors are not applied, as they have a negligible effect upon the constraining power of the model survey – i.e. with perfect knowledge of source redshifts, such a survey could self-calibrate for intrinsic alignments beyond the precision of our direct analysis. The difference between the red/blue unfilled contours in Figs. 8 and 9 is then the potential gain in precision from even tighter IA model constraints, which is seen to be particularly large for the dark energy equation of state w0.
The advantages of informative priors on intrinsic alignment model parameters are clearly demonstrated here, especially when considering that the current modes of modelling are too simple – our colour-split analysis is already more complex than most. Alignment models with additional freedoms must be used, in order to characterise the variable contributions of galaxies of different types and in different environments – e.g. the mixed alignment perturbative model of Blazek et al. (2017), recently applied to DES Y1 data (Troxel et al. 2018) and accompanied by losses in constraining power. The mitigation of such losses demands dedicated IA studies, producing reliable priors for model parameters.
6. Conclusions
We have measured the galaxy position-intrinsic shear and position-position correlations in the GAMA and SDSS Main galaxy samples, selecting subsamples by colour and redshift. We undertook a detailed consideration of reliable subsample covariance estimation, implementing a 3-dimensional jackknife routine for the relatively small-area GAMA samples. We jointly fit to our intrinsic alignment and clustering measurements with several models; the non-linear and linear alignment models (N/LA), and luminosity-dependent analogues (N/LA-β).
Our NLA fits yield constraints (quoted to 1σ) upon the intrinsic alignment amplitude AIA for 3 cases; unselected, early-type and late-type galaxies, each representing a step forward in precision for constraints of their type from dedicated, spectroscopic studies of intrinsic alignments. Our findings agree with the literature, wherein red galaxies exhibit significant, positive (radial) alignments, and blue galaxy alignments are thus far undetectable. We also fit the LA model to our data, finding comfortable consistency with each of our results for the NLA. As noted in the text, this is largely due to our restriction to linear scales >6 h−1 Mpc where the N/LA difference is minimal.
Our red galaxy alignment constraint 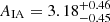 appears to demonstrate that fainter, non-LRG galaxies are still privy to a radial alignment mechanism on large scales (up to 60 h−1 Mpc in this analysis), although not as strongly as LRGs (e.g. Joachimi et al. 2011, Singh et al. 2015). We are able to improve constraints upon the blue galaxy alignment amplitude to
appears to demonstrate that fainter, non-LRG galaxies are still privy to a radial alignment mechanism on large scales (up to 60 h−1 Mpc in this analysis), although not as strongly as LRGs (e.g. Joachimi et al. 2011, Singh et al. 2015). We are able to improve constraints upon the blue galaxy alignment amplitude to 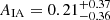 , consistent with the work of Mandelbaum et al. (2011), and still consistent with a null signal. This result, from scales >6 h−1 Mpc15, supports the quadratic alignment picture of weak spiral galaxy alignments on linear scales. Fitting jointly to the wg+ (and wgg) signals measured in GAMA and SDSS, without any colour or redshift selections, yields
, consistent with the work of Mandelbaum et al. (2011), and still consistent with a null signal. This result, from scales >6 h−1 Mpc15, supports the quadratic alignment picture of weak spiral galaxy alignments on linear scales. Fitting jointly to the wg+ (and wgg) signals measured in GAMA and SDSS, without any colour or redshift selections, yields 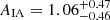 , signifying a net radial alignment of galaxies in the combined dataset.
, signifying a net radial alignment of galaxies in the combined dataset.
In the context of contaminations to weak lensing, the result for blue galaxies may be the most pertinent – whilst our flux-limited samples offer the most representative dataset we can muster, the difficulties of spectroscopy limit them to relatively bright galaxies at low redshifts. Thus our model constraints for the unselected case are likely to over-predict red galaxy contributions – photometric cosmic shear datasets extend to greater depths and hence higher redshifts, where faint, blue galaxies dominate samples. While the results of our fitting to individual galaxy samples reveal weak/non-existent correlations between IA and galaxy luminosity/redshift, we also find significant, scale-dependent variability of IA when separating central/satellite contributions. In GAMA, red central and satellite galaxies align with their local galaxy distribution, i.e. that of the group halo, whilst red central shapes are solely responsible for the linear-scale correlation. Any blue central/satellite galaxy alignments remain undetectable. A full consideration is beyond the scope of this work, however our derived IA constraints remain the most representative for shear-like samples, and should be instructive for future studies.
We recommend the use of our colour-specific alignment constraints, and our interpolation between them (Eq. (22)), in formulating a prior range on AIA for future cosmic shear signal fitting. An average of our constraints, weighted by the relative red/blue galaxy populations, is likely to provide a more realistic description of the alignments present in a dataset – noting the GAMA satellite fraction of ∼27%, one can consider the AIA interpolation to serve as a conservative upper-limit for similarly satellite-heavy samples.
Our fits of the luminosity-dependent NLA resulted in null detections for the β power-law, at 95% confidence. The blue galaxy β parameter is poorly constrained by the data, as the luminosity baseline of the samples is sparse and ineffectual, and the signals are close to zero. The red galaxy result is interesting, as it seems to contradict previous works which have found a roughly linear scaling of alignments with sample luminosity (Joachimi et al. 2011; Singh et al. 2015). The reason for this is that the red galaxy alignments show little/no evolution over a luminosity baseline of (rescaled to start at unity) ∼[1, 1.67, 5]. This observation might be partly explained by the density weighting and consequent bias-dependent signal enhancement described by Blazek et al. (2015), and certainly lends support to the notion that the current methods of modelling for IA are insufficient to grasp the complexity of contributions from galaxies in different environments.
We forecasted the cosmological parameter constraining capabilities of red/blue-split cosmic shear in a completed KiDS survey, assuming that alignments in the simulated data were described by the NLA or LA models. Applying our IA nuisance parameter constraints as informative priors, we find reductions of up to ∼50% (or ∼20% for the LA) in the size of confidence intervals for the S8 parameter and w0, dependent on the freedoms of photometric redshift bias parameters. Our forecasts demonstrate the potential utility of independent intrinsic alignment model constraints as informative priors in cosmic shear analyses, particularly as IA parameterisations become more complex and impactful.
In the era of LSST, Euclid and WFIRST, our current prescriptions for the intrinsic alignment contamination of cosmic shear would lag behind greatly increased statistical power – one fears that the limit of cosmological inference could be determined by the uncertainty in models for IA (and other systematics), and open to strong biases as a result. Our work has attempted to characterise the alignment signatures of a purely flux-limited sample, finding complexity beyond the divergent behaviour of elliptical and spiral galaxies, extending to the non-trivial contributions of red centrals and satellites. These findings motivate us to explore IA models with galaxy red- and satellite-fraction considerations, and to constrain such models with representative spectroscopic data – such work will aid in the maximisation of potential for the next generation of lensing surveys.
Looking forward, we hope to perform this analysis with a halo model for intrinsic alignments, adapted from the formalism of Schneider & Bridle (2010), fitting to all scales, including a satellite-alignment prescription, and taking full advantage of the high completeness of these data (Fortuna et al., in prep.). In the meantime, our derived NLA model constraints will provide useful priors for current and future shear surveys, improving cosmological constraints and blocking the influence of unknown systematics on IA parameterisations. New, narrow-band photometric datasets are currently being amassed (PAUS; Benítez et al. 2009, J-PAS; Benítez et al. 2014), with the potential for the production of unprecedented IA model constraints, for use in future weak lensing analyses. Furthermore, the statistical power and associated precision of these datasets will enable the use of intrinsic-intrinsic shear (II) correlations in studying the type- and environment-dependence of galaxy alignment mechanisms. Powerful and additional statistics, cross-correlations between galaxy types, and increased depths in these analyses will shed new light on the intrinsic alignment contamination of cosmic shear, and on the physics of galaxy formation and evolution.
Publicly available through CosmoHub: http://cosmohub.pic.es
In practice, one could affix weights ws to the shear components, to allow for down-weighting of noisier shapes – we do not apply any weights in our analysis (nor do previous direct-measurement studies of IA), as our use of elliptical weight functions in shape estimation poses problems for the estimation of ellipticity errors (see Sect. 2.3 of Georgiou et al. 2019).
Hui & Zhang (2008) and Blazek et al. (2017) theorise linear alignment scaling for all galaxies on sufficiently large scales, arising from non-Gaussian structure fluctuations.
Hirata et al. (2007) also studied LRGs – we only discuss their work on the flux-limited SDSS Main sample.
We note that the Z1B amplitude is consistent with zero at 95% confidence, and that this signal (downward cyan triangles in the top panel of Fig. 3) is not found to be a particularly significant detection, at <2σ (Table 3). Additionally, the signal becomes comfortably consistent with zero upon removal of the faint-limit we apply to our GAMA density samples (explained in Appendix A.2), which affects the Z1B sample far more significantly than each of the others combined. This could be interpreted as follows; the Z1B sample shows a net tangential alignment at ∼1.7σ, but only when excluding the faintest (∼27% here) galaxies from the density sample. However, the faint-limit is part of our clustering covariance estimation (see Appendix A.2) – removing it may invalidate the clustering fits which anchor the galaxy bias, so this interpretation must be taken with moderation. A linear-scale tangential alignment of blue galaxies, dependent on the bias of the density tracer, is an interesting result which would call for further work. However, it should be noted that (i) tidal torquing mechanisms ought to be weak on these scales, so this signal is not expected, (ii) the significance of the negative amplitude is low, and (iii) the signal itself lacks a clear detection.
Acknowledgments
We thank Rachel Mandelbaum and Sukhdeep Singh for sharing data products and insights. We also thank members of the KiDS consortium for many helpful discussions. HJ acknowledges support from a UK Science and Technology Facilities Council (STFC) Studentship. HH and MCF acknowledge support from Vici grant 639.043.512, financed by the Netherlands Organisation for Scientific Research (NWO). NEC acknowledges support from a Royal Astronomical Society Research Fellowship. CH acknowledges support from the European Research Council under grant number 647112. KK acknowledges support by the Alexander von Humboldt Foundation. This work is based on data products from observations made with ESO Telescopes at the La Silla Paranal Observatory under programme IDs 177.A-3016, 177.A-3017 and 177.A-3018, and on data products produced by Target/OmegaCEN, INAF-OACN, INAF-OAPD and the KiDS production team, on behalf of the KiDS consortium. We also work with data products from GAMA: a joint European-Australasian project based around a spectroscopic campaign using the Anglo-Australian Telescope. The GAMA input catalogue is based on data taken from the Sloan Digital Sky Survey and the UKIRT Infrared Deep Sky Survey. Complementary imaging of the GAMA regions is being obtained by a number of independent survey programmes including GALEX MIS, VST KiDS, VISTA VIKING, WISE, Herschel-ATLAS, GMRT and ASKAP providing UV to radio coverage. GAMA is funded by the STFC (UK), the ARC (Australia), the AAO, and the participating institutions. The GAMA website is http://www.gama-survey.org/. Part of this work was made possible thanks to CosmoHub. CosmoHub has been developed by the Port d’Informació Científica (PIC), maintained through a collaboration of the Institut de Física d’Altes Energies (IFAE) and the Centro de Investigaciones Energéticas, Medioambientales y Tecnológicas (CIEMAT). The work was partially funded by the “Plan Estatal de Investigación Científica y Técnica y de Innovación” program of the Spanish government. Author Contributions: All authors contributed to the development and writing of this paper. The authorship list is given in two groups: the lead authors (HJ, CG, BJ, HH), followed by an alphabetical group including those who are key contributors to either the scientific analysis, or to the data products.
References
- Abbott, T. M. C., Abdalla, F. B., Alarcon, A., et al. 2018, Phys. Rev. D, 98, 043526 [Google Scholar]
- Alam, S., Albareti, F. D., Prieto, C. A., et al. 2015, ApJS, 219 [Google Scholar]
- Bacon, D. J., Refregier, A. R., & Ellis, R. S. 2000, MNRAS, 318, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Benítez, N., Gaztañaga, E., Miquel, R., et al. 2009, ApJ, 691, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Benítez, N., Dupke, R., Moles, M., et al. 2014, ArXiv e-prints [arXiv:1403.5237] [Google Scholar]
- Blazek, J., Vlah, Z., & Seljak, U. 2015, JCAP, 2015, 015 [NASA ADS] [CrossRef] [Google Scholar]
- Blazek, J., MacCrann, N., Troxel, M. A., & Fang, X. 2017, ArXiv e-prints [arXiv:1708.09247] [Google Scholar]
- Bridle, S., & King, L. 2007, New J. Phys., 9, 444 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, M. L., Taylor, A. N., Hambly, N. C., & Dye, S. 2002, MNRAS, 333, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Carretero, J., Castander, F. J., Gaztañaga, E., Crocce, M., & Fosalba, P. 2015, MNRAS, 447, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Catelan, P., Kamionkowski, M., & Blandford, R. D. 2001, MNRAS, 320, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Cervantes-Sodi, B., Hernandez, X., & Park, C. 2010, MNRAS, 402, 1807 [NASA ADS] [CrossRef] [Google Scholar]
- Chisari, N., Codis, S., Laigle, C., et al. 2015, MNRAS, 454, 2736 [NASA ADS] [CrossRef] [Google Scholar]
- Coupon, J., Kilbinger, M., McCracken, H. J., et al. 2012, A&A, 542, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crocce, M., Castander, F. J., Gaztañaga, E., Fosalba, P., & Carretero, J. 2015, MNRAS, 453, 1513 [NASA ADS] [CrossRef] [Google Scholar]
- Croft, R. A. C., & Metzler, C. A. 2000, ApJ, 545, 561 [NASA ADS] [CrossRef] [Google Scholar]
- de Jong, J. T. A., Verdoes Kleijn, G. A., Kuijken, K. H., & Valentijn, E. A. 2013, Exp. Astron., 35, 25 [Google Scholar]
- de Jong, J. T. A., Kleijn, G. A. V., Erben, T., et al. 2017, A&A, 604, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drinkwater, M. J., Jurek, R. J., Blake, C., et al. 2010, MNRAS, 401, 1429 [Google Scholar]
- Driver, S. P., Hill, D. T., Kelvin, L. S., et al. 2011, MNRAS, 413, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Efstathiou, G., & Lemos, P. 2018, MNRAS, 476, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Farrow, D. J., Cole, S., Norberg, P., et al. 2015, MNRAS, 454, 2120 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Fosalba, P., Crocce, M., Gaztañaga, E., & Castander, F. J. 2015, MNRAS, 448, 2987 [NASA ADS] [CrossRef] [Google Scholar]
- Georgiou, C., Johnston, H., Hoekstra, H., et al. 2019, A&A, 622, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunn, J. E., Carr, M., Rockosi, C., et al. 1998, ApJ, 116, 3040 [Google Scholar]
- Hambly, N., MacGillivray, H., Read, M., et al. 2001, MNRAS, 326, 18 [Google Scholar]
- Heavens, A., Refregier, A., & Heymans, C. 2000, MNRAS, 319, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Heymans, C., Brown, M., Heavens, A., et al. 2004, MNRAS, 347, 895 [NASA ADS] [CrossRef] [Google Scholar]
- Heymans, C., Grocutt, E., Heavens, A., et al. 2013, MNRAS, 432, 2433 [NASA ADS] [CrossRef] [Google Scholar]
- Hikage, C., Oguri, M., Hamana, T., et al. 2019, PASJ, in press [arXiv:1809.09148] [Google Scholar]
- Hilbert, S., Xu, D., Schneider, P., et al. 2017, MNRAS, 468, 790 [NASA ADS] [CrossRef] [Google Scholar]
- Hildebrandt, H., Viola, M., Heymans, C., et al. 2017, MNRAS, 465, 1454 [Google Scholar]
- Hildebrandt, H., Köhlinger, F., van den Busch, J. L., et al. 2018, A&A, submitted [arXiv:1812.06076] [Google Scholar]
- Hirata, C., & Seljak, U. 2003, MNRAS, 343, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Hirata, C. M., & Seljak, U. 2004, Phys. Rev. D, 70, 063526 [NASA ADS] [CrossRef] [Google Scholar]
- Hirata, C. M., Mandelbaum, R., Ishak, M., et al. 2007, MNRAS, 381, 1197 [NASA ADS] [CrossRef] [Google Scholar]
- Hoffmann, K., Bel, J., Gaztañaga, E., et al. 2015, MNRAS, 447, 1724 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, H.-J., Mandelbaum, R., Freeman, P. E., et al. 2018, MNRAS, 474, 4772 [NASA ADS] [CrossRef] [Google Scholar]
- Hui, L., & Zhang, J. 2008, ApJ, 688, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Jee, M. J., Tyson, J. A., Hilbert, S., et al. 2016, ApJ, 824, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Joachimi, B., & Bridle, S. L. 2010, A&A, 523, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Joachimi, B., Mandelbaum, R., Abdalla, F. B., & Bridle, S. L. 2011, A&A, 527, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Joudaki, S., Blake, C., Heymans, C., et al. 2016, MNRAS, 000, stw2665 [Google Scholar]
- Joudaki, S., Blake, C., Johnson, A., et al. 2018, MNRAS, 474, 4894 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, N., Wilson, G., & Luppino, G. A. 2000, ArXiv e-prints [arXiv:astro-ph/0003338] [Google Scholar]
- Kiessling, A., Cacciato, M., Joachimi, B., et al. 2015, Space Sci. Rev., 193, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, D., Rassat, A., Host, O., & Bridle, S. 2012, MNRAS, 424, 1647 [NASA ADS] [CrossRef] [Google Scholar]
- Köhlinger, F., Viola, M., Joachimi, B., et al. 2017, MNRAS, 471, 4412 [NASA ADS] [CrossRef] [Google Scholar]
- Krause, E., Eifler, T., & Blazek, J. 2016, MNRAS, 456, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Kuijken, K., Heymans, C., Hildebrandt, H., et al. 2015, MNRAS, 454, 3500 [NASA ADS] [CrossRef] [Google Scholar]
- Landy, S. D., & Szalay, A. S. 1993, ApJ, 412, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, ArXiv e-prints [arXiv:1110.3193] [Google Scholar]
- Lee, J. 2011, ApJ, 732, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J., & Erdogdu, P. 2007, ApJ, 671, 1248 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J., & Pen, U.-L. 2002, ApJ, 567, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Li, C., Jing, Y. P., Faltenbacher, A., & Wang, J. 2013, ApJ, 770, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Liske, J., Baldry, I. K., Driver, S. P., et al. 2015, MNRAS, 452, 2087 [NASA ADS] [CrossRef] [Google Scholar]
- LSST Science Collaboration, Abell, P. A., Allison, J., et al. 2009, ArXiv e-prints [arXiv:0912.0201] [Google Scholar]
- Mandelbaum, R., Hirata, C. M., Seljak, U., et al. 2005, MNRAS, 361, 1287 [NASA ADS] [CrossRef] [Google Scholar]
- Mandelbaum, R., Hirata, C. M., Ishak, M., Seljak, U., & Brinkmann, J. 2006, MNRAS, 367, 611 [NASA ADS] [CrossRef] [Google Scholar]
- Mandelbaum, R., Blake, C., Bridle, S., et al. 2011, MNRAS, 410, 844 [NASA ADS] [CrossRef] [Google Scholar]
- Melchior, P., Viola, M., Schäfer, B. M., & Bartelmann, M. 2011, MNRAS, 412, 1552 [NASA ADS] [CrossRef] [Google Scholar]
- Piras, D., Joachimi, B., Schäfer, B. M., et al. 2018, MNRAS, 474, 1165 [NASA ADS] [CrossRef] [Google Scholar]
- Roche, N., & Eales, S. A. 1999, MNRAS, 307, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Samuroff, S., Blazek, J., Troxel, M. A., et al. 2018, MNRAS, submitted [arXiv:1811.06989] [Google Scholar]
- Schäfer, B. M. 2009, Int. J. Mod. Phys. D, 18, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, M. D., & Bridle, S. 2010, MNRAS, 402, 2127 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, P., van Waerbeke, L., Kilbinger, M., & Mellier, Y. 2002, A&A, 396, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sifón, C., Hoekstra, H., Cacciato, M., et al. 2015, A&A, 575, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Singh, S., & Mandelbaum, R. 2016, MNRAS, 457, 2301 [NASA ADS] [CrossRef] [Google Scholar]
- Singh, S., Mandelbaum, R., & More, S. 2015, MNRAS, 450, 2195 [NASA ADS] [CrossRef] [Google Scholar]
- Singh, S., Mandelbaum, R., Seljak, U., Slosar, A., & Vazquez Gonzalez, J. 2017, MNRAS, 471, 3827 [NASA ADS] [CrossRef] [Google Scholar]
- Smail, I., Hogg, D. W., Yan, L., & Cohen, J. G. 1995, ApJ, 449, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D., Gehrels, N., Breckinridge, J., et al. 2013, ArXiv e-prints [arXiv:1305.5422] [Google Scholar]
- Strauss, M. A., Weinberg, D. H., Lupton, R. H., et al. 2002, AJ, 124, 1810 [NASA ADS] [CrossRef] [Google Scholar]
- Tegmark, M., Taylor, A. N., & Heavens, A. F. 1997, ApJ, 480, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Tenneti, A., Mandelbaum, R., & Di Matteo, T. 2016, MNRAS, 462, 2668 [NASA ADS] [CrossRef] [Google Scholar]
- Tonegawa, M., Totani, T., Okada, H., et al. 2015, PASJ, 67, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Tonegawa, M., Okumura, T., Totani, T., et al. 2018, PASJ, 70, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Troxel, M. A., MacCrann, N., Zuntz, J., et al. 2018, Phys. Rev. D, 98, 043528 [NASA ADS] [CrossRef] [Google Scholar]
- van Uitert, E., Joachimi, B., Joudaki, S., et al. 2018, MNRAS, 476, 4662 [NASA ADS] [CrossRef] [Google Scholar]
- Van Waerbeke, L., Mellier, Y., Erben, T., et al. 2000, A&A, 594, A13 [Google Scholar]
- Velliscig, M., Cacciato, M., Schaye, J., et al. 2015, MNRAS, 454, 1 [Google Scholar]
- Wittman, D. M., Tyson, J. A., Kirkman, D., Dell’Antonio, I., & Bernstein, G. 2000, Nature, 405, 143 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Wright, A. H., Robotham, A. S. G., Driver, S. P., et al. 2017, MNRAS, 470, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, A. H., Hildebrandt, H., Kuijken, K., et al. 2018, A&A, submitted [arXiv:1812.06077] [Google Scholar]
- York, D. G., Adelman, J., Anderson, Jr., J. E., et al. 2000, AJ, 120, 1579 [CrossRef] [Google Scholar]
- Zuntz, J., Paterno, M., Jennings, E., et al. 2015, Astron. Comput., 12, 45 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Covariances
To quantify sample variance, one would ideally prefer to use many realisations of simulated data in estimating errors on a statistic. Unfortunately, there remain qualitative disagreements between the latest hydrodynamical simulations with respect to the form of late-type galaxy intrinsic alignments (Tenneti et al. 2016). More fundamental road-blocks are small volumes and a lack of multiple realisations of these simulations, making them unsuitable for covariance purposes, as yet. We prefer our IA measurement errors to come from the data.
With an eye to include the largest possible transverse scales in our analysis, we implement a 3-dimensional delete-one jackknife. The jackknife covariance is estimated as
where wα is the signal of interest, as measured from jackknife sample α, and w̄ is the average over N samples. T denotes the conjugate transpose of the mean-subtracted signal vector. N jackknife samples are defined by dividing the survey into N subvolumes and excluding one at a time, measuring wα in the rest of the survey. The performance of jackknife covariance estimation relies on a balance between (i) the number of jackknife subvolumes N, and (ii) the angular scale of their corresponding “patches” in the RA − Dec plane, where one always compromises the other. N should be ≫ the size of the data vector, or else the covariance becomes noisy and eventually singular. And yet, the scale of the subvolumes must be greater than the largest scales of interest, or the variance over those scales will not be captured and errors will be underestimated.
Figure A.1 illustrates the mapping from an angular scale on the sky to a comoving transverse scale at a given redshift, with our log-spaced rp-bin edges shown as horizontal black lines. This plot is interpreted as follows: coloured lines give the maximum comoving separations captured by an angular scale, thus anything below each line is correctly sampled by a sky-patch of that size, at that redshift. Normalised redshift distributions of GAMA and SDSS Main are overlaid, along with the redshift boundary defining our high- and low-z GAMA samples (vertical red line). At high redshift, the GAMA jackknife demands patches of scale ≳4.5 degrees for all rp scales to be captured, whilst the lower redshifts, which include all of the SDSS sample, are significantly hamstrung by the jackknife requirement. Contiguous regions of equatorial GAMA are 12 deg × 5 deg in size, rendering ideal patches too few in number. SDSS Main covers a much larger area, but requires even larger patches at lower redshift. Thus we define a series of redshift slices, each with comparable numbers of galaxies, and subdivide jackknife patches into “cubes”. We take care to ensure that the resulting cubes are of more than sufficient depth to be considered statistically independent, and to accomodate the largest line-of-sight separations under consideration – |Πmax| = 60 h−1 Mpc, so we ensure that all cubes are deeper than 150 h−1 Mpc. This requirement, along with the need for many jackknife regions of roughly equal galaxy numbers, is what informs our GAMA samples’ shared redshift boundary at z = 0.26. The large-Π systematics test extends to |Πmax| = 90 h−1 Mpc, and we opt for a standard 2D jackknife in this case, reducing the binning of the measured signal in order to stabilise the covariance matrix.
 |
Fig. A.1. As a function of redshift, the comoving transverse vs. on-sky angular scale relation, for a range of scales in degrees. The rp bin edges we employ are plotted as horizontal black lines, highlighting the limitations of too-small patches to sample larger rp pairs, esp. at lower redshifts. The vertical dotted line indicates the z = 0.26 redshift division for our GAMA samples, and redshift distributions of red and blue galaxies in SDSS (z ∼ [ 0.02 , 0.3 ]) and GAMA (z ∼ [ 0.02 , 0.5 ]) are overlaid as coloured, dashed histograms. Grey shading indicates z < 0.02, which we exclude from our analysis. |
We note that by slicing subvolumes in redshift, we are assuming that we can approximate the variance over a redshift bin by the combined variance of its sub-bins, and thus that any redshift evolution is subdominant to the variance over different pointings. Since previous studies (Joachimi et al. 2011; Mandelbaum et al. 2011; Tonegawa et al. 2018) support weakly- or non-evolving alignments – albeit for differently selected samples – and our redshift baseline is short, we believe this assumption is reasonable.
Figure A.2 compares the performance of various 2D and 3D jackknife configurations. For our GAMA intrinsic alignment measurements we choose to work with (3 × 5) deg2 patches, sliced into cubes – the performance of this configuration is indicated by solid lines in the top-middle-right panel of Fig. A.2. Subvolumes of this size combat the noise evident for (6 × 5) deg2 patches (top-right panel), and remain large enough to sample all but the largest transverse scales at low redshifts – we opt to drop only the largest-rp data point for low-redshift measurements. We describe our method for estimating clustering covariances in GAMA in Appendix A.2. For SDSS, we estimate both IA and clustering covariances with a (10 × 10) deg2 jackknife cube configuration (Fig. A.2, bottom-right, solid lines) – the largest scales allowing for acceptable numbers of patches in the irregular SDSS footprint. We choose to retain all data points for SDSS measurements.
 |
Fig. A.2. Performance of the 3D (solid lines) and 2D (dashed lines) jackknife in various configurations, plotted as ratios to analytical (shot-noise) errors estimated for the wg+ statistic. GAMA configurations are plotted on the top row, with SDSS on the bottom. Colour/redshift sample error ratios are vertically offset by increments of 0.5 (equivalent to a 50% difference in the error on wg+ ) for clarity, and σjack./σshot. = 1 is indicated for each sample by a dotted horizontal line. Also shown are the Z2R and SR samples’ 2D (left-in-panel) and 3D (right-in-panel) jackknife estimates of absolute correlation matrices |
Our chosen configurations yield 36 , 24 and 74 jackknife cubes per low-redshift GAMA, high-redshift GAMA and SDSS sample, respectively. Large-Π test jackknife errors are derived from 12 and 37 patches (2D) for GAMA and SDSS, respectively.
A.1. Masking
While patches are chosen to be roughly equal in area, this is not always achieved due to masking and irregular survey edges. A patch covering less area translates into a less variant jackknife sample upon deletion. Thus when estimating the covariance from jackknife measurements, the noise at large scales is spuriously lowered, and inter-bin correlations are biased.
We quantify this effect using data from the MICE Simulation. The Marenostrum Institut de Ciéncies de l’Espai (MICE) Grand Challenge galaxy catalogue (Carretero et al. 2015, Hoffmann et al. 2015) was assembled from a 7 × 1010 dark matter particle, ∼(3 h−1 Gpc)3 comoving volume simulation (Fosalba et al. 2015), with halo occupation and abundance matching techniques (Crocce et al. 2015). The resulting catalogue spans a 5000 deg2 octant, complete down to an absolute r-band magnitude of Mr < −18.9.
For a GAMA-sized patch of MICE, we generate a random ellipticity distribution and mask-out chunks of area in a similar fashion to the real masking in our KiDS images, estimating the jackknife alignment covariance before and after masking. We find that, whilst off-diagonal covariance elements can be severely mis-estimated, on-diagonal elements are recovered at ∼23% or better. We can lower this margin of error – with a particular impact on the larger scales we use in fitting – to ∼18% or better by applying weights to jackknife samples, equal to the relative areas of their respective deleted subvolumes (we apply an approximate re-normalisation incorporating the weights).
To test whether the more serious mis-estimation of off-diagonal covariance elements biases our results significantly, we set them all to zero and repeat our likelihood analysis. In comparison with our results quoted in Table 2, we find consistency at 68% confidence in all cases, with our fitted LA parameter values shifting as follows; 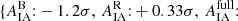 +0.30σ}. Whilst red- and all-galaxy amplitude shifts are small at just ∼0.3σ, the larger, negative shift of ∼1.2σ in the blue-galaxy amplitude fit acts to strengthen consistency with zero. For the LA-β, the red- and all-galaxy β parameters shift to centre on zero, with small shifts taking the amplitudes toward the 1-parameter LA centres. The blue-galaxy β parameter is relatively unchanged, with the amplitude centre shifting close to zero. Since none of these shifts contradict our original findings, the omission of inter-bin correlations can be said not to affect the conclusions of this work. We know that the worst biases of the off-diagonal covariance in our MICE test were equivalent to shifts in correlation coefficients of ≲0.2, thus we further conclude that biases of the signal covariance due to survey masking are subdominant to statistical errors for these data.
+0.30σ}. Whilst red- and all-galaxy amplitude shifts are small at just ∼0.3σ, the larger, negative shift of ∼1.2σ in the blue-galaxy amplitude fit acts to strengthen consistency with zero. For the LA-β, the red- and all-galaxy β parameters shift to centre on zero, with small shifts taking the amplitudes toward the 1-parameter LA centres. The blue-galaxy β parameter is relatively unchanged, with the amplitude centre shifting close to zero. Since none of these shifts contradict our original findings, the omission of inter-bin correlations can be said not to affect the conclusions of this work. We know that the worst biases of the off-diagonal covariance in our MICE test were equivalent to shifts in correlation coefficients of ≲0.2, thus we further conclude that biases of the signal covariance due to survey masking are subdominant to statistical errors for these data.
A.2. GAMA clustering covariance
We make further use of MICE in estimating clustering covariances for GAMA – for consistency, we impose the MICE faint-limit (Mr ⩽ −18.9) on our GAMA density samples, for losses of { Z1B : 27.3% , Z1R : 5.6% , Z2B : 0.1% , Z2R : 0.1% } – see Table 1 for sample details.
We apply the GAMA flux-limit r < 19.8 to MICE and make a flat cut in absolute rest-frame g − r to isolate the red sequence. Dividing the MICE area (with declination ⩽40 deg) into 18 rectangular patches, each ∼180 deg2, we measure the clustering signals in each patch and find the spread to be slightly disagreeable with the clustering of analogous samples in GAMA (Fig. A.3). Thus we choose to validate the SWOT clustering jackknife routine (SWOT-jk), and its sensitivity to the jackknife subvolume numbers-vs.-size trade-off, using MICE.
 |
Fig. A.3. Clustering measurements from our defined GAMA galaxy samples (open circles) overlaid with corresponding measurements from individual, ∼180 deg2 MICE subvolumes (dotted lines). Filled triangles show the means of the MICE clustering signals. We see significant differences between MICE and GAMA, particularly at low redshift and large scales, and so choose not to estimate covariances directly from MICE – see Appendix A.2 for details. |
We first obtain SWOT-jk estimates of the MICE sample clustering signals and covariances, per patch. We then estimate total MICE sample clustering covariances by constructing 2D jackknifes with all 18 patches. The variance16 over SWOT-jk estimates then approximates the sample variance of a 180 deg2 – i.e. GAMA-like – survey. If this is greater than any systematic offset between the mean covariance over the patches and the (area-scaled) total jackknife covariance, then the bias of the SWOT-jk is subdominant to the statistical error of a GAMA-like survey. This is indeed the case for smaller transverse pair separations, which are well-sampled even by small angular scales. Samples at high redshift also do well in this regard, as smaller angular scales trace large spatial volumes. As Fig. A.4 illustrates, however, the SWOT-jk significantly underestimates large-scale covariance elements for low-redshift samples (bottom panels; green lines & shading vs. solid coloured lines). As discussed in Appendix A above, this is due to poor sampling of these pairs, and thus diminished variation across jackknife samples.
Since the jackknife performance differential is dominated by sample redshift, rather than colour, we attempt to quantify the lost variance by fitting 1 scaling variable to each of the 3 largest transverse separation bins i under consideration. Boosting each covariance element with the product aij of the 2 relevant scaling variables, we are able to bring the mean-over-patches (pink lines and hatching in Fig. A.4) into closer agreement with the total MICE jackknife. We take these scaling factors to be approximately representative of the large-scale performance drop-off inherent to the SWOT-jk at low redshift, and apply them to our low-z GAMA clustering covariances.
 |
Fig. A.4. A comparison of clustering covariance elements (columns), estimated for each redshift/colour galaxy sample (rows) with the SWOT internal jackknife per MICE patch (X, green) and the total jackknife over all patches (Y, solid coloured lines), plotted as X/Y − 1. The 0.16 , 0.5 , 0.84 percentiles over the patch estimates are indicated by dashed lines and shading. Pink solid lines and hatching indicate covariance elements scaled by the fitted variables aij described in Appendix A.2. |
Appendix B: Individual sample fits
Table B.1 details the individual fits of the 1-parameter NLA model to galaxy samples, as described in Sect. 4.2.2, along with the relevant sample properties displayed in Fig. 6, and constraints upon the galaxy biases of corresponding density samples.
1D marginalised constraints (to 1σ) upon the 1-parameter NLA amplitude AIA for each sample under consideration – each of the points shown in Fig. 6 corresponds to a row here.
Appendix C: Linear alignment model fits
Here we present fits of the linear alignment model to our IA data. Table C.1 shows the results of our LA fitting, which are discussed in Sect. 4.2.3.
The same as Table 2, here for the parameters of the linear alignment (LA) model (Sect. 3.1) and its luminosity-dependent analogue (LA-β).
Appendix D: Photo-Z bias parameter contours
Here we include our Fisher forecasted constraints for all IA and photo-z nuisance parameters considered (Sect. 5), before and after application of our derived IA model priors (Sect. 4). Figs. D.1 and D.2 accompany the LA/LA-β model forecasts of Figs. 8 and 9, respectively.
All Tables
Details of our density (bracketed numbers) and intrinsic shape field tracer samples, composed of GAMA and SDSS galaxies split by redshift and/or colour.
NLA model parameter and galaxy bias 1D marginalised constraints for our samples, with 68% confidence intervals and the reduced χ2 (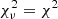 per degree of freedom) statistics for the global fit.
per degree of freedom) statistics for the global fit.
Reduced χ2 statistics to assess the significance of signal detections against the null hypothesis (i.e. a zero-signal), for wg+ and for systematics tests; wg× and wg+ limited to large line-of-sight separations (60 ⩽ |Π| ⩽ 90 h−1 Mpc), denoted Π+.
Gaussian priors on cosmological and IA/photo-z nuisance parameters adopted for our Fisher forecasts.
Forecasted improvements in constraining power for key cosmological parameters when employing IA model constraints as informative prior ranges on IA nuisance parameters.
1D marginalised constraints (to 1σ) upon the 1-parameter NLA amplitude AIA for each sample under consideration – each of the points shown in Fig. 6 corresponds to a row here.
The same as Table 2, here for the parameters of the linear alignment (LA) model (Sect. 3.1) and its luminosity-dependent analogue (LA-β).
All Figures
 |
Fig. 1. Left panel: galaxy rest-frame colour–magnitude diagram, where we choose a cut in g − r to isolate the red sequence in GAMA and SDSS. Right panel: sample absolute r-band magnitude-redshift diagram. The total distribution of GAMA and SDSS galaxies is shown, binned in hexagonal cells with a colour scale corresponding to the counts in cells. Coloured contours indicate 75% and 95% of galaxies in a sample. Colour/redshift cuts are shown as dashed green lines, and the apparent leakage of contours is due to the grid-size used in kernel density estimation. |
| In the text | |
 |
Fig. 2. Measured galaxy clustering for our blue (top panel) and red (bottom panel) galaxy samples. Solid curves illustrate the best-fit linear clustering per sample (Eq. (19)). The vertical dashed line indicates rp = 6 h−1 Mpc, below which scales are excluded from fitting (Sect. 3.3). |
| In the text | |
 |
Fig. 3. Measured galaxy position-intrinsic shear correlations for our blue (top panel) and red (bottom panel) galaxy samples. Best-fit NLA models are shown as solid curves, and the vertical dashed line indicates rp = 6 h−1 Mpc, below which scales are excluded from fitting (Sect. 3.3). The best-fit LA model to SR is shown as a dot-dashed line. |
| In the text | |
 |
Fig. 4. Galaxy clustering (top panel) and position-intrinsic shear correlations (bottom panel) measured in the full KiDS+GAMA and SDSS Main datasets. Solid lines illustrate the best-fit NLA model, and dot-dashed lines the LA. The vertical dashed line indicates rp = 6 h−1 Mpc, below which scales are excluded from fitting (Sect. 3.3). |
| In the text | |
 |
Fig. 5. Posterior probability contours of our fitted galaxy bias bg, NLA amplitude A and luminosity power-law β parameters, for red (left panel) and blue (right panel) galaxies. The filled (unfilled) contours are for the NLA (NLA-β) models. Dashed grey lines mark values of zero for IA parameters. |
| In the text | |
 |
Fig. 6. Constraints on the NLA model alignment amplitude AIA, from various subsamples of GAMA and SDSS (Table 1), plotted against sample properties. The constraints illustrated here are also given in Table B.1. Top left panel: AIA vs. shape sample red galaxy fraction. We interpolate (green line/shading) between our fits to blue (blue square) and red (red square) galaxy samples, according to |
| In the text | |
 |
Fig. 7. Various position-intrinsic shear correlations measured between GAMA samples of exclusively central or satellite galaxies, with errors estimated via jackknife. The title of each panel indicates the central/satellite composition of the position-shear (i.e. density-shape) samples, and we measure correlations in the mixed samples, and for red- (red dashed) and blue-only (blue dashed) subsets. |
| In the text | |
 |
Fig. 8. Fisher forecasted cosmological constraints for a KiDS-like survey, with (cyan) and without (grey) the application of our derived IA priors, assuming intrinsic alignments obey the non-linear alignment (NLA) model. Filled contours correspond to forecasts without any priors upon photo-z bias parameters (cf. the “Modest” and “Informative” prior cases in Table 4). Forecasts with photo-z bias fixed to zero are represented by navy and red unfilled contours, where navy also assumes perfect knowledge of IA model parameters. Dashed grey lines mark values of zero for nuisance parameters. |
| In the text | |
 |
Fig. 9. The same as Fig. 8, but assuming luminosity-dependent non-linear alignments (NLA-β) in the data. |
| In the text | |
 |
Fig. 10. Comparison of marginalised 68% confidence intervals on |
| In the text | |
 |
Fig. A.1. As a function of redshift, the comoving transverse vs. on-sky angular scale relation, for a range of scales in degrees. The rp bin edges we employ are plotted as horizontal black lines, highlighting the limitations of too-small patches to sample larger rp pairs, esp. at lower redshifts. The vertical dotted line indicates the z = 0.26 redshift division for our GAMA samples, and redshift distributions of red and blue galaxies in SDSS (z ∼ [ 0.02 , 0.3 ]) and GAMA (z ∼ [ 0.02 , 0.5 ]) are overlaid as coloured, dashed histograms. Grey shading indicates z < 0.02, which we exclude from our analysis. |
| In the text | |
 |
Fig. A.2. Performance of the 3D (solid lines) and 2D (dashed lines) jackknife in various configurations, plotted as ratios to analytical (shot-noise) errors estimated for the wg+ statistic. GAMA configurations are plotted on the top row, with SDSS on the bottom. Colour/redshift sample error ratios are vertically offset by increments of 0.5 (equivalent to a 50% difference in the error on wg+ ) for clarity, and σjack./σshot. = 1 is indicated for each sample by a dotted horizontal line. Also shown are the Z2R and SR samples’ 2D (left-in-panel) and 3D (right-in-panel) jackknife estimates of absolute correlation matrices |
| In the text | |
 |
Fig. A.3. Clustering measurements from our defined GAMA galaxy samples (open circles) overlaid with corresponding measurements from individual, ∼180 deg2 MICE subvolumes (dotted lines). Filled triangles show the means of the MICE clustering signals. We see significant differences between MICE and GAMA, particularly at low redshift and large scales, and so choose not to estimate covariances directly from MICE – see Appendix A.2 for details. |
| In the text | |
 |
Fig. A.4. A comparison of clustering covariance elements (columns), estimated for each redshift/colour galaxy sample (rows) with the SWOT internal jackknife per MICE patch (X, green) and the total jackknife over all patches (Y, solid coloured lines), plotted as X/Y − 1. The 0.16 , 0.5 , 0.84 percentiles over the patch estimates are indicated by dashed lines and shading. Pink solid lines and hatching indicate covariance elements scaled by the fitted variables aij described in Appendix A.2. |
| In the text | |
 |
Fig. D.1. The same as Fig. 8, for nuisance parameters only. |
| In the text | |
 |
Fig. D.2. The same as Fig. 9, for nuisance parameters only. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



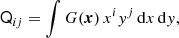
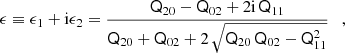
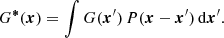
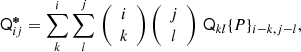
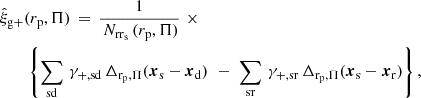
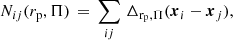
![$$ \begin{aligned} \gamma _{+,ij} \, = \, \frac{1}{\mathcal{R} } \, \mathfrak{R} \mathrm{e} \left[\epsilon _{i} \, {\mathrm{exp}}\left(-2\mathrm{i} \varphi _{ij} \right) \right], \end{aligned} $$](/articles/aa/full_html/2019/04/aa34714-18/aa34714-18-eq10.gif)
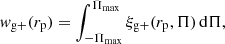
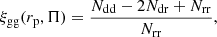
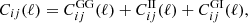
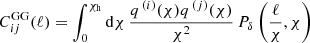
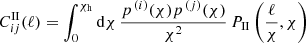
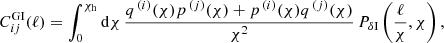
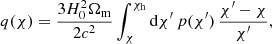
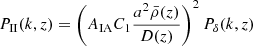
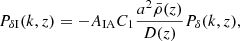
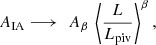
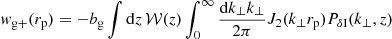
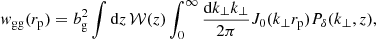
![$$ \begin{aligned} \mathcal{W} (z) = \frac{p_{i}(z)p_{j}(z)}{\chi ^{2}(z)\chi ^{\prime }(z)} \left[ \int \mathrm{d}z \frac{p_{i}(z)p_{j}(z)}{\chi ^{2}(z)\chi ^{\prime }(z)} \right]^{-1}, \end{aligned} $$](/articles/aa/full_html/2019/04/aa34714-18/aa34714-18-eq27.gif)
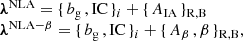
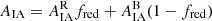
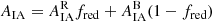
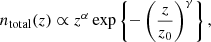
![$$ \begin{aligned} {\boldsymbol{d}} = \{\,&C_{i_{\mathrm{B} }j_{\mathrm{B} }}(\ell ) \quad \forall \quad i \,, j \in [1\,,5] \, \cap \, i \leqslant j , \nonumber \\&C_{i_{\mathrm{B} }j_{\mathrm{R} }}(\ell ) \quad \forall \quad i \,, j \in [1\,,5] , \nonumber \\&C_{i_{\mathrm{R} }j_{\mathrm{R} }}(\ell ) \quad \forall \quad i \,, j \in [1\,,5]\, \cap \, i \leqslant j \, \} , \end{aligned} $$](/articles/aa/full_html/2019/04/aa34714-18/aa34714-18-eq54.gif)