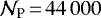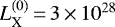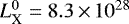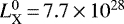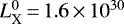| Issue |
A&A
Volume 624, April 2019
|
|
|---|---|---|
| Article Number | A101 | |
| Number of page(s) | 9 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201834491 | |
| Published online | 18 April 2019 | |
Photo-evaporation of close-in gas giants orbiting around G and M stars
INAF – Osservatorio Astronomico di Palermo,
Piazza del Parlamento 1,
90134
Palermo,
Italy
e-mail: daniele.locci@inaf.it
Received:
23
October
2018
Accepted:
28
February
2019
Context. X-rays and extreme ultraviolet radiation impacting a gas produce a variety of effects that, depending on the electron content, may provide significant heating of the illuminated region. In a planetary atmosphere of solar composition, stellar high energy radiation can heat the gas to very high temperatures and this could affect the stability of planetary atmospheres, in particular for close-in planets.
Aims. We investigate the variations with stellar age in the occurring frequency of gas giant planets orbiting G and M stars, taking into account that the high energy luminosity of a low mass star evolves in time, both in intensity and hardness.
Methods. Using the energy-limited escape approach we investigated the effects induced by the atmospheric mass loss on giant exoplanet distribution that is initially flat, at several distances from the parent star. We followed the dynamical evolution of the planet atmosphere, tracking the departures from the initial profile due to the atmospheric escape, until it reaches the final mass-radius configuration.
Results. We find that a significant fraction of low mass Jupiter-like planets orbiting with periods lower than ~3.5 days either vaporize during the first billion years or lose a relevant part of their atmospheres. The planetary initial mass profile is significantly distorted; in particular, the frequency of occurrence of gas giants, less massive than 2 MJ, around young stars can be considerably greater than their occurrence around older stellar counterparts.
Key words: planets and satellites: atmospheres / planets and satellites: dynamical evolution and stability / planet-star interactions / planets and satellites: gaseous planets
© ESO 2019
1 Introduction
X-rays and extreme ultraviolet radiation impacting a gas produce a variety of effects that, depending on the electron content, may provide a significant heating of the illuminated region. In a planetary atmosphere of solar composition X-rays penetrate much deeper than ultraviolet radiation (e.g. Cecchi-Pestellini et al. 2009), where due to the large fractional ionization can heat the gas to very high temperatures, having consequences on the stability of planetary atmospheres, in particular for close-in planets.
After the dispersal of the protoplanetary disc, extrasolar planets generally cool and contract to their currently observed sizes. In planets close enough to the host star, the atmosphere may instead go through a long phase of efficient hydrodynamic escape, or even blow off, and the atmosphere final fate depends mainly on the atmospheric mass and stellar irradiation (e.g. Lammer et al. 2003). The transiting exoplanet HD 209458b is the first planet with an observed ongoing atmospheric hydrodynamic escape, estimated to be ~1010 g s−1 (Vidal-Madjar et al. 2003). A few other planets with escaping atmospheres, such as hot Neptune GJ 436b (Kulow et al. 2014; Ehrenreich et al. 2015; Lavie et al. 2017) and hot Jupiter HD 189733b (Lecavelier des Étangs et al. 2010; Bourrier et al. 2013), have been subsequently discovered mainly via Lyα transit spectroscopy.
At very early phases of planetary evolution, atmospheres are subjected to extremely intense high energy stellar fluxes beyond the Lyman continuum edge (hereafter XUV radiation). This is the time when atmospheric escape is strongest and may shape the planetary envelope, before setting the atmosphere onto its final evolutionary path. In fact, photo-evaporation of low-density atmospheres may be the dominant evolutionary mechanism in planet size distribution (Fulton & Petigura 2018). There is less of a consensus whether planetary evaporation is driven by extreme ultraviolet or X-ray heating. Owen & Jackson (2012) pointed out that these two energy sources might give rise to separate effects. Evaporation driven by X-rays generally occurs at high X-ray luminosities, low planetary densities, high planetary masses, and small separations, while extreme ultraviolet seems dominate at low X-ray luminosities, high planetary densities, low planetary masses, and large separations. These authors also found that the evaporative flow may undergo a transition from X-ray-driven at early times to extreme ultraviolet-driven at late times.
To recover a planetary evolutionary path, we might start from the current mass of the planet and retrace its evolution back in time (e.g. Lopez et al. 2012 in the case of low mass planets), obtaining the mass of the planet when the star was much younger. Taking the opposite view, we might consider a sample of giant planets with a uniform distribution in mass, assigning to each of the planets a radius from existing numerical calculations at the initial time of the simulation, and follow the resulting evolution.
The general characteristics of the mass loss process can be studied in a statistical sense without modelling in detail individual planets using a method put forward by Lecavelier des Étangs et al. (2007). Through this approach consisting in the comparison of the stellar high energy received by the upper atmosphere to the planetary potential energy in an energy diagram, several studies (e.g. Lecavelier des Étangs et al. 2007; Davis & Wheatley 2009; Ehrenreich & Désert 2011) discussed the effects of the mass loss on the evolutionary history of a population of known exoplanets.
Among the methods proposed to describe the hydrodynamical instability of a planetary atmosphere exposed to strong high energy irradiation, the concept of energy-limited escape has been widely used in literature (e.g. Erkaev et al. 2007; Sanz-Forcada et al. 2010; Lopez & Fortney 2013; Jin et al. 2014). In such a model put forward by Watson et al. (1981), the planetary thermosphere is considered as a closed system, and the mass loss rate is derived by equating the radiative energy input to the energy gain of the evaporated atmospheric material. By using the energy-limited escape description, we investigate the effects in time of the atmospheric mass loss on a synthetic sample of giant exoplanets with an initial uniform (flat) planetary mass distribution at several distances from a parent star. We extend the studies of Penz et al. (2008a) and Penz & Micela (2008), who addressed such a problem exploiting synthetic planetary populations around dG and dM stars, respectively. We take into account the variations of the planetary size with time in response to gravitational contraction and mass loss processes. Moreover, we assign to each planet a specified stellar luminosity evolving with time.
We assume an initial time of 10 Myr when planets are supposed to have already reached their final orbit through migration (we neglect type III migration). Then, we follow the dynamical evolution of the planet atmosphere, tracking the departures from the initial profile due to the atmospheric escape, until it reaches the final mass-radius configuration. On this basis we derive the fractional occurrence frequency of giants planets around young dwarf stars. Recent advances in detection techniques allow us to reveal planets even around active young T Tauri stars (Donati et al. 2017); the result is that a larger incidence of hot Jupiter seems to occur at young stellar ages than in older phases. In our study we therefore investigate gas giant frequency variations at different orbital periods, from the T Tauri phase to more evolved main sequence stages. Planetary periods are taken from the work of Fressin et al. (2013), which used a catalogue of more than 2300 candidate transiting planets, released in February 2013 by the mission Kepler (Batalha et al. 2013). These authors take into account five classes of exoplanets with orbital periods in the range 0.8–418 days. Such distribution does not depend on the spectral type of parent stars and it is valid from F to M spectral types.
In the following section we present an outline of the method together with a description of computational approximations and shortcuts. Section 3 contains a collection of results, while the conclusions we reach are presented in the last Section.
2 Model
We studied a population of synthetic giant planets orbiting around dG and dM stars. We initially assumed a uniform mass distribution for a population of 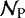 giant planets with masses MP in the range 0.2–16 MJ, MJ being the Jupiter mass. We subdivided the mass interval into 20, evenly spaced mass bins. We also considered the 11 orbital period bins selected by Fressin et al. (2013). At the initial time, ti = 10 Myr, planet radii, RP were taken from Fortney et al. (2007), who derived the radius as a function of time given a planetary mass in the range MP = 0.24− 11.3 MJ, and a planet mean orbital distance, dP ranging from 0.02 to 9.5 AU. We extrapolated planetary radii corresponding to masses laying beyond the limits. For any mass bin, we chose 200 evenly spaced masses; then, for a given planetary mass we randomly assigned one orbital period in each interval provided by Fressin et al. (2013). The number of selected planets adds to a total
giant planets with masses MP in the range 0.2–16 MJ, MJ being the Jupiter mass. We subdivided the mass interval into 20, evenly spaced mass bins. We also considered the 11 orbital period bins selected by Fressin et al. (2013). At the initial time, ti = 10 Myr, planet radii, RP were taken from Fortney et al. (2007), who derived the radius as a function of time given a planetary mass in the range MP = 0.24− 11.3 MJ, and a planet mean orbital distance, dP ranging from 0.02 to 9.5 AU. We extrapolated planetary radii corresponding to masses laying beyond the limits. For any mass bin, we chose 200 evenly spaced masses; then, for a given planetary mass we randomly assigned one orbital period in each interval provided by Fressin et al. (2013). The number of selected planets adds to a total 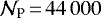 .
.
The model put forward by Fortney et al. (2007) was developed for solar-like stars. Nevertheless, we extended this model to cover stellar types up to M, scaling the stellar flux accordingly to the different orbital distances owned by planets with identical orbital periods revolving around different stars. In order to chose a suitable Fortney’s track for the case of dM stars, we opportunely scaled the distance from the star by a factor 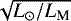 , where L⊙ and LM are the luminosity of the dG and the dM stars, respectively. Figure 1 shows the initial MP −RP distribution of the
, where L⊙ and LM are the luminosity of the dG and the dM stars, respectively. Figure 1 shows the initial MP −RP distribution of the  model planets. Close-in planets are located in the upper part of the figure.
model planets. Close-in planets are located in the upper part of the figure.
In the energy limited escape approach, the thermal planetary mass loss rate results (e.g. Sanz-Forcada et al. 2011)
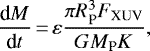 (1)
(1)
where FXUV is XUV radiation flux at the planet orbit, G the gravitational constant, K the potential energy reduction factor due to stellar tidal forces (Erkaev et al. 2007), and ε the escape efficiency. This latter quantity incorporates the details of the escape process, representing the efficiency of conversion of the energy of the incident XUV radiation into effective escape of gas. Selsis et al. (2007) considered such an efficiency as the product of the heating efficiency and the fraction of the deposited energy that is eventually lost through escaping gas. While this latter fraction has been estimated to be around 0.5 or lower (e.g. Penz et al. 2008b), the heating efficiency depends on the spectral shape of theincoming radiation (Cecchi-Pestellini et al. 2009).
The high energy luminosity of solar-type stars evolves in time, both in intensity and hardness (e.g. Micela 2001). We define an average heating efficiency weighted over the shape of a chosen stellar spectrum as follows:
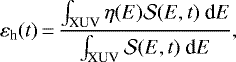 (2)
(2)
where η is the heating efficiency for a hydrogen-ionizing photon of energy E (Dalgarno et al. 1999), and 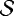 the spectral shape (Locci et al. 2018). The variation in time of the spectral shape is estimated as
the spectral shape (Locci et al. 2018). The variation in time of the spectral shape is estimated as
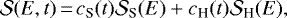 (3)
(3)
where cS and cH, such that cS (t) + cH(t) = 1 are evolving coefficients taking into account the different evolution of the shapes of the emitted spectrum in the soft and hard XUV spectral bands (see Micela 2001 for details). The adopted spectral shapes are models for the thermal emission of hot plasmas with energies 0.5 (soft band S) and 1 keV (hard band H), derived by Raymond & Smith (1977). We obtain ε(t) = 0.5 × εh(t)≲0.4.
Young solar type stars emit X-rays at a level 3–4 orders of magnitude higher than the present-day Sun, during both the pre-main sequence phase, when the emission is dominated by intense flares, and the first phases of the main sequence (Feigelson et al. 2003; Favata et al. 2005). In order to account for this effect in the X-ray band, we use the prescriptions given in Penz et al. (2008a) and Penz & Micela (2008). We use as reference the stars in the Pleiades, a widely studied young stellar cluster that has an estimated age of 80 Myr. The evolution of the X-ray luminosity results
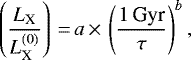 (4)
(4)
where 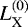 is the initial luminosity of the star and τ the star age in Gyr. The parameters a and b in Eq. (4) are reported in Table 1.
is the initial luminosity of the star and τ the star age in Gyr. The parameters a and b in Eq. (4) are reported in Table 1.
The X-ray luminosity of a star at specific stellar ages follows a distribution whose mean value is determined by Eq. (4) and has a spread of about one order of magnitude. This probability density function may be represented by a log-normal profile, whose cumulative distribution function is written as (Penz et al. 2008a)
![\begin{equation*}{\cal P}[\textrm{ln} (L_{\textrm{X}}/{\textrm{erg~s}^{-1}})]\,{=}\,\frac{1}{2} \left[ 1+ \textrm{erf} \biggl( \frac{\textrm{ln}(L_{\textrm{X}}/{\textrm{erg~s}^{-1}})-\mu}{\sqrt{2}\sigma} \biggr) \right] ,\end{equation*}](/articles/aa/full_html/2019/04/aa34491-18/aa34491-18-eq11.png) (5)
(5)
where 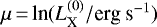 and σ is the standard deviation of the logarithm variable (Penz & Micela 2008; Penz et al. 2008a). The adopted values for the initial X-ray luminosities are
and σ is the standard deviation of the logarithm variable (Penz & Micela 2008; Penz et al. 2008a). The adopted values for the initial X-ray luminosities are 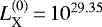 and 1028.75 erg s−1 for dG and dM stars, respectively (Preibisch & Feigelson 2005).
and 1028.75 erg s−1 for dG and dM stars, respectively (Preibisch & Feigelson 2005).
We consider 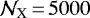 X-ray luminosity bins and we derive the fractional number of stars falling within each bin exploiting Eq. (5). Then, for each of the 11 planet orbital bins, we randomly assign 4000 X-ray luminosity (corresponding to the number of planets in each period bin), and follow their evolution in time through Eq. (4).
X-ray luminosity bins and we derive the fractional number of stars falling within each bin exploiting Eq. (5). Then, for each of the 11 planet orbital bins, we randomly assign 4000 X-ray luminosity (corresponding to the number of planets in each period bin), and follow their evolution in time through Eq. (4).
The extreme ultraviolet luminosity is given by the relation (Sanz-Forcada et al. 2011)
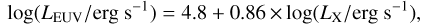 (6)
(6)
where it is assumed that the evolution of the extreme ultraviolet radiation follows that of the X-ray band. The total luminosity LXUV is then the superposition of the luminosities in the extreme ultraviolet and X-ray spectral bands.
The stellar irradiation contrasts with the natural contraction of the radius of a giant planet under its own weight. The rate at which the radius decreases is determined by the bond albedo, the presence of clouds and their optical depths, the gas-phase abundances and their opacities, and the intensity of the stellar radiation (Burrows et al. 2000). Isolated giant planets or brown dwarfs contract more rapidly than irradiated close-in planets (e.g. Burrows et al. 1997). For this reason the mass-radius depends on the orbital distance. In our simulation the radius is then allowed to change with time in response to the mass loss induced by the XUV radiation, together with the natural contraction of the planetary atmosphere due to the radiative losses.
We let the planet lose mass at time t following the overflow from the Roche lobe induced by XUV radiation, and then we derive the radius (and therefore the density) corresponding to the new mass at the time t + dt, scaling appropriately along the Fortney et al. (2007) tracks. We iterate until we reach the final time tf = 4.5 Gyr.
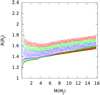 |
Fig. 1 InitialMP−RP distribution at 10 Myr according to Fortney et al. (2007) for a sample of |
3 Results
We consider the cases of a dG star with mass M⋆ = 1 M⊙, and a dM star with M⋆ = 0.3 M⊙. Unless otherwise stated, each planet of mass MP is characterized by two random parameters (simulated as explained above), namely the stellar X-ray luminosity LX, and the mean orbital period TP (or the orbital distance dP).
3.1 Energy diagrams
Following Lecavelier des Étangs et al. (2007), we constructed energy diagrams, in which the potential energy, Ep of a planet is plotted versus the power received by its upper atmosphere, d EXUV∕dt. Such an approach allows us to estimate the planetary lifetime and the atmospheric mass loss rate, Ṁ (g s−1).
In Fig. 2 we show the energy diagrams for our set of 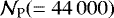 models, orbiting around dG and dM stars. All the planets that have completely lost their envelope lie in the evaporation-forbidden region delimited by the lifetime line.
models, orbiting around dG and dM stars. All the planets that have completely lost their envelope lie in the evaporation-forbidden region delimited by the lifetime line.
The lifetime in the case of dM stars is slightly greater than the case of dG stars, implying that planets survive longer around dM stars, as shown in Fig. 3. The mass loss rate has been calculated by means of Eq. (1) via the model described in Sect. 2. The ratio of the stellar fluxes received by planets orbiting around dG and dM stars at the same orbital period is 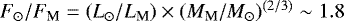 .
.
3.2 Planetary mass distribution
The main objective of this work is to study the effects of high energy stellar radiation on planetary mass distribution. Distant planets are poorly subjected to mass loss events and their radii are mainly constrained by natural contraction, while closer planets, andamong this group those with lower densities, may be significantly affected.
In Fig. 4 we show the effects of XUV irradiation over the initial, flat mass distribution of planets orbiting either dG and dM stars for several period bins. The number of planets of each mass bin is normalized at the number of planets for bin of the initial flat mass distribution. We find that for periods longer than six days, the effects of high energy radiation are negligible. Low mass Jupiter-like planets close to the star are instead strongly perturbed. A large fraction of planets with MP ≲0.6 MJ located very close to their parent stars (first Fressin’s period bin) are vaporized. The most affected planets are those with a large radius (low density), orbiting around X-ray bright stars. Over the entire planetary mass distribution the percentage of planets that are lost, i.e. with final masses outside the range 0.2− 13 MJ never exceeds 4% (2%) for dG (dM) stars in the first period bin (0.8–2 days). However, the number of lost planets is not evenly distributed over the entire range of masses, but is concentrated at lower masses. At the shortest assumed orbital periods (TP = 0.8−2 days), 36% (20%) of planets in the 0.2–1 MJ mass bin around dG (dM) stars are lost and thus removed from the initial distribution; the same fate occurs to 18% (8%) of planets falling in the 1–2 MJ mass bin. The small bump located at low mass values in the mass profile shown in Fig. 4 is produced by planets falling outside the lower boundary of the original mass distribution, which still maintains residual atmospheres. The cores of vaporized planets are not shown in the Fig. 4.
In orderto investigate the effects of extreme ionizing fluxes, we consider model planets orbiting with rather short periods, i.e. TP = 0.5–0.8 days. The top left panel of Fig. 4 represents the final mass distribution. In the case of dG (dM) stars, 11% (7%) of planets are lost in the full mass range (0.2−13MJ) and completely lose their atmosphere in ~9% (~ 6%) of the total number of planets. We also find that 81% (62%) are removed from the mass range 0.2− 1 MJ, while 49% (24%) are removed from the 1−2 MJ mass bin. Of the original 200 planets initially present in the first mass bin 0.2− 1 MJ, 49.5% (8%) of these are removed as they are inside the Roche limit; 49% (78%) are vaporized, while the remaining 0.5% (14%) survive. These planets are not of course the only population of the 0.2− 1 MJ mass bin, as this small fraction of planets is increased by the overflow from higher mass bins.
In Fig. 5 we include all orbital periods and we show the behaviour of the mass distribution for both dG and dM stars. For the sake of simplicity we include three ages, 0.5, 1.5, and 4.5 Gyr, adding to a total of 44 000 × 3 model points. As expected the more affected planets are those with low mass and small orbital periods. This is consistent with, for example findings by Szabó & Kiss (2011), which described the so-called evaporation sub-Jupiter desert in the range mass of 0.02–0.8 MJ. For periods lower than 2.5 days, our result reproduces the sub-Jovian desert, but we also find a scarcity of planets for masses lower than 0.8 MJ and periods lower than 1 day (see e.g. Owen 2018).
Figure 6 shows the final versus the initial masses of close (first period bin) and far (last period bin) planets for the surviving atmospheres: low mass close-in planets loose a substantial fraction of their initial masses, while far planets lie mainly on the bisector of the diagram (i.e. they are virtually unperturbed). We point out that we consider as vaporized, planets completely devoid of their gaseous envelopes showing thus their bare rocky core (Lecavelier des Étangs et al. 2004); these are the so-called chthonian planets (Hébrard et al. 2004). In our simulations, we selected Fortney et al. (2007) models with a constant 10 M⊕ rocky core. Thus, vaporization produces rocky planets with such a final constant value for their masses. This is of course an oversimplification; for example Lammer (2013) argued that at distances dP ~ 0.1−1 AU, in solar-likeenvironments the critical mass to accrete a gaseous envelope is MP ~ 5−20 M⊕. Thus, at shorter orbital distances, rocky planets of lower mass are expected.
We estimate the frequency of giant planets at the age of 10 Myr per star of given spectral type and each period bin given in Fressin et al. (2013). To this aim we use the distributions shown in Fig. 4 as corrections to the current planetary mass profile;the latter is assumed to be dominated by 4.5 Gyr old planets. In the case of dG (dM) stars, in the orbital period bin 0.8–2 days, we find 4% (2%) more giant planets at early times than at the nominal final evolutionary time, and 1% (~ 0.5%) in the period bin 2–3.4 days. At larger periods basically no differences occur. Such differences are small and likely unobservable, even in future much larger planetary samples. However, these differences are specifically concentrated in the 0.2–2 MJ range, rather than over the full mass range. For instance, in the period bin TP = 0.8−2 days, around young stars we find ~36%(~20%) more planets have masses in the range of those of Saturn to Jupiter. This value increases up to a factor of at least 2 when we consider closer gaseous giants. These predictions may be confirmed or disproved by the project GAPS2 (Global Architecture of Planetary Systems), the extension of the programme GAPS (Covino et al. 2013), for which the determination of the frequency of massive hot planets around young stars constitutes one of the main objectives. Finally, we note that all of the vaporized planets lie below the lifetime line in the energy diagrams shown in Fig. 2.
 |
Fig. 2 Energy diagram for planets orbiting dG (left panel) and dM (right panel) stars. Red dots represent planets surviving with some fraction of the initial envelope, while blue dots show planets that lost the entire envelope. The solid black line indicates the lifetime line. |
 |
Fig. 3 Colour map of the mass loss rate at 0.5 and 4.5 Gyrs in planets orbiting dG (top panels) and dM (bottom panels) stars. |
 |
Fig. 4 Normalized number of planets per mass bin. Each panel corresponds to an orbital period interval. The initial (flat) mass distribution: blue line; final mass distribution for planets around dG stars: red line; and final mass distribution for planet around dM stars: green line. Since radiative effects are negligible, orbital periods longer than ~ 6 days have not been shown. |
 |
Fig. 5 Normalized number of planets as functions of the mass and orbital period; the plot summarizes the data for three different ages: 0.5 (red dots), 1.5 (green dots), and 4.5 (blue dots) Gyr. |
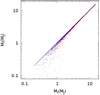 |
Fig. 6 Final mass distribution of our planetary sample as a function of initial planetary mass. Planets in the range TP = 0.8–2 days are labelledwith red (blue) dots when orbiting dG (dM) stars; black dots on the bisector indicate planets in the 245–418 days period range. |
3.3 Temporal evolution of the mass–radius relation
In Fig. 7 we highlight the effects of the high energy radiation on the temporal evolution of planetary mass and radius. We show the temporal evolution in two cases: (i) three masses, MP = 0.55, 1, and 2 MJ, with respective orbital periods 1.7, 1.5, and 1.8 days, which receive a common initial XUV flux FXUV = 1.1 × 106 erg cm−2 s−1; and (ii) a single planetary mass MP = 1 MJ with a period of 1.8 days and three initial X-ray luminosities 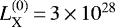 , 3 × 1029, and 1.6 × 1030 erg s−1. All the planets are in the first period bin. From the results reported in the figure, it is clear that lighter planets lose more mass that the more massive ones (top left panel), while planets around the more bright stars lose more mass (top right panel). An interesting point is the mass loss of 1 MJ planets may be significantly affected if the central star is very bright (middle right panel). Comparing the fates of irradiated planets with unperturbed planets, we find again that the most affected planets are those with lower masses and those orbiting around brighter stars (see bottom panels).
, 3 × 1029, and 1.6 × 1030 erg s−1. All the planets are in the first period bin. From the results reported in the figure, it is clear that lighter planets lose more mass that the more massive ones (top left panel), while planets around the more bright stars lose more mass (top right panel). An interesting point is the mass loss of 1 MJ planets may be significantly affected if the central star is very bright (middle right panel). Comparing the fates of irradiated planets with unperturbed planets, we find again that the most affected planets are those with lower masses and those orbiting around brighter stars (see bottom panels).
Finally, in Fig. 8 we show the mass–radius evolutionary tracks of three planets orbiting around the dG star. Their initial masses are MP = 0.3, 1, and 1.2 MJ, and we locate these in two different orbital period bins, TP = 0.8−2 and 245–418 days. In the first period bin, we select planets with (almost) identical periods, i.e. TP = 1.7 days. The initial stellar X-ray luminosities are 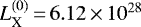 , 3.12 × 1028 and 1.7 × 1030 erg s−1. The first planet is selected to explore the effects of low densities; in fact, such a planet vaporizes after roughly 100 Myr even thoughthe high energy flux of its parent star is relatively modest. The other two planets, possessing similar initial mass and density, follow different evolutionary tracks because of the different amount of impinging stellar high energy radiation. No effects are seen for distant planets. The results shown in Fig. 8 imply that during the first 1 Gyr, both radius and mass undergo large variations, remaining unaffected at longer times. In the presence of a population of planets with an age spread, we expect a spread in the mass–radius relation: younger planets lie in the higher radius–higher mass part of the diagram. Figure 8 reveals that the evolution of the planetary radius is dominated by gravitational contraction, especially during the first 0.5 Gyr. Generally, the modification to the radius in response to atmospheric losses introduces a small correction, with the exception ofplanets orbiting stars with a strong high energy emission, when the mass loss mechanism becomes important during the whole simulation. This implies a greater correction to the radius due to the mass loss (see also Fig. 7).
, 3.12 × 1028 and 1.7 × 1030 erg s−1. The first planet is selected to explore the effects of low densities; in fact, such a planet vaporizes after roughly 100 Myr even thoughthe high energy flux of its parent star is relatively modest. The other two planets, possessing similar initial mass and density, follow different evolutionary tracks because of the different amount of impinging stellar high energy radiation. No effects are seen for distant planets. The results shown in Fig. 8 imply that during the first 1 Gyr, both radius and mass undergo large variations, remaining unaffected at longer times. In the presence of a population of planets with an age spread, we expect a spread in the mass–radius relation: younger planets lie in the higher radius–higher mass part of the diagram. Figure 8 reveals that the evolution of the planetary radius is dominated by gravitational contraction, especially during the first 0.5 Gyr. Generally, the modification to the radius in response to atmospheric losses introduces a small correction, with the exception ofplanets orbiting stars with a strong high energy emission, when the mass loss mechanism becomes important during the whole simulation. This implies a greater correction to the radius due to the mass loss (see also Fig. 7).
In Fig. 9 we show in an energy diagram the position of some well-known real exoplanets, together with synthetic evolutionary tracks obtained by our modelling technique, as an indication of the evolutionary paths followed by the real planets during their lifetimes. We assume all the planets orbit around G stars, although some of these planets actually orbit K stars. In Table 2 we show the mass loss rate for the planets reported in Fig. 9, calculated by means of Eq. (1). We also compare this results with those present in literature, from both theoretical models and measurements.
Since the X-ray emission of dM stars decreases at a slower rate than for dG, we compare in the energy diagram the evolutionary tracks of two planets, with mass MP = 1 and 2 MJ, orbiting around dG and dM stars. The stars are assumed to have the same initial X-ray luminosities, namely 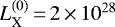 and 1 × 1029 erg s−1, while the planets are orbiting at the same distance from the parent stars, i.e. they receive the same XUV flux. The results reported in Fig. 10 show that the evolutionary tracks tend to get closer and closer as the time increases. As a consequencethe fate of an exoplanet population at the age at which planets do not evolve anymore, does not depend significantly on the stellar type.
and 1 × 1029 erg s−1, while the planets are orbiting at the same distance from the parent stars, i.e. they receive the same XUV flux. The results reported in Fig. 10 show that the evolutionary tracks tend to get closer and closer as the time increases. As a consequencethe fate of an exoplanet population at the age at which planets do not evolve anymore, does not depend significantly on the stellar type.
3.4 Massdistribution with a constant birth rate
In the previous subsections we analysed the evolution of a sample of planets that are identical in age, evolving from 10 to 4.5 Gyr. To provide a more realistic picture, we now consider planets at different evolutionary stages. We assume that during the simulation time (~ 10 Gyr) the planet birth rate remains constant. To cover the parameter space more densely, we extend the number of simulated planets to 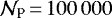 . Planet orbital periods are within the period bin 0.8–2 days.
. Planet orbital periods are within the period bin 0.8–2 days.
Far planets are unaffected by high energy radiation; their final mass distribution coincides with the initial mass distribution.The mass distribution results are shown in Fig. 11. Close-in planets – in particular Jovian and sub-Jovian – show a final mass distribution departing significantly from the original profile, emphasizing both the efficiency and speed of radiation-induced evaporation processes. Assuming that the initial mass distribution does not depend on the orbital distance (this is not unquestionable and depends on planetary migration, e.g. Trilling et al. 2002), the present results suggest that planets in the 0.2−1 MJ range occur less frequently close to than far away from a XUV emitting star. Such discrepancy (~ 41%(33%) in the case of the dG (dM) stars) in the occurring frequencies of close and far planets could be observable after correcting for the observational biases that all too often favour the detection of close-in planets. In the present calculations we find a milder difference between the occurrence frequencies of planets orbiting dG and dM stars with respect to the case of planets with identical ages (cf. Figs. 4, top left panel, and 11). This is consistent with the results shown in Fig. 10.
 |
Fig. 7 Evolving mass loss (top panels), mass (middle panels) and radius (bottom panels). Left panels: case of three planets of different masses, MP = 0.55 (red line), 1 (green line), and 2 MJ (blue line), subjected to identical irradiation FXUV = 1.1 × 106 erg cm−2 s−1. Right panels: the planetary mass is taken constant to MP = 1 MJ, while the initial X-ray luminosity is varied, |
 |
Fig. 8 Mass–radius relation for near (left panel) and far (right panel) exoplanets at different ages: 10 Myr (red dots), 0.5 Gyr (green dots), 1.5 Gyr (yellow dots), 2.5 Gyr (blue dots), 3.5 Gyr (purple dots), and 4.5 Gyr (light blue dots). In both panels, black lines refer to the evolutionary paths followed by three planets with initial masses MP = 0.6 MJ ( |
 |
Fig. 9 Energy diagrams for five observed exoplanets together with the corresponding evolutionary track. Each simulation is labelled with the initial mass of the planet. The dashed part of the lines indicates the section of the curve that is an extrapolation, as our model is unable to calculate the planetary radius of planets with masses much lower than 0.2 MJ. |
 |
Fig. 10 Energy diagrams for two planets of mass MP = 1 and 2 MJ orbiting around dG (dashed lines) and dM (solid lines) stars of identical initial X-ray luminosities and fluxes. |
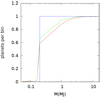 |
Fig. 11 Number of planets per mass bin for a sample of |
4 Discussion and conclusions
The presentmodel simulates the hydrodynamic escape of planetary atmospheres embedded in intense XUV radiation fluxes from parent stars. The model is based on the energy-limited approximation. During the simulations the planetary radius changes in response to gravitational contraction and photo-evaporation. The relevant factors in the simulation are the planetary distance and magnitude of stellar XUV luminosity. This latter parameter depends on time as low mass stars are known to have evolving radiation environments. Mass escape depends implicitly, but significantly on the stellar mass, as this last parameter is crucial in determining the planet distance (in a fixed period bin), and thus the flux impinging at the top of the atmosphere, and the variation in time of the strength of XUV radiation (see Eqs. (4) and (6)).
The general results from this work are as follows:
- (i)
A significant fraction (4% around dG stars and 2% around dM stars) of low mass Jupiter-like planets orbiting with periods lower than six days vaporize during the first billion years, and 1% around dG stars and 2% around dM stars of planets loose a relevant part of their atmospheres.
- (ii)
The planetary initial mass profile is significantly distorted in stellar radiation environments dominated by high energy photons; in particular, the frequency of occurrence of planets in the 0.2–2 MJ mass range around young star can be considerably greater (20% and 10% in the case of the dG and dM stars, respectively) than the planetary occurring frequency around older counterparts.
- (iii)
We find that the mass loss rates around dG and dM stars differ significantly at early times, but such differences decrease with time.
The results of the present calculation provide a correction factor, that if applied to the current frequency of exoplanets, allows us to retrieve the frequency around young stars.
In conclusion, XUV stellar illumination may have important consequences on the mass distribution of close-in planets, heating the outer layers of a planets envelope and driving mass loss. However, other mechanisms may have significant impact on the planetary mass distribution. Moreover, all these processes might operate simultaneously. A possible diagnostics may be the mass loss dependence on stellar mass (Fulton & Petigura 2018) because of its tight link to high energy luminosity, in particular during the pre-main sequence phase when the emission is dominated by intense flares (e.g. Favata et al. 2005).
Acknowledgements
We acknowledge support from INAF through the Progetto Premiale: A Way to Other Worlds? of the Italian Ministry of Education. We would like to thank the anonymous referee for her/his comments, suggestions, and criticisms that contributed to improve the manuscript.
References
- Batalha, N. M., Rowe, J. F., Bryson, S. T., et al. 2013, VizieR Online Data Catalog: J/ApJS/204/24 [Google Scholar]
- Bourrier, V., Lecavelier des Étangs, A., Dupuy, H., et al. 2013, A&A, 551, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burrows, A., Marley, M., Hubbard, W. B., et al. 1997, ApJ, 491, 856 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, A., Guillot, T., Hubbard, W. B., et al. 2000, ApJ, 534, L97 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cecchi-Pestellini, C., Ciaravella, A., Micela, G., & Penz, T. 2009, A&A, 496, 863 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Covino, E., Esposito, M., Barbieri, M., et al. 2013, A&A, 554, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dalgarno, A., Yan, M., & Liu, W. 1999, ApJS, 125, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, T. A., & Wheatley, P. J. 2009, MNRAS, 396, 1012 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J. F., Yu, L., Moutou, C., et al. 2017, MNRAS, 465, 3343 [NASA ADS] [CrossRef] [Google Scholar]
- Ehrenreich, D., & Désert, J. M. 2011, A&A, 529, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ehrenreich, D., Bourrier, V., Wheatley, P. J., et al. 2015, Nature, 552, 459E [Google Scholar]
- Erkaev, N. V., Kulikov, Y. N., Lammer, H., et al. 2007, A&A, 472, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Favata, F., Flaccomio, E., Reale, F., et al. 2005, ApJS, 160, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Feigelson, E. D., Gaffney, J. A., Garmire, G., Hillenbrand, L. A., & Townsley, L. 2003, ApJ, 584, 911 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., Marley, M. S., & Barnes, J. W. 2007, ApJ, 659, 1661 [NASA ADS] [CrossRef] [Google Scholar]
- Fressin, F., Torres, G., Charbonneau, D., et al. 2013, ApJ, 766, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Fulton, B. J., & Petigura, E. A. 2018, AJ, 156, 264 [NASA ADS] [CrossRef] [Google Scholar]
- Haswell, C. A. 2017, in Handbook of Exoplanets (Switzerland: Springer International Publishing), 97 [Google Scholar]
- Hébrard, G., Lecavelier des Étangs, A., Vidal-Madjar, A., Désert, J.-M., & Ferlet, R. 2004, ASP Conf. Ser., 321, 203 [NASA ADS] [Google Scholar]
- Jin, S., Mordasini, C., Parmentier, V., et al. 2014, ApJ, 795, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Kubyshkina, D., Fossati, L., Erkaev, N. V., et al. 2018, ApJ, 866, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Kulow, J. R., France, K., Linsky, J., & Loyd, R. O. P. 2014, ApJ 786, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Lai, D., Helling, C., & van den Heuvel, E. P. J. 2010, ApJ, 721, 923 [NASA ADS] [CrossRef] [Google Scholar]
- Lammer, H. 2013, Origin and Evolution of Planetary Atmospheres (Switzerland: Springer) [CrossRef] [Google Scholar]
- Lammer, H., Selsis, F., Ribas, I., et al. 2003, ApJ, 598, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Lavie, B., Ehrenreeich, D., Lecavelier des Étangs, A., et al. 2017, A&A 605, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lecavelier des Étangs, A. 2007, A&A, 461, 1185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lecavelier des Étangs, A., Vidal-Madjar, A., McConnell, J.C., & Hébrard, G. 2004, A&A, 418, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lecavelier des Étangs, A., Ehrenreeich, D., Vidal-Madjar, A., et al. 2010, A&A, 514, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Locci, D., Cecchi-Pestellini, C., Micela, G., Ciaravella, A., & Aresu, G. 2018, MNRAS, 473, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Lopez, E. D., & Fortney, J. J. 2013, ApJ, 776, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Lopez, E. D., Fortney, J. J., & Miller, N. 2012, ApJ, 761, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Micela, G. 2001, in X-ray Astronomy 2000, eds. R. Giacconi, S. Serio, & L. Stella, ASP Conf. Ser., 234, 143 [NASA ADS] [Google Scholar]
- Owen, J. E. 2018, ARA&A, in press [Google Scholar]
- Owen, J. E., & Jackson, A. P. 2012, MNRAS, 425, 2931 [NASA ADS] [CrossRef] [Google Scholar]
- Penz, T., & Micela, G. 2008, A&A, 479, 579 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Penz, T., Micela, G., & Lammer, H. 2008a, A&A, 477, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Penz, T., Langmayr, D., Erkaev, N.V., et al. 2008b, Planet. Space Sci., 56, 1260 [NASA ADS] [CrossRef] [Google Scholar]
- Preibisch, T., & Feigelson, E. D. 2005, ApJS, 160, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Raymond, J. C., & Smith, B. W. 1977, ApJS, 35, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Sanz-Forcada, J., Ribas, I., Micela, G., et al. 2010, A&A, 511, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanz-Forcada, J., Micela, G., Ribas, I., et al. 2011, A&A, 532, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Selsis, F., Chazelas, B., Bordé, P., et al. 2007, Icarus, 191, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Szabó, G. M., & Kiss, L. L. 2011, ApJ, 727, L44 [NASA ADS] [CrossRef] [Google Scholar]
- Trilling, D. E., Lunine, J. I., & Benz, W. 2002, A&A, 394, 241 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vidal-Madjar, A., Lecavelier des Étangs, A., Désert, J. M., et al. 2003, Nature, 422, 143 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Watson, A. J., Donahue, T. M., & Walker, J. C. G. 1981, Icarus, 48, 150 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 InitialMP−RP distribution at 10 Myr according to Fortney et al. (2007) for a sample of |
| In the text | |
 |
Fig. 2 Energy diagram for planets orbiting dG (left panel) and dM (right panel) stars. Red dots represent planets surviving with some fraction of the initial envelope, while blue dots show planets that lost the entire envelope. The solid black line indicates the lifetime line. |
| In the text | |
 |
Fig. 3 Colour map of the mass loss rate at 0.5 and 4.5 Gyrs in planets orbiting dG (top panels) and dM (bottom panels) stars. |
| In the text | |
 |
Fig. 4 Normalized number of planets per mass bin. Each panel corresponds to an orbital period interval. The initial (flat) mass distribution: blue line; final mass distribution for planets around dG stars: red line; and final mass distribution for planet around dM stars: green line. Since radiative effects are negligible, orbital periods longer than ~ 6 days have not been shown. |
| In the text | |
 |
Fig. 5 Normalized number of planets as functions of the mass and orbital period; the plot summarizes the data for three different ages: 0.5 (red dots), 1.5 (green dots), and 4.5 (blue dots) Gyr. |
| In the text | |
 |
Fig. 6 Final mass distribution of our planetary sample as a function of initial planetary mass. Planets in the range TP = 0.8–2 days are labelledwith red (blue) dots when orbiting dG (dM) stars; black dots on the bisector indicate planets in the 245–418 days period range. |
| In the text | |
 |
Fig. 7 Evolving mass loss (top panels), mass (middle panels) and radius (bottom panels). Left panels: case of three planets of different masses, MP = 0.55 (red line), 1 (green line), and 2 MJ (blue line), subjected to identical irradiation FXUV = 1.1 × 106 erg cm−2 s−1. Right panels: the planetary mass is taken constant to MP = 1 MJ, while the initial X-ray luminosity is varied, |
| In the text | |
 |
Fig. 8 Mass–radius relation for near (left panel) and far (right panel) exoplanets at different ages: 10 Myr (red dots), 0.5 Gyr (green dots), 1.5 Gyr (yellow dots), 2.5 Gyr (blue dots), 3.5 Gyr (purple dots), and 4.5 Gyr (light blue dots). In both panels, black lines refer to the evolutionary paths followed by three planets with initial masses MP = 0.6 MJ ( |
| In the text | |
 |
Fig. 9 Energy diagrams for five observed exoplanets together with the corresponding evolutionary track. Each simulation is labelled with the initial mass of the planet. The dashed part of the lines indicates the section of the curve that is an extrapolation, as our model is unable to calculate the planetary radius of planets with masses much lower than 0.2 MJ. |
| In the text | |
 |
Fig. 10 Energy diagrams for two planets of mass MP = 1 and 2 MJ orbiting around dG (dashed lines) and dM (solid lines) stars of identical initial X-ray luminosities and fluxes. |
| In the text | |
 |
Fig. 11 Number of planets per mass bin for a sample of |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.