| Issue |
A&A
Volume 623, March 2019
|
|
|---|---|---|
| Article Number | A108 | |
| Number of page(s) | 11 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201834693 | |
| Published online | 12 March 2019 | |
Age determination for 269 Gaia DR2 open clusters⋆
1
INAF–Osservatorio Astronomico di Padova, Vicolo Osservatorio 5, 35122 Padova, Italy
e-mail: diego.bossini@gmail.com
2
INAF–Osservatorio di Astrofisica e Scienza dello Spazio, Via Gobetti 93/3, 40129 Bologna, Italy
3
Institut de Ciències del Cosmos, Universitat de Barcelona (IEEC-UB), Martí Franquès 1, 08028 Barcelona, Spain
4
SIM, Faculdade de Ciências, Universidade de Lisboa, Ed. C8, Campo Grande, 1749-016 Lisboa, Portugal
5
Laboratoire d’Astrophysique de Bordeaux, Univ. Bordeaux, CNRS, B18N, Allée Geoffroy Saint-Hilaire, 33615 Pessac, France
6
Observational Astrophysics, Department of Physics and Astronomy, Uppsala University, Box 516 75120 Uppsala, Sweden
Received:
20
November
2018
Accepted:
28
January
2019
Context. The Gaia Second Data Release provides precise astrometry and photometry for more than 1.3 billion sources. This catalog opens a new era concerning the characterization of open clusters and test stellar models, paving the way for better understanding of the disk properties.
Aims. The aim of the paper is to improve the knowledge of cluster parameters, using only the unprecedented quality of the Gaia photometry and astrometry.
Methods. We have made use of the membership determination based on the precise Gaia astrometry and photometry. We applied an automated Bayesian tool, BASE-9, to fit stellar isochrones on the observed G, GBP, GRP magnitudes of the high probability member stars.
Results. We derive parameters such as age, distance modulus, and extinction for a sample of 269 open clusters, selecting only low reddening objects and discarding very young clusters, for which techniques other than isochrone-fitting are more suitable for estimating ages.
Key words: methods: statistical / open clusters and associations: general / Galaxy: stellar content / catalogs
Full Tables A.1–A.3 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/623/A108
© ESO 2019
1. Introduction
The study of the formation and evolution of open clusters (OC) and their stellar populations represents a backbone of research in modern astrophysics. Indeed, they have a strong impact on our understanding of key open issues, from the star formation process, to the assembly and evolution of the Milky Way disk and galaxies in general (Friel 1995; Jacobson et al. 2016; Cantat-Gaudin et al. 2016; Janes & Adler 1982). As their ages cover the entire lifespan of the Milky Way thin disk, OCs can be used for tracing the Galactic structure. It is therefore essential to have precise information on a significant number of OCs, located at different Galactocentric distances together with the determination of their parameters (e.g., age, kinematics, distances, and chemistry). In the pre-Gaia era we were still far from an ideal situation: the OC census is in fact poorly known. Currently, about 3000 OCs are listed in the most recent versions of Kharchenko et al. (2013, hereafter MWSC) and Dias et al. (2002, hereafter DAML) catalogs. However, the sample is far from being complete even in the local environment (within 1.6–2 kpc, Joshi et al. 2016), where new nearby clusters are still being discovered (see e.g., Cantat-Gaudin et al. 2018a,b; Castro-Ginard et al. 2018). At the faint end of the OC distribution, small and sparse objects and remnants of disrupted clusters can escape detection (Bica & Bonatto 2011). It is also not straightforward to distinguish true clusters from asterisms without high quality kinematic information (Kos et al. 2018). Moreover, studies on OCs may be affected by very large uncertainties on the membership, distance, and metallicity and this reflects on the age determination (Netopil et al. 2016; Cantat-Gaudin et al. 2018a).
Gaia has opened a new era in Galactic astronomy and in cluster science, in particular, thanks to the recent second data release (Gaia Collaboration 2018a,c, hereafter GDR2). GDR2 not only provides homogeneous photometric data covering the whole sky, but also unprecedented high precision kinematics and parallax information, that are fundamental to obtain accurate membership and to identify new clusters. This will, in turn, allow more precise age determinations.
This paper is part of a series devoted to improve the OCs census and their parameter determination, based on Gaia data. Cantat-Gaudin et al. (2018c) has derived membership probability and parameters for 128 OCs, by combining 2MASS photometry (Skrutskie et al. 2006), Gaia First Data Release (GDR1) TGAS parallaxes, and proper motions from either GDR1 or UCAC4 data (Zacharias et al. 2012). Castro-Ginard et al. (2018), Cantat-Gaudin et al. (2018a,b) discovered a large number of new OCs using GDR2, and reclassified a significant number of objects that turned out to be likely asterisms and not true clusters. Cantat-Gaudin et al. (2018a, hereafter Paper I) also updated the cluster census in the solar neighborhood, deriving memberships, mean distances and proper motions for 1229 OCs from GDR2. Soubiran et al. (2018) have made use of GDR2 to derive the kinematics of a sample of 861 OCs in the Milky Way, confirming that OCs have a similar velocity distribution to field stars in the solar neighborhood. The aim of this work is to carry out automated determination of OC parameters (age, distance, extinction) by isochrone fitting using BASE-9 (von Hippel et al. 2006, see also Jeffery et al. 2016) on Paper I clusters. The final catalog contains bona-fide parameters for 269 clusters. This constitutes an impressive data base to understand not only the formation and evolution of OCs, but also the disk properties.
Section 2 presents the data and the cluster selection. Section 3 summarizes the method and the priors used to derive OC parameters (i.e., BASE-9). In Sect. 4 we present the ages and the cluster parameters obtained for our sample of OCs. Finally, in Sect. 5 we compare our results with other surveys.
2. Data: Gaia cluster selection, membership, and photometry
We make use of the cluster membership derived in Paper I on the basis of the GDR2 photometry, proper motions and parallaxes. The catalog includes 1229 objects. Paper I has indeed improved the determination of membership for their clusters, thanks to Gaia very precise multidimensional astrometric data, with proper motions precision typically of 0.05–0.3 mas yr−1 (for G = 14−18) and parallaxes with precision of ∼0.02 mas. We recall that to discard sources with overly large photometric uncertainties, the membership derived in Paper I is limited to sources brighter than G ∼ 18 (see Evans et al. 2018, for details). ite This corresponds to the turnoff of a 3 Gyr cluster seen at 10 kpc, assuming no interstellar extinction. The more distant and older OCs are therefore out of our detection threshold. We restrict our analysis to a selection of OCs, having low extinction (AV < 2.5 mag) and ages older than 10 Myr (according to MWSC and DAML catalogs). For younger clusters, for which the unclear identification of the main-sequence turnoff (TO), contamination of Pre-MS stars, and possible age spread can compromise the isochrone-fitting method, other independent techniques are more suitable to estimate the age (see, e.g., Bouvier et al. 2018; Jeffries et al. 2017; Jeffries 2017; David & Hillenbrand 2015). The final sample counts 269 OCs, located within 4.5 kpc. Due to the selection criteria we applied, our sample is clearly far from being complete.
In this work we have made use only of the photometry from GDR2 in its three bands G, GBP, and GRP. This is motivated by the exceptional quality of this photometry, having a precision on the order of a few millimag (see for instance Gaia Collaboration 2018b). Figure 1 presents color-magnitude diagrams (CMD) of a few poorly studied clusters, namely ASCC 23, Alessi 8, and Gulliver 21. In all these objects, the main sequence and the equal mass binary sequence can be clearly identified.
 |
Fig. 1. CMDs of a sample of OCs from GDR2 data, namely ASCC 23, Alessi 8, and Gulliver 21. Blue curves are the isochrones corresponding to the cluster parameters derived in this work. |
3. Method: Bayesian parameter determination
Handling the large, three-dimensional GDR2 datasets requires automated methods in order to characterize the OCs. To determine the parameters of our sample we used an open-source software suite known as BASE-9 (von Hippel et al. 2006), that introduces a Bayesian approach to compare observational distribution of magnitudes of stellar members of a cluster in different bands with a set of theoretical isochrones. The Bayesian method requires a likelihood function, that is, the distribution of the data given the model parameters. The knowledge about the model parameters before considering the current data defines the prior distribution, while the combined information in the data and our prior knowledge give the posterior distribution.
BASE-9 can adjust four parameters (age, metallicity, absorption, and distance modulus) at each iteration, using a Monte Carlo-Markov chain algorithm (MCMC). BASE-9 provides estimate of the posterior probability distribution (PDF) for a given number of iterations. Each iteration point is linked to the next by a “random walk” process described in von Hippel et al. (2006) and van Dyk et al. (2009), to which we also refer for a deeper description of BASE-9. The introduction of priors is very useful to avoid or at least reduce local minima. Our choice of priors is described in the Sect. 3.3. Visual inspection of the trace plot (parameter value against iteration number) shows that all the iteration chains reach their apparent stationary distributions within the first 1000 steps. This tuning period (called burn-in phase) is then discarded from the subsequent analysis. Each chain continues for another 10 000 iterations in order to ensure statistical relevance of the results. The clear advantage of this automated Bayesian approach for model fitting is to provide principled and reproducible estimates and uncertainties on all parameter.
3.1. Stellar models and isochrones
By default, BASE-9 comes with a large library of isochrones computed by different stellar-evolution groups. However none of this set of models include photometry in Gaia DR2 passbands (Evans et al. 2018, revised version). Therefore we replaced the BASE-9-implemented PARSEC set (Bressan et al. 2012) with an updated version where also GDR2 passbands are available1. Our grid consists of isochrones in the range of log(age)2 between 6.60 and 10.13 with a step of 0.01, and [Fe/H] between −2.10 and +0.50 with a step of 0.05. For this work we have used the release PARSEC v1.2S with the bolometric corrections described by Chen et al. (2014). These authors implement the relation between the temperature T and Rosseland mean optical depth τ across the atmosphere from PHOENIX BT-Settl models as the outer boundary conditions for low temperatures. In addition the PARSEC isochrones include a re-calibration of the mass-radius relation for cool dwarfs as derived from eclipsing binaries. This isochrone set has been proven to reproduce not only the lower main sequence, but also all the CMD features in more than 30 nearby OCs in GDR2 (see Gaia Collaboration 2018b).
3.2. Interstellar extinction
In BASE-9 the absorption is described using the parameter AV, which is the extinction in the V band. However, using different set of bands (i.e., the Gaia bands), it is necessary to translate AV into a proper measure of the extinction in the specific bands. Due to the large width of the Gaia bands, the coefficients AM/AV, where M can be G, GBP, and GRP, are dependent on the stellar effective temperature (Jordi et al. 2010; Danielski et al. 2018; Gaia Collaboration 2018b). Therefore, we can expect a deviation in the shape of the reddened isochrone if a fixed relation AM/AV is adopted. A more sophisticated approach is introduced in Danielski et al. (2018) and implemented in Gaia Collaboration (2018b). In this case the extinction coefficients of the Gaia bands are defined as functions of the absorption AV itself and the stellar effective temperature, in terms of the color (GBP − GBP):
where c1…7M belong to a set of coefficients defined in Gaia Collaboration (2018b) for G, GBP, and GRP. The terms c1M represents also the fixed extinction coefficients calibrated for a A0V star. All the coefficients are listed in Table 1. The results presented in Tables A.1–A.3 are given in terms of AGTO, the extinction in G at the turnoff of the cluster, and AV, the extinction parameter to be used in Eq. (1) to derive the dependence on color (and therefore temperature).
Summary of extinction coefficients used in this work.
3.3. Choice of priors
The Bayesian approach has the advantage that previous independent results can be incorporated through the joint prior distribution, that can be specified via independent priors on each parameter. BASE-9 needs priors on the age, metallicity ([Fe/H]), AV, and on the distance modulus. To set those values we refer to the literature where possible. Concerning extinction, we used the values from DAML or MWSC catalogs (prioritizing the first), where available, otherwise we set AV prior to 0.1 mag, respectively. AV has been marginalized within a σAV = 1/3 ⋅ AV (or 0.033 mags if AV = 0). No restriction is applied on the age and the variable is left free to vary inside the whole isochrone grid. The prior on the distance modulus is estimated through parallax inversion, which is equivalent to the equation
where (m − M)0 is the intrinsic distance modulus and 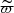 is the median value of the parallax of the cluster members. As discussed by Luri et al. (2018), such determination of distance is a very poor approximation, since systematics and correlations in the Gaia astrometric solution tend to overestimate the true distance, that should instead be obtained by Bayesian inferences (see, e.g., Bailer-Jones et al. 2018). Equation (2) gives more consistent results for very close objects, having uncertainties on the parallax lower than 5–6% (see Gaia Collaboration 2018a,b) This justifies our assumption that for clusters closer than 1 kpc and having almost no extinction, the distance modulus is assumed to be fixed to the value of Eq. (2). This is the case for the clusters in common with Gaia Collaboration (2018b) Table 2 (see also Sect. 5). In all the other cases, the distance modulus is derived from the posterior distribution of the BASE-9 solutions, as recommended by Luri et al. (2018). We must stress that BASE-9 looks for the observed modulus, and therefore we set the (m − M)V prior to include the contributions of both distance and extinction:
is the median value of the parallax of the cluster members. As discussed by Luri et al. (2018), such determination of distance is a very poor approximation, since systematics and correlations in the Gaia astrometric solution tend to overestimate the true distance, that should instead be obtained by Bayesian inferences (see, e.g., Bailer-Jones et al. 2018). Equation (2) gives more consistent results for very close objects, having uncertainties on the parallax lower than 5–6% (see Gaia Collaboration 2018a,b) This justifies our assumption that for clusters closer than 1 kpc and having almost no extinction, the distance modulus is assumed to be fixed to the value of Eq. (2). This is the case for the clusters in common with Gaia Collaboration (2018b) Table 2 (see also Sect. 5). In all the other cases, the distance modulus is derived from the posterior distribution of the BASE-9 solutions, as recommended by Luri et al. (2018). We must stress that BASE-9 looks for the observed modulus, and therefore we set the (m − M)V prior to include the contributions of both distance and extinction:
We finally chose to keep [Fe/H] fixed during the BASE-9 runs, in order to reduce the degeneracy within the variables. We divide our sample in three categories having different uncertainties on the [Fe/H] determination: (1) clusters with high (HRS) and low resolution spectroscopy (LRS) determination of metallicity, (2) clusters with other determination of metallicity (photometric determination, PHC), and (3) clusters with no information on metallicity (NC). High resolution metallicity determinations include data from Netopil et al. (2016) and Gaia-ESO (Spina et al. 2017; Magrini et al. 2017). Concerning LRS and PHC clusters, we make use of the compilations by Heiter et al. (2014) (using spectroscopy), Paunzen et al. (2010) (using photometry) as homogenized and recalibrated by Netopil et al. (2016), who bring them onto a common scale, producing the largest homogeneous compilation of OC metallicities by far. To this group we added a few clusters whose metallicity information is taken from DAML. When this is not available we used the MWSC catalog. If no other information is found in the literature (NC clusters), we set [Fe/H] = 0.0. This is a reasonable assumption, looking at the metallicity of the OCs that are in the range [Fe/H] ∈ [−0.3, +0.3] (Netopil et al. 2016). The number of clusters in each group is reported in Table 2. Since using different sources for [Fe/H] can introduce several biases, we discuss the implication of all the above priors on the OC parameter determination in Sect. 4.2.
Reference source for the metallicity priors.
3.4. Post-process analysis
The probability distribution of the posteriors in BASE-9 are calculated during the post-process analysis. For each run, once the chain converges, the iterations are generally distributed around a single high-probability solution. We estimated this solution through the medians for the three variables (i.e., age, extinction, and distance modulus), neglecting low probability solutions when present. Runs having multiple (very different) solutions of comparable probability are regarded as unreliable and discarded.
It is important to notice that in principle red giant branch (RGB) and red clump (RC) stars could be used to set constrains on the metallicity. In fact, the locations of these phases on the CMD are sensitive to the change of [Fe/H]. However the majority of our clusters, with a few exceptions, show CMDs without these features or with only a few red giant stars (RG), therefore the fit is largely dominated by main sequence stars. As a final note, we point out that each result has been checked visually, and clusters with a poor isochrone fit have been discarded.
4. Results
The final sample of OCs span a range of 7.0 < log(age) < 10.0. Figure 2 shows an example of the output for NGC 2251. On the three diagonal panels we show the probability distribution function of the variables with their median values (red solid line), while in the top-right panel we present the CMD of the cluster where the isochrone corresponding to the median values of the solutions is overplotted.
 |
Fig. 2. Solutions for NGC 2251. On the three diagonal panels we show the probability distribution functions of the variables with their medians (red solid line) and the 16th and 84th percentiles of the distribution (red dashed lines). The panels with the maps show instead the 2D-probability for each couple of parameters, highlighting possible correlations (e.g., between distance modulus and absorption). Finally, in the top-right panel we present the CMD of the cluster with the isochrone corresponding to the median parameters. |
The parameter determination for the three groups of clusters including the priors on [Fe/H] are listed in Table A.1 (44 OCs), Table A.2 (46 OCs), and finally Table A.3 (179 OCs) for HRS+LRS, PHC, NC objects, respectively. The values are referred to the median of each posterior distribution, while the uncertainties correspond to the 16th and 84th percentiles. Figure 3 presents the age distribution of the studied clusters.
 |
Fig. 3. Age distribution of the studied clusters. The dashed line represents the median value of the distribution (log(age) = 8.2) while the dotted lines represent the 84th and 16th percentiles (log(age)84th = 8.8, log(age)16th = 7.6). |
In the following paragraphs we estimate the random errors on the solutions and the systematics resulting from our assumptions on.
4.1. BASE-9 internal uncertainties
Estimation of parameter uncertainties has been done by considering the 16th and 84th percentiles (corresponding to ±1σ) of the iterations distribution for each posterior (see Fig. 2). The distribution of the internal uncertainties for all the parameters is given in Fig. 4.
 |
Fig. 4. Distribution of 1σ (estimated through percentiles) of the internal uncertainties on the age (left panel), extinction (middle panel), and distance modulus (right panel). |
We find that 90% of the clusters have sigmas smaller than, respectively, σlog(age) = 0.10, σAV = 0.033, and σ(m − M)0 = 0.037, while their medians are 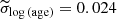 ,
, 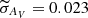 , and
, and  . While the extinction and the distance modulus determination are well confined, the distribution of the uncertainties on the log(age) presents a tail of about 30 OCs having 0.1 < σlog(age) < 0.25. Typical examples of this category of objects are Gulliver 20, IC 2157, and Ruprecht 29. These clusters are characterized by having no information on [Fe/H] (i.e., we assume [Fe/H] = 0.0); high extinction (AV > 1.0) and a low number of members. For these reasons, their fits are not well constrained, and the solutions present a high degree of degeneracy between the extinction and the distance modulus. Figure 5 and Table 3 shows the distribution of the relative error on log(age). HRS and LRS clusters have smaller internal uncertainties, while clusters belonging to the PHC group present larger errors. We detect no trend of σlog(age) as a function of the log(age).
. While the extinction and the distance modulus determination are well confined, the distribution of the uncertainties on the log(age) presents a tail of about 30 OCs having 0.1 < σlog(age) < 0.25. Typical examples of this category of objects are Gulliver 20, IC 2157, and Ruprecht 29. These clusters are characterized by having no information on [Fe/H] (i.e., we assume [Fe/H] = 0.0); high extinction (AV > 1.0) and a low number of members. For these reasons, their fits are not well constrained, and the solutions present a high degree of degeneracy between the extinction and the distance modulus. Figure 5 and Table 3 shows the distribution of the relative error on log(age). HRS and LRS clusters have smaller internal uncertainties, while clusters belonging to the PHC group present larger errors. We detect no trend of σlog(age) as a function of the log(age).
 |
Fig. 5. BASE-9 relative error on log(age) against log(age). |
Internal uncertainties on the BASE-9 log(age) determination for the different groups of OCs, namely those having [Fe/H] from spectroscopy (both HRS and LRS), photometry, or no information respectively.
4.2. Impact of fixed-metallicity prior
As discussed in Sect. 3.3, we used a fixed metallicity in our BASE-9 calculations, and this can have an impact on results. The aim of this section is to estimate the degree of degeneracy between the parameter determination and [Fe/H].
We select from our catalog a sample of ∼100 clusters spanning the whole age range we consider, and we run BASE-9 on them using three different priors on the metallicity, [Fe/H] = −0.3, −0.1, +0.1. In this test, the metallicity is let free to vary within a σ[Fe/H] = 0.05. Using these three runs, we calculate for the three solutions of each cluster the regression line on the plane log(age)-[Fe/H]. The slope dlog(age)/d[Fe/H] gives the predicted variation of the log(age) within 1 dex in metallicity for that specific cluster. Considering the overall distribution, we find a median slope of 0.18 with a median absolute deviation (MAD) of 0.22 (see Fig. 6). Clearly the systematics we introduce on the OC parameter determination are different depending on the uncertainties on the [Fe/H] priors (see Table 2). The effect can be negligible in the case of objects having metallicity determination from high resolution spectroscopy. Assuming as typical the sigma of 0.06 dex on [Fe/H] determination as derived from high resolution spectroscopy in the Gaia ESO public survey (see for instance Jacobson et al. 2016), we obtain
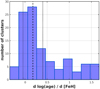 |
Fig. 6. Distribution of d log(age)/d[Fe/H], imposing several [Fe/H] values as prior for a sample of about 100 objects. Dashed line correspond to the median, while dot lines are the median ± the MAD. |
As we mentioned, for the NC group we assume [Fe/H] = 0.0. Looking at the distribution of the metallicity of Galactic clusters, we expect that all objects are inside a Δ[Fe/H] = ±0.3. In this case we estimate an effect on log(age) of ±0.05, which, translated in linear age, corresponds to about 13%. Clusters having [Fe/H] from photometry or low resolution spectroscopy can be regarded as having intermediate uncertainties. In the case of PHC objects, we find a median value of σ[Fe/H] = 0.15−0.20, resulting in Δ log(age) = 0.03−0.04, while for the LRS sample we derive σ[Fe/H] = 0.12, corresponding to Δ log(age) = 0.02.
The apparent distance modulus variations at changing [Fe/H] are quite small, with a median value Δ(m − M) = 0.012 ± 0.007 for the extreme case when we assumed [Fe/H] = 0.0. However, the extinction and the absolute distance modulus solutions are more affected by the assumption on [Fe/H], with a clear degeneracy. We find a median value of ΔAV = 0.19 ± 0.02 and Δ(m − M)0 = 0.2 ± 0.03 for the extinction and the absolute distance modulus respectively.
5. Discussion
5.1. Comparison with benchmark clusters
We compare our results with a set of well studied clusters for which we have high quality determination of the parameters.
5.1.1. Nearby OCs
In our sample we have 20 nearby clusters already studied by the Gaia Collaboration (2018b) using GDR2 data. In Fig. 7 we compare the age determination in both papers. Both determinations agree within a few percent, showing however a small systematic underestimate for the younger objects. This deviation is mainly due to the fact that the majority of the clusters are inconspicuous (see Fig. 8). In some cases differences between the two ages can be ascribed to the membership determination. One example can be NGC 6793 (see Fig. 8). In this very poorly studied cluster, the bright star at G ∼ 9 has a high probability membership from Paper I, while in the Gaia Collaboration (2018b) it is not considered as a member: this changes the position of the MSTO and, therefore, the age from log(age) = 8.78 to 8.65. We find a similar trend also when comparing with MWSC and DAML (see Sect. 5.2).
 |
Fig. 7. Comparison between the age derived in this work against Gaia Collaboration (2018b) for 20 clusters in common. Δ log(age) = log(age)thiswork − log(age)ref versus log(age)thiswork. |
 |
Fig. 8. CMDs of the clusters in common with Gaia Collaboration (2018b). Blue and red lines represent, respectively, isochrones with ages proposed in this work and by Gaia Collaboration (2018b). |
5.1.2. Comparison with asterosesimic data
Our sample contains also three OCs studied by Kepler (Borucki et al. 2010): NGC 6791, NGC 6811, and NGC 6819. In many of their red-giant stars, solar-like oscillations have been detected, providing global seismic parameters such as the large separation Δν and the frequency of maximum oscillation power νmax. These quantities, combined with the effective temperature, can be used to derive stellar masses through the so-called scaling relations (see, e.g., Kallinger et al. 2010 and Mosser et al. 2010).
In turn, the mass can be used to provide an indirect validation of our age determination. We compare previous estimations of RG masses for these clusters with the range of values corresponding to the same evolutionary phases along our isochrones.
NGC 6791. Seismic determination of the average RGB mass for NGC 6791 gives a value of M = 1.22 ± 0.01 M⊙ (Miglio et al. 2012, considering stars up to the RC luminosity). However, it was demonstrate that scaling relations tend to overestimate the value of the mass of RGB stars (White et al. 2011, Brogaard et al. 2018 and reference therein), therefore an additional calibration is required (Rodrigues et al. 2017). This introduces a systematic on the mass of ±0.10 M⊙. The estimation of the mass from RGB eclipsing binaries is M = 1.15 ± 0.02, in agreement with the previous seismic determination (Brogaard et al. 2012).
Both measures are perfectly compatible with the mass of M = 1.13 ± 0.01 M⊙, as derived averaging the masses from the bottom of the RGB up to the RC luminosity for an isochrone of the age of log(age) = 9.927 ± 0.002, which corresponds to our solution.
NGC 6811. Sandquist et al. (2016) determined the masses for six stars, five of them belonging to the red-clump phase, plus 1 RC candidate. The average value is M = 2.24 ± 0.07 M⊙, which is compatible with our average mass determination of M = 2.31 ± 0.08 M⊙ for the red-clump phase in an isochrone of log(age) = 8.94.
NGC 6819. Handberg et al. (2017) derived seismic parameters for 54 RG stars in NGC 6819. Within the sample, they were able to distinguish between RGB and RC stars. They also identified three non-member stars, six stars classified as overmassive, five uncertain cases, and one Li-rich RC. In a subsequent work, Rodrigues et al. (2017) estimated individual masses and ages for 52 RC stars. They compared observational data, including seismic constrains from Handberg et al. (2017), with a grid of models through a Bayesian method (PARAM, da Silva et al. 2006). Using only single RGBs they found an average mass of MRGB = 1.61 ± 0.04 M⊙. Our BASE-9 solution for NGC 6819 corresponds to an isochrone of log(age) = 9.30, that gives an average mass for the RGB of M = 1.675 ± 0.005. This values shows only a partial compatibility with Rodrigues et al. (2017) determination, lying within 1.5σ, since they find an age of log(age) = 9.35 ± 0.03 using a different set of stellar models by Bossini et al. (2015).
5.2. Comparison with MWSC and DAML catalogs
We have 242 clusters in common with MWSC and 234 with DAML. Figures 9 and 10, and Table 4 show the difference among our determination of age, extinction, and distance for those clusters included in these catalogs.
 |
Fig. 9. Age differences between our catalog with MWSC (upper panel) and DAML (lower panel). Triangles are clusters with spectroscopic determination of [Fe/H]. Dashed lines correspond to the median deviations. Right panel: histograms (in gray) show the difference in age distribution between our sample and the two catalogs. |
 |
Fig. 10. Extinction and distance modulus differences between our catalog and MWSC (upper panel) and DAML (lower panel). Triangles are clusters with spectroscopic determination of [Fe/H]. Dashed lines correspond to the median deviations from each cluster. |
Comparison of the age, AV, and distance modulus determination in the present work with literature catalogs, namely DAML and MWSC.
The median value of the age distribution is mainly consistent with DAML catalog, and shows a systematic of ∼−0.09 with MWSC. The dispersion is very large in both cases, especially for young clusters, but it is smaller for objects belonging to the HRS group. In addition a clear trend of the age difference with age is present, in the sense that results from BASE-9 are generally younger for OCs below log(age) < 8.5. These deviations are not surprising and might be ascribed to the quality of the cluster membership determination. Previous membership determinations are based on ground based photometry and/or proper motions and are severely hampered by field star contamination. This problem is particularly age-related. In fact, while old clusters can count on better populated features (MS, RGB, and RC) that help the age determination from isochrone fitting, in young clusters the fit is generally based on the luminosity of the MSTO, which may be not well defined, due to the lack in the number of bright near-TO stars. In such a scenario, a different determination of membership, with the addition of bright TO stars, can change the estimation of the age (as seen in Sect. 5.1.1 for NGC 6793).
Figure 10 compares globally our estimates of AV and (m − M)0 with the MWSC and DAML. Overall, no systematic difference, or a very small one, is present between this work and the literature concerning the value of AV, but with a large dispersion. The distance modulus exhibits a median difference (m − M)0, thiswork − (m − M)0, lit ∼ −0.1 for both catalogs, getting worse at (m − M)0 > 10, where it becomes ∼0.37, 0.27 for MWSC and DAML catalogs respectively.
Figure 11 shows the difference between the distance moduli derived from the analysis of BASE-9 results ((m − M)0, med, i.e., the posteriors) and from the inversion of the median parallax ((m − M)0, par, see Eq. (2)). We derive a median offset of ((m − M)0, BASE − 9 − (m − M)0, par = −0.11. As already discussed in previous sections, the inverse of the parallax tends to overestimate the distance modulus. This is specially true when the relative uncertainty on the parallax is higher than 20%, but it holds also when the uncertainties are lower than that. Here the majority of the clusters are more distant than 1 kpc, in a regime where the uncertainties on the single star parallaxes are higher than 20%. Averaging the uncertainties on the number of stars in a cluster does not reduce systematics and correlations. The offset we find corresponds to a medium offset of +0.021 mas in parallax. This value is in good agreement with the well-known systematic found in Gaia parallaxes and reported in Gaia Collaboration (2018d).
 |
Fig. 11. Differences of the distance modulus between posteriors ((m − M)0, med) and priors ((m − M)0, par), where the first have been derived from BASE-9 output and the latter from Eq. (2). Blue triangles are clusters with spectroscopic determination of [Fe/H], while the red dashed line is the median deviation corresponding to Δ(m − M)0, med − par = −0.11 mag. |
In addition, the results show a large dispersion, with differences up to ±0.5 mag. We cannot exclude the possibility that this is due to some other effects, such as uncertainties on the extinction coefficients, or on the assumptions on the metal content. Stochastic effects on the color-magnitude diagrams of the less populated clusters can also play a significant role, as well as effects related to stellar evolution (rotation, convection) and binarity.
6. Conclusions
In this work we have made use of an automated method based on Bayesian classification, BASE-9, to derive the age of 269 OCs using GRD2 photometry. The parameter determination precision is σlog(age) = 0.100, σAV = 0.033, and σ(m − M)0 = 0.037, while, their medians are  ,
, 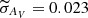 , and
, and  . In all the calculations we assume a fixed value of the metallicity [Fe/H], taking it either from high or low resolution spectroscopy or from photometry. When no information is available, we assume [Fe/H] = 0.0. We discuss the effect that the prior has on our results through a series of numerical sensitivity experiments. We find that in the worst case (no information on [Fe/H]), we have a Δlog(age) = ±0.05. Comparing our results with existing literature data, we find a large dispersion on age, and AV with no or a little systematics. On average, younger objects are affected by large differences with existing catalogs. This could well be due to the high quality of the Gaia data, meaning that it has more reliable membership determination and photometry. However, we cannot exclude that BASE-9 tends to underestimate the ages of young clusters. We point out that this is the largest data base of OC parameters derived using homogeneous and high quality data and this method. In this work we make use only of the information from the three Gaia bands. This is motivated by the high quality of the Gaia photometry. However, BASE-9 runs show that using only these magnitudes is not possible to resolve the degeneracy between the four cluster parameters, mainly the distance modulus and the extinction (see also Andrae et al. 2018). For this reason we have analyzed only low extinction objects. A further development will be to use information from complementary photometry to alleviate the degeneracy and extend the present catalog to higher extinction regimes.
. In all the calculations we assume a fixed value of the metallicity [Fe/H], taking it either from high or low resolution spectroscopy or from photometry. When no information is available, we assume [Fe/H] = 0.0. We discuss the effect that the prior has on our results through a series of numerical sensitivity experiments. We find that in the worst case (no information on [Fe/H]), we have a Δlog(age) = ±0.05. Comparing our results with existing literature data, we find a large dispersion on age, and AV with no or a little systematics. On average, younger objects are affected by large differences with existing catalogs. This could well be due to the high quality of the Gaia data, meaning that it has more reliable membership determination and photometry. However, we cannot exclude that BASE-9 tends to underestimate the ages of young clusters. We point out that this is the largest data base of OC parameters derived using homogeneous and high quality data and this method. In this work we make use only of the information from the three Gaia bands. This is motivated by the high quality of the Gaia photometry. However, BASE-9 runs show that using only these magnitudes is not possible to resolve the degeneracy between the four cluster parameters, mainly the distance modulus and the extinction (see also Andrae et al. 2018). For this reason we have analyzed only low extinction objects. A further development will be to use information from complementary photometry to alleviate the degeneracy and extend the present catalog to higher extinction regimes.
Acknowledgments
This work makes use of data products from: the ESA Gaia mission (gea.esac.esa.int/archive/), funded by national institutions participating in the Gaia Multilateral Agreement. This work was supported by ASI (Italian Space Agency) under contract 2014-025-R.1.2015. AB acknowledges funding from PREMIALE 2015 MITiC. This work was supported by the MINECO (Spanish Ministry of Economy) through grant ESP2016-80079-C2-1-R (MINECO/FEDER, UE) and MDM-2014-0369 of ICCUB (Unidad de Excelencia “María de Maeztu”). C.S. and L.C. acknowledge support from the CNES and from the “programme national cosmologie et galaxies” (PNCG) of CNRS/INSU. A.M. acknowledges the Portuguese Fundação para a Ciência e a Tecnologia (FCT) through the Strategic Programme UID/FIS/00099/2013 for CENTRA UH acknowledges support from the Swedish National Space Agency (SNSA/Rymdstyrelsen).
References
- Andrae, R., Fouesneau, M., Creevey, O., et al. 2018, A&A, 616, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Mantelet, G., & Andrae, R. 2018, AJ, 156, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Bica, E., & Bonatto, C. 2011, A&A, 530, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bossini, D., Miglio, A., Salaris, M., et al. 2015, MNRAS, 453, 2290 [NASA ADS] [CrossRef] [Google Scholar]
- Bouvier, J., Barrado, D., Moraux, E., et al. 2018, A&A, 613, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Brogaard, K., VandenBerg, D. A., Bruntt, H., et al. 2012, A&A, 543, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brogaard, K., Hansen, C. J., Miglio, A., et al. 2018, MNRAS, 476, 3729 [NASA ADS] [CrossRef] [Google Scholar]
- Cantat-Gaudin, T., Donati, P., Vallenari, A., et al. 2016, A&A, 588, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cantat-Gaudin, T., Jordi, C., Vallenari, A., et al. 2018a, A&A, 618, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cantat-Gaudin, T., Krone-Martins, A., Sedaghat, N., et al. 2018b, A&A, submitted [arXiv:1810.05494] [Google Scholar]
- Cantat-Gaudin, T., Vallenari, A., Sordo, R., et al. 2018c, A&A, 615, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castro-Ginard, A., Jordi, C., Luri, X., et al. 2018, A&A, 618, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, Y., Girardi, L., Bressan, A., et al. 2014, MNRAS, 444, 2525 [NASA ADS] [CrossRef] [Google Scholar]
- da Silva, L., Girardi, L., Pasquini, L., et al. 2006, A&A, 458, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Danielski, C., Babusiaux, C., Ruiz-Dern, L., Sartoretti, P., & Arenou, F. 2018, A&A, 614, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- David, T. J., & Hillenbrand, L. A. 2015, ApJ, 804, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Dias, W. S., Alessi, B. S., Moitinho, A., & Lépine, J. R. D. 2002, A&A, 389, 871 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, D. W., Riello, M., De Angeli, F., et al. 2018, A&A, 616, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Friel, E. D. 1995, ARA&A, 33, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Arenou, F., et al.) 2018a, A&A, 616, A17 [Google Scholar]
- Gaia Collaboration (Babusiaux, C., et al.) 2018b, A&A, 616, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018c, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Lindegren, L., et al.) 2018d, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Handberg, R., Brogaard, K., Miglio, A., et al. 2017, MNRAS, 472, 979 [NASA ADS] [CrossRef] [Google Scholar]
- Heiter, U., Soubiran, C., Netopil, M., & Paunzen, E. 2014, A&A, 561, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jacobson, H. R., Friel, E. D., Jílková, L., et al. 2016, A&A, 591, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Janes, K., & Adler, D. 1982, ApJS, 49, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffery, E. J., von Hippel, T., van Dyk, D. A., et al. 2016, ApJ, 828, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffries, R. D. 2017, Mem. Soc. Astron. It., 88, 637 [NASA ADS] [Google Scholar]
- Jeffries, R. D., Jackson, R. J., Franciosini, E., et al. 2017, MNRAS, 464, 1456 [NASA ADS] [CrossRef] [Google Scholar]
- Jordi, C., Gebran, M., Carrasco, J. M., et al. 2010, A&A, 523, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Joshi, Y. C., Dambis, A. K., Pandey, A. K., & Joshi, S. 2016, A&A, 593, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kallinger, T., Weiss, W. W., Barban, C., et al. 2010, A&A, 509, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kharchenko, N. V., Piskunov, A. E., Schilbach, E., Röser, S., & Scholz, R.-D. 2013, A&A, 558, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kos, J., de Silva, G., Buder, S., et al. 2018, MNRAS, 480, 5242 [NASA ADS] [CrossRef] [Google Scholar]
- Luri, X., Brown, A. G. A., Sarro, L. M., et al. 2018, A&A, 616, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magrini, L., Randich, S., Kordopatis, G., et al. 2017, A&A, 603, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miglio, A., Brogaard, K., Stello, D., et al. 2012, MNRAS, 419, 2077 [NASA ADS] [CrossRef] [Google Scholar]
- Mosser, B., Belkacem, K., Goupil, M. J., et al. 2010, A&A, 517, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Netopil, M., Paunzen, E., Heiter, U., & Soubiran, C. 2016, A&A, 585, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paunzen, E., Heiter, U., Netopil, M., & Soubiran, C. 2010, A&A, 517, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodrigues, T. S., Bossini, D., Miglio, A., et al. 2017, MNRAS, 467, 1433 [NASA ADS] [Google Scholar]
- Sandquist, E. L., Jessen-Hansen, J., Shetrone, M. D., et al. 2016, ApJ, 831, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Soubiran, C., Cantat-Gaudin, T., Romero-Gomez, M., et al. 2018, A&A, 619, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spina, L., Randich, S., Magrini, L., et al. 2017, A&A, 601, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Dyk, D. A., Degennaro, S., Stein, N., Jefferys, W. H., & von Hippel, T. 2009, Ann. Appl. Stat., 3, 117 [NASA ADS] [CrossRef] [Google Scholar]
- von Hippel, T., Jefferys, W. H., Scott, J., et al. 2006, ApJ, 645, 1436 [NASA ADS] [CrossRef] [Google Scholar]
- White, T. R., Bedding, T. R., Stello, D., et al. 2011, ApJ, 743, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Zacharias, N., Finch, C. T., Girard, T. M., et al. 2012, VizieR Online Data Catalog: I/322 [Google Scholar]
Appendix A: Cluster tables
First ten of the 44 HRS+LRS clusters.
First ten of the 46 PHS clusters.
First ten of the 179 NC clusters.
All Tables
Internal uncertainties on the BASE-9 log(age) determination for the different groups of OCs, namely those having [Fe/H] from spectroscopy (both HRS and LRS), photometry, or no information respectively.
Comparison of the age, AV, and distance modulus determination in the present work with literature catalogs, namely DAML and MWSC.
All Figures
 |
Fig. 1. CMDs of a sample of OCs from GDR2 data, namely ASCC 23, Alessi 8, and Gulliver 21. Blue curves are the isochrones corresponding to the cluster parameters derived in this work. |
| In the text | |
 |
Fig. 2. Solutions for NGC 2251. On the three diagonal panels we show the probability distribution functions of the variables with their medians (red solid line) and the 16th and 84th percentiles of the distribution (red dashed lines). The panels with the maps show instead the 2D-probability for each couple of parameters, highlighting possible correlations (e.g., between distance modulus and absorption). Finally, in the top-right panel we present the CMD of the cluster with the isochrone corresponding to the median parameters. |
| In the text | |
 |
Fig. 3. Age distribution of the studied clusters. The dashed line represents the median value of the distribution (log(age) = 8.2) while the dotted lines represent the 84th and 16th percentiles (log(age)84th = 8.8, log(age)16th = 7.6). |
| In the text | |
 |
Fig. 4. Distribution of 1σ (estimated through percentiles) of the internal uncertainties on the age (left panel), extinction (middle panel), and distance modulus (right panel). |
| In the text | |
 |
Fig. 5. BASE-9 relative error on log(age) against log(age). |
| In the text | |
 |
Fig. 6. Distribution of d log(age)/d[Fe/H], imposing several [Fe/H] values as prior for a sample of about 100 objects. Dashed line correspond to the median, while dot lines are the median ± the MAD. |
| In the text | |
 |
Fig. 7. Comparison between the age derived in this work against Gaia Collaboration (2018b) for 20 clusters in common. Δ log(age) = log(age)thiswork − log(age)ref versus log(age)thiswork. |
| In the text | |
 |
Fig. 8. CMDs of the clusters in common with Gaia Collaboration (2018b). Blue and red lines represent, respectively, isochrones with ages proposed in this work and by Gaia Collaboration (2018b). |
| In the text | |
 |
Fig. 9. Age differences between our catalog with MWSC (upper panel) and DAML (lower panel). Triangles are clusters with spectroscopic determination of [Fe/H]. Dashed lines correspond to the median deviations. Right panel: histograms (in gray) show the difference in age distribution between our sample and the two catalogs. |
| In the text | |
 |
Fig. 10. Extinction and distance modulus differences between our catalog and MWSC (upper panel) and DAML (lower panel). Triangles are clusters with spectroscopic determination of [Fe/H]. Dashed lines correspond to the median deviations from each cluster. |
| In the text | |
 |
Fig. 11. Differences of the distance modulus between posteriors ((m − M)0, med) and priors ((m − M)0, par), where the first have been derived from BASE-9 output and the latter from Eq. (2). Blue triangles are clusters with spectroscopic determination of [Fe/H], while the red dashed line is the median deviation corresponding to Δ(m − M)0, med − par = −0.11 mag. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



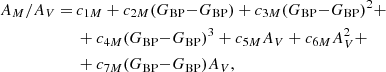
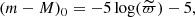

![$$ \begin{aligned} \Delta \log \mathrm{(age)}=\dfrac{d\,\mathrm{log(age)}}{{d}{[\mathrm{{Fe}}/\mathrm{{H}}]}}\cdot \Delta {[\mathrm{{Fe}}/\mathrm{{H}}]}= \pm 0.01. \end{aligned} $$](/articles/aa/full_html/2019/03/aa34693-18/aa34693-18-eq8.gif)