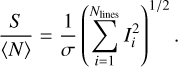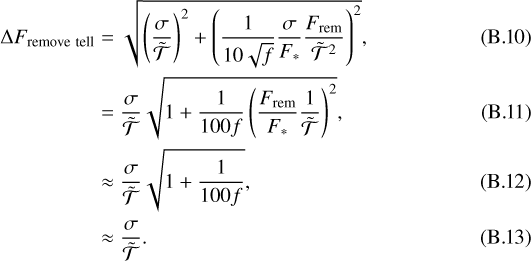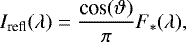| Issue |
A&A
Volume 622, February 2019
|
|
|---|---|---|
| Article Number | A139 | |
| Number of page(s) | 22 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201834169 | |
| Published online | 12 February 2019 | |
Detecting isotopologues in exoplanet atmospheres using ground-based high-dispersion spectroscopy
Leiden Observatory, Leiden University,
Postbus 9513,
2300
RA Leiden,
The Netherlands
e-mail: molliere@strw.leidenuniv.nl
Received:
31
August
2018
Accepted:
19
December
2018
Context. The cross-correlation technique is a well-tested method for exoplanet characterization, having lead to the detection of various molecules, to constraints on atmospheric temperature profiles, wind speeds, and planetary spin rates. A new, potentially powerful application of this technique is the measurement of atmospheric isotope ratios. In particular D/H can give unique insights into the formation and evolution of planets, and their atmospheres.
Aims. In this paper we aim to study the detectability of molecular isotopologues in the high-dispersion spectra of exoplanet atmospheres, to identify the optimal wavelength ranges to conduct such studies, and to predict the required observational efforts – both with current and future ground-based instrumentation.
Methods. High-dispersion (R = 100 000) thermal emission spectra, and in some cases reflection spectra, were simulated by self-consistent modeling of the atmospheric structures and abundances of exoplanets over a wide range of effective temperatures. These were synthetically observed with a telescope equivalent to the VLT and/or ELT, and analyzed using the cross-correlation technique, resulting in signal-to-noise ratio predictions for the 13CO, HDO, and CH3D isotopologues.
Results. We find that for the best observable exoplanets, 13CO is well in range of current telescopes. We predict it will be most favorably detectable at 2.4 μm, just longward of the wavelength regions probed by several high-dispersion spectroscopic observations presented in the literature. CH3D can be best targeted at 4.7 μm, and may be detectable using 40 m-class telescopes for planets below 600 K in equilibrium temperature. In this case, the sky background becomes the dominating noise source for self-luminous planets. HDO is best targeted at 3.7 μm, and is less affected by sky background noise. 40 m-class telescopes may lead to its detection for planets with Tequ below 900 K. It could already be in the range of current 8 m-class telescopes in the case of quenched methane abundances. Finally, if Proxima Cen b is water-rich, the HDO isotopologue could be detected with the ELT in ~1 night of observing time in its reflected-light spectrum.
Conclusions. Isotopologues will soon be a part of the exoplanet characterisation tools. Measuring D/H in exoplanets, and ratios of other isotopes, could become a prime science case for the first-light instrument METIS on the European ELT, especially for nearby temperate rocky and ice giant planets. This can provide unique insights in their history of icy-body enrichment and atmospheric evaporation processes.
Key words: methods: numerical / planets and satellites: atmospheres / radiative transfer
© ESO 2019
1. Introduction
The cross-correlation technique is a well established tool for detecting the presence of molecular absorbers in exoplanet atmospheres. In addition, it can constrain a planet’s atmospheric temperature profile, planetary spin rate and wind patterns, as well as its mass − in the case of a non-transiting planet. Examples are the detection of CO in HD 209458 b (which also constrained the planet’s wind speed, see Snellen et al. 2010), CO in β Pic b (which also constrained the planet’s spin rate, see Snellen et al. 2014), CO in τ Boötis b (Brogi et al. 2012; Rodler et al. 2012), H2O in 51 Peg b (Birkby et al. 2017), H2O in HD 88133 b and Ups And b (Piskorz et al. 2016, 2017), H2O and CO in HD 179949 b (Brogi et al. 2014), H2O (Birkby et al. 2013) and CO in HD 189733b (Rodler et al. 2013; de Kok et al. 2013), and TiO in the temperature-inverted part of WASP-33b’s atmosphere (Nugroho et al. 2017). Bryan et al. (2018) measured the rotation rates for a set of planets and brown dwarfs by cross-correlating with atmospheric models containing, among others, H2O and CO opacities. Recently, atomic and ionized species were detected using cross-correlation techniques in the optical transmission spectrum of the hottest known planet Kelt-9b (Hoeijmakers et al. 2018). Also, the techniques for extracting physical parameters from observations are improving, with the first study of high-resolution spectral retrieval presented recently by Brogi & Line (2018).
In the study presented here, we have investigated how the cross-correlation technique may be used to identify isotopologues in planetary atmospheres. Isotopologues are molecular chemical species with different numbers of neutrons in the nuclei of their constituent atoms. We have studied the feasibility of such a detection using current and next-generation instruments, in particular CRIRES+ (Follert et al. 2014) on the Very Large Telescope, and METIS (Brandl et al. 2014) on the ELT.
Most ofthe near-infrared (NIR) molecular opacity of (hot) Jupiters originates from H-, C- and O- bearing species. In this study, we therefore concentrate on the isotopologues of CO, H2O and CH4. H2O and CH4 are expected to be abundant in temperate, low-mass planets, with H2O playing a key role in planet habitability. Isotopologue detections and subsequent measurements of isotop(ologu)e-ratios from these species can provide interesting insights in planet formation and atmospheric processes. In principle, this requires benchmarking the inferred ratios with those observed in the host star or the surrounding interstellar medium. However, although there exists scatter in our local neighborhood (~ 1 kpc), the carbon, oxygen and hydrogen isotope ratio variations are usually not larger than a factor of a few (see, e.g. Milam et al. 2005; Polehampton et al. 2005; Linsky et al. 2006)1. Hence, if exoplanet isotope ratios are found to be very different from the average local ISM values, this would make the planet stand out already without having to compare to the isotope ratios of its host star.
Typical isotope ratios in the neighborhood of the sun are 12C/13C ~ 70 (Milam et al. 2005), 16 O/17O ~ 1600 (Romano et al. 2017), 16O/18O ~ 400 (Polehampton et al. 2005), and deuterium to hydrogen (D/H) ~ 2 × 10−5 (Linsky et al. 2006; Asplund et al. 2009). We note that in the solar system the oxygen and carbon isotope ratios are ~ 30% larger, probably because the sun formed 4.5 Gyr ago, conserving the higher isotope ratios from that period (Clayton & Nittler 2004; Ayres et al. 2013).
Variations in the isotope ratios may provide clues on how planets form from the condensed and gaseous material in proto-planetary disks. In the solar system, such variations are most prominent in D/H (see Fig. 1 of Altwegg et al. 2015). Volatile-rich primitive meteorites are found to be enriched in D by about a factor six compared to the proto-solar nebula. This enrichment is found to be comparable or higher for Jupiter-family comets, and to be a factor 10−20 for Oort-cloud comets. We note, however that significant scatter exists, and the D/H value found in the Jupiter family comet 67P/GC is actually consistent with the highest D/H values found in Oort cloud comets, see Altwegg et al. (2015). This trend of enrichment in D within the condensed volatiles appears to increase with distance from the Sun. This may be explained by a temperature-dependent fractionation of D into water ice (see, e.g., Geiss & Reeves 1981), but we note that the Oort comets may have formed in the inner Solar System, and then been scattered outward by the giant planets (see, e.g., Morbidelli 2005, and the references therein).
The gas giants Jupiter and Saturn are found to have D/H values of (2.6 ± 0.7) × 10−5 and 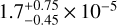 , respectively (Mahaffy et al. 1998; Lellouch et al. 2001), roughly in line with the proto-solar value (2 × 10−5). In contrast, the ice giants Uranus and Neptune have measured ratios of (4.4 ± 0.4) × 10−5 and (4.1 ± 0.4) × 10−5 (Feuchtgruber et al. 2013), hence they are D-enriched by a factor of approximately two. This is thought to be caused by atmospheric contamination by icy planetesimals. While the fraction of such contamination is low for Jupiter and Saturn, having no effect on their D/H values, this is significant for Uranus and Neptune. Assuming that these icy planetesimals had an intrinsic D/H enrichment of an order of magnitude, similar to that of comets (i.e. D/H ~ 2 × 10−4), and assuming anatmospheric enrichment as indicated by Guillot & Gautier (2014) for Uranus and Neptune, this can have caused the overall D-enrichment of their atmospheres by a factor of two.
, respectively (Mahaffy et al. 1998; Lellouch et al. 2001), roughly in line with the proto-solar value (2 × 10−5). In contrast, the ice giants Uranus and Neptune have measured ratios of (4.4 ± 0.4) × 10−5 and (4.1 ± 0.4) × 10−5 (Feuchtgruber et al. 2013), hence they are D-enriched by a factor of approximately two. This is thought to be caused by atmospheric contamination by icy planetesimals. While the fraction of such contamination is low for Jupiter and Saturn, having no effect on their D/H values, this is significant for Uranus and Neptune. Assuming that these icy planetesimals had an intrinsic D/H enrichment of an order of magnitude, similar to that of comets (i.e. D/H ~ 2 × 10−4), and assuming anatmospheric enrichment as indicated by Guillot & Gautier (2014) for Uranus and Neptune, this can have caused the overall D-enrichment of their atmospheres by a factor of two.
However, it is not yet known whether this scheme generally applies to planet formation processes. Numerous studies address atmospheric composition (relative to H–He), and its connection to a planet’s formation history, often assuming that it is governed by gas that the planet accretes, instead of planetesimals (Öberg et al. 2011; Ali-Dib et al. 2014; Thiabaud et al. 2014; Helling et al. 2014; Marboeuf et al. 2014b,a; Madhusudhan et al. 2014, 2017; Mordasini et al. 2016; Öberg & Bergin 2016; Cridland et al. 2016). Among these Mordasini et al. (2016) is a notable exception, assuming planetesimal, rather than gas enrichment. In the case of gas enrichment, volatiles in the gas phase of thedisk are expected to be partly sequestered into condensates, resulting in lower metallicities but unchanged isotopologue ratios in the disk gas. Hence, it is expected that isotopologue ratios in the atmospheres of extrasolar planets will not be significantly different from that of their host stars or local ISM, except if they are strongly contaminated by icy planetesimals, which have increased D/H values. The inferred trends of increasing planetary bulk metallicity as a function of decreasing planetary mass may be seen as a sign of planetesimal and solid body enrichment dominating over gas enrichment (Miller & Fortney 2011; Thorngren et al. 2016). Recently, synthetic planet formation calculations by Marboeuf et al. (2018) have been able to reproduce the planetary mass – D/H correlation in the Solar System, when applying the envelope pollution by planetesimals as advocated by Mordasini et al. (2016).
In contrast to deuterium and hydrogen, there is no evidence for strong fractionation of either oxygen or carbon. The 16O/18O values inferred from comets such as 1P/Halley, 67P/Churyumov-Gerasimenko and C/2014 Q2 (Lovejoy; see Altwegg & Bockelée-Morvan 2003; Altwegg et al. 2015; Biver et al. 2016, and the references therein) are broadly consistent with the Solar System abundances. The same holds for the oxygen isotopic abundances of primitive and differentiated meteorites (systematic variations do exist, but only of the order of single digit percentage values, see, e.g., Clayton 1993; Yurimoto et al. 2007). Also, the 12C/13C ratios observed in 11 different comets (see Altwegg & Bockelée-Morvan 2003; Biver et al. 2016, and the references therein) and chondrites of different types (see, e.g., Halbout et al. 1986; Pearson et al. 2006) are all consistent with the Solar System abundances.This means that neither C nor O condensates have a significant preference for a certain isotope, resulting in the gas and condensate phase C and O isotope ratios to be unaffected, at least down to a percentage level (e.g., Clayton 1993; Yurimoto et al. 2007).
A process that can further affect the D/H value is atmospheric escape: thermal or ion pick-up escape processes preferentially retain more massive isotopologues (see, e.g., Jakosky & Phillips 2001). Hence D is expected to be relatively more abundant than H in planets which have undergone significant (non-hydrodynamic) atmospheric loss. This seems to be indeed the case for Mars, which exhibits a D/H value of at least five to seven times larger than the terrestrial value (see, e.g., Krasnopolsky 2015; Villanueva et al. 2015; Clarke et al. 2017). The primordial value inferred for Mars is about twice the terrestrial value (Leshin 2000). Identifying water as the major hydrogen carrier, the above values correspond to equivalent ocean depths between at least 60 and 130 m having been lost from the Martian surface (Krasnopolsky 2015; Villanueva et al. 2015). For Venus the process of evaporation may have been even more extreme, because its atmospheric D/H is about 1000 times higher than the protosolar value of 2 × 10−5 (Kulikov et al. 2006).
There is also a particularly interesting prospect that isotopologue measurements could shed light on biological processes and help to provide evidence for the presence of extraterrestrial life. Living matter on Earth tends to favor 12C over 13C when building organic carbon molecules: for organic carbon compounds the 13C/12C ratio is 3% lower than for inorganic compounds (see, e.g., Langmuir & Broecker 2012, and the references therein). For Earth, the absolute 13C/12C values in the organic and inorganic reservoirs depend on the fractionation of carbon between these two reservoirs, as well as on the total 13C/12C (crustal) average. A possible tracer of life would thus be to compare the 13C/12C ratios of atmospheric methane (mostly organic origin on Earth, see, e.g., Quay et al. 1991) and CO2 (inorganic origin, if not derived from burning fossil fuels, see, e.g., Ghosh & Brand 2003). Alternatively, if the 13C/12C crustal average of a terrestrial exoplanet was known, and the 13C/12C in its oxidized (e.g. CO, CO2) or reduced (CH4) atmospheric components could be measured, then the carbon fractionation into organic (i.e. living, or recently living) matter could be inferred. However, assuming these processes would be the same as on Earth, these effects are very difficult to measure, requiring a precision in absolute 13C abundance of ~ 10−4. For exoplanets, we expect this to be out of scope of any present or future planned instrument or telescope.
In this paper, we focus on the detectability of carbon monoxide (13CO), methane (CH3 D) and water (HDO), because we expect (13CO) the least difficult to measure, and CH3D and HDO to bear the greatest significance when seeking to probe a planet’s formation and evolution history. In Sect. 2 we describe how the planetary high-resolution spectra are modeled, and how the observationsare simulated. In Sect. 3 we present our calculations for the detectability of 13CO in hot Jupiters, as a function of wavelength. In Sect. 4 we show how HDO may be found in self-luminous and irradiated planets, as a function of effective temperature, with and without methane quenching in the atmosphere. In Sect. 5 we study the detectability of CH3D, with the same planetary setup. Finally, the case of HDO in terrestrial exoplanet atmospheres is studied in Sect. 6, where we assume a twin Earth as an input model for Proxima Cen b. Our results are summarised and discussed in Sect. 7.
2. Model description
2.1. Atmospheric structure
The atmospheric temperature and abundance structures used to generate the high resolution spectra are derived from self-consistent atmospheric models. In the calculations presented here, structures are obtained with petitCODE (Mollière et al. 2015, 2017), except for the results shown in Sect. 6. petitCODE calculates the atmospheric structures of exoplanets in 1-d in radiative-convective and chemical equilibrium. The radiative transfer considers both absorption and scattering processes. Only gas opacities are considered in the calculations presented here, but clouds can optionally be included in petitCODE calculations, in a self-consistent fashion. The gas opacity species considered here are H2O, CO, CO2, OH (HITEMP, see Rothman et al. 2010), CH4, NH3, PH3, HCN (ExoMol, see Tennyson & Yurchenko 2012), as well as H2, H2 S, C2 H2 (HITRAN, see Rothman et al. 2013), Na, K (VALD3, see Piskunov et al. 1995), and CIA of H2 –H2 and H2–He (Borysow & Frommhold 1989; Borysow et al. 1989; Richard et al. 2012). For H2 and CO, also the UV electronic transitions by Kurucz (1993) are included, as well as the Rayleigh scattering opacities for H2, He, CO2, CO, CH4 and H2O. For the cross-sections, the values reported in Dalgarno & Williams (1962; H2), Chan & Dalgarno (1965; He), Sneep & Ubachs (2005; CO2, CO, CH4) and Harvey et al. (1998; H2O) are used.
petitCODE is a well-tested tool for calculating exoplanet atmospheric structures, and has recently been benchmarked against the ATMO (Tremblin et al. 2015) and Exo-REM (Baudino et al. 2015) codes (Baudino et al. 2017). It was used for a parameter study of irradiated atmospheres (Mollière et al. 2015), and for generating predictions of exoplanet observationswith the James Webb Space Telescope (JWST) for high-priority targets (Mollière et al. 2017). Moreover, petitCODE enabled the atmospheric characterization of the self-luminous planet 51 Eri b (Samland et al. 2017), and constrained the atmospheric properties of several transiting exoplanets (Mancini et al. 2016a,b, 2017; Southworth et al. 2017). Finally, it connected planet formation models with synthetic atmospheric observations in Mordasini et al. (2016).
2.2. High resolution spectra
The high resolution spectra were calculated with a new radiative transfer code, based on petitCODE, that we report on here for the first time. It usesthe same molecular opacity database as petitCODE, in which pressure and temperature-dependent opacities are stored at a resolution ofν∕Δν = 106. The atmospheric structure calculations in petitCODE are carried out at a lower resolution, making use of the correlated-k approximation (Goody et al. 1989; Lacis & Oinas 1991; Fu & Liou 1992), as described in Appendix B of Mollière et al. (2015). The new high resolution radiative transfer code presented here uses the opacity database of petitCODE at its intrinsic resolution, and in a line-by-line, rather than a correlated-k treatment. Identical to the capabilities of petitCODE, both transmission and emission spectra can be calculated. Because the work presented in this paper focuses on the high-resolution NIR to MIR emission spectra of cloudless atmospheres, scattering is currently neglected, but scattering is included in the atmospheric structure calculations, as described in Sect. 2.1 above.
2.3. Synthetic observations
For a given set of planet–star parameters (stellar effective temperature and radius, planetary semi-major axis, radius, mass and atmospheric composition) self-consistent atmospheric structures are calculated, and used for generating the high-resolution emission flux FPlanet(ν) in the planet’s rest frame, where ν denotes the frequency. In order to generate the planet’s signal as it would be seen by an instrument on Earth, the rest frame frequency values are first shifted according to ν↦ν(1 − vrad∕c), where vrad is the radial velocity between the planet and the observer, and c is the speed of light. Subsequently, the host star’s flux is included by adding a flat white spectrum to the planetary flux,
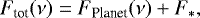 (1)
(1)
where the contrast between planet and star is a free parameter. We assume that the stellar lines can be perfectly removed during the data analysis. A second free parameter is the signal-to-noise-ratio (S/N) of the stellar flux, S/N*. For convenient numerical modeling, we set 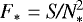 (assuming Poisson noise), and replace FPlanet(ν) with
(assuming Poisson noise), and replace FPlanet(ν) with 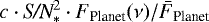 , where
, where 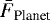 is the average planetary flux and c is the desired average contrast in the considered wavelength region. Subsequently, the total flux Ftot(ν) is multiplied with a transmission model for the Earth’s atmosphere,
is the average planetary flux and c is the desired average contrast in the considered wavelength region. Subsequently, the total flux Ftot(ν) is multiplied with a transmission model for the Earth’s atmosphere, 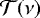 , such that the total flux that reaches the ground-based telescope is
, such that the total flux that reaches the ground-based telescope is
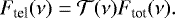 (2)
(2)
Subsequently, the spectrum is convolved to the intrinsic spectral resolution of the instrument, and binned to the wavelength steps of the instrument. Both the instrument resolution and the number of pixels per resolution element are free parameters. We follow the convention of defining the instrumental resolution ν∕Δν such that Δν is the full width half maximum (FWHM) of the line spread function (LSF) of the instrument’s dispersing element. We assume a Gaussian distribution for the LSF, hence the relation between its standard deviation and the instrument resolution is  . In the following, the result of convolving and re-binning Ftel(ν) will be denoted
. In the following, the result of convolving and re-binning Ftel(ν) will be denoted 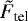 , where ν′ is the frequency corresponding to the instrument pixel, with the uncertainty being
, where ν′ is the frequency corresponding to the instrument pixel, with the uncertainty being
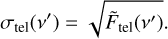 (3)
(3)
The final simulated observation Fobs(ν′) is obtained by perturbing 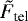 with a Gaussian with standard deviation equal to σtel.
with a Gaussian with standard deviation equal to σtel.
3. 13CO in hot Jupiter atmospheres
The prescription for generating simulated observations described above is used for a case study of 13CO in a hot Jupiter atmosphere. The HD 179949b system was chosen as a benchmark. It hosts a non-transiting gas giant (discovered by Tinney et al. 2001) with an equilibrium temperature of Tequ = 1519 K (see Table 1). Ground-based high-dispersion spectroscopic observations with CRIRES onESO’s Very Large Telescope (VLT) have already shown the presence of both water (S/N = 3.9) and CO (S/N = 5.8) in the planet’s atmosphere Brogi et al. (2014).
Parameters used for the self-consistent structure calculations for HD 179949b.
3.1. Synthetic HD 179949b observations
A self-consistent atmospheric structure was calculated as described in Sect. 2.1, assuming the input parameters from Table 1. Synthetic observations consisting of 100 high-resolution observations in orbital phase from − 45° to + 45° around superior conjunction were generated as described in Sects. 2.2 and 2.3, taking into account the appropriate Doppler shifts of the planetary spectrum due to the radial component of its orbital velocity, and the waxing and waning of the planet. Also, the geometric effect of the orbital inclination on the area of the visible dayside was included. The flux of the visible part of the dayside was assumed to be uniform and equal to the average dayside flux obtained from petitCODE, and to be zero on the nightside. For the high resolution spectra, only the line opacities of H2O, CO2 and CO were included, as well as H2 –H2 and H2–He CIA. For the planet-to-star contrast we used the values stemming from the self-consistent calculations.
The S/N* as function of wavelength was calculated relative to the value at 2.3 μm following
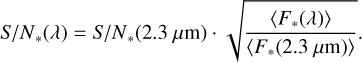 (4)
(4)
Here 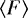 denotes the average fluxes in the wavelength ranges of interest. The telluric transmission model was generated using the ESO SkyCalc2 tool (Noll et al. 2012; Jones et al. 2013), assuming a stellar altitude of 60° (airmass = 2). The elevation was set to 2640 m, corresponding to the summit of Cerro Paranal, adopting also the median precipitable water vapor amount of Paranal (2.5 mm). An instrument resolution of ν∕Δν = 105 was assumed with wavelength steps corresponding to 3 pixels per resolution element Δν.
denotes the average fluxes in the wavelength ranges of interest. The telluric transmission model was generated using the ESO SkyCalc2 tool (Noll et al. 2012; Jones et al. 2013), assuming a stellar altitude of 60° (airmass = 2). The elevation was set to 2640 m, corresponding to the summit of Cerro Paranal, adopting also the median precipitable water vapor amount of Paranal (2.5 mm). An instrument resolution of ν∕Δν = 105 was assumed with wavelength steps corresponding to 3 pixels per resolution element Δν.
The COisotopologue ratios were assumed to be the same as in the HITRAN/HITEMP databases (their molparam.txt file): 12C16O constitutes 98.7%, while 13C16O constitutes 1.1% of all CO molecules. The HITRAN/HITEMP values are based on the compilation of telluric isotopic abundances by De Biévre et al. (1984). We note that in the case of 12C/13C, variations inthe Solar System and its neighborhood are small (as discussed in Sect. 1), justifying the use of the telluric values, given in Table D.1.
3.2. Analysis of the synthetic observations
For the analysis of the synthetic observations, standard methods, as have been used for real high-dispersion observations, were applied (see, e.g., Brogi et al. 2012, 2014). The main steps of the analysis are briefly described below. The data (emission spectra of star and planet) are organized as a two-dimensional matrix (see, e.g., uppermost panel of Fig. 1), where the columns represent the wavelength steps, and rows the spectra taken at different orbital phases.
The goal of the data reduction is to construct a nominal data set, containing the planet flux, from observationsobtained with the procedure described in Sect. 2.3. This will be called data set A, it is the planetary flux that an observer would measure, after a successful data reduction. We also will create a data set B, which is identical to A, except that the lines of all spectroscopically active molecules, except for 13C16O, have been removed: this is done by calculating planet spectra which contain all species, except the targeted 13C16O isotopologue. Multiplying this new spectrum with the telluric transmission model3, the new spectrum is then subtracted from the synthetic observation, prior to reduction. After reduction, this will result in data set B. Hence, data set B only contains the lines of the targeted 13C16O, at the correct relative line strengths as they are present in data set A. Using data set B significantly simplifies the analysis of the contribution of the 13C16O isotopologuein the spectra, because with it we can directly measure the signal strength imprinted onto the observation by 13C16O alone. This is different from the analysis of real observations, where all available information on the planet spectrum, including those from other observations, will be used to constrain the atmospheric structure and relative volume mixing ratios of therelevant spectroscopically-active molecules (Brogi & Line 2018). Subsequently, spectra will need to be modeled assuming a range of isotope ratios and compared to the data. If the data are significantly better fitted by models for which the secondary isotopologue is included, this isotopologue is detected and an isotope-ratio can be inferred. Hence, here we do not study the retrievability of isotopologue abundances for atmospheres, instead we study the strength of the signal that a given isotopologue imprints on the observation. We will also show the 13C16O detection S/Ns, obtained from a classical analysis, when, for example, cross-correlating a pure 13C16O model with data set A. All the necessary procedures for the data reduction are described in the following two steps, which are identical for the data sets A and B.
The synthetic observations are shown in panel a of Fig. 1. For every column the median value is calculated which will be used to normalise the data. This value as function of wavelength is the best estimate of the telluric absorption line spectrum, which in oursimulations is kept constant throughout the observations, implying, within noise-limits, a perfect telluric subtraction. Panels a and b in Fig. 1 show a small cutout of the simulated observations before and after the telluric correction. For clarity, an extremely high signal-to-noise of S/N* = 10 000 is used, with c = 4 × 10−4, making the effects of the different analysis steps visible. The full orbital phase is shown to demonstrate the effect of the waxing and waning of the planet, but for the analysis below only phase angles varying between − 45° and + 45° around superior conjunction are considered.
Finally, to obtain data set A, the data shown in panel b of Fig. 1 is scaled by its standard deviation in each column, suppressing the parts of the data affected by strong telluric absorption. This is achieved by first calculating the total flux-average of all points in panel b (over all columns and lines), and subtracting that value from all points in panel b. All points in a given column are then divided by their column-wide standard deviation. Panel c in Fig. 1 shows the simulated data after this step. This is data set A. This step is done to prevent the cross-correlation signal to be dominated by the more noisy data. Panel d of Fig. 1 shows the same as panel c, but now for data set B, hence showing only the lines of 13C16O isotopologue.
 |
Fig. 1. Different analysis steps of the simulated observations. Panel a: raw synthetic observation (number of photons as a function of wavelength and phase). Panel b: data after the telluric correction, as described in the text. Panel c: data of panel b after subtracting the total wavelength and phase mean, and normalising each column byits standard deviation, to suppress noisy wavelength regions. This is data set A. Panel d: same as panel c, but with the signal of all contaminant line absorbers removed, making the lines originating from 13C16O visible. Thisis data set B. |
3.3. Cross-correlation signal at 2.4 μm
We first demonstrate the use of the cross-correlation technique to detect the 13C16O isotopologue of carbon monoxide, considering a wavelength range of 2.32–2.45 μm, just redward of the wavelength regions probed by several previous observations targeting CO in hot-Jupiter atmospheres (e.g. Brogi et al. 2014). Since these observations only probed out to 2.345 μm, they just missed the band head of 13C16O. In Fig. 2, we show the opacities of 12C16O (blue) and 13C16O (orange) between 2.29 and 2.40 μm. The 13C16O band head at 2.345 μm is clearly visible.
The 100 simulated high-dispersion spectra were each given a signal-to-noise of S/N* = 200 per wavelength step. First we consider the cross-correlation of data set A (which includes the lines from all molecules and isotopologues) with a pure 12C16O template spectrum, assuming that the radial velocity curve of the planet is perfectly known. For the pure 12C16O template spectrum we assumed the same atmospheric structure as used for creating the full planetary spectrum, but include only the 12C16O opacity in the spectral calculation. This results in a cross-correlation signal with an S/N of ~ 13 (see left panel of Fig. 3). This is as expected. The planet-to-star contrast of this system is 7 × 10−4 at 2.3 μm, and the S/N of the combined 100 spectra is 2 × 103, implying an S/N on the planet spectrum of ~1.4 per wavelength step. This is very similar to precisions already reached with existing observations, albeit for a smaller and slightly blueward wavelength region (Brogi et al. 2014). With on the order of 100 strong CO lines in the targeted wavelength region, this combines to an overall S/N of  (see Appendix A.1 for a derivation), which is in good agreement with the S/N resulting from our more detailed simulations. As a control, we also cross-correlated data set B (from which all spectral lines of the main isotopologue were removed) in the same way, and naturally no signal was detected (see left panel of Fig. 3).
(see Appendix A.1 for a derivation), which is in good agreement with the S/N resulting from our more detailed simulations. As a control, we also cross-correlated data set B (from which all spectral lines of the main isotopologue were removed) in the same way, and naturally no signal was detected (see left panel of Fig. 3).
Subsequently, we cross-correlated data set B, that is the observation from which all lines of molecules and isotopes other than 13C16O have been subtracted, with two different models. First, with a pure template spectrum, containing lines only from 13C16O. This is shown in the right panel of Fig. 3. 13C16O is the most abundant of the secondary isotopologues (1.1% of all CO molecules, see Table D.1), and therefore studied here. This results in a cross-correlation signal with an S/N of ~ 5. A better matching cross-correlation template is given by the difference between a full planet spectrum model minus the same constructed without the opacity of 13C16O, a noiseless model B spectrum. This takes potential shielding of 13C16O lines by the other isotopologues or molecules into account. This results in a cross-correlation signal with an S/N of ~ 7, and is expected in the case that sufficient spectral information is available such that the planet atmosphere can be well modeled. Even in the worst case, that is without removal of the main isotopologue and other molecules from the data (using data set A), the signal from the 13C16O, correlating with the pure 13C16O template spectrum, is still detected at an S/N of ~3.5, see right panel of Fig. 3.
 |
Fig. 2. Opacities of 12C16O (blue) and 13C16O (orange), shown at T = 1200 K and P = 10−4 bar, which are representative values for the pressures and temperatures probed by CO lines at high resolution, in HD 179949b. The opacities have been scaled such that 12C16O constitutes 98.7% and 13C16O 1.1% of all CO molecules. |
 |
Fig. 3. Results from simulated observations of HD 179949 b consisting of 100 spectra with an S/N* of 200 each, with a R = 100 000 spectrograph covering the wavelength range λ = 2.32–2.45 μm. Left panel: cross-correlation function (CCF) using a pure 12C16O template spectrum on data set A (black solid line) which contains all species, and data set B (grey dashed line) which contains lines of 13C16O only. Data set A gives a signal with an S/N of ~13, while the main isotope, as expected, is not detected in data set B. Right panel: CCF using a pure 13C16O template spectrum on data set A (black dotted line) and data set B (solid blue line). In addition, we show the CCF using a noiseless telluric-free model for data set B as a template (red solid line). The 13C16O isotope is detected at an S/N of ~3.5 and ~5 in data set A and B, respectively. By using the perfect noiseless input model as a template, 13C16O’s detection S/N is further increased to an S/N of ~7. To reach the latter significance, the planet atmosphere needs to be well constrained. |
3.4. Wavelength and S/N study
In the previous section we showed that 13C16O should be readily detectable at 2.4 μm. Here we investigate how such detectability varies as function of wavelength. This is shown in Fig. 4, where the expected S/N of 13C16O (and 12C16O) for the same benchmark hot Jupiter is shown as function of wavelength, for blocks of λ∕Δλ of 20, at a resolving power of R = 100 000, with a wavelength sampling of three pixels, a stellar S/N*(2.3 μm) of 200 per step per exposure, and 100 exposures. The stellar S/N at wavelengths different from 2.3 μm was obtained using Eq. (4) (using PHOENIX models, Hauschildt et al. 1999, for the host star, as described in Mollière et al. 2015). It changes from roughly 300 at 1 μm to 80 at 6 μm.
The sky background will rise steeply for ground-based observations at wavelengths longer than 4.2 μm. To study the importance of this effect we additionally added the wavelength-dependent photon noise of the sky to the noise budget. The sky radiance was obtained from the SkyCalc tool, with the same settings as used for the telluric transmission model. Moreover, we assumed an 8 m-class telescope with 0.1 total throughput, which resulted in an exposure time of 28 s for each of the individual 100 spectra, if requiring to reach S/N*(2.3 μm) = 200. The thermal emission of the telescope was not included. The grey and orange lines indicate the S/N as function of wavelength for the detection of the 12C16O and 13C16O isotopologues, respectively.
For 13C16O we show the S/N arising from correlating data set B with a pure 13C16O spectral template, which is conservative, corresponding to the solid blue line in Fig. 3. When using the noise-free data set B spectrum as a cross-correlation template, the S/N at, for example, 4.7 μm would increase from ~ 4.5 to ~ 6.5. For the 12C16O detection we show the S/N arising from correlating data set A with a pure 12C16O spectral template. The simulations at each wavelength were run multiple times to reduce the stochastic scatter. In Fig. 4 the 16 to the 84 percentiles of the S/N distributions are indicated as orange or gray boxes, corresponding to the 1σ uncertainty ranges. The pure isotopologue models were chosen to cross-correlate with the data, to allow direct comparison to the CO detection by Brogi et al. (2014), who used pure (multi-isotopologue) CO models.
For reference, Fig. 4 also shows the transmission of the Earth atmosphere (light grey) and the logarithm of the opacity of the carbon monoxide molecule as function of wavelength (light red). As expected, because the isotope-mass differences are small, the main and secondary isotopologue can only be detected where the CO opacity is high, that is at ~ 2.4 μm and around ~ 4.7 μm. Our simulations are shown for fixed exposure times (28 s per spectrum), and include the stellar and sky photon noise variations as a function of wavelength. With this we find that the 2.4-μm region is more efficient for the 13C16O detection, with an expected S/N of 5 for the assumptions given above. In the case studied here, sky background and stellar photon noise are of equal importance at 4.7 μm, leading to an S/N of ~4.5 for the 13C16O detection.
Figure 4 also shows the literature S/N of the CO detection in the 2.3 μm region, as reported by Brogi et al. (2014). Their S/N value (5.8) was scaled up to 9 to account for the fact that our wavelength bins are broader. Their detection S/N is broadly consistent at roughly 80% of the prediction presented here, resulting from data with overall a somewhat lower signal to noise. Hence we expect 13C16O to be detectable with CRIRES+ on the VLT.
 |
Fig. 4. Wavelength-dependent detection S/N for the secondary 13C16O (orange boxes) and the main 12C16O isotopologue (gray boxes). The box widths correspond to the wavelength range of the synthetic observations, while the height corresponds to the 16 and 84 percentiles of themeasured S/Ns, as derived by running the simulations multiple times. For 13C16O the S/N of data set B cross-correlated with the pure isotopologue template spectrum are shown, which is conservative, corresponding to the solid blue line in Fig. 3. For 12C16O the S/N of data set A cross-correlated with the pure isotopologue template spectrum are shown. We assumed 100 observationswith S/N*(2.3 μm) = 200, used to calculate the stellar S/N as function of wavelength. In the background, we show the telluric transmission model (gray solid line), as well as the scaled and offset logarithm of the CO opacity at T = 1200 K and P = 10−4 bar (light red solid line). The CO detection by Brogi et al. (2014) is shown in cyan. The actual S/N value of the CO detection in Brogi et al. (2014) is 5.8, but due to the larger wavelength coverage of our bins one has to scale this value up to a S/N of 9. This is somewhat lower than our prediction for 12C16O, but the S/Nof their observations is also smaller. |
4. Detecting HDO in atmospheres of self-luminous and irradiated planets
In this section, we mainly focus on the detectability of HDO in the thermal spectra of young, self-luminous, gas-dominated planets. In the light of planet formation and evolution, a planet’s D/H value is arguably the most interesting isotope ratio to study. Both atmospheric evaporation and icy planetesimal accretion can have a noticeable impact, both tending to increase the atmospheric D/H. In contrast, substellar objects more massive than 13 M♃ can burn their deuterium, regardless of their formation pathway (Saumon et al. 1996; Chabrier & Baraffe 2000; Burrows et al. 2001; Baraffe et al. 2003; Mollière & Mordasini 2012; Bodenheimer et al. 2013), and observations of deuterium in these objects has been suggested as a test for whether their mass is above or below the deuterium burning threshold (Béjar et al. 1999; Pavlenko et al. 2008).
The main wavelength region of interest for HDO measurements is around 3.7 μm, where at low temperatures (T ≲ 600 K), and for galactic abundances (HDO/H2O ≈ 4 × 10−5) the HDO opacity protrudes through a minimum of the opacity of the main isotopologue of H2O. For example, this wavelength region has been used to study the HDO abundances on Mars (see, e.g., Villanueva et al. 2015). The detectability of HDO at a given D/H is expected to strongly depend on atmospheric temperature. While it is obvious that thermal emission from cool planets is more difficult to detect than that from warm planets, the 3.7 μm region is, in contrast, relatively clean from H2O opacity at low temperature, but largely blanketed by it in hotter atmospheres. This is shown in Fig. 5, where the water opacities in the 3.7 μm region are plotted relative to those of HDO for different temperatures4. We therefore expect that HDO will be best detected in relatively cool, directly imaged planets, such that the angular separation from their host star leads to a much decreased stellar flux and noise in the planet spectrum. We note that we also study the cases of two irradiated planets, within the framework of this section. This is only an approximation, because the planetary spectra used in the analysis below assumed self-luminous planets.
Unfortunately, HDO measurements may be hampered by blanketing by CH4 absorption in the same wavelength range. However, the latter may be quenched, meaning that methane-poor gas is mixed up from deeper, hotter regions in the atmosphere. This particular case is therefore also studied below (see Sect. 4.4). We investigate the detectability of CH3D in Sect. 5.
 |
Fig. 5. Opacities of H2O (blue) and HDO (orange) at T = 300 K (upper panel), T = 700 K (middle panel) and T = 1100 K (lower panel), at P = 10−2 bar, which is a representative pressure value probed by water and HDO in the calculations considered here. The opacities have been scaled such that H2O constitutes 99.7% and HDO 4 × 10−5 of all H2O molecules. The higher the temperature, the more shielding of HDO occurs by H2O. |
4.1. Synthetic observations
The atmospheric structures were calculated using the petitCODE as introduced in Sect. 2.1, for which we assumed self-luminous planets, with a surface gravity of log10(g) = 3.5 (cgs), a solar composition ([Fe/H] = 0), and equilibrium temperatures varying from 300 to 1500 K in ΔT = 100 K steps. Clouds were neglected in the calculations. These are models modified from the atmosphere grid calculated for Samland et al. (2017), where HITRAN opacities are used for NH3 and PH3 in the structure calculations. Here we use their Exomol counterparts for the high-resolution calculations.
Since non-equilibrium chemistry can quench the CO, CH4 and H2O abundances in lower temperature planets, by mixing up CO-rich and CH4-poor material from high-temperature, high-pressure regions of the planets (see, e.g., Zahnle & Marley 2014), we consider models both with equilibrium abundances, as well as models where CH4 (and CO2) has been excluded in the chemical equilibrium calculations, constituting an extreme quenching scenario (see Sect. 4.4). The exclusion of CO2 was necessary because equilibrium chemistry would otherwise lock up oxygen in this molecule, which should stay in H2O in the real quenching case. We also found that the carbon in CO is preferentially moving into C2 H2 at low pressures and temperatures (T ≲ 140 K), but CO does nothave any features in the 3.7 μm region, so this effect was neglected here.
Subsequently, high-resolution spectra for the planets were calculated as described in Sect. 2.2, taking into account the opacities of H2O, CO, H2S, NH3, PH3, CH4 and CO2, as well as H2 –H2 and H2–He CIA. Nominally, the HDO/H2O ratio was assumed to be twice the cosmic D/H value of 2 × 10−5. The factor two arises from combinatorics, that is the fact that every water molecule has two locations where D may be placed, instead of H, when forming HDO instead of forming H2O (this will be a factor four for CH3D). The wavelength region considered here was from 3.6 to 3.8 μm. As before, we assumed a resolution of 105, and three wavelength steps per resolution element.
4.2. Analysis of the synthetic observations
The analysis of the synthetic observations is similar to that for CO described in Sect. 3.2. The main difference is that the planet does not exhibit any measurable change in its radial velocity offset during the observations (assuming a long >year orbital period). Therefore, it is not the change in Doppler shift that is used to separate the planet spectral features from that of the star and the Earth atmosphere. Instead, both the planet and star are observed simultaneously, but angularly separated, allowing the stellar spectrum to be used for removing the stellar and telluric contributions from the planet spectrum (Snellen et al. 2015).
Template planet spectra FP(λ) and FP - HDO(λ) are created, which are identical except that the latter has its HDO opacity removed. Comparing to Sect. 3.2, FP (λ) corresponds to data set A (without tellurics and noise) and FP(λ) − FP - HDO(λ) to data set B. In principle, subsequent analysis would involve the addition of noise and telluric absorption, followed by reduction steps similar as for the hot Jupiter case described in Sect. 2.3. However, since this procedure must be performed many times, we derived, tested, and used the following equation to approximate the statistical detection level of HDO for an observation with a certain S/N per wavelength step:
![\begin{align*} \nonumber S/N & \,{=}\, \frac{1}{\sigma} \left\{ \sum_{i=1}^{N_{\lambda}} \left[ F_{\textrm{P}}(\lambda_i) - F_{\textrm{P - HDO}}(\lambda_i) \right]^2 \right\}^{1/2} \\[3pt] & = \frac{1}{\left\langle F_{\textrm{P}}\right\rangle}\left(S/N\right)_{\textrm{pix}}\left\{\sum_{i=1}^{N_{\lambda}}\left[F_{\textrm{P}}(\lambda_i)-F_{\textrm{P-HDO}}(\lambda_i)\right]^2\right\}^{1/2} \ ,\vspace*{-4pt}\end{align*}](/articles/aa/full_html/2019/02/aa34169-18/aa34169-18-eq15.png) (5)
(5)
where σ is the error in the spectrum per wavelength step, Nλ is the number of spectral points, (S/N)pix is the average S/N per wavelength step, and 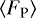 is the average flux per wavelength step in the targeted spectrum. The derivation of Eq. (5) is given in Appendix A.2. This approximative formula predicts the S/N of the HDO detection when cross-correlating data set B with the noiseless B model (corresponding to the red solid line in the right panel of Fig. 3).
is the average flux per wavelength step in the targeted spectrum. The derivation of Eq. (5) is given in Appendix A.2. This approximative formula predicts the S/N of the HDO detection when cross-correlating data set B with the noiseless B model (corresponding to the red solid line in the right panel of Fig. 3).
This formula was tested by comparing it to the full synthetic analysis (i.e. adding tellurics and noise, reducing the data, cross-correlating with an HDO template), leading to a good agreement, see Appendix B.1. The reader should note that due to the complexity of the HDO spectrum, and methane absorption that causes a quasi-continuum depending on the atmospheric temperature, even simpler S/N estimates as mentioned for CO in Sect. 3.3 (S/N scaling with 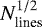 , where Nlines is the number of lines) are not adequate.
, where Nlines is the number of lines) are not adequate.
We also want to point out that Eq. (5) predicts the S/N accurately, when compared to the full analysis in Appendix B.1, even though the effects of telluric absorption are not included in Eq. (5). The full analysis in Appendix B.1 includes the effect of telluric absorption, the spectrum of which is actually dominated by telluric HDO. The telluric HDO does not absorb the exoplanet HDO signal because we assumed a Doppler shift of 30 km s−1 between the exoplanet and Earth, see Appendix B.1, which shifts the HDO lines enough to fall outside the telluric HDO lines.
4.3. Required spectral S/N to detect HDO
In Fig. 6 we show the required S/N per pixel of a planet spectrum for detecting HDO at a S/N of 5, in the 3.6–3.8 μm region, as a function of planetary Tequ and D/H value. These were calculated using Eq. (5).
The required S/N per pixel increases as function of temperature, for example for the cosmic D/H value from ~ 1 at 400 K to ~ 15 at 1200 K, due to the increased shielding by H2O absorption at higher temperatures. The 3.7 μm region is relatively clear of water absorption at low temperatures. The reader should note, however, that it is generally more difficult to reach a certain S/N level for a cooler planet than for a warmer planet. The required S/N per pixel flattens out at higher temperatures due to the expected decrease in methane abundance. Obviously, HDO is easier to detect if the atmospheric D/H value is higher. At 400 K, only an S/N per pixel of 0.1 is needed if the D/H value is 100 times the cosmic value (e.g. that of Mars).
It is instructive to compare the results presented in Fig. 6 with the expected S/N limits of known exoplanets achievable with the current 10 m-class telescopes and the future Extremely Large Telescopes (ELTs). For this we concentrate on the CRIRES+ instrument (Follert et al. 2014) on ESO’s VLT (cyan symbols) and METIS (Brandl et al. 2014; red symbols) on the European ELT, and a few prototypical exoplanets indicated in Fig. 6, assuming a single night (10 h) of observations. The planetary parameters used for this study are given in Table E.1.
For CRIRES+ on the VLT, we assumed an instrument resolution of R = 100 000, three pixels per resolution element, a mirror surface area of 52 m2, and a total telescope + instrument throughput of 0.15. For METIS on the ELT, identical specifications were assumed, but the mirror surface area was changed to 976 m2. The planetary flux was estimated by interpolating our synthetic, self-luminous exoplanet models to the planets’ published equilibrium temperature, and subsequently using the planet radius and distance to the Solar System to scale the flux accordingly. The effect of the planetary log(g), composition, and cloudiness are hence neglected in the S/N estimates presented here. The stellar flux was obtained in the same way, using PHOENIX models (Hauschildt et al. 1999) for the host star spectra, as described in Mollière et al. (2015). Finally, the expected S/N per pixel for one night of observations was obtained by computing the mean number of photons per instrument pixel of planet, star, and the sky emission, and then calculating
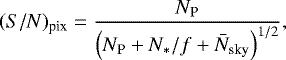 (6)
(6)
where NP, N*, and 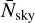 are the number of photons per pixel of planet, star, and the wavelength median of the sky background, respectively. The factor f denotes the amount of starlight reduction at the planet position. In the case that planet and star are not angularly separated, denoted as VLT-1d and ELT-1d, there is no starlight reduction and f = 1. For directly imaged planets, denoted as VLT-2d and ELT-2d in Fig. 6, f is assumed to be 100 and 1000 for VLT-2d and ELT-2d observations, respectively, using slit spectroscopy (e.g. Snellen et al. 2014), or the integral field unit in the case of METIS (e.g. Snellen et al. 2015). As discussed in the end of Sect. 4.2 above, the telluric absorption, and hence emission, is dominated by telluric HDO, which is Doppler-shifted with respect to the planet signal. We are hence interested in the average sky emission between the telluric HDO lines, which we estimated by calculating the median sky emission in the 3.6–3.8 μm region.
are the number of photons per pixel of planet, star, and the wavelength median of the sky background, respectively. The factor f denotes the amount of starlight reduction at the planet position. In the case that planet and star are not angularly separated, denoted as VLT-1d and ELT-1d, there is no starlight reduction and f = 1. For directly imaged planets, denoted as VLT-2d and ELT-2d in Fig. 6, f is assumed to be 100 and 1000 for VLT-2d and ELT-2d observations, respectively, using slit spectroscopy (e.g. Snellen et al. 2014), or the integral field unit in the case of METIS (e.g. Snellen et al. 2015). As discussed in the end of Sect. 4.2 above, the telluric absorption, and hence emission, is dominated by telluric HDO, which is Doppler-shifted with respect to the planet signal. We are hence interested in the average sky emission between the telluric HDO lines, which we estimated by calculating the median sky emission in the 3.6–3.8 μm region.
While the sky background is negligible for the VLT-1d and ELT-1d cases, where f = 1, we find that the photon noise of star and planet can often be comparable to the sky background noise for the VLT-2d and ELT-2d cases, which have f = 100 and 1000, respectively.
 |
Fig. 6. Contour map showing the required S/N of the planetary spectrum per pixel, as function of planetary equilibrium temperature and D/H value, for an HDO detection at an S/N of five. The considered wavelength region is 3.6 to 3.8 μm. The D/H values of the Solar System planets are indicated by the horizontal white dotted lines. The colored symbols indicate the lowest detectable D/H values for various exoplanets. Cyan and red symbols indicate limits for CRIRES+ at VLT and METIS at ELT, respectively, assuming a single night of observation (10 h). Filled circles stand for those targets which can be angularly separated from their host star, assuming a stellar flux reduction at the planet position by a factor 100 and 1000 for the VLT and ELT, respectively. Star-symbols denote planets that cannot be spatially resolved, for example hot Jupiters, hence no flux suppression is possible. * GJ 1214 b-like planet is a hypothetical non-transiting twin of GJ 1214 b at half the distance from Earth. The hatched area indicates the region where the required S/N per pixel is larger than 5, implying very weak HDO lines, which may be difficult to recover accurately with planet atmospheric modeling. |
Individual planets: GJ 504b, 51 Eri b, HR 8799 cde
For the directly imaged planets GJ 504b, 51 Eri b, and HR 8799 cde, assuming equilibrium chemistry, we expect that galactic D/H values will be out of reach for 10 m class telescopes. With the ELT, galactic D/H values are all in reach within a single night.
Super Earths: GJ 1214b-like planets
GJ 1214 b (and other planets like it) is an interesting target since it is of low mass (6.5 M⊕; Charbonneau et al. 2009), significantly irradiated (Tequ = 604 K, see Table E.1), and potentially highly enriched in icy planetesimals, and therefore could have a high D/H value. It is not expected that recently formed, self-luminous planets of this mass would ever exhibit such temperature, due to the low amount of formation heat retained (Linder et al. 2019). While GJ 1214 b itself is too faint, similar non-transiting systems should be found at smaller distances from the Solar System. With a transit probability of ~ 7%, the nearest non-transiting GJ 1214 b-like system is expected to be found at approximatly half the distance, with a host star 1.5 magnitudes brighter, which we used for our simulations.
Using METIS on the ELT, we expect that atmospheric D/H values ≥30 times the galactic mean value may allow for the detection of HDO in a single night. Current theories point to GJ 1214 b being strongly enriched in metals (by a factor 100 to 1000 w.r.t. solar, see Morley et al. 2013, 2015; Mollière et al. 2017), a large D/H value may well be expected for this type of planet (see the discussion in Sect. 1), although probably not as high as 30. We assume solar abundances in the spectral models used here, so only D/H varies. Moreover, the spectral models used here were for self-luminous planets, while the GJ 1214 b-twin planet is irradiated. We will revisit this planet in the methane quenching and CH3D detection cases in Sects. 4.4 and 5.
51 Peg b
Similar to the GJ 1214b-like case studied above, we use our self-luminous atmospheric grid to study the detectability of HDO in the atmosphere of the hot Jupiter 51 Peg b. While this planet is not a self-luminous planet, our analysis gives a first estimate of the single-pixel S/N to be expected for hot Jupiters. Here we predict that one night of observations with VLT CRIRES+ will allow to detect HDO if the atmospheric D/H value is 15 times the galactic value or higher, while ELT METIS would allow detecting HDO down to D/H values of twice the galactic value. For a gas giant like 51 Peg b one would expect a D/H value similar to the galactic value (see Sect. 1), which could be reached in four nights with ELT METIS, thus remaining a challenge.
It is important to note that, for the hotter planets, large S/Ns per pixel are required to detect HDO. For HR 8799 cde and 51 Peg b, the required S/N per pixel is >10 for the detection of HDO at galactic D/H values, implying intrinsicly very weak HDO lines. This requires very accurate and complete planet atmospheric modeling, since all weak planet lines need to be accounted for at this level. This is something which has to be investigated in future studies. The region where the required S/N per pixel is larger than 5 is hence indicated by the hatched area in Fig. 6. If trying to avoid this hatched region, HDO at galactic abundances may be detectable in planets out to equilibrium temperatures of 900 K.
4.4. HDO detection with methane quenching
The results for the methane-depleted calculations (see Sect. 4.1) are shown in Fig. 7. As expected, the required single-pixel S/N to detect HDO decreases substantially: HDO at galactic abundances can now be detected in a single night of VLT CRIRES+ observations in all example planets, except for the GJ 1214 b-like case, which would require ELT observations. But we note that a higher D/H value is likely to be expected for such a planet, as discussed in Sect. 4.3.
The required S/N per pixel for these cases is lower than 5 out to 1200 K, implying significantly stronger HDO lines than in the default non-quenching case. The gain in sensitivity is due to the fact that methane is not blanketing the HDO lines, but also because we effectively peer into the deeper, warmer and therefore brighter regions of the planet atmosphere.
Moreover, the required S/N in the quenching case is a monotonously increasing function of Tequ for all D/H values. The plateau seen in the non-quenching case is not present and therefore evidently caused by the decrease in methane absorption with temperature.
 |
Fig. 7. Same as Fig. 6, but neglecting both CH4 (and CO2) in thechemistry and for the opacities, in order to mimic an atmosphere where CH4, CO, and H2O are quenched at high pressures (i.e. high temperatures). |
5. Detecting CH3D in self-luminous and irradiated planets
In this section, we study the detectability of the methane isotopologue CH3D, which has been used to infer the D/H value in Uranus, Neptune, Saturn, and Jupiter, and in the atmosphere of Saturn’s moon Titan (see, e.g., de Bergh 1995; Owen & Encrenaz 2003).
Here we focus on the rovibrational CH3D band centered around 4.6 μm. This band has the advantage that both the expected planet CH4 and H2O opacity are comparatively low, making this wavelength range appear ideal for the detection of CH3D. Consequently, this wavelength region has been recently advertised for detecting CH3D in WISE 0855 (Skemer et al. 2016; Morley et al. 2018a,b). One complication of the 4.6 μm region is that the telluric background emission will become the dominating noise source, especially for self-luminous planets, where the planet can be angularly separated from the star.
Figure 8 shows the opacities of CH3D and CH4 at temperatures of 300 and 700 K, and the telluric transmission in the 4.6 μm region. Similar to the behaviour seen for HDO and H2O (see Fig. 5 and the discussion in Sect. 4), CH3D is weaker with respect to CH4 at higher temperatures, because the lines in the opacity minimum of CH4 are stronger at high temperature and blanket the CH3D opacity. We use the HITRAN line list for CH3D, and Exomol for CH4. As the telluric absorption and emission is quite strong shortward of 4.6μm, our analysis concentrates on the range between 4.6 and 4.8 μm. Future analyses may include the relatively strong CH3D feature at 4.55μm, requiring highly accurate telluric corrections.
In terms of opacity and chemical abundances, we expect CH3D to be most easily detected in cool exoplanets, where CH3D is sufficiently strong compared to CH4, and equilibrium chemistry predicts high methane abundances for H2 /He dominated atmospheres. Hotter planets are expected to have a lower methane abundance both due to chemical equilibrium effects and methane quenching (see, e.g. Zahnle & Marley 2014), as discussed earlier.
 |
Fig. 8. Opacities of CH4 (blue) and CH3D (orange), shown at T = 300 K (upper panel) and T = 700 K (lower panel), at P = 0.1 bar, which is a representative pressure value probed by methane and CH3D in the calculations considered here. The opacities have been scaled such that CH4 and CH3D constitute 98.8% and 8 × 10−5 of all CH4 isotopologues, respectively. The telluric transmission is shown in black. |
5.1. Synthetic observations and analysis
The same atmospheric models of self-luminous gas giant planets were used as for the HDO study, focussing on the wavelength range from 4.6 to 4.8 μm, and assuming a nominal CH3D abundance of 8 × 10−5, relative to CH45. All nominal isotopologue abundances used in this paper can be found in Table D.1.
We use the same analysis technique as described in Sect. 4.2. However, Eq. (5) was modified, since this wavelength region is more strongly affected by telluric absorption and emission. The derivation follows the same principles outlined in Appendix A.2, but accounts for the flux attenuation by tellurics, leading to scaling of the flux with  . For irradiated planets around bright hosts, where the stellar photon noise still dominates, the noise is scaled with
. For irradiated planets around bright hosts, where the stellar photon noise still dominates, the noise is scaled with 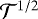 , where
, where 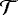 is the telluric transmission. For self-luminous planets the stellar photon noise is replaced by the photon noise of the sky background:
is the telluric transmission. For self-luminous planets the stellar photon noise is replaced by the photon noise of the sky background:
![\begin{align} &S = \sum_{i=1}^{N_{\lambda}} \mathcal{T}(\lambda_i)\left[ F_{\textrm{P}}(\lambda_i) - F_{\textrm{P - CH}_3\textrm{D}}(\lambda_i) \right]^2,\\ &N_{\textrm{irrad}} = \left\{\sum_{i=1}^{N_{\lambda}} \left[ F_{\textrm{P}}(\lambda_i) - F_{\textrm{P - CH}_3\textrm{D}}(\lambda_i) \right]^2\sigma_{\textrm{telluric}}^2(\lambda_i)\right\}^{1/2},\\ &N_{\textrm{sky}} = \left\{\sum_{i=1}^{N_{\lambda}} \left[ F_{\textrm{P}}(\lambda_i) - F_{\textrm{P - CH}_3\textrm{D}}(\lambda_i) \right]^2\sigma_{\textrm{sky}}^2(\lambda_i)\right\}^{1/2},\end{align}](/articles/aa/full_html/2019/02/aa34169-18/aa34169-18-eq24.png)
where the effective single-pixel noise for cases dominated by stellar photons is defined by 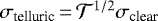 , with σclear being the photon noise when neglecting the impact of the Earth’s atmosphere. In the background dominated case, the wavelength-dependent form of σsky is again obtained from SkyCalc. The S/N of the CH3D detection is subsequently given by the ratio of Eqs. (7) and (8), or (7) and (9), depending on whether stellar or sky background emission dominates the noise budget.
, with σclear being the photon noise when neglecting the impact of the Earth’s atmosphere. In the background dominated case, the wavelength-dependent form of σsky is again obtained from SkyCalc. The S/N of the CH3D detection is subsequently given by the ratio of Eqs. (7) and (8), or (7) and (9), depending on whether stellar or sky background emission dominates the noise budget.
Analogous to the HDO detection case, this approximation for a wavelength-dependent noise source was tested by comparing to the full synthetic analysis (i.e. adding tellurics and noise, reducing the data, cross-correlating with a CH3D template), again leading to good agreement, see Appendix B.2.
5.2. Required S/N to detect CH3D
In Fig. 9 we show the required S/N per pixel of planetary spectra, to detect CH3D at an S/N of 5, as a function of D/H and planetary equilibrium temperature, in the 4.6–4.8 μm region. Analogous to the HDO study in Sect. 4, we overplot the expected S/Ns for known planetary systems, assuming a single night (10 h) of observations for the VLT and ELT. The plot is presented for cases dominated by sky background emission, so only the self-luminous planets are shown here. For producing this plot, the single pixel S/N was defined by dividing the mean planet signal per pixel in the 4.6–4.8 μm region by the median sky background noise, in the same wavelength region. Thus, although the underlying predictions account for the full wavelength dependence of the planet and background spectrum, a single scalar S/N value can be assigned to every (Tequ, D/H) pair.
For cooler planets (Tequ ≲ 600 K), CH3D may be detectable using METIS on the ELT. Hence, due to the sky background emission, we expect that CH3D is slightly more difficult to detect than HDO. In the case of strong methane quenching (cf. Fig. 7), HDO is significantly easier to detect than CH3D, and potentially even VLT-class telescopes could achieve this.
We findthat the irradiated GJ 1214 b-like planet, when studied with the ELT, as well as the hot Jupiter 51 Peg b, when studied with the VLT or ELT, should stay in the regime dominated by stellar photon noise. For the GJ 1214 b-twin, a single night of ELT observations could probe D/H values down to 1.5 times the galactic mean value. For the hotter 51 Peg b, even the ELT will only probe down to D/H values of ~5 in a single night, requiring a mean S/N of 20 per pixel, which is an unlikely precision to be reached from a modeling standpoint alone. Moreover, D/H values of 5 times the galactic mean value are not expected for gas giant planets.
We thus find that CH3D is a disfavored isotopologue when trying to infer D/H values in self-luminous planets, when compared to HDO, because the sky background emission in the 4.7 μm region is too strong. From the ground, HDO represents the better choice at all temperatures, regardless of whether methane is quenched or not. From space, and in the absence of methane quenching, the situation is reversed, however, and the associated CH3D detectability has been advertised for medium resolution spectra with the upcoming JWST (Morley et al. 2018b). For irradiated nearby super-Earths, such as the GJ 1214b-like planet studied here, a ground-based CH3D detection may be feasible, especially as a large atmospheric metal enrichment inferred for GJ 1214b (Morley et al. 2013, 2015; Mollière et al. 2017) may lead to increased D/H values.
 |
Fig. 9. Same as Fig. 6, but for CH3D. The single pixel S/N is defined as the mean planet signal per pixel, in the 4.6–4.8 μm range, divided by the median sky background noise per pixel, in the same wavelength range. |
6. Detecting HDO in Proxima Centauri b
Proxima Centauri b is a recently discovered planet in the habitable zone of the Sun’s closest stellar neighbor (Anglada-Escudé et al. 2016). With Mmin = 1.27 M⊕, only slightly more massive than the Earth, it has likely a mainly rocky composition with a climate allowing possibly liquid water on its surface (Ribas et al. 2016; Turbet et al. 2016). In this section, we investigate whether HDO could be detected in the spectrum of Proxima Cen b, assuming atmospheric properties identical to that of Earth.
The properties of the planet atmosphere remain yet unknown. However, extreme irradiation conditions and (partial) atmospheric loss likely play or have played an important role on this planet: models estimate stellar wind pressures multiple orders of magnitudes higher than experienced by Earth (Garraffo et al. 2016). In addition, stellar X-ray and EUV fluxes could have caused loss of water by evaporating Proxima Cen b’s atmosphere, especially when its host star was still in he pre-main-sequence phase. The total loss of water was likely less than an Earth’s ocean, however (Ribas et al. 2016).
If Proxima b has retained sufficient water, partly in liquid form on its surface, life could possibly have formed and developed. However, any lifeforms that Proxima Cen b was or is hypothetically harboring may have had to develop a UV tolerance much higher than organisms with even the highest UV tolerance on Earth (e.g. Deinococcus radiodurans). Assuming an Earth-like atmosphere, the recently observed super-flare from its host star and its derived flare rate spectrum suggests that no ozone could survive in the atmosphere of Proxima b, ending all hypothetical life on Proxima Cen b with a single super flare (Howard et al. 2018).
It is unclear what types of climate the planet’s orbit and assumed tidally-locked or resonating spin rate allow, which also depends on the atmospheric composition. This has, for example, been studied in Turbet et al. (2016), with as main conclusion that conditions on the planet may allow for the existence of liquid water on its surface, for example on the dayside for a tidally locked case, with a 1 bar N2 and slightly enriched in CO2 w.r.t. Earth, or all along the equator in the case of a 3:2 resonance between spin and orbital motion (with 1 bar N2 and enriched in CO2).
With Proxima Cen b’s actual atmospheric state unknown, we study the case of an Earth-twin in emitted and reflected light assuming a circular orbit with a radius of 0.0485 AU (Anglada-Escudé et al. 2016). For modeling the planet spectrum, we used the P-T structure of Earth as shown in Fig. 1.3 in Bigg (2004). Motivated by the values in Table 1.1 in Bigg (2004), we chose very simple abundance models for the planet atmosphere: for water, a uniform volume mixing ratio of 0.5% within the troposphere (P > 0.3 bar); for ozone 0.7 ppm within the stratosphere (P < 0.3 bar), and for CO2 and CH4, vertically homogeneous volume mixing ratios of 400 (including alien fossil fuel emission) and 1.75 ppm, respectively. We assumed the a D/H value of 2 × 10−4, similar to that of Earth.
In the left panel of Fig. 10 the resulting low-resolution (λ∕Δλ = 1000) synthetic emission spectrum (black solid line) is plotted over the observed average Earth emission spectrum (pink solid line) as measured by the Nimbus 4 satellite between 6.25 and 25 μm (Hanel et al. 1972). The agreement is close enough for the study presented here. The synthetic spectrum has been obtained with petitCODE (Mollière et al. 2015, 2017). The reflected light spectrum is shown in red, assuming a planetary surface albedo of 30%.
The only atmospheric process we consider for the calculation of the reflected light spectrum is attenuation of the stellar light due to scattering and absorption. Atmospheric emission and scattering into the ray that is propagating through the atmosphere is neglected. Hence, we assume that the stellar flux is reflected at the planet’s surface, and attenuated on its way to and from the surface. In this case, the reflected flux measured by an observer at distance d from a planet, when viewing its dayside, is
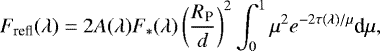 (10)
(10)
where A is the surface albedo of the planet (assuming a Lambertian surface), F* is the stellar flux measured at the substellar point of the planet, RP is the planetary radius, and τ is the optical depth from the planetary surface to space, parallel to the surface normal vector. See Appendix C for a derivation of this expression. For an airless planet with a surface albedo of unity, one recovers that 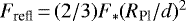 , hence a geometric albedo of 2/3, as expected.
, hence a geometric albedo of 2/3, as expected.
For the stellar flux, a Proxima Cen-like stellar spectrum was taken from PHOENIX models (Hauschildt et al. 1999). We assumed an effective temperature and radius of 3042 K (Ségransan et al. 2003) and 0.1542 R⊙ (Kervella et al. 2017).
For the high resolution study in emitted light we calculate the spectrum in the same way as in the low resolution case above, this time using our high resolution code described in Sect. 2.2. The corresponding high-resolution emission and reflection spectra for an Earth-like Proxima Cen b are shown in the right panel of Fig. 10 for the relevant wavelength range of 3.6–3.8 μm. As is evident from the right panel of Fig. 10, the reflected flux is favorable over the emitted by a factor ~ 15. Since this is a function of the albedo, the various available choices of the latter are discussed below. Moreover, more and deeper lines appear to be visible in the reflected spectrum when compared to the emission spectrum. This can be understood from the fact that in the emission case isothermal regions in the P–T structure tend to decrease the line contrasts, whereas in the reflection case stellar light is simply attenuated as it moves through the planet’s atmosphere. The full observed planetary spectrum is simply the sum of the reflected and emitted flux, due to the linear nature of the radiative transfer equation.
Our S/N prediction, using Eq. (5), suggests that HDO can be detected (at 5σ) if a planet spectrum can be obtained with an S/N per pixel of 0.23 and 0.11 for the emitted and reflected components, respectively. Making use of Eq. (6), we calculate that a single night (10 h) of ELT METIS observations should result in an S/N of ~ 0.1 per pixel, when observed in reflected light and assuming a stellar flux reduction at the planet position of a factor f = 1000. This suggests that if Proxima Cen b is an Earth twin and is similarly enriched in deuterium, HDO could be detectable in ~ 1 night of observations. However, it will have to be seen how well ELT coronagraphy will work at only 1.8 λ∕D, the star-planet separation at longest elongation. Assuming a maximum practical integration time of 10 nights, a minimum star-light suppression of f = 100 needs to be achieved to detect HDO in Proxima Cen b. We note that we neglected the phase illumination of the planet, assuming full visibility of the planet dayside. If only half of the visible hemisphere of the planet is illuminated by the star during observations, the required observing time increases by a factor 4.
We stress possible limitations of our study. First on the non-exhaustive list of effects that should be included in future studies, is the choiceof the surface albedo, which was taken to be 30%. This is the bolometric value expected for ice or snow when considering an M-dwarf host star (Turbet et al. 2016). For comparison, ice and snow on Earth have an albedo of ~ 60%, desert sand has ~40%, whereas oceans and vegetation have albedos of about 5 and 15%, respectively (see, e.g., Table 2.2 in Marshall & Plumb 2007). Next, one may consider the effect of scattering the stellar light in the atmosphere itself, and Turbet et al. (2016) found that the local bolometric albedo for Proxima Cen b may increase from 30% (ice/snow) to 50% in regions where waterclouds may form. This adds the effect of clouds to the list of processes not considered here. Increasing the albedo due to clouds may seem like an advantage, because a higher albedo increases the reflected flux. At the same time, if the majority of the reflection flux stems from water clouds, then the sharp lines of the water vapor opacity will weaken, as the vapor-richest regions are hidden below the clouds. Of course, using an Earth atmosphere to model the HDO detectability should be kept in mind as an important limitation, because Proxima Cen b’s atmospheric temperature and chemical abundance structure could be very different from what was assumed here.
 |
Fig. 10. Apparent spectrum of Proxima Cen b at a distance of 1.29 pc, assuming it is identical to Earth. Left panel: planet synthetic thermal spectrum, assuming the Earth’s P–T profile and abundances is shown as a black solid line. As a comparison, measurements by the Nimbus 4 satellite are shown as a pink solid line, which largely overlap. The red solid line shows the reflected light assuming a surface albedo of 30%, including the attenuation of the planetary atmosphere. The two vertical black dashed lines denote the wavelength region of interest for probing HDO (3.6–3.8 μm). Right panel: same but focused on the 3.6–3.8 μm region, and showing high-resolution spectra. At these wavelength, the reflected starlight is ~15 times stronger than the intrinsic thermal emission from the planet. |
7. Summary and outlook
In this paper we have studied the potential of detecting the 13C16O, HDO, and CH3D isotopologues in exoplanet atmospheres using ground-based high-dispersion spectroscopy. For the 13C16O case we considered the dayside emission spectra of hot Jupiters, while mostly concentrating on self-luminous planets for the HDO and CH3D isotopologues. In addition, a HDO reflection study was carried out for Proxima Cen b. In particular the HDO and CH3D isotopologues are interesting, since their detection will lead to constraints on atmospheric D/H values, providing insights to planet accretion histories and possible atmospheric evaporation processes. In addition, for massive substellar objects, constraints on the D/H value may shed light on their possible deuterium burning history, and hence mass.
We expect that 13C16O will be readily detectable with instruments such as CRIRES+ on the VLT. Particularly observations in the 2.4 μm range, in the first CO overtone band, will lead to high detection S/Ns for 13C16O, with only a few nights of observations.
Excitingly, HDO will be detectable at 3.7 μm with the ELTs over a broad range of atmospheric temperatures, for planets up to 900 K in equilibrium temperature, when assuming D/H values as low as the galactic mean value. Since methane tends to blanket the HDO features, atmospheres in which methane is strongly quenched may be significantly more accessible, potentially even with 10 m class telescopes, in this case for planets up to 1200 K in equilibrium temperature. If sufficient coronagraphic starlight reduction can be reached with METIS on the ELT at 2λ∕D, an HDO detection in Proxima b will be possible, if its atmosphere is water-rich and Earth-like.
The CH3D isotopologue, the detection of which will also constrain the D/H value in a planet atmosphere, would be clearly favorable if the sky background emission at ~4.7μm could be neglected. However, due to sky background, only the ELT will likely detect CH3D, for planets with equilibrium temperatures below 600 K. Also for irradiated or transiting planets in the super-Earth regime, if in the solar neighbourhood, a CH3D detection is likely possible.
Isotopologues will soon be a part of the exoplanet characterisation tools. Here we studied only three isotopologues, 13C16O, HDO, and CH3D, and only consider the signal strength they imprint onto the observed planet spectra. Future studies should also consider different molecules, look into different techniques such as transmission spectroscopy (which we avoided due to the high uncertainty of their cloud and haze properties), and most importantly try to answer how well one can retrieve the actual isotopologue abundance (ratios) from high-resolution observations. The question is whether such observations must be complemented by lower resolution spectroscopy to better constrain, for example, the atmospheric temperature profile. Another unanswered question is whether current line lists have the required precision for carrying out such studies. If line positions of any important atmospheric absorber are wrong, or lines are missing altogether, then the noise arising from pseudo-random line overlap between the observations and models may make the successful isotopologue detection more difficult when using the cross-correlation technique. Striving for the detection of isotopologues in exoplanet atmospheres will challenge the exoplanet modeling community to refine their modeling and retrieval techniques.
Acknowledgements
We thank our referee Bruno Bézard for his many useful comments, which helped improving this paper. P.M. thanksJ. Kasting and R. Pierrehumbert for helpful discussions. P.M. also thanks C. Morley and M. Line, whose comments greatly improved the quality of this work. This work benefited from the 2018 Exoplanet Summer Program in the Other Worlds Laboratory (OWL) at the University of California, Santa Cruz, a program funded by the Heising-Simons Foundation. P.M and I.S. acknowledge support from the European Research Council under the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 694513.
Appendix A: Cross-correlation signal-to-noise
A.1. Lines of equal strength
Here we derive the signal-to-noise characteristics when trying to identify a line species in noisy data. We start with the case of spectral lines which all have the same strength in the spectral data. The cross-correlation is defined as
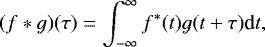 (A.1)
(A.1)
it is thus the integral of the product of the function f and the function g, where g has been shifted to the “left” (i.e. toward more negative t values) by the distance τ. For real valued functions it holds that (f * g)(τ) = (g * f)(−τ).
We now consider a planetary spectrum observed at high resolution within a spectral range [−ν, ν]. Here we assume that we have a perfect model for the noise-free spectrum of the planet, f(ν). However, the observation will not give f(ν), it will give the planetary spectrum plus noise n(ν). The total observed signal is then o(ν) = f(ν) + n(ν). Throughout this section, for clarity, we will describe the noise assuming a Gaussian with a mean value of zero, and we assume that the planetary spectrum is zero outside the lines, while the lines are assumed to be positive. Because we expect the noise to be fully dominated by the planet’s host star, assuming Gaussian-distributed noise is appropriate, as the Poisson distribution transitions to a Gauss distribution at large mean values. Assuming that the noise has a constant standard deviation σ for every pixel, a single line within the planetary spectrum, of strength I, will only be visible if I ≫ σ. Moreover, the S/N of a single line observation will be S/Nsingle = I∕σ.
Now, instead, we carry out a cross-correlation between the observation and the model spectrum, across the range where we have data:
![\begin{align*} (o*f)(\nu_0) & = \int_{-\nu}^{\nu} \left[f(\nu)+n(\nu)\right]f(\nu+\nu_0)\textrm{d}\nu \\ & = \int_{-\nu}^{\nu} f(\nu)f(\nu+\nu_0)\textrm{d}\nu +\int_{-\nu}^{\nu}n(\nu)f(\nu+\nu_0)\textrm{d}\nu.\end{align*}](/articles/aa/full_html/2019/02/aa34169-18/aa34169-18-eq29.png)
Here we neglect the complex conjugate notation, as all functions are real-valued. If one has a perfect (in reality: good) model, then the first integral in Eq. (A.3) will be maximal for ν0 = 0. We call this value the signal S. This is the signal to be extracted by means of cross-correlation. If the planet has a density of ρ lines per frequency interval in the observed spectral region, with all lines of roughly equal strength I, then the height of the peak S at ν0 = 0 can be approximated as
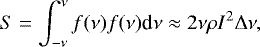 (A.4)
(A.4)
where Δν is the approximate line width of the lines within the studied frequency range and 2νρ is the number of lines probed across [−ν, ν]. The second integral in Eq. (A.3), which we will call noise N, can be approximated by noticing that the integral will be dominated by the locations where f(ν + ν0) is maximal (i.e. where the lines are). The mean value, for arbitrary ν0 (assuming that the properties of the planet lines stay constant across the range probed by shifting ν0) can hence be written as
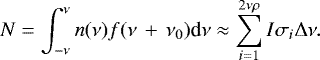 (A.5)
(A.5)
Here, σi denotes an actual sampled value of the noise with standard deviation σ. Now, because we assume the noise values to be independent and random (following a Poisson distribution), we find that the average magnitude of the noise N is
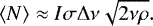 (A.6)
(A.6)
The S/N measured at the peak of the cross-correlation function of model and observation is thus
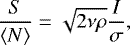 (A.7)
(A.7)
and one sees that the S/N grows with the square root of the number of lines being probed.
In reality the data will contain not only the planetary signal, and the photon noise of the observation, but also lines belonging to the planet’s host star, telluric lines, or planetary lines not included in the model f(ν). If these contaminant lines are uncorrelated with respect to the distribution of the lines in the model spectrum, then they merely correspond to an additional noise source. If this is not the case, and there is some non-negligible correlation, then this will be visible in the form of secondary peaks in the cross-correlation function.
A.2. Lines of varying strength
If every line i has a different strength Ii, then the signal in the first term of Eq. (A.3) can be approximated as
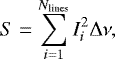 (A.8)
(A.8)
whereas for the noise it holds that
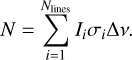 (A.9)
(A.9)
Because the noise values at the Nlines line positions are independent, it holds for the average noise magnitude that
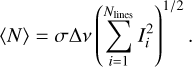 (A.10)
(A.10)
Hence, the strongest lines will be most important. Moreover, when evaluating Eq. (A.11) for estimating the expected signal-to-noise for a given model f(ν) = I(ν), and a given noise level σ, one can simply set
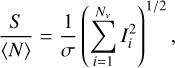 (A.12)
(A.12)
that is taking the sum over all frequency points, rather than just the line positions.
Appendix B: Testing the cross-correlation S/N approximation (Eq. (5)) for trace species
B.1. Testing the S/N approximation for HDO
Here we present full simulations of the HDO detection for the self-luminous, directly imageable planets, as described in Sect. 4.1. This is done to validate our approximative S/N calculations (see Eq. (5)) used for the HDO detection in Sects. 4 and 6. “Full simulation” here means that we included telluric absorption, added photon noise, and then carried out a synthetic reduction step, followed by cross-correlating with an HDO model.
For the full simulation we first obtained synthetic observations as described in Sect. 2.3. As before, we assumed to record the data as 100 individual spectra, at a resolution of 105, and three wavelength steps per resolution element6. Our benchmark calculations are for young, directly imaged planets, and we therefore assumed that the star-light at the planet’s position is reduced by a factor of f = 1000. Similar to the CO detection study (see Sect. 3), we treated the stellar flux as featureless, assuming any features can be readily removed. For the velocity offset between the telluric absorption and the planet–star system we assumed a value of 30 km s−1, which for all systems near the ecliptic can be achieved due to the barycentric motion of the Earth.
Here we will analyse the characteristics of the HDO detection S/N in planets as a function of Tequ at a very large signal-to-noise level, and compare this to the prediction made with the approximation enabled by Eq. (5), described in Sect. 4.2. We chose to work with a high signal-to-noise, in order to be able to compare the full and approximative methods properly, otherwise most of the cases would simply lead to non-detections, with the S/Ns scattering around zero. The calculations here assume that at the location of the star the spectral single-pixel S/N at 2.3 μm is S/N*(2.3 μm) = 5000 per single spectrum (we will evaluate 100 spectra later), leading to S/N* = 3317 at 3.7 μm (assuming a sun-like host star). Identically to Sect. 3.1, Eq. (4), we use a stellar flux model to calculate the corresponding stellar S/N* at 3.7 μm. Moreover, because we assume that at the location of the planet the stellar flux is lower by a factor 1000, the photon noise is lower by a factor  . The data reduction process is described in Appendix B.3.
. The data reduction process is described in Appendix B.3.
The results for the HDO detection S/N are shown in Fig. B.1. We show both the S/Ns obtained for cross-correlating the synthetic observation with a pure HDO isotopologue template spectrum (i.e. taking the full self-consistent atmospheric structure but considering only the HDO opacity for the spectrum), and the detection S/N obtained when using the better cross-correlation model FP − FP-HDO, which will have the HDO line ratios at correct relative strength. This corresponds to the noiseless and telluric-free model of data set B, described in Sect. 3.2. The synthetic observation we correlated the models with was the contaminant corrected data set, analogous to data set B in Fig. 1. The cross-correlation functions of the 100 synthetic observationswe added before calculating the detection S/N. As is evident, using the noiseless and telluric-free model for data set B, instead of the pure HDO isotopologue template spectrum, gives a S/N which is on average better by ΔS/N ~ 7.
 |
Fig. B.1. S/N of the HDO detection in the spectrum of a directly imaged gas planet as a function of the planetary Tequ. The HDO/H2O ratio was 4 × 10−5. Here we assumed S/N*, at 3.7μm = 3317 per spectrum, a stellar flux 1000 times smaller at the position of the planet, considering 100 spectral observations. Orange boxes: detection S/N when correlating the contaminant removed observation (data set B) with a pure HDO isotopologue template. Black boxes: detection S/N when correlating with the noiseless, telluric-free model B spectrum. The box height corresponds to the measured 16 and 84 percentiles of the measured S/Ns, when running the simulation multiple times. The black dotted line denotes the S/N scaling expected purely from the increasing planet–star contrast as the planet becomes hotter. This assumes that the ratio of the HDO and H2O opacities isnot temperature dependent. The black dashed line shows the prediction of the S/N signal following Eq. (5), indicating good agreement. |
It can be seen that the detection S/N first increases with temperature, in a way which we find to be linear in the increasing planet–star contrast (black dotted line in Fig. B.1) at 3.7 μm, as expected, as the planet becomes hotter. From Tequ ≈ 700 K on this behavior stops and the S/N stagnates, due to the fact the HDO opacity is weaker with respect to the H2O opacity at high temperatures. For higher Tequ ≳ 1200 K the HDO detection S/N starts rising again. This is caused by methane, the main absorber in the 3.7 μm atmosphericwindow, being less abundant at higher temperatures (see the discussion of Fig. 7 in Sect. 4.4).
The black dashed line in Fig. B.1 shows the predicted detection S/N results when using Eq. (5). For the spectral signal-to-noise per pixel, used in Eq. (5), we evaluated
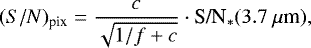 (B.1)
(B.1)
where f = 1000 is the flux stellar flux reduction at the position of the planet, and c is the mean planet to star contrast in the wavelength region of interest.
This makes use of our estimate from Appendix B.3, namely that the data reduction process itself is not expected to increase the error of the final spectrum of the target species considerably. One expects Eq. (5) to follow the detection S/N for cross-correlating the observation with the noiseless and telluric-free model for data set B, and indeed the agreement is very good until equilibrium temperatures of 1100 K. Then Eq. (5) starts to slightly overpredict the detection S/N. We do not attribute this to the failing of Eq. (5) at these higher temperatures. Rather, we suspect that the detailed simulation of the HDO detection, which we compare to here, may give rise to additional noise. The noise-free auto-correlation we calculate for the telluric-free data set B is even higher (≈ 45 in this temperature range), that is cannot be the reason for the S/N differences we observe here. The S/N approximation method (Eq. (5)) has thus been verified successfully.
B.2. Testing the S/N approximation for CH3D
In Fig. B.2 we show the test of the S/N-approximation for CH3D (Eqs. (7) and (8) in Sect. 5), analogous to the test shown for HDO in Fig. B.1. One sees that we can reach a good agreement, with differences never larger than 30%.
 |
Fig. B.2. Analogous to Fig. B.1, but this time testing the S/N-approximation (Eqs. (7) and (8)) for CH3D. |
B.3. Data reduction and estimated error magnitude
Here we describe the data reduction used in Appendix B.1, and discuss the resulting magnitude of the planet flux error bars, for a single spectral pixel.
For every of the 100 individual spectra considered here, the observed flux at the Earth’s surface is
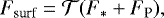 (B.2)
(B.2)
where 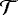 is the telluric transmission, F* the stellar flux at the location of the planet, and FP is the planet’s flux (planet and star are velocity-shifted with respect to the telluric transmission). The model input error of a single-pixel and spectrum is supposed to be constant in the approximation here, and given by
is the telluric transmission, F* the stellar flux at the location of the planet, and FP is the planet’s flux (planet and star are velocity-shifted with respect to the telluric transmission). The model input error of a single-pixel and spectrum is supposed to be constant in the approximation here, and given by
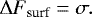 (B.3)
(B.3)
The telluric transmission model (also see Sect. 3.2) will be constructed by observing the star directly, that is not at the location of the planet. We assume that the star, when observed directly, is brighter by a factor f. Hence the estimate of the telluric transmission, if assuming that the star’s flux without telluric absorption, F*, is perfectly known, is:
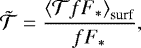 (B.4)
(B.4)
where 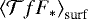 is the median observed flux in a given pixel, taking all 100 spectra into account. Because the star is brighter by a factor f when observed directly, with the error scaling with
is the median observed flux in a given pixel, taking all 100 spectra into account. Because the star is brighter by a factor f when observed directly, with the error scaling with 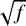 , we find that
, we find that
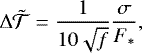 (B.5)
(B.5)
where the factor 1∕10 stems from combining the 100 spectra to get the transmission estimate. Now, using the measured transmission model, the model flux, taking into account the contaminant species only, is subtracted from the observation (see Sect. 3.2), leading to
![\begin{align*} F_{\textrm{rem}} & = F_{\textrm{surf}}-\tilde{\mathcal{T}}F_{\textrm{P-HDO}} \\ & \approx \mathcal{T}[F_*+(F_{\textrm{P}}-F_{\textrm{P-HDO}})]. \end{align*}](/articles/aa/full_html/2019/02/aa34169-18/aa34169-18-eq48.png)
The expected error then works out to be
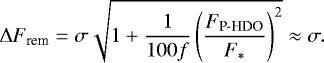 (B.8)
(B.8)
Next, we remove the telluric lines, in order to not be dominated by these in the cross-correlation function:
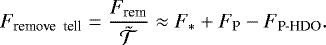 (B.9)
(B.9)
We note that we implicitly assumed here that the errors introduced by the transmission model estimate  , when obtaining Frem, and then Fremove tell, are independent. Only then would it be allowed to carry out two consecutive, and independent error propagation analyses. However, the error introduced by
, when obtaining Frem, and then Fremove tell, are independent. Only then would it be allowed to carry out two consecutive, and independent error propagation analyses. However, the error introduced by 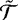 is negligible in both steps, and the same would result from a more correct analysis.
is negligible in both steps, and the same would result from a more correct analysis.
Finally, we remove the influence of very strong telluric lines by setting (see Sect. 3.2)
 (B.14)
(B.14)
where 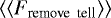 denotes the average over all spectral channels and all 100 spectra, and σcolumn is the standard flux deviation of a given spectral channel, when considering all
denotes the average over all spectral channels and all 100 spectra, and σcolumn is the standard flux deviation of a given spectral channel, when considering all 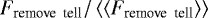 values for all 100 spectra, Hence, if there was no HDO line signal, then Ffinal would be simply a flat spectrum around zero, with a standard deviation of 1. One finally gets
values for all 100 spectra, Hence, if there was no HDO line signal, then Ffinal would be simply a flat spectrum around zero, with a standard deviation of 1. One finally gets
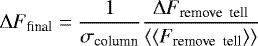 (B.15)
(B.15)
such that the expected signal-to-noise on the HDO-associated planetary flux per spectral pixel is
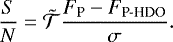 (B.16)
(B.16)
The step for obtaining Ffinal (i.e. dividing by σcolumn) will effectively remove the wavelength regions of strong telluric lines from the analysis. If one assumes that σ itself scales with 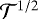 , one gets theexpected behaviour for photon noise, namely that the S/N of the observation scales with
, one gets theexpected behaviour for photon noise, namely that the S/N of the observation scales with 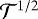 .
.
Hence, the reduction and contaminant removal step is not a significant noise source, with the total S/N given simply by the flux difference due to the target species, divided by the observational uncertainties.
Appendix C: Derivation of the reflected flux as a function of surface albedo and atmospheric absorption
The reflected flux seen by an observer, viewing the dayside of a planet, can be expressed as
 (C.1)
(C.1)
where Irefl is the intensity of the reflected ray at the top of the exoplanet’s atmosphere, ndetect is the normal vector of the detector, and nP is the direction of travel of the reflected light. Because of the large distances between observer and planet, the angle between the
two vectors is negligibly small. Neglecting the atmospheric attenuation, the intensity of the scattered light at the surface of the planet can be found by equating
 (C.2)
(C.2)
where ϑ is the angle between the normal vector of the planet’s surface and the incoming radiation. Here a Lambertian surface was assumed, because for isotropic intensities it holds that F = πI, which follows from F = ∫ Icos(ϑ)dΩ, integrated over a solid angle of 2π.
The area of an annulus on the planet’s sphere, at an angle ϑ away from the substellar point, is
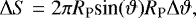 (C.4)
(C.4)
where RP is the planetary radius. The effective area seen by the observer is equal to cos (ϑ)ΔS. Hence the total reflected flux, using ΔΩ = cos(ϑ)ΔS∕d2 for the annulus’ solid angle, where d is the distance between planet and observer, is
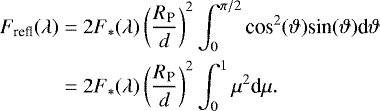 (C.5)
(C.5)
For a variable surface albedo A(λ), as well as using that the ray will be attenuated by e−τ(λ)∕μ twice as it travels through the atmosphere, one obtains
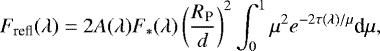 (C.6)
(C.6)
where τ(λ) is the optical depth of a ray from the planetary surface to space, running parallel to the normal vector of the planetary surface.
Appendix D: Nominal isotopologue abundances
In Table D.1 we list the default isotopologue ratios assumed in our calculations, if not otherwise noted in the text.
Default isotopologue ratios used in this study.
Appendix E: Parameters assumed for the planets in the HDO and CH3D detection studies
In Table E.1 we list the parameters assumed for the planets in the HDO and CH3D detection studies (Sects. 4 and 5).
Parameters assumed for the planets in the HDO and CH3D detection studies (Sects. 4 and 5).
References
- Ali-Dib, M., Mousis, O., Petit, J.-M., & Lunine, J. I. 2014, ApJ, 785, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Altwegg, K., & Bockelée-Morvan, D. 2003, Space Sci. Rev., 106, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Altwegg, K., Balsiger, H., Bar-Nun, A., et al. 2015, Science, 347, 1261952 [Google Scholar]
- Anglada-Escudé, G., Amado, P. J., Barnes, J., et al. 2016, Nature, 536, 437 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Ayres, T. R., Lyons, J. R., Ludwig, H.-G., Caffau, E., & Wedemeyer-Böhm, S. 2013, ApJ, 765, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Chabrier, G., Barman, T. S., Allard, F., & Hauschildt, P. H. 2003, A&A, 402, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barber, R. J., Tennyson, J., Harris, G. J., & Tolchenov, R. N. 2006, MNRAS, 368, 1087 [NASA ADS] [CrossRef] [Google Scholar]
- Baudino, J.-L., Bézard, B., Boccaletti, A., et al. 2015, A&A, 582, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baudino, J.-L., Mollière, P., Venot, O., et al. 2017, ApJ, 850, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Béjar, V. J. S., Osorio, M. R. Z., & Rebolo, R. 1999, ApJ, 521, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Bigg, G. R. 2004, The Oceans and Climate (Cambridge: Cambridge University Press), 286 [Google Scholar]
- Birkby, J. L., de Kok, R. J., Brogi, M., et al. 2013, MNRAS, 436, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Birkby, J. L., de Kok, R. J., Brogi, M., Schwarz, H., & Snellen, I. A. G. 2017, AJ, 153, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Biver, N., Moreno, R., Bockelée-Morvan, D., et al. 2016, A&A, 589, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bodenheimer, P., D’Angelo, G., Lissauer, J. J., Fortney, J. J., & Saumon, D. 2013, ApJ, 770, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnefoy, M., Perraut, K., Lagrange, A.-M., et al. 2018, A&A, 618, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borysow, A., & Frommhold, L. 1989, ApJ, 341, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Borysow, A., Frommhold, L., & Moraldi, M. 1989, ApJ, 336, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Brandl, B. R., Feldt, M., Glasse, A., et al. 2014, in Ground-Based and Airborne Instrumentation for Astronomy V, Proc. SPIE, 9147, 914721 [CrossRef] [Google Scholar]
- Brogi, M., & Line, M. R. 2018, ArXiv e-prints [arXiv:1811.01681] [Google Scholar]
- Brogi, M., Snellen, I. A. G., de Kok, R. J., et al. 2012, Nature, 486, 502 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Brogi, M., de Kok, R. J., Birkby, J. L., Schwarz, H., & Snellen, I. A. G. 2014, A&A, 565, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bryan, M. L., Benneke, B., Knutson, H. A., Batygin, K., & Bowler, B. P. 2018, Nat. Astron., 2, 138 [Google Scholar]
- Burrows, A., Hubbard, W. B., Lunine, J. I., & Liebert, J. 2001, Rev. Mod. Phys., 73, 719 [Google Scholar]
- Chabrier, G., & Baraffe, I. 2000, ARA&A, 38, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Chan, Y. M., & Dalgarno, A. 1965, Proc. Phys. Soc., 85, 227 [Google Scholar]
- Charbonneau, D., Berta, Z. K., Irwin, J., et al. 2009, Nature, 462, 891 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Clarke, J. T., Mayyasi, M., Bhattacharyya, D., et al. 2017, J. Geophys. Res. Space Phys., 122, 2336 [NASA ADS] [Google Scholar]
- Clayton, R. N. 1993, Annu. Rev. Earth Planet. Sci., 21, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Clayton, D. D., & Nittler, L. R. 2004, ARA&A, 42, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Cridland, A. J., Pudritz, R. E., & Alessi, M. 2016, MNRAS, 461, 3274 [Google Scholar]
- Dalgarno, A., & Williams, D. A. 1962, ApJ, 136, 690 [NASA ADS] [CrossRef] [Google Scholar]
- de Bergh C. 1995, Adv. Space Res., 15, 427 [NASA ADS] [CrossRef] [Google Scholar]
- De Biévre, P., Gallet, M., Holden, N. E., & Barnes, I. L. 1984, J. Phys. Chem. Ref. Data, 13, 809 [NASA ADS] [CrossRef] [Google Scholar]
- de Kok, R. J., Brogi, M., Snellen, I. A. G., et al. 2013, A&A, 554, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feuchtgruber, H., Lellouch, E., Orton, G., et al. 2013, A&A, 551, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Follert, R., Dorn, R. J., Oliva, E., et al. 2014, in Ground-Based and Airborne Instrumentation for Astronomy V, Proc. SPIE, 9147, 914719 [CrossRef] [Google Scholar]
- Fu, Q., & Liou, K. N. 1992, J. Atm. Sci., 49, 2139 [NASA ADS] [CrossRef] [Google Scholar]
- Garraffo, C., Drake, J. J., & Cohen, O. 2016, ApJ, 833, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Geiss, J., & Reeves, H. 1981, A&A, 93, 189 [Google Scholar]
- Ghosh, P., & Brand, W. A. 2003, Int. J. Mass Spectrom., 228, 1 [CrossRef] [Google Scholar]
- Goody, R., West, R., Chen, L., & Crisp, D. 1989, J. Quant. Spectr. Rad. Transf., 42, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Guillot, T., & Gautier, D. 2014, ArXiv e-prints [arXiv:1405.3752] [Google Scholar]
- Halbout, J., Mayeda, T. K., & Clayton, R. N. 1986, Earth Planet. Sci. Lett., 80, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Hanel, R. A., Conrath, B. J., Kunde, V. G., et al. 1972, J. Geophys. Res., 77, 2629 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, A. H., Gallagher, J. S., & Levelt Sengers J. M. H. 1998, J. Phys. Chem. Ref. Data, 27, 761 [NASA ADS] [CrossRef] [Google Scholar]
- Hauschildt, P. H., Allard, F., & Baron, E. 1999, ApJ, 512, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Helling, C., Woitke, P., Rimmer, P. B., et al. 2014, Life, 4, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, C., Yurchenko, S. N., & Tennyson, J. 2013, Icarus, 226, 1673 [NASA ADS] [CrossRef] [Google Scholar]
- Hoeijmakers, H. J., Ehrenreich, D., Heng, K., et al. 2018, Nature, 560, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, W. S., Tilley, M. A., Corbett, H., et al. 2018, ApJ, 860, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Jakosky, B. M., & Phillips, R. J. 2001, Nature, 412, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, A., Noll, S., Kausch, W., Szyszka, C., & Kimeswenger, S. 2013, A&A, 560, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Thévenin, F., & Lovis, C. 2017, A&A, 598, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krasnopolsky, V. A. 2015, Icarus, 257, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Kulikov, Y. N., Lammer, H., Lichtenegger, H. I. M., et al. 2006, Planet. Space Sci., 54, 1425 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. 1993, SYNTHE Spectrum Synthesis Programs and Line Data. Kurucz CD-ROM No. 18 (Cambridge, MA: Smithsonian Astrophysical Observatory), 1993, 18 [Google Scholar]
- Lacis, A. A., & Oinas, V. 1991, J. Geophys. Res., 96, 9027 [NASA ADS] [CrossRef] [Google Scholar]
- Langmuir, C., & Broecker, W. 2012, How to Build a Habitable Planet: The Story of Earth from the Big Bang to Humankind (Princeton: Princeton University Press) [Google Scholar]
- Lellouch, E., Bézard, B., Fouchet, T., et al. 2001, A&A, 370, 610 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leshin, L. A. 2000, Geophys. Res. Lett., 27, 2017 [NASA ADS] [CrossRef] [Google Scholar]
- Linder, E. F., Mordasini, C., Molliere, P., et al. 2019, A&A, DOI: 10.1051/0004-6361/201833873 [Google Scholar]
- Linsky, J. L., Draine, B. T., Moos, H. W., et al. 2006, ApJ, 647, 1106 [NASA ADS] [CrossRef] [Google Scholar]
- Madhusudhan, N., Amin, M. A., & Kennedy, G. M. 2014, ApJ, 794, L12 [Google Scholar]
- Madhusudhan, N., Bitsch, B., Johansen, A., & Eriksson, L. 2017, MNRAS, 469, 4102 [NASA ADS] [CrossRef] [Google Scholar]
- Mahaffy, P. R., Donahue, T. M., Atreya, S. K., Owen, T. C., & Niemann, H. B. 1998, Space Sci. Rev., 84, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Mancini, L., Giordano, M., Mollière, P., et al. 2016a, MNRAS, 461, 1053 [NASA ADS] [CrossRef] [Google Scholar]
- Mancini, L., Kemmer, J., Southworth, J., et al. 2016b, MNRAS, 459, 1393 [NASA ADS] [CrossRef] [Google Scholar]
- Mancini, L., Southworth, J., Raia, G., et al. 2017, MNRAS, 465, 843 [NASA ADS] [CrossRef] [Google Scholar]
- Marboeuf, U., Thiabaud, A., Alibert, Y., Cabral, N., & Benz, W. 2014a, A&A, 570, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marboeuf, U., Thiabaud, A., Alibert, Y., Cabral, N., & Benz, W. 2014b, A&A, 570, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marboeuf, U., Thiabaud, A., Alibert, Y., & Benz, W. 2018, MNRAS, 475, 2355 [NASA ADS] [CrossRef] [Google Scholar]
- Marshall, J., & Plumb, R. 2007, Atmosphere, Ocean and Climate Dynamics: An Introductory Text, International Geophysics (New York: Elsevier Science) [Google Scholar]
- Milam, S. N., Savage, C., Brewster, M. A., Ziurys, L. M., & Wyckoff, S. 2005, ApJ, 634, 1126 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, N., & Fortney, J. J. 2011, ApJ, 736, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Mollière, P., & Mordasini, C. 2012, A&A, 547, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mollière, P., van Boekel, R., Dullemond, C., Henning, T., & Mordasini, C. 2015, ApJ, 813, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Mollière, P., van Boekel, R., Bouwman, J., et al. 2017, A&A, 600, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morbidelli, A. 2005, ArXiv e-prints [astro-ph/0512256] [Google Scholar]
- Mordasini, C., van Boekel, R., Mollière, P., Henning, T., & Benneke, B. 2016, ApJ, 832, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Morley, C. V., Fortney, J. J., Kempton, E. M.-R., et al. 2013, ApJ, 775, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Morley, C. V., Fortney, J. J., Marley, M. S., et al. 2015, ApJ, 815, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Morley, C. V., Skemer, A. J., Allers, K. N., et al. 2018a, ApJ, 858, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Morley, C. V., Skemer, A. J., Miles, B. E., et al. 2018b, ApJL, submitted [arXiv:1810.04241] [Google Scholar]
- Noll, S., Kausch, W., Barden, M., et al. 2012, A&A, 543, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nugroho, S. K., Kawahara, H., Masuda, K., et al. 2017, AJ, 154, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., & Bergin, E. A. 2016, ApJ, 831, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., Murray-Clay, R. A., & Bergin, E. A. 2011, ApJ, 743, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, T., & Encrenaz, T. 2003, Space Sci. Rev., 106, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Pavlenko, Y. V., Harris, G. J., Tennyson, J., et al. 2008, MNRAS, 386, 1338 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, V. K., Sephton, M. A., Franchi, I. A., Gibson, J. M., & Gilmour, I. 2006, Meteorit. Planet. Sci., 41, 1899 [NASA ADS] [CrossRef] [Google Scholar]
- Piskorz, D., Benneke, B., Crockett, N. R., et al. 2016, ApJ, 832, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Piskorz, D., Benneke, B., Crockett, N. R., et al. 2017, AJ, 154, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [NASA ADS] [Google Scholar]
- Polehampton, E. T., Baluteau, J.-P., & Swinyard, B. M. 2005, A&A, 437, 957 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quay, P. D., King, S. L., Stutsman, J., et al. 1991, Global Biogeochem. Cycles, 5, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Rajan, A., Rameau, J., De Rosa, R. J., et al. 2017, AJ, 154, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Ribas, I., Bolmont, E., Selsis, F., et al. 2016, A&A, 596, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richard, C., Gordon, I. E., Rothman, L. S., et al. 2012, J. Quant. Spectr. Rad. Transf., 113, 1276 [NASA ADS] [CrossRef] [Google Scholar]
- Rodler, F., Lopez-Morales, M., & Ribas, I. 2012, ApJ, 753, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Rodler, F., Kürster, M., & Barnes, J. R. 2013, MNRAS, 432, 1980 [NASA ADS] [CrossRef] [Google Scholar]
- Rothman, L. S., Gordon, I. E., Barber, R. J., et al. 2010, J. Quant. Spectr. Rad. Transf., 111, 2139 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, D., Matteucci, F., Zhang, Z.-Y., Papadopoulos, P. P., & Ivison, R. J. 2017, MNRAS, 470, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Rothman, L. S., Gordon, I. E., Babikov, Y., et al. 2013, J. Quant. Spectr. Rad. Transf., 130, 4 [Google Scholar]
- Samland, M., Mollière, P., Bonnefoy, M., et al. 2017, A&A, 603, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Israelian, G., & Mayor, M. 2004, A&A, 415, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saumon, D., Hubbard, W. B., Burrows, A., et al. 1996, ApJ, 460, 993 [NASA ADS] [CrossRef] [Google Scholar]
- Ségransan, D., Kervella, P., Forveille, T., & Queloz, D. 2003, A&A, 397, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skemer, A. J., Morley, C. V., Allers, K. N., et al. 2016, ApJ, 826, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Sneep, M., & Ubachs, W. 2005, J. Quant. Spectr. Rad. Transf., 92, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Snellen, I. A. G., de Kok, R. J., de Mooij, E. J. W., & Albrecht, S. 2010, Nature, 465, 1049 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Snellen, I. A. G., Brandl, B. R., de Kok, R. J., et al. 2014, Nature, 509, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Snellen, I., de Kok, R., Birkby, J. L., et al. 2015, A&A, 576, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Southworth, J., Mancini, L., Madhusudhan, N., et al. 2017, AJ, 153, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Tennyson, J., & Yurchenko, S. N. 2012, MNRAS, 425, 21 [Google Scholar]
- Thiabaud, A., Marboeuf, U., Alibert, Y., et al. 2014, A&A, 562, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thorngren, D. P., Fortney, J. J., Murray-Clay, R. A., & Lopez, E. D. 2016, ApJ, 831, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Tinney, C. G., Butler, R. P., Marcy, G. W., et al. 2001, ApJ, 551, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Tremblin, P., Amundsen, D. S., Mourier, P., et al. 2015, ApJ, 804, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Turbet, M., Leconte, J., Selsis, F., et al. 2016, A&A, 596, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Villanueva, G. L., Mumma, M. J., Novak, R. E., et al. 2015, Science, 348, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Voronin, B. A., Tennyson, J., Tolchenov, R. N., Lugovskoy, A. A., & Yurchenko, S. N. 2010, MNRAS, 402, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Wittenmyer, R. A., Endl, M., & Cochran, W. D. 2007, ApJ, 654, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Yurimoto, H., Kuramoto, K., Krot, A. N., et al. 2007, Protostars and Planets V (Tucson, AZ: University of Arizona Press), 849 [Google Scholar]
- Zahnle, K. J., & Marley, M. S. 2014, ApJ, 797, 41 [NASA ADS] [CrossRef] [Google Scholar]
We note that for carbon and oxygen the isotopic ratios 12C/13C, 16O/17O and 16O/18O decrease toward the galactic center (see, e.g., Milam et al. 2005; Romano et al. 2017). This is thought to be caused by dredge-up of heavier C and O isotopes as reaction-intermediates of the CNO cycle in AGB stars, which are later ejected into the ISM with the stars’ outer layers.
We use HITEMP water opacities, for which the secondary isotopologue lines are taken from the HITRAN line list. HITRAN is known to be incomplete at high temperatures, but also the high-temperature Exomol line lists both for H2O (Barber et al. 2006) and HDO (Voronin et al. 2010) exhibit this behaviour when inspected with the Exomol cross-section service (Hill et al. 2013).
All Tables
Parameters assumed for the planets in the HDO and CH3D detection studies (Sects. 4 and 5).
All Figures
 |
Fig. 1. Different analysis steps of the simulated observations. Panel a: raw synthetic observation (number of photons as a function of wavelength and phase). Panel b: data after the telluric correction, as described in the text. Panel c: data of panel b after subtracting the total wavelength and phase mean, and normalising each column byits standard deviation, to suppress noisy wavelength regions. This is data set A. Panel d: same as panel c, but with the signal of all contaminant line absorbers removed, making the lines originating from 13C16O visible. Thisis data set B. |
| In the text | |
 |
Fig. 2. Opacities of 12C16O (blue) and 13C16O (orange), shown at T = 1200 K and P = 10−4 bar, which are representative values for the pressures and temperatures probed by CO lines at high resolution, in HD 179949b. The opacities have been scaled such that 12C16O constitutes 98.7% and 13C16O 1.1% of all CO molecules. |
| In the text | |
 |
Fig. 3. Results from simulated observations of HD 179949 b consisting of 100 spectra with an S/N* of 200 each, with a R = 100 000 spectrograph covering the wavelength range λ = 2.32–2.45 μm. Left panel: cross-correlation function (CCF) using a pure 12C16O template spectrum on data set A (black solid line) which contains all species, and data set B (grey dashed line) which contains lines of 13C16O only. Data set A gives a signal with an S/N of ~13, while the main isotope, as expected, is not detected in data set B. Right panel: CCF using a pure 13C16O template spectrum on data set A (black dotted line) and data set B (solid blue line). In addition, we show the CCF using a noiseless telluric-free model for data set B as a template (red solid line). The 13C16O isotope is detected at an S/N of ~3.5 and ~5 in data set A and B, respectively. By using the perfect noiseless input model as a template, 13C16O’s detection S/N is further increased to an S/N of ~7. To reach the latter significance, the planet atmosphere needs to be well constrained. |
| In the text | |
 |
Fig. 4. Wavelength-dependent detection S/N for the secondary 13C16O (orange boxes) and the main 12C16O isotopologue (gray boxes). The box widths correspond to the wavelength range of the synthetic observations, while the height corresponds to the 16 and 84 percentiles of themeasured S/Ns, as derived by running the simulations multiple times. For 13C16O the S/N of data set B cross-correlated with the pure isotopologue template spectrum are shown, which is conservative, corresponding to the solid blue line in Fig. 3. For 12C16O the S/N of data set A cross-correlated with the pure isotopologue template spectrum are shown. We assumed 100 observationswith S/N*(2.3 μm) = 200, used to calculate the stellar S/N as function of wavelength. In the background, we show the telluric transmission model (gray solid line), as well as the scaled and offset logarithm of the CO opacity at T = 1200 K and P = 10−4 bar (light red solid line). The CO detection by Brogi et al. (2014) is shown in cyan. The actual S/N value of the CO detection in Brogi et al. (2014) is 5.8, but due to the larger wavelength coverage of our bins one has to scale this value up to a S/N of 9. This is somewhat lower than our prediction for 12C16O, but the S/Nof their observations is also smaller. |
| In the text | |
 |
Fig. 5. Opacities of H2O (blue) and HDO (orange) at T = 300 K (upper panel), T = 700 K (middle panel) and T = 1100 K (lower panel), at P = 10−2 bar, which is a representative pressure value probed by water and HDO in the calculations considered here. The opacities have been scaled such that H2O constitutes 99.7% and HDO 4 × 10−5 of all H2O molecules. The higher the temperature, the more shielding of HDO occurs by H2O. |
| In the text | |
 |
Fig. 6. Contour map showing the required S/N of the planetary spectrum per pixel, as function of planetary equilibrium temperature and D/H value, for an HDO detection at an S/N of five. The considered wavelength region is 3.6 to 3.8 μm. The D/H values of the Solar System planets are indicated by the horizontal white dotted lines. The colored symbols indicate the lowest detectable D/H values for various exoplanets. Cyan and red symbols indicate limits for CRIRES+ at VLT and METIS at ELT, respectively, assuming a single night of observation (10 h). Filled circles stand for those targets which can be angularly separated from their host star, assuming a stellar flux reduction at the planet position by a factor 100 and 1000 for the VLT and ELT, respectively. Star-symbols denote planets that cannot be spatially resolved, for example hot Jupiters, hence no flux suppression is possible. * GJ 1214 b-like planet is a hypothetical non-transiting twin of GJ 1214 b at half the distance from Earth. The hatched area indicates the region where the required S/N per pixel is larger than 5, implying very weak HDO lines, which may be difficult to recover accurately with planet atmospheric modeling. |
| In the text | |
 |
Fig. 7. Same as Fig. 6, but neglecting both CH4 (and CO2) in thechemistry and for the opacities, in order to mimic an atmosphere where CH4, CO, and H2O are quenched at high pressures (i.e. high temperatures). |
| In the text | |
 |
Fig. 8. Opacities of CH4 (blue) and CH3D (orange), shown at T = 300 K (upper panel) and T = 700 K (lower panel), at P = 0.1 bar, which is a representative pressure value probed by methane and CH3D in the calculations considered here. The opacities have been scaled such that CH4 and CH3D constitute 98.8% and 8 × 10−5 of all CH4 isotopologues, respectively. The telluric transmission is shown in black. |
| In the text | |
 |
Fig. 9. Same as Fig. 6, but for CH3D. The single pixel S/N is defined as the mean planet signal per pixel, in the 4.6–4.8 μm range, divided by the median sky background noise per pixel, in the same wavelength range. |
| In the text | |
 |
Fig. 10. Apparent spectrum of Proxima Cen b at a distance of 1.29 pc, assuming it is identical to Earth. Left panel: planet synthetic thermal spectrum, assuming the Earth’s P–T profile and abundances is shown as a black solid line. As a comparison, measurements by the Nimbus 4 satellite are shown as a pink solid line, which largely overlap. The red solid line shows the reflected light assuming a surface albedo of 30%, including the attenuation of the planetary atmosphere. The two vertical black dashed lines denote the wavelength region of interest for probing HDO (3.6–3.8 μm). Right panel: same but focused on the 3.6–3.8 μm region, and showing high-resolution spectra. At these wavelength, the reflected starlight is ~15 times stronger than the intrinsic thermal emission from the planet. |
| In the text | |
 |
Fig. B.1. S/N of the HDO detection in the spectrum of a directly imaged gas planet as a function of the planetary Tequ. The HDO/H2O ratio was 4 × 10−5. Here we assumed S/N*, at 3.7μm = 3317 per spectrum, a stellar flux 1000 times smaller at the position of the planet, considering 100 spectral observations. Orange boxes: detection S/N when correlating the contaminant removed observation (data set B) with a pure HDO isotopologue template. Black boxes: detection S/N when correlating with the noiseless, telluric-free model B spectrum. The box height corresponds to the measured 16 and 84 percentiles of the measured S/Ns, when running the simulation multiple times. The black dotted line denotes the S/N scaling expected purely from the increasing planet–star contrast as the planet becomes hotter. This assumes that the ratio of the HDO and H2O opacities isnot temperature dependent. The black dashed line shows the prediction of the S/N signal following Eq. (5), indicating good agreement. |
| In the text | |
 |
Fig. B.2. Analogous to Fig. B.1, but this time testing the S/N-approximation (Eqs. (7) and (8)) for CH3D. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.