EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 621 (January 2019) A&A, 621 (2019) A128 Full HTML
Open Access
Issue
A&A
Volume 621, January 2019
Article Number A128
Number of page(s) 13
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/201833963
Published online 17 January 2019

© ESO 2019

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1 Introduction

With the advent of a new generation of space- and ground-based instruments, the constraints on the interior structure of planets and exoplanets have been continuously improving. This is for example the case with Jupiter where the Juno space mission (Bolton et al. 2017) is currently measuring gravitational moments to an unprecedented accuracy, or the various transit and radial velocity programs such as HARPS or Kepler that provide, when combined, density measurements for more than 600 exoplanets (Exoplanet Team 2018). These continuously improving observational constraints on the inner structure of planets and exoplanets call for a proportional effort on the modeling side to achieve a better understanding of the nature of these objects. The modeling of planetary interiors directly relies on the thermodynamic properties of matter at the extreme temperature and pressure conditions encountered within a planet. These can reach several hundreds of megabars (1 Mbar = 100 GPa) and up to 500 000 K for the brown dwarfs and giant planets several times the size of Jupiter (see, e.g., Baraffe et al. 2010, for review).

Great progress has been made over the past ten years in understanding this extreme state of matter, which is not directly accessible to laboratory experiments, by using first principles or ab initio simulations based on density functional theory (Benuzzi-Mounaix et al. 2014). This computational intensive approach, which can be validated on the limited density-temperature range accessible to shock or high-pressure experiments, provides a fully quantum mechanical description for the electronic structure of this state of matter without adjustable parameters. With computational resources greatly increasing, this approach provides the most reliable means to calculate the properties of matter in the thermodynamical range most relevant to planetary modeling, extending from the experimentally accessible thermodynamic conditions to the ones where analytical and semi-analytical approaches become valid. This method has recently been applied to provide comprehensive equations of state (EOSs) for the two most abundant elements, hydrogen and helium (Caillabet et al. 2011; Becker et al. 2014; Militzer 2013), which brought about a renewed understanding of the internal structure of Jupiter (Nettelmann et al. 2012; Hubbard & Militzer 2016; Militzer et al. 2016; Wahl et al. 2017; Guillot et al. 2018). A similar effort is underway for water, and ab initio simulations are now probing the physical properties of water at conditions encountered in planetary interiors.

Following the pioneering work of Cavazzoni et al. (1999), Mattsson & Desjarlais (2006) and French et al. (2009) calculated the properties of the superionic phase for dense water at conditions encountered within Uranus and Neptune. For water, the superionic phase is defined as oxygen atoms locked into either a body-centered cubic (BCC) or face-centered cubic (FCC) crystalline structure with the hydrogen atoms diffusing as in a liquid. This particular phase, which appears at pressures and temperatures above the regular solid ice phases, provides electrical conductivities compatible with the unusual magnetic fields observed for these objects (Redmer et al. 2011). Subsequent works attempted to identify the stable solid phase underlying the superionic region of the phase diagram (Wilson et al. 2013; French et al. 2016) and investigated the miscibility of water in a H-He dense plasma anticipated near Jupiter’s core (Soubiran & Militzer 2015). While the debate is ongoing regarding the precise localization and nature of the superionic phase for dense water (Millot et al. 2018), there is still no comprehensive EOS of dense water available for planetary modeling.

As the focus in exoplanetary science is now turning to the characterization of the Earth-like to Neptune-like continuum, there is a great need for an EOS for water that spans thermodynamic conditions ranging from the atmosphere of an Earth-like planet to the core of a giant planet or brown dwarf several times the size of Jupiter. In the following section, we expand on the work of French et al. (2009) and apply ab initio molecular dynamics simulations and the high-pressure high-temperature Thomas-Fermi limit to calculate the properties of water up to a density of 100 g cm−3 and reach conditions encountered in these massive objects. We supplement this data set by the free-energy parametrization developed by the International Association for Properties of Water and Steam (IAPWS1; Wagner &Pruß 2002) that provides an accurate account of the behavior of water in the vapor and liquid phases at pressures below 1 GPa. Using these data sets, we built a wide-range EOS that covers the complete thermodynamical state relevant to planetary modeling. We approximate this EOS by an analytical fit of the free energy, whose derivatives simultaneously provide the fits to pressure and internal energy in agreement with the data, and provide an estimation for the total entropy.

We apply this EOS to probe the effect of temperature on the standard mass-radius diagram used to identify exoplanets by considering wet, Earth-like, ocean planets and pure water planets. Finally, we use this EOS for dense water to calculate the gravitational moments of Jupiter currently measured by the Juno probe (Guillot et al. 2018).

2 Ab initio simulations

The EOS developed in the present work is based on ab initio molecular dynamics simulations for densities ρ between 1 and 50 g cm−3 and temperatures T between 1000 and 50 000 K, complemented with the free-energy parametrization of Wagner & Pruß (2002) at lower densities and temperatures. At ρ > 50 g cm−3, we used the Thomas-Fermi molecular dynamics (TFMD) simulations (Lambert et al. 2006; Mazevet et al. 2007).

2.1 Computational details

To complement the data obtained previously for water using ab initio molecular dynamics simulations (French et al. 2009, 2016; Wilson et al. 2013), we carried out simulations using the ABINIT (Gonze et al. 2009) electronic structure package. This consists in treating the electrons quantum mechanically using finite temperature density functional theory (DFT) while propagating the ions classically on the resulting Born-Oppenheimer surface by solving the Newton equations of motion. We used the generalized gradient approximation (GGA) formulation of the DFT with the parametrization of the exchange-correlation functional provided by Perdew et al. (1996; PBE).

We used two sets of pseudopotentials to cover the density range from 1 to 50 g cm−3. For densities up to 5 g cm−3, we used two projector augmented wave (PAW) pseudopotentials generated by Jollet et al. (2014). These pseudopotentials are designed to accurately reproduce the all-electrons results obtained for the individual atomic species. This provides a gaurantee that the use of the pseudopotential does not cause any important spurious effect. For the two atomic species considered here, hydrogen and oxygen, this consists in cutoff radii of 0.7a0 and 1.2a0, respectively, where a0 = ℏ2∕(mee2) is the Bohr radius, and an oxygen pseudopotential with the 1s state treated as a core state. To reach densities above 7 g cm−3, we use the ATOMPAW (Holzwarth et al. 2001) package to generate pseudopotentials with cutoff radii of rpaw = 0.4a0 and rpaw = 0.6a0 for the hydrogen and oxygen atomic species, respectively. We further find that the oxygen 1s state needs to be included as a valence state to reach the highest density treated, 50 g cm−3. The accuracy of the two pseudopotentials produced was inferred by directly comparing the cold curves obtained for the individual atomic species in the FCC phase with the corresponding all-electrons calculations (Jollet et al. 2014). This significant reduction in the cutoffradius requires an increase of the plane wave cutoff from 30 to 100 Ha to reach convergence in pressure and energy below 1%.

The convergence tests performed regarding the number of particles in the simulation cell and the k-point grids in momentum space confirm the results reported by French et al. (2009, 2016). We paid particular attention to the influence of the superionic phase and performed calculations using both the FCC and BCC crystallographic structures.

Wilson et al. (2013) pointed out that a superionic phase where the oxygen ions remain in an FCC rather than BCC structure may be more stable at intermediate temperature. For the EOS points, we used 54 atoms in the BCC superionic phase. For the FCC superionic phase, we used 108 atoms for densities up to 15 g cm−3 while we found 32 atoms to be sufficient at the highest densities. For both phases, we performed the simulations at the Γ-point and integrated the equations of motion with a time-step of 5 au (1 au = 0.024 fs). We attribute this slight difference with the simulation parameters reported by French et al. (2016) to the level of accuracy required in their calculations to evaluate the thermodynamic potentials in the superionic FCC and BCC phases.

2.2 Ab initio simulation results

Figure 1 displays the pressure P and temperature T values at which ab initio simulations were performed. We have also included sample points from the IAPWS free energy formulation (Wagner & Pruß 2002) for completeness. For the internal energy and pressure, we found a good agreement between our calculations and the previous results of French et al. (2009). We have therefore directly included these points in our ab initio set. Figure 1 also shows that a superionic phase remains stable up to the highest pressures for temperatures up to 16 000 K.

The superionic phase is identified in our molecular dynamics simulations by looking at the mean square displacement of the hydrogen and oxygen ions as a function of time. Figure 1 shows that at ρ > 15 g cm−3 the superionic phase remains stable up to T = 16 000 K when considering either the BCC or FCC structures. With the temperature grid used here, this suggests that the superionic-plasma phase boundaries for both the BCC and FCC structures vary slowly in this pressure range and are both located between 16 000 and 20 000 K. We also point out that the simulations performed here do not allow us to identify the superionic phase that is the most stable in this thermodynamic regime; nor do they indicate whether or not another superionic phase exists in this thermodynamical range.

Here, we do not further explore the exact determination of either the superionic-plasma boundary or the nature of the superionic state. The results previously obtained at low pressures indicated that this issue has little consequence for the EOS (French et al. 2016). To confirm that this remains the case for the entire density range considered here, we show in Table 1 the results obtained for the internal energy and pressure at representative densities and considering both the BCC and FCC superionic states. We see in Table 1 that the pressure and internal energy values agree to within 1.5%. We thus started our simulations with the BCC superionic lattice at ρ > 20 g cm−3, as this enables smaller simulation cells. Using larger simulation cells, we verified that convergence is reached for pressure and internal energy up to 50 g cm−3.

thumbnail Fig. 1

Phase diagram of dense water obtained using the ab initio and Thomas-Fermi simulations. Each symbol represents a simulation point. The phase state is indicated by a colored symbol according to the legend. Previous ab initio points obtained by French et al. (2009) as well as representative points of Wagner & Pruß (2002) are also shown.
Table 1

Pressure PBCC and internal energy UBCC obtained for the BCC superionic phase and the differences ΔP = PFCC − PBCC and ΔU = UFCC − UBCC between the FCC and BCC superionic phases, as well as fractional differences.

2.3 Thomas-Fermi extension

Beyond 50 g cm−3, we switch from full ab initio simulations to Thomas-Fermi molecular dynamics (TFMD) simulations (Lambert et al. 2006). This consists in using the Thomas-Fermi approximation to describe the electrons while propagating the ions on the resulting Born-Oppenheimer surface. In this framework, the kinetic energy operator in the electronic Hamiltonian is replaced by a functional of the density (Martins 2004). This greatly simplifies the calculation, as a plane wave basis is no longer needed and the electronic density is obtained by simply solving the Poisson equation. This represents the natural high-density limit to the DFT and hence to the ab initio simulations. Figure 2 shows the relative difference for the pressure P and internal energy U between the full ab initio and the TFMD simulations at densities between 34 and 50 g cm−3. For both quantities, we see that the difference between the two methods is rapidly reducing as the density increases to be well under 1% at 50 g cm−3. This result clearly shows that the high-density limit is reached and justifies the use of the Thomas-Fermi approximation beyond this density.

We further point out that the Thomas-Fermi approximation requires the use of a regularization potential. We make the choice of using the pseudopotential determined at ρ = 75 g cm−3 and T = 2000 K throughout the entire range of interest. This approximation introduces an uncertainty on the internal energy of a few percent as the regularization formally breaks the transferability of the pseudopotential in density and temperature (Lambert et al. 2006). The internal energy obtained by the TFMD method is adjusted to the ab initio one at ρ = 50 g cm−3 and T = 6000 K. While the simulations were all started in the FCC phase, we make the choice of not recording the stability of the superionic phase as quantum effects for the protons may start to play a non-negligible role in its stability (French et al. 2016); the effect on the pressure and internal energy is a higher order effect.

3 Analytical fit of the Helmholtz free energy

The full ab initio simulation results presented in the previous section were used to construct a functional form of the Helmholtz free energy valid over the entire density-temperature domain relevant to planetary modeling. Such an analytical fit of the free energy provides a convenient means to combine various data for use in simulations of interior structure or evolution of planets. For water, this includes the ab initio results presented above, valid down to a few gigapascals, and the low-energy IAPWS formulation (Wagner & Pruß 2002) that provides the EOS of water at P < 1 GPa in the vapor and liquid phases as constrained by experimental measurements.

3.1 Formulation

The parametrization of the Helmholtz free energy is expressed as (1)

where each term has its own physical meaning.

The first term, (2)

is the translational (ideal molecular gas) contribution. Here, is the number of H2 O molecules, is the total number of H and O atomic nuclei in volume V, g is the mass of the molecule, kB is the Boltzmann constant, and (3)

is the thermal wavelength of a molecule.

In the second and third terms of Eq. (1), (4)

and (5)

are the analytical expressions for the excess free energy in the moderate-density liquid regime (i.e., at ρ ≲ 1 g cm−3 and 300 K ≲ T ≲ 2000 K) and at high densities (ρ ≫ 1 g cm−3), respectively, which, together with Ftran, provide the fit to the pressure as a function of density through the thermodynamic relation (6)

Furthermore, (7)

is an interpolating function, which varies from 0 to 1 and ensures fitting the pressure as a function of density in the entire ρ − T domain considered. In Eq. (5), Fe(Ne, T, V) is the Helmholtz free energy of the ideal nonrelativistic Fermi gas of Ne = neV electrons at temperatureT, and Z* is an effective charge number, which is expressed as an analytical fitting function so as to adjust the pressure derived through Eq. (6) to the pressure data from the ab initio calculations. Explicitly, (8)

where (9)

is the effective (ideal Fermi gas) electron pressure, is the electron thermal wavelength, 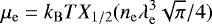(10)

is the effective electron chemical potential, and (11)

In Eq. (9), 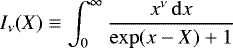(12)

is the standard Fermi integral, and Xν(I) in Eq. (10) is the inverse function. For both Iν(X) and Xν(I) we use the Padé-type approximations of Antia (1993). In Eq. (11), Γe and rs are the usual electron Coulomb parameter and density parameter, respectively: Γe = e2∕(aekBT) in the CGS system, and rs = ae∕a0, where is the electron-sphere radius, and is the total number density of all electrons (free and bound). In Eq. (4), avdW and bvdW are the van der Waals constants (respectively, 5.524 × 1012 erg cm3 mol−2 and 30.413 cm3 mol−1; Grigoriev & Meilikhov 1997). The first line in Eq. (4) reproduces the van der Waals EOS, which is sufficiently accurate at ρ ≪ 1 g cm−3, and the second line adjusts the EOS at ρ ~ 1 g cm−3.

The fourth term in Eq. (1) reads (13)

where b1 = 3 × 10−13 erg, b2 = 1.35 × 10−13 erg, b3 = 2.43 × 10−13 erg, and τ = T∕Tcrit = T∕647 K. It is derived from the fitting correction to the residual internal energy, 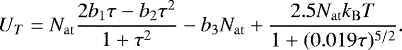(14)

This correction does not affect pressure but improves the fit to the internal energy, through the thermodynamic relation 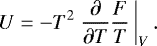(15)

We note that we measure the total internal energy from its minimum at the ground state of the molecular phase so that U > 0 at any ρ and T. This definition is the same as in Wagner & Pruß (2002) but differs from the definition adopted in Table 1 and Fig. 2 by the ground-state energy value of 11.14 MJ g−1. It also differs by a constant of 77 kJ g−1 from the internal energy given in French et al. (2009), French & Redmer (2015), and Soubiran & Militzer (2015).

The last term in Eq. (1), − S0T is an additional correction, which affects neither P nor U, but shifts the entropy, 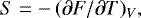(16)

by constant S0. We find that the value S0 = 4.9kBNat provides the best fit (within 10%) to the results presented for S by Soubiran &Militzer (2015) at ρ ≈ (1–2.5) g cm−3 and T =(1000–6000) K. However, entropy evaluation from our present fit should be used with caution especially when crossing the boundaries of different phases, where one can expect a discontinuity. This may lead to a value of S0 that differs from one phase to the other.

The present analytical fit describes the EOS of liquid water at ρ ≲ 1 g cm−3 and T ≲2000 K, as well as plasma at 1 g cm−3 ≲ ρ ≲ 102 g cm−3 and 103 K ≲ T ≲×105 K. While not including the super-ionic phase as a different phase, the single-phase approximation used here provides a satisfactory description of the thermodynamical properties in this super-ionic regime. It has, however, a limited applicability for the ice VII and ice X phases that occur at T ≲ 2000 K in the range (0.02–0.5) Mbar ≲ P ≲ 3 Mbar (Petrenko & Whitworth 1999). We also point out that quantum effects for the ions, which could be relevant at the highest densities and for low temperatures, are not included in the current parametrization. To build a fully multi-phase EOS for water, one can supplement our fit by the parametrizations constructed specifically for the ice and super-ionic phases (French & Redmer 2015; French et al. 2016). This will be the topic of future work. Finally, we also point out that our analytical fit is less reliable in the domain of thermal ionization and dissociation of molecular water, where ρ ≪ 1 g cm−3 and T ≫ 103 K. This regime is indeed poorly constrained by either the ab initio simulations or the IAPWS parametrization.

thumbnail Fig. 2

Panel a: relative difference between the ab initio and Thomas-Fermi internal energies as a function of density. Panel b: as in panel a but for the pressures.

3.2 Validation of the analytical fit

We first verify the ability of the analytical fit to reproduce both the results of theoretical calculations and the IAPWS free energy model. In Figs. 3 and 4, we compare the behavior of pressure and internal energy obtained with the input data at low and high densities and temperatures, respectively.

As we are primarily interested in planetary interiors, the accurate description of the liquid-vapor transition below the critical point located at Tcrit = 647 K and Pcrit = 22.064 MPa is beyond the scope of this study. Furthermore, these conditions are tied to an accurate modeling of the atmosphere of the planet that do not directly involve an EOS such as the one developed here. Figures 3a and b suggest that without atmospheric treatment, interior models should consider the liquid state for surface conditions when the surface temperature is below the critical point. We expand on this point in the following sections.

At the lowest densities, we see in Fig. 3a that the pressure turns negative along the 300 and 600 K isotherms for densities below 1 g cm−3. Figure 3b indicates that this translates to a minimum for the internal energy. This corresponds to the crossing of the liquid–vapor phase boundary and a region where the pressures are formally negative, which in fact corresponds to phase coexistence. For instance, for the 300 K isotherm the analytical fit gives a region of negative pressures expanding from 0.9 to 0.1 g cm−3. We note that the IAPWS data (Wagner & Pruß 2002) indicate a wider phase-transition region, with low density of ~10−3 g cm−3 on this isotherm. The agreement improves for the 600 K isotherm. We see that the analytical fit reproduces the overall behavior of the pressure across the liquid-vapor boundary. However, it extends this boundary to a higher temperature, giving the critical point at 683 K and 0.331 g cm−3 (to be compared with the experimental values of 647 K and 0.322 g cm−3).

Figures 3a and b also indicate that the agreement with the ab initio data at higher temperatures is satisfactory up to 6000 K. We note that the ab initio results and the free energy model predictions are not in perfect agreement at 1000 K. As the ab initio method becomes less reliable as density decreases, mainly due to the deficiency of density functional theory in under-dense regime, the ab initio results fail to match the IAPWS formulation at low density. Our analytical fit eliminates this mismatch by interpolation between the low-density IAPWS and high-density ab initio data.

Figures 4a and b show the data and fitted isotherms for the pressure and internal energy across the entire density range at higher temperatures, 1000 K ≤ T ≤ 50 000 K. Figure 4a displays the pressure normalized to the atomic ideal gas contribution nat kBT. As noted above, the fit does not perfectly reproduce the ab initio data for the ice X phase along the 1000 K isotherm at 2.5 g cm−3 ≤ ρ ≤ 4 g cm−3. However, it satisfactorily reproduces the thermodynamical properties, despite the fact that the system crosses a number of various phases in the ρ–T domain displayed in the figures.

We also point out that the data represented in Figs. 3 and 4 by empty symbols (the ice phase, the data by Soubiran & Militzer 2015, and the Thomas-Fermi results) have not been explicitly included to construct the analytical fit. We see that the data by Soubiran & Militzer (2015) is in good agreement with the prediction of the analytical fit. Furthermore, the good agreement found with the Thomas-Fermi results up to 100 g cm−3 shows the validity of the analytical fit up to this high density.

Figures 5 summarizes the applicability of the current analytical EOS for planetary modeling. We display the accuracy of the analytical fit as a color code corresponding to the residual difference between the predicted and input P and U values. On the same figure, we also show representative interior profiles for Jupiter, Saturn, and Neptune that display a significant amount of water in their interior. This shows that the analytical fit is accurate for modeling these objects. For comparison, the profile of a 9MJ planet is also shown. As pointed out before, the single-phase approximation used for this analytical fit ignores the discontinuities due to the phase changes between the different phase states. For the phase transition between the liquid state and ice X, the discrepancies increase to tens of percent. Otherwise we see that the fit remains a reasonable approximation for both the pressure and internal energy throughout the relevant thermodynamical domain.

thumbnail Fig. 3

Comparison between the input data and the analytical fitted isotherms for the pressure P (panel a) and for the internal energy U (panel b) atrelatively low densities. Symbols show the data: the IAPWS (Wagner & Pruß 2002) published table for P < 1 GPa (straight crosses) and extension to P > 1 GPa according to the IAPWS free-energy model (squares); results of ab initio calculations by Soubiran & Militzer (2015; empty diamonds) and by French et al. (2009; oblique crosses for liquid, inverted triangles for ice X, filled diamonds for the superionic [SI] phase). Solid lines represent the present fit; dotted lines represent the fit of French & Redmer (2015) for ice X.

4 Comparison with experimental data and previous EOSs

We now turn to compare the predictions of the analytical fit developed in Sect. 3 with existing experimental data from both static and dynamical experiments. We compare these predictions with EOSs commonly used in planetary interior models. In Fig. 6, we compare the predictions of the analytical fit developed with the static high-pressure data obtained using diamond anvil cells (Hemley et al. 1987; Sugimura et al. 2008). We also show in Fig. 6 the 1000 K isotherm and its corresponding ab initio data to further illustrate the approximation made by not accounting explicitly for the solid ice phases and extending the liquid throughout the solid phases. We see that the analytical fit thus misses the jump between the liquid and ice X phases at ρ ~ 2.5 g cm−3, as we have already seen in Fig. 4.

The T = 300 K isotherm behaves similarly. We see that both the IAPWS free energy formulation and our analytical fit, being continued from the low-density region at T = 300 K, overestimate the pressure (underestimate the density) in the ice phases at higher densities. At P = 10 GPa, the resulting density is about 7% lower than in the ice phases. This should be compared with the predictions of Seager et al. (2007) who used T = 0 K DFT calculations for the various ice phases to construct their EOS. By neglecting the effect of temperature and the phonon contribution, they overestimate the density of dense water by about 3% at 10 GPa. We also note that this difference with the experimental data tends to decrease as the pressure increases for both EOSs. Therefore, the most significant difference resulting from neglecting the ice phases that we can anticipate for interior structure calculations could be for the pressure profile of the outer layer of a planet, if it had T ~ 103 K at ρ ~ 3 g cm−3. From Fig. 5 we see that this is not the case for the giant planets, for which the temperature is much higher and therefore the temperature profile passes well above this phase jump.

We also point out some differences between the two ab initio calculations beyond 4 g cm−3. We attribute these differences to the use of different functionals in the Thomas-Fermi approximation; we further investigate their impact on the interior structure models in the following sections.

Figure 7 shows a comparison between the predictions of our analytical fit deduced from ab initio simulations and the measured experimental data along the principal shock Hugoniot line. For a given initial state, the Rankine-Hugoniot relation determines the final states allowed by conservation of energy and momentum during a shock. It is directly related to the EOS and reads 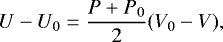(17)

where subscript 0 indicates the initial state. The principal Hugoniot corresponds to a single shock, obtained with initial state at rest in normal conditions. Figure 7 shows that shock experiments probe a range of pressures almost an order of magnitude higher than when using diamond anvil cells (Fig. 6). This also corresponds to a significant increase in temperature. The temperature reaches about 5000 K around 100 GPa for a shock, while it remains near 300 K in diamond anvil cell experiments. With the increase of the shock pressure beyond 500 GPa, the temperature exceeds 50 000 K. Since the input ab initio data that underlie our fit have been obtained for T ≤50 000 K, the accuracy of the fit at higher temperatures is not guaranteed (the corresponding part of the Hugoniot line is drawn by long dashes in Fig. 7).

Figure 7 shows a good agreement at low pressures with early data obtained using explosion (Volkov et al. 1980)and gas-gun techniques (Mitchell & Nellis 1982; Lyzenga et al. 1982). The unique measurement of the water EOS at P > 1000 GPa, published long ago by Podurets et al. (1972), is satisfactorily described by the above-mentioned continuation of our fit beyond the range where it has been constrained by the data. The first laser shock data obtained in the 100–1000 GPa range by Celliers et al. (2004) are much softer than the analytical fit. This experimental data set is in good agreement with SESAME 7150 predictions. In contrast, we see that the analytical fit agrees very nicely with the more recent experimental data of Knudson et al. (2012) obtained using the Z-pinch techniques, as well as with the latest results of Kimura et al. (2015). This confirms that earlier laser shock experiments likely suffer from systematic errors which could be caused by the standard used in the impedance-matching method (Knudson & Desjarlais 2009). This experimental set is therefore not considered here to validate the behavior of water at high pressures and temperatures. This also highlights that the SESAME 7150 predictions, which are in good agreement with the data of Celliers et al. (2004), should be ruled out for planetary modeling. The SESAME 7150 model is not considered a reliable EOS nowadays, but it is still in use for planetary modeling (Miguel et al. 2016). This is also the case for the ANEOS model (Thomson & Lauson 1972). Figure 7 shows that ANEOS predictions depart from the data of Knudson et al. (2012) at ρ > 2.5 g cm−3 significantly outside the experimental error bars.

Figure 8 shows a comparison between the predictions of our analytical fit and the EOS measurements obtained using double-shock experiments (Volkov et al. 1980; Knudson et al. 2012), where the initial shock wave is reflected from a surface of a standard material (aluminum or quartz). In this case, the initial state in Eq. (17) lies on the principal Hugoniot line and represents the initial condition for the secondary Hugoniot. Since the latter initial condition is measured with some uncertainties, the position of the secondary Hugoniot is not firmly defined. We therefore show the 1σ limits for each secondary Hugoniot that arise from these uncertainties in the initial state.

Figure 9 shows a comparison between the predictions of our analytical fit with two EOS measurements in experiments using laser-induced shock in statically compressed water. We find a better agreement with the latest dataset of Kimura et al. (2015) compared to that of Lee et al. (2006). We show these for completeness as the scatter in the experimental data cannot further constrain the validity of the analytical fit.

Overall, we find that our present analytical fit provides a satisfactory description of both the static and dynamical experimental results available to date for dense water. We now turn to illustrate the applications of the EOS developed for the interior structure of different classes of planets.

thumbnail Fig. 4

Comparison of the data with the analytical fitted isotherms at high densities for the pressure normalized to the ideal atomic gas value, P∕natkBT (panel a), and for the internal energy U (panel b). Symbols show the data: the IAPWS table (Wagner & Pruß 2002, straight crosses); results of ab initio calculations by Soubiran & Militzer (2015; empty diamonds); ab initio calculations by French et al. (2009; oblique crosses for liquid, inverted triangles for ice X, filled diamonds for the superionic [SI] phase, asterisks for the plasma phase); and the results of our present ab initio calculations (filled triangles for the SI phase and filled dots for the plasma phase), supplemented with our TFMD calculations at ρ > 50 g cm−3 (empty circles). Solid lines represent the present fit; the dotted line represents the fit of French & Redmer (2015) for ice X at T = 1000 K.
thumbnail Fig. 5

Pointsin the ρ–T plane where the input data have been used to construct the analytical fit. Different symbols correspond to different phase states: crosses for liquid, asterisks for plasma, upright triangles for superionic state, and reverted triangles for ice X. The colors of the symbols represent the accuracy of the fit (for both P and U, i.e., the maximum of the two residuals) according to the palette above the legend. The lines show isentropes of Jupiter (J), according to the models of Leconte & Chabrier (2012) and Nettelmann et al. (2012; the solid and dashed lines, respectively), Saturn (S), according to Leconte & Chabrier (2012), Neptune (N) according to two models of Nettelmann et al. (2013; solid and dashed lines), and a planet with M = 9 MJ (see Baraffe et al. 2008, 2010).
thumbnail Fig. 6

Comparison of the analytical fit predictions with high-pressure data at T = 300 K.
thumbnail Fig. 7

Principal Hugoniot line in the ρ–P plane calculated using the present fit (solid line for T < 50 000 K, continued bylong-dashed line for T > 50 000 K) compared with experimental data (dots with error bars) of Podurets et al. (1972; as reanalyzed by Knudson et al. 2012; the original result of Podurets et al. 1972 is also shown with dotted error bars), Volkov et al. (1980); Mitchell & Nellis (1982); Lyzenga et al. (1982); Celliers et al. (2004); Knudson et al. (2012), and Kimura et al. (2015). For comparison, the principal Hugoniot lines predicted by the SESAME (Lyon & Johnson 1992) and ANEOS (Thomson & Lauson 1972) models are shown by the dotted line and short-dashed line, respectively. Inset panel: principal Hugoniot line in the ρ– T plane calculated from the fit and the experimental data points from Lyzenga et al. (1982) and Kimura et al. (2015).
thumbnail Fig. 8

Comparison of experimental data for reshocked water (points with error bars) with corresponding Hugoniot lines calculated from the analytical fit (solid lines). The principal Hugoniot is shown by the dot-dashed line. Dashed lines show the theoretical regions defined by taking into account 1σ experimental uncertainties for the initial (primary-shock) states. Panels a and b: comparison for the data of Volkov et al. (1980) and of Knudson et al. (2012), respectively.
thumbnail Fig. 9

Comparison between the calculations based on our analytical fit and the experimental shock data for initially precompressed water. Panel a: points measured by Lee et al. (2006). Panel b: points obtained by Knudson et al. (2012). The inset ineach panel shows the initial pressures and densities measured.

5 Implication for planetary interiors

The internalstructure calculations are performed by solving the standard hydrostatic, mass, and energy conservation equations (e.g., Schwarzschild 1958; Kippenhahn et al. 2012),

where P is the pressure, ρ the density, g = Gm∕r2 the gravity, G is the gravitational constant, m is the mass enclosed within a sphere of radius r, and ∇T = dlnT∕dlnP depends on the mechanism of energy transport. If the medium is stable against convection, then (21)

where Teff is the effective surface temperature and K is the effective opacity. If the transport of energy is dominated by convection, then in the simplest (Schwarzschild) approximation ∇T = ∇ad, where (22)

is the adiabatic gradient.

The interior structure of a planet of a given mass, M, is obtained by integrating inward the set of Eqs. (18)–(20), starting from a boundary condition defined by a fixed surface temperature and pressure. This is formally given by either in situ measurements for planets of the solar system or full atmospheric calculations for exoplanets. As we are primarily interested in testing our EOS for dense water, we devise strategies to overcome this difficulty for each type of planet that we consider.

5.1 Water planets

In order to test the accuracy of our EOS, we first turn to the calculation of the inner structure and mass-radius relationship of a planet entirely made of water. This is a purely academic exercise disconnected from the outcomes of planetary formation but the resulting mass-radius relationship remains a well-used benchmark to classify exoplanets (Seager et al. 2007). It also allows us to decipher the influence of temperature on both the inner structure and mass-radius relationship. Figure 10 shows the effect of temperature on isothermal interior structure models for planets of 0.5 and 5 MEarth, respectively. In this situation, the temperature throughout the planet is constant and equal to the surface temperature, Tsurf. The outer boundary conditions are chosen as 1 bar for temperature above the critical point and at the liquid-vapor boundary below. This corresponds to different surface densities and close to 1 g cm−3 for the two models using a surface temperature below the critical value.

Figure 10 shows that within this model, the effect of temperature is twofold. As the EOS developed fully accounts for temperature throughout the density range covered by the conditions existing in planetary interiors, it affects the extent of the outer edge boundary as well as the compressibility deeper within the planet. Figure 10 shows that both these effects are important for low-mass planets where we notice a radius increasing by a factor of two when the surface temperature varies from 300 to 2000 K. This increase in radius comes from a significant expansion of the low-density outer edge beyond 1.5 REarth that follows the rapid expansion of the supercritical liquid at high temperatures and low surface gravity. It also comes from the significant temperature dependence of the water EOS for densities below 2 g cm−3 previously pointed out in Fig. 6. For a planet of 0.5 MEarth, the maximum pressure reached at the center of the planet is 0.18 Mbar for a temperature of 2000 K and 0.27 Mbar for a temperatureof 300 K.

Figure 10 shows that the effect of temperature decreases significantly when the planet size increases. This comes from both a smaller expansion of the outer edge resulting from a larger surface gravity, and a reduced temperature dependence of the EOS as the density increases. Figure 10 shows that the density profile of the planet is dominated by densities between 2 and 4 g cm−3 for a planet of 5 MEarth. Figure 6 shows that the temperature dependence of the EOS is almost negligible in this density range. The effect of temperature is therefore reduced to a small expansion of the outer edge that leads to an increase of 10% of the radius. This suggests that the effect of temperature becomes negligible as the mass of the planet increases.

Figures 11a and b give the mass-radius relationship obtained with the current EOS and calculated for the complete range of planets detected to date, and a zoom for planets below 10 MEarth (Exoplanet Team 2018). As anticipated above, we see that the temperature dependence decreases as the mass of the planet increases. Figure 11b shows that the temperature effect is rather important for planets smaller than 10 MEarth. We also see in Fig. 11a that the temperature dependence for pure-water planets can be neglected for planets larger than 15 MEarth when considering an isothermal temperature profile. We also find that the mass–radius relationship obtained with the EOS developed in the current work is consistent with the calculations of Seager et al. (2007) for the entire range of planets detected. Figures 11a and b show that the radius obtained with the EOS developed here and for an isothermal model with surface temperature of 250 K is 3% higher than the results of Seager et al. (2007) for planets less than 10 MEarth and 2% lower above this planetary mass. This latter result comes from the difference in the behavior of the two EOS at high densities already mentioned in the previous section. For low-mass planets, where inspection of Fig. 7 indicates the largest difference between the EOS developed here with both the experimental data and the zero temperature EOS of Seager et al. (2007), we also find a rather satisfactory agreement. This indicates that neglecting the ice phases has a minimal impact on the resulting mass–radius relationship even for low-mass planets. For benchmarking purposes, we also show in Fig. 11b that the zero temperature results of Seager et al. (2007) can be recovered with the current EOS by considering a surface pressure of 10 GPa (0.1 Mbar).

Finally, we notice in Fig. 11b that several detected planets fall within the temperature-dependent range of the isothermal pure-water model. This suggests that temperature-dependent effect on the mass-radius relationship needs to be included when considering the interior structure to identify the nature of these objects. We pursue further this suggestion using more realistic interior structure models and by considering wet super-Earths and ocean planets.

thumbnail Fig. 10

Isothermal density profiles of pure-water planets for varying surface temperatures. The values of the surface temperature, Tsurf, are indicated in the figure for a planet of mass M = 0.5 MEarth (panel a) and for a planet of mass M = 5 MEarth (panel b). REarth is the radiusof the Earth.
thumbnail Fig. 11

Mass-radius relationship for pure-water planets in an isothermal model. The surface temperature and pressure are indicated in the figure and compared to the result of Seager et al. (2007) over the entire range of planets currently detected (panel a); for planets with mass less than 10 MEarth (panel b). Isothermal models for pure silicates (MgSiO3) and iron (Fe) (Bouchet et al. 2013; Mazevet et al. 2015) are also displayed.

5.2 Wet super-Earth planets or ocean planets

Wet super-Earth or ocean planets are objects that have no equivalent in the solar system. They have been introduced to interpret the continuum of planets detected between pure water and Earth-like object. Earth-like planets consist of objects of varying mass but following the Earth composition (33% Fe, 66% MgSiO3 by mass). Wet Super-Earths consist of an Earth-like core made of 33% iron and 66% silicates and a significant fraction of water outside the core (Valencia et al. 2006; Thomas & Madhusudhan 2016). To test the validity of our EOS at describing these objects, we show in Fig. 13 the mass–radius relationship obtained by considering isothermal models and wet super-Earth planets constituted of 50% water. The iron and silicates EOSs used are temperature dependent and, similarly to the water EOS developed here, are described by free-energy functional forms adjusted directly to ab initio calculations (Bouchet et al. 2013; Mazevet et al. 2015).

Figure 12 shows the mass–radius relationship for isothermal models obtained using two different surface temperatures. For a surface temperatureof Tsurf = 500 K, we obtained a rather satisfactory agreement with the previous calculations of Thomas & Madhusudhan (2016). We point out that the outer boundary condition used in the current work follows a somewhat different prescription. As mentioned before, we do not consider the vapor phase for surface temperature below the critical point and use the liquid-vapor boundary at 1 bar as outer boundary conditions. Figure 12 shows that the temperature dependence of the mass–radius relationship is rather significant and cannot be neglected when assessing the interior structure of these objects, in agreement with the conclusions of Baraffe et al. (2008). Indeed, we see in Fig. 12 that several planets lie between the boundaries delimited by the two surface temperatures. As for the case of the pure water planets, the temperature dependence decreases as the mass of the planet increases and becomes negligible beyond 15 MEarth.

The wet Earth-like model that is 50% water is at a midpoint between the dry Earth-like planets and pure-water planets. By extension of the temperature dependence shown for planets that are 50% water, we can anticipate that this also needs to be taken into account to deduce the composition of objects such as Kepler-18b or 55Cnc that hold a significant fraction of water themselves. In this case, the amount of water deduced will directly depend on the surface temperature considered. Along the same line of reasoning, we can also anticipate that the overlap between the pure water and wet Earth-like planet with a surface temperature of Tsurf = 2000 K shown below 2 MEarth for a composition of 50% water will expand to planets with larger mass when the fraction of water is increased. To make a more quantitativestatement on this issue requires to go beyond the internal structure calculations and to account for an accurate modeling of the atmosphere as well as the amount of light received from the host star. Both these topics are beyond the scope of this study that aims at validating the EOS for dense water developed here. We instead turn to the evaluation of the effect of temperatureon the mass–radius relationship beyond the simple isothermal model where the temperature is kept constant throughout the planet.

The EOS developed in the current work provides the total entropy thanks to the parametrization of the Helmholtz free energy using the ab initio results. This allows us to calculate more realistic interior models by considering a water layer undergoing nearly adiabatic convection. The uncertainty in defining S0 pointed out in Sect. 3 does not affect these results as long as the convective layer remains within a single thermodynamic phase. The previous isothermal models and the adiabatic ones bracket the maximum impact of the water EOS upon the mechanical structure of the body. We see in Fig. 13 that the effect of temperature on the mass–radiusrelationship is almost two times more important when considering the water layer as adiabatic rather than isothermal. When considering a surface pressure of 1 bar, Fig. 13 shows that the radius obtained up to 10 MEarth is significantly larger than that in the pure-water case at zero temperature. This effect is the most spectacular for surface temperatureabove the critical temperature. It remains limited when the surface temperature is below the critical point. We also point out that the surface pressure tends to reduce this effect. Figure 13 shows that the radius decreases by 20% at 1200 K when the surface pressure increases from 1 to 100 bars. This suggests that neglecting the effect of temperature when identifying the internal structure of exoplanets leads to overestimatations of the overall amount of water, especially for objects close to their parent star and receiving a significant amount of light. This needs to be tempered by the probable escape of the atmosphere under these particular conditions and will need to be assessed on a case by case basis with a proper treatment of the atmosphere.

thumbnail Fig. 12

Temperature dependence of the mass–radius relationship for isothermal models of wet super-Earth planets containing 50% water denoted as Wet. The surface temperatures are indicated in the figure. The dots represent detected planets in this range of planetary mass. Isothermal models: pure water (water), silicates (MgSiO3), iron (Fe), Earth-like composition containing 66% silicates and 33% iron (Earth-like; Bouchet et al. 2013; Mazevet et al. 2015). The benchmark calculations for wet super-Earth planets are from Thomas & Madhusudhan (2016).
thumbnail Fig. 13

Temperature dependence of the mass–radius relationship for adiabatic models of wet super-Earth planets containing 50% water as solid lines. The surface temperatures and pressures are indicated in the figure. The dots represent detected planets in this range of planetary mass. The isothermal models for pure-water planets (dashed) and wet super-Earth planets (purple) with the corresponding surface temperatures are also displayed in the figure. These correspond to the data shown in Figs. 11 and 12, respectively.

5.3 Core of giant planets

We now turn to the last situation where a temperature-dependent EOS for dense water is important for planetary modeling the core of giant planets. Following the well-accepted core-accretion scenario (Pollack et al. 1996), a significant amount of water is expected in the core of giant planets. This potentially significant amount of water stems from the likely composition of the initial core that triggered the accretion of a large fraction of hydrogen and helium. The exact amount of water as well as the size of the core for a planet like Jupiter is a matter of debate and one of the main scientific goals of the Juno mission (Bolton et al. 2017). The probe is currently measuring Jupiter’s high-order gravitational moments for Jupiter to decipher the amount of metallic element present in the interior as well as their distribution throughout the planet (Wahl et al. 2017). This goal requires an accurate modeling of the EOS for all the elements potentially constituting the planet, including water.

Figure 14 shows the dependence of Jupiter’s first two gravitational moments, J2 and J4, on the dense water EOS used in the modeling of the interior. Jupiter’s interior is obtained by solving the standard hydrostatic equilibrium Eqs. (18)–(20) and by considering the planet as composed of an H-He envelope and a pure-water core (we note the assumption of a fully adiabatic interior profile here). The hydrogen and helium EOSs used for the envelope are also based on ab initio simulation results (Caillabet et al. 2011; Soubiran 2012). The gravitational moments are calculated using the theory of figures to the third order (Zharkov & Trubitsyn 1978).

Figure 14 shows the values of the first two gravitational moments obtained using two different water EOSs, namely the present and the widely used ANEOS ones, to describe the core and by considering two different helium concentrations. The size of the core is varied to the values indicated in the graph. The first mass fraction of helium, YHe = 0.2384, correspondsto the Galileo measurements, while a slightly higher mass fraction, YHe = 0.26, allows us to reproduce the values of the two gravitational moments J2 and J4. Within a two-layer model of Jupiter, the first case reproduces the observed radius of the planet as well as the value of J2 measured but, as shown in Fig. 14, it misses the J4 moment by slightly more than 1%. Conversely, in the case where the mass fraction of helium is increased to YHe = 0.26, the observed radius is underestimated by slightly more than 1% while matching the first two gravitational moments. This shortcoming of the two-layer model for Jupiter, namely a central core surrounded by a homogeneous gaseous envelope, has been well documentedelsewhere (Miguel et al. 2016). We point out here that this issue is not resolved by using different water EOSs for the core.

We see in Fig. 14 that using different water EOSs leads to different predictions regarding the size of the core. These two predictions in the size of the core differ by close to 20%, and do not depend on the helium concentration. We note that this also translates into different average and maximum densities reached in the central core. The EOS developed here predicts a pure-water core density more than 25% higher than in the case of the widely used ANEOS one. The highest density reached in the former case is close to 12.45 g cm−3, while it remains close to 9.67 g cm−3 in the latter case. This difference is comparable with the variation of the core density when a pure-ice core is replaced by a core of pure rock, as pointed out by Guillot (1999). In our case, this can be traced back to significant discrepancies between the two EOSs, which predict different compressibilities for pressures and temperatures relevant to Jupiter’s inner core. These conditions correspond to pressures above 40 Mbar and temperatures between 15 000 and 20 000 K depending on the hydrogen-helium EOSs used, Miguel et al. (2016). In this thermodynamical region, the two water EOSs predict pressures that differ by more than 10%. This shows that the current EOS is useful to accurately calculate the exact size of the core that is potentially present at the center of giant planets.

thumbnail Fig. 14

Dependence of Jupiter’s first two gravitational moments on the dense-water EOS used, namely the present and ANEOS ones. The calculations are performed in a two-layer model for a fixed value of the mass fraction of He in the envelope, YHe, indicated inthe graph where the mass of the dense water core varies. The size of the pure water core is indicated for a few sample points in the figure. The pre-Juno values of the gravitational moments are the values collected in Miguel et al. (2016) while the Juno data are from Folkner et al. (2017).

6 Summary

In summary, we developed an EOS for water applicable to the full range of thermodynamic conditions relevant to planetary modeling. This encompasses the range from outer layers of wet super-Earth to the core of giant planets. This EOS includes an evaluation of the entropy (within an arbitrary constant value S0, Sect. 3, which can differ from one phase to another but has no impact on all other thermodynamic quantities) thanks to the parametrization of the Helmholtz free-energy functional form on the ab initio results. Using this EOS, we show that the temperature dependence of the EOS needs to be accounted for when analyzing the composition and nature of exoplanets using the standard mass–radius relationship, a point already stressed by Baraffe et al. (2008). We also show that an accurate description of the thermodynamic properties of dense water is required to deduce the mass of the core of giant planets from gravitational moments as it is currently measured for Jupiter by the Juno mission. As discussed in Sect. 3, the EOS developed here is not very accurate for the solid ice phases. This does not noticeably affect the planetary gross properties, such as the mass–radius relationship, but may produce an error of several percent in calculations of temperature profiles. To include explicitly all the ice phases as well as treating the super-ionic phase will be the topic of further development of the present EOS.

Acknowledgements

Part of this work was supported by the SNR grant PLANETLAB 12-BS04-0015 and the Programme National de Planetologie (PNP) of CNRS-INSU co-funded by CNES. Funding and support from Paris Sciences et Lettres (PSL) university through the project origins and conditions for the emergence of life is also acknowledged. This work was performed using HPC resources from GENCI- TGCC (Grant 2017- A0030406113) and was granted access to the HPC resources of MesoPSL financed by the Region Ile de France and the project Equip@Meso (reference ANR-10-EQPX-29-01) of the programme Investissements d’Avenir supervised by the Agence Nationale pour la Recherche.

References

  1. Antia, H. M. 1993, ApJS, 84, 101 [NASA ADS] [CrossRef] [Google Scholar]
  2. Baraffe, I., Chabrier, G., & Barman, T. 2008, A&A, 482, 315 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Baraffe, I., Chabrier, G., & Barman, T. 2010, Rep. Prog. Phys., 73, 016901 [NASA ADS] [CrossRef] [Google Scholar]
  4. Becker, A., Lorenzen, W., Fortney, J. J., et al. 2014, ApJS, 215, 21 [NASA ADS] [CrossRef] [Google Scholar]
  5. Benuzzi-Mounaix, A., Mazevet, S., Ravasio, A., et al. 2014, Phys. Scr., T161, 014060 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bolton, S. J., Adriani, A., Adumitroaie, V., et al. 2017, Science, 356, 821 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bouchet, J., Mazevet, S., Morard, G., Guyot, F., & Musella, R. 2013, Phys. Rev. B, 87, 094102 [NASA ADS] [CrossRef] [Google Scholar]
  8. Caillabet, L., Mazevet, S., & Loubeyre, P. 2011, Phys. Rev. B, 83, 094101 [NASA ADS] [CrossRef] [Google Scholar]
  9. Cavazzoni, C., Chiarotti, G. L., Scandolo, S., et al. 1999, Science, 283, 44 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  10. Celliers, P. M., Collins, G. W., Hicks, D. G., et al. 2004, Phys. Plasmas, 11, L41 [CrossRef] [Google Scholar]
  11. Exoplanet Team. 2018, The Extrasolar Planets Encyclopaedia, http://www.exoplanet.eu [Google Scholar]
  12. Folkner, W. M., Iess, L., Anderson, J. D., et al. 2017, Geophys. Res. Lett., 44, 4694 [NASA ADS] [CrossRef] [Google Scholar]
  13. French, M., & Redmer, R. 2015, Phys. Rev. B, 91, 014308 [NASA ADS] [CrossRef] [Google Scholar]
  14. French, M., Mattsson, T. R., Nettelmann, N., & Redmer, R. 2009, Phys. Rev. B, 79, 054107 [NASA ADS] [CrossRef] [Google Scholar]
  15. French, M., Desjarlais, M. P., & Redmer, R. 2016, Phys. Rev. E, 93, 022140 [NASA ADS] [CrossRef] [Google Scholar]
  16. Gonze, X., Amadon, B., Anglade, P. M., et al. 2009, Comput. Phys. Commun., 180, 2582 [NASA ADS] [CrossRef] [Google Scholar]
  17. Grigoriev, I. S., & Meilikhov, E. Z. 1997, Handbook of Physical Quantities (Boca Raton: CRC-Press) [Google Scholar]
  18. Guillot, T. 1999, Planet. Space Sci., 47, 1183 [NASA ADS] [CrossRef] [Google Scholar]
  19. Guillot, T., Miguel, Y., Militzer, B., et al. 2018, Nature, 555, 227 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  20. Hemley, R. J., Jephcoat, A. P., Mao, H. K., et al. 1987, Nature, 330, 737 [NASA ADS] [CrossRef] [Google Scholar]
  21. Holzwarth, N. A. W., Tackett, A. R., & Matthews, G. E. 2001, Comput. Phys. Commun., 135, 329 [NASA ADS] [CrossRef] [Google Scholar]
  22. Hubbard, W. B., & Militzer, B. 2016, ApJ, 820, 80 [NASA ADS] [CrossRef] [Google Scholar]
  23. Jollet, F., Torrent, M., & Holzwarth, N. 2014, Comput. Phys. Commun., 185, 1246 [NASA ADS] [CrossRef] [Google Scholar]
  24. Kimura, T., Ozaki, N., Sano, T., et al. 2015, J. Chem. Phys., 142, 164504 [NASA ADS] [CrossRef] [Google Scholar]
  25. Kippenhahn, R., Weigert, A., & Weiss, A. 2012, Stellar Structure and Evolution, 2nd edn, Astronomy and Astrophysics Library (Berlin, Heidelberg: Springer) [CrossRef] [Google Scholar]
  26. Knudson, M. D., & Desjarlais, M. P. 2009, Phys. Rev. Lett., 103, 091102 [CrossRef] [Google Scholar]
  27. Knudson, M. D., Desjarlais, M. P., Lemke, R. W., et al. 2012, Phys. Rev. Lett., 108, 091102 [NASA ADS] [CrossRef] [Google Scholar]
  28. Lambert, F., Clérouin, J., & Zérah, G. 2006, Phys. Rev. E, 73, 016403 [NASA ADS] [CrossRef] [Google Scholar]
  29. Leconte, J., & Chabrier, G. 2012, A&A, 540, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Lee, K. K. M., Benedetti, L. R., Jeanloz, R., et al. 2006, J. Chem. Phys., 125, 014701 [NASA ADS] [CrossRef] [Google Scholar]
  31. Lyon, S. P., & Johnson, J. D. 1992, SESAME: The Los Alamos National Laboratory Equation of State Database, Tech. Rep. LA-UR-92-3407, Los Alamos National Laboratory, Los Alamos, NM [Google Scholar]
  32. Lyzenga, G. A., Ahrens, T. J., Nellis, W. J., & Mitchell, A. C. 1982, J. Chem. Phys., 76, 6282 [NASA ADS] [CrossRef] [Google Scholar]
  33. Martins, R. M. 2004, Electronic Structure (Cambridge: Cambridge University Press) [Google Scholar]
  34. Mattsson, T. R., & Desjarlais, M. P. 2006, Phys. Rev. Lett., 97, 017801 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  35. Mazevet, S., Lambert, F., Bottin, F., Zérah, G., & Clérouin, J. 2007, Phys. Rev. E, 75, 056404 [NASA ADS] [CrossRef] [Google Scholar]
  36. Mazevet, S., Tsuchiya, T., Taniuchi, T., Benuzzi-Mounaix, A., & Guyot, F. 2015, Phys. Rev. B, 92, 014105 [Google Scholar]
  37. Miguel, Y., Guillot, T., & Fayon, L. 2016, A&A, 596, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Militzer, B. 2013, Phys. Rev. B, 87, 014202 [NASA ADS] [CrossRef] [Google Scholar]
  39. Militzer, B., Soubiran, F., Wahl, S. M., & Hubbard, W. 2016, J. Geophys. Res. Planets, 121, 1552 [NASA ADS] [CrossRef] [Google Scholar]
  40. Millot, M., Hamel, S., Rygg, J. R., et al. 2018, Nat. Phys., 14, 297 [CrossRef] [Google Scholar]
  41. Mitchell, A. C., & Nellis, W. J. 1982, J. Chem. Phys., 76, 6273 [NASA ADS] [CrossRef] [Google Scholar]
  42. Nettelmann, N., Becker, A., Holst, B., & Redmer, R. 2012, ApJ, 750, 52 [NASA ADS] [CrossRef] [Google Scholar]
  43. Nettelmann, N., Helled, R., Fortney, J. J., & Redmer, R. 2013, Planet. Space Sci., 77, 143 [NASA ADS] [CrossRef] [Google Scholar]
  44. Perdew, J. P., Burke, K., & Wang, Y. 1996, Phys. Rev. B, 54, 16533 [NASA ADS] [CrossRef] [Google Scholar]
  45. Petrenko, V. F., & Whitworth, R. W. 1999, The Physics of Ice (Oxford: Oxford University Press) [Google Scholar]
  46. Podurets, M. A., Simakov, G. V., Trunin, R. F., Popov, L. V., & Moiseev, B. N. 1972, Sov. Phys. JETP, 35, 375 [NASA ADS] [Google Scholar]
  47. Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
  48. Redmer, R., Mattsson, T. R., Nettelmann, N., & French, M. 2011, Icarus, 211, 798 [NASA ADS] [CrossRef] [Google Scholar]
  49. Schwarzschild,M. 1958, Structure and Evolution of the Stars (Princeton: Princeton University Press) [CrossRef] [Google Scholar]
  50. Seager, S., Kuchner, M., Hier-Majumder, C. A., & Militzer, B. 2007, ApJ, 669, 1279 [NASA ADS] [CrossRef] [Google Scholar]
  51. Soubiran, F. 2012, Ph.D. Thesis, ENS Lyon, Lyon, France [Google Scholar]
  52. Soubiran, F., & Militzer, B. 2015, ApJ, 806, 228 [NASA ADS] [CrossRef] [Google Scholar]
  53. Sugimura, E., Iitaka, T., Hirose, K., et al. 2008, Phys. Rev. B, 77, 214103 [NASA ADS] [CrossRef] [Google Scholar]
  54. Thomas, S. W., & Madhusudhan, N. 2016, MNRAS, 458, 1330 [NASA ADS] [CrossRef] [Google Scholar]
  55. Thomson, S. L. & Lauson, H. S. 1972, Improvements in the CHARTD Radiation-Hydrodynamics Code III: Revised Analytic Equation of State, Tech. Rep. SC-RR-710714, Sandia National Laboratories, Albuquerque, NM [Google Scholar]
  56. Valencia, D., O’Connell, R. J., & Sasselov, D. 2006, Icarus, 181, 545 [NASA ADS] [CrossRef] [Google Scholar]
  57. Volkov, L. P., Voloshin, N. P., Mangasarov, R. A., et al. 1980, JETP Lett., 31, 513 [NASA ADS] [Google Scholar]
  58. Wagner, W., & Pruß, A. 2002, J. Phys. Chem. Ref. Data, 31, 387 [NASA ADS] [CrossRef] [Google Scholar]
  59. Wahl, S. M., Hubbard, W. B., Militzer, B., et al. 2017, Geophys. Res. Lett., 44, 4649 [NASA ADS] [CrossRef] [Google Scholar]
  60. Wilson, H. F., Wong, M. L., & Militzer, B. 2013, Phys. Rev. Lett., 110, 151102 [NASA ADS] [CrossRef] [Google Scholar]
  61. Zharkov, V. N., & Trubitsyn, V. P. 1978, Physics of Planetary Interiors, Astronomy and Astrophysics Library (Tucson: Pachart) [Google Scholar]

All Tables

Table 1

Pressure PBCC and internal energy UBCC obtained for the BCC superionic phase and the differences ΔP = PFCC − PBCC and ΔU = UFCC − UBCC between the FCC and BCC superionic phases, as well as fractional differences.

In the text

All Figures

thumbnail Fig. 1

Phase diagram of dense water obtained using the ab initio and Thomas-Fermi simulations. Each symbol represents a simulation point. The phase state is indicated by a colored symbol according to the legend. Previous ab initio points obtained by French et al. (2009) as well as representative points of Wagner & Pruß (2002) are also shown.
In the text
thumbnail Fig. 2

Panel a: relative difference between the ab initio and Thomas-Fermi internal energies as a function of density. Panel b: as in panel a but for the pressures.
In the text
thumbnail Fig. 3

Comparison between the input data and the analytical fitted isotherms for the pressure P (panel a) and for the internal energy U (panel b) atrelatively low densities. Symbols show the data: the IAPWS (Wagner & Pruß 2002) published table for P < 1 GPa (straight crosses) and extension to P > 1 GPa according to the IAPWS free-energy model (squares); results of ab initio calculations by Soubiran & Militzer (2015; empty diamonds) and by French et al. (2009; oblique crosses for liquid, inverted triangles for ice X, filled diamonds for the superionic [SI] phase). Solid lines represent the present fit; dotted lines represent the fit of French & Redmer (2015) for ice X.
In the text
thumbnail Fig. 4

Comparison of the data with the analytical fitted isotherms at high densities for the pressure normalized to the ideal atomic gas value, P∕natkBT (panel a), and for the internal energy U (panel b). Symbols show the data: the IAPWS table (Wagner & Pruß 2002, straight crosses); results of ab initio calculations by Soubiran & Militzer (2015; empty diamonds); ab initio calculations by French et al. (2009; oblique crosses for liquid, inverted triangles for ice X, filled diamonds for the superionic [SI] phase, asterisks for the plasma phase); and the results of our present ab initio calculations (filled triangles for the SI phase and filled dots for the plasma phase), supplemented with our TFMD calculations at ρ > 50 g cm−3 (empty circles). Solid lines represent the present fit; the dotted line represents the fit of French & Redmer (2015) for ice X at T = 1000 K.
In the text
thumbnail Fig. 5

Pointsin the ρ–T plane where the input data have been used to construct the analytical fit. Different symbols correspond to different phase states: crosses for liquid, asterisks for plasma, upright triangles for superionic state, and reverted triangles for ice X. The colors of the symbols represent the accuracy of the fit (for both P and U, i.e., the maximum of the two residuals) according to the palette above the legend. The lines show isentropes of Jupiter (J), according to the models of Leconte & Chabrier (2012) and Nettelmann et al. (2012; the solid and dashed lines, respectively), Saturn (S), according to Leconte & Chabrier (2012), Neptune (N) according to two models of Nettelmann et al. (2013; solid and dashed lines), and a planet with M = 9 MJ (see Baraffe et al. 2008, 2010).
In the text
thumbnail Fig. 6

Comparison of the analytical fit predictions with high-pressure data at T = 300 K.
In the text
thumbnail Fig. 7

Principal Hugoniot line in the ρ–P plane calculated using the present fit (solid line for T < 50 000 K, continued bylong-dashed line for T > 50 000 K) compared with experimental data (dots with error bars) of Podurets et al. (1972; as reanalyzed by Knudson et al. 2012; the original result of Podurets et al. 1972 is also shown with dotted error bars), Volkov et al. (1980); Mitchell & Nellis (1982); Lyzenga et al. (1982); Celliers et al. (2004); Knudson et al. (2012), and Kimura et al. (2015). For comparison, the principal Hugoniot lines predicted by the SESAME (Lyon & Johnson 1992) and ANEOS (Thomson & Lauson 1972) models are shown by the dotted line and short-dashed line, respectively. Inset panel: principal Hugoniot line in the ρ– T plane calculated from the fit and the experimental data points from Lyzenga et al. (1982) and Kimura et al. (2015).
In the text
thumbnail Fig. 8

Comparison of experimental data for reshocked water (points with error bars) with corresponding Hugoniot lines calculated from the analytical fit (solid lines). The principal Hugoniot is shown by the dot-dashed line. Dashed lines show the theoretical regions defined by taking into account 1σ experimental uncertainties for the initial (primary-shock) states. Panels a and b: comparison for the data of Volkov et al. (1980) and of Knudson et al. (2012), respectively.
In the text
thumbnail Fig. 9

Comparison between the calculations based on our analytical fit and the experimental shock data for initially precompressed water. Panel a: points measured by Lee et al. (2006). Panel b: points obtained by Knudson et al. (2012). The inset ineach panel shows the initial pressures and densities measured.
In the text
thumbnail Fig. 10

Isothermal density profiles of pure-water planets for varying surface temperatures. The values of the surface temperature, Tsurf, are indicated in the figure for a planet of mass M = 0.5 MEarth (panel a) and for a planet of mass M = 5 MEarth (panel b). REarth is the radiusof the Earth.
In the text
thumbnail Fig. 11

Mass-radius relationship for pure-water planets in an isothermal model. The surface temperature and pressure are indicated in the figure and compared to the result of Seager et al. (2007) over the entire range of planets currently detected (panel a); for planets with mass less than 10 MEarth (panel b). Isothermal models for pure silicates (MgSiO3) and iron (Fe) (Bouchet et al. 2013; Mazevet et al. 2015) are also displayed.
In the text
thumbnail Fig. 12

Temperature dependence of the mass–radius relationship for isothermal models of wet super-Earth planets containing 50% water denoted as Wet. The surface temperatures are indicated in the figure. The dots represent detected planets in this range of planetary mass. Isothermal models: pure water (water), silicates (MgSiO3), iron (Fe), Earth-like composition containing 66% silicates and 33% iron (Earth-like; Bouchet et al. 2013; Mazevet et al. 2015). The benchmark calculations for wet super-Earth planets are from Thomas & Madhusudhan (2016).
In the text
thumbnail Fig. 13

Temperature dependence of the mass–radius relationship for adiabatic models of wet super-Earth planets containing 50% water as solid lines. The surface temperatures and pressures are indicated in the figure. The dots represent detected planets in this range of planetary mass. The isothermal models for pure-water planets (dashed) and wet super-Earth planets (purple) with the corresponding surface temperatures are also displayed in the figure. These correspond to the data shown in Figs. 11 and 12, respectively.
In the text
thumbnail Fig. 14

Dependence of Jupiter’s first two gravitational moments on the dense-water EOS used, namely the present and ANEOS ones. The calculations are performed in a two-layer model for a fixed value of the mass fraction of He in the envelope, YHe, indicated inthe graph where the mass of the dense water core varies. The size of the pure water core is indicated for a few sample points in the figure. The pre-Juno values of the gravitational moments are the values collected in Miguel et al. (2016) while the Juno data are from Folkner et al. (2017).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.