| Issue |
A&A
Volume 620, December 2018
|
|
|---|---|---|
| Article Number | A200 | |
| Number of page(s) | 10 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201833512 | |
| Published online | 17 December 2018 | |
Limits on stable iron in Type Ia supernovae from near-infrared spectroscopy★
1
European Southern Observatory,
Karl-Schwarzschild-Straße 2,
85748
Garching bei München,
Germany
e-mail: afloers@eso.org
2
Max-Planck-Institut für Astrophysik,
Karl-Schwarzschild-Straße 1,
85748
Garching bei München,
Germany
3
Physik-Department,
Technische Universität München,
James-Franck-Straße 1,
85748 Garching bei München, Germany
4
Astrophysics Research Centre, School of Mathematics and Physics, Queen’s University Belfast,
Belfast BT7 1NN,
UK
5
Oskar Klein Centre, Department of Physics, Stockholm University,
SE 106 91 Stockholm,
Sweden
Received:
28
May
2018
Accepted:
10
October
2018
We obtained optical and near infrared spectra of Type Ia supernovae (SNe Ia) at epochs ranging from 224 to 496 days after the explosion. The spectra show emission lines from forbidden transitions of singly ionised iron and cobalt atoms. We used non-local thermodynamic equilibrium (NLTE) modelling of the first and second ionisation stages of iron, nickel, and cobalt to fit the spectra using a sampling algorithm allowing us to probe a broad parameter space. We derive velocity shifts, line widths, and abundance ratios for iron and cobalt. The measured line widths and velocity shifts of the singly ionised ions suggest a shared emitting region. Our data are fully compatible with radioactive 56Ni decay as the origin for cobalt and iron. We compare the measured abundance ratios of iron and cobalt to theoretical predictions of various SN Ia explosion models. These models include, in addition to 56Ni, different amounts of 57Ni and stable 54,56Fe. We can exclude models that produced only 54,56Fe or only 57Ni in addition to 56Ni. If we consider a model that has 56Ni, 57Ni, and 54,56Fe then our data imply that these ratios are 54,56Fe / 56Ni = 0.272 ± 0.086 and 57Ni / 56Ni = 0.032 ± 0.011.
Key words: supernovae: general / line: formation / line: identification / radiation mechanisms: thermal
© ESO 2018
1 Introduction
Type Ia supernovae (SNe Ia) are a remarkably uniform class of objects. Exceptions such as overly bright (e.g. SN 1991T Filippenko et al. 1992b; Phillips et al. 1992; Ruiz-Lapuente et al. 1992) or overly faint (e.g. SN 1991bg Filippenko et al. 1992a; Leibundgut et al. 1993; Turatto et al. 1996) supernovae have been extensively studied (see Taubenberger 2017, for a recent overview of the various Type Ia subtypes). High-cadence all sky surveys (e.g. Kulkarni 2012; Shanks et al. 2015; Chambers et al. 2016; Kochanek et al. 2017) have discovered that members of the class exhibit a broad spectrum of disorders. However, the Branch-normal Type Ias (Branch et al. 2006) remain the dominant detected class and one of the best distance indicators at the disposal of astronomers. Following calibration procedures, for example, the one by Phillips (1993), that correlate the width of the light curve with the peak brightness, SNe Ia exhibit a very small dispersion in their absolute magnitudes. As such, their use in cosmology is extensive and understanding them is of general interest (Leibundgut & Sullivan 2018).
Colgate & McKee (1969) proposed powering of the optical and infrared (IR) displays of SNe to originate in energy deposition from the decay of radioactive 56Ni to 56Co and subsequently to 56Fe. Depending on the temperature and density, burning to nuclear statistical equilibrium converts much of the progenitor white dwarf to iron group elements (Hoyle & Fowler 1960; see Seitenzahl et al. 2013 for a recent calculation of yields). Many studies have provided both direct and indirect evidence for this scenario. Direct evidence can be found in Churazov et al. (2014) who detected γ-ray lines from the decay of 56Co at 847 and 1238 keV. Indirect evidence was shown by Kuchner et al. (1994) who, in Type Ia late-time optical spectra ≈200 days, observed that the doubly ionised emission lines of Co and Fe evolved according to the expected ratio that would result from the production of Fe as the daughter product of the radioactive decay of 56Co. The total energy of the explosion maps onto the mass of nucleosynthesised 56Ni and the luminosity at maximum light is directly linked to the mass of 56Ni (Arnett 1982). The determination of the mass of 56Ni based on optical and IR photometry and spectroscopy has been the subject of many papers and almost as many models. In general, of order 0.4 M⊙–0.8 M⊙ of 56Ni is found to be produced in Branch-normal SNe Ia (Arnett 1982; for a more recent study see Childress et al. 2015).
The post maximum optical and near-infrared (NIR) spectra of SNe Ia exhibit a plethora of iron group emission lines, predominantly in the singly and doubly ionised states (Axelrod 1980; Fransson & Chevalier 1989; Kozma et al. 2005; Fransson & Jerkstrand 2015). Many authors have provided an extensive analysis of the physical conditions in the ejecta and the processes that generate the spectrum. Post-maximum spectra have been published by many authors and show remarkable similarity in features and evolution (Mazzali et al. 1998). Maeda et al. (2010) made the startling discovery that often the singly ionised emission lines of the iron group elements exhibit a different systemic velocity when compared to their doubly ionised counterparts and proposed that there exists a region within the core of the ejecta where electron capture processes dominate the nucleosynthetic yield.
In this paper, we fit late-time NIR observations with emission lines from NLTE level populations to derive the evolution of the mass ratio of Co II to Fe II. We aim to place limits on the stable Fe and 57Ni in the ejecta by observing the evolution in the mass ratio of Co to Fe. In Sect. 2, we briefly describe the observations and in Sect. 3, we present our NLTE emission line fit code. In Sect. 4, we present the results of our spectral fits and derive the mass ratio MCo II ∕ MFe II. In Sect. 5, we compare the mass ratio results of our SN sample with explosion model predictions within the Bayesian framework. The results are discussed in Sect. 6.
2 Observations
Four sets of data are included in this work (see Table 1). One set from the GNIRS instrument on Gemini-North, two from the X-shooter instrument at ESO’s Paranal observatory and the fourth from SOFI at the New Technology Telescope (NTT) and ISAAC+FORS1 at the Very Large Telescope (VLT). GNIRS, SOFI, and ISAAC cover the NIR bands, FORS1 covers the optical while X-shooter covers both the optical and NIR bands. As we are mainly interested in the abundances of various radioactive isotopes all epochs in this work are given in days after the explosion, assuming a rise time of ~ 18 days (Ganeshalingam et al. 2011).
We use two NIR spectra of SN2014J obtained with GNIRS at Gemini-North (see Dhawan et al. 2018). Optical+NIR spectra of SN 2013cg, SN 2012fr, SN 2013aa, SN 2013cs and SN 2013ct were obtained by Maguire et al. (2016) at the VLT. Maguire et al. (2018) also obtained a spectrum of PSNJ11492548-0507138 (hereafter PSNJ1149) and a second spectrum of SN 2013aa. We also use two spectra of SN 1998bu (Spyromilio et al. 2004). For details of the reduction see the publication papers.
A number of broad (≈ 7000–9000 km s−1) emission lines at 1.55 and 1.65 μm are evident in the data. We identify these as emission by the 1.644 μm [Fe II] line arising from the a4 F–a4D multiplet and the 1.547 μm [Co II] line from the a5 F–b3F multiplet. The a4 F-a4D [Fe II] multiplet includes the 1.533 μm [Fe II] line. The identification of the various features has been extensively covered in the literature. The detection of the 1.257 μm a6 D9∕2–a4D7∕2 confirms the identification and strength of the a4 F9∕2–a4D7∕2 1.644 μm line as they arise from the same upper level. Similarly, the detection in many of our spectra of the 1.090 μm (a3 F4–b3F4) line of [Co II] which shares an upper level with the 1.547 μm (a5 F4–b3F4) line also secures the identification.
Overview of spectra in our sample.
3 Fitting the spectra
3.1 Emission line model
We use a one zone model with Fe II, Ni II, and Co II; it also includes Co III if the spectrum covers the 6000Å region. For this set of ions, we solve the NLTE rate equations treating only collisional excitation and de-excitation by collisional and radiative processes to compute energy level populations and derive forbidden line emissivities. For the collisional processes we use a thermal electron gas characterised by a Boltzmann distribution and an electron density. We ignore radiative transfer effects as the optical depths of the lines under consideration are very low at the observed epochs. We also do not consider non-thermal excitations as the energy going into this channel at the relatively high electron densities we determine is also very low (Fransson & Chevalier 1989). We do not include charge exchange and time-dependent terms in the NLTE rate equations. Even though we do not treat continuum processes directly, we include a parametrized smooth continuum in the model (see Sect. 3.2). We use such a smooth continuum to include uncertainties due to true continuum processes in the early spectra and potentially low-level light echoes. We do not treat energy deposition in the ejecta, and as a result our model does not match the emitted radiation over all wavelengths, but only for certain lines. We do not solve the ionisation balance but treat the number of emitting ions as a fit parameter. Effectively, we solve a simplified and parametrized NLTE problem.
A one-zone model, by default spherically symmetric, convolved with a Gaussian line profile serves to fit the spectra and extract the salient properties of the lines (flux, rest velocity, and Doppler broadening). One evident limitation of the one-zone model is that different ionisation stages, not necessarily co-located in the ejecta (see Sect. 4.2), are likely to have different excitation conditions in some fraction of the emitting regions. This work, which concentrates on the singly ionised species, is not significantly affected by this limitation.
The features at 4700 and 5200 Å are a blend of singly and doubly ionised iron, with possibly asymmetric line profiles. Changes of the velocity offset and width of the 4700Å feature with time suggest that this wavelength region is not optically thin until 400 days after the explosion (Black et al. 2016). A detailed analysis of this feature would require a more sophisticated model process. As [Fe III] only slightly influences the rest of the Optical+NIR spectrum we do not attempt to fit spectral features below 5500Å.
We fit the 5900Å region with [Co III] and the double-peaked feature between 7000 and 7800Å with [Fe II]+[Ni II]. All spectra exhibit a strong emission feature between 8500 Å and 9900 Å. We can reproduce the feature at 8600 Å with lines from the Fe II a4 F–a4P and Co II a3 F–b3F multiplets, but in spectra which are less than one year old the red part of the feature between 8800 and 9900 Å cannot be well explained by emission from only ions in our sample. Models by Botyánszki & Kasen (2017), among other authors, suggest the presence of S III in this region. We only use the 8600 Å feature for spectra of SN 2014J, but we do not use the 8800–9900 Å region.
The strongest lines of the considered ions are given in Table 2. An overview of the model ions with their respective atomic data is given in Table 3. For Fe II we use the atomic data from Bautista et al. (2015) as they provide collision strengths for the higher levels responsible for optical transitions. The spectra are displayed in Fig. 1 in chronological order. The data are corrected for the redshift of the host, as well as Galactic, and, if applicable, host galaxy extinction according to Table 1. The simple model of Fe II, Co II, Co III and Ni II fits the data well above 5500Å.
Strongest lines of the included ions in the optical and NIR.
Ions included in the fits and their atomic data sets.
 |
Fig. 1 Optical (left panel) and NIR (right panel) spectra of SNe Ia obtained with X-shooter, FORS1, and ISAAC at the VLT, SOFI at the NTT, and GNIRS at Gemini-North. The spectra are arranged in epoch starting with the youngest at the top and corrected for redshift and extinction. Fluxes are normalized to the 7300 Å [Fe II] + [Ni II] feature (optical) and 12 600 Å [Fe II] feature (NIR). The red line indicates the mean flux of all fit models at each wavelength, the orange shaded area marks the 68% uncertainty of the fit. Dashed vertical lines indicate the strongest lines as given in Table 2 ([Fe II]: - - - -, [Ni II]: ⋯ ⋯⋯ [Co II]: —⋅—, [Co III]: — ⋅ ⋅— ⋅). The subtracted background is shown as a grey band. Fits were performed for the optical and NIR spectra at the same time. The lines/ions composing the features below 5500Å are not included in our fits. |
3.2 Parameter estimation
We explore the parameter space using the nested-sampling algorithm Nestle1 (Shaw et al. 2007). The algorithm allows us to sample from our flat priors over a large range by optimising the selection of variables based on the quality of the earlier fits. To compare the model with the data we assume a χ2 likelihood. Our set of four ions shares the same temperature and electron density. Each ion is allowed to have its own line width, velocity offset, and strength. Uniform priors are used for all parameters except the electron density, for which we use a log-uniform distribution.There exists a significant body of work in the literature starting with Axelrod (1980), and a plethora of other authors (see e.g. Kuchner et al. 1994; Kozma et al. 2005; Fransson & Jerkstrand 2015; Botyánszki & Kasen 2017) that have shown that temperatures for the ejecta of a SNe Ia during the first year after explosion lie in the range of 2000−15 000 K. For our modelling we adopt the following boundaries for the priors: temperature range (2000–15 000 K), electron densities between 104 and 107 cm−3, Doppler widths between 2 and 15 × 103 km s−1, and shifts between − 3 and 3 × 103 km s−1. The very large allowed range for the temperature prior does not affect the resulting fit. We note the presence of a weak continuum in some spectra bluewards of 9500 Å; in those cases, we subtract a linear background (grey bands in Fig. 1) in the optical. Widths and shifts of individual ions are determined using a global fit where the individual species are allowed to vary within the prior space.
Besides the fit parameters noted above, the fits provide us with the individual emission line emissivities. The ratios of the transitions arising from within the a4 F–a4D Fe II multiplet show little variation with temperature as the difference in the energy levels within a4 D is less than 1000 cm−1 and for the strongest lines at 1.644 μm and 1.533 μm less than 500 cm−1. The higher-lying states responsible for lines in the optical vary significantly in strength over the considered temperature range and thus allow us to estimate the electron temperature. However, there is a degeneracy between electron density and temperature. Good fits can be achieved with high temperature and low densities, and vice versa. Some of these high temperatures and low densities would not be compatible with a prior of ~ 0.4−0.8 M⊙ of iron group elements. We have not adopted such a prior for the fitting as absolute mass estimates suffer considerably from systematics (e.g. distance). We want to emphasise that the uncertainties from this degeneracy are much smaller than the priors (see Table 4).
68% posterior probability intervals of the fit parameters.
4 Fit results
4.1 Fit parameters and MCo II/ MFe II
The ratio of the H-band [Co II] to [Fe II] lines places limits on the temperature of the ejecta of above 1500 K. Below this temperature, the blue wing of the 1.55 μm spectral feature is underproduced and the blend of the 1.634 [Co II] and 1.644 [Fe II] lines which accounts for the 1.65-μm feature is unable to reproduce the spectra. The presence of the shoulder from the a4 F7∕2−a4D3∕2 [Fe II] line at1.599 μm in spectra at all epochs indicates that the emission originates from a high-density region (ne > 105 cm−3).
The absolute mass of the emitting material strongly depends on the assumed temperature in the ejecta and the distance to the object. We do not consider that our model is sophisticated enough to provide detailed constraints on these parameters (see for example Fransson & Jerkstrand 2015 or Diamond et al. 2018 for such work). On the other hand, mass ratios are only weakly dependent on the temperature. In particular, from the line ratio of 1.547 μm [Co II] to 1.533 μm [Fe II] (see Fig. 2) we can determine the mass fraction of Co II to Fe II (Varani et al. 1990):
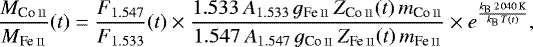 (1)
(1)
where T is the temperature of the gas in degrees Kelvin reflecting the difference in the upper energy levels of the two transitions, A are the transition probabilities between the a4 F9∕2−a4D5∕2 Fe II and a5 F5−b3F4 Co II levels, g are the statistical weights of the upper levels, m are the atomic masses and
![\begin{equation*} Z{\left(t\right)} = \sum_i \left( g_i\,\exp{[-E_i/ (k_{\text{B}}T{\left(t\right)})]}\right)\end{equation*}](/articles/aa/full_html/2018/12/aa33512-18/aa33512-18-eq2.png) (2)
(2)
are the atomic partition functions. The flux ratio, partition functions, temperature and the inferred mass ratio are functions of time after explosion. For the atomic data used in this work Eq. (1) reduces to
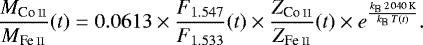 (3)
(3)
As the SN 1998bu 269 d spectrum covers only the NIR we cannot determine the temperature and electron density from the ratio of optical to NIR Fe II lines. To determine the line widths and velocity offsets we fit the spectrum for a fixed temperature T =7200 K and electron density log (ne / cm−3) = 6.2. These numbers lie between the fit results of SN 2013ct at 247 d and SN 2013cs at 321 d. The mass ratio is then computed for T =(7200 ± 1500) K and log (ne / cm−3) = (6.20 ± 0.15). The uncertainties of the density and temperature are reflected in an increased uncertainty of the derived mass ratio MCo II / MFe II for this spectrum.
The spectrum of SN1998bu at 364 d does not cover the 1.019μm Co II line, which affects the uncertainty of the inferred mass ratio significantly as the Co II 1.547 μm line is rather weak compared tothe Fe II 1.533 μm line. Good fits can be achieved for a wide range of cobalt masses in this case.
The spectra of SN 2014J only cover the NIR wavelengths down to 8500 Å. We therefore cannot use the 7200 Å [Fe II] + [Ni II] complex to determine the density and temperature in the ejecta. We find that the 8600 Å feature is well reproduced (best at late epochs > 350 d) by our emission model for other SNe in our sample with both optical and NIR wavelength coverage. We estimate the temperature and density of our SN 2014J spectra by fitting the 8600 Å feature.
In Table 4, we present the 68% credibility interval for the electron density, temperature, Co II / Fe II mass ratio, widths and shifts of [Fe II], [Co II] and [Co III]. The evolution of the mass ratio with the time since the supernova explosion is shown in Fig. 3. The error bars in the plot reflect mainly the uncertainty of the degenerate density and temperature, and, for very late spectra (> 400 d), the Doppler width of singly ionised cobalt. Superimposed on the data points is the change of the mass ratio of cobalt to iron as expected from the radioactive decay of 56Ni (black curve). The line is not a fit to the data but rather the evolution of the mass ratio assuming the established decay half-lives of 6.08 and 77.27 days for 56Ni and 56Co respectively:
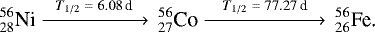 (4)
(4)
 |
Fig. 2 Best fit model of SN 2013aa at 378 d in the H-band. Shown is the extinction and redshift corrected spectrum (black line) and individual contributions from the ions Fe II (orange), Co II (green) and Co III (red) as solid curves. The purple line is the combined emission of the three ions. The two solid vertical lines are used to compute MCo II ∕ MFe II. Dashed curves indicate the contribution of the individual lines in the blended region. We do not show Ni II as it does not have any lines in this region. |
 |
Fig. 3 Evolution of the inferred MCo II ∕ MFe II ratio with time. We assumed a rise time of 18 days (Ganeshalingam et al. 2011). The error bars reflect the 68% posterior interval of the mass ratio. The coloured lines show the expected mass ratio MCo ∕ MFe of the MCh delayed-detonation model “N100” (Seitenzahl et al. 2013, green), the sub-MCh CO detonation model “det_2010_1.06” (Sim et al. 2010, orange) and the MCh “W7 Z⊙” model (Nomoto & Leung 2018, red). The black line is not a fit to the data and represents the MCo ∕ MFe ratio assuming only radioactive decay from 56Ni to 56Co to 56Fe. The same ionisation fractions of Co II and Fe II allow us to generalise MCo II ∕ MFe II to MCo ∕ MFe and compare the two ratios (see Sect. 5). |
4.2 Shifts and widths of singly and doubly ionised material
We can use the velocity shifts of [Fe II], [Co II], and [Co III] to perform a similar study to Maguire et al. (2018). We present our results in Figs. 4 and 5. Different velocity shifts between stable material ([Ni II]), singly ionised decay products ([Fe II], [Co II]) and doubly ionised decay products ([Fe III], [Co III]) would suggest their production in spatially separated regions of the ejecta (Maeda et al. 2010). As we fit the forbidden Co II lines at 1.019 and 1.547 μm we can directly compare velocity offsets and widths of singly and doubly ionised cobalt. For Fe III and Fe II this cannot be done as the 4700Å Fe III-dominated feature exhibits a shift of its central wavelength with time.
We find that the absolute velocity shifts of [Fe II], (1.1 ± 0.5) × 103 km s−1, are very similar to the absolute velocity shifts of [Co II] (0.9 ± 0.7) × 103 km s−1. Deviations of the velocity shift between the two ions are less than 500 km s−1 for most spectra and likely the result of noise near the 1.019 μm [Co II] feature. Velocity shifts of singly ionised ions can be either positive or negative for the observed sample.
Lines ofFe II and Co II exhibit comparable widths. Line widths of [Co II] usually have a higher uncertainty than line widths of [Fe II] as there is only one unblended Co II feature in our spectra, but multiple features of [Fe II] can be found at 7200, 8600, 12 600 and 16 400 Å. We find widths of (7.9 ± 1.0) × 103 km s−1 for [Co II] and (7.9 ± 0.8) × 103 km s−1 for [Fe II].
We find that [Co III] shows lower velocity offsets from its rest wavelength than singly ionised iron and cobalt. While there are spectra in which the [Co III] velocity shift is similar to [Fe II] and [Co II] (SN 2013cs, SN 1998bu), for the majority of spectra in our sample we get different velocity shifts between [Co III] and [Co II]. We find (0.5 ± 0.6) × 103 km s−1 for the mean absolute [Co III] velocity shift, compared to (0.9 ± 0.7) × 103 km s−1 for [Co II]. As noted in Maguire et al. (2018), shifts of [Co III] seem to be consistent with zero offset from the rest wavelength.
On average, [Co III] lines also appear to be broader than [Co II] lines by about 3000 km s−1 ((10.7 ± 1.8) × 103 km s−1 for [Co III] compared to (7.9 ± 1.0) × 103 km s−1 for [Co II]). We note that supernovae which exhibit a strong continuum in the 5900 Å region (SN 2012cg, SN 1998bu at 364 d, SN 2013aa at 443 d) tend to have higher line widths than supernovae without continuum in this region. In these cases, the line widths appear to be strongly affected by the manual continuum subtraction. [Co III] widths determined in this work are compatible within their uncertainties with results from Maguire et al. (2018). [Co III] lines in our fits are redshifted by ~ 500 km s−1 compared to Maguire et al. (2018). This systematic shift is mostly due to the presence of [Fe II] lines from the a4 F − a2D multiplet (5335, 5377, 5528Å) on the blue side of the 5 900 Å feature which are not included in the work of Maguire et al. (2018). We note that the choice of the continuum differs between this work and Maguire et al. (2018).
 |
Fig. 4 Velocity shifts of [Fe II], [Co II], and [Co III] as a function of time after explosion. |
 |
Fig. 5 Line widths of [Fe II], [Co II], and [Co III] as a function of time after explosion. |
5 Comparison of MCo II/MFe II with explosion model yields
Besides 56Ni, explosion models predict the presence of the isotopes 54,56Fe, 57Ni and 58Ni. If the explosive burning in the white dwarf occurs at high densities (e.g. MCh models) stable 54,56Fe and 58Ni and rapidly decaying 57Ni can be produced directly. Sub-MCh models lack a high enough central density to produce neutron-rich material. However, if the progenitor has a high metallicity (several times solar) there is an excess of neutrons, resulting in the synthesis of 54,56Fe, 57Ni, and stable 58Ni with masses comparable to those of MCh explosions (Sim et al. 2010; Ruiter et al. 2013).
In Fig. 3 the prediction of the MCo / MFe ratio is shown in the case of pure 56Ni to 56Co to 56Fe decay and for nucleosynthetic yields of the MCh deflagration model “W7 Z⊙ ” (Nomoto & Leung 2018), the MCh delayed-detonation model “N100” (Seitenzahl et al. 2013), and the sub-MCh CO detonation model “det_2010_1.06” (Sim et al. 2010). The “W7 Z⊙ ” model produces 2.8% 57Ni and 35% 54,56Fe, the MCh delayed detonation model “N100” produces 3.1% 57Ni and 19.4% 54,56Fe, and the sub-MCh CO detonation model ‘det_2010_1.06’ produces 0.6% 57Ni and no stable iron, each given in fractions of the 56Ni mass. As mentioned before, a high metallicity progenitor like in the “det_2010_1.06_0.075Ne” model (Sim et al. 2010) produces similar masses of 54,56Fe and 57Ni as the “N100” model.
Stable iron produced in the explosion has the strongest effect on MCo / MFe while not all of the 56Co has yet decayed to 56Fe (< 300 d). 57Ni decays within a few days to 57 Co, which has a much longer half-life than 56Co:
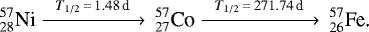 (5)
(5)
Due to the longer half-life it can still be found late in the nebular phase (> 400 d) when almost no 56Co remains.
Co II and Fe II have similar ionisation potentials and appear to be co-located within the ejecta (see Sect. 4). We therefore assume that the relative ionisation fraction between Co II and Fe II does not change with time, allowing us to generalise MCo II ∕ MFe II to MCo ∕ MFe. This ratio measures the total mass of cobalt to iron at a given time, with possible contributions from stable 54,56Fe and decay products according to Eqs. (4) and (5). We compare the predicted MCo ∕ MFe ratio of different models with the results from our fits by determining their likelihood based on their Bayes factors. The Bayes factor quantifies the evidence of data D for model Ma compared to model Mb. In our analysis we consider the nested models M0 to M3 (see Table 5). The possible parameters of these models are initial abundances of the isotopes 56Ni, 54,56Fe, and 57Ni.
For nested models, the Bayes factor can be computed analytically if the priors are separable and the more complicated model Mb becomes the simpler model Ma for θ = θ0:
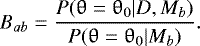 (6)
(6)
We use the mass ratio results from our individual spectral fits to compute the Bayes factor between models M0 and M3. Prior odds are set to one as we do not have an initial preference for any model. For 54,56Fe and 57Ni we adopt flat priors 0 ≤ M54,56Fe ∕ M56Ni ≤ 0.5 and 0 ≤ M57Ni ∕ M56Ni ≤ 0.05. The covariances and posterior densities of the models are shown in Fig. 6 for M3 and in Fig. 7 for M1 and M2. Due to the introduction of additional degrees of freedom all models fit the data reasonably well.
To determine the best fitting model given the data we compute the Bayes factors between the models as shown in Table 6. The MCo ∕ MFe ratio of bothMCh and sub-MCh explosion models follows closely the mass ratio from pure 56Ni decay between 250 and 350 days after the explosion. Data points between these epochs cannot distinguish between either model.
Most MCh explosion models that predict between 0.4 and 0.8 M⊙ of 56Ni (filled symbols in Fig. 6) lie in the 3σ error ellipse of model M3. The error ellipse also contains the aforementioned high-metallicity CO detonation model “det_2010_1.06_0.075Ne” (Sim et al. 2010). Models, that yield less than 0.4 M⊙ or more than 0.8 M⊙ of 56Ni are marked with empty symbols. The models with only 57Ni or only 54,56Fe in addition to the 56Ni are not allowed as the gain in fit quality is small compared to the added parameter space (see Fig. 7). A comparison between models 56Ni only (M0) and our more complex M3 model favours the complex model.
Models and their included isotopes produced in the explosion.
 |
Fig. 6 Covariances and normalized posterior densities of model M3. Theoretical predictions of the initial 54,56Fe and 57Ni fraction of various explosion models are indicated by green (Near-Ch-mass) and orange (sub-Ch-mass) symbols. Theoretical predictions with too little (<0.4 M⊙) or too much (>0.8 M⊙) 56Ni compared to Branch-normal SNe Ia are marked as empty symbols. Black lines show the 1, 2, and 3σ credibility regions. Numbers next to the 1D histograms indicate the 68% credibilityrange of the individual parameters. Models: Del. Det. (Seitenzahl et al. 2013; Ohlmann et al. 2014; Nomoto & Leung 2018), Deflag. (Fink et al. 2014), new W7 (Nomoto & Leung 2018), CONe Defl. (Kromer et al. 2015), Grav. Conf. (Seitenzahl et al. 2016), CO Det. (Sim et al. 2010; Nomoto & Leung 2018), ONe Det. (Marquardt et al. 2015), Double Det. (Sim et al. 2012), V. Merger (Pakmor et al. 2010, 2012; Kromer et al. 2013, 2016). |
 |
Fig. 7 Panel a: normalized posterior density of model M1 with only stable iron 54,56Fe and radioactive 56Ni. Panel b: normalized posterior density of model M2 with only radioactive 57Ni and 56Ni. |
Bayes factors and their interpretation between the nested models and relative probabilities of the models.
6 Discussion
6.1 Emission line widths and velocity shifts
Maguire et al. (2018) found that the velocity shifts and line widths of [Fe II] and [Ni II] of SNe in the sample are compatible within their uncertainties. We measure an average [Fe II] velocity shift of (1.1 ± 0.5) × 103 km s−1, across the sample, compared to (0.9 ± 0.7) × 103 km s−1 for [Co II]. Lines of [Fe II] and [Co II] are either both redshifted or both blueshifted. The average line widths are (7.9 ± 1.0) × 103 km s−1 in the case of [Co II] and (7.9 ± 0.8) × 103 km s−1 for [Fe II]. This indicates that the emission from all singly ionised iron-group ions originates from the same spatial region in the ejecta. The emitting region of singly ionised material appears to be located off-centre and is smaller than the emitting region of doubly ionised cobalt by about 3000 km s−1. We do not find significant velocity shift and line width offsets between [Fe II] emission in the optical and NIR. We confirm the results of Maguire et al. (2018) that the absolute velocity shift of [Co III] is lower than that of the singly ionised species and for most spectra in our sample compatible with no offset from the rest wavelength.
Nucleosynthetic calculations for delayed detonations including multiple ignition points by Seitenzahl et al. (2013) show the stable iron group 54Fe, 56Fe, and 58Ni to be distributed within the supernova in close association with 56Ni. At the epochs of our observations (~200–500 days), the γ-rays still deposit energy into the ejecta and any stable iron, whether in the core or distributed within the ejecta, should be heated and contribute to the emission. If stable and radioactive materials are co-located in the same region, the stable material can also be heated by positrons. In fact, evidence for heating of stable elements is found in the late-time optical spectra where the line of [Ni II] is evident at 7378 Å (e.g. Maeda et al. 2010; Maguire et al. 2018). No significant amount of 56Ni can be expected to be present in the ejecta 100 days after the explosion.
It is possible to hide a large amount of material if it is not heated and therefore not emitting. At epochs later than 350 days, when the mean free path for the γ-rays from the decay of 56Co is larger than the radius of the supernova and the bulk of the γ-rays do not deposit their energy in the ejecta, the energy deposition within the ejecta is almost exclusively via the β+ channel (e.g. Axelrod 1980; Woosley et al. 1989, 2007; Leibundgut & Pinto 1992). It is assumed, due to trapping by magnetic fields, that the positron energy deposition is local to the emission region. It is, therefore, possible to have pockets of cold gas. In such a case those regions would not contribute to the spectra. Unlike the observations of SN 2003hv (Motohara et al. 2006; Maeda et al. 2010; Mazzali et al. 2011), as discussed in Maguire et al. (2018) our spectra do not exhibit flat-topped profiles of emission features and there is no evidence for an ashes bubble in the centre of, or off-centre, in the ejecta. A more sophisticated analysis of the line profiles of these species in the context of energy deposition scenarios and distributions can be found in Diamond et al. (2018).
6.2 The origin of iron and cobalt
Doubly ionised cobalt and iron lines have been used in the past by other authors (see Kuchner et al. 1994) to derive that the mass ratio MCo ∕ MFe in SNe Ia is governed by the radioactive decay of 56Co to 56Fe. That work relied on iron and cobalt lines below 5500 Å. Singly ionised lines above 7000 Å become optically thin after about 150 days.
Our work determines that the singly ionised lines observed in the spectra arise from the daughter products of the radioactive 56Ni. Even though we can only constrain the temperature weakly, it is evident that the mass ratio evolution is not a temperature effect. While it is plausible to assume variations in the temperature of the ejecta from one SN to another, these are unlikely to be extreme as the heating and cooling are fundamentally dictated by the same elements (the daughter products of the decay of 56Ni). Furthermore, the production of 56Ni is tightly linked to the density and temperature of the progenitor. Simply put, the inner ejecta of normal SNe Ia should be very similar in terms of their excitation within the boundaries of this analysis. This is borne out by the very strong similarity of the emission line spectra obtained during the first year after the explosion (Mazzali et al. 1998).
By fitting the spectra with forbidden emission lines of our set of NLTE atoms we find a decline of the temperature in the ejecta from ~ 8000 K at 200 days to ~4000 K at 500 days. Such a temperature evolution is consistent with predictions from simulations (Fransson & Jerkstrand 2015). We also find that the density of the emitting material decreases from a few times 106 cm−3 to about 105 cm−3 between the youngest and oldest spectrum in our sample. These densities are consistent with a simple distribution of roughly half a solar mass of singly and doubly ionised iron group material in a volume expanding at ~ 8000 km s−1 for the age of the SN.
We ruled out models containing only stable iron or only 57Ni in addition to 56Ni. Theoretical predictions of the cobalt to iron mass ratio from MCh and sub-MCh explosion simulations differ only slightly from the pure 56Ni decay chain. Within the Bayesian framework we find evidence (B03 = −3.8) for a model with 56Ni, stable iron and 57Ni produced during the explosion similar to most MCh models, compared to a purely 56Ni origin of iron.
Due to largely unknown ejecta densities and temperatures, the uncertainties of the derived cobalt to iron mass ratio are quite large. Future observations of the relative strength of the [Co II] 10.52, 14.74 and 15.46 μm lines (e.g. with JWST) would also allow for a direct measurement of the density and temperature of the emitting material in the range 104 –106 cm−3 and 3000–10 000 K (Storey et al. 2016). A more accurate Co II / Fe II mass ratio could be used to determine the amount of 57Ni and 54,56Fe for individual SNe rather than assuming similar progenitor scenarios for a sample of SNe.
The presence of 57Ni was also discussed for the nearby SN 2011fe (Dimitriadis et al. 2017; Kerzendorf et al. 2017; Shappee et al. 2017) and SN 2012cg (Graur et al. 2016). For these two objects photometric measurements were obtained at extremely late phases (> 1000 days after explosion) to construct a pseudo-bolometric light curve. Graur et al. (2016) claimed that 57Ni is required to explain the late-time light curve of SN 2012cg. Both Dimitriadis et al. (2017) and Shappee et al. (2017) argued for a detection of 57Ni in SN 2011fe, albeit with very different abundances, pointing to either near-MCh (Dimitriadis et al. 2017)or sub-MCh explosions (Shappee et al. 2017). Kerzendorf et al. (2017) tested the effect of various isotopic abundances and physical processes on the light curve and came to the conclusion that one cannot determine the 57Ni abundance from the light curve without detecting the mid-IR cooling lines.
7 Conclusions
We fitted late time spectra of SNe Ia with broadened emission profiles from NLTE level populations using a Bayesian sampler. We computed good fits with similar widths and velocity offsets among the singly ionised atoms, indicating a common emission region. We find that doubly ionised cobalt is located in a broader and more centred region of the ejecta. We have shown that the singly ionised iron group elements in the late-time spectra of SNe Ia change their flux ratios in agreement with an evolution of their mass ratios that would be governed by the radioactive decay of 56Co to 56Fe. This result disfavours the presence of only stable iron or only the decay products of 57Ni in the ejecta in addition to 56Ni, at least for the SNe observed here. For a model that produced both stable iron and 57Ni in addition to 56Ni during the explosion we find 54,56Fe/56Ni = 0.272 ± 0.086 and 57Ni/56Ni = 0.032 ± 0.011 with a ratio of stable iron to 57Ni of ~ 8.5: 1.
Acknowledgements
We would like to thank the anonymous referee for the helpful comments. We thank the staff at Gemini and Paranal observatories. This research would not be possible without their efforts in supporting queue/service mode observing. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. This work made use of the Heidelberg Supernova Model Archive (HESMA), https://hesma.h-its.org. We would like to thank Johannes Buchner for helpful discussions and comments. A.F. acknowledges the support of an ESO Studentship. K.M. is supported by the UK STFC through an Ernest Rutherford fellowship. S.T. acknowledges support by TRR33 “The Dark Universe” of the German Research Foundation (DFG). W.E.K. acknowledges the Excellence Cluster Universe, Technische Universität München, Boltzmannstrasse 2, D-85748 Garching, Germany and acknowledges the support of an ESO Fellowship.
References
- Amanullah, R., Goobar, A., Johansson, J., et al. 2014, ApJ, 788, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Arnett, W. D. 1982, ApJ, 253, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Axelrod, T. S. 1980, Ph.D. Thesis, California University, Santa Cruz, USA [Google Scholar]
- Bautista, M. A., Fivet, V., Ballance, C., et al. 2015, ApJ, 808, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Black, C. S., Fesen, R. A., & Parrent, J. T. 2016, MNRAS, 462, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Botyánszki, J., & Kasen, D. 2017, ApJ, 845, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Branch, D., Dang, L. C., Hall, N., et al. 2006, PASP, 118, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellaro, E., Patat, F., Mazzali, P. A., et al. 2001, ApJ, 549, L215 [NASA ADS] [CrossRef] [Google Scholar]
- Cassidy, C. M., Ramsbottom, C. A., Scott, M. P., & Burke, P. G. 2010, A&A, 513, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cassidy, C. M., Hibbert, A., & Ramsbottom, C. A. 2016, A&A, 587, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chambers, K. C., Magnier, E. A., Metcalfe, N., et al. 2016, ArXiv e-prints [arXiv:1612.05560] [Google Scholar]
- Childress, M. J., Hillier, D. J., Seitenzahl, I., et al. 2015, MNRAS, 454, 3816 [NASA ADS] [CrossRef] [Google Scholar]
- Churazov, E., Sunyaev, R., Isern, J., et al. 2014, Nature, 512, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Colgate, S. A., & McKee, C. 1969, ApJ, 157, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Dhawan, S., Flörs, A., Leibundgut, B., et al. 2018, A&A, 619, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Diamond, T. R., Hoeflich, P., Hsiao, E. Y., et al. 2018, ApJ, 861, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Dimitriadis, G., Sullivan, M., Kerzendorf, W., et al. 2017, MNRAS, 468, 3798 [NASA ADS] [CrossRef] [Google Scholar]
- Filippenko, A. V., Richmond, M. W., Branch, D., et al. 1992a, AJ, 104, 1543 [NASA ADS] [CrossRef] [Google Scholar]
- Filippenko, A. V., Richmond, M. W., Matheson, T., et al. 1992b, ApJ, 384, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Fink, M., Kromer, M., Seitenzahl, I. R., et al. 2014, MNRAS, 438, 1762 [NASA ADS] [CrossRef] [Google Scholar]
- Fransson, C., & Chevalier, R. A. 1989, ApJ, 343, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Fransson, C., & Jerkstrand, A. 2015, ApJ, 814, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Ganeshalingam, M., Li, W., & Filippenko, A. V. 2011, MNRAS, 416, 2607 [NASA ADS] [CrossRef] [Google Scholar]
- Graur, O., Zurek, D., Shara, M. M., et al. 2016, ApJ, 819, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyle, F., & Fowler, W. A. 1960, ApJ, 132, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jha, S., Garnavich, P. M., Kirshner, R. P., et al. 1999, ApJS, 125, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Kass, R. E. & Raftery, A. E. 1995, J. Am. Stat. Assoc., 90, 773 [Google Scholar]
- Kerzendorf, W. E., McCully, C., Taubenberger, S., et al. 2017, MNRAS, 472, 2534 [NASA ADS] [CrossRef] [Google Scholar]
- Kochanek, C. S., Shappee, B. J., Stanek, K. Z., et al. 2017, PASP, 129, 104502 [NASA ADS] [CrossRef] [Google Scholar]
- Kozma, C., Fransson, C., Hillebrandt, W., et al. 2005, A&A, 437, 983 [Google Scholar]
- Kramida, A., Yu. Ralchenko, Reader, J., & NIST ASD Team 2018, NIST Atomic Spectra Database (ver. 5.5.6), Available at https://physics. nist.gov/asd (Gaithersburg, MD: National Institute of Standards and Technology). [Google Scholar]
- Kromer, M., Pakmor, R., Taubenberger, S., et al. 2013, ApJ, 778, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Kromer, M., Ohlmann, S. T., Pakmor, R., et al. 2015, MNRAS, 450, 3045 [NASA ADS] [CrossRef] [Google Scholar]
- Kromer, M., Fremling, C., Pakmor, R., et al. 2016, MNRAS, 459, 4428 [NASA ADS] [CrossRef] [Google Scholar]
- Kuchner, M. J., Kirshner, R. P., Pinto, P. A., & Leibundgut, B. 1994, ApJ, 426, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Kulkarni, S. R. 2012, ArXiv e-prints [arXiv:1202.2381] [Google Scholar]
- Leibundgut, B. & Pinto, P. A. 1992, ApJ, 401, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Leibundgut, B. & Sullivan, M. 2018, Space Sci. Rev., 214, A57 [NASA ADS] [CrossRef] [Google Scholar]
- Leibundgut, B., Kirshner, R. P., Phillips, M. M., et al. 1993, AJ, 105, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Maeda, K., Taubenberger, S., Sollerman, J., et al. 2010, ApJ, 708, 1703 [NASA ADS] [CrossRef] [Google Scholar]
- Maguire, K., Taubenberger, S., Sullivan, M., & Mazzali, P. A. 2016, MNRAS, 457, 3254 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maguire, K., Sim, S. A., Shingles, L., et al. 2018, MNRAS, 477, 3567 [NASA ADS] [CrossRef] [Google Scholar]
- Marquardt, K. S., Sim, S. A., Ruiter, A. J., et al. 2015, A&A, 580, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mazzali, P. A., Cappellaro, E., Danziger, I. J., Turatto, M., & Benetti, S. 1998, ApJ, 499, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Mazzali, P. A., Maurer, I., Stritzinger, M., et al. 2011, MNRAS, 416, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Motohara, K., Maeda, K., Gerardy, C. L., et al. 2006, ApJ, 652, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K., & Leung, S.-C. 2018, Space Sci. Rev., 214, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Ohlmann, S. T., Kromer, M., Fink, M., et al. 2014, A&A, 572, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pakmor, R., Kromer, M., Röpke, F. K., et al. 2010, Nature, 463, 61 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Pakmor, R., Kromer, M., Taubenberger, S., et al. 2012, ApJ, 747, L10 [Google Scholar]
- Phillips, M. M. 1993, ApJ, 413, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, M. M., Wells, L. A., Suntzeff, N. B., et al. 1992, AJ, 103, 1632 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiter, A. J., Sim, S. A., Pakmor, R., et al. 2013, MNRAS, 429, 1425 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiz-Lapuente, P., Cappellaro, E., Turatto, M., et al. 1992, ApJ, 387, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Seitenzahl, I. R., Ciaraldi-Schoolmann, F., Röpke, F. K., et al. 2013, MNRAS, 429, 1156 [Google Scholar]
- Seitenzahl, I. R., Kromer, M., Ohlmann, S. T., et al. 2016, A&A, 592, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shanks, T., Metcalfe, N., Chehade, B., et al. 2015, MNRAS, 451, 4238 [NASA ADS] [CrossRef] [Google Scholar]
- Shappee, B. J., Stanek, K. Z., Kochanek, C. S., & Garnavich, P. M. 2017, ApJ, 841, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Shaw, J. R., Bridges, M., & Hobson, M. P. 2007, MNRAS, 378, 1365 [NASA ADS] [CrossRef] [Google Scholar]
- Silverman, J. M., Ganeshalingam, M., Cenko, S. B., et al. 2012, ApJ, 756, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Sim, S. A., Röpke, F. K., Hillebrandt, W., et al. 2010, ApJ, 714, L52 [Google Scholar]
- Sim, S. A., Fink, M., Kromer, M., et al. 2012, MNRAS, 420, 3003 [NASA ADS] [CrossRef] [Google Scholar]
- Spyromilio, J., Gilmozzi, R., Sollerman, J., et al. 2004, A&A, 426, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Storey, P. J., & Sochi, T. 2016, MNRAS, 459, 2558 [NASA ADS] [CrossRef] [Google Scholar]
- Storey, P. J., Zeippen, C. J., & Sochi, T. 2016, MNRAS, 456, 1974 [NASA ADS] [CrossRef] [Google Scholar]
- Taubenberger, S. 2017, Handbook of Supernovae, ed. A. W. Alsabti & P. Murdin, 317 [CrossRef] [Google Scholar]
- Turatto, M., Benetti, S., Cappellaro, E., et al. 1996, MNRAS, 283, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Varani, G. F., Meikle, W. P. S., Spyromilio, J., & Allen, D. A. 1990, MNRAS, 245, 570 [NASA ADS] [Google Scholar]
- Woosley, S. E., Pinto, P. A., & Hartmann, D. 1989, ApJ, 346, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Kasen, D., Blinnikov, S., & Sorokina, E. 2007, ApJ, 662, 487 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Bayes factors and their interpretation between the nested models and relative probabilities of the models.
All Figures
 |
Fig. 1 Optical (left panel) and NIR (right panel) spectra of SNe Ia obtained with X-shooter, FORS1, and ISAAC at the VLT, SOFI at the NTT, and GNIRS at Gemini-North. The spectra are arranged in epoch starting with the youngest at the top and corrected for redshift and extinction. Fluxes are normalized to the 7300 Å [Fe II] + [Ni II] feature (optical) and 12 600 Å [Fe II] feature (NIR). The red line indicates the mean flux of all fit models at each wavelength, the orange shaded area marks the 68% uncertainty of the fit. Dashed vertical lines indicate the strongest lines as given in Table 2 ([Fe II]: - - - -, [Ni II]: ⋯ ⋯⋯ [Co II]: —⋅—, [Co III]: — ⋅ ⋅— ⋅). The subtracted background is shown as a grey band. Fits were performed for the optical and NIR spectra at the same time. The lines/ions composing the features below 5500Å are not included in our fits. |
| In the text | |
 |
Fig. 2 Best fit model of SN 2013aa at 378 d in the H-band. Shown is the extinction and redshift corrected spectrum (black line) and individual contributions from the ions Fe II (orange), Co II (green) and Co III (red) as solid curves. The purple line is the combined emission of the three ions. The two solid vertical lines are used to compute MCo II ∕ MFe II. Dashed curves indicate the contribution of the individual lines in the blended region. We do not show Ni II as it does not have any lines in this region. |
| In the text | |
 |
Fig. 3 Evolution of the inferred MCo II ∕ MFe II ratio with time. We assumed a rise time of 18 days (Ganeshalingam et al. 2011). The error bars reflect the 68% posterior interval of the mass ratio. The coloured lines show the expected mass ratio MCo ∕ MFe of the MCh delayed-detonation model “N100” (Seitenzahl et al. 2013, green), the sub-MCh CO detonation model “det_2010_1.06” (Sim et al. 2010, orange) and the MCh “W7 Z⊙” model (Nomoto & Leung 2018, red). The black line is not a fit to the data and represents the MCo ∕ MFe ratio assuming only radioactive decay from 56Ni to 56Co to 56Fe. The same ionisation fractions of Co II and Fe II allow us to generalise MCo II ∕ MFe II to MCo ∕ MFe and compare the two ratios (see Sect. 5). |
| In the text | |
 |
Fig. 4 Velocity shifts of [Fe II], [Co II], and [Co III] as a function of time after explosion. |
| In the text | |
 |
Fig. 5 Line widths of [Fe II], [Co II], and [Co III] as a function of time after explosion. |
| In the text | |
 |
Fig. 6 Covariances and normalized posterior densities of model M3. Theoretical predictions of the initial 54,56Fe and 57Ni fraction of various explosion models are indicated by green (Near-Ch-mass) and orange (sub-Ch-mass) symbols. Theoretical predictions with too little (<0.4 M⊙) or too much (>0.8 M⊙) 56Ni compared to Branch-normal SNe Ia are marked as empty symbols. Black lines show the 1, 2, and 3σ credibility regions. Numbers next to the 1D histograms indicate the 68% credibilityrange of the individual parameters. Models: Del. Det. (Seitenzahl et al. 2013; Ohlmann et al. 2014; Nomoto & Leung 2018), Deflag. (Fink et al. 2014), new W7 (Nomoto & Leung 2018), CONe Defl. (Kromer et al. 2015), Grav. Conf. (Seitenzahl et al. 2016), CO Det. (Sim et al. 2010; Nomoto & Leung 2018), ONe Det. (Marquardt et al. 2015), Double Det. (Sim et al. 2012), V. Merger (Pakmor et al. 2010, 2012; Kromer et al. 2013, 2016). |
| In the text | |
 |
Fig. 7 Panel a: normalized posterior density of model M1 with only stable iron 54,56Fe and radioactive 56Ni. Panel b: normalized posterior density of model M2 with only radioactive 57Ni and 56Ni. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


