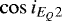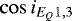| Issue |
A&A
Volume 620, December 2018
|
|
|---|---|---|
| Article Number | A45 | |
| Number of page(s) | 13 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201833435 | |
| Published online | 27 November 2018 | |
The “memory” of the Oort cloud
1
LAL-IMCCE, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Universités, UPMC Univ. Paris 06, Univ. Lille.,
1 Impasse de l’Observatoire,
59000
Lille,
France
e-mail: marc.fouchard@univ-lille1.fr
2
RISE Project Office, National Astronomical Observatory of Japan, 2-12 Hoshigaoka-cho,
Mizusawa,
Iwate
023-0816, Japan
3
CfCA, NAOJ, Mitaka, Tokyo 181-8588, Japan
Received:
16
May
2018
Accepted:
21
September
2018
Aims. Our aim in this paper is to try to discover if we can find any record of the Oort cloud formation process in the orbital distribution of currently observable long-periodic comets.
Methods. Long-term simulations of tens of millions of comets from two different kinds of proto-Oort clouds (isotropic and disk-like) were performed. In these simulations we considered the Galactic tides, stellar passage, and planetary perturbations.
Results. In the case of an initially disk-like proto-Oort cloud, the final Oort cloud remains anisotroic inside of about 13 200 au. A record of the initial shape is preserved, here referred to as the “memory”, even on the final distribution of observable comets. This memory is measurable in particular for observable comets for which the previous perihelion was beyond 10 au and that were significantly affected by Uranus or Neptune at that moment (the so-called Kaib-Quinn jumpers observable class). Indeed, these comets are strongly concentrated along an extended scattered disk that is the remnant of the initial population 1 Gyr before the comets are observable. In addition, for this class of comets, the distributions of ecliptic inclination and Galactic longitude of the ascending node at the previous perihelion preceding the observable perihelion highlight characteristics that are not present in the isotropic model. Furthermore, the disk-like model produces four times more observable comets than the isotropic one, and its flux is independent of the initial distribution of orbital energy. Also for the disk-like model, the region beyond Neptune up to ~40 au gives the major contribution to the final flux of observable comets.
Conclusions. The disk-like model sustains a flux of observable comets that are more consistent with the actually observed flux than using the isotropic model. However, further investigations are needed to reveal whether a fingerprint of the initial proto-Oort cloud, such as those highlighted in the present article, is present in the sample of known long-period comets.
Key words: comets: general / Oort Cloud
© ESO 2018
1 Introduction
Since the keystone work of Oort (1950), it has been well accepted that “new” long-period comets, that is, comets for which the original semi-major axis is greater than 10 000 au come from the region beyond several tens of thousand of astronomical units. In addition, to supply the present flux of such comets, the Oort cloud should contain about 1012 objects. Since the era of Jan Oort, the mechanisms that make an Oort cloud comet observable have been widely investigated. At the time of Jan Oort, passing stars were the unique process that could make Oort cloud comets observable. In the 1980s, as we see in the work of Heisler & Tremaine (1986) and Byl (1986) among others, the Galactic tides appear to have been very efficient at producing observable long-period comets, mainly because the dynamic involved is quasi-integrable. Delsemme (1987) showed that the fingerprint of the Galactic tides was present in the distribution of the orbital element of the known long-period comets. Since then, passing stars have been disregarded and only the Galactic tides have been taken into account. However, Rickman et al. (2008) showed that in long-term evolution, that is, evolution on the order of the Gyr, passing stars are fundamental in maintaining an almost constant flux of observable comets over the age of the solar system. This synergy between the Galactic tides and passing stars is now well understood (Fouchard et al. 2011a) on a long timescale, but also in short-term evolution (Fouchard et al. 2011b).
However, even if the mechanisms at work are much better known than at the time of Oort, the estimated number of comets in the present Oort cloud has only slightly decreased from the initially estimated value (several 1011 of objects; e.g., Francis 2005; Kaib & Quinn 2009). This huge number of comets, compared to the number of objects required in the scattered disk to supply the flux of Jupiter family comets (Duncan & Levison 1997), still poses a problem for describing the Oort cloud formation.
Two main scenarios are usually proposed for the Oort cloud formation. The first is the formation of the cloud while the Sun is still in its birth cluster (Fernández & Brunini 2000). This scenario has grown more attractive with the discovery of Sedna, since such an object could be a natural outcome of this kind of formation (Brasser et al. 2006, 2012; Kaib & Quinn 2008; Levison et al. 2010; Brasser & Schwamb 2015). The second is a formation of the cloud by planetary scattering as performed by Leto et al. (2008). Such a formation process was recently investigated in Brasser & Morbidelli (2013), in the frame of the late migration of the giant planets (Levison et al. 2011). This later study has the advantage of significantly reducing the problem of the ratio between the Oort cloud and scattered disk population. The aim of the present paper is to investigate whether some memory of the processes that formed the Oort cloud could persist throughout the age of the solar system until the flux of observable long-period comets.
To do so, we consider two different possible initial proto-Oort clouds: one with a disk-like shape that is more consistent with a formation through planetary scattering by the giant planets, and one with a fully isotropic and thermalized shape, that is more consistent with a formation in a dense stellar cluster. In both cases, the initial distribution of orbital energy will also be a parameter of our results.
The article is organized as follows. The initial conditions and the simulations are described in Sect. 2. In Sect. 3, the evolution of the different Oort clouds is described, while Sect. 4 is devoted to the final flux of observable comets. The influence of the initial orbital energy distribution on the final flux of observable comets is discussed in Sect. 5. We give our conclusions in Sect. 6.
2 Initial conditions and simulations
2.1 Initial conditions
We have used two different sets of initial conditions. The first has a disk-like shape. We used the following uniform distributions: the orbital energy zi = −1∕ai for semi-major axis ai between 500 and 20 000 au, the perihelion distance qi between 3 and 45 au, the ecliptical inclination 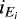 between 0 and 20°, the ecliptical argument of perihelion
between 0 and 20°, the ecliptical argument of perihelion 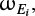 , longitude of the ascending node
, longitude of the ascending node 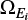 and mean anomaly Mi between 0 and 360°. The total number of objects for this set is 13 428 570. This set will be referred to as D0, or the D0 model.
and mean anomaly Mi between 0 and 360°. The total number of objects for this set is 13 428 570. This set will be referred to as D0, or the D0 model.
The second set has an isotropic shape and is fully thermalized (Hills 1981). Apart from the eccentricity ei that as a law of distribution proportional to e de, with a perihelion distance qi greater than 15 au, all the other following quantities are drawn from uniform distributions: the orbital energy zi for semi-major axis ai between 500 au and 50 000 au, 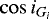 between −1 and 1 where
between −1 and 1 where 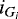 is the Galactical inclination, the Galactical argument of perihelion
is the Galactical inclination, the Galactical argument of perihelion 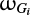 , the Galactical longitude of the ascending node
, the Galactical longitude of the ascending node 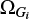 and the mean anomaly Mi between 0 and 360°. For this set, the total number of comets is 20 307 700. This set will be referred to as I0 or the model I0.
and the mean anomaly Mi between 0 and 360°. For this set, the total number of comets is 20 307 700. This set will be referred to as I0 or the model I0.
Our initial conditions D0 and I0 were such that the quantity zi = −1∕ai has a uniform distribution; in other words, the density function of the initial orbital energy is constant. If we want a density function of this orbital energy proportional to 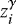 , we simply have to weight each comet by
, we simply have to weight each comet by
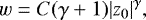 (1)
(1)
with zmin and zmax being the limiting values of the initial range of orbital energy.
Our initial sets D0 and I0 correspond to γ = 0. For γ = 1, …, 8, we easily defined the sets Dγ and Iγ, from the sets D0 and I0 by applying the proper weight to each comet.
2.2 Simulations
For each set, the evolution of the comets is performed using the same strategy as in Fouchard et al. (2017). Each comet is initially placed into the proto-Oort cloud at a random time, between zero and one revolution of the solar system around the center of the Galaxy so the distribution of the initial Galactic longitude is uniform. With our choice of parameters used for the Galactic tides (Levison et al. 2001), we have TG ≈ 236 Myr. Then, the comets evolve under the action of the Galactic tides, passing stars and planetary perturbations (Fouchard et al. 2014)1. A single sequence of passing stars was used. It contains about 200 000 stellar encounters at less than 2 pc from the Sun in a 5 Gyr time-span. The sequence is built following the procedure in Rickman et al. (2008). The evolution of a comet is stopped when it impacts the Sun or a giant planet, or goes beyond 400 000 au from the Sun or has a semi-major axis smaller than 100 au.
Then at five different instants, between 3.75 and 4.75 Gyr with 250 Myr between each instant, all the comets that remain in the cloud were stored. After each recording time, the evolution of each comet was continued for 30 Myr under the action of Galactic tides, passing stars and planetary perturbations, but then all the stars that may produce a significant cometary shower are removed, following the procedure described in Fouchard et al. (2017). This precaution was taken since it is unlikely that we are now experiencing a cometary shower (Wiegert & Tremaine 1999).
Then, the first perihelion passage after this additional 30 Myr evolution was considered. When at perihelion, if a comet is found at less than 5 au from the Sun, then it is considered observable. Each recorded final Oort cloud produces a set of observable comets. With such a procedure, for each set of observable comets the position of the Galactic center in the ecliptic reference frame is similar to the actual position. Hence, the influence of the radial Galactic tide is similar to the present one. Indeed, in Levison et al. (2006) a correlation between the position of the Galactic center and the Oort cloud dynamics was highlighted.
As in Fouchard et al. (2017), we considered that 250 Myr is enough for the single orbits in the cloud to be uncorrelated. Consequently, summing all the observable comets from the five different recording times is equivalent to multiplying by five the number of initial objects into the Oort cloud.
Here we make a general remark about the quantitative results given in the present paper. All the results have been obtained using a single sequence of stellar encounter (this sequence corresponds to the sequence #2 in Fouchard et al. 2017). However, it has been observed in Fouchard et al. (2017) that, using 10 different sequences, final results may differ by about 20%. Consequently, all results given here should be considered with such an error bar with respect to the stellar sequence.
3 Evolution and final state of the Oort clouds
3.1 The I0 proto-Oort cloud
First we turn our attention to the I0 proto-Oort cloud. Initially the cloud contains 20 307 700 comets. Then the number of comets is slightly decreasing, and only 4% of the comets are ejected from the cloud at 4 Gyr.
Figure 1 shows the distribution of comets in (z, q), (z, cos(iE), (z, ωG) and (z, ΩG) planes at four different epochs t = 250 Myr and 1, 2, and 4 Gyr. Each plane is evenly split into cells in which, for clarity of the figures, an equal bin size was used in log q and log a (instead of q and z = −1∕a). Then the number of comets in each bin is converted in number density per au for q and per au−1 for z. The distributions were then normalized with respect to the total number of comets that remain into the cloud.
We recall that initially all the distributions are uniform, except for q. The cloud shows no strong evolution during the four-billion-years time span. The main long-term evolution is the transport of orbital energy for perihelion distance smaller than 70 au. At the beginning, this transport is mainly caused by direct planetary scattering from the giant planets and thus it is more efficient for orbits close to the ecliptic. Afterward, this transport is also at work for perihelion distance beyond Neptune and mainly for cos iE close to ± 0.5, i.e., for iE ≈ 60° and iE ≈ 120°. These inclinations are close to the values that allow a perihelion distance libration that can be as large as 16 au because of the Lidov–Kozai mechanism induced by Neptune (Saillenfest et al. 2017). Consequently, when q ≤ 45 au, this libration can lead the orbit of the comet to cross the orbit of Neptune, where the comet can be scattered by the planet. For higher perihelion distance, interaction of the Lidov–Kozai mechanism with mean-motion resonances with Neptune can lead to much higher perihelion excursion. In addition, very weak planetary perturbations can induce a weak orbital energy transport on long-term period (Gladman et al. 2002; Gallardo et al. 2012).
We also note that the transport of orbital energy is such that after 1 Gyr the Oort cloud is evenly filled for semi-major axes between 50 000 au and 105 au. This transport of orbital energy is mainly caused by passing stars that have the effect of flattening the orbital energy distribution (Higuchi & Kokubo 2015).
We then want to investigate whether the cloud remains isotropic at any epoch and any distance from the Sun. Three indicators will be used: (i) is the first, second (median), and third quartiles of cos iE, noted 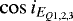 , (ii) is derived from the Kolmogorv–Smirnov test, and corresponds to the maximal distance d between our cumulative distribution of cosiE and a cumulative uniform distribution, and (iii) is the normalized ratio of the sums of the square of the vertical axis distance and the radial axis distance defined by (Higuchi & Kokubo 2015):
, (ii) is derived from the Kolmogorv–Smirnov test, and corresponds to the maximal distance d between our cumulative distribution of cosiE and a cumulative uniform distribution, and (iii) is the normalized ratio of the sums of the square of the vertical axis distance and the radial axis distance defined by (Higuchi & Kokubo 2015):
 (2)
(2)
where the sum is performed over all objects found at heliocentric distance r. At a given heliocentric distance, αr = 0.5 for a fully isotropic distribution of objects, and αr = 0 for a flat distribution of objects.
Figure 2 shows the evolution of 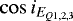 and d versus the semi-major axis, and the evolution of αr versus the heliocentric distance r after an evolution of 4 Gyr. Clearly, the cloud is fully isotropic at any distance from the Sun. Again, the unique departure from an isotropic state is for semi-major axes smaller than 500 au as seen in Fig. 1.
and d versus the semi-major axis, and the evolution of αr versus the heliocentric distance r after an evolution of 4 Gyr. Clearly, the cloud is fully isotropic at any distance from the Sun. Again, the unique departure from an isotropic state is for semi-major axes smaller than 500 au as seen in Fig. 1.
 |
Fig. 1 From top to bottom panels: distribution of comets in (a, q), (a, cos (iE), (a, ωG) and (a, ΩG) planes at four different epochs t = 250 Myr and 1, 2 and 4 Gyr. For visibility, the bin sizes are constant along any axis. However, the density function is computed in number of comets per au for the perihelion distance and per au−1 for the semi-major axis. The data come from the evolution of the I0 proto-Oort cloud. |
3.2 The D0 proto-Oort cloud
Here we consider the evolution of the comets for the D0 proto-Oort cloud. The number of comets still in the Oort cloud is continuously decreasing. However, in contrast to the I0 proto-Oort cloud, only 38% of the comets are still in the cloud at 4 Gyr, of which 43% are ejected before 500 Myr. Because the comets are placed into the cloud with a random time between 0 and 264 Myr, it means that most of the comets are ejected in a time span between 200 My and 500 Myr. This is consistent with the timescale for planetary scattering due to Uranus and Neptune that is about 200 Myr (Brasser & Morbidelli 2013).
Figure 3 shows the distribution of the comets on the four different planes already considered for Fig. 1 but for the D0 proto-Oort cloud. In less than 250 Myr, the Oort cloud already highlights the two components already described in Fouchard et al. (2017). The Uranus–Neptune region needs a bit more time to be emptied, and between 1 and 4 Gyr no significant change is observed. The main evolution is a shift toward smaller semi-major axes of the threshold between the inner flat component and the Oort cloud-like component as it has been already investigated in Fouchard et al. (2017). This threshold is found at about 1500 au at 4 Gyr.
A second evolution is observed on the (z, ΩG) plane of Fig. 3. Because initially the orbits are closed to the ecliptic, it induces that ΩG is concentrated toward 180°. This concentration is well observed in the figure for t = 250 Myr, and as time goes one, it erodes. It addition, one notes that ΩG is decreasing overall with increasing speed for higher semi-major axis. This is a direct consequence of the effect Galactic tides considering an integrable model (Breiter & Ratajczak 2005; Higuchi et al. 2007).
Clearly, the Oort cloud is not globally isotropic. Many features result from the initial condition shape after an evolution of several billion years under the dominant effect of the Galactic tides (see Higuchi et al. 2007, for more details). However, after one billion years, and for the outermost part of the cloud no structure is clearly visible. To evaluate the isotropy of this outermost part, we have plotted in Fig. 4 the evolution versus the semi-major axis a or the heliocentric distance r, of our three different isotropic indicators: the three quartiles of cosiE noted 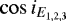 , the maximal distance d with a uniform distribution of cosiE and the αr indicator.
, the maximal distance d with a uniform distribution of cosiE and the αr indicator.
First we comment on the evolution of αr. The wave shape observed for r ≈ 13 000 au is typical of the tidal action on an initial disk-like population. The wave moves inward as time passes. This behavior has been discussed in Higuchi & Kokubo (2015). In our case we are more interested in the behavior of αr beyond the wave structure.
From all three evolutions, the Oort cloud appears to be at least statistically isotropic only for semi-major axis a beyond about 50 000 au (i.e., r ≈ 100 000 au). However, a transition seems to occur between 10 000 and 20 000 au. Indeed, 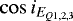 converge toward values characteristic of a uniform distribution, d goes below 0.1 and seems to reach a slightly decreasing plateau and αr starts to increase regularly with r, from 0.4 to 0.5. To more precisely evaluate this threshold, we consider the evolution of d, which is a decreasing function of a for a greater than 1000 au. From these observations, d = 0.1 appears to be a good estimate for the threshold between an Oort cloud that is clearly not isotropic and an Oort cloud that may be considered qualitatively isotropic. The value of a, noted aisot, where d goes below 0.1 is 13 200 au.
converge toward values characteristic of a uniform distribution, d goes below 0.1 and seems to reach a slightly decreasing plateau and αr starts to increase regularly with r, from 0.4 to 0.5. To more precisely evaluate this threshold, we consider the evolution of d, which is a decreasing function of a for a greater than 1000 au. From these observations, d = 0.1 appears to be a good estimate for the threshold between an Oort cloud that is clearly not isotropic and an Oort cloud that may be considered qualitatively isotropic. The value of a, noted aisot, where d goes below 0.1 is 13 200 au.
Here we consider the evolution of the Oort cloud with time. We consider the evolution of aisot as it has just been defined, and the exponent ϵ of two power-law fits to the distribution of semi-major axes (i.e., dn(a) ∝ aϵda): the first fit is made for semi-major axes between 5000 and 30 000 au, noted simply ϵ, and the second for semi-major axes between aisot and 30 000 au, noted ϵisot. Figure 5 shows the evolution of these three parameters with time.
During the first billion years, the evolution is very drastic for all parameters, whereas after less than two billion years, one notes that the Oort cloud is already very similar to its final shape. Indeed, at 1.75 Gyr, aisot ≈ 15 000 au2, ϵ ≈ −1.09 and then smoothly decreases toward its final value ϵ ≈−1.33 at t = 3.75 Gyr, and ϵisot ≈−1.32 at 1.75 Gyr and then remains almost constant.
The final values of the power-law exponent ϵ and ϵisot, are consistent with previous estimates of the orbital energy distribution of the Oort cloud. For instance, Duncan et al. (1987) and Brasser et al. (2006) found ϵ = −1.5 and Kaib & Quinn (2008) found ϵ = −1.4.
 |
Fig. 2 Top panel: evolution of the median |
3.3 Changing the initial energy distributions
The main quantitative characteristics of the clouds for the D0, D8, I0 and I8 proto-Oort cloud after four billion years are given in Table 1.
For the disk-like proto-Oort clouds, one remarks that the final shape of the Oort cloud and the whole amount of comets ejected are nearly independent of the initial distribution of orbital energy. A similar result is obtained for a similar initial Oort cloud in Fouchard et al. (2017).
Regarding the isotropic proto-Oort clouds, its initial shape has been poorly altered during the four-billion-years simulation. On the contrary, for the I8, the threshold from which the Oort cloud can be considered isotropic tells us that the cloud is not isotropic at any distance. The reason is that initially the I8 proto-Oort cloud is strongly concentrated toward 500 au. Hence, because stellar perturbations are poorly efficient at such distance (except during very rare close stellar encounters), the transport toward larger semi-major axes is then mainly caused by the Galactic tides and/or Lidov–Kozai mechanism that decrease the perihelion distance toward the planetary region and then by planetary scattering. As such, the efficiency of this transport is not uniform and consequently it generates an outer part of the Oort cloud that is not isotropic with respect to our definition. However, it is nevertheless very close to being isotropic since the quantity d used to define an isotropic state oscillates sporadically between 0 and 0.2.
 |
Fig. 5 Upper panel: evolution of aisot with time for the D0 model. Lower panel: evolution versus time of the power law exponent for the best fit to the orbital energy distribution for 5000 < a < 30 000 au (black line) and for aisot < a < 30 000 au (gray line). |
General characteristics of the Oort cloud at t = 4 Gyr.
4 Observable comets
4.1 Four different classes
As in previous papers (Fouchard et al. 2014, 2017), the observable comets are classified according to their recent history before they acquireobservability. We have considered the variation of the perihelion distance and the orbital energy during the last orbital period of the comets.
In Fouchard et al. (2017), we consider that a comet was a “jumper” in the case where the perihelion distance at the previous perihelion passage was greater than qj = 15 au. However, in Fouchard et al. (2013), it appears that the solar system is still quite transparent at this distance. Indeed, the opacity factor (the proportion of comets ejected from the Oort cloud) is smaller than 5% on average, although this factor is strongly dependent on the inclination. Consequently, we have decided to shift qj at 10 au in this paper, where the opacity factor is about 40% on average.
We are then able to define our two first classes of observable comets: if the previous perihelion is greater than qj = 10 au, then the comet is a jumper, otherwise it is called a “creeper”.
We also made a distinction depending on the variation of the original orbital energy, in other words, the barycentric orbital energy at 250 au from the Sun before reaching perihelion, during the most recent orbital period. Let us suppose that a comet has an original semi-major axis at the previous perihelion passage ap that is not large enough for the tides and background passing stars to inject the comet directly into the observable region. From numerical experiments and with qj = 15 au, it corresponds more or less to ap < 20 000 au (Fouchard et al. 2011b). Let us now suppose that, during the previous perihelion passage, this comet received a planetary kick such that its orbital energy after perihelion is now large enough for the tides alone to inject the comet into the observable region. In Fouchard et al. (2011b), this corresponds more or less to ap > 25 000 au. Consequently, this comet may become observable because of the help of the planetary kick at the previous perihelion passage. Such a process was highlighted by Kaib & Quinn (2009) in the frame of Oort cloud comets, and it turns out that a majority of observable comets may support such a process (Kaib & Quinn 2009; Fouchard et al. 2014, 2017).
The two thresholds correspond to an increase of the orbital energy equal to 10−5 au−1 for qj = 15 au. In our case, qj has been reduced to 10 au which affects both thresholds of the semi-major axis that became respectively 16 407 and 20 508 au (we just used the fact that the variation of the perihelion distance over on orbital period using an integrable model of the Galactic tide scales as a7∕2), which induces an increase of the orbital energy equals to 1.2 × 10−5 au−1 during the last orbital period. This is rather similar to the threshold already used in Fouchard et al. (2014, 2017). Consequently, we will keep the same threshold. Thus, for an observable comet, when the original orbital energy z = −1∕a has increased for more than 10−5 au−1 over the lastorbital period, the comet is called a Kaib–Quinn comet (KQ).
Consequently, we have four classes of observable comets: jumpers, KQ-jumpers, creepers, and KQ-creepers.
4.2 General statistics
We first turn our attention to the observable comets obtained from the D0 and I0 models. Table 2 summarizes the key characteristics of each model, where the flux of observable comets is extrapolated to an initial proto-Oort cloud containing 1012 comets.
The main difference between the D0 and I0 models is observed on the total flux. Indeed, the D0 model produces nearly four times more observable comets than the I0 model and has a total flux similar to the fluxes obtained in Fouchard et al. (2017). The low efficiency of the I0 model is easily explained by the fact that initially the comets are very far from the planetary region of the solar system, and this makes the realization of observability of the comets less likely. Whereas for D0 even if the comets travel far from the planetary system, they will keep the memory of their initial position because of the quasi-integrability of the tides. Hence, they are more likely to come back to the planetary region and become observable.
Regarding the proportion of comets in the different observable classes, some differences are observed, although less significant than for thetotal flux. These are mainly due to the fact that it is more complicated to be a KQ-creeper for the D0 model than for the I0 model. Indeed, as observed in Fouchard et al. (2014), KQ-creepers exhibit a very slow transport oforbital energy before they receive the good planetary kick that will make them observable. Such slow and long-term transport is easier when the orbit is retrograde in order to avoid direct ejection by the planets. Because the D0 model starts with orbits that are all close to the ecliptic, unlike the I0 model, it is more difficult to produce KQ-creepers for the D0 model. This scenario is confirmed by the proportion of retrograde orbits for KQ-creepersthat is significantly more than 50% for both models, but higher for the I0 model than for the D0 model.
The same argument could be applied to creepers. They are, however, less numerous in both models, and their transport in the semi-major axis is generally faster than for the KQ-creepers. Indeed, it has been seen in Fouchard et al. (2014) that most of the creepers are fast creepers, meaning that they made only on passage at less than 10 au before being observable, on the contrary to KQ-creepers that should make many passages at less than 10 au before they receive the good planetary kick]FOUetal:14a. This “fast” creeping weakens the constraint on the protection with respect to the planetary scattering. This difference affects the other proportions – more jumpers and KQ-jumpers for the D0 model than for the I0 model – and also the overall proportion of retrograde comets – an excess of retrograde comets for the I0 model.
Regarding the seven threshold values of the semi-major axis, they are rather similar for the two models. Jumpers have a median semi-major axis about 45 000 au, whereas for KQ-jumpers the median is about 33 000 au. Creepers and KQ-creepers are found at much lower semi-major axes, with a median at about 22 000 au for KQ-creepers and smaller than 18 500 au for creepers. On the contrary, no jumpers or KQ-jumpers are found for original semi-major axes smaller than 21 400 au.
These observations are consistent with previous results (Fouchard et al. 2014) and also with the characteristic of each class. For instance, for a comet to be a jumper or a KQ-jumper, its original semi-major axis should be greater than 16 500 au in case background stars help for the jump, or 20 500 au, in case the tides alone produce the jump. This is not the case for creepers and KQ-creepers. We note that these characteristics are independent of the models.
We plotted a histogram of the distribution of original semi-major axis where the step limits are given by the minimal, maximal and the 10th, 25th, 50th, 75th, and 90th percentiles of the original semi-major axis, and the step height is such that the area of each bar is proportional to the number of observable comets with original orbital energy within the step borders. The scale factor is such that a flat distribution induces a step height equals to about 1 (it depends on the minimal and maximal values) for all steps.
Such distributions are found at the top of Fig. 6 for the D0 and I0 models. In addition, each bar has been colored depending on the proportion of comets in each class. These distributions are a good illustration of the data shown in Table 2, where we see that the Oort spike is very similar in both cases, with jumpers and KQ-jumpers located on the outer part of the spike whereas the inner part contains mainly creepers and KQ-creepers.
For the three lower rows of plots in Fig. 6, the set of observable comets has been split into four groups according to the original semi-major axis, using the following ranges in astronomical units: ∈ [10 000, 17 000], [17 000, 20 500], [20 500, 40 000] and > 40 000 or negative. Then for each range of original semi-major axis, we have computed the median (50th percentile), first (25th percentile) and third quartile (75th percentile) of cosiE, where iE is the ecliptical inclination, the proportion of retrograde comets (in each class and considering all the comets) and the proportion of comets in each class.
Again, the plots are a good illustration of the data shown in Table 2. In particular, we note that for both models the innermost part of the Oort cloud (a < 17 000 au) contains a majority of retrograde comets, and this is easily explained by the fact that this region contains exclusively creepers and KQ-creepers. For semi-major axes greater than 20 500 au, because of the domination of jumper and KQ-jumpers, the preference for retrograde orbits vanishes. Such results are consistent with the results in Fernández (2002) where a preference for retrograde orbits is observed for observed “new” comets with semi-major axes smaller than 22 000 au.
General statistics for observable comets.
4.3 cos iE, ΩG and ωG distributions
Next, we investigated in more detail how the initial proto-Oort cloud affects the distributions of some orbital elements of interest. The ecliptic inclination iE is fundamental because it is directly related to the effect of planetary scattering. However, it says little about the effect of Galactic tides. We know from Heisler & Tremaine (1986) that the Galactic argument of perihelion ωG is a crucial parameter since according to its value one can say whether the perihelion distance decreases or increases with time. This is due to the integrable characteristics of the tides model. This property has also been highlighted on observed long-period comets by Delsemme (1987) that showed for the first time that observed long-period comets prefer to have a Galactic argument of perihelion in [0°, 90°] and [180°, 270°] just becausein such ranges the perihelion distance is decreasing under the effect of the tides.
The third angle considered here is the Galactic longitude of the ascending node ΩG already taken into account in Sect. 2. Indeed, we see in Fig. 3 that the distribution of ΩG for the comets that remain in the Oort cloud keep a memory of its initial distribution even after four billion years for semi-major axes smaller than 13 200 au. Consequently, it is likely that such a memory is still observed even considering the set of observable comets.
In addition, the distributions of cosiE, ωG and ΩG were computed at two different epochs: for the original orbit at the observable perihelion (using the subscript o), and for the original orbit at the previous perihelion passage (using the subscript p). Figures 7 and 8 show the distributions obtained for the D0 and I0 models, respectively. The distributions for the different classes have also been plotted.
First of all, we note that in any case the distributions are flattened between the previous perihelion and the observable perihelion passage. This can be explained by the two following arguments:
- (i)
At the observable perihelion, the perihelion distance is not necessarily decreasing. This was not the case at the previous perihelion (even though some peculiar cases can always be found). And it explains the fact that almost no comet has
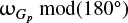 in [90°, 180°], which is not the case for
in [90°, 180°], which is not the case for 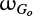 .
. - (ii)
The original orbital elements at the previous perihelion passage determine whether the comet can receive or not a planetary kick. This is crucial for the Kaib–Quinn process to work. At the observable perihelion, the original orbital element has been affected by the planets at the previous perihelion and also by the tides and passing stars during the whole orbital period between the two perihelion passages. Consequently, some of the information leading to the Kaib–Quinn process has been lost.
Let us now discuss the distributions class by class.
-
For the jumpers, any distribution is nearly flat, except for ωG. Indeed, for a comet to be a jumper the perihelion distance must decrease, at least at the previous perihelion passage, whereas iE and ΩG are much less important.
-
For the KQ-jumpers, considering the distribution at the previous perihelion, we note that for the D0 model, the comets are strongly concentrated toward the ecliptic, as it is observed on the
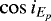 and
and 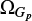 distribution. Because of the large proportion of KQ-creepers, this concentration is still observed on the overall population, even if weakened. At the observable perihelion such a concentration has been significantly erased. It is also remarkable that for the I0 model this concentration is much less pronounced. Hence, this concentration comes not only from the process required for a comet to be a KQ-jumper; in other words, it must have received a planetary kick from Uranus or Neptune at the previous perihelion, which is more likely for trajectories close to the ecliptic, but also, and even mainly, from the memory of the initial conditions.
distribution. Because of the large proportion of KQ-creepers, this concentration is still observed on the overall population, even if weakened. At the observable perihelion such a concentration has been significantly erased. It is also remarkable that for the I0 model this concentration is much less pronounced. Hence, this concentration comes not only from the process required for a comet to be a KQ-jumper; in other words, it must have received a planetary kick from Uranus or Neptune at the previous perihelion, which is more likely for trajectories close to the ecliptic, but also, and even mainly, from the memory of the initial conditions. -
For the creepers, it is observed again on the cosiE distributions that this class of comets has a preference for retrograde orbits. This also induces the small excess of comets with ΩG close to 0° mod(360°) for the I0 model in particular.
-
For the KQ-creepers, as for the creepers, they have a preference for retrograde orbits, but the distribution of cosiE is less concentrated toward −1. For ΩG, the distribution for the I0 model features also an accumulation toward 0° mod(360°), but here again less concentrated than the creeper class. Whereas for the D0 model, the ΩG distribution shows a preference for ΩG < 180° which indicates that this class of comets comes from the region of the Oort cloud with a ≤ 13 200 au, where ΩG is indeed in this range after four billion years as observed in Fig. 3.
-
 |
Fig. 6 Panels a and e: distributions of the original orbital energy z = 1∕a (see text for details). The remaining panels give quantity for four different range of semi-major axes (see text for details). Panels b and f: median of cos iE (black line) and first and third quartiles (boundary of gray area). Panels c and g: proportion of retrograde orbits (black line: all comets, red line: jumpers, blue line: creepers, orange line: KQ-jumpers, magenta line: KQ-creepers). Panels d and h: proportions of comets in each observable class is given (same color code as for the third row). Panels a–d: D0 proto-Oort cloud. Panels e and f: I0 proto-Oort cloud. |
4.4 Comets in the cloud long before they become observable
Clearly observable comets keep the memory of the initial shape of the Oort cloud, mainly in the D0 model. Figures 9 and 10 show the position of the observable comets at t = 3.5 Gyr in different planes superposed on the overall population of the Oort clouds. Because these comets are observable at epochs ranging between 3.75 and 4.75 Gyr, it means that we are looking at the position of the observable comets in the cloud 0.25 to 1.25 Gyr before they become observable. This gives us an idea of how this memory is conserved with time and on the late evolution of the observable comets.
Here again, we discuss the results for each class:
-
For the jumpers, in both cases they are found in the outermost region of the Oort cloud, i.e. for a > 20 000 au. This region may be considered isotropic for both models.
-
The KQ-jumpers on the contrary, occupy a very different region according to the model. For the I0 model, they are found for semi-major axes smaller than 20 000 au. We note that if the majority of them have prograde orbits, they do not accumulate along the ecliptic. For the D0 model, the situation changes completely. Indeed, a large proportion of the future KQ-jumpers are still placed ina kind of extended scattered disk extended until a ≈ 2 000 au, whereas the remaining KQ-jumpers with larger semi-major axes has already started to follow the Galactical perihelion, cycle. When they return to the minimal value of the perihelion, they likely go back to an orbit close to the ecliptic. It then depends on ΩG for such an event to occur, but because we are considering future KQ-jumpers, we know that this is more likely.
-
For the creepers, no structure is clearly seen also because they are less numerous. However, this point means that for the creepers, their final characteristics is mainly caused by the constraint put on the way they become observable rather than from a memory of the initial shape of the Oort cloud.
-
Then for the KQ creepers, in both cases they have semi-major axes generally smaller than 20 000 au. For the I0 model, the only additional feature is that ωG is in the range where the perihelion distance is decreasing under the effect of the integrable Galactic tides model. On the contrary, for the D0 model, one notes that the KQ-creepers are significantly gathered in rather distinctive region for the different orbital elements except for the ecliptic inclination. This means that until t = 3.5 Gyr, their evolution seems to follow rather well the ideal evolution caused by the integrable tides, and thus the memory of the initial shape is still very strong.
 |
Fig. 7 Panels a and d: distributions of cosiE where iE is the ecliptic inclination; panels b and e: distributions of the Galactic argument of perihelion ωG ; panels c and f: distributions of the Galactic longitude of the ascending node ΩG. Panels a–c:original orbit at the observable perihelion passage; panels e–g: orginal orbit at the previous perihelion passage. Foreach plot the black line is for all observable comets, the red line for jumpers, the blue line for creepers, the orange line for KQ-jumpers, and the magenta line for the KQ-creepers. The data are obtained from observable comets from the D0proto-Oort cloud. |
5 Changing the initial orbital energy distribution
5.1 Flux, initial orbital energy, and Oort peak
Here we consider the influence of the initial distribution of orbital energy on the main properties of the flux of observable comets. Figure 11 shows the evolution versus γ of the flux of comets per year, the median, first and third quartiles of the initial semi-major axis, the median, first, and third quartiles of the original semi-major axis at the observable perihelion and the proportion of comets in each class.
For the D models the flux is almost independent of γ, and this confirms the result already obtained in Fouchard et al. (2017). And, as in Fouchard et al. (2017), the unique quantity that is strongly affected by γ is in the initial semi-major axis, where we note that observable comets are initially strongly concentrated toward 500 au when γ increases.
Regarding the original semi-major axis, a weak shift toward smaller original semi-major axes when γ increases is observed. However, this shift is not significant enough to draw any conclusion.
The evolution of the different class proportions is more significant. Indeed, when γ increases, the proportion of jumpers decreases while the proportions of KQ-creepers and KQ-jumpers increase. This tells us that KQ comets have a preference for initially moderate semi-major axis, whereas this is not the case for the jumpers. Indeed, for a jumper to be an observable comet, the key parameter is the semi-major axis that has to be large enough so the tides can sufficiently decrease the perihelion distance. On the contrary, for the KQ comets the key parameter is the planetary kick that they received at the perihelion before they become observable. For this event to occur, a moderate semi-major axis can be advantageous since the comets will make more passages close to the planets. And in fact, we observe in Fig. 9 that about 1 Gyr before KQ comets become observable, they are more concentrated to small semi-major axis (especially KQ-jumpers) rather than jumpers.
For the I models, the evolution of the same parameters with respect to γ is quite different. Indeed, considering an isotropic initial Oort cloud, the main parameter that affects the future evolution is the semi-major axis, and the transport of the semi-major axis for these models is mainly caused by passing stars. Since the major axis has to be large enough for a comet to be observable, and the work to be done by the stars is more important for larger values of γ, it explains why the flux of observable comets is almost divided by 2 for values of γ ranging from 0 to 2. Afterward, the flux increases slightly, but not significantly. It seems that at this point the concentration does not make much difference for the stars to bring the semi-major axis to the outer part of the Oort cloud. Regarding the evolution of median of the original semi-major axis and the proportion of observable comets in the different classes, no significant behavior is observed.
 |
Fig. 9 Density of comets and position of final observable comets in the (q, a) (panel a), (cos iE, a) (panel b), (ωG, a) (panel c) and (ΩG, a) planes (panel d). For each plot, the grayscale gives the density of comets scaled to the whole population as for Fig. 1, and the color dots correspond to the position of the final observable comets. Red points are for jumpers, blue points for creepers, orange points for KQ-jumpers and magenta points for KQ-creepers. Data are obtained from the D0 proto-Oort cloud at t = 3.5 Gyr. |
 |
Fig. 11 Behaviors with respect to γ (exponent of the power law for the initial orbital energy distribution). Panels a and e: flux of observable comets per year (normalized for an initial Oort cloud with 1012 comets. Panels b and f: first, second (black line) and third quartiles for the initial semi-major axis. Panels c and g: first, second (black line) and third quartiles for the original semi-major axis. Panels d and h: proportion of observable comets in each class (red for jumpers, blue for creepers, orange for KQ-jumpers and magenta for KQ-creepers). Panels a–d: disk-like proto-Oort cloud. Panels e–h: isotropic proto-Oort cloud. |
5.2 Initial perihelion distance for the D0 and D8 models
Here we make some specific remarks about the initial values of the perihelion distances for the observable comets for the disk-like proto-Oort clouds. Figure 12 shows the distributions of the initial perihelion distance for the observable comets for the D0 and the D8 models. The distributions are computed for the whole sample and for each class of observable comets.
The contribution of the region between 30 and 40 au is clearly the major one (36% for the D0 model and 38% forthe D8 model). Beyond 40 au, the contribution decreases drastically. This can be explained by the fact that planetary scattering, which is the key mechanism for transport of orbital energy, has an efficiency that is drastically decreasing beyond 40 au (Torbett & Smoluchowski 1990; Gladman et al. 2002).
Inside Neptune’s orbit, the contribution to the final production of observable comets is increasing with the initial perihelion distance to the Sun. The increase seems to be steeper for the D8 model than for the D0 model. However, one has to be careful about this difference: for instance, the large increase for the contribution to creepers for 20 < qi < 25 au is coming from a single comet whose weight has been increased by several orders between the D0 and the D8 models, whereas only seven creeper objects are found in this bin.
It is remarkable that the initial perihelion distance appears to affect the final observing class of the comets: if jumpers seem to come evenly throughout our all range of initial perihelion distance, the KQ comets (either creepers or jumpers) are more commonly coming from the Uranus–Neptune region and even more from the region beyond Neptune, the so-called extended scattered disk (Gladman et al. 2002). The creepers show the same pattern, butto a lesser extent. Such a memory of the initial perihelion distance was also highlighted in Paulech et al. (2010) but it was more closely related to the formation of the inner-Oort cloud itself rather than to the flux of observable comets and mainly affects the efficiency of the formation itself rather than the structure of the inner cloud.
For our work, the explanation for these preferences is the same as for the initial semi-major axis. A KQ comet needs to receive a planetary kick at the perihelion one orbital period before the observable perihelion. While the comet is waiting for this planetary kick it has to remain under the control of the planets (at least for some periods) without being ejected for the cloud. A perihelion between Neptune’s orbit and about 40 au from the Sun is clearly the preferred region.
 |
Fig. 12 Initial perihelion distance distribution for all observable comets (black line) and for the four different observable classes: red for jumpers, blue for creepers, orange for KQ-jumpers and magenta for KQ-creepers. Top panel is for the D0 model and bottom panel is for the D8 model. |
6 Conclusions
We carried out long-term simulation of tens of millions of objects in two different kinds of initial proto-Oort cloud. The first had an initial shape more consistent with an Oort cloud born from the scattering of objects caused by passing stars when the Sun was still in its birth stellar cluster. This means that the trajectories of the objects have been randomized in such a way that the cloud can be considered fully thermalized (Hills 1981). The second is more consistent with objects scattered by the giant planets and consists in an initial population with small inclination and perihelion distance inside or close to the planetary region of the solar system.
In the case of the fully thermalized proto-Oort cloud, one can consider that any memory of how the cloud formed has been already wiped out by the stellar cluster. And in fact, the cloud did not exhibit any evolution at any distance from the Sun (except for semi-major axes smaller than 500 au). Consequently, one can consider the results from this simulation as the typical situation where the long-term evolution of comets into the cloud and the inherent flux of observable comets hold no trace of memory of their initial condition.
On the contrary, it appears that for the initial disk-like population, the memory of the initial shape is still present over the whole simulation, that lasts 4 Gyr, for semi-major axes that are smaller than 13 200 au. The two main features coming from this memory are as follows: (i) a concentration of comets along the ecliptic plane for semi-major axes smaller than 7000 au, and (ii) beyond this and before the isotropic region, the typical wave structure coming from the Galactic tides action on an initial disk of objects (Higuchi et al. 2007).
Considering the final flux of observable comets, we have seen that the initial disk-like population induces a flux that is four to eight times higher than the isotropic initial population according to the initial energy distribution used. From these data alone can one conclude that an Oort cloud formed through stellar scattering, at least as far as the flux of observable comets is concerned. In addition, Nordlander et al. (2017) showed that the Oort cloud would not survive in a relatively rich stellar cluster except an inner shell. But in this case the inner shell could be isotropic, which may be a problem for the final flux of observable comets. The scenario proposed in Brasser & Morbidelli (2013) with an Oort cloud formed from a late migration of the giant planets once the Sun has left the cluster seems to be more viable with the present flux. However, in the case where this late migration was not so late, as proposed by Kaib & Chambers (2016), the birth cluster should be much less massive (hundreds of stars) in order that the cluster dispersed before the migration occurred.
Such conclusions are driven only from the number of observable comets per year, which is not a big constraint. However, from our numerical results, it turns out that a detailed investigation on the properties of the known new long-period comet could give a much better suggestion of the scenario that leads to the formation of the Oort cloud.
Indeed, one of the major results of the present study is considering the so-called KQ jumpers. The fingerprint of their initial position is still strongly present with an accumulation of the longitude of the Galactic ascending node and ecliptic inclination at previous perihelion that accumulate respectively toward 180° and 0°. Indeed, it appears that about 1 Gyr before the observable perihelion this class of comets is still strongly concentrated in an extended scattered disk that is the remnant of the initial population. Such a long-term memory is still also present in the KQ-creepers. But KQ-creepers need mainly to avoid planetary scattering from the Jupiter and Saturn so as not to be ejected from the Oort cloud. Consequently, they have a preference for retrograde orbits, which makes it difficult to make a distinction between KQ-creepers from an initial isotropic population and KQ-creepers from an initial disk-like population.
A special investigation was made on the initial perihelion distance of observable comets for the initial disk-like population. It appears that the region between Neptune and 40 au gives the major contribution to the flux of observable comets. Because of the stability of this region, comets can remain there for billions of years before a major perturbation by Neptune places them on track to the observable region.
In conclusion, it appears that the long-term dynamics of the Oort cloud involved by the Galactic tides, passing stars and planetary perturbations are such that a memory of the initial shape of the population is still present even in the flux of observable long-period comets after4 Gyr. A careful investigation of the known long period comets properties, could give us a key to how the Oort cloud was formed, as could the reconstruction of their orbit at the previous perihelion passage. Obviously, we do not hope to be able to identify among known long-period comets the class they belong to. Indeed, at the present time we are unable to reproduce the real stellar perturbations during the last orbital period of known comets, and the determination of the original orbital energy is subject to different kinds of errors (eventual non-gravitational forces, a small arc of the trajectory is observed). However, we know that a KQ-jumper has its previous perihelion in the region of Uranus and Neptune, creepers (KQ or not) in the Jupiter–Saturn region, and a comet with a previous perihelion beyond the planetary region is certainly a jumper. Even if the uncertainties concerning the previous perihelion distance coming from the two above sources of error introduce a significant noise, using such a criterion should help to highlight an imprint of the initial shape of the Oort cloud if any. This is not straightforward and will be the content of our forthcoming papers.
Finally, the effect of a massive planet in the innermost part of the cloud as suggested by Batygin & Brown (2016) should be investigated. Indeed, Nesvorný et al. (2017) shows that such a planet would significantly affect the extended scattered disk. Then, the question of whether the memory of the initial shape is still conserved naturally arises. We will also deal with this subject in our forthcoming publications.
Acknowledgements
This work was partly supported by the JSPS Kakenhi Grant (JP25400458 and JP16K05546), and by the Programme National de Planétologie (PNP) of CNRS/INSU, co-funded by CNES. Some part of the numerical integration was performed at CfCA, NAOJ. We would like to thank the reviewer Julio A. Fernández and the editor Tristan Guillot for constructive comments on improving this manuscript.
References
- Batygin, K., & Brown, M. E. 2016, AJ, 151, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Brasser, R., & Morbidelli, A. 2013, Icarus, 225, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Brasser, R., & Schwamb, M. E. 2015, MNRAS, 446, 3788 [NASA ADS] [CrossRef] [Google Scholar]
- Brasser, R., Duncan, M. J., & Levison, H. F. 2006, Icarus, 184, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Brasser, R., Duncan, M. J., Levison, H. F., Schwamb, M. E., & Brown, M. E. 2012, Icarus, 217, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Breiter, S., & Ratajczak, R. 2005, MNRAS, 364, 1222 [NASA ADS] [CrossRef] [Google Scholar]
- Byl, J. 1986, Earth Moon and Planets, 36, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Delsemme, A. H. 1987, A&A, 187, 913 [NASA ADS] [Google Scholar]
- Duncan, M., Quinn, T., & Tremaine, S. 1987, AJ, 94, 1330 [NASA ADS] [CrossRef] [Google Scholar]
- Duncan, M. J., & Levison, H. F. 1997, Science, 276, 1670 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fernández, J. A. 2002, in Asteroids, Comets, and Meteors: ACM 2002, ed. B. Warmbein, ESA SP, 500, 303 [NASA ADS] [Google Scholar]
- Fernández, J. A., & Brunini, A. 2000, Icarus, 145, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Fouchard, M., Froeschlé, C., Rickman, H., & Valsecchi, G. B. 2011a, Icarus, 214, 334 [NASA ADS] [CrossRef] [Google Scholar]
- Fouchard, M., Rickman, H., Froeschlé, C., & Valsecchi, G. B. 2011b, A&A, 535, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fouchard, M., Rickman, H., Froeschlé, C., & Valsecchi, G. B. 2013, Icarus, 222, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Fouchard, M., Rickman, H., Froeschlé, C., & Valsecchi, G. B. 2014, Icarus, 231, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Fouchard, M., Rickman, H., Froeschlé, C., & Valsecchi, G. B. 2017, Icarus, 292, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Francis, P. J. 2005, ApJ, 635, 1348 [NASA ADS] [CrossRef] [Google Scholar]
- Gallardo, T., Hugo, G., & Pais, P. 2012, Icarus, 220, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Gladman, B., Holman, M., Grav, T., et al. 2002, Icarus, 157, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Heisler, J., & Tremaine, S. 1986, Icarus, 65, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Higuchi, A., & Kokubo, E. 2015, AJ, 150, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Higuchi, A., Kokubo, E., Kinoshita, H., & Mukai, T. 2007, AJ, 134, 1693 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Hills, J. G. 1981, AJ, 86, 1730 [NASA ADS] [CrossRef] [Google Scholar]
- Kaib, N. A., & Chambers, J. E. 2016, MNRAS, 455, 3561 [NASA ADS] [CrossRef] [Google Scholar]
- Kaib, N. A., & Quinn, T. 2008, Icarus, 197, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Kaib, N. A., & Quinn, T. 2009, Science, 325, 1234 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Leto, G., Jakubík, M., Paulech, T., Neslušan, L., & Dybczyński, P. A. 2008, MNRAS, 391, 1350 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H. F., Dones, L., & Duncan, M. J. 2001, Astron. J, 121, 2253 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H. F., Duncan, M. J., Dones, L., & Gladman, B. J. 2006, Icarus, 184, 619 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H., Duncan, M., Brasser, R., & Kaufmann, D. 2010, Science, 329, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H. F., Morbidelli, A., Tsiganis, K., Nesvorný, D., & Gomes, R. 2011, AJ, 142, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., Vokrouhlický, D., Dones, L., et al. 2017, ApJ, 845, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Nordlander, T., Rickman, H., & Gustafsson, B. 2017, A&A, 603, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oort, J. H. 1950, Bull. Astron. Inst. Neth., 11, 91 [Google Scholar]
- Paulech, T., Jakubík, M., Neslušan, L., Dybczyński, P. A., & Leto, G. 2010, A&A, 509, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rickman, H., Fouchard, M., Froeschlé, C., & Valsecchi, G. B. 2008, Celest. Mech. Dyn. Astron., 102, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Saillenfest, M., Fouchard, M., Tommei, G., & Valsecchi, G. B. 2017, Celest. Mech. Dyn. Astron., 127, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Torbett, M. V., & Smoluchowski, R. 1990, nature, 345, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Wiegert, P., & Tremaine, S. 1999, Icarus, 137, 84 [NASA ADS] [CrossRef] [Google Scholar]
For the planetary perturbations, they are applied when a comet passes at less than 70 au from the Sun and computed on the portion of the orbit at less than 250 au from the Sun. These two parameters are different from those used in Fouchard et al. (2014).
Changes in the evolution of aisot might be related to a very close stellar encounters that occur around 650 Myr and 3 Gyr. For details on this stellar sequence, it corresponds to the stellar sequence #2 in Fouchard et al. (2017).
All Tables
All Figures
 |
Fig. 1 From top to bottom panels: distribution of comets in (a, q), (a, cos (iE), (a, ωG) and (a, ΩG) planes at four different epochs t = 250 Myr and 1, 2 and 4 Gyr. For visibility, the bin sizes are constant along any axis. However, the density function is computed in number of comets per au for the perihelion distance and per au−1 for the semi-major axis. The data come from the evolution of the I0 proto-Oort cloud. |
| In the text | |
 |
Fig. 2 Top panel: evolution of the median |
| In the text | |
 |
Fig. 3 As Fig. 1 but for the D0 proto-Oort cloud. |
| In the text | |
 |
Fig. 4 As Fig. 2 but for the D0 proto-Oort cloud. |
| In the text | |
 |
Fig. 5 Upper panel: evolution of aisot with time for the D0 model. Lower panel: evolution versus time of the power law exponent for the best fit to the orbital energy distribution for 5000 < a < 30 000 au (black line) and for aisot < a < 30 000 au (gray line). |
| In the text | |
 |
Fig. 6 Panels a and e: distributions of the original orbital energy z = 1∕a (see text for details). The remaining panels give quantity for four different range of semi-major axes (see text for details). Panels b and f: median of cos iE (black line) and first and third quartiles (boundary of gray area). Panels c and g: proportion of retrograde orbits (black line: all comets, red line: jumpers, blue line: creepers, orange line: KQ-jumpers, magenta line: KQ-creepers). Panels d and h: proportions of comets in each observable class is given (same color code as for the third row). Panels a–d: D0 proto-Oort cloud. Panels e and f: I0 proto-Oort cloud. |
| In the text | |
 |
Fig. 7 Panels a and d: distributions of cosiE where iE is the ecliptic inclination; panels b and e: distributions of the Galactic argument of perihelion ωG ; panels c and f: distributions of the Galactic longitude of the ascending node ΩG. Panels a–c:original orbit at the observable perihelion passage; panels e–g: orginal orbit at the previous perihelion passage. Foreach plot the black line is for all observable comets, the red line for jumpers, the blue line for creepers, the orange line for KQ-jumpers, and the magenta line for the KQ-creepers. The data are obtained from observable comets from the D0proto-Oort cloud. |
| In the text | |
 |
Fig. 8 As Fig. 7 for observable comets obtained from the I0 proto-Oort cloud. |
| In the text | |
 |
Fig. 9 Density of comets and position of final observable comets in the (q, a) (panel a), (cos iE, a) (panel b), (ωG, a) (panel c) and (ΩG, a) planes (panel d). For each plot, the grayscale gives the density of comets scaled to the whole population as for Fig. 1, and the color dots correspond to the position of the final observable comets. Red points are for jumpers, blue points for creepers, orange points for KQ-jumpers and magenta points for KQ-creepers. Data are obtained from the D0 proto-Oort cloud at t = 3.5 Gyr. |
| In the text | |
 |
Fig. 10 As Fig. 9 for data obtained from the T0 proto-Oort cloud for t = 3.5 Gyr. |
| In the text | |
 |
Fig. 11 Behaviors with respect to γ (exponent of the power law for the initial orbital energy distribution). Panels a and e: flux of observable comets per year (normalized for an initial Oort cloud with 1012 comets. Panels b and f: first, second (black line) and third quartiles for the initial semi-major axis. Panels c and g: first, second (black line) and third quartiles for the original semi-major axis. Panels d and h: proportion of observable comets in each class (red for jumpers, blue for creepers, orange for KQ-jumpers and magenta for KQ-creepers). Panels a–d: disk-like proto-Oort cloud. Panels e–h: isotropic proto-Oort cloud. |
| In the text | |
 |
Fig. 12 Initial perihelion distance distribution for all observable comets (black line) and for the four different observable classes: red for jumpers, blue for creepers, orange for KQ-jumpers and magenta for KQ-creepers. Top panel is for the D0 model and bottom panel is for the D8 model. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\[ C=\frac{z_{\textrm{max}}-z_{\textrm{min}}}{|z_{\textrm{min}}|^{\gamma+1}-|z_{\textrm{max}}|^{\gamma+1}}, \]](/articles/aa/full_html/2018/12/aa33435-18/aa33435-18-eq10.png)