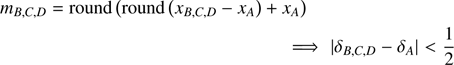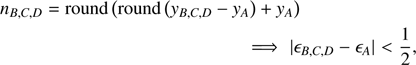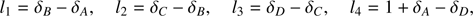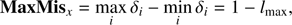| Issue |
A&A
Volume 619, November 2018
|
|
|---|---|---|
| Article Number | A56 | |
| Number of page(s) | 13 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201833685 | |
| Published online | 06 November 2018 | |
Assessing and mitigating alignment defects of the pyramid wavefront sensor: a translation insensitive control method
1
LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Univ. Paris Diderot, Sorbonne Paris Cité, 5 place Jules Janssen, 92195 Meudon, France
e-mail: vincent.deo@obspm.fr
2
GEPI, Observatoire de Paris, Université PSL, CNRS, 5 place Jules Janssen, 92195 Meudon, France
Received:
20
June
2018
Accepted:
20
August
2018
The pyramid wavefront sensor (PWFS) is the currently preferred design for adaptive optics (AO) systems for extremely large telescopes, as focal plane wavefront sensing bears potential for a large intrinsic sensitivity gain when compared to Shack–Hartmann (SH) sensors. Yet, obtaining a high quality pyramidal prism and a model-consistent assembly remains a critical design factor. We demonstrate that the traditional gradient sensing controller is extremely sensitive to prism shape defects and assembly misalignments. We show that even optimal registration of quadrants on the detector may be insufficient to prevent misalignment induced performance loss through a theoretical analysis of the impact of detection plane quadrants sampling errors and individual translations, which may be induced by a variety of mechanical defects. These misalignments displace wavefront information to terms not included in the conventional gradient-like slopes maps and high spatial frequencies become invisible to the sole X− and Y− axis differences. We introduce expanded space control (ESC) for quad-cell signal by generalizing output measurements of the PWFS and demonstrate its insensitivity to misalignment-induced information loss, therefore dramatically relaxing machining and alignment constraints for PWFS engineering. This work presents the theoretical developments leading to ESC design, along with validating performance and robustness results, both in end-to-end numerical simulations and on a PWFS demonstrator bench at LESIA.
Key words: instrumentation: adaptive optics / techniques: high angular resolution / telescopes
© ESO 2018
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
This paper presents novel research about pyramid wavefront sensor (PWFS; Ragazzoni 1996) control, conducted within the MICADO SCAO module (Davies et al. 2010; Clénet et al. 2014) development at LESIA. Developing a PWFS-based adaptive optics (AO) system with more than 80 × 80 pupil points resolution for the European Extremely Large Telecope (the ELT) brings up unprecedented scalability challenges to state-of-the-art focal plane sensing, making of paramount importance the current effort to gather experience, data, and thorough knowledge of PWFSs. Since its introduction, the PWFS was demonstrated to provide a valuable sensitivity increase over equivalent Shack–Hartmann (SH) sensors (Ragazzoni & Farinato 1999; Esposito et al. 2010). However, theoretical and experimental developments on the PWFS remain an active and open research topic. Knowledge of modulation impact (Ragazzoni et al. 2002b), signal normalization, edge-diffracted photons usage (Vérinaud 2004), theoretical models (Shatokhina 2014; Fauvarque et al. 2016a,b), optimal modal control (Gendron & Léna 1994; Korkiakoski et al. 2008a; Deo et al. 2018), or phase reconstruction algorithms do not yet converge into a unique, well-established set of operation guidelines.
This paper presents a possible improvement to PWFS control, called expanded space control (ESC). Through expanding the dimension of the sensor data space, ESC provides an operating mode that is robust to independent translations of the four sensor quadrants and therefore to several PWFS defects. First, Sect. 2 describes in detail the mathematics of extracting PWFS signal from the detector and a generalized formalism to describe different preprocessing options. Section 3 covers how pyramid prism defects propagate into detector plane misalignments and why models requiring well-defined subapertures do not hold for PWFS. Section 4 covers a statistical analysis of misalignment distribution and proposes an optimal method to preselect detector data given the misalignment. Sections 5 and 6 introduce an approach similar to system transfer function (TF) to shed light on the reconstruction completeness issue with conventional control and ESC, and propose quantitative figures of merit for design risk assessment. Finally, Sect. 7 presents end-to-end performance results, depending on signal normalization and misalignment, through simulations with the COMPASS software (Gratadour et al. 2014; Carlotti et al. 2014), and end-to-end runs on a laboratory demonstrator bench.
2. Measurements of the pyramid wavefront sensor
Imaging the telescope pupil, or an altitude layer meta-pupil in layer-oriented AO (Ragazzoni et al. 2002a), through a PWFS or a conceptually similar focal plane optical design (Horwitz 1994; Gendron et al. 2010) generates four pupil-like images (quadrants) in the detection plane, as shown in Fig. 1. These quadrants can generally be assumed to be optically independent, for example, when using a focal-point splitting prism with sufficient angular deviation (Fauvarque et al. 2016b). Pupil quadrant intensity maps ARaw, BRaw, CRaw, and DRaw, referred to as “Raw” before preprocessing, are extracted by selecting geometrically relevant areas of the detection plane and cropping to the illuminated pupil-shaped quadrant area as follows:
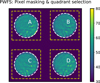 |
Fig. 1. Typical observation on the PWFS detector – here on the laboratory bench–, illustrating a priori requirements for the pixel mask. White: conventional control requires subpixel precision in estimating contours and centers of quadrants. Yellow: with ESC, an estimated selection zone containing all illuminated pixels of each quadrant is sufficient. Irrelevant pixels can be eliminated from the selection zone afterward. |
where (xi, yi)i = A, B, C, D are quadrants geometrical centers and I(x, y) is the spatially continuous intensity map in the detection plane. Quadrant intensities ARaw, BRaw, CRaw, DRaw(x, y) are binned and discretized by the detector pixel matrix into two-dimensional matrices •[m, n], which we alternately consider in a vectorized form •[k], i.e., as a list of pixel values, possibly restricted only to a subset of sufficiently illuminated pixels. Valid [m, n] (or [k]) indices are defined by the selected pixel/subaperture mask, which must be identical for all four quadrants, as shown in Fig. 1. We inherit the term of subaperture from its usual acceptance with SH sensors: the projected footprint of the [m, n] pixel of each quadrant in the entrance pupil, although it must be assumed those four footprints are identical.
Different approaches exist to process the quadrant pixels into meaningful measurements. First, the quadrants need to be normalized: the “local” normalization (noted •Loc), originally introduced by Ragazzoni (1996), proposes normalizing by the total intensity per subaperture as follows:
so as to bring a convenient closed form expression for relevant measurements (Eq. (5)) within the ray optics modelization of the PWFS. Another normalization method, referred to as the “global” method hereafter (noted •Glob) was first proposed by Vérinaud (2004), using the spatially averaged intensity,
where ⟨X[k]⟩k is the average of vector X over all indices k. This normalization was motivated by more recent small-signal linearized models of the PWFS, and is now widely adopted in the community. Normalized quadrants, either local or global, are
In this formalism, the traditional gradient-like measurements along the axes are therefore noted XLoc, YLoc or XGlob, YGlob depending on the normalization. The derivation in the ray optics approximation in Ragazzoni (1996) establishes the relationship between the continuous measurements XLoc, YLoc and the gradient of the wavefront in the pupil,
where δ(x, y) is the optical path difference in the entrance pupil and α is the circular modulation half-angle. This leads to consider in discretized space,
to obtain, assuming derivation approximations and leaving discretization aside, a sensible measurement of 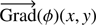 .
.
We propose generalizing measurement methods by considering additional terms beyond gradient-like XLoc/Glob and YLoc/Glob. ESC (Deo et al. 2017) of the PWFS considers sensor output to be a combination of the former X, Y terms with two newly defined terms: a cross-coupling term ZLoc/Glob and an intensity term FLoc/Glob, defined by the following linear transform:
The typical structure of these four ESC measurements is shown in Fig. 2, for a perfectly aligned PWFS (top) and a misaligned system (bottom). The example in Fig. 2 is obtained from interaction matrices of end-to-end simulations, whose setups and parameters are covered in detail in Sect. 7.1.
 |
Fig. 2. Simulated small-signal differential response (interaction matrix measurement) of the PWFS in the four ESC measurement maps for 3 aberrations: tilt (left), spherical (center), and higher frequency Karhunen–Loëve #103 (right). Top row: the system is perfectly aligned and differential signals in ZGlob and FGlob are zero. Bottom row: exaggerated misalignment case (up to ≈5% of pupil diameter for each quadrant), illustrating how information is now spread across all four X, Y, Z, FGlob ESC measurements. |
This formalism allows us to define a variety of measurement computation options; possibly any combination of terms A, B, C, D and X, Y, Z, F with either local or global normalization. A synthesis of end-to-end performance with various PWFS measurements is presented in Sect. 7.2. In this section we obtain results for an ideal PWFS with perfect alignment, using the end-to-end AO simulator COMPASS (Gratadour et al. 2014) and we conclusively validate the superior performance of global measurement methods over local measurement methods, or XYLoc, Sine (Eq. (6)), at all illuminations.
3. Misalignments of pyramid quadrants
Theoretical models of the PWFS usually rely on matching •[m, n] quadrant pixels to be exactly superimposed, i.e., in a comparison with a quad-cell SH, such that they correspond to a given well-defined subaperture (Sect. 2). However, the PWFS optical concept introduces additional degrees of freedom due to both machining and alignment uncertainties, which do not have equivalents in the quad-cell SH framework, such as independent translations of each of the four quadrants with respect to the detector sampling. This study thoroughly covers this case, and leaves aside other potential effects such as differential pupil magnification, rotation, or distortion, which we believe to be at worst of a second order, if not non-existent, in classical refractive optical designs. With these restrictions stated, we believe that the conclusions of this research should apply to those defects as well were they to be encountered in some hypothetical future experimental design. The schematics in Fig. 3 synthesize how archetypal pyramid apex defects introduce quadrant translations and modify the intensity at the PWFS zero aberration operating point, thus introducing signals unphysical to a perfect PWFS.
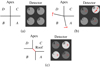 |
Fig. 3. Schematic representations of common defects on the prism apex and their impact on quadrant positioning. Panel a: nominal design of the pyramid apex: quadrants lie on a perfect square, although the side length of the square needs not match an integer multiple of the pixel size. Panel b: polishing angle of facet B is excessive, shifting outward edges of facet B; quadrant B is moved away from the optical axis and receives more flux, whereas A and D receive less. Panel c: facet polishing depth is unequal, creating a roof apex. Intensities at zero-phase point are modified. |
Even with major effort given to machining pyramidal prisms with the greatest precision, the latest investigations (Pinna et al. 2017) report quadrant positioning up to a precision of only ≈1% of the pupil diameter, which still represents a significant portion of a subaperture for ELT-sized PWFS designs. For that reason, we assume that risk mitigation procedures are required on the basis of lack of accurate subpixel positioning capability of the quadrants.
After the translation and cropping process (Eq. (1)), quadrants are sampled and discretized by the pixel matrix. We define the “true” quadrants as the would-be measurements if the quadrant centers (xi, yi)i = A, B, C, D were to lie exactly at the center of pixels, defining the following discretization:
and similarly for quadrants B, C, and D, where Π(x, y) is the unit rectangular function (Π(x, y)=1 if |x| <  and |y| <
and |y| < 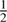 ; 0 otherwise), and assuming a lattice of identical, square pixels completely covering the detector surface. However, as geometrical centers need not match any pixel center, the actual measurement becomes
; 0 otherwise), and assuming a lattice of identical, square pixels completely covering the detector surface. However, as geometrical centers need not match any pixel center, the actual measurement becomes
where [mi, ni]i = A, B, C, D are the indices of the detector pixel retained as approximate center for quadrant i. The idealized versus actual pixel sampling issue is illustrated in Fig. 4a, and the misalignment-inducing decision issue that arises with a second quadrant in Fig. 4b.
 |
Fig. 4. Schematized selection of the detector pixels corresponding to the centers of the first two quadrants A and B. Information is priorly obtained that (xA, yA)=(37.57, 41.84) and (xB, yB)=(120.33, 41.42) for this example. Panel a: idealized [0, 0] central pixel for quadrant A (red) and nearest detector pixel (black) chosen as [0, 0] reference. Panel b: at the center of quadrant B; red: idealized [0, 0] pixel for quadrant B; black: subaperture footprint of the [0, 0] pixel chosen for quadrant A; blue and green: possible pixel choices for [0, 0] of B: pixel “1” (blue) minimizes absolute misalignment (|δB|,|ϵB|), whereas pixel “2” (green) minimizes the differential misalignment (|δB − δA|,|ϵB − ϵA|). Solid grid on panels a and b: detector pixel boundaries. |
We define the following quantity for all quadrants:
which is not a misalignment indicator yet, but the offset between the geometric centers of quadrants (xi, yi) and the coordinates [mi, ni] on the pixel matrix considered as such. We establish the link between these offsets and misalignment quantities in the following sections.
The importance of selecting appropriate central pixels to have subaperture-like correspondence when processing quadrants into measurement maps is critical and is discussed in detail in Sect. 5. Selection methods given knowledge of the center (xi, yi) are discussed below in Sect. 4, looking toward (a) an optimal way to select the central pixels (mi, ni) and (b) indicators of worst and average-case scenarios for random alignment configurations.
4. Pixel selection and misalignment distributions
Beyond the opto-mechanical causes of PWFS quadrant translations, the question arises of how to perform pixel selection – computing [mi, ni] – to obtain the smallest amount of misalignments (δi, ϵi), and the best possible PWFS operating conditions. Working hypotheses are that (1) we assume a design where no extensive mechanical or optical effort was undertaken to guarantee subpixel quadrant positioning, and therefore the fractional parts of (xi, yi) are uniformly distributed and (2) quadrant positions in the detecting planes (xi, yi) are accurately measured.
We quantify the amount of misalignment in the system with the maximum position difference between any two quadrants, on a single axis and on both axes, as follows:
and we use this metric in the next paragraphs, where we analyze three pixel selection methods, comparing their performance regarding the distribution of MaxMis on average and worst case scenarios.
Naive approach. The most common approach for finding central pixels, referred to as the naive method thereafter, is to simply round off each quadrant’s center independently to the nearest detector pixel,
which leads to δi, ϵi uniformly distributed in [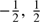 ]. As illustrated in Fig. 4b, this method may lead to suboptimal pixel choices starting with two quadrants: the naive method makes selection of pixel “1”, while choosing pixel “2” allows for reduced MaxMis values on both axes. This early arising issue with pixel selection in terms of differential quadrant misalignment appears striking enough to justify seeking more suitable techniques.
]. As illustrated in Fig. 4b, this method may lead to suboptimal pixel choices starting with two quadrants: the naive method makes selection of pixel “1”, while choosing pixel “2” allows for reduced MaxMis values on both axes. This early arising issue with pixel selection in terms of differential quadrant misalignment appears striking enough to justify seeking more suitable techniques.
Reference quadrant method. The reference quadrant method consists in selecting an arbitrary quadrant, for example, A, to round off (xi, yi)i = B, C, D in the idealized pixel frame of quadrant A, and finally replacing quadrants on the pixel grid of the detector by a common translation. It is therefore guaranteed that misalignments are less than 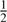 px with the reference quadrant,
px with the reference quadrant,
but yet misalignments between non-reference quadrants may remain larger than  px. While misalignments are statistically smaller than with the naive method (Table 1) the upper bound MaxMis ≤ 1 remains unchanged.
px. While misalignments are statistically smaller than with the naive method (Table 1) the upper bound MaxMis ≤ 1 remains unchanged.
Optimal method. We propose an optimal method to obtain [mi, ni] values systematically minimizing MaxMis, whose implementation and proof of optimality are detailed in Appendix A. With optimal pixel choice, the upper bound is reduced to  , reached only for evenly-spaced cases,
, reached only for evenly-spaced cases,
demonstrating worst-case PWFS alignment scenarios with a pair of quadrant having  px relative misalignment.
px relative misalignment.
Using David & Nagaraja (2005), we derived analytical distributions for MaxMisx, y and MaxMisboth ax., for all three methods with results synthesized in Fig. 5 and Table 1. In particular for the optimal method, we obtain:
 |
Fig. 5. Probability density functions (pdf) for top: MaxMisx, y and bottom: MaxMisboth ax. for pixel centering performed with naive, reference quadrant (qref.) or optimal methods (opt.). Solid (dashed) vertical lines highlight the average (median) of the corresponding pdf. Opt. and qref. pdfs overlap below 0.5, which is their common single-axis median. |
showing that even with optimized pixel selection, a misalignment of  px or more along either axis is to be expected and accounted for in PWFS operation. This underlines not only the importance of assessing the performance impact of such misalignments, but also of proposing risk mitigating methods regarding those impacts.
px or more along either axis is to be expected and accounted for in PWFS operation. This underlines not only the importance of assessing the performance impact of such misalignments, but also of proposing risk mitigating methods regarding those impacts.
5. Misalignments: an analytical transform
5.1. Definition
As mentioned in Sects. 1 and 2, several models have been established around the PWFS since its introduction (Ragazzoni 1996; Vérinaud 2004; Shatokhina et al. 2013; Shatokhina 2014; Fauvarque et al. 2016a). Although it is beyond the scope of this paper to discuss the analytical validity of these models, we briefly summarize our hypotheses in this matter as follows: that the signals 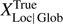 and
and 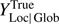 are (1) direction-sensitive operators along the axes, which may be linearized in a small signal regime compatible with AO closed loop operation and (2) contain sufficient information to perform a complete and unambiguous (besides piston mode) phase reconstruction. This latter point has been recently demonstrated in Fauvarque et al. (2016a) in the small-signal context: XTrue and YTrue signals contain all available phase information, whereas ZTrue and FTrue small-signal linearizations are analytically null, and thus convey no information. This demonstration however holds only if (1) the pyramidal apex is ideal and (2) quadrants are ideally sampled and referenced, i.e., if MaxMisboth ax. = 0.
are (1) direction-sensitive operators along the axes, which may be linearized in a small signal regime compatible with AO closed loop operation and (2) contain sufficient information to perform a complete and unambiguous (besides piston mode) phase reconstruction. This latter point has been recently demonstrated in Fauvarque et al. (2016a) in the small-signal context: XTrue and YTrue signals contain all available phase information, whereas ZTrue and FTrue small-signal linearizations are analytically null, and thus convey no information. This demonstration however holds only if (1) the pyramidal apex is ideal and (2) quadrants are ideally sampled and referenced, i.e., if MaxMisboth ax. = 0.
We show that when either condition above fails – thus inducing unforeseen independent translations of the quadrants – information is shifted out from X and Y signals into ZMeas. and FMeas.. Let us express the relationship between idealized quadrants and actual measurements before pixel discretization occurs; we can express the translation of each quadrant (with abusive notations),
but this relationship does not conveniently transform through pixel discretization. However, taking the spatial Fourier transform of Eq. (16) (strictly, of Eqs. (8) and (9)), a relationship is obtained that also expresses conveniently after discretization as
where f̂(u, v) is the two-dimensional discrete space Fourier transform of f[m, n] (zero-padded at will), and u, v are spatial frequencies in ![$ [-\frac{1}{2},\,\frac{1}{2}]\,\mathrm{px}^{-1} $](/articles/aa/full_html/2018/11/aa33685-18/aa33685-18-eq29.gif) . Using the P transform (Eq. (7)) between normalized quadrants and ESC measurements X, Y, Z, and F, and using
. Using the P transform (Eq. (7)) between normalized quadrants and ESC measurements X, Y, Z, and F, and using 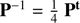 , we obtain:
, we obtain:
where Δ is the complex linear phasor corresponding to quadrant translations
The complex-valued, Fourier domain M̂is transformation (Eq. (18)) provides us with a block-wise TF from the four perfect alignment measurements •True to the PWFS actual measurements •Meas.. The M̂is operator is a unitary transform at all frequencies with specific structure,
and with coefficients additionally verifying |p + q + r + s|(u, v)=1 for any frequency (u, v). Additionally, each of the terms is Hermitian in (u, v), for example, p(−u, −v)=conj(p(u, v)).
5.2. Simulated impact on real AO systems
We present numerical demonstrations of the impact of M̂is on PWFS measurements through a numerical simulation on a realistic AO design. System parameters are similar to those presented in Table 3 of an 18 m telescope with a 39 × 39 deformable mirror (DM). In this section only, the PWFS follows exact Fried geometry, i.e., with an actuator placed at each pixel corner in order to obtain identically sized PWFS and DM Nyquist domains for the sake of clarity. We use more realistic PWFS configurations starting at the end of Sect. 6. Using this system, we measure the response of the PWFS to each spatial frequency through interaction matrices over Fourier modes of the DM, thus computing a pseudo-TF between the input phase and measurement terms. This small signal TF on all four components X, Y, Z, F is shown in Fig. 6, illustrating the alteration of measurements when the system suffers quadrant misalignments. For this example, a misalignment scenario with MaxMis = 0.75 px was chosen in compliance with Eq. (14), specifically,
 |
Fig. 6. Simulated TF of the PWFS in the four measurement terms, (top) without misalignment and (bottom) with MaxMis = 0.75 as per Eq. (21). All 8 heat maps are shown over the Nyquist domain of the system, i.e. |
Numerical simulations of the response confirm no information is within the small signal approximations of 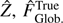 (Fig. 6, top), well validating the theoretical demonstrations in Fauvarque et al. (2016a). We note that the nullity of
(Fig. 6, top), well validating the theoretical demonstrations in Fauvarque et al. (2016a). We note that the nullity of 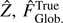 – both from the theoretical developments and from all simulations we conducted without misalignment – is completely independent of the system design, including the modulation radius used, as long as a perfect four-faced PWFS is used. On the other hand, misalignments (Fig. 6, bottom) induce a signal attenuation in the NW-SE corners of
– both from the theoretical developments and from all simulations we conducted without misalignment – is completely independent of the system design, including the modulation radius used, as long as a perfect four-faced PWFS is used. On the other hand, misalignments (Fig. 6, bottom) induce a signal attenuation in the NW-SE corners of 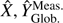 , where |p(±0.5, ∓0.5)| = |q(±0.5, ∓ 0.5)| = 0 (Fig. 7, top), while the information at these frequencies seems to be transferred to
, where |p(±0.5, ∓0.5)| = |q(±0.5, ∓ 0.5)| = 0 (Fig. 7, top), while the information at these frequencies seems to be transferred to 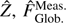 measurements.
measurements.
 |
Fig. 7. Top: magnitudes of the 4 terms of M̂is(u, v) for the case shown in Fig. 6. The |p(u, v)| term goes to 0 in the NW and SE corners, where measurement in XTrue is shifted in ZMeas. (YTrue in FMeas.) by the r(u, v) term. Bottom: frequency dependent measurement energy ratio of [ZMeas., FMeas.] cumulative energy to total energy. Edge effects are induced by pixel area integration. White pixel: undefined value for piston mode. |
The M̂is transform corresponding to the example in Fig. 6 is shown in Fig. 7 (top). For this misalignment, a total of 22.6% of the simulated TF energy is borne by the ZMeas. and FMeas. terms. As seen in Fig. 7 (bottom), this energy fraction highly depends on the spatial frequency and follows the structure of s(u, v) and r(u, v), reaching a maximum value of ≈75.5% energy in the NW and SE corner areas of the Nyquist domain. Without considering the pixel integration (Eq. (9)) TF damping that at these corners, this energy fraction would reach 100% on the corner points, where p = q = 0 and 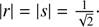
From the observations above, it is expected that using an XYGlob. measurement method, misalignment significantly affects the sensing ability of the PWFS for input phase spatial frequencies at a −45° angle, and corresponding speckles should persist in the long exposure point spread function (PSF). This behavior was confirmed with numerical simulations with nominal and misalignment-altered PSFs as shown in Fig. 8. When using XYGlob. control with misalignments (Fig. 8b), the correction zone is reduced, principally along the NW-SE axis, as we need to filter out 15% of the modes based on the fraction of their response contained in Z and F, a filtering required just to ensure loop stability. As shown in Fig. 8c, when comparing to the nominal PSF (Fig. 8a) we observe that besides the geometrical distortion of the PSF, the background within the correction zone of the DM is amplified by up to 10, an unsatisfactory reduction of AO performance.
 |
Fig. 8. Panels a and b: long exposure H-band PSFs for the 0.75 px MaxMis misalignment case detailed in Figs. 6 and 7: with XYZFGlob. measurement control (panel a) and with XYGlob. (panel b). Panel c: Log10-scaled relative difference between the latter PSFs. |
More dramatic examples and their impact on PSFs were presented in a previous work (Deo et al. 2017), showing multiple residual speckle stripes due to several zero-valued bands in p(u, v) for extreme misalignment situations.
6. Misalignment figure of merit
Not all misalignments are equivalent because the magnitude |M̂is(u, v)| is determined through six degrees of freedom, and different misalignments – even with identical MaxMis – impact PWFS operation with conventional XYGlob. at various degrees. Our main focus is to emphasize the theoretical inability of XYGlob. nominal operation past a certain degree of misalignment, and we also investigate the compromise of using XYZGlob. as a trade-off between reconstruction ability and computational cost. First, unitarity of M̂is(u, v) ensures that unit gain in XTrue and YTrue is split within all four ESC measurements without loss, distributed depending on the four terms p, q, r, s (see Eq. (20)), as follows:
-
The diagonal term p(u, v) is the amount of accurate measurement from XYTrue in XYMeas..
-
The q(u, v) term cross-couples or swaps information between x and y axes, however overall without loss between XYTrue and XYMeas..
-
The r(u, v) and s(u, v) terms are the critical quantities, representing an information displacement from X, YTrue to Z, FMeas..
It is useful to synthesize the phase reconstruction information available within a given measurement mode, by introducing a quantitative frequency dependent figure of merit fom(u, v), representing the fraction of information conserved from X̂True and ŶTrue at a given spatial frequency. As we hypothesize knowledge of both XTrue and YTrue is required for reconstruction, it follows that we consider the least of the two singular values (s.v.; real-valued, positive) of the M̂is transform sub-matrix between [XTrue, YTrue] and the considered measurements, i.e.,
where σ2(M) is smallest singular value of matrix M with two rows. Further along this numerical reduction, a global figure of merit expressed as a single scalar value for a given misalignment ought to be provided. We estimated that the average or median values were not suitable; we decided to quantify globally the S/N value by the first quartile of fom• over the frequency domain, which represents a S/N value guaranteed for 75% of the Fourier modes of the system. Our global figure of merit is hence the FOM• value such that
The FOM ranges from 100% for nominal transfer between •Meas. and •True measurements down to (theoretically) 0% for complete signal loss. As a global S/N indicator, FOM is expected to strongly correlate with the number of modes requiring to be filtered out to ensure loop stability, and therefore AO performance.
We performed an extensive Monte Carlo analysis of FOM values for XY and XYZ measurement modes, which are shown in Figs. 9a and d. The median value of FOMXY drops dramatically past MaxMis = 0.25 px, down to 0.37 at fixed tolerances of MaxMis = 1 px. When using XYZ measurement, FOMXYZ median is maintained at 0.67 for such cases, which demonstrates the retrieval of information that had leaked into ZMeas. domain. This statistical approach also lets us rank the FOM yielded by pixel selection methods, with from best to worst optimal, reference quadrant and naive, correlatively with the MaxMis tolerances obtained with these. For reference, the misalignment case example presented in Sect. 5, which has MaxMis = 0.75 px, yields a FOMXY value of 0.49 and requires filtering 15% of controlling modes just to permit loop stability, in a noiseless simulation and yet with the degraded PSF shown in Fig. 8b.
 |
Fig. 9. Statistical distribution of FOMXY (panels a–c) and FOMXYZ (panels d–f) for random misalignments either with fixed MaxMis from 0.1 px to 1 px or distributed as the output of the 3 pixel selection methods (naive, qref., opt.) presented in Sect. 4. Boxes show the median and quartiles of the distribution and whiskers the 1st and 9th deciles. From left to right for both rows: without noise on (xi, yi)i = A, B, C, D determination, with 0.1 px and with 0.3 px RMS noise. |
Beyond our Sect. 4 hypothesis that quadrants centers can be exactly known, we also investigated the final impact on FOM of uncertainties in quadrant referencing. The stability and biases of the many methods to fit quadrants on the detector, depending on quadrant resolution, illumination conditions or noise levels, are not documented to our knowledge, and final reliability may vary depending on each PWFS AO design and calibration protocols. With quadrant referencing errors, the pixel selection procedure is performed on erroneous quadrant centers with coordinates
While the δi, ϵi obtained through pixel selection on the values of Eq. (24) comply with the statistics discussed in Sect. 4, actual quadrant misalignment values of the system are δi − errix , ϵi − erriy . These errors can lead to a different and suboptimal pixel choice for quadrant referencing, and further to the AO having a strongly degraded M̂is transform compared to the optimal quadrant referencing. Using the optimal method, and assuming the center finding error is a zero-mean Gaussian process of standard deviation σ, we simulated that the pixel selection is altered to a suboptimal alternative in 50% (respectively 90%) of cases when σ = 0.1 px (resp. 0.3 px).
The results of the impact study of calibration errors of (xi, yi) using our FOM• indicator are presented in Figs. 9b, c, e and f, allowing us to compare putative phase reconstruction capability of measurement modes XY, XYZ, and XYZF (FOMXYZF = 1) for various misalignment and uncertainty error scenarios. The impact of subpixel positioning uncertainty is significant; the M̂is transform unknowingly affects reconstruction capability.
Another critical question arising concerning misalignment impact is the possibility of zeros occurring in fomXY(u, v), i.e., potential reconstructor incapacity zones. With the optimal pixel selection algorithm, only the special cases of Eq. (14) lead to two zeros in opposite corners of the Nyquist domain. However, with the reference quadrant or the naive methods, or with errors on quadrant centers, the probability of zero-valued stripes crossing fomXY(u, v) may be significant, with values reported on Table 2 (section“1 px to 1 actu”).
Probability of a zero-valued zone occurring in fomXY(u, v) depending on pixel selection method, error on quadrant finding, and PWFS pixels to DM actuators oversampling factor.
The values in Table 2 also include probability estimates regarding PWFS to DM oversampling. Our mathematical developments so far focus on misalignment impact within the PWFS Nyquist domain, implicitly assuming the latter matches the correction area of the DM. Because of the enhanced behavior of PWFS in oversampling regimes rather than rigorous Fried geometry (Vidal et al. 2017), most PWFS-based systems currently in development are designed with oversampled PWFS. In this case, metrics should be corrected to only take into account the correction area of the system. Although this work does not propose an extensive analysis of oversampled behavior, we include in Table 2 the probabilities of zeros occurring in the AO correction zone with oversampling ratios of the current designs of the MICADO SCAO system (96 px to 80 actu) and the NFIRAOS AO facility of the Thirty Meter Telescope International Observatory (TMT; 96 px. to 60 actu) (Wang et al. 2017). These values show that misalignment-induced performance loss is well mitigated simply by system geometry when reaching oversampling ratios above ≈1.5. Such a design decision may however not generally be a satisfactory trade-off for PWFS designs because it is bound to enhance readout noise impact for dimmest guide stars.
7. Numerical simulations and laboratory results
7.1. Experimental setup and protocols
We performed end-to-end simulations and optical bench runs to assess the performance of various measurement methods and their stability regarding PWFS misalignment. To perform these experiments at a realistic high-order AO scale, yet to maintain acceptable computing times, we considered an 18 m diameter telescope equipped with a 39 × 39 square-pitch DM, targeting half the dimensions of ELT SCAO systems. The PWFS is sampled with a 13–18% oversampling factor, consistent with the current value of the MICADO SCAO design. Detailed information on bench experimental setup and end-to-end run algorithms are identical to previous work (Deo et al. 2017); major parameters are recalled in Table 3.
Parameters for measurement method comparison and quadrant misalignment experimental runs.
For each controller mode and misalignment values (δi, ϵi), end-to-end long exposure Strehl ratios (S.R.) are obtained by (1) computing a reference modal interaction matrix I0 in Airy spot regime; (2) bootstrapping the AO loop for 0.8 s (i.e., 400 frames) with command matrix 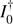 , reaching a suboptimal stationary regime; (3) computing the sensitivity loss compensation modal coefficients Gmodal; and (4) running the AO loop and recording telemetry data for 2.0 s (1000 frames) with the optical gain corrected command matrix Gmodal ×
, reaching a suboptimal stationary regime; (3) computing the sensitivity loss compensation modal coefficients Gmodal; and (4) running the AO loop and recording telemetry data for 2.0 s (1000 frames) with the optical gain corrected command matrix Gmodal × 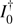 . This procedure applies to numerical simulations and bench experiments.
. This procedure applies to numerical simulations and bench experiments.
It is to be noted that our computations do not include optical throughput, and therefore stellar magnitudes should be scaled accordingly for real system projective performances. We use a zero-point value of 2.62 × 010 ph s−1 m−2, yielding the flux values given in Table 4.
Section 7.2 presents results of numerical simulations comparing a variety of measurement and normalization options for a perfect PWFS to be conclusive regarding (1) the relative performance of •Glob. and •Loc. normalizations and (2) conservation of system sensitivity when adding ESC measurements to X and Y. Section 7.3 covers numerical simulations and optical bench experiments regarding robustness of XYGlob., XYZGlob., and XYZFGlob. methods relative to PWFS misalignments, toward confirming the intrinsic robustness of XYZFGlob. to any amount of misalignment.
7.2. Comparing measurement methods for a perfect PWFS: Numerical simulations
We compared the end-to-end performance of •Glob., •Loc. and XYLoc.,Sine measurement methods, at modulation radii ranging from 2 to 6 λ/D, and for guide star magnitudes 14–19. We tested an extensive number of centroiding options to assess performance discrepancies, namely: (global) XYGlob., XYZGlob., XYFGlob., XYZFGlob., ABCDGlob.; (local): XYLoc., XYZLoc., ABCDLoc.; and (local-sine): XYLoc.,Sine. The ABCDnorm modes are operated by considering PWFS output as the direct concatenation of valid pixels of the four quadrants. These modes are fully equivalent to the corresponding XYZFnorm modes: the P transform preliminary operation from A, B, C, and D to X, Y, Z, and F becomes factored into the system command matrix. Numerical simulations confirmed this equivalence, with identical outputs down to floating point precision.
In all fairness regarding measurement methods, in particular discrepancies in the normalization of modal sensitivity compensation coefficients, we performed all experiments after an optimization of the integrator scalar gains given all other parameters, thus eliminating this factor for result interpretation. Figure 10 shows simulated performance for XY measurement modes. Others methods listed above (XYZ•, XYF•, XYZF•, ABCD•) could not be drawn due to excessive similarity: all •Glob. methods, on the one hand, and all •Loc. and XYLoc.,Sine, on the other hand, yield identical performance within two points of Strehl ratio, at all guide star magnitudes and modulation radii.
 |
Fig. 10. End-to-end simulation performance comparison of measurement methods, in particular the normalization employed, after optimization of the loop gain, for a perfect PWFS design. Shaded area: error bars as ±1 standard deviations of the instantaneous short exposure S.R. |
ESC use preserves PWFS sensitivity. We previously discussed that for a perfect PWFS prism and assembly, F and Z bear no information, and even that FLoc. = 1 analytically and was not considered. However the perfect similarity in performance with or without adding terms Z and F satisfactorily demonstrates that their addition to the processing does not degrade the noise propagation, i.e., has no impact whatsoever on PWFS sensitivity.
Global outperforms Local. Finally, the results in Fig. 10 demonstrate the superior performance of •Glob. methods over •Loc. me
thods. A limiting magnitude increase of up to  is measured, and benefits are observed over the complete magnitude range – even for magnitudes < 17, where 0-photon count pixels do not yet cause normalization issues to •Loc. methods.
is measured, and benefits are observed over the complete magnitude range – even for magnitudes < 17, where 0-photon count pixels do not yet cause normalization issues to •Loc. methods.
7.3. Misalignment impact on end-to-end performance
We analyze the impact of quadrant misalignments for various MaxMis specifications and for stellar magnitudes 14–18.5, both in numerical simulations and on the optical bench, currently restricting our study to global normalization. We compare the performance of conventional XYGlob. and ESC Modes XYZGlob. and XYZFGlob.. The misalignments selected correspond to values of (δi, ϵi) deduced from Eq. (14) but multiplied by a scaling factor to vary MaxMis as desired. In numerical simulations, quadrants are misaligned by altering the orientations of the refracting planes within the PWFS phase mask, allowing us to set (xi, yi) with arbitrary precision. On the optical bench, the high-resolution design of the PWFS detector is such that a WFS pixel information is obtained by binning camera pixels by 6, and therefore misalignments can be introduced with a  pixel-wide uniformly distributed precision, i.e., with a standard deviation of 0.048 px.
pixel-wide uniformly distributed precision, i.e., with a standard deviation of 0.048 px.
Numerical simulation results are shown in Fig. 11, which includes two operational behaviors:
-
Solid lines: all DM modes are driven by the controller
-
Dashed lines: mode filtering is performed based on a rejection criterion in order to maintain loop stability.
 |
Fig. 11. Numerical simulation performance results for various misalignment scenarios. Solid lines: all DM modes controlled (error as shaded areas, defined as in Fig. 10); dashed lines: modes with dominant energy in Z and F filtered (error as solid bars), only shown when relative difference to unfiltered control is larger than 1%. The Strehl ratio (S.R.) is measured at 1650 nm. Results are shown for rMod = 2 λ/D; simulations for 4 λ/D and 6 λ/D achieve similar performance. |
which is the complementary quantity to Fig. 7 (bottom). A threshold value of 40% was manually adjusted, trading off between insufficient and excessive mode filtering; both choices reduce the final performance.
We investigated the responses to misalignments up to MaxMis = 1.5 px. Although this is beyond the worst case scenario even for naive quadrant referencing, these cases largely cover possible errors on quadrant centers adjustments, and we also believe the stability of XYZFGlob. at large misalignments – with previous work (Deo et al. 2017) investigating up to MaxMis = 5.0 px – is, if not of operational utility, at least of theoretical interest.
At all magnitudes tested, conventional XYGlob. shows dramatic performance loss for misalignments larger than MaxMis = 0.5 px. While mode filtering allows us to avoid critical AO failure (S.R. down to 0%), it remains an insufficient compromise that does not mitigate the misalignment-induced performance loss.
Simulations with XYZFGlob. show no significant sensitivity to misalignments, aside from extreme noise of MagR = 18.5, and therefore offers a satisfactory solution to cancel out misalignment effects, hence confirming theoretical developments of Sect. 5, and paving the way for relaxing PWFS specifications to favor this software-based solution. Finally, XYZGlob. provides an intermediate misalignment mitigating ESC method at only 75% the computational cost of XYZFGlob..
End-to-end runs with similar parameters were successfully performed on the optical bench; the results are shown in Fig. 12. Because the bench is operated with a spatial light modulator (SLM) rather than a conventional DM, we use the following process to generate phase screens: (1) the turbulence screen is generated numerically; (2) DM shape is generated; and (3) DM and turbulence buffers are summed and displayed on the SLM. Also, the SLM imposes a strictly monochromatic operation, making actual H-band images unavailable, and in place these were synthetically computed from the difference between turbulent and DM phase screens. Another SLM-specific behavior constrained us to discard data points for which emulated phase maps diverge beyond 1.5 μm RMS during AO loop operation. This leads to artifacts of amplitude 2% S.R. to build up and dominate the PSF recording. However, other data points with lower S.R. are deemed valid, as the RMS residual is kept within 600 nm RMS and no artifacts are observed.
 |
Fig. 12. Adaptive optics bench performance results for various misalignment scenarios. Solid and dashed lines, shaded areas: same as in Fig. 11; top row: H-band S.R. computed from the phase residuals; bottom row: measured S.R. in the R band, relative to bench focal camera nominal alignment (≈80% absolute S.R.). Results are shown for rMod = 6 λ/D, which is close to minimal operational radius on bench due to PWFS prism edge roughnesses of approximately 30 μm (1 λ/D) width. Cross markers: measured R-band S.R. is undetermined (explanations in the text). |
Showing a flat phase screen on the SLM does not induce a flat wavefront in the bench pupil, and the residual computation is biased by a residual aberration. After best effort calibration, we estimate this aberration to an unmeasured 50 nm RMS, i.e., 4 pts of H-band S.R. at most, which is little compared to the experimental results shown in Fig. 12 (H-band S.R. of 56% mapping to 200 nm RMS residual through the Maréchal approximation). Long-exposure S.R. in the R band were also measured using an imaging camera, and confirm AO loop operability even when lacking a coherent PSF core at the pyramid pin for guide star magnitudes ≥17. R-band S.R. are satisfactorily consistent with trends in computed H-band S.R. at magnitudes 14 and 17. Bench experiments confirm numerical simulation results with a consistent relative difference of 10 pts. H-band S.R. ceiling performance.
The predicted absolute stability of XYZFGlob. control with quadrant misalignments is experimentally confirmed by our optical bench results.
8. Conclusions
In this work, the authors propose a thorough analysis of (1) how quadrants on the PWFS detector are extracted and normalized from sensor data and (2) quadrant misalignments depending on the quadrant pixel referencing algorithm. Simulation and bench runs bring conclusive information regarding the better performance of the global normalization (Vérinaud 2004) over the local normalization (Ragazzoni 1996) with a sensitivity limit gain of 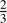 of a magnitude.
of a magnitude.
Our theoretical analysis of independent quadrant translations in the Fourier domain leads us into introducing ESC, generalizing the notion of output measurements for the PWFS. We theorize, and measure through experimental small-signal TFs, that frequency information is shifted from gradient-like terms X and Y into ESC terms Z and F due to the relative misalignments of the quadrants. As zero-gain frequency zones may appear within the XY-only TF, it is expected that (a) past a certain misalignment, conventional XY control is unable to sense all frequencies of the PWFS domain and (b) that ESC should be insensitive to any relative misalignments. Furthermore, through a Monte Carlo statistical analysis of realistic quadrant misalignments, and by introducing a scalar figure of merit to quantify performance loss with conventional control, it is pointed out that realistic misalignment situations may lead to significant AO performance loss, therefore requiring risk mitigation procedures other than for extremely tight pyramid prism specifications. As a conceptually simple extension of conventional XY PWFS control, ESC provides a fitting candidate for misalignment impact mitigation.
Simulations and optical bench runs confirm that ESC with four measurement maps XYZF is insensitive to misalignments, as long as illuminated pixels are not cropped out by the quadrant mask, and is thus up to the sensitivity limit. It is also demonstrated that adding in the extra terms Z and F does not worsen noise propagation, even if made unnecessary by low misalignment situations.
Generally, this study attempts to bring additional arguments to PWFS systems design trade-offs; along with prism quality and price, oversampling factor choice, or RTC dimensioning. With XYZF measurements twice as large, instrumental RTCs specifications should be adapted. However, the command matrix – slopes vector multiplication is well within the scope of parallel computing, and the computational impact should be well mitigated using GPU-based RTC architectures (Gratadour et al. 2016). The authors therefore believe XYZF or ABCD PWFS control is a satisfactory risk mitigation choice and has the benefit of dramatically relaxing PWFS design constraints.
Acknowledgments
This research is performed in the frame of the development of MICADO, first light instrument of the ELT (ESO), with the support of ESO, INSU/CNRS and Observatoire de Paris. The authors wish to thank the fruitful contributions of D. Gratadour, F. Ferreira, and A. Sevin to the COMPASS simulation tool and of Z. Hubert to the experimental bench.
References
- Carlotti, A., Vérinaud, C., Gratadour, D., Westphal, M., & Beuzit, J.-L. 2014, Proc. SPIE, 9148, 91486R [CrossRef] [Google Scholar]
- Clénet, Y., Buey, T. M., Rousset, G., et al. 2014, Proc. SPIE, 9148, 91480Z [CrossRef] [Google Scholar]
- David, H. A., & Nagaraja, H. N. 2005, Order Statistics, 3rd edn eds. W. A. Shewhart, & S. S. Wilks (John Wiley& Sons, Inc.) [Google Scholar]
- Davies, R., Ageorges, N., Barl, L., et al. 2010, Proc. SPIE, 7735, 77352A [CrossRef] [Google Scholar]
- Deo, V., Vidal, F., & Gendron, E. 2017 5th AO4ELT conference-Adaptive Optics for Extremely Large Telescopes. [Google Scholar]
- Deo, V., Gendron, E., Rousset, G., Vidal, F., & Buey, T. 2018, Proc. SPIE, 10703, 1070320 [Google Scholar]
- Esposito, S., Riccardi, A., Fini, L., et al. 2010, Proc. SPIE, 7736, 773609 [CrossRef] [Google Scholar]
- Fauvarque, O., Neichel, B., Fusco, T., Sauvage, J.-F., & Girault, O. 2016a, Optica, 3, 1440 [NASA ADS] [CrossRef] [Google Scholar]
- Fauvarque, O., Neichel, B., Fusco, T., Sauvage, J.-F., & Girault, O. 2016b, Proc. SPIE, 9909, 990960 [CrossRef] [Google Scholar]
- Ferreira, F., Gendron, E., Rousset, G., & Gratadour, D. 2018, A&A, 616, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gendron, E., & Léna, P. 1994, A&A, 291, 337 [NASA ADS] [Google Scholar]
- Gendron, E., Brangier, M., & Chenegros, G. 2010, in 1st AO4ELT conference-Adaptive Optics for Extremely Large Telescopes , 05003 [Google Scholar]
- Gratadour, D., Puech, M., Vérinaud, C., et al. 2014, Proc. SPIE, 9148, 91486O [CrossRef] [Google Scholar]
- Gratadour, D., Dipper, N., Biasi, R., et al. 2016, Proc. SPIE, 9909, 99094I [CrossRef] [Google Scholar]
- Horwitz, B. A. 1994, in 1994 Symposium on Astronomical Telescopes & Instrumentation for the 21st Century, International Society for Optics and Photonics , 496 [Google Scholar]
- Inoue, T., Tanaka, H., Fukuchi, N., et al. 2007, Proc. SPIE, 6487, 64870Y [CrossRef] [Google Scholar]
- Korkiakoski, V., Vérinaud, C., & Le Louarn, M. 2008a, Appl. Opt., 47, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Korkiakoski, V., Vérinaud, C., & Le Louarn, M. 2008b, Proc. SPIE, 7015, 701554 [CrossRef] [Google Scholar]
- Pinna, E., Briguglio, R. A., & Bonaglia, M. 2017, Pyramid Prototyping for the GMT, Wavefront Sensing in the VLT era II. [Google Scholar]
- Ragazzoni, R. 1996, J. Mod. Opt., 43, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Ragazzoni, R., & Farinato, J. 1999, A&A, 350, L23 [Google Scholar]
- Ragazzoni, R., Diolaiti, E., Farinato, J., et al. 2002a, A&A, 396, 731 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ragazzoni, R., Diolaiti, E., & Vernet, E. 2002b, Opt. Commun., 208, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Shatokhina, I. 2014, PhD Thesis, Johannes Kepler Universität Linz, Austria. [Google Scholar]
- Shatokhina, I., Obereder, A., Rosensteiner, M., & Ramlau, R. 2013, Appl. Opt., 52, 2640 [NASA ADS] [CrossRef] [Google Scholar]
- Vérinaud, C. 2004, Opt. Commun., 233, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Vidal, F., Ferreira, F., & Deo, V., 2017, in 5th AO4ELT conference-Adaptive Optics for Extremely Large Telescopes [Google Scholar]
- Wang, L., Véran, J. P., & Ellerbroek, B. 2017, 5th AO4ELT conference-Adaptive Optics for Extremely Large Telescopes. [Google Scholar]
Appendix A: Quadrant central pixel selection methods
A.1. Preselected reference quadrant method
Within the reference quadrant method described succinctly in Sect. 4, one of the quadrants is priorly chosen, here A, and central pixels are selected through
with the inner rounding corresponding to nearest-pixel selection for B, C, D for an idealized pixel lattice in which xA, yA are integers; and the outer rounding operations being a common nearest-pixel roundoff of this idealized lattice on the actual detector pixel matrix.
A.2. Optimal method
We consider the values of mi, ni, δi, ϵi after a naive method roundoff. There are plenty of ways to modify this output to minimize MaxMis. One method, for instance, is experimenting with the reference quadrant method using all four possible references and selecting the best outcome, which will be the optimum. However we prefer the following three-step algorithmic description as it is insightful about the intrinsic geometry of the problem being discussed: the minimization the total span of an arbitrary number of real values only using integer translations.
Without loss of generality, the demonstration is restricted to the x-axis, and we assume sorted values at the beginning of the process,
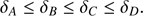 (A.2)Length testing. We define the four lengths that correspond to separations between δi values
(A.2)Length testing. We define the four lengths that correspond to separations between δi values
as shown in Fig. A.1. We seek which of these four lengths is maximal, with value lmax. Two outcomes are possible:
-
l4 = lmax, in which case the algorithm skips to the termination
-
l4 < lmax, and we perform a pixel shifting.
 |
Fig. A.1. Beginning of the optimal misalignment algorithm. In this example, δA = −0.35, δB = −0.15, δC = 0.10, δD = 0.40, such that l3 = 0.3 = lmax. The optimal value with this example is |
Pixel shifting. If lmax = l1, we shift the reference pixel for quadrant A one pixel to the left, i.e., mA, δA are changed to mA − 1, δA + 1. In case lmax = l2 (resp. lmax = l3), this shift is performed on both quadrants A and B (resp. A, B, and C), resulting as on Fig. A.2.
 |
Fig. A.2. After the pixel shifting step, with quadrants A, B, and C offset one pixel to the left from the initial situation of Fig. A.1. |
Termination. All four quadrants are offset identically to minimize the largest |δi|, so as to avoid offsets larger than 1 between the quadrant center xi and the assumed central pixel mi. Between Figs. A.2 and A.3, a 1 px right-shift is made, finally yielding δi ∈ [ − 0.60, 0.10].
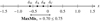 |
Fig. A.3. Final value of δi misalignments at the optimal choice of central pixels mi. |
The situation at the end of the optimal algorithm is such that
which is also the minimal sum of any three of the li, ensuring the optimality of MaxMisx over choices of mi.
All Tables
Probability of a zero-valued zone occurring in fomXY(u, v) depending on pixel selection method, error on quadrant finding, and PWFS pixels to DM actuators oversampling factor.
Parameters for measurement method comparison and quadrant misalignment experimental runs.
All Figures
 |
Fig. 1. Typical observation on the PWFS detector – here on the laboratory bench–, illustrating a priori requirements for the pixel mask. White: conventional control requires subpixel precision in estimating contours and centers of quadrants. Yellow: with ESC, an estimated selection zone containing all illuminated pixels of each quadrant is sufficient. Irrelevant pixels can be eliminated from the selection zone afterward. |
| In the text | |
 |
Fig. 2. Simulated small-signal differential response (interaction matrix measurement) of the PWFS in the four ESC measurement maps for 3 aberrations: tilt (left), spherical (center), and higher frequency Karhunen–Loëve #103 (right). Top row: the system is perfectly aligned and differential signals in ZGlob and FGlob are zero. Bottom row: exaggerated misalignment case (up to ≈5% of pupil diameter for each quadrant), illustrating how information is now spread across all four X, Y, Z, FGlob ESC measurements. |
| In the text | |
 |
Fig. 3. Schematic representations of common defects on the prism apex and their impact on quadrant positioning. Panel a: nominal design of the pyramid apex: quadrants lie on a perfect square, although the side length of the square needs not match an integer multiple of the pixel size. Panel b: polishing angle of facet B is excessive, shifting outward edges of facet B; quadrant B is moved away from the optical axis and receives more flux, whereas A and D receive less. Panel c: facet polishing depth is unequal, creating a roof apex. Intensities at zero-phase point are modified. |
| In the text | |
 |
Fig. 4. Schematized selection of the detector pixels corresponding to the centers of the first two quadrants A and B. Information is priorly obtained that (xA, yA)=(37.57, 41.84) and (xB, yB)=(120.33, 41.42) for this example. Panel a: idealized [0, 0] central pixel for quadrant A (red) and nearest detector pixel (black) chosen as [0, 0] reference. Panel b: at the center of quadrant B; red: idealized [0, 0] pixel for quadrant B; black: subaperture footprint of the [0, 0] pixel chosen for quadrant A; blue and green: possible pixel choices for [0, 0] of B: pixel “1” (blue) minimizes absolute misalignment (|δB|,|ϵB|), whereas pixel “2” (green) minimizes the differential misalignment (|δB − δA|,|ϵB − ϵA|). Solid grid on panels a and b: detector pixel boundaries. |
| In the text | |
 |
Fig. 5. Probability density functions (pdf) for top: MaxMisx, y and bottom: MaxMisboth ax. for pixel centering performed with naive, reference quadrant (qref.) or optimal methods (opt.). Solid (dashed) vertical lines highlight the average (median) of the corresponding pdf. Opt. and qref. pdfs overlap below 0.5, which is their common single-axis median. |
| In the text | |
 |
Fig. 6. Simulated TF of the PWFS in the four measurement terms, (top) without misalignment and (bottom) with MaxMis = 0.75 as per Eq. (21). All 8 heat maps are shown over the Nyquist domain of the system, i.e. |
| In the text | |
 |
Fig. 7. Top: magnitudes of the 4 terms of M̂is(u, v) for the case shown in Fig. 6. The |p(u, v)| term goes to 0 in the NW and SE corners, where measurement in XTrue is shifted in ZMeas. (YTrue in FMeas.) by the r(u, v) term. Bottom: frequency dependent measurement energy ratio of [ZMeas., FMeas.] cumulative energy to total energy. Edge effects are induced by pixel area integration. White pixel: undefined value for piston mode. |
| In the text | |
 |
Fig. 8. Panels a and b: long exposure H-band PSFs for the 0.75 px MaxMis misalignment case detailed in Figs. 6 and 7: with XYZFGlob. measurement control (panel a) and with XYGlob. (panel b). Panel c: Log10-scaled relative difference between the latter PSFs. |
| In the text | |
 |
Fig. 9. Statistical distribution of FOMXY (panels a–c) and FOMXYZ (panels d–f) for random misalignments either with fixed MaxMis from 0.1 px to 1 px or distributed as the output of the 3 pixel selection methods (naive, qref., opt.) presented in Sect. 4. Boxes show the median and quartiles of the distribution and whiskers the 1st and 9th deciles. From left to right for both rows: without noise on (xi, yi)i = A, B, C, D determination, with 0.1 px and with 0.3 px RMS noise. |
| In the text | |
 |
Fig. 10. End-to-end simulation performance comparison of measurement methods, in particular the normalization employed, after optimization of the loop gain, for a perfect PWFS design. Shaded area: error bars as ±1 standard deviations of the instantaneous short exposure S.R. |
| In the text | |
 |
Fig. 11. Numerical simulation performance results for various misalignment scenarios. Solid lines: all DM modes controlled (error as shaded areas, defined as in Fig. 10); dashed lines: modes with dominant energy in Z and F filtered (error as solid bars), only shown when relative difference to unfiltered control is larger than 1%. The Strehl ratio (S.R.) is measured at 1650 nm. Results are shown for rMod = 2 λ/D; simulations for 4 λ/D and 6 λ/D achieve similar performance. |
| In the text | |
 |
Fig. 12. Adaptive optics bench performance results for various misalignment scenarios. Solid and dashed lines, shaded areas: same as in Fig. 11; top row: H-band S.R. computed from the phase residuals; bottom row: measured S.R. in the R band, relative to bench focal camera nominal alignment (≈80% absolute S.R.). Results are shown for rMod = 6 λ/D, which is close to minimal operational radius on bench due to PWFS prism edge roughnesses of approximately 30 μm (1 λ/D) width. Cross markers: measured R-band S.R. is undetermined (explanations in the text). |
| In the text | |
 |
Fig. A.1. Beginning of the optimal misalignment algorithm. In this example, δA = −0.35, δB = −0.15, δC = 0.10, δD = 0.40, such that l3 = 0.3 = lmax. The optimal value with this example is |
| In the text | |
 |
Fig. A.2. After the pixel shifting step, with quadrants A, B, and C offset one pixel to the left from the initial situation of Fig. A.1. |
| In the text | |
 |
Fig. A.3. Final value of δi misalignments at the optimal choice of central pixels mi. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



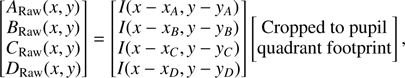
![$$ \begin{aligned} \begin{bmatrix} A_{\mathrm{Loc}}[k] \\ B_{\mathrm{Loc}}[k] \\ C_{\mathrm{Loc}}[k] \\ D_{\mathrm{Loc}}[k] \end{bmatrix} = \dfrac{1}{\displaystyle \sum _{Q=A,B,C,D}Q_{\mathrm{Raw}}[k]} \begin{bmatrix} A_{\mathrm{Raw}}[k] \\ B_{\mathrm{Raw}}[k] \\ C_{\mathrm{Raw}}[k] \\ D_{\mathrm{Raw}}[k] \end{bmatrix}, \end{aligned} $$](/articles/aa/full_html/2018/11/aa33685-18/aa33685-18-eq2.gif)
![$$ \begin{aligned} \begin{bmatrix} A_{\mathrm{Glob}}[k] \\ B_{\mathrm{Glob}}[k] \\ C_{\mathrm{Glob}}[k] \\ D_{\mathrm{Glob}}[k] \end{bmatrix} = \dfrac{1}{\left\langle \displaystyle \sum _{Q=A,B,C,D}Q_{\mathrm{Raw}}[k]\right\rangle _k} \begin{bmatrix} A_{\mathrm{Raw}}[k] \\ B_{\mathrm{Raw}}[k] \\ C_{\mathrm{Raw}}[k] \\ D_{\mathrm{Raw}}[k] \end{bmatrix}, \end{aligned} $$](/articles/aa/full_html/2018/11/aa33685-18/aa33685-18-eq3.gif)
![$$ \begin{aligned}&\begin{bmatrix} X_{\rm norm} \\ Y_{\rm norm} \end{bmatrix}[k] = \begin{bmatrix} A_{\mathrm{norm}}- B_{\mathrm{norm}}+ C_{\mathrm{norm}}- D_{\mathrm{norm}}\\ A_{\mathrm{norm}}+ B_{\mathrm{norm}}- C_{\mathrm{norm}}- D_{\mathrm{norm}}\end{bmatrix}[k] \nonumber \\&=\begin{bmatrix} 1&-1&1&-1\\ 1&1&-1&-1 \end{bmatrix} \cdot \begin{bmatrix} A_{\mathrm{norm}}\\ B_{\mathrm{norm}}\\ C_{\mathrm{norm}}\\ D_{\mathrm{norm}}\end{bmatrix}[k],\nonumber \\&\mathrm{where\ norm} \in \{\mathrm{Loc},\,\mathrm{Glob}\}. \end{aligned} $$](/articles/aa/full_html/2018/11/aa33685-18/aa33685-18-eq4.gif)
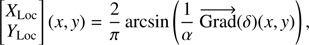
![$$ \begin{aligned} \begin{bmatrix} X_{\rm Loc, Sine} \\ Y_{\rm Loc, Sine} \end{bmatrix}[k] = \sin \left(\dfrac{\pi }{2} \begin{bmatrix}X_{\rm Loc}\\ Y_{\rm Loc} \end{bmatrix}[k]\right), \end{aligned} $$](/articles/aa/full_html/2018/11/aa33685-18/aa33685-18-eq6.gif)

![$$ \begin{aligned} A_{\rm Raw}^\mathrm{True}[m,n] = \int \int _{x,{y}} A_{\rm Raw}(x,\,{y})\,{\times }\,\Pi (x-x_A-m,\,{y}-{y}_A-n)\ \mathrm{dx}\ \mathrm{d}{y}, \end{aligned} $$](/articles/aa/full_html/2018/11/aa33685-18/aa33685-18-eq9.gif)
![$$ \begin{aligned} A_{\rm Raw}^\mathrm{Meas.}[m,n] = \int \int _{x,{y}} A_{\rm Raw}(x,\,{y})\,{\times }\,\Pi (x-m_A-m,\,{y}-n_A-n)\ \mathrm{dx}\ \mathrm{d}{y}, \end{aligned} $$](/articles/aa/full_html/2018/11/aa33685-18/aa33685-18-eq12.gif)
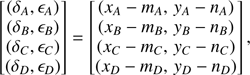
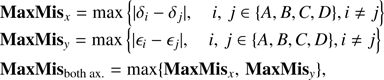
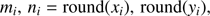
![$$ \begin{aligned}&\delta _A,\,\epsilon _A \in [-\frac{1}{2}, \frac{1}{2}], \quad \delta _{B,C,D} \in [\delta _A - \frac{1}{2}, \delta _A + \frac{1}{2}], \nonumber \\&\epsilon _{B,C,D} \in [\epsilon _A - \frac{1}{2}, \epsilon _A + \frac{1}{2}], \end{aligned} $$](/articles/aa/full_html/2018/11/aa33685-18/aa33685-18-eq18.gif)

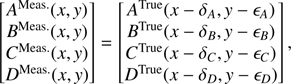
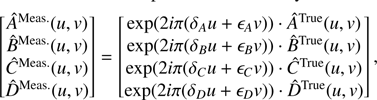
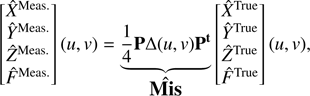
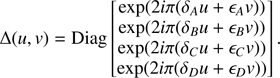
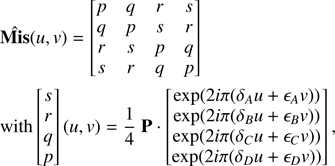
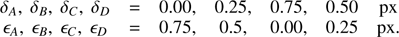
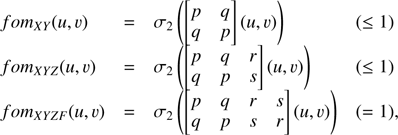
![$$ \begin{aligned} \displaystyle \int \int _{u,{v}\,{=}\,-0.5}^{0.5} \left[1\ \mathrm{if} \ fom_\bullet (u,{v}) \le {\mathrm{\mathbf{FOM}}_{\bullet }}\right] \mathrm{d} u \mathrm{d} {v} = 0.25. \end{aligned} $$](/articles/aa/full_html/2018/11/aa33685-18/aa33685-18-eq42.gif)

![$$ \begin{aligned} \begin{array}{ll}&\text{ Mode} \text{ ratio} =\dfrac{\text{ norm}([X^\mathrm{Meas.}, Y^\mathrm{Meas.}])}{\text{ norm}([X^\mathrm{True}, Y^\mathrm{True}])}\\&\qquad \qquad \quad =\dfrac{\text{ norm}([X^\mathrm{Meas.}, Y^\mathrm{Meas.}])}{\text{ norm}([X^\mathrm{Meas.}, Y^\mathrm{Meas.}, Z^\mathrm{Meas.}, F^\mathrm{Meas.}])}, \end{array} \end{aligned} $$](/articles/aa/full_html/2018/11/aa33685-18/aa33685-18-eq49.gif)
![$$ \begin{aligned} m_A,\,n_A = \mathrm{round} (x_A, {y}_A)\\ \implies \delta _A, \epsilon _A \in \left[-\frac{1}{2}, \frac{1}{2}\right] \end{aligned} $$](/articles/aa/full_html/2018/11/aa33685-18/aa33685-18-eq51.gif)