| Issue |
A&A
Volume 646, February 2021
|
|
|---|---|---|
| Article Number | A27 | |
| Number of page(s) | 18 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/202039584 | |
| Published online | 03 February 2021 | |
Multi-CCD modelling of the point spread function⋆
1
AIM, CEA, CNRS, Université Paris-Saclay, Université de Paris, 91191 Gif-sur-Yvette, France
e-mail: tobias.liaudat@cea.fr
2
Department of Astrophysical Sciences, Princeton University, 4 Ivy Ln., Princeton, NJ 08544, USA
3
Institut d’Astrophysique de Paris, UMR7095 CNRS, Université Pierre & Marie Curie, 98 bis boulevard Arago, 75014 Paris, France
4
NRC Herzberg Astronomy and Astrophysics, 5071 West Saanich Road, Victoria, BC V9E 2E7, Canada
Received:
2
October
2020
Accepted:
20
November
2020
Context. Galaxy imaging surveys observe a vast number of objects, which are ultimately affected by the instrument’s point spread function (PSF). It is weak lensing missions in particular that are aimed at measuring the shape of galaxies and PSF effects represent an significant source of systematic errors that must be handled appropriately. This requires a high level of accuracy at the modelling stage as well as in the estimation of the PSF at galaxy positions.
Aims. The goal of this work is to estimate a PSF at galaxy positions, which is also referred to as a non-parametric PSF estimation and which starts from a set of noisy star image observations distributed over the focal plane. To accomplish this, we need our model to precisely capture the PSF field variations over the field of view and then to recover the PSF at the chosen positions.
Methods. In this paper, we propose a new method, coined Multi-CCD (MCCD) PSF modelling, which simultaneously creates a PSF field model over the entirety of the instrument’s focal plane. It allows us to capture global as well as local PSF features through the use of two complementary models that enforce different spatial constraints. Most existing non-parametric models build one model per charge-coupled device, which can lead to difficulties in capturing global ellipticity patterns.
Results. We first tested our method on a realistic simulated dataset, comparing it with two state-of-the-art PSF modelling methods (PSFEx and RCA) and finding that our method outperforms both of them. Then we contrasted our approach with PSFEx based on real data from the Canada-France Imaging Survey, which uses the Canada-France-Hawaii Telescope. We show that our PSF model is less noisy and achieves a ∼22% gain on the pixel’s root mean square error with respect to PSFEx.
Conclusions. We present and share the code for a new PSF modelling algorithm that models the PSF field on all the focal plane that is mature enough to handle real data.
Key words: methods: data analysis / techniques: image processing / cosmology: observations / gravitational lensing: weak
Code available at https://github.com/CosmoStat/mccd
© T. Liaudat et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Current galaxy imaging surveys, such as DES (Jarvis et al. 2016), KIDS (Kuijken et al. 2015), and CFIS (Ibata et al. 2017), as well as future surveys, such as the Vera C. Rubin Observatory’s LSST (Tyson et al. 2006), the Euclid mission (Laureijs et al. 2011), or the Roman Space Telescope, require an estimated determination of the instrument’s point spread function (PSF). For some scientific applications, such as weak gravitational lensing (Kilbinger 2015), low-surface brightness studies (Infante-Sainz et al. 2019), or analyses of diffraction-limited images in crowded stellar fields (Beltramo-Martin et al. 2020), the PSF must be reconstructed with a high level of accuracy. A preliminary approach is to derive a PSF model using available information about the instrument, whereupon the model parameters are then chosen by fitting observed stars in the field to yield a PSF model. This has been widely used for the Hubble Space Telescope (HST) as in the case of TinyTim software (Krist et al. 1995), although it was later shown that a relatively simple PSF estimation based on the data, which does not assume a model for the instrument, provides better fits to stars with regard to both photometry and astrometry measurements (Hoffmann & Anderson 2017). Furthermore, such a solution cannot readily be applied to ground-based observations, where the atmosphere plays an important role and adds a stochastic aspect to the PSF. Other methods, based on imaging-data only, use unresolved stars in the field as direct measurements of the PSF, reconstructing an accurate PSF from these observed stars. A very impressive range of methodologies have been proposed in the past to perform this task: Moffat modelling (Bendinelli et al. 1988), polynomial models (Piotrowski et al. 2013; Bertin 2011), principal component analysis (Jee et al. 2007; Schrabback et al. 2010; Gentile et al. 2013), sparsity (Ngolè et al. 2015), neural networks (Herbel et al. 2018; Jia et al. 2020a,b), and optimal transport (Ngolè & Starck 2017; Schmitz et al. 2018). The PSFEx software (Bertin 2011) is the most widely used. The resolved components analysis (RCA) method (Ngolè et al. 2016; Schmitz et al. 2020) was proposed within the framework of the Euclid space mission to deal with PSFs that are both undersampled and spatially varied in the field. Cameras are often mosaics of several charge-coupled devices (CCDs), but all the above-mentioned methods can only build one PSF model per CCD, with the exception of the approach used by Miller et al. (2013), and the recently proposed approach by Jarvis et al. (2021). Since the models they build within each detector are independent from each other, it is difficult to capture global patterns of variation in the PSF. For example, upon observing PSFEx’s shape residuals maps from the DES Year 1 results (Fig. 8 in Zuntz et al. 2018), we can see global patterns.
In this paper, we present a new method based on RCA that can capture large patterns spreading across several or all CCDs. We compare the results with both RCA and PSFEx based on simulations and real data. Section 2 reviews these two existing methods, while the proposed MCCD methods are described in Sect. 3. Experiments on simulated images are shown in Sect. 4 and tests on real data are presented in Sect. 5. We give our conclusions in Sect. 7. In addition, Table 1 provides a glossary of variables used throughout this article.
Important variables used in this article.
2. PSFEx and RCA
PSFEx (Bertin 2011) is a standard and widely-used software1. RCA (Ngolè et al. 2016) is a more recent method that was developed with the Euclid Visible Imager’s PSF in mind in order to deal with the undersampling of the observed star images. The software is also freely available2. It is important to remark that these two approaches rely solely on the observed data: they are blind with respect to the optical system involved in the image acquisition process.
2.1. The observation model
Let us define ℋ(u) as the PSF field involved in our problem. It is a continuous function of a two-dimensional position, u = (x, y), which, in principle, could be image coordinates based on the camera’s CCD pixels or could also be celestial coordinates such as right ascension and declination. Throughout this paper, we assume that this PSF field accounts for the contribution of all effects from optical aberrations and diffraction to atmospheric distortions.
Our observation model consists of images, Ik, the pixels in one CCD chip, k, which contains  noisy stars at positions,
noisy stars at positions,  . We define a ‘stamp’ as a square small image cutout centred on a single star. Each star observation stamp, i, on the CCD’s k can be written as:
. We define a ‘stamp’ as a square small image cutout centred on a single star. Each star observation stamp, i, on the CCD’s k can be written as:
where ni, k accounts for a noise image that we will consider to be white and Gaussian, and ℱ is the degradation operator. Three main effects are taken into account in this operator: (i) the discrete sampling into a finite number of pixels, namely an image stamp of ny × ny pixels; (ii) a sub-pixel shift that depends on where the centroid of the image is placed with respect to the pixel grid; and (iii) a downsampling that affects the pixels in the stamp by a factor of D leaving a D ny × D ny stamp. For example, to handle the Euclid mission sampling rate (Cropper et al. 2013), a factor D = 1/2 is required to achieve Nyquist sampling rate. Henceforth, and throughout this article, we use a unitary value for D.
We write each of these stamps into a one-dimensional column vector and, therefore, ![$ Y_k = [\mathbf{y}_{k, 1} \cdots \mathbf{y}_{k, n_{\mathrm{star}}^{k}}] $](/articles/aa/full_html/2021/02/aa39584-20/aa39584-20-eq18.gif) is the matrix containing all the observed stamps in CCD’s k. It contains
is the matrix containing all the observed stamps in CCD’s k. It contains  columns and D ny × D ny rows. Finally, we concatenate all CCD matrices and obtain Y = (Y1⋯YK).
columns and D ny × D ny rows. Finally, we concatenate all CCD matrices and obtain Y = (Y1⋯YK).
2.2. PSFEx
For a given exposure, this method builds one independent model for each CCD. It was designed as a companion software for SExtractor (Bertin & Arnouts 1996), which builds catalogues of objects from astronomical images. Each object contains several measurements that PSFEx then uses to describe the variability of the PSF. Each selected attribute follows a polynomial law up to some user-defined maximum polynomial degree d. The model for CCD k can be written as:
where Ak has m rows corresponding to the number of polynomials used, and  columns corresponding to the number of observed stars used to train the PSF model. The matrix, Sk, is learned during training and has
columns corresponding to the number of observed stars used to train the PSF model. The matrix, Sk, is learned during training and has  rows (the number of pixels in each image), and m columns.
rows (the number of pixels in each image), and m columns.
For example, if d is set to 2 and the attributes chosen are the pixel coordinates (x, y), each column i of the Ak matrix corresponding to the star i at location  is
is ![$ \boldsymbol{a}^{k}_{i} = [1, x^k_i, \mathit{y}^k_i, (x^k_i)^2, (\mathit{y}^k_i)^2, x^k_i \mathit{y}^k_i]^{T} $](/articles/aa/full_html/2021/02/aa39584-20/aa39584-20-eq24.gif) . The number of monomials m corresponding to a maximum degree d can be computed as (d + 1)(d + 2)/2.
. The number of monomials m corresponding to a maximum degree d can be computed as (d + 1)(d + 2)/2.
The training of the model amounts to solving an optimisation problem that takes the form:
where  represents the estimated per-pixel variances, and T is a scalar weighting. The matrix Sk is decomposed as S0, k + ΔSk, where the first term corresponds to a first guess of the PSF. The optimisation is carried out on the difference between this first guess and the observations. The second term in Eq. (3) acts as a Tikhonov regularisation which, in this case, favours smoother PSF models.
represents the estimated per-pixel variances, and T is a scalar weighting. The matrix Sk is decomposed as S0, k + ΔSk, where the first term corresponds to a first guess of the PSF. The optimisation is carried out on the difference between this first guess and the observations. The second term in Eq. (3) acts as a Tikhonov regularisation which, in this case, favours smoother PSF models.
Finally, the PSF recovery at one galaxy position, uj, is straightforward and can be done by using the learned Sk matrix and directly calculating a vector,  , corresponding to the monomials of the chosen attributes. The recovered PSF is then computed as
, corresponding to the monomials of the chosen attributes. The recovered PSF is then computed as
2.3. Resolved components analysis
The RCA method is based on a matrix factorisation scheme. It was first presented in Ngolè et al. (2016) and later evaluated on Euclid image simulations in Schmitz et al. (2020). As with PSFEx, this method also builds independent models for each CCD within an exposure and is able to handle under-sampled images. Any observed star i from CCD k is modelled as a linear combination of PSF features, called eigenPSFs in the following, as
where Sk is the matrix composed of the eigenPSFs, ak, i a vector containing the set of linear weights, and  is the reconstructed PSF.
is the reconstructed PSF.
The modelling is recast into an optimisation problem where the Sk and Ak matrices are estimated simultaneously. The problem is ill-posed due to the undersampling and the noise, meaning that many PSF fields can reproduce the observed stars. In order to break this degeneracy, the RCA uses a series of regularisers during the optimisation procedure to enforce certain mild assumptions on the PSF field: (i) the low-rankness of the solution, enforced by setting the number of eigenPSFs learned, N, to be small; (ii) the positivity of the reconstructed PSFs; (iii) the sparsity of the PSF representation on an appropriate basis; and iv) the spatial constraints that account for imposing a certain structure within the Ak matrix. This last constraint is imposed by a further factorisation of Ak into  . The computation of the
. The computation of the  matrix is addressed in Sect. 3.4. Finally, the PSF model reads:
matrix is addressed in Sect. 3.4. Finally, the PSF model reads:
and the optimisation problem that the RCA method solves is:
where wk, i are weights, Φ represents a transformation allowing the eigenPSFs to have a sparse representation, ⊙ denotes the Hadamard product, ι+ is the indicator function of the positive orthant, and ιΩ is the indicator function over a set Ω defined to enforce the spatial constraints.
The PSF recovery at a position uj is carried out by a radial basis function (RBF) interpolation of the learned columns of the Ak matrix, issuing a vector, ak, j. In this way, the spatial constraints encoded in the Ak matrix are preserved when estimating the PSF at galaxy positions. Finally, the reconstructed PSF is:
3. A new family of MCCD methods
The MCCD methods we propose in this study are aimed at exploiting all the information available in a single exposure, which requires the handling of all CCDs simultaneously. The main advantage of this approach is that we can build a more complex model since the number of stars available for training is much larger as compared to a model based on individual CCDs. We aim to construct a model that is capable of capturing PSF features following a global behaviour, in spite of the fact that the PSF field is discontinuous at CCD boundaries. The main reason behind this discontinuity effect is in the misalignment between various CCDs. Methods such as PSFEx or RCA, which process each CDD independently, avoid the discontinuity problem through construction, but have difficulties capturing global patterns of PSF variability that occur on scales larger than a single CCD. The main idea behind our MCCD approach is to include both a global model that provides a baseline estimation of the PSF and a local model that provides CCD-specific corrections.
3.1. The MCCD data model
In a typical wide-field setting, the PSF field, ℋ, exhibits a certain regularity that we translate into spatial correlations of the PSFs. The model we build for a specific CCD k is the matrix  , which is composed by the concatenation of the estimations of the different stars encountered in that CCD. Each postage stamp column of length,
, which is composed by the concatenation of the estimations of the different stars encountered in that CCD. Each postage stamp column of length,  , corresponds to the model for a specific flattened star from the
, corresponds to the model for a specific flattened star from the  stars present in CCD k.
stars present in CCD k.
The PSF field at star positions is reconstructed as a linear combination of PSF features, called eigenPSFs, which are learned from the observations. As previously stated, we want to have both a global and a local component for the model, so we need different eigenPSFs for each component. Hence, the model is based on a matrix factorisation scheme as follows:
where  contains rk local eigenPSFs and
contains rk local eigenPSFs and  contains
contains  global eigenPSFs. The matrices,
global eigenPSFs. The matrices,  and
and  , correspond to the local and global weights of the linear combinations, respectively. We can see that for a given CCD k, the final model,
, correspond to the local and global weights of the linear combinations, respectively. We can see that for a given CCD k, the final model,  , is made up of the sum of the contributions of the local,
, is made up of the sum of the contributions of the local,  , and global,
, and global,  , models.
, models.
Now, let us build a single model for all the K CCDs in the focal plane. We start by building a single matrix containing all the PSF models by concatenating the model  for each CCD as follows:
for each CCD as follows:
where  and
and  is the total number of stars in one camera exposure. Then we can concatenate the different eigenPSF matrices, k, into a single matrix:
is the total number of stars in one camera exposure. Then we can concatenate the different eigenPSF matrices, k, into a single matrix:
where  and we concatenated the global eigenPSF matrix,
and we concatenated the global eigenPSF matrix,  , at the end. This leaves a total of
, at the end. This leaves a total of  columns for the S matrix. We can follow a similar procedure to define A as a block matrix:
columns for the S matrix. We can follow a similar procedure to define A as a block matrix:
where A ∈ ℝr × N and 0 is used for matrices made up of zeros. The last row of the A block matrix is composed by the global model weights  . Having already defined the Multi-CCD matrices,
. Having already defined the Multi-CCD matrices,  , S and A, we can write the final model as:
, S and A, we can write the final model as:
where we include all the CCDs. Expanding it leads to a formula, as shown in Eq. (9), for each CCD.
3.2. Inverse problem and regularisation
The estimation of our model, summarised in the matrices S and A of Eq. (13), is posed as an inverse problem. Given the observation and MCCD data models presented above, this problem amounts to the minimisation of  , where ∥ ⋅ ∥F denotes the Frobenius matrix norm. This problem is ill-posed due to the noise in the observations and to the degradation operator, ℱ, meaning that there are many PSF models that would match the star observations. In order to break this degeneracy, we enforce several constraints, based on basic knowledge of the PSF field, which we use to regularise our inverse problem. Similarly to the ones exploited in the RCA method (Schmitz et al. 2020), we use the following constraints: (i) Low-rankness of the model; (ii) Positivity of the model; (iii) Sparsity in a given domain; (iv) Spatial variations. We give a more detailed description of these in Appendix A. These constraints are used by both parts of our model, namely, the global and the local components.
, where ∥ ⋅ ∥F denotes the Frobenius matrix norm. This problem is ill-posed due to the noise in the observations and to the degradation operator, ℱ, meaning that there are many PSF models that would match the star observations. In order to break this degeneracy, we enforce several constraints, based on basic knowledge of the PSF field, which we use to regularise our inverse problem. Similarly to the ones exploited in the RCA method (Schmitz et al. 2020), we use the following constraints: (i) Low-rankness of the model; (ii) Positivity of the model; (iii) Sparsity in a given domain; (iv) Spatial variations. We give a more detailed description of these in Appendix A. These constraints are used by both parts of our model, namely, the global and the local components.
As mentioned above, the spatial constraint is enforced by further factorisation of the coefficient matrices, A. However, since we want to enforce different properties for the global and the local contributions, the factorisation used differs for each case.
3.3. Global model
We want the global component to provide a baseline estimation of the PSF and for that we propose that the coefficients follow a polynomial variation of the position. The global coefficient matrix,  , is factorised into
, is factorised into  , where
, where  is a weight matrix and
is a weight matrix and  contains each considered monomials evaluated at global star positions. The dimension,
contains each considered monomials evaluated at global star positions. The dimension,  , is determined by the maximum allowed degree in the polynomials: for all monomials of degree less than a given d, we have
, is determined by the maximum allowed degree in the polynomials: for all monomials of degree less than a given d, we have  . For example, for d = 2 (i.e.
. For example, for d = 2 (i.e.  ), we have:
), we have:
where  are the global pixel coordinates of the observed stars distributed in the kth CCD. The global component of the model for a specific CCD k are as follows:
are the global pixel coordinates of the observed stars distributed in the kth CCD. The global component of the model for a specific CCD k are as follows:
It is important to mention that despite our choice, throughout this paper, to use position polynomials for building the global space constraint, the model is not necessarily restricted to that choice. The Πk matrix could be constructed using other parameters of the observations in order to facilitate the capture of other dependencies and could also follow other types of functions.
3.4. Local model
It is possible to define different types of local models. In this paper, we discuss three options that depend on how we enforce the local spatial constraint. More specifically, they depend on how we factorise the local Ak matrix in the relation:
Nevertheless, the MCCD framework does not restrict us to these three options and it is possible to define other local models. It is worth remarking that all the framework and optimisation procedures are maintained throughout the different flavours of the MCCD algorithms. The main difference is the way the spatial constraints are enforced in the local and global models.
3.4.1. MCCD-RCA
One motivation for the local model is to provide CCD-specific corrections and to do so, our first choice is RCA’s spatial constraint strategy which leads to the MCCD-RCA algorithm. The motivation for this choice is the capability of the RCA spatial constraint to handle different types of PSF variations. On the one hand, it can capture smooth variations over the CCD and on the other hand, it can account for localised changes that affect a reduced number of PSFs. If the PSFs were sampled on a regular grid, this would mean capturing variations occurring at different spatial frequencies. Unfortunately, the PSF locations do not coincide with a regular grid but on what could be seen as a fully connected undirected weighted graph where the weights can be defined as a function of the distance between the different nodes (PSF locations)3. However, the RCA spatial constraint exploits the graph harmonics in order to capture the different PSF variations. These harmonics are represented by the eigenvectors of the graph’s Laplacian matrix (Chung 1997), which depend on how we define the graph’s weights. A parametric function of the PSF distances can serve as the graph’s weights, as in Schmitz et al. (2020), and the selection of the function’s parameters can be done following Ngolè et al. (2016). For each local model (i.e. each CCD in the mosaic), we define rk graphs, each corresponding to one of the rk local parameters. For each graph, we can extract the mk most useful eigenvectors of its Laplacian matrix and present all of them as the columns of the matrix  . In this way, we can write:
. In this way, we can write:
where  is a weight matrix that is used to enforce the spatial constraints. In other words, the sparsity of
is a weight matrix that is used to enforce the spatial constraints. In other words, the sparsity of  ’s rows in the dictionary
’s rows in the dictionary  . Full details are available in Ngolè et al. (2016) and Schmitz et al. (2020).
. Full details are available in Ngolè et al. (2016) and Schmitz et al. (2020).
3.4.2. MCCD-POL
The second local model, referred to as MCCD-POL, follows a polynomial spatial constraint. Similar to PSFEx, we factorise the the local weights into two matrices as follows:
where  has the same form as the matrix in Eq. (14), with the difference that in this case, the positions are represented in local coordinates of its corresponding CCD k. As with d in the global model, a parameter is chosen to define the maximum order of the polynomial used.
has the same form as the matrix in Eq. (14), with the difference that in this case, the positions are represented in local coordinates of its corresponding CCD k. As with d in the global model, a parameter is chosen to define the maximum order of the polynomial used.
3.4.3. MCCD-HYB
The third option consists of using the two local models we presented above, namely, the RCA and polynomial, to work together in an hybrid algorithm we will refer to as MCCD-HYB. The idea behind it is that the addition of the polynomial space constraint could help the original graph constraint to capture the different features found. In this case, we factorise the local weights with block matrices as:
where  and
and  are the matrices defined in the polynomial version and
are the matrices defined in the polynomial version and  and
and  are the matrices defined in the original MCCD-RCA algorithm.
are the matrices defined in the original MCCD-RCA algorithm.
Finally, generically including the spatial constraints in Eq. (9), we get the following description of our model for a specific CCD:
which we can also write in a global form,  , where
, where  and S have already been defined in Eqs. (10) and (11), and where α and V⊤ are the following matrices:
and S have already been defined in Eqs. (10) and (11), and where α and V⊤ are the following matrices:
3.5. Optimisation problem
Combining the regularisations enumerated in Sect. 3.2 and the data model described in Sect. 3.1, we can construct the optimisation problem in an elegant way by reformulating Eq. (7). However, we can split the optimisation problem into a more convenient form:
In the previous equation, the columns of  are the stars distributed in the kth CCD sensor, ℱk is the degradation operator, wk, i and
are the stars distributed in the kth CCD sensor, ℱk is the degradation operator, wk, i and  are weight vectors, Φ is a transform that allows a sparse representation of our eigenPSFs, and Ωk and
are weight vectors, Φ is a transform that allows a sparse representation of our eigenPSFs, and Ωk and  are sets to enforce sparsity and normalisation of the rows of αk and
are sets to enforce sparsity and normalisation of the rows of αk and  , respectively. The indicator function of a set 𝒞 is written as ι𝒞(⋅), that is equal to 0 if the argument belongs to 𝒞 and +∞ otherwise. For example, ι+ is the indicator function over the positive orthant. More explicitly, the sets Ωk and
, respectively. The indicator function of a set 𝒞 is written as ι𝒞(⋅), that is equal to 0 if the argument belongs to 𝒞 and +∞ otherwise. For example, ι+ is the indicator function over the positive orthant. More explicitly, the sets Ωk and  are defined the following way:
are defined the following way:
where (ηk, i)1 ≤ i ≤ rk and  are appropriately chosen integers, and ∥ ⋅ ∥0 is the pseudo-norm ℓ0 that returns the number of non-zero elements of a vector. So we are enforcing, in the global case, the row
are appropriately chosen integers, and ∥ ⋅ ∥0 is the pseudo-norm ℓ0 that returns the number of non-zero elements of a vector. So we are enforcing, in the global case, the row  of
of  to have at most
to have at most  non-zero elements. An interpretation could be that we are forcing each eigenPSF to follow a small number of positional polynomials as
non-zero elements. An interpretation could be that we are forcing each eigenPSF to follow a small number of positional polynomials as  ’s rows will be sparsely represented over the Πk matrices.
’s rows will be sparsely represented over the Πk matrices.
The Φ transform used throughout this paper is the starlet transform (Starck et al. 2011). We enforce the sparsity on the different decomposition levels excluding the coarse scale. The ℓ1 term promotes the sparsity of the eigenPSFs with respect to Φ while the weights wk, i and  regulate the sparsity penalisation against the other constraints and should be adapted throughout the optimisation algorithm depending on the noise level.
regulate the sparsity penalisation against the other constraints and should be adapted throughout the optimisation algorithm depending on the noise level.
The second term in each of the Ω sets (e.g.  ) was not mentioned in the regularisation Sect. 3.2, but they are needed to avoid a degenerated solution, for example ∥Sk∥F → ∞ and ∥Ak∥F → 0, due to the usual scale indeterminacy when doing a matrix factorisation. To avoid this, we normalise the Ak and
) was not mentioned in the regularisation Sect. 3.2, but they are needed to avoid a degenerated solution, for example ∥Sk∥F → ∞ and ∥Ak∥F → 0, due to the usual scale indeterminacy when doing a matrix factorisation. To avoid this, we normalise the Ak and  columns. This translates to forcing the normalisation of the eigenPSF weights contributing to model each observed star. This does not mean that the eigenPSF weights will be the same for each star, but that the norms of the weight vectors are equal.
columns. This translates to forcing the normalisation of the eigenPSF weights contributing to model each observed star. This does not mean that the eigenPSF weights will be the same for each star, but that the norms of the weight vectors are equal.
3.6. Algorithm
The optimisation in Eq. (22) is non-convex as we are facing a matrix factorisation problem. To overcome this situation we use an alternating minimisation scheme where we optimise one variable at a time, iterating over the variables as studied in Xu & Yin (2013) or Bolte et al. (2014). In consequence, we can at most expect them to converge towards a local minima. The main iteration is performed over the different variables occurring in Eq. (22), first over the global  and then over the local S1, α1, …, SK, αK.
and then over the local S1, α1, …, SK, αK.
The method is shown in Algorithm 1, which contains the four main optimisation problems derived from the alternating scheme. There exists a wide literature on minimisation schemes involving non-smooth terms, specifically proximal methods (Parikh & Boyd 2014), which we can exploit in order to handle the four cases. Notably, we use the algorithm proposed by Condat (2013) for problems (II), (III), and (IV). For problem (I), we use the method proposed by Liang et al. (2018) which is an extension of the well-known FISTA algorithm (Beck & Teboulle 2009). Even though the ℓ0 pseudo-norm is non-convex and, therefore, not adapted to the general scenario of the aforementioned algorithms, we can alleviate this issue by combining the application of its proximal operator and a given heuristic.
With regard to the algorithm’s initialisation, we start by a preprocessing where we reject stars that are strong outliers in terms of shape or size. We run the shape measurement algorithm mentioned in Sect. 4.4 on the training stars and discard those that are several sigmas away from nearby stars. At this moment, we can assign a specific weight for each training star. There are three available options: (i) to use a unitary weight for each training star; (ii) to use a weight provided by the user; (iii) to compute a weight ωi as a function of the star’s signal-to-noise-ratio (S/N) based on ωi ∝ S/Ni/(S/Ni + median(S/N)) and bound to a specific interval to avoid bright stars from dominating the optimisation.
Next, we continue with all the local eigenPSFs set to zero, as seen in line 4 of Algorithm 1; and the  matrix set to the identity, favouring the specialisation of each global eigenPSF to one specific monomial. By following this procedure, we are training a global polynomial model that fits the stars as best as it can. Later on, the local models work with the residuals between the observed stars and the global model, trying to capture variations missed in the previous step.
matrix set to the identity, favouring the specialisation of each global eigenPSF to one specific monomial. By following this procedure, we are training a global polynomial model that fits the stars as best as it can. Later on, the local models work with the residuals between the observed stars and the global model, trying to capture variations missed in the previous step.
There are four iteration loops in Algorithm 1. In line 8, this is the main iteration, and in line 15, the iteration over the CCDs for the training of the local model. The other two iterations on lines 9 and 14 correspond to a refinement of the estimation. Our objective is to correctly estimate the global and the local contributions for the model and to do this, we alternate the minimisation between the global and the local contributions, which we call outer minimisation. On top of that, each of these two contributions include an inner alternating minimisation scheme as we are performing a matrix factorisation for the local and for the global models. For example, we are simultaneously minimising over Sk, αk for the local model and over  for the global model. We want to refine this inner minimisation, meaning that the optimisation of the two variables separately approaches the joint optimisation of both variables. To accomplish this, we need to go through a small number of iterations, which are described by the n superscript variables, before continuing the iteration of the next alternating scheme. The optimisation strategy can be seen as a compound alternating minimisation scheme considering the outer and the inner alternations. More information about the optimisation strategy can be found in Appendix D.
for the global model. We want to refine this inner minimisation, meaning that the optimisation of the two variables separately approaches the joint optimisation of both variables. To accomplish this, we need to go through a small number of iterations, which are described by the n superscript variables, before continuing the iteration of the next alternating scheme. The optimisation strategy can be seen as a compound alternating minimisation scheme considering the outer and the inner alternations. More information about the optimisation strategy can be found in Appendix D.
| Initialisation: | |
| 1: Preprocessing() | |
| 2: for k = 1 to K do | |
3: Harmonic constraint parameters (ek, i, ak, i)1 ≤ i ≤ rk → 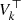 , , 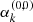
|
|
4: 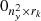 → → 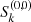
|
|
| 5: end for | |
6: Global coordinates → Πk, 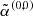
|
(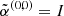 ) ) |
7: 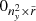 → → 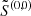
|
|
| Alternate minimisation: | |
| 8: for l = 0 to lmax do | Algorithm’s main iterations |
| 9: for n = 0 to nG do | Global alternating iterations |
10: Noise level, 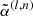 → update → update 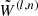
|
|
11: 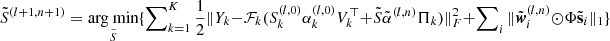
|
(I) |
12: 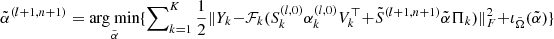
|
(II) |
| 13: end for | |
| 14: for n = 0 to nL do | Local alternating iterations |
| 15: for k = 1 to K do | CCD iterations Noise level |
16: Noise level, 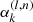 → update → update 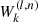
|
|
17: 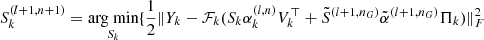
|
|
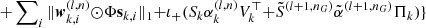 |
(III) |
18: 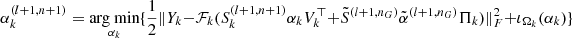
|
(IV) |
| 19: end for | |
| 20: end for | |
| 21: end for | |
3.7. PSF recovery
Once the training of the model on the observed stars is complete, we can continue with the problem of estimating the PSF field at galaxy positions. We call this problem PSF recovery. Gentile et al. (2013) conducted a study on PSF interpolation techniques and Ngolè & Starck (2017) proposed a sophisticated approach based on optimal transport theory (Peyré & Cuturi 2018). We will follow a RBF (Radial Basis Function) interpolation scheme with a thin plate kernel4, as in Schmitz et al. (2020), due to its simplicity and good performance. This choice comes with the assumption that the influence of each observation does not depend on the direction but only on the distance to the target which is well described by the RBF kernel.
The RBF interpolation of a function f on a position u works by building a weighted linear combination of RBF kernels (ϕ(⋅)) centred in each of the available training star positions ui. The interpolation function reads
where  are the linear weights that need to be learnt and NRBF is the number of elements used to estimate the interpolant. In order to learn the weights, we force the exact reconstruction of the interpolant on the known positions, that is
are the linear weights that need to be learnt and NRBF is the number of elements used to estimate the interpolant. In order to learn the weights, we force the exact reconstruction of the interpolant on the known positions, that is  . By fixing the aforementioned constraint we have a system of NRBF equations with NRBF unknown that are the λi weights. Once the system is solved, it is just a matter of evaluating the interpolant on the desired position u following Eq. (25).
. By fixing the aforementioned constraint we have a system of NRBF equations with NRBF unknown that are the λi weights. Once the system is solved, it is just a matter of evaluating the interpolant on the desired position u following Eq. (25).
At this point, we need to choose the function f over which we go on to interpolate. A straightforward choice would be to use the reconstructed PSFs at the training positions as the f(ui). Nevertheless, this would not take into account the specificities and structure of our model. Following the discussion in Sect. 4.2 of Schmitz et al. (2020), we use the learnt Ak and  matrices. They encompass all the spatial distribution properties of the learned features, that is, our eigenPSFs; thus it is natural for our framework to use these values as the function to interpolate.
matrices. They encompass all the spatial distribution properties of the learned features, that is, our eigenPSFs; thus it is natural for our framework to use these values as the function to interpolate.
We continue with a brief explanation of the interpolation procedure. For one given target position u in CCD k, we consider the NRBF closest observed stars to that position that also belong to the CCD k. We call Ak(NRBF) to the Ak matrix composed only with the columns of the aforementioned NRBF stars. We want to estimate the interpolated column vector Ak, u. For this, we use a RBF interpolation scheme for each row of the Ak(NRBF) matrix. The elements of the row t represent the  evaluations and the element
evaluations and the element  represents the interpolated value
represents the interpolated value  . The same procedure is repeated for each row of the Ak(NRBF) matrix so as to obtain the column vector Ak, u. This is illustrated in Fig. 1. We repeat the procedure with the global component matrix,
. The same procedure is repeated for each row of the Ak(NRBF) matrix so as to obtain the column vector Ak, u. This is illustrated in Fig. 1. We repeat the procedure with the global component matrix,  , in order to obtain
, in order to obtain  , another column vector with the interpolated values. At this point, we note that we handle the global and the local contributions independently. Once we have calculated the two interpolated vectors, the reconstructed PSF is obtained following the MCCD data model as can be seen in the next equation
, another column vector with the interpolated values. At this point, we note that we handle the global and the local contributions independently. Once we have calculated the two interpolated vectors, the reconstructed PSF is obtained following the MCCD data model as can be seen in the next equation
 |
Fig. 1. Example of the interpolation procedure involved in the PSF recovery. |
We found that restricting the NRBF neighbours to a single CCD for the global components gives better results. This might be due to the fact that the global components are able to capture some of the discontinuities from one CCD to another and, therefore, the interpolation is degraded when using stars from different CCDs. The number of neighbours NRBF should be chosen as a function of the available number of stars per CCD in the training set and as the RBF kernel chosen. Henceforth, and given the training set we handle in this study, NRBF is set to 20.
4. Numerical experiments
4.1. Data
The simulated data set we create to evaluate MCCD set is based on a Canada-France Imaging Survey (CFIS)5 MegaCam6 exposure from the Canada-France-Hawaii Telescope (CFHT). It contains 2401 stars distributed along 40 CCDs over a field of view of ∼1 deg2 as shown in Fig. 2. Each CCD consists of a matrix of 2048 by 4612 pixels with some given gaps between the different CCDs. The horizontal gap length consist of ∼70 pixels while vertical gaps contain ∼425 pixels.
 |
Fig. 2. Star positions in CFHT’s MegaCam used for the simulated dataset. The positions were taken from a real CFIS exposure. |
4.2. Training set
Our simulation pipeline considers a Moffat PSF profile with normalised flux drawn using the Galsim software7 (Rowe et al. 2015) for each position in the exposure. To simulate the PSF shape variation, we used two radial analytic functions which define our ground truth shape ellipticities distortions. Shearing stars leads naturally to a size variation. Figure 3 shows the resulting e1, e2 and size maps. Our pipeline performs the following steps:
-
Simulate Moffat stars with a size fixed to the mean size measured in the real exposure.
-
Shear the simulated stars as a function of their position using the two analytical functions.
-
Apply a random sub-pixel shift following a uniform distribution centred on zero.
-
Apply a binning to get a 51 × 51 pixel image, with a pixel size equivalent to CFIS MegaCam’s maps, that is, 0.187 arcsec.
-
Add a constant white Gaussian noise to the images, with standard deviation σ, derived from the desired S/N level
 |
Fig. 3. Shape measurement results of the simulated test star catalogue following the analytical ellipticities. |
where y is the image postage stamp consisting of p2 pixels. Each experience will consist of a constant S/N value, as we later see, which is drawn from the set {10, 30, 50, 70}.
Since PSFEx was designed as a companion software to SExtractor, we need to follow a different procedure to generate the simulated data. We first need to process our simulations with SExtractor, so that the catalogue produced can be used as inputs for PSFEx. To accomplish this, we mimic a complete CCD so that SExtractor is able to process it. We create star images as we already described for the MCCD method but without noise as it will be added later. Then we distribute them on a mock image of 2048 × 4612 pixels. The corresponding positions will be the pixel coordinates that are presented in Fig. 2. Once the mock image is created, we add the noise value according to the desired S/N to the whole image. When the mock image is created, we run SExtractor in order to have a star catalogue that PSFEx can use as input.
4.3. Testing data set
For the testing, we want to observe how well the different models capture the ellipticity maps when trained on real star positions. Therefore, the positions in each CCD are taken from a regular grid of 20 × 40 and considering that the total amount of CCDs is 40, we finally obtain a total of 32 000 stars with which to test our model. These stars are simulated following the same ellipticity maps (see Fig. 3), without any sub-pixel shift and without any noise. The goal is now to use the training data (i.e. simulated observed stars) to learn the model, and then to predict the PSFs at positions of test stars. As we have the ground truth at these positions, without noise and sub-pixel shift, it is easy to get a robust evaluation of model predictions.
4.4. Quality criteria
In order to correctly assess the performance of our PSF modelling algorithm, we consider several criteria:
-
Pixel root mean square error (RMSE): calculated between the pixel images of the recovered PSFs and the noiseless test stars. The expression of the pixel RMSE is the following:
where Yi, j is the pixel j of test star i that has a total of
 pixels, N is the total number of test stars,
pixels, N is the total number of test stars,  is the estimation of the test star’s pixel and ⟨ ⋅ ⟩ denotes the mean over all the elements in the array.
is the estimation of the test star’s pixel and ⟨ ⋅ ⟩ denotes the mean over all the elements in the array. -
Shape (ellipticity) error: We estimate the ellipticities of reconstructed stars using the adaptive moments’ ellipticity estimator from Galsim’s HSM module (Hirata & Seljak 2003; Mandelbaum et al. 2005). The shape and size definitions can be found in Appendix B. For each of the ellipticity components, the RMSE is calculated as:
-
Size error: We use the measurements from HSM and the definition in Appendix B to compute the following RMSE:
-
Moment residual maps: To visualise the shape and size errors, we plot these quantities as a function of their position on the focal plane.
When comparing two methods, we define the relative gain with regard to the metric, m, of method 1 with respect to the method 2 as:
4.5. Model parameters
Based on experiments with simulated and real data, we have chosen the following parameters
-
PSFEx: we use the following configuration:
PSF_SAMPLING 1.0 PSF_SIZE 51,51 PSFVAR_KEYS XWIN_IMAGE,YWIN_IMAGE PSFVAR_GROUPS 1,1 PSFVAR_DEGREES 2 PSFVAR_DEGREES refers to the maximum polynomial degree, and, XWIN_IMAGE and YWIN_IMAGE, to the windowed centroid positions in pixel coordinates. The PSFEx software8 does not include publicly an interpolation method, so we use an available PSFEx interpolation module9.
-
RCA: we set r equal to eight local components, the denoising parameters
 to 1, and the other parameters to their default value from its official repository10.
to 1, and the other parameters to their default value from its official repository10. -
MCCD: we use the same parameters as RCA for the local component and a maximum polynomial degree of eight for the global components. The denoising parameters
 and
and  are set to 1 for the local and the global contributions.
are set to 1 for the local and the global contributions.
The MCCD parameters that most affect its behaviour are mentioned above. Their choice greatly relies on the training data set used. Depending on the number of stars available and the complexity of the instrument’s PSF, it may be preferable to adopt a more complex model by augmenting the number of local components, r, and the maximum polynomial degree. However, if the stars are not enough to constrain the model, we may end with a model that overfits the training stars. A proper selection of the denoising parameters can control the bias-variance tradeoff in the estimation. A high value of the denoising parameter, namely, 3, leads to an extremely denoised model. It will contain a high estimation bias that can be related with a model that cannot capture some spatial variations and fine details of the PSF. On the contrary, if the denoising parameter is close to zero, the only denoising performed by the MCCD is due to the low-rank constraint and therefore the estimations can be rather noisy.
4.6. Results
4.6.1. Comparison between PSFEX, RCA and MCCD-RCA
The first results can be seen in Figs. 4 and 5, where we compare the PSFEx, RCA, and MCCD-RCA algorithms. We observe that MCCD-RCA outperforms the other methods, with an average pixel RMS improvement over PSFEx of 51% and ellipticity RMS improvement ranging from 15% for stars with S/N 10 to 36% for a S/N of 70. The RCA is almost as good as MCCD-RCA for the pixel error, but does not provide good results for the other metrics. This behaviour can be explained by the fact that the model strongly deteriorates for some CCDs, giving extreme ellipticities and sizes values. These deteriorations of the model are not strong enough to produce a large pixel error but causes much more significant errors on the moments. We include in Appendix C RCA’s R2 residual map that shows the catastrophic failure in the modelling of some CCDs.
 |
Fig. 4. RMSE on pixels, shape, and size metrics as a function of stars S/N for the three main methods. The RMSE are plotted with solid lines and the gain of the methods with respect to PSFEx are plotted with dashed lines. |
 |
Fig. 5. Moment residual maps comparing the MCCD-RCA algorithm on the left and the PSFEx algorithm on the right. They are obtained by subtracting the model’s and the test star’s measured shape and size metrics and plotting them on their corresponding position over the focal plane. The S/N value of the star dataset is 50. |
We can see on the right column of the residual maps in Fig. 5 that PSFEx’s ellipticity residuals follow the global pattern from the dataset. This means that the ellipticity is not captured in the model, showing some of the difficulties found when modelling a global ellipticity pattern using independent models for each CCD. The MCCD-RCA algorithm, which builds up a model for the whole focal plane, does a better job in capturing the global ellipticity pattern. The MCCD-RCA’s residuals are smaller and less correlated with the pattern of the dataset. With regard to the third row of Fig. 5, where the size of the simulated PSFs is practically constant, we observe that the MCCD-RCA has slightly larger errors when the training star density is low, as in the bottom-right corner (see Fig. 2).
4.6.2. Comparison between MCCD-POL, MCCD-RCA, and MCCD-HYB
The comparison between the MCCD-POL, MCCD-RCA, and MCCD-HYB methods is shown in Fig. 6. First, we notice that MCCD-POL presents poor performance in most of the metrics. This indicates that the local polynomial model is not able to capture the PSF variations that are left over from the difference of the global model and the observed stars. Hence, even if MCCD-POL has a lower pixel error than PSFEx (see Fig. 4), it has greater ellipticity errors. Capturing these PSF variations properly is essential for obtaining good ellipticity performances. The MCCD-RCA and MCCD-HYB have similar behaviours, but MCCD-HYB uses a mixed approach of a polynomial and graph-based local model outperforms the original MCCD-RCA method in terms of ellipticity components. The average gain in both components of MCCD-HYB with respect to MCCD-RCA is around 18%, proving the utility of using the hybrid approach. This suggests that there are some features related to the PSF shape that can be captured by a simple polynomial model and not by the graph-based model alone. Examples of global and local eigenPSF from the MCCD-HYB model can be seen in Appendix C.
 |
Fig. 6. Comparison of the performance of MCCD-POL, MCCD-RCA, and MCCD-HYB methods in terms of the RMSE on the pixels, the shape and the size metric of the star’s S/N. The RMSE are plotted on a solid line and the gain of the method with respect to PSFEx is plotted on dashed lines. |
4.7. Comparison of computing resources
The MCCD methods take ∼2.9× more CPU-time than PSFEx when compared on the same machine. We evaluate it on the fitting and validation procedures, that is, the estimation of the PSF model and the recovery of PSF at test positions. A relevant detail is that the PSFEx package is coded in the C programming language, while the MCCD methods are completely coded in Python.
5. UNIONS/CFIS experiments
In this section, we compare the MCCD-HYB method with PSFEx using real data from the Ultra-violet Near-Infrared Optical Northern Sky (UNIONS) survey, which is a collaboration between the Panoramic Survey Telescope and Rapid Response System (Pan-STARRS) and CFIS. We use the r-band data from the latter.
5.1. Dataset
We analysed a subset of around 50 deg2 from the whole CFIS survey area that, in total, will eventually span 5000 deg2. It corresponds to the subset named W3 described in Erben et al. (2013), and includes 217 exposures. Each CCD from each exposure has been processed independently with SExtractor. The stars were selected in a size-magnitude diagram, in the magnitude range between 18 and 22, and a Full-Width Half Maximum (FWHM) range between 0.3 and 1.5 arcsec. In order to validate the PSF models, we randomly split the stars into a testing and a training dataset, trying to estimate the first set of stars while constructing our model only with the second. The training dataset is composed of 80% of the detected stars and the test dataset of the remaining 20%. We consider a fixed threshold on the number of training stars per CCD, meaning that if the number of training stars in a given CCD is less than 30, we discard the CCD. The star density of the training dataset is presented in Fig. 7. The ellipticity and the size of the training stars can be seen in Fig. 8. Each bin represents the mean shape measurement over all the stars with a centroid located within the bin.
 |
Fig. 7. Star density of all the training dataset with respect to their position on the MegaCam’s focal plane. We have on average 1560 training stars per exposure. |
 |
Fig. 8. Ellipticities and size maps measured on the training stars of our CFIS dataset. |
5.2. Model parameters
The setup of PSFEx for this experiment is similar to the one used for the simulated images, which can be found in Sect. 4.5. The MCCD-HYB method uses a maximum global polynomial degree of 3, with 16 local components and the denoising parameters Kσ set up to 0.1. In order to compare the star images with the different methods (PSFEx and MCCD-HYB), the models need to match the flux as well as the centre of the star. Hence, after estimating a PSF model at a given star location, the PSF is normalised and shifted to match the star. For this purpose, we use the same intra-pixel shift and flux estimation methods for both PSF models: (i) we estimate the star and the PSF centroids, (ii) we calculate the shift needed by the PSF to match the star and construct a shifting kernel, and (iii) the PSFs are convolved by their corresponding shifting-kernel. To match the flux, we calculate an α parameter for each test star and PSF that corresponds to the argument that minimises the function, f(α) = ∥I1 − αI2∥2, where I1 and I2 are the star and the PSF, respectively.
5.3. Metric on real data: the Qp criteria
Performing a comparison between two PSF models with real data is an arduous task since we do not know the shapes and pixel values of the observed stars. However, subtracting our estimated model from an observed star (i.e. pixel residual) should lead to a residual map containing only noise if the model is perfect. The probability of having our model correlated with the noise is extremely small. Therefore, from this point of view, the method with the smallest pixel RMS residual error can be considered as the best. Using all the test stars ys and our estimates  , we calculate the pixel RMS residual error:
, we calculate the pixel RMS residual error:  , where Ns is the number of stars and Ni is the number of pixels we consider in a given image when we use a 10 pixel radius circle from the centre of the residual images. The noise standard deviation σnoise is calculated from the stars only using the pixels outside the aforementioned circle. For a perfect modelling, we would have Err ≈ σnoise, and we define the Qp1 metric as:
, where Ns is the number of stars and Ni is the number of pixels we consider in a given image when we use a 10 pixel radius circle from the centre of the residual images. The noise standard deviation σnoise is calculated from the stars only using the pixels outside the aforementioned circle. For a perfect modelling, we would have Err ≈ σnoise, and we define the Qp1 metric as:
We next introduce two metrics to quantify how noisy the models are. The variance of the PSF model for the test stars s reads ![$ \sigma_{s}^{2} = [ \text{Var}(\mathit{y}_{s} - \hat{y}_{s}) - \sigma_{\text{noise}}^{2}(\mathit{y}_{s}) ]_{+} $](/articles/aa/full_html/2021/02/aa39584-20/aa39584-20-eq147.gif) , where Var(⋅) is a usual variance estimator, the operator [ ⋅ ]+ sets to zero negative values and
, where Var(⋅) is a usual variance estimator, the operator [ ⋅ ]+ sets to zero negative values and  is the noise variance estimation for a single star. We present the Qp2 and Qp3 metrics in the following equations:
is the noise variance estimation for a single star. We present the Qp2 and Qp3 metrics in the following equations:
The Qp2 metric represents the modelling error expectation for a given star and the Qp3 metric indicates the fluctuation of the modelling error. A perfect PSF model would give values close to zero for the three metrics.
5.4. Results
The main results of the experiment are synthesised in Table 2, where the Qp criteria are given. In the Qp1 column, we can observe a 22% gain of the MCCD-HYB method with respect to PSFEx. From Qp2 and Qp3 metrics, we also conclude that the MCCD-HYB model is considerably less noisy than the one from PSFEx.
Qp criterion using all test stars of the W3 dataset from CFIS.
In order to explore potential remaining structure in the residuals, we stack together the residuals for all 534 test stars from a random exposure. These are shown, along with the stacking of the test stars themselves, in Fig. 9. We can see that PSFEx has a sharper stacked error compared to MCCD-HYB. This could indicate that our algorithm is better at capturing the size of the PSF, as the peak of the residual is directly related to it. Considering that there is no trace of shifting errors and that we are calculating the flux optimally, a greater mismatch in the size of the PSF equals to a greater peak pixel error on the residual. The third row presents the mean of the stacked absolute value of the residuals for both of the PSF models so that the residuals can not cancel themselves. We observe the same behaviour described above with the PSFEx pixel error distribution being sharper but more centred. It is also possible to notice the higher noise PSFEx has when compared to the MCCD-HYB model.
 |
Fig. 9. Stacked star profile from all 534 test stars in a random CFIS exposure (id. 2099948) (top), corresponding stacked residuals after subtraction by the PSFEx (middle left) or MCCD-HYB (middle right) PSF models. The bottom row includes the stacked absolute value of the residuals. |
Figure 10 presents examples of star image reconstructions by the two different PSF models, PSFEx and MCCD-HYB, and their corresponding residuals. The proposed method yields a near noiseless model when compared to PSFEx, as can clearly be seen on the top-left and bottom-right stars of Fig. 10, where the stars have low S/N of 19.3 and 4.2, respectively. Both models share a good estimation of the bottom-right star, which comes a low-stellar-density region of the focal plane (the bottom-right corner, as can be seen in Fig. 7). On the bottom-left star of Fig. 10, we observe a similar type of error as that appearing in Fig. 9.
 |
Fig. 10. Examples of real CFIS test stars, the estimations of both methods, and the pixel residuals. The exposures are the same as in Fig. 9. We present four test stars with the estimated PSF models and the corresponding residuals. Top-left star: a star extracted from the top-left corner of the focal plane with a S/N of 19. Top-right star: a star leading to a high error for both methods. Bottom-left star: a star located in the centre of the focal, with a relatively high S/N of 160. Bottom-right star: a star located in the bottom-right corner of the focal plane, with a low S/N of 4. |
It is difficult to derive conclusions of different PSF model performances based on the shape measurement of noisy stars due to its high stochasticity. Nevertheless, driven by the comments from DES Y1 (Zuntz et al. 2018) on the residual mean size offset from the PSFEx model, we conducted a study with our data. We measured the size from the training stars and from both calculated PSF models, PSFEx and MCCD-HYB, and then computed the residual. The RMS residual size of the ΔR2/R2 value gave 4.82 × 10−2 for PSFEx and 4.02 × 10−2 for MCCD-HYB. This represents a 16% gain of our proposed algorithm.
Figure 11 presents in the left column the histogram of the residuals and in the right column the histograms of the size metrics. We notice that the MCCD-HYB algorithm has a sharper residual size around zero. The figure also includes the mean of the residuals for each PSF model. This shows that both models tend to overestimate the size of the PSF. However, the MCCD-HYB model presents a 30% gain in the mean residual size with respect to PSFEx, indicating a smaller bias in the shape.
 |
Fig. 11. Histograms showing the distribution of the size metric over the training stars and their residuals for both PSF models, PSFEx and MCCD-HYB. |
6. Reproducible research
In the spirit of reproducible research, the MCCD-RCA algorithm is to be publicly available on the CosmoStat’s Github11, including the material needed to reproduce the simulated experiences. The MCCD PSF modelling software will be included in the CFIS shape measurement pipeline Guinot et al. (in prep.).
7. Conclusion
In this work, we present a family of non-parametric PSF (Point Spread Function) modelling methods coined MCCD, including its best-performing extension MCCD-HYB, which are built upon the existing Resolved Component Analysis (RCA) method and are capable of constructing PSF models that span all the charge-coupled devices (CCDs) from an instrument’s focal plane at once. Naturally, the use of more stars for the training allows us to build more complex models that can capture evasive features. Our model is composed of global components, spanning all the CCDs, and local components that are CCD-specific. By using this structure, we can better capture global patterns and features that might be lost when using only a local model like in RCA or, the widely used algorithm, PSFEx.
The method was first tested with a set of simulated PSFs following a real star spatial distribution over MegaCam’s focal plane, an instrument from the Canada-France-Hawaii Telescope(CFHT). Its use leads to better performance in all the evaluated metrics when compared to PSFEx. We then tested the method on a set of real CFIS images, an imaging survey based on CFHT, in order to confirm that it can handle real data. Our method achieves a smaller pixel root mean square (RMS) residual than PSFEx and the estimated model is considerably less noisy.
The performance gain of the MCCD methods over PSFEx is higher when using our simulated dataset than when using the real dataset. This can be explained by the fact that our simulated dataset shows more intricate variations in the PSF than the real data does and MCCD is better at capturing such strong variations.
The proposed method can naturally handle more complex PSF profiles, such as those expected from space-based instruments. The RCA method was tested with Euclid-like simulated PSFs and has demonstrated a better performance than PSFEx (Ngolè et al. 2016; Schmitz et al. 2020). Therefore, we expect to have an even superior performance in this scenario with MCCD. Thanks to its formulation, it can also handle super-resolution, making it suitable for undersampled data.
Despite the good performance of the method, there is still room for improvement. A natural straightforward extension for the MCCD algorithms would be to replace the denoising strategy by one more suited for the specificities of the PSFs we work with. This could be accomplished by using a deep neural network as the denoiser (Ronneberger et al. 2015; Ye et al. 2018).
A graph G can be defined as a pair (V, E), where V is the set of vertices and E the set of edges that connects the different vertices. In our case, each star position constitutes a vertex and there is one edge for each pair of vertices. The edges have no preferred direction and its value depends on the distance between the two vertices it connects.
We use the implementation found in the python package https://github.com/CEA-COSMIC/ModOpt from Farrens et al. (2020).
Acknowledgments
The authors would like to thank the anonymous referee for the fruitful comments on the paper. This work is based on data obtained as part of the Canada-France Imaging Survey, a CFHT large program of the National Research Council of Canada and the French Centre National de la Recherche Scientifique. Based on observations obtained with MegaPrime/MegaCam, a joint project of CFHT and CEA Saclay, at the Canada-France-Hawaii Telescope (CFHT) which is operated by the National Research Council (NRC) of Canada, the Institut National des Science de l’Univers (INSU) of the Centre National de la Recherche Scientifique (CNRS) of France, and the University of Hawaii. This research used the facilities of the Canadian Astronomy Data Centre operated by the National Research Council of Canada with the support of the Canadian Space Agency. This work has made use of the CANDIDE Cluster at the Institut d’Astrophysique de Paris and made possible by grants from the PNCG and the DIM-ACAV. Software: Numpy (van der Walt et al. 2011), Scipy (Virtanen et al. 2020), Astropy (Astropy Collaboration 2013, 2018), GalSim (Rowe et al. 2015), IPython (Perez & Granger 2007), Jupyter (Kluyver et al. 2016), Matplotlib (Hunter 2007), PySAP (Farrens et al. 2020).
References
- Aliprantis, C., & Border, K. 2007, Infinite Dimensional Analysis A Hitchhiker’s Guide (Springer) [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Beck, A. 2017, First-Order Methods in Optimization, MOS-SIAM Series on Optimization (Society for Industrial and Applied Mathematics) [Google Scholar]
- Beck, A., & Teboulle, M. 2009, SIAM J. Img. Sci., 2, 183 [Google Scholar]
- Beltramo-Martin, O., Marasco, A., Fusco, T., et al. 2020, MNRAS, 494, 775 [Google Scholar]
- Bendinelli, O., Parmeggiani, G., & Zavatti, F. 1988, J. Astrophys. Astron., 9, 17 [Google Scholar]
- Bertin, E. 2011, in Astronomical Data Analysis Software and Systems XX, eds. I. N. Evans, A. Accomazzi, D. J. Mink, & A. H. Rots, ASP Conf. Ser., 442, 435 [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bolte, J., Sabach, S., & Teboulle, M. 2014, Math. Program., 146, 459 [Google Scholar]
- Chung, F. R. K. 1997, Spectral Graph Theory (American Mathematical Society) [Google Scholar]
- Condat, L. 2013, J. Optim. Theor. Appl., 158, 460 [Google Scholar]
- Cropper, M., Hoekstra, H., Kitching, T., et al. 2013, MNRAS, 431, 3103 [Google Scholar]
- Erben, T., Hildebrandt, H., Miller, L., et al. 2013, MNRAS, 433, 2545 [Google Scholar]
- Farrens, S., Grigis, A., El Gueddari, L., et al. 2020, Astron. Comput., 32, 100402 [Google Scholar]
- Gentile, M., Courbin, F., & Meylan, G. 2013, A&A, 549, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Golub, G. H., & Van Loan, C. F. 1996, Matrix Computations, 3rd edn. (USA: Johns Hopkins University Press) [Google Scholar]
- Herbel, J., Kacprzak, T., Amara, A., Refregier, A., & Lucchi, A. 2018, JCAP, 07, 054 [Google Scholar]
- Hirata, C., & Seljak, U. 2003, MNRAS, 343, 459 [Google Scholar]
- Hoffmann, S. L., & Anderson, J. 2017, A Study of PSF Models for ACS/WFC, Instrument Science Report ACS, 2017-8 [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R. A., McConnachie, A., Cuillandre, J. C., et al. 2017, ApJ, 848, 128 [Google Scholar]
- Infante-Sainz, R., Trujillo, I., & Román, J. 2019, MNRAS, 491, 5317 [Google Scholar]
- Jarvis, M., Sheldon, E., Zuntz, J., et al. 2016, MNRAS, 460, 2245 [Google Scholar]
- Jarvis, M., Bernstein, G. M., Amon, A., et al. 2021, MNRAS, 501, 1282 [Google Scholar]
- Jee, M. J., Blakeslee, J. P., Sirianni, M., et al. 2007, PASP, 119, 1403 [Google Scholar]
- Jia, P., Wu, X., Yi, H., Cai, B., & Cai, D. 2020a, AJ, 159, 183 [Google Scholar]
- Jia, P., Li, X., Li, Z., Wang, W., & Cai, D. 2020b, MNRAS, 493, 651 [Google Scholar]
- Kilbinger, M. 2015, Rep. Prog. Phys., 78, 086901 [Google Scholar]
- Kluyver, T., Ragan-Kelley, B., Pérez, F., et al. 2016, ELPUB [Google Scholar]
- Krist, J. 1995, in Astronomical Data Analysis Software and Systems IV, eds. R. A. Shaw, H. E. Payne, & J. J. E. Hayes, ASP Conf. Ser., 77, 349 [NASA ADS] [Google Scholar]
- Kuijken, K., Heymans, C., Hildebrandt, H., et al. 2015, MNRAS, 454, 3500 [Google Scholar]
- Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, ArXiv e-prints [arXiv:1110.3193] [Google Scholar]
- Liang, J., Luo, T., & Schönlieb, C. B. 2018, ArXiv e-prints [arXiv:1811.01430] [Google Scholar]
- Mandelbaum, R., Hirata, C. M., Seljak, U., et al. 2005, MNRAS, 361, 1287 [Google Scholar]
- Miller, L., Heymans, C., Kitching, T., et al. 2013, MNRAS, 429, 2858 [Google Scholar]
- Ngolè, F., & Starck, J.-L. 2017, SIAM J. Imaging Sci., 10, 1549 [Google Scholar]
- Ngolè, F., Starck, J.-L., Ronayette, S., Okumura, K., & Amiaux, J. 2015, A&A, 575, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ngolè, F., Starck, J.-L., Okumura, K., Amiaux, J., & Hudelot, P. 2016, Inverse Prob., 32, 124001 [Google Scholar]
- Parikh, N., & Boyd, S. 2014, Found. Trends Optim., 1, 127 [Google Scholar]
- Perez, F., & Granger, B. E. 2007, Comput. Sci. Eng., 9, 21 [Google Scholar]
- Peyré, G., & Cuturi, M. 2018, Comput. Trans. Optim. [Google Scholar]
- Piotrowski, L. W., Batsch, T., Czyrkowski, H., et al. 2013, A&A, 551, A119 [EDP Sciences] [Google Scholar]
- Ronneberger, O., Fischer, P., & Brox, T. 2015, International Conference on Medical Image Computing and Computer-assisted Intervention (Springer), 234 [Google Scholar]
- Rowe, B., Jarvis, M., Mandelbaum, R., et al. 2015, Astron. Comput., 10, 121 [Google Scholar]
- Schmitz, M. A., Heitz, M., Bonneel, N., et al. 2018, SIAM J. Imaging Sci., 11, 643 [Google Scholar]
- Schmitz, M. A., Starck, J. L., Mboula, F. N., et al. 2020, A&A, 636, A78 [CrossRef] [EDP Sciences] [Google Scholar]
- Schrabback, T., Hartlap, J., Joachimi, B., et al. 2010, A&A, 516, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Starck, J.-L., Murtagh, F., & Bertero, M. 2011, Handbook of Mathematical Methods in Imaging (Springer), 1489 [Google Scholar]
- Starck, J.-L., Murtagh, F., & Fadili, J. 2015, Sparse Image and Signal Processing: Wavelets and Related Geometric Multiscale Analysis, 2nd edn. (Cambridge University Press) [Google Scholar]
- Tyson, J. A., Zhan, H., Knox, L., & LSST Collaboration 2006, Am. Astron. Soc. Meeting Abstracts, 209, 86.08 [Google Scholar]
- van der Walt, S., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Meth., 17, 261 [Google Scholar]
- Xu, Y., & Yin, W. 2013, SIAM J. Imaging Sci., 6, 1758 [Google Scholar]
- Ye, J. C., Han, Y., & Cha, E. 2018, SIAM J. Imag. Sci., 11, 991 [Google Scholar]
- Zuntz, J., Sheldon, E., Samuroff, S., et al. 2018, MNRAS, 481, 1149 [Google Scholar]
Appendix A: RCA regularisations
In this section, we provide more detailed descriptions for each regularisation that we use in our local RCA model:
-
Low rank: PSF variations can be explained by a small number of eigenPSFs. This constraint can be enforced by the proper choice of two parameters, the number of local, rk, and global,
 , eigenPSFs. These parameters are directly linked with the complexity of the model we are addressing for each given case and its selection naturally depends on the PSF field we will be facing. It is important to allow the model a certain complexity so that it can correctly capture the PSF field’s variations but it should not be much more complex as the model will tend to overfit the noisy observations and, therefore, lose its generalising power for estimating the PSF in galaxy positions.
, eigenPSFs. These parameters are directly linked with the complexity of the model we are addressing for each given case and its selection naturally depends on the PSF field we will be facing. It is important to allow the model a certain complexity so that it can correctly capture the PSF field’s variations but it should not be much more complex as the model will tend to overfit the noisy observations and, therefore, lose its generalising power for estimating the PSF in galaxy positions. -
Positivity: the reconstructed PSFs
 should only contain non-negative pixel values.
should only contain non-negative pixel values. -
Sparsity: the observed PSFs are structured images; a way to promote our model to follow this structured behaviour is to enforce the sparsity of the eigenPSFs in an appropriate basis.
-
Spatial constraints: the regularity of the PSF field ℋ means that the smaller the distance between two PSFs positions ui, uj the smaller the difference between their representations should be ℋ(ui),ℋ(uj). This regularity can be achieved by enforcing constraint in the coefficient matrices
 ; for example, the line l of Ak corresponds to the contribution of eigenPSF l to the
; for example, the line l of Ak corresponds to the contribution of eigenPSF l to the  stars in CCD k located in positions
stars in CCD k located in positions  . The closer the positions, the closer the coefficient values should be.
. The closer the positions, the closer the coefficient values should be.
Appendix B: Shape and size definitions
The ellipticity parameters and the size are defined in terms of the moments of the surface brightness profile I(x, y) following (Hirata & Seljak 2003):
where μ, ν ∈ {x, y} and w(x, y) is weight window to avoid noise related issues. The size is defined as:
and the ellipticities are defined as:
The adaptive moment measurement from HSM gives σ as output which relates to our size metric as R2 = 2σ2.
Appendix C: Additional figures
In this appendix, we include the additional figures, Figs. C.1 and C.2.
 |
Fig. C.1. Residual ΔR2/R2 map of the RCA algorithm of stars with a S/N of 50. The CCDs where the RCA model is having degeneracies that can be clearly spotted on the map. |
 |
Fig. C.2. Example eigenPSFs extracted from the MCCD-HYB PSF model trained on the simulated dataset with a S/N of 70. The local eigenPSFs were extracted from the graph’s spatial constraint of a central CCD. It can be seen from the eigenPSFs that the global model is specialising on the shape of the PSF while the local model specialises on capturing its ellipticity. It is also worth to mention that the first global eigenPSF found on the first row provides the baseline isotropic PSF the model uses. (a) Global eigenPSFs. (b) Local eigenPSFs. |
Appendix D: Optimisation methods
In this appendix, we include details on the practical resolution of the four optimisation problems seen in Algorithm 1. For more information about proximal operators and proximal algorithms, we refer to Parikh & Boyd (2014) and Beck (2017).
D.1. Problem (III)
As in most of the optimisation problems, the algorithm used depends on the objective function we work with. In this case, we use the primal-dual algorithm 3.1 in Condat (2013)12. The main motivation resides in the nature of the constraints we use when optimising over Sk, as we face one smooth and two non-smooth terms, and a linear operator. The optimisation algorithm aims at solving the following problem:
where: (i) F is convex, differentiable and its gradient is L-Lipschitz continuous; (ii) G and H are proximable functions that should have closed form proximal operators; (iii) L is a bounded linear operator; and (iv) the set of minimisers of the aforementioned optimisation problem is nonempty. It is straightforward to identify the different functions in the optimisation of the local Sk matrix which match the formulation of Eq. (D.1). Following the notation we use throughout the paper, let  , with
, with  , and G(Sk) = ∑i∥wk, i ⊙ Φsk, i∥1. Let H(Sk) = ι+(Sk) and the linear operator L be
, and G(Sk) = ∑i∥wk, i ⊙ Φsk, i∥1. Let H(Sk) = ι+(Sk) and the linear operator L be  . For the moment, we consider Φ to be the identity.
. For the moment, we consider Φ to be the identity.
To solve the algorithm, we need the proximal operator of H*, the adjoint function of H, the proximal operator of G, and the gradient of F with its Lipschitz constant.
Starting with H, the proximal operator of H* can be calculated directly using the proximal operator of the function H itself by means of the Moreau decomposition (Beck 2017, Theorem 6.44). The proximal operator of an indicator function over a set 𝒞 is the orthogonal projection over that set. Therefore, we note [X]+ the projection of X ∈ ℝn × m onto the positive orthant, that is,
Continuing with G, the proximal operator of the ℓ1 norm is the soft thresholding operator which can be defined component-wise, for x, λ ∈ ℝ, as
We name L∇SkF(⋅) the Lipschitz constant of F’s gradient. The next equations resume what we need to use the chosen optimisation algorithm:
where the proximal operator of G is defined component-wise, the notation [sk, i]j represents the element j of the i column vector of matrix Sk,  is the adjoint operator of ℱk, and ρ(⋅) is the spectral radius13 that we calculate using the power method (Golub & Van Loan 1996). For the algorithm’s parameters τ and σ, based on Theorem 3.1 from Condat (2013), we use:
is the adjoint operator of ℱk, and ρ(⋅) is the spectral radius13 that we calculate using the power method (Golub & Van Loan 1996). For the algorithm’s parameters τ and σ, based on Theorem 3.1 from Condat (2013), we use:
where ∥ ⋅ ∥op is the operator norm (Aliprantis & Border 2007) and α is a parameter we set to 3/2. Being L a bounded linear operator we can calculate ∥L∥op as  being L* its adjoint operator.
being L* its adjoint operator.
We now consider the case where Φ is not the identity, but it is orthonormal, ΦTΦ = I. We can adapt the soft thresholding operator in order to cope with the G term. This would be  . When using undecimated wavelets as the starlets, the orthonormal condition is not met. Nevertheless, they are tight frames whose Gram matrix is close to the identity which means that the presented formulation will be a good approximation. We refer to Starck et al. (2015) for more information on wavelets.
. When using undecimated wavelets as the starlets, the orthonormal condition is not met. Nevertheless, they are tight frames whose Gram matrix is close to the identity which means that the presented formulation will be a good approximation. We refer to Starck et al. (2015) for more information on wavelets.
D.2. The remaining optimisation problems
We deal in a similar way with the problems (II) and (IV) from Algorithm 1 using the same optimisation method proposed in Condat (2013). On the other hand, for problem (I), we use the optimisation algorithm in Liang et al. (2018). This is due to the fact that we are neglecting the positivity constraint as we account for it when optimising over the other variables. In order to use these algorithms we need to compute the gradients of the differentiable term of each problem as follows:
where  . Concerning the global optimisation over
. Concerning the global optimisation over  and
and  we need to consider all the CCDs when computing the gradient. So we can reformulate the global formulas as:
we need to consider all the CCDs when computing the gradient. So we can reformulate the global formulas as:
An approximation for the Lipschitz constants of the different gradients can be calculated as:
where ρ(⋅) is the spectral radius.
Finally, we also need the proximal operator of the indicator function over the unit-ball ιℬ(⋅), where ℬ = {x∈ℝn | ∥x∥2 = 1}. It can be computed as:
D.3. Sparsity enforcement parameters
There are two moments when we enforce sparsity during the optimisation. First, when we denoise the eigenPSFs by the use of the ℓ1 norm as in Eq. (22). The w weights are set depending on a noise estimation of the observed images, and the parameters  and
and  . The noise standard deviation is estimated using the median absolute deviation. The higher the Kσ parameters are set, the higher the thresholding and the denoising will be. Second, when we enforce the spatial constraints through α sparsity. In this case, we follow the sparsity enforcement proposed in Ngolè et al. (2016).
. The noise standard deviation is estimated using the median absolute deviation. The higher the Kσ parameters are set, the higher the thresholding and the denoising will be. Second, when we enforce the spatial constraints through α sparsity. In this case, we follow the sparsity enforcement proposed in Ngolè et al. (2016).
All Tables
All Figures
 |
Fig. 1. Example of the interpolation procedure involved in the PSF recovery. |
| In the text | |
 |
Fig. 2. Star positions in CFHT’s MegaCam used for the simulated dataset. The positions were taken from a real CFIS exposure. |
| In the text | |
 |
Fig. 3. Shape measurement results of the simulated test star catalogue following the analytical ellipticities. |
| In the text | |
 |
Fig. 4. RMSE on pixels, shape, and size metrics as a function of stars S/N for the three main methods. The RMSE are plotted with solid lines and the gain of the methods with respect to PSFEx are plotted with dashed lines. |
| In the text | |
 |
Fig. 5. Moment residual maps comparing the MCCD-RCA algorithm on the left and the PSFEx algorithm on the right. They are obtained by subtracting the model’s and the test star’s measured shape and size metrics and plotting them on their corresponding position over the focal plane. The S/N value of the star dataset is 50. |
| In the text | |
 |
Fig. 6. Comparison of the performance of MCCD-POL, MCCD-RCA, and MCCD-HYB methods in terms of the RMSE on the pixels, the shape and the size metric of the star’s S/N. The RMSE are plotted on a solid line and the gain of the method with respect to PSFEx is plotted on dashed lines. |
| In the text | |
 |
Fig. 7. Star density of all the training dataset with respect to their position on the MegaCam’s focal plane. We have on average 1560 training stars per exposure. |
| In the text | |
 |
Fig. 8. Ellipticities and size maps measured on the training stars of our CFIS dataset. |
| In the text | |
 |
Fig. 9. Stacked star profile from all 534 test stars in a random CFIS exposure (id. 2099948) (top), corresponding stacked residuals after subtraction by the PSFEx (middle left) or MCCD-HYB (middle right) PSF models. The bottom row includes the stacked absolute value of the residuals. |
| In the text | |
 |
Fig. 10. Examples of real CFIS test stars, the estimations of both methods, and the pixel residuals. The exposures are the same as in Fig. 9. We present four test stars with the estimated PSF models and the corresponding residuals. Top-left star: a star extracted from the top-left corner of the focal plane with a S/N of 19. Top-right star: a star leading to a high error for both methods. Bottom-left star: a star located in the centre of the focal, with a relatively high S/N of 160. Bottom-right star: a star located in the bottom-right corner of the focal plane, with a low S/N of 4. |
| In the text | |
 |
Fig. 11. Histograms showing the distribution of the size metric over the training stars and their residuals for both PSF models, PSFEx and MCCD-HYB. |
| In the text | |
 |
Fig. C.1. Residual ΔR2/R2 map of the RCA algorithm of stars with a S/N of 50. The CCDs where the RCA model is having degeneracies that can be clearly spotted on the map. |
| In the text | |
 |
Fig. C.2. Example eigenPSFs extracted from the MCCD-HYB PSF model trained on the simulated dataset with a S/N of 70. The local eigenPSFs were extracted from the graph’s spatial constraint of a central CCD. It can be seen from the eigenPSFs that the global model is specialising on the shape of the PSF while the local model specialises on capturing its ellipticity. It is also worth to mention that the first global eigenPSF found on the first row provides the baseline isotropic PSF the model uses. (a) Global eigenPSFs. (b) Local eigenPSFs. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.








































![$$ \begin{aligned} \text{Find } \hat{x} \in \underset{x \in \mathcal{X}}{\text{arg min}} \left[ F(x) + G(x) + H(L(x)) \right], \end{aligned} $$](/articles/aa/full_html/2021/02/aa39584-20/aa39584-20-eq159.gif)
![$$ \begin{aligned} \text{prox}_{\iota _{+}(\cdot )}(X) = [X]_{+} \rightarrow [X_{i,j}]_{+} = {\left\{ \begin{array}{ll} X_{i,j}&\mathrm{if} X_{i,j} \ge 0 ,\\ 0&\mathrm{otherwise}. \end{array}\right.} \end{aligned} $$](/articles/aa/full_html/2021/02/aa39584-20/aa39584-20-eq163.gif)



![$$ \begin{aligned}&\text{prox}_{\tau G(\cdot )}([\mathbf s _{k,i}]_{j}) = \text{SoftThresh}_{\tau [\boldsymbol{w}_{k,i}]_{j}}([\mathbf s _{k,i}]_{j} ), \end{aligned} $$](/articles/aa/full_html/2021/02/aa39584-20/aa39584-20-eq167.gif)












