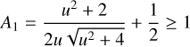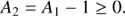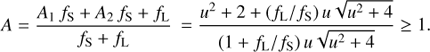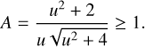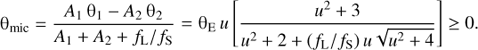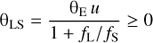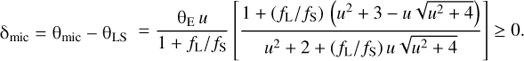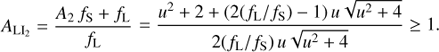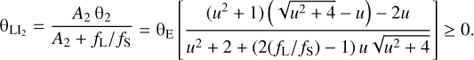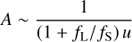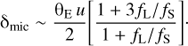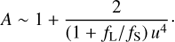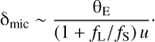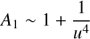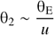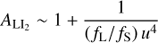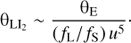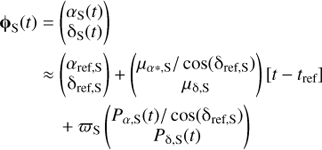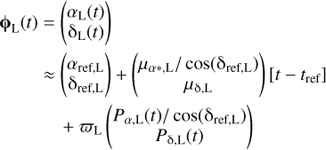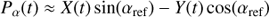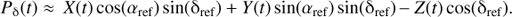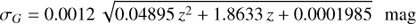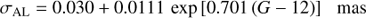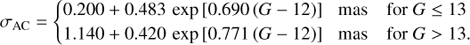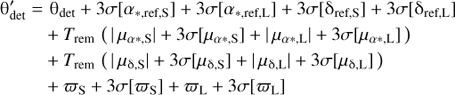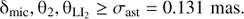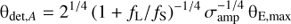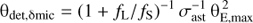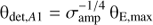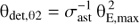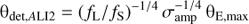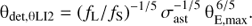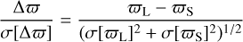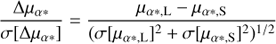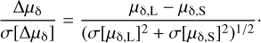| Issue |
A&A
Volume 618, October 2018
|
|
|---|---|---|
| Article Number | A44 | |
| Number of page(s) | 25 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201833505 | |
| Published online | 11 October 2018 | |
Predicted microlensing events from analysis of Gaia Data Release 2⋆
New York University Abu Dhabi, PO Box 129188, Saadiyat Island, Abu Dhabi, UAE
e-mail dan.bramich@hotmail.co.uk
Received:
26
May
2018
Accepted:
5
July
2018
Context. Astrometric microlensing can be used to make precise measurements of the masses of lens stars that are independent of their assumed internal physics. Such direct mass measurements, obtained purely by observing the gravitational effects of the stars on external objects, are crucial for validating theoretical stellar models. Specifically, astrometric microlensing provides a channel to direct mass measurements of single stars for which so few measurements exist. Microlensing events that also exhibit a detectable photometric signature provide even stronger lens mass constraints.
Aims. I use the astrometric solutions and photometric measurements of ~1.7 billion stars provided by Gaia Data Release 2 (GDR2) to predict microlensing events during the nominal Gaia mission and beyond. This will enable astronomers to observe the entirety of each event, including the peak, with appropriate observing resources. The data collected will allow precise lens mass measurements for white dwarfs and low-mass main sequence stars (K and M dwarfs) helping to constrain stellar evolutionary models.
Methods. I search for source-lens pairs in GDR2 that could potentially lead to microlensing events between 25th July 2014 and 25th July 2026. I estimate the lens masses using GDR2 photometry and parallaxes, and appropriate model stellar isochrones. Combined with the source and lens parallax measurements from GDR2, this allows the Einstein ring radius to be computed for each source-lens pair. By considering the source and lens paths on the sky, I calculate the microlensing signals that are to be expected.
Results. I present a list of 76 predicted microlensing events. Nine and five astrometric events will be caused by the white dwarf stars LAWD 37 and Stein 2051 B, respectively. A further nine events will exhibit detectable photometric and astrometric signatures. Of the remaining events, ten will exhibit astrometric signals with peak amplitudes above 0.5 mas, while the rest are low-amplitude astrometric events with peak amplitudes between 0.131 and 0.5 mas. Five and two events will reach their peaks during 2018 and 2019, respectively. Five of the photometric events have the potential to evolve into high-magnification events, which may also probe for planetary companions to the lenses.
Key words: gravitational lensing: micro / methods: data analysis / catalogs / astrometry / stars: fundamental parameters
Table A.5. is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/618/A44
© ESO 2018
1. Introduction
Gravitational lensing involves the bending of light rays from a source by a massive object (referred to as the lens; Einstein 1915). When a single compact lens object passes close enough to the line of sight between the source and the observer, then the observer typically views two distorted and magnified images of the background source (Einstein 1936; Liebes 1964; Refsdal 1964). Within our own Galaxy, sources and lenses are usually stars and the lensed images are separated by less than a few milliarcseconds1 (mas). This is unresolvable with currently available telescopes (both ground and space) and the effect is referred to as microlensing (Petrou 1981; Paczyński 1986).
As the source and lens move relative to each other, the strength of the lensing effect changes, leading to observable deviations in source brightness (photometric microlensing; e.g. Beaulieu et al. 2006) and centroid position (astrometric microlensing; e.g. Sahu et al. 2017). For a lens that is too faint to be detected, observation of both the photometric and astrometric microlensing signals allows important parameter degeneracies to be broken (Høg et al. 1995; Miyamoto & Yoshii 1995; Walker 1995), although no microlensing event has yet been detected via both channels to date. For bright lenses where both the source and the lens have known distances via trigonometric parallax measurements, the astrometric lensing signal alone enables the mass of the lens to be determined. This has recently been achieved for the first time ever by Sahu et al. (2017) for the white dwarf Stein 2051 B. They used Hubble Space Telescope (HST) observations acquired at eight epochs over 2 yr to measure a ~3 mas deflection in the position of an 18.3 mag (V band) background source star. Combined with the parallax measurements for the source and the lens, the mass of Stein 2051 B was measured as ~0.675 M⊙ with uncertainty ~8%, which provided a new sorely-needed datum for comparison with white dwarf evolutionary models.
The validation of theoretical models of stars requires mass measurements that are independent of the assumed internal physics. Direct mass measurements, obtained purely by observing the gravitational effects of stars on external objects, fulfill these requirements. However, most directly measured stellar masses come from observations of the orbital motion of binary stars (Torres et al. 2010), and stars in binary systems evolve differently to single stars. Hence, direct mass measurements of single stars are highly desirable and exceptionally important. Astrometric microlensing provides a powerful technique for the direct determination of masses of single stars proven to yield uncertainties below ~10%, and that has the potential to achieve uncertainties of ~1%. This compares favourably with the best uncertainties in mass estimates for stars in binary systems (~1– 3%) and from asteroseismology (~1–10%; Chaplin et al. 2014; Silva Aguirre et al. 2017).
Given that microlensing events are intrinsically rare occurrences that depend on chance stellar alignments, predicting when and where they will occur is highly advantageous for the collection of data throughout an event. The first attempt at predicting a microlensing event was made by Feibelman (1966). Frustratingly for Feibelman2, subsequent observations showed that the potential lens star 40 Eridani A would not pass close enough to the source star to yield a detectable signal (Feibelman 1986). Nowadays, thousands of photometric microlensing events towards the Galactic bulge are routinely detected each year by dedicated surveys (Optical Gravitational Lensing Experiment – OGLE, Udalski 2003; Microlensing Observations in Astrophysics – MOA, Bond et al. 2001) which alert the astronomical community to the events as early as possible to enable followup observations in the search for extrasolar planets (e.g. RoboNet-II, Tsapras et al. 2009). Unfortunately, due to the small signals involved, there are no dedicated ground-based surveys for discovering astrometric microlensing events, while from space, targeted efforts are ongoing (Kains et al. 2017).
The Gaia satellite (see Sect. 2), with its unprecedented combination of all-sky coverage, sample volume (depth), and astrometric precision and accuracy, is predicted to serendipitously detect thousands of astrometric microlensing events during its five-year mission (Dominik & Sahu 2000; Belokurov & Evans 2002). However, the prediction of exactly which stars will undergo microlensing deviations is only possible for the subset of events with bright lenses3. This task was attempted by Proft et al. (2011, hereafter P11) using a patchwork of the best stellar proper motion catalogues available at the time. Unfortunately, the precision of the stellar positions and proper motions in the catalogues that were used, which are limited by the ground-based observations from which they are derived, is not good enough for predicting microlensing events with a high certainty. Furthermore, parallax measurements, and therefore distances, were unavailable for the majority of the candidate lens stars listed in P11, substantially increasing the uncertainty in any supposed microlensing geometry. The combined effect of these unavoidable limitations resulted in highly uncertain estimates of the timings and amplitudes of the astrometric signals for the candidate events (see Table 2 in P11). Finally, due to the fact that the Gaia launch was delayed, and since the mission is also likely to be extended, a reanalysis of the predicted events during the revised observational window is required anyway.
A few days before Gaia Data Release 2 (Brown et al. 2018, hereafter GDR2; Sect. 2) and the submission of this paper, McGill et al. (2018, hereafter M18) reported on a predicted astrometric microlensing event that will be caused by the white dwarf LAWD 37 (WD 1142−645). M18 predict that the event will exhibit a peak astrometric signal on 11th November 2019 (±4 d), which is just after the end of the Gaia nominal five-year mission. It was the only candidate event discovered from an analysis of the Tycho-Gaia Astrometric Solution and Gaia Data Release 1 catalogues (Lindegren et al. 2016). In fact, it turns out that LAWD 37 will cause nine microlensing events during the time baseline of any extended Gaia mission (see Sect. 6.1).
In this paper, I use GDR2 as a precise and accurate astrometric and photometric catalogue of stars to predict microlensing events with detectable signals during the (extended) lifetime of the Gaia satellite. In Sect. 3, I review the essential aspects of microlensing relevant to this paper. In Sect. 4, I describe the methods I use to identify source-lens pairs from GDR2 that could potentially lead to detectable microlensing events. I estimate lens masses and search for microlensing events in Sect. 5, and I present my results in Sect. 6. I provide a brief summary and conclusions in Sect. 7.
2. The Gaia satellite and Data Release 2
The Gaia satellite (Prusti et al. 2016, hereafter P16), launched on 19th December 2013, aims to measure the three-dimensional spatial and velocity distribution of stars over a large fraction of the volume of the Galaxy, and to determine their properties such as effective temperature and surface gravity. These measurements for ~109 stars will enable a vastly improved understanding of (i) the structure, dynamics, and evolution of our Galaxy, including its star formation history, (ii) stellar physics and evolution, (iii) binary and multiple stars, and (iv) stellar variability and the distance scale (see Perryman et al. 2001). This list of science applications is not exhaustive. Science observations for the nominal five-year mission started on 25th July 2014. However, it has already been announced4 that Gaia operations will likely continue until at least the end of 2020, although the principal science mission lifetime is limited to 10 ± 1 yr by the amount of fuel available for the fine attitude control thrusters (P16).
Gaia operates at the second Lagrange point (L2) of the Sun-Earth-Moon system, and it scans the entire sky using uniform revolving scanning with two identical telescopes separated by a constant angle of 106°̣5 on the sky along the scanning circle. The spin rate around the spacecraft spin axis is one revolution every 6 h (or equivalently 60″ s−1), and the spin axis precesses slowly around the Sun (5.8 revolutions per year) at a fixed solar-aspect angle of 45°. Hence the scanning law provides at least six distinct epochs of observation per year for any object in the sky (and two observations at each epoch), although the number of times any particular object is observed depends on its position in the sky (especially the ecliptic latitude). The sky-averaged end-of-mission number of observations is ~80. Objects scan across the 106 charge-coupled device (CCD) detectors in the shared focal plane of the two telescopes while the CCDs are operated in time-delayed integration mode. Pixel windows around objects of interest are kept and binning is performed in the across-scan direction.
Gaia performs absolute astrometry in the International Celestial Reference System (ICRS; Arias et al. 1995) for objects between 3 mag and 21 mag. A single observation of an object yields an astrometric measurement derived from the transit of the object over both a sky mapper CCD and nine astrometric field CCDs. The along-scan positional error is much smaller than the across-scan positional error (by a factor of ~7–70; Sect. 4.1.4). However, the varying scanning angles executed by Gaia ensure that precise two-dimensional astrometric information can be recovered from what are effectively one-dimensional measurements. The standard errors on the positional measurement for a single observation in the along- and across-scan directions are typically ~0.03 and 0.32 mas at 10 mag, ~0.12 and 5.4 mas at 15 mag, and ~3.1 and 200 mas at 20 mag, respectively.
The satellite also performs white-light photometry (G pass-band, 330–1050 nm), and low-resolution spectroscopy which integrates to magnitudes in broad blue and red passbands GBP (330–680 nm) and GRP (630–1050 nm), respectively (Carrasco et al. 2016; Evans et al. 2018). The standard error on the G magnitude for a single observation is ~0.4 mmag for G < 12 mag, ~1.7 mmag at G = 15 mag, and ~31 mmag at G = 20 mag (Sect. 4.1.3).
The astrometric crowding limit for Gaia is ~1 050 000 objects per deg2 for G-band photometry, and ~750 000 objects per deg2 for GBP- and GRP-band photometry (P16). Stars with equal brightness can be resolved down to ~100 mas since the along-scan point-spread function (PSF) full-width at half-maximum (FWHM) has values that fall mostly between ~90 and 108 mas (median value ~103 mas; see Fig. 9 of Fabricius et al. 2016). Larger separations are required to resolve stars with brightness differences.
GDR2 corresponds to all science data obtained by Gaia between 25th July 2014 (10:30 UTC) and 23rd May 2016 (11:35 UTC). It contains 1 692 919 135 objects of which 1 331 909 727 have 5-parameter astrometric solutions (position, proper motion, and parallax), and 361 009 408 have 2-parameter astrometric solutions (position only). The astrometric solutions are based on Gaia data alone. All objects have a mean G magnitude measurement, and ~82% of objects also have mean GBP and GRP photometric measurements. Typical uncertainties in the proper motions range from ~0.05 mas yr−1 for G < 14 mag to ~1.2 mas yr−1 at G = 20 mag. For parallaxes and positions at the reference epoch J2015.5, the uncertainties range from ~0.04 mas for G < 14 mag to ~0.7 mas at G = 20 mag (Lindegren et al. 2018).
Some of the limitations of GDR2 have a negative impact on predicting the microlensing events that Gaia will observe. GDR2 has a faint limit that varies across the sky due mainly to the inhomogeneous scanning coverage over the corresponding time period and the spatial variations in stellar density. This adversely affects the number of potential source stars available to my study. GDR2 also reports that a fraction of stars brighter than G = 7 mag are missing from the catalogue and that the completeness near bright objects is not yet optimal, which affects both potential source and lens stars in my analysis. Finally, ~17% of stars with proper motions greater than ~0.6 arcsec yr−1 are missing from GDR2 (Brown et al. 2018), which adversely affects stars that are potentially some of the best lens candidates. Hence the list of predicted microlensing events with bright lenses set forth in this paper is likely to be somewhat incomplete when compared in hindsight to the actual list of such events detected by Gaia.
3. Microlensing essentials
The theoretical treatment of microlensing has been explored in detail throughout the relevant literature (e.g. Paczyński 1996). Consequently, I limit myself to summarising and developing the important concepts and equations directly relevant to this paper. Specifically I follow Dominik & Sahu (2000, hereafter D00; see also references therein).
3.1. Point-source point-lens lensing
Let a (point-like) source S and (point-like) lens L be at distances DS and DL, respectively, from an observer such that 0 < DL < DS. Given angular position vectors ϕS and ϕL on the celestial sphere for the source and lens, respectively, one can define the dimensionless distance vector:
where θE is the Einstein radius:
The mass M is the mass of the lens. The major and minor images, I1 and I2, respectively, of the source as seen by the observer are located on either side of the lens along the straight line I2-L-S-I1 in the sky plane (Fig. 1). I1 and I2 lie outside and inside, respectively, of the Einstein ring around the lens. They are separated by an angular distance on the sky of:
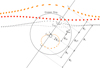 |
Fig. 1 Configuration of a microlensing event as seen by the observer, who does not resolve any of the components. The filled red circles represent the source S at equal time intervals as it moves relative to the lens L (black circle). The relative motion of the source consists of uniform proper motion in a straight line combined with annual parallax, which is why the source appears to move in a non-linear fashion. The major and minor images, I1 and I2, respectively, of the source are plotted as orange ellipses. Although S, L, I1 and I2 are all plotted with a finite size for illustrative purposes, the analysis in this paper ignores finite-size effects. At any single instant, I1, S, L and I2 form a straight line on the sky along with the centroids Cmic (asterisks), CLS (plus signs) and CLI2 (crosses). The centroids Cmic, CLS and CLI2 have been plotted for fL/ fS = 1. Angular distances defined in the text are marked in the diagram. |
where u = |u|. The angular distances θ1 and θ2 on the sky corresponding to L-I1 and L-I2, respectively, are given by:
The flux ratios A1 and A2, relative to the source, of the images I1 and I2, respectively, are:
3.2. Microlensing
In microlensing, the source images I1 and I2, and the lens L, are all unresolved. Furthermore, it is possible that the lens is luminous5. Adopting fS and fL as the source and lens fluxes, respectively, then one may write the observed overall magnification (brightening) of the microlensing system as:
For a non-luminous (dark) lens, one has fL = 0, which yields the standard result:
Now consider the observed centroid Cmic of the microlensing system (i.e. the centroid of I1, I2 and L). It lies on the line L-I1 (Fig. 1) at an angular distance from L of:
In the absence of lensing effects, the observed centroid CLS of S and L, which also lies on the line L-I1, would be at an angular distance from L of:
which is only coincident with the source position when fL = 0. The centroid shift due to microlensing may then be derived as:
For a dark lens, one has fL = 0, which yields the well-known result:
It is worth noting that incorrect results for δmic in Eq. (12) have been derived in the literature by calculating the centroid shift relative to the source position (e.g. Boden et al. 1998) or by failing to take into account the source image splitting (e.g. Goldberg & Woźniak 1998; Goldberg 1998). The only authors to have presented the correct expression for δmic are D00 and Lee et al. (2010). Unfortunately, one also finds that many derivations in the literature of δmic for the special case where fL = 0 (Eq. (13)) are accompanied by the potentially misleading statement that the centroid shift is being calculated relative to the source position as opposed to the observed source-lens centroid (e.g. Gould 2001; Han 2002; Nucita et al. 2016).
3.3. Partially-resolved microlensing
With the resolution and precision of Gaia, it is possible that microlensing signals are detectable even when θEu is large enough for L and I1 to be resolved. In this case, L and I2 remain blended, and the ratio ALI2 of the blend flux relative to the lens flux is given by:
Furthermore, the observed centroid CLI2 of L and I2 lies on the line L-I2 (Fig. 1) at an angular distance from L of:
For a dark lens, one has fL = 0 and θLI2 = θ2 while ALI2 is ill-defined.
I refer to this situation as partially-resolved microlensing6 because lensing effects are detectable while some, but not all, of the components L, I1 and I2 are resolved. In this regime, for a luminous lens (fL > 0), the lensing has two observable photometric and astrometric effects. Firstly, the major source image I1 is magnified by A1 relative to the source flux and it is shifted from the nominal source position S by an angular distance of θ2. Secondly, the blend of L and I2 is magnified by ALI2 relative to the lens flux and the centroid CLI2 is shifted from the nominal lens position L by an angular distance of θLI2 along the line L-I2.
3.4. Behaviour of the observed signals
Figure 2 shows the variation of the photometric and astrometric signals during a microlensing event as a function of the normalised source-lens separation u. A microlensing event can potentially reach magnifications above A ≳ 1000 for very small values of u ≲ 0.001, and it is only finite-source effects (Witt & Mao 1994) that limit the peak magnification (e.g. Dong et al. 2006). In contrast, the normalised centroid shift δmic/θE reaches a maximum near u ≈ 1 and it tends to zero for very small values of u. Both A − 1 and δmic/θE tend to zero for very large values of u, albeit at considerably different rates. Curves are plotted in Fig. 2 for a dark lens (continuous black lines) and for a luminous lens with fL/ fS = 1 (dotted black lines). The effect of a luminous lens is to decrease the amplitude of both the photometric and astrometric signals. Furthermore, the maximum centroid shift occurs at a smaller value of u for a luminous lens.
 |
Fig. 2 Variation of the magnification above baseline A − 1 and the normalised centroid shift δmic/θE during a microlensing event as a function of the normalised source-lens separation u. Continuous and dotted black curves correspond to the cases of a dark lens (fL = 0) and a luminous lens with fL/ fS = 1, respectively. The asymptotic behaviour of the photometric and astrometric signals for the specific case of a dark lens is plotted using red and blue curves, respectively, and these asymptotic curves are labelled with their functional form. |
More formally, the asymptotic behaviour of A and δmic for u ≪ 1 is:
For u ≫ 1, the asymptotic behaviour is:
It is useful to note from these equations that as u increases from 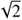 , the magnification above baseline A − 1 decreases at a much faster rate than the centroid shift δmic.
, the magnification above baseline A − 1 decreases at a much faster rate than the centroid shift δmic.
For a dark lens, the maximum centroid shift occurs when 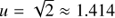 with the value δmic ≈ 0.354 θE. For a luminous lens with fL/fS = 1, the maximum centroid shift occurs when u ≈ 0.827 with the value δmic ≈ 0.267 θE. In general, computing the value of u that corresponds to the maximum centroid shift for a luminous lens requires the solution of a high-degree polynomial.
with the value δmic ≈ 0.354 θE. For a luminous lens with fL/fS = 1, the maximum centroid shift occurs when u ≈ 0.827 with the value δmic ≈ 0.267 θE. In general, computing the value of u that corresponds to the maximum centroid shift for a luminous lens requires the solution of a high-degree polynomial.
In the partially-resolved microlensing regime, the most relevant asymptotic behaviour for the two photometric and astrometric signals is for u ≫ 1 where:
Up to this point, only the dependence of the microlensing signals on the normalised source-lens separation u has been discussed. However, u is fundamentally a function of time as the source and lens move on the celestial sphere relative to each other, principally due to their proper motions and annual parallaxes (Fig. 1). The relative motion is typically dominated by the relative proper motion, which leads to characteristic variations in u, and therefore also characteristic variations in the observed magnification and centroid shift of the microlensing event as a function of time. For uniform rectilinear (straight line) relative proper motion, and no other relative motion components, the time-dependent magnification and centroid shift variations are symmetric around the time of closest approach between the source and the lens (i.e. the time t = t0 at which u = u0 is a minimum; see Fig. 2 in Paczyński 1986 and Fig. 1 in D00).
Astrometric microlensing events are characterised by a slowing of the (apparent) relative source-lens motion as u decreases towards u0, a rapid acceleration and deceleration of the relative motion as u passes through its minimum value u = u0 (including a rotational component to the relative motion), a further slowing of the relative motion as u increases away from u0, and a final recovery to the original relative source-lens motion in the absence of lensing (Chitre & Saslaw 1989; D00). This motion signature can be identified as being due to microlensing, and correctly distinguished from induced motion by a nearby source companion, as long as the closest approach u = u0 occurs during the observational time baseline (Belokurov & Evans 2002). Even so, the presence of a massive companion to either the source and/or the lens will make the modelling of an astrometric microlensing event considerably more challenging (e.g. An & Han 2002; Sajadian 2014; Nucita et al. 2016).
3.5. Examples specific to Gaia
For microlensing events with u0 > 8.5, the peak values of A − 1 and A1 − 1 are less than the equivalent of 0.4 mmag above baseline, which is below the G-band photometric precision of Gaia for bright stars (Eq. (28)). Even though these signals cannot be detected in Gaia photometry, it is still possible that the associated centroid shifts δmic and θ2 are detectable because, for large and increasing u, they follow a much slower u−1 asymptotic decline than the u−4 declines of A − 1 and A1 − 1 (Sect. 3.4). The predicted microlensing event from M18 falls into this category. The predicted event has u0 ≈ 11.6, θE ≈ 32.8 mas, and θEu0 ≈ 380 mas for a G ≈ 18 mag source star. Since the median spatial resolution of Gaia is ~103 mas (Sect. 2), the event will unfold completely in the partially-resolved microlensing regime. The maximum centroid shift θ2 ≈ 2.8 mas of the major source image I1 can be detected by Gaia in a single observation at ~3.6 σAL for the most favourable scanning angles (Eq. (30)), while the remaining signals A1 − 1, ALI2 − 1 and θLI2 are all undetected. Interestingly, for similar event parameters u0 = 8.5, θE = 32.8 mas, θEu0 ≈ 279 mas, and “swapped” source and lens G magnitudes of 10 and 18 mag, respectively, the peak signals are A1 − 1 0.2 mmag (~0.5 σG; Eq. (28)), θ2 ≈ 3.8 mas (~116 σAL), ALI2 − 1 0.27 mag (~42 σG), and θLI2 ≈ 0.85 mas (~1.3 σAL). In other words, for I1, the peak centroid shift is securely detected while the peak magnification above baseline is undetected, and for the LI2 blend, the peak magnification above baseline and centroid shift are securely and border-line detected, respectively.
Taking this last example further, for a dark lens, at u = u0, the major and minor source images have a separation of ~286 mas and they are resolved by Gaia. More importantly though, the minor image is also bright enough to be detected by Gaia as it has a G magnitude of ~19.4 mag. Since Gaia performs on-the-fly object detection, I strongly recommend that whenever a microlensing event of a bright source due to an invisible massive object is identified by Gaia (e.g. Harding et al. 2018), the data are checked for a transient object detection near the expected position of the minor source image. If the minor source image is successfully recorded and measured, then this will be the first time that a fully resolved lensing event is observed for a source and lens within our Galaxy.
In Fig. 3, I plot A − 1 (black curves), δmic (red curves) and θ2 (blue curves) as a function of time for two fictitious microlensing events. For both events, I assume that the source star is at a distance of DS = 4 kpc. The lens is taken to be the 0.675 M⊙ white dwarf Stein 2051 B (Sahu et al. 2017) moved out to a distance of DL = 60 pc. At this distance, the lens would have an apparent V magnitude of ~17.6 mag and a proper motion of ~0.218″ yr−1. I assume a source star proper motion of 1 mas yr−1 in the same direction as the lens. I also assume that the source has the same apparent magnitude as the lens so that fL/ fS = 1 (which is the case for a Sun-like star at 4 kpc). The Einstein radius for this microlensing configuration is θE ≈ 9.5 mas. In the absence of the parallactic motions, I set u0 = 0.6 (left-hand panel) and u0 = 1.6 (right-hand panel), and this is set to occur at time t0 = 2 457 776.5 d (BJD[TDB]; mid-mission for Gaia). Annual parallax is then included in the source and lens motions by adopting the celestial coordinates of Stein 2051 B and by assuming that the proper motions are at constant declination (Sect. 4.1.1).
 |
Fig. 3 Variation of the magnification above baseline A − 1 (black curve) and the centroid shifts δmic (mas; red curve) and θ2 (mas; blue curve) as a function of time (d) for the two fictitious microlensing events described in Sect. 3.5. The events differ only in that u0 = 0.6 and u0 = 1.6 for the left- and right-hand panels, respectively. The vertical dashed lines in each panel indicate when an event switches between unresolved and partially-resolved microlensing based on the median Gaia spatial resolution of ~103 mas. The dotted curves indicate the photometric (G-band) and astrometric (along-scan) precisions for a single observation with black, red and blue colours corresponding to A − 1, δmic and θ2, respectively. |
For Gaia, both the unresolved and partially-resolved microlensing regimes are relevant to these example events. The vertical dashed lines in each panel of Fig. 3 indicate a regime change. In the unresolved regime, the blend has a baseline magnitude of ~16.8 mag. The corresponding photometric (G-band) and astrometric (along-scan) precisions for a single observation (Eqs. (28) and (30)) are plotted in the panels of Fig. 3 as horizontal curves (black, red, and blue for A − 1, δmic, and θ2, respectively). Both events have essentially the same detectability characteristics despite the different values of u0 and the different amplitudes/shapes of the signals at their peaks. From a single observation, Gaia can recover A − 1 and δmic above 3-sigma in a time-window of ~100 d centred on t = t0. At least two observations are guaranteed during this window. Hence, for the most favourable scanning angles, the photometric and astrometric signals are securely detected in the unresolved microlensing regime. In the partially-resolved microlensing regime, A1 − 1, ALI2 − 1 and θLI2 are negligible, and these signals go undetected by Gaia. However, θ2 is in the range ~1–1.5 σAL for time periods of ~65 d immediately before and after the unresolved regime. Hence one of the astrometric signals has a small chance of being border-line detected in the partially-resolved regime.
4. Needles in a haystack
In this section, I describe the methods I use to identify sourcelens pairs from GDR2 that could potentially lead to microlensing events that are detectable by Gaia or other observing facilities. To perform such an analysis, one needs certain ingredients. The previous section already dealt with microlensing effects as a function of M, DL, DS, u and fL/ fS (or alternatively θE, u and fL/ fS). Further essential ingredients are detailed in Sect. 4.1, while the analysis of GDR2 is described in Sect. 4.2.
4.1. Ingredients
4.1.1. Stellar paths across the celestial sphere
Let the angular position vectors ϕS and ϕL on the celestial sphere for the source and lens, respectively, be formulated as functions of time t. Taking into account proper motion and annual parallax, one may write:
where the subscripts S and L correspond to the source and the lens, respectively. The vector ϕ(t) has components of right ascension α(t) and declination δ(t). The coordinates (αref, δref) are celestial coordinates at the reference epoch t = tref. For GDR2, tref = J2015.5 = 2 457 206.375 d (BJD[TDB]). The quantities μα* and μδ are the tangent plane projections of the proper motion vector in the directions of increasing right ascension and declination, respectively, and ϖ is the annual parallax. The functions Pα(t) and Pδ(t) are the parallax factors specified by:
Here X(t), Y(t) and Z(t) are the Solar-system barycentric coordinates of the Earth in astronomical units at the J2000.0 reference epoch (see Sect. 7.2.2.3 in Urban & Seidelmann 2013). I used the Jet Propulsion Laboratory HORIZONS on-line ephemeris computation service7 to obtain tabulated values of X(t), Y(t) and Z(t) at daily intervals over the date ranges relevant to this paper. I then employ cubic spline interpolation to calculate X(t), Y(t) and Z(t) from these data for any time t.
4.1.2. Observational time baseline of Gaia
All times t listed in this paper are Barycentric Julian Dates (BJD) in Barycentric Dynamical Time (TDB). Science observations for Gaia started on 25th July 2014 (t = 2 456 863.5 d). For the purpose of predicting microlensing events, I adopt an optimistic end-date for the Gaia mission of 25th July 2026 (t = 2 461 246.5 d; maximal mission duration of 12 yr).
4.1.3. Photometric precision of Gaia
An estimate of the standard error σG on the G magnitude for a single observation, which includes a 20% contingency margin for unknown systematic errors, is given by P16 as:
where:
For stars brighter than G = 12 mag, these formulae yield σG ≈ 0.4 mmag.
4.1.4. Astrometric precision of Gaia
The astrometric precision of Gaia is typically quantified by the end-of-mission parallax standard error (e.g. P16). However, for this work, I instead require an estimate of the astrometric precision for a single observation. Let the standard errors on the positional measurement for a single observation in the along- and across-scan directions be denoted by σAL and σAC, respectively. Rybicki et al. (2018, hereafter R18) performed Monte Carlo centroiding simulations to estimate σAL and σAC as a function of V magnitude and V − I colour. They note that the colour dependence of their results disappears when considering G magnitudes. Using the relation between G − V and V − I detailed in Appendix A of Evans et al. (2018), one may convert the V and V − I values in Tables 1 and 2 from R18 into G magnitudes. In Fig. 4, I plot σAL (mas; left-hand panel) and σAC (mas; right-hand panel) from these tables against G (black dots).
 |
Fig. 4 Plot of σAL (mas; left-hand panel) and σAC (mas; right-hand panel) versus G magnitude. The data from R18 are plotted as black dots and the formal errors reported by Fabricius et al. (2016) are plotted as plus signs in the left-hand panel. The best fit curves are plotted in red. |
Fabricius et al. (2016) state that the formal error along-scan for a single astrometric field CCD is 0.06 mas for G < 12 mag, reaching 0.6 mas at G = 17 mag, and 3 mas at G = 20 mag. To compare this with the results from R18, one must inflate these errors by 50% and then divide by 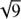 to account for the combination of independent measurements from nine CCDs. These adjusted errors are plotted in the left-hand panel of Fig. 4 (plus signs) where it is clear that they are somewhat smaller than the values from R18. Erring on the side of caution, I choose to fit the data from R18 and I employ functions of the form f (G) = σmin + B exp [C (G − 12)], where σmin, B and C are parameters to be determined. The data for σAC exhibit a jump8 at G ≈ 13 mag, and accordingly I fit the data on either side of the jump independently. For σAL, σAC with G 13 mag, and σAC with G > 13 mag, the noise-floor parameter σmin is fixed at 0.030, 0.200, and 1.140 mas, respectively. The fits are plotted in Fig. 4 using red curves. The corresponding formulae for estimating σAL and σAC as a function of G magnitude are:
to account for the combination of independent measurements from nine CCDs. These adjusted errors are plotted in the left-hand panel of Fig. 4 (plus signs) where it is clear that they are somewhat smaller than the values from R18. Erring on the side of caution, I choose to fit the data from R18 and I employ functions of the form f (G) = σmin + B exp [C (G − 12)], where σmin, B and C are parameters to be determined. The data for σAC exhibit a jump8 at G ≈ 13 mag, and accordingly I fit the data on either side of the jump independently. For σAL, σAC with G 13 mag, and σAC with G > 13 mag, the noise-floor parameter σmin is fixed at 0.030, 0.200, and 1.140 mas, respectively. The fits are plotted in Fig. 4 using red curves. The corresponding formulae for estimating σAL and σAC as a function of G magnitude are:
Constraints that need to be satisfied in order for a GDR2 object to be selected as a lens star.
Constraints that need to be satisfied in order for a GDR2 object with a 5-parameter astrometric solution to be selected as a source star.
4.2. Selecting source-lens pairs
Throughout this section and the rest of the paper, GDR2 data column names are written in TYPEWRITER font.
4.2.1. Corrections to GDR2 quantities
The astrometric solution for GDR2 is described in Lindegren et al. (2018), and they found that there is an overall negative bias in the parallax measurements of −0.029 mas. Furthermore, the published uncertainties on the parameters of the astrometric solutions are underestimated by different amounts for different object populations, ranging anywhere from ~7 to 50% (Brown et al. 2018). Consequently, I correct the GDR2 parallaxes by adding 0.029 mas to the PARALLAX entries, and I inflate the uncertainties on the astrometric parameters by 25% (i.e. the entries RA_ERROR, DEC_ERROR, PMRA_ERROR, PMDEC_ERROR and PARALLAX_ERROR). The astrometric parameter covariances are provided in GDR2 as correlation coefficients, and therefore no adjustment of these entries is required. The inflated uncertainties are conservative for faint objects (G > 16 mag) outside the Galactic plane, and also for objects brighter than G = 12 mag. However, for 12 < G < 15 mag, the uncertainties may still be too small for some objects. Hereafter, references to Gaia parallax measurements and the astrometric parameter uncertainties always refer to the corrected parallax values and the inflated uncertainties.
4.2.2. Lens star selection
The first task in identifying potential microlensing events from GDR2 is to select a set of lens stars from the data. For a reliable microlensing prediction, a lens must have a well-constrained mass, distance (or equivalently, parallax), and path on the sky. To meet these requirements, I conservatively select lens stars from GDR2 using the constraints listed in Table 1. The constraints on ASTROMETRIC_PARAMS_SOLVED and the parallax signal-to-noise ratio (S/N) ϖ/σ[ϖ] limit the lens sample to those stars with well-determined distances and paths on the sky, while the filter on DUPLICATED_SOURCE ensures that the astrometric solutions are derived from reliable data. Furthermore, the constraint on 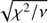 has been proposed in Appendix C of Lindegren et al. (2018), and adopted by Arenou et al. (2018) and Babusiaux et al. (2018), as a way of rejecting stars with spurious astrometric solutions. While inspecting plots of ASTROMETRIC_EXCESS_NOISE_SIG versus mean G magnitude (PHOT_G_MEAN_MAG), it also became clear that a filter on this quantity with an appropriate threshold is required as suggested in Chapter 14 of the GDR2 documentation (ESA & DPAC 2018). This constraint rejects lens stars whose motion is not well-described by proper motion and parallax alone (e.g. binary stars with periods of up to ~10× the GDR2 time baseline). Microlensing predictions from such stars would be unreliable. Note that although the constraint on non-positive parallaxes is actually contained within the constraint on the parallax S/N, it is listed in Table 1 for added clarity on the implemented filters. Finally, it stands to reason that lens stars cannot be extra-galactic, which justifies the filter on FRAME_ROTATOR_OBJECT_TYPE, and they also cannot be closer to us than our closest neighbour Proxima Centauri. Application of these constraints to GDR2 yields NL = 132 944 121 potential lens stars.
has been proposed in Appendix C of Lindegren et al. (2018), and adopted by Arenou et al. (2018) and Babusiaux et al. (2018), as a way of rejecting stars with spurious astrometric solutions. While inspecting plots of ASTROMETRIC_EXCESS_NOISE_SIG versus mean G magnitude (PHOT_G_MEAN_MAG), it also became clear that a filter on this quantity with an appropriate threshold is required as suggested in Chapter 14 of the GDR2 documentation (ESA & DPAC 2018). This constraint rejects lens stars whose motion is not well-described by proper motion and parallax alone (e.g. binary stars with periods of up to ~10× the GDR2 time baseline). Microlensing predictions from such stars would be unreliable. Note that although the constraint on non-positive parallaxes is actually contained within the constraint on the parallax S/N, it is listed in Table 1 for added clarity on the implemented filters. Finally, it stands to reason that lens stars cannot be extra-galactic, which justifies the filter on FRAME_ROTATOR_OBJECT_TYPE, and they also cannot be closer to us than our closest neighbour Proxima Centauri. Application of these constraints to GDR2 yields NL = 132 944 121 potential lens stars.
4.2.3. Source star selection
I also use GDR2 as a catalogue of source stars. The constraints that I adopt for selecting source stars are somewhat more relaxed than those that I adopt for lens stars. This is mainly because source stars are likely to be much more distant than lens stars for the majority of microlensing geometries, and the parallax signal for the source star in such cases may be too small for Gaia to detect with a reasonable S/N. Fortunately, when ϖS ≪ ϖL, the estimated size of the Einstein ring is not affected by a lack of the source parallax measurement and corresponding distance estimate (Eq. (2) and noting that ϖ = 1/D). Therefore I do not place any constraints on whether an object has a 2- or 5-parameter astrometric solution, or on the parallax S/N ϖ/σ[ϖ], when selecting potential source stars.
For stars with a 5-parameter astrometric solution, I select source stars from GDR2 using the constraints listed in Table 2. Compared to the constraints listed in Table 1 for lens stars, the filter on FRAME_ROTATOR_OBJECT_TYPE has been dropped, since extra-galactic sources can be lensed, and the constraint on ϖ/σ[ϖ] has also been dropped for the reasons already stated. Application of these constraints to GDR2 yields 1 127 324 197 potential source stars.
For stars with only a 2-parameter astrometric solution, I select source stars from GDR2 using the constraints listed in Table 3. Most stars with only a 2-parameter astrometric solution are faint (G > 20 mag) and I found it necessary to relax the thresholds on 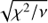 and ASTROMETRIC_EXCESS_NOISE_SIG by inspecting the distributions of these quantities as a function of mean G magnitude. I also introduce a filter on VISIBILITY_PERIODS_USED similar to that which is applied by Lindegren et al. (2018) for accepting 5-parameter astrometric solutions. Application of these constraints to GDR2 yields 238 748 126 more source stars, for a grand total of NS = 1 366 072 323 potential source stars.
and ASTROMETRIC_EXCESS_NOISE_SIG by inspecting the distributions of these quantities as a function of mean G magnitude. I also introduce a filter on VISIBILITY_PERIODS_USED similar to that which is applied by Lindegren et al. (2018) for accepting 5-parameter astrometric solutions. Application of these constraints to GDR2 yields 238 748 126 more source stars, for a grand total of NS = 1 366 072 323 potential source stars.
Constraints that need to be satisfied in order for a GDR2 object with a 2-parameter astrometric solution to be selected as a source star.
4.2.4. Initial source-lens pair selection
Finding the microlensing events that will occur during the mission lifetime of Gaia from GDR2 is essentially a very large cross-matching problem between the NS potential source stars and NL potential lens stars already selected from the catalogue. Its solution requires considering NL(NS − 1) source-lens pairs, which is an extremely large number. Fortunately, one can immediately use spatial information to reject the vast majority of pairs. A conservative upper limit θE,max on the value of the Einstein radius for any particular source-lens pair can be estimated by assuming a maximum lens mass of Mmax = 10 M⊙, a maximum lens parallax of ϖL,max = ϖL + 3σ[ϖL] (where σ[ϖL] is the uncertainty on ϖL), and a source parallax of zero (Eq. (2)). To translate θE,max into a maximum source-lens angular separation θdet within which a microlensing signal can be detected, I only consider the astrometric signals, since, for large and increasing u, they decline at a much slower rate than the photometric signals. Specifically, for large u, the deflection θ2 of the major source image has the greatest amplitude. The best astrometric precision achievable by any current observing facility in a single observation (excluding radio interferometry) is Gaia’s ~0.030 mas precision in the along-scan direction for bright objects (Eq. (30)). Requiring θ2 ≥ 0.030 mas, and using Eqs. (4) and (5), one obtains an upper limit 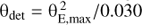 mas.
mas.
For each potential lens star, I calculate the value of θdet. The minimum, median, and maximum values of θdet over all lens stars are ~0.27, 2.75, and 2092 arcsec, respectively. To account (very) conservatively for source and lens motions, and for errors in the astrometric parameters, I compute the following quantity for each source-lens pair:
where σ[α*,ref]/ cos(δref), σ[δref], σ[μδ], σ[μδ], and σ[ϖ] are the uncertainties on αref (RA), δref (DEC), μα* (PMRA), μδ (PMDEC), and ϖ (PARALLAX), respectively, and Trem ≈ 11.1 yr is the maximum remaining time for the Gaia mission as counted from the GDR2 reference epoch (Sect. 4.1.2). I reject all source-lens pairs for which the angular distance between them at t = tref exceeds 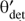 . This leaves 85 135 565 source-lens pairs, with 22 616 138 unique lenses, for further consideration, which is a much more manageable number.
. This leaves 85 135 565 source-lens pairs, with 22 616 138 unique lenses, for further consideration, which is a much more manageable number.
4.2.5. Refined source-lens pair selection
The list of source-lens pairs can be filtered further by considering more carefully the upper limit on the lens mass Mmax on a case-by-case basis. For a main sequence lens star more massive than the Sun, the relation L/L⊙ ≈ (M/M⊙)4 holds. Using the lens parallax and its mean G magnitude, and assuming an absolute bolometric magnitude for the Sun of Mbol,⊙ ≈ 4.74 mag, one may estimate the lens luminosity, and therefore its mass. The fact that extinction and bolometric corrections have been ignored imply that the mass is underestimated. Accounting for ample extinction (AG ≈ 2 mag) and maximal bolometric corrections (BC ≈ −4 mag), I set Mmax to 100.6 ≈ 4 times the lens mass estimate. For giant stars, Mmax is over-estimated since they are more luminous than main sequence stars, and hence the value of Mmax computed in this way also serves as a maximum lens mass for giant stars. If Mmax is less than the Chandrasekhar limit, then I increase it to 1.44 M⊙ to cover the possibility that the lens is a white dwarf, which also serves as an upper limit to the lens mass for sub-solar mass main sequence stars and brown dwarfs. Using this improved upper limit on the lens mass Mmax, and again adopting ϖL,max = ϖL +3σ[ϖL] and a source parallax of zero, I calculate a new value of E,max for each source-lens pair.
Considering the six possible microlensing signals A, δmic, A1, θ2, ALI2, and θLI2, one finds that their asymptotic behaviours for u ≫ 1, as described by Eqs. (18)–(23), always bound-above their corresponding exact expressions in Eqs. (8), (12), (6), (5), (14), and (15), respectively. By comparing the asymptotic amplitude of each signal to a best-achievable photometric or astrometric precision, then one may compute a new maximum sourcelens angular separation θdet within which at least one of the signals can be detected. The bright-limit photometric precision for Gaia of σG ≈ 0.4 mmag for a single observation in the G-band (Eq. (28)) is also widely applicable to ground-based telescopes and it is of the correct order of magnitude for various space telescopes (e.g. HST). The bright-limit astrometric precision for Gaia of σAL ≈ 0.030 mas for a single observation in the along-scan direction (Eq. (30)) is the best for any current observing facility, although it requires a very specific orientation of the scanning angle. Averaging over all possible scanning angles, the bright-limit astrometric precision per-observation for Gaia is ~0.131 mas (Eqs. (30) and (31)), which is similar to the best astrometric precision achievable by HST of ~0.2 mas (e.g. Kains et al. 2017). Therefore, I adopt the following requirements for each signal:
By using Eqs. (18)–(23), the following upper limits can then be derived:
For θdet, I adopt:
The minimum, median, and maximum values of θdet over all source-lens pairs are ~0.13, 0.59, and 68.8 arcsec, respectively.
For each source-lens pair, I consider their paths on the sky during the maximal time baseline of the Gaia mission (Sect. 4.1.1). I reject all source-lens pairs that do not approach each other to within an angular distance of less than θdet during this time window. After performing this highly efficient, and yet conservative, filtering step for each source-lens pair, I have 51 379 source-lens pairs remaining, with 14 067 unique lenses.
4.2.6. Spurious astrometric solutions
By exploring scatter plots of various quantities from GDR2 for the lens sample in the latest set of source-lens pairs, I found that the majority of these lenses have spurious astrometric solutions. This is most easily observed in Fig. 5 where the lens parallax S/N ϖL/σ[ϖL] is plotted against lens parallax ϖL. There is a well-defined group of lenses for which the parallax error is ~30–50 times larger than that of other lenses at the same parallax. Further investigation of this group of lenses revealed that they typically lie in highly crowded fields near the Galactic plane or the Magellanic clouds where Gaia struggles to perform reliable astrometric measurements. I therefore clean the sample by rejecting all source-lens pairs with σ[ϖL] > 0.4 mas. This limit is plotted in Fig. 5 as a continuous straight line, and the cut leaves me with 2882 source-lens pairs, including 2600 unique lenses.
 |
Fig. 5 Parallax S/N ϖL/σ[ϖL] against parallax ϖL for the lens stars in a set of 51 379 source-lens pairs. The continuous line corresponds to σ[ϖL] = 0.4 mas. Rejected lenses fall below this line. The dashed lines representing ϖL/σ[ϖL] = 4 and ϖL = 769 mas correspond to the constraints applied to GDR2 to select the initial lens sample (Table 1). |
4.2.7. Binary and co-moving stars
At this stage, it became clear that about half of the source-lens pairs so far selected are either binary stars or co-moving stars at approximately the same distance from the Sun. Furthermore, the parallaxes indicate that for some of the source-lens pairs, the lens is more distant than the source. Neither of these source-lens geometries will produce a microlensing event.
In Fig. 6, I plot histograms of relative source-lens parallax S/N, and relative source-lens proper motion S/N for each coordinate direction (black histograms). These quantities are defined by:
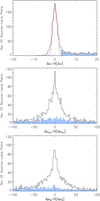 |
Fig. 6 Histograms of Δϖ/σ[Δϖ] (top panel), Δμα*/σ[Δμα*] (middle panel) and Δμδ/σ[Δμδ] (bottom panel) for 2882 source-lens pairs (black histograms). In the top panel, the red curve is a Gaussian with zero mean and standard deviation of unity, scaled to match the histogram of Δϖ/σ[Δϖ]. In each panel, the blue histogram with striped bars is for the source-lens pairs satisfying Δϖ/σ[Δϖ] > 3. |
In the top panel, the histogram of Δϖ/σ[Δϖ] shows a Gaussian-like core that is a little wider than a Gaussian with zero mean and standard deviation of unity (red curve). This implies that many of the source-lens pairs consist of stars at the same distance from the Sun, and that the parallax errors are only slightly underestimated. In the middle and bottom panels, the histograms of Δμα*/σ[Δμα*] and Δμδ/σ[Δμδ] show the broad peaked distributions expected for a sample of source-lens pairs including binary and co-moving stars.
To filter out binary and co-moving source-lens pairs, I reject all source-lens pairs with Δϖ/σ[Δϖ] < 3. In each panel of Fig. 6, I over-plot a blue histogram with striped bars for the accepted source-lens pairs. The filter on Δϖ/σ[Δϖ] cleanly removes the peaks from the distributions of Δϖ/σ[Δϖ], Δμα*/σ[Δμα*] and Δμδ/σ[Δμδ]. A quick inspection of the S/Ns of the total relative proper motions for the accepted source-lens pairs reveals two pairs with S/N < 3, which I also reject. I now have 1533 source-lens pairs remaining, with 1257 unique lenses.
4.2.8. Final source-lens pair selection
Returning to the calculation of the improved maximum detection radius described in Sect. 4.2.5, I recompute the values of θdet for the latest set of source-lens pairs using the improved upper limit on the lens mass Mmax and adopting Δϖmax = Δϖ + 3σ[Δϖ], which takes into account the source parallax (when available). This modification is now possible because of the constraint applied to Δϖ/σ[Δϖ] in Sect. 4.2.7. By rejecting all sourcelens pairs that do not approach each other to within an angular distance of less than θdet during the maximal time baseline of the Gaia mission, I am left with a final sample that consists of 1470 source-lens pairs, with 1194 unique lenses.
5. Threading the needles
In Sect. 4.2.8, I made a final selection of source-lens pairs from GDR2 that could potentially lead to microlensing events by using conservative upper limits on the lens mass and the sourcelens relative parallax, while also considering their paths on the sky. However, to be able to predict a set of microlensing events and their properties from these source-lens pairs, it is essential to have a reasonable estimate of the lens mass in each case.
5.1. Lens mass estimates
In the left-hand panel of Fig. 7, I plot absolute G-band magnitude MG against GBP − GRP colour (using PHOT_BP_MEAN_MAG and PHOT_RP_MEAN_MAG) for the 1194 lens stars in the final sample of source-lens pairs from Sect. 4.2.8. The absolute G magnitude is calculated from:
 |
Fig. 7 Left panel: Hertzsprung-Russell diagram of MG versus GBP−GRP for the 1194 lens stars in the final sample of source-lens pairs from Sect. 4.2.8. The continuous black line joining (−1, 5) and (5, 25) mag separates white dwarf stars from main sequence dwarfs/subdwarfs (Kilic et al. 2018). The lens masses are indicated by the colour of the plot points (see the scale at the bottom of the panel). The 55 lenses that are present in 58 of the source-lens pairs that do not have GBP or GRP magnitudes in GDR2 are plotted with black points at fixed colour GBP−GRP = −0.3 mag and using their computed absolute magnitudes MG. Right panel: same as the left-hand panel for the 64 lens stars in the 76 microlensing events found in Sect. 5.2, except that the only lens that does not have a GBP or GRP magnitude is plotted in colour to indicate its estimated mass using photometry from external catalogues. The points from the left-hand panel are plotted in the background in light grey. |
where G is the apparent G-band mean magnitude (PHOT_G_MEAN_MAG). No attempt has been made to account for reddening and extinction in this plot since ~80% of the lenses are at distances of less than 200 pc, and the most distant lens is at ~1.01 kpc. The plot is essentially a Hertzsprung-Russell diagram for the lens stars and it reveals that the lens sample consists of main sequence and white dwarf stars with a few stars on the giant branch. The main sequence lens stars are dominated by K and M dwarfs/subdwarfs although their full range covers from late M dwarfs up to early A stars. The white dwarf lens stars lie below the continuous black line joining (−1, 5) and (5, 25) mag defined by Kilic et al. (2018). Unfortunately, 55 lenses that are present in 58 of the source-lens pairs do not have GBP or GRP magnitudes in GDR2 and I plot them in Fig. 7 at fixed colour GBP−GRP = −0.3 mag using their computed absolute magnitudes MG (black points).
For the 1 075 main sequence and giant stars that lie above the continuous line in Fig. 7, I use the isochrones Python package (Morton 2015) to estimate the lens masses. The package employs the MESA (Paxton et al. 2011, 2013, 2015) Isochrones and Stellar Track Library (MIST; Dotter 2016; Choi et al. 2016) and maximises the posterior probability of the fundamental parameters (mass, age, metallicity, distance, and extinction) given the data. For each lens star, I compute Sloan g and i magnitudes from G, GBP and GRP via the relevant transformations given in Evans et al. (2018), and I provide ϖL, G, g and i, along with their uncertainties, as input to the isochrones package. I also use the dustmaps Python package with the Bayestar17 three-dimensional dust maps (Green et al. 2015, 2018) to bound-above the extinction prior in isochrones for each lens star where possible. The posterior distributions are sampled using the MCMC ensemble sampler emcee (Foreman-Mackey et al. 2013) with 300 walkers. Each walker executes a burn-in of 300 steps, and then iterates through 500 subsequent steps of which the last 100 steps are recorded. I adopt the median of the posterior sample as the estimate of the lens mass in each case. The scatter in the lens mass posterior samples is typically ~2–10%, which is comparable to the systematic errors in the MESA evolutionary tracks (~5–10% differences with other evolutionary track libraries; Paxton et al. 2011). In fact, MIST isochrones are known to predict colours that are too blue for stars with masses below ~0.6–0.7 M⊙ (Choi et al. 2016), which implies that the mass estimates for the lower mass stars may be systematically underestimated. Hence the estimated masses may be in error by up to ~15% in the worst cases with a tendency towards underestimation. However, these errors are too small to substantially affect the microlensing predictions presented in this paper. The lens masses estimated by this method are indicated in Fig. 7 by the colours of the plot points.
There are 337 white dwarf lenses below the continuous line in Fig. 7 with distances ranging from ~4.3 to 237 pc. To estimate their masses, I interpolate the evolutionary cooling sequences for DA- and DB-type white dwarfs computed specifically for the Gaia passbands (Pierre Bergeron, priv. comm.; Holberg & Bergeron 2006; Kowalski & Saumon 2006; Bergeron et al. 2011; Tremblay et al. 2011). The mass estimates from the DA and DB cooling sequences are always very similar (to within ~1–15%) and for the purposes of predicting microlensing events, these differences are unimportant. Therefore, for each white dwarf lens star, I adopt the greater of the two mass estimates. Again, in Fig. 7, the lens masses estimated by this method are indicated by the colours of the plot points.
For the 55 lens stars that do not have GBP or GRP magnitudes in GDR2, I continue to adopt for the moment the improved upper limit on the lens mass Mmax computed in Sect. 4.2.5.
5.2. Finding microlensing events
I now have all of the ingredients necessary for each source-lens pair to be able to predict microlensing events and their properties. For each of the 1470 source-lens pairs from Sect. 4.2.8, I perform 1000 Monte Carlo simulations of the source and lens paths on the sky. Each simulation is generated using the following procedure:
-
(i)
I draw a set of astrometric parameters for the lens star from a multi-variate Gaussian distribution defined by the lens astrometric solution parameter values and their covariance matrix provided in GDR2. I do the same for the source star.
-
(ii)
I calculate the Einstein radius θE (Eq. (2)) using the lens mass estimate from Sect. 5.1, and the lens and source parallaxes ϖL and ϖS, respectively, drawn in step (i).
-
(iii)
I compute the path of the source relative to the lens (Sect. 4.1.1) in units of normalised source-lens separation u for the time period from t = 2 456 863.5 d to t = 2 461 246.5 d (Sect. 4.1.2).
-
(iv)
I adopt Gaia’s resolution of 103 mas and I calculate the maximum change in each of the six microlensing signals A, δmic, A1, θ2, ALI2, and θLI2 over the 12-yr time baseline. To do this, I use the lens-to-source flux ratio fL/ fS derived from the Gaia G-band photometry and the relevant equations from Sect. 3. I refer to these values as “delta” microlensing signals.
I then calculate the median of each of the delta microlensing signals over all of the simulations for the source-lens pair. Collecting these results for the 1470 source-lens pairs, I reject all source-lens pairs for which none of the median delta microlensing signals exceed 0.4 mmag for photometric signals or 0.131 mas for astrometric signals (Sect. 4.2.5).
For the 55 lens stars in 58 source-lens pairs that do not have GBP or GRP magnitudes in GDR2, only 16 lens stars in 16 sourcelens pairs remain after this procedure. For these 16 lenses, I looked up their counterparts in the PPMXL (Roeser et al. 2010) and Pan-STARRS1 (Chambers et al. 2016) catalogues, and I used the photometry from these catalogues, combined with their GDR2 parallaxes and G magnitudes, to estimate their masses using the methods described in Sect. 5.1 (the 16 lenses consist of 15 main sequence stars and one white dwarf). I then re-ran the above procedure, which left only one of these lenses in a single source-lens pair that exhibits a detectable delta microlensing signal (microlensing event ME28; Sect. 6.4).
The final set of predicted microlensing events consists of 76 events caused by 64 unique lens stars. I name these events ME1-ME76. One lens causes nine events (ME1-ME9; Sect. 6.1), while another lens causes five events (ME10-ME14; Sect. 6.2). The remaining 62 events are caused by 62 unique lens stars. The 64 lenses are at distances ranging from ~3.29 to 366 pc. The lenses are typically considerably brighter than the sources with differences ranging from ~12.2 mag brighter to ~1.8 mag fainter. The lens proper motions range from ~23.1 mas yr−1 to 6.896 arcsec yr−1. In the right-hand panel of Fig. 7, I plot the Hertzsprung-Russell diagram for the lenses in these microlensing events, with the lenses from the left-hand panel plotted in the background in light grey. The lenses break down into 34 main sequence stars and 30 white dwarf stars.
For each microlensing event, I use the results of the Monte Carlo simulations to calculate the median values of the event properties θE, u0, and t0, and of all of the delta microlensing signals. I also calculate the median full-width duration at half-maximum signal for each signal. I compute 1-sigma confidence intervals for each quantity, which may be asymmetric. The results are reported in Tables A.1–A.5. Asymmetric uncertainties are only reported where necessary.
6. Sewing the future
In this section, I present and discuss the 76 microlensing events that have been identified. Nine events are gold events in the sense that they will exhibit both photometric and astrometric signals above the precision limits discussed in Sect. 4.2.5. The 67 remaining events will exhibit purely astrometric signals, with 12 of these giving rise to astrometric shifts of more than 0.5 mas.
6.1. Nine microlensing events caused by LAWD 37
The microlensing event presented by M18, and discussed in Sects. 1 and 3.5, is the event ME4. The improved parameters of the astrometric solutions from GDR2 for the white dwarf lens star LAWD 37 and the source star yield a refined prediction of their separation at closest approach of ~368.1 ± 1.6 mas which will occur on 14th November 2019 at 5 h (±3 h). The mass that I estimate for LAWD 37 in Sect. 5.1 is ~28% larger than that adopted by M18, which means that θE ≈ 36.97 ± 0.02 mas and u0 ≈ 9.95 ± 0.05 are larger and smaller, respectively, than their corresponding values predicted by M18. For the same reason, I also predict a larger change in the deflection of the source position of Δθ2 ≈ 3.600 ± 0.018 mas over the 12-yr baseline. The event has a full-width duration at half-maximum signal of ~122.2 ± 0.6 d.
These results support the conclusion that the astrometric microlensing signal can be detected by Gaia for the most favourable scanning angles (M18; Sect. 3.5 in this paper). However, I note that the astrometric noise model for Gaia observations in M18 is considerably more optimistic than that of R18 adopted here (Sect. 4.1.4). M18 quote 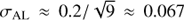 mas for the G ≈ 18.6 mag source star whereas Eq. (30) yields σAL ≈ 1.17 mas. Clearly, if the R18 astrometric noise model is correct, then the astrometric signal will only be revealed at ≳1σAL for a small range of scan angles, and it will certainly be impossible for Gaia to measure the mass of LAWD 37 to within ~3% as claimed by M18. The HST has a much better outlook for observing this event because the observational setup can be optimised for the lens and source properties.
mas for the G ≈ 18.6 mag source star whereas Eq. (30) yields σAL ≈ 1.17 mas. Clearly, if the R18 astrometric noise model is correct, then the astrometric signal will only be revealed at ≳1σAL for a small range of scan angles, and it will certainly be impossible for Gaia to measure the mass of LAWD 37 to within ~3% as claimed by M18. The HST has a much better outlook for observing this event because the observational setup can be optimised for the lens and source properties.
ME4 is not the only microlensing event to be caused by LAWD 37 between 2014 and 2026, although it does have the largest peak amplitude. In total there are nine astrometric microlensing events ME1-ME9 that will all unfold completely in the partially-resolved regime (Table A.1 and Fig. 8). Events ME1-ME3 are low-amplitude events with Δθ2 ≈ 0.13–0.15 mas that are already, or currently, finishing. Apart from ME4, the most promising remaining event is ME79 which will achieve Δθ2 ≈ 0.386 ± 0.004 mas, although it will unfold slowly between 2020 and 2026. All of these events overlap in time and they highlight the fact that when performing astrometry on the stars in the near-field of LAWD 37, the lensing effect will need to be modelled as part of the astrometric solution. However, this approach has the advantage that multiple stars can be used simultaneously to measure the mass of LAWD 37.
 |
Fig. 8 Top panel: path on the sky of the white dwarf lens star LAWD 37 (WD 1142−645), and nine source stars in the microlensing events ME1-ME9, over the time baseline of an extended Gaia mission. The coordinate axes are measured relative to (αref,L, δref,L). Middle panel: time-evolution of the normalised source-lens separation u for each microlensing event. Bottom panel: time-evolution of the deflection θ2 (mas) of the major source image. The horizontal black line indicates the astrometric precision limit of 0.131 mas from Sect. 4.2.5. |
6.2. Five microlensing events caused by Stein 2051 B
ME10 happens to be the tail-end of the microlensing event observed by Sahu et al. (2017) for the white dwarf lens star Stein 2051 B (WD 0426+588). The lens is part of a binary system where the other component Stein 2051 A is at a separation of ~10.22″. However, the binary orbital motion (P ≳ 1000 yr) is too slow to affect the microlensing predictions presented here (Heintz 1990). Stein 2051 B will cause four more astrometric microlensing events ME11-ME14 between 2020 and 2026 that will all unfold completely in the partially-resolved regime (Table A.2 and Fig. 9). Three of these events will reach peak signals of Δθ2 ≈ 0.3 mas and above in relatively quick succession. Unfortunately, Gaia will not be able to detect any of them, even with the observations already acquired of the tail-end of ME10, because σAL is too large for such faint source stars. However, HST will be able to repeat what it has already achieved for ME10, and observations of multiple lensed source stars will help to further constrain the mass of Stein 2051 B.
 |
Fig. 9 Top panel: path on the sky of the white dwarf lens star Stein 2051 B (WD 0426+588), and five source stars in the microlensing events ME10-ME14, over the time baseline of an extended Gaia mission. The coordinate axes are measured relative to (αref,L, δref,L). Middle panel: time-evolution of the normalised source-lens separation u for each microlensing event. Bottom panel: time-evolution of the deflection θ2 (mas) of the major source image. The horizontal black line indicates the astrometric precision limit of 0.131 mas from Sect. 4.2.5. |
6.3. Nine photometric microlensing events
The nine events ME15-ME23 are predicted to yield both photometric and astrometric signals as they unfold (Table A.3), and all of them will unfold in both the partially-resolved and unresolved regimes when considering the resolution of Gaia (Figs. 10 and 11). ME18, ME19 and ME22 each have better than a ~33% probability that the source will pass within the Einstein ring of the lens. However, the prediction of the exact amplitude of the photometric signal that will be observed is quite uncertain in most cases simply because the uncertainties on the relative source-lens motions are similar to, or larger than, the Einstein radius. Specifically, ME17-ME19, ME21 and ME22 could potentially evolve into high-magnification microlensing events. In the unresolved regime, both the photometric and astrometric signals can be boosted by observing the event in a passband for which fL/ fS is minimised (Eqs. (8) and (12)). The Gaia G-band used in this analysis is sub-optimal for most events and a tailored follow-up observing strategy can greatly improve the observed signals.
 |
Fig. 10 Photometric microlensing events ME15-ME18. In all panels, five curves are plotted with the colours yellow, red, black, blue, and cyan. Each curve corresponds to the 2.3, 15.9, 50, 84.1, and 97.7 percentiles, respectively, of the results of the Monte Carlo simulations performed in Sect. 5.2 after they have been ordered by increasing u0. The yellow and cyan curves are plotted first, followed by the red and blue curves, and finally the black curve, which is why the black curve is the most visible when the individual curves are hard to distinguish. Left-hand panels: path of the source star relative to the lens star. The Einstein ring is shown as a circle of radius θE centred on the lens position (also plotted five times with five different colours). The resolution of Gaia is indicated as a circle of radius 103 mas centred on the lens position (dashed curve). Middle left-hand panels: time-evolution of the normalised source-lens separation u. Middle right-hand panels: time-evolution of the photometric signals 2.5 log(A) (mag; unresolved regime) and 2.5 log(A1) (mag; partially-resolved regime). The horizontal black line indicates the photometric precision limit of 0.4 mmag from Sect. 4.2.5. Right-hand panels: time-evolution of the astrometric signals δmic (mas; unresolved regime) and θ2 (mas; partially-resolved regime). The horizontal black line indicates the astrometric precision limit of 0.131 mas from Sect. 4.2.5. |
 |
Fig. 11 Photometric microlensing events ME19-ME23. The format of the figure is the same as in Fig. 10. |
Assessing whether Gaia will be able to detect the photometric signals of any of the microlensing events presented in this section is very difficult because of the satellite’s complicated scanning law. The durations of the photometric signals range from ~7–133 d, and Gaia returns to the same field every ~63 d on average, which implies that the photometric events can easily be missed. It is much more advisable to target these events with an appropriate telescope during the predicted event duration in order to characterise them properly. With regards to the accompanying astrometric signals, Gaia can only detect ME15, ME19 and ME20 at ~2−4σAL (i.e. for the most favourable scanning angles).
ME15. The lens star OGLE SMC115.5.319 is a high proper motion white dwarf star (Poleski et al. 2011). It lies in the direction of the Small Magellanic Cloud (SMC) and it is a member of a binary system, the other component of which is the M5 dwarf OGLE SMC115.5.12 (separation ~13.10″; P ≳ 7300 yr). The lens has G ≈ 17.65 mag which is only ~0.5 mag brighter than the source star. The event will peak on 30th June 2021 at 5 h (±1 d) with a photometric amplitude of ~1 mmag and it will achieve a maximum source deflection of ~1.64 mas (detectable by Gaia at ~2σAL). In Fig. 10, the jumps in the astrometric curve are due to the event switching between partiallyresolved and unresolved microlensing at the Gaia resolution of 103 mas. The lens flux suppresses both the photometric and astrometric signals in the unresolved regime. Observing in GBP would boost the peak photometric signal by a factor of ~1.3.
ME16. The lens star SDSS J035037.54+112707.9 is a spectroscopically confirmed M2 dwarf star (West et al. 2011) at a distance of ~366 pc (the most distant lens star in my sample). The photometric signal is somewhat diluted by the lens star, but it may still peak at ~0.01 mag (+2σ) on 31st October 2022 (±7 d).
ME17. Peaking on 27th December 2023 (±20 d), this event will be caused by an M dwarf lens star (not in SIMBAD10) and it may reach a peak magnification of ~0.15 mag (+2σ). This is the second most distant lens star in my sample (~270 pc).
ME18. The lens star G192-52 is a spectroscopically confirmed M1 subdwarf (Bai et al. 2016) that is part of a visual binary (Mason et al. 2001; binary separation of ~596″), and it is ~6 mag brighter than the source star. Even though the photometric signal will be highly suppressed by the lens blend flux, there is still a resonable chance that the photometric signal will peak at above ~0.06 mag (+2σ) on 23rd October 2025 (±15 d) since the source has a ~42% probability of passing within the Einstein ring. Observing in GBP would boost the peak photometric signal by a factor of ~3.6.
ME19. This is by far the most promising photometric microlensing event presented here. The source has a ~33% probability of passing within the Einstein ring of the M dwarf lens star and the ±1-sigma range for the photometric magnification is between ~0.039–0.158 mag, with the possibility of reaching above ~0.45 mag (+2σ). The event is favourable because the lens star at G ≈ 17.18 mag is only ~1.0 mag brighter than the source star, it will have a relatively short duration of ~7.7 d, and the peak is well-constrained to occur on 3rd November 2019 at 15 h (±32 h). Furthermore, the astrometric signal is detectable by Gaia at ~2σAL. Observing in GBP would boost the peak signals by a factor of ~1.3.
ME20. The lens star is a white dwarf (not in SIMBAD) at ~40.6 pc that is approximately the same brightness as the source star. The photometric magnification at peak is well-constrained to lie in the ±2-sigma range ~0.006–0.04 mag which is easily detectable from both ground- and space-based telescopes. The peak will occur on 31st January 2025 (±3 d) and the photometric event will last ~43 d. The astrometric event will be much slower and it is detectable by Gaia at ~4σAL.
ME21. The source has positional uncertainties of ~29 mas in each coordinate direction, which is ~5 times larger than the Einstein radius. Consequently the source path relative to that of the lens is rather uncertain. Unfortunately, this makes any predictions for this event unreliable (e.g. the photometric signal can be anything from below 0.4 mmag to 1 mag). The lens is a lowmass white dwarf star (not in SIMBAD), and the event will peak during April 2024 (±2 months).
ME22. The lens star Wolf 851 is a spectroscopically confirmed K7 subdwarf (Gizis 1997). The source has a ~40% probability of passing within the Einstein ring. However, since the lens is ~9 mag brighter than the source, the photometric signal will be highly suppressed and it may only reach ~6 mmag (+2σ). The peak will occur on 28th August 2023 (±4 d). Observing in GRP would boost the peak photometric signal by a factor of ~1.5.
ME23. The M dwarf lens star (not in SIMBAD) at G ≈ 18.2 mag is of approximately the same brightness as the source. Since the event will happen near the end of the time period considered, the source path relative to that of the lens is somewhat uncertain, and the peak photometric signal of ~1 mmag (+2σ) is predicted to occur on 28th February 2026 (±12 d).
6.4. Ten astrometric microlensing events
The ten events ME24-ME33 will exhibit astrometric signals as they unfold (Table A.4). However, their predicted photometric signals are too small to be significant because u0 > 6 for all of these events. ME26 and ME28 will unfold in both the partiallyresolved and unresolved regimes when considering the resolution of Gaia (Figs. 12 and 13), while the other events will all unfold completely in the partially-resolved regime. Gaia will be able to detect ME26, ME28, ME31 and ME33 at ~11, 3, 1 and 1σAL, respectively (i.e. for the most favourable scanning angles), while the remaining events will be undetectable. However, all of the events presented in this section are within the detection capabilities of HST.
 |
Fig. 12 Astrometric microlensing events ME24-ME28. The format of the figure is the same as in Fig. 10 except that the panels for the non-existent photometric signals have been dropped. |
 |
Fig. 13 Astrometric microlensing events ME29-ME33. The format of the figure is the same as in Fig. 10 except that the panels for the non-existent photometric signals have been dropped. |
ME24. The white dwarf lens star LSPM J0024+6834N (Lépine & Shara 2005) at ~36.1 pc has a brighter visual companion (G 242-54; Gaia source ID 529594417069407744; M dwarf) with similar proper motion and parallax at a separation of 2.34″, which corresponds to a projected orbital separation of ~84 au. Fortunately, the orbital motion (P ≳ 800 yr) is too slow to affect the microlensing prediction presented here. The event will peak on 19th October 2024 at 10 h (±25 h).
ME25. The M3 dwarf lens star Ross 322 (Bidelman 1985) will cause a relatively fast-unfolding (duration ~124 d) astrometric microlensing event during mid-2018, peaking on 10th August 2018 at 7 h (±17 h). The signal will reach nearly 1 mas and the event is a great target for observations starting immediately.
ME26. Unfortunately this event in the direction of the SMC is currently declining, although Gaia will already have taken useful observations for which the astrometric signal is detectable at ~11σAL. Due to the brightness difference between the lens (M3-4 dwarf; Massey & Olsen 2003) and the source, the signal is only significant in the partially-resolved microlensing regime, with a maximum source deflection of ~1.2 mas. The peak occurred on 25th January 2018 at 15 h (±2 h) and by mid-2018 the signal will have dropped to ~0.3 mas. Observations are encouraged immediately to catch this event before the signal becomes too weak.
ME27. The lens star is a white dwarf (not in SIMBAD) that will cause an astrometric signal of ~0.55 mas on 25th November 2025 (±5 d).
ME28. This is one of only two events in the sample of 76 microlensing events for which the source is significantly brighter than the lens (fL/ fS ≈ 0.20). Unfortunately, in this case, the lens does not have a GBP or GRP magnitude in GDR2. However, using data from the PPMXL catalogue (Roeser et al. 2010), I was able to surmise that this is a ~0.46 M⊙ M-dwarf star (not in SIMBAD). Interestingly, the photometric signal ALI2 will nearly reach 0.4 mmag in the partially-resolved regime. Observing this event in passbands where fL/ fS is even smaller than ~0.20 will potentially enable the first detection of the minor source image in a microlensing event in our galaxy (Eq. (14)). The event will peak on 12th June 2025 (±2 d).
ME29. The peak of this event will occur towards the end of the Gaia extended mission on 5th February 2026 (±4 d) with an astrometric signal of ~0.61 mas. The lens star Ross 528 is a spectroscopically confirmed K4 dwarf (Bidelman 1985).
ME30. The lens star LAWD 66 (WD 1708−147) is a spectroscopically confirmed DQ6 white dwarf (McCook & Sion 1999) at a distance of ~22.66 pc. The event will peak on 23rd August 2024 at 10 h (±15 h) with a peak signal of ~1.4 mas. Unfortunately the source is rather faint at G ≈ 20.8 mag.
ME31. The nearby (~13.51 pc) spectroscopically confirmed DC-type white dwarf lens WD 1743−545 (Subasavage et al. 2017) will cause a peak astrometric signal of ~0.55 mas on 5th November 2025 at 7 h (±1 h). The time of closest approach is very well constrained because of the form of the path taken by the source relative to the lens.
ME32. On 26th September 2025 (±4 d), the event caused by the spectroscopically confirmed DA-type white dwarf lens LSPM J1913+2949 (Limoges et al. 2013) will peak with an astrometric signal of ~1.1 mas.
ME33. This event will still be rising towards its peak at the end of the time period considered in this paper (25th July 2026). The peak signal will be a little above ~0.56 mas. The lens star Ross 213 is a spectroscopically confirmed K5 dwarf (Bidelman 1985).
6.5. Low-amplitude astrometric microlensing events
The 43 astrometric microlensing events ME34-ME76 will give rise to peak astrometric signals with amplitudes in the range 0.131-0.5 mas. I present these low-amplitude astrometric events in Table A.5 (provided at the CDS) for exploration by the astronomical community. No further analysis is performed here.
7. Summary and conclusions
I selected 1470 source-lens pairs, with 1194 unique lenses, from GDR2 that could potentially lead to microlensing events during the time baseline of an extended Gaia mission lasting from 25th July 2014 until 25th July 2026. Analysing these pairs in detail, I found that 76 microlensing events caused by 64 unique lenses will occur that exhibit microlensing signals exceeding the precision limits of 0.4 mmag (photometric) and 0.131 mas (astrometric). Nine and five astrometric microlensing events will be caused by LAWD 37 and Stein 2051 B, respectively. These lens stars are very nearby white dwarfs passing through relatively crowded fields which explains their efficiency at producing microlensing events.
A further nine events will yield both photometric and astrometric signals. These are highly desirable events for follow-up observations at the correct moment since they have the potential to constrain the lens mass much better than events that only exhibit an astrometric signal. Five of these photometric events, ME17-ME19, ME21 and ME22 could potentially achieve highmagnification which can be used to probe lens binarity or for planetary companions. Specifically, ME19, which will peak at the beginning of November 2019, is the most promising microlensing event presented in this paper, and its characterisation will allow a precise measurement of the mass of a late-type M dwarf.
Ten microlensing events will yield astrometric signals with amplitudes above 0.5 mas, and two of these events (ME25 and ME26) are ongoing during 2018, requiring immediate observation. The 43 remaining events are all low-amplitude astrometric events with amplitudes between 0.131 and 0.5 mas reported for further exploration by the astronomical community.
The Gaia satellite has ushered in an era of being able to reliably predict gravitational microlensing events for (at least) the next decade. The third data release scheduled for 2020, with improved astrometric solutions and completeness for the high proper motion stars, will enable more predictions much further into the future.
In Feibelman (1986), he concludes: “It is hoped that this 20-year exercise in frustration will encourage others to conduct systematic searches … for stars with large proper motions that eventually may eclipse a background star and give rise to the elusive gravitational lens effect”. My work in this paper is a contemporary realisation of this sentiment.
It is interesting to note that the idea of predicting microlensing events can be traced back at least as far as Refsdal (1964) who concluded that “By comparing photographs of the sky taken at different times, the angular velocity of a great number of stars can be determined, and passages may be predicted.”
Acknowledgments
I acknowledge the support of the NYU Abu Dhabi Research Enhancement Fund under grant RE124. I thank the referee for taking the time to read this paper in detail and make insightful comments. Many of the calculations performed in this paper employed code from the DanIDL library of IDL routines (Bramich 2017) available at http://www.danidl.co.uk. Martin Dominik gave very useful advice on references for the introduction and Lasha Ephremidze kindly checked some of my mathematical derivations. I am grateful to Pierre Bergeron for providing the white dwarf cooling models in the Gaia passbands. This research was carried out on the High Performance Computing resources at New York University Abu Dhabi. Thanks goes to Nasser Al Ansari, Muataz Al Barwani, Guowei He and Fayizal Mohammed Kunhi for their excellent support. I would also like to thank the Solar System Dynamics Group at the Jet Propulsion Laboratory for providing the Horizons On-Line Ephemeris System. I made extensive use of the SIMBAD and VizieR web-resources as provided by the Centre de Données astronomiques de Strasbourg, for which I am exceptionally grateful. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. Various people have encouraged and inspired me during my work on this topic. Thanks goes to Irene Skuballa, Martin Bo Nielsen, Jasmina Blecic, Yanping Chen, Dave Russell, Mallory Roberts, Andrea Macciò, and Rocio and Lucia Muñiz Santacoloma. I dedicate this work to my most wonderful daughters Phoebe and Chloe Bramich Muñiz. Without their patience and support, this paper would have taken much longer to write.
References
- An, J. H., & Han, C. 2002, ApJ, 573, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Arenou, F., Luri, X., Babusiaux, C., et al. 2018, A&A, 616, A17 [Google Scholar]
- Arias, E. F., Charlot, P., Feissel M., & Lestrade, J.-F. 1995, A&A, 303, 604 [NASA ADS] [Google Scholar]
- Bai, Y., Luo, A.-L., Comte, G., et al. 2016, Res. Astron. Astrophys., 16, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Beaulieu, J.-P., Bennett, D. P., Fouqué, P., et al. 2006, Nature, 439, 437 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Belokurov, V. A., & Evans, N. W. 2002, MNRAS, 331, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Bergeron, P., Wesemael, F., Dufour, P., et al. 2011, ApJ, 737, 28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bidelman, W. P. 1985, ApJS, 59, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Boden, A. F., Shao, M., & van Buren, D. 1998, ApJ, 502, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Bond, I. A., Abe, F., Dodd, R. J., et al. 2001, MNRAS, 327, 868 [NASA ADS] [CrossRef] [Google Scholar]
- Bramich, D. M. 2017, Astrophysics Source Code Library [record ascl: 1709.005] [Google Scholar]
- Bramich, D. M., & Nielsen, M. B. 2018, Acta Astron., submitted [arXiv:1806.10003] [Google Scholar]
- Carrasco, J. M., Evans, D. W., Montegriffo, P., et al. 2016, A&A, 595, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chambers, K. C., Magnier, E. A., Metcalfe, N., et al. 2016, ArXiv e-prints [arXiv:1612.05560] [Google Scholar]
- Chaplin, W. J., Lund, M. N., Handberg, R. et al. 2014, ApJS, 210, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Chitre, S. M., & Saslaw, W. C. 1989, Nature, 341, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Choi, J., Dotter, A., Conroy, C., et al. 2016, ApJ, 823, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Dominik, M., & Sahu, K. C. 2000, ApJ, 534, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Dong, S., DePoy, D. L., Gaudi, B. S., et al. 2006, ApJ, 642, 842 [NASA ADS] [CrossRef] [Google Scholar]
- Dotter, A. 2016, ApJS, 222, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Einstein, A. 1915, Sitzungsber. Preuss. Akad. Wiss., 47, 831 [Google Scholar]
- Einstein, A. 1936, Science, 84, 506 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- European Space Agency (ESA), & Gaia Data Processing and Analysis Consortium (DPAC) 2018, Gaia Data Release 2, Documentation Release 1.0 [Google Scholar]
- Evans, D. W., Riello, M., De Angeli, F., et al. 2018, A&A, 616, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabricius, C., Bastian, U., Portell, J., et al. 2016, A&A, 595, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feibelman, W. A. 1966, Science, 151, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Feibelman, W. A. 1986, PASP, 98, 1199 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Gaia Collaboration (Babusiaux, C., et al.) 2018, A&A, 616, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gizis, J. E. 1997, AJ, 113, 806 [NASA ADS] [CrossRef] [Google Scholar]
- Goldberg, D. M. 1998, ApJ, 498, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Goldberg, D. M., & Woźniak, P. R. 1998, Acta Astron., 48, 19 [NASA ADS] [Google Scholar]
- Gould, A. 2001, PASP, 113, 903 [NASA ADS] [CrossRef] [Google Scholar]
- Green, G. M., Schlafly, E. F., Finkbeiner, D. P., et al. 2015, ApJ, 810, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Green, G. M., Schlafly, E. F., Finkbeiner, D., et al. 2018, MNRAS, 478, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Han, C. 2002, MNRAS, 335, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Harding, A. J., Di Stefano R., Lépine S. et al. 2018, MNRAS, 475, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Heintz, W. D. 1990, AJ, 99, 420 [NASA ADS] [CrossRef] [Google Scholar]
- Høg, E., Novikov, I. D., & Polnarev, A. G. 1995, A&A, 294, 287 [NASA ADS] [Google Scholar]
- Holberg, J. B., & Bergeron, P. 2006, AJ, 132, 1221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kains, N., Calamida, A., Sahu, K. C., et al. 2017, ApJ, 843, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Kilic, M., Hambly, N. C., Bergeron, P., Genest-Beaulieu, C., & Rowell, N. 2018, MNRAS, 479, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Kowalski, P. M., & Saumon, D. 2006, ApJ, 651, 137 [Google Scholar]
- Lee, C. H., Seitz, S., Riffeser, A., & Bender, R. 2010, MNRAS, 407, 1597 [NASA ADS] [CrossRef] [Google Scholar]
- Lépine, S., & Shara, M. M. 2005, AJ, 129, 1483 [NASA ADS] [CrossRef] [Google Scholar]
- Liebes, S. 1964, Phys. Rev., 133, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Limoges, M.-M., Lépine, S., & Bergeron, P. 2013, AJ, 145, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Lindegren, L., Lammers, U., Bastian, U., et al. 2016, A&A, 595, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mason, B. D., Wycoff, G. L., Hartkopf, W. I., Douglass, G. G., & Worley, C. E. 2001, AJ, 122, 3466 [Google Scholar]
- Massey, P., & Olsen, K. A. G. 2003, AJ, 126, 2867 [NASA ADS] [CrossRef] [Google Scholar]
- McCook, G. P., & Sion, E. M. 1999, ApJS, 121, 1 [NASA ADS] [CrossRef] [Google Scholar]
- McGill, P., Smith, L. C., Evans, N. W., Belokurov, V., & Smart, R. L. 2018, MNRAS, 478, 29 [Google Scholar]
- Miyamoto, M., & Yoshii, Y. 1995, AJ, 110, 1427 [NASA ADS] [CrossRef] [Google Scholar]
- Morton, T. D. 2015, Astrophysics Source Code Library [record ascl:1503.010] [Google Scholar]
- Nucita, A. A., De Paolis, F., Ingrosso, G., Giordano, M., & Manni, L. 2016, ApJ, 823, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Paczyński, B. 1986, ApJ, 304, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Paczyński, B. 1996, ARA&A, 34, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
- Perryman, M. A. C., de Boer, K. S., Gilmore, G., et al. 2001, A&A, 369, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petrou, M. 1981, PhD Thesis, University of Cambridge, UK [Google Scholar]
- Poleski, R., Soszyński, I., Udalski, A., et al. 2011, Acta Astron., 61, 199 [NASA ADS] [Google Scholar]
- Proft, S., Demleitner, M., & Wambsganss, J. 2011, A&A, 536, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prusti, T., de Bruijne, J. H. J., Brown, A. G. A., et al. 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Refsdal, S. 1964, MNRAS, 128, 295 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Roeser, S., Demleitner, M., & Schilbach, E. 2010, AJ, 139, 2440 [NASA ADS] [CrossRef] [Google Scholar]
- Rybicki, K. A., Wyrzykowski, Ł., Klencki, J., et al. 2018, MNRAS, 476, 2013 [NASA ADS] [CrossRef] [Google Scholar]
- Sahu, K. C., Anderson, J., Casertano, S., et al. 2017, Science, 356, 1046 [NASA ADS] [CrossRef] [Google Scholar]
- Sajadian, S. 2014, MNRAS, 439, 3007 [NASA ADS] [CrossRef] [Google Scholar]
- Silva Aguirre, V., Lund, M. N., Antia, H. M., et al. 2017, ApJ, 835, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Subasavage, J. P., Jao, W. C., Henry, T. J., et al. 2017, AJ, 154, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
- Tremblay, P.-E., Bergeron, P., & Gianninas, A. 2011, ApJ, 730, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Tsapras, Y., Street, R., Horne, K., et al. 2009, Astron. Nachr., 330, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Udalski, A. 2003, Acta Astron., 53, 291 [NASA ADS] [Google Scholar]
- Urban, S. E., & Seidelmann, P. K. 2013, Explanatory Supplement to the Astronomical Almanac, 3rd edn. (Mill Valley, CA: University Science Books) [Google Scholar]
- Walker, M. A. 1995, ApJ, 453, 37 [NASA ADS] [CrossRef] [Google Scholar]
- West, A. A., Weisenburger, K. L., Irwin, J., et al. 2011, AJ, 141, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Witt, H. J., & Mao, S. 1994, ApJ, 430, 505 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Additional tables
Characteristics of the nine microlensing events ME1-ME9 caused by the white dwarf lens star LAWD 37.
Characteristics of the five microlensing events ME10-ME14 caused by the white dwarf lens star Stein 2051 B.
Characteristics of the nine photometric microlensing events ME15-ME23.
Characteristics of the ten astrometric microlensing events ME24-ME33.
All Tables
Constraints that need to be satisfied in order for a GDR2 object to be selected as a lens star.
Constraints that need to be satisfied in order for a GDR2 object with a 5-parameter astrometric solution to be selected as a source star.
Constraints that need to be satisfied in order for a GDR2 object with a 2-parameter astrometric solution to be selected as a source star.
Characteristics of the nine microlensing events ME1-ME9 caused by the white dwarf lens star LAWD 37.
Characteristics of the five microlensing events ME10-ME14 caused by the white dwarf lens star Stein 2051 B.
All Figures
 |
Fig. 1 Configuration of a microlensing event as seen by the observer, who does not resolve any of the components. The filled red circles represent the source S at equal time intervals as it moves relative to the lens L (black circle). The relative motion of the source consists of uniform proper motion in a straight line combined with annual parallax, which is why the source appears to move in a non-linear fashion. The major and minor images, I1 and I2, respectively, of the source are plotted as orange ellipses. Although S, L, I1 and I2 are all plotted with a finite size for illustrative purposes, the analysis in this paper ignores finite-size effects. At any single instant, I1, S, L and I2 form a straight line on the sky along with the centroids Cmic (asterisks), CLS (plus signs) and CLI2 (crosses). The centroids Cmic, CLS and CLI2 have been plotted for fL/ fS = 1. Angular distances defined in the text are marked in the diagram. |
| In the text | |
 |
Fig. 2 Variation of the magnification above baseline A − 1 and the normalised centroid shift δmic/θE during a microlensing event as a function of the normalised source-lens separation u. Continuous and dotted black curves correspond to the cases of a dark lens (fL = 0) and a luminous lens with fL/ fS = 1, respectively. The asymptotic behaviour of the photometric and astrometric signals for the specific case of a dark lens is plotted using red and blue curves, respectively, and these asymptotic curves are labelled with their functional form. |
| In the text | |
 |
Fig. 3 Variation of the magnification above baseline A − 1 (black curve) and the centroid shifts δmic (mas; red curve) and θ2 (mas; blue curve) as a function of time (d) for the two fictitious microlensing events described in Sect. 3.5. The events differ only in that u0 = 0.6 and u0 = 1.6 for the left- and right-hand panels, respectively. The vertical dashed lines in each panel indicate when an event switches between unresolved and partially-resolved microlensing based on the median Gaia spatial resolution of ~103 mas. The dotted curves indicate the photometric (G-band) and astrometric (along-scan) precisions for a single observation with black, red and blue colours corresponding to A − 1, δmic and θ2, respectively. |
| In the text | |
 |
Fig. 4 Plot of σAL (mas; left-hand panel) and σAC (mas; right-hand panel) versus G magnitude. The data from R18 are plotted as black dots and the formal errors reported by Fabricius et al. (2016) are plotted as plus signs in the left-hand panel. The best fit curves are plotted in red. |
| In the text | |
 |
Fig. 5 Parallax S/N ϖL/σ[ϖL] against parallax ϖL for the lens stars in a set of 51 379 source-lens pairs. The continuous line corresponds to σ[ϖL] = 0.4 mas. Rejected lenses fall below this line. The dashed lines representing ϖL/σ[ϖL] = 4 and ϖL = 769 mas correspond to the constraints applied to GDR2 to select the initial lens sample (Table 1). |
| In the text | |
 |
Fig. 6 Histograms of Δϖ/σ[Δϖ] (top panel), Δμα*/σ[Δμα*] (middle panel) and Δμδ/σ[Δμδ] (bottom panel) for 2882 source-lens pairs (black histograms). In the top panel, the red curve is a Gaussian with zero mean and standard deviation of unity, scaled to match the histogram of Δϖ/σ[Δϖ]. In each panel, the blue histogram with striped bars is for the source-lens pairs satisfying Δϖ/σ[Δϖ] > 3. |
| In the text | |
 |
Fig. 7 Left panel: Hertzsprung-Russell diagram of MG versus GBP−GRP for the 1194 lens stars in the final sample of source-lens pairs from Sect. 4.2.8. The continuous black line joining (−1, 5) and (5, 25) mag separates white dwarf stars from main sequence dwarfs/subdwarfs (Kilic et al. 2018). The lens masses are indicated by the colour of the plot points (see the scale at the bottom of the panel). The 55 lenses that are present in 58 of the source-lens pairs that do not have GBP or GRP magnitudes in GDR2 are plotted with black points at fixed colour GBP−GRP = −0.3 mag and using their computed absolute magnitudes MG. Right panel: same as the left-hand panel for the 64 lens stars in the 76 microlensing events found in Sect. 5.2, except that the only lens that does not have a GBP or GRP magnitude is plotted in colour to indicate its estimated mass using photometry from external catalogues. The points from the left-hand panel are plotted in the background in light grey. |
| In the text | |
 |
Fig. 8 Top panel: path on the sky of the white dwarf lens star LAWD 37 (WD 1142−645), and nine source stars in the microlensing events ME1-ME9, over the time baseline of an extended Gaia mission. The coordinate axes are measured relative to (αref,L, δref,L). Middle panel: time-evolution of the normalised source-lens separation u for each microlensing event. Bottom panel: time-evolution of the deflection θ2 (mas) of the major source image. The horizontal black line indicates the astrometric precision limit of 0.131 mas from Sect. 4.2.5. |
| In the text | |
 |
Fig. 9 Top panel: path on the sky of the white dwarf lens star Stein 2051 B (WD 0426+588), and five source stars in the microlensing events ME10-ME14, over the time baseline of an extended Gaia mission. The coordinate axes are measured relative to (αref,L, δref,L). Middle panel: time-evolution of the normalised source-lens separation u for each microlensing event. Bottom panel: time-evolution of the deflection θ2 (mas) of the major source image. The horizontal black line indicates the astrometric precision limit of 0.131 mas from Sect. 4.2.5. |
| In the text | |
 |
Fig. 10 Photometric microlensing events ME15-ME18. In all panels, five curves are plotted with the colours yellow, red, black, blue, and cyan. Each curve corresponds to the 2.3, 15.9, 50, 84.1, and 97.7 percentiles, respectively, of the results of the Monte Carlo simulations performed in Sect. 5.2 after they have been ordered by increasing u0. The yellow and cyan curves are plotted first, followed by the red and blue curves, and finally the black curve, which is why the black curve is the most visible when the individual curves are hard to distinguish. Left-hand panels: path of the source star relative to the lens star. The Einstein ring is shown as a circle of radius θE centred on the lens position (also plotted five times with five different colours). The resolution of Gaia is indicated as a circle of radius 103 mas centred on the lens position (dashed curve). Middle left-hand panels: time-evolution of the normalised source-lens separation u. Middle right-hand panels: time-evolution of the photometric signals 2.5 log(A) (mag; unresolved regime) and 2.5 log(A1) (mag; partially-resolved regime). The horizontal black line indicates the photometric precision limit of 0.4 mmag from Sect. 4.2.5. Right-hand panels: time-evolution of the astrometric signals δmic (mas; unresolved regime) and θ2 (mas; partially-resolved regime). The horizontal black line indicates the astrometric precision limit of 0.131 mas from Sect. 4.2.5. |
| In the text | |
 |
Fig. 11 Photometric microlensing events ME19-ME23. The format of the figure is the same as in Fig. 10. |
| In the text | |
 |
Fig. 12 Astrometric microlensing events ME24-ME28. The format of the figure is the same as in Fig. 10 except that the panels for the non-existent photometric signals have been dropped. |
| In the text | |
 |
Fig. 13 Astrometric microlensing events ME29-ME33. The format of the figure is the same as in Fig. 10 except that the panels for the non-existent photometric signals have been dropped. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.